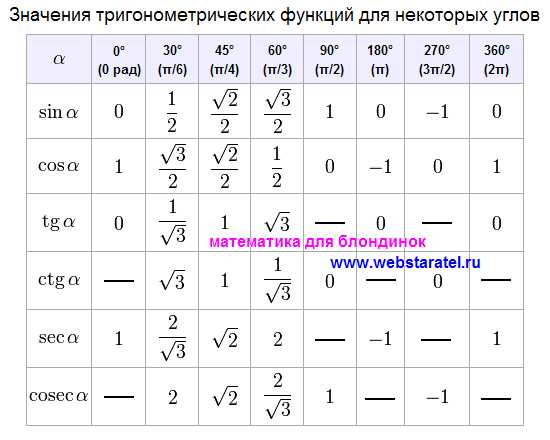
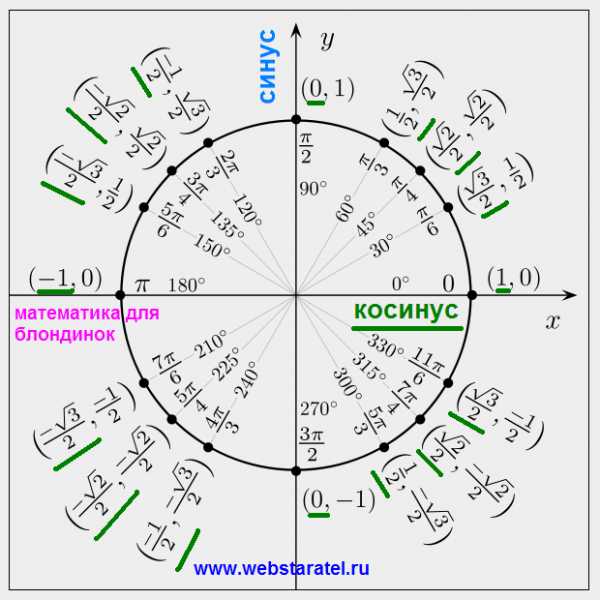
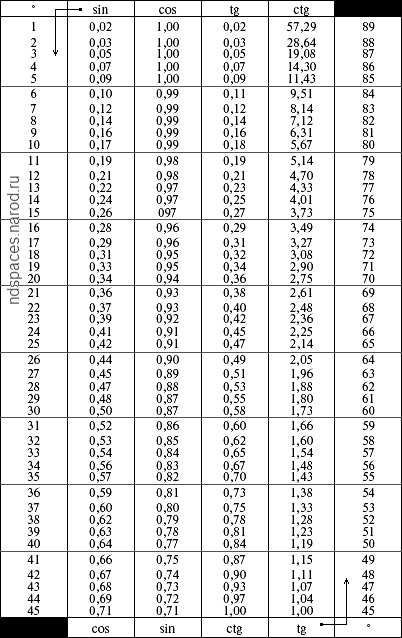
Сложение и вычитание положительных и отрицательных чисел. 6-й класс
Разделы: Математика
Цели и задачи урока:
образовательные:
— систематизация и обобщение знаний, умений и
навыков сложения и вычитания положительных и
отрицательных чисел;
— отработка навыков решения задач;
— усовершенствование навыков решения
уравнений;
развивающие:
— развитие навыков анализа, синтеза и обобщения;
— повышение общей культуры учащихся;
— расширение умственного кругозора учащихся;
воспитательные:
воспитывать у школьников
ответственность, аккуратность и
дисциплинированность.
Ход урока
1. Организационный этап (3 мин.).
Проверить готовность учащихся к уроку,
сообщить учащимся тему и цель урока.
2. Актуализация знаний и устная работа (10 мин.).
1) Учитель задает учащимся вопросы:
а) Как выполняется сложение чисел с одинаковыми
знаками?
б) Как выполняется сложение чисел с разными
знаками?
в) Как выполняется вычитание?
2) Вычислить устно:
| -2+(-5) |
-1,2+(-3,4) |
| -4+(-10) |
-7,8-2,8 |
| 7+(-12) |
6,4+(-14) |
| 15-21 |
3,9-5,1 |
| -5+23 |
-1,7+5 |
| 3-(-14) |
4,1-(-6,9) |
| -24-(-65) |
-3,7-(-2,1) |
| -35-35 |
-3,2+3,2 |
3) Учитель предлагает учащимся расположить
числа в порядке возрастания и узнать, какое слово
зашифровано в таблице.
| -6,5 |
-2,75 |
-6,8 |
-6,6 |
2,1 |
2,75 |
-1,2 |
3,5 |
-0,9 |
6,6 |
| о |
р |
к |
о |
н |
а |
д |
т |
и |
а |
Ответ: координата.
Учащиеся вспоминают определение координаты.
4) Даны числа -12 и 3.
а) назвать модули этих чисел;
б) назвать целые числа, расположенные между
этими числами;
в) назвать несколько целых чисел меньших, чем -12;
г) чему равна сумма этих чисел? Разность?
5) Отметить на координатной прямой точки А(-5),
В(-3,5), Д(2,5), Е(5), С(-0,5)
3. Решение примеров на сложение и вычитание
положительных и отрицательных чисел (7 мин.).
1) Решив данные примеры, вы разгадаете имя
древнегреческого ученого, зашифрованное в
данной таблице.
1) -1+ И
2) -3—(-1) Г
3) -3,2- 2,9 Ф
4) -3,3 + 1,8 О
5) -4+3 П
6) -5,5 + 5,5 А
7) -2,5 -2,5 Р
| -1 |
— |
-5,7 |
0 |
-1,75 |
-1,8 |
-5 |
| |
|
|
|
|
|
|
2) Учащиеся решают примеры самостоятельно.
1)-0,81+0,66
2) 3+(-)
3) -5+(-2)
4) +(-)
5) -7-(-9)
6) 3-4
4. Решение уравнений, использующих операции над
числами (7 мин.).
1) В каком веке жил древнегреческий ученый
Пифагор? Мы узнаем, если решим данное уравнение.
(х-3,4)-13= -10,4
Ответ: в VI веке до н.э.
2) В каком веке появилась десятичная система
счисления?
(х-3,5)-6= -3,5
Ответ: в VI веке н.э.
3)В каком веке дроби стали восприниматься как
числа?
(30-х)-12,4= — 4,4
Ответ: в XVIII веке н.э.
5. Решение задачи, содержащей положительные и
отрицательные числа (4 мин.).
Из задуманного числа Таня вычла 16,2 и прибавила
4,8. В результате получила -5,1. Найдите задуманное
число.
Ответ: 6,3
6. Самостоятельная работа (10 мин.).
1 вариант
Решите уравнения:
а) х+3,8=2,7
б) 7,1+у= -1,8
в) -1,2 -а=3
г) (х+2,4)+10,3= -1,5
2 вариант
Решите уравнения:
а) -3,2+х=5,2
б) 6,7+у= — 4,3
в) 5,7-х=8,9
г) (х-6,8)+9,3=1,7
7. Домашнее задание (2 мин.).
“Дидактические материалы по математике, 6
класс” А.С.Чесноков, К.И.Нешков стр.20 № 236, 237, 238.
8. Подведение итогов урока (2 мин.).
Учащиеся заканчивают предложения:
- чтобы сложить два числа с одинаковыми знаками,
надо …
- чтобы сложить два числа с разными знаками, надо
…
- вычитание всегда можно представить как …
- вычесть отрицательное число, значит …
6.02.2011
Поделиться страницей:
xn--i1abbnckbmcl9fb.xn--p1ai
Сложение и вычитание положительных и отрицательных чисел. 6-й класс
Разделы: Математика
Цели:
- Образовательные: повторить и обобщить изучаемый материал;
закрепить у обучающихся умение выполнять действия сложения и вычитания чисел
с разными знаками; проверить умения и навыки ребят в работе с положительными
и отрицательными числами;
- Развивающие: развитие памяти, речи, познавательного интереса за
счет вовлечения обучающихся в игру; формирование представлений о
математическом языке, его компонентах, историческом развитии;
- Воспитательные: воспитание аккуратности, дисциплины,
настойчивости, умению внимательно выслушивать мнение других, уважительно
относиться к ответам одноклассников.
Об уроке: Данный урок является заключительным в теме “Сложение,
вычитание положительных и отрицательных чисел”. Цель устного счёта – подготовить
учащихся к продуктивной работе на протяжении всего урока. В ходе урока
проводится работа по поддержанию и совершенствованию ранее сформированных знаний
и умений, в частности, вычислительных навыков. Предлагаются задания, требующие
сообразительности, внимания, анализа и обобщения имеющихся знаний.
Структура урока:
- Постановка цели урока
- Устный счёт
- Путешествие по планетам
- Самостоятельная работа
- Итог, домашнее задание
Оборудование урока: маршрутные листы
(Приложение 1), презентация (Приложение 2)
Ход урока
1. Организационный момент.
У: Здравствуйте, ребята. Сегодня у нас с вами необычный урок. Урок,
который даст нам возможность получить новую и интересную информацию и
одновременно поможет повторить все, что вы знаете о сложении и вычитании
положительных и отрицательных чисел. Наш урок будет проходить в форме
космического путешествия. И совершим мы этот полет вот на таком космическом
корабле (слайд, Презентация). Девиз урока: “ Дорогу осилит идущий, а математику
мыслящий”. Вы побываете на разных планетах: сделайте остановку на планете
“Исторической”, посетите планету “Сложения и вычитания”, побываете на планете
“Уравнения”, не останутся без внимания и другие планеты.
В начале нашего путешествия мне бы хотелось обратиться к словам известного
российского математика Александра Мордковича: “Кто с детских лет занимается
математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает
в себе настойчивость и упорство в достижении цели”. Именно это потребуется нам
на уроке: внимание, настойчивость, упорство, чтобы достичь поставленных целей.
2. Постановка целей и задач урока.
3. Актуализация опорных знаний и умений учащихся.
Каждому из вас, как великому путешественнику, выдается звездный маршрутный
лист (Приложение 1), где указаны планеты и
задания в той последовательности, в которой вам нужно их посетить.
У: Но, чтобы воспользоваться маршрутным листом вам ребята нужно пройти
устое испытание.
Устное испытание:
1.Сравните числа:
а) -58 и 145; б) 63,2 и -62,3; в) -8,58 и -8,5; г) -1\2 и -0,5
В: Какими вы правилами пользовались для сравнения чисел?
2.Вычислите:
- -22 + 35
- -3,7 + 2,8
- 1,5 + (-6,3)
- 8,2 + (-8,2)
- 22 – 27
- -13 – 8
- 19– (-2)
- -27 – (-3)
- -35 + (-9)
В: Какими правилами вы пользовались при сложении и вычитании
положительных и отрицательных чисел?
У: Мы повторили правила, которые нам пригодятся для успешного
путешествия. Я считаю, что устное испытание вы прошли и наше путешествие
начинается. В добрый путь друзья! Возьмите в руки звездный маршрутный лист,
посмотрите, с какой планеты мы начнем свое путешествие.
О: Правильно, с планеты “Исторической”.
Попасть на другие планеты, минуя историческую, нельзя. Поэтому мы делаем
первую остановку, здесь мы познакомимся с историей возникновения положительных и
отрицательных чисел (рассказ одного из учеников).
История возникновения положительных и отрицательных чисел.
Отрицательные числа появились значительно позже натуральных чисел и
обыкновенных дробей. Первые сведения об отрицательных числах встречаются у
китайских математиков во II в. до н. э. Положительные числа тогда толковались
как имущество, а отрицательные – как долг, недостача. Но ни египтяне, ни
вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VII в.
индийские математики начали широко использовать отрицательные числа, но
относились к ним с некоторым недоверием.
В Европе отрицательными числами начали пользоваться с XII–XIII вв., но до XVI
в., как и в древности, они понимались как долги, большинство ученых считали их
“ложными”, в отличие от положительных чисел – “истинных”.
Признанию отрицательных чисел способствовали работы французского математика,
физика и философа Ренё Декарта. Он предложил геометрическое истолкование
положительных и отрицательных чисел – ввел координатную прямую.
Складывать и вычитать отрицательные числа научились древнекитайские ученые
еще до нашей эры.
Индийские математики представляли себе положительные числа как, “имущества”,
а отрицательные числа как “долги”. Вот как индийский математик Брахмагупта
излагал правила сложения и вычитания: “Сумма двух имуществ есть имущество”,
“сумма двух долгов есть долг”, “сумма имущества и долга равна их разности” и т.
д. Попробуйте перевести эти древнеиндийские правила на современный язык.
У: Ребята мы познакомились с историей возникновения положительных и
отрицательных чисел и продолжаем наш путь на планету “Сложения и вычитания”.
Воспользуйтесь маршрутным листом для выполнения задания на этой планете.
В: Какие задания ждут вас на этой планете?
О: Выполнить сложение и вычитание чисел с разными знаками.
У: Приступаем к выполнению заданий.
У: Давайте проверим ваши решения.
У: Мы покидаем планету “Сложения и вычитания” и держим свой путь к
планете “Уравнения”.
Задания:
1) х + 1,2 = -0,17
2) 14 – х = -28
3) х – 9 = – 3,1
4) -2,1 – х = -2
У: На решение каждого уравнения 2 минуты. Приступайте.
У: Ребята давайте проверим ваши решения (ответы и решения с
комментариями). Мы говорим планете “Уравнения” до свидания и держим наш курс к
планете “Ребусная”.
У: Обратимся к маршрутному листу, что вам предстоит разгадать?
О: Найти ошибки в вычислениях и восстановить решение.
1-е задание: Заполните пропуски
1) -14 + … = -37
2) -4,8 + … = -8,6
3) -2,13 + … = -17
4) -3,8 + … = -4,08
2-е задание: Найдите ошибки в вычислениях
1) 25+ (-17) = -8
2) -30,5 – 12,6 = 43,1
3) 15, 73 – 20,5 = 4,77
У: Проверяем свои решения.
У: Молодцы ребята, вы справились с испытанием. А мы подлетаем к
планете “Мудрецов”
1-е задание: Даны числа: -1, -2, -3, -4, -5, -6, -7, -8, -9, -10
Составьте из них три верных равенства, используя каждое число по одному разу.
2-е задание: Замените звездочки знаками “+” или “ – ” так, чтобы получились
верные равенства:
1) -6,1 * (-2,3 ) * 3,8 = 0
2) 3,9 * 7,4 * (-9,3) = -12,8
У: Ну, что посмотрим кто у нас самый мудрый.
У: Мы покидаем планету “Мудрецов” и держим курс на самую творческую
планету “Творчество”.
У: Ребята, вашим домашним заданием было написать сочинение на тему
“Положительные и отрицательные числа в моей жизни”
У: По желанию представьте свои работы (ребята представляют свои
работы).
У: Спасибо всем, кто представил свои творческие работы, а мы
приближаемся к “Финальной планете”.
Задания финальной планеты:
Найти значение алгебраической суммы
- (-18) + 48 – 34 – (– 18) + 35 –28 =
- 30,5 – 12,4 + (-7,5) – 30,5 + 19,9 =
- (-45,56) + 66, 53 – (-13,47) + 45,56 =
- 87 – 54 + 43 – (-55) + 39 – 87 =
- Уменьшаемое 17, вычитаемое -10, найдите разность
- Запишите разность чисел 14 и 6, вычислите её.
- Число -24 уменьшите на 12
- Число -15 увеличьте на 19
4. Итог урока. Рефлексия.
У: Наше путешествие подходит к концу. Сегодня вы хорошо потрудились. И
каждый из вас оценит свой труд сам. У вас на парте две звездочки разного цвета:
желтая звезда означает, что тема “Сложение и вычитание положительных и
отрицательных чисел” вами полностью усвоена, а зеленая звезда – что есть вопросы
в данной теме, на которые следует обратить внимание. Сейчас вы создадите свой
звездный небосвод. Каждый из вас крепит на небосвод звезду того цвета, которую
считает он заслужил.
5. Домашнее задание.
Наше путешествие подошло к своему завершению, но с планетами мы не прощаемся,
и домашнее задание вам будет подготовить задания для планеты “Любознательность”.
У: Урок хочется закончить стихами:
Есть, науки хороши
Для развития души,
Их и сами все вы знаете, конечно.
Для развития ума предназначена она –
Математика.
Это было, это будет, это вечно!
11.01.2011
xn--i1abbnckbmcl9fb.xn--p1ai
Методика изучения темы «Сложение и вычитание положительных и отрицательных чисел» в 6-м классе
Разделы: Математика
Тема “Сложение и вычитание положительных и
отрицательных чисел” является традиционно
трудной для усвоения шестиклассниками. Вместе с
тем, это тот фундамент, на котором строится
дальнейшее изучение математики. Без прочного
овладения этим материалом ученики будут
испытывать значительные сложности при обучении
в последующих классах.
Для того чтобы облегчить восприятие этого
материала, я предлагаю помимо традиционного
учебника “Математика 6” под редакцией
Н.Я.Виленкина, в котором явно недостаточно
примеров на сложение и вычитание целых чисел,
использовать вкладыш для классов
коррекционно-развивающего обучения
“Арифметика. Задания для учащихся 6 класса” Л.В.
Кузнецовой и др. Пособие это было издано в 1994 году
в издательстве “Галс Плюс” и с тех пор,
насколько мне известно, не переиздавалось,
поэтому я приведу в своей работе полностью те
задания, которые считаю целесообразным
использовать при организации работы с учащимися.
Планирование учебного материала.
| № урока |
Тема урока |
| 1. |
Сложение чисел с помощью координатной
прямой. |
| 2. |
Сложение отрицательных чисел. |
| 3. |
Сложение чисел с разными знаками. |
| 4. |
Сложение чисел с разными знаками. |
| 5. |
Обучающая самостоятельная работа по
теме “Сложение положительных и отрицательных
чисел”. |
| 6. |
Вычитание. |
| 7. |
Вычитание. |
| 8. |
Вычитание. |
| 9. |
Обучающая самостоятельная работа по
теме “Сложение и вычитание положительных и
отрицательных чисел”. |
| 10. |
Обобщающее повторение темы “Сложение и
вычитание положительных и отрицательных чисел”. |
| 11. |
Контрольная работа. |
Учебники и учебные пособия.
1. “Математика 6” Н.Я. Виленкин и др. Москва, 2003.
2. “Арифметика. Задания для учащихся 6 класса”
Л.В. Кузнецова и др., Москва, 1994.
3. “Самостоятельные и контрольные работы.
Математика 6”. А.П. Ершова и В.В. Голобородько,
Москва, 2003.
4. “Карточки для проведения контрольных работ.
Математика 6.” В.И. Жохов, Л.Б. Крайнева. Москва, 2003.
Методический комментарий.
Сложение чисел с помощью координатной прямой
обычно не вызывает сложностей и является
введением к изучению новой темы, наглядным
материалом, на который будет опираться
дальнейшая работа. Обычно к концу этого урока
учащиеся уже видят определённые закономерности
при сложении чисел и могут обходиться без
координатной прямой. К этому надо их поощрять.
На втором уроке на закономерность, возникшую
при сложении отрицательных чисел, надо обратить
особое внимание и сформулировать правило. Для
закрепления удобно использовать в качестве
устных упражнений №№ 390, 391 и 392 из вкладыша
“Арифметика”.
№ 390.
Выполните сложение:
а) (- 12) + (- 9)
б) (- 13) + (- 8)
в) (- 18) + (- 5)
г) (- 15) + (- 7)
д) — 100 + (- 20)
е) — 362 + (- 300)
ж) – 110 + (- 10)
з) – 99 + (- 1)
№ 391.
Сложите числа:
а) – 7, — 13 и – 22
б) – 5, — 12 и – 17
в) – 6, — 19 и 0
г) – 13, — 17 и – 30.
№ 392
Представьте в виде суммы двух отрицательных
слагаемых числа:
а) – 10
б) – 23
в) – 99
г) – 101
Аналогично можно поступить при изучении темы
“Сложение чисел с разными знаками”. Для устных
упражнений при закреплении подойдёт № 394 из
указанного пособия.
№ 394
Выполните сложение:
а) 6 + (- 7)
б) (- 5) + 14
в) (- 1) + 8
г) (- 20) + 13
д) (- 7) + 7
е) 9 + (- 14)
ж) (– 8) + 11
з) 17 + (- 9)
и) (- 22) + 22
к) 8 + (- 13)
л) (- 7) + 9
м) (- 20) + 4
При выполнении этого задания от учащихся
следует добиваться чёткой аргументации
постановки знака и выбора действия с модулями
(сложение или вычитание).
Более сложное задание № 1050 из учебника следует
выполнить письменно с комментариями. На этом же
уроке можно предложить задание творческого
характера № 398 из вкладыша, в котором требуется
представить числа – 2, 0, 3 и – 1 в виде суммы
положительного и отрицательного чисел.
Следующий урок по данной теме надо посвятить
закреплению темы “сложение положительных и
отрицательных чисел”, обратив особое внимание
на дифференцирование случаев сложения
отрицательных чисел и чисел с разными знаками.
На пятом уроке темы проводится обучающая
самостоятельная работа С-22 по сборнику А.П.
Ершовой и В.В. Голобородько “Самостоятельные и
контрольные работы. Математика 6”. Работа дана в
шести вариантах трёх уровней сложностей, что
позволяет осуществить дифференцированный
подход к учащимся. Во время работы учащиеся
получают индивидуальные консультации, что даёт
возможность учителю уже на этом этапе выявить
затруднения и произвести необходимую коррекцию.
Вычитание положительных и отрицательных чисел
– это наиболее трудное для учащихся действие.
Перед тем как формулировать правило, о том, что
для вычитания некоторого числа, нужно прибавить
число, противоположное данному, следует
обязательно провести мотивацию на примерах с
координатной прямой. Для первичного закрепления
можно использовать № 400 из вкладыша
“Арифметика”.
№ 400
Замените вычитание сложением:
а) – 4 – (- 7)
б) 7 – (+ 9)
в) – 7 – (- 2)
г) – 3 – (+ 3)
д) – 18 – (+ 5)
е) 6 – (- 6)
ж) – 19 – (- 3)
з) – 4 – (+ 1)
При выполнении этого задания следует
добиваться от учащихся чёткой аргументации
действий: “Чтобы отнять от числа –4 число –7,
надо к числу –4 прибавить число 7”. Вслед за этим
надо письменно выполнить № 401 и только потом
перейти к решению №1075 из учебника.
№ 401
Выполните вычитание:
а) – 3 – (- 5)
\б) 5 – (- 7)
в) – 8 – (+ 3)
г) – 4 – (+ 4)
д) – 13 – (+ 9)
е) 1 – (- 1)
ж) 10 – (+ 18)
з) – 24 – (+ 12)
Седьмой урок темы можно посвятить понятию
“сумма”. Восприятие выражений вида –3 + 8 – 6 + 71 + 5
– 6 как суммы достаточно сложно для учащихся, но
имеет очень большое значение для дальнейшей
работы с положительными и отрицательными
числами. Во вкладыше “Арифметика” этому вопросу
уделено гораздо большее внимание, чем в учебнике.
Объяснительный материал можно прочитать с
учащимися на страницах 77-78. Я приведу его здесь
полностью:
“При выполнении упражнений мы вычитание
заменяли сложением. Любое выражение, в котором
только действия сложения и вычитания, можно
записать в виде суммы:
— 3 – (-5) = — 3 + (+5)
— 1 – (- 4) – (+ 8) = — 1 + (+ 4) + (- 8)
Договорились такие суммы записывать без
скобок: знак сложения между числами опускается
(он подразумевается), а числа выписываются друг
за другом со своими знаками:
— 1 + (+ 4) + (- 8) = — 1 + 4 – 8.
Запись — 3 – 5 + 4 – 7 + 2 называют суммой. Она
означает сумму чисел: — 3, — 5, + 4. – 7 и + 2, т.е. — 3 – 5 + 4
– 7 + 2 = (- 3) + ( – 5 ) + (+ 4) + ( – 7) + ( + 2).”
Вслед за этим целесообразно выполнить
упражнения № 403, 404. При работе с каждым из заданий
надо добиться от учащихся, чтобы они безошибочно
называли слагаемые в сумме.
№ 403.
Запишите без скобок выражение:
а) – 2 – (- 4)
б) 5 – (- 6)
в) – 3 – (+ 8)
г) – 1 — (+1)
д) – 15 + (- 6) – (+ 20)
е) – 5 – (- 17) + (+ 4) – (- 3)
ж) 7 – (+ 3) + (- 1) – (- 5)
з) – 1 – (- 2) + (- 3) – (+ 4)
№ 404.
Запишите, какие числа складываются:
а) – 3 – 4
б) 8 – 11
в) – 1 + 3
г) – 10 – 2
д) – 1 – 4 + 2
е) 7 + 5 – 16
ж) – 13 – 17 – 20
з) 5 – 8 – 5
и) 0 – 3 + 11 – 8
к) – 2 + 1 + 7 – 20
л) 12 – 30 – 31 + 4
м) – 1 – 2 – 3 – 4
Далее следует объяснить, что слагаемые в сумме
подчиняются переместительному свойству и что
сумму, состоящую из двух слагаемых, можно свести
к одному из четырёх случаев:
- сложение двух положительных чисел
- сложение двух отрицательных чисел
- вычитание из большего числа меньшего
- вычитание из меньшего числа большего,
На стенде к началу изучения темы я вывешиваю
следующую таблицу.
| СЛОЖЕНИЕ И ВЫЧИТАНИЕ 3 + 5 = 8
–3 – 5 = –8
5 – 3 = 2
3 – 5 = –2
–5 + 3 = 3 – 5
3 + (– 5) = 3 – 5
3 – (– 5) = 3 + 5 |
На этом этапе уместно обратить внимание
учащихся на неё и ещё раз разобрать по таблице
все возможные случаи сложения и вычитания
положительных и отрицательных чисел.
После этого учащиеся выполняют № 406 из
вкладыша.
№ 406.
Вычислите:
а) 5 – 7
б) – 4 – 8
в) – 13 – 9
г) 1 – 10
д) – 5 – 5
е) – 3 + 18
ж) – 19 + 2
з) 17 – 20
и) 0,5 – 1
к) – 0,2 – 0,4
л) 1,7 – 2,7
м) – 2,3 + 3,4
В качестве устных упражнений на следующем
уроке предлагаются различные примеры на
сложение и вычитание положительных и
отрицательных чисел. В случае затруднений
школьники учатся использовать таблицу на стенде
и аргументировать свои действия.
На 8-м уроке работа над понятием “сумма”
продолжается. Для повторения можно предложить №
1079 из учебника, в котором просят составить сумму
из данных слагаемых. Затем нужно перейти к
изучению правила вычисления больших сумм,
изложенного во вкладыше на странице 79.
“При вычислении значения выражения 4 – 8 + 3 – 9 +
6 – 16 можно не записывать его в виде суммы
слагаемых с разными знаками, а выполнять
вычисления сразу. При этом удобно поступать так.
Сначала сложить все числа со знаком +:
4 + 3 + 6 = 13;
потом сложить все числа со знаком — :
— 8 – 9 – 16 = — 33;
затем найти сумму 13 и – 33:
13 – 33 = — 20.”
Для закрепления выполняются упражнения № 407 и
408 из вкладыша.
№ 407.
Найдите значение выражения:
а) – 14 – 7 – 9
б) 7 – 12 – 8
в) 5 – 13 + 6
г) 24 – 31 – 9
д) – 5 – 3 + 6 + 8 + 4
е) 6 – 2 + 5 – 7
ж) 7 – 4 – 9 + 8 – 6
з) 4 – 8 + 3 – 9 + 6 – 16
№ 408.
Вычислите:
а) 17 – 21 – 50 + 43 + 37 – 11
б) – 31 + 42 + 12 – 14 – 60
в) 10 – 1 + 8 + 4 – 25
г) – 1,2 – 2 + 3,5 – 4,1 + 6
На девятом уроке проводится обучающая
разноуровневая самостоятельная работа С-23 по
сборнику А.П. Ершовой и В.В. Голобородько
“Самостоятельные и контрольные работы.
Математика 6”.
Последний урок темы можно посвятить
обобщающему повторению изученной темы. На этом
уроке следует обратить особое внимание на
решение заданий, вызвавших наибольшие
затруднения у учащихся в процессе изучения темы
и во время самостоятельных работ.
Завершается изучение темы контрольной работой,
которую можно провести по карточкам В.И. Жохова и
Л.Б. Крайневой (К-10).
23.01.2007
xn--i1abbnckbmcl9fb.xn--p1ai
«Сложение и вычитание положительных и отрицательных чисел». 6-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (7,2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок закрепления, обобщения
и совершенствования знаний с применением
компьютерных технологий.
Вид урока: космическое путешествие
Цели:
- Образовательная: обобщить и закрепить
знания, умения и навыки учащихся при решении
конкретных упражнений и заданий по данной теме.
- Развивающая: способствовать развитию
воображения, творческой активности учащихся,
памяти, внимания, логического мышления. Обобщить
и систематизировать знания путём создания
условий для интеллектуального развития личности
ребёнка на уроке; развивать математическую
культуру речи и письма.
- Воспитательная: воспитывать
доброжелательное отношение к коллективу,
интерес к предмету.
Задачи:
1. Обобщить и закрепить знания, умения и навыки
учащихся при решении конкретных упражнений и
заданий по данной теме.
2. Проверить усвоение учебного материала,
применяя фронтальную, групповую и
индивидуально-дифференциальную формы работы
Раздаточный материал: карточки с
заданиями, карта учёта полёта.
Техническое обеспечение:
Интерактивная доска модели InterWriter,
мультимедийный проектор, программы OO Writer, OO Calc.
Для проведения урока необходимо:
- запустить интерактивный режим работы доски;
- открыть файл Приложение1.gwb
- на компьютеры учеников скопировать файл Приложение2.ods
- открыть презентацию, файл Презентация.odp
- далее следовать плану урока.
План урока
Ребята, тема нашего урока: “Сложение и
вычитание положительных и отрицательных чисел”.
Но проходить он будет в необычной форме. Наш урок
будет проходить в форме космического
путешествия.
А отправимся в этот полёт мы вот на этом
космическом корабле.
Знаменитый лётчик Валерий Павлович Чкалов
сказал: “Полёт – это математика”. Пусть эти
слова станут девизом нашего урока.
Я желаю вам интересного путешествия и удачного
приземления, а для этого вы …
| Что должны знать? 1. Понятие модуля
Понятие противоположных чисел.
2. Правила:
— сложения отрицательных чисел;
— сложения чисел с разными знаками;
— вычитания положительных и отрицательных
чисел;
— действий с обыкновенными дробями;
— сравнения чисел. |
Что должны уметь? 1. Грамотно
формулировать правила на сложение и вычитание
отрицательных и положительных чисел.
2. Решать примеры на использование данных
правил.
3. Видеть рациональные пути решения.
4. Внимательно, аккуратно оформлять решение
заданий. |
Думаю вы все готовы к полёту. Удачи вам ребята!
Ни пуха, ни пера!
этап.
Я уже говорила, что в полёт вы отправитесь вот
на этом космическом корабле. Но прежде всего вы
должны пройти “допуск” к полёту. Первый этап
нашего полёта называется “Зачисление в члены
экипажа корабля”. Для этого вам нужно ответить
на вопросы, которые напечатаны на красных
карточках и лежат у каждого на парте.
1. Чему равен модуль положительного числа?
Отрицательного числа? Нуля?
2. Какие числа называются противоположными?
Приведите примеры.
3. Как сложить два отрицательных числа?
4. Как сложить числа с разными знаками?
5. Чему равна сумма двух противоположных чисел?
6. Сформулируйте переместительный закон
сложения?
7. Как сравнить два отрицательных числа?
За каждый правильный ответ в карточку учёта в 1
колонку ставите 1 балл, которая тоже находится на
парте, нет 0 баллов.
Все справились с заданием у всех имеется
необходимый запас теоретических знаний и все
зачислены в члены экипажа.
II. этап.
А сейчас мы узнаем на какую планету совершим
путешествие. Для этого вы должны будете
выполнить следующее задание.
Вы видите записанные примеры нужно к каждому
примеру найти и перетащить правильный ответ. Но
будьте внимательны, т. к. кроме правильных
ответов есть и неправильные!
Если всё будет сделано правильно, то мы сможем
прочитать название планеты.
| 1. — 22 + 35 = 2. — 3,7 + 2,8 =
3. 1,5 + (- 6,3) =
4. 8,2 + (-8,2) =
5. 22 – 27 =
6. -14 + 8 =
7. 19 + (- 2) =
8. – 27 + (- 3) =
9. -35 + (- 9) =
10. -1,6 + (- 4,7) =
11. -2,5 + (-3,6) = |
| 10 |
Е |
-0,9 |
Л |
63 |
Д |
-5 |
Е |
| — 4,8 |
А |
-30 |
М |
-6,3 |
Р |
17 |
А |
| 0 |
Н |
— 6,1 |
С |
-41 |
З |
13 |
П |
| — 6 |
Т |
5,3 |
У |
-44 |
А |
5,9 |
К |
|
Итак мы с вами отправляемся на планету “Марс”.
В средствах массовой информации в последние
годы много говорится о готовящемся полете
человека на Марс. Мы сегодня тоже совершим полет
на Марс, в этом нам поможет математика. Слайды о
Марсе
III. этап. Следующий этап называется
“Заполни карту готовности”. Для этого вам
нужно решить интерактивный тест на компьютере.
1. Выполни сложение: (-3,9 + 3,9) + (- 8,2)
а) -5,6 б) – 8,2 в) -6,6 г) другой ответ
2. Реши уравнение : x – 8 = — 5
а) 2 б) 3 в) -13 г) другой ответ
3. Выполни действия: (4,8 – 10,8) + 2,7
а) -8,7 б) – 4,1 в) 4,1 г) другой ответ
4. Найдите значение выражения: — 0,75 + 3,87 – 3,99 + 0,75
а) 0,12 б) – 12 в) – 0,12 г) другой ответ
5. Найдите длину отрезка АВ, если А (- 10), В (- 6)
а) 4 б) 16 в) -16 г) – 4
За каждый правильный ответ 1 балл. Выставление
баллов в карточку учёта.
Динамическая пауза.
Учитель: Любая работа требует перерыва!
Выполним восстановительные упражнения:
Сложите руки в замок и положите их на затылок.
Отклоните голову назад, слегка сопротивляясь
замком рук.
Быстро поморгайте, закройте глаза и посидите
так, считая до пяти. Повторите 3 раза.
Крепко зажмурьте глаза, досчитайте до трёх,
откройте их и посмотрите вдаль, считая до пяти.
Повторите три раза.
IV. Пятый этап путешествия называется
“Посадка разрешается”
Для совершения посадки на планете Марс нужно
найти ошибки, которые допущены при нахождении
значения выражений.
– 37 +25 + (- 18) = 30 ( — 30)
6,8 + (- 9,5) +1,4 = 17,7 (- 1,3)
– 7,2 + (-3,5) +10,6 = — 0,1 (0,1)
-3,2 + (-2,9) + (- 8,5) = 2,4 (-14,6)
“Посадка разрешается”
V. Следующий этап “Высадка на Марс”
Марсиане приглашают ваш экипаж в кафе “Олимп”
на обед из 4-х блюд. Как вы думаете, почему он так
называется? Показывается слайд вулкана Олимп.
Работать вы будете в парах. Каждая пара получит
меню из 4 блюд. Вы можете выбрать любые три блюда.
Каждое блюдо имеет свою цену. Вы сами выбираете
какие примеры вы будете решать:
- Сравните значение выражение: 3,87 + (- 2,63) и 5,29 + ( -
3,59) (1 балл)
- Вычислите: 5,4 + (-3,7) + (- 4,2) (1балл)
- Решите уравнение: 3,7 – X = -2,3 (2 бала)
- Замените * знаком “+” или “-”, так, чтобы было
верное равенство: — 6,1 * (- 2,3) * 3,8 = 0 (4 балла)
Проверка самостоятельной работы по образцу
(меняются пары заданиями)
А сейчас марсиане приглашают вас на прогулку в
долины “Маринера”.
Но во время прогулки на склоне каньона
“Кандор” мы увидели записи математических
терминов, но от времени некоторые буквы плохо
видны, а марсиане не могут восстановить записи.
Давайте им поможем
- Разн…..сть
- Ум…..ньшаемое
- Выч…..таемое
- Выч….сть
- …..тнять
- Су….ма
- …..трицательное ч…сло
- Сл….гаемое
- П….ол…..жительное ч…сло
- К….рдинатная прямая
По очереди выходят к доске и вставляют
пропущенные буквы
Этап “Возвращение на землю”
Наше путешествие подходит к концу. Пора
возвращаться. “В гостях хорошо, а дома лучше”.
Для этого вы по ступенькам лестницы должны
совершить посадку на космический корабль.
Выходите по очереди к доске вместо * поставить
знак “+” или “-”, чтоб получилось верное
равенство
- (* 10) + ( * 5) = — 5
- (* 8) + ( * 9) = 1
- (* 10) + ( * 10) = — 20
- (* 30) + ( * 10) = 40
- (* 5) + ( * 5) = 0
- (* 15) + ( * 2) = — 13
- (* 20) + ( * 15) = 5
VII. Последний этап “Разбор полётов”
Вам нужно подсчитать по карточкам учёта
количество баллов и выставить оценку за урок.
- 7 баллов – “ 3 ”
- 8 -10 баллов – “ 4 ”
- 11 баллов и выше – “ 5 ”
Домашнее задание:
Задача № 1
Среднее расстояние от Марса до Солнца
составляет — 35, 5 — (- 263, 5) млн. км (228 млн. км)
Задача № 2
Период обращения вокруг Солнца равен 541,36 — (-
145,64) земным суткам. (687 земным суткам)
Задача № 3
Экваториальный
радиус равен (101 — 605,3) + 3901,2 км (3396,9 км)
Задача № 4
Найди минимальное расстояние от Марса до Земли
(когда Земля находится
точно между Солнцем и Марсом)
Для этого реши уравнение: 20 — X = — 35,75. Ответ
запиши в млн. км. ( 55,75 млн км)
Задача № 5
Найди максимальное расстояние от Марса до
Земли (когда Солнце находится точно между Землёй
и Марсом)
Для этого реши уравнение: 10x — 9x + (- 120) = 281. Ответ
запиши в млн. км. ( 401млн. км)
Рефлексия: Мне хочется, чтобы вы поделились
впечатлениями о сегодняшнем уроке. А для этого я
вам расскажу одну притчу.
Шел мудрец, а навстречу ему три человека,
которые везли под горячим солнцем тележки с
камнями для строительства. Мудрец остановился и
каждому задал по вопросу. У первого спросил: “Что
ты делал целый день?”. И тот с ухмылкой ответил,
что целый день возил проклятые камни. У второго
мудрец спросил: “А что ты делал целый день?”, и
тот ответил: “А я добросовестно выполнял свою
работу”. А третий улыбнулся, его лицо
засветилось радостью и удовольствием: “А я
принимал участие в строительстве храма!”.
— Ребята! Давайте мы попробуем оценить каждый
свою работу за урок.
— Кто работал так, как первый человек, поднимают
синие квадратики.
— Кто работал добросовестно, поднимают зеленые
квадратики.
— Кто принимал участие в строительстве храма
“Знаний”, поднимают красные квадратики.
СПАСИБО ЗА УРОК!!!
Карточка учета
| Название этапа |
Количество баллов |
| Зачисление в члены экипажа корабля |
|
| Название планеты |
|
| Заполнение карты готовности |
|
| Посадка разрешается |
|
| Обед в кафе “Олимп” |
|
| Посещение долины “Маринер” |
|
| Возвращение на Землю |
|
| Разбор полёта |
|
| Всего: |
|
1. Чему равен модуль положительного числа?
Отрицательного числа? Нуля?
2. Какие числа называются противоположными?
Приведите примеры.
3. Как сложить два отрицательных числа?
4. Как сложить числа с разными знаками?
5. Чему равна сумма двух противоположных чисел?
6. Сформулируйте переместительный закон
сложения?
7. Как сравнить два отрицательных числа?
Домашнее задание:
Задача № 1
Среднее расстояние от Марса до Солнца
составляет — 35, 5 — (- 263, 5) млн. км
Задача № 2
Период обращения вокруг Солнца равен 541,36 — (-
145,64) земным суткам.
Задача № 3
Экваториальный
радиус равен (101 — 605,3) + 3901,2 км
Задача № 4
Найди минимальное расстояние от Марса до Земли
(когда Земля находится
точно между Солнцем и Марсом)
Для этого реши уравнение: 20 — X = — 35,75. Ответ
запиши в млн. км.
Задача № 5
Найди максимальное расстояние от Марса до
Земли (когда Солнце находится точно между Землёй
и Марсом)
Для этого реши уравнение: 10x — 9x + (- 120) = 281. Ответ
запиши в млн. км.
Домашнее задание:
Задача № 1
Среднее расстояние от Марса до Солнца
составляет — 35, 5 — (- 263, 5) млн. км
Задача № 2
Период обращения вокруг Солнца равен 541,36 — (-
145,64) земным суткам.
Задача № 3
Экваториальный
радиус равен (101 — 605,3) + 3901,2 км
Задача № 4
Найди минимальное расстояние от Марса до Земли
(когда Земля находится
точно между Солнцем и Марсом)
Для этого реши уравнение: 20 — X = — 35,75. Ответ
запиши в млн. км.
Задача № 5
Найди максимальное расстояние от Марса до
Земли (когда Солнце находится точно между Землёй
и Марсом)
Для этого реши уравнение: 10x — 9x + (- 120) = 281. Ответ
запиши в млн. км.
1. Минимальное расстояние от Марса до Земли
составляет 55,75 млн км (когда Земля находится
точно между Солнцем и Марсом)
2. Максимальное расстояние от Марса до Земли —
около 401млн. км (когда Солнце находится точно
между Землёй и Марсом)
3. Среднее расстояние от Марса до Солнца
составляет 228 млн. км.
4. Период обращения вокруг Солнца равен 687
земным суткам
5. Экваториальный
радиус – 3396,9 км
“Посадка разрешается”
Найти ошибки, которые допущены при нахождении
значения выражений.
1. – 37 +25 + (- 18) = 30
2. 6,8 + (- 9,5) +1,4 = 17,7
3. – 7,2 + (-3,5) +10,6 = — 0,1
4. -3,2 + (-2,9) + (- 8,5) = 2,4
————————————————————————————
“Посадка разрешается”
Найти ошибки, которые допущены при нахождении
значения выражений.
1. – 37 +25 + (- 18) = 30
2. 6,8 + (- 9,5) +1,4 = 17,7
3. – 7,2 + (-3,5) +10,6 = — 0,1
4. -3,2 + (-2,9) + (- 8,5) = 2,4
————————————————————————————-
“Посадка разрешается”
Найти ошибки, которые допущены при нахождении
значения выражений.
1. – 37 +25 + (- 18) = 30
2. 6,8 + (- 9,5) +1,4 = 17,7
3. – 7,2 + (-3,5) +10,6 = — 0,1
-3,2 + (-2,9) + (- 8,5) = 2,4
Кафе “ОЛИМП”
МЕНЮ
№1. Сравните значение выражение: 3,87 + (- 2,63) и 5,29 + (
— 3,59) (1 балл)
№ 2. Вычислите: 5,4 + (-3,7) + (- 4,2) (1 балл)
№3. Решите уравнение: 3,7 – X = — 2,3 (2 бала)
№4. Замените * знаком “+” или “- так, чтобы
было верное равенство:
— 6,1 * (- 2,3) * 3,8 = 0 (4 балла)
19.03.2014
xn--i1abbnckbmcl9fb.xn--p1ai
Люди с давних времен используют медь в повседневной жизни. Очень важным параметром для современных людей является ее плотность и удельный вес.
Медь — это цветной металл красноватого цвета с розовым отливом, наделенный высокой плотностью. В природе насчитывается более 170 видов минералов, имеющих в своем составе Cuprum. Только из 17 ведется промышленная добыча этого элемента. Основная масса этого химического элемента содержится в составе рудных металлов: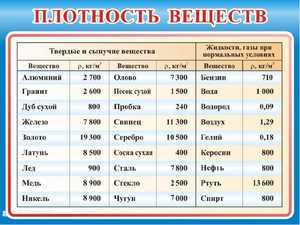
Удельный вес меди будет равняться 8,94 г/см3. Параметры удельной плотности и веса у меди совпадают, однако такое совпадение не характерно для других металлов. Удельная масса очень важна не только при производстве изделий с ее содержанием, но и при переработке лома. Существует много методик, с помощью которых можно рационально подобрать материалы для формирования изделий. В международных системах СИ параметр удельного веса выражается в ньютонах на 1 единицу объема.
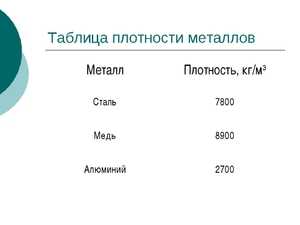обладают следующими характеристиками:
