Схема (метод) Горнера
Схема Горнера — способ деления многочлена
anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0 на бином x — a.
Чтобы выполнить деление составляется таблица:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится число a. Во второй строке пишутся коэффициенты полученного многочлена, которые считаются так:
| an | an-1 | an-2 | … | a1 | a0 | |
| a | bn-1 | bn-2 | bn-3 | … | b0 | r |
bn-1 = an
bn-2 = abn-1 + an-1
bn-3 = abn-2 + an-2
b0 = ab1 + a1
r (остаток от деления) = ab0 + a0
Таким образом можно деление превратить в сумму:
(anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0)/(x — a) = bn-1xn-1 + bn-2xn-2 + … + b1x + b0 + r/(x — a)Если r = 0, то исходный многочлен можно разложить на множители:
anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0 = (x — a)(bn-1xn-1 + bn-2xn-2 + … + b1x + b0)
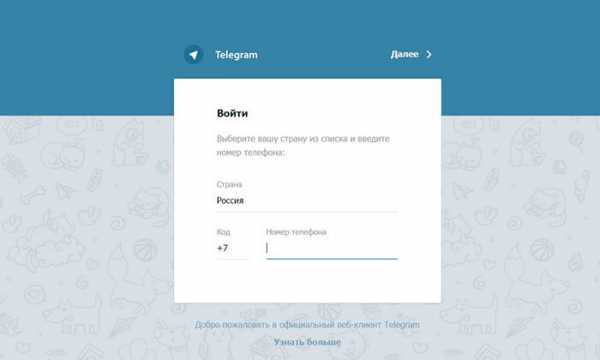
Применение схемы Горнера проще всего понять на примерахtutata.ru
Схема Горнера
Схема Горнера – способ деления многочлена Pn(x)=∑i=0naixn−i=a0xn+a1xn−1+a2xn−2+…+an−1x+an на бином x−a. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a, взятое из бинома x−a:
После деления многочлена n-ой степени на бином x−a, получим многочлен, степень которого на единицу меньше исходного, т.е. равна n−1. Непосредственное применение схемы Горнера проще всего показать на примерах.
Пример №1
Разделить 5x4+5x3+x2−11 на x−1, используя схему Горнера.
Решение
Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x4+5x3+x2−11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x−1, то во второй строке запишем единицу:
Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки:
Следующую ячейку заполним по такому принципу: 1⋅5+5=10:
Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11:
Для пятой ячейки получим: 1⋅11+0=11:
И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0:
Задача решена, осталось только записать ответ:
Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5x4+5x3+x2−11 на x−1. Естественно, что так как степень исходного многочлена 5x4+5x3+x2−11 равнялась четырём, то степень полученного многочлена 5x3+10x2+11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остачу от деления многочлена 5x4+5x3+x2−11 на x−1. В нашем случае остача равна нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена 5x4+5x3+x2−11 при x=1 равно нулю.
Можно сформулировать вывод и в такой форме: так как значение многочлена 5x4+5x3+x2−11 при x=1равно нулю, то единица является корнем многочлена 5x4+5x3+x2−11.
Пример №2
Разделить многочлен x4+3x3+4x2−5x−47 на x+3 по схеме Горнера.
Решение
Сразу оговорим, что выражение x+3 нужно представить в форме x−(−3). В схеме Горнера будет учавствовать именно −3. Так как степень исходного многочлена x4+3x3+4x2−5x−47 равна четырём, то в результате деления получим многочлен третьей степени:
Полученный результат означает, что
x4+3x3+4x2−5x−47=(x+3)(x3+0⋅x2+4x−17)+4=(x+3)(x3+4x−17)+4
В этой ситуации остача от деления x4+3x3+4x2−5x−47 на x+3 равна 4. Или, что то самое, значение многочлена x4+3x3+4x2−5x−47 при x=−3 равно 4. Кстати, это несложно перепроверить непосредственной подстановкой x=−3 в заданный многочлен:
x4+3x3+4x2−5x−47=(−3)4+3⋅(−3)3−5⋅(−3)−47=4.
Т.е. схему Горнера можно использовать, если необходимо найти значение многочлена при заданном значении переменной. Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.
Пример №3
Найти все целочисленные корни многочлена x6+2x5−21x4−20x3+71x2+114x+45, используя схему Горнера.
Решение
Коэффициенты рассматриваемого многочлена есть целые числа, а коэффициент перед старшей степенью переменной (т.е. перед x6) равен единице. В этом случае целочисленные корни многочлена нужно искать среди делителей свободного члена, т.е. среди делителей числа 45. Для заданного многочлена такими корнями могут быть числа 45;15;9;5;3;1 и −45;−15;−9;−5;−3;−1. Проверим, к примеру, число 1:
Табл. №1
Как видите, значение многочлена x6+2x5−21x4−20x3+71x2+114x+45 при x=1 равно 192(последнее число в второй строке), а не 0, посему единица не является корнем данного многочлена. Так как проверка для единицы окончилась неудачей, проверим значение x=−1. Новую таблицу для этого составлять не будем, а продолжим использование табл. №1, дописав в нее новую (третью) строку. Вторую строку, в которой проверялось значение 1, выделим красным цветом и в дальнейших рассуждениях использовать её не будем.
Можно, конечно, просто переписать таблицу заново, но при заполнении вручную это займет немало времени. Тем более, что чисел, проверка которых окончится неудачей, может быть несколько, и каждый раз записывать новую таблицу затруднительно. При вычислении «на бумаге» красные строки можно просто вычёркивать.
Табл. №2
Итак, значение многочлена x6+2x5−21x4−20x3+71x2+114x+45 при x=−1 равно нулю, т.е. число −1 есть корень этого многочлена. После деления многочлена x6+2x5−21x4−20x3+71x2+114x+45 на бином x−(−1)=x+1 получим многочлен x5+x4−22x3+2x2+69x+45, коэффициенты которого взяты из третьей строки табл. №2 (см. пример №1). Результат вычислений можно также представить в такой форме:
x6+2x5−21x4−20x3+71x2+114x+45=(x+1)(x5+x4−22x3+2x2+69x+45)(1)
Продолжим поиск целочисленных корней. Теперь уже нужно искать корни многочлена x5+x4−22x3+2x2+69x+45. Опять-таки, целочисленные корни этого многочлена ищут среди делителей его свободного члена, – числа 45. Попробуем ещё раз проверить число −1. Новую таблицу составлять не будем, а продолжим использование предыдущей табл. №2, т.е. допишем в нее еще одну строку:
Итак, число −1 является корнем многочлена x5+x4−22x3+2x2+69x+45. Этот результат можно записать так:
x5+x4−22x3+2x2+69x+45=(x+1)(x4−22x3+24x+45)(2)
Учитывая равенство (2), равенство (1) можно переписать в такой форме:
x6+2x5−21x4−20x3+71x2+114x+45=(x+1)(x5+x4−22x3+2x2+69x+45)==(x+1)(x+1)(x4−22x3+24x+45)=(x+1)2(x4−22x3+24x+45)(3)
Теперь уже нужно искать корни многочлена x4−22x2+24x+45, – естественно, среди делителей его свободного члена (числа 45). Проверим еще раз число −1:
Число −1 является корнем многочлена x4−22x2+24x+45. Этот результат можно записать так:
x4−22x2+24x+45=(x+1)(x3−x2−21x+45)(4)
С учетом равенства (4), равенство (3) перепишем в такой форме:
x6+2x5−21x4−20x3+71x2+114x+45=(x+1)2(x4−22x3+24x+45)=(x+1)2(x+1)(x3−x2−21x+45)=(x+1)3(x3−x2−21x+45)(5)
Теперь ищем корни многочлена x3−x2−21x+45. Проверим еще раз число −1:
Проверка окончилась неудачей. Выделим шестую строку красным цветом и попробуем проверить иное число, например, число 3:
В остаче ноль, посему число 3 – корень рассматриваемого многочлена. Итак, x3−x2−21x+45=(x−3)(x2+2x−15). Теперь равенство (5) можно переписать так:
x6+2x5−21x4−20x3+71x2+114x+45==(x+1)3(x3−x2−21x+45)=(x+1)3(x−3)(x2+2x−15)(6)
Проверим ещё раз число 3:
Полученный результат можно записать так (это продолжение равенства (6)):
x6+2x5−21x4−20x3+71x2+114x+45=(x+1)3(x−3)(x2+2x−15)==(x+1)3(x−3)(x−3)(x+5)=(x+1)3(x−3)2(x+5)(7)
Из последней скобки видно, что число −5 также является корнем данного многочлена. Можно, конечно, формально продолжить схему Горнера, проверив значение x=−5, но необходимости в этом нет. Итак,
x6+2x5−21x4−20x3+71x2+114x+45=(x+1)3(x−3)(x2+2x−15)=(x+1)3(x−3)2(x+5)
Числа −1;3;5 – корни данного многочлена. Причем, так как скобка (x+1) в третьей степени, то −1 – корень третьего порядка; так как скобка (x−3) во второй степени, то 3 – корень второго порядка; так как скобка (x+5) в первой степени, то x=−5 – корень первого порядка (простой корень).
Вообще, обычно оформление таких примеров состоит из таблицы, в которой перебираются возможные варианты корней, и ответа:
Из таблицы следует вывод, полученный нами ранее с подробным решением:
x6+2x5−21x4−20x3+71x2+114x+45=(x+1)3(x−3)(x2+2x−15)=(x+1)3(x−3)2(x+5)
Пример №4
Убедиться, что числа 2 и −5 являются корнями многочлена 3x6+9x5−28x4+6x3−30x2−30x+100. Разделить заданный многочлен на биномы x−2 и x+5.
Решение
Степень многочлена 3x6+9x5−28x4+6x3−30x2−30x+100 равна 6. После деления на два заданных бинома степень заданного многочлена уменьшится на 2, т.е. станет равна 4.
Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.
studfiles.net
Тема урока «Теорема Безу. Схема Горнера и ее применение»
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (81 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: Урок усвоения и закрепления первичных знаний.
Цель урока:
- Ознакомить учеников с понятием корней многочлена, научить находить их. Усовершенствовать навыки применения схемы Горнера по разложению многочлена по степеням и деления многочлена на двучлен.
- Научиться находить корни уравнения с помощью схемы Горнера.
- Развивать абстрактное мышление.
- Воспитывать вычислительную культуру.
- Развитие межпредметных связей.
Ход урока
1. Организационный момент.
Сообщить тему урока, сформулировать цели.
2. Проверка домашнего задания.
3. Изучение нового материала.
Пусть Fn(x)= anxn +a n-1xn-1+…+ a1x +a0 —многочлен относительно x степени n, где a0, a1,…,an –данные числа, причем a0 не равно 0. Если многочлен Fn(x) разделить с остатком на двучлен x-a, то частное (неполное частное) есть многочлен Qn-1(x) степени n-1, остаток R есть число, при этом справедливо равенство Fn(x)=(x-a) Qn-1(x) +R. Многочлен Fn(x) делится нацело на двучлен (x-a) только в случае R=0.
Теорема Безу: Остаток R от деления многочлена Fn(x) на двучлен (x-a) равен значению многочлена Fn(x) при x=a, т.е. R= Pn(a).
Немного истории. Теорема Безу, несмотря на внешнюю простоту и очевидность, является одной из фундаментальных теорем теории многочленов. В этой теореме алгебраические свойства многочленов (которые позволяют работать с многочленами как с целыми числами) связываются с их функциональными свойствами (которые позволяют рассматривать многочлены как функции). Одним из способов решения уравнений высших степеней является способ разложения на множители многочлена, стоящего в левой части уравнения. Вычисление коэффициентов многочлена и остатка записывается в виде таблицы, которая называется схемой Горнера.
Схема Горнера – это алгоритм деления многочленов, записанный для частного случая, когда частное равно двучлену x–a.
Горнер Уильям Джордж (1786 — 1837), английский математик. Основные исследования относятся к теории алгебраических уравнений. Разработал способ приближенного решения уравнений любой степени. В 1819 г. ввёл важный для алгебры способ деления многочлена на двучлен х — а (схема Горнера).
Вывод общей формулы для схемы Горнера.
Разделить с остатком многочлен f(x) на двучлен (x-c) значит найти такой многочлен q(x) и такое число r, что f(x)=(x-c)q(x)+r
Запишем это равенство подробно:
f0xn + f1 xn-1 + f2 xn-2 + …+fn-1 x + fn =(x-c) (q0 xn-1 + q1 xn-2 + q2 xn-3 +…+ qn-2 x + qn-1 )+r
Приравняем коэффициенты при одинаковых степенях:
xn : f0 = q0 => q0 = f0 xn-1 : f1 = q1 — c q0 => q1 = f1 + c q0 xn-2 : f2 = q2 — c q1 => q2 = f2 + c q1 … … x0 : fn = qn — c q n-1 => qn = fn + c qn-1.
Демонстрация схемы Горнера на примере.
Задание 1. С помощью схемы Горнера разделим с остатком многочлен f(x) = x3 — 5x2 + 8 на двучлен x-2.
| 1 | -5 | 0 | 8 | |
| 2 | 1 | 2*1+(-5)=-3 | 2*(-3)+0=-6 | 2*(-6)+8=-4 |
f(x) = x3 — 5x2 + 8 =(x-2)(x2-3x-6)-4, где g(x)= (x2-3x-6), r = -4 остаток.
Разложение многочлена по степеням двучлена.
Используя схему Горнера, разложим многочлен f(x)=x3+3x2-2x+4 по степеням двучлена (x+2).
В результате должны получить разложение f(x) = x3+3x2-2x+4 = (x+2)(x2+x-4)+12 = (x+2)((x-1)(x+2)-2)+12 = (((1*(x+2)-3)(x+2)-2)(x+2))+12 = (x+2)3 -3(x+2)2 -2(x+2)+12
Схему Горнера часто используют при решении уравнений третьей, четвертой и выших степеней, когда удобно разложить многочлен на двучлен x-a. Число a называют корнем многочлена Fn(x) = f0xn + f1 xn-1 + f2 xn-2 + …+fn-1 x + fn , если при x=a значение многочлена Fn(x) равно нулю: Fn(a)=0, т.е. если многочлен делится нацело на двучлен x-a.
Например, число 2 является корнем многочлена F3(x)=3x3-2x-20, так как F3(2)=0. это означает. Что разложение этого многочлена на множители содержит множитель x-2.
F3(x)=3x3-2x-20=(x-2)(3x2+6x+10).
Любой многочлен Fn(x) степени n 1 может иметь не более n действительных корней.
Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.
Если старший коэффициент уравнения равен 1, то все рациональные корни уравнения, если они существуют, целые.
Закрепление изученного материала.
Для закрепления нового материала учащимся предлагается выполнить номера из учебника 2.41 и 2.42 (стр. 65).
(2 ученика решают у доски, а остальные, решив, в тетради задания сверяются с ответами на доске).
Подведение итогов.
Поняв структуру и принцип действия схемы Горнера, ее можно использовать и на уроках информатики, когда рассматривается вопрос о переводе целых чисел из десятичной системы счисления в двоичную и обратно. В основе перевода из одной системы счисления в другую лежит следующая общая теорема
Теорема. Для перевода целого числа Ap из p-ичной системы счисления в систему счисления с основанием d необходимо Ap последовательно делить с остатком на число d, записанное в той же p-ичной системе, до тех пор, пока полученное частное не станет равным нулю. Остатки от деления при этом будут являться d-ичными цифрами числа Ad, начиная от младшего разряда к старшему. Все действия необходимо проводить в p-ичной системе счисления. Для человека данное правило удобно лишь при p = 10, т.е. при переводе из десятичной системы. Что касается компьютера, то ему, напротив, “удобнее” производить вычисления в двоичной системе. Поэтому для перевода “2 в 10” используется последовательное деление на десять в двоичной системе, а “10 в 2” — сложение степеней десятки. Для оптимизации вычислений процедуры “10 в 2” компьютер использует экономную вычислительную схему Горнера. [1]
Домашнее задание. Предлагается выполнить два задание.
1-е. Используя схему Горнера разделить многочлен f(x)=2x5-x4-3x3+x-3 на двучлен (x-3).
2-е. Найти целые корни многочлена f(x)=x4-2x3+2x2-x-6.(учитывая, что любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена)
Литература.
- Курош А.Г. “Курс высшей алгебры”.
- Никольский С.М, Потапов М.К. и др. 10 класс “Алгебра и начала математического анализа”.
- [1] http://inf.1september.ru/article.php?ID=200600907.
16.12.2013
xn--i1abbnckbmcl9fb.xn--p1ai
Онлайн калькулятор схема горнера — PDF
Многочлены и их корни
Многочлены и их корни 2018 г. Гущина Елена Николаевна Определение: Многочленом степени n n N называется всякое выражение вида: P & z = a & z & + a &+, z &+, + + a, z + a., где a &, a &+,, a,, a. R, a &
ПодробнееМногочлены и их корни
Многочлены и их корни Определение: Многочленом степени n (n N) называется всякое выражение вида: P n (z) = a n z n + a n 1 z n 1 + + a 1 z + a 0, где a n, a n 1, a 1, a 0 R, a n старший коэффициент, a
ПодробнееАлгебраические уравнения
Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами
ПодробнееКОРНИ МНОГОЧЛЕНОВ, ТЕОРЕМА БЕЗУ
ЛЕКЦИЯ 20 КОРНИ МНОГОЧЛЕНОВ, ТЕОРЕМА БЕЗУ ДИФФЕРЕНЦИРОВАНИЯ МНОГОЧЛЕНОВ ФОРМУЛЫ ВИЕТА 1 КОРНИ МНОГОЧЛЕНОВ Займемся тем, ради чего в прошлом изучали алгебру, корнями многочленов. Дело в том, что многие
ПодробнееУпростите выражение калькулятор онлайн
Упростите выражение калькулятор онлайн >>> Упростите выражение калькулятор онлайн Упростите выражение калькулятор онлайн Наши партнеры собирают ваши данные используют файлы cookie для персонализации и
ПодробнееУпростите выражение калькулятор онлайн
Упростите выражение калькулятор онлайн >>> Упростите выражение калькулятор онлайн Упростите выражение калькулятор онлайн Наши партнеры собирают ваши данные используют файлы cookie для персонализации и
ПодробнееПояснительная записка.
Пояснительная записка. Рабочая программа элективного курса «Алгебра плюс» для 10 «А» класса составлена на основе авторской программы А.Н. Землякова по элективному курсу «Алгебра плюс: рациональные и иррациональные
ПодробнееP x x Qx ( ) + r или
Лекция Разложение рациональной дроби на простейшие Аннотация: Доказывается, что из неправильной дроби можно выделить целую часть, а правильную дробь разложить на простейшие Рациональной дробью (рациональной
ПодробнееАлгебраические многочлены.
Алгебраические многочлены. 1 Алгебраические многочлены степени n над полем K Определение 1.1 Многочленом степени n, n N {0}, от переменной z над числовым полем K называется выражение вида: fz = a n z n
ПодробнееМАТЕМАТИЧЕСКИЙ ПРАКТИКУМ
МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ Ю.Л.Калиновский Введение Решение квадратных уравнений Решение квадратных уравнений c помощью разложения на множители. Решение квадратных уравнений c помощью дополнения до полного
ПодробнееЛЕКЦИЯ N11. Методы интегрирования.
ЛЕКЦИЯ. Методы интегрирования..интегрирование по частям..рациональные дроби. Разложение правильной дроби на простейшие…интегрирование рациональных дробей..интегрирование по частям. Пусть u и v две непрерывные
ПодробнееПриложение 1. ГРУППЫ, КОЛЬЦА, ПОЛЯ
Приложение 1 ГРУППЫ, КОЛЬЦА, ПОЛЯ Для криптографии алгебра является одним из основных инструментов в теоретических исследованиях и практических построениях криптографических преобразований Поэтому в этом
Подробнеесайты:
Федеральное агентство по образованию Уральский государственный экономический университет Ю. Б. Мельников Стратегия составления уравнений Раздел электронного учебника для сопровождения лекции Изд. 3-е,
ПодробнееЛЕКЦИЯ 10 СРАВНЕНИЯ СТЕПЕНЕЙ ВЫШЕ ПЕРВОГО
ЛЕКЦИЯ 10 СРАВНЕНИЯ СТЕПЕНЕЙ ВЫШЕ ПЕРВОГО Переходя от сравнений первой степени к сравнениям более высоких степеней, целесообразно сначала рассмотреть тот случай, когда модуль простое число В этом случае
ПодробнееИррациональные уравнения и неравенства 2
Иррациональные уравнения и неравенства Оглавление Иррациональные уравнения Метод возведения обеих частей уравнения в одну и ту же степень Задание Задание Задание Замена иррационального уравнения смешанной
ПодробнееРЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ
РЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ Обозначим через значение некоторого выражения при подстановке в него целого числа Тогда зависимость члена последовательности от членов последовательности F F со значениями
ПодробнееОнлайн конвертер cdw в dwg
Онлайн конвертер cdw в dwg >>> Онлайн конвертер cdw в dwg Онлайн конвертер cdw в dwg Реклама помогает поддерживать и развивать наш сервис. Зарегистрировался — Все отлично. Забудьте о проблеме несовместимости
ПодробнееЛекция 2: Многочлены
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Понятие многочлена Определения Многочленом от одной переменной называется выражение вида
ПодробнееМЕТОД НАХОЖДЕНИЯ КОРНЕЙ МНОГОЧЛЕНОВ. I
Детерминированные системы 4(34) ностью параметров объекта управления Система уравнений описывающая КЭМП в виде обобщенной электрической машины может быть использована только для предварительного анализа
ПодробнееПримеры и комментарии
72 Глава2 Многочлены Примеры и комментарии Алгоритмы А-01 Запись многочлена в стандартном виде А-02 Действия над многочленами А-03 Устные преобразования А-04 Формулы сокращенного умножения А-05 Бином Ньютона
ПодробнееПояснительная записка
Статус документа Пояснительная записка Настоящая рабочая программа по алгебре для 8 класса (углубленный уровень) основной общей общеобразовательной школы составлена на основе федерального компонента государственного
ПодробнееЗАДАЧИ ПО АЛГЕБРЕ (часть 1)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Нижегородский государственный университет им НИ Лобачевского Национальный исследовательский университет ЗАДАЧИ ПО АЛГЕБРЕ часть ) Учебно-методическое
ПодробнееТестовые задания и диктанты
Глава4 Уравнения 1 Тестовые задания и диктанты Т-01 Решение линейного уравнения Т-02 Решение уравнений разложением на множители Т-03 Рациональные уравнения, сводящиеся к линейным Т-04 Замена неизвестного
ПодробнееТема 5 Рациональные системы уравнений
Тема 5 Рациональные системы уравнений F ( x, x,…, ) 0, F ( x, x,…, ) 0, Система уравнений вида где… Fk ( x, x,…, ) 0, F i( x, x,…, ), i,…, k, некоторые многочлены, называется системой рациональных
ПодробнееЛЕКЦИЯ 10 ПОСТРОЕНИЕ СПЛАЙНОВ
ЛЕКЦИЯ 10 ПОСТРОЕНИЕ СПЛАЙНОВ На прошлой лекции было доказано, что интерполяционные многочлены в форме Лагранжа и Ньютона эквивалентны. Были введены функция Лебега и константа Лебега. Было показано, что
ПодробнееПояснительная записка
1 Пояснительная записка Рабочая программа элективного курса «МИР, МАТЕМАТИКА, МАТЕМАТИКИ» Для10-11 классов, составлена в соответствии с программой А.Н. Землякова «Элективные курсы в профильном обучении.
ПодробнееИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Первообразная функция и неопределённый интеграл первообразной Лемма Функция F( называется первообразной для функции f( на промежутке X, если F ( = f( X Функция,
ПодробнееЕ. Н. ФИЛАТОВ АЛГЕБРА
Заочный физико-математический лицей «Авангард» Е. Н. ФИЛАТОВ АЛГЕБРА 8 Экспериментальный учебник Часть МОСКВА 06 Заочный физико-математический лицей «Авангард» Е. Н. Филатов АЛГЕБРА 8 Экспериментальный
ПодробнееМатематика 8 класс Многочлены
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
ПодробнееЗадача 11. Деление с остатком
XVIII Республиканский Турнир Юных Математиков Задача 11. Деление с остатком Лицей БГУ — 1 Автор: Пчелинцев Илья Научный руководитель: Шабан Светлана Аннотация Полностью решены пункты 1-3, 5 исходной постановки
ПодробнееТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ В результате изучения курса ученик должен знать/понимать определение модуля числа, свойства модуля, геометрический смысл модуля; алгоритм решения линейных, квадратных,
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа составлена на основе программы А.Н.Землякова «Алгебра +: рациональные и иррациональные алгебраические задачи». Факультативный курс «Рациональные и иррациональные
Подробнее8 класс Алгебра. Тема «Рациональные дроби»
8 класс Алгебра Тема «Рациональные дроби» 1. ОСНОВНЫЕ ПОНЯТИЯ Понятие алгебраической дроби знакомо вам из курса алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей.
ПодробнееТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ
Лекции по Математике Вып ТММ- Ю В Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 00 УДК 5+5 ББК Ч35 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С-Петерб техн ун-та М А Салль Кандидат
Подробнееdocplayer.ru
Методика преподавания темы «Схема Горнера, теорема Безу и деление уголком».
Репетитор по математике не всегда может объяснить материал, который неудачно изложен в учебнике.
Ксожалению, таких тем становится все больше и больше, и ошибки изложения вслед за авторами пособий совершаются в массовом порядке. Это относится не только к начинающим репетиторам по математике и репетиторам по совместительству (репетиторы — студенты и репетиторы ВУЗов), но и к опытным преподавателям, репетиторам — профессионалам, репетиторам со стажем и квалификацией. Талант грамотного корректора шероховатостей школьных учебников имеют далеко не все репетиторы математики. Не все также понимают, что эти коррекции (или дополнения) необходимы. Адаптацией материала для его качественного восприятия детьми занимаются единицы. Ксожалению, ушло то время, когда преподаватели математики вместе с методистами и авторами изданий в массовом порядке обсуждали каждую букву учебника. Раньше, прежде чем пустить учебник в школы, проводили серьезные анализы и исследования результатов обучения. Пришло время дилетантов, стремящихся сделать пособия универсальными, подгоняя их под стандарты сильных математических классов.Гонка за увеличением количества информации приводит только к снижению качества ее усвоения и, как следствие, к снижению уровня реальных знаний по математике. Но на это никто не обращает внимание. И наши дети вынуждены уже в 8 классе изучать то, что мы с вами проходили в институте: теорию вероятности, решение уравнений высоких степеней и кое-что еще. Адаптация материала в книжках для его полноценного восприятия ребенком оставляет желать лучшего и репетитор по математике вынужден как-то с этим бороться.
Поговорим о методике преподавания такой специфической темы, как «деление уголком многочлена на многочлен», более известной во взрослой математике как «теорема Безу и схема Горнера». Еще каких-нибудь пару лет назад вопрос не стоял перед репетитором по математике так остро, ибо он не входил в основную школьную программу. Теперь уважаемые авторы учебника под редакцией Теляковского внесли изменения в последнее издание лучшего, на мой взгляд, учебника, и, окончательно испортив его, только добавили репетитору лишних забот. Преподаватели школ и классов, не имеющих статус математических, ориентируясь на нововведения авторов, стали чаще включать дополнительные параграфы в свои уроки, а любознательные дети, рассматривая красивые странички их учебника математики, все чаще спрашивают репетитора: «Что это за деление уголком? Мы будем это проходить? Как делить уголком?» От таких прямых вопросов уже не спрятаться. Репетитору придется что-то рассказывать ребенку.
А как? Наверное, я бы не стал описывать метод работы с темой, если бы в учебниках она грамотно преподносилась. У нас ведь как все происходит? Учебники нужно печатать и продавать. А для этого их надо регулярно обновлять. Преподаватели Вузов жалуются, что дети приходят к ним с пустыми головами, без знаний и навыков? Требования к математическим знаниям растут? Отлично! Давайте мы уберем некоторые упражнения, а вместо них вставим темы, которые изучаются по другим программам. Чем наш учебник хуже? Включим какие-нибудь дополнительные главы. Школьники не знают правило деления уголком? Это же элементарная математика. Надо сделать такой параграф необязательным, озаглавив его «для тех, кто хочет знать больше». Репетиторы против? А какое нам дело до репетиторов вообще? Методисты и преподаватели школ тоже против? Мы не будем усложнять материал и рассмотрим наиболее простую его часть.
И вот тут начинается. Простота темы и качество ее усвоения заключатся, прежде всего, в понимании ее логики, а не в том, чтобы согласно предписанию авторов учебника выполнить некий набор не понятно как связанных друг с другом операций. Иначе туман в голове школьника будет обеспечен. Если расчет авторов идет на относительно сильных учеников (но обучающихся по обычной программе), то не стоит подавать тему в командной форме. А что мы видим в учебнике? Дети, надо делить по такому правилу. Получите многочлен под уголком. Таким образом, первоначальный многочлен разложится на множители. Однако, понять, почему именно так подбираются слагаемые под уголком, почему их надо умножать на многочлен над уголком, а затем вычитать из текущего остатка — непонятно. И самое главное не понятно, почему подобранные одночлены надо в итоге сложить и почему получившиеся скобки будут разложением первоначального многочлена. Любой грамотный математик поставит жирный знак вопроса над теми объяснениями, которые даются в учебнике.
Я предлагаю вниманию репетиторов и преподавателей математики свое решение проблемы, которое практически делает для ученика очевидным все то, что изложено в учебнике. Фактически мы докажем теорему Безу: если число а — корень многочлена, то этот многочлен можно разложить на множители, один из который x-a, а второй получается из первоначального одним из трех способов: выделением линейного множителя через преобразования, делением уголком или по схеме Горнера. Именно с такой форомулировкой репетитору по математике будет легче работать.
Что такое методика преподавания? Прежде всего это четкий порядок в последовательности объяснений и примеров, на основе которых делаются математические выводы. Данная тема не исключение. Репетитору по математике очень важно познакомить ребенка с теоремой Безу до того, как будет выполняться деление уголком. Это очень важно! Добиться понимания лучше всего на конкретном примере. Возьмем какой-нибдуь многочлен с подобранным корнем и показажем технику его разложения на множители при помощи знакомого школьнику еще с 7 класса метода тождественных преобразований. При соответствующих сопроводительных пояснениях, акцентах и подсказках репетитора по математике вполне реально донести материал без каких-либо общих математических выкладок, произвольных коэффициентов и степеней.
Важный совет репетитору по математике — следовать инструкциям от начала и до конца и не менять эту последовательнотсь.
Итак, допустим, что перед нами многочлен . Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить на два слагаемых так, чтобы одно из них было произведением линейного выражения и некоторого одночлена, а второе имело бы степень на единицу меньше, чем . То есть представим его в видеОдночлен для красного поля подберем так, чтобы при при умножении его на старший член полностью совпадал со старшим членом первоначального многочлена. Если ученик не самый слабый, то он вполне способен будет назвать репетитору по математике искомое выражение: . Репетитору следует тут же предложить вставить его в красное поле и показать что будет получаться при их раскрытии. Лучше всего этот виртуальный временный многочлен подписать под стрелочками (под фотанчиком), выделяя его каким-нибудь цветом, например, синим. Это поможет подоборать слагаемое для красного поля, называемое остатком от выделения. Я бы советовал репетиторам именно здесь указывать на то, что этот остаток можно находить вычитанием. Выполняя такую операцию получим:
Репетитор по математике должен обратить внимание ученика на то, что подставляя единицу в данное равенство, мы гарантировано получим нуль в его левой части (так как 1 — корень первоначального многочлена), а в правой, очевидно, тоже обнулим первое слагаемое. Значит без всякой проверки можно сказать, что единица — корень «зеленого остатка».
Поступим с ним так же, как мы это сделали с первоначальным многочленом, выделяя из него такой же линейный множитель . Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо. Ученик подбирает репетитору одночлен для красного поля так, чтобы он при умножении на старшее слагаемое линейного выражения давал старшее слагаемое раскладывающегося многочлена. Вписываем в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем И, наконец, проделывая тоже самое с последним остаткомполучим окончательно
Теперь вынесем выражение за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень». Для того, чтобы ученику не казалось, что последний «зеленый остаток» случайно разложился на нужные множители, репетитор по математкие должен указать на важное свойство всех зеленых остатков — каждый из них имеет корень 1. Поскольку степени этих остатков убывают, то какая бы степень начального многочлена ни была нам дана, рано или поздно, мы получим линейный «зеленый остаток» с корнем 1, а следовательно он обязательно разложиться на произведение некоторого числа и выражения .После такой подготовительной работы репетитору по математкие не составит труда объяснить ученику, что происходит при делении уголком. Это тот же самый процесс, только в более краткой и компактной форме, без знаков равно и без переписываний одних и тех же выделенных слагаемых. Многочлен из которого выделяется линейный множитель записываем слева от уголка, подбираемые красные одночлены собираем под уголом (теперь становится понятно, почему они должны складываться), для получения «синих многочленов» надо «красные» умножать на x-1, а затем вычитать из текущего выделяемого как это делается при обычном делении чисел в столбик (вот она аналогия с раннее изученным). Получаемые «зеленые остатки» подвергаются новому выделению и подбору «красных одночленов» . И так до получения нулевого «зеленого остатка». Самое главное, что ученику становится понятна дальнейшая судьба записанных многочленов над и под уголком. Очевидно, это скобки, произведение которых равно первоначальному многочлену.
Следующий этап работы репетитора по математике — формулирование теоремы Безу. Cобственно ее формулировка при таком подходе репетитора становится очевидной: если число а — корень многочлена, то его можно разложить на множители, один из которых , а другой получается из первоначального одним из трех способов:- непосредственным разложением (аналогом метода группировки)
- делением уголком (в столбик)
- через схему Горнера
Корень умножается на последний снесенный «красный коэффициент», прибавляется к следующему коэффициенту верхней строки и результат сносится в нижнюю строчку . В последней колонке гарантированно получим старший коэффициент последнего «зеленого остатка», то есть нуль. После завершения процесса, числа, зажатые между подобранным корнем и нулевым остатком оказываются коэффициентами второго (нелинейного) множителя.
Поскольку корень а дает в конце нижней строки нуль, то схему Горнера можно использовать для проверки чисел на звание корень многочлена. Если специальная теорема о подборе рационального корня. Все кандидаты на это звание, полученные с ее помощью, просто вставляются по очереди слева в схему Горнера. Как только мы получим нуль, тестируемое число будет корнем, и одновременно в его строчке получим коэффициенты разложения первоначального многочлена на множители. Очень удобно.
В завершение хотелось бы отметить, что для аккуратного введения схемы Горнера , а также для практического закрепления темы, репетитор по математике должен иметь в своем распоряжении достаточное количество часов. Репетитору, работающему с режимом «раз в неделю» не стоит заниматься делением уголком. На Егэ по математике и на ГИА по математике вряд ли в первой части когда-нибудь встретится уравнение третьей степени, решаемое такими средствами. Если репетитор готовит ребенка экзамену по математике в МГУ — изучение темы становится обязательным. Очень уж любят преподаватели ВУЗов, не в пример составителям ЕГЭ, проверить глубину знаний абитуриента. В общем случае уравнение степени выше четвертой не разрешимо в радикалах. Однако, иногда можно отыскать корни многочлена, который находится в левой части уравнения высшей степени, представив его в виде призведения многочленов степени не выше четвертой. Таким образом, разложение многочлена на множители лежит в основе решения таких уравнений, поэтому, рекомендуем подробно изучить этот раздел, прежде чем двигаться дальше.Достаточно часто рассматриваются уравнения высших степеней с целыми коэффициентами. В этом случае можно попытаться найти рациональные корни уравнения, после чего можно разложить на множители многочлен, находящийся в левой части исходного уравнения, тем самым перейти к нахождению корней уравнения, степень которого будет ниже.
В этой статье как раз разберемся с решением уравнений высших степеней с целыми коэффициентами.
Уравнения высших степеней с целыми коэффициентами.
Любое уравнение вида можно свести к приведенному уравнению той же степени домножив обе его части на и выполнив замену переменной вида :Полученные коэффициенты тоже будут целыми. Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида .
Алгоритм решения.
Находим целые корни уравнения.
И так продолжаем перебор делителей, начиная с . В итоге найдем все m целых корней уравнения и оно представится в виде , где — многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.
- Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения любым способом.
Разберем алгоритм на примере.
Решить уравнение .Во-первых, найдем все целые корни данного уравнения.
Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3.
Будем подставлять их по очереди в исходное равенство до получения тождества.
При х=1 имеем . То есть х=1 является корнем уравнения. Разделим многочлен на (х-1) столбиком: Следовательно, . Продолжим перебор делителей, но уже для равенства :
Следовательно, . Продолжим перебор делителей, но уже для равенства :При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения.
Разделим на (х+1) столбиком: Таким образом,
Таким образом,Продолжаем перебор делителей для равенства , начиная с х = -1:
Получили неверные равенства, следовательно, целых корней уравнение больше не имеет.
Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена . , то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных .Замечание.
Можно было использовать схему Горнера вместо деления многочленов столбиком.
Решение было бы следующим.
Как только выяснили, что x=1 является корнем уравнения, то имеемТаблица коэффициентов схемы Горнера сразу дает коэффициенты частного от деления многочленов, то есть . Как только выясняем, что х = -1 является следующим решением уравнения, то по схеме Горнера имеем
После этого шага метода Горнера приходим к разложению . После проверки оставшихся делителей для равенства переходим к нахождению оставшихся корней. х = -1, х=1, . Найти корни уравнения .
Делителями свободного члена являются числа 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12 и -12.
Проводим проверку:То есть, х=2 является корнем уравнения. Делим на х-2 по схеме Горнера:
Получаем . Продолжаем проверку делителей для равенства , начиная с х=2.
То есть, х=2 опять является корнем. Делим на х-2
Получаем . Проверять оставшиеся делители для равенства нет смысла, так как быстрее найти корни этого квадратного трехчлена через дискриминант. Решаем квадратное уравнение:
.
Следовательно, корнями является комплексно сопряженная пара . х=2, . Найти действительные корни уравнения . Для вычисления коэффициентов частного и остатка от деления многочлена на линейный двучлен x-s очень удобно использоватьсхему Горнера (иногда называют метод Горнера). Заполняется таблица:Полученные числа являются коэффициентами частного от деления многочлена на двучлен x-s, а — остатком. То есть,
В следующем примере не будем давать такие подробные пояснения.
Убедиться, что многочлен делится на двучлен без остатка и найти частное. Проверим это с использованием схемы Горнера:Получили остаток равный нулю, что говорит о делимости исходного многочлена без остатка на двучлен. Частным является многочлен Когда , то можно говорить о делимости многочлена на двучлен x-s, другими словами, s – корень исходного многочлена. По следствию из теоремы Безу, такой многочлен представляется в виде произведения:
Найти корни уравнения и разложить многочлен в левой части уравнения на множители.
Если это уравнение имеет целые корни, то они находятся среди делителей свободного члена. Запишем эти делители 1,-1,2,-2,3,-3,6,-6.
Проверим их по схеме Горнера.То есть, х=1 корнем не является.
Продолжаем схему Горнера.То есть, х=-1 является корнем, и исходный многочлен представится в виде Продолжим проверку делителей, начиная с х=-1 (так как корни могут повторяться), но в схеме Горнера коэффициентами будем считать значения последней полученной строки:
То есть, х=-1 не является повторяющимся (кратным) корнем. Проверяем следующий делитель:
То есть, х=2 не является корнем. Продолжаем схему Горнера для х=-2:
То есть, х=-2 является корнем уравнения, многочлен представляется в виде
Таким образом, получили требуемое разложение. Из него видно, что последним третьим корнем является х=3. Завершим таблицу, в качестве коэффициентов будем использовать уже значения последней полученной строки:
Вывод: последняя таблица, заполненная по схеме Горнера, по сути, является решением рассмотренного примера.
х=-1, х=-2, х=3, .matematika-2014elena-viktorovna.blogspot.com
Решение кубических уравнений методом Горнера
Если не удается решить кубическое уравнение группировкой, то можно попробовать разложить многочлен на множители по схеме Горнера. Разберем на примере:
Дано уравнение
x3 + 6x2 — 25x + 18 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 18 являются ±1, ±2, ±3, ±6, ±9, ±18.
Подставим число 1: 1 + 6 — 25 + 18 = 0. Мы выяснили, что число 1 является корнем уравнения. Если бы делитель 1 не подошел, то мы бы проверяли все делители, пока не нашли тот, который бы являлся корнем.
Мы нашли 1 из корней многочлена. Корнем многочлена является 1, а значит исходный многочлен должен делиться на x — 1. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 1. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 1, просто перенеся его из соответствующей ячейки первой строки. | |
| 1 ∙ 1 + 6 = 7 | |
| 1 ∙ 7 — 25 = -18 | |
| 1 ∙ (-18) + 18 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Таким образом мы исходный многочлен разложили на множители:
x3 + 6x2 — 25x + 18 = (x — 1)(x2 + 7x — 18)
И теперь, всего лишь, осталось найти корни квадратного уравнения
x2 + 7x — 18 = 0
D = b2 — 4ac = 72 — 4 ∙ 1 ∙ (-18) = 121
D > 0 ⇒ уравнение имеет 2 корня
| x1,2 = | -b ± √ D |
= | -7 ± 11 | = -9; 2 |
| 2a | 2∙1 |
Мы нашли все корни уравнения:
x = 1; 2; -9
tutata.ru
Метод Горнера. Деление многочлена.
| Заданный многочлен имеет вид |
| если разделим его |
| Получим многочлен |
| и остаток |
на бином вида
результат деления есть функция вида
Такой результат получается только в результате деления исходного многочлена на бином без остатка.
В общем же случае говорится, что функцию можно представить в виде
где r — это остаток от деления.
Коэффициенты функции рассчитываются по реккурентым формулам
Схема Горнера очень удобна своей простой и отсутствием функции деления. Это позволяет решать с повышенной точностью подобные уравнения, а также решать целочисленные уравнения, без каких либо машинных(компьютерных) погрешностей.
Кстати!
Есть новый калькулятор который осуществляет деление многочлена на многочлен с остатком . Работает в том числе и в комплексном поле, кроме того, делящий многочлен может быть на самом деле многочленом(!), а не биномом, как в этой статье.
Кроме этого, эта же схема позволяет решать задачу определения значения функции при каком либо значении. «Фи!» — скажете Вы. «Это же элементарно, любой калькулятор это может».
да конечно, поставивив вместо неизвестного x необходимое значение мы получим нам нужный результат, но какой ценой?
Нам придется возводить значения в степень, что несомненно внесет свою погрешность в расчеты.
Это явно проявляется при работе в поле комплексных чисел, при делении многочлена на комплексный бином.
Нам проще воспользоватся теоремой Безу, которая гласит: Остаток r от деления многочлена на на линейный двучлен равен значению многочлена при
Бот созданный на этом сайте, позволяет Вам решать поставленную задачу методом Горнера, не только для действительных чисел, но и для комплексных. Это расширяет возможности применения бота и позволяет более полно исследовать функцию.
Если делящий многочлен не является одночленом, то стоит воспользоватся калькулятором который делит произвольные многочлены друг на друга с вычислением остатка.Деление многочлена на многочлен.Division of complex polynomials
Синаксис
Для пользователей XMPP клиентов
horner коэффициенты полинома; значение с
Теперь рассмотрим примеры.
разделить с остатком
Пишем коэффициенты 2 0 -3 2 и через точку запятой -2. Надеюсь понятно почему пишем -2, а не+2 ?
Получаем ответ
| Заданный многочлен имеет вид |
| если разделим его |
| Получим многочлен |
| и остаток |
Следующий пример исходный полином тот же, но значение С будет комплексным например 1+i
Пишем коэффициенты 2 0 -3 2 и через точку запятой 1+i
Получаем
| Заданный многочлен имеет вид |
| если разделим его |
| Получим многочлен |
| и остаток |
Таким образом мы можем писать любые значения, в том числе и комплексные, в коэффицентах как делимого полинома так и делящего бинома
Удачных расчетов!
- Многочлен и матрица как аргумент >>
abakbot.ru






























 Видео 360 градусов обеспечивает полный обзор всего происходящего
Видео 360 градусов обеспечивает полный обзор всего происходящего