Задачи в стихах на сложение и вычитание в пределах 10
Муниципальное бюджетное общеобразовательное учреждение
города Новосибирска Дзержинского района
«Лицей №113»
630089 город Новосибирск, улица Бориса Богаткова, д.241/1
т. (383) 267-69-07; 267-74-01 sch_113_nsk@nios.ru
Задачи в стихах
на сложение и вычитание в пределах 10
1 класс
Автор: Птицына Наталья Васильевна,
учитель начальных классов
Новосибирск
2016
И ребят он угощал:
Одну сливу дал Наташе,
Одну – Лене, одну – Саше.
Две осталось у него.
Сколько было слив всего?
В магазине купить соли,
Вымыть пол,
Покрасить стол,
Привести из сада Сашу,
Сварить рисовую кашу.
Не ленился если в школе,
Скажи, сколько дел у Оли?
Гости за столом сидят.
Правильно чтоб торт разрезать,
Считает Лена всех подряд:
Я и папа с мамой,
Катя со Светланой,
Бабушка и Оля,
Кареглазый Коля.
На сколько частей должна разрезать торт Лена?
Встретить белку и лису,
Встретить волка и лося,
Встретить зайца у куста.
Сколько животных можно встретить зимой в лесу?
Уселась белочка на сук,
Вспорхнул на ветку воробей,
На тропку выполз муравей –
Все улыбнулись солнцу!
Сколько всего животных улыбнулись солнцу?
Два да три…
Их будет…?
Бродили по местам грибным.
И нашли под елью скоро
Два огромных мухомора.
Походили у осин и нашли ещё один.
Сколько грибов нашли друзья?
Строили в поле себе теремок.
Сделали крышу, крыльцо и окошки
И протоптали к дому дорожки.
Сколько животных строили теремок?
Сидели на опушке.
Одна им подмигнула
И в озеро нырнула.
Сколько лягушек осталось на опушке?
Им навстречу муравей.
Сколько будет насекомых?
Сосчитай – ка поскорей!
За малиной в лес спешат.
Испугался вдруг один,
Убежал и след простыл.
Сколько смелых медвежат
За малиной в лес спешат?
Подарил одну матрёшку.
Мы её открыли, а там ещё четыре.
Сколько же всего матрёшек у Серёжи?
Строит домик на воде.
И пришли ему помочь:
Папа, мама, сын и дочь.
И приплыл паучок.
Посчитай –ка всех, дружок!
Пять орешков в мешке,
Ещё три на полке.
Посчитай их, сколько?
В вазе четыре,
У Саши одно.
Сколько всего?
Прилетела мама.
Сколько птиц стало?
Белая козочка и два индюшонка.
Если нам их сосчитать,
Всех их будет ровно…(пять).
Золотой гребешок
Зёрна отыскал,
Курочек позвал.
Прибежали курочки:
Две из переулочка,
Три из-за поворота,
Одна из огорода.
А сейчас проверь,
Сколько курочек теперь?
Ищет всех своих сынишек:
Двое спрятались на ветке
У кукушки, у соседки;
Трое спрятались в цветах;
Трое – в ягодных кустах.
А один, ленивый самый,
Дома спит под одеялом.
Растерялась мама – мышь.
Сосчитай мышат, малыш!
Помоги их всех найти,
К маме – мышке привести!
Десять лисят к ним прибежали.
Восемь лисят скрылись у речки,
Двое в канаве, в тёмном местечке.
Трое котят за забор убежали.
Четверо – в будку, их видно едва ли.
Ну – ка, проверь – все разбежались?
Или немногие всё же остались?
Крот увидел два грибка,
А подальше у осин
Он нашёл ещё один.
Кто ответить нам готов,
Сколько крот нашёл грибов?
Своим детям семь котлет.
За обедом съели детки
Всего лишь три котлетки.
А сколько котлет
Не съели дети на обед?
Покатился Колобок,
Встретил серого зайчишку,
Встретил волка, встретил мишку,
Да плутовку лису
Повстречал ещё в лесу.
Отвечайте скорей,
Колобок сколько встретил зверей?
Три забрались под ушат,
Два мышонка спят под ёлкой,
Сосчитать мышей недолго.
Продавали рукавички.
Прилетело ещё пять,
Сколько будут продавать?
И сестрёночка Ириша.
Сосчитайте поскорей,
Сколько же в семье детей?
— Ты откуда, непоседа?
— Запасаюсь я к зиме:
Видишь яблоки на мне.
Собираю их в лесу,
6 принёс да 3 несу.
Призадумался сосед:
Это много или нет?
Обезьянок там видала:
3 сидели на песке,
2 качались на доске,
А ещё 3 спинки грели.
Сосчитать вы всех успели?
Волк, лиса, малышка крот
Были дружные соседи.
На пирог пришли к медведю.
Вы, ребята, не зевайте:
Сколько всех зверей считайте.
Подосиновик нашёл.
Походил вокруг осин
И нашёл ещё один.
Сколько всего подосиновиков нашёл зайчик?
Мышке тапочки купил.
И на все четыре лапки
Натянула мышка тапки.
Побежала по тропинке
Да споткнулась о травинку.
С лапки тапочка упала
И куда –то запропала.
Тапку мышка не нашла
И без тапочки пошла.
Сколько тапочек осталось у мышки?
На песочке в ряд лежат.
Одному из пяти братцев
Захотелось искупаться.
Остальным же неохота
Возвращаться вновь в болото.
Сколько лягушат осталось лежать на песке?
Вышло десять малышей.
Пять из них на травку сели,
Остальные — на качели.
Сколько ребят село на качели?
Десять спелых груш нашёл.
Семь из них он дал ежатам,
Остальные же – зайчатам.
Сколько груш дядя ёж дал зайчатам?
Шли толпой на водопой.
А навстречу три тигрёнка
С водопоя шли домой.
Сосчитайте поскорей,
Сколько встретилось зверей?
Собрала десяток шишек.
Сразу все не отдала,
По одной всего дала.
Старшему – еловую,
Среднему – сосновую,
Младшему – кедровую.
Сколько шишек осталось у мамы белки?
Животных имеет, а счёт не ведёт.
Я буду, ребята, их называть,
А вы постарайтесь быстрей сосчитать:
Корова, телёнок, два сереньких гуся,
Овца, поросёнок и кошка Катуся.
Сколько всего животных у бабушки Нади?
Белых бусинок – горошин.
А росточков из земли
Показалось только три.
Три горошинки взошло!
Сколько их не проросло?
Греет свой пушистый бок.
Прибежал ещё один
И уселся рядом с ним.
Сколько стало щенят?
Этой покупкой довольна была.
Если морковку ещё ей купить,
Сколько их будет?
Ты сможешь сложить?
Прибежала с праздника — и молчок.
Стали ей потерянный примерять.
Сколько же у Золушки их опять?
Не приложат ума,
Сколько тарелок
Нужно подать,
Чтоб каждому щи
Из отдельной хлебать?
Карандаш один у Гриши.
Сколько же карандашей
У обоих малышей?
И одинок, и грустен он.
Но подошёл к нему сынок,
И больше слон не одинок.
Сколько слонов теперь, ребята?
Два зайца сидели
И дружно весёлую песенку
Пели.
Один убежал,
А второй вслед глядит.
Сколько у домика
Зайцев сидит?
А за ней – Аринка.
А потом пришёл Игнат.
Сколько стало всех ребят?
В зоопарке звери сели.
Два пятнистых леопарда
Солнцу улыбаются
И со старым добрым львом
Весело качаются.
Сколько всего зверей?
Повстречал ещё там двух.
Сколько стало петухов?
У кого ответ готов?
Ёжик притащил.
Самое румяное белке подарил.
С радостью подарок
Получила белка.
Сосчитайте яблоки
У ежа в тарелке!
Два голубя снялись и улетели.
Ну –ка, скажите мне поскорей,
Сколько осталось сидеть голубей?
Играли в прятки у бочонка.
Один в бочонок еле влез.
А сколько убежало в лес?
На горе катается?
Трое в саночках сидят,
Один дожидается.
Червячка с крючка сняла.
Наварила щука щей,
Пригласила трёх ершей.
Говорили всем ерши:
— Щи у щуки хороши!
Сколько было всего рыбок?
Два мяча у Вани.
Два мяча да два. Малыш!
Сколько их сообразишь?
Утка удочку нашла.
По траве, росой умытой,
Утка к озеру пришла.
Долго клёва ожидала,
Подсекла трёх сазанов,
Одного ерша поймала…
Сосчитай её улов.
Шёл баран на водопой.
Трёх овечек за собою
Вёл он важно к водопою.
Сколько вместе их? Считайте!
Ответ быстро называйте!
Улеглись в лукошечке.
Тут одна к ним прибежала.
Сколько вместе кошек стало?
Одна из сорок не знала урок.
Сколько прилежно
Трудилось сорок?
А крольчата лежат и молчат:
За кадушкой — один,
За кормушкой — один,
Под листом — один,
Под кустом – один.
Как детей поскорее найти?
Их должно быть чуть меньше пяти.
Лишь три только птицы.
Но к ним прилетели
Ещё две синицы.
Так сколько же птиц
Здесь в кормушке у нас?
Покажет на карточке
Каждый из вас.
Два грибка и три морковки.
Прибежал хорёк, утащил грибок.
Съел зайчонок две морковки.
Что осталось на верёвке?
Подосиновик нашла,
Две лисички, боровик
И зелёный моховик.
Сколько я нашла грибов?
У кого ответ готов?
Решили попробовать сыру.
Тут следом явились подружки –
Три сереньких мышки – норушки.
Кот спал в это время на крыше,
Про этот не ведая пир.
А ну, сосчитай, сколько мышек
Съели оставленный сыр?
Возле кадки три лопатки.
Все лопатки сосчитать!
Сколько будет?
Ровно…(пять).
На скорлупку глядят.
Два яичка в гнезде
У наседки лежат.
Сосчитай поскорей:
Сколько будет цыплят
У наседки моей?
Товарных два вагона,
А три других в сцеплении
Готовы к отправлению.
Прибавь – ка к двум вагонам три
И сколько станет – назови!
Плавать и нырять хотят?
Три уплыли далеко,
Два нырнули глубоко.
Сколько их всего в пруду?
Сосчитать я не могу.
Бегают, резвятся.
К шалунишкам три дружка
С громким лаем мчатся.
Вместе будет веселей.
Сколько же всего друзей?
Волна их весело качала.
Три лодки взяли рыбаки,
Чтоб переплыть простор реки.
А сколько лодок у причала
Волна по – прежнему качала?
Одного домой позвали.
Он в окно глядит, считает,
Сколько их теперь играет?
Куклы Танины сидят:
Два медведя, Буратино
И весёлый Чипполино,
И котёнок, и слонёнок.
Помогите вы Танюшке
Сосчитать её игрушки!
Другой лежит – трава над головой.
А четверо на солнечной опушке
Играют в прятки – ушки на макушке.
Пересчитать, дружочек мой, сумей – ка,
Всю заячью весёлую семейку.
Маленьких, удаленьких –
Целая семья опят.
Сколько их на пне сидят?
Что – то рисуют старательно.
Соседу задачку про водоём
Нужно решить обязательно.
Вот и тебе задачка, мой друг:
Сколько друзей собралось вокруг?
Вышиты узорами.
Сколько вышить нам осталось –
Подсчитаем скоро мы.
На ней тыква большая,
А пониже тоже
Три тыквы моложе.
А под горкою в траве
Ещё две.
Ну – ка, кто скажет сейчас,
Сколько тыкв всего у нас?
К блюдцу с молоком приник.
Вот другой. Ему смешно
Видеть пса через окно.
Вот ещё один сидит,
Тихо мышку сторожит.
Три других моих котёнка
Спят, мурлыча потихоньку.
Вот задача для ребят –
Всех пересчитать котят!
Шесть детей на луг гулять.
Все гусята, как клубочки.
Три сынка, а сколько дочек?
Плюс мама лайка.
Сколько будет?
Сосчитай – ка!
Шесть ярко – красных помидоров.
Потом четыре оторвалось,
А сколько на кусте осталось?
Две утки плывут неизвестно куда,
Три рыбки у берега тихо плеснули
И в синюю воду обратно нырнули.
Сколько их всех?
Две птички – невелички.
Потом за ними заодно
Ещё четыре птички.
Порхали птички над столом,
Чирикали и пели
Почти минуту, а потом
Куда – то улетели.
Обратно – порх –через окно
Одна, за ней четыре.
Так сколько ж с девочкою той
Осталось их в квартире?
Пять лесных орешков мелких.
Вот ещё один лежит,
Мхом заботливо укрыт.
Ну и белка! Вот хозяйка!
Все орешки посчитай – ка.
Четыре – у Наташи.
Вы кубики все эти
Скорей считайте, дети.
И работа закипела.
Побежали за лозой
Суслик с рыжею Лисой,
Мячиком катился Ёжик,
Белка с Лаской мчались тоже,
Даже Мишка – хвастунишка
Следом кинулся вприпрыжку.
Сколько здесь зверят трудилось?
Что в ответе получилось?
Стерегут поплавки.
Рыбак Корней
Поймал трёх окуней,
Рыбак Евсей –
Четырёх карасей.
Сколько рыб рыбаки
Натаскали из реки?
На пирог пришли соседи:
Ёж, барсук, енот, косой,
Волк с плутовкою лисой.
А медведь никак не мог
Разделить на всех пирог.
От труда медведь вспотел,
Он считать ведь не умел.
Помоги ему скорей,
Посчитай – ка всех зверей.
Песни распевали.
Вскоре пять кузнечиков
Голос потеряли.
Сосчитай без лишних слов,
Сколько в хоре голосов?
Во дворе – две курочки,
Два гуся – в пруду,
Один индюк в саду.
Сколько птиц всего? Считайте!
Ответ быстро называйте!
Попало немало:
Три окуня, три карася,
Один ершок – и того в горшок.
Уху сварю, всех – всех угощу.
Сколько рыб я сварю?
Прилетело семь сорок.
А из них лишь три сороки
Приготовили уроки.
Сколько лодырей – сорок
Прилетело на урок?
Две ещё к ним прилетели.
Отвечайте быстро, смело,
Сколько всех их прилетело?
Со своих сбежали веток.
Все повисли до одной
На хвостах вниз головой.
Раскричались, раскачались,
Меж собой передрались.
Больше всех досталось в драке
Самой главной забияке.
С ветки сбросили её.
Сколько будет без неё?
А потом ещё один.
Вы ответьте на вопрос:
Сколько он грибов принёс?
Четыре конфеты.
Ещё дала три Алла.
Сколько всего стало?
Голосистый певунок,
Шесть хохлаток тоже там.
Сколько всех их?
Скажешь сам?
Под высокою сосной
К медвежонку в день рожденья
Собрался народ лесной:
Ёжик, волк, енот, барсук,
Заяц, лось, лисёнок – друг.
Посчитайте поскорей,
Сколько было всех гостей?
Дал вчера семь штук конфет.
Съел одну конфетку внук.
Сколько же осталось штук?
Пять огурцов уже съели.
Осталось сколько их, ребятки?
Вы сосчитать сумели?
Вид их очень уж красив.
Съел четыре сливы Павел.
Сколько мальчик слив оставил?
Три других за облаками.
Два спустились на ручей.
Сколько было всех гусей?
Паровоз и два коня,
Серебристый самолёт,
Три ракеты, вездеход…
Сколько вместе?
Как узнать?
Помогите сосчитать!
Восемь рыжиков нашёл.
Шесть грибов в корзинку,
Остальных – на спинку.
— Сколько рыжиков везёшь
На своих иголках, ёж?
Ехать в Кошкино хотят.
Сели кошки у окошек.
Восемь окон, сколько кошек?
И под ёлкой три.
Сколько будет всех грибочков?
Ну – ка, говори!
Мы отведать их успели:
Пять румяных, наливных,
Три с кислинкой. Сколько их?
Восемь резвых коз,
Беленьких и сереньких,
Вверх задравши хвост.
Пять козочек белых.
Сколько было серых?
Ребята, сколько всего птиц?
Пять дали товарищи в школе.
Яблок сколько всего
Стало, друзья, у него?
Четыре Наташки
Под солнцем весенним
Играли в пятнашки.
Так сколько, ребята, ответьте скорей,
Под солнцем осенним играло детей?
Пироги с капустой печь.
Для Наташи, Коли, Вовы
Пироги уже готовы,
Да ещё один пирог
Кот под лавку уволок.
Да ещё из печки пять
Маме нужно вынимать.
Если сможешь, помоги –
Сосчитай – ка пироги!
И без дела не снуют.
Три несут травинку,
Три несут былинку,
Три несут иголки.
Сколько их под ёлкой?
Собрала своих цыплят.
Шесть бежали впереди,
Три остались позади.
Беспокоится их мать
И не может сосчитать.
Посчитайте – ка, ребята,
Сколько было всех цыплят.
Рыбак Корней поймал трёх окуней,
Рыбак Евсей – четырёх карасей.
А рыбак Михаил двух сомов изловил.
Сколько рыб рыбаки
Натаскали из реки?
Надо сосчитать наседке:
Шесть — на грядках, три — во ржи.
Сколько их всего, скажи?
На ветке рядком
Весело чирикали –
Каждый о своём.
Трактор проехал,
Разлетелись все;
Шесть летят к деревне,
А сколько в траве?
Нам подарки принесла:
Гречку загорелую,
И пшеницу зрелую,
И бруснику спелую,
Дыню полосатую,
Свёклу бородатую,
И морковь хвостатую.
Яблоки душистые,
Персики пушистые,
Груши золотистые
Осень принесла.
Сколько всего подарков осени вы насчитали?
Восемь маслят и один мухомор.
Сколько всего грибов?
Греметь?
Ульи строит наш
Медведь.
Ульев сделал он
Лишь семь –
На два меньше, чем
Хотел.
Сколько ульев хотел сделать мишка?
Два других за облаками,
Пять спустились на ручей.
Сколько было всех гусей?
Болтая вечерком,
Дойти до самых жарких стран
Задумали пешком.
— А я, пожалуй, не пойду, —
Промолвил павиан, —
В зоологическом саду
Не станет обезьян.
Сколько обезьян отправилось в жаркие страны?
Поймал шесть окуней.
А друг его Сергей
Трёх небольших ершей.
Сосчитай без лишних слов
Этих мальчиков улов.
Два листика Алёша дал.
Скажите сколько у него
Осенних листиков всего?
Четыре каштана,
В другом кармане
Их пять.
Мы просим, дети,
Каштаны эти
Пересчитать.
А с ними три мышонка,
А с ними три весёлых
Умытых поросёнка
Бежали спозаранку
Из дома на полянку.
Посчитайте поскорей,
Сколько было всех друзей,
Что утром спозаранку
Играли на полянке?
Одну из них взяла Наташа.
Теперь уж сколько чашек там?
Подумай и ответишь сам.
Девять маленьких ребят.
В первом едут двое только,
Во втором детишек сколько?
И угостил своих друзей:
Четыре вишни дал он Вите,
А остальные все Никите.
Сколько вишен дал Никите?
Вы сосчитайте и скажите.
Одна из них на клумбу села.
Все остальные через сад
К себе на пасеку спешат.
Так сколько ж пчёл летит из сада?
Нам сосчитать тех пчёлок надо.
Девять ягодок малины,
Пять дала своей подружке.
Сколько ягод стало в кружке?
Диме нет ещё шести.
Дима всё ещё не может
До Серёжи дорасти.
На сколько лет Дима младше Серёжи?
И плясали, и резвились.
После добрый Дед Мороз
Нам подарки преподнёс.
Дал большущие пакеты,
В них же – вкусные предметы.
Стала я пакет вскрывать,
Содержимое считать:
Две конфеты в бумажках синих,
Пять орехов рядом с ними,
Груша с яблоком, один
Золотистый мандарин.
Всё лежит в пакете этом!
Сосчитайте все предметы!
Собрала своих цыплят.
Семь бежали впереди,
Три остались позади.
Беспокоится их мать
И не может сосчитать.
Сосчитайте – ка, ребята,
Сколько было там цыпляток.
Прыгают в поле десять сорок.
Девять взлетели, сели на ели.
Сколько осталось в поле сорок?
По дорожке идут.
За ними вдогонку
Двое бегут.
Так сколько ж всего
По дорожке лесной
Торопится в школу
Зайчишек зимой?
Вдоль тропинки
И несла грибы в корзинке:
Пять опят
И пять лисичек
Для лисят и для лисичек.
Сколько всего грибов несла лисица?
Белка сделала качели.
И на белкины качели
Собрались лесные звери:
Заяц, куница,
Рыжая лисица,
Ёж и шестеро зайчат –
На качели все спешат.
Вы, ребята, не зевайте,
Всех зверей пересчитайте.
Ну и в дождь, конечно, мокли:
Двое жёлтеньких маслят,
Пять тоненьких опят
Да три рыжие лисички –
Очень милые сестрички.
Вы, ребята, не молчите.
Сколько всех грибов?
Скажите!
И увидел мухомор,
Два опёнка,
Два сморчка,
Три маслёнка,
Два строчка…
У кого ответ готов:
Сколько я нашёл грибов?
Десять счётных палочек.
Две из них сломались.
Сколько же осталось?
Как зелены они, стройны!
Деревьев сколько тут? Узнайте
И хорошенько сосчитайте.
Окон очень много в нём.
Тут их шесть, четыре там.
Посчитай все окна сам.
Здесь пять мешков, там тоже пять.
Так сколько же мешков собрали?
Десять кукол на витрине.
Куколку одну купили
Папа с мамою для Лили.
Сколько кукол на витрине
Осталось в детском магазине?
Десять крошечных цыплят.
Здесь три только.
Деток сколько
Под наседкою сидят?
Четыре пингвина,
Совёнок и мама сова
Однажды в июле
В Москву заглянули
Всего на денёк или два.
Сколько птиц захотели Москву посмотреть?
Посчитай поверней и скорее ответь!
Подарили Пете книжку о ракете.
Прочитал Петя, подарил Свете.
Света – Ване, Ваня – Тане,
Таня – маленькой Марьяне.
Сколько детей прочитали книгу?
Дали каждому обед:
Собачке – в миске,
В блюдечке киске,
Курочке – несушке
Пшена в черепушке,
Машеньке – в тарелочке
Голубой не маленькой.
Сколько их обедает?
Играли ребята в прятки.
Прятались все:
Коля – в овсе,
Оля – за Колей,
Егорка – за горкой,
Андрейка – за лейкой,
Тимошка – за кошкой,
Лена – за сено,
Светка – за веткой,
Филипп – за гриб.
А Барбос пришёл.
Сразу всех нашёл.
Сколько детей нашёл пёс?
У Маши были конфеты.
Она угостила Свету,
Наташу, Иру, Сережу,
Таню и Петю тоже.
Одна конфета осталась,
А Машенька растерялась:
Сколько же было конфет?
Кто может дать ответ?
У Сашки в кармашке
Конфеты в бумажке.
Он дал по конфете
Свете и Пете,
Ирине, Галине,
Марине и Нине.
И сам съел конфету.
Сколько было конфет?
Много зверей в зоопарке живет:
Белый медведь, жираф, бегемот,
Тигр, шимпанзе, лиса и енот,
Слон, леопард, снежный барс и койот.
Кто потрудился зверей сосчитать,
Прошу вас ответ немедленно дать!
Пой–ка, подпевай-ка!
Птичек посчитай-ка!
Эта птичка – соловей,
Эта птичка – воробей,
Эта птичка – совушка – сонная головушка.
Эта птичка свиристель,
Эта птичка – коростель,
Эта птичка скворушка – серенькое пёрышко.
Это – зяблик,
Это стриж,
Это – развесёлый чиж.
Ну а это – злой орлан.
Птички, птички – по домам.
Сколько птиц насчитали вы, дети?
Кто быстрее всех ответит?
В класс пришли ученики
И по рисунку принесли.
Вы, ребята, не зевайте –
Все рисунки посчитайте:
У Вики – гвоздики,
У Никитки – маргаритки,
У Анютки – незабудки,
У Андрея – орхидея,
Ландыши – у Саши,
Георгины – у Марины,
У Алены – пионы,
У Наташки – ромашки,
Тюльпаны – у Оксаны,
Нарциссы – у Ларисы.
В первом классе нашей школы
Учатся Егорка, Коля,
Шесть Сергеев, две Наташи.
Скажет кто-нибудь сейчас,
Сколько девочек у нас?
На забор уселась галка,
Начинается считалка:
Раз, два, три, четыре , пять…
Буду всех ребят считать.
Юлю, Мишу, Свету, Колю,
Петю, Иру, Витю, Олю.
Если я считать устану,
На минуту перестану.
Помолчу, передохну,
И опять считать начну.
Считала, считала.
А не понятно галке,
Сколько ребят в считалке?
У мамы моей пять сыновей.
Начну я считать – выходит не пять.
Смотрите: Володя – мой первый брат,
Вот Костя – второй,
Вот и третий – Игнат,
Четвёртый Гришутка.
А пятого нет.
Считаю сначала.
Всё тот же ответ.
Всё время четыре выходит на счёт.
Кто пятого сына, ребята найдёт?
Мы большущая семья.
Самый младший – это я.
Таня есть и Вася есть,
Юра, Шура, Зина, Маша,
И Наташа тоже наша.
Сколько детей в семье?
Сидят рыбаки, стерегут поплавки.
Рыбак Корней поймал окунька.
Другой рыбак – башмак,
Евсей – карася,
Рыбаку Кирюше попалась галоша.
А рыбак Михаил Сома изловил.
Сколько рыбок рыбаки
Натаскали из реки?
Разноцветные клубки
Бабушка достала
И для внуков дорогих
Подарочки связала:
Шапочку – для Маши,
Кофточку – Наташе,
Варежки – Илюше,
Носочки – для Андрюши,
Шарфик – для Ромочки
Перчатки – для Томочки.
Рады внучата подаркам таким,
Сказали спасибо все как один.
Сколько же всего ребят
Бабушку благодарят?
У Алёнки в гостях
Два цыплёнка в лаптях,
Петушок в сапожках,
Курочка в серёжках,
Селезень в кафтане,
Утка в сарафане
И корова в юбке
В тёплом полушубке.
Сколько всего гостей у Алёнки?
Ксюша съела барбариску,
А Илья жуёт ириску.
И Олеся очень рада
Вкусной дольке мармелада.
А у Олечки сюрприз!
Ей достался главный приз:
В длинном фантике красивом
Две конфеты с черносливом.
Посчитай скорей ответ,
Сколько было всех конфет.
Я, Серёжа, Коля, Ванда —
Волейбольная команда.
Женя с Игорем пока
Запасных два игрока.
А когда подучатся,
Сколько нас получится?
В снег упал Серёжа,
А за ним Алёша,
А за ним Ирина,
А за ней Марина,
А потом упал Игнат.
Сколько на снегу ребят?
На качелях две Елены.
А с мячом Иван, Игнат.
Две Ирины прибежали
На скакалках поскакать.
Валя, Зина и Егор.
Вот и в сборе весь наш двор.
А теперь скажите мне,
Сколько деток во дворе?
По лесу охотник шёл,
В чащу леса он зашёл.
Повстречались ему здесь
Заяц, волк, лиса, медведь.
Звери все до одного
Убежали от него.
Сосчитайте всех зверей!
И как можно поскорей.
Сколько яблок у ребят
Солнышком в руках горят?
У Наташи и у Ромы,
У Серёжи и у Томы,
На столе ещё одно солнышком напоено.
Ну- ка, сколько яблок, братцы?
Кто сумеет догадаться?
Над рекой летали птицы:
Голубь, щука, две синицы,
Два стрижа и пять угрей.
Сколько птиц? Ответь скорей.
У утенка день рожденья,
Игры, танцы, угощенья.
В гости все друзья пришли
И подарки принесли.
Мячик подарил баран.
Ослик – звонкий барабан.
А подарок от зайчишки
Не морковка, а две книжки.
Все подарки хороши,
Рад утенок от души.
Стал подарки он считать
И решил: их ровно пять.
Посчитай и дай ответ,
Он ошибся или нет.
Молоточками стуча,
Веселясь и хохоча,
Шли по лесу гномики,
Чтоб построить домики.
Гном Седая Борода
Дом построил у пруда,
Круглый, толстенький Ватрушка
Дом построил на опушке,
Гномик озорной Егорка
Дом построил у пригорка,
А веселый гном Незнайка
Дом построил на лужайке.
А Ворчалка, хмурый гном,
Прямо в чаще строит дом.
Сколько было гномиков,
И сколько было домиков?
Как под ёлкой встали в круг
Зайка, белка и барсук,
Встали ёжик и енот,
Лось, кабан, лиса и кот.
А последним встал медведь,
Сколько всех зверей? Ответь!
Список литературы
Веденина В.П. Творческие работы учащихся //Нач.шк. — №6.- 1996.
Волина В.В. Праздник числа.- М., 1996.
Герасимова М. А я делаю так… //Нач.шк. — №8. – 1994.
Дроздова В.Е. Весёлые задачи //Нач.шк. -№6 – 1991.
Егорова О.А. Задачи в стихах //Нач.шк. — №3. – 2005.
Капустинская И.Ю. Весёлые задачи //Нач.шк. — №2. – 1992.
Кострюкова Задачки в стихах //Нач.шк. — №10. – 2009.
Матющенко Е.В. Какие оценки в школе? //Нач.шк. — №8. – 1996.
Михайлова А.В. Хорошо зимой в лесу! //Нач.шк.- №1.- 2004.
Михайлова Н.А. Весёлые задачи //Нач.шк. — №2.- 1995.
Полончук О.Г. Задачи в стихах //Нач.шк. — №6. – 2004.
Сорочинская О.Л. Весёлые задачи //Нач.шк. — №6. – 1993.
Широких О.С.Весёлые задачи // Нач.шк. -№6 – 1991.
infourok.ru
Сложение и вычитание в пределах 10. Решение задач. 1-й класс
Разделы: Начальная школа
Цели урока:
- Познавательные:
- закрепление изученных приёмов сложения и
вычитания вида +, – 3;
- формирование умений решать простые задачи на
сложение и вычитание в приделах первого десятка.
- Личностные: ориентация на понимание причин
успеха в учебной деятельности, на понимание
предложений и оценок учителей, одноклассников.
- Регулятивные:
- принятие и сохранение учебной задачи;
- планирование своих действий в соответствии с
поставленной задачей и условиями реализации.
- Коммуникативные:
- нахождение общего решения в совместной
деятельности, сотрудничество с
одноклассниками и учителем.
ХОД УРОКА
1. Организация начала урока
Прозвенел звонок и смолк.
Начинается урок.
Проверь, дружок,
Готов ли ты начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка и тетрадки?
Все ли правильно сидят?
Все ль внимательно глядят?
Тут затеи и задачи,
Игры, сказки всё для вас!
Пожелаем всем удачи –
За работу, в добрый час!
2. Мотивация
– Дети, сегодня мы с вами побываем в сказке.
Главный герой её – царь, который очень любил
математику: задачи, ребусы математические на
досуге решать, хитроумные книги читать по
математике. Но вот прошли годы, состарился
царь-математик. Настала пора о наследнике ему
подумать. И решил царь – наследником царства
будет тот из его родственников, кто покажет себя
лучшим знатоком математики.
Приказал царь в главном зале дворца столы
поставить, доски развесить. «Управлять
государством нелегко – думал царь, – много
приходится размышлять. Знания нужны. Вот и выберу
того, кто лучше других умеет соображать, мыслить,
математику любить».
– Ребята, а кто из вас желает побывать во дворце у
царя и стать претендентом на престол? Поднимите
руки.
– Тогда возьмите волшебные палочки и вместе со
мной произнесите волшебные слова:
«Крибле-крабле-бумс!» (Приложение
1, слайд 1)
Слова царя: «Я рад видеть вас,
первоклассники, в моём царстве. И повелеваю вам,
претендентам на царский престол, начать работу с
«Гимнастики» мозга.
3. Устный счёт
– Посчитайте от 1 до 10 и обратно;
– Что происходит при счёте до 10? А при обратном?
– Какое число идёт при счёте за числом 8?
– Какое число стоит при счёте перед числом 5?
– Какое число стоит при счёте перед числом 10?
– Какое число встречается раньше: 0 или 10? 3 или 5?
– Назовите соседей числа 7, 4, 6.
– Какое число больше чем 5 на 1?
– Какое число меньше чем 5 на 1?
4. Игра «Отвечай – не зевай» (разрезные
цифры).
7 + 2
8 уменьшить на 1
5 увеличить на 3
6 – 3
4 + 2, полученный результат уменьшить на 3
Первое слагаемое 6, второе слагаемое 3. Найти
сумму.
У Коли и Марины
4 мандарина.
Из них у брата – 3.
А сколько у сестры?
5 лодок было у причала,
Волна их весело качала.
3 лодки взяли рыбаки,
Чтоб переплыть простор реки.
И сколько лодок у причала
Волна по-прежнему качала?
У маленькой Светы
4 конфеты.
Ещё дала 2 Алла.
Сколько всего стало?
Молодцы! (Приложение 1,
слайд 2).
– А теперь посмотрите на геометрические фигуры
и скажите, как можно назвать одним словом все эти
фигуры?
– Как называют каждую фигуру?
– Как можно провести в каждом четырёхугольнике
отрезок так, чтобы из каждой фигуры получилось
два треугольника?
– Какая фигура называется треугольником?
Физминутка (Приложение
1, слайд 3)
(бег на месте).
А сейчас хочу я, дети
Прокатить вас на карете.
Ну-ка, братцы, не зевайте –
Все к карете подбегайте.
Учитель: Мы с вами много трудились
и нам пора подкрепиться. Чтобы быть сильным и
здоровым, необходимо правильно питаться. А
именно нам необходимы витамины. А где содержится
много витаминов?
Сейчас я двум группам дам рисунки, по которым вы
составите задачи. А с остальными ребятами мы
поработаем по учебнику. Страница 105 №4.
Проверка задач.
Итак, мои дорогие претенденты, витаминами мы с
вами подкрепились, а сейчас мы с вами отдохнём.
Физминутка (под музыку)
– Чтобы быть наследником надо много знать (Приложение 1, слайд 4).
Выберите себе задание, с которым вы считаете, что
можете справиться сами.
У-1 У-2 У-3
7 + 2 = 1
8 + =
10 3
+
=
9 – 3 = 2
– 2 = 8
10
–
=
6 – 2 = 3
+ 3 =
10 + = 10
Проверка.
5. Самостоятельная работа
В тетрадях на печатной основе страница 38.
Взаимопроверка.
6. Итог урока
– Наш конкурс подходит к концу. Но прежде, чем
объявить наследника престола, царь хочет
услышать:
– Понравилось ли вам, уважаемые претенденты, в
математическом царстве?
– Какое задание было самым интересным?
– А какое – самым трудным? (Приложение
1, слайд 5 и магнитофон)
Ребята, вы меня поразили.
Сердце моё вы покорили.
Желаю и впредь так держать –
пятёрки одни получать!
– Утешили вы меня, старика. Есть, кому царство
оставить, кому управление доверить. Назначаю
наследником престола (ученик), который лучше и
быстрее всех считает, решает сложные задачи. Не
боится трудностей.
Поздравляю наследника. А вам, уважаемые
претенденты, ваш учитель вручит ордена моего
государства (6 слайд).
18.07.2012
Поделиться страницей:
xn--i1abbnckbmcl9fb.xn--p1ai
Сложение и вычитание в пределах 10
Конспект по ФЭМП в подготовительной к школе группе «Сложение и вычитание до 10»
Калимуллина Сания Фагимовна — воспитатель МБДОУ «Детский сад общеразвивающего вида «Светофорик» города Буинска Буинского муниципального района Республики Татарстан»
Конспект по ФЭМП в подготовительной к школе группе
«Сложение и вычитание до 10»
Программное содержание:
• Продолжать учить, самостоятельно составлять и решать задачи на сложение и вычитание в пределах 10.
• Упражнять в умении ориентироваться на листе бумаги в клетку.
• Совершенствовать умение ориентироваться в окружающем пространстве относительно себя и другого лица.
• Развивать внимание, память, логическое мышление.
Методические приёмы:
Игровые
Наглядные (использование демонстрационного и раздаточного материала).
Словесные (напоминание, указание, вопросы, индивидуальные ответы детей).
Поощрение, анализ занятия.
Оборудование и материалы: ноутбук, интерактивная доска, презентация в среде Power Point
Раздаточный материал: простые карандаши (по 1 на каждого ребёнка, карточки с заданиями.
Ход ООД:
1.Приветствие. (Эмоциональный настрой)
Дружно за руки возьмёмся
И друг другу улыбнёмся.
Ты мой друг и я твой друг.
Дружат все друзья вокруг.
2.Сообщение темы.
Воспитатель: Ребята, вы любите путешествовать?
(Ответы детей)
Воспитатель: У меня есть мечта – я хочу полететь на Луну. А вы хотите? Предлагаю вам сегодня отправиться со мной в путешествие на Луну. В космосе происходят очень невероятные вещи и поэтому в полёт могут отправиться только внимательные, находчивые, сообразительные ребята. А сейчас, я вас проверю на внимательность, сообразительность и смекалку.
3. Разминка для ума.
1) Наступил долгожданный апрель. Сначала зацвела 1 яблоня, а потом еще 3 сливы. Сколько деревьев зацвело?
Дети: В апреле деревья не цветут.
2) В вазе было 7 тюльпанов, 3 нарцисса. Сколько тюльпанов было в вазе?
Дети: В вазе было 7 тюльпанов.
Воспитатель: Кто летает на ракете на Луну? (профессия)
(Ответы детей)
Воспитатель: Каким должен быть космонавт?
Дети: Здоровым, умным, сильным.
Воспитатель: А еще космонавт должен хорошо считать, отгадывать загадки и не бояться трудностей. Сейчас мы и узнаем, кто из вас может стать космонавтом и отправиться в полёт.
1,2,3,4,5. В мире можно всё пересчитать.
Сколько в комнате углов? (4)
Сколько ног у воробьёв? (2)
Сколько пальцев на руках? (10)
Сколько пальцев на ногах?(10)
Сколько солнышек на небе? (1)
Сколько глаз у человека? (2)
Сколько огоньков у светофора? (3)
Сколько колёс у машины? (4)
Воспитатель: Вот какие молодцы! Быстро пересчитали. Можно всех брать в полёт! Теперь я полностью уверена, что вы находчивые, внимательные, сообразительные ребята и с вами можно отправиться в космическое путешествие без опасения.
Воспитатель: Вот мы и готовы, но только на чём мы доберёмся до Луны, ведь среднее расстояние от Земли до Луны составляет 384400 километров ?
Дети: На ракете.
Воспитатель: А кто был главным конструктором строительства ракет?
Дети: Сергей Алексеевич Королёв.
Воспитатель: Мы тоже будем конструкторами и соберём свой космический корабль для путешествия.
4. Графический диктант (ракета) «Нарисуйте космический корабль по клеточкам»
Воспитатель: Ребята, через минуту мы с вами должны быть в полной готовности. Командиром корабля буду я, а вы членами экипажа.
Воспитатель: Экипаж, внимание! Обратный отсчёт за запуск корабля от 10 до 1 – пошёл!
Дети: 10,9,8,7,6,5,4,3,2,1. – Полетели!
(Музыка)
Воспитатель: Посмотрите, как красиво наша Земля!
Воспитатель: Ребята, какие планеты вы знаете? В нашей солнечной системе 9 планет. Но вот беда: все они перепутались. Давайте расставим их по порядку, но для начала вспомним считалочку про планеты.
На земле жил звездочёт
Он планетам вёл отчёт.
Меркурий раз
Венера два
Три Земля
Четыре Марс
Пять Юпитер
Шесть Сатурн
Семь Уран
Восьмой Нептун
Девятый дальше всех Плутон
Кто не видеть – выйди вон
5. Расставь планеты по порядку.
Воспитатель: Внимание экипаж. Метеориты преградили нам путь. Что же делать? Ребята, их надо сравнить, ведь метеориты бывают разные: одни большие, другие маленькие.
6. Задание «Расставь знаки»
А сравнить мы их сможем, если расставим знаки: > = <
9 5
5 3
3 2
7
8
0
10
3 3
Воспитатель: Смотрите, еще больше метеоритов. Что же делать? Надо их сложить и вычитать.
(Дети выполняют задания на сложение и вычитание.)
Воспитатель: Путь свободен.
7. Физминутка.
Ждут нас быстрые ракеты
Для прогулок по планетам
На какую захотели, на такую полетели,
Но у нас один секрет
Опоздавшим места нет.
8. Воспитатель: Экипаж внимание! На нас движется какой – то объект! Кого напоминает вам этот объект!
Дети: Робота.
Воспитатель: Ребята, робот необычный. Вам не кажется, что детали что – то нам напоминают?
Дети: Геометрических фигур.
Воспитатель: А из каких геометрических фигур он выложен?
Дети: Из прямоугольников, квадратов, треугольников.
Воспитатель: Правильно. А теперь ребята, давайте сосчитаем, сколько всего геометрических фигур понадобилось для того, чтобы выложить робота?
Дети: Для того, чтобы выложить робота понадобилось 10 геометрических фигур.
Воспитатель: Вот мы прилетели на Луну.
Луна – спутник Земли. Это самое близкое к нам космическое тело.
Кто это встречает нас на Луне?
Дети: Лунтик
Воспитатель: Он любит считать звезды, изучать их. Ребята, Лунтик приготовил нам некоторые созвездия, которые он увидел в свою подзорную трубу, но вот беда: все линии стерлись. Как нам быть? Нам надо соединить цифры по порядку от меньшего к большему и узнать, что увидел Лунтик.
9. «Соедини по точкам»
Воспитатель: Что же, ребята, время нашего полёта закончилось. Нам пора возвращаться на Землю.
Внимание экипаж! Ведём обратный отсчёт от 10 до 1
Дети: 10,9,8,7,6,5,4,3,2,1! – Полетели!
Воспитатель: Есть касание! Мы снова на Земле! С удачным возвращением. Разрешите мне, как командиру корабля, поздравить вас и наградить медалями за отличный полёт.
10. Итог занятия.
1) Понравился вам наш полёт на Луну?
2) Что самое трудное было?
3) Что показалось лёгким?
4) Хотите еще отправиться в такой полёт?
Воспитатель: Ребята, мне было интересно вместе с вами полетать на Луну. Спасибо вам, что вы согласились со мной путешествовать. На этом наше занятие окончено.
infourok.ru
Весёлые задачи 1 класс. Сложение и вычитание в пределах 10
Весёлые задачи
Сложение и вычитание в пределах 10
1. 2 жучка бежали в домик
Им на встречу муравей.
Сколько будет насекомых?
Сосчитай-ка поскорей?
(2+1=3 насекомых)
2. 5 весёлых медвежат
За малиной в лес спешат.
Испугался вдруг один,
Убежал и след простыл.
Сколько смелых медвежат
за малиной в лес спешат?
(5 -1=4 медвежонка)
3. В день рожденья я Серёжке
Подарил одну матрёшку.
Мы её открыли, а там ещё четыре
Сколько матрёшек у Серёжи?
(1+4=5 матрёшек)
4. Сосед бобёр на речке
Строит домик на воде.
И пришли ему помочь:
Папа, мама, сын и дочь.
И приплыл паучок.
Посчитай-ка всех дружок!
(1+1+1+1+1++1=6 штук )
5.У белки в дупле
5 орешков в мешке
ещё 3 на полочке.
Посчитай-ка их, сколько ?
(5+3=8 орешек)
6. 5яблок в корзине в вазе 4,
У Саши одно.
Сколько всего?
(5+4+1=10 штук)
7. 9 совят в гнезде сидят
Прилетела мама
Сколько птиц стало ?
(9+1=10 сов)
8.Петя — петушок
Золотой гребешок.
Зерна отыскал,
Курочек позвал.
Прибежали курочки:
2-из переулочка,
3-из-за поворота,
1-из огорода.
А сейчас проверь,
Сколько курочек теперь?
(2+3+1=6 курочек)
9. Полевая мама -мышка.
Ищет всех своих сынишек:
2 спрятались за веткой,
3 спрятались в цветах ;
3 в ягодных кустах,
А 1 ленивый самый,
Дома спит под одеялом.
Растерялась мама-мышь!
Сосчитай мышат, малыш!
Помоги их всех найти,
маме мышки привести.
(2+3+3+1=9мышат)
10. 9 мышек жили в норке.
Ели сыр, таскали корки .
Жили мышки не тужили
Вперёд хозяйству приносили
И хозяин рассердился.
Всех мышей поймать решил:
Кошку злобную завёл.
Мышеловку приобрёл.
Мышки не остерегались
В первый день 6 штук поймались
Во второй и третий день,
Все попрятались они.
На четвёртый день опять
Вышли мышки погулять,
Кошка их подстерегла
И ещё 1 поймала.
Сколько же мышей опять
выйдет завтра погулять.
(9-6-1=2 мышки )
11. Мне 10 лет, а брат Серёжа
На 8 лет меня моложе.
Узнайте сколько лет ему,
Серёже, брату моему?
(10-8=2 года )
12. Мы большущая семья,
Самый младший-это я!
Сразу нас не перечесть:
Маня есть и Ваня есть,
Юра, Шура, Клаша, Даша,
И Наташа тоже наша.
Мы по улице идём-
Говорят, что детский дом,
Посчитайте поскорей,
Сколько нас в семье детей? (1++1+1+1+1+1+1+1=8 детей)
13. 7 воробышек спустились на грядки,
Скачут и что-то клюют без оглядки.
Котик-хитрюга внезапно подкрался,
Мигом схватил одного и умчался.
Вот как опасно клевать без оглядки.
Сколько теперь их осталось на грядке ?
(7-1=6 воробушек )
14. 2 цыплёнка стоят,
2 в скорлупках сидят.
6 яиц под крылом
У наседки лежат.
Посчитай поверней,
Отвечай поскорей:
Сколько будет цыплят
У наседки моей?
(2+2+6=10цыплят )
15. Кто то вечером к медведю
На пирог пришли соседи:
Ёж,барсук,енот,»косой»
Волк с плутовкою лисой.
А медведь никак не мог,
Разделить на всех порог.
От труда медведь вспотел,-
Он считать ведь не умел
Помоги ему скорей,
Посчитай-ка всех зверей. (1+1+1+1+1+1+1=7зверей)
16. Я сегодня рано встала,
Кукол всех пересчитала:
3 матрёшки на окошке,
2 матрёшки на перинке,
Пупсик с Катей, Буратино
И Петрушка в колпаке.
На зелёном сундучке.
Я считала, я трудилась ,
Но потом со счёту сбилась.
Помогите мне опять
Кукол всех пересчитать! (3+2+1+1+1+1=9 кукол)
17. Нам из Гомеля тётя
Ящик яблок прислала.
В этом ящике яблок
Было, в общем немало.
Начал яблоки эти
Спозаранок считать я.
Помогали мне сёстры,
Помогали мне братья…
И пока мы считали
8 раз отдыхали,
8 раз мы сидели
И по яблоку съели.
И осталось их столько?
Ох, осталось их столько,
Что ,когда в этот ящик
Мы опять поглядели,
Там на дне его чистом
Только стружки белели…
Вот прошу угадать я
Сколько было нас братьев?
Сколько было сестёр?
Поделили мы яблоки
Все без остатка.
А всего то их было
50 без десятка.
(8+8=16 отдыхали
50-10=40 яблок было
40:16= 3 брата и 2 сестры)
18.Ветер дунул, лист сорвал.
И ещё один упал.
А потом упало 5.
Кто их может сосчитать? (1+1+5=7 листьев)
19.Ёжик по грибы пошёл ,
10 рыжиков нашёл.
8 положил в корзину,
Остальное же на спину.
Сколько рыжиков везёшь
на своих иголках ёж? ( 10-8=2 гриба )
20. 3 ромашки-желтоглазки,
2 весёлых василька
Подарили дети маме
Сколько же цветов
в букете? (3+2= 5 цветов)
21.Группа малышей утят.
Плавать и нырять хотят.
6 уплыли далеко,
2 нырнули глубоко.
Сколько же утят в пруду?
Сосчитать я не могу? (6+2=8 утят)
22.-5 малышек медвежат
Мама уложила спать.
Одному никак не спится ,
а скольким хороший сон
сниться . (5-1=4 медвежатам )
23.Цапя по воде шагала,
Лягушат себе искала,
2 спрятались в траве.
6 под кочкой.
Сколько лягушат спаслось?
Только точно! (2+6=8 лягушат)
24.-2 розы Маша сорвала
В подарок маме принесла
Сорви ещё и подари
Ты мамочке не две, а…… (2+1=3)
25.У куклы 5 нарядных платьев.
Какое нынче одевать?
Есть у меня для куклы шерсть
Свяжу, и платьев будет………… (5+1=6)
26. 5 щенят в футбол играли
Одного домой позвали, он в окно глядит
Считает, сколько их теперь играет?
(5-1=4 щенка)
27. 5ворон на крышу сели
2 ещё к ним прилетели,
Отвечайте быстро, смело.
Сколько всех их прилетело? (5+2=7 ворон)
28.В снег упал Серёжа,
Зина и Антоша,
А за ними Лена,
Катенька и Гена.
А потом Игнат.
Сколько на снегу ребят? (1+1+1+1+1+1+1=7 ребят)
29 . На качелях 2 Елены.
А с мячом Иван, Игнат.
2 Ирины прибежали
На скакалках поскакать.
Валя, Зина и Егор.
Вот и в сборе весь наш двор.
А теперь скажите мне,
сколько деток во дворе? (2+1+1+2+1+1+1=9 ребят)
30.Белка, ёжик и енот
Волк, лиса, малышка крот.
Были дружные соседи.
На пирог пришли к медведю.
Вы, ребята не зевайте.
Сколько всех зверей, Считайте? (1+1+1+1+1+1+1=7 зверей)
31.-2 щенка баловника.
Бегают, резвятся.
К шалунишкам 3 дружка
С громким лаем мчатся.
Вместе будет веселей.
Сколько же теперь друзей? (2+3= 5 щенков)
32.В шкафу на полке 5 книг.
Я прочитала 2 из них.
Осталось сколько книг читать?
Вы это можете узнать? (5-2=3 книги)
33.Красиво вышила Татьяна
2 лилии и 2 тюльпана.
Какие чудные цветы!
А сколько их, нам подскажи? (2+2=4 цветка)
34.Я нашёл в дупле у белки
5 лесных орехов мелких.
Вот ещё один лежит,
Мхом заботливо укрыт,
Ну, и белка, вот хозяйка!
Все орешки сосчитай-ка! (5+1=6 орехов)
35.В шкафу стояло 9 чашек.
Одну из них взяла Наташа.
Сколько чашек теперь там?
Подумай и скажи нам .(9-1=8 чашек )
36.Мурка ,кошка-мышеловка,
Съела 3 мышей в кладовке,
И опять к норе подкралась.
Цап! Ещё 1 попалась.
Вот так Мурка! Сколько ей
Удалось поймать мышей? (3+1=4 мышки)
37.Дружно Муравьи живут
И без дела не снуют:
2 несут травинку,
3 несут былинку,
5 несут от ёлки колючие иголки.
Сколько муравьишек занято работой. (2+3+5=10 муравьёв)
38.На снежные горке
Катался Егорка,
Антон и Саша.
Скажи скорей,
Сколько каталось детей ?
Антона и Сашу с горы
столкнула Наташа.
Сколько теперь на горе детей?
(1+1+1+1=4 детей 4-2=2 осталось)
39.У хохлатки есть ребятки:
10 крошечных цыплят.
Здесь 3 только.
Деток сколько под крылом её сидят?
(10-3 =7 деток)
40.Сегодня 10 лет Серёже,
Диме нет ещё 6.
Дима всё никак не может
до Серёжи дорасти.
А на сколько лет моложе
мальчик Дима, чем Серёжа?(10-6= на 4 года )
41.Над рекой летали птицы.
Голубь, щука, 2 синицы,
2 стрижа и 5 угрей.
Сколько птиц ответь скорей!
(щука, угорь – рыбы 1+2+2=5 птиц)
42.Просят Колю сосчитать
сколько будет 5 да 5
Коля фыркнул: «Пустяки,
это будет……. 2 руки! (5+5=10)
infourok.ru
Веселые задачки в стихотворной форме по математике на тему «Сложение и вычитание в пределах 10» (1 класс)
ПРИБАВИТЬ И ВЫЧЕСТЬ 1
Карандаш один у Миши, карандаш один у Гриши.
Сколько же карандашей у обоих малышей? (1+1=2)
Утка морковку в корзине несла, этой покупкой довольна была.
Если морковку ещё ей купить, сколько их будет? Ты можешь сложить? (1+1=2)
Ёжик по лесу шел, на обед грибы нашел: два — под берёзой, один — у осины.
Сколько их будет в плетёной корзине? (2+1=3)
На поляне у дубка крот увидел 2 грибка.
А подальше, у осин, он нашел ещё один.
Кто ответить нам готов, сколько крот нашел грибов? (2+1=3)
3 яблока из сада ёжик притащил. Самое румяное белке подарил.
С радостью подарок получила белка. Сосчитайте яблоки у ежа в тарелке! (3-1=2)
2 петуха на жердь взлетели, ударив крыльями, запели: — Ку-ка-ре-ку!
Потом ещё один взлетел и тоже радостно запел.
Теперь, дружочек мой, давай-ка, всех петухов пересчитай-ка! (2+1=3)
На пасеке 3 медвежонка играли в прятки у бочонка.
Один в бочонок еле влез. А сколько убежало в лес? (3-1=2)
В класс вошла Маринка, А за ней — Иринка,
А потом пришёл Игнат. Сколько стало всех ребят? (1+1+1=3)
3 яблока… Одно сорвать ручонка так и тянется.
Но прежде надо сосчитать! А сколько же останется? (3-1=2)
Ну-ка, сколько здесь ребят, на горе катается?
Трое в саночках сидят, один дожидается. (3+1=4)
Я рисую кошкин дом: 3 окошка, дверь с крыльцом.
Наверху ещё окно, чтобы не было темно.
Посчитай окошки в домике у кошки. (3+1=4)
4 сороки пришли на уроки, одна из сорок не знала урок.
Сколько ж прилежно трудилось сорок? (4-1=3)
3 пушистых кошечки улеглись в лукошечке.
Тут одна к ним прибежала. Сколько вместе кошек стало? (3+1=4)
К речке бежало трое утят, свежей воды все напиться хотят!
Уточка — мама за ними спешит. Сколько их вместе? Скорее скажи. (3+1=4)
4 краски есть у Сани, одна у маленького брата.
Все краски посчитайте сами. Ну, постарайтесь-ка, ребята! (4+1=5)
На блюдце у Андрюши 4 жёлтых груши.
Есть мальчик захотел, одну из груш он съел.
Теперь считайте груши на блюдце у Андрюши. (4-1=3)
6 весёлых медвежат за малиной в лес спешат.
Но один малыш устал, от товарищей отстал.
А теперь ответ найди: сколько мишек впереди? (6-1=5)
.
В кормушке сидели лишь 3 только птицы, но к ним прилетела ещё и синица.
Так сколько же птиц на кормушке у нас? Скажет словами каждый из вас! (3+1=4)
5 щенят в футбол играли, одного домой позвали.
Он в окно глядит, считает. Сколько их теперь играет? (5-1=4)
8 храбрых малышей переходят вброд ручей.
Один отстал: «Домой хочу!» Сколько их пришло к ручью? (8-1=7)
Я нашёл в дупле у белки 5 лесных орешков мелких.
Вот ещё один лежит, мхом заботливо укрыт.
Ну и белка! Вот хозяйка! Все орешки посчитай-ка. (5+1=6)
7 воробьев опустились на грядки, скачут и что-то клюют без оглядки.
Котик-хитрюга внезапно подкрался, мигом схватил одного и умчался.
Вот как опасно клевать без оглядки. Сколько же птиц осталось на грядке? (7-1=6)
6 грибов нашёл Вадим, а потом ещё один.
Вы ответьте на вопрос: сколько он грибов принёс? (6+1=7)
Внуку Шуре добрый дед дал вчера 7 штук конфет.
Съел одну конфету внук. Сколько же осталось штук? (7-1=6)
В шкафу стояло 9 чашек. Одну из них взяла Наташа.
Сколько чашек теперь там? Подумай и ответишь сам! (9-1=8)
В сад 9 пчёлок прилетело. Одна из них на клумбу села.
Все остальные через сад к себе на пасеку спешат.
Так сколько ж пчёл летит из сада? Нам сосчитать тех пчёлок надо! (9-1=8)
Было в детском магазине 10 кукол на витрине.
Куколку одну купили папа с мамою для Лили.
Сколько кукол на витрине осталось в детском магазине? (10-1=9)
Я дыню разрезал на 10 кусков. Теперь, посчитай-ка, вопрос мой таков:
Все 10 кусков ароматны и сладки. Один дам тебе. Сколько будет в остатке? (10-1=9)
5 весёлых медвежат за малиной в лес спешат.
Испугался вдруг один, убежал — и след простыл.
Сколько смелых медвежат за малиной в лес спешат? (5-1=4)
5 малышек- медвежат мама уложила спать. Одному никак не спится.
А скольким сон хороший снится? (5-1=4)
2 жучка бежали в домик. Им навстречу муравей.
Сколько будет насекомых? Сосчитай-ка поскорей! (2+1=3)
9 совят в гнезде сидят. Прилетела мама. Сколько птиц стало? (9+1=10)
7 мартышек, 7 соседок со своих сбежали веток.
Все повисли до одной на хвостах вниз головой.
Раскачались, раскричались, меж собою передрались.
Больше всех досталось в драке самой главной забияке.
С ветки сбросили её. Сколько будет без неё? (7-1=6)
5 щенят, плюс мама-лайка. Сколько будет? Сосчитай-ка! (5+1=6)
.
ПРИБАВИТЬ И ВЫЧЕСТЬ 2
3 голубя белых на крыше сидело, 2 голубя вдруг улетело.
Ну, скажите мне поскорей, сколько осталось голубей? (3-2=1)
4 зайца шли из школы, и вдруг на них напали пчёлы.
2 зайчика спаслись едва. А сколько не успело? (4-2=2)
В садике гулял павлин, подошёл ещё один.
2 павлина за кустами. Сколько их? Считайте сами! (1+1+2=4)
4 спелых груши на веточке качалось.
2 груши снял Павлуша. А сколько груш осталось? (4-2=2)
Как-то четверо ребят с горки покатились.
Двое в саночках сидят. Сколько в снег свалились? (4-2=2)
3 цыплёнка стоят, на скорлупки глядят.
2 яичка в гнезде у наседки лежат. Сосчитай поскорей:
Сколько будет цыплят у наседки моей? (3+2=5)
Над рекой летели птицы: голубь, щука, 2 синицы,
2 стрижа и 5 угрей. Сколько птиц? Ответь скорей! (1+2+2=5)
Наша Маша рано встала, кукол всех пересчитала:
2 матрёшки на окошке, 2 Маринки на перинке,
2 Танюшки на подушке, а Петрушка в колпачке — на дубовом сундучке.
Игрушки быстро сосчитайте и ответ мне называйте! (2+2+2+1=7)
7 гусей пустились в путь, 2 решили отдохнуть.
Сколько их под облаками? Сосчитайте, дети, сами! (7-2=5)
Красиво вышила Татьяна 2 лилии и 2 тюльпана.
Какие чудесные цветы! А сколько их — нам скажешь ты? (2+2=4)
Сколько маленьких утят плавать и нырять хотят?
3 уплыли далеко, 2 нырнули глубоко.
Сколько их всего в пруду? Сосчитать я не могу! (3+2=5)
3 лисёнка играли на травке лесной, 2 зайчонка спешили с рыбалки домой.
А если прибавим ещё и лису, сколько зверей мы увидим в лесу? (3+2+1=6)
Вот 8 зайчат по дорожке идут, за ними вдогонку ещё 2 бегут.
Так сколько всего по дорожке лесной торопится в школу зайчишек зимой? (8+2=10)
Решила старушка ватрушки испечь, поставила тесто, печь затопила,
А сколько их надо — совсем позабыла.
2 штучки — для внучки, 2 штучки — для деда,
2 штучки — для Тани, дочурки соседа.
Считала, считала, да сбилась, а печь-то совсем протопилась.
Помогите старушке — сосчитайте ватрушки! (2+2+2=6)
На воде — 2 уточки, во дворе — 2 курочки, 2 гуся — в пруду, 1 индюк в саду. Сколько птиц всего? Считайте! Ответ быстро называйте! (2+2+2+1=7)
Повёл ротозей в поле гусей: 5 белых, 2 серых, 1 конопатый!
А сколько их было? Кто скажет, ребята? (5+2+1=8)
5 ворон на крышу сели, 2 ещё к ним прилетели.
Отвечайте быстро, смело. Сколько всех их прилетело? (5+2=7)
7 листьев Вася сам собрал, 2 листика Алёша дал.
Скажите, сколько у него осенних листиков всего? (7+2=9)
5 синиц на ветку сели, к ним 2 галки прилетели.
Сосчитайте быстро, детки, сколько птиц сидит на ветке? (5+2=7)
У меня и Аллочки 10 счётных палочек.
2 из них сломалось. Сколько же осталось? (10-2=8)
-Бабушка, милая, хочу пирожок!
-Хорошо, испеку! Сколько надо, дружок?
-2 для мамы, 2 для папы, для сестрёнки тоже 2,
2 тебе, 2 мне испечь. Ох, мне всех не перечесть!
Кто малышу помочь готов? Сколько надо пирогов? (2+2+2+2+2=10)
Если знаешь ты таблицу, на вопрос ответишь смело.
Сколько птичек-невеличек на кормушку прилетело?
Воробьёв драчливых пара, и синичек тоже пара,
Пара сизых голубей, ну, и пара снегирей. (2+2+2+2=8)
Мы ходили на базар, выбирали там товар: 3 морковки, 2 петрушки,
Тыква, свёкла, сельдерей. Сколько будет овощей? (3+2+1+1+1=8)
Жили-были под дубочком 10 пухленьких грибочков.
Прискакал бельчонок вдруг — и грибов не стало 2-х.
У кого ответ готов? Сколько там теперь грибов? (10-2=8)
В деревне у бабушки 2 поросёнка, белая козочка и 2 индюшонка.
Если нам их сосчитать, всех их будет ровно… (2+1+2=5)
У меня стоят на полке: 2 зелёных лягушонка,
2 медведя и мышонок и чудесный кукушонок.
А ещё стоит слонёнок и щенок с зашитым ухом,
Розовенький поросёнок с красной пуговкой на брюхе.
А теперь хочу послушать: сколько у меня игрушек? (2+2+1+1+1+1+1=9)
Как-то раз в лесу густом ёж построил себе дом.
Пригласил лесных зверей. Сосчитай их поскорей:
3 зайчонка, 2 лисёнка, 2 бельчонка, 2 бобра. Называть ответ пора! (3+2+2+2=9)
2 мяча у Ани, 2 мяча у Вани.
Сколько, дети, всех мячей? Отвечайте мне скорей! (2+2=4)
В 2-х автобусах сидят 8 маленьких ребят.
В первом едут двое только. Во втором их будет сколько? (8-2=6)
У маленькой Светы — 4 конфеты. Ещё дала 2 Алла.
Сколько всего стало? (4+2=6)
.
ПРИБАВИТЬ И ВЫЧЕСТЬ 3
Возле грядки 2 лопатки, возле кадки 3 лопатки.
Все лопатки сосчитать! Сколько будет? Ровно … (2+3=5)
Через поле по прямой шёл баран на водопой,
Трёх овечек за собою вел он важно к водопою.
Сколько вместе их? Считайте! Ответ быстро называйте! (1+3=4)
Белка сушит на верёвке 2 грибка и 3 морковки.
Прибежал хорёк, утащил грибок.
Съел зайчонок 2 морковки. Что осталось на верёвке? (2+3-1-2=2)
К двум пушистеньким зайчишкам прибежали 3 братишки.
Всем пора бы это знать, что их будет ровно … (2+3=5)
Две мышки проникли в квартиру, решили попробовать сыру.
Тут следом явились подружки — 3 сереньких мышки — норушки.
Сколько мышек, считайте? Ответ быстро называйте! (2+3=5)
На рельсах перегона товарных 2 вагона,
А 3 других в сцеплении, готовы к отправлению.
Прибавь-ка к 2 вагонам 3 и сколько станет — назови! (2+3=5)
2 щенка – баловника бегают, резвятся.
К шалунишкам 3 дружка с громким лаем мчатся.
Вместе будет веселей. Сколько же всего друзей? (2+3=5)
5 лодок было у причала, волна их весело качала.
3 лодки взяли рыбаки, чтоб переплыть простор реки.
А сколько лодок у причала волна по-прежнему качала? (5-3=2)
Посадил я 5 хороших белых бусинок — горошин,
А росточков из земли показалось только 3.
3 горошины взошло. Сколько их не проросло? (5-3=2)
Яблочки в саду поспели. Мы отведать их успели:
5 румяных, наливных, три с кислинкой. Сколько их? (5+3=8)
Вышла курочка гулять, собрала своих цыплят:
7 бежали впереди, 3 осталось позади.
Беспокоится их мать и не может сосчитать.
Сосчитайте-ка, ребята, сколько было всех цыплят? (7+3=10)
К серой цапле на урок прилетело 7 сорок.
А из них лишь 3 сороки приготовили уроки.
Сколько лодырей – сорок прилетело на урок? (7-3=4)
Сеть тяну, рыбу ловлю. Попало немало:
2 окунька, 3 карася, 1 ершок — и того в горшок.
Уху сварю, всех угощу. Сколько рыб я сварю? (2+3+1=6)
3 больших, 3 маленьких, маленьких, удаленьких —
Целая семья опят. Сколько их на пне сидят? (3+3=6)
Стоит горка крутая, на ней тыква большая,
А пониже тоже 3 тыквы моложе. А под горкою в траве ещё 2.
Ну-ка, кто скажет сейчас? Сколько тыкв всего у нас? (1+3+2=6)
3 гуся летят над нами, 3 других за облаками.
2 спустились на ручей. Сколько было всех гусей? (3+3+2=8)
Есть игрушки у меня: паровоз и 2 коня,
Серебристый самолёт, 3 ракеты, вездеход…
Сколько вместе? Как узнать? Помогите сосчитать? (1+2+1+3+1=8)
Ёж спросил ежа — соседа:
-Ты откуда, непоседа?
-Запасаюсь я к зиме, видишь яблоки на мне? Собираю их в лесу: 6 принёс да 3 несу.
Призадумался сосед:
-Это мало или нет?
Поскорей мне дай ответ! (6+3=9)
У пенёчков 5 грибочков и под ёлкой 3.
Сколько будет всех грибочков? Ну-ка, говори! (5+3=8)
На удочку Андрей поймал 6 окуней.
А друг его Сергей трёх небольших ершей.
Сосчитай без лишних слов этих мальчиков улов. (6+3=9)
Вот 7 дубков и 3 сосны. Как зелены они, стройны!
Деревьев сколько тут? Узнайте! И хорошенько сосчитайте! (7+3=10)
Вот котёнок – озорник к блюдцу с молоком приник.
Вот другой — ему смешно видеть пса через окно.
Вот ещё один сидит — тихо мышку сторожит.
3 других моих котёнка — спят, мурлыча потихоньку.
Вот задача для ребят: всех пересчитать котят! (1+1+1+3=6)
Все ли здесь цыплятки — детки? Надо сосчитать наседке:
6 — на грядках, 3 — во ржи. Сколько их всего, скажи? (6+3=9)
Однажды 3 цыплёнка, а с ними 3 мышонка,
А с ними 3 весёлых умытых поросёнка
Бежали спозаранку из дома на полянку.
Посчитайте поскорей, сколько было всех друзей,
Что утром спозаранку, играли на полянке? (3+3+3=9)
Я вошёл в тенистый бор и увидел мухомор,
опёнка, 2 сморчка, 3 маслёнка, 2 строчка…
У кого ответ готов? Сколько я нашёл грибов? (1+2+2+3+2=10)
Сбежала от Федоры посуда: 3 стакана, 3 чашки, 3 блюдца.
Кто сосчитать готов? Сколько всего беглецов? (3+3+3=9)
В зоопарке я бывала, обезьянок я видала:
3 сидели на песке, 2 качались на доске, а ещё 3 спинки грели.
Сосчитать вы всех успели? (3+2+3=8)
.
Белка с рынка возвращалась и с лисою повстречалась:
-Что ты, белочка, несешь? — задала лиса вопрос.
-Я несу своим детишкам: 2 ореха и 3 шишки.
Ты, лиса, мне подскажи: сколько будет 2+3?
Лиса быстро сосчитала, ровно 10 насчитала.
Ах ты, рыжая плутовка, обманула белку ловко!
Вы, ребята, ей не верьте! И ответ её проверьте. (2+3=5)
5 котят песок копают, 3 на солнце загорают,
2 купаются в золе. Сколько всех? Скажите мне! (5+3+2=10)
У белки в дупле 5 орешков в мешке,
Ещё 3 на полке. Посчитай-ка их, сколько? (5+3=8)
Петя — петушок, золотой гребешок,
Зёрна отыскал, курочек позвал.
Прибежали курочки: две из переулочка,
Три из-за поворота, одна из огорода.
А сейчас проверь! Сколько курочек теперь? (2+3+1=6)
Полевая мама — мышка ищет всех своих сынишек:
Двое спрятались на ветке. Трое спрятались в цветах.
Трое — в ягодных кустах. А один, ленивый самый,
Дома спит под одеялом.
Помоги их всех найти, к маме-мышке привести! (2+3+3+1=9)
Майским вечером к пеструшке на блины пришли подружки:
3 несушки, 3 клохтушки. Сколько курочек в избушке? (3+3=6)
Дружно муравьи живут, они без дела не снуют.
Два несут травинку, три несут былинку, три несут иголки.
Сколько их у ёлки? (2+3+3=8)
Привела гусыня-мать 6 детей на луг гулять.
Все гусята, как клубочки: 3 сынка. А сколько дочек? (6-3=3)
У Коли и Маринки 4 мандаринки.
Из них у Коли — 3. А сколько у сестры? (4-3=1)
У маленькой Светы 4 конфеты, ещё дала 3 Алла.
Сколько всего стало? (4+3=7)
В садик тёти Гали 5 гусей забралось.
Троих прогнали. Сколько там осталось? (5-3=2)
На кустике перед забором 7 красных помидоров.
Потом 3 оторвалось. А сколько на кусте осталось? (7-3=4)
7 кубиков у Маши, а 3 у Наташи.
Вы кубики все эти скорей считайте, дети! (7+3=10)
.
.
.
.
ПРИБАВИТЬ И ВЫЧЕСТЬ 4
Сидят рыбаки, стерегут поплавки. Рыбак Корней поймал 3-х окуней,
Рыбак Евсей – 4-х карасей, а рыбак Михаил 2-х сомов изловил.
Сколько рыб рыбаки натаскали из реки? (3+4+2=9)
Рада Алёнка — нашла 2 маслёнка, да 4 в корзинке. Сколько грибов на картинке? (2+4=6)
Влетели к девочке в окно 2 птички-невелички, потом за ними заодно ещё 4 птички.
Сколько вместе их? Считайте! Ответ быстро называйте! (2+4=6)
3 ягнёнка дружно жили, да козлят ещё четыре.
Вместе им-то веселей! Сколько же всего друзей? (3+4=7)
На тарелочке 7 слив, вид их очень уж красив.
Съел 4 сливы Павел. Сколько мальчик слив оставил? (7-4=3)
Посадила бабка в печь пирожки с капустой печь.
Для Наташи, Кати, Вовы пирожки уже готовы.
Да ещё один пирог — кот под лавку уволок.
Да в печи — 4 штуки. Пироги считают внуки.
Если можешь, помоги сосчитать все пироги! (1+1+1+1+4=8)
4 Алёнки, 4 Наташки под солнцем весенним играли в пятнашки.
Так сколько, ребята, ответьте скорей, под солнцем весенним играло детей? (4+4=8)
Есть у Нади 5 тетрадей, папа девочке их дал.
Дал и Ире он 4. Ты б тетради посчитал! (5+4=9)
Взял 9 вишенок Сергей, он угостил своих друзей.
4 дал он Вите, а остальные все Никите.
Сколько вишен дал Никите? Вы сосчитайте и скажите! (9-4=5)
5 яблок в корзине, в вазе четыре, у Саши одно. Сколько всего? (5+4+1=10)
Ниночка рисует дом. Окон много- много в нём.
Тут их 6, 4 — там. Посчитай все окна сам! (6+4=10)
Шла овчарка по дорожке, у неё — 4 ножки.
Ей навстречу — чёрный дог. Сколько всех собачьих ног? (4+4=8)
В день рожденья я Серёжке подарил одну матрёшку.
Мы её открыли, а там ещё 4.
Так сколько же матрёшек получилось у Серёжки? (1+4=5)
7 антенн на этой крыше. Наш электрик, дядя Миша,
Лишь 4 укрепил, остальные — брат Кирилл.
Сколько же Кирилл антенн установил? (7-4=3)
4 павлина, 4 пингвина, совёнок и мама-сова.
Однажды в июле в Москву заглянули всего на денёк или два.
Сколько же птиц в июле в Москву заглянули? (4+4+1+1=10)
.
.
.
ПРИБАВИТЬ И ВЫЧЕСТЬ 5
Завтракали на привале. Нам с собой яичек дали.
Всмятку 2 и 5 крутых. Посчитай-ка, сколько их? (2+5=7)
7 огурцов собрали с грядки. 5 огурцов уж съели.
Осталось сколько их, ребятки? Вы б сосчитать сумели? (7-5=2)
3 яблока было у Коли, 5 дали товарищи в школе.
Яблок сколько всего стало, друзья, у него? (3+5=8)
В хоре 7 кузнечиков песни распевали. Вскоре 5 кузнечиков голос потеряли.
Сосчитай без лишних слов, сколько в хоре голосов? (7-5=2)
Бегали по лесу 8 резвых коз: беленьких и сереньких, вверх задравши хвост.
5 козочек белых. Сколько было серых? (8-5=3)
В одном кармане 4 каштана, в другом кармане их 5.
Мы просим, дети, каштаны эти пересчитать! (4+5=9)
Стала курица считать маленьких цыпляток:
Жёлтых 5 и чёрных 5, а всего … (5+5=10)
2 гуся летят над нами, 2 других за облаками,
5 спустились за ручей. Сколько было всех гусей? (2+2+5=9)
Вот задумал ёж друзей пригласить на юбилей.
Пригласил 2-х медвежат, 3-х зайчат и 5 бельчат.
Посчитайте поскорей, сколько у ежа друзей? (2+3+5=10)
В кружку сорвала Марина 8 ягодок малины,
5 дала своей подружке. Сколько ягод стало в кружке? (8-5=3)
У деревьев грибы сохли, ну, и в дождь, конечно, мокли.
Двое жёлтеньких маслят, 5 тоненьких опят.
Да 3 рыжие лисички, очень милые сестрички.
Вы, ребята, не молчите, Сколько всех грибов? Скажите! (2+5+3=10)
Мама-курица цыплят привела в фруктовый сад.
-Посмотрите, детки, груша упала с ветки.
Вот ещё упало 5, кто их может сосчитать?
Но цыплята маловаты, помогите им, ребята! (1+5=6)
4 мышки — крохотушки, очень дружные подружки
Вышли в поле погулять. Прибежали ещё 5.
Очень дружно они пели. Всех их было ровно… (4+5=9)
Мы на ёлке веселились, и плясали, и резвились.
После добрый Дед Мороз нам подарки приподнёс.
Дал большущие пакеты, в них же — вкусные предметы.
Стала я пакет вскрывать, содержимое считать:
2 конфеты в бумажках синих, 5 орехов рядом с ними.
Груша с яблоком, один — золотистый мандарин.
Всё лежит в пакете этом! Сосчитайте все предметы! (2+5+1+1+1=10)
.
Шла лисица вдоль тропинки и несла грибы в корзинке:
5 опят и 5 лисичек для лисят и для лисичек.
Кто ответить готов? Сколько грибов? (5+5=10)
infourok.ru
Сложение и вычитание в пределах 10.Решение задач
Я Абдикова Нургуль Галымтаевна. 2005 году закончила АРПИ. В данное время учитель начальных классов в школе имени Б.Колдасбаева. На уроках пременяю новые технологии. Детям даю разно уровневые задания. В неделе начальных классов урок путешествие по математике на тему «Приём вычисления с переходом через десяток » учителя отценили на отлично.
Просмотр содержимого документа
«сложение и вычитание в пределах 10.Решение задач»
Тема: Сложение и вычитание в пределах 10 и решение задач. Цель: закрепить приемы сложения и вычитание; основанные на составе чисел, и решение задач. -совершенствовать навыки быстрого и стабильного счета в пределах 10; -совершенствовать умение решать задачи; -активизация мыслительной деятельности, развитие логического мышления, грамотной математической речи. -воспитывать доброжелательность, взаимопомощь и аккуратность. Тип урока: урок-закрепление. Вид урока: Путешествие Формы урока: коллективная, индивидуальная. Методы урока: словесный, практический, наглядный, игровой, частично –поисковый, Оборудование: карточки с примерами. полоски бумаги, солнышко, рисунки паровозика . Ход урока: Организационный момент: Поздоровались: психологический настрой к уроку: Сколько времени в году? Назовите их? А какое сейчас время года? Посмотрите в окно на улице снег, мороз, холодно. А в нашем классе тепло и уютно. Так — как нас согревает, ласковое, теплое солнышко. Посмотрите друг на друга, улыбнитесь и пожелайте удачи. Сообщение темы и целей урока: Сегодня на уроке, мы повторим ранее изученный материал. Но урок наш будет не совсем обычным. Мы отправимся с вами в увлекательное путешествие, где будем решать, соображать, удивляться, думать и обязательно считать. А на чем мы отправимся в путь, вы узнаете если отгадаете загадку: Братцы в гости снарядились. Друг за друга уцепились. И помчались в путь далекий. Лишь оставили дымок. (поезд) Правильно. На поезде. И так приобретайте билеты, а затем поудобней садитесь в вагоны . ( вагон 1 : вагон 2) Открываем тетради пишем. Дату отправления. Сегодняшнее число. Классная работа. Разминка 1.Счет прямой, обратный. 2.Назовите соседей чисел 7,5,3. 3.Какие цифры потерялись? Мы отправляемся дальше. Следующая станция «Помогай-ка » мы должны помочь нашему хорошему другу Незнайке решить задачу. Для этого открываем учебник. И читаем задачу. Было 6 кукол. Отдала 2 куклы Осталось -?к 6-2= 4 (к) Ответ : осталось 4 куклы. Остальные работают в тетрадях.
Физкультминутка: Мы работали, устали. А теперь тихонько встали. Сколько раз в ладоши хлопнем (5) Сколько раз ногою топнем (3) Мы присядем сколько раз (6) Я прошу вас тихо сесть. Отправляемся в путь, следующая станция «Посчитай- ка». И здесь нас встречает Буратино, давайте вместе с Буратино вспомним мы с вами состав чисел:
8 10 9
4537 7352 1327
6371 4913 6452
8012 5828 1864
4467 4553 5236
8526 3964 4409
Остальные дети в это время играют в игру «Засели домики» Молодцы ребята!
Игра. Кто быстрее? Решение примеров с учебника
Следующая станция «Логиков» -Ребята, Мы подъехали к трем дорогам. По какой из них нам поехать дальше? Верная та дорога, которая длиннее синей, но короче красной (зеленая). -Вот и попали мы на поляну Радости, на которой растут необычные цветы с записанными выражениями. Сравните эти выражения.
2-1*4 5*3+1 2+2*4
Итог урока: Рефлексия . Ну, что же дети, виднеется остановка «Школа», с которой мы начинали свой путь. Наше путешествие подходит к концу. -Есть такая традиция – оставлять о себе на память доброе имя. А теперь, ребята, давайте посадите свои цветочки на поляне Радость, если урок понравилось красные цветочки если не понравилось синие. Понравилось вам наше путешествие? Где мы сегодня побывали? Молодцы! Наш урок закончен. Спасибо вам за хорошую работу. Выставления оценок. Домашнее задание.
Костанайская область
Село Амангельды
kopilkaurokov.ru
«Нумерация чисел первого десятка», «Сложение и вычитание в пределах 10», «Решение задач».
Конспект урока математики в 1 классе
Место проведения: ГБОУ школа-интернат № 17 г. Самары
Разработала и провела: Смолина Наталья Владимировна
Тема: Урок-закрепление по темам: «Нумерация чисел первого десятка», «Сложение и вычитание в пределах 10», «Решение задач».
Цель: закрепить знания о числах 0 и 10, умение соотносить их с цифрами и количеством предметов, умение выполнять действия сложения и вычитания в пределах 10, умеие решать задачи.
Обучающие:
1) закреплять навык прямого и обратного счета в пределах 10,
2)закреплять вычислительные навыки в пределах 10 без перехода через разряд,
3)продолжать вырабатывать умение решать задачи на уменьшение на несколько единиц, на сравнение.
4)вырабатывать умение называть и различать геометрические линии.
Коррекционно-развивающие:
1)коррекция зрительного восприятия на основе упражнений в сравнении,
2)развитие и коррекция способности к соцальной адаптации в общественных местах,
3) коррекция и развитие воображения учащихся через задания с воображаемой ситуацией.
Воспитывающие:
1) воспитание интереса к предмету «Математика»,
2)воспитание активного интереса к изучению окружающей действительности.
Оборудование:
карточки с числовым рядом,
иллюстрации овощей, фруктов, продуктов,
иллюстрации к задачам,
плакат с изображением геометрических линий,
плакат со словом «геометрия»
плакат с высказываниями: «Математика — точная наука», «Математика — царица наук»
плакат с ребусами
Ход урока.
1. Психологический настрой.
У нас на уроке много гостей. Издавна русские люди говорили: «Гости в дом — радость в дом». Улыбкой друг другу создадим хорошее настроение и начнём работу.
2. Актуализация знаний.
— Сегодня мы отправимся в путешествие. Как вы думаете, куда? Не на Луну, не в космос, ни на необитаемый остров. Мы прогуляемся по городу и зайдем в те места, где люди бывают ежедневно. А знаете, почему? Прежде чем человек может отправиться в столь далекие и опасные путешествия, он должен научиться хорошо ориентироваться в окружающем его пространстве. А что это — окружающее нас пространство? Это наш класс, школа, улица, общественные места города.
3. Постановка проблемной ситуации.
— А какие занания должны быть у человека, который выходит из дома один? (выслушиваются ответы детей). Правильно. А еще даже, чтобы ответить на простейшие вопросы, сколько этажей в твоем доме, сколько людей тебе встретилось и т. п., что надо уметь делать ? Конечно, уметь считать, и не приблизительно, примерно уметь считать, а точно, потому что математика — точная наука (показать детям плакат с этим высказываением).
— А в каких профессиях нужна математика? Да, ребята, практически во всех. Послушайте:
Чтоб врачом, моряком
или летчиком стать,
Надо прежде всего
математику знать.
И на свете нет профессии,
вы заметьте-ка,
Где бы вам не пригодилась математика.
4. Основная часть урока.
4.1.Числовой ряд натуральных чисел.
— Ну что ж, в путь. Итак, мы выходим из квартиры и заходим в лифт. Но вот проблема: многие из кнопок стерлись и их не видно. Надо восстановить числовой ряд. (Детям раздаются листочки с числовым рядом от 0 до 10, в котором пропущены числа.). Вставьте пропущенные числа.
— Пока мы спускаемся, давацте сосчитаем ступени (показываю рисунок лестницы со ступенями), а вот нам навстречу идут соседи. Сосчитайте. Какие числа нам помогли сосчитать? Правильно, натуральные. Что это за числа? (выслушать ответ). Правильно, посмотрите на плакат:
Натуральные числа — это числа, которые используют для счета предметов
или для указания порядкового номера
4.2. Нумерация в пределах 10 (четные и нечетные числа)
Вот мы вышли из дома и идем вдоль домов по улице. Мы помним, что с одной стороны улицы идут четные номера домов, с другой — нечетные. Назовите четные номера от 0 до 10. Теперь нечетные.
4.3. Сложение и вычитание в пределах 10.
Дошли до магазина. Нам нужно кое-что купить. Догадываетесь, какие знания мы будем опять использовать? Действительно, математические знания и умения нам нужны на каждом жизненном шагу. В магазине нас ждут примеры на сложение и вычитание в пределах 10.
Все задачи сопровождаются иллюстрациями.
1. Нам надо купить 3 кабачка и 2 баклажана. Сколько всего овощей купили?
2. Еще мы возьмем 6 яблок и 4 груши. Сколько всего фруктов возьмем?
3. Из кассеты яиц, в которой лежит 3 десятка яиц, возьмем только 2 десятка. Сколько десятков останется в кассете?
4. С полки, на которой стоят 9 бутылок молока, возьмем себе 2 бутылки. Сколько бутылок молока останется на полке?
5. 10 разных булочек разложили в 2 пакета. Как это можно сделать? Что надо вспомнить? Правильно, состав числа 10.
4.4. Решение задачи на уменьшение на несколько единиц.
Выходим из магазина, относим покупки домой. А теперь отдохнем? Поедем в цирк?
Нам нужно проехать 9 остановок на автобусе до цирка. Считаем до 9 по цепочке.
Ну, вот и цирк! Заходим, показываем билеты, раздеваемся в гардеробе и проходим на свои места. Чтобы найти свой ряд и место, знания какой науки нам пригодятся? Разумеется, математики.
В цирке нас ждут задачи. А что такое задача? (Это математический рассказ, в котором есть условие и вопрос). А что такое условие задачи? (это то, что нам известно). Что такое вопрос задачи ? (то, что надо узнать, найти).
Итак, выступление диких зверей. Кто изображен на иллюстрации? (тигры и львы). Послушайте задачу: На арене цирка выступали 6 львов, а тигров на 2 меньше. Сколько тигров выступало на арене цирка?
О ком задача? (о львах и тиграх)
Что нам известно о львах? (их было 6)
Известно, сколько было тигров? (нет, не известно)
Но что сказано про тигров? (их было на 2 меньше, чем львов)
Что значит «на 2 меньше»? (столько же, но без двух)
Что надо узнать в задаче, какой вопрос? (сколько тигров выступало)
Какие слова возьмем для краткой записи? (львы и тигры)
Что напишем напротив слова «львы»? (6)
Что напишем напротив слова «тигры»? (их количество нам неизвестно, значит, ставим занк вопроса, но сказано, что на 2 меньше, значит, после знака вопроса ставим запятую и пишем на 2 меньше)
Каким действием узнаем, сколько выступало тигров? (вычитанием). Почему? (тигров было меньше). Один ученик записывает решение на доске, остальные с помощью красно-зеленых светофоров показывают, согласны они с записанным решением или нет.
Какой будет ответ? (4 тигра выступало на арене цирка).
4.5. Физминутка.
4.6. Математические ребусы.
ПО2Л
ВИ3НА
О5
7Я
Р1НА
4.7. Решение задачи на сравнение.
Антракт! Идем в буфет. Смотрите, на одном подносе лежит 5 пирожных, а на другом -8 пирожков. Чего больше? Чего меньше? Как узнать, на сколько пирожков больше, чем пирожных? (чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее).
А чтобы проверить, действительно ли на 3 меньше, что надо сделать? (соединить пирожные и пирожки в пары с помощью линий). (Ребята окружают первую парту и соединяют в пары). Сколько пирожков осталось без пары? (3). Значит, чего больше? (пирожков). На сколько? (на 3).
4.8. Геометрический материал.
Повеселились? Поедем домой. Едем на остановке обратно 9 остановок. Считаем в обратном порядке от 9 до 1 по цепочке.
Проезжаем мимо стройки. А вы занете, какая наука помогает строить дома, чертить чертежи? (на доске плакат со словом «геометрия»). Это геометрия, что в переводе означает «гео» — земля, «метрио» — измеряю. Давайте, пока едем, повторим названия линий, которые мы изучили.
Перед вами пронумерованные линии. Назовите линию под номером 1 (отрезок). Что такое отрезок (прямая, у которой есть начало и конец). Под цифрой два? (луч). Что такое луч? (прямая, у которой есть начало и нет конца). Как назвается эта линия? (ломаная). Из чего состоит ломаная? (из отрезков). А эта фигура? (многоугольник). Как по-другому называется многоугольник? (замкнутая ломаная).
4.9. Задачи на логическое мышление.
Вот мы и дома! Нам надо приготовить себе ужин. Одно яйцо варится 4 минуты. Сколько минут будут варится два таких яйца? (4 минуты).
Пойдемте чистить зубы. Вот вам задача: пока мальчик чистил зубы, он оставил включенным кран с водой. За 1 минуту из крана вылилось 3 литра воды. Сколько литров выльется за 2 минуты? (6 литров).
Подведение итогов.
— Какие вы молодцы, ребята. Очень хорошо потрудились!
— Понравилась вам прогулка?
— Где мы побывали?
— Знания каких наук мы использовали? Да, знания математики, чтобы считать, русского языка, чтобы общаться и понимать друг друга, чтения, чтобы читать названия остановок, вывески, ценники и другую полезную нам информацию, окружающего мира, геометрии).
— Да, все ж без математики
Нам невозможно жить!
Любите математику
И вы поймете вдруг,
Что правда математика —
Царица всех наук.
infourok.ru





















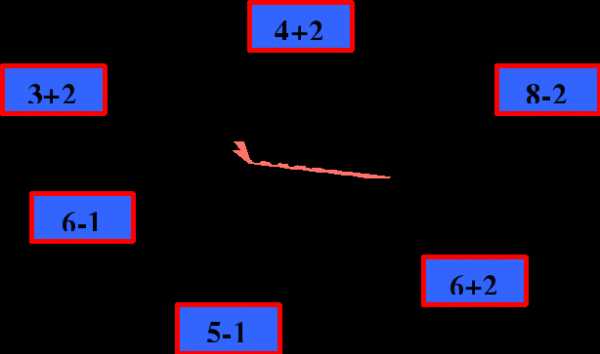

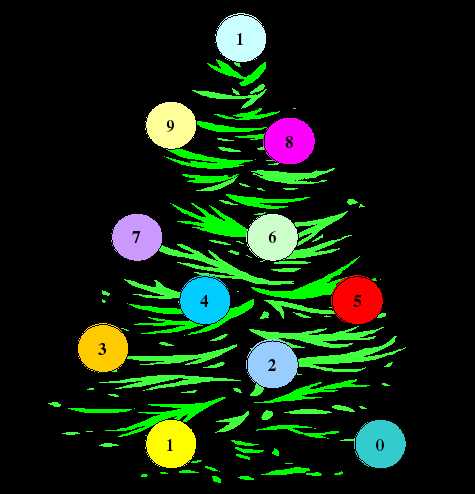


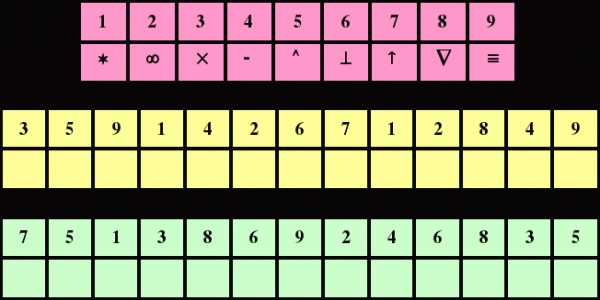
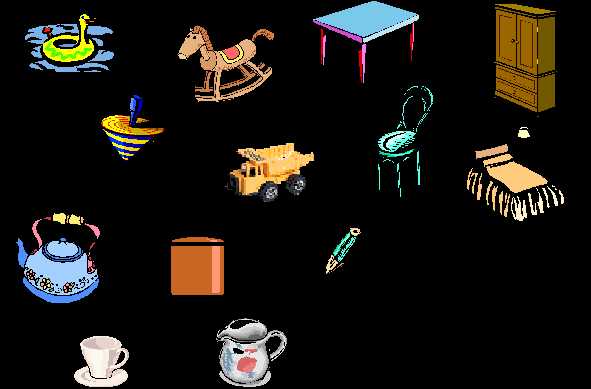






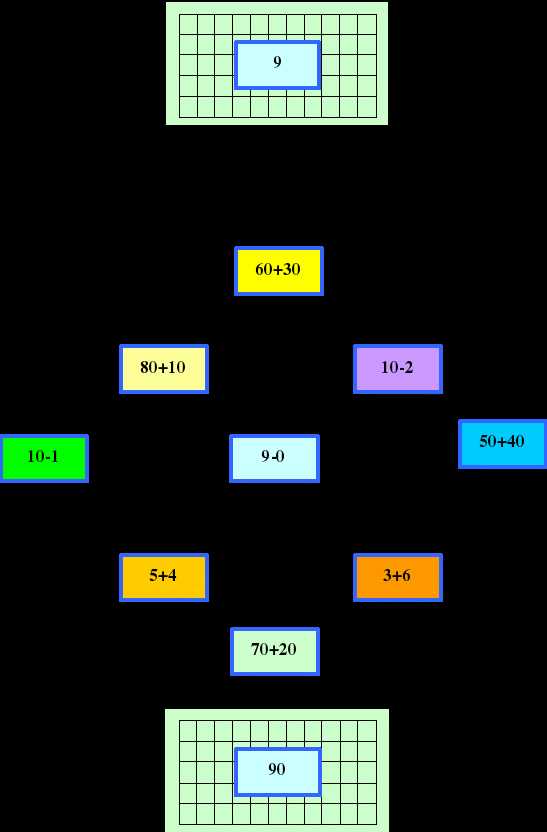




 вокруг данной прямой (оси вращения)называется
такое движение, при котором каждая точка
фигуры
вокруг данной прямой (оси вращения)называется
такое движение, при котором каждая точка
фигуры  описывает
окружность с центром на оси вращения,
лежащую в плоскости, перпендикулярной
к оси вращения.
описывает
окружность с центром на оси вращения,
лежащую в плоскости, перпендикулярной
к оси вращения. ,
, ,
, и параллельным переносом осей координат
приводится к каноническому виду подобно
тому, как это делалось для линий второго
порядка (см. Исследование общего уравнение
линии второго порядка). Поверхности
второго порядка и их канонические
уравнения представлены в табл. 3.
и параллельным переносом осей координат
приводится к каноническому виду подобно
тому, как это делалось для линий второго
порядка (см. Исследование общего уравнение
линии второго порядка). Поверхности
второго порядка и их канонические
уравнения представлены в табл. 3.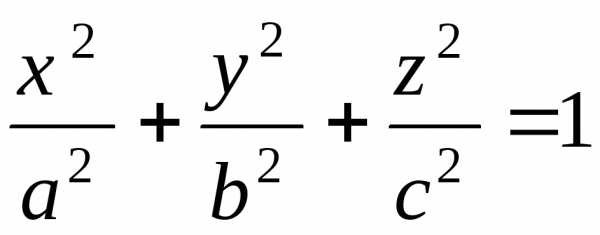
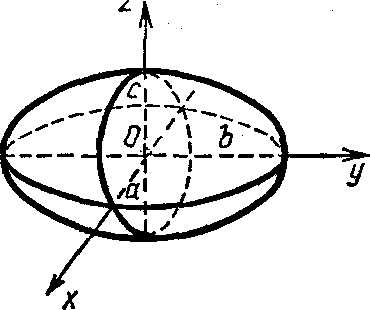
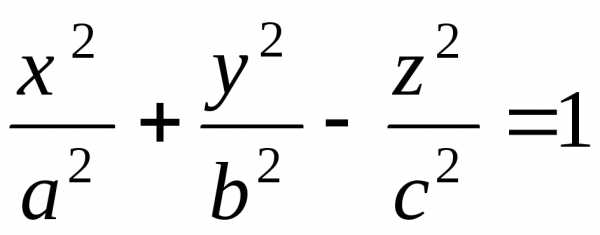
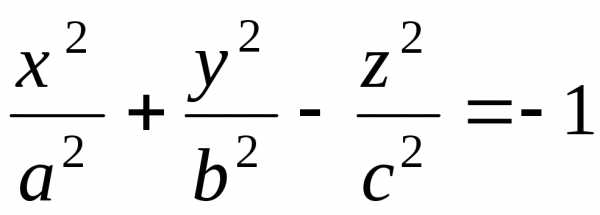
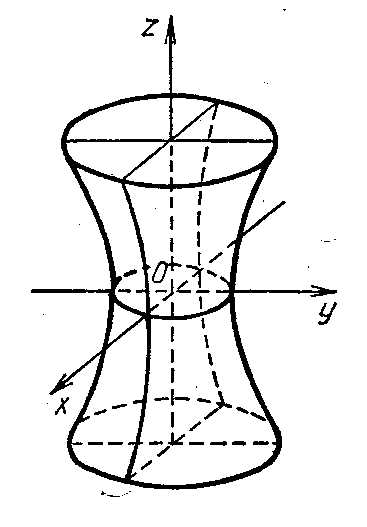
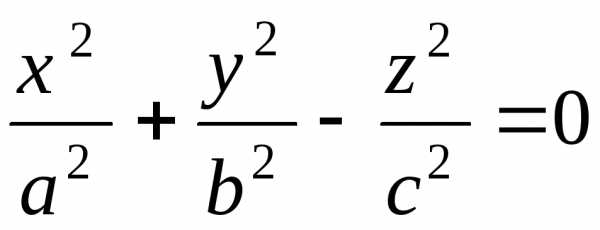
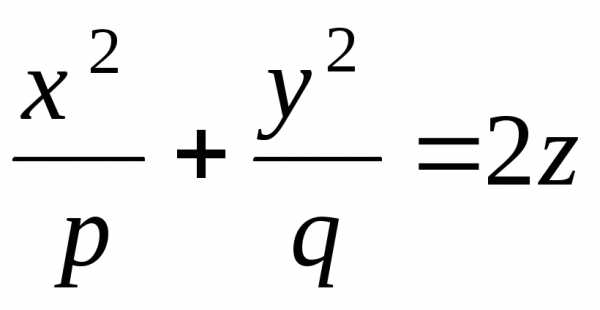
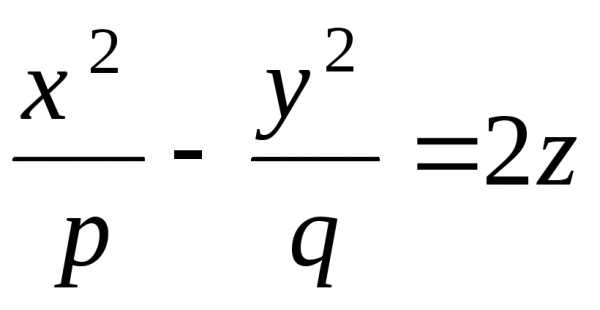
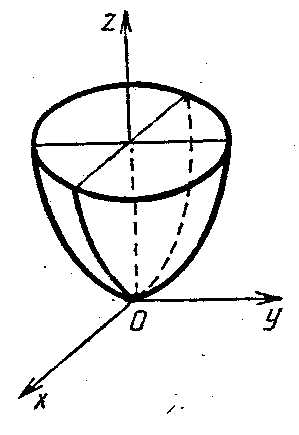
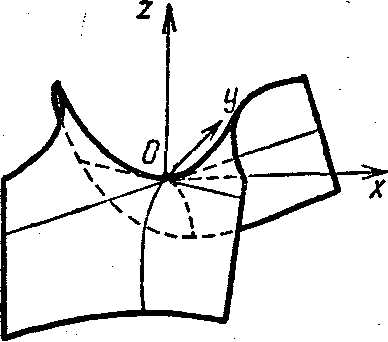
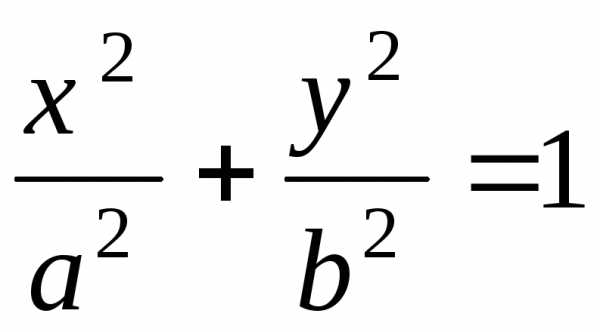
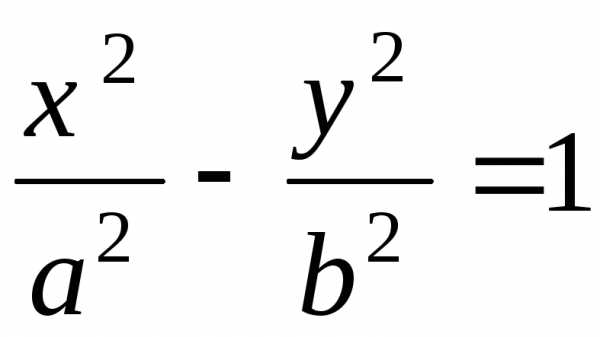
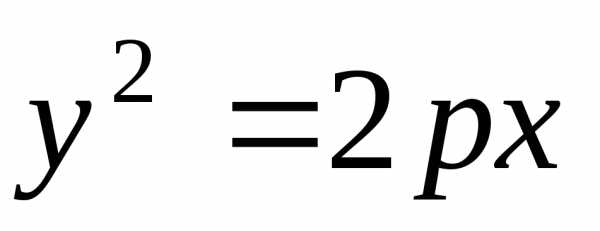
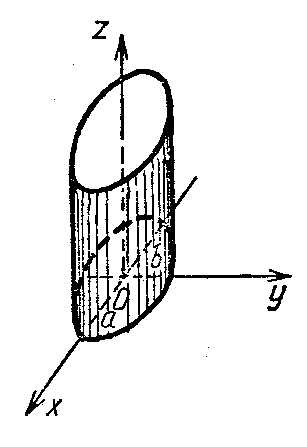
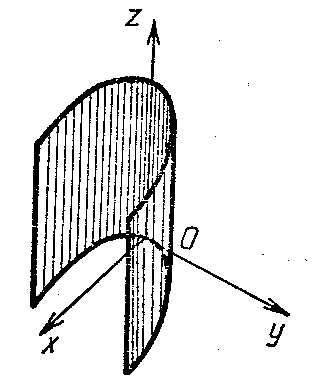
 ,
а центр находится в точке.
,
а центр находится в точке.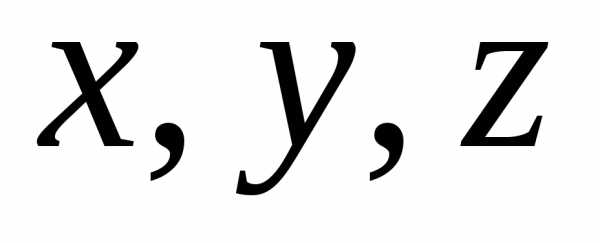 координаты произвольной точки
координаты произвольной точки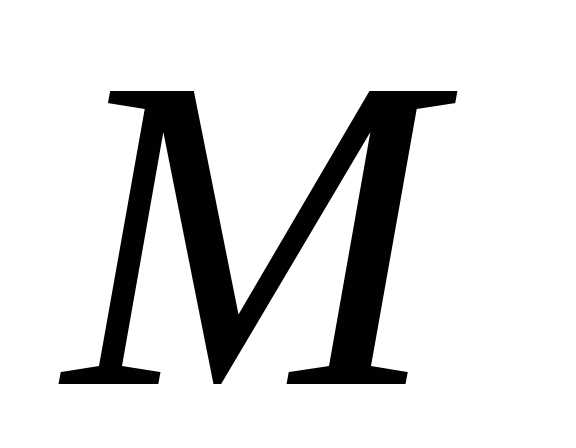 сферы и выразив через них равенство
сферы и выразив через них равенство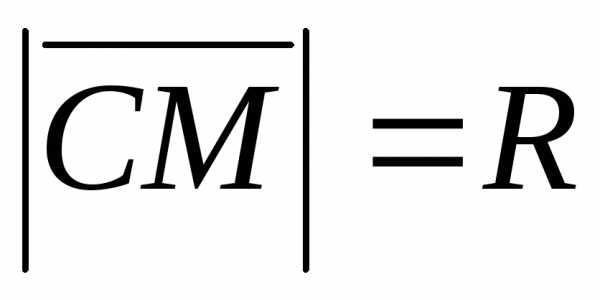 ,
будем иметь
,
будем иметь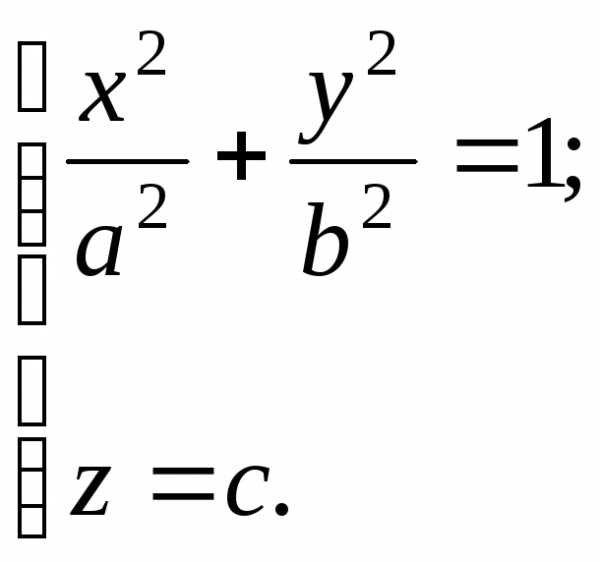 (7.1)
(7.1)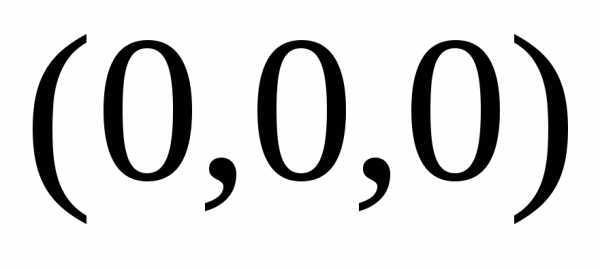 и точку
и точку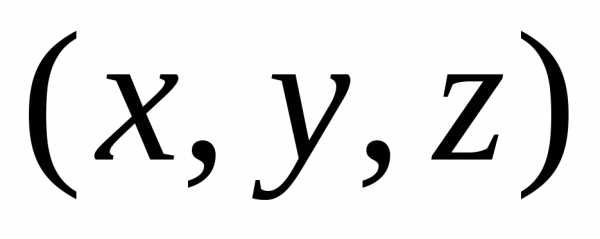 направляющей, имеет вид
направляющей, имеет вид (7.2)
(7.2)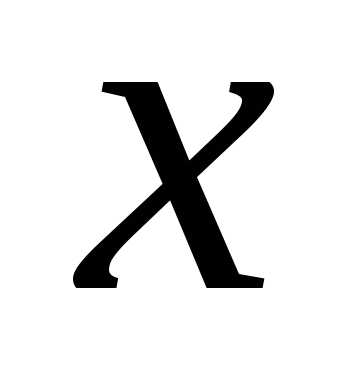 ,
, ,
, из уравнений (7.1) и (7.2). Для этого в
уравнениях (7.2) заменим
из уравнений (7.1) и (7.2). Для этого в
уравнениях (7.2) заменим на
на и определим
и определим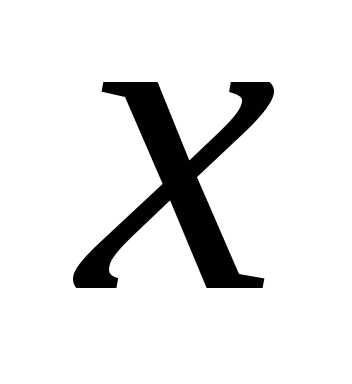 и
и :
: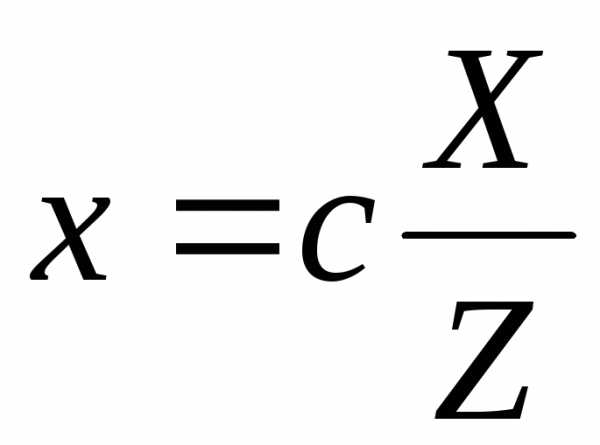 ;
; 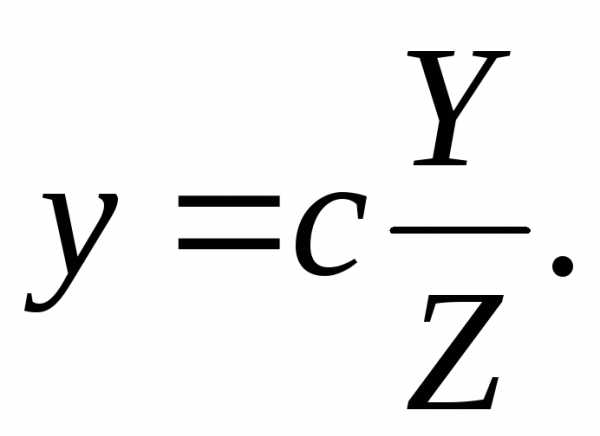
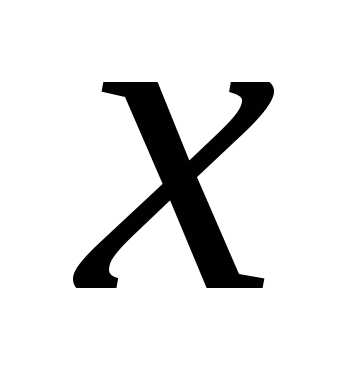 и
и в первое уравнение системы (7.1), будем
иметь:
в первое уравнение системы (7.1), будем
иметь: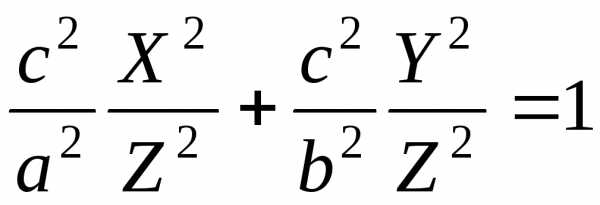 или
или 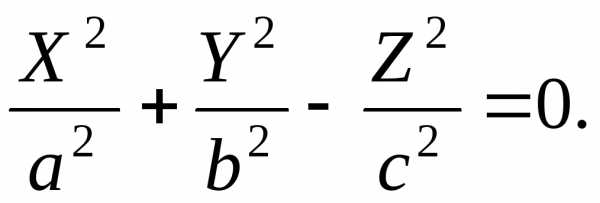
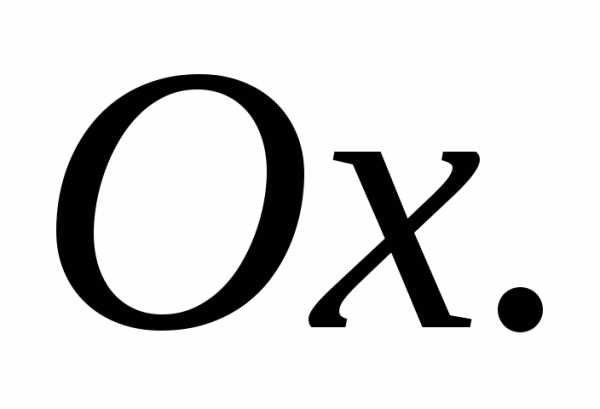 Действительно, данное уравнение не
содержит
Действительно, данное уравнение не
содержит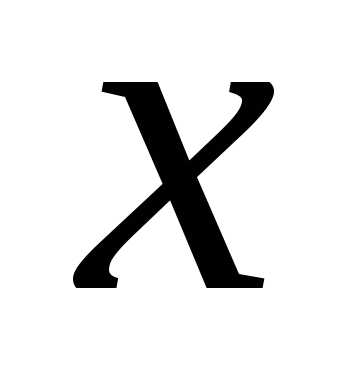 ,
а направляющая цилиндра есть гипербола
,
а направляющая цилиндра есть гипербола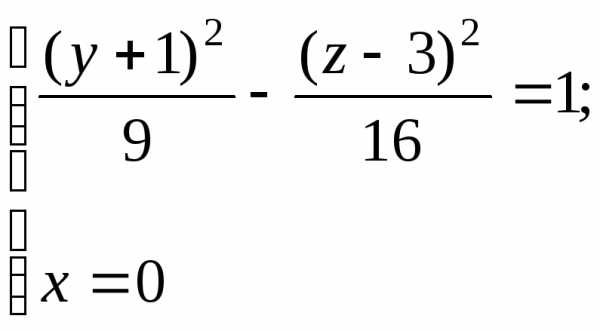
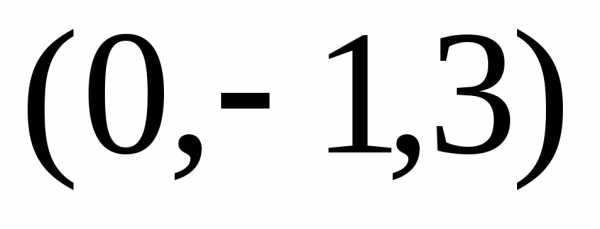 и действительной осью, параллельной
оси
и действительной осью, параллельной
оси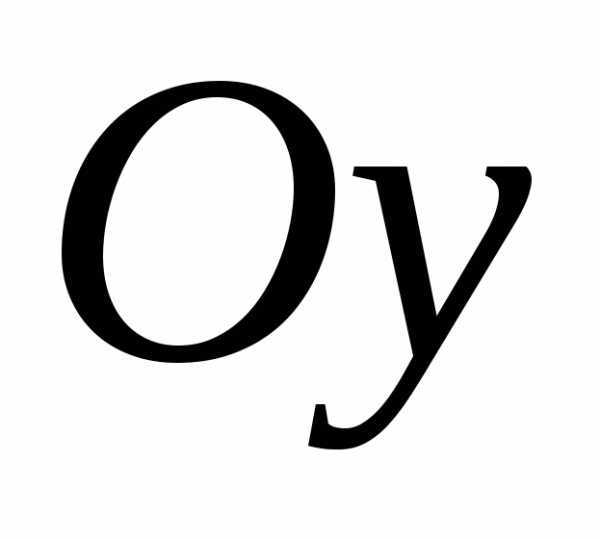 .
.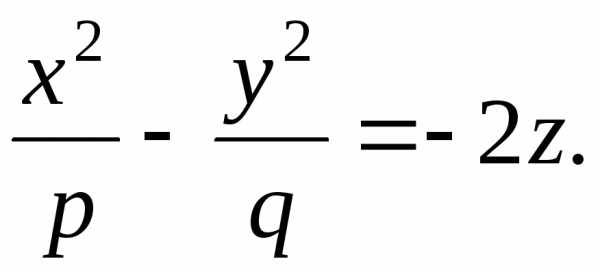
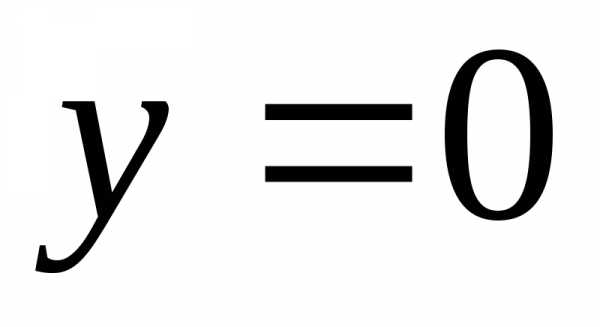 .
В результате имеем
.
В результате имеем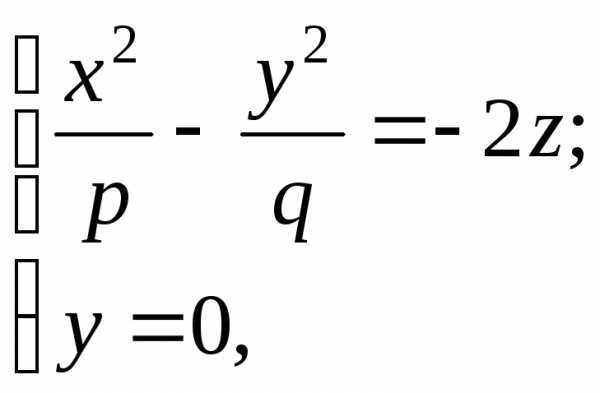
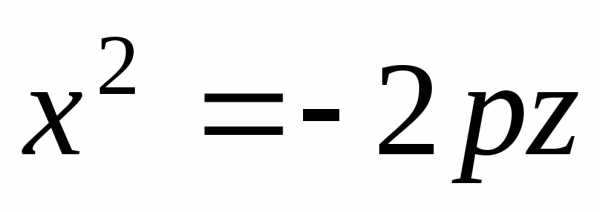 .
Это уравнение параболы в плоскости
.
Это уравнение параболы в плоскости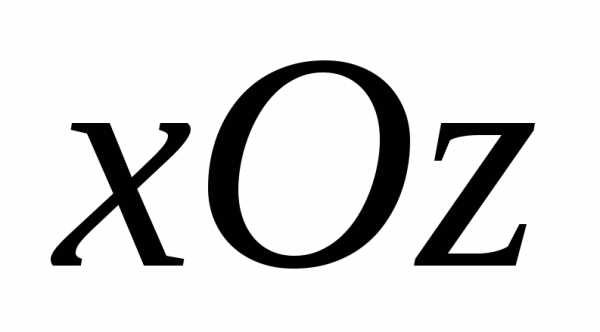
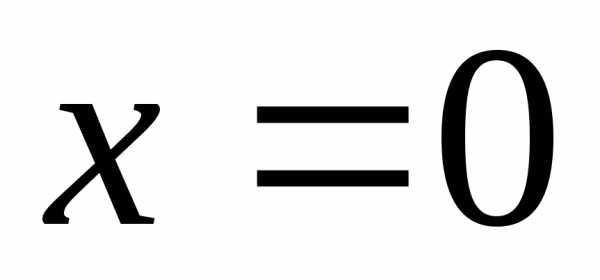 есть парабола
есть парабола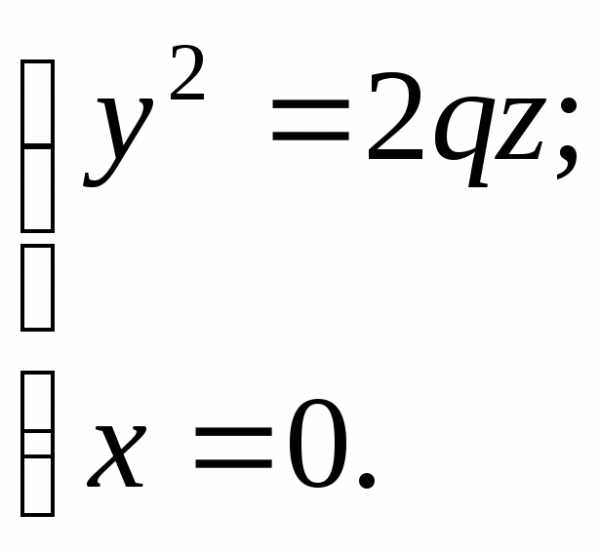
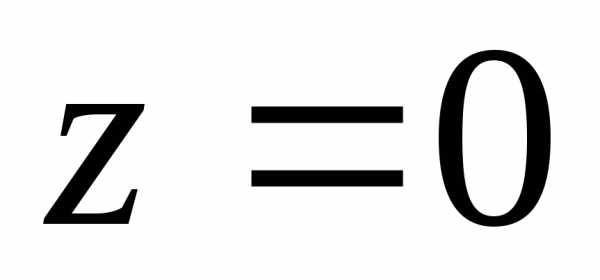 есть пара пересекающихся прямых:
есть пара пересекающихся прямых: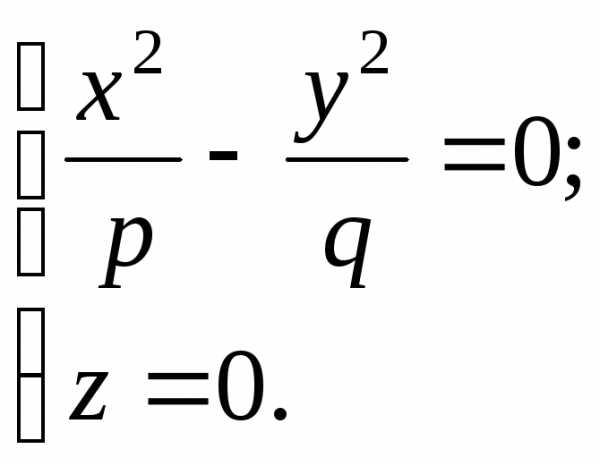
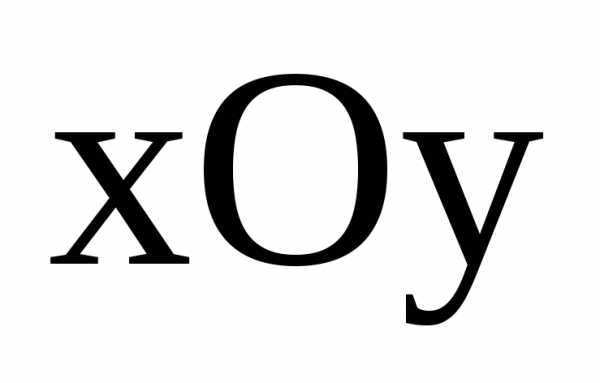 ,
есть гиперболы:
,
есть гиперболы: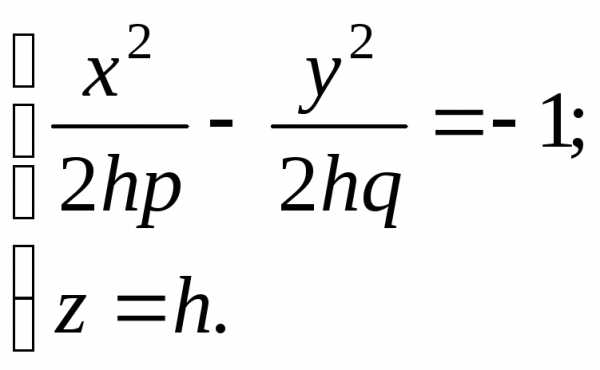
 действительная ось гиперболы параллельна
оси
действительная ось гиперболы параллельна
оси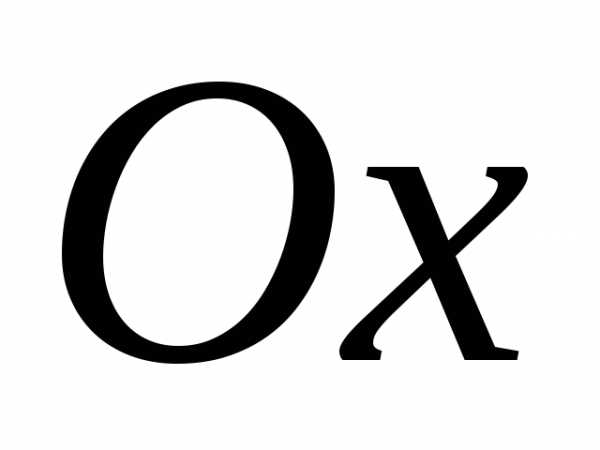 ,
при
,
при оси
оси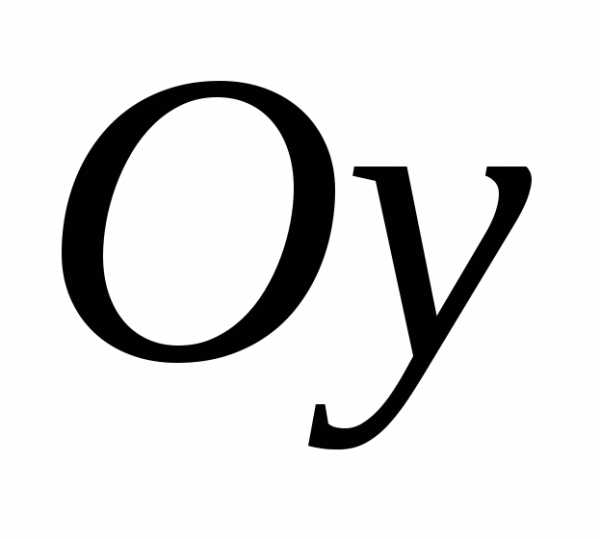 .
Исследуемая поверхность является
гиперболическим параболоидом (по
ассоциации с формой, поверхность получила
название «седло»).
.
Исследуемая поверхность является
гиперболическим параболоидом (по
ассоциации с формой, поверхность получила
название «седло»).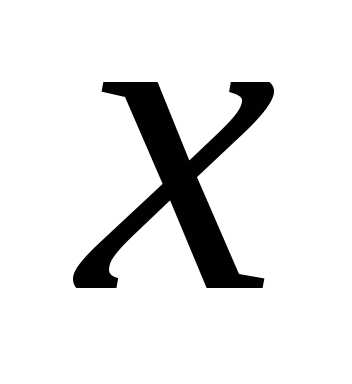 ,
, ,
, :
: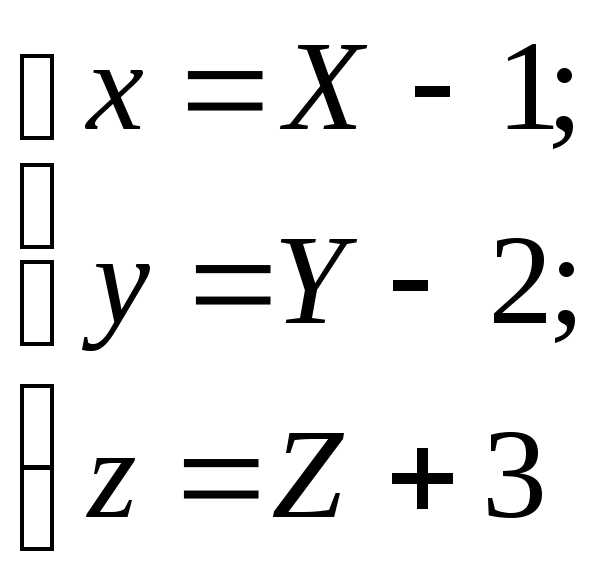
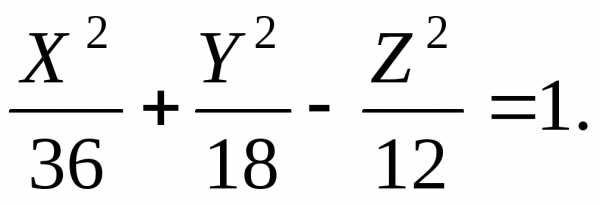
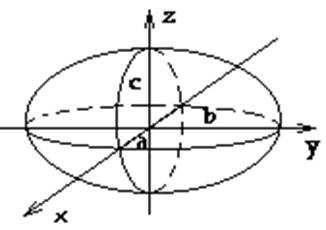 Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :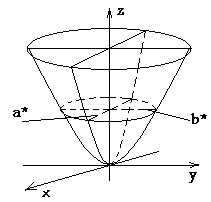 (7)
(7)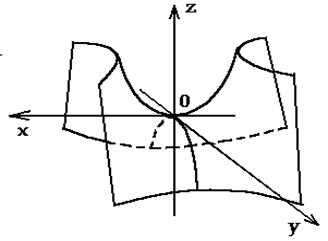
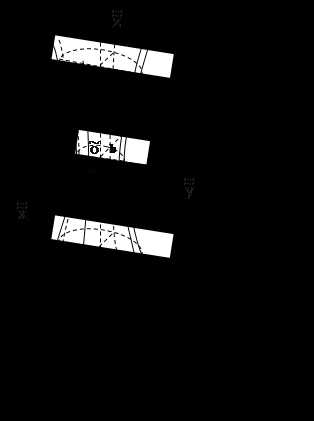


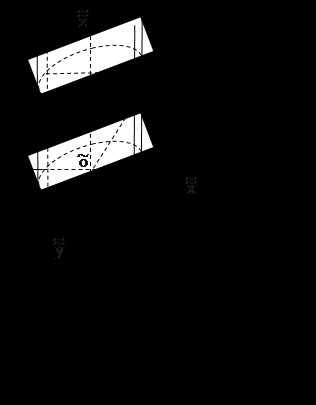
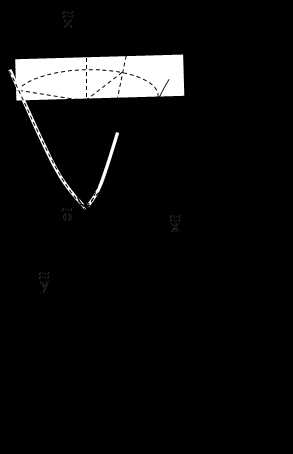

 ,
,