Рубрика: Школьная жизнь

Самостоятельная работа на тему «Округление чисел» (5 класс)

Самостоятельная работа №34 «Округление чисел»

Вариант I

1) Округлите числа:

а) 6,713; 2,385; 16,051; 0,849; 49,25 до десятых;

б) 0,526; 3,964; 2,408; 7,663 и 8,555 до сотых;

в) 417, 3; 213,58 и 664,3 до десятков;

г) 801,9, 1267, 1 и 2405 до сотен.

2. Выполните действия

2. Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного поезда 42 км/ч, а скорость пассажирского поезда на 32 км/ч больше. Сейчас между ними 20,6 км. Какое расстояние будет между ними через 0,4 ч.

Вариант II

1) Округлите числа:

а) 4,822; 5,265; 16,058; 0,847 и 6,35 до десятых;

б) 3,537; 0,973; 11,307; 5,554 и 4,555 до сотых;

в) 836,5; 304,1 и 735,2 до десятков;

г) 749,9; 579,2 и 550,1 до сотен.

2. Выполните действия

2. Легковая и грузовая машины движутся в противоположных направлениях. Скорость легковой автомашины 72 км/ч, а грузовой 54 км/ч. Сейчас между ними 12,2 км. Какое расстояние будет между машинами через 0,3 ч

1

1)42+32=74 км/час скорость пассажирского

2)42+74=116 км/час скорость удаления

3)116*0,4=46,4 км пройдут за 0,4 часа

4)20,6+46,4=67 км будет расстояние между ними

2

72+54=126 км\час скорость удаления
126*0,3=37,8 км удаление за 0,3 часа
37,8+12,2=50 км будет между ними

infourok.ru

Урок на тему «Округление чисел» (5 класс)

ПЛАН-КОНСПЕКТ УРОКА ПО МАТЕМАТИКЕ В 5 КЛАССЕ (2 урока)
учитель: Немченко Наталья Викторовна

Тип урока: урок изучения нового материала.

Формы работы учащихся: фронтальная работа, математический

диктант (самостоятельная работа), работа в парах,

взаимопроверка.

Цель урока: формирование умения округлять натуральные числа.

Задачи:

— образовательные (познавательные УУД)

формировать умение в процессе реальной ситуации использовать определение следующих понятий «округление чисел, приближенное значение».

— воспитательные (коммуникативные и личностные УУД)

формировать умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группе сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность

—развивающие (регулятивные УУД)

формировать умение обрабатывать информацию и ранжировать ее по указанным основаниям; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Структура урока

1. Организационный момент

2. Актуализация опорных знаний и умений (повторение)

3. Организация познавательной деятельности

4. Постановка проблемы (создание проблемной ситуации)

5. Открытие новых знаний

6. Физкультминутка

7. Первичное закрепление

8. Самостоятельная работа с самопроверкой по образцу

9. Включение нового знания в систему знаний

10. Рефлексия деятельности (подведение итогов)

11. Задание на дом

Оборудование: компьютер, проектор, экран

Ход урока

I. Организационный момент. 1)включить учащихся в учебную деятельность;

II. Актуализация опорных знаний и умений.

Фронтальный опрос
1. Сколько вы знаете цифр?
2. Какие классы чисел вы знаете?
3. Как называются разряды, входящие в класс единиц? В класс тысяч? Миллионов?
Вспомнить таблицу разрядов. Приложение 1. Слайд1

4. Прочитать число: 37569104578. Приложение 1. Слайд 2

5. Ответить на следующие вопросы:

а) Какая цифра стоит в разряде единиц тысяч;

б) В каких разрядах, каких классах стоит цифра 7;

в) Какой разряд, какого класса отсутствует?

III. Организация познавательной деятельности
1). Организация учебного процесса на этапе

Приложение 1. Слайд 3

В жизни мы часто имеем дело с приближенными значениями. Иногда просто невозможно точно сосчитать, а иногда не нужно точно знать, сколько чего либо. Например: всего на планете живет около 350 тысяч видов растений; в словаре русского языка Ожегова на титульном листе указано, что в нем около 57000 слов (хотя можно было бы подсчитать их точное количество).

Текст №1 Слайд 4. Приложение 1.

Полярный радиус Земли составляет 6357 км, а экваториальный – 6378 км. Однако, обычно говорят, что радиус Земли равен приблизительно 6400 км.

Текст №2 Слайд 5. Приложение 1.

Когда мы включаем выключатель, вся комната сразу же озаряется светом. Кажется, что свету совсем не надо времени, чтобы добраться до стен. Делались многочисленные попытки определить скорость света. В 17 веке считали, что скорость света равна 300 000 км/с, в 19 веке – 313 000 км/с. А современные исследования показали, что скорость света равна 299 792 458 м/с. Однако, если вы спросите у образованного человека какова скорость света, он ответит, что она приближенно равна 300 000 км/ч

Текст №3 Слайд 6. Приложение 1.

Представим себе, что длина пути между двумя железнодорожными станциями равна 7980 км. В таком случае обычно говорят, например, так:   «Расстояние между станциями около 8000 (восьми тысяч) километров». Если же длина пути – 7032 км, то говорят, что расстояние равно примерно 7000 (семи тысячам) километров.

— Какие слова вам показались новыми? (примерно, приближённо, около).

Слайд 7. Приложение 1.

— 350 000, 57000, 6400, 300 000, 313 000, 7000 Что интересного в полученном ряде? ( все числа круглые). Слайд 8. Приложение 1.

— Что значит «круглое число»? ( Число, оканчивающееся нулем или нулями)

— Когда, по – вашему, происходит замена точного значения величины близким к нему круглым числом?

— Как вы считаете какой будет тема нашего урока? (Приближённые значения. Округление чисел).

Слайд 9. Приложение 1.

Тема фиксируется на доске и в тетрадях учащихся.

— Что теперь будем делать? (попробуем выполнить задание)

Задание классу. Выбрать предложения, в которых речь идет о приближенных значениях. Слайд 10. Приложение 1.

В корзине 15 яблок.

Расстояние между с. Потудань и г. Старый Оскол 25 км.

На полке 40 книг.

Население города 42000 человек

В алфавите 33 буквы

В нашей реке обитают 42000 рыбы.

IV. Постановка проблемы( создание проблемной ситуации )

Как же округлять натуральные числа? (Учитель помогает учащимся ставить проблему урока)

V. Открытие новых знаний

1). Работа на координатном луче, чтобы вывести правило округления натуральных чисел. Слайд 2-5. Приложение 2.

К какому круглому числу ближе число 21,224, 134, 144,154,164, 174,184,194

— Какой вывод можно сделать?

— Если величина имеет значение после целых 1,2,3,4 то мы округляем ее с недостатком, если значение 6,7,8,9 то с избытком

— А как поступить если значение равно 5?

Выслушивается ответ учащихся. Если ученики ответят не верно то учитель ответ корректирует. Учащиеся формулируют правило округления натуральных чисел.

— Учитель показывает на доске как нужно округлять натуральные числа

Округлить до десятков 467; 1832. 46/7; 183/2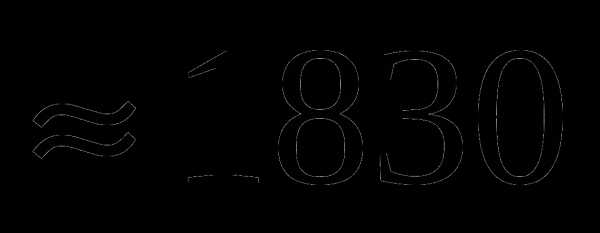

Округлить до сотен 2765; 6241. 27/65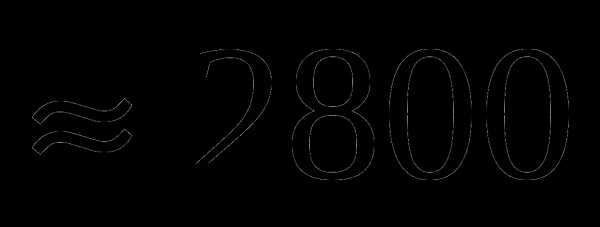62/41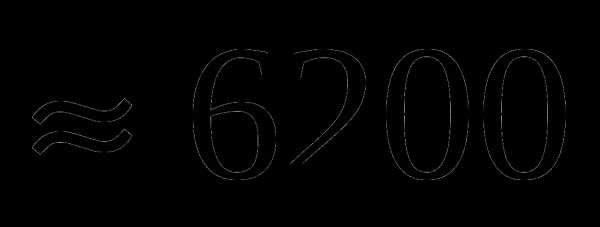

VI. Физкультминутка

VII. Первичное закрепление.

1). Примеры на округление натуральных чисел.

К доске вызываются учащиеся по очереди, все остальные выполняют задание в тетрадях После каждого примера учитель включает приложение 2 слайды 6-18, проверяют правильность выполнения.

Задания: а) округлить до десятков: 732, 568, 480732, 9569.

б) округлить до сотен: 85 157, 923537.

в) округлить до тысяч: 53702, 923068.

г) округлить до десятков тысяч: 614017, 2682039.

д) округлить до миллионов: 2537858, 31000509

е) округлить до сотен: 68, 43

ж) округлить до тысяч: 848, 321

з) округлить до сотен число 3961, округлить до десятков число 2995

Работа проверяется всем классом.

2). В начале второго урока учитель предлагает рассмотреть

Задачи шутки. Приложение 2. Слайды 19-25

3). Работа в парах, устно. Задача.

Задача №1

Марина задумала число и, округлив его до десятков, получила 470. Какое число могла задумать Марина? Назовите самое большое из возможных вариантов. Назовите самое маленькое.

(Учитель записывает ответы учащихся на доске, чтобы учащиеся могли видеть полученный ряд чисел. (465,466, 467, 468,469,470,471,472,473,474),(474),(465) )

Задача №2.
Коля задумал число и, округлив его до десятков, записал: 380. Которое из указанных чисел мог задумать Коля?

(Числа записаны на доске).
375; 376; 377; 378; 379; 371; 372
Задача №3.
В поезде едут 228 пассажиров. Какое приближение точнее: 220 или 230 пассажиров?
Задача №4.
Запишите ряд чисел, который получится при последовательном округлении числа 37 602 до десятков, сотен, тысяч.

Ответ: до десятков 37600

до сотен 37600

до тысяч 38000
Ответы проверяются коллективно.

VIII. Самостоятельная работа на два варианта с взаимопроверкой в парах.

http://school-collection.edu.ru

IX. Включение нового знания в систему знаний.

1). Задача:

246+6258+781+305

а) найдите сумму и результат округлить до десятков

б) округлите слагаемые до десятков, после чего найдите сумму.

в) сравните результаты

XI. Рефлексия деятельности ( подведение итогов)

Чему научились, что нового и интересного узнали на уроке?

Что называют округлением чисел? Округлить это значит заменить точные данные числами с нулями.

Зачем нужно округлять числа?

Удобство работы с круглыми числами, если точное значение числа не важно

— Оцени свои ощущения и работу на уроке на листе самооценки.

Дата

Мне было интересно на уроке

Я был внимателен на уроке

Я понял тему урока

Я частично понял тему урока

Я не понял тему урока

Выставление отметок.

XII. Домашнее задание .№ 134-на «3», № 132- на «4», № 132, 135 –на «5».

Используемая литература:

1). Математика 5 класс; учебник для общеобразовательных учреждений / И.И. Зубарева, А.Г. Мордкович — 14-ое изд.- М.: Мнемозина, Москва 2014 г.

2). Математика поурочные планы по учебнику И. И. Зубаревой, А. Г Мордковича

5 класс. Автор-составитель Е.А Ким 2010 г.

3). Е.Е Тульчинская математика 5-6 классы тесты для учащихся общеобразовательных учреждений, 3-е издание, Москва 2011 г.

ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ ЭОР НА ДАННОМ УРОКЕ:

1. Приложение 1. Презентация.

2. Приложение 2. Презентация.
3. le-savchen.ucoz.ru›Файлы›13-1-0-184 

4. Математический диктант по теме «Округление натуральных чисел» Контрольный тест -презентация http://files.school-collection.edu.ru/dlrstore/843df329-4a88-4b68-86d1-09ed1819a155/08_2_md%282%29.ppt

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА.

Этап урока

Название используе-мых ЭОР

Деятельность учителя

Деятельность ученика

Время

(в мин.)

Формируемые УУД

Познавательные

Регулятивные

Коммуника-

тивные

Личностные

I.

Организационный момент

Приветствие класса, проверка готовности к уроку, организация внимания детей.

Создать психологический настрой на работу

Настраиваются на активную учебную деятельность. Записывают число, классная работа в тетрадях

1 мин

Осознанное построение речевого высказывания

Прогнозиро-

вание своей деятельности

Планирование

учебного сотрудничества с учителем и сверстниками.

Мотивация необходимости учения.

Умение слушать.

II. Актуализация опорных знаний и умений (повторение)

Прило-жение1.

Округле-ние чисел. Слайд 1-2

Предлагает

материал для повторения.

Участвуют в работе по повторению в беседе с учителем отвечают на поставленные вопросы.

5 мин

Смысловое чтение, структурирование собственных знаний, умение строить высказывания

Целепологание (постановка учебной задачи)

Контроль и оценка процесса и результатов деятельности.

Организовывать и планировать учебное сотрудничество с учителем и сверстниками

Самоопре-деление (Оценивание усвоенного материала )

III.

Организация познавательной деятельности

Прило-жение1.

Округле-ние чисел.

Слайды 3-10

Предоставляет материал, ставит перед учащимся практическую познавательную задачу (учитель подводит учащихся к понятию «круглые числа»)

Участвуют в диалоге. Отвечают на вопросы учителя. Формулируют определение «круглого числа». Формулируют тему урока и записывают её в тетради.

5 мин

Смысловое чтение. Поиск информации. Структурирование знаний.

Подведение под понятие. Анализ объектов с целью выявления признаков

Целепологание (Постановка учебной задачи Проявляют инициативу,

осознают возникшее затруднение, цель предстоящей деятельность дачи)

Постановка вопросов, разрешение конфликтов, умение выражать свои мысли

Мотивация учения, интерес к новому

IV.

Постановка пробле-мы

Помогает учащимся сформулировать проблему урока.

Ставят проблему. Проявляют инициативу,

осознают возникшее затруднение, цель предстоящей деятельности.

1 мин

Формулировка проблемы

Умение строить высказывания.

Рефлексия деятельности

Целепологание

Планирование.

Саморегуляция

Постановка вопросов, умение выражать свои мысли, планирование учебного сотрудничества. Рефлексия своих действий

Формирование навыков индивидуаль-ной и коллективной исследователь-ской деятельности.

V.

Открытие новых знаний. Работа на координатном луче, чтобы вывести правило округле-ния натураль-ных чисел

Предоставляет материал, ставит перед учащимся практическую познавательную задачу (с помощью числовой оси подводит учащихся к выводу правила округления натуральных чисел) Помогает учащимся сформулировать правило округления натуральных чисел.

На примерах у доски показывает как правильно округлять натуральные числа

Рассматривают слайды. Участвуют в диалоге. Формулируют правила округления натуральных чисел, проверяют текст правила. Слушают объяснение учителя

8 мин

Знако-символические средства (числовая ось).

Составление плана решения (определить способ решения, определить последователь-ность действий, запись решения)

Целепологание

Планирование. Прогнозиро-вание.

Контроль.

Коррекция.

Оценка.

Саморегуляция

Планирование учебного сотрудничества

постановка вопроса, разрешение конфликтов, умение выражать свои мысли, планирование учебного сотрудничества

Формирование способности к волевому усилию в преодоление трудностей

VI.

Физкультминутка

Сменить деятельность, обеспечить эмоциональную разгрузку учащихся

Учащиеся сменили вид деятельности и готовы продолжить работу

2 мин

Волевая саморегуляция

Самооценка

Понимание основ здорового образа жизни

VII. Первич-ное закрепле-ние

1) Округле-ние чисел.

Слайды 6-18

2)Задачи шутки Округле-ние чисел.

Слайды

19-25

1) Даёт задание учащимся.

Вызывает их по одному к доске.

Затем включает приложение 2, для того, чтобы учащиеся могли проверить свой ответ. Ответы учащихся корректирует.

2) в начале второго урока предлагает учащимся задачи -шутки

3) предлагает задания для устного выполнения, задачи №1-№4

1) В рабочей тетради и у доски, проговаривая правило округления, выполняют округление чисел.

По приложению 2 исправляют свои ответы.

2) разбирают задачи шутки

3) отвечают на вопросы учителя устно. Работают в парах

18

мин

на пер-вом уроке.

10 мин на вто-ром уроке

Составление плана решения (определить способ решения, определить последователь-ность действий, запись решения)

Целепологание

Планирование.

Контроль.

Коррекция.

Оценка.

Саморегуляция

Планирование учебного сотрудничества,

постановка вопроса, разрешение конфликтов, умение выражать свои мысли, планирование учебного сотрудничества

Самооценка.

VIII.

Самостоятельная работа с самопро-веркой по образцу

http://school-collection.edu.ru

Предлагает задание для самостоятельной работы с единой коллекции цифровых образовательных ресурсов.

Выполняют самостоятельную работу, затем проверяют коллективно.

13 мин

Смысловое чтение. Поиск информации.

Составление плана решения (определить способ решения, определить последовательность действий, запись решения)

Целепологание

Планирование. Прогнозиро-вание.

Контроль.

Коррекция.

Оценка.

Саморегуляция

Определять цель поставленной учебной задачи.

Формирование терпения и настойчивости

IX.

Включе-ние нового знания в систему знаний

Даёт задание на округление суммы. Один ученик вызывается к доске

Выполняют задание.

10 мин

Смысловое чтение,

умение строить высказывания,

формулировка проблемы, рефлексия деятельности,

структурирование знаний, поиск информации, смысловое чтение

Целепологание

Планирование. Прогнозиро-вание.

Контроль.

Коррекция.

Оценка.

Планирование учебного сотрудничества с учителем и сверстниками,

постановка вопроса, разрешение конфликтов, умение выражать свои мысли.

Формирование мотивации к самосовершенствованию

X.

Рефлек-сия деятель-ности

( подве-дение итогов)

1). Организовывает фиксацию нового содержания, изученного на уроке.

2). Организовывает оценивание учащимися собственной деятельности на уроке.

3). Организовать фиксацию неразрешённых затруднений на уроке как направление будущей учебной деятельности. Просить учащихся заполнить лист самоанализа.

Выставляет оценки комментируя.

Подводят итоги совместно с учителем.

Заполняют лист

самоанализа

5 мин

Оценка процесса и результатов деятельности

Волевая саморегуляция; оценка-выделение и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению, прогнозиро-вание

Умение с достаточной полнотой и точностью выражать свои мысли

Самооценка

XI.

Домаш-нее задание

Озвучивает домашнее задание с учебника. Комментирует Д/З

Записывают в дневниках д/з

2 мин

Умение слушать

infourok.ru

Тесты для 5 класса. Округление чисел. Проценты.

Математика. 5 класс.             Тест 7. Вариант 2.

1. Чтобы разделить десятичную дробь на натуральное число, надо: 1) разделить дробь на это число, не обращая внимания на запятую; 2) поставить в частном запятую тогда, когда закончится деление целой части. Выполнить деление: 434,2:26.

A) 17,7; B) 16,7; C) 18,7; D) 17,6; E) 18,6.

2. Чтобы разделить число на десятичную дробь, надо: 1) в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе; 2) выполнить деление десятичной дроби на натуральное число. Выполнить деление: 2,496:3,2.

A) 7,8; B) 78; C) 780; D) 0,078; E) 0,78.

3. Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр. Вычислить:  43,17·10.

A) 4317; B) 4,317; C) 431,7; D) 0,4317; E) 43,17.

4. При округлении числа до какого-либо разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой — отбрасывают. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру не изменяют. Если первая замененная нулем или отброшенная цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на единицу. Округлить до десятков число: 73,5462.

A) 73,546; B) 70; C) 73,5; D) 73,55; E) 74.

5. Найти среднее арифметическое ряда чисел: 6,5; 7,5; 7,6; 7,4.

A) 8,5; B) 8,75; C) 6,75; D) 7,25; E) 8,25.

6. Найти размах ряда:

A) 3,25; B) 3,15; C) 3,35; D) 3,3; E) 3,5.

7. Найти моду ряда чисел: 6,2; 0,7; 5,8 и 6,2.

A) 0,7; B) 5,8; C) 5,5; D) 3,3; E) 6,2.

8. Процентом называется … часть.

А) одна вторая; В) одна сотая; С) одна десятая; D) одна тысячная; Е) одна пятая.

9. Чтобы найти процент от числа, надо: 1) выразить проценты обыкновенной или десятичной дробью; 2) умножить данное число на эту дробь. Найти 40% от числа 150.

А) 60; В) 50; С) 70; D) 600; Е) 400.

10. Записать 95% в виде дроби.

А) 1,95; В) 1,05; С) 95; D) 0,95; Е) 0,095.

11. Записать в виде процентов число:

А) 120%; В) 150%; С) 140%; D) 130%; Е) 15%.

12. Найти число по его проценту, если 7% его составляют 42.

А) 600; В) 400; С) 300; D) 500; E) 700.

Ответы к тестам Вы найдете на странице «Ответы«.

 

www.mathematics-repetition.com

округление 5 класс | математика-повторение

Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения. Если первая замененная нулем или отброшенная цифра равна 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.

Примеры.

Округлить до целых:

1) 12,5;   2) 28,49;   3) 0,672;  4) 547,96;   5) 3,71.

Решение. Подчеркиваем цифру, стоящую в разряде единиц (целых) и смотрим на цифру, стоящую за ней. Если это цифра 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения, а все цифры после нее отбрасываем. Если же за подчеркнутой цифрой стоит цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на единицу.

1) 12,5≈13;

2) 28,49≈28;

3) 0,672≈1;

4) 547,96≈548;

5) 3,71≈4.

Округлить до десятых:

6) 0, 246;   7) 41,253;   8 ) 3,81;   9) 123,4567;   10) 18,962.

Решение. Подчеркиваем цифру, стоящую в разряде десятых, а затем поступаем согласно правилу: все стоящие после подчеркнутой цифры отбросим. Если за подчеркнутой цифрой была цифра 0 или 1 или 2 или 3 или 4, то подчеркнутую цифру не изменяем. Если за подчеркнутой цифрой шла цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на 1.

6) 0, 246≈0,2;

7) 41,253≈41,3;

8 ) 3,81≈3,8;

9) 123,4567≈123,5;

10) 18,962≈19,0.  За девяткой стоит шестерка, поэтому, девятку увеличиваем на 1. (9+1=10) нуль пишем, 1 переходит в следующий разряд и будет 19. Просто 19 мы в ответе записать не можем, так как должно быть понятно, что мы округляли до десятых — цифра в разряде десятых должна быть. Поэтому, ответ: 19,0.

Округлить до сотых:

11) 2, 045;   12) 32,093;   13) 0, 7689;   14)  543, 008;  15)  67, 382.

Решение. Подчеркиваем цифру в разряде сотых и, в зависимости от того, какая цифра стоит после подчеркнутой, оставляем подчеркнутую цифру без изменения (если за ней 0, 1, 2, 3 или 4) или  увеличиваем подчеркнутую цифру на 1 (если за ней стоит 5, 6, 7, 8 или 9).

11) 2, 045≈2,05;

12) 32,093≈32,09;

13) 0, 7689≈0,77;

14)  543, 008≈543,01;

15)  67, 382≈67,38.

Важно:  в ответе последней должна стоять цифра в том разряде, до которого вы округляли.

 

www.mathematics-repetition.com

Приближенные значения чисел Округление чисел Математика 5 класс Задания

Правила.        Приближенные значения чисел
Округление чисел

         В жизни мы часто пользуемся неточными (приближенными) значениями чисел. Например, про арбуз, который весит 7,150 кг мы можем сказать, что он весит примерно 7 килограмм. В данном случае это приближенное значение массы арбуза с недостатком. А если в 13:58 на вопрос: «Который час?» — мы ответим: «Около двух» — это приближенное значение времени с избытком (в данном случае на две минуты).

         На рисунке видно, что значение длины отрезка 10 см 3,5 мм Значит 10 см — это приближенное значение длины отрезка с недостатком, а 11 см — это приближенное значение с избытком. В данном случае длина отрезка ближе к 10, чем к 11, значит 10 — это округленное значение длины отрезка до целых.

         Округлить число можно и до других разрядов (десятых, сотых, тысячных). Например, округлим число 123,238 до сотых, получится 123,24. Округлим 3456 до десятков — 3460.

         При округлении числа до какого-нибудь разряда, цифры во всех следующих разрядах заменяют нулями, а стоящие после запятой, отбрасывают.

         Если следующая за остающемся разрядом цифра равна 5, 6, 7, 8 или 9, то остающийся разряд увеличивают на 1. Если она равна 0, 1, 2, 3 или 4, то остающийся разряд оставляют без изменения.
        Округлим до десятков 128 — 130;
        Округлим до десятых 237,23 — 237,2;
        Округлим до сотых 22,187 — 22,19;
        Округлим до сотых 22,197 — 22,20 = 22,2 ;

www.matematika-na.ru

Урок для 5 класса по теме «Округление чисел»

КОНСПЕКТ УРОКА для 5 класса

Урок № 1 по теме «Округление натуральных чисел»

1. Учитель математики Филатова Алла Анатольевна

2. Место работы МБОУ «Одинцовская средняя общеобразовательная

школа № 5» Одинцовского муниципального района Московской области

3. Базовый учебник Математика. 5 класс: учеб. для общеобразоват. учреждений / И. И. Зубарева и др. – 11-е изд., — М.: Мнемозина, 2014. – 270 с.

4. Обобщенная цель урока: формирование познавательных учебных действий и способностей учащихся при округлении натуральных чисел;

5. Задачи:

предметные: ввести понятия «круглое число», «округление числа»; изучить правило округления натуральных чисел; формировать умение применять правило округления натуральных чисел при выполнении различных заданий;

метапредметные: развивать умение анализировать, сравнивать, делать выводы, развивать устную и письменную речь;

личностные: формировать внимательность и аккуратность в вычислениях, требовательное отношение к себе и своей работе, умение высказывать свою точку зрения, слушать других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству.

6. Тип урока: урок открытия «нового» знания.

7. Формы работы учащихся: фронтальная работа, математический диктант (самостоятельная работа), работа в парах, взаимопроверка.

8. Необходимое техническое оборудование: персональный компьютер, проектор, экран.

9. Структура и ход урока представлены в таблице 1. На каждом этапе урока учитель и учащиеся выполняют конкретные действия (табл. 1), связанные с задачами этапов и познавательными УУД.

10. Перечень используемых ЦОР и ЭОР на данном уроке (таблица 2).

Таблица 1.

Структура и ход урока «Округление натуральных чисел»

Содержание

этапа

Название

используемых ЦОР и ЭОР

(с указанием порядкового номера из Таблицы 2)

Деятельность

учителя

Деятельность

учащихся

Познавательные

универсальные учебные действия

Время, мин

1. Организационный этап

1

Организационный момент

Приветствует  учащихся, проверяет  готовность           к уроку, организует внимание детей. Раздаёт листы самооценивания

Приветствуют учителя, проверяют готовность к уроку, слушают учителя

Ставят перед собой цель: «Что я хочу получить сегодня от урока»

1

2. Актуализация знаний

2

Проверка домашнего задания, воспроизведение и коррекция опорных знаний

Задает вопросы обучающимся, комментирует ответы, корректируя их

Выполняют задания. Устно отвечают на вопросы учителя

Анализ; построение логической цепочки; установление причинно-следственных связей; выведение следствий

5

3. Мотивация учебной деятельности учащихся

3

Организация познавательной деятельности

Организует работу учащихся над заданиями.

Участвуют в диалоге. Отвечают на вопросы учителя

Смысловое чтение; поиск информации; структурирование знаний; подведение под понятие.

5

4

Постановка проблемы (создание проблемной ситуации)

Выводит на формулировку темы и целей урока. Помогает сформулировать тему и цель урока

Формулируют тему и цель урока

Формулировка проблемы; умение строить высказывания; рефлексия деятельности

1

5

Открытие новых знаний

Правило округления натуральных чисел(№1)

Демонстрирует презентацию. Руководит деятельностью учащихся. Анализирует ответы учащихся, корректирует их. Показывает образец записи решения.

Выполняют задания. Отвечают на вопросы учителя. Учащиеся формулируют правило округления натуральных чисел.

Анализ; построение логической цепочки; установление причинно-следственных связей; выведение следствий

7

4. Физкультминутка

6

Физкультминутка

Обеспечивает эмоциональную разгрузку учащихся

Учащиеся сменили вид деятельности и готовы продолжить работу.

2

5. Закрепление в знакомой или измененной ситуации

7

Решение заданий на округление натуральных чисел

Организует выполнение заданий, проверяет правильность выполнения

Учащиеся выполняют по очереди задания у доски, все остальные выполняют задания в тетрадях. Работа проверяется всем классом.

Смысловое чтение;

умение строить высказывания; составление плана решения

11

8

Работа в парах. Устное решение задач

Организует и контролирует процесс решения задач

Работают в парах над поставленными задачами.

Смысловое чтение; умение строить высказывание; выбор эффективных способов решения задачи

5

9

Самостоятельная работа на два варианта с взаимопроверкой в парах

Математический диктант «Округление натуральных чисел»(№2)

Предлагает задание для самостоятельной работы из единой коллекции цифровых образовательных ресурсов.

Выполняют самостоятельную работу. Обмениваются тетрадями и проверяют работу товарища

Смысловое чтение; поиск информации; составление плана решения

5

6. Информация о домашнем задании

10

Постановка

домашнего

задания

Дает комментарий к домашнему заданию

Учащиеся записывают домашнее задание в дневники

1

7. Рефлексия

11

Рефлексия.

Подведение

итогов

урока

Организует обсуждение: Какова была тема урока? Какую задачу ставили? Каким способом решали поставленную задачу? Я сегодня…

Выставляет отметки

Проводят самооценку результатов своей деятельности и деятельности всего класса. Сдают листы самооценивания

Самоконтроль и самооценка процесса и результатов деятельности

2

Всего

45

Таблица 2.

Перечень используемых ЦОР и ЭОР на данном уроке

Гиперссылка на ресурс,

обеспечивающая доступ к ЦОР и ЭОР

1

Правило округления натуральных чисел (№206812)

Информационный

Презентация к уроку.

Фронтальная работа на этапе введения новых знаний

http://school-collection.edu.ru/catalog/res/ff0b9a17-07b5-41d4-a208-057a70439883/?from=608887c4-68f4-410f-bbd4-618ad7929e22&interface=pupil&class=47&subject=16

2

математический диктант «Округление натуральных чисел», 2 варианта (№206644)

Первичный контроль

Презентация к уроку.

http://school-collection.edu.ru/catalog/res/843df329-4a88-4b68-86d1-09ed1819a155/?from=608887c4-68f4-410f-bbd4-618ad7929e22&interface=pupil&class=47&subject=16

infourok.ru

Округление чисел. Прикидка и оценка результатов вычислений. Математика, 5 класс: уроки, тесты, задания.

1.	Округли число Сложность: лёгкое	1
2.	Округли число до указанного разряда Сложность: лёгкое	1
3.	Устный счёт Сложность: лёгкое	1
4.	Найди предложение с приближённым значением Сложность: среднее	2
5.	До какого разряда выполнили округление Сложность: среднее	2
6.	Назови старший разряд частного Сложность: среднее	2
7.	Назови самое большое или самое маленькое число Сложность: сложное	3
8.	Текстовая задачи на сумму денег Сложность: сложное	3
9.	Замени символ * на нужную цифру Сложность: сложное	3

www.yaklass.ru

Как найти ширину прямоугольника?

Решение задач с четырехугольниками — один из наиболее обширных разделов геометрии, доставляющий школьникам немало трудностей. Предлагаем вам разобраться с типичными задачами, в которых требуется найти ширину прямоугольника.

Прежде всего, необходимо вспомнить, что это за фигура и какие ее основные свойства. Прямоугольником называется четырехугольник, у которого все углы прямые, а противоположные стороны равны. Горизонтальную сторону называют шириной прямоугольника, а вертикальную – длиной.

Задача 1. Вычисляем ширину, зная периметр

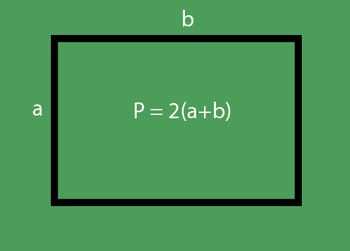Разберем этот тип задач на примере следующего задания. Дан прямоугольник, периметр которого равен 36 см, а длина – 16 см. Необходимо найти ширину. Периметр – это сумма сторон фигуры. Поскольку противоположные стороны прямоугольника равны, то формула его периметра имеет следующий вид: Р = 2(а+b), где а и b стороны прямоугольника.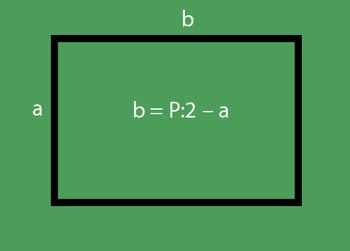

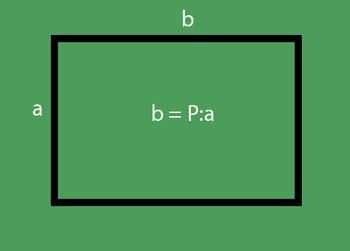Получаем:

• b = Р:2 – а = 36:2-16=2 (см)

Ответ: ширина прямоугольника равна 2 см.

Задача 2. Находим ширину, зная длину и периметр

Немного усложним задание. Теперь необходимо найти ширину прямоугольника, если известно, что она в 5 раз меньше его длины, а периметр треугольника равен 120 см.

Из условия задачи:

Мы уже знаем, что b = Р:2 – а. Подставляем значения Р и а. Получаем:

• b = 120:2 – 5b;
• 6b = 60;
• b = 60:6
• b = 10 (см).

Ответ: ширина прямоугольника равна 10 см. 

Задача 3. Определяем ширину, если известна площадь

Условие задачи: огород имеет прямоугольную форму. Его площадь равна 400 000 м2, а длина 400 м. Какова ширина огорода?

Огород по условию — прямоугольник. Площадь прямоугольника равна произведению его сторон. Если нам известна длина и площадь, то ширина будет равняться:

• b = P:a = 400 000:400 = 1000 (м)

Ответ: ширина огорода 1000 м.

Задача 4. Как найти ширину, зная диагональ

Эта задача уже немного сложнее предыдущих. В ней, кроме свойств прямоугольника, необходимо будет вспомнить формулы прямоугольных треугольников.

elhow.ru

Чему равна длина прямоугольника?

Задача на нахождение длины прямоугольника может быть сформулирована по-разному. Разберемся, как найти длины сторон прямоугольника для каждой конкретной формулировки. Длина прямоугольника – длинная его сторона, ширина прямоугольника, — его короткая сторона.

• Дан прямоугольник. Известно значение его периметра P, известна ширина B прямоугольника. Требуется найти длину прямоугольника.

  Периметр P– сумма длин всех сторон прямоугольника. Пусть L-неизвестная длина прямоугольника. Тогда P=2B+2L. Отсюда: 2L=P-2B. L = (P-2B)/2.

• Дан прямоугольник. Известно значение его площади S. Известна ширина прямоугольника B. Требуется найти длину прямоугольника.

  Площадь прямоугольника – произведение его длины на ширину. Пусть L – неизвестная длина прямоугольника. Тогда S=L*B.  Отсюда узнаем, чему равна длина прямоугольника: L=S/B.

• Дан прямоугольник. Известно значение ширины прямоугольника В и значение длины диагонали А. Требуется узнать, чему равна длина прямоугольника.

  Когда прямоугольник разделен диагональю, он состоит из двух прямоугольных треугольников. Для прямоугольного треугольника действует теорема Пифагора: «Квадрат гипотенузы равен сумме квадратов катетов». В данном конкретном случае катетами являются ширина прямоугольника В и длина прямоугольника L. Гипотенуза – диагональ прямоугольника. Анализируя все вышесказанное, получаем: А²=В²+L². Отсюда  L²=A²— B². L=v(A²-B²).

• Дан прямоугольник. Известна длина диагонали прямоугольника А.Известно, какой угол ? образует диагональ с шириной прямоугольника. Найти длину прямоугольника.

  Диагональ делит прямоугольник на два прямоугольных треугольника. Значит, отношение длины прямоугольника к его диагонали дают синус известного угла. Отсюда: sin α=L/A, здесь L-длина прямоугольника. L=sin α/A

• Дан прямоугольник. Известна длина диагонал

elhow.ru

где ширина а где длина у прямоугольника



Где длина а где ширина у прямоугольника

В разделе Школы на вопрос Помогите по математике 4 класса заданный автором черносотенный лучший ответ это Если я не ошибаюсь, периметр прямоугольника равен удвоенной сумме высоты и ширины. Высота х, ширина 3, след. 24=2*(3+х) , след. х=9. Тогда площадь ровна 9*3=27 квадратных см.

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Помогите по математике 4 класса

Ответ от Ђатьяна Акимова[гуру]
Сначала необходимо найти длину. Идём по формуле P= a+a+b+b, где a- длина, b- ширина . Значит 24- (3+3)= 18, Итак, 18 -это две длины, значит длина 9 см. Теперь ищем площадь. по формуле S= ab.

Ответ от Невролог[гуру]
двадцать семь смпериметр — это сумма всех сторон. 2 стороны по 3см. 2 другие по 9 (проверка: 3+9*2=24)площадь прямоугольника: 3*9=27

Ответ от Опроститься[гуру]
т. е. периметр Р=24 см, ширина b=3 см, надо найти а.P = 2*a + 2*b24 = 2*а + 2*3; 2а = 24 — 6, 2а = 18, а = 18/2= 9 см.площадь S = а*b. S= 9 * 3, S = 27 cм^2 (квадратных сантиметров)

Ответ от Алексей[новичек]
— — — — — —|                            ||                            ||                            |— —————Периметр — это две длины и две ширины.Чтобы найти площадь, надо длину умножить на ширину.Длины у нас нету, а ширина есть.Чтобы найти длину, надо из периметра вычесть две ширины, так как коротких сторон у прямоугольника две.Остаток надо разделить пополам, потому что длины у прямоугольника тоже две.После этого длину умножить на ширину.

Ответ от Crazy Girl[новичек]
Если я не ошибаюсь, периметр прямоугольника равен удвоенной сумме высоты и ширины. Высота х, ширина 3, след. 24=2*(3+х) , след. х=9. Тогда площадь ровна 9*3=27 квадратных см.

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Прямоугольник на Википедии
Посмотрите статью на википедии про Прямоугольник

 

Ответить на вопрос:

22oa.ru

Как найти длину прямоугольника 🚩 формула ширины прямоугольника 🚩 Образование 🚩 Другое

6 апреля 2011

Автор КакПросто!

Стройка, ремонт, изготовление мебели в домашних условиях, творческий процесс или решение задачек в ребенком-школьником, все это может заставить вас вспоминать, как найти длину прямоугольника.

Статьи по теме:

Инструкция

Длину прямоугольника можно найти несколькими способами. Все зависит от исходных данных.

Вариант первый, пожалуй, самый простой.

Если известны ширина прямоугольника и его площадь, воспользуемся формулой нахождения площади. Известно, что площадь прямоугольника равна произведению ширины и длины прямоугольника.

Соответственно, разделив площадь прямоугольника на ширину, мы получим его длину. Вариант второй, известны ширина и периметр прямоугольника. Значит, можно использовать формулу нахождения периметра.

Периметр прямоугольника возможно найти сложив величины ширины и длины и помножив полученное число на два. Находим неизвестную сторону.

Периметр делим на два и от полученного отнимаем ширину.

Если известна только ширина прямоугольника и длина диагонали, можно воспользоваться теоремой Пифагора. Разделим прямоугольник на два равных прямоугольных треугольника.

Помним, что квадрат гипотенузы равен сумме квадратов катетов. Значит длину (в данной ситуации один из катетов) находится по формуле: корень квадратный из разности величины гипотенузы в квадрате и величины катета в квадрате.

Следующий способ: известен угол меж диагоналями прямоугольника и диагональ. Рассмотрим треугольник, образованный стороной прямоугольника и половинками диагоналей. По теореме косинусов вы и найдете эту сторону прямоугольника.

Источники:

• найти ширину прямоугольника
• Какова длина прямоугольника, если известна его ширина

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

как найти длину прямоугольника, зная площадь и ширина

Вам понадобится калькулятор. Инструкция 1 Чтобы найти длину стороны прямоугольника, если известна ширина и площадь, разделите числовое значение площади на числовое значение ширины. То есть воспользуйтесь формулой: Д = П / Ш, где: Д – длина стороны прямоугольника, Ш – ширина прямоугольника, П – его площадь. Например, если площадь прямоугольника равна 20 см², а его ширина – 5 см, то длина его стороны будет: 20 / 5 = 4 см. 2 Перед началом вычислений переведите ширину и площадь прямоугольника в одну систему измерений. То есть, площадь должна выражаться в соответствующих ширине квадратных единицах измерения. При этом, длина получится в тех же единицах, что и ширина. Так, если ширина задана в метрах, то площадь необходимо перевести в метры квадратные. Особенно актуален такой перевод при измерении земельных участков, где площадь обычно задана в гектарах, арах и «сотках» . 3 Например, пусть площадь дачного участка равняется шести соткам, а его ширина – 30 метров. Требуется найти длину участка. Так как «соткой» называют 100 квадратных метров, то площадь «стандартных» шести соток можно записать как 600 м². Отсюда длину земельного участка можно найти разделив 600 на 30. Получается – 20 метров. 4 Иногда заданы площадь и ширина фигуры, имеющей не прямоугольную, а произвольную форму. При этом, также требуется найти ее длину. Как правило, в это случае подразумеваются габаритные размеры фигуры, то есть параметры прямоугольника, в который эту фигуру можно заключить. Если большая точность вычислений не требуется, то воспользуйтесь вышеприведенной формулой (Д = П / Ш) . Однако, значение длины при этом получится заниженным. Чтобы получить более точное значение длины фигуры, оцените насколько полно фигура заполняет свой габаритный прямоугольник и разделите полученную длину на коэффициент заполнения. 5 Так, например, если озеро имеет площадь 100 квадратных километров, его ширина равна 5 километров и оно занимает примерно половину габаритного прямоугольника, то его длина будет: 100 / 5 / 0,5 = 40 километров.

Надо площадь минус ширина.

P разделить на B = A

touch.otvet.mail.ru

Как найти ширину и длину прямоугольника, зная его периметр и площадь!?

Решить систему. Х — ширина, у — длина. 2(х+у) = Р х*у=S Р, S — периметр, площадь.

Система двух уравнений. Площадь равна a x b, где a, b — стороны прямоугольника. Периметр равен 2a + 2 b. И решай. Одну сторону вырази через Х и находи Х.

Пусть длина a, ширина b, площадь S, периметр P. Тогда: S = a*b P=2*(a+b) Решаем систему уравнений: из второго a=P/2-b подставляем в первое S=b*(P/2-b) 2*b^2-P*b+2*S=0 Решаем квадратное уравнение: D=P^2-16*S Если D<0 — уравнение корней не имеет, задача решений не имеет D=0 — a=b — это квадрат сос тороной a=P/4 D>0 — два корня уравнения, стороны прямоугольика: a=(P+sqr(P^2-16*S))/4 b=(P-sqrt(P^2-16*S))/4 Примеры: S=8, P=10 — D<0 — решений нет S=4, P=8 — D=0 — квадрат, со стороной a=8/4=2 S=4, P=10 — D=6>0 — прямоугольник со сторонами: a=(10+6)/4=4 a=(10-6)/4=1

touch.otvet.mail.ru

длина прямоугольника — это… Что такое длина прямоугольника?



длина прямоугольника

мат. length of rectangle

Большой англо-русский и русско-английский словарь. 2001.

• длина проходки
• длина пути

Смотреть что такое «длина прямоугольника» в других словарях:

• БЕЛЬЁ ДЕТСКОЕ — БЕЛЬЁ ДЕТСКОЕ. К детскому белью относятся: сорочки дневные и ночные, трусы, кальсоны, лифчики, пижамы и т.д. Широко распространено трикотажное детское бельё: фуфайки, сетки, майки и т. п. К белью для новорождённых относятся: распашонки, рубашечки …   Краткая энциклопедия домашнего хозяйства

• БЛУЗКА — женская кофточка. Блузки шьют преимущественно из тех же тканей, что и платья, самых разнообразных фасонов: с закрытым или открытым воротом, фантази лёгкие с оборками, буфами и другими отделками, а также с различного рода вышивками (см. Вышивка… …   Краткая энциклопедия домашнего хозяйства

• ДЕТСКАЯ ОДЕЖДА — ДЕТСКАЯ ОДЕЖДА. К детской одежде относятся: платья, кофты, юбки, фартуки, матроски, верхние рубашки (в том числе ковбойки), куртки, брюки короткие и длинные и т. п., а также изделия из трикотажа жакеты, свитеры, спортивные гарнитуры и т. д. В… …   Краткая энциклопедия домашнего хозяйства

• ВОРОТНИК — ВОРОТНИК. Воротники костюмов, платьев, блузок, мужских рубашек и др. могут быть самых разнообразных фасонов.Воротник мужской рубашки может быть двойным и одинарным. Двойной воротник делается пристежным или пришитым к сорочке, состоит из стойки и… …   Краткая энциклопедия домашнего хозяйства

• Флаг РСФСР — Флаг Российской Советской Федеративной Социалистической Республики РСФСР СССР …   Википедия

• КОМБИНЕЗОН — рабочая одежда. Состоит из брюк и верха в форме блузы или нагрудника с бретелями. Делается одинаково для мужчин и женщин из рубчатого вельвета, холста или другого плотного материала тёмных цветов. Комбинезон удобен и практичен для работы на… …   Краткая энциклопедия домашнего хозяйства

• БЕЛЬЁ ЖЕНСКОЕ — БЕЛЬЁ ЖЕНСКОЕ. К женскому белью относятся: сорочки дневные и ночные, спальные пижамы, комбинации, трусы, трико, бюстгальтеры и мягкие пояса для резинок. Наиболее красиво выглядит бельё в гарнитурах. В гарнитур входят комбинация, трусы, иногда и… …   Краткая энциклопедия домашнего хозяйства

• Флаг Российской СФСР — Флаг РСФСР  государственный символ РСФСР. После Октябрьской революции, встала необходимость принятия флага Российской Советской Республики (после II съезда Советов, определившего федерацию  РСФСР). В качестве национального (государственного) и… …   Википедия

• Знак ранения — (Знак числа ранений)[1]  отличительный наградной знак (нагрудный знак и не только) военнослужащих ВС России (Русской Армии и Флота, Вооружённых Сил СССР (ВС СССР)), получивших ранения на фронтах Великой войны, Великой Отечественной войны и… …   Википедия

• Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> …   Энциклопедия инвестора

• БЕЛЬЕ МУЖСКОЕ — подразделяется на верхнее и нижнее. К верхнему белью относятся всевозможные рубашки, к нижнему нижние сорочки, сетки, трусы, кальсоны, спальные пижамы, плавки, майки. В зависимости от назначения мужское бельё шьют из различных тканей: бязи,… …   Краткая энциклопедия домашнего хозяйства

dic.academic.ru

размер, нормы и отклонения у мужчин и парней таблица средних

Размер члена заключается в совокупности длины и объёма органа в спокойном состоянии, а также при эрекции, возникшей в результате повышения притока крови. Для мужской самооценки и полноценности величина имеет значение.

Измеряется по таким параметрам: диаметр, объем и окружность члена. Нормы и отклонения выясняем здесь.

Страсти и комплексы

Порой даже образованные и успешные мужчины определяют размер достоинства, как показатель лидерства и мужественности. Наблюдая со стороны, они прикидывают, у кого больше и считают себя заведомо проигравшими. Чтобы опровергнуть или убедиться в собственной неполноценности, представители сильного пола измеряют своего «друга» ладонью, либо определяют длину стопы для «точных» показателей.

По статистике, около 30% опрошенных мужчин удовлетворены габаритами, остальные же комплексуют и думают, что он мал. Есть и те, кто скупают виагру пачками и ломятся в клиники пластической хирургии в надежде, что их поймут и учтут пожелания.

Есть ли«эталонный» стандарт пениса с точки зрения медицины? Узнаем под следующим заголовком.

Эталонный стандарт

Норма для всех возрастов

У новорождённых он едва доходит до 5 сантиметров. В активную фазу роста переходит у подростков, причём пиком резкого увеличения считается 14-15 лет. После 17 лет пенис растёт медленно, но стабильно.

По медицинским данным, стандартный норматив балансирует в амплитуде от 12 до 18 см. Малым считают величину меньше 12 см., но расстраиваться не стоит, жить с таким показателем ещё можно. Больше 18 см. считается увеличенным, а менее 8 сантиметров врачи определяют как микропенис. Такие размеры считают аномальными, они-то и требуют повышенного внимания со стороны сексопатологов, эндокринологов, урологов.

Параметры нормального габарита также зависят от принадлежности к определённой расе. У африканцев чаще всего фиксируют более увеличенные, чем у европеоидной расы, пропорции тогда как у монголоидной расы он немного меньше.

Диаметр

Средний диаметр члена — от 10 до 16 сантиметров. 

Таблица позволит определить максимальные и минимальные значения, а также их распространённость среди лиц мужского пола.  

 

Количество мужчин (в процентах)	Окружность (см)
3	Меньше, чем 7,5 сантиметров
1	7 — 9
7	9 — 10
23	10- 11
36	11- 13
21	13 — 14
7	14 — 15
0,5	Больше 15

 

 

 

 

 

 

 

 

Длина

Второй столбец в таблице размеров члена указывает на усреднённые показатели, а третий – на нижний порог.

Возраст	Величина члена в сантиметрах
	Средние значения	Средние пропорции с отклонением
Недоношенные новорожденные дети	—	—
30 недель	2.5+0.4	1.5
34 недели	3.0+0.4	2.0
Доношенные новорожденные дети	3.5+0.4	2.5
От 0 до 5 месяцев	3.9+0.4	1.9
От 6 до 12 месяцев	4.3+0.8	2.3
От 1 до 2 лет	4.7+0.9	2.6
От 2 до 3 —	5.1+0.9	2.9
От 3 до 4 —	5.5+0.9	3.3
От 4 до 5 —	5.7+0.9	3.5
От 5 до 6 —	6.0+0.9	3.8
От 6 до 7 —	6.1+0.9	3.9
От 7 до 8 —	6.2+1.0	3.7
От 8 до 9 —	6.3+1.0	3.8
От 9 до 10 —	6.3+1.0	3.8
От 10 до 11 —	6.4+1.1	3.7
Старше 11 —	13.3+1.6	9.3

Нарушения в росте связаны множественными причинами, такими как:

• предрасположенность на генетическом уровне;
• сбои в развитии;
• нарушение выработки гормонов;
• недоразвитие пещеристых тел.

Иногда фактор недоразвитости не выявляется.

Причины необоснованных комплексов и страхов

Основными причинами приуменьшения истинной величины считаются неудачи в личной жизни. Большинство дам удовлетворены достоинством своих мужчин. Однако, есть придирчивые, которые также мечтают о «кинг сайзе». 

Порноиндустрия также закладывает стереотипы, вводящие в заблуждение. Особенно восприимчивы к данной теме парни подросткового возраста (преимущественно 13-17 лет).

Каков истинный размер у микропениса?

По результатам исследований, американский урологический журнал с характерным названием Journal of Urology напечатал данные о маленьком пенисе:

«Величина фаллоса меньше четырёх см в спокойном положении и меньше семи с половиной в эрегированном состоянии считается недостаточной. Подобные размеры являются весомыми основаниями для увеличения полового члена»

Какая длина считается нормальной или средней?

Цитируем данные того же издания:

• 8,8 см выдаёт нормальная величина в обычном положении;
• до 12,9 см вырастает в возбуждённом состоянии;
• 9-10 см составляют нормальные параметры толщины члена.

Установлено отсутствие взаимосвязи между габаритами фаллоса в отдыхающих и напряжённых моментах из-за индивидуальных особенностей у мужчин. Увеличение возраста тоже не играет важной роли (уменьшение к 70-ти годам не превышает 1 см).

Размер XXL – мечта в реальности или сказочные пытки?

Большие габариты поднимают самооценку до просторов галактики. Как на самом деле живётся с Великим и Могучим?

Минусы:

• дискомфорт во время секса;
• сложность при выборе брюк и нижнего белья; 
• казусы на пляже, в общественном транспорте.

Измерение

Длина измеряется при полной эрекции, желательно при натяжении, засекая момент кульминации. Это зависит от физического состояния, и от психологического.

При эрекции фаллос творит чудеса, увеличиваясь в 2-3 раза. При спокойном состоянии не стоит делать поспешных выводов, ведь небольшие пенисы в эрегированном виде зачастую обгоняют достоинства побольше.

Для измерения нужно сделать замер линейкой от лобка до конца головки. Диаметр полового члена измеряется сантиметровой лентой, приложив к серединке органа, выводят конечный результат в виде окружности.

Но окружность и обхват – это не одно и то же. Поэтому результат нужно поделить на число пи (3,14). Объясняется это тем, что орган не имеет идеальных контуров.

Особо любопытные берутся за такую формулу:

(Длина органа*окружность в квадрате)/(12,5). Наиболее высокую точность чисел можно вывести только неоднократно проверяя параметры в разных состояниях, внешних факторах, временных промежутках. После получения нескольких данных можно вывести среднее значение.

Влияние внешних, возрастных факторов

За изучение темы серьёзно взялась группа учёных из Саудовской Аравии. В анализе смогли поучаствовать 778 добровольцев от 20 до 82 лет в урологических лабораториях. От исследования исключили несовершеннолетних и парней со специфическими болезнями половых органов. Участникам вводили лекарство, повышающее эрекцию, проводили замеры и вывели такие результаты:

• величина члена начиная с кожи на лобке и заканчивая его колпаком достигла результата 12,53 сантиметра;
• величина пениса от лобкового симфиза до конца составила 14,34;
• утолщение фаллоса – 11,5.

По результатам подсчёта соотношения массы тела с его ростом (значение равно 29,09) выяснили, что чем выше ИМТ, тем 

меньше габариты фаллоса. Слабое уменьшение органа происходит с увеличением возраста.

Длина VS Ширина

Сильный пол часто предполагает, что всё решает длина. Женщины, напротив, обращают внимание на ширину.

Причина — влагалище девушки, достигающим всего 10 см в глубину, что с большим достоинством не всегда удобно. При широком органе происходит интенсивное надавливание на клитор, половые губы, при вхождении во влагалище, что помогает достичь удовольствия без дополнительной стимуляции.

Что думают специалисты?

Правильно измерять фаллос необходимо врачам, особенно при обращении пациента за хирургическим вмешательством. Точные данные помогают при подборе протеза. Затруднения вызывают только пациенты с эректильной дисфункцией, но опытный глаз уже намётан в данном вопросе.

Микропенис встречается очень редко, большинство мужчин имеют нормальный средний диаметр члена. Причина лишь в психоэмоциональном состоянии: стеснительность, мнительность, закомплексованность.

Даже если самооценка в полном порядке, измерения нужны для себя.

Точные знания своих показателей помогают подобрать презервативы, ведь соскальзывание приводит к протечке спермы, а сдавливание – к разрыву материала.

Заключение

Не важно, насколько велик или мал, мужчина не всегда способен оценить его объективно. Имеют значение не параметры сами по себе, а способность грамотно управлять им, а также нежность и забота, которую мужчина дарит своей партнёрше. Если он и она несовместимы вне секса, то таблица размеров точно тут не поможет.

 Всё ещё недоволен внешним достоинством? Трясёшься перед сближением с любимой? Значит, пора работать над собой. Если не справляешься, то услуги психолога, сексопатолога в помощь. Остановись, пойми, что природа не просто так создала именно твою внешность, твой организм. Ты уникален, в этом твоя фишка.

Автор статьи

Журналист-практик, рецепты проверяет на себе.
Знает все про мужчин и народную медицину.

Написано статей

879

Рейтинг автора

5

annahelp.ru

Что представляет собой диаметр окружности :: SYL.ru

Прежде чем рассматривать диаметр окружности, поговорим о ее длине. Под данным термином подразумевают произведение диаметра на число «пи». К примеру, при заданном радиусе круга можно определить не только длину, но и вычислить его площадь. Для любых видов постоянной величиной является дробь, в которой числителем является длина, а знаменатель — это диаметр окружности.

Определение

Для всех круглых геометрических фигур одинаковым будет отношение длины к диаметру. Например, зная величину радиуса круглой фигуры, вполне можно найти ее длину, диаметр, а также площадь. Длина круга — это произведение числа «πи» на диаметр окружности.

Такой величиной считают в геометрии кривую линию, ограничивающую круг. Так как фигуры представлены на плоскости, то подобное определение характеризует двухмерное изображение. Точки рассматриваемой кривой на одинаковом расстоянии удалены от центра выбранного круга.

Расчеты

Зная, что представляет собой радиус нашей планеты, несложно определить длину круговой орбиты спутника Земли. На практике проведение подобных вычислений осуществляется редко, так как число «пи» является приблизительным, поэтому высока вероятность погрешности. Для того чтобы определить ее длину в быту через диаметр окружности, используется такой прибор, как курвиметр.

Применение и формула

Зная диаметр окружности, можно осуществлять строительство жилых домов, развлекательных центров, супермаркетов. Инженеры-конструкторы, занимающиеся разработкой разнообразных машин, агрегатов, механизмов, постоянно сталкиваются с подобными вычислениями. Какова формула диаметра данной кривой? Вычерчивают ее с помощью циркуля. В математике применяется прием косвенного вычисления длины окружности.

Самым простым способом является использование радиуса. Диаметр вычисляется как два радиуса. При заданной длине окружности можно определить ее диаметр путем деления длины на число «пи». К примеру, при длине 10 сантиметров диаметр будет составлять 10 : 3,14 = 3,18 сантиметра.

При заданной площади круга, вычисление диаметра проводят путем извлечения квадратного корня из данного числа, затем деления полученного ответа на число «пи». К примеру, при площади круга 25 квадратных сантиметров, квадратный корень составит 5 сантиметров, а после деления этого числа на 3,14, получим 1,59 см. Это и есть диаметр данной в задаче окружности.

Справиться с такими несложными вычислениями может и рядовой ученик школы, и инженер конструкторского бюро.

www.syl.ru

как узнать диаметр, если длина окружности 30 см.?

Разделить на число Пи 3,14, получить радиус и умножить на 2

В П раз меньше, то есть в 3,14 раза. Для простоты считаем, что в 3, значит, диаметр 10 см

длина окр — 2пиR. R=30\2пи=приблиз 4,8см тогда диаметр будет = 9,6см школьный курс

Народ, у вас что, Яндекса нет? или лень?

Владимир! Открываем «Стандартные программы», находим «Калькулятор». Вспоминаем, что L = 2 pi x R или pi x D. Всех делов! А в Калькуляторе уже заложено число Пи. Результат: 9,5492965855137201461330258023509… Ну, приблизительно, естественно. Ибо Пи — число иррациональное. То бишь — бесконечная непериодическая дробь.

вот и меня интересует-чему обучают в школе?

Начертите окружность длинной в 30 см и измерьте расстояние от одной стороны до другой (через центр круга) получите диаметр!

touch.otvet.mail.ru

Правила для аббревиатуры модулей

Правила для аббревиатуры модулей Удаленные или переименованные модули
К сожалению, не существует определенных стандартов для аббревиатуры версий переводов Библии.
Как правило, каждое издание (комментарии, словари, другая христианская литература) делало свое сокращение и если издание становилось популярным, напр. NASB или KJV. Такие сокращения (аббревиатуры) принимались и использовались в других местах.
Только в последнее время начали создавать не только уникальное название перевода, но и уникальную аббревиатуру, даже регистрировать ее, напр. ESV, NET, NIV, WEB… Не редко можно встретить одинаковую аббревиатуру для различных переводов на разных языках.
Так как они практически не пересекались, то проблемы в этом не было. С появлением компьютерных программ, возникла необходимость иметь уникальный код для каждого перевода Библии.
Каждая программа решает это по-своему. Мы изучили принципы создания различных аббревиатур и определили свой принцип, который един для всех модулей программы.

Правила для аббревиатуры модулей MyBible

1. Аббревиатура должна быть уникальной по всем модулям на всех языках.
2. Если существует официальная аббревиатура, то она должна быть использована для модуля. Если нет официальной аббревиатуры, используются устойчивые существующие аббревиатуры.
3. Модуль аббревиатура может включать в себя модификацию/уточнения разделенные тире, например: SDK-C, SDK-L, NHEB-JM, NHEB-ME, NHEB-Y, NHEB-YS,
4. Если есть в модуле код языка, он идет в конце в нижнем регистре после тире, напр., PMP-cz, PMP-sk, ERV-th …, кроме случаев, когда код является частью официального общепринятого названия, напр. ThKJV, TgB …
5. Первый или единственный модуль конкретного перевода — только аббревиатура.
6. Последующие модули того же перевода — к аббревиатуре добавляем справа апостроф и после него год издания или номер издания (что более узнаваемо).
7. Год издания — предпочтительно четыре цифры, для устранения неоднозначностей, напр. KJ’1769, KJ’1611+. В случаях, когда перевод хорошо узнаваем и широко упоминаем по двум цифрам года, и это год 20 или 21 столетия — используем две цифры, напр. NRT’14.
8. Команда MyBible имеет решающий голос при определении аббревиатуры для модулей.

mybible.zone

Урок 3. Создание модуля с нуля за 5 минут

В этом уроке мы создадим простой модуль для OpenERP, который пока не будет иметь никакой функциональности (которую мы будем добавлять в следующих уроках), но который можно будет устанавливать в систему. Он будет содержать минимальный код, требуемый для модуля OpenERP.

Все используемые в системе модули должны находится в папке addons установленной системы. Каждый модуль представляет из себя папку, которая может быть заархивирована в формате ZIP. Имя папки или архива соответствует имени модуля.

Совет

Если вы не можете найти где находится папка с модулями, откройте файл конфигурации openerp-server.conf и найдите параметр addons_path. В нем указан текущий путь к модулям OpenERP. При необходимости можно задать другую папку, изменив этот параметр.

Рассмотрим структуру типичного модуля. Например зайдем в папку модуля crm.

Здесь можно увидеть папки и файлы с различными расширениями. Все эти файлы и папки мы будем рассматривать более подробно в наших уроках, по мере их использования. В общем виде они могут описывать следующие элементы модуля:

• Бизнес объекты: описывают записи в базе данных и методы работы с ними.
• Пользовательские интерфейсы: описывают меню, действия, представления объектов в различных видах, информационные панели и т.д.
• Переводы: описывают перевод терминов модуля на различные языки.
• Отчеты: описывают создание различных отчетов на основе записей в базе данных.
• Правила доступа: описывают уровни доступа различных групп пользователей к объектам.
• Бизнес процессы: описывают движение объектов через различные этапы состояний.
• Помощники: описывают пошаговые последовательности взаимодействия пользователя с системой.
• Данные: данные для инициализации и демонстрационные данные.
• Тесты: описывают автоматизированные сценарии тестов.

Поскольку мы создаем скелет модуля, без всякой функциональности, то мы пока не будем использовать перечисленные выше элементы. Тогда минимальный модуль OpenERP будет состоять из папки и двух файлов. Итак, приступим к созданию нашего первого модуля!

Первым делом необходимо придумать имя модулю. Оно должно состоять из строчных латинских букв, каждое слово должно быть отделено знаком подчеркивания. Начинаться имя должно с наиболее значимых слов. Если модуль зависит от других модулей, то необходимо чтобы имя начиналось с названий модулей, от которых он зависит. Например:
hr (модуль управления кадрами)
hr_contract (модуль управления трудовыми договорами, зависит от hr)

Создаем папку и даем ей имя модуля .

Теперь в любом текстовом редакторе (например Notepad++) создаем два файла:
__init__.py
__openerp__.py

Совет

Чтобы избежать в дальнейшем проблем с отображением русских букв, все текстовые файлы создавайте в кодировке UTF-8.

Файл дескриптора модуля Python __init__.py

Файл __ init__.py, как и для любого модуля на языке Python, выполняется в начале программы. Он необходим для импорта файлов, которые должны быть загружены. Поэтому, если вам необходимо загрузить файл с кодом, то вы здесь создаете строку для импорта этого файла. Например:

import module

В нашем случае, пока оставляем файл пустым.

Файл дескриптора модуля OpenERP __openerp__.py

Этот файл определяет файлы с данными, которые анализируются на этапе инициализации сервера системы, и зависимости для создаваемого модуля. Он должен содержать словарь со следующими параметрами.

Параметр	Описание	Значение по умолчанию
name	Название модуля на английском языке.	»
version	Версия модуля. В соответствии со спецификацией Semantic Versioning.	‘0.0.0’
description	Описание модуля.	»
author	Автор модуля.	»
website	Сайт поддержки модуля.	»
license	Лицензия модуля.	‘Affero GPL-3’
category	Категория модуля. Модули из категории Hidden по умолчанию не отображаются в представлениях списка и канбана.	‘Uncategorized’
sequence	Определяет порядок отображения модулей в представлениях списка и канбана.	100
complexity	Уровень сложности использования модуля для пользователя. easy: интуитивный и легкий для использования любым пользователем. normal: необходимы бизнес знания в области использования модуля. expert: требует технических навыков.	‘normal’
images	Ссылки на используемые изображения. Путь должен быть относительным к директории модуля. По соглашению файлы необходимо располагать внутри папки /images/.	[]
depends	Список модулей, от которых зависит этот модуль. Модуль base всегда неявно входит в список зависимостей, даже если он не указан здесь явно.	[‘base’]
external_dependencies	Определяет внешние зависимости от софта, установленного на сервере. python — необходимые модули на Python bin — необходимые исполняемые файлы postgres — необходимые возможности СУБД PostgreSQL	[]
data	Список файлов с данными (в формате CSV, YAML или XML), необходимыми при установке или обновлении модуля. Путь должен быть относительным к директории модуля.	[]
demo	Список файлов с демонстрационными данными (в формате CSV, YAML или XML), загружаемыми при создании демонстрационной базы данных. Путь должен быть относительным к директории модуля.	[]
test	Список .yml файлов со сценариями автоматизированных тестов, выполняемых после создания демонстрационной базы данных. После завершения тестов все совершенные транзакции отменяются. Путь должен быть относительным к директории модуля. По соглашению файлы необходимо располагать внутри папки /test/.	[]
js	Упорядоченный список .js файлов (включая зависимости) со сценариями для браузеров. Порядок важен, поскольку веб сервер может их объединять для оптимизации. Путь должен быть относительным к директории модуля. По соглашению файлы необходимо располагать внутри папки /static/src/js/, а файлы в составе сторонних библиотек внутри static/lib/.	[]
css	Упорядоченный список .css файлов с таблицами стилей для браузеров. Порядок важен, поскольку веб сервер может их объединять для оптимизации. Путь должен быть относительным к директории модуля. По соглашению файлы необходимо располагать внутри папки /static/src/css/, а файлы в составе сторонних библиотек внутри static/lib/.	[]
qweb	Список .xml файлов с шаблонами для генерации HTML страниц. Путь должен быть относительным к директории модуля. По соглашению файлы необходимо располагать внутри папки /static/src/xml/.	[]
installable	Значение True определяет, что модуль устанавливаемый.	True
auto_install	Значение True определяет, что модуль устанавливается системой автоматически. Модуль не будет установлен, пока не будут установлены все модули, от которых он зависит. Если модуль независим, то он установится сразу после создания базы данных.	False
application	Значение True определяет, что модуль является приложением, а не дополнением.	False
certificate	Номер сертификата модуля, если модуль сертифицирован издателем.	»
icon	Неявный параметр. Адрес иконки модуля в представлении канбан. Автоматически создается при размещении файла /static/src/img/icon.png в модуле. Желательно чтобы изображение имело прозрачный фон.	‘/base/static/src/img/icon.png’

Создадим словарь для нашего модуля. Поскольку наш модуль еще ничего не делает, добавим только те параметры, которые отвечают за визуальное представление в системе.

Визуальные параметры модуля в представлении канбан.

 

Визуальные параметры модуля в представлении форма.

 

Словарь дескриптора нашего модуля.

{
    'name': 'Первый модуль',
    'description': """Самый маленький модуль для OpenERP.""",
    'author': 'Иванов Иван Иваныч',
    'website': 'http://codup.com',
    'sequence': 0,
    'application': True,
}

Параметры sequence и application используем для удобства разработки, чтобы модуль был виден по умолчанию в представлении канбан в самом верху. Также неявно зададим параметр icon, разместив иконку в папке модуля /static/src/img/icon.png.

Все! Наш первый модуль готов. Скопируйте его в папку с модулями системы и обновите список модулей (Настройки->Модули->Обновить список модулей). Новый модуль теперь доступен в системе и с ним можно производить все действия, как и с другими модулями: устанавливать, обновлять, удалять и т.д.

Примечание

Если вы не знаете как устанавливать модули в OpenERP, вы можете узнать как это сделать в Уроке №2.

Вы можете скачать готовый модуль здесь.

Примечание

Если вы скопируете модуль в заархивированном виде, то возможно не будет отображаться иконка модуля (баг на момент написания статьи). Если хотите, чтобы отображалась иконка разархивируйте модуль перед копированием.

codup.com

Общие правила структурного построения программных модулей.

1. Каждый модуль характеризуется функциональной законченностью, автономностью и независимостью в оформлении от модулей, которые его используют и которые он вызывает. Высокую степень независи­мости модулей можно достичь с помощью двух методов оптимизации:

— усилением внутренних связей в каждом модуле, т.е. реализовать от­дельные функции отдельными модулями (высокая прочность модуля).

— ослаблением взаимосвязи между модулями, применяя формальный механизм передачи параметров (слабое сцепление модулей).

2. Применяются стандартные правила организации связей по управ­ле­нию и информации с другими модулями (смотри далее).

3. Комплексы программ разрабатываются в виде совокупности не­боль­ших по количеству (до 100) программных модулей, связанных иерархическим образом, что дает возможность полностью и относи­тельно просто уяснить функцию и правила работы отдельных частей и комплекса программ в целом.

4. Как правило, модуль содержит от 10 до 1000 выполняемых опера­то­ров языка высокого уровня. Размеры модуля влияют на степень независимости программы, легкость ее чтения и тестирования.

5. Модуль прочный. Прочность модуля измеряется его внутренними свя­зями. Модуль — это замкнутая программа, которая выполняет одну или несколько функций, обладает некоторой логикой.

6. Модуль предсказуемый, т.е. модуль, работа которого не зависит от предыстории его использования. Модули не должны сохранять никаких «воспоминаний» о предыдущем вызове.

7. Определена структура принятия решений. Желательно, чтобы те модули, на которые прямо влияет принятое решение, были подчиненными (вызываемыми) по отношению к принимающему решение модулю.

8. Объем данных, на которые модуль может ссылаться, должен быть сведен к минимуму.

9. Внутренняя процедура (или подпрограмма) — это замкнутая ­прог­рам­ма, физически расположенная в вызывающем ее модуле. Их следует избегать, т.к.  их трудно изолировать  для  автономного тестирования и они не могут быть вызваны из модулей, отличных от тех, которые их физически содержат. Когда возникает потреб­ность во внутренней процедуре, проектировщик должен рассмотреть возможность оформления ее в виде отдельного модуля.

10. В параметры процедуры следует включать только те переменные, че­рез которые идет обмен информацией с другими программными единицами. Другие переменные — это внутреннее дело процедуры. Процедуры, которые выдают в качестве результата только одно значение, оформляются как функции. Функция удобнее в использо­вании, так как ее результат непосредственно можно использовать в арифметическом и/или в логическом выражениях.

Правила связи программных модулей по управлению.

1.   Передача управления вызываемому модулю всегда осуществляется через его начало,  т.е. через  первый  оператор.

2.   Выход из вызываемого модуля всегда происходит через  его естественное окончание, т.е. после нормального его завершения.

3.   По окончании исполнения вызываемого модуля управление передается в вызывающий модуль на оператор, следующий непосред­ственно за оператором вызова.

4.   Модули низших уровней или одного уровня иерархии могут вызываться для исполнения только модулями высших уровней, т.е. модули низших уровней не могут вызывать модули высших уровней, а модули одного уровня — вызывать друг друга.

5.   Если все же необходимо исполнить модуль с некоторой внутренней точки, то вызов все равно осуществляется стандартным образом (через его первый оператор), а точка начала задается в виде пара­метра. При этом в начале вызываемого модуля должен стоять пе­реключатель, который обеспечивает передачу управления программой к его внут­ренним точкам по параметру, указанному при обращении к модулю.

6.   В каждом модуле  должна  быть  предусмотрена  возможность подклю­чения контрольных и отладочных средств; операторы, ре­али­зующие эти средства, обычно сосредотачиваются в конце модуля.

studfiles.net

Ответы@Mail.Ru: что такое модульное программирование?

Модульное программирование является развитием и совершенствованием процедурного программирования и библиотек специальных программ. Основная черта модульного программирования — стандартизация интерфейса между отдельными программными единицами. Модуль — это отдельная функционально-законченная программная единица, которая структурно оформляется стандартным образом по отношению к компилятору и по отношению к объединению ее с другими аналогичными единицами и загрузке. Как правило, каждый модуль содержит паспорт, в котором указаны все основные его характеристики: язык программирования, объем, входные и выходные переменные, их формат, ограничения на них, точки входа, параметры настройки и т. д. Объем модуля обычно не превышает 1000 команд ЭВМ или операторов языка программирования. В противном случае модуль становится громоздким и трудным к восприятию и использованию. Модульное программирование — это искусство разбиения задачи на некоторое число различных модулей, умение широко использовать стандартные модули путем их параметрической настройки, автоматизация сборки готовых модулей из библиотек, банков модулей. Основные концепции модульного программирования: — Каждый модуль реализует единственную независимую функцию; — Каждый модуль имеет единственную точку входа и выхода; — Размер модуля по возможности должен быть минимизирован; — Каждый модуль может быть разработан и закодирован различными членами бригады программистов и может быть отдельно протестирован; — Вся система построена из модулей; — Модуль не должен давать побочных эффектов; — Каждый модуль не зависит от того, как реализованы другие модули. При таком подходе сложная система разделяется на несколько частей, одновременно создаваемых различными программистами. Каждый модуль реализует единственную функцию. Размер модуля невелик, поэтому тестирование управляемо и может быть проведено тщательным образом. После кодирования и тестирования всех модулей происходит их интеграция, и тестируется вся система. При сопровождении тестируется и отлаживается только тот модуль, который плохо работает. Очевидны преимущества в облегчении написания и тестирования программ, уменьшается стоимость их сопровождения. Концепция модульного программирования реализована в ряде языков, таких как Modula 2, Turbo Pascal 5.0 и выше, C, и др. Отличие в реализации процедурного программирования от модульного состоит в том, что модуль не виден программе. В отличие от стандартных языков процедурного программирования, в модульных языках лишние модули просто не прикомпановываются на этапе сборки.

модульное програмирование — это искуство

touch.otvet.mail.ru

Как сложить модуль 🚩 как сложить модуль 🚩 Математика

Поделки своими руками всегда есть и будут в цене, особенно если они сделаны мастерски. Очень интересной идеей для творчества является модульное оригами, которое изготавливается из бумаги и других вспомогательных материалов.

Модульное оригами представляет собой фигурки из листов-модулей. Для изготовления 3D-фигурок подойдет обычная офисная бумага формата А4 с плотностью, которая подходит для печати на принтерах. Такая бумага будет отличным материалом для создания модулей, потому что она не отличается идеальной гладкостью, но при этом достаточно плотная. Модули, сделанные из офисной цветной бумаги, надежно держатся между собой, а также не скользят при соединении. На сгибах офисная бумага не белеет, что, безусловно, очень важно.

Также для изготовления модульных оригами подойдут страницы из глянцевых журналов. Именно из глянцевых страниц можно сделать самые яркие и красочные оригами, которые издалека будут напоминать разноцветные стеклянные фигурки. Но не стоит выбирать слишком тонкую глянцевую бумагу, так как она будет рваться на сгибах.

Многие дети не хуже взрослых могут сделать красивое модульное оригами, но их работы все равно не будут настолько профессиональны. Поэтому для детского творчества можно купить несколько наборов цветной бумаги, но обязательно, чтобы листы были достаточно плотными. Почему несколько наборов? Потому что для изготовления модулей понадобится не один и не два листа одного цвета. Качественная детская цветная бумага не будет рваться и «белеть» на сгибах.

В продаже имеется и специальная бумага для модульного оригами, которая называется «ками». Специфичность такой бумаги заключается в том, что листы уже имеют квадратную форму, а также оптимальную плотность для создания модульных шедевров. В наборах «ками» находится по несколько листов одного цвета, при этом одна сторона является цветной, а другая белой. Есть также специальные наборы, где лист бумаги с обеих сторон цветной.

Для модульного оригами могут использоваться не только листы формата А4. Для данного вида творчества подойдет бумага самых различных размеров. Если модули предполагается делать треугольные, рекомендуется брать бумагу размером 1/16 или 1/32 от обычного формата А4.

www.kakprosto.ru

Что такое модуль?

Термин «модуль» можно встретить в самых разных сферах деятельности: в математике, информатике, технике и так далее. В школе на уроках мы пытались понять, чему, например, равен модуль числа -15. Дома по телевизору мы смотрим новости о том, что происходит на российском модуле международной космической станции. А что такое модуль? В каких сферах жизни еще используется это понятие?

Модуль в математике

В математике модулем называется абсолютная величина какого-либо числа. Если представить себе расположение любого числа на координатной прямой, то модулем этого числа будет расстояние от него до нулевой точки. Таким образом, модулем положительного числа а (записывается как |а|) будет само это число. Модулем отрицательного числа -а будет число, ему противоположное, то есть а.

О том, как проводить вычисления с модулями, читайте в статье Как решать модули.

Также в математике есть такое понятие «модуль вектора». Если вы помните, то вектором называется отрезок прямой, имеющий не только длину, но и направление. Так вот, модулем вектора называется длина этого направленного отрезка.

Модуль в технике

В технике модулем называется самостоятельный узел сложной инженерной системы, выполняющий собственную индивидуальную задачу. Как правило, модули могут быть отсоединены от целой системы.

Классическим примером технических модулей являются космические модули. По модульному принципу построена международная космическая станция (МКС). Новый модуль, доставляемый на орбиту, пристыковывается к уже работающим. На МКС в настоящий момент работают 5 российских, 7 американских, 1 европейский и 1 японский модули.

Космические летательные аппараты имеют также такие составные элементы, как стыковочный модуль, спускаемый модуль. С помощью спускаемого модуля на Землю с орбиты возвращаются космонавты. Спускаемые модули могут выполнять и исследовательские функции. Так, спускаемый модуль «Филы» космического аппарата «Розетта» в ноябре 2014 года совершил посадку на одной из комет Солнечной системы с целью изучения поверхности этой кометы.

Однако модули не всегда представляют собой такие сверхсложные технические объекты. Мод

elhow.ru

система национальных счетов снс это мти



Показатели снс

В разделе Макроэкономика на вопрос МАКРОЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ СНС??? (система национальных счетов) Какая взаимосвязь между ними? заданный автором Вопросник лучший ответ это Суть СНС сводится к формированию обобщающих показателей функционирования экономики на различных стадиях процесса воспроизводства и взаимной вязке этих показателей между собой. В основе национального счетоводства лежит характеристика процессов создания, распределения, перераспределения, и использования дохода в рамках экономической системы с определенной структурой и закономерностью функционирования. Каждой стадии воспроизводственного цикла производству продуктов и услуг и связанных с этим процессов образование доходов, первичному и вторичному их распределению и использованию – соответствует счет или группа счетов. Счета являются счетами потоков то есть в них отражается сквозное движение стоимости товаров и услуг через все стадии воспроизводственного цикла – от производства до конечного потребления и накопления. Система завершается построением балансовых таблиц отражающих итоговое изменение национального богатства в результате труда данного года, и меж отраслевого баланса производства и использования продукции и услуг. Для экономики в целом предусматривается составление всех счетов. Они образуют сводные счета и отражают, с одной стороны, отношения между национальной экономикой и другими странами, а с другой – отношения между различными показателями системы. Он дает возможность проанализировать объем и структуру валового выпуска по нескольким направлениям. Во-первых, позволяет определить долю продуктов и материальных услуг и долю нематериальных услуг в общем объеме валового выпуска и валового внутреннего продукта всей экономики, что дает возможность судить о развитии сфер деятельности. Во-вторых, предоставляет возможность исчислит долю валового выпуска и валовой добавленной стоимости отдельных секторов и отраслей в общем валовом выпуске продуктов и услуг; выявить их натурально-вещественную и стоимостную структуру с целью оценки доли затрат живого и овеществленного труда на производство продукции отрасли, сектора, страны в целом, а также на производство различного вида услуг. Объем налогов в сопоставлении с валовой добавленной стоимостью позволяет определить, сколько на каждую единицу конечного результата уплачено налогов. Анализ показателей налогов позволяет получить информацию о налоговой системе: о видах, источниках поступлений налогов и сделать вывод о том, на кого возложено основное налоговое бремя. Теневая экономика, в принципе, должна учитываться в СHС, так как в этой сфере производятся продукты, услуги и доходы, участвующие в экономическом обороте. Большинство стран делает поправки к данным, собранным с помощью налоговых деклараций, с учетом сокрытия части доходов. Hо в любом случае уголовно наказуемые деяния не рассматриваются как производственная деятельность (типа наркобизнеса) .Выделяют следующие основные счета:Счет производства — показывает результаты производственной деятельности (затраты, промежуточное потребление, производство добавленной стоимости) . В итоге счет дает добавленную стоимость в рыночных ценах. Счет образования доходов — характеризует процесс образования прибыли, заработной платы, доходов от собственности, социальных выплат, других доходов. Счет распределения доходов — показывает, как доходы распределяются между основными получателями – домашними хозяйствами, фирмами, учреждениями, административными структурами. Счет использования доходов — отражает соответствующий процесс: из располагаемого валового дохода образуются конечное потребление и валовое накопление. Счет капитала — содержит показатели сбережения, изменения запасов, амортизации основного капитала, перечисления капитала. Финансовый счет — показывает итоговые изменения финансовых активов и пассивов, образование сальдо долговых требований и обязательств. Ну вот, это в кратце. Надеюсь помогла. Удачи юное создание.

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: МАКРОЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ СНС??? (система национальных счетов) Какая взаимосвязь между ними?

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Система национальных счетов на Википедии
Посмотрите статью на википедии про Система национальных счетов

Скотт Уильям Белл на Википедии
Посмотрите статью на википедии про Скотт Уильям Белл

Скотт Шонн Уильям на Википедии
Посмотрите статью на википедии про Скотт Шонн Уильям

 

Ответить на вопрос:

22oa.ru

V3:Система национальных счетов Понятие, содержание и общие принципы построения снс

1. К элементам системы национальных счетов не относят …

–: совокупность счетов СНС

–: совокупность хозяйственных единиц

–: совокупность секторов экономики

+: план счетов бухгалтерского учета

2. Совокупность накопленных ресурсов страны, ее экономических активов, необходимых для осуществления процесса производства и обеспечения жизни ее жителей называется …

–: институциональным сектором

–: системой национальных счетов

+: национальным богатством

–: валовым национальным продуктом

3. В СНС не требуется составления полного набора счетов для сектора экономики …

–: некоммерческие организации, обслуживающие домашние хозяйства

–: нефинансовые предприятия

+: остальной мир

–: финансовые учреждения

4. Резидентами России являются …

+: иностранные компании и банки, находящиеся на экономической территории страны более года

–: иностранные студенты

–: сотрудники иностранных посольств

–: иностранные военнослужащие

5. В структуру СНС входит баланс …

+: денежных доходов и расходов населения

–: трудовых ресурсов

–: активов и пассивов

–: основных фондов

6. К группам счетов для секторов экономики в СНС относятся …

+: счета накопления

–: счета образования доходов

–: финансовые счета

+: балансы активов и пассивов

7. К консолидированному счету производства балансирующей статьей является …

–: валовой национальный располагаемый доход

+: валовой внутренний продукт

–: валовая прибыль и валовые смешанные доходы

–: валовой национальный доход

8. Оплата труда и факторы производства отражаются в графе «Использование» счета …

–: распределения первичных доходов

+: образования доходов

–: счета конечного использования

–: производства товаров и услуг

9. Счета в СНС составляются …

+: по секторам, отраслям и по экономике в целом

–: только по отраслям экономики

–: только по экономике в целом

–: только по секторам экономики

10. В странах с развитой рыночной экономикой макростатистические показатели рассчитываются на основании …

–: платежной системы государства

– платежного баланса

+: системы национальных счетов

–: баланса народного хозяйства

11. Какие важнейшие приемы бухгалтерского учета использованы в СНС?

+: принцип двойной записи операций

–: записи в счетах относятся к каждой отдельной хозяйственной операции

–: использование учетных регистров, формы которых разрабатываются Минфином РФ

–: в счетах СНС различают две части: дебет и кредит

12. Экономическая территория страны не охватывает …

–: посольства страны и других государств

–: территориальные воды

+: военные и научные базы других государств

–: национальное воздушное пространство

13. Экономическим оборотом в СНС называется …

–: территориальное перемещение институциональных единиц

–: обмен экономической информацией между хозяйствующими субъектами

+: движение товаров и доходов в стоимостной форме

–: отражение активов и обязательств товаропроизводителей на счетах бухгалтерского учета

Группировки и классификации в системе национальных счетов

1. Система классификации в СНС включает …

+: экономические операции

–: временя выполнения операций

–: счета

–: формы собственности

2. В состав капитальных трансфертов включаются…

–: прямые текущие налоги на доходы

–: взносы по социальному страхованию

+: безвозмездные ассигнования в виде экономической помощи на капитальное строительство в других странах

–: возмещение убытков от стихийных бедствий

3. В статистике системы национальных счетов в составе сектора «Экономика в целом» выделяются (согласно КИЕС) следующие из нижеперечисленных секторов …

–: дальнее зарубежье

+: финансовые корпорации

+: государственное управление

–: ближнее зарубежье

4. Операции с доходами не включают…

+: экспорт товаров и услуг

+: приобретение финансовых активов

–: перераспределение доходов

+: распределение добавленной стоимости

5. В статистике системы национальных счетов к операциям с товарами и услугами относят …

+: субсидии

+: выпуск продукции

+: импорт товаров и услуг

studfiles.net

43 Система национальных счетов (снс). Институциональные единицы. Макроэкономические агенты экономики.

Система национальных счетов представляет собой определённый способ упорядочения информации об экономических операциях, совершаемых субъектами хозяйствования в процессе общественного воспроизводства; совокупность взаимосвязанных показателей, характеризующих производство, распределение, перераспределение, обмен и использование конечного продукта и национального дохода.

Под экономической операцией в СНС понимается добровольное взаимодействие двух хозяйствующих субъектов в связи с производством и использованием продукции, распределением и перераспределением доходов, приобретением финансовых активов, принятием финансовых обстоятельств. В СНС изучаются экономические операции между институциональными единицами – хозяйствующими субъектами, которые владеют и распоряжаются активами, от своего имени принимают обязательства, вступают в экономические операции с др. институциональными единицами, составляют полный набор счетов. Существует 2 типа институциональных единиц: юридические лица и домашние хозяйства. В СНС институциональные единицы группируются в институциональные секторы экономики – агрегированные группы хозяйствующих субъектов со сходными целями, функциями и источниками финансирования. Выделяют 6 секторов.

Сектор нефинансовых предприятий объединяет субъектов экономики независимо от форм собственности и организационно-правовых норм, но с общей функцией производства материальных благ и услуг нефинансового характера.

Сектор финансовых учреждений охватывает институциональные единицы, занятые финансовыми операциями.

Сектор государственного управления включает институциональные единицы, которые оказывают услуги, реализуемые не за деньги, т.е. для которых не существует рынка.

Сектор домашних хозяйств состоит их домашних хозяйств и некорпоративных предприятий, владельцами которых являются домашние хозяйства.

Сектор некоммерческих организаций, обслуживающих домашние хозяйства, образован из субъектов, не контролируемых и не финансируемых государством.

Сектор заграницы (остальной мир) является внешним по отношению к перечисленным внутренним секторам национальной экономики и включает институциональные единицы, которые, работая за границей, осуществляют операции с субъектами внутри страны.

44 Валовой внутренний продукт (ввп). Принципы и методы расчета ввп. Другие показатели системы национальных счетов.

ВВП – совокупная рыночная стоимость всего объема конечных продуктов (товаров и услуг), произведенных на территории данной страны как отечественными, так и зарубежными производителями за определенный период времени (год)

Расчёт ВВП производится по территориальным признакам. Под конечными продуктами понимаются товары и услуги, которые приобретаются для конечного пользования, накопления и экспорта, а не для перепродажи либо дальнейшей переработки. В ВВП не включаются :

• Продажа подержанных вещей

• Частные и государственные трансфертные платежи

• Сделки с ценными бумагами

На базе ВВП можно рассчитать другой показатель СНС (ВНД).

ВНД – совокупная рыночная стоимость всего объёма конечных продуктов, созданных отечественными производителями как на территории данной страны, так и за рубежом за определенный период времени (год)

ВНД – ВВП + сальдо первичных доходов из-за рубежа

Расчёт ВВП по расходам предполагает суммирование расходов всех субъектов нац.экономики на конечное потребление

ВВП = G+lg+C+Xn;

G – расходы государства, связанные с закупкой товаров и услуг

С – расход домохозяйств на приобретение товаров и услуг

L – валовые частные внутренние инвестиции или инвестиционные расходы фирм

Xn – чистый экспорт, или разница между экспортом и импортом

В соответствии с производственным методом ВВП рассчитывается путем определения и суммирования добавленной стоимости, созданной всеми субъектами нац.экономики

Добавленная стоимость отдельной фирмы – разница между выручкой от реализации произведенной ею продукции и текущими материальными издержками

Расчёт ВВП по доходам предполагает суммирование всех доходов созданных факторами производства, а также 2х элементов, не связанных с выплатой доходов – амортизации (А) и чистых косвенных налогов на бизнес (Тn)

Расчёт ВВП по доходам :

ВВВ = W + r + Pr + I + A + Tn

r – рентные доходы

W – вознаграждение за труд наемных работников

I – процент собственника денежного капитала

Прибыль делится на :

1) Прибыль корпоративного сектора

2)Прибыль некорпоративного сектора

studfiles.net

Вопрос 31. Система национальных счетов (СНС)

Сущность и задачи СНС.

Система национальных счетов представляет собой построенный определенным образом набор счетов и балансовых таблиц, на основе которых вычисляются взаимосвязанные макроэкономические показатели, характеризующие результаты деятельности национальной экономики за определенный период времени (как правило за год), ее структуру и важнейшие взаимосвязи. Набор этот одинаковый для всех стан, использующих СНС.

СНС дает возможность сопоставления экономических показателей всех стран, использующих СНС,сводимость макроэкономических показателей на мировом уровне, позволяет определить место национальной экономики в мировой экономике, решает проблему международных сопоставлений. Это достигается единством методологии расчета макроэкономических показателей, и тем самым содействует международной интеграции и экономическому сотрудничеству.

СНС выполняет несколько важных функций, среди которых:

— измерение объемов производства за определенный промежуток времени;

— выявление существующих тенденций в экономике;

— организация экономической политики государства.

Категории и структура СНС.

СНС представляет экономику в виде институционных единиц, связанных между собой экономическими операциями.

Институционные единицы — это хозяйствующие субъекты, обладающие автономией в принятии экономических решений по всем вопросам хозяйственной деятельности. Существуют два типа институционных единиц: 1) юридические лица – предприятия, корпорации, квазикорпорации(единицы, сходные с корпорациям, но формально не имеющие их статуса) государственные учреждения, банки, страховые компании и др.

2)домашние хозяйства, рассматриваются как институционные единицы, так как самостоятельно принимают экономические решения, определяющие их поведение.

Все институционные единицы являются так называемыми резидентами страны. Это понятие включает в себя те институционные единицы, которые связаны с экономической территорией страны экономическим интересом в течение относительно длительного периода (обычно год или более).

Экономическая территория – это территория административно управляемая правительством страны, в пределах которой лица, товары и деньги свободно перемещаются.

На практике резидентами данной страны выступают все юридические лица, функционирующие на ее территории, независимо от того, контролируются они иностранным капиталом или нет. Понятие резидента не связанно с понятием национальности или гражданства.

Национальная экономика охватывает деятельность резидентов независимо от их местонахождения: на территории данной страны или за ее пределами. Например, строительные бригады, работающие временно в других странах, рассматриваются как резиденты страны, из которой они прибыли.

Внутренняя экономика учитывает деятельность на экономической территории страны как резидентов, так и нерезидентов.

Основные классификации СНС

В СНС используется несколько классификаций.
Первая классификация — группировка хозяйственных единиц по отраслям. В группировке хозяйственных единиц по отраслям единицей классификации является заведение — предприятие или его часть, занятое преимущественно одним видом производственной деятельности, по которой имеется статистическая информация о затратах и выпуске продукции.
Отраслью в СНС называется совокупность заведений, которые расположены территориально в одном месте и заняты одним видом основной производственной деятельности.
Отрасли классифицируются по четырем категориям:
1) отрасли, производящие товары и рыночные услуги;
2) отрасли, производящие нерыночные услуги силами государственных учреждений;
3) отрасли, производящие нерыночные услуги силами частных коммерческих организаций;
4) отрасли, оказывающие нерыночные услуги, производимые домашними хозяйствами.

Вторым типом классификации при построении СНС является группировка единиц по институциональным секторам. Она осуществляется с целью исследования потоков доходов и расходов, финансовых активов и пассивов. Классификационной единицей в секторной группировке является институциональная единица — хозяйственная единица, которая ведет полный набор бухгалтерских счетов, может Самостоятельно принимать решение и распоряжаться своими материальными и финансовыми ресурсами. Исключение составляют считающиеся инсти­туциональными единицами домашние хозяйства. Они не ведут счетов, но могут распоряжаться своими ресурсами, от своего имени владеть активами и принимать обязательства, и являются хозяйствующими субъектами.
Сектор – это группа институциональных единиц, однородных с точки зрения выполняемых ими функций в экономическом процессе и способа финансирования затрат.
Институциональные единицы группируются по шести секторам:
• «Нефинансовые предприятия»;
• «Финансовые учреждения»;
• «Государственные учреждения»;
• «Некоммерческие организации, обслуживающие домашние хозяйства»;
• «Домашние хозяйства»;
• «Остальной мир».

 

Классификация счетов

СНС РФ включает следующие группы счетов:

-секторов экономики

-отраслей экономики

-отдельных экономических операций

-экономики в целом (консолидированные счета)

Счета для секторов экономики подразделяются на текущие счета, счета накопления, балансы активов и пассивов.

Текущие счета секторов экономики включают:

-счет производства

-счет образования доходов

-счет распределения первичных доходов

-счет распределения вторичных доходов

-счет использования располагаемого дохода

-счет операций с капиталом.

Счет производства разрабатывается с целью характеристики результатов производства продукции и услуг. Он является ключевым с точки зрения содержания.

Вопрос 32. Макроэкономические показатели и их взаимосвязь. Расчет ВВП производственным, распределительным методом и методом конечного использования

Макроэкономические показатели и их взаимосвязь

Макроэкономические показатели— сводные, агрегированные, усредненные по экономике в целом показатели объемов производства и потребления, доходов и расходов, структуры, эффективности, уровня благосостояния, экспорта и импорта, темпов экономического роста и др. Макроэкономические показатели отражают общие тенденции в экономике. Их можно разделить на три группы: потоки, запасы (активы) и показатели экономической конъюнктуры. Потоки отражают передачу ценностей субъектами друг другу в процессе экономической деятельности, запасы – накопление и использование ценностей субъектами. Потоки представляют собой экономические параметры, значение которых измеряется в единицу времени, как правило, в расчете на год, значение экономических параметров запасов измеряется на определенный момент. Пример потоков – сбережения и инвестиции, бюджетный дефицит, пример запасов – накопленный в результате капитал, государственный долг.

Между запасами и потоками в экономике существует взаимосвязь: изменения в одних величинах, как правило, сопровождаются соответствующими изменениями в других. Однако при определенных обстоятельствах показатели запасов и потоков могут изменяться независимо друг от друга.

 

Валовый внутренний продукт

Основным показателем системы макроэкономических показателей является Валовый внутренний продукт, характеризующий стоимость конечных товаров и услуг, произведенных резидентами страны за определенный период времени, за вычетом стоимости промежуточного потребления. Валовый внутренний продукт исчисляется в рыночных ценах конечного потребления, то есть в ценах, оплачиваемых покупателем, включая все торгово-транспортные наценки и налоги на продукты.

 

Валовый национальный доход

ВНД представляет собой сумму первичных доходов, полученных резидентами данной страны за тот или иной период в связи с их прямым или косвенным участием в производстве ВВП своей страны и ВВП других стран. Таким образом, ВНД больше ВВП на сумму первичных доходов, полученных резидентами данной страны из-за границы (за вычетом первичных доходов, выплаченных нерезидентам).

К первичным доходам относятся оплата труда, прибыль, налоги на производство, доходы от собственности (проценты, дивиденды, рента и т. д.).

 



infopedia.su

14. Система национальных счетов (Снс) и её показатели

Система национальных счетов (СНС) — это система взаимоувязанных показателей, применяемая для описания и анализа макроэкономических процессов. Она дает сведения о всех стадиях экономического кругооборота — производстве и обмене, первичном и вторичном распределении (перераспределении), потреблении и сбережении (накоплении). СНС ООН 1993 г. включает оценку теневой экономики, которая, как уже отмечалось, представляет собой производство обычных товаров и услуг, осуществляемое подпольным образом с целью сокрытия доходов от налогообложения. Более того, она предлагает учитывать даже производство юридически незаконных товаров и услуг (наркотики, проституция и т.п.), а также труд по ведению домашнего хозяйства (приготовление пищи, уборка жилищ, воспитание детей и т.д.), хотя большинство стран мира, в том числе Россия, не готовы включать в свои расчеты оценки этой деятельности.

Структура СНС исходит из того, что каждой стадии экономического кругооборота соответствует специальный счет или группа счетов. СНС России в настоящее время включает следующие счета:

• Счет производств показывает результаты производственной деятельности (затраты, промежуточное потребление, производство добавленной стоимости). В итоге счет дает добавленную стоимость в рыночных ценах.

• Счет образования доходов характеризует процесс образования прибыли, заработной платы, доходов от собственности, социальных выплат, других доходов.

• Счет распределения доходов показывает, как доходы распределяются между основными получателями – домашними хозяйствами, фирмами, учреждениями, административными структурами.

• Счет использования доходов отражает соответствующий процесс: из располагаемого валового дохода образуются конечное потребление и валовое накопление.

• Счет капитала содержит показатели сбережения, изменения запасов, амортизации основного капитала, перечисления капитала.

• Финансовый счет показывает итоговые изменения финансовых активов и пассивов, образование сальдо долговых требований и обязательств.

Св-ва СНС: 1.охват большого кол-ва информации, 2.замкнутость(единая матрица)

15. Валовой внутренний продукт (Ввп): понятие, принципы и способы расчёта

Валовой внутренний продукт (ВВП) измеряет стоимость конечной продукции, произведенной на территории данной страны за определенный период, независимо от того, находятся факторы производства в собственности граждан данной страны или принадлежат иностранцам.

16. Модель кругооборота с участием иностранного сектора экономики

Иностранный сектор экономики

Импорт

Чистый приток капитала

Экспорт

Рынки продуктов

Расходы на потребление

Расходы на НП

Гос.закупки

Чистые налоги

Государство

Домохозяйства

Фирмы

Инвестиц. расходы

Гос.займы

Сбережения

Финансовые рынки

Инвестиц. средства

НД

Платежи за ресурсы

Рынки ресурсов

Рис.4. Модель кругооборота с участием иностранного сектора

Иностранный сектор связан с экономической системой 3 способами: импорт, экспорт и чистый приток капитала.

Импорт отражает платежи за импортируемые данной страной товары и услуги. Экспорт отражает платежи данной стране. Разница между экспортом и импортом называется чистым экспортом.

Третий способ связи экономики с внешним миром состоит в осуществлении международных финансовых операций: получение или предоставление кредитов, сделки по купле-продаже реальных и финансовых активов. Если страна импортирует больше, чем экспортирует, то имеет место реальный чистый приток капитала (напр., страна много занимает). В обратном случае наблюдается чистый отток капитала.

НП = Расходы на потребление + Расходы на инвестиции + Госзакупки + Экспорт – Импорт = =Потребление + Сбережения + Чистые налоги = НД.

studfiles.net

Система национальных счетов

7.СИСТЕМА  НАЦИОНАЛЬНЫХ СЧЕТОВ 

7.1 Основные понятия, принципы и правила построения системы национальных счетов (СНС) 

1. В анализе экономики по методологии СНС центральной является классификация хозяйственных единиц по

      1. отраслям экономики

      2. секторам экономики

      3. формам собственности

      4. организационно-правовым формам 

2. Субъектом  экономического оборота в СНС   являются

      1. товары и услуги

      2. денежные средства и другие носители стоимости

      3. хозяйствующие единицы

      4. экономические операции 

3.Внутренней (национальной) экономикой в СНС называется деятельность

1. резидентов только  на экономической территории страны

2. резидентов  на экономической территории страны и за её  

3. резидентов и нерезидентов страны на её экономической территории

4. Единица,  расположенная  территориально  в одном месте и занятая  преимущественно одним видом  производственной деятельности, в  СНС называется

      1. отраслью

      2. заведением

      3. институциональной единицей

      4. сектором экономики 

5.  Неверным  признаком институциональной единицы  является

      1. владение активами

      2. ответственность по своим обязательствам

      3. совместное владение доходами

          4. право распоряжаться своими материальными и финансовыми

        ресурсами 
 
 
 

6. Резидентами  России являются

      1. сотрудники иностранных посольств

      2. иностранные студенты

      3. иностранные военнослужащие

7. Экономическая  территория страны не охватывает 

      1. национальное воздушное пространство

      2. территориальные воды

      3. посольства страны в других государствах

      4. военные и научные базы других государств 

8. Экономической  операцией называется изменение стоимости активов и обязательств институциональных единиц  под влиянием

9. В системе  национальных счетов не применяется  принцип

       1. двойной записи каждой операции

2. учёта операций не по начисленным, а  по фактически   

3.оценки операций в текущих рыночных ценах на момент их

4.уравнивания итогов операций по каждой стороне счёта путём    

10.  Экономическим  оборотом в СНС называется

  3. обмен экономической  информацией между хозяйствующими субъектами

  4. отражение активов и обязательств товаропроизводителей на счетах бухгалтерского учёта 

11. Экономические   потоки  возникают

1. только по взаимному соглашению между институциональными единицами

3. по взаимному соглашению между институциональными единицами и в одностороннем порядке

12. Трансфертом  не является

      1. выплата пенсии

      2. предоставление гуманитарной помощи

      3. получение наследства

      4. выплата заработной платы наёмным работникам 

13. Представление  одной институциональной единицей  товаров, услуг и активов другой  единице на безвозмездной основе  называется

      1. субсидией

      2. трансфертом

      3. пособием

      4. дотацией 

14. Текущие некомпенсируемые  выплаты из государственного  бюджета хозяйственным единицам, производящим определённые виды товаров и услуг называются

 

15. Счета  в  СНС составляются

      1. только по экономике в целом

      2. только по секторам экономики

      3. только по отраслям экономики

      4. по секторам, отраслям и по экономике в целом  

16.  В структуру  СНС входит баланс

17. Завершающим  блоком СНС являются

      1. счета для отраслей экономики

      2. счета для отдельных видов деятельности

      3. счета внешних операций

      4. балансовые таблицы и межотраслевой баланс 
 
 

stud24.ru

Система национальных счетов 17

СИСТЕМА НАЦИОНАЛЬНЫХ СЧЕТОВ (СНС)

1. Основные понятия СНС.

2. Система сводных национальных счетов.

1. Основные понятия СНС.

Система национальных счетов(СНС) – представляет собой систему взаимосвязанных статистических показателей, характеризующих макроэкономические процессы.

Суть СНС сводится к формированию показателей развития экономики на различных стадиях воспроизводства и взаимной увязке этих показателей. Каждой стадии воспроизводства соответствует специальный счет или группа счетов. Счета используются для регистрации экономических операций, осуществляемых институциональными единицами (предприятиями, учреждениями, домашними хозяйствами), являющимися резидентами данной страны. Отражаются также и операции между резидентами данной страны и нерезидентами.

Национальные счета – набор взаимосвязанных таблиц, имеющих вид балансовых построений. Каждый счет представляет собой баланс в виде двусторонней таблицы, в которой каждая операция отражается дважды: один раз – в ресурсах, другой – в использовании (табл. 1).

Схема сета Таблица 1

Итоги операций на каждой стороне счета балансируются или по определению, или с помощью балансирующей статьи, которая является ресурсной статьей следующего счета.

Балансирующая статья счета, обеспечивающая баланс (равенство) его правой и левой частей, рассчитывается как разность между объемами ресурсов и их использованием. Иначе говоря, балансирующая статья предыдущего счета, отраженная в разделе «Использование», является исходным показателем раздела «Ресурсы» последующего счета (табл. 2). Этим достигается увязка счетов между собой и образование СНС.

Балансирующие статьи национальных счетов Таблица 2

2. Система сводных национальных счетов.

Система национальных счетов, реализуемая в РФ, основана на новой версии Системы национальных счетов ООН, пересмотренной и принятой Статистической комиссией ООН в 1993 г. (СНС – 93).

СНС в РФ в настоящее время включает следующие основные счета:

1. Счет товаров и услуг.

2. Счет производства.

3. Счет образования (первичных) доходов.

4. Счет распределения первичных доходов.

5. Счет вторичного распределения доходов.

6. Счет использования располагаемого дохода.

7. Счет операций с капиталом.

8. Финансовый счет.

Схемы основных счетов приведены в табл. 3 – 9.

Таблица 3

Счет товаров и услуг

Выпуск продуктов и услуг в рыночных ценах =

= Выпуск продуктов и услуг в основных ценах +

+ Налоги на продукты и импорт –

— Субсидии на продукты и импорт.

Статистическое расхождение характеризует суммарную ошибку при построении всех счетов, которая не должна превышать 4-5% ВВП.

Таблица 4

Счет производства

ВВП = ВВ – ПП

Таблица 5

Счет образования доходов

ВП / ВСД = ВВП – ОТ – Н + С

Таблица 6

Счет распределения первичных доходов

ВНД = ВП / ВСД + ОТ + Н – С + Дпо – ДПр

Таблица 7

Счет вторичного распределения доходов

ВНРД = ВНД + ТТПо – ТТПр

Таблица 8

Счет использования располагаемого доходов

ВС = ВНРД – КП

Таблица 9

Счет операций с капиталом

ЧК/ЧЗ = ВС + КТПо – КТПр – ВНОК – ИЗМОб – ЧПц – ЧПЗННА

Все счета являются консолидированными, т.е. построенными для экономики в целом, и отражают, с одной стороны, отношения между национальной экономикой и другими странами, а с другой – взаимосвязь различных показателей системы счетов.

Для каждого сектора внутренней экономики предусматривается составление секторальных счетов экономики. Существуют также счета секторов «Домашние хозяйства», «Органы государственного управления» и «остальной мир».

3. Методы расчета макроэкономических показателей.

Валовый внутренний продукт может быть определен на разных стадиях воспроизводственного цикла соответствующими методами:

· производственным;

· распределительным;

· конечного использования.

На стадии производства товаров и услуг ВВП рассчитывается производственным методом как сумма ВДС всех отраслей или секторов экономики по рыночным ценам, включая чистые налоги на продукты и импорт:

ВВП = Σ ВДС + ЧНП + ЧНИ

На стадии распределения доходов ВВП определяется как сумма первичных доходов, выплаченных производственными единицами-резидентами, и включает: оплату труда наемных работников (ОТ), чистые налоги на производство (ЧНП) и импорт (ЧНИ), валовую прибыль экономики (ВПЭ) и валовые смешанные доходы (от собственности и предпринимательства) (ВСД):

ВВП = ОТ + ЧНП + ЧНИ + ВПЭ + ВСД

На стадии использования ВВП рассчитывается как сумма конечного потребления продуктов и услуг (КП), валового накопления (ВН) и чистого экспорта товаров и услуг, который представляет разницу между экспортом и импортом (Э – И):

ВВП = КП + ВН + (Э – И)

Каждый метод исчисления ВВП имеет самостоятельное значение в экономическом анализе.

Расчет ВВП на стадии производства позволяет отразить отраслевую структуру и характер развития экономики.

Валовый внутренний продукт, рассчитанный на стадии распределения, отражает состав и структуру доходов.

Валовый внутренний продукт, вычисленный методом конечного использования, позволяет определить вклад результатов труда данного года в увеличение национального богатства (валового сбережения).

Для оценки качества расчетов ВВП и других показателей различными методами используют специфический показатель – статистическое расхождение между произведенным и использованным ВВП. ВВП, скорректированный на инфляцию, называется реальным ВВП . Для корректировки используют индекс-дефлятор ВВП – это отношение ВВП, исчисленное в текущих ценах, к объему ВВП, исчисленного в сопоставимых ценах предыдущего периода.

mirznanii.com

Масштаб 1 5000 означает что

Масштаб

Масшта́б (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем случае отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.

Понятие наиболее распространено в геодезии, картографии и проектировании — отношение величины изображения объекта к его натуральной величине. Человек не в состоянии изобразить большие объекты, например дом, в натуральную величину, поэтому при изображении большого объекта в рисунке, чертеже или макете величину объекта уменьшают в несколько раз: в два, пять, десять, сто, тысячу и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину её изображения в несколько тысяч раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.

Масштаб в геодезии, картографии и проектировании

Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.

Масштабы на картах и планах могут быть представлены численно или графически.

Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1 : 5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.

План города (более крупный масштаб)

Карта Мира (более мелкий масштаб)

Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1 : 1 000 крупнее, чем масштаб 1 : 25 000. Иначе говоря, при более крупном масштабе объект изображается крупнее (больше), при более мелком масштабе — тот же объект изображается мельче (меньше).

Именованный масштаб показывает, какое расстояние на местности соответствует 1 см на плане. Записывается, например: «В 1 сантиметре 100 километров», или «1 см = 100 км».

Графические масштабы подразделяются на линейные и поперечные.

• Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части.
• Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла. Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД=0,2 мм, а точность 0,1.

Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).

Масштабы изображений на чертежах должны выбираться из следующего ряда:[1]

Масштабы уменьшения	1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1 000
Натуральная величина	1:1
Масштабы увеличения	2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1

При проектировании генеральных планов больших объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.

Масштаб в фотографии

Основная статья: Линейное увеличение

При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.

Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.

Масшт

zna4enie.ru

5000 его длина составляет 10 см

1: 50 000 — это означает, что в одном сантиметре 5000 и умножаете это число на 10. Итого = 50 000))))

ответ 10*5 000=50 000

1:5’000=10*5’000=50’000(см) 1 см-5’000

Мы умножаем длину ручья на масштаб 1:5000: 10*5000=50000

М 1:5000 в 1 см — 5000 см в 10 см 5000*10 = 50000 см = 500 м = 0,5 км Протяженность ручья составляет 50000 см или 500 м, или 0,5 км

10 умножить на 5000

touch.otvet.mail.ru

Ответы@Mail.Ru: Как начертить отрезок длиной 200м в масштабе 1:5000? помогите плиз

Это будет отрезок длиной 4см. Дели длину на 5000 — это будет количество метров и переводи в более удобную единицу измерения — сантиметр.

рома, слушай здесь: масштаб означает, что на карте 1 см будет на местности отражать 5000 см (50м) значит 200 м на местности будут на карте 4 см.

Если я не ошибаюсь.. . 4см И запомни, все размеры в миллиметрах!

В машиностроении — измерение в масштабе в миллиметрах, в строительстве и географии — в сантиметрах, и цифры будут разные. Если строительство — то 1:5000=Х : 20000(см)

touch.otvet.mail.ru

Ответы@Mail.Ru: что значит масштаб 1:100000

Масшта́б (нем. Maßstab, от Maß — мера, размер и Stab — палка) — в общем случае отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта. Это степень уменьшения горизонтального проложения линий местности на карте. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности. Для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м) , 0,1 мм — 100 см (1 м) . Для масштаба 1:100000 точность масштаба будет равна соответственно 1 км.

Один см на бумаге соответствует 1 км в натуре

в 1см на карте 1000метров

Это степень уменьшения горизонтального проложения линий местности на карте. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности. Для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м) , 0,1 мм — 100 см (1 м) . Для масштаба 1:100000 точность масштаба будет равна соответственно 1 км.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют МАСШТАБОМ карты . Вот что такое масштаб . В рассматриваемом нам примере масштаб карты равен 1:100 000. Говорят, что карта сделана в масштабе одна стотысячная .

1:100.000 ЭТО: 1 КМ.

Масштабы топографических карт Крупномасштабные планы 1 : 1 000 000 — в 1 см 10 км 1 : 500 000 — в 1 см 5 км 1 : 200 000 — в 1 см 2 км 1 : 100 000 — в 1 см 1 км 1 : 50 000 — в 1 см 500 м 1 : 25 000 — в 1 см 250 м 1 : 10 000 — в 1 см 100 м 1 : 5000 — в 1 см 50 м 1 : 2000 — в 1 см 20 м 1 : 1000 — в 1 см 10 м 1 : 500 — в 1 см 5 м

touch.otvet.mail.ru

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ К РАБОТЕ 1 — КиберПедия

 

При составлении планов и карт горизонтальные проекции линий местности уменьшают в определенное число раз в зависимости от требований и точности, предъявляемым к планам и картам.

Степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте называется масштабом. Иными словами, масштаб есть отношение длины отрезка ℓ на плане или карте к горизонтальной проекции соответствующего отрезка L на местности, т.е.

ℓ/L – масштаб. Различают численный и графические масштабы.

Ч и с л е н н ы й м а с ш т а б . Численный масштаб – это правильная дробь, числитель которой есть единица, а знаменатель – число, показывающее, во сколько раз горизонтальные проекции линии местности уменьшены на плане или карте:

= = ,

 

где М – знаменатель численного масштаба.

Чем больше значение знаменателя численного масштаба М, тем больше степень уменьшения горизонтальных проекций линий местности и тем мельче масштаб плана или карты. Численный масштаб – безразмерная величина, поэтому им можно пользоваться при измерениях в любых линейных мерах.

В геодезии наиболее часто применяются следующие масштабы: 1:500, 1:1000, 1:2000, 1:5000 – для планов и 1:10000, 1:25000, 1:50000, 1:100000, 1:200000, 1:300000, 1:500000, 1:1000000 – для карт. Указанные отношения показывают, что горизонтальные проекции линий местности уменьшены на плане соответственно в 500, 1000, 2000 и т.д. раз, т.е. отрезку в 1 см на плане соответствуют на местности длины: 500 см или 5 м, 1000 см или 10 м,

2000 см или 20 м и т.д. На картах ниже подписи численного масштаба (например, 1:10000) приводится пояснительный масштаб: «в 1 сантиметре 100 м».

 

При помощи масштабов можно решить следующие задачи:

 

1. По длине горизонтальной проекции линии L на местности определить длину соответствующего отрезка ℓ на плане масштаба .

 

Пусть L = 275,5 м, = 1:5000.

Из соотношения = находим ℓ= = = 5,51 см

По длине отрезка ℓ на плане масштаба определить длину линии L на местности.

Пусть ℓ = 3,62 см, =1:2000

Тогда L = ℓ∙М = 3,62 cм × 2000 = 7240 см = 72,4 м

 

При большом объеме работ для исключения вычислений в решении указанных задач удобнее пользоваться графическими масштабами, к которым относятся линейныйи поперечный(трансверсальный) масштабы.

Л и н е й н ы й м а с ш т а б . Линейным масштабом называется графическое изображение численного масштаба в виде прямой линии с делениями для отсчета расстояний ( рис. 1 а, б, в ).

а)

 

б)

 

 

в)

 

Рисунок 1 — Масштабы

 

а) — линейный с основанием 1 см;

б) — линейный с основанием 2 см;

в) — поперечный.

 

Для построения линейного масштаба на прямой линии откладывают ряд отрезков одинаковой длины а (например, а = 2 см), называемые основанием линейного масштаба. Крайний левый отрезок делят на 10 равных частей и на правом его конце ставят 0, а на левом – число метров (километров), которое на плане соответствует основанию в заданном масштабе. Вправо от 0 деления масштаба подписывают значениями соответствующих расстояний на местности. Размерность ставится один раз в правом конце линейного масштаба.

На рисунке 1а показан линейный масштаб для численного масштаба 1:2000, основание равно а=1 см. На рисунке 1б показан масштаб для численного масштаба 1:2000, основание а=2 см, на котором раствором циркуля-измерителя найден отрезок на плане, соответствующий линии местности L=106 м. При этом десятые доли малого деления оцениваются на глаз. В связи с этим линейный масштаб во многих случаях не позволяет измерять расстояние с необходимой точностью.

Т о ч н о с т ь м а с ш т а б о в. При оценке точности нанесения точек на план следует исходить из физиологических возможностей человеческого глаза. Как известно, глаз человека способен отчетливо различать две точки, если они располагаются под углом не менее 60«^{к наблюдателю. При меньшем угле зрения глаз воспринимает две точки слившимися в одну. Для расстояния наилучшего зрения равного 25 см, углу 60«соответствует отрезок, равный 0,1 мм. Таков, например, диаметр кружка от укола остро отточенной иглы. Отсюда следует, что на плане (карте) в самом благоприятном случае можно изобразить лишь такие горизонтальные проекции линии местности, которым в данном масштабе соответствует отрезок 0,1мм и более.}

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1мм на плане, называется точностью масштаба t,т.е.

 

t = = 0,0001 · М, м (1.1)

 

где М – знаменатель численного масштаба.

Значения точностей различных масштабов, найденных по формуле (1), приведены ниже.

 

Численные масштабы	1:500	1:1000	1:2000	1:5000	1:10000	1:25000
Точность масштаба, м	0,05	0,10	0,20	0,50	1,00	2,50

 

Такая точность определения расстояний на плане или карте не может быть достигнута при использовании линейного масштаба. Поэтому для повышения точности измерений расстояний на плане или карте применяют поперечный (трансверсальный) масштаб.

П о п е р е ч н ы й м а с ш т а б. Поперечный масштаб является разновидностью линейного масштаба. Для его построения на отрезке прямой АВ (рис. 1в) несколько раз откладывают основание масштаба, равное обычно 2 см. В полученных точках восстанавливают перпендикуляры к линии АВ произвольной, но равной длины. Два крайних перпендикуляра делят на m равных частей и через одноименные точки проводят линии, параллельные прямой АВ. Левые нижнее АО и верхнее СD основания делят на n равных частей; точку О нижнего основания соединяют наклонной линией с первой точкой Е верхнего основания СD, а через все остальные точки проводят линии, параллельные ОЕ (трансверсали).

Для определения величины наименьшего деления ed поперечного масштаба из подобия треугольников ОЕD и Оed можно записать:

 

отсюда ed = .

 

Поскольку ED= , а Od= , то ed = = = P,

 

где Р = e · d — наименьшее деление поперечного масштаба.

 

Если основание поперечного масштаба а = 2 см, а левое основание и перпендикуляры разделены на 10 частей, т.е. m · n = 100, то имеем нормальный сотенный поперечный масштаб.У такого масштаба отрезки между перпендикуляром OD и трансверсалью ОЕ (см. рис. 1в) составляют сотые доли основания масштаба.

Поперечный масштаб обычно гравируют на металлических пластинках, которые закрепляются на некоторых геодезических приборах (геодезических транспортирах, масштабных линейках, кипрегелях). Оцифровка поперечного масштаба производится так же, как и линейного – в соответствии с численным масштабом. С помощью поперечного масштаба можно решить те же задачи, что и по численному или линейному масштабам.

Каждая линия, откладываемая на плане или карте с помощью поперечного масштаба, слагается из трех частей: а) числа целых оснований, взятых от нулевого перпендикуляра до правой ножки циркуля; б) числа десятых долей основания, взятых от нулевого перпендикуляра до левой ножки измерителя; в) сотых долей основания, расположенных между вертикальной линией и трансверсалью.

Аналогично можно решать обратную задачу — по длине отрезка на плане или карте определить длину соответствующей линии местности.

Для примера на поперечном масштабе, который соответствует численному 1:2000 (см. рис. 1в), показано положение ножек циркуля-измерителя при взятии отрезков длиной 62,8 м и 131,4 м.

1 : 2000 в 1 см – 20 м; в 1 осн. – 40 м.

62,8 м : 40 м = 1,57 (осн)

131,4 м : 40 м = 3,285 (осн)

 

При пользовании поперечным масштабом необходимо следить, чтобы концы обеих ножек циркуля-измерителя располагались на одной горизонтальной линии масштаба либо в середине между одноименными горизонтальными линиями.

Топографические планы создают в крупных масштабах 1:500; 1:1000; 1:2000 и 1:5000. Предназначаются они для составления генеральных планов, технических проектов и рабочих чертежей при обеспечении строительства различных инженерных сооружений.

Карты по масштабам подразделяются на крупномасштабные – 1:10000; 1:25000; 1:50000; 1:100000, среднемасштабные – 1:200000; 1:300000; 1:500000 и мелкомасштабные 1:1000000 и мельче. Крупномасштабные топографические карты могут быть использованы для предварительных изысканий строительства, для выбора территорий, намечаемых под строительство промышленных сооружений, жилых поселков, городов.

После изучения теоретических сведений по данной теме можно переходить к выполнению заданий по теме «Масштабы».

 

 

Задание к работе 1. Масштабы, их точность

Задание 1.Оцифровать линейный масштаб с основанием а=1см для численного масштаба 1:

 

 

Задание 2.Изобразить на плане следующие длины отрезков:

 

Масштабы	Длина отрезка
на местности, м	на плане
1:200
1:500
1:1000
1:25000

 

Задание 3. Определить длины отрезков (м), взятых с планов следующих масштабов

 

Масштабы	Длина отрезка
на плане	на местности, м
1:500
1:2000
1:10000
1:50000

 

Задание 4.Определить графическую точность нижеперечисленных масштабов:

 

Масштаб	Точность, м	Масштаб	Точность, м
1:200		1:5000
1: 500		1:10000
1:1000		1:25000
1:2000		1:500000

 

 

Задание 5. Вычертить поперечный масштаб с основанием 2 см

 

 

РАБОТА 2

 

cyberpedia.su

Ответы@Mail.Ru: что такое именованный масштаб

Именованный (словесный) масштаб — вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке. Это то пояснение, указывающее соотношение длин линий на карте и на местности. Например, если численный масштаб 1: 100 000, именованный масштаб выглядит так> в 1см — 1км>, так как 1 см на карте соответствует 100 000 см, т. е. 1 км, на местности. Линейный масштаб служит для измерения по картам длин линий в реальности. Он представляет собой прямую линию, разделенную на равные отрезки, соответствующие десятичным числам расстояний на местности. Отрезки, а называют основанием масштаба. А расстояние на местности, соответствующее основанию, называют величиной линейного масштаба. Для повышения точности определения расстояний крайнее слева основание делят на более мелкие части б, называемые наименьшими делениями линейного масштаба. При работе с планом и картой часто приходиться переводить численный масштаб в именованный или линейный. Для этого необходимо знаменатель численного масштаба перевести в более крупные меры — метры и километры. Например, если численный масштаб плана 1:5000, это значит что в 1 см на плане соответствует на местности 5000 см или 50 метрам.

Именованный (словесный) масштаб — вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке. Это то пояснение, указывающее соотношение длин линий на карте и на местности. Например, если численный масштаб 1: 100 000, именованный масштаб выглядит так> в 1см — 1км>, так как 1 см на карте соответствует 100 000 см, т. е. 1 км, на местности. Линейный масштаб служит для измерения по картам длин линий в реальности. Он представляет собой прямую линию, разделенную на равные отрезки, соответствующие десятичным числам расстояний на местности. Отрезки, а называют основанием масштаба. А расстояние на местности, соответствующее основанию, называют величиной линейного масштаба. Для повышения точности определения расстояний крайнее слева основание делят на более мелкие части б, называемые наименьшими делениями линейного масштаба. При работе с планом и картой часто приходиться переводить численный масштаб в именованный или линейный. Для этого необходимо знаменатель численного масштаба перевести в более крупные меры — метры и километры. Например, если численный масштаб плана 1:5000, это значит что в 1 см на плане соответствует на местности 5000 см или 50 метрам. Источник: ► Тема «Масштаб» — География

а зачем он не понимаю

touch.otvet.mail.ru

Характеристика и мантисса десятичного логарифма.

2015-06-14   

Десятичный логарифм
Характеристика и мантисса

Десятичным логарифмом числа называется его логарифм по основанию 10. Кроме общего обозначения $log_{10} N$ для десятичных логарифмов обычно применяют сокращенное обозначение $lg N$.

Десятичные логарифмы широко применяются в приближенных вычислениях; в связи с этим имеются подробные и весьма точные таблицы десятичных логарифмов.

Для применения к приближенным вычислениям нам потребуются некоторые свойства и понятия, относящиеся к десятичным логарифмам.

Рассмотрим все числа вида $10^{n}$, где $n$ — целое число:

$\cdots; 10^{-3} = 0,001; 10^{-2} = 0,01; 10^{-1} = 0,1; 10^{0} = 1; 10^{1}=10; 10^{2}=100; 10^{3} = 1000; \cdots$

Будем говорить, что эти числа представляются единицей с нулями (с последующими нулями, если $n > 0$, и с предшествующими нулями, если $n

Десятичный логарифм числа, представляемого единицей с нулями, равен числу нулей в этом числе, если оно есть единица с последующими нулями, и числу нулей с противоположным знаком, если оно есть единица с предшествующими нулями.

Например:

$lg 0,0001=-4, lg 0,01=-2, lg 1000 = 3, lg 1000000 = 6$.

Десятичный логарифм любого числа, не равного целой степени десяти, является числом дробным (вообще говоря, иррациональным).

Напомним, что всякое число (рациональное или иррациональное) однозначно разлагается на сумму своей целой части и дробней части. При этом целой частью данного числа называется наибольшее целое число, не превосходящее данного; дробная часть любого числа заключена между нулем и единицей:

$3,176 = 3 + 0,176; — 2,143 = — 3 + 0,857 = \overline{3},857$.

Введем теперь следующее.

Определение. Для любого положительного числа целая часть десятичного логарифма называется характеристикой, а дробная часть—мантиссой этого логарифма.

Характеристику логарифма любого положительного числа можно найти точно, и делается это с помощью простого правила. Действительно, пусть дано число $N > 0$; тогда можно указать такие две степени числа 10 с последовательными целыми показателями $n$ и $n + 1$, между которыми находится данное число $N$:

$10^{n}

Прологарифмируем эти неравенства по основанию 10:

$n \leq lg N

в соответствии со свойством 5 логарифмов (Определение и свойства логарифмов). Отсюда следует, что целая часть, т. е. характеристика $lg N$, равна $n: lg N = n, \cdots$ Многоточием обозначены неизвестные десятичные знаки мантиссы, т. е. дробной части $lg N$. При этом в случае $n

Для формулировки соответствующего правила рассмотрим два случая: $N > 1$ и $N

Пусть $N > 1$ (десятичный логарифм $lg N$ в этом случае положителен). Обозначим через $k$ число цифр в записи целой части $N$. Ясно, что в этом случае

$10^{k-1} \leq N

Например, для $N = 378,6$ (трехзначная целая часть)

$10^{2} \leq 378,6

Логарифмируя неравенства (1), получаем

$k – 1 \leq lg N

и видим, что характеристика $lg N$ равна $k – 1$ (например, характеристика логарифма 378,6 равна 2).

Итак, характеристика десятичного логарифма числа, большего единицы, на единицу меньше количества цифр его целой части.

Например:

$lg 3,524 = 0, \cdots; lg 47,01 = 1; \cdots, lg 936,3 = 2, \cdots$

Пусть теперь положительное число $N$ меньше единицы: $0

Запись числа $N$ начинается в этом случае с нуля целых; за этим нулем может следовать еще несколько нулей перед первой отличной от нуля цифрой числа. Если число нулей перед первой ненулевой цифрой (включая и нуль целых) равно $l$, то

$1^{-l} \leq N

Например:

$10^{-1} \leq 0,32 $10^{-2} \leq 0,032 $10^{-3} \leq 0,0032 $\cdots \cdots$

Неравенства (3) показывают, что

$- l \leq lg N

т. е. характеристика логарифма $lg N$ равна $-l$.

Итак, характеристика десятичного логарифма положительного числа, меньшего единицы, равна взятому со знаком минус числу нулей в данном числе, предшествующих первой значащей цифре, включая и нуль целых.

Например:
$lg 0,3052 = \overline{1}, \cdots; lg 0,0587 = \overline{2} \cdots; lg 0,0096 = \overline{3}, \cdots$

Мы выяснили, что характеристика десятичного логарифма числа определяется непосредственно по виду самого числа, если оно целое или представлено в виде десятичной дроби. Для определения характеристики, таким образом, не нужны никакие вычисления (и таблицы). Что же касается мантиссы, то она, как правило, берется из таблиц (например, из таблиц Брадиса). При этом следует пользоваться одним замечательным свойством мантиссы: если в логарифмируемом числе перенести запятую на любое количество знаков влево или вправо, то мантисса десятичного логарифма от этого не изменится (изменится только характеристика логарифма). В самом деле, перенести в числе запятую — это значит умножить его на некоторую целую (положительную или отрицательную) степень числа 10. Например, при переносе запятой на 2 знака вправо число умножится на $10^{2} = 100$, а при переносе запятой на 2 знака влево оно умножится на $10^{-2} = 1/100$. Пусть

$lg N = n + m$,

где $n$ — характеристика, а $m$ — мантисса этого логарифма. После переноса запятой в числе $N$ на $k$ знаков получится число $N \cdot 10^{ \pm k}$t (верхний знак относится к случаю переноса запятой вправо, а нижний — к случаю переноса запятой влево). На основании правил логарифмирования имеем

$lg (N \cdot 1^{\pm k}) = lg N \pm k lg 10 = lg N \pm k$.

Но $k$ — целое число, так что прибавление $\pm k$ к $lg N$ может отразиться лишь на его характеристике:

$lg (N \cdot 10^{\pm k}) = n + m \pm k = (n \pm k) + m$.

Из рассмотренного можно заключить, что если числа записаны с помощью одних и тех же и одинаково расположенных цифр и отличаются одно от другого только местоположением в них запятой, то десятичные логарифмы таких чисел имеют одну и ту же мантиссу (но, конечно, разные характеристики!). Таковы, например, числа $42,59, 4,259, 0,4259, 0,04259$ и т. д.

В качестве примера найдем без таблиц разность $lg 28,76 — lg 0,002876$.

Логарифмы, из которых составлена данная разность, отличаются лишь характеристиками, а мантиссы у них одинаковы и при вычитании взаимно уничтожаются. Поэтому искомая разность логарифмов равна разности их характеристик: $lg 28,76 – lg 0,002876 = 1 — ( — 3) = 1 + 3 = 4$. Этот пример можно решить и так:

$lg 28,76 — lg 0,002876 = lg \frac{28,76}{0,002876} = lg 10000 = lg 10^{4} = 4$.

earthz.ru

Таблица и формула для перехода от десятичных логарифмов к натуральным.

Таблица и формула для перехода от десятичных логарифмов к натуральным. Если Вам известен десятичный логарифм какого-то числа Х (равный lg(X)), то натуральный логарифм этого числа (равный ln(X)) будет равен, согласно основным свойствам логарифмов : ln(X)=In10*lg(X)=(1/Ig(e))*lg(X)=(1/M)*lg(X), т.е. натуральный логарифм числа, равен десятичному логарифму этого числа умноженному на «число 1/М»=1/Ig(e). Для быстрых оценок приводим табличку: Таблица для перехода от десятичных логарифмов к натуральным (таблица умножения на «число 1/М» (у англосаксов это «число 1/A») = In 10 = 2,3025851). Таблица для перехода от десятичных логарифмов к натуральным (таблица умножения на «число 1/М» (у англосаксов это «число 1/A») = In 10 = 2,3025851).   0 10 20 30 40 50 60 70 80 90 0 0,0000 23,026 46,052 69,078 92,103 115,129 138,155 161,181 184,207 207,233 1 2,3026 25,328 48,354 71,380 94,406 117,431 140,458 163,484 186,509 209,535 2 4,6052 27,631 50,657 73,683 96,709 119,734 142,760 165,786 188,812 211,838 3 6,9078 29,934 52,959 75,985 99,011 122,037 145,062 166,089 191,115 214,140 4 9,2103 32,236 55,262 78,288 101,314 124,340 147,365 170,391 193,417 216,443 5 11,513 34,539 57,565 80,590 103,616 126,642 149,668 172,694 195,720 218,746 6 13,816 36,841 59,867 82,893 105,919 128,945 151,971 174,997 198,022 221,048 7 16,118 39,144 62,170 85,196 108,221 131,247 154,273 177,299 200,325 223,351 8 18,421 41,447 64,472 87,498 110,524 133,550 156,576 179,602 202,627 225,653 9 20,723 43,749 66,775 89,801 112,827 135,853 158,878 181,904 204,930 227,956

tehtab.ru

Таблица Брадиса — натуральные логарифмы.

Таблица Брадиса — натуральные логарифмы. Десятки Единицы 0 0,6931 1,0986 1,3863 1,6094 1,7918 1,9459 2,0794 2,1972 2,3026 2,3979 2,4849 2,5649 2,6391 2,7081 2,7726 2,8332 2,8904 2,9444 2,9957 3,0445 3,091 3,1355 3,1781 3,2189 3,2581 3,2958 3,3322 3,3673 3,4012 3,434 3,4657 3,4965 3,5264 3,5553 3,5835 3,6109 3,6376 3,6636 3,6889 3,7136 3,7377 3,7612 3,7842 3,8067 3,8286 3,8501 3,8712 3,8918 3,912 3,9318 3,9512 3,9703 3,989 4,0073 4,0254 4,0431 4,0604 4,0775 4,0943 4,1109 4,1271 4,1431 4,1589 4,1744 4,1897 4,2047 4,2195 4,2341 4,2485 4,2627 4,2767 4,2905 4,3041 4,3175 4,3307 4,3438 4,3567 4,3694 4,382 4,3944 4,4067 4,4188 4,4308 4,4427 4,4543 4,4659 4,4773 4,4886 4,4998 4,5109 4,5218 4,5326 4,5433 4,5539 4,5643 4,5747 4,5850 4,5951 4,6052 4,6151 4,625 4,6347 4,6444 4,654 4,6634 4,6728 4,6821 4,6913

tehtab.ru

    Терминология
    Отыскание логарифма данного числа
    Отыскание числа по данному логарифму
Логарифмы применяются для замены сложных математических действий более простыми, например возвышение в степень приводится при помощи логарифмов к умножению, извлечение корня — к делению и т. д.

Терминология. Если Ab = N, то b = log a N; логарифм числа N при основании «a» есть степень, в которую нужно возвести число «а», чтобы получить число N; «а» называется основанием логарифма. Логарифмы, употребляемые обычно в вычислениях, называются десятичными (обыкновенными, Бригговыми) и имеют основание а = 10.
Десятичный логарифм какого-нибудь числа N представляет собой степень, в которую нужно возвести число 10, чтобы получить число N; например log10 100 = 2, так как 100 = 10 в квадрате. Вместо log10N всегда применяется обозначение lg N.

Логарифмы при основании е = 2,7182818284… называются натуральными или неперовыми и вместо lg е N принято обозначение ln N.

Между натуральными и десятичными логарифмами существуют следующие зависимости:

Отыскание логарифма данного числа

Логарифм состоит из целой части, называемой характеристикой, и дробной части, называемой мантиссой, например, lg 25 = 1,39794, здесь 1 — характеристика, 39794 — мантисса.
Мантисса находится по таблицам логарифмов, а характеристика определяется в зависимости от количества цифр целой части числа N > 1, логарифм которого отыскивается, или в зависимости от положения запятой в случае, если N Логарифмы целых чисел не выше трехзначных находятся непосредственно в таблице имеющейся на этом сайте; для того же, чтобы отыскать логарифм числа N 1, имеющего не более трех значащих цифр и на конце несколько нулей, отбрасывают запятую и нули справа и слева, затем ищут в таблице для полученного таким образом числа логарифм, из которого берут только мантиссу, характеристику же определяют по правилу, поясненному ниже:

Мантисса логарифмов всех этих чисел одна и та же, так как, если отбросить запятую и нули справа и слева у этих чисел, то получится одно и то же трехзначное число 758. Мантисса равна 87967. Характеристика логарифма каждого числа равна его значности минус единица.
Если после отбрасывания запятой и нулей останется число, содержащее больше трех значащих цифр, то логарифм его можно найти приближенно, отбрасывая при отыскании мантиссы все цифры, кроме первых трех.
Пример. Найти приближенно lg 40,536. Находим мантиссу логарифма числа 405, она равняется 60746 это приблизительно равно 6075; характеристика равняется 1, следовательно, lg 40,536, что приблизительно равно 1,6075.

Отыскание числа по данному логарифму.

По мантиссе логарифма отыскивается число. Количество цифр и положение запятой определяются по правилу, указанному выше. Пример, lg N =3,2380. По мантиссе 2380 находим число 173. Так как характеристика равна 3, то число должно быть четырехзначным, следовательно, N приблизительно равняется 1730.
Из определения логарифма числа следует:

Натуральные и десятичные логарифмы отрицательных чисел мнимы.
Действия с логарифмами:

Эти зависимости сохраняют силу при любом основании логарифмов.

cnc.im

Выруби AdBlock ! ! !

ШВЕЦОВ К.И., БЕВЗ Г.П. СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ АРИФМЕТИКА, АЛГЕБРА, 1965  СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ Решения. а) б) в) 36. Десятичные логарифмы 1. Свойства десятичных логарифмов а) Логарифм целого числа, изображенного единицей с последующими нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в данном числе. Примеры, lg 100 = 2; lg 10000 = 4. б) Логарифм десятичной дроби, изображаемой единицей с предшествующими нулями, есть целое отрицательное число, содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая и 0 целых. Примеры. lg 0,00001 = -5; lg 0,001 = -3. в) Логарифм рационального числа, которое не является степенью 10 с целым показателем (положительным, отрицательным или нулевым), есть иррациональное число. Логарифм иррационального числа может быть как рациональным, так и иррациональным числом. Например, (рациональное число), (иррациональное число). Целая часть логарифма называется его характеристикой, а дробная — мантиссой. г) Характеристика логарифма числа, большего единицы, на единицу меньше числа цифр его целой части. Примеры. lg 3,15 = 0,…; lg 375 = 2,…; lg 2000 = 3,… д) Характеристика логарифма числа, меньшего единицы, содержит столько отрицательных единиц, сколько нулей в этом числе предшествует первой значащей цифре, считая и нуль целых. При этом мантисса логарифма положительна. Примеры. е) От умножения числа на 10, 100, 1000,…, вообще на единицу с последующими нулями, мантисса логарифма не меняется, а характеристика увеличивается на столько единиц, сколько нулей в множителе. От деления числа на единицу с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе. Поэтому перенесение запятой в десятичной дроби на несколько знаков вправо или влево не изменяет мантиссы логарифма этой дроби, а только характеристику. Таким образом, логарифмы чисел 0,00423; 0,0423; 4,23; 423 отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны). Мантиссы логарифмов чисел, имеющих одну и ту же значащую часть, одинаковы. 2. Преобразование отрицательного логарифма. Известно, что десятичные логарифмы чисел, меньших 1, отрицательны. Такие логарифмы всегда можно преобразовать так, что мантисса у них будет положительная, а характеристика — отрицательной. Это выполняется по следующему правилу. Чтобы преобразовать логарифм с отрицательной мантиссой в логарифм с положительной мантиссой, надо к характеристике прибавить минус единицу, а к мантиссе прибавить плюс единицу. Так, например, если мы имеем логарифм -2,3781, то можно его преобразовать так: -2,3781 = -2 — 0,3781 = (-2 — 1) + (1 — 0,3781) = -3 + 0,6219 = . Кратко эти действия записывают так: Примеры. 3. Таблицы десятичных логарифмов. Существуют таблицы, в которых даются десятичные логарифмы всех чисел с точностью до трех, четырех, пяти и т.д. десятичных знаков. Соответственно этому их называют трехзначными, четырехзначными, пятизначными и т.д. Чаще всего пользуются четырехзначными таблицами десятичных логарифмов. Эти таблицы содержат мантиссы логарифмов всех целых чисел от 1 до 9999 включительно, вычисленные с четырьмя десятичными знаками. Этими таблицами пользуются так. Пример 1. Найдем десятичный логарифм трехзначного числа 73,3. Его характеристика 1, так как в числе 73 две цифры. Чтобы найти мантиссу, отбрасываем запятую и ищем мантиссу числа 733. В столбце, обозначенном буквой N, находим число 73. Двигаясь по строке, в которой находится число 73, до пересечения ее со столбцом, обозначенным цифрой 3, находим 8651. Число 0,8651 и будет искомой мантиссой. Итак, lg 73,3 = 1,8651. ⇦ Ctrl предыдущая страница / страница 132 из 168 / следующая страница Ctrl ⇨ мобильная версия страницы Смотрите также на этом сайте: ГАДАНИЯ, СОННИКИ, ЗАГОВОРЫ, НУМЕРОЛОГИЯ, ХИРОМАНТИЯ, ВУДУ, МАЯТНИК, ДЕНЕЖНАЯ МАГИЯ ВЯЗАНИЕ НА СПИЦАХ, КРЮЧКОМ, ТУНИССКОЕ ВЯЗАНИЕ, МОДЕЛИ ВЯЗАНОЙ ОДЕЖДЫ; ШИТЬЕ; МАШИННОЕ ВЯЗАНИЕ РАЗНООБРАЗНЫЕ КУЛИНАРНЫЕ РЕЦЕПТЫ; ГОРШОЧКИ, МИКРОВОЛНОВКА; КОНСЕРВИРОВАНИЕ СПРАВОЧНИКИ ПО ФИЗИКЕ, МАТЕМАТИКЕ, АНГЛИЙСКОМУ ЯЗЫКУ; ПОХУДЕНИЕ, АКУПУНКТУРА; НЕИСПРАВНОСТИ АВТОМОБИЛЯ МНОЖЕСТВО ИСТОРИЧЕСКИХ ФАКТОВ О СОБЫТИЯХ, ОРУЖИИ И ОБМУНДИРОВАНИИ ВТОРОЙ МИРОВОЙ ВОЙНЫ; АРМЕЙСКИЕ БОТИНКИ ВСЕХ ВРЕМЕН ПОПУЛЯРНЫЕ ПЕСЕННИКИ 1963-1987 гг.; ТОСТЫ, РОЗЫГРЫШИ, КОНКУРСЫ Пользуйтесь поиском вверху страницы! Все, что будет найдено со значком Ł — относится к данному сайту 

cartalana.org

Мантиссы десятичных логарифмов, таблицы — Энциклопедия по машиностроению XXL

Таблица V. МАНТИССЫ ДЕСЯТИЧНЫХ ЛОГАРИФМОВ

Отыскание чисел по их десятичным логарифмам. Для отыскания числа по его логарифму может быть использована та же таблица мантисс (табл. V, стр. 34). Если мантисса меньше 0,3030, то соответ-  [c.107]

Мантисса находится по таблицам логарифмов, а характеристика определяется в зависимости от количества цифр целой части числа, логарифм которого разыскивается, или в зависимости от положения запятой в случае десятичной дроби, как указано в табл. 1.  [c.85]

Логарифмы целых чисел не выше трехзначных находятся непосредственно в этой таблице для того же, чтобы отыскать логарифм числа N десятичной дроби) или числа 1, имеющего не более трех значащих цифр и на конце несколько нулей, отбрасывают запятую и нули справа и слева, затем ищут в таблице для полученного таким образом числа логарифм, из которого берут только мантиссу, характеристику же определяют по правилу, поясненному ниже  [c.67]

Нахождение логарифма (десятичного) трехзначного числа производится непосредственно по таблице, а для числа с тремя значащими цифрами из таблицы берется мантисса, характеристика же устанавливается по правилам алгебры. Например,  [c.34]

Математические таблицы даны, соответственно обычной практике технических справочников, в нижеследующем объёме степени, корни, натуральные логарифмы, длины окружностей, площади кругов и обратные величины (табл. I), мантиссы десятичных логарифмов (таблица 2), натуральные значения тригонометрических функций (табл. 3), характеристики дуг (табл. 4—6), специальные фужции (табл. 7 и 8), важнейщие постоянные (табл. 9) и сводка расчётных характеристик плоских фигур и тел (табл. 10 и 11).  [c.9]

Мантиссы десятичных логарифмов (табл. 2) и натуральные значения тригонометрических функций (табл. 3) даны в расширенном объёме шестизначные мантиссы десятичных логарифмов для аргументов от 1 до 10000, шести-и семизначные таблицы тригонометрических функций через Г. Столь подробные таблицы исключают необходимость применения специальных математических справочников и позволяют осуществлять с необходимой точностью даже наиболее строгие вычисления по геодезии, механике, электротехнике и т. п.  [c.9]

Десятичные, или бригговы, логарифмы имеют основанием число 10 и обозначаются символом Ig. Правила вычислений с десятичными логарифмами см. стр. 107. Таблица мантисс, т. е. дробной части числа, представляющего логарифм, приведена на стр. 34.  [c.113]

В шестой графе таблицы, помещённой на стр. 14, указаны десятичные логарифмы целых чисел от 1 до 1000. Таким образом логарифмы целых чисел не выше трёхзначных отыскиваются непосредственно по таблицам. Для того же, чтобы разыскать логарифм десятичной дроби или числа, имеющего на конце несколько нулей, отбрасывают запятую и нули справа и слева и, обратив его в целое трехзначное число, ищут по таблицам (стр. 14) его логарифм, из которого берут только мантиссу, характеристику же опреде- ляют по правилу, пояснённому в табл. 1.  [c.85]

Для определения десятичных логарифмов чисел сначала для данного числа находят характеристику его логарифма, а затем — мантиссу по таблице. Для трехзначных чисел мантиссу находят на пересечении строки, в начале которой (графа Щ стоят две первые цифры данного числа, и столбца-, озаглавленного третьей цифрой. Если заданное число имеет больше трех значапщх цифр, необходимо применить линейную интерполяцию.  [c.442]

Для нахождения числа по его десятичному логарифму служит таблица вдагаржфмов. Аргументом в этой таблице является мантисса заданного логарифма. На пересечении строки, определяемой двумя Первыми  [c.449]

Десятичные логарифмы записываются в виде десятичной дроби с точностью до определённого десятичного знака её целая часть называется характеристикой логарифма, а дробная —мант и сс ой например, Ig 285 = 2,454845, здесь 2 —характеристика, а 454845 — мантисса. Если число больше единицы, то характеристика положительна и на единицу меньше числа его цифр, стоящих перед запятой если число меньше единицы, то характеристика отрицательна и по абсолютной величине равна числу нулей слева, включая и нуль целых. Мантисса отыскивается по таблицам логарифмов, причём на положение запятой и на нули слева и справа не обращают внимания, так как числа, получающиеся из данного путём умножения или деления на 10 имеют одинаковые мантиссы. Мантисса всегда берётся положительной, поэтому если логарифм отрицательный, то знак минус ставится над характеристикой (3,820714= —3+0,820714= — 2,179286).  [c.107]

---

mash-xxl.info

Мантиссы логарифмов — Справочник химика 21

    Четырехзначные мантиссы логарифмов приведены в таблице п. 76. Пользование таблицей иллюстрируется примерами  [c.524]

    ЧЕТЫРЕХЗНАЧНЫЕ МАНТИССЫ ЛОГАРИФМОВ [c.220]

    Четырехзначные мантиссы логарифмов [c.791]

    Нахождение логарифмов чисел. Пусть требуется найти логарифм числа 456,78. Так как это число содержит пять значащих цифр, а четырехзначные таблицы логарифмов дают точность только до четвертой цифры, округляем это число до 456,8. Пишем характеристику логарифма, равную числу целых цифр без одной 2. Далее, не обращая внимания на запятую, находим мантиссу логарифма числа 4568. Для этого отыскиваем в таблице логарифмов точку пересечения горизонтального ряда, отвечающего перным двум цифрам этого [c.237]

    Правила пользования таблицей 14. В таблице приведены трехзначные мантиссы логарифмов. Для вычисления [Н» ] по известному pH находят в первом вертикальном столбце первый знак мантиссы величины pH и в первой горизонтальной строке — второй знак этой мантиссы. Затем в точке пересечения линий, идущих от найденных цифр, получают значение [Н ], которое надо еще умножить на 10 в степени, равной характеристике pH, взятой в отрицательным знаком. Например, [c.260]

    Следует учитывать, что при пользовании таблицами десятичных логарифмов числа будут определяться с относительной погрешностью, равной —где п — число знаков мантиссы логарифмов, [c.774]

    Представления о значащих цифрах применимы и в том случае, когда для вычислений используются логарифмы. Используя правила, аналогичные изложенным выше, следует сохранять в мантиссе логарифма такое же число значащих цифр, какое содержится в исходной численной величине, или еще одну значащую цифру, если исходная величина ближе к следующей степени 10, чем к предыдущей степени 10. Например, логарифм числа 2,472 должен быть записан с мантиссой, содержащей три цифры, а логарифм числа 9,236 — с мантиссой, содержащей четыре цифры. Обычно для подобных вычислений используют таблицы четырехзначных логарифмов. Логарифмическая линейка дает одинаковую точность во всех частях шкалы. [c.519]

    В графе определяют указана формула вещества, процентное содержание которого определяют в графе получено — состав весовой формы в графе множитель — число, представляющее собой величину отношения атомного или молекулярного веса определяемого соединения к молекулярному весу весовой формы или к ее кратному значению в гра([ое логарифм приводится значение мантиссы логарифма множителя (фактора) в вычислениях, требующих перемножения нли деления многозначных чисел, необходимо пользоваться логари( )мами или логарифмической линейкой. [c.151]

    По таблице пропорциональных частей при табличной разности, равной 7, на 3 единицы числа нужно прибавить 2,1 к мантиссе (см. пятизначные мантиссы логарифмов, таблицу). [c.247]

    Определено Ищут Фактор Мантисса логарифма Определено Ищут Фактор Мантисса логарифма [c.357]

    Логарифм числа состоит из характеристики (цифра перед запятой) и мантиссы (цифры после запятой). Логарифмы чисел с рядом одинаковых цифр различаются только характеристикой, мантисса же числа остается одной и той же. Например, числа 6265,3 62,653 0,0062653 0,000062653 будут иметь мантиссу 79 694. Ее берут из таблицы мантисс логарифмов. Характеристику определяют по числу цифр, стоящих перед запятой. Если число начинается не с нуля, то характеристика будет на единицу меньше числа цифр, стоящих до запятой, например 6265,3=3,79694 1 62,653== = 1,79694. [c.246]

    Взамен обычной таблицы пятизначных логарифмов в конце книги приведена упрощенная таблица пятизначных логарифмов и антилогарифмов. Она занимает такой же объем, какой имеют таблицы четырехзначных логарифмов. Это достигнуто тем, что взамен действительных значений разностей между мантиссами даны средние их значения для каждой строки таблицы. Ошибки, возникающие при работе с этой таблицей, не превышают 0,00002. В других таблицах справочника приведены точные значения пятизначных мантисс логарифмов. [c.8]

    Если данные, предназначенные для хранения, выражены обычно в их натуральной форме, то для построения стебля с листьями можно (а иногда и необходимо) использовать преобразованные числа, в наиболее простом случае — логарифмы исходных данных. Шкала логарифмов как бы расширяет диапазон распределений последних цифр разрядов (фактически — мантисс логарифмов). [c.149]

    Для нахожд

www.chem21.info

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида. Графики тригонометрических функций. Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах. Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже. График функции y=sinA (синусоида) График функции y=cosA (косинусоида) График функции y=tgA (тангенсоида) Из графиков видно что: Графики синуса и косинуса колеблются в пределах между -1 и 1 Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90o Кривые синуса и косинуса непрерывны и повторяются с периодом 360o , кривая тангенса имеет разрывы и повторяется с периодом 180o . Углы произвольной величины На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О — отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке — отрицательным. График. Положительное или отрицательное направление при движении по окружности. Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.) Пусть ОА вращается дальше таким образом, что Θ2 — любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ . График. Поcтроение углов в различных квадрантах. Пусть ОА вращается дальше таким образом, что Θ4— любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -. В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева. График. Положительные и отрицательные значения синусов, косинусов и тангенсов. Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0o и 360o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin-1, получим ответ 19,03o . Однако существует второй угол между 0o и 360o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180o — 19,03o = 160,97o . Таким образом, 19,03o и 160,97o — это углы в диапазоне от 0o до 360o , синус которых равен 0,3261. Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. График. Нахождение всех углов по заданному значению синуса (пример) Пример 1 Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071

dpva.ru

Гармоническое колебание, уравнения, графики движения. Изменение координаты, скорости, ускорения со временем. Примеры, тесты

Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Находим производную сложной функции.

fizmat.by

график косинуса — с русского на английский

См. также в других словарях:

• Интегральный косинус — График интегрального косинуса для 0 < x ≤ 8π. Интегральный косинус  специальная функция, определяемая интегралом …   Википедия

• История тригонометрии — Геодезические измерения (XVII век) …   Википедия

• Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… …   Энциклопедия инвестора

• Отрицательная частота — Понятие отрицательной и положительной частоты может быть показано на примере вращающегося в ту или другую сторону вектора. Частота со знаком отражает как скорость, так и направление вращения. Скорость выражена в оборотах (циклах) в секунду… …   Википедия

• Полярная система координат — Полярная сетка, на которой отложено несколько углов с пометками в градусах. Полярная система координат  двумерная система координат, в которой каждая точка на плоскости определяется двумя числами  полярным углом и полярны …   Википедия

• Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение …   Википедия

• Sh x — Гиперболические функции  семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение 2 Свойства …   Википедия

• Синус-верзус — Определение тригонометрических функций на единичной окружности. Отрезок CD описывает версинус. Синус верзус (sinus versus  обращённый синус; другие написания: версинус, синус версус, называется также «стрелка дуги»)  одна из редко… …   Википедия

• КОСИНУС — (cosine) В прямоугольном треугольнике отношение катета и гипотенузы, образующих угол. Косинус угла х записывается как cos х. Если начертить окружность радиусом, равным единице, то при измерении величины угла против часовой стрелки, начиная с… …   Экономический словарь

• Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике  элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции …   Википедия

translate.academic.ru

график косинуса — это… Что такое график косинуса?



график косинуса

cosine curve

Большой англо-русский и русско-английский словарь. 2001.

• график косеканса
• график котангенса

Смотреть что такое «график косинуса» в других словарях:

• Интегральный косинус — График интегрального косинуса для 0 < x ≤ 8π. Интегральный косинус  специальная функция, определяемая интегралом …   Википедия

• История тригонометрии — Геодезические измерения (XVII век) …   Википедия

• Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… …   Энциклопедия инвестора

• Отрицательная частота — Понятие отрицательной и положительной частоты может быть показано на примере вращающегося в ту или другую сторону вектора. Частота со знаком отражает как скорость, так и направление вращения. Скорость выражена в оборотах (циклах) в секунду… …   Википедия

• Полярная система координат — Полярная сетка, на которой отложено несколько углов с пометками в градусах. Полярная система координат  двумерная система координат, в которой каждая точка на плоскости определяется двумя числами  полярным углом и полярны …   Википедия

• Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение …   Википедия

• Sh x — Гиперболические функции  семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение 2 Свойства …   Википедия

• Синус-верзус — Определение тригонометрических функций на единичной окружности. Отрезок CD описывает версинус. Синус верзус (sinus versus  обращённый синус; другие написания: версинус, синус версус, называется также «стрелка дуги»)  одна из редко… …   Википедия

• КОСИНУС — (cosine) В прямоугольном треугольнике отношение катета и гипотенузы, образующих угол. Косинус угла х записывается как cos х. Если начертить окружность радиусом, равным единице, то при измерении величины угла против часовой стрелки, начиная с… …   Экономический словарь

• Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике  элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции …   Википедия

dic.academic.ru

Вычитание дробей | Формулы с примерами

Вычитание дробей

С одинаковыми знаменателями

Определение
Что бы найти разность дробей с одинаковыми знаменателями, нужно просто вычесть их числители. Знаменатель останется прежним.

Наглядный пример
Найдем, во сколько раз каждый знаменатель меньше общего
и умножим каждую дробь на это число.

Пример 1131 —  431 = 11 — 431 = 7  31;

92 —  32 = 9 — 32 = 62 =  3;1

186 —  126 = 18 — 126 = 66 =  1.1

С разными знаменателями

Определение
Чтобы вычесть дроби с разными знаменателями, надо привести их к общему знаменателю.

Порядок действий

1. Преобразуем смешанную дробь в неправильную;
2. Найдем общий знаменатель;
3. Приведем дроби к общему знаменателю;
4. Выполним действия с числителями;
5. Приведем получившуюся неправильную дробь к смешанной.

Пример
1417 —  23 =  4251 —  3451 =  8  51;

2119 —  12 =  2238 —  1938 =  3  38;

3223 —  43 =  9669 —  9269 =  4  69.

formula-xyz.ru

Деление дробей | Формулы с примерами

Деление правильных дробей

Определение
Чтобы разделить дробь на целое число, нужно преобразовать целое число в дробь (1), полученную дробь перевернуть (2) и умножить на первую дробь (3).

Иными словами: чтобы разделить дробь на целое число, нужно числитель оставить прежним, а знаменатель исходной дроби умножить на данное число.

Пример
35 :  33= 35 :  31 =  35 •  13 =  3 • 15 • 3 =   3 15 =  15;

89 :  43= 89 :  41 =  89 •  14 =  8 • 19 • 4 =   8 36 =   2 9;

15 :  43= 15 :  41 =  15 •  14 =  1 • 15 • 4 =   1 20.

Правило
Чтобы разделить одну правильную дробь на другую, нужно также
применить умножение на обратную дробь.

Пример
47 :  14 =  47 •  41 =  4 • 47 • 1 =  167 =  227;

68 :  36 =  68 •  63 =  6 • 68 • 3 =  3624 =  112;

79 :  47 =  79 •  74 =  7 • 79 • 4 =  4936 =  11336.

Деление смешанных дробей

Определение
Чтобы разделить смешанные дроби, сначала нужно
преобразовать их в неправельные (1), а затем перевернуть
вторую дробь (2) и умножить на первую (3).

Пример
243 :  314 =  2 • 3 + 43 :  3 • 4 + 14 =  103 :  134 =  103 •  413 =  4039 =  1 1 39;

113 :  212 =  1 • 3 + 13 :  2 • 2 + 12 =  43 :  52 =  43 •  25 =   8 15;

352 :  514 =  3 • 2 + 52 :  5 • 4 + 14 =  112 :  214 =  112 •   4 21 =  4442 =  2221 =  1 1 21.

Обратная дробь

Правило
Дробь  ba — обратная к дроби  ab.

Дроби  ab и  ba — взаимно обратные дроби.

Пример (взаимно обратные) 34 и  43;

72 и  27;

125 и   5 12.

formula-xyz.ru

Сравнение дробей | Формулы с примерами

Сравнение с одинаковыми знаменателями

Больше та дробь,
числитель которой больше.

Пример 23 44, т.к. 2

79 109, т.к. 7

2011>  1611, т.к. 20

Сравнение на числовом луче

Пример

Больше та дробь, которая находится правее.

Сравнение с разными знаменателями

Значит привести дроби к общему знаменателю и сравнить новые числители.

Пример 1.   54 и   65:     54 =   2520, 65 =   2420, 25 54 65;

2.   59 и   37:     59 =   3563, 37 =   2763, 35 > 27, значит    59 >    37;

3.   913 и   87:     913 =   6391, 87 =   10491, 63 913 87;

Сравнение смешанных чисел

Правило 1. Сравнить целые части. Если k > n, то :

2. Если целые части равны (k = n), сравнить дробные части:

Пример 537 > 283 , т.к. 5 > 2;

727 78  10 , т.к. 27 810.

Формулы по алфавиту:

© 2019 Все права защищены
При использовании материалов данного сайта обязательно указывать ссылку на источник

formula-xyz.ru

Умножение дробей | Формулы с примерами

Умножение правильных дробей

Определение
Произведение правильных дробей — это дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей.

Пример 54 •  311 =  5 • 3 4 • 11 = 1544;

73 •  45 = 7 • 49 • 5 = 2815;

93 —  74 = 9 • 73 • 4 = 3612 =  3.1

Правило

Если нужно умножить целое число на дробь, то умножаем это число на
числитель, так как любое целое число можно представить в виде
неправильной дроби со знаменателем 1.

Умножение смешанных дробей

Определение
Чтобы умножить правильную дробь на смешанную, нужно сначала преобразовать смешанную дробь в неправильную.

Порядок действий

1. Преобразуем смешанную дробь в неправильную;
2. Перемножаем числители и знаменатели;
3. Приводим получившуюся неправильную дробь к смешанной.

Пример
534 •  25 =  234 •  25 =  23 • 24 • 5 =  4620 =  2310 =  2 3 10;

313 •  12 =  103 •  12 =  10 • 13 • 2 =  106 =  53 =  1 2 3;

724 •  13 =  304 •  13 =  30 • 14 • 3 =  3012 =  52 =  2 1 2.

formula-xyz.ru

Десятичная дробь | Формулы с примерами

Что такое десятичные дроби?

Определение
Десятичная дробь (число) — то же самое, что десятичные числа, т.е. правильные или неправильные дроби со знаменателем, кратным 10. Их принято писать без знаменателя, в строчку, отделяя целую часть (слева) запятой.

Первая цифра справа от запятой соответствует десятым долям, вторая — сотым и т.д. Они называются десятичной частью числа.

Где a — натуральное число или 0;
b, c, d … — цифры.

Как читать?

Правило 3, 345 — 3 целых 345 тысячных,
целая часть — 3, дробная часть 345;

365, 0957 — 365 целых 957 десятитысячных,
целая часть — 365, дробная часть 0957;

0,4 — 0 целых 4 десятых,
целая часть — 0, дробная часть 3;

Правило

! Если дробная часть десятичной дроби оканчивается нулями, то их можно не писать — значение дроби не изменится:

Пример 534, 543 00 = 534, 543;

1654, 43267 00 = 1654, 43267;

9374, 8763456 00000 = 9374, 8763456.

! Если к дробной части приписать любое число нулей, то значение десятичной дроби не изменится:

Пример 12, 324 = 12, 324 00;

362, 970 = 362, 970 00 = 362, 970 000 000;

569, 261 = 569, 261 000 000 000 = 569, 261 000 000 000 000 000 ….

! Любое целое число можно представить в виде десятичной дроби с любым числом нулей справа от запятой:

Пример 1 = 1,0 = 1,00 = 1, 000 000 000 000 … ;

3 = 3,000 = 3,000 000 000 000 000 … ;

9 = 9,000 = 9,000 000 000 000 000 000 … .

Разряды целой и дробной части числа

Таблица разрядов целой и дробной части числа

formula-xyz.ru

Действия с дробями: правила, примеры, решения

Данная статья рассматривает действия над дробями. Будут  сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида AB, где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.

Yandex.RTB R-A-339285-1

Правила выполнения действий с числовыми дробями общего вида

Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 35, 2,84, 1+2·34·(5-2), 34+782,3-0,8, 12·2, π1-23+π, 20,5ln 3, то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.

Определение 1

Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:

• При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: ad±cd=a±cd, значения a, c и d≠0 являются некоторыми числами или числовыми выражениями.
• При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями.  Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
• При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим ab·cd=a·cb·d, где a, b≠0, c, d≠0 выступают в роли действительных чисел.
• При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: ab:cd=ab·dc.

Обоснование правил

Определение 2

Существуют следующие математические моменты, на которые следует опираться при вычислении:

• дробная черта означает знак деления;
• деление на число рассматривается как умножение на его обратное значение;
• при

zaochnik.com

Обыкновенные дроби | Формулы с примерами

Правило обыкновенных дробей

1n — это одна из n равных частей, на которые разделяется единица (отрезок единичной величины) — n-ая часть единицы.

Запись дробей

Число вверху дроби показывает, с каким количеством равных частей целого мы имеем дело, а число внизу — это полное число равных частей, на которое было разделено целое.

12 — половина — одна вторая:

13 — треть — одна третья:

14 — четверть — одна четвертая:

15 — одна пятая,

123 — одна двадцать третья, …

mn — m n-ных частей единицы: mn = k • 1n

35 — три пятых:

533 — gпять тридцать третьих

14 — четыре третьих:

0n — нисколько n-ных частей единицы: 0n = 0

formula-xyz.ru

4000 примеров по математике, 5 класс, Часть 3, Узорова О.В., Нефёдова Е.А., 2006

По кнопке выше «Купить бумажную книгу» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.

По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.

По кнопке «Найти похожие материалы на других сайтах» можно искать похожие материалы на других сайтах.

On the buttons above you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.

4000 примеров по математике, 5 класс, Часть 3, Узорова О.В., Нефёдова Е.А., 2006.

  Пособие содержит около 4000 именованных математических примеров по темам, изучаемым в первой четверти 5 класса. Оригинальное построение материала позволяет обеспечить более глубокое его усвоение.
На каждой странице приведены 3-4 столбика в среднем по 50 примеров. Если ученик решает столбик за 4-6 минут, это свидетельствует о хорошем уровне подготовки. На целую страницу у него должно уходить не более 30 минут. Чтобы достичь отличных результатов, каждый день следует решать по одной странице.
Пособие может быть использовано на уроках математики, а также для работы дома.

Дата публикации: 14.04.2014 07:44 UTC

Теги: задачник по математике :: математика :: Узорова :: Нефёдова :: 5 класс

---

Смотрите также учебники, книги и учебные материалы:

Следующие учебники и книги:

• 30000 примеров по математике, 4 класс, Узорова О.В., Нефёдова Е.А., 2003
• 3000 примеров по математике, 3 класс, Табличное умножение и деление, Узорова О.В., Нефёдова Е.А., 2006
• 3000 примеров по математике, 4 класс, Сложение и вычитание в пределах 1000, Узорова О.В., Нефёдова Е.А., 2003
• 4000 примеров по математике, 6 класс, Часть 1, Узорова О.В., Нефёдова Е.А., 2006

Предыдущие статьи:

• Сборник задач по математике для ВТУЗов, Часть 2, Специальные разделы математического анализа, Болгов В.А., Ефимов А.В., Каракулин А.Ф., 2010
• ГИА, Математика, 11 класс, Сборник заданий, Истер А.С., Глобин А.И., Панкратова И.Е.
• Математика, 9 класс, Решебник, Подготовка к ГИА 2014, Войта Е.А., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
• Нестандартные задачи по математике, 2 класс, Левитас Г.Г., 2010

---

nashol.com

Математические примеры для 5 класса. Узорова О.В., Нефедова Е.А.

Несформированность навыков перевода именованных единиц, счета, действий с дробями и так далее приводит к тому, что дети работают в тетрадках и у доски долго, оставляя самое невыгодное впечатление о своих знаниях. Зачастую умные дети оказываются в рядах отстающих по весьма обидному поводу. Освоить азы математики, без которых «никуда», поможет сборник для решения примеров, составленный Узоровой О.

Ликвидировать некоторые проблемы в обучении возможно только многократной тренировкой навыков. В данном случае это решение примеров по различным темам в специальных тренинговых сборниках. Посвятив занятиям всего полчаса в день, ребенок сделает заметный шаг вперед уже через несколько недель. Это не останется без внимания у педагога-предметника и отразится на оценках в журнале в самом положительном смысле.

Математические примеры для 5 класса состоят из трех частей, каждая из которых отличается набором тем и отрабатываемых навыков. В короткой записке для родителей и учителей автор поясняет практическое значение решения такого количества примеров (по странице в день – около 50 заданий). Следует отметить, что сборники лишены готовых ответов, что позволяет родителям оставить ребенка решать задания самостоятельно.

Такой прием отработки решения примеров по математике в 5 классе, как многократное повторение имеет большое значение учебы. Дети усваивают все способы решения и доводят их до автоматизма.

Издательство: АСТ
Год издания: 2006
Авторы: Узорова О.В., Нефедова Е.А.
Формат: PDF
Количество страниц: 18+18+18
Язык: Русский

 

Скачать бесплатно Часть_1_primeri_matematika_5_klass_uchebnik.PDF

Скачать бесплатно Часть_3_primeri_matematika_5_klass_uchebnik.PDF

Скачать бесплатно Часть_4_primeri_matematika_5_klass_uchebnik.PDF

www.vse-dlya-detey.ru

Математика 5 класс. Задания и упражнения. Натуральные числа.

Натуральные числа

Сравнение, сложение и вычитание натуральных чисел.



Базовый уровень

Задание 1

Какое из чисел 2/7, 837, 9/15, 1592 может означать количество кирпичей на строительном складе? Как называются эти числа?

Решение
• 837, 1592.
• Эти числа называются натуральными.

Задание 2

Прочитайте каждое из чисел:

1) 385	2) 703	3) 1 907	4) 34 856
5) 591	6) 862	7) 8 057	8) 82 930

Решение
• 1 — триста восемьдесят пять,
• 2 — семьсот три,
• 3 – тысяча девятьсот семь,
• 4 – тридцать четыре тысячи восемьсот пятьдесят шесть,
• 5 – пятьсот девяносто один,
• 6 – восемьсот девяносто два,
• 7 — восемь тысяч пятьдесят семь,
• 8 – восемьдесят две тысячи девятьсот тридцать.

Задание 3

Назовите сколько единиц, десятков, сотен и тысяч в каждом из чисел:

1) 793	2) 6 004	3) 201
4) 39 862	5) 856 398	6) 6 836 539

Решение
• 1 – 793 единицы, 79 десятков, 7 сотен;
• 2 – 6 004 единицы, 600 десятков, 60 сотен, 6 тысяч;
• 3 — 201 единица, 20 десятков, 2 сотни;
• 4 – 39 862 единицы, 3 986 десятков, 398 сотен, 39 тысяч;
• 5 – 856 398 единиц, 85 639 десятков, 8 563 сотен, 856 тысяч;
• 6 — 6 836 539 единиц, 683 653 десятков, 68 365 сотен, 6 836 тысяч.



Задание 4

Запишите числа цифрами:

• 1) Семьсот девяносто четыре;
• 2) Три тысячи триста сорок восемь;
• 3) Восемьсот двадцать один;
• 4) Триста восемь тысяч семьдесят четыре;
• 5) Один миллион пятьсот тридцать одна тысяча шестьсот семьдесят три;
• 6) Тринадцать миллионов 98 тысяч сто тридцать один.

Решение

1) 794	2) 3 348	3) 821
4) 308 074	5) 1 531 673	6) 13 098 131

Задание 5

Запишите каждое из чисел словами:
30, 857, 208, 1029, 14845.

Решение

Тридцать, восемьсот пятьдесят сем, двести восемь, тысяча двадцать девять, четырнадцать тысяч восемьсот сорок пять.

Задание 6

Расставьте знаки больше или меньше:

308 … 380	7 591 … 7 951	47 805 … 91 000	359 000 … 68 000
192 … 180	3 829 … 6 350	71 003 … 17 300	296 038 … 269 380

Решение

308 < 380	7 591 < 7 951	47 805 < 91 000	359 000 < 68 000
192 > 180	3 829 < 6 350	71 003 > 17 300	296 038 > 269 380

Задание 7

Выполните сложение:

200 + 300 =	700 + 59 =	340 + 60 =	37 + 163 =
417 + 162 =	417 + 82 =	3002 + 6003 =	450 + 540 =

Решение

200 + 300 = 500	700 + 59 = 759	340 + 60 = 400	37 + 163 = 200
417 + 162 = 579	417 + 82 = 499	3002 + 6003 = 9005	450 + 540 = 990

Задание 8

Выполните вычитание:

133 — 33 =	860 — 177 =	500 — 387 =	1384 — 1262 =
457 — 391 =	293 — 290 =	5827 — 2268 =	7545 — 5676 =

Решение

133 — 33 = 100	860 — 177 = 683	500 — 387 = 113	1384 — 1262 = 122
457 — 391 = 66	293 — 290 = 3	5827 — 2268 = 3559	7545 — 5676 = 1869

Задание 9

Решите задачу:
До обеда в магазине было продано 48 кг помидор, а после обеда на 14 кг меньше. Сколько кг помидор было продано в магазине после обеда?

Решение
• 1) 48 – 14 = 34 (кг).
• Ответ: после обеда в магазине было продано 34 кг помидор.

Задание 10

Найдите значение выражения:

(34 + 15) — 24 =	64 — (25 + 14) =	(36 + 34) — 24 =
(13 + 58) — 28 =	36 — (16 + 29) =	(43 + 29) — 23 =

Решение

(34 + 15) — 24 = 25	64 — (25 + 14) = 25	(36 + 34) — 24 = 46
(13 + 58) — 28 = 43	36 — (16 + 19) = 1	(43 + 29) — 23 = 49

Задание 11

В вазе было 37 конфет. Шестеро детей съели по 3 конфеты и двое по 4 конфеты. Сколько конфет осталось в вазе?

Решение
• 1) 6 * 3 = 18 (конфет) съели шестеро детей;
• 2) 3 * 4 = 12 (конфет) съели четверо детей;
• 3) 18 + 12 = 30 (конфет) всего съели дети;
• 4) 37 – 30 = 7 (конфет).
• Ответ: в вазе осталось 7 конфет.

Средний уровень

Задание 1

Запишите числа цифрами:

• 1. Восемьсот семьдесят миллионов девять;
• 2. Два миллиарда четыреста пятьдесят девять миллионов триста шестьдесят восемь тысяч пятьсот семьдесят девять;
• 3. Тридцать миллиардов четыре миллиона двадцать три;
• 4. Восемьсот миллиардов шесть;
• 5. 248 миллиарда 6 миллионов 18 тысяч сто;
• 6. 503 миллиарда 241 тысяча 64.

Решение

1) 87 000 009

2) 2 459 368 579

3) 30 004 000 023

4) 800 000 000 006

5) 248 006 018 100

6) 503 000 241 064

Задание 2

Запишите числа, как сумму разрядных слагаемых:

1) 349

2) 809

3) 2475

4) 3008

Решение

1) 349 = 300 + 40 + 9

2) 809 = 800 + 9

3) 2475 = 2000 + 400 + 70 + 5

4) 3008 = 3000 + 8

Задание 3

Расставьте знаки больше или меньше:

852 618 … 852 681

2 545 033 … 2 545 300

300 300 003 … 300 003 300

Решение

852 618 < 852 681

2 545 033 < 2 545 300

300 300 003 > 300 003 300

Задание 4

Запишите числа в порядке возрастания:
98362, 6395, 1103672, 492031, 10238, 2958, 300271, 300713, 490952, 192, 74.

Решение

74,  192,  2 958,  6 395,  10 238,  98 362,  300 271,  300 713,  490 952,  492 031,  1 103 672.

Задание 5

Запишите натуральные числа, которые меньше 82 и больше 74.

Решение

75,  76,  77,  78,  79,  80,  81.

Задание 6

Какое количество натуральных чисел расположено между числами:

1) 57 и 64;

2) 238 и 261;

3) 167 и 192;

4) 342 и 409;

Решение

1) 6;

2) 21;

3) 24;

4) 66.

Задание 7

Выполните сложение:

27 592 + 593 089 =	59 003 + 12 903 =	129 301 + 739 912 =
60 018 + 224 983 =	30 283 + 45 037 =	884 916 + 294 001 =

Решение

27 592 + 593 089 = 620 681	59 003 + 12 903 = 71 906	129 301 + 739 912 = 869 213
60 018 + 224 983 = 285 001	30 283 + 45 037 = 75 320	884 916 + 294 001 = 1 178 917

Задание 8

Вычислите:

18м 48см + 26м 39см = ;

45т 390 кг + 21т 31кг = .

Решение

18м 48см + 26м 39см = 44м 87 см;

45т 390 кг + 21т 31кг = 66т 421кг.

Задание 9

Выполните вычитание:

49 081 — 19 090 =	18 928 — 18 098 =	397 802 — 65 834 =
72 305 — 50 923 =	25 730 — 21 829	450 038 — 375 340 =

Решение

49 081 — 19 090 = 29 991	18 928 — 18 098 = 830	397 802 — 65 834 = 331 968
72 305 — 50 923 = 21 382	25 730 — 21 829 = 3 901	450 038 — 375 340 = 74 698

Задание 10

Найдите значения выражений:

469 + 1 843 — 1 992 =	4 578 — 2640 + 3 654 =
9 029 — 6 230 — 1 389 =	19 463 + 7 356 + 35 230 =

Решение

469 + 1 843 — 1 992 = 320	4 578 — 2640 + 3 654 = 5 592
9 029 — 6 230 — 1 389 = 1 410	19 463 + 7 356 + 35 230 = 62 049

Задание 11

Вычислите:

6 036 — (1 343 + 2 876) =	9 803 — (6 357 + 1 996) =
4 378 — (2 195 — 1 880) =	6 306 — (4 381 — 2 270) =

Решение

6 036 — (1 343 + 2 876) = 1 817	9 803 — (6 357 + 1 996) = 1 450
4 378 — (2 195 — 1 880) = 4 063	6 306 — (4 381 — 2 270) = 4 195

Задание 12

В швейную мастерскую привезли 150 м ткани. В первую неделю было израсходовано 46 метров, а во вторую 38 метров. Сколько метров ткани осталось в мастерской?

Решение

• 1) 46 + 38 = 84 (м) ткани израсходовали за 2 недели;
• 2) 150 – 84 = 66 (м) ткани.
• Ответ: в мастерской осталось 66 метров ткани.

Задание 13

Сравните не вычисляя:

1 487 + 372 … 183 + 1 394	48 391 + (3 409 + 2 809) … (2 893 + 1 908) + 48 391
8 934 + 490 … 822 + 8 943	17 429 + (6 830 + 3 402) … (7 620 + 3 420) + 17 429

Решение

1 487 + 372 > 183 + 1 394	48 391 + (3 409 + 2 809) > (2 893 + 1 908) + 48 391
8 934 + 490 < 822 + 8 943	17 429 + (6 830 + 3 402) < (7 620 + 3 420) + 17 429

Задание 14

Решите задачу:
В овощной магазин привезли картофель и лук. Картофеля привезли 185 кг, а лука на 48 кг меньше. Сколько всего картофеля и лука привезли в магазин?

Решение

• 1) 185 — 48 = 137 (кг) лука привезли в магазин;
• 2) 185 + 137 = 322 (кг).
• Ответ: всего привезли 322 кг лука и картофеля?



mat-zadachi.ru

Персональный сайт учителя математики — Задания для 5 класса

Натуральные числа и шкалы

1. Натуральные числа

2. Отрезок. Длина отрезка. Треугольник

3. Плоскость. Прямая. Луч

4. Шкалы и координаты

5. Сравнение чисел

Сложение и вычитание натуральных чисел

6. Сложение натуральных чисел и его свойства

7. Вычитание натуральных чисел и его свойства

8. Уравнение

Умножение и деление натуральных чисел

9. Умножение натуральных чисел и его свойства

10. Деление натуральных чисел и его свойства

11. Деление с остатком

12. Порядок выполнения действий

13. Упрощение выражений

14. Степень числа. Квадрат и куб числа

Формулы скорости, площади и объема

15. Формулы. Формула скорости, пути

16. Площадь. Формула площади прямоугольника

17. Прямоугольный параллелепипед. Объем

Обыкновенные дроби

18. Окружность и круг

19. Доли. Обыкновенные дроби

20. Правильные и неправильные дроби

21. Сравнение дробей

22. Сложение и вычитание дробей с одинаковыми знаменателями

23. Деление и дроби

24. Смешанные числа

Десятичные дроби. Сложение и вычитание десятичных дробей

25. Десятичная запись дробных чисел

26. Сравнение десятичных дробей

27. Сложение и вычитание десятичных дробей

28. Приближенные значения чисел. Округление чисел

Умножение и деление десятичных дробей

29. Умножение десятичных дробей

30. Деление десятичных дробей

31. Среднее арифметическое

32. Проценты

ksjusche-holodowa.narod.ru

Книга «4000 примеров по математике. 5 класс. Часть 4»

Добавить

• Читаю
• Хочу прочитать
• Прочитал

Жанр: Учебная литература

ISBN: 978-5-17-018944-3, 978-5-17-013391-X, 978-5-271-06505-7, 978-5-271-06568-5

Год издания: 2003

Серия: Как научиться быстро считать

Издательство: АСТ

Фрагмент книги

Оцените книгу

Скачать книгу

373 скачивания

Читать онлайн

О книге «4000 примеров по математике. 5 класс. Часть 4»

Пособие содержит 4000 математических примеров по темам, изучаемым в четвертой четверти 5 класса. Оригинальное построение материала позволяет обеспечить более глубокое его усвоение. Как показывает практика, ученик полностью освоил программу, если решает пример и записывает ответ по истечении 4-7 секунд. В этом случае можно говорить, что навык счета доведен до автоматизма. На каждой странице приведены 4-7 столбиков по 52 примера. Если ученик решает столбик за 4-6 минут, это свидетельствует о хорошем уровне подготовки. На целую страницу у него должно уходить 30 минут. Чтобы достичь отличных результатов, каждый день следует решать по одной странице. Пособие может быть использовано на уроках математики, а также для работы дома.

На нашем сайте вы можете скачать книгу «4000 примеров по математике. 5 класс. Часть 4» Узорова Ольга Васильевна бесплатно и без регистрации в формате fb2, rtf, epub, pdf, txt, читать книгу онлайн или купить книгу в интернет-магазине.

Отзывы читателей

Подборки книг

Похожие книги

Другие книги автора

Информация обновлена: 19.01.2018

avidreaders.ru

Математика 5 класс

Интерактивный учебник. Математика 5 класс. Описание

        Наш интерактивный учебник «Математика 5 класс» рассчитан на повторение, закрепление и проверку ваших знаний по школьному курсу математики в пятом классе. Это отличная тренировка навыков решения задач и примеров. Особенностью учебника является интерактивная проверка ответов на задачи и задания, что позволяет исключить ошибки в ответах, а также возможность подсмотреть ответ.

        Все мы порой сталкиваемся с опечатками и ошибками в учебной литературе, что порой весьма огорчает. Мы прикладываем все свои силы и знания, что бы исключить ошибки на наших страницах. В нашем учебнике заложена программная защита от собственных ошибок, которая гарантирует правильную проверку ваших ответов. И все же, если вы заметили опечатку или ошибку, мы будем вам очень признательны за сообщение о ней, которое вы можете отправить, заполнив форму на странице «Контакты».

        Пользоваться «Математикой 5 класс» просто. На этой странице в «Оглавлении» находятся ссылки на тематические страницы учебника, где вы можете, нажав на красную ссылку прочитать правила по теме. Ниже расположены задачи и задания, первое из которых открыто по умолчанию, а следующие вы можете открыть, кликнув по их заголовкам мышью. Под заданиями находятся ссылки на соседние темы учебника, что позволяет переходить от темы к теме, не заходя на страницу «Математика 5 класс».

        Еще мы хотим развеять ваши сомнения по поводу нагрузки на глаза ребенка, во время занятий на нашем сайте. Основное время ребенок смотрит в тетрадку, которую обязательно надо иметь под рукой для решения задач, а шрифт заданий подобран таким образом, чтобы он легко читался. И все же мы рекомендуем пользоваться кнопками Ctrl+ и Ctrl- для увеличения (уменьшения) размера шрифта.

        Несколько важных рекомендаций: Во время решения задач делайте все расчеты на бумаге в столбик, прочерчивайте графические задачи карандашом. В пятом классе это очень важно. Тренируйте устный счет. Ну, вот, пожалуй, и все. Успехов вам на нелегком, но интересном учебном фронте, в том числе и на страницах нашего проекта «Математика 5 класс».

www.matematika-na.ru

Примеры заданий по математике 5 класс

На слайдах примеры материалов для практических занятий по математике для учащихся 5 класса. Памятки умножение и деление десятичных дробей, тесты, правила, математические диктанты. Тест на знание свойств сложения и умножения натуральных чисел. 

Просмотр содержимого документа
«Примеры заданий по математике 5 класс»

Инструкция

Сложение и вычитание ДД «в столбик».

		15,3 + 9,138	72,6 – 6,24
1	Уравнять в дробях количество знаков после запятой:	15,300 и 9,138	72,60 и 6,24
2	Записать их друг под другом так, чтобы запятая была подписана под запятой:		-72,60 6,24
3	Выполнить сложение (вычитание), не обращая внимания на запятую:		-72,60 6,24 6636
4	Поставить в ответе запятую под запятой в данных дробях:		-72,60 6,24 66,36

Самостоятельно:

1) Найти разность:

а) 9,3 – 3,4 б) 8,6 – 6,9 в) 10,3 – 8,15

г) 35,6 – 9 д) 12 – 2,68 е) 7 – 0,37

ж) 4,1 – 1,754 з) 0,43 – 0,3291

Самостоятельная работа

Вариант I
1) Найдите сумму:
а) 4,9 + 1,6 б) 8,3 + 0,8 в) 7,9 + 4 г) 13 + 4,2 д) 5,7 + 3,28 е) 1,27 + 24,3 ж) 10,09 + 0,208 з) 0,596 + 0,83
2) Найдите разность:
а) 4,7 – 2,8 б) 5,1 – 4,7 в) 12,1 – 8,7 г) 45,6 – 13 д) 3 – 2,4 е) 17 – 0,87 ж) 6,5 – 4,837 з) 0,12 – 0,0856

Самостоятельная работа

Вариант II

1) Найдите сумму:

а) 3,8 + 1,9 б) 3,6 + 0,5 в) 8 + 3,6 г) 3,7 + 16 д) 2,58 + 1,4 е) 7,2 + 15,68 ж) 0,906 + 12,8 з) 0,47 + 0,741

2) Найдите разность:

а) 6,5 – 2,7 б) 4,3 – 3,5 в) 11,2 – 9,4 г) 34,7 – 4 д) 21 – 3,49 е) 5 – 0,61 ж) 7,3 – 4,568 з) 0,16 – 0,0911

Решите уравнения:

а) 6,7 – х = 2,8 д) х – 2,9 = 3,93

б) у – 2,7 = 3,4 е) (z – 3,48) + 2,15 = 3,9

в) (х + 3,5) – 4,8 = 2,4 ж) у + 3,54 = 8,2

г) (7,1 – х) + 3,9 = 4,5 з) (у – 8,48) + 2,16 = 3,9

Самостоятельная работа.

Вариант I

1. Выполните действия: (43,4 – 7,87) – (4,3 + 27,83) 2. Решите задачу: В первый день клевер был скошен с площади 18,37 га, что на 5,7 га больше, чем во второй день, и на 2,21 га больше, чем в третий день. С какой площади был скошен клевер за эти три дня? 3. Решите уравнение: а) y – 2,9 = 3,93 б) (x – 8,48) + 2,16 = 3,9

Самостоятельная работа.

Вариант II

1. Выполните действия:

(26,72 + 4,9) + (35,8 – 6,98)

2. Решите задачу: В первый день было вспахано 14,25 га, что на 3,6 га больше, чем во второй день, и на 4,15 га меньше, чем в третий день. Сколько гектаров было вспахано за три дня?

3. Решите уравнение:

а) у + 3,54 = 8,2 б) (x – 3,48) + 2,15 = 3,9

multiurok.ru