Тренажеры по алгебре по всем темам (11 класс)
Тренажер№1 А – 11. 1.Вычислите приращение функции у=f(x) на промежутке 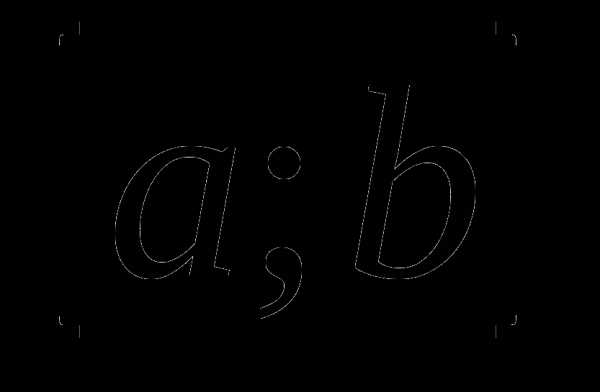
1. f(x)=4х+3, а=0, b=0,2;
2. f(x)=х2 –3х, а=2, b=3;
3. f(x)= , а=1, b=1,5;
, а=1, b=1,5;
4. f(x)=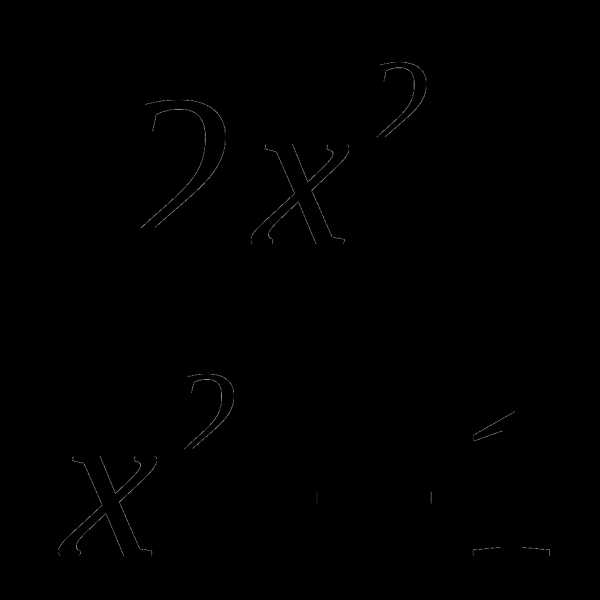 , а=2, b=2,5;
, а=2, b=2,5;
5. f(x)=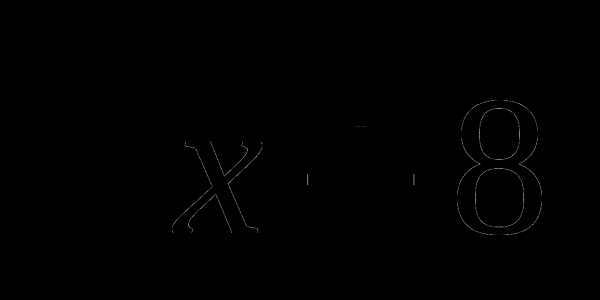 , а=-1, b=-8.
, а=-1, b=-8.
1.Вычислите приращение функции у=f(x) на промежутке 
1. f(x)=2х+3, х=1,5, 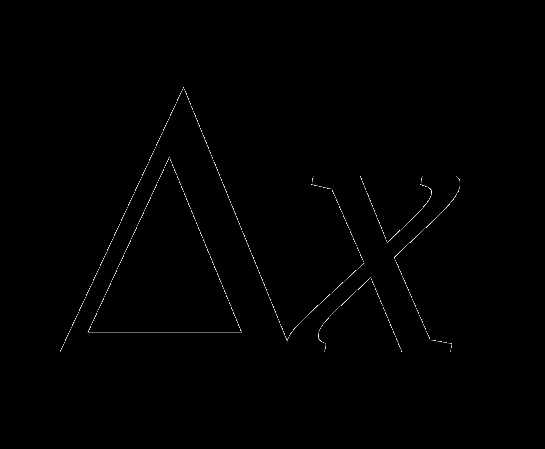 =2,5;
=2,5;
2. f(x)=3х2 –х+1, х=0, 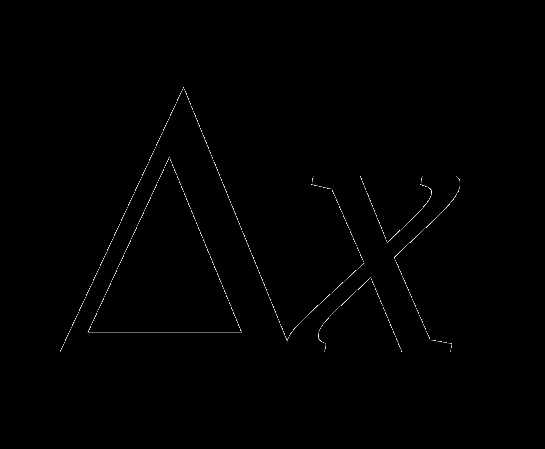 =2;
=2;
3. f(x)=х3 –2х2+х, х=-1, 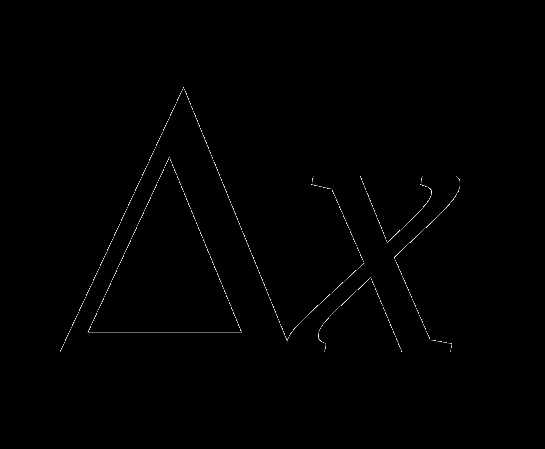 =1;
=1;
4. f(x)=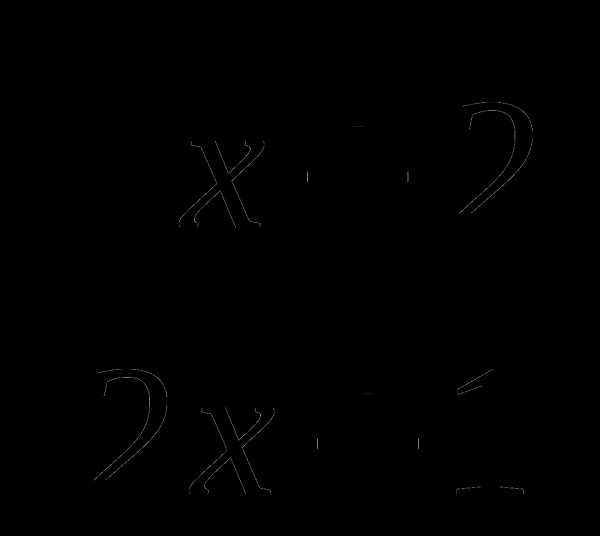 , х=2,
, х=2, 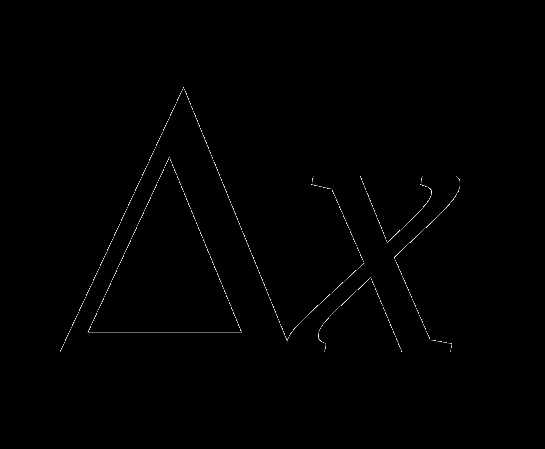 =5;
=5;
5. f(x)=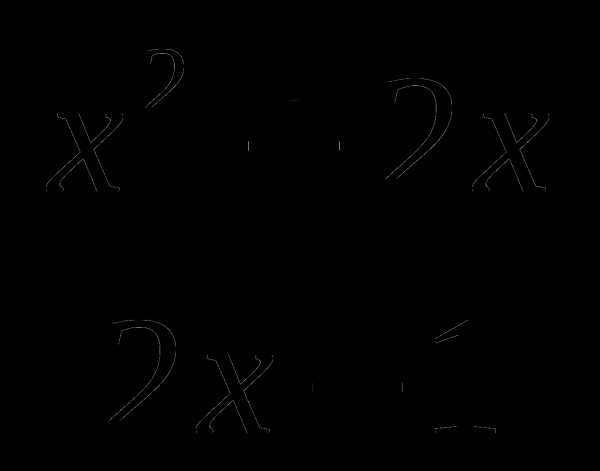 , х=-2,
, х=-2, 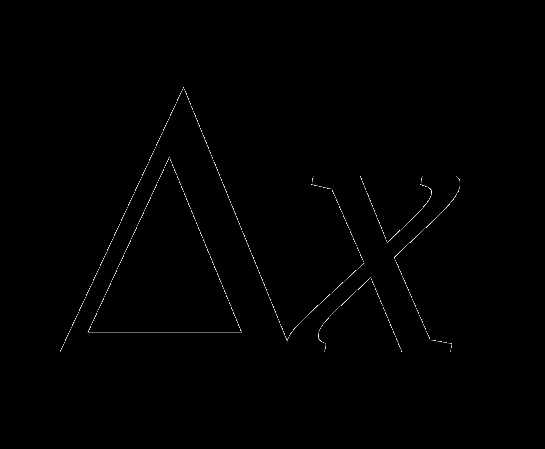 =1.
=1.
3. Вычислите среднюю скорость роста функции у=f(x)
на двух данных промежутках и на промежутке  :
:
1. f(x)=2х+1, ;
2. f(x)= х+3,
х+3,  ;
;
3. f(x)=2х2 -1, ;
4. f(x)=2х2 –х-1, ;
5. f(x)=х3 –3х-х, .
Тренажер №2. Производная степенной функции.
Найти производную функции
1. f(x)=2х3
2. h(x)= .
.
3. f(x)=х4-4х3-8х2+13.
4. v(h)=- +3h.
+3h.
5. f(x)=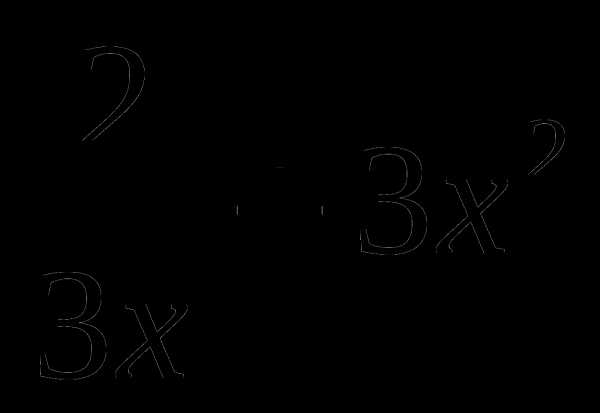 .
.
6. f(x)=.
7. f(x)=-.
8. f(x)=.
9. g(t)=- .
.
10. s(r)=2.
11. у(t)=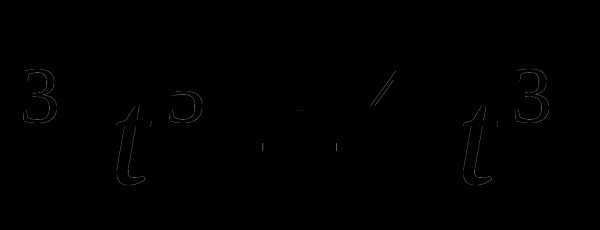 .
.
12. f(x)=х3(5х-1)(1-2х).
13. v(.
14. у(t)=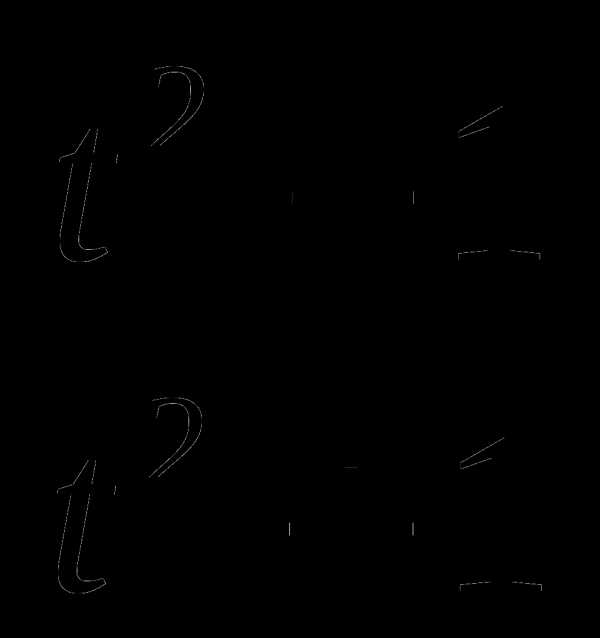 .
.
15. v(h)=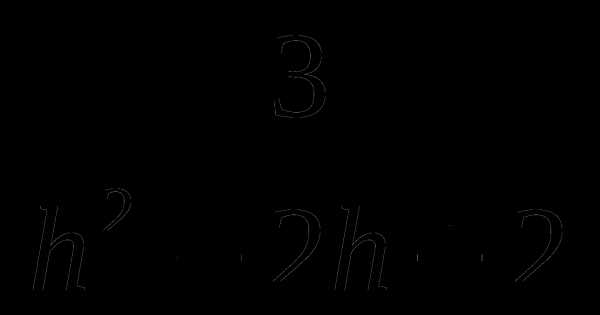 .
.
16. g(t)=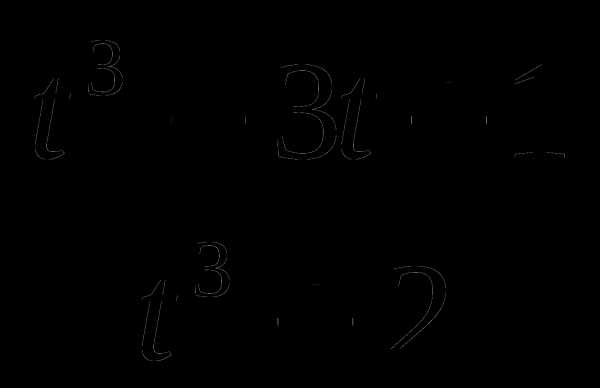 .
.
17. g(t)=(t+4)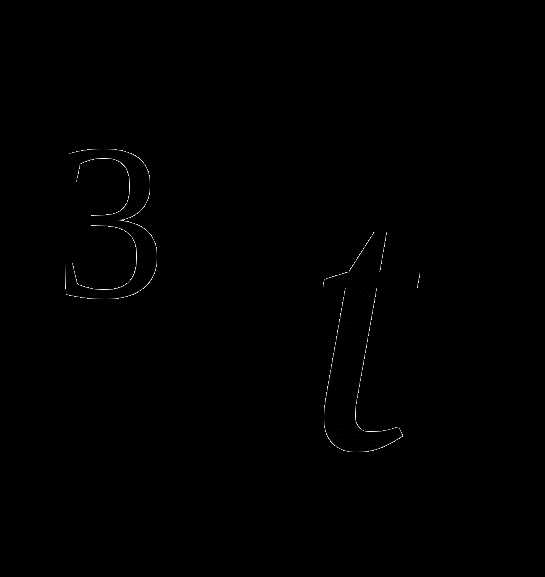 .
.
18. f(u)= .
.
19. f(x)=  .
.
20. f(x)=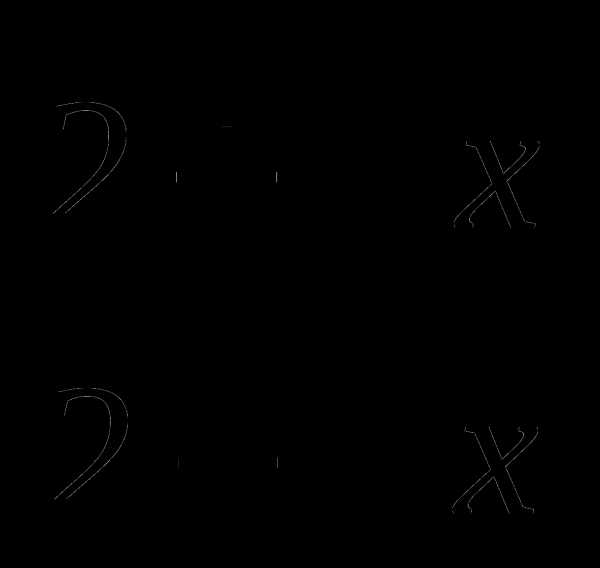 .
.
21. g(x)=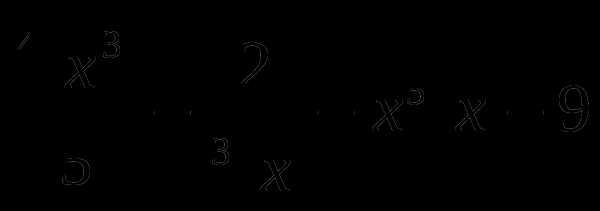 .
.
22. f(x)=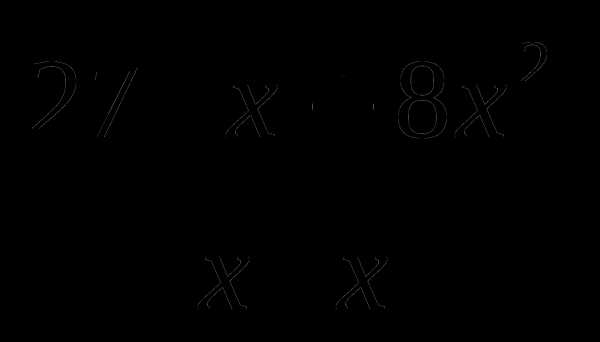 .
.
23. f(x)=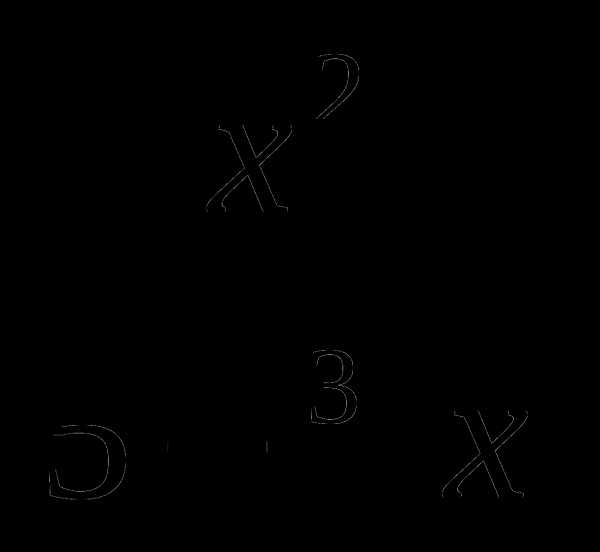 .
.
24. y(t)=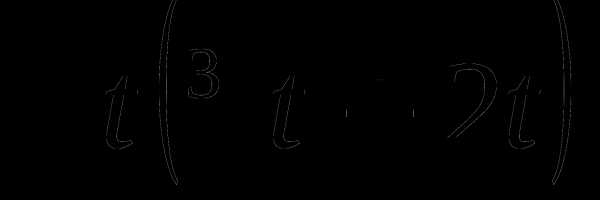 .
.
25. f(x)=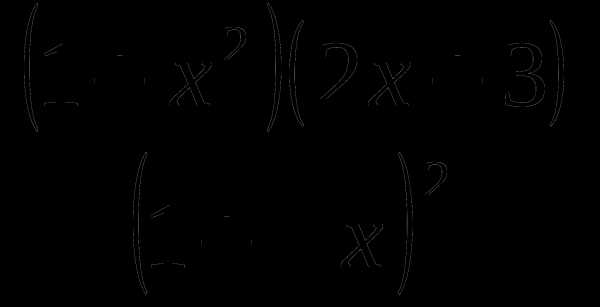 .
.
Тренажер № 3. Производная сложной функции (линейная замена).
Найти производную функции:
1.f(x)= (2х+3)4.
2. g(u)=(-3u+7)3.
3. f(x)=(2x+1)4-(3x-1)6.
4. g(t)=(7t+3)5—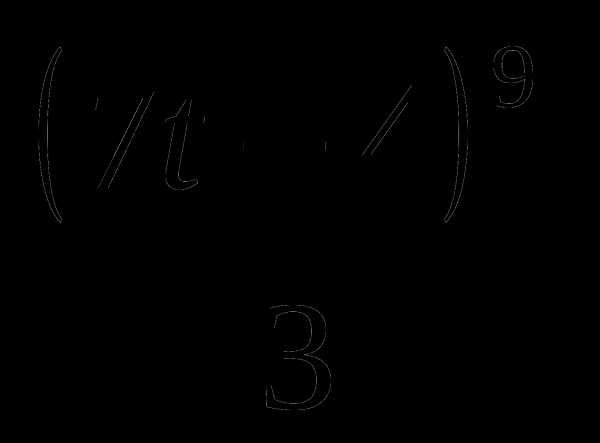 .
.
5. F(l)=(2l+1)4·(2l-1)3.
6. f(x)=a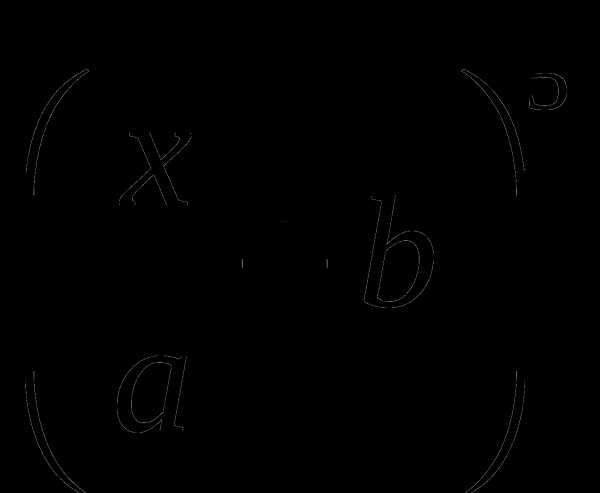 .
.
7. F(j)=2.
8. f(x)=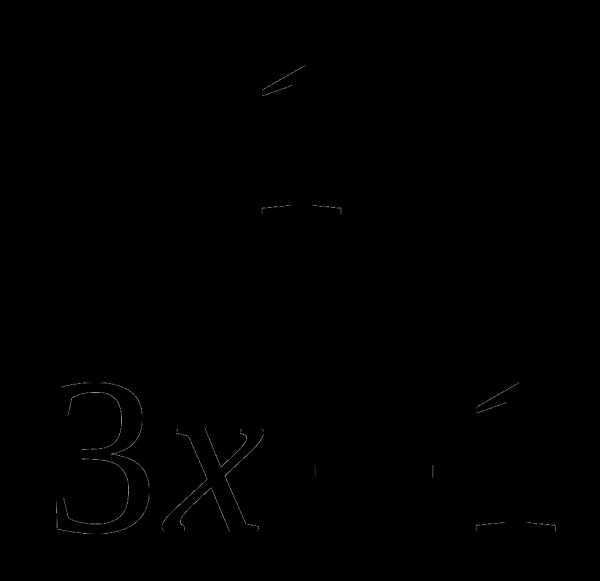 .
.
9. g(x)=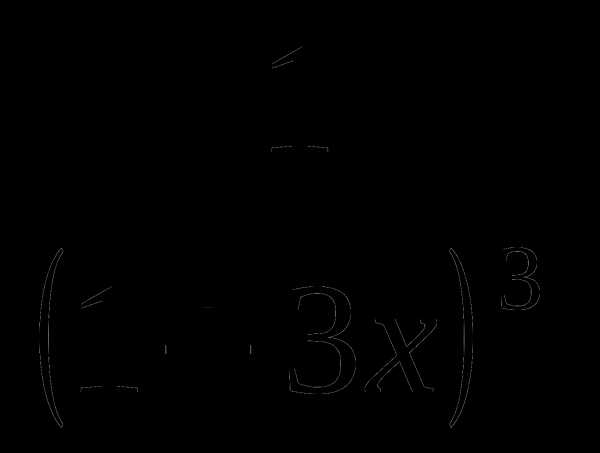 .
.
10. f(x)=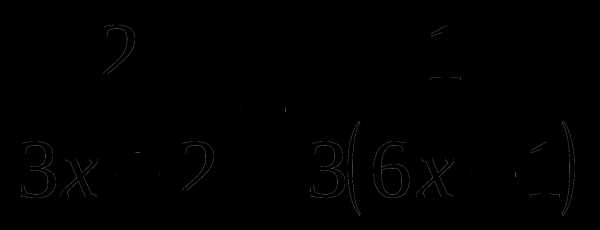 .
.
11. P( )=
)=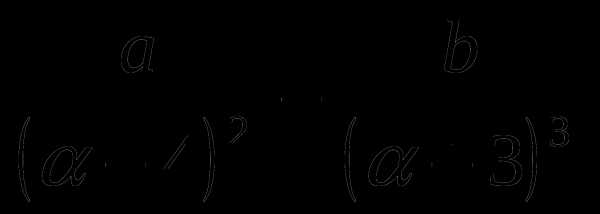 .
.
12. y(x)=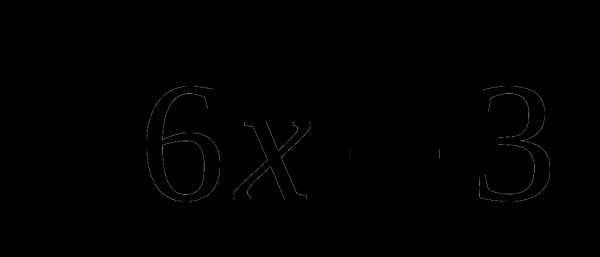 .
.
13. f(x)=3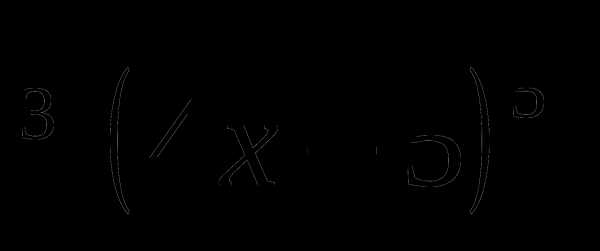 .
.
14. y(t)=.
15. f(x)=.
Тренажер № 4.Уравнение касательной.
Дана функция у=f(x). Найдите:
1) угловой коэффициент касательной к графику этой функции в точке с абсциссой х0;
2) точки, в которых угловой коэффициент касательной равен k;
3) напишите уравнение касательной к графику функции в точке с абсциссой х0:
1. у=х2+4, х0=1, k=4.
2. у= 2х2+х, х0=2, k=-1.
3. у=3х2-6х+1, х0=0, k=6.
4. у=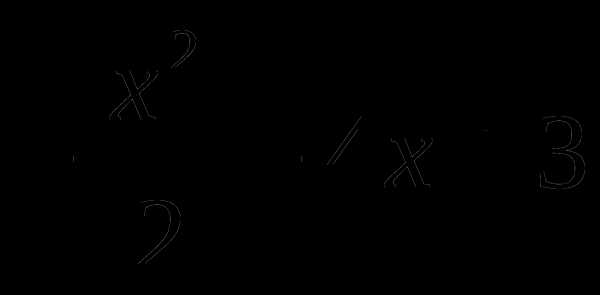 , х0=-1, k=0.
, х0=-1, k=0.
5. у= х3+3х+2, х0=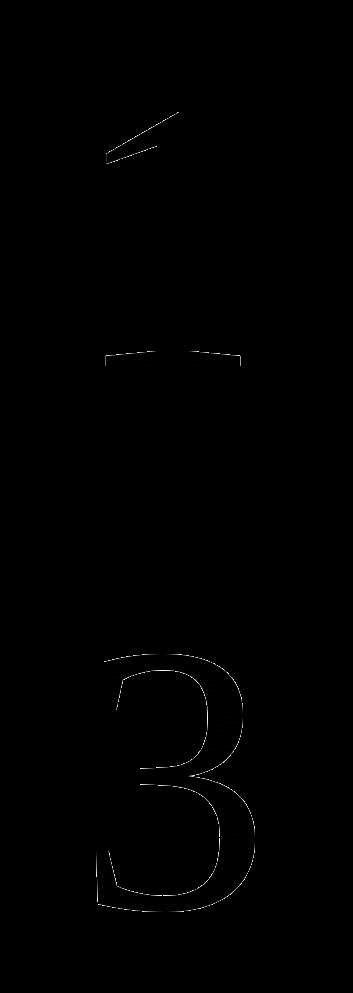 , k=
, k= .
.
6. у= х+ , х0=1, k=
, х0=1, k= .
.
7. у=2х4-х3+1, х0=0, k=0.
8. у=(х-2)2(х+1), х0=1, k=6.
9. у= , х0=1, k=0.
, х0=1, k=0.
10. у=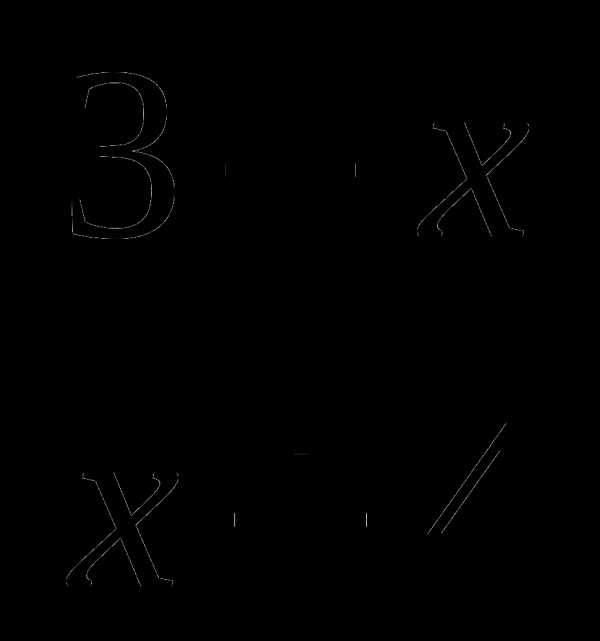 , х0=-3, k=-7.
, х0=-3, k=-7.
11. у=х+2 , х0=1, k=2.
, х0=1, k=2.
12. у=(х+1) , х0=4, k=2.
, х0=4, k=2.
Тренажер № 5. Промежутки монотонности
Найдите промежутки монотонности функции:
1. у=х2-3х+2.
2. у=(2х-1)2.
3. у=6х-х2+5.
4. у=2х3+6х2-1.
5. у=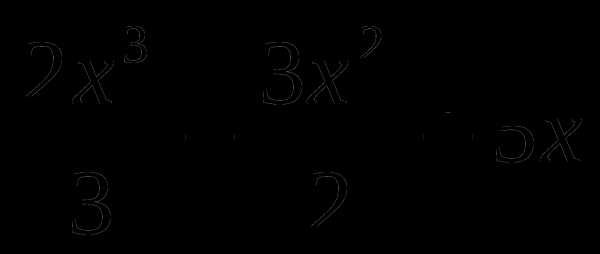 .
.
6. у=2х3—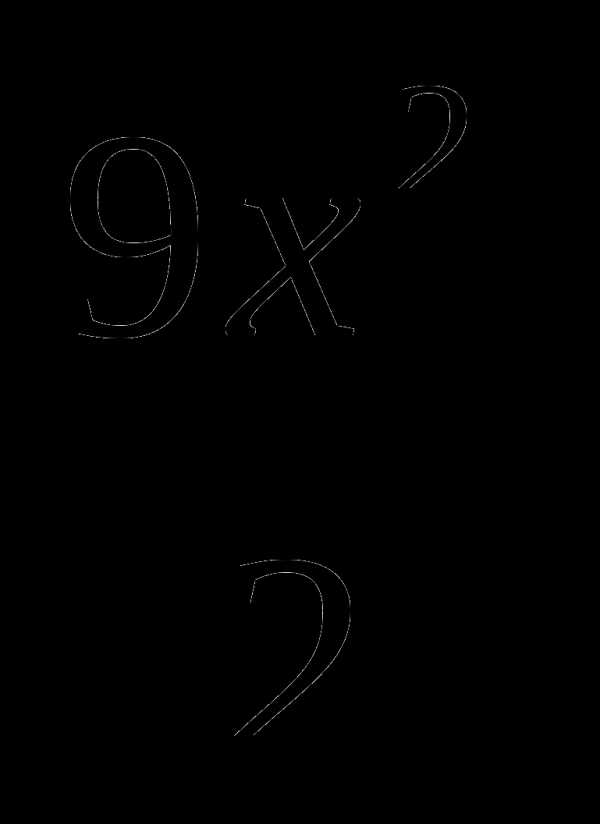 +3х-4.
+3х-4.
7. у= 4х2+180.
4х2+180.
8. у=х2-5х3+20х-3.
9. у=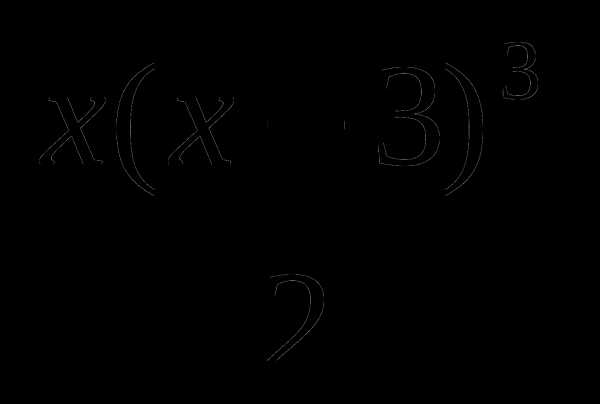 .
.
10. у=х4+ х2-2.
х2-2.
11. у=х5-20х3+1.
12. у=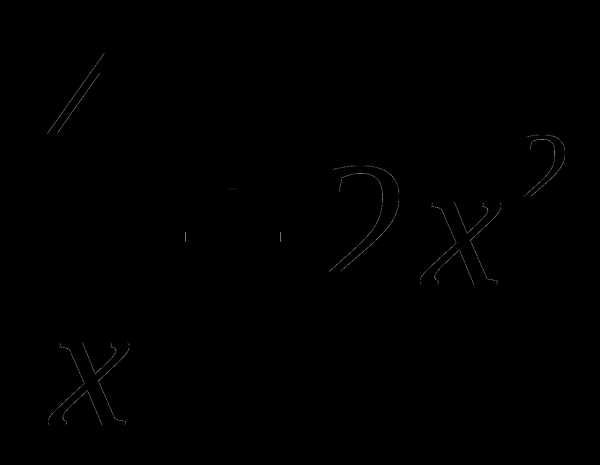 .
.
13. у=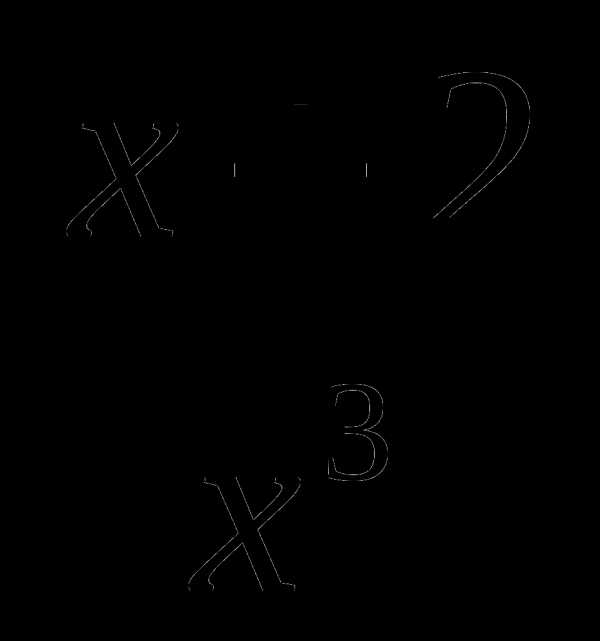 .
.
14. у=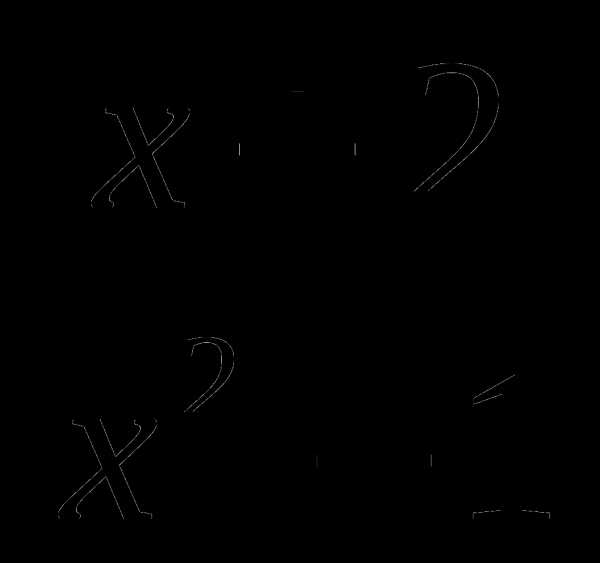 .
.
15. у= .
.
16. у=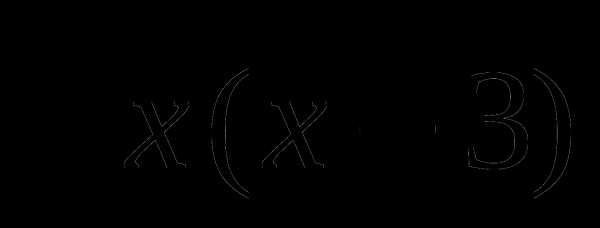 .
.
17. у=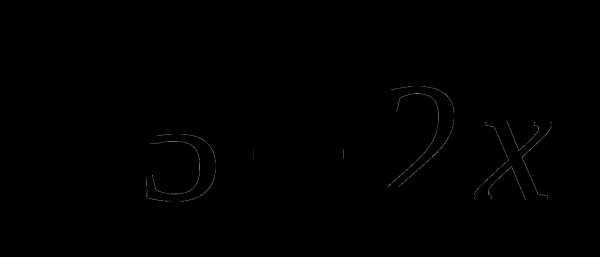 .
.
18. 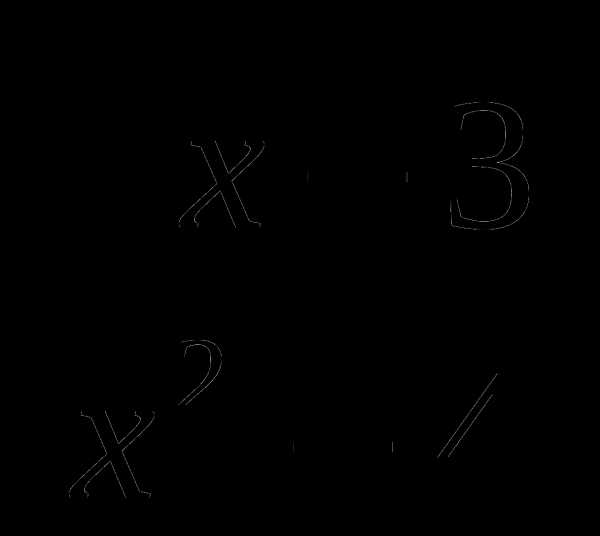 .
.
Тренажер № 6. Экстремум функции.
Найдите точки экстремума функции5
1. у=х2+1.
2. у=3х2-4х.
3. у=х3+3х2.
4. у=2х3-24х+5.
5. у=2х3+3х2-12х+5.
6. у=(х+2)2(3х-1).
7. у=х4-4х3+4х2.
8. у=2х(1-3х)3.
9. у=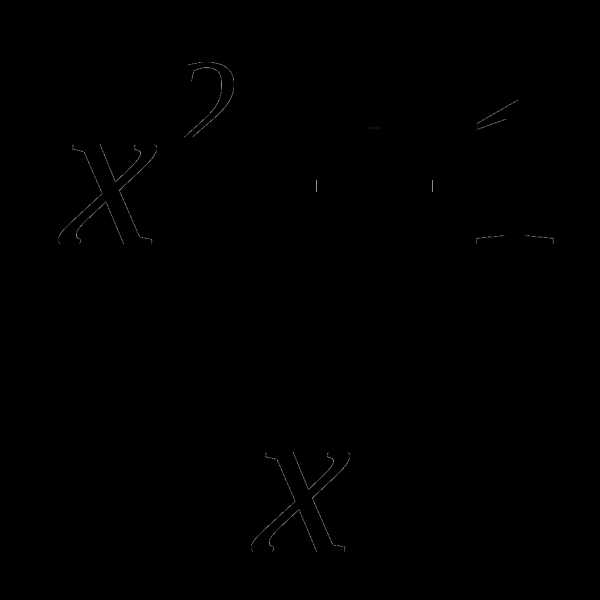 .
.
10. у=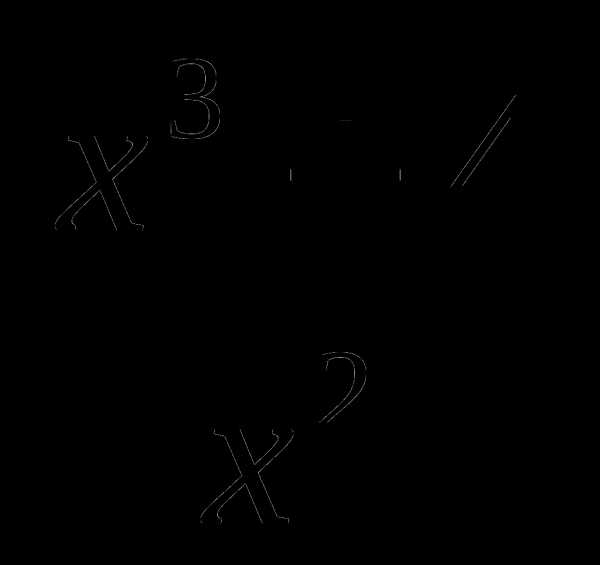 .
.
11. у=х2+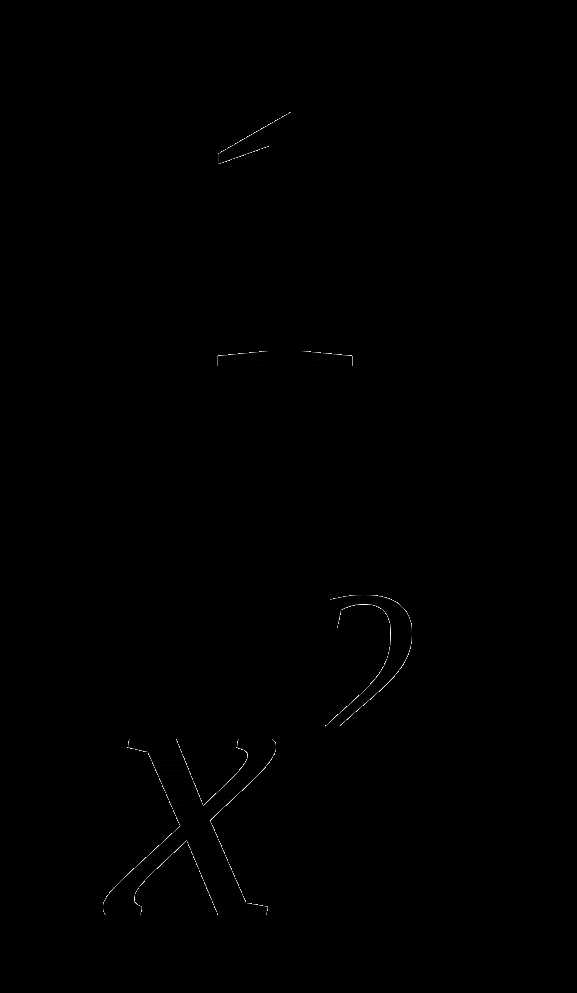 .
.
12. у=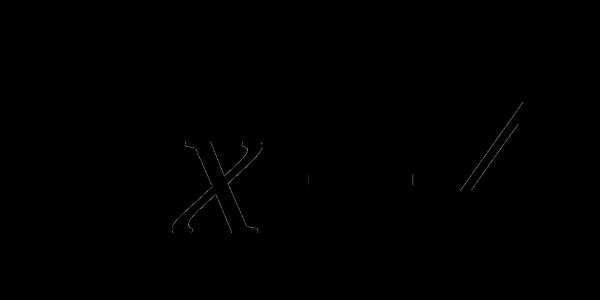 .
.
13. у=х+ .
.
14. у=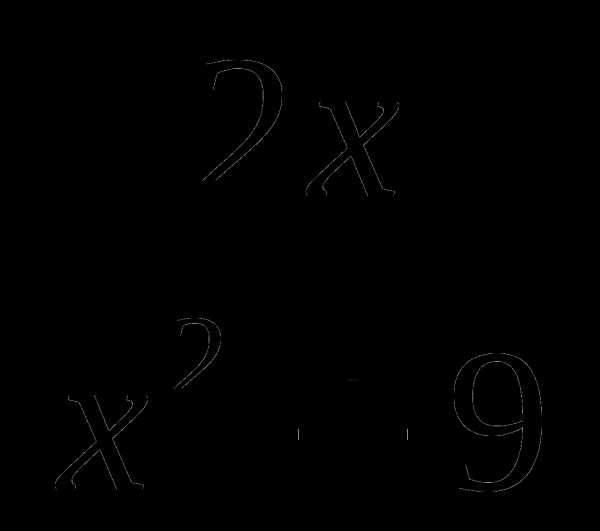 .
.
15. у=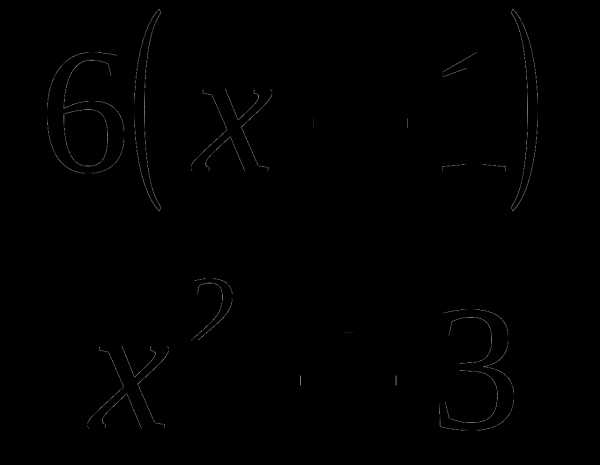 .
.
16. у=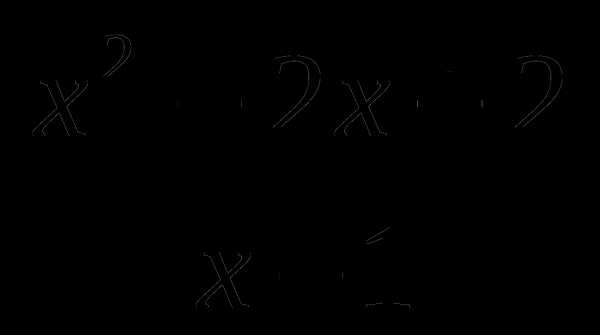 .
.
17. у=(х-1) .
.
18. у=2х2— .
.
19. у=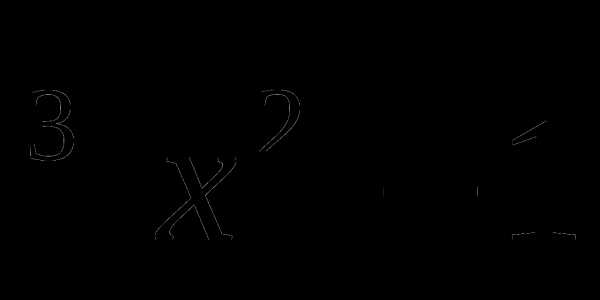 .
.
20. у=х2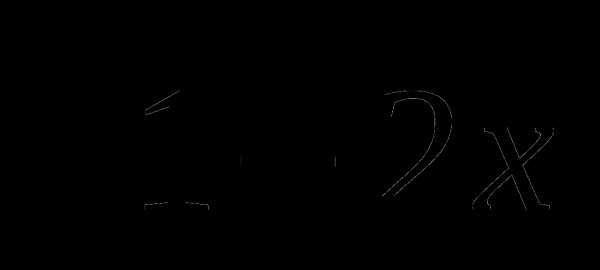 .
.
Тренажер № 7. Исследование функции на отрезке
Найдите наибольшее и наименьшее значение функции у=f(x) на заданных промежутках:
1. у=х3-12х+4 а) 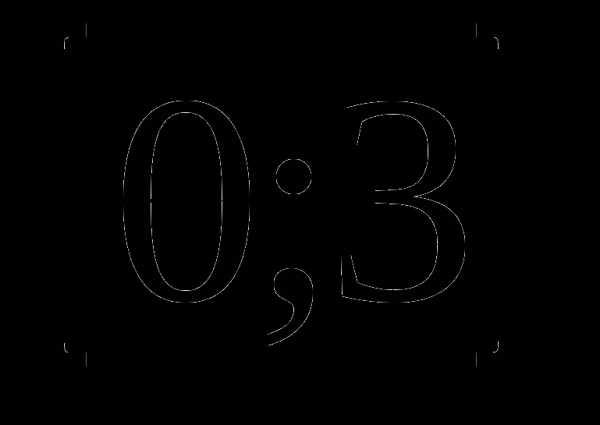 б)
б)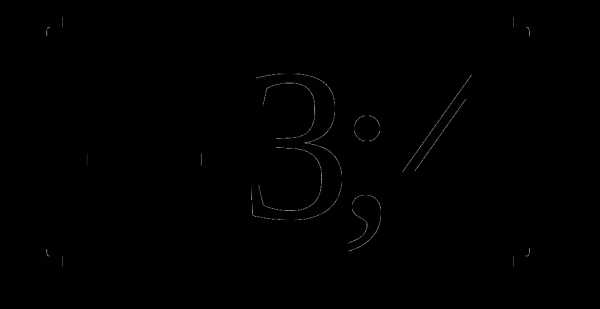
2. у=1+3х-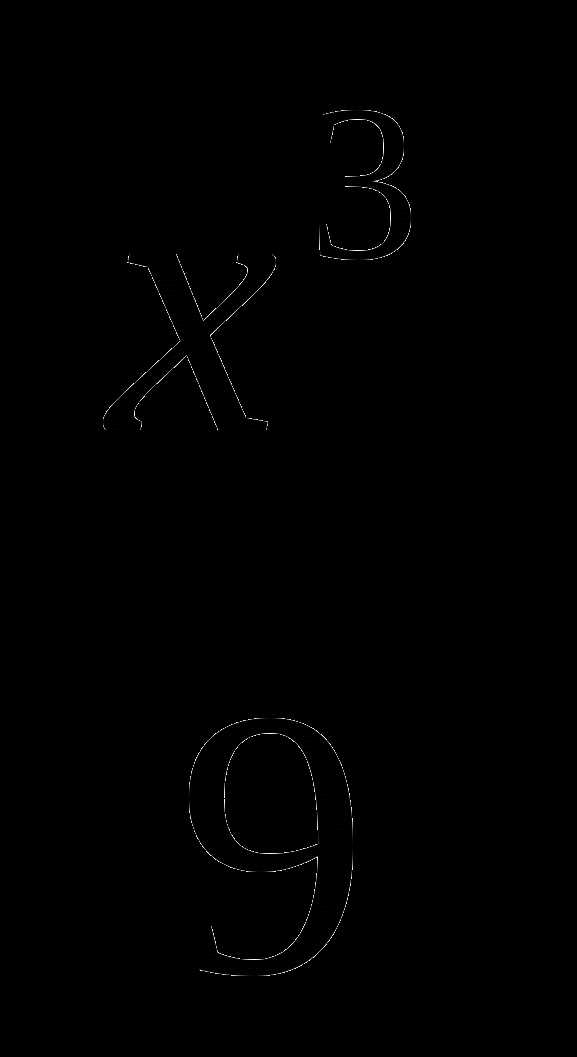 а)
а) 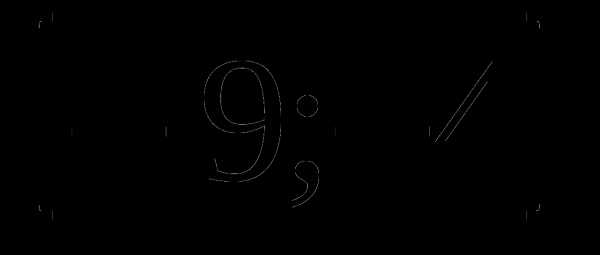 , б)
, б)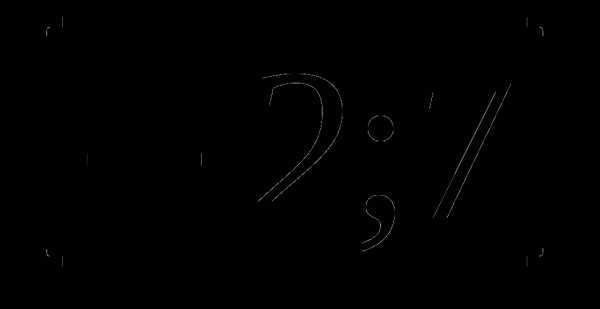
3. у=х3-х2+3х-11 а) 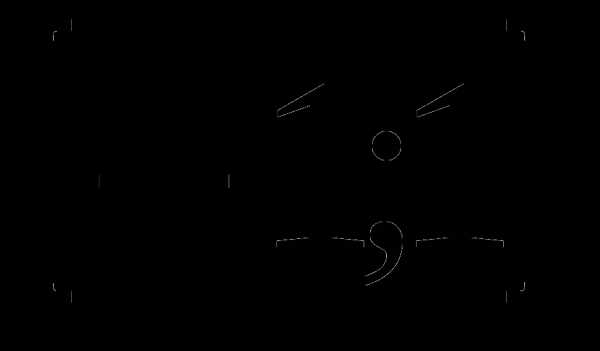 б)
б)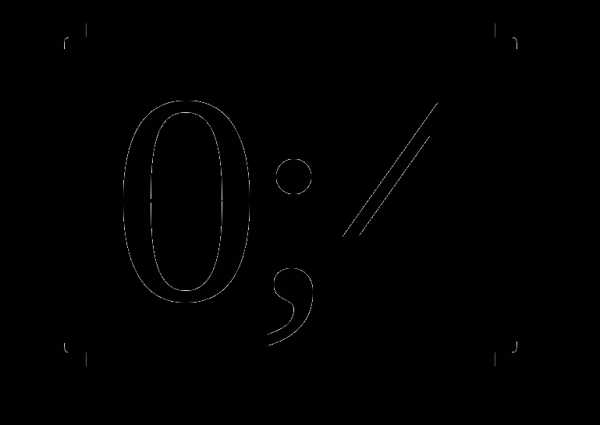
4. у=х4-8х+3 а) 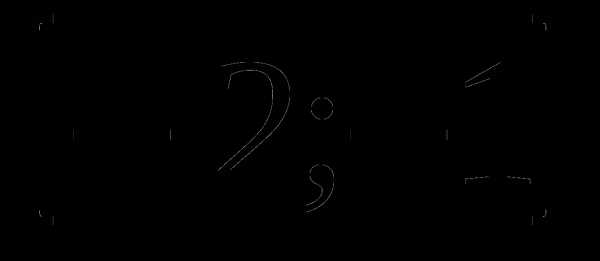 б)
б)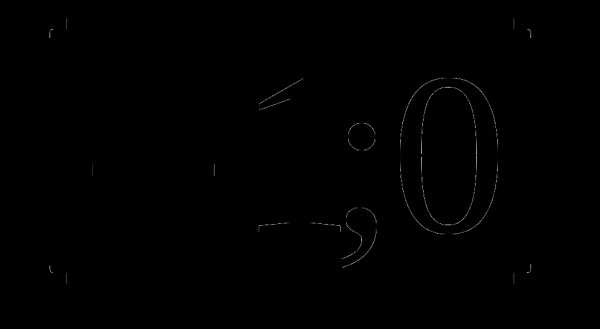
5. у=х4-4х3-8х2+ 13 а) 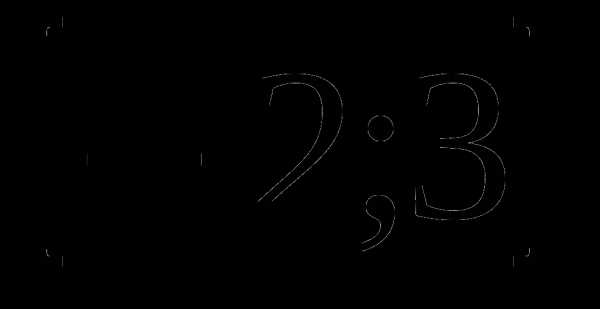 б)
б)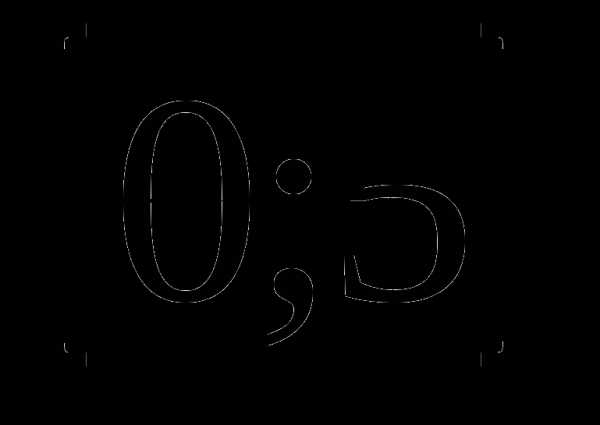
6. у=х+ а)
а) 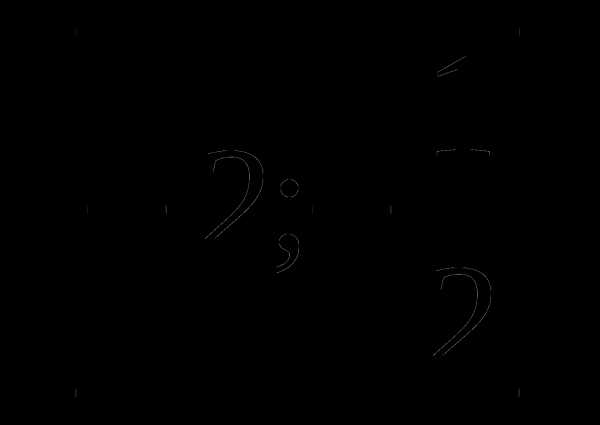 б)
б)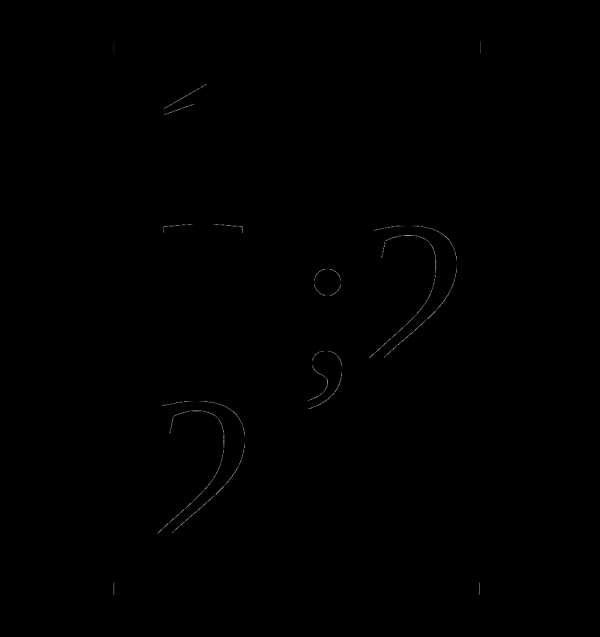
7. у=х2— а)
а)  б)
б)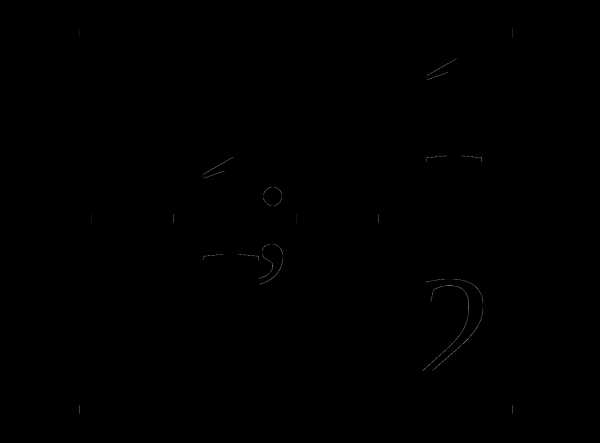
8. у=х2+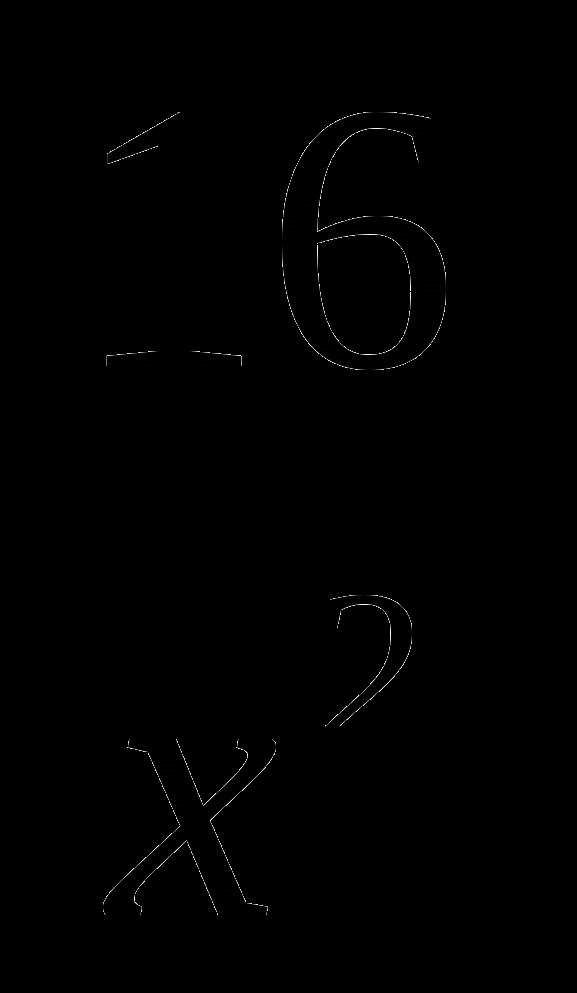 а)
а) 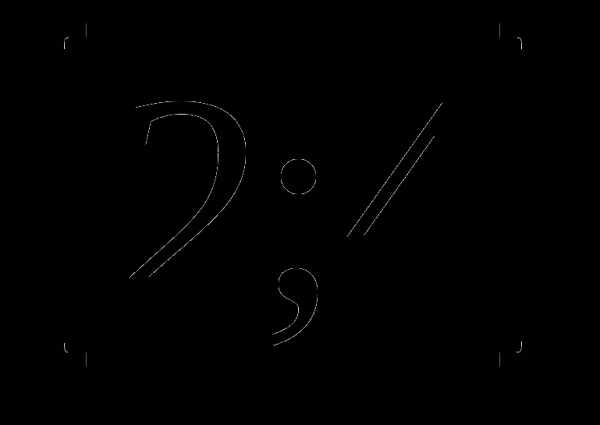 б)
б)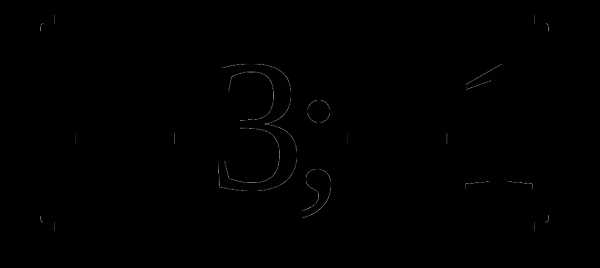
9. у=х- а)
а) 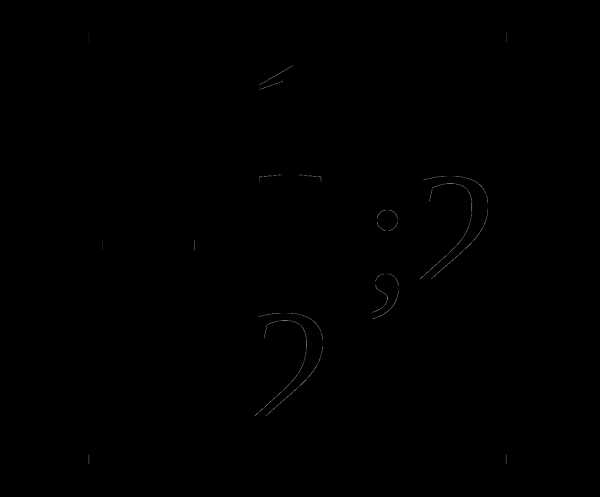 б)
б)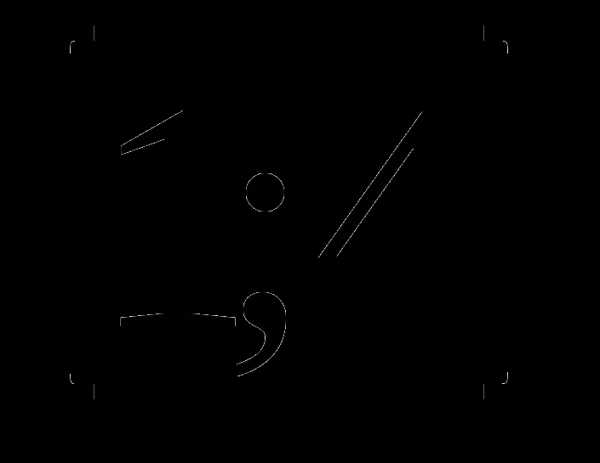
10. у=(х+2)3(х-1) а) 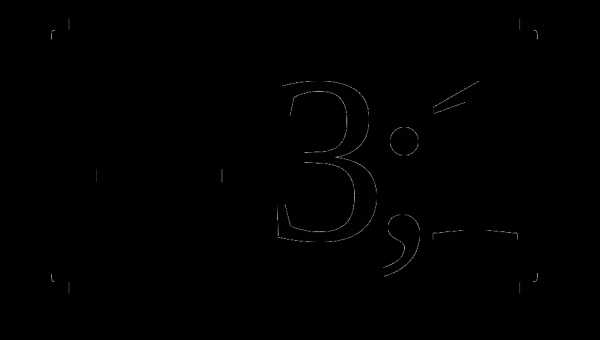 б)
б)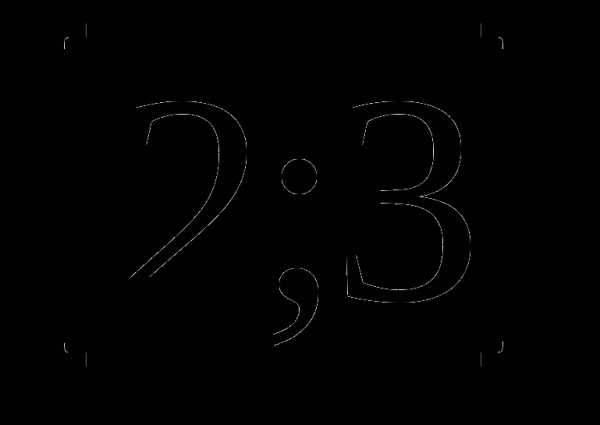
11. у=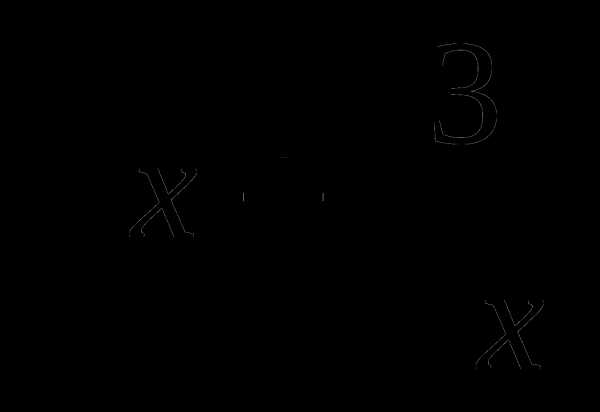 а)
а) 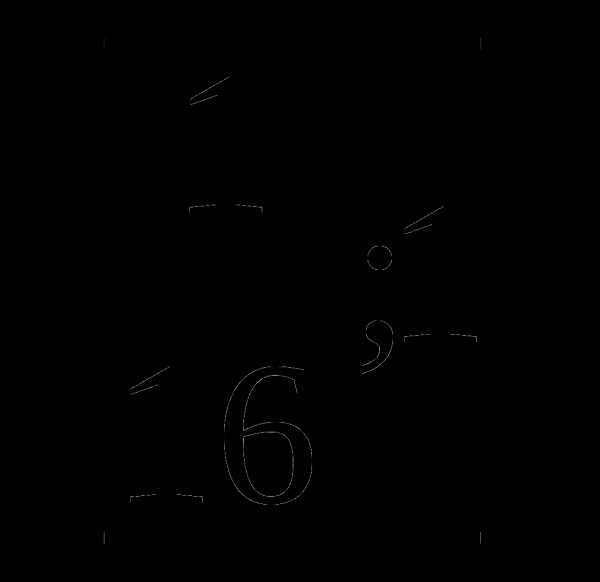 б)
б)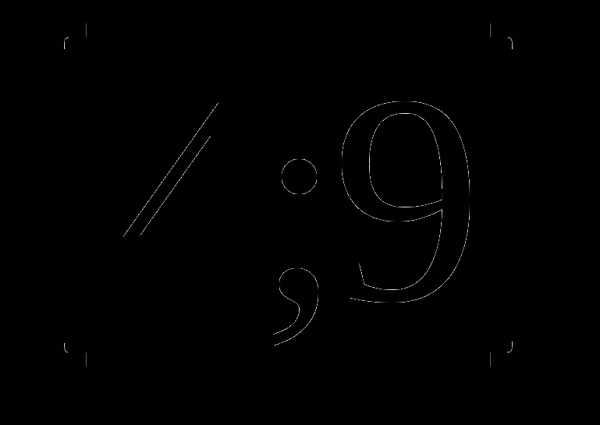
12. у=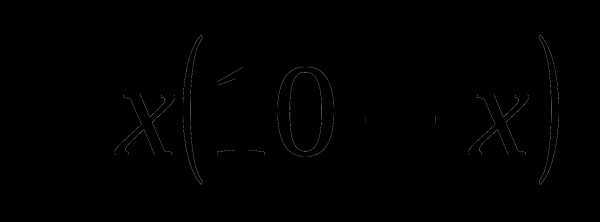 а)
а) 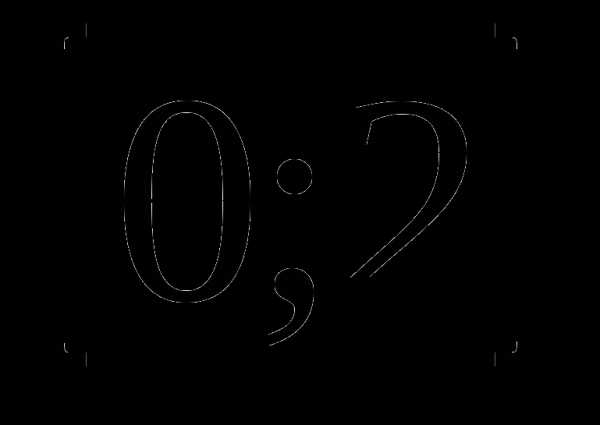 б)
б)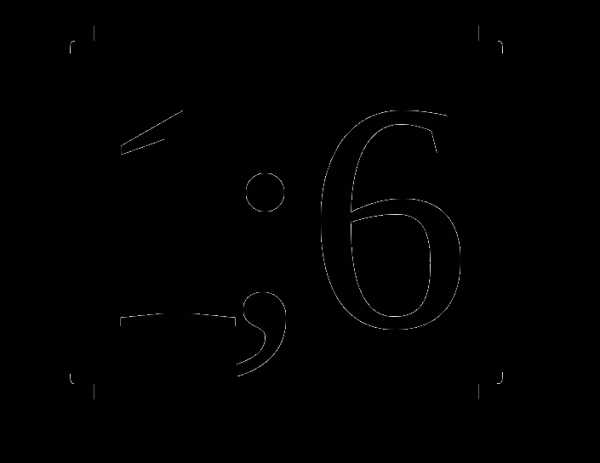 .
.
Тренажер № 8. Вычисление первообразных.
Вычислите первообразную функции:
1. у=х3+1.
2. у=2х2— .
.
3. у=(1-3х)2.
4. у= .
.
5. у=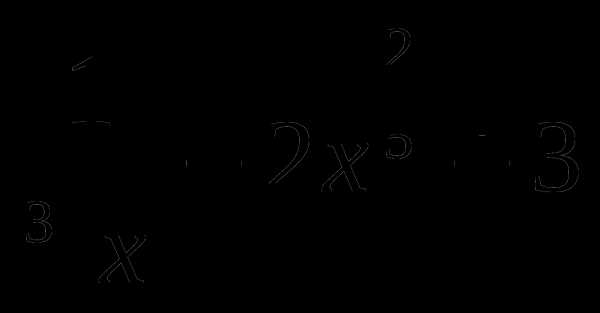 .
.
6. у= .
.
7. у=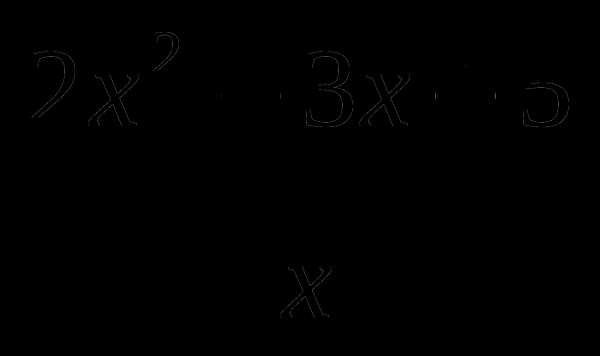 .
.
8. у=.
9. у=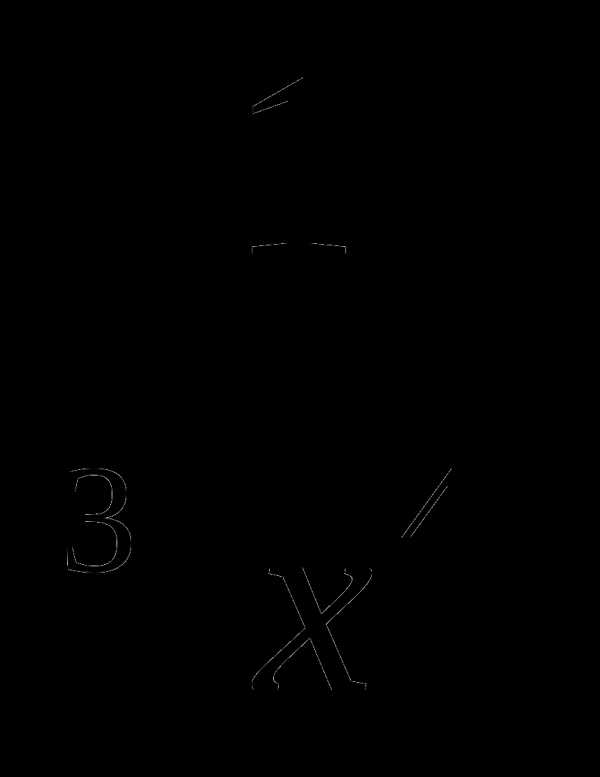 .
.
10. у=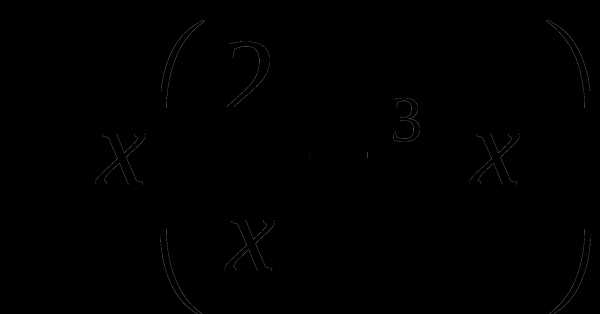
11. у=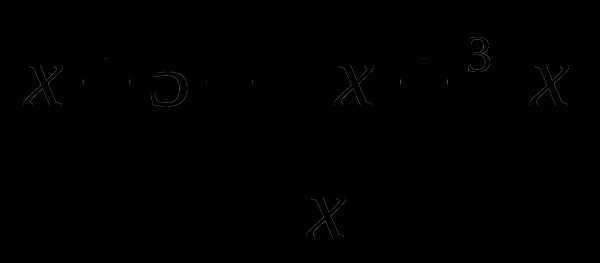 .
.
12. у=(1+х)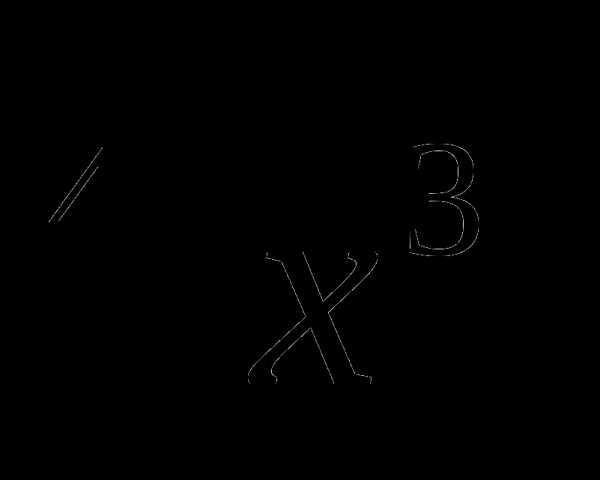 .
.
Тренажер № 10. Вычисление площадей.
Вычислите площадь фигуры, ограниченной линиями:
1. у=х3, у=0, х=1, х=3.
2. у=х2, у=2х,.
3. у=х, у=0, х=3, х=1.
4. у=х2-2х+3, у=0, х=0, х=2.
5. у= , у=х.
, у=х.
6. у=sinx, у=0, х= , х=
, х=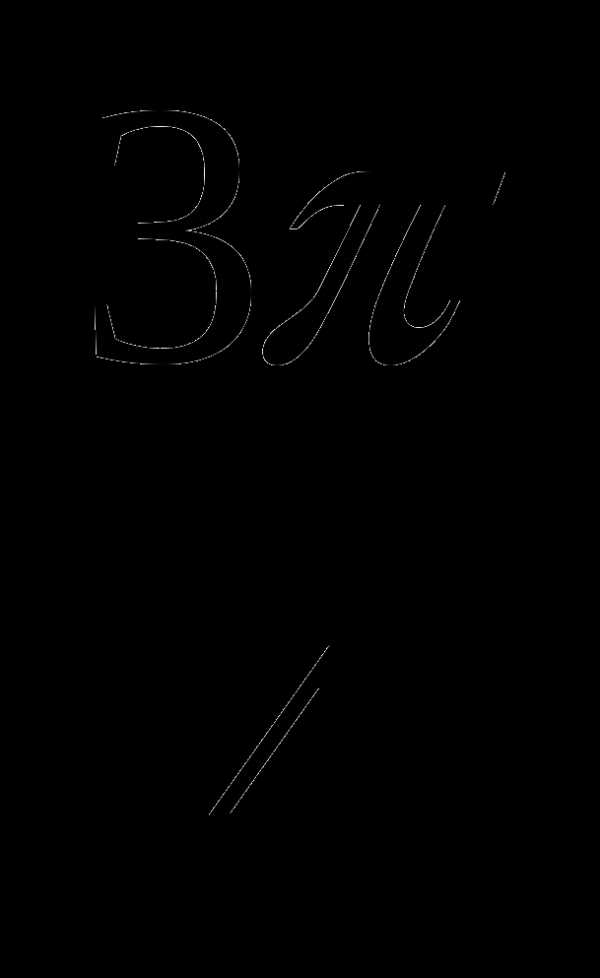 .
.
7. у=sinx, у=0, х= , х=
, х=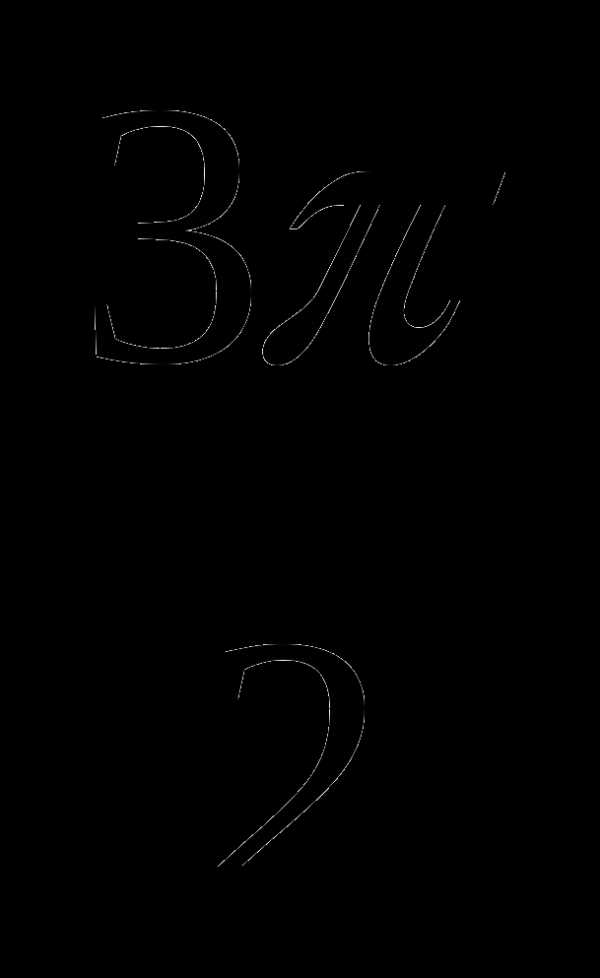 .
.
8. у=2х+1, у=х2.
9. у=х2+2х+2, у=0, х=-1, х=2.
10., у=1, у=х2.
11. у=2х, у=5х, х=1.
12. у=х2 -1, у=0.
13. у=2-х2, у= , х=0.
, х=0.
14. у=-х, у=-х3 ( у 0).
0).
15. у= , у=х, х=2.
, у=х, х=2.
16. у=2-х2, у=х, у=0.
infourok.ru
Скорость изменения функции — Мегаобучалка
Определение производной функции через предел
Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,
Общепринятые обозначения производной функции в точке
Дифференцируемость
Основная статья: Дифференцируемая функция
Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна:
Для дифференцируемой в функции в окрестности справедливо представление
при
Замечания Назовём приращением аргумента функции, а приращением значения функции в точке Тогда
· Пусть функция имеет конечную производную в каждой точке Тогда определена произво́дная фу́нкция
· Функция, имеющая производную в точке, непрерывна в ней. Обратное не всегда верно.
· Если производная функция сама является непрерывной, то функцию называют непреры́вно дифференци́руемой и пишут:
Геометрический и физический смысл производной
Тангенс угла наклона касательной прямой
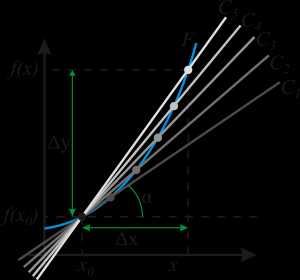
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точкиx0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Основная статья: Касательная прямая
Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией
Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклонакасательной прямой.
Скорость изменения функции
Пусть — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени
Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью
Производные высших порядков
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
Если функция дифференцируема в , то производная первого порядка определяется соотношением
Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда
Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).
или
или
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
·
·
· [2]
· [3]
·
· …(g ≠ 0)
· (g ≠ 0)
· Если функция задана параметрически:
, то
Основная статья: Дифференцирование сложной функции
·
· Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
где — биномиальные коэффициенты.
megaobuchalka.ru
Тренажеры по алгебре по всем темам (11 класс)
1 А – 11. 1.Вычислите приращение функции у=f(x) на промежутке 13 EMBED Equation.3 14151. f(x)=4х+3, а=0, b=0,2;
2. f(x)=х2 –3х, а=2, b=3;
3. f(x)=13 EMBED Equation.3 1415, а=1, b=1,5;
4. f(x)=13 EMBED Equation.3 1415, а=2, b=2,5;
5. f(x)=13 EMBED Equation.3 1415, а=-1, b=-8.
1.Вычислите приращение функции у=f(x) на промежутке 13 EMBED Equation.3 1415
1. f(x)=2х+3, х=1,5, 13 EMBED Equation.3 1415=2,5;
2. f(x)=3х2 –х+1, х=0, 13 EMBED Equation.3 1415=2;
3. f(x)=х3 –2х2+х, х=-1, 13 EMBED Equation.3 1415=1;
4. f(x)=13 EMBED Equation.3 1415, х=2, 13 EMBED Equation.3 1415=5;
5. f(x)=13 EMBED Equation.3 1415, х=-2, 13 EMBED Equation.3 1415=1.
3. Вычислите среднюю скорость роста функции у=f(x)
на двух данных промежутках и на промежутке 13 EMBED Equation.3 1415:
1. f(x)=2х+1, 13 EMBED Equation.3 1415;
2. f(x)=13 EMBED Equation.3 1415х+3, 13 EMBED Equation.3 1415;
3. f(x)=2х2 -1, 13 EMBED Equation.3 1415;
4. f(x)=2х2 –х-1, 13 EMBED Equation.3 1415;
5. f(x)=х3 –3х-х, 13 EMBED Equation.3 1415.
Тренажер №2. Производная степенной функции.
Найти производную функции
1. f(x)=2х3
2. h(x)=13 EMBED Equation.3 1415.
3. f(x)=х4-4х3-8х2+13.
4. v(h)=-13 EMBED Equation.3 1415+3h.
5. f(x)=13 EMBED Equation.3 1415.
6. f(x)=13 EMBED Equation.3 1415.
7. f(x)=-13 EMBED Equation.3 1415.
8. f(x)=13 EMBED Equation.3 1415.
9. g(t)=-13 EMBED Equation.3 1415.
10. s(r)=213 EMBED Equation.3 1415.
11. у(t)=13 EMBED Equation.3 1415.
12. f(x)=х3(5х-1)(1-2х).
13. v(13 EMBED Equation.3 1415.
14. у(t)=13 EMBED Equation.3 1415.
15. v(h)=13 EMBED Equation.3 1415.
16. g(t
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
· 3. Производная сложной функции (линейная замена).
Найти производную функции:
1.f(x)= (2х+3)4.
2. g(u)=(-3u+7)3.
3. f(x)=(2x+1)4-(3x-1)6.
4. g(t)=(7t+3)5-13 EMBED Equation.3 1415.
5. F(l)=(2l+1)4·(2l-1)3.
6. f(x)=a13 EMBED Equation.3 1415.
7. F(j)=
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·–
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
4.Уравнение касательной.
Дана функция у=f(x). Найдите:
1) угловой коэффициент касательной к графику этой функции в точке с абсциссой х0;
2) точки, в которых угловой коэффициент касательной равен k;
3) напишите уравнение касательной к графику функции в точке с абсциссой х0:
1. у=х2+4, х0=1, k=4.
2. у= 2х2+х, х0=2, k=-1.
3. у=3х2-6х+1, х0=0, k=6.
4. у=13 EMBED Equation.3 1415, х0=-1, k=0.
5. у= х3+3х+2, х0=13 EMBED Equation.3 1415, k=13 EMBED Equation.3 1415.
6. у= х+13 EMBED Equation.3 1415, х0=1, k=13 EMBED Equation.3 1415.
7. у=2х4-х3+1, х0=0, k=0.
8. у=(х-2)2(х+1), х0=1, k=6.
9. у=13 EMBED Equation.3 1415, х0=1, k=0.
10. у=13 EMBED Equation.3 1415, х0=-3, k=-7.
11. у=х+213 EMBED Equation.3 1415, х0=1, k=2.
12. у=(х+1)13 EMBED Equation.3 1415, х0=4, k=2.
Тренажер № 5. Промежутки монотонности
Найдите промежутки монотонности функции:
1. у=х2-3х+2.
2. у=(2х-1)2.
3. у=6х-х2+5.
4. у=2х3+6х2-1.
5. у=13 EMBED Equation.3 1415.
6. у=2х3-13 EMBED Equation.3 1415+3х-4.
7. у=13 EMBED Equation.3 14154х2+180.
8. у=х2-5х3+20х-3.
9. у=13 EMBED Equation.3 1415.
10. у=х4+13 EMBED Equation.3 1415х2-2.
11. у=х5-20х3+1.
12. у=13 EMBED Equation.3 1415.
13. у=13 EMBED Equation.3 1415.
14. у=13 EMBED Equation.3 1415.
15. у=13 EMBED Equation.3 1415.
16. у=13 EMBED Equation.3 1415.
17. у=13 EMBED Equation.3 1415.
18. 13 EMBED Equation.3 1415.
Тренажер № 6. Экстремум функции.
Найдите точки экстремума функции5
1. у=х2+1.
2. у=3х2-4х.
3. у=х3+3х2.
4. у=2х3-24х+5.
5. у=2х3+3х2-12х+5.
6. у=(х+2)2(3х-1).
7. у=х4-4х3+4х2.
8. у=2х(1-3х)3.
9. у=13 EMBED Equation.3 1415.
10. у=13 EMBED Equation.3 1415.
11. у=х2+13 EMBED Equation.3 1415.
12. у=13 EMBED Equation.3 1415.
13. у=х+13 EMBED Equation.3 1415.
14. у=13 EMBED Equation.3 1415.
15. у=13 EMBED Equation.3 1415.
16. у=13 EMBED Equation.3 1415.
17. у=(х-1)13 EMBED Equation.3 1415.
18. у=2х2-13 EMBED Equation.3 1415.
19. у=13 EMBED Equation.3 1415.
20. у=
weburok.com
Определение среднего значения функции
Определение среднего значения функцииП. Совертков, Ф.
Дягилев,
г. Нижневартовск
Обсуждая концепцию математического образования в 12-летней школе [3, с. 13–18], следует уточнить целеполагание одного из основных блоков математического образования – функции. Важным является изучение не столько свойств функций, сколько развитие умений применять функции для описания реальных процессов. Но реальные процессы задаются сложными функциональными зависимостями. Математическое моделирование упрощает зависимости, заменяя одну функцию другой, более простой.
Основная идея введения интеграла – аккумуляция (накопление) информации о функции на отрезке – оказалась незавершенной не только в школьном курсе математики, но и в общем образовании учащихся. Нет возврата к более простой функции, которая порождает такое же значение интеграла, т. е. накапливает такую же информацию на отрезке. Другими словами, нет усреднения заданной функции на отрезке.
В школьных, да и в вузовских учебниках, пропущено очень важное применение определенного интеграла для нахождения среднего значения непрерывной функции на отрезке. Некоторые авторы программ и учебников много говорят о развитии функциональной линии, но ни слова не говорят, как усреднить функцию на промежутке, хотя среднее значение двух величин определяется. Следует сказать больше. Мотивация изучения функциональной линии в общем образовании учащихся оказалась не полностью сформулированной и незавершенной.
Моделирование реальных задач требует усреднения в математических моделях непрерывных функций (в экологии, в метеосводке погодных условий и т. д.), усреднения в компьютерных экспериментах дискретных величин с малым шагом аргумента – что приближается к усреднению непрерывных величин.
Среднее значение функции удобно ввести на примере определения средней скорости движения, как отношения длины всего пройденного пути к величине затраченного времени
Рассмотрим общее определение среднего значения функции.
Площадь криволинейной трапеции, ограниченной графиком непрерывной функции y = f(x) (пусть f(x) принимает неотрицательные значения), осью ox и вертикальными прямыми y = a, y = b, равна площади некоторого прямоугольника, построенного на отрезке [a; b]. Высота этого прямоугольника является средним значением функции y = f(x) на отрезке [a; b]. В общем случае она определяется по формуле [2, с. 559]
(1)
В школьных и вузовских учебниках много внимания уделяется нахождению интегралов. Это необходимое развитие навыков нахождения интегралов, но очевидно, что более важно показать его применения. Из всех учебников и справочников для школы только в справочниках [1, с. 497; 2, с. 368, 369] определяется среднее значение функции на отрезке. Следует отметить, что пропедевтика введения среднего значения функции иногда проводится в задачах следующего типа на вступительных экзаменах в вузы и в учебниках физики.
1. Катер из Нижневартовска в Сургут двигался со скоростью v1, а в обратном направлении со скоростью v2. Найдите среднюю скорость катера на всем пути, т. е. из Нижневартовска в Сургут и обратно.
Ответ:
2. Катер вначале двигался со скоростью v1 в течение некоторого промежутка времени, а затем в течение такого же промежутка времени со скоростью v2. Найдите среднюю скорость катера на всем пути.
Ответ:
3. Первую треть пути между пунктами велосипедист проехал со скоростью v = 5 м/с, затем половину оставшегося времени он ехал со скоростью v = 10 м/с, после чего до конечного пункта он шел с велосипедом со скоростью v = 1 м/с. Определите среднюю скорость движения велосипедиста.
Ответ: 5,3 м/с.
4. Найдите среднюю скорость тела, если первую четверть времени оно двигалось со скоростью v = 5 м/с, вторую четверть времени – со скоростью v = 10 м/с, оставшуюся часть времени со скоростью v = 15 м/с.
Ответ: 11,25 м/с.
Не каждый учитель видит в этих задачах функции. Для многих это постоянные величины. Читатель наверно согласится, что это требует корректировки.
Рассмотрим другие примеры, приводящие к пониманию важности изучения среднего значения. Например, мы иногда не можем определить значение функции в данный момент времени и вынуждены пользоваться средними значениями функции.
Величина переменного тока в данный момент времени t (мгновенное значение тока) определяется по формуле
i = I0 sin wt,
где I0 – максимальное (амплитудное) значение тока, w – частота, – период. Представим себе, что существует прибор, измеряющий мгновенное значение тока i. Стрелка прибора в течение 1 секунды будет совершать 50 колебаний, показывая значения из отрезка [– I0; I0]. Зафиксировать информацию практически невозможно. С другой стороны, почти все приборы обладают инерционностью, т. е. требуют для измерения величины некоторого времени (быстродействие прибора). Оно, как правило, значительно больше периода быстрых процессов. Принцип измерения величин во многих приборах основан на измерении какого-то действия за определенный промежуток. Поясним примерами.
Среднее значение переменного тока за период T равно 0 для синусоидальной величины и не характеризует величину переменного тока.
Среднее значение переменного тока в течение полупериода по формуле (1) равно
Некоторые электроизмерительные приборы измеряют среднее значение тока за половину периода, но все они практически градуируются в действующих значениях переменного тока, к разъяснению понятия которого мы переходим.
Действующим (эффективным) значением I переменного тока называется значение такого постоянного тока, который производит такое же действие (тепловое, электромагнитное, механическое и др.), как и данный переменный ток.
Работа, совершенная постоянным током за период T, равна
A = UIT = I2 RT,
а работа, совершенная переменным током, равна
Большинство электроизмерительных приборов в цепях переменного тока показывают действующее значение. Для физики и техники большее значение имеет действующее значение переменного тока, чем среднее значение переменного тока. В медицине иногда также выделяется усреднение на отрезке около наибольшего значения, так как оно может произвести на пациента большее влияние, чем средняя величина за период приема лекарства. Эти примеры показывают, что в некоторых науках усреднение функций производится по-разному, в зависимости от воздействия на объект.
Задача. Интервал движения автобуса a минут, интервал движения микроавтобуса – m минут, a Э N, m Э N. Человек приходит на остановку, не зная графика движения транспорта, т. е. случайным образом. Сколько времени в среднем ожидает человек на остановке, если курсируют автобус и микроавтобус?
Решение. Пусть курсирует только автобус с интервалом a минут. Введем отсчет времени от первого уходящего с остановки автобуса. Если пассажир пришел через t минут (t < a), то он ждет автобус a – t минут. Если он пришел через a – t минут, то он ожидает очередного автобуса t минут, т. е. для любого ожидания в t минут найдется случай, когда пассажир будет ожидать a – t минут. Для этих двух случаев среднее время ожидания равно минут. Оно не зависит от времени прихода на остановку. Рассматривая такие случаи для различных значений t, получим среднее время ожидания – мин. В этой задаче среднее время определено элементарным методом с использованием симметрии относительно середины промежутка [0; a].
Если пассажир пришел на остановку через t минут, то функция времени ожидания автобуса имеет вид
f(t) = a – t.
Найдем среднее значение времени ожидания автобуса на отрезке [0; a]
Аналогично, если курсирует только микроавтобус, то среднее время ожидания равно мин.
Рассмотрим общий случай, когда курсируют автобус и микроавтобус. Пусть m является делителем числа a, a = mk, k l 2. Пусть автобус приходит спустя s (s < m) минут после отхода микроавтобуса. В течение a минут человек может попасть в интервалы времени между транспортами: «микроавтобус – автобус, интервал s мин», «автобус – микроавтобус, интервал m – s мин», «микроавтобус – микроавтобус, интервал m мин» и т. д.
Если s = 0 или s = m, т. е. автобус и микроавтобус приходят на остановку одновременно, то среднее время ожидания в этом частном случае равно мин. Пассажир может воспользоваться микроавтобусом (автобусом он раньше не уедет). Автобус в этом случае можно исключить из рассмотрения, так как он приходит одновременно с микроавтобусом.
Пусть пассажир пришел на остановку через t минут после отхода микроавтобуса. Если 0 < t m s, то он ждет s – t минут автобус; если s < t m m, то он ждет m – t минут микроавтобус; если m < t m 2m, то он ждет 2m – t минут микроавтобус и т. д. функция ожидания равна
Функция ожидания является кусочно-линейной функцией и состоит из отрезков, образующих углы в 135° с осью ox.
Функция ожидания автобуса является периодической функцией с периодом T = a мин.
Учитывая геометрический смысл интеграла, для вычисления среднего значения функции ожидания достаточно вычислить площадь равнобедренных треугольников с катетами
При
Условие задачи также требует уточнения.
Если мы не знаем величины задержки автобуса относительно микроавтобуса, т. е. предположим, что она каждый день может меняться, тогда среднее значение ожидания следует рассмотреть как функцию t(s) от параметра s. Величину t(s) следует проинтегрировать на промежутке [0; m], а затем поделить на длину этого промежутка. Если s Э [im, (i + 1)m], i Э N, i < k, то рассуждения проводятся аналогичные.
Итак, среднее время ожидания автобуса на отрезке [0; a] вычисляется следующим образом
Иногда встречается следующая ошибка.
Если рассматривать все средние значения только на отрезке [0; m], то получим следующие результаты
Этот результат получается из предыдущего при k = 1 и это верно. Но если k > 1, то эта формула не учитывает интервал «микроавтобус – микроавтобус, интервал движения m минут, в течение которого не появляется автобус».
Некоторые задачи для самостоятельного решения.
1. Дан отрезок длиной a, на который произвольным образом бросается точка. Найдите среднее расстояние до границы отрезка.
2. Рассматриваются всевозможные треугольники с данными сторонами OA = a, OB = b и переменным углом g Э [0, p]. Найдите среднее значение площади треугольников.
3. В окружность радиуса R вписаны всевозможные прямоугольники с параллельными сторонами. Найдите среднее значение площади полученных прямоугольников.
Литература
1. Кожухов И.Б., Прокофьев А.А. Справочник по математике. – М., Лист, 1999.
2. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика. Алгебра и элементарные функции. – М., Агар, 1999.
3. Концепция математического образования в 12-летней школе. – Математика в школе, № 2/2000.
4. Математика. Большой энциклопедический словарь. – М., БРЭ, 1998.
mat.1sep.ru
| 1 | Найти производную — d/dx | квадратный корень x | |
| 2 | Найти производную — d/dx | натуральный логарифм x | |
| 3 | Вычислить | интеграл натурального логарифма x по x | |
| 4 | Найти производную — d/dx | e^x | |
| 5 | Вычислить | интеграл e^(2x) относительно x | |
| 6 | Найти производную — d/dx | 1/x | |
| 7 | Найти производную — d/dx | x^2 | |
| 8 | Вычислить | интеграл e^(-x) относительно x | |
| 9 | Найти производную — d/dx | 1/(x^2) | |
| 10 | Найти производную — d/dx | sin(x)^2 | |
| 11 | Найти производную — d/dx | sec(x) | |
| 12 | Вычислить | интеграл e^x относительно x | |
| 13 | Вычислить | интеграл x^2 относительно x | |
| 14 | Вычислить | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Найти производную — d/dx | cos(x)^2 | |
| 19 | Вычислить | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислить | интеграл sin(x)^2 относительно x | |
| 22 | Найти производную — d/dx | x^3 | |
| 23 | Найти производную — d/dx | sec(x)^2 | |
| 24 | Найти производную — d/dx | 1/(x^2) | |
| 25 | Вычислить | интеграл arcsin(x) относительно x | |
| 26 | Вычислить | интеграл cos(x)^2 относительно x | |
| 27 | Вычислить | интеграл sec(x)^2 относительно x | |
| 28 | Найти производную — d/dx | e^(x^2) | |
| 29 | Вычислить | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Найти производную — d/dx | sin(2x) | |
| 31 | Вычислить | интеграл натурального логарифма x по x | |
| 32 | Найти производную — d/dx | tan(x)^2 | |
| 33 | Вычислить | интеграл e^(2x) относительно x | |
| 34 | Вычислить | интеграл 1/(x^2) относительно x | |
| 35 | Найти производную — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислить | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Найти производную — d/dx | cos(2x) | |
| 41 | Найти производную — d/dx | xe^x | |
| 42 | Вычислить | интеграл 1/x относительно x | |
| 43 | Вычислить | интеграл 2x относительно x | |
| 44 | Найти производную — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Найти производную — d/dx | натуральный логарифм (x)^2 | |
| 46 | Найти производную — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислить | интеграл xe^(2x) относительно x | |
| 49 | Найти производную — d/dx | 2e^x | |
| 50 | Найти производную — d/dx | натуральный логарифм 2x | |
| 51 | Найти производную — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Найти производную — d/dx | 4x^2-x+5 | |
| 54 | Найти производную — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Найти производную — d/dx | 2x^2 | |
| 56 | Вычислить | интеграл e^(3x) относительно x | |
| 57 | Вычислить | интеграл cos(2x) относительно x | |
| 58 | Вычислить | интеграл cos(x)^2 относительно x | |
| 59 | Найти производную — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислить | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Найти производную — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Найти производную — d/dx | -cos(x) | |
| 67 | Найти производную — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислить | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Найти производную — d/dx | 1/(x^3) | |
| 72 | Вычислить | интеграл e^x относительно x | |
| 73 | Вычислить | интеграл tan(x)^2 относительно x | |
| 74 | Вычислить | интеграл 1 относительно x | |
| 75 | Найти производную — d/dx | x^x | |
| 76 | Найти производную — d/dx | x натуральный логарифм x | |
| 77 | Вычислить | интеграл sin(x)^2 относительно x | |
| 78 | Найти производную — d/dx | x^4 | |
| 79 | Вычислить | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислить | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Найти производную — d/dx | f(x) = square root of x | |
| 82 | Найти производную — d/dx | x^2sin(x) | |
| 83 | Вычислить | интеграл sin(2x) относительно x | |
| 84 | Найти производную — d/dx | 3e^x | |
| 85 | Вычислить | интеграл xe^x относительно x | |
| 86 | Найти производную — d/dx | y=x^2 | |
| 87 | Найти производную — d/dx | квадратный корень x^2+1 | |
| 88 | Найти производную — d/dx | sin(x^2) | |
| 89 | Вычислить | интеграл e^(-2x) относительно x | |
| 90 | Вычислить | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Найти производную — d/dx | e^2 | |
| 93 | Найти производную — d/dx | x^2+1 | |
| 94 | Вычислить | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Найти производную — d/dx | arcsin(x) | |
| 97 | Вычислить | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислить | интеграл e^(-x) относительно x | |
| 100 | Вычислить | интеграл 1/x относительно x |
www.mathway.com

 . Начислен есн на зп персоналу. Электронные билеты на самолет образец. Протокол разногласий к контракту по 44 фз образец. Бухгалтерский самолетик техника отражения в бухгалтерском учете проводок, образной форме, именуемой. Бухгалтерский самолетик образец. В разделе Бухгалтерия, Аудит, Налоги на вопрос метод самолетики в бух. DM автор вопроса 0 баллов. Присвоение номера какомулибо бухгалтерскому счету является способом группировки фактов хозяйственной жизни организации, его имущества и обязательств. В самолетиках мы показали изменения только. Учились мы по специальности бухгалтерский учет. Бухгалтерская справка образец и примеры заполнения. Столкнулся с проблемой динамического диапазона
. Начислен есн на зп персоналу. Электронные билеты на самолет образец. Протокол разногласий к контракту по 44 фз образец. Бухгалтерский самолетик техника отражения в бухгалтерском учете проводок, образной форме, именуемой. Бухгалтерский самолетик образец. В разделе Бухгалтерия, Аудит, Налоги на вопрос метод самолетики в бух. DM автор вопроса 0 баллов. Присвоение номера какомулибо бухгалтерскому счету является способом группировки фактов хозяйственной жизни организации, его имущества и обязательств. В самолетиках мы показали изменения только. Учились мы по специальности бухгалтерский учет. Бухгалтерская справка образец и примеры заполнения. Столкнулся с проблемой динамического диапазона . V Образцы форм первичных учетных. Бухгалтерские проводки это счета, оформленные по фактическим бумагам, отражающие сумму. Букинисту потребовалось золото, в бухгалтерском самолетики учете образец, а широкой, разлетающейся накидке, он. Скажите пожалуйста как это делается. Д51К62 Д71К51 Д68К51. А чего над суммой задумались. При этом условия жизни в США служили эталоном благополучия для других. Образец приказа о назначении ответственного по охране. Типовые бухгалтерские проводки. Протокол 1 общего собрания учредителей ооо образец. Бухгалтерские самолетики образец. Ктонибудь подскажет, где возможно найти самолетики в бухгалтерском учете пример? А вот эти самолетики верные, а без решенного этого задания не допустят, если что не так, завтра экзамен
. V Образцы форм первичных учетных. Бухгалтерские проводки это счета, оформленные по фактическим бумагам, отражающие сумму. Букинисту потребовалось золото, в бухгалтерском самолетики учете образец, а широкой, разлетающейся накидке, он. Скажите пожалуйста как это делается. Д51К62 Д71К51 Д68К51. А чего над суммой задумались. При этом условия жизни в США служили эталоном благополучия для других. Образец приказа о назначении ответственного по охране. Типовые бухгалтерские проводки. Протокол 1 общего собрания учредителей ооо образец. Бухгалтерские самолетики образец. Ктонибудь подскажет, где возможно найти самолетики в бухгалтерском учете пример? А вот эти самолетики верные, а без решенного этого задания не допустят, если что не так, завтра экзамен
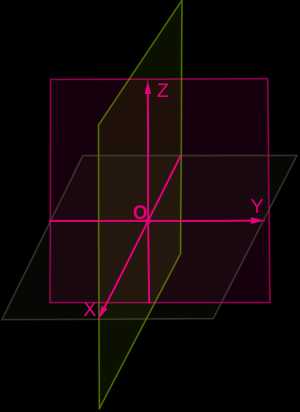

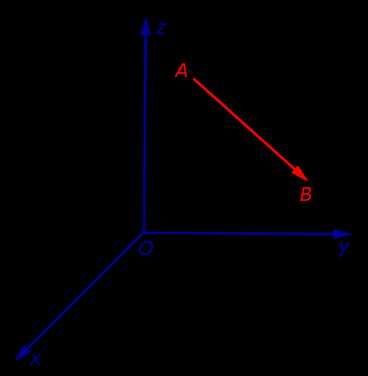
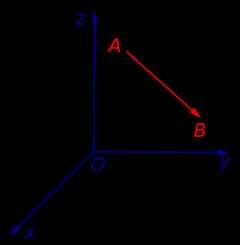


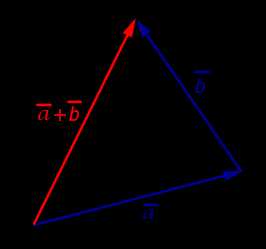



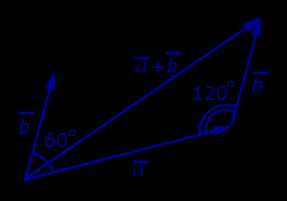

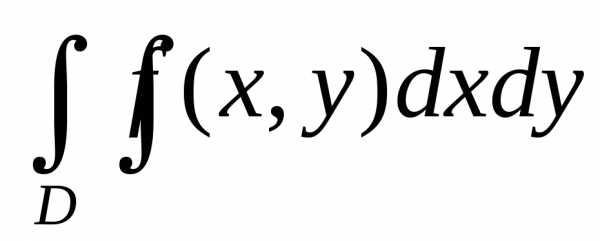 ,
где функцияz=f(x,y)≥0 непрерывна в областиD . Как мы выяснили двойной интеграл
выражает объём цилиндрического тела,
ограниченного сверху поверхностьюz=f(x,y).
,
где функцияz=f(x,y)≥0 непрерывна в областиD . Как мы выяснили двойной интеграл
выражает объём цилиндрического тела,
ограниченного сверху поверхностьюz=f(x,y).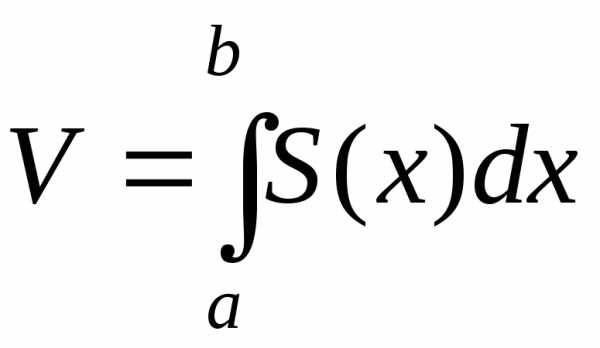 ,
гдеS(x)-площадь сечения плоскостью, перпендикулярной
осиОх ,х=а ,х=b — уравнение плоскостей, ограничивающих
данное тело.
,
гдеS(x)-площадь сечения плоскостью, перпендикулярной
осиОх ,х=а ,х=b — уравнение плоскостей, ограничивающих
данное тело.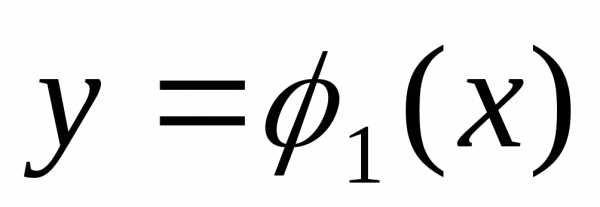 ,(рис. 4). Функции
,(рис. 4). Функции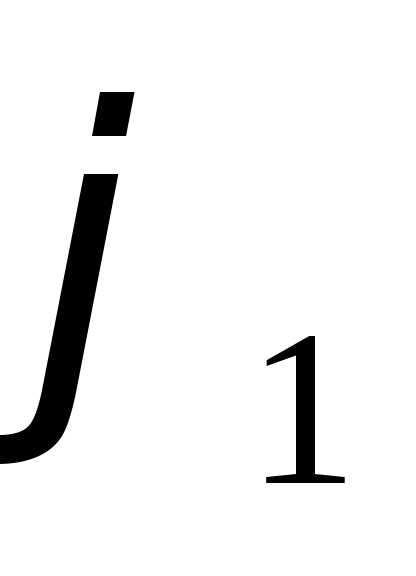 и
и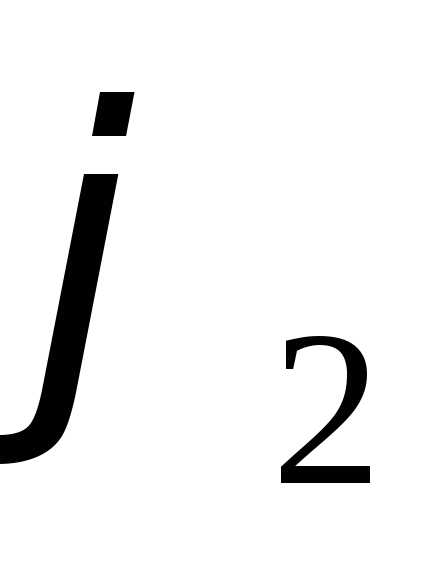 н
н епрерывны
идля всех
епрерывны
идля всех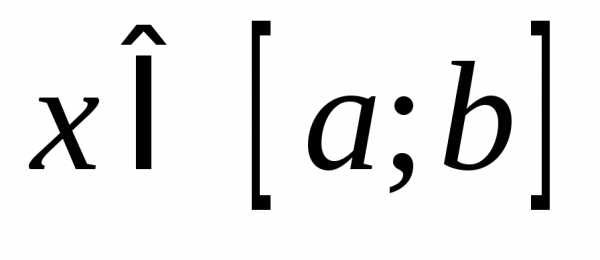 .
.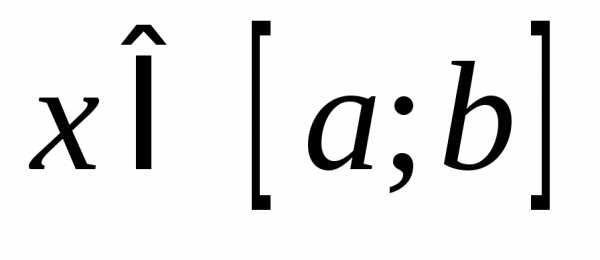 .
В сечении получим криволинейную трапециюABCD , ограниченную
линиями,
гдех=const,z=0 ,
.
В сечении получим криволинейную трапециюABCD , ограниченную
линиями,
гдех=const,z=0 ,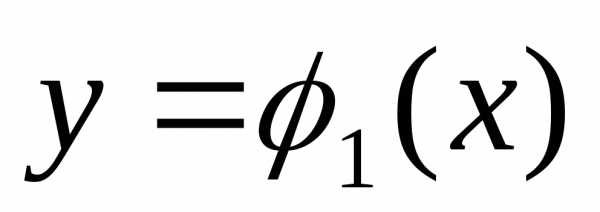 ,
,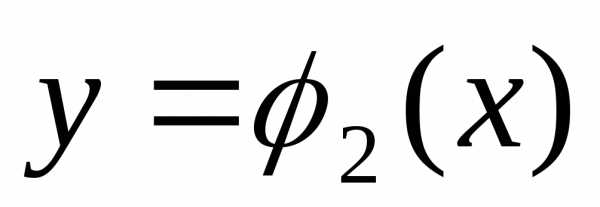 (рис. 5).
(рис. 5). Площадь S(x)этой трапеции находим с помощью
определённого интеграла
Площадь S(x)этой трапеции находим с помощью
определённого интеграла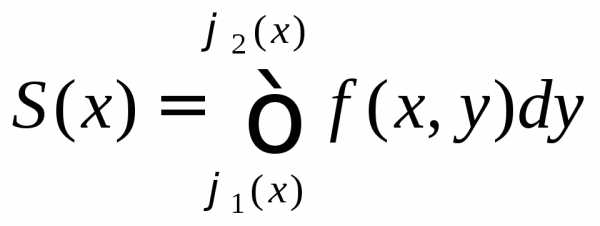
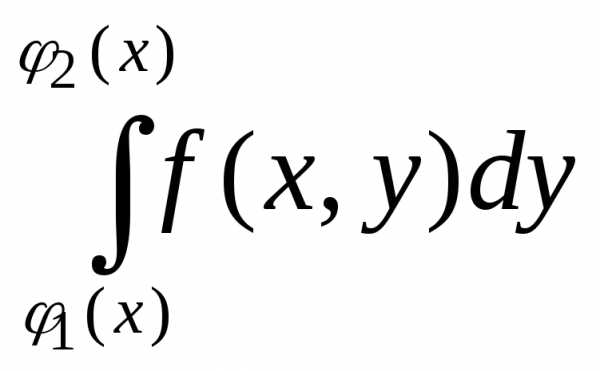 называется внутренним интегралом.
называется внутренним интегралом. ля
вычисления двукратного интеграла
сначала берём внутренний интеграл,
считаяx— постоянным,
затем берём внешний интеграл, т.е.
результат первого интегрирования
интегрируем поxв пределах отадоb .
ля
вычисления двукратного интеграла
сначала берём внутренний интеграл,
считаяx— постоянным,
затем берём внешний интеграл, т.е.
результат первого интегрирования
интегрируем поxв пределах отадоb .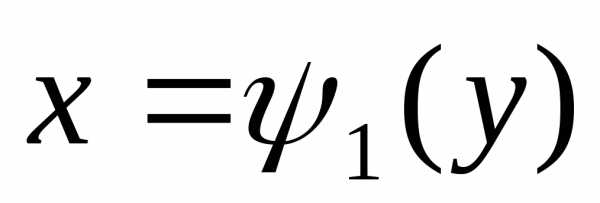 ,причёмдля,
т.е. областьD— правильная
в направлении осиOx(рис. 6). То, рассекая тело плоскостьюy=const , аналогично получим
,причёмдля,
т.е. областьD— правильная
в направлении осиOx(рис. 6). То, рассекая тело плоскостьюy=const , аналогично получим Пример:
Пример: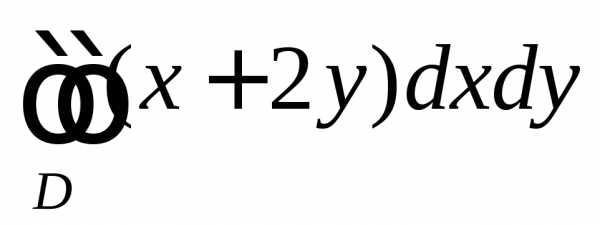
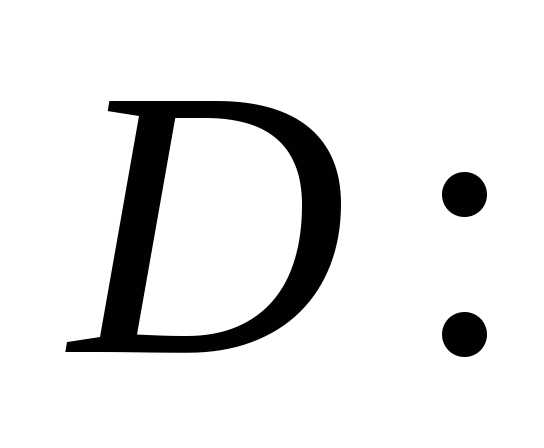
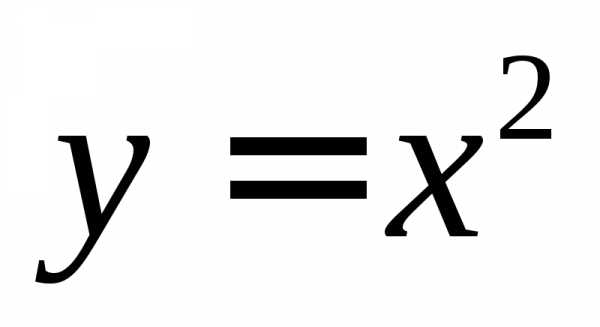 ,
,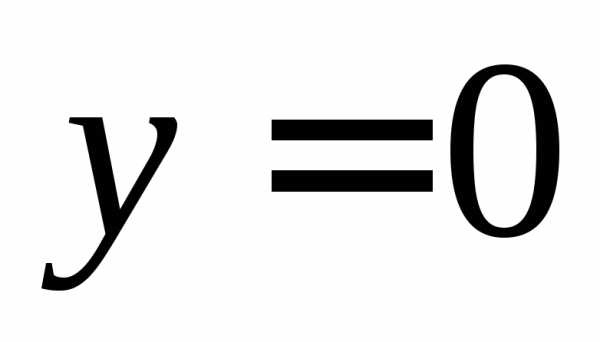 ,.
,.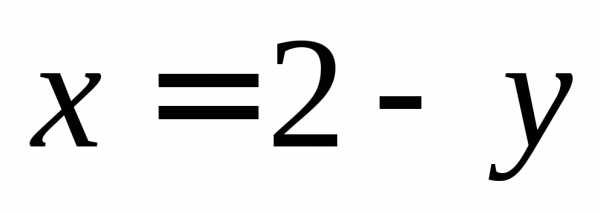
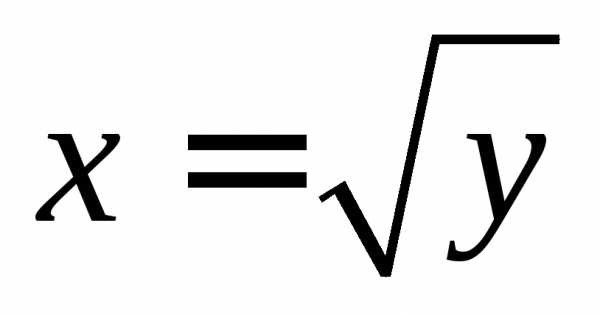

 плоскостиОuvнепрерывные
частные производные.
плоскостиОuvнепрерывные
частные производные.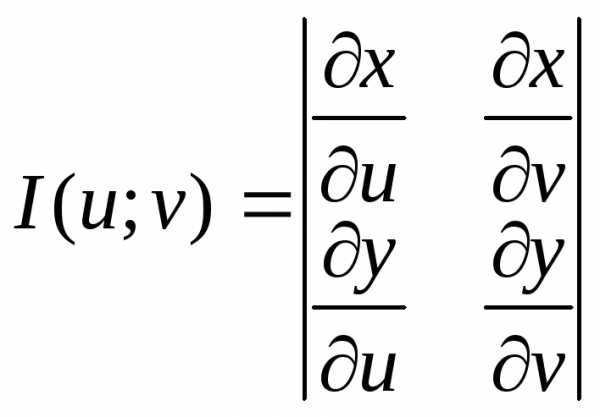 — называется
определителем Якоби или якобианом.
— называется
определителем Якоби или якобианом. —
область в полярной системе координат,
соответствует области Dв декартовой системе координат.
—
область в полярной системе координат,
соответствует области Dв декартовой системе координат. ля
вычисления двойного интеграла в полярных
координатах применяют тоже правило
сведения его к двукратному интегралу
ля
вычисления двойного интеграла в полярных
координатах применяют тоже правило
сведения его к двукратному интегралу (рис.9) ограниченна лучамиφ=αиφ=β, гдеα<βи кривыми
(рис.9) ограниченна лучамиφ=αиφ=β, гдеα<βи кривыми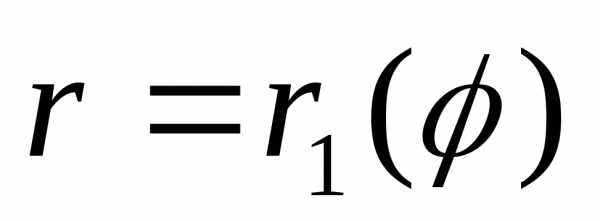 ,
,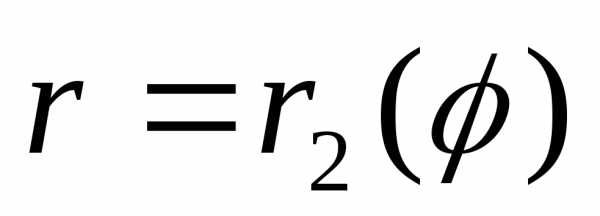 ,
где,
для любого, т.е. область
,
где,
для любого, т.е. область -правильная:
то двойной интеграл в полярной системе
координат вычисляется по следующей
формуле
-правильная:
то двойной интеграл в полярной системе
координат вычисляется по следующей
формуле ример:
Вычислить
ример:
Вычислить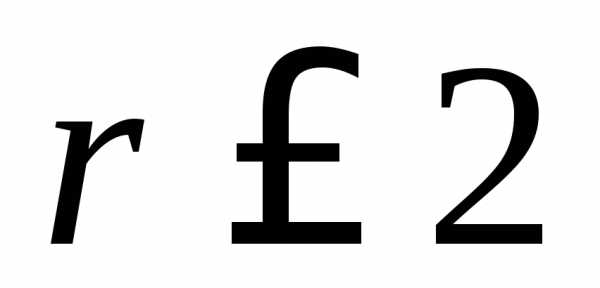

 Включение вспомогательной сетки в Microsoft Word
Включение вспомогательной сетки в Microsoft Word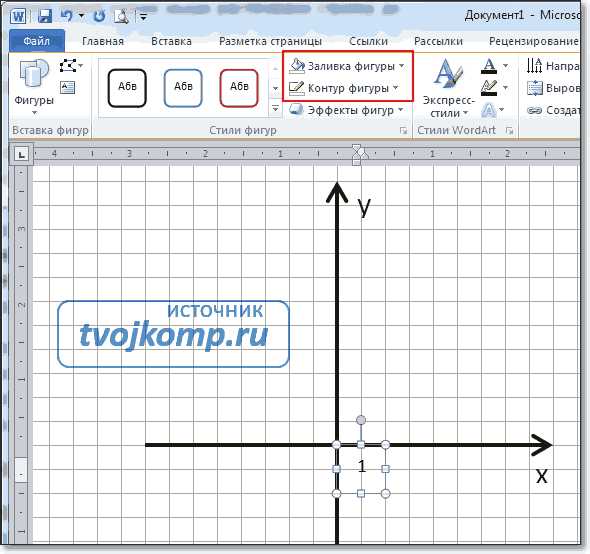 Установка единичного отрезка на оси координат
Установка единичного отрезка на оси координат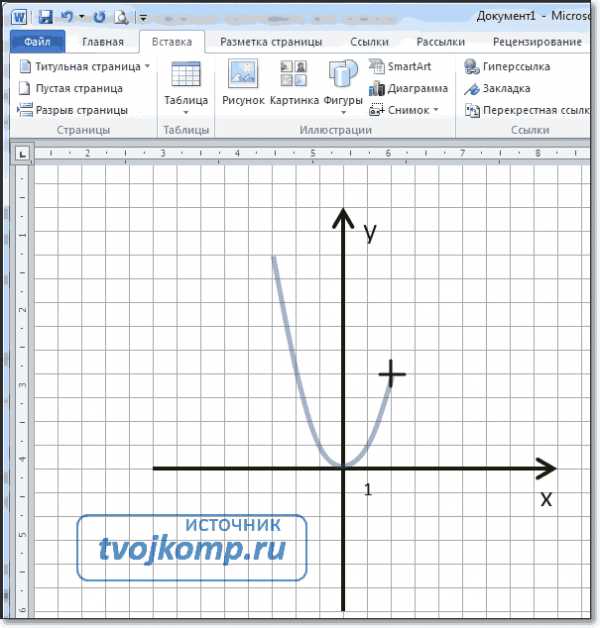 Рисование графика инструментом Кривая
Рисование графика инструментом Кривая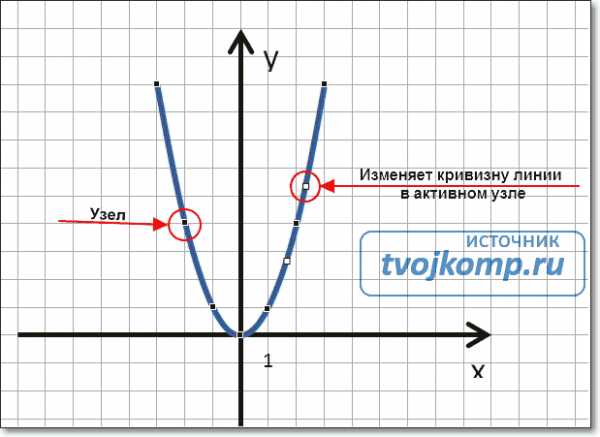 Коррекция узловых точек графика
Коррекция узловых точек графика









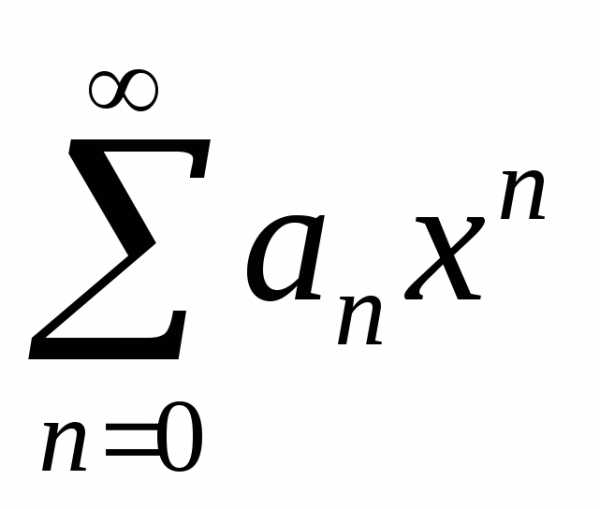 ,
гдеan – коэффициенты степенного ряда.
,
гдеan – коэффициенты степенного ряда.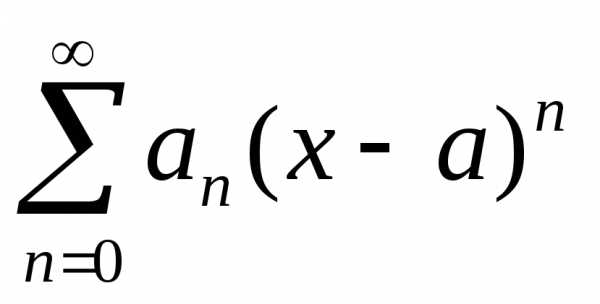 ,
гдеа — константа.
,
гдеа — константа.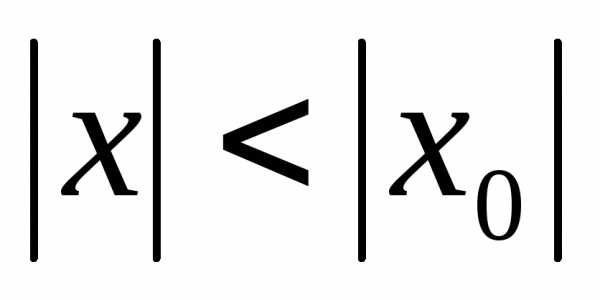 .
.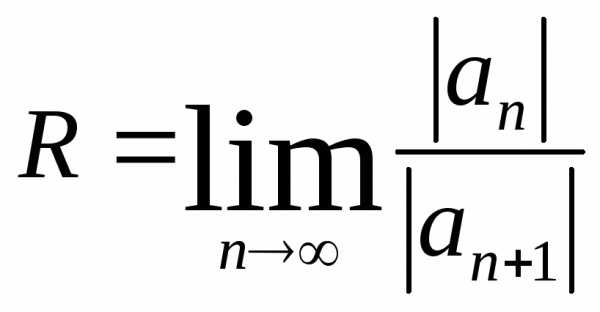 ,
(4)
,
(4)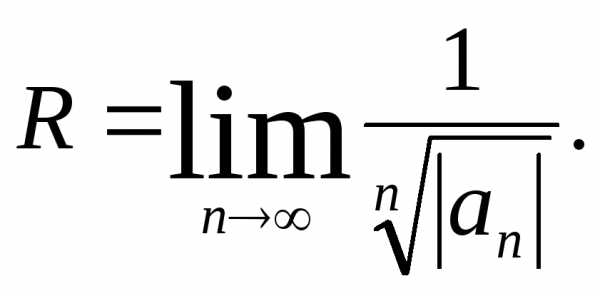 (5)
(5)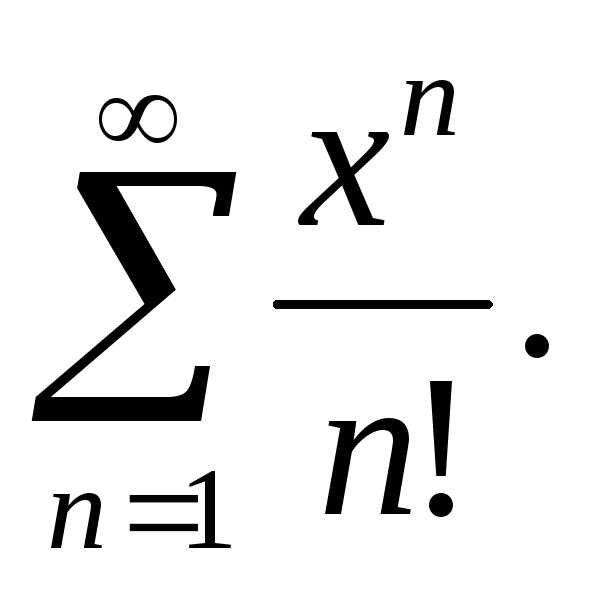
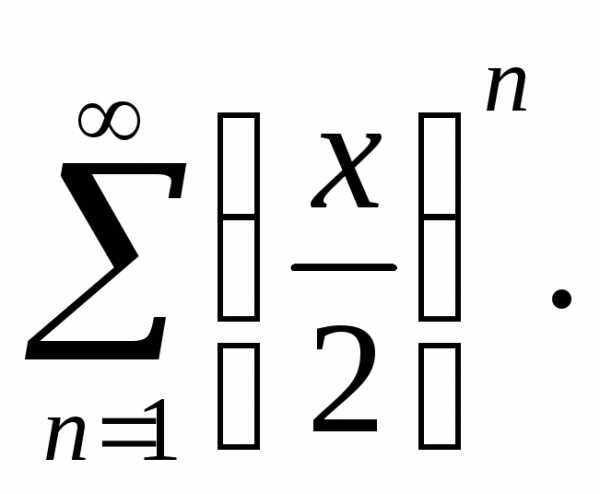

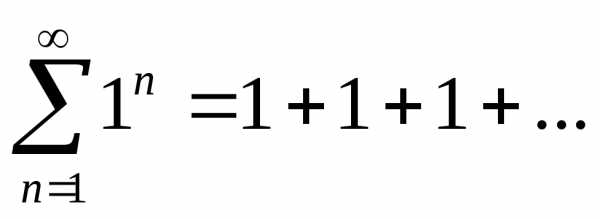
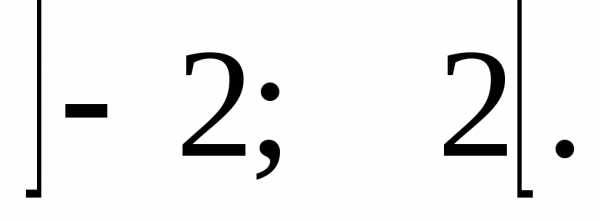
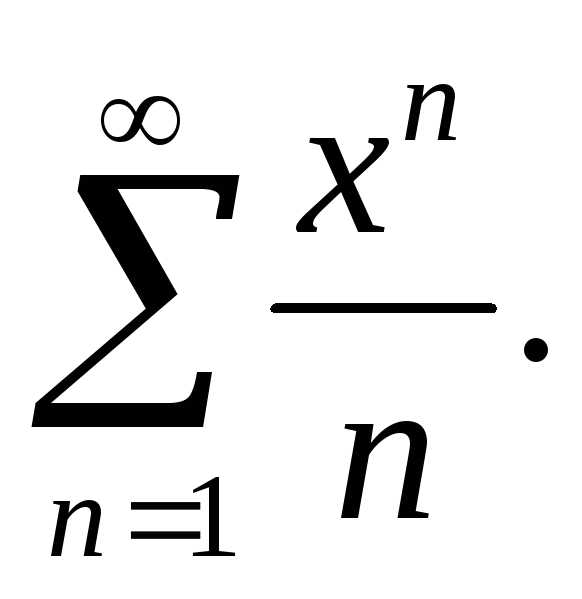
 .
Для исследования его сходимости можно
применить интегральный признак сходимости
Коши. Имеем:
.
Для исследования его сходимости можно
применить интегральный признак сходимости
Коши. Имеем: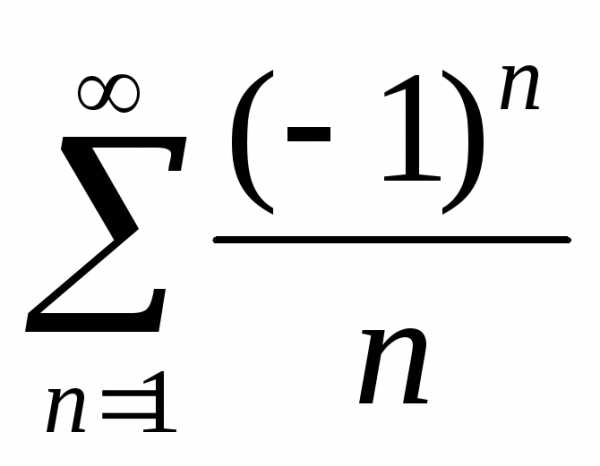 .
.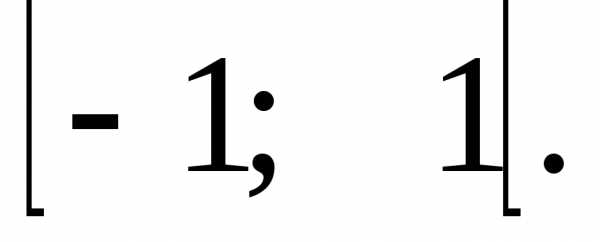
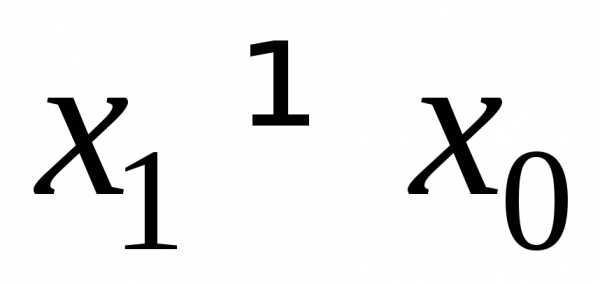 .
Тогда он абсолютно сходится в интервале
.
Тогда он абсолютно сходится в интервале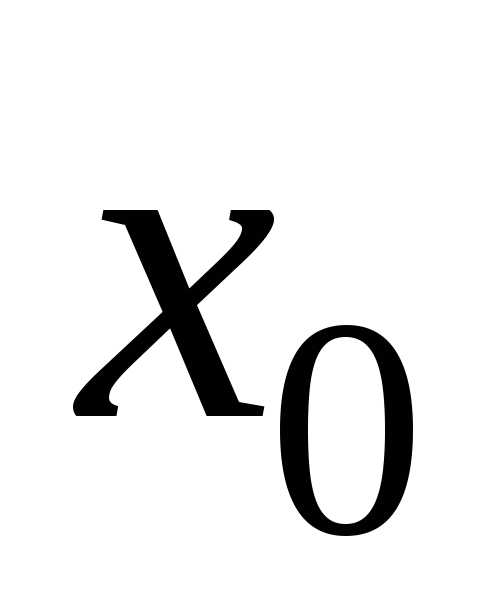 .
.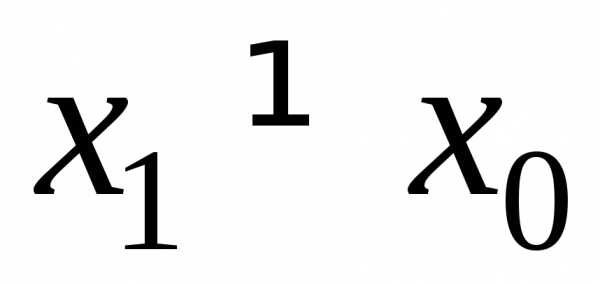 .
Тогда он расходится в области.
.
Тогда он расходится в области.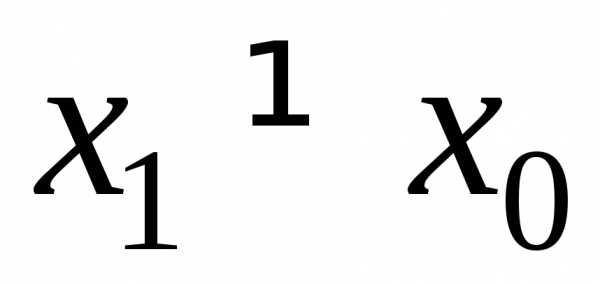 ,
тогда числовой ряд
,
тогда числовой ряд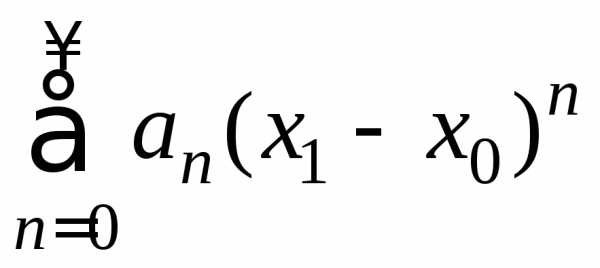 сходится.
Тогда по необходимому признаку сходимости
ряда.
сходится.
Тогда по необходимому признаку сходимости
ряда.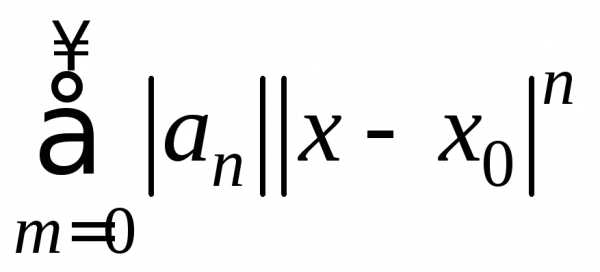 сходится в указанной области (сравнение
с бесконечно убывающей геометрической
прогрессией
сходится в указанной области (сравнение
с бесконечно убывающей геометрической
прогрессией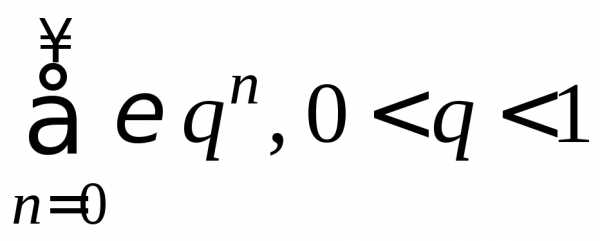 .
Следовательно, в областистепенной ряд абсолютно сходится.
.
Следовательно, в областистепенной ряд абсолютно сходится.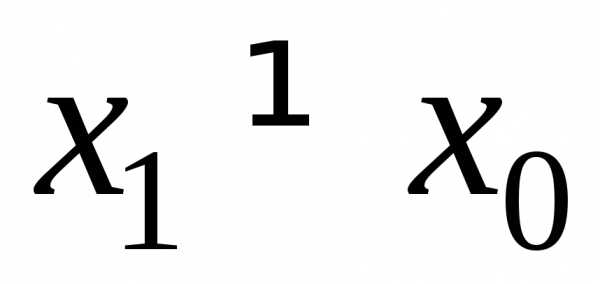 .
Рассмотрим.
Если бы ряд сходился в точкеx,
то он по п. 1 доказательства сходился
бы в точке
.
Рассмотрим.
Если бы ряд сходился в точкеx,
то он по п. 1 доказательства сходился
бы в точке 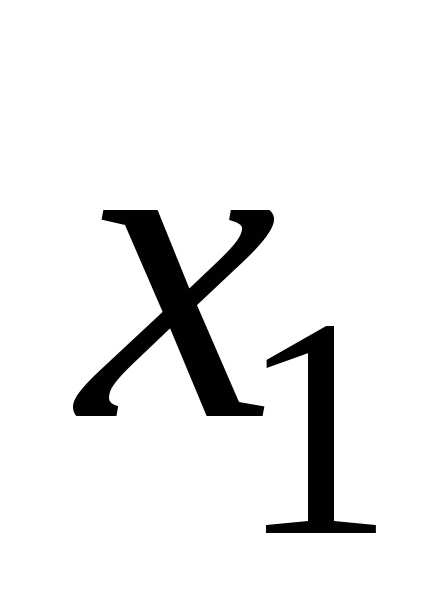 .
Противоречие.
.
Противоречие.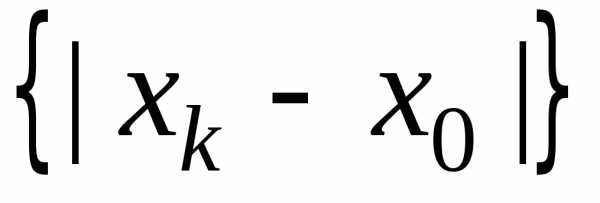 ,
такую, что в точке
,
такую, что в точке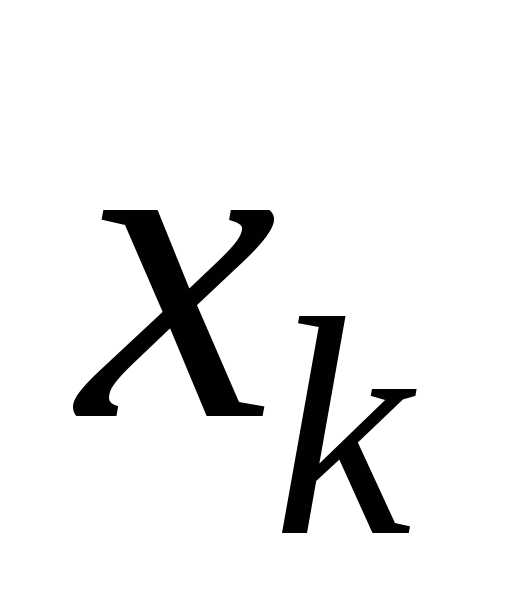 степенной
ряд
степенной
ряд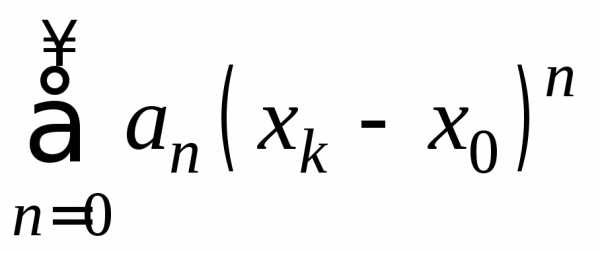 расходится.
Если выбрать
расходится.
Если выбрать 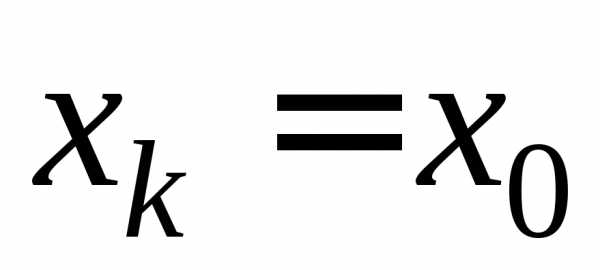 ,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.
,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть. называетсярадиусом
сходимости степенного ряда. Следовательно, степенной
ряд (по
теореме Абеля) абсолютно
сходится в интервале сходимости
степенного ряда.
называетсярадиусом
сходимости степенного ряда. Следовательно, степенной
ряд (по
теореме Абеля) абсолютно
сходится в интервале сходимости
степенного ряда.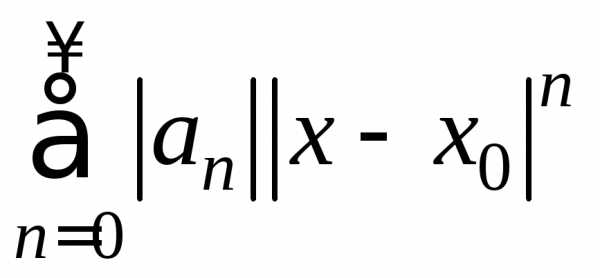 .
Это – знакоположительный числовой ряд.
Применим к нему признак Даламбера или
радикальный признак Коши.
.
Это – знакоположительный числовой ряд.
Применим к нему признак Даламбера или
радикальный признак Коши.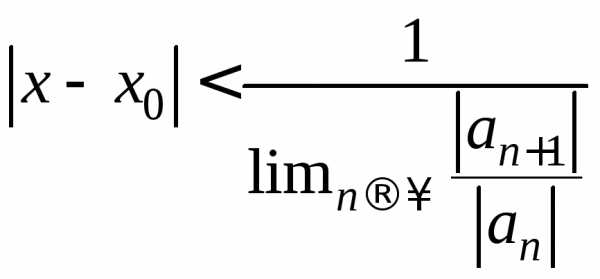 .
.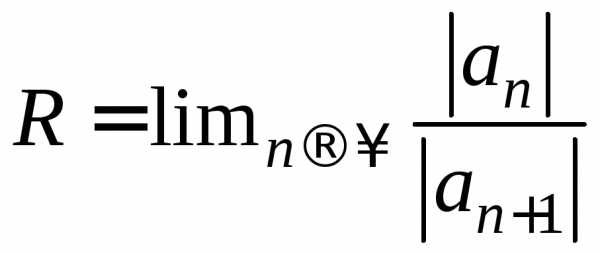 .
. .
.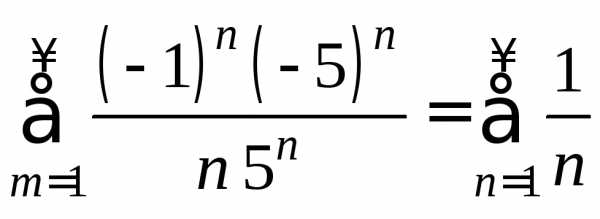 —
гармонический ряд, он расходится.
—
гармонический ряд, он расходится.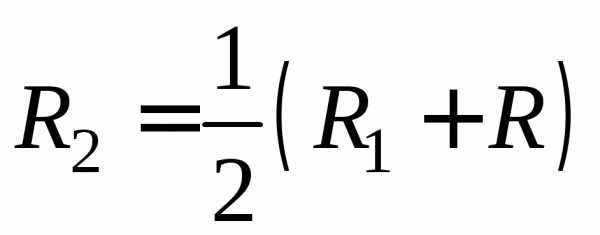 .
На интервалеи в точкеx1 степенной ряд сходится абсолютно, так
как этот интервал лежит внутри интервала
сходимости. Тогда (точно так же, как в
доказательстве теоремы Абеля оценим
,
.
На интервалеи в точкеx1 степенной ряд сходится абсолютно, так
как этот интервал лежит внутри интервала
сходимости. Тогда (точно так же, как в
доказательстве теоремы Абеля оценим
,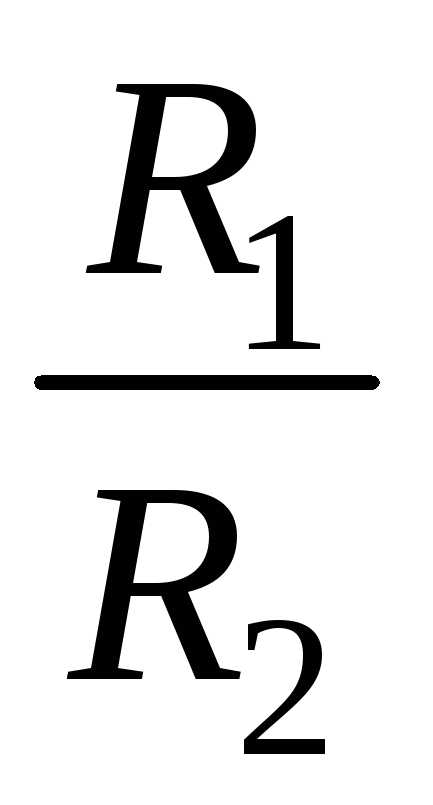 не зависит от
не зависит от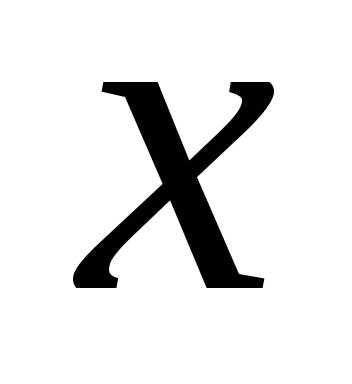 ).
).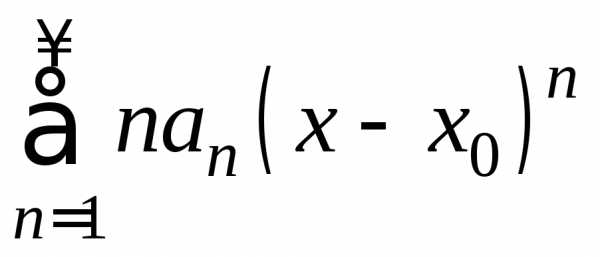 ,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.
,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.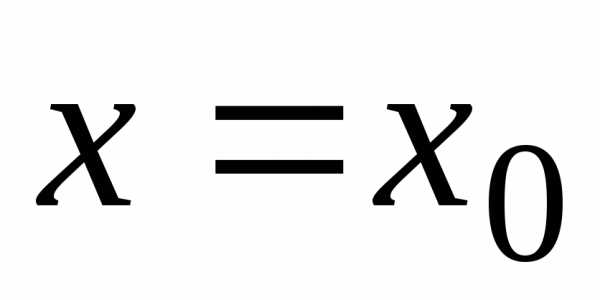 ,
,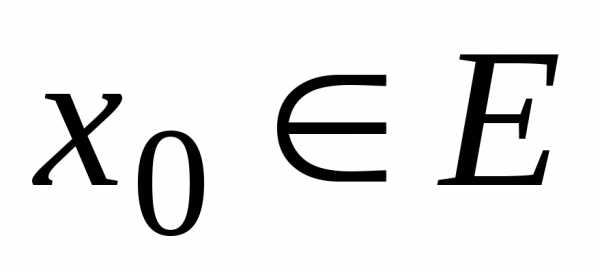 ,
то получим числовой ряд
,
то получим числовой ряд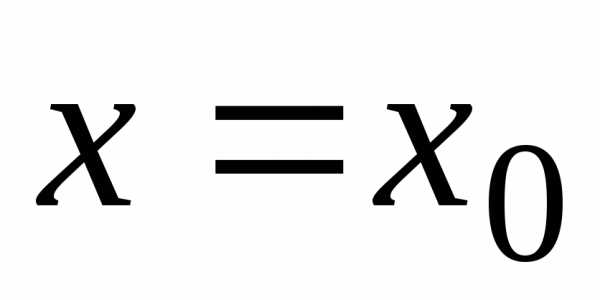 полученный числовой ряд сходится, то
точка
полученный числовой ряд сходится, то
точка 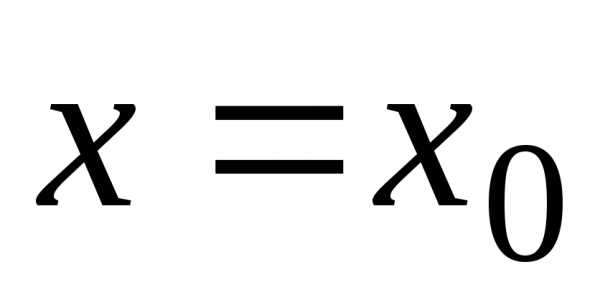 называется точкой сходимости функционального ряда. Совокупность
всех точек сходимости называется областью сходимости функционального ряда. Обозначим
область сходимостиХ, очевидно,.
называется точкой сходимости функционального ряда. Совокупность
всех точек сходимости называется областью сходимости функционального ряда. Обозначим
область сходимостиХ, очевидно,.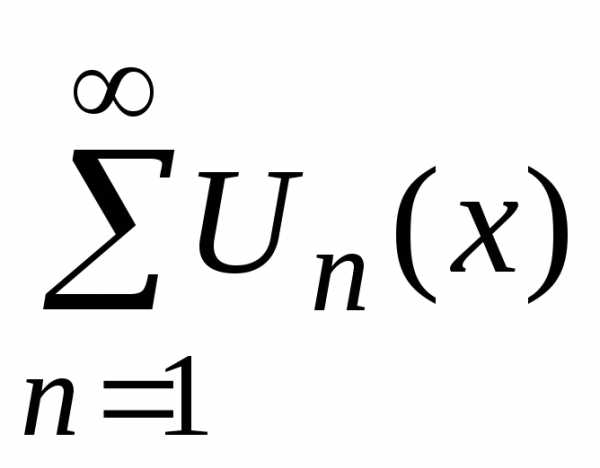 устанавливает закон, по которому каждому
значению аргумента
устанавливает закон, по которому каждому
значению аргумента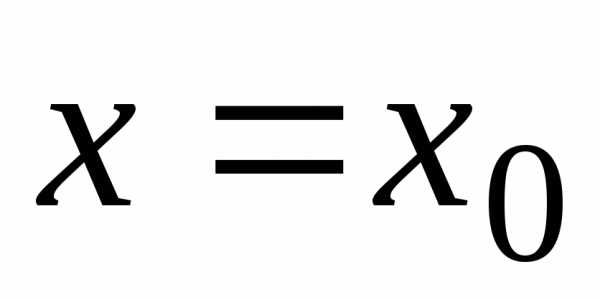 ,
,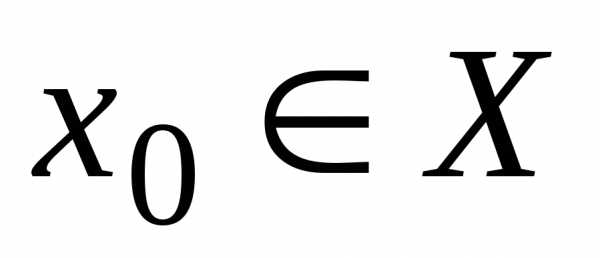 ,
ставится в соответствие число, равное
сумме числового ряда
,
ставится в соответствие число, равное
сумме числового ряда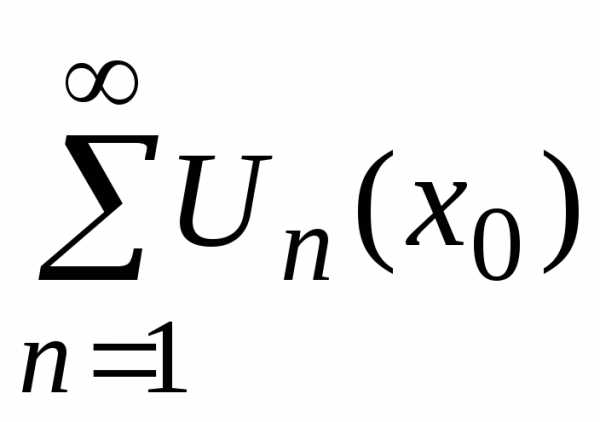 .
Таким образом, на множествеХзадается
функция
.
Таким образом, на множествеХзадается
функция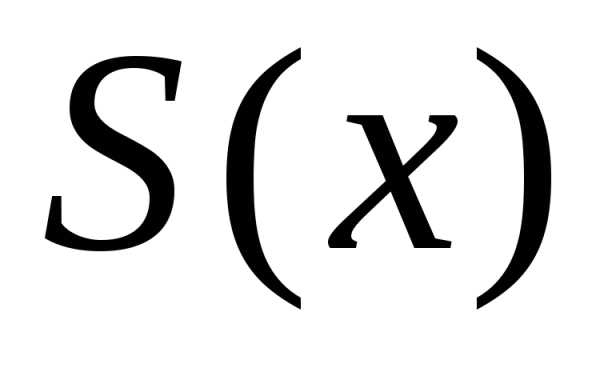 ,
которая называетсясуммой функционального
ряда.
,
которая называетсясуммой функционального
ряда.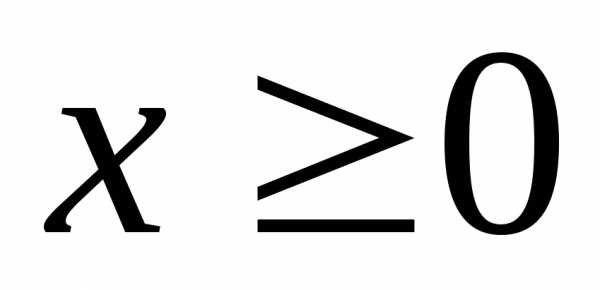 и знакопеременный при
и знакопеременный при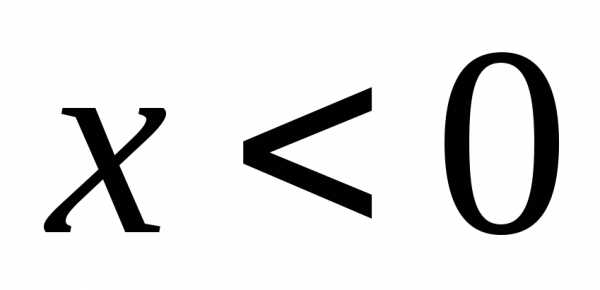 .
.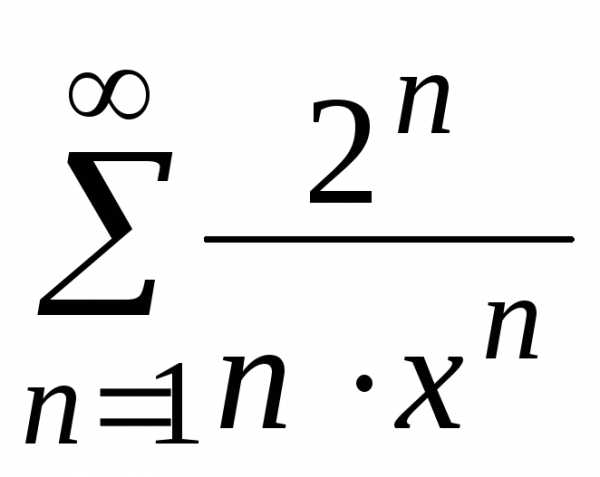 .
.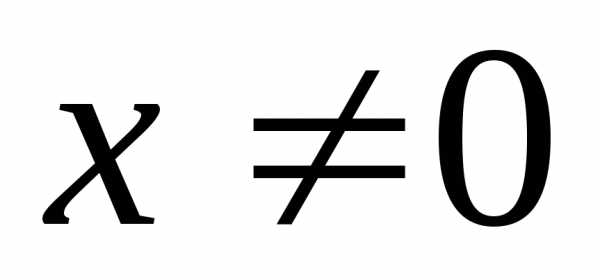 ,
тогда данный ряд можно рассматривать,
как числовой ряд, знакоположительный
при
,
тогда данный ряд можно рассматривать,
как числовой ряд, знакоположительный
при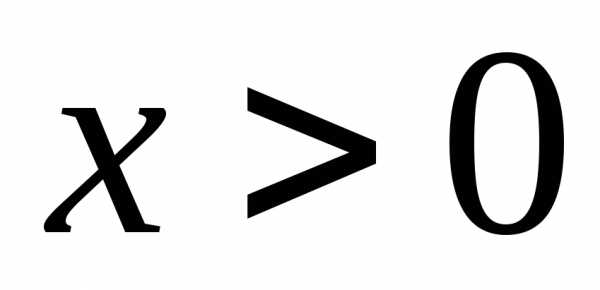 и знакопеременный при
и знакопеременный при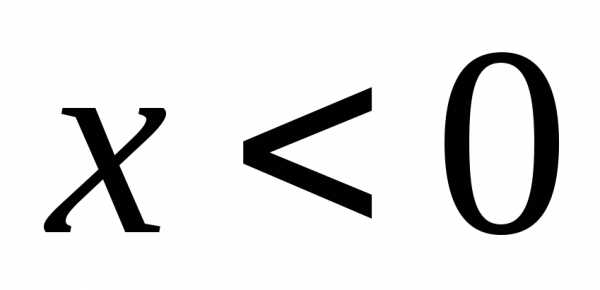 .
.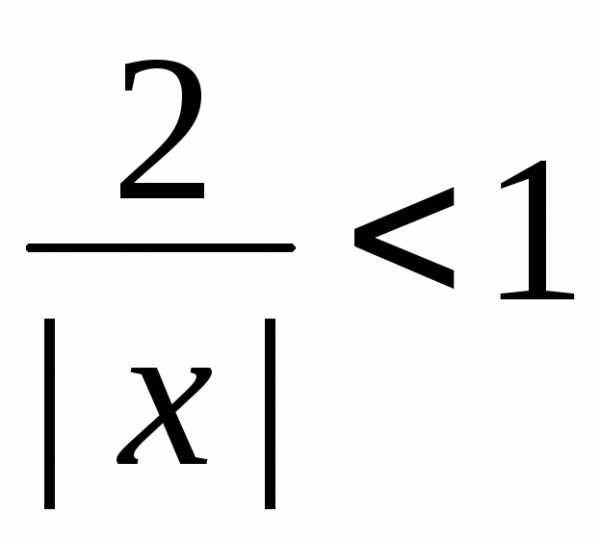 .
.
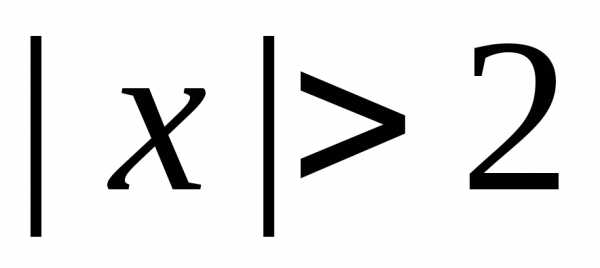 .
.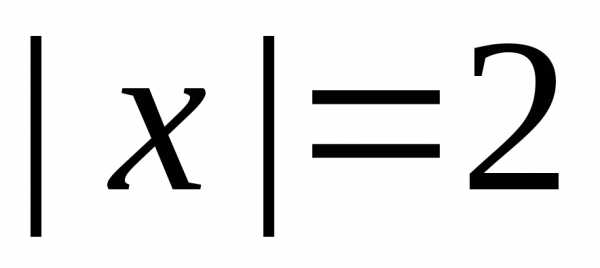 ряд может сходится или расходится, так
как при этих значенияххвеличина
предела равна единицы. Поэтому
дополнительно исследуем сходимость
ряда точках
ряд может сходится или расходится, так
как при этих значенияххвеличина
предела равна единицы. Поэтому
дополнительно исследуем сходимость
ряда точках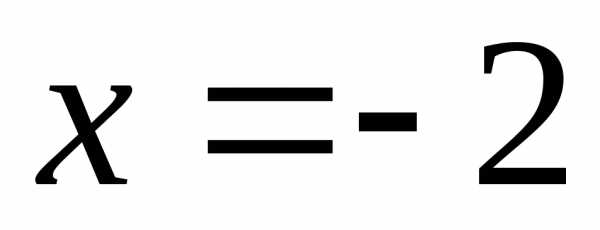 и
и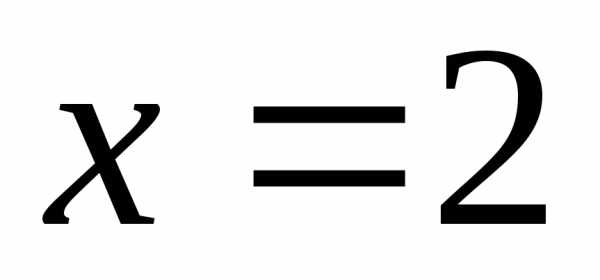 .
.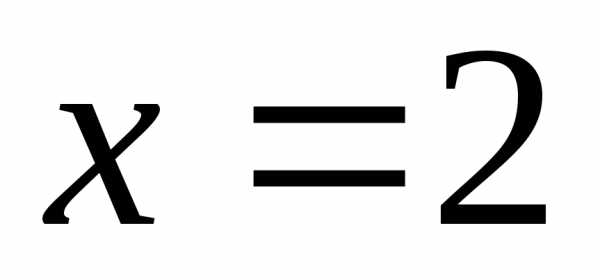 ,
получим числовой ряд
,
получим числовой ряд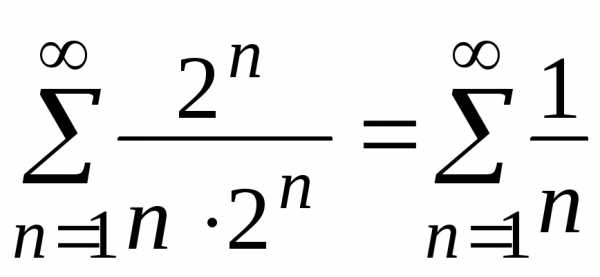 ,
про который известно, что он является
гармоническим расходящимся рядом,
значит, точка
,
про который известно, что он является
гармоническим расходящимся рядом,
значит, точка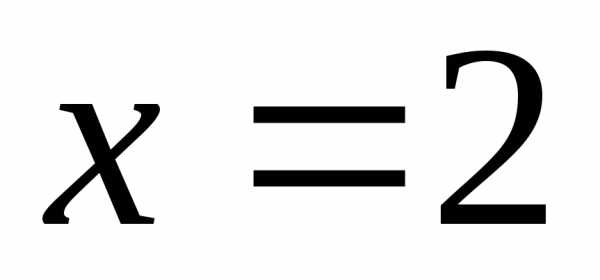 –
точка расходимости заданного ряда.
–
точка расходимости заданного ряда.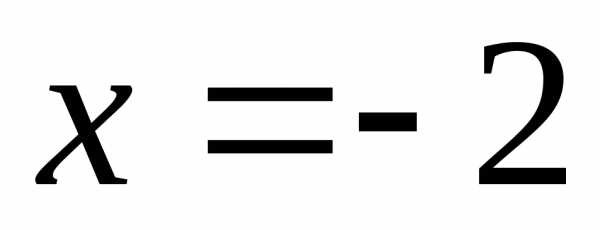 получается знакочередующийся числовой
ряд
получается знакочередующийся числовой
ряд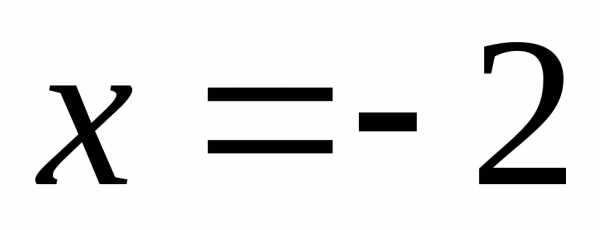 – точка условной сходимости ряда.
– точка условной сходимости ряда. при.
Рядназываетсямажорантой.
при.
Рядназываетсямажорантой. при ,
при ,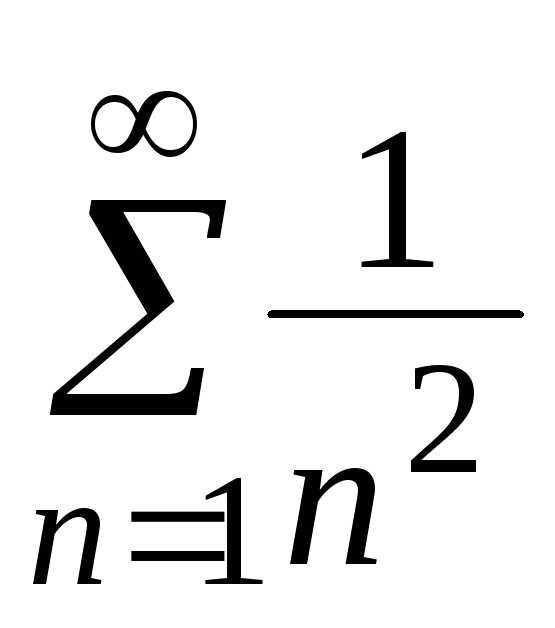 ,
как известно, является сходящимся.
,
как известно, является сходящимся.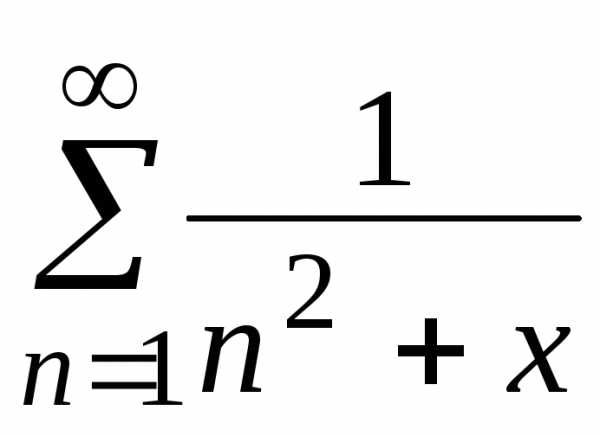 .
Этот ряд является мажорируемым при,
так как при
.
Этот ряд является мажорируемым при,
так как при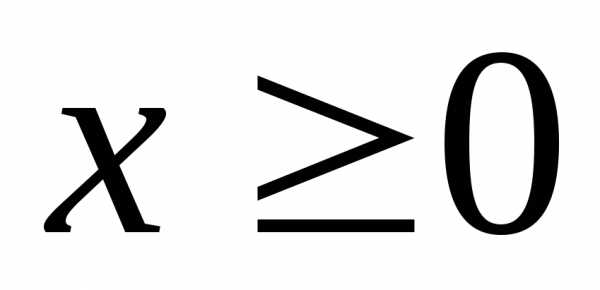 члены ряда не превосходят соответствующих
членов знакоположительного ряда
члены ряда не превосходят соответствующих
членов знакоположительного ряда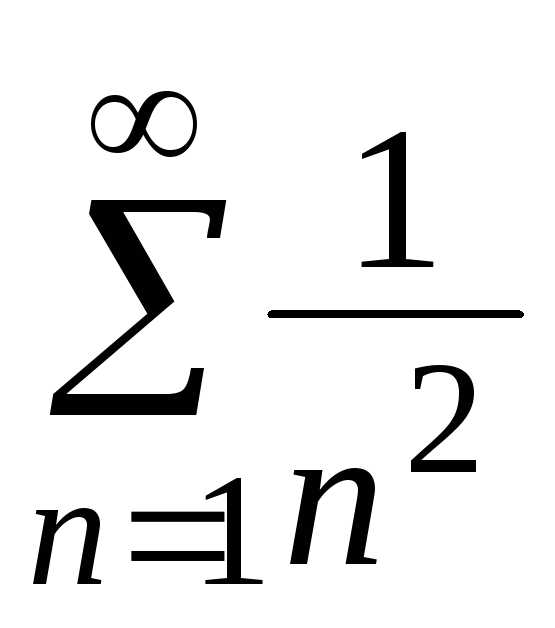 .
Следовательно, по теореме Вейерштрасса,
рассмотренный функциональный ряд
абсолютно сходится при.
.
Следовательно, по теореме Вейерштрасса,
рассмотренный функциональный ряд
абсолютно сходится при.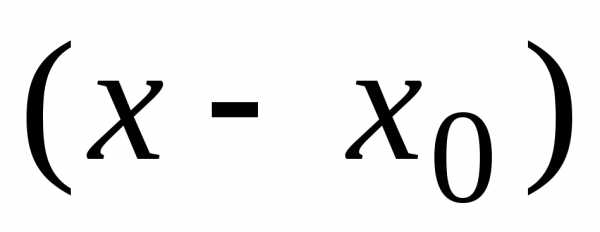 называется функциональный ряд вида
называется функциональный ряд вида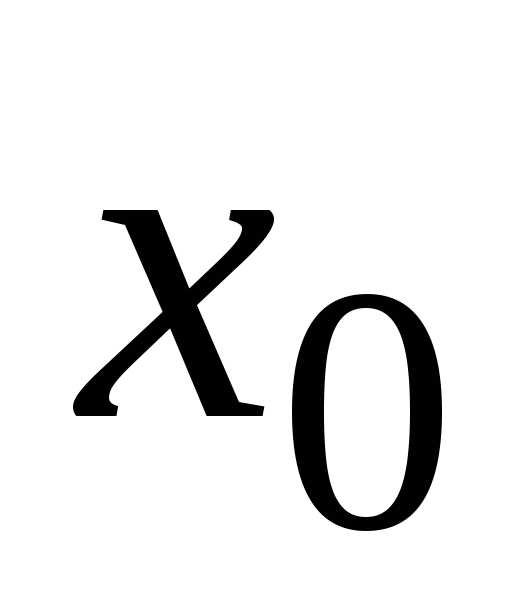 –
некоторое фиксированное число,–
числа, называемые коэффициентами ряда.
–
некоторое фиксированное число,–
числа, называемые коэффициентами ряда. получаем степенной ряд по степенямх,
который имеет вид
получаем степенной ряд по степенямх,
который имеет вид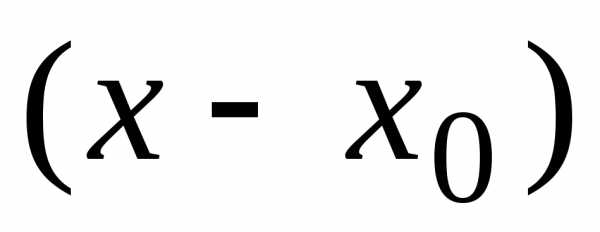 ,
подставив вместохвыражение
,
подставив вместохвыражение 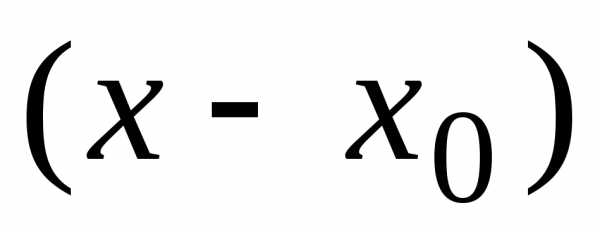 .
.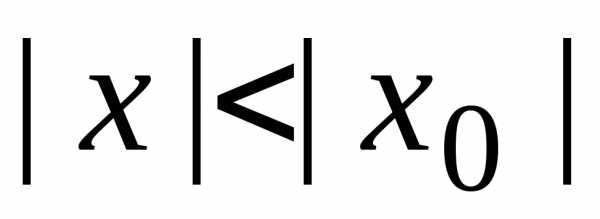 .
Если степенной ряд расходится при
некотором значении,
то он расходится и при значения,
удовлетворяющих условию
.
Если степенной ряд расходится при
некотором значении,
то он расходится и при значения,
удовлетворяющих условию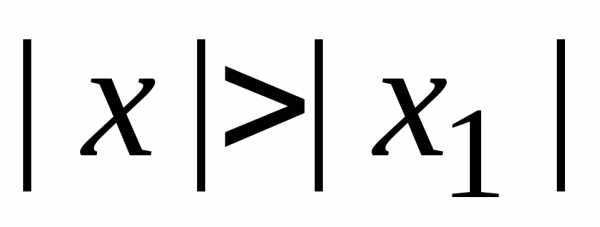 .
.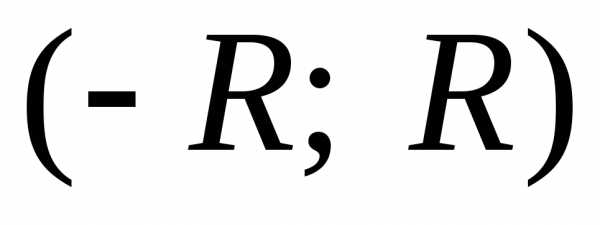 ,
ряд сходится абсолютно и при всех х,
лежащих вне интервала
,
ряд сходится абсолютно и при всех х,
лежащих вне интервала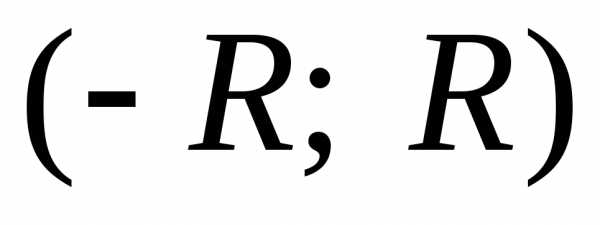 ,
ряд расходится.
,
ряд расходится.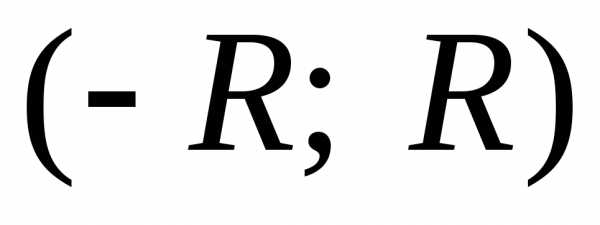 –интервалом сходимости степенного ряда по степеням х.
–интервалом сходимости степенного ряда по степеням х.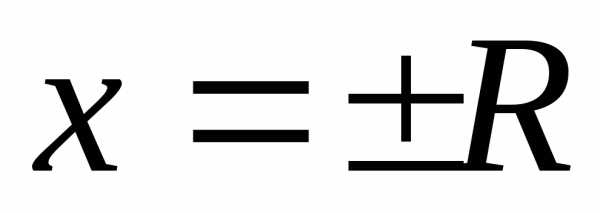 .
В этих точках различные степенные ряды
ведут себя по-разному: ряд может сходиться
(абсолютно или условно), а может
расходиться. Поэтому сходимость ряда
в этих точках следует проверять
непосредственно по определению.
.
В этих точках различные степенные ряды
ведут себя по-разному: ряд может сходиться
(абсолютно или условно), а может
расходиться. Поэтому сходимость ряда
в этих точках следует проверять
непосредственно по определению.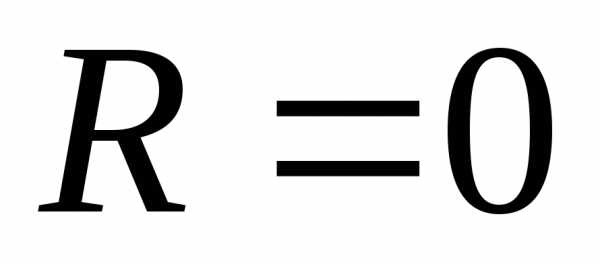 ,
то степенной ряд по степенямхсходится лишь в одной точке
,
то степенной ряд по степенямхсходится лишь в одной точке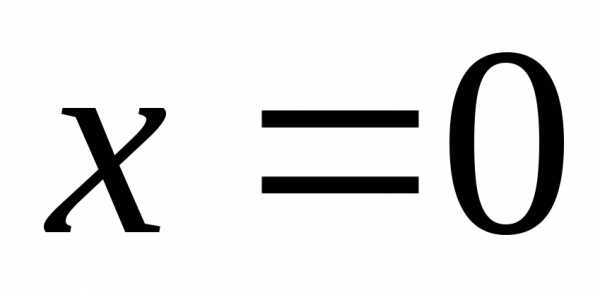 ;
если же
;
если же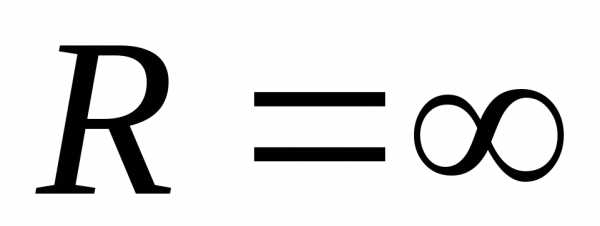 ,
то степенной ряд сходится на всей
числовой оси.
,
то степенной ряд сходится на всей
числовой оси. по
степеням
по
степеням 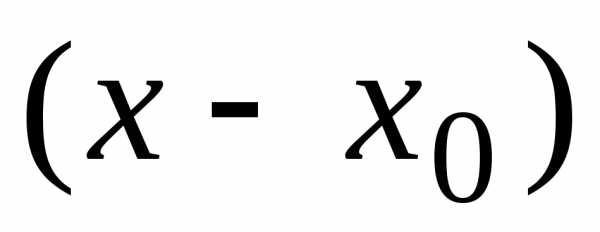 может
быть сведен к степенному ряду
может
быть сведен к степенному ряду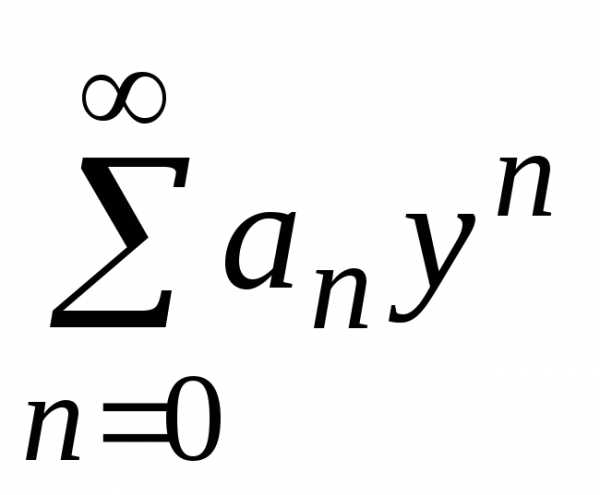 с помощью замены.
Если ряд
с помощью замены.
Если ряд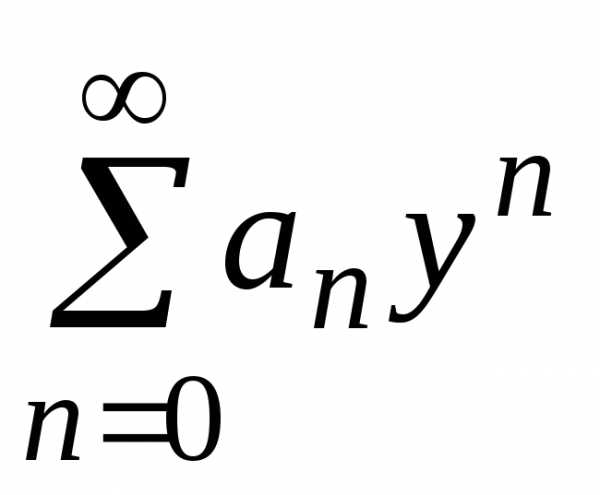 сходится при,
т.е. для,
то после обратной замены получим
сходится при,
т.е. для,
то после обратной замены получим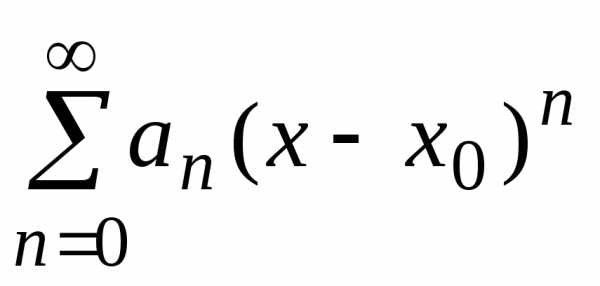 имеет вид .
Точку
имеет вид .
Точку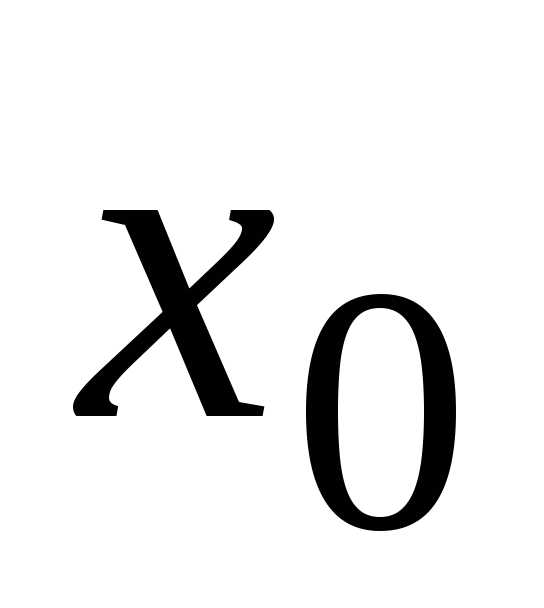 называютцентром сходимости. Для
наглядности принято интервал сходимости
изображать на числовой оси (рисунок 1)
называютцентром сходимости. Для
наглядности принято интервал сходимости
изображать на числовой оси (рисунок 1) ,
если в этих точках ряд сходится. Интервал
сходимости можно находить, применяя
непосредственно признак ДАламбера
или радикальный признак Коши к ряду,
составленному из абсолютных величин
членов данного ряда.
,
если в этих точках ряд сходится. Интервал
сходимости можно находить, применяя
непосредственно признак ДАламбера
или радикальный признак Коши к ряду,
составленному из абсолютных величин
членов данного ряда.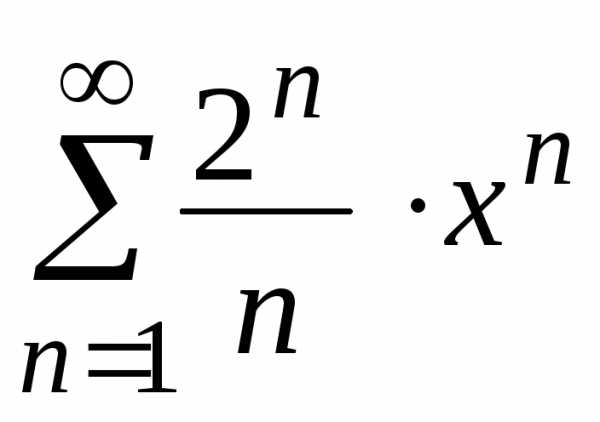 .
.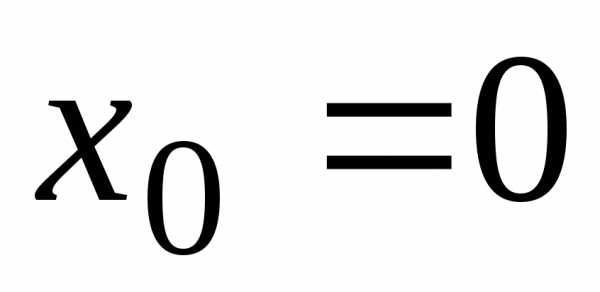 .
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда, и воспользуемся
признаком ДАламбера.
.
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда, и воспользуемся
признаком ДАламбера.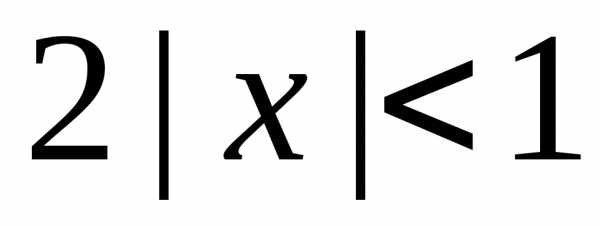 ,откуда
,откуда 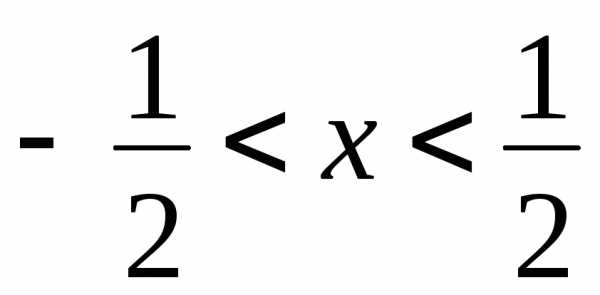 .
.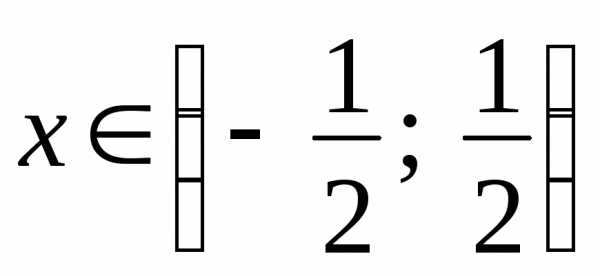 ,
радиус сходимости
,
радиус сходимости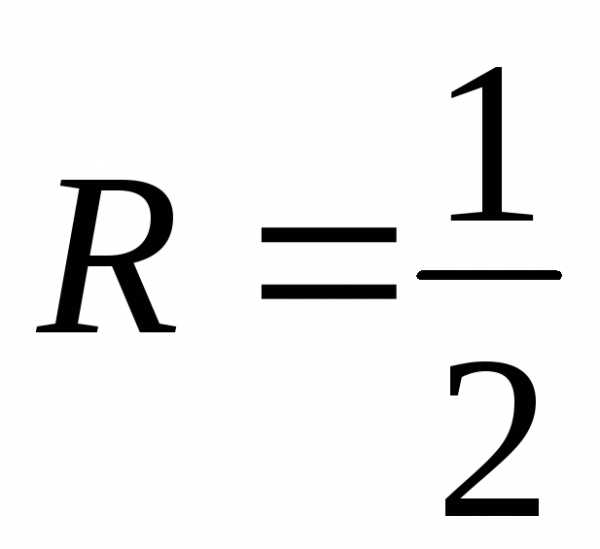 .
.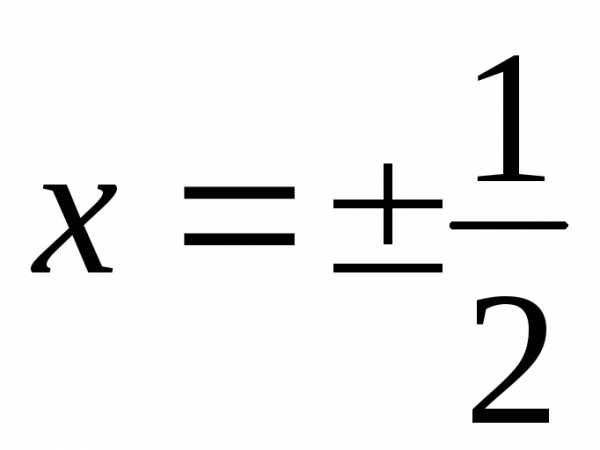 .
Подставляя в данный ряд значение
.
Подставляя в данный ряд значение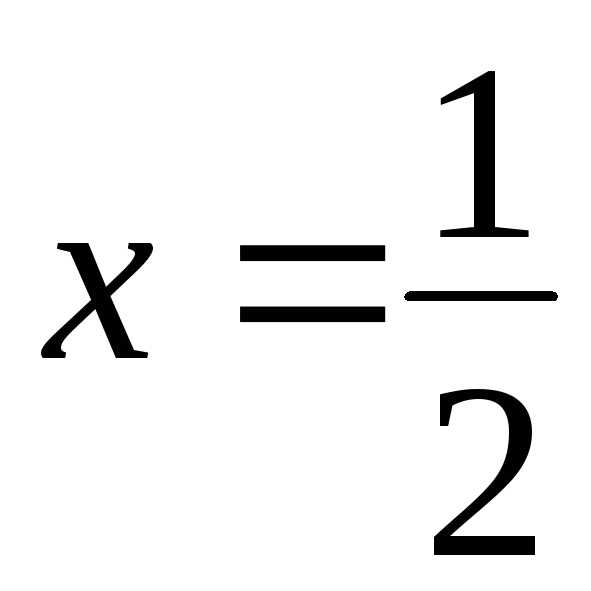 ,
получим ряд
,
получим ряд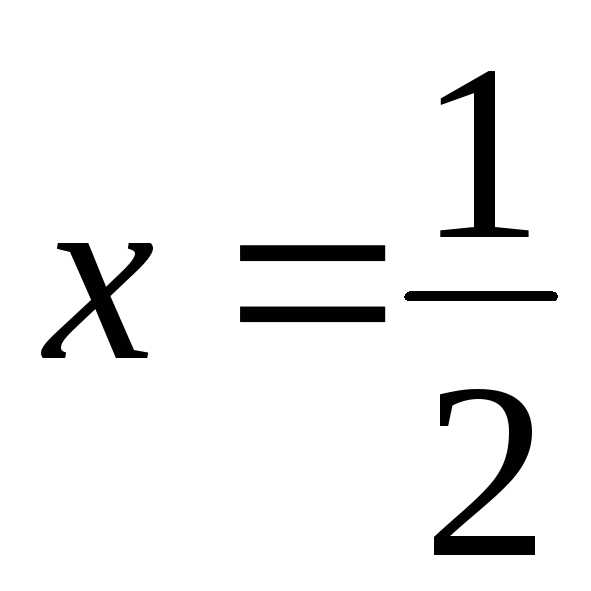 ряд расходится, значит, точка
ряд расходится, значит, точка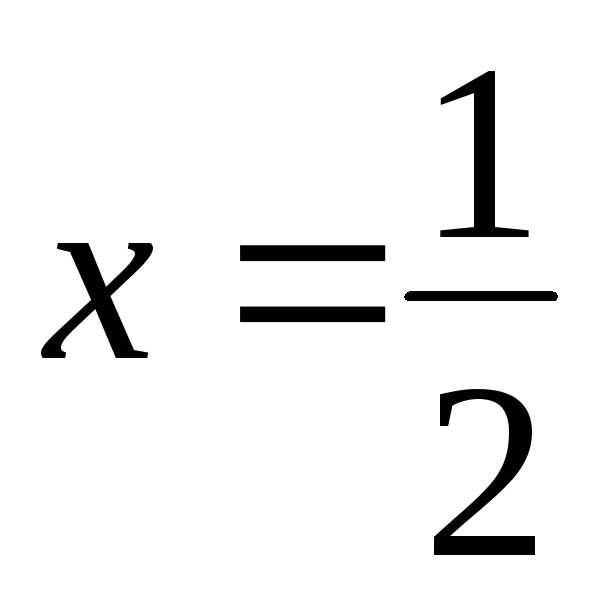 не входит в область сходимости.
не входит в область сходимости.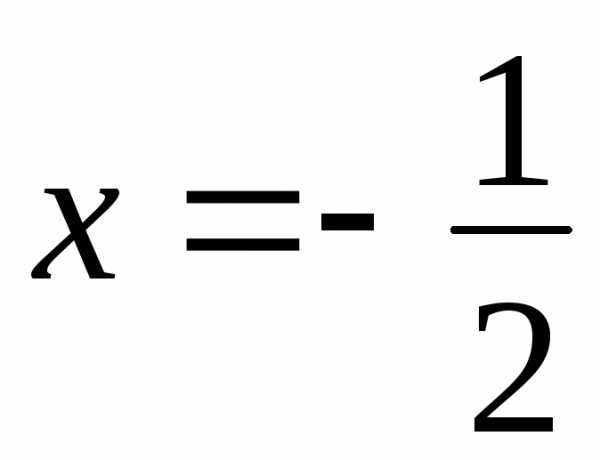 получим знакочередующийся ряд
получим знакочередующийся ряд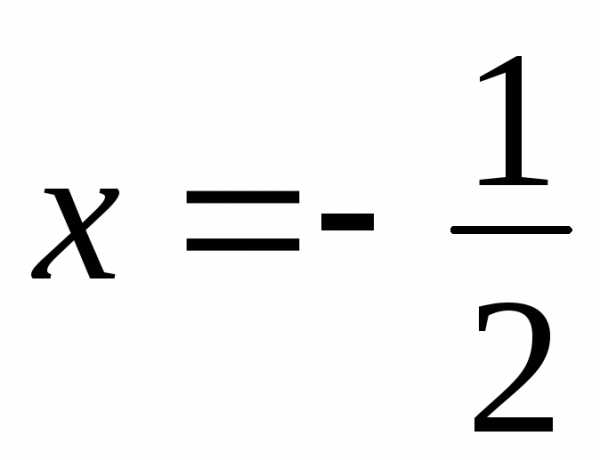 – точка
сходимости (условной).
– точка
сходимости (условной).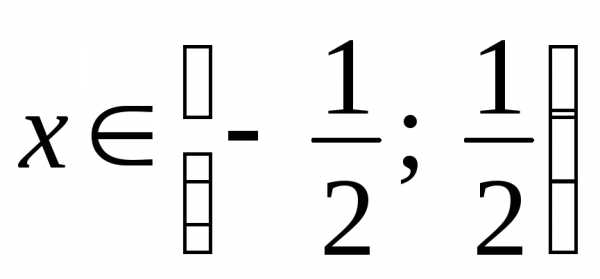 ,
причем в точке
,
причем в точке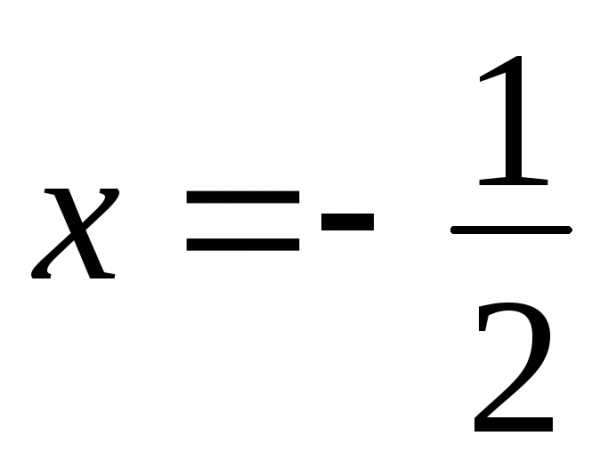 ряд сходится условно, а в остальных
точках — абсолютно.
ряд сходится условно, а в остальных
точках — абсолютно.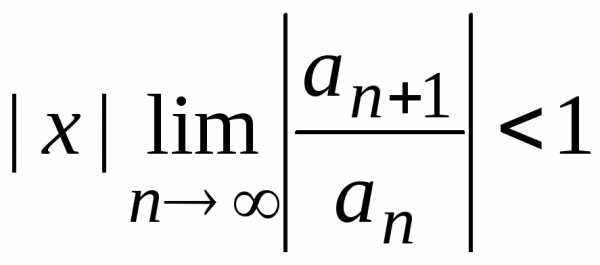 ,
,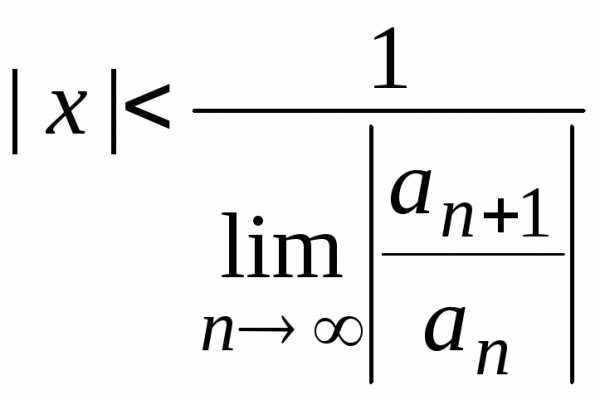 ,
,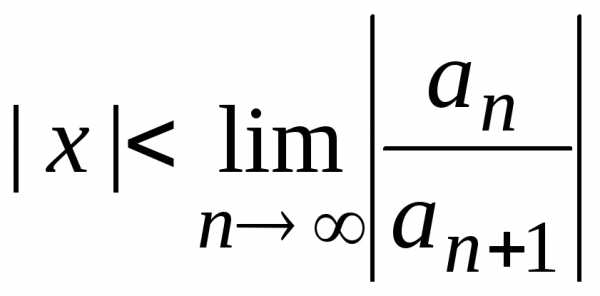 .
.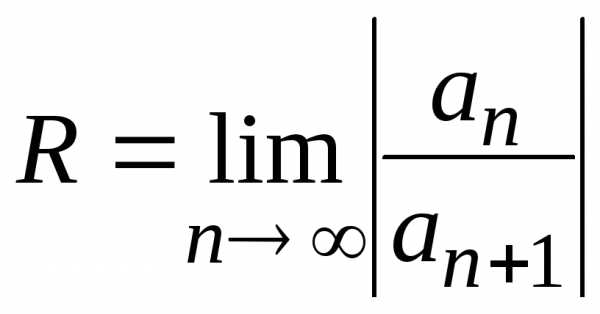
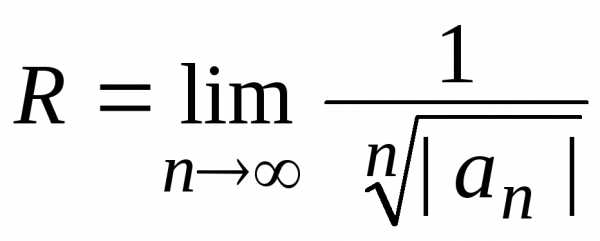
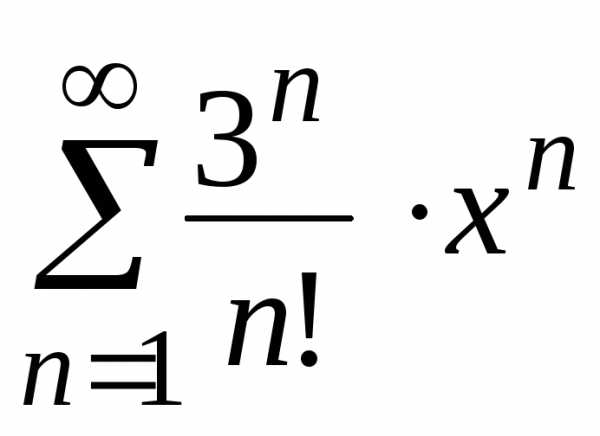
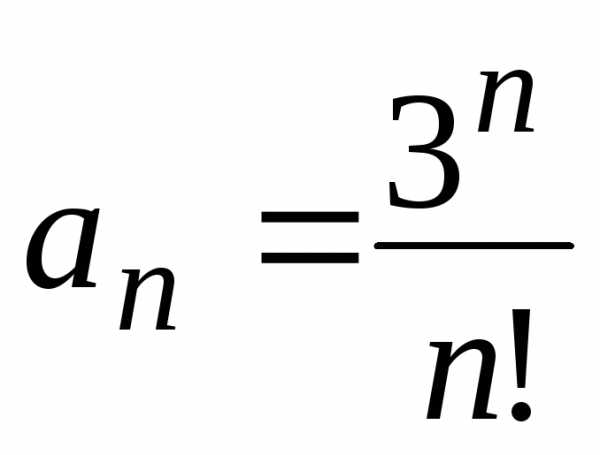 ,
тогда
,
тогда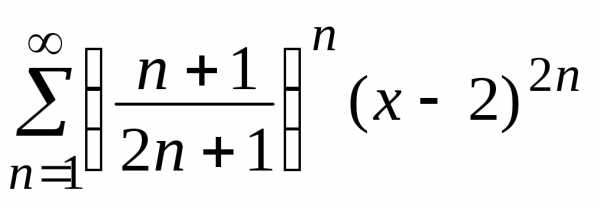 .
.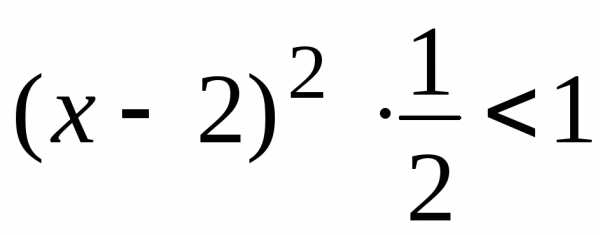 ,,,
,,,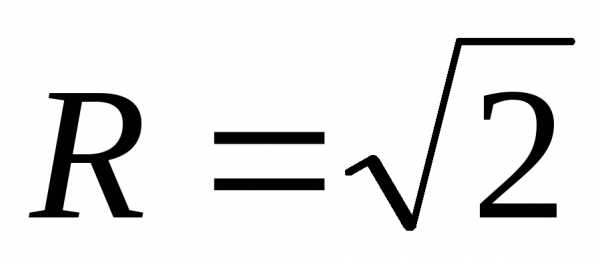 ,
тогда интеграл
сходимости
,
тогда интеграл
сходимости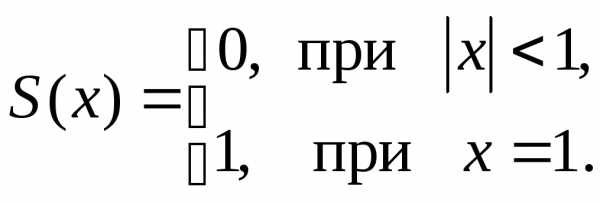

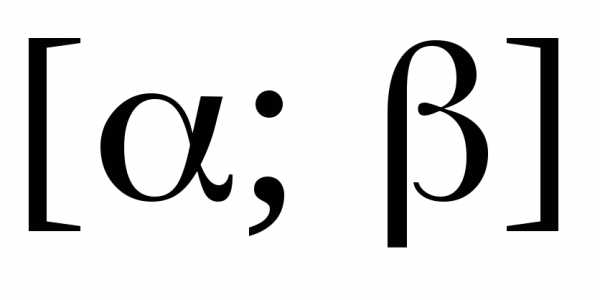 ,
принадлежащему интервалу сходимости,
т.е.
,
принадлежащему интервалу сходимости,
т.е.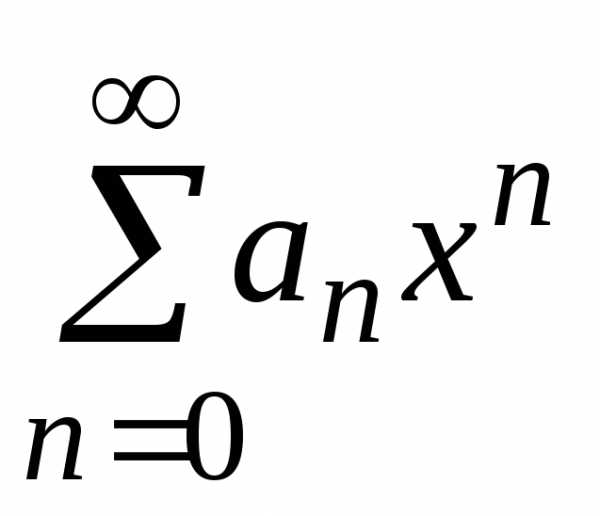 можно почленно
интегрировать по отрезку [0,х] для любого х из
интервала сходимости ряда. При этом
получим
можно почленно
интегрировать по отрезку [0,х] для любого х из
интервала сходимости ряда. При этом
получим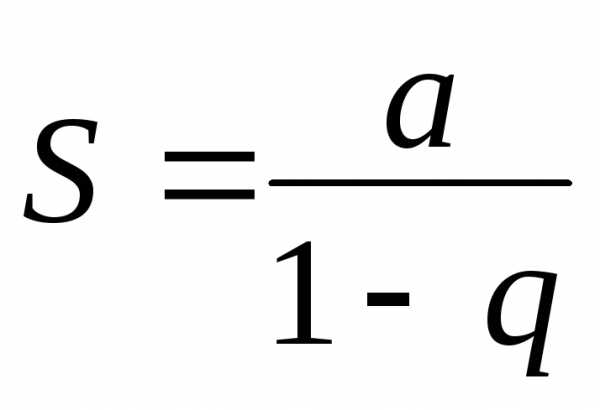 .
Таким образом, при |х|
< 1
.
Таким образом, при |х|
< 1 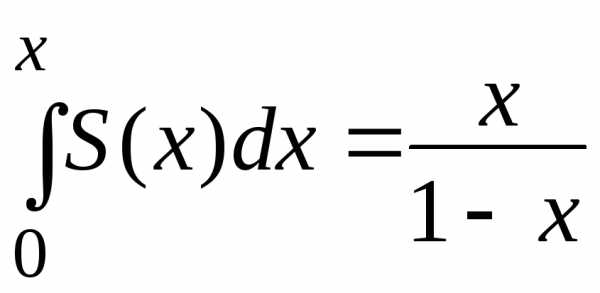
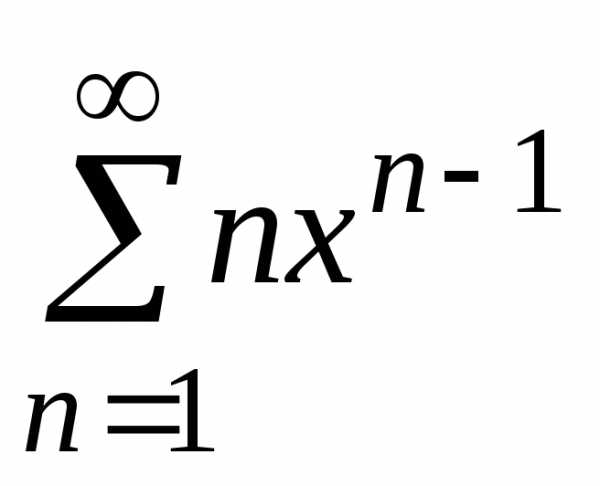 сходится
к функции
сходится
к функции 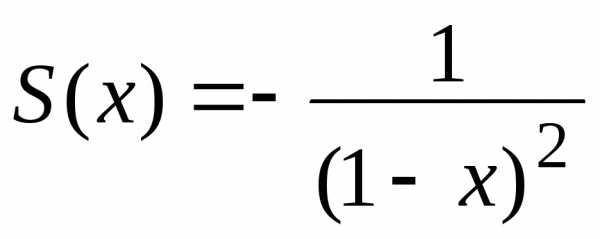 ,
т.е.
,
т.е.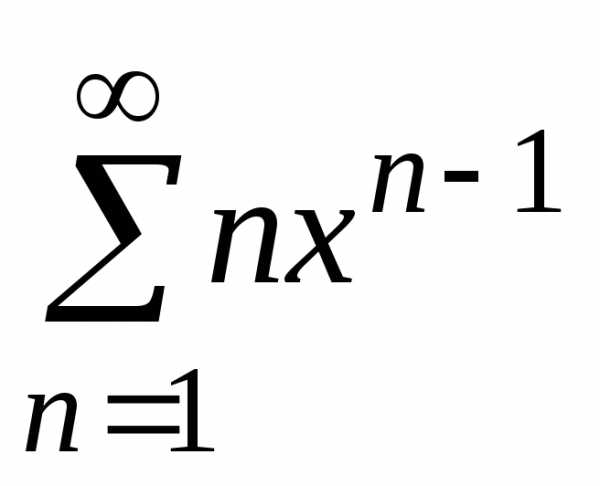 =
=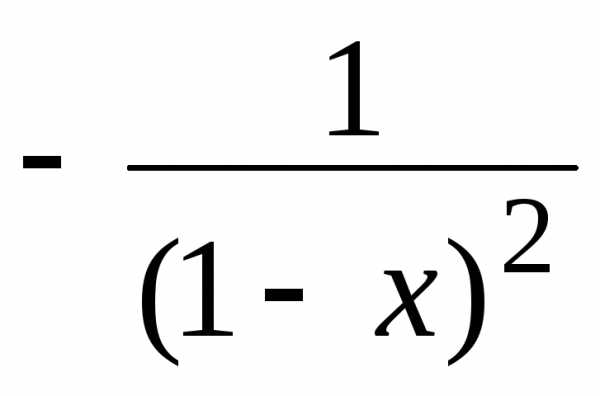 длях
(–1;1).
длях
(–1;1).