Свойства четырехугольника, с примерами
Рис. 1
Рис. 2
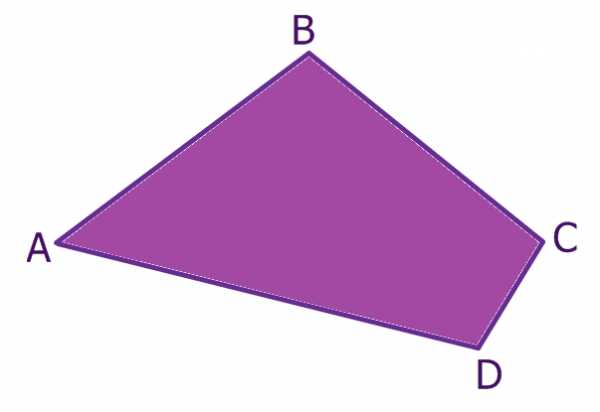
Четырехугольники бывают выпуклые (если они расположены в одной полуплоскости относительно прямой, которая содержит одну из его сторон) (рис. 1) и невыпуклые (рис. 2).
Основные виды четырехугольников: параллелограмм, прямоугольник, квадрат, ромб, трапеция.
Свойства четырехугольников
- Сумма углов четырехугольника равна .
- Четырехугольник можно вписать в окружность, если суммы его противоположных углов равны .
- Четырехугольник можно описать вокруг окружности, если суммы длин его противоположных сторон равны: .
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон:
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Справочник олимпиадника. Планиметрия. Четырехугольник
Справочник олимпиадника. Четырехугольник
к содержанию справочника
1. Сумма диагоналей выпуклого четырёхугольника больше суммы его двух противоположных сторон.
2. Если отрезки, соединяющие середины противоположных сторон четырёхугольника
а) равны, то диагонали четырёхугольника перпендикулярны;
б) перпендикулярны, то диагонали четырёхугольника равны.
3. Биссектрисы углов при боковой стороне трапеции пересекаются на её средней линии.
4. Стороны параллелограмма равны и . Тогда четырёхугольник, образованный пересечениями биссектрис углов параллелограмма, является прямоугольником, диагонали которого равны .
5. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований трапеции, равен их полуразности.
6. На сторонах АВ и AD параллелограмма ABCD взяты точки М и N так, что прямые МС и NC делят параллелограмм на три равновеликие части. Найдите MN, если BD=d.
7. Отрезок прямой, параллельной основаниям трапеции, заключённый внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой.
8. Через точку пересечения диагоналей трапеции с основаниями и проведена прямая, параллельная основаниям. Отрезок этой прямой, заключенный между боковыми сторонами трапеции, равен .
9. Трапеция разделена прямой, параллельной её основаниям, равным и , на две равновеликие трапеции. Тогда отрезок этой прямой, заключённый между боковыми сторонами, равен .
10. Если выполняется одно из следующих условий, то четыре точки А, В, С и D лежат на одной окружности.
а) CAD=CBD = 90°.
б) точки А и В лежат по одну сторону от прямой CD и угол CAD равен углу CBD.
в) прямые АС и BD пересекаются в точке О и О А•ОС=ОВ•OD.
11. Прямая, соединяющая точку Р пересечения диагоналей четырехугольника ABCD с точкой Q пересечения прямых АВ и CD, делит сторону AD пополам. Тогда она делит пополам и сторону ВС.
12. Каждая сторона выпуклого четырёхугольника поделена на три равные части. Соответствующие точки деления на противоположных сторонах соединены отрезками. Тогда эти отрезки делят друг друга на три равные части.
13. Две прямые делят каждую из двух противоположных сторон выпуклого четырёхугольника на три равные части. Тогда между этими прямыми заключена треть площади четырёхугольника.
14. Если в четырёхугольник можно вписать окружность, то отрезок, соединяющий точки, в которых вписанная окружность касается противоположных сторон четырёхугольника, проходит через точку пересечения диагоналей.
15. Если суммы противоположных сторон четырёхугольника равны, то в такой четырёхугольник можно вписать окружность.
16. Свойства вписанного четырёхугольника со взаимно перпендикулярными диагоналями. Четырёхугольник ABCD вписан в окружность радиуса R. Его диагонали АС и BD взаимно перпендикулярны и пересекаются в точке Р. Тогда
а) медиана треугольника АРВ перпендикулярна стороне CD;
б) ломаная АОС делит четырёхугольник ABCD на две равновеликие фигуры;
в) АВ2+CD2=4R2;
г) АР2+ВР2+СР2+DP2=4R2 и АВ2+ВС2+CD2+AD2=8R2;
д) расстояние от центра окружности до стороны четырёхугольника вдвое меньше противоположной стороны.
е) если перпендикуляры, опущенные на сторону AD из вершин В и С, пересекают диагонали АС и BD в точках Е и F, то BCFE — ромб;
ж) четырёхугольник, вершины которого — проекции точки Р на стороны четырёхугольника ABCD, — и вписанный, и описанный;
з) четырёхугольник, образованный касательными к описанной окружности четырёхугольника ABCD, проведёнными в его вершинах, можно вписать в окружность.
17. Если a, b, c, d — последовательные стороны четырёхугольника, S — его площадь, то , причем равенство имеет место только для вписанного четырёхугольника, диагонали которого взаимно перпендикулярны.
18. Формула Брахмагупты. Если стороны вписанного четырехугольника равны a, b, с и d, то его площадь S может быть вычислена по формуле ,
где — полупериметр четырехугольника.
19. Если четырёхугольник со сторонами а, b, с, d можно вписать и около него можно описать окружность, то его площадь равна .
20. Точка Р расположена внутри квадрата ABCD, причем угол PAB равен углу РВА и равен 15°. Тогда треугольник DPC — равносторонний.
21. Если для вписанного четырёхугольника ABCD выполнено равенство CD=AD+ВС, то биссектрисы его углов А и В пересекаются на стороне CD.
22. Продолжения противоположных сторон АВ и CD вписанного четырёхугольника ABCD пересекаются в точке М, а сторон AD и ВС — в точке N. Тогда
а) биссектрисы углов AMD и DNC взаимно перпендикулярны;
б) прямые МQ и NQ пересекают стороны четырёхугольника в вершинах ромба;
в) точка пересечения Q этих биссектрис лежит на отрезке, соединяющем середины диагоналей четырёхугольника ABCD.
23. Теорема Птолемея. Сумма произведений двух пар противоположных сторон вписанного четырёхугольника равна произведению его диагоналей.
24. Теорема Ньютона. Во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности расположены на одной прямой.
25. Теорема Монжа. Прямые, проведённые через середины сторон вписанного четырёхугольника перпендикулярно противоположным сторонам, пересекаются в одной точке.
27. Четыре круга, построенных на сторонах выпуклого четырёхугольника как на диаметрах, покрывают весь четырёхугольник.
29. Два противоположных угла выпуклого четырёхугольника — тупые. Тогда диагональ, соединяющая вершины этих углов, меньше другой диагонали.
30. Центры квадратов, построенных на сторонах параллелограмма вне его, сами образуют квадрат.
www.itmathrepetitor.ru
Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике
Здесь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе. Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие. Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.
1) Площади четырехугольников
Площадь параллелограмма
произведение основания на высоту
пороизведение сторон на синус угла между ними
полупроизведение диагоналей на синус угла между ними
Площадь трапеции
произведение полусуммы оснований на высоту
произведение средней линии на высоту
полупроизведение диагоналей на синус угла между ними
Площадь произвольного четырехугольника
Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними
2) Свойства параллелограмма
В параллелограмме:
противолежащие стороны и углы равны
диагонали пересекаются и в точке пересечения делятся пополам
3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть
3) Cредняя линия в трапеции
Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
То есть и
4) Средняя линия в равнобедренной трапеции
Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.
То есть
5) Теорема с сдвиге диагонали в трапеции
Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:
трапеция — равнобедренная равнобедренный
6) Четыре замечательные точки в трапеции
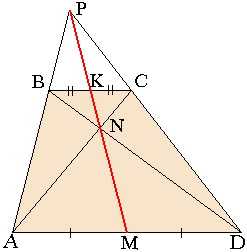
Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.
То есть точки M, N, K и P лежат на одной прямой
Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан. Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список. Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией. В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.
Колпаков Александр Николаевич. Репетитор по математике.
Метки: Геометрия, Справочник репетитора
ankolpakov.ru
Четырехугольник — это… Что такое Четырехугольник?
- Четырехугольник
Четырёхугольник — это многоугольник, содержащий четыре вершины и четыре стороны. Различают выпуклые и невыпуклые четырёхугольники (см. рис.).Свойства
Площадь произвольного выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними.
Сумма углов четырёхугольника равна .
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° ().
Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
Виды четырёхугольников
- Параллелограмм — четырёхугольник, у которого все противоположные стороны параллельны
- Прямоугольник — четырёхугольник, у которого все углы прямые
- Ромб — четырёхугольник, у которого все стороны равны
- Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны
- Трапеция — четырехугольник, у которого две противоположные стороны параллельны
- Дельтоид — четырёхугольник, у которого две пары смежных сторон равны
Литература
- Параллелограмм — четырёхугольник, у которого все противоположные стороны параллельны
Wikimedia Foundation. 2010.
- Четырехугольный волосатый краб
- Четырехтактный двигатель
Смотреть что такое «Четырехугольник» в других словарях:
четырехугольник — четырехсторонник; каре, параллелограмм, трапеция, прямоугольник, четыреугольник, многоугольник, трапецея, тетрагон Словарь русских синонимов. четырехугольник сущ., кол во синонимов: 11 • антипараллелограм … Словарь синонимов
четырехугольник — (4 угольник) … Орфографический словарь-справочник
четырехугольник — ▲ многоугольник ↑ имеющий, четыре, угол четырехугольник многоугольник с четырьмя сторонами. четырехугольный. трапецоид четырехугольник, не имеющий параллельных сторон. выпуклый четырехугольник. дельтоид, ромбоид выпуклый четырехугольник,… … Идеографический словарь русского языка
Четырехугольник — частный случай многоугольника (см.). Он называется плоским, если его вершины лежат в одной плоскости; в противном же случае Ч. называется косым. В данный плоский Ч. можно вписать круг, если суммы противоположных сторон его равны. Около данного… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Четырехугольник — четырёхугольник м. 1. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей четыре угла. 2. Пространство или предмет такой формы. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
четырехугольник — ‘фигура’ Syn: четырехсторонник … Тезаурус русской деловой лексики
четырехугольник — ЧЕТЫРЁХУГОЛЬНИК а; м. 1. Геометрическая фигура, ограниченная замкнутой линией, звенья которой образуют четыре угла. Построиться четырёхугольником, в ч. 2. (чего). О чём л., имеющем такую форму. Ч. двора. Ч. раскрытой двери. Ровные… … Энциклопедический словарь
четырехугольник — ЧЕТЫРЕХУГОЛЬНИК, а, м Геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой образуют четыре угла. Войска построились четырехугольником … Толковый словарь русских существительных
четырехугольник противоположных полюсов — opposite pole quadrilateral Четырехугольник, образованный соединением двух пар противоположных полюсов так, что противоположные полюсы непосредственно не соединяются. Шифр IFToMM: 2.3.29 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
Четырехугольник Ламберта — Четырёхугольник Ламберта или трипрямоугольник четырёхугольник, в котором при трёх вершинах прямые углы. Рассматривался Иоганном Ламбертом в 1766 при попытках доказать постулат Евклида о параллельных. Из трёх возможных предположений о величине… … Википедия
dic.academic.ru
Какие четырехугольники могут иметь прямые углы? (2 прямых угла)
Если ровно 2 угла прямые, то возможны два случая. 1. Либо прямые углы — при одной стороне, и тогда это прямоугольная трапеция. 2. Либо прямые углы противолежат друг другу, и тогда это…. впрочем, специального названия нет. Можно назвать это кривой прямоугольник, или полупрямоугольник (полуквадрат). <a rel=»nofollow» href=»https://otvet.mail.ru/question/83653011″ target=»_blank»>https://otvet.mail.ru/question/83653011</a> Если хотя бы 3 угла прямые, то и 4-й угол тоже прямой, и это прямоугольник (в частном случае квадрат). Ну а если прямой только один угол, то тогда вариаций слишком много, и для каждого из них особого названия, конечно, нет. Просто четырёхугольник с прямым углом (может быть как выпуклым, так и невыпуклым).
шизой попахивает
Естественно. Возьмите два угольника и складывайте их как угодно. А ромбы тут не в кассу.
Неравнобокая трапеция.
Разумеется могут быть… пересеките противоположные стороны квадрата или прямоугольника прямой и Вы получите 2 четырехугольника с 2 прямыми углами и любыми двумя другими… Ну или в качестве ещё одного варианта с прямыми противолежащими углами — ромбоид. <img src=»https://otvet.imgsmail.ru/download/73610362_f7c005055a72bb26a806e06396c6fcd1_800.jpg» alt=»» data-big=»1″ data-lsrc=»//otvet.imgsmail.ru/download/73610362_f7c005055a72bb26a806e06396c6fcd1_120x120.jpg»>
Возможен невыпуклый четырёхугольник, кроме уже перечисленных <img src=»//otvet.imgsmail.ru/download/8353180_dec9ff624e8bab5a5c86d9c93a77c2ce_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/8353180_dec9ff624e8bab5a5c86d9c93a77c2ce_120x120.jpg» data-big=»1″>
touch.otvet.mail.ru
Всё о четырехугольниках …… или почти всё
Муниципальная общеобразовательная школа № 114На тему:
Всё о четырехугольниках …… или почти всё.
Выполнила:
Ученица 8 класса
Патюткина Елена Анатольевна
Учитель Тюрнина Т.Ю.
Волгоград 2009г.
Четырёхугольник — это многоугольник, содержащий четыре вершины и четыре стороны. Различают выпуклые и невыпуклые четырёхугольники (см. рис.).
ABCD — выпуклый четырёхугольник, A1B1C1D1 — невыпуклый
Четырехугольник — геометрическая фигура с четырьмя сторонами. Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки — сторонами четырехугольника.
Четырехугольники
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными.
Четырехугольники. Четырехугольником является всякая плоская фигура, ограниченная четырьмя прямыми (рис. 4). Параллелограммом называется четырехугольник, у которого противоположные стороны имеют равную длину. Ромб (рис. 4,г) – это параллелограмм, все стороны которого равны, а прямоугольник (рис. 4,д) – это параллелограмм, у которого все углы прямые. Диагонали параллелограмма (рис. 4,ж) в точке пересечения делятся пополам; в прямоугольнике диагонали равны. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – непараллельны. Параллельные стороны называются основаниями. Площадь трапеции равна произведению высоты на полусумму ее оснований: A = h [(b + d)/2]. Площадь параллелограмма A = bh. Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны параллельны
Прямоугольник — четырёхугольник, у которого все углы прямые
Ромб — четырёхугольник, у которого все стороны равны
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны
Трапеция — четырехугольник, у которого две противоположные стороны параллельны
Дельтоид — четырёхугольник, у которого две пары смежных сторон равны
Свойства
Площадь произвольного выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними.
Сумма углов четырёхугольника равна .
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° ().
Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны (AB + CD = BC + AD)
Свойства четырехугольников:
1. Пусть ABCE параллелограмм, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
2. Пусть ABCE прямоугольник, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
e) Диагонали равны
3. Пусть ABCE ромб, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
e) Диагонали перпендикулярны
f) Все стороны равны
g) Диагонали ромба делят его углы пополам
4. Пусть ABCE квадрат, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
f) Диагонали перпендикулярны
g) Диагонали квадрата делят его углы пополам
h) Все стороны равны
Свойства параллелограмма
противолежащие стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180°;
сумма квадратов диагоналей равна сумме квадратов всех сторон:
d12+d22=2(a2+b2).
Признаки параллелограмма
Четырехугольник является параллелограммом, если:
Две его противоположные стороны равны и параллельны.
Противоположные стороны попарно равны.
Противоположные углы попарно равны.
Диагонали точкой пересечения делятся пополам.
Трапеция.
Трапеция, у которой боковые стороны равны, называется равнобокой.
Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. Трапеция, у которой боковые стороны равны, называется равнобокой.
На данном рисунке изображена равнобокая трапеция ABCE. Параллельные стороны, BC и AE, являются основаниями. AB и CE — равные боковые стороны.
Следующие теоремы описывают свойства равнобоких трапеций.
В равнобокой трапеции углы при основании равны.
Диагонали равнобокой трапеции равны.
Средняя линяя трапеции: отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.
Свойства трапеции
ее средняя линия параллельна основаниям и равна их полусумме;
если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
если трапеция равнобокая, то около нее можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Основные формулы
Произвольный выпуклый четырехугольник d1, d2 — диагонали; — угол между ними; S — площадь.
S =d1d2 sin
Параллелограмм
a и b — смежные стороны; — угол между ними; ha — высота, проведенная к стороне a.
S = aha
S = ab sin
S =d1d2 sin
Трапеция
a и b — основания; h — расстояние между ними; l — средняя линия.
S = lh
Прямоугольник
S = ab
S =d1d2 sin
Ромб
S = aha
S = a2sin
S =d1d2
Квадрат
d — диагональ.
S = a2
S =d2
birmaga.ru



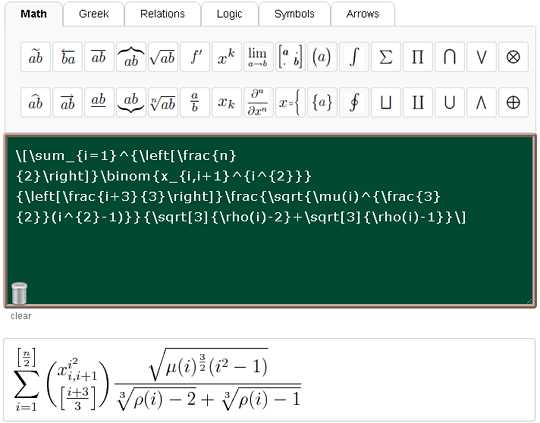



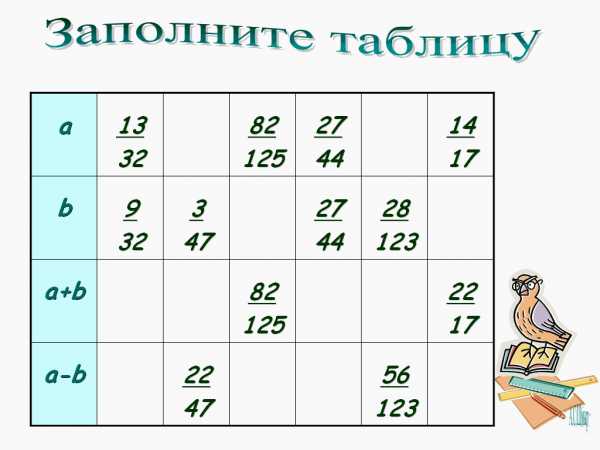

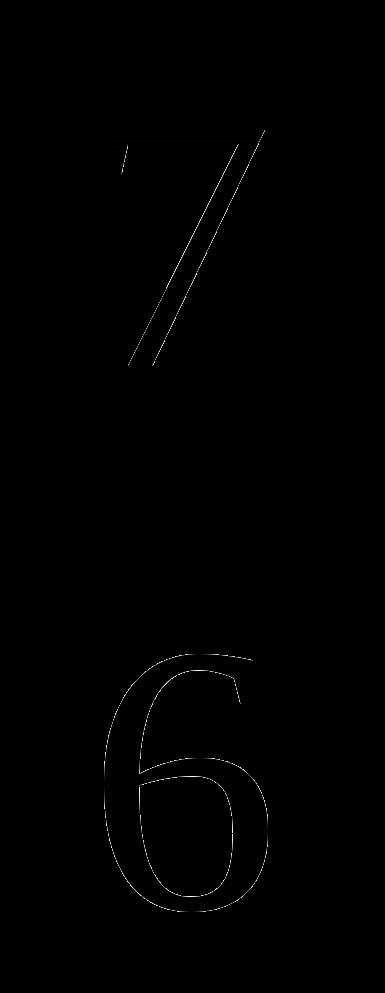 ; ;
; ;  ;
;  . Выберите правильную дробь.
. Выберите правильную дробь. и , выберите наибольшее.
и , выберите наибольшее. всей книги. Сколько страниц во всей книги, если она прочитала 240 страниц?
всей книги. Сколько страниц во всей книги, если она прочитала 240 страниц? +
+ 
 см. Ширина его на
см. Ширина его на  см меньше длины. Вычислите ширину прямоугольника?
см меньше длины. Вычислите ширину прямоугольника?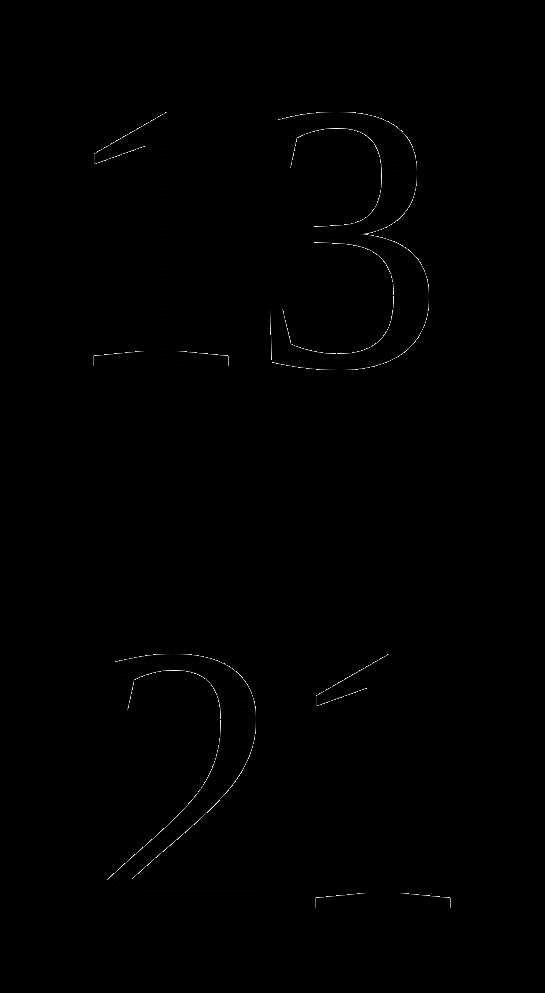 —
— 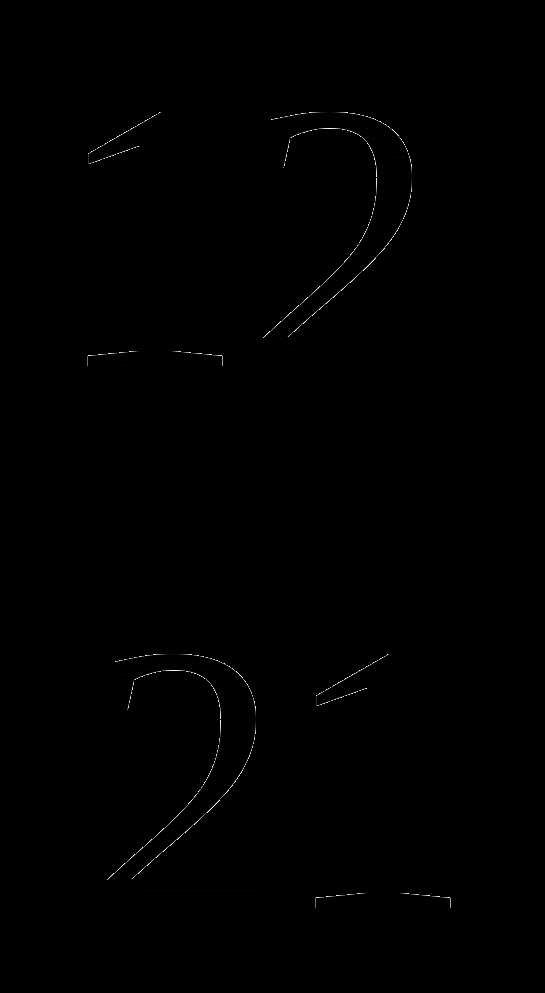 +
+ 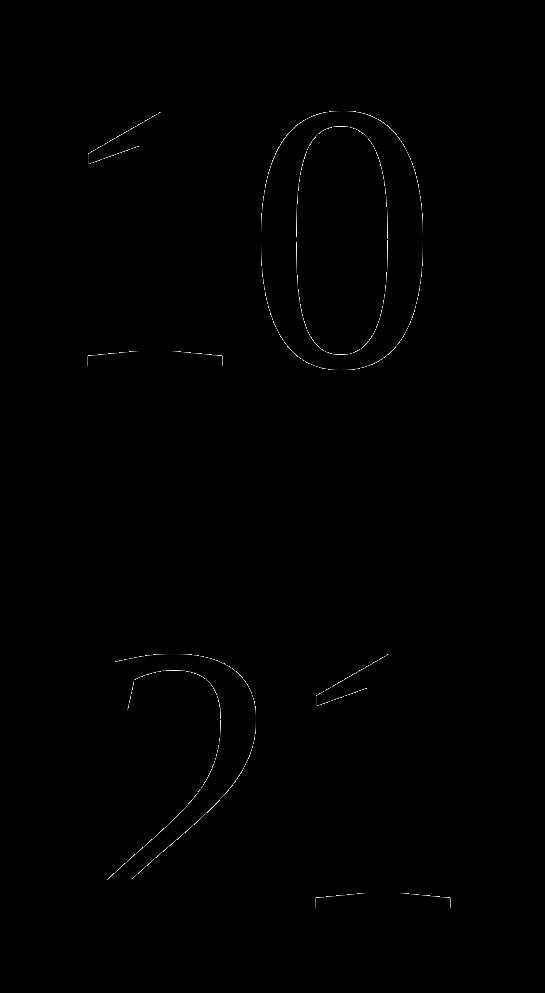

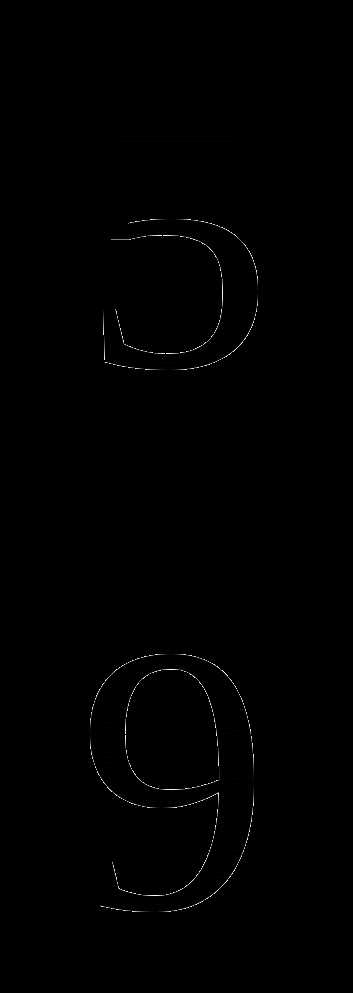




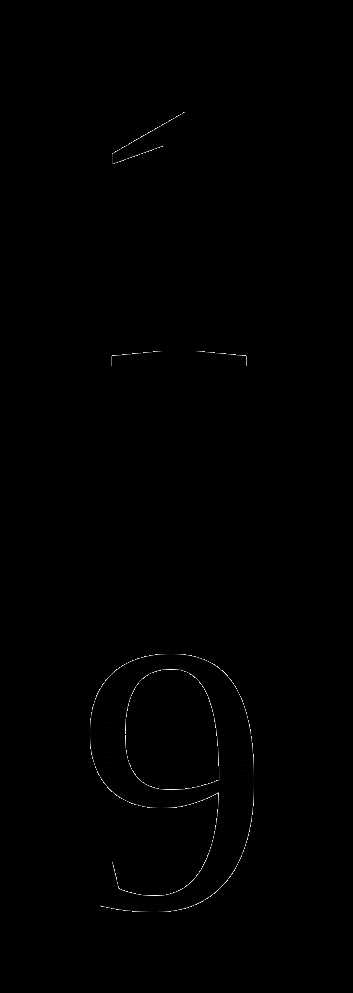

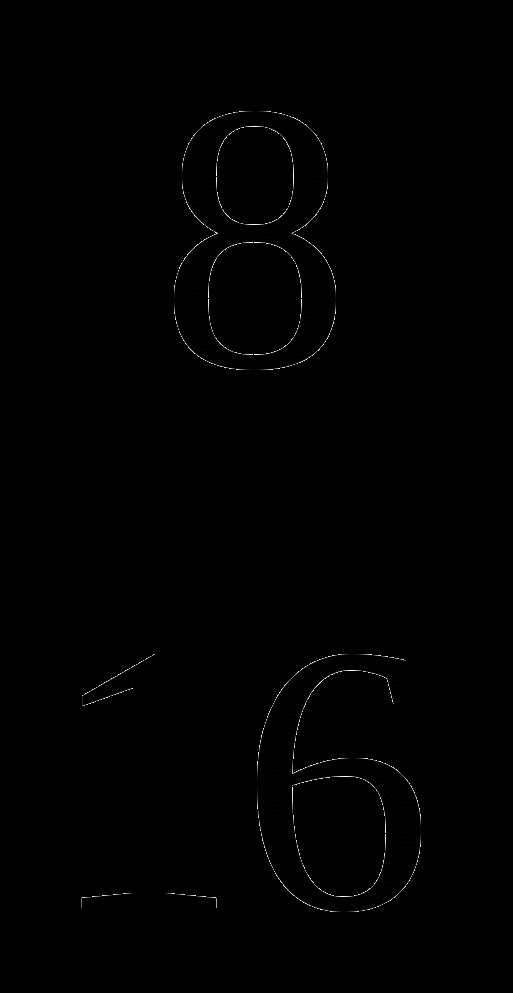
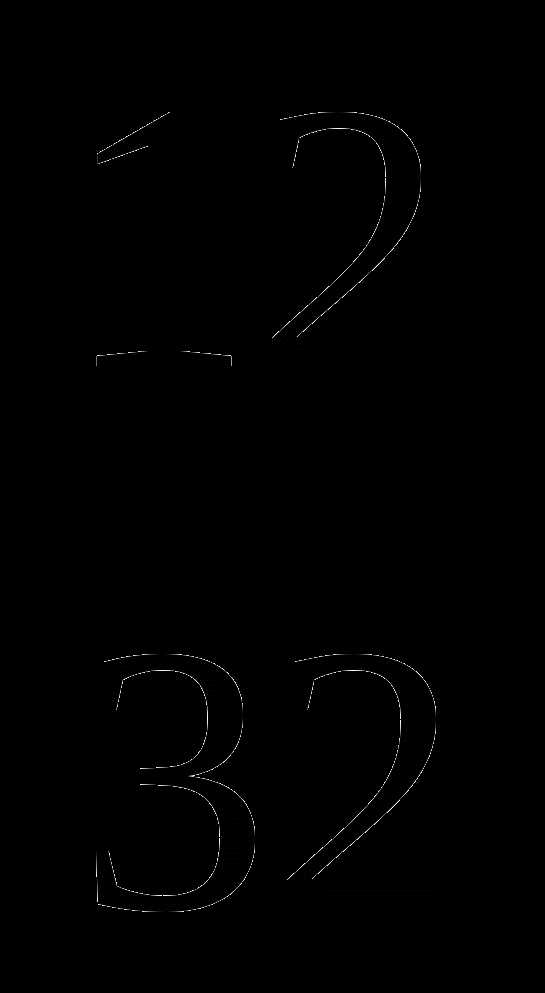




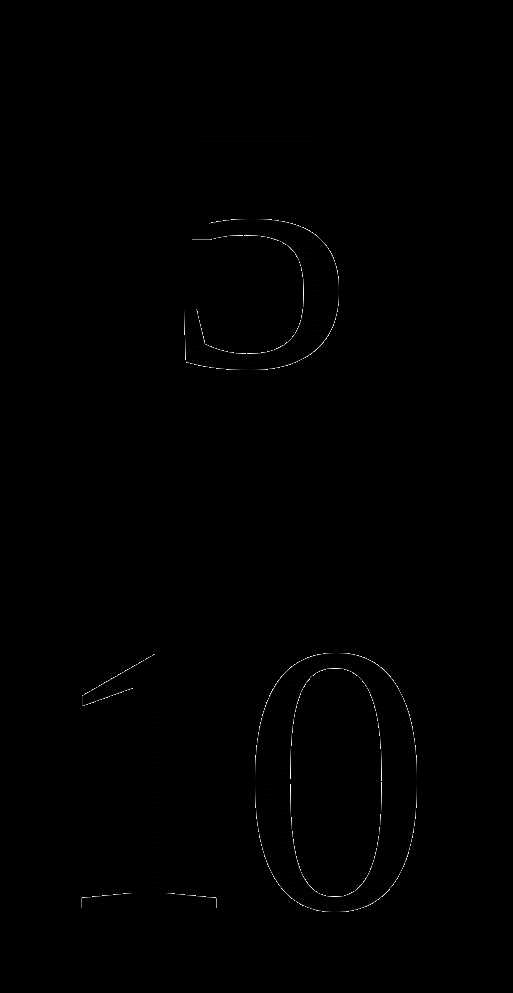
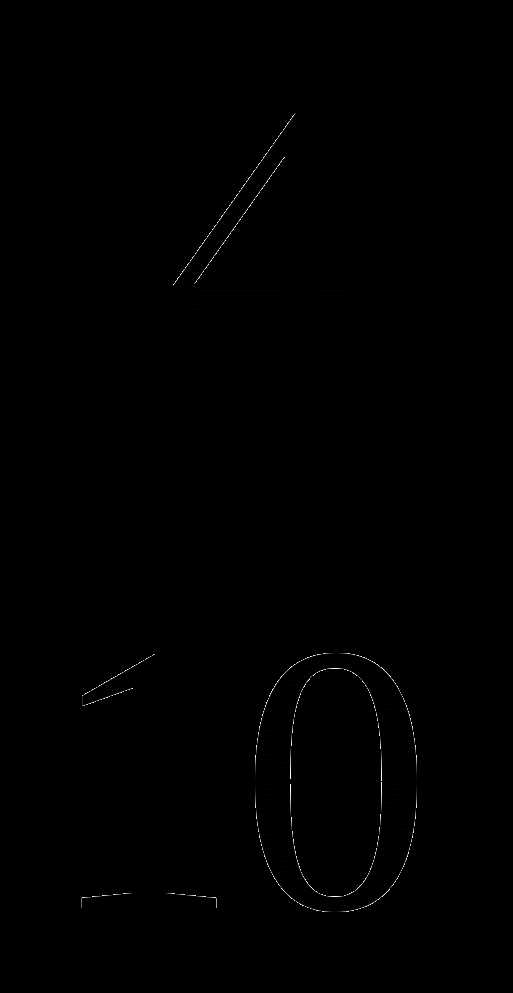



 ;
;  ;
; 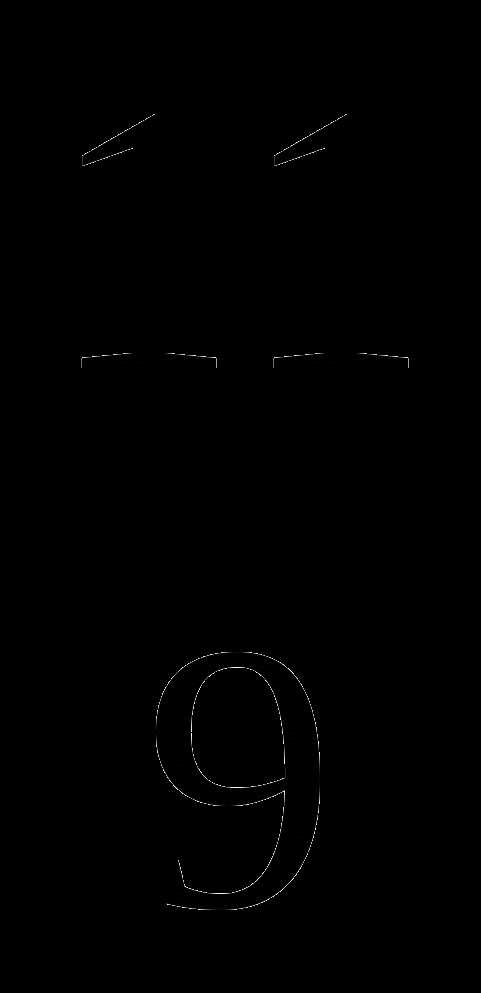 ;
; 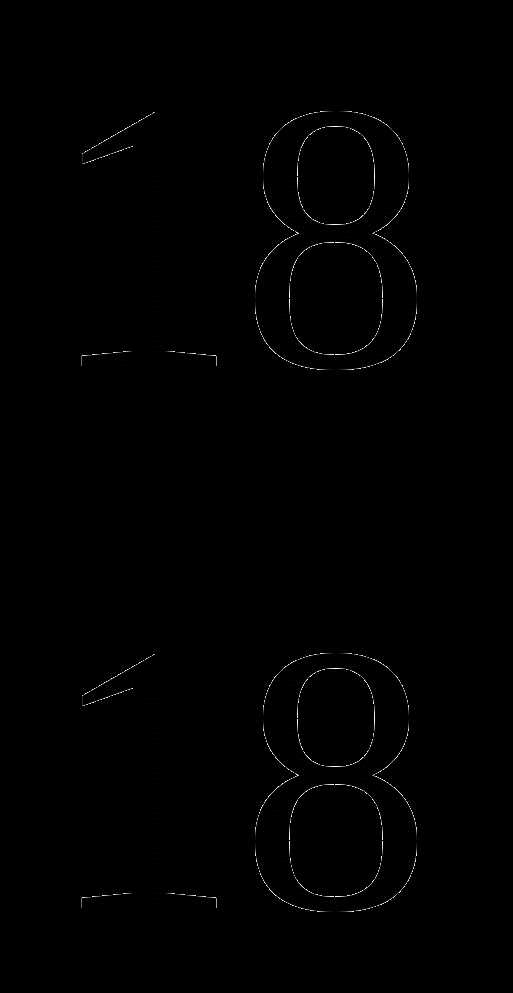 . Выберите правильную дробь.
. Выберите правильную дробь. , выберите большее.
, выберите большее. книги. Сколько страниц ему осталось прочитать?
книги. Сколько страниц ему осталось прочитать? +
+ 
 —
— 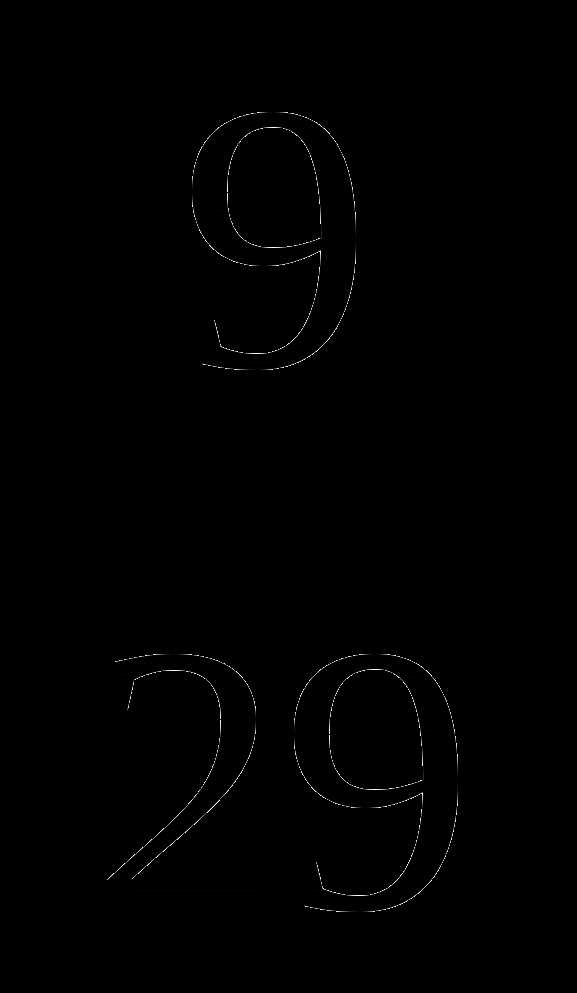 .
. +
+ 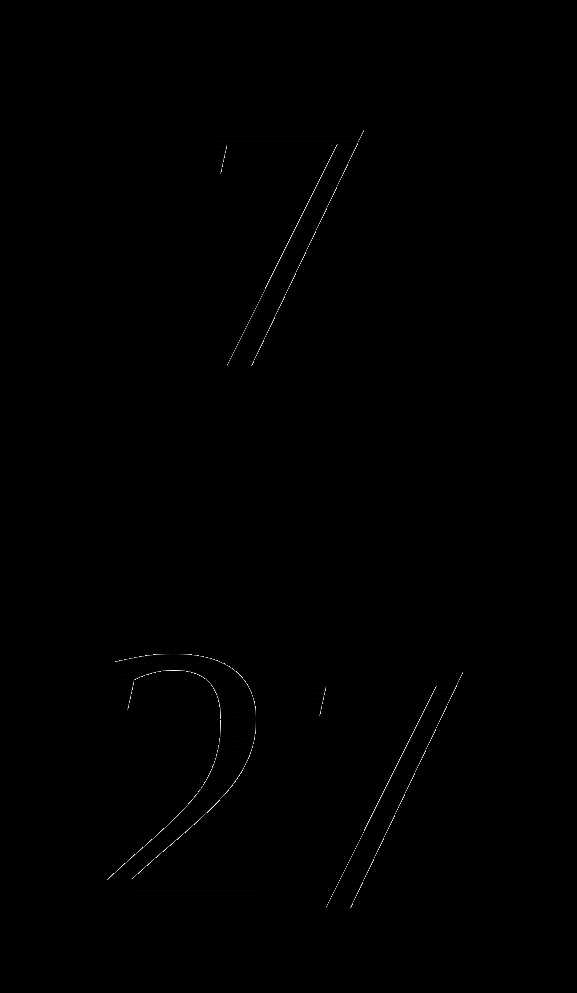 —
—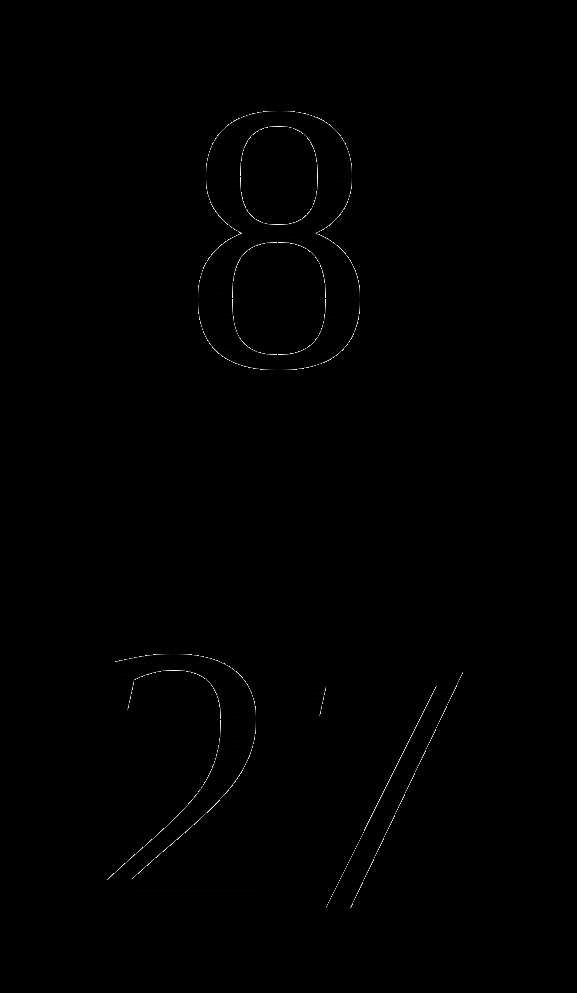 .
.
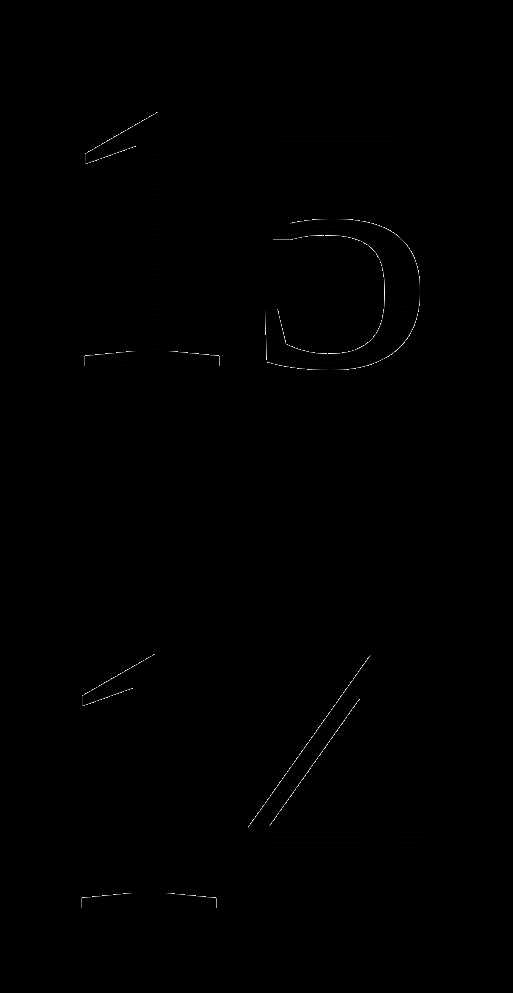









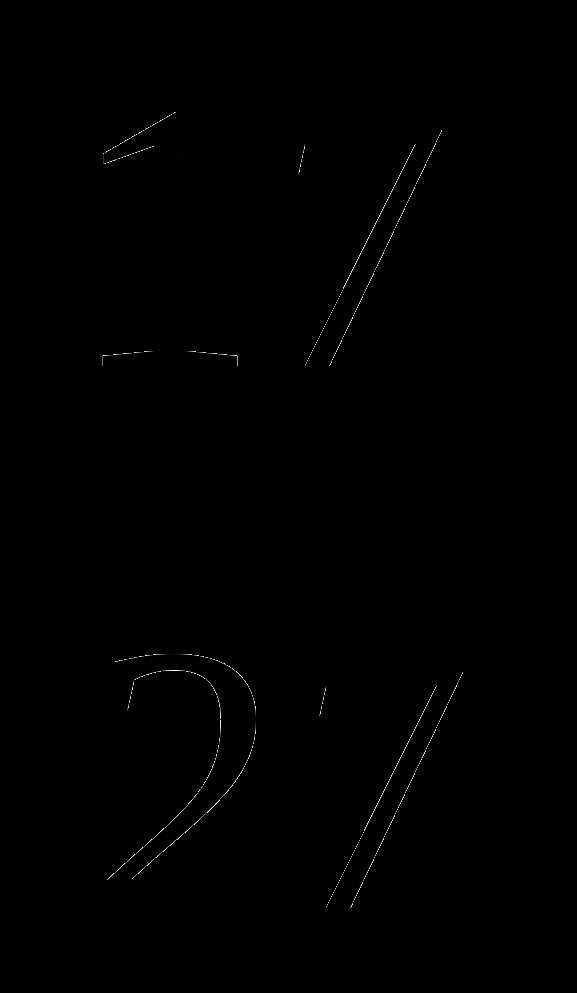
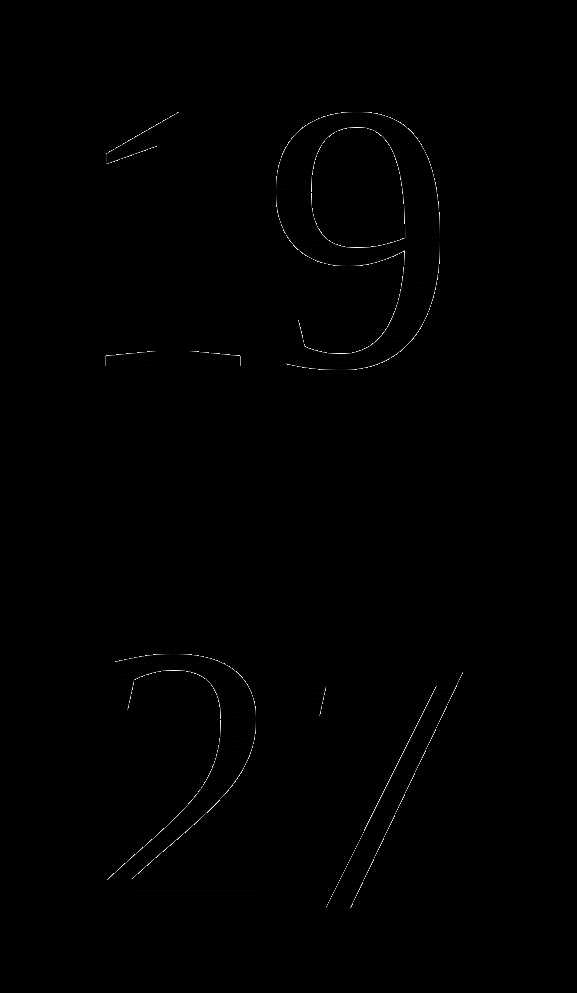























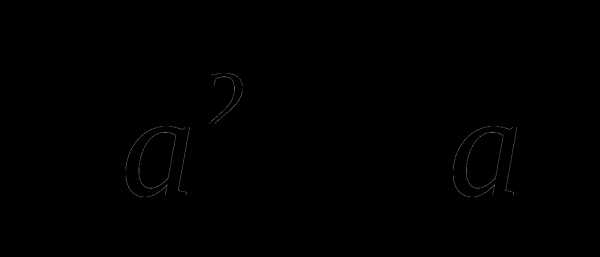 , применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей.
, применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей.
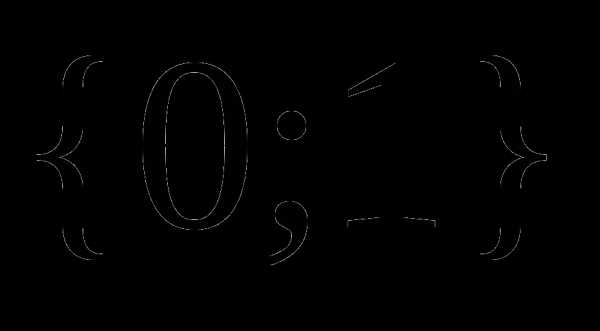 .
.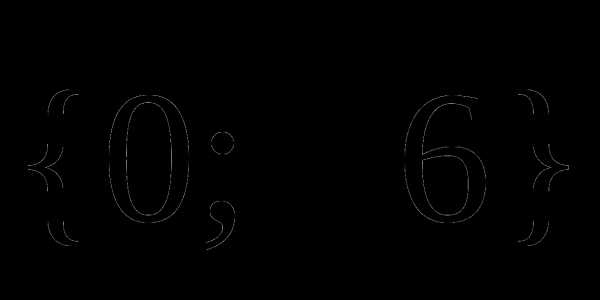 .
.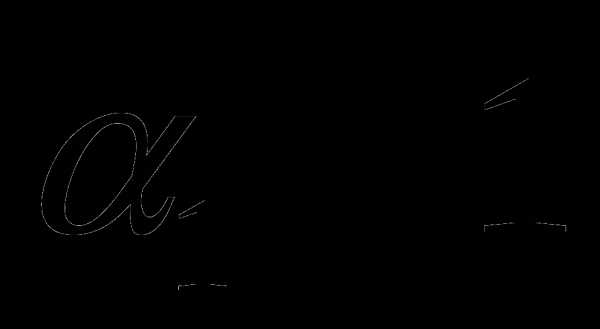 ,
,  . Поэтому исходное уравнение равносильно системе:
. Поэтому исходное уравнение равносильно системе: .
. достаточно, чтобы избавиться от знака модуля в любых неравенствах.
достаточно, чтобы избавиться от знака модуля в любых неравенствах.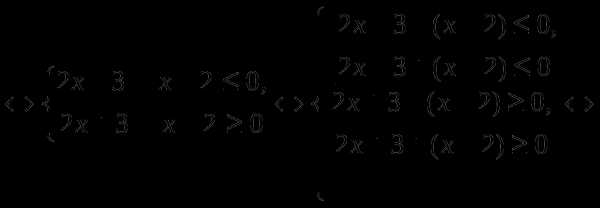
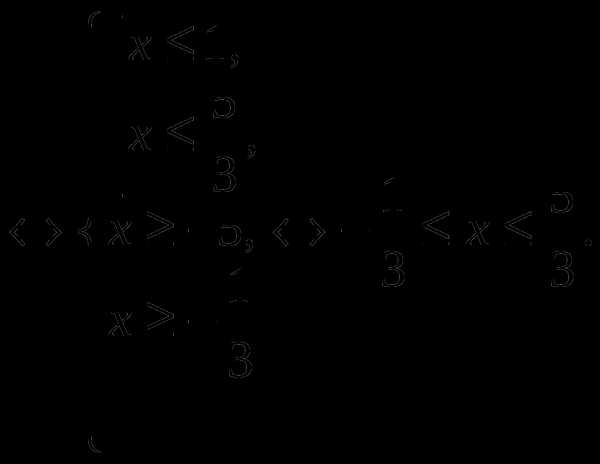
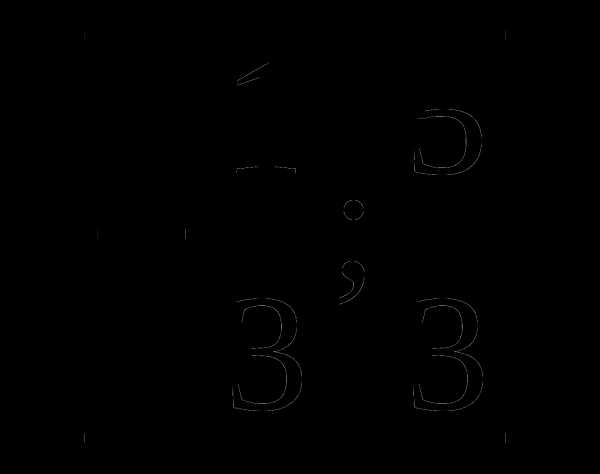 .
. с горизонтальными прямыми у = а равно числу решений уравнения.
с горизонтальными прямыми у = а равно числу решений уравнения.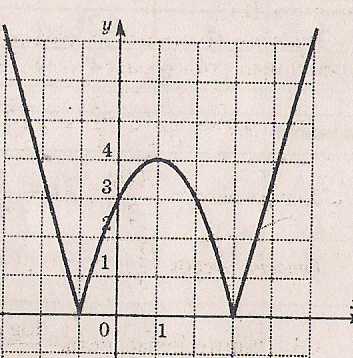 твет: если
твет: если  < 0, то решений нет; если а= 0, то два решения, если
< 0, то решений нет; если а= 0, то два решения, если  0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения. ; ,
; , 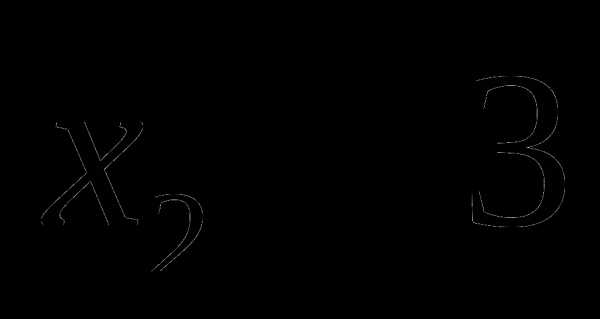 ; ,
; ,  .
.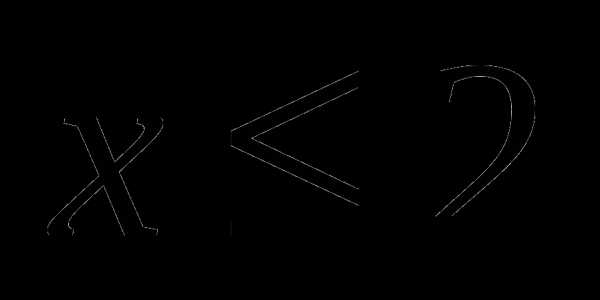 или . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение
или . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение  из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех
из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех  из промежутка
из промежутка 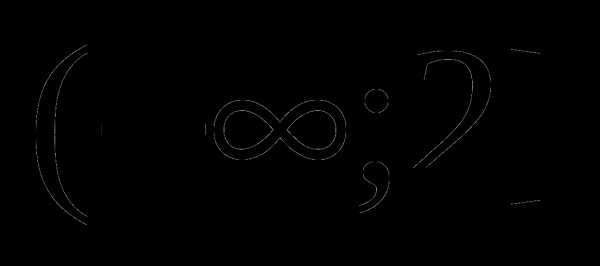 и подставим его значение в выражение
и подставим его значение в выражение 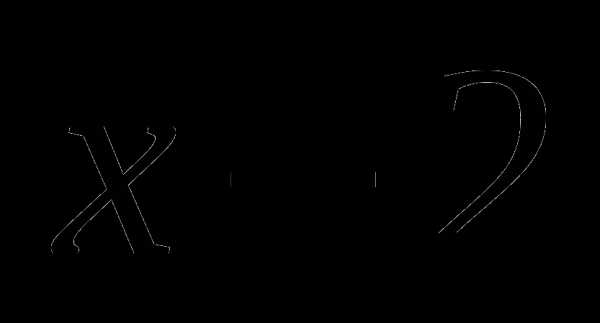 , получаем , значит на этом промежутке
, получаем , значит на этом промежутке 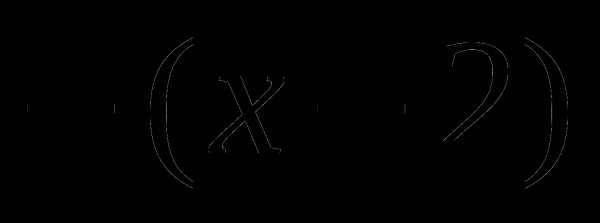 .
.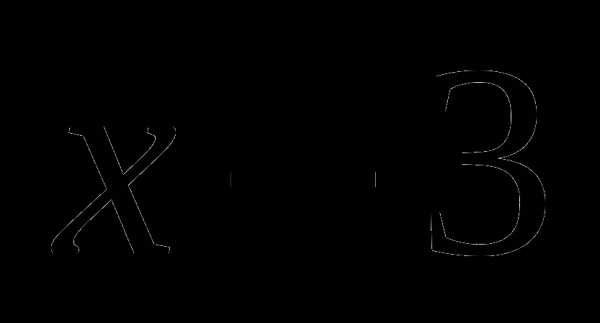 получит значение , значит, оно на промежутке
получит значение , значит, оно на промежутке 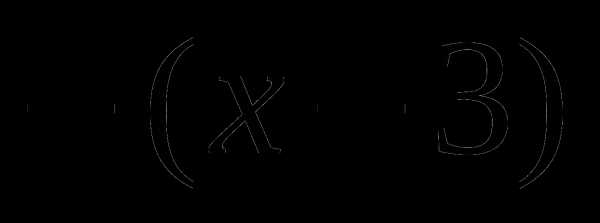 .
. получит значение и «выйдет» из под модуля со знаком «минус»: .
получит значение и «выйдет» из под модуля со знаком «минус»: . .
.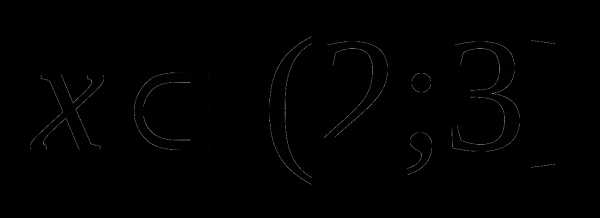 . Выбираем любое значение
. Выбираем любое значение  . Определяем знак каждого из выражений под модулем при этом значении
. Определяем знак каждого из выражений под модулем при этом значении 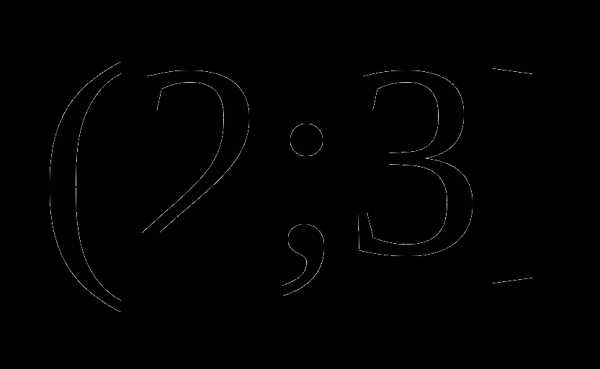 , а значит, не является корнем уравнения.
, а значит, не является корнем уравнения.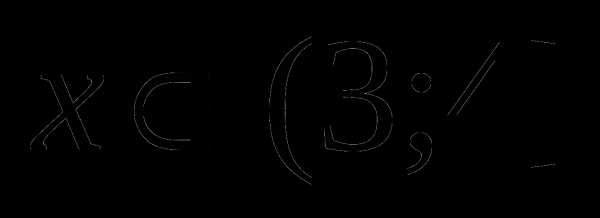 . Выбираем произвольное значение
. Выбираем произвольное значение 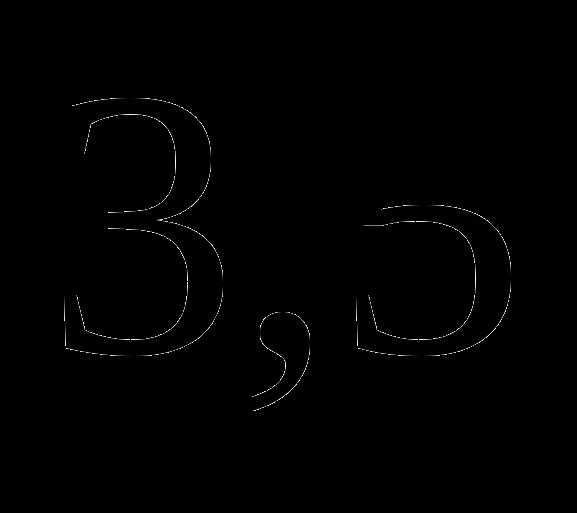 и подставляем в каждое из выражений. Находим, что выражения
и подставляем в каждое из выражений. Находим, что выражения 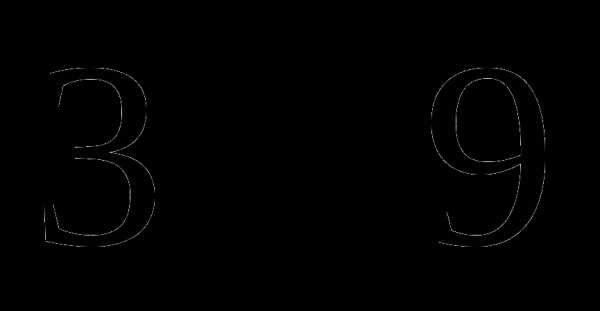 , а значит, уравнение не имеет корней на этом промежутке.
, а значит, уравнение не имеет корней на этом промежутке. ,
,  которое входит в промежуток и является корнем уравнения.
которое входит в промежуток и является корнем уравнения.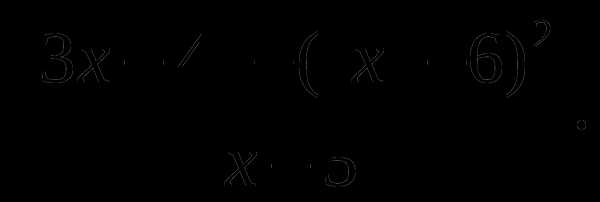
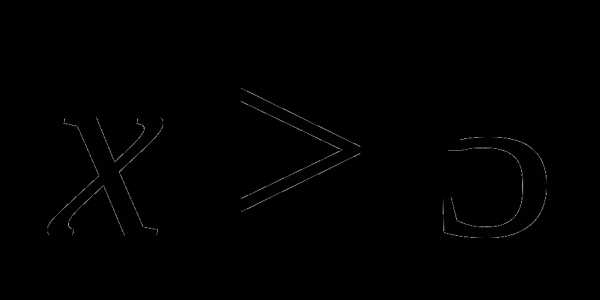 . Получим уравнение, равносильное исходному:
. Получим уравнение, равносильное исходному: .
.
 , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение . Решая его и учитывая ограничение
, на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение . Решая его и учитывая ограничение 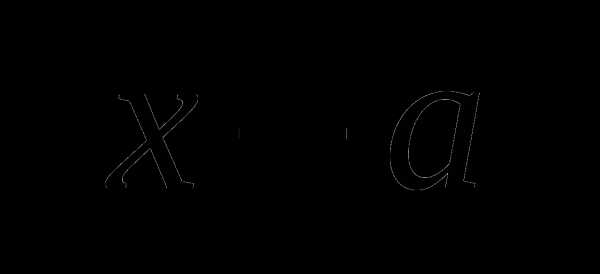 — длина отрезка координатной оси, соединяющего точки с абсциссами
— длина отрезка координатной оси, соединяющего точки с абсциссами  . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.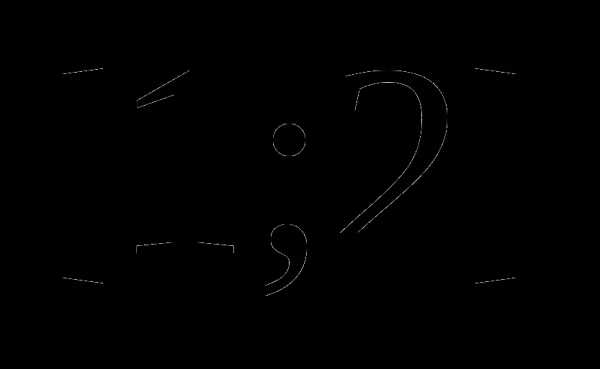 обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет.
обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет. и
и  в точности равна
в точности равна 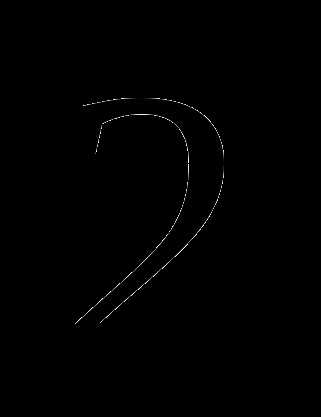 . Это все точки отрезка
. Это все точки отрезка 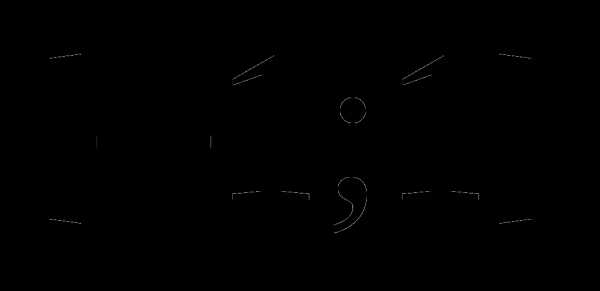 . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
. Для всех чисел вне данного отрезка сумма расстояний будет больше двух.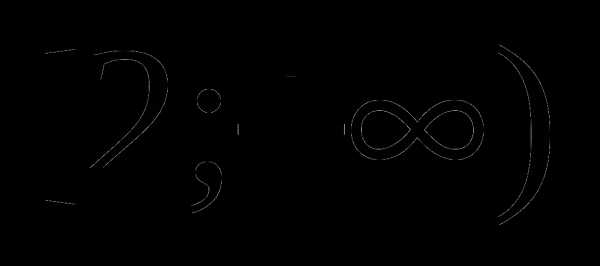 .
.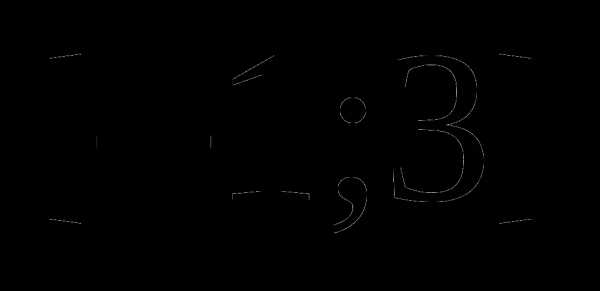 .
.

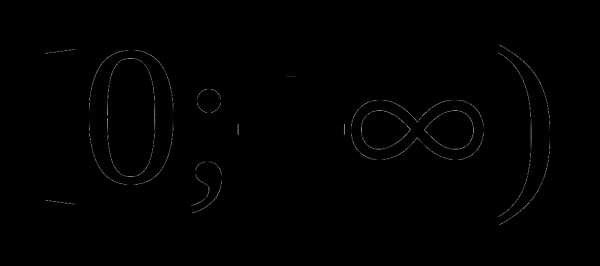 . Решая уравнение получим, что функция
. Решая уравнение получим, что функция 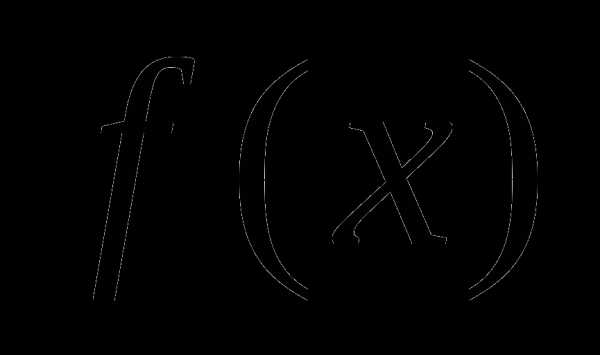 не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например,
не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например,  , получаем, что функция принимает только положительные значения.
, получаем, что функция принимает только положительные значения.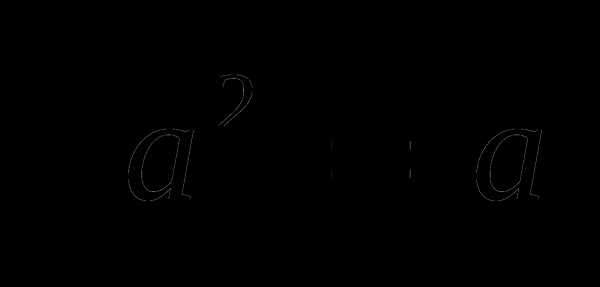 ; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов.
; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов. stroyday.ru
stroyday.ru stroyday.ru
stroyday.ru stroyday.ru
stroyday.ru remont-otdelka-m.ru
remont-otdelka-m.ru remont-otdelka-m.ru
remont-otdelka-m.ru