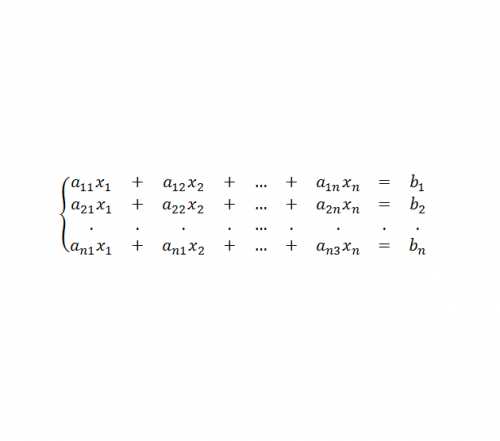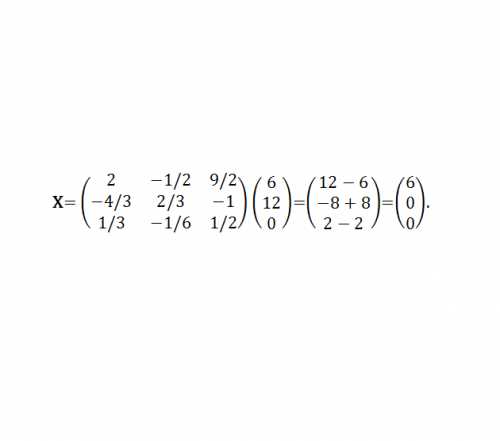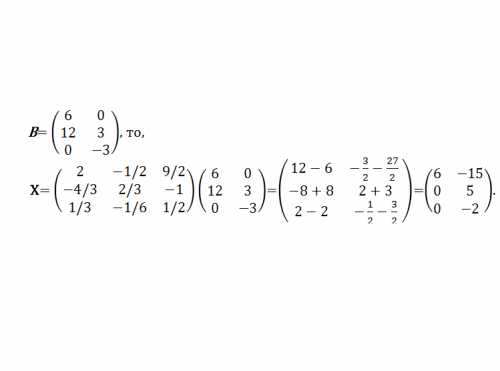Формула Бернулли / Теория вероятности [Калинин В.М., Тихомиров С.Р.] / 3dstroyproekt.ru
Схема испытаний Бернулли. Формула Бернулли
Пусть производится несколько испытаний. Причем, вероятность появления события $A$ в каждом испытании не зависит от исходов других испытаний. Такие испытания называются независимыми относительно события А. В разных независимых испытаниях событие А, может иметь либо различные вероятности, либо одну и туже. Мы будем рассматривать лишь такие независимые испытания, в которых событие $A$ имеет одну и ту же вероятность.
Под сложным событием будем понимать совмещение простых событий. Пусть производится n-испытаний. В каждом испытании событие $A$ может появиться или не появиться. Будем считать, что в каждом испытании вероятность появления события $A$ одна и та же и равна $p$. Тогда вероятность $\overline A $ { или не наступления А } равна $P( { \overline A } )=q=1-p$.
Пусть требуется вычислить вероятность того, что в n -испытаниях событие $A$ наступит k — раз и $n-k$ раз — не наступит. Такую вероятность будем обозначать $P_n ( k )$. Причем, последовательность наступления события $A$ не важна. Например: $( { AAA\overline A , AA\overline A A, A\overline A AA, \overline A AAA } )$
$P_5 ( 3 )-$ в пяти испытаниях событие $A$ появилось 3 раза и 2 — не появилось. Такую вероятность можно найти по формуле Бернулли.
Вывод формулы Бернулли
По теореме умножения вероятностей независимых событий, вероятность того, что событие $A$ наступит $k$ раз и $n-k$ раз не наступит, будет равна $p^k\cdot q^ { n-k } $. И таких сложных событий может быть столько, сколько можно составить $C_n^k $. Так как, сложные события несовместны, то по теореме о сумме вероятностей несовместных событий, нам надо сложить вероятности всех сложных событий, а их ровно $C_n^k $. Тогда вероятность появления события $A$ ровно k раз в n испытаниях, есть $P_n ( { A,\,k } )=P_n ( k )=C_n^k \cdot p^k\cdot q^ { n-k } $ формула Бернулли.
Пример. Игральная кость подбрасывается 4 раза. Найти вероятность того, что единица появится в половине случаев.
Решение. $A=$ { появление единицы }
$ P( A )=p=\frac { 1 } { 6 } \,, \,P( { \overline A } )=q=1-\frac { 1 } { 6 } =\frac { 5 } { 6 } $ $ P_4 ( 2 )=C_4^2 \cdot p^2\cdot q^ { 4-2 } =\frac { 4! } { 2!\cdot 2! } \cdot 6^2\cdot ( { \frac { 5 } { 6 } } )^2=0,115 $
Легко видеть, что при больших значениях n достаточно трудно подсчитать вероятность из-за громадных чисел. Оказывается эту вероятность можно посчитать не только с помощью формулы Бернулли.
3dstroyproekt.ru
Глава 3. Основные формулы теория вероятностей
§ 1. Операции над событиями.
Суммой двух событий А и В называется событие АВ (А+В), заключающееся в том, что произойдет хотя бы одно из событий А или В (либо событие А, либо событие В либо А и В одновременно).
Произведением (или пересечением) двух событий А и В называется событие АВ (АВ), состоящее в одновременном появлении и события А и события В.
Вероятность суммы двух событий вычисляется по формуле (теорема сложения)
.
События А1,А2,…,Ак образуют полную группу
событий,
если в результате испытания непременно
произойдет одно из них , т.е. 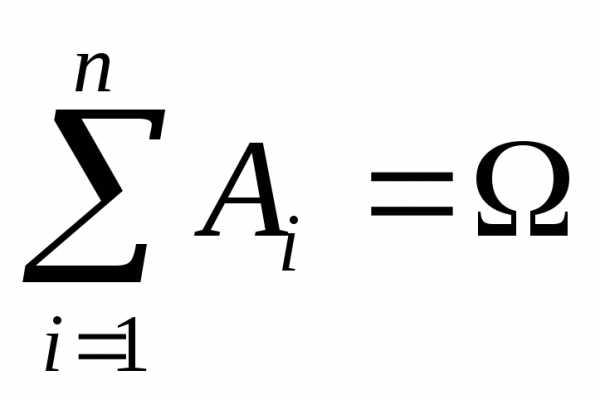 .
.
События А и В называются несовместными (непересекающимися), если они не могут произойти одновременно АВ=. Если события несовместны, то
Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).
Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение.
Событие A={вынуты
пуговицы одного цвета} можно представить
в виде суммы
,
где события и
и означают выборку пуговиц красного и
синего цвета соответственно. Вероятность
вытащить две красные пуговицы равна
означают выборку пуговиц красного и
синего цвета соответственно. Вероятность
вытащить две красные пуговицы равна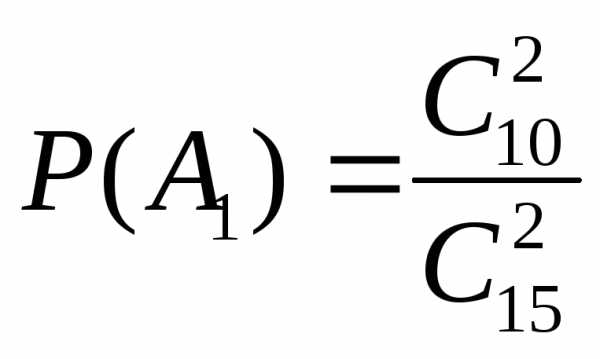 ,
а вероятность вытащить две синие пуговицы
,
а вероятность вытащить две синие пуговицы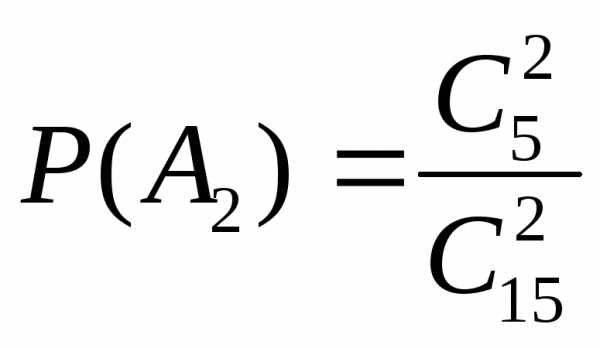 .
Так как события
.
Так как события и
и не
могут произойти одновременно, то в силу
теоремы сложения
не
могут произойти одновременно, то в силу
теоремы сложения
§ 2. Условная вероятность и теорема умножения.
Помимо обычной (безусловной) вероятности можно рассматривать так называемую условную вероятность, вычисляемую при условии, что событие B произошло. Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:
Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)
.
Формула умножения для трех событий:
.
Задача 2. В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?
Решение. Пусть А={старший ребенок – мальчик}, B={в семье есть дети обоего пола}. Будем считать, что рождения мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар: . В этом пространстве лишь два исхода (МД и ДМ) отвечают событиюB. Событие AB означает, что в семье есть дети обоего пола и старший ребенок – мальчик, это значит, что второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и
Задача 3. Мастер, имея 10 деталей, из которых 3 – нестандартных, берет и проверяет детали одну за другой, пока нему не попадется стандартная. Какова вероятность, что он проверит ровно две детали.
Решение. Событие А={мастер проверил ровно две
детали} означает, что при такой проверке
первая деталь оказалась нестандартной,
а вторая – стандартная. Значит, 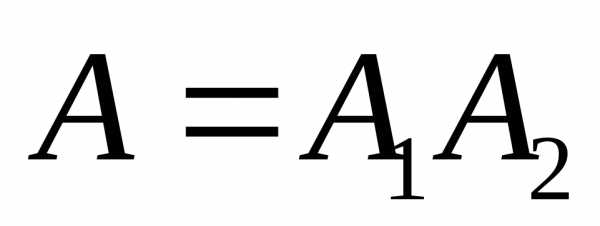 ,
где
,
где ={
первая деталь оказалась нестандартной
} и
={
первая деталь оказалась нестандартной
} и ={вторая
деталь – стандартная}. Очевидно, что
вероятностькроме
того,(так
как перед взятием второй детали у мастера
осталось 9 деталей, из которых только 2
нестандартные и 7 стандартных). По теореме
умножения
={вторая
деталь – стандартная}. Очевидно, что
вероятностькроме
того,(так
как перед взятием второй детали у мастера
осталось 9 деталей, из которых только 2
нестандартные и 7 стандартных). По теореме
умножения
studfiles.net
Теория вероятностей. Формулы по теории вероятностей
Высшая математика | Теория вероятностей | Общая теория Статистики | Социально экономическая статистика Онлайн калькуляторы1/Основные понятия теории вероятностей
1.1. Классическое и статистическое определение вероятности
1.2. Основные формулы комбинаторики
1.3. Геометрические вероятности
2. Основные теоремы
2.1. Теоремы сложения и умножения вероятностей
2.2. Вероятность появления хотя бы одного события
2.3. Формула полной вероятности
2.4. Формула Байеса (Бейеса)
3. Повторение испытаний
3.1. Формула Бернулли
3.2. Локальная и интегральная теоремы Лапласа
3.3. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
3.4. Наивероятнейшее число появлений события в независимых испытаниях
4. Дискретные случайные величины
4.1. Числовые характеристики дискретных случайных величин
4.2. Закон распределения вероятностей дискретной случайной величины.
4.3. Теоретические моменты
5. Закон больших чисел
5.1. Неравенство Чебышева
5.2. Теорема Чебышева
6. Непрерывные случайные величины
6.1. Числовые характеристики непрерывных случайных величин
6.2. Равномерное распределение
6.3. Нормальное распределение
6.4. Показательное распределение
7. Распределение функции случайных аргументов
7.1. Функция одного случайного аргумента
8. Системы двух случайных величин
8.1. Закон распределения двумерной случайной величины
8.2. Условные законы распределения вероятностей составляющих дискретной двумерной случайной величины
Приведенные Формулы по Теории вероятностей приведены в данном справочнике в помощь студентам.
При решении задач по Теории вероятностей, очень часто возникает ситуация, что под рукой нет необходимой формулы. В данном справочнике мы постарались собрать основные формулы по теории вероятностей и Математической статистике, а также привести примеры решения задач по Теории вероятностей и математической статистике с использованием этих формул.
primer.by
Формула полной вероятности. Вероятность гипотез / Теория вероятности [Калинин В.М., Тихомиров С.Р.] / 3dstroyproekt.ru
Формула полной вероятности
Теорема Вероятность события $A$, которое может наступить лишь при появлении одного из несовместных событий $B_1 ,B_2 ,\ldots B_n $, образующих полную группу равна сумме произведений вероятности каждого из событий на соответствующую условную вероятность. \begin{equation} \label { eq5 } P( A )=P( { B_1 } )\cdot P_ { B_1 } ( A )+P( { B_2 } )\cdot P_ { B_2 } ( A )+\ldots +P( { B_n } )\cdot P_ { B_n } ( A ) \qquad (5) \end{equation} Формула полной вероятности.
Вероятность полной группы несовместных событий $ P( { B_1 } )+P( { B_2 } )+\ldots +P( { B_n } )=1 $
Пример. Имеется два набора ламп. Вероятность того, что лампа 1-го набора стандартна, равна 0,8, второго — 0,7. Найти вероятность того, что взятая наудачу лампа { из наудачу взятого набора } — стандартна.
Решение } : пусть событие $A=$ { извлеченная лампа стандартна }
$B_1 =$ { лампа извлечена из 1-го набора }
$B_2 =$ { лампа извлечена из 2-го набора }
эти события попарно — несовместны.
Вероятность того, что лампа вынута из 1-го набора $P( { B_1 } )=\frac { 1 } { 2 } =0,5$.
Вероятность того, что лампа вынута из 2-го $P( { B_2 } )=\frac { 1 } { 2 } =0,5$.
Вероятность полной группы несовместных событий $\sum\limits_i { P( { B_i } )=0,5+0,5=1 } $.
Вероятность того, что вынутая из 1-го набора лампа является стандартной, есть условная вероятность $P_ { B_1 } ( A )=0,8$
Вероятность того, что вынутая из 2-го набора лампа является стандартной, есть условная вероятность $P_ { B_2 } ( A )=0,7$
Искомая вероятность того, что вынутая наудачу лампа является стандартной, есть $ P( A )=P( { B_1 } )\cdot P_ { B_1 } ( A )+P( { B_2 } )\cdot P_ { B_2 } ( A )=\frac { 1 } { 2 } \cdot 0,8+\frac { 1 } { 2 } \cdot 0,7=\frac { 1 } { 2 } \cdot 1,5=0,75 $
Вероятность гипотез. Формула Байеса
При рассмотрении формулы полной вероятности событие $A$наступает при условии появления одного из несовместных событий $B_i $, следовательно, события $A$ и $B_i$ — зависимы. Поскольку заранее неизвестно какое из событий наступит, то будем события $B_i$ называть гипотезами.
Допустим теперь, что событие $A$ — наступило. Этот факт изменит вероятность гипотез $P_A ( { B_1 } )\ldots P_A ( { B_n } )$
Найдем условные вероятности в предположении, что событие $A$ наступило т.е. $P_A ( { B_1 } )\,,\,P_A ( { B_2 } )\ldots $ { переоценка гипотезы }
Для этого используем теорему умножения.
$P(AB_1)=P(A)\cdot P_A(B_1)=P(B_1)\cdot P_ { B_ { 1 } } (A)$
$P_A ( { B_1 } )=\frac { P( { B_1 } )\cdot P_ { B_1 } ( A ) } { P( A ) } $, Формула Байеса
где $P( A )$ находится по формуле полной вероятности.
Формула Байеса позволяет переоценить вероятности гипотез после того, как событие $A$ произошло.
В формуле Байеса есть контроль $ \sum\limits_i { P( { B_i } )=1 } $
Пример. Сверла попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что сверло попало к первому контролеру, равна 0,6. Ко второму — 0,4. Вероятность того, что сверло будет признано стандартным 1-м контролером, равна 0,95 — вторым 0,97. Готовое сверло было признано стандартным. Найти вероятность того, что это сверло проверил 1-й контролер.
Решение. Через $A$, обозначим событие, которое произошло. $A=$ { готовое сверло признано стандартным }
Сделаем два предположения, две гипотезы:
$B_1 =$ { сверло проверил 1 -й контролер } , $P(B_1 )=0,6$,
$B_2 =$ { сверло проверил 2 -й контролер } , $P(B_2 )=0,4$,
Контроль $\sum\limits_i { P( { B_i } )=0,6+0,4=1 } $
Вероятность того, что сверло будет признано стандартным 1-м контролером $P_ { B_1 } (A)=0,95$,
Вероятность того, что сверло будет признано стандартным 1-м контролером $P_ { B_2 } (A)=0,97$,
Искомую вероятность, т.е. вероятность того, что стандартное сверло проверил } 1-й контролер, $P_A ( { B_1 } )$ найдем по формуле Байеса, $P( A )$ — находится по формуле полной вероятности.
$ P_A ( { B_1 } )=\frac { P( { B_1 } )\cdot P_ { B_1 } ( A ) } { P( A ) } =\frac { P( { B_1 } )\cdot P_ { B_1 } ( A ) } { P( { B_1 } )\cdot P_ { B_1 } ( A )+P( { B_2 } )\cdot P_ { B_2 } ( A ) } =\frac { 0,6\cdot 0,95 } { 0,6\cdot 0,95+0,4\cdot 0,97 } =\frac { 0,57 } { 0,57+0,388 } =\frac { 0,57 } { 0,958 } \approx 0,595$
До испытания вероятность гипотезы $B_1 $ равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы { т.е. условная вероятность } изменилась и стала 0,595.
3dstroyproekt.ru
Основные термины и формулы теории вероятностей
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Основные понятия математической статистики Совокупность — это множество объектов (элементов совокупности), обладающих общим свойством. Объем совокупности — это число
ПодробнееПРИМЕР РЕШЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ 6 (МПМ, 2 курс, 3 семестр) Тема «Математическая статистика»
Задача 1. ПРИМЕР РЕШЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ 6 (МПМ, 2 курс, 3 семестр) Тема «Математическая статистика» В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0,
ПодробнееМедицинская статистика
Лукьянова Е.А. Медицинская статистика Специальность «Лечебное дело» 3 Проверка статистических гипотез Критерии согласия Критерий Стьюдента для связанных выборок Критерий Стьюдента для несвязанных выборок
ПодробнееПроверка статистических гипотез
Проверка статистических гипотез 1. Статистические гипотезы; 2. Критерии проверки гипотез; 3. Проверка параметрических гипотез; 4. Критерий Пирсона Завершить показ Статистические гипотезы. Статистические
ПодробнееМодель парной регрессии
Модель парной регрессии 30 25 20 15 10 В статистических данных редко встречаются точные линейные соотношения: y x 1 2 Обычно они бывают приближенными: y x 1 2 5 0 2 4 6 8 10 12 14 16 18 20
ПодробнееЗадачи статистической проверки гипотез.
Задачи статистической проверки гипотез. Статистическая проверка гипотез является вторым после статистического оценивания параметров распределения и в то же время важнейшим разделом математической статистики.
ПодробнееЛекция 20. Проверка статистических гипотез
Лекция. Проверка статистических гипотез Понятие о статистических гипотезах и методах их проверки При решении многих задач возникает необходимость оценки того, подчиняется ли распределение генеральной совокупности
Подробнее1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
3 1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В связи с возросшей ролью математической статистики в современной науке и технике, будущие специалисты в области энергоэффективных технологий нуждаются в серьезных знаниях теории
ПодробнееПоказательное распределение.
Показательное распределение. 1) Распределение с.в. X подчинено показательному закону с параметром 5. Записать вычислить M X DX. f x Показательное распределение с параметром имеет плотность вероятности:
ПодробнееЛекция 5. Доверительные интервалы
Лекция 5. Доверительные интервалы Грауэр Л.В., Архипова О.А. CS Center Санкт-Петербург, 2014 Грауэр Л.В., Архипова О.А. (CSC) Лекция 5. Доверительные интервалы Санкт-Петербург, 2014 1 / 31 Cодержание Содержание
ПодробнееУЧЕБНАЯ ПРОГРАММА ПО ДИСЦИПЛИНЕ
Учреждение образования «Белорусский государственный педагогический университет имени Максима Танка» Институт повышения квалификации и переподготовки Факультет переподготовки специалистов образования Кафедра
ПодробнееJohann Carl Friedrich Gauß
ПРИЛОЖЕНИЕ 1 Все вероятности равны 50%. Либо случится, либо нет. Мерфология, Логические предложения Кольварда Типовые распределения При проверке гипотез широкое применение находит ряд теоретических законов
ПодробнееПроверка статистических гипотез. Грауэр Л.В.
Проверка статистических гипотез Грауэр Л.В. Статистические гипотезы Гипотеза о равенстве математических ожиданий двух генеральных совокупностей Гипотеза о равенстве дисперсий нескольких генеральных совокупностей
ПодробнееЛекция 12.Байесовский подход
Лекция 12.Байесовский подход Буре В.М., Грауэр Л.В. ШАД Санкт-Петербург, 2013 Буре В.М., Грауэр Л.В. (ШАД) Байесовский подход Санкт-Петербург, 2013 1 / 36 Cодержание Содержание 1 Байесовский подход к статистическому
ПодробнееМАТЕМАТИЧЕСКАЯ СТАТИСТИКА. Лекция 14
ЧАСТЬ 8 МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Лекция 4 ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ЦЕЛЬ ЛЕКЦИИ: определить понятие генеральной и выборочной совокупности и сформулировать три типичные задачи
ПодробнееПлан лекций 1 семестр
План лекций 1 семестр 1. Введение. 1.1. Предмет, метод и задачи статистики; источники статистической информации. 1.2. Кратка история развития статистики. Структура статистических органов на современном
ПодробнееАНАЛИЗ МАЛОЙ ВЫБОРКИ
Б. И. СУХОРУЧЕНКОВ АНАЛИЗ МАЛОЙ ВЫБОРКИ Прикладные статистические методы Москва «Вузовская книга» 2010 УДК 519.2 ББК 22.17 С91 С91 Сухорученков Б. И. Анализ малой выборки. Прикладные статистические методы
ПодробнееПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Понятие статистической гипотезы Статистическая гипотеза это предположение о виде распределения или о величинах неизвестных параметров генеральной совокупности, которая может
Подробнее4 Проверка параметрических гипотез
4 Проверка параметрических гипотез Статистическая гипотеза Параметрическая гипотеза 3 Критерии проверки статистических гипотез Статистической называют гипотезу о виде неизвестного распределения или о параметрах
Подробнее(, ) (, ) ( ) x y. F x y = P X Y D
4 СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН КОРРЕЛЯЦИОННЫЙ АНАЛИЗ Многомерной случайной величиной (векторной случайной величиной, случайным вектором или случайной точкой) называют упорядоченный набор нескольких случайных
Подробнее= (3) 2 1. КРАТКАЯ ТЕОРИЯ.
ИЗУЧЕНИЕ СТАТИСТИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ РАДИОАКТИВНОГО РАСПАДА Лабораторная работа 8 Цель работы: 1. Подтверждение случайного, статистического характера процессов радиоактивного распада ядер.. Ознакомление
Подробнее5. ОЦЕНКА ГЕНЕРАЛЬНЫХ ПАРАМЕТРОВ
Оценка параметров 30 5. ОЦЕНКА ГЕНЕРАЛЬНЫХ ПАРАМЕТРОВ 5.. Введение Материал, содержащийся в предыдущих главах, можно рассматривать как минимальный набор сведений, необходимых для использования основных
ПодробнееОглавление. От автора… 9
Оглавление От автора………………………………. 9 Глава 1. Терминология……………………. 13 1.1. Основные термины математической статистики… 12 1.2. Смысл понятия «случайная величина»……….
Подробнее6. КРИТЕРИИ ЗНАЧИМОСТИ И ПРОВЕРКА ГИПОТЕЗ
Проверка статистических гипотез 37 6. КРИТЕРИИ ЗНАЧИМОСТИ И ПРОВЕРКА ГИПОТЕЗ 6.. Введение В этой главе рассматривается группа статистических методов, которые получили наибольшее распространение в статистических
ПодробнееТеоретические задания
Вопросы к зачёту ОУИТ для групп П-1, П- и П- Специальность: 0115 Программирование в компьютерных системах По дисциплине: ЕН.0 Теория вероятностей и математическая статистика 7 семестр 015/16 учебный год
ПодробнееМатематическая статистика
Математическая статистика 1 Выборка X x, x,, x Опр.1 Пусть одномерная с.в., а 1 значения с.в.,полученные в результате испытания. Будем называть полученные значения выборкой из генеральной совокупности
Подробнее5 Гипотезы и критерии согласия
5 Гипотезы и критерии согласия Гипотезы и критерии согласия Критерий согласия — Пирсона Пусть,,, выборка из распределения теоретической случайной величины с неизвестной функцией распределения F ( Проверяется
ПодробнееРавномерное распределение.
Равномерное распределение. Равномерным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид, если xa ; b f x b a 0, если xa ; b Математическое ожидание M X
ПодробнееПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
Подробнее5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Основной принцип проверки ПРОВЕРКА ГИПОТЕЗ О ЧИСЛОВЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ дисперсия известна дисперсия неизвестна t распределение распределение
Подробнееdocplayer.ru
Лекции по теории вероятностей и математической статистике
В. М. Калинин, С. Р. Тихомиров
Теория вероятностей
Классическое определение вероятности. Основные формулы исчисления вероятностей
Разберём весьма частный, однако, часто встречающийся случай: состоит из конечного числа N равновероятных событий.
Понятие »равновероятности» здесь является исходным, неопределяемым. Основанием для суждения о равновозможности, равновероятности обычно служит физическая симметрия, равноправие исходов. Понятие «вероятность» здесь уже является производным, определяемым: вероятностью P(A) события A называется
P(A),
где N(A) – число элементарных событий, благоприятствующих событию A.
В этих условиях выведем основные формулы исчисления вероятностей.
1. Вероятность достоверного события равна 1: P()1. Это очевидно, так как N()N.
2. Вероятность невозможного события равна 0: P()0. Это ясно, поскольку N()0.
3. P()1P(A). Справедливость равенства следует из равенства N(A) N()N.
4. 0P(A)1 для A, поскольку 0N(A)N.
5. AB P(A)P(B), поскольку в этом случае N(A)N(B).
6. Для любых событий A и B: P(AB)P(A), так как N(AB)N(A).
7. Теорема сложения для несовместимых событий. Если события A и B несовместимы, то вероятность их суммы равна сумме вероятностей:
P(AB)P(A)P(B).
Действительно, N(AB)N(A)N(B) и остаётся разделить это равенство на N.
8. Теорема сложения в общем случае:
P(AB)P(A)P(B)P(AB).
Действительно, из определения суммы событий: N(AB)N(A)N(B) N(AB). Деля почленно это равенство на N, убеждаемся в справедливости теоремы.
9. Обобщение теоремы сложения на n событий:
P(A1A2An)(1)k1P(Aj1Aj2Ajk).
Формула доказывается методом математической индукции несложно, но громоздко. Во внутренней сумме число слагаемых, очевидно, равно и суммирование ведётся по всевозможным наборам различных натуральных индексов j1, j2, , jk.
10. Условная вероятность.
Добавим к комплексу условий, реализация которых интерпретируется как опыт, ещё одно условие: произошло событие B; это возможно практически лишь в случае, когда P(B)0. Все опыты, в которых B не произошло, мы как бы игнорируем. Считаем, что добавление события B к комплексу условий не нарушает равновероятности исходов и не меняет природы самих исходов. Теперь опыт может иметь лишь один из N(B) исходов, а из них событию A благоприятствуют N(AB) исходов. В соответствии с классическим определением, вероятность события A при условии, что произошло событие B, равна:
P(A|B).
Таким образом, по существу, условная вероятность ничем не отличается от обычной, безусловной вероятности.
В случае, если AB, формула для условной вероятности упрощается:
P(A|B),
так как здесь ABA.
11. Теорема умножения: вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло:
P(AB)P(B)P(A|B)P(A)P(B|A).
Первая из этих формул для P(B)0 является лишь формой записи формулы пункта 10 для условной вероятности; вторая получена из неё перестановкой местами A и B, что для P(A)0 возможно. Вместе с тем ясно, что теорема умножения верна и для случая P(A)0 или P(B)0, но при этом она становится тривиальной и бессодержательной.
12. Независимость событий.
Будем говорить, что событие A не зависит от события B, если P(A|B)P(A). В этом случае теорема умножения упрощается: P(AB)P(A)P(B).
И наоборот, для событий, имеющих положительную вероятность, из последней формулы следует независимость события A от B:
P(A|B)P(A).
Таким образом, второе эквивалентное определение независимости: события A и B, имеющие положительные вероятности, независимы, если вероятность их произведения равна произведению их вероятностей: P(AB)P(A)P(B). События A и B в этом определении симметричны: если событие A не зависит от B, то и B не зависит от A.
Если события A и B независимы, то независимы также и события A и .
Действительно:
P(|A)P(B|A)1,
откуда:
P(|A)1P(B|A)1P(B),
а это и доказывает наше утверждение.
Ясно, что независимы также и события ,.
Если события A и B независимы, то они не могут быть несовместимыми: если A и B – одновременно несовместимы и независимы, то, с одной стороны, AB и P(AB)0, а, с другой, – P(AB)P(A)P(B), что противоречит предположению о положительности вероятностей P(A) и P(B).
Обобщение понятия независимости на n событий: события A1, A2, , An называются независимыми в совокупности, если для любого набора различных индексов j1, j2, , jk вероятность произведения событий Aj1Aj2Ajk равна произведению вероятностей событий Aj1, Aj2, , Ajk:
P(Aj1Aj2Ajk)P(Aj1)P(Aj2)P(Ajk).
Можно думать, что для независимости событий в совокупности достаточно попарной независимости, Конкретные примеры, однако, доказывают, что это не так.
Таким образом, для независимых событий легко вычислять вероятность произведения, а для несовместимых событий легко вычислять вероятность суммы.
Если события A1, A2, , An независимы, то
P(A1A2An)P()1P()P()P().
Если события A1, A2, , An несовместимы, то
P()P()1P(A1A2An)1P(Ak).
13. Теорема умножения для n событий:
P(A1A2An)P(A1)P(A2An|A1).
Учитывая, что условные вероятности ничем не отличаются от безусловных – лишь добавляется к комплексу условий ещё одно, которое в дальнейшем терять или отбрасывать нельзя, – можем продолжить:
P(A1A2An)P(A1)P(A2|A1)P(A3An|A1A2) .
Окончательно:
P(A1A2An)P(A1)P(A2|A1)P(A3|A1A2)P(An|A1A2An1).
Эта теорема позволяет дать ещё одно определение независимости в совокупности: события A1, A2, , An, имеющие положительные вероятности, независимы в совокупности, если для любого набора неравных индексов
P(Aj1Aj2Ajk|Ai1Ai2Aim)P(Aj1Aj2Ajk),
что легко устанавливается по теореме умножения и формуле для условных вероятностей.
14. Формула полной вероятности.
Пусть A1, A2, , An – любое разбиение пространства , B – любое событие. Тогда BBB(A1A2An)BA1BA2BAn и получаем формулу полной вероятности:
P(B)P(BAk)P(Ak)P(B|Ak).
Обычно A1, A2, , An – взаимоисключающие друг друга ситуации, в которых может происходить событие B.
15. Формулы Байеса.
В обозначениях предыдущего пункта:
P(Ak|B),k1, 2, , n,
и мы получили формулы Байеса, которые называют также формулами вероятностей гипотез: если событие B может произойти лишь с одним и только одним из событий A1, A2, , An и оно действительно произошло, то, спрашивается, с каким из событий Ak оно произошло? Можно сделать n гипотез и, соответственно, формулы Байеса дают апостериорные вероятности P(Ak|B) для этих гипотез, выражая их через априорные вероятности P(Am) и условные вероятности P(B|Am) того, что в условиях m-ой гипотезы произойдёт событие B.
Таковы основные формулы исчисления вероятностей. Они получены в условиях весьма частного случая – классической схемы, т. е. для пространства конечного числа N равновероятных элементарных событий. В этой схеме число событий, которым благоприятствуют ровно k исходов, равно , а общее число различных событий, следовательно, равно2N.
Весьма неожиданно, что все полученные формулы являются общими и в действительности сохраняют свою силу для любого пространства элементарных событий. Покажем это.
studfiles.net
Теория вероятности. Основные формулы — online presentation
Теория вероятностиПонятие
Формула
PA =
Вероятность, мера вероятности
n( A)
n
Объединение событий
AÈB={x|xÎAÚxÎB}
Пересечение событий
AÇB={x|xÎAÙxÎB}
Противоположное событие
Ā={xÏA}
Разность, или дополнение события
A\B={xÎA|xÏB}
Включение
AÍBÛ»aÎA:aÎB
Равенство
A=BÛ(AÍB)Ù(BÍA)
Строгое включение
AÌBÛ(AÍB)Ù(A¹B)
Несовместимость
AÇB=Æ Û «aÎA:aÏB
Относительная частота события
n( A)* *
n( A)*
n( A)
P =
; PA Þ PA ; * Þ
*
n
n
n
n®¥
*
A
n®¥
Правило умножения несовместных
событий
n*m
Перестановка n элементов
P = n!
Размещение m элементов n способами
Anm =
n!
= n(n — 1)(n — 2)(n — 3)…(n — m + 1)
(n — m)!
n!
m!(n — m)!
Сочетание m элементов n способами
Cnm =
Условная вероятность события B при
условии, что событие A уже имело место
P( A | B) =
«…есть k объектов, из которых l
обладают интересующим нас признаком;
вероятность
того,
что
среди
m
выбранных объектов данным признаком
будет обладать n объектов, равна…»
PA =
P( A Ç B )
P( B )
n( A)
; n = Ckm ; n( A) = Cln ´ Ckm—l n
n
n
Формула полной вероятности
P( B) = å P( Ai ) P( B | Ai ) = P( A1 ) P( B | A1 ) + P( A2 ) P( B | A2 ) + ..
i =1
Теорема Байеса
P( Bk | A) =
P( Bk ) P( A | Bk )
n
å P( B ) P( A | B )
i =1
i
i
Вероятность k исходов в n
повторяющихся событиях
P( A) = Cnk ´ p k ´ (1 — p ) n-k
Вероятность возникновения исхода
в событии с порядковым номером l
P(t = l ) = p ´ q l -1 = p ´ (1 — p )l -1
Математическая статистика
Понятие
Формула
Размах
R = max(x1;x2;…;xn)-min(x1;x2;…;xn)
X =
Среднее арифметическое
( X + X 2 + X 3 + … + X n )
1 n
Xi = 1
å
n i =1
n
1 n
D=
( X i — X )2
å
n — 1 i =1
Дисперсия
s =
Стандартное отклонение
Коэффициент линейной корреляции
1 n
( X i — X )2
å
n — 1 i =1
å (x — x ) × ( y — y )
å (x — x ) × å ( y — y )
rx , y =
i
i
en.ppt-online.org

 {1,
2, 3, …}
{1,
2, 3, …} ;
; 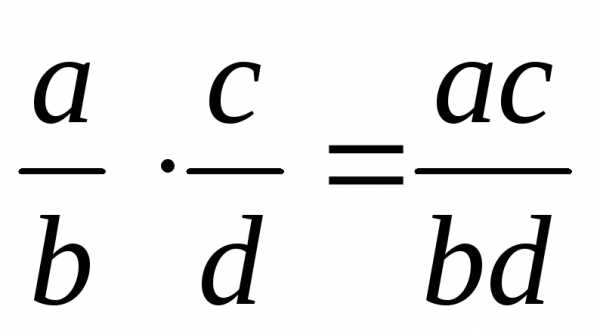 ;
; ;
;  ;
; ;
; ;
; ;
;  ; ;
; ; ;x
;x ;
;  ; ;;
; ;; ;
; ;
;  ;
; ;
;
 ,
где
,
где —
дискриминант.
—
дискриминант. ;
; .
. .
.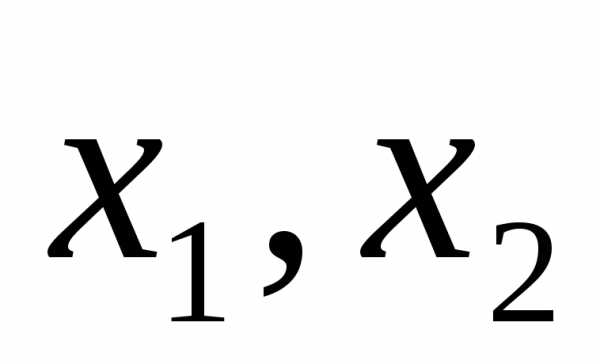 -корни
квадратного
трехчлена,
-корни
квадратного
трехчлена,  ,
то
,
то —
разность
прогрессии;
—
разность
прогрессии; — знаменатель
прогрессии;
— знаменатель
прогрессии; ):
):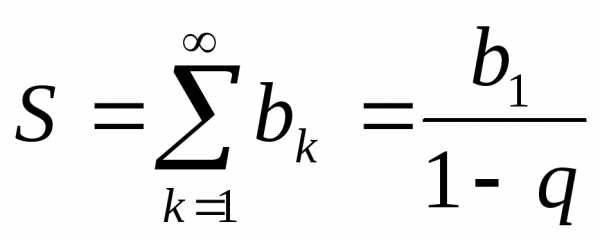 .
. по
основанию
по
основанию :
: .
. ; ;.
; ;. :.
:. ;
;  ;
; ;
;  ;;
;; ;
;  ;
; ;
;  ;
; ;
;  ;
; ; ;
; ; ;
;  ;
; ;
; ;
;  ;
;  ;
;  ;
;
 ;.
;.
 ;
; .
. ;.
;. ;
; ;
; ,;.
,;.
 ;
;  ;
;

 ,
, ,
то:
,
то: ;
; ,
, ;
; 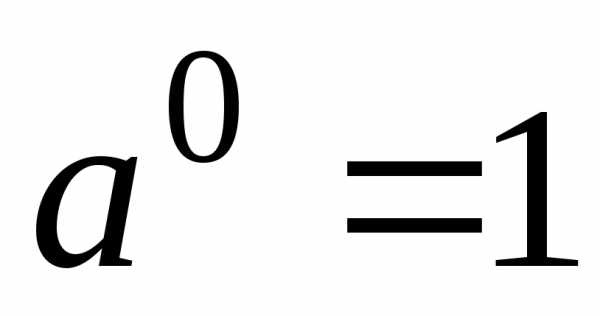 ;
; ,
, ;,
;, ;
;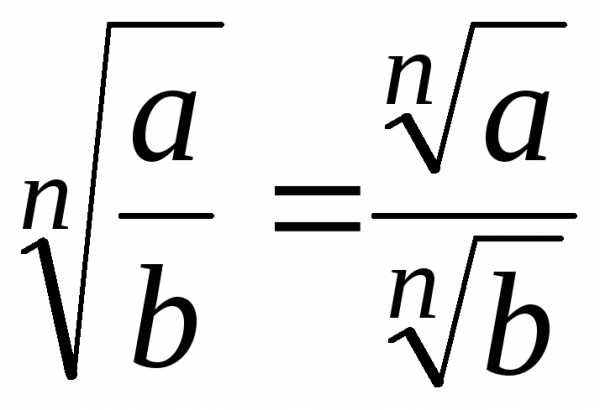 ,
, .
. и
и — корни квадратного уравнения,
то
— корни квадратного уравнения,
то ,
, ,
,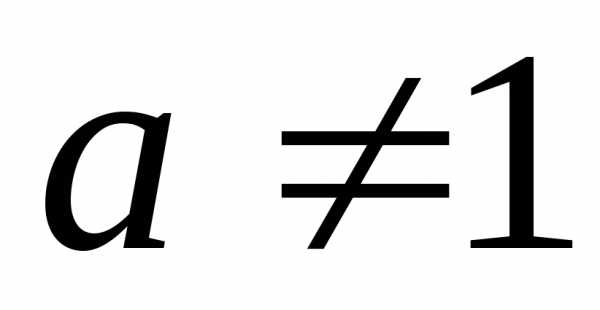 ,
то:
,
то: – основное логарифмическое тождество;
– основное логарифмическое тождество; – формула перехода;
– формула перехода; ,;
8)
,;
8) ;
9)
;
9)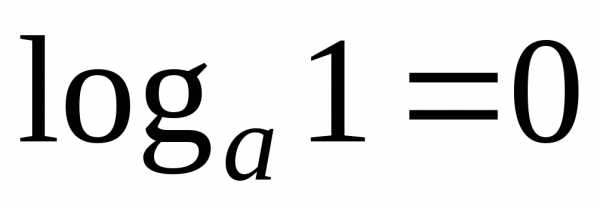 .
. 3)
3)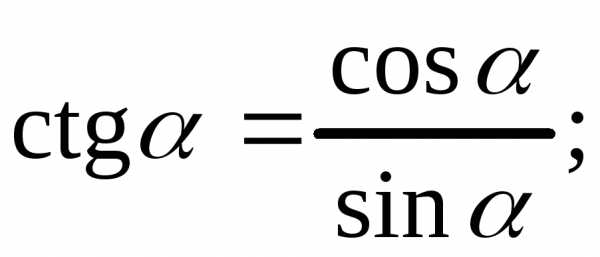
 5) 6)
5) 6) 4)
4) 5)
5)








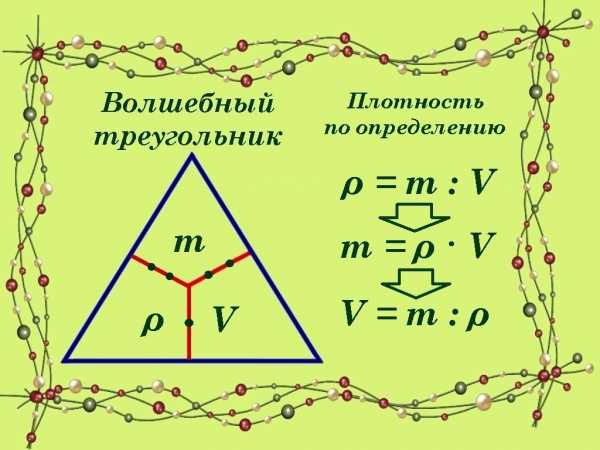
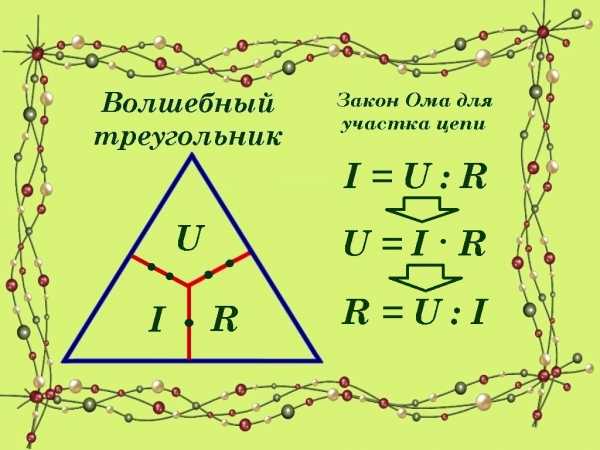

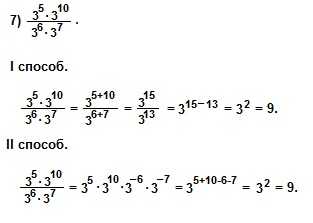 При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .



 Здесь Аij – алгебраическое дополнение соответствующего элемента определителя матрицы А. Аij получают удалением из определителя |A| i-строки и j-столбца, на пересечении которых лежит а(ij), и умножением вновь полученного определителя на (-1)^(i+j).
Здесь Аij – алгебраическое дополнение соответствующего элемента определителя матрицы А. Аij получают удалением из определителя |A| i-строки и j-столбца, на пересечении которых лежит а(ij), и умножением вновь полученного определителя на (-1)^(i+j).