Что изучает эконометрика?
Поиск ЛекцийЭконометрика
Учебное пособие для студентов
экономических специальностей гуманитарных вузов
Москва 2001
Минзов А.С. Эконометрика. – М.: Из-во МФА, 2001. C. 54.
Настоящее учебное пособие содержит краткий курс лекций, контрольные задания, систему тестов, учебную программу, вспомогательные материалы и статистические таблицы, а также методические указания по дисциплине «Эконометрика». Оно подготовлено в строгом соответствие с авторской программой, соответствующей государственным образовательным стандартам высшего профессионального образования экономических специальностей. Пособие адресовано преподавателям и студентам всех форм обучения экономических специальностей Московской финансово-юридической академии.
Ó А.С. Минзов, 2001
Ó МФА, 2001
Содержание
От редактора…………………………………………………………………………………………………………….. 4
От автора………………………………………………………………………………………………………………….. 6
1. Основные задачи, цели и последовательность проведения
эконометрического анализа………………………………………………………………………………………. 7
1.1. Что изучает эконометрика ?…………………………………………………………………………….. 7
1.2. Краткая история развития эконометрики…………………………………………………………. 8
1.3. Классификация эконометрических моделей…………………………………………………….. 8
1.3.1. Регрессионные модели…………………………………………………………………………….. 8
1.3.2. Системы взаимозависимых моделей………………………………………………………… 9
1.3.3. Рекурсивные системы……………………………………………………………………………… 9
1.3.4. Модели временных рядов………………………………………………………………………… 9
1.4. Постановки некоторых эконометрических задач……………………………………………. 10
1.5. Последовательность разработки эконометрических моделей………………………….. 12
Резюме………………………………………………………………………………………………………………… 13
2. Эконометрический анализ на основе моделей линейной регрессии……………………… 15
2.1. Однофакторная линейная регрессия………………………………………………………………. 15
2.2. Многофакторная линейная регрессия…………………………………………………………….. 23
2.3. Некоторые особенности применения многофакторных
регрессионных моделей в эконометрическом анализе………………………………………….. 27
2.3.1. Мультиколлинеарность………………………………………………………………………….. 27
2.3.2. Использование фиктивных переменных………………………………………………… 28
2.3.3. Проблемы гетероскедастичности……………………………………………………………. 29
Резюме………………………………………………………………………………………………………………… 29
3. Эконометрический анализ на основе временных рядов………………………………………… 30
3.1. Основные понятия в теории временных рядов………………………………………………. 30
3.2. Цели, этапы и методы анализа временных рядов……………………………………………. 31
3.3. Модели тренда и методы его выделения из временного ряда………………………….. 32
3.4. Порядок анализа временных рядов………………………………………………………………… 33
3.5. Графические методы анализа временных рядов……………………………………………… 34
3.6. Пример анализа временных рядов…………………………………………………………………. 35
Резюме………………………………………………………………………………………………………………… 41
Литература……………………………………………………………………………………………………………… 42
Приложение 1…………………………………………………………………………………………………………. 43
Приложение 2…………………………………………………………………………………………………………. 46
Приложение 3…………………………………………………………………………………………………………. 47
Приложение 4…………………………………………………………………………………………………………. 48
Сегодня высокие информационные технологии превращают бизнес в высокоинтеллектуальное занятие, а бизнесмену дают такую степень свободы, которая превращает его в главную личность нового столетия.
Из разговора двух олигархов
От редактора
Переход к рыночной экономике вызвал всплеск социальной потребности общества в квалифицированных экономистах и менеджерах. Основная образовательная задача стала заключаться в том, чтобы не просто дать студентам знания по рыночной экономике, но и научить их современному экономическому мышлению, умению прогнозировать развитие экономических и бизнес – процессов, принимать научно обоснованные решения.
В соответствие с государственным образовательным стандартом в учебных планах МФА предусматривается знакомство студентов факультета экономики и управления с дисциплинами, позволяющими овладеть современными математическими методами, широко используемыми в лучших университетах России и мира.
В настоящее время существует несколько подходов к изучению новой математической дисциплины «Эконометрика», определенной в качестве обязательной дисциплины государственных образовательных стандартов для экономических специальностей.
Первый основан на достаточно «узком» понимании понятия Эконометрика, как науки, занимающейся изучением количественных закономерностей и взаимозависимостей в экономике с использованием методов корреляционно-регрессионного анализа [1]. Такой подход характерен для западных экономических школ, которые ориентируются на другие образовательные программы и более низкий уровень математической культуры студентов экономических специальностей. Прикладной курс эконометрики в западных вузах изучается по программам подготовки магистров экономических специальностей, специализирующихся на углубленном изучении математических методов. Рекомендованный в этой образовательной концепции учебник Кристофера Доугерти «Введение в эконометрику», к сожалению, достаточно слабо отражает специфику, опыт и национальные достижения в этой области Российских научных школ. Кроме того, он использует терминологию, практически не применяемую в России. Но, самое главное заключается в том, что эта прикладная наука должна изучаться на реальных или псевдореальных примерах задач, возникающих в экономике и бизнесе России, что, вполне естественно невозможно в рекомендованной литературе. Если этого нет, то трудно убедить студентов в полезности этой, безусловно, необходимой современному экономисту, дисциплины. Этот упрощенный подход породил еще одну проблему: модное слово «эконометрика» вызвало появление большого количества преподавателей в этой области (я имею ввиду Россию, на Западе это не так). Практически любой подготовленный в области математической статистики преподаватель считает для себя возможным прочитать курс «Эконометрика», уходя от решения экономических задач к чисто технологическим (математическим) и, как правило, без связи с реальными ситуациями, возникающими в работе экономиста. Таким образом, этот подход не решает главной задачи – научить студентов работе в реальной ситуации и отражает западные образовательные концепции без связи с образовательными концепциями в России.
Второй подход к изучению «Эконометрики» основан на более широком понимании концепции изучения «Эконометрики», как науки о построении прикладных экономико – математических моделей на основе эмпирических данных для обоснования управленческих и экономических решений. В этом основное отличие концепции изучении дисциплины от других образовательных концепций, реализуемых в других вузах России. Программа изучения экономико-математических методов включает: методы эконометрического анализа при прогнозировании экономических и бизнес процессов и методы прогнозирования динамики процессов с использованием математических методов анализа временных рядов.
Настоящее учебное пособие разработано для студентов, изучающих дисциплину «Эконометрика» всех форм обучения: очной, очно-заочной, заочной и, в том числе, с использованием дистанционных технологий. В состав пособия включены:
учебная программа по дисциплине «Эконометрика», адекватно отражающая современные требования государственных стандартов для студентов экономических специальностей и раскрывающая образовательную концепцию Московской финансово-юридической академии;
краткий курс лекций по основным темам программы с примерами, контрольными вопросами к каждой теме;
сборник контрольных заданий, которые выполняются студентами всех форм обучения и охватывают наиболее значимые разделы этой дисциплины;
методические указания по выполнению контрольных заданий и справочные материалы по основным разделам эконометрического анализа.
Контрольные задания могут быть выполнены как с использованием ручных методов, так и использованием пакета электронных таблиц EXCEL и пакета статистических программ STATISTICA.
Автор сборника – профессор Минзов Анатолий Степанович, специалист в области статистических методов обработки результатов эксперимента и математического моделирования в бизнесе. А.С. Минзов — автор 120 научных трудов, в числе которых научные статьи, учебные пособия и учебники, монографии и другие издания. В МФА читает курсы «Информатика», «Глобальная информационная сеть и ее применение в науке, бизнесе и межкультурных коммуникациях», «Математические методы и информационные технологии в психологических исследованиях», «Математические методы в экономике», «Методы решения оптимизационных задач в бизнесе», «Статистика» и др.
Сборник может представлять интерес и для студентов, выполняющих курсовые и дипломные работы и использующих статистические методы для обработки результатов эксперимента.
Полагаем, что теоретические знания, полученные Вами в ходе аудиторных занятий, помогут успешно справиться с представленными в сборнике контрольными заданиями.
От редактора
От автора
Освоение техники современного экономического моделирования — основа для решение более сложных и актуальных практических задач, решаемых в экономике и управлении. Это пособие предназначено для студентов экономических специальностей гуманитарных вузов. Концепция этого пособия основана на прагматических стремлениях автора показать практическое применение методов эконометрического анализа на конкретных примерах, которые возникают в работе современного экономиста, менеджера и маркетолога. Это видно из тех примеров, которые используются в пособии.
В учебном пособии представлены основные учебные материалы по дисциплине «Эконометрика». В этом смысле оно самодостаточно, но для более глубокого понимания методов эконометрического анализа рекомендуется ознакомиться с рекомендованной автором литературой.
В приложении приведены контрольные задания с методическими указаниями по их выполнению. Задания построены таким образом, что обеспечивают естественную связь с изученными ранее дисциплинами. При выполнении этих заданий можно использовать как обычные ручные методы и калькуляторы, так и ПЭВМ. Для этого в сборник включены в необходимом количестве справочные материалы и статистические таблицы. При выполнении контрольной работы с использованием ПЭВМ рекомендуется использовать пакет статистических программ STATISTICA.
Для работы с контрольным заданием необходимо выбрать вариант задания, который соответствует порядковому номеру студента в журнале и, ознакомившись с методическими указаниями, выполнить его. Наиболее важная часть обработки результатов эксперимента – это выводы. Они должны быть достаточно аргументированы и убедительны.
Контрольная работа выполняется на отдельных листах бумаги, либо на ПЭВМ в редакторе WORD 7.0, либо пишется от руки аккуратным подчерком. На титульном листе должна быть полная информация о студенте (курс, филиал, вариант). Студенты заочной формы, обучающиеся по дистанционной технологии, результаты решения задач оформляют в установленной специальной форме.
Если в ходе выполнения задания возникают вопросы, на которые после изучения рекомендуемой литературы вы все же не можете найти ответ, можно обратиться к автору пособия за консультацией по E-mail: [email protected]
Профессор, доктор технических наук А.Минзов
1. Основные задачи, цели и последовательность
проведения эконометрического анализа
Что изучает эконометрика?
В настоящее время не существует однозначного понимания термина «эконометрика». Можно лишь говорить о смысловом значении этого термина как «науки об экономических измерениях». Однако такое определение вряд ли кого-либо может устроить, так как становится непонятно что, зачем и кому надо измерять в экономике? Авторы учебников и пособий по эконометрике не старались отвечать на эти вопросы, считая, что ответ на них очевиден. Все это так, если бы мы видели очень заметные достижения в области эконометрического анализа в экономике и бизнесе, особенно в условиях нестабильного Российского рынка. Но этого сегодня пока нет, по крайней мере, автор о заметных достижениях в этой области не слышал. Наиболее полное из имеющихся в литературе определений термина «эконометрика» предложено в работе [3]: Эконометрика – наука, исследующая количественные закономерности и взаимозависимости в экономике при помощи методов математической статистики. Основа этих методов — корреляционно-регрессионный анализ. С этим определением можно было бы согласиться, но второе предложение, выделенное курсивом, резко уменьшает круг задач, решаемых в эконометрике. Очень большое количество экономических процессов протекает во времени с определенной регулярностью, например спрос. Для этих процессов используется другой математический аппарат, основанный на анализе временных рядов. С учетом этого, в более широком смысле можно сказать, что Эконометрика – наука, исследующая закономерности и взаимозависимости между различными факторами в экономике и бизнесе при помощи методов статистического анализа. При этом под фактором понимаются измеряемые и не измеряемые экономические показатели, например уровень инфляции, покупательский спрос, цена, объем продаж и т.д. Основная задача эконометрики – проверка экономических теорий на фактическом (эмпирическом) материале при помощи методов математической статистики. По сути, работая с этими моделями, мы предполагаем, что вся информация о сути экономического явления содержится в эмпирическом материале, вполне естественно допуская при этом определенные ошибки. Эконометрический анализ позволяет предвидеть только те экономические процессы, которые сохраняют основные тенденции развития, либо повторялись несколько раз в прошлом. Нельзя ожидать от него чего-то большего.
Цель эконометрического анализа – разработка эконометрических моделей, позволяющих прогнозировать тенденции развития экономических и бизнес процессов для получения наиболее эффективных и обоснованных решений. Эконометрические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказывать будущее его поведение при изменении каких-либо параметров. Предсказание будущих изменений, например, повышение обменного курса, ухудшение экономической конъюнктуры, падение прибыли может опираться и на интуицию. Однако при этом могут быть упущены, неправильно определены или неверно оценены важные взаимосвязи экономических показателей, влияющие на рассматриваемую ситуацию. В модели все взаимосвязи переменных могут быть оценены количественно, что позволяет получить более качественный и надежный прогноз. Для любого экономического субъекта возможность прогнозирования ситуации означает, прежде всего, получение лучших результатов, избежание потерь или минимизации рисков.
Кто проводит эконометрический анализ? Ответ на этот вопрос также неоднозначен. На Западе это делает специалист в области эконометрического анализа – аналитик или эконометрист. В России, в соответствие с новыми государственными стандартами это должен делать экономист и менеджер по любой специализации. В России аналитиков не готовят, ими становятся только те, кто владеет эконометрическими методами анализа.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Предмет эконометрики
Понятие эконометрики
Эконометрика представляет собой базовую дисциплину экономического направления, которой присущи следующие особенности:
- Прямое отношение к экономике и экономической теории, по которому к эконометрике относят все, что связано с измерениями в данных науках;
- Узко-инструментальная ориентированность, то есть определенный набор математических и статистических средств, позволяющих проводить верификацию модельных соотношений анализируемых экономических показателей.
Определение 1
Эконометрика занимается определением наблюдаемых в экономической жизни конкретных количественных закономерностей с применением статистических методов для осуществления своей цели.
Эконометрика включает любое приложение математики или статистики к исследованию явлений экономического характера.
Отправными точками эконометрики можно считать три науки, которые в единстве образуют эконометрику:
- Статистика,
- Экономическая теория,
- Математика.
При этом эконометрика не то же самое, что экономическая статистика. Она не идентична и экономической теории, хотя опирается на нее.
Замечание 1
Объект исследования эконометрики в качестве самостоятельного раздела математической экономики — экономико-математические модели, выстраиваемые с учетом случайных факторов. Данные модели именуются эконометрическими моделями, их исследование проводят на основе методов статистики и математики.
Экономические модели считаются важнейшим инструментом эконометрики
Задачи эконометрики
Исследование эконометрики предполагает решение следующих основных задач:
- Процесс построения эконометрических моделей путем представления экономических моделей в математической форме, которая является удобной для проведения эмпирического анализа.
- Оценить параметры построенных моделей, которые делают выбранную модель наиболее адекватной реальным условиям.
- Проверить качество определяемых параметров модели и самой модели в совокупности.
- Использовать построенную модель в процессе объяснения поведения изучаемых экономических показателей, прогнозирования и планирования, а также с целью осмысленного проведения экономической политики.
Предмет эконометрики
После рассмотрения определений эконометрики, можно сказать, что ее предметом являются количественное выражение экономических взаимосвязей.
Предметом исследования эконометрики также считаются массовые экономические процессы и явления.
Эконометрика является наукой, которая эмпирически связана с выводом экономических законов, при этом используются данные или «наблюдения» для получения количественных зависимостей экономических соотношений.
Экономические явления как предмет эконометрики (в отличие от экономической теории) рассматриваются в большей мере в количественном аспекте.
Например, спрос на продукцию с ростом цен падает. В экономической теории не рассматривается, насколько быстро это происходит. Для каждого конкретного случая данные задачи решает эконометрика.
Математическая экономика выстраивает и анализирует модели экономических процессов, не используя реальные числовые значения, а эконометрика исследует модели, опираясь на эмпирические данные.
Замечание 2
Эконометрика в большей мере использует аппарат математической статистики. Чаще всего это происходит в процессе установления связей экономических показателей.
Но, в то же время, в экономике не проводятся управляемые эксперименты, а специалисты эконометрики применяют собственные приемы анализа, не встречаемые в математической статистике.
spravochnick.ru
Эконометрика как самостоятельное знание
ЭКОНОМЕТРИКА
Лекция №1
Эконометрическое знание выделилось и сформировалось как закономерный результат развития и взаимодействия экономической теории, математической экономики, экономической статистики, математической статистики и теории вероятностей. Эконометрика формулирует собственные предмет, цель и задачи исследования. При этом содержание эконометрики, ее структура и область применения тесно связаны с перечисленными науками.
Взаимосвязь эконометрики с другими науками
Эконометрика | Другие науки |
Изучаются экономические явления с точки зрения количественных характеристик Осуществляется опытная проверка экономических законов | Экономическая теория Изучаются качественные аспекты экономических явлений Математическая экономика Получают выражение экономических законов в форме математических моделей |
Применяется инструментарий экономической статистики для анализа и прогноза экономических взаимосвязей Применяется аппарат математической статистики в силу случайного характера большей части экономических показателей | Экономическая статистика Собираются, обрабатываются и представляются экономические данные в наглядном виде Математическая статистикаРазрабатываются методы анализа данных в зависимости от целей исследования |
Эконометрика – это наука, предметом изучения которой является количественное выражение взаимосвязей экономических явлений и процессов.
Понятие «эконометрика»
Термин «эконометрика»экономисты начали применять благодаря исследованиям П. Цъемпы (1910), Й. Шумпетера (1923), Р. Фриша (1930). Этот термин появился в результате соединения двух слов: «экономика» и «метрика». В переводе с греческогоoikonomos(экономист) — это управляющий домом, метрика(metrihe, metron) —мера, размер.
Ученые-эконометристы, признанные авторитеты в области эконометрических исследований, по-разному подходили к определению эконометрики. Приведем примеры их высказываний.
Формулировки определений понятия «эконометрика»
Автор | Содержание понятия «эконометрика» |
Р. Фриш | «…есть единство трех составляющих — статистики, экономической теории и математики» |
Ц. Грилихес | «…является одновременно нашим телескопом и нашим микроскопом для изучения окружающего экономического мира» |
Э. Маленво | «…наполняет эмпирическим содержанием априорные экономические рассуждения» |
С. Фишер | «…занимается разработкой и применением статистических методов для измерения взаимосвязей между экономическими переменными» |
С. Айвазян | «…объединяет совокупность методов и моделей, позволяющих придавать количественные выражения качественным зависимостям» |
Анализ подходов к определению эконометрики, а также состояние эконометрической науки позволяют сформулировать цель эконометрики, которая достигается решением определенных задач.
Цель эконометрики– разработка способов моделирования и количественного анализа реальных экономических объектов
studfiles.net
Тема 1. Основные понятия эконометрики………………………..5
Министерство образования республики Беларусь
УО Белорусский государственный университет
Л.Ф.Дежурко
Эконометрика
Учебно-методическое пособие
Для студентов всех специальностей
Минск 2009
Содержание
Содержание курса………………………………………………….3
Тема 2. Парная линейная регрессия……………………………….7
Тема 3. Нелинейная регрессия……………………………………..21
Тема 4. Множественная регрессия…………………………………27
Тема 5. Временные ряды……………………………………………32
Тема 6 Эконометрический анализ при нарушении предпосылок
метода наименьших квадратов……………………………………..35
Литература……………………………………………………………41
Содержание курса
Тема 1. Основные понятия эконометрики
Определение эконометрики и ее задачи.
Типы данных.
Терминология
Классификация экономических моделей.
Этапы экономического моделирования.
Виды зависимостей.
Тема 2. Парная линейная регрессия
Истинное и выборочное уравнения регрессии.
Метод наименьших квадратов.
Геометрическая интерпретация метода наименьших квадратов.
Экономическая интерпретация коэффициентов парной линейной регрессии.
Основные предпосылки регрессионного анализа. Теорема Гаусса-Маркова.
Расчет стандартных ошибок коэффициентов регрессии.
Проверка значимости коэффициентов регрессии.
Построение доверительных интервалов для параметров теоретической регрессии.
Проверка общего качества уровня регрессии. Коэффициент детерминации.
Проверка значимости коэффициента детерминации.
Оценка тесноты связи между переменными. Коэффициент корреляции.
Проверка значимости коэффициента корреляции.
Прогнозирование.
Тема 3. Нелинейная регрессия
Регрессии, нелинейные по переменным.
Регрессии, нелинейные по параметрам.
Индекс корреляции и индекс детерминации.
Эластичность функции.
Тема 4. Множественная регрессия
Оценка параметров линейной модели множественной регрессии.
Оценка качества множественной линейной регрессии.
Анализ и прогнозирование на основе многофакторных моделей.
Тема 5. Временные ряды
Основные понятия временных рядов.
Основная тенденция развития – тренд.
Построение аддитивной модели.
Тема 6 Эконометрический анализ при нарушении предпосылок
метода наименьших квадратов
Понятие мультиколлинеарности.
Понятие автокорреляции.
Понятие гетероскедастичности.
Тема1:
Основные понятия эконометрики.
Вопросы:
Определение эконометрики и ее задачи.
Типы данных.
Терминология
Классификация экономических моделей.
Этапы экономического моделирования.
Виды зависимостей.
1.
Эконометрика – это наука, изучающая количественные закономерности и взаимосвязи в экономике.
Она зародилась и получила свое развитие на основе слияния экономической теории, математической экономики, экономической и математической статистики. В современной эконометрике широко используются информатика, статистические пакеты прикладных программ.
Объект – экономика, различные экономические явления и взаимосвязи.
Предмет – их количественные характеристики.
Задачи: 1. построение эконометрических моделей и оценивание их параметров.
2. проверка гипотез, о свойствах показателей и формах их связей.
Эконометрический анализ — основа для экономического анализа и прогнозирования.
2.
Эконометрика базируется на реальных экономических данных.
2 типа данных:
1. пространственные данные – данные о каком-либо экономическом показателе, полученные от однотипных объектов и относящиеся к одному моменту (периоду времени). Модели, построенные по пространственным данным, называются пространственными моделями.
2. временные ряды – данные об экономическом показателе, характеризующем какой-либо объект в различные моменты времени. Модели, построенные на временных рядах , называются моделями временных рядов.
3.
Исследуемый экономический показатель называют результативным, объясняемым, зависимым экономическим показателем. Соответствующую переменную – объясняемой или зависимой. Экономические показатели, воздействие которых на исследуемый экономический показатель изучается, называют факторами, объясняющими или независимыми показателями (переменными).
4.
В эконометрике выделяют следующие основные 3 класса моделей:
1. Модели временных рядов:
1. Модели тренда (описывают устойчивые изменения экономического показателя в течение длительного времени).
2. Модели сезонности (описывают устойчивые внутригодовые колебания).
3. Модели авторегрессии (в них описываются влияния значения объясняемого экономического показателя в прошедший момент времени на его значение в текущий момент времени).
2. Регрессионные модели с одним уравнением. В них объясняемый экономический показатель представляется в виде функции от объясняющих экономических показателей (факторов). В зависимости от вида функции эти модели бывают: линейные и нелинейные.
3. Системы одновременных уравнений – это системы регрессионных уравнений, в которых в качестве объясняющих переменных используются объясняемые переменные из других уравнений системы.
5.
1 этап: постановочный. Формулируется цель исследования. Целью может служить анализ возможного развития экономического явления, прогноз экономических показателей, выработка на этой основе управленческих решений).
2 этап: априорный. Проводится анализ связей экономических переменных, выделяются зависимые и независимые переменные.
3 этап: информационный. Осуществляется сбор необходимой статистической информации о значениях экономических переменных.
4 этап: спецификация моделей. Для описания выявленных между экономическими показателями связей, подбирается математическая функция.
5 этап: параметризация. На основе собранных статистических данных об экономических переменных оцениваются параметры (коэффициенты) математических функций.
6 этап: верификация. Проводится проверка адекватности модели, т.е. насколько построенная модель соответствует реальному экономическому явлению.
6.
Все зависимости между экономическими переменными можно разделить на 2 вида:
Функциональные. Если каждому значению независимой переменной или нескольким независимых переменных соответствует одно строго определенное значение зависимой переменной, то такая зависимость называется функциональной. В ней отсутствует воздействие случайных факторов, поэтому в экономике функциональная зависимость встречается редко.
Статистические. В экономике каждому значению независимых переменных может соответствовать несколько значений зависимой переменной в зависимости от воздействия неучтенных и случайных факторов. Например, пусть исследуется зависимость прибыли предприятия от объема производства и цены за единицу продукции. При одном и том же объеме производства и цене за единицу продукции прибыль предприятия может быть различна, т.к. на нее воздействуют множество других факторов, в том числе случайных.
Зависимость между переменными, на которую накладывается воздействие случайных факторов, называется статистической. Для нее характерно то, что изменение независимой переменной приводит к изменению математического ожидания зависимой переменной. Уравнение регрессии – математическая формула, описывающая статистическую зависимость между переменными. Если формула описывается линейной функцией, то регрессия называется линейной. Если нелинейной функцией – нелинейной регрессией. Если регрессия связывает одну зависимую и одну независимую переменную, то такая регрессия называется парной (простой). Если рассматривается зависимость экономической переменной от нескольких экономических переменных, то такая регрессия называется множественной.
studfiles.net
Тема 1. Предмет изучения дисциплины «эконометрика», ее место в экономике
«Эконометрику» наряду с микро- и макроэкономикой в настоящее время относят к числу базовых дисциплин экономического образования, считают их основой экономической теории. Причём, методы эконометрики применяются и в рамках микро- и макроэкономики.
Термин «эконометрика» впервые был введен в 1926 г. норвежским учёным Рагнаром Фришем. Изначально широкая трактовка термина предполагала «измерения, то есть любые количественные методы, в экономике», узкая – экономические приложения математико-статистических моделей и методов. Предполагалось, что «эконометрика» позволит осуществлять количественный анализ экономических явлений, процессов, основываясь на современном развитии теории и наблюдениях, с применением формальных (количественных) методов обоснования содержательных выводов.
В период возникновения эконометрики С.Фишер представлял её как раздел экономики, связанный с применением статистических методов для характеристики взаимосвязей между экономическими показателями. По Л.Клейну основная задача эконометрики – наполнить эмпирическим (основанным на опыте) содержанием априорные экономические рассуждения. Э. Маленво утверждал, что цель эконометрики – эмпирический вывод экономических законов. Приводились и образные сравнения, характеризовавшие место новой дисциплины среди других наук. Например, Ц.Грилихес замечал, что эконометрика является одновременно телескопом и микроскопом для изучения окружающего экономического мира. В целом, пролагали, что математическая экономика помогает описывать экономические закономерности с применением формальных соотношений, а эконометрика позволяет осуществлять их опытную проверку. Точнее, эконометрика позволила применять данные экономической статистики для исследований, анализа взаимосвязей между соответствующими показателями.
Таким образом, в целом – в прошлом веке в рамках экономики появилась обособленная дисциплина (на стыке дисциплин «экономическая статистика», «экономическая теория», «теория вероятностей и математическая статистика»). Появление эконометрики обусловлено необходимостью количественного обоснования содержательно (экономически) интерпретируемых выводов на разных исследовательских уровнях. Эконометрика предназначена для формального (алгоритмического) описания зависимостей между показателями согласно имеющимся данным предшествующих периодов или аналогов (с учетом выявляемых погрешностей). Эконометрические модели зависимостей между показателями наряду с оценкой ожидаемых ошибок применимы как обособленно при исследованиях макро- и микроэкономических систем (для прогнозирования), так и в виде модельных блоков (для имитации) в рамках сложных модельных комплексов, а также применяемых при выборе и количественном обосновании управленческих решений (для интерпретации), для поиска наиболее выгодных решений (для оптимизации).
В последнее время неуклонно расширяются условия для использования на практике формальных методов систематизации данных, так как интенсивно совершенствуются вычислительная техника (компьютерные технологии). Соответствующие методы могут быть основаны на применении профилированного в определенной предметной сфере математического моделирования. В рамках экономико-математического моделирования традиционно выделяют параллельно применяемые виды: оптимизационное, имитационное, балансовое (модели математической экономики). Эконометрика представляет основу осуществления сложного моделирования всех указанных видов.
Следующая характеристика эконометрики в настоящее время считается наиболее общепринятой. «Эконометрика-это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе
-экономической теории,
-экономической статистики,
-математико-статистического инструментария
придавать количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией» (см.[4, с.598]).
Предметом изучения эконометрики выступают социально-экономические системы (объекты, явления) в их элементарных проявлениях. То есть, прежде всего, в форме зависимостей между экономическими показателями (в частности, одного показателя от одного или нескольких других, включая предполагаемую ошибку из-за отсутствия данных о нужных показателях или вследствие стохастичности). Уместно выделять как описывающие зависимости (функции, прогнозирующие значение опосредованно управляемого показателям при заданных значениях непосредственно управляемых показателей), так и диагностирующие (классифицирующие объекты-наборы данных).
Соответственно, в первую очередь, содержание эконометрики определяют методы выявления функциональных зависимостей одного показателя от других (возможно, одного), с получением потенциально применимых на практике количественных характеристик качества соответствия ожидаемых приложений этих зависимостей фактическим результатам. Во вторых, это методы анализа указанного вида зависимостей, оценок соответствующих погрешностей в совокупности.
Основная цель практических приложений эконометрики – обеспечение возможности совмещения конструктивной сущности ряда принципиально различных дисциплин: экономики, математики, информатики. Базисный характер эконометрики проявляется в том, что обеспечивается формирование знаний о конкретном объекте (явлении) с целью управления прообразом моделирования. Обеспечивается экономическое познание, позволяющее совмещать формальные методы и содержательные аспекты. В экономике, как, например, в физике, эксперименты невозможны, так как изучаемые объекты, явления потенциально изменчивы с течением временем, и зачастую весьма интенсивно меняются. Поэтому, в частности, хорошо апробированной на практике методы математической статистики нуждаются в адаптации. И эконометрика развивается адекватно потребностям практики, индуцируемая техническим прогрессом (прежде всего, совершенствованием компьютерных технологий). А свободная рыночная конкуренция диктует необходимость расширять приложения эконометрики, стимулирует развитие соответствующих теоретических методов.
Вопросы по введению и 1-ой теме:
Каковы традиции применения содержания дисциплины «эконометрика» в рамках российского экономического высшего образования?
Чем исторически обосновывается актуальность эконометрики?
Какова общая характеристика современной эконометрики?
Какое место в экономическом образовании занимает дисциплина «эконометрика»?
Как появился термин «эконометрика», как он трактовался изначально (широко, узко)?
Как характеризовали эконометрику разные специалисты в период становления дисциплины?
Какие научные дисциплины определили появление эконометрики? Чем обусловлено её обособление в рамках экономики?
Каким образом и параллельно с какими видами моделирования в экономике применяется эконометрическое моделирование в современных условиях?
Как принято определять понятие «эконометрика» в наше время?
Что выступает предметом изучения эконометрики?
Какие методы, в первую очередь, определяют содержание эконометрики?
В чем основная цель практических приложений эконометрики и чем стимулируется развитие эконометрики?
studfiles.net
Определение эконометрики. Метод эконометрики
ОПРЕДЕЛЕНИЕ ЭКОНОМЕТРИКИ. МЕТОД ЭКОНОМЕТРИКИ 2
Эконометрический метод и этапы эконометрического исследования. 2
ПАРНАЯ РЕГРЕССИЯ. СПОСОБЫ ЗАДАНИЯ УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ. 4
ЛИНЕЙНАЯ МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ. СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ. 9
ОЦЕНКА СУЩЕСТВЕННОСТИ УРАВНЕНИЯ В ЦЕЛОМ НА ОСНОВЕ ДИСПЕРСИОННОГО АНАЛИЗА (-КРИТЕРИЙ ФИШЕРА). 11
ОЦЕНКА СУЩЕСТВЕННОСТИ ОТДЕЛЬНЫХ ПАРАМЕТРОВ РЕГРЕССИИ (-КРИТЕРИЙ СТЬЮДЕНТА). 12
ПРОГНОЗ ПО ЛИНЕЙНОМУ УРАВНЕНИЮ РЕГРЕССИИ. СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ. 14
НЕЛИНЕЙНАЯ РЕГРЕССИЯ. КЛАССЫ НЕЛИНЕЙНЫХ РЕГРЕССИЙ. ОЦЕНКА НЕЛИНЕЙНОЙ РЕГРЕССИИ В ЦЕЛОМ 14
РЕГРЕССИИ НЕЛИНЕЙНЫЕ ОТНОСИТЕЛЬНО ВКЛЮЧЕННЫХ В АНАЛИЗ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ. 15
РЕГРЕССИИ НЕЛИНЕЙНЫЕ ПО ОЦЕНИВАЕМЫМ ПАРАМЕТРАМ. 16
КОЭФФИЦИЕНТЫ ЭЛАСТИЧНОСТИ ДЛЯ РАЗНЫХ ВИДОВ РЕГРЕССИОННЫХ МОДЕЛЕЙ. 17
КОРРЕЛЯЦИЯ И -КРИТЕРИЙ ФИШЕРА ДЛЯ НЕЛИНЕЙНОЙ РЕГРЕССИИ. 18
ОТБОР ФАКТОРОВ ПРИ ПОСТРОЕНИИ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. 20
ОТБОР ФАКТОРОВ НА ОСНОВЕ КОРРЕЛЯЦИОННОГО АНАЛИЗА. КОЛЛИНЕАРНОСТЬ 21
ОТБОР ФАКТОРОВ НА ОСНОВЕ КОРРЕЛЯЦИОННОГО АНАЛИЗА. МУЛЬТИКОЛЛИНЕАРНОСТЬ 22
ОЦЕНКА ПАРАМЕТРОВ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. СТАНДАРТИЗИРОВАННАЯ ФОРМА УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ 23
ЭЛАСТИЧНОСТЬ В МНОЖЕСТЕННОЙ РЕГРЕССИИ. 25
МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ. 26
ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ. 28
-КРИТЕРИЙ ФИШЕРА И ЧАСТНЫЙ -КРИТЕРИЙ ФИШЕРА ДЛЯ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. 30
-КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. 31
Эконометрика – одна из базовых дисциплин экономического образования во всем мире. Однако до недавнего времени она не была признана в СССР и России. Это было связано с тем, что из трех основных составляющих эконометрики – экономической теории, экономической статистики и математики – две первые были представлены в нашей стране неудовлетворительно. Но теперь ситуация изменилась коренным образом.
Существуют различные варианты определения эконометрики:
расширенные, при которых к эконометрике относят все, что связано с измерениями в экономике;
узко инструментально ориентированные, при которых понимают определенный набор математико-статистических средств, позволяющих верифицировать модельные соотношения между анализируемыми экономическими показателями.Существуют следующие определения эконометрики:
«Эконометрика занимается определением наблюдаемых в экономической жизни конкретных количественных закономерностей, применяя для этой цели статистические методы» (О. Ланге)
«Эконометрика – любое приложение математики или статистических методов к изучению экономических явлений» (Э. Маленво).
Эконометрика – это статистико-математический анализ экономических отношений (Д. Лайтхилл).
Наиболее полное определение дал Р. Фриш в 1933 г.:
«Эконометрика – это не то же самое, что экономическая статистика. Она не идентична и тому, что мы называем экономической теорией, хотя значительная часть этой теории носит количественный характер. Эконометрика не является синонимом приложений математики к экономике. Как показывает опыт, каждая из трех отправных точек: статистика, экономическая теория и математика – необходимое, но недостаточное условие для понимания соотношений в современной экономической жизни. Это – единство всех трех составляющих. И это единство образует эконометрику».
Исходя из приведенных определений, предметом изучения эконометрики является количественное выражение взаимосвязей в экономике. Таким образом,
Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории, экономической статистики и экономических измерений, математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией.
Эконометрический метод и этапы эконометрического исследования.
Эконометрический метод складывался в преодолении следующих трудностей, искажающих результаты применения классических статистических методов (сущность новых терминов будет раскрыта в дальнейшем):
асимметричности связей;
мультиколлинеарности связей;
эффекта гетероскедастичности;
автокорреляции;
ложной корреляции;
наличия лагов.
Познание в эконометрике осуществляется в форме эконометрического исследования. Его основные этапы представлены на рисунке 1.2.
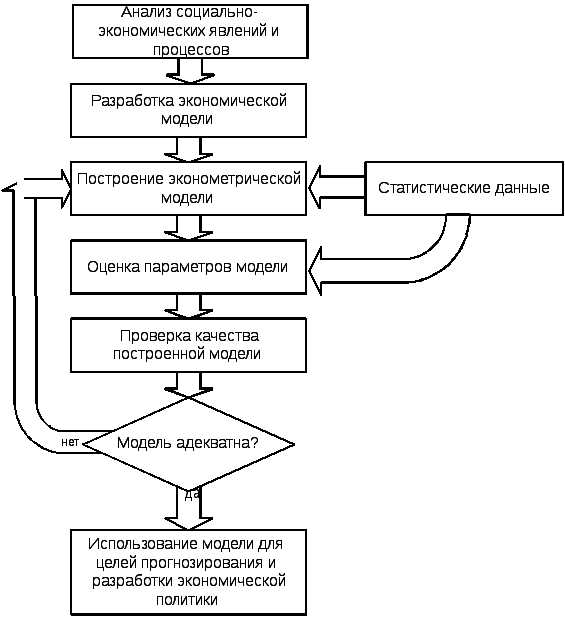
Рис. 1.2 Основные этапы эконометрического исследования
Рассмотрим последовательно выделенные этапы.
1. Эконометрическое исследование начинается с констатации определенного факта социально-экономической жизни. Это может быть какая-либо проблема, например, высокий уровень инфляции, макроэкономическая нестабильность, угроза банкротства, или логически определеннаякачественная зависимость: «объем спроса обратно пропорционален цене», или же продиктованная практическими потребностяминеобходимость решения какой-либо задачи: прогнозирования курсов валют, ценных бумаг и других экономических показателей.
2. На втором этапе на основе метода научной абстракции формируется описательная экономическая модель, базирующаяся на выбранных или разработанных исследователем экономических теориях и концепциях (неоклассической, институциональной, кейнсианской, монетаристской и т.п.). Формирование экономической модели не зависит от имеющихся в распоряжении исследователя эмпирических данных.
3. В центре любого эконометрического исследования находится эконометрическая модель, разрабатываемая на третьем этапе. Различают два основных подхода к формированию эконометрической модели: «сверху вниз» и «снизу вверх».
Подход «сверху вниз»состоит в том, что изначально в модель включается максимально возможное число переменных-факторов. Затем происходит оценка значимости переменных, и те переменные, которые не оказывают существенного влияния на изучаемое явление, исключаются.
При применении подхода «снизу вверх», напротив, изначально выбирается максимально простая модель, содержащая только один основной фактор. Затем, если эта модель недостаточно точна, в нее вводят новые переменные. Процесс усложнения модели осуществляется до тех пор, пока она не будет иметь удовлетворительную точность.
Необходимо отметить, что все переменные можно разделить на полезные, лишние и вредные. Полезные – это переменные, введение которых в модель значительно улучшало ее качество. Лишними называются переменные, не оказывающие существенного влияния ни на качество модели, ни на ее параметры, а вредные переменные, в случае их добавления в модель, изменяют значения параметров в ней без существенного изменения качества.
Таким образом, подход «сверху вниз» заключается в обнаружении и исключении из модели лишних и вредных переменных, а подход «снизу вверх» – в поиске и добавлении в модель полезных переменных.
Сравнительный анализ достоинств и недостатков этих подходов приведены на рисунке 1.3
На практике из-за своей сравнительной простоты чаще используется подход «снизу вверх», в то время как серьезное фундаментальное исследование должно основываться на подходе «сверху вниз», поскольку только с его помощью возможен всесторонний анализ явления и установление всех существующих связей.
Рис. 1.3 Достоинства и недостатки основных подходов к построению эконометрической модели
Эконометрическое моделирование реальных социально-экономических процессов и систем обычно преследует два типа конечных прикладных целей (или одну из них): 1) прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы; 2) имитацию различных возможных сценариев социально-экономического развития анализируемой системы (многовариантные сценарные расчеты, ситуационное моделирование).
При постановке задач эконометрического моделирования следует определить их иерархический уровень и профиль. Анализируемые задачи могут относиться к макро- (страна, межстрановой анализ), мезо- (регионы внутри страны) и микро- (предприятия, фирмы, семьи) уровням и быть направленными на решение вопросов различного профиля инвестиционной, финансовой или социальной политики, ценообразования, распределительных отношений и т.п.
studfiles.net
|
Поиск Лекций
В настоящее время не существует однозначного понимания термина «эконометрика», более того, существует точка зрения, что и сам термин «эконометрика» переведен с английского неверно правильнее было бы назвать «эконометрия», тем более, что родственный предмет изучающий количественные методы в биологии называется «Биометрия». Можно лишь говорить о смысловом значении этого термина как «науки об экономических измерениях» или «о количественных методах измерения социально – экономических процессов и явлений». Однако такое определение вряд ли кого-либо может устроить, так как становится непонятно, что, зачем и кому надо измерять в экономике? Авторы учебников и пособий по эконометрике не старались отвечать на эти вопросы, считая, что ответ на них очевиден. Все это так, если бы мы видели очень заметные достижения в области эконометрического анализа в экономике и бизнесе, особенно в условиях нестабильной российской экономической жизни. Наиболее распространенное и полное из имеющихся в литературе определений термина «эконометрика» выглядит примерно так: Эконометрика – наука, исследующая количественные закономерности и взаимозависимости в экономике при помощи методов математической статистики. Основа этих методов — корреляционно-регрессионный анализ. Однако очень большое количество экономических процессов протекает во времени с определенной регулярностью, например спрос. Для этих процессов используется не только корреляционно – регрессионный анализ но и математический аппарат, основанный на анализе временных рядов. С учетом этого, в более широком смысле можно сказать, что Эконометрика – наука, исследующая закономерности и взаимозависимости между различными факторами в экономике и бизнесе при помощи методов статистического анализа. При этом под фактором понимаются измеряемые и не измеряемые экономические показатели, например уровень инфляции, покупательский спрос, цена, объем продаж, качество обслуживания, моральный климат в коллективе и т.д. До сих пор считалось что основная задача эконометрики – проверка экономических теорий на фактическом (эмпирическом) материале при помощи методов математической статистики. Именно для этих целей и создавалась эконометрика в 30 – е годы прошлого столетия. По сути, работая с этими моделями, мы предполагаем, что вся информация о сути экономического явления содержится в эмпирическом материале, вполне естественно допуская при этом определенные ошибки. Эконометрический анализ позволяет предвидеть только те экономические процессы, которые сохраняют основные тенденции развития, либо повторялись несколько раз в прошлом. Нельзя ожидать от него чего-то большего. Однако в последнее время появилась возможность предлагать фактический материал для создания , как новых экономических теорий, так и использовать эконометрическую теорию в практике предприятий. Это связано с возможностями современных информационных технологий. Используя традиционную методологию эконометристы, как правило, в постановочной части использовали идеи теоретиков и либо доказывали, либо опровергали их. А частенько , чего греха таить, подгоняли результаты по принципу – «чего угодно». Благо, в достаточно сложном для теоретиков математическом аппарате никто разбираться, как правило, и не собирался. Цель эконометрического анализа – разработка эконометрических моделей, позволяющих прогнозировать тенденции развития экономических и бизнес процессов для получения наиболее эффективных и обоснованных решений. Эконометрические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказывать будущее его поведение при изменении каких-либо параметров. Предсказание будущих изменений, например, повышение обменного курса, ухудшение экономической конъюнктуры, падение прибыли может опираться и на интуицию. Однако при этом могут быть упущены, неправильно определены или неверно оценены важные взаимосвязи экономических показателей, влияющие на рассматриваемую ситуацию. В модели все взаимосвязи переменных могут быть оценены количественно, что позволяет получить более качественный и надежный прогноз. Для любого экономического субъекта возможность прогнозирования ситуации означает, прежде всего, получение лучших результатов, избежание потерь или минимизации рисков. Кто проводит эконометрический анализ? Ответ на этот вопрос также неоднозначен. На Западе это делает специалист в области эконометрического анализа – аналитик или эконометрист. В России, в соответствие с новыми государственными стандартами это должен делать экономист и менеджер по любой специализации. В России аналитиков не готовят, более того большинство уверено, что экономисты это гуманитарии. Аналитиками становятся только те, кто владеет эконометрическими методами анализа и методами исследования операций.
Рекомендуемые страницы: Поиск по сайту |
|
poisk-ru.ru
А или х 
В }
{1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.
А и х 
В}.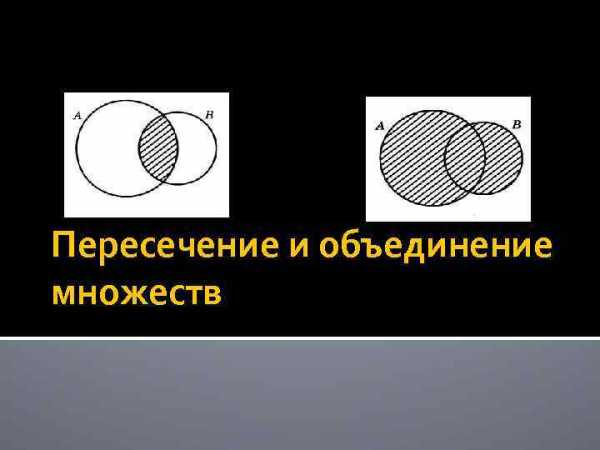
Пересечение и объединение множеств
Что значит объединение? Объединением двух множеств называется множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначают A U B и читают «объединение A и B». Операции объединения и пересечения множеств обладают многими свойствами сложения и умножения чисел, например переместительным, сочетательным и распределительным свойствами. Пусть А – множество простых двузначных чисел, В – множество двузначных чисел, оканчивающихся цифрой 1. Рассмотрим теперь мн-во К, которому принадлежат все элементы множества А и все элементы мн-ва В. Мн-во К составлено из всез двузначных чисел, которые являются простыми или оканчиваются цифрой 1, т. е. К = {11, 13, 17, 19, 21, …, 83, 89, 91, 97} Говорят, что мн-во К является объединением множеств А и В
Что значит пересечение? Пересечением двух множеств называется множество, состоящее из всех общих элементов этих множеств. Обозначают A∩B и читают «пересечение A и B». Понятия объединения и пересечения множеств дос
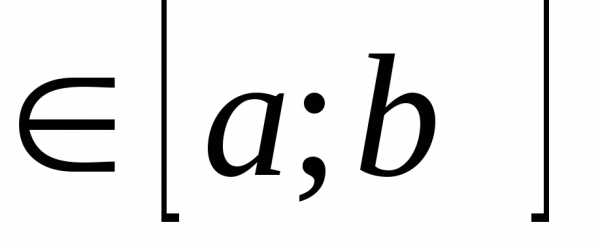
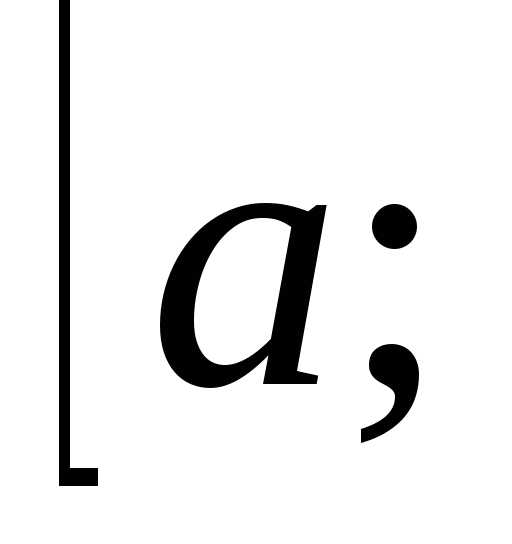
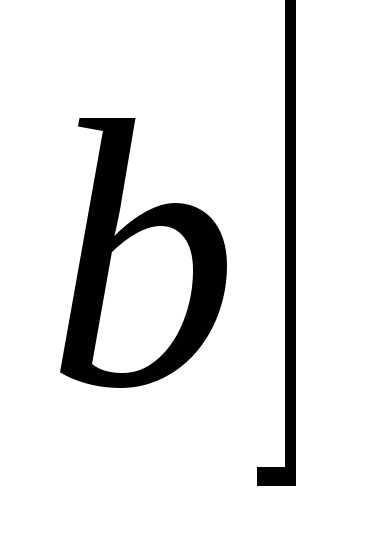
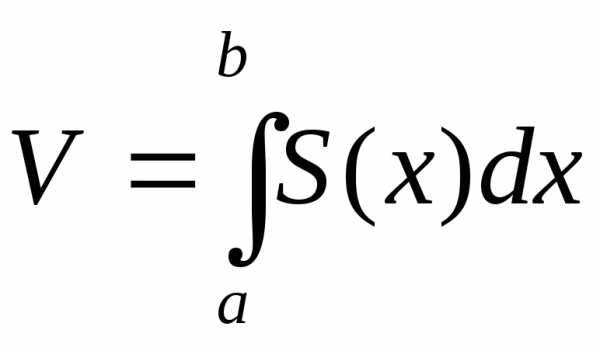
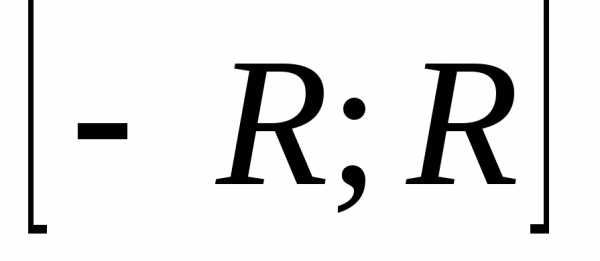
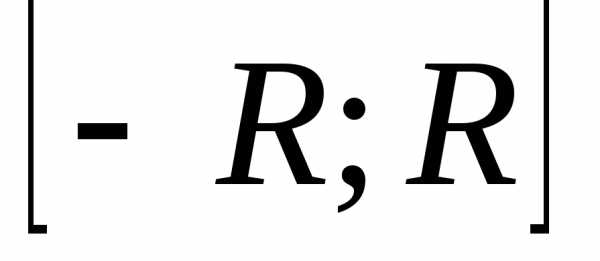
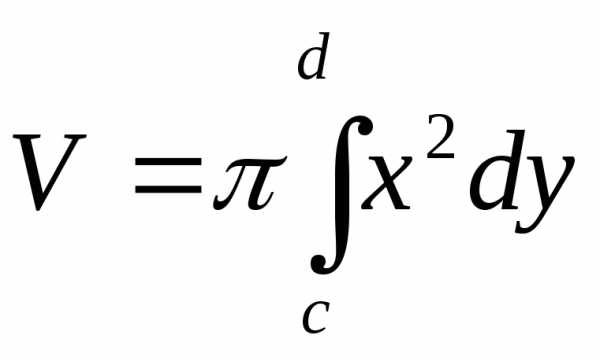
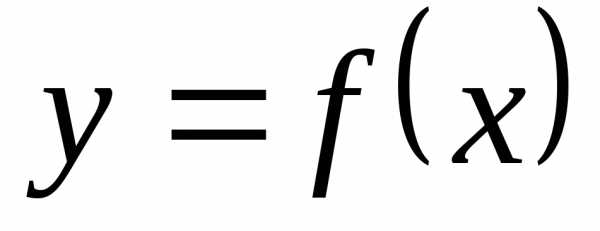
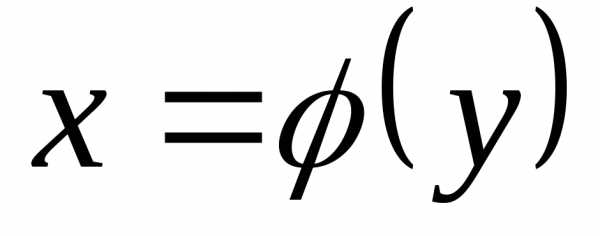
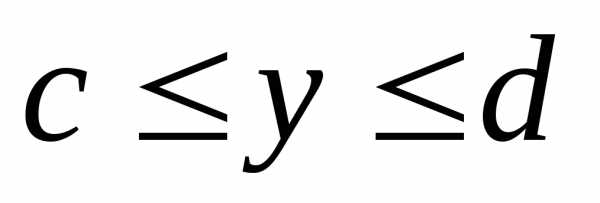
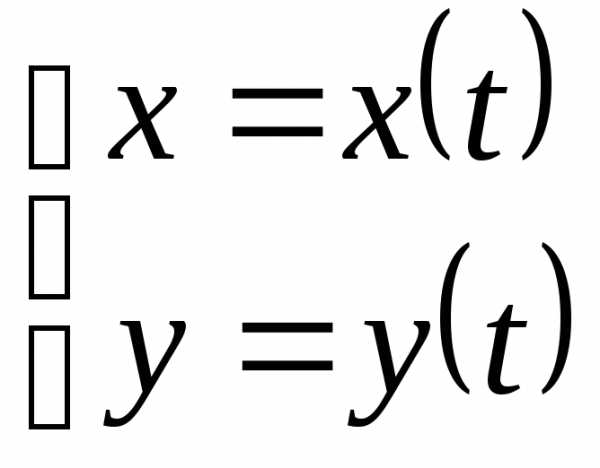
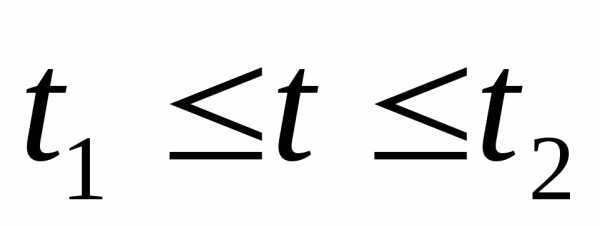
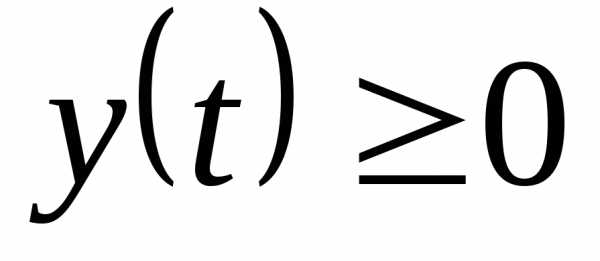
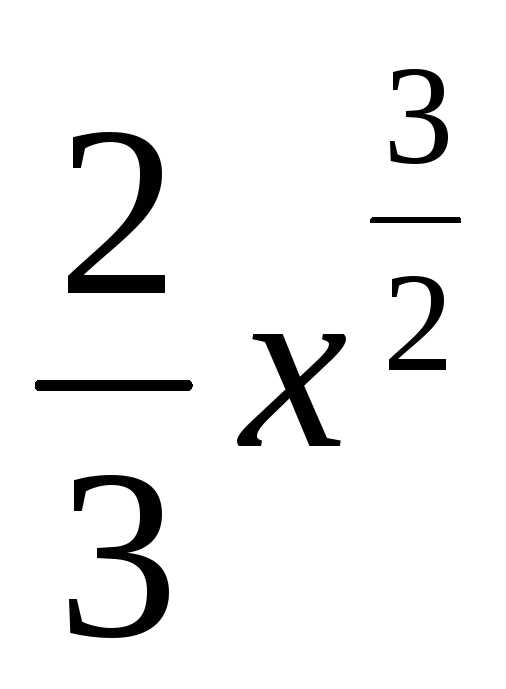
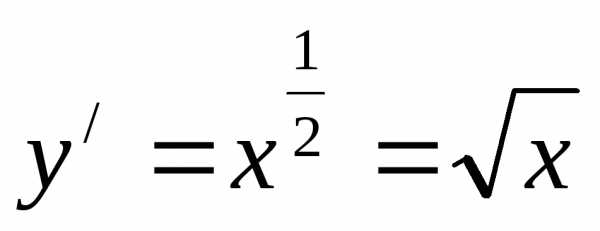
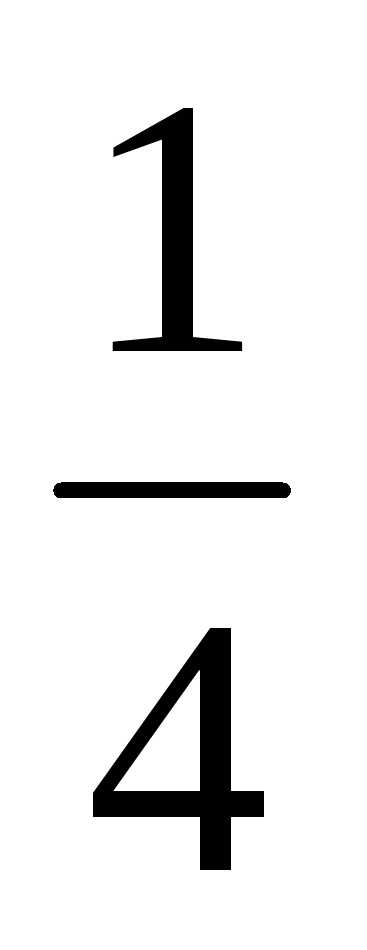
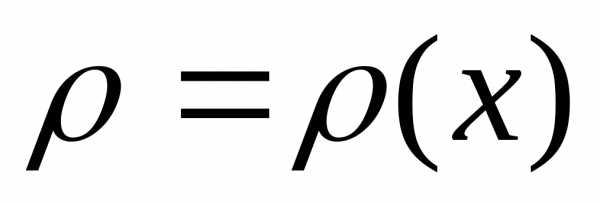
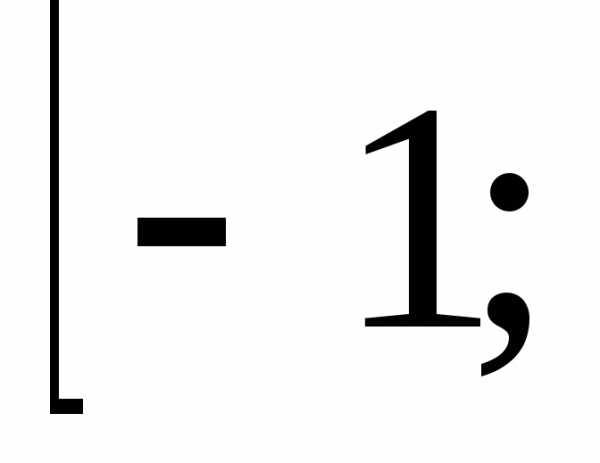
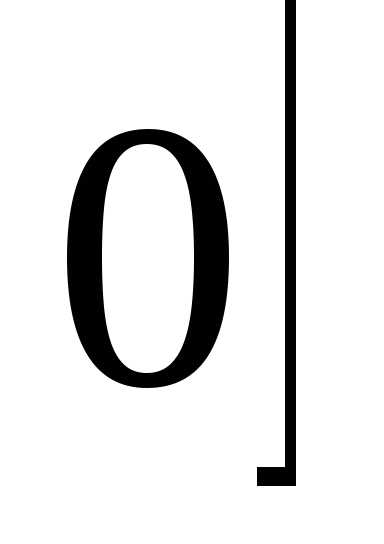
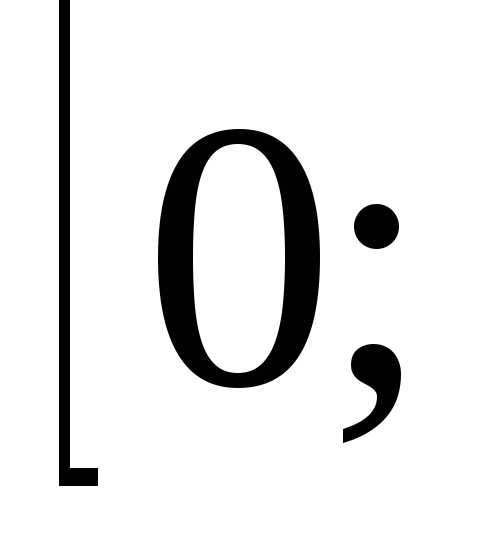
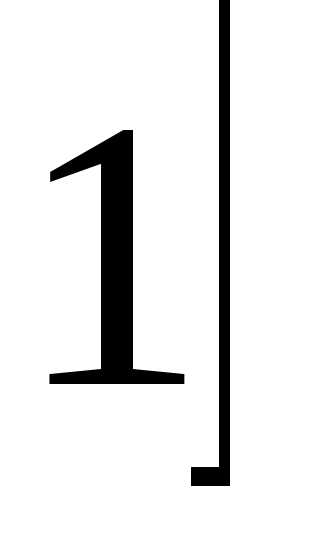=18(куб.ед.)
dx
dx=lim
dx=lim(-
)
=lim(-
+1)=1,
dx
еслиm>1 и расходящимся,
еслиm1.
гиперболаy= 
является своеобразным “порогом”.
(m1)
dx 
dx=2
dx
dx=
lim 1/(1+x2)
dx= lim arctg x
= lim arctg b=
dx=
сходится.
exd(-x2)]=lim[
e-x]=
lim[-
e-b+
]=
,
dx= lim 
dx= lim(lnx)=lim(ln(1)-ln(a))=+
.
меньше нуля, то действительных корней трехчлен не имеет.
— корень уравнения, , , D=36-4=32,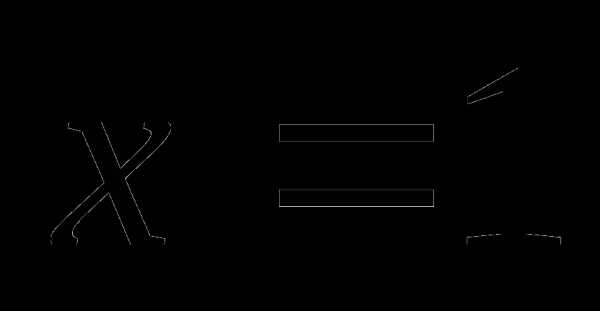
и сводится к квадратному.
,
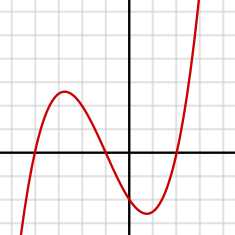График кубической функции y=(x3+3×2−6x−8)/4{\displaystyle y=(x^{3}+3x^{2}-6x-8)/4}, у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0). Имеются 2 критические точки
Уравнение 8×3+7×2−4x+1{\displaystyle 8x^{3}+7x^{2}-4x+1} имеет один действительный и два мнимых корня.