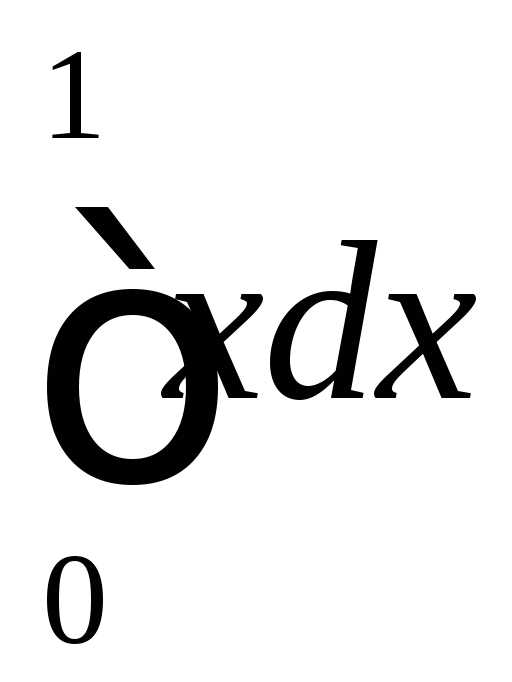Math2.ru — Помощь по высшей математике
Добро пожаловать на сайт, посвящённый оказанию помощи в изучении математики. Основные направления деятельности сайта:
Занятия высшей математикой в онлайне
Зачем тратить время на поездки к репетитору? Занимайтесь в удобное Вам время, – по доступным ценам. Дистанционное обучение гораздо предпочтительнее заказа контрольной работы, так как Вы вкладываетесь в свои знания, работаете на долгосрочную перспективу. Занятия высшей математикой онлайн (с помощью Skype) – это просто технически и эффективнее чем стандартные занятия на дому. Это подтверждается моим многолетним опытом работы. Как репетитор по высшей математике, я могу помочь Вам в подготовке к экзаменам, контрольным и зачётам. Моё искреннее убеждение состоит в том, что дистанционное образование имеет немало преимуществ перед «классическим» вариантом подготовки студента. Подробная информация про удалённое обучение высшей математике размещена в разделе «Онлайн-обучение».Помощь в самостоятельном изучении математики
Надеюсь, что Вы найдете на сайте информацию или услугу, которая Вам требуется. Если у Вас возникнут какие-то пожелания по поводу выложенных материалов или добавления новых, пишите на почту, в ICQ или Skype. Можно также написать мне на аккаунт Контакте. Все пожелания будут учтены.
Также буду рад Вашим отзывам или пожеланиям относительно размещаемых на сайте материалов на форуме. Помощь на форуме оказывается совершенно бесплатно :)
Немного про меня

Меня зовут Алексей. Так сложилось, что математика – это не только моё профильное образование, но и хобби. Коротко о моём образовании: в 2006 году закончил с отличием магистратуру физико-математического факультета в Николаевском государственном университете им. В.О. Сухомлинского, специальность «ПМСО. Математика». Магистр педагогического образования, преподаватель математики.
Также у меня за плечами опыт преподавания в Национальном университете кораблестроения им. адмирала Макарова. Работал преподавателем (впоследствии – старшим преподавателем) на кафедре высшей математики в течении семи лет. В соавторстве издал два учебника с грифом МОН Украины: «Математическое программирование» и «Практикум по решению прикладных задач интегрального исчисления», а также методическое пособие по теории вероятностей для студентов экономических специальностей.
Окончил аспирантуру КНУ им. Т.Г. Шевченко (факультет кибернетики), сейчас работаю над диссертацией. Полагаю, теперь сомнений в моей компетенции возникнуть не должно. Уверен, что наше сотрудничество будет плодотворным! Найти меня можно так:
math1.ru
Полезные сайты / math5school.ru
Math.ru
Math.ru — сайт для школьников, студентов, учителей и для всех, кто интересуется математикой.
На сайте вы найдёте книги, видео-лекции, занимательные математические факты, различные по уровню и тематике задачи, отдельные истории из жизни учёных – всё то, что поможет окунуться в удивительный и увлекательный мир математики.
Для коллег, которые учат (или помогают учить и учиться), собраны материалы для уроков, официальные документы и другое полезное в работе.
Allmath.ru. Вся математика в одном месте
Allmath.ru. Вся математика в одном месте — это математический портал, на котором вы найдете любой материал по математическим дисциплинам.
Высшая математика: математический анализ, линейная алгебра, аналитическая геометрия, дискретная математика, теория вероятностей и математическая статистика, эконометрика, дифференциальная геометрия, математическая логика, теория графов, уравнения математической физики и др.
Прикладная математика: исследование операций и математическое программирование, математическая экономика, финансовая математика, актуарная математика, теория управления, теория систем, прикладная математика в информатике, численные методы, микроэкономика, макроэкономика и др.
Школьная математика: алгебра и начала анализа, планиметрия, стереометрия, комбинаторика и др.
Олимпиадная математика: школьные и студенческие олимпиады, «олимпиадные лекции».
Математика, которая мне нравится
Математика, которая мне нравится – материалы для самостоятельного изучения математики со множеством примеров и задач для самостоятельного решения, олимпиадные задачи, интересные статьи о математике, обучении и образовании.
По словам автора сайта: «В школе есть единственный предмет, который помогает научиться думать, – и это именно математика. И это вовсе не сухой набор формул, как считают многие. Увы, просто не нашлось того, кто бы им открыл всю красоту этой науки.»
Образовательный портал ФИЗ/МАТ класс
Образовательный портал ФИЗ/МАТ класс — на сайте представлены справочный материал, задачи, литература и лекции соответствующие школьному курсу физики и математики.
Широко представлены нормативные документы сферы образования, методические разработки для учителей, примерные программы школьного курса для некоторых учебников.
Здесь вы найдете ссылки на образовательные ресурсы по математике, а также на другие сайты, которые будут интересны и полезны как школьникам, так и учителям.
Архив номеров «Кванта»
Архив номеров «Кванта» — Первый номер журнала «Квант» вышел в 1970 году. Материалы, накопленные в журнале за четыре десятилетия, бесценны. Не раз молодые ученые, многого добившиеся в науке, и замечательные учителя, на вопрос: «Что повлияло на выбор профессии?» – отвечали, – «Учитель (школьный учитель, сумевший увлечь своим предметом) и «Квант».
Сейчас старые номера журнала «Квант» практически недоступны читателям. Имеется ничтожное число библиотек, в которых есть полное собрание вышедших журналов. Данный проект призван открыть путь к богатому архиву журнала всем, кто этого пожелает.
Московский центр непрерывного математического образования
МЦНМО — Центр ставит своей целью сохранение и развитие традиций математического образования в городе Москве, поддержку различных форм внеклассной работы со школьниками (кружков, олимпиад, турниров и т.д.), методическую помощь руководителям кружков и преподавателям классов с углубленным изучением математики, поддержку программ в области преподавания математики в высшей школе и аспирантуре, научной работы.
На сайте Центра представлен обширный материал, соответствующий целям, стоящим перед ним.
Интернет библиотека МЦНМО
Интернет библиотека МЦНМО — Публикация в сети золотого фонда популярной физико-математической литературы.
Замечательные книги, бывшие в течение десятков лет настольными для многих школьных учителей математики, руководителей кружков, школьников, интересующихся точными науками, стали в последние годы физически недоступны читателям (несмотря на большие тиражи, издания давно стали библиографической редкостью, недоступной, к сожалению, в большинстве библиотек; переиздать все эти книги – непростая техническая и финансовая задача).
На сайте для свободного ознакомления представлены многие десятки электронных версий любимых книг и журналов, прежде всего, математического направления.
Открытый банк заданий по математике
Открытый банк заданий по математике — Экзамен по математике является обязательным для всех выпускников российских школ. ЕГЭ по математике позволяет вузам отобрать тех абитуриентов, которые способны использовать математику в своем дальнейшем образовании и в профессиональной деятельности.
На сайте представлены: тренировочные и диагностические работы, опубликованные в формате PDF, каталоги, структурирующие тренировочные материалы ЕГЭ по видам заданий, содержанию и умениям.
Задачи
Задачи — Интернет-проект предназначен для учителей и преподавателей, как помощь при подготовке уроков, кружков и факультативных занятий в школе. Система «Задачи» поможет и школьнику, заинтересовавшемуся какой-то задачей, найти и её, и множество похожих примеров; поможет глубже понять данную тему и расширить свой кругозор.
В настоящее время проект включает в себя в основном задачи по математике (есть и особые разделы, посвященные лингвистике и криптографии). В системе содержатся задачи олимпиад и турниров по математике разного уровня и разных регионов. В систему постоянно добавляются новые задачи и новые решения.
Большинство задач приводится вместе с решениями, задачи по геометрии снабжены чертежами.
Matholymp.org.ua
Matholymp.org.ua (укр.) — создан с целью освещения событий и информирования о шагах, предпринимаемых математическим олимпиадным движением Киева и Украины, для расширения общения между участниками движения – учащимися, студентами и преподавателями.
На сайте: приведена информация об олимпиадах, сборах и турнирах, проводимых движением; подробно описан каждый тур олимпиады или игровой день турнира математических боев; анализируются решения олимпиадных задач; публикуются фоторепортажи о соревнованиях; перечислены школы и университеты, которые принимают активное участие или помогают проводить математические олимпиадные соревнования.
Международная Математическая Oлимпиада
Международная математическая олимпиада (MMO) — это Чемпионат мира по математике среди школьников старших классов, проводящийся каждый год в одной из стран. Первая MMO прошла в 1959 году в Румынии с участием семи стран. В последние годы в ММО участвуют более 100 стран с 5 континентов. Консультативный совет ММО утверждает страну, принимающую ММО, следит за соблюдением правил и поддерживает традиции ММО.
На сайте представлена разнообразная статистическая, хронологическая и архивная информация о Международных математических олимпиадах за все годы.
В разделе Страны представлены Сайты Национальных МО многих стран мира.
Математические олимпиады и математические задачи
Математические олимпиады и математические задачи — База данных задач математических олимпиад различных уровней России и зарубежья. Задачники, методические материалы и пр. Подборка ссылок на родственные интернет-ресурсы.
Арбуз
АРБУЗ. Занимательный мир чисел, слов, пикселей и заблуждений — Материалы по популярной математике и занимательному программированию, картинки математического содержания, различные сведения о числе π и др.
Занимательная математика
Занимательная математика — на сайте вы найдете занимательные математические факты, истории из жизни математиков, формулы, таблицы, решения задач.
Данный веб-ресурс содержит задачи, направленных на воспитание гибкости математического мышления и развитие инициативы и сообразительности.
Материал на сайте будет полезен для школьников, студентов, абитуриентов, преподавателей.
Formula.co.ua – математика для школы
Formula.co.ua – математика для школы (укр.) — сайт посвящен элементарной математике, то есть математике, которую преподают в школе. Материал, размещенный на нем, пригодится не только ученикам и учителям, но и тем, кто желает восстановить знания по математике в объеме программы средней школы.
Сайт содержит онлайн сервисы для решения задач (например, решение квадратного уравнения, нахождение гипотенузы и катетов прямоугольного треугольника и т.п.), позволяющие без лишних усилий, просто введя известные параметры, одним нажатием кнопки вычислить искомое значение.
Теорию на сайте дополняют математические факты, былины из жизни математиков, интересные высказывания, логические флеш игры, детские шутки, для любителей поломать голову над каверзными загадками присутствует головоломки, каталог математических рефератов, словарь математических терминов.
Webmath.ru. Образовательные онлайн сервисы
Webmath.ru — образовательный портал для студентов, абитуриентов и школьников. На сайте находятся более 50 онлайн калькуляторов, которые могут помочь учащимся решить задачи по математике, алгебре, геометрии, физике, теории вероятности и многим другим предметам.
По словам администрации сайта: «Наша цель: сделать сайт, на котором любой учащийся сможет найти все необходимое для решения проблем связанных с учебой, свободный от лишней информации и вредных советов!»
Учителям информатики и математики и их любознательным ученикам
Учителям информатики и математики и их любознательным ученикам — Школьные олимпиадные задачи и тесты по программированию за 1989-2002 годы. Материалы по информатике и математике. Методическая копилка заданий. Тренажер для подготовки к ЕГЭ по математике. Ссылки на интернет-ресурсы соответствующей тематики.
Lineyka
Lineyka — справочные материалы, подборка учебной литературы и рефератов по высшей и школьной математике; методические разработки уроков, уроки-презентации, календарное планирование, рабочие программы, нестандартные уроки для учителей; олимпиадные задачи с решениями; методические разработки лабораторных работ по эконометрии и математическому программированию, лекционный материал по этим дисциплинам, решения некоторых задач математического программирования; сведения о выдающихся математиках.
Математические этюды
Математические этюды — На сайте представлены этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях. Посетителя сайта приглашают совершить познавательные экскурсии по красивым математическим задачам. Их постановка понятна школьнику, но до сих пор некоторые задачи не решены учёными.
f(x y z).ru
f(x y z).ru — Интерактивный справочник формул, содержащий в концентрированной форме основные формулы и сведения по математике, геометрии, физике. Интерактивность позволяет производить вычисления формул онлайн.
Данный справочник обеспечивает простой доступ ко всему арсеналу формул и вычислений современной науки, позволяя не перегружать свою память избытком данных. Его цель, дать короткий и точный ответ, и произвести вычисления.
Интерактивный справочник формул поможет вам в вопросах изучения теории, а также позволит значительно сэкономить время, при поиске формул, данных и на процессе вычисления значений по этим формулам.
Теорема Пифагора
Теорема Пифагора — На этом сайте вы сможете найти сведения об истории открытия и доказательства теоремы Пифагора, а так же о самом Пифагоре. Приведены около 30 различных доказательств этой теоремы от древнеиндийского математика Басхары до векторного доказательства. Вы сможете узнать, как использовали свойства и теорему прямоугольного треугольника древние египтяне, архитекторы средневековья и как она используется в наше время.
Сайт элементарной математики Дмитрия Гущина
Сайт элементарной математики Дмитрия Гущина — Этот сайт для всех, кто интересуется элементарной математикой: школьников, абитуриентов, слушателей подготовительных курсов, студентов педагогических вузов и учителей.
Здесь вы найдете варианты выпускных экзаменов, задачи по математике, предлагавшиеся на вступительных экзаменах, задачи математических олимпиад вузов и методические пособия по математике, информацию о математических мероприятиях в Санкт-Петербурге.
На сайте опубликованы все задания ЕГЭ по математике 2013 года с решениями. Для каждой задачи открытого банка заданий (В1 – B14) приведено полное решение или решение аналогичной задания-прототипа, отличающегося только конкретными числовыми данными.
Internet-задачник «1000 задач»
Internet-задачник «1000 задач» — Этот сайт задуман как электронный сборник задач по математике, или даже онлайн-репетитор по школьному курсу математики.
Главная часть сайта – это сборник задач по школьному курсу математики, отобранных авторами сайта вследствие многолетнего репетиторства с выпускниками средней школы. Задач в сборнике ровно 1000 соответственно названию сайта (хотя на всем сайте их значительно больше). К задачам прилагаются ответы, а также решения с подробными объяснениями.
Задачник можно использовать как для проверки своих знаний по математике так и для онлайн-обучения в виде практикума.
www-FORMULA.ru
www-FORMULA.ru — Девиз сайта: «Любая формула в один клик с главной страницы».
Представлены разделы:площадь плоских фигур, периметр фигур, радиус описанной и вписанной окружности, тригонометрия, формулы для параллелограмма, окружности и круга, ромба, квадрата и прямоугольника, различных видов трапеции, объёмы и площади поверхности тел, алгебраические формулы, производные и др.
Великие математики
Великие математики — Сайт посвящён знаменитым математикам, предлагается материал об их жизненном пути и вкладе в науку.
История математики. Биографии великих математиков
История математики. Биографии великих математиков — Сведения про ученых разных времен и народов, которые своими трудами обогатили математическую науку.
Тот, кто любит математику и имеет к ней призвание, в примерах из жизни многих ученых найдет живительную поддержку своим устремлениям и с большей настойчивостью будет заниматься своим любимым делом.
Вся элементарная математика
Вся элементарная математика — Этот сайт – средняя математическая интернет-школа, в которой вы можете учиться, не выходя из дому.
Сайт ответит на многие вопросы, станет помощником и консультантом в учёбе. Здесь вы найдёте всю необходимую информацию, сможете постоянно расширять и углублять свои знания по всем основным разделам элементарной математики: арифметике, алгебре, геометрии, тригонометрии, функциям и графикам, основам анализа и т.д.
Математика – это просто!
Математика – это просто! — Цель сайта помочь научиться решать математические задачи, освоить разные методы решений, закрепить пройденный материал, а также получить консультацию квалифицированных специалистов по способам решения задач.
Представлены: книги по алгебре, геометрии, логике и математике в общем; биографии ученых; таблицы значений различных функций стандартных аргументов и инструмент для получения любых других значений; обширный справочный материал.
Математическое образование: прошлое и настоящее
Математическое образование: прошлое и настоящее — Сайт имеет своей целью накопление и систематизацию методического наследия в области преподавания математики. Современные информационные технологии позволяют хранить и передавать на расстояния книги, журнальные и газетные публикации. Создатели сайта стремятся сделать наиболее интересные из них доступными для широкой аудитории: учителей, методистов, преподавателей и учащихся педагогических вузов.
Представлены книги по методике преподавания математики в школе, внеклассной работе по математике, очерки из истории математики, биографии ученых, библиографические пособия. Имеются архивы журналов и сборников (журналы «Математика в школе», «Математическое образование», сборники «Математическое просвещение» и др.). Основная часть материалов представлена в виде электронных версий печатных изданий в формате djvu.
Решение задач по математике онлайн
Решение задач по математике онлайн – сайт обращён к учащимся изучающим математику и призван помочь школьникам и студентам и освободить их от многих рутинных вычислений, и подсказать метод решения. Основу сайта составляют математические программы (калькуляторы) для решения задач онлайн.
Все вычисления производятся на сайте, программы не нужно скачивать и устанавливать на компьютер. На каждую задачу приводится поэтапный процесс получения ответа, т.е. подробное решение с объяснениями этапов решения данной задачи.
Решение задач приводится в виде, принятом в большинстве школ и вузов, некоторые задачи решаются двумя способами.
math4school.ru
| Автор(ы) | Название | Год | Стр. | Загрузить, Mb | ||||
| djvu | ps | html | TeX | |||||
| И. Б. Абельсон | Две прогрессии | 1938 | 163 | 4.03 | — | — | — | — |
| И. Б. Абельсон | Максимум и минимум | 1935 | 108 | 2.18 | — | — | — | — |
| И. Б. Абельсон | Рождение логарифмов | 1948 | 232 | 5.26 | — | — | — | — |
| С. А. Абрамов | Элементы программирования | 1982 | 96 | 1.02 | — | — | — | — |
| А. К. Айзенберг, К. У. Асимов | Тематический указатель статей журнала «Математика в школе» (1937—1966 rr.) | 1970 | 200 | 16.23 | 8.21 | — | — | — |
| А. В. Акопян, А. А. Заславский | Геометрические свойства кривых второго порядка. | 2007 | 136 | — | 3.71 | — | — | — |
| П. С. Александров | Введение в теорию групп. | 1980 | 144 | 3.48 | — | — | — | — |
| Б. И. Александров, М. В. Лурье | Задачи на составление уравнений. | 1990 | 96 | 1.37 | — | — | — | — |
| И. И. Александров | Сборник геометрических задач на построение. | 1950 | 176 | 2.75 | — | — | — | — |
| П. С. Александров, А. И. Маркушевич, А. Я. Хинчин | Энциклопедия элементарной математики. Книга 1 (арифметика) |
1951 | 448 | 6.63 | — | — | — | — |
| П. С. Александров, А. И. Маркушевич, А. Я. Хинчин | Энциклопедия элементарной математики. Книга 2 (алгебра) |
1951 | 424 | 5.44 | — | — | — | — |
| П. С. Александров, А. И. Маркушевич, А. Я. Хинчин | Энциклопедия элементарной математики. Книга 3 (функции и пределы, основы анализа) |
1952 | 559 | 7.61 | — | — | — | — |
| П. С. Александров, А. И. Маркушевич, А. Я. Хинчин | Энциклопедия элементарной математики. Книга 4 (геометрия) |
1963 | 568 | 8.80 | — | — | — | — |
| П. С. Александров, А. И. Маркушевич, А. Я. Хинчин | Энциклопедия элементарной математики. Книга 5 (геометрия) |
1966 | 624 | 8.68 | — | — | — | — |
| В. Б. Алексеев | Теорема Абеля в задачах и решениях. | 2001 | 192 | — | 1.78 | — | — | — |
| Н. Б. Алфутова, А. В. Устинов | Алгебра и теория чисел для математических школ. | 2001 | 264 | — | 2.00 | — | — | — |
| Д. В. Аносов | Взгляд на математику и нечто из нее. | 2003 | 24 | — | 0.19 | — | — | — |
| Д. В. Аносов | От Ньютона к Кеплеру | 2006 | 272 | — | 1.92 | — | — | — |
| П. Р. Аракелян, М. Ю. Зубченко, В. М. Радченко | Шоста Соросiвська олiмпiада з математики. | 2000 | 31 | 0.46 | — | — | — | — |
| Б. И. Аргунов, М. Б. Балк | Геометрические построения на плоскости. | 1957 | 268 | 4.38 | — | — | — | — |
math.ru
| Автор(ы) | Название | Год | Стр. | Загрузить, Mb | ||||
| djvu | ps | html | TeX | |||||
| И. Б. Абельсон | Две прогрессии | 1938 | 163 | 4.03 | — | — | — | — |
| И. Б. Абельсон | Максимум и минимум | 1935 | 108 | 2.18 | — | — | — | — |
| И. Б. Абельсон | Рождение логарифмов | 1948 | 232 | 5.26 | — | — | — | — |
| А. К. Айзенберг, К. У. Асимов | Тематический указатель статей журнала «Математика в школе» (1937—1966 rr.) | 1970 | 200 | 16.23 | 8.21 | — | — | — |
| П. С. Александров | Введение в теорию групп. | 1980 | 144 | 3.48 | — | — | — | — |
| Б. И. Александров, М. В. Лурье | Задачи на составление уравнений. | 1990 | 96 | 1.37 | — | — | — | — |
| П. С. Александров, А. И. Маркушевич, А. Я. Хинчин | Энциклопедия элементарной математики. Книга 2 (алгебра) |
1951 | 424 | 5.44 | — | — | — | — |
| В. Б. Алексеев | Теорема Абеля в задачах и решениях. | 2001 | 192 | — | 1.78 | — | — | — |
| Н. Б. Алфутова, А. В. Устинов | Алгебра и теория чисел для математических школ. | 2001 | 264 | — | 2.00 | — | — | — |
| В. И. Арнольд | Задачи для детей от 5 до 15 лет | 2007 | 16 | — | 0.31 | — | — | — |
| В. И. Арнольд | Задачи для детей от 5 до 15 лет. | 2004 | 16 | — | 0.17 | — | — | — |
| В. И. Арнольд | Математическое понимание природы | 2011 | 144 | — | 2.45 | — | — | — |
| И. В. Арнольд | Отрицательные числа в курсе алгебры. | 1947 | 80 | 1.53 | — | — | — | — |
| К. У. Асимов, Р. Н. Котельникова | Тематический указатель статей журнала «Математика в школе» (1967—1975 rr.) | 1978 | 148 | 11.00 | 4.42 | — | — | — |
| И. И. Богданов, П. А. Кожевников, О. К. Подлипский, Д. А. Терёшин, | Всероссийские олимпиады школьников по математике 1993–2006 | 2007 | 472 | — | 3.00 | — | — | — |
| И. И. Баврин, Е. А. Фрибус | Старинные задачи. | 1994 | 128 | 1.86 | — | — | — | — |
| А. С. Барсов | Что такое линейное программирование. | 1959 | 104 | 1.29 | — | — | — | — |
| М. И. Башмаков, Б. М. Беккер, В. М. Гольховой | Задачи по математике. Алгебра и анализ. | 1982 | 192 | 6.29 | — | — | — | — |
| М. И. Башмаков | Уравнения и неравенства. | 1976 | 96 | 1.07 | — | — | — | — |
| Л. Беран | Упорядоченные множества. | 1981 | 64 | 0.59 | — | — | — | — |
math.ru
| # | Автор(ы) | Название | Год | Стр. | Загрузить, Mb | ||||
| djvu | ps | html | TeX | ||||||
| 1 | А. И. Маркушевич | Возвратные последовательности. | 1950 | 52 | 0.35 | — | — | — | — |
| 2 | И. П. Натансон | Простейшие задачи на максимум и минимум. | 1950 | 32 | 0.20 | — | — | — | — |
| 3 | И. С. Соминский | Метод математической индукции. | 1965 | 58 | 1.42 | — | — | — | — |
| 4 | А. И. Маркушевич | Замечательные кривые. | 1952 | 32 | 0.28 | — | — | — | — |
| 5 | П. П. Коровкин | Неравенства. | 1966 | 58 | 0.37 | — | — | — | — |
| 6 | Н. Н. Воробьев | Числа Фибоначчи. | 1978 | 144 | 0.95 | — | — | — | — |
| 7 | А. Г. Курош | Алгебраические уравнения произвольных степеней. | 1975 | 32 | 0.33 | — | — | — | — |
| 8 | А. О. Гельфонд | Решение уравнений в целых числах. | 1978 | 63 | 0.43 | — | — | — | — |
| 9 | А. И. Маркушевич | Площади и логарифмы. | 1979 | 64 | 0.45 | — | — | — | — |
| 10 | А. С. Смогоржевский | Метод координат. | 1952 | 40 | 0.47 | — | — | — | — |
| 11 | Я. С. Дубнов | Ошибки в геометрических доказательствах. | 1961 | 70 | 0.66 | — | — | — | — |
| 12 | И. П. Натансон | Суммирование бесконечно малых величин. | 1960 | 58 | 0.31 | — | — | — | — |
| 13 | А. И. Маркушевич | Комплексные числа и конформные отображения. | 1954 | 52 | 0.38 | — | — | — | — |
| 14 | А. И. Фетисов | О доказательствах в геометрии. | 1954 | 60 | 0.36 | — | — | — | — |
| 15 | И. Р. Шафаревич | О решениях уравнений высших степеней. | 1954 | 22 | 0.28 | — | — | — | — |
| 16 | В. Г. Шерватов | Гиперболические функции. | 1954 | 58 | 0.48 | — | — | — | — |
| 17 | В. Г. Болтянский | Что такое дифференцирование? | 1955 | 64 | 0.63 | — | — | — | — |
| 18 | Г. М. Миракьян | Прямой круговой цилиндр. | 1955 | 40 | 0.42 | — | — | — | — |
| 19 | Л. А. Люстерник | Кратчайшие линии. | 1955 | 104 | 0.65 | — | — | — | — |
| 20 | А. М. Лопшиц | Вычисление площадей ориентированных фигур. | 1956 | 60 | 0.43 | — | — | — | — |
math.ru
Math.ru
Анастасия Борисовна Калинина, Евгения Марковна Кац, Антон Михайлович ТилипманМ.: ВАКО, 2013. 384 с.
ISBN 978-5-408-01282-4; Тираж 5000 экз.
| |||||||||||
Как познакомить ребёнка с математикой? Как показать, что математика — это красиво? Как не напугать, а увлечь? Эти и многие другие вопросы ставят перед собой авторы книги. В книге множество задач самой разной сложности. К каждой задаче даётся ответ, к большинству — подробное решение.
Книга адресована всем тем родителям и педагогам, кто занимается подготовкой детей к школе, учителям начальных классов, руководителям математических кружков, организаторам олимпиад.
Мы рады выложить эту книгу с любезного письменного согласия всех трех авторов книги
(при окончившихся правах издательства).
Естественно, файлы эти предполагают лишь некоммерческое использование в образовательных целях.
О любом коммерческом использовании надо общаться с правообладателями.
В.Д.Арнольд
октябрь 2016
Содержание
| Предисловие | 3 | ||
| Задачи | Ответы и Решения | ||
| 1. | Четвёртый лишний | 6 | 190 |
| 2. | Заплатки | 7 | 192 |
| 3. | Ребусы | 8 | 193 |
| 4. | Братья и сёстры | 9 | 193 |
| 5. | Я старше тебя | 11 | 195 |
| 6. | От буквы к букве | 13 | 197 |
| 7. | Я больше тебя | 18 | 197 |
| 8. | Возрастание и убывание | 24 | 200 |
| 9. | Последовательности | 25 | 200 |
| 10. | Удобный подсчёт | 27 | 203 |
| 11. | Цифры в масках | 28 | 205 |
| 12. | Шаловливый Лёва | 31 | 208 |
| 13. | Чётность | 33 | 210 |
| 14. | Нарисуй схему | 36 | 213 |
| 15. | Распилы | 40 | 224 |
| 16. | Интервалы | 42 | 230 |
| 17. | Сосчитай все прямоугольники | 45 | 235 |
| 18. | Сосчитай все треугольники | 49 | 236 |
| 19. | Задачи на разрезание | 53 | 238 |
| 20. | Тетрамино | 55 | 242 |
| 21. | Пентамино | 61 | 247 |
| 22. | Танграм | 65 | 249 |
| 23. | Задачи про Мишу и Тимошу | 70 | 254 |
| 24. | Кирпичики | 73 | 256 |
| 25. | Объёмные и плоские фигуры | 77 | 259 |
| 26. | Развёртки | 79 | 260 |
| 27. | Предметы и их свойства | 83 | 261 |
| 28. | Множества и их пересечения | 87 | 262 |
| 29. | Клинопись | 94 | 265 |
| 30. | Римские числа | 95 | 265 |
| 31. | Задачи со спичками | 102 | 267 |
| 32. | Судоку | 104 | 268 |
| 33. | Числовая змея | 105 | 274 |
| 34. | Координаты | 113 | 277 |
| 35. | Словесное описание чисел | 120 | 283 |
| 36. | Составь таблицу | 124 | 290 |
| 37. | Размещение предметов | 126 | 296 |
| 38. | Известны сумма и разность | 127 | 297 |
| 39. | Головы и ноги | 129 | 300 |
| 40. | Взвешивание | 133 | 303 |
| 41. | Сравнения | 137 | 311 |
| 42. | Деньги | 138 | 313 |
| 43. | Возраст | 140 | 316 |
| 44. | Календарь | 143 | 319 |
| 45. | Время на часах | 147 | 323 |
| 46. | Дороги и перекрёстки | 153 | 329 |
| 47. | Мосты и берега | 158 | 333 |
| 48. | Графы | 160 | 335 |
| 49. | Моя семья | 161 | 340 |
| 50. | Задачи, решаемые с конца | 163 | 341 |
| 51. | Делимость | 164 | 342 |
| 52. | Части и целое | 166 | 344 |
| 53. | Дроби | 169 | 352 |
| 54. | Задачи про совместную работу | 172 | 355 |
| 55. | Три рыбака и три судака | 173 | 357 |
| 56. | Задачи на движение | 174 | 358 |
| 57. | Невезучий Петя | 175 | 362 |
| 58. | Лилипуты и Гулливер | 178 | 364 |
| 59. | Рыцари и лжецы | 181 | 367 |
| 60. | Комбинаторика | 182 | 368 |
| 61. | Разные задачи | 183 | 370 |
| 62. | Ханойские башни | 185 | 375 |
| 63. | Лист Мёбиуса | 186 | |
| 64. | Как пролезть сквозь тетрадный листок? | 187 | |
| Скачать: всю книгу — PDF, 10.2 M |
PDF, 5.2 M |
PDF, 5.4 M |
ПРЕДИСЛОВИЕ
Дорогие учителя! Мамы и папы! Бабушки и дедушки!
Перед вами не совсем обычная книга. Мы собрали в ней множество довольно трудных задач, но хотим показать, что математика — это не сложно. Мы нарисовали для этой книги более полутора тысяч незатейливых схематичных картинок, но хотим показать, что математика — это красиво. Эта книга содержит множество слов и мыслей, но главная наша мысль записывается всего четырьмя словами: математика — в ваших руках!
Наш задачник рассчитан на возраст от 6 до 10 лет, но книга может оказаться полезной и некоторым пятилетним малышам, и школьникам постарше. Эта книга доступна буквально каждому. Она не для вундеркиндов, хотя содержит ряд задач, над которыми поломают голову и многие взрослые. Наша книга не только и не столько для тех, кому математика уже интересна. Напротив, наша главная цель — заинтересовать даже такого ребёнка, кто считает, что математика — это сложно, скучно и не для него. Настоящая книга не заменяет существующие школьные учебники, но служит весомым дополнением к любому из них.
Книга состоит из двух частей: первая содержит задачи, вторая — ответы и подробные решения. Задачи сгруппированы по 64 разделам. Каждый следующий раздел, как правило, немного сложнее предыдущего. Задачи внутри разделов также расположены по возрастанию сложности.
Большинство разделов предваряется двумя отдельными вступлениями для взрослых и для детей. Чтобы их различать, используются следующие условные обозначения:
| — для взрослых; | — для детей. |
Вступления для взрослых представляют собой методические рекомендации, обращения к детям содержат пояснения к заданию. Если дети ещё не умеют читать, эти вступления им могут прочитать взрослые.
Многие школьники думают, что математика — это таблица умножения и сотни однотипных примеров и задач. Механические манипуляции с числами и клеточками в тетради вырабатывают у детей стойкую и незаслуженную неприязнь к математике. Наша цель — побороть эту неприязнь, не дать ей сформироваться.
Мы с помощью этой книги не пытаемся развить у детей автоматизм, не ставим своей целью натаскать их на задачи того или иного сорта. Наши задачи не шаблонны, их не надо решать на скорость или на количество — они учат рассуждать. Учиться этому можно и нужно вне зависимости от того, пошёл ли ребёнок в школу или ещё нет, умеет ли ребёнок читать и даже считать.
Математика — это не только умение пересчитывать предметы и сравнивать числа, это, прежде всего, умение мыслить логически. Это умение нужно повсюду: в биологии и в языкознании, в магазине и в горах, на уроке и на необитаемом острове, — и именно поэтому математика фундаментальна.
Сложность задач в этом сборнике варьируется в широких пределах. Это даёт возможность включиться в работу ребёнку с любым уровнем математической подготовки. Но следует остерегаться соблазна давать ребёнку задачи как можно более сложные, на пределе его возможностей. Трудные задачи, стоящие особняком, вызывают у многих детей растерянность, неуверенность в своих силах. С разбега можно прыгнуть дальше, чем с места, и поэтому не забывайте, что и простыми задачами не стоит пренебрегать. Уверенность в себе помогает закрепить интерес, неуверенность его уничтожает.
Во многих учебниках встречаются задачи повышенной сложности, так называемые «задачи со звёздочкой». Сложность этих задач, как правило, не вычислительная, — их невозможно решить, применяя стандартные, заранее известные шаблоны. «Звёздочка» означает необходимость озарения, необходимость догадаться до чего-то нового. Но как научиться догадываться?
Один из способов догадаться — нарисовать вспомогательную схематичную картинку. Важно научить детей видеть, что с математической точки зрения отношение «Денис старше Гриши» означает в точности то же самое, что «у Гали коса толще, чем у Жени». Правильно нарисованная схема выявляет математический смысл задачи и заметно упрощает её решение. Схема способна сделать даже очень сложную задачу простой, а непонятное и длинное условие — коротким и доступным. Может даже случиться, что сама схема окажется ответом к задаче.
Вот почему мы оцениваем задачи в нашей книге по двум параметрам: «сложность» и «наглядность». Уровень сложности мы традиционно обозначаем звёздочками (*), от одной до пяти. Уровень наглядности обозначаем «солнышком» (☼) — задаче может быть присвоено от нуля до трёх таких символов. Сложная и ненаглядная задача — труднее, чем сложная и наглядная.
Многим детям для решения ряда задач бывает полезен дополнительный наглядный материал, который можно потрогать руками: счётные палочки, заранее вырезанные геометрические фигуры. Иногда может потребоваться и другой реквизит: полоски бумаги, бумажные цепочки, ножницы, клей, степлер, спички, горошины, пластилиновые шарики. Всё это полезно приготовить заранее и использовать по мере необходимости.
Задачи некоторых типов (разделы 2, 4, 5, 6, 7, 8, 11, 20, 21, 29, 33, 34, 38) дети могут придумывать и сами — друг для друга, на обмен. Такая форма работы усиливает интерес к предмету и мотивацию.
Главное, что нужно помнить взрослым: ребёнку должно быть интересно! Мы можем этого не замечать, но математикой пронизан весь окружающий мир: снежинки и ананасы, радуга и музыка, — красота нашего мира во многом описывается математикой. Этот мир не должен вызывать у детей уныние и неприязнь. Математика — это красиво! Давайте поможем детям увидеть эту красоту!
В заключение хотим сказать, что будем благодарны всем, кто сообщит нам, как использовалась наша книга: каков был возраст детей, формат занятий, какие разделы вы использовали в своей работе, какие вызвали у детей наибольший интерес. Мы также примем с благодарностью ваши замечания, пожелания и предложения, направленные на улучшение книги в последующих изданиях.
| А.Б. Калинина
[email protected]u |
Е.М. Кац
mouse.jane@gmail.com |
А.М. Тилипман
[email protected] |
| |||||||||||
math.ru
| Для проведения поиска по авторам введите начальный фрагмент фамилии или фрагменты нескольких фамилий авторов через пробел без симолов усечения («*»). Для поиска по ключевым словам используется язык запросов, описанный ниже.
Несколько примеров:
|
Алфавитный каталог Тематический каталог Архивы журналов |
math.ru








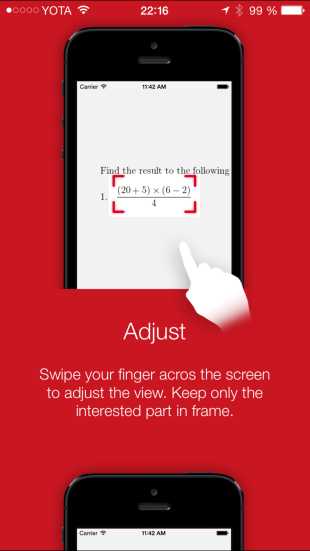
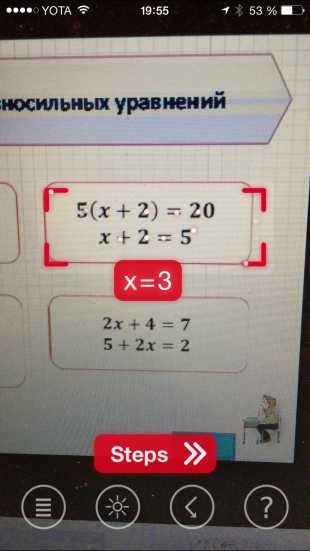
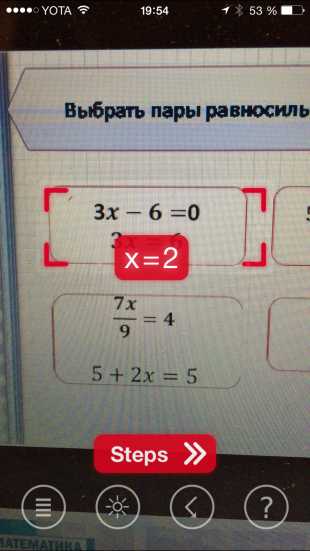

 .
. .
.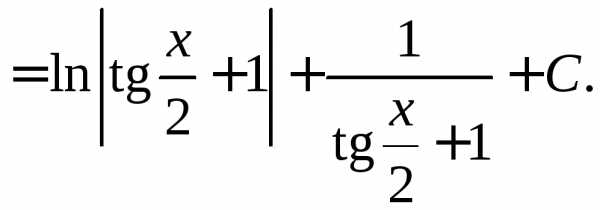 ►
►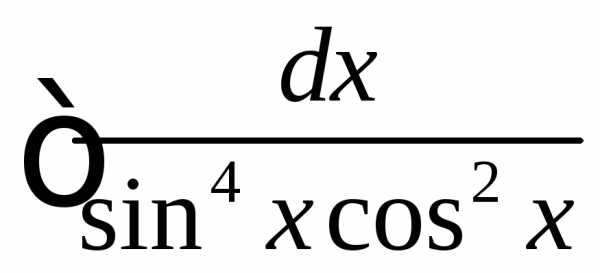 .
.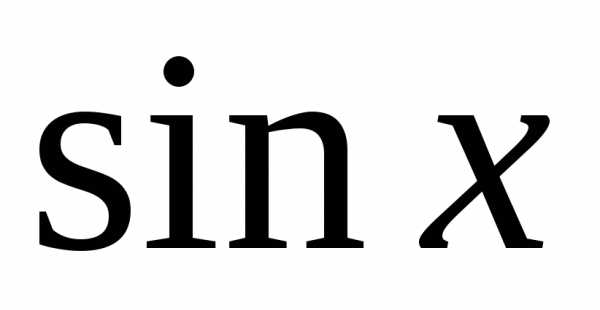 и
и входят в подынтегральную функцию в
чётных степенях, то можно сделать
подстановку
,
входят в подынтегральную функцию в
чётных степенях, то можно сделать
подстановку
, 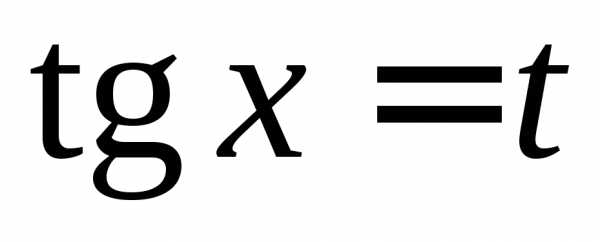 .
Используя формулы , получаем
.
Используя формулы , получаем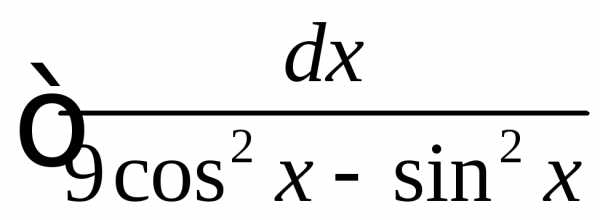 .
.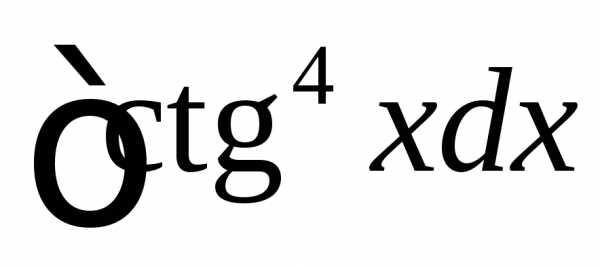 .
.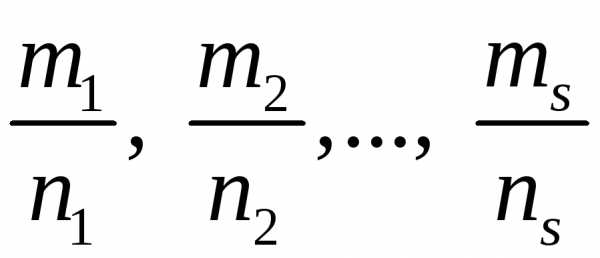 сводятся к интегралам от рациональных
функций переменнойt.
сводятся к интегралам от рациональных
функций переменнойt.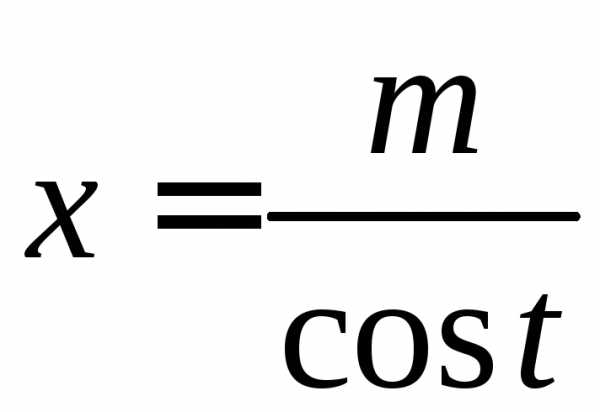 в
в 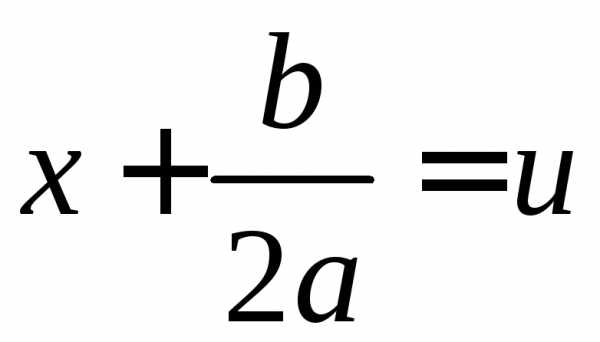 ,
получим интеграл одного из видов ,
или .
,
получим интеграл одного из видов ,
или .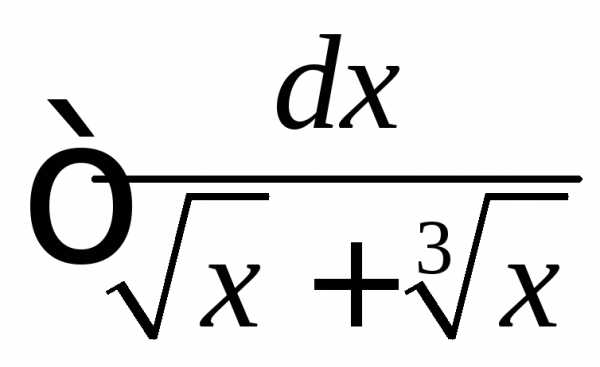 .
.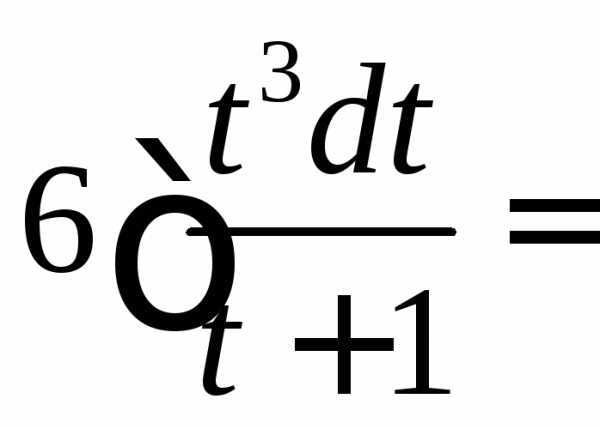
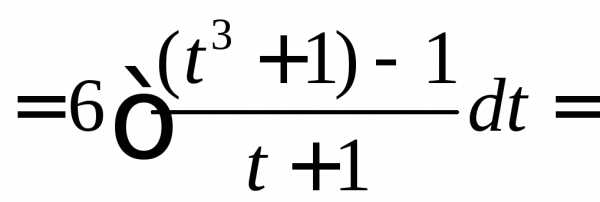
 .
.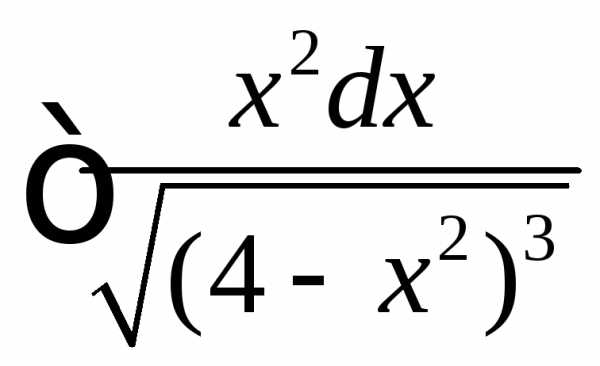 .
.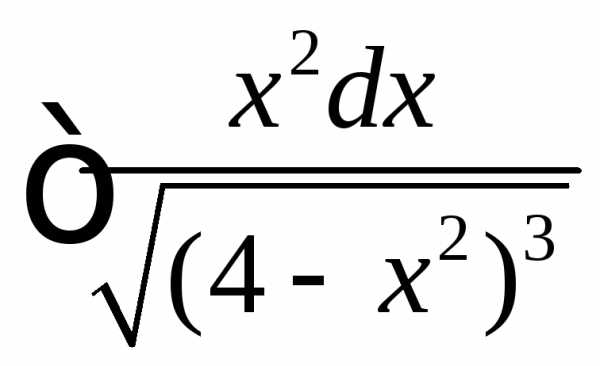 =
=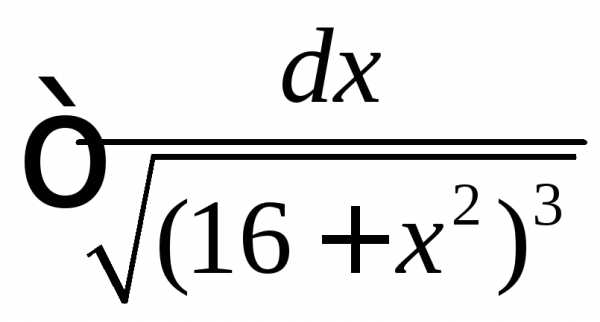 .
.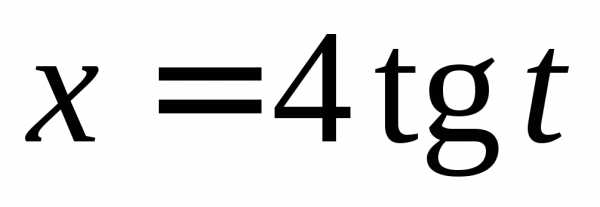 ,.
,.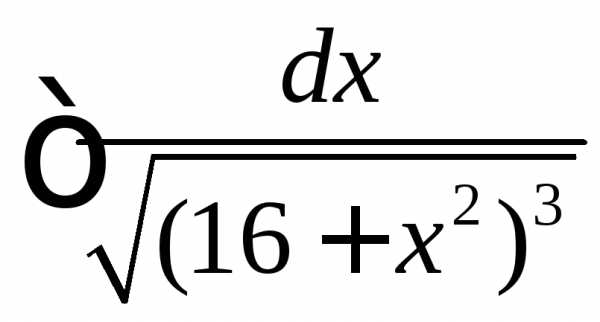 =
=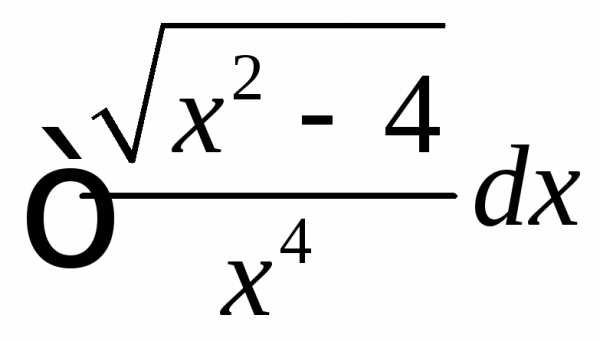 ,
,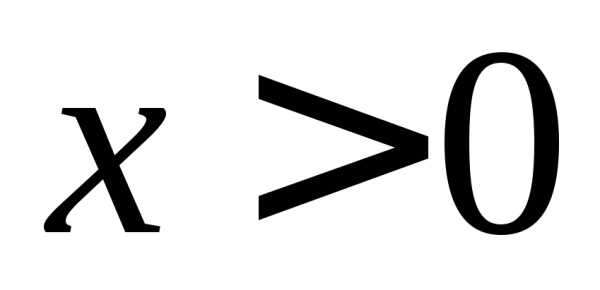 .
.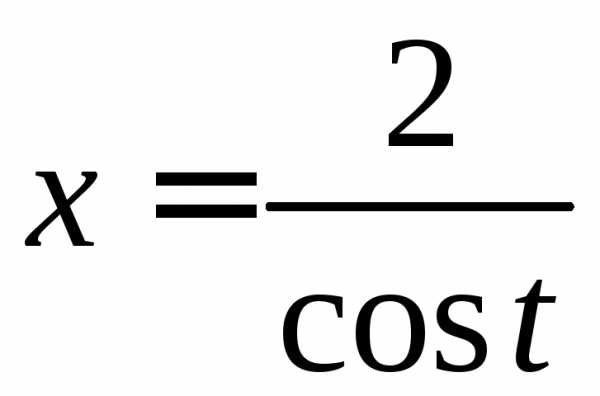 (.
(.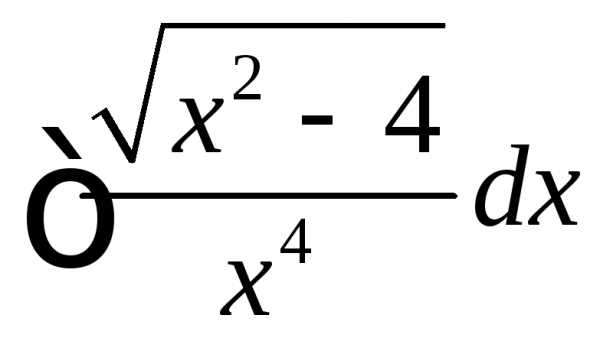
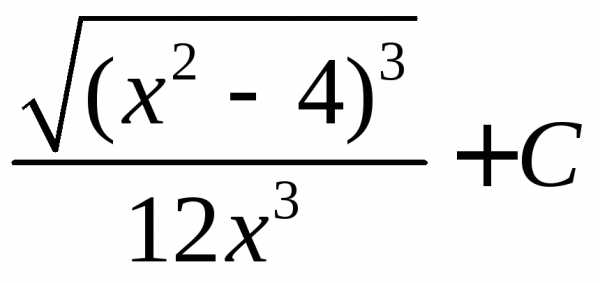 .
►
.
►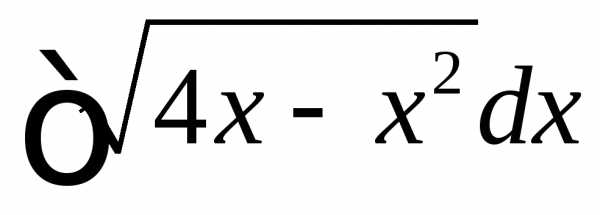 .
.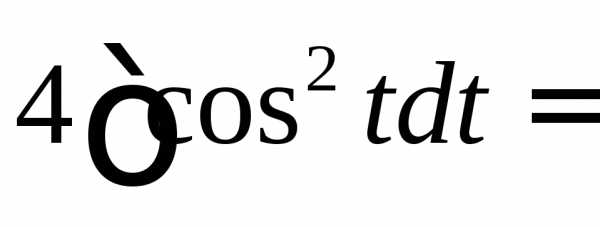
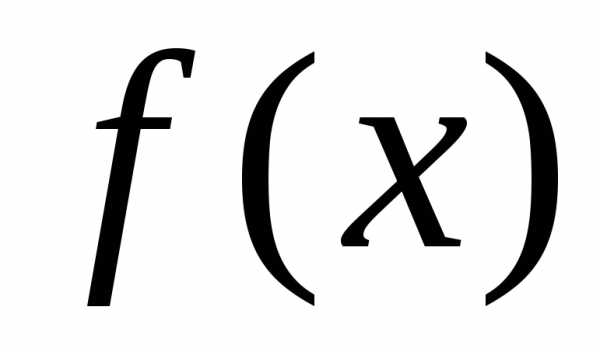 определена на отрезке
определена на отрезке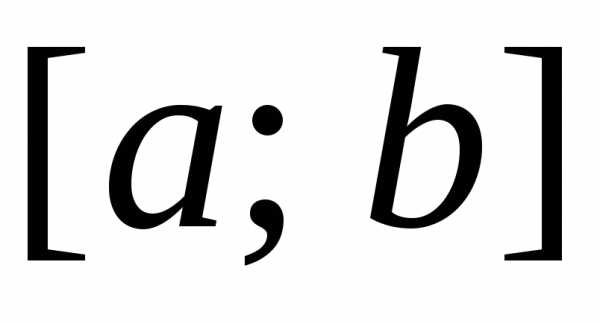 .
Разобьем этот отрезок точкамина частичные отрезки
.
Разобьем этот отрезок точкамина частичные отрезки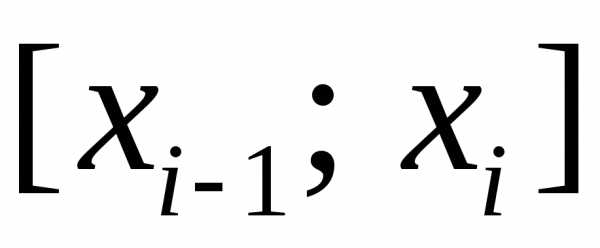 ,,
длины.
Наибольшую из этих длин
,,
длины.
Наибольшую из этих длин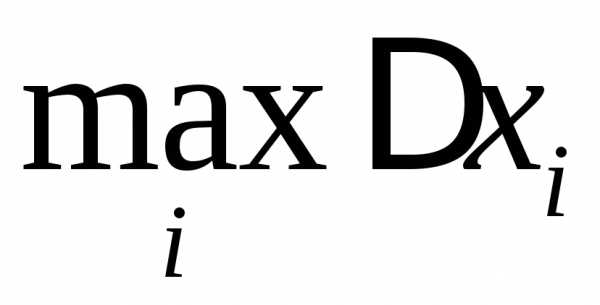 назовеммелкостью
разбиения.
В каждом из частичных отрезков
назовеммелкостью
разбиения.
В каждом из частичных отрезков 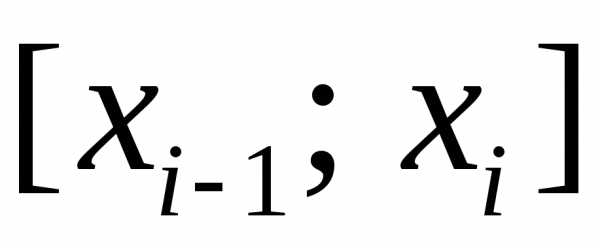 выберем точку
выберем точку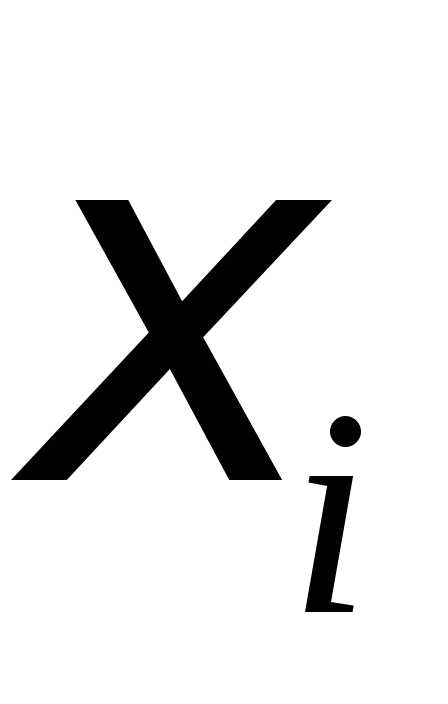 (рис. 1). Составим интегральную сумму
(рис. 1). Составим интегральную сумму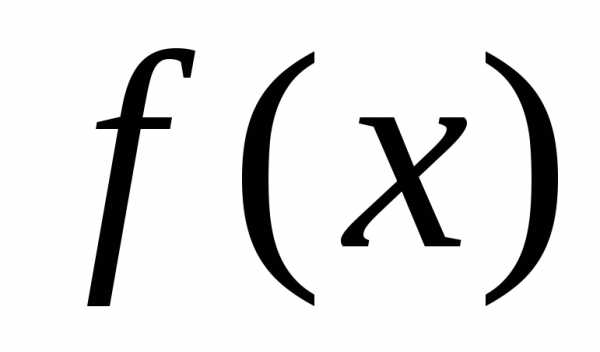 по отрезку (в пределах от
по отрезку (в пределах от до
до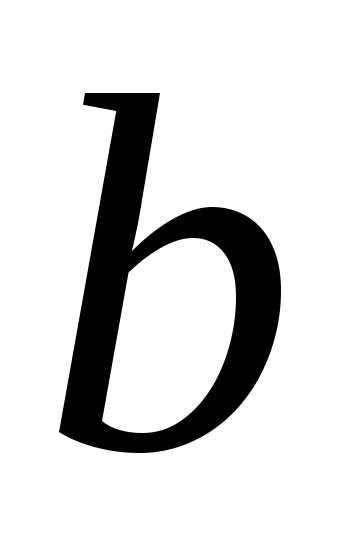 )
называется число (оно обозначается
)
называется число (оно обозначается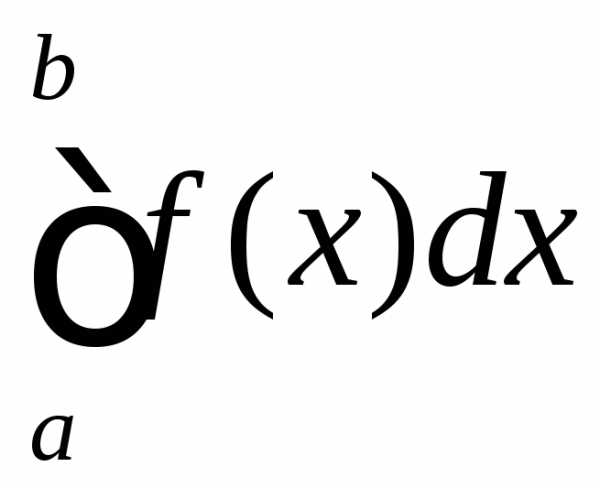 ),
равное пределу интегральных сумм при
неограниченном измельчении разбиения:
),
равное пределу интегральных сумм при
неограниченном измельчении разбиения: найдется такое
найдется такое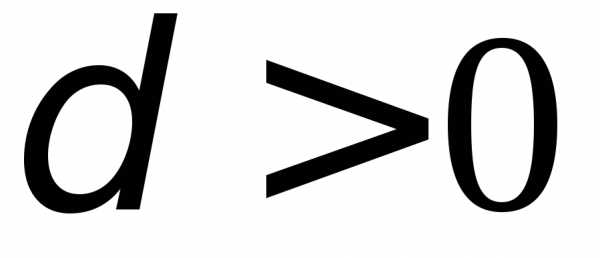 ,
что для любого разбиения с мелкостью
,
что для любого разбиения с мелкостью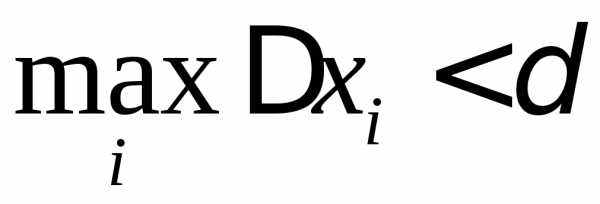 при любом выборе точек
при любом выборе точек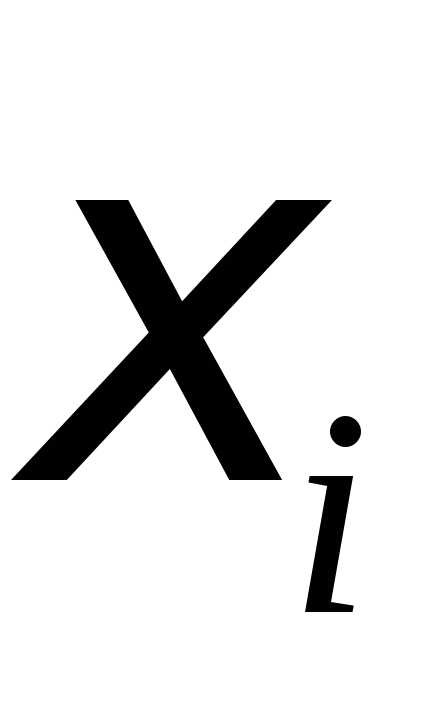 выполняется неравенство
выполняется неравенство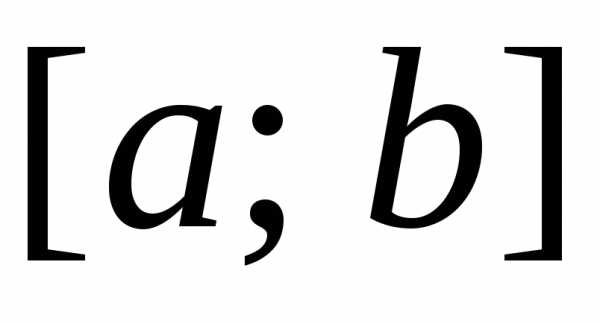 ,
определенный интеграл по этому отрезку
существует –функция
интегрируема по отрезку
,
определенный интеграл по этому отрезку
существует –функция
интегрируема по отрезку 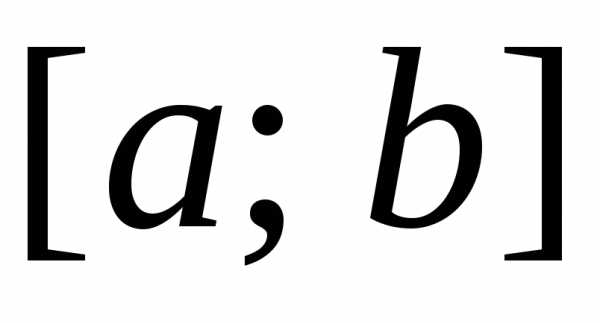 .
.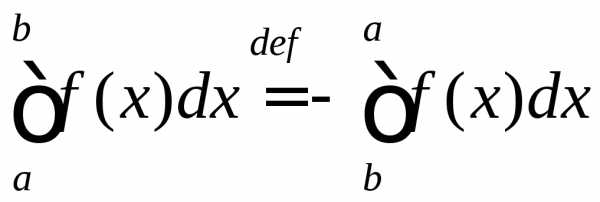 при
при  ;
и
;
и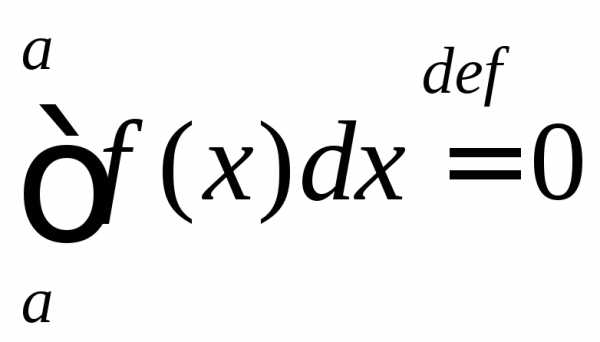 .
.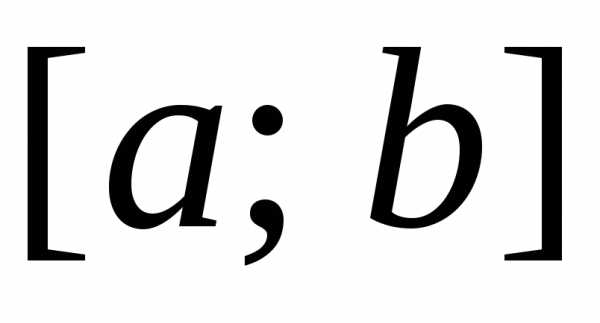 на достаточно большое число
на достаточно большое число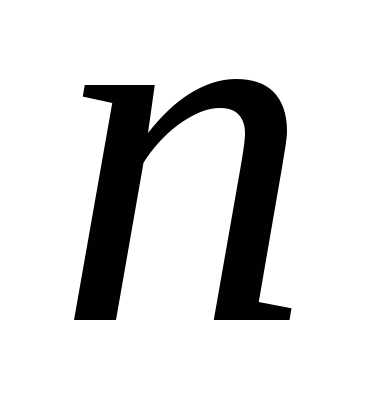 равных отрезков длины
равных отрезков длины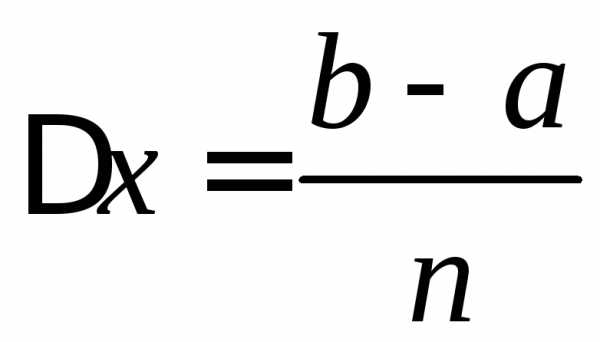 ,
за
,
за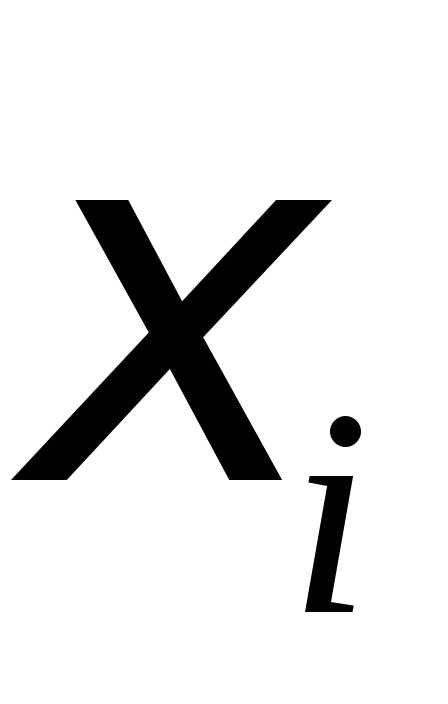 берем середину
берем середину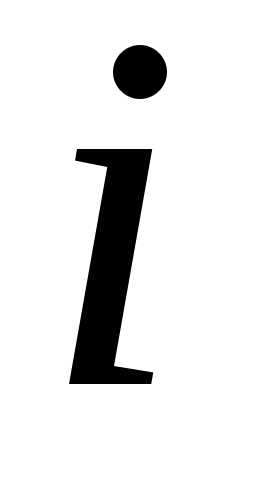 -го
отрезка1
-го
отрезка1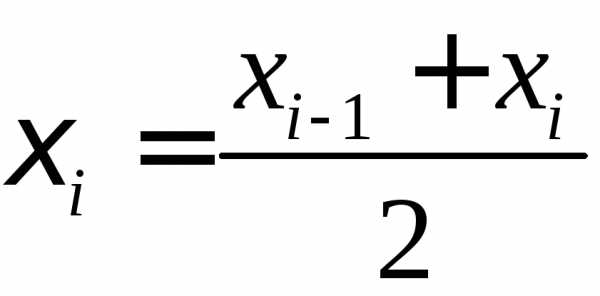 .
В качестве приближенного значения
интеграла принимаем интегральную сумму:
.
В качестве приближенного значения
интеграла принимаем интегральную сумму: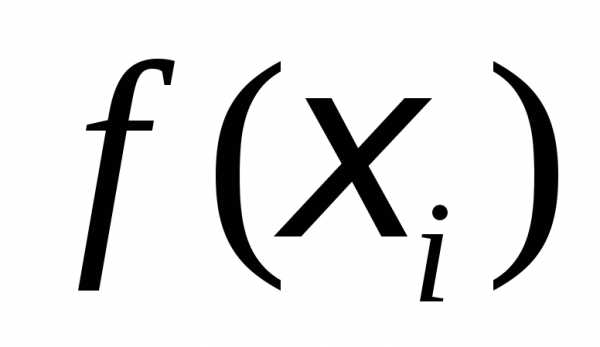 и основанием(рис.1),
откуда и происходит название метода.
и основанием(рис.1),
откуда и происходит название метода.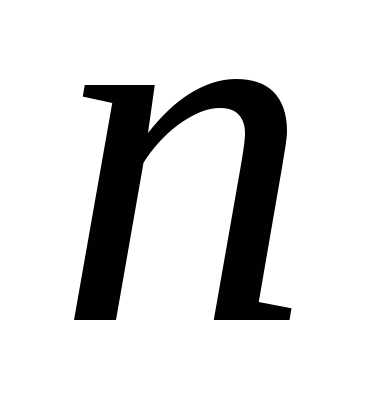 ,
то
,
то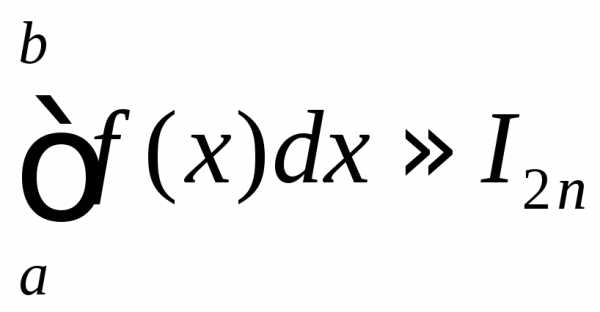 с точностью до
с точностью до .
.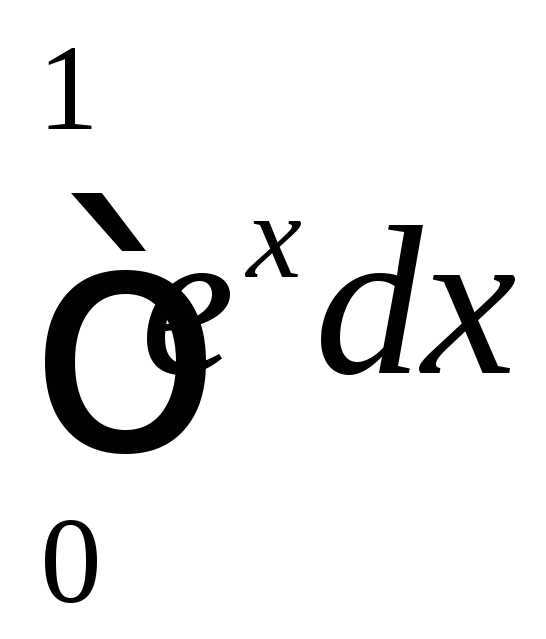 по определению, как предел интегральных
сумм.
по определению, как предел интегральных
сумм.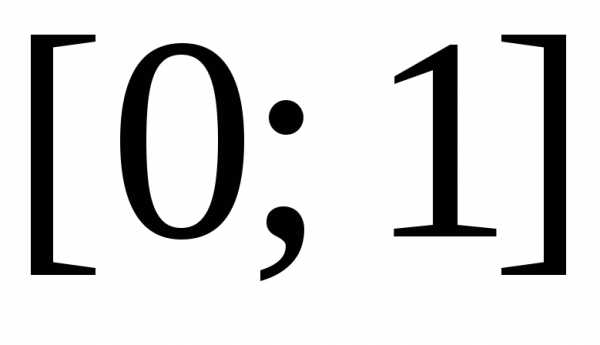 разобьем точками
разобьем точками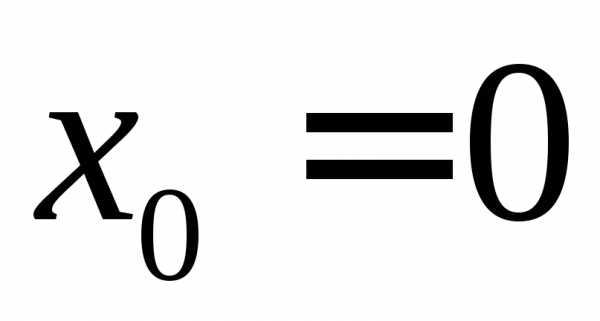 ,
,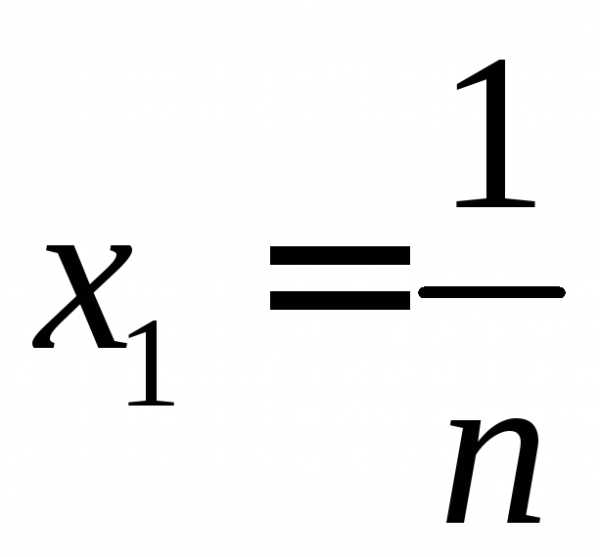 ,на частичные отрезки
,на частичные отрезки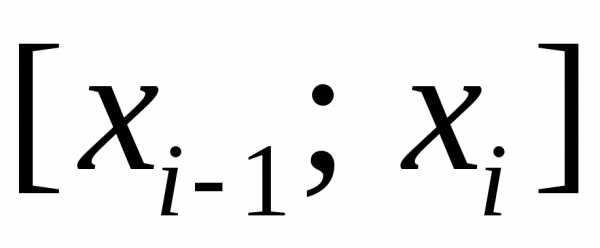 ,,
одинаковой длины
,,
одинаковой длины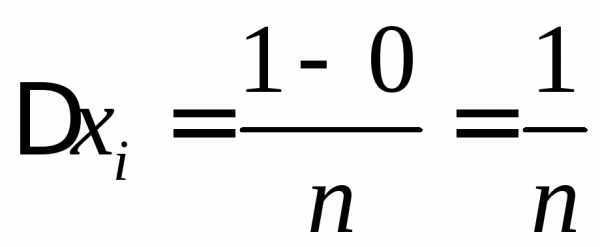 .
Возьмем
.
Возьмем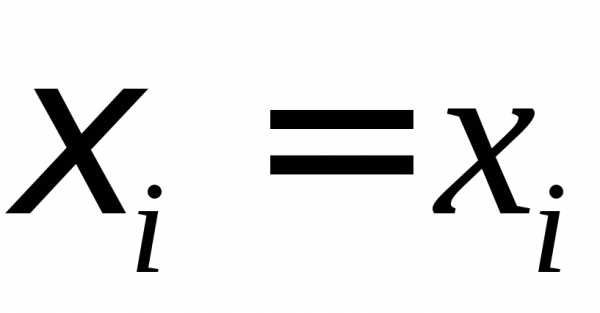 ,.
Составим интегральную сумму для функции
,.
Составим интегральную сумму для функции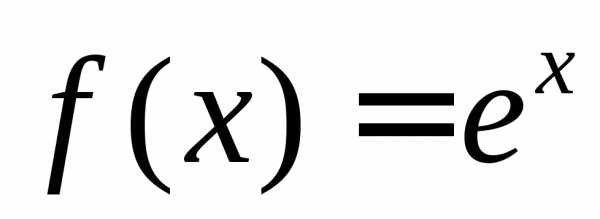
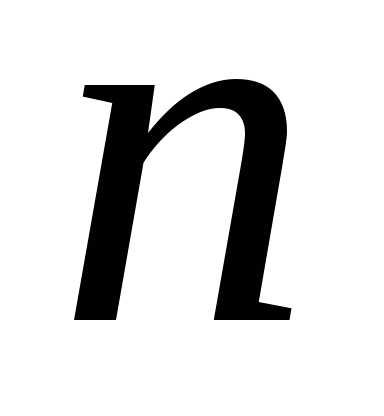 членов геометрической прогрессии со
знаменателем
членов геометрической прогрессии со
знаменателем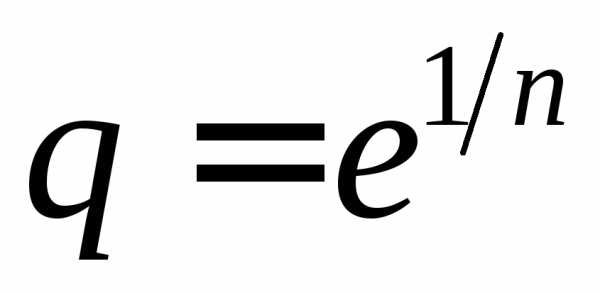 и первым членом
и первым членом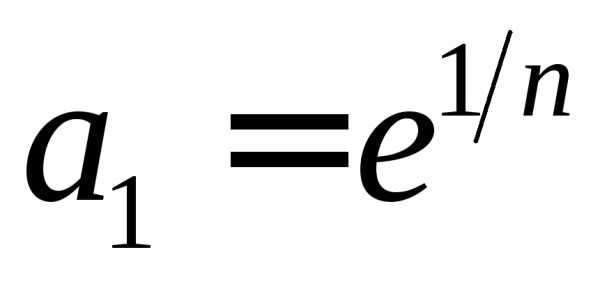 .
Она равна
.
Она равна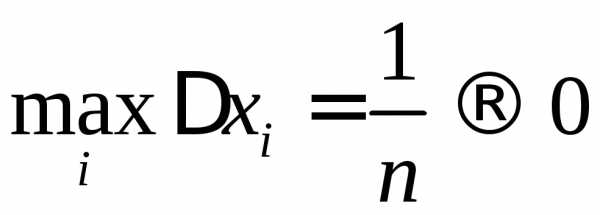 ().
().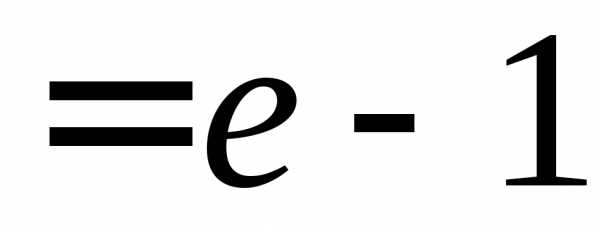 .►
.►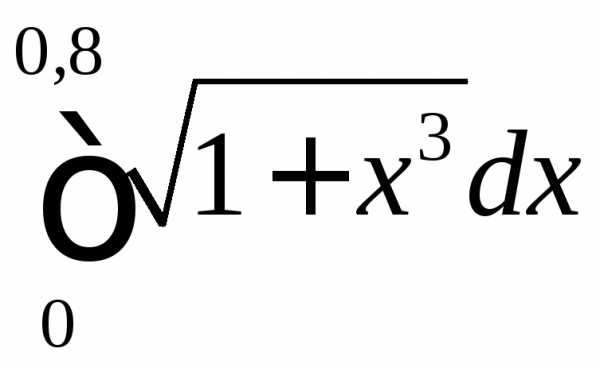 методом прямоугольников (методом
средних) с точностью до.
методом прямоугольников (методом
средних) с точностью до.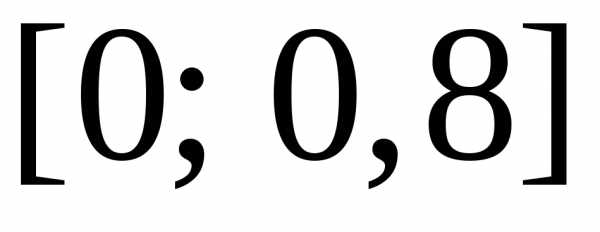 на
на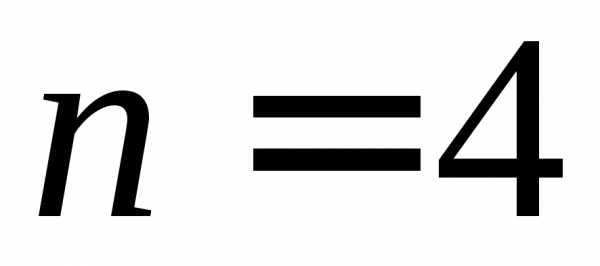 равных отрезков. Их длина
равных отрезков. Их длина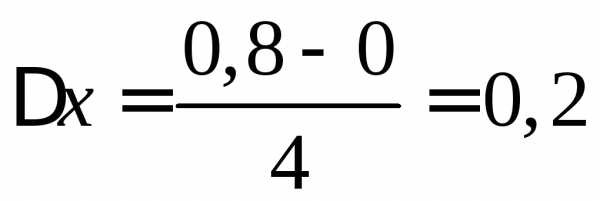 .
Поэтому точки деления
.
Поэтому точки деления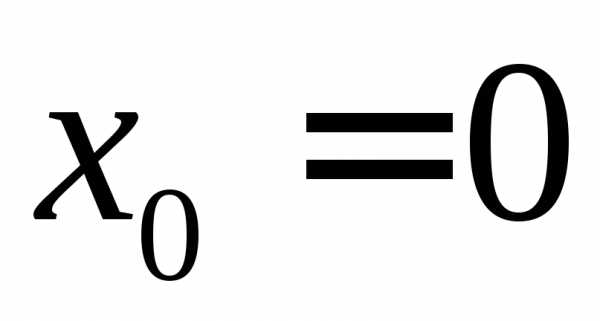 ,
,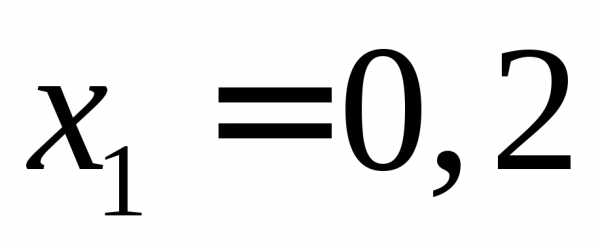 ,
,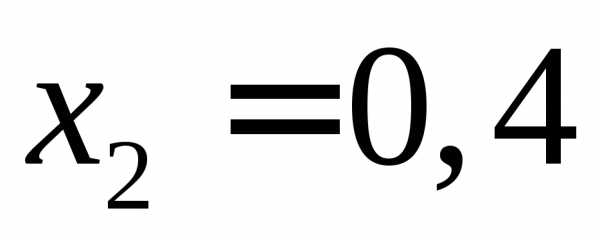 ,
,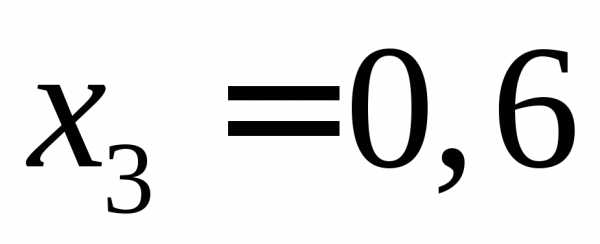 ,
,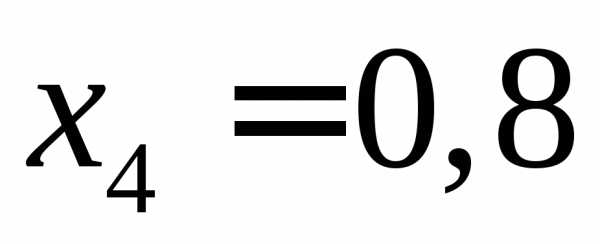 .
Составим табл. 1.
.
Составим табл. 1.
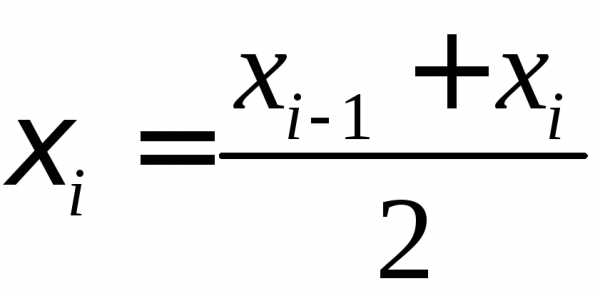
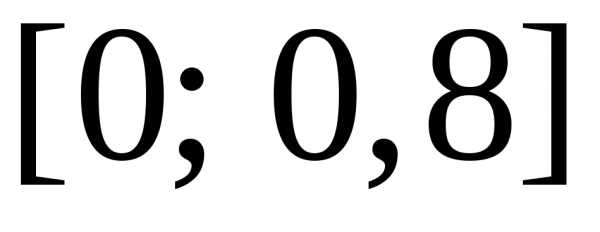 на
на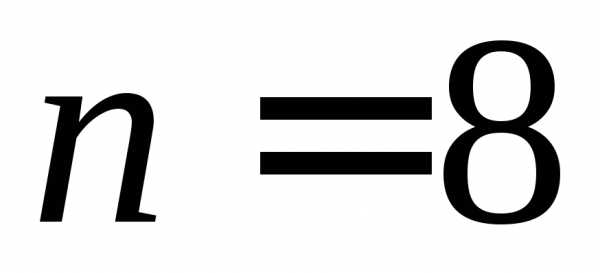 равных отрезков. Их длина
равных отрезков. Их длина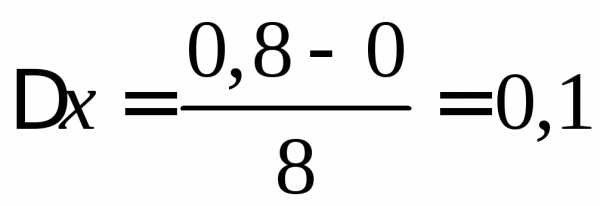 .
Поэтому точки деления
.
Поэтому точки деления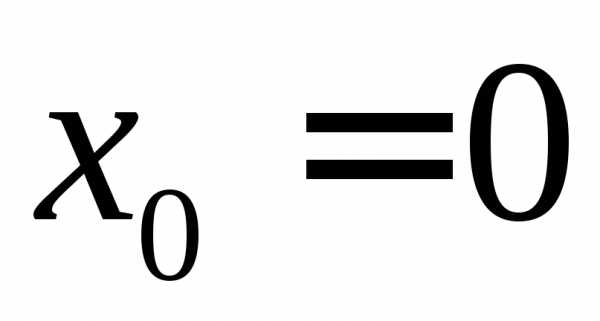 ,,
,,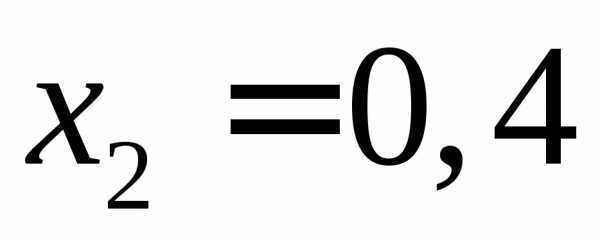 ,
…,
,
…,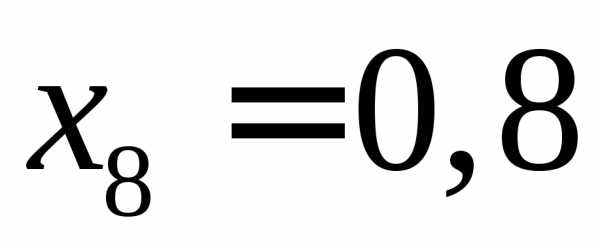 .
Составим табл. 2.
.
Составим табл. 2.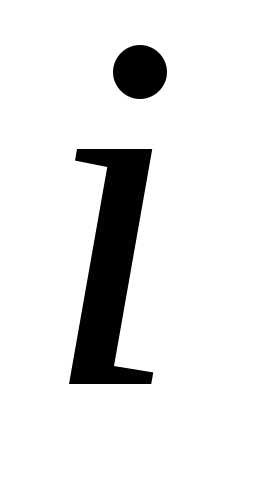
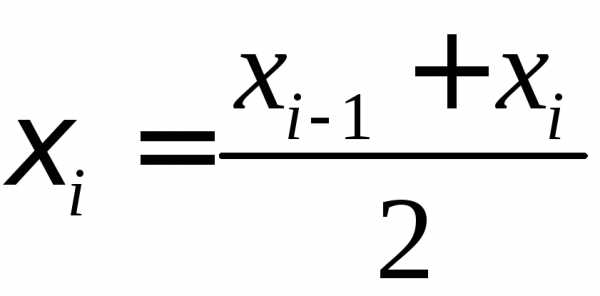
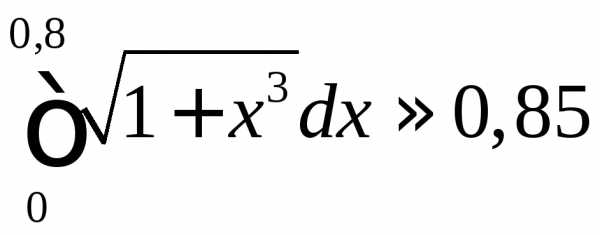 .
. могло бы оказаться, что.
Тогда для достижения заданной точности
могло бы оказаться, что.
Тогда для достижения заданной точности следует продолжить вычисление интегральных
сумм
следует продолжить вычисление интегральных
сумм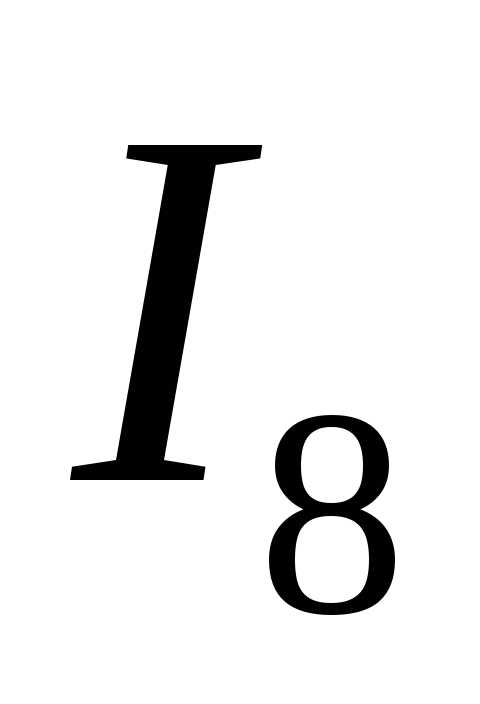 ,
,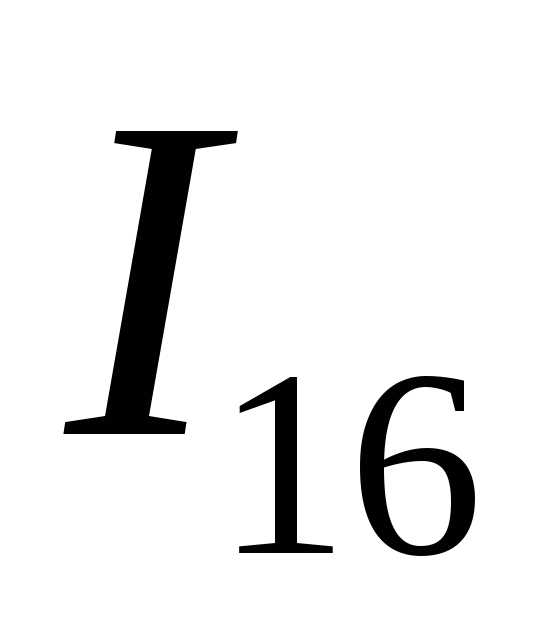 ,
,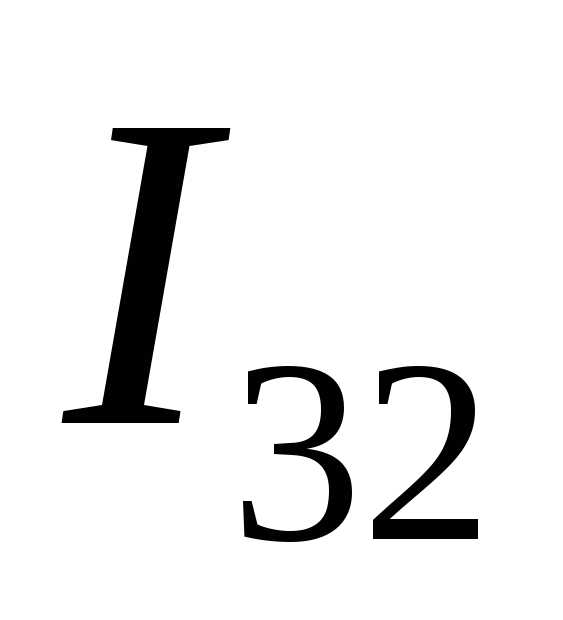 ,
… до тех пор, пока абсолютная величина
разности двух соседних членов этой
последовательности не станет
,
… до тех пор, пока абсолютная величина
разности двух соседних членов этой
последовательности не станет .
►
.
►