Тест: Умножение и деление на 2 и 3
Данный тест можно использовать для закрепления или проверки умения решать задачи на умножение, умение устанавливать связи между компонентами и результатами действий.
Математика 2 класс | Автор: Хусаинова Суембика Вахитовна | ID: 1963 | Дата: 7.4.2014
«;} else {document.getElementById(«torf1″).innerHTML=»»;};
if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;};
if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;};
if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;};
if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;};
if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;};
if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;};
if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;};
}
}
Получение сертификата
о прохождении теста
testedu.ru
Умножение и деление чисел на 2 и на 3.(закрепление)
Умножение и деление чисел на 2 и на 3.(закрепление)
05.06.2012, 16:12
Урок математики во 2 классе .Образовательная программа «Начальная школа 21 века»
Тема: Умножение и деление чисел на 2 и на 3.
Цели:
1) Закрепить знание табличного умножения и деления на 2 и на 3.
Развивать вычислительные навыки учащихся.
2) Продолжить обучение решению задач с использованием действий умножения и деления.
3) Работать над формированием универсальных учебных действий (УУД), повышением познавательной активности обучающихся.
4) Воспитывать у учащихся чувство взаимовыручки.
Презентация сказки «Гуси- лебеди» , аудиозапись сказки «Гуси-лебеди»,презентация «Львёнок ищет друзей»
Этап урока
Планируемые результаты (общеучебные умения и действия – УУД)
1.Организационный момент
Формирование внутренней позиции школьника на уровне положительного отношения к урокам математики.
2. Устный счёт
Умение формулировать выводы на основе сравнения, обобщения.
3. Объявление темы и задач урока
Умение проявлять инициативу в учебно-познавательной деятельности.
4. Актуализация опорных знаний
Умение кодировать информацию в знаково — символической форме.
В сотрудничестве с учителем проводить классификацию изучаемых объектов,
формулировать выводы на основе сравнения, обобщения.
5. Повторение таблицы умножения и деления на 2,на 3.
Принимать активное участие в работе группами.
Контролировать свои действия в коллективной работе.
Принимать учебную задачу и следовать инструкции учителя.
Ориентация на понимание оценок учителя и одноклассников.
Проявлять инициативу в учебно- познавательной деятельности.
6. Проверка знания таблицы умножения и деления на 2,на 3.
Принимать учебную задачу и следовать инструкции учителя.
Контролировать свои действия в коллективной работе.
Принимать учебную задачу и следовать инструкции учителя.
Ориентация на понимание оценок учителя и одноклассников.
Понимание чувств одноклассников.
7. Физминутка
Формирование коммуникативных умений.
8. Решение задач с использованием действий умножения и деления.
Понимание нравственного содержания поступков окружающих людей.
Умение строить простые индуктивные и дедуктивные рассуждения
Умение стремиться к координации различных мнений в сотрудничестве; умение договариваться, приходить к общему решению.
Формирование интереса к познанию математических фактов.
Умение осуществлять поиск нужной информации,
строить небольшие математические сообщения в устной форме.
Интерес к различным видам учебной деятельности, включая элементы предметно- исследовательской деятельности.
Умение планировать свои действия в соответствии с учебными задачами и инструкцией учителя
Умение моделировать задачи на основе анализа жизненных сюжетов.
Умение принимать установленные правила в планировании и контроле способа решения.
Формирование самооценки на основе заданных критериев успешности учебной деятельности
9.Подведение итога урока.
Понимание причин успеха в учёбе.
Самооценка на основе заданных критериев успешности учебной деятельности
10.Домашнее задание.
11.Рефлексия
Понимание причин успеха в учёбе.
Ход урока:
1. Организационный момент.
Слайд 2
-Я хочу начать урок следующими словами:
«Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” (Ж.Ж.Руссо)
— Пусть эти слова будут напутствием на уроке.
2. Устный счёт.
Слайд 3
-Посчитаем устно.
60-48= 58+6= 50+29= 3*6= 45-7=
(Объясняют способ вычисления, заменяя числа, где необходимо, суммой разрядных или удобных слагаемых)
-Какой пример лишний? Почему?
(3*6=18 – лишний, т. к. он на умножение)
-Составьте по данному примеру другой пример на умножение и примеры на деление.
(6*3=18, 18:3=6, 18:6=3)
(При перестановке слагаемых произведение не изменяется.
Если произведение разделить на 1 множитель, то получится 2 множитель и наоборот)
3. Объявление темы и задач урока.
— Догадались ли вы, какова тема нашего урока?
(Умножение и деление чисел.)
-Умножение и деление чисел на 2 и на 3.
-Давайте вместе подумаем, что нам нужно повторить и чему учиться на уроке.
-Повторить правила (законы) умножения и деления
-Закрепить знание таблицы умножения и деления на 2 и на 3
-Учиться решать задачи с использованием действий умножения и деления.
Слайд 4
-Таковы задачи нашего урока и мы должны их выполнить.
4. Актуализация опорных знаний.
-Какие правила и законы нам могут пригодиться на уроке? Лишние мы уберём, а нужные разделим на группы.
а*в = в*а а+в = в+а
а*1 = а а+(в+с) = (а+в)+с
а:1 = а а:а = 1
а+0 = а а*0 = 0
а:0 а:2- половина
а:3- треть
-Какие группы мы получили?
Деление Умножение
а:1 = а а*в = в*а
а:а = 1 а*1 = а
а:0 (на 0 делить нельзя) а*0 = 0
а:2- половина
а:3- треть
-Что мы повторили?
( Правила и законы умножения и деления.)
-Мы выполнили одну из поставленных задач.
5. Повторение таблицы умножения и деления на 2,на 3.
-Повторим таблицу умножения на 2 и на 3. Работать будем в группах.
а) Повторение правил работы в группах.
( Работать без шума. Не ссориться, не спорить, работать дружно, помогать друг другу…)
-Подберите синонимы к слову помогать.
(Помогать, спасать, выручать)
-Я очень хотела бы, чтобы вы всегда выручали друг друга не только на уроке, но и в жизни. Это очень важно для нас всех.
б) Повторение таблицы умножения на 2 и на 3.
-Мы повторим таблицу умножения на 2 и на 3. Кто будет затрудняться, группа тому поможет.
(Дети работают в группах. По цепочке, по очереди задают друг другу примеры на табличные случаи умножения на 2, на 3.)
-Вы уже не первый раз проверяете знание таблицы умножения. Кто из членов вашей группы лучший знаток таблицы?
(Каждая группа называет ученика.)
-Аплодисменты лучшим знатокам.
в) Повторение таблицы деления на 2.
-Встаньте, пожалуйста, поиграем в игру «Горячий мяч». Ведущий называет пример и подаёт мяч кому-то из детей. Стараемся ответить и передать мяч водящему очень быстро, он горячий.
г) Повторение таблицы деления на 3.
(Используется презентация «Львёнок ищет друзей»)
— Выручите Львёнка, помогите ему собрать друзей. А вместе с тем повторим таблицу деления на 3.
-Молодцы, вы выручили Львёнка, у него теперь много друзей.
д) Подведение итога работы на данном этапе.
-Что мы повторили и закрепили?
-(Таблицы умножения и деления на 2,на 3.)
-Мы справились ещё с одной задачей урока.
6. Проверка знания таблицы умножения и деления на 2,на 3.
-А сейчас мы проверим свои знания.
Математический диктант:
-2 умножить на 7.
-По 3 взять 5 раз.
-Запишите произведение чисел 5 и 2.
-3 разделить на 3
-Первый множитель 3, второй множитель 9, запишите произведение.
-12 разделить на 2
-Чему равно произведение чисел 2 и 0?
-Поменялись тетрадями по кругу, взаимопроверка, проверяем работу соседа.
-Правильные ответы на доске: 14,15, 10, 1, 27, 6, 0.
-Поменялись тетрадями опять по кругу, но в обратном направлении.
-Посмотрите свои работы. У кого нет ошибок? Это будущие отличники.
( Во 2 классе оценки пока не выставляются).
-У кого 1-2 ошибки? Будущие хорошисты.
-У кого ошибок было больше, руку поднимать не нужно, мысленно скажите себе: « Я должен повторить таблицу умножения и деления на 2, на3»
— Что мы проверили?
(Знание таблицы умножения и деления на 2, на 3.)
-Результатами я осталась довольна, спасибо, вы старались.
7.Физминутка.
-Я предлагаю отдохнуть.
(Выполняются танцевальные упражнения под музыку, которые показывает одна из подготовленных учениц.)
8. Решение задач с использованием действий умножения и деления.
а) Беседа по сказке. Слайды 5, 6, 7, 8, 9, 10
-Конечно, все вы знаете эту сказку, но я вам её напомню.
(Слушают отрывок из сказки «Гуси- лебеди»(запись прилагается) и просматривают слайды.)
-К кому обращалась за помощью девочка?
-К печке, яблоньке, речке. Слайд 11
-Почему они не выручили девочку?
(Она была невежлива, отказывалась от угощения)
-У нас на уроке эта сказка на новый лад. Кроме угощения герои приготовили девочке задачи. Выручим девочку, поможем ей решить задачи?
б) Решение задач. (Работа в группах)
-Задача печки.Слайд 12
Испекла я 24 пирожка.
Разложила их на 3 тарелки.
Сколько пирожков на каждой тарелке?
-Посовещайтесь в группе, каким действием решается задача? Выберите карточку с верным решением.
(Показывают карточку (действие : ) 24:3=8(п))
-Задача речки. Слайд 13
За день путники выпивают по 2 кувшина киселя.
Сколько кувшинов киселя они выпьют за неделю?
— Что такое неделя?
( 7 дней)
-Почему неделю так назвали? Ребята поработали заранее и нашли ответ на вопрос. Послушайте. (Использовались Интернет и толковый словарь)
(Особым почётом в древности была окружена семёрка. Отголоски почитания числа 7 дошли до наших дней. Вспомните пословицы: Семь бед — один ответ. Семеро одного не ждут. Наша неделя состоит из 7 дней. Древние заметили, что 7 нельзя поделить на равные части. Вот и назвали 7- не – деля. (Интернет)
-Неделя — образовано от словосочетания «не делать», то есть отдыхать. Неделя — означало «день отдыха». (Толковый словарь.)
-Ещё раз посмотрите на задачу. Каким действием решается? Посовещайтесь в группе и выберите верное решение.
(Показывают карточку (действие *) 2*7=14 (к)
-Задача ёжика в учебнике, с. 90 №21. Слайд 14
Маша нашла 27 грибов. Треть из них – подосиновики. Сколько подосиновиков нашла Маша?
(Совещаются. Показывают карточку (действие : ) 27:3=9(п) )
в) Решение задач коллективно.
-Задача яблоньки. Слайд 15
В корзине было несколько яблок. Девочка с братцем съели по 3 яблочка и ещё осталось 5 яблок. Сколько яблок было сначала?
(Задача подробно анализируется коллективно и решается письменно.)
(Чтобы узнать сколько яблок было, нужно знать, сколько их съели и сколько осталось. Сколько осталось известно, а сколько съели мы не знаем, но известно, что съели 2 человека по 3 яблока. Значит, можно узнать.
-Расскажите план решения задачи.
-Что узнаем 1 действием?
(Сколько яблок съели.)
-Что узнаем 2 действием?
(Сколько яблокбыло.)
-Запишем решение вместе.
1) 3*2=6(яб.) — съели.
2) 6+5=11(яб.) — было.
-Мы выручили девочку, решили все задачи, она обязательно спасёт братца. Слайд 16
г) Составление и решение задачи.
-Теперь вернёмся из сказки в нашу жизнь. Пойдём в кино.
(Встали, имитация ходьбы.)
-Займите места. Смотрим немое кино. Вы ничего не услышите, а всё, что увидите, считайте.
( Дети показывают сценку:
Мама покупает в магазине конфеты, продавец даёт ей 14 штук. Мама приходит домой. Сидят 3 детей. Мама даёт каждому по 2 конфеты. Остальные лежат в пакете.)
-Расскажите, что вы увидели?
(Мама купила 14 конфет. Дома она дала трём детям по 2 конфеты.)
-Можно ли это назвать задачей? Чего не хватает?
(Вопроса.)
-Поставьте к задаче вопрос.
(Сколько конфет осталось у мамы?)
(Анализ задачи:
Чтобы узнать сколько конфет осталось у мамы, нужно знать сколько конфет мама купила и сколько она отдала детям. Сколько конфет купили известно, а сколько отдали мы не знаем, но знаем, что трём детям по 2 конфеты, а значит можем узнать.
-Обсудите план решения в группах.
-Что узнаем 1 действием?
( Сколько конфет мама отдала.)
-Что узнаем 1 действием?
( Сколько конфет осталось у мамы.)
— Один из вас за доской будет решать задачу, а остальные решат её самостоятельно.
1) 2*3=6(к.) – отдала.
2) 14-6=8(к.)- осталось.
-Самопроверка. Сверьте соё решение с решением ученика на доске.
-А теперь проверим, сколько конфет лежит в пакете. Вывод?
(Задача решена верно)
-Чему мы учились?
(Решать задачи)
-Мы выполнили ещё одну задачу, которую поставили перед собой в начале урока.
Значит, все задачи выполнены. Молодцы!
9. Подведение итога урока.
-Подведём итог нашей работы.
Нам поможет карточка – помощница.
-На уроке я повторил…
-Я учился…
-На уроке мне было…
-Я понял, что…
-Я радовался…
-Я всегда буду…
(Дети читают начало в карточке и сами заканчивают мысль)
-На уроке я повторил… таблицу умножения и деления на 2, на 3.
-Я учился… решать задачи.
-На уроке мне было… (интересно, скучно, легко, трудно…)
-Я понял, что… надо знать таблицу, уметь решать задачи
-Я радовался… (успехам товарищей, своим успехам, полученным знаниям)
-Я всегда буду… выручать своих товарищей.
10. Домашнее задание.
-Просмотрите домашнее задание. Что вам не понятно?
с.90 №25, с. 88 №11.
11. Рефлексия.
-Поднимите тот смайлик, который выражает ваше настроение после урока.
-Спасибо за урок.
infourok.ru
Умножение и деление на 2 и 3.
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ШКОЛА № 47 ГОРОДА ДОНЕЦКА»
учитель начальных классов
Мужецкая Светлана Дмитриевна
высшая категория
Математика
2 класс
Тема: Закрепление. Умножение и деление на 2 и 3.
Цели: закрепить таблицу умножения и деления на 2 и 3, отрабатывать вычислительные навыки, умение решать задачи и уравнения, развивать умение рассуждать, доказывать, работать в парах развивать творческое мышление и формировать интерес к предмету, воспитывать навыки культурного поведения, дружелюбия, взаимопомощи.
Ход урока
Подготовка и мотивация
2. Контроль подготовленности учащихся к восприятию основного. Слайд 1
— Ребята, к нам пришло письмо.
— От кого оно? Откуда? Мы узнаем, если решим примеры
На доске:
2х3 4х2 5х3 7х2 1х2
6:3 9:3 12:6 8:2
— От кого это письмо?
— Откуда оно?
Урок математики мы проведём вместе с героями книги Э. Успенского…..
(показ книги)
3. Сообщение темы и целей урока. Слайд 2
— Кто догадался, по какой теме мы будем работать?
— Правильно. Тема урока: Закрепление. Умножение и деление на 2 и 3.
Вместе с героями мы повторим таблицу умножения и деления на 2 и 3, закрепим умения решать задачи и уравнения, будем учиться думать и другу помогать.
4. Устный счёт.
1. а) Работа с тренажёрами.
— А чтобы собраться в путь, мы проведём разминку в парах и проверим таблицу умножения
б) Проверка.
— Поднимите руку те, кто не допустил ошибок. Молодцы!
А что мы посоветуем тем ребятам, кто допустил ошибки?
Минутка чистописания.
3. а) Работа по карточкам с разно уровневыми заданиями.
— Итак, мы направляемся в деревню Простоквашино. Слайд 3
У нас есть карта, на ней 3 маршрута: красный, синий, жёлтый. Возьмите на парте карточку с маршрутом и устно посчитайте протяжённость каждого участка. Ответы запишите в тетрадь. Пишите красиво и аккуратно.
б) Самопроверка. (ответы на доске) Слайд 4
5. Решение задачи. Повторение компонентов при умножении и делении. Слайд 5
— Вот мы и в деревне. А тут всё кувырком. Пока кот Матроскин смотрел телевизор, по двору разбежались цыплята. Нужно помочь ему собрать и сосчитать цыплят самым быстрым способом. Каким?
Запись: 3х4=12
— Как называются компоненты при умножении?
— А теперь поможем рассадить кроликов в клетки. Слайд 6
Составьте задачу, можем узнать сразу, каким действием?
Запись: 8:2=4
Проверка с доски.
— Как называются компоненты при делении?
Молодцы! Из книги Э. Успенского мы узнали, «…что дядя Фёдор был серьёзным, самостоятельным мальчиком. В 4 года читать научился, а в 6 лет уже суп варил…» (показ книги)
Физкультминутка
6. Игра-разминка для ума от дяди Фёдора «Домики», сидя за партами.
7. Тест «Верите ли вы…»
— Верите ли вы, что произведение чисел 3 и 0 равно 0?
— …что если какое-либо число разделить на 1. то получится это же число?
— …что если число разделить на это же число, то получится 0?
— …что если какое-нибудь число умножить на 0, то получится это же число?
— …что если какое-нибудь число умножить на единицу, то получится это же число?
— Молодцы!
8. Решение уравнений.
1. Работа по учебнику.
– Как-то раз дядя Фёдор рассказывал своим друзьям удивительную историю про математические иероглифы. А что это за иероглифы, мы узнаем, открыв учебники.
Это уравнения. Решаем их по рядам:
1 ряд — 1 столбик, 2 ряд — 2 столбик, 3 ряд — 3 столбик
3 ученика работают у доски.
2. Проверка с проговариваем компонентов.
9. Решение геометрических задач.
— Пока мы с вами решали уравнения, пёс Шарик трудился на огороде.
— Какую геометрическую фигуру напоминает его участок? Слайд 7
— Что такое прямоугольник?
10. Работа по слайду 8.
— Шарик разметил участок для посадки овощей на равные части. Сколько прямоугольников у него получилось?
— Проверим.
— Эта грядка для посадки капусты. Что известно о сторонах прямоугольника?
— Что надо узнать?
— Что такое Р?
Составим задачу про грядку.
— Можем ли мы сразу вычислить периметр?
— Что сказано о ширине?
— Каким действием найдём длину? Запись решения по действиям.1 ученик работает у доски.
— Найдите периметр этой грядки разными способами.
1 ученик у доски.
Физкультминутка
Мы капусту режем,
Мы капусту трём.
Мы капусту солим,
Мы капусту жмём.
11. Закрепление «Игра». Слайд 9, 10, 11, 12, 13
После работы наши герои любили собраться за столом и пить чай. Конфеты они всегда делили поровну. На экране вы увидим число, разделите его пополам на 2 и покажите ответ веером цифр.
12. Итог урока. Рефлексия. Слайд 14
— Ребята, вот и подошёл к концу наш урок. Что мы повторили и закрепили? У кого из вас появилось желание прочитать книги Э. Успенского, которые стоят на книжной полке?
На доске картинка — домик.
— Если вы считаете, что работали на уроке хорошо, с полной отдачей, наклейте на небо нашей картины солнышко, если работали не в полную силу, то наклейте солнышко с тучкой, если вы не понравились себе, то наклейте тучку.
13. Домашнее задание.
Работать с карточками-тренажёрами.
kopilkaurokov.ru
«Умножение и деление на 3». 2-й класс
Разделы: Начальная школа
Цель урока:
- закрепить навыки табличного умножения и деления на 3;
- закрепить умения называть геометрические фигуры;
- отрабатывать вычислительные навыки и решение текстовых задач;
- развивать внимание, зрительную и слуховую память, сообразительность,
логическое мышление, интерес к математике;
- воспитывать чувство взаимовыручки, самостоятельность и
дисциплинированность.
Оборудование: изображение Буратино, Мальвины, лисы Алисы, кота Базилио,
черепахи Тортиллы, нарисованный Буратино из геометрических фигур, 3 сундучка
разных цветов, ключик, разрезанная картинка Буратино в чулане, карточки с
примерами.
Ход урока
I. Организационный момент.
Быть должны у нас в порядке
Книжки, ручки и тетрадки.
А девиз у нас такой:
«Все, что надо, под рукой».
II. Сообщение темы урока, целей.
– Я предлагаю на сегодняшнем уроке математики побывать в сказке. Если вы
отгадаете загадку, то узнаете главного героя.
У отца был мальчик странный,
Необычный, деревянный,
На земле и под водой,
Ищет ключик золотой,
Всюду нос сует свой длинный.
Кто же это? (Буратино Рисунок 1)
– Буратино по-итальянски означает деревянная кукла. Ребята, а как, называется
сказка и кто ее написал? (Алексей Толстой “Золотой ключик, или Приключения
Буратино”.)
– Если вы сегодня будете хорошо работать, то узнаете тайну “Золотого
ключика”. Вы хотите узнать тайну, тогда начнем нашу сказку.
III. Устный счет.
Задание от Буратино.
Посчитаем по порядку в арифметической зарядке. Сейчас я буду показывать вам
карточки, а вы должны быстро решить примеры:
30 – 27 = (3)
13 + 6 = (19)
40 + 35 = (75) |
44 – 20 = (24)
25 + 8 = (33)
99 – 13 = (86) |
80 – 20 = (60)
32 + 11 = (43)
75 – 25 = (50) |
IV. Актуализация знаний.
– Шел Буратино по тропинке и пришел к домику Мальвины. Мальвина пригласила
Буратино в гости, напоила чаем и решила проверить его знания по математике.
Рисунок 2.
Задача от Мальвины.
12 яблок нужно разложить на тарелки, по 3 яблока на каждую. Сколько тарелок
займут эти яблоки?
– О чем эта задача?
– Что известно о яблоках?
– Что нужно сделать с яблоками?
V. Закрепление табличного умножения и деления на 3.
– Буратино справился с заданием, но за плохое поведение его заперли в чулане.
Чтобы выбраться из чулана, ему нужно собрать картинку, которую подкинула
Мальвина. Давайте поможем Буратино и решим примеры.
Рисунок 3.
VI. Физкультминутка.
Буратино потянулся,
Раз – нагнулся,
Два – нагнулся,
Руки в стороны развел,
Ключик, видно, не нашел.
Чтобы ключик нам достать,
Нужно на носочки встать.
VII. Самостоятельная работа.
– Буратино вышел из чулана, но он хочет доказать Мальвине, что он умный
мальчик. Для этого необходимо решить задачу.
В чулане было 5 паучков, каждый паучок сплел по 3 паутинки. Сколько всего
паутинок в чулане? (Ученики записывают у себя в тетрадях краткую запись и
решение.)
VIII. Работа с геометрическим материалом.
Буратино оставил Мальвине решенную задачу, а сам побежал по дорожке. Но тут
он встретил разбойников лису Алису и кота Бизилио.
(Рисунок 4). Они его хотели ограбить и отнять монеты, если он не
скажет, из каких геометрических фигур он состоит. Рисунок 5.
(Буратино состоит из кругов, треугольников, прямоугольников, квадратов.)
– Сколько кругов?
– Сколько квадратов? и т.д.
IX. Повторение и закрепление изученного.
Правильно сказав, из каких геометрических фигур он состоит, пошел Буратино к
черепахе Тортилле. Тортилла отдаст ключик, если он отгадает в каком из 3
сундуков он лежит. Для этого необходимо решить примеры в столбик и отгадать
полученное слово. Рисунок 6.
X. Итог урока.
Буратино получил ключик, теперь он может открыть дверь. Рисунок 7.
Когда, он открыл дверь, он видел надпись: В ЗНАНИИ СИЛА.
– Как вы понимаете пословицу?
– Что показалось трудным?
– Что считаете самым интересным?
7.03.2013
Поделиться страницей:
urok.1sept.ru
Умножение и деление на 2 и на 3 » Мир учителя
Россия, Саратовская область, г Энгельс
МБОУ «СОШ № 9»
Учитель начальных классов
Хирная Татьяна Юрьевна
Умножение и деление чисел на 2 и на 3
Цели:
1) Закрепить знание табличного умножения и деления на 2 и на 3.
Развивать вычислительные навыки учащихся.
2) Продолжить обучение решению задач с использованием действий умножения и деления.
3) Работать над формированием универсальных учебных действий (УУД), повышением познавательной активности обучающихся.
4) Воспитывать у учащихся чувство взаимовыручки.
Урок подготовлен и проведён учителем начальных классов Хирной Т.Ю. На уроке используется презентация учителя Хирной Т.Ю. ,
Урок нацелен на формирование универсальных учебных действий (УУД).
Этап урока | Планируемые результаты (общеучебные умения и действия – УУД) |
1.Организационный момент | Формирование внутренней позиции школьника на уровне положительного отношения к урокам математики. |
2. Устный счёт | Умение формулировать выводы на основе сравнения, обобщения. |
3. Объявление темы и задач урока | Умение проявлять инициативу в учебно-познавательной деятельности. |
4. Актуализация опорных знаний | Умение кодировать информацию в знаково — символической форме. В сотрудничестве с учителем проводить классификацию изучаемых объектов, формулировать выводы на основе сравнения, обобщения. |
5. Повторение таблицы умножения и деления на 2,на 3. | Принимать активное участие в работе группами. Контролировать свои действия в коллективной работе. Принимать учебную задачу и следовать инструкции учителя. Ориентация на понимание оценок учителя и одноклассников. Проявлять инициативу в учебно- познавательной деятельности. |
6. Проверка знания таблицы умножения и деления на 2,на 3. | Принимать учебную задачу и следовать инструкции учителя. Контролировать свои действия в коллективной работе. Принимать учебную задачу и следовать инструкции учителя. Ориентация на понимание оценок учителя и одноклассников. Понимание чувств одноклассников. |
7. Физминутка | Формирование коммуникативных умений. |
8. Решение задач с использованием действий умножения и деления. | Понимание нравственного содержания поступков окружающих людей. Умение строить простые индуктивные и дедуктивные рассуждения Умение стремиться к координации различных мнений в сотрудничестве; умение договариваться, приходить к общему решению. Формирование интереса к познанию математических фактов. Умение осуществлять поиск нужной информации, строить небольшие математические сообщения в устной форме. Интерес к различным видам учебной деятельности, включая элементы предметно- исследовательской деятельности. Умение планировать свои действия в соответствии с учебными задачами и инструкцией учителя Умение моделировать задачи на основе анализа жизненных сюжетов. Умение принимать установленные правила в планировании и контроле способа решения. Формирование самооценки на основе заданных критериев успешности учебной деятельности |
9.Подведение итога урока. | Понимание причин успеха в учёбе. Самооценка на основе заданных критериев успешности учебной деятельности |
10.Домашнее задание. | |
11.Рефлексия | Понимание причин успеха в учёбе. |
Урок математики, 2 класс.
Образовательная программа «Начальная школа 21 века»
Тема: Умножение и деление чисел на 2 и на 3.
Цели:
1) Закрепить знание табличного умножения и деления на 2 и на 3.
Развивать вычислительные навыки учащихся.
2) Продолжить обучение решению задач с использованием действий умножения и деления.
3) Работать над формированием универсальных учебных действий (УУД), повышением познавательной активности обучающихся.
4) Воспитывать у учащихся чувство взаимовыручки.
Ход урока:
- 1. Организационный момент.
Улыбнитесь друг другу. Пожелайте успеха. Подарите и мне свои улыбки. Спасибо. Проверьте свою готовность к уроку. Возьмите с собой на урок три «волшебных» слова: А-активность, В-внимание, С-старание.
-Я хочу начать урок следующими словами:
“Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” (Ж.Ж.Руссо)
— Пусть эти слова будут напутствием на уроке.
2. Устный счёт.
-Посчитаем устно.
60-48= 58+6= 50+29= 3*6= 45-7=
(Объясняют способ вычисления, заменяя числа, где необходимо, суммой разрядных или удобных слагаемых)
-Какой пример лишний? Почему?
(3*6=18 – лишний, т. к. он на умножение)
-Составьте по данному примеру другой пример на умножение и примеры на деление.
(6*3=18, 18:3=6, 18:6=3)
(При перестановке слагаемых произведение не изменяется.
Если произведение разделить на 1 множитель, то получится 2 множитель и наоборот)
3. Объявление темы и задач урока.
— Догадались ли вы, какова тема нашего урока?
(Умножение и деление чисел.)
-Умножение и деление чисел на 2 и на 3.
-Давайте вместе подумаем, что нам нужно повторить и чему учиться на уроке.
-Повторить правила (законы) умножения и деления
-Закрепить знание таблицы умножения и деления на 2 и на 3
-Учиться решать задачи с использованием действий умножения и деления.
-Таковы задачи нашего урока и мы должны их выполнить.
4. Актуализация опорных знаний.
-Какие правила и законы нам могут пригодиться на уроке? Лишние мы уберём, а нужные разделим на группы.
а*в = в*а а+в = в+а
а*1 = а а+(в+с) = (а+в)+с
а:1 = а а:а = 1
а+0 = а а*0 = 0
а:0 а:2- половина
а:3- треть
-Какие группы мы получили?
Деление Умножение
а:1 = а а*в = в*а
а:а = 1 а*1 = а
а:0 (на 0 делить нельзя) а*0 = 0
а:2- половина
а:3- треть
-Что мы повторили?
( Правила и законы умножения и деления.)
-Мы выполнили одну из поставленных задач.
5. Повторение таблицы умножения и деления на 2,на 3.
-Повторим таблицу умножения на 2 и на 3. Работать будем в группах.
а) Повторение правил работы в группах.
( Работать без шума. Не ссориться, не спорить, работать дружно, помогать друг другу…)
-Подберите синонимы к слову помогать.
(Помогать, спасать, выручать)
-Я очень хотела бы, чтобы вы всегда выручали друг друга не только на уроке, но и в жизни. Это очень важно для нас всех.
б) Повторение таблицы умножения на 2 и на 3.
-Мы повторим таблицу умножения на 2 и на 3. Кто будет затрудняться, группа тому поможет.
(Дети работают в группах. По цепочке, по очереди задают друг другу примеры на табличные случаи умножения на 2, на 3.)
-Вы уже не первый раз проверяете знание таблицы умножения. Кто из членов вашей группы лучший знаток таблицы?
(Каждая группа называет ученика.)
-Аплодисменты лучшим знатокам.
в) Повторение таблицы деления на 2.
-Встаньте, пожалуйста, поиграем в игру «Горячий мяч». Ведущий называет пример и подаёт мяч кому-то из детей. Стараемся ответить и передать мяч водящему очень быстро, он горячий.
г) Подведение итога работы на данном этапе.
-Что мы повторили и закрепили?
-(Таблицы умножения и деления на 2,на 3.)
-Мы справились ещё с одной задачей урока.
6. Проверка знания таблицы умножения и деления на 2,на 3.
-А сейчас мы проверим свои знания.
Математический диктант:
-2 умножить на 7.
-По 3 взять 5 раз.
-Запишите произведение чисел 5 и 2.
-3 разделить на 3
-Первый множитель 3, второй множитель 9, запишите произведение.
-12 разделить на 2
-Чему равно произведение чисел 2 и 0?
-Поменялись тетрадями по кругу, взаимопроверка, проверяем работу соседа.
-Правильные ответы на доске: 14,15, 10, 1, 27, 6, 0.
-Поменялись тетрадями опять по кругу, но в обратном направлении.
-Посмотрите свои работы. У кого нет ошибок? Это будущие отличники.
( Во 2 классе оценки пока не выставляются).
-У кого 1-2 ошибки? Будущие хорошисты.
-У кого ошибок было больше, руку поднимать не нужно, мысленно скажите себе: « Я должен повторить таблицу умножения и деления на 2, на3»
— Что мы проверили?
(Знание таблицы умножения и деления на 2, на 3.)
-Результатами я осталась довольна, спасибо, вы старались.
7.Физминутка.
-Я предлагаю отдохнуть.
(Выполняются танцевальные упражнения под музыку, которые показывает одна из подготовленных учениц.)
8. Решение задач с использованием действий умножения и деления.
а) Беседа по сказке.
-Конечно, все вы знаете эту сказку, но я вам её напомню.
(просматривают слайды.)
-К кому обращалась за помощью девочка?
-К печке, яблоньке, речке.
-Почему они не выручили девочку?
(Она была невежлива, отказывалась от угощения)
-У нас на уроке эта сказка на новый лад. Кроме угощения герои приготовили девочке задачи. Выручим девочку, поможем ей решить задачи?
б) Решение задач. (Работа в группах)
-Задача печки.
Испекла я 24 пирожка.
Разложила их на 3 тарелки.
Сколько пирожков на каждой тарелке?
-Посовещайтесь в группе, каким действием решается задача? Выберите карточку с верным решением.
(Показывают карточку (действие : ) 24:3=8(п))
-Задача речки.
За день путники выпивают по 2 кувшина киселя.
Сколько кувшинов киселя они выпьют за неделю?
— Что такое неделя?
( 7 дней)
-Почему неделю так назвали? Ребята поработали заранее и нашли ответ на вопрос. Послушайте. (Использовались Интернет и толковый словарь)
(Особым почётом в древности была окружена семёрка. Отголоски почитания числа 7 дошли до наших дней. Вспомните пословицы: Семь бед — один ответ. Семеро одного не ждут. Наша неделя состоит из 7 дней. Древние заметили, что 7 нельзя поделить на равные части. Вот и назвали 7- не – деля. (Интернет)
-Неделя — образовано от словосочетания «не делать», то есть отдыхать. Неделя — означало «день отдыха». (Толковый словарь.)
-Ещё раз посмотрите на задачу. Каким действием решается? Посовещайтесь в группе и выберите верное решение.
(Показывают карточку (действие *) 2*7=14 (к)
-Задача ёжика в учебнике, с. 90 №21.
Маша нашла 27 грибов. Треть из них – подосиновики. Сколько подосиновиков нашла Маша?
(Совещаются. Показывают карточку (действие : ) 27:3=9(п) )
в) Решение задач коллективно.
-Задача яблоньки.
В корзине было несколько яблок. Девочка с братцем съели по 3 яблочка и ещё осталось 5 яблок. Сколько яблок было сначала?
(Задача подробно анализируется коллективно и решается письменно.)
(Чтобы узнать сколько яблок было, нужно знать, сколько их съели и сколько осталось. Сколько осталось известно, а сколько съели мы не знаем, но известно, что съели 2 человека по 3 яблока. Значит, можно узнать.
-Расскажите план решения задачи.
-Что узнаем 1 действием?
(Сколько яблок съели.)
-Что узнаем 2 действием?
(Сколько яблокбыло.)
-Запишем решение вместе.
1) 3*2=6(яб.) — съели.
2) 6+5=11(яб.) — было.
-Мы выручили девочку, решили все задачи, она обязательно спасёт братца.
г) Составление и решение задачи.
-Теперь вернёмся из сказки в нашу жизнь. Пойдём в кино.
(Встали, имитация ходьбы.)
-Займите места. Смотрим немое кино. Вы ничего не услышите, а всё, что увидите, считайте.
( Дети показывают сценку:
Мама покупает в магазине конфеты, продавец даёт ей 14 штук. Мама приходит домой. Сидят 3 детей. Мама даёт каждому по 2 конфеты. Остальные лежат в пакете.)
-Расскажите, что вы увидели?
(Мама купила 14 конфет. Дома она дала трём детям по 2 конфеты.)
-Можно ли это назвать задачей? Чего не хватает?
(Вопроса.)
-Поставьте к задаче вопрос.
(Сколько конфет осталось у мамы?)
(Анализ задачи:
Чтобы узнать сколько конфет осталось у мамы, нужно знать сколько конфет мама купила и сколько она отдала детям. Сколько конфет купили известно, а сколько отдали мы не знаем, но знаем, что трём детям по 2 конфеты, а значит можем узнать.
-Обсудите план решения в группах.
-Что узнаем 1 действием?
( Сколько конфет мама отдала.)
-Что узнаем 1 действием?
( Сколько конфет осталось у мамы.)
— Один из вас за доской будет решать задачу, а остальные решат её самостоятельно.
1) 2*3=6(к.) – отдала.
2) 14-6=8(к.)- осталось.
-Самопроверка. Сверьте соё решение с решением ученика на доске.
-А теперь проверим, сколько конфет лежит в пакете. Вывод?
(Задача решена верно)
-Чему мы учились?
(Решать задачи)
-Мы выполнили ещё одну задачу, которую поставили перед собой в начале урока.
Значит, все задачи выполнены. Молодцы!
9. Подведение итога урока.
worldofteacher.com
Урок математики «Таблица умножения и деления на 3». 3-й класс
Разделы: Начальная школа, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (9,9 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
1.Развивающие:
- развивать мыслительные операции (анализ,
синтез, обобщение), психические процессы
(внимание, память), творческие способности.
2. Образовательные:
- формировать понятие о таблице умножения и
деления на 3;
- тренировать способность умножать и делить на 2 и
3;
- тренировать способность решать задачи с
использованием таблицы умножения;
- закреплять переместительное свойство
умножения, взаимосвязь умножения и деления,
порядок действий в выражениях без скобок,
- тренировать вычислительные навыки.
3. Воспитательные:
- прививать интерес к математике,
- воспитывать чувство сотрудничества и дружбы.
Оборудование урока:
- учебник “Математика 2 класс”, часть 3, автор Л.Г.
Петерсон,
- презентация Microsoft PowerPoint.
- компьютер;
- проектор.
Ход урока
I. Оргмомент.
2 слайд. Ребята, сегодня мы с
вами отправимся в на необитаемый остров к
Робинзону Крузо на корабле. Этот моряк прожил 28
лет в полном одиночестве на необитаемом острове,
у берегов Америки, куда был выброшен
кораблекрушением.И мы должны спасти его.
Путешествие далекое, интересное, но опасное,
поэтому с собой берем самых смелых и находчивых
математиков.
– Ребята, начинаем урок. Если вы знаете, о чем
идет речь, хлопните в ладоши:
- переместительное свойство умножения;
- таблица умножения и деления на 2
- компоненты умножения;
- компоненты деления.
– Как много вы уже знаете! А сегодня узнаете еще
больше. Будьте старательными, активными,
внимательными и у вас все получится.3
слайд.
– Мы подплывем к острову и Робинзон Крузо уже
ждёт нас.4 слайд.
– Но что случилось? Наш корабль наткнулся на
рифы и разбился. Что бы выбраться на берег мы
должны выполнить задание.
II. Актуализация.
1. – Рассмотрите числа, записанные на доске.
10, 12 , 14, ……
11, 13, 15, ……
12, 15, 18……
– Что их объединяет? ( они двузначные)
– Найдите лишнее. Почему? (10 –круглое0
– Найдите закономерность каждой строки.
(счёт идет через 2, счёт идёт через 3)
Продолжите ряды в тетрадях.
– Проверим первый ряд. Как получили следующее
число? (16, 18)
– Проверим второй ряд. Как получили следующее
число? (17, 19)
– Проверим третий ряд. Как получили следующее
число? (21, 24)
– Чем первая строка отличается от второй? (1
строка – чётные, вторая – нечётные; первая
строка – числа кратные 2)
– Мы выбрались на берег. Теперь нам нужно
построить корабль, чтобы выбраться с острова.А
без математики мы с вами этого сделать не сможем.
Давайте вспомним таблицу умножения на 2.
5 слайд.
6 слайд.
– На острове вместе с Робинзоном жил его друг
Пятница.Он любит кататься на лианах.Но что за
запись на них. (это пример с пропущенным
вторым множителем)
2) Взаимосвязь умножения и деления
– Итак, на сколько нужно умножить 2, чтобы
получить 16?(на 8)
На доске:
– Какое свойство умножения использовали? (переместительное)
– Назовите компоненты умножения. (Первый
множитель, второй множитель, произведение)
– Какая операция обратна операции умножения? (деление)
– Как связаны между собой умножение и деление?
(если произведение разделить на один из
множителей, то получим другой множитель)
– Назовите компоненты деления. (делимое,
делитель, частное)
– Составьте равенства на деление с данными
числами.
7 слайд.
– Корпус лодки готов.
III. Создание проблемной ситуации.
8 слайд.
– А сейчас давайте поиграем в “робинзонскую
математическую молчанку”. Действуйте по
алгоритму:
- внимательно рассмотрите выражение;
- вспомни порядок действий в выражениях без
скобок
- выполните действия по порядку;
- запишите ответ в тетради и молча покажите, что
вы закончили.
9 слайд.
Начинаем игру
6*2+2*7
18:2-12:6
3*8+27:3
– Кто нашел значение выражения? (записываю все
варианты ответов)
– У кого вызвали затруднения решение
какого-либо выражения? (№)
– Почему? (Не знаем таблицу умножения и
деления на 3)
Какова тема урока? ( таблица умножения и
деления на 3)(фиксируем)10 слайд.
| Таблица умножения и
деления на 3 |
Какие цели поставим перед собой? (Составить
таблицу умножения и деления на 3 и научиться её
использовать)(фиксирую)
| Составить таблицу
умножения и деления на 3 и научиться её
использовать |
IV. “Открытие” новых знаний.
– Я предлагаю объединится в команды и
поработать.
Как вы думаете, с какого случая начнем
составление таблицы умножения на 3? Обсудите в
гуппах. (Ответы разные 3*0, 3*1, 3*2)
– Почему мы не будем начинать со случая 3*1? (Знаем
правило, при умножении любого числа на 0=0)
– Почему не будем начинать со случая 3*1? (Знаем
правило, что при умножении любого числа на 1
получается тоже число)
– Почему не начнём со случая 3*2? (От перемены
мест множителей произведение не изменяется)
– Значит начнём со случая 3*3.
– Какая закономерность будет наблюдаться в
результатах таблицы умножения на 3?(произведение
увеличивается на 3)
– Откройте учебники на странице 106.Заполним 1
столбик .
– первая группа прочитайте ответы.
Продолжим заполнение таблицы по строкам.
(Проверка 1,2,3,4 строки – вторая группа
5,6,7 строки – третья группа.)
– Рассмотрите 1 и 2 столбики.
– Как изменяется произведение, если
увеличивается один из множителей? (произведение
увеличивается)
– Рассмотрите 3 столбик.
– Что происходит с частным, если делимое
увеличивается, а делитель не меняется? (частное
увеличивается)
– Молодцы! А теперь послушайте такое задание. Я
буду называть вам разные числа. Если вы услышите
число, кратное 3 – хопайте.12, 10. 15, 18, 22 ,21, 25, 27.
– Какую операцию мы с вами выполнили? (составили
таблицу)
– И вот мачта с флагом корабля готова .
11 слайд.
Робинзон предлагает немного отдохнуть.
V. Физминутка
12-21 слайд.
22 слайд.
VI.
Первичное закрепление.
– Для чего нужно знать таблицу умножения на 3? (Что
бы решать примеры, задачи)
– И, прежде всего мы вернемся к тому выражению,
которое вызвало у нас затруднение.
– Давайте вместе найдем ответ, используя
таблицу умножения и деления на 3.
– Теперь я могу убрать вопрос, а вы проверьте
себя.(33) У кого все правильно – молодцы, а
тем, кто ошибся – спасибо за ошибку – вы помогли
нам разобраться.
– Продолжим находить значения выражений,
выполняя задание № 2.
– С выражениями 1 столбика работаем вместе (1
ученик проговаривает)
Значения выражений2-го столбика вы найдете,
работая в парах
VII.
Самостоятельная работа с проверкой по
образцу.
А значения выражений из 3-го столбика найдите
самостоятельно. (Проверка по образцу)
– Что нам помогло успешно справиться с
заданием?(Знание таблицы умножения на 3)
23 слайд.
– Вот и паруса на корабле готовы.
VIII.Закрепление.
– Где мы можем применить таблицу умножения на 3?
(В решении задач и примеров, уравнений)
– Вы правы. И сейчас мы решим задачу вместе с
Робинзоном.
24 слайд.
№ 10.
– Прочитаем задачу (1 ученик)
– Что в задаче известно? (Было 52 конфеты,
брал 6 дней по 3 конфеты)
– Что нужно узнать? (Сколько осталось)
– Начертим схему.
– Можно ли сразу ответить на вопрос задачи? (Нет)
– Почему? (не знаем сколько съел)
– Можем узнать? (Да)
– Как? (3*6=18 (К.) съел)
– Теперь можем ответить на вопрос задачи? (Да)
– Как? (52-18=24 (к.) – осталось)
– Кто сможет решить задачу самостоятельно –
поднимите руку. Приступайте к решению задачи в
тетради.
– Кому нужна помощь? (Раздаю карточки с
заготовкой схемы, и пояснением к действиям).
– Оцените свою работу с задачей.Если всё
получилось-нарисуйте зелёный круг. Если
испытывали затруднения – жёлтый, а если не
смогли справиться с задачей – красный.
– В каком действии вы применили табличный
случай на 3? (В 1)
VIII. Рефлексия.
25 слайд.
– Вот и спасательный круг на корабль повесили.
– Достигли мы цели нашего урока? (Да)
– Обоснуйте. (Мы составили таблицу
умножения и деления на 3 и научились её применять)
– Что удалось выполнить?
– Можем ли мы утверждать, что научились
уверенно применять таблицу умножения и деления
на 3? (Нет)
Какую цель каждый из вас должен поставить перед
собой? (выучить таблицу умножения на 3
наизусть)
26 слайд.
– Корабль готов.Мы помогли Робинзону Крузо.
Оцените свою работу на уроке. Если всё
получилось и у вас отличное настроение-нарисуйте
весёлый смайлик, если было трудно и вам нужно ещё
поработать над этой темой – грустный.
27 слайд.
– Спасибо за урок!
Аудио-приложение
2.01.2012
urok.1sept.ru
Конспект урока на тему:»Умножение и деление на 2 и 3″
Тип урока. Урок закрепления ( технология деятельностного подхода)
Цель. Закрепить знание табличных случаев умножения и деления на 2 и на 3, совершенствовать вычислительные навыки.
Задачи.
1) Продолжить обучение решению задач с использованием действий умножения и деления.
2) Работать над формированием универсальных учебных действий (УУД), повышением познавательной активности обучающихся.
3) Воспитывать у учащихся чувство взаимовыручки.
Ход урока:
- Организационный момент.
Приветствие между учениками.
Желаю больших успехов
Везде и во всем.
Удачи тебе на уроке.
Садитесь, дети.
-Я хочу начать урок следующими словами:
«Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению.” (Ж.Ж.Руссо)
— Пусть эти слова будут нашим напутствием на уроке.
Покажите свой настрой к уроку. (Хорошо — вверх большой палец, плохо – вниз большой палец) И у меня хорошее настроение.
2. Устный счёт.
Ребята, посмотрите на примеры и посчитайте
4*3 6*2 6*3 9*2 12:2 12:3 18:2 18:3
— Что объединяет эти примеры? (Они взаимосвязаны компонентами, если произведение разделить на 1 множитель, то получится 2 множитель и наоборот.)
3. Объявление темы и задач урока.
— Определите, какова тема нашего урока?
(Умножение и деление чисел на 2 и на 3)
-Давайте вместе подумаем, что нам нужно повторить и чему учиться на уроке.
(Повторить правила (законы) умножения и деления. Закрепить знание таблицы умножения и деления на 2 и на 3. Учиться решать задачи с использованием действий умножения и деления)
-Вы правильно определили тему урока и что должны повторить и закрепить. Таковы задачи нашего урока и мы должны их выполнить.
4. Актуализация опорных знаний.
— Ребята, мы повторим правила и законы умножения и деления. На ваших столах карточки, распределите их на группы.
а*в = в*а
а*1=а
а:1 = а
а:а = 1
а*0 = 0
а:2- половина
а:3- треть
-На какие группы поделили? Покажите свой успех, если вы распределили карточки. (Берутся за руки и поднимают вверх)
Деление Умножение
а:1 = а а*в = в*а
а:а = 1 а*1 = а
а:2- половина, а*0 = 0
а:3- треть
Показывают на доске. Объясняют каждую запись.
5. Повторение таблицы умножения и деления на 2 и на 3.
а) Ребята, повторите правила работы в группах.
( Быть терпеливыми, доброжелательными, вежливыми. Не спорить, работать дружно, помогать друг другу, не переговариваться.)
-Подберите синонимы к слову помогать.
(спасать, выручать, оказать помощь, содействовать)
-Я очень хотела бы, чтобы вы всегда выручали друг друга не только на уроке, но и в жизни. Это очень важно для нас всех.
Создайте группу из 4 человек.
-Повторим таблицу умножения на 2 и на 3.
Дети работают в группах, по цепочке. Ученик задает пример рядом сидящему, а вся группа внимательно слушает ответ, если верно, то кивают головой, а если неверно, то помогают ему. Теперь отвечающий задает пример следующему, примеры не повторяются. И так продолжают. (1 круг совершают, поднимают руки)
б) Повторение таблицы деления на 2 и на 3.
Игра «Найди пару»
Половина класса берут карточки с примерами, а другая – ответы. По команде учителя, ученики находят правильный пример с ответом.
6. Проверка знания таблицы умножения и деления на 2 и на 3.
Открыли тетради. Минутка чистописания. Запись чисел 22 и 33.
— Дайте характеристику числу 22.
( натуральное, двухзначное, четное, в этом числе 2 дес. 2 ед.)
— Как можно записать умножением этот пример, если бы
между 33 стоя знак сложения. 3+3= 3х2
Запишите числа.
Математический диктант. Цветограмма:
12 21 14
9 15 6
10 12 8
20 4 2
9 3 6
24 27 15
-2 умножить на 7.
-По 3 взять 3 раза.
-Найдите частное чисел24 и 3.
-16 разделить на 8
-Делимое 9, делитель 3.Найди частное.
— Чему равен периметр треугольника со стороной 5 см?
Правильные ответы читает ученица: 14,9, 8, 2,3,15.
Работа с партнером по лицу.
( лицом ко мне отвечают.) Четные числа
Найдите половину числа
( спиной ко мне отвечают) Нечетные числа
Найдите треть числа
Открыли учебник стр. 93. Запишите № 6.
— В каких столбиках повторим умножение и деление?
— Какой способ применим во втором столбике? (удобный способ сложения)
Сосчитайте, запишите только ответы.
14 57 16 3
18 48 18 2
9 68 18 3
Самопроверка. Показать успех.
7.Физминутка.
-Я предлагаю отдохнуть.
В нашем классе Гузель ходит в танцевальный кружок, и она научит некоторым танцевальным упражнениям под музыку.
8. Решение задач с использованием действий умножения и деления.
а) Решение задач.
Запишите в тетрадь стр. 93 № 3. Прочитайте задачу.
— Что означает рабочие дни?
— Что такое неделя? ( 7 дней)
— Почему неделю так назвали?
Старикова Вика и Закирова Гульназ нашли ответ на вопрос. Послушайте. (Использовались Интернет и толковый словарь)
Вика. Я искала ответ в интернете. Особым почётом в древности была окружена семёрка. Отголоски почитания числа 7 дошли до наших дней. Вспомните пословицы: Семь бед — один ответ. Семеро одного не ждут. Наша неделя состоит из 7 дней. Древние люди заметили, что 7 нельзя поделить на равные части. Вот и назвали 7- не – деля, то есть не делится.
Гульназ. Я нашла ответ в толковом словаре. Неделя — образовано от словосочетания «не делать», то есть отдыхать. Неделя — означало «день отдыха». (Толковый словарь.)
-Ещё раз посмотрите на задачу. Подумайте, каким действием решается? Посовещайтесь в группе и выберите верное решение.
Выполним задачу в тетрадях.
б) Ребята, сейчас мы выполним задачи на умножение и деление. (Работа в группах, по 4 ученика. В каждой группе даны задачи)
- В одном доме 9 этажей. Сколько этажей в 3 домах.
- Сколько нужно заплатить за 8 тетрадей, если одна тетрадь стоит 2 рубля?
- Веревку длиной 18 м разрезали на 3 одинаковые части. Сколько метров веревки в каждой части?
Проверка. Один читает задачу и говорит решение, ответ. Согласие всех остальных групп – хлопок.
в) Задача на построение ломаной линии и прямоугольника.
Группа, состоящая из одного ряда, читает задание на листе и распределяет обязанности, чтобы выполнить правильно задание.
Начерти ломаную линию, длину которой можно найти
9 * 3 + 3 =30 см
Начерти прямоугольник, периметр которого равен длине этой ломаной.
Один из команды, показывает на доске. (на листе)
9. Игра « Будь внимательным»
Сейчас вы послушаете знакомую песню «Дважды два четыре». Запишите примеры, которые вы услышите, повторные примеры не записывайте.
2*2=4, 3*3=9, 5*5=25, 6*8=48, 6*6=36
Сколько записали примеров?
Помогите партнеру по плечу дописать.
Покажите успех, если у вас правильно. Молодцы!
10. Подведение итога урока.
-Подведём итог нашей работы. Поделитесь своими высказываниями. Нам поможет карточка – помощница.
-На уроке я повторил…
-Я учился…
-На уроке мне было трудно…
-Я понял, что…
-Я радовался…
-Я всегда буду…
Теперь я могу….
— Достигли мы цели урока?
— Возьмите цветик и укажите свой ответ. Если ДА – красный цвет, Нет – синий, ЗАТРУДНЯЮСЬ – желтый.
— Я знаю таблицу умножения и деления на 2 и на 3.
— Я умею решать задачи на умножение и деление.
— Я испытывал затруднения при решении примеров и задач.
_ Ребята, я вам предлагаю, сегодня дома быть экспертами и проверить родителей на умножение и деление на 2 и на 3.
11. Домашнее задание.
-Просмотрите домашнее задание. Где вызывает затруднение?
стр. 93 №2,№ 4
12. Рефлексия.
— Покажите свое настроение.(с помощью большого пальца)
— Спасибо за урок.
Просмотр содержимого документа
«Конспект урока на тему:»Умножение и деление на 2 и 3″»
Тема урока. Умножение и деление чисел на 2 и на 3
Тип урока. Урок закрепления ( технология деятельностного подхода)
Цель. Закрепить знание табличных случаев умножения и деления на 2 и на 3, совершенствовать вычислительные навыки.
Задачи. 1) Продолжить обучение решению задач с использованием действий умножения и деления.
2) Работать над формированием универсальных учебных действий (УУД), повышением познавательной активности обучающихся.
3) Воспитывать у учащихся чувство взаимовыручки.
Ход урока:
Организационный момент.
Приветствие между учениками.
Желаю больших успехов
Везде и во всем.
Удачи тебе на уроке.
Садитесь, дети.
-Я хочу начать урок следующими словами:
«Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” (Ж.Ж.Руссо)
— Пусть эти слова будут нашим напутствием на уроке.
Покажите свой настрой к уроку. (Хорошо — вверх большой палец, плохо – вниз большой палец) И у меня хорошее настроение.
2. Устный счёт.
Ребята, посмотрите на примеры и посчитайте
4*3 6*2 6*3 9*2 12:2 12:3 18:2 18:3
— Что объединяет эти примеры? (Они взаимосвязаны компонентами, если произведение разделить на 1 множитель, то получится 2 множитель и наоборот.)
3. Объявление темы и задач урока.
— Определите, какова тема нашего урока?
(Умножение и деление чисел на 2 и на 3)
-Давайте вместе подумаем, что нам нужно повторить и чему учиться на уроке.
(Повторить правила (законы) умножения и деления. Закрепить знание таблицы умножения и деления на 2 и на 3. Учиться решать задачи с использованием действий умножения и деления)
-Вы правильно определили тему урока и что должны повторить и закрепить. Таковы задачи нашего урока и мы должны их выполнить.
4. Актуализация опорных знаний.
— Ребята, мы повторим правила и законы умножения и деления. На ваших столах карточки, распределите их на группы.
а*в = в*а
а*1=а
а:1 = а
а:а = 1
а*0 = 0
а:2- половина
а:3- треть
-На какие группы поделили? Покажите свой успех, если вы распределили карточки. (Берутся за руки и поднимают вверх)
Деление Умножение
а:1 = а а*в = в*а
а:а = 1 а*1 = а
а:2- половина, а*0 = 0
а:3- треть
Показывают на доске. Объясняют каждую запись.
5. Повторение таблицы умножения и деления на 2 и на 3.
а) Ребята, повторите правила работы в группах.
( Быть терпеливыми, доброжелательными, вежливыми. Не спорить, работать дружно, помогать друг другу, не переговариваться.)
-Подберите синонимы к слову помогать.
(спасать, выручать, оказать помощь, содействовать)
-Я очень хотела бы, чтобы вы всегда выручали друг друга не только на уроке, но и в жизни. Это очень важно для нас всех.
Создайте группу из 4 человек.
-Повторим таблицу умножения на 2 и на 3.
Дети работают в группах, по цепочке. Ученик задает пример рядом сидящему, а вся группа внимательно слушает ответ, если верно, то кивают головой, а если неверно, то помогают ему. Теперь отвечающий задает пример следующему, примеры не повторяются. И так продолжают. (1 круг совершают, поднимают руки)
б) Повторение таблицы деления на 2 и на 3.
Игра «Найди пару»
Половина класса берут карточки с примерами, а другая – ответы. По команде учителя, ученики находят правильный пример с ответом.
6. Проверка знания таблицы умножения и деления на 2 и на 3.
Открыли тетради. Минутка чистописания. Запись чисел 22 и 33.
— Дайте характеристику числу 22.
( натуральное, двухзначное, четное, в этом числе 2 дес. 2 ед.)
— Как можно записать умножением этот пример, если бы
между 33 стоя знак сложения. 3+3= 3х2
Запишите числа.
Математический диктант. Цветограмма:
12 21 14
9 15 6
10 12 8
20 4 2
9 3 6
24 27 15
-2 умножить на 7.
-По 3 взять 3 раза.
-Найдите частное чисел24 и 3.
-16 разделить на 8
-Делимое 9, делитель 3.Найди частное.
— Чему равен периметр треугольника со стороной 5 см?
Правильные ответы читает ученица: 14,9, 8, 2,3,15.
Работа с партнером по лицу.
( лицом ко мне отвечают.) Четные числа
Найдите половину числа
( спиной ко мне отвечают) Нечетные числа
Найдите треть числа
Открыли учебник стр. 93. Запишите № 6.
— В каких столбиках повторим умножение и деление?
— Какой способ применим во втором столбике? (удобный способ сложения)
Сосчитайте, запишите только ответы.
14 57 16 3
18 48 18 2
9 68 18 3
Самопроверка. Показать успех.
7.Физминутка.
-Я предлагаю отдохнуть.
В нашем классе Гузель ходит в танцевальный кружок, и она научит некоторым танцевальным упражнениям под музыку.
8. Решение задач с использованием действий умножения и деления.
а) Решение задач.
Запишите в тетрадь стр. 93 № 3. Прочитайте задачу.
— Что означает рабочие дни?
— Что такое неделя? ( 7 дней)
— Почему неделю так назвали?
Старикова Вика и Закирова Гульназ нашли ответ на вопрос. Послушайте. (Использовались Интернет и толковый словарь)
Вика. Я искала ответ в интернете. Особым почётом в древности была окружена семёрка. Отголоски почитания числа 7 дошли до наших дней. Вспомните пословицы: Семь бед — один ответ. Семеро одного не ждут. Наша неделя состоит из 7 дней. Древние люди заметили, что 7 нельзя поделить на равные части. Вот и назвали 7- не – деля, то есть не делится.
Гульназ. Я нашла ответ в толковом словаре. Неделя — образовано от словосочетания «не делать», то есть отдыхать. Неделя — означало «день отдыха». (Толковый словарь.)
-Ещё раз посмотрите на задачу. Подумайте, каким действием решается? Посовещайтесь в группе и выберите верное решение.
Выполним задачу в тетрадях.
б) Ребята, сейчас мы выполним задачи на умножение и деление. (Работа в группах, по 4 ученика. В каждой группе даны задачи)
В одном доме 9 этажей. Сколько этажей в 3 домах.
Сколько нужно заплатить за 8 тетрадей, если одна тетрадь стоит 2 рубля?
Веревку длиной 18 м разрезали на 3 одинаковые части. Сколько метров веревки в каждой части?
Проверка. Один читает задачу и говорит решение, ответ. Согласие всех остальных групп – хлопок.
в) Задача на построение ломаной линии и прямоугольника.
Группа, состоящая из одного ряда, читает задание на листе и распределяет обязанности, чтобы выполнить правильно задание.
Начерти ломаную линию, длину которой можно найти
9 * 3 + 3 =30 см
Начерти прямоугольник, периметр которого равен длине этой ломаной.
Один из команды, показывает на доске. (на листе)
9. Игра « Будь внимательным»
Сейчас вы послушаете знакомую песню «Дважды два четыре». Запишите примеры, которые вы услышите, повторные примеры не записывайте.
2*2=4, 3*3=9, 5*5=25, 6*8=48, 6*6=36
Сколько записали примеров?
Помогите партнеру по плечу дописать.
Покажите успех, если у вас правильно. Молодцы!
10. Подведение итога урока.
-Подведём итог нашей работы. Поделитесь своими высказываниями. Нам поможет карточка – помощница.
-На уроке я повторил…
-Я учился…
-На уроке мне было трудно…
-Я понял, что…
-Я радовался…
-Я всегда буду…
Теперь я могу….
— Достигли мы цели урока?
— Возьмите цветик и укажите свой ответ. Если ДА – красный цвет, Нет – синий, ЗАТРУДНЯЮСЬ – желтый.
— Я знаю таблицу умножения и деления на 2 и на 3.
— Я умею решать задачи на умножение и деление.
— Я испытывал затруднения при решении примеров и задач.
_ Ребята, я вам предлагаю, сегодня дома быть экспертами и проверить родителей на умножение и деление на 2 и на 3.
11. Домашнее задание.
-Просмотрите домашнее задание. Где вызывает затруднение?
стр. 93 №2,№ 4
12. Рефлексия.
— Покажите свое настроение.(с помощью большого пальца)
— Спасибо за урок.
kopilkaurokov.ru



 вестие о приезде настоящего ревизора и разоблачение Хлестакова.
вестие о приезде настоящего ревизора и разоблачение Хлестакова.
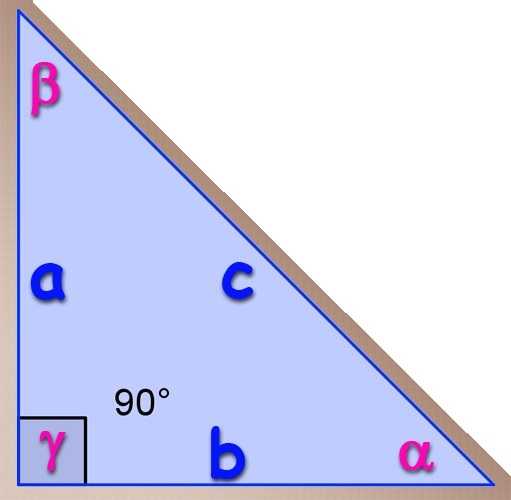
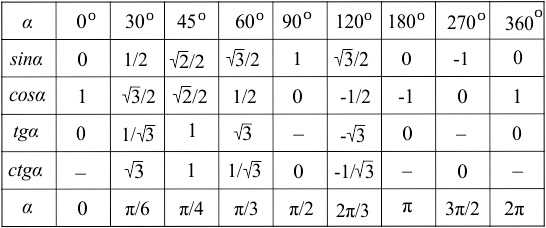
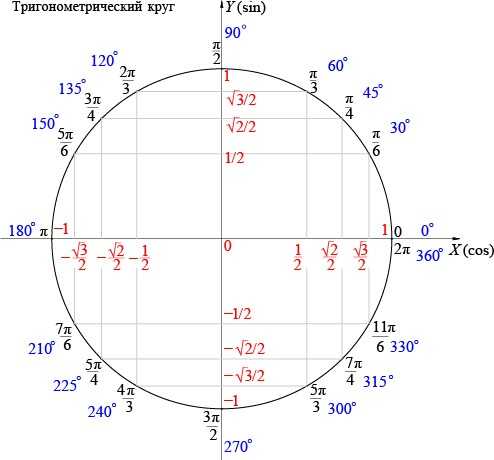
 Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.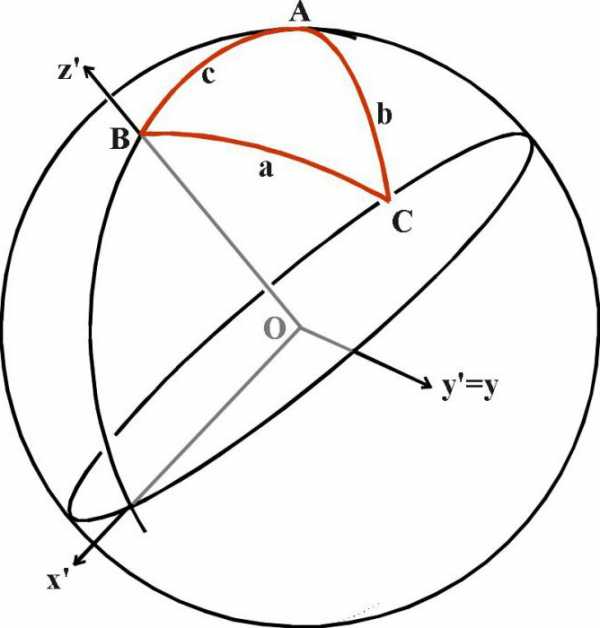 Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание – она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
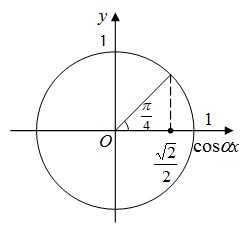
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание – она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях. Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза – это по умолчанию самая длинная сторона прямоугольного треугольника. Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза – это по умолчанию самая длинная сторона прямоугольного треугольника. Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.