Тема 10. Математические понятия Контрольные вопросы по теории
Какие свойства считают существенными и несущественными для объекта?
Что понимают под объемом понятия?
Что понимают под содержанием понятия?
В каком отношении находятся объемы понятий, если понятия несовместимы, совместимы, тождественны, одно понятие является видовым по отношении к другому понятию?
Что значит – определить понятие?
Какие определения относят к явным и неявным?
Какие правила необходимо соблюдать, формулируя определения понятий через род и видовое отличие?
Практические задания
Назовите несколько элементов, принадлежащих объему понятия: а) «целое число»; б) «многоугольник»; в) «часть речи»; г) «хвойное дерево»; д) «геометрическая фигура».
Укажите какие-нибудь свойства, присущие всем параллелограммам. Какие из названных вами свойств принадлежат и другим фигурам?
Назовите несколько свойств, входящих в содержание понятия: а) «правильный многоугольник»; б) «ломаная линия»; в) «прямоугольник»; г) «ромб»; д) «биссектриса угла»; е) «треугольник».
Какие из следующих свойств входят в содержание понятия «трапеция», а какие – нет? а) Иметь пару равных сторон; б) иметь пару параллельных сторон; в) иметь все равные углы; г) иметь равные диагонали.
Назовите свойства: а) присущие и прямоугольнику, и ромбу; б) присущие прямоугольнику и не присущие ромбу; в) присущие ромбу и не присущие прямоугольнику.
Назовите фигуру со следующими свойствами: а) иметь 4 вершины; б) иметь 2 пары параллельных сторон; в) иметь 4 равные стороны; г) иметь 4 стороны и прямой угол.
Какие из следующих понятий являются совместимыми, а какие – несовместимыми:
а: «четное число»,
b: «нечетное число»,
с: «число, кратное 3»,
d: «двузначное число» ?
Изобразите отношения между объемами следующих понятий на кругах Эйлера:
а) а: «целое число»; b: «натуральное число»; с: «отрицательное число»;
б) а: «квадрат»; b : «ромб с прямым углом»;
в) а: «четырехугольник», b: «трапеция», с: «прямоугольник»;
г) а: «натуральное число, кратное 3», b: «натуральное число, кратное 4», с: «натуральное число»;
д) а: «треугольник», b: «равнобедренный треугольник», с: «равносторонний треугольник».
Приведите примеры понятий, отношения между которыми могут быть изображены с помощью кругов Эйлера, приведенных на рисунке.
С с с с
а) б) в) г)
Укажите три понятия, являющиеся родовыми по отношению к понятию «прямоугольник». Какое из них является ближайшим?
Для каждого из следующих понятий укажите ближайшее родовое понятие: а) хвойное дерево; б) имя существительное; в) квадрат; г) биссектриса угла; д) нечетное число; е) окружность.
Назовите понятие, являющееся родовым по отношению к данной группе понятий: а) квадрат, трапеция, ромб; б) круг, окружность, многоугольник, отрезок; в) деревья, кустарники, травы.
Для каждого из следующих понятий укажите видовое понятие: а) животное; б) растение; в) многоугольник; г) параллелограмм; д) дерево; е) часть речи.
Назовите несколько свойств, общих для прямоугольника и квадрата. Выясните, какое из высказываний истинно: «всякое свойство прямоугольника присуще квадрату»; «всякое свойство квадрата присуще прямоугольнику». В каком отношении находятся содержания понятий «прямоугольник» и «квадрат» и их объемы?
Может ли одно и то же понятие быть родовым по отношению к некоторому понятию аи видовым по отношению к понятиюb?
Находятся ли в отношении рода и вида следующие пары понятий: а) многоугольник и треугольник; б) угол и острый угол; в) луч и прямая; г) ромб и квадрат; д) круг и окружность; е) отрезок и прямая?
Можно ли отождествить понятия: а) число и цифра; б) окружность и граница круга; в) выражение и значение выражения?
Среди понятий, изучаемых в начальном курсе математики, есть такие, как «четное число», «треугольник», «многоугольник», «число», «трехзначное число», «прямой угол», «сумма», «слагаемое», «выражение». Есть ли среди них понятия, находящиеся в отношении: а) рода и вида; б) целого и части?
В следующих определениях выделите определяемое и определяющее понятия, родовое понятие (по отношению к определяемому) и видовое отличие:
а) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
б) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Назовите все свойства, которые содержатся в видовом отличии каждого из следующих определений:
а) Биссектрисой угла называется луч, выходящий из вершины угла и делящий угол пополам.
б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Дайте определения следующих понятий: а) четырехугольник; б) прямоугольник; в) ромб; г) равнобедренный треугольник; д) равносторонний треугольник; е) трапеция. Выделите в каждом из определений родовое понятие и видовое отличие.
Дайте определение понятия «квадрат», указав в качестве родового понятия понятие: а) «прямоугольник», б) «ромб».
Можно ли при помощи свойства «иметь прямой угол» выделить подмножество квадратов из множества: а) четырехугольников б) ромбов; в) параллелограммов? Если нет, то укажите свойства, при помощи которых это можно сделать.
Сформулируйте определение трапеции. Пользуясь им, сформулируйте условие, при котором: а) четырехугольник будет являться трапецией: б) четырехугольник не будет являться трапецией.
Учащийся определил прямой угол как угол, стороны которого взаимно перпендикулярны, а взаимно перпендикулярные прямые как прямые, образующие при пересечении прямые углы. Какую ошибку допустил учащийся?
Есть ли логические ошибки в следующих определениях? Исправьте их.
а) Прямоугольником называется четырехугольник, у которого противоположные стороны равны.
б) Прямоугольник –это когда все углы прямые.
в) Биссектрисой угла называется прямая, делящая угол пополам.
г) Диаметром круга называется хорда, проходящая через центр круга.
д) Сложением называется действие, при котором числа складываются.
е) Простое число –это когда оно имеет только два натуральных делителя.
ж) Равносторонним треугольником называется треугольник, у которого равны все стороны и все углы.
з) Луч –это прямая, ограниченная с одной стороны.
и) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.
к) Отрезок – это прямая, ограниченная с двух сторон.
л) Касательной к окружности называется прямая, которая касается окружности.
м) Остроугольным треугольником называется треугольник, у которого есть острый угол.
Какие из следующих обоснований правильны, а какие –нет: а) треугольникАВСне равнобедренный, так какАВВС; б) треугольникABCне равнобедренный, так какАВВСиВС АС; в) треугольникABCне равнобедренный, так какАВВС;ВС АСиАВ АС.
Учащийся по аналогии с определением остроугольного треугольника сформулировал такое определение остроугольного четырехугольника: «Остроугольным четырехугольником называется выпуклый четырехугольник, все углы которого острые». Можно ли считать это определение правильным?
Понятие «противоположные стороны прямоугольника» в начальном курсе математики можно определить так: «Красным цветом обозначены две противоположные стороны прямоугольника, а синим цветом – две другие противоположные стороны» (все это показано на рисунке). Какой способ определения понятия использован?
Понятие «трехзначное число» вводится в начальных классах так: учащимся предлагается ответить на вопрос: «Сколько всего цифр (знаков) используется для записи каждого из чисел: 573, 982, 700, 403, 777, 585?» затем учитель делает заключение: «Это трехзначные числа». Каким образом в этом случае определено понятие трехзначного числа?
Выясните, каким способом определяются в различных учебниках по математике для начальных классов понятия: а) выражение; б) сумма; в) слагаемое; г) четное число; д) периметр; е) однозначное число.
Приведите примеры генетических и индуктивных определений из курса алгебры.
studfiles.net
Строить определения математических понятий
Стр 1 из 4Следующая ⇒Математические понятия.
Задания на формирование умения
строить определения математических понятий
Типовые задания с решениями
Пример 1.Назовите несколько элементов, принадлежащих объему понятия «металл».
Решение. В объем понятия «металл» входят элементы, охватываемые этим понятием. К ним относятся, например, железо, никель, медь, цинк, золото, серебро, титан.
Пример 2.Назовите несколько свойств, принадлежащих содержанию понятия «дерево». Принадлежит ли содержанию этого понятия свойство «иметь листья»?
Решение. Содержание понятия «дерево состоит из тех свойств, которые являются общими для всех деревьев». К таким свойствам относятся, например, следующие: «быть растением», «иметь корень», «иметь ствол», «иметь ветви», «имеет кору».
Свойство «иметь листья» не входит в содержание понятия «дерево», поскольку этим свойством обладают не все деревья. Так, хвойные деревья не имеют листьев.
Пример 3.Определите, в каких отношениях находятся понятия:
а) трапеция и параллелограмм;
б) четное число и простое число;
в) телефон и средство связи.
Решение.
а) Объемом понятия а — «трапеция» является множество А, состоящее из четырехугольников, у которых две стороны параллельны, а две другие не параллельны. Объемом понятия в –«параллелограмм» является множество В, состоящее из четырехугольников, у которых противоположные стороны попарно параллельны. Поскольку никакой четырехугольник не может удовлетворять тем и другим требованиям одновременно, то объемы этих понятий не пересекаются. Следовательно, сами понятия являются несовместимыми (рис а).
б) Объемы понятий а – «четное число» и в – « простое число» содержат общий элемент. Этим числом является число 2, одновременно четное и простое. Поскольку объемы понятий находятся в отношении пересечения, сами понятия являются совместимыми. (рис б).
в) Объем А понятии «телефон» является подмножеством множества В – объема понятия «средства связи». Причем А не совпадает с В. Поэтому АÌВ, т.е. объемы понятий находятся в отношении включения. Понятие «телефон» является видовым, а понятие «средство связи» -родовым. (рис в).
Задания для самостоятельной работы (базовый уровень)
1. Назовите несколько элементов, принадлежащих объему понятия:
а) посуда; б) мебель;
в) автомобиль; г)часть речи;
д) город; е) геометрическая фигура;
ж) планета; з) наука;
и) университет; к)библиотека.
2. Укажите несколько свойств, принадлежащих содержанию понятия:
а) птица; б) книга;
в) поезд; г)студент;
д) существительное; е) треугольник;
ж) праздник; з) рыба.
3. Укажите свойства, которые присущи:
а) прямоугольнику и ромбу;
б) прямоугольнику и не присущи ромбу;
в) ромбу и не присущи прямоугольнику.
4.Для каждого из следующих понятий укажите родовое и видовое понятия:
а) цветок; б) город; в) стол;
г) стакан; д) самолет; е) треугольник;
ж) собака; з) тюльпан; и) существительное;
к) кошка; л) уравнения; м) трактор.
5. Следующие понятия разбейте на группы. Для каждой группы назовите родовое понятие:
а) роза; б) береза; в) серебро;
г) лев; д) баран; е) липа;
ж) корова; з) тюльпан; и) медведь;
к) олово; л) жасмин; м) цинк.
6. Изобразите с помощью диаграмм Эйлера-Венна отношения между объемами понятий a, b и c, если:
а) a – «треугольник», b – «прямоугольный треугольник», c –«равнобедренный прямоугольник»;
б) a – «ромб», b – «квадрат», c – «прямоугольник»;
в) a – «образовательное учреждение», b — «школа» c – «ВУЗ»;
г) a – «натуральное число», b – «четное число», c – «нечетное число»;
д) a — «жилое помещение», b — «дом», c – «комната».
7. Сформулируйте определение данного понятия через род и видовое отличие. В каждом определении выделите родовое понятие и видовой признак, если рассматриваются:
а) «равнобедренный треугольник»;
б) «диаметр окружности»;
в) «существительное»;
г) «прилагательное».
8. Сформулируйте определение прямоугольного треугольника и выявите его структуру.
Задания для самостоятельной работы (повышенный уровень)
1.Выясните, соизмеримы ли следующие определения:
а) квадратом называется четырехугольник, у которого все стороны равны;
б) прямоугольником называется ромб, имеющий прямой угол;
в) равнобедренный треугольник – это треугольник, у которого хотя бы две стороны равны;
г) прилагательным называется часть речи, обозначающая признак предмета и отвечающая на вопрос «какой».
В случае отрицательного ответа внесите соответствующие изменения в определение.
2.Учащийся определилпрямой угол как угол, стороны которого взаимно перпендикулярны, а взаимно перпендикулярные прямые как прямые, образующие при пересечении прямые углы. Какую ошибку допустил учащийся?
3. Учащийся по аналогии с определением остроугольного треугольника сформулировал такое определение остроугольного четырехугольника: «Остроугольным четырехугольником называется выпуклый четырехугольник, все углы которого острые». Можно ли считать это определение правильным?
4.Один учащийся определил понятие прямоугольника так: «Прямоугольником называется четырехугольник, у которого все углы прямые и стороны попарно равны».
Второй учащийся сказал: «Прямоугольником называется четырехугольник, у которого все углы прямые».
А третий дал такое определение: «Прямоугольником называется четырехугольник, у которого противоположные стороны равны».
Какой из учащихся дал верное определение понятия прямоугольника? Можно ли это понятие определить еще каким либо образом?
5.В каких из приведенных ниже определениях математических понятий имеются ошибки? Исправьте их, если это возможно.
а) Биссектрисой треугольника называется прямая, делящая угол треугольника пополам.
б) Диаметром круга называется хорда, проходящая через центр круга.
в) Касательной к окружности называется прямая, которая касается окружности.
г) Ромбом называется параллелограмм, две смежные стороны которого равны.
д) Сложение называется действие, при котором числа складываются.
е) Равносторонним треугольником называется треугольник, у которого равны все его стороны и все его углы.
ж) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.
6. Проанализируйте логическую структуру определения прямоугольника (через четырехугольник) и установите, какие из фигур являются прямоугольниками.
7.Дайте определение биссектрисы угла и установите, на каком рисунке луч ВD является биссектрисой угла (рис. 6).
8.Сформулируйте определение понятия «квадрат», указав в качестве родового понятия «прямоугольник». Пользуясь данным определением, укажите условия, при которых:
а) фигура будет являться квадратом;
б) фигура не будет являться квадратом.
9.Достаточно ли нижеприведенное условие для того, чтобы четырехугольник был прямоугольником:
а) он имеет две пары параллельных сторон;
б) три его угла являются прямыми;
в) его диагонали равны;
г) две его стороны параллельны.
mykonspekts.ru
1. Начертите три геометрические фигуры, принадлежащие объ… -reshimne.ru
2. Назовите пять существенных свойств понятия: а) треугольник; б) круг.
3. Каков объем понятия: а) однозначное число; б) натуральное число; в) луч?
4. Назовите несколько свойств, общих для прямоугольника и квадрата. Какое из следующих утверждений верное: а) Всякое свойство квадрата присуще прямоугольнику. б) Всякое свойство прямоугольника присуще квадрату?
5. Находятся ли в отношении рода и вида следующие пары понятий: а) многоугольник и треугольник; б) угол и острый угол; в) луч и прямая; г) ромб и квадрат; д) круг и окружность?
6. Изобразите при помощи кругов Эйлера отношения между объемами понятий а, в и с, если: а) а – «четырехугольник», в – «трапеция», с – «прямоугольник»; б) а – «натуральное число, кратное 3», в – «натуральное число, кратное 4», с – «натуральное число»; в) а – «треугольник», в – «равнобедренный треугольник», с – «равносторонний треугольник».
7. Приведите примеры понятий, отношения между которыми изображены на рисунке.
а) б)
8. Среди понятий, изучаемых в начальном курсе математики, есть такие, как «четное число», «треугольник», «многоугольник», «число», «трехзначное число», «прямой угол», «сумма», «слагаемое», «выражение». Есть ли среди них понятия, находящиеся в отношении: а) рода и вида; б) целого и части?
9. Какие свойства понятий «прямоугольник» и «сложение» изучают в начальном курсе математики?
10. Переформулируйте следующие определения, используя слова «тогда и только тогда, когда»:
а) Четным называется число, которое делится на 2.
б) Множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
в) Множества А и В называются равными, если А Ì В и В Ì А.
г) Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.
11. В следующих определениях выделите определяемое и определяющее понятие, родовое понятие (по отношению к определяемому) и видовое отличие: а) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны; б) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
12. Назовите все свойства, которые содержатся в видовом отличии каждого из следующих определений: а) Биссектрисой угла называется луч, выходящий из вершины угла и делящий угол пополам; б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
13. Соразмеримы ли следующие определения: а) Остроугольным треугольником называется треугольник, у которого есть острый угол; б) Прямоугольным треугольником называется треугольник, у которого есть прямой угол.
14. Учащийся определил прямой угол, стороны которого взаимно перпендикулярны, а взаимно перпендикулярные прямые как прямые, образующие при пересечении прямые углы. Какую ошибку допустил учащийся?
15. Есть ли логические ошибки в следующих определениях? Если есть, то исправьте их.
а) Прямоугольником называется четырехугольник, у которого противоположные стороны равны.
б) Биссектрисой угла называется прямая, делящая угол пополам.
в) Сложением называется действие, при котором числа складываются.
г) Равносторонним треугольником называется треугольник, у которого равны все стороны и все углы.
д) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.
reshimne.ru
Виды углов. Прямой угол. 2-й класс
Разделы: Начальная школа, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (9,7 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: объяснение нового материала.
Место урока в структуре по теме: данная тема изучается в разделе “Табличное сложение однозначных чисел с переходом через десяток”.
Цель урока: Познакомить учащихся с понятием “прямой угол” и научить применять полученные знания на практике.
Задачи урока:
1. Образовательные:
- Познакомить учащихся с понятием “прямой угол”;
- Сформировать практические навыки определения прямого угла при помощи треугольника и без него;
- Продолжить работу по совершенствованию навыка устного счёта в пределах 100;
2. Развивающие:
- Развитие логического мышления, внимания, памяти, пространственного воображения;
- Развитие творческих умений и навыков по теме для успешного выполнения заданий;
- Развитие культуры речи и эмоций учащихся.
3. Воспитательные:
- В целях решения задач нравственного воспитания содействовать воспитанию гуманности и коллективизма, наблюдательности и любознательности, развитию познавательной активности, формированию навыков самостоятельной работы;
- В целях решения задач эстетического воспитания содействовать развитию у учащихся чувства прекрасного.
ХОД УРОКА
I. Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте
Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
— Ребята, сегодня мы опять отправимся в путешествие по королевству Геометрия.
3. Устный счёт.
2 слайд
– У ворот нас встречают король Точка и его дочь – принцесса Прямая. Прежде чем король и принцесса познакомят нас с жителями своего королевства, они хотят вас испытать.
II. Устный счет.
(Слайд 3)
1) Игра “Гусеница-растеряша”.
— Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому правилу можно продолжить ряд чисел. (Дети называют правило: это чётные числа; каждое последующее число на 2 больше предыдущего).
— Какие же числа растеряла гусеница? (2,4,6,8,10,12,14,16)
(Слайд 4)
2) Игра “Математический баскетбол”.
Баскетбол — командная спортивная игра, цель которой забросить руками мяч в подвешенную корзину.
— Любой из вас забьёт гол, если правильно решит пример. (Дети по цепочке решают примеры). 30 + 7 25 + 5 32 – 12 66 + 4 80 – 7 28 – 10 45 – 45 53 + 7 59 – 9 90 + 9
Слайд 5
Задание на логику
— Сколько пятачков у 15 поросят? (15)
— Когда гусь стоит на двух ногах, то весит 4 кг. Сколько будет весить гусь, когда встанет на одну ногу?
6 слайд
– Вы прошли все испытания. Король и принцесса очень довольны вами и готовы познакомить вас с жителями королевства “Геометрия”!
(По щелчку створки ворот открываются.)
(Слайд 7)
— Ребята, перед вами жители королевства “Геометрия”.
— Посмотрите на фигуры в каждой рамке. Какая из них лишняя? Почему?
(Учащиеся называют лишние фигуры, обосновывают свой выбор).
— Разделите все оставшиеся фигуры на две группы. Как это можно сделать? (Оставшиеся фигуры можно разделить на две группы: линии и многоугольники.)
— Назовите виды линий и многоугольников, известные вам. (Линии: прямая, ломаная, кривая. Многоугольники: квадрат, трапеция, прямоугольник, четырёхугольник, пятиугольник, шестиугольник, многоугольник).
IV. Работа над новым материалом.
(Слайд 8)
1) — Тему урока вам подскажет кроссворд. Кроссворд “Геометрический”.
1) Часть прямой, у которой есть начало, но нет конца. (Луч).
2) Геометрическая фигура, не имеющая углов. (Круг).
3) Самая маленькая геометрическая фигура. (Точка).
4) Геометрическая фигура, имеющая форму вытянутого круга. (Овал).
— Тема нашего урока спряталась по вертикали. Найдите её. (Угол). (щелчок вылетают геометрические фигуры).
— Сформулируйте пожалуйста тему нашего урока.
— Ребята, а зачем мы будем изучать углы?
— Как Вы думаете, вам эти знания пригодятся?
(Ответы детей)
— Углы окружают нас и в повседневной жизни. Приведите свои примеры, где можно найти углы вокруг нас.
— Ребята, а может, кто-то знает, что такое угол? (выслушиваются мнения детей)
Правильность нашей формулировки, мы проверим чуть позже.
— Люди, каких профессий чаще всего встречаются с углами? (конструктор, инженер, дизайнер, строитель, архитектор, моряк, астроном, архитектор, портной и т.д.)
Слайд 9.
Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван.
— Ребята, а сейчас Король и Принцесса предлагают немного поиграть.
Слайд 10.
Игра “Им угол имя подарил”.
— Угол важная фигура. Многим фигурам он помог дать имя. Назовите фигуры.
— Что общего в названиях фигур? (что они имеют угольник – общая часть)
— Почему первая часть слов везде разная? (потому что углов разное количество)
Физминутка 11-16 слайды
Открываем тетради, записываем 18 января, классная работа. (слайд 17)
Слайд 18.
— Ребята, а теперь от красных полей отступите одну клеточку и поставьте точку О. От этой точки проведите два луча.
На доске заранее нарисовать точку О (4-5). Вызвать 4-5 детей, чтобы они провели лучи на доске.
— Что за фигуры у нас получилась? (угол)
— Посмотрите, какие разные эти углы.
— Ребята, а теперь соберите правило из слов.
Работа в парах.
(Вывод: угол — это геометрическая фигура, образованная двумя разными лучами
с общим началом).
— Ребята, а теперь посмотрите на фигуру, которую нарисовала я.
— Это угол, или нет.
(Дети говорят – нет, еще раз возвращаемся к правилу, после этого делаем вывод о том, что это тоже угол – развернутый)
Слайд 19. (вывод по углу)
Плакат на доске
Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда? (На листе чертеж таких углов)
Ответы детей.
— В таких случаях если называть разные углы одной буквой, то будет непонятно, о каком угле идёт речь. Что этого не произошло, на каждой стороне угла можно отметить по одной точке, поставить около неё букву и обозначить угол тремя буквами, при этом всегда в середине записывают букву, обозначающую вершину угла. Угол АОВ. Лучи АО и ОВ – стороны угла.
Плакат на доске
Слайд 20.
— Ребята, у вас на столах лежат разные виды углов. Найдите пожалуйста одинаковые виды углов.
— Как будете искать? (Ответы детей)
Один человек на моих моделях ищет одинаковые углы.
— Ребята, смотрите, номера 6 и 7 совпали полностью, а 1 и 5 — нет. № 5 больше.
— Какой можно сделать вывод? После ответа детей появляется слайд.
ВЫВОД: слайд 21
- Равные углы при наложении совпадают
- Если один угол наложить на другой и они совпадут, то эти углы равны
Слайд 22.
Изготовление модели прямого угла.
Слайд 23
Не всегда удобно определять прямой угол на глаз. Для этого используют линейку-угольник.
— Каким цветом выделен угол больше прямого? (Голубым).
— Меньше прямого? (Зелёным).
— Какой же угол из трёх предложенных прямой?
— Почему вы так решили? (Вершина и стороны угла совпали с прямым углом на линейке-угольнике).
— Как же определить вид угла?
ВЫВОД:
- Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике.
Слайд 24
— Каждый из углов имеет своё название. Острый угол – это угол, который меньше прямого. Тупой угол – это угол, который больше прямого.
(На доске появляются таблички с названием углов)
— Какой угол мы будем считать главным?
Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется ПРЯМЫМ.
Если угол уже — ОСТРЫМ,
Если шире, то — ТУПЫМ.
Слайд 25.
— Ребята, а всегда возможно наложить углы?
— Нет. (Если начерчены в тетради…)
— Для этого существует транспортир, с помощью которого измеряют углы. Углы измеряют в градусах. Посмотрите на виды транспортиров.
Слайд 26.
Очень часто углы мы можем наблюдать на часах. Углы образуют часовые стрелки.
Работа по учебнику.
Задание: Используя модель прямого угла, найди прямые углы и выпиши их номера. (Дети выполняют задание самостоятельно, затем один ученик называет свой вариант ответа, все проверяют работу).
— С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол, каждый сам назовёт его одной или тремя буквами.
Слайд 27-29 (Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется взаимопроверка в парах).
Я ОСТРЫЙ — начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим ОСТРЫЙ УГОЛ мы,
как остриё меча.А для УГЛА ТУПОГО
Всё повторяем снова:
Из точки две прямых ведём,
Но их пошире разведём.
На чертёж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
Практическая работа по закреплению изученного.
На партах у вас проволока. Сделайте из нее прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой.
7. Итог урока.
— Расскажите мне по схеме о том, что вам дал сегодняшний урок математики?
8. Домашнее задание.
17.03.2011
urok.1sept.ru
Урок математики «Прямой угол (практическая работа). Обозначение угла. Острые и тупые углы. Угольник»
ТемаПрямой угол (практическая работа). Обозначение угла. Острые и тупые углы. Угольник
Цель
знакомство с понятием «угол», сформировать представление о видах угла: «прямой, тупой, острый»
Задачи
— образовательная: формировать общее понятие угла как геометрической фигуры, познакомить учащихся с различными видами углов и приёмом сравнения углов (острого и тупого) как результат их сравнения с прямым углом;
— развивающая: создать условия для развития математической речи учащихся, работать над формированием и развитием приёмов анализа и сравнения;
— воспитательная: создать условия для развития культуры общения, адекватной самооценки результатов деятельности учеников.
Тип урока
урок открытия нового знания
Методы
частично-поисковый, самостоятельная работа и работа с учебником, парная и индивидуальная работа.
Основное содержание темы, термины и понятия
Представление о видах углов.
Термины: прямой, острый, тупой угол; стороны угла; вершина угла;
Планируемый результат
Предметные умения
УУД
Знать:
-термин «угол»;
-понятия «сторона угла», «вершина угла»;
-виды углов, элементы угла
Уметь:
-строить угол;
-распознавать и сравнивать виды углов, элементы угла.
Личностные:
—готовность целенаправленно использовать математические знания, умения и навыки в учебной деятельности и в повседневной жизни; -способность осознавать и оценивать свои мысли, действия и выражать их в речи.
Регулятивные:-в сотрудничестве с учителем ставить новые учебные задачи;
-проявлять познавательную инициативу в учебном сотрудничестве.
Познавательные:
1. Общеучебные:
-описывать взаимное расположение предметов в пространстве и на плоскости;
-распознавать, называть, изображать прямой, острый и тупой углы,
-распознавание и изображение на чертеже углов
2. Логические:
-умение определять признаки сходства и различия предметов; — развитие пространственного мышления.
Коммуникативные: — аргументировать свою позицию и координировать её с позициями партнеров в совместной деятельности;
— осуществлять взаимный контроль и оказывать в сотрудничестве необходимую помощь.
Оборудование
учебники, тетради на печатной основе, ПК, презентация урока на флешке, мультимедиа проектор, интернет.
Этапы урокаДеятельность
учеников
УУД
Деятельность
учителя
I. Мотивация к учебной деятельности
Цели:
— актуализировать требования к ученику со стороны учебной деятельности;
— создание условий для возникновения у учеников внутренней потребности включения в учебную деятельность;
— организовать планирование учебной деятельности на уроке.
Формулируют правила поведения на уроке, аргументируют их.
Слушают музыку
Слушают учителя
Личностные УУД
(Осмысление внутренней позиции ученика на уровне положительного отношения к уроку)
Регулятивные УУД
(Самоорганизация и организация своего рабочего места)
Встало солнышко давно,
Заглянуло к нам в окно.
Нас оно торопит в класс,
Вновь урок у нас сейчас!
Посмотрите друг на друга, улыбнитесь, пожелайте успехов в освоении нового. Пусть хорошее настроение поможет совершить вам открытие на уроке математике. Крепко обнимите себя и скажите: У меня всё получится! Садитесь.
Работа с пословицей:
НЕ КРАСНА ИЗБА УГЛАМИ, А КРАСНА ПИРОГАМИ.
— Как понимаете эту пословицу?
(Дом хорош не внешней красотой, а гостеприимством хозяев)
— Как встречают гостей радушные хозяева?
(Хлебом-солью, приветливыми улыбками, аплодисментами (артистов, например))
— У нас сегодня тоже гости. Давайте, как гостеприимные хозяева встретим их улыбками.
— Чем можем их порадовать?
(Дружной работой на уроке,…)
— Как вы думаете, нужно ли вам изучать математику?
— Где в повседневной жизни вы встречались с математикой?
— Математика нужна во многих областях.
И ни одна из профессий, которую вы выберете, став взрослыми, не может обойтись без знания математики.
Строителю она нужна, чтобы рассчитать, сколько материалов нужно для строительства здания; врачу, чтобы рассчитать норму лекарства или создать новое лекарство от всех болезней; инженеру, чтобы создать новую совершенную машину. Без математики не может обойтись ни одна наука: ни химия, ни физика, ни астрономия
— Что мы развиваем на уроках математики? 
II. Актуализация знаний.
Цель: Повторение изученного материала
Выполняют устный счёт
Познавательные УУД
(Актуализация изученных способов действий, развитие мыслительных операций)
Личностные УУД
(Осознание своих эмоций, интереса к изучению математики)
Регулятивные УУД
(Учатся работать по предложенному учителем плану)
Познавательные УУД
(Сравнение математических записей по нескольким основаниям; нахождение закономерности; самостоятельное продолжение их по установленному правилу)
Соблюдая все правила каллиграфии, запишите в тетради число, классную работу.
Минутка чистописания
—Найдите закономерность и продолжите ряд чисел.
-Посмотрите на ряд чисел, что можете сказать о расположении чисел?
-А что значит в порядке возрастания?, а убывания?
— На какие две группы мы можем разделить все полученные числа?
— А почему мы их так называем?
– Чтобы узнать что-то новое, что надо сделать сначала?
— А разве может быть математика без устного счёта?
Заполните таблицу
Уменьшаемое70
42
80
98
Вычитание
4
6
12
Разность
20
10
41
Что неизвестно в первом столбике? Как находили?
Что неизвестно во втором столбике? Как находили? (Чтобы найти уменьшаемое, нужно к вычитаемое прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.)
— Что такое задача?
* В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых деревьев росло в саду? (9)
*На проводе сидели 12 ласточек. Через некоторое время четвёртая и седьмая ласточки улетели. Сколько ласточек осталось сидеть на проводе? (10)
* Винни-Пух, Кролик и Пятачок ожидали поезд три часа. Сколько часов ожидал поезд каждый из них? (3)
* Из половины муки бабушка испекла пирожки, а остальные 2кг муки ушло на ватрушки. Сколько килограммов муки было у бабушки? ( 4)
III.Постановка проблемы.
Цель: вывести тему и цели урока
IV.Музыкальная физминутка (для глаз)
Формулирование темы и целей урока.
Участвуют в обсуждении проблемных вопросов, формулируют собственное мнение и аргументируют его.
Участвуют в исследовательской практической работе
в ходе практической работы, определить что такое угол, виды углов, способы их построения;
Выполняют движения под музыку.
Познавательные УУД
(Использование простейших приемов анализа различных видов записей, умение устанавливать аналогии)
Регулятивные УУД
(Умение принимать цель урока и следовать ей в учебной деятельности)
Личностные УУД
(Умение применять правила охраны своего здоровья)
Говорите название и в какую группу надо отнести. (В первую группу фигуры 1, 3, 5; во вторую — фигуры 2, 4.)
Как называется наука, изучающая геометрические фигуры? ( ГЕОМЕТРИЯ)
— Как вы понимаете, что такое ГЕОМЕТРИЯ?
В переводе с греческого слово «Геометрия» означает «землемерие».
— Что изучает наука геометрия?
— С какими понятиями из этой страны вы уже знакомы? (точка, отрезок, прямая, геометрические фигуры)
— Какие геометрические фигуры вы знаете?
Сегодня нас приглашает царица Математика в путешествие по области Геометрия. Чтобы узнать цель путешествия, надо разгадать кроссворд «Геометрический».
1) Часть прямой, у которой есть начало, но нет конца. (Луч).
2) Геометрическая фигура, не имеющая углов. (Круг).
3) Самая маленькая геометрическая фигура. (Точка).
4) Геометрическая фигура, имеющая форму вытянутого круга. (Овал).
По вертикали вы можете прочитать ещё название геометрической фигуры. (угол)
— Есть ли угол на экране? Сколько их? (1 – красный)
— Как вы думаете: какая тема нашего урока? Какие учебные задачи поставим на урок?
— Ребята, а зачем мы будем изучать углы?
— Как Вы думаете, вам эти знания пригодятся?
V. Первичное закрепление. Рефлексия учебной деятельности
Цели:
— организовать первичное применение нового знания.
— зафиксировать новое содержание урока;
— организовать рефлексию собственной учебной деятельности;
Решают учебную задачу: выводят переместительный закон умножения.
Участвуют в обсуждении проблемных вопросов, формулируют собственное мнение и аргументируют его
Сравнивают собственные выводы с выводами учебника
Регулятивные УУД
(Проявление самостоятельности и инициативы в разных видах деятельности)
Познавательные УУД
(Умение следовать образцу и правилу)
— Могли бы мы обойтись без углов в жизни?
Без углов предметы принимали бы форму круга или овала.
Кто из вас слышал слово угол в обыденной жизни? Углы окружают нас и в повседневной жизни. Приведите свои примеры, где есть углы вокруг нас. (Посмотрите на экран). Здесь показан металлический угол для соединения труб, канцелярский уголок, чертёжные угольники, угловая мебель: стол, диван.
— В тетради отметьте точку и обозначьте её буквой О. Проведите из точки О два луча.
— Что такое луч?
— На сколько частей лучи разделили плоскость? Меньшую часть заштрихуйте цветным карандашом.
-Какую фигуру вы заштриховали? (Угол).слайд
— Сформулируйте определение.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
— Из чего же состоит угол? (точка-вершина угла, лучи- стороны угла )
— А как можно обозначить угол? /1-одной буквой в вершине, 2-цифрой, 3- тремя буквами/ слайд
— А какие инструменты нам понадобились для построения углов?
-Но еще мы можем построить угол без использования данных инструментов.
Сгибание разных по размеру листов бумаги с целью построения углов.
-У тебя получилась модель прямого угла. Какое из высказываний будет верным?
1. Синий угол больше красного.
2. Красный угол больше синего.
3.Синий и красный углы равны. /высказывания детей/
— Прочитаем, что об этом думают Миша и Маша. стр.85 учебника
Прямой угол в тетради можно начертить с помощью инструмента, который называется «угольник». Рассмотрите угольник и найдите прямой угол.
На какие вопросы уже нашли ответы? ( что такое угол, и из чего он состоит)
-Какие затруднения испытывали? Что помогло ответить на вопросы?
VI. Закрепление материала.
Цель: закрепить знания по пройденному материалу
Осуществляют опору на прошлый опыт и знания
Личностные УУД
(Формирование личного отношения к содержанию задания)
Коммуникативные УУД
(Умение с достаточной полнотой и точностью выражать свои мысли)
Одинаковые углы вы видите на экране? (Нет.)
Пришло время узнать виды углов.
1 2 3 4 5
Практическая работа. Построение модели прямого угла.
— Углы бывают разные, но сначала мы познакомимся с самым главным углом. Возьмите лист бумаги. Сложите лист пополам, а потом ещё раз пополам. Обведите линии сгиба карандашом. На сколько частей прямые линии разделили плоскость? (На четыре).
— Сколько углов получилось? (Четыре).
— Это особенные углы. Может быть, кто-то знает название этих углов? (Эти углы прямые).
— Не всегда удобно определять прямой угол на глаз. Для этого используют линейку-угольник. Чтобы определить прямой угол или нет угла, нужно совместить вершину и одну сторону угла с вершиной и стороной прямого угла на линейке-угольнике. учебник стр.86
— На рисунке видно, что бывают и другие углы — не прямые. Можно ли сравнивать углы по величине. Каждый из углов имеет своё название.
С помощью модели прямого угла узнайте, будут ли прямыми остальные углы угольника. Видим, что угол угольника меньше прямого угла, значит он какой? Острый угол – это угол, который меньше прямого.
— Проверим третий угол. Видим, что угол угольника больше прямого угла, значит он какой? Тупой угол – это угол, который больше прямого.
Если стороны угла и прямого угла угольника совпали, то это какой угол? (прямой) Если угол меньше, чем прямой угол угольника, то это…? (острый угол) Если угол больше, чем прямой угол угольника, то это угол…?(тупой)
Какие же виды углов бывают? (таблички)
VII. Физминутка
Под музыку выполняют
движения
Личностные УУД
(Умение применять правила охраны своего здоровья)
VIII. Самостоятельная работа.
Цель:
-организовать выполнение учащимися самостоятельной работы на новое знание;
— организовать самопроверку по эталону, самооценку;
— организовать выявление места и причины затруднений, работу над ошибками.
Выполняет каждый самостоятельно и проверка в парах
Познавательные УУД
(Понимание смысла задания; возможность применить первоначальные способы поиска информации)
Коммуникативные
УУД
(Участие в работе группы, распределение роли, общение друг с другом)
Положи три карандаша так, чтобы получились три угла – острый, прямой и тупой. 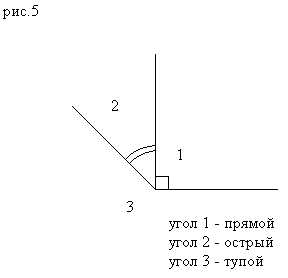
Работа в печатной тетради. № 112( слайд)
— Ребята, вы научились чертить углы?
—Решите мне задачу.
-Вова начертил на листе бумаги 9 углов, а Саша на 3 угла меньше. Сколько углов начертили мальчики вместе?
Что это такое?
— А что такое задача?
— Повторите условие, а теперь вопрос.
-О чём эта задача?
-Что известно?
— Что сказано о Вове?
-Что нужно узнать?
— Можем, мы ли сразу ответить на вопрос?
-Почему?
— А можем ли узнать, сколько углов начертил Саша?
-Каким действием?
— Почему вычитанием?
— Мы узнали, сколько углов начертил Саша. Как узнать, сколько углов мальчики начертили вместе?
-Почему сложением?
-Запишите решение задачи в тетрадь.
IX. Самооценка. Рефлексия деятельности.
Цель:
подвести итог проделанной работы на уроке.
Систематизируют полученные знания, высказывают свои впечатления от урока
Формулируют конечный результат своей работы на уроке.
Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты, степень их соответствия.
Личностные УУД
(Оценивание разного вида деятельности на уроке)
Регулятивные УУД
(Формирование умение адекватно оценивать свою деятельность)
Пришло время подвести итог урока.
-Был ли урок полезен, для вас?
Какое задание вам понравилось?
Какое задание было самым интересным?
А какое — самым трудным?
-Какую задачу ставили на урок?
-Достигли ли её?
-Каким способом?
-Где можете применить новые знания?
— Из каких элементов состоит угол?
-Какие углы бывают?
–– Кто доволен сегодня своей работой?
– Кто хотел бы что-нибудь исправить?
— Что для этого нужно сделать
-Оцените свою работу на уроке?
X. Домашнее задание, выставление оценок, комментирование
Цель:
— организовать выполнение д/з
Записывают задание, задают вопросы
П.Т. стр 47 № 115-116
infourok.ru
Конспект урока по математике на тему «Прямой угол»
Муниципальное бюджетное общеобразовательное учреждение
«Заинская средняя общеобразовательная школа №6»
Заинского муниципального района Республики Татарстан.
Открытый урок в 1″в» классе
по математике
( УМК «Школа 2100»)
«Прямой угол»
Чернова Людмила Михайловна
Учитель начальных классов
первой квалификационной категории
МБОУ ЗСОШ № 6
г. Заинск Республики Татарстан
2014 г
Тема : Угол. Прямой угол
Педагогические задачи: познакомить с понятиями угол, прямой угол; учить делать модель прямого угла и выделять прямые углы из множества других углов путем сравнения с моделью прямого угла.
Планируемые результаты образования:
Предметные: знают: понятия угол, прямой угол; умеют: делать модель прямого угла и выделять прямые углы из множества других углов путем сравнения с моделью прямого угла.
Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД):
Регулятивные: проговаривают последовательность действий на уроке, работают по предложенному учителем плану.
Познавательные: ориентируются в своей системе знаний: отличают новое от уже известного с помощью учителя.
Коммуникативные: владеют диалогической формой речи и способами совместной деятельности в группе, слушают и понимают речь других (одноклассников, учителя).
Личностные УУД: имеют представление о причинах успеха в учебе, проявляют интерес к учебному материалу, имеют целевую установку на отработку математических навыков.
Оборудование: небольшие листы кальки на каждого ученика, линейки, цветные карандаши.
Ход урока
Приветствие:
Улыбнитесь друг другу, улыбка — хороший настрой на работу. На уроке мы будем рассуждать, мыслить, решать, раскроем секреты математики.
I. Организационный момент.
– Проверьте наличие необходимых предметов на парте. Я буду читать загадку, а вы должны поднять этот предмет:
Если ты его отточишь,
Нарисуешь всё что хочешь:
Солнце, море, горы, пляж.
Что же это? …
(Карандаш.)
То я в клетку, то в линейку.
Написать по мне сумей-ка!
Можешь и нарисовать…
Что такое я? …
(Тетрадь.)
Прямота – моя главная черта. (Линейка.)
Зря страницы не листай,
Там где я – вот там читай.
Я нужна вам для порядка.
Кто такая я? …
(Закладка.)
Хотя я и не свинка,
У меня чумазенькая спинка.
Но совесть у меня чиста –
Помарку стёр ведь я с листа.
(Ластик.)
Сегодня мы с вами будем путешествовать по необычной стране. Эта страна называется Геометрия. А вы – путешественники на протяжении всего пути должны быть очень внимательны и находчивы. Для этого выполним задания.
II. Актуализация опорных знаний.
Минутка чистописания .
1. Работа в тетради: задание 1 на с. 26.
– С какими числами уже знакомы? (1, 2, 3, 4.) Какое из них обозначает самое большое количество предметов? Самое маленькое количество предметов?
– Потренируемся записывать цифры 1, 2, 3, 4. Какие цифры написаны в первом ряду? во втором ряду? Продолжите ряды.
2. Фронтальная работа (счет по числовому отрезку).
– С какой фигурой познакомились на прошлом уроке? Что помогает нам делать числовой отрезок? Давайте вспомним, как надо правильно считать по числовому отрезку. (Если перемещаться влево, числа увеличиваются, вправо – уменьшаются.)
– Сосчитайте от 3 до 8, от 9 до 1. Назовите последующее число для 1, 3 (ответ 2,4). На сколько следующее число больше предыдущего? (на 1) Назовите предыдущее число для 4, 2.(3,1) На сколько предыдущее число меньше последующего?( на 1) . Какое число стоит справа от 2, слева от 4?
– Какие фигуры нарисованы на доске?
В старших классах
Каждый школьник
Изучает треугольник.
Три каких-то уголка,
А работы – на века.
– Почему эти фигуры так называются? Докажите что это треугольники !? (У них три вершины и три стороны.)
Включается проектор (1 слайд)
– Посмотрите, что происходит с треугольниками. (Учитель стирает часть фигур.) Непослушные Ластики стерли часть фигур и утверждают, что это тоже фигуры. А как вы думаете? Давайте посмотрим может быть у нас в классе есть то, на что похоже эти фигуры. (Предположения учащихся.)(Слайд №2)
– Сколько проведено лучей из каждой точки? Как бы вы назвали эти фигуры? (Предположения детей.)
Ребята давайте мы подумаем , что мы сегодня будем изучать (Углы, угол)
. С чем мы познакомимся? (С прямыми углами.) Какие задачи поставим перед собой ?
Это углы. Точки – это вершины углов. Лучи – стороны углов.
III. «Открытие» нового знания.
Практическая работа.
– Сегодня на уроке будем заниматься на с. 54–55. Сейчас я вам предлагаю побыть маленькими исследователями и проведем небольшой эксперимент.
У вас на партах лежат листы кальки самой разной формы. Перегните свой лист пополам и еще раз пополам – получается модель прямого угла. Разверните листы, обведите сгибы цветным карандашом при помощи линейки. Сверните обратно. Какая фигура у вас получилась? (Прямой угол.)
– Проверьте предположения. (Учащиеся читают статью учебника на с. 54.) (Да, это прямой угол.)
– Сравните свою модель с моделью товарища по парте.
Учащиеся накладывают модели друг на друга.
– Можно ли сказать, что они равны? (Углы равны, если при наложении их стороны совпадают. Все прямые углы равны.)
Учитель накладывает свою модель на модели учеников, совмещая при этом вершину и стороны.
– Мы получили модель прямого угла и будем с ней работать.
А чтобы лучше нам работалось мы проведем небольшую разминку.
Физминутка
Сейчас будет музыка вы будете под нее танцевать, двигаться и образовывать пару , когда музыка прекращается вы будете обсуждать данный вопрос.
Вопрос 1. Сколько сторон у квадрата? Начинает тот у кого светлые волосы или выше ростом.
2. Сколько точек у луча.
3. Назовите замкнутые ломанные линии.
IV. Первичное закрепление.
1. Работа с учебником: задание 4 на с. 55.
– У вас на столах есть листочки с заданиями.
Какие углы начертили Катя, Петя, Лена и Вова? Давайте проверим, кто начертил прямой угол? Как это сделать? (Наложить модель прямого угла на чертеж.)
– Как будем накладывать? (Так, чтобы совпали вершины и стороны.)
Учащиеся накладывают и определяют, что прямые углы начертили Катя и Вова.
– Чем непрямые углы отличаются от прямых? (У непрямых углов одна сторона находится или внутри модели, или снаружи.)
– Так как можно найти прямые углы?
— Обведите только прямые углы.
— Возьмите линейку, цветные карандаши.
— Как вы можете проверить свою работу?
Какие углы вы обвели?
Выполняют самостоятельно путем наложения модели фигур на сами фигуры. Проводится взаимопроверка.
V. Тренировочные упражнения.
1. Работа с учебником: задания 5, 6 на с. 55. (Слайд №3)
– Посмотрите на числовую прямую (задание 5). Какое действие выполнила Катя? (Из 3 вычла 1.) Запишите числовое равенство.
Ученик выполняет задание на доске, остальные в тетради. Получаются записи: 3 – 1 = 2 3 + 1 = 4 2 – 1 = 1 4 – 1 = 3
Самостоятельно записывают результаты действий в порядке возрастания.
Учащиеся самостоятельно записывают нужные выражения (задание 6), а затем устно объясняют выбор.
VI. Итог урока.
Вот и закончилось наше путешествие. Что нового узнали во время путешествия? Понравилось ли вам оно?
– С какими фигурами познакомились? Что интересного узнали об углах? Где могут пригодиться наши знания?
У вас на столах лежат листочки разного цвета красные зеленые и желтые.
— Оцените свою работу на уроке на «Дереве успехов».
— Если кому было интересно и все понятно поднимите зеленый листочек.
— Если у вас были сомнения поднимите желтый листочек.
-Если кому было трудно и нужна помощь, поднимите красный листочек. Поблагодарили друг друга за работу на уроке и прекрипите свои листочки на наше дерево.
Всем спасибо за урок. Молодцы!
infourok.ru
План-конспект урока по математике (2 класс) на тему: Угол. Прямой угол.
ТЕМА: Угол. Прямой угол
Цель: помочь детям уяснить понятие угла, прямого угла, учить делать модель прямого угла и выделять прямые углы из множества других углов путём сравнения с моделью прямого угла.
Планируемые результаты:
Личностные УУД:
— способность к самооценке на основе критерия успешности учебной деятельности.
Метапредметные:
— уметь определять и формулировать; проговаривать последовательность действий на уроке; уметь высказывать своё предположение на основе работы с материалом учебника; уметь работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной оценки; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; планировать своё действие в соответствии с поставленной задачей (Регулятивные УУД).
— уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им; учиться работать в группе, формулировать собственное мнение и позицию (Коммуникативные УУД).
— уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке; осуществлять синтез как составление целого из частей. (Познавательные УУД).
Предметные:
— Понимать смысл угол, прямой угол.
— Уметь делать модель прямого угла.
— Уметь выделять прямые углы из множества других углов путём сравнения с моделью прямого угла.
Ход урока:
I. Мотивация к учебной деятельности
Цели:
— актуализировать требования к ученику со стороны учебной деятельности;
— создать условия для возникновения у учеников внутренней потребности включения в учебную деятельность;
-установить тематические рамки;
— уточнить тип урока;
— наметить шаги учебной деятельности.
-Наш урок хотелось бы начать словами известного американского математика Нивена:
Математику нельзя изучать, наблюдая, как это делает сосед.
-Как вы понимаете эту фразу?
II. Актуализация и фиксирование индивидуального затруднения в пробном действии.
Цели:
-организовать актуализацию умений выполнять операции и обратные операции;
-организовать выполнение учащимися пробного учебного действия;
-организовать фиксирование учащимися индивидуального затруднения;
-уточнить следующий шаг учебной деятельности.
Найдите операцию, объект и результат операции и запишите только ответы:(Слайд)
— 33 больше задуманного числа на 8
— 42 больше задуманного числа на 10
— 17 увеличить на 22
— 66 уменьшить на 20
— какое число надо прибавить к 20, чтобы получить 73?
(взаимопроверка по эталону: 25, 32, 39, 46, 53)
— кто заметил закономерность? Запишите следующее число (60)
— Назовите известные вам геометрические фигуры (Слайд)
III. Выявление места и причины затруднения
Цели:
— выявить место затруднения;
— зафиксировать во внешней речи причину затруднения.
— Отметьте на листе бумаги точку А, проведите два луча АВ и АС.
IV. Построение проекта выхода из затруднения
Цели:
-организовать постановку цели урока;
-организовать составление совместного плана действий;
-определить средства;
-уточнить следующий шаг учебной деятельности.
— Продолжите их до конца листа. На сколько частей они делят плоскость? Закрасьте меньшую часть и вырежьте. Какая фигура получилась?
— Над какой темой будем работать?
— Чему должны научиться?
V.Реализация построенного проекта
Цели:
-реализовать построенный проект в соответствии с планом;
-зафиксировать новое знание в речи и знаках;
-организовать устранение и фиксирование преодоления затруднения;
-уточнить тему урока.
Работа по учебнику стр. 38 урок 13.
Чтение правила.
VI. Первичное закрепление с проговариванием во внешней речи
Цель:
-организовать выявление места и причины затруднений, работу над ошибками.
Физминутка
Работа по стр. 38 № 2
Практическая работа по построению прямых углов № 3, 4. Проверка по эталону (слайд)
VIII. Включение в систему знаний и повторение
Цели:
-организовать повторение умений составлять равенства, используя связь целого и частей.
-Угол дал имя многим геометрическим фигурам. Каким?
— Решение задачи на нахождение периметра прямоугольника. стр. 40 № 9.
— Прочитайте задачу, выполните построение в тетради.
-Что необходимо знать, для решения задачи? (что такое периметр)
— Как найти периметр?
VIII. Рефлексия учебной деятельности на уроке
Цели:
-зафиксировать новое содержание урока;
-организовать рефлексию и самооценку учениками собственной учебной деятельности
-Над какой темой работали?
— Какие цели ставили в начале урока?
— Что показалось интересным?
— Оцените свою работу на уроке.
Домашнее задание: стр. 40 № 8.
nsportal.ru


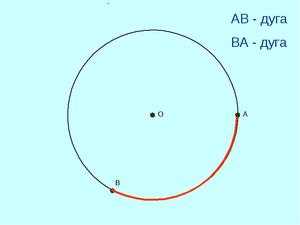 Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.
Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.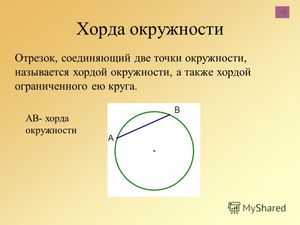 Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.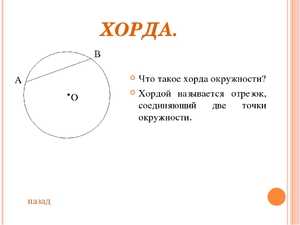 Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.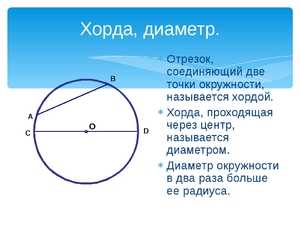 Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.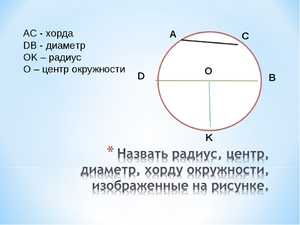 Две равные между собой хорды стягивают равные дуги.
Две равные между собой хорды стягивают равные дуги.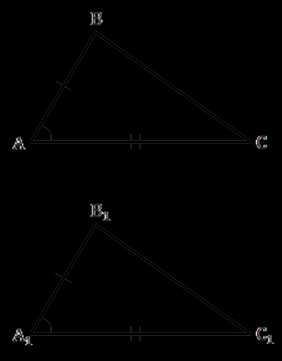

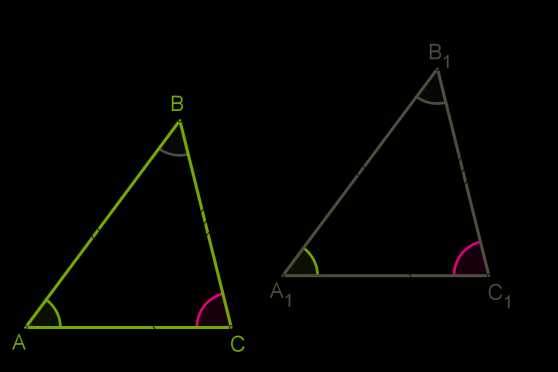 При этом совпадают все стороны и все углы.
При этом совпадают все стороны и все углы.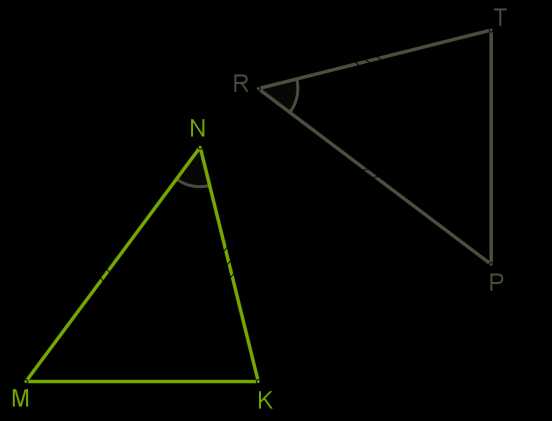
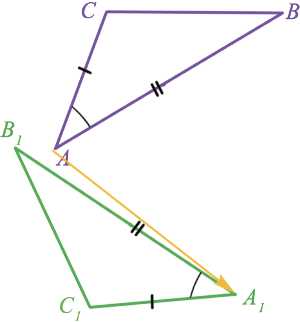
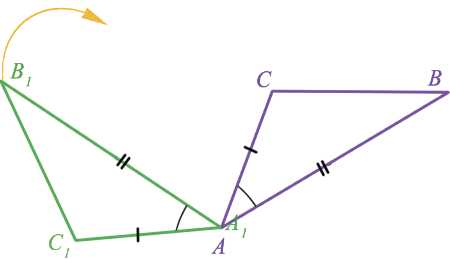
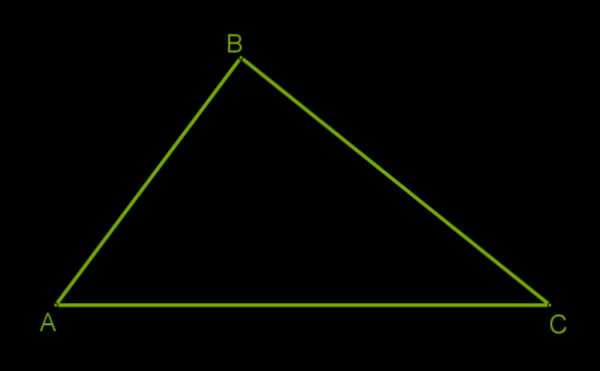
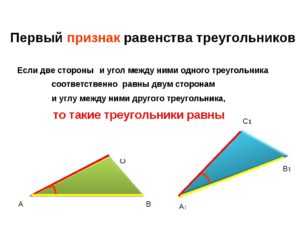 Предположим, что у нас есть фигура, начерченная на листе бумаги. При этом у нас есть линейка и транспортир, с помощью которых мы можем замерять длины отрезков и углы между ними. Как перенести на второй лист бумаги фигуру таких же размеров или увеличить ее масштаб в два раза.
Предположим, что у нас есть фигура, начерченная на листе бумаги. При этом у нас есть линейка и транспортир, с помощью которых мы можем замерять длины отрезков и углы между ними. Как перенести на второй лист бумаги фигуру таких же размеров или увеличить ее масштаб в два раза.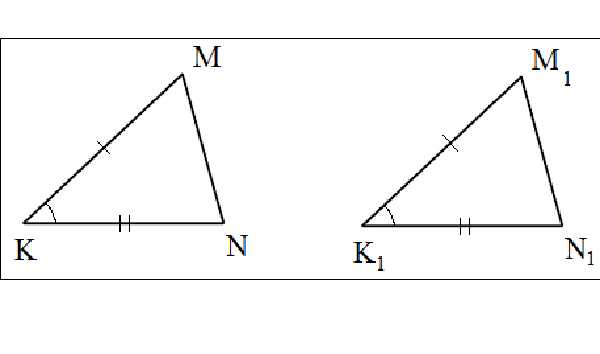

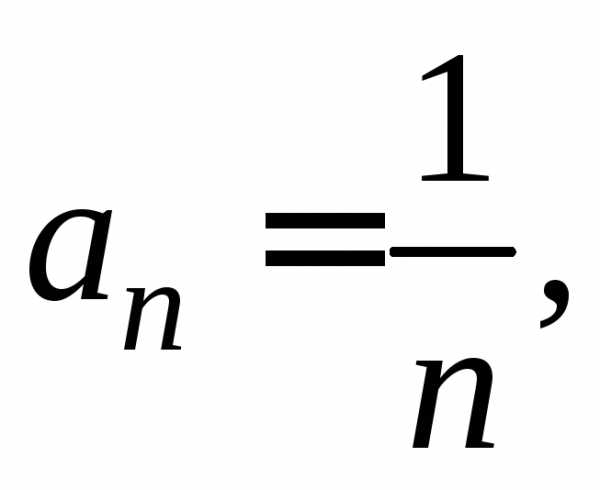

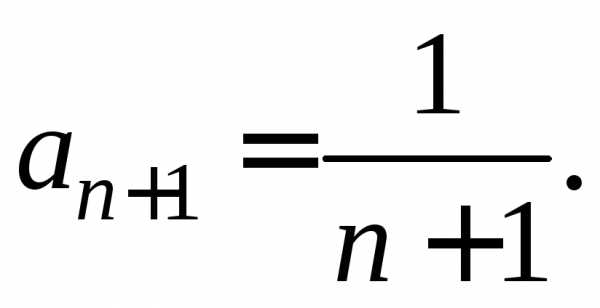 Найдем радиус сходимости ряда:
Найдем радиус сходимости ряда:
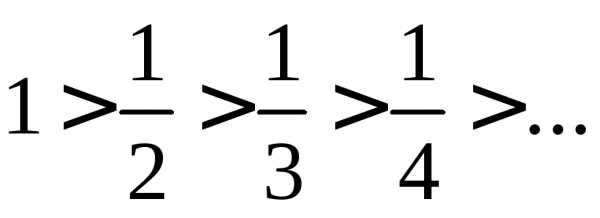 ;
2).
;
2).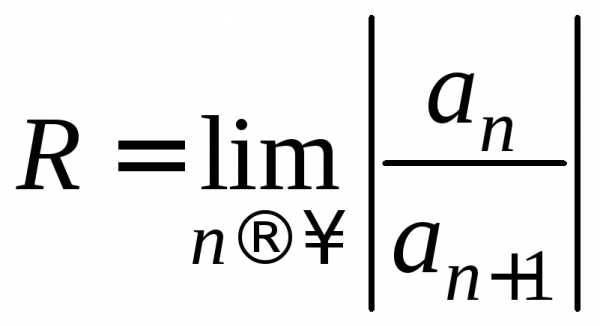 .
.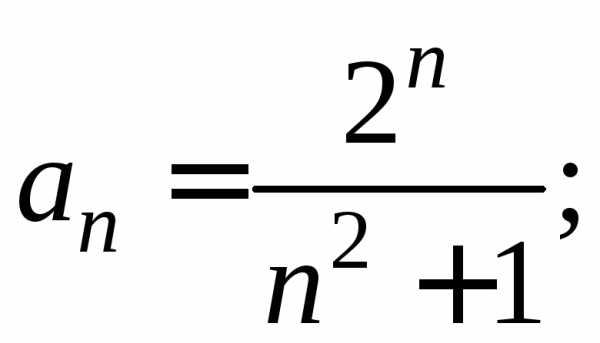
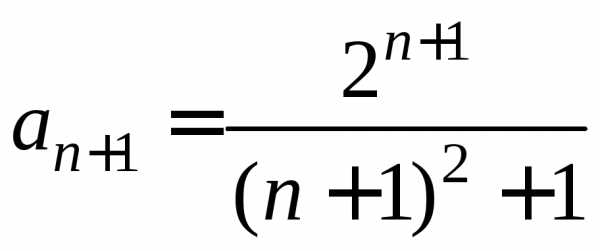 ;
;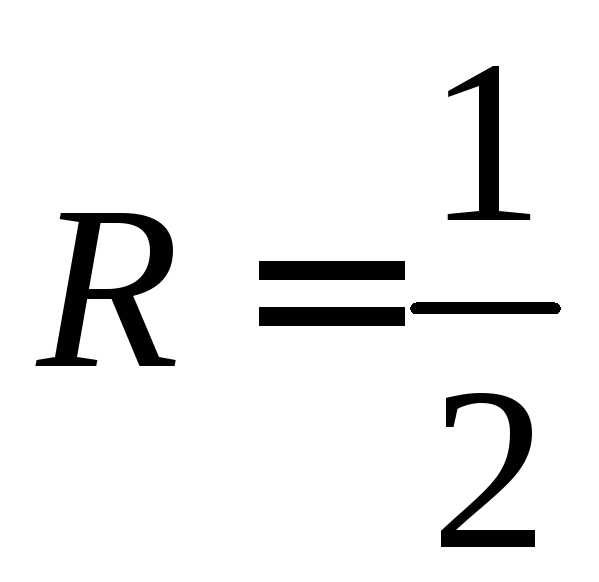 ,
а интервал сходимости (-
,
а интервал сходимости (-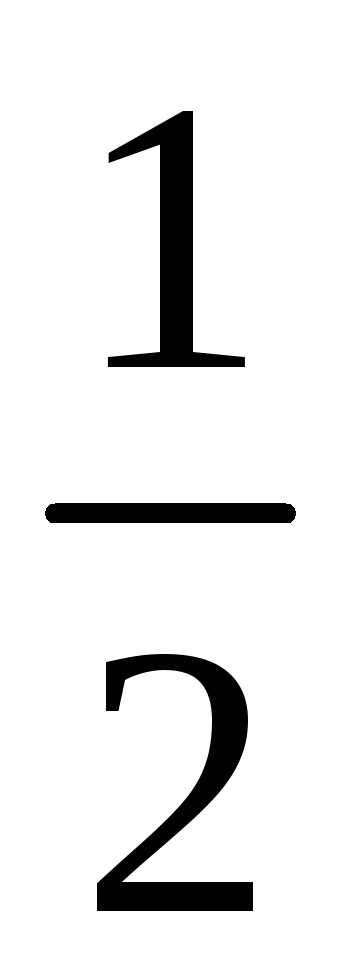 ;
;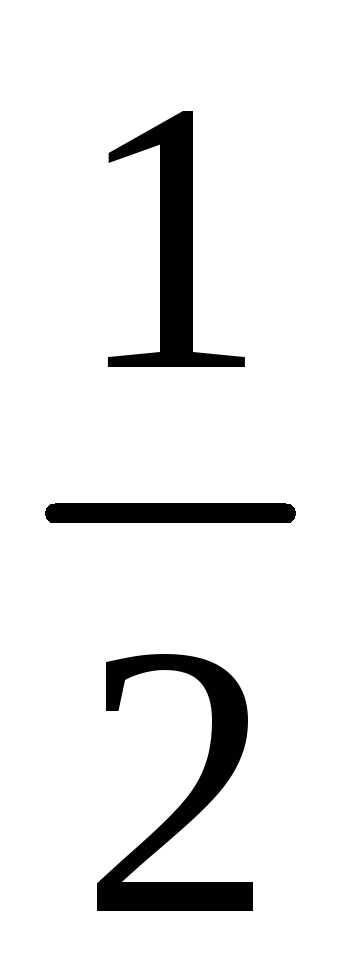 ).
Геометрически это выглядит так:
).
Геометрически это выглядит так: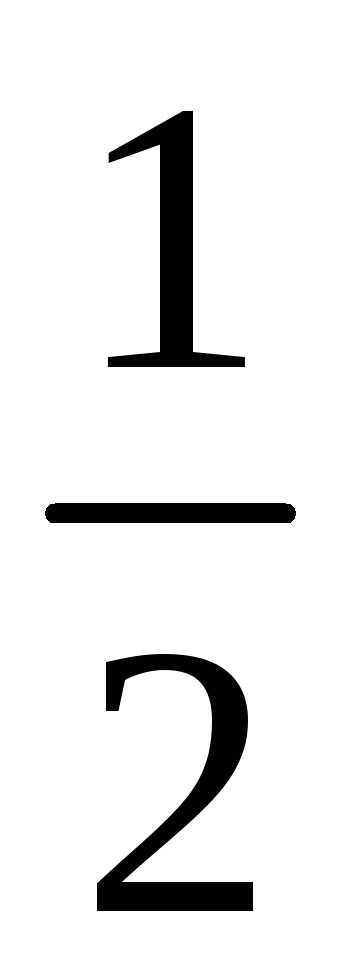 , данный степенной ряд превращается в
числовой ряд вида:
, данный степенной ряд превращается в
числовой ряд вида: ,
данный степенной ряд превращается в
знакочередующийся рядкоторый сходится абсолютно, так как
сходится соответствующий ряд из
абсолютных величин:.
,
данный степенной ряд превращается в
знакочередующийся рядкоторый сходится абсолютно, так как
сходится соответствующий ряд из
абсолютных величин:.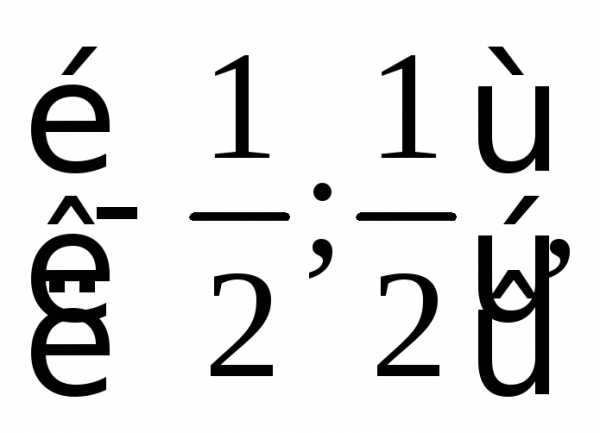 т.е.
т.е.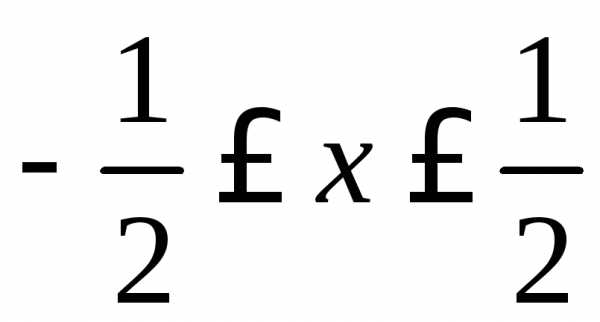 .
.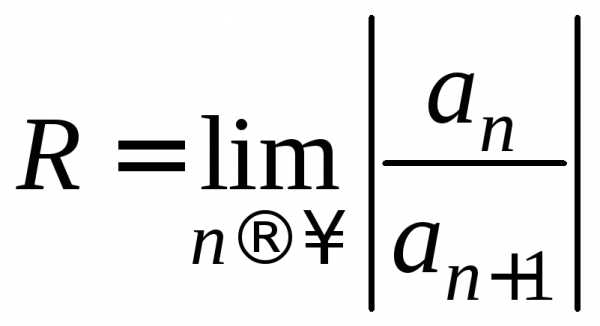 .
.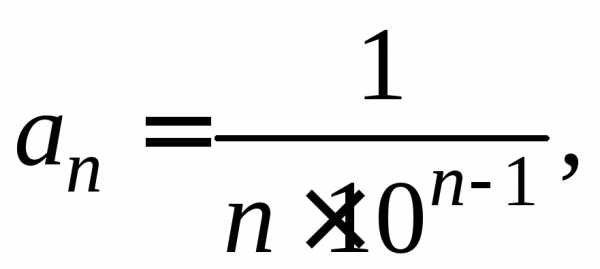
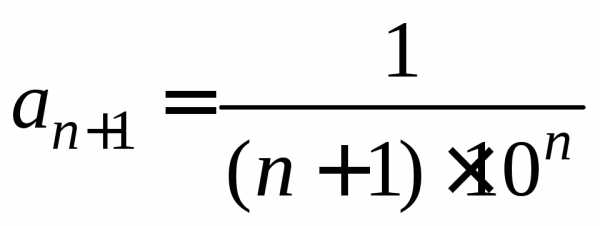
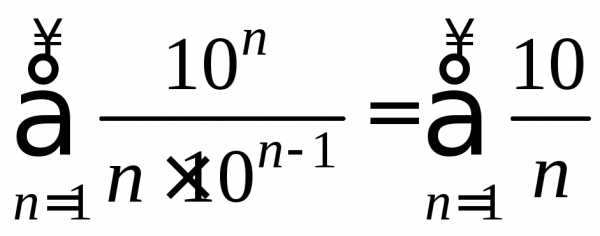 ,
, .
.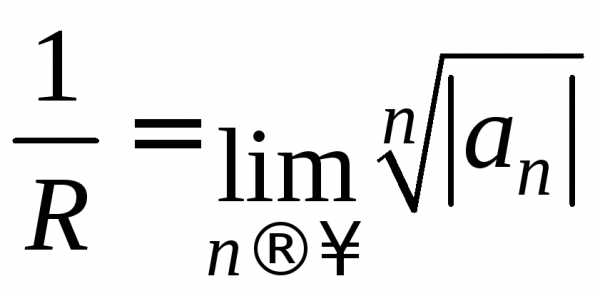 :
: .
Ряд сходится при всехх,
т.е. в интервале (-;
+).
.
Ряд сходится при всехх,
т.е. в интервале (-;
+). для отыскания радиуса сходимости ряда,
так как он не содержит четных степенейх.
Поэтому промежуток сходимости ряда
найдем, воспользовавшись признаком
Даламбера.
для отыскания радиуса сходимости ряда,
так как он не содержит четных степенейх.
Поэтому промежуток сходимости ряда
найдем, воспользовавшись признаком
Даламбера.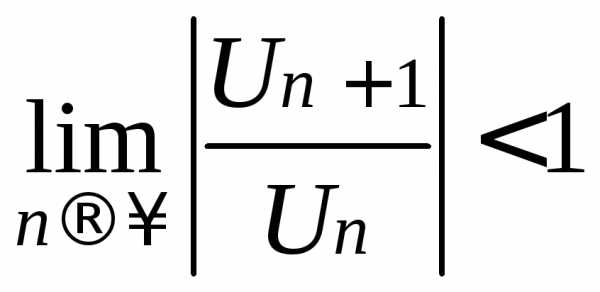 т.е.
т.е. 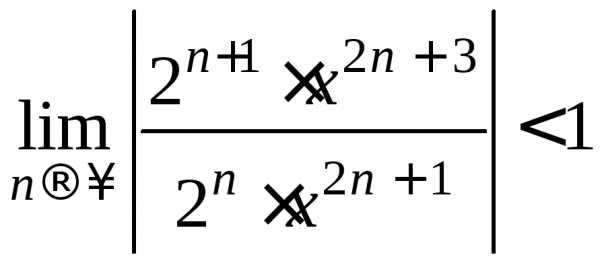 .
.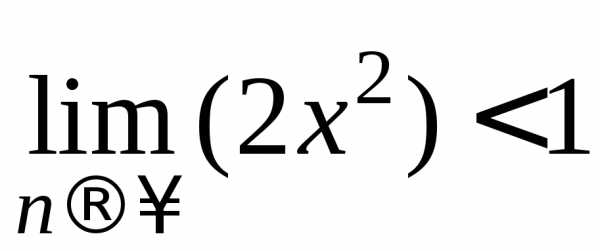 .
.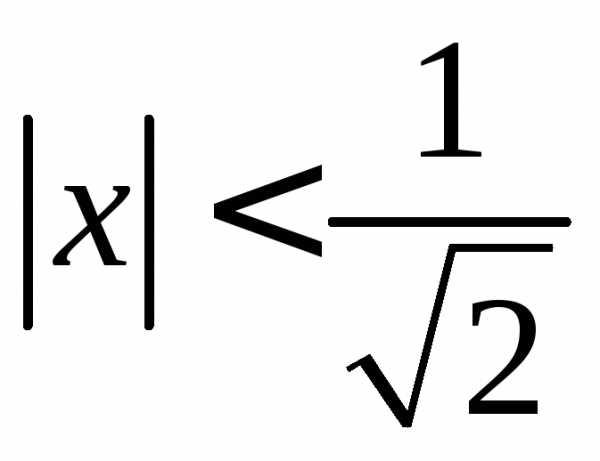 ,
т.е.
,
т.е.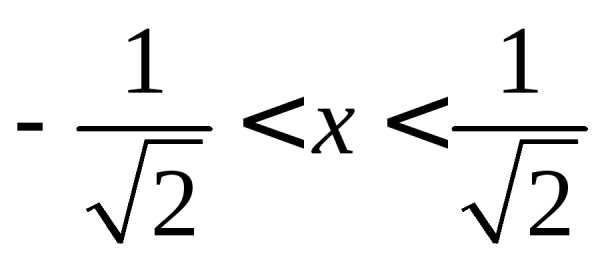 .
.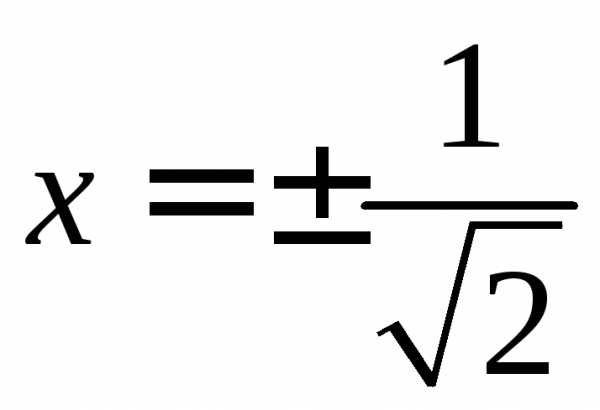 получим расходящийся числовой ряд
1+1+1+1+…+1+…
получим расходящийся числовой ряд
1+1+1+1+…+1+…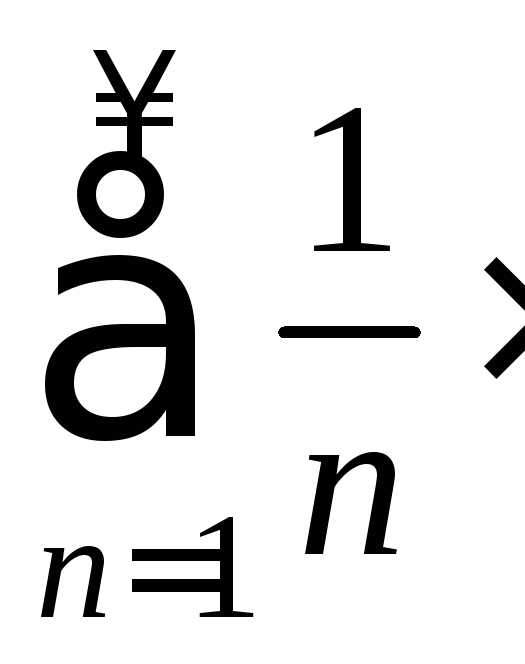
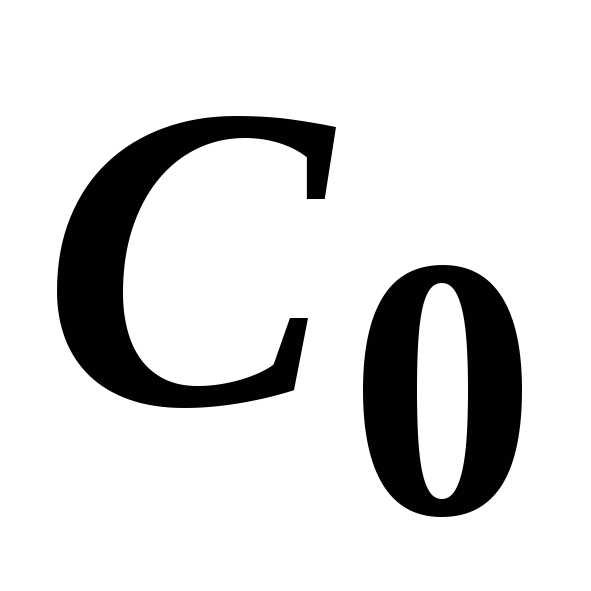 ,
, ,
…,
,
…,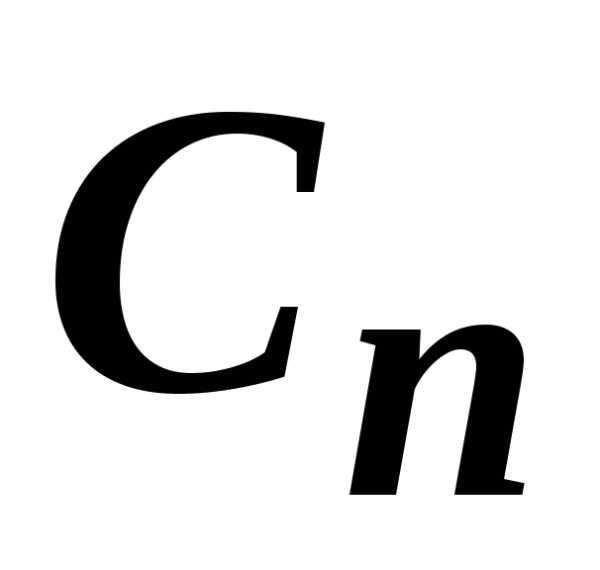 ,…
на степенные функции от разности
,…
на степенные функции от разности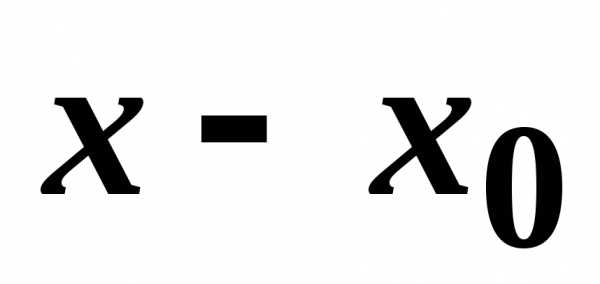 с целыми неотрицательными показателями
степеней.
с целыми неотрицательными показателями
степеней.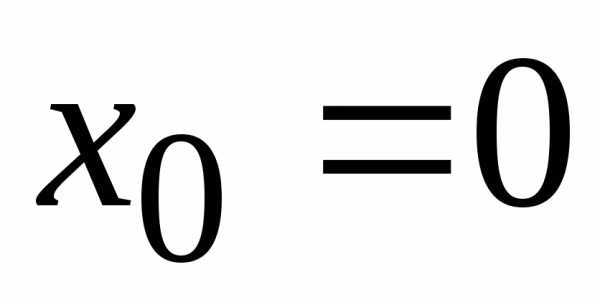 .
.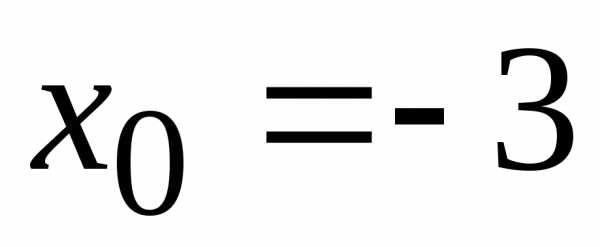 .
.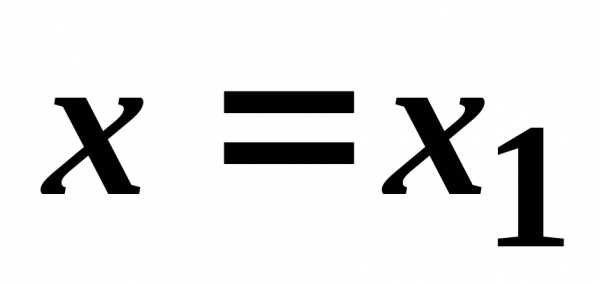 ,
то он сходится, и притом абсолютно, для
всех
,
то он сходится, и притом абсолютно, для
всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ,
то он расходится для всех
,
то он расходится для всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству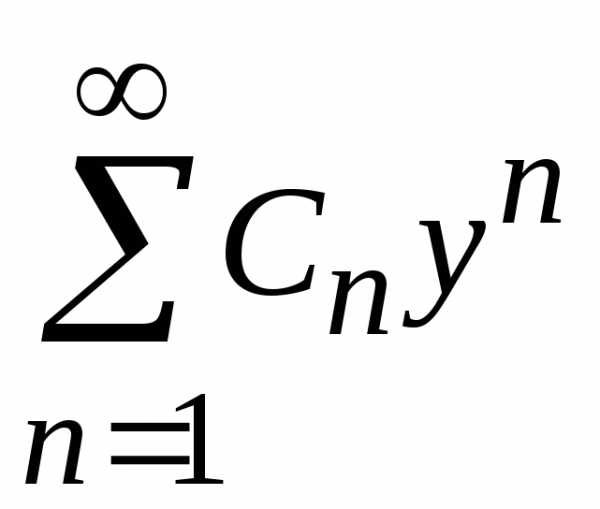 ,
точка сходимости которого,
а неравенство, описывающее область
сходимости, примет вид
,
точка сходимости которого,
а неравенство, описывающее область
сходимости, примет вид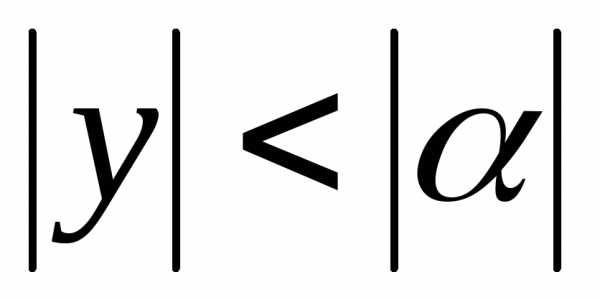 .
.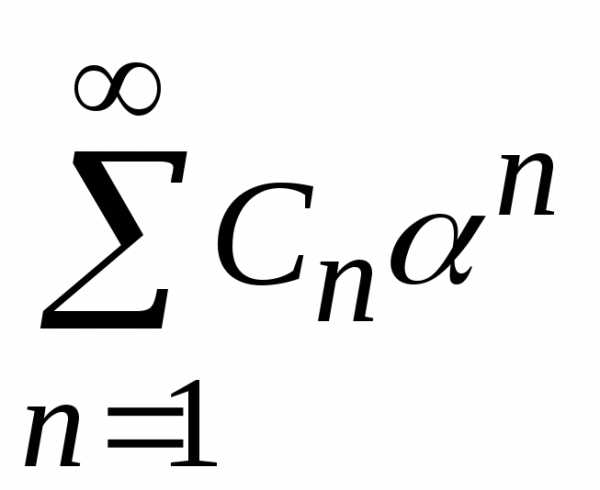 сходится,
следовательно общий член
сходится,
следовательно общий член 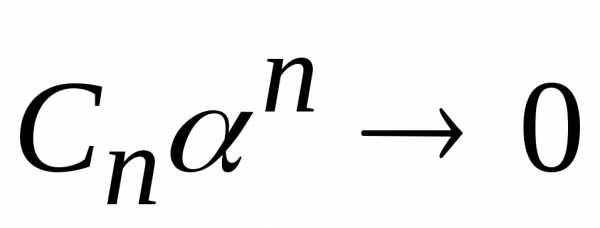 при,
но любая последовательность, имеющая
предел ограничена, т.е. существует такое
при,
но любая последовательность, имеющая
предел ограничена, т.е. существует такое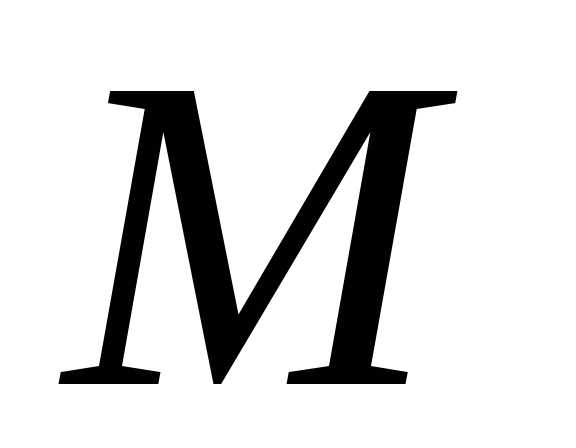 ,
что
,
что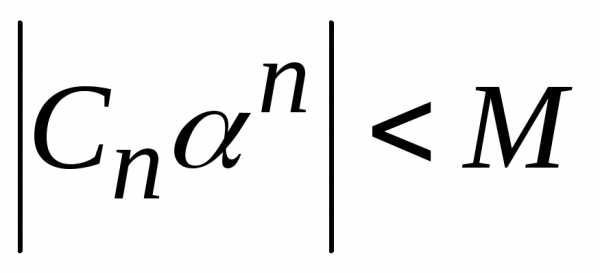 для всех
для всех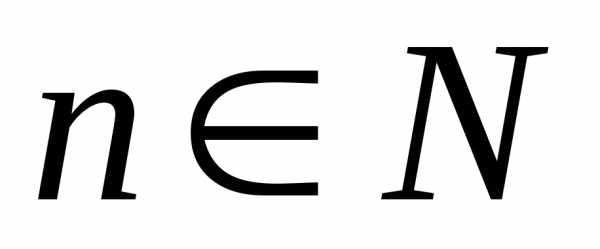 .
.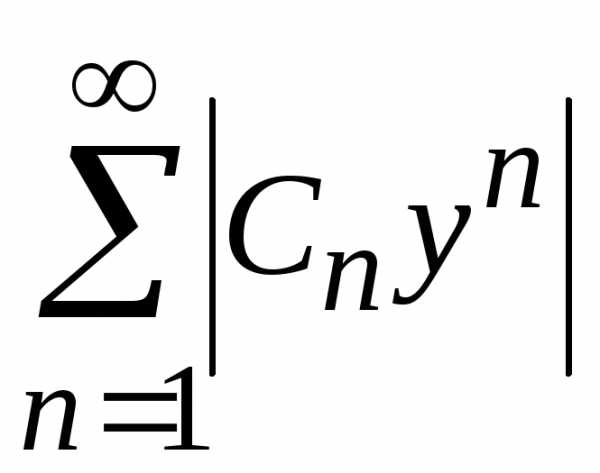 .
.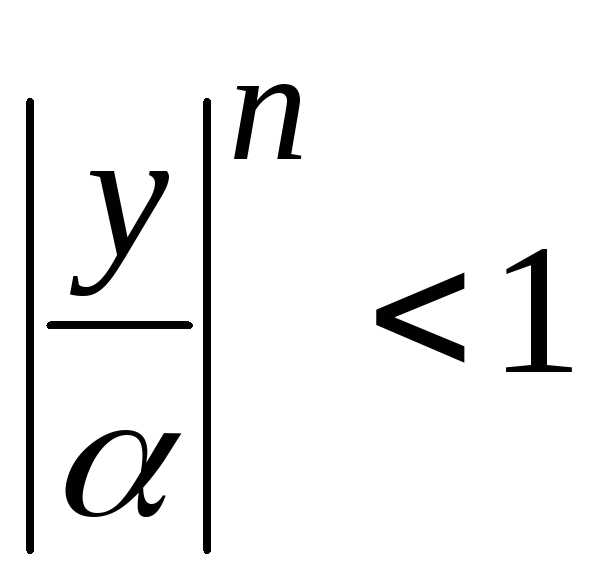 ,
так как
,
так как 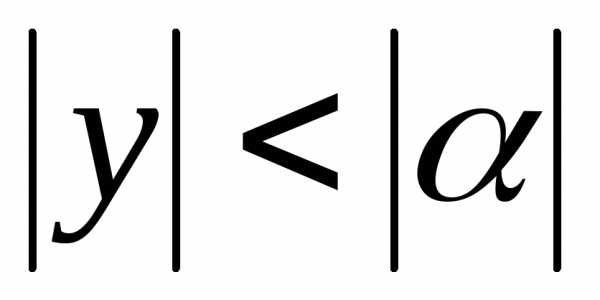 .
.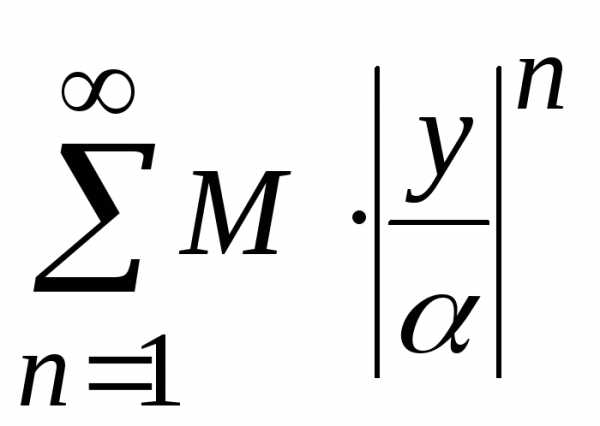 ,
который является геометрической
прогрессией со знаменателем
,
который является геометрической
прогрессией со знаменателем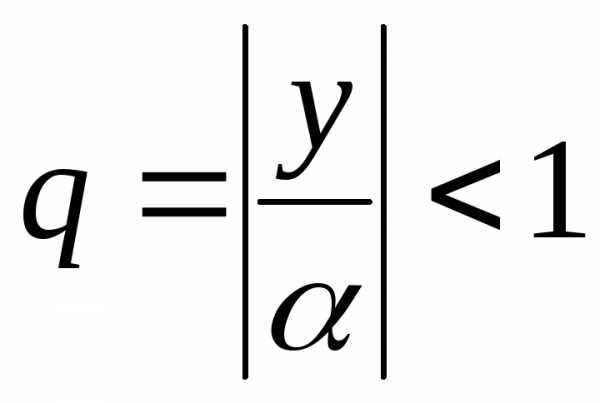 ,
следовательно, он сходится. Так как
,
следовательно, он сходится. Так как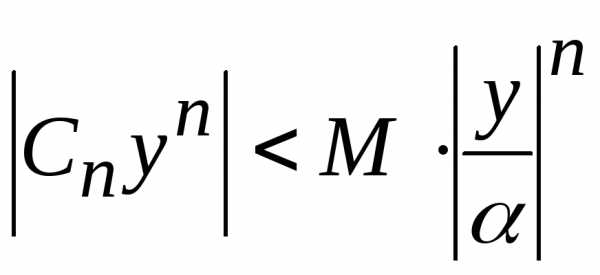 ,
то из первого признака сравнения следует
абсолютная сходимость исходного
степенного ряда.
,
то из первого признака сравнения следует
абсолютная сходимость исходного
степенного ряда.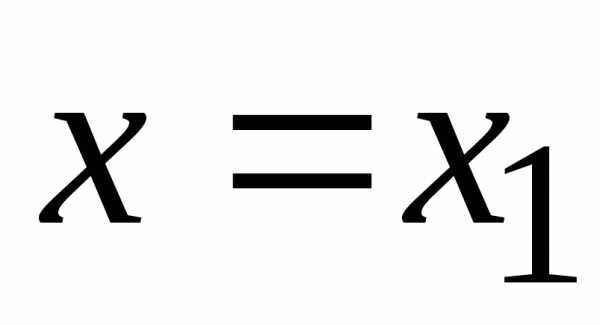 ,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда
,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда 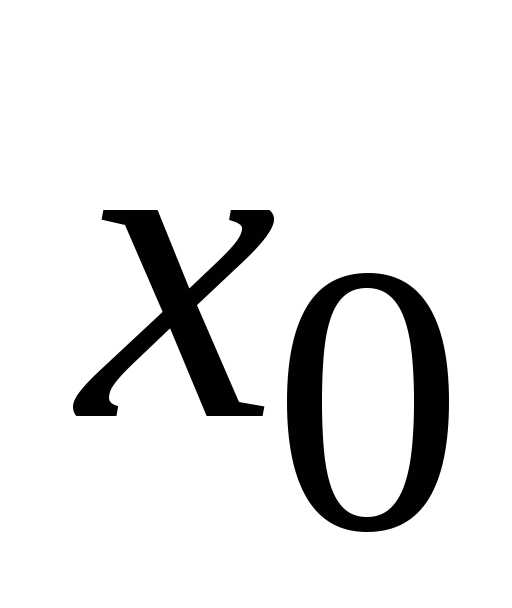 ,
чем
,
чем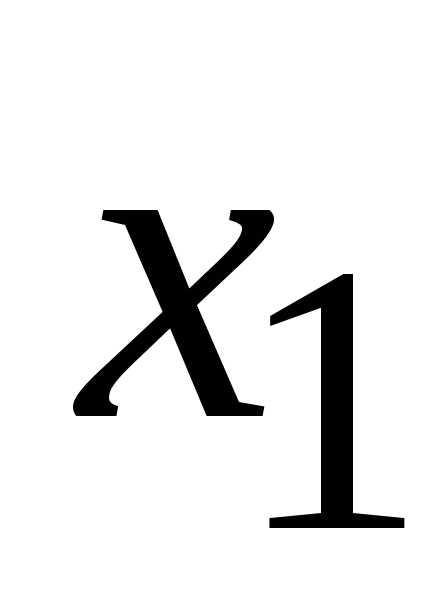 .
Если же ряд расходится при
.
Если же ряд расходится при 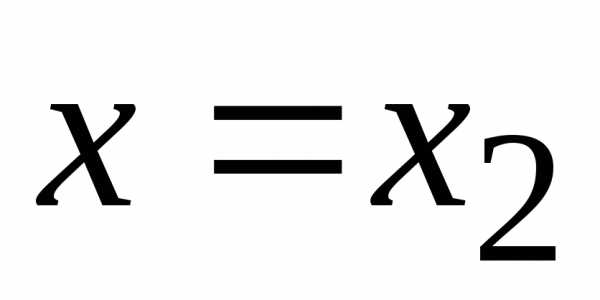 ,
то он расходится и во всех более удаленных
от центра ряда точках.
,
то он расходится и во всех более удаленных
от центра ряда точках. ,
что для всех
,
что для всех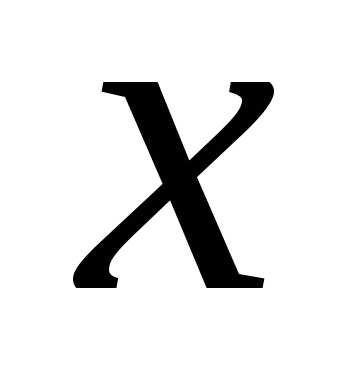 ,
удовлетворяющих неравенству ,
ряд сходится абсолютно и расходится
при всех
,
удовлетворяющих неравенству ,
ряд сходится абсолютно и расходится
при всех 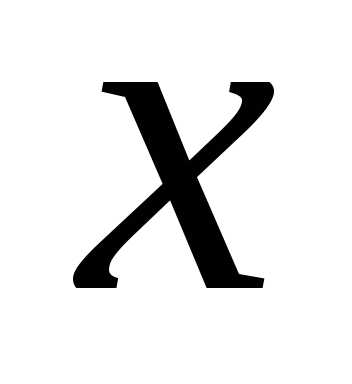 ,
для которых .
,
для которых . называетсярадиусом
сходимости ряда
называетсярадиусом
сходимости ряда 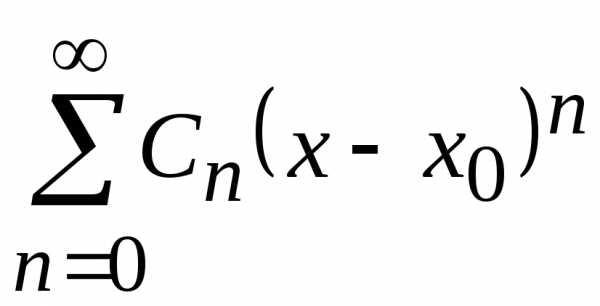 ,
а интервал
–интервалом
сходимости.
,
а интервал
–интервалом
сходимости.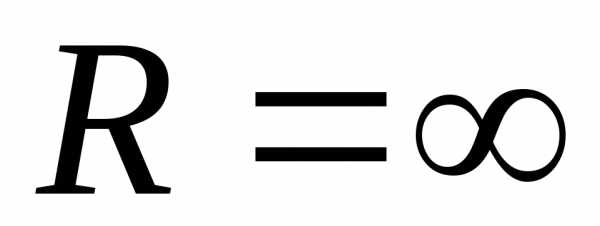 )
или может превращаться в точку (в этом
случае
)
или может превращаться в точку (в этом
случае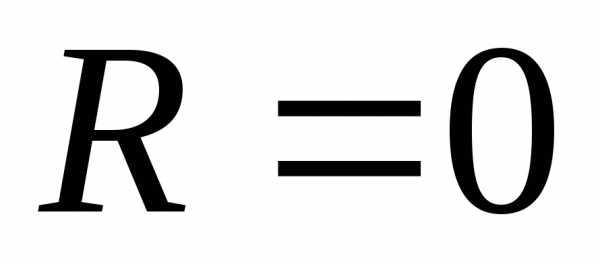 ).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.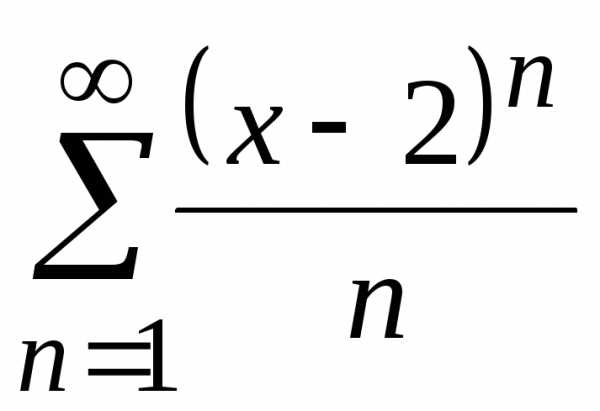 .
.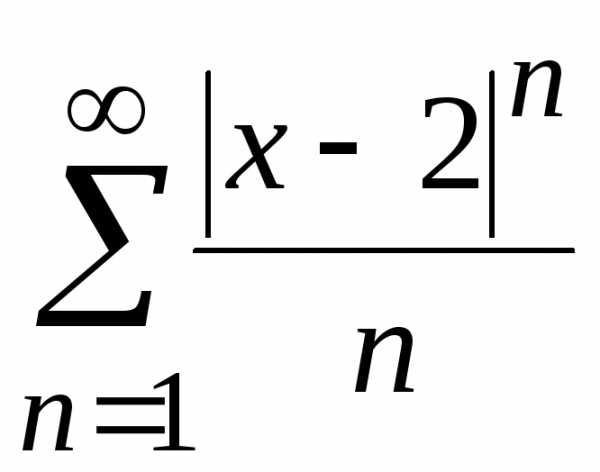 .
Применим признак Даламбера:
.
Применим признак Даламбера: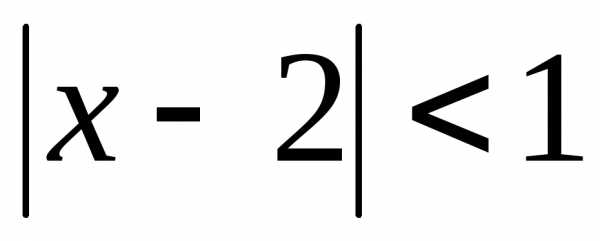 ,
то ряд сходится. Итак,,–
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках
,
то ряд сходится. Итак,,–
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках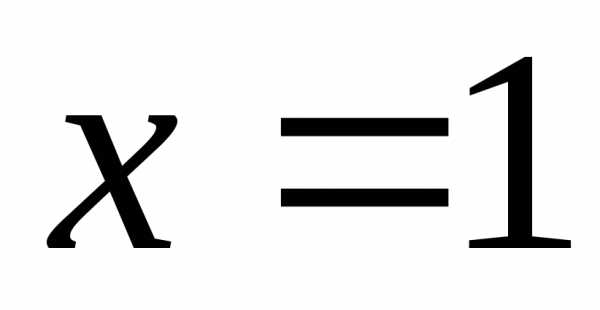 и
и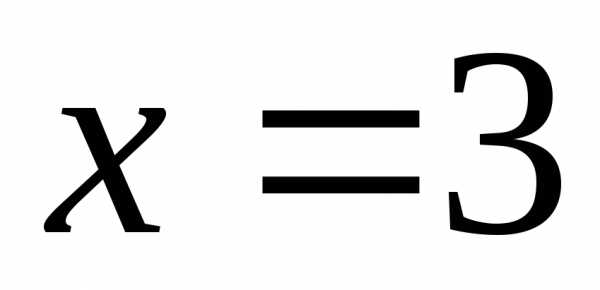 ,
исследуется отдельно.
,
исследуется отдельно.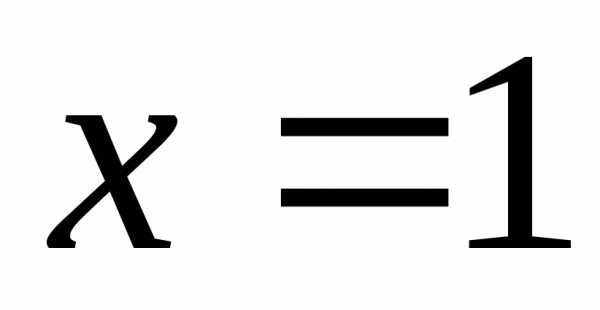 из данного ряда получаем ряд
из данного ряда получаем ряд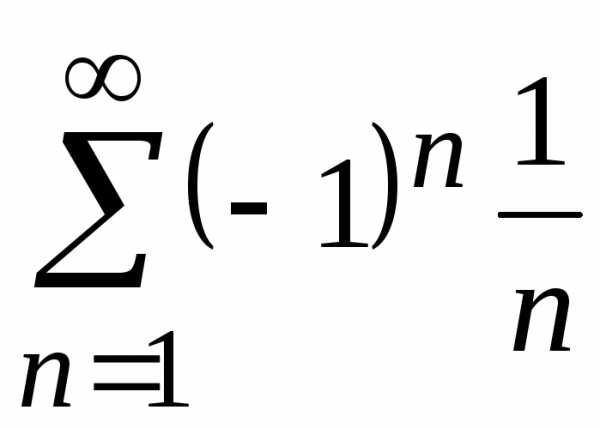 ,
который условно сходится.
,
который условно сходится.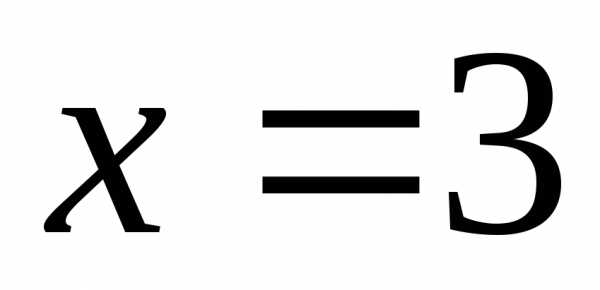 получаем гармонический ряд
получаем гармонический ряд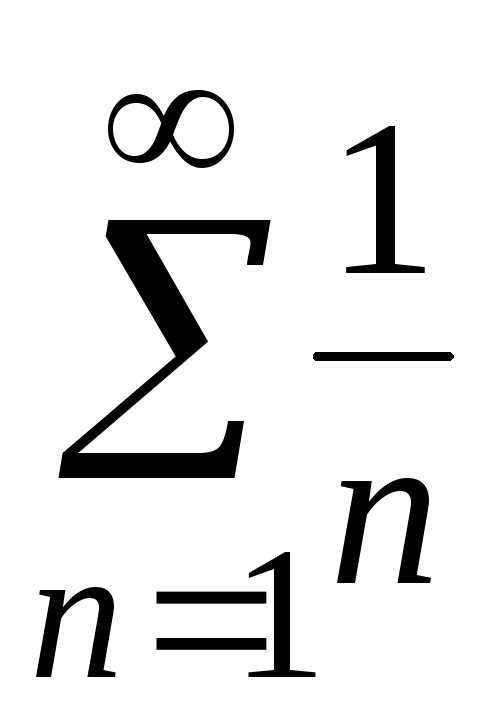 ,
который расходится.
,
который расходится.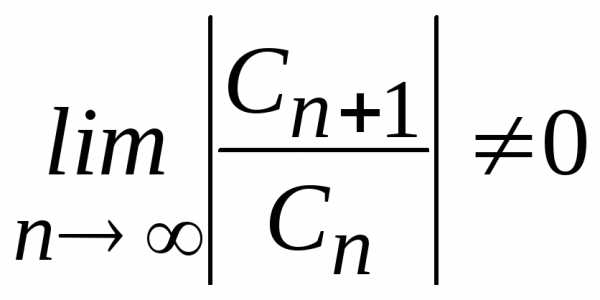 ,
то радиус сходимости степенного ряда
можно вычислить по формуле
,
то радиус сходимости степенного ряда
можно вычислить по формуле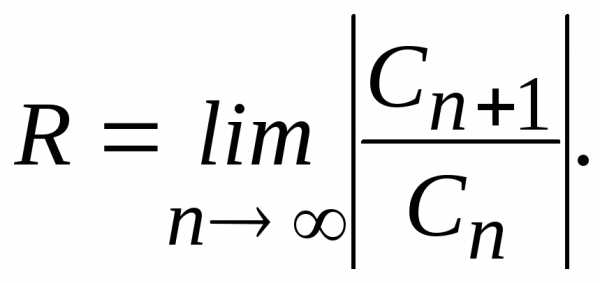
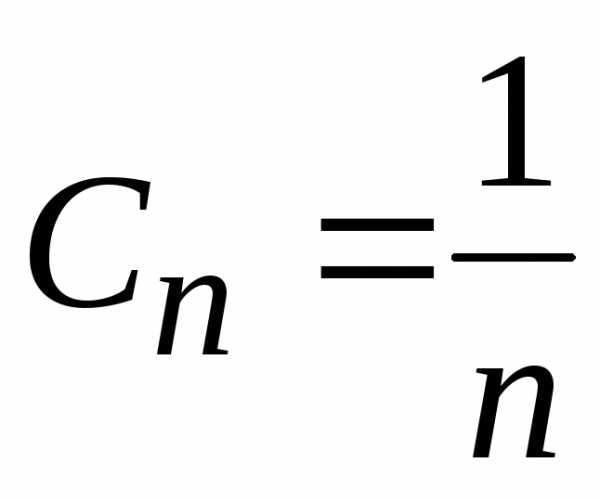 и
и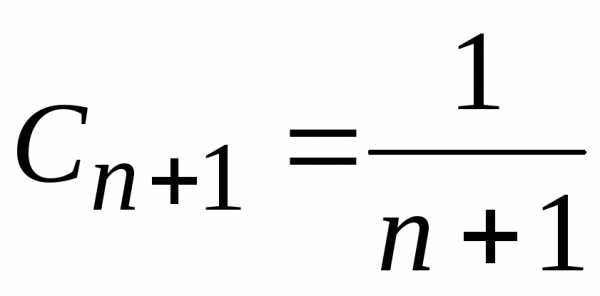 ,
поэтому
,
поэтому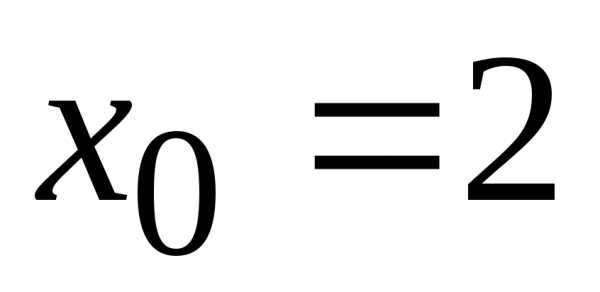 – центр степенного ряда, то– интервал сходимости данного ряда.
– центр степенного ряда, то– интервал сходимости данного ряда.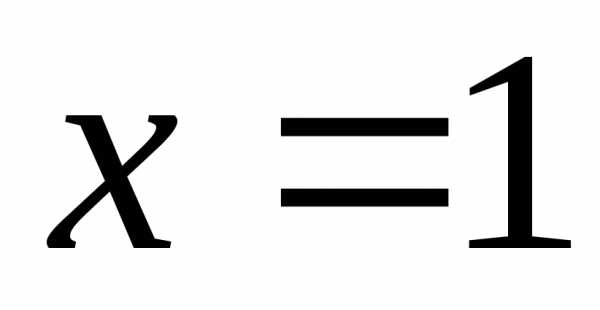 .
.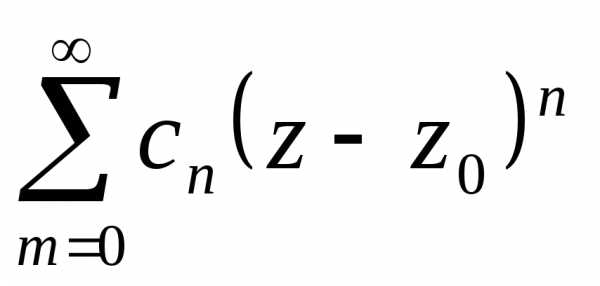 — это частный случай функциональных
рядов, в котором члены ряда представляют
собой степени отклонения переменной
— это частный случай функциональных
рядов, в котором члены ряда представляют
собой степени отклонения переменной от некоторой фиксированной точки
плоскости
от некоторой фиксированной точки
плоскости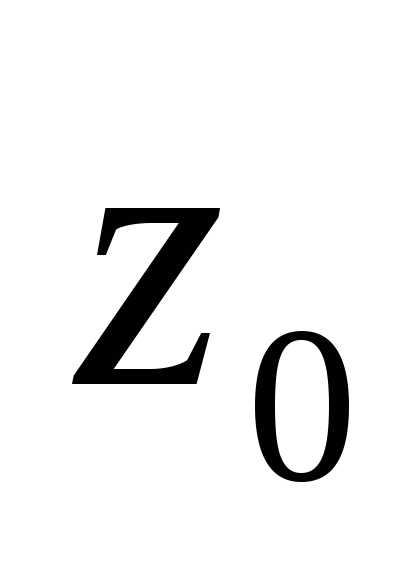 (центра сходимости ряда). Степенные ряды
действительной переменной сходятся в
интервале
(центра сходимости ряда). Степенные ряды
действительной переменной сходятся в
интервале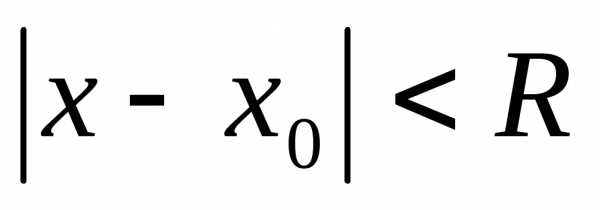 ,
где
,
где 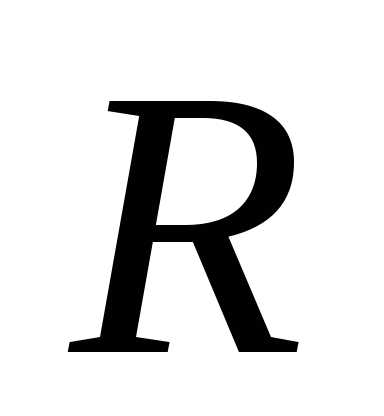 —
радиус сходимости ряда. Точно так же
степенной ряд комплексной переменной
сходится на множестве
—
радиус сходимости ряда. Точно так же
степенной ряд комплексной переменной
сходится на множестве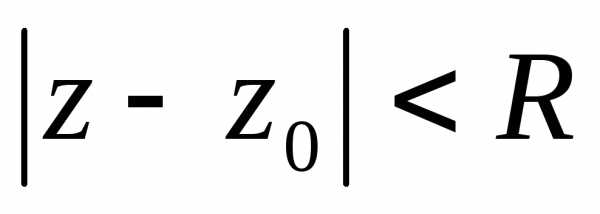 ,
только в комплексных числах это множество
представляет собой круг без границы.
Сходимость ряда на границе исследуется
отдельно.
,
только в комплексных числах это множество
представляет собой круг без границы.
Сходимость ряда на границе исследуется
отдельно.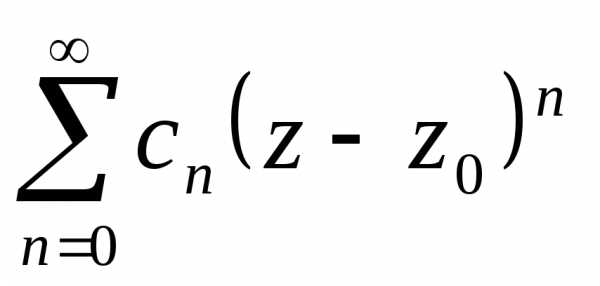 сходится в точке
сходится в точке ,
то он абсолютно сходится в круге.
Если степенной ряд
,
то он абсолютно сходится в круге.
Если степенной ряд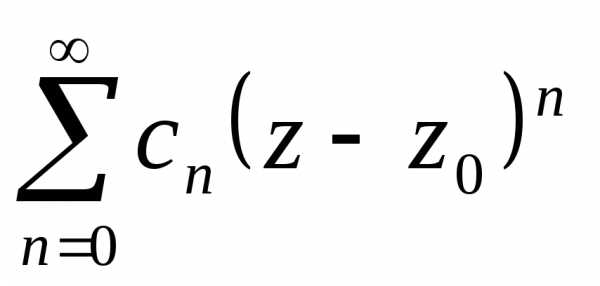 расходится в точке
расходится в точке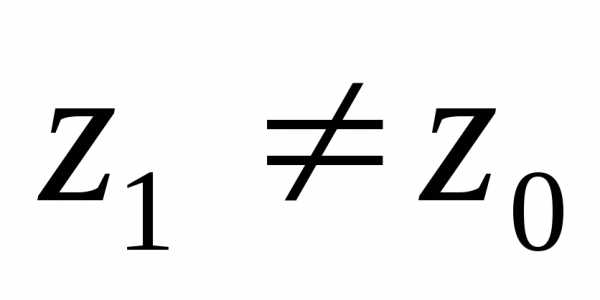 ,
то он расходится во внешности круга.
,
то он расходится во внешности круга.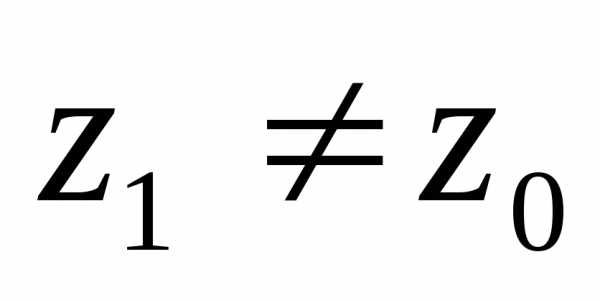 и.
и.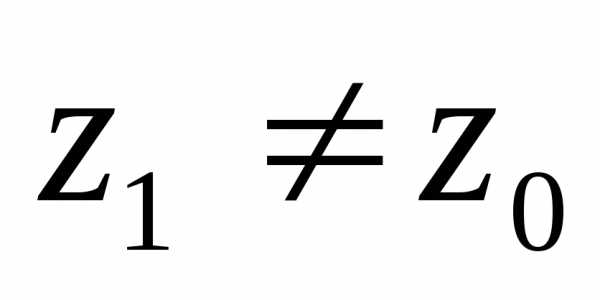 ,
то по необходимому признаку сходимости
ряда.
,
то по необходимому признаку сходимости
ряда.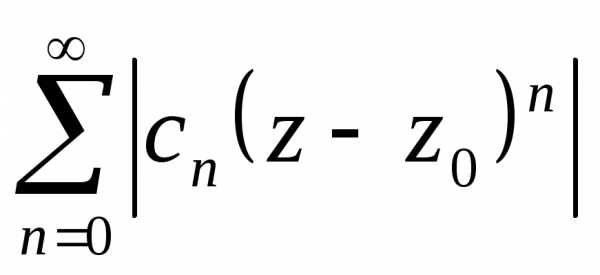 Оценим
общий член ряда из модулей.
Оценим
общий член ряда из модулей.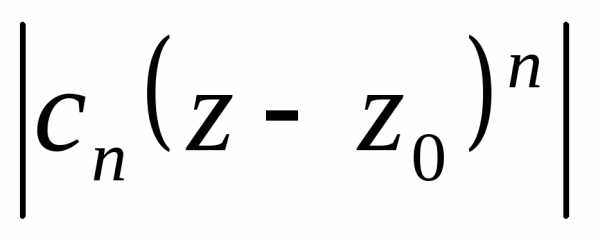 .
.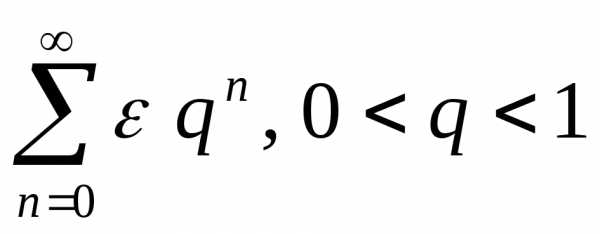 ).
Следовательно, исходный ряд в областисходится абсолютно.
).
Следовательно, исходный ряд в областисходится абсолютно. 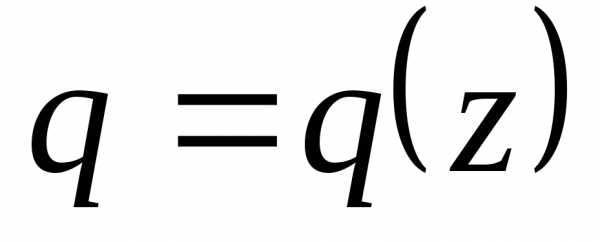 ,
а в признаке Вейерштрасса требуется
указать один мажорирующий ряд для всех
точек
,
а в признаке Вейерштрасса требуется
указать один мажорирующий ряд для всех
точек рассматриваемой
области, то есть
рассматриваемой
области, то есть не
должно зависеть от
не
должно зависеть от .
Поэтому равномерную сходимость ряда в
областиутверждать нельзя. Однако если взять
.
Поэтому равномерную сходимость ряда в
областиутверждать нельзя. Однако если взять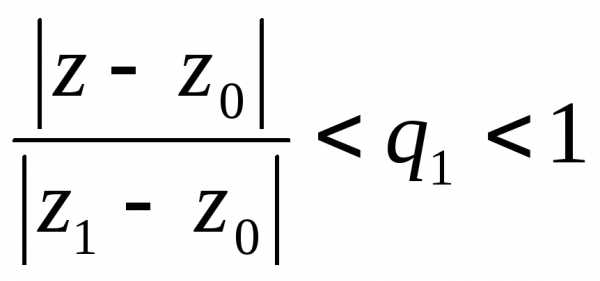 (
(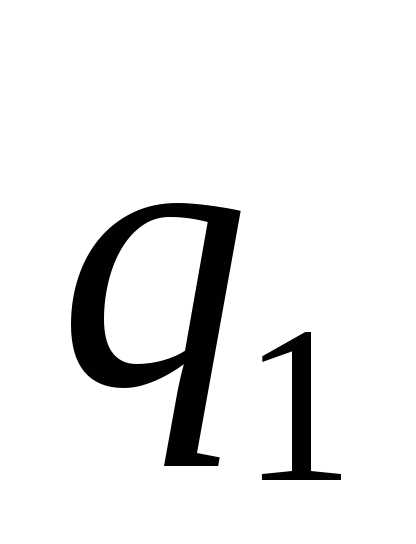 не зависит от
не зависит от ),
то в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса.
),
то в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса.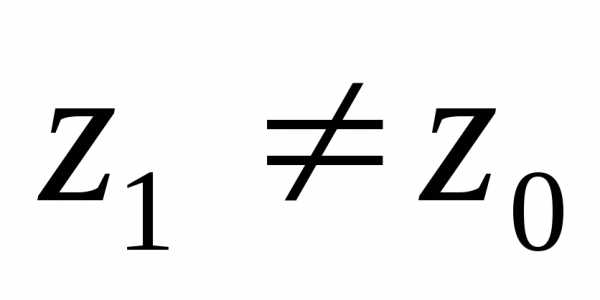 и.
и. ,
то по доказанному в пункте 1), он должен
абсолютно сходиться в точке
,
то по доказанному в пункте 1), он должен
абсолютно сходиться в точке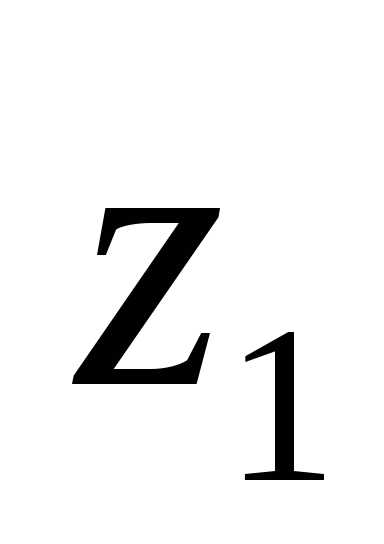 ,
следовательно, сходиться в точке
,
следовательно, сходиться в точке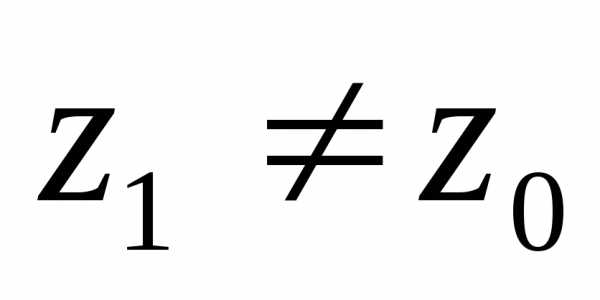 .
Это противоречит тому, что исходный ряд
расходится в точке
.
Это противоречит тому, что исходный ряд
расходится в точке ,
следовательно исходный ряд расходится
в области.
,
следовательно исходный ряд расходится
в области.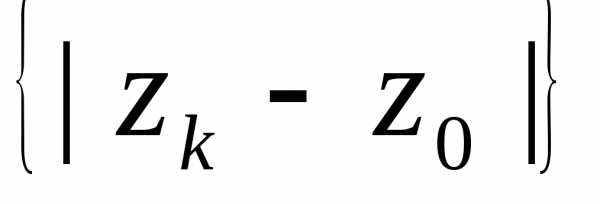 ,
такую, что в точке
,
такую, что в точке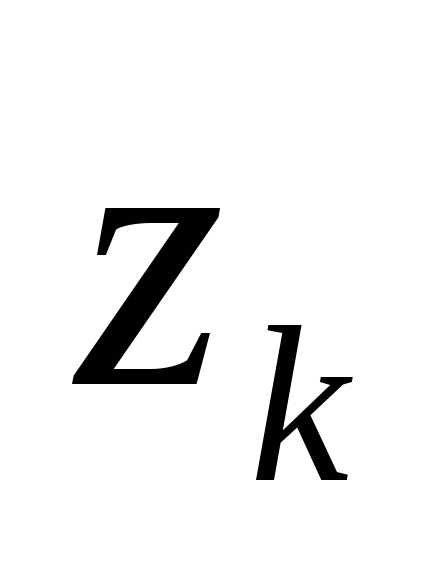 степенной
ряд
степенной
ряд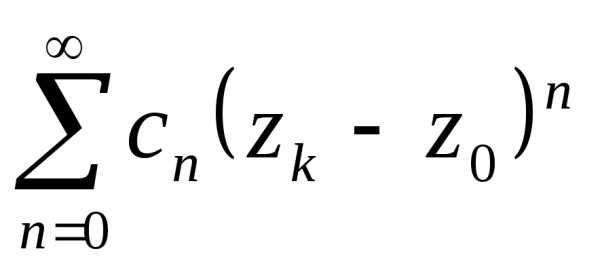 расходится.
Если выбрать
расходится.
Если выбрать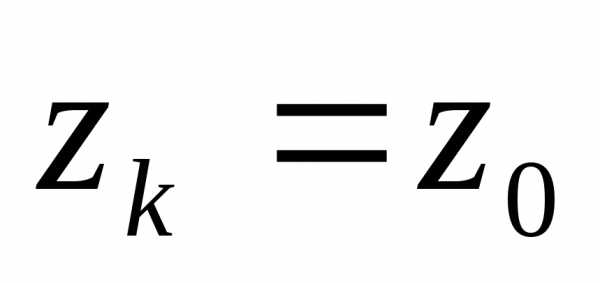 ,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.
,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.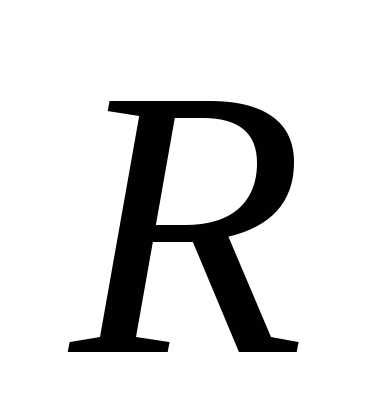 называетсярадиусом сходимости
степенного ряда.Следовательно,степенной ряд абсолютно сходится в
круге
называетсярадиусом сходимости
степенного ряда.Следовательно,степенной ряд абсолютно сходится в
круге 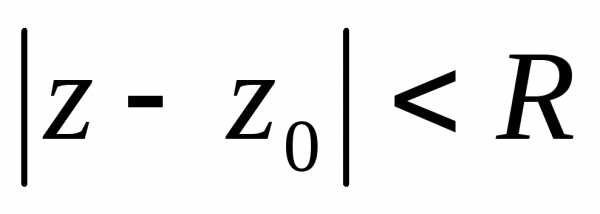 сходимости степенного ряда.
сходимости степенного ряда.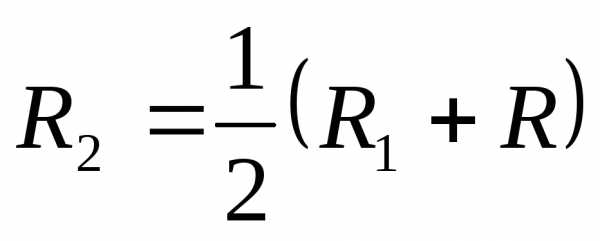 .
На окружностистепенной ряд сходится абсолютно, так
как эта окружность лежит внутри круга
сходимости. Тогда
.
На окружностистепенной ряд сходится абсолютно, так
как эта окружность лежит внутри круга
сходимости. Тогда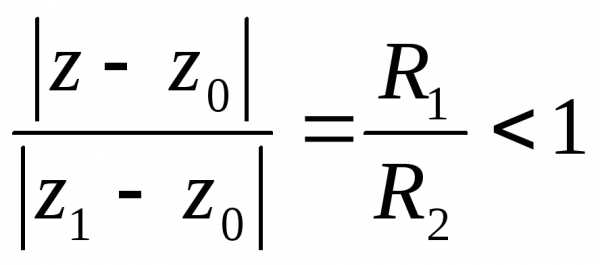 (
(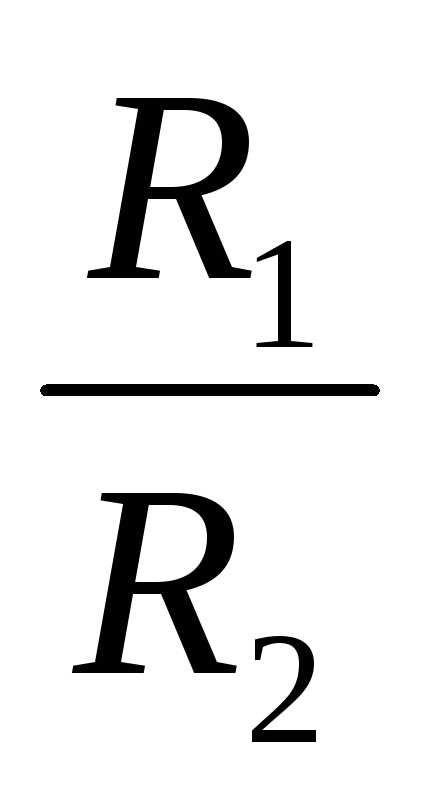 не зависит от
не зависит от ),
тогда в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса (замечание в
доказательстве теоремы Абеля).
),
тогда в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса (замечание в
доказательстве теоремы Абеля).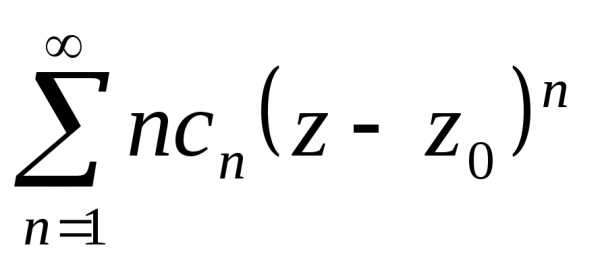 ,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.
,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.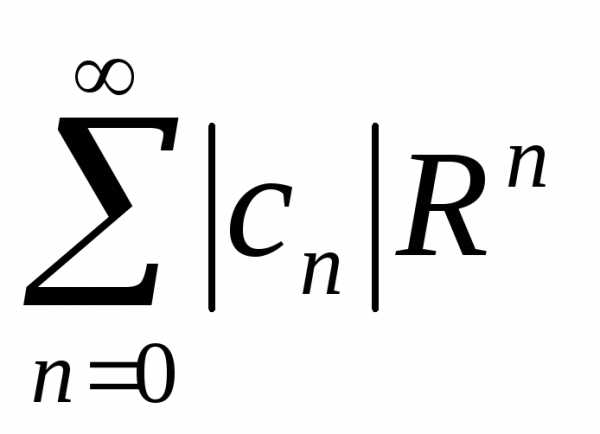 .
. в степенной ряд и исследовать сходимость
полученного числового ряда.
в степенной ряд и исследовать сходимость
полученного числового ряда.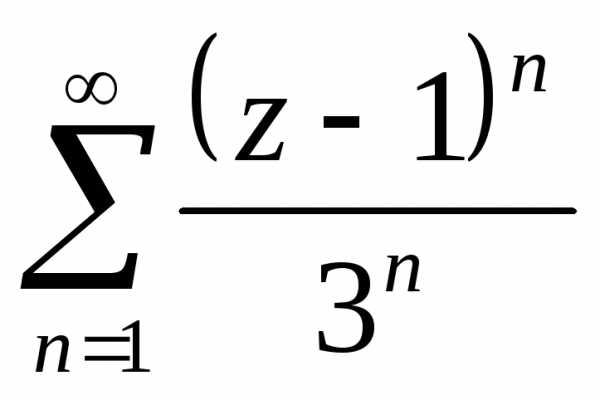 ,
ряд
,
ряд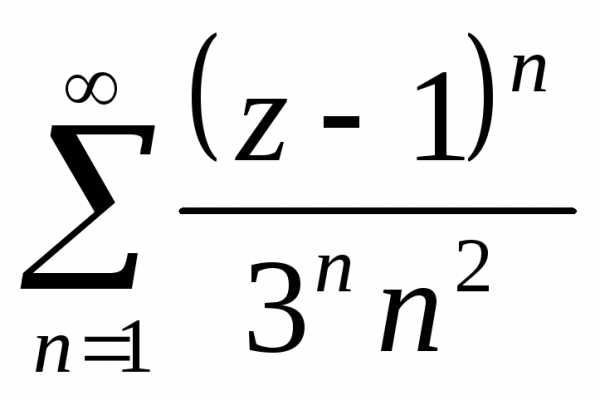 ,
ряд
,
ряд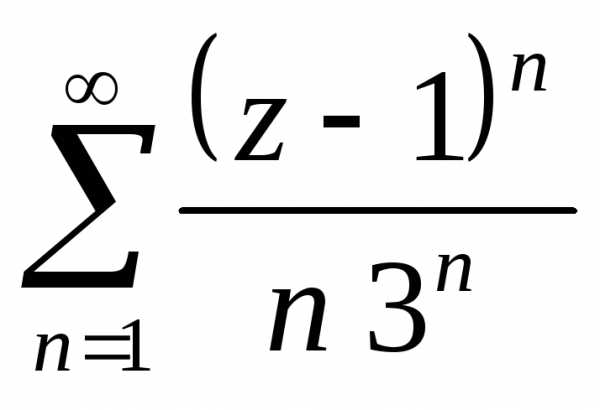 иллюстрируют все три случая. Первый ряд
расходится на всей границе
иллюстрируют все три случая. Первый ряд
расходится на всей границе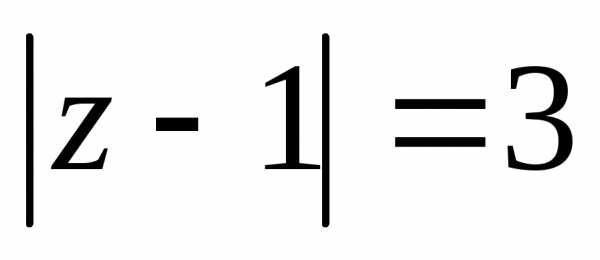 ,
так как на ней не выполняется необходимый
признак сходимости ряда. Второй ряд
сходится на всей границе, третий ряд
сходится в одних точках границы и
расходится в других.
,
так как на ней не выполняется необходимый
признак сходимости ряда. Второй ряд
сходится на всей границе, третий ряд
сходится в одних точках границы и
расходится в других.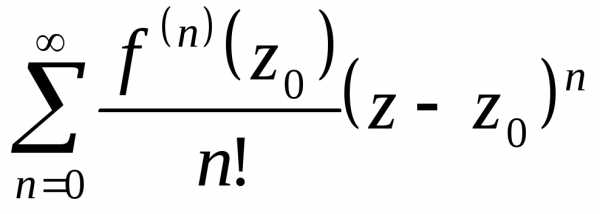 (предполагается,
что функция
(предполагается,
что функция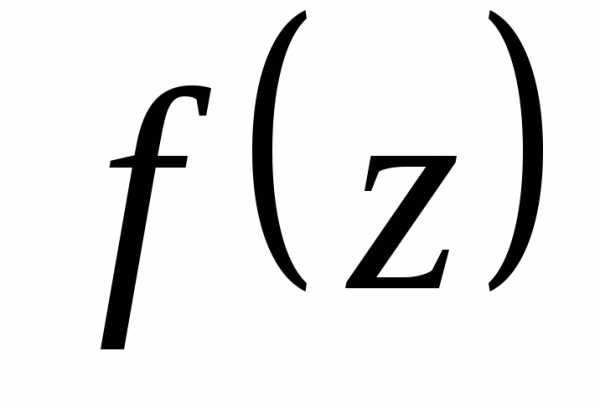 является бесконечно дифференцируемой).
является бесконечно дифференцируемой).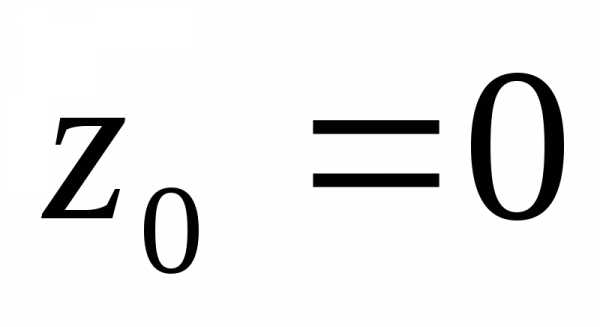 ,
то есть ряд
,
то есть ряд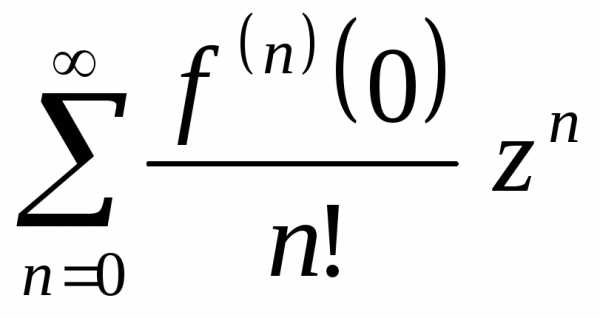 .
.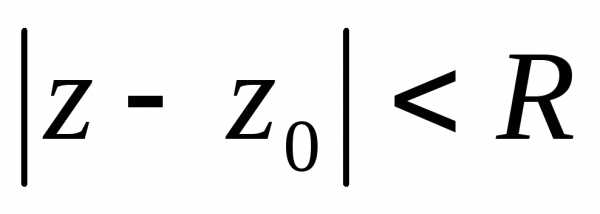 .
Подставим в разложение
.
Подставим в разложение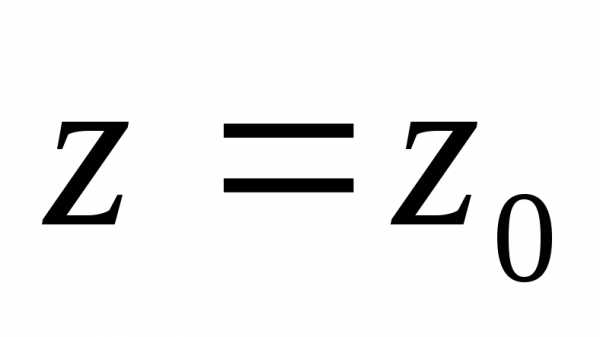 ,
получим
,
получим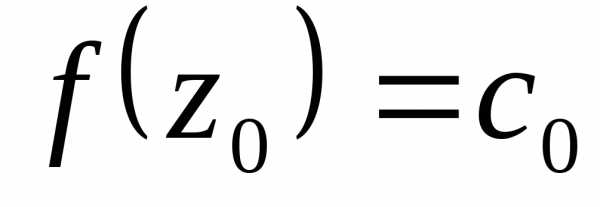 .
.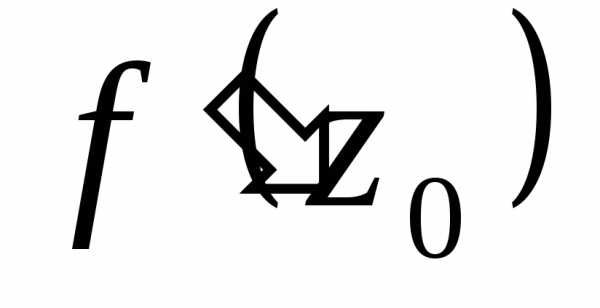 =
=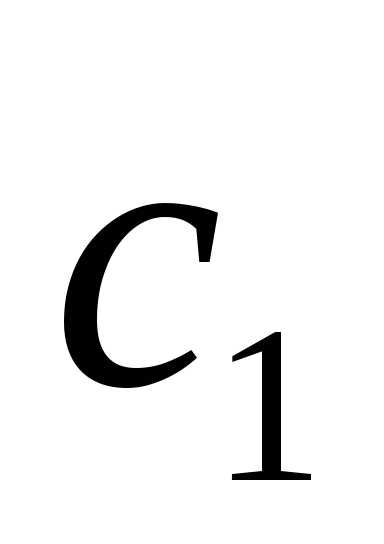 ,
,
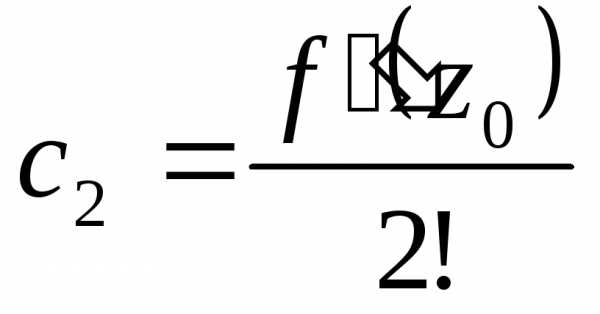 ,
,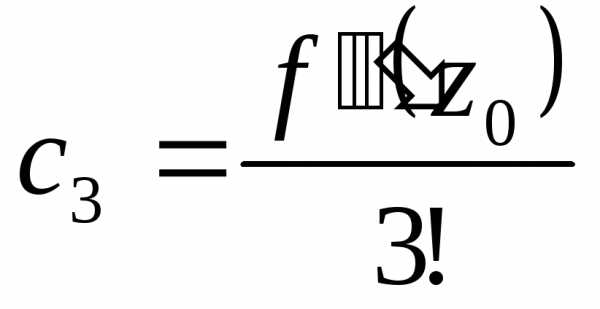 ,
,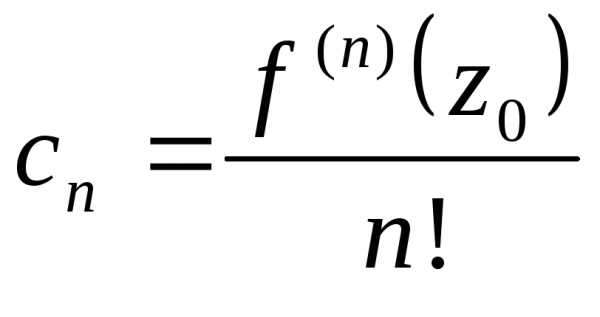 .
Это – коэффициенты ряда Тейлора.
.
Это – коэффициенты ряда Тейлора.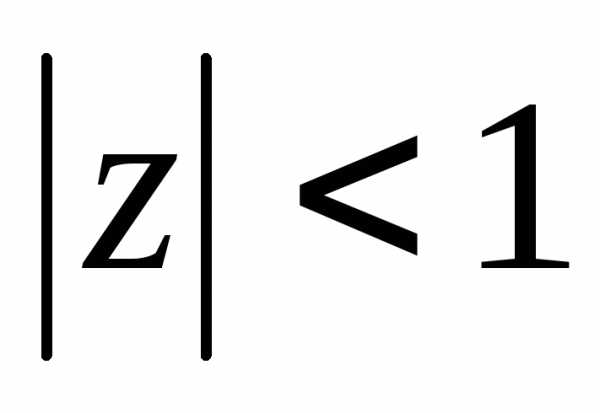 .
.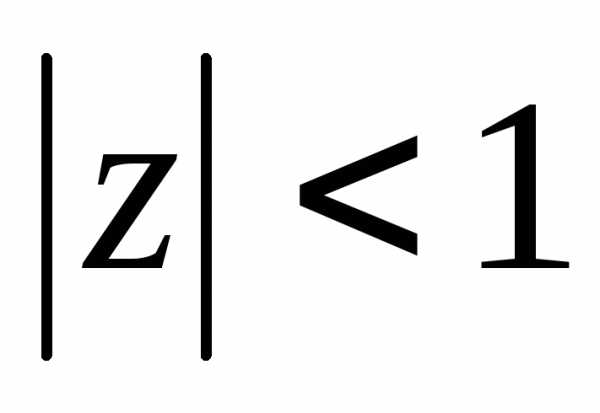 .
.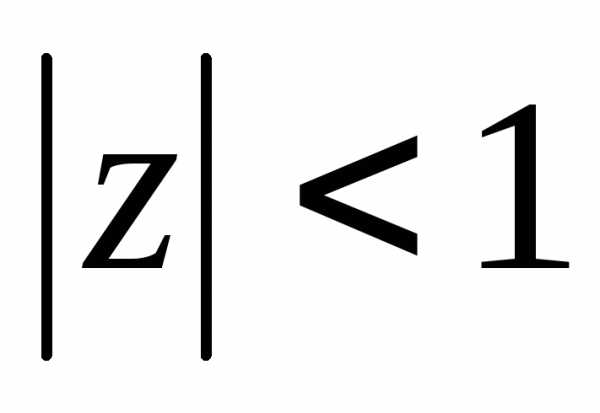 ,
,

 Решите полученное уравнение. Корни уравнения будут являться критическими точками функции.
Решите полученное уравнение. Корни уравнения будут являться критическими точками функции.  Определите, какими критическими точками — минимума или максимума — являются полученные корни. Для этого найдите вторую производную f’’(x) от исходной функции. Подставьте в нее по очереди значения критических точек и высчитайте выражение. Если вторая производная от функции в критической точке больше нуля, то это будет точка минимума. Иначе – точка максимума.
Определите, какими критическими точками — минимума или максимума — являются полученные корни. Для этого найдите вторую производную f’’(x) от исходной функции. Подставьте в нее по очереди значения критических точек и высчитайте выражение. Если вторая производная от функции в критической точке больше нуля, то это будет точка минимума. Иначе – точка максимума. 




