Тесты по бюджетному учету с ответами
Тесты по курсу «Особенности бухгалтерского учета в бюджетных организациях».Тема 1. «Бюджетная система РФ. Бюджетная классификация РФ».
1.1: «Бюджетная система РФ».
1.Документ о поквартальном распределении доходов и расходов бюджета и поступлений из источников финансирования его дефицита, устанавливающий распределение бюджетных ассигнований между получателями бюджетных средств и составляемый в соответствии с бюджетной классификацией РФ, называется:
а) бюджетная роспись;
б) поквартальная смета доходов и расходов;
в) трансферт;
г) лимит бюджетных обязательств.
2. Бюджетные средства, предоставляемые бюджету другого уровня бюджетной системы РФ или юридическому лицу на безвозмездной основе для осуществления определённых целевых расходов, носят название:
а) субвенция;
б) субсидия;
в) дотация;
г) бюджетные ассигнования.
3. Бюджетные средства, предоставляемые бюджету другого уровня бюджетной системы РФ, физическому или юридическому лицу на условиях долевого финансирования целевых расходов, называется:
а) субвенция;
б) субсидия;
в) дотация;
г) бюджетные ассигнования.
.4. Форма финансирования бюджетных расходов, которая предусматривает предоставление средств юридическим лицам или другому бюджету на возвратной и возмездной основе, называется:
а) дотация;
б) бюджетный кредит;
в) государственный или муниципальный заем;
г) бюджетные ассигнования.
5. Средства одного бюджета бюджетной системы РФ, перечисляемые другому бюджету бюджетной системы РФ, — это:
а) бюджетные ассигнования,
б) бюджетные обязательства;
в) межбюджетные трансферты;
г) бюджетный кредит.
.6. Бюджетная система РФ:
а) четырёхуровневая;
б) двухуровневая;
в) пятиуровневая;
г) трёхуровневая.
.7. Недопустимость непосредственного исполнения расходных обязательств органов государственной власти и органов местного самоуправления за счёт средств бюджетов других уровней отражает принцип:
а) самостоятельности бюджетов,
б) равенство бюджетных прав субъектов РФ, муниципальных образований,
в) сбалансированности бюджета,
г) достоверности бюджета.
.8. Орган государственной власти РФ, имеющий право распределять средства федерального бюджета по подведомственным распорядителям и получателям бюджетных средств, а также наиболее значимое бюджетное учреждение науки, образования, культуры, здравоохранения и средств массовой информации носит название:
а)главный распорядитель средств федерального бюджета,
б) главный распорядитель средств бюджета субъекта РФ, средств местного бюджета;
в) распределитель бюджетных средств, Казначейство РФ.
9. Федеральное казначейство обладает следующими бюджетными полномочиями:
а) производит распределение доходов и иных поступлений между бюджетами бюджетной системы РФ,
б) открывает в банке России и кредитных организациях счета по учёту средств федерального бюджета и иных средств,
в) устанавливает порядок кассового обслуживания исполнения бюджетов бюджетной системы РФ,
г) утверждает сводную бюджетную роспись,
д) верны все ответы кроме ответа г).
10. Органом денежно-кредитного регулирования является:
а) банк России,
б) Министерство финансов РФ,
в)Казначейство,
Счётная палата РФ.
11. Организация, созданная органами государственной власти РФ, органами государственной власти субъектов РФ, местного самоуправления для осуществления управленческих, социально-культурных, научно-технических и иных функций некоммерческого характера, деятельность которого финансируется из соответствующего бюджета или бюджета государственного внебюджетного фонда на основе сметы доходов и расходов, называется:
а) благотворительной
edudocs.net
Тест с ответами по бюджетной системе
1. Какие доходы от местных налогов зачисляются в бюджеты поселений :
1. земельный налог +
2. НДС
3. налог на имущество физических лиц
4. транспортный налог +
2. Кто определяет назначения и структуру кодов бюджетной классификации РФ :
1. Государственная Дума РФ
2. Министерство финансов РФ +
3. Совет Министров РФ
4. Совет Федерации РФ
3. По каким нормативам распределяются между бюджетами РФ акцизы на алкогольную продукцию:
1. 75%
2. 100%
3. 60% +
4. В каком году в России был составлен первый бюджет :
1. 1551
2. 1641 +
3. 1861
5. Классификация расходов бюджетов РФ- это :
1. группировка социальных программ, финансируемых бюджетами всех уровней
2. группировка объектов, финансируемых бюджетами всех уровней
3. группировка расходов бюджетов всех уровне бюджетной системы РФ +
6. Основной принцип бюджетных полномочий государственных органов власти субъектов РФ и органы местного самоуправления — это:
1. самостоятельность +
2. подотчетность
3. бессрочность
7. Бюджет выполняет следующую главную задачу:
1. Предоставление международного кредита
2. Перераспределение ВВП +
8. К безвозмездным поступлениям относятся:
1. иные межбюджетные трансферты из других бюджетов бюджетной системы РФ +
2. дотации из других бюджетов бюджетной системы РФ +
3. субвенции из федерального бюджета или из бюджетов субъектов РФ +
4. доходы в виде прибыли, приходящейся на доли в уставных капиталах обществ
5. прибыли государственных и муниципальных унитарных предприятий
9. Средства резервных фондов исполнительных органов государственной власти направляются:
1. на финансирование обеспечение непредвиденных расходов +
2. на финансирование учебных заведений
3. на финансирование капитального строительства
10. Размер резервных фондов исполнительных органов государственной власти не может превышать:
1. 3% утвержденного общего объема расходов, установленных законами о соответствующих бюджетах +
2. 10 % утвержденного общего объема расходов, установленных законами о соответствующих бюджетах
3. 5 % утвержденного общего объема расходов, установленных законами о соответствующих бюджетах
11. Бюджетная классификация РФ- это:
1. группировка источников финансирования дефицитов бюджета бюджетной системы РФ
2. группировка бюджетов бюджетной системы РФ
3. группировка доходов, расходов и источников финансирования дефицита бюджета бюджетной системы РФ +
12. Какая особенность расходов бюджетов государственных внебюджетных фондов:
1. свободное инвестирование средств
2. расходование в соответствие с текущими потребностями исполнительных органов
3. строгое целевое назначение расходов +
13. Средства обязательного социального страхования являются:
1. федеральной государственной собственностью +
2. смешанной собственностью
3. собственностью страховщика
14. Какой федеральный орган осуществляет внешнюю проверку годового отчета об исполнение федерального бюджета:
1. Счетная палата РФ +
2. Министерство финансов РФ
3. Федеральное казначейство
15. С каким понятием связан механизм перераспределения бюджетных ассигнований:
1. бюджетным федерализмом +
2. возвратности
3. открытости
16. Какие доходы подлежат зачислению в бюджет:
1. межбюджетные трансферты
2. налоговые доходы +
3. неналоговые доходы +
17. Не позднее скольких дней до дня внесения проекта закона о федеральном бюджете в ГД РФ вносится закон в правительство РФ:
1. 20
2. 15 +
3. 30
18. Для изъятия избыточной денежной массы из экономики были созданы:
1. фонд поддержки экономики
2. резервный фонд +
3. фонд национального благосостояния +
4. фонд финансирования дорожного строительства
19. Цель создания федерального фонда финансовой поддержки субъектов РФ:
1. выравнивание бюджетной обеспеченности субъектов РФ +
2. повышение благосостояния населения субъекта РФ
3. повышение инвестиционной привлекательности субъекта РФ
20. Страховые взносы на обязательное пенсионное страхование — это:
1. индивидуально безвозмездные обязательные платежи, которые выплачиваются в бюджет Пенсионного Фонда РФ
2. индивидуально возмездные обязательные платежи, которые выплачиваются в бюджет Пенсионного Фонда РФ +
3. индивидуально безвозмездные не обязательные платежи, которые выплачиваются в бюджет Пенсионного Фонда РФ
21. Перечислите доходы, формирующие бюджет федеральным фондом обязательного медицинского страхования:
1. неналоговые доходы +
2. налоговые доходы +
3. межбюджетные трансферты
22. Государственный бюджет — это:
1. Золотовалютный резерв государства
2. Общегосударственные финансы, территориальные финансы, финансы хозяйствующих субъектов
3. важнейшее звено хозяйственной системы, обеспечивающее перераспределение национального дохода +
23. Расходы бюджета — это:
1. денежные средства, выплачиваемые из бюджета, за исключением средств, являющихся источниками финансирования дефицита бюджета +
2. денежные средства, выплачиваемые из бюджета, включая источники, финансирования дефицита бюджета
3. денежные средства, выплачиваемые из бюджета, государственной корпорации
24. Количество уровней бюджетной системы зависит:
1. принципов построения бюджетной системы
2. государственного устройства страны +
3. экономической целесообразности
4. полномочий органов власти и управления
25. Денежные фонды, имеющие строго целевое назначение- это:
1. бюджет предприятия,
2. государственный бюджет
3. внебюджетные специальные фонды. +
refdocx.ru
Бюджетная система тесты с ответами 61-100
Тесты по бюджетной системе
61. Формы финансирования расходов бюджета
+А)сметное финансирование, бюджетные инвестиции, государственные трансферты, бюджетные кредиты
Б)сметное финансирование, портфельные инвестиции, международные трансферты, бюджетные кредиты
В)бюджетное финансирование, бюджетные инвестиции, межбюджетные трансферты, банковские кредиты
Г)бюджетное финансирование, бюджетные инвестиции, межбюджетные трансферты, межбанковские кредиты
Д) сметное финансирование, бюджетные инвестиции, государственные трансферты
Тест. 62. Принципы распределения расходов между бюджетами
А) единства, сбалансированности
+ Б) ведомственной подчиненности, территориального расположения
В) самостоятельности, полноты
Г) обоснованности, эффективности
Д) целевого использования бюджетных средств, справедливости
63. Расходы бюджета на экономическую деятельность охватывают
А) государственные субсидии и дотации предприятиям
Б) государственные капитальные вложения
+В)государственные субсидии и дотации предприятиям, государственные капитальные вложения, операционные расходы
Г)государственные субсидии и дотации предприятиям, операционные расходы
Д)государственные субсидии и дотации предприятиям, капитальные и операционные расходы
64. Расходы бюджета на социальную защиту включают расходы на
А) образование
Б) охрану здоровья
В) духовное и физическое воспитание
+ Г) субсидии и помощь отдельным гражданам
Д) государственное обеспечение граждан, которые не могут себя содержать самостоятельно
Тест — 65. Расходы бюджета на социальную сферу включают расходы на
+ А) образование, охрану здоровья, физическое воспитание
Б) науку и образование
В) управление
Г) субсидии и помощь отдельным гражданам
Д) государственное обеспечение граждан, которые не могут себя содержать самостоятельно
66. Расходы бюджета на социальное обеспечение включают расходы
А) образование, охрану здоровья, физическое воспитание
Б) науку и образование
В) управление
Г) субсидии и помощь отдельным гражданам
+ Д) государственное обеспечение граждан, которые не могут себя содержать самостоятельно
67. Расходы бюджета на науку включают расходы на
А) финансирование общеобразовательных школ и высших учебных заведений
Б) финансирование фундаментальных исследований
В) финансирование детских дошкольных учреждений
Г) финансирование государственных и межгосударственных научно – технических программ
+Д) финансирование государственных и межгосударственных научно – технических программ, финансирование фундаментальных исследований
68. Расходы бюджета на оборону охватывают расходы на
+А) закупку вооружения, военной техники, содержание воинских частей, выплату пенсий военнослужащим
Б) содержание воинских частей, выплату пенсий военнослужащим
В)закупку вооружения, военной техники, обеспечение правопорядка
Г) содержание воинских частей, выплату пенсий военнослужащим, финансирование фундаментальных исследований
Д) финансирование государственных и межгосударственных оборонных программ
69. Расходы бюджета в сфере международной деятельности включают
А) содержание международных организаций
+Б) оплату взносов в международные организации
В) международные расчеты
Г) международные кредиты
Д) финансирование международных мероприятий
70. Расходы на обслуживание государственного долга включают
А) расходы на содержание международных организаций
Б) финансирование международных расчетов
+В) расходы на погашение задолженности и процентов
Г) расходы на погашение международных кредитов
Д) финансирование международных мероприятий
71. Сметное финансирование – форма финансирования при которой
А) бюджетные ассигнования выделяются на основании счетов
Б) бюджетные ассигнования выделяются на основании расчетных документов
В) бюджетные ассигнования выделяются на основании договора
Г)бюджетные ассигнования выделяются на основании соглашения
+Д) бюджетные ассигнования выделяются на основании смет
72. Бюджетное финансирование инвестиционных проектов характеризует выделение государственных ассигнований на
А) непроизводственную сферу
+Б) производственную сферу
В) социальную сферу
Г) государственные инвестиционные проекты
Д) негосударственные инвестиционные проекты
73. Государственные субсидии – форма предоставления государственной финансовой помощи
А) международным организациям
Б) коммерческим банкам
В) центральному банку
+ Г) физическим и юридическим лицам
Д) целевым государственным фондам
74. Государственные субвенции предполагают
А) паевое участие международных организаций в финансировании отдельных расходов и проектов
Б)паевое участие коммерческих банков в финансировании отдельных расходов и проектов
В) паевое участие страховых организаций в финансировании отдельных расходов и проектов
Г) паевое участие физических лиц в финансировании отдельных расходов и проектов
+ Д) паевое участие субъектов предпринимательской деятельности в финансировании отдельных расходов и проектов
75 — Тест. Государственные дотации – это выделение средств из бюджета на
А) финансирование государственных предприятий
+Б) покрытие убытков предприятий
В) финансирование центрального банка
Г) финансирование государственных целевых программ
Д) финансирование социальных расходов
76. Бюджетные кредиты – это предоставление
+А) коммерческим предприятиям временной финансовой помощи на условиях возвратности
Б)коммерческим банкам временной финансовой помощи на условиях возвратности
В)государственным предприятиям временной финансовой помощи на условиях возвратности
Г) международным организациям временной финансовой помощи на условиях возвратности
Д) центральному банку временной финансовой помощи на условиях возвратности
77. Главное задание бюджетного планирования
А) Бюджетный дефицит
Б) бюджетный профицит
+В) равновесие доходов и расходов
Г) планирование доходной части бюджета
Д) планирование расходной части бюджета
78. Равновесие доходов и расходов бюджета – это
А) планирование расходов без гарантированных поступлений
+Б)расходы бюджета имеют соответствующие источники финансирования
В) превышение расходов над постоянными доходами бюджета
Г) отсутствие превышения расходов над постоянными доходами бюджета
Д) излишек средств, подлежащий выделению из бюджета высшего уровня
79. Признаки бюджетного дефицита
А) формы проявления, источники погашения
Б) формы проявления, источники финансирования
В) формы проявления, причины возникновения
+Г)формы проявления, причины возникновения, направления средств
Д) формы проявления, причины возникновения, межбюджетные отношения
80. Формы проявления бюджетного дефицита
А) официальный, фиктивный
Б) утвержденный, скрытый
В) не утвержденный, официальный
Г) открытый, закрытый
+Д) открытый, скрытый
81.По причинам возникновения бюджетного дефицита различают
+ А) вынужденный, сознательный
Б) фальсифицированный, сознательный
В) нереальный, открытый
Г) скрытый, сознательный
Д) полу прикрытый, возможный
82. Вынужденный бюджетный дефицит является следствием
А) политики «заемных» финансов
+Б) экономического и социального кризиса
В) нерационального планирования
Г) скрытого завышения расходной части бюджета
Д) финансовой политики
Тест — 83. Источники покрытия бюджетного дефицита
А) государственный кредит
Б) межбанковский кредит
+В) государственные займы, эмиссия денег
Г) внешние, внутренние
Д) мобилизация свободных денежных средств предприятий и населения
84.Эмиссия денег является
А) обеспеченным источником покрытия бюджетного дефицита
+ Б) необеспеченным источником покрытия бюджетного дефицита
В) реальным источником покрытия бюджетного дефицита
Г) полноценным источником покрытия бюджетного дефицита
Д) оправданным источником покрытия бюджетного дефицита
85. Государственные займы являются
А) обеспеченным источником покрытия бюджетного дефицита
Б) необеспеченным источником покрытия бюджетного дефицита
В) нереальным источником покрытия бюджетного дефицита
+ Г) полноценным источником покрытия бюджетного дефицита
Д) оправданным источником покрытия бюджетного дефицита
86. Вертикальная структура бюджета характеризуются
А) межбюджетными отношениями
Б) организацией взаимоотношений между разными бюджетами
В) вариантами структурного построения бюджета
Г) принципами построения бюджетной системы
+Д) бюджетным устройством, бюджетной системой
87. Бюджетное устройство показывает
+ А) способы построения бюджетной системы
Б) совокупность бюджетов, формирующихся в государстве
В) межбюджетные отношения
Г) разделение доходов и расходов между звеньями бюджетной системы
Д) виды бюджетов
88.Вертикальные уровни бюджетов устанавливаются соответственно
А) автономности бюджетов
+Б) политического устройства государства и административного – территориального деления
В) децентрализации бюджетов
Г)объединения централизованных и децентрализованных бюджетов
Д) создания нескольких уровней бюджета
89. Виды бюджетов
А) централизованные, децентрализованные
Б) консолидированный, местные
+В) центральные, местные
Г) высшие, низшие
Д) крупные, мелкие
90.Важнейшее направление бюджетного устройства
А) покрытие бюджетного дефицита
Б) обеспечение равновесия доходов и расходов
В) вертикальное деление бюджетов
+Г) размежевание доходов и расходов между бюджетами
Д) построение бюджетной системы
91. Подходы распределения расходов бюджета
А) централизованный, децентрализованный
Б) социальный, из ведомственной подчиненности
В) по территориальному признаку, социальный
Г) бюджетного регулирования, закрепления
+Д)по территориальному признаку, из ведомственной подчиненности
92. Все доходы делятся на группы
+А) закрепленные, регулирующие
Б) государственные, местные
В) централизованные, децентрализованные
Г) вертикальные, горизонтальные
Д) высшие, низшие
93 -Тест. Межбюджетные отношения делятся на
А) закрепленные, регулирующие
+ Б) вертикальные, горизонтальные
В) государственные, местные
Г) централизованные, децентрализованные
Д) внешние, внутренние
94. Бюджетная система Украины включает уровни
А) государственный, местный
Б) вертикальные, горизонтальные
+В) общегосударственный, областной, районный, нижний
Г) автономные, подчиненные
Д) межбюджетные, общие
95. Структура бюджетной системы характеризуется
А) удельным весом отдельных видов бюджетов в бюджетной системе
Б) удельным весом отдельных видов бюджетов в финансовой системе
В) удельным весом отдельных видов бюджетов в финансовом рынке
+Г) удельным весом отдельных видов бюджетов в сведенном бюджете
Д) удельным весом отдельных видов бюджетов в общегосударственном уровне бюджетной системы
96.Каждое звено бюджетной системы является
А) централизованным фондом денежных средств
Б) децентрализованным фондом денежных средств
В) государственным фондом денежных средств
Г) межбюджетным фондом денежных средств
+Д) обособленным фондом денежных средств
97. Бюджетное субсидирование – это
+ А) выделение средств из бюджета высшего уровня бюджетам низшего уровня
Б) перечисление средств из одного бюджета другому для предоставления ему финансовой помощи
В) паевое участие нескольких бюджетов в финансировании определенных расходов или проектов
Г) выделение средств из бюджета высшего уровня для сбалансирования бюджетов низшего уровня
Д) перераспределение доходов и расходов между бюджетами после их утверждения
98. Бюджетные субсидии – это
А) выделение средств из бюджета высшего уровня бюджетам низшего уровня
+ Б) перечисление средств из одного бюджета другому для предоставления ему финансовой помощи
В) паевое участие нескольких бюджетов в финансировании определенных расходов или проектов
Г) выделение средств из бюджета высшего уровня для сбалансирования бюджетов низшего уровня
Д) перераспределение доходов и расходов между бюджетами после их утверждения
99. Бюджетные субвенции – это
А) выделение средств из бюджета высшего уровня бюджетам низшего уровня
Б) перечисление средств из одного бюджета другому для предоставления ему финансовой помощи
+ В) паевое участие нескольких бюджетов в финансировании определенных расходов или проектов
Г) выделение средств из бюджета высшего уровня для сбалансирования бюджетов низшего уровня
Д) перераспределение доходов и расходов между бюджетами после их утверждения
100. Тест. Бюджетные дотации – это
А) выделение средств из бюджета высшего уровня бюджетам низшего уровня
Б) перечисление средств из одного бюджета другому для предоставления ему финансовой помощи
В) паевое участие нескольких бюджетов в финансировании определенных расходов или проектов
+Г) выделение средств из бюджета высшего уровня для сбалансирования бюджетов низшего уровня
Д) перераспределение доходов и расходов между бюджетами после их утверждения
test-otvet.com.ua
Тест с ответами по финансам и бухгалтерскому учету
410. За счет налога на имущество организаций, транспортного налога, налога на игорный бизнес, единого налога взимаемого в связи с применением упрощенной системы налогообложения формируются налоговые доходы бюджетов … … (2 слова)
Ответ: субъектов РФ
Ответ: субъекта РФ
411. Начинается 1 января, заканчивается 31 декабря текущего года … … в РФ (2 слова)
Ответ: бюджетный период
412. Общий объем доходов федерального бюджета, с выделением объема нефтегазовых доходов, общий объем расходов, нормативы распределения доходов между бюджетами бюджетной системы РФ, если они не утверждены БК РФ, дефицит являются предметом рассмотрения в ……… чтении (1 слово)
Ответ: первом
413. Перечень главных администраторов доходов федерального бюджета, бюджетные ассигнования по разделам, распределение между субъектами РФ межбюджетных трансфертов, перечень главных администраторов источников финансирования дефицита федерального бюджета являются предметом рассмотрения … … чтении (2 слова)
Ответ: во втором
414. Пособия по временной нетрудоспособности, на погребение, выплаты в рамках обязательного социального страхования от несчастных случаев на производстве, создание резерва для обеспечения финансовой устойчивости Фонда – это виды расходов, осуществляемые из Фонда … … … (3 слова)
Ответ: социального страхования РФ
415. Муниципальные займы, кредиты, полученные от кредитных организаций, бюджетные кредиты, полученные от бюджетов других уровней бюджетной системы – это источники финансирования дефицита … … (2 слова)
Ответ: местного бюджета
416. Договор о предоставлении муниципальных гарантий, займы осуществляемые путем выпуска муниципальных ценных бумаг, кредитные договора с кредитными организациями – это формы … … муниципального образования (2 слова)
Ответ: долговых обязательств
417. Договора о получении субъектом РФ бюджетных кредитов от бюджетов других уровней бюджетной системы, кредитные договора с кредитными организациями, государственные займы субъектов РФ путем выпуска ценных бумаг субъекта РФ – это формы … … субъекта РФ (2 слова)
Ответ: долговых обязательств
418. Взносы государств-членов в соответствии с устанавливаемой для каждой страны квоты является источником образования … … Международного валютного фонда (2 слова)
Ответ: уставного капитала
419. Государственные и муниципальные контракты размещаются на …………основе (1 слово)
Ответ: конкурсной
420. Размещение новых государственных займов для погашения задолженности по уже выпущенным займам — это ………… государственного долга (1 слово)
Ответ: рефинансирование
421. Превышение расходов бюджета над его доходами – это… … (2 слова)
Ответ: дефицит бюджета
422. Превышение доходов бюджета над его расходами – это … … (2 слова)
Ответ: профицит бюджета
423. Выплачиваемые из бюджета денежные средства, за исключением средств, являющихся в соответствии с Бюджетным Кодексом источниками финансирования дефицита бюджета – это … … (2 слова)
Ответ: расходы бюджета
424. Документ, который составляется и ведется главным распорядителем бюджетных средств (главным администратором источников финансирования дефицита бюджета) в соответствии с Бюджетным кодексом в целях исполнения бюджета по расходам (источникам финансирования дефицита бюджета) — это … … (2 слова)
Ответ: бюджетная роспись
425. Предельные объемы денежных средств, предусмотренных в соответствующем финансовом году для исполнения бюджетных обязательств – это … … (2 слова)
Ответ: бюджетные ассигнования
426. Форма финансирования проектов, включенных в программу государственных внешних заимствований Российской Федерации, которая предусматривает предоставление средств в иностранной валюте на возвратной и возмездной основах путем оплаты товаров, работ и услуг в соответствии с целями этих проектов – это … … … (3 слова)
Ответ: целевой иностранный кредит
427. Документ, который составляется и ведется финансовым органом (органом управления государственным внебюджетным фондом) в соответствии с Бюджетным кодексом в целях организации исполнения бюджета по расходам бюджета и источникам финансирования дефицита бюджета – это … … …(3 слова)
Ответ: сводная бюджетная роспись
428. Обязательства, возникающие из государственных или муниципальных заимствований, гарантий по обязательствам третьих лиц, другие обязательства в соответствии с видами долговых обязательств, установленными Бюджетным Кодексом, принятые на себя Российской Федерацией, субъектом Российской Федерации или муниципальным образованием – это … … … … (4 слова)
Ответ: государственный или муниципальный долг
429. Обязательства, возникающие в иностранной валюте, за исключением обязательств субъектов Российской Федерации и муниципальных образований перед Российской Федерацией, возникающих в иностранной валюте в рамках использования целевых иностранных кредитов (заимствований) – это … … (2 слова)
Ответ: внешний долг
430. Обязательства, возникающие в валюте Российской Федерации, а также обязательства субъектов Российской Федерации и муниципальных образований перед Российской Федерацией, возникающие в иностранной валюте в рамках использования целевых иностранных кредитов (заимствований) – это … … (2 слова)
Ответ: внутренний долг
431. Расходные обязательства, подлежащие исполнению в соответствующем финансовом году – это … … (2 слова)
Ответ: бюджетные обязательства
432. Взаимоотношения между публично-правовыми образованиями по вопросам регулирования бюджетных правоотношений, организации и осуществления бюджетного процесса – это … … (2 слова)
Ответ: межбюджетные отношения
433. Средства, предоставляемые одним бюджетом бюджетной системы Российской Федерации другому бюджету бюджетной системы Российской Федерации – это … … (2 слова)
Ответ: межбюджетные трансферты
434. Межбюджетные трансферты, предоставляемые на безвозмездной и безвозвратной основе без установления направлений и (или) условий их использования – это ……. (1 слово)
Ответ: дотации
435. Документ, устанавливающий требования к составу, качеству и (или) объему, условиям, порядку и результатам оказания государственных (муниципальных) услуг – это … … (2 слова)
Ответ: государственное задание
Ответ: муниципальное задание
436. Бюджетные средства, направляемые на создание или увеличение за счет средств бюджета стоимости государственного (муниципального) имущества – это … … (2 слова)
Ответ: бюджетные инвестиции
437. Документ, устанавливающий в соответствии с классификацией расходов бюджетов лимиты бюджетных обязательств бюджетного учреждения – это … … (2 слова)
Ответ: бюджетная смета
438. Объем прав в денежном выражении на принятие бюджетным учреждением бюджетных обязательств и (или) их исполнение в текущем финансовом году (текущем финансовом году и плановом периоде) – это … … … (3 слова)
Ответ: лимит бюджетных обязательств
439. Год, в котором осуществляется исполнение бюджета, составление и рассмотрение проекта бюджета на очередной финансовый год (очередной финансовый год и плановый период)- это … … … (3 слова)
Ответ: текущий финансовый год
440. Следующий за текущим финансовым годом – это … … … (3 слова)
Ответ: очередной финансовый год
441. Два финансовых года, следующие за очередным финансовым годом — это … … (2 слова)
Ответ: плановый период
442. Предшествующий текущему финансовому году – это … … … (3 слова)
Ответ: отчетный финансовый год
443. Прогнозируемая в определенный период текущего финансового года недостаточность на едином счете бюджета денежных средств, необходимых для осуществления кассовых выплат из бюджета — это … … … (3 слова)
Ответ: временный кассовый разрыв
444. Бюджет государственного … … Российской Федерации – фонд денежных средств, образуемый вне федерального бюджета и предназначенный для реализации конституционных прав граждан на пенсионное обеспечение, социальное страхование, охрану здоровья и медицинскую помощь (2 слова)
Ответ: внебюджетного фонда
445. Бюджет … … – фонд денежных средств находящийся в распоряжении органов местного самоуправления и предназначенный для решения вопросов местного значения (2 слова)
Ответ: муниципального образования
Ответ: местный бюджет
446. … … … – фонд денежных средств, находящийся в распоряжении органов государственной власти субъектов РФ и предназначенный для выполнения их функций и задач (3 слова и 2 слова )
Ответ: Бюджет субъекта РФ
Ответ: Региональный бюджет
447. …….. – процедура составления финансовых планов (1 слово)
Ответ: Бюджетирование
448. … … — законодательно устанавливаемая группировка доходов, расходов и источников финансирование дефицита бюджетов, используемая для составления и исполнения бюджетов, составления бюджетной отчетности и обеспечивающая сопоставимость показателей бюджетов бюджетной системы РФ (2 слова)
Ответ: Бюджетная классификация
449. … … — составная часть финансовой политики государства, определяющая условия и принципы организации финансовых отношений при формировании доходов бюджетов, в ходе осуществления бюджетных расходов, при организации межбюджетных отношений (2 слова)
Ответ: Бюджетная политика
450. … … … – совокупность бюджетов государственно-территориальных и административно – территориальных образований, находящихся в определенной взаимосвязи друг с другом на основе принципов, установленных законодательством (3 слова)
Ответ: Бюджетная система государства
451. … … Российской Федерации – основанная на экономических отношениях и государственном устройстве Российской Федерации, регулируемая законодательством РФ совокупность федерального бюджета, бюджетов субъектов РФ, местных бюджетов и бюджетов государственных внебюджетных фондов (2 слова)
Ответ: Бюджетная система
452. … … – совокупность федеральных законов, законов субъектов РФ, муниципальных правовых актов представительных органов муниципальных образований, регулирующих бюджетные правоотношения (2 слова)
Ответ: Бюджетное законодательство
453. … … – совокупность процессов, связанных с формированием бюджетных фондов, включающая составление, рассмотрение и утверждение бюджетов, а так же вопросы теории и методологии их осуществления (2 слова)
Ответ: Бюджетное планирование
454. … … – совокупность юридических нор, определяющих основы бюджетного устройства страны и бюджетного процесса на всех уровнях бюджетной системы (2 слова)
Ответ: Бюджетное право
455. … … — организационно – правовое построение бюджетной системы, позволяющее выделить в ее составе структурные подразделения (виды бюджетов и звенья) и определить формы взаимосвязей между ними (2 слова)
Ответ: Бюджетное устройство
456. … … — государственное (муниципальное) учреждение , финансовое обеспечение выполнения функций которого, в том числе по оказанию государственных и (муниципальных) услуг юридическим и физическим лицам в соответствии с государственным (муниципальных) заданием, осуществляется за счет средств соответствующего бюджета на основе бюджетной сметы (2 слова)
Ответ: Бюджетное учреждение
457. … … – обособленная часть средств бюджетов, предназначенных для обеспечения бесперебойного финансирования как запланированных, так и непредвиденных расходов, возникших внезапно и имеющих чрезвычайный или случайный характер (2 слова)
Ответ: Бюджетные резервы
458. … … – денежные средства, предоставляемые бюджетом другому бюджету бюджетной системы РФ, юридическому лицу (за исключением государственных и муниципальных учреждений), иностранному государству, иностранному юридическому лицу на возвратной и возмездной основе (2 слова)
Ответ: Бюджетный кредит
459. … … – совокупность методов мобилизации доходов, форм предоставления бюджетных средств и их межбюджетного перераспределения (2 слова)
Ответ: Бюджетный механизм
460. … … – срок, в течение которого действует утвержденный бюджет (2 слова)
Ответ: Бюджетный период
461. … … — регламентируемая законодательством РФ деятельность органов государственной власти, органов местного самоуправления и иных участников бюджетного процесса по составлению и рассмотрению проектов бюджетов, утверждению и исполнению бюджетов, контролю за их исполнением, осуществлению бюджетного учета, составлению, внешней проверке, рассмотрению и утверждению бюджетной отчетности (2 слова)
Ответ: Бюджетный процесс
462. … … – форма организации бюджетных отношений, позволяющая органично сочетать фискальные интересы федерации, субъектов РФ и муниципальных образований в режиме реальной самостоятельности всех бюджетов, входящих в бюджетную систему (2 слова)
Ответ: Бюджетный федерализм
463. … … – обособленная часть стоимости ВВП, доходов от внешнеэкономической деятельности и части национального богатства, концентрируемая в распоряжении соответствующего органа государственной власти и органа местного самоуправления и используемая для выполнения функций и задач, отнесенных к его компетенции (2 слова)
Ответ: Бюджетный фонд
464. … … расходов бюджета – распределение бюджетных ассигнований, предусмотренных законом (решением) о бюджете на соответствующий финансовый год главным распорядителям бюджетных средств по разделам, подразделам, целевым статьям и видам расходов бюджетной классификации РФ (2 слова)
Ответ: Ведомственная структура
465. … … – форма образования и расходования бюджетных ресурсов определенного органа государственной власти или органа местного самоуправления (2 слова)
Ответ: Вид бюджета
466. … … – обязательства, возникающие в иностранной валюте, за исключением обязательств субъектов РФ и муниципальных образований перед РФ, возникающих в иностранной валюте в рамках использования целевых иностранных кредитов (заимствований) (2 слова)
Ответ: Внешний долг
467. Государственные и муниципальные …… – передача в распоряжение заемщика средств путем приобретения заимодателями государственных и муниципальных ценных бумаг (1слово)
Ответ: займы
468. Государственные и муниципальные ……… – денежные отношения, возникающие в ходе формирования и использования денежных средств органами государственной власти и местного самоуправления (1 слово)
Ответ: финансы
469. … … – денежные средства, направляемые из бюджетов органов государственной власти разных уровней и государственных внебюджетных фондов на финансовое обеспечение функций и задач государства (2 слова)
Ответ: Государственные расходы
470. Денежные ……. коммерческой организации – прибыль от продаж товаров (работ, услуг), прибыль от прочей реализации имущества, сальдо прочих доходов и расходов (1 слово)
Ответ: доходы
471. Денежные ……. коммерческой организации – амортизация, резервные и аналогичные им фонды, образованные за счет прибыли прошлых лет (1 слово)
Ответ: накопления
472. Денежные ………… коммерческой организации — бюджетные средства; средства, привлеченные за счет операций на финансовом рынке; средства, поступающие в порядке перераспределения от основной (материнской) компании, вышестоящей организации, за счет внутри- и межотраслевого перераспределения (1 слово)
Ответ: поступления
473. …… финансовой системы – группы финансовых отношений внутри сфер финансовой системы, классифицируемые в соответствии с целью деятельности субъектов хозяйствования или с формой организации государственных и муниципальных финансов (1 слово)
Ответ: Звенья
474. Исполнение бюджета по ……….. – процесс принятия бюджетных обязательств; подтверждения денежных обязательств, санкционирования оплаты денежных обязательств и подтверждения исполнения денежных обязательств (1 слово)
Ответ: расходам
475. …… государственный или муниципальный долг – сумма выпущенных и непогашенных органом государственной власти или органом местного самоуправления долговых обязательств и гарантированных ими обязательств других лиц, включая проценты, которые должны быть выплачены по этим обязательствам (1 слово)
Ответ: Капитальный
476. … … исполнения бюджета – проведение и учет операций по кассовым поступления в бюджет и кассовым выплатам из бюджета(2 слова)
Ответ: Кассовое обслуживание
477. …… государственного внешнего долга – реализация всех механизмов, обеспечивающих замещение внешнего долга другими видами обязательств, менее обременительными для экономики страны – должника (1 слово)
Ответ: Конверсия
478. …… государственного или муниципального займа – изменение доходности государственного или муниципального займа (1 слово)
Ответ: Конверсия
479. …… государственного или муниципального займа – увеличение срока функционирования выпущенного государственного или муниципального займа (1 слово)
Ответ: Консолидация
480. … …. – свод бюджетов бюджетной системы РФ на соответствующей территории (за исключением бюджетов государственных внебюджетных фондов) без учета межбюджетных трансфертов между этими бюджетами (2 слова)
Ответ: Консолидированный бюджет
481. ……… перераспределение средств – ежегодная передача средств из одного бюджета другому бюджету бюджетной системы РФ для выравнивания бюджетной обеспеченности, финансового обеспечения передаваемых государственных полномочий, покрытия временных кассовых разрывов (1 слово)
Ответ: Межбюджетное
482. ……… финансового контроля – конкретные способы осуществления контрольных действий и операций (1 слово)
Ответ: Методы
483. … … бюджета – предусмотренные налоговым законодательством РФ федеральные региональные и местные налоги сборы, а также пени и штрафы, возникшие в результате налоговых правонарушений, поступающие в соответствующий бюджет (2 слова)
Ответ: Налоговые доходы
484. ……… финансовый контроль – вид финансового контроля, представленный аудиторским, внутрихозяйственным и общественным контролем (1 слово)
Ответ: Негосударственный
485. … … международных финансовых организаций – форма привлечения средств на возвратной и возмездной основе для закупок преимущественно на конкурсной основе товаров, работ и услуг с целью осуществления инвестиционных проектов структурных реформ при участии и за счет средств международных финансовых организаций (2 слова)
Ответ: Нефинансовые кредиты
486. ……… бюджетных ассигнований – документ, характеризующий бюджетные ассигнования в очередном финансовом году (1 слово)
Ответ: Обоснование
487. … … – вид финансового контроля, осуществляемого непосредственно гражданами, а также общественными организациями и объединениями (2 слова)
Ответ: Общественный контроль
488. ……… финансовой политики – совокупность финансовых отношений и финансовых ресурсов, образующих сферы и звенья финансовой системы государства (1 слово)
Ответ: Объекты
489. … … бюджета – превышение расходов бюджета (уменьшенных на расходы по обслуживанию государственного или муниципального долга) над доходами бюджета (2 слова)
Ответ: Первичный дефицит
490. … бюджета – превышение доходов бюджета над расходами бюджета (уменьшенными на расходы по обслуживанию государственного или муниципального долга) (2 слова)
Ответ: Первичный профицит
491. … … бюджета – налоговые и неналоговые доходы бюджета, зачисляемые в бюджеты в соответствии с бюджетным и иным законодательством РФ , законодательством о налогах и сборах, а также доходы, полученные бюджетами в виде безвозмездных поступлений, за исключением субвенций (2 слова)
Ответ: Собственные доходы
492. … … – система мер по непосредственно материальному обеспечению нетрудоспособных и малообеспеченных в рамках социальной защиты (2 слова)
Ответ: Социальное обеспечение
493. … … процесса – совокупность последовательно проводимых этапов бюджетного процесса, включающая составление проекта бюджета, рассмотрение и утверждение бюджет, исполнение бюджета; контроль за его исполнением, осуществление бюджетного учета, составление, внешнюю проверку, рассмотрение и утверждение бюджетной отчетности (2 слова)
Ответ: Стадии бюджетного
494. ………… – межбюджетные трансферты, предоставляемые для финансового обеспечения расходных обязательств РФ (субъектов РФ, муниципальных образований), возникающих при выполнении органами государственной власти (органами местного самоуправления) переданных им полномочий (1 слово)
Ответ: Субвенции
495. ……… – межбюджетные трансферты, предоставляемые с целью софинансирования расходных обязательств РФ (субъектов РФ, муниципальных образований), возникающих в ходе осуществления органами государственной власти (органами местного самоуправления) своих полномочий (1 слово)
Ответ: Субсидия
496. … … системы – группы финансовых отношений, выделяемые в соответствии с ролью субъектов этих отношений в общественном воспроизводстве (2 слова)
Ответ: Сфера финансовой
497. … … акционерного общества – сумма номинальной стоимости акций общества, приобретенных акционерами (2 слова)
Ответ: Уставный капитал
498. … … … – органы государственной власти и органы местного самоуправления, а также другие органы и организации, на которые возложены полномочия по осуществлению бюджетного процесса (3 слова)
Ответ: Участники бюджетного процесса
499. … … – исследование конкретных перспектив развития финансов экономических субъектов и субъектов власти в будущем, научно обоснованное предположение об объемах и направлениях использования финансовых ресурсов на перспективу (2 слова)
Ответ: Финансовое прогнозирование
500. … … – совокупность видов и форм организации финансовых отношений, условий и методов исчисления, применяемых при формировании финансовых ресурсов, образовании и использовании денежных фондов целевого назначения (2 слова)
Ответ: Финансовый механизм
refdocx.ru
Тест бюджетный учет и отчетность ответы — Правозащита
Для того, чтобы оценить ресурс, необходимо авторизоваться.
Учебное пособие по дисциплине «Бюджетный учет и отчетность» включает руководство по изучению дисциплины, теоретический материал, глоссарий. Предназначено для студентов, обучающихся по специальности 08010965 «Бухгалтерский учет, анализ и аудит», изучающих дисциплину «Бюджетный учет и отчетность». Подготовлено на кафедре «Бухгалтерский учет, анализ и аудит» УлГТУ.
Тест бюджетный учет и отчетность ответы
Ответы на тесты для бюджетх организаций
1. Классификация операций сектора государственного управления (далее КОСГУ) используется:
Вариант 2: для ведения бюджетного (бухгалтерского) учета, составления бюджетной (бухгалтерской) и иной финансовой отчетности
2. Какие разряды кода классификации доходов бюджетов, расходов бюджетов, источников финансирования дефицитов бюджетов использует бюджетное учреждение при формировании первых 17-ти разрядов счета рабочего плана счетов:
Вариант 1: с 4 по 20 разряд
3. Какими разрядами представлен показатель «Вид расходов» в классификации расходов бюджетов:
Вариант 3: с 18 по 20 разряд
4. Какие статьи (подстатьи) КОСГУ соответствуют следующему виду расходов классификации расходов бюджетов: 119 — Взносы по обязательному социальному страхованию на выплаты по оплате труда работников и иные выплаты работникам учреждений:
Вариант 2: 213, 262
5. Какие сроки установлены для хранения квартальной бюджетной отчетности?
Вариант 2: 5 лет
6. Номер счета Плана счетов (Рабочего плана счетов) состоит из:
Вариант 1: 26 разрядов
7. По какой статье КОСГУ следует отразить доходы государственных (муниципальных) учреждений от поступлений субсидий на финансовое обеспечение выполнения ими государственного (муниципального) задания.
Вариант 2: 130 «Доходы от оказания платных услуг»
8. К какому виду расходов классификации расходов бюджетов следует отнести услуги по уборке снега с территории бюджетного учреждения?
Вариант 1: 244 «Прочая закупка товаров, работ и услуг для обеспечения государственных (муниципальных) нужд»
9. На
pzpspb.ru
ответы по бюджету — Стр 2
Тесты по дисциплине «Бухгалтерский учет в бюджетных организациях» для студентов специальности «Бухгалтерский учет, анализ и аудит»
Вариант 1.
1.Нормативный документ, на основании которого осуществляется ведение бухгалтерского учета в бюджетных организациях:
а) Налоговый кодекс; б) Гражданский кодекс;
в) Закон «О бухгалтерском учете и отчетности».
2. Бюджетная классификация – это:
а) систематизированная группировка доходов и расходов бюджета;
б) плановый документ, отражающий расходы на содержание организации;
в) финансовый план бюджетной организации.
3. Поступление денежных средств в кассу по чеку с текущего счета в учреждении банка отражается проводкой:
а) Дт 120 «Касса» Кт 144 «Внутриведомственные расчеты»;
б) Дт 120 «Касса» Кт 100 «Текущий счет по бюджету»;
в) Дт 121 «Валютные средства в кассе» Кт 173 «Расчеты с бюджетом».
4. Поступления и выдачи наличных денег по кассе учитываются:
а) в смете расходов по бюджету; б) в Книге журнал-главная;
в) в кассовой книге.
5. Для учета операций по расчетам с подотчетными лицами используется субсчет:
а) 160 «Расчеты с подотчетными лицами»;
б) 140 «Расчеты по финансированию из бюджета»;
в) 144 «Внутриведомственные расчеты».
6. Командированному работнику возмещаются следующие расходы:
а) суточные; б) по найму жилья;
в) согласно счету гостиницы.
7. Стоимость поступивших от поставщиков строительных материалов для капитального строительства отражается проводкой:
а) Дт 067 «Прочие материалы» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 041 «Строительные материалы для капитального строительства» Кт 150 «Расчеты с поставщиками и подрядчиками»;
в) Дт 063 «Хозяйственные материалы» Кт 178 «Расчеты с прочими дебиторами и кредиторами».
8. Для учета расчетов с родителями за содержание детей в детских учреждениях предназначен субсчет:
а) 172 «Расчеты по специальным видам платежей»;б) 180 «Расчеты с персоналом»;
в) 187 «Расчеты по исполнительным листам».
9. Дебетовое сальдо по субсчету 170 «Расчеты по недостачам» означает:
а) суммы, поступившие в возмещение причиненного ущерба;
б) результат инвентаризации материальных ценностей;
в) сумму задолженности виновных лиц бюджетной организации.
10. Списание недостачи основных средств, отнесенной на материально-ответственное лицо, отражается проводкой:
а) Дт 019 «Прочие основные средства» Кт 170 «Расчеты по недостачам»;
б) Дт 170 «Расчеты по недостачам» Кт 019 «Прочие основные средства»;
в) Дт 200 «Расходы по бюджету» Кт 019 «Прочие основные средства».
11. Способы проведения переоценки основных средств в бюджетных организациях:
а) путем индексации первоначальной стоимости объектов основных средств;
б) путем определения первоначальной стоимости объектов основных средств;
в) путем определения фактической себестоимости объектов основных средств.
12. Списание остаточной стоимости ликвидируемого оборудования отражается проводкой:
а) Дт 200 «Расходы по бюджету» Кт 013 «Машины и оборудование»;
б) Дт 250 «Фонд в основных средствах» Кт 013 «Машины и оборудование»;
в) Дт 210 «Расходы к распределению» Кт 013 «Машины и оборудование».
13. На объекты основных средств, подлежащие ликвидации, составляется:
а) накладная на внутреннее перемещение; б) товарно-транспортная накладная;
в) акт ликвидации по форме, установленной в организации.
14. Для учета нематериальных активов в бюджетных организациях предназначен субсчет:
а) 067 «Прочие материалы»; б) 019 «Прочие основные средства»;
в) 030 «Продукция на складе».
15. Поступление предметов от поставщика отражается проводкой:
а) Дт 070 «Предметы на складе» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 200 «Расходы по бюджету» Кт 070 «Предметы на складе»;
в) Дт 070 «Предметы на складе» Кт 144 «Внутриведомственные расчеты».
16. Начисление взносов от ФЗП в Белгосстрах отражается проводкой:
а) Дт 171 «Расчеты по социальному страхованию» Дт 200 «Расходы по бюджету»;
б) Дт 180 «Расчеты с персоналом» Кт 171 «Расчеты по социальному страхованию»;
в) Дт 200 «Расходы по бюджету» Кт 171 «Расчеты по социальному страхованию».
17. Внебюджетные средства, принадлежащие бюджетной организации:
а) суммы по поручениям; б) доходы от реализации продукции;
в) депозитные суммы.
18. Накладные расходы подсобных хозяйств, от выполнения научно-исследовательских работ по договорам с заказчиками учитываются на субсчете:
а) 210 «Расходы к распределению»; б) 080 «Затраты на производство»;
в) 200 «Расходы по бюджету».
19. Фактическая себестоимость готовой продукции, сданной на склад, отражается проводкой:
а) Дт 080 «Затраты на производство» Кт 030 «Продукция на складе»;
б) Дт 030 «Продукция на складе» Кт 080 «Затраты на производство»;
в) Дт 030 «Продукция на складе» Кт 211 «Расходы по внебюджетным средствам».
20. Перед составлением годовой бухгалтерской отчетности для обеспечения достоверности данных проводится:
а) ревизия; б) аудит; в) инвентаризация.
Вариант 2.
1. Форма бухгалтерского учета, применяемая в бюджетных организациях:
а) мемориально-ордерная; б) книжно-журнальная;
в) журнально-ордерная.
2. Основной источник средств бюджетных организаций:
а) прибыль; б) ассигнования из государственного бюджета;
в) уставный капитал.
3. Для учета наличия и движения денежных средств в кассе в национальной валюте предназначен субсчет:
а) 130 «Аккредитивы»; б) 100 «Текущий счет по бюджету»;
в) 120 «Касса».
4. Суммы аванса, выданные из кассы под отчет подотчетным лицам, отражаются проводкой:
а) Дт 160 «Расчеты с подотчетными лицами» Кт 120 «Касса»;
б) Дт 160 «Расчеты с подотчетными лицами» Кт 173 «Расчеты с бюджетом»;
в) Дт 160 «Расчеты с подотчетными лицами» Кт 100 «Текущий счет по бюджету».
5. По возвращении из командировки работник представляет в бухгалтерию:
а) товарную накладную; б) смету расходов по бюджету;
в) авансовый отчет.
6. Для расчетов с поставщиками и подрядчиками за строительные материалы, конструкции, детали, оборудование к установке предназначен субсчет:
а) 179 «Расчеты в порядке плановых платежей»;
б) 178 «Расчеты с прочими дебиторами и кредиторами»;
в) 150 «Расчеты с поставщиками и подрядчиками».
7. Суммы, отраженные по кредиту субсчета 170 «Расчеты по недостачам» означают:
а) суммы, поступившие в возмещение причиненного ущерба;
б) суммы ущерба, причиненного виновником;
в) суммы недостачи по результатам инвентаризации.
8. Поступление хозяйственных материалов от поставщика отражается проводкой:
а) Дт 067 «Прочие материалы» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 063 «Хозяйственные материалы и канцелярские принадлежности» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
в) Дт 068 «Материалы в пути» Кт 150 «Расчеты с поставщиками и подрядчиками».
9. Расчеты с бюджетом в бюджетных организациях отражаются на субсчете:
а) 100 «Текущий счет по бюджету»; б) 200 «Расходы по бюджету»;
в) 173 «Расчеты с бюджетом».
10. Объекты основных средств бюджетных организаций:
а) объекты жилищного фонда; б) сценические и постановочные средства;
в) экспонаты животного мира.
11. При проведении переоценки основных средств составляется:
а) товарно-транспортная накладная; б) ведомость переоценки основных средств;
в) сличительная ведомость.
12. Поступление транспортных средств от поставщика отражается проводкой:
а) Дт 015 «Транспортные средства» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 200 «Расходы по бюджету» Кт 015 «Транспортные средства»;
в) Дт 015 «Транспортные средства» Кт 200 «Расходы по бюджету».
13. Способ начисления амортизации объектов основных средств в бюджетных организациях:
а) ускоренный; б) производительный;
в) линейный.
14. Счета для учета материальных запасов:
а) 06 «Материалы и продукты питания»; б) 01 «Основные средства»;
в) 07 «Отдельные предметы в составе оборотных средств».
15. Списание продуктов, израсходованных на питание контингента, отражается проводкой:
а) Дт 200 «Расходы по бюджету» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 200 «Расходы по бюджету» Кт 061 «Продукты питания»;
в) Дт 061 «Продукты питания» Кт 200 «Расходы по бюджету».
16. Начисление взносов на профессиональное пенсионное страхование отражается проводкой:
а) Дт 171 «Расчеты по социальному страхованию» Кт 200 «Расходы по бюджету»;
б) Дт 180 «Расчеты с персоналом» Кт 171 «Расчеты по социальному страхованию»;
в) Дт 200 «Расходы по бюджету» Кт 171 «Расчеты по социальному страхованию».
17. Внебюджетные средства, не принадлежащие бюджетной организации:
а) суммы по поручениям; б) доходы от реализации продукции;
в) доходы от аренды имущества.
18. Стоимость израсходованных материалов на производство в подсобных хозяйствах промышленного характера отражается проводкой:
а) Дт 200 «Расходы по бюджету» Кт 067 «Прочие материалы»;
б) Дт 080 «Затраты на производство» Кт 067 «Прочие материалы»;
в) Дт 067 «Прочие материалы» Кт 080 «Затраты на производство».
19. Фактическая себестоимость отгруженной продукции покупателям отражается проводкой:
а) Дт 280 «Реализация продукции» Кт 030 «Продукция на складе»;
б) Дт 031 «Продукция отгруженная» Кт 080 «Затраты на производство»;
в) Дт 280 «Реализация продукции» Кт 200 «Расходы по бюджету».
20. Формы бухгалтерской отчетности бюджетных организаций:
а) отчет об исполнении бюджетной сметы;
б) кассовый отчет; в) материальный отчет.
Вариант 3.
1. Бюджетная организация – это организация созданная:
а) учредителями для осуществления производственной деятельности и получения прибыли;
б) государственными органами для осуществления управленческих, социально-культурных, научно-технических и иных функций некоммерческого характера, которая финансируется из соответствующего бюджета;
в) индивидуальным предпринимателем для получения дохода.
2. Счета, применяемые для учета бюджетного финансирования и расчетов по финансированию подведомственных бюджетных организаций:
а) 23 «Финансирование и займы»;
б) 14 «Внутриведомственные расчеты по финансированию»;
в) 10 «Текущие счета по бюджету».
3. Учет фактических расходов ведется на счете:
а) 200 «Расходы по бюджету»; б) 210 «Расходы к распределению»
в) 080 «Затраты на производство».
4. Направление работников в служебную командировку оформляется:
а) отчетом о командировке; б) авансовым отчетом;
в) приказом (распоряжением) руководителя организации.
5. Списание израсходованных подотчетных сумм согласно авансовым отчетам отражается проводкой:
а) Дт 200 «Расходы по бюджету» Кт 180 «Расчеты с персоналом»;
б) Дт 200 «Расходы по бюджету» Кт 160 «Расчеты с подотчетными лицами»;
в) Дт 160 «Расчеты с подотчетными лицами» Кт 200 «Расходы по бюджету».
6. Для расчетов с поставщиками за материальные ценности предназначен субсчет:
а) 144 «Внутриведомственные расчеты»;
б) 178 «Расчеты с прочими дебиторами и кредиторами»;
в) 183 «Расчеты по вкладам в банках».
7. Суммы, отраженные по дебету субсчета 170 «Расчеты по недостачам» означают:
а) суммы ущерба, причиненного виновником;
б) суммы, поступившие в возмещение причиненного ущерба;
в) суммы недостачи по результатам инвентаризации.
8. Поступление продуктов питания от поставщика при наличии постоянных хозяйственных связей отражается проводкой:
а) Дт 067 «Прочие материалы» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 061 «Продукты питания» Кт 179 «Расчеты в порядке плановых платежей»;
в) Дт 061 «Продукты питания» Кт 150 «Расчеты с поставщиками и подрядчиками».
9. Списание недостачи денежных средств в кассе, отнесенной на кассира, отражается проводкой:
а) Дт 120 «Касса» Кт 170 «Расчеты по недостачам»;
б) Дт 200 «Расходы по бюджету» Кт 120 «Касса»;
в) Дт 170 «Расчеты по недостачам» Кт 120 «Касса».
10. Объекты основных средств отражаются в бухгалтерском учете:
а) по первоначальной стоимости; б) по стоимости приобретения;
в) по учетной стоимости.
11. Аналитический учет основных средств ведется:
а) в сличительной ведомости;
б) в инвентарной карточке учета объектов основных средств;
в) в карточке складского учета.
12. Разница между переоцененной стоимостью зданий и их стоимостью до переоценки отражается проводкой:
а) Дт 010 «Здания» Кт 250 «Фонд в основных средствах»;
б) Дт 010 «Здания» Кт 200 «Расходы по бюджету»;
в) Дт 200 «Расходы по бюджету» Кт 010 «Здания».
13. Период, за который осуществляется начисление амортизации по основным средствам:
а) ежемесячно; б) ежеквартально; в) за полный календарный год.
14. Поступление медикаментов от поставщика отражается проводкой:
а) Дт 062 «Медикаменты и перевязочные средства» Кт 178 «Расчеты с прочими дебиторами и кредиторами»;
б) Дт 062 «Медикаменты и перевязочные средства» Кт 200 «Расходы по бюджету»;
в) Дт 062 «Медикаменты и перевязочные средства» Кт 173 «Расчеты с бюджетом».
15. Начисление заработной платы работникам бюджетных организаций отражается проводкой:
а) Дт 180 «Расчеты с персоналом» Кт 200 «Расходы по бюджету»:
б) Дт 200 «Расходы по бюджету» Кт 180 «Расчеты с персоналом»;
в) Дт 080 «Затраты на производство» Кт 180 «Расчеты с персоналом».
16. Удержание подоходного налога из заработной платы отражается проводкой:
а) Дт 200 «Расходы по бюджету» Кт 173 «Расчеты с бюджетом»;
б) Дт 173 «Расчеты с бюджетом» Кт 180 «Расчеты с персоналом»;
в) Дт 180 «Расчеты с персоналом» Кт 173 «Расчеты с бюджетом».
17. Затраты на производство в подсобных хозяйствах бюджетных организаций учитываются на субсчете:
а) 080 «Затраты на производство»; б) 200 «Расходы по бюджету»;
в) 230 «Финансирование из бюджета».
18. Стоимость израсходованных материалов на выполнение научно-исследовательских работ по договорам с заказчиками отражается проводкой:
а) Дт 200 «Расходы по бюджету» Кт 060 «Материалы для учебных, научных и других целей»;
б) Дт 082 «Затраты на научно-исследовательские работы по договорам» Кт 060 «Материалы для учебных, научных и других целей»;
в) Дт 068 «Материалы в пути» Кт 082 «Затраты на научно-исследовательские работы по договорам».
19. Финансовый результат деятельности подсобных хозяйств, от выполнения научно-исследовательских работ по договорам с заказчиками формируется на субсчете:
а) 280 «Реализация продукции»; б) 272 «Внебюджетные фонды»;
в) 410 «Прибыли и убытки».
20. Прибыль от внебюджетной деятельности, остающаяся в распоряжении бюджетной организации, направляется:
а) на выплату заработной платы;
б) на образование фондов экономического стимулирования;
в) на выплату дивидендов.
Вариант 4.
1. Объекты бухгалтерского учета бюджетных организаций:
а) материальные ценности и денежные средства;
б) расходы по исполнению смет расходов по бюджету;
в) финансирование из бюджета.
2. Расходы бюджетных организаций подразделяются:
а) кассовые, фактические; б) прямые, косвенные;
в) одноэлементные, комплексные.
3. Учет кассовых расходов ведется на счете:
а) 20 «Расходы по бюджету»; б) 10 «Текущие счета по бюджету»;
в) 08 «Затраты на производство».
4. Работнику при направлении в служебную командировку выдается:
а) командировочное удостоверение; б) удостоверение личности;
в) авансовый отчет.
5. Поступление неиспользованных подотчетных сумм в кассу отражается проводкой:
а) Дт 160 «Расчеты с подотчетными лицами» Кт 120 «Касса»;
б) Дт 173 «Расчеты с бюджетом» Кт 160 «Расчеты с подотчетными лицами»;
в) Дт 120 «Касса» Кт 160 «Расчеты с подотчетными лицами».
6. Для расчетов с поставщиками за материальные ценности при наличии постоянных хозяйственных связей предназначен субсчет:
а) 150 «Расчеты с поставщиками и подрядчиками»;
б) 178 «Расчеты с прочими дебиторами и кредиторами»;
в) 179 «Расчеты в порядке плановых платежей»;
7. Для расчетов по недостачам денежных средств, товарно-материальных ценностей предназначен субсчет:
а) 170 «Расчеты по недостачам»; б) 080 « Затраты на производство»;
в) 200 «Расходы по бюджету».
8. Начисление родительской платы за содержание детей, находящихся на государственном обеспечении, отражается проводкой:
а) Дт 120 «Касса» Кт 172 «Расчеты по специальным видам платежей»;
б) Дт 172 «Расчеты по специальным видам платежей» Кт 173 «Расчеты с бюджетом»;
в) Дт 173 «Расчеты с бюджетом» Кт 172 «Расчеты по специальным видам платежей».
9. Списание недостачи хозяйственных материалов, отнесенной на материально-ответственное лицо, отражается проводкой:
а) Дт 063 «Хозяйственные материалы и канцелярские принадлежности» Кт 170 «Расчеты по недостачам»;
б) Дт 170 «Расчеты по недостачам» Кт 200 «Расходы по бюджету»;
в) Дт 170 «Расчеты по недостачам» Кт 063 «Хозяйственные материалы и канцелярские принадлежности».
10. Объекты основных средств, которые подвергались переоценке, отражаются в бухгалтерском учете:
а) по переоцененной стоимости; б) по учетной стоимости;
в) по средневзвешенной стоимости.
11. При поступлении объектов основных средств от поставщика составляется:
а) товарная накладная; б) акт приема-передачи основных средств;
в) карточка складского учета.
12. При начислении амортизации объектов основных средств составляется проводка:
а) Дт 01 «Основные средства» Кт 020 «Амортизация основных средств»;
б) Дт 200 «Расходы по бюджету» Кт 020 «Амортизация основных средств»;
в) Дт 250 «Фонд в основных средствах» Кт 020 «Амортизация основных средств».
13. Для оформления и учета приема объектов основных средств из ремонта оформляется:
а) накладная на внутреннее перемещение; б) приходный ордер;
в) акт по форме, установленной в организации.
14. Материальные запасы отражаются в учете:
а) по фактической себестоимости; б) по первоначальной стоимости;
в) по остаточной стоимости.
15. Начисление взносов органам социального страхования отражается проводкой:
а) Дт 171 «Расчеты по социальному страхованию» Кт 180 «Расчеты с персоналом»;
б) Дт 200 «Расходы по бюджету» Кт 171 «Расчеты по социальному страхованию»;
в) Дт 171 «Расчеты по социальному страхованию» Кт 200 «Расходы по бюджету».
16. Удержание взносов в пенсионный фонд из заработной платы отражается проводкой:
а) Дт 180 «Расчеты с персоналом» Кт 171 «Расчеты по социальному страхованию»;
б) Дт 171 «Расчеты по социальному страхованию» Кт 180 «Расчеты с персоналом»;
в) Дт 200 «расходы по бюджету» Кт 171 «Расчеты по социальному страхованию».
17. Затраты на выполнение научно-исследовательских работ учитываются на субсчете:
а) 080 «Затраты на производство»; б) 200 «Расходы по бюджету»;
в) 082 «Затраты на научно-исследовательские работы по договорам».
18. Стоимость реализованной продукции и предъявление счета покупателю отражается проводкой:
а) Дт 154 «Расчеты с покупателями и заказчиками» Кт 280 «Реализация продукции»;
б) Дт 280 «Реализация продукции» Кт 200 «Расходы по бюджету;
в) Дт 111 «Текущий счет по внебюджетным средствам» Кт 280 «Реализация продукции».
19. Дебетовый оборот по субсчетам 080 «Затраты на производство», 082 «Затраты на научно-исследовательские работы по договорам» означает:
а) сумму затрат, связанных с производством продукции, работ, услуг;
б) величину незавершенного производства;
в) фактическую себестоимость продукции, работ, услуг.
20. Использование прибыли подсобных хозяйств, от выполнения научно-исследовательских работ по договорам с заказчиками отражается на субсчете:
а) 410 «Прибыли и убытки»; б) 230 «Финансирование из бюджета»;
в) 411 «Использование прибыли».
Вариант 5.
1. Основной источник средств бюджетных организаций:
а) средства государственного и местных бюджетов;
б) прибыль;
в) кредиты банка и займы физических лиц.
2. Поступление денежных средств в кассу по чеку с текущего счета в учреждении банка отражается проводкой:
а) Дт 100 «Текущий счет по бюджету» Кт 120 «Касса»;
б) Дт 120 «Касса» Кт 100 «Текущий счет по бюджету»;
в) Дт 120 «Касса» Кт 144 «Внутриведомственные расчеты».
3. Бюджетная классификация – это:
а) состав затрат по калькуляционным статьям;
б) состав затрат по экономическим элементам;
в) систематизированная группировка доходов и расходов бюджета.
4. Объекты бухгалтерского учета бюджетных организаций:
а) расходы по исполнению смет расходов по бюджету;
б) финансирование из бюджета;
в) материальные ценности и денежные средства.
5. Для расчетов с поставщиками и подрядчиками за строительные материалы, конструкции, детали, оборудование к установке предназначен субсчет:
а) 150 «Расчеты с поставщиками и подрядчиками»;
б) 144 «внутриведомственные расчеты»;
в) 179 «Расчеты в порядке плановых платежей».
6. Дебетовое сальдо по субсчету 170 «Расчеты по недостачам» означает:
а) суммы, поступившие в возмещение причиненного ущерба;
б) сумму задолженности виновных лиц бюджетной организации;
в) результат инвентаризации материальных ценностей.
7. Начисление родительской платы за содержание детей, находящихся на государственном обеспечении, отражается проводкой:
а) Дт 120 «Касса» Кт 172 «Расчеты по специальным видам платежей»;
б) Дт 173 «Расчеты с бюджетом» Кт 172 «Расчеты по специальным видам платежей»;
в) Дт 172 «Расчеты по специальным видам платежей» Кт 173 «Расчеты с бюджетом».
8. Недостача денежных средств в кассе, отнесенная на кассира, отражается проводкой:
а) Дт 170 «Расчеты по недостачам» Кт 120 «Касса»;
б) Дт 120 «Касса» Кт 170 «Расчеты по недостачам»;
в) Дт 200 «Расходы по бюджету» Кт 120 «Касса».
9. Объекты основных средств бюджетных организаций:
а) материалы, готовая продукция; б) библиотечные фонды, музейные ценности;
в) денежные средства в кассе, на счетах в банке.
10. Объекты основных средств отражаются в бухгалтерском учете:
а) по стоимости приобретения; б) по учетной стоимости;
в) по первоначальной стоимости.
11. При начислении амортизации объектов основных средств составляется проводка:
а) Дт 020 «Амортизация основных средств» Кт 01 «Основные средства»;
б) Дт 250 «Фонд в основных средствах» Кт 020 «Амортизация основных средств».
в) Дт 200 «Расходы по бюджету» Кт 020 «Амортизация основных средств»;
12. На объекты основных средств, подлежащие ликвидации, составляется:
а) акт ликвидации по форме, установленной в организации;
б) накладная на внутреннее перемещение; в) коммерческий акт;
13. Разница между переоцененной стоимостью зданий и их стоимостью до переоценки отражается проводкой:
а) Дт 010 «Здания» Кт 200 «Расходы по бюджету»;
б) Дт 010 «Здания» Кт 250 «Фонд в основных средствах»;
в) Дт 200 «Расходы по бюджету» Кт 010 «Здания».
14. Счета для учета материальных запасов:
а) 01 «Основные средства»; б) 06 «Материалы и продукты питания»;
в) 07 «Отдельные предметы в составе оборотных средств».
15. Начисление заработной платы работникам бюджетных организаций отражается проводкой:
а) Дт 180 «Расчеты с персоналом» Кт 200 «Расходы по бюджету»;
б) Дт 080 «Затраты на производство» Кт 180 «Расчеты с персоналом»;
в) Дт 200 «Расходы по бюджету» Кт 180 «Расчеты с персоналом».
16. Удержание подоходного налога из заработной платы отражается проводкой:
studfiles.net
Онлайн-тесты на oltest.ru: Бухгалтерский учёт в бюджетных организациях
Онлайн-тестыТестыБухгалтерский учёт и аудитБухгалтерский учёт в бюджетных организацияхвопросы1-151. Аналитический учет белья, одежды и обуви, находящихся на складе и в эксплуатации, в бухгалтерии ведется на карточках формы:
• ОС-9 или вкладных листах формы 402
2. Аналитический учет ведется в расчетных регистрах:
• карточках
• книгах
• накопительных ведомостях
3. Аналитический учет молодняка животных ведется:
• по видам и возрастным группам
4. Аналитический учет основных средств ведется на инвентарных карточках форм:
• ОС-6 и ОС-8
5. Арендованные основные средства учитываются на:
• забалансовом счете 01
6. Бухгалтерский учет ведется:
• на основе единого классификатора по всем синтетическим и аналитическим счетам
7. Бухгалтерский учет исполнения смет осуществляется по форме бухгалтерского учета:
• мемориально-ордерной или журнально-ордерной
• бухгалтерскими службами учреждений и централизованными бухгалтериями
9. Бухгалтерский учет исполнения смет учреждений, независимо от источников финансирования, ведется:
• на едином балансе по утвержденному плану счетов
10. В кассовых и банковских документах исправления:
• не допускаются
11. В том случае, когда имеются расхождения с данными документов поставщика, составляется акт приемки по форме:
• 429
12. В учреждениях все бухгалтерские документы, связанные с исполнением смет подписываются:
• главным бухгалтером или его заместителем
• заместителем руководителя
• руководителем
13. Все мемориальные ордера — накопительные ведомости вместе с относящимися к ним документами должны быть подобраны в хронологическом порядке и сброшюрованы, по истечении каждого отчетного:
• месяца
14. Для белья, постельных принадлежностей, одежды и обуви применяются номенклатурные номера, которые состоят из _____________ значков.
• 7
15. Для бухгалтерского учета операций в бюджетных организациях применяется план счетов, который может включать _____________ счетов.
• 41
oltest.ru
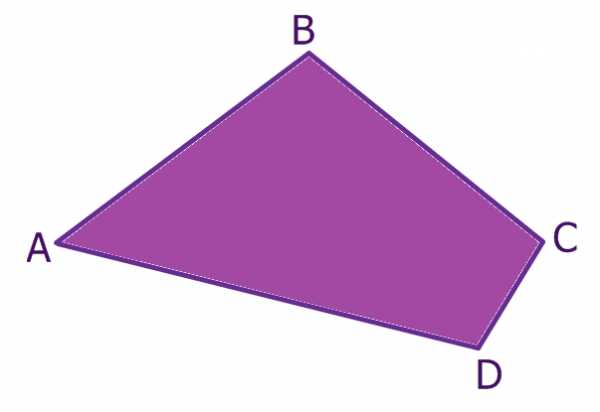
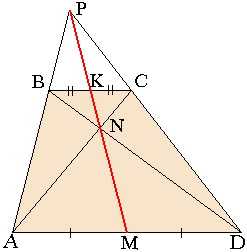
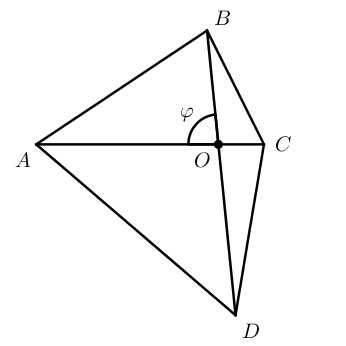
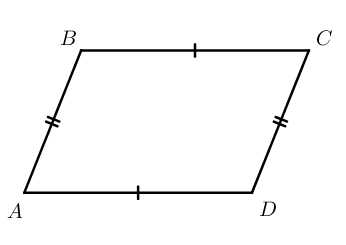
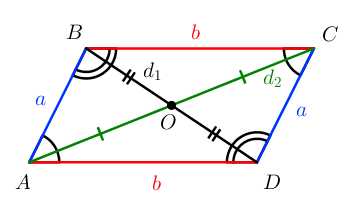
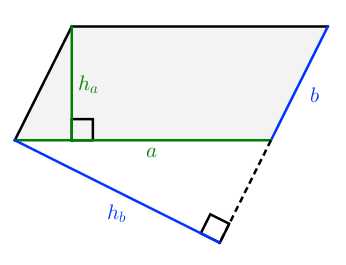S=a⋅ha=b⋅hb
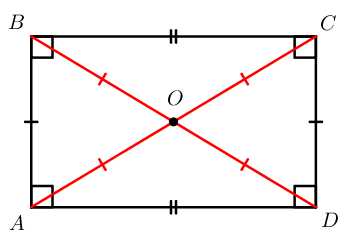
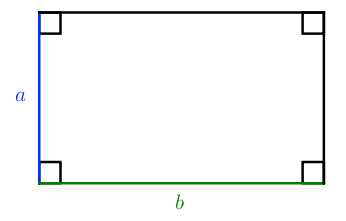S=a⋅b
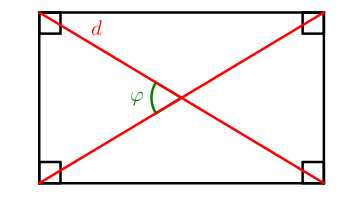S=12⋅d2⋅sinφ
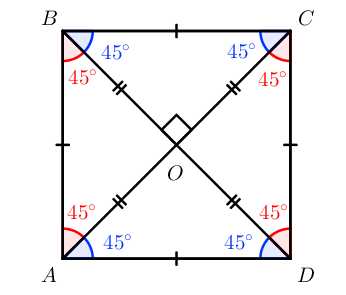
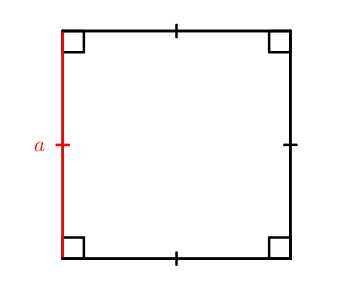S=a2
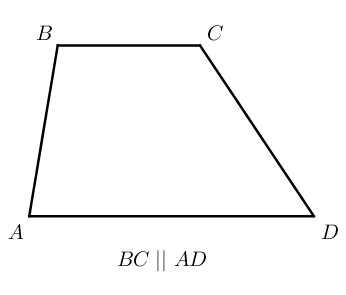
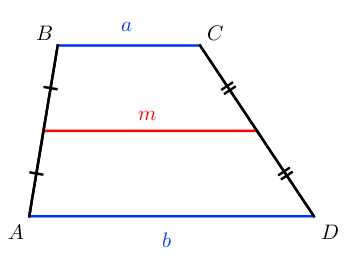
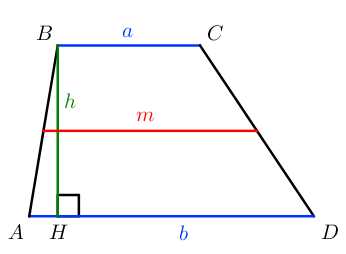S=a+b2⋅h=m⋅h
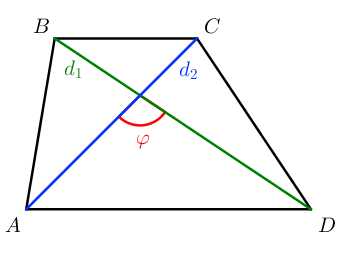S=12d1⋅d2⋅sinφ
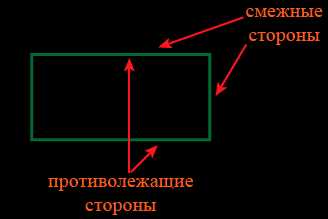
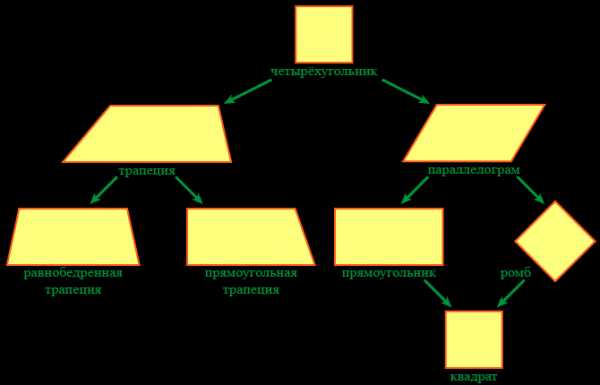
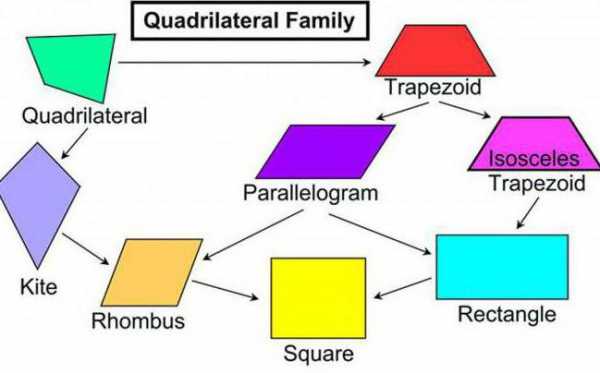Однако из-за слишком сложных свойств некоторых из них на уроках геометрии школьников знакомят только с двумя видами.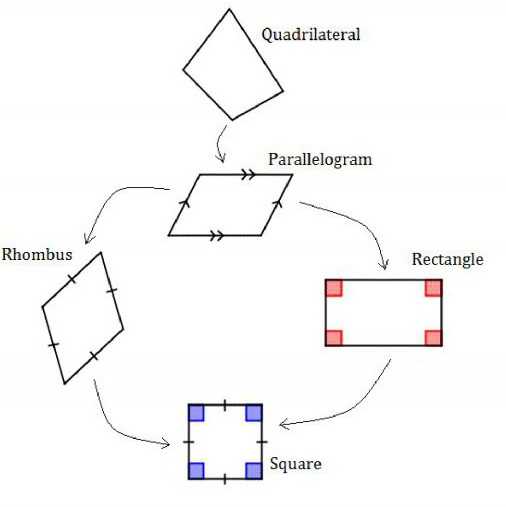
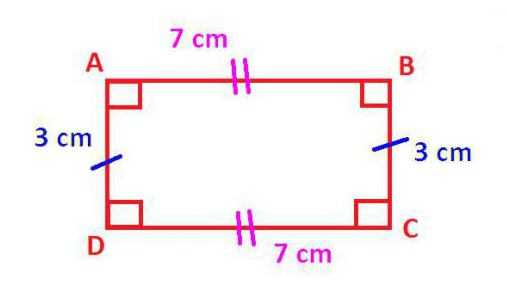
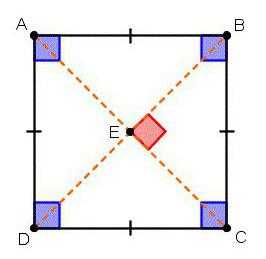
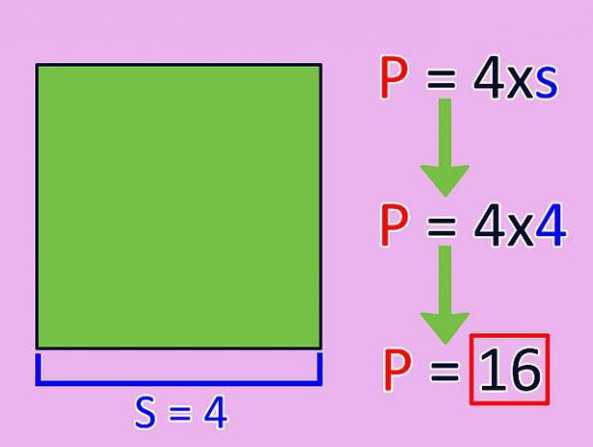
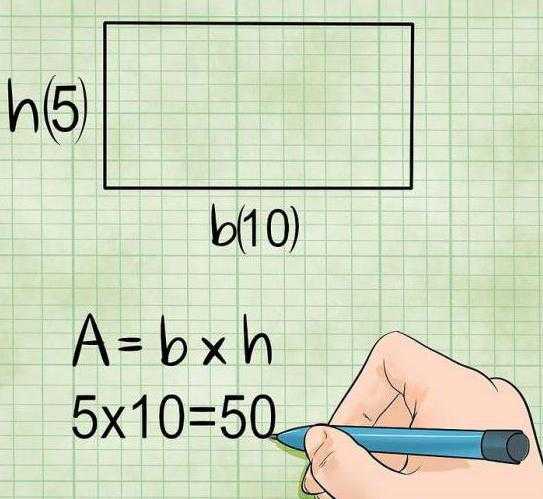
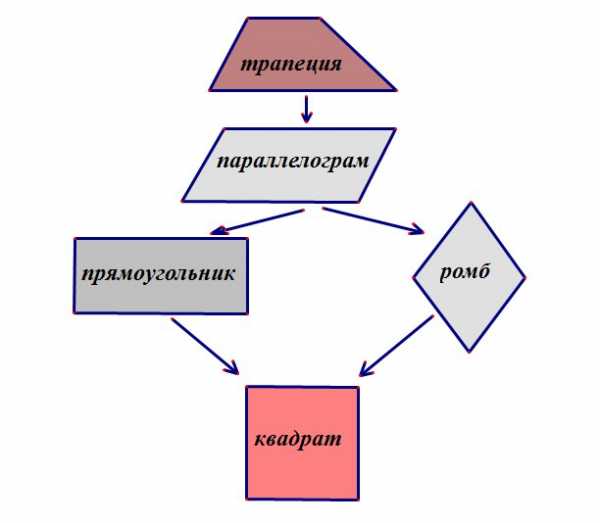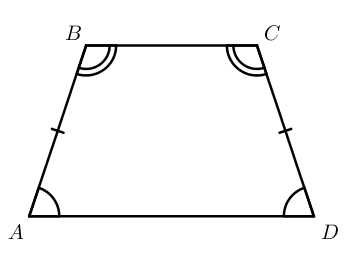
Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.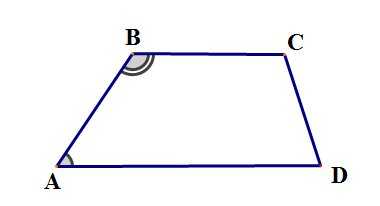
1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°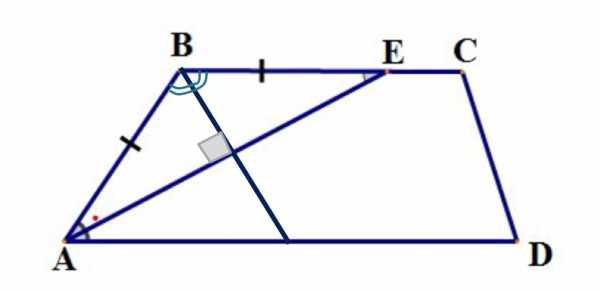
Приветствую!
