Плотность машинного масла — как измерить и что нужно знать?
Формула расчета плотности или удельного веса известна еще со школьной программы по физике. Определение плотности можно представить в виде массы какого-либо вещества, находящейся в единице объема. Поэтому измеряется плотность в килограммах на кубический метр (кг/м3). По этой формуле можно рассчитать плотность любого вещества: твердого, жидкого, газообразного. Нас же интересует плотность машинного масла, которая так же представлена во всех таблицах с измерением кг на кубометр.
Содержание статьи
Плотность, как важный параметр масла
Плотность, как в моторном, так и в трансмиссионном машинном масле такой же важный параметр, как и вязкость. Чем плотнее структура масла, тем лучше оно образует защитную пленку на деталях. Чем выше его текучесть, тем пленка будет тоньше, но быстрее закроются все микротрещинки в механизмах силовых агрегатов и трансмиссии.

Идеальная формула текучести и плотности нефтепродуктов достигается исключительно с помощью присадок, так как в итоге надо чтобы масло быстро пролилось во все уголки двигателя и коробки передач, а затем надежно покрыло механизмы, защищая их от трения и износа (все те же противозадирные присадки).
Плотность масла не одинакова, она зависит напрямую от класса смазочных продуктов: минеральное, полусинтетическое, синтетическое и т.п. Помимо этого, на плотность влияют процессы получения продукта, новые технологии способны создать уникальную текучесть синтетических моторных и трансмиссионных масел в купе с надежным защитным покрытием. Минеральные и полусинтетические масла имеют более высокую плотность, так как относятся к природным или частично природным продуктам нефтепереработки. Соответственно качество нефти и ее состав напрямую влияет на конечный продукт, такой как машинное масло.
Не последнюю роль в плотности машинных масел так же играет степень очистки их базового продукта и присадочные пакеты, добавляемые при производстве смазочных материалов. Стандартная плотность машинного масла равна 910 кг/м3, что можно увидеть в любой таблице измерения плотностей большинства веществ.
Для машинных масел можно вывести формулу, чем чище масло, тем меньше оно содержит фракций, соответственно его плотность будет ниже и выкипать они будут при более низких температурах с небольшим временным интервалом. И наоборот, чем больше содержит машинное масло фракций, которые имеют высокую плотность, тем выше будут температуры закипания.
Зачем это нужно знать, — затем что бы прочитать на канистре при какой температуре машинное масло может дать вспышку, а так же какое из масел необходимо применить, что бы надежно защищало автомобиль при высоких температурах под нагрузкой.
Как измерить плотность масла?

Для измерения всех масел используют приборы, называемые ареометрами. Они представляют собой стеклянную запаянную трубку со шкалой делений, которая погружается в исследуемую жидкость.
В чем то ареометры похожи на спиртометры и термометры для воды, принцип измерения примерно тот же. В промышленности ареометры используют редко, возможно потому, что они сделаны из стекла и часто бьются, а возможно и потому что уже давно изобрели электронные плотномеры, которые точнее и быстрее предоставляют необходимые данные и достаточно безопасны в использовании.
В любом случае, чем бы не измерялась плотность машинного масла, она будет относительная. Измерение проводится при температуре 20 градусов по Цельсию. Температурный режим измерения других нефтепродуктов отличается от машинного масла, с эталонами можно ознакомится в таблице эталонных измерений. К примеру, масло для авиационной техники имеет плотность от 880 до 905 кг/м3, для дизельных двигателей от 890 до 920 кг/м3, а для моторов на бензине порог изменяется в рамках 910 — 930.
Важные особенности
Всем уже известно, что вязкость машинного масла — это основной параметр, определяющий его использование. Не смотря на то, что плотность не менее важна, классификации ее как таковой нет, в отличии обиходного SAE. Тем не менее практика и многочисленные тесты позволили увязать значение по SAE и плотность.

Пример! Определяем по марке машинного масла плотность и вязкость. Зимнее моторное масло 10W имеет плотность 857 кг/м3 или 0,857 кг/л при вязкости равной 32 сантистокса. Измерения проводились опытным путем при температуре в 40 градусов по Цельсию и занесены в табличные данные основных характеристик машинных масел. Естественно это не эталон и за счет присадок такое масло может иметь более жидкое состояние с меньшей плотностью. Смотрим далее, зимнее моторное масло 20W имеет уже совершенно другие показатели, вязкость его равна 68 сантистоксов, а плотность 865 кг/м3. Закономерность прослеживается, шаг вязкости увеличил плотность продукта. Летние машинные масла имеют еще большую плотность, чем зимние. Интервал таких марок, как 20 — 50, в соответствии даст плотность масла 861 — 875, при интервале вязкости от 46 до 220 снт.
Любые проводимые опыты и таблицы эталонов — это условность. Покупая машинное масло обязательно нужно внимательно читать этикетку, так как присадки и добавки в базовое масло способны кардинально изменить его параметры, не смотря на то, что буквы и классификация по SAE могут быть одинаковыми.
avtotehnar.ru
Плотность моторного масла. Таблица | АвтоЖидкость
 Физическое отношение массы к объёму жидкости определяет плотность моторного масла. Наряду с вязкостью параметр имеет прямую зависимость от температуры, влияет на работу двигателей и обеспечивает заявленную мощность при гидропередаче. Некачественное моторное масло содержит вредные присадки, а отработанное — примеси, которые повышают плотностные параметры. Расскажем, как влияют высокие и низкие показатели плотности синтетических масел на работу поршневых или роторных двигателей авто.
Физическое отношение массы к объёму жидкости определяет плотность моторного масла. Наряду с вязкостью параметр имеет прямую зависимость от температуры, влияет на работу двигателей и обеспечивает заявленную мощность при гидропередаче. Некачественное моторное масло содержит вредные присадки, а отработанное — примеси, которые повышают плотностные параметры. Расскажем, как влияют высокие и низкие показатели плотности синтетических масел на работу поршневых или роторных двигателей авто.
Высокоплотные смазочные материалы
Плотность автомобильных масел варьируется на уровне 0,68–0,95 кг/л. Смазочные жидкости с показателем выше 0,95 кг/л относят к высокоплотным. Такие масла снижают механическую нагрузку при гидравлической передаче без потери производительности. Однако в силу повышенной густоты смазка не проникает в труднодоступные участки поршневых цилиндров. Как результат: увеличивается нагрузка на кривошипно-шатунный механизм (коленвал). Также растёт расход смазочного материала и чаще образуются коксовые отложения.
Через 1,5–2 года смазочная жидкость уплотняется на 4–7% от первоначального значения, что сигнализирует о необходимости замены смазочного материала.

Низкоплотные моторные масла
Снижение массо-объёмного параметра ниже 0,68 кг/л обусловлено введением низкоплотных примесей, например, легковесных парафинов. Некачественные смазки в подобном случае приводят к быстрому износу гидромеханических элементов двигателя, а именно:
- Жидкость не успевает смазать поверхность движущихся механизмов и стекает в картер.
- Повышенное выгорание и коксоотложение на металлических деталях ДВС.
- Перегрев силовых механизмов вследствие увеличения силы трения.
- Повышенный расход смазочного материала.
- Загрязнение масляных фильтров.
Таким образом, для правильной работы связки «цилиндр-поршень» необходимо моторное масло оптимальной плотности. Значение определяется для конкретного типа двигателя и рекомендуется согласно классификациям SAE и API.

Таблица плотности зимних моторных масел
Смазки, обозначаемые индексом 5w40–25w40, относят к зимним типам (W – Winter). Плотность подобных продуктов варьируется в диапазоне 0,85–0,9 кг/л. Цифра перед «W» указывает на температуру, при которой обеспечивается проворачивание и прокручивание поршневых цилиндров. Вторая цифра — индекс вязкости нагретой жидкости. Плотностный показатель смазки класса 5W40 минимальный среди зимних типов — 0,85 кг/л при 5 °C. У аналогичного продукта класса 10W40 значение на уровне 0,856 кг/л, а для 15w40 параметр равен 0,89–0,91 кг/л.
| Класс моторного масла по SAE | Плотность, кг/л |
| 5w30 | 0,865 |
| 5w40 | 0,867 |
| 10w30 | 0,865 |
| 10w40 | 0,865 |
| 15w40 | 0,910 |
| 20w50 | 0,872 |
 Из таблицы видно, что показатель зимних минеральных смазок колеблется на уровне 0,867 кг/л. При эксплуатации смазочных жидкостей важно следить за отклонениями плотностных параметров. Измерить значение поможет обычный ареометр.
Из таблицы видно, что показатель зимних минеральных смазок колеблется на уровне 0,867 кг/л. При эксплуатации смазочных жидкостей важно следить за отклонениями плотностных параметров. Измерить значение поможет обычный ареометр.
Плотность отработанного моторного масла
По истечении 1–2 лет использования ухудшаются физические свойства технических смазок. Окраска продукта меняется от светло-жёлтой до бурой. Причина — образование продуктов распада и появление загрязняющих примесей. Асфальтены, производные карбена, а также несгораемая сажа — главные компоненты, ведущие к уплотнению технических смазок. К примеру, жидкость класса 5w40 с номинальным показателем 0,867 кг/л спустя 2 года имеет значение 0,907 кг/л. Устранить деградационные химические процессы, ведущие к изменению плотности моторного масла, невозможно.
avtozhidkost.ru
Что означает показатель плотности у моторого масла
Плотность масла — одна из важнейших характеристик наряду с коэффициентом вязкости. Эти показатели влияют на рабочие свойства моторных жидкостей. Нередко из-за нарушений рекомендуемых допусков смазочных материалов автомобили снимают с гарантийного обслуживания. Потому следует внимательно относится к выбору жидкостей, отвечающих за исправную долговечную работу.
Выбирая моторное масло, автомобилисты ориентируются на главные его свойства. К ним относятся:
- плотность. Этот показатель — отношение объема к массе, измеряемый в килограммах на кубический метр. Значение плотности моторного масла находится в прямой зависимости от температуры;
- удельный вес — отношение массы вещества к массе воды. Так же зависит от температурных показателей;
- вязкость — показатель текучести жидкости при различных температурных режимах. Ее измеряют в нескольких единицах: стокс, сантистокс, м₂ или мм₂ на секунду;
- температура вспышки. Этот параметр показывает при какой максимальной температуре происходит вспышка при контакте с открытым огнем;
- температура застывания — показатель минимума, при котором масло застывает;
- кислотное и щелочное число. Влияют на нейтрализацию образующихся кислот в процессе работы мотора. От этих параметров зависят антиоксидантные свойства смазочных смесей.
Что такое плотность
Густота и вязкость смазки в картере является плотностью. Ее значение показывает сколько молекул вещества находится в определенном объеме, и увеличивается при повышении давления. При высоком коэффициенте появляется возможность снижения гидропередачи без изменения мощности.
Однако если плотность высокая, то смазка хуже проникает в зазоры двигателя, усложняя вращение коленвала. Такое явление можно наблюдать при запуске мотора в морозное утро. Кроме того, по той же причине увеличивается расход топливных ресурсов. Густое масло вызывает налипание нагара и повышенный расход моторной жидкости.

Но низкий показатель плотности так же имеет свои недостатки. При сниженной вязкости возникают такие проблемы:
- жидкость быстро стекает в картер, не успев смазать все зазоры;
- если в ДВС значительные зазоры между стенками цилиндра и поршнем, такая смазка не эффективна;
- загрязнение силового агрегата отработанными продуктами вследствие чрезмерного выгорания моторной жидкости;
- активная циркуляция приводит к быстрому загрязнению масляных фильтров;
- как результат плохой смазки — повышенный износ деталей и механизмов.
Правильно выбранный продукт с соответствующей маркировкой не причинит вреда сердцу вашего автомобиля, поможет увеличить рабочий ресурс. Для качественного обслуживания необходимо выбирать только проверенные торговые марки.
Соотношение плотности и вязкости
Выбирая масло для своего автотранспортного средства водитель ориентируется на классификацию SAE, характеризующую жидкость по показателю вязкости. Отдельной классификации по плотности не существует. В условиях нашего климата актуальны всесезонные продукты.
Так, буква W в маркировке означает зимнюю смазку. Зимние масла имеют диапазон от 5W до 25W. При значении 5W продукт не теряет своих рабочих качеств до показателя -30C, а при 20W смазка эффективна лишь при небольших морозах. Летние смазочные продукты обладают низкой вязкостью. Их маркировка — от 10 до 60.
Измерение плотности
Для определения плотности используется ареометр. Конструкция состоит из стеклянного поплавка с трубкой, на которую нанесена шкала. Показания фиксируют при температуре 20C в кг/л.
Отношение показателя плотности масла к плотности воды является относительным значением. Его определяют следующим образом: ингредиенты берутся в равных количествах при температуре 40C.
Плотность синтетики и полусинтетики
По сути, показатель данного параметра синтетических и полусинтетических жидкостей идентичен. Отличие имеются только в способности менять состояние. Полусинтетика, имея минеральную составляющую, блокирует поршневую систему при низких температурах. Такие продукты подвержены термическому влиянию.

Несмотря на то, что синтетика менее подвержена зависимости от температур, не всегда показатель плотности может быть оптимален. Зависит это от нескольких моментов:
- количество и качество пакета присадок. В некоторых случаях масса присадочных компонентов может быть вредна для двигателя;
- на синтетические смеси негативно влияют максимальные температуры и длительная непрерывная эксплуатация;
- в условиях максимальных температурных показателей возникает риск отказа системы охлаждения, и защита мотора становится неэффективной;
- при высокой стоимости таких продуктов цикл их работы невысок. Срок годности — 12 месяцев, после чего жидкость становится бесполезной;
- большое количество контрафактных продуктов в торговых точках.
Но даже при всех этих минусах синтетические машинные масла обеспечивают достойный уровень защиты двигателя в линейке аналогичных продуктов.
Выбор смазочной жидкости
Выбор смазки должен быть ориентирован согласно допускам, указанным производителем силового агрегата. Учитывать необходимо и сезонность, что важно для климатических условий региона. В маркировке продукта плотность масел указывается цифрой вначале, например, из двух продуктов — 5W40 и 10W40 последнее будет наиболее плотным.

При выборе смазочного состава необходимо учитывать такие моменты:
- максимальная идентичность с продуктами, рекомендованными допусками моторных масел;
- фирменная тара. Следует избегать приобретения на розлив из бочки;
- оригинальный продукт. Внимательно изучайте товар на предмет подделки;
- свежесть и срок годности.
На показания плотности оказывают влияние посторонние вещества, которые могут проникать в масла при износе или разгерметизации соединений. Определить такое явление можно с помощью масляного щупа (посторонние пятна) и контроля расходования смазки. Поможет в этом прибор под названием ареометр.
Показатели плотности горюче-смазочных продуктов:
- бензин ~ 760 кг/м3;
- диз. топливо ~ 840 кг/м3;
- антифриз — 1035-1085 кг/м3;
- вода — 1000 кг/м3;
- моторное масло — 880-930 кг/м3.
Учитывая эти показатели, просто определить наличие посторонних примесей, используя ареометр. При разгерметизации систем охлаждения значение увеличивается, а уменьшается при неисправности поршневой.
Чтобы быть уверенным в качестве смазочных материалов автолюбители могут воспользоваться маслотестером. Этот прибор позволяет узнать не только плотность с точностью до единиц, но и тип масел (синтетика, минералка, полусинтетика).
Правильный выбор смазочных материалов увеличит ресурс службы двигателя и избавит от дополнительных трат на ремонт и обслуживание.
oavtomasle.ru
На что влияет плотность моторного масла и как ее измерить
Любая техническая жидкость (моторное масло – не исключение) имеет химические и физические свойства. Эти характеристики закладываются производителем, и влияют на качество работы расходного материала.
Например, от плотности моторного масла зависят гидравлические параметры: насколько эффективно будет нагнетаться давление, а соответственно поступление смазки к рабочим точкам по маслопроводам.

Измерение плотности жидкостей в лаборатории
Кроме того, от этой величины зависит теплообмен. Как известно, с помощью моторной смазки отводится тепло от деталей трения, поскольку система охлаждения двигателя не задействована в этом процессе.
Производитель делает масла определенной плотности для обеспечения заданных значений кинематической вязкости. Собственно, это значение получают из величин динамической вязкости и плотности жидкости.
Что такое плотность масла?
Для покупателя привычно видеть на упаковке такие параметры, как вязкость по SAE, классификации качества по API или ACEA. Удельная плотность моторного не относится к основным характеристикам, ее значение можно узнать из расширенной классификации или по результатам тестов.
С точки зрения физики, эта величина определяется отношением массы вещества к его объему. То есть, чем больше единиц массы умещается в определенный объем – тем выше значение.
Чтобы понять, как работает система измерения, обратимся к эталону:
Величину 1 кг/л имеет дистиллированная вода при температуре 4°C.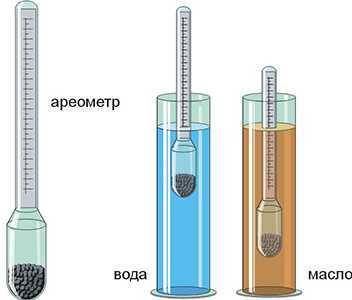
Поскольку в смазочных материалах содержатся различные вещества, многие из которых легче воды – плотность масла ниже.
Обратите внимание
Разговорная форма «легче» имеет прямое отношение к плотности материала. Употребляя это слово, мы как раз имеем в виду, что при одном и том же объеме, вещества имеют разный вес.
Плотность отработанного моторного масла будет отличаться от свежего, скорее всего в сторону увеличения. Это связано с тем, что часть легких жидкостей улетучивается, а тяжелые примеси добавляются. Это шлаки, взвесь твердых частиц, сажа, и пр.
Таким образом, понятно, что базовое значение зависит от основы масла, и состава его присадок.
Для сведения
Мошенники часто производят очистку отработанных масел, для повторной продажи в упаковках известных брендов. При этом, даже после тщательного удаления всех примесей, которыми «богата» отработка, такие характеристики, как плотность, не восстанавливаются.

Зная правильное значение этого параметра, вы легко сможете проверить приобретаемый продукт «на подлинность».
Есть еще одна зависимость величины: от температуры
Казалось бы, в чем тут связь? Но ведь эталонное значение (см. выше: плотность дистиллированной воды) получают при определенной температуре: 4°C. Для тестирования нефтепродукта, за эталонную температуру принимается 20°C.
Это легко объяснимо с точки зрения физики:
- Вода относительно стабильна, величина практически не меняется в зависимости от температуры. Однако при около нулевом значении, начинается процесс кристаллизации льда. Поэтому эталонная температура выше.
- Масло – это сложный состав. Густота автомобильной смазки определяется различными компонентами, у которых различная температура замерзания и кипения. Поэтому, в качестве эталонной температуры установлено промежуточное значение для средней полосы климата.

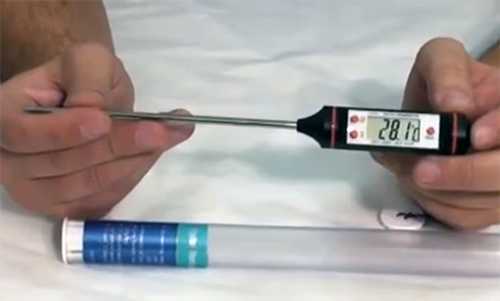
Электронный градусник для замера температур
Зависимость от внешних градусов следующая: от минуса до эталонного значения – цифры растут. Затем, по мере увеличения температуры, значение плотности снижается. Мы знаем, что вязкость зависит от плотности напрямую. При этом по мере снижения температуры масло густеет.
Это не связано с плотностью: зависимость этих величин требуется только для измерения (возвращаемся к эталонной температуре).
Снижение вязкости при понижении температуры
Разумеется, при измерении параметров невозможно обеспечить идеальные условия. Эталонные замеры производятся только в лабораториях. Поэтому для поправки на изменение внешней температуры, разработана таблица плотности масел.
| Плотноть (кг/м3) | Температурная поправка (кг/м3*С) | Плотноть (кг/м3) | Температурная поправка (кг/м3*С) |
|---|---|---|---|
| 690,0 …699,9 | 0,91 | 850,0… 859,9 | 0,699 |
| 700,0…709,9 | 0,897 | 860,0…869,9 | 0,686 |
| 710,0… 719,9 | 0,884 | 870,0… 879,9 | 0,673 |
| 720,0 …729,9 | 0,87 | 880,0… 889,9 | 0,66 |
| 730,0 …739,9 | 0,857 | 890,0… 899,9 | 0,647 |
| 740,0 …749,9 | 0,844 | 900,0…909,9 | 0,633 |
| 750,0 …759,9 | 0,831 | 910,0…919,9 | 0,62 |
| 760,0…769,9 | 0,818 | 920,0…929,9 | 0,607 |
| 770,0…779,9 | 0,805 | 930,0…939,9 | 0,594 |
| 780,0 …789,9 | 0,792 | 940,0…949,9 | 0,581 |
| 790,0 …799,9 | 0,778 | 950,0…959,9 | 0,567 |
| 800,0…809,9 | 0,765 | 960,0…969,9 | 0,554 |
| 810,0…819,9 | 0,752 | 970,0…979,9 | 0,541 |
| 820,0…829,9 | 0,738 | 980,0…989,9 | 0,528 |
| 830,0 …839,9 | 0,725 | 990,0…999,9 | 0,515 |
| 830,0…839,9 | 0,712 |
Зависимость нелинейная, если построить график – получится парабола. Поэтому поправка на 1°C рассчитывается в каждом диапазоне. Чем плотнее жидкость, тем меньше зависимость от внешних условий.
Это хорошо заметно на примере простой воды. При идеальных показателях 1 кг/литр, плотность изменится лишь тогда, когда жидкость будет на грани закипания или замерзания.
Как и в чем измеряется плотность масла?
Согласно формуле (отношение массы к объему), величина фиксируется в килограммах на кубометр (кг/м³).
Для справки: плотность моторных масел лежит в пределах 750 — 995 кг/м³ (при 20°C).
Для измерения нам необходимо знать паспортные характеристики проверяемого продукта. На этикетках это значение не указано, поэтому необходимо получить эту информацию дополнительно.
Рассмотрим пример вычислений значения:
- Допустим, что согласно паспортным данным, диапазон тестируемого машинного масла лежит в пределах 990-999 кг/м³. Соответственно, поправка на каждый градус: 0,515 (см. таблицу выше).
- Выполняем измерение, фиксируя текущую температуру. Удобнее проводить процедуру с помощью комбинированного прибора.
Он сразу показывает две величины: температуру и плотность масла, в реальном времени. Хотя можно воспользоваться ареометром и термометром, особенно в бытовых условиях: покупка прибора – дорогое удовольствие.
- Получаем следующие значения: 997,8 кг/м³ при температуре 24,2°C.
- Разница 4,2°C перемножается с величиной поправки 0,515. Получаем значение 2,16.
- Поскольку температура выше эталонной, отнимаем полученную поправку от измеренного значения 997,8 кг/м³.
- Полученное значение 995,6 кг/м³ и есть реальный показатель плотности масла.
Сравнив эти данные с информацией в паспорте продукта, вы легко сможете определить, насколько покупаемый расходник соответствует заявленным характеристикам.
Отличается ли плотность синтетики и минерального масла?
Разумеется, есть связь между базовой основой и плотностью продукта. Тип и количество присадок играют второстепенную роль. У минеральных масел это значение выше. Естественный продукт несколько тяжелее. Обычно производитель устанавливает диапазон 875 – 856 кг/м³.
Лабораторный эксперимент показывающий плотность масла — виде
Синтетические смазки легче, можно считать, что легкость связана с сырьем – их в основном синтезируют из природного газа. На самом деле, связи с газом нет. Тем не менее, значение ниже, чем у минералки: 840 – 860 кг/м³ (за редким исключением).
Кстати, малый вес синтезированных смазочных материалов позиционируется в качестве конкурентного преимущества. На самом деле важно не то, какая плотность установлена производителем.
Для двигателя главное – сохранение этого значения при смене рабочих температур. Мы знаем, что от величины плотности зависит одна их главных характеристик: кинематическая вязкость моторного масла по SAE.
Вывод:
Сила не в абсолютных значениях, а в стабильности этого параметра.
prosmazku.ru
Плотность моторного масла – изучаем характеристики

Как и любое другое химическое вещество, моторное масло обладает определенной плотностью. Для большинства современных масел показатель плотности составляет 0,7–0,93 кг на один литр. Однако существуют варианты моторного масла с большей или меньшей плотностью, а отработанное моторное масло всегда характеризуется избыточной плотностью из-за наличия в своем составе дополнительных веществ.
1 Свойства моторного масла и варианты классификации
На сегодняшний день не существует определенной классификации моторных масел по физической плотности, однако их принято разделять по степени вязкости (SAE). Именно к этому показателю производители современных смазочных материалов привязывают и плотность, несмотря на то, что с физической точки зрения эти два показателя напрямую не связаны. Но перед тем как обозначить различия между маслами по вязкости и понять, для чего необходимо знать плотность отработанного и нормального масла, необходимо разобраться, что собой представляет моторное масло и от чего зависят его конечные показатели.

Моторное масло, помимо снижения коэффициента трения и антифрикционных свойств, выполняет целый ряд дополнительных функций, за которые отвечают специальные вещества, именуемые присадками, которые добавляются в нефтяную основу вещества. Присадки необходимы в первую очередь для того, чтобы максимально оптимизировать характеристики смазочной жидкости, расширить температурный диапазон, улучшить защитные свойства, уменьшить трение в системе двигателя и т. д.

В процессе работы ДВС и под воздействием высоких температур поршневая группа очень сильно нагревается, поэтому качественное моторное масло должно иметь показатели вязкости, при которых оно обеспечит надежную смазку узлов и создание масляного уплотнителя между стенками цилиндра и поршня. С помощью присадок производитель делает масла определенной плотности и вязкости, которые предназначены для бензиновых или дизельных двигателей, либо универсальные продукты, которые могут использоваться на любых типах моторов. Доля присадок в моторном масле составляет от 5 до 30 процентов, что также влияет на конечную плотность продукта.
2 Вязкость – основное свойство смазочного материала
Что в конечном итоге представляет собой вязкость моторного масла? Данный показатель позволяет определить степень текучести смеси, который изменяется прямо пропорционально изменениям температуры окружающей среды. По вязкости современные масла делятся на «зимние» и «летние». В первом случае масло имеет приставку «W», например, 5W или 10W и имеет более густой состав. Как правило, производители, включая Лукойл, Mobil, Elf, Liqui-Moly и др. дают гарантию на использование своей продукции только согласно рекомендациям. Так, масло 5W может быть использовано при температурах не ниже –30 градусов, тогда как 20 W выдерживает температуру до –9 градусов. Данные виды масел нельзя использовать в летнее время, для этого классификация предусматривает «летние» варианты более низкой вязкости, которые обозначаются просто цифрами. Кроме того, от вязкости моторного масла зависят и такие показатели, как:
- скорость поступления жидкости к поверхностям при трении,
- образование защитной маслянистой пленки на узлах двигателя,
- скорость «прокручивания» двигателя при холодном пуске,
- степень работы насоса, стойкость к протечкам через негерметичные соединения и т. д.

Во время эксплуатации моторного масла его свойства, и в частности вязкость, могут как увеличиваться, так и уменьшаться в зависимости от конкретных реакций, которые происходят во время работы мотора. При попадании в масло «посторонних» веществ, например, антифриза или частиц топлива, его вязкость резко увеличивается, что ухудшает смазочные свойства и характеристики. Поэтому в случае обнаружения увеличения или уменьшения вязкости более, чем на 20 процентов при средней температуре в сторону, противоположную первоначальному значению, необходимо в срочном порядке проводить замену масла в двигателе и диагностику системы на выявление неисправностей.

Как правило, показатели вязкости, плотность и другие характеристики смазочного материала определяются с помощью специального прибора, который называется маслотестер. Данный прибор позволяет определить изменение вязкости и сделать выводы об износе или выходе из строя некоторых узлов двигателя авто. Именно плотность может служить своего рода индикатором негерметичности различных соединений двигателя или износа цилиндро-поршневой группы.
3 Плотность отработанных масел
Как и вязкость, плотность смазочного материала также зависит от изменения температурных показателей окружающей среды, однако влияние температуры на плотность нельзя назвать столь явным. Плотность зависит от попадания в вещество частиц хладагента или отработанного топлива на молекулярном уровне. В среднем плотность современных масел составляет 830–930 кг/м3 в зависимости от их состава (минеральное, синтетическое или полусинтетическое) и температуры. Зная плотность бензина и дизельного топлива, воды и антифриза, можно определить степень изменения с помощью ареометра или маслотестера.

Отработанное масло характеризуется повышенной плотностью как раз из-за присутствия в составе различных механических примесей, воды и т. д. При этом отработанное масло любой плотности, в составе которого присутствует много воды, грязи и других неперерабатываемых остатков, не подлежит утилизации и переработке. Хранить отработанное масло необходимо с соблюдением всех условий, в определенных резервуарах и при постоянной температуре в помещении для хранения.
Источник
pippip.ru
Плотность веществ
| Вещество | Плотность г/мл = 103 кг/м3 |
Вещество | Плотность г/мл = 103 кг/м3 |
|---|---|---|---|
| Агат | 2,6 | Пробка | 0,25 |
| Алебастр | 1,8 | Ртуть | 13,6 |
| Алюминий | 2,7 | Сало | 0,9 |
| Алмаз | 3,5 | Свинец | 11,3 |
| Асбест | 2,4 | Серебро | 10,3 |
| Асфальт | 1,4 | Скипидар | 0,85 |
| Ацетон | 0,8 | Слюда | 2,8 |
| Бензин | 0,7 | Смола (камедь) | 1,1 |
| Бура | 1,7 | → черная | 1,1 |
| Вар | 1 | Спирт денатурированный | 0,8 |
| Вода морская | 1,03 | → этиловый | 0,8 |
| Воск (лабораторный) | 1 | Спирт | 0,79 |
| → пчелиный | 0,95 | Сталь мягкая | 7,9 |
| Германий | 5,4 | → углеродистая (<1% C) | 7,8 |
| Глицерин | 1,3 | Сургуч | 1,8 |
| Гранит | 2,7 | Сплавы | |
| Графит | 2,3 | → Альни | 6,9 |
| Дерево сухое | → Альнико | 7,1 | |
| → Бакаут | 1,3 | → Баббит (80% Sn) | 7,3 |
| → Бальза (пробковое) | 0,2 | → Бронза алюминиевая (8% Al) | 7,7 |
| → Бамбук | 0,4 | → → фосфористая | 8,9 |
| → Бук | 0,75 | → Дюралюминий | 2,8 |
| → Дуб | 0,7 | → Железо нержавеющее (12% Cr) | 7,7 |
| → Кедр | 0,55 | → Зеркальная бронза | 8,4 |
| → Красное дерево | 0,8 | → Инвар | 8 |
| → Самшит | 1 | → Инконель | 8,5 |
| → Сосна (белая) | 0,5 | → Константан | 8,9 |
| → Тиковое дерево | 0,85 | → Кронит | 8,1 |
| → Черное дерево | 1,2 | → Латунь (60/40) | 8,4 |
| Желатин | 1,3 | → → (70/30) | 8,5 |
| Железо кремнистое | 6,9 | → Ло–Экс | 2,7 |
| → сварочное | 7,8 | → Магналий | 2,6 |
| Зола (древесная) | 0,75 | → Мазак (№2) | 6,7 |
| Золото (22 карата) | 17,5 | → Манганин | 8,5 |
| → (9 каратов) | 11,3 | → Медь бериллиевая | 8,2 |
| Карбид вольфрама (6% СО) | 15 | → Монель | 8,8 |
| → вольфрама (12% СО) | 14,2 | → Мю–металл | 8,8 |
| Кварц кристаллический | 2,6 | → Нейзильбер | 8,4 |
| → плавленный полупрозрачный | 2,1 | Никель–серебро | 8,8 |
| → → прозрачный | 2,2 | Никель–хром | 8,4 |
| Кварцевый песок (чистый) | 2,6 | Никоник | 8,2 |
| Керамот | 1,6 | Пермаллой | 8,6 |
| Керосин | 0,8 | Платина–иридий (90/10) | 21,5 |
| Каолин | 2,6 | Приной мягкий (70% Sn, 30% Pb) | 8,3 |
| Корунд | 4 | Сплав «Y» | 2,8 |
| Кость | 1,9 | Супермаллой | 8,9 |
| → слоновая | 1,8 | Пушечный металл | 8,2 |
| Кремний | 2,4 | Элинвар | 8,1 |
| Ксилол | 0,85 | Тиокол | 1,4 |
| Лед | 0,92 | Уголь (антрацит) | 1,6 |
| Масло животное | 0,9 | → (битуминозный) | 1,4 |
| → касторовое | 0,95 | → (древесный) | 0,4 |
| → льняное | 0,95 | → (ретортный) | 1,9 |
| → оливковое | 0,9 | Уайт–спирт | 0,85 |
| → парафиновое | 0,8 | Фарфор | 2,3 |
| Медь | 8,9 | Хром | 7,2 |
| Микалекс | 2,4 | Чугун | 7 |
| Молоко | 1,03 | Шифер | 2,8 |
| Мрамор | 2,7 | Эбонит | 1,2 |
| Наждак | 4 | Янтарь | 1,1 |
| Нефть | 0,8 | ||
| Нихром | 8,4 | ||
| Олово | 7,3 | ||
| Парафин | 0,9 | ||
| Песок (сухой) | 1,6 | ||
| Вещество | Формула | Плотность г/мл = 103 кг/м3 |
Вещество | Формула | Плотность г/мл = 103 кг/м3 |
|---|---|---|---|---|---|
| Азот | N2 | 1.2505 | Неон | Ne | 0.8999 |
| Аммиак | NH3 | 0.7714 | Нитрозил | ||
| Аргон | Ar | 1.7839 | → фтористый | NOF | 2.176* |
| Ацетилен | C2H2 | 1.1709 | → хлористый | NOCl | 2.992 |
| Бор фтористый | BF3 | 2.99 | Озон | O3 | 2.22 |
| n-Бутан | C4H10 | 2.703 | Окись азота | NO | 1.3402 |
| i-Бутан | C4H10 | 2.673 | Пропан | C3H8 | 2.0037 |
| Водород | H2 | 0.08987 | Пропилен | C3H6 | 1.915 |
| → бромистый | HBr | 3.664 | Радон | Rn | 9.73 |
| → иодистый | Hl | 5.789 | Сера | ||
| → мышьяковистый | H3As | 3.48 | → двуокись | SO2 | 2.9263 |
| → селенистый | H2Se | 3.6643 | → гексафторид | SF6 | 6.50* |
| → сернистый | H2S | 1.5392 | Силан | ||
| → теллуристый | H2Te | 5.81 | → диметил | SiH2(CH3)2 | 2.73 |
| → фосфористый | H3P | 1.53 | → метил | SiH3CH3 | 2.08 |
| → хлористый | HCl | 1.6391 | → хлористый | SiH3Cl | 3.03 |
| Воздух | — | 1.2928 | → трифтористый | SiHF3 | 3.89 |
| Гелий | He | 0.1785 | Стибин (15°С, 754 мм.рт.ст.) | SbH3 | 5.3 |
| Германия тетрагидрид | GeH4 | 3.42 | Cульфурил фтористый | SO2F2 | 3.72* |
| Диметилсульфид | C2H6S | 0.848* | Триметиламин | (CH3)3N | 2.580* |
| Диметилдисульфид | (CH3S)2 | 1.062* | Триметилбор | (CH3)3B | 2.52 |
| Диметиламин | (CH3)2NH | 1.966* | Углерод | ||
| Дифтордихлорметан | CF2Cl2 | 5.51 | → двуокись | CO2 | 1.9768 |
| Дициан | C2N2 | 2.335* | → окись | CO | 1.25 |
| Закись азота | N2O | 1.978 | → серокись | COS | 2.72 |
| Кислород | O2 | 1.42904 | Фосфор | ||
| Кремний | → фтористый | PF3 | 3.907* | ||
| → фтористый | SiF4 | 4.9605 | → оксифторид | POF3 | 4.8 |
| → гексагидрид | Si2H6 | 2.85 | → пентафторид | PF5 | 5.81 |
| → тетрагидрид | SiH4 | 1.44 | Фтор | F2 | 1.695 |
| Криптон | Kr | 3.74 | Фторокись азота | NO2F | 2.9 |
| Ксенон | Xe | 5.89 | Хлор | Cl2 | 3.22 |
| Метан | CH4 | 0.7168 | → двуокись | ClO2 | 3.09* |
| Метилеихлорид | CH3Cl | 2.307 | → окись | Cl2O | 3.89* |
| Метиламин | CH5N | 1.388 | Хлорокись азота | NO2Cl | 2.57 |
| Метилмеркаптан | CH3SH | 0.87 | Этан | C2H6 | 1.356 |
| Метиловый эфир | C2H6O | 2.1098 | Этилен | C2H4 | 1.2605 |
| Метилфторид | CH3F | 1.545 | |||
| Метилхлорид | CH3Cl | 2.307 | |||
| Мышьяк фтористый | AsF5 | 7.71 | |||
Примечание: источниками справочных данных являются публикации в Интернете, поэтому они не могут считаться «официальными» и «абсолютно точными». Как правило, в Интернет справочниках не приводятся ссылки на научные работы, являющиеся основой опубликованных данных. Мы стараемся брать информацию из наиболее надежных научных сайтов. Однако если кого-то интересуют ссылки на эксперименты, советуем произвести самостоятельно углубленный поиск в Интернете. Будем признательны за любые комментарии к нашим справочным таблицам, а особенно за уточнения существующей информации или дополнение справочных данных.
temperatures.ru
Как и для чего нужно определять плотность моторного масла
 Смазка должна быть нормальной плотности
Смазка должна быть нормальной плотностиМногим владельцам машин известно, что моторное масло является непременным атрибутом нормального функционирования двигателя. Оно смазывает трущиеся узлы, охлаждает систему, препятствует коррозии, очищает детали. Масла, заливаемые в поршневые двигатели внутреннего сгорания (ДВС), изготавливают из высококипящих фракций нефти различных способов очистки.
Поскольку моторные антифрикционные средства, помимо снижения коэффициента трения, должны выполнять еще целый ряд функций, в нефтяную основу добавляют синтетические вещества, называемые присадками. Вносимые примеси оптимизируют характеристики конечного продукта, позволяют реже проводить замену смазки, расширяют температурный диапазон применения без потерь полезных качеств. Температура вспышки питающей смеси внутри камеры сгорания топлива достигает 2000 оС, в результате чего поршневая группа сильно нагревается. При данных жестких условиях композитное масло должно сохранять вязкость, достаточную для смазывания узлов и создания надежного уплотнения между стенками цилиндра и поршня.
Доля присадок в современных составах для снижения трения подвижных частей двигателя составляет от 5 до 25% от общего объема. Вносимые добавки и технология изготовления позволяют выпускать продукты, применяемые либо в бензиновых, либо в дизельных ДВС, а также универсальные средства, пригодные для эксплуатации в любых типах моторов.
Виды и свойства присадок
Присадки помогают изготавливать смазки требуемого производителями автомобилей уровня качества. По характеру взаимодействия с узлами ДВС различают следующие виды присадок:
- противоизносные;
- антифрикционные;
- противозадирные;
- моюще-диспергирующие;
- противокоррозионные;
- депрессионные;
- вязкостные;
- антипенные.
Высокая температура вспышки горючей смеси приводит к тому, что частицы газообразной взвеси сгорают, оставляя после себя золу. В настоящее время ведется борьба за повышение экологической чистоты масел, в частности, изучается такой параметр, как сульфатная зольность. В соответствии с нормативными документами данная характеристика не должна превышать:
- 2% от общего объема для мощных дизелей грузовых автомобилей;
- 1,8% для малолитражных дизельных моторов;
- 1-1,5% для бензиновых агрегатов.
Если при испытаниях лабораториями сульфатная зольность оказывается больше вышеприведенных значений, выпуск новой разработки запрещается.
Перед производителями антифрикционных составов для ДВС стоят две задачи:
- Увеличить количество присадок, придающих изделию свойства, удовлетворяющие все возрастающим требованиям разработчиков современных моторов.
- Придерживаться норм экологической чистоты при эксплуатации автомобиля на изготовленных смесях.
Во время воспламенения топлива резко увеличивается температура в рабочем объеме, которая является катализатором окислительных процессов. Кислоты, возникающие при сгорании частиц масляного тумана и горючей смеси, вызывают коррозию деталей мотора и снижают вязкость смазки. Нейтрализовать влияние агрессивной среды производители стараются при помощи введения добавок на основе щелочных металлов. Сульфатная зольность конечного продукта увеличивается пропорционально доле вводимых антикоррозийных примесей. С одной стороны, введение синтетических добавок улучшает характеристики антифрикционного средства. В то же время это ухудшает его экологичность и приводит к риску образования излишней зольности, ведущей к устойчивому отложению сажи на узлах агрегата.
В результате антиокислительных реакций снижается количество нейтрализующих примесей в начальном продукте и, соответственно, щелочное число изделия. По достижении минимального значения данного параметра лавинообразно возрастают коррозионные процессы, но зольность выхлопа сильно снижается.
Высокая температура вспышки приводит не только к сжиганию полезных присадок, она вызывает незначительную деформацию головки блока цилиндров. Это может привести к поломке агрегата и потере герметичности изолированных систем. Неисправность ДВС значительно влияет на такие качества смазывающего нефтепродукта, как вязкость и плотность.
Чрезмерное загущение или разжижение недопустимы
Вязкость является одним из основополагающих качеств моторного масла. Она определяет степень текучести смеси, характеризуя сопротивление жидкой среды течению – перемещению одного слоя субстанции относительно другого под воздействием внешних сил. На данный параметр сильно влияет окружающая температура: при её увеличении смазка становится более жидкой, а при понижении – густой.
Вязкость характеризует такие свойства моторного масла:
- поступление смазки к трущимся поверхностям;
- образование на узлах защитной пленки;
- облегчение прокручивания двигателя при холодном старте;
- легкость прокачки насосом при низких температурах;
- устойчивость к вытеканию через неплотные соединения.
 Будьте осторожны с присадками
Будьте осторожны с присадкамиВ процессе эксплуатации двигателя вышеперечисленное качество антифрикционного средства может как увеличиваться, так и уменьшаться. Изменение вызывают физические и химические реакции, происходящие в моторе. Например, масло становится более густым из-за попадания в него нерастворимых веществ, ухудшающих смазывающие свойства и работоспособность продукта. С другой стороны даже высокая температура вспышки не обеспечивает полного сгорания газовой смеси в рабочей камере. Остатки топлива попадают в картер и взаимодействуют со смазкой, ухудшая её характеристики.
При изменении вязкости более чем на 25% в любую сторону от начального значения специалисты рекомендуют провести внеплановую замену моторного масла и выяснить причины, повлиявшие на изменение параметра.
Существует специальный прибор для определения различных характеристик смазки для мотора, в числе прочих параметров измеряющий вязкость – маслотестер. С его помощью определяют время заполнения тестового объема исследуемым маслом и густоту опытного образца. Имея данные об изменении вязкости относительно начальной величины, можно определить неисправность узлов ДВС или оставшийся ресурс работы исследуемого продукта.
Индикатор герметичности соединений мотора
Не менее важной характеристикой масла, чем вязкость, является плотность. Она выражается в кг/м3 и показывает, сколько молекул вещества находится в определенном объеме. Температура окружающей среды оказывает влияние на плотность смазки, как и на её вязкость, но в гораздо меньшей степени.
 Лаборатория анализирует смазку
Лаборатория анализирует смазкуСущественно на плотность влияют попадающие в состав продукта посторонние вещества, например, частицы топлива или охлаждающей жидкости. Они могут попадать в смазку через негерметичные прокладки или при износе поршневой группы. Визуально определить наличие инородных веществ в составе практически невозможно. Попадание в смазку топлива или охлаждающей жидкости можно выявить при ее контроле с помощью измерительного щупа. Однако если двигатель начал “есть масло”, этот метод не принесет ощутимых результатов – расход будет компенсировать пополнение, оставляя общий уровень неизменным.
Зная плотность бензина (~ 760 кг/м3), дизельного топлива (~ 840 кг/м3), воды (1000 кг/м3), антифриза (1035-1085 кг/м3), а также моторного масла (880-930 кг/м3), можно диагностировать попадание посторонних примесей с помощью ареометра. Увеличение плотности смазки сигнализирует о нарушении герметичности охлаждающей двигатель системы, снижение говорит о неисправности поршневой группы.
Более точные результаты изменения характеристик смазки можно получить при помощи маслотестера. Данный прибор измеряет величины с точностью до единиц. Он позволяет не только вычислить плотность исследуемого образца, но и определяет тип залитого в двигатель продукта (минеральное, синтетика, полусинтетика). Последнее обстоятельство приобретает большое значение, если вы собираетесь поменять смазку в подержанном автомобиле, купленном с рук.
Специалисты не рекомендуют при замене масла использовать разные его типы без предварительной промывки двигателя специальными составами. Даже если слив старой смазки длительный, оставшиеся на деталях компоненты могут вступить в реакцию с присадками другого типа, образуя соединения, наносящие вред двигателю. Использование при замене специальных промывочных средств позволяет переходить на смазку другого типа, но приводит к лишним финансовым затратам. Избежать потерь времени и денежных средств можно, анализируя залитый ранее продукт при помощи маслотестера.
maslomotors.ru








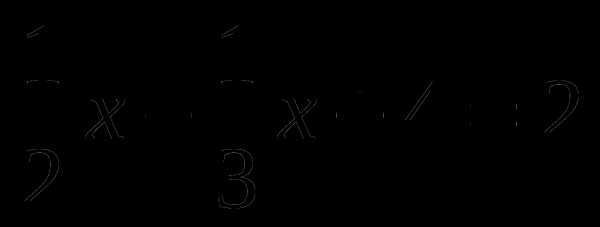 ;
;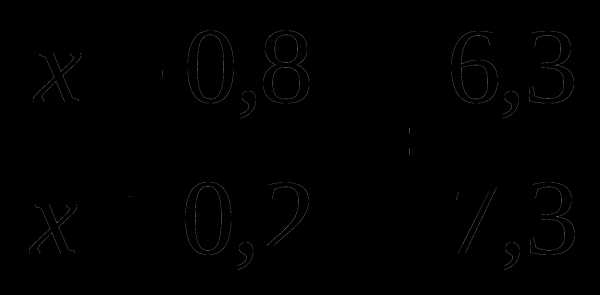


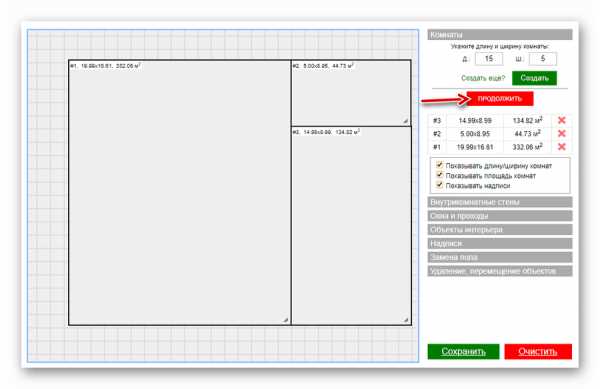
 Сегодня застройщику-любителю нет необходимости карандашом на бумаге самому чертить примитивные схемы будущего дома
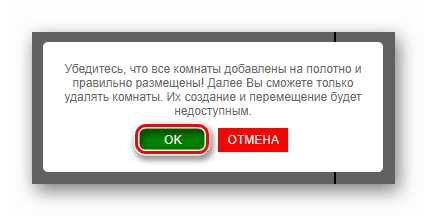
Сегодня застройщику-любителю нет необходимости карандашом на бумаге самому чертить примитивные схемы будущего дома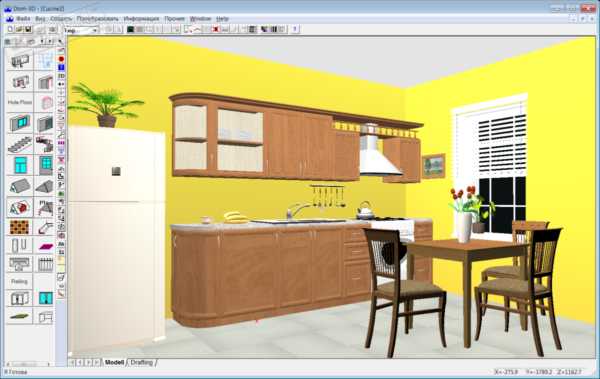 Интерфейс софта Дом-3D
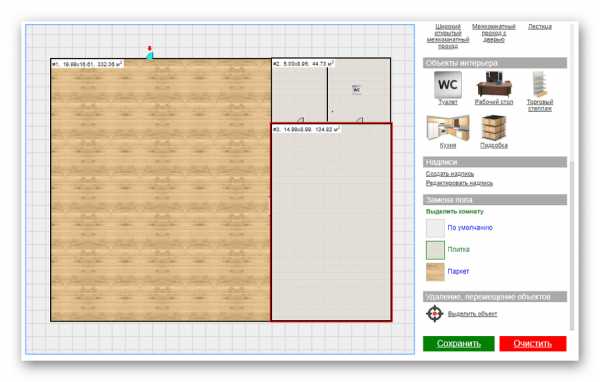
Интерфейс софта Дом-3D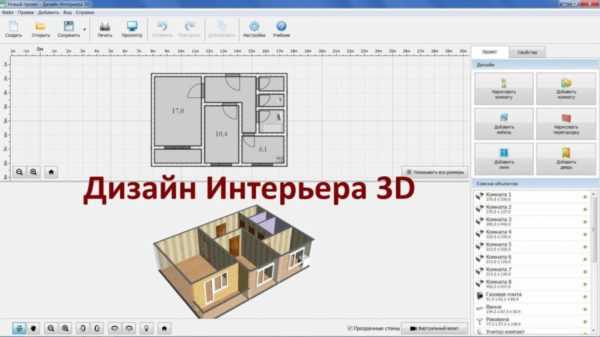 Для создания интерьера разработан каталог более чем 120 отделочных материалов
Для создания интерьера разработан каталог более чем 120 отделочных материалов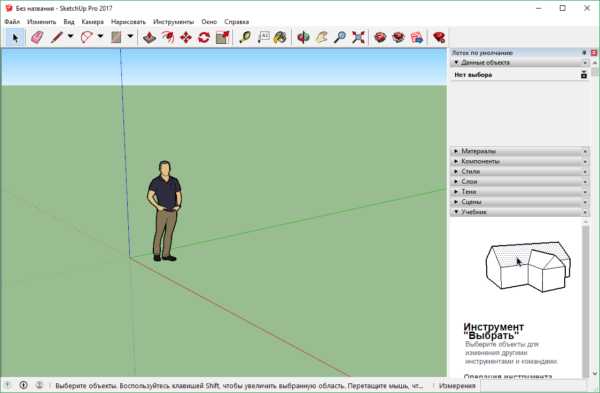 Новый проект, который создан в SkatchUp
Новый проект, который создан в SkatchUp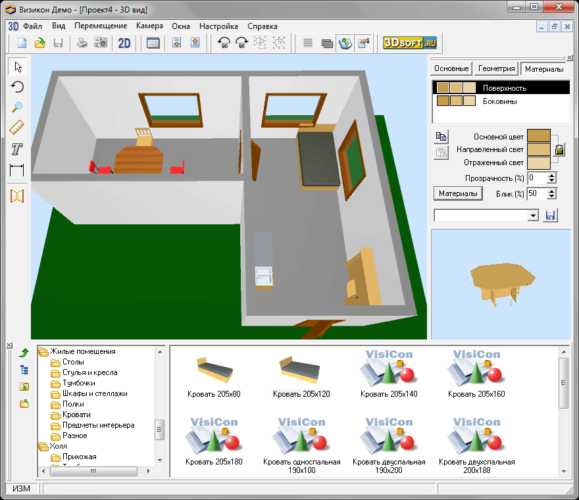 Готовый проект можно увидеть на плоскости и в трехмерной модели с разных точек зрения, разного расстояния
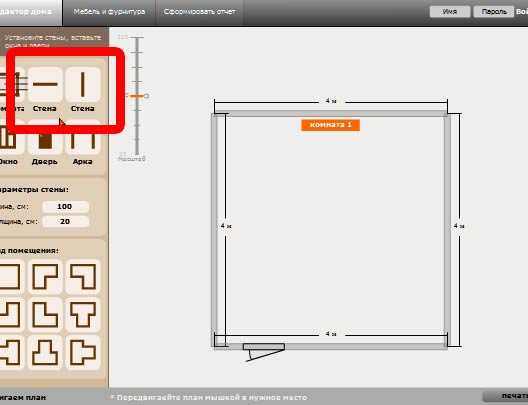
Готовый проект можно увидеть на плоскости и в трехмерной модели с разных точек зрения, разного расстояния Каждый шаг моделирования сопровождается подсказками, поэтому в ней способен разобраться пользователь, не имеющий навыков компьютерного дизайна
Каждый шаг моделирования сопровождается подсказками, поэтому в ней способен разобраться пользователь, не имеющий навыков компьютерного дизайна Софт позволяет спроектировать дом, стены, окна, двери, полы, потолки, крыши, изменять внутреннюю и внешнюю отделку по цвету и текстуре
Софт позволяет спроектировать дом, стены, окна, двери, полы, потолки, крыши, изменять внутреннюю и внешнюю отделку по цвету и текстуре
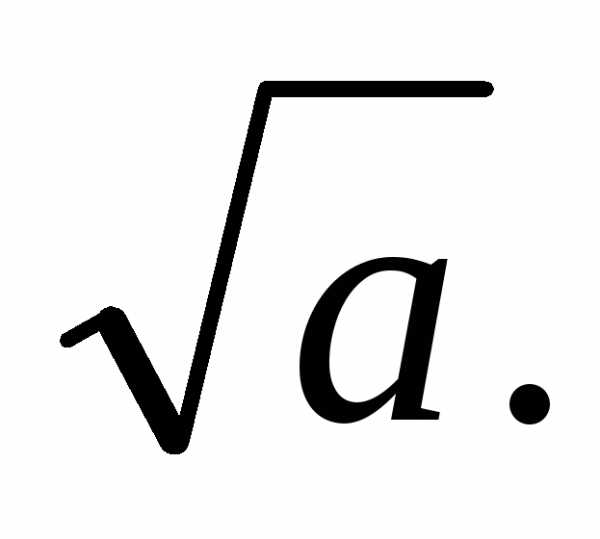
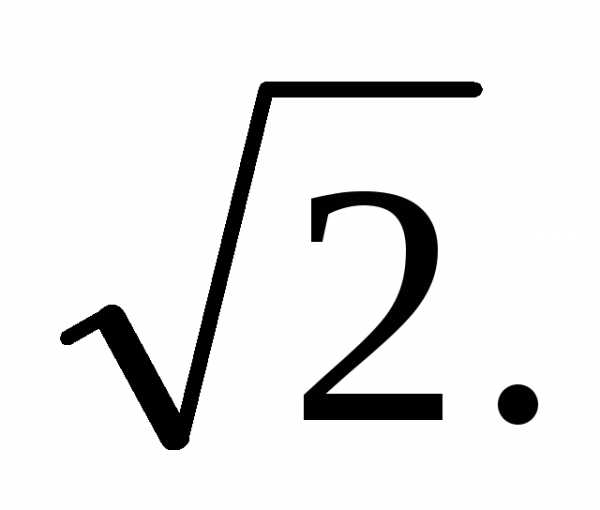
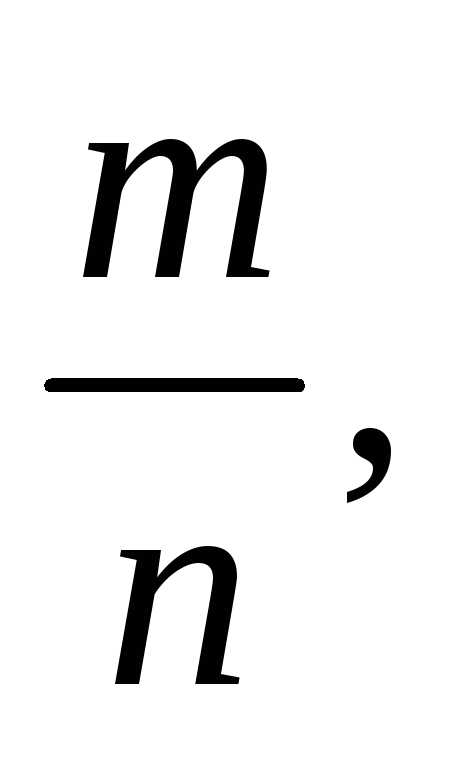 де
де 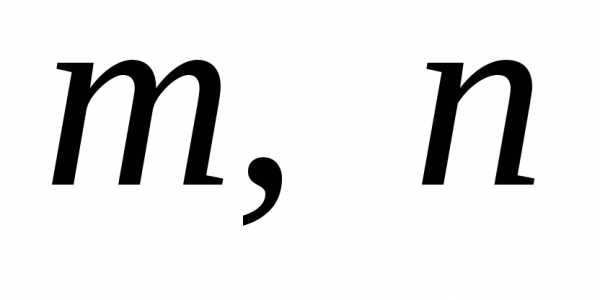 — натуральні числа. Тоді Оскільки число
— натуральні числа. Тоді Оскільки число 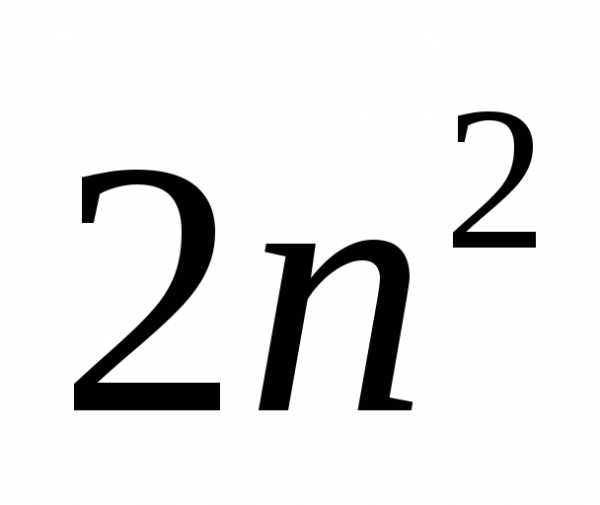 — парне, то й число
— парне, то й число 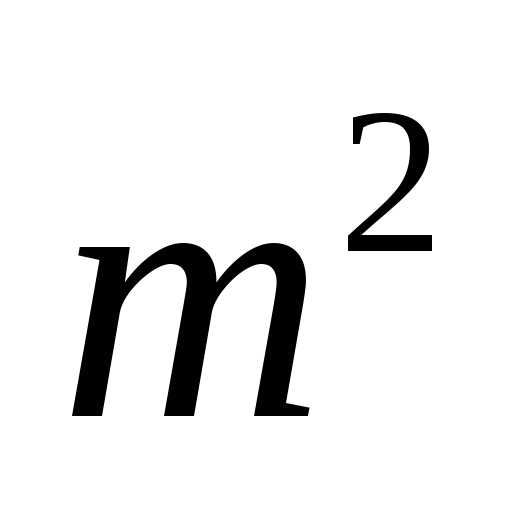 ,
що йому дорівнює також парне, а тому
число
,
що йому дорівнює також парне, а тому
число 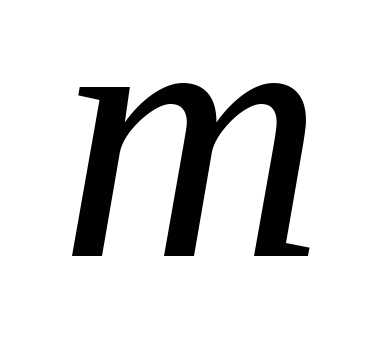 — також парне (адже квадрат непарного
числа є непарне число), тобто
— також парне (адже квадрат непарного
числа є непарне число), тобто 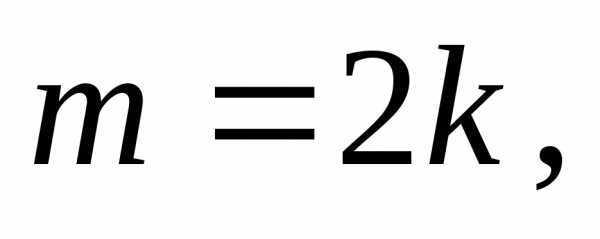 де
де  — натуральне число. Підставивши цей
вираз у рівність
— натуральне число. Підставивши цей
вираз у рівність 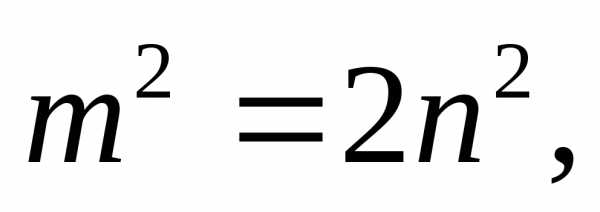 дістанемо
дістанемо 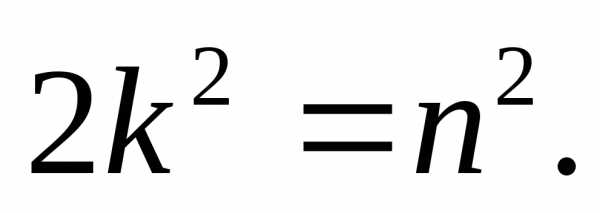 Оскільки
Оскільки  — парне число, то
— парне число, то 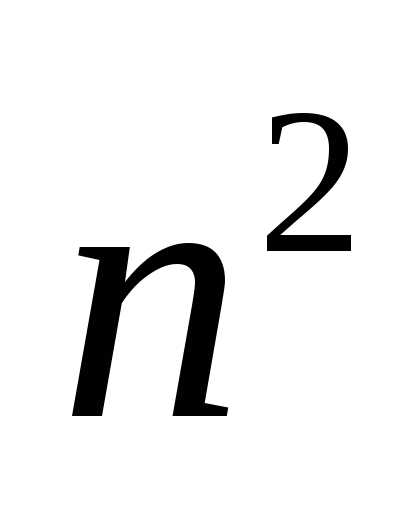 — також парне, тому і
— також парне, тому і 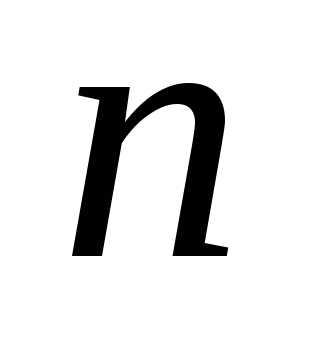 — парне число. Отже,
— парне число. Отже, 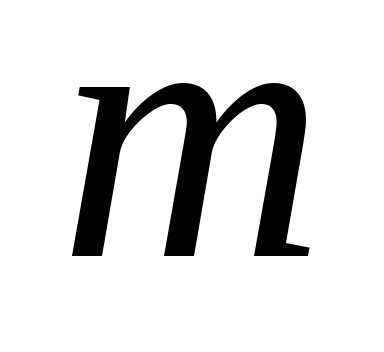 і
і 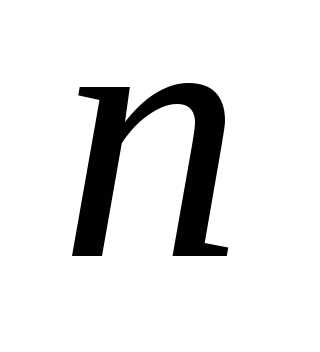 — парні числа, а це суперечить припущенню,
що дріб
— парні числа, а це суперечить припущенню,
що дріб  нескоротний. Звідси випливає, що не
існує раціонального числа, квадрат
якого дорівнює 2. Таким чином,
нескоротний. Звідси випливає, що не
існує раціонального числа, квадрат
якого дорівнює 2. Таким чином,  не є раціональним числом.
не є раціональним числом.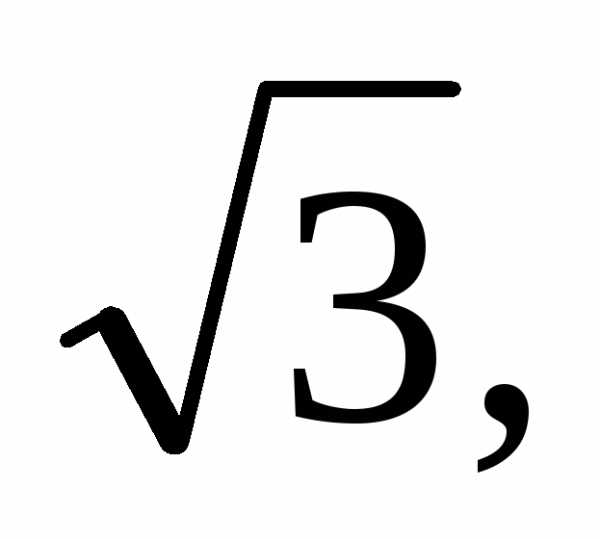


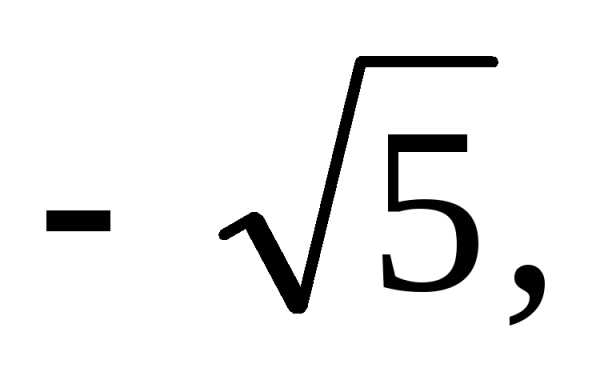

 і т. ін.
і т. ін.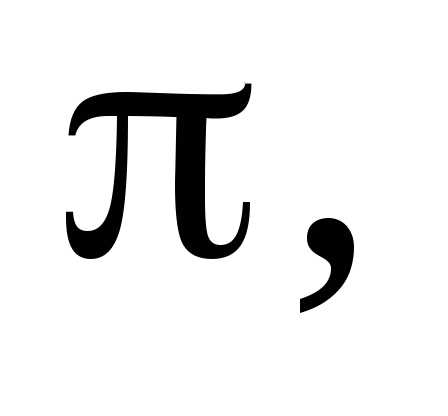 яке виражає відношення довжини кола до
його діаметра.
яке виражає відношення довжини кола до
його діаметра.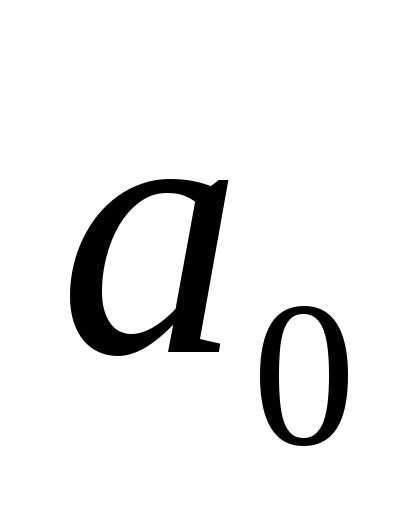 — ціла частина числа х; —
десяткові знаки, є поданням деякого
нового (не раціонального) числа, що
називається ірраціональним. Множину
всіх таких чисел називають множиною
ірраціональних чисел.
— ціла частина числа х; —
десяткові знаки, є поданням деякого
нового (не раціонального) числа, що
називається ірраціональним. Множину
всіх таких чисел називають множиною
ірраціональних чисел.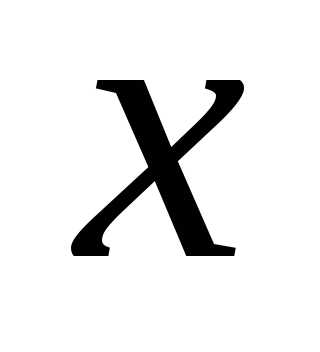 і
і  справджується лише одне і лише одне із
співвідношень:
справджується лише одне і лише одне із
співвідношень: 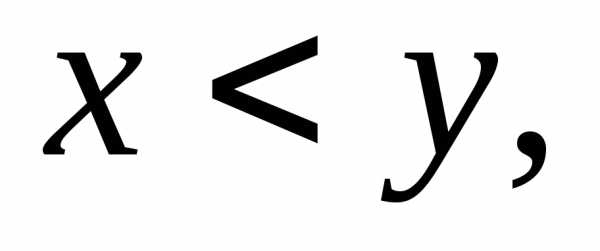

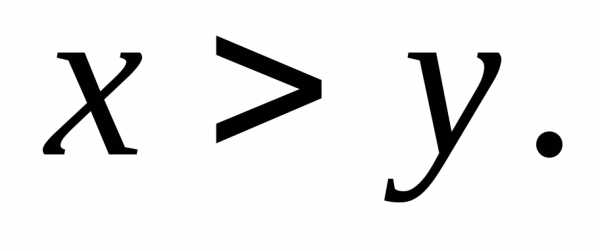 Сенс нерівності між дійсними числами
визначається правилом порівняння
нескінченних десяткових дробів.
Сенс нерівності між дійсними числами
визначається правилом порівняння
нескінченних десяткових дробів.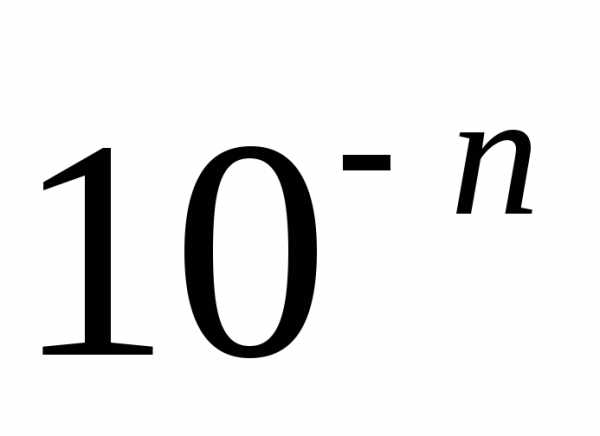 з недостачею
з недостачею 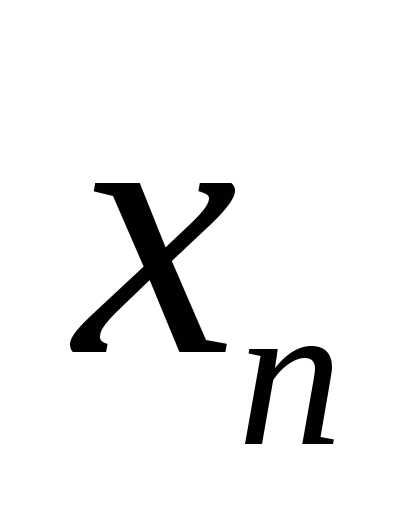 і з надлишком
і з надлишком 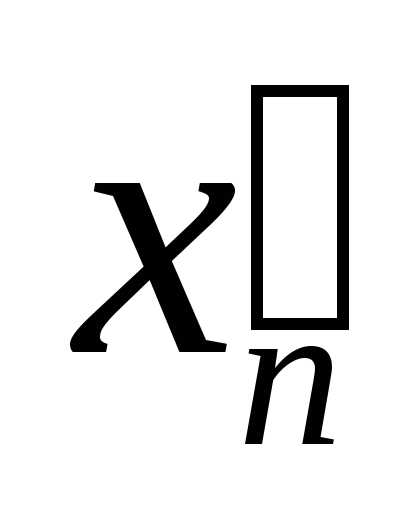 визначаються так:
визначаються так: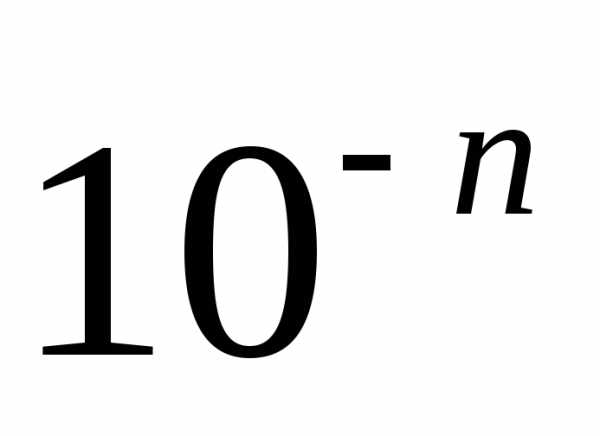 рівносильне збільшенню
останньої цифри дробу на одиницю.
Зауважимо, що кожне з десяткових наближень
рівносильне збільшенню
останньої цифри дробу на одиницю.
Зауважимо, що кожне з десяткових наближень 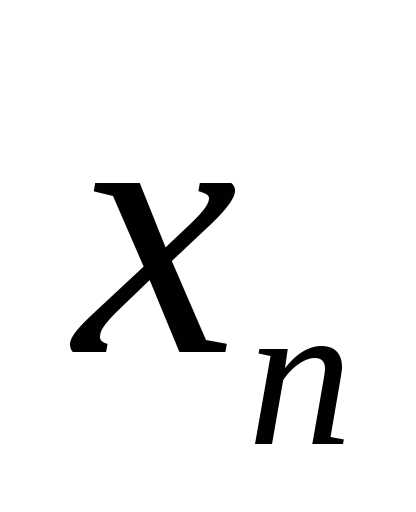 і
і 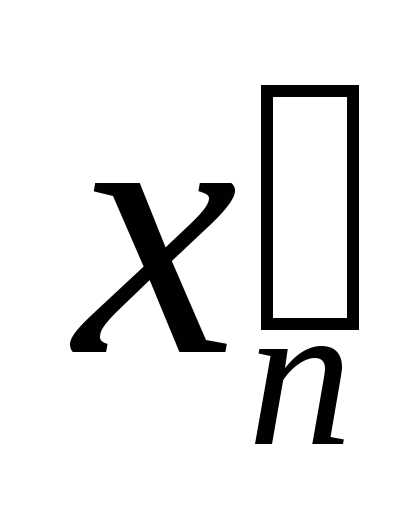 дійсного числа
дійсного числа 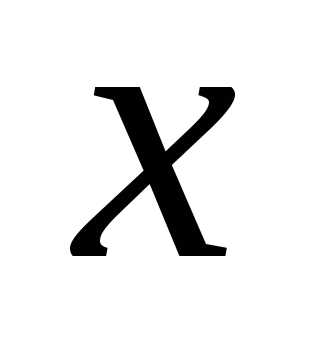 є раціональним числом.
є раціональним числом.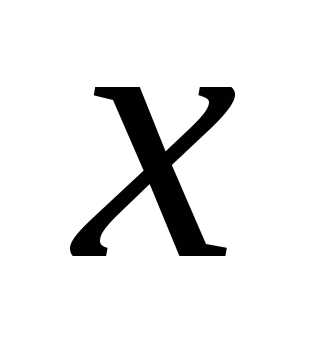 і
і  Для їхніх наближень з недостачею та
надлишком із точністю до
Для їхніх наближень з недостачею та
надлишком із точністю до 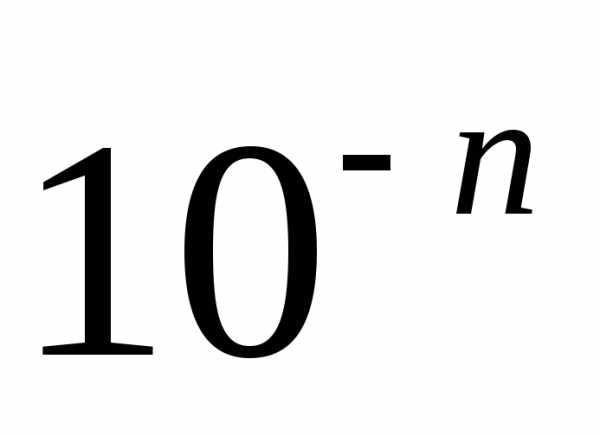 справджуються такі нерівності
справджуються такі нерівності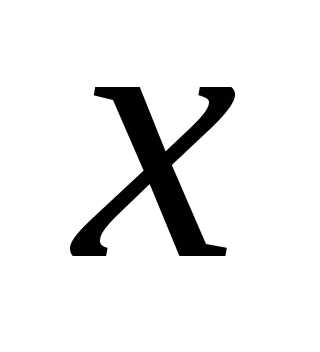 і
і  називають таке дійсне число
називають таке дійсне число 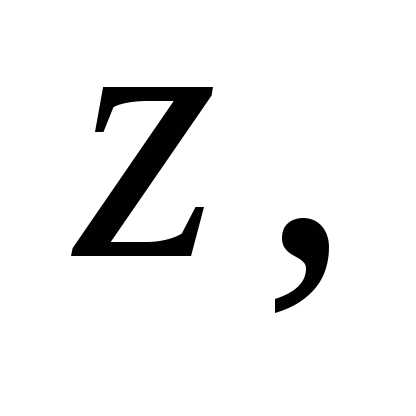 яке при будь-якому цілому невід’ємному
яке при будь-якому цілому невід’ємному 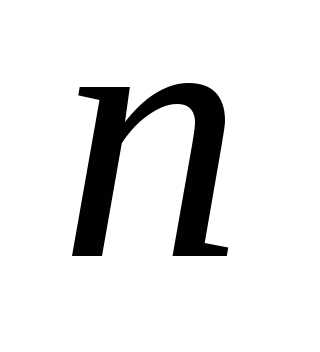 задовольняє нерівності Можна довести, що таке число існує і
єдине.
задовольняє нерівності Можна довести, що таке число існує і
єдине.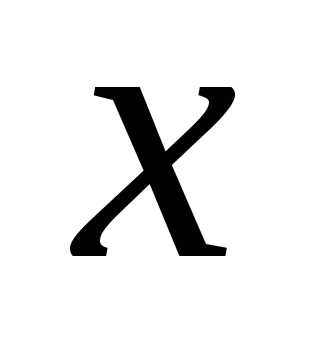 і
і  називають таке дійсне число
називають таке дійсне число 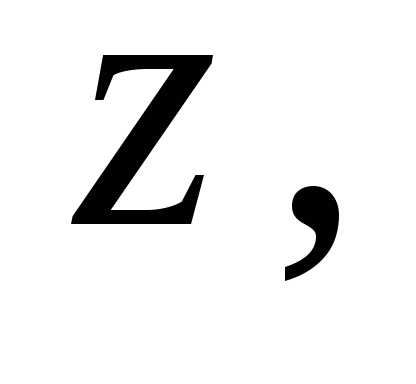 яке при будь-якому цілому невід’ємному
яке при будь-якому цілому невід’ємному 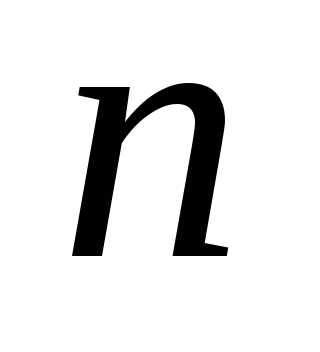 задовольняє нерівності Можна довести, що таке число існує і
єдине.
задовольняє нерівності Можна довести, що таке число існує і
єдине. (читається: «проміжок від
(читається: «проміжок від  до
до  ».
».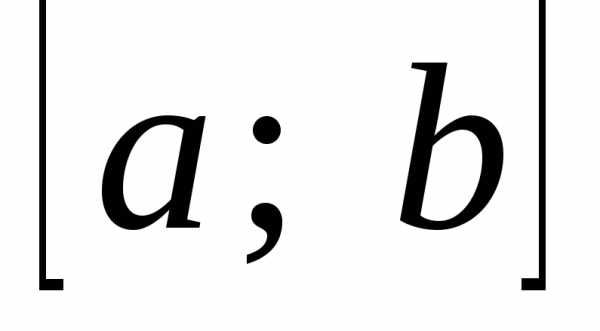 (читається: «проміжок від
(читається: «проміжок від  до
до 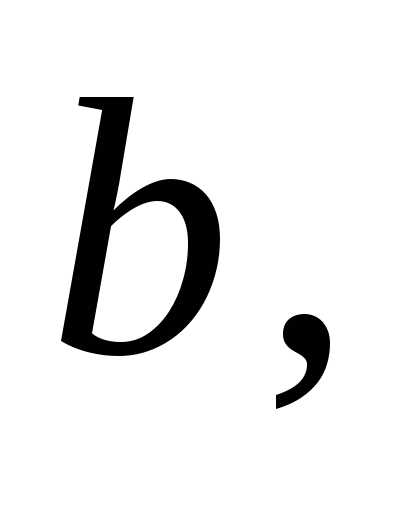 включаючи
включаючи  та
та 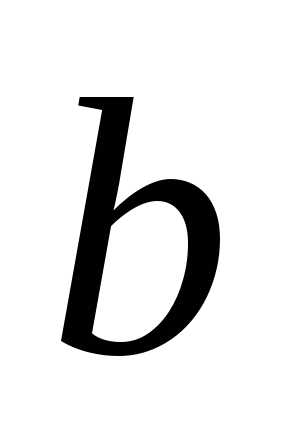 »),
[a; b)
і (a; b].
»),
[a; b)
і (a; b]. називають інтервалом,
проміжок
називають інтервалом,
проміжок  — відрізком або сегментом,
а проміжки [a; b)
і (a; b]
— напівінтервалами.
— відрізком або сегментом,
а проміжки [a; b)
і (a; b]
— напівінтервалами.


 Число 2{\displaystyle \scriptstyle {\sqrt {2}}} є ірраціональним числом.
Число 2{\displaystyle \scriptstyle {\sqrt {2}}} є ірраціональним числом. — Правило Лопиталя для вычисления
пределов с неопределенными выражениями
вида
— Правило Лопиталя для вычисления
пределов с неопределенными выражениями
вида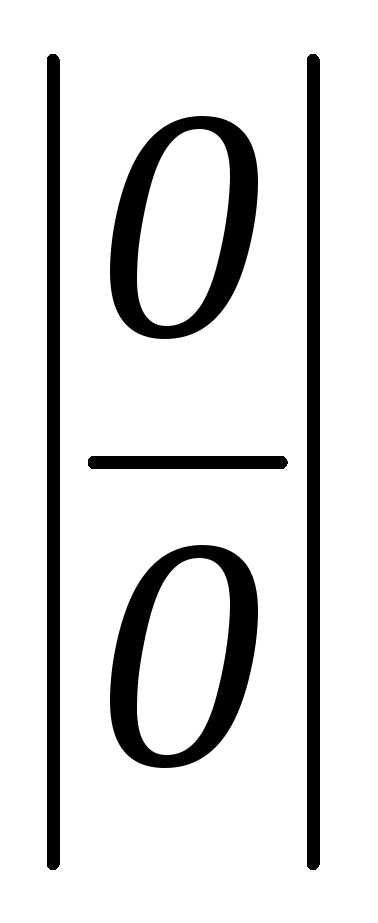 или
или можно сформулировать в виде теоремы.
можно сформулировать в виде теоремы.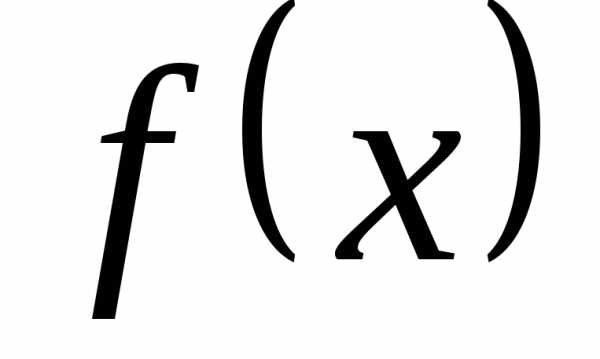 и
и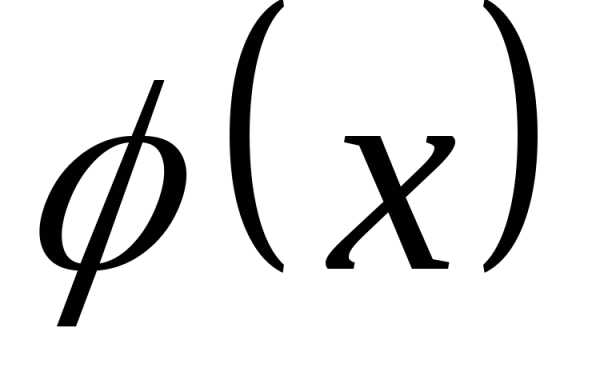 дифференцируемы в некоторой окрестности
точки
дифференцируемы в некоторой окрестности
точки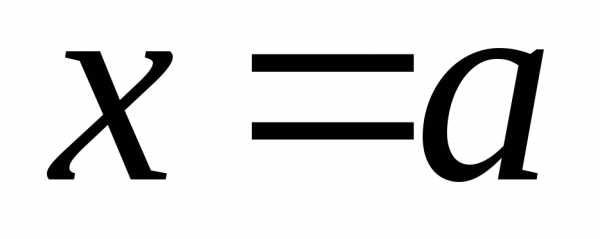 ,
причем
,
причем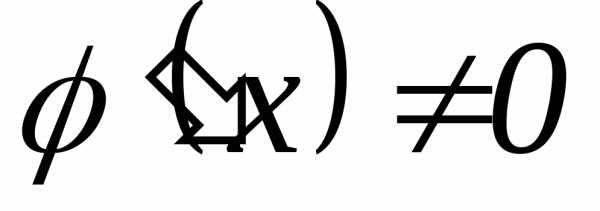 .
Тогда, если существует предел (конечный
или бесконечный) отношения производных
этих функций, то существует равный ему
предел отношения самих функций.
.
Тогда, если существует предел (конечный
или бесконечный) отношения производных
этих функций, то существует равный ему
предел отношения самих функций.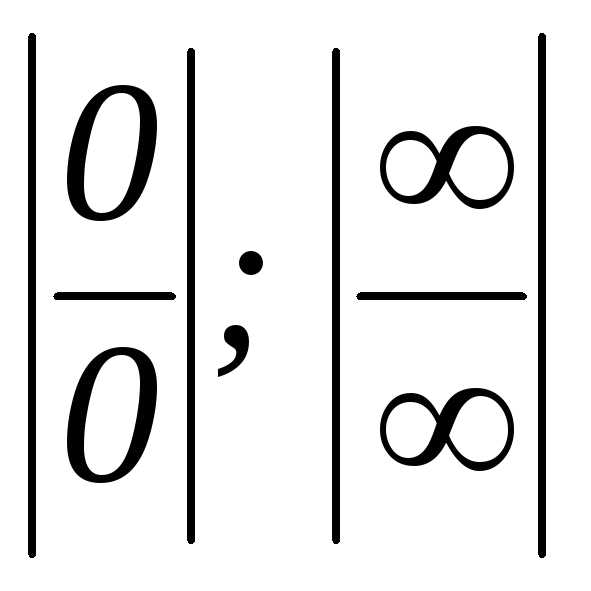 и применяют правило Лопиталя.
и применяют правило Лопиталя.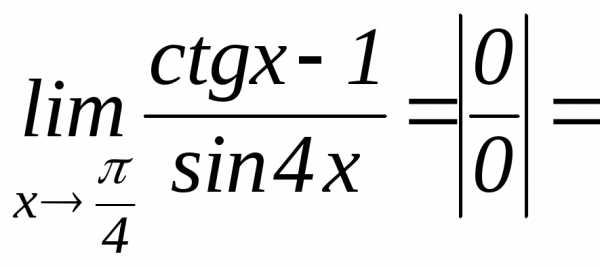
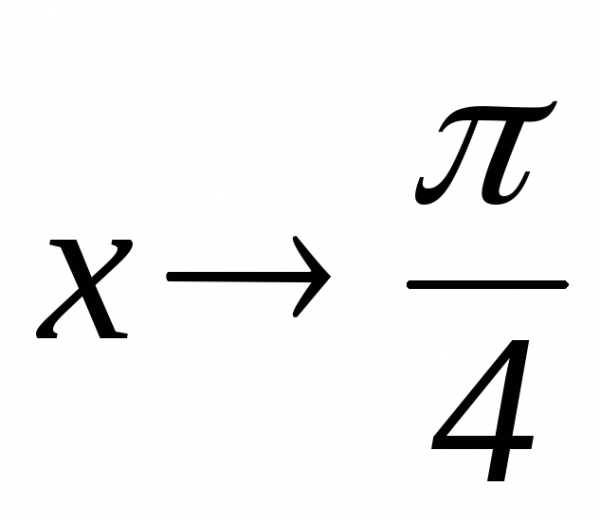 ,
а не к0.
,
а не к0.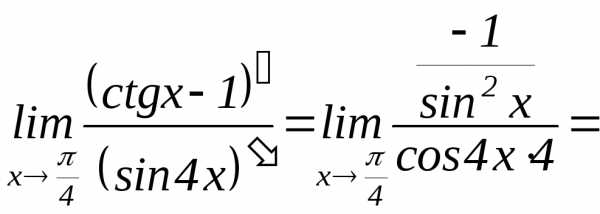
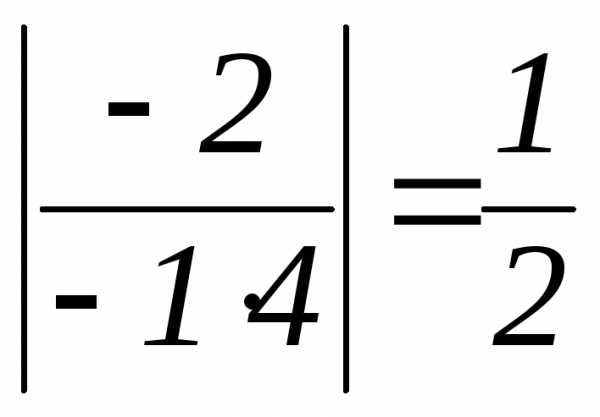

 — Раскрытие степенных неопределенных
выражений вида
— Раскрытие степенных неопределенных
выражений вида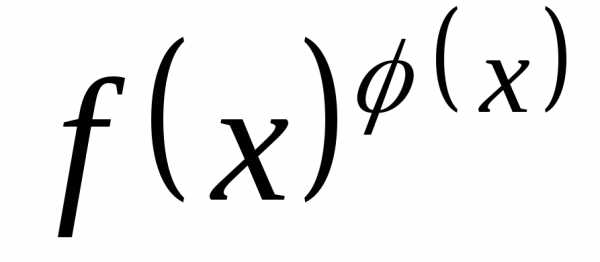 (см. раздел о логарифмическом
дифференцировании, тема 5). Обозначим
его
(см. раздел о логарифмическом
дифференцировании, тема 5). Обозначим
его
 .
.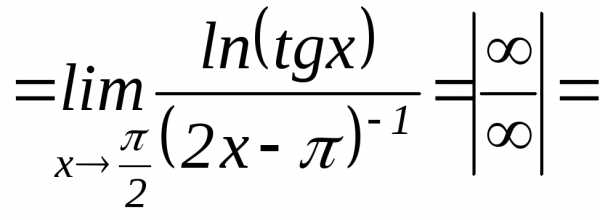
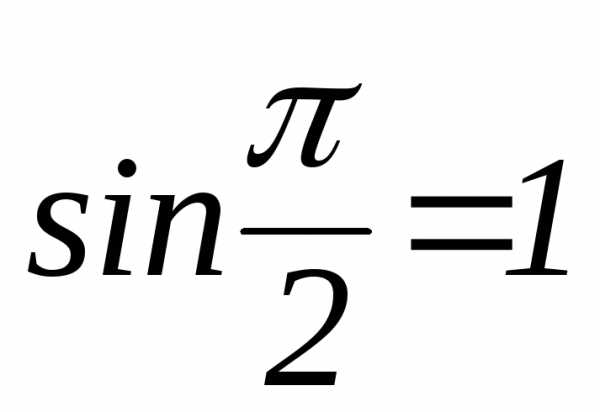 и снова применяем правило Лопиталя.
и снова применяем правило Лопиталя.


 Мото
Мото Ралли
Ралли