Тупой угол рисунок (46 фото) » Рисунки для срисовки и не только
Острый угол тупой угол прямой угол
Скачать
Тупой угол фото
Скачать
Тупой угол
Скачать
Угол прямой угол
Скачать
Острый угол тупой угол прямой угол
Скачать
Острые углы прямые углы тупые углы
Скачать
Тупой угол без фона
Скачать
Прямой острый и тупой углы 2 класс
Скачать
Математика 2 класс острые прямые и тупые углы
Скачать
Тупой угол
Скачать
Углы острый тупой прямой развернутый
Скачать
Острый тупой и прямой углы
Скачать
Углы острый тупой прямой развернутый
Скачать
Прямой острый тупой угол 3 класс правило
Скачать
Виды углов прямой острый тупой
Скачать
Острый тупой и прямой углы
Скачать
Острый угол тупой угол прямой угол
Скачать
Угол рисунок
Скачать
Как выглядит острый угол и тупой угол и прямой угол
Скачать
Прямой угол
Скачать
Прямой угол рисунок
Скачать
Тупой угол
Скачать
1 Острый угол изображён на рисунке
Скачать
Острый угол прямой угол тупой угол развёрнутый угол
Скачать
Прямой угол рисунок
Скачать
Развернутый угол рисунок
Скачать
Углы 2 класс
Скачать
Острые углы прямые углы тупые углы
Скачать
Угол прямой тупой острый для детей
Скачать
Углы прямой тупой острый развернутый градусы
Скачать
Прямой угол на прозрачном фоне
Скачать
Прямой и тупой угол математика 2 класс
Скачать
Тупой угол
Острый угол
Скачать
Угол тупого угла
Скачать
Прямой острый и тупой углы 2 класс
Скачать
Прямой острый и тупой углы 3 класс математика
Скачать
Развернутый угол тупой угол острый угол
Скачать
Острый угол тупой угол прямой угол
Скачать
Острый тупой и прямой углы
Угол без фона
Скачать
Острый угол прямой угол тупой угол развёрнутый
45 Угол тупой
Скачать
Прямой угол рисунок
Скачать
Тупой угол картинка
Выясните, какой угол (острый, прямой или тупой) между векторами.
 .. ГДЗ, вопросы и задачи 446, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/классВыясните, какой угол (острый, прямой или тупой) между векторами… ГДЗ, вопросы и задачи 446, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс
.. ГДЗ, вопросы и задачи 446, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/классВыясните, какой угол (острый, прямой или тупой) между векторами… ГДЗ, вопросы и задачи 446, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Даны векторы Выясните, какой угол (острый, прямой или тупой) между векторами:
Лучший ответ
Лови
далее если 0< α<90° (острый угол), тο cosα>0, если cosα=0, то α=90°, если 90°<α<180°, то cosα<0.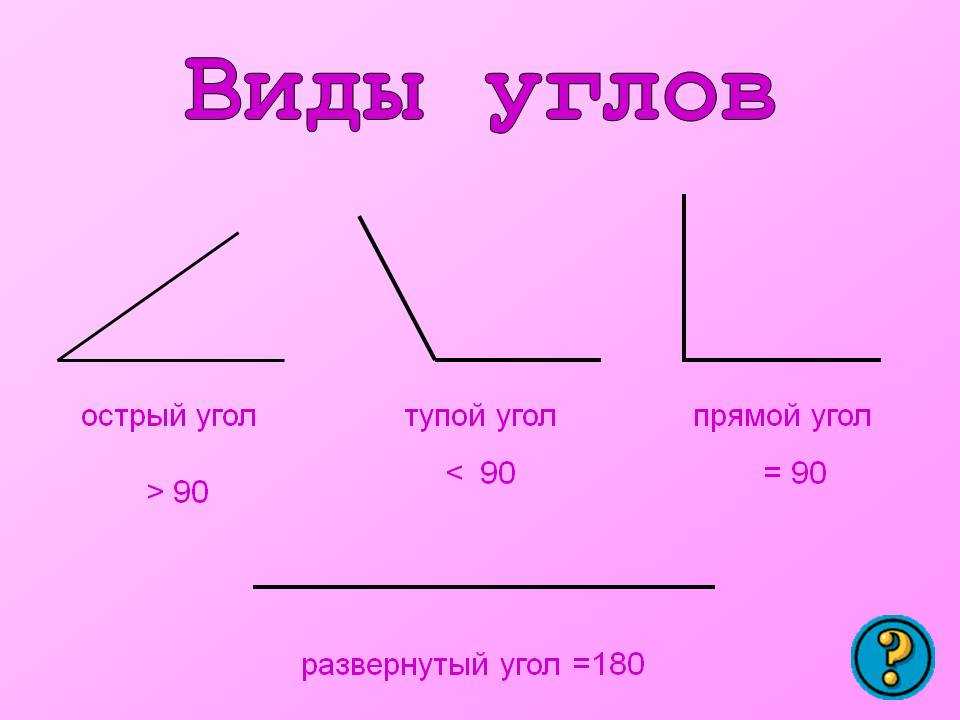
для любых векторов, отличных от нулевого. Тогда знак cosα совпадает со знаком числителя.
т.к. 3 ∙(-5)+(-1)·1+(0·1)= -15-1= -16<0, следовательно. угол тупой;
т.к. -5· (-1)+1· (-2)-0 · 1=5·2=3>0, следовательно, угол острый;
т.к. 3∙(-1)+(-1)∙(-2)+(1∙1) = -3+2+1=0, следовательно. угол прямой
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
Компьютерные игры
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее..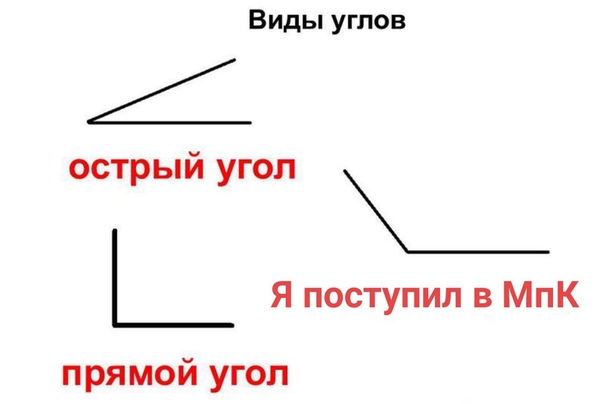 .)
.)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
Какой был проходной балл в вузы в 2017 году?
Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)
Поступление11 классЕГЭНовости
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
определений тупого угла, примеры — Club Z! Репетиторство
Слово «тупой» часто используется для описания того, кто не является самым острым инструментом в сарае. Но в геометрии тупой угол — это просто угол, размер которого больше 90 градусов, но меньше 180 градусов. Тупой угол может быть как острым, так и прямым. Это просто зависит от того, как вы на это смотрите. Разделив тупой угол пополам, вы получите два конгруэнтных острых угла. И если вы продлите отрезки тупого угла, вы в конечном итоге создадите прямую линию, которая даст вам угол в 180 градусов. В этом сообщении блога мы рассмотрим определение тупого угла, его степень и некоторые примеры.
Что такое тупой угол?
Тупой угол — это угол, который больше 90 градусов, но меньше 180 градусов. Термин «тупой» происходит от латинского слова «тупой», что подходит, потому что тупой угол шире, чем острый угол, который острее.
Углы бывают двух видов: острые и тупые. Острый угол меньше 90 градусов, а тупой угол больше 90 градусов, но меньше 180 градусов. (Углы, равные ровно 90 или 180 градусам, называются прямыми углами или прямыми углами соответственно.) Таким образом, тупой угол — это просто любой угол, который находится между этими двумя крайностями.
Тупой угол можно представить как «закругленный». Представьте себе лист бумаги, сложенный пополам; складка будет линией с углом 90 градусов. Теперь представьте, что снова сложите бумагу так, чтобы края сошлись, но не совсем выровнялись; эта складка образует тупой угол.
Тупые углы относительно распространены в природе; например, локтевой сустав человека образует тупой угол. Но в геометрии, особенно при работе с многоугольниками, гораздо более распространены острые углы, поскольку легче создавать фигуры с преимущественно острыми углами, чем с тупыми углами.
Как выглядит тупой угол?
Тупой угол – это угол, величина которого больше 90° и меньше 180°. Это противоположность острого угла. Тупые углы иногда называют «тупыми» углами, потому что они кажутся менее острыми, чем острые углы.
Это противоположность острого угла. Тупые углы иногда называют «тупыми» углами, потому что они кажутся менее острыми, чем острые углы.
Тупой угол может быть образован двумя прямыми линиями, которые пересекаются в одной точке, но не пересекаются (их называют косыми). Точка пересечения прямых называется вершиной угла. Две прямые, образующие угол, называются сторонами угла.
Градус тупого угла измеряется в градусах, как и любой другой угол. Символ степени — маленький кружок °. Итак, если вы видите угол, представленный как 45°, это означает, что угол имеет меру 45°.
Примеры тупых углов: 135°, 150°, 160°
Тупой угол Градус
Тупой угол — это угол, величина которого больше 90 градусов, но меньше 180 градусов. Считается разновидностью острого угла. Градус тупого угла — это расстояние между двумя линиями, образующими угол. Самый распространенный способ измерения углов — в градусах, при этом полный круг равен 360 градусам.
Как построить тупой угол?
Тупой угол – это угол, величина которого больше 90 градусов и меньше 180 градусов. Это считается типом рефлекторного угла.
Это считается типом рефлекторного угла.
Есть несколько способов построить тупой угол. Один из способов — использовать транспортир для измерения желаемого градуса угла. Другой способ — использовать циркуль, чтобы нарисовать две дуги, которые пересекаются под нужным углом.
Если вы хотите построить тупой угол без использования каких-либо инструментов, вы можете сделать это, нарисовав две линии, которые встречаются в одной точке, а затем идут наружу под разными углами. Чем дальше друг от друга будут две линии, тем больше будет угол.
Тупоугольный треугольник
Тупоугольный треугольник — это треугольник, в котором один из углов больше 90 градусов. Два других угла меньше 90 градусов. Стороны тупоугольного треугольника не равны.
Как определить, является ли треугольник тупоугольным?
Есть несколько способов определить, является ли треугольник тупым. Первый способ — посмотреть на углы треугольника. Если какой-либо из углов больше 90 градусов, то треугольник тупоугольный. Другой способ определить, является ли треугольник тупоугольным, — посмотреть на длины сторон. Если какая-либо из сторон длиннее двух других, то треугольник тупоугольный. Вы также можете использовать теорему Пифагора, чтобы определить, является ли треугольник тупым. Если длина любой стороны больше суммы двух других сторон, то треугольник тупоугольный.
Другой способ определить, является ли треугольник тупоугольным, — посмотреть на длины сторон. Если какая-либо из сторон длиннее двух других, то треугольник тупоугольный. Вы также можете использовать теорему Пифагора, чтобы определить, является ли треугольник тупым. Если длина любой стороны больше суммы двух других сторон, то треугольник тупоугольный.
Примеры вопросов о тупых углах
Тупой угол — это угол, величина которого больше 90 градусов и меньше 180 градусов. Примером тупого угла является угол в 100 градусов.
Существует несколько типов вопросов о тупых углах, которые вам могут задать на уроках математики или на стандартных тестах. Один тип вопросов может попросить вас определить, является ли данный угол тупым, прямым или острым. Другой тип вопроса может попросить вас найти меру тупого угла. Вот несколько примеров вопросов, иллюстрирующих эти концепции:
1. Какой из следующих углов тупой?
а) 45 градусов
б) 90 градусов
в) 135 градусов
Заключение
Тупой угол – это угол, который больше 90 градусов, но меньше 180 градусов. Тупой угол также называют рефлекторным углом. Рефлекторный угол образуется, когда стороны угла направлены в противоположные стороны.
Тупой угол также называют рефлекторным углом. Рефлекторный угол образуется, когда стороны угла направлены в противоположные стороны.
Степень тупого угла составляет от 91 до 179 градусов. Наиболее распространенным примером тупого угла является прямой угол. Прямой угол имеет степень 90 градусов.
Некоторые другие примеры тупых углов включают:
Угол 135 градусов
Угол 145 градусов
Угол 155 градусов
Острый угол — определение, свойства, градус, формула, примеры чем 90°. Например, когда время 11 часов, угол, образованный между часовой и минутной стрелками, является острым углом. Другими словами, 30°, 40°, 57° и т. д. — все это острые углы.
| 1. | Что такое острый угол? |
| 2. | Реальные примеры острых углов |
| 3. | Свойства остроугольного треугольника |
| 4. | Часто задаваемые вопросы об остром угле |
Что такое острый угол?
Угол образуется, когда два луча встречаются в вершине. Когда этот угол меньше 90° называется острым углом. На рисунке ниже угол, образованный между «Лучами 1» и «Лучами 2», является острым. Кроме того, когда прямой угол делится на два, он образует два острых угла.
Когда этот угол меньше 90° называется острым углом. На рисунке ниже угол, образованный между «Лучами 1» и «Лучами 2», является острым. Кроме того, когда прямой угол делится на два, он образует два острых угла.
Определение острого угла
Острый угол определяется как угол, величина которого меньше 90 градусов, т. е. мера составляет от 0° до 90°. Некоторые из примеров: 60 °, 30 °, 45 градусов и т. Д. Треугольник, образованный всеми внутренними углами, меньшими 90 °, называется остроугольным треугольником. Например, равносторонний треугольник является остроугольным, так как его внутренние углы равны 60°.
Острый угол Градус
В предыдущем разделе мы читали, что угол, который измеряется меньше 90 градусов, то есть меньше прямого угла, является острым углом. Примеры градусов острого угла: 63°, 31°, 44°, 68°, 83°, 85°. Следовательно, градус острого угла лежит в пределах от 0° до менее 90°. Вот несколько схематических изображений острых углов.
Реальные примеры острых углов
Мы знаем, что углы больше 0° и меньше 90° в геометрии называются острыми углами. Следовательно, 45°, 5°, 28°, 49°, 89° являются примерами острых углов.
Следовательно, 45°, 5°, 28°, 49°, 89° являются примерами острых углов.
Вот несколько реальных примеров острых углов.
- Ломтик арбуза, разрезанный на небольшие части, как показано ниже.
- Несколько примеров образования углов между часовой и минутной стрелками часов.
- Клюв птицы, когда он открыт.
- Угол образуется, когда пасть крокодила открыта.
Свойства остроугольного треугольника
В остроугольном треугольнике все углы меньше 90°. Когда все три угла треугольника равны 60°, он образует особый треугольник, называемый равносторонним треугольником. Остроугольные треугольники можно разделить на остроугольные, равнобедренные и равнобедренные. Существует много типов треугольников, и остроугольный треугольник является одним из них. В показанном ниже треугольнике все внутренние углы меньше 90°. Поэтому его называют остроугольным треугольником.
Формула острого угла
Точно так же, как теорема Пифагора для прямоугольных треугольников, у нас есть формула треугольника острого угла, которая часто известна как теорема неравенства треугольников для остроугольных треугольников. Он гласит, что сумма квадратов двух сторон треугольника больше, чем квадрат наибольшей стороны. В Δ ABC, если стороны измеряются a,b,c так, что c является наибольшей стороной, то a 2 + b 2 > с 2 . Другими словами, в треугольнике, если a 2 + b 2 > c 2 , треугольник является остроугольным.
Он гласит, что сумма квадратов двух сторон треугольника больше, чем квадрат наибольшей стороны. В Δ ABC, если стороны измеряются a,b,c так, что c является наибольшей стороной, то a 2 + b 2 > с 2 . Другими словами, в треугольнике, если a 2 + b 2 > c 2 , треугольник является остроугольным.
☛Темы, связанные с острым углом
Ознакомьтесь с некоторыми интересными темами, связанными с острым углом.
- Геометрия
- Уголки
- Треугольники
- Тупой угол
- Транспортир
Примеры острого угла
Пример 1: Выберите углы, которые можно классифицировать как острые.
Решение:
Вариант а) и вариант d) измеряют менее 90°. Следовательно, это острые углы.
Пример 2: Посмотрите на часы, показанные ниже, и определите моменты времени, когда стрелки образуют острый угол.

Решение:
Мы можем заметить, что в 10 и 11 часов угол, образованный между часовой и минутной стрелками, является острым углом. Таким образом, часы, которые показывают 10 и 11 часов, образуют острый угол.
Пример 3: Является ли следующий треугольник остроугольным?
Решение:
Все 3 угла внутри остроугольного треугольника должны быть меньше 90°. Из рисунка видно, что два угла равны 45° каждый, а ∠Y равен 90°. Следовательно, это не остроугольный треугольник.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу по математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по острому углу
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об остром угле
Что такое острый угол?
Острый угол – это угол, величина которого меньше 90°. Его можно измерить с помощью транспортира. Например, 35°, 60°, 72° и т. д. — все это острые углы.
Его можно измерить с помощью транспортира. Например, 35°, 60°, 72° и т. д. — все это острые углы.
Каковы некоторые примеры острых углов?
Острые углы — это углы, градусная мера которых меньше 90°. Таким образом, 10°, 30°, 45°, 70° являются примерами острых углов.
Как найти меру острого угла?
Острые углы можно измерять с помощью транспортира. Чтобы измерить острый угол, поместите нижнюю линию транспортира на базовую линию и поместите центр транспортира на вершину, где пересекаются линии двух углов. Теперь рассмотрим нижнюю шкалу транспортира и измерим угол.
Что такое остроугольный треугольник?
Остроугольный треугольник — это треугольник, все внутренние углы которого меньше 90°. Например, у равностороннего треугольника все внутренние углы равны 60°. Таким образом, его можно назвать остроугольным треугольником.
Каковы свойства остроугольного треугольника?
Есть несколько важных свойств, которые отличают остроугольный треугольник от других типов треугольников.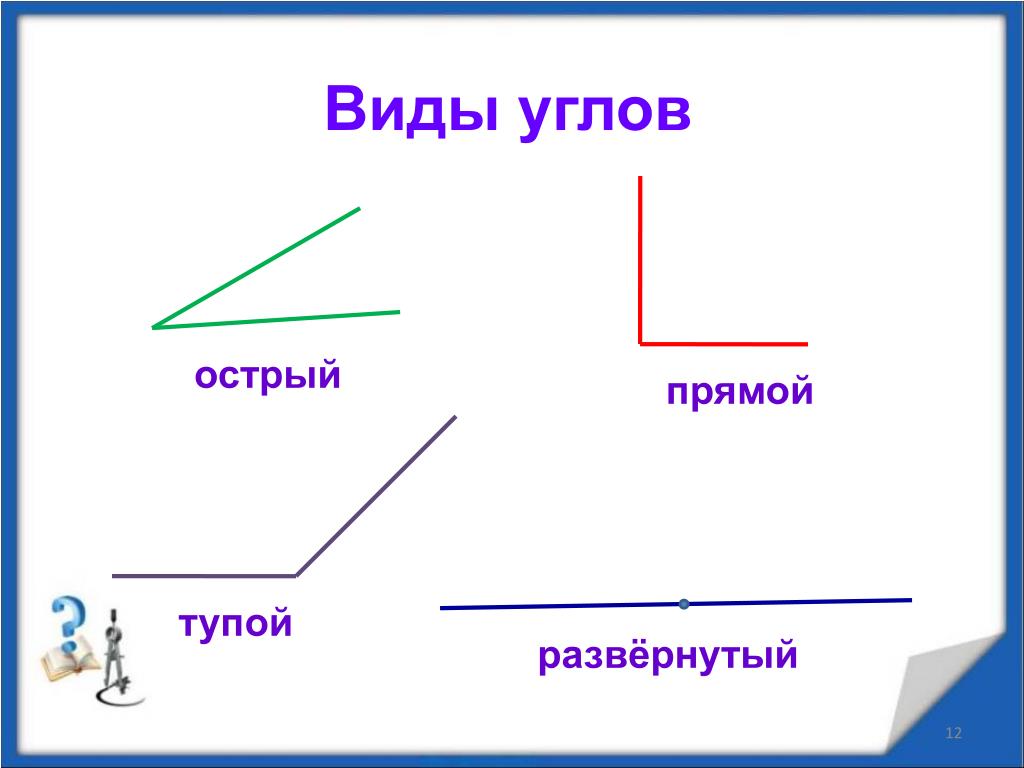
- Три внутренних угла остроугольного треугольника в сумме дают 180°.
- Треугольник не может быть остроугольным и прямоугольным одновременно.
- Треугольник не может быть одновременно тупоугольным и остроугольным.
- Все три угла остроугольного треугольника всегда меньше 90° или лежат между (от 0° до 90°).
Каковы характеристики острого угла?
Основная характеристика острого угла заключается в том, что его измерение лежит в пределах от 0° до 9°0°. В случае остроугольного треугольника мера всех трех внутренних углов остроугольного треугольника лежит в пределах от 0° до 90°, но сумма всех внутренних углов всегда равна 180°.
Какое наименьшее количество острых углов у прямоугольного треугольника?
В прямоугольном треугольнике должно быть не менее двух острых углов. Один угол должен быть равен 90°, а два других всегда лежат в пределах от 0° до 90°.
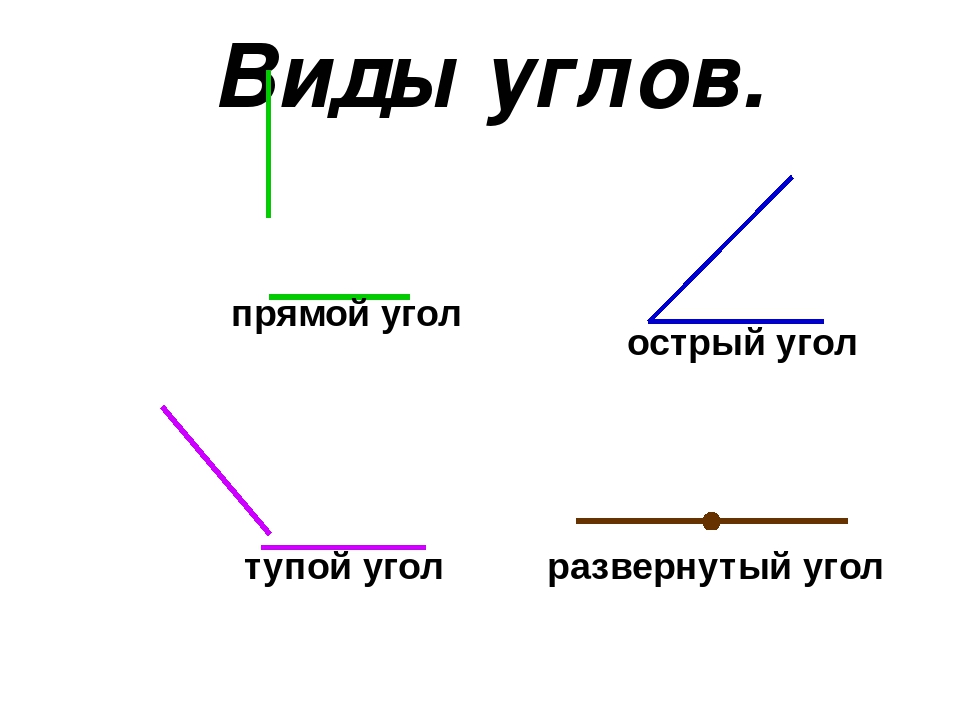
Как выглядит острый угол?
Размер острого угла лежит между 0° и 9°0°.

 Совершив Mostbet логин, вы сможете делать ставки в тенге и установить для интерфейса казахский язык, чтобы удобно ориентироваться по сайту и в приложении.
Совершив Mostbet логин, вы сможете делать ставки в тенге и установить для интерфейса казахский язык, чтобы удобно ориентироваться по сайту и в приложении.  Мостбет регистрация доступна для всех игроков, которые исполнилось 18 лет. Есть пять вариантов, с помощью которых вы сможете создать аккаунт на этом сайте:
Мостбет регистрация доступна для всех игроков, которые исполнилось 18 лет. Есть пять вариантов, с помощью которых вы сможете создать аккаунт на этом сайте: Совершив Мостбет вход, новые игроки могут получить бонус на первый депозит или бесплатную ставку, а также участвовать в программе лояльности и получать дополнительные бонусы за активность на сайте. Вот пример бонусов, доступных в Mostbet:
Совершив Мостбет вход, новые игроки могут получить бонус на первый депозит или бесплатную ставку, а также участвовать в программе лояльности и получать дополнительные бонусы за активность на сайте. Вот пример бонусов, доступных в Mostbet: Этот Мостбет бонус доступен, если вы делаете экспресс ставку на три и более исхода. После этого вы можете получить + 40% к ставке.
Этот Мостбет бонус доступен, если вы делаете экспресс ставку на три и более исхода. После этого вы можете получить + 40% к ставке. 2 Ghz и выше;
2 Ghz и выше; 000 тенге
000 тенге В 16 веке из Турции данное растение было привезено в Англию и обрело там большую популярность у цветоводов. Однако с конца 19 века оно утратило былую популярность, но в настоящее время данные цветы с каждым годом пользуются все большим спросом. На данный момент такой род объединяет больше 600 разнообразных видов ранункулюса. Если срезать цветок такого растения и поместить в вазу, то он будет сохранять свою свежесть на протяжении полумесяца. Итальянцы садовый лютик именуют «золотыми пуговками лугов». Имеется известная легенда о том, что Иисус превратил небольшие звездочки в лютики и подарил их своей матери в знак любви и уважения…
В 16 веке из Турции данное растение было привезено в Англию и обрело там большую популярность у цветоводов. Однако с конца 19 века оно утратило былую популярность, но в настоящее время данные цветы с каждым годом пользуются все большим спросом. На данный момент такой род объединяет больше 600 разнообразных видов ранункулюса. Если срезать цветок такого растения и поместить в вазу, то он будет сохранять свою свежесть на протяжении полумесяца. Итальянцы садовый лютик именуют «золотыми пуговками лугов». Имеется известная легенда о том, что Иисус превратил небольшие звездочки в лютики и подарил их своей матери в знак любви и уважения… 1 Как посадить в комнатных условиях
1 Как посадить в комнатных условиях
 В самом начале своего раскрытия цветки схожи с розами. А после полного раскрытия они очень похожи на махровые маки. Очень часто ранункулюс розовый и ранункулюс белый используют при составлении букета невесты. Но при этом не стоит забывать, что сок такого растения является ядовитым.
В самом начале своего раскрытия цветки схожи с розами. А после полного раскрытия они очень похожи на махровые маки. Очень часто ранункулюс розовый и ранункулюс белый используют при составлении букета невесты. Но при этом не стоит забывать, что сок такого растения является ядовитым.
 Дело в том, что там у такого цветка сохраняется более насыщенная окраска соцветий, при этом продолжительность цветения заметно увеличивается. Также лютик следует оградить от влияния сквозняков. Такое растение не переносит минусовую температуру, в связи с этим его надо сажать только после того, как минует угроза заморозков.
Дело в том, что там у такого цветка сохраняется более насыщенная окраска соцветий, при этом продолжительность цветения заметно увеличивается. Также лютик следует оградить от влияния сквозняков. Такое растение не переносит минусовую температуру, в связи с этим его надо сажать только после того, как минует угроза заморозков. А также произвести обработку почвы при помощи фундазола.
А также произвести обработку почвы при помощи фундазола. Когда вырастут 2 пары настоящих листочков, ранункулюс надо будет пикировать по индивидуальным горшочкам. Когда весной минует угроза заморозков, данные цветы следует пересадить в сад. Цветение будет наблюдаться лишь на следующий год, так что если вы хотите получить быстрый результат, такой способ размножения ранункулюса для вас не подходит.
Когда вырастут 2 пары настоящих листочков, ранункулюс надо будет пикировать по индивидуальным горшочкам. Когда весной минует угроза заморозков, данные цветы следует пересадить в сад. Цветение будет наблюдаться лишь на следующий год, так что если вы хотите получить быстрый результат, такой способ размножения ранункулюса для вас не подходит. В некоторых случаях в жидкость рекомендуется всыпать вещество, стимулирующее рост. Выбирайте для такого цветка сразу наиболее подходящее для него места, так как пересаживать его не рекомендуется.
В некоторых случаях в жидкость рекомендуется всыпать вещество, стимулирующее рост. Выбирайте для такого цветка сразу наиболее подходящее для него места, так как пересаживать его не рекомендуется. Узнать о том, что цветок начал гнить, можно по плесени на листовых пластинах и по опадению бутончиков. Пораженные части цветка следует обрезать, грунт вокруг него надо взрыхлить и непременно уменьшить полив. Своевременно надо убирать отцветшие цветочки, так как они будут препятствовать цветению других соцветий. Данному растению необходимо регулярное рыхление грунта, а также его надо подкармливать, используя для этого органические удобрения. Так, 2 раза в месяц в почву нужно вносить калийное удобрение (на 1 квадратный метр от 40 до 50 грамм вещества), а во время цветения для этого подойдет сульфат калия, калийная соль либо древесная зола. Паутинный клещ может поселиться на кустике лютика (особенно во время летней засухи). На листочках и побегах могут поселиться трипсы и тли. Когда вы увидите на листве беловатые либо серебристые пятнышки, то незамедлительно примите меры по уничтожению вредителей. Для этого кустики надо обработать подходящими инсектицидными средствами. В профилактических целях 2 либо 3 раза в неделю ранункулюс нужно обрабатывать раствором меркаптофоса (0,2%).
Узнать о том, что цветок начал гнить, можно по плесени на листовых пластинах и по опадению бутончиков. Пораженные части цветка следует обрезать, грунт вокруг него надо взрыхлить и непременно уменьшить полив. Своевременно надо убирать отцветшие цветочки, так как они будут препятствовать цветению других соцветий. Данному растению необходимо регулярное рыхление грунта, а также его надо подкармливать, используя для этого органические удобрения. Так, 2 раза в месяц в почву нужно вносить калийное удобрение (на 1 квадратный метр от 40 до 50 грамм вещества), а во время цветения для этого подойдет сульфат калия, калийная соль либо древесная зола. Паутинный клещ может поселиться на кустике лютика (особенно во время летней засухи). На листочках и побегах могут поселиться трипсы и тли. Когда вы увидите на листве беловатые либо серебристые пятнышки, то незамедлительно примите меры по уничтожению вредителей. Для этого кустики надо обработать подходящими инсектицидными средствами. В профилактических целях 2 либо 3 раза в неделю ранункулюс нужно обрабатывать раствором меркаптофоса (0,2%).
 Их необходимо засыпать почвой таким образом, чтобы лишь верхушки возвышались над поверхностью. При достаточном объеме цветочного горшочка в него можно высадить сразу несколько клубеньков. Хорошенько полейте и уберите на первое время в достаточно прохладное место (около 12 градусов). По мере необходимости надо проводить увлажнение грунта.
Их необходимо засыпать почвой таким образом, чтобы лишь верхушки возвышались над поверхностью. При достаточном объеме цветочного горшочка в него можно высадить сразу несколько клубеньков. Хорошенько полейте и уберите на первое время в достаточно прохладное место (около 12 градусов). По мере необходимости надо проводить увлажнение грунта. Они нуждаются в систематическом поливе, при этом во время интенсивного роста в воду рекомендуется всыпать удобрения. Полив верхний, однако при этом постарайтесь, чтобы не произошло переувлажнение грунта. Время от времени нужно увлажнять листву из опрыскивателя. Когда растение начнет увядать, поливать его нужно намного меньше.
Они нуждаются в систематическом поливе, при этом во время интенсивного роста в воду рекомендуется всыпать удобрения. Полив верхний, однако при этом постарайтесь, чтобы не произошло переувлажнение грунта. Время от времени нужно увлажнять листву из опрыскивателя. Когда растение начнет увядать, поливать его нужно намного меньше. Такое многолетнее растение в местах с мягкими зимами можно и не выкапывать, их просто накрывают опавшими листьями либо лапником.
Такое многолетнее растение в местах с мягкими зимами можно и не выкапывать, их просто накрывают опавшими листьями либо лапником. Большинство малоопытных цветоводов в связи с этим каждый год приобретают свежие клубеньки.
Большинство малоопытных цветоводов в связи с этим каждый год приобретают свежие клубеньки. 02+17.19
02+17.19 $ )
$ ) 2} \
\cssId{s38}{=\ (-1)(p)} \
\cssId{s39}{=\-р}
$$
2} \
\cssId{s38}{=\ (-1)(p)} \
\cssId{s39}{=\-р}
$$

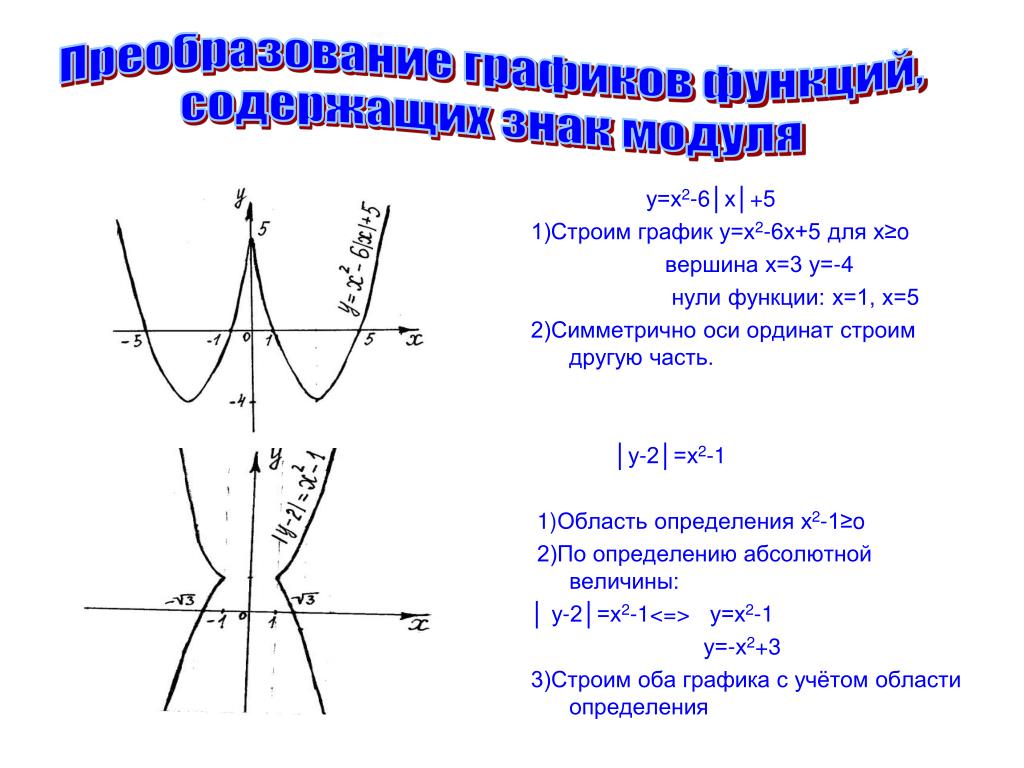
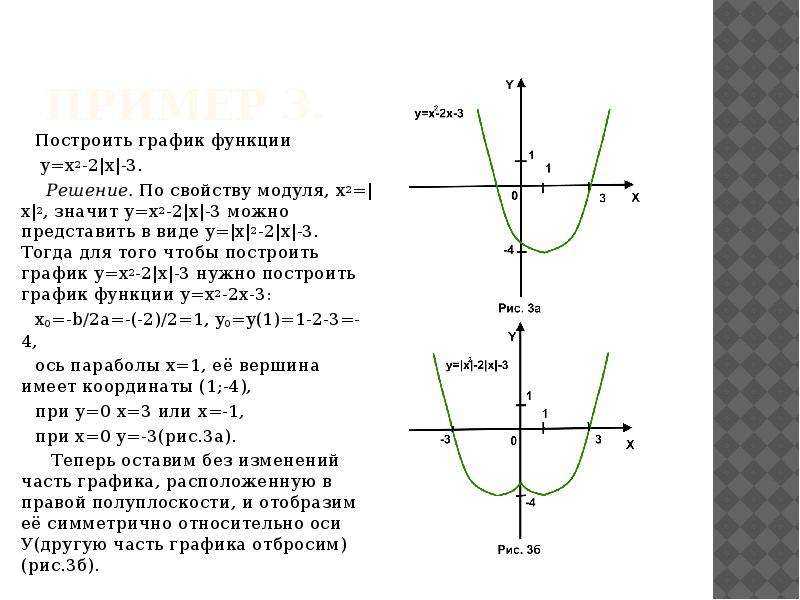 Сравнивая оба графика, видим что они одинаковые.
Сравнивая оба графика, видим что они одинаковые. Получаем график функции у = (|х| — 2) 2 – 3
Получаем график функции у = (|х| — 2) 2 – 3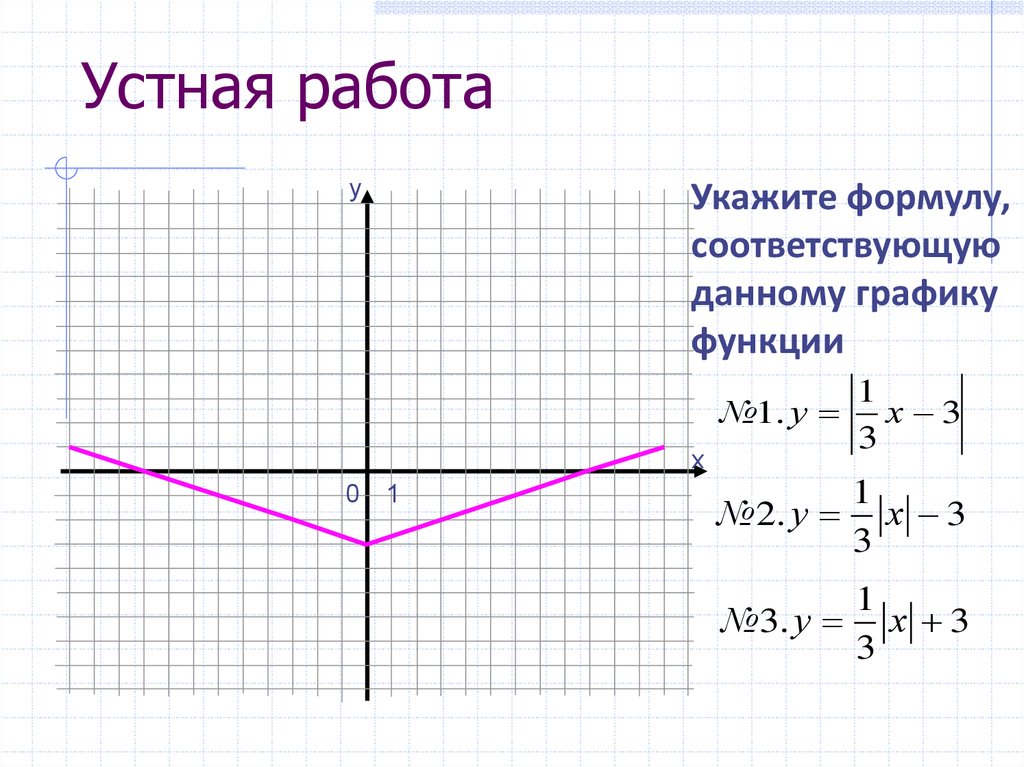 Функции и графики
Функции и графики Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
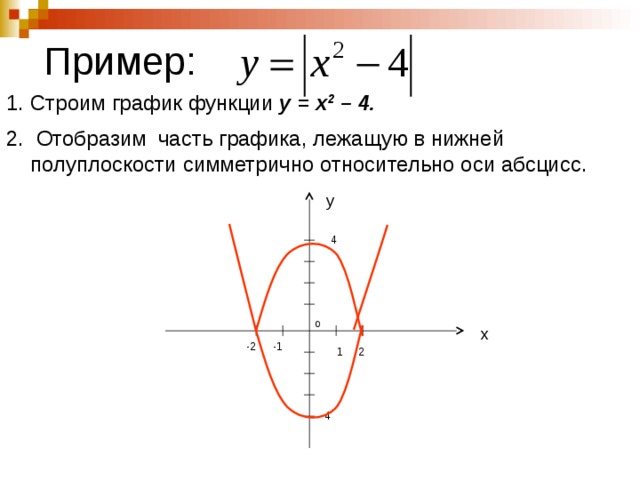
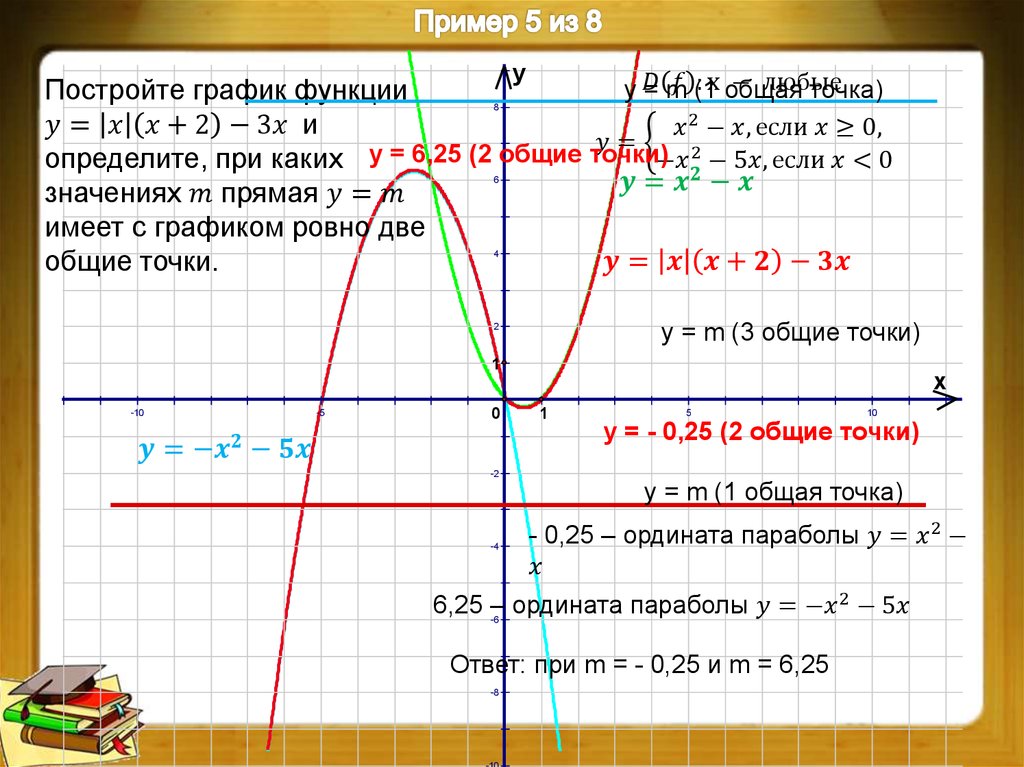
 Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки? д.
д.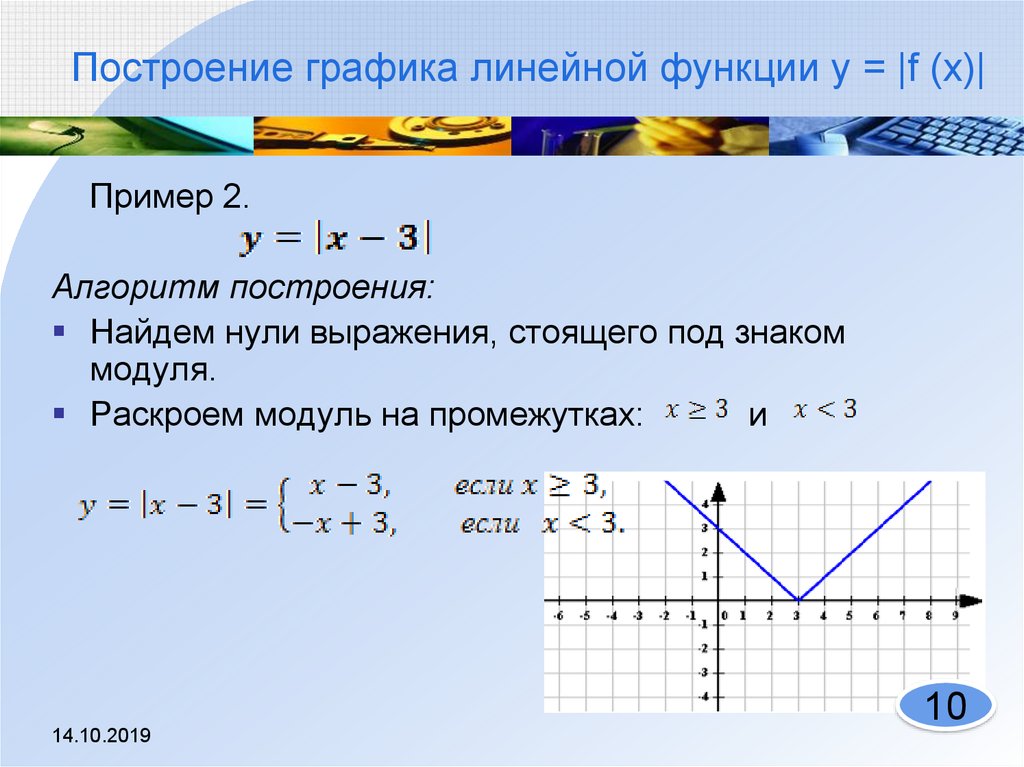 Давайте разберемся, что же это за алгоритмы.
Давайте разберемся, что же это за алгоритмы.

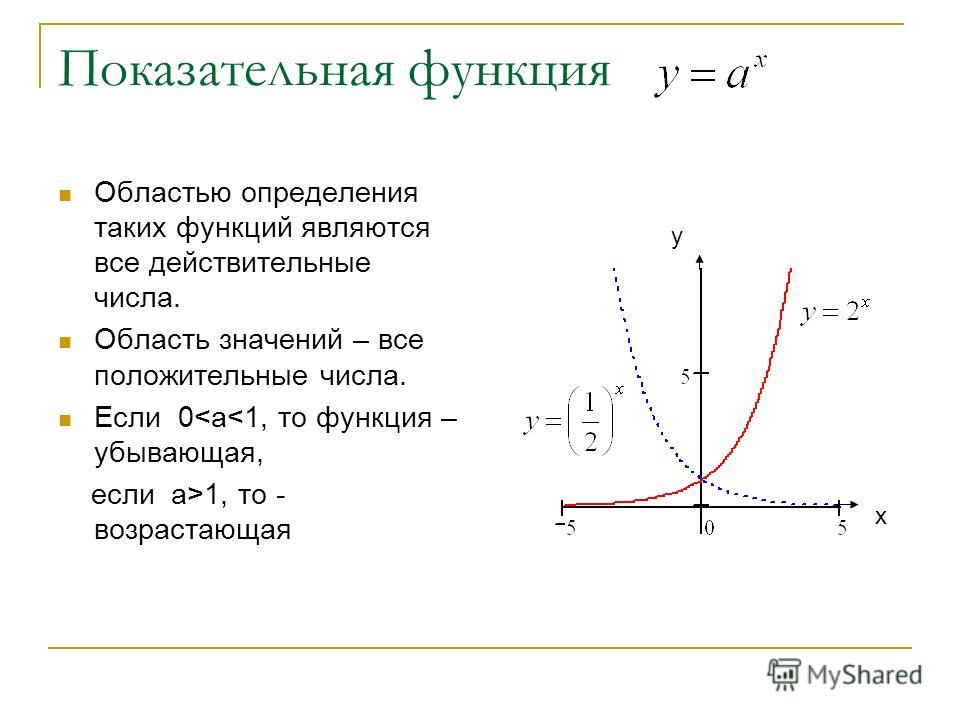
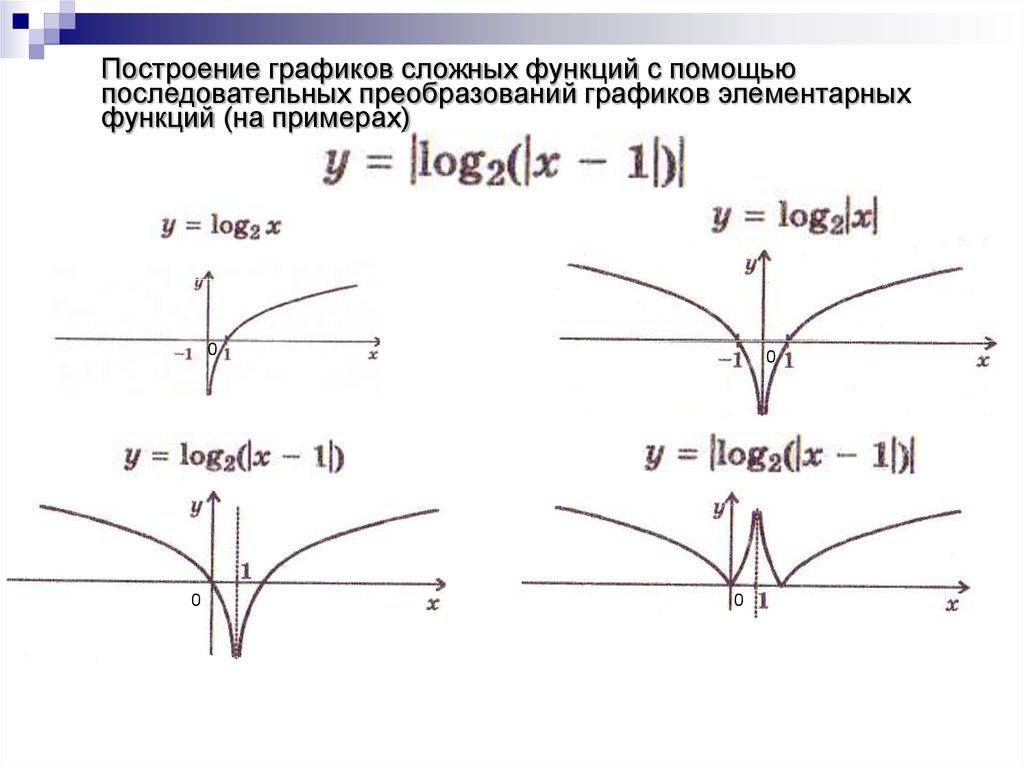 Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
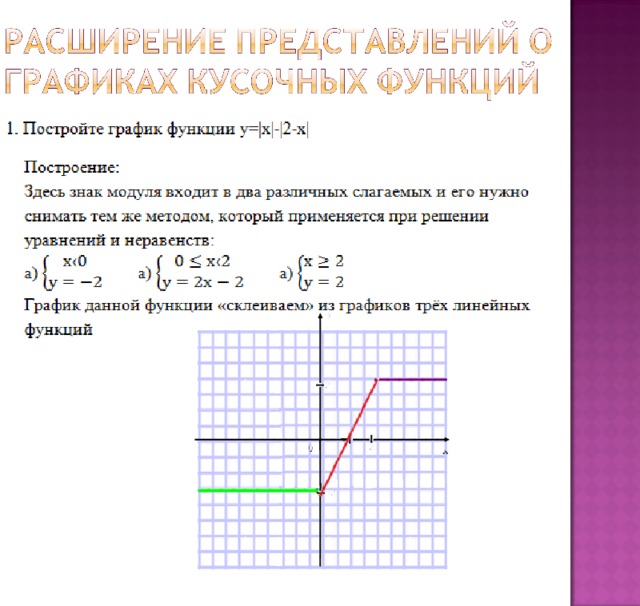 3$.
3$.
 API для этих функций был тщательно разработан, чтобы быть как можно более последовательным и простым в освоении, что позволяет легко переключаться с точечной диаграммы на гистограмму, гистограмму и диаграмму солнечных лучей во время сеанса исследования данных. Прокрутите вниз, чтобы увидеть галерею графиков Plotly Express, каждый из которых создается с помощью одного вызова функции.
API для этих функций был тщательно разработан, чтобы быть как можно более последовательным и простым в освоении, что позволяет легко переключаться с точечной диаграммы на гистограмму, гистограмму и диаграмму солнечных лучей во время сеанса исследования данных. Прокрутите вниз, чтобы увидеть галерею графиков Plotly Express, каждый из которых создается с помощью одного вызова функции. 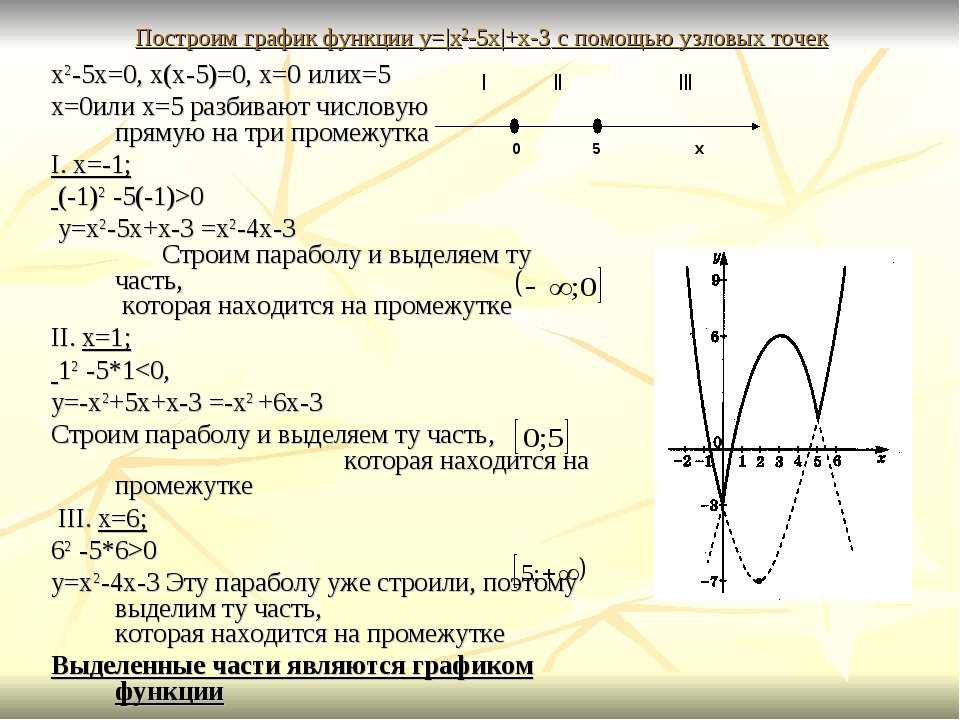 express как px
express как px  Атрибуты traces
Атрибуты traces 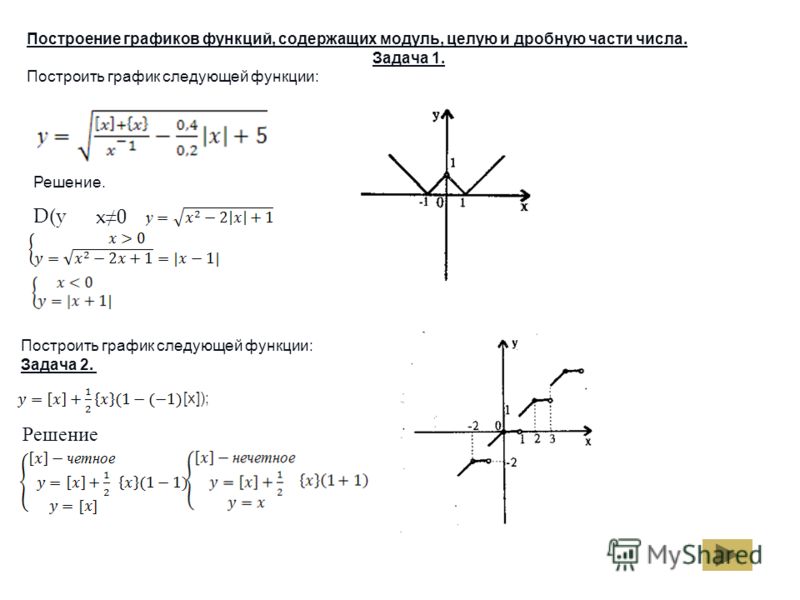

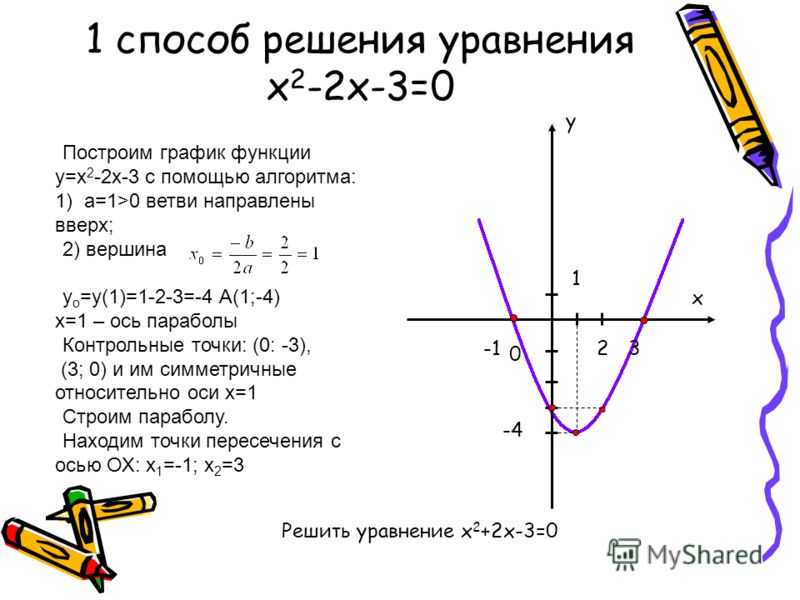 express как px
df = px.data.iris()
рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species")
рис.шоу()
express как px
df = px.data.iris()
рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species")
рис.шоу()
 bar(df, x="медаль", y="количество", цвет="нация",
pattern_shape="нация", pattern_shape_sequence=[".", "x", "+"])
рис.шоу()
bar(df, x="медаль", y="количество", цвет="нация",
pattern_shape="нация", pattern_shape_sequence=[".", "x", "+"])
рис.шоу()
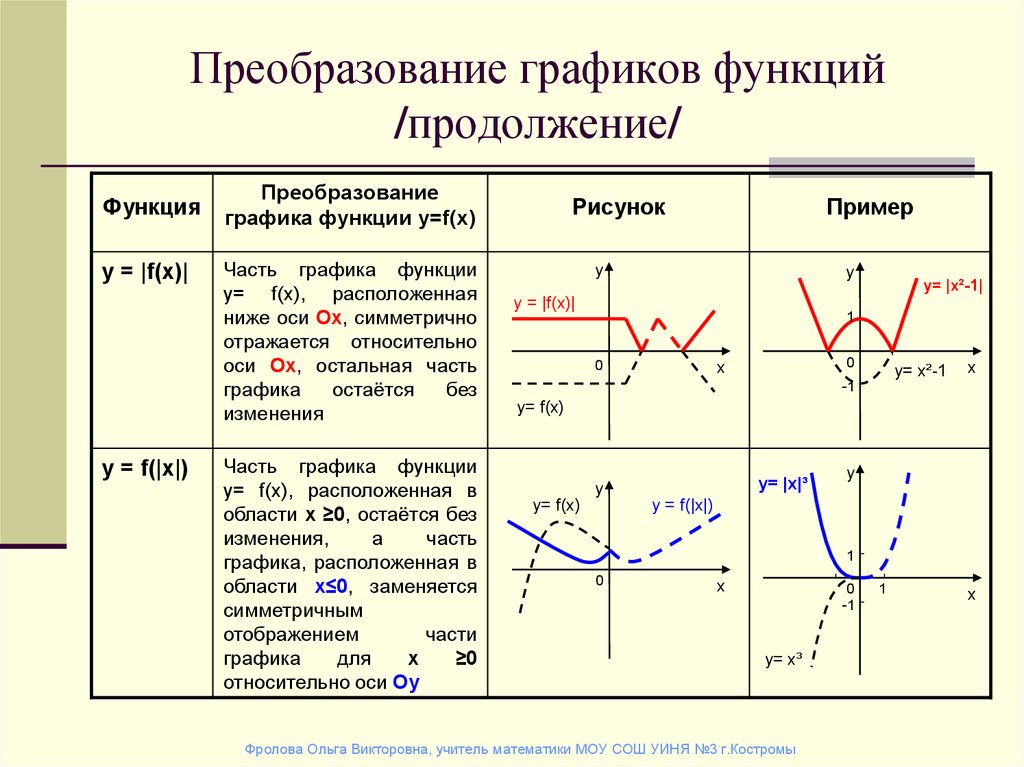 parallel_coordinates(df, color="species_id", labels={"species_id": "Виды",
"sepal_width": "Ширина чашелистика", "sepal_length": "Длина чашелистика",
"petal_width": "Ширина лепестка", "petal_length": "Длина лепестка", },
color_continuous_scale=px.colors.diverging.Tealrose, color_continuous_midpoint=2)
рис.шоу()
parallel_coordinates(df, color="species_id", labels={"species_id": "Виды",
"sepal_width": "Ширина чашелистика", "sepal_length": "Длина чашелистика",
"petal_width": "Ширина лепестка", "petal_length": "Длина лепестка", },
color_continuous_scale=px.colors.diverging.Tealrose, color_continuous_midpoint=2)
рис.шоу()
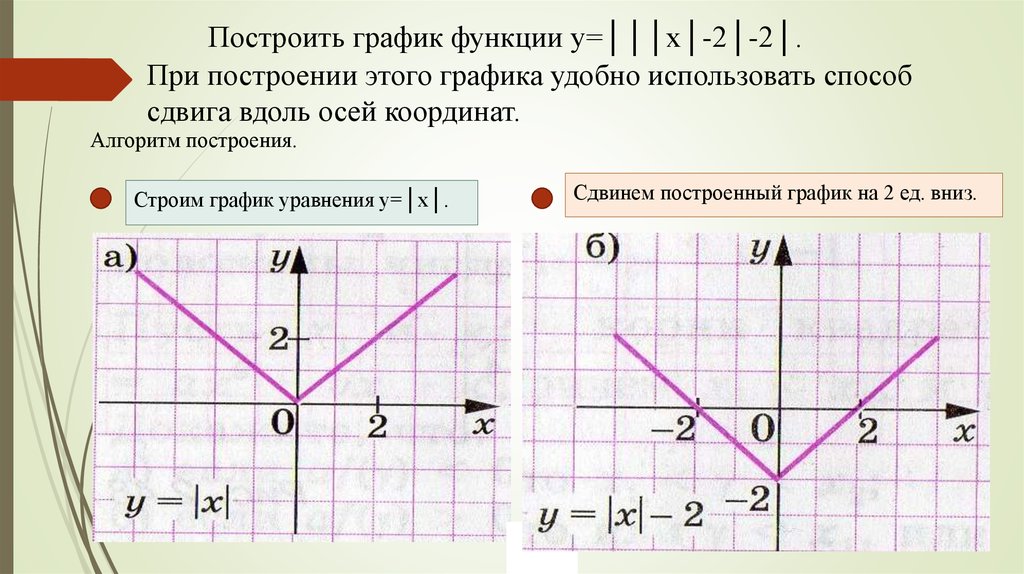 data.gapminder()
рис = px.scatter(df, x="gdpPercap", y="lifeExp", анимация_frame="год", анимация_группа="страна",
размер = "поп", цвет = "континент", hover_name = "страна", facet_col = "континент",
log_x=Истина, size_max=45, range_x=[100,100000], range_y=[25,90])
рис.шоу()
data.gapminder()
рис = px.scatter(df, x="gdpPercap", y="lifeExp", анимация_frame="год", анимация_группа="страна",
размер = "поп", цвет = "континент", hover_name = "страна", facet_col = "континент",
log_x=Истина, size_max=45, range_x=[100,100000], range_y=[25,90])
рис.шоу()
 импортировать панд как pd
df = pd.DataFrame([
dict(Task="Job A", Start='2009-01-01', Finish='2009-02-28', Resource="Alex"),
dict(Task="Job B", Start='2009-03-05', Finish='2009-04-15', Resource="Alex"),
dict(Task="Job C", Start='2009-02-20', Finish='2009-05-30', Resource="Max")
])
fig = px.timeline(df, x_start="Начало", x_end="Готово", y="Ресурс", color="Ресурс")
рис.шоу()
импортировать панд как pd
df = pd.DataFrame([
dict(Task="Job A", Start='2009-01-01', Finish='2009-02-28', Resource="Alex"),
dict(Task="Job B", Start='2009-03-05', Finish='2009-04-15', Resource="Alex"),
dict(Task="Job C", Start='2009-02-20', Finish='2009-05-30', Resource="Max")
])
fig = px.timeline(df, x_start="Начало", x_end="Готово", y="Ресурс", color="Ресурс")
рис.шоу()
 e6, 'country'] = 'Другие страны' # Представляет только большие страны
fig = px.pie(df, values='pop', names='country', title='Население европейского континента')
рис.шоу()
e6, 'country'] = 'Другие страны' # Представляет только большие страны
fig = px.pie(df, values='pop', names='country', title='Население европейского континента')
рис.шоу()
 data.gapminder().query("год == 2007")
fig = px.icicle(df, path=[px.Constant('мир'), 'континент', 'страна'], values='pop',
color='lifeExp', hover_data=['iso_alpha'])
рис.шоу()
data.gapminder().query("год == 2007")
fig = px.icicle(df, path=[px.Constant('мир'), 'континент', 'страна'], values='pop',
color='lifeExp', hover_data=['iso_alpha'])
рис.шоу()
 express как px
df = px.data.tips()
рис = px.ecdf(df, x="total_bill", color="sex")
рис.шоу()
express как px
df = px.data.tips()
рис = px.ecdf(df, x="total_bill", color="sex")
рис.шоу()
 express как px.
данные = [[1, 25, 30, 50, 1], [20, 1, 60, 80, 30], [30, 60, 1, 5, 20]]
рис = px.imshow (данные,
labels=dict(x="День недели", y="Время дня", color="Производительность"),
x=['Понедельник', 'Вторник', 'Среда', 'Четверг', 'Пятница'],
y=['Утро', 'День', 'Вечер']
)
fig.update_xaxes (сторона = "сверху")
рис.шоу()
express как px.
данные = [[1, 25, 30, 50, 1], [20, 1, 60, 80, 30], [30, 60, 1, 5, 20]]
рис = px.imshow (данные,
labels=dict(x="День недели", y="Время дня", color="Производительность"),
x=['Понедельник', 'Вторник', 'Среда', 'Четверг', 'Пятница'],
y=['Утро', 'День', 'Вечер']
)
fig.update_xaxes (сторона = "сверху")
рис.шоу()
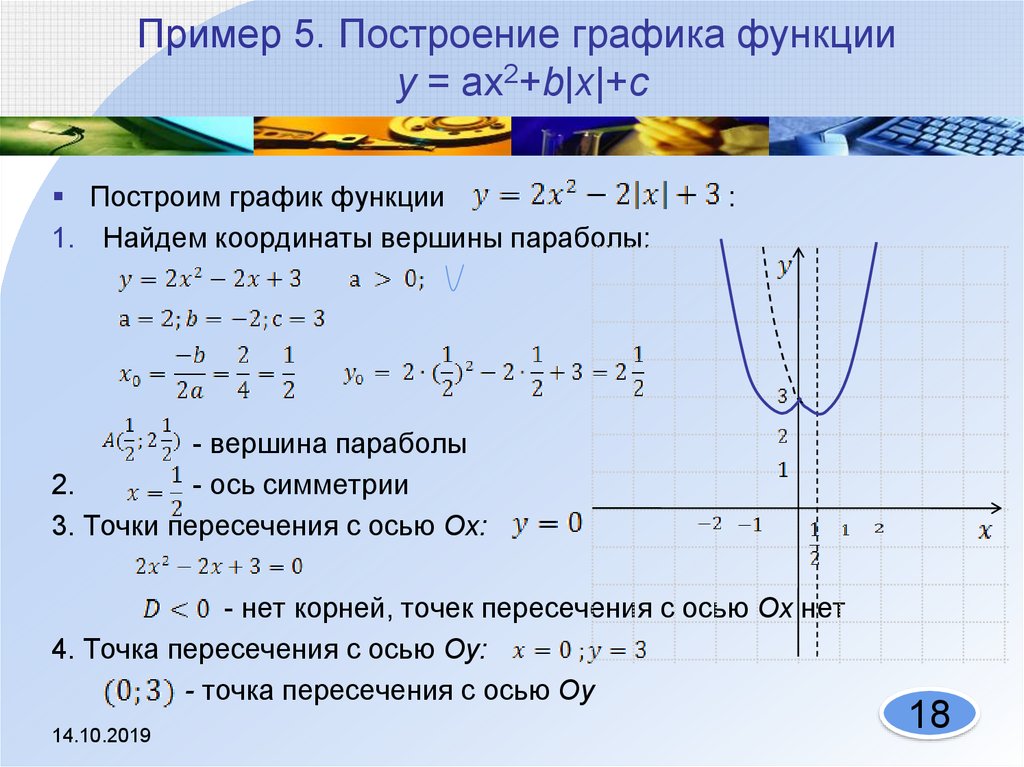 IceFire, size_max=15, масштаб=10,
mapbox_style="карто-позитрон")
рис.шоу()
IceFire, size_max=15, масштаб=10,
mapbox_style="карто-позитрон")
рис.шоу()
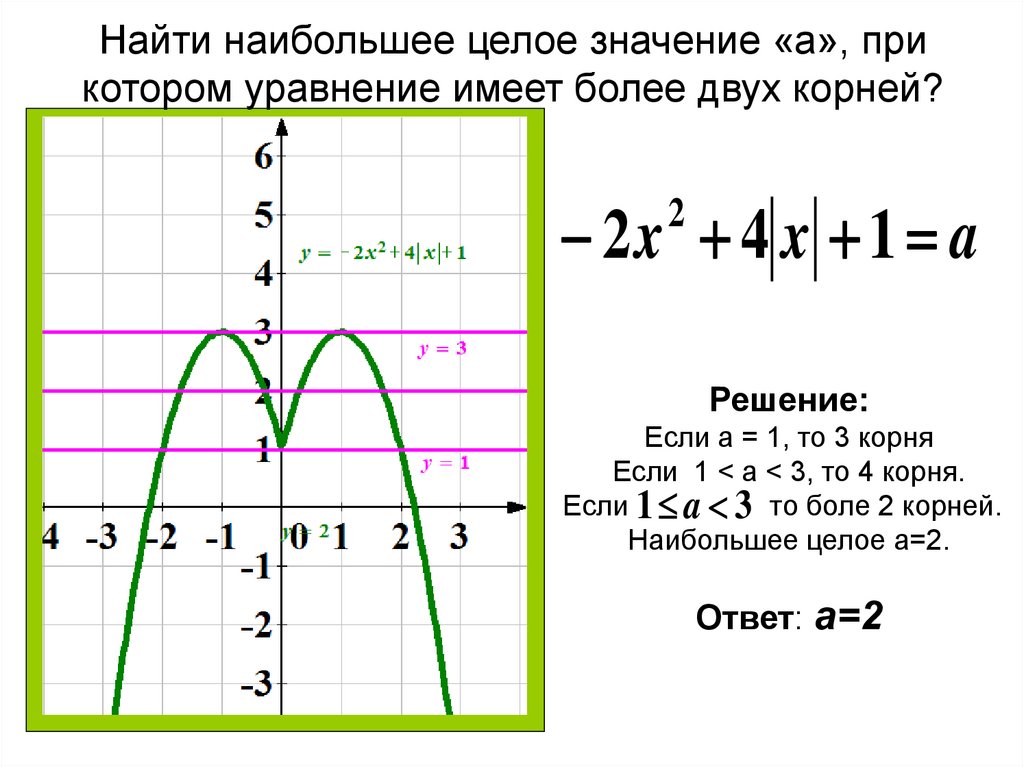
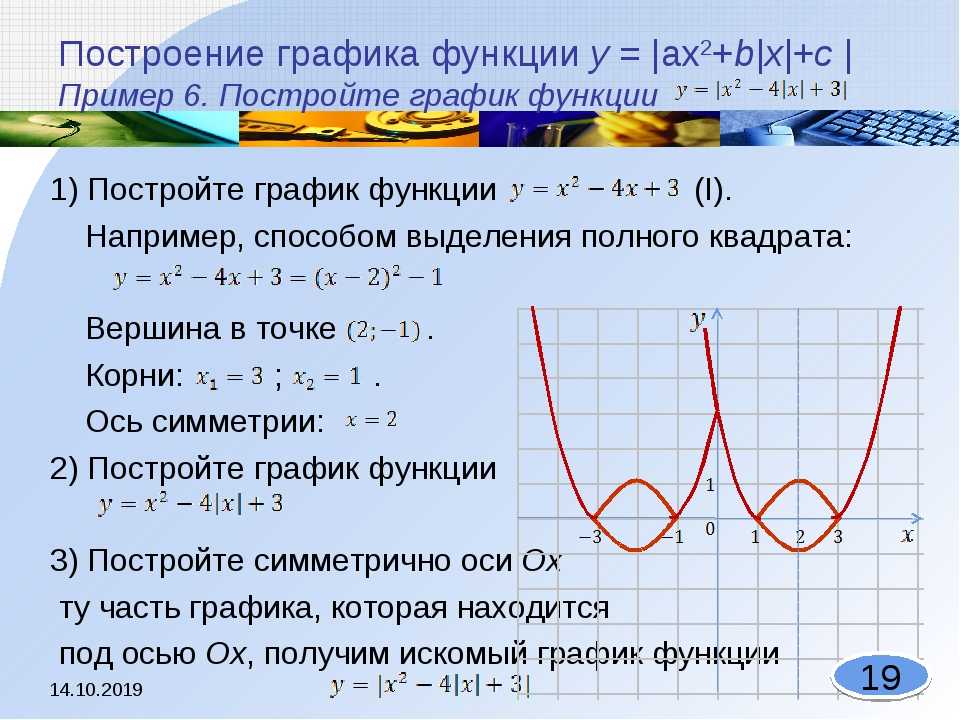 bar_polar(df, r="частота", theta="направление", цвет="сила", template="plotly_dark",
color_discrete_sequence= px.colors.sequential.Plasma_r)
рис.шоу()
bar_polar(df, r="частота", theta="направление", цвет="сила", template="plotly_dark",
color_discrete_sequence= px.colors.sequential.Plasma_r)
рис.шоу()
 шоу()
шоу()
 09.2019
09.2019 Нажмите OK, чтобы получить график. Подробнее [примеры 3D-функций]
Нажмите OK, чтобы получить график. Подробнее [примеры 3D-функций]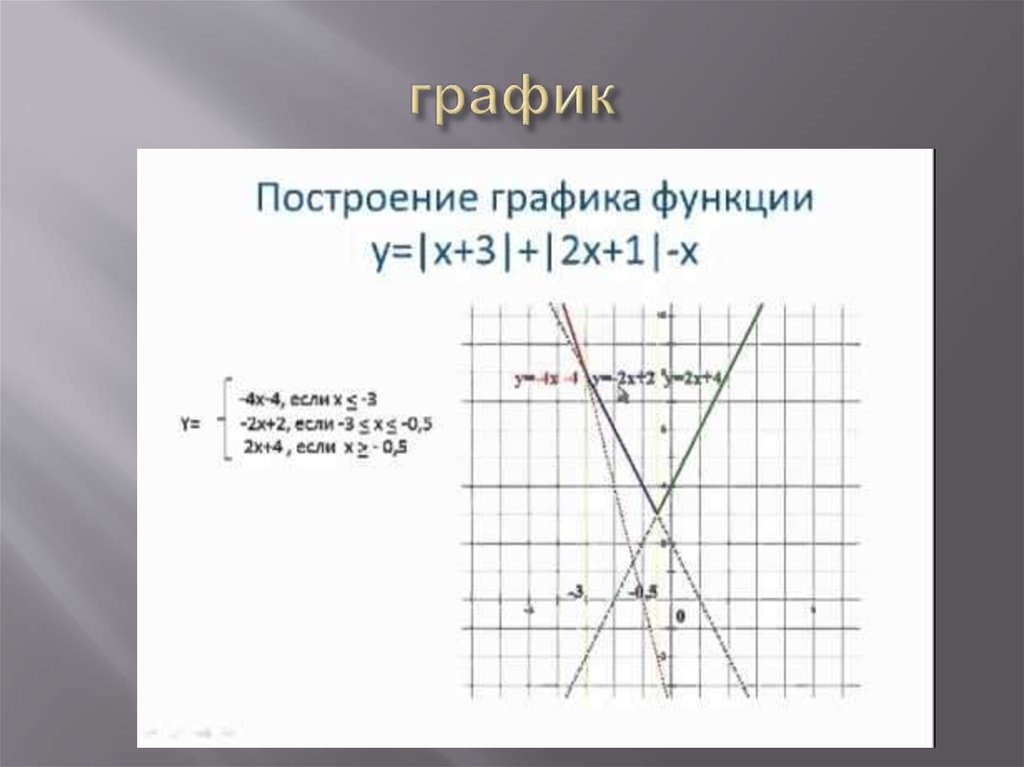
 Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Область значений функции E(у) = [-1; 1]. Ответ: E(у) = [-1; 1].
Область значений функции E(у) = [-1; 1]. Ответ: E(у) = [-1; 1]. Множество всех значений функции \(y = f(x)\), x ∈ X, называют областью значений функции.
Множество всех значений функции \(y = f(x)\), x ∈ X, называют областью значений функции.

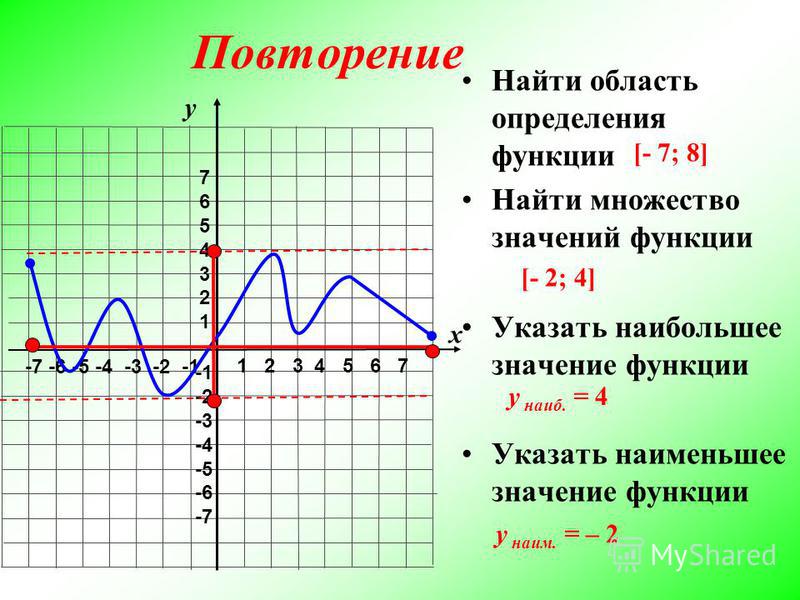 10 класс. Колмогоров А.Н.№101 – Рамблер/классНайдите область определения и область значений функции: Алгебра и начала анализа. 10 класс. Колмогоров А.Н.№101 – Рамблер/класс
10 класс. Колмогоров А.Н.№101 – Рамблер/классНайдите область определения и область значений функции: Алгебра и начала анализа. 10 класс. Колмогоров А.Н.№101 – Рамблер/класс В какой момент времени (Подробнее…)
В какой момент времени (Подробнее…)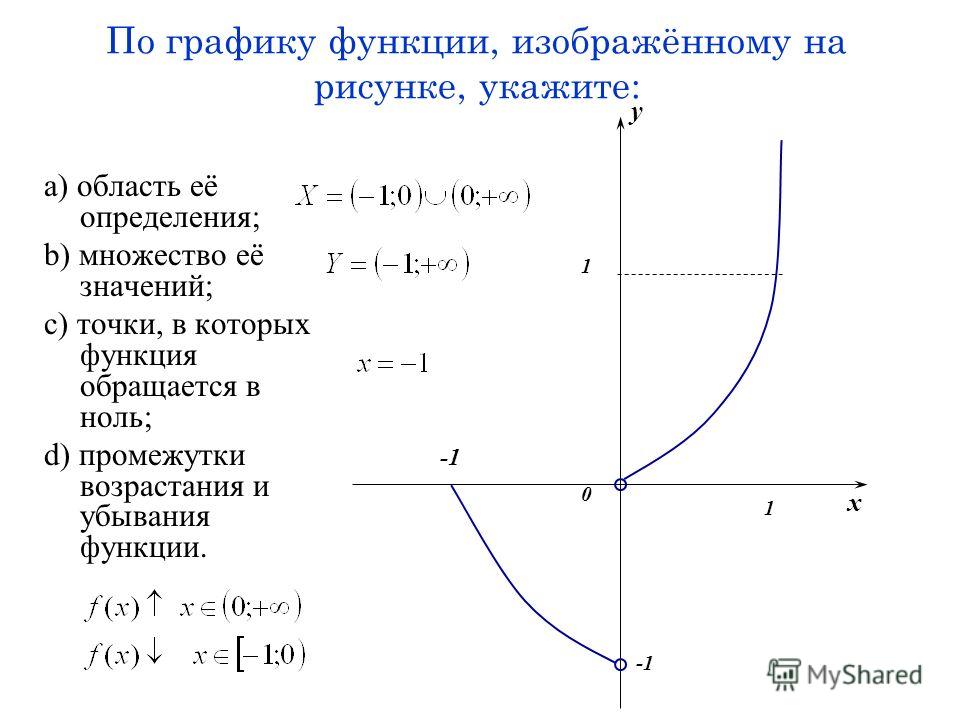 ..
..

 (0,0, значение), предел)
# лимит = 100
# значение = ---
значение = -22,5 # значение = -22,5, предел = 100
print(clip(value)) # результат равен 0.0
# значение = -22,5
# лимит = 100
(0,0, значение), предел)
# лимит = 100
# значение = ---
значение = -22,5 # значение = -22,5, предел = 100
print(clip(value)) # результат равен 0.0
# значение = -22,5
# лимит = 100
 ")
print("Но, по крайней мере, Python говорит нам о них!")
print("Поэтому их обычно не так уж сложно исправить.")
")
print("Но, по крайней мере, Python говорит нам о них!")
print("Поэтому их обычно не так уж сложно исправить.")
 py в print_message(день)
9"sunday": "Ой, выходные почти закончились."
10 }
---> 11 print(сообщения[день])
12
13
KeyError: «Пятница»
py в print_message(день)
9"sunday": "Ой, выходные почти закончились."
10 }
---> 11 print(сообщения[день])
12
13
KeyError: «Пятница»
 К счастью, ответ краток и прост.
К счастью, ответ краток и прост.  Когда вы используете ключевое слово «var» внутри функции, инициализируемая вами переменная является приватной для этой функции и не может быть видна вне этой функции. Но если внутри этой функции есть функции, то эти «внутренние» функции могут «видеть» эту переменную, и говорят, что эта переменная находится «в области видимости». Функции могут «видеть» переменные, объявленные внутри них. Они также могут «видеть» все, что объявлено вне их, но никогда не могут видеть те, которые объявлены внутри функций, вложенных в эту функцию. Это область видимости в JavaScript.
Когда вы используете ключевое слово «var» внутри функции, инициализируемая вами переменная является приватной для этой функции и не может быть видна вне этой функции. Но если внутри этой функции есть функции, то эти «внутренние» функции могут «видеть» эту переменную, и говорят, что эта переменная находится «в области видимости». Функции могут «видеть» переменные, объявленные внутри них. Они также могут «видеть» все, что объявлено вне их, но никогда не могут видеть те, которые объявлены внутри функций, вложенных в эту функцию. Это область видимости в JavaScript. Если объект «foo» имеет метод с именем «bar», когда ключевое слово JavaScript «this» используется внутри «bar», это относится к «foo». Если функция «bar» выполнялась в глобальной области видимости, то «this» относится к объекту окна (кроме строгого режима). Важно помнить, что, используя методы JavaScript call() или apply(), вы можете изменить контекст, в котором выполняется функция. Это, в свою очередь, изменяет значение «этого» внутри этой функции при ее выполнении.
Если объект «foo» имеет метод с именем «bar», когда ключевое слово JavaScript «this» используется внутри «bar», это относится к «foo». Если функция «bar» выполнялась в глобальной области видимости, то «this» относится к объекту окна (кроме строгого режима). Важно помнить, что, используя методы JavaScript call() или apply(), вы можете изменить контекст, в котором выполняется функция. Это, в свою очередь, изменяет значение «этого» внутри этой функции при ее выполнении.
 Записать это можно с помощью уравнения:
Записать это можно с помощью уравнения:
 {c_{3}} f(x) dx\)
{c_{3}} f(x) dx\)
 2 + x + C\)
2 + x + C\)
 Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.

 Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
 Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
 Результат интегрирования называется интегралом .
Результат интегрирования называется интегралом .  4
4 
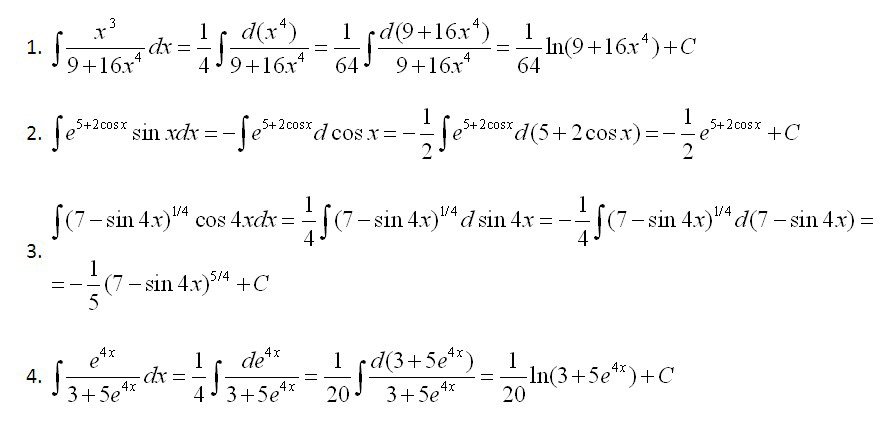





 \circ}) = — 5 \cdot 1 = — 5\)
\circ}) = — 5 \cdot 1 = — 5\) 2 α = ?
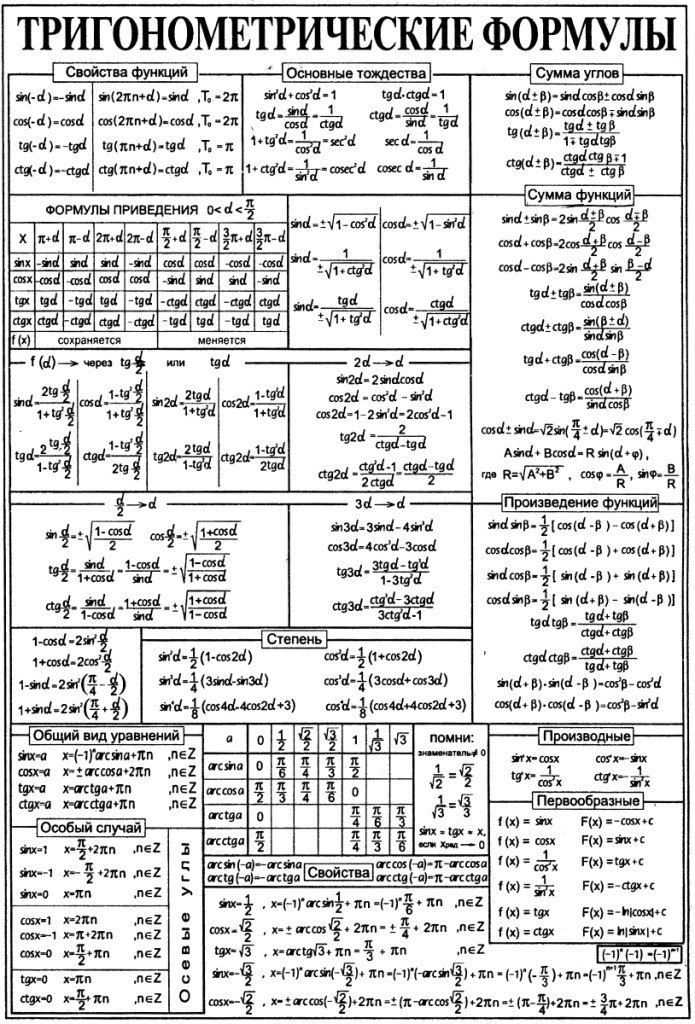
16:34 Итого получили 20 формул тригонометрии.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.ru/video/b99256c0e2a5f1411c87731142e2a822/
Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии. Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/
Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/
Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Как найти значения sin, cos, tg и ctg для углов в 30°, 45° и 60°.
2 α = ?
16:34 Итого получили 20 формул тригонометрии.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.ru/video/b99256c0e2a5f1411c87731142e2a822/
Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии. Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/
Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/
Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Как найти значения sin, cos, tg и ctg для углов в 30°, 45° и 60°. Тригонометрические функции в геометрии. Часть 5. Геометрия 9 класс. https://rutube.ru/video/9393cb6043b9878b49883195db02d251/
Как найти противо- и прилежащие катеты по углу и гипотенузе. Как найти площадь треугольника, параллелограмма и трапеции. Тригонометрические функции. Часть 6. Геометрия 9 класс. https://rutube.ru/video/01cfdff903c6c37227f510c5f4bf7984/
Как найти объем пирамиды (конуса) по боковому ребру (образующей) и углу между боковым ребром (образующей) и плоскостью основания. Тригонометрические функции. Часть 7. Геометрия 10-11 класс. https://rutube.ru/video/a246217e2de6f5960fb55a3e77b904d0/
Как найти противо- и прилежащие катеты по углу и другому катету. Как найти площадь треугольника и параллелограмма. Тригонометрические функции. Часть 8. Геометрия 9 класс. https://rutube.ru/video/5b374b4961980532582185a1803b6be0/
Тангенс и котангенс в решении задач по стереометрии. Тригонометрические функции. Часть 9. Геометрия 10-11 класс. https://rutube.ru/video/22ce4c90678e252c22f2084eb1ec14a3/
Как найти гипотенузу по катету и противолежащему или прилежащему углу.
Тригонометрические функции в геометрии. Часть 5. Геометрия 9 класс. https://rutube.ru/video/9393cb6043b9878b49883195db02d251/
Как найти противо- и прилежащие катеты по углу и гипотенузе. Как найти площадь треугольника, параллелограмма и трапеции. Тригонометрические функции. Часть 6. Геометрия 9 класс. https://rutube.ru/video/01cfdff903c6c37227f510c5f4bf7984/
Как найти объем пирамиды (конуса) по боковому ребру (образующей) и углу между боковым ребром (образующей) и плоскостью основания. Тригонометрические функции. Часть 7. Геометрия 10-11 класс. https://rutube.ru/video/a246217e2de6f5960fb55a3e77b904d0/
Как найти противо- и прилежащие катеты по углу и другому катету. Как найти площадь треугольника и параллелограмма. Тригонометрические функции. Часть 8. Геометрия 9 класс. https://rutube.ru/video/5b374b4961980532582185a1803b6be0/
Тангенс и котангенс в решении задач по стереометрии. Тригонометрические функции. Часть 9. Геометрия 10-11 класс. https://rutube.ru/video/22ce4c90678e252c22f2084eb1ec14a3/
Как найти гипотенузу по катету и противолежащему или прилежащему углу. Тригонометрические функции. Часть 10. Геометрия 9 класс. https://rutube.ru/video/d4f247808a953357f1ed1c2a66e6fe73/
Как найти значения длин сторон прямоугольного треугольника по значениям тригонометрических функций. Тригонометрические функции. Часть 11. Геометрия 9 класс. https://rutube.ru/video/3f37a5cab19ba4a197de56e09b20237f/
Основное тригонометрическое тождество. Упрощение тригонометрических выражений. Тригонометрия. Геометрия 9 класс. Алгебра 10 класс. Часть 12. https://rutube.ru/video/458402dea2fc63846652e01cf35d69f3/
#ОсновныеФормулыТригонометрии #ОсновныеФормулыТригонометрии9 #ОсновныеФормулыТригонометрии10 #ОсновныеТригонометрическиеТождества #ДоказатьОсновныеТригонометрическиеТождества #ТождестваТригонометрии #ОсновныеТригонометрическиеТождестваФормулы #ОсновноеТригонометрическоеТождествоСинус #ОсновноеТригонометрическоеТождествоКосинус #ТригонометрическоеТождествоТангенс #ТригонометрическоеТождествоКотангенс #МатематикаОтБаканчиковой
доказать основные тригонометрические тождества, тождества тригонометрии, основное тригонометрическое тождество формулы, основное тригонометрическое тождество синус, основное тригонометрическое тождество косинус, тригонометрическое тождество тангенс, тригонометрическое тождество котангенс, основные тригонометрические формулы, тригонометрические формулы 9 класс, тригонометрические формулы 10 класс
Тригонометрические функции. Часть 10. Геометрия 9 класс. https://rutube.ru/video/d4f247808a953357f1ed1c2a66e6fe73/
Как найти значения длин сторон прямоугольного треугольника по значениям тригонометрических функций. Тригонометрические функции. Часть 11. Геометрия 9 класс. https://rutube.ru/video/3f37a5cab19ba4a197de56e09b20237f/
Основное тригонометрическое тождество. Упрощение тригонометрических выражений. Тригонометрия. Геометрия 9 класс. Алгебра 10 класс. Часть 12. https://rutube.ru/video/458402dea2fc63846652e01cf35d69f3/
#ОсновныеФормулыТригонометрии #ОсновныеФормулыТригонометрии9 #ОсновныеФормулыТригонометрии10 #ОсновныеТригонометрическиеТождества #ДоказатьОсновныеТригонометрическиеТождества #ТождестваТригонометрии #ОсновныеТригонометрическиеТождестваФормулы #ОсновноеТригонометрическоеТождествоСинус #ОсновноеТригонометрическоеТождествоКосинус #ТригонометрическоеТождествоТангенс #ТригонометрическоеТождествоКотангенс #МатематикаОтБаканчиковой
доказать основные тригонометрические тождества, тождества тригонометрии, основное тригонометрическое тождество формулы, основное тригонометрическое тождество синус, основное тригонометрическое тождество косинус, тригонометрическое тождество тангенс, тригонометрическое тождество котангенс, основные тригонометрические формулы, тригонометрические формулы 9 класс, тригонометрические формулы 10 класс Можно сказать, что отношения сторон по отношению к любому из его острых углов представляют собой тригонометрическое отношение этого конкретного угла.
Можно сказать, что отношения сторон по отношению к любому из его острых углов представляют собой тригонометрическое отношение этого конкретного угла.

 Прямоугольный треугольник имеет три стороны: гипотенузу, противоположную сторону (перпендикуляр) и прилежащую сторону (основание). Самая длинная сторона известна как гипотенуза, противоположная сторона перпендикулярна, а смежная сторона находится там, где лежат и гипотенуза, и противоположная сторона.
Прямоугольный треугольник имеет три стороны: гипотенузу, противоположную сторону (перпендикуляр) и прилежащую сторону (основание). Самая длинная сторона известна как гипотенуза, противоположная сторона перпендикулярна, а смежная сторона находится там, где лежат и гипотенуза, и противоположная сторона. Их называют тригонометрическими функциями. Синус, косинус, секанс, косеканс, тангенс и котангенс — шесть тригонометрических функций.
Их называют тригонометрическими функциями. Синус, косинус, секанс, косеканс, тангенс и котангенс — шесть тригонометрических функций.
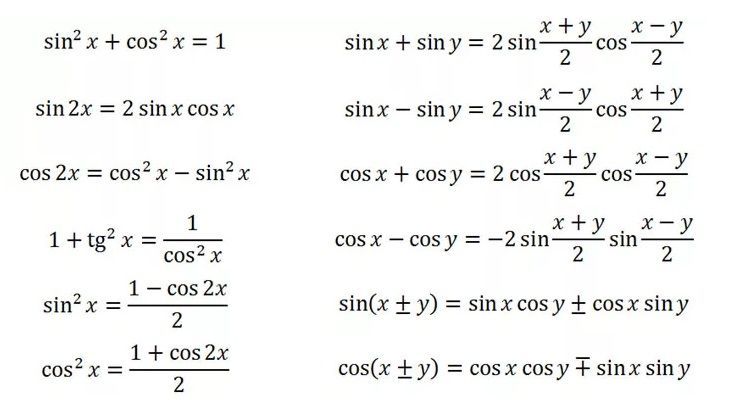
 )
) )
) )
) )
) )
) )
) )
) )
) )/3
)/3
 $
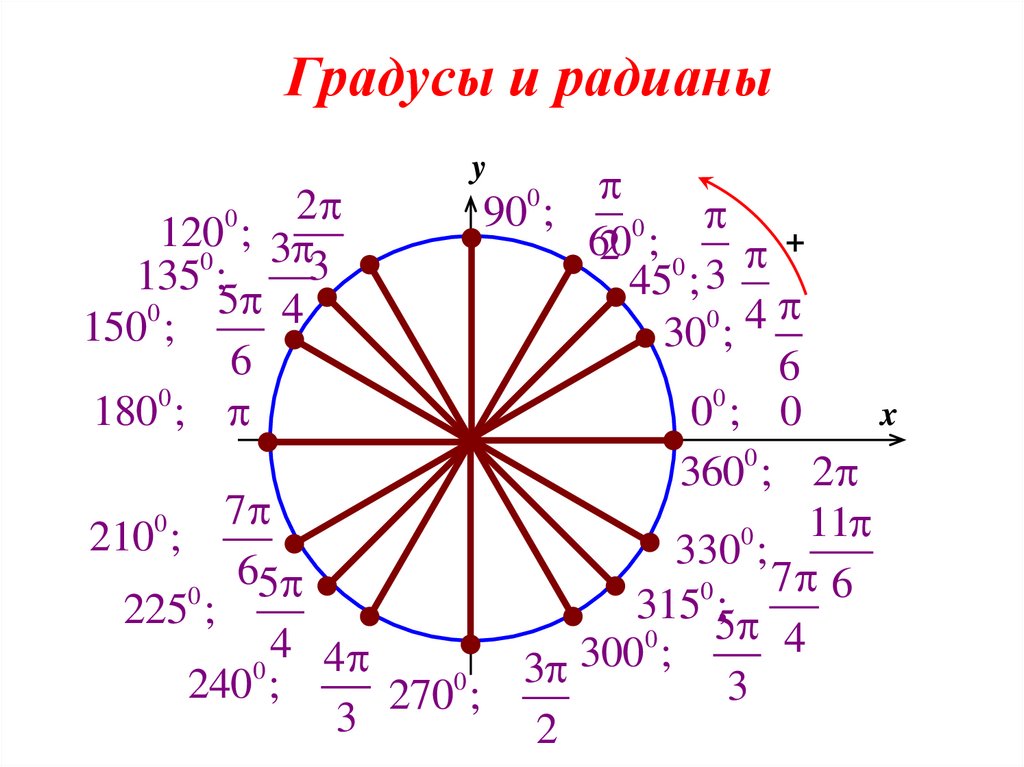
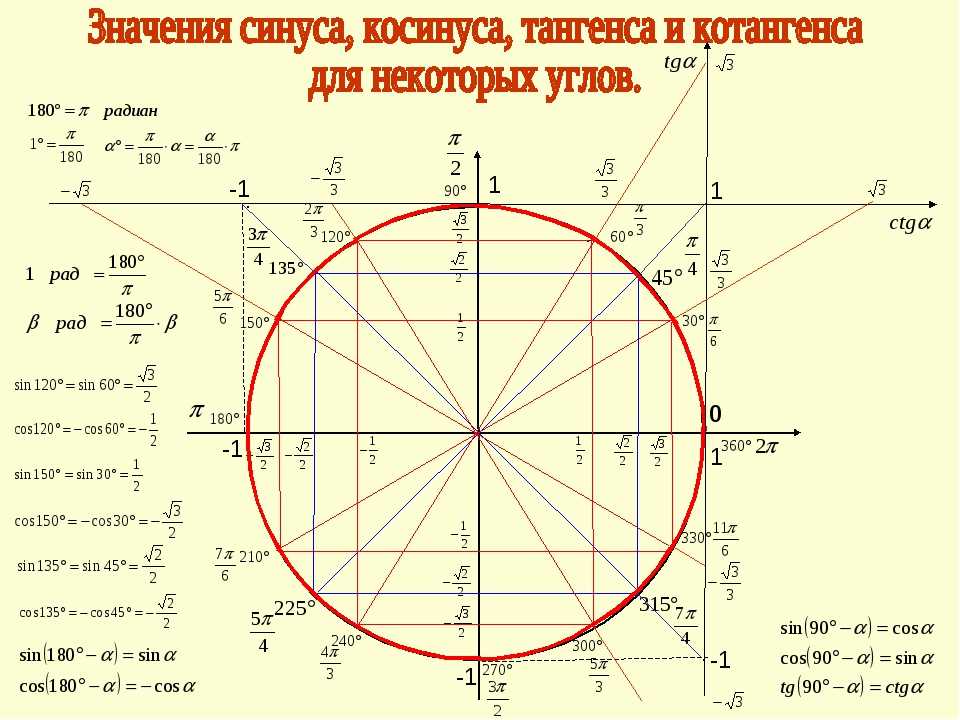
Радианная мера спешит на помощь!
$
Радианная мера спешит на помощь!

 (Причудливый набор текста — это запоминающее устройство!)
(Причудливый набор текста — это запоминающее устройство!)  $
$ 


 Эта информация важна для выбора прибора учета электроэнергии. Обладая данными о коэффициенте трансформации используемого оборудования, можно понять, во сколько раз снижена электрическая нагрузка. Узнать эти показатели, можно проведя определенные расчеты.
Эта информация важна для выбора прибора учета электроэнергии. Обладая данными о коэффициенте трансформации используемого оборудования, можно понять, во сколько раз снижена электрическая нагрузка. Узнать эти показатели, можно проведя определенные расчеты. Умножаем обе цифры
Умножаем обе цифры 


 Полный ответ приведен ниже (упрощенный до самой низкой формы):
Полный ответ приведен ниже (упрощенный до самой низкой формы):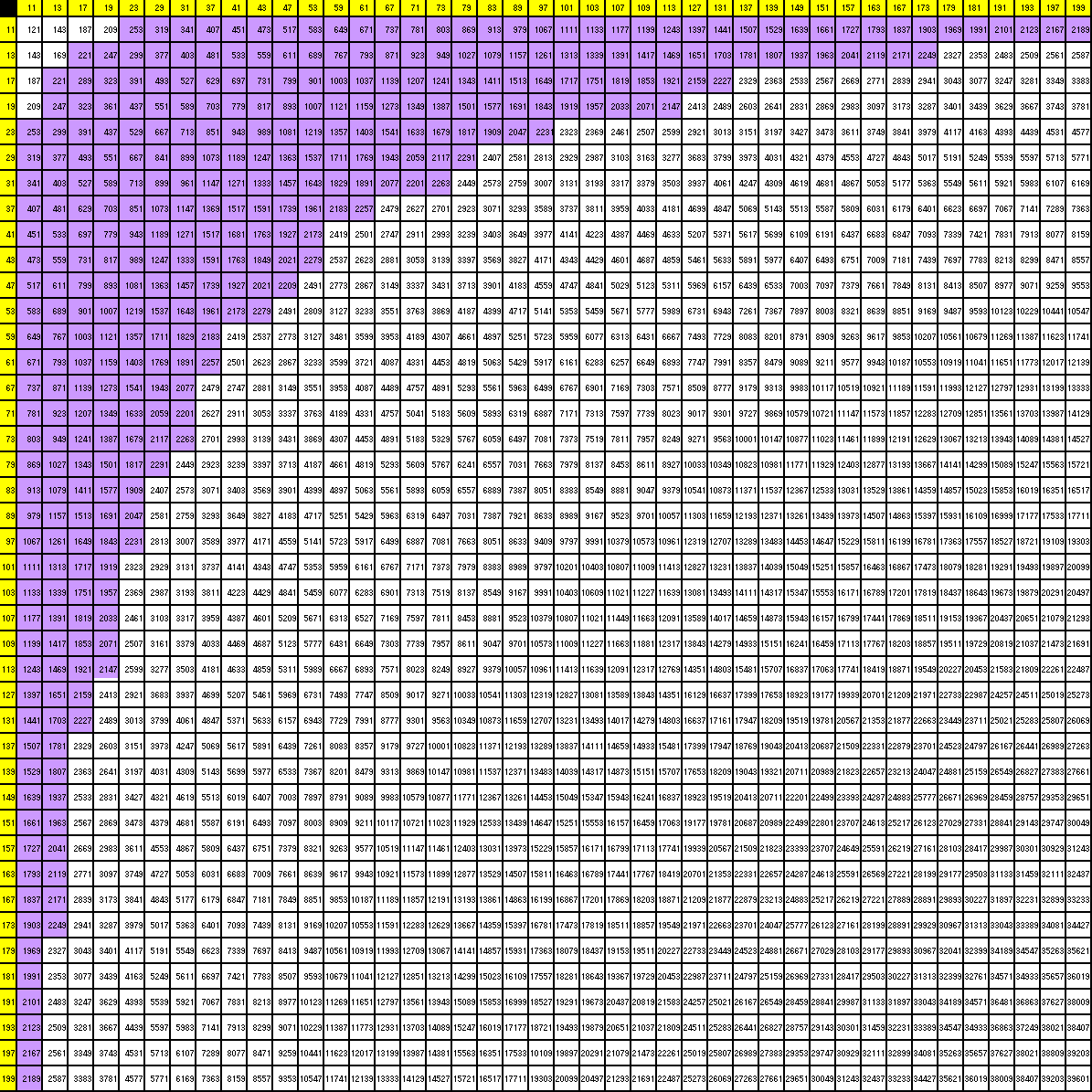
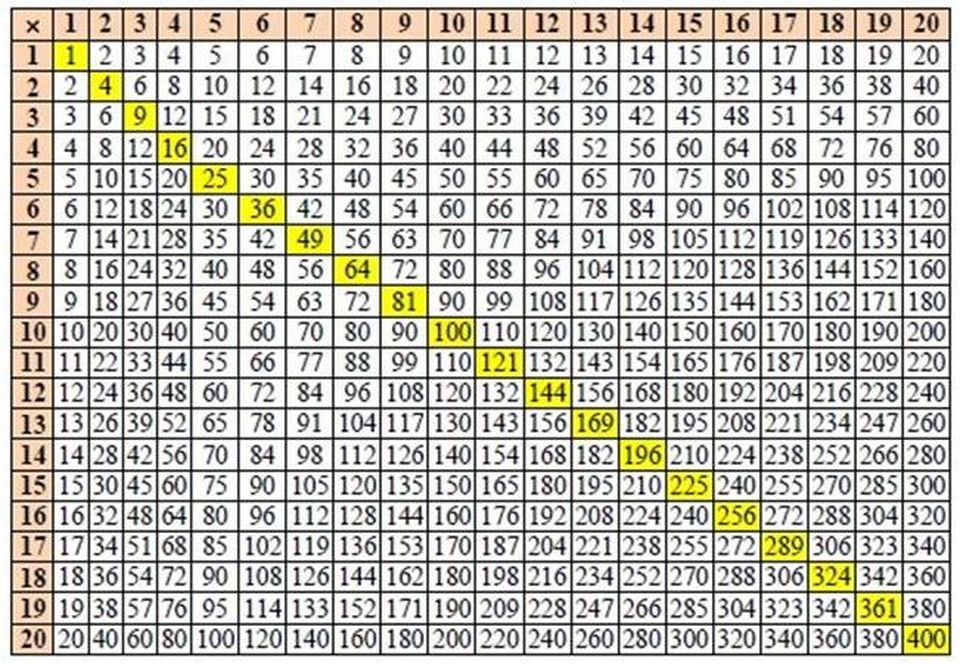 Они являются результирующим произведением натуральных чисел и 60. Другими словами, мы можем сказать, что числа, кратные 60, — это числа, которые можно разделить на 60 без остатка. Мы можем создать n число, кратное 60, просто умножив 60 на n натуральных чисел.
Они являются результирующим произведением натуральных чисел и 60. Другими словами, мы можем сказать, что числа, кратные 60, — это числа, которые можно разделить на 60 без остатка. Мы можем создать n число, кратное 60, просто умножив 60 на n натуральных чисел. Первые пять кратных 6 равны 6, 12, 18, 24 и 30. Путем умножения каждого кратного 6 на 10, мы можем получить числа, кратные 60.
Первые пять кратных 6 равны 6, 12, 18, 24 и 30. Путем умножения каждого кратного 6 на 10, мы можем получить числа, кратные 60.