Исследование функции онлайн. Решение задач на построение графика и полное исследование функции он-лайн
Исследование функции производится по четкой схеме и требует от студента твердых знаний основных математических понятий таких, как область определения и значений, непрерывность функции, асимптота, точки экстремума, четность, периодичность и т.п. Студент должен свободно дифференцировать функции и решать уравнения, которые порой бывают очень замысловатыми.
То есть данное задание проверяет существенный пласт знаний, любой пробел в которых станет препятствием к получению правильного решения. Особенно часто сложности возникают с построением графиков функций. Эта ошибка сразу бросается в глаза преподавателю и может очень сильно подпортить вашу оценку, даже если все остальное было сделано правильно. Здесь вы можете найти задачи на исследование функции онлайн: изучить примеры, скачать решения, заказать задания.
Исследовать функцию и построить график: примеры и решения онлайн
Мы приготовили для вас множество готовых исследований функций, как платных в решебнике, так и бесплатных в разделе Примеры исследований функций. На основе этих решенных заданий вы сможете детально ознакомиться с методикой выполнения подобных задач, по аналогии выполнить свое исследование.
Мы предлагаем готовые примеры полного исследования и построения графика функции самых распространенных типов: многочленов, дробно-рациональных, иррациональных, экспоненциальных, логарифмических, тригонометрических функций. К каждой решенной задаче прилагается готовый график с выделенными ключевыми точками, асимптотами, максимумами и минимумами, решение ведется по алгоритму исследования функции.
Решенные примеры, в любом случае, станут для вас хорошим подспорьем, так как охватывают самые популярные типы функций. Мы предлагаем вам сотни уже решенных задач, но, как известно, математических функций на свете — бесконечное количество, а преподаватели — большие мастаки выдумывать для бедных студентов все новые и новые заковыристые задания. Так что, дорогие студенты, квалифицированная помощь вам не помешает.
Решение задач на исследование функции на заказ
На этот случай наши партнеры предложат вам другую услугу — полное исследование функции онлайн на заказ. Задание будет выполнено для вас с соблюдением всех требований к алгоритму решения подобных задач, что очень порадует вашего преподавателя.
Мы сделаем для вас полное исследование функции: найдем область определения и область значений, исследуем на непрерывность и разрывность, установим четность, проверим вашу функцию на периодичность, найдем точки пересечения с осями координат. Ну и, конечно же, дальше с помощью дифференциального исчисления: разыщем асимптоты, вычислим экстремумы, точки перегиба, построим сам график.
Представьте себе: вы получите готовое, гарантированно правильно решенное задание за скромную сумму! Может быть, вам осталось решить только один, самый сложный пример, с которым вы сами никак не справитесь? Не затягивайте, закажите его или скачайте и сдавайте зачет на отлично!
Еще про задачи исследования функции:
Исследовать функцию и построить график
Краткая теория
Наиболее наглядное представление о ходе изменения функции дает ее график. Поэтому построение графика является заключительным этапом исследования функции, в котором используются все результаты ее исследования.
Схема исследования функции с последующим построением графика такова:
- Исследование области определения функции.
- Исследование функции на четность и нечетность.
- Нахождение точек пересечения графика с осями координат
- Исследование функции на точки разрыва. Нахождение вертикальных асимптот. Нахождение горизонтальных и наклонных асимптот.
- Исследование функции на экстремум и интервалы монотонности функции.
- Исследование функции на интервалы выпуклости и вогнутости графика функции. Нахождение точек перегиба графика функции.
- Построение графика функции.
Полученные данные следует использовать для построения графика функции. Если исследуемая функция является четной или нечетной, то ее достаточно исследовать при неотрицательных значениях аргумента из множества ее задания и принять во внимание, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Если, например, функция имеет период , то следует построить график на отрезке , а затем продолжить его периодически на всю числовую ось.
Кроме того, если полученных данных окажется недостаточно, то следует, воспользовавшись уравнением , найти дополнительные точки графика, в которых его изменение менее ясно.
Разумеется, в процессе исследования функции не обязательно придерживаться приведенной схемы, иногда порядок исследования полезно выбрать, исходя из конкретных особенностей данной функции.
Примеры решения задач
Задача 1
Исследовать функцию и построить ее график:
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция является четной
3) Находим точки пересечения с осями координат:
График функции пересекает ось в точках и . Ось график функции не пересекает.
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
В точке существует разрыв 2-го рода.
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–горизонтальная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Первая производная на области определения в нуль не обращается
-функция возрастает
-функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции вогнутый
– график функции вогнутый
7) График функции имеет вид:
Задача 2
Исследовать функцию и построить ее график:
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция является нечетной
3) График функции оси координат не пересекает
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
В точке существует разрыв 2-го рода.
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–наклонная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Приравняем найденную производную к нулю и решим полученное уравнение:
-функция возрастает
-функция убывает
-функция убывает
-функция возрастает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции выпуклый
– график функции вогнутый
7) График функции имеет вид:
Задача 3
Исследовать функцию и построить ее график.
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция не обладает свойствами четности — нечетности
3) Находим точки пересечения с осями координат:
График пересекает ось в точке (-0618, 0) и (1.618, 0)
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.
Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.
Для нахождения наклонной асимптоты вычисляем пределы:
Прямая –горизонтальная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Приравняем найденную производную к нулю и решим полученное уравнение:
Полученное уравнение действительных корней не имеет
– функция убывает
– функция убывает
– функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
– график функции выпуклый
– график функции вогнутый
– график функции выпуклый
– график функции вогнутый
7) График функции имеет вид:
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.
Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.
Исследование функции онлайн, функции третьей , четвертой степени
Исследование функции онлайн, функции третьей , четвертой степени
Исследуем функции онлайн, заданной формулой: Область определения: Данная функция определена для: Переносим известные величины в правую часть неравенства c противоположным знаком. Полученное решение отметим на рисунке. Ответ: . Для исследовании функции онлайн найдем первую производную: Воспользуемся формулой производной частного. Воспользуемся свойством степеней, Воспользуемся правилом нахождения производной для сложной функции. Раскрываем скобки. Выносим общий множитель. Воспользуемся свойством степеней. Вторая производная: Для исследования функции оналай найдём вторую производную. Вторая производная это производная от первой производной. Воспользуемся формулой производной частного. Воспользуемся свойством степеней. Воспользуемся правилом нахождения производной для сложной функции. Выносим общий множитель. Воспользуемся свойством степеней. Точек пересечения с осью х нет Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю. Дробь обращается в нуль тогда, когда числитель равен нулю. Левая часть уравнения принимает только положительные значения. Ответ: нет решений. Точки пересечения с осью y: Пусть Вертикальные асимптоты: Определим значения аргумента, при которых знаменатель функции обращается в ноль Перенесем известные величины в правую часть уравнения. Горизонтальные асимптоты: нет. Наклонные асимптоты: Для нахождения наклонных асимптот преобразуем исходное выражение. Для возведения в степень воспользуемся биноминальной формулой. Раскрываем скобки. Предел разности исходной функции и функции на бесконечности равен нулю. Критические точки: Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение. Дробь обращается в нуль тогда, когда числитель равен нулю. Решаем уравнение методом разложения на множители. Разложим одночлены в сумму нескольких. Изменяем порядок действий. Производим группировку. Выносим общий множитель. Выносим общий множитель. Теперь решение исходного уравнения разбивается на отдельные случаи. Случай . Перенесем известные величины в правую часть уравнения. Итак,ответ этого случая: нет решений. Случай . Находим дискриминант. Дискриминант положителен, значит уравнение имеет два корня. Воспользуемся формулой корней квадратного уравнения. Ответ этого случая: Ответ: Возможные точки перегиба: нет Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение. Дробь обращается в нуль тогда, когда числитель равен нулю. Следующее уравнение равносильно предыдущему. Находим дискриминант. Дискриминант отрицателен, значит уравнение не имеет корней. Ответ: нет решений. Точки разрыва: Симметрия относительно оси ординат: нет Функция f(x) называется четной, если f(-x)f(x). Выносим знак минус из произведения. Выносим знак минус из произведения. Приводим дроби к общему знаменателю. Производим сложение дробей с одинаковыми знаменателями. Для возведения в степень воспользуемся биноминальной формулой. Раскрываем скобки. Изменяем порядок действий. Приводим подобные члены. Раскрываем скобки. Приводим подобные члены. Разложим числитель дроби на множители. Симметрия относительно начала координат: нет Функция f(x) называется нечетной, если f(-x)=-f(x) Выносим знак минус из произведения. Выносим знак минус из произведения. Приводим дроби к общему знаменателю. Производим сложение дробей с одинаковыми знаменателями. Для возведения в степень воспользуемся биноминальной формулой. Изменяем порядок действий. Приводим подобные члены. Выносим знак минус из произведения. Разложим числитель дроби на множители. Тестовые интервалы: Относительные экстремумы: Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум Проходя через точку максимума. производная функции меняет знак с (+) на (-). Относительный максимум . Данные таблицы нанесем на координатную плоскость. Используя результаты исследования функции, построим ее график. Множество значений функции следующее:
Урок 48. функции. свойства функций и их графики. исследование функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
- функция, аргумент функции, значение функции
- график функции, преобразование графика функции
- свойства функции, исследование свойств функции
Глоссарий по теме урока
Определение
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
у — зависимая переменная, значение функции
Определение
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Определение
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Определение
Функция у = f(х) называется четной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
- для любого х из области определения выполняется равенство f(-х)=f(х).
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=-f(х).
Определение
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Определение
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1<х2, выполняется неравенство у1<у2.
Функция у=f(x) убывает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких что, х1<х2, выполняется неравенство у1>у2.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Дополнительная литература:
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
https://mathb-ege.sdamgia.ru/test?theme=177
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
- Множество значений функции
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
- Четность / нечетность функции
D(y)= — симметрична относительно нуля
,
следовательно, функция четная и ее график симметричен относительно оси ОУ
- Нули функции
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
- Промежутки знакопостоянства
у>0 при
у<0 при
- Монотонность
Найдем производную
Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.
Определим знаки производной в полученных промежутках.
точки -1, 1 – выколоты, 0 — закрашена
Производная положительна, а значит, функция возрастает при .
Производная отрицательна, а значит, функция убывает при
- Экстремум
х=0 – стационарная точка.
В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.
Значение функции в точке максимума
- Дополнительные точки
у(0,5)= у(-0,5)=-5/3; у(2)=у(-2)=5/3; у(3)= у(-3)=5/4
- Отразим найденные свойства графически, построим график функции
2. Решение задачи на оптимизацию
Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.
В решении таких задач выделяют 3 основных этапа:
1 этап. «Перевод» задачи на язык функций:
- вводят независимую переменную х
- выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
- выражают у через х и другие известные величины
- устанавливают по условию задачи границы изменения переменной х
2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.
Рассмотрим план решения на примере задачи.
Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
Решение:
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x2 у.е.
Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x)2 (у.е.)
Всем рабочим нужно заплатить 4x2+(24 — x)2 = 5x2 -48x+576 (у.е.)
Причем 0≤ x ≤ 24, x ϵ N.
2 этап.
Рассмотрим функцию f(x)=5x2-48x+576.
Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x0 = 4,8 .
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
Функции |
у=0 |
у=sin(x+5π/2) |
у=lg(x+10) |
Решение:
- у=0
область определения – множество действительных чисел – симметрична относительно нуля
у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.
Данная функция одновременно четна и нечетна.
- у=sin(x+5π/2)
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
- у=lg(x+10)
логарифмируемое выражение должно быть положительным
x+10>0; x>-10
D(y): x>-10
Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
Зайдем с другого конца, выразим -f(x):
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
Ответ:
Функции | Четность / нечетность |
у=0 | и четная, и нечетная |
у=sin(x+5π/2) | четная |
у=lg(x+10) | общего вида |
нечетная |
2.
Решение:
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у<7
Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:
Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.
Выполним построения выделенных функций.
Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.
Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.
Ответ:
Исследование функции на экстремум (примеры). Практикум по математическому анализу. Урок 53
Примеры. Исследовать на максимум и минимум функции:
1) ; 2) ; 3) ; 4) ; 5) ; 6) .
Решение. 1) Согласно правилу исследования функции на экстремум:
I. Находим производную: и критические точки. Полагая , получим . Функция определена и непрерывна на всей числовой оси. Поэтому точки и являются критическими.
Других критических точек нет, так как производная существует всюду.
II. Исследуем критические точки, определяя знак слева и справа от каждой этой точки (по правилу IIа). Для сокращения вычислений и для наглядности это исследование удобно записать в виде следующей таблицы:
В первой строке помещены все критические точки в порядке расположения их на числовой оси; между ними вставлены промежуточные точки, расположенные слева и справа от критических точек. Во второй строке помещены знаки производной в указанных промежуточных точках, т. е. знаки и .
В третьей строке — заключение о поведении функции. Исследуемая функция имеет одну точку экстремума — точку максимума , где . До этой точки в интервале функция неизменно возрастает, а после нее в интервале она неизменно убывает (рис. 45).
2) I. Ищем критические точки. Производная обращается в нуль при и не существует (разрывна) при . Однако критическими точками являются только точки и : они лежат внутри области определения функции , которая представляет отрезок [ — 1; 1], и в них эта функция непрерывна. Точки и не являются критическими, так как они лежат не внутри области определения функции , а на ее границах.
II. Исследуем критические точки по знаку производной в соседних с ними точках. Составим следующую таблицу:
Согласно этой таблице функция и имеет две точки экстремума: точку минимума , где и точку максимума ,где (рис. 46).
3) I. Находим производную
и критические точки: при ; не существует (равна ) при . Функция определена и непрерывна на всей числовой оси. Поэтому обе найденные точки являются критическими.
II. Исследуем критические точки по знаку производной в соседних с ними точках. Составим таблицу:
Из таблицы следует, что функция имеет две точки экстремума: точку максимума , где , и точку минимума , где (рис. 47).
4) I. Найдем критические точки. Производная равна нулю в точках . Эти точки являются критическими, так как функция определена и непрерывна на всей числовой оси. Производная существует всюду. Поэтому других критических точек функция не имеет.
II. Исследуем критические точки по знаку второй производной в самих этих точках (по правилу II б): , следовательно, критическая точка есть точка максимума, где , поэтому критическая точка есть точка минимума, где (рис. 48).
5) I. Ищем производную и критические точки: обращается в нуль в точке . В этой точке функция непрерывна, но она не лежит внутри области определения функции , которая представляет интервал .
Поэтому точка не является критической; не обращается в нуль в других точках и существует во всей области определения функции. Поэтому функция , как не имеющая ни одной критической точки, не имеет экстремума. Во всей своей области определения она неизменно (монотонно) возрастает, ибо во всей этой области (рис. 49).
Если не учесть, что точка не лежит внутри области определения функции , то, применяя правило IIб, , приходим к ошибочному заключению, что в этой точке функция имеет минимум.
6) I. Находим критические точки: при .
Все точки являются критическими, так как функция определена и непрерывна на всей числовой оси; существует всюду, поэтому других критических точек нет.
II. Исследуем критические точки по знаку второй производной в самих этих точках: . При четном , , точки являются точками минимума, где ; при нечетном , , точки являются точками максимума, где (рис. 50). Здесь оказалось, что у функции максимумы и минимумы строго чередуются. То же будет и у любой непрерывной функции, имеющей несколько экстремумов.
Исследовать функцию на непрерывность онлайн с подробным решением. Точки разрыва функции и их виды
Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!
На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность . Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.
Что нужно знать и уметь? Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции . Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций . Также желательно ознакомиться с геометрическими преобразованиями графиков , поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!
Непрерывность функции. Точки разрыва и их классификация
Понятие непрерывности функцииРассмотрим некоторую функцию , непрерывную на всей числовой прямой:
Или, говоря лаконичнее, наша функция непрерывна на (множестве действительных чисел).
Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.
При этом следует чётко отличать два простых понятия: область определения функции и непрерывность функции . В общем случае это не одно и то же . Например:
Данная функция определена на всей числовой прямой, то есть для каждого значения «икс» существует своё значение «игрека» . В частности, если , то . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: .
Однако эта функция не является непрерывной на ! Совершенно очевидно, что в точке она терпит разрыв . Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги. Немного позже мы рассмотрим классификацию точек разрыва.
Непрерывность функции в точке и на интервалеВ той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке .
Теория математического анализа даёт определение непрерывности функции в точке с помощью «дельта» и «эпсилон» окрестностей, но на практике в ходу другое определение, которому мы и уделим самое пристальное внимание.
Сначала вспомним односторонние пределы , ворвавшиеся в нашу жизнь на первом уроке о графиках функций . Рассмотрим будничную ситуацию:
Если приближаться по оси к точке слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси к точке (малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела :
Обратите внимание на запись (читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует , по сути это и обозначает, что мы подходим к числу с левой стороны.
Аналогично, если приближаться к точке «ка» справа (синяя стрелка), то «игреки» придут к тому же значению , но уже по зелёной стрелке, и правосторонний предел оформится следующим образом:
«Добавка» символизирует , и запись читается так: «икс стремится к ка справа».
Если односторонние пределы конечны и равны (как в нашем случае): , то будем говорить, что существует ОБЩИЙ предел . Всё просто, общий предел – это наш «обычный» предел функции , равный конечному числу.
Заметьте, что если функция не определена при (выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях , выражения означают, что «икс» бесконечно близко приближается к точке , при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ , определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция .
Определение : функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке: .
Определение детализируется в следующих условиях:
1) Функция должна быть определена в точке , то есть должно существовать значение .
2) Должен существовать общий предел функции . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: .
3) Предел функции в данной точке должен быть равен значению функции в этой точке: .
Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке .
Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале , если она непрерывна в каждой точке данного интервала.
В частности, многие функции непрерывны на бесконечном интервале , то есть на множестве действительных чисел . Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения , так, например, логарифмическая функция непрерывна на интервале . Надеюсь, к данному моменту вы достаточно хорошо представляете, как выглядят графики основных функций. Более подробную информацию об их непрерывности можно почерпнуть у доброго человека по фамилии Фихтенгольц.
С непрерывностью функции на отрезке и полуинтервалах тоже всё несложно, но об этом уместнее рассказать на уроке о нахождении минимального и максимального значений функции на отрезке , а пока голову забивать не будем.
Классификация точек разрываУвлекательная жизнь функций богата всякими особенными точками, и точки разрыва лишь одна из страничек их биографии.
Примечание : на всякий случай остановлюсь на элементарном моменте: точка разрыва – это всегда отдельно взятая точка – не бывает «несколько точек разрыва подряд», то есть, нет такого понятия, как «интервал разрывов».
Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода . У каждого типа разрыва есть свои характерные особенности, которые мы рассмотрим прямо сейчас:
Точка разрыва первого родаЕсли в точке нарушено условие непрерывности и односторонние пределы конечны , то она называется точкой разрыва первого рода .
Начнём с самого оптимистичного случая. По первоначальной задумке урока я хотел рассказать теорию «в общем виде», но чтобы продемонстрировать реальность материала, остановился на варианте с конкретными действующими лицами.
Уныло, как фото молодожёнов на фоне Вечного огня, но нижеследующий кадр общепринят. Изобразим на чертеже график функции :
Данная функция непрерывна на всей числовой прямой, кроме точки . И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
(Условие №2 непрерывности выполнено).
Но функция не определена в точке , следовательно, нарушено Условие №1 непрерывности, и функция терпит разрыв в данной точке.
Разрыв такого вида (с существующим общим пределом ) называют устранимым разрывом . Почему устранимым? Потому что функцию можно доопределить в точке разрыва:
Странно выглядит? Возможно. Но такая запись функции ничему не противоречит! Теперь разрыв устранён и все счастливы:
Выполним формальную проверку:
2) – общий предел существует;
3)
Таким образом, все три условия выполнены, и функция непрерывна в точке по определению непрерывности функции в точке.
Впрочем, ненавистники матана могут доопределить функцию нехорошим способом, например :
Любопытно, что здесь выполнены первые два условия непрерывности:
1) – функция определена в данной точке;
2) – общий предел существует.
Но третий рубеж не пройден: , то есть предел функции в точке не равен значению данной функции в данной точке.
Таким образом, в точке функция терпит разрыв.
Второй, более грустный случай носит название разрыва первого рода со скачком . А грусть навевают односторонние пределы, которые конечны и различны . Пример изображён на втором чертеже урока. Такой разрыв возникает, как правило, в кусочно-заданных функциях , о которых уже упоминалось в статье о преобразованиях графиков .
Рассмотрим кусочную функцию и выполним её чертёж. Как построить график? Очень просто. На полуинтервале чертим фрагмент параболы (зеленый цвет), на интервале – отрезок прямой (красный цвет) и на полуинтервале – прямую (синий цвет).
При этом в силу неравенства значение определено для квадратичной функции (зелёная точка), и в силу неравенства , значение определено для линейной функции (синяя точка):
В самом-самом тяжёлом случае следует прибегнуть к поточечному построению каждого куска графика (см. первый урок о графиках функций ).
Сейчас нас будет интересовать только точка . Исследуем её на непрерывность:
2) Вычислим односторонние пределы.
Слева у нас красный отрезок прямой, поэтому левосторонний предел:
Справа – синяя прямая, и правосторонний предел:
В результате получены конечные числа , причем они не равны . Поскольку односторонние пределы конечны и различны : , то наша функция терпит разрыв первого рода со скачком .
Логично, что разрыв не устраним – функцию действительно не доопределить и «не склеить», как в предыдущем примере.
Точки разрыва второго родаОбычно к данной категории хитро относят все остальные случаи разрыва. Всё перечислять не буду, поскольку на практике в 99%-ти процентах задач вам встретится бесконечный разрыв – когда левосторонний или правосторонний, а чаще, оба предела бесконечны.
И, конечно же, самая напрашивающаяся картинка – гипербола в точке ноль. Здесь оба односторонних предела бесконечны: , следовательно, функция терпит разрыв второго рода в точке .
Я стараюсь наполнять свои статьи максимально разнообразным содержанием, поэтому давайте посмотрим на график функции , который ещё не встречался:
по стандартной схеме:
1) Функция не определена в данной точке, поскольку знаменатель обращается в ноль.
Конечно, можно сразу сделать вывод о том, что функция терпит разрыв в точке , но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:
Напоминаю, что под записью понимается бесконечно малое отрицательное число , а под записью – бесконечно малое положительное число .
Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке . Ось ординат является вертикальной асимптотой для графика.
Не редка ситуация, когда оба односторонних предела существуют, но бесконечен только один из них, например:
Это график функции .
Исследуем на непрерывность точку :
1) Функция не определена в данной точке.
2) Вычислим односторонние пределы:
О методике вычисления таких односторонних пределов поговорим в двух последних примерах лекции, хотя многие читатели всё уже увидели и догадались.
Левосторонний предел конечен и равен нулю (в саму точку мы «не заходим»), но правосторонний предел бесконечен и оранжевая ветка графика бесконечно близко приближается к своей вертикальной асимптоте , заданной уравнением (чёрный пунктир).
Таким образом, функция терпит разрыв второго рода в точке .
Как и для разрыва 1-го рода, в самой точке разрыва функция может быть определена. Например, для кусочной функции смело ставим чёрную жирную точку в начале координат. Справа же – ветка гиперболы, и правосторонний предел бесконечен. Думаю, почти все представили, как выглядит этот график.
То, чего все с нетерпением ждали:
Как исследовать функцию на непрерывность?Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:
Пример 1
Исследовать функцию
Решение :
1) Под прицел попадает единственная точка , в которой функция не определена.
2) Вычислим односторонние пределы:
Односторонние пределы конечны и равны.
Таким образом, в точке функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение , и вроде бы получается обычная парабола. НО исходная функция не определена в точке , поэтому обязательна следующая оговорка:
Выполним чертёж:
Ответ : функция непрерывна на всей числовой прямой кроме точки , в которой она терпит устранимый разрыв.
Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.
Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.
Разделаемся с любимыми модулями:
Пример 2
Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение : почему-то студенты боятся и не любят функции с модулем, хотя ничего сложного в них нет. Таких вещей мы уже немного коснулись на уроке Геометрические преобразования графиков . Поскольку модуль неотрицателен, то он раскрывается следующим образом: , где «альфа» – некоторое выражение. В данном случае , и наша функция должна расписаться кусочным образом:
Но дроби обоих кусков предстоит сократить на . Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке , так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие , и первое неравенство сделать строгим:
Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения : перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.
Выполним чертёж. В соответствии с нашими выкладками, слева от точки необходимо начертить фрагмент параболы (синий цвет), а справа – кусок параболы (красный цвет), при этом функция не определена в самой точке :
Если есть сомнения, возьмите несколько значений «икс», подставьте их в функцию (не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.
Исследуем функцию на непрерывность аналитически:
1) Функция не определена в точке , поэтому сразу можно сказать, что не является в ней непрерывной.
2) Установим характер разрыва, для этого вычислим односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Ещё раз заметьте, что при нахождении пределов не имеет значения, определена функция в точке разрыва или нет.
Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования;-)) и завершить задание:
Ответ : функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком.
Иногда требуют дополнительно указать скачок разрыва. Вычисляется он элементарно – из правого предела нужно вычесть левый предел: , то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).
Пример 3
Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
Это пример для самостоятельного решения, примерный образец решения в конце урока.
Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:
Пример 4
Исследовать функцию на непрерывность и построить график функции .
Решение : очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства значение принадлежит прямой (зелёная точка), и в силу неравенство значение принадлежит параболе (красная точка):
Ну вот, в принципе, всё понятно =) Осталось оформить решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
I) Исследуем на непрерывность точку
1)
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Вычислим скачок разрыва как разность правого и левого пределов:
, то есть, график рванул на одну единицу вверх.
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
– односторонние пределы конечны и равны, значит, существует общий предел.
3) – предел функции в точке равен значению данной функции в данной точке.
На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:
Ответ : функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.
Пример 5
Исследовать функцию на непрерывность и построить её график .
Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.
Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:
Пример 6
Дана функция . Исследовать функцию на непрерывность в точках . Построить график.
Решение : и снова сразу выполним чертёж на черновике:
Особенность данного графика состоит в том, что при кусочная функция задаётся уравнением оси абсцисс . Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение относится к ветке тангенса (красная точка), а значение принадлежит прямой .
Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4 подобных примеров:
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Вычислим односторонние пределы:
, значит, общий предел существует.
На всякий пожарный напомню тривиальный факт: предел константы равен самой константе. В данном случае предел нуля равен самому нулю (левосторонний предел).
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
И здесь – предел единицы равен самой единице.
– общий предел существует.
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
Как обычно, после исследования переносим наш чертёж на чистовик.
Ответ : функция непрерывна в точках .
Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).
Небольшая математическая «скороговорка» для самостоятельного решения:
Пример 7
Дана функция . Исследовать функцию на непрерывность в точках . Классифицировать точки разрыва, если они есть. Выполнить чертёж.
Постарайтесь правильно «выговорить» все «слова» =) И график нарисовать поточнее, точность, она везде лишней не будет;-)
Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:
Пример 8
Исследовать на непрерывность функцию и построить её схематический график.
Решение : нехорошие точки очевидны: (обращает в ноль знаменатель показателя) и (обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование.
Определение точки разрыва функции
Конечная точка x 0 называется точкой разрыва функции f(x) ,
если функция определена на некоторой проколотой окрестности точки x 0 ,
но не является непрерывной в этой точке.
То есть, в точке разрыва, функция либо не определена, либо определена, но хотя бы один односторонний предел в этой точке или не существует, или не равен значению f(x 0 ) функции в точке x 0 . См. «Определение непрерывности функции в точке ».
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода , если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва , если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .
Таким образом, точка устранимого разрыва — это точка разрыва первого рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка разрыва называется точкой разрыва второго рода , если она не является точкой разрыва 1-го рода.
То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Исследование функций на непрерывность
При исследовании функций на непрерывность мы используем следующие факты.
- Элементарные функции и обратные к ним непрерывны на своей области определения. К ним относятся следующие функции:
, а также постоянная и обратные к ним функции. См. «Справочник по элементарным функциям ». - Сумма, разность и произведение непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве.
Частное двух непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве, за исключением точек, в которых знаменатель дроби обращается в нуль. См. «Арифметические свойства непрерывных функций » - Сложная функция непрерывна в точке , если функция непрерывна в точке , а функция непрерывна в точке . См. «Предел и непрерывность сложной функции »
Примеры
Пример 1
Задана функция и два значения аргумента и .
Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа, установить вид разрыва; 3) сделать схематический чертеж.
.
Заданная функция является сложной. Ее можно рассматривать как композицию двух функций:
,
.
Тогда
.
Рассмотрим функцию .
Она составлена из функции и постоянных с помощью арифметических операций сложения и деления. Функция является элементарной — степенной функцией с показателем степени 1 . Она определена и непрерывна для всех значений переменной .
Поэтому функция определена и непрерывна для всех ,
кроме точек, в которых знаменатель дроби обращается в нуль. Приравниваем знаменатель к нулю и решаем уравнение:
.
Получаем единственный корень .
Итак, функция определена и непрерывна для всех ,
кроме точки .
Рассмотрим функцию .
Это показательная функция с положительным основанием степени. Она определена и непрерывна для всех значений переменной .
Поэтому заданная функция определена и непрерывна для всех значений переменной ,
кроме точки .
Таким образом, в точке , заданная функция является непрерывной.
График функции y = 4 1/(x+2) .
Рассмотрим точку . В этой точке функция не определена. Поэтому она не является непрерывной. Установим род разрыва. Для этого находим односторонние пределы.
Используя связь между бесконечно большими и бесконечно малыми функциями , для предела слева имеем:
при ,
,
,
.
Здесь мы использовали следующие общепринятые обозначения:
.
Также мы использовали свойство показательной функции с основанием :
.
Аналогично, для предела справа имеем:
при ,
,
,
.
Поскольку один из односторонних пределов равен бесконечности, то в точке разрыв второго рода.
В точке функция непрерывна.
В точке разрыв второго рода,
.
Пример 2
Задана функция .
Найти точки разрыва функции, если они существуют. Указать род разрыва и скачек функции, если есть. Сделать чертеж.
.
График заданной функции.
Функция является степенной функцией с целым показателем степени, равным 1 . Такую функцию также называют линейной. Она определена и непрерывна для всех значений переменной .
В входят еще две функции: и .
Они составлены из функции и постоянных с помощью арифметических операций сложения и умножения:
,
.
Поэтому они также непрерывны для всех .
Поскольку функции, входящие в состав непрерывны для всех , то может иметь точки разрыва только в точках склейки ее составляющих. Это точки и . Исследуем на непрерывность в этих точках. Для этого найдем односторонние пределы.
Рассмотрим точку .
Чтобы найти левый предел функции в этой точке, мы должны использовать значения этой функции в любой левой проколотой окрестности точки .
Возьмем окрестность .
На ней .
Тогда предел слева:
.
Здесь мы использовали тот факт, что функция является непрерывной в точке (как и в любой другой точке). Поэтому ее левый (как и правый) предел равен значению функции в этой точке.
Найдем правый предел в точке .
Для этого мы должны использовать значения функции в любой правой проколотой окрестности этой точки. Возьмем окрестность .
На ней .
Тогда предел справа:
.
Здесь мы также воспользовались непрерывностью функции .
Поскольку, в точке ,
предел слева не равен пределу справа, то в ней функция не является непрерывной — это точка разрыва. Поскольку односторонние пределы конечны, то это точка разрыва первого рода. Скачек функции:
.
Теперь рассмотрим точку .
Тем же способом вычисляем односторонние пределы:
;
.
Поскольку функция определена в точке и левый предел равен правому, то функция непрерывна в этой точке.
Функция имеет разрыв первого рода в точке . Скачек функции в ней: . В остальных точках функция непрерывна.
Пример 3
Определить точки разрыва функции и исследовать характер этих точек, если
.
Воспользуемся тем, что линейная функция определена и непрерывна для всех .
Заданная функция составлена из линейной функции и постоянных с помощью арифметических операций сложения, вычитания, умножения и деления:
.
Поэтому она определена и непрерывна для всех ,
за исключением точек, в которых знаменатель дроби обращается в нуль.
Найдем эти точки. Приравниваем знаменатель к нулю и решаем квадратное уравнение :
;
;
;
.
Тогда
.
Используем формулу:
.
С ее помощью, разложим числитель на множители:
.
Тогда заданная функция примет вид:
(П1) .
Она определена и непрерывна для всех ,
кроме точек и .
Поэтому точки и являются точками разрыва функции.
Разделим числитель и знаменатель дроби в (П1) на :
(П2) .
Такую операцию мы можем проделать, если .
Таким образом,
при .
То есть функции и отличаются только в одной точке: определена при ,
а в этой точке не определена.
Чтобы определить род точек разрыва, нам нужно найти односторонние пределы функции в точках и . Для их вычисления мы воспользуемся тем, что если значения функции изменить, или сделать неопределенными в конечном числе точек, то это не окажет ни какого влияние на величину или существование предела в произвольной точке (см. «Влияние значений функции в конечном числе точек на величину предела »). То есть пределы функции в любых точках равны пределам функции .
Рассмотрим точку .
Знаменатель дроби в функции ,
при в нуль не обращается. Поэтому она определена и непрерывна при .
Отсюда следует, что существует предел при и он равен значению функции в этой точке:
.
Поэтому точка является точкой устранимого разрыва первого рода.
Рассмотрим точку .
Используя связь бесконечно малых и бесконечно больших функций , имеем:
;
.
Поскольку пределы бесконечные, то в этой точке разрыв второго рода.
Функция имеет точку устранимого разрыва первого рода при , и точку разрыва второго рода при .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Подборка онлайн калькуляторов для полного исследования функции и построение графика.
Найти Область определения функции
Вычислить Четность функции
Вычисление точек пересечения графика с осью (нули функции)
Найти экстремумы функции
Точки перегиба, интервалы выпуклости и вогнутости
Построить график функции
Данный калькулятор предназначен для нахождения точек разрыва функции онлайн.
Точки разрыва функции – это точки, в которых функция имеет разрыв, при этом функция в этих точках не является непрерывной.
Существует определенная классификация точек разрыва функции. Точки разрыва функции делятся на точки разрыва первого рода и точки разрыва второго рода.
Точки разрыва первого рода при x=a имеют место быть, если существуют левосторонний и правосторонний пределы: lim(x→a-0)f(x) и lim(x→a+0)f(x). Эти пределы должны быть конечны. Если хотя бы один из односторонних пределов равен нулю или бесконечности, то в таком случае функция имеет точки разрыва второго рода.
Для того чтобы найти точки разрыва функции онлайн, необходимо указать функцию и значение аргумента.
Для получения полного хода решения нажимаем в ответе Step-by-step.
Исследовать функцию, построить график
План исследования функций и построения графика .
Ответ означает следующее: even — функция четная, odd — функция нечетная, neither even nor odd — функция ни четная ни нечетная.
3. Точки пересечения графика функции с осями координат;
4. Непрерывность функции, точки разрыва;
5. Асимптоты графика функции;
6. Интервалы монотоности и критические точки;
7 . Интервалы выпуклости и точки перегиба;
8. Посторение графика на основании проведённого исследования.
Образовательные онлайн сервисы: теория и практика
Решения типовых задач — Математический анализ
Исследовать функцию на непрерывность, определить характер разрыва.
Пример 1 .
Функция не определена в точках, уже нарушено первое условие непрерывности, следовательно, в этих точках функция испытывает разрыв.
Для выяснения характера разрыва нужно вычислить односторонние пределы в точках.
Так как левый предел в точке равен бесконечности, то в ней разрыв II рода.
Так как правый предел в точке равен бесконечности, то в ней разрыв II рода.
Пример 2 Функция определена на всей числовой прямой, но при этом она не является непрерывной, так как, т.е. правый и левый пределы в нуле не равны между собой и не равны значению функции в нуле, нарушены 2 и 3 условия непрерывности. Так как правый и левый пределы в нуле существуют и конечны, то это разрыв I рода.
Пример 3 Функция неопределена в нуле, следовательно, – точка разрыва.
Так как и, то это устранимый разрыв, функцию можно в нуле доопределить “по непрерывности”, положив равной единице.
Пример 4
Функция является элементарной, поэтому она непрерывна в области её определения. В область определения не входят точки, следовательно, они являются точками разрыва данной функции.
Определим тип точек разрыва.
Так как, то точка является точкой
разрыва второго рода функции.
Односторонние пределы функции в точке равны, но функция при не определена, следовательно, является устранимой точкой разрыва первого рода.
Так как заданная функция является четной функцией, то, очевидно, что
И является точкой разрыва второго рода функции.
Для построения эскиза графика функции исследуем поведение функции при
и. Так как функция четная, то
Построим эскиз графика функции.
Предлагаем наиболее хорошие на наш взгляд учебники для самостоятельного изучения математики и экономики
Компактные справочные материалы, формулы по различным разделам высшей математики и экономической статистики.
Некоторые задачи можно решить онлайн, введя числовые значения, с подробным решением.
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно : a должно быть меньше b , иначе график не сможет построиться. Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения a и b
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции.3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Контрольная работа РУ — калькуляторы онлайн
Непрерывность и построение графиков кусочно-заданных функций – сложная тема. Учиться строить графики лучше непосредственно на практическом занятии. Здесь в основном показано исследование на непрерывность.
Известно, что элементарная функция (см. с. 16) непрерывна во всех точках, в которых определена. Поэтому нарушение непрерывности у элементарных функций возможно только в точках двух типов:
а) в точках, где функция «переопределяется»;
б) в точках, где функция не существует.
Соответственно только такие точки и проверяются при исследовании на непрерывность, что показано в примерах.
Для неэлементарных функций исследование сложнее. Например, функция (целая часть числа) определена на всей числовой оси, но терпит разрыв при каждом целомx . Подобные вопросы выходят за рамки пособия.
Перед изучением материала следует повторить по лекции или учебнику, какими (какого рода) бывают точки разрыва.
Исследование кусочно-заданных функций на непрерывность
Функция задана кусочно , если она на разных участках области определения задаётся разными формулами.
Основная идея при исследовании таких функций – выяснить, задана ли функция в тех точках, в которых переопределяется, и как. Затем проверяется, совпадают ли значения функции слева и справа от таких точек.
Пример 1. Покажем, что функция
непрерывна.
Функция
элементарна и потому непрерывна в тех
точках, в которых определена. Но, очевидно,
она определена во всех точках.
Следовательно, во всех точках она и
непрерывна, в том числе при
,
как требует условие.
То же справедливо
для функции
,
и при
она непрерывна.
В таких случаях
непрерывность может нарушаться только
там, где функция переопределяется. В
нашем примере это точка
.
Проверим её, для чего найдём пределы
слева и справа:
Пределы слева и справа совпадают. Остаётся узнать:
а) определена ли
функция в самой точке
;
б) если да, то
совпадает ли
со значениями пределов слева и справа.
По условию, если
,
то
.
Поэтому
.
Видим, что
(все равны числу 2). Это означает, что в
точке
функция
непрерывна .
Итак, функция непрерывна на всей оси,
включая точку
.
Замечания к решению
а) При вычислениях
не играло роли, подставляем мы в конкретную формулу число
или
.
Обычно это важно, когда получается
деление на бесконечно малую величину,
поскольку влияет на знак бесконечности.
Здесь же
и
отвечают только завыбор
функции;
б) как правило,
обозначения
и
равноправны, то же касается обозначений
и
(и справедливо для любой точки, а не
только для
).
Дальше для краткости применяются
обозначения вида
;
в) когда пределы слева и справа равны, для проверки на непрерывность фактически остаётся посмотреть, будет ли одно из неравенств нестрогим . В примере таковым оказалось 2-е неравенство.
Пример 2. Исследуем на непрерывность функцию
.
По тем же причинам,
что в примере 1, непрерывность может
нарушаться только в точке
.
Проверим:
Пределы слева и
справа равны, но в самой точке
функция не определена (неравенства
строгие). Это означает, что
– точкаустранимого
разрыва .
«Устранимый
разрыв» означает, что достаточно или
сделать любое из неравенств нестрогим,
или придумать для отдельной точки
функцию, значение которой при
равно –5, или просто указать, что
,
чтобы вся функция
стала непрерывной.
Ответ: точка
– точка устранимого разрыва.
Замечание 1. В литературе устранимый разрыв обычно считается частным случаем разрыва 1-го рода, однако студентами чаще понимается как отдельный тип разрыва. Во избежание разночтений будем придерживаться 1-й точки зрения, а «неустранимый» разрыв 1-го рода оговаривать особо.
Пример 3. Проверим, непрерывна ли функция
В точке
Пределы слева и
справа различны:
.
Независимо от того, определена ли функция
при
(да) и если да, то чему равна (равна 2),
точка
–точка
неустранимого разрыва 1-го рода .
В точке
происходитконечный
скачок (от
1 к 2).
Ответ: точка
Замечание 2. Вместо
и
обычно пишут
и
соответственно.
Возможен вопрос: чем отличаются функции
и
,
а также их графики? Правильный ответ:
а) 2-я функция не
определена в точке
;
б) на графике 1-й
функции точка
«закрашена», на графике 2-й – нет
(«выколотая точка»).
Точка
,
где обрывается график
,
не закрашена на обоих графиках.
Сложнее исследовать функции, по-разному определённые на трёх участках.
Пример 4. Непрерывна ли функция
?
Так же, как в
примерах 1 – 3, каждая из функций
,
инепрерывна на всей числовой оси, в том
числе – на участке, на котором задана.
Разрыв возможен только в точке
или (и) в точке
,
где функция переопределяется.
Задача распадается на 2 подзадачи: исследовать на непрерывность функции
и
,
причём точка
не представляет интереса для функции
,
а точка
– для функции
.
1-й
шаг. Проверяем
точку
и функцию
(индекс не пишем):
Пределы совпадают.
По условию,
(если пределы слева и справа равны, то
фактически функция непрерывна, когда
одно и из неравенств нестрогое). Итак,
в точке
функция непрерывна.
2-й
шаг. Проверяем
точку
и функцию
:
Поскольку
,
точка
– точка разрыва 1-го рода, и значение
(и то, есть ли оно вообще) уже не играет
роли.
Ответ: функция непрерывна во всех точках, кроме
точки
,
где имеет место неустранимый разрыв
1-го рода – скачок от 6 к 4.
Пример 5. Найти точки разрыва функции
.
Действуем по той же схеме, что в примере 4.
1-й
шаг. Проверяем
точку
:
а)
,
поскольку слева от
функция постоянна и равна 0;
б)
(
– чётная функция).
Пределы совпадают,
но при
функция по условию не определена, и
получается, что
– точка устранимого разрыва.
2-й
шаг. Проверяем
точку
:
а)
;
б)
– значение функции не зависит от
переменной.
Пределы различны:
,
точка
– точка неустранимого разрыва 1-го рода.
Ответ:
– точка устранимого разрыва,
– точка неустранимого разрыва 1-го рода,
в остальных точках функция непрерывна.
Пример 6. Непрерывна ли функция
?
Функция
определена при
,
поэтому условие
превращается в условие
.
С другой стороны,
функция
определена при
,
т.е. при
.
Значит, условие
превращается в условие
.
Получается, что
должно выполняться условие
,
и область определения всей функции –
отрезок
.
Сами по себе
функции
и
элементарны и потому непрерывны во всех
точках, в которых определены – в
частности, и при
.
Остаётся проверить,
что происходит в точке
:
а)
;
Поскольку
,
смотрим, определена ли функция в точке
.
Да, 1-е неравенство – нестрогое относительно
,
и этого достаточно.
Ответ: функция определена на отрезке
и непрерывна на нём.
Более сложные случаи, когда одна из составляющих функций неэлементарна или не определена в какой-либо точке своего отрезка, выходят за рамки пособия.
НФ1. Постройте графики функций. Обратите внимание, определена ли функция в той точке, в которой переопределяется, и если да – каково значение функции (слово «если » в определении функции для краткости пропущено):
1) а)
б)
в)
г)
2) а)
б)
в)
г)
3) а)
б)
в)
г)
4) а)
б)
в)
г)
Пример 7. Пусть
.
Тогда на участке
строим горизонтальную прямую
,
а на участке
строим горизонтальную прямую
.
При этом точка с координатами
«выколота», а точка
«закрашена». В точке
получается разрыв 1-го рода («скачок»),
и
.
НФ2. Исследуйтена непрерывность функции, по-разному определённые на 3-х интервалах. Постройте графики:
1) а)
б)
в)
г)
д)
е)
2) а)
б)
в)
г)
д)
е)
3) а)
б)
в)
г)
д)
е)
Пример 8. Пусть
.
На участке
строим прямую
,
для чего находим
и
.
Соединяем точки
и
отрезком. Сами точки не включаем,
поскольку при
и
функция по условию не определена.
На участке
и
обводим осьOX
(на ней
),
однако точки
и
«выколоты». В точке
получаем устранимый разрыв, а в точке
– разрыв 1-го рода («скачок»).
НФ3. Постройте графики функций и убедитесь в их непрерывности:
1) а)
б)
в)
г)
д)
е)
2) а)
б)
в)
г)
д)
е)
НФ4. Убедитесь в непрерывности функций и постройте их графики:
1) а)
б)
в)
2 а)
б)
в)
3) а)
б)
в)
НФ5. Постройте графики функций. Обратите внимание на непрерывность:
1) а)
б)
в)
г)
д)
е)
2) а)
б)
в)
г)
д)
е)
3) а)
б)
в)
г)
д)
е)
4) а)
б)
в)
г)
д)
е)
5) а)
б)
в)
г)
д)
е)
НФ6. Постройте графики разрывных функций. Обратите внимание на значение функции в той точке, где функция переопределяется (и существует ли оно):
1) а)
б)
в)
г)
д)
е)
2) а)
б)
в)
г)
д)
е)
3) а)
б)
в)
г)
д)
е)
4) а)
б)
в)
г)
д)
е)
5) а)
б)
в)
г)
д)
е)
НФ7. То же задание, что и в НФ6:
1) а)
б)
в)
г)
д)
е)
2) а)
б)
в)
г)
д)
е)
3) а)
б)
в)
г)
д)
е)
4) а)
б)
в)
г)
д)
е)
Непрерывность функции в точке. Функция y = f (x ) называется непре-
рывной в точке x 0 , если:
1) эта функция определена в некоторой окрестности точки x 0 ;
2) существует предел lim f (x ) ;
→ x 0
3) этот предел равен значению функции в точке x 0 , т.е. limf (x )= f (x 0 ) . | ||
x→ x0 | ||
Последнее условие равносильно условию lim | y = 0 , гдеx = x − x 0 – при- | |
x→ 0 | ||
ращение аргумента, y = f (x 0 + | x )− f (x 0 ) – приращение функции, соответст- | |
вующее приращению аргумента | x , т.е. функция | f (x ) непрерывна в точкеx 0 |
тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Односторонняя непрерывность. Функцияy = f (x ) называется непрерыв-
ной слева в точкеx 0 , если она определена на некотором полуинтервале(a ;x 0 ]
и lim f (x )= f (x 0 ) .
x→ x0 − 0
Функция y = f (x ) называется непрерывнойсправа в точкеx 0 , если она оп-
ределена на некотором полуинтервале [ x 0 ;a ) и limf (x )= f (x 0 ) .
x→ x0 + 0
Функция y = f (x ) | непрерывна в точке x 0 | тогда и только тогда, когда она | ||||||
непрерывна | ||||||||
lim f (x )= limf (x )= limf (x )= f (x 0 ) . | ||||||||
x→ x0 + 0 | x→ x0 − 0 | x→ x0 | ||||||
Непрерывность функции на множестве. Функция y = f (x ) называется
непрерывной на множестве X , если она является непрерывной в каждой точкеx этого множества. При этом если функция определена в конце некоторого промежутка числовой оси, то под непрерывностью в этой точке понимается непрерывность справа или слева. В частности, функцияy = f (x ) называетсяне-
прерывной на отрезке [ a; b] , если она
1) непрерывна в каждой точке интервала (a ;b ) ;
2) непрерывна справа в точке a ;
3) непрерывна слева в точке b .
Точки разрыва функции. Точкаx 0 , принадлежащая области определения функцииy = f (x ) , или являющаяся граничной точкой этой области, называется
точкой разрыва данной функции , еслиf (x ) не является непрерывной в этой точке.
Точки разрыва подразделяются на точки разрыва первого и второго рода:
1) Если существуют конечные пределы lim f (x )= f (x 0 − 0) и
x→ x0 − 0
f (x )= f (x 0 + 0) , причем не все три числаf (x 0 − 0) ,f (x 0 + 0) , | f (x 0 ) равны | ||
x→ x0 + 0 | |||
между собой, то x 0 | называется точкой разрыва I рода. | ||
В частности, если левый и правый пределы функции в точке x 0 | равны меж- | ||
собой, но | не равны значению функции в этой точке: | ||
f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , то x 0 называется точкой устранимого разрыва.
В этом случае, положив f (x 0 )= A , можно видоизменить функцию в точкеx 0
так, чтобы она стала непрерывной (доопределить функцию по непрерывности ). Разностьf (x 0 + 0)− f (x 0 − 0) называетсяскачком функции в точке x 0 .
Скачок функции в точке устранимого разрыва равен нулю.
2) Точки разрыва, не являющиеся точками разрыва первого рода, называются точками разрыва II рода . В точках разрыва II рода не существует или бесконечен хотя бы один из односторонних пределовf (x 0 − 0) иf (x 0 + 0) .
Свойства функций, непрерывных в точке.
f (x) | и g (x ) непрерывны в точкеx 0 , то функции | ||
f (x )± g (x ) , | f (x )g (x ) и | f (x) | (где g (x )≠ 0) также непрерывны в точкеx . |
g(x) | |||
2) Если функция u (x ) непрерывна в точкеx 0 , а функцияf (u ) непрерывна
в точке u 0 = u (x 0 ) , то сложная функцияf (u (x )) непрерывна в точкеx 0 .
3) Все основные элементарные функции (c , x a ,a x , loga x , sinx , cosx , tgx , ctgx , secx , cosecx , arcsinx , arccosx , arctgx , arcctgx ) непрерывны в каж-
дой точке своих областей определения.
Из свойств 1)–3) следует, что все элементарные функции (функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и операции композиции) также непрерывны в каждой точке своих областей определения.
Свойства функций, непрерывных на отрезке.
1) (теорема о промежуточных значениях) Пусть функция f(x) определе-
на и непрерывна на отрезке [ a ;b ] . Тогда для любого числаC , заключенного
между числами f (a ) иf (b ) , (f (a )
2) (теорема Больцано – Коши
рывна на отрезке [ a ;b ] и принимает на его концах значения различных знаков.
Тогда найдется хотя бы одна точка x 0 [ a ;b ] , такая, чтоf (x 0 )= 0 .
3) (1-я теорема Вейерштрасса ) Пусть функцияf (x ) определена и непре-
рывна на отрезке [ a ;b ] . Тогда эта функция ограничена на этом отрезке.
4) (2-я теорема Вейерштрасса ) Пусть функцияf (x ) определена и непре-
рывна на отрезке | [ a ;b ] . Тогда эта функция достигает на отрезке[ a ;b ] | |||||
наибольшего | наименьшего | значений, т.е. | существуют | |||
x1 , x2 [ a; b] , | для любой | точки x [ a ;b ] | справедливы | неравенства | ||
f (x 1 )≤ f (x )≤ f (x 2 ) .
Пример 5.17. Пользуясь определением непрерывности, доказать, что функцияy = 3x 2 + 2x − 5 непрерывна в произвольной точкеx 0 числовой оси.
Решение: 1 способ: Пусть x 0 – произвольная точка числовой оси. Вы-
числим сначала предел функции f (x ) приx → x 0 , применяя теоремы о пределе суммы и произведения функций:
lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2 | − 5. | ||||||
x→ x0 | x→ x0 | x→ x0 | x→ x0 | ||||
Затем вычисляем значение функции в точке x :f (x )= 3x 2 | − 5 . | ||||||
Сравнивая полученные результаты, видим, | lim f (x )= f (x 0 ) , что согласно | ||||||
x→ x0 | |||||||
определению и означает непрерывность рассматриваемой функции в точке x 0 .
2 способ: Пусть | x – приращение аргумента в точкеx 0 . Найдем соот- | |||
ветствующее | приращение | y = f(x0 + x) − f(x0 ) = | ||
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5) | ||||
6 x x+ (x) 2 | 2x = (6x + 2)x + (x )2 . | |||
Вычислим теперь предел приращения функции, когда приращение аргу- | ||||
стремится | ||||
y = lim (6x + 2) | x + (x )2 = (6x + 2) lim | x + (limx )2 = 0 . | |||
x→ 0 | x→ 0 | x→ 0 | x→ 0 | ||
Таким образом, lim y = 0 , что и означает по определению непрерывность
x→ 0
функции для любого x 0 R .
Пример 5.18. Найти точки разрыва функцииf (x ) и определить их род. В
случае устранимого разрыва доопределить функцию по непрерывности:
1) f (x ) = 1− x 2 приx
5x приx ≥ 3
2) f (x )= x 2 + 4 x + 3 ;
x + 1
f (x) = | |||||
x4 (x− 2) | |||||
f (x )= arctg | |||||
(x − 5) | |||||
Решение: 1) Областью определения данной функции является вся число-
вая ось (−∞ ;+∞ ) . На интервалах(−∞ ;3) ,(3;+∞ ) функция непрерывна. Разрыв возможен лишь в точкеx = 3 , в которой изменяется аналитическое задание функции.
Найдем односторонние пределы функции в указанной точке:
f (3− 0)= lim (1− x 2 )= 1− 9= 8;
x →3 −0
f (3+ 0)= lim 5x = 15.
x →3 +0
Мы видим, что левый и правый пределы конечны, поэтому x = 3 | |||||
разрыва I | f (x ) . Скачок функции в | ||||
f (3+ 0)− f (3− 0)= 15− 8= 7 . | |||||
f (3)= 5 3= 15= f (3+ 0) , поэтому в точке | x = 3 | ||||
f (x ) непрерывна справа.
2) Функция непрерывна на всей числовой оси, кроме точки x = − 1, в которой она не определена. Преобразуем выражение дляf (x ) , разложив числитель
дроби на множители: | f (x) = | 4 x +3 | (x + 1)(x + 3) | X + 3 приx ≠ − 1. | |||||
x + 1 | x + 1 | ||||||||
Найдем односторонние пределы функции в точке x = − 1: | |||||||||
f (x )= lim | f (x )= lim(x + 3)= 2 . | ||||||||
x →−1 −0 | x →−1 +0 | x →−1 | |||||||
Мы выяснили, что левый и правый пределы функции в исследуемой точке существуют, конечны и равны между собой, поэтому x = − 1 – точка устранимо-
прямую y = x + 3 с «выколотой» точкойM (− 1;2) . Чтобы функция стала непре-
рывной, следует положить f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .
Таким образом, доопределив f (x ) по непрерывности в точкеx = − 1, мы получили функциюf * (x )= x + 3 с областью определения(−∞ ;+∞ ) .
3) Данная функция определена и непрерывна для всех x , кроме точек
x = 0 ,x = 2 , в которых знаменатель дроби обращается в ноль.
Рассмотрим точку x = 0:
Поскольку в достаточно малой окрестности нуля функция принимает толь-
ко отрицательные значения, то f (− 0)= lim | = −∞ = f (+0) | Т.е. точка | |||
(x − 2) | |||||
x →−0 | |||||
x = 0 является точкой разрыва II рода функции | f (x ) . | ||||
Рассмотрим теперь точку x = 2:
Функция принимает отрицательные значения вблизи слева от рассматри-
ваемой точки и положительные – справа, поэтому | f (2− 0)= | = −∞, | ||||||
x4 (x− 2) | ||||||||
x →2 −0 | ||||||||
f (2+ 0)= lim | = +∞ . Как и в предыдущем случае, в точкеx = 2 | |||||||
(x − 2) | ||||||||
x →2 +0 | ||||||||
ция не имеет ни левого, ни правого конечного пределов, т.е. терпит в этой точке разрыв II рода.
x = 5 . | ||||||||||||||||||
f (5− 0)= lim arctg | π ,f (5+ 0)= lim arctg | x = 5 | ||||||||||||||||
(x − 5) | (x − 5) | |||||||||||||||||
x →5 −0 | x →5 +0 | |||||||||||||||||
ка разрыва | ||||||||||||||||||
f (5+ 0)− f (5− 0)= | π − (− | π )= π (см. рис. 5.2). | ||||||||||||||||
Задачи для самостоятельного решения
5.174. Пользуясь лишь определением, доказать непрерывность функцииf (x ) в
каждой точке x 0 R :
а) f(x) = c= const; | б) f (x )= x ; | ||
в) f (x )= x 3 ; | г) f (x )= 5x 2 − 4x + 1; | ||
д) f (x )= sinx . | |||
5.175. Доказать, что функция | f (x) = x 2 | 1 приx ≥ 0, | является непрерывной на |
1 при x | |||
всей числовой оси. Построить график этой функции. | |||
5.176. Доказать, что функция | f (x) = x 2 | 1 приx ≥ 0, | не является непрерывной |
0 при x | |||
в точке x = 0 , но непрерывна справа в этой точке. Построить график функцииf (x ) .
рывной в точке x = | Но непрерывна слева в этой точке. Построить график | |||||||||||||
функции f (x ) . | ||||||||||||||
5.178. Построить графики функций | ||||||||||||||
а) y = | x + 1 | б) y= x+ | x + 1 | |||||||||||
x + 1 | x + 1 | |||||||||||||
Какие из условий непрерывности в точках разрыва этих функций выполнены, и какие не выполнены?
5.179. Указать точку разрыва функции
sin x | При x ≠ 0 | ||
при x = 0 | |||
Какие из условий непрерывности в этой точке выполнены, и какие не выполнены?
Общая схема исследования функции и построения графиков (Лекция №11)
- Найти ОДЗ и точки разрыва функции.
- Найти точки пересечения графика функции с осями координат.
- Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
- Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
- Найти асимптоты графика функции: а) вертикальные, b) наклонные.
- На основании проведенного исследования построить график функции.
Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.
Примеры. Исследовать функции и построить их графики.
- .
1. Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: x = 0,у=0.
Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).
2. . Критические точки: x1 = 1; x2= –1. 3. 4. а) Вертикальных асимптот нетб) . Асимптота – y = 0.
- .
- D(y)=(–∞; +∞). Точек
разрыва нет.
Пересечение с осью Ox: .
- .
- а) Вертикальных асимптот нет
б).
Наклонных асимптот нет.
- D(y)=(–∞; +∞). Точек
разрыва нет.
- .
- D(y)=(0; +∞). Функция
непрерывна на области определения.
Пересечение с осью :
- а) .
Вертикальная асимптота x = 0.
б).Наклонная асимптота y = 0.
- D(y)=(0; +∞). Функция
непрерывна на области определения.
- .
- D(y)=(
–∞;0)È(0;1)È(1;+∞).
Функция имеет две точки разрыва x= 0 и x= 1.
Точек пересечения с осями координат нет.
- при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.
-
а)
Вертикальные асимптоты x = 0, x = 1.
б)
Наклонная асимптота y = x + 1.
- D(y)=(
–∞;0)È(0;1)È(1;+∞).
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Во многих приложениях математического анализа встречаются комбинации показательных функций. Эти комбинации рассматриваются как новые функции и обозначаются:
– гиперболический синус.
– гиперболический косинус.
С помощью этих функций можно определить еще две функции.
– гиперболический тангенс.
– гиперболический котангенс.
Функции sh x, ch x, th x определены, очевидно, для всех значений x, т.е. их область определения (–∞; +∞). Функция же cthx определена всюду за исключением точки x = 0.
Между гиперболическими функциями существуют следующие соотношения, аналогичные соответствующим соотношениям между тригонометрическими функциями.
Найдем: .
Т.е. .
.
Итак, .
Следовательно, .
Найдем производные гиперболических функций
.
Аналогично можно показать .
.
Т.е. и .
Графики гиперболических функций. Для того чтобы изобразить графики функций
shx и chx нужно вспомнить графики функций y = ex и y = e—x
Проведем исследования функции y = th x.
- D(f) = (–∞; +∞), точек разрыва нет.
- Точка пересечения с осями координат .
-
, функция возрастает на (–∞; +∞).
- Вертикальной асимптоты нет.
.
y = cth x
- D. Точка разрыва x = 0 cth x = 0 – нет
-
убывает на .
- При x → +∞
Dynamic Consent: потенциальное решение некоторых проблем современных биомедицинских исследований | BMC Medical Ethics
Европейский научный фонд. Взгляд в будущее ESF: персонализированная медицина для гражданина Европы. http://archives.esf.org/fileadmin/Public_documents/Publications/Personalised_Medicine.pdf. По состоянию на 25 ноября 2016 г.
Андерсон Н., Брэгг С., Хартцлер А., Эдвардс К. Инициативы, ориентированные на участников: инструменты для облегчения участия в исследованиях.Appl Transl Genom. 2012; 1: 25–9.
Артикул Google Scholar
Флетчер Б., Георге А., Мур Д., Уилсон С., Дэмери С. Улучшение набора врачей в рандомизированных контролируемых исследованиях: систематический обзор. BMJ Open. 2012; 2 (1): e000496.
Артикул Google Scholar
Джонссон Л., Хельгессон Г., Рафнар Т., Халлдорсдоттир И., Чиа К.С., Эрикссон С. и др.Гипотетическая и фактическая готовность участвовать в исследованиях биобанка. Eur J Hum Genet. 2010. 18 (11): 1261–4.
Артикул Google Scholar
Мацуи К., Кита Ю., Уэшима Х. Информированное согласие, участие в популяционном когортном исследовании, включающем генетический анализ, и отказ от него. J Med Ethics. 2005. 31 (7): 385–92.
Артикул Google Scholar
Росс С., Грант А, Советник С., Гиллеспи В., Рассел И., Прескотт Р.Препятствия для участия в рандомизированных контролируемых испытаниях: систематический обзор. J Clin Epidemiol. 1999. 52 (12): 1143–56.
Артикул Google Scholar
Ньюингтон Л., Меткалф А. Факторы, влияющие на набор персонала для исследования: качественное изучение опыта и восприятия исследовательских групп. BMC Med Res Methodol. 2014; 14: 10.
Артикул Google Scholar
Боден-Альбала Б., Карман Х., Саутвик Л., Парик Н.С., Робертс Э., Вадди С. и др. Изучение барьеров и методов набора и удержания в клинических испытаниях по инсульту. Гладить. 2015; 46 (8): 2232–7.
Артикул Google Scholar
Perry J, Wohlke S, Hessling AC, Schicktanz S. Почему нужно принимать участие в индивидуальных исследованиях рака? Генетическое заблуждение пациентов, генетическая ответственность и непонимание стратификации — эмпирически-этическое исследование.Eur J Cancer Care (Engl) 2016.
Д’Абрамо Ф., Шильдманн Дж., Фоллманн Дж. Восприятие и взгляды участников исследования на согласие на исследование биобанка: обзор эмпирических данных и этический анализ. BMC Med Ethics. 2015; 16:60.
Артикул Google Scholar
Budin-Ljosne I, Bentzen HB, Solbakk JH, Myklebost O. Секвенирование генома в исследованиях требует нового подхода к согласию. Tidsskr Nor Laegeforen.2015; 135 (22): 2031–2.
Артикул Google Scholar
Khaleel SL. В кн .: Clinical Leader. Набор и удержание пациентов с редкими заболеваниями. http://www.clinicalleader.com/doc/rare-disease-patient-recruitment-and-retention-0001. По состоянию на 25 ноября 2016 г.
Penckofer S, Byrn M, Mumby P, Ferrans CE. Улучшение набора, удержания и участия субъектов в исследованиях с помощью теории межличностных отношений Пеплау.Nurs Sci Q.2011; 24 (2): 146–51.
Артикул Google Scholar
Бронштейн М.Г., Каккис Э.Д. Пациенты как ключевые партнеры в разработке лекарств от редких заболеваний. Nat Rev Drug Discov. 2016; 15 (11): 731–2.
Артикул Google Scholar
Николсон Л.М., Швириан П.М., Кляйн Э.Г., Скайбо Т., Мюррей-Джонсон Л., Энели И. и др. Стратегии набора и удержания в лонгитюдных клинических исследованиях с группами населения с низким доходом.Клинические испытания Contemp. 2011. 32 (3): 353–62.
Артикул Google Scholar
Пульезе Л., Вудриф М., Кроули О., Лам В., Сон Дж., Брэдли С. Осуществимость модели «принеси свое собственное устройство» в клинических исследованиях: результаты рандомизированного контролируемого пилотного исследования мобильного взаимодействия с пациентами Орудие труда. Cureus. 2016; 8 (3): e535.
Google Scholar
Ханссон М.Г., Диллнер Дж., Бартрам С.Р., Карлсон Дж. А., Хельгессон Г.Следует ли разрешить донорам дать широкое согласие на будущие исследования биобанка? Ланцет Онкол. 2006; 7 (3): 266–9.
Артикул Google Scholar
Хофманн Б. Расширение согласия — и ослабление этики? J Med Ethics. 2009. 35 (2): 125–9.
Артикул Google Scholar
Грейди С., Экштейн Л., Беркман Б., Брок Д., Кук-Диган Р., Фуллертон С.М. и др. Широкое согласие на исследования биологических образцов: выводы семинара.Am J Bioeth. 2015; 15 (9): 34–42.
Артикул Google Scholar
Плуг Т., Холм С. Выход за рамки ложной дихотомии широкого или конкретного согласия: мета-перспектива выбора участников в исследованиях с использованием человеческих тканей. Am J Bioeth. 2015; 15 (9): 44–6.
Артикул Google Scholar
Колфилд Т., Апшур Р. Э., Даар А. Банки данных ДНК и согласие: предлагаемый вариант политики, включающий модель авторизации.BMC Med Ethics. 2003; 4: E1.
Артикул Google Scholar
Lind A-S. В кн .: Уппсальский университет. Новый закон для исследователей Биобанка http://www.crb.uu.se/biobank-perspectives/item/?tarContentId=496836. По состоянию на 25 ноября 2016 г.
Lind A-S. LifeGene — закрытое дело? В: Информация и право в переходный период: свобода слова, Интернет, конфиденциальность и демократия в 21 веке. Под редакцией Lind AS RJ, Österdahl I.Стокгольм: Liber; 2015. с. 339–50.
Кэй Дж., Уитли Э.А., Лунд Д., Моррисон М., Тир Х., Мелхэм К. Динамическое согласие: интерфейс пациента для исследовательских сетей двадцать первого века. Eur J Hum Genet. 2015; 23 (2): 141–6.
Артикул Google Scholar
Уилбанкс Дж., Друг Ш. Во-первых, дизайн для обмена данными. Nat Biotechnol. 2016; 34 (4): 377–9.
Google Scholar
Диксон В.Г., Спенсер К., Уильямс Х., Сандерс К., Лунд Д., Уитли Е.А. и др. Динамическая модель согласия пациента на совместное использование данных медицинской карты. BMJ. 2014; 348: g1294.
Артикул Google Scholar
Javaid MK, Forestier-Zhang L, Watts L, Turner A, Ponte C, Teare H, et al. Платформа исследований RUDY — новый подход к исследованиям редких заболеваний опорно-двигательного аппарата, ориентированным на пациентов. Orphanet J Rare Dis. 2016; 11 (1): 150.
Артикул Google Scholar
Паттаро С., Гогеле М., Маскальцони Д., Мелотти Р., Швинбахер С., Де Гранди А. и др. Исследование Cooperative Health Research в Южном Тироле (CHRIS): обоснование, цели и предварительные результаты. J Transl Med. 2015; 13 (1): 348.
Артикул Google Scholar
Тир Х.Дж., Моррисон М., Уитли Э.А., Кей Дж. На пути к «Вовлечению 2.0»: выводы из исследования динамического согласия участников биобанка. Цифровое здоровье. 2015; 0 (0): 1–13.
Тиль Д.Б., Платт Дж., Платт Т., Кинг С.Б., Фишер Н., Шелтон Р. и др. Тестирование онлайн-портала динамического согласия для исследования биобанков большого населения. Геномика общественного здравоохранения. 2015; 18 (1): 26–39.
Артикул Google Scholar
Бутин Н.Т., Матье К., Хоффнагл А.Г., Аллен Н.Л., Кастро В.М., Мораш М. и др. Внедрение электронного согласия в биобанке: возможность для исследований в области точной медицины.J Pers Med. 2016; 6 (2): 17.
Коатуп В., Тир Х. Дж., Минари Дж., Йошизава Дж., Кэй Дж., Такахаши М. П. и др. Использование цифровых технологий для проведения медицинских исследований: взгляды пациентов с миотонической дистрофией в Японии. BMC Med Ethics. 2016; 17 (1): 51.
Артикул Google Scholar
Спенсер К., Сандерс К., Уитли Э.А., Лунд Д., Кэй Дж., Диксон В.Г. Перспективы пациентов в отношении обмена анонимными личными данными о здоровье с использованием цифровой системы для динамического согласия и обратной связи с исследованиями: качественное исследование.J Med Internet Res. 2016; 18 (4): e66.
Артикул Google Scholar
Кэй Дж., Каррен Л., Андерсон Н., Эдвардс К., Фуллертон С.М., Канеллопулу Н. и др. От пациентов к партнерам: инициативы в области биомедицинских исследований, ориентированные на участников. Nat Rev Genet. 2012. 13 (5): 371–6.
Артикул Google Scholar
Каньяда Дж. А., Тупасела А., Снелл К. За пределами и в рамках общественного участия: расширенный подход к участию в биобанкинге.New Genet Soc. 2015; 34 (4): 355–76.
Артикул Google Scholar
Д’Абрамо Ф. Исследование биобанка, информированное согласие и общество. К новому альянсу? J Epidemiol Community Health. 2015; 69 (11): 1125–8.
Артикул Google Scholar
Уильямс Х., Спенсер К., Сандерс С., Лунд Д., Уитли Э.А., Кей Дж и др. Динамическое согласие: возможное решение для повышения уверенности пациентов и доверия к тому, как электронные карты пациентов используются в медицинских исследованиях.ИМИР Мед Информ. 2015; 3 (1): e3.
Артикул Google Scholar
Эло С., Кынгас Х. Процесс качественного контент-анализа. J Adv Nurs. 2008. 62 (1): 107–15.
Артикул Google Scholar
Исследование Руди. https://research.ndorms.ox.ac.uk/rudy/. По состоянию на 25 ноября 2016 г.
Исследование CHRIS (Совместные исследования в области здравоохранения в Южном Тироле).В: Исследование EURAC. http://www.eurac.edu/en/research/health/biomed/projects/Pages/default.aspx. Accssed 25 ноября 2016 г.
Гарвардский персональный геномный проект. http://www.personalgenomes.org/. По состоянию на 25 ноября 2016 г.
Ball MP, Bobe JR, Chou MF, Clegg T, Estep PW, Lunshof JE, et al. Гарвардский персональный геномный проект: уроки открытого общественного исследования. Genome Med. 2014; 6 (2): 10.
Артикул Google Scholar
Мелхам К., Морая Л.Б., Митчелл С., Моррисон М., Тир Х., Кэй Дж. Эволюция абстиненции: переговоры об исследовательских отношениях в биобанкинге. Политика Life Sci Soc. 2014; 10 (1): 16.
Артикул Google Scholar
Платформа для ответственного взаимодействия со всеми (PEER). В: Генетический альянс. http://www.geneticalliance.org/programs/biotrust/peer. По состоянию на 25 ноября 2016 г.
Genetic Alliance. http: // www.geneticalliance.org/. По состоянию на 25 ноября 2016 г.
Private Access, Inc. https://www.privateaccess.info/. По состоянию на 25 ноября 2016 г.
Хага С.Б., О’Дэниел Дж. Общественные взгляды на практику совместного использования данных в исследованиях геномики. Геномика общественного здравоохранения. 2011. 14 (6): 319–24.
Артикул Google Scholar
Нильстун Т., Хермерен Г. Образцы человеческих тканей и этика — отношение широкой общественности Швеции к исследованиям биобанков.Философия медицинского обслуживания. 2006. 9 (1): 81–6.
Артикул Google Scholar
Кричли К., Николь Д., Отловски М. Влияние мер коммерциализации и обмена генетическими данными на общественное доверие и намерение участвовать в исследованиях биобанков. Геномика общественного здравоохранения. 2015; 18 (3): 160–72.
Артикул Google Scholar
Маскальцони Д. Проекты ELSI по психиатрии в народонаселении.В: Неделя европейских биобанков: 13–16 сентября 2016 г .; Вена, Австрия. 2016.
Ludman EJ, Fullerton SM, Spangler L, Trinidad SB, Fujii MM, et al. Рад, что вы спросили: мнения участников о повторном согласии на отправку данных dbGap. J Empir Res Hum Res Этика. 2010. 5 (3): 9–16.
Артикул Google Scholar
Бурштейн М.Д., Робинсон Дж.О., Хильзенбек С.Г., Макгуайр А.Л., Лау К.С. Обмен педиатрическими данными в геномных исследованиях: отношение и предпочтения родителей.Педиатрия. 2014; 133 (4): 690–7.
Артикул Google Scholar
Trinidad SB, Fullerton SM, Bares JM, Jarvik GP, Larson EB, Burke W. Геномные исследования и широкий обмен данными: мнения потенциальных участников. Genet Med. 2010. 12 (8): 486–95.
Артикул Google Scholar
Budin-Ljosne I, Soye KJ, Tasse AM, Knoppers BM, Harris JR. Вербовка на основе генотипа: стратегия, время которой пришло? BMC Med Genomics.2013; 6 (1): 19.
Артикул Google Scholar
23andMe. https://www.23andme.com/. По состоянию на 25 ноября 2016 г.
Biankin AV, Piantadosi S, Hollingsworth SJ. Ориентированные на пациента исследования для терапевтического развития в точной онкологии. Природа. 2015; 526 (7573): 361–70.
Артикул Google Scholar
Винн Б. Неопределенность и экологическое обучение.Glob Environ Chang. 1992. 2 (2): 111–27.
Артикул Google Scholar
Голубь Е.С., Джоли Ю., Кнопперс БМ. Власть народу: модель управления биобанками через вики. Genome Biol. 2012; 13 (5): 158.
Артикул Google Scholar
Steinsbekk KS, Kare MB, Solberg B. Широкое согласие против динамического согласия в исследованиях биобанка: является ли пассивное участие этической проблемой? Eur J Hum Genet 2013.
Фернандес-Алеман Дж. Л., Сеньор И. К., Лозоя П. А., Товаль А. Безопасность и конфиденциальность в электронных медицинских картах: систематический обзор литературы. Дж Биомед Информ. 2013. 46 (3): 541–62.
Артикул Google Scholar
Бейкер ДБ, Кэй Дж., Терри С.Ф. Управление через конфиденциальность, справедливость и уважение к людям. EGEMS (Мойка DC). 2016; 4 (2): 1207.
Google Scholar
Beskow LM, Dombeck CB, Thompson CP, Watson-Ormond JK, Weinfurt KP. Информированное согласие на использование биобанков: основанные на консенсусе рекомендации для адекватного понимания. Genet Med. 2015; 17 (3): 226–33.
Артикул Google Scholar
Sonne SC, Andrews JO, Gentilin SM, Oppenheimer S, Obeid J, Brady K, et al. Разработка и пилотное тестирование процесса информированного согласия с помощью видео. Клинические испытания Contemp. 2013. 36 (1): 25–31.
Артикул Google Scholar
Секвенирование генома: что думают пациенты? Хартия пациента. В: Genetic Alliance UK. 2016. https://www.geneticalliance.org.uk/media/2493/my-cancer-my-dna-patient-charter-edits-sept2016.pdf, дата обращения 25 ноября 2016 г.
Trinidad SB, Фуллертон С. М., Барес Дж. М., Ярвик Г. П., Ларсон Э. Б., Берк В. Информированное согласие в исследованиях в масштабе генома: что думают предполагаемые участники? AJOB Prim Res. 2012; 3 (3): 3–11.
Артикул Google Scholar
Tabor HK, Stock J, Brazg T., McMillin MJ, Dent KM, Yu JH и др. Информированное согласие на секвенирование всего генома: качественный анализ ожиданий участников и восприятия рисков, преимуществ и вреда. Am J Med Genet A. 2012; 158A (6): 1310–9.
Артикул Google Scholar
Президентская комиссия по изучению биоэтических вопросов: конфиденциальность и прогресс в секвенировании всего генома. 2012. http://bioethics.gov/sites/default/files/PrivacyProgress508_1.pdf. По состоянию на 25 ноября 2016 г.
Когортная программа инициативы Precision Medicine Initiative. В: Национальные институты здоровья. https://www.nih.gov/precision-medicine-initiative-cohort-program. По состоянию на 25 ноября 2016 г.
Когортная программа Инициативы по прецизионной медицине — Создание исследовательского фонда для медицины 21 века — Отчет рабочей группы Инициативы по прецизионной медицине (PMI) Консультативному комитету при директоре NIH. https://www.nih.gov/precision-medicine-initiative-cohort-program/pmi-working-group.По состоянию на 25 ноября 2016 г.
Faglig Prioriterte områder i 2016: Interessekonflikter, samtykke og vitenskapelig integritet. В: De nasjonale forskningsetiske komiteene. https://www.etikkom.no/hvem-er-vi-og-hva-gjor-vi/komiteenes-arbeid/faglig-prioritert-omrade-i-2016-interessekonflikter/. На норвежском. По состоянию на 25 ноября 2016 г.
Nishimura A, Carey J, Erwin PJ, Tilburt JC, Murad MH, McCormick JB. Улучшение понимания процесса получения информированного согласия в ходе исследования: систематический обзор 54 вмешательств, протестированных в рандомизированных контрольных исследованиях.BMC Med Ethics. 2013; 14:28.
Артикул Google Scholar
Шабани М., Борри П. Проблемы обмена персональными геномными данными через Интернет. Политика Life Sci Soc. 2015; 11: 3.
Артикул Google Scholar
Джонссон Л., Эрикссон С. Автономия — это право, а не подвиг: как теоретические заблуждения запутали дискуссию о динамическом согласии на исследования биобанка.Bioethics 2016.
Mascalzoni D, Hicks A, Pramstaller P, Wjst M. Информированное согласие в эпоху геномики. PLoS Med. 2008; 5 (9): e192.
Артикул Google Scholar
McCormack P, Kole A, Gainotti S, Mascalzoni D, Molster C, Lochmuller H, et al. «Ты должен хотя бы спросить». Ожидания, надежды и опасения пациентов с редкими заболеваниями в отношении крупномасштабных данных и обмена биоматериалами для исследований в области геномики. Eur J Hum Genet.2016; 24 (10): 1403–8.
Lunshof JE, Chadwick R, Vorhaus DB, Church GM. От генетической конфиденциальности до открытого согласия. Nat Rev Genet. 2008. 9 (5): 406–11.
Артикул Google Scholar
Освободите данные. http://www.free-the-data.org/. По состоянию на 25 ноября 2016 г.
12 лучших инструментов для исследователей в 2021 году
Прошли те времена, когда приходилось ходить в библиотеку, изучать многочисленные книги, делать заметки на бумаге и проводить исследования.Благодаря технологиям нам больше не нужно выполнять эту утомительную рутину для проведения исследований. Однако исследование по-прежнему представляет собой кропотливый и кропотливый процесс.
Вот почему мы решили раскрыть некоторые из лучших программных инструментов для исследователей, которые помогут вам с легкостью проводить и поддерживать ваши исследования. Читайте дальше…
Список 12 лучших инструментов для исследователей для получения лучших результатов:
Сегодняшние исследования динамичны. Мы часто используем Интернет для просмотра веб-сайтов, просмотра видео, изучения аналитики и проведения наших исследований, исследуя различные типы цифрового контента, что делает технологии одним из основных участников успеха наших исследований.Хотя Интернет облегчил нам доступ к мирской информации одним нажатием кнопки (или мыши!), Он создал целый ряд новых проблем.
Сортировка, казалось бы, бесконечного количества веб-сайтов, проверка содержимого и подбор только лучших материалов может занять много времени и усилий. Вот почему мы представили вам 12 основных исследовательских инструментов, которые каждый исследователь должен использовать при работе в Интернете.
1. Bit.aiОнлайн-исследования — это просмотр множества веб-сайтов, статей, блогов, изображений, видео, инфографики и многого другого, чтобы найти то, что вы ищете.Для наших динамических, интерактивных и мультимедийных исследований нам нужен инструмент, который объединяет все аспекты современного исследования под одной крышей. Простые текстовые редакторы прошлого просто не справятся! Здесь на помощь приходит Bit.
Bit позволяет исследователям и командам сотрудничать, обмениваться, отслеживать и управлять всеми знаниями и исследованиями в одном месте. Это идеальный инструмент исследования, чтобы делиться многомерными исследованиями с коллегами, а не просто скучным текстом и слайдами. Добавляйте статьи, PDF-файлы, видео, официальные документы, электронные книги, образцы аудио — в общем, все, что вы можете придумать — и легко делитесь ими со своими коллегами!
Другие примечательные особенности Bit включают:
- Простой в использовании, минималистичный редактор, поддерживающий Markdown.
- Совместное редактирование в реальном времени и общение с коллегами.
- Добавьте в свой битовый документ цифровой контент любого типа (изображения, видео и т. Д.).
- Библиотека содержимого для сохранения всех медиафайлов для быстрого доступа.
- Интеллектуальный поиск, который позволяет любому быстро находить любые файлы, изображения, документы, ссылки и т. Д.
В целом Bit — незаменимый инструмент для письма для исследователей и авторов!
Основные характеристики Bit:
- Рабочие пространства для удобного хранения различного исследовательского контента
- Библиотека контента для хранения медиаресурсов
- Сотрудничество в реальном времени с коллегами-исследователями
Стоимость:
- Бесплатно с ограниченной функциональностью
- Платные планы начинаются с Pro (8 долларов в месяц), Business (15 долларов в месяц), Enterprise (свяжитесь с отделом продаж)
Подробнее: Научная статья: что это и как писать? (Шаги и формат)
2.elink.ioИсследование часто включает просмотр сотен ссылок и статей и их объединение в одно безопасное место для использования в будущем или их публикации для вашей аудитории. Вот почему многие исследователи используют инструменты закладок и курирования, такие как elink, чтобы быстро сохранять свои ссылки под одной крышей и делиться ими со своими коллегами. elink позволяет исследователям легко сохранять контент со всего Интернета. Они могут сохранять ссылки на статьи, видео, облачные файлы, сообщения в социальных сетях и многое другое!
Исследователи могут сохранять контент в свою библиотеку ссылок или добавлять их непосредственно в коллекции материалов и делиться своими исследованиями со своими коллегами.Чтобы упростить процесс создания закладок, у elink также есть хромированное расширение. Просто щелкните расширение или щелкните правой кнопкой мыши любую веб-страницу, чтобы сохранить содержимое прямо на панели управления elink. Исследователи могут редактировать заголовок и описание, чтобы добавить свой голос или заметки. Они даже могут объединять ссылки и делиться своей коллекцией ссылок с другими в виде информационного бюллетеня или встраивать коллекцию в ваш блог / веб-сайт!
Основные характеристики elink:
- Быстрое сохранение ссылок с помощью расширения chrome
- Создание и публикация ссылок на исследования в виде информационного бюллетеня или встраивания его на свой веб-сайт
- Простой пользовательский интерфейс
Цена:
- Бесплатно с ограниченной функциональностью
- Платные планы начинаются с Pro ежемесячно (15 долларов в месяц), Pro 1 год (12 долларов в месяц), Pro 2 года (10 долларов в месяц).
3. GanttPRO
Независимо от того, какое исследование вы проводите, вам необходимо организовать, спланировать и сосредоточиться на всех своих действиях. Без надежного инструмента планирования исследователи могут отставать от графика и терять прогресс. Инструмент управления проектами и задачами GanttPRO позволяет отдельным исследователям и группам любого размера легко планировать свои задачи на визуально привлекательной временной шкале диаграммы Ганта, отслеживать их прогресс и все сроки.
GanttPRO позволяет исследователям создавать неограниченное количество задач, групп задач и подзадач на одной временной шкале.Кроме того, это идеальный инструмент планирования для назначения задач вашим коллегам-исследователям или создания виртуальных ресурсов, кем бы они ни были. Программное обеспечение — хороший выбор для совместной работы, учета рабочего времени, а также для обмена и экспорта ваших расписаний.
Ключевые особенности GanttPRO:
- Десятки готовых шаблонов.
- Сотрудничество в реальном времени с коллегами-исследователями.
- Элегантный пользовательский интерфейс с короткой кривой обучения.
Стоимость:
- Бесплатная 14-дневная пробная версия со всеми доступными функциями.
- Платные планы начинаются с групповых (4,5 доллара США за пользователя в месяц), индивидуальных (15 долларов США в месяц), корпоративных (контактные данные).
Исследовательская работа часто включает часы корректуры и проверки орфографии, чтобы сделать ваше исследование профессиональным. Говоря грамматически, инструмент для улучшения письма сэкономит вам массу времени и усилий при выполнении этой ужасной задачи! Помимо базовой проверки орфографии и исправлений, Grammarly включает в себя средство проверки грамматики, средство проверки пунктуации, средство улучшения словарного запаса и даже средство проверки плагиата!
Этот замечательный инструмент сканирует ваше исследование на предмет более чем 250 типов грамматических ошибок в шести различных жанрах письма и оставляет вас безошибочным письмом.С подробными объяснениями всех ваших ошибок и еженедельными отчетами о проделанной работе. Grammarly — незаменимый инструмент для исследователей. Он доступен как расширение для браузера, настольное приложение, веб-приложение и надстройка Microsoft. Многие альтернативы Grammarly также доступны на рынке, которые одинаково хороши.
Основные характеристики Grammarly:
- Работает с большинством онлайн-инструментов, таких как Word, Slack и т.д.
- Платные планы начинаются с: Премиум ($ 11.66 / месяц), Business (12,50 $ / месяц)
Подробнее: 10 лучших приложений для письма, которые сделают вас лучшим писателем!
5. Typeset.ioTypeset.io утверждает, что является более умной альтернативой Word и Latex, которую должны использовать все исследователи. Начните исследование с простого в использовании интерфейса или импортируйте существующие файлы Word. Благодаря более чем 100 000 проверенных форматов журналов на выбор, Typeform упрощает процесс исследования! Быстро скопируйте-вставьте или загрузите свою статью на Typeset и следуйте любому стилю цитирования, который вам нужен.
Typeset также имеет встроенную программу проверки грамматики и плагиата, чтобы гарантировать, что ваше письмо безошибочно. После завершения загрузки и цитирования нажмите автоформат, чтобы сгенерировать отчет за секунды. Вы также можете загрузить свое исследование в формате PDF, Docx, LaTeX или даже в виде Zip-файла. Благодаря встроенным функциям совместной работы вы можете приглашать на платформу своих коллег-исследователей и работать вместе.
Основные характеристики набора:
- Более 100 000+ форматов журналов на выбор
- Инструмент для проверки плагиата и грамматики
- Услуги редактирования для повышения шансов публикации
Стоимость:
- бесплатно с ограниченной функциональностью
- Платные планы начинаются с: исследователя (8 долларов в месяц), группы (6 долларов в месяц), журналов / издателей (связаться с отделом продаж)
Scrivener — еще один отличный инструмент для написания исследований и организации заметок. Scrivener используется исследователями, сценаристами, романистами, публицистами, студентами, журналистами, учеными, юристами, переводчиками и т. Д. И предназначен для написания длительных проектов. При регистрации вам быстро предоставляется его редактор с боковой панелью, чтобы все было на месте. Вы также можете разбить свой контент на управляемые разделы любого размера и позволить Scrivener объединить их вместе.
Для писателей и рассказчиков есть пробковая доска, на которой можно визуализировать сюжетную линию и перемещать карты по своему усмотрению. В планировщике хранится синопсис того, что вы уже написали, а также данные о количестве слов и метаданные. Пользователи могут размещать свои исследовательские статьи и другие файлы в папках и подпапках.
Основные характеристики Scrivener:
- Настольные и мобильные приложения
- Создатель схемы
- Простая организация
Цена:
- Бесплатно с ограниченной функциональностью
- Платные планы начинаются от 40 долларов США.84 / единовременная плата
Далее идет замечательный исследовательский инструмент от Google под названием Google Scholar. Google Scholar предоставляет быстрый способ поиска научной литературы из одного места. Ищите статьи, тезисы, книги, рефераты и заключения судов в профессиональных сообществах, онлайн-репозиториях, университетах, академических издательствах и других веб-сайтах.
Исследователи также могут легко изучить связанные работы, цитаты, авторов и публикации.Создайте общедоступный профиль автора и узнайте, кто цитирует вашу недавнюю публикацию. Google Scholar также позволяет своим пользователям быть в курсе последних событий в любой области исследований.
Основные возможности Google Scholar:
- Создание общедоступной страницы автора
- Ищите информацию в базе данных Google
- Простота использования
Цена:
8. Сноска3332Endnote хочет, чтобы вы занимались более умными исследованиями, упростив утомительную работу по форматированию библиографий, поиску полного текста и поиску ссылок.Endnote носит совместный характер, поскольку позволяет вам делиться выбранными группами ссылок, управлять доступом группы, а также отслеживать активность и изменения с единой панели инструментов. Благодаря более продуманному анализу Endnote автоматически находит влияние ваших ссылок и находит наиболее подходящий журнал для ваших статей.
Платформа также позволяет пользователям автоматически создавать, форматировать и обновлять библиографии. Быстро экспортируйте свои ссылки и полнотекстовые PDF-файлы в EndNote и сразу же приступайте к работе. С помощью набора шаблонов и подключаемых модулей EndNote исследователи могут улучшить свой опыт работы с Endnote и получить максимальную отдачу от платформы.
Основные характеристики сноски:
- Фильтры импорта для предыдущих исследований
- Отслеживайте активность ваших товарищей по команде в общей библиотеке
- Автоматическое обновление ссылок и ссылок
Стоимость:
- Бесплатно с ограниченной функциональностью
- Платные планы начинаются с 249 долларов США
Evernote — это приложение для создания заметок, которое может быть очень полезным при проведении исследований.Приложение поможет вам хранить все ваши личные идеи, списки дел4, заметки и ссылки на исследования в одном месте. Создайте отдельные теги и папки для различных типов информации, которую вы сохраняете, и держите ее в порядке. Evernote автоматически синхронизируется на всех ваших устройствах, включая настольный компьютер, смартфон и планшет, поэтому вы можете переключаться между устройствами без потери данных.
Его расширение для браузера Chrome под названием Evernote web clipper — отличное дополнение для сохранения статей или другого контента в Интернете во время исследования.Просто щелкните расширение браузера, чтобы сохранить всю страницу или выделить ее в блокноте Evernote вместе с любыми заметками об этой странице.
Основные характеристики Evernote:
- Храните заметки, статьи и другой контент в одном месте
- Расширение Chrome для вырезания контента
- Установка напоминаний
Цена:
- Бесплатно с ограниченной функциональностью
- Платные планы начинаются с Plus (34,99 доллара США в год или 3 доллара США.99 в месяц), Premium (69,99 долларов США в год или 7,99 долларов США в месяц) и Evernote Business (свяжитесь с отделом продаж)
Mendeley — это программное обеспечение для управления ссылками, которое позволяет исследователям создавать ссылки, цитаты, и библиографии в нескольких стилях журналов с помощью всего нескольких щелчков мышью. Получите быстрый доступ к своей библиотеке откуда угодно — откуда угодно. Windows, Mac, Linux и т. Д. И добавляйте документы прямо из браузера несколькими щелчками мыши или импортируйте любые документы со своего рабочего стола в свою библиотеку.
Благодаря своей исследовательской сети, исследователи соединяются и объединяются в сеть с более чем 6 миллионами пользователей. Пользователи могут создавать группы, чтобы проводить обсуждения, находить исследования и следить за избранной библиографией. Есть также более 250 000+ вакансий в области науки, технологий и здравоохранения для продвижения вашей карьеры и предоставления информации от более чем 5000 организаций для финансирования ваших следующих исследований!
Основные возможности Mendeley:
- Аннотируйте и систематизируйте документы
- Находите и создавайте группы с коллегами-исследователями
- Информация о грантах от более чем 5000 организаций
Стоимость:
- Бесплатно с ограниченной функциональностью
- планы начинаются от 55 долларов в год за 5 ГБ до 165 долларов в год при неограниченном хранилище
ContentMine предлагает различные службы интеллектуального анализа текста, чтобы помочь исследователям находить, загружать, анализировать и извлекать знания из научных статей. ContentMine создает собственный открытый исходный код, чтобы помочь исследователям находить статьи и не тратить на это время в Интернете. Они также могут конвертировать академические статьи, PDF-файлы в HTML или почти в любой формат.
ContentMine также может извлекать данные из таблиц и графиков, сокращая время, необходимое для проведения метаанализа.Платформа также предлагает консультации, а также обучающие семинары для обучения людей тому, что они делают и как.
Ключевые особенности ContentMine:
- Извлечение данных из таблиц и графиков
- Быстро извлекайте текст из сотен статей
- Семинары и тренинги
Цены:
3
12. ResearchGateПоследний инструмент в нашем списке замечательных инструментов для исследователей — это платформа под названием ResearchGate.ResearchGate предоставляет вам доступ к более чем 135 миллионам страниц публикаций, позволяя вам быть в курсе того, что происходит в вашей области. Благодаря встроенному сообществу исследователи могут делиться своими исследованиями, сотрудничать с коллегами и открывать новые статьи и библиографии.
ResearchGate также обеспечивает глубокую аналитику тех, кто читал вашу работу, и отслеживает ваши ссылки. ResearchGate — это исследовательское сообщество, к которому нужно присоединиться с более чем 17 миллионами пользователей!
Ключевые особенности ResearchGate:
- Делитесь и находите исследователей
- Аналитика, чтобы узнать, кто читает вашу работу
- Отслеживание цитирования
Ценообразование:
Заключительные слова
наш список удивительных веб-сайтов, приложений и программного обеспечения, которые можно использовать при проведении исследования.Исследования — это тяжелая работа — от поиска и управления контентом до организации и публикации — исследование требует много времени и усилий.
Тем не менее, с нашим потрясающим списком инструментов, исследователи наверняка потратят большую часть своего времени и усилий и выполнят работу более эффективно. Пропустили ли мы какой-нибудь замечательный инструмент для исследователей? Дайте нам знать, написав нам в Твиттере @bit_docs.
Дополнительные чтения:
AWS Lambda — Serverless Compute
Обработка данных
AWS Lambda можно использовать для выполнения кода в ответ на триггеры, такие как изменения данных, сдвиги в состоянии системы или действия пользователей.Lambda может напрямую запускаться сервисами AWS, такими как S3, DynamoDB, Kinesis, SNS и CloudWatch, может подключаться к существующим файловым системам EFS или может быть организован в рабочие процессы с помощью AWS Step Functions. Это позволяет создавать различные системы бессерверной обработки данных в реальном времени.
Обработка файлов в реальном времени
Amazon S3 можно использовать для запуска AWS Lambda для обработки данных сразу после загрузки. Вы также можете напрямую подключиться к существующей файловой системе Amazon EFS, что обеспечивает массовый параллельный общий доступ для крупномасштабной обработки файлов.Например, вы можете использовать Lambda для эскизов изображений, перекодирования видео, индексных файлов, обработки журналов, проверки содержимого, а также агрегирования и фильтрации данных в режиме реального времени.
The Seattle Times использует AWS Lambda для изменения размера изображений для просмотра на различных устройствах, таких как настольные компьютеры, планшеты и смартфоны. Прочитать пример использования »
Обработка потоков в реальном времени
AWS Lambda и Amazon Kinesis можно использовать для обработки потоковых данных в реальном времени для отслеживания активности приложений, обработки заказов транзакций, анализа потока кликов, очистки данных, генерации метрик, фильтрации журналов, индексации, анализа социальных сетей, а также телеметрии данных устройств IoT и замер.
Localytics обрабатывает миллиарды точек данных в режиме реального времени и использует Lambda для обработки исторических и текущих данных, хранящихся в S3 или передаваемых из Kinesis. Прочитать пример использования »
Машинное обучение
AWS Lambda можно использовать для предварительной обработки данных перед их передачей в модель машинного обучения.Имея Lambda-доступ к EFS, вы также можете использовать свою модель для прогнозирования в масштабе без необходимости выделять или управлять какой-либо инфраструктурой.
«В Aible мы сосредоточены на предоставлении самых мощных технологий искусственного интеллекта с минимально возможными эксплуатационными расходами. Поэтому мы используем AWS Lambda и Serverless для обучения машинному обучению и прогнозирования. С помощью бессерверного режима мы можем выполнять широкий спектр рабочих нагрузок машинного обучения с меньшими затратами. эффективно, используя при этом большие вычислительные ресурсы, необходимые для быстрой итерации и масштабирования, чтобы создать ИИ для оптимального воздействия на бизнес.»
Род Баттерс, технический директор — Aible
Бэкэнд
Вы можете создавать бессерверные серверные ВМ с помощью AWS Lambda для обработки веб-запросов, мобильных приложений, Интернета вещей (IoT) и сторонних API-запросов. Воспользуйтесь преимуществами согласованных средств управления производительностью Lambda, таких как несколько конфигураций памяти и Provisioned Concurrency, для создания чувствительных к задержкам приложений в любом масштабе.
Веб-приложения
Объединив AWS Lambda с другими сервисами AWS, разработчики могут создавать мощные веб-приложения, которые автоматически масштабируются вверх и вниз и запускаются в конфигурации с высокой доступностью в нескольких центрах обработки данных — с нулевыми административными усилиями, необходимыми для масштабируемости, резервного копирования или нескольких центров обработки данных избыточность.
Серверные модули Интернета вещей
Вы можете создавать бессерверные серверные ВМ с помощью AWS Lambda для обработки веб-запросов, мобильных приложений, Интернета вещей (IoT) и сторонних API-запросов.
Мобильные серверные части
AWS Lambda упрощает создание насыщенных, персонализированных приложений. Вы можете создавать серверные части с помощью AWS Lambda и Amazon API Gateway для аутентификации и обработки запросов API. Используйте AWS Amplify, чтобы легко интегрировать серверную часть с интерфейсами iOS, Android, Web и React Native.
Bustle использует бессерверный бэкэнд для своего приложения и веб-сайтов Bustle iOS, используя AWS Lambda и Amazon API Gateway.Бессерверные архитектуры позволяют Bustle никогда не заниматься управлением инфраструктурой, поэтому каждый инженер может сосредоточиться на создании новых функций и внедрении инноваций. Прочитать пример использования »
AlphaFold: решение грандиозной проблемы биологии 50-летней давности
Мы также увидели признаки того, что прогнозирование структуры белка может быть полезным в будущих усилиях по реагированию на пандемию, как один из многих инструментов, разработанных научным сообществом.Ранее в этом году мы предсказали несколько белковых структур вируса SARS-CoV-2, включая ORF3a, структура которого ранее была неизвестна. В CASP14 мы предсказали структуру другого белка коронавируса, ORF8. Впечатляюще быстрая работа экспериментаторов подтвердила структуры как ORF3a, так и ORF8. Несмотря на их сложный характер и наличие очень небольшого количества связанных последовательностей, мы достигли высокой степени точности обоих наших прогнозов по сравнению с их экспериментально определенными структурами.
Мы не только ускоряем понимание известных болезней, но и рады возможности этих методов исследовать сотни миллионов белков, для которых у нас в настоящее время нет моделей, — обширную территорию с неизвестной биологией. Поскольку ДНК определяет аминокислотные последовательности, которые составляют структуры белков, революция в геномике сделала возможным считывание последовательностей белков из естественного мира в массовом масштабе — с 180 миллионами последовательностей белков и подсчетом в базе данных Universal Protein (UniProt).Напротив, учитывая экспериментальную работу, необходимую для перехода от последовательности к структуре, только около 170 000 белковых структур находятся в банке данных о белках (PDB). Среди неопределенных белков могут быть некоторые с новыми интересными функциями, и — так же, как телескоп помогает нам заглянуть глубже в неизвестную вселенную — такие методы, как AlphaFold, могут помочь нам найти их.
Открывая новые возможности
AlphaFold — одно из наших самых значительных достижений на сегодняшний день, но, как и во всех научных исследованиях, есть еще много вопросов, на которые нужно ответить.Не всякая структура, которую мы прогнозируем, будет идеальной. Еще многое предстоит узнать, в том числе о том, как несколько белков образуют комплексы, как они взаимодействуют с ДНК, РНК или небольшими молекулами, и как мы можем определить точное местоположение всех боковых цепей аминокислот. В сотрудничестве с другими можно многое узнать о том, как лучше всего использовать эти научные открытия при разработке новых лекарств, о способах управления окружающей средой и многом другом.
Для всех нас, работающих над вычислительными методами и методами машинного обучения в науке, такие системы, как AlphaFold, демонстрируют потрясающий потенциал ИИ как инструмента для фундаментальных открытий.Так же, как 50 лет назад Анфинсен поставил задачу, выходящую далеко за пределы возможностей науки в то время, многие аспекты нашей Вселенной остаются неизвестными. Объявленный сегодня прогресс вселяет в нас уверенность в том, что ИИ станет одним из самых полезных инструментов человечества в расширении границ научных знаний, и мы с нетерпением ждем впереди многих лет упорной работы и открытий!
Пока мы не опубликуем статью об этой работе, пожалуйста, цитируйте:
Высокоточное прогнозирование структуры белка с использованием глубокого обучения
Джон Джампер, Ричард Эванс, Александр Прицель, Тим Грин, Майкл Фигурнов, Кэтрин Туньясувунакул, Олаф Роннебергер, Расс Бейтс, Огюстин Жидек, Алекс Бриджленд, Клеменс Мейер, Саймон А.А. Коль, Анна Потапенко, Эндрю Дж. Баллард, Эндрю Ромера, Бернардино -Паредес, Станислав Николов, Ришуб Джейн, Йонас Адлер, Тревор Бэк, Стиг Петерсен, Дэвид Рейман, Мартин Штайнеггер, Михалина Пачольска, Дэвид Сильвер, Ориол Виньялс, Эндрю У. Старший, Корай Кавукчуоглу, Пушмит Кохли, Демис Хассабис.
в Четырнадцатой критической оценке методов прогнозирования структуры белка (тезисы), 30 ноября — 4 декабря 2020 г. Получено отсюда.
Мы находимся в самом начале изучения того, как лучше всего дать возможность другим группам использовать наши предсказания структуры, наряду с подготовкой рецензируемой статьи для публикации. Хотя наша команда не сможет ответить на все запросы, если AlphaFold может иметь отношение к вашей работе, отправьте несколько строк об этом на alphafold @ deepmind.com. Мы свяжемся с вами, если появятся возможности для дальнейшего изучения.
Защита и безопасность конечных точек Apex One ™
Защита и безопасность конечных точек Apex One ™ | Trend MicroНовое определение безопасности конечных точек
Автоматизированная, интуитивно понятная комплексная защита
Автоматизированный
Защита Trend Micro Apex One ™ обеспечивает расширенное автоматическое обнаружение угроз и реагирование на постоянно растущий спектр угроз, включая бесфайловые программы и программы-вымогатели.Наше сочетание современных методов, предназначенных для разных поколений, обеспечивает тщательно настроенную защиту конечных точек, которая максимизирует производительность и эффективность.
проницательный
Получите полезную информацию, расширенные возможности расследования и централизованный контроль с помощью расширенного набора инструментов EDR, сильной интеграции SIEM и открытого набора API. У вас есть возможность проводить коррелированные расширенные исследования угроз, выходящие за рамки конечной точки, и дополнять ваши группы безопасности управляемой службой обнаружения и реагирования.
МФУ
В постоянно меняющемся технологическом ландшафте вам нужна безопасность, выходящая за рамки традиционного антивируса. Apex One предлагает обнаружение угроз, реагирование и расследование в рамках одного агента. Избавьтесь от множества поставщиков и консолей и получите гибкость развертывания с помощью вариантов развертывания как SaaS, так и локального развертывания.
Системные требования Apex OneМинимальные рекомендуемые требования к агенту
Операционные системы агентов
- Windows 7 (6.1)
- Windows 8.1 (6.2 / 6.3)
- Windows 10 (10.0)
- Windows Server 2008 R2 (6.1)
- Windows Server 2012 (6.2)
- Windows Server 2012 R2 (6.3)
- Windows Server 2016 (10)
- Windows Server 2019
- macOS® High Sierra 10.13
- macOS Sierra 10.12
- OS X® Эль-Капитан 10.11
- OS X Yosemite 10.10 или новее
- OS X Mavericks 10.9 или новее
- OS X Mountain Lion 10.8.3 или новее
- OS X Lion 10.7.5 или новее (только 64-разрядная версия)
Agent Platform Процессор
: Intel Pentium с тактовой частотой 300 МГц или аналогичный (Windows 7, 8.1, 10 семей) и процессор Intel® Core ™ для Mac
- минимум 1,0 ГГц (рекомендуется 2,0 ГГц) Intel Pentium или аналогичный (Windows Embedded POSReady7)
- Минимум 1,4 ГГц (рекомендуется 2,0 ГГц) Intel Pentium или эквивалентный (Windows 2008 R2, семейство Windows 2016, семейство Windows 2019)
Память:
- Не менее 512 МБ (2.Рекомендуется 0 ГБ) и не менее 100 МБ исключительно для Apex One (Windows 2008 R2, семейство 2012)
- Минимум 1,0 ГБ (рекомендуется 2,0 ГБ) и не менее 100 МБ исключительно для Apex One (Windows 7 (x86), 8.1 (x86), Windows Embedded POSReady 7, семейство 10 (x64))
- Минимум 2,0 ГБ (рекомендуется 4,0 ГБ) и не менее 100 МБ исключительно для Apex One (семейство Windows 7 (x64), 8.1 (x64), 10 (x64))
- Минимум 512 МБ для Apex One на Mac
Дисковое пространство: 1.Минимум 5 ГБ (рекомендуется 3 ГБ для всех продуктов) для Windows, минимум 300 МБ для Mac
Расширенные методы обнаружения
Apex One использует сочетание методов защиты от угроз разных поколений, чтобы обеспечить широчайшую защиту от всех типов угроз, предоставляя вам:
Машинное обучение перед выполнением и во время выполнения
Более точное обнаружение сложных вредоносных программ, таких как бесфайловые угрозы, живущие вне земли и вымогатели
Методы шумоподавления, такие как перепись и создание безопасных списков, на всех уровнях обнаружения для значительного уменьшения количества ложных срабатываний
Эффективная защита от сценариев, инъекций, атак программ-вымогателей, памяти и браузера за счет инновационного анализа поведения
Максимальная защита от уязвимостей
Больше, чем просто сканирование, Apex One Vulnerability Protection использует систему предотвращения вторжений (HIPS) на основе хоста для виртуального исправления известных и неизвестных уязвимостей до того, как исправление станет доступным или развернутым:
Устранение рисков путем защиты уязвимостей с помощью инновационных возможностей виртуального исправления и исследований мирового уровня
Расширение защиты на критически важные платформы и физические или виртуальные устройства
Сокращение времени простоя при восстановлении и исправлении ошибок
Выявление уязвимостей на основе CVE, MS-ID и степени серьезности
Обнаружение большего количества уязвимостей, чем любой другой поставщик, благодаря нашему ведущему в отрасли исследованию уязвимостей
Интегрированное обнаружение и реагирование
Используйте передовые методы обнаружения, которые позволяют обнаруживать угрозы и реагировать на них до того, как они скомпрометируют данные.С Trend Micro Vision One ™ вы получаете полнофункциональные возможности XDR, которые расширяют возможности обнаружения и реагирования и расширяют их на несколько уровней безопасности для широкой видимости и реагирования на угрозы, влияющие на всю организацию.
Испытайте XDR с Trend Micro Vision One с автоматическим бесплатным доступом для 10% лицензированных пользователей *. Защитите тех, кто подвергается наибольшему риску, и улучшите обнаружение и реагирование для вашей организации.
* Бесплатные лицензии XDR не включают интегрированные ответные действия
Поиск индикаторов атаки (IoA) и определение намерений злоумышленника в режиме реального времени
Проверка пользовательских временных шкал (телеметрия) для индикаторов компрометации (IoC) для определения воздействия целевых атак
Используйте интерактивную диаграмму анализа первопричин для детализации обнаружения и реагирования путем изоляции или завершения процессов и обновления точек защиты
Есть возможность выйти за рамки единого векторного подхода путем корреляции событий по электронной почте, конечным точкам, серверам, облачным рабочим нагрузкам и сетям.
Эффективная защита ваших конфиденциальных данных Защитите ваши конфиденциальные данные как в сети, так и за ее пределами, чтобы обеспечить максимальную видимость и контроль.Шифрование конечных точек, * встроенный DLP и управление устройствами:
- Охватывает самый широкий спектр устройств, приложений и типов файлов
- Помощь в соблюдении большинства нормативных требований, включая GDPR
- Защита данных с помощью шифрования всего диска, папки, файла и съемного носителя
- Установка детальных политик для контроля устройств и управления данными
- Управление ключами шифрования Microsoft ® BitLocker ® и Apple ® FileVault ®
* Шифрование конечной точки доступно как отдельный агент.
Улучшенный контроль приложений против вредоносного программного обеспечения. Предотвращение запуска неизвестных и нежелательных приложений на корпоративных конечных точках. Приложение Trend Micro Apex One ™ Application Control позволяет:
- Блокировать запуск вредоносных программ с помощью настраиваемых политик блокировки, списков надежных отправителей и запретов
- Создавайте динамические политики, используя возможности категоризации приложений и аналитики репутации Trend Micro для сокращения накладных расходов на управление
- Корреляция данных из миллионов событий приложений для выявления угроз и поддержки актуальной базы данных проверенных приложений
Централизованный обзор и контроль
Обеспечьте согласованное управление безопасностью, видимость и отчетность на нескольких уровнях взаимосвязанной безопасности с помощью централизованной консоли.
Расширение контроля и прозрачности для локальных, облачных и гибридных моделей
Повышение защиты, снижение сложности и устранение избыточности
Обеспечьте доступ к аналитическим данным об угрозах с помощью Trend Micro ™ Smart Protection Network ™
TrendConnect позволяет пользователям оставаться в курсе событий в реальном времени с помощью предупреждений о продуктах и информации об угрозах. С помощью приложения TrendConnect клиенты смогут:
- Мгновенно просматривайте статус развертывания, чтобы не запускать устаревшие версии Trend Micro Apex One
- Согласование развертываний с лучшими практиками Trend Micro Apex One для обеспечения оптимальной защиты конечных точек
- Будьте на шаг впереди с уведомлениями в режиме реального времени о новых уязвимостях / угрозах и уведомлениями о новых важных и критических исправлениях
Как это работает
Ряд возможностей многоуровневого обнаружения, наряду с расследованием и реагированием, защищает конечную точку на всех этапах
В очередной раз признан лидером в Магическом квадранте Gartner 2021 года для платформ защиты конечных точек
Признан лидером в конкурсе The Forrester Wave ™: ПО для обеспечения безопасности конечных точек как услуга, 2 квартал 2021 г.
Захвачено Trend Micro 10.5% рынка безопасности конечных точек 2020 года, самая высокая доля.
Названа лидером в области Forrester Wave ™ : Enterprise Detection and Response, Q1 2020
Apex One доступен вместе с XDR в простых упаковках.
Apex One с XDR
Одноагентное облачное управляемое решение с лучшими возможностями защиты конечных точек и XDR.
XDR для пользователей
Добавляет Microsoft ® Office 365 ® и Google G Suite ™ для защиты электронной почты и обмена файлами в облаке, а также объединяет возможности обнаружения конечных точек и электронной почты и реагирования для борьбы с методом атаки номер один — фишингом.
«С момента развертывания Trend Micro мы зафиксировали миллионы атак, остановили 117 000 угроз за один день и не зарегистрировали ни одного заражения за 18 месяцев.Trend Micro всегда работает, даже когда я сплю ». более
Ян Келлер
Начальник службы безопасности, SBV Services
Начало работы с Trend Micro Apex One Endpoint Security
Полная защита пользователя
Для дополнительной функциональности, надстроек:
Обнаружение и отклик конечной точки (EDR): включите расширенные возможности обнаружения и отклика (XDR) с помощью Trend Micro Vision One.Увеличьте ценность XDR с помощью коррелированных обнаружений, интегрированных исследований и ответных мер в различных решениях Trend Micro.
Управляемое обнаружение и ответ (MDR): Trend Micro ™ Managed XDR предоставляет экспертные услуги по обнаружению, расследованию и поиску угроз для конечных точек, а также электронной почты, серверов, облачных рабочих нагрузок и / или сети.
Cloud Sandbox: предложение «песочница как услуга» анализирует многоступенчатые загрузки, URL-адреса, C&C и многое другое в «безопасном режиме реального времени».
sXpIBdPeKzI9PC2p0SWMpUSM2NSxWzPyXTMLlbXmYa0R20xk
Искусственный интеллект и будущее людей
Система распознавания транспортных средств и людей для использования правоохранительными органами продемонстрирована на прошлогодней конференции GPU Technology Conference в Вашингтоне, округ Колумбия.C., в котором рассказывается о новых применениях искусственного интеллекта и глубокого обучения. (Saul Loeb / AFP / Getty Images)Цифровая жизнь расширяет человеческие возможности и разрушает вековую человеческую деятельность. Системы, основанные на коде, распространились на более чем половину жителей планеты благодаря внешней информации и возможности подключения, предлагая ранее невообразимые возможности и беспрецедентные угрозы. По мере того как новый искусственный интеллект (ИИ), управляемый алгоритмами, продолжает распространяться, будут ли люди жить лучше, чем сегодня?
Около 979 пионеров технологий, новаторов, разработчиков, руководителей бизнеса и политики, исследователей и активистов ответили на этот вопрос в ходе опроса экспертов, проведенного летом 2018 года.
Эксперты предсказали, что сетевой искусственный интеллект повысит эффективность человека, но также поставит под угрозу его автономию, возможности и возможности. Они говорили о широких возможностях; что компьютеры могут соответствовать или даже превосходить человеческий интеллект и возможности в таких задачах, как принятие сложных решений, рассуждение и обучение, сложная аналитика и распознавание образов, острота зрения, распознавание речи и языковой перевод. Они заявили, что «умные» системы в сообществах, в транспортных средствах, в зданиях и коммунальных службах, на фермах и в бизнес-процессах сэкономят время, деньги и жизни и предоставят людям возможность наслаждаться более индивидуализированным будущим.
Многие из них сосредоточили свои оптимистические замечания на здравоохранении и множестве возможных применений ИИ для диагностики и лечения пациентов или помощи пожилым людям жить более полной и здоровой жизнью. Они также с энтузиазмом восприняли роль ИИ в содействии широким программам общественного здравоохранения, основанным на огромных объемах данных, которые могут быть собраны в ближайшие годы обо всем, от личных геномов до питания. Кроме того, ряд этих экспертов предсказывали, что ИИ будет способствовать долгожданным изменениям в формальных и неформальных системах образования.
Тем не менее, большинство экспертов, независимо от того, оптимистичны они или нет, выражали озабоченность по поводу долгосрочного воздействия этих новых инструментов на основные элементы человеческого бытия. Всех респондентов в этом ненаучном опросе попросили подробно рассказать, почему, по их мнению, ИИ улучшит положение людей или нет. Многие разделяли глубокие переживания и предлагали пути решения. Основные озвученные ими темы об угрозах и средствах защиты изложены в прилагаемой таблице.
ИИ и будущее человека: эксперты выражают озабоченность и предлагают решения
| ПРОБЛЕМЫ | Человеческое агентство: Люди теряют контроль над своей жизнью | Принятие решений по ключевым аспектам цифровой жизни автоматически передается инструментам «черного ящика», основанным на коде.Людям не хватает информации и они не изучают контекст того, как работают инструменты. Они жертвуют независимостью, конфиденциальностью и властью перед выбором; они не контролируют эти процессы. Этот эффект будет усиливаться по мере того, как автоматизированные системы станут более распространенными и сложными. |
| Злоупотребление данными: Использование данных и наблюдение в сложных системах предназначены для получения прибыли или для реализации власти | Большинство инструментов искусственного интеллекта находятся и будут находиться в руках компаний, стремящихся к прибыли, или правительств, стремящихся к власти.Ценности и этика часто не закреплены в цифровых системах, которые принимают решения за них. Эти системы объединены в глобальную сеть, и их нелегко регулировать или ограничивать. | |
| Потеря работы: Захват рабочих мест искусственным интеллектом приведет к увеличению разрыва в экономике, что приведет к социальным потрясениям | Эффективность и другие экономические преимущества машинного интеллекта на основе кода будут и дальше нарушать все аспекты человеческой работы. В то время как некоторые ожидают появления новых рабочих мест, другие обеспокоены массовой потерей рабочих мест, увеличением экономического разрыва и социальными потрясениями, включая популистские восстания. | |
| Блокировка зависимости: Снижение когнитивных, социальных навыков и навыков выживания у людей | Многие считают ИИ расширением человеческих возможностей, но некоторые предсказывают обратное: растущая зависимость людей от сетей, управляемых машинами, подорвет их способность думать самостоятельно, действовать независимо от автоматизированных систем и эффективно взаимодействовать с другими. | |
| Mayhem: Автономное оружие, киберпреступность и информация о вооружении | Некоторые предсказывают дальнейшую эрозию традиционных социально-политических структур и возможность больших человеческих жертв из-за ускоренного роста автономных военных приложений и использования информации, лжи и пропаганды в качестве оружия для опасной дестабилизации человеческих групп.Некоторые также опасаются проникновения киберпреступников в экономические системы. | |
| ПРЕДЛАГАЕМЫЕ РЕШЕНИЯ | Глобальное благо — номер 1: Улучшение человеческого сотрудничества через границы и групп заинтересованных сторон | Цифровое сотрудничество в интересах человечества является высшим приоритетом. Необходимо найти способы, позволяющие людям во всем мире прийти к общему пониманию и соглашению — объединить усилия, чтобы способствовать внедрению широко распространенных подходов, направленных на решение серьезных проблем и поддержание контроля над сложными человеческими и цифровыми сетями. |
| Система, основанная на ценностях: Разработка политики, гарантирующей, что ИИ будет направлен на «человечность» и общее благо | Примите «лунный менталитет» для создания инклюзивных, децентрализованных интеллектуальных цифровых сетей, «пропитанных эмпатией», которые помогают людям активно обеспечивать соответствие технологий социальным и этическим обязанностям. Потребуется какой-то новый уровень процесса регулирования и сертификации. | |
| Расставьте приоритеты для людей: Измените экономические и политические системы, чтобы лучше помочь людям «гоняться с роботами» | Реорганизовать экономические и политические системы с целью расширения способностей и возможностей людей, чтобы усилить взаимодействие между людьми и ИИ и упрочить тенденции, которые могут поставить под угрозу человеческую значимость перед лицом запрограммированного интеллекта. | |
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ЦЕНТР PEW И УНИВЕРСИТЕТ ЭЛОН В ПРЕДСТАВЛЕНИИ ИНТЕРНЕТ-ЦЕНТРА
В частности, участникам было предложено рассмотреть следующее:
«Пожалуйста, подумайте, что впереди до 2030 года. Аналитики ожидают, что люди станут еще более зависимыми от сетевого искусственного интеллекта (ИИ) в сложных цифровых системах. Некоторые говорят, что мы продолжим исторический путь улучшения нашей жизни с в основном положительными результатами, поскольку мы широко внедряем эти сетевые инструменты.Некоторые говорят, что наша растущая зависимость от этого ИИ и связанных с ним систем, вероятно, приведет к повсеместным трудностям.
Наш вопрос: как вы думаете, наиболее вероятно, что к 2030 году развитие ИИ и связанных с ним технологических систем расширит человеческий потенциал и расширит его возможности? То есть будет ли большинству людей в большинстве случаев лучше, чем сегодня? Или наиболее вероятно, что развитие ИИ и связанных с ним технологических систем уменьшит человеческую автономию и свободу действий до такой степени, что большинству людей не будет лучше, чем сегодня? »
В целом, несмотря на опасения по поводу недостатков, 63% респондентов в этом опросе заявили, что они надеются, что большинству людей будет в основном лучше в 2030 году, а 37% заявили, что людям будет лучше , а не .
Ряд мыслителей, участвовавших в этом опросе, заявили, что растущая зависимость людей от технологических систем будет успешной только в том случае, если пристальное внимание будет уделяться тому, как эти инструменты, платформы и сети проектируются, распространяются и обновляются. Некоторые из мощных, всеобъемлющих ответов включали ответы:
Соня Катяль , содиректор Берклиского центра права и технологий и член первого совета консультантов Министерства торговли США по цифровой экономике, предсказала: «В 2030 году самый большой набор вопросов будет касаться того, как восприятие ИИ и их применение повлияет на развитие гражданских прав в будущем.Вопросы о конфиденциальности, свободе слова, праве на собрания и технологическом построении личности снова возникнут в этом новом контексте ИИ, поставив под сомнение наши глубочайшие убеждения о равенстве и возможностях для всех. Кто выиграет, а кто окажется в невыгодном положении в этом новом мире, зависит от того, насколько широко мы анализируем эти вопросы сегодня, на будущее ».
Нам необходимо активно работать, чтобы технология соответствовала нашим ценностям. Эрик Бриньольфссон
Эрик Бриньолфссон , директор Инициативы Массачусетского технологического института по цифровой экономике и автор книги «Машины, платформы, толпа: использование нашего цифрового будущего», сказал: «ИИ и связанные с ним технологии уже достигли сверхчеловеческой производительности во многих областях, и есть Нет сомнений в том, что к 2030 году их возможности, вероятно, значительно улучшатся.… Я думаю, что более вероятно, что мы воспользуемся этой силой, чтобы сделать мир лучше. Например, мы можем практически искоренить глобальную бедность, значительно снизить заболеваемость и обеспечить лучшее образование почти всем на планете. Тем не менее, AI и ML [машинное обучение] также могут использоваться для все большей концентрации богатства и власти, оставляя позади многих людей, и для создания еще более ужасающего оружия. Ни один из результатов не является неизбежным, поэтому правильный вопрос — не «Что произойдет?», А «Что мы выберем делать?». Нам нужно активно работать, чтобы обеспечить соответствие технологий нашим ценностям.Это можно и нужно делать на всех уровнях, от правительства до бизнеса, до академических кругов и до индивидуального выбора ».
Брайан Джонсон , основатель и генеральный директор Kernel, ведущего разработчика передовых нейронных интерфейсов, и OS Fund, венчурной компании, сказал: «Я твердо верю, что ответ зависит от того, сможем ли мы сместить наши экономические системы в сторону приоритета радикальных человеческих ресурсов. улучшение и остановка тенденции к тому, что человечество неуместно перед лицом ИИ. Я не имею в виду только работу; Я имею в виду истинную экзистенциальную неуместность, которая является конечным результатом отсутствия приоритета человеческого благополучия и познания.”
Марина Горбис , исполнительный директор Института будущего, сказала: «Без значительных изменений в нашей политической экономике и режимах управления данными [ИИ], вероятно, приведет к еще большему экономическому неравенству, большему слежению и большему количеству программ и нечеловеческих факторов. центрические взаимодействия. Каждый раз, когда мы программируем нашу среду, мы в конечном итоге программируем себя и свои взаимодействия. Люди должны стать более стандартизированными, устраняя интуицию и двусмысленность нашего взаимодействия.И в этой неоднозначности и сложности и заключается суть человека ».
Джудит Донат , автор книги «Социальная машина, дизайн для жизни в Интернете» и преподаватель Центра Интернета и общества Беркмана Кляйна Гарвардского университета, прокомментировала: «К 2030 году большинство социальных ситуаций будет облегчаться с помощью ботов — на первый взгляд разумных программы, которые взаимодействуют с нами по-человечески. Дома родители будут привлекать опытных ботов, чтобы помогать детям с домашними заданиями и стимулировать разговоры за ужином.На работе боты будут проводить встречи. Доверенное лицо бота будет считаться важным для психологического благополучия, и мы все чаще будем обращаться к таким товарищам за советом, начиная от того, что надеть, на кого выйти замуж. Мы, люди, глубоко заботимся о том, как нас видят другие, а те, чье одобрение мы ищем, будут все более искусственными. К тому времени разница между людьми и ботами значительно исчезнет. Через экран и проекцию голос, внешний вид и поведение ботов будут неотличимы от человеческих, и даже физические роботы, хотя и явно нечеловеческие, будут настолько убедительно искренними, что наше впечатление о них как о мыслящих, чувствующих существах на одном уровне. с нами или выше нас, будут непоколебимы.В дополнение к двусмысленности, наше собственное общение будет сильно расширено: программы будут составлять многие из наших сообщений, а наш внешний вид в сети / дополненной реальности будет [создаваться] с помощью вычислений. (Грубая человеческая речь и поведение без посторонней помощи будут казаться смущающе неуклюжими, медленными и бесхитростными.) Благодаря доступу к огромным массивам данных о каждом из нас, боты намного превзойдут людей в своей способности привлекать и убеждать нас. Способные искусно имитировать эмоции, они никогда не будут подавлены чувствами: если они что-то выпалит в гневе, это произойдет потому, что такое поведение было рассчитано как наиболее эффективный способ достижения тех целей, которые они «наметили».’Но каковы эти цели? Компаньоны с искусственным интеллектом будут создавать впечатление, что социальные цели, аналогичные нашим собственным, мотивируют их — чтобы к ним относились с уважением, будь то любимый друг, уважаемый начальник и т. Д. Но их реальное сотрудничество будет с людьми и учреждениями, которые их контролируют. . Как и их сегодняшние предки, они будут продавцами товаров, которые используют их для стимулирования потребления, и политиками, которые уполномочивают их влиять на общественное мнение ».
Эндрю Маклафлин , исполнительный директор Центра инновационного мышления Йельского университета, ранее занимавший должность заместителя главного технологического директора США при президенте Бараке Обаме и ведущий специалист по глобальной государственной политике Google, написал: «2030 год не за горами.Я считаю, что такие инновации, как Интернет и сетевой ИИ, приносят огромные краткосрочные выгоды, наряду с долгосрочными недостатками, которые могут занять десятилетия, прежде чем их можно будет распознать. ИИ будет способствовать широкому спектру оптимизаций эффективности, но также позволит скрыть дискриминацию и произвольное наказание людей в таких областях, как страхование, поиск работы и оценка эффективности ».
Майкл М. Робертс , первый президент и главный исполнительный директор Интернет-корпорации по присвоению имен и номеров (ICANN) и член Зала славы Интернета, написал: «Диапазон возможностей интеллектуальных агентов по увеличению человеческого интеллекта по-прежнему практически неограничен.Основная проблема заключается в том, что чем удобнее агент, тем больше ему нужно знать о вас — предпочтения, время, возможности и т. Д. — что создает компромисс: дополнительная помощь требует большего вмешательства. Это не черно-белый вопрос — оттенки серого и связанные с ним лекарства будут спорить бесконечно. На сегодняшний день установлено, что удобство преобладает над конфиденциальностью. Я подозреваю, что так будет и дальше ».
Дана Бойд , главный исследователь Microsoft, основатель и президент Исследовательского института данных и общества, сказал: «ИИ — это инструмент, который люди будут использовать для самых разных целей, в том числе в погоне за властью.Произойдут злоупотребления властью, связанные с использованием ИИ, точно так же, как будут достигнуты успехи в науке и гуманитарных усилиях, которые также будут связаны с ИИ. К сожалению, есть определенные линии тренда, которые могут создать массивную нестабильность. Возьмем, к примеру, изменение климата и миграцию климата. Это еще больше дестабилизирует Европу и США, и я ожидаю, что в панике мы увидим, что ИИ будет использоваться во вредных целях в свете других геополитических кризисов ».
Эми Уэбб , основатель Future Today Institute и профессор стратегического предвидения в Нью-Йоркском университете, прокомментировала: «Структуры социальной защиты, существующие в настоящее время в США.S. и многие другие страны по всему миру не были предназначены для нашего перехода на ИИ. Переход через ИИ продлится следующие 50 лет или больше. По мере того, как мы продвигаемся дальше в эту третью эру вычислений и по мере того, как каждая отдельная отрасль все больше внедряется в системы искусственного интеллекта, нам потребуются новые квалифицированные специалисты, обладающие гибридной квалификацией, которые смогут выполнять работу, которой никогда раньше не было. Нам понадобятся фермеры, умеющие работать с большими наборами данных. Онкологи прошли обучение на роботов. Биологи получили образование инженеров-электриков.Нам не нужно будет готовить персонал только один раз, если внести несколько изменений в учебную программу. По мере развития ИИ нам потребуется отзывчивая рабочая сила, способная адаптироваться к новым процессам, системам и инструментам каждые несколько лет. Потребность в этих областях возникнет быстрее, чем признают наши отделы труда, школы и университеты. Легко оглянуться на историю через призму настоящего и не заметить социальные волнения, вызванные повсеместной технологической безработицей. Нам нужно обратиться к трудной истине, которую немногие готовы высказать вслух: искусственный интеллект в конечном итоге приведет к тому, что большое количество людей навсегда останутся без работы.Так же, как предыдущие поколения стали свидетелями радикальных изменений во время и после промышленной революции, быстрый темп развития технологий, вероятно, будет означать, что бэби-бумеры и старейшие представители поколения X — особенно те, чьи рабочие места могут быть воспроизведены роботами — не будут возможность переквалифицироваться на другую работу без значительных затрат времени и сил ».
Барри Чудаков , основатель и руководитель Sertain Research, прокомментировал: «К 2030 году сотрудничество человека и машины / искусственного интеллекта станет необходимым инструментом для управления и противодействия эффектам нескольких одновременных ускорений: широкий технологический прогресс, глобализация, изменение климата и сопутствующие глобальные миграции.В прошлом человеческие общества управляли изменениями благодаря интуиции и интуиции, но, как сказал Эрик Теллер, генеральный директор Google X, «наши социальные структуры не успевают за темпами изменений». справиться с растущим списком «злых проблем» к 2030 году, ИИ — или, используя фразу Джой Ито, «расширенный интеллект» — будет ценить и переоценивать практически все области человеческого поведения и взаимодействия. Искусственный интеллект и прогрессивные технологии изменят наши рамки и временные рамки реагирования (что, в свою очередь, изменит наше чувство времени).Там, где раньше социальное взаимодействие происходило в разных местах — работе, школе, церкви, семье — социальные взаимодействия все чаще будут происходить в непрерывном, одновременном времени. Если нам повезет, мы будем следовать 23 принципам искусственного интеллекта Азиломара, изложенным в Институте будущего жизни, и будем работать над «не беспристрастным разведывательным, а полезным разведыванием». Подобно ядерному сдерживанию, проистекающему из взаимно гарантированного уничтожения, ИИ и связанные технологические системы представляют собой сила для морального возрождения.Мы должны принять это моральное возрождение, иначе мы столкнемся с моральными загадками, которые могут привести к гибели людей. … Моя самая большая надежда на сотрудничество человека, машины и искусственного интеллекта представляет собой моральное и этическое возрождение — мы перенимаем менталитет луны и сцепляем руки, чтобы подготовиться к приближающимся ускорениям. Я больше всего боюсь, что мы примем логику наших новых технологий — мгновенный отклик, изоляция за экранами, бесконечное сравнение самооценки, фальшивая самопрезентация — не думая и не реагируя умно.”
Джон К. Хэвенс , исполнительный директор Глобальной инициативы IEEE по этике автономных и интеллектуальных систем и Совета по расширенному интеллекту, написал: «Теперь, в 2018 году, большинство людей во всем мире не могут получить доступ к своим данным. , поэтому любые дискуссии о «улучшении человеческого ИИ» игнорируют критический контекст того, кто на самом деле контролирует информацию и личность людей. Вскоре будет чрезвычайно сложно идентифицировать какие-либо автономные или интеллектуальные системы, алгоритмы которых не взаимодействуют с человеческими данными в той или иной форме.”
На карту поставлено не что иное, как то, в каком обществе мы хотим жить и как мы воспринимаем нашу человечность. Батья Фридман
Батья Фридман , профессор взаимодействия человека и компьютера в информационной школе Вашингтонского университета, написала: «Наши научные и технологические возможности намного превосходят и будут намного превосходить наши моральные — это наша способность мудро и гуманно использовать знания. и инструменты, которые мы разрабатываем. … Автоматизированная война — когда автономное оружие убивает людей без участия человека — может привести к отсутствию ответственности за отнятие жизни у врага или даже к осознанию того, что у врага отняли жизнь.На карту поставлено не что иное, как то, в каком обществе мы хотим жить и как мы воспринимаем нашу человечность ».
Грег Шеннон , главный научный сотрудник отдела CERT Университета Карнеги-Меллона, сказал: «Лучше / хуже будет 4: 1 с долгосрочным соотношением 2: 1. ИИ хорошо справится с повторяющейся работой, когда «близко» будет достаточно, а людям эта работа не нравится. … Жизнь определенно станет лучше, поскольку искусственный интеллект продлевает время жизни, от приложений для здоровья, которые разумно «подталкивают» нас к здоровью, до предупреждений о надвигающихся сердечных приступах / инсультах, до автоматизированного медицинского обслуживания для малообеспеченных (удаленных) и тех, кто нуждается в расширенном уходе (пожилые уход).Что касается свободы, здесь есть очевидные риски. ИИ влияет на агентство, создавая сущности со значительными интеллектуальными способностями для мониторинга, принуждения и даже наказания людей. Те, кто знает, как его использовать, будут иметь огромную потенциальную власть над теми, кто не может / не может. Будущее счастье действительно неясно. Некоторые уступят свое агентство ИИ в играх, на работе и в сообществе, как сегодня агентство по краже опиоидного кризиса. С другой стороны, многие будут освобождены от рутинных, непривлекательных задач / заданий. Если элементы общественного счастья являются частью целевых функций ИИ, то ИИ может стать катализатором взрыва счастья.”
Костас Александридис , автор книги «Изучение сложной динамики в многоагентных интеллектуальных системах», предсказал: «Многие из наших повседневных решений будут автоматизированы с минимальным вмешательством конечного пользователя. Автономия и / или независимость будут принесены в жертву и заменены удобством. Новые поколения граждан будут все больше и больше зависеть от сетевых структур и процессов ИИ. Есть проблемы, которые необходимо решать с точки зрения критического мышления и неоднородности.Сетевая взаимозависимость, скорее всего, повысит нашу уязвимость к кибератакам. Также существует реальная вероятность того, что будет существовать более резкое разделение между цифровыми «имущими» и «неимущими», а также между технологически зависимыми цифровыми инфраструктурами. Наконец, возникает вопрос о новых «командных высотах» владения и контроля над инфраструктурой цифровой сети ».
Оскар Ганди , заслуженный профессор коммуникации в Университете Пенсильвании, ответил: «Мы уже сталкиваемся с необоснованным предположением, когда нас просят представить сотрудничество человека и машины.Взаимодействие немного отличается, но все же испорчено предоставлением формы идентичности — возможно, даже личности — машинам, которые мы будем использовать, чтобы преодолевать всевозможные возможности и проблемы. Проблемы, с которыми мы столкнемся в будущем, очень похожи на проблемы, с которыми мы сталкиваемся в настоящее время, когда полагаемся на « других » (включая технологические системы, устройства и сети) в приобретении вещей, которые мы ценим, и избегаем этих других вещей (которые мы могли бы или могли бы не знать).
Джеймс Скофилд О’Рурк , профессор менеджмента в Университете Нотр-Дам, сказал: «На протяжении всей истории человечества технология была в основном нейтральным понятием.Вопрос о его ценности всегда зависел от его применения. С какой целью будет использоваться ИИ и другие технологические достижения? Все, от пороха до двигателей внутреннего сгорания и ядерного деления, применялось как полезными, так и разрушительными способами. Если предположить, что мы можем сдерживать или контролировать ИИ (а не наоборот), ответ на вопрос, станет ли нам лучше, полностью зависит от нас (или нашего потомства). «Дорогой Брут, вина не в наших звездах, а в нас самих, в том, что мы подчиняемся.’”
Саймон Биггс , профессор междисциплинарных искусств в Эдинбургском университете, сказал: «ИИ будет расширять возможности человека. Проблема не в ИИ, а в людях. Как вид, мы агрессивны, склонны к соперничеству и ленивы. Мы также эмпатичны, общаемся и (иногда) жертвуем собой. У нас есть много других атрибутов. Все это будет усилено. Учитывая исторический прецедент, можно предположить, что будут усилены наши худшие качества.Я ожидаю, что в 2030 году ИИ будет регулярно использоваться для ведения войн и убийства людей, гораздо более эффективно, чем мы можем убивать в настоящее время. Как общества, мы будем в меньшей степени затронуты этим, чем мы в настоящее время, поскольку мы не будем сражаться и убивать себя. Наша способность изменять свое поведение с учетом эмпатии и связанных с этим этических рамок будет уменьшена из-за диссоциации между нашей свободой действий и актом убийства. Мы не можем ожидать, что наши системы искусственного интеллекта будут этичными от нашего имени — они не будут такими, поскольку они будут разработаны, чтобы убивать эффективно, а не продуманно.Другая моя главная забота — наблюдение и контроль. Появление Китайской системы социального кредитования (SCS) является индикатором того, что она может произойти. Мы будем существовать в SCS, поскольку ИИ конструирует гибридные экземпляры нас самих, которые могут напоминать, а могут и не походить на нас. Но наши права и возможности как физических лиц будут определяться SCS. Это воплощение оруэлловского кошмара ».
Марк Сурман , исполнительный директор Mozilla Foundation, ответил: «ИИ продолжит концентрировать власть и богатство в руках нескольких крупных монополий, основанных на U.С. и Китай. Большинству людей — и в некоторых частях мира — будет хуже ».
Уильям Уриккио , медиа-исследователь и профессор сравнительных медиа-исследований в Массачусетском технологическом институте, прокомментировал: «ИИ и связанные с ним приложения сталкиваются с тремя проблемами: развитие со скоростью закона Мура, развитие в руках технологической и экономической элиты и развитие без выгоды информированной или заинтересованной общественности. Публика сводится к коллективу потребителей, ожидающих появления следующей технологии. Чье понятие «прогресс» будет преобладать? У нас есть достаточно доказательств того, что ИИ используется для увеличения прибыли, независимо от последствий для давно удерживаемых ценностей; усилить государственный контроль и даже получить «социальный кредит» граждан без участия самих граждан.Как и предшествующие технологии, ИИ агностик. Его развертывание находится в руках общества. Но в отсутствие общественности, грамотной в области ИИ, решение о том, как лучше всего развернуть ИИ, будет зависеть от особых интересов. Будет ли это означать справедливое развертывание, устранение социальной несправедливости и ИИ на государственной службе? Поскольку ответ на этот вопрос скорее социальный, чем технологический, я настроен пессимистично. Исправление? Нам необходимо развивать общественность, грамотную в области искусственного интеллекта, что означает сосредоточенное внимание в образовательном секторе и в публичных СМИ.Нам необходимо обеспечить разнообразие в развитии технологий искусственного интеллекта. И до тех пор, пока общественность, ее избранные представители и их правовые и нормативные режимы не смогут освоить эти стремительные разработки, нам необходимо проявлять осторожность и надзор за развитием ИИ ».
Остальная часть этого отчета разделена на три раздела, которые основаны на обнадеживающих и критических наблюдениях сотен дополнительных респондентов: 1) озабоченность по поводу эволюции человеческого ИИ, 2) предлагаемые решения по устранению воздействия ИИ, и 3) ожидания относительно того, что будет с жизнью.

 Сокращение дробей». Алгебра 8 класс
Сокращение дробей». Алгебра 8 класс Масса
плоской пластины m определяется формулой (1), статические
моменты плоской пластины можно вычислить
по формулам (3) и (4). Тогда, согласно
формулам (5), получаем выражение для
координат центра масс плоской пластины:
Масса
плоской пластины m определяется формулой (1), статические
моменты плоской пластины можно вычислить
по формулам (3) и (4). Тогда, согласно
формулам (5), получаем выражение для
координат центра масс плоской пластины: Выбрать систему координат, в
которой будут вычисляться двойные
интегралы.
2. Записать область в виде
системы неравенств в выбранной системе
координат.
3. Вычислить площадь S и массу m пластины по формулам (1) и (2).
4. Вычислить
статические моменты My , Mx по формулам (3) и (4).
5. Вычислить
координаты центра масс
,
по
формулам (6). Нанести центр масс на чертеж.
При этом возникает визуальный
(качественный) контроль полученных
результатов.
Численные ответы должны
быть получены с тремя значащими цифрами.
Выбрать систему координат, в
которой будут вычисляться двойные
интегралы.
2. Записать область в виде
системы неравенств в выбранной системе
координат.
3. Вычислить площадь S и массу m пластины по формулам (1) и (2).
4. Вычислить
статические моменты My , Mx по формулам (3) и (4).
5. Вычислить
координаты центра масс
,
по
формулам (6). Нанести центр масс на чертеж.
При этом возникает визуальный
(качественный) контроль полученных
результатов.
Численные ответы должны
быть получены с тремя значащими цифрами. Эта область может
быть описана системой неравенств:
Эта область может
быть описана системой неравенств:
 Разобьем область D на п «элементарных областей» площади которых обозначим через а диаметры (наибольшее расстояние между точками области) — через (см. рис. 214).
Разобьем область D на п «элементарных областей» площади которых обозначим через а диаметры (наибольшее расстояние между точками области) — через (см. рис. 214).
 2) можно записать в виде
2) можно записать в виде В своей совокупности они составляют тело V. Обозначив объем столбика с основанием через , получим
В своей совокупности они составляют тело V. Обозначив объем столбика с основанием через , получим зная, что ее поверхностная плотность есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей площади которых обозначим через . В каждой области возьмем произвольную точку и вычислим плотность в ней:
зная, что ее поверхностная плотность есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей площади которых обозначим через . В каждой области возьмем произвольную точку и вычислим плотность в ней:


 Следовательно,
Следовательно,
 8):
8): 10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде 12), перейдем к полярным координатам:
12), перейдем к полярным координатам: Получаем формулу для вычисления площади S области D:
Получаем формулу для вычисления площади S области D: Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3). ru
ru 2)\cdot \mu (P)ds } =I_x +I_y $ { относительно начала координат } .
2)\cdot \mu (P)ds } =I_x +I_y $ { относительно начала координат } . 1 } = { 2\pi \left( { \frac { 1 } { 2 } + \frac { 1 } { 4 } }\right) } = { \frac { { 3\pi } } { 2 } \;\left( { \text { Кл } }\right). } $
1 } = { 2\pi \left( { \frac { 1 } { 2 } + \frac { 1 } { 4 } }\right) } = { \frac { { 3\pi } } { 2 } \;\left( { \text { Кл } }\right). } $ Примеры.
Примеры.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 Вычислить моменты инерции однородного треугольника со сторонами х+у=1, х+2у=2 , у=0, относительно координатных осей.
Вычислить моменты инерции однородного треугольника со сторонами х+у=1, х+2у=2 , у=0, относительно координатных осей.
 , где D – параллелограмм со сторонами у=х, у=х+3, у=-2х+1, у=-2х+5.
, где D – параллелограмм со сторонами у=х, у=х+3, у=-2х+1, у=-2х+5.


 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.014 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.014 с.) 18)
18) 19)
19) В силу симметрии кривой относительно координатных осей
можно вычислить сначала ту часть, которая расположена первой четверти. В этом случае угол φ будет изменяться от 0 до, а радиус r от 0 до . По формуле (6.20) получим:
В силу симметрии кривой относительно координатных осей
можно вычислить сначала ту часть, которая расположена первой четверти. В этом случае угол φ будет изменяться от 0 до, а радиус r от 0 до . По формуле (6.20) получим: Также с помощью Acrobat можно преобразовать файлы PDF в форматы PNG или TIFF.
Также с помощью Acrobat можно преобразовать файлы PDF в форматы PNG или TIFF. Несмотря на то, что существует несколько веб-сайтов и приложений, чтобы позаботиться об этом, вы должны найти те, которым вы можете доверять.
Несмотря на то, что существует несколько веб-сайтов и приложений, чтобы позаботиться об этом, вы должны найти те, которым вы можете доверять.
 Используйте опцию «Открыть файлы», присутствующую в программном обеспечении.
Используйте опцию «Открыть файлы», присутствующую в программном обеспечении. Он предлагает расширенные формы управления и инструменты OCR для обработки любого типа документооборота.
Он предлагает расширенные формы управления и инструменты OCR для обработки любого типа документооборота.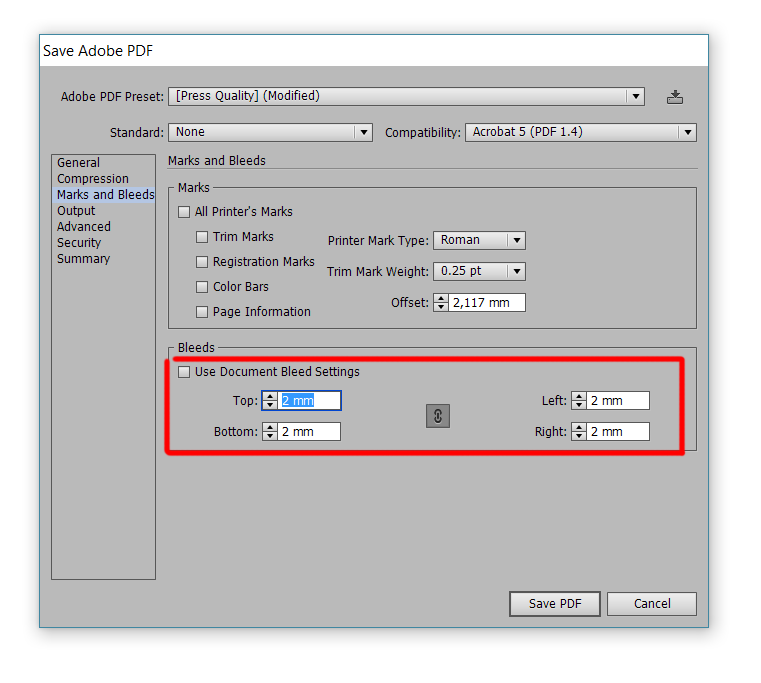 Одним из лучших инструментов, которые вы можете использовать для этой цели, является конвертер pdf2go. При использовании этого инструмента вы получите следующие преимущества. Благодаря этому вам не нужно заморачиваться с загрузкой программного обеспечения. Следовательно, он не требует ни времени, ни пространства. Кроме того, отсутствие загрузки означает наличие вредоносного ПО.
Одним из лучших инструментов, которые вы можете использовать для этой цели, является конвертер pdf2go. При использовании этого инструмента вы получите следующие преимущества. Благодаря этому вам не нужно заморачиваться с загрузкой программного обеспечения. Следовательно, он не требует ни времени, ни пространства. Кроме того, отсутствие загрузки означает наличие вредоносного ПО. Вверху вы найдете вкладку «Все инструменты», нажмите на нее.
Вверху вы найдете вкладку «Все инструменты», нажмите на нее. Итак, это плоский документ с фиксированным макетом.
Итак, это плоский документ с фиксированным макетом. Однако с помощью такого инструмента, как PDFelement, вы можете преобразовать файл размером менее 50 КБ/100 КБ/200 КБ с помощью функции сжатия перед преобразованием в формат JPG. Итак, скачайте его и конвертируйте столько файлов, сколько хотите.
Однако с помощью такого инструмента, как PDFelement, вы можете преобразовать файл размером менее 50 КБ/100 КБ/200 КБ с помощью функции сжатия перед преобразованием в формат JPG. Итак, скачайте его и конвертируйте столько файлов, сколько хотите.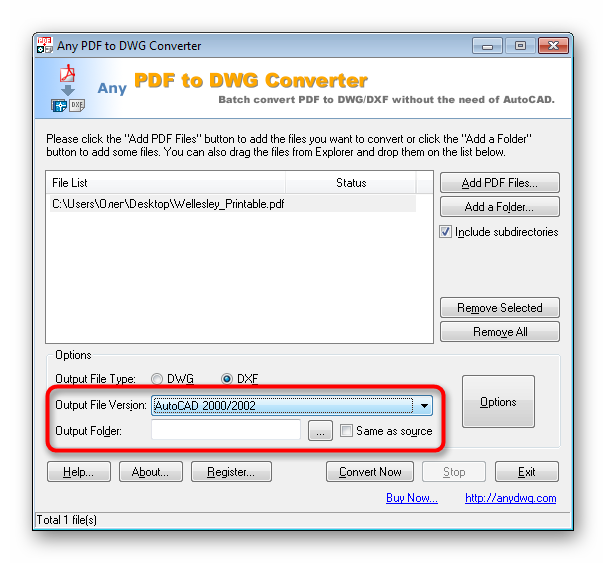
 Третий недостаток заключается в том, что он использует много данных для этапов загрузки и выгрузки. Если у вас ограниченный тариф, это не очень удобно. Однако самым большим недостатком является то, что это небезопасный метод. Если вы имеете дело с личными или конфиденциальными файлами, есть вероятность, что они могут быть взломаны во время загрузки или скачивания. Это не вина файла iLovePDF, потому что он достаточно безопасен; ошибка может быть в вашем собственном интернет-соединении, которое не всегда безопасно. Это особенно верно, если вы используете общедоступный Wi-Fi.
Третий недостаток заключается в том, что он использует много данных для этапов загрузки и выгрузки. Если у вас ограниченный тариф, это не очень удобно. Однако самым большим недостатком является то, что это небезопасный метод. Если вы имеете дело с личными или конфиденциальными файлами, есть вероятность, что они могут быть взломаны во время загрузки или скачивания. Это не вина файла iLovePDF, потому что он достаточно безопасен; ошибка может быть в вашем собственном интернет-соединении, которое не всегда безопасно. Это особенно верно, если вы используете общедоступный Wi-Fi.
 Фактически, это один из аспектов PDFelement, который делает его настолько популярным среди всех, от отдельных пользователей до крупных корпораций, которые используют его для своих PDF-документов и других рабочих процессов.
Фактически, это один из аспектов PDFelement, который делает его настолько популярным среди всех, от отдельных пользователей до крупных корпораций, которые используют его для своих PDF-документов и других рабочих процессов. Атрибуты аннотации, такие как толщина линии, размер шрифта, цвет, заливка фона могут быть изменены с помощью набора инструментов, предоставленного для этой цели.
Атрибуты аннотации, такие как толщина линии, размер шрифта, цвет, заливка фона могут быть изменены с помощью набора инструментов, предоставленного для этой цели.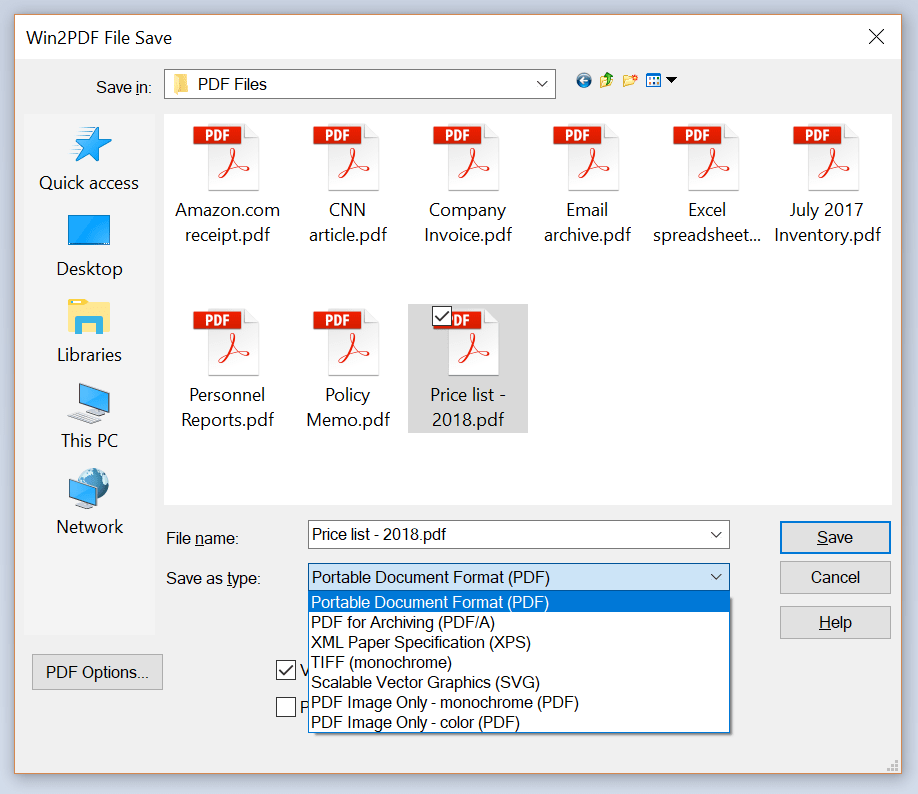 Цифровые подписи могут быть добавлены, и они имеют юридическую силу и имеют обязательную силу, что отлично подходит для контрактов и подобных документов.
Цифровые подписи могут быть добавлены, и они имеют юридическую силу и имеют обязательную силу, что отлично подходит для контрактов и подобных документов.
 Вы не почувствуете никакой двусмысленности при использовании этой онлайн-утилиты.
Вы не почувствуете никакой двусмысленности при использовании этой онлайн-утилиты.
 Скачайте с официального сайта PDFCreator Free: https://www.pdfforge.org/pdfcreator/download, а затем становите программу на компьютер.
Скачайте с официального сайта PDFCreator Free: https://www.pdfforge.org/pdfcreator/download, а затем становите программу на компьютер.
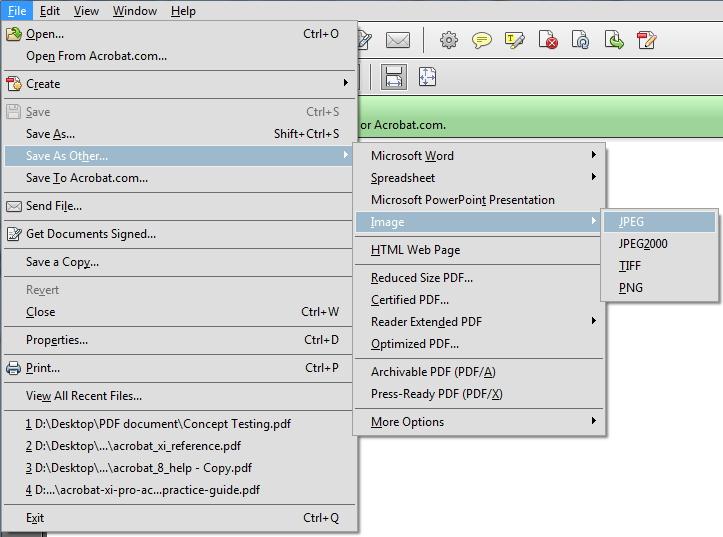
 Поэтому вы можете воспользоваться услугам данного приложения для конвертирования ПДФ в Джипег.
Поэтому вы можете воспользоваться услугам данного приложения для конвертирования ПДФ в Джипег. io/ru/pdf2jpg/.
io/ru/pdf2jpg/.
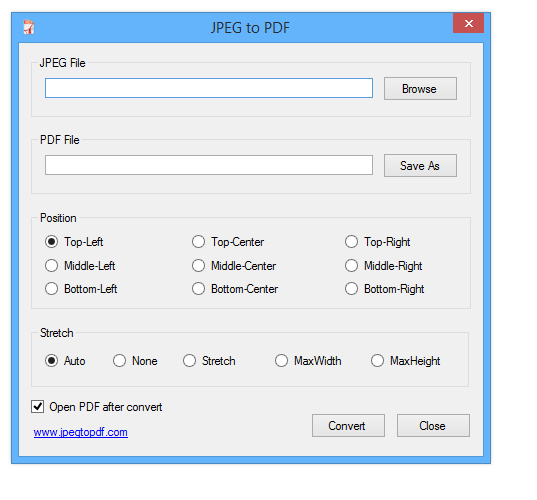 Здесь можно решать разные задачи, в том числе по интересующему нас вопросу.
Здесь можно решать разные задачи, в том числе по интересующему нас вопросу.
 Современный бесплатный инструмент для слияния PDF в JPG создан для быстрого объединения нескольких файлов в один PDF в JPG документ. Это PDF в JPG объединение приложение отвечает на запрос, чтобы облегчить отправку, совместное использование, печать и просмотр документов. Вы не должны тратить свое время, выполняя эти операции вручную на настольном программном обеспечении. Наша цель состоит в том, чтобы предоставить вам наиболее эффективные решения для оптимизации рабочего процесса вашего офиса с помощью онлайн-приложений.
Современный бесплатный инструмент для слияния PDF в JPG создан для быстрого объединения нескольких файлов в один PDF в JPG документ. Это PDF в JPG объединение приложение отвечает на запрос, чтобы облегчить отправку, совместное использование, печать и просмотр документов. Вы не должны тратить свое время, выполняя эти операции вручную на настольном программном обеспечении. Наша цель состоит в том, чтобы предоставить вам наиболее эффективные решения для оптимизации рабочего процесса вашего офиса с помощью онлайн-приложений. 
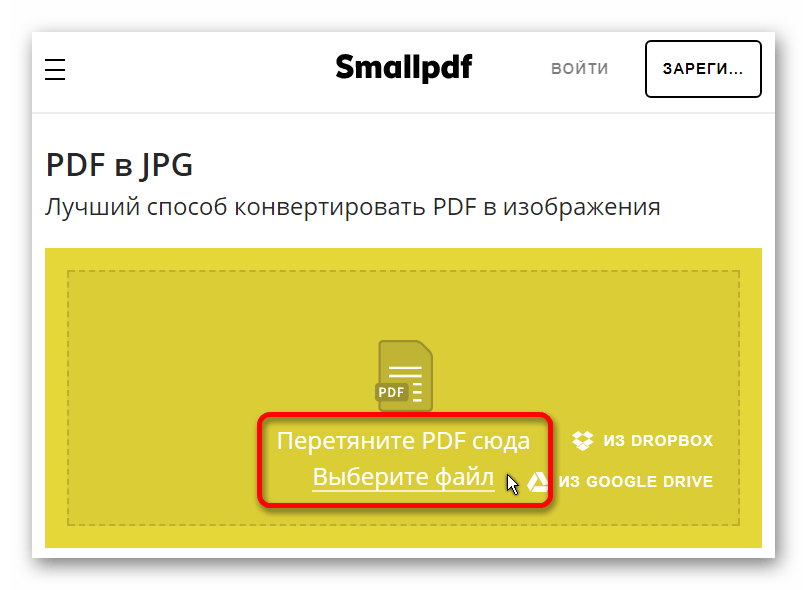 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать после этого периода времени. Никто не имеет доступа к вашим файлам. Слияние файлов (включая PDF и JPG) абсолютно безопасно.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать после этого периода времени. Никто не имеет доступа к вашим файлам. Слияние файлов (включая PDF и JPG) абсолютно безопасно.
 innerHTML = »
innerHTML = » innerHTML = »
innerHTML = »
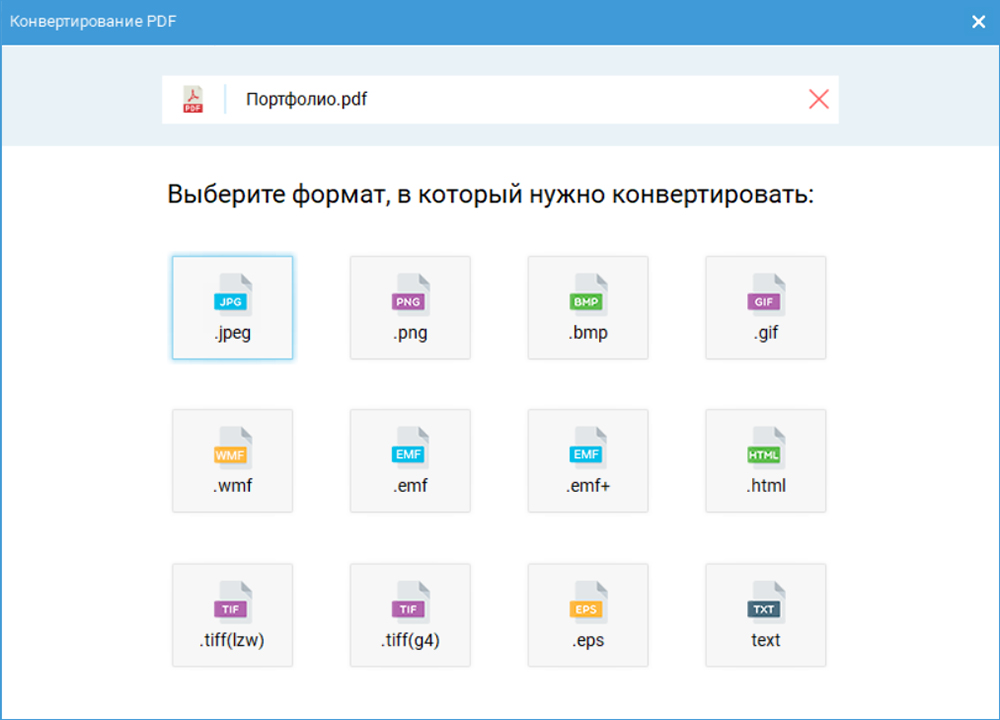
 PDF
PDF Две разные вещи. Действительно, PDF и JPG — это разные форматы файлов, которые не часто используются взаимозаменяемо. Однако это не исключает возможности, что вам может понадобиться изменить PDF на JPG.
Две разные вещи. Действительно, PDF и JPG — это разные форматы файлов, которые не часто используются взаимозаменяемо. Однако это не исключает возможности, что вам может понадобиться изменить PDF на JPG. Уверяем вас, что нет! Многие люди хотят знать, как конвертировать PDF в JPG. В этой статье мы покажем вам, как конвертировать PDF в JPG, как редактировать PDF-файлы Mac, а также покажем вам несколько приложений для конвертации PDF в JPG, которые нам очень нравятся.
Уверяем вас, что нет! Многие люди хотят знать, как конвертировать PDF в JPG. В этой статье мы покажем вам, как конвертировать PDF в JPG, как редактировать PDF-файлы Mac, а также покажем вам несколько приложений для конвертации PDF в JPG, которые нам очень нравятся. Сначала вы увидите экран выбора, где вы выбираете файл, который хотите открыть. Это выложено так же, как ваше приложение Finder, показывая ваш рабочий стол и папки с документами. Это очень просто и понятно, как все приложение Preview воспринимается пользователями.
Сначала вы увидите экран выбора, где вы выбираете файл, который хотите открыть. Это выложено так же, как ваше приложение Finder, показывая ваш рабочий стол и папки с документами. Это очень просто и понятно, как все приложение Preview воспринимается пользователями.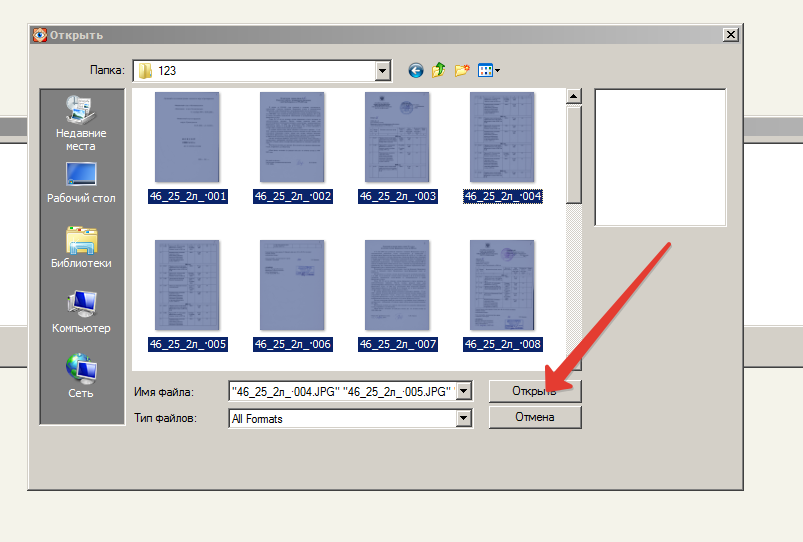 Пользователям, вероятно, потребуется увеличить масштаб, чтобы просмотреть мелкий шрифт или детали, а предварительный просмотр может не отображать эти точные детали. Это когда отдельное приложение наиболее полезно — и вы найдете его более полезным, чем вы думаете, чаще, чем вы думаете.
Пользователям, вероятно, потребуется увеличить масштаб, чтобы просмотреть мелкий шрифт или детали, а предварительный просмотр может не отображать эти точные детали. Это когда отдельное приложение наиболее полезно — и вы найдете его более полезным, чем вы думаете, чаще, чем вы думаете. Его минималистичный интерфейс позволяет легко добавлять файлы и просматривать предварительный просмотр того, что вы добавляете, после загрузки файла. Больше не нужно запоминать имена файлов и выбирать их из списка, что может привести к гораздо большему количеству ошибок, чем мы готовы признать.
Его минималистичный интерфейс позволяет легко добавлять файлы и просматривать предварительный просмотр того, что вы добавляете, после загрузки файла. Больше не нужно запоминать имена файлов и выбирать их из списка, что может привести к гораздо большему количеству ошибок, чем мы готовы признать. Когда вы пытаетесь преобразовать несколько файлов для нескольких клиентов или уникальных вариантов использования, Permute поможет вам сэкономить время.
Когда вы пытаетесь преобразовать несколько файлов для нескольких клиентов или уникальных вариантов использования, Permute поможет вам сэкономить время.
 Выберите «Файл» > «Сохранить» в строке меню Automator. Затем выберите Сохранить. После этого вы можете закрыть приложение Automator
Выберите «Файл» > «Сохранить» в строке меню Automator. Затем выберите Сохранить. После этого вы можете закрыть приложение Automator
 Если мы критичны, просмотр файлов может быть единственным «реальным» использованием для предварительного просмотра. Опытные пользователи определенно захотят большего от своего Mac, особенно если они используют его для редактирования или преобразования PDF-файлов и нуждаются в детальном контроле разрешения и качества изображения. Большинство тех, кто действительно нуждается в выполнении задач, на которые способен Preview, по-прежнему ищут помощи в приложениях.
Если мы критичны, просмотр файлов может быть единственным «реальным» использованием для предварительного просмотра. Опытные пользователи определенно захотят большего от своего Mac, особенно если они используют его для редактирования или преобразования PDF-файлов и нуждаются в детальном контроле разрешения и качества изображения. Большинство тех, кто действительно нуждается в выполнении задач, на которые способен Preview, по-прежнему ищут помощи в приложениях. Есть множество приложений, которые требуют большего — и это только для одного приложения!
Есть множество приложений, которые требуют большего — и это только для одного приложения!
 Есть несколько достойных приложений, которые вы можете получить в магазине Microsoft, которые защитят вас от любых ненадлежащих действий приложений, и мы объясним их ниже.
Есть несколько достойных приложений, которые вы можете получить в магазине Microsoft, которые защитят вас от любых ненадлежащих действий приложений, и мы объясним их ниже. С помощью приложения Preview вы можете конвертировать файлы в несколько различных форматов, включая PNG, TIFF и, конечно же, JPG.
С помощью приложения Preview вы можете конвертировать файлы в несколько различных форматов, включая PNG, TIFF и, конечно же, JPG.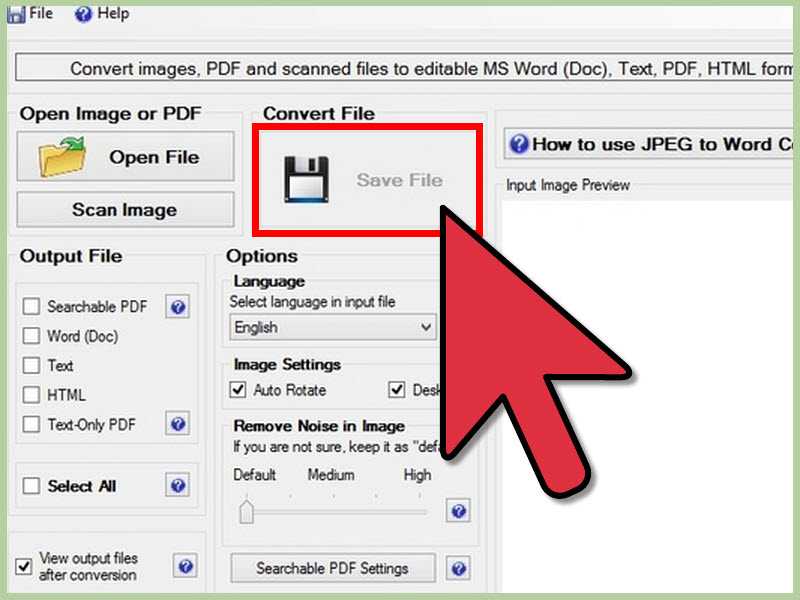


 Вы должны выбрать целевые форматы: В изображение (.jpg/.png / .jpeg) и установить диапазон страниц.
Вы должны выбрать целевые форматы: В изображение (.jpg/.png / .jpeg) и установить диапазон страниц. Во-первых, вы должны найти PDF-файл на своем компьютере, щелкнуть правой кнопкой мыши PDF-файл и выбрать вариант «Открыть», а затем Adobe Acrobat Reader DC.
Во-первых, вы должны найти PDF-файл на своем компьютере, щелкнуть правой кнопкой мыши PDF-файл и выбрать вариант «Открыть», а затем Adobe Acrobat Reader DC.
 Вы даже можете конвертировать свои файлы из онлайн-сервисов, которые вы используете, не выходя из приложения.
Вы даже можете конвертировать свои файлы из онлайн-сервисов, которые вы используете, не выходя из приложения. в любом другом приложении. Вы также можете отправить свои новые файлы по электронной почте из приложения. Безопасность файлов должна быть наименьшей из ваших забот, поскольку все файлы, преобразованные на наших серверах, удаляются в течение следующих 24 часов.
в любом другом приложении. Вы также можете отправить свои новые файлы по электронной почте из приложения. Безопасность файлов должна быть наименьшей из ваших забот, поскольку все файлы, преобразованные на наших серверах, удаляются в течение следующих 24 часов.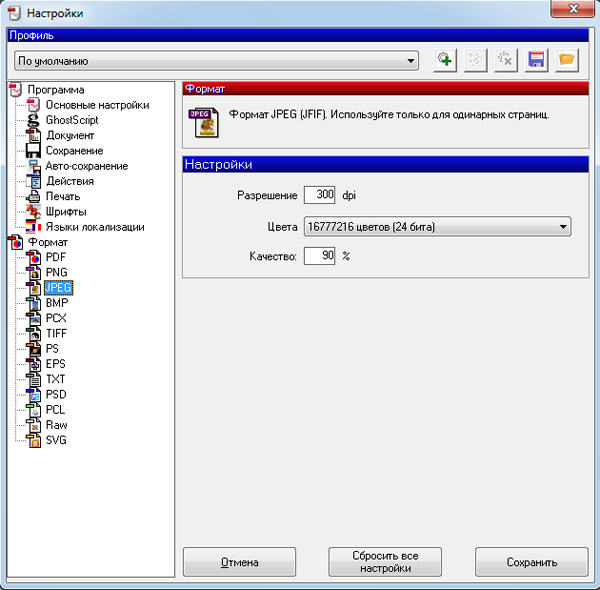 Если получится обновлю по глупости 60-90 минут, чтобы доказать, что оно на самом деле работает, когда ни одно другое приложение не делает то, что оно говорит … йоу, если бы я был разработчиком приложения, давал бы людям одно в день, а затем запрашивал бы обновление. Восприятие потребителей — это единственный способ убедить людей купить.
Если получится обновлю по глупости 60-90 минут, чтобы доказать, что оно на самом деле работает, когда ни одно другое приложение не делает то, что оно говорит … йоу, если бы я был разработчиком приложения, давал бы людям одно в день, а затем запрашивал бы обновление. Восприятие потребителей — это единственный способ убедить людей купить. Наконец-то я могу конвертировать файл. Но тогда… WTFrick??… Я могу либо заплатить 10 долларов, чтобы преобразовать его за секунды, либо подождать 60-9.0 минут бесплатно!! Это безумно. И плохой клиентский опыт. И чтобы дать вам пощечину еще раз, последний вариант, который у вас есть, если вы действительно хотите подождать 60 минут, — это кнопка ОТМЕНА. Это означает, что вы ничего не получите за все ваше разочарование. Уволить команду дизайнеров пользовательского интерфейса!! Ужасно.
Наконец-то я могу конвертировать файл. Но тогда… WTFrick??… Я могу либо заплатить 10 долларов, чтобы преобразовать его за секунды, либо подождать 60-9.0 минут бесплатно!! Это безумно. И плохой клиентский опыт. И чтобы дать вам пощечину еще раз, последний вариант, который у вас есть, если вы действительно хотите подождать 60 минут, — это кнопка ОТМЕНА. Это означает, что вы ничего не получите за все ваше разочарование. Уволить команду дизайнеров пользовательского интерфейса!! Ужасно. После оплаты премиум версии я узнал, что программа не работает.
После оплаты премиум версии я узнал, что программа не работает. com Inc.
com Inc. Мощный бесплатный онлайн-конвертер документов PDF в JPG очень прост. Не требуется установка программного обеспечения для настольных компьютеров, такого как Microsoft Word, OpenOffice или Adobe Acrobat. Все конвертации вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мощный бесплатный онлайн-конвертер документов PDF в JPG очень прост. Не требуется установка программного обеспечения для настольных компьютеров, такого как Microsoft Word, OpenOffice или Adobe Acrobat. Все конвертации вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. 
 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать по истечении этого периода времени. Никто не имеет доступа к вашим файлам. Преобразование файлов (в том числе PDF в JPG) абсолютно безопасно.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать по истечении этого периода времени. Никто не имеет доступа к вашим файлам. Преобразование файлов (в том числе PDF в JPG) абсолютно безопасно.

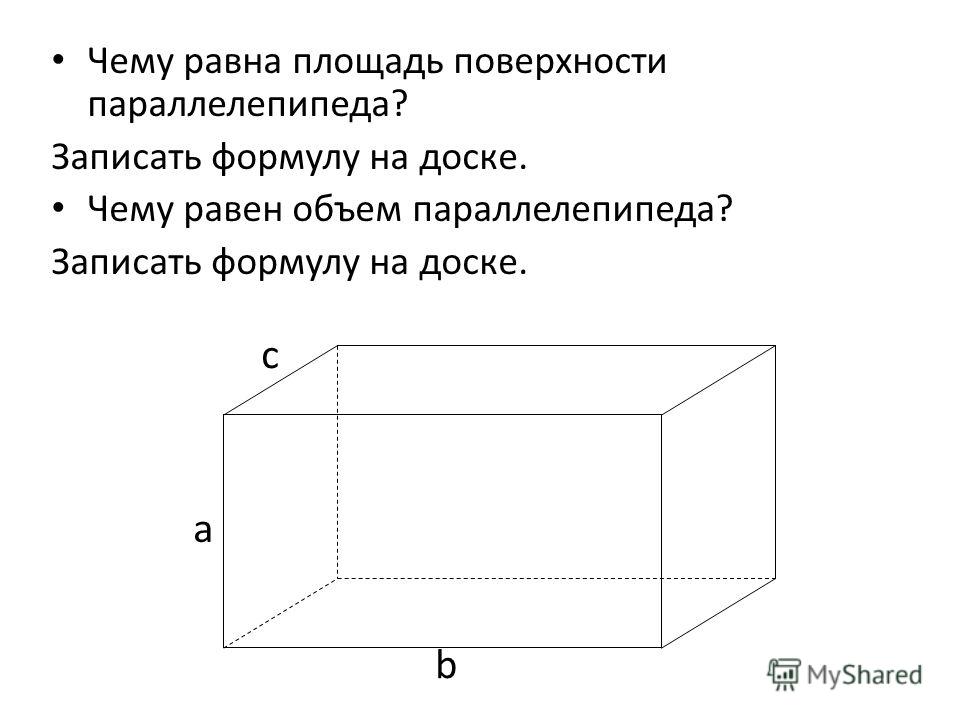 Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
 Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объём тела или вместимость сосуда определяется его формой и линейными размерами.
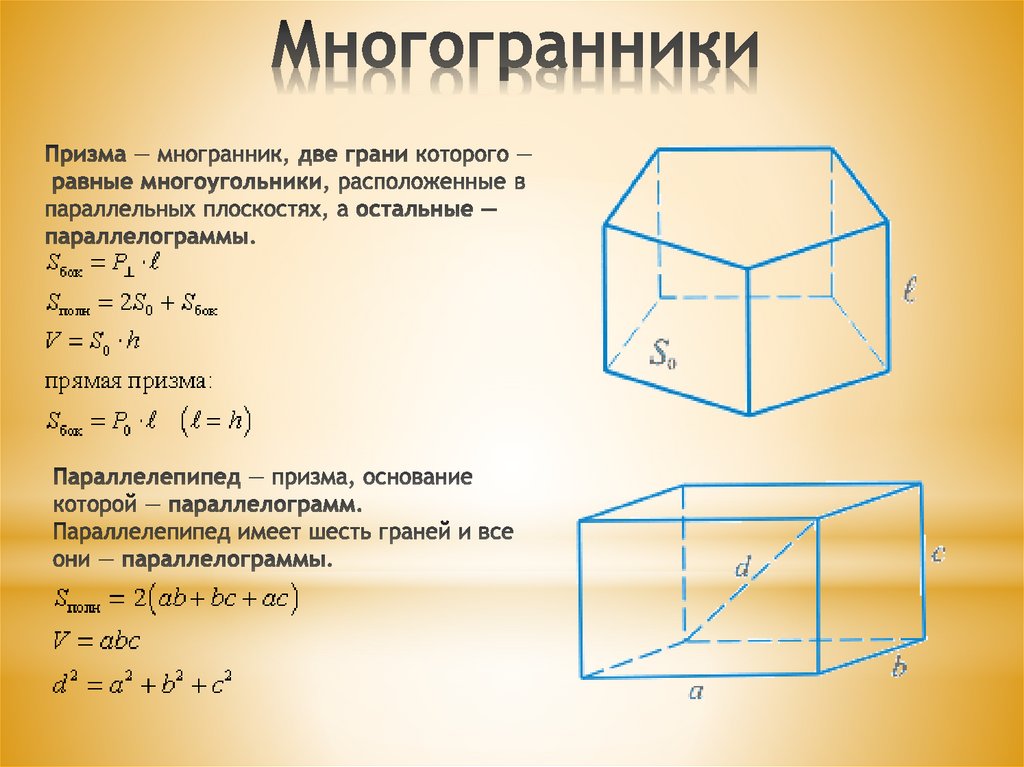 141592.
141592. 141592.
141592. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Такой куб называют единичным (смотри рисунок ниже).
За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Такой куб называют единичным (смотри рисунок ниже).

 Объем куба
Объем куба

 141592
141592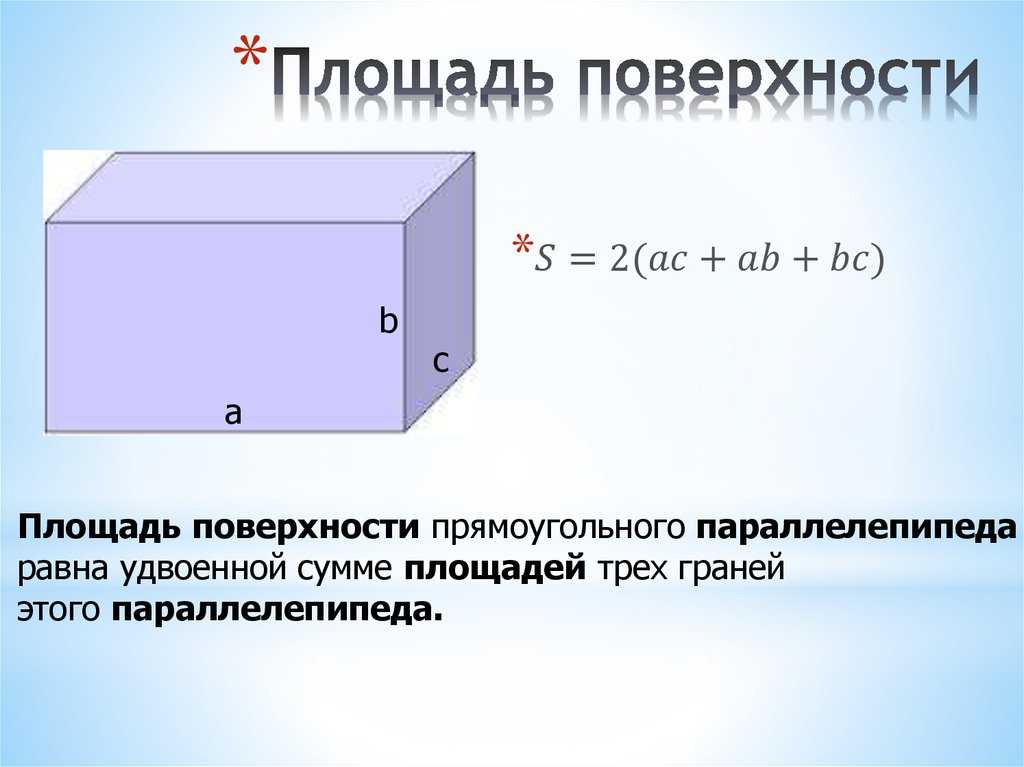


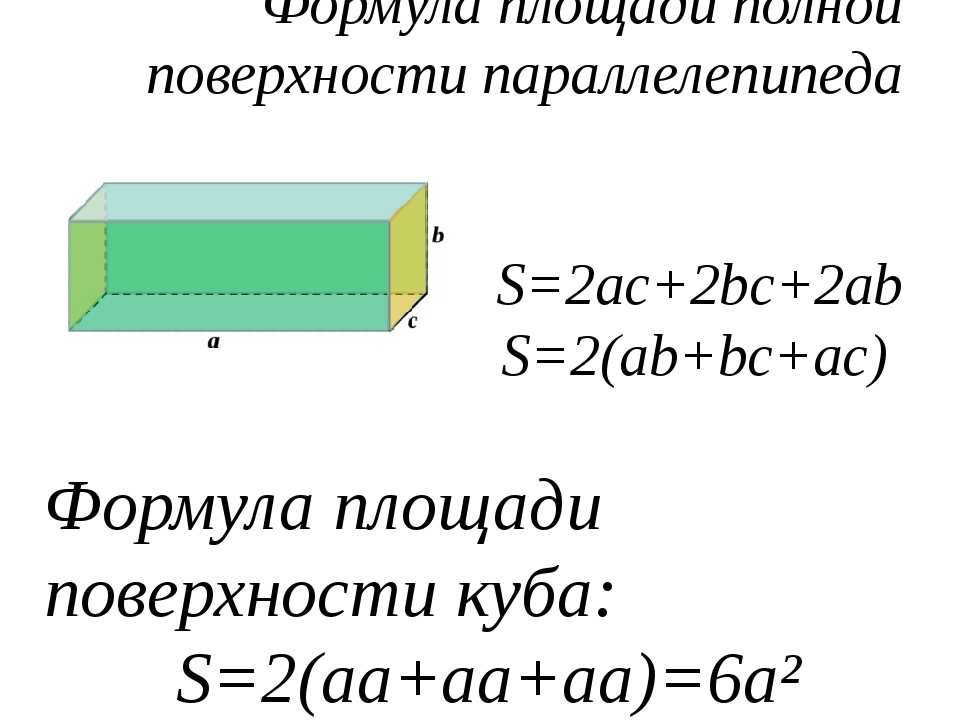 141592
141592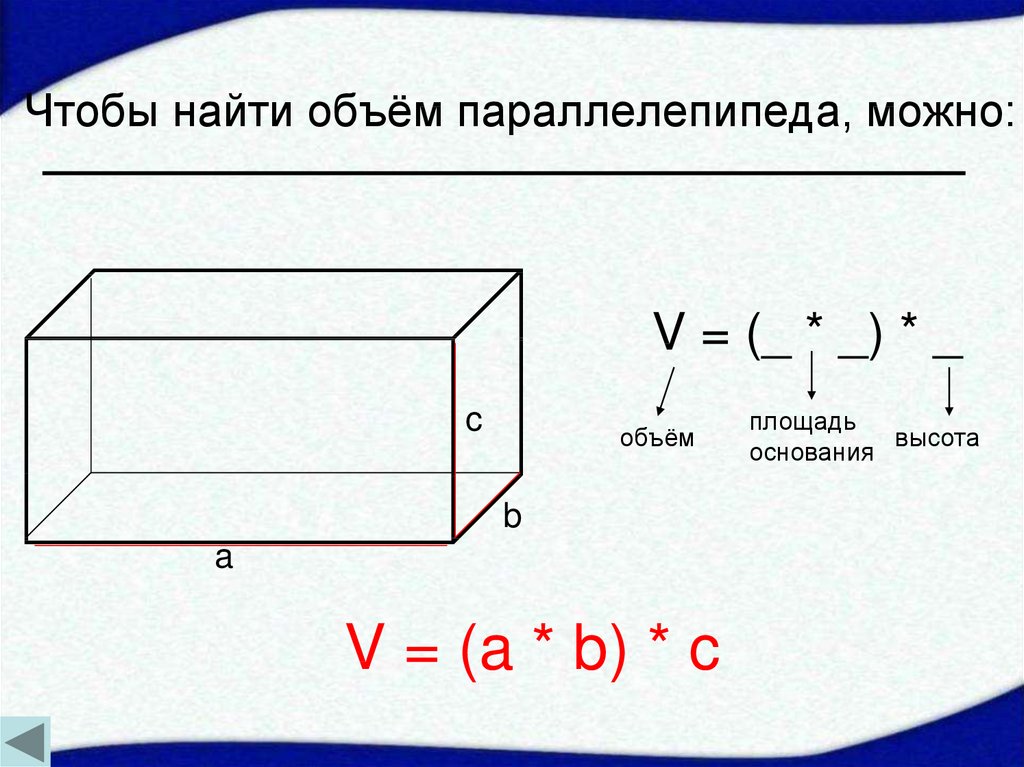
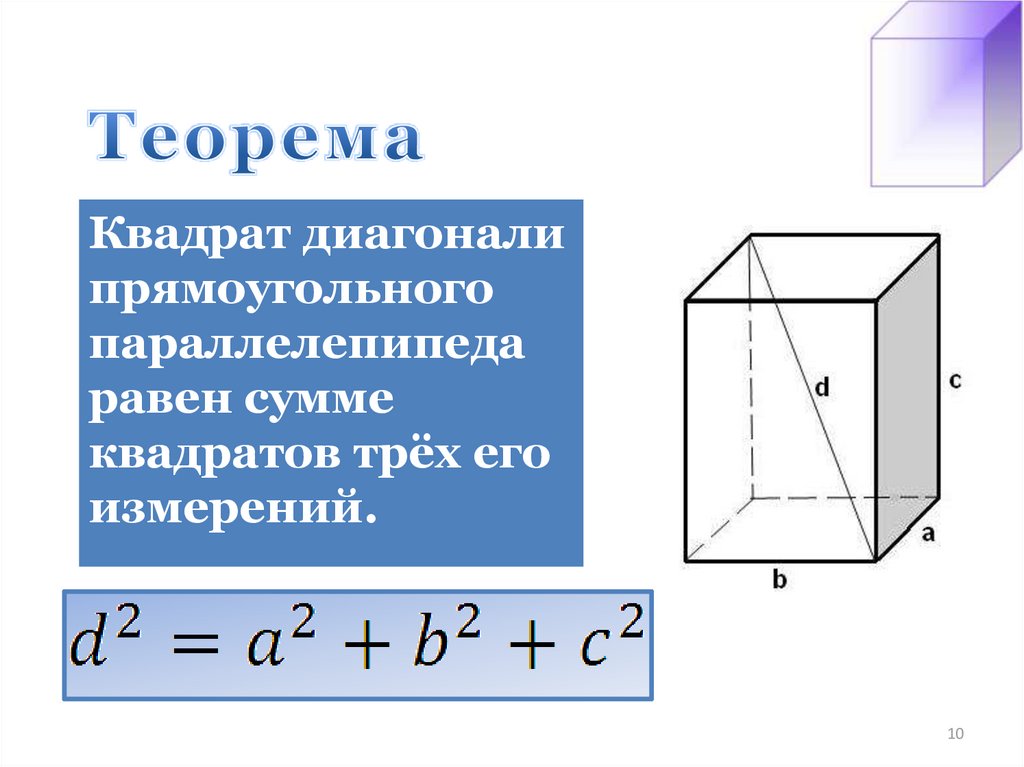
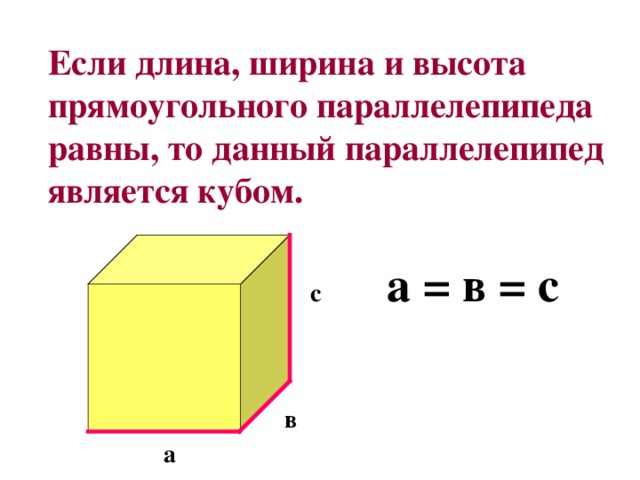
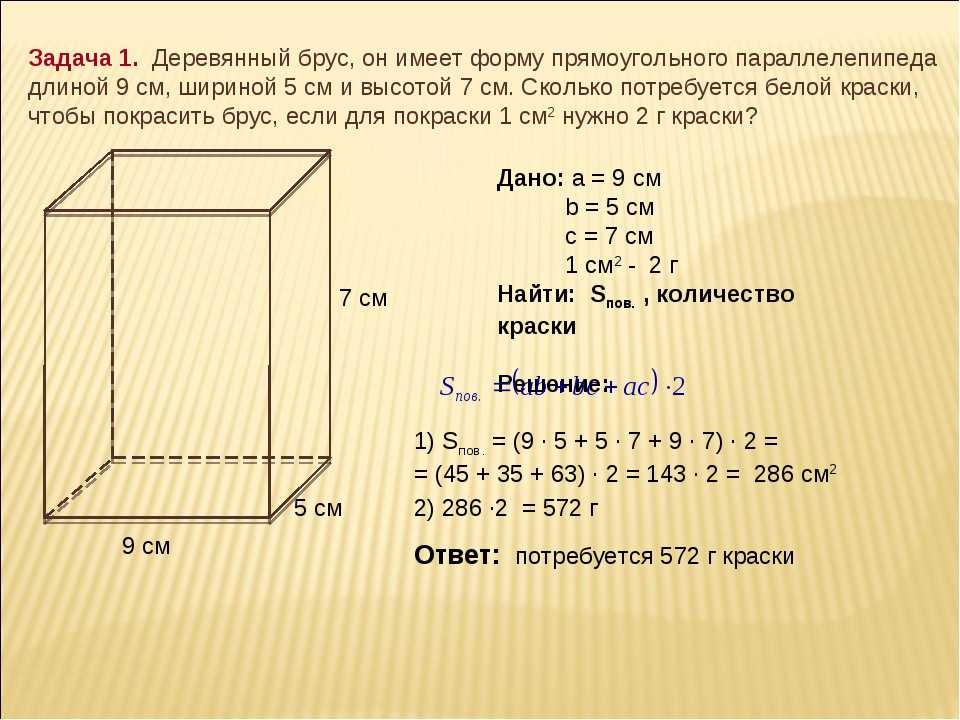

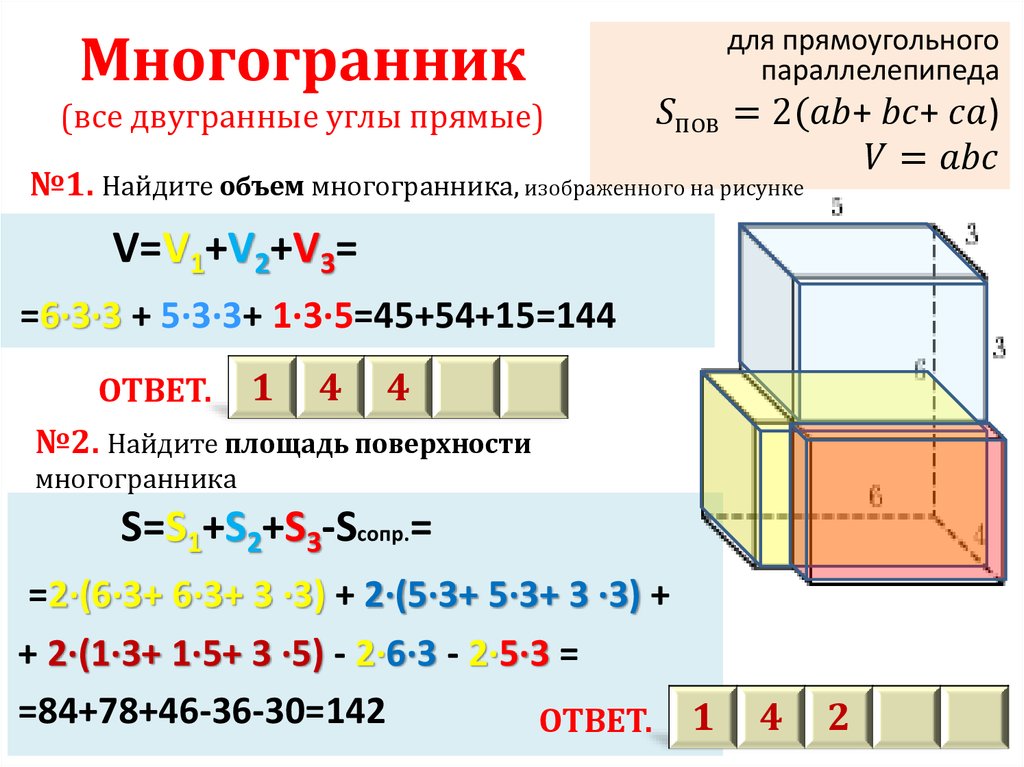
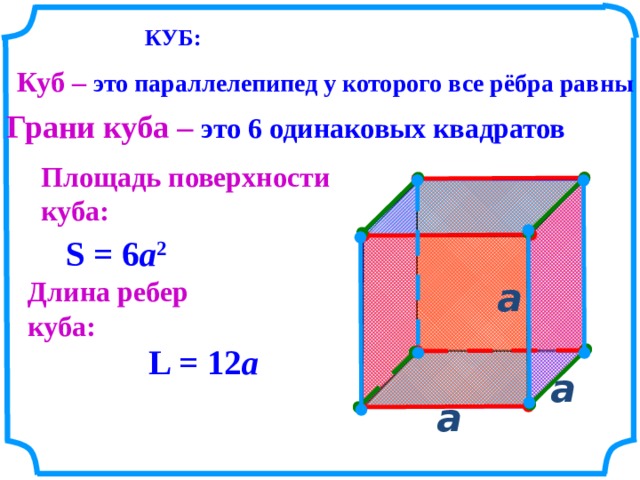 3 $$
3 $$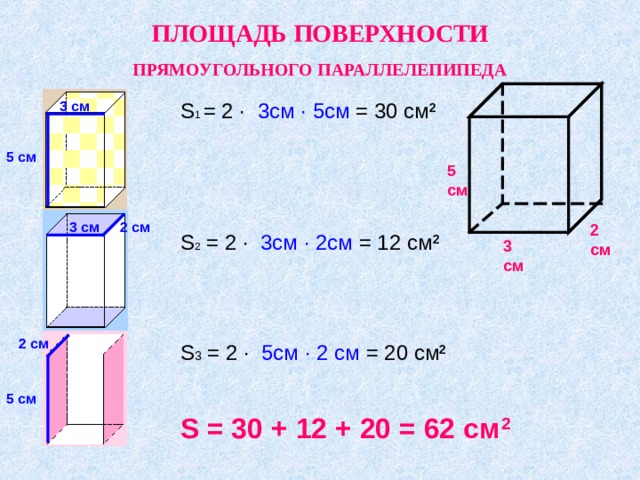
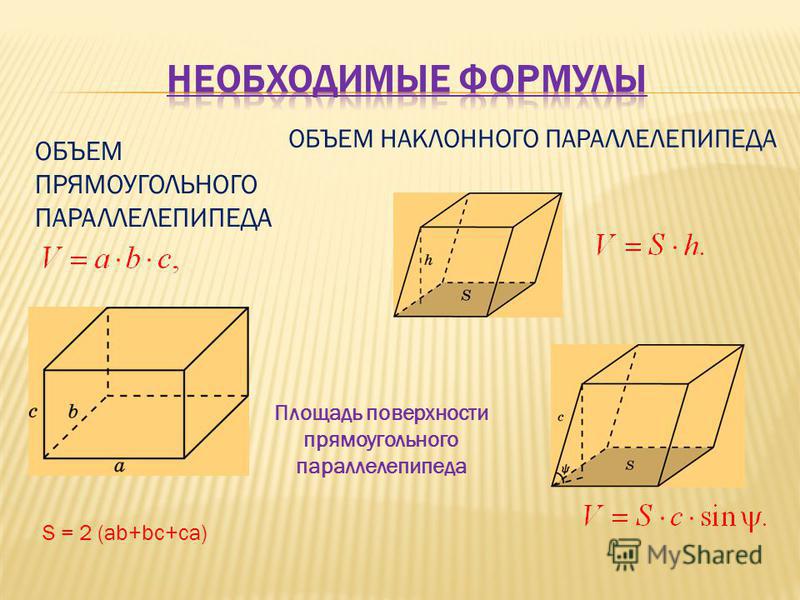
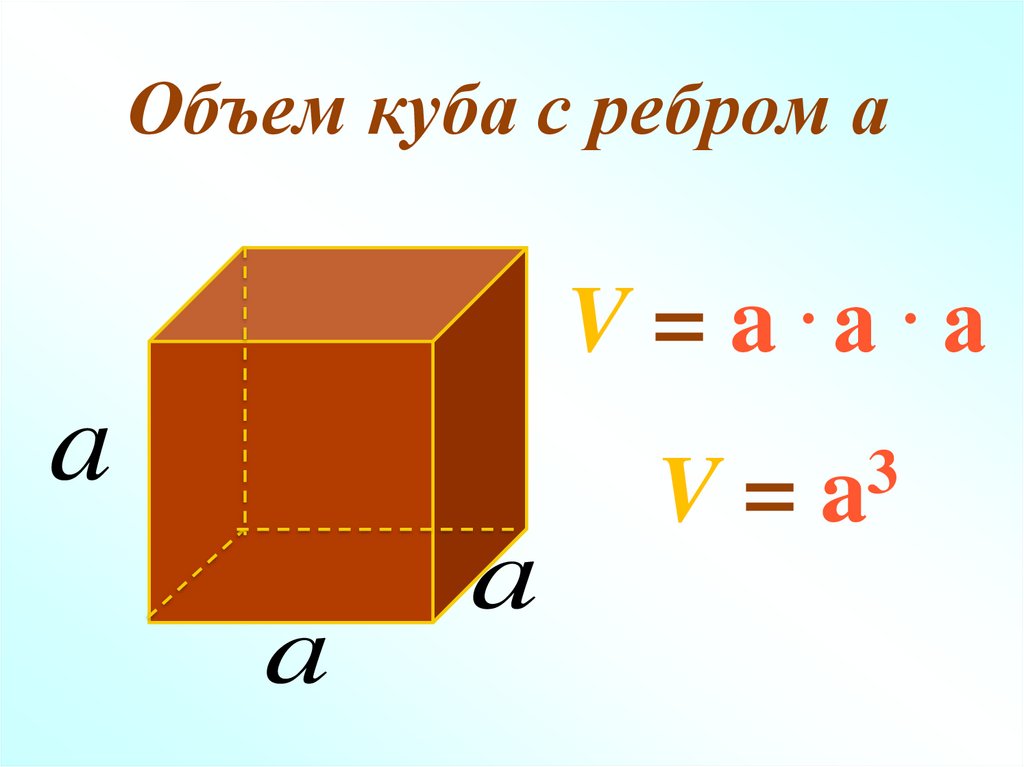
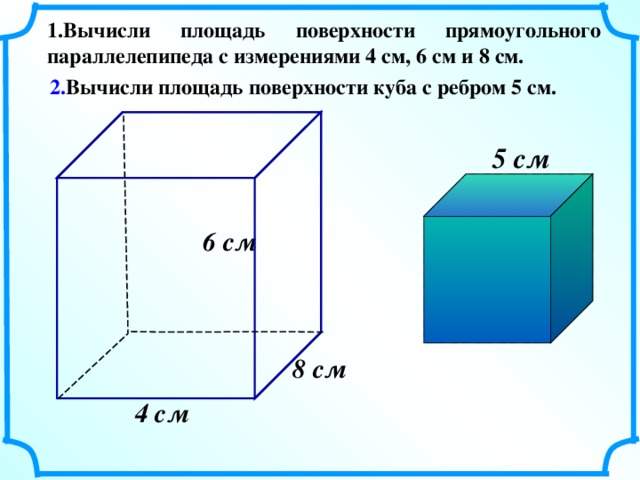 Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями. д.
д. Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки? Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.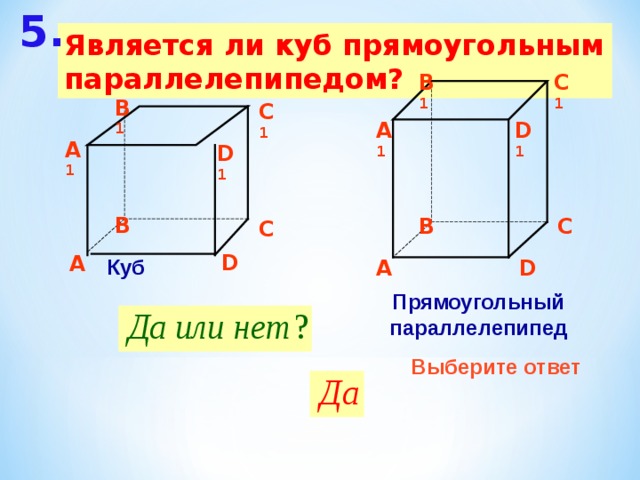 Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.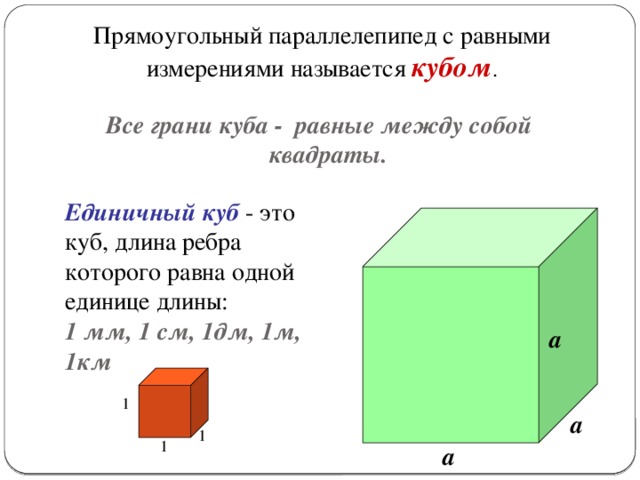
 Мы можем нарисовать параллелепипеды, используя закон параллелограмма для сложения векторов.
Мы можем нарисовать параллелепипеды, используя закон параллелограмма для сложения векторов.
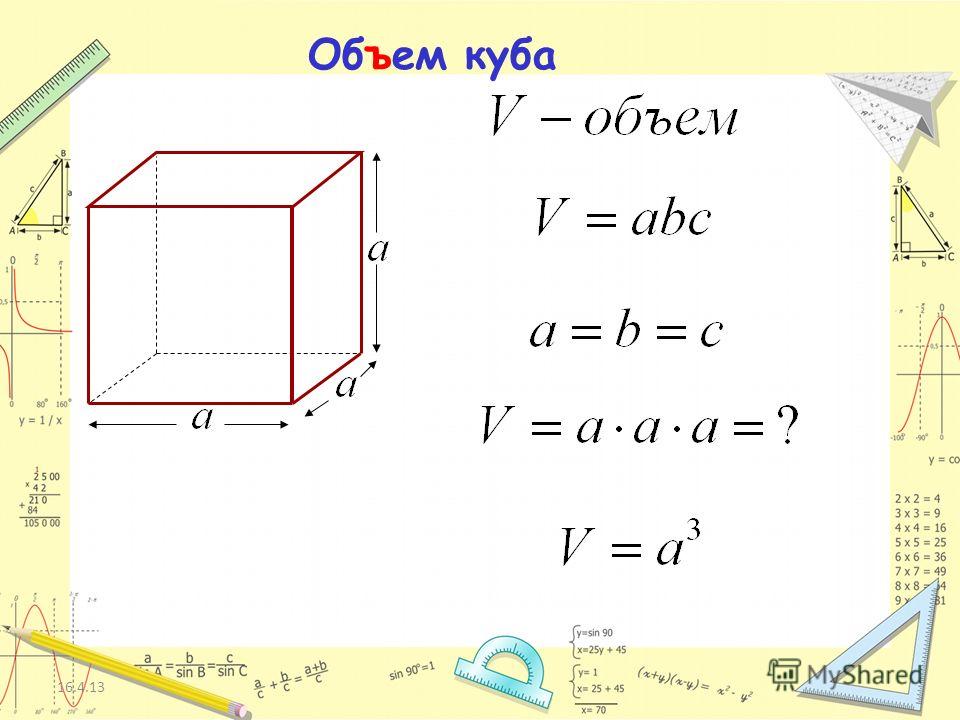
 Таким образом, vol(A) масштабируется как |c|.basev2v1height—-→base34v2v134heightbaseheightv1v2v3—-→base43heightv1v243v3
Таким образом, vol(A) масштабируется как |c|.basev2v1height—-→base34v2v134heightbaseheightv1v2v3—-→base43heightv1v243v3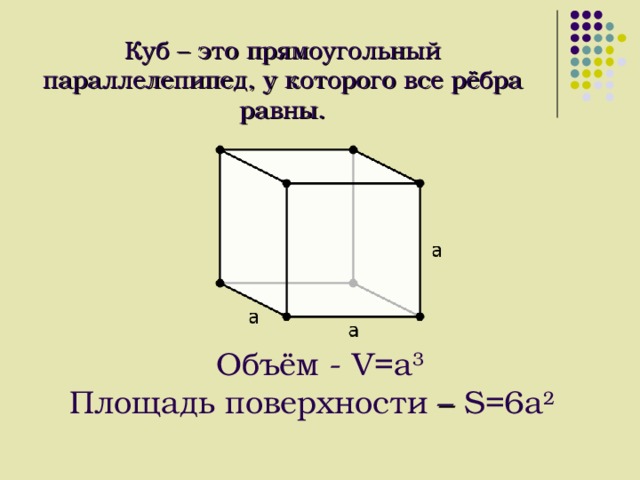 В этом случае параллелепипед P, определяемый одной своей строкой, представляет собой как раз отрезок [0,a] (или [a,0], если a<0). «Объем» области в R1=R — это просто ее длина, поэтому в данном случае ясно, что vol(P)=|a|.
В этом случае параллелепипед P, определяемый одной своей строкой, представляет собой как раз отрезок [0,a] (или [a,0], если a<0). «Объем» области в R1=R — это просто ее длина, поэтому в данном случае ясно, что vol(P)=|a|. Если вы прошли курс интегрального исчисления, вы, вероятно, вычисляли отрицательные площади под кривыми; идея здесь похожа.
Если вы прошли курс интегрального исчисления, вы, вероятно, вычисляли отрицательные площади под кривыми; идея здесь похожа.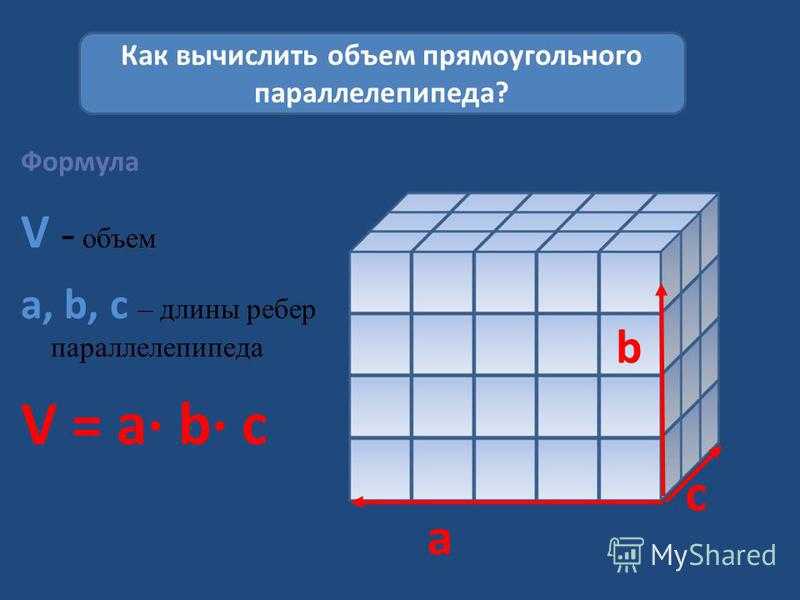 Если S — любая область в Rn, то
Если S — любая область в Rn, то Любую область S можно аппроксимировать набором очень маленьких кубов вида x+AC. Затем образ T(S) аппроксимируется образом этого набора кубов, который представляет собой набор очень маленьких параллелепипедов вида T(x)+AP.
Любую область S можно аппроксимировать набором очень маленьких кубов вида x+AC. Затем образ T(S) аппроксимируется образом этого набора кубов, который представляет собой набор очень маленьких параллелепипедов вида T(x)+AP.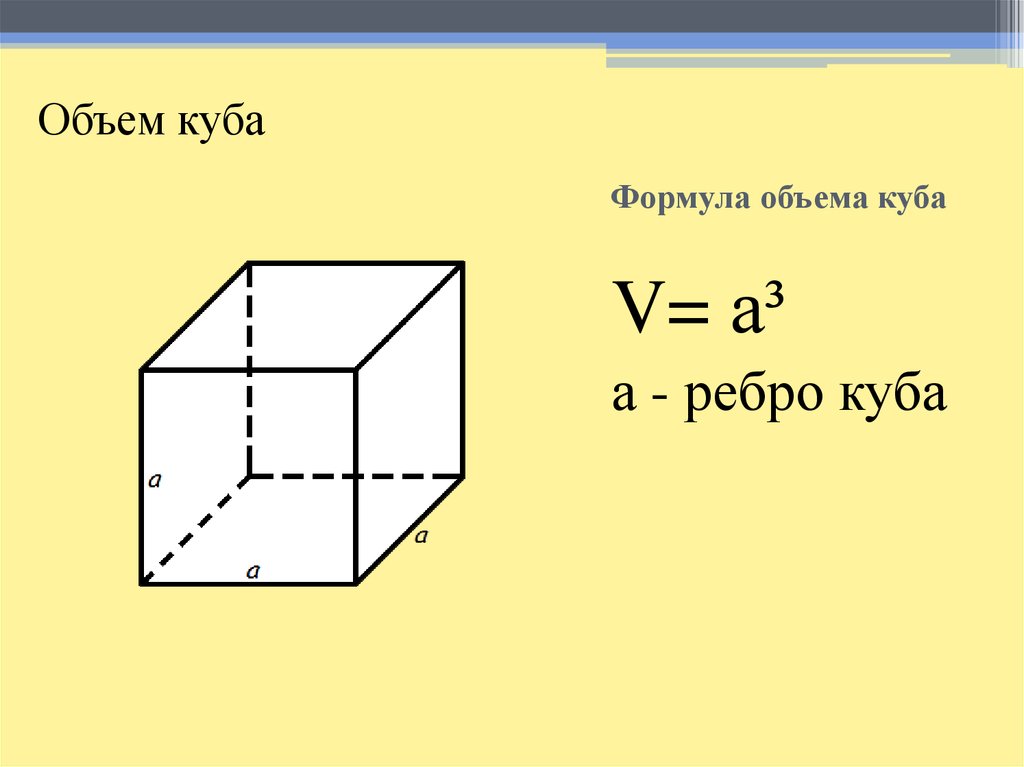 Оно происходит от греческой фразы «параллелепидон», означающей «объект, имеющий параллельную плоскость». По определению, это трехмерная фигура или призма с основанием в виде параллелограмма, образованным шестью сторонами параллелограмма. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. В этой статье мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Оно происходит от греческой фразы «параллелепидон», означающей «объект, имеющий параллельную плоскость». По определению, это трехмерная фигура или призма с основанием в виде параллелограмма, образованным шестью сторонами параллелограмма. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. В этой статье мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами. Прямоугольный кубоид с шестью прямоугольными гранями, куб с шестью квадратными гранями и ромбоэдр с шестью ромбовидными гранями — все это частные случаи параллелепипеда.
Прямоугольный кубоид с шестью прямоугольными гранями, куб с шестью квадратными гранями и ромбоэдр с шестью ромбовидными гранями — все это частные случаи параллелепипеда.

 Площадь боковой поверхности (LSA) параллелепипеда равна произведению периметра основания на высоту параллелепипеда. Таким образом, формула площади боковой поверхности параллелепипеда имеет вид:
Площадь боковой поверхности (LSA) параллелепипеда равна произведению периметра основания на высоту параллелепипеда. Таким образом, формула площади боковой поверхности параллелепипеда имеет вид: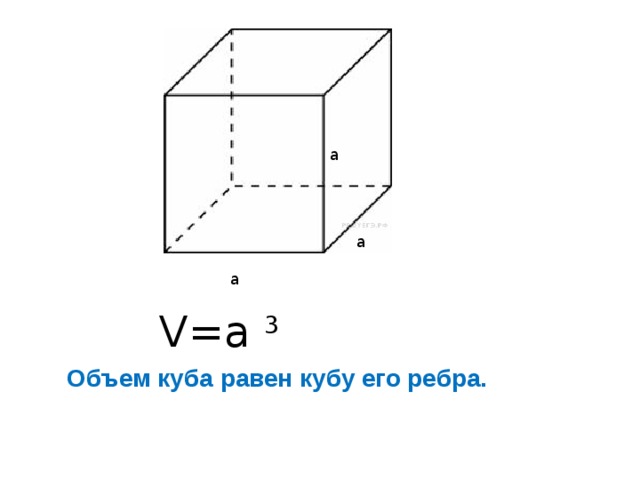
 Давайте посмотрим, как мы можем это вычислить.
Давайте посмотрим, как мы можем это вычислить.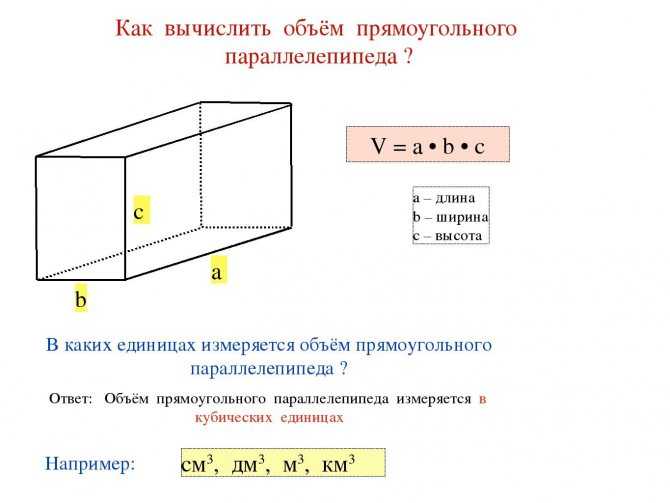
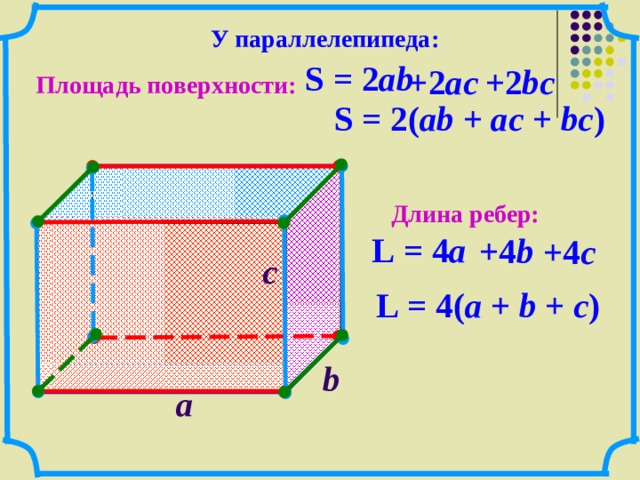


 Проседанный Стивеном Вудинг
Проседанный Стивеном Вудинг

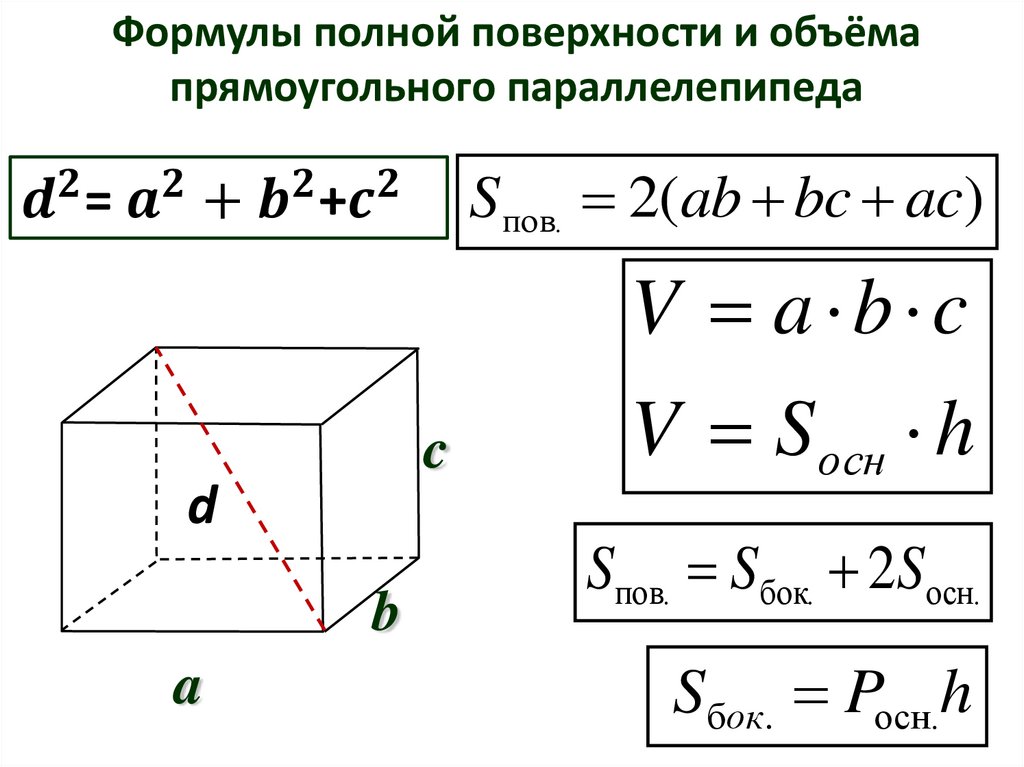


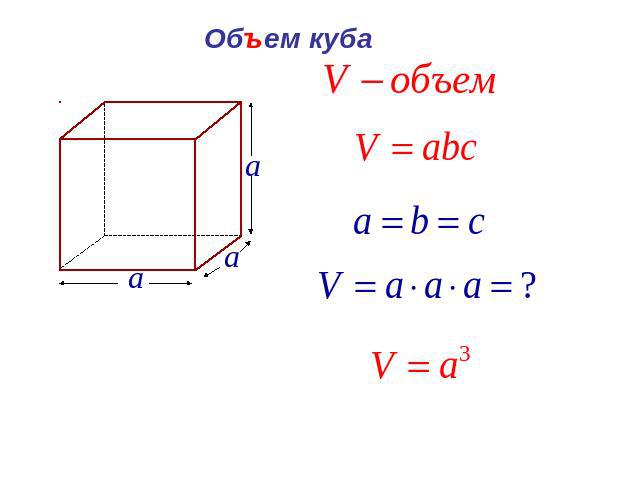

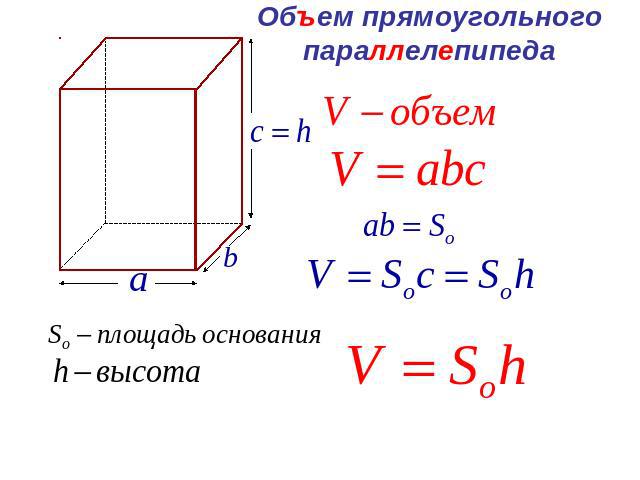
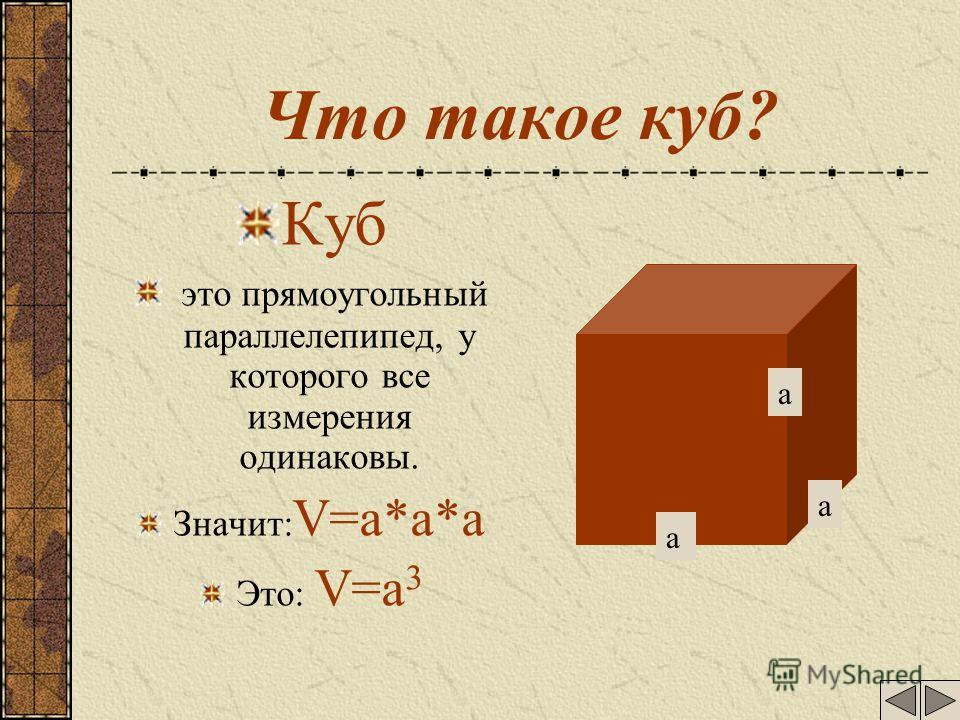
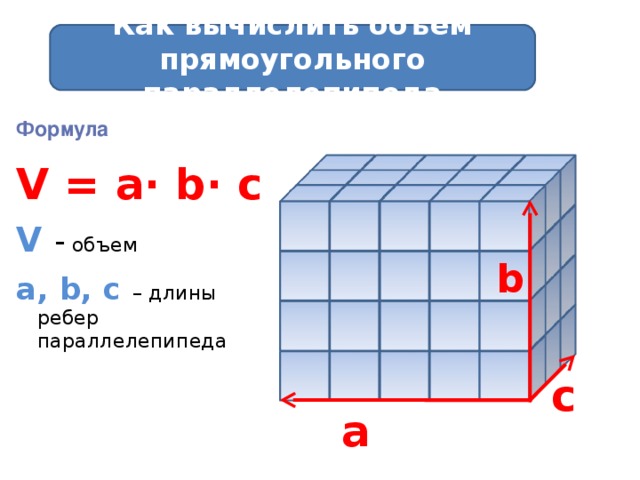 Другими словами, векторы
Другими словами, векторы  ..
..
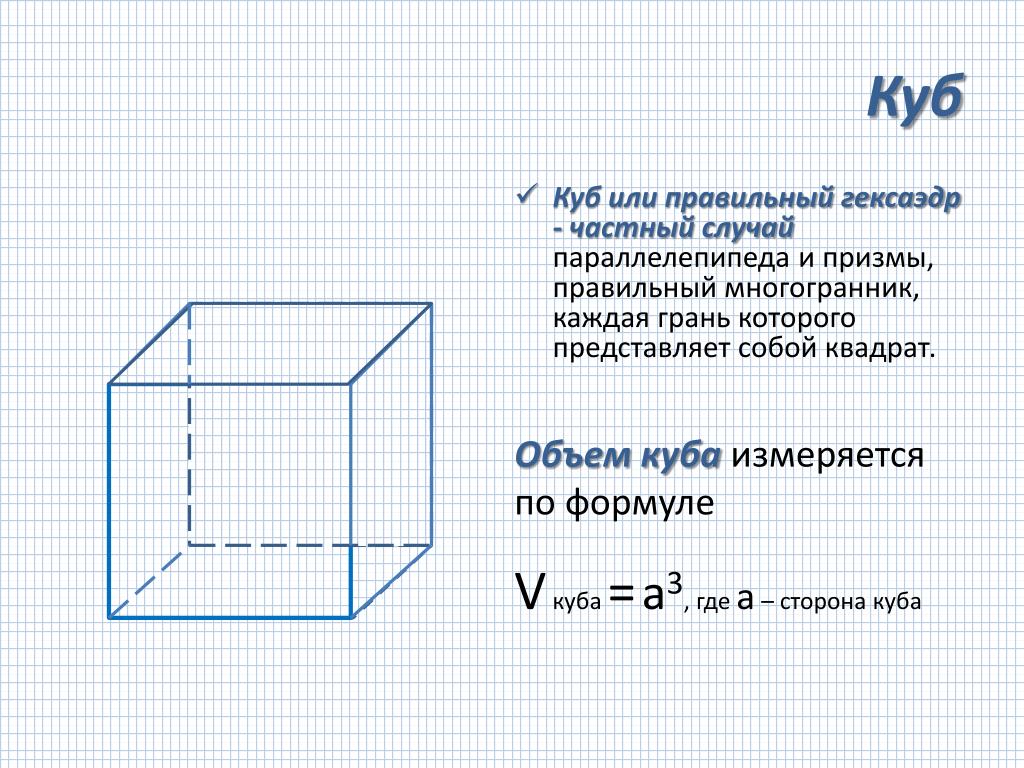

 Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус. Формулы, характеристики и свойства конуса
Область. Формулы площади
Периметр. Формулы периметра
Объем. Формулы объема
Формулы площади поверхности
Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус. Формулы, характеристики и свойства конуса
Область. Формулы площади
Периметр. Формулы периметра
Объем. Формулы объема
Формулы площади поверхности
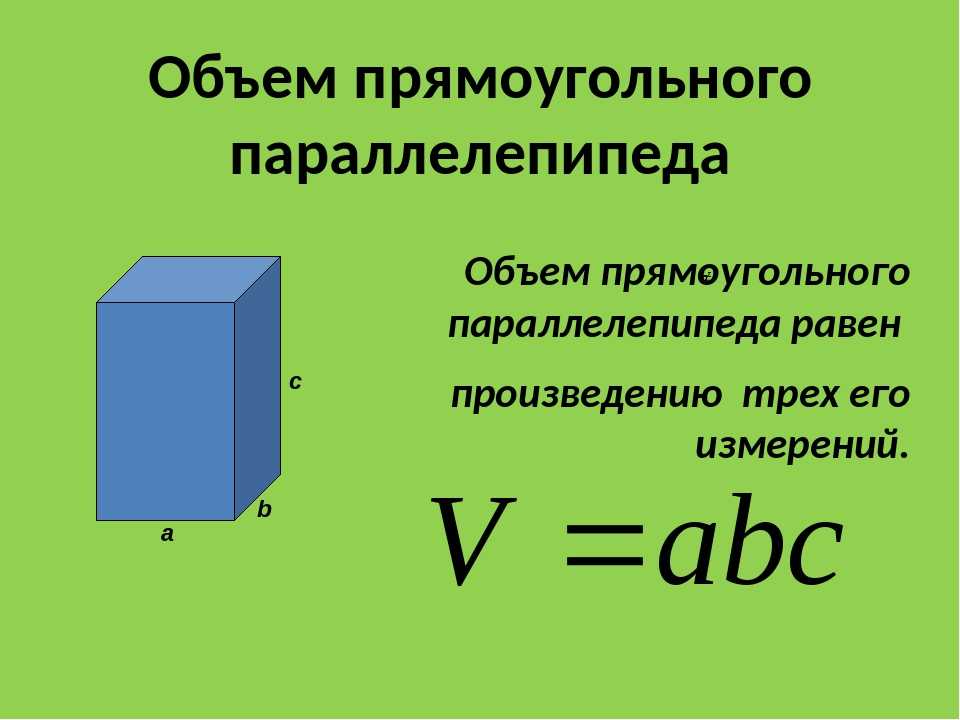 Но математика показывает нам закономерность, эта закономерность соответствует нашей интуиции в простом случае, и, учитывая, что трехмерный объем представляет собой сумму кратных двумерных объемов, кажется правдоподобным, что N-мерный объем может быть суммой кратных (N-1)-мерных объемов.
Но математика показывает нам закономерность, эта закономерность соответствует нашей интуиции в простом случае, и, учитывая, что трехмерный объем представляет собой сумму кратных двумерных объемов, кажется правдоподобным, что N-мерный объем может быть суммой кратных (N-1)-мерных объемов. Однако мы можем использовать этот факт, чтобы показать, что изменение масштаба второго вектора также приводит к изменению масштаба объема.
Однако мы можем использовать этот факт, чтобы показать, что изменение масштаба второго вектора также приводит к изменению масштаба объема.
 5cm} x_1 &= \left< 3,4 \right> \\ x_2 &= \left< −1,2 \right> \end{align*}$
5cm} x_1 &= \left< 3,4 \right> \\ x_2 &= \left< −1,2 \right> \end{align*}$ 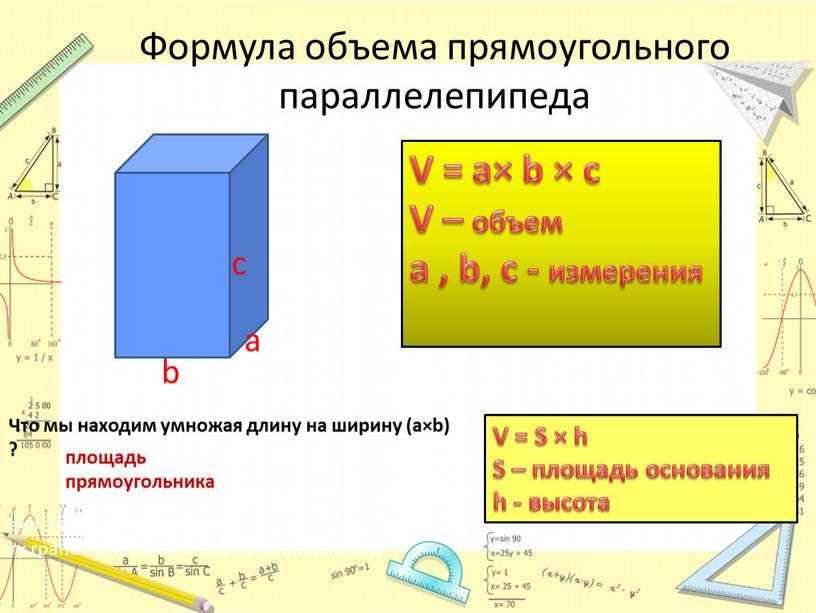
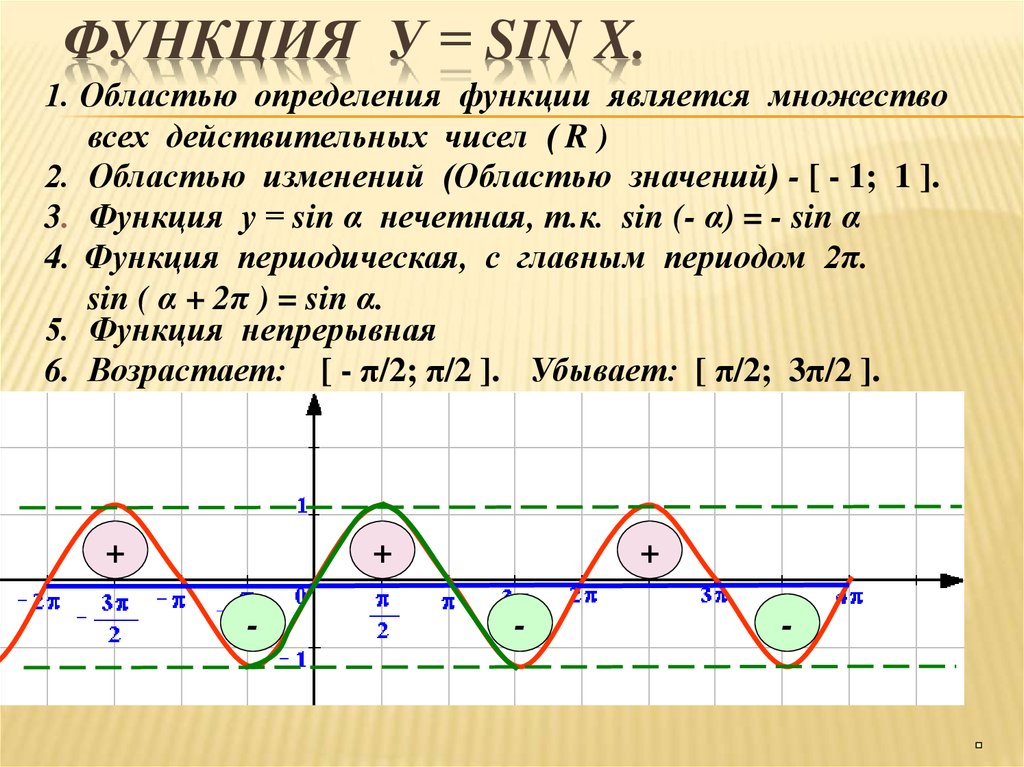
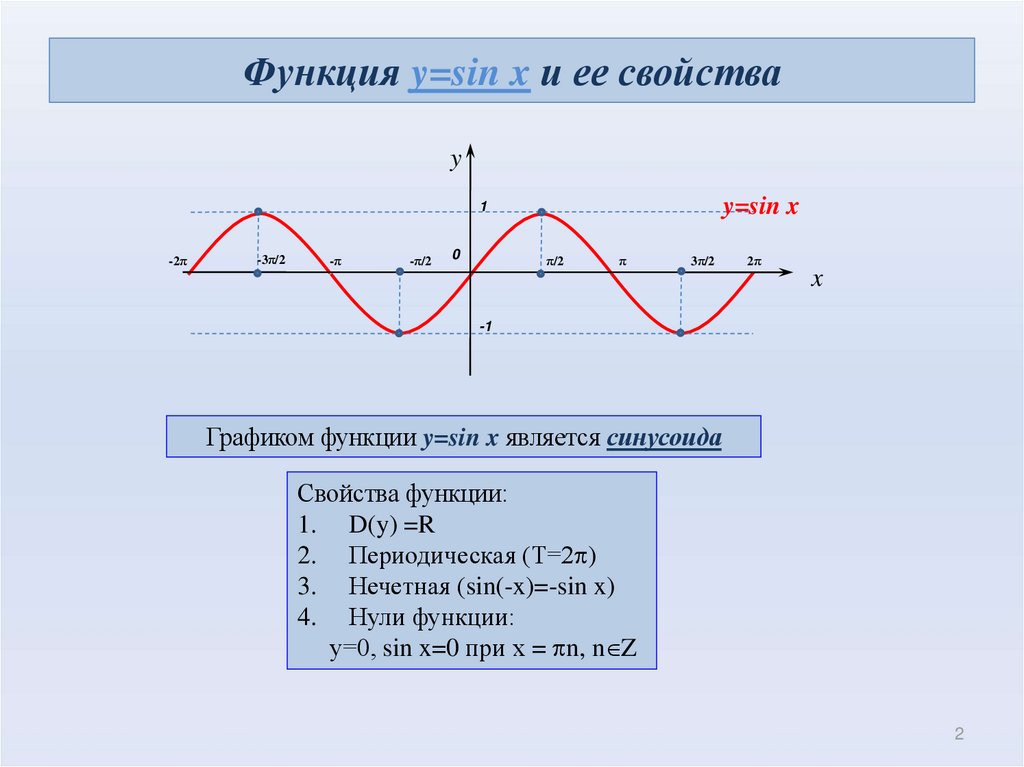 На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.  График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц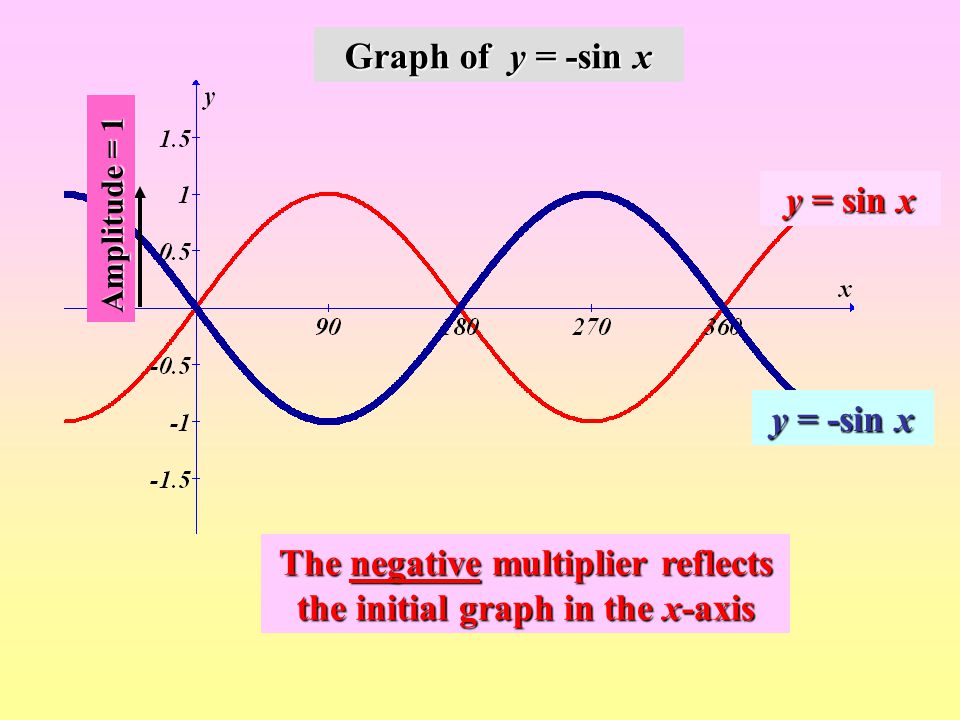 Четность
Четность  Организация домашнего задания
Организация домашнего задания  1).
1). Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач.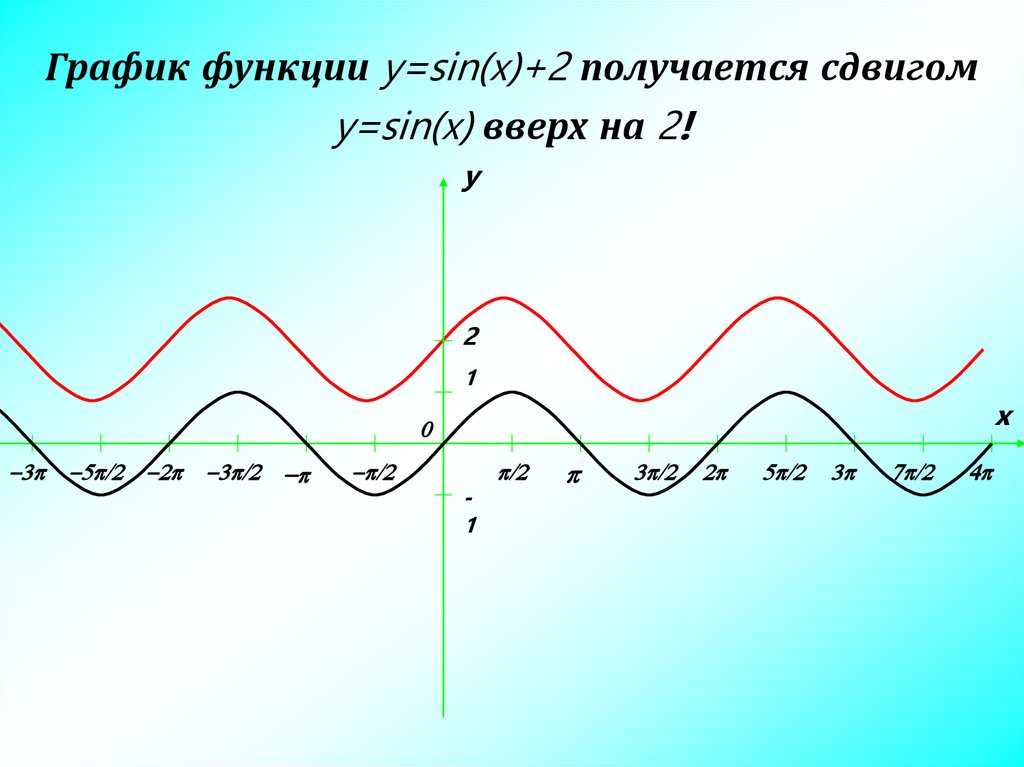 Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003. Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2  y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз  Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если 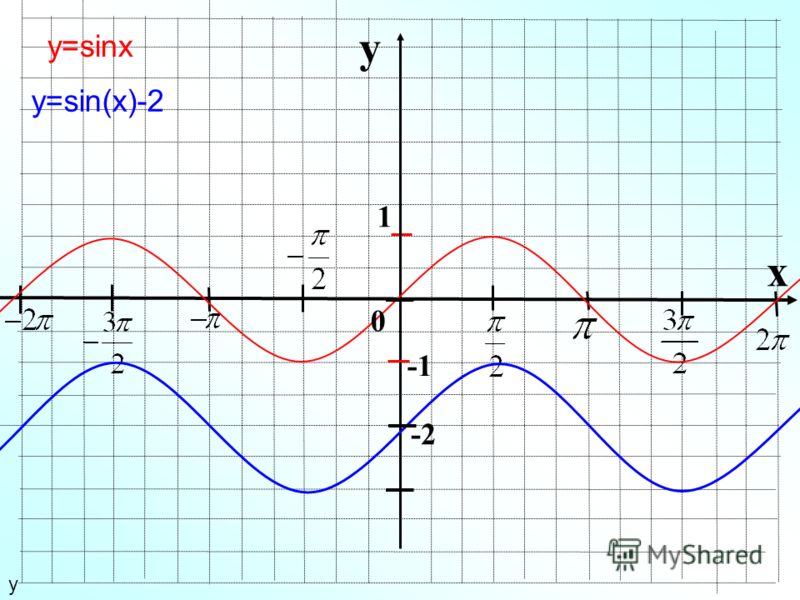 1).
1).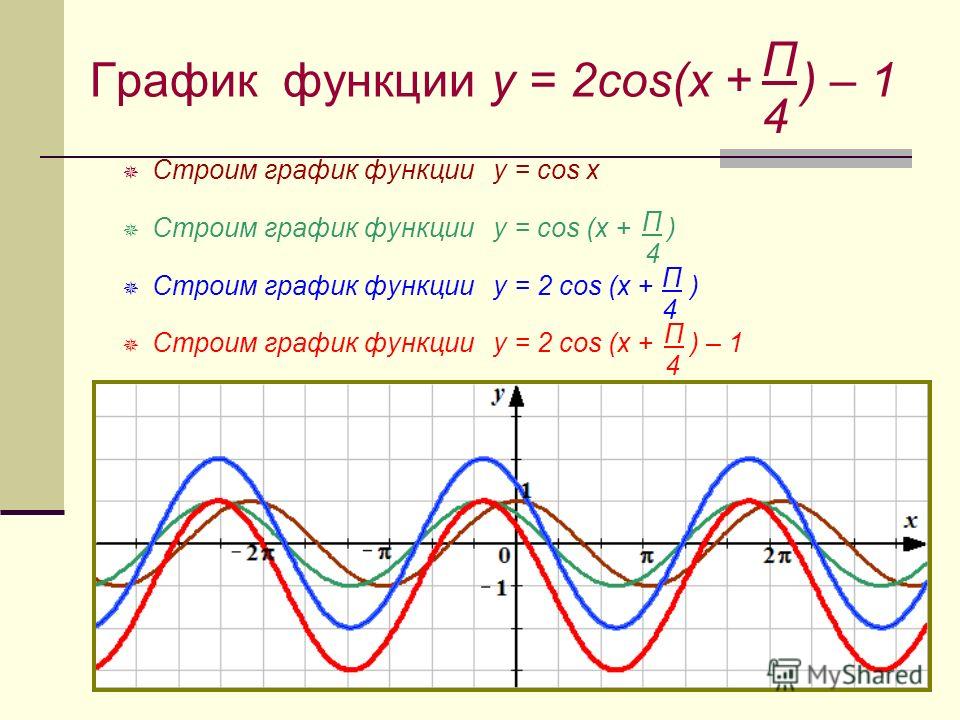 Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.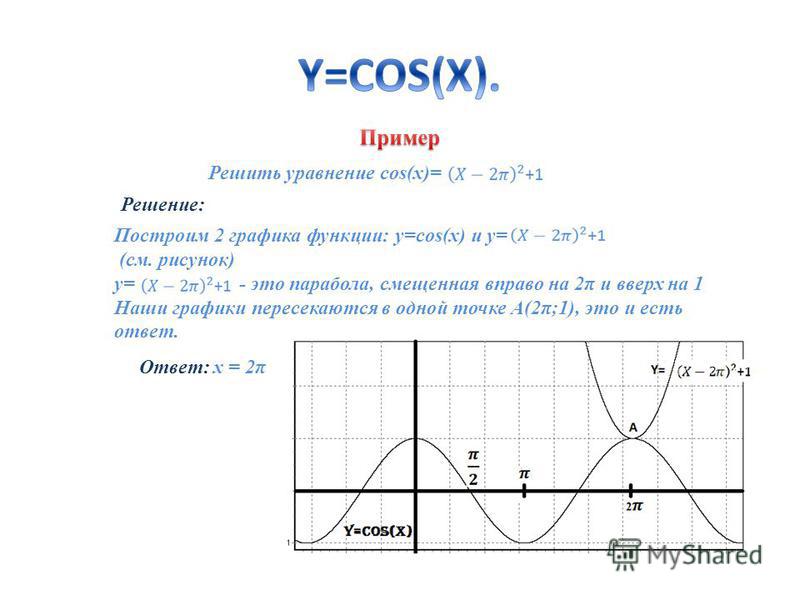
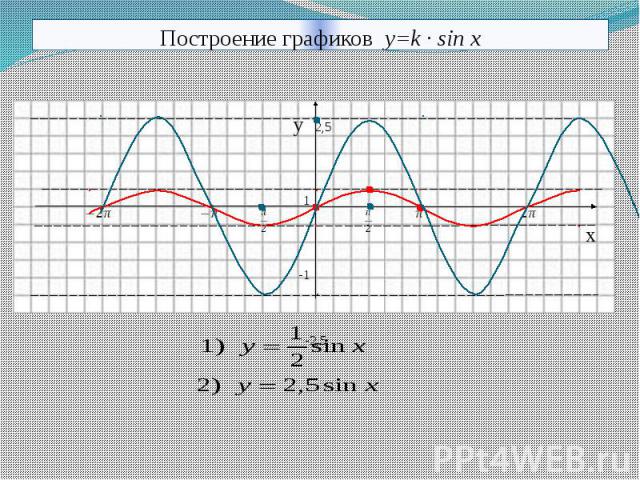 Это значения x .
Это значения x . Это график функции y = sin x на отрезке [-π; π].
Это график функции y = sin x на отрезке [-π; π].
 Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Если m > 1, то синусоида растягивается от оси x на коэффициент m. 
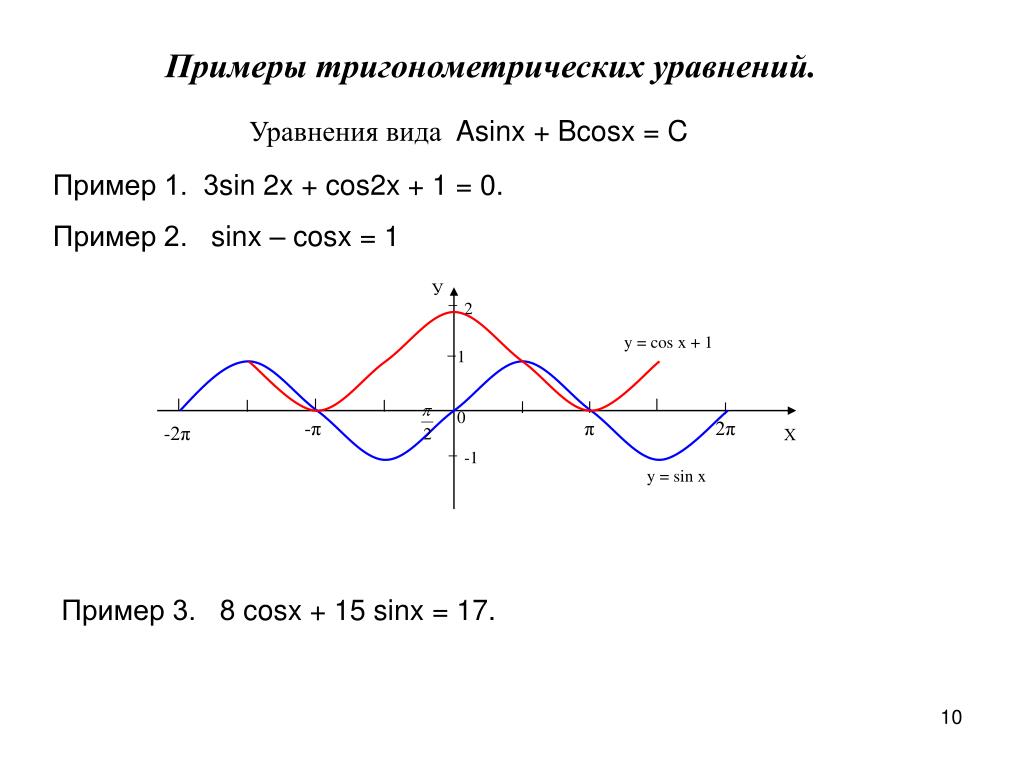 Этот закон соответствия и называется функцией.
Этот закон соответствия и называется функцией.
 Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007. Задачник для общеобразовательных учреждений (профильный уровень) под ред.
Задачник для общеобразовательных учреждений (профильный уровень) под ред. Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x
Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x 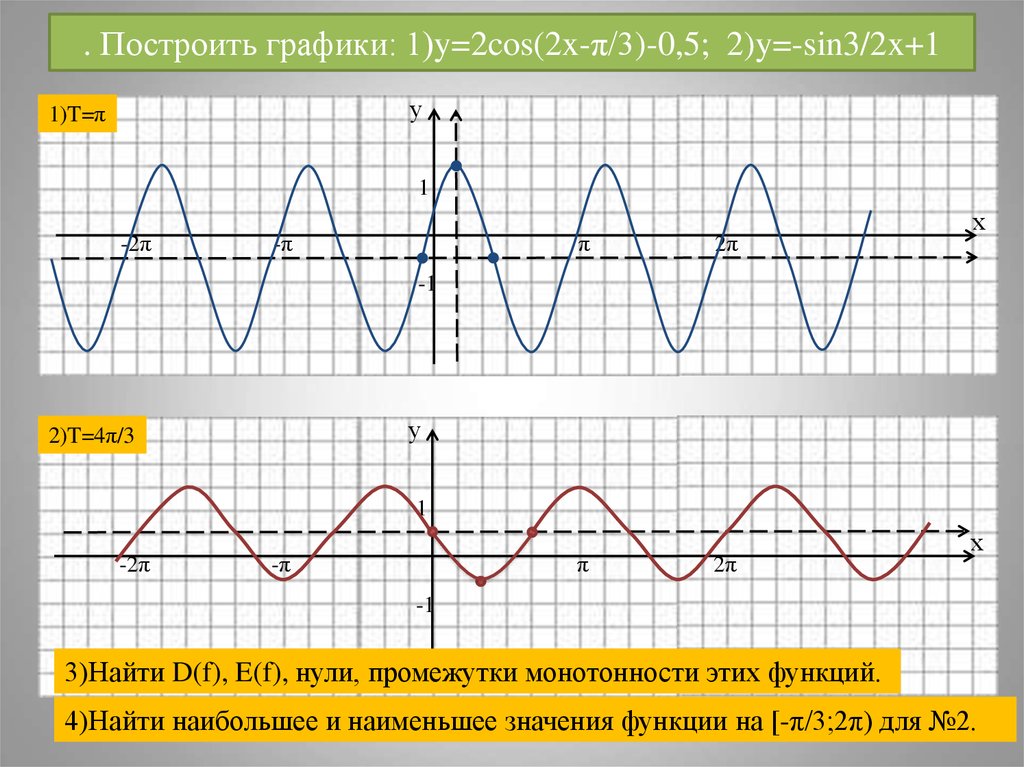 Функция y=sin x существует при всех действительных значениях x, причем, график ее является сплошной линией (без разрывов), т.е. функция непрерывна. 2.Функция y=sin x нечетная, ее график симметричен относительно начала координат 3.Наибольшие и наименьшие значения. Все возможные значения функции sinx ограничены неравенством -1 sinx 1, причем 4. Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
Функция y=sin x существует при всех действительных значениях x, причем, график ее является сплошной линией (без разрывов), т.е. функция непрерывна. 2.Функция y=sin x нечетная, ее график симметричен относительно начала координат 3.Наибольшие и наименьшие значения. Все возможные значения функции sinx ограничены неравенством -1 sinx 1, причем 4. Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если 

 е. тангенс — функция неограниченная .
е. тангенс — функция неограниченная .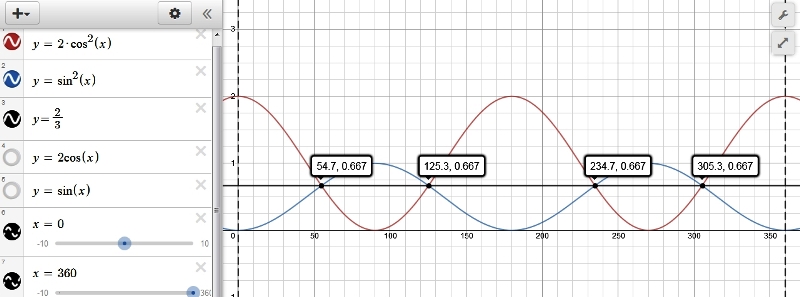
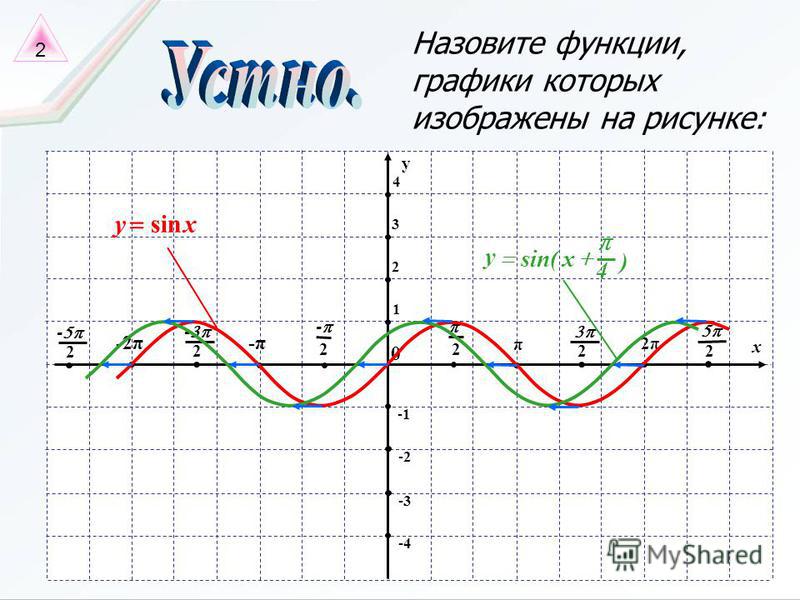 Как это связано с
монотонностью функции? (функция s = sin t возрастает
на отрезке и
убывает на отрезке ).
Как это связано с
монотонностью функции? (функция s = sin t возрастает
на отрезке и
убывает на отрезке ).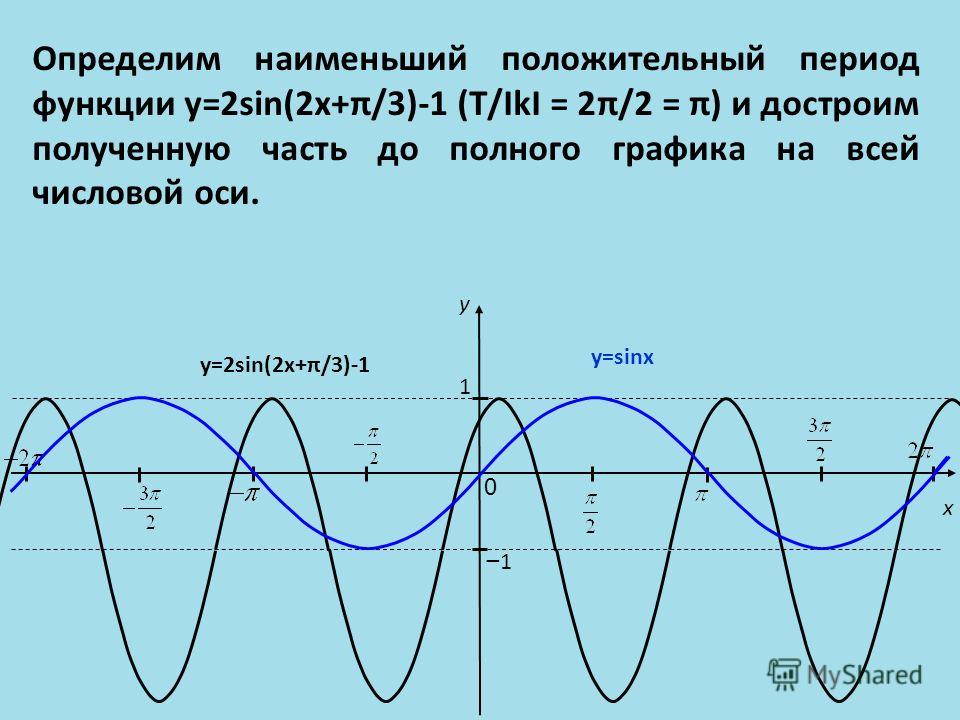 № 10.18 (б,в)
№ 10.18 (б,в) Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов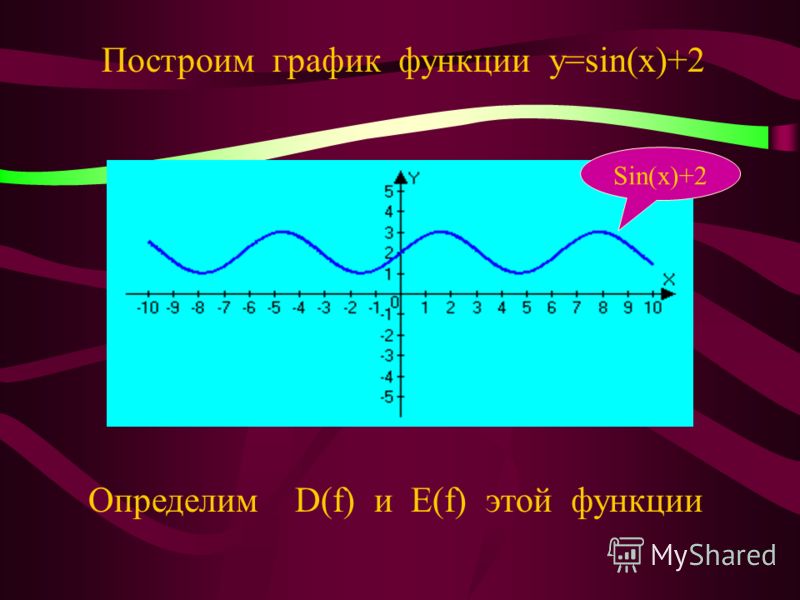 Мультимедийный проектор
Мультимедийный проектор Определение четности
Определение четности
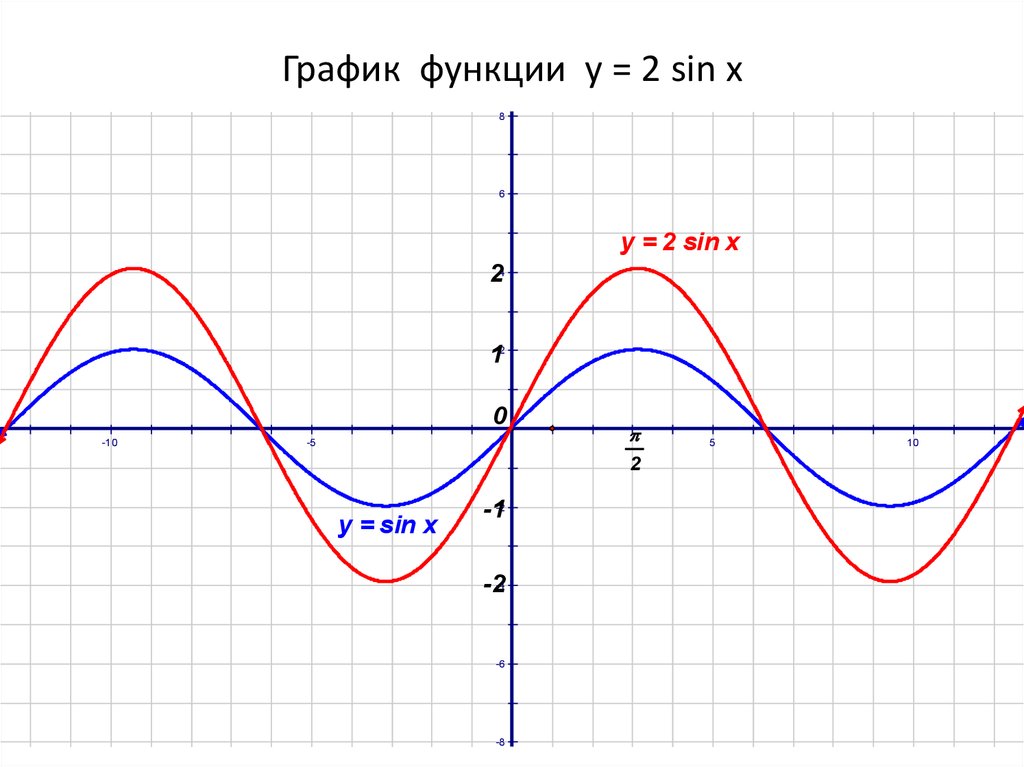 Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)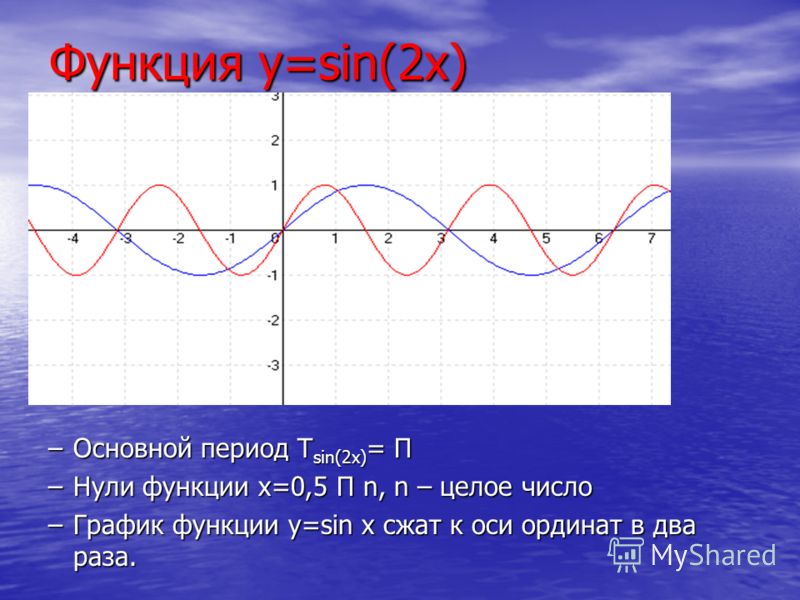 Область определения
Область определения