«Особенности построения графиков функций заданных неявно и параметрически»
Полякова О.Л.
Доклад
ОСОБЕННОСТИ Построения графиков функций
заданных неявно и параметрически
Из курса математического анализа известен стандартный алгоритм исследования явно заданных функций (область определения; множество значений; четность – нечетность; асимптоты; периодичность; нули; экстремумы; интервалы монотонности, выпуклости и вогнутости; точки перегиба). При параметрическом или неявном задании функции существует ряд специфических особенностей, отличающих построение графиков этих функций. Рассмотрим эти особенности на примерах.
Пример 1. Построить график функции [2, с. 126].
Сначала строим графики функций и соответственно в системах координат и .
1 а)Рис. 1 б)
Учитывая графическое изображение функций и , исследуем функцию по схеме [3].
Область определения функции: .
Множество значений функции: .
Таккак — функция общего вида, а — нечетная функция, то симметрииграфик не имеет.
При исследовании функции заданной параметрически, необходимо найти
особые точки (точка особая точка кривой, если ) и определить их вид.
Пусть, — первая отличная от нуля производная и — первая из производных, не коллинеарных вектору . Тогда если:
Рис. 2 а)Рис. 2 б)
Точка является особой точкой кривой, так как производные первого порядка: равны нулю при . Определяем тип особой точки, для этого вычисляем вторую и третью производные:
Таким образом, точка – точка возврата первого рода.
Точки самопересечения находим из условия , решая систему:
.
Так как , значит, кривая не имеет точек самопересечения.
Угловой коэффициент касательной:
.
При и при , т.е. в точках с координатами , и касательные параллельны оси абсцисс; при , т.е. в точке с координатами касательная параллельна оси ординат.
Экстремумы функции и интервалы монотонности.
Точка – точка минимума; точки , – точки максимума; при и при функция убывает; при , и при функция возрастает.
Интервалы выпуклости и точки перегиба. Так как вторая производная
отлична от нуля, следовательно кривая не имеет точек перегиба; при и при кривая выпукла вверх; при и при кривая выпукла вниз.
Асимптоты.
Прямая является наклонной асимптотой, т.к.
; .
Прямая наклонная асимптота, так как при , , и .
Прямая вертикальная асимптота, т.к. при .
Горизонтальных асимптот кривая не имеет.
График функции (рис. 3):
Рисунок 3 — График функции
При исследовании и построении графика функции заданной неявно также определяют особые точки кривой.
Точка кривой называется особой точкой, если ее координаты одновременно удовлетворяют трем уравнениям:
Если в особой точке производные второго порядка не равны одновременно нулю, тогда точка является двойной точкой кривой, причем форма кривой у ее двойной точки зависит от знака определителя
.
Возможные случаи изображены на рисунке [1, с. 271]:
а) узловая точкаРис. 4 б) изолированная точка
Рис. 4 в) точка возврата первого рода
4 г) точка возврата второго родаРис. 4 д) точка самокасания
Пример 2. Построить график функции [1, с.182].
Область определения находим, решая уравнение:
Откуда, область определения первой ветви , второй ветви —
Кривая симметрична относительно координатных осей.
Точки пересечения кривой с осями координат:
Асимптоты. Горизонтальных и вертикальных асимптот кривая не имеет, так как коэффициенты при высших степенях и постоянные величины. Наклонные асимптоты находим из условия:
,
приравнивая к нулю коэффициенты при , . Получаем и — наклонные асимптоты искомой кривой.
Особые точки:
Точка является особой двойной точкой, так как и производные второго порядка в этой точке одновременно не равны нулю. Т.к. точка с координатами узловая точка.
Найдем касательные к кривой в особой точке, для этого приравняем к нулю коэффициенты при низших степенях:
,
Таким образом, прямые и – две касательные к кривой в особой точке.
Координаты точек, в которых касательные параллельны оси абсцисс, найдем, решив систему:
.
В точках , касательные параллельны оси абсцисс. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение
в точке с координатами принимает положительные значения, то в этой точке максимум; а в точках с координатами произведение , следовательно это точки минимума.
Координаты точек, в которых касательные параллельны оси ординат, найдем, решив систему:
.
В точках с координатами , касательные параллельны оси ординат. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение
в точке с координатами , принимает положительные значения, то в этой точке максимум; а в точке с координатами – минимум, так как произведение .
Точкиперегиба находим, приравняв к нулю вторую производную:
,
очевидно, точка перегиба.
График функции (рис. 5):
Рис. 5 — График функции
Исследовать кривую – значит выявить совокупность важнейших свойств, дающих исчерпывающую информацию для изображения графика этой кривой. В целом, алгоритм исследования параметрических и неявно заданных функций совпадает с алгоритмом исследования функций заданных явно. Однако, существуют следующая специфическая особенность отличающая исследование этих функций от функций заданных явно, заключающаяся в нахождении особых точек и точек самопересечения.
При исследовании параметрических функций часто возникают сложности при определении точек перегиба и промежутков вогнутости, так как это исследование требует нахождения второй производной функции, которая представляет собой громоздкое выражение и решить уравнение точными методами не удается, необходимо прибегать к численным методам. Аналогичные сложности возникают и при исследовании неявно заданных функций: из-за сложных выражений второй производной определять точки перегиба приходится методом подбора (интуитивно) или же не определять вовсе.
Библиографический список:
Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. – Киев: Наук. думка, 1979. – 320 с.
Райхмист Р. Б. Графики функций: Справ. пособие для вузов. – М., «Высшая школа», 1991. – 160 с.
Иллюстрированный самоучитель по Mathematica 5 › Мультимедиа: геометрия, графика, кино, звук › Построение графиков функций, заданных параметрически (функция ParametricPlot) [страница — 203] | Самоучители по математическим пакетам
Построение графиков функций, заданных параметрически (функция ParametricPlot)
Функция ParametricPlot позволяет рисовать кривые и семейства кривых, заданных параметрически. Эта функция имеет те же опции, что и функция Plot. В некотором смысле эта функция универсальна. Если не учитывать неявно заданных функций, то именно функция ParametricPlot позволяет построить графики всех мыслимых функций, включая и многозначные.
Без проблем строятся и графики, заданные в полярной системе координат. Фигуры Лиссажу, кривые Уатта, овалы Кассини, Декарта, Мюнгера, улитки Паскаля, однолистники, листы Декарта, всевозможные розы и розетки, рулеты, годографы, эволюты и эвольвенты всех мыслимых и немыслимых кривых, циклоиды, всевозможные спирали, циссоиды, конхоиды, строфоиды, астроиды, кардиоиды, неоиды, лемнискаты, узлы, квадратрисы, клотоиды, кохлеоиды, трохоиды, элипсиды, катакаустики, всевозможные параболы, локсодромы и лоциклики, трезубцы, трисектрисы, трилистники, верзиеры, брахистохроны, подэры, кривые с именами древнегреческих и средневековых ученых – вот далеко не полный перечень всевозможного зверья, которое может быть нарисовано функцией ParametricPlot.
Пример 9.3. Фигуры Лиссажу.
Это классический пример применения функции ParametricPlot. Рисуются эти фигуры совсем просто, и потому мы нарисуем сразу несколько.
Пример 9.4. Розы и розетки.
Эти цветы весьма многочисленны, выглядят, как правило, очень мило и легко рисуются. Процесс вычерчивания совсем прост, если предварительно определить следующую функцию.
PolarR[a1,a2_,omega_,phi_] := Module[{r=a1+a2*Cos[omega*phi]},<r*Coi[phi],r*Sin[phi]}]
Вот как, например, с помощью этой функции рисуется многолепестковая роза.
А вот еще один милый цветок.
Цветы эти столь разнообразны, что согласия относительно количества их видов нет. Одни насчитывают более полтора десятка видов, другие – не менее сотни.
Построение графика функции, заданной в параметрической форме. — Студопедия
Государственное образовательное учреждение высшего профессионального образования
Московский авиационный институт
(национальный исследовательский университет)
РАДИОВУЗ МАИ
О.М.Данченко
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
МОСКВА
О.М. ДАНЧЕНКО
Методические указания по выполнению индивидуальных заданий по математическому анализу – М.; РАДИОВТУЗ, 2012г., — 36 с.
Данное пособие содержит типовые задачи для индивидуальных заданий студентов-заочников по курсу «Математический анализ» часть 1. Ко всем задачам приводятся подробные решения и указания. Приведенные задания в равной степени могут использоваться студентами очного отделения при подготовке к экзамену. В приложении приведена подробная программа курса по «Математическому анализу» часть 1.
РАДИОВТУЗ 2012
Содержание
Введение…………………………………………………………………………….
Построение графиков функций, заданных в полярной системе координат или в параметрической форме……………………………………………………………
Вычисление пределов последовательностей и функций…………………………
Исследование функций на непрерывность………………………………………..
Вычисление производных………………………………………………………….
Исследование функций с помощью производных, построение графиков функций……………………………………………………………………………..
Задания на вычисление интегралов……………………………………………….
Приложения…………………………………………………………………………
Введение
В процессе изучения курса «Математический анализ» предусмотрено выполнение студентами индивидуальных домашних заданий в каждом семестре. Индивидуальное домашнее задание 1-ого семестра содержит следующие задачи:
1. Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме.
2. Вычисление пределов последовательностей и функций.
3. Исследование функций на непрерывность.
4. Вычисление производных от сложных функций, функций, заданных неявно или в параметрической форме.
5. Исследование функций с помощью производных, построение графика функции.
6. Вычисление неопределенного и определенного интегралов.
Рассмотрим далее типовые примеры на каждое из заданий и укажем методы их решения.
Построение графиков функций, заданных в простой полярной системе координат.
Простая полярная система координат характеризуется следующим:
ρ=ρ(φ); 0≤ρ<+∞; 0≤φ≤2π(1)
Положительные углы φотсчитываются от полярной оси (совпадающей с положительным направлением оси ОХ) против часовой стрелки, отрицательные – по часовой стрелке. При построении графика функции в соответствии с уравнениями (1) следует придерживаться следующего порядка действий:
а) указать область допустимых значений (О.Д.З.), т.е. определить при каких углах φфункция ρ(φ) – неотрицательна, т.е. ρ(φ)≥ 0;
б) найти область изменения функции;
в) указать является ли функция четной или нечетной, т.е. если ρ(-φ) = ρ(φ),то график функции симметричен относительно полярной оси и, следовательно, достаточно сделать исследования для φ≥0.После данных исследований следует построить кривую по точкам.
Пример: построить график функции в простой полярной системе координатρ=2cos2φ
Так как в простой полярной системе координат ρ≥0, то О.Д.З. будут являться только те углы φ,для которых cos2φ≥0,т.е. 0≤φ≤π/4; 3π/4≤φ≤5π/4; 7π/4≤φ≤2π. Функция будет ограничена, т.к. |cos2φ|≤1,т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4.Для 0≤φ≤π/4функция монотонно убывает от двух до нуля, для 3π/4≤φ≤πфункция монотонно возрастает от нуля до двух (рис. 1).
Построение графика функции, заданной в параметрической форме.
Пусть x=X(t)и y=Y(t), где параметр tизменяется в определенных заданных пределах. График функции, заданной в параметрической форме, строится по характерным точкам.
Пример: x=t², y= t∙(t²-3)/3
а) Заметим, что для любых значений аргумента t функция x(t)=t²≥0, следовательно, график функции расположен в правой полуплоскости.
б) В силу нечетности функции y(t), так как y(-t)=-y(t), график функции симметричен относительно оси ОХ.
в) Определим точки, в которых y(t) = 0: при t=0, y(0)=0 и x(0)=0
при t= + и t= — y=0, а x(+ ) = 3 – т.е. это точки пересечения графика функции с осью ОХ. Для более точного построения графика функции достаточно добавить еще 2-3 точки, например при t=1 y(1)=-2/3, x(1)=1; при t=2 y(2)=2/3, x(2)=4; при t =3 y(3)=6, x(3)=9 (рис.2.).
рис. 1 рис. 2
Построение графиков функций, заданных параметрически — Мегаобучалка
Задание: Построить график функции
1. Решение этой задачи сведём к предыдущей задаче.
2. Запишем заголовки: в А1: t, в ячейку В1: х, в ячейку С1: у.
3. В столбце А с помощью маркера автозаполнения создать ряд значений для t от 0 до с шагом (либо при помощи набора команд: Правка Þ Заполнить Þ Црогрессия (шаг 0,314, предельное значение 6,28)).
4. В ячейку В2 вводим формулу =COS(2*A2)*SIN(A2)и копируем её в диапазоне В3:В22.
5. В ячейку С2 вводим формулу =COS(A2)*SIN(3*A2)и копируем её в диапазоне С3:С22.
6. Выделяем диапазон данных В2:С22 со значениями х и у, строим точечную диаграмму.
7. Результат работы представлен на рис. 7.
Построение графиков кусочно-непрерывной функции
Задание: Построить график функции , заданной тремя ветками на отрезке .
.
Для построения этого графика шаг изменения желательно выбирать поменьше, например, , и т. д. Далее в мастере диаграмм выбирать точечную диаграмму (первую в первой строке).
1. В ячейке A1 записываем заголовок X.
2. В ячейке В1 записываем заголовок f1.
3. В ячейке С1 записываем заголовок f2.
4. В ячейке D1 записываем заголовок f3.
5. В ячейке E1 записываем заголовок F(x).
6. В столбце А создаём ряд значений для х от -0,2 до 2,41 с шагом 0,03. Такой диапазон изменения взят с учётом промежутков, на которых задан каждый «кусок» функции. Так, по условию, у нас , поэтому можно взять в качестве крайнего левого значения аргумента. Кроме того, из третьего участка функции видно, что . Поэтому в качестве крайнего правого участка взято .2+4*A2+11)и копируем её в столбце D.
10. В Е2 запишем формулу:
=ЕСЛИ(А2<0,47;В2;ЕСЛИ(А2>=2;D2;С2))
Скопируем её в столбце Е до конца диапазона изменения аргумента функции.
11. Выделим диапазон, состоящий из данных в столбце А и данных в столбце Е (используя клавишу CTRL) и строим точечную диаграмму.
12. Результат работы представлен на рис. 8.
Задания для самостоятельной работы
1. Построить график функции в прямоугольной системе координат. Диапазон изменения и шаг выберите самостоятельно:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
2. Построить график функции, заданной в полярной системе координат:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
3. Построить график функции, заданной параметрическим способом:
1. ,
2. ,
3. ,
4. ,
5. ,
6. ,
7. ,
8. ,
9. ,
10. ,
11. ,
12. ,
13. ,
14.
15.
4.Построить графики функций, используя функцию ЕСЛИ( )
а) Случай двух ветвей:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
б) Случай трёх ветвей:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Лабораторный практикум № 4
gnuplot / parametric (E)
В обычном двумерном построении в gnuplot координата Y выражается y=f(x), однако можно использовать параметрическое задание функции, использующее параметр t,
x = f(t) y = g(t)
С помощью этого выражения gnuplot может рисовать более сложные функции. Отметим, что 3D построения параметрической поверхности, задаваемой параметрами u,v, дается в разделе построения сферических гармоник.
В первую очередь необходимо использовать команду set parametric, чтобы gnuplot определил параметрическую переменную для функции. Затем, команда plot, выполняющая построение функции f(t) координаты X и функцит g(t) для координаты Y, задается как plot f(t),g(t).
Чтобы провести простейшую вертикальную линию, не выражающуюся формой y=f(x), а заданную как x=const. Эта функция может быть определена как:
x=const y=t
с параметром t, когда t различен. Диапазон t контролируется командой set trange.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> const=3
gnuplot> set trange [1:4]
gnuplot> set xrange [0:5]
gnuplot> set yrange [0:5]
gnuplot> plot const,t
В данном случае вертикальная линия нарисованна в x=3. Использование set trange [1:4] , определило диапазон от 1 до 4. Если trange не установлен, вертикальная линия будет отрисована от верхней до нижней границы.
Параметрическое задание окружности:
x=sin(t) y=cos(t)
окружность может быть нарисована при изменении параметра t от 0 до 2pi. График принимает вид «квадрата» и диапазон t задается опцией команды plot.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> set size square
gnuplot> set xrange [-1:1]
gnuplot> set yrange [-1:1]
gnuplot> plot [0:2*pi] sin(t),cos(t)
Параметр t не изменяется непрерывно и фактически управляется значениями, установленными командой set samples. По умолчанию значение равно 100. В случае set samples 8, gnuplot вычисляет только 8 значений t от 0 до 2*pi, и график становиться семиугольником. Если необходим построить N-угольник, задается set samples N+1.
2D параметрическое представление удобно для рисования функции, которая находится в полярных координатах. 2D полярная координатаимеет 2 переменные: r и угловую theta. gnuplot выражает параметр t для theta, а радиус r выражается через функцию угла, а именно r(t). Координата (x,y) дается из:
x=r(t)*cos(t) y=r(t)*sin(t)
Окружность — особый случай, когда r(t)=const. Когда радиус пропорционален t, получается спираль.
gnuplot> set xrange [-10*pi:10*pi] gnuplot> set yrange [-10*pi:10*pi] gnuplot> plot [0:10*pi] t*sin(t),t*cos(t)
Следующий пример показывает график кардиоды r(t)=const*(1+cos(t)).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> r(t) = 1+cos(t)
gnuplot> plot [0:2*pi] r(t)*cos(t),r(t)*sin(t)
Обычная функция имеет вид y=f(x), но параметрическая позволяет делать график x=f(y). Значения Y такие же как и t и значения x вычисляются функцией f(t).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> c=2*pi
gnuplot> set size square
gnuplot> set trange [-c:c]
gnuplot> set xrange [-c:c]
gnuplot> set yrange [-c:c]
gnuplot> plot c*sin(t),t with lines, t,c*cos(t) with impulses
Показаны 2 функции, одна (зеленые линии) y=2pi*cos(x), другая (красная толстая линия) x=f(t)=2pi*sin(y).
Опция with impulse рисует вертикальную линию от оси Y=0. Если используется with impulses для красной кривой x=2pi*sin(y), то получается вертикальная линия, не горизонтальная.
Производная функции, заданной неявно
Дифференцирование функций, заданных неявно, опирается на возможность почленного дифференцирования тождеств.
В общем случае уравнение почленно дифференцировать нельзя.
Пусть функция задана неявно уравнением и известно, что существует решение этого уравнения в виде ; подставив это решение в уравнение, получим тождество .
Продифференцировав по х, получим уравнение для нахождения производной .
Пример
Найти производную функции, заданной неявно: .
Решение
Продифференцируем обе части данного уравнения по аргументу х:
Дифференцирование функций, заданных параметрически
Пусть функция задана параметрически уравнениями
(1) — параметр.
Требуется найти производную .
Имеет место формула
или .
Пример
Найти производную функции, заданной параметрически: .
Решение
Найдем производные функций х и у по переменной t:
,
.
Согласно формуле , получим
.
Исследование функций и построение графиков функций
Одна из возможных схем исследования функции и построения ее графика включает следующие этапы решения задачи:
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Определить четность, нечетность, периодичность функции.
4. Исследовать функцию на экстремум, найти интервалы монотонности функции, точки максимума и минимума.
5. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба.
6. Найти точки разрыва функции и асимптоты графика функции.
7. Построить график функции.
Пример
С помощью методов дифференциального исчисления исследовать и построить график функции .
Решение
1. Область определения функции находится из условия: , т.е. .
2. Точки пересечения графика функции с осями координат:
с осью Оу, , точка ,
с осью Ох, , точка .
3. Четность, нечетность, периодичность функции.
Функция называется четной, если для любого х из области определения справедливо равенство . Функция называется нечетной, если для любого х из области определения справедливо равенство . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
В нашем случае, , следовательно, функция нечетная, а ее график симметричен относительно начала координат.
Функция непериодическая.
4. Исследование функции на экстремум.
Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную:
.
Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель к нулю:
, т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
_ _ _
х
-6 6 у
5. Исследование на выпуклость, вогнутость. Точки перегиба.
Вычислим производную второго порядка:
Необходимое условие точки перегиба: или не существует. Равенство выполняется при , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
_ + _ +
х
-6 0 6 у
Так как при переходе через точку вторая производная меняет знак, то точка с абсциссой является точкой перегиба. Итак, точка перегиба имеет координаты .
6. Точки разрыва функции и асимптоты графика функции.
1) Вертикальные асимптоты. Прямая является вертикальной асимптотой графика функции , если хотя бы один из пределов
или
равен или . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
Заданная функция имеет две точки разрыва второго рода и , так как
, ,
, ,
следовательно, график функции имеет две вертикальных асимптоты и .
2) Наклонные асимптоты. Пусть прямая является асимптотой графика функции . Такую асимптоту называют наклонной. Для того, чтобы график функции имел при наклонную асимптоту , необходимо и достаточно, чтобы существовали оба предела:
.
Аналогично находится асимптота при .
Так как , то наклонных асимптот нет.
3) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда .
Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы:
.
Если эти пределы конечны и различны, то прямые будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен , то не существуют и соответствующие асимптоты.
Так как
,
то график функции имеет горизонтальную асимптоту .
7. Построение графика функции.
Для уточнения построения графика функции можно найти ряд вспомогательных точек
| х | -9 | -4 | ||
| у | -1,4 | 1,4 | -1,4 | 1,4 |
после чего строим график функции.
Графики параметрических функций — Интеллектуальная Кобринщина
Plot Parametric Functions — Wolfram MathematicaГрафики параметрических функций
Mathematica может строить графики параметрических функций в двух и трех измерениях. Воспользуйтесь параметрическим графиком, если Вы можете выразить координаты x, y или x, y, z в каждой точке Вашей кривой как функцию одного или более параметров.
Построим график параметрической кривой (x,y)=(2 sin(t),cos(t)), с параметром t изменяющимся от 0 до 2 ?:
In[1]:=
Out[1]=
Вы можете построить график двух параметрических кривых, поместив их в список:
In[2]:=
Out[2]=
Чтобы отобразить еще больше графиков кривых, просто добавьте их в список:
In[3]:=
Out[3]=
Воспользуемся командой ParametricPlot3D для построения графика поверхности, заданной функцией :
In[4]:=
Out[4]=
Построим график параметрической кривой (x,y,z)=(5 cos(u),5 sin(u),u+sin(u)) в трех измерениях:
In[5]:=
Out[5]=
Графики — Алгебра и тригонометрия
Дальнейшие применения тригонометрии
Цели обучения
В этом разделе вы будете:
- Графические плоские кривые, описываемые параметрическими уравнениями путем нанесения точек.
- Графические параметрические уравнения.
Это конец девятого иннинга с двумя аутами и двумя игроками на базе. Хозяева проигрывают с разницей в два раунда. Бэттер раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом примерно к горизонту.Как далеко полетит мяч? Сможет ли он очистить забор для выигрышного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрические уравнения. В этом разделе мы обсудим параметрические уравнения и некоторые общие приложения, такие как задачи о движении снаряда.
Рис. 1. Параметрические уравнения могут моделировать траекторию полета снаряда. (Источник: Пол Крехер, Flickr)Совместное построение графиков параметрических уравнений и прямоугольной формы
Постройте график параметрических уравнений и сначала постройте график, используя точки данных, сгенерированные из параметрической формы.Затем изобразите прямоугольную форму уравнения. Сравните два графика.
Анализ
На (Рисунок) данные параметрических уравнений и прямоугольного уравнения нанесены вместе. Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического в виде пунктирной линии красного цвета. Ясно, что обе формы дают один и тот же график.
Рисунок 5.Попробуйте
Нарисуйте график параметрических уравнений вместе с прямоугольным уравнением на той же сетке.
[show-answer q = ”fs-id1165137807092 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137807092 ″]
График параметрических уравнений выделен красным цветом, а график прямоугольного уравнения нарисован синими точками поверх параметрических уравнений.
[/ hidden-answer]
Приложения параметрических уравнений
Многие преимущества параметрических уравнений становятся очевидными при решении реальных задач. Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не показывают положение объекта в конкретное время.Однако параметрические уравнения иллюстрируют, как значения x и y изменяются в зависимости от t как местоположения движущегося объекта в конкретный момент времени.
Обычное применение параметрических уравнений — решение задач, связанных с движением снаряда. В этом типе движения объект продвигается вперед в направлении вверх, образуя угол к горизонтали, с начальной скоростью и на высоте выше горизонтали.
Путь объекта, движущегося под наклоном к горизонтали с начальной скоростью и на высоте над горизонтом, определяется как
, где учитывается влияние силы тяжести, а — начальная высота объекта.В зависимости от единиц измерения, участвующих в задаче, useorThe уравнение допускает горизонтальное расстояние, а уравнение для дает вертикальное расстояние.
Нахождение параметрических уравнений для описания движения бейсбольного мяча
Решите проблему, указанную в начале этого раздела. Попадает ли тесто в выигрышную игру? Предположим, что мяч ударяется с начальной скоростью 140 футов в секунду под углом к горизонтали, при этом происходит контакт на высоте 3 футов над землей.
- Найдите параметрические уравнения для моделирования траектории бейсбольного мяча.
- Где мяч через 2 секунды?
- Как долго мяч находится в воздухе?
- Это хоумран?
[скрытый-ответ a = ”fs-id1165137453386 ″]
Используйте формулы, чтобы составить уравнения. Горизонтальное положение определяется с помощью параметрического уравнения для Таким образом,
Таким образом,Подставьте 2 в уравнения, чтобы найти горизонтальное и вертикальное положение мяча.
Через 2 секунды мяч оказывается на расстоянии 198 футов от бокса бьющего и на высоте 137 футов над землей.
Чтобы вычислить, как долго мяч находится в воздухе, мы должны выяснить, когда он ударится о землю или когда. Таким образом,
Через секунду мяч коснулся земли. (Квадратное уравнение можно решить разными способами, но эта задача была решена с помощью компьютерной математической программы.)
Мы не можем подтвердить, что попадание было хоумраном, не принимая во внимание размер дальнего поля, который варьируется от поля к полю.Однако для простоты предположим, что внешняя стена находится в 400 футах от домашней плиты в самой глубокой части парка. Предположим также, что высота стены составляет 10 футов. Чтобы определить, касается ли мяч стены, нам нужно вычислить, насколько высок мяч, когда x = 400 футов. Итак, мы установим x = 400, найдем и введем в
.Мяч находится на высоте 141,8 фута, когда вылетает за пределы поля. Это был действительно хоумран. См. (Рисунок).
Рисунок 7.[/ hidden-answer]
Упражнения по разделам
Устный
Какие два метода используются для построения графиков параметрических уравнений?
[show-answer q = ”fs-id1165135194726 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135194726 ″]
точек с помощью стрелки ориентации и графического калькулятора
[/ hidden-answer]
В чем отличие параметрических уравнений точечного построения от декартовых уравнений?
Почему на некоторых графиках нарисованы стрелки?
[show-answer q = ”fs-id1165137758269 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137758269 ″]
Стрелки показывают ориентацию, направление движения согласно возрастающим значениям
[/ hidden-answer]
Назовите несколько распространенных типов графиков параметрических уравнений.
Почему параметрические графики важны для понимания движения снаряда?
[show-answer q = ”fs-id1165137715148 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137715148 ″]
Параметрические уравнения показывают различные вертикальные и горизонтальные движения во времени.
[/ hidden-answer]
Графический
Для следующих упражнений нарисуйте каждый набор параметрических уравнений в виде таблицы значений. Включите ориентацию на графике.
[show-answer q = ”fs-id1165135188326 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135188326 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134583390 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134583390 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165135237047 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135237047 ″] [/ скрытый-ответ]
Для следующих упражнений нарисуйте кривую и укажите ее ориентацию.
[show-answer q = ”fs-id1165134069188 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134069188 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137417002 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137417002 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137936702 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137936702 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134081386 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134081386 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137805783 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137805783 ″] [/ скрытый-ответ]
Для следующих упражнений нарисуйте уравнение и укажите ориентацию.Затем напишите декартово уравнение.
[show-answer q = ”fs-id1165135149887 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135149887 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165135512730 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135512730 ″] [/ скрытый-ответ] [show-answer q = ”fs-id11651323 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651323 ″] [/ скрытый-ответ]
Для следующих упражнений нарисуйте уравнение и укажите ориентацию.
[detect-answer q = ”211246 ″] Показать решение [/ show-answer][hidden-answer a = ”211246 ″] [/ hidden-answer] [show-answer q = ”fs-id1165135252162 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135252162 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137680409 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137680409 ″] [/ скрытый-ответ]
Для следующих упражнений используйте параметрические уравнения для целых чисел a и b :
График по домену и включению ориентации.
График по домену где и, включая ориентацию.
[show-answer q = ”fs-id1165137409296 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137409296 ″] [/ скрытый-ответ]
График по домену где и, включая ориентацию.
График по домену где и, включая ориентацию.
[show-answer q = ”fs-id1165137551247 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137551247 ″] [/ скрытый-ответ]
Ifis 1 более чем описывает влияние значений andhave на график параметрических уравнений.
Опишите график ifand
[show-answer q = ”fs-id1165135189746 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135189746 ″]
Произойдет 100 возвратно-поступательных движений.
[/ hidden-answer]
Что произойдет, если на 1 больше, чем Опишите график.
Если параметрические уравнения и имеют график горизонтальной параболы, раскрывающейся вправо, что изменит направление кривой?
[show-answer q = ”fs-id1165135499919 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135499919 ″]
Возьмем противоположное уравнению.
[/ hidden-answer]
Для следующих упражнений опишите график системы параметрических уравнений.
и линейный
и линейный
[show-answer q = ”fs-id1165135609231 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135609231 ″]
Парабола открывается.
[/ hidden-answer]
и линейный
Напишите параметрические уравнения круга с центральным радиусом 5 и направлением против часовой стрелки.
[show-answer q = ”fs-id1165135352460 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135352460 ″]
[/ hidden-answer]
Напишите параметрические уравнения эллипса с большой центральной осью длиной 10, малой осью длиной 6 и ориентацией против часовой стрелки.
Для следующих упражнений используйте графическую утилиту, чтобы построить график в области окна для следующих значений и, а также включить ориентацию.
[show-answer q = ”fs-id1165132960728 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165132960728 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134386554 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134386554 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165133349420 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165133349420 ″] [/ скрытый-ответ]
Расширения
Объект подбрасывается в воздух с вертикальной скоростью 20 футов / с и горизонтальной скоростью 15 футов / с.Высота объекта может быть описана уравнением, в то время как объект движется по горизонтали с постоянной скоростью 15 футов / с. Напишите параметрические уравнения для положения объекта, а затем избавьтесь от времени, чтобы записать высоту как функцию горизонтального положения.
[show-answer q = ”fs-id1165132079269 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165132079269 ″]
[/ hidden-answer]
Скейтбордист, едущий по ровной поверхности с постоянной скоростью 9 футов / с, подбрасывает в воздух мяч, высоту которого можно описать уравнением. Напишите параметрические уравнения для положения мяча, а затем исключите время, чтобы записать высоту в виде функция горизонтального положения.
Для следующих упражнений используйте этот сценарий: Дротик бросается вверх с начальной скоростью 65 футов / с под углом возвышения 52 °. Учитывайте положение дротика в любое время и не обращайте внимания на сопротивление воздуха.
Найдите параметрические уравнения, моделирующие проблемную ситуацию.
[show-answer q = ”fs-id1165134371099 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134371099 ″]
[/ hidden-answer]
Найдите все возможные значения, которые представляют ситуацию.
Когда дротик упадет на землю?
[show-answer q = ”fs-id1165135445722 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135445722 ″]
примерно 3,2 секунды
[/ hidden-answer]
Найдите максимальную высоту дротика.
В какое время дротик достигнет максимальной высоты?
[show-answer q = ”fs-id1165135444043 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135444043 ″]
1,6 секунды
[/ hidden-answer]
Для следующих упражнений посмотрите на графики каждого из четырех параметрических уравнений.Хотя они выглядят необычно и красиво, они настолько распространены, что имеют названия, указанные в каждом упражнении. Используйте графическую утилиту для построения графика каждого в указанном домене.
Эпициклоида: в домене.
Гипоциклоида: в домене.
[show-answer q = ”fs-id1165134569130 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134569130 ″] [/ скрытый-ответ]
Гипотрохоид: в домене.
Роза: на домене.
[show-answer q = ”fs-id1165134134026 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134134026 ″] [/ скрытый-ответ]
Нахождение параметрических уравнений для графика
Набор параметрических уравнений не уникален для данного графа.Например, следующие наборы параметрических уравнений приводят к одному и тому же прямоугольному уравнению и, таким образом, представляют один и тот же график.Первое параметрическое уравнение | Второе параметрическое уравнение | Прямоугольное уравнение |
х = 4t2−4 | у = т | х = 4y2−4 |
х = t2−4 | у = t2 2y = t | х = (2у) 2 — 4 х = 4y2−4 |
Чтобы найти набор параметрических уравнений для графика, представленного как y = x 2 + 2 при t = x + 2, пусть t = x. Переключение ролей t и x в этом уравнении дает одно из параметрических уравнений:
t = x + 2 → x = t + 2
Теперь подставьте выражение для x в прямоугольное уравнение y = x 2 + 2, чтобы получить второе параметрическое уравнение.
y = x2 + 2
y = (t + 2) 2 + 2
y = t2 + 4t + 4 + 2
y = t2 + 4t + 6
Таким образом, набор параметрических уравнений для графика, представленного как y = x 2 + 2, имеет вид
x = t + 2
y = t2 + 4t + 6
Теперь, когда определены оба параметрических уравнения, можно построить общий график с выбранными значениями параметра.
т | -2 | -1 | 0 | 1 | 2 |
х = т + 2 | 0 | 1 | 2 | 3 | 4 |
у = т 2 + 4т + 6 | 2 | 3 | 6 | 11 | 18 |
РЕКОМЕНДАЦИИ ПО ПОИСКУ ПАРАМЕТРИЧЕСКИХ УРАВНЕНИЙ ДЛЯ ГРАФИКА:
1.Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. В результате получится одно параметрическое уравнение.
2. Подставьте выражение для переменной на шаге 1 в прямоугольное уравнение. В результате получится второе параметрическое уравнение.
3. Нарисуйте кривую.
Попробуем пару примеров.
Пример 1. Найдите набор параметрических уравнений для прямоугольного уравнения y = x 2 + 1, учитывая t = 2 — x.Затем нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой.
Шаг 1: Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. Пусть t = x и перепишем уравнение параметров, переключив t и x. | т = 2 — х Оригинал х = 2 — т Переключить t и x | |||||||||||||||
Шаг 2: подставьте выражение для переменной на шаге 1 в прямоугольное уравнение | y = x2 + 1 Оригинал y = (2 − t) 2 + 1 Заменить y = (4−4t + t2) + 1 Квадрат y = 5−4t + t2 Добавить | |||||||||||||||
Шаг 3: Нарисуйте кривую. Перечислите два параметрических уравнения и нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой. Прямоугольное уравнение: у = х2 + 1 Параметрические уравнения: х = 2 — т, у = 5−4t + t2
| ||||||||||||||||
Пример 2: Найдите набор параметрических уравнений для прямоугольного уравнения y = 2×2 + 1 при t = x.Затем нарисуйте график с точками в точке t = {0,1,2,3,4} и укажите ориентацию кривой.
Шаг 1: Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. | t = xОригинал x = t Переключить t и x | ||||||||||||||||||
Шаг 2: подставьте выражение для переменной на шаге 1 в прямоугольное уравнение | y = 2×2 + 1 Оригинал y = 2t2 + 1 Заменить y = 2t + 1 квадрат | ||||||||||||||||||
Шаг 3: Нарисуйте кривую. Перечислите два параметрических уравнения и нарисуйте график с точками в t = {0, 1, 2, 3, 4} и укажите ориентацию кривой. Прямоугольное уравнение: у = 2×2 + 1 Параметрические уравнения: х = т, у = 2т + 1
Обратите внимание, что область графика — x≥0, потому что область параметрического уравнения t = x ограничивает x значениями от нуля или выше. | |||||||||||||||||||
Параметрическая диаграмма — обзор
15.2 Деформация, вызванная ползучестью
При устойчивом растягивающем напряжении при температурах выше 0,4 T м большинство металлов и сплавов демонстрируют нормальные кривые деформации ползучести / времени. Таким образом, после начальной деформации нагружения скорость деформации ползучести (ε˙ = dε / d t ) непрерывно уменьшается со временем в течение первичной стадии, достигая минимальной или вторичной скорости (ε˙m) перед ускорением во время третичной стадии, которая приводит к разрушению через некоторое время ( t f ).Произведение ε˙mtf часто, но не всегда, является постоянным ( M ), что означает, что разрушение при ползучести контролируется деформацией, поскольку t f увеличивается по мере того, как ε˙m падает с уменьшением напряжения и температуры.
Было предложено множество соотношений для количественной оценки изменений деформации ползучести во времени. Некоторые из этих уравнений стремятся описать только ранние стадии кривых ползучести, в то время как другие пытаются определить форму всех траекторий ε / t , но не было достигнуто согласия относительно соотношений, которые следует использовать.Несмотря на характерную форму нормальных кривых, поэтому стало обычной практикой игнорировать первичную и третичную стадии, предполагая, что вторичная скорость остается постоянной с увеличением времени и деформации. Уравнение [15.3] затем сводится к:
[15.4] ε˙m = f3σ, T
с дальнейшим упрощением, дающим:
[15.5] ε˙m = f4σf5T
, поэтому переменные рассматриваются как отдельные и независимые.
В уравнении [15.5] при фиксированной температуре зависимость ε˙m от напряжения может быть определена как:
[15.6] ε˙m∝f4σ∝σn
, где n — показатель степени напряжения. В качестве альтернативы:
[15,7] ε˙m∝f4σ∝expσ
, что дает экспоненциальную зависимость ε˙m от напряжения. И наоборот, при фиксированном напряжении температурная зависимость ε˙m в уравнении [15.5] обычно представляется уравнением Аррениуса вида:
[15.8] ε˙m∝f5T∝exp − Qc / RT
, где Q c — энергия активации ползучести в единицах Дж моль -1 при газовой постоянной R = 8.314 Дж моль −1 K −1 . Комбинируя уравнения [15.5], [15.7] и [15.8], получаем:
[15.9] M / tf = ε˙m = Bexp − Qc − Vσ / RT
, где B и V рассматриваются как константы. . Однако в большинстве теоретических и практических исследований, проведенных за последние полвека, уравнения [15.5], [15.6] и [15.8] были объединены для получения стандартной степенной зависимости:
[15.10] M / tf = ε˙ m = Aσnexp − QcRT
, но значения параметра A , а также n и Q c различаются в зависимости от режима нагрузки / температуры.
15.2.1 Параметрические подходы к анализу данных
Хотя лист данных NIMS по ползучести № 43 (1996) описывает только характеристики разрушения под напряжением, 1 результаты доступны из других источников 3 , 4 допускают ползучесть срок службы, который следует учитывать в связи с характеристиками скорости ползучести образцов труб из Gr. 91 сталь. Таким образом, используя уравнение [15.10], графики logε˙m / logσ на рис. 15.1 могут быть представлены 3 набором прямых линий, показывающих уменьшение от n 16 при 848 K до n 9 при 923 К.Точно так же отношения напряжение / срок ползучести, определенные в расширенных диапазонах напряжений при 773–973 K для нескольких партий Gr. 91 трубка 1 показывает градиентные изменения, соответствующие уменьшению от n 17 до n 4,5 с повышением температуры (рис. 15.2). При Q c в диапазоне от 600 до 700 кДж моль −1 эти аномально большие значения n и Q c типичны для моделей поведения, описанных для сталей для электростанций и других закаленных частицами сплавы.
15.1. Зависимость минимальных скоростей ползучести от напряжения, зарегистрированная для Gr. 91 труба стальная 3 при 848–923 К.
15.2. Зависимость продолжительности ползучести от напряжения, записанная для нескольких партий Gr. 91 трубная сталь 1 при 773–973 К.
Из-за сложных напряжений и температурных зависимостей ε˙m и t f (рис. 15.1 и 15.2) оценка долговременных свойств путем экстраполяции Кратковременные измерения предполагают постоянное использование различных параметрических методов, введенных в 1950-х годах. 5–7 Эти эмпирические подходы определяют «параметры корреляции», включающие как продолжительность ползучести, так и температуру, которые могут быть нанесены на график как функции напряжения, чтобы наложить результаты нескольких партий на единую «эталонную кривую» для данной стали. К сожалению, ни один параметрический метод не смог подобрать экспериментальные данные, представленные для большинства сталей для электростанций, и даже при выборе наилучшей процедуры подгонки достигаемая точность не всегда бывает удовлетворительной. 8
Одно ограничение, присущее параметрическим методам, связано с «переменными константами», встречающимися в стандартных степенных отношениях (уравнение [15.10]). Например, уравнение [15.10] можно переписать, чтобы получить параметр ( P OSD ), предложенный Orr, et al. , 7 как:
[15,11] POSD = logtf − P1 / T
, где P 1 включает Q c . Следовательно, вариации в Q c гарантируют, что наложенные параметрические графики являются нелинейными. Кривизна графиков, основанных на уравнении [15.11], затем не удаляется заменой уравнения [15.10] с уравнением [15.9]. Фактически, уравнение [15.9] может быть преобразовано в параметр ( P LM ), предложенный Ларсоном и Миллером 5 как
[15.12] PLM = Tlogtf + P2
, где P 2 теперь содержит Q c .
В сочетании с широкими полосами разброса, обычно связанными с наборами данных из нескольких пакетов, неизвестные кривизны традиционных параметрических графиков ограничивают экстраполяцию примерно до трех значений самых длинных доступных надежных тестовых измерений.По этой причине испытания продолжительностью до 30 000 часов и более обычно должны проводиться для оценки прочности на разрыв в 100 000 часов.
15.2.2 Альтернативные процедуры для рационализации данных
Для чистых металлов, переформулируя уравнение [15.10] и используя ожидаемые энергии активации для диффузии, отношения напряжение / скорость ползучести, записанные при различных температурах, накладываются друг на друга 9 просто путем построения зависимостей on (σ / E ) скорости ползучести с температурной компенсацией ε˙m exp ( Q c / RT ).Аналогичным образом, соответствующие характеристики разрушения под напряжением рационализированы путем построения графика продолжительности ползучести с температурной компенсацией: t f exp (- Q c / RT ) против (σ / E ). Однако этот подход неприменим к сталям для электростанций, поскольку незначительные изменения в условиях термомеханической обработки, выбранных для изготовления компонентов, могут изменить получаемую микроструктуру.
Модули упругости зависят от температуры, но не сильно изменяются при изменении микроструктуры, тогда как свойства ползучести и разрушения закаленных частицами сплавов чувствительны как к температуре, так и к микроструктуре, как и σ Y и σ TS .Следовательно, ранние процедуры рационализации, основанные на нормализации σ до E 9 , обновляются путем нормализации σ до σ Y или σ TS . 10–13 Таким образом, используя значения σ TS , измеренные для каждой партии Gr. 91 исследуемая сталь, 1 данные о многосерийном разрушении под напряжением на рис. 15.2 наложены на рис. 15.3 с использованием модифицированного выражения степенного закона: 11–13
15.3. Зависимость срока ползучести с температурной компенсацией от (σ / σ T S ) с использованием значений σ T S для каждой партии Gr.91 исследована трубная сталь, 1 с Q c * = 300 кДж моль −1 .
[15,13] M / tf = ε˙m = A * σ / σTSnexp − Qc * / RT
, где A * ≠ A и Q c * получается из температурной зависимости ε ˙m при постоянной (σ / σ TS ), а не при постоянной σ, как при определении Q c в уравнении [15.10]. Из рис. 15.3 видно, что Q c * = 300 кДж моль −1 , значение, близкое к значению для решеточной диффузии в матрице легированной стали.С Гр. 91, как и в случае с другими металлами и сплавами, наборы свойств ползучести 10–14 также эффективно рационализируются путем нормализации σ до σ Y , так что (σ / σ TS ) можно заменить на (σ / σ Y ) в уравнении [15.13]. Независимо от того, выбрано ли σ Y или σ TS , результирующая «эталонная кривая» на рис. 15.3, по крайней мере, столь же впечатляющая, как и полученная с использованием параметрических методов. Кроме того, с помощью уравнения [15.13] эмпирические члены в параметрических отношениях (уравнения [15.11] и [15.12] заменены физически значимыми свойствами, а именно ощутимой энергией активации и измеренными значениями σ Y и σ TS .
15.2.3 Интерпретация поведения степенного закона
Уравнение [15.13] позволяет избежать больших и переменных значений Q c , наблюдаемых при наборах данных для Gr. 91 описываются с помощью уравнения [15.10] (рис. 15.2), но не устраняют уменьшение с n 20 до n 4 (рис.15.3), обычно ожидается, что тенденция сохранится к n ± 1 или менее по мере увеличения продолжительности испытания и увеличения температуры.
Одна ранняя попытка объяснить аномально большие значения n предположила 15 , что ползучесть происходит не при полном приложенном напряжении (σ), а при пониженном напряжении (σ — σ o ), так что
[15.14 ] ε˙m∝σ − σom
, где м = 4, при этом σ o теперь называется «пороговым напряжением». Сравнение уравнений [15.10] и [15.14], n ≅ m ≅ 4, когда σ o ≅ 0 или когда σ o ∝ σ, тогда как n > m , когда σ o большое. Этот подход широко применялся для ползучести сплавов с упрочненными частицами, 16 , но был достигнут незначительный прогресс, поскольку σ o нельзя надежно измерить или спрогнозировать.
Чаще всего вариации значений n интерпретируются на основании того, что различные механизмы ползучести становятся доминирующими в различных режимах напряжения и температуры.Таким образом, хотя наложенные результаты на рис. 15.3 предполагают, что градиент непрерывно изменяется по мере уменьшения (σ / σ TS ), такие кривые можно аппроксимировать серией отрезков прямых линий, соответствующих n >> 4, n 4 и в конечном итоге n ≅ 1, причем каждое изменение градиента связано с переходом механизма. Тем не менее, не было достигнуто согласия по детальным рассматриваемым процессам, и с практической точки зрения текущие теории не позволяют прогнозировать свойства ползучести и разрушения конструкционных сталей.Более того, принимая концепции нескольких механизмов, анализ результатов, записанных в одном режиме механизма, не позволил бы прогнозировать свойства в другом режиме, что потребовало бы завершения долгосрочных программ испытаний. В этом контексте, поэтому кажется разумным рассмотреть, предлагают ли стандартные отношения степенного закона действительную основу для представления и интерпретации свойств ползучести.
С помощью уравнения [15.10] тот факт, что n и Q c сами являются функциями напряжения и температуры, означает, что при упрощении уравнения [15.4], чтобы получить уравнение [15.5], переменные не являются отдельными и независимыми. Кроме того, предположение о том, что изменения деформации ползучести со временем, напряжением и температурой (уравнение [15.3]) можно адекватно количественно оценить с помощью напряжений и температурных зависимостей вторичной или «установившейся» скорости ползучести (уравнение [15.4]): весьма сомнительно. По этим причинам, без привлечения переключений механизмов, альтернативный подход 17 утверждает, что модели поведения, проявляемые сталями для электростанций (рис.2 = 1 $.
Несколько вопросов, которые стоит задать себе:
- С чего начать? То есть, когда $ \ theta = 0 $, , где на единичной окружности — это вы?
- Что происходит с точкой $ (x, y) = (\ sin \ theta, \ cos \ theta) $ по мере увеличения $ \ theta $ от $ 0 $ до $ \ pi $?
- Где ты находишься, когда $ \ theta $ достигает $ \ pi $?
Теперь вы знаете , какие частей единичной окружности задаются параметрической кривой.
Добавлен. Как и многие студенты на начальном этапе, вам кажется, что вы хотите построить несколько точек, а затем выполнить интерполяцию; это не лучшая идея, потому что она полагается на то, что вы просто случайно попадете в нужные точки, чтобы получить точную картину того, что происходит.Чтобы дать вам пример, если вы пытались построить график для функции $ y = \ sin (\ pi x) $ и попробовали несколько точек, скажем, $ x = 0 $, $ x = 1 $, $ x = 2 $, $ x = 3 $ и т. д., вы можете подумать, что ваша функция — это постоянная функция $ 0 $, потому что при выборе точек упускается все важное, что происходит с $ y $.
Вы, , не хотите, этого делать. Вместо этого вы хотите подумать о том, что делают эти функции.
Один из способов, которым я считаю наиболее плодотворным размышление о параметрических уравнениях, — это думать о параметре как о дающем время , а об уравнениях как о движении точки; Представьте себе анимацию со светящейся точкой, движущейся по плоскости и оставляющей за собой «след» света.Этот след — параметрическая кривая, точка — это положение в «текущем $ t $». Вы хотите подумать о том, что делает эта точка, когда ваш параметр варьируется от своего начального значения до конечного значения (то есть, когда анимация идет от начала до конца).
Итак, начнем с $ \ theta = 0 $, первого кадра вашей анимации. Ваша светящаяся точка будет в $ x (0) = \ sin (0) = 0 $ и $ y (0) = \ cos (0) = 1 $. Итак, вы начинаете с точки $ (0,1) $.
Теперь нажмите кнопку PLAY .Что происходит, когда $ \ theta $ начинает продвигаться от $ 0 $ к $ \ pi $? Координата $ x $ будет следовать графику $ y (\ theta) = \ sin (\ theta) $, поэтому сначала она повысится с $ 0 $ до $ 1 $ (при $ \ theta = \ frac {\ pi} {2 } $), а затем снова упасть с $ 1 $ на $ 0 $ (при $ \ theta = \ pi $). Он будет делать это без скачков и перерывов. Итак, если вы смотрели только на «тень» нашей светящейся точки на оси $ x $, она начинается с $ x = 0 $, затем плавно перемещается вправо (без рывков, без скачков, без пропусков). ), пока он не достигнет $ 1 $ в середине фильма, а затем вернется к $ 0 $, пока не вернется к $ 0 $ в конце фильма.
А что насчет $ y $? Он начинается с 1 доллара США; он будет вести себя как график $ \ cos \ theta $. Когда вы нажмете PLAY , он начнется с 1 доллара, а затем упадет до 0 долларов, снова плавно, без скачков, рывков и пропусков, пока не достигнет 0 долларов в середине фильма (при $ \ theta = \ frac {\ pi} {2} $). Затем продолжит движение в том же направлении, от $ 0 $ до $ -1 $, и достигнет $ -1 $ в конце «фильма» (когда $ \ theta = \ pi $). Итак, если вы посмотрите на «тень» светящейся точки на оси $ y $, она начнется с $ 1 $, затем опустится до $ 0 $ и продолжит снижаться до $ -1 $, и все это в целом гладко. манерой, без скачков, рывков, колебаний, откатов и т. д.
Теперь сложите эти два движения вместе: вы начнете с $ (0,1) $, вершины единичного круга. Затем, когда $ \ theta $ перемещается от $ 0 $ к $ \ pi / 2 $, светящаяся точка начинает двигаться вправо и вниз, всегда по единичной окружности, до тех пор, пока $ \ theta = \ pi / 2 $ не окажется в точке <заполните поле> . Нажмите ПАУЗА на видео и подведите итоги. Где мы? Какую часть единичного круга мы нарисовали? Сколько раз? Любой возврат? Сколько времени вы проводите без движения? Было ли движение в целом «плавным»?
Хорошо, готовы продолжить? Снова нажмите PLAY , и наш $ \ theta $ начнет увеличиваться с $ \ pi / 2 $ в сторону $ \ pi $.Эта светящаяся точка, представляющая $ (x (\ theta), y (\ theta)) $, перемещается, но теперь вниз и влево, всегда вдоль единичной окружности, пока, наконец, не $ \ theta = \ pi $, «конец фильм «, он достигает своего конечного пункта назначения в точке <заполните другой бланк> .
Все это время движение было без прыжков, колебаний или возвратов, потому что функции $ x = \ sin \ theta $ и $ y = \ cos \ theta $ имеют эти движения: без прыжков, без пропусков, без рывков, без колебаний , никаких возвратов, просто плавное движение (представьте, что ваша рука рисует их графики).Эта светящаяся точка теперь проследила часть единичной окружности ровно один раз, без возврата. Какая часть?
параметрический график / индекс | Система ресурсов Wolfram
Результаты поиска
144 экспоната
Ресурс функции: & emsp14; НаправлениеПараметрический участок
Создайте параметрический график кривой на плоскости с направлением, указанным стрелками и цветом
Ресурс функции: & emsp14; Раздел ParametricPlot3D
Постройте параметрическую определенную поверхность вместе с различными типами сечений поверхности.
Ресурс функции: & emsp14; Направление Параметрический участок3D
Создайте параметрический график кривой в пространстве с направлением, указанным стрелками и цветом
Ресурс функции: & emsp14; ConicSectionPlot
Классифицирует и строит любой полином степени два или меньше от двух или меньшего числа переменных.
Ресурс функции: & emsp14; ParametricSurfaceTangentPlane
Вычислить касательную плоскость параметрической поверхности
Ресурс функции: & emsp14; SuggestPlotRange
Получить диапазон переменных, против которого строить заданную функцию
Ресурс функции: & emsp14; EnhancedPlot
График с несколькими улучшениями, добавленными для сингулярностей, асимптот, значений surd и неинтервальных областей
Ресурс функции: & emsp14; ManipulatePlot
Создание графика, на котором диапазоны графика и параметры функции могут управляться динамически
Ресурс функции: & emsp14; УчастокВектор
Постройте список векторов на плоскости
Ресурс функции: & emsp14; KeywordPlot
Постройте плотность ключевых слов в фрагменте текста
Ресурс функции: & emsp14; Участок
Постройте две кривые и выделите их точки пересечения
Ресурс функции: & emsp14; HypergraphPlot
Постройте гиперграф, заданный списком гиперребер
Ресурс функции: & emsp14; InteractiveConicPlot
Отображение интерактивного графика со всей необходимой информацией для данного конического сечения
Ресурс функции: & emsp14; BenchmarkPlot
Постройте тайминги эталонного теста
Ресурс функции: & emsp14; Комбинированные участки
Комбинируйте графики, позволяя создавать графики с двумя наборами осей и объединять прологи и эпилоги.
Ресурс функции: & emsp14; Кривизна Участок
Постройте кривую, определяемую ее кривизной
Ресурс функции: & emsp14; PairwiseScatterPlot
Постройте матрицу точечной диаграммы
Ресурс функции: & emsp14; PlotGrid
Создавайте составные графики и другие расширенные сеточные макеты графиков
Ресурс функции: & emsp14; Древовидная картаПлощадь
Постройте вложенный список значений в виде древовидной карты
Ресурс функции: & emsp14; MilkyWayPlot3D
Постройте положение астрономических объектов в галактике Млечный Путь или рядом с ней.
Ресурс функции: & emsp14; Функция PeriodPlot
Постройте заданное количество периодов периодической функции
Ресурс функции: & emsp14; SimpleHypergraphPlot
Постройте гиперграф, заданный списком гиперребер и изолированных вершин
Ресурс функции: & emsp14; Приблизительная кривая
Получите приближение к параметрической кривой
Ресурс функции: & emsp14; VennGraphPlot
Визуализируйте пересечения перекрывающихся множеств
Ресурс функции: & emsp14; CobwebPlot
Визуализируйте одномерные повторяющиеся функции
Ресурс функции: & emsp14; PolygonMarker
Создавайте маркеры, тщательно разработанные для создания графиков публикационного качества.
Ресурс функции: & emsp14; LabelListPlot
Постройте вхождения меток в список
Ресурс функции: & emsp14; PolarDendrogramPlot
Постройте полярную дендрограмму кластеризации
Ресурс функции: & emsp14; Участок
Постройте состав циклов, имеющих разные радиусы, частоты и фазы.
Ресурс функции: & emsp14; DragZoomPlot
Версия графика, которая позволяет увеличивать график с помощью мыши.
Ресурс функции: & emsp14; Мясной участок
Деревья условий порядка построения графиков для метода Рунге – Кутта
Ресурс функции: & emsp14; Внутри
Сделайте график функции изнутри и снаружи
Ресурс функции: & emsp14; FittedModelPlot
Постройте построенные модели вместе с их необработанными данными
Ресурс функции: & emsp14; EigenvectorPlot
Визуализируйте собственные векторы матрицы 2 x 2 или 3 x 3
Ресурс функции: & emsp14; NFAPlot
Постройте недетерминированный конечный автомат
Ресурс функции: & emsp14; CombinatorPlot
Визуализируйте выражение статического комбинатора
Ресурс функции: & emsp14; Приблизительная поверхность
Аппроксимировать параметрическую поверхность с помощью различных графических примитивов
Ресурс функции: & emsp14; DiscreteIntegralPlot
Постройте и найдите площадь области, определяемую списком точек, осью x и типом границы.
Ресурс функции: & emsp14; ParallelCoordinatesPlot
Наносит на график наборы данных большой размерности по параллельным осям
Ресурс функции: & emsp14; BiPlot
Визуализируйте основные компоненты табличных данных
Ресурс функции: & emsp14; TessellationPlot
Создание мозаики плоскости с заданными формами ячеек
Ресурс функции: & emsp14; SaundersDigitPlot
Постройте график функции Сондерса
Ресурс функции: & emsp14; РазделКонтурПлощадь
Возвращает контурный график функции вместе с проекциями на плоскость x-y заданных участков графика.
Ресурс функции: & emsp14; ListGrowthPlot
Постройте график роста списков и временных данных
Ресурс функции: & emsp14; ComplexBubblePlot
Визуализируйте сложную функцию в виде множества пузырьков
Ресурс функции: & emsp14; LeeInterpolatingNodes
Создание узлов интерполяции из точек на кривой
Ресурс функции: & emsp14; LinearDescriptionPlotQuiz
Создайте интерактивную графическую викторину по построению линейных функций.
Ресурс функции: & emsp14; Кубический ОписаниеPlotQuiz
Создайте интерактивную графическую викторину по построению кубических функций
Ресурс функции: & emsp14; Квадратичный ОписаниеPlotQuiz
Создайте интерактивную графическую викторину по построению квадратичных функций.
Ресурс функции: & emsp14; GeneralRationalInterpolation
Найдите рациональную интерполяцию параметрически определенной функции
Ресурс функции: & emsp14; FrenetSerretPlot
Постройте систему отсчета Френе – Серре кривой
Ресурс функции: & emsp14; RuledSurfacePlot
Постройте линейчатую поверхность
Ресурс функции: & emsp14; CatacausticCurvePlot
Постройте катастрофу кривой
Ресурс функции: & emsp14; GraphFunctionPlot
Постройте значения функции в вершинах графика
Ресурс функции: & emsp14; CrossRecurrencePlot
Визуализируйте перекрытие двух дискретных временных рядов
Ресурс функции: & emsp14; MultiwayEvolutionPlot
Постройте график эволюции многоходовой системы
Ресурс функции: & emsp14; PursuitCurvePlot
Постройте кривую преследования хищник-жертва
Ресурс функции: & emsp14; MultipleAxesPlot
Отображение разных вертикальных осей для двух построенных выражений
Ресурс функции: & emsp14; LeastSquaresPlot
Постройте данные вместе с визуализацией квадратов ошибок по сравнению с подгонкой
Ресурс функции: & emsp14; IteratedAffinePlot
Постройте полигоны после итеративного применения перемещения, масштабирования и поворота
Ресурс функции: & emsp14; DottedArrayPlot
Постройте массив значений с точками в указанных позициях
Ресурс функции: & emsp14; SinusoidPlotQuiz
Создайте тест, чтобы оценить понимание графиков функций синуса и косинуса
Ресурс функции: & emsp14; Принцип Парето, участок
Постройте графики соблюдения принципа Парето
Ресурс функции: & emsp14; График интегрального приближения
Вычислить и построить аппроксимацию интеграла функции на интервале
Ресурс функции: & emsp14; ExtractPlotImageData
Извлечь данные из графического изображения
Ресурс функции: & emsp14; RaggedDigitsPlot
Постройте массив цифр так, чтобы они были неровными слева.
Ресурс функции: & emsp14; NewtonMethodPlot
Постройте функцию вместе с графическим отображением итераций Ньютона, приближающих ее корень
Ресурс функции: & emsp14; MoleculeValuePlot
Получите график молекулы с атомами или связями, окрашенными в соответствии со значениями свойств
Ресурс функции: & emsp14; Филогенетический участок
Постройте дендрограмму для набора нуклеотидных последовательностей генома
Ресурс функции: & emsp14; MillerIndicesPlot
Постройте кристаллографические плоскости кубической решетки с индексами Миллера h, k, l
Ресурс функции: & emsp14; QuadricSurfacePlot
Классифицируйте и постройте любой многочлен второй степени или менее от трех или менее переменных.
Ресурс функции: & emsp14; PolarTreemapPlot
Постройте полярную древовидную карту данного вложенного списка
Ресурс функции: & emsp14; РазделPlot3D
Постройте поверхность вместе с различными типами участков поверхности.
Ресурс функции: & emsp14; Кривизна TorsionPlot3D
Постройте кривую, определяемую ее кривизной и кручением
Ресурс функции: & emsp14; GalileanSatellitesPlot
Постройте относительное положение четырех крупнейших спутников Юпитера, если смотреть с Земли.
Ресурс функции: & emsp14; MoleculePrincipalMomentPlot
Визуализируйте распределение форм молекул на 2D-диаграмме рассеяния
Ресурс функции: & emsp14; ОбщиеМиниМаксПриближение
Найдите минимальное и максимальное приближение функции, определенной параметрически.
Ресурс функции: & emsp14; КомбинаторEvolutionPlot
Визуализируйте эволюцию комбинаторного выражения
Ресурс функции: & emsp14; SubstitutionSystemPlot
Визуализируйте эволюцию одномерной системы замещения, не зависящей от соседей.
Ресурс функции: & emsp14; WolframModelPlot
Создание визуального отображения гиперграфа
Ресурс функции: & emsp14; StemLeafPlot
Постройте диаграмму стволовых и листовых
Ресурс функции: & emsp14; КомбинаторБрекетыPlot
Визуализируйте согласованные скобки комбинатора
Ресурс функции: & emsp14; ДНКAlignmentPlot
Создание визуализации для выравнивания последовательностей ДНК
Ресурс функции: & emsp14; FindMinimumPlot
Визуализируйте оценки функций, выполненные FindMinimum
Ресурс функции: & emsp14; ByteArrayPlot
Визуализируйте содержимое двоичных данных
Ресурс функции: & emsp14; MobileAutomatonPlot
Визуализация эволюции мобильного автомата
Ресурс функции: & emsp14; ГенеалогияTreePlot
Создайте генеалогическое генеалогическое древо, показывающее отношения между вами и другим родственником
Ресурс функции: & emsp14; FindRootPlot
Визуализируйте оценки функций, выполненные FindRoot
Ресурс функции: & emsp14; RegressionListPlot
Отображение линии регрессии набора данных
Ресурс функции: & emsp14; LSystemPlot
Показать L-систему
Ресурс функции: & emsp14; MultispacePlot3D
Постройте мультипространство в 3D
Ресурс функции: & emsp14; OrderedGraphModelPlot
Графики упорядоченных трехвалентных графов
Ресурс функции: & emsp14; DateListPlotRanged
Постройте временной ряд, который включает штриховку, чтобы указать диапазоны нанесенного значения.
Ресурс функции: & emsp14; УчастокVector3D
Постройте список векторов в пространстве
Ресурс функции: & emsp14; Интерактивная графика
Создавайте интерактивную версию графического выражения с масштабированием, панорамированием и всплывающими подсказками.
Ресурс функции: & emsp14; TabViewListPlot
Создайте TabView для ListPlot, используя линейные и логарифмические оси
Ресурс функции: & emsp14; Подстановка Система Причинно-следственная связь
Постройте график, иллюстрирующий причинно-следственные особенности эволюции системы замещения.
Ресурс функции: & emsp14; QuadricPlot3D
Постройте квадратную поверхность, автоматически определяя интересующие области, направление взгляда и масштаб
Ресурс функции: & emsp14; MultipleAxesListPlot
Версия ListPlot, которая отображает два списка данных с разными осями y
Ресурс функции: & emsp14; RiemannSphereComplexPlot
Версия ComplexPlot с трехмерной вращающейся сферой Римана
Ресурс функции: & emsp14; Аллювиальный график
График изменения веса с течением времени
Ресурс функции: & emsp14; DirectionalDerivativePlot3D
Визуализируйте производную по направлению на трехмерном графике
Ресурс функции: & emsp14; CheckboxLegended
Добавьте к графику легенду с флажками, которая динамически включает и выключает отдельные наборы данных.
Ресурс функции: & emsp14; SubstitutionSystemRulePlot
Создание значка правила для одномерной системы подстановки, не зависящей от соседей
Ресурс функции: & emsp14; LayeredGraphPlot3D
Создание многослойного трехмерного графика графика
Ресурс функции: & emsp14; TagSystemRulePlot
Создайте значок правила для системы тегов
Ресурс функции: & emsp14; MobileAutomatonRulePlot
Создайте значок правила для мобильного автомата
Ресурс функции: & emsp14; SequenceGraph
Создать график из последовательности данных
Ресурс функции: & emsp14; Последовательный участок замещения системы
Визуализация эволюции системы последовательного замещения
Ресурс функции: & emsp14; LinearFunctionQuiz
Создайте тест, чтобы оценить понимание линейных функций
Ресурс функции: & emsp14; Повернутый Эллипс Матрица
Создайте двоичную матрицу с повернутой эллиптической областью единиц
Ресурс функции: & emsp14; SolarSystemPlot3D
Постройте положение объектов солнечной системы в 3D
Ресурс функции: & emsp14; MoleculeValuePlot3D
Получите трехмерный график молекулы с атомами или связями, окрашенными в соответствии со значениями свойств
Ресурс функции: & emsp14; RiemannSurfacePlot3D
Постройте римановы поверхности композиций элементарных функций
Ресурс функции: & emsp14; Луна, положение, участок, 3D,
Постройте относительное положение Луны и Земли в 3D, освещенное Солнцем.
Ресурс функции: & emsp14; Интегральное приближениеPlot3D
Вычислить и построить аппроксимацию интеграла функции двух переменных на прямоугольнике, используя различные методы и типы разбиения.
Ресурс функции: & emsp14; QuadraticResidueAcousticDiffuserPlot
Постройте трехмерный рельеф, представляющий диффузор с квадратичным остатком.
Ресурс функции: & emsp14; RadarChart
Отображение числовых данных на диаграмме в стиле радара
Ресурс функции: & emsp14; Спирограф
Постройте спирограф
Ресурс функции: & emsp14; MoleculeSymmetryPlot3D
Покажите молекулу в 3D вместе с ее элементами симметрии
Ресурс функции: & emsp14; SequentialSubstitutionSystemRulePlot
Создание значка правила для системы последовательной замены
Ресурс функции: & emsp14; Оценить Benchmark
Измерьте время оценки функции на заданном наборе входов.
Ресурс функции: & emsp14; ДойлСпираль
Постройте спирали Дойла
Ресурс функции: & emsp14; РешеткаUnitCellPlot3D
Отображение конкретных элементарных ячеек в трехмерной решетке
Ресурс функции: & emsp14; EnlargeBoundingBox
Увеличить ограничивающую рамку на дробную величину
Ресурс функции: & emsp14; РешеткаVoronoiCellPlot3D
Отображение ячеек Вороного для определенных точек решетки в трехмерной решетке
Ресурс функции: & emsp14; RandomMandala
Создавайте случайные графики мандалы
Ресурс функции: & emsp14; Пенроуз Плитка
Сделайте участки из плиток Пенроуза
Ресурс функции: & emsp14; LifetimeChart
Визуализируйте жизнь в неделях или месяцах
Ресурс функции: & emsp14; Среднее значение
Создайте тест, чтобы оценить понимание теоремы о среднем значении для производных
Ресурс функции: & emsp14; WolframPhysicsProjectStyleData
Найдите стили, используемые в проекте Wolfram Physics Project
Ресурс функции: & emsp14; ХофштадтерБабочка
Постройте последовательные шаги бабочки Hofstadter & CloseCurlyQuote
Ресурс функции: & emsp14; GraphMouseMagnify
Динамически увеличивайте графики с помощью мыши
Ресурс функции: & emsp14; ГрафикаOptionQ
Проверить, является ли выражение графическим параметром
Ресурс функции: & emsp14; Герцшпрунг-Рассел Схема
Постройте положение звезд на диаграмме Герцшпрунга – Рассела.
Ресурс функции: & emsp14; ChaosGame
Итерации сюжета для 2D-игры с хаосом
Ресурс функции: & emsp14; ГрафикаBounds
Получите диапазон сюжета, используемый в части графики
Ресурс функции: & emsp14; TreeGrid
Отобразить дерево с сеткой
Ресурс функции: & emsp14; ContinentalPlateMaps
Постройте положение континентальных плит в различные геологические периоды.
Ресурс функции: & emsp14; CurveAnalysis
Получите динамический график одномерной функции вместе с дополнительными алгебраическими и основанными на исчислении свойствами функции.
Ресурс функции: & emsp14; Выбрать Atoms3D
Интерактивный выбор индексов атомов на трехмерном графике молекулы
Ресурс функции: & emsp14; МолекулаМешRegion
Создайте сетку из молекулы
Ресурс функции: & emsp14; ScaledRankChart
Отображение диаграммы масштабированного количества элементов в списке
Ресурс функции: & emsp14; ГрафикаИнформация
Возвращает информацию о визуализированной форме объекта Graphics, такую как размер отступа изображения и фактический используемый диапазон графика.
Графики · Алгебра и тригонометрия
Параметрические уравнения: графики · Алгебра и тригонометрияВ этом разделе вы будете:
- Графические плоские кривые, описываемые параметрическими уравнениями путем нанесения точек.
- Графические параметрические уравнения.
Это конец девятого иннинга с двумя аутами и двумя игроками на базе. Хозяева проигрывают с разницей в два раунда. Бэттер раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом примерно 45 °
к горизонтали. Как далеко полетит мяч? Сможет ли он очистить забор для выигрышного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрических уравнений .В этом разделе мы обсудим параметрические уравнения и некоторые общие приложения, такие как задачи о движении снаряда.
Построение параметрических уравнений по точкам
Вместо графического калькулятора или компьютерной программы построения графиков, нанесение точек на график для представления графика уравнения является стандартным методом. Пока мы тщательно вычисляем значения, точечное построение очень надежно.
Для пары параметрических уравнений нарисуйте график с помощью точек.
- Создайте таблицу из трех столбцов: t, x (t) и y (t).
- Оценить
х
и
yдля значений
tна интервале, для которого определены функции.
- Постройте получившиеся пары (х, у).
Построение графика пары параметрических уравнений по точкам построения
Нарисуйте график параметрических уравнений x (t) = t2 + 1, y (t) = 2 + t.
Построить таблицу значений t, x (t),
и у (т),
, как в [ссылка], и нанесите точки на плоскости.
График представляет собой параболу с вершиной в точке (1,2),
открытие вправо. См. [Ссылка].
Анализ
Как значения для t
прогрессируют в положительном направлении от 0 до 5, нанесенные точки очерчивают верхнюю половину параболы.В качестве значений т
становятся отрицательными, они очерчивают нижнюю половину параболы. Ограничений по домену нет. Стрелки указывают направление в соответствии с возрастающими значениями t.
График не представляет функцию, так как он не пройдет проверку вертикальной линии. График состоит из двух частей: положительные значения t,
и отрицательные значения для t.
Нарисуйте график параметрических уравнений x = t, y = 2t + 3, 0≤t≤3.
! [График заданных параметрических уравнений с ограниченной областью — он выглядит как правая половина восходящей параболы.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_003.jpg)
Построение графа тригонометрических параметрических уравнений
Создайте таблицу значений для заданных параметрических уравнений и нарисуйте график:
x = 2cos ty = 4sin t
Создайте таблицу, подобную приведенной в [ссылка], используя угловую меру в радианах в качестве входных данных для t,
и оценивая x
и г.
Использование углов с известными значениями синуса и косинуса для t
упрощает расчеты.
[ссылка] показывает график.
По симметрии, показанной в значениях x
и у,
мы видим, что параметрические уравнения представляют собой эллипс . Эллипс отображается в направлении против часовой стрелки, как показано стрелками, указывающими на увеличение t
.значений.
Анализ
Мы видели, что параметрические уравнения могут быть построены на графике по точкам. Однако графический калькулятор сэкономит время и выявит нюансы на графике, которые могут быть слишком утомительными, чтобы обнаружить их, используя только ручные вычисления.
Обязательно измените режим на калькуляторе на параметрический (PAR). Чтобы подтвердить, Y =
Окнодолжно показать
X1T = Y1T =
вместо Y1 =.
Изобразите параметрические уравнения: x = 5cos t, y = 3sin t.
! [График заданных уравнений — горизонтальный эллипс.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_005.jpg)
Совместное построение графиков параметрических уравнений и прямоугольной формы
Постройте параметрические уравнения x = 5cos t
и y = 2sin t.
Сначала постройте график, используя точки данных, сгенерированные из параметрической формы . Затем изобразите прямоугольную форму уравнения.Сравните два графика.
Создайте таблицу значений, как в [ссылка].
Постройте (x, y)
значений из таблицы. См. [Ссылка].
Затем преобразуйте параметрические уравнения в прямоугольную форму. Для этого решаем для t
в любом x (t)
или y (t),
, а затем подставим выражение для t
в другом уравнении.Результатом будет функция y (x)
при решении для t
как функция от x,
или x (y)
при решении для t
как функция от y.
x = 5cos tx5 = cos t Решить для cos t. y = 2sin t Решить относительно sin t.y2 = sin t
Затем используйте теорему Пифагора .
cos2t + sin2t = 1 (x5) 2+ (y2) 2 = 1×225 + y24 = 1
Анализ
В [ссылка] данные параметрических уравнений и прямоугольного уравнения отображаются вместе.Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического в виде пунктирной линии красного цвета. Ясно, что обе формы дают один и тот же график.
Построение графиков параметрических и прямоугольных уравнений в системе координат
Постройте параметрические уравнения x = t + 1
и y = t, t≥0,
и прямоугольный эквивалент y = x − 1
в той же системе координат.
Создайте таблицу значений для параметрических уравнений, как мы делали в предыдущем примере, и график y = t, t≥0
в той же сетке, что и в [ссылка].
Анализ
С доменом на т.
ограничено, мы наносим только положительные значения t.
Параметрические данные отображаются синим цветом, а график прямоугольного уравнения — красным пунктиром.И снова мы видим, что эти две формы пересекаются.
Изобразите график параметрических уравнений x = 2cos θ и y = 4sin θ,
вместе с прямоугольным уравнением на той же сетке.
График параметрических уравнений выделен красным цветом, а график прямоугольного уравнения нарисован синими точками поверх параметрических уравнений.
Приложения параметрических уравнений
Многие преимущества параметрических уравнений становятся очевидными при решении реальных задач.Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не показывают положение объекта в конкретное время. Однако параметрические уравнения иллюстрируют, как значения x и y изменяются в зависимости от t как местоположения движущегося объекта в конкретный момент времени.
Обычное применение параметрических уравнений — решение задач, связанных с движением снаряда. При этом типе движения объект продвигается вперед в направлении вверх, образуя угол θ
.к горизонтали, с начальной скоростью v0,
и на высоте h
выше горизонтали.
Путь объекта, движущегося под углом θ
к горизонтали, с начальной скоростью v0,
и на высоте h
выше горизонтали, равно
х = (v0cosθ) t y = −12gt2 + (v0sinθ) t + h
где g
учитывает влияние силы тяжести и h
— начальная высота объекта. В зависимости от устройств, участвующих в проблеме, используйте g = 32 фут / с2
или g = 9,8 м / с2.
Уравнение для x
дает горизонтальное расстояние, а уравнение для y
дает вертикальное расстояние.
Для решения задачи о движении снаряда используйте параметрические уравнения.
- Горизонтальное расстояние определяется выражением
х = (v0cos θ) т.
Заменить
начальную скорость объекта. v0. - Выражение
cos θ
указывает угол, под которым объект перемещается.Замените этот угол в градусах на
. cos θ. - Вертикальное расстояние определяется по формуле
y = −12gt2 + (v0sin θ) t + h.
Срок
−12gt2представляет эффект силы тяжести. В зависимости от задействованных единиц используйте
. g = 32 фут / с2или
g = 9,8 м / с2.Снова замените начальную скорость на
v0,и высота, на которой объект двигался, на
час - Рассчитайте каждый член для решения т.
Нахождение параметрических уравнений для описания движения бейсбольного мяча
Решите проблему, указанную в начале этого раздела. Попадает ли тесто в выигрышную игру? Предположим, что мяч ударяется с начальной скоростью 140 футов в секунду под углом 45 °
в горизонтальное положение, установив контакт на высоте 3 фута над землей.
- Найдите параметрические уравнения для моделирования траектории бейсбольного мяча.
- Где мяч через 2 секунды?
- Как долго мяч находится в воздухе?
- Это хоумран?
Используйте формулы, чтобы составить уравнения. Горизонтальное положение определяется с помощью параметрического уравнения для x.
Таким образом,
x = (v0cos θ) tx = (140cos (45 °)) t
Вертикальное положение определяется с помощью параметрического уравнения для y.
Таким образом,
y = −16t2 + (v0sin θ) t + hy = −16t2 + (140sin (45 °)) t + 3
Подставьте 2 в уравнения, чтобы найти горизонтальное и вертикальное положение мяча.
x = (140cos (45 °)) (2) x = 198 футов = −16 (2) 2+ (140sin (45 °)) (2) + 3y = 137 футов
Через 2 секунды мяч оказывается на расстоянии 198 футов от бокса бьющего и на высоте 137 футов над землей.
Чтобы вычислить, как долго мяч находится в воздухе, мы должны выяснить, когда он ударится о землю или когда y = 0.
Таким образом,
y = −16t2 + (140sin (45∘)) t + 3y = 0 Установите y (t) = 0 и решите квадратное уравнение t = 6,2173
При t = 6,2173
секунды, мяч коснулся земли. (Квадратное уравнение можно решить разными способами, но эта задача была решена с помощью компьютерной математической программы.)
Мы не можем подтвердить, что попадание было хоумраном, не принимая во внимание размер дальнего поля, который варьируется от поля к полю.Однако для простоты предположим, что внешняя стена находится в 400 футах от домашней плиты в самой глубокой части парка. Предположим также, что высота стены составляет 10 футов. Чтобы определить, касается ли мяч стены, нам нужно вычислить, насколько высок мяч, когда x = 400 футов. Таким образом, мы установим x = 400, решим для t,
и ввод т
в г.
x = (140cos (45 °)) t400 = (140cos (45 °)) t t = 4.04 y = −16 (4,04) 2+ (140sin (45 °)) (4,04) +3 y = 141,8
Мяч находится на высоте 141,8 фута, когда вылетает за пределы поля. Это был действительно хоумран. См. [Ссылка].
Ключевые понятия
- Когда есть третья переменная, третий параметр, по которому
х
и
yзависит, можно использовать параметрические уравнения.
- Чтобы построить график параметрических уравнений путем нанесения точек, составьте таблицу с тремя столбцами, обозначенными
t, x (t),
и
у (т).Выберите значения для
tв порядке возрастания. Постройте последние два столбца для
. хи
у.См. [Ссылка] и [ссылка].
- При построении параметрической кривой путем нанесения точек отметьте соответствующие значения t и покажите на графике стрелки, указывающие ориентацию кривой. См. [Ссылка] и [ссылка].
- Параметрические уравнения позволяют отображать направление или ориентацию кривой на графике. Уравнения, которые не являются функциями, можно изобразить в виде графиков и использовать во многих приложениях, связанных с движением.См. [Ссылка].
- Движение снаряда зависит от двух параметрических уравнений:
x = (v0cos θ) t
и
y = −16t2 + (v0sin θ) t + h.Начальная скорость обозначена как
v0. θпредставляет начальный угол объекта при броске, а
hпредставляет высоту, на которой объект перемещается.
Упражнения по разделам
Устный
Какие два метода используются для построения графиков параметрических уравнений?
точек с помощью стрелки ориентации и графического калькулятора
В чем отличие параметрических уравнений точечного построения от декартовых уравнений?
Почему на некоторых графиках нарисованы стрелки?
Стрелки показывают ориентацию, направление движения согласно возрастающим значениям t.
Назовите несколько распространенных типов графиков параметрических уравнений.
Почему параметрические графики важны для понимания движения снаряда?
Параметрические уравнения показывают различные вертикальные и горизонтальные движения во времени.
Графический
Для следующих упражнений нарисуйте каждый набор параметрических уравнений в виде таблицы значений. Включите ориентацию на графике.
{x (t) = ty (t) = t2−1| t | x | y |
| −3 | ||
| -2 | ||
| -1 | ||
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
| т | −3 | -2 | -1 | 0 | 1 | 2 |
| x | ||||||
| y |
! [График приведенных уравнений — имеет вид раскрывающейся вверх параболы.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_202.jpg)
! [График заданных уравнений — прямая, наклон отрицательный.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_204.jpg)
! [График данных уравнений — выглядит как боковая парабола, открывающаяся вправо.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_206.jpg)
Для следующих упражнений нарисуйте кривую и укажите ее ориентацию.
{x (t) = — ty (t) = t
! [График данных уравнений — выглядит как левая половина открывающейся вверх параболы.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_208.jpg)
{x (t) = — t + 2y (t) = 5− \ | t \ |
! [График данных уравнений — выглядит как открывающаяся вниз функция абсолютного значения.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_210.jpg)
{x (t) = 4sin ty (t) = 2cos t
{x (t) = 2sin ty (t) = 4cos t
! [График приведенных уравнений — вертикальный эллипс.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_212.jpg)
{x (t) = 3cos2ty (t) = — 3sin t
{x (t) = 3cos2ty (t) = — 3sin2t
! [График заданных уравнений — прямая от (0, -3) до (3,0). Он проходит в обоих направлениях, с положительным и отрицательным наклоном.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_214.jpg)
{x (t) = sec ty (t) = tan t
{x (t) = sec ty (t) = tan2t
! [График приведенных уравнений — имеет вид раскрывающейся вверх параболы.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_216.jpg)
Для следующих упражнений нарисуйте уравнение и укажите ориентацию. Затем напишите декартово уравнение.
{x (t) = t − 1y (t) = — t2
! [График данных уравнений — выглядит как открывающаяся вниз парабола.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_218.jpg)
{x (t) = 2cos ty (t) = — sin t
! [График заданных уравнений — горизонтальный эллипс.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_220.jpg)
{x (t) = 7cos ty (t) = 7sin t
{x (t) = e2ty (t) = — e t
! [График данных уравнений — выглядит как нижняя половина боковой параболы, открывающейся вправо] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_222.jpg)
Для следующих упражнений нарисуйте уравнение и укажите ориентацию.
х = t2, y = 3t, 0≤t≤5
х = 2t, у = t2, −5≤t≤5
! [График данных уравнений — выглядит как открывающаяся вверх парабола] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_224.jpg)
х = т, у = 25-т2, 0 <т≤5
х (t) = — t, y (t) = t, t≥0
! [График данных уравнений — выглядит как верхняя половина боковой параболы, открывающейся влево] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_226.jpg)
x = −2cos t, y = 6 sin t, 0≤t≤π
x = −sec t, y = tan t, — π2 ! [График данных уравнений — левая половина гиперболы с диагональными асимптотами] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_228.jpg) Для следующих упражнений используйте параметрические уравнения для целых чисел a и b : х (t) = acos ((a + b) t) y (t) = acos ((a − b) t) График в области [−π, 0], , где a = 2 и b = 1, и включить ориентацию. График в области [−π, 0], , где a = 3 и b = 2 , и включить ориентацию. ! [График заданных уравнений — периодическая вертикальная траектория] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_230.jpg) График в области [−π, 0], , где a = 4 и b = 3 , и включить ориентацию. График в области [−π, 0], , где a = 5 и b = 4 , и включить ориентацию. ! [График заданных уравнений — периодическая вертикальная траектория] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_232.jpg) Если на 1 больше, чем b, описать влияние значений и б имеют на графике параметрические уравнения. Опишите график, если a = 100 и b = 99. Произойдет 100 возвратно-поступательных движений. Что будет, если b больше чем на 1? Опишите график. Если параметрические уравнения x (t) = t2 и y (t) = 6−3t есть график горизонтальной параболы, раскрывающейся вправо, что бы изменило направление кривой? Возьмем противоположность x (t) уравнение. Для следующих упражнений опишите график системы параметрических уравнений. и y (t) линейный и x (t) линейный и x (t) линейный Напишите параметрические уравнения круга с центром (0,0), радиус 5 и ориентация против часовой стрелки. {x (t) = 5costy (t) = 5sint Запишите параметрические уравнения эллипса с центром (0,0), большая ось длиной 10, малая ось длиной 6 и ориентация против часовой стрелки. Для следующих упражнений используйте графическую утилиту для построения графика в окне [−3,3] по [−3,3] в домене [0,2π) для следующих значений и б , и включить ориентацию. {x (t) = sin (at) y (t) = sin (bt) а = 1, б = 2 ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_233.jpg) а = 3, б = 3 ! [График приведенных уравнений — прямые, идущие в Q1 и Q3 (в обоих направлениях) от начала координат до 1 единицы.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_235.jpg) а = 2, б = 5 ! [График данных уравнений — линии, идущие в Q1 и Q3 (в обоих направлениях) от начала координат на 3 единицы.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_237.jpg) Для следующих упражнений посмотрите на графики, созданные с помощью параметрических уравнений вида {x (t) = acos (bt) y (t) = csin (dt). Используйте параметрический режим графического калькулятора, чтобы найти значения a, b, c, и d для достижения каждого графика. ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_239.jpg) а = 4, б = 3, с = 6, г = 1 ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_240.jpg) ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_241.jpg) а = 4, б = 2, с = 3, г = 3 ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_242.jpg) Для следующих упражнений используйте графическую утилиту для построения графиков заданных параметрических уравнений. Изобразите все три набора параметрических уравнений в области [0, 2π]. ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_243.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_244.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_245.jpg) Изобразите все три набора параметрических уравнений в области [0,4π]. Изобразите все три набора параметрических уравнений в области [−4π, 6π]. ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_249.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_250.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_251.jpg) Кажется, что график каждой системы параметрических уравнений «ползет» по одной из осей. Что контролирует, по какой оси ползет график? Объясните влияние на график параметрического уравнения, когда мы переключили sin t и cos t . Y — перехват изменений. Объясните влияние на график параметрического уравнения, когда мы изменили домен. Объект подбрасывается в воздух с вертикальной скоростью 20 футов / с и горизонтальной скоростью 15 футов / с. Высота объекта описывается уравнением y (t) = — 16t2 + 20t , а объект движется по горизонтали с постоянной скоростью 15 футов / с. Напишите параметрические уравнения для положения объекта, а затем избавьтесь от времени, чтобы записать высоту как функцию горизонтального положения. у (х) = — 16 (х15) 2 + 20 (х15) Скейтбордист, едущий по ровной поверхности с постоянной скоростью 9 футов / с, подбрасывает в воздух мяч, высоту которого можно описать уравнением y (t) = — 16t2 + 10t + 5. Напишите параметрические уравнения для положения мяча, а затем исключите время, чтобы записать высоту как функцию горизонтального положения. Для следующих упражнений используйте этот сценарий: Дротик бросается вверх с начальной скоростью 65 футов / с под углом возвышения 52 °. Рассмотрим положение дротика в любой момент времени t. Сопротивлением воздуха пренебречь. Найдите параметрические уравнения, моделирующие проблемную ситуацию. {x (t) = 64tcos (52 °) y (t) = — 16t2 + 64tsin (52 °) Найдите все возможные значения x , которые представляют ситуацию. Когда дротик упадет на землю? примерно 3,2 секунды Найдите максимальную высоту дротика. В какое время дротик достигнет максимальной высоты? Для следующих упражнений посмотрите на графики каждого из четырех параметрических уравнений. Хотя они выглядят необычно и красиво, они настолько распространены, что имеют названия, указанные в каждом упражнении. Используйте графическую утилиту для построения графика каждого в указанном домене. Эпициклоида: {x (t) = 14cos t − cos (14t) y (t) = 14sin t + sin (14t) в домене [0,2π] . Гипоциклоида: {x (t) = 6sin t + 2sin (6t) y (t) = 6cos t − 2cos (6t) в домене [0,2π] . ! [График заданных уравнений — гипоциклоида] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_253.jpg) Гипотрохоид: {x (t) = 2sin t + 5cos (6t) y (t) = 5cos t − 2sin (6t) в домене [0,2π] . Роза: {x (t) = 5sin (2t) sinty (t) = 5sin (2t) стоимость в домене [0,2π] . ! [График заданных уравнений — четырехлепестковая роза] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_255.jpg) Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected] Атрибуция: Построение графиков — одна из основных сильных сторон систем компьютерной алгебры.
Мы различаем построение формул и функций.
Подобно функции и выражениям в одной переменной,
кривые на плоскости лучше всего строить, когда они заданы в параметрической форме.
Для кривых с особенностями в начале координат преобразование в
полярная форма может привести к гораздо лучшим результатам, потому что тогда мы можем
исключить особую точку в полярной формулировке. Плоская кривая может быть задана четырьмя различными способами.3 — x), — 2,2, ymin = -5, ymax = 5, detect_poles = ‘show’, figsize = 4) На рис. 35 мы видим вертикальные асимптоты на графике. Рис. 35 График функции с несколькими полюсами. Некоторые кривые даны явными представлениями для координат
\ ((x (t), y (t)) \), как функции от некоторой переменной \ (t \).
Мы строим такие представления с помощью Хотя сюжет из 2000 точек выглядит очень хорошо,
может создаться впечатление, что кривая дважды проходит через начало координат. Переведем в полярные координаты.
В полярных координатах каждая точка представлена радиусом и углом.
Радиус — это расстояние от точки до начала координат.
Угол — это угол, который образует вектор, заканчивающийся в точке.
с горизонтальной осью. Прежде чем решать это выражение для r, хорошо бы упростить. Даже без факторизации мы видим, что r = 0 — двойной корень. Мы выбираем первое решение и наносим две части разными цветами.
Для кривых, заданных в полярных координатах, как \ (r = f (t) \),
мы используем Полярный график показан на рис. 39. Рис. 39 Две половины полярного графика для \ (t \ in [0, \ pi] \)
и для \ (t \ in [\ pi, 2 \ pi] \). Это все? Ну, не забыли ли мы о компоненте r = 0?
Точка (0, 0) является изолированной особенностью вещественной кривой. Полный полярный график показан на рис. 40. Рис. 40 Полный полярный график с добавлением начала координат в виде точки. Технологии
Расширения
Эта работа находится под международной лицензией Creative Commons Attribution 4.0. Двумерные графики — Введение в символьные вычисления 1.0.0 документация
Кривые на плоскости
Parametric_plot .
Кривая Лиссажу определяется параметрическим способом,
показано на рис.36.2
implicit_plot (f, (x, -2, 2), (y, -2, 2)). show (figsize = 4)
implicit_plot (f, (x, -2, 2), (y, -2, 2), plot_points = 2000, \
color = ‘red’). показать (figsize = 4) г, т = var ('г, т')
g = f.subs ({x: r * cos (t), y: r * sin (t)})
печать g
sg = g.trig_simplify ()
печать sg
polar_plot , обеспечивая диапазон для \ (t \). s0 = s [0].rhs ()
first = polar_plot (s0, (t, 0, pi), axes = False, color = 'красный')
second = polar_plot (s0, (t, pi, 2 * pi), оси = False, color = 'green')
(первый + второй) .show (figsize = 4)
p0 = точка ((0, 0), color = 'blue', size = 50)
(p0 + первый + второй).показать()

 Пожалуйста, не путайте с неравенствами двух переменных, где геометрически задействована вся координатная плоскость. Однако есть и приятные совпадения! Итак, для неравенства равносильны следующие преобразования:
Пожалуйста, не путайте с неравенствами двух переменных, где геометрически задействована вся координатная плоскость. Однако есть и приятные совпадения! Итак, для неравенства равносильны следующие преобразования: В данном случае:
В данном случае:
 А основной способ – метод интервалов мы детально разберём в статье Нули функции. Интервалы знакопостоянства.
А основной способ – метод интервалов мы детально разберём в статье Нули функции. Интервалы знакопостоянства. Такая функция не определена вообще (разумеется, график тоже иллюзорен).
Такая функция не определена вообще (разумеется, график тоже иллюзорен). 2-25/x+7 — Учеба и наука
2-25/x+7 — Учеба и наука 05.16
05.16 3
3 {2}-3 x+2=0
\) По теореме Вета: \(\
x_{1}+x_{2}=3 ; x_{1} \cdot x_{2}=2
\),поэтому \(\
x_{1}=1, x_{2}=2
\) .Таким образом, неравенство примет вид
{2}-3 x+2=0
\) По теореме Вета: \(\
x_{1}+x_{2}=3 ; x_{1} \cdot x_{2}=2
\),поэтому \(\
x_{1}=1, x_{2}=2
\) .Таким образом, неравенство примет вид Существует система неравенств
Существует система неравенств
 Исследование функции — естественный процесс, который встречается в различных дисциплинах.
Исследование функции — естественный процесс, который встречается в различных дисциплинах.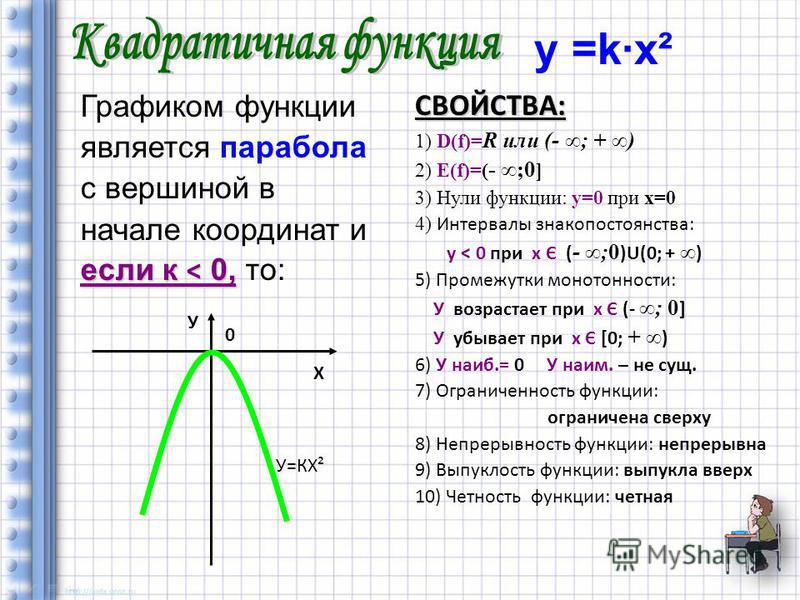
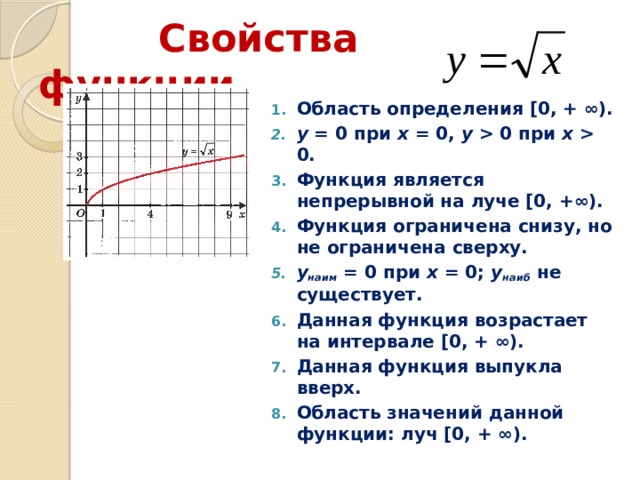 Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.
Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.
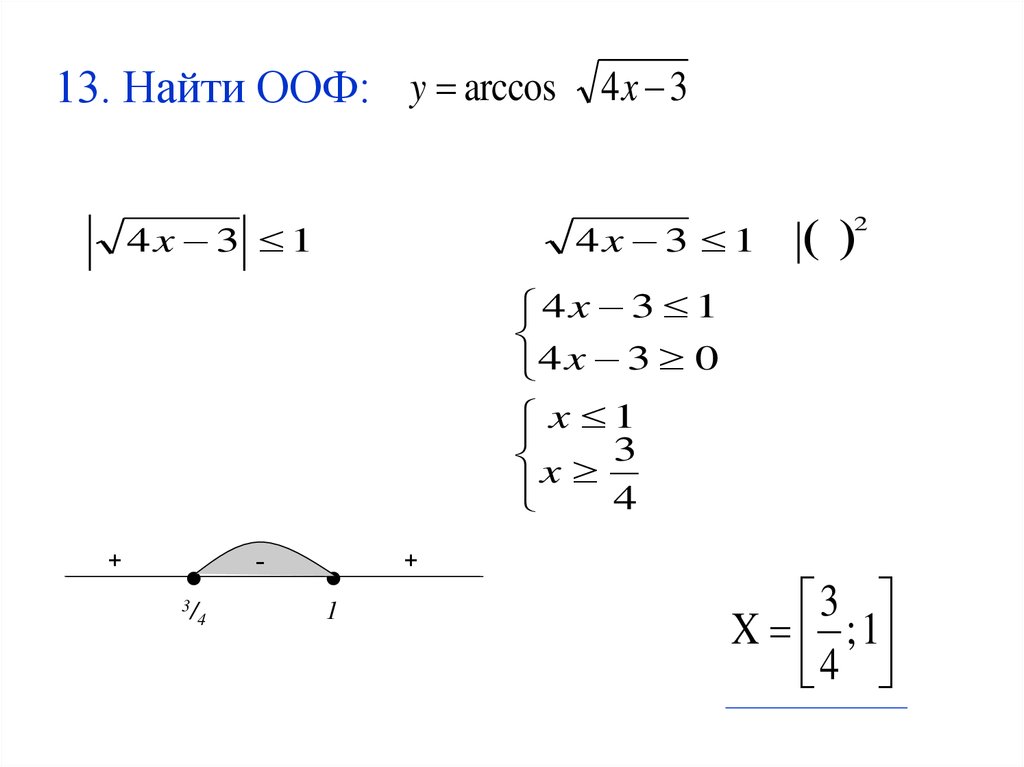
 Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.
Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.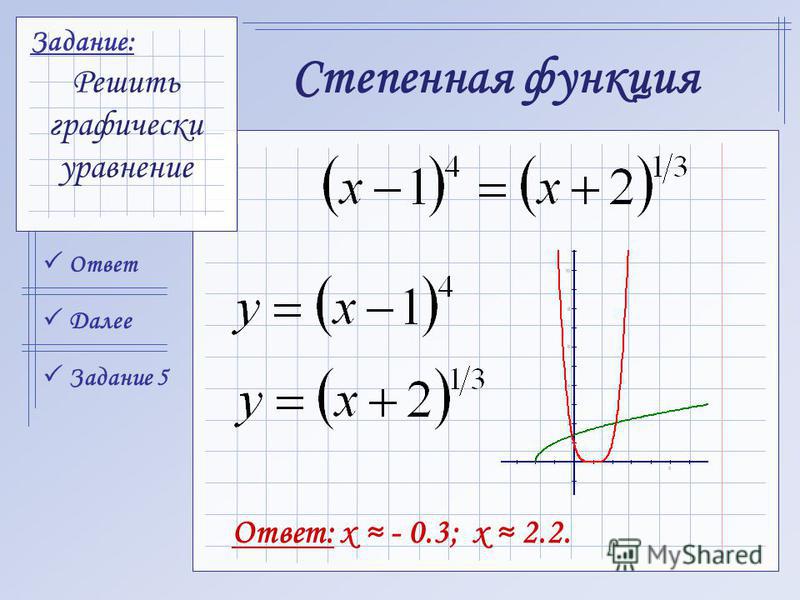 В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.
В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.

 2] — (4 * 4 * 9) = 144 — 144 = 0.
2] — (4 * 4 * 9) = 144 — 144 = 0. Можно сказать, что это строгий математический закон, который связывает два числа определенным образом.
Можно сказать, что это строгий математический закон, который связывает два числа определенным образом.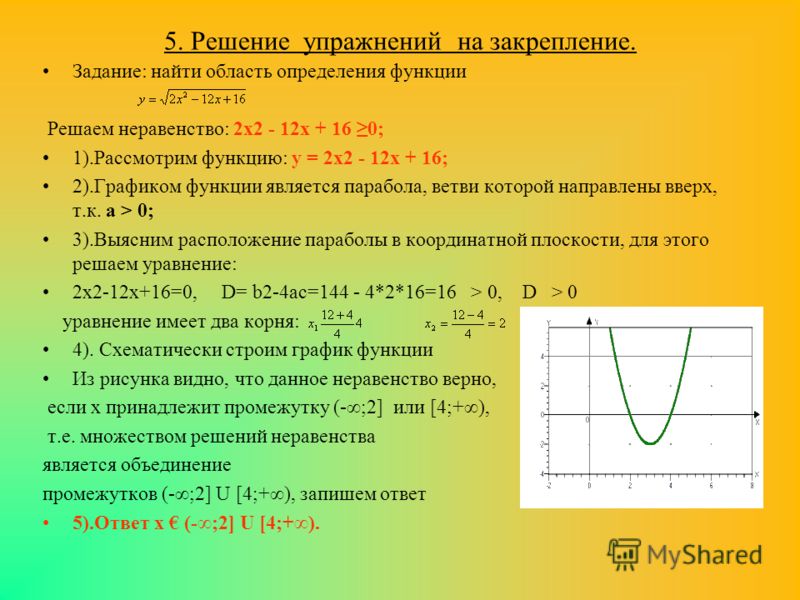
 Областью определения являются все значения аргумента, при котором f(x) имеет смысл.
Областью определения являются все значения аргумента, при котором f(x) имеет смысл.
 Найти область определения.
Найти область определения.
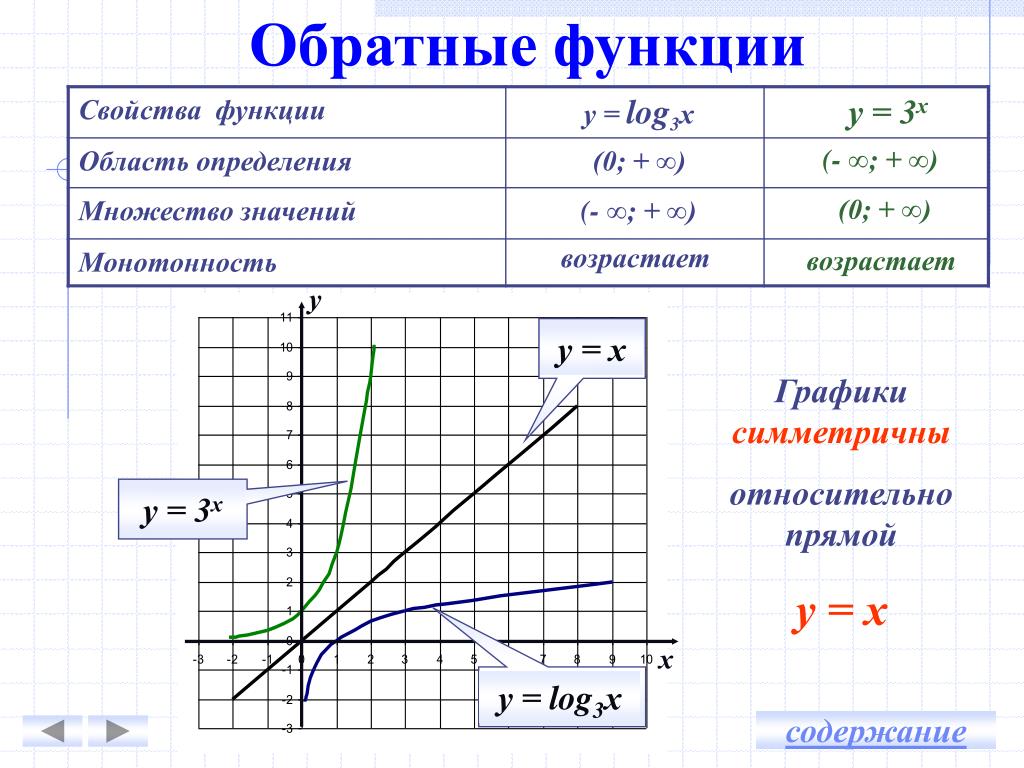

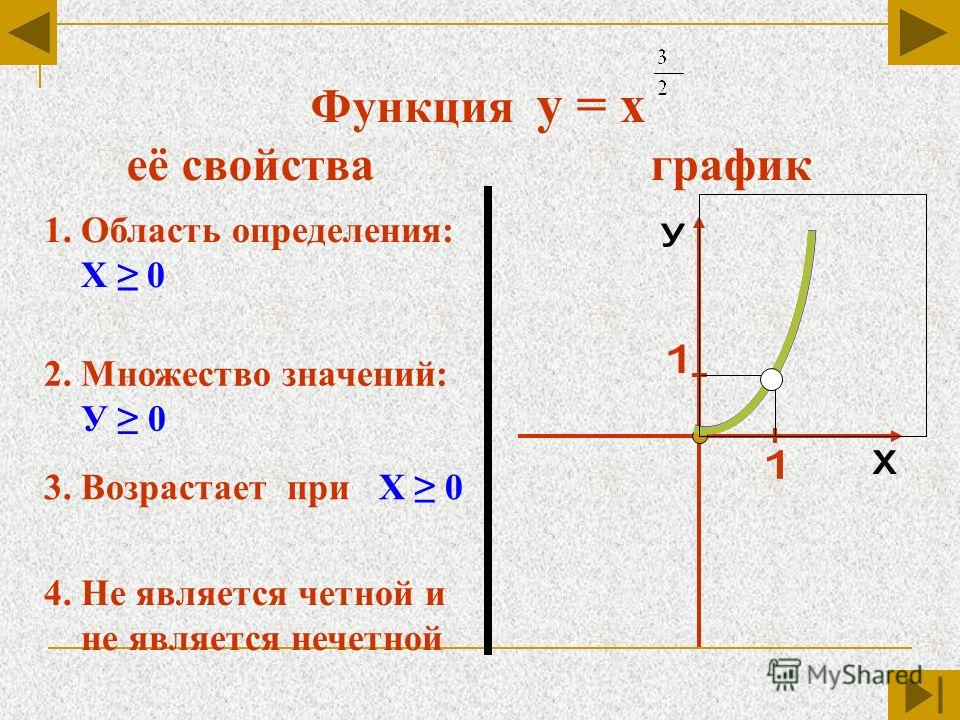
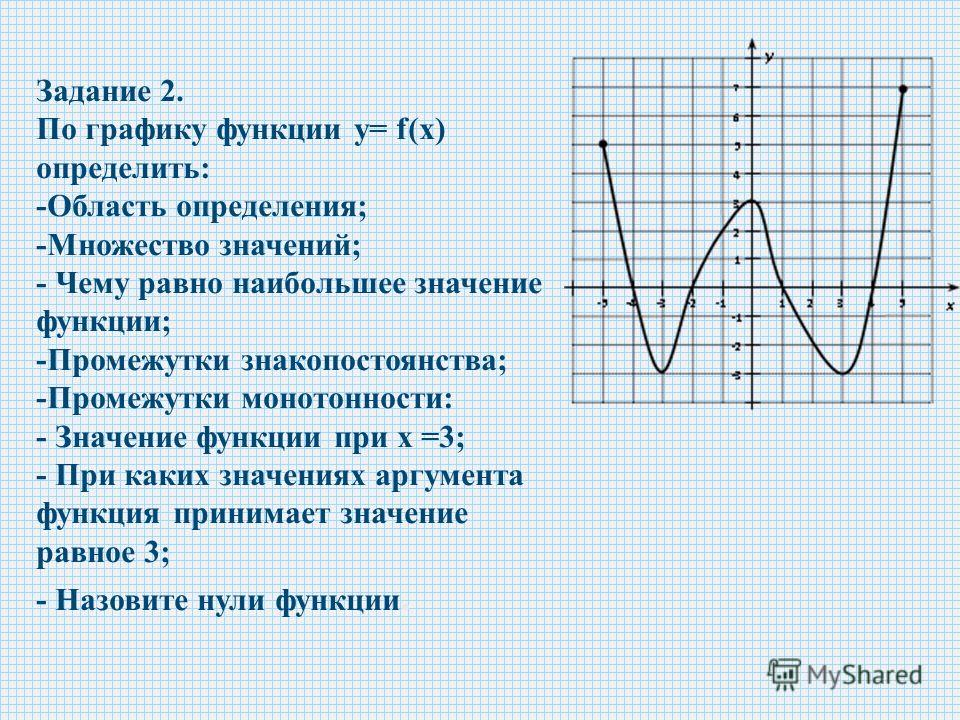 Тогда зависимость импульса от времени является сложной функцией .
Но ее, для краткости, обозначают так: .
При таком подходе и — это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например .
Тогда явно видно, что и — это разные функции.
Тогда зависимость импульса от времени является сложной функцией .
Но ее, для краткости, обозначают так: .
При таком подходе и — это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например .
Тогда явно видно, что и — это разные функции. Множество значений состоит из двух элементов — “истина” и “ложь”.
Множество значений состоит из двух элементов — “истина” и “ложь”.
 Но не всякая функция имеет максимум и минимум.
Но не всякая функция имеет максимум и минимум. Различными цветами обозначены ее ветви. Каждая ветвь является функцией.
Различными цветами обозначены ее ветви. Каждая ветвь является функцией. В результате, для каждого значения n
,
мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией . А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функцией .
В результате, для каждого значения n
,
мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией . А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функцией .
 Однако, чтобы найти область
определения функции, нам не нужно перебирать все пары иксов и игреков.
Однако, чтобы найти область
определения функции, нам не нужно перебирать все пары иксов и игреков. Такое сообщение
предусмотрено авторами программы, если выражение для вычисления ответа достаточно сложно или касается
какой-то узкой предметной области, или же предусмотрено авторами языка программирования, если дело
касается общепринятых норм, например, что нельзя делить на нуль.
Такое сообщение
предусмотрено авторами программы, если выражение для вычисления ответа достаточно сложно или касается
какой-то узкой предметной области, или же предусмотрено авторами языка программирования, если дело
касается общепринятых норм, например, что нельзя делить на нуль.
 Следовательно, область определения данной функции — вся числовая прямая, то есть
]- ∞; + ∞[
.
Следовательно, область определения данной функции — вся числовая прямая, то есть
]- ∞; + ∞[
.



 е. функции первой степени:
е. функции первой степени:



 Модули имеют собственное состояние сеанса, связанное с глобальной областью.
Весь код модуля выполняется в специфической для модуля иерархии областей видимости, которая имеет свои особенности.
собственная корневая область.
Модули имеют собственное состояние сеанса, связанное с глобальной областью.
Весь код модуля выполняется в специфической для модуля иерархии областей видимости, которая имеет свои особенности.
собственная корневая область.

 Область по умолчанию для
функции и псевдонимы являются локальной областью действия, даже если они определены в
сценарий.
Область по умолчанию для
функции и псевдонимы являются локальной областью действия, даже если они определены в
сценарий.
 Следующая команда ссылается на переменную
Следующая команда ссылается на переменную  В удаленных и
внепроцессные сеансы, они всегда являются независимыми копиями.
В удаленных и
внепроцессные сеансы, они всегда являются независимыми копиями. Он имеет свойства и методы типа. Для простых типов, таких как System.Version , копия точная. Для сложных типов копия
несовершенный. Например, повторно гидратированные объекты сертификата не включают
закрытый ключ.
Он имеет свойства и методы типа. Для простых типов, таких как System.Version , копия точная. Для сложных типов копия
несовершенный. Например, повторно гидратированные объекты сертификата не включают
закрытый ключ.
 Следующая команда создает
псевдоним в глобальной области:
Следующая команда создает
псевдоним в глобальной области:
 ps1,
недоступно в текущей области.
ps1,
недоступно в текущей области. За
Например, вы можете запустить сценарий для создания дочерней области в сеансе.
За
Например, вы можете запустить сценарий для создания дочерней области в сеансе. Все экспорты помещаются в глобальные таблицы.
Если вы загружаете модуль2 из в модуль1, модуль2 загружается в сеанс
состояние модуля1, а не глобальное состояние сеанса. Любой экспорт из модуля2
размещен в верхней части состояния сеанса module1. Если вы используете
Все экспорты помещаются в глобальные таблицы.
Если вы загружаете модуль2 из в модуль1, модуль2 загружается в сеанс
состояние модуля1, а не глобальное состояние сеанса. Любой экспорт из модуля2
размещен в верхней части состояния сеанса module1. Если вы используете 
 Использование модификатора глобальной области видимости в этом случае
не отображает приватную переменную.
Использование модификатора глобальной области видимости в этом случае
не отображает приватную переменную.
 ps1, содержащий следующие команды:
ps1, содержащий следующие команды: ps1, определяющий переменную
ps1, определяющий переменную  ps1, определяющий переменную
ps1, определяющий переменную  ps1, содержащий следующие команды.
Команда пытается отобразить и изменить значение
ps1, содержащий следующие команды.
Команда пытается отобразить и изменить значение  0. В PowerShell 2.0 для
указать, что переменная была создана в локальном сеансе, используйте следующие
формат команды.
0. В PowerShell 2.0 для
указать, что переменная была создана в локальном сеансе, используйте следующие
формат команды.



 Если вы хотите попрактиковаться в области видимости, просто отслеживайте, какая у вас текущая локальная область видимости и к каким переменным, типам и т. д. у вас есть доступ.
Если вы хотите попрактиковаться в области видимости, просто отслеживайте, какая у вас текущая локальная область видимости и к каким переменным, типам и т. д. у вас есть доступ. Теперь мы собираемся добавить в этот класс перечисление как вложенный тип. Вот так:
Теперь мы собираемся добавить в этот класс перечисление как вложенный тип. Вот так:


 Вы можете получить доступ к тому, что выше, на более низких уровнях, но не к тому, что ниже, на более высоких уровнях.
Вы можете получить доступ к тому, что выше, на более низких уровнях, но не к тому, что ниже, на более высоких уровнях.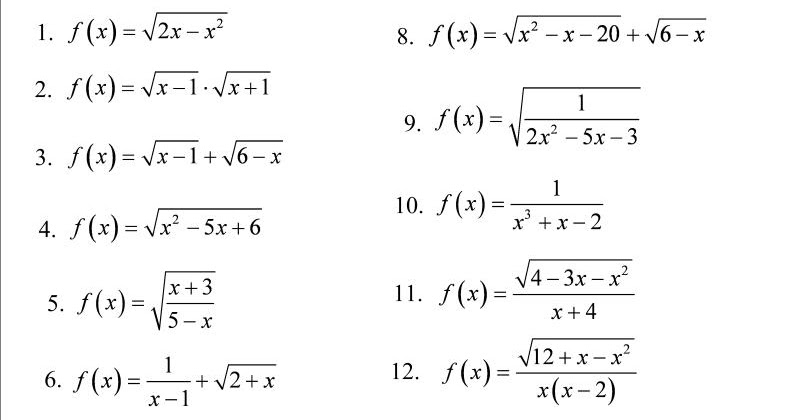 Вы можете узнать больше об управлении доступом в Swift в этом руководстве: Управление доступом, объясненное в Swift
Вы можете узнать больше об управлении доступом в Swift в этом руководстве: Управление доступом, объясненное в Swift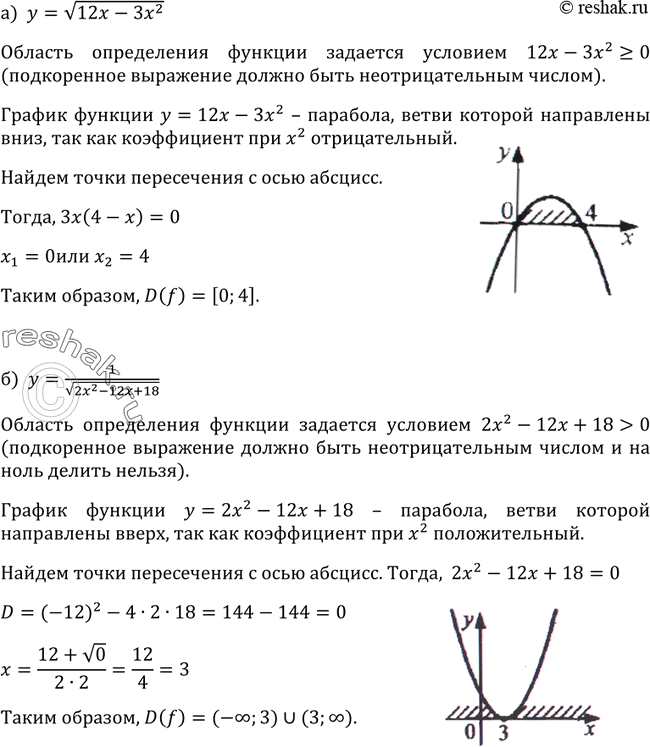 Когда загрузка завершится, в будущем мы хотим выполнить некоторый код для отображения изображения. Мы определяем этот код в замыкании и передаем его функции, загружающей изображение. Затем эта функция выполняет закрытие после завершения загрузки.
Когда загрузка завершится, в будущем мы хотим выполнить некоторый код для отображения изображения. Мы определяем этот код в замыкании и передаем его функции, загружающей изображение. Затем эта функция выполняет закрытие после завершения загрузки.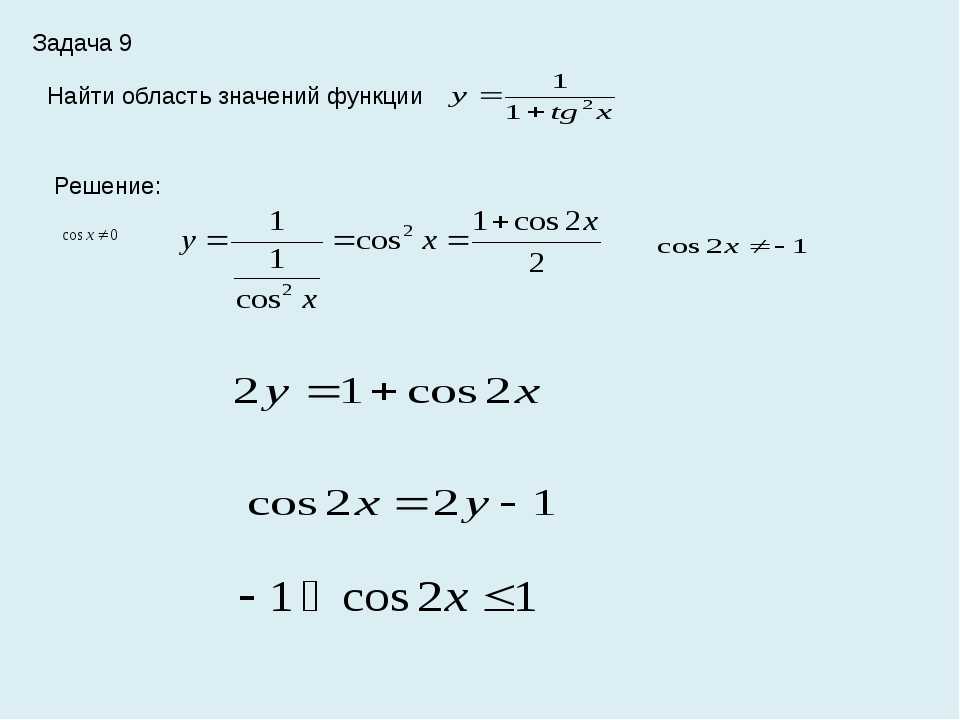 Его второй параметр, обработчик завершения, расположенный между самыми внутренними волнистыми скобками, является замыканием. Когда загрузка изображения завершена, мы присваиваем значение загруженного изображения свойству image объекта imageView, которое будет отображать изображение.
Его второй параметр, обработчик завершения, расположенный между самыми внутренними волнистыми скобками, является замыканием. Когда загрузка изображения завершена, мы присваиваем значение загруженного изображения свойству image объекта imageView, которое будет отображать изображение. То же самое верно для наблюдателей свойств, вычисляемых свойств и другого кода блочного уровня.
То же самое верно для наблюдателей свойств, вычисляемых свойств и другого кода блочного уровня.
 Это понятная опечатка: текст должен быть строкой, которая является входным параметром для функции reverse().
Это понятная опечатка: текст должен быть строкой, которая является входным параметром для функции reverse().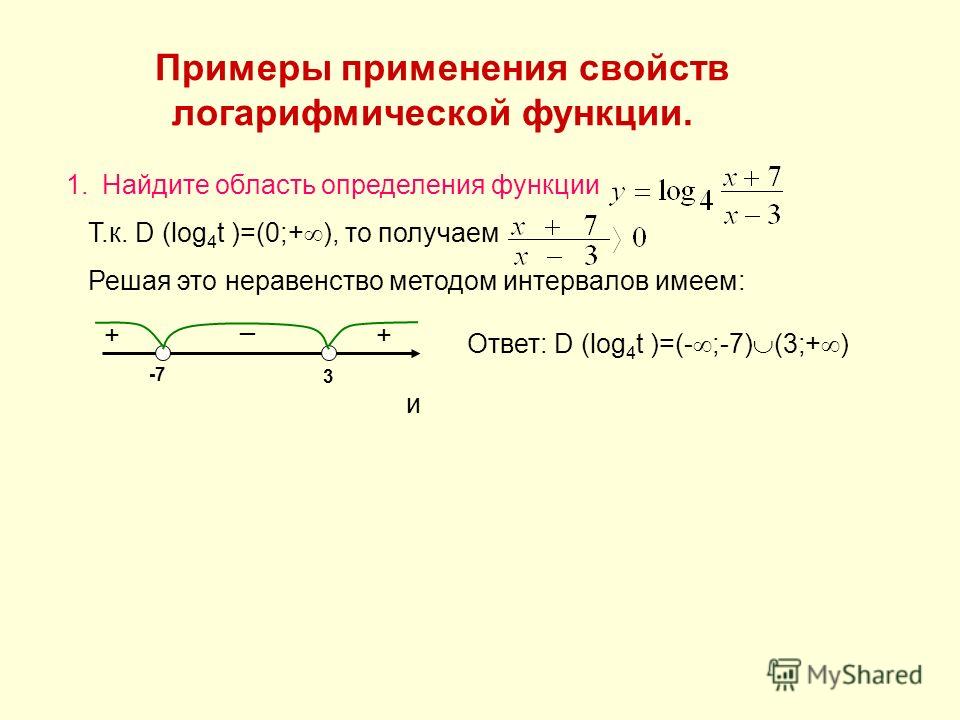 Например, если вам не хватает типа представления, вам, вероятно, потребуется импортировать SwiftUI. Документация iOS SDK может помочь вам в этом.
Например, если вам не хватает типа представления, вам, вероятно, потребуется импортировать SwiftUI. Документация iOS SDK может помочь вам в этом. У нас есть семантическое управление версиями, теги выпуска, привязка версий и так далее, но в какой-то момент вам придется обновить приложение с версии 1.0 библиотеки до версии 2.0. Между тем, API для этой библиотеки изменился, и они переименовали некоторые классы, которые вы используете. Что случается? Не удается найти … в объеме. В этом сценарии важно помнить о своих предположениях, потому что вы собираетесь искать тот класс, который наверняка существовал в версии 1.0!
У нас есть семантическое управление версиями, теги выпуска, привязка версий и так далее, но в какой-то момент вам придется обновить приложение с версии 1.0 библиотеки до версии 2.0. Между тем, API для этой библиотеки изменился, и они переименовали некоторые классы, которые вы используете. Что случается? Не удается найти … в объеме. В этом сценарии важно помнить о своих предположениях, потому что вы собираетесь искать тот класс, который наверняка существовал в версии 1.0! Допустим, у вас есть 2 представления — как вы можете получить эту переменную отсюда туда? Вот тут-то и начинается передача данных из одного компонента в другой. Ознакомьтесь с этими руководствами: Как: передавать данные между представлениями с помощью SwiftUI и Как: передавать данные между контроллерами представлений в Swift
Допустим, у вас есть 2 представления — как вы можете получить эту переменную отсюда туда? Вот тут-то и начинается передача данных из одного компонента в другой. Ознакомьтесь с этими руководствами: Как: передавать данные между представлениями с помощью SwiftUI и Как: передавать данные между контроллерами представлений в Swift 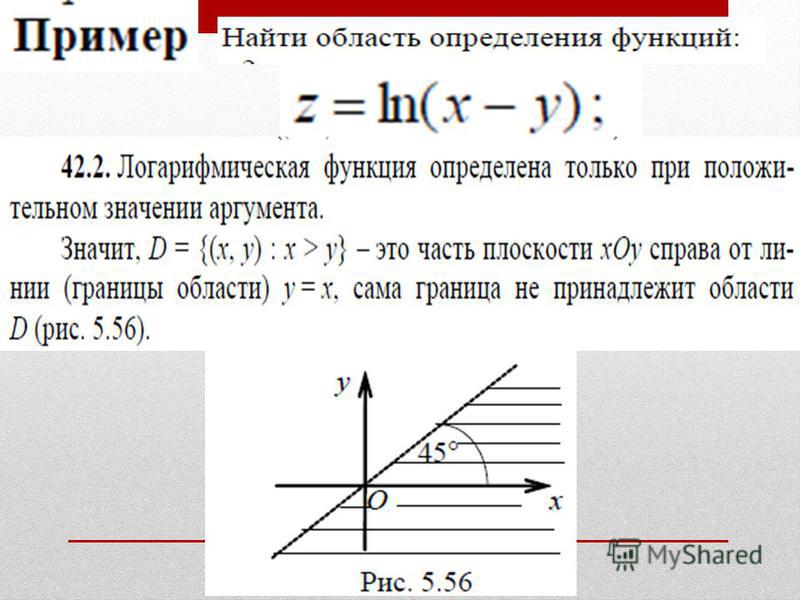

 Например, переменные, определенные в области скрипта, считаются ее локальной областью.
Например, переменные, определенные в области скрипта, считаются ее локальной областью. Другой элемент с тем же именем в другой области может скрывать исходный элемент, но не переопределяет и не изменяет исходный элемент.
Другой элемент с тем же именем в другой области может скрывать исходный элемент, но не переопределяет и не изменяет исходный элемент. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Если при наложении одного угла на другой они совпадут, то эти углы равны.
 Транспортир. Виды углов
Транспортир. Виды углов Прямой, тупой, острый и развернутый угол
Прямой, тупой, острый и развернутый угол Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.


 Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой .
Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой . Такой угол имеет свое название.
Такой угол имеет свое название. Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).


 Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .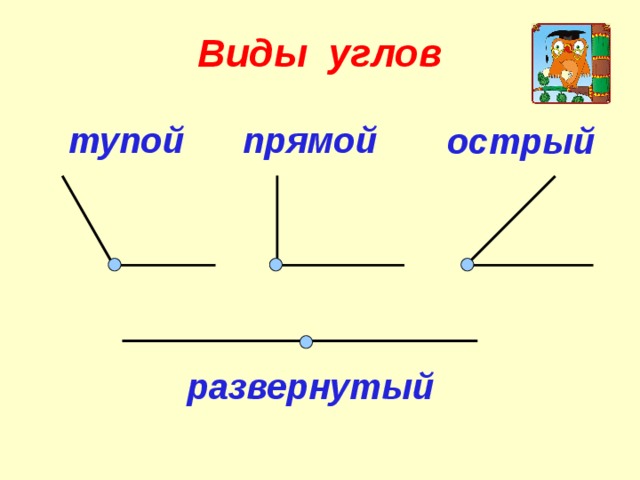 Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.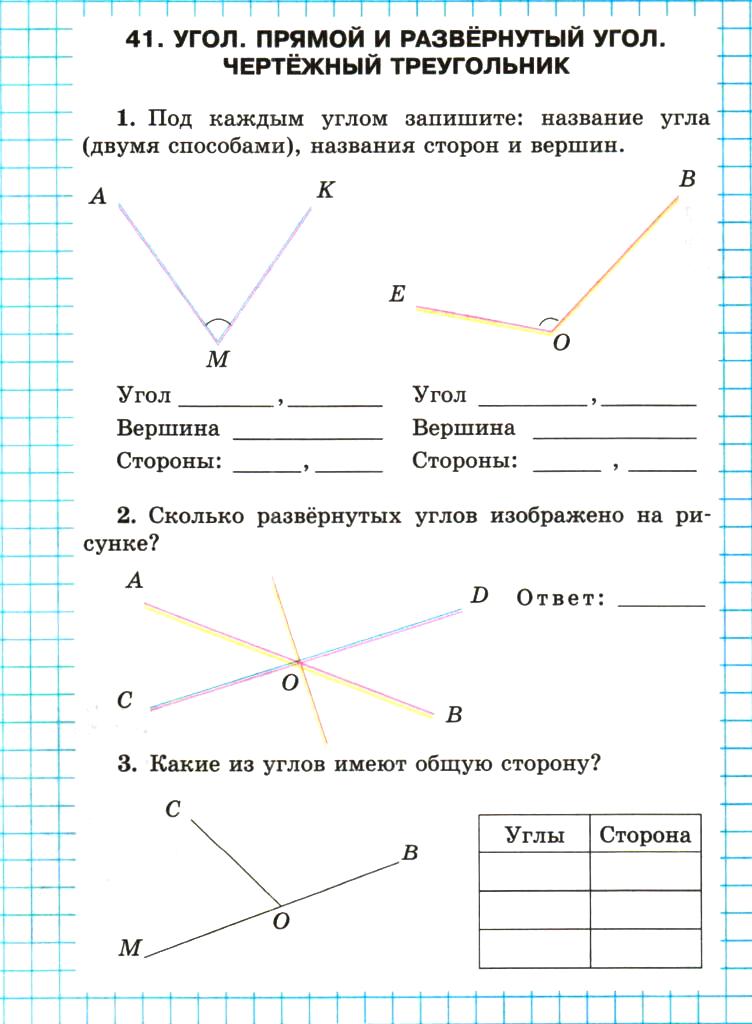
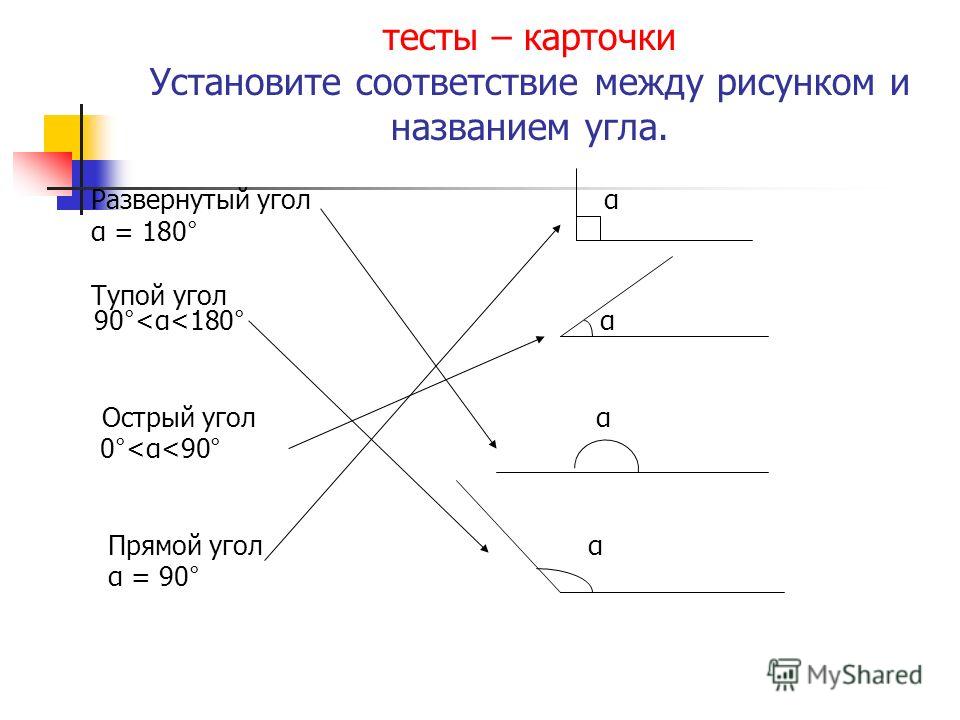
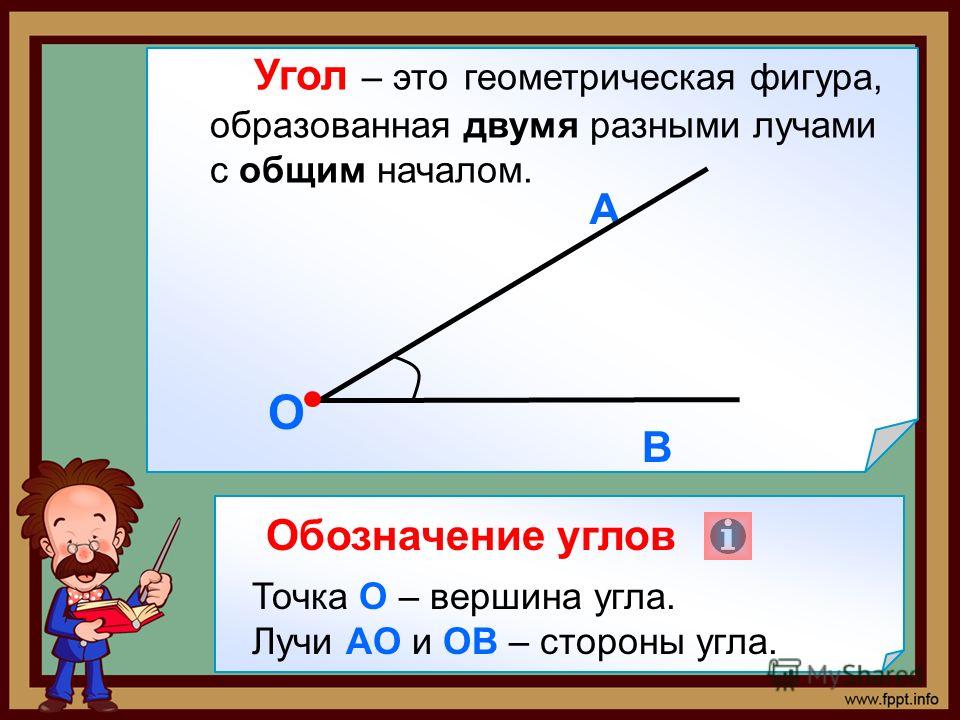 На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
 Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

 Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
 Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° . Что же называют радианом.
Что же называют радианом.
 Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

 Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ? Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха? В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
 Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений  Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
Развертка кривой см. Эвольвента … Большой Энциклопедический словарь Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера Очень важной с практической точки зрения является проблема о конформном… … Википедия
Очень важной с практической точки зрения является проблема о конформном… … Википедия *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
*РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь Фигура делит плоскость… … Математическая энциклопедия
Фигура делит плоскость… … Математическая энциклопедия 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
 166).
166). То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
 Это и есть развернутый угол.
Это и есть развернутый угол.
 Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? 


 Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять: е. их сумма 90 о.
е. их сумма 90 о. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.

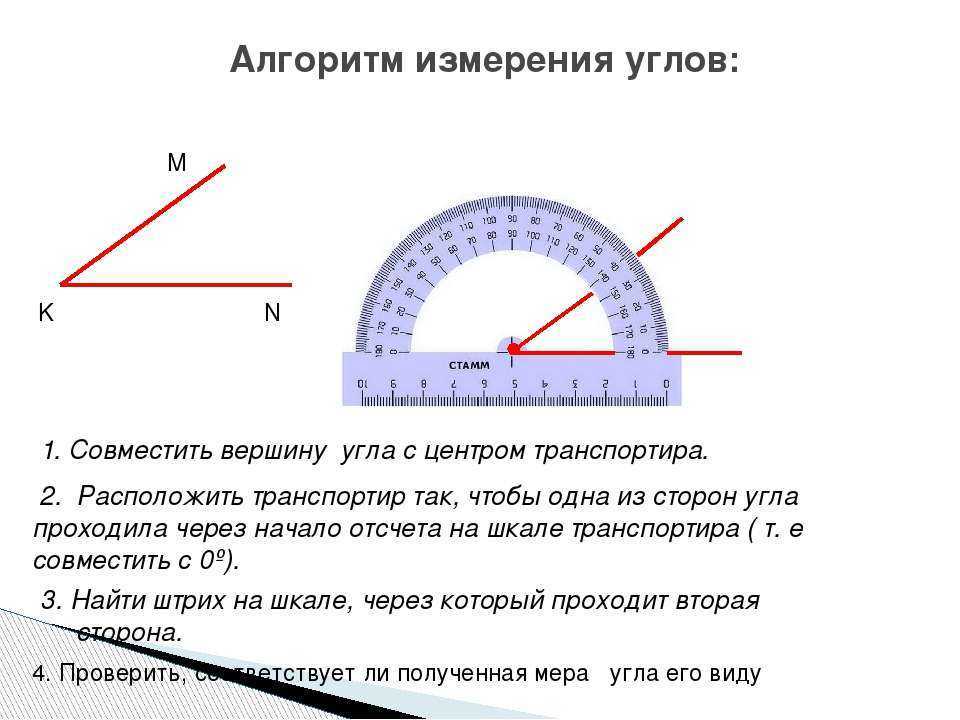

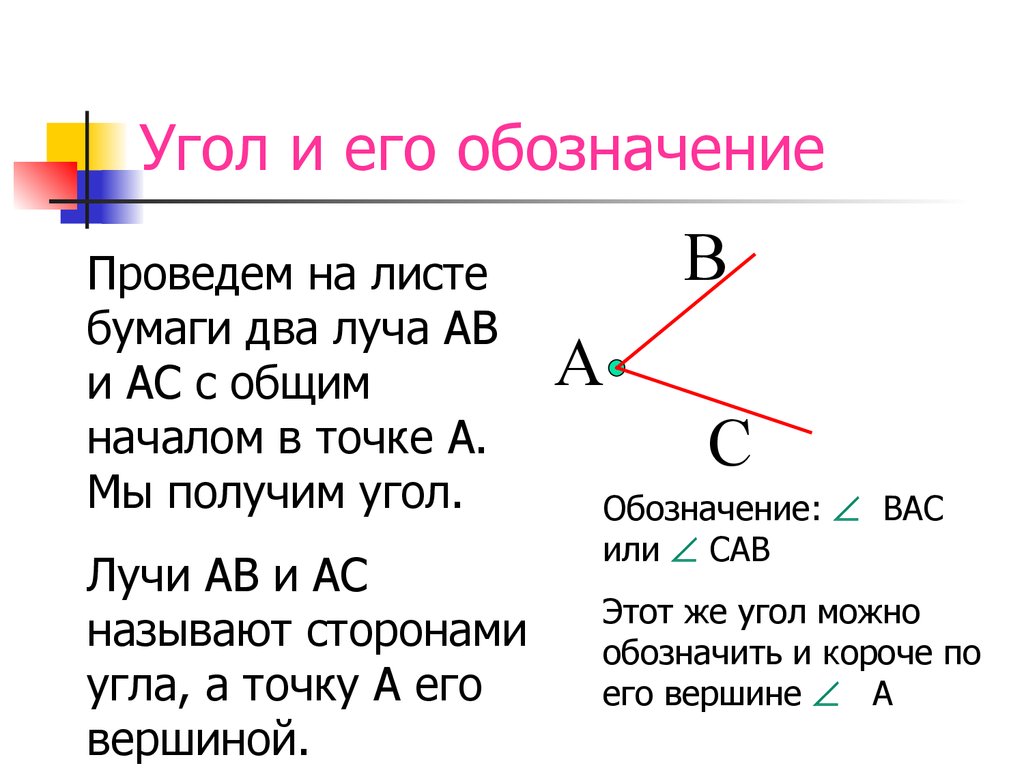
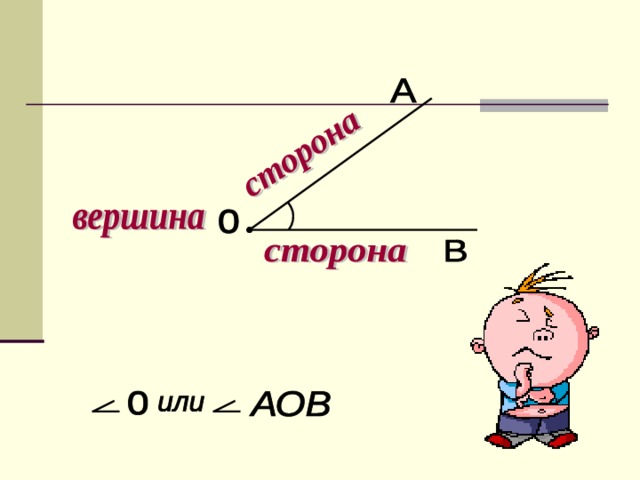

 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
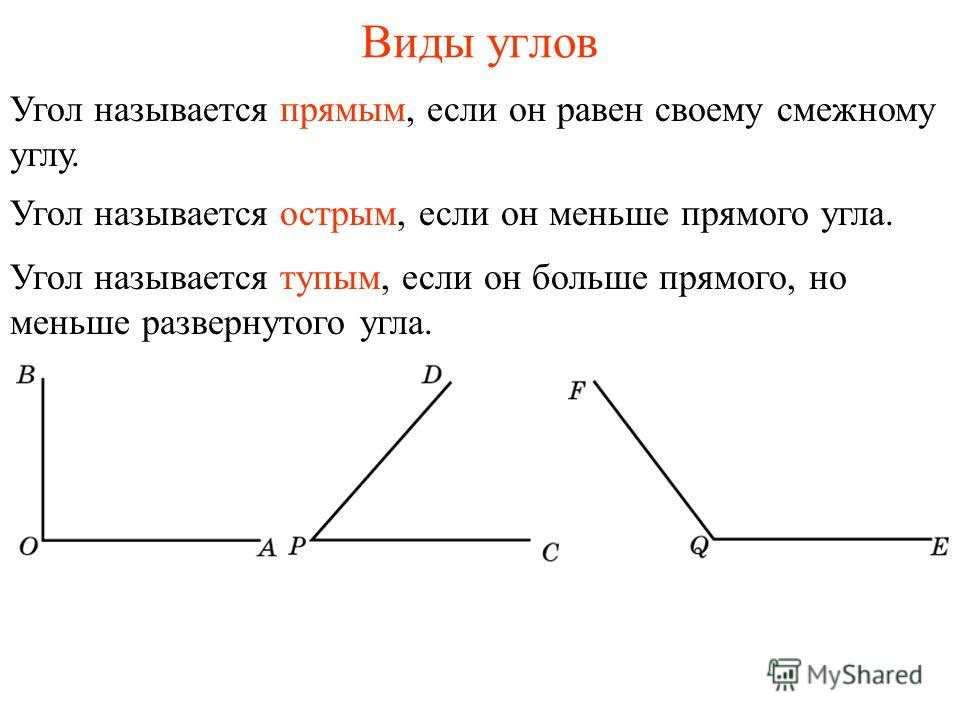
 Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
 Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей. до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
 УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
 164).
164). Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
 Это и есть развернутый угол.
Это и есть развернутый угол.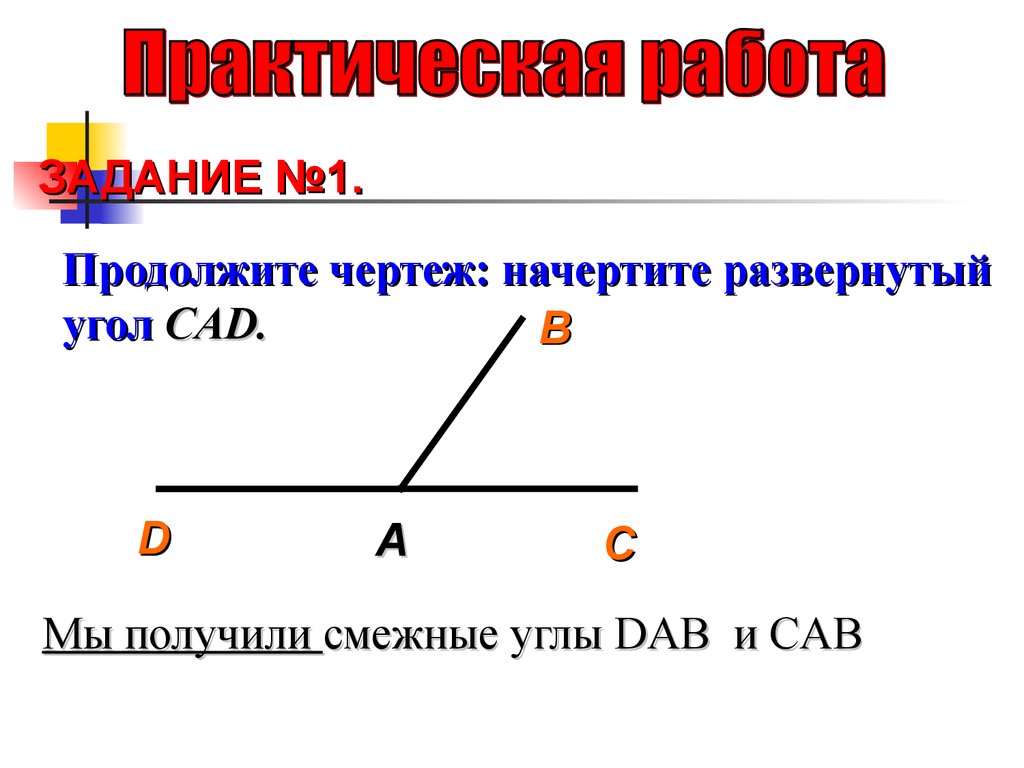
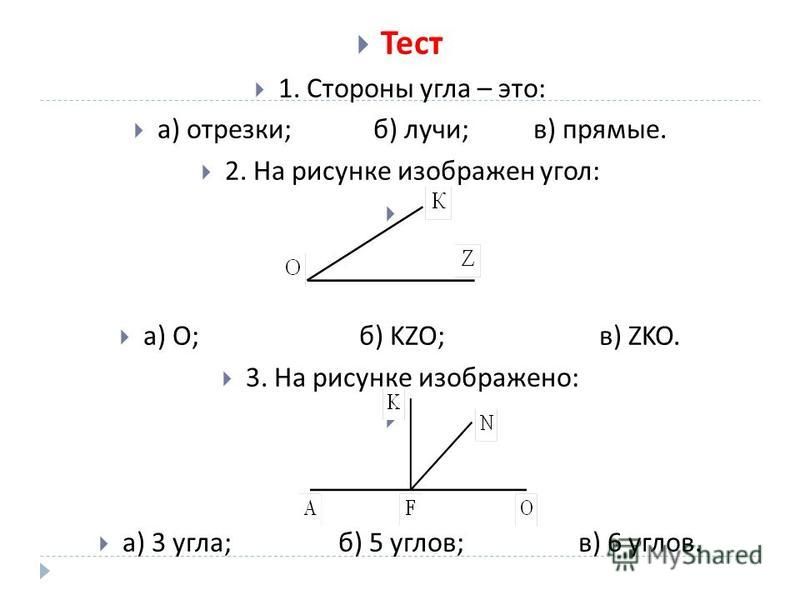 Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.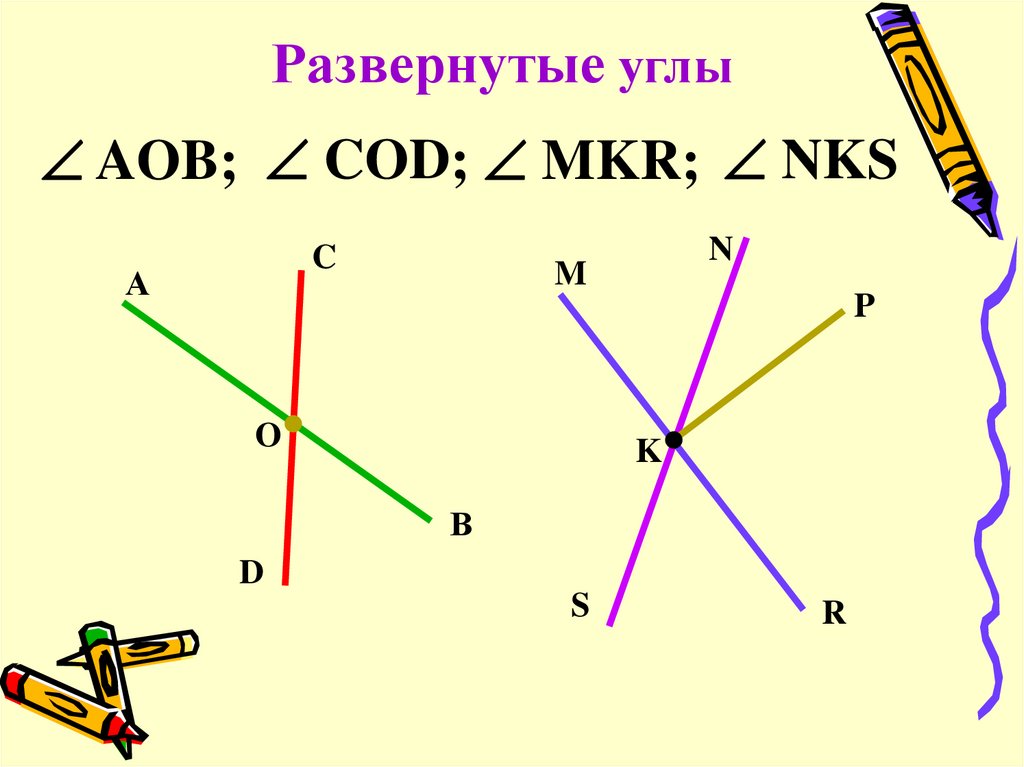 Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? 
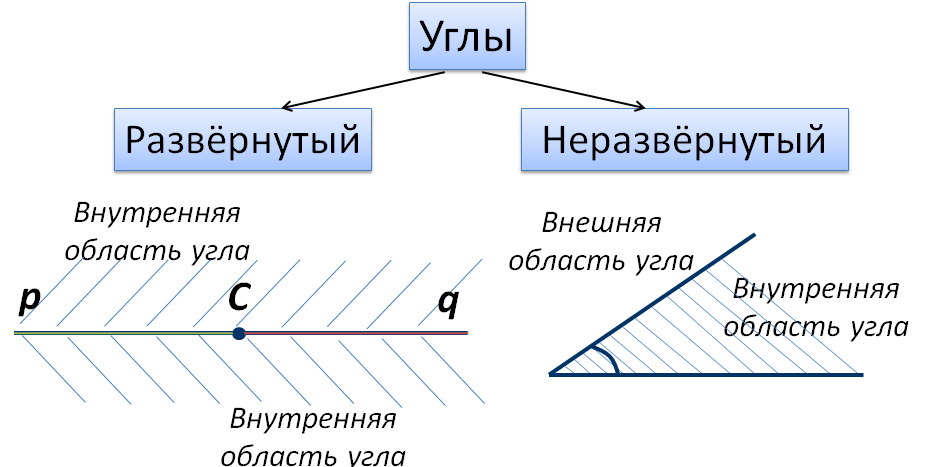



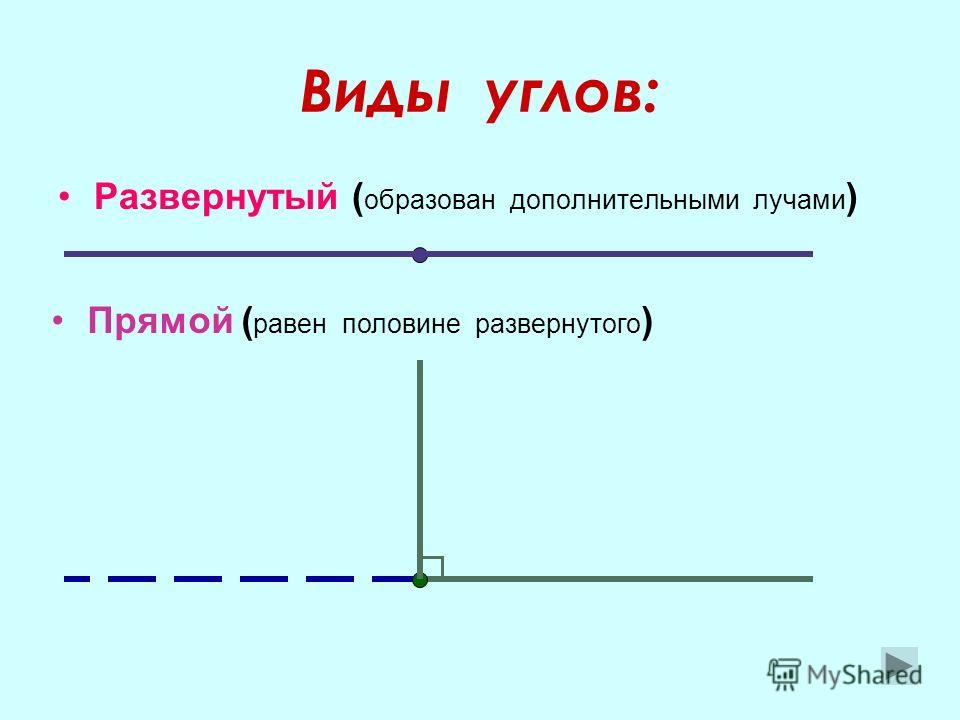


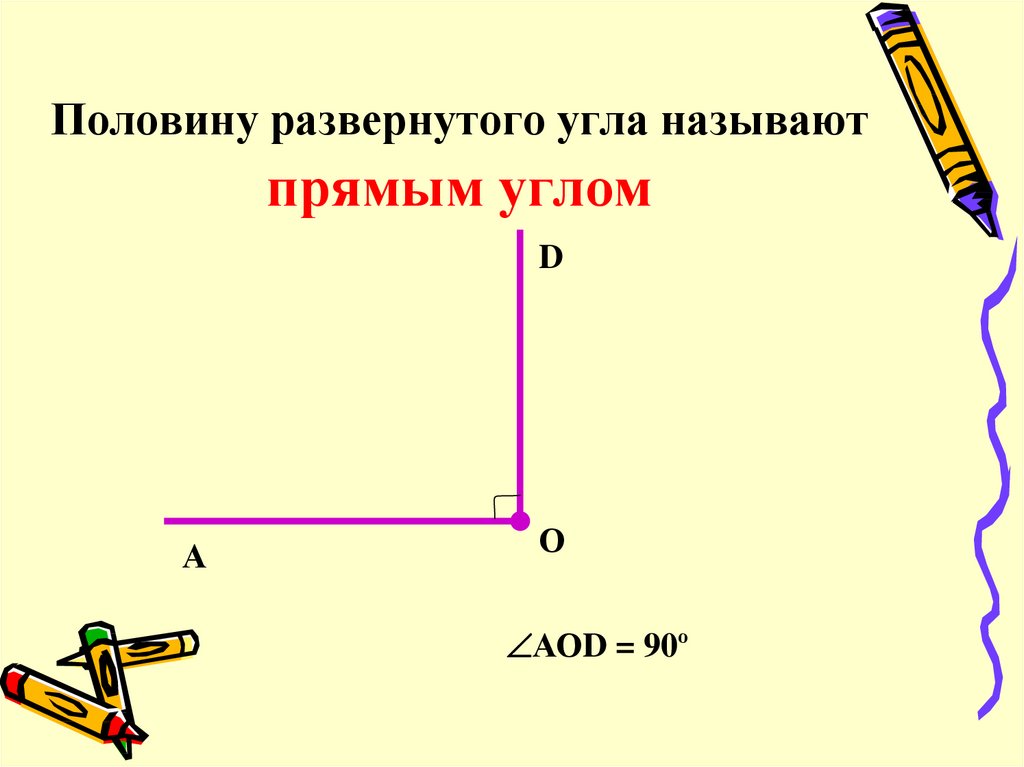 Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.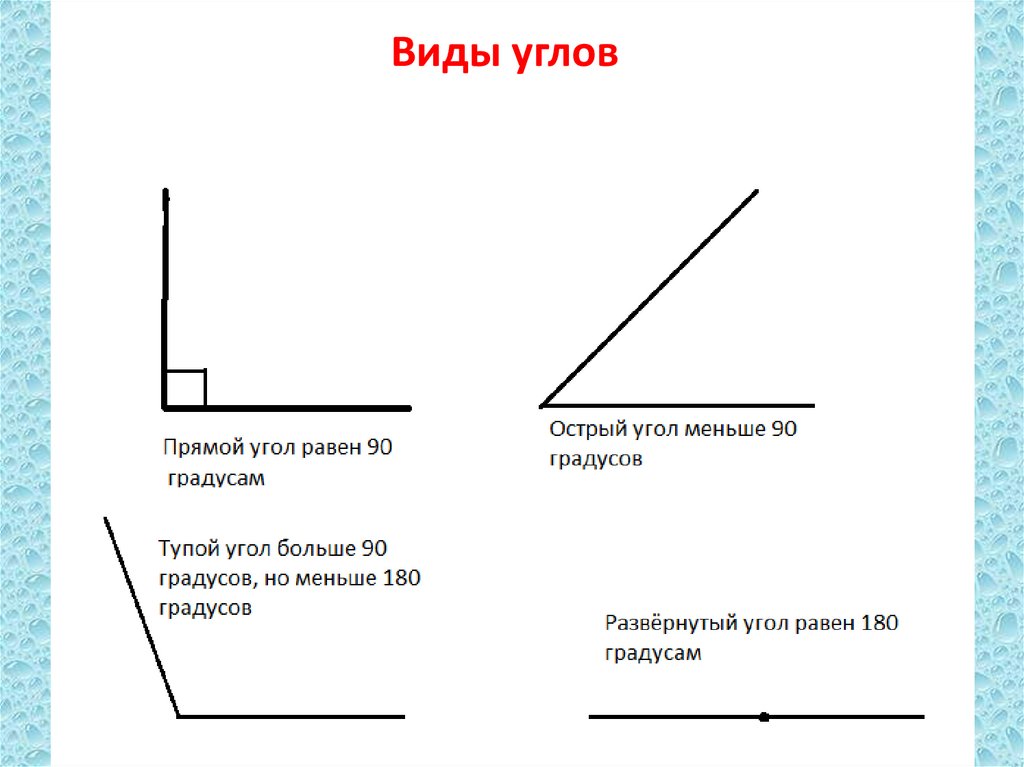 Они считаются подобными.
Они считаются подобными.
 На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
Теперь рассмотрим их виды по расположению на плоскости относительно друг друга. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.



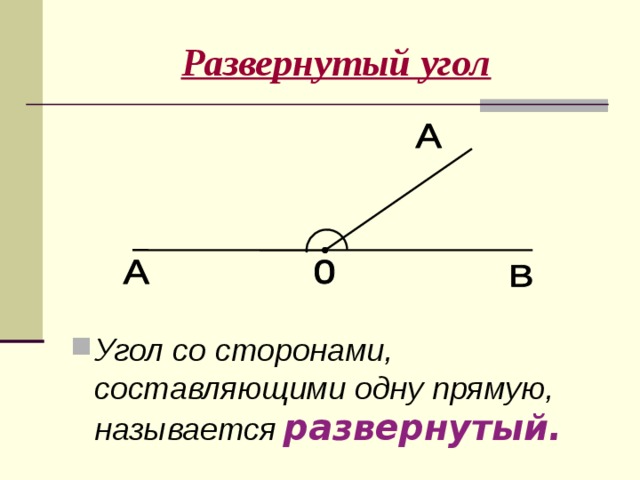 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.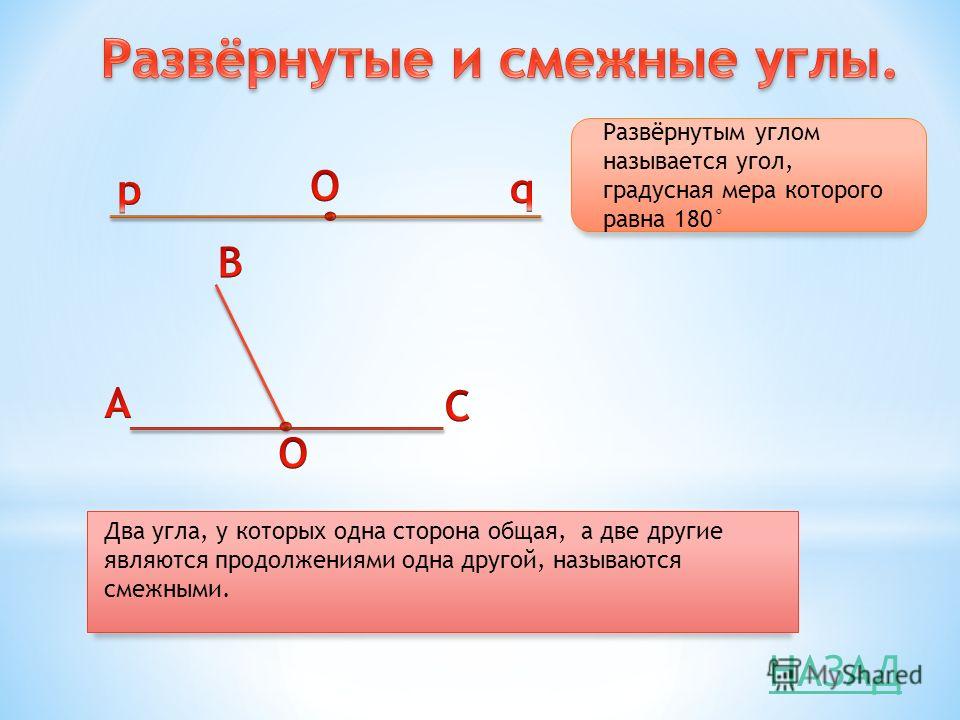 Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.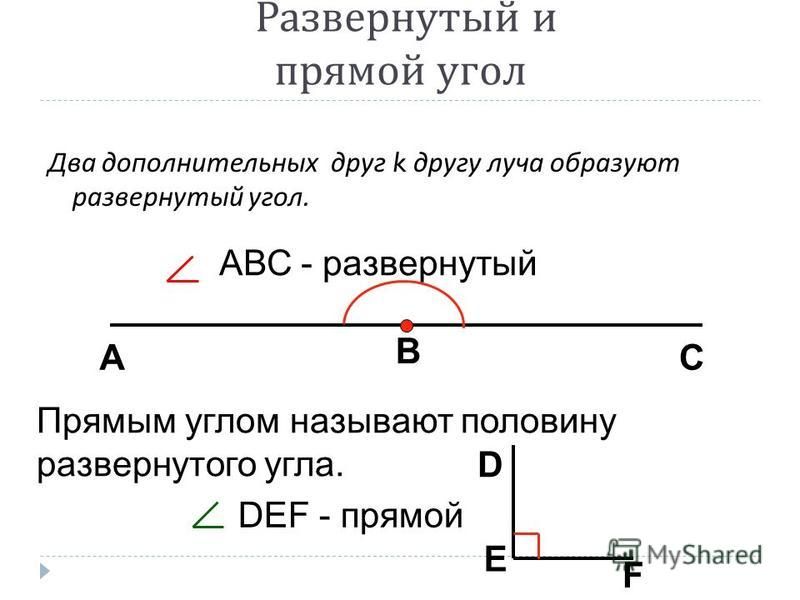
 Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .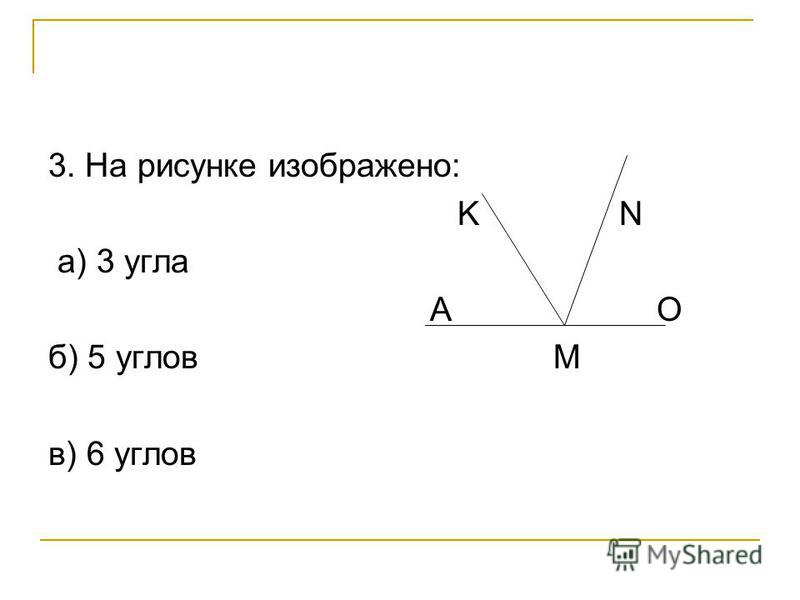
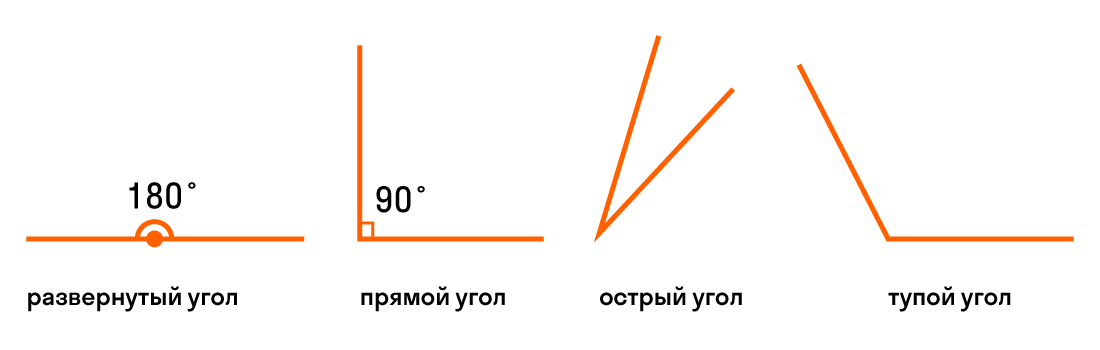
 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).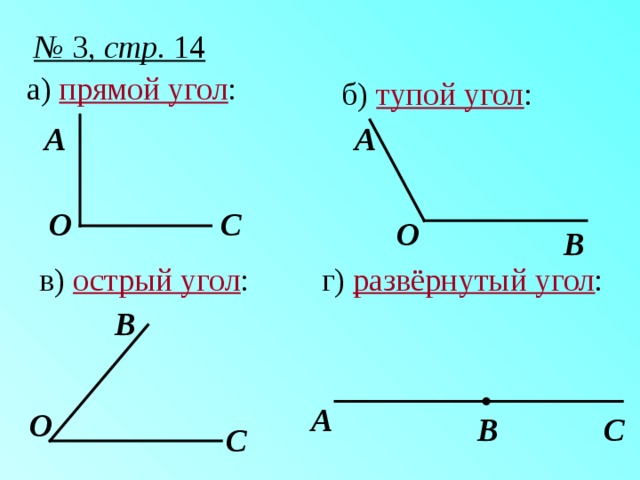 Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)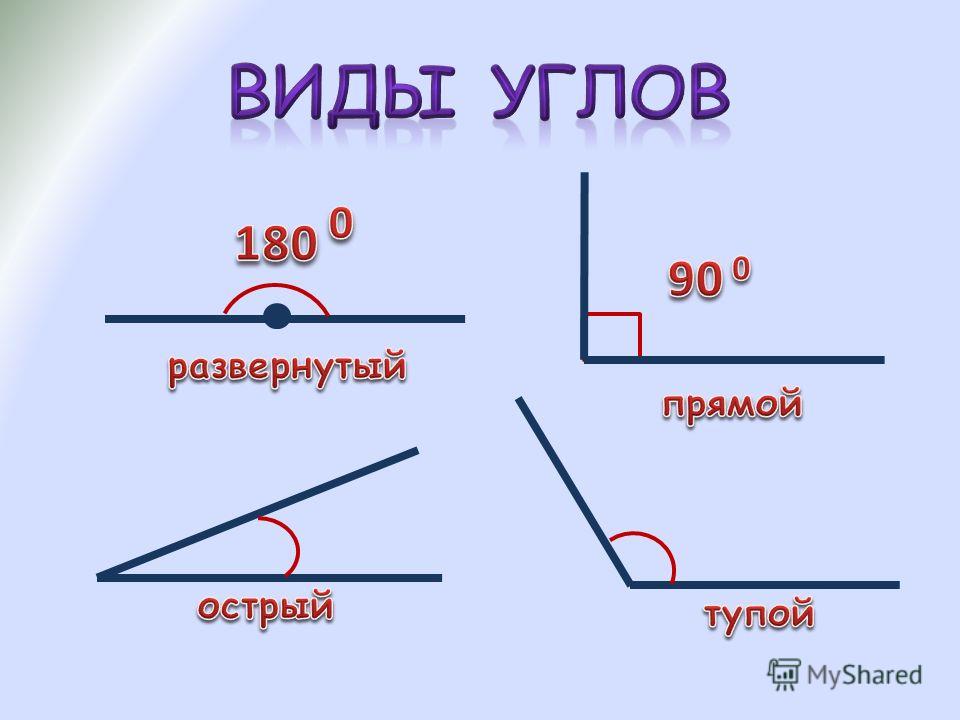 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2). Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…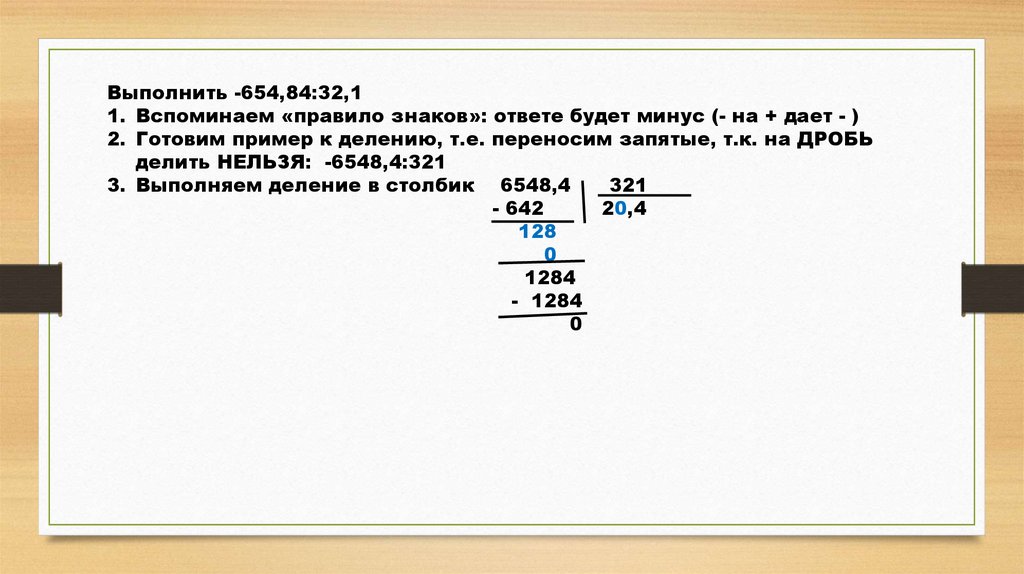 Делить на ноль нельзя.
Делить на ноль нельзя. Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас! Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели. Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку. Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
 Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!). Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
 Значит, B = C.
Значит, B = C. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать. Всегда.
Всегда. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике. Математики не правильно записали свое правило.
Математики не правильно записали свое правило. Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными». 2
2 А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
 В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу. Деление рациональных чисел
Деление рациональных чисел
 Например, для вычисления дроби
Например, для вычисления дроби

 Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

 Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.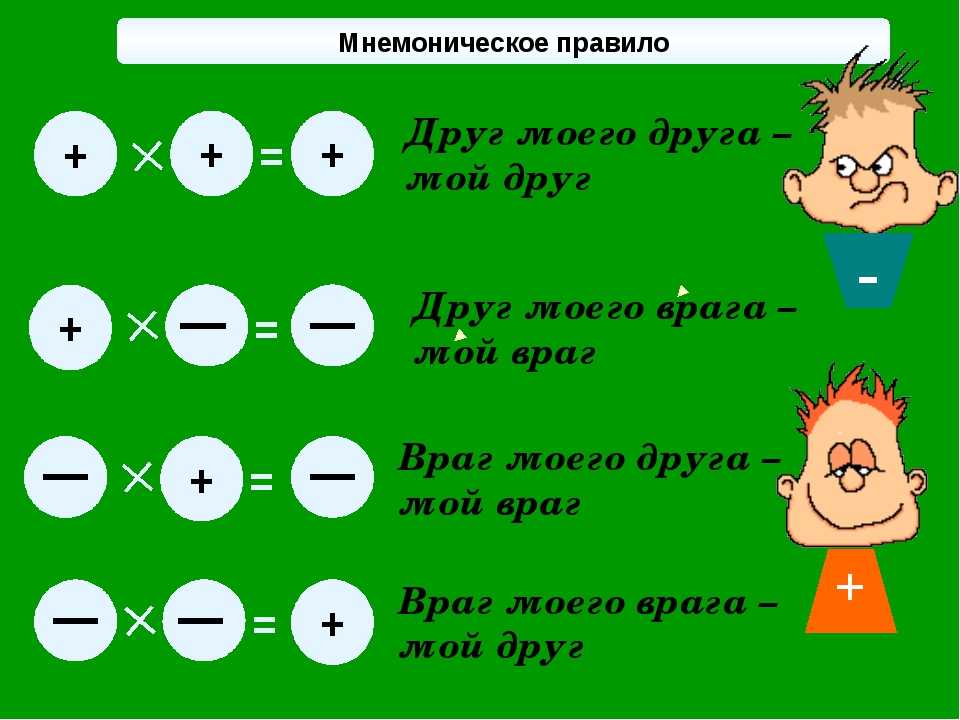 То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак! В таких случаях применяется следующее правило:
В таких случаях применяется следующее правило:


 То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.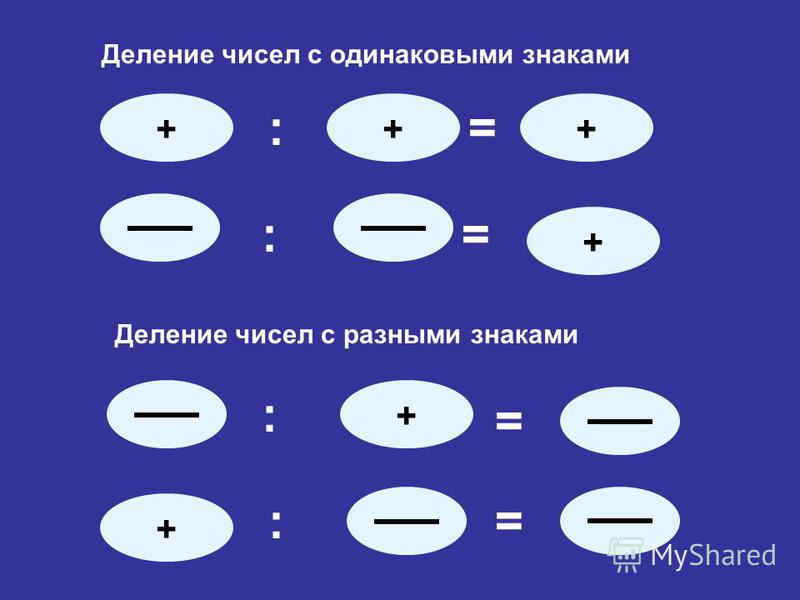

 Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс. com
com
 Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:
Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:

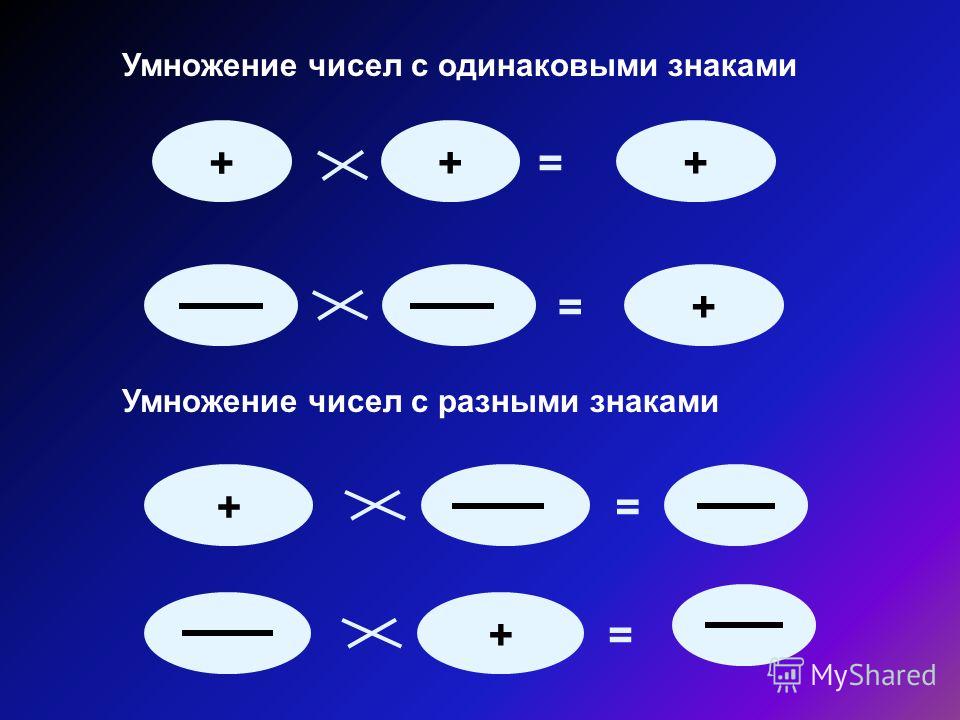 Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ.
Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ. Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями!
Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями!
 Тогда сумма будет равна −10+10 = 0.
Тогда сумма будет равна −10+10 = 0.

 е. в том направлении, в котором смотрели), положительное движение.
е. в том направлении, в котором смотрели), положительное движение.
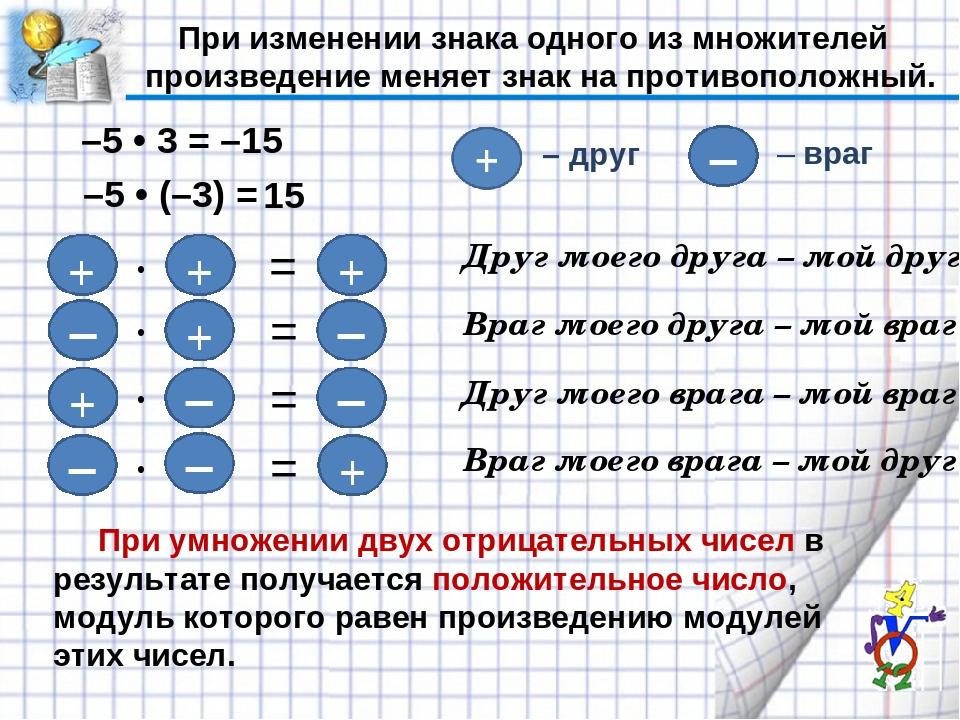 Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике. Например:
Например: Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например: При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
 В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.
В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.


 Сколько воды было в баке 3 дня назад ?
Сколько воды было в баке 3 дня назад ? Получая 4 больше каждый раз.
Получая 4 больше каждый раз.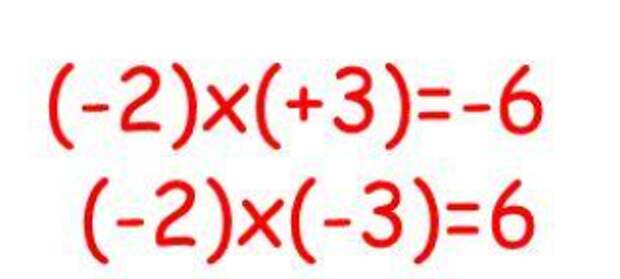 Получая 4 больше каждый раз.
Получая 4 больше каждый раз. Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.
Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел. Они могут использовать его для проверки перед экзаменами или для изучения темы.
Они могут использовать его для проверки перед экзаменами или для изучения темы.
 )
) От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.
От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.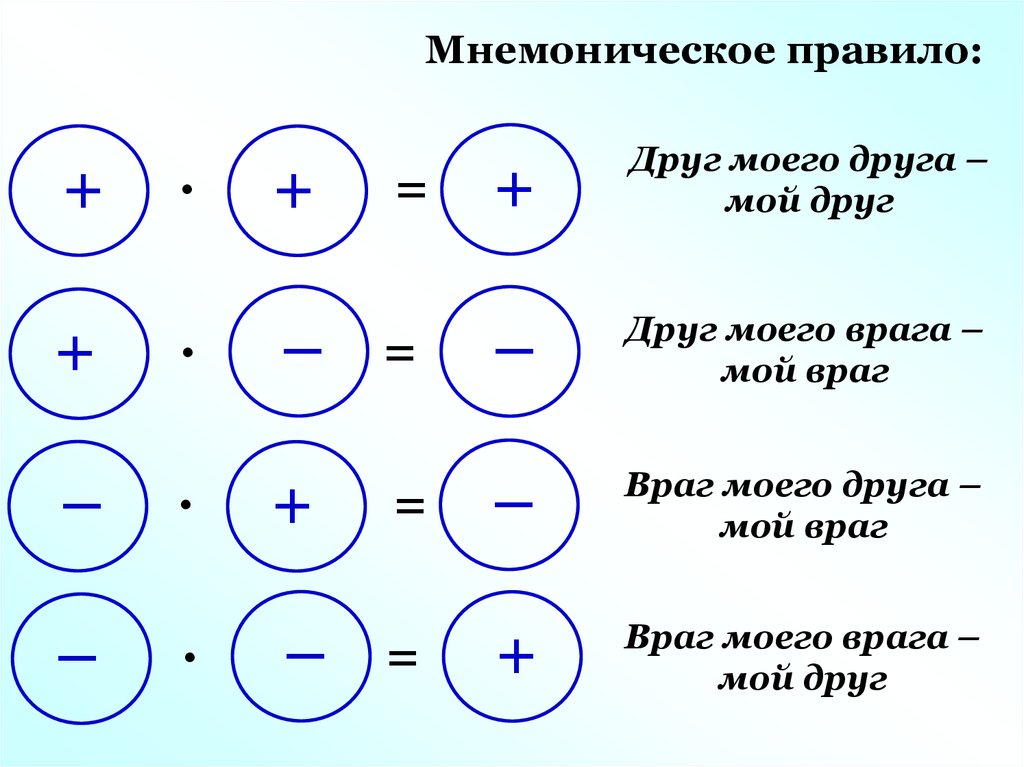 Отрицательное значение матрицы получается путем ее умножения на -1.
Отрицательное значение матрицы получается путем ее умножения на -1.
 Отрицательные пять, умноженные на отрицательные семь, дают положительное число 35,9.0003
Отрицательные пять, умноженные на отрицательные семь, дают положительное число 35,9.0003
 И на самом деле, наш расчет не включает ничего из этого. Затем мы выполняем любое умножение или деление. Опять же, в расчете их нет. Однако необходимо выполнить некоторые дополнительные вычитания. Мы заменяем отрицательное число три минус два, бит, который мы вычислили ранее, на отрицательное значение.
пять. Помните, что в противном случае мы сохраняем вычисления в том же порядке. Итак, мы собираемся оценить минус пять минус три.
И на самом деле, наш расчет не включает ничего из этого. Затем мы выполняем любое умножение или деление. Опять же, в расчете их нет. Однако необходимо выполнить некоторые дополнительные вычитания. Мы заменяем отрицательное число три минус два, бит, который мы вычислили ранее, на отрицательное значение.
пять. Помните, что в противном случае мы сохраняем вычисления в том же порядке. Итак, мы собираемся оценить минус пять минус три. Так или иначе, мы бы начали с вычисления минус три минус два, а затем
вычли из этого три.
Так или иначе, мы бы начали с вычисления минус три минус два, а затем
вычли из этого три.
 И довольно просто умножить на 10. Мы также знаем, что отрицательное число, умноженное на другое отрицательное число, дает
положительный. Итак, минус пять раз минус два тоже плюс 10.
И довольно просто умножить на 10. Мы также знаем, что отрицательное число, умноженное на другое отрицательное число, дает
положительный. Итак, минус пять раз минус два тоже плюс 10. И когда мы это делаем, мы создаем пробел, который заполняем нулем. Таким образом, отрицательное число 361, умноженное на 10, равно отрицательному числу 3610. Таким образом, ответ на отрицательное число 19умножить на 19 умножить на минус пять раз на минус два
отрицательный 3610.
И когда мы это делаем, мы создаем пробел, который заполняем нулем. Таким образом, отрицательное число 361, умноженное на 10, равно отрицательному числу 3610. Таким образом, ответ на отрицательное число 19умножить на 19 умножить на минус пять раз на минус два
отрицательный 3610. Прибавление минуса равносильно вычитанию плюса. Итак, 13 прибавить минус 19 — это то же самое, что 13 минус 19. И это минус шесть. Мы заменяем выражение в наших скобках на минус шесть, гарантируя, что мы
держите наш вопрос в том же порядке. И получается четыре минус минус шесть.
Прибавление минуса равносильно вычитанию плюса. Итак, 13 прибавить минус 19 — это то же самое, что 13 минус 19. И это минус шесть. Мы заменяем выражение в наших скобках на минус шесть, гарантируя, что мы
держите наш вопрос в том же порядке. И получается четыре минус минус шесть. что делаем и в каком порядке. Итак, давайте вспомним, что означают буквы. Первая буква обозначает скобки или квадратные скобки. Мы выполняем любые вычисления внутри пары круглых скобок. Теперь, если в этих скобках есть довольно сложная задача, мы еще раз
посмотрите, чтобы выполнить порядок операций над этим битом.
что делаем и в каком порядке. Итак, давайте вспомним, что означают буквы. Первая буква обозначает скобки или квадратные скобки. Мы выполняем любые вычисления внутри пары круглых скобок. Теперь, если в этих скобках есть довольно сложная задача, мы еще раз
посмотрите, чтобы выполнить порядок операций над этим битом. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
 Последнему научиться можно только решив тысячи задач.
Последнему научиться можно только решив тысячи задач. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным. 5
5 Это нужно, если описание к товару добавляется на стороне «Магазина».
Это нужно, если описание к товару добавляется на стороне «Магазина».
 Необходимо создать «Вес» через дополнительное поле и указать название этого поля в поле на стороне модуля в магазине. В данном случае вес будет загружен в карточку товара на стороне магазина в стандартное поле «Вес».
Необходимо создать «Вес» через дополнительное поле и указать название этого поля в поле на стороне модуля в магазине. В данном случае вес будет загружен в карточку товара на стороне магазина в стандартное поле «Вес». На стороне модуля необходимо прописать название поля и на стороне «МойСклад» прописать как дополнительное поле у товаров, название может быть произвольным, тип — дробное число.
На стороне модуля необходимо прописать название поля и на стороне «МойСклад» прописать как дополнительное поле у товаров, название может быть произвольным, тип — дробное число. Интернет-магазин заполнен, МойСклад пустой
Интернет-магазин заполнен, МойСклад пустой
 ..
..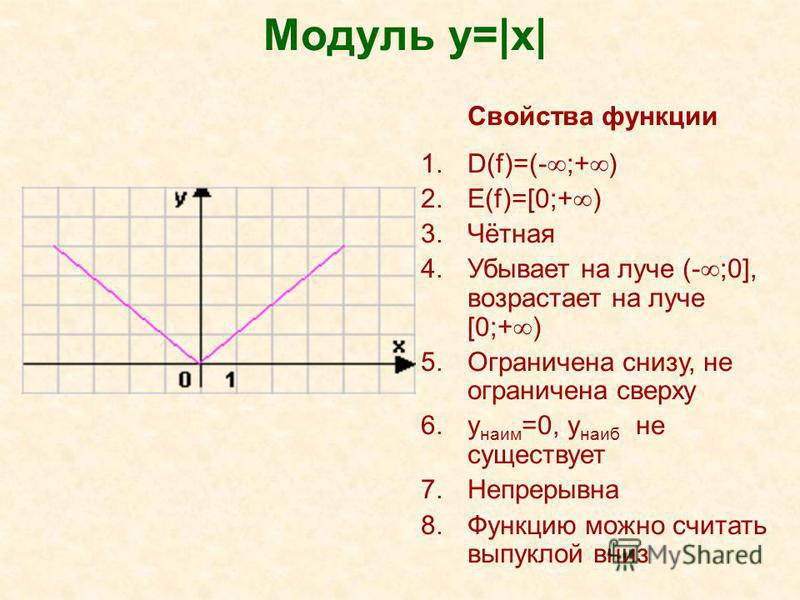 Комплексным числомz=x+iy называется упорядоченная пара действительных чисел : .
Комплексным числомz=x+iy называется упорядоченная пара действительных чисел : . 1) По предыдущей теореме имеем:
1) По предыдущей теореме имеем: Тогда точка имеет декартовыекоординаты , а и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
Тогда точка имеет декартовыекоординаты , а и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д. Поменяв местами и , получаем
Поменяв местами и , получаем 2.1 Определение Абсолютное значение или модуль действительного числа a (обозначается как |a|) определяется как
2.1 Определение Абсолютное значение или модуль действительного числа a (обозначается как |a|) определяется как  .
. -3| = |-6| = 6 = |2|.|3| = 6
-3| = |-6| = 6 = |2|.|3| = 6 2.5 ТЕОРЕМА — (Неравенство треугольника)
2.5 ТЕОРЕМА — (Неравенство треугольника) Последние версии модулей можно бесплатно скачать на странице загрузок.
Последние версии модулей можно бесплатно скачать на странице загрузок.

 Для удаления последней отмеченной точки при построении многоугольника нажмите «Esc» на клавиатуре.
Для удаления последней отмеченной точки при построении многоугольника нажмите «Esc» на клавиатуре.
 05.2011 00:00. По истечению заданного времени отображение объекта на карте прекратится. Чтобы убрать период отображения, щелкните «Сбросить» в справочнике «Дополнительные слои» или во вкладке «Описание расширенных настроек объекта».
05.2011 00:00. По истечению заданного времени отображение объекта на карте прекратится. Чтобы убрать период отображения, щелкните «Сбросить» в справочнике «Дополнительные слои» или во вкладке «Описание расширенных настроек объекта».



 Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
 Модуль положительного числа равен самому числу. Модуль нуля равен нулю. То есть для любого числа n, которое больше либо равно нулю, будет справедлива следующая формула |n| = n. Например, |15| = 15, то есть модуль числа 15 равен 15-ти.
Модуль положительного числа равен самому числу. Модуль нуля равен нулю. То есть для любого числа n, которое больше либо равно нулю, будет справедлива следующая формула |n| = n. Например, |15| = 15, то есть модуль числа 15 равен 15-ти. Кроме того, |a — b| = |b — a|, так как расстояние от точки a до точки b и расстояние от b до a равны друг другу. Например, |25 — 5| = |5 — 25|, то есть |20| = |- 20|.
Кроме того, |a — b| = |b — a|, так как расстояние от точки a до точки b и расстояние от b до a равны друг другу. Например, |25 — 5| = |5 — 25|, то есть |20| = |- 20|. 7.13
7.13 lua (по умолчанию /etc/lmod/lmodrc.lua)
lua (по умолчанию /etc/lmod/lmodrc.lua) Таблица — это общее название
хэш-таблица, словарь или ассоциативный массив. То есть хранит
пары ключ-значение. Это соглашение Lmod, что таблица называется с
завершающая буква T, чтобы напомнить нам, что это таблица.
Таблица — это общее название
хэш-таблица, словарь или ассоциативный массив. То есть хранит
пары ключ-значение. Это соглашение Lmod, что таблица называется с
завершающая буква T, чтобы напомнить нам, что это таблица. На
с другой стороны файл модуля может иметь два или более свойств.:
На
с другой стороны файл модуля может иметь два или более свойств.: поля в таблице управляют тем, как отображается свойство. За
пример:
поля в таблице управляют тем, как отображается свойство. За
пример: Если значение
разделена двоеточием, тогда каждая строка между двоеточиями должна быть
действительные ключи.
Если значение
разделена двоеточием, тогда каждая строка между двоеточиями должна быть
действительные ключи.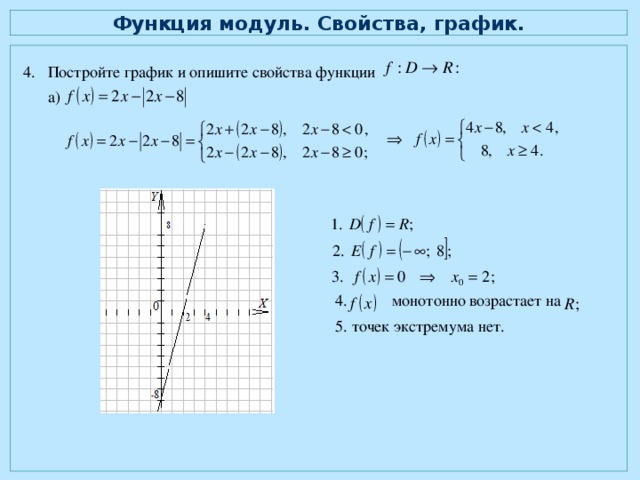 ХтмлДокумент, XmlDocument.
ХтмлДокумент, XmlDocument. «Повторное использование XModuleAttributes в TestCase»).
«Повторное использование XModuleAttributes в TestCase»).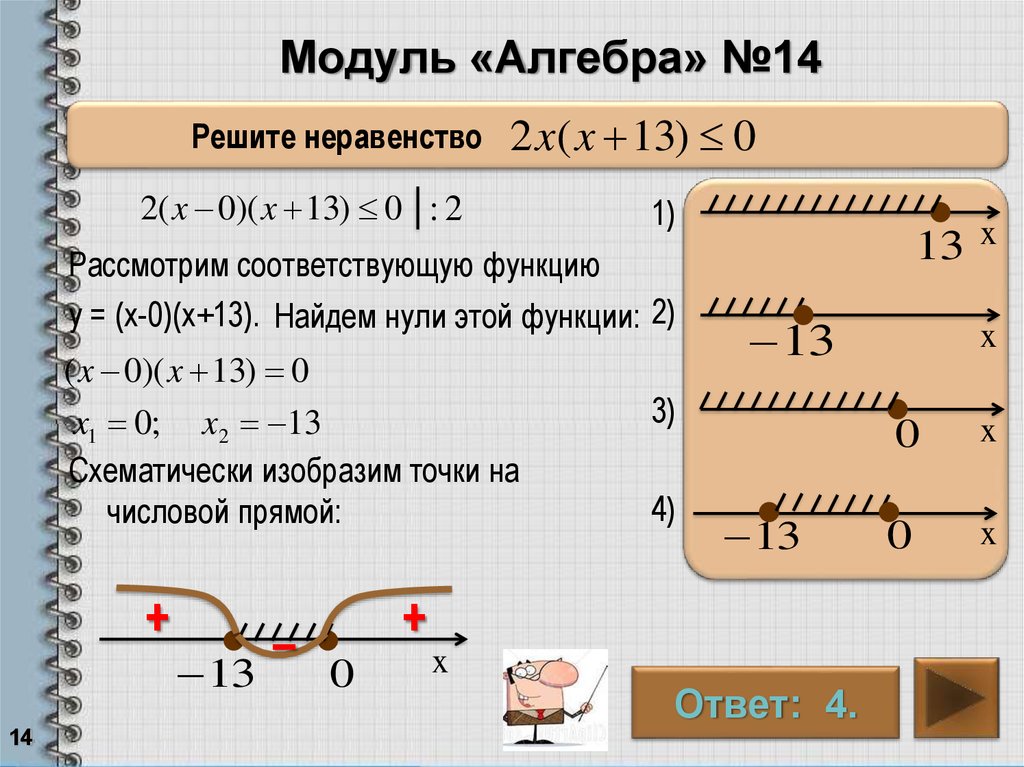 Может быть создано любое количество XTestStepValues.
Может быть создано любое количество XTestStepValues.

 д.). DataType указывает тип записи, указанный в поле Value TestStepValue.
д.). DataType указывает тип записи, указанный в поле Value TestStepValue. Затем это значение наследуется для специализаций и ссылок на модули (см. главу «Структура XModules»).
Затем это значение наследуется для специализаций и ссылок на модули (см. главу «Структура XModules»).
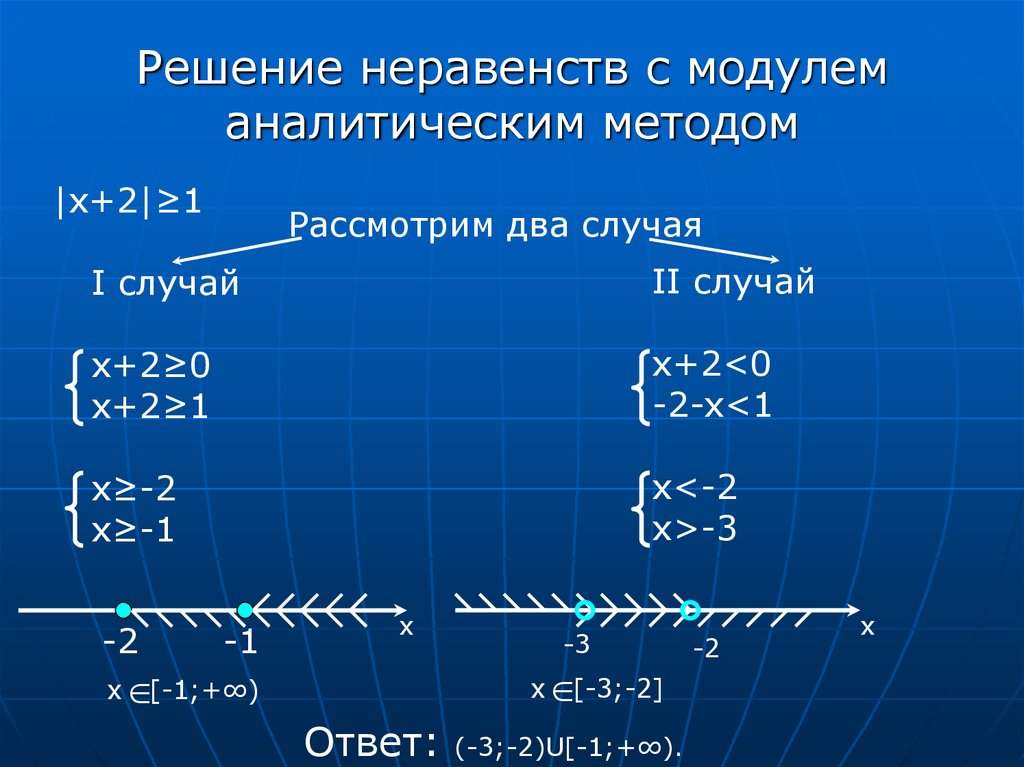 д.).
д.). «Значения TestStep, использование значений XTestStep»).
«Значения TestStep, использование значений XTestStep»). Абстрактные модули нельзя использовать в TestCase (см. главу «Обобщения и специализации»).
Абстрактные модули нельзя использовать в TestCase (см. главу «Обобщения и специализации»).
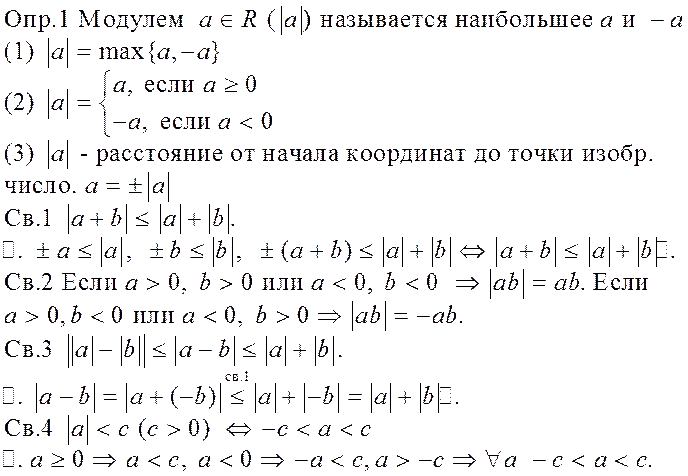
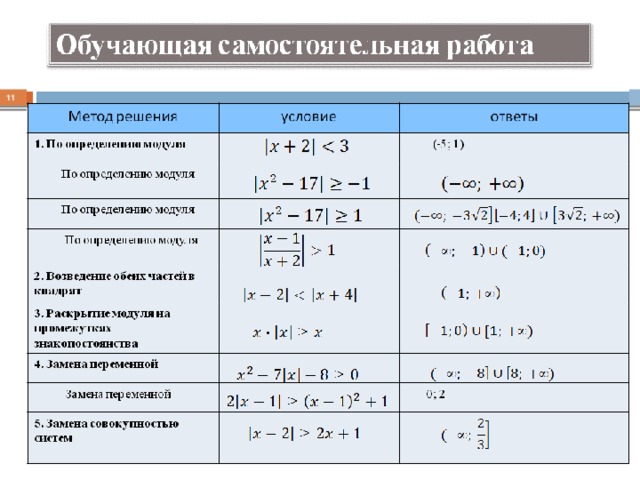 главу »
Назначить права пользователям или группам пользователей»).
главу »
Назначить права пользователям или группам пользователей»). Тип элемента управления (BusinessType) должен быть указан в качестве значения для этого свойства. Это никак не влияет на автоматизированное рулевое управление.
Тип элемента управления (BusinessType) должен быть указан в качестве значения для этого свойства. Это никак не влияет на автоматизированное рулевое управление. главу «Синхронизация — включить/отключить»).
главу «Синхронизация — включить/отключить»).
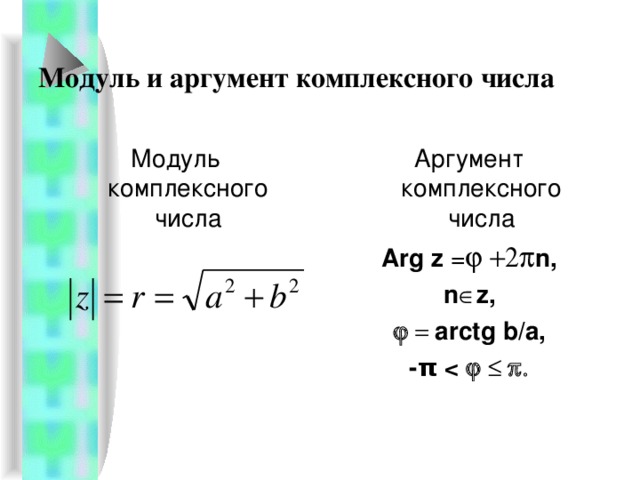 главу »
Назначение прав пользователям или группам пользователей»).
главу »
Назначение прав пользователям или группам пользователей»).

 03.2012)
03.2012) > Невозможно запросить значение этого свойства, так как оно не имеет доступного значения.
> Невозможно запросить значение этого свойства, так как оно не имеет доступного значения.
 applicationId
целевойSdk = 32
код_версии = код_версии_конфигурации
имя_версии = Config.имя_версии
proguardFiles(
getDefaultProguardFile("proguard-android-optimize.txt"),
"proguard-rules.pro",
)
}
типы сборки {
отлаживать {
signingConfig = signingConfigs.getByName («отладка»)
versionNameSuffix = "-отладка"
исшринкресаурцес = ложь
}
выпускать {
isShrinkResources = истина
signingConfig = signingConfigs.getByName («релиз»)
}
}
applicationId
целевойSdk = 32
код_версии = код_версии_конфигурации
имя_версии = Config.имя_версии
proguardFiles(
getDefaultProguardFile("proguard-android-optimize.txt"),
"proguard-rules.pro",
)
}
типы сборки {
отлаживать {
signingConfig = signingConfigs.getByName («отладка»)
versionNameSuffix = "-отладка"
исшринкресаурцес = ложь
}
выпускать {
isShrinkResources = истина
signingConfig = signingConfigs.getByName («релиз»)
}
}
 Это помогло, но теперь мои библиотечные модули не обфусцированы, что не является приемлемым решением
Это помогло, но теперь мои библиотечные модули не обфусцированы, что не является приемлемым решением
 4 of this series, I recommend you to check this link → Constructors and Access modifiers in TypeScript
4 of this series, I recommend you to check this link → Constructors and Access modifiers in TypeScript ..👇
..👇  setColor("Red")
setColor("Red") 
 ts
ts 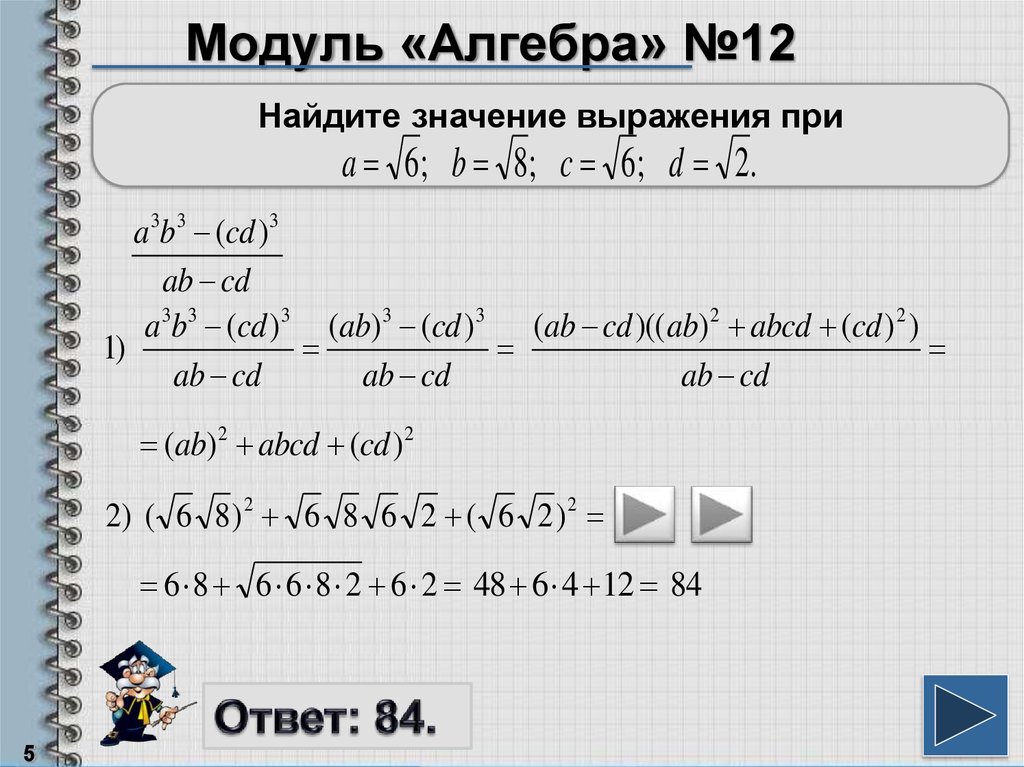

 В этом случае разработчик модуля может захотеть убедиться, что только те поля свойств, которые соответствуют контексту (то есть макету), отображаются в конструкторе сайтов, когда редактор страниц настраивает модуль.
В этом случае разработчик модуля может захотеть убедиться, что только те поля свойств, которые соответствуют контексту (то есть макету), отображаются в конструкторе сайтов, когда редактор страниц настраивает модуль. В качестве альтернативы, если для свойства макета установлено значение richTextWithImage , должны отображаться свойства featureRichText , featureImage и imageAlignment (но свойство featureText не должно отображаться).
В качестве альтернативы, если для свойства макета установлено значение richTextWithImage , должны отображаться свойства featureRichText , featureImage и imageAlignment (но свойство featureText не должно отображаться). "
}
},
"обязательно": ["название продукта"]
}
}
}
"
}
},
"обязательно": ["название продукта"]
}
}
}
 "
}
},
"обязательно": ["название продукта"]
}
}
}
"
}
},
"обязательно": ["название продукта"]
}
}
}
 ",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"область": "модуль",
"group": "Свойства макета"
}
}
}
{
"$type": "модуль контента",
"friendlyName": "Видимость конфигурации",
"имя": "конфиг-видимость",
"description": "Модуль проверки видимости конфигурации",
"categories": ["config-visibility"],
"теги": [""],
"действия данных": {
},
"конфигурация": {
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
}
}
",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"область": "модуль",
"group": "Свойства макета"
}
}
}
{
"$type": "модуль контента",
"friendlyName": "Видимость конфигурации",
"имя": "конфиг-видимость",
"description": "Модуль проверки видимости конфигурации",
"categories": ["config-visibility"],
"теги": [""],
"действия данных": {
},
"конфигурация": {
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
}
}
 ",
"тип": "строка"
},
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
},
"зависимые схемы": {
"название продукта": {
"характеристики": {
"подзаголовок": {
"тип": "строка",
"friendlyName": "Подзаголовок продукта",
"description": "Подзаголовок продукта."
}
},
"обязательно": ["название продукта"]
},
"макет": {
"один из": [
{
"характеристики": {
"макет": {
"перечисление": {
"Только обычный текст": "Только обычный текст"
}
},
"текст функции" : {
"тип": "строка",
"friendlyName": "Текст функции",
"description": "Заголовок основного текста для отображения в модуле.
",
"тип": "строка"
},
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
},
"зависимые схемы": {
"название продукта": {
"характеристики": {
"подзаголовок": {
"тип": "строка",
"friendlyName": "Подзаголовок продукта",
"description": "Подзаголовок продукта."
}
},
"обязательно": ["название продукта"]
},
"макет": {
"один из": [
{
"характеристики": {
"макет": {
"перечисление": {
"Только обычный текст": "Только обычный текст"
}
},
"текст функции" : {
"тип": "строка",
"friendlyName": "Текст функции",
"description": "Заголовок основного текста для отображения в модуле. "
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"ричтекстонли": "ричтекстонли"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле."
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"богатый текст с изображением": "богатый текст с изображением"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле.
"
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"ричтекстонли": "ричтекстонли"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле."
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"богатый текст с изображением": "богатый текст с изображением"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле. "
},
"изображение функции" : {
"тип": "изображение",
"friendlyName": "Название функции",
"description": "Изображение для отображения в модуле."
},
"выравнивание изображения": {
"friendlyName": "Выравнивание изображения",
"description": "Устанавливает желаемое выравнивание изображения по левому или правому краю текста.",
"тип": "строка",
"перечисление": {
"левый": "левый",
"верно-верно"
},
"по умолчанию": "слева"
}
}
}
]
}
}
}
"
},
"изображение функции" : {
"тип": "изображение",
"friendlyName": "Название функции",
"description": "Изображение для отображения в модуле."
},
"выравнивание изображения": {
"friendlyName": "Выравнивание изображения",
"description": "Устанавливает желаемое выравнивание изображения по левому или правому краю текста.",
"тип": "строка",
"перечисление": {
"левый": "левый",
"верно-верно"
},
"по умолчанию": "слева"
}
}
}
]
}
}
}









 Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

 Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям. Имеем:
Имеем:
 д. заменяются их значениями.
д. заменяются их значениями.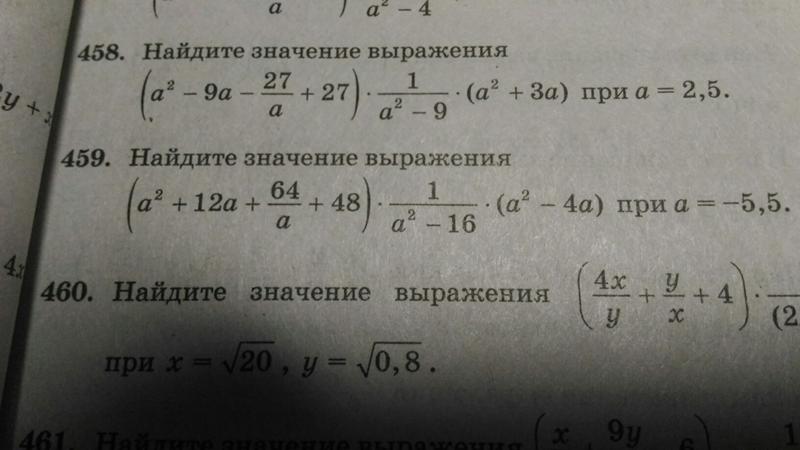
 При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
 Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
 Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.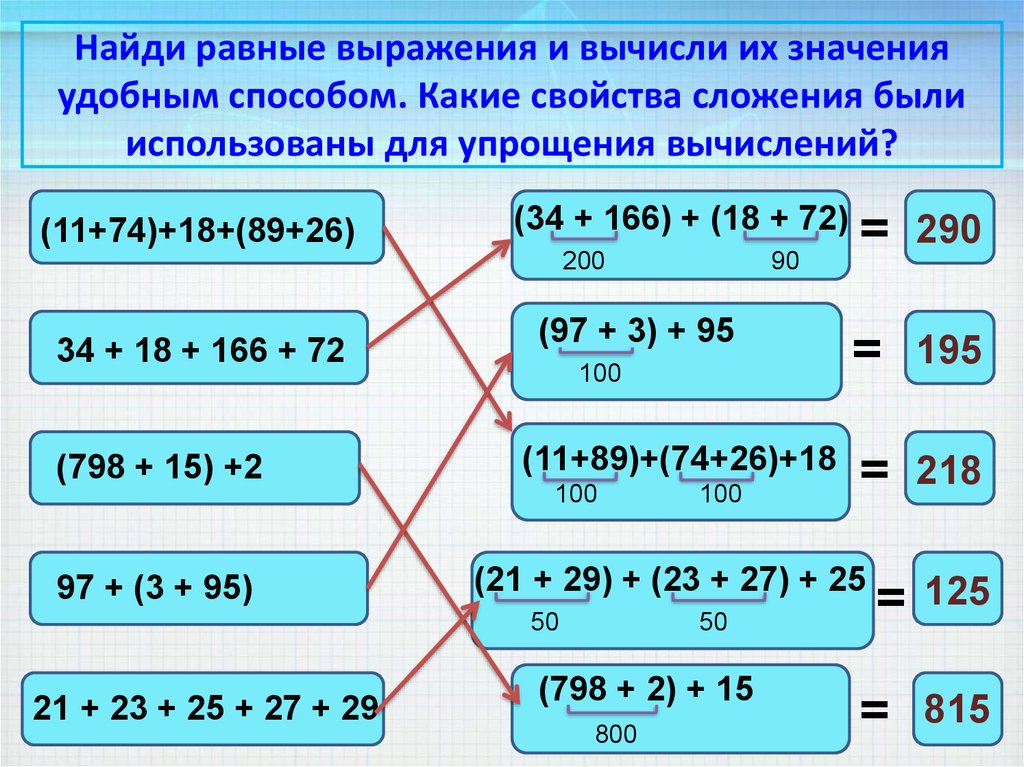


 Поясним на примере.
Поясним на примере. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
 Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.  Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
 Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.


 Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается. Сформулируем общее правило нахождения значений таких выражений.
Сформулируем общее правило нахождения значений таких выражений.
 С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
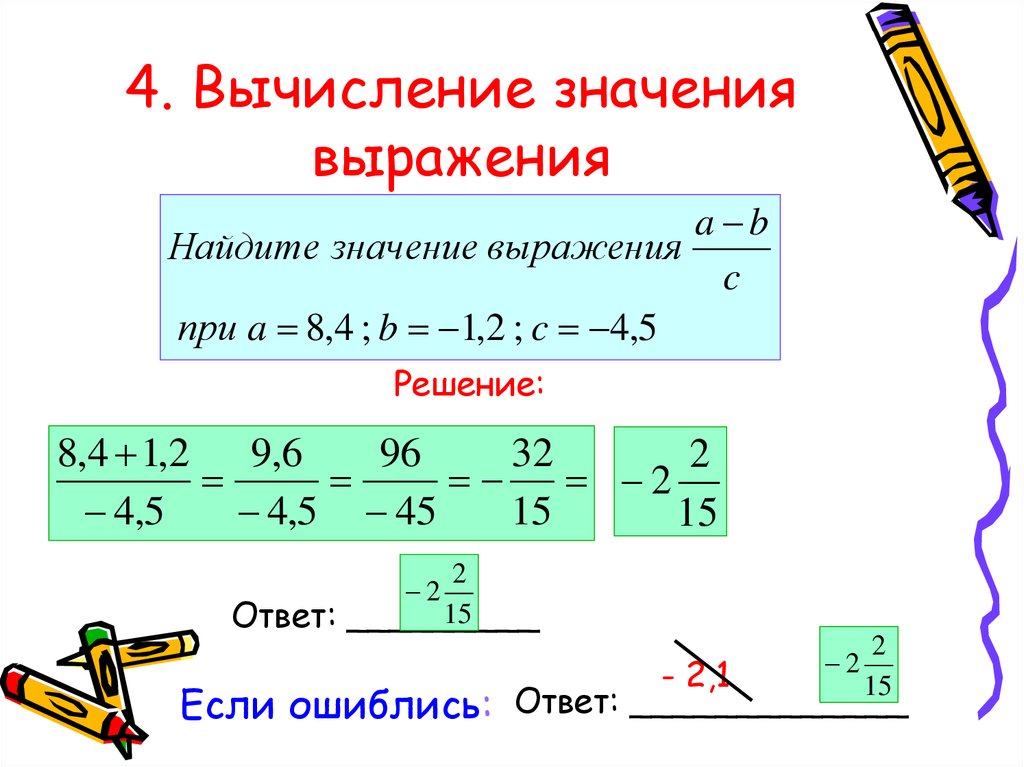




 Однако, в данном случае можно применить формулу сокращенного умножения.
Однако, в данном случае можно применить формулу сокращенного умножения. Упростим исходное выражение, чтобы найти его значение.
Упростим исходное выражение, чтобы найти его значение. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям. Имеем:
Имеем:
 д. заменяются их значениями.
д. заменяются их значениями.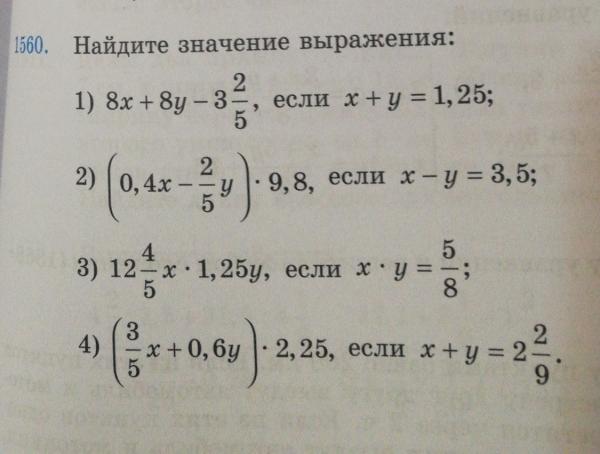
 При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
 Алгебра 8 класс
Алгебра 8 класс Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.

 Поясним это на еще одном примере.
Поясним это на еще одном примере.
 Рассмотрим решение примера.
Рассмотрим решение примера.


 Сначала — умножение и деление, затем — сложение и вычитание.
Сначала — умножение и деление, затем — сложение и вычитание.
 С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.




 Например, следующие выражения являются буквенными:
Например, следующие выражения являются буквенными: Например, запишем следующее выражение:
Например, запишем следующее выражение: Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.