Тесты МФПУ Синергия: Квалифицированная помощь в решении
Мировая система школьного и университетского образования постепенно переходит на тестовый способ контроля знаний обучающихся. Университет и колледж «Синергия» одними из первых разработали тесты по всем направлениям и специальностям. Поскольку дистанционный способ обучения является в вузе самым популярным, то и система тестов в МФПУ (МФПА) «Синергия» с каждым годом претерпевает качественные изменения.
На первый взгляд молодым людям, обучающимся в университете, кажется, что такой вид контроля прост, иногда нужно только лишь угадать правильный ответ. Это неверное мнение, онлайн тесты составлены с опорой на новые технологии, пройти их, не зная предмет, невозможно.
После неудачного прохождения испытания, тестирование начинает казаться молодым людям гораздо сложнее традиционного экзамена. В аудитории есть возможность подсмотреть конспект или другую шпаргалку, взять другой билет или разжалобить преподавателя. Сидя у собственного компьютера, такой возможности нет, на это не хватает времени.
Решить тесты факультетов «Синергии» требуется в определенный период времени. Если процент неверных ответов большой, система прекращает сеанс, а следующий возможен через определенное время. При таком положении дел учебная задолженность постепенно накапливается, что может привести к отчислению из университета.
Способы поиска решений онлайн тестов МФПУ «Синергия»
Начало сессии обычно знаменуется активным поиском верных ответов на вопросы тестов. Студенты ищут платные и бесплатные варианты помощи, их достаточно много, но все обладают определенными минусами.
- Выучить предмет от начала до конца и постараться пройти испытание самостоятельно. Такой вариант хорош для тех, кто имеет возможность учиться в течение семестра. Для этого должно быть соблюдено много условий: наличие времени, отсутствие лени, умение сосредоточиться на учебном процессе и выделить в потоке сетевой информации главные составляющие. Бывшим школьникам самостоятельная работа дается тяжело, слишком большое количество заданий кажется неподъемной ношей.

- Найти правильные ответы бесплатно на форуме «Синергии». Такой путь выбирают многие студенты, но обычно теряют на поиск верных решений слишком много времени, а по факту они оказываются неправильными либо устаревшими. Размещенные на форуме ответы и контрольные работы выполняли такие же студенты, а им свойственно ошибаться в процессе учебы.
- Попросить бесплатной помощи у друзей пройти испытание, либо заплатить специалисту, разбирающемуся в дисциплине. На деле бывает, что друзья сами не до конца разбираются в предмете и знания рекомендованного специалиста невозможно заранее проверить.
Получается, что все способы приводят к потере времени и разочарованию в своих действиях. К сожалению, бесплатный сыр бывает только в мышеловке, и эта пословица подходит для студенческих проблем.
Решить тестирование, сдать экзамен или зачет в МФПУ Синергии на “отлично” с помощью экспертов
Опыт студентов и их многочисленные отзывы показывают, что решение тестовых задач, написание рефератов, контрольных и дипломных работ лучше доверить профессионалам.
Схема общения с нашими менеджерами проста. Поняв, какие проблемы могут подстерегать его в ближайшую сессию, он может поделиться этой информацией на нашем сайте. Для этого нужно заполнить подготовленную форму. Заказчик указывает имя, адрес электронной почты, номер мобильного телефона. Затем заполняются графы, относящиеся к теме тестов: нужно указать курс, факультет и направление, а также название тестового учебного блока. В дополнительном поле можно указать важные требования.
Если у наших менеджеров задание не вызовет вопросов, они сразу запускают его в работу. Если вопросы появятся, перезвонят и уточнят все необходимые детали. Мы предлагаем также пройти тесты за обучающегося в «Синергии» студента. Для этого нам нужно доверить логин и пароль от «Личного кабинета», чтобы эксперты прошли тесты онлайн. Заказчики оплачивают сначала половину стоимости работы, вторую половину нужно доплатить при ее загрузке в «Личный кабинет».
За короткий промежуток времени мы пришлем заказчику абсолютно верные ответы на вопросы тестов и уникальные выпускные и текущие работы. Многолетнее сотрудничество с опытными преподавателями и научными работниками позволяет отвечать за качество выполняемых работ. Мы гарантируем конфиденциальность нашего сотрудничества и низкие цены на услуги. Учитесь с нами с удовольствием!
Многолетнее сотрудничество с опытными преподавателями и научными работниками позволяет отвечать за качество выполняемых работ. Мы гарантируем конфиденциальность нашего сотрудничества и низкие цены на услуги. Учитесь с нами с удовольствием!
Тесты Синергия.
 Ответы на тесты синергияТесты Синергия МФПУ ответы
Ответы на тесты синергияТесты Синергия МФПУ ответыБольше всего студентов волнуют не только итоговые экзамены в МФПУ «Синергия», но и промежуточные зачеты. Пугают не только сложные вопросы, но и умная система «безопасности» в мегакампус 2.0. Все это необходимо, чтобы обеспечить контроль уровня знаний обучающихся и выпустить действительно грамотных профессионалов своего дела.
Но бывают разные ситуации, когда срочно необходима помощь, чтобы качественно решить тесты «Синергии». Даже самый ответственный пользователь, студент Синергии может не разобраться с темой или оказаться в ситуации острой нехватки времени, а оказываться на грани отчисления – совсем не хочется.
Приобрести готовые работы можете в магазине
ПЕРЕЙТИ В КАТАЛОГ ГОТОВЫХ ОТВЕТОВМы поможем безопасно справиться с любым зачетом и экзаменом на высоком уровне. Но сначала разберемся:
Как же происходит сдача теста в мфпу «Синергия»?У каждого студента есть свой кабинет в системе megacampus 2.0, вход туда осуществляется с использованием личных логина и пароля. Допустим, вам необходимо сдать тесты синергия за 1 семестр, и вы выбираете тест психология синергия. Прежде чем приступить, нужно будет ознакомиться с правилами прохождения итоговых испытаний, временными ограничениями, количеством допустимых «промахов» и попыток начать все сначала.
А дальше вы нажимаете кнопку «Идентификация». Что же происходит?
Вебкамера считает ваше изображение, обычно такое сканирование длится не больше минуты, и только тогда вы сможете отвечать на вопросы тестов Синергии.
Такая технология онлайн-контроля используется уже во многих дистанционных образовательных учреждениях, чтобы исключить возможность помощи студенту иных лиц, при решении тестов мфпу. Ваше изображение с вебкамеры моментально отправляется в центр аналитики, где благодаря «умным» алгоритмам происходит сравнение снимка с исходными данными. Ведь ваша фотография хранится в базе университета еще с момента вашей регистрации на сайте. Обойти эту многоэтапную систему сканирования сложно, но мы контролируем, чтобы именно ваша фотография была отправлена алгоритму на проверку. Все это, благодаря открытым и легальным методам, позволяет убедить систему в подлинности и избежать блокировки на сайте мегакампуса во время вашей сессии.
И если вы обращаетесь к нам за помощью при решении тестов, мы гарантируем прохождение идентификации личности без проблем и неприятных последствий.
Сколько раз можно «завалить»?На тестирование по одному предмету дается всего лишь 3 попытки. Но обхитрить систему не получится ведь каждый раз, запуская новую попытку, вы будете получать совсем другой набор вопросов.
Так что, не спешите искать в интернете, где можно купить тесты синергии с ответами. Это не всегда поможет, ведь комбинация заданий каждый раз разная, и даже если у вас будет список решений на все существующие в системе вопросы, вы просто не успеете отыскать нужные, потому что время тест мфпу жестко ограничил.
Например, на поиск верных ответов по маркетингу, экономической теории, макроэкономике, русскому языку или элективной физической культуре в синергии вам будет предложено всего лишь 40 минут на одну попытку. Ни одной лишней секунды, чтобы замешкаться.
А вот на тест по математике в синергии отводится уже целых 2 часа, но не обольщайтесь, ведь в нем большая часть времени уйдет на решение сложных задач и примеров, с использованием множества формул. Такое же время дается и на тест по математическому анализу.
И за такое короткое время вы должны безошибочно справиться с половиной теста! Необходимое количество балов для сдачи зачета/экзамена по любому предмету – минимум 50.
Если во время экзамена в Синергии вы сумеете набрать от 90 до 100 баллов, система оценит вас «отлично». Если ваш итоговый результат окажется в промежутке между 70 и 89 баллами, рассчитывайте на оценку «хорошо». А набравшим от 50 до 69 светит только «удовлетворительно». С зачетом все еще проще: нужно лишь попытаться превысить порог в 50 баллов. Все, что меньше 50 баллов, автоматически приравнивается к оценке «неудовлетворительно».
Что, если не сдал даже за три попытки?В мегакампусе тест автоматически считается незачетным, если вы не набрали нужное количество верных ответов ни за один подход. А в случае с проваленным трижды экзаменом, вы получите оценку «неудовлетворительно».
Возможность пересдать, конечно, есть, но придется запрашивать пересдачу уже через деканат.
Почему студенты выбирают нас?- У наших специалистов большой опыт в решении тестов Синергия любой сложности.
- Мы помогаем с любыми дисциплинами университета «Синергия» и Московского открытого института.
- Сжатые сроки – не проблема.
- Расценки на помощь и консультацию вас устроят. Комфортный прайс, без переплат.
- Оказание помощи полностью конфиденциальное.
- Мы помогаем не только с тестами, а так же поможем закрыть полностью семестр (курсовые работы, бизнес практикумы, отчеты по практике).
- Качество выполнения всегда на высоте.
Так что, если вы совсем не уверены в своих знаниях, лучше выбрать надежный способ получить желанный «зачет»! Мы даем гарантию оценки хорошо/отлично в основных гуманитарных тестах синергии по русскому языку, истории, иностранному языку, и в сложных испытаниях по предметам как математика синергия, экономика и по другим предметам, и видам работ.
А это значит, что вы точно получите от 70 до 100 баллов по выбранным дисциплинам, и никаких проблем с пересдачами!
Выбирайте только надежных профессионалов для решения предметных тестов, бизнес практикумов, курсовых в Синергии. А главное, заранее оценивайте свои знания и возможности, чтобы успеть подтянуть слабые места в теории или вовремя обратиться к нам за помощью!
Обращайтесь к нам через контактные данные:Форма заказа через сайт: узнать стоимость и заказатьГотовы работы Тесты Синергия. Практики. Курсовые работы
МАГАЗИН ГОТОВЫХ РАБОТОтветы на тесты Синергия | заказать работу для МФПУ
СИНЕРГИЯ: ОТВЕТЫ НА ТЕСТЫ ПО ЛЮБОМУ ПРЕДМЕТУ
Вам скоро предстоит сдача онлайн-теста, но вы не уверены в своих силах? Боитесь, что не сдадите предмет с первого раза? Не волнуйтесь, мы здесь, чтобы помочь! История, экономика, эконометрика, финансовые стратегии и финансовое право, денежное обращение и кредит, основы юридической техники, экономический анализ деятельности банка, физическая культура и спорт – это лишь часть предметов, с которыми мы работаем. С нами студент уверенно сдаст сессию, несмотря на пробелы в знаниях и нехватку времени для подготовки к экзаменам.
КТО МЫ?
Наша компания работает официально, оказывая услуги студентам высших учебных заведений более 8 лет. Мы помогаем решить проблемы с усвоением знаний при минимальных усилиях и временных затратах. В наши услуги входит:
· выполнение индивидуальных заданий, независимо от их темы, сложности и вида;
· предоставление готовых ответов к тестам;
· выполнение любого типа контрольно-проверочных работ: эссе, контрольных, курсовых, рефератов;
· доработка готовых работ, доведение их до необходимого процента уникальности;
· помощь со сдачей зачетов и экзаменов;
· разработка дипломного проекта, включая составление речи для его защиты;
· решение проблем с прохождением практики, включая подготовку отчета по ней.
ЧЕМ МЫ МОЖЕМ ВАМ ПОМОЧЬ?
Одной из наших специализаций является подготовка ответов на имеющиеся по различным дисциплинам тесты. Поэтому, если у Вас есть проблемы с изучением какого-либо предмета, не стоит затягивать, ведь преодолевать трудности все равно придется. Обращайтесь за помощью к нам. Мы сможем помочь вам следующими способами:
1. Обеспечить Вас готовыми решениями. Обладая доступом к тестам МФПУ «Синергия», а также базе готовых ответов, мы предоставим Вам гарантированно правильный результат. Риск, неточности или ошибки полностью исключены.
2. Сдать тест за Вас, но в этом случае Вы предоставляете нам данные для входа в Ваш личный кабинет электронной системы учебного заведения. Вместо Вас сдавать тест будет наш специалист.
КАКОЙ СПОСОБ ВЫБРАТЬ?
Более удобным и надежным способом, по мнению специалистов, является второй. Объясним почему:
· В прохождении онлайн-тестов наш специалист обладает огромным опытом. Он не допустит случайных ошибок, поскольку всегда внимателен, собран, спокоен. Он гарантирует правильность ответов.
· Рассмотрим вариант, когда Вы, имея на руках готовые ответы к тестам, разволновались, не выспались, или что-то забыли. В этом случае существует риск допустить ошибки. Да и время тестирования ограничено – Вам попросту его может не хватить.
Исходя из этого, прибегнуть к помощи специалиста для получения положительной оценки – наиболее верное решение. В этом случае Вы избежите стресса, сэкономите личное время. Пока наш сотрудник проходит за Вас тест, Вы можете спокойно заниматься более важными делами. Это выгодно и удобно, поскольку исключает ненужные волнения.
ГАРАНТИЯ 100% РЕЗУЛЬТАТА
Для студентов на современном рынке сегодня довольно много возможностей для поиска исполнителей. Встречаются и недобросовестные, в полной мере не выполняющие свои обязательства перед клиентами. Нам понятно Ваше недоверие и настороженность, но в помощи с нашей стороны Вы можете быть уверены.
Сотрудничая с нами, Вы получите необходимую помощь и успешно пройдете тестирование. Хороший результат мы Вам гарантируем, поскольку:
· наш штат состоит из прошедших строгий отбор преподавателей, хорошо разбирающихся в предмете;
· наши сотрудники всегда на связи и ответят на интересующий Вас вопрос, помогут решить возникшие проблемы;
· мы обладаем доступом к учебно-методической базе «Синергия», поэтому правильность ответов гарантирована;
· наша компания официально зарегистрирована, с каждым клиентом заключается договор.
Мы те, кому стоит доверять. Свяжитесь с нами, и мы поможем решить проблемы с учебой!
Как сдать тесты в «Синергии» без лишних нервов
Как сдать тесты в «Синергии» без лишних хлопот, как лучше готовиться.
Когда приходит время сессии и сдачи экзаменов в «Синергии» для многих наступают непростые времена. К тестированию надо хорошо подготовиться, полезно также подробно разобраться, как именно устроен процесс экзаменации и сдачи зачетов в МФПУ Синергия.
После того, как студент освоил определенную тему, ему предоставляют доступ ко всем материалам для контроля знаний. Это тесты с заданиями, на выполнение которых дается ограниченное количество времени. Задания нужно выполнять сразу после проведения идентификации через вебкамеру, а время на выполнение ограничено, так что просто искать ответы через интернет не получится. На помощь придет решение тестов синергия, подробнее об этом можно прочитать на сайте тестсинергия.рф.
Среди итоговых испытаний, предусмотренных университетом есть такие виды:
Зачетные тесты в МФПУ
Эти испытания имеют промежуточный характер, их проводят после прохождения каждого семестра, они касаются всего объема знаний по определенной дисциплине. Если изучение дисциплины рассчитано на несколько семестров, то зачетное тестирование проводят только по одному пройденному за семестр блоку, а потом еще надо сдавать заключительный экзамен по всей дисциплине.
Зачетные тесты от экзаменов отличаются системой оценки. Зачетные тесты в МФПУ «Синергия» считаются успешно пройденными, если набрано больше 50 баллов. Это равняется оценке «удовлетворительно», то есть «тройке», но этого достаточно для получения зачета.
Экзаменационные тесты
К этим тестам понадобится более длительная и тщательная подготовка. Чтобы получить по ним положительную отметку понадобится набрать более чем 70 баллов. И, для получения оценки «хорошо» или «отлично», надо основательно готовиться. Часто студенты приобретают варианты с готовыми ответами, чтобы сдача экзамена была с гарантированным успехом.
Ответы на тесты МФПУ «Синергия» – помощь студентам
Невозможно сдать зачет или экзамен без предварительной подготовки. И вовсе не обязательно, чтобы она заключалась исключительно в выучивании заданного материала, ведь не всегда есть столько времени на учебу, не всегда бывает все понятно. Если нет времени все выучить самостоятельно, а предмет сдать хочется, то в этом могут помочь готовые ответы. Преимущество дистанционного обучения в университете «Синергия» в том, что экзамен сдается не лично преподавателю, а удаленно через интернет. Всегда есть возможность воспользоваться шпаргалкой, если плохо знаешь. Главное, чтобы шпора была, и чтобы ответы на вопросы в ней были правильными, иначе экзамен будет завален, а Вы отправитесь на пересдачу.
Где взять ответы на вопросы МФПУ «Синергия»
Заполучить готовые ответы на вопросы университета «Синергия» можно несколькими способами, каждый из которых имеет свои плюсы и недостатки:
- Составить их самостоятельно. Поступая таким образом, Вы сможете запомнить часть материала, пока будете искать нужную информацию, и абсолютно ничего не заплатите. Однако потратите уйму времени, причем без гарантии, что все Ваши ответы будут правильными и устроят Вашего преподавателя. Все же дисциплину Вы знаете не очень хорошо, а потому легко можете допустить ошибки, неточности, не раскроете полностью поставленный вопрос.
- Поиск бесплатных ответов на тесты МФПУ «Синергия», а также на зачеты или экзамены в интернете или у ребят со старших курсов. Преимущества этого метода заключаются в том, что не придется ничего платить, да и времени на поиск уйдет гораздо меньше, чем, если бы пришлось составлять их самостоятельно. Недостаток же состоит в том, что нет гарантии, что удастся найти шпаргалки по всем вопросам, которые могут быть на экзамене, к тому же не факт, что найденные варианты будут абсолютно правильными.
- Заказать ответы на вопросы Университета «Синергия» у нас. Вы получите полный перечень их на все вопросы, которые могут Вам встретиться. Все они будут правильными, полными и без ошибок. Вы сэкономите время, легко сдадите предмет, не будете испытывать стресс. Однако минус такого способа решения проблемы – плата за готовые варианты ответов. Однако плата небольшая. И это определено стоит того, учитывая, что Вы гарантированно сдадите зачет или экзамен, сэкономите уйму времени, будете чувствовать себя спокойно и уверенно.
Какой способ выберете Вы? Тот, который бесплатный, но при этом не несет никаких гарантий, или же тот, за который пусть и понадобится немного заплатить, но зато голова не будет болеть о том, что придется отправиться на пересдачу?
Наши ответы на вопросы университета «Синергия» — уверенность в сдаче сессии
Если Вы выбрали второй вариант, то Вы сделали правильный выбор. Зачем рисковать там, где можно получить гарантированный результат? Причем результат положительный! Мы можем предложить Вам готовые ответы для МФПУ «Синергия» абсолютно по всем дисциплинам, благодаря наработанной базе за время многолетнего сотрудничества с этим учебным заведением, а также благодаря наличию в штате специалистов в различных областях. Какой бы предмет Вы не сдавали, знайте, что мы рядом и всегда готовы помочь Вам с ним.
8 причин заказать ответы на вопросы университета «Синегрия» у нас
- Все ответы составлены специалистами, преподающими в ВУЗах. Они лаконичны, грамотно построены, не содержат ни единой ошибки, полностью раскрывают поставленный вопрос. При их составлении используется только актуальная информация.
- Предоставляем Вам ответы в течение 1-2 суток, поэтому если сдача предмета назначена на завтра, Вы успеете вовремя подготовиться к ней.
- Невысокие цены по сравнению с другими компаниями, предлагающими такие же услуги.
- Помогаем сдать любой предмет, независимо от того, какую специальность Вы осваиваете.
- Всегда на связи и готовы в любой момент прийти к Вам на выручку.
- Если нужно сдать тест, можем пройти его вместо Вас, что сэкономит Вам время и позволит избежать риска случайных ошибок по невнимательности, которые случаются, даже если используется шпаргалка.
- Соблюдаем конфиденциальность своих клиентов.
- Добросовестно выполняем взятые на себя обязательства и внимательно относимся к каждому студенту, обратившемуся к нам за помощью.
Когда нет времени подготовиться к зачету или экзамену самим, лучше не рисковать и не пробовать сдать его, отвечая наугад или пытаясь во время него пользоваться интернетом для поиска ответов. Так Вы вряд ли сдадите предмет, но вот то, что перенервничаете – это наверняка! Да еще и будете направлены на пересдачу. Лучше закажите у нас готовые ответы для МФПУ «Синергия», и успешно сдайте Ваш зачет, ни о чем не беспокоясь. Гарантированная положительная оценка, отсутствие стресса, простота сдачи предмета, значительная экономия времени – вот почему стоит обратиться к нам за помощью.
Психология. Ответы к тесту МФПУ Синергия — Тест
Психология. Ответы к тесту МФПУ Синергия
Тип: Тест Предмет: Психология Год сдачи: 2017 Итоговая оценка: 93 % 30 вопросов. Правильные ответы выделены маркером. Тест сдан в 2017 году на оценку «отлично» (93 балла), скриншот с результатом прилагается.
Тип темперамента, отличающийся подвижностью, склонностью к частой смене впечатлений, отзывчивостью и общительностью, — …
холерик
сангвиник
флегматик
меланхолик
Человек как представитель биологического вида называется
индивидуальностью
индивидом
личностью
субъектом деятельности
Человек как субъект межличностных и социальных отношений и сознательной деятельности называется
личностью
индивидом
индивидуальностью
субъектом деятельности
Чувства, связанные с переживанием прекрасного, возвышенного и способствующие личностному развитию, называются …
эстетическими
моральными
практическими
Ранее всего у ребенка проявляется … мышление
наглядно-образное
наглядно-действенное
пространственное
словесно-логическое
Сплоченность группы — это …
неоднозначное явление, т.к. она положительно влияет на психологический климат и мотивацию членов группы, но нередко препятствует самовыражению неординарных личностей
во всех отношениях положительное явление
нейтральное явление, само по себе не влияющее на продуктивность группы, отрицательное явление, т.к. всегда препятствует самовыражению личности
Акцентирование, типизация, агглютинация, аналогия — это приемы
внимания
воображения
памяти
мышления
Направленная сосредоточенность психической деятельности на определенных значимых сигналах — это…
ощущения
внимание
воображение
представление
Сторона общения, связанная с процессами взаимодействия партнеров, называется
перцептивной
коммуникативной
интерактивной
Тип темперамента, характеризующийся легкой ранимостью, способностью глубоко переживать даже незначительные события, -…
сангвиник
холерик
меланхолик
флегматик
К психическим процессам относится …
восприятие
направленность
темперамент
ощущения
Наглядный образ предмета или явления, возникающий на основе прошлого опыта путем его воспроизведе в памяти, — это …
припоминание
представление
узнавание
реминисценция
Свойство внимания, выражающееся в возможности более или менее легкого перехода от одного вида деятельности к другому, называется …
переключаемостью
рассеянностью
объемом
Мыслительная операция, направленная на выделение элементов, составляющих целый предмет или явление, это …
обобщение
анализ
синтез
сравнение
Вид памяти, сохраняющей информацию на время решения конкретной задачи (набора телефонного номера и пр.), — это… память
долговременная
оперативная
кратковременная
Примером направленности внимания является …
художественный образ
оптимизм
экстраверсия
интроверсия
Тип темперамента, проявляющийся в медлительности, устойчивости, слабом внешнем выражении эмоциональных состояний, -…
меланхолик
флегматик
сангвиник
холерик
Сторона общения, под которой подразумевают процессы восприятия человека человеком, называется
перцептивной
коммуникативной
интерактивной
Устойчивое эмоциональное отношение человека к явлениям действительности, возникающее при удовлетворении или неудовлетворении потребностей, называется …
направленностью
волей
эмоциями
чувствами
Психические явления, придающие своеобразие протеканию психических процессов, — это…
психические свойства личности
психические состояния
психические процессы
волевые процессы
К функциям воображения относится ..
регулирование эмоциональных состоянии
произвольная регуляция познавательных процессов и состояний человека образное представление действительности
формирование внутреннего плана действий
образное представление действительности, регулирование эмоциональных состояний, произвольная регуляция познавательных процессов и состояний человека и формирование внутреннего плана действий
Стремительные, бурно протекающие эмоциональные процессы — это
Чувства
аффект
фрустрация
стресс
Ощущения — это чувственное отражение
объективной реальности в виде отдельных свойств предметов и явлений
субъективной реальности в виде отдельных свойств предметов и явлений
объективной реальности в виде целостных образов
объективной реальности в виде целостных образов
Стандартизированный метод определения количественных показателей, направленный на выявление одного или нескольких взаимосвязанных параметров личности, — это …
анкетирование
контент-анализ
интервьюирование
тестирование
Группа, в которой выстраиваются эмоциональные отношения, но совместная деятельность направлена на удовлетворение личных интересов, называется …
командой
диффузной
ассоциацией
корпорацией
Восприятие-это…
субъективное отражение реальности в виде отдельных свойств предметов и явлений объективное отражение реальности в виде целостных образов объективное отражение реальности в виде отдельных свойств предметов и явлений субъективное отражение реальности в виде целостных образов
Неосознаваемое состояние готовности личности конкретным образом восприним действовать по отношению к окружающим его людям или объектам — это…
интерес
мировоззрение
установка
убеждение
Психические явления, устойчиво отображающиеся в принятии решений и поведении, называются
психическими процессами
психическими свойствами личности
неосознаваемыми психическими процессами
психическими состояниями
Активным видом воображения являются
непреднамеренное воображение
мечты
сны
грезы
Индивидуально-психологические особенности человека, проявляющиеся в деятельности и являющиеся условием успешности ее выполнения, называются …
способностями
направленностью темпераментом
характером
Свойство внимания, выражающееся в возможности выполнения одновременно двух работ, называется
переключаемостью
объемом
распределением
рассеянностью
отвлечением
устойчивостью
Помощь с тестами МФПУ Синергия от 50 руб.
Если у вас нет времени на выполнение теста для МФПУ Синергия, вы всегда можете попросить меня, пришлите тесты мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.Ответы на вопросы по заказу тестов для МФПУ Синергия:
Сколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.
Какой срок выполнения?
- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
Если требуется доработка, это бесплатно?
- Доработка бесплатна. Срок выполнения от 1 до 2 дней.
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости бесплатна.
Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.
Какие у вас гарантии?
- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.
В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время! Я стараюсь быть всегда онлайн.
Содержание:
- Ответы на вопросы по заказу тестов для МФПУ Синергия:
- Синергия (университет)
- Как происходит сдача тестов Синергии
- Как заказать тесты
Синергия (университет)
Вы учитесь в Synergy и пытаетесь пройти онлайн-тест? Есть два способа решения проблемы. Пока вы полностью не разберетесь в предмете или вместо этого обращайтесь за помощью к эксперту, который помжет с тестами.
Сегодня студенты, которые выбирают дистанционное обучение, чаще всего выбирают МФПУ Синергия. Дистанционная технология, используемая для обучения в этом университете, позволила тысячам студентов получить высшее образование. Обучение осуществляется через оболочку Megacampus 2.0.
Обращение за помощью ко мне экономит вам много времени и усилий и позволяет сосредоточиться на своих исследованиях по более важной и необходимой теме или заняться другими важными вопросами.
Я работаю строго под VPN. То есть невозможно определить IP и место входа в личный кабинет.
Как происходит сдача тестов Синергии
- Вы напишите мне логин/пароль и фото инструкцию куда нажимать и на какой тест, я или преподаватель самостоятельно проходит за Вас все интересующие предметы в мегакампус.
- Вы сфотографируете вопросы. Преподаватель выделит правильные ответы и вышлим вам.
Как заказать тесты
Напишите мне в воцап, и напишите подробно с чем вам помочь и мы с вами всё согласуем.
Наиболее часто заказывают тесты из этих Вузов и учебных систем:
- Витте (МИЭМП)
- Педкампус
- РАНХиГС
- ТюмГУ
- ЮУрГУ
- УрФУ
- МГСУ
- СПбГТИ
- СДО Прометей
- МФЮА
- МЭИ
- ТулГУ
- МЭСИ
- ТУСУР (ФДО)
- СДО ФЭМ
- УГНТУ
- ТОГУ
- Росдистант
- РГСУ
- МИИТ
- ВлГУ
- Мегакампус
- EDUCON
- РосНОУ
- Тесты по высшей математике
- Тесты по теории вероятности
- Тесты по физике
- Тесты по химии
Synergy — это сертификат испытаний, который дает. Мфпу «Синергия» отзывы
Недостатки:
- Грубость со стороны Анны Макаровой. Общение нецензурными словами.
Не так давно я поступил в Университет Синергия на дистанционное обучение, специальность — лингвистика. Мне очень понравилось удобство получения такого образования. Еще на этапе учебы в политехническом учебном заведении нам рассказали об этом вузе, и я был уверен, что обязательно туда поеду, так как это было большое количество преимуществ.
Поступило. Все было очень круто, мне предоставили данные для входа в личный кабинет с учебными материалами и тестами. Но не успев по-настоящему включиться в учебный процесс, столкнулся с проблемами, которые заставили меня подать заявление на вычет, подразумевающий возврат денег. Сотрудница Анна Макарова работала со мной на протяжении всего процесса. Этот несовершеннолетний был приставлен ко мне для того, чтобы периодически помогать в случае каких-либо затруднений. Увы, с возвратом денег возникли сложности. Этот сотрудник стал меня игнорировать, отвечая на вопросы, что называется «отвали».«Поскольку все документы на возврат уже поданы, по рекомендации Анны я решила подождать еще немного. Через пару месяцев я решила пойти в деканат этого вуза, чтобы разобраться в этой ситуации. В результате выяснилось, что в поданных на возврат документов были ошибки, и нужно было их перевыпустить. Потом после переоформления попросили подождать еще 45 дней. И эти 45 дней тоже прошли, еще несколько прошли месяцы.Проблема не решалась, пока я не оставил комментарии в группе этого вуза в соцсети … Через пару дней со мной связался сотрудник Аллева Рината. Этот неожиданно быстро решил мой вопрос, и я действительно поверил, что мир не без добрых людей … Сотрудник попал в ситуацию, был лоялен и с ним приятно общаться. Конечно, мои надежды почти не оправдались, но Ринат доказал обратное. В течение недели (опять же из-за задержек в финансовом отделе) деньги вернулись на мой счет.Спасибо большое, Ринат! Больше таких, как ты!
Преимущества:
- на лекции ходить не надо
- заметок на сайте
- сдача в виде тестов
Недостатки:
- есть сбои в личном кабинете
- не дозвонились до деканата
Я перевелась в этот вуз на дистанционное обучение с вечернего отделения другого вуза, потому что совсем не было времени ходить на лекции и ездить туда-сюда сначала в связи с беременностью, а потом с появлением ребенка.Я перешел на тот же 3-й курс, с которого ушел, но некоторые предметы пришлось закончить. В университете за меня подписали договор, оформили меня, дали логин и пароль к личному кабинету образовательного сайта. Как это работает: захожу в личный кабинет, вижу несколько дисциплин, у каждой есть план тренировок, конспекты лекций, список дополнительных. литературу, которую можно прочитать для дальнейшего изучения предмета. Затем, прочитав лекции, вы можете приступить к тесту.На тестирование в зависимости от тематики отводится около 40-60 минут. Вы можете использовать лекции и Интернет, если что-то не помните. Если вы не знаете, где искать в лекциях хоть немного теории, пройти ее проблематично. После прохождения теста оценка появится в журнале успеваемости. Помимо тестов, есть мастер-классы (что-то вроде зачетной работы) и курсовые работы. Все отправляется в электронном виде. Скачанные из Интернета работы не оцениваются. Недавно я прошел первую сессию, в которой были тесты, 4 мастер-класса и одна курсовая работа… Пришлось поработать, что-то даже осталось в памяти.
Считаю, что этот вуз рассчитан на тех, кто не может ходить на вечернее или дневное обучение, но хочет учиться, что при желании вполне возможно, и для тех, кто хочет быстрее получить «корочку». Например, тот предмет, который мне нужен, я изучил и понял, и сдал на отлично. Вещи, которые мне не нужны на работе, сдавал как-то «для галочки». Для тех, кто хочет, чтобы их сверлили, заставляли учиться, силой выколачивали знания из головы, этот вуз не подходит.
Цена на обучение вполне доступная — 15 750 руб. за семестр.
Когда я получила первое высшее образование по специальности экономист, она два года работала секретарем в адвокатской конторе. Она не собиралась работать по специальности, потому что уже имела солидный опыт работы в другой сфере. Я не хотел уезжать за меньшие деньги и начинать все сначала.
Сначала была секретарем, потом помощником юриста. И она уже могла работать самостоятельно — юристом, но не имела соответствующего образования.Не хотелось снова учиться, проходить этот нелегкий путь. К тому же образование требует времени. Большинство вузов Самары предлагают вечернее обучение: нужно посещать занятия по пятницам и субботам. Моему работодателю не нравится отсутствие сотрудника каждую пятницу. А еще придется брать отпуск во время сеансов, который иногда длится больше месяца и практически не оплачивается.
Но даже без юридического образования не было бы дальнейшего роста. Несколько лет искала подходящий вариант и нашла — это дистанционное обучение.
Университет Синергии находится в Москве. Я сформировалась такой, какой должна быть, когда поступила в университет. Был заключен договор об оказании платных образовательных услуг … Оригинал моего первого диплома забрали на время учебы. Оплата производится заранее за семестр. Оплачивать можно сразу за год.
После зачисления ключи из личного кабинета на сайте вуза. Туда отправляются задачи, которые необходимо выполнить до указанного срока.Задания были самые разные: вопросы, тесты, практические задания, сочинения. Как правило, указывались требования к их выполнению — объем, шрифт и т.д.
Задачи сложные. В Интернете особо нечего найти. Теоретические вопросы построены таким образом, что на них сложно дать однозначный ответ. Создан для интеллекта, логики и, конечно же, знаний ученика. Пришлось выразить свои мысли. В то же время было интересно.
Если бы это было мое первое образование, я не уверен, что сделал бы его сам. Мне, вероятно, придется связаться с фирмами, которые помогают выполнять задания в колледже. Но хорошо, что к тому времени у меня уже был солидный опыт практической работы … Но и это иногда не помогало, я обращалась за советом к коллегам.
Задания отнимали много времени, хотелось выполнять их как можно лучше, чтобы получить хорошие баллы. Некоторые предметы, как и в большинстве вузов, не оценивались, выставлялся только зачет.
Большой плюс — возможность выполнять задания по выходным, вечером, в общем, когда есть свободное время. Вам не нужно никуда идти.
Так прошло два года, я оплачивал обучение по семестрам и выполнял задания. Вы должны быть осторожны с оплатой в университете и не пропускать сроки. В противном случае бухгалтерия Synergy может наложить штраф. Иногда они намеренно путают студентов со сроками, чтобы оштрафовать. Ну это один из минусов, они везде.В любом университете придумывают всевозможные расходы, кроме обучения.
Когда дело дошло до моего диплома, я получил список тем на выбор и целую брошюру на нескольких страницах с требованиями для диплома. Тема оговаривается заранее примерно за полгода. Но есть проблемы с условиями защиты в Synergy. По учебному плану у меня должна была быть охрана в мае, но она была перенесена на начало марта, и об этом сообщили только в феврале.Диплом надо было писать за месяц. В этом институте очень строгие требования к литературе, используемой в дипломе — она должна быть новой. Если в списке есть учебники и книги, возраст которых превышает пять лет с момента публикации, то оценка защиты может быть понижена. После того, как диплом будет полностью заполнен, вам необходимо получить отзыв от научного руководителя и отзыв от рецензента. Текст диплома проверяется в программе антиплагиата; он должен содержать не менее 70% самостоятельного текста.Остальные 30 — цитаты из книг.
Мне вручили настоящий диплом государственного образца об окончании школы.
Так что получить второе высшее образование вполне возможно.
Преимущества:
- Вы можете выполнять задачи в любое удобное время
- в наличии
- нет необходимости посещать занятия
- недорогая плата за обучение
Недостатки:
- необоснованно начислить штрафы
- неточные сроки защиты диплома
Я студент 3 курса ООО «Синергия» в Москве по направлению «Менеджмент в ресторанном и гостиничном сервисе».Меня все устраивает, проблем с прохождением сеансов нет. В классах тоже все учителя не только читают лекции, но и сами работали и работают в этой сфере. По учебе претензий нет. Нас постоянно водят на форумы, которые проводит институт, что тоже очень здорово. Интерьер тоже очень современный, кофейни, магазины, места для ночлега. Люди вокруг интересные. Дети со многих факультетов трудоустраиваются в университете и проходят стажировку.Минусов не видел уже три года. Учусь на Соколе, единственное пешком до метро 15 минут
Как успешный выпускник университета на факультете информационных технологий, я расскажу вам, как это на самом деле, и дам несколько советов.
Было МФПА, теперь МФПУ «Синергия». Есть разница, качественно высокий уровень стал. Что ж, я не могу назвать синергию редакцией шараша. Сейчас все нарядно подкрутили и без включения мозга учиться будет сложно, ну а тех, у кого его нет, обычно отчисляют.В начале 1-го курса в группе было 35 человек, затем к 5-му году было ликвидировано много людей + были реабилитированные после армии или переведенные. В итоге на защиту диплома вышло около 15 человек из первоначального коллектива! Мои друзья учились в штате. учреждения и там они реально перепугались.
Первое и самое главное правило, которое нужно запомнить будущим школьникам: никто не будет тащить вас за ручку, все вопросы нужно решать нам самим, высшее учебное заведение изначально подразумевает, что у человека есть зачаток мозга и у него есть Уникальное достоинство (в нынешнем тренде это так) — независимость.
Второе правило вы хотите выучить? — см. первое правило. Знания даны и современные, а не так, как я пытался сделать в одном государстве. университет на красной линии с обшарпанными стенами и компьютерными «гробами» 15 дюймов, до сих пор пользовался Эльбрусом.
Правило третье — общайтесь с людьми и будьте в курсе всех событий. Вы не можете? Ты не знаешь? Вы застенчивы? — Неважно, жизнь научит или, чаще всего, заставит.
Правило четвертое — не груби с незнакомцами… Некоторые очень «лестно» отзываются о деканате. У меня лично с деканатом проблем не было, но были организационные вопросы и довольно часто, но сразу запомнил правило 1 и 3. Конечно, были люди, которые скачивали права и все остальное, но обычно те, что в Интернете называются ваша школота.
А теперь подробнее об обучении.
Есть много разных предметов, и из всего, что мы рассмотрели, главное, что из вас получается лидер с базовыми обширными знаниями, разными направлениями… Вам дается база, с которой можно начать углубленное самостоятельное (см. Правило 1) обучение.
Экзамены, курсовые, государственные, диплом.
Здесь все совсем иначе. Но в целом будет так: здесь плохо, это не по ГОСТу, здесь тема не раскрывается, нет описания, нет ссылок на литературу, нет графика или графика другого, нет расчетов и формул, но как вы это получили, и почему вы это сделали, а не иначе.В общем, в процессе будет чем заняться и если учесть правило 1, если знаний не получишь, вгонят, как говорится — плохая голова, в ногах нет покоя: ) Именно поэтому вы часто будете лично встречаться с преподавателями и деканатом, а потом воспользуетесь правилами 3 и 4, а потом, осознав все, снова переходите к правилу 1.
ГОС конечно удивила, жестоко было. В гос. uni не часто бывает. Ну, как получилось, что вы пришли с бумажкой, тут же взяли и рассказали, а потом достали мобильник, можно лететь из штата.Как по мне, GOS в целом не так уж и сложна, например:
1. Стандарты MRP, MRP II, ERP, ERP II: основные принципы применения
2. Национальные и международные стандарты и рекомендации по аудиту информационной безопасности.
3. Основные виды средств несанкционированного доступа и методы противодействия им.
4. Выполните криптографическое преобразование шифрования сообщения с заданными параметрами, используя полиалфавитный шифр (шифр Viginer).
5. Определите минимальное количество ключей, необходимых для обеспечения безопасности связи с системой симметричного шифрования и связи «каждый с каждый».
Около 100 вопросов, ну что на них ответить прямо сейчас? 🙂
Это я выделил такие посредственные вопросы, вопросы типа: Обзор возможностей версий MS WINDOWS, даже не рассматриваю.
Ну например шифр Вижинер, страшно? Погуглить там ничего сложного, требуется лишь минимальный зачаток мозга.
Что самое интересное, при подготовке к ГСН есть отдельные издания для подготовки, это сухая выписка из тонны книг, супер удобно.
Ну и в заключение хочу сказать, что статус вуза растет, как среди студентов, так и среди работодателей. Причиной тому является синергетический эффект, поэтому он получил название МФПУ «Синергия». Есть и бюджетные места, где Дмитрий Медведев лично приехал в вуз, и тенденция развития очень перспективная, и если мыслить глобально, а действовать локально, то все будет хорошо.
———
Удачи и успехов.
Итак, наша проклятая школа — Одинцовская гимназия №7 (которую я, слава богу, окончила) сотрудничает с Университетом Синергия.Я просто ненавидел свою школу, в которой якобы преподают, и поэтому больше не мог думать ни о чем хорошем об университете Synergy.
В 9 классе к нам пришли два представителя этого вуза. Вместо одного урока нам дали печатные задания по трем разным предметам: русский язык, математика и, на мой взгляд, еще история.
Я выбрал математику. Эти задачи необходимо было решать. Естественно, нужно было указать контактную информацию. Тех, кто набрал наибольшее количество баллов, вызывали и приглашали в институт для получения сертификата.Конечно, во время разговора хвалили, но как насчет того, чтобы без этого звонить будущим школьникам? Конечно, обрадовалась и поехала по указанному адресу с мамой и сестрой (во время звонка сказали, что можно брать с собой родителей). Мы пошли в Университет «Синергия» возле метро Семеновская.
Я училась в классе «Б», когда приехала и собралась в других людях, увидела еще двух девочек из нашей школы только из параллельного класса «С». В общем, часа два, а может и больше, всем собравшимся показали презентацию, рассказали о Synergy и похвалили свой университет.Было так скучно и скучно. Потом нам выдали сертификаты. По математике набрала 48 баллов (но, поверьте, для честного ученика нашей школы это совсем не мелочи!).
Кстати, у нас уже были контракты на столах. Лично я просто хотела получить аттестат, а после 9 класса уходить совсем не собиралась.
Потом нам обещали чаепитие, но на чаепитие мало кто пришел, кто-то просто не слышал, куда идти, кто-то вообще ничего не слышал о чаепитии.В целом чаепитие Synergy Business School было очень и очень экономичным.
В общем, после таких «открытых дверей», где-то через день-два все равно звонили, спрашивали, нравятся ли они, выбрали ли мы какую-то специальность для себя. Я не скрывал, что мне с ними совсем не нравится. Мне все это не нравилось с самого начала. потому что это выглядело так, как будто они уже были студентами, как привлечь студентов к себе, но все эти бесполезные «привлечь больше студентов для оплаты» еще не закончились.
В этом году я закончил школу (11 класс). После поступления в университет она взяла академический отпуск из-за болезни.
Недавно нам позвонили из Министерства образования на дом. И стали говорить, что сейчас дипломы дают отличный заработок, второе высшее образование — это поощряется, потому что сейчас так сложно устроиться на работу и все такое бла-бла-бла. Когда я сказал, на какую специальность поступил, человек из отдела образования сразу стал говорить: «Да, сейчас высокооплачивается» и стал предлагать мне дистанционное обучение.Долгое время он был убежден, что дипломы и второе высшее образование так важны. Лично меня не волнуют мои дипломы, даже если я работаю дворником, главное, чтобы вы себя не продавали, а дело не в этом … Среди университетов, которые они продвигали, была Synergy.
Да, это довольно известный университет, но то, как они пытаются обмануть своих студентов, вызывает у меня отвращение. Аттестат якобы что-то дает при поступлении, якобы больше шансов.Я закрашу и выложу что-нибудь, чтобы показать, как выглядит их сертификат.
Видеообзор
Synergy — это сертификат испытаний, который выдает. Мфпу «Синергия» отзывы
Недостатки:
- Грубость со стороны Анны Макаровой. Общение нецензурными словами.
Не так давно я поступил в Университет Синергия на дистанционное обучение, специальность — лингвистика. Мне очень понравилось удобство получения такого образования.Еще на этапе учебы в политехническом учебном заведении нам рассказали об этом вузе, и я был уверен, что обязательно туда поеду, так как это было большое количество преимуществ.
Поступило. Все было очень круто, мне предоставили данные для входа в личный кабинет с учебными материалами и тестами. Но не успев по-настоящему включиться в учебный процесс, столкнулся с проблемами, которые заставили меня подать заявление на вычет, подразумевающий возврат денег. Сотрудница Анна Макарова работала со мной на протяжении всего процесса.Этот несовершеннолетний был приставлен ко мне для того, чтобы периодически помогать в случае каких-либо затруднений. Увы, с возвратом денег возникли сложности. Этот сотрудник стал меня игнорировать, отвечая на вопросы, что называется «отвали». Поскольку все документы на возврат уже поданы, по рекомендации Анны я решила подождать еще немного. Через пару месяцев я решил пойти в деканат этого вуза, чтобы разобраться в этой ситуации. В результате выяснилось, что в поданных на возврат документов были ошибки, и необходимо их переоформить.Затем, после перевыпуска, меня попросили подождать еще 45 дней. И те 45 дней тоже прошли, прошло еще несколько месяцев. Проблема не решалась, пока я не оставил комментарии в группе этого вуза в соцсети … Через пару дней со мной связался сотрудник Аллева Рината. Этот неожиданно быстро решил мой вопрос, и я действительно поверил, что мир не без добрых людей … Сотрудник попал в ситуацию, был лоялен и с ним приятно общаться. Конечно, мои надежды почти не оправдались, но Ринат доказал обратное.В течение недели (опять же из-за задержек в финансовом отделе) деньги вернулись на мой счет. Спасибо большое, Ринат! Больше таких, как ты!
Преимущества:
- на лекции ходить не надо
- заметок на сайте
- сдача в виде тестов
Недостатки:
- есть сбои в личном кабинете
- не дозвонились до деканата
Я перевелась в этот вуз на дистанционное обучение с вечернего отделения другого вуза, потому что совсем не было времени ходить на лекции и ездить туда-сюда сначала в связи с беременностью, а потом с появлением ребенка.Я перешел на тот же 3-й курс, с которого ушел, но некоторые предметы пришлось закончить. В университете за меня подписали договор, оформили меня, дали логин и пароль к личному кабинету образовательного сайта. Как это работает: захожу в личный кабинет, вижу несколько дисциплин, у каждой есть план тренировок, конспекты лекций, список дополнительных. литературу, которую можно прочитать для дальнейшего изучения предмета. Затем, прочитав лекции, можно переходить к тесту.На тестирование в зависимости от тематики отводится около 40-60 минут. Вы можете использовать лекции и Интернет, если что-то не помните. Если вы не знаете, где искать в лекциях хоть немного теории, пройти ее проблематично. После прохождения теста оценка появится в журнале успеваемости. Помимо тестов, есть мастер-классы (что-то вроде зачетной работы) и курсовые работы. Все отправляется в электронном виде. Скачанные из Интернета работы не оцениваются. Недавно я прошел первую сессию, в которой были тесты, 4 мастер-класса и одна курсовая работа… Пришлось поработать, что-то даже осталось в памяти.
Считаю, что этот вуз рассчитан на тех, кто не может ходить на вечернее или дневное обучение, но хочет учиться, что при желании вполне возможно, и для тех, кто хочет быстрее получить «корочку». Например, тот предмет, который мне нужен, я изучил и понял, и сдал на отлично. Вещи, которые мне не нужны на работе, сдавал как-то «для галочки». Для тех, кто хочет, чтобы их сверлили, заставляли учиться, силой выколачивали знания из головы, этот вуз не подходит.
Цена на обучение вполне доступная — 15 750 руб. за семестр.
Когда я получила первое высшее образование по специальности экономист, она два года работала секретарем в адвокатской конторе. Она не собиралась работать по специальности, потому что уже имела солидный опыт работы в другой сфере. Я не хотел уезжать за меньшие деньги и начинать все сначала.
Сначала была секретарем, потом помощником юриста. И она уже могла работать самостоятельно — юристом, но не имела соответствующего образования.Не хотелось снова учиться, проходить этот нелегкий путь. К тому же образование требует времени. Большинство вузов Самары предлагают вечернее обучение: нужно посещать занятия по пятницам и субботам. Моему работодателю не нравится отсутствие сотрудника каждую пятницу. А еще придется брать отпуск во время сеансов, который иногда длится больше месяца и практически не оплачивается.
Но даже без юридического образования не было бы дальнейшего роста. Несколько лет искала подходящий вариант и нашла — это дистанционное обучение.
Университет Синергии находится в Москве. Я сформировалась такой, какой должна быть, когда поступила в университет. Был заключен договор об оказании платных образовательных услуг … Оригинал моего первого диплома забрали на время учебы. Оплата производится заранее за семестр. Оплачивать можно сразу за год.
После зачисления ключи из личного кабинета на сайте вуза. Туда отправляются задачи, которые необходимо выполнить до указанного срока.Задания были самые разные: вопросы, тесты, практические задания, сочинения. Как правило, указывались требования к их выполнению — объем, шрифт и т.д.
Задачи сложные. В Интернете особо нечего найти. Теоретические вопросы построены таким образом, что на них сложно дать однозначный ответ. Создан для интеллекта, логики и, конечно же, знаний ученика. Пришлось выразить свои мысли. В то же время было интересно.
Если бы это было мое первое образование, не уверен, что я бы получил его самостоятельно. Мне, вероятно, придется связаться с фирмами, которые помогают выполнять задания в колледже. Но хорошо, что к тому времени у меня уже был солидный опыт практической работы … Но и это иногда не помогало, я обращалась за советом к коллегам.
Задания отнимали много времени, хотелось выполнять их как можно лучше, чтобы получить хорошие баллы. Некоторые предметы, как и в большинстве вузов, не оценивались, выставлялся только зачет.
Большой плюс — возможность выполнять задания по выходным, вечером, в общем, когда есть свободное время. Вам не нужно никуда идти.
Так прошло два года, я оплачивал обучение по семестрам и выполнял задания. Вы должны быть осторожны с оплатой в университете и не пропускать сроки. В противном случае бухгалтерия Synergy может наложить штраф. Иногда они намеренно путают студентов со сроками, чтобы оштрафовать. Ну это один из минусов, они везде.В любом университете придумывают всевозможные расходы, кроме обучения.
Когда дело дошло до моего диплома, я получил список тем на выбор и целую брошюру на нескольких страницах с требованиями для диплома. Тема оговаривается заранее примерно за полгода. Но есть проблемы с условиями защиты в Synergy. По учебному плану у меня должна была быть охрана в мае, но она была перенесена на начало марта, и об этом сообщили только в феврале.Диплом надо было писать за месяц. В этом институте очень строгие требования к литературе, используемой в дипломе — она должна быть новой. Если в списке есть учебники и книги старше пяти лет со дня публикации, то оценка защиты может быть понижена. После того, как диплом будет полностью заполнен, вам необходимо получить отзыв от научного руководителя и отзыв от рецензента. Текст диплома проверяется в программе антиплагиата; он должен содержать не менее 70% самостоятельного текста.Остальные 30 — цитаты из книг.
Мне вручили настоящий диплом государственного образца об окончании школы.
Так что получить второе высшее образование вполне возможно.
Преимущества:
- Вы можете выполнять задачи в любое удобное время
- в наличии
- нет необходимости посещать занятия
- недорогая плата за обучение
Недостатки:
- необоснованно начислить штрафы
- неточные сроки защиты диплома
Я студент 3 курса ООО «Синергия» в Москве по направлению «Менеджмент в ресторанном и гостиничном сервисе».Меня все устраивает, проблем с прохождением сеансов нет. В классах тоже все учителя не только читают лекции, но и сами работали и работают в этой сфере. По учебе претензий нет. Нас постоянно водят на форумы, которые проводит институт, что тоже очень здорово. Интерьер тоже очень современный, кофейни, магазины, места для ночлега. Люди вокруг интересные. Дети со многих факультетов трудоустраиваются в университете и проходят стажировку.Минусов не видел уже три года. Учусь на Соколе, единственное пешком до метро 15 минут
Как успешный выпускник университета на факультете информационных технологий, я расскажу вам, как это на самом деле, и дам несколько советов.
Было МФПА, теперь МФПУ «Синергия». Есть разница, качественно высокий уровень стал. Что ж, я не могу назвать синергию редакцией шараша. Сейчас все нарядно подкрутили и без включения мозга учиться будет сложно, ну а тех, у кого его нет, обычно отчисляют.В начале 1-го курса в группе было 35 человек, затем к 5-му году было ликвидировано много людей + были реабилитированные после армии или переведенные. В итоге на защиту диплома вышло около 15 человек из первоначального коллектива! Мои друзья учились в штате. учреждения и там они реально перепугались.
Первое и самое главное правило, которое нужно запомнить будущим школьникам: никто не будет тащить вас за ручку, все вопросы нужно решать нам самим, высшее учебное заведение изначально подразумевает, что у человека есть зачаток мозга и у него есть Уникальное достоинство (в нынешнем тренде это так) — независимость.
Второе правило вы хотите выучить? — см. первое правило. Знания даны и современные, а не так, как я пытался сделать в одном государстве. Университет на красной линии с обшарпанными стенами и компьютерными «гробами» 15 дюймов, до сих пор пользовался Эльбрусом.
Правило третье — общайтесь с людьми и будьте в курсе всех событий. Вы не можете? Ты не знаешь? Вы застенчивы? — Неважно, жизнь научит или, чаще всего, заставит.
Правило четвертое — не груби с незнакомцами… Некоторые очень «лестно» отзываются о деканате. У меня лично с деканатом проблем не было, но были организационные вопросы и довольно часто, но сразу запомнил правило 1 и 3. Конечно, были люди, которые скачивали права и все остальное, но обычно те, что в Интернете называются ваша школота.
А теперь подробнее об обучении.
Есть много разных предметов, и из всего, что мы рассмотрели, главное, что из вас получается лидер с базовыми обширными знаниями, разными направлениями… Вам дается база, с которой можно начать углубленное самостоятельное (см. Правило 1) обучение.
Экзамены, курсовые, государственные, диплом.
Здесь все совсем иначе. Но в целом будет так: здесь плохо, это не по ГОСТу, здесь тема не раскрывается, нет описания, нет ссылок на литературу, нет графика или графика другого, нет расчетов и формул, но как вы это получили, и почему вы это сделали, а не иначе.В общем, в процессе будет чем заняться и если учесть правило 1, если знаний не получишь, вгонят, как говорится — плохая голова, в ногах нет покоя: ) Именно поэтому вы часто будете лично встречаться с преподавателями и деканатом, а потом воспользуетесь правилами 3 и 4, а потом, осознав все, снова переходите к правилу 1.
ГОС конечно удивила, жестоко было. В гос. uni не часто бывает. Ну как приехали с бумажкой, взяли, тут же написали и рассказали, а потом мобильник достали, можно лететь из штата.Как по мне, GOS в целом не так уж и сложна, например:
1. Стандарты MRP, MRP II, ERP, ERP II: основные принципы применения
2. Национальные и международные стандарты и рекомендации по аудиту информационной безопасности.
3. Основные виды средств несанкционированного доступа и методы противодействия им.
4. Выполните криптографическое преобразование шифрования сообщения с заданными параметрами, используя полиалфавитный шифр (шифр Viginer).
5. Определите минимальное количество ключей, необходимых для обеспечения безопасности связи с системой симметричного шифрования и связи «каждый с каждый».
Около 100 вопросов, ну что на них ответить прямо сейчас? 🙂
Это я выделил такие посредственные вопросы, вопросы типа: Обзор возможностей версий MS WINDOWS, даже не рассматриваю.
Ну например шифр Вижинер, страшно? Погуглить там ничего сложного, требуется лишь минимальный зачаток мозга.
Что самое интересное, при подготовке к ГСН есть отдельные издания для подготовки, это сухая выписка из тонны книг, супер удобно.
Ну и в заключение хочу сказать, что статус вуза растет, как среди студентов, так и среди работодателей. Причиной тому является синергетический эффект, поэтому он получил название МФПУ «Синергия». Есть и бюджетные места, где Дмитрий Медведев лично приехал в вуз, и тенденция развития очень перспективная, и если мыслить глобально, а действовать локально, то все будет хорошо.
———
Удачи и успехов.
Итак, наша проклятая школа — Одинцовская гимназия №7 (которую я, слава богу, окончила) сотрудничает с Университетом Синергия.Я просто ненавидел свою школу, в которой якобы преподают, и поэтому больше не мог думать ни о чем хорошем об университете Synergy.
В 9 классе к нам пришли два представителя этого вуза. Вместо одного урока нам дали печатные задания по трем разным предметам: русский язык, математика и, на мой взгляд, еще история.
Я выбрал математику. Эти задачи необходимо было решать. Естественно, нужно было указать контактную информацию. Тех, кто набрал наибольшее количество баллов, вызывали и приглашали в институт для получения сертификата.Конечно, во время разговора хвалили, но как насчет того, чтобы без этого звонить будущим школьникам? Конечно, обрадовалась и поехала по указанному адресу с мамой и сестрой (во время звонка сказали, что можно брать с собой родителей). Мы пошли в Университет «Синергия» возле метро Семеновская.
Я училась в классе «Б», когда приехала и собралась в других людях, увидела еще двух девочек из нашей школы только из параллельного класса «С». В общем, часа два, а может и больше, всем собравшимся показали презентацию, рассказали о Synergy и похвалили свой университет.Было так скучно и скучно. Потом нам выдали сертификаты. По математике набрала 48 баллов (но, поверьте, для честного ученика нашей школы это совсем не мелочи!).
Кстати, у нас уже были контракты на столах. Лично я просто хотела получить аттестат, а после 9 класса уходить совсем не собиралась.
Потом нам обещали чаепитие, но на чаепитие мало кто пришел, кто-то просто не слышал, куда идти, кто-то вообще ничего не слышал о чаепитии.В целом чаепитие Synergy Business School было очень и очень экономичным.
В общем, после таких «открытых дверей», где-то через день-два все равно звонили, спрашивали, нравятся ли они, выбрали ли мы какую-то специальность для себя. Я не скрывал, что мне с ними совсем не нравится. Мне все это не нравилось с самого начала. потому что это выглядело так, как будто они уже были студентами, как привлечь студентов к себе, но все эти бесполезные «привлечь больше студентов для оплаты» еще не закончились.
В этом году я закончил школу (11 класс). После поступления в университет она взяла академический отпуск из-за болезни.
Недавно нам позвонили из Министерства образования на дом. И стали говорить, что сейчас дипломы дают отличный заработок, второе высшее образование — это поощряется, потому что сейчас так сложно устроиться на работу и все такое бла-бла-бла. Когда я сказал, на какую специальность поступил, человек из отдела образования сразу стал говорить: «Да, сейчас высокооплачивается» и стал предлагать мне дистанционное обучение.Долгое время он был убежден, что дипломы и второе высшее образование так важны. Лично меня не волнуют мои дипломы, даже если я работаю дворником, главное, чтобы вы себя не продавали, а дело не в этом … Среди университетов, которые они продвигали, была Synergy.
Да, это довольно известный университет, но то, как они пытаются обмануть своих студентов, вызывает у меня отвращение. Аттестат якобы что-то дает при поступлении, якобы больше шансов.Я закрашу и выложу что-нибудь, чтобы показать, как выглядит их сертификат.
Видеообзор
Купить Econometrics Synergy MFPU Tests и скачать
Оценка отлично
Если модуль линейного коэффициента корреляции близок к нулю, то …
Проверьте правильный ответ:
связь между переменными сильная
в линейной форме связь между переменными слабая
связь между переменными слабая
В результате компонентного анализа временного ряда он не может быть получен… модель
Проверьте правильный ответ:
дано
мультипликативный
множественная регрессия
Косвенный MNK используется, если …
Проверьте правильный ответ:
опознаваемый
сверхидентифицируемый
неопознанный
Неправильный с точки зрения экономической теории знак коэффициента линейной регрессии может быть обнаружен …
Проверьте правильный ответ:
о гетероскедастичности остатков
о мультиколлинеарности факторов
об автокорреляции остатков
Стационарный…
Проверьте правильный ответ:
есть постоянная и переменная
можно рассматривать как узко, так и широко
бывает много и мало
Белый шым — это …
Проверьте правильный ответ:
свойство коэффициента регрессионной модели
Модель временных рядов
с независимыми одинаково распределенными наблюдениями
модель авторегрессии первого порядка
Гомостатичность означает …
Проверьте правильный ответ:
Отсутствие корреляции между случайным членом и независимыми переменными регрессионной модели
Отсутствие автокорреляции случайного члена уравнения регрессии
Постоянство дисперсии случайного члена в уравнении регрессии
По количеству объясняющих факторов регрессии они…
Проверьте правильный ответ:
двухместные, трехместные и т. Д.
простой и сложный
парные и множественные
По характеристикам связи между перегруппировками переменных в общем прошу прощения за две группы — …
Проверьте правильный ответ:
равномерно увеличивается и равномерно уменьшается
одинаково ускорен и одинаково медленен
положительные и отрицательные
Для стационарного процесса в узком смысле этого не может быть …
Проверьте правильный ответ:
процесс не является стационарным в широком смысле
константа случайного ожидания
корреляционная функция зависит только от запаздывания между уровнями ряда.
При проверке используется критерий Фишера…
Проверьте правильный ответ:
статистическая значимость модели в целом
автокорреляция в ряду фактической ошибки
модель факторов независимости
Нулевая гипотеза при проверке коэффициента уравнения регрессии на статическое значение говорит, что …
Проверьте правильный ответ:
оценка положительного коэффициента
Оценка коэффициента
равна нулю
Значение коэффициента
равно нулю
При построении моделей рекомендуется, чтобы количество выборок превышало количество факторов не менее чем на…
Проверьте правильный ответ:
десять раз
дважды
трижды
В условиях гетероактивности остатков для оценки параметров экономической модели использовать …
Проверьте правильный ответ:
метод моментов
метод максимального правдоподобия
обобщенный метод наименьших квадратов
Ранг тождества духа — это уровень производительности расширенной матрицы параметров на
транспортируемая матрица, ограничивающая количество эндогенных переменных…
Проверьте правильный ответ:
система
систем минус один
уравнений
Двухступенчатый MNK не применяется, если настройка …
Проверьте правильный ответ:
сверхидентифицируемый
опознаваемый
неопознанный
Оценки коэффициентов классической модели, полученные методом наименьшей цены, имеют …
Проверьте правильный ответ:
только свойство эффективности
свойств неподвижности, постоянства и эффективности
только платежеспособное имущество
Функция регрессии — это математическое выражение… между переменными
Проверьте правильный ответ:
исключительно линейная связь
корреляционная связь
функциональная зависимость
Студенческие приемы используются для …
Проверьте правильный ответ:
проверка независимости факторов
отзывов. Московский финансово-промышленный университет «Синергия»
МФПУ «Синергия» — один из многих московских вузов, в котором преподают в сфере современного менеджмента, финансов, информатики и экономики.Он привлекает студентов невысокой стоимостью обучения, качественным образованием, а также многочисленными международными проектами, в которых может принять участие абсолютно каждый.
НОУ «МФПУ Синергия»: история
Вуз был основан в 1995 году, тогда он назывался Московский международный институт эконометрики, информатики, финансов и права. Получив лицензию Министерства образования, новый вуз начал осуществлять прямую деятельность. Спустя четыре года МИИЭИФиП получил государственную аккредитацию.
В начале 2000 года учебное заведение получило статус члена Европейского фонда, занимающегося развитием современного менеджмента. В 2005 году вуз проходит переаттестацию и получает новый статус, теперь он называется Московская финансово-промышленная академия.
Два года спустя в учебном заведении формируется Международный наблюдательный совет, который занимается интеграцией вуза в мировую образовательную среду.Благодаря этой внутренней организации студенты могут принимать участие в программах обмена, а также совет организует лекции, читаемые иностранными экспертами.
В 2011 году вуз снова проходит аккредитацию и только теперь получает свое нынешнее название — Московский финансово-промышленный университет («Синергия»). По результатам проверки качества образования, проведенной Минобрнауки РФ в 2012 году, учебное заведение признано действующим, в 2013 году вновь прошло аккредитацию, получив право на проведение образовательных мероприятий. работай.
Факультеты университета
Главное, на что обращают внимание студенты и родители при изучении материалов об университете под названием Synergy (MFPU), — это обратная связь. В большинстве случаев они положительные, поскольку обучение проводят профессионалы своего дела, которые предоставляют студентам самую актуальную и актуальную информацию.
Сейчас в университете девять факультетов, в будущем их количество планируется увеличить. Помимо факультетов информационных систем, экономики и бизнеса, существуют также факультеты спортивного менеджмента, психологии, рекламы, лингвистики, права и Интернета.Именно поэтому университет популярен не только среди студентов, решивших связать свою жизнь с экономикой.
Возможности для студентов
По состоянию на 2015 год штат МФПУ «Синергия» (Москва) насчитывает 600 специалистов разного уровня подготовки, подавляющее большинство из которых — доктора наук, кандидаты и аспиранты. Благодаря этому в университете действует восемь уровней обучения, наиболее популярными из которых являются программы колледжа, бакалавриата и магистратуры.
Также в университете можно получить бизнес-образование, второе высшее образование, пройти курсы повышения квалификации или переподготовки, а также окончить аспирантуру.Те, кто хочет учиться в университете, но по каким-то причинам не может приехать в Москву, могут воспользоваться программами дистанционного обучения.
Московский финансово-промышленный университет сотрудничает с столичными вузами, образуя в них дополнительные кафедры. Так, преподаватели Колледжа связи № 54 и МФПУ уже несколько лет вместе готовят телекоммуникационных специалистов.
Международные проекты университета
Synergy (MFPU), отзывы о которых давно разошлись по России и за ее пределами, также активно участвует в международных образовательных проектах.По состоянию на 2015 год за пределами Российской Федерации есть четыре представительства этого университета: в Бразилии, Великобритании, Китае и Сингапуре.
МФПУ является партнером пяти зарубежных университетов, которые также готовят современных менеджеров и экономистов. В 2010 году один из факультетов учебного заведения установил партнерские отношения с Университетом Нортумбрии (Великобритания). В 2013 году исследовательские институты Университета Циньхуа также стали партнерами Synergy.
Сколько стоит обучение?
МФПУ «Синергия», стоимость обучения в котором несколько дешевле, чем в других столичных вузах, пользуется большой популярностью у провинциалов.Для получения степени бакалавра нужно будет платить от 30 до 90 тысяч рублей за семестр в зависимости от специальности. Самые дорогие очные специальности — предпринимательство, лингвистика, дизайн.
Стоимость обучения на заочном отделении значительно ниже, по состоянию на 2014/2015 учебный год она составляла 24 тысячи рублей за семестр по всем специальностям, кроме предпринимательской (30 тысяч рублей). Актуальные цены на обучение необходимо уточнять в приемной комиссии учебного заведения, так как они изменились.
Бюджетные места, конечно, есть, но их количество ограничено и с каждым годом сокращается. Подробную и актуальную информацию о количестве таких мест можно получить в приемной комиссии вуза по телефонам +7 (495) 545 43 45 или 8 (800) 100 00 11. Звонок по второму номеру бесплатный.
Филиалы
Для тех, кто не может приехать в Москву, но хочет получить образование, одним из вариантов, которые может предложить МФПУ Synergy, являются филиалы. Университет имеет более 50 филиалов и отделений по всей стране, 9 филиалов расположены в Астрахани, Волгодонске, Краснознаменске, Ноябрьске, Омске, Подольске, Тамбове, Черкесске и Элисте.
Также есть филиалы университета, расположенные в странах СНГ. На территории Беларуси действуют 9 единиц, один филиал в Тбилиси (Грузия), один в Бишкеке (Кыргызстан) и один в Алматы (Казахстан). Подробный перечень кафедр университета и всю необходимую информацию о них можно уточнить по бесплатному телефону горячей линии — 8 (800) 100 00 11.
Как поступить?
Для поступления в муниципальное образовательное учреждение высшего образования «Синергия» абитуриенту необходимо предоставить ряд документов.В первую очередь, речь идет о школьном аттестате, а также об экзаменах. Также необходимо предоставить медицинскую справку по форме 086-у (выдается в школах), военный билет (для мальчиков) плюс две фотографии 3 на 4.
Также рекомендуется предоставить портфель писем, благодарственных писем и других документов, подчеркивающих исключительность студента, поскольку отборочная комиссия рассматривает в первую очередь наиболее успешных кандидатов. Если абитуриент поступает сразу в несколько вузов, он имеет право предоставить копии своих документов, а оригиналы — при окончательном зачислении.
В случае, если будущий студент не сдал экзамен, он может пойти сдавать его в вуз, а также сдать дополнительные внутренние экзамены, это обсуждается индивидуально при поступлении. Проходной балл вуз устанавливает самостоятельно, его можно уточнить в приемной комиссии при поступлении.
студенческая жизнь
Synergy University (MFPU), отзывы о студенческой жизни которого исключительно положительные, постоянно участвует в различных внеклассных мероприятиях. Ежегодно проводится «Студенческая весна», где лучшие студенты факультетов демонстрируют свое мастерство, самые интересные номера выставляются на городской конкурс.
Кроме того, ежегодно на каждом факультете проводятся церемонии посвящения первокурсников в студенты, а также проводятся внутрифакультетские и общеуниверситетские каникулы. Каждый желающий может вступить в профком, чтобы быть в курсе жизни вуза и помогать одноклассникам в решении возникающих вопросов.
Общежитие
Если будущий студент Synergy все же переезжает в столицу и находится в поисках жилья, он имеет право подать заявление на место в общежитии. Однако есть условие: иногородний студент, проживающий на расстоянии 10 и более километров от Москвы, должен поступить на бюджетное место, то есть получить образование бесплатно.
Кроме того, проживание в общежитии платное, однако его стоимость намного ниже арендного жилья в Москве. По состоянию на 2015 год в университете действуют два студенческих общежития по адресам Погонный проезд, 5/1 и Балтийская, 10/3. Подробную стоимость проживания можно уточнить в приемной комиссии вуза.
Однако, если бюджетных мест не хватило, а общежитие получить не удалось, не стоит унывать. При приемной комиссии университета есть центр размещения студентов, который помогает студентам найти доступное жилье рядом с университетом.Центр постоянно следит за тем, чтобы студенты жили в комфортных условиях, поэтому, если абитуриенту не понравится выбранное жилье, ему в кратчайшие сроки предложат другой вариант. Таким образом, Университет «Синергия» (МФПУ), оценивая положительное отношение к студентам, в котором он распространился по всей России, формирует комфортные для его подопечных условия.
Можно ли работать и учиться?
Многие студенты вузов вынуждены совмещать работу и учебу, и MFPU Synergy University встречает их.При учебном заведении работает центр занятости, куда может подать заявку любой студент университета, желающий устроиться на работу. Благодаря многочисленным связям с работодателями центр помогает найти работу в кратчайшие сроки.
Наряду с поиском вакансий специалисты центра помогают соискателям подготовиться к собеседованию, обучить их навыкам успешной самопрезентации, а также помогают развивать профессиональные качества. Кроме того, центр занятости контролирует процесс регистрации студента в той или иной компании, играя роль посредника, это помогает гарантировать, что новоиспеченный сотрудник сможет совмещать учебу и работу.
Отставка из армии
Synergy (MFPU), отзывы студентов о которой весьма положительны, предусматривает отсрочку от службы в армии на период обучения всем, кто планирует закончить очное обучение в бакалавриате, магистратуре или аспирантуре. Однако при поступлении в вуз необходимо будет предъявить военный билет, чтобы специалисты вуза могли передать информацию в военкоматы.
Помимо прочего, в университете действует программа «Призывник», которая позволяет всем военнослужащим стать слушателями «Синергии» во время прохождения службы.После получения военного билета и окончания службы такой студент имеет право продолжить учебный процесс в статусе второкурсника.
Довузовская подготовка
Если абитуриент хочет подтянуть свои знания, то МФПУ «Синергия», тесты которого помогают подготовиться к ЕГЭ и внутренним экзаменам, готово помочь. Подготовительные курсы открыты в апреле-мае, дату их проведения и стоимость необходимо уточнить в приемной комиссии вуза.
Помимо прочего, любой желающий может пройти аналогичные курсы, целью которых может быть повышение собственного образования. В университете постоянно проводятся краткосрочные курсы MBA, которые рассчитаны на тех, кто планирует стать высокооплачиваемым и успешным руководителем предприятия.
МФПУ «Синергия», расположенное по адресу г. Москва, Ленинградский проспект, дом 80, постоянно совершенствуется и развивается. В ближайшие годы планируется открыть еще несколько факультетов и филиалов в городах России и СНГ, чтобы каждый мог получить качественное высшее образование.
Купить Management Synergy MFPU тестовые ответы и скачать
Оценка отлично
Функция менеджера, которая входит в постановку целей и определение цели их достижения, называется …
Проверьте правильный ответ:
мотивация
планирование
организация
контроль
Целенаправленное администрирование объекта управления из объекта управления в условиях ограничения и в
называется соответствие выбранному критерию эффективности…
Проверьте правильный ответ:
планирование
координация
менеджмент
анализ
По концепции Б. Герчикова, человек с экономической мотивацией …
Проверьте правильность вариантов ответа:
НЕСКОЛЬКО ВАРИАНТОВ
стремится взять на себя полную ответственность за дело
требует высокой заработной платы
ищет возможности доказать, что он способен выполнять работу, которую не каждый может делать
не настаивает на том, что работа очень интересная или высокооплачиваемая.
готов выполнить работу с максимальной отдачей без какого-либо контроля со стороны
Согласно модели Pterter-Loyler, достигаемые результаты зависят от…
Проверьте правильность вариантов ответа:
НЕСКОЛЬКО ВАРИАНТОВ
точность и детализация плана деятельности сотрудника
способностей сотрудников
усилий сотрудников
характеристик сотрудников
строгость системы контроля сотрудников
В теорию и практику управления введено понятие «иерархия потребностей» …
Проверьте правильный ответ:
Дуглас МакГрегор
Абрахам Маслоу
Виктор Врум
Фредерик Герцберг
Консенсус сотрудников относительно организации, выражение благодарности или неудовлетворенности, слухи и т. Д.ОТНОСИТЕЛЬНО ИНФОРМАЦИИ
… персонаж
Проверьте правильный ответ:
финансовый
социально-психологический
технический
управленческий
Экспертиза появляется, когда: …
Проверьте правильность вариантов ответа:
НЕСКОЛЬКО ВАРИАНТОВ
подчиненных соглашаются с указаниями руководителя, поскольку признают его превосходство в знаниях и опыте.
лидер обладает такими личными качествами, которые заставляют его выделяться и уважать, восхищаться им и хотят быть похожими на него
руководитель способен быстро и точно определить, кто из его подчиненных является экспертом в том или ином деле
руководитель — самый высококвалифицированный специалист в своей сфере деятельности.
Согласно теории жизненного цикла P.Херси и К. Бланчапа, термин «зрелость исполнителей» будет понят …
Проверьте правильность вариантов ответа:
НЕСКОЛЬКО ВАРИАНТОВ
желание достичь цели
образование и опыт в отношении конкретной задачи, которую необходимо выполнить
возраст
общее образование и стаж работы по профессиям
способность брать на себя ответственность за свое поведение
Менеджеры, вовлеченные в непреднамеренное управление сотрудниками, контактами с клиентами и информацией
Обеспечивая процесс контроля, связанный с… уровень
Проверьте правильный ответ:
выше
первичный
средний
Прямые методы управления, недирективные (первичные), обязательные, связанные с … методами контроля
Проверьте правильный ответ:
социально-психологический
экономичный
организационно-распорядительный
Удобный доступ к результатам отличает … контроль
Проверьте правильный ответ:
графический
селективный
скрыто
предварительный
Организованная структура компании, которая делит компанию по признаку термической, производственной продукции.
, а для клиентов он называется…
Проверьте правильный ответ:
линейный
матрица
дивизионный
функциональный
Принцип … предполагает, что каждый член организации становится участником запланированной деятельности незаменим
вместимость
Проверьте правильный ответ:
участие
непрерывность
гибкость
единство
Согласно теории … устранение факторов, вызывающих рост неадекватной деятельности человека, не обязательно приводит к
Повышение удовлетворенности и наоборот
Проверьте правильный ответ:
Д.Макклелланд
две группы факторов Ф. Герцберга
справедливость (равенство) J.S. Адамс
иерархия потребностей А. Маслоу
В организации с внутренними переменными из
отзывов. Московский финансово-промышленный университет «Синергия»
МФПУ «Синергия» — один из многих московских вузов, который занимается преподаванием современного менеджмента, финансов, информатики и экономики. Он привлекает студентов невысокой стоимостью обучения, качественным образованием, а также многочисленными международными проектами, в которых может принять участие абсолютно каждый.
Негосударственное образовательное учреждение «МФПУ Синергия»: история
Высшее учебное заведение создано в 1995 году, тогда носило название Московский международный институт эконометрики, информатики, финансов и права. Получив лицензию Министерства образования, новый вуз начал осуществлять прямую деятельность. Спустя четыре года МИФП получил государственную аккредитацию.
В начале 2000 года учебное заведение получило статус члена Европейского фонда, занимающегося развитием современного менеджмента.В 2005 году вуз проходит переаттестацию и получает новый статус, теперь он называется Московская финансово-промышленная академия.
Два года спустя в школе формируется Международный наблюдательный совет, который занимается интеграцией вуза в мировую образовательную среду. Благодаря такой внутренней организации студенты могут принимать участие в программах обмена, а также совет организует лекции, которые читают иностранные специалисты.
В 2011 году вуз снова аккредитован, и теперь он получает свое нынешнее название — Московский финансово-промышленный университет («Синергия»).По результатам контроля качества образования, проведенного Минобрнауки РФ в 2012 году, учебное заведение признано действующим, в 2013 году вновь прошло аккредитацию на право ведения воспитательной работы.
Факультеты университета
Главное, чтобы студенты обращали внимание на родителей, изучая материалы об университете под названием «Синергия» (МФПУ) — отзывы. В большинстве случаев они положительные, так как учебную работу проводят профессионалы, которые предоставляют студентам наиболее актуальную и необходимую информацию.
Сейчас в университете девять факультетов, в дальнейшем их количество планируется увеличить. Помимо факультетов информационных систем, экономики и бизнеса здесь также функционируют факультеты спортивного менеджмента, психологии, рекламы, лингвистики, права и Интернета. Поэтому университет популярен не только среди студентов, решивших связать свою жизнь с экономикой.
Возможности для студентов
По состоянию на 2015 год штат МФПУ «Синергия» (г. Москва) состоит из 600 специалистов разного уровня подготовки, подавляющее число среди которых составляют доктора наук, кандидаты и аспиранты.Благодаря этому в университете действует восемь уровней обучения, наиболее популярными из которых являются колледж, бакалавриат и магистратура.
Также в университете можно получить бизнес-образование, второе высшее образование, пройти курсы повышения квалификации или повышения квалификации, а также закончить аспирантуру. Те, кто хочет учиться в университете, но по каким-то причинам не может приехать в Москву, могут воспользоваться программами дистанционного обучения.
Московский финансово-промышленный университет сотрудничает со столичными вузами, формируя в них дополнительные кафедры.Так, преподаватели Колледжа связи № 54 и МФПУ уже несколько лет совместными усилиями готовят специалистов по телекоммуникациям.
Международные университетские проекты
«Синергия» (МФПУ), отзывы о которых давно распространены по всей России и за ее пределами, также активно участвует в международных образовательных проектах. По состоянию на 2015 год за пределами Российской Федерации есть четыре представительства этого учреждения: в Бразилии, Великобритании, Китае и Сингапуре.
МФПУ является партнером пяти зарубежных университетов, которые также занимаются подготовкой современных менеджеров и экономистов. В 2010 году один из факультетов учебного заведения установил партнерские отношения с Университетом Нортумбрии (Великобритания). В 2013 году партнером Synergy стал Институт науки Университета Циньхуа.
Сколько стоит обучение?
МФПУ «Синергия», стоимость обучения в котором несколько дешевле, чем в остальных столичных вузах, пользуется большой популярностью у провинциалов.Для получения степени бакалавра нужно будет платить от 30 до 90 тысяч рублей за семестр в зависимости от специальности. Самые дорогие специальности на дневном отделении — это предпринимательство, лингвистика и дизайн.
Стоимость обучения на заочном отделении значительно ниже, по состоянию на 2014/2015 учебный год она составляла 24 тысячи рублей за семестр по всем специальностям, кроме предпринимательской (30 тысяч рублей). Актуальные цены на обучение необходимо уточнять в приемной комиссии учебного заведения, так как они могут быть изменены.
Бюджетные места, конечно, есть, но их количество ограничено и с каждым годом уменьшается. Подробную и актуальную информацию о количестве таких мест можно получить в приемной комиссии вуза по телефону +7 (495) 545 43 45 или 8 (800) 100 00 11. Звонок на второй номер бесплатный.
Филиалы
Для тех, кто не может приехать в Москву, но хочет получить образование, один из вариантов, которые могут предложить МФУ «Синергия» — филиалы. Университет имеет более 50 филиалов и офисов по всей стране, 9 филиалов расположены в Астрахани, Волгодонске, Краснознаменске, Ноябрьске, Омске, Подольске, Тамбове, Черкесске и Элисте.
Также есть филиалы университета, расположенные на территории СНГ. На территории Беларуси действуют 9 подразделений, один филиал в Тбилиси (Грузия), один в Бишкеке (Кыргызстан) и один в Алматы (Казахстан). Подробный перечень кафедр вуза и всю необходимую информацию о них можно уточнить по телефону бесплатной горячей линии — 8 (800) 100 00 11.
Как действовать?
Для поступления в МГУ «Синергия» абитуриенту необходимо предоставить ряд документов.В первую очередь, речь идет о школьном аттестате, а также о свидетельстве о ЕГЭ. Также необходимо предоставить медицинскую справку по форме 086-у (выдается в школах), военный билет (для мальчиков) плюс две фотографии с 3 по 4.
Также рекомендуется подать портфель писем, благодарственных писем и другие документы, подчеркивающие исключительность студента, поскольку отборочная комиссия сначала рассмотрит наиболее успешных кандидатов. Если абитуриент поступает сразу в несколько вузов, он имеет право предоставить копии своих документов, а уже при окончательном зачислении подать оригиналы.
В случае, если будущий студент не сдал ЕГЭ, он может сдать его в вузе, а также сдать дополнительные внутренние экзамены, это оговаривается индивидуально при поступлении. Вуз устанавливает проходной балл самостоятельно, его можно уточнить в приемной комиссии при приеме.
студенческая жизнь
Университет «Синергия» (ФПУ), отзывы о студенческой жизни в котором исключительно положительные, постоянно участвует в различных внеклассных мероприятиях.Ежегодно проводится «Студенческая весна», где лучшие студенты факультетов демонстрируют свое мастерство, самые интересные номера выдвигаются на городской конкурс.
Кроме того, ежегодно на каждом факультете проводятся церемонии посвящения в новобранец среди студентов, организуются внутрифакультетские и общеуниверситетские каникулы. Любой желающий может вступить в профсоюзный комитет, чтобы быть в курсе университетской жизни и помогать однокурсникам в решении возникающих вопросов.
Общежитие
Если будущий студент «Синергии» все же переезжает в столицу и находится в поисках жилья, он имеет право подать заявление на место в общежитии.Однако здесь есть условие: иногородний студент, проживающий на расстоянии 10 и более километров от Москвы, должен поступить на бюджетное место, то есть получить образование бесплатно.
Кроме того, проживание в общежитии платное, однако его стоимость намного ниже арендного жилья в Москве. По состоянию на 2015 год в университете действуют два студенческих общежития по адресу: Погонный проезд, 5/1 и Балтийский, 10/3. Подробную стоимость проживания можно уточнить в приемной комиссии вуза.
Однако, если бюджетных мест не хватило, и хостел получить не удалось, не расстраивайтесь.При приемной комиссии университета работает центр размещения студентов, который помогает студентам найти доступное жилье рядом с университетом. Центр постоянно следит за тем, чтобы студенты жили в комфортных условиях, поэтому, если абитуриенту не понравится выбранное жилье, ему в кратчайшие сроки предложат другой вариант. Таким образом, Synergy University (FPA), отзывы о положительном отношении к студентам, в котором оно распространилось по всей России, создает условия, комфортные для их подопечных.
Можно ли работать и учиться?
Многие студенты вузов вынуждены совмещать работу и учебу, и Университет ФПА «Синергия» идет им навстречу. В образовательном центре есть центр занятости, куда может подать заявку любой студент университета, желающий устроиться на работу. Благодаря многочисленным связям с работодателями центр помогает найти работу в кратчайшие сроки.
Специалисты Центра параллельно с поиском вакансий помогают соискателям подготовиться к собеседованию, обучить их навыкам успешной самопрезентации и помогают развивать профессиональные навыки.Помимо прочего, центр занятости контролирует процесс регистрации студента в той или иной компании, играя роль посредника, он помогает обеспечить, чтобы новоявленный сотрудник мог совмещать учебу и работу.
Отставка из армии
«Синергия» (FPA), отзывы студентов о которой весьма полезны, предусматривает отсрочку от армии на период обучения всем, кто планирует получить степень бакалавра, магистра или аспирантуру на дневном отделении. .Однако при поступлении в вуз в обязательном порядке необходимо будет предоставить военный билет, чтобы специалисты вуза могли передать информацию в военкоматы.
Помимо прочего, в университете существует программа «Призывник», которая позволяет всем военнослужащим стать слушателями «Синергии» во время прохождения службы. После получения военного билета и окончания службы такой студент имеет право продолжить учебный процесс в статусе второкурсника.
Довузовская подготовка
Если абитуриент желает подтянуть свои знания, то ФПП «Синергия», тесты которой помогают подготовиться к сдаче экзамена, и внутренние экзамены готовы прийти на помощь. Подготовительные курсы открыты в апреле-мае, дату их проведения и стоимость необходимо уточнять в приемной комиссии вуза.
Помимо прочего, любой желающий может пройти аналогичные курсы, целью которых может быть повышение собственного образования. В университете постоянно проходят краткосрочные курсы MBA, которые рассчитаны на тех, кто планирует стать высокооплачиваемым и успешным менеджером компании.
ФПА «Синергия», адрес которой — г. Москва, Ленинградский проспект, дом 80, постоянно совершенствуется и развивается. В ближайшие годы планируется открыть еще несколько факультетов и филиалов в городах России и СНГ, чтобы каждый мог получить качественное высшее образование.
бакалавр психологии | Московский финансово-промышленный университет «Синергия» Краснознаменский филиал
Необходимые документы
При поступлении в Краснознаменский филиал Московского финансово-промышленного университета «Синергия» в России необходимо подготовить все необходимые документы.Запросите список необходимых документов непосредственно в университете, так как он может отличаться для разных стран. В нашем чате вы также можете запросить образцы документов.
- Все академические документы
- Форма онлайн-заявки
- Паспорт
- Контакт Нет
- Email ID
- Семейные данные
- Фотографии
- Подтверждение оплаты комиссии
- Плата за подачу заявления
- Резюме / CV (выпускник, аспирант)
- Страхование здоровья и жизни
- Студенческая виза
- Медицинский сертификат
- Декларация о финансовой поддержке
- Мотивирующее письмо
- План исследовательского предложения (магистр, доктор философии)
- Свидетельство о тестировании на ВИЧ



 {2} \alpha=\frac{1+\cos 2 \alpha}{2}
\)
{2} \alpha=\frac{1+\cos 2 \alpha}{2}
\)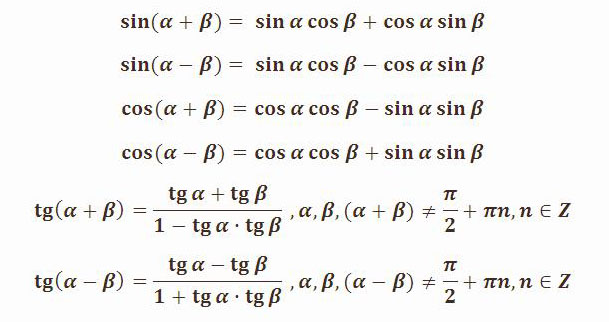 {4} \alpha
\)
{4} \alpha
\)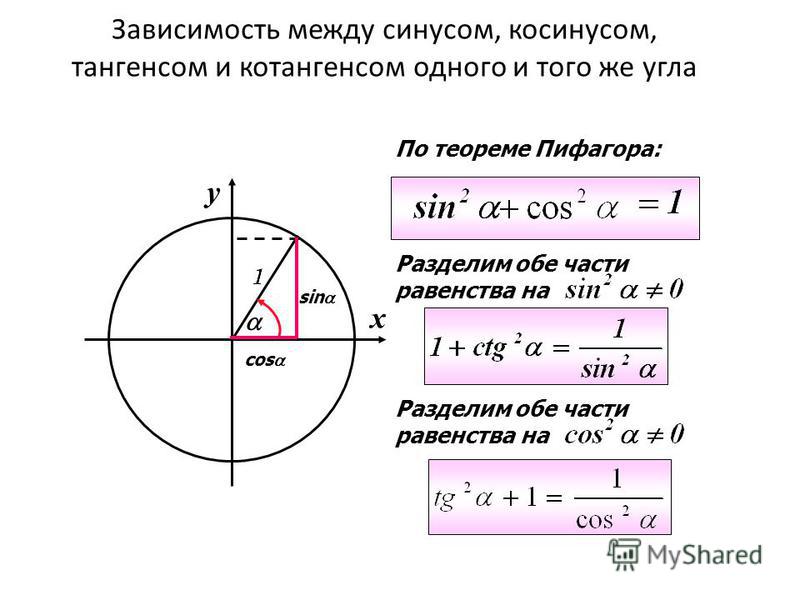





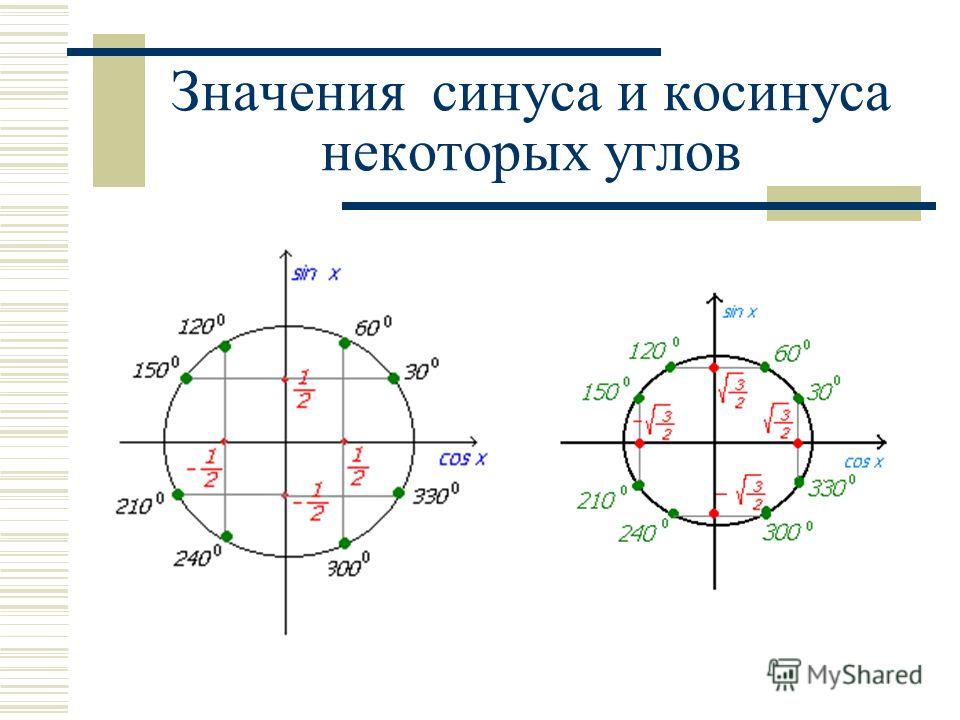 Найти по формулам длину биссектрисы из острого угла на катет:
Найти по формулам длину биссектрисы из острого угла на катет:
 β – второй острый угол).
β – второй острый угол).
 Подставив значение α в формулу синуса, получим:
Подставив значение α в формулу синуса, получим:


 Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения. Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
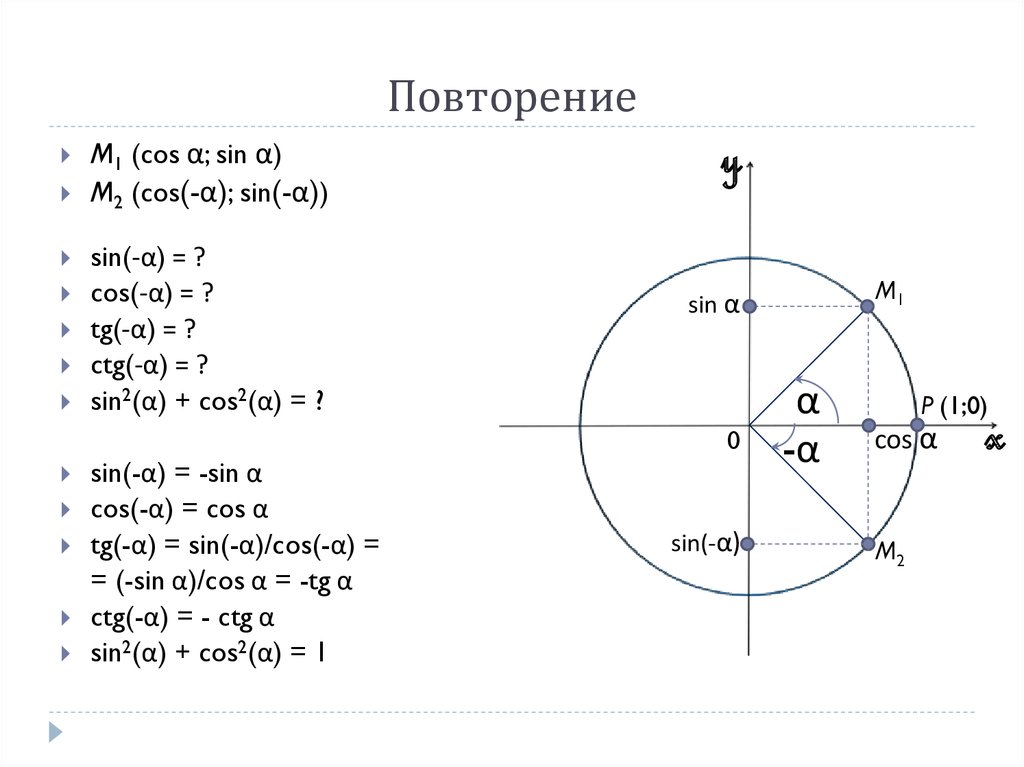 Так что такое синус и косинус?
Так что такое синус и косинус?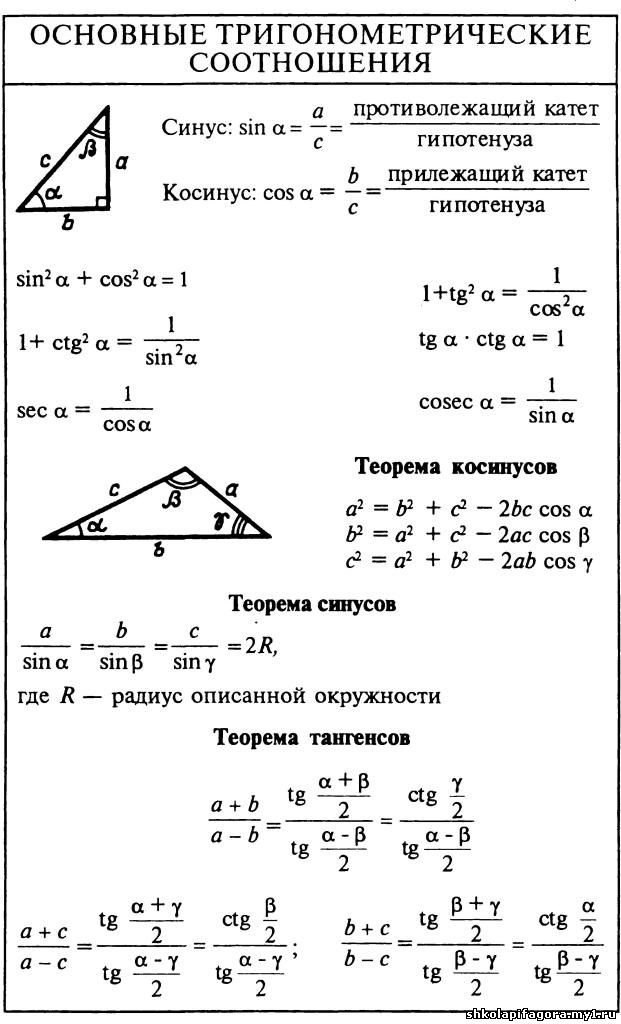 Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.
Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.
Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.
Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.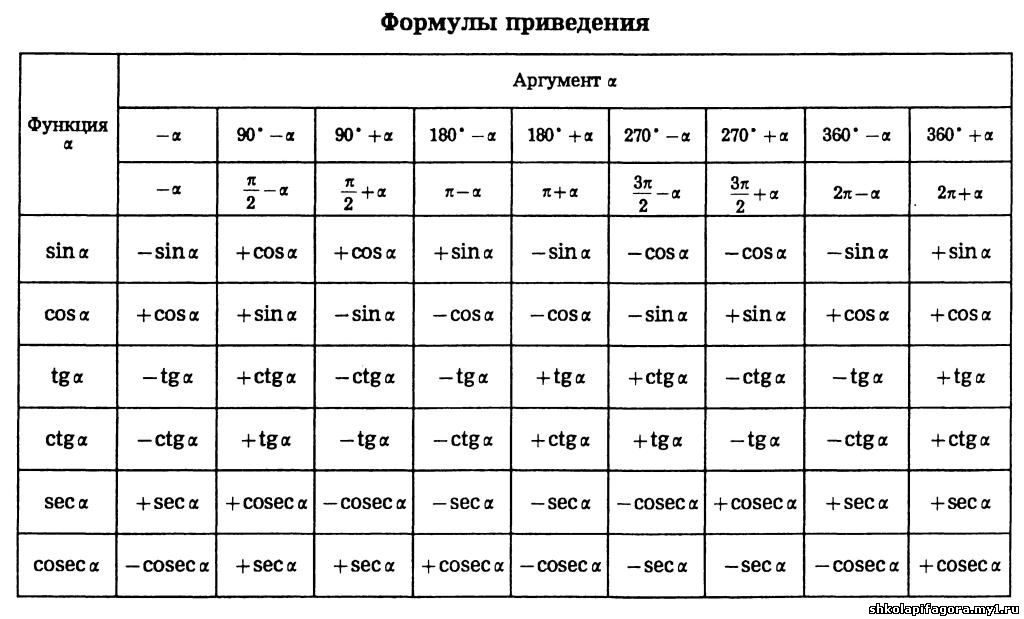 Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.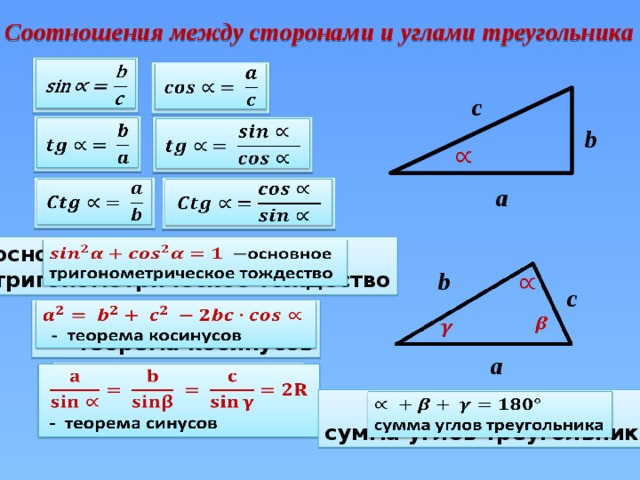 А ведь некоторые специалисты решают такие задачи ежедневно.
А ведь некоторые специалисты решают такие задачи ежедневно.
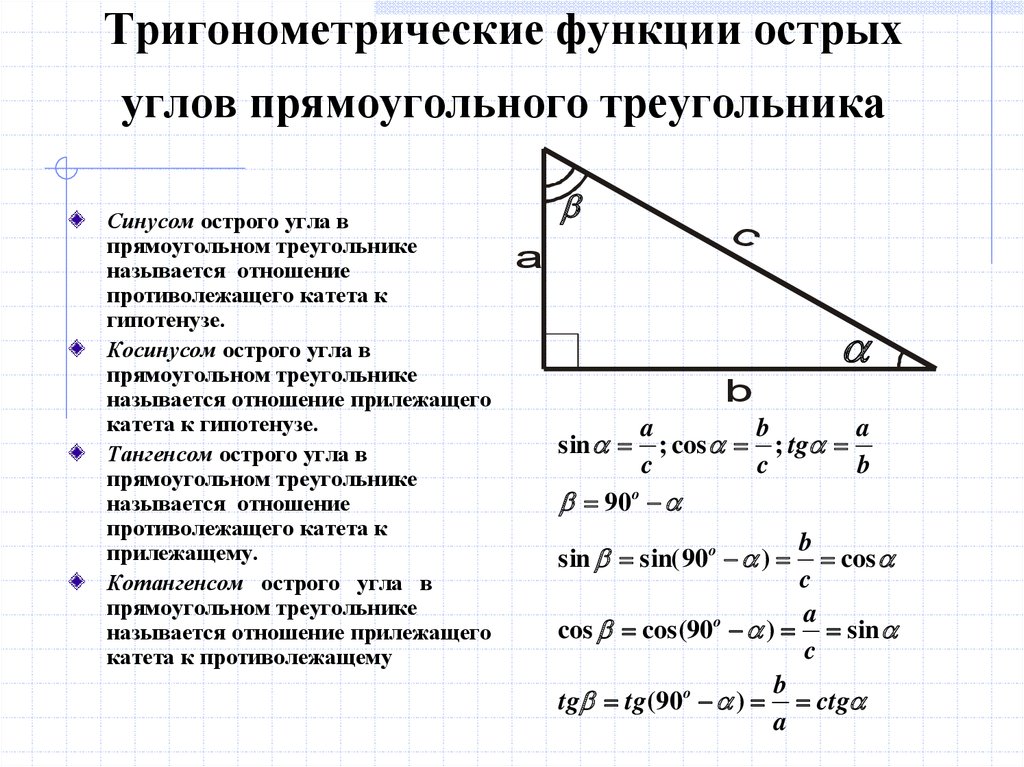 Если угол обозначить буквой α, в общем виде решение можно записать так: α = arcsin(sin(α)).
Если угол обозначить буквой α, в общем виде решение можно записать так: α = arcsin(sin(α)).
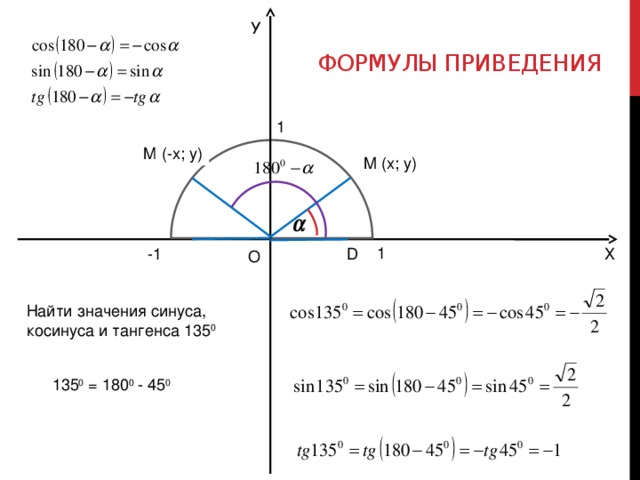 Чтобы запустить раскройте главное меню на кнопке «Пуск» ( или нажатием клавиши WIN), перейдите в раздел «Все программы», а затем в подраздел «Стандартные» и щелкните пункт «Калькулятор».
Чтобы запустить раскройте главное меню на кнопке «Пуск» ( или нажатием клавиши WIN), перейдите в раздел «Все программы», а затем в подраздел «Стандартные» и щелкните пункт «Калькулятор». Рядом с ним стоит короткая надпись Inv.
Рядом с ним стоит короткая надпись Inv. е. 90°). Закономерности соотношений именно этих углов и длин сторон и описывают тригонометрические функции.
е. 90°). Закономерности соотношений именно этих углов и длин сторон и описывают тригонометрические функции.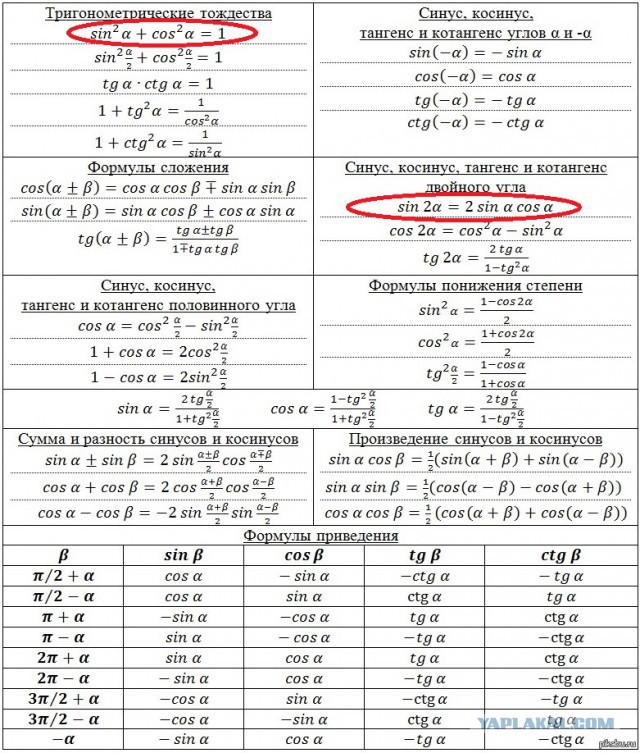 Нулевыми значения функции становятся при 0°, 180°, 360° и т.д. Из всего этого вытекает, что синус является функцией периодической и период ее равен 360° или удвоенному числу Пи.
Нулевыми значения функции становятся при 0°, 180°, 360° и т.д. Из всего этого вытекает, что синус является функцией периодической и период ее равен 360° или удвоенному числу Пи.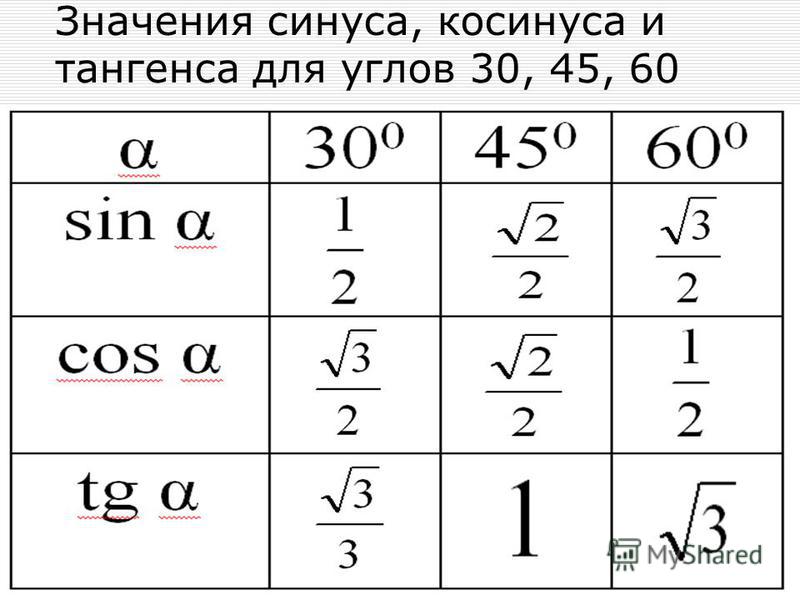 Согласно определению, синус угла (α) должен быть отношению длины стороны (a), лежащей напротив него — катета — к длине стороны (c), противолежащей прямому углу — гипотенузы: sin(α) = a/c.
Согласно определению, синус угла (α) должен быть отношению длины стороны (a), лежащей напротив него — катета — к длине стороны (c), противолежащей прямому углу — гипотенузы: sin(α) = a/c. На этом задачу можно решенной в общем виде.
На этом задачу можно решенной в общем виде.
 Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности». Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов. зависимость между синусом, косинусом и тангенсом одного и того же угла — Алгебра и начала математического анализа — 10 класс
зависимость между синусом, косинусом и тангенсом одного и того же угла — Алгебра и начала математического анализа — 10 класс
 Она связывает синус с косинусом. А это значит, чо зная значения синуса, можно найти значения косинуса и наоборот.
Она связывает синус с косинусом. А это значит, чо зная значения синуса, можно найти значения косинуса и наоборот.
 Эти формулы являются тождествами.
Эти формулы являются тождествами.

 Поэтому квадрат расстояния между ними равен:
Поэтому квадрат расстояния между ними равен:
 Это стимулирует их на хорошую подготовку к уроку, детям всегда хочется побывать в роли учителя, тем более, что дети послабее опрашивают тех, кто лучше разбирается в данном предмете. Все ученики класса, кроме этих пятерых, достают листки и делают на них чертежи к теореме, и пишут дано. На первый взгляд дети работают сами, но на самом деле вся работа хорошо спланировано учителями. Весь класс у него на контроле. Как только работа с листочками закончена, учащиеся готовые отвечать поднимают руки и им учитель предлагает занять место рядом с одним из пятерых, уже ответивших теорему. Дети начинают тихим шепотом отвечать друг другу. Через 3-4 минуты в классе уже 10 человек, которые спрашивают, и так по нарастающей. Когда все ответили, учитель называет всех учеников по списку, и отметку говорит тот, кто его опрашивал. Отметки, как правило, бывают хорошими, двоек нет совсем, так как дети знают, что спросят всех. (Если оценки чуть завышены, это не страшно, важно, что они с желанием готовятся, следовательно учат теорию, владеют ей начинают лучше решать задачи, а это то, чего мы хотим добиться на уроках геометрии.
Это стимулирует их на хорошую подготовку к уроку, детям всегда хочется побывать в роли учителя, тем более, что дети послабее опрашивают тех, кто лучше разбирается в данном предмете. Все ученики класса, кроме этих пятерых, достают листки и делают на них чертежи к теореме, и пишут дано. На первый взгляд дети работают сами, но на самом деле вся работа хорошо спланировано учителями. Весь класс у него на контроле. Как только работа с листочками закончена, учащиеся готовые отвечать поднимают руки и им учитель предлагает занять место рядом с одним из пятерых, уже ответивших теорему. Дети начинают тихим шепотом отвечать друг другу. Через 3-4 минуты в классе уже 10 человек, которые спрашивают, и так по нарастающей. Когда все ответили, учитель называет всех учеников по списку, и отметку говорит тот, кто его опрашивал. Отметки, как правило, бывают хорошими, двоек нет совсем, так как дети знают, что спросят всех. (Если оценки чуть завышены, это не страшно, важно, что они с желанием готовятся, следовательно учат теорию, владеют ей начинают лучше решать задачи, а это то, чего мы хотим добиться на уроках геометрии.
 АОВ = треугол. COD
АОВ = треугол. COD т.д.
т.д. е. < AEB = < СFD.
е. < AEB = < СFD.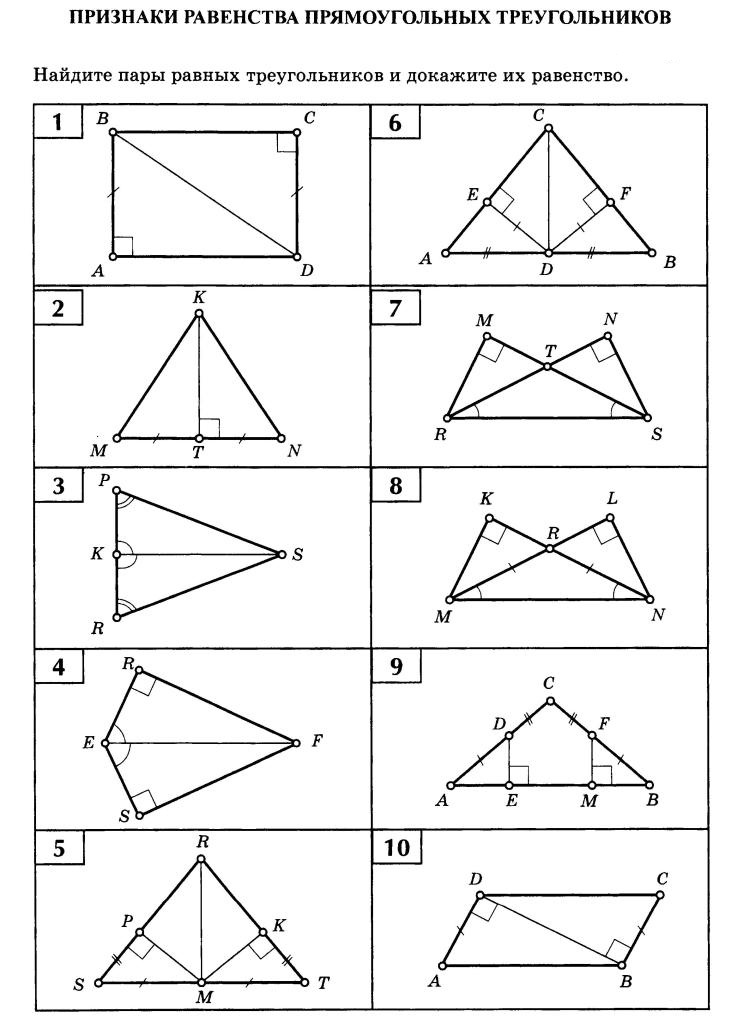
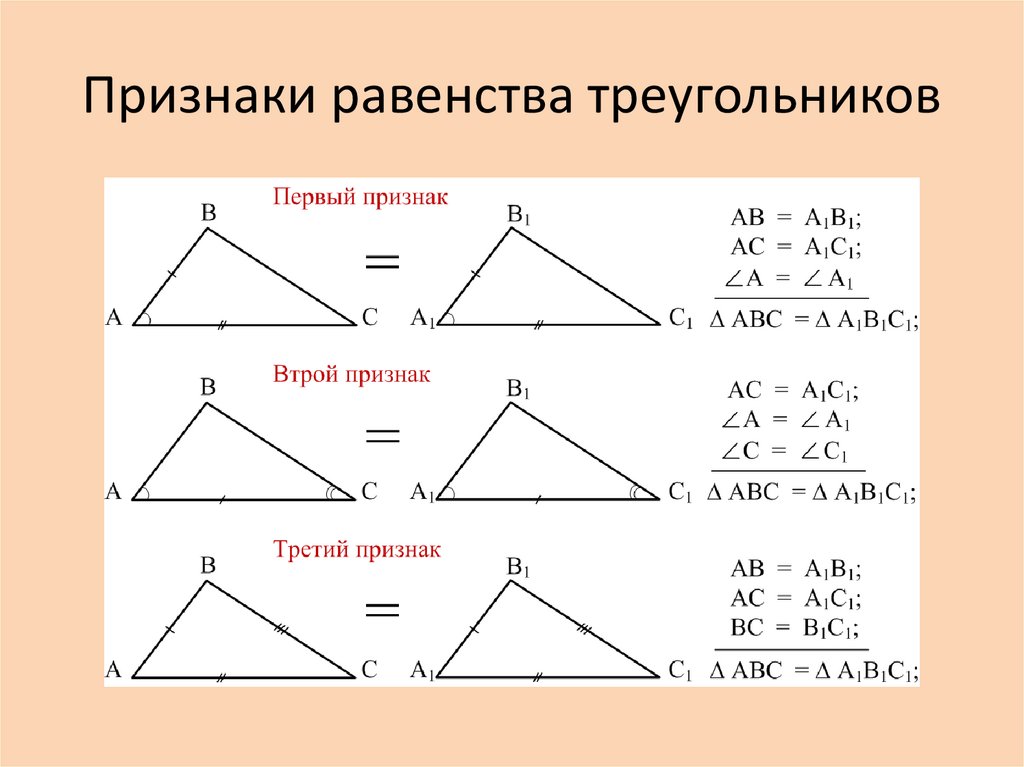

 к. у них АК = СР , ВК = ВР по условию , ے АКВ = ے СРВ как углы смежные с углами ВКР и ВРК , равными по условию.
к. у них АК = СР , ВК = ВР по условию , ے АКВ = ے СРВ как углы смежные с углами ВКР и ВРК , равными по условию. 37.
37.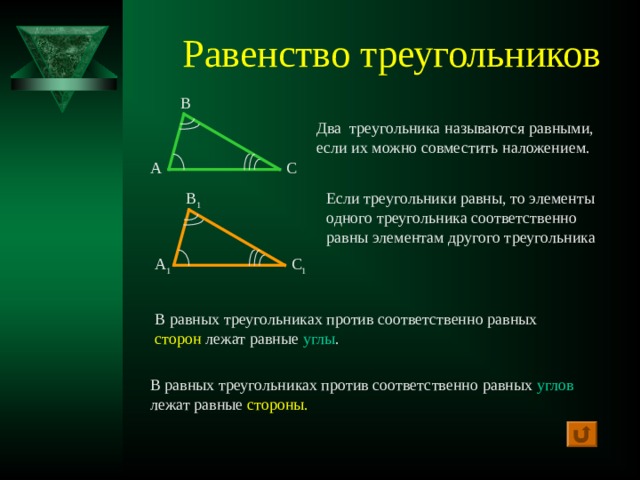 yandex.ru
yandex.ru
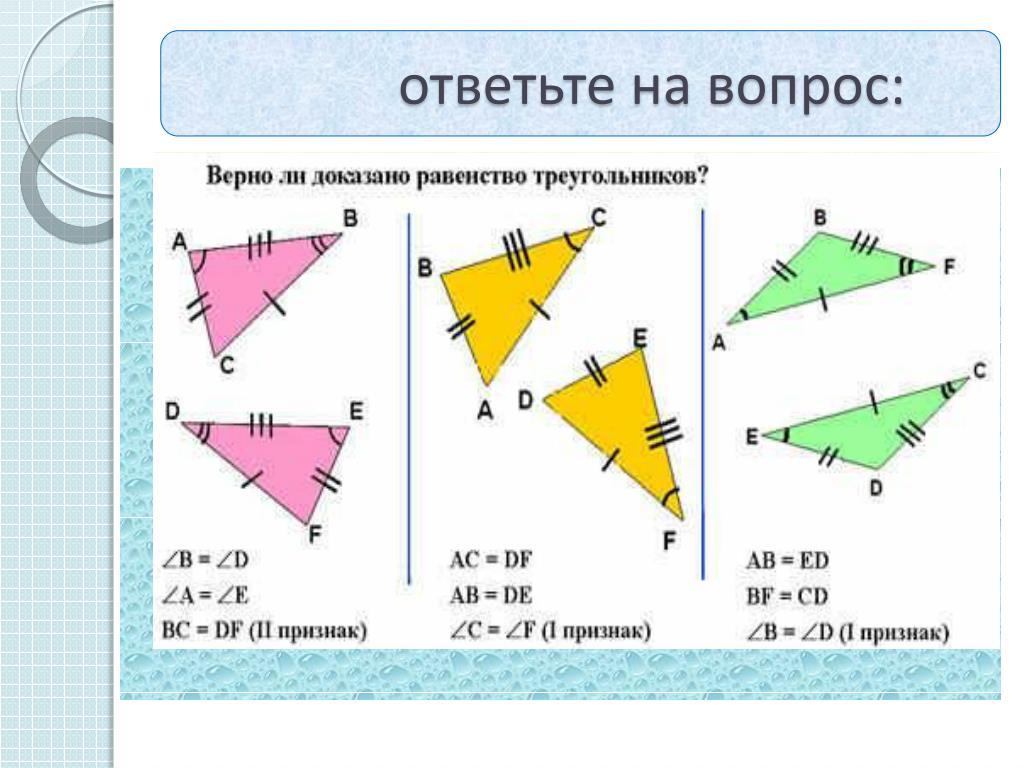



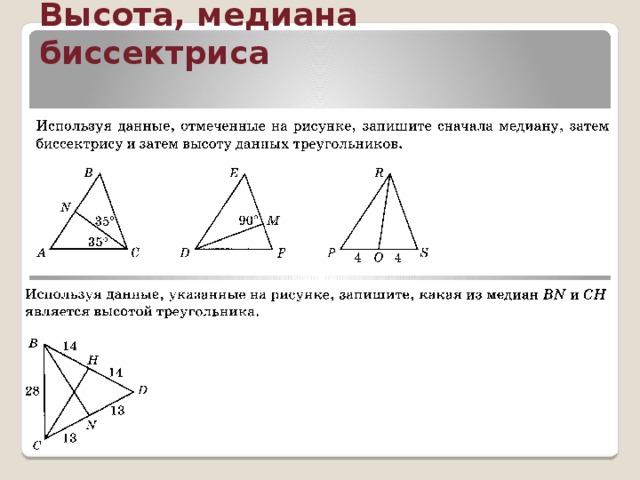
 (–)
(–)

 )
)
 С. и др. – М.: Вербум-М, 2004.
С. и др. – М.: Вербум-М, 2004.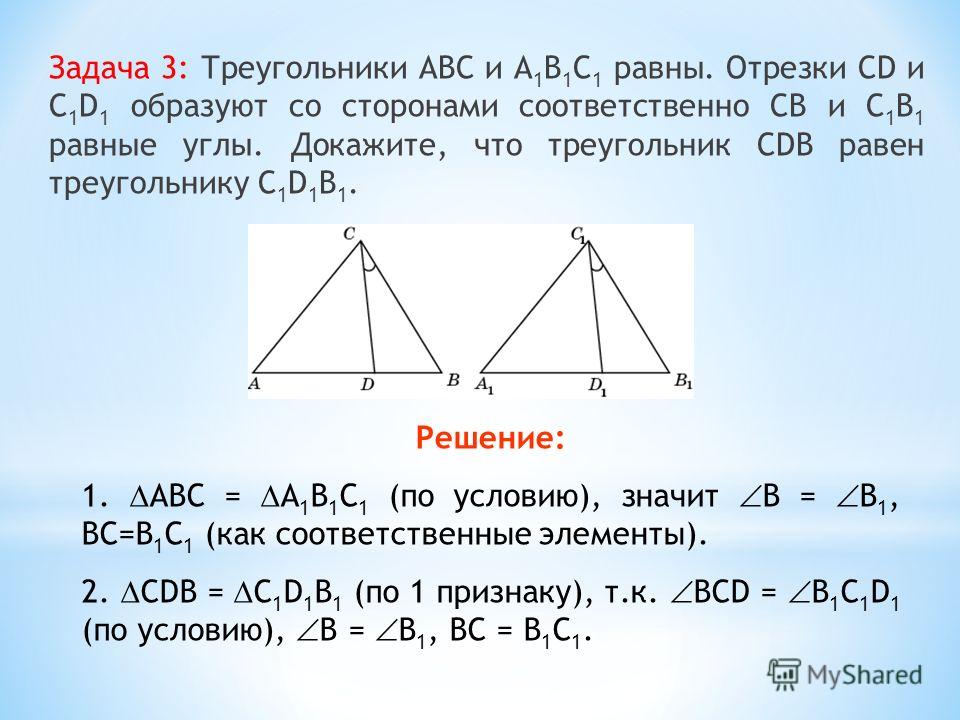
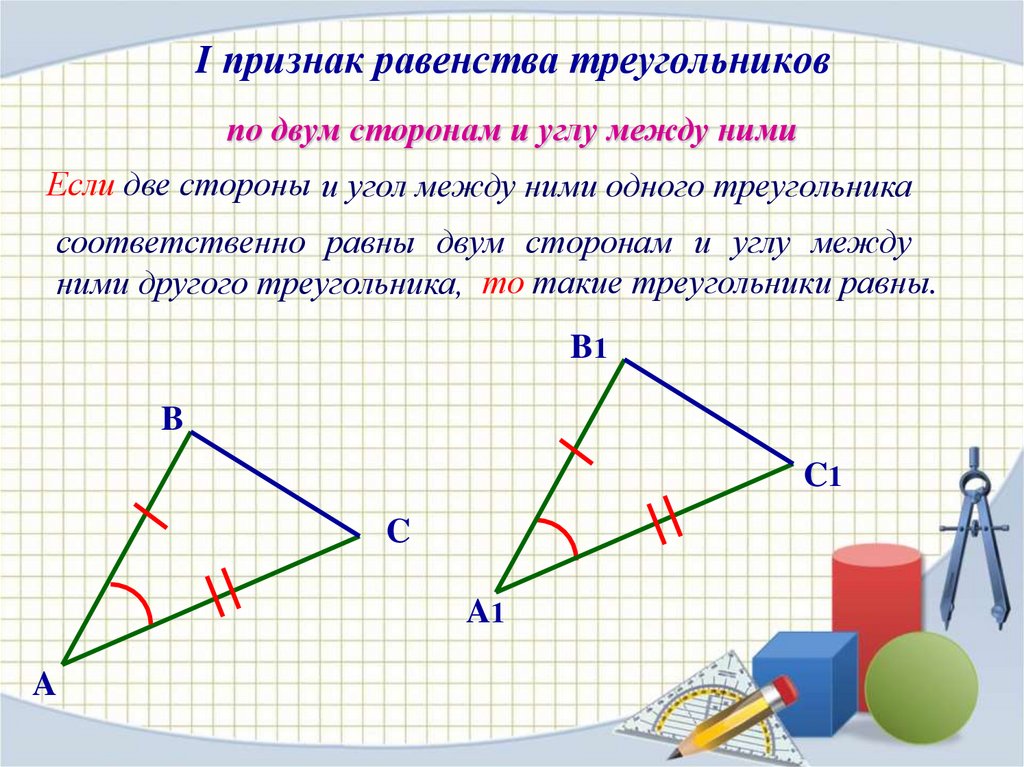 Прошло более двух тысяч лет, а определение не изменилось. Это определение о равенстве фигур можно отнести и к треугольникам.
Прошло более двух тысяч лет, а определение не изменилось. Это определение о равенстве фигур можно отнести и к треугольникам.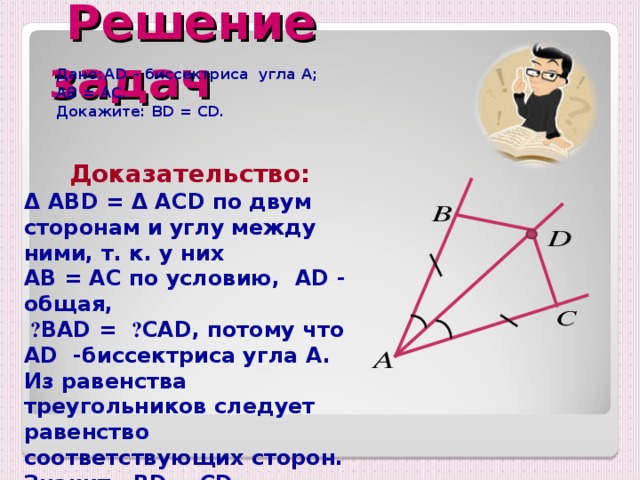 Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников). school-collection.edu.ru/dlrstore/70da6388-da75-4ba7-9be6-20b942428b30/1_priznak.swf
school-collection.edu.ru/dlrstore/70da6388-da75-4ba7-9be6-20b942428b30/1_priznak.swf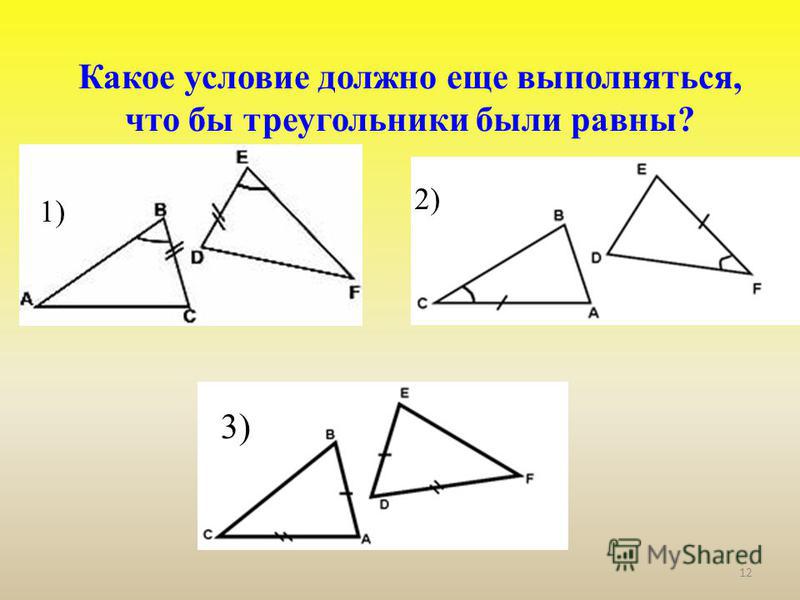 Найдите величину угла ACE, если
Найдите величину угла ACE, если  Тогда AB= BK+ AK= 5.
Тогда AB= BK+ AK= 5.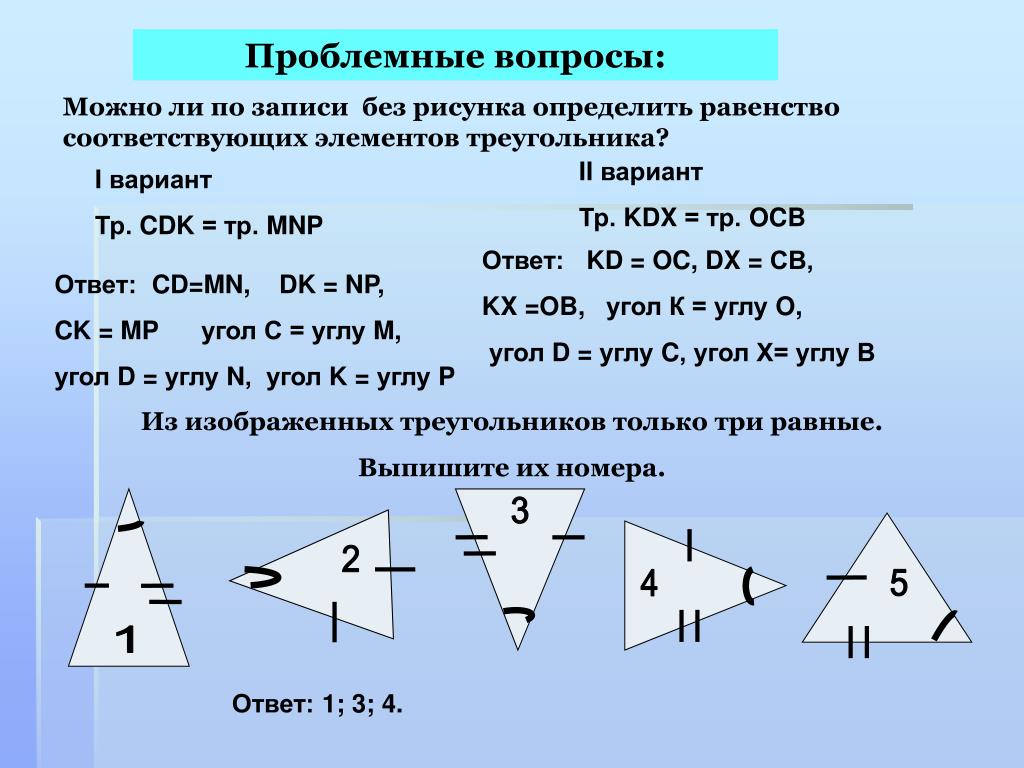 Вот она.
Вот она. Комплексная зачетная тетрадь. Стадник Л. Г.
Комплексная зачетная тетрадь. Стадник Л. Г. 

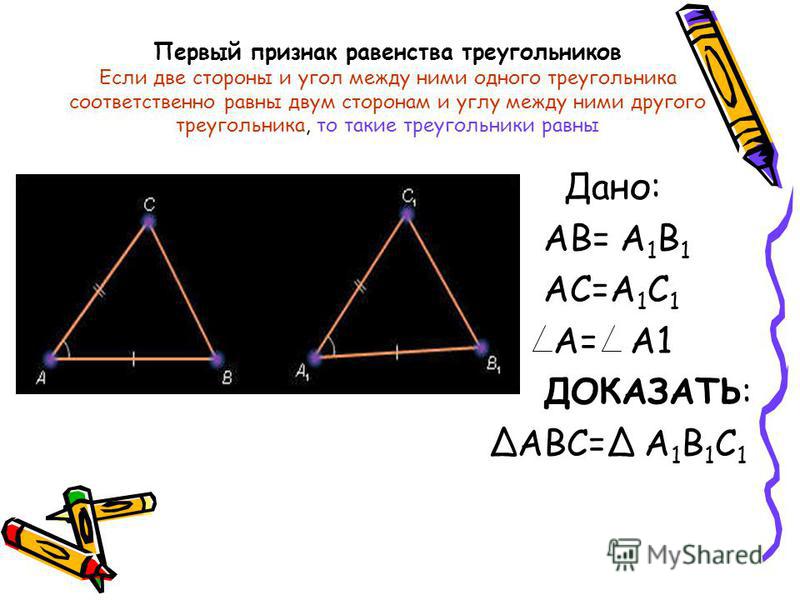
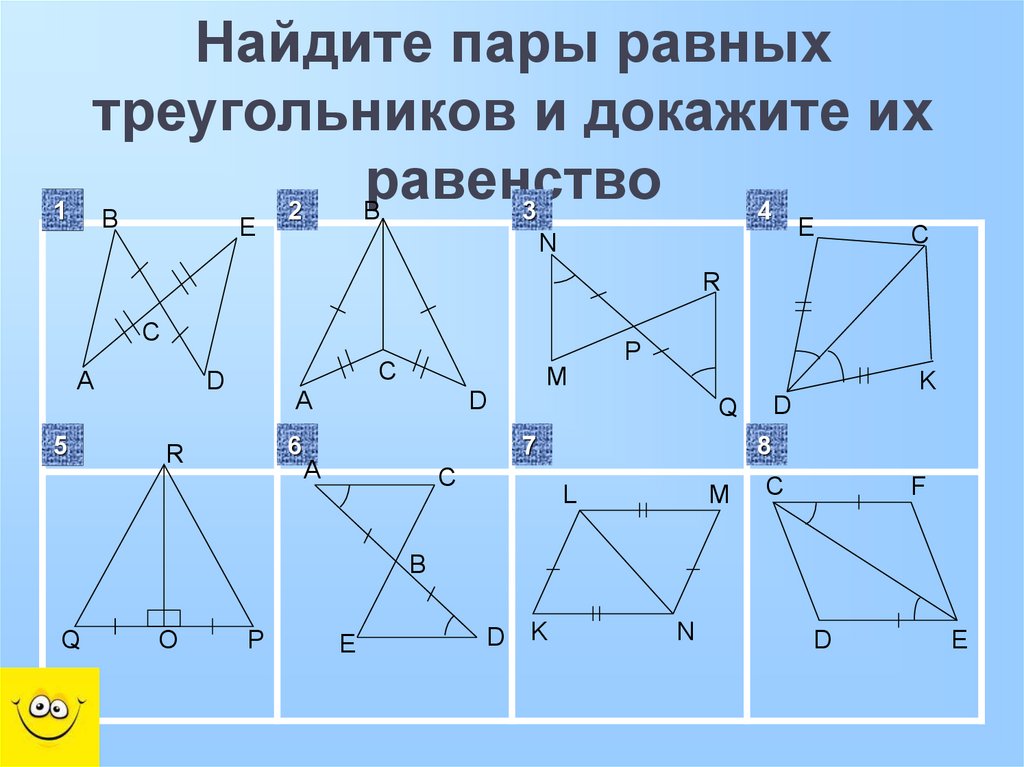
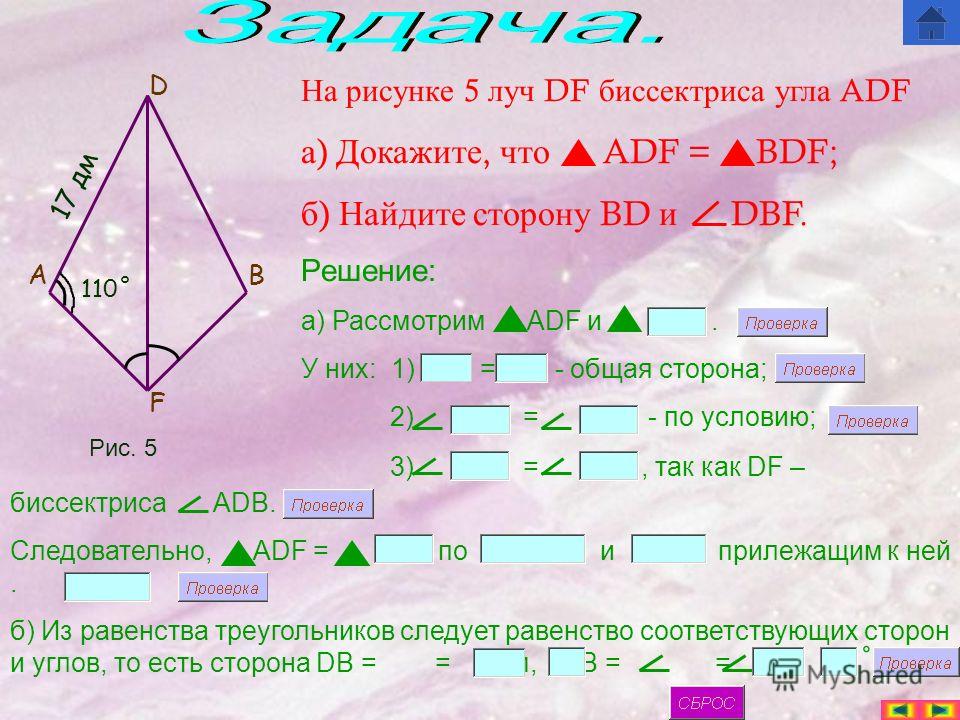 Но треугольники не равны. Итак, условие утверждения выполнено, а заключение – нет. Значит утверждение не верно. Обратите особое внимание, на то, что условие «между ними» необходимо!
Но треугольники не равны. Итак, условие утверждения выполнено, а заключение – нет. Значит утверждение не верно. Обратите особое внимание, на то, что условие «между ними» необходимо!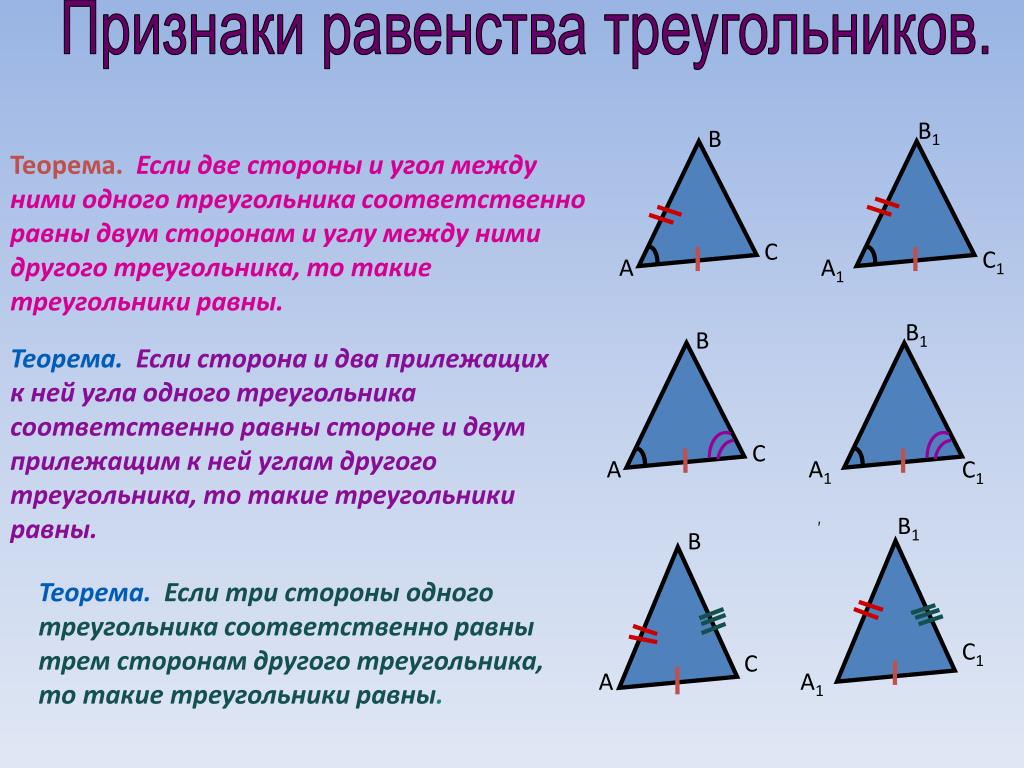
 А затем записываем решение задачи: я на доске, ученики в тетради.
А затем записываем решение задачи: я на доске, ученики в тетради.
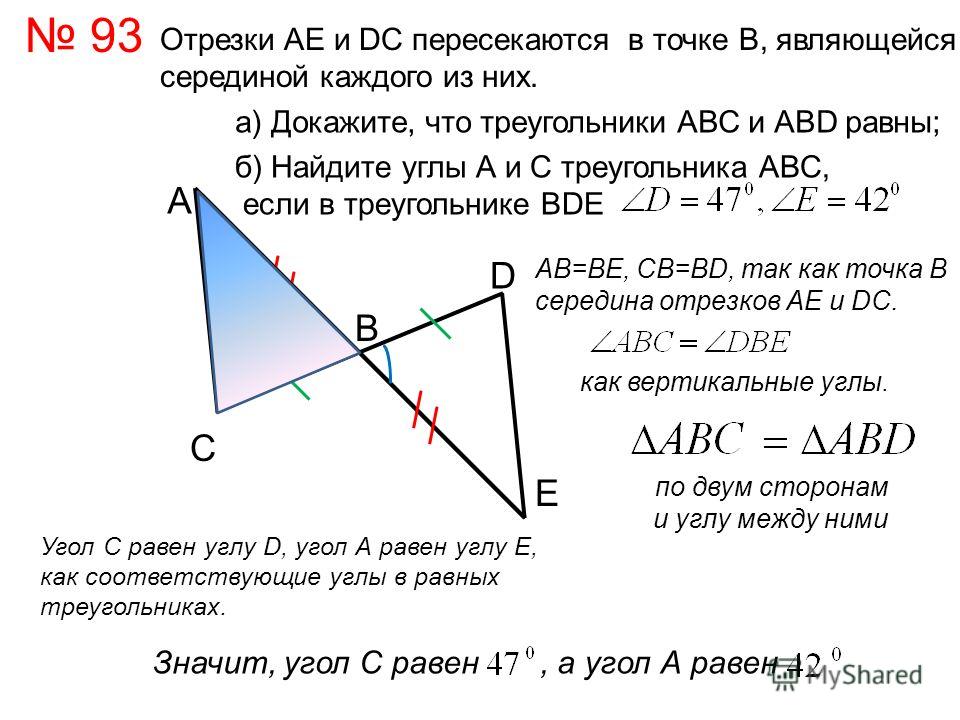 ВС=АD, 1 = 2, а) Докажите, что треугольники АВС и СDА равны; б)Найдите АВ и ВС, если АD =17см, DС=14см.
ВС=АD, 1 = 2, а) Докажите, что треугольники АВС и СDА равны; б)Найдите АВ и ВС, если АD =17см, DС=14см.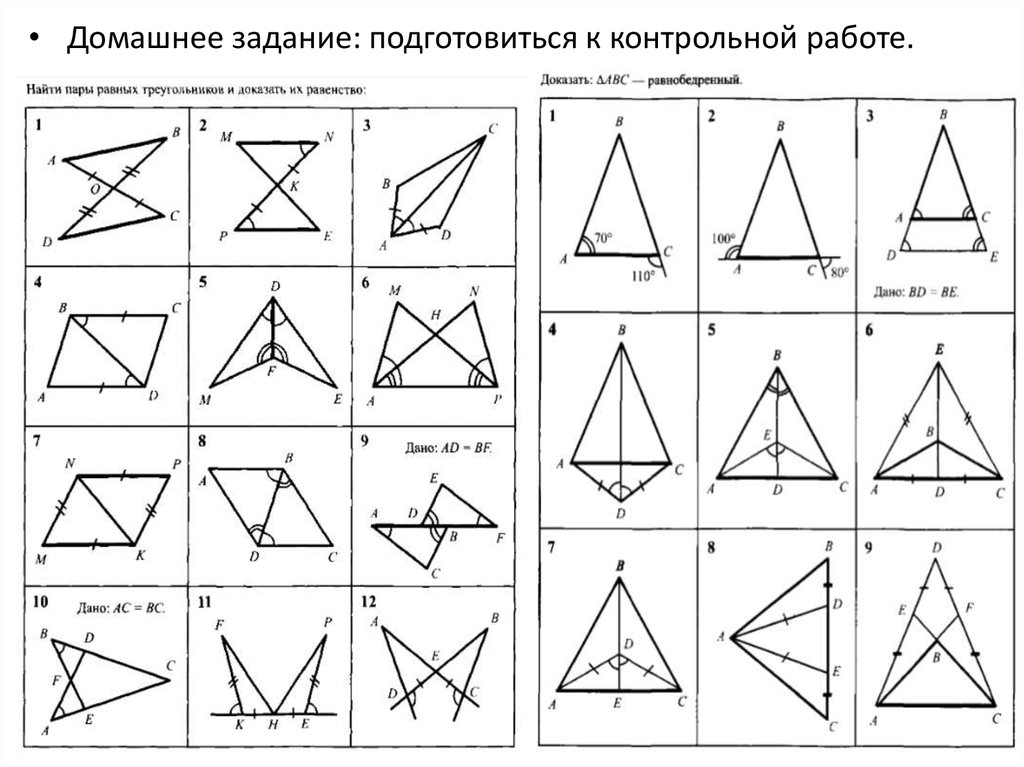
 (Вертикальные, смежные углы, треугольник ) – 15 мин.
(Вертикальные, смежные углы, треугольник ) – 15 мин.


 На данный момент большинство из нас знакомы с тем фактом, что треугольник имеет три стороны.
На данный момент большинство из нас знакомы с тем фактом, что треугольник имеет три стороны. Проще говоря, он не будет формировать треугольник, если указанные выше 3 условия неравенства треугольника неверны.
Проще говоря, он не будет формировать треугольник, если указанные выше 3 условия неравенства треугольника неверны.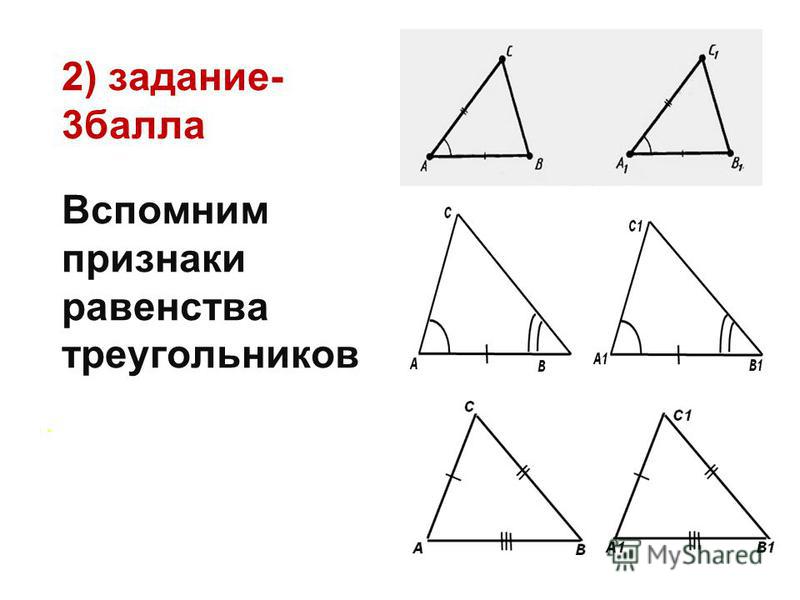 (неверно, 17 не меньше 16)
(неверно, 17 не меньше 16)
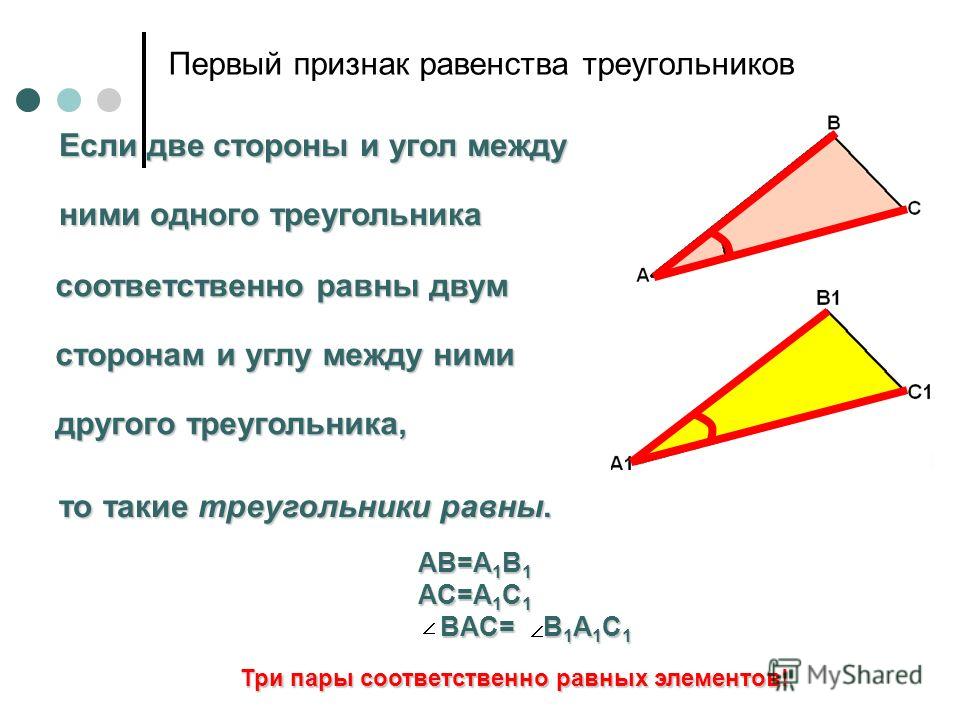
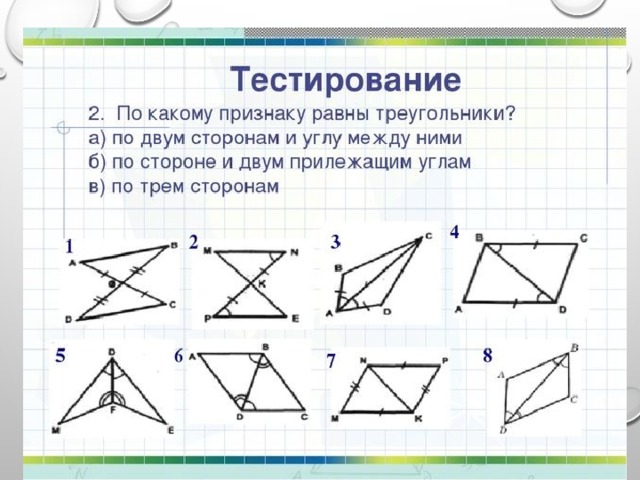 Обратите внимание, что в первых двух случаях мы используем те же самые части, которые мы использовали для доказательства конгруэнтности треугольников в геометрии, но в последнем случае мы не смогли доказать
конгруэнтные треугольники
учитывая эти части. Это потому, что остальные части могли быть разных размеров. Это называется неоднозначным случаем, и мы обсудим его чуть позже.
Обратите внимание, что в первых двух случаях мы используем те же самые части, которые мы использовали для доказательства конгруэнтности треугольников в геометрии, но в последнем случае мы не смогли доказать
конгруэнтные треугольники
учитывая эти части. Это потому, что остальные части могли быть разных размеров. Это называется неоднозначным случаем, и мы обсудим его чуть позже.
 52
см
а также
б
знак равно
22
грех
75
°
грех
63
°
≈
23,85
см
52
см
а также
б
знак равно
22
грех
75
°
грех
63
°
≈
23,85
см (Высота
час
от вершины
Б
в сторону
А
С
¯
, по определению синусов равен
б
грех
А
.)
(Высота
час
от вершины
Б
в сторону
А
С
¯
, по определению синусов равен
б
грех
А
.)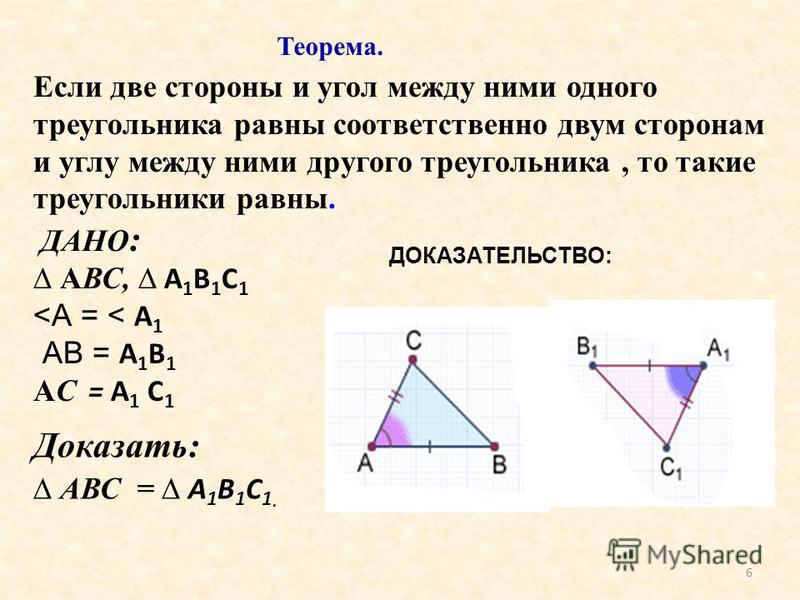
 Так что получается, что решения нет. Проверьте это, используя закон синусов.
Так что получается, что решения нет. Проверьте это, используя закон синусов. Следовательно, никакого треугольника не существует.
Следовательно, никакого треугольника не существует.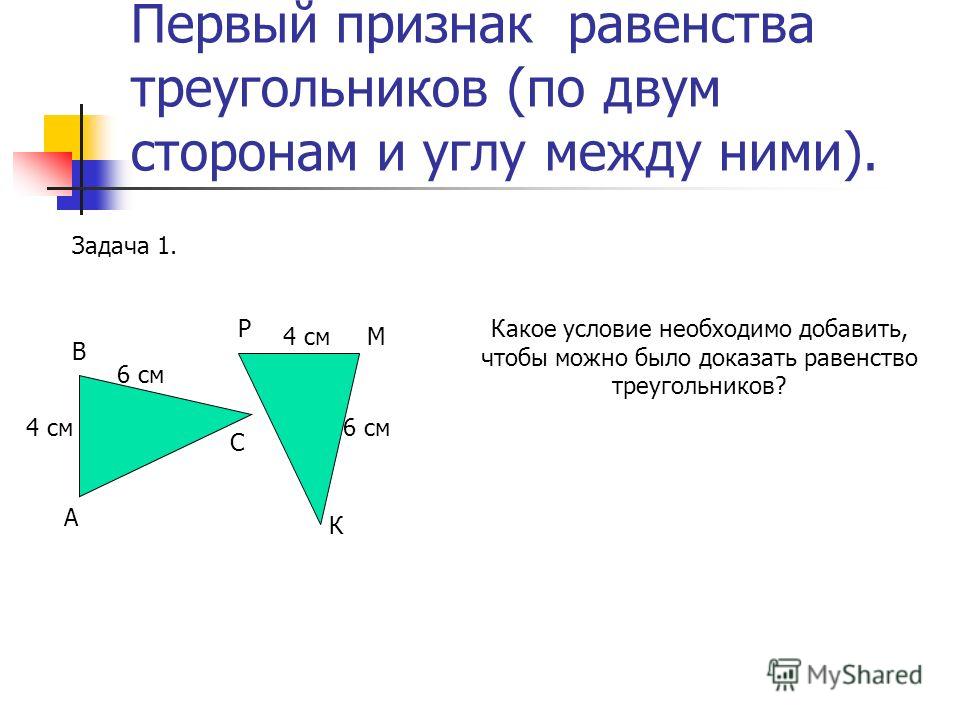

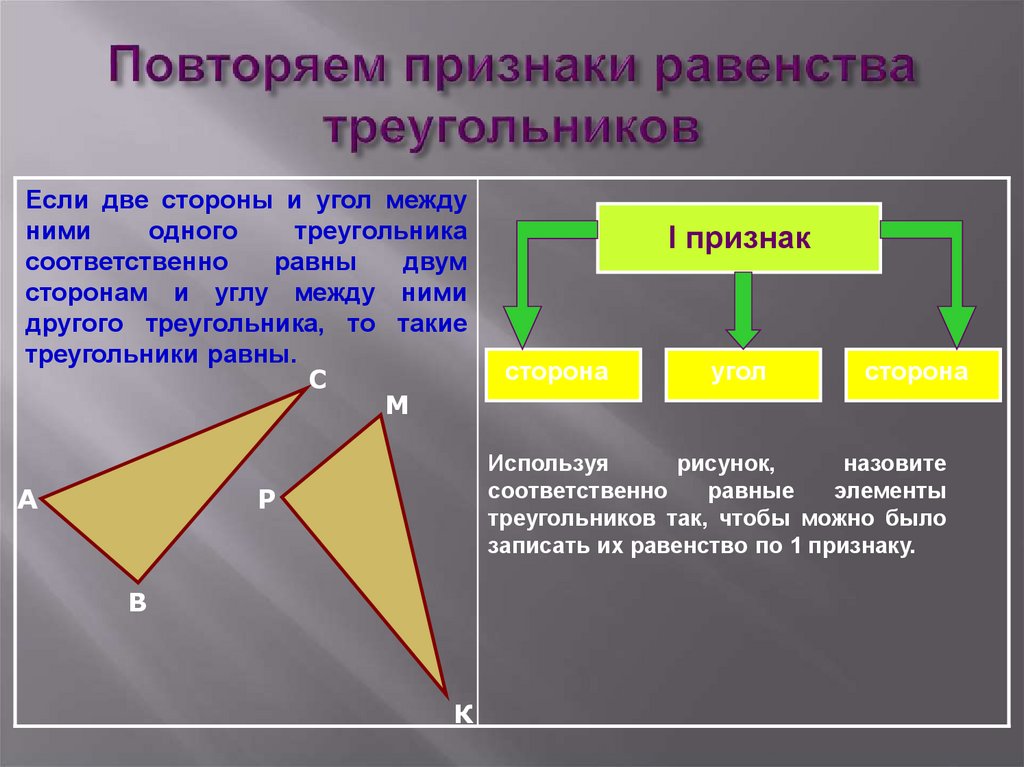 19
19 Найдите остальные углы и сторону.
Найдите остальные углы и сторону. 52
°
52
°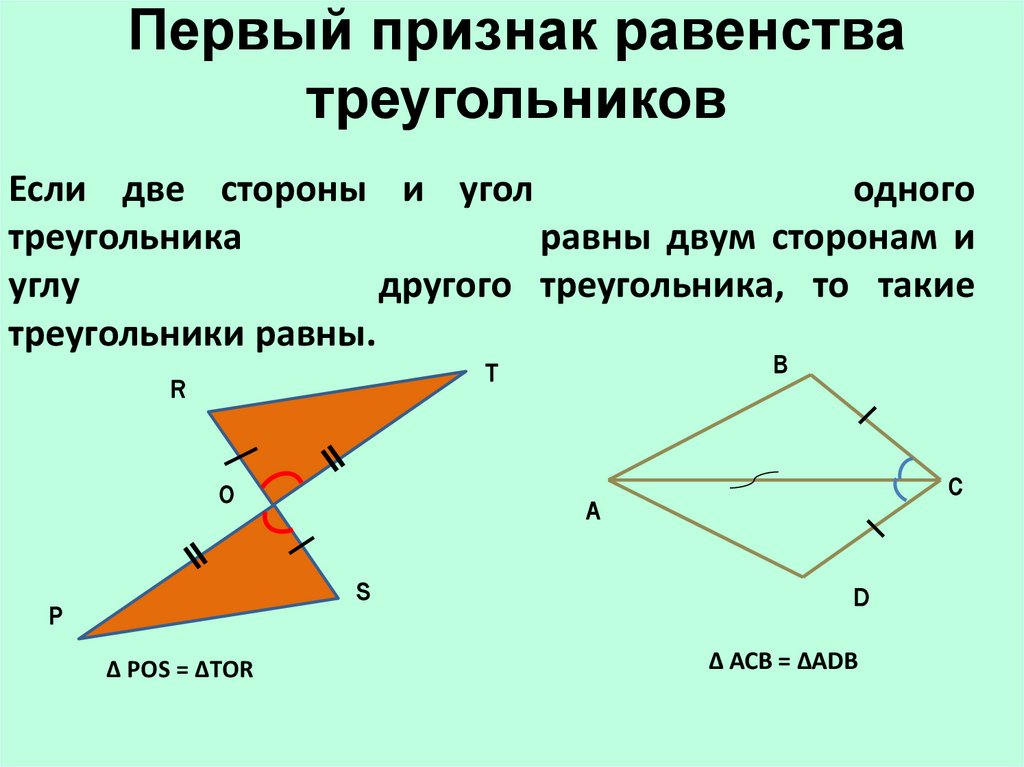 52
°
знак равно
290,79
°
52
°
знак равно
290,79
°  В этих двух случаях мы должны использовать
Закон косинусов
.
В этих двух случаях мы должны использовать
Закон косинусов
.
 Вас попросили найти
другой угол и две другие стороны.
Вас попросили найти
другой угол и две другие стороны. )
)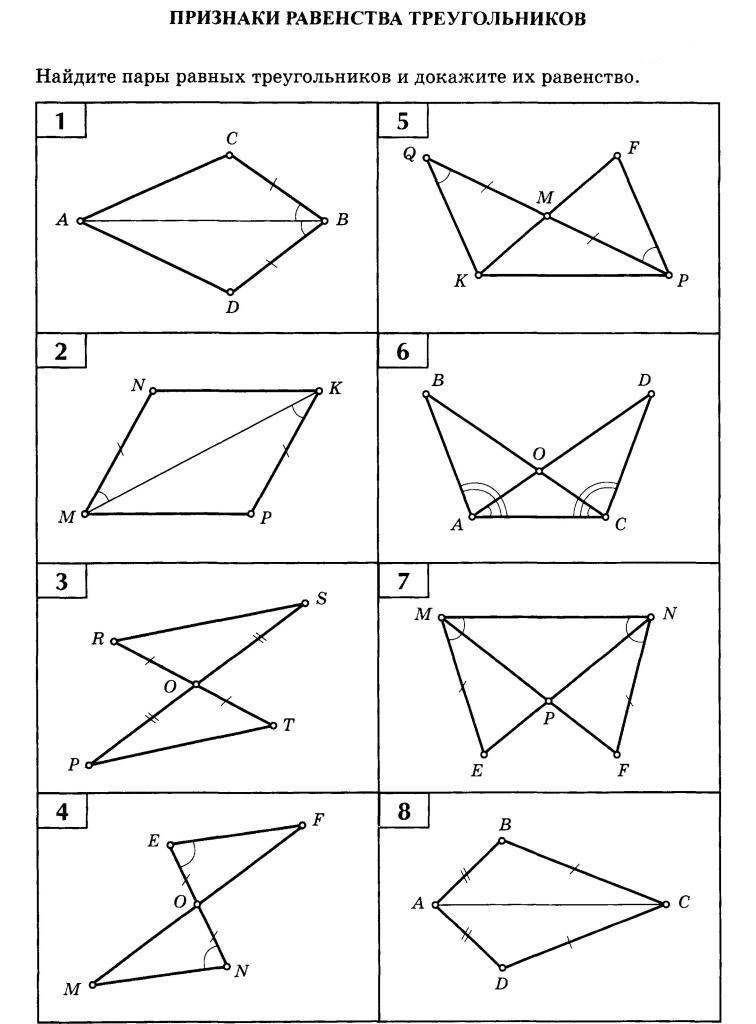 Опускание перпендикуляра CD в
Диаграмма делит большой треугольник (который вы не знаете, как
решить) на два прямоугольных треугольника ACD и BCD с общей стороной CD.
И вы можете решить эти прямоугольные треугольники.
Опускание перпендикуляра CD в
Диаграмма делит большой треугольник (который вы не знаете, как
решить) на два прямоугольных треугольника ACD и BCD с общей стороной CD.
И вы можете решить эти прямоугольные треугольники.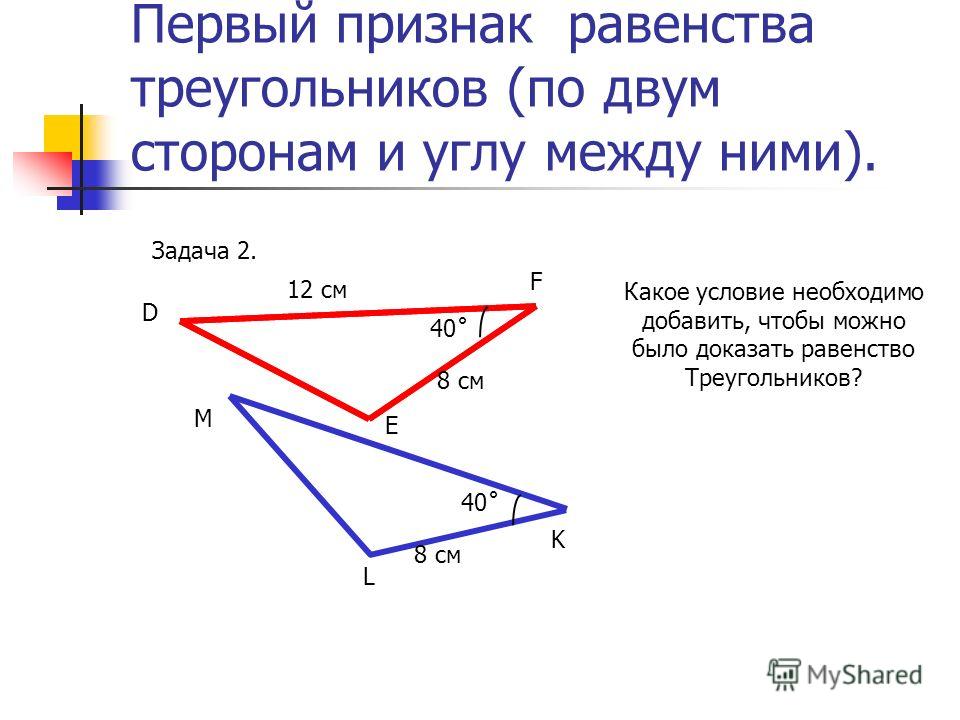 Вы помните, как записывать
длины катетов прямоугольного треугольника?
катет всегда равен гипотенузе умноженной на либо косинус
прилежащего угла или синус противолежащего угла. (Если
для тебя это пустые слова, или даже если ты не на 100%
уверен в этом, пожалуйста, вернитесь и просмотрите
этот раздел, пока не почувствуете себя уверенно.)
Вы помните, как записывать
длины катетов прямоугольного треугольника?
катет всегда равен гипотенузе умноженной на либо косинус
прилежащего угла или синус противолежащего угла. (Если
для тебя это пустые слова, или даже если ты не на 100%
уверен в этом, пожалуйста, вернитесь и просмотрите
этот раздел, пока не почувствуете себя уверенно.) Но вещи, равные одной и той же вещи, равны друг другу.
Это означает, что
Но вещи, равные одной и той же вещи, равны друг другу.
Это означает, что
 Угол С принадлежит исходному треугольнику ABC.
Угол С принадлежит исходному треугольнику ABC. Этот закон справедлив для любого треугольника.
Этот закон справедлив для любого треугольника.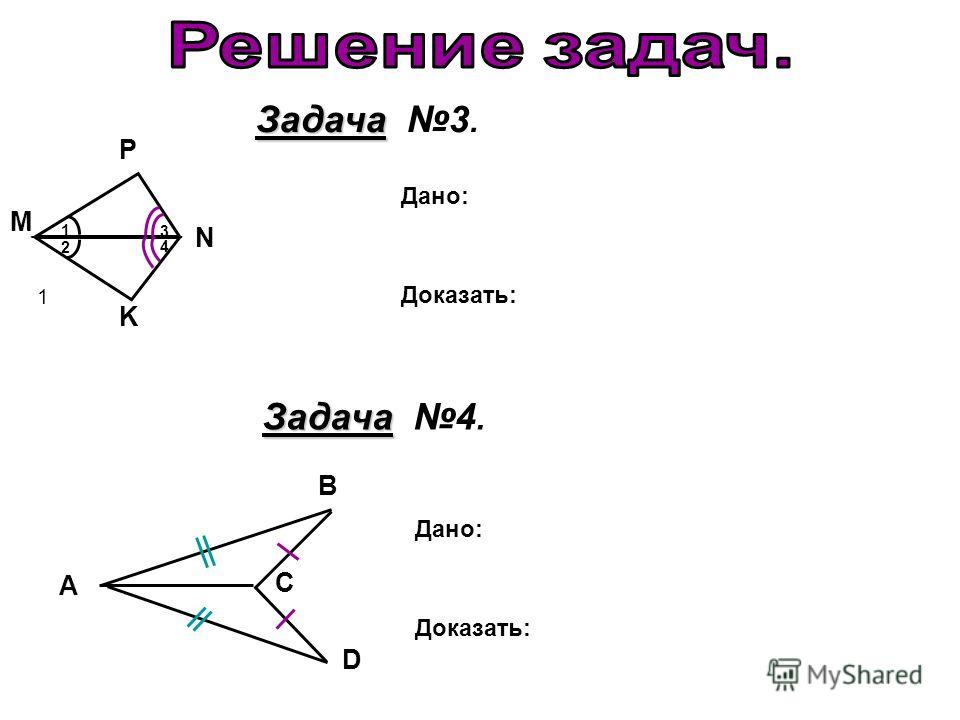
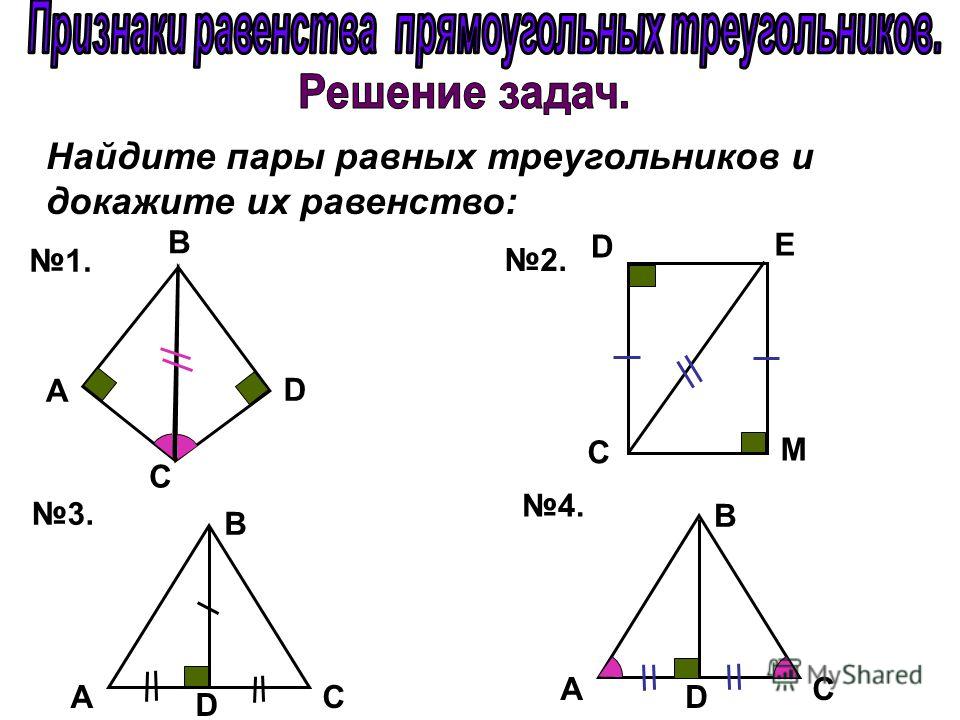
 э.)
э.) Мы можем решить это с помощью небольшой алгебры:
Мы можем решить это с помощью небольшой алгебры: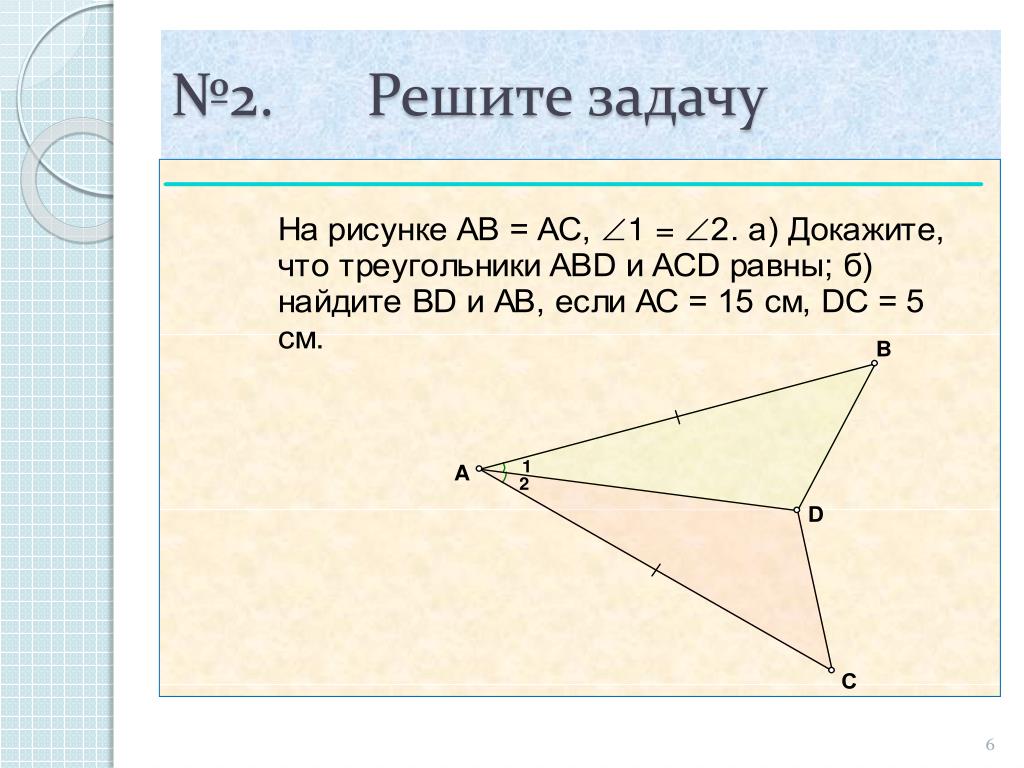
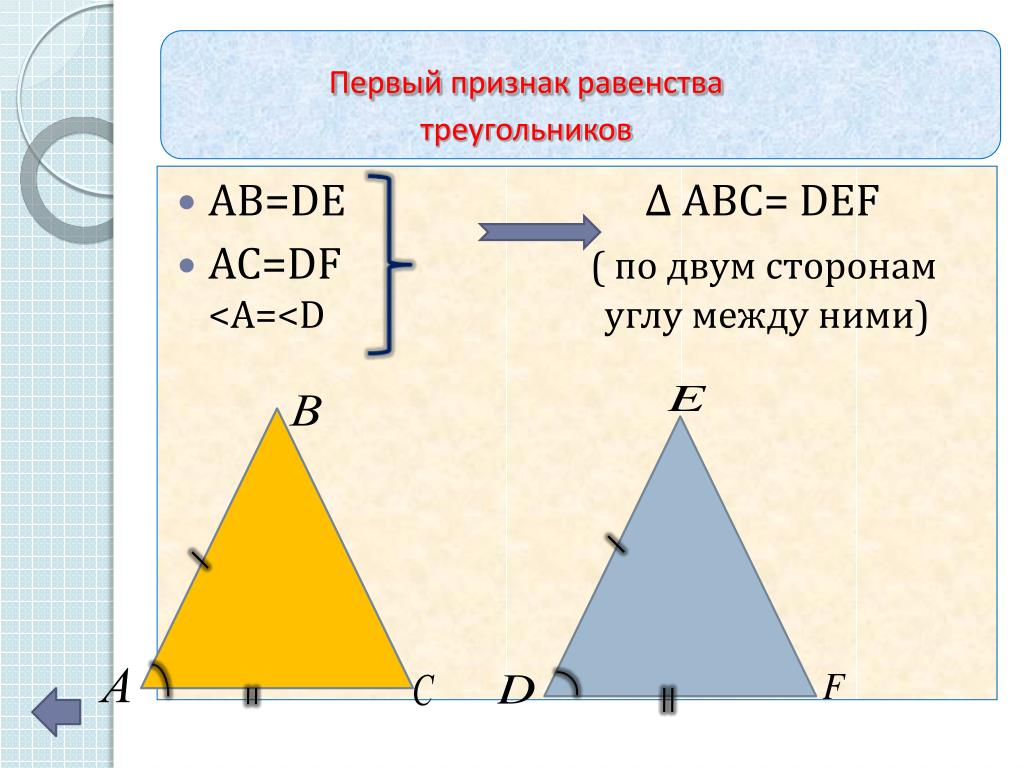 Поскольку косинус имеет уникальные значения от 0 до
180, вам никогда не придется беспокоиться о нескольких решениях одной задачи.
треугольник, когда вы используете закон косинусов.
Поскольку косинус имеет уникальные значения от 0 до
180, вам никогда не придется беспокоиться о нескольких решениях одной задачи.
треугольник, когда вы используете закон косинусов.
 )
)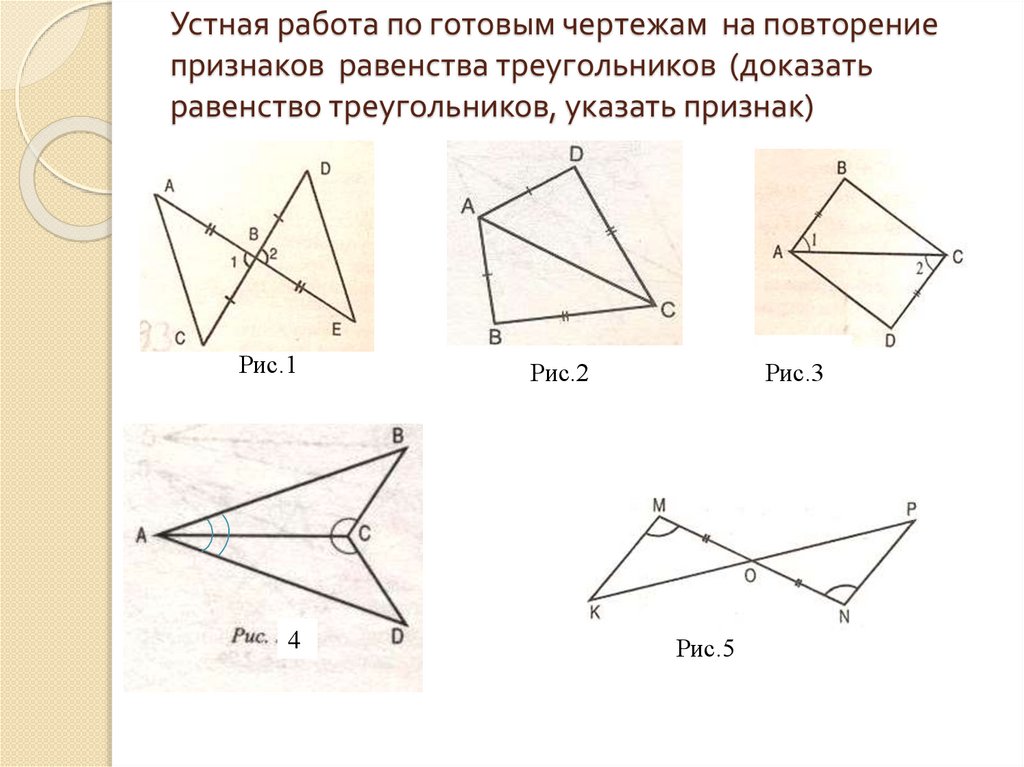 Без хотя бы одной стороны у вас есть
форма треугольника, но нет возможности правильно масштабировать ее. За
например, те же самые углы могут дать вам треугольник со сторонами 7-12-13,
35-60-65 или любой другой кратный.
Без хотя бы одной стороны у вас есть
форма треугольника, но нет возможности правильно масштабировать ее. За
например, те же самые углы могут дать вам треугольник со сторонами 7-12-13,
35-60-65 или любой другой кратный.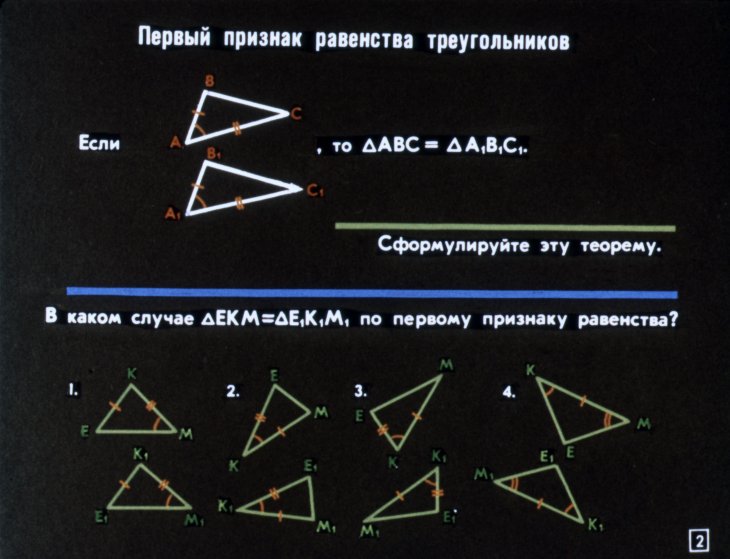 Обратите внимание, ниже.
Обратите внимание, ниже. Просто примените определения синуса и косинуса
(уравнение 1) и тангенс (уравнение 4), чтобы найти другую
стороны и углы.
Просто примените определения синуса и косинуса
(уравнение 1) и тангенс (уравнение 4), чтобы найти другую
стороны и углы.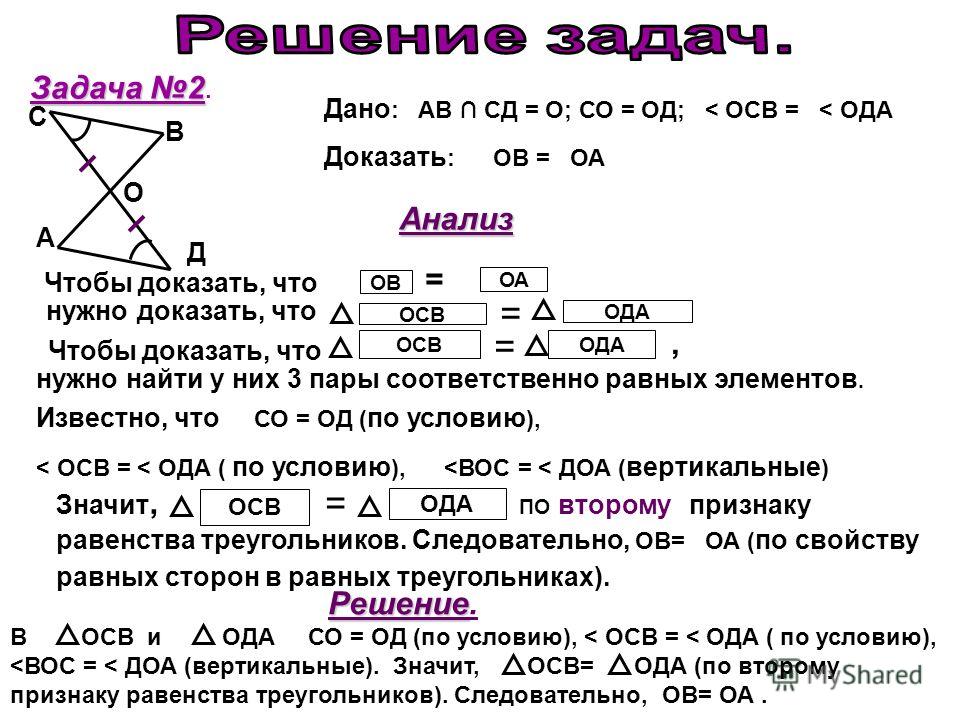 Эти два положения дают два разных значения угла A ,
два разных значения для угла C и два разных значения для стороны c .
Подумайте об этом некоторое время и
Вы увидите, что эта неоднозначность может возникнуть только тогда, когда известный угол
острая, а прилежащая сторона длиннее противоположной стороны, и
противоположная сторона больше высоты.
Эти два положения дают два разных значения угла A ,
два разных значения для угла C и два разных значения для стороны c .
Подумайте об этом некоторое время и
Вы увидите, что эта неоднозначность может возникнуть только тогда, когда известный угол
острая, а прилежащая сторона длиннее противоположной стороны, и
противоположная сторона больше высоты.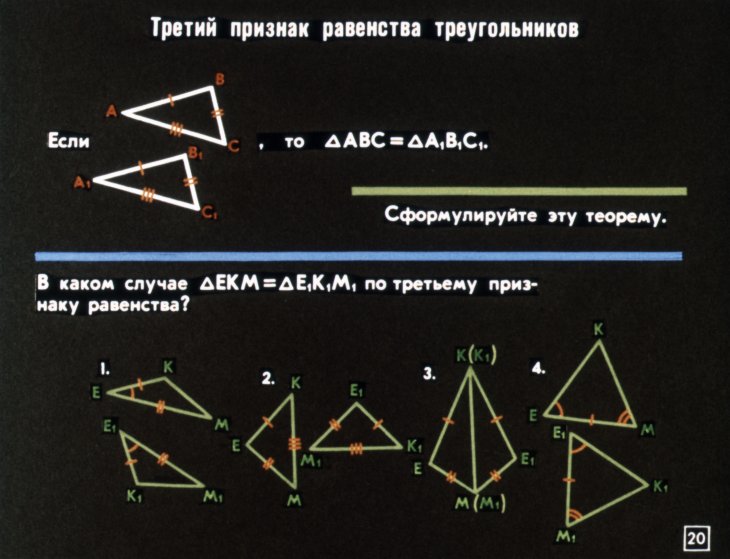
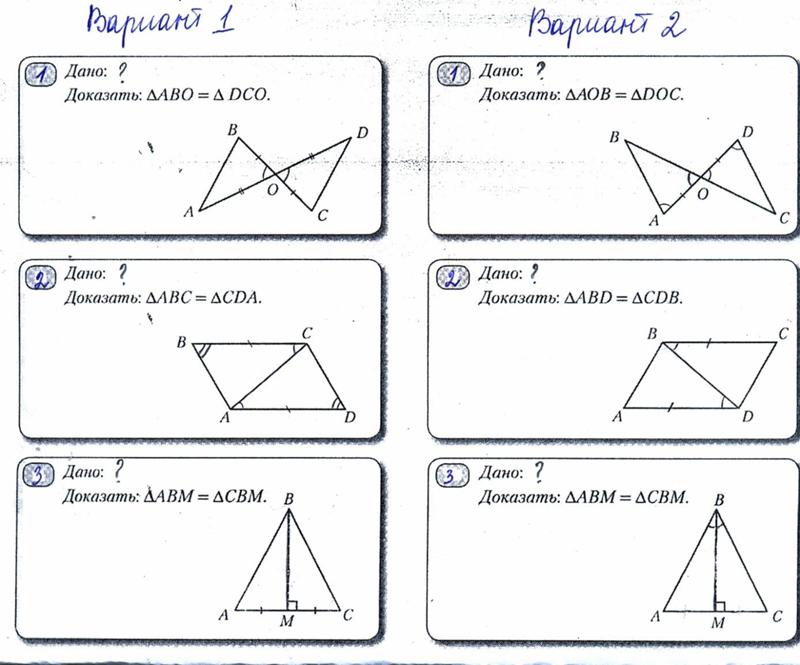 В этом
случай, когда ваше решение ограничено, и вы отклоняете решение, которое
не соответствует ограничениям.
В этом
случай, когда ваше решение ограничено, и вы отклоняете решение, которое
не соответствует ограничениям.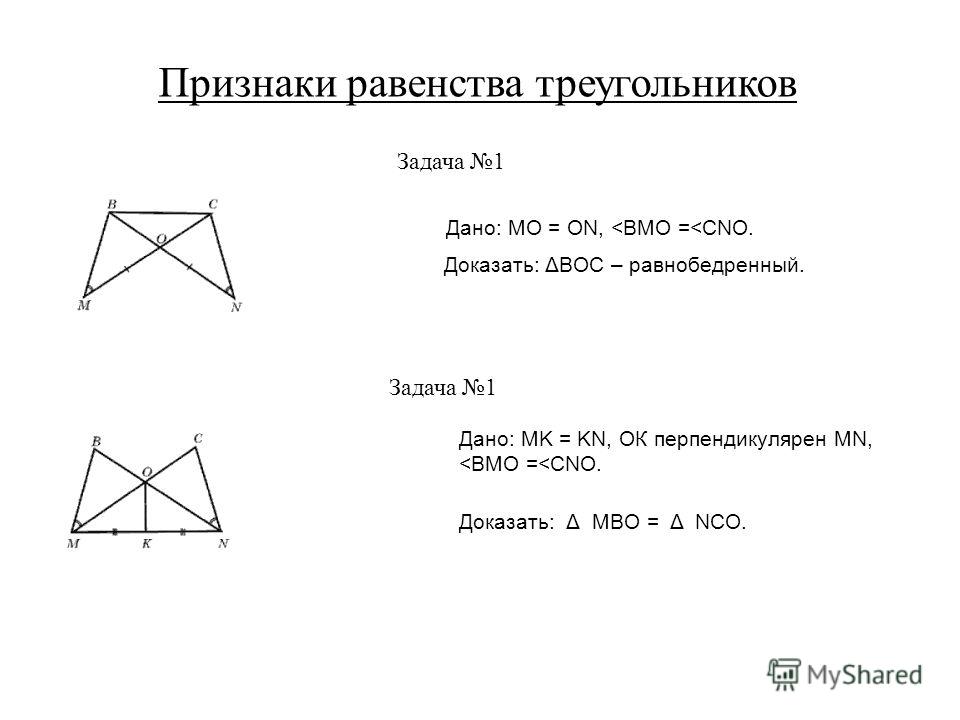 ..
..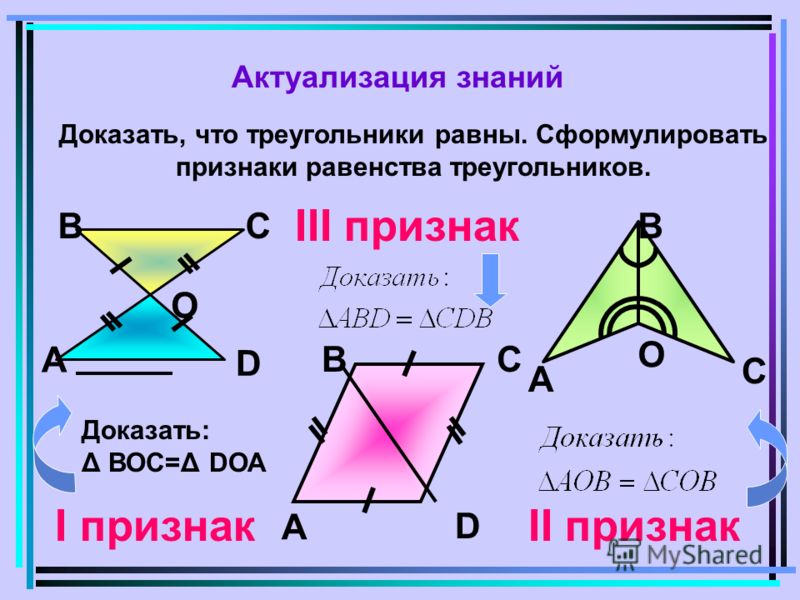
 Ответ находится в законе синусов:
Ответ находится в законе синусов: Просто найдите грех A :
Просто найдите грех A : )
В государственном парке река течет практически прямо
1800 м. Вы хотите построить монорельс из A , один конец
этот участок, до точки C на дальнем берегу. Вы также хотите
построить пешеходный мост от B , на другом конце этого участка
реки, до той же точки C на дальнем берегу.
В A угол между вашими линиями взгляда и B и C равен 67. В B угол между вашим прицелом
строк A и C 38.
)
В государственном парке река течет практически прямо
1800 м. Вы хотите построить монорельс из A , один конец
этот участок, до точки C на дальнем берегу. Вы также хотите
построить пешеходный мост от B , на другом конце этого участка
реки, до той же точки C на дальнем берегу.
В A угол между вашими линиями взгляда и B и C равен 67. В B угол между вашим прицелом
строк A и C 38. Вы решили покрасить треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
три стороны.
Вы решили покрасить треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
три стороны.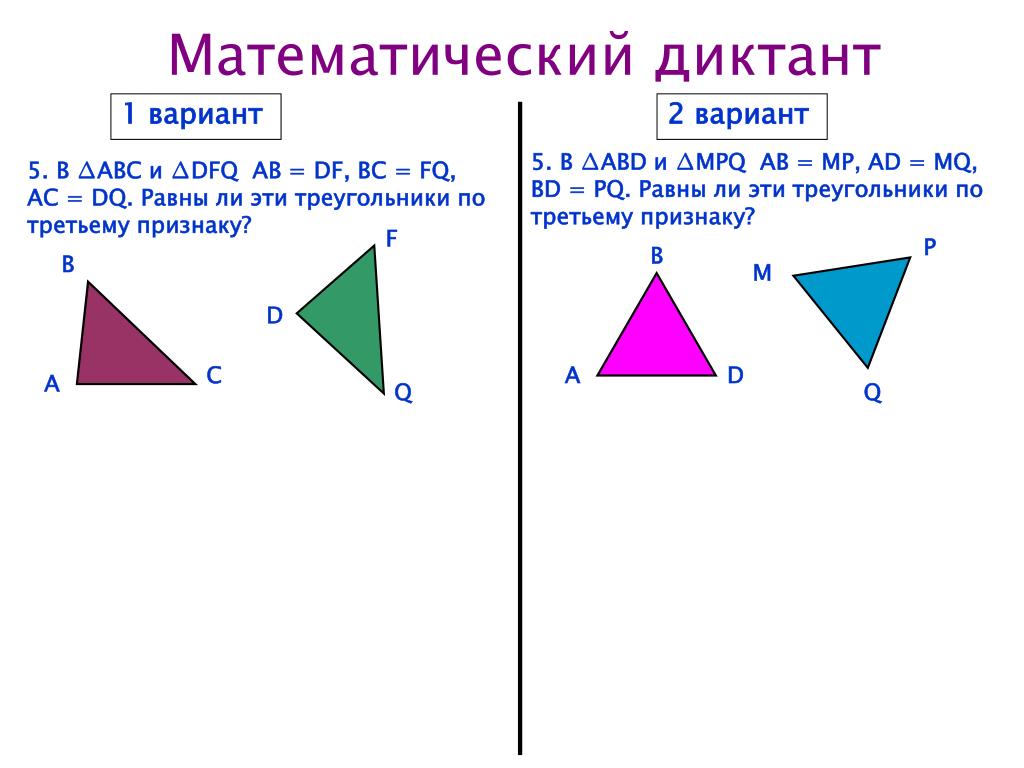 Поля. Большинство учителей не очень хорошо учат вас
как решать задачи и делать доказательства. Они показывают вам, как они делать их, и ожидать, что вы подберете их методы своего рода
осмос. Но большинство из них не очень хорошо объясняют мысль
процесс, в ходе которого выполняется геометрическое доказательство или решается страшная
проблема истории.
Поля. Большинство учителей не очень хорошо учат вас
как решать задачи и делать доказательства. Они показывают вам, как они делать их, и ожидать, что вы подберете их методы своего рода
осмос. Но большинство из них не очень хорошо объясняют мысль
процесс, в ходе которого выполняется геометрическое доказательство или решается страшная
проблема истории. Если вы не можете получить его
из книжного магазина, идите в библиотеку и возьмите экземпляр. ты не будешь
Извините.
Если вы не можете получить его
из книжного магазина, идите в библиотеку и возьмите экземпляр. ты не будешь
Извините.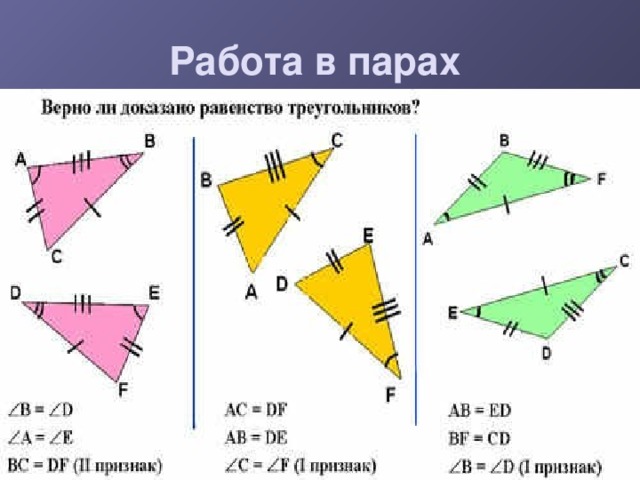 На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.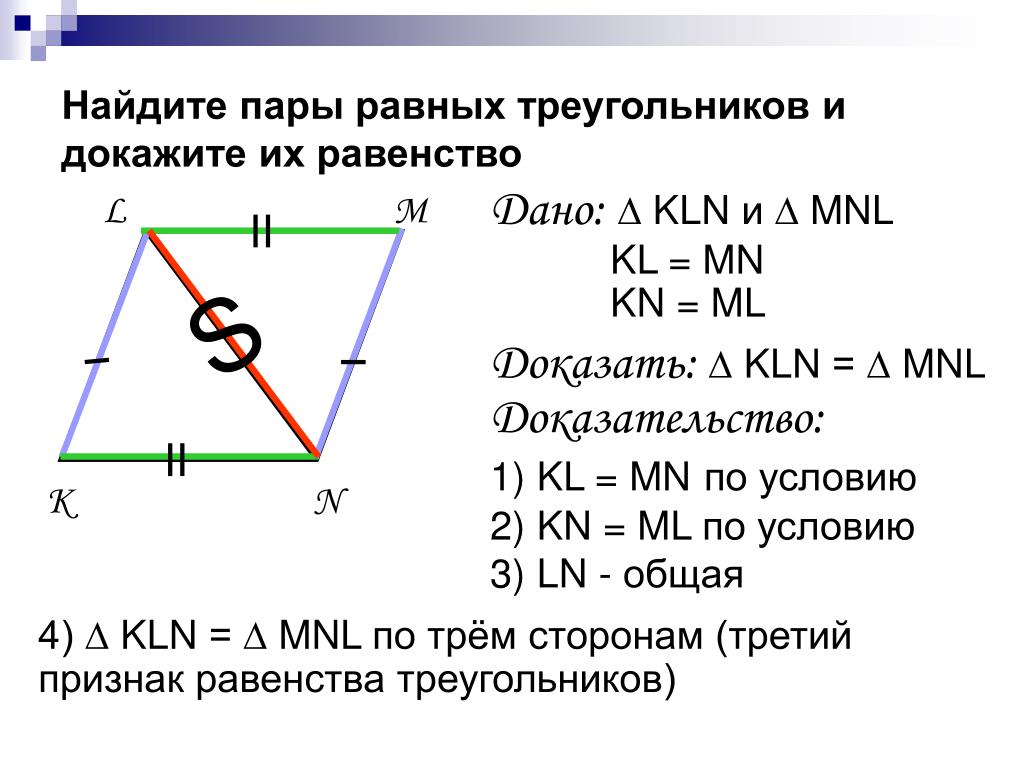 Теорема Пифагора.
Теорема Пифагора.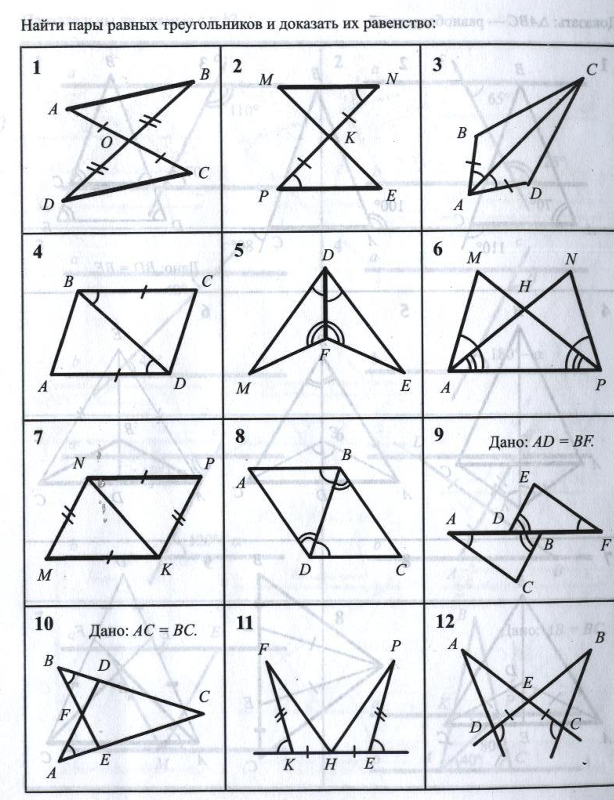
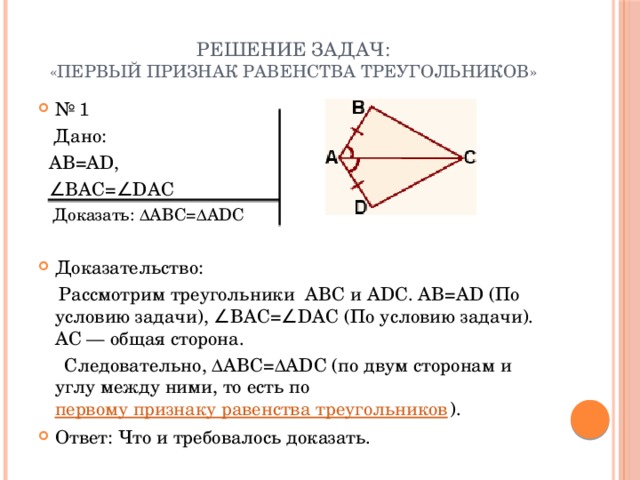
 A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.  Какова длина PQ ?
Какова длина PQ ? Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, по нужным точкам на АВ ?
Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, по нужным точкам на АВ ? Это означает, что вы опускаете перпендикуляр из C на эту линию и определяете ее длину. Вы можете использовать угол A и прямую AC , чтобы найти его, или вы можете использовать угол B и прямую BC , чтобы найти его.
Это означает, что вы опускаете перпендикуляр из C на эту линию и определяете ее длину. Вы можете использовать угол A и прямую AC , чтобы найти его, или вы можете использовать угол B и прямую BC , чтобы найти его. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.  Тогда для каждого из правильных положений лодки P, вы знаете две стороны и угол между ними треугольника PAC, , так что вы можете определить нужный угол по закону косинусов.
Тогда для каждого из правильных положений лодки P, вы знаете две стороны и угол между ними треугольника PAC, , так что вы можете определить нужный угол по закону косинусов.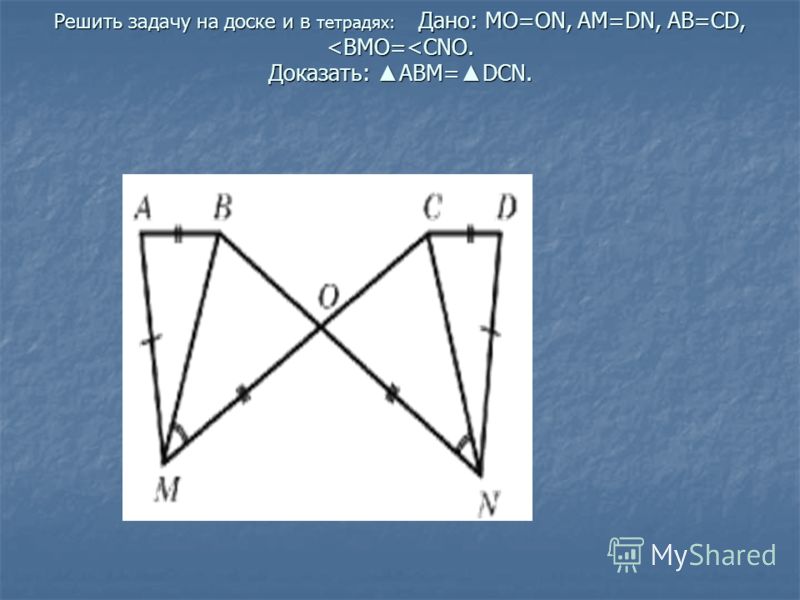
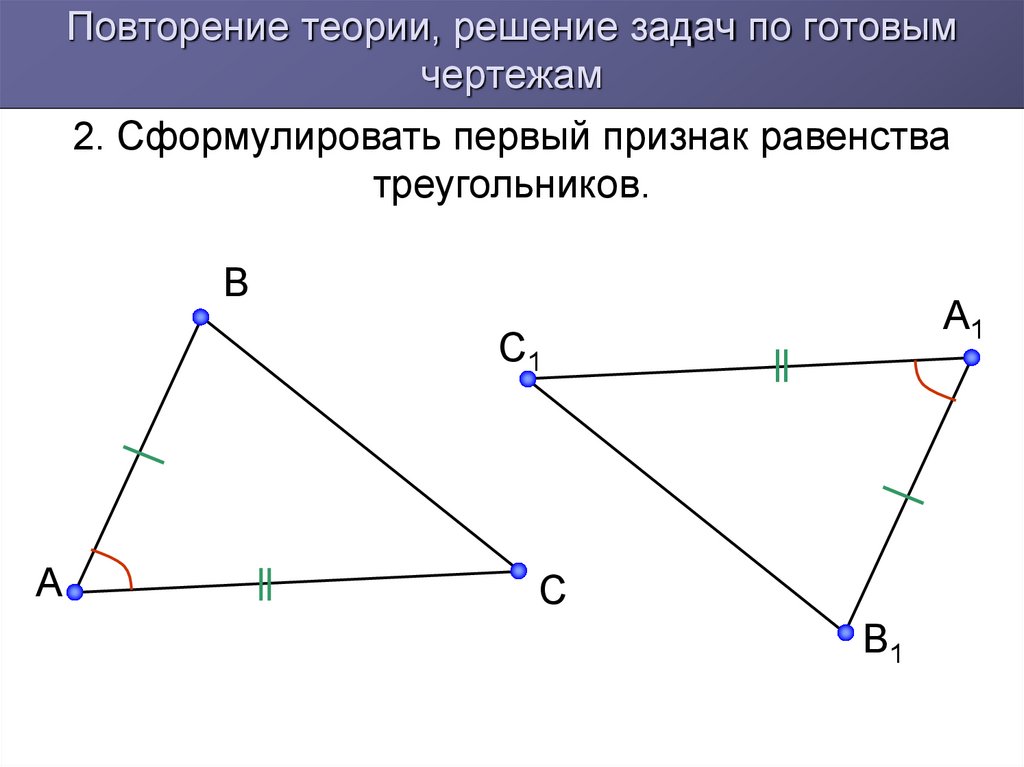
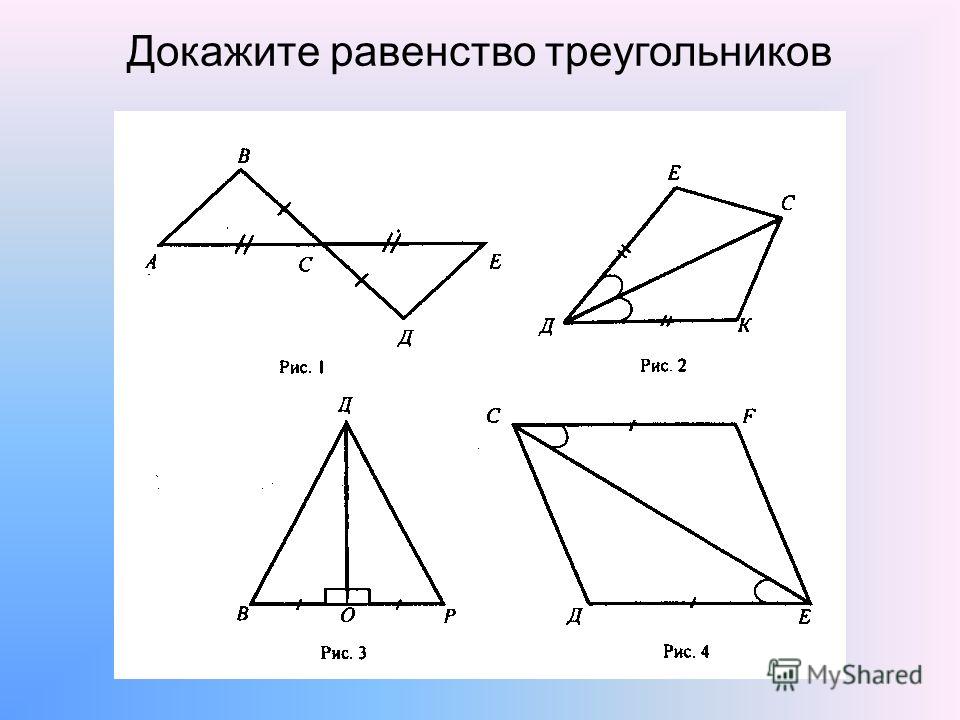 Если вы сначала пойдете в C, а затем в B, то расстояние, которое вы преодолеете, AC + CB, несомненно, будет больше, чем AB. В качестве альтернативы, давайте попробуем понять теорему о неравенстве треугольника через построение. Предположим, что вам даны три длины: x , y и z . Вас просят построить треугольник с этими сторонами. Вы действуете следующим образом:
Если вы сначала пойдете в C, а затем в B, то расстояние, которое вы преодолеете, AC + CB, несомненно, будет больше, чем AB. В качестве альтернативы, давайте попробуем понять теорему о неравенстве треугольника через построение. Предположим, что вам даны три длины: x , y и z . Вас просят построить треугольник с этими сторонами. Вы действуете следующим образом:
 Дополнительно можем заключить, что в треугольнике:
Дополнительно можем заключить, что в треугольнике: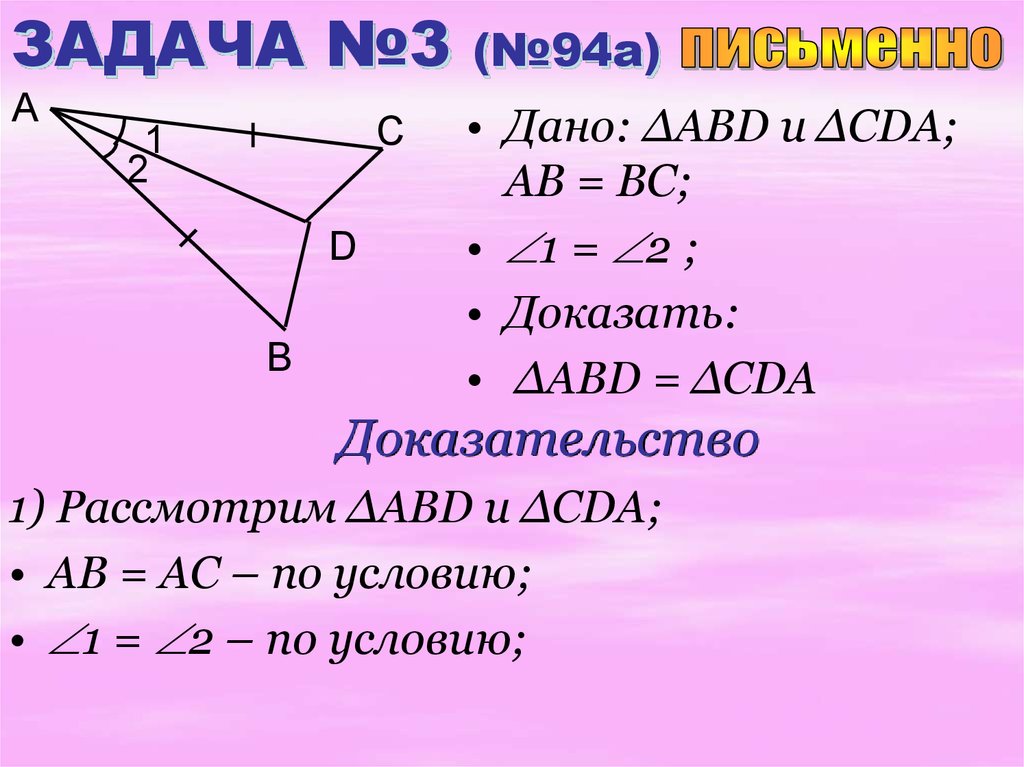
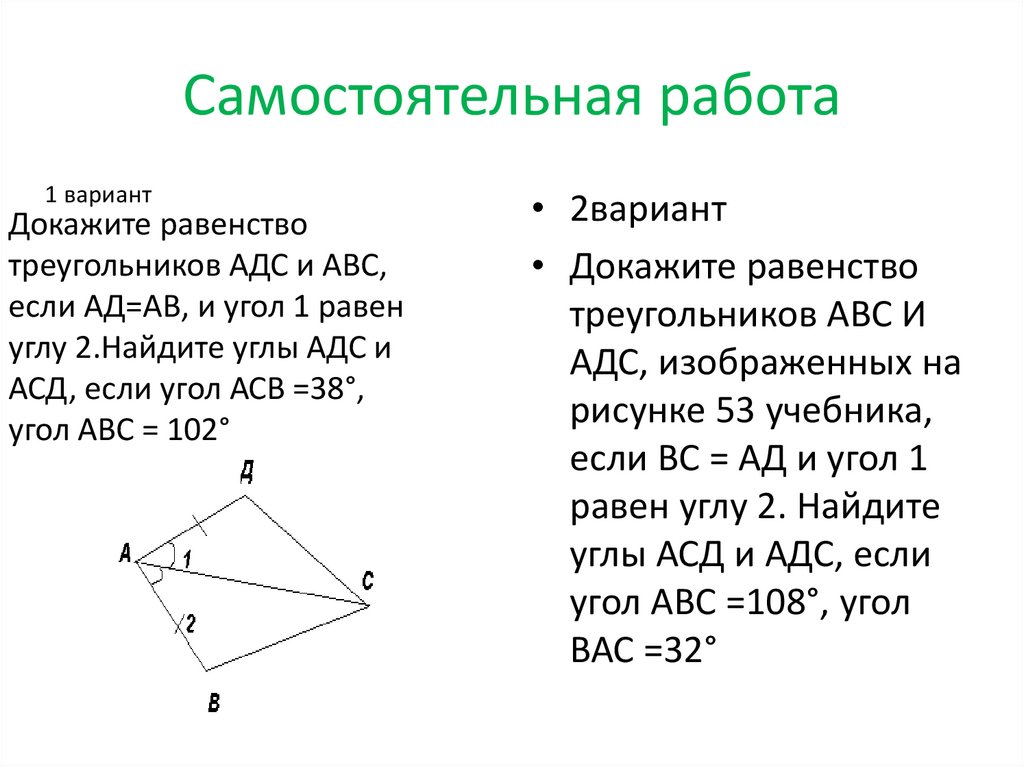 Сможет ли он составить треугольник с этими тремя измерениями?
Сможет ли он составить треугольник с этими тремя измерениями?
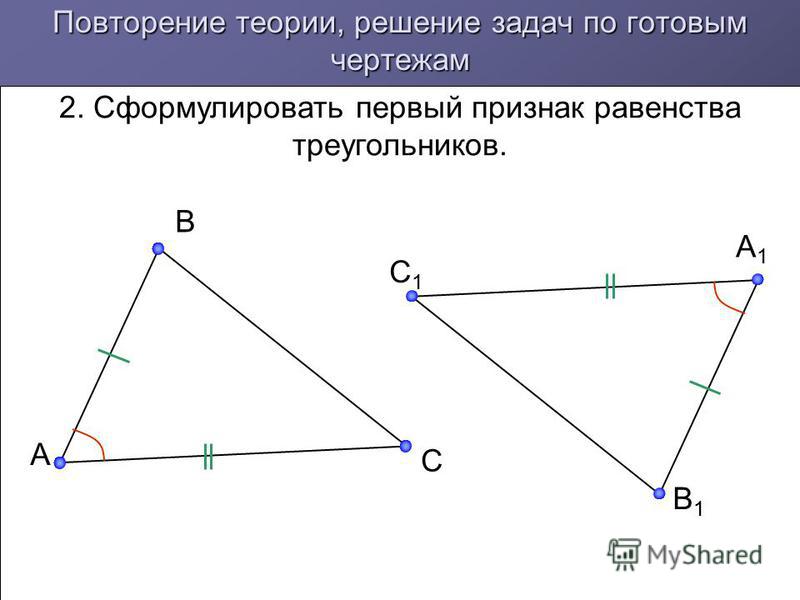
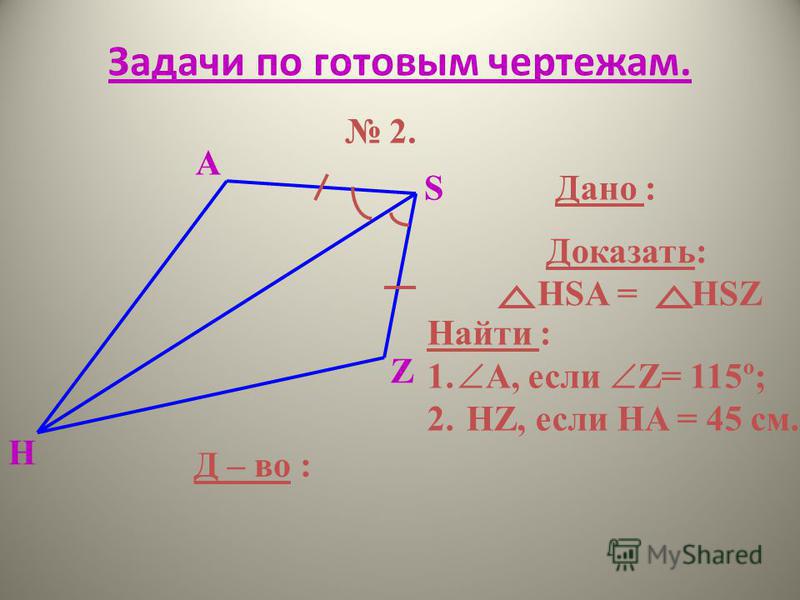 Исходя из классификации по внутренним углам, различают три типа – равнобедренные, равнобедренные и разносторонние. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, являются прямоугольным, остроугольным и косоугольным. Вот типы треугольников:
Исходя из классификации по внутренним углам, различают три типа – равнобедренные, равнобедренные и разносторонние. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, являются прямоугольным, остроугольным и косоугольным. Вот типы треугольников: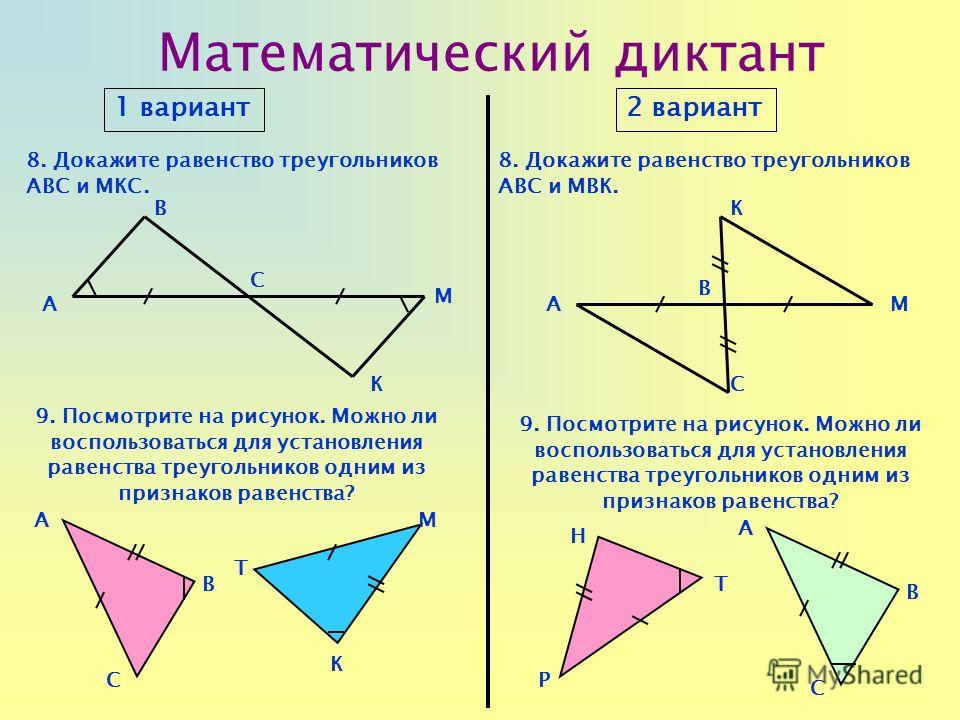 Итак, когда замкнутая фигура имеет три угла?
Итак, когда замкнутая фигура имеет три угла?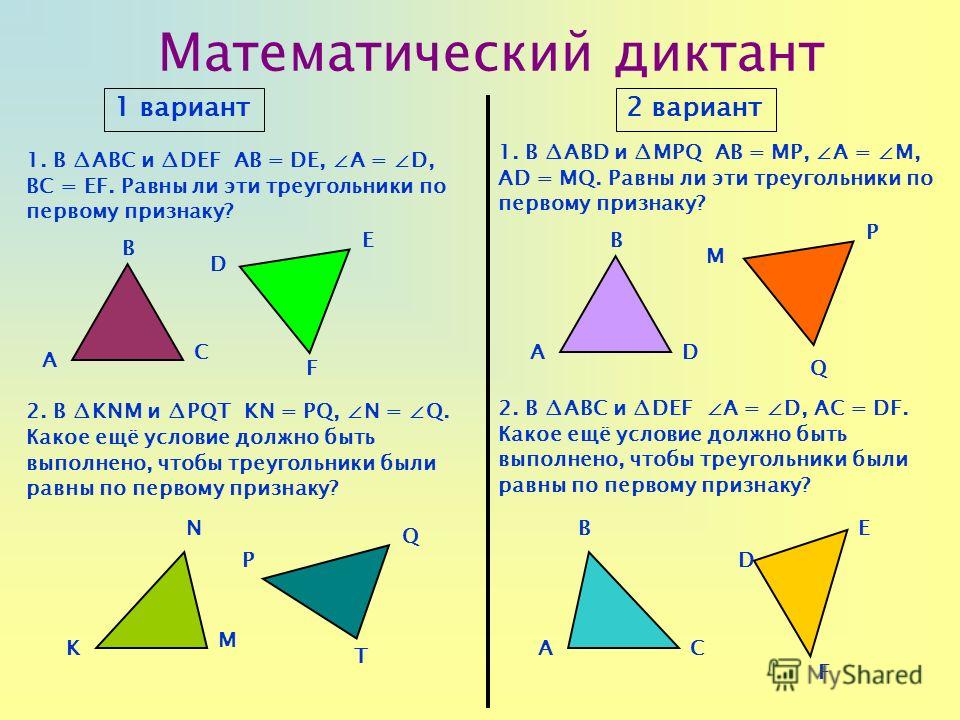
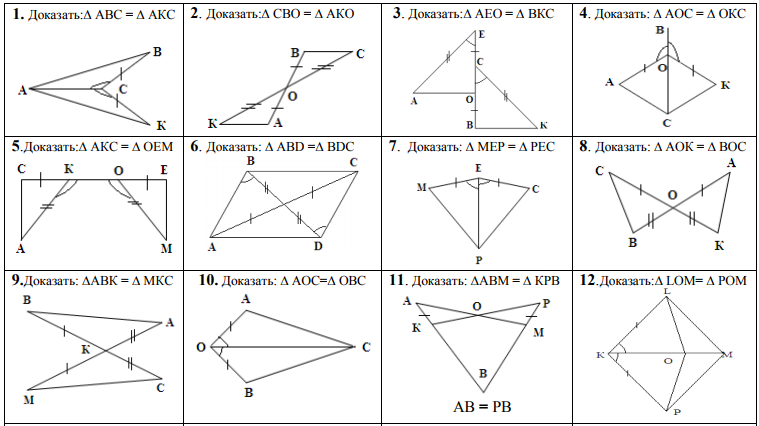
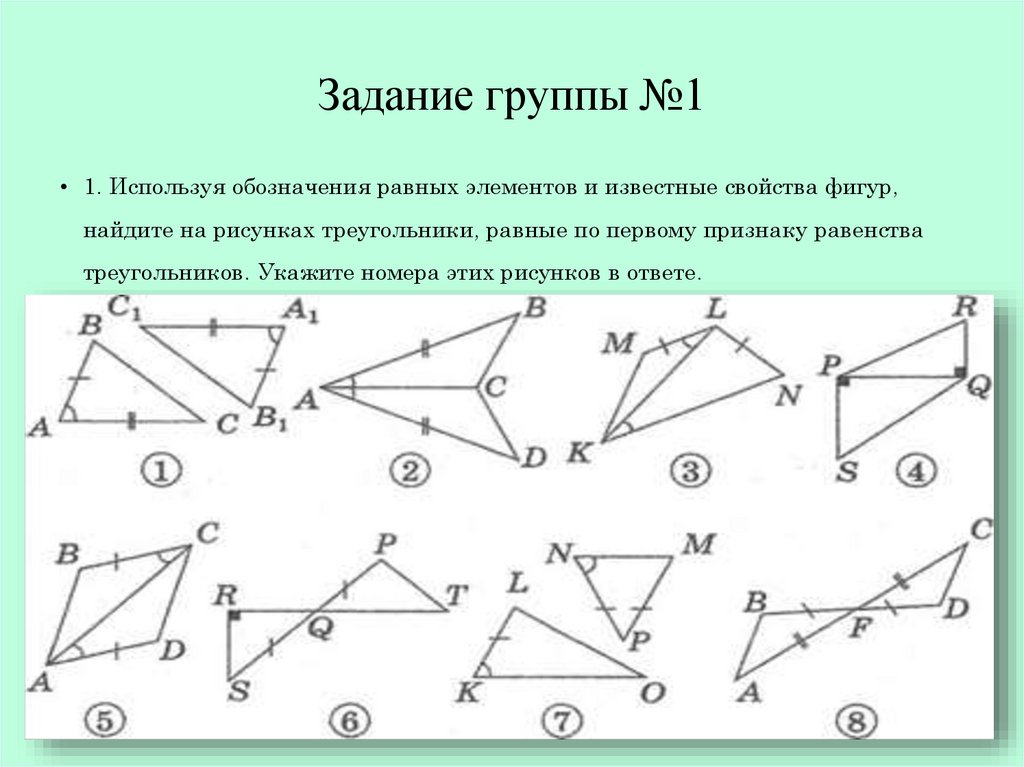
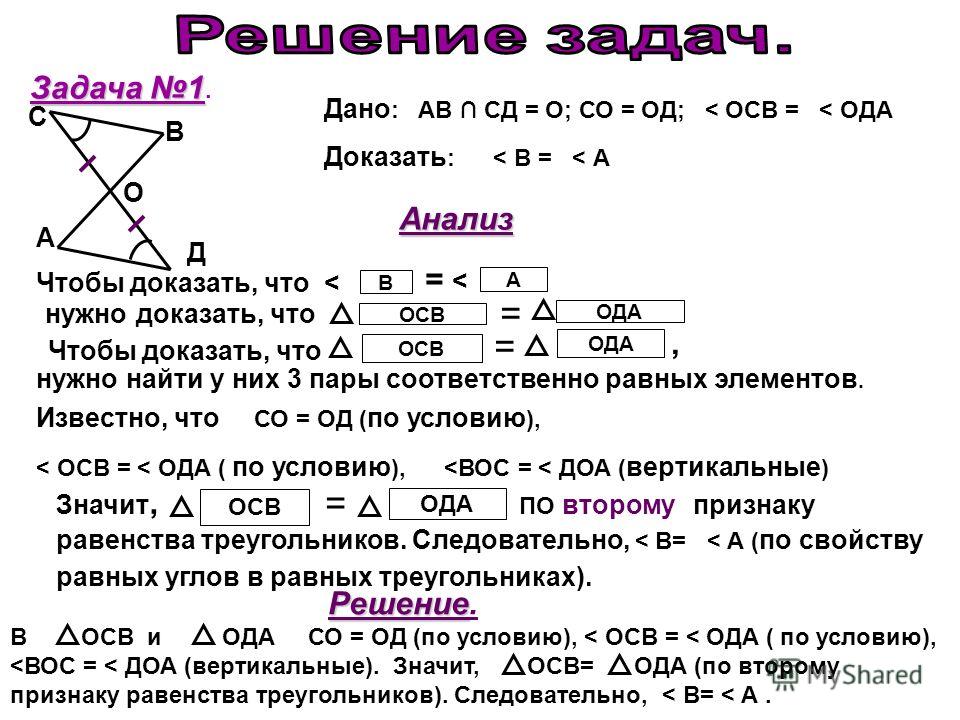

 И угадайте, на какой марке компьютеров вы могли бы найти VisiCalc? На Apple II, которая стала популярной благодаря этой программе.В течение 1980-х годов Lotus 1-2-3 стал лидером на рынке электронных таблиц для персональных компьютеров, которые работали под управлением операционной системы Microsoft MS-DOS и быстро обогнали VisiCalc по продажам.
И угадайте, на какой марке компьютеров вы могли бы найти VisiCalc? На Apple II, которая стала популярной благодаря этой программе.В течение 1980-х годов Lotus 1-2-3 стал лидером на рынке электронных таблиц для персональных компьютеров, которые работали под управлением операционной системы Microsoft MS-DOS и быстро обогнали VisiCalc по продажам. 3695868907363
3695868907363 3639702343
3639702343 color-mn { color: #005B7C; }
color-mn { color: #005B7C; } 
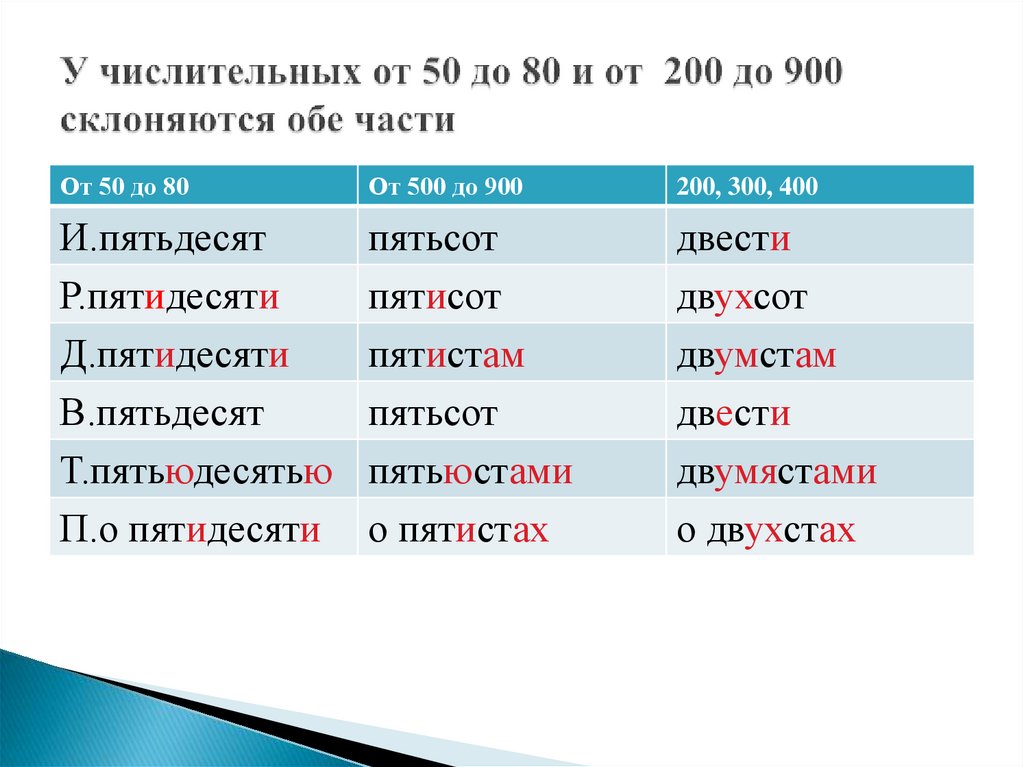
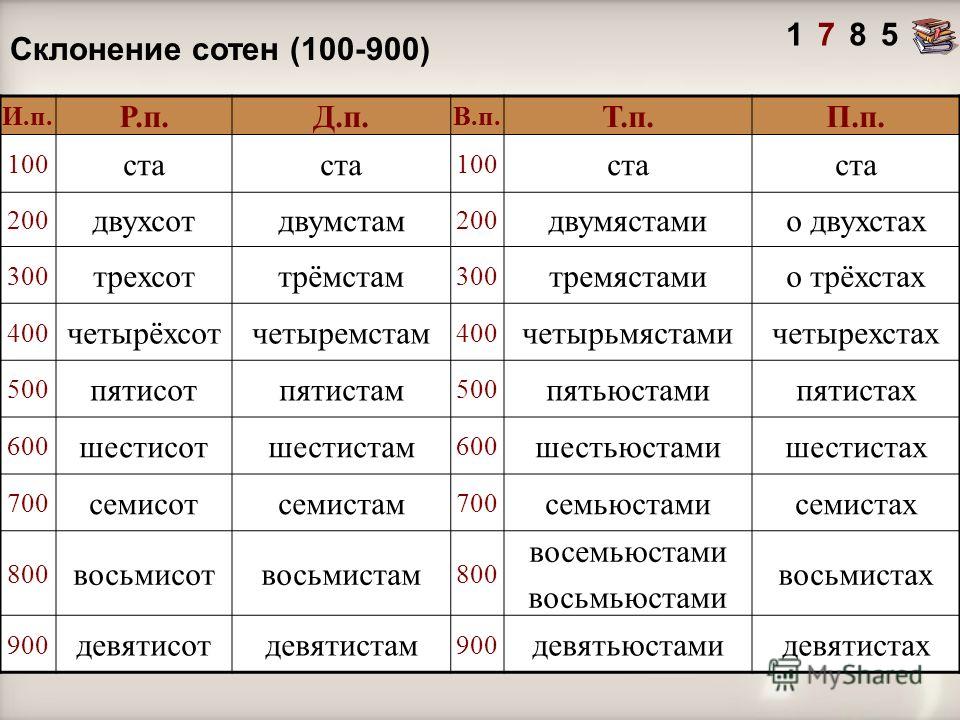

 — Ну здравствуй, Витольд. Хмм, гляжу семейным стал. Поздравляю! — пожал я следом на своё приветствие, изрядно меня удивившего своим ненаигранным смущением на мои слова, руку ведьмаку, которого поставил над всеми своими вассалами во главе ордена в своё отсутствие. Хотя кому ещё быть главным среди них, как не самому первому в их расе. Тут надо кое-что прояснить. Тот, кого я зову Витольдом и кого в ордена знают как Вольда, есть тот самый сын Альзура, которого он сделал химерой, желая дать своему ребенку возможность творить магию. После отравления Альзура, а именно так церковь смогла убить, как я подозреваю Архимага, у Ватикана в те годы было не мало умельцев магов, кому было по силам сообща одолеть даже Архимага, но этого и не потребовалось, всё сделал яд, в общем после того как Архимага или очень сильно магистра, не суть важно, не стало, дела у Витольда с его товарищами, кто также прошел инициацию, пошли очень скверно. Их стали загонять по всей христианской Европе и скрываясь от церкви, они перебрались в Норвегию, где затаились на десятки лет.
— Ну здравствуй, Витольд. Хмм, гляжу семейным стал. Поздравляю! — пожал я следом на своё приветствие, изрядно меня удивившего своим ненаигранным смущением на мои слова, руку ведьмаку, которого поставил над всеми своими вассалами во главе ордена в своё отсутствие. Хотя кому ещё быть главным среди них, как не самому первому в их расе. Тут надо кое-что прояснить. Тот, кого я зову Витольдом и кого в ордена знают как Вольда, есть тот самый сын Альзура, которого он сделал химерой, желая дать своему ребенку возможность творить магию. После отравления Альзура, а именно так церковь смогла убить, как я подозреваю Архимага, у Ватикана в те годы было не мало умельцев магов, кому было по силам сообща одолеть даже Архимага, но этого и не потребовалось, всё сделал яд, в общем после того как Архимага или очень сильно магистра, не суть важно, не стало, дела у Витольда с его товарищами, кто также прошел инициацию, пошли очень скверно. Их стали загонять по всей христианской Европе и скрываясь от церкви, они перебрались в Норвегию, где затаились на десятки лет. Там же они практически сразу получили признание и уважение, всё таки на землях Скандинавов ещё существовало язычество, а христианство только делало робкие шаги и вроде как даже добились некоторых успехов. Аристократия уже прошла крещение, вот только стоило им оказаться на борту драккара, кнорра или в сече на суше, как они забывали о христианских добродетелях и взывали к Одину или Тору.
Сама Норвегия тех лет была местом очень неспокойным, так что различных монстров там водилось не мало. Начиная от стай одичавших оборотней, потерявших всё человеческое в себе, до льдистых драконов и драургов. Витольд славно покуролесил в тех краях со своими товарищами, да только за те пятьдесят лет, что они там скрывались, все его друзья отошли в мир иной. Всё таки они занимались опасным делом и каждый из прожитый там день был наполнен сражениями и битвами с различными порождениями магии.
К тому времени, когда сын Альзура решил возвращаться на континент, рядом с ним не было никого, кто бы знал его настоящее происхождения и для всех он стал Вольдом, а не Витольдом.
Там же они практически сразу получили признание и уважение, всё таки на землях Скандинавов ещё существовало язычество, а христианство только делало робкие шаги и вроде как даже добились некоторых успехов. Аристократия уже прошла крещение, вот только стоило им оказаться на борту драккара, кнорра или в сече на суше, как они забывали о христианских добродетелях и взывали к Одину или Тору.
Сама Норвегия тех лет была местом очень неспокойным, так что различных монстров там водилось не мало. Начиная от стай одичавших оборотней, потерявших всё человеческое в себе, до льдистых драконов и драургов. Витольд славно покуролесил в тех краях со своими товарищами, да только за те пятьдесят лет, что они там скрывались, все его друзья отошли в мир иной. Всё таки они занимались опасным делом и каждый из прожитый там день был наполнен сражениями и битвами с различными порождениями магии.
К тому времени, когда сын Альзура решил возвращаться на континент, рядом с ним не было никого, кто бы знал его настоящее происхождения и для всех он стал Вольдом, а не Витольдом. Несколько лет ему понадобилась на то, чтобы попасть в Цитадель. Церковники тогда крепко обложили все подступы к ней и все порталы ведущие на земли близ Цитадели были под плотным наблюдением. Это уже позднее он смог открыть законсервированные, скрытые порталы, о которых никому не было известно и таким образом орден получил базу и тихую пристань. А местонахождение этих неучтённых выходов охранялось принесением клятвы неразглашения. От меня же, Архимага и сильнейшего менталиста, ему не удалось скрыть правду о себе. Так что я уже через несколько дней после нашего с ним знакомства узнал его истинную историю и происхождение. И думается мне, что он оказался самым сильным из своей расы потому, что ритуал который ему оставил отец для инициации ведьмаков был откорректирован и у него на руках оказалась бюджетная версия, так сказать эконом класс.
— И ты будь здрав, Святозар. Хмм, да. Уже тридцать лет как женился. — запустив руку в свою роскошную бороду, которая сейчас была распущена, а не как обычно заплетена в косы, прогудел здоровяк.
Несколько лет ему понадобилась на то, чтобы попасть в Цитадель. Церковники тогда крепко обложили все подступы к ней и все порталы ведущие на земли близ Цитадели были под плотным наблюдением. Это уже позднее он смог открыть законсервированные, скрытые порталы, о которых никому не было известно и таким образом орден получил базу и тихую пристань. А местонахождение этих неучтённых выходов охранялось принесением клятвы неразглашения. От меня же, Архимага и сильнейшего менталиста, ему не удалось скрыть правду о себе. Так что я уже через несколько дней после нашего с ним знакомства узнал его истинную историю и происхождение. И думается мне, что он оказался самым сильным из своей расы потому, что ритуал который ему оставил отец для инициации ведьмаков был откорректирован и у него на руках оказалась бюджетная версия, так сказать эконом класс.
— И ты будь здрав, Святозар. Хмм, да. Уже тридцать лет как женился. — запустив руку в свою роскошную бороду, которая сейчас была распущена, а не как обычно заплетена в косы, прогудел здоровяк. — Даже не буду спрашивать, кто твоя избранница. Тебя уже можно поздравлять с счастливым отцовство или я поторопился? — хотя будет точнее сказать, чей избранник он. Олаф мне поведал о влюбленности в Витольда его ученицы Агнешки, которую тот спас от костра инквизиции, ещё девятилетней соплюшкой и привёл в орден. А уже позже взял над ней опеку и обучил её всем необходимым в их трудной профессии знаниям, умениям и премудростям.
И с того дня, как Агнешка осознала свои чувств к своему учителю и спасителю, когда вошла в возраст половозрелой девушки, она не оставляла надежды затащить своего обожаемого и любимого наставника к себе в постель. Ну а после обретения возможности иметь детей, она смогла его дожать и сделать своим мужчиной. Молодец!
Меня уже мучило любопытство, родились ли у них уже дети и если да, то очень хотелось взглянуть на него или их. У них явно получатся неординарные детки. Всё-таки Витольд самый сильный в своей расе представитель, а Агнешка истинная ведьма и плод их любви явно возьмёт от своих родителей самое лучшее.
— Даже не буду спрашивать, кто твоя избранница. Тебя уже можно поздравлять с счастливым отцовство или я поторопился? — хотя будет точнее сказать, чей избранник он. Олаф мне поведал о влюбленности в Витольда его ученицы Агнешки, которую тот спас от костра инквизиции, ещё девятилетней соплюшкой и привёл в орден. А уже позже взял над ней опеку и обучил её всем необходимым в их трудной профессии знаниям, умениям и премудростям.
И с того дня, как Агнешка осознала свои чувств к своему учителю и спасителю, когда вошла в возраст половозрелой девушки, она не оставляла надежды затащить своего обожаемого и любимого наставника к себе в постель. Ну а после обретения возможности иметь детей, она смогла его дожать и сделать своим мужчиной. Молодец!
Меня уже мучило любопытство, родились ли у них уже дети и если да, то очень хотелось взглянуть на него или их. У них явно получатся неординарные детки. Всё-таки Витольд самый сильный в своей расе представитель, а Агнешка истинная ведьма и плод их любви явно возьмёт от своих родителей самое лучшее. Тут не нужно быть пророк, чтобы это предугадать. Будучи любящей женой, Агнешка всем сердцем будет ждать рождения своего дитя и желать ему только лишь блага. А мне известно насколько мир благосклонен к истинным ведьмам и как легко откликается на их искренние чувства.
— Можно! — просиял этот гигант, что был на пол головы выше меня. А я ведь далеко не низкий представитель мужского пола и ростом сто девяносто сантиметров, а у Витольда все двести десять, — Агнешка нарадоваться не может нашей Любавушке. Ей уже второй год. — и всё было сказано с гордостью, хвастовством и обожанием, обращённое сразу же и на любимую женщину и на их ребёнка. Ранее весь его внешний вид и внутреннее содержание говорили, просто кричали о том, что этот разумный взвалил на себя тяжёлое бремя и будет его нести до своего последнего вздоха. Все силы его души, его чувства, разум, воля, тело, дух, были сосредоточены на уничтожение тварей.
Но что я вижу теперь? Мужа, который наконец таки обрёл семейное счастье, о котором запретил себе когда-то мечтать.
Тут не нужно быть пророк, чтобы это предугадать. Будучи любящей женой, Агнешка всем сердцем будет ждать рождения своего дитя и желать ему только лишь блага. А мне известно насколько мир благосклонен к истинным ведьмам и как легко откликается на их искренние чувства.
— Можно! — просиял этот гигант, что был на пол головы выше меня. А я ведь далеко не низкий представитель мужского пола и ростом сто девяносто сантиметров, а у Витольда все двести десять, — Агнешка нарадоваться не может нашей Любавушке. Ей уже второй год. — и всё было сказано с гордостью, хвастовством и обожанием, обращённое сразу же и на любимую женщину и на их ребёнка. Ранее весь его внешний вид и внутреннее содержание говорили, просто кричали о том, что этот разумный взвалил на себя тяжёлое бремя и будет его нести до своего последнего вздоха. Все силы его души, его чувства, разум, воля, тело, дух, были сосредоточены на уничтожение тварей.
Но что я вижу теперь? Мужа, который наконец таки обрёл семейное счастье, о котором запретил себе когда-то мечтать.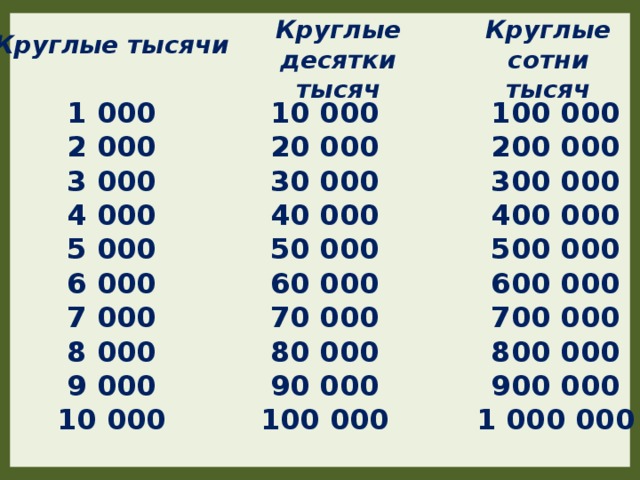 Достойнейший из моих вассалов, хотя все они тут достойные разумные. Даже будучи гонимыми и осуждаемыми обывателями, они не отказались от своего добровольно взятого на себя долга противостоять угрозам человечеству, хотя сами отринули его ради этой цели, пройдя инициацию и перестав быть людьми.
Среди Ведьмаков не было случайных людей. Для всех них, это был собственный и непростой выбор, который они сделали осознанно, перед этим пройдя жесточайшие тренировки в качестве послушников. У них было достаточно времени понять, что путь ведьмака лишён всякой романтики и рыцарства. Это тяжкий труд, за который ты ещё будешь презираем глупцами и быть под постоянным гнётом предубеждений в отношении себя, стоит тебе перестать быть человеком. Расизм в природе человечества со времён их столкновения с фейри, для большинства из которых люди были забавными зверушками или вовсе пищей.
— Поздравляю и обязательно зайду к Вам в гости, хочу поглядеть на Ваше маленькое чудо! — нужно будет ещё подарки им подготовить.
Достойнейший из моих вассалов, хотя все они тут достойные разумные. Даже будучи гонимыми и осуждаемыми обывателями, они не отказались от своего добровольно взятого на себя долга противостоять угрозам человечеству, хотя сами отринули его ради этой цели, пройдя инициацию и перестав быть людьми.
Среди Ведьмаков не было случайных людей. Для всех них, это был собственный и непростой выбор, который они сделали осознанно, перед этим пройдя жесточайшие тренировки в качестве послушников. У них было достаточно времени понять, что путь ведьмака лишён всякой романтики и рыцарства. Это тяжкий труд, за который ты ещё будешь презираем глупцами и быть под постоянным гнётом предубеждений в отношении себя, стоит тебе перестать быть человеком. Расизм в природе человечества со времён их столкновения с фейри, для большинства из которых люди были забавными зверушками или вовсе пищей.
— Поздравляю и обязательно зайду к Вам в гости, хочу поглядеть на Ваше маленькое чудо! — нужно будет ещё подарки им подготовить.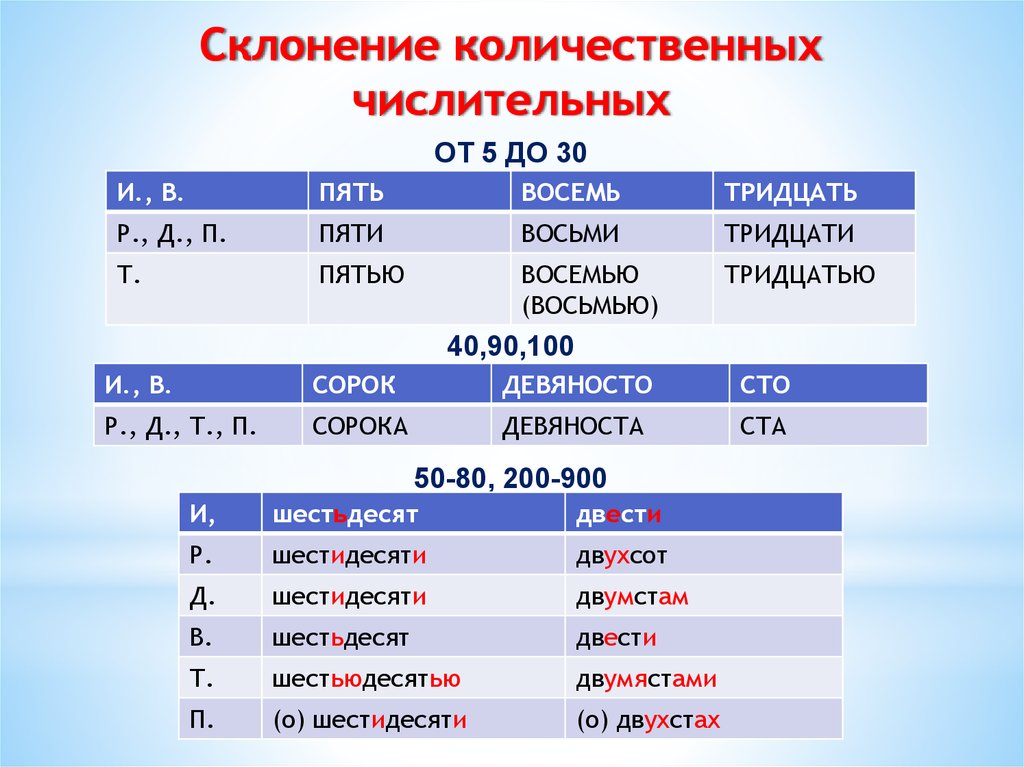 Всё-таки он и Агнешка не рядовые члены моего ордена и мои вассалы, а его руководящий состав и моя опора. Так что я обязан как-то отметить их и проявить своё внимание к их жизни и радостям.
— Хорошо. Мы с радостью примем Вас в гостях, сюзерен. Всё уже в сборе, мне объявить собрание и созвать всех руководителей? -
— Да, будь любезен. Очень уж мне любопытно послушать от Вас о том, как обстоят дела у ордена. — многое мне уже поведал Альфонсо, но он сам знает лишь то, что на поверхности. Ведьмаки на протяжении всей своей истории научились очень хорошо хранить свои секреты и внутренние дела всегда оставались в стенах цитадели, а для остального мира тайной.
Не прошло и десяти минут, как в зале собраний собрались мои старые знакомые. Тут присутствовали Витольд, Агнешка, Маркус и Олаф. Ничего как я погляжу не изменилось. Мы разместились за столом, который оказался новым и если ранее он здесь был круглым, то теперь прямоугольный и я естественно сел во главе его.
Всё-таки он и Агнешка не рядовые члены моего ордена и мои вассалы, а его руководящий состав и моя опора. Так что я обязан как-то отметить их и проявить своё внимание к их жизни и радостям.
— Хорошо. Мы с радостью примем Вас в гостях, сюзерен. Всё уже в сборе, мне объявить собрание и созвать всех руководителей? -
— Да, будь любезен. Очень уж мне любопытно послушать от Вас о том, как обстоят дела у ордена. — многое мне уже поведал Альфонсо, но он сам знает лишь то, что на поверхности. Ведьмаки на протяжении всей своей истории научились очень хорошо хранить свои секреты и внутренние дела всегда оставались в стенах цитадели, а для остального мира тайной.
Не прошло и десяти минут, как в зале собраний собрались мои старые знакомые. Тут присутствовали Витольд, Агнешка, Маркус и Олаф. Ничего как я погляжу не изменилось. Мы разместились за столом, который оказался новым и если ранее он здесь был круглым, то теперь прямоугольный и я естественно сел во главе его. Видимо после того, как мною была установлена понятная иерархия с четкой вертикалью власти, стол и сменили. Как только все разместились, после того как я занял своё место, слово взял Витольд.
— За прошедшие годы число наших братьев и сестер значительно увеличилось. Сейчас нас шесть тысяч двести тридцать шесть разумных. Из них семьсот двадцать три ребенка. Две тысячи триста двадцать один ведьмак состоит в боевом крыле из которых триста разумных находятся на постоянном дежурстве и охране цитадели и двести в Скалистом Приюте. Остальная часть занята ремеслами, производством и иной хозяйственной деятельностью. Сейчас среди нас имеются уже тридцать три магистра и шестьсот двадцать один мастер магии по шумерской шкале. — я уже довольно потирал у себя в уме руки ( Кто молодец? Я молодец! ), а спрашивать о том, что ещё за Приют, не пришлось.
— Скалистый Приют, это земли и крепость, которые нам в вечное владение передала церковь в благодарность за уничтожение угрозы вампиров роду людскому.
Видимо после того, как мною была установлена понятная иерархия с четкой вертикалью власти, стол и сменили. Как только все разместились, после того как я занял своё место, слово взял Витольд.
— За прошедшие годы число наших братьев и сестер значительно увеличилось. Сейчас нас шесть тысяч двести тридцать шесть разумных. Из них семьсот двадцать три ребенка. Две тысячи триста двадцать один ведьмак состоит в боевом крыле из которых триста разумных находятся на постоянном дежурстве и охране цитадели и двести в Скалистом Приюте. Остальная часть занята ремеслами, производством и иной хозяйственной деятельностью. Сейчас среди нас имеются уже тридцать три магистра и шестьсот двадцать один мастер магии по шумерской шкале. — я уже довольно потирал у себя в уме руки ( Кто молодец? Я молодец! ), а спрашивать о том, что ещё за Приют, не пришлось.
— Скалистый Приют, это земли и крепость, которые нам в вечное владение передала церковь в благодарность за уничтожение угрозы вампиров роду людскому. Этому очень поспособствовал покойный кардинал Амати, аргументируя в Риме тем, что число братьев и сестер нашего ордена стало превышать три тысячи разумных. — да, мой старый товарищ уже сорок лет, как отошёл в мир иной и я даже не знаю как на это реагировать, но кардинала и магистра Ордена Творца, Венченцо Амати захоронили в Венеции в склепе под церковью имени меня — Святозара Защитника! Вот такие вот дела, но вернёмся к отчёту моих вассалов — А так как уже назревал вопрос ухода магического мира в тень, желательным было бы чтобы мы как можно меньше стали мелькать в мире простецов. Находятся наши земли и крепость Скалистый Приют в магическом мире. Когда их нам отдали, то они были не пригодны для жизни. Когда-то это был форпост Римской империи в волшебном мире, перешедший так сказать по наследству Ватикану. Вот только во время развала империи, легион который там когда-то нёс службу, был отозван и крепость с близлежащими землями остались без присмотра, а естественный портал с земли туда был запечатан.
Этому очень поспособствовал покойный кардинал Амати, аргументируя в Риме тем, что число братьев и сестер нашего ордена стало превышать три тысячи разумных. — да, мой старый товарищ уже сорок лет, как отошёл в мир иной и я даже не знаю как на это реагировать, но кардинала и магистра Ордена Творца, Венченцо Амати захоронили в Венеции в склепе под церковью имени меня — Святозара Защитника! Вот такие вот дела, но вернёмся к отчёту моих вассалов — А так как уже назревал вопрос ухода магического мира в тень, желательным было бы чтобы мы как можно меньше стали мелькать в мире простецов. Находятся наши земли и крепость Скалистый Приют в магическом мире. Когда их нам отдали, то они были не пригодны для жизни. Когда-то это был форпост Римской империи в волшебном мире, перешедший так сказать по наследству Ватикану. Вот только во время развала империи, легион который там когда-то нёс службу, был отозван и крепость с близлежащими землями остались без присмотра, а естественный портал с земли туда был запечатан. — Витольд кивнул Олафу и теперь рассказ продолжил уже он.
— Так как нам не было известно о том, какая там обстановка и что сейчас там происходит, портал ведь в те земли был запечатан в пятьсот одиннадцатом году, то первая экспедиция туда состояла из трехсот ветеранов наше братства. — нет, всё-таки это была прекрасная идея взять орден под свою руку и сделать их новой расой. Для них любой ведьмак в первую очередь это брат или сестра и только после соплеменник, — И это оказалось верным решением. Там творилась жуть. Сама крепость была занята сильным личом и умертвиями. Личом оказался древний римский маг, который служил когда-то в Скалистом Приюте и после естественной смерти был похоронен на кладбище там же, так как не принадлежал к знатным родам и был сиротой, что всю свою жизнь посвятил службе в легионе. Когда крепость покинули и она осталась на долгое время брошенной, то за отсутствием должного ухода за источником магии, на котором стоит Скальный Приют, тот вышел из под контроля и вновь стал диким.
— Витольд кивнул Олафу и теперь рассказ продолжил уже он.
— Так как нам не было известно о том, какая там обстановка и что сейчас там происходит, портал ведь в те земли был запечатан в пятьсот одиннадцатом году, то первая экспедиция туда состояла из трехсот ветеранов наше братства. — нет, всё-таки это была прекрасная идея взять орден под свою руку и сделать их новой расой. Для них любой ведьмак в первую очередь это брат или сестра и только после соплеменник, — И это оказалось верным решением. Там творилась жуть. Сама крепость была занята сильным личом и умертвиями. Личом оказался древний римский маг, который служил когда-то в Скалистом Приюте и после естественной смерти был похоронен на кладбище там же, так как не принадлежал к знатным родам и был сиротой, что всю свою жизнь посвятил службе в легионе. Когда крепость покинули и она осталась на долгое время брошенной, то за отсутствием должного ухода за источником магии, на котором стоит Скальный Приют, тот вышел из под контроля и вновь стал диким.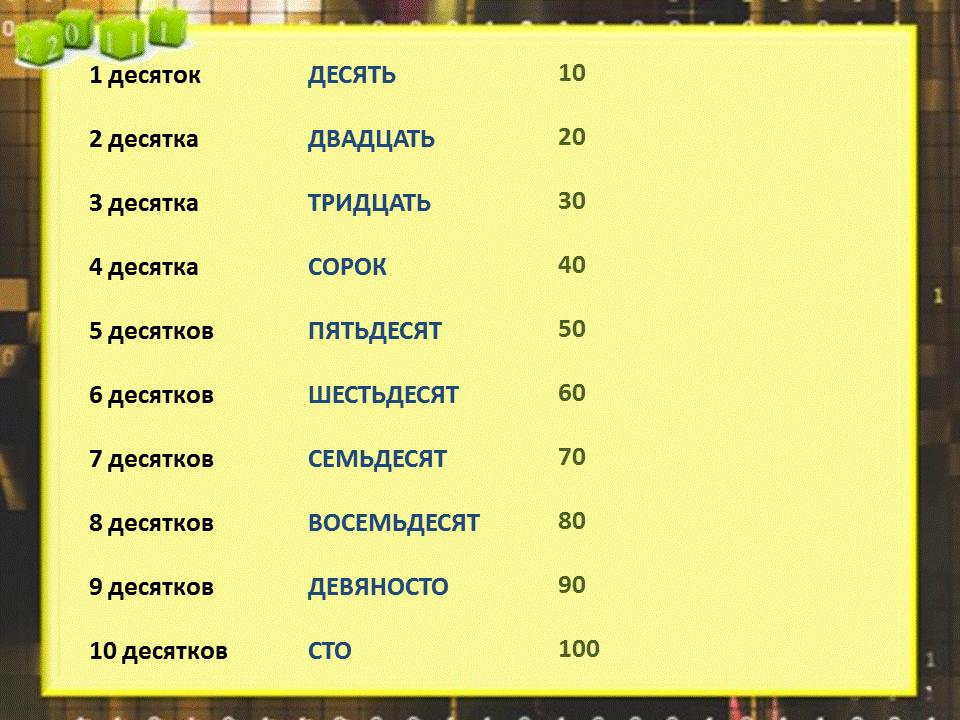 — что вполне логично. Раз этот источник магии стоял на балансе имперской собственности, то он не привязывался к крови чьего-либо рода и право администраторского управление источником и чарами завязанными на него передавались при помощи артефакта, который обычно выглядел как широкий медальон и привязывался он к ауре уполномоченного разумного.
Промочив горло, Олаф продолжил.
— После того, как источник вышел из под подчинения, дикая магия из него пробудила Виктора. Так зовут лича, который после своего восстания поднял себе в услужение всех похороненных рядом с собой воинов легиона. Нам очень повезло, что в число разумных входящих в экспедицию находилась Иоланта, обладающая даром мага смерти и которая смогла подчинить лича, а также взять под контроль остальных умертвий. Даже боюсь представить, что было бы, если бы нам пришлось принять бой. Ведь за тысячелетие своего существования в крепости Виктора в виде лича, он не только инферналов поднимал, а трупы всех магических тварей, которые ранее обитали поблизости от крепости и были убиты его мертвыми слугами.
— что вполне логично. Раз этот источник магии стоял на балансе имперской собственности, то он не привязывался к крови чьего-либо рода и право администраторского управление источником и чарами завязанными на него передавались при помощи артефакта, который обычно выглядел как широкий медальон и привязывался он к ауре уполномоченного разумного.
Промочив горло, Олаф продолжил.
— После того, как источник вышел из под подчинения, дикая магия из него пробудила Виктора. Так зовут лича, который после своего восстания поднял себе в услужение всех похороненных рядом с собой воинов легиона. Нам очень повезло, что в число разумных входящих в экспедицию находилась Иоланта, обладающая даром мага смерти и которая смогла подчинить лича, а также взять под контроль остальных умертвий. Даже боюсь представить, что было бы, если бы нам пришлось принять бой. Ведь за тысячелетие своего существования в крепости Виктора в виде лича, он не только инферналов поднимал, а трупы всех магических тварей, которые ранее обитали поблизости от крепости и были убиты его мертвыми слугами. Общая численность нежити насчитывала более трёх тысяч единиц, из которых треть была одаренной и имела магические способности. После того, как Лич был подчинён, следом был взят под контроль источник крепости, а самого лича и всех его умертвий привязали к нему в качестве стражи. Благодаря им, дальнейшая зачистка близлежащих территорий не составила никакого труда и мы не понесли потерь, даже раненных не было. -
Хм. Что-то я не припомню среди ведьмаков магов смерти. Видимо она из нового набора, но больно уж имя у неё говорящие. Нужно будет проверить девочку и узнать о её происхождение.
Слово взял брат Маркус и о слава Творцу, его ершистость и шило в одном месте куда-то подевались, а всё это время, что я слушал Витольда и Олафа, он сидел смирно и не демонстрировал своего буйного нрава.
— Сейчас Скалистый Приют стал нашим тренировочным лагерем. Также мы построили там теплицы и выращиваем немало полезных и редких растений и трав.
Общая численность нежити насчитывала более трёх тысяч единиц, из которых треть была одаренной и имела магические способности. После того, как Лич был подчинён, следом был взят под контроль источник крепости, а самого лича и всех его умертвий привязали к нему в качестве стражи. Благодаря им, дальнейшая зачистка близлежащих территорий не составила никакого труда и мы не понесли потерь, даже раненных не было. -
Хм. Что-то я не припомню среди ведьмаков магов смерти. Видимо она из нового набора, но больно уж имя у неё говорящие. Нужно будет проверить девочку и узнать о её происхождение.
Слово взял брат Маркус и о слава Творцу, его ершистость и шило в одном месте куда-то подевались, а всё это время, что я слушал Витольда и Олафа, он сидел смирно и не демонстрировал своего буйного нрава.
— Сейчас Скалистый Приют стал нашим тренировочным лагерем. Также мы построили там теплицы и выращиваем немало полезных и редких растений и трав. Часть из них остаётся у нас и идёт на нужды ордена, а часть мы продаём Ватикану, а также гильдии зельеваров. За прошедшие шестьдесят лет, которые нам принадлежит Скалистый Приют, мы полностью восстановили крепость и все постройки прилегающие к ней, значительно их расширив и модернизирована. За прошлый год мы смогли заработать на продаже ингредиентов сто двадцать тысяч галлеонов. В этом году мы собираемся открыть в Скалистом Приюте фермы по выращиванию мандрагор, пегасов и гиппогрифов. На местном кладбища неподалеку от крепости пробудился источник смерти, который идеально подходит для этих целей. Заодно мандрагоры поглощая ману смерти снизят некрофон вокруг источника смерти и будут сдерживать его негативное влияние на близлежащие территории. Сейчас для этих целей используются барьеры. Этим проектом занимается Иоланта, как самая сильная магиня с соответствующим даром в наших рядах. — не понял, а что это сейчас была за интонация в голосе на имени Иоланта? Хм, неужели и эта колючка нашла своё семейное счастье?
— Сто лет назад среди Вас не было ведьмачки с таким именем.
Часть из них остаётся у нас и идёт на нужды ордена, а часть мы продаём Ватикану, а также гильдии зельеваров. За прошедшие шестьдесят лет, которые нам принадлежит Скалистый Приют, мы полностью восстановили крепость и все постройки прилегающие к ней, значительно их расширив и модернизирована. За прошлый год мы смогли заработать на продаже ингредиентов сто двадцать тысяч галлеонов. В этом году мы собираемся открыть в Скалистом Приюте фермы по выращиванию мандрагор, пегасов и гиппогрифов. На местном кладбища неподалеку от крепости пробудился источник смерти, который идеально подходит для этих целей. Заодно мандрагоры поглощая ману смерти снизят некрофон вокруг источника смерти и будут сдерживать его негативное влияние на близлежащие территории. Сейчас для этих целей используются барьеры. Этим проектом занимается Иоланта, как самая сильная магиня с соответствующим даром в наших рядах. — не понял, а что это сейчас была за интонация в голосе на имени Иоланта? Хм, неужели и эта колючка нашла своё семейное счастье?
— Сто лет назад среди Вас не было ведьмачки с таким именем.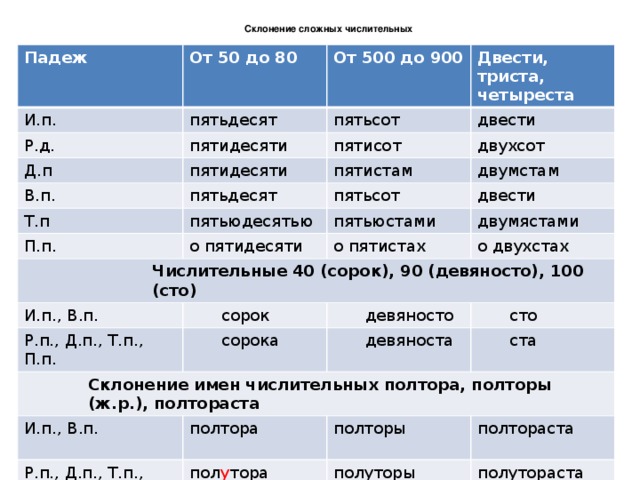 Кто она, откуда прибыла и как оказалась среди Вас? — и задавал я этот вопрос Маркусу. Так как уже заглянула в его разум и узнал, что Иоланта является его женой. Но так как у всех ведьмаков очень сильные от природы окклюментные щиты, то глубоко заглянуть не удалось, плюс у каждого из здесь присутствующих на собрание ведьмаков были артефакты защиты разума. И судя по тому, что они у всех имеет одинаковую структуру и унифицированный вид, то думается мне, что делает их один из Ведьмаков. Прелестно!
— В 1607 году в орден поступил заказ на устранение расплодившихся волколаков, что каким-то образом смогли просочиться из магического мира в шотландское нагорье, где стали кошмарить местных крестьян. Местные маги своими силами не смогли справиться, — ан нет, вот теперь узнаю старину Маркуса, всё та же неприязнь к магам, — туда отправился я и ещё двадцать братьев. Около месяца мы занимались этим и в одной из деревенек, под завалом разрушенного дома мы нашли живую, но подранную и истекающую кровью девочку одиннадцати лет.
Кто она, откуда прибыла и как оказалась среди Вас? — и задавал я этот вопрос Маркусу. Так как уже заглянула в его разум и узнал, что Иоланта является его женой. Но так как у всех ведьмаков очень сильные от природы окклюментные щиты, то глубоко заглянуть не удалось, плюс у каждого из здесь присутствующих на собрание ведьмаков были артефакты защиты разума. И судя по тому, что они у всех имеет одинаковую структуру и унифицированный вид, то думается мне, что делает их один из Ведьмаков. Прелестно!
— В 1607 году в орден поступил заказ на устранение расплодившихся волколаков, что каким-то образом смогли просочиться из магического мира в шотландское нагорье, где стали кошмарить местных крестьян. Местные маги своими силами не смогли справиться, — ан нет, вот теперь узнаю старину Маркуса, всё та же неприязнь к магам, — туда отправился я и ещё двадцать братьев. Около месяца мы занимались этим и в одной из деревенек, под завалом разрушенного дома мы нашли живую, но подранную и истекающую кровью девочку одиннадцати лет. Мы спасли ребёнка, а так как в этой деревеньке мы добили последних взрослых особей стаи этих людоедов, после отчёта перед заказчиком и получения расчёта, мы отправились обратно в цитадель, забрав девочку Иоланту с собой. А уже спустя пять лет она прошла инициацию и стала ведьмаком. Также она уже тридцать лет является моей женой. — в этот раз он постарался удержать свои эмоции в узде, но они всё равно были мною легко читаемы. Маркуса распирали чувства любви к Иоланта и гордости за то, что смог заполучить себе такое сокровище. Эти его чувства просто фонтанировали из его чувственного духа, что даже абсолютно лишенный эмпатического дара разумный мог их прочувствовать. Был бы этот мир мультяшным, вокруг него бы сейчас летали сердечки и амурчики.
— А почему её тогда нет с нами? Раз она в скором времени будет руководить собственным проектом, который предполагает большую ответственность, мандрагоры это Вам не фиалки выращивать, мне необходимо познакомиться с нею лично. — и пока я говорил, Олаф подал сигнал через очередной артефакт, которые имелись у всех здесь присутствующих и вышедшие из под руки одного и того же мастера и стоило мне закончить говорить, как дверь в зал собраний отворилась и в неё вошла очаровательная девушка.
Мы спасли ребёнка, а так как в этой деревеньке мы добили последних взрослых особей стаи этих людоедов, после отчёта перед заказчиком и получения расчёта, мы отправились обратно в цитадель, забрав девочку Иоланту с собой. А уже спустя пять лет она прошла инициацию и стала ведьмаком. Также она уже тридцать лет является моей женой. — в этот раз он постарался удержать свои эмоции в узде, но они всё равно были мною легко читаемы. Маркуса распирали чувства любви к Иоланта и гордости за то, что смог заполучить себе такое сокровище. Эти его чувства просто фонтанировали из его чувственного духа, что даже абсолютно лишенный эмпатического дара разумный мог их прочувствовать. Был бы этот мир мультяшным, вокруг него бы сейчас летали сердечки и амурчики.
— А почему её тогда нет с нами? Раз она в скором времени будет руководить собственным проектом, который предполагает большую ответственность, мандрагоры это Вам не фиалки выращивать, мне необходимо познакомиться с нею лично. — и пока я говорил, Олаф подал сигнал через очередной артефакт, которые имелись у всех здесь присутствующих и вышедшие из под руки одного и того же мастера и стоило мне закончить говорить, как дверь в зал собраний отворилась и в неё вошла очаровательная девушка. Брюнетка, с черными словно бездна глазами, алыми губками, римским профилем и алебастровой кожей. Росточком она была не велика, чуть выше полутора метров, зато очень грациозная и она не двигалась при ходьбе, пока приближалась к нам, а словно перетекала как скатывающаяся по поверхности капля ртути. Уххх! Хороша девчонка. Взгляд волевой, с небольшой стервозинкой искрящейся в глазах и судя по тому как она двигается, она великолепный мастер по оружию и амбидекстр впридачу.
Она обвела взглядом стол, за которым сейчас находилось всё руководства ордена и её муж, но удивилась тому, что место во главе стола занято неизвестным ей разумным, а Витольд, что видимо ранее занимал его, сидит по правую руку от меня.
Она не проронила и слова, ожидая когда ей объяснят происходящее. Слово взял Маркус.
— Мессир, позвольте Вам представить мою жену Иоланту. Иоланта, это наш сюзерен и глава ордена, Святозар Змиев. — теперь я удостоился более пристально взгляда и очень выверенного, безукоризненного книксена, который был в ходу ещё лет четыреста назад.
Брюнетка, с черными словно бездна глазами, алыми губками, римским профилем и алебастровой кожей. Росточком она была не велика, чуть выше полутора метров, зато очень грациозная и она не двигалась при ходьбе, пока приближалась к нам, а словно перетекала как скатывающаяся по поверхности капля ртути. Уххх! Хороша девчонка. Взгляд волевой, с небольшой стервозинкой искрящейся в глазах и судя по тому как она двигается, она великолепный мастер по оружию и амбидекстр впридачу.
Она обвела взглядом стол, за которым сейчас находилось всё руководства ордена и её муж, но удивилась тому, что место во главе стола занято неизвестным ей разумным, а Витольд, что видимо ранее занимал его, сидит по правую руку от меня.
Она не проронила и слова, ожидая когда ей объяснят происходящее. Слово взял Маркус.
— Мессир, позвольте Вам представить мою жену Иоланту. Иоланта, это наш сюзерен и глава ордена, Святозар Змиев. — теперь я удостоился более пристально взгляда и очень выверенного, безукоризненного книксена, который был в ходу ещё лет четыреста назад. Маги такие ретрограды, а если моя догадка верна, то она воспитывалась в древнейшем и благороднейшем доме. Он был выполнен безупречно, но создавалось впечатление, будто ей пришлось очень быстро вспоминать как он выполняется. Её реверанс говорил о многом. Если она попала к ведьмакам в возрасте двенадцати лет, то эти знания и умения явно из её жизни вне ордена, вот только откуда они могут быть у деревенской девочки?
— Очень приятно Иоланта Певерелл. Святозар Змиев! — что и требовалось доказать. Девочка вздрогнула на том моменте, когда я встал из-за стола и сделав к ней навстречу несколько шагов, произнёс фамилию «ужасных некромантов» и её расширившиеся в удивление и страхе глаза говорят о том, что я попал в точку.
— Покиньте нас все. Мне нужно поговорить с Иолантой наедине. — только лишь Маркус немного запнулся на исполнении моего приказа, да только у него не было выбора и как бы он не хотел остаться здесь с нами, он не мог себе этого позволить.
Маги такие ретрограды, а если моя догадка верна, то она воспитывалась в древнейшем и благороднейшем доме. Он был выполнен безупречно, но создавалось впечатление, будто ей пришлось очень быстро вспоминать как он выполняется. Её реверанс говорил о многом. Если она попала к ведьмакам в возрасте двенадцати лет, то эти знания и умения явно из её жизни вне ордена, вот только откуда они могут быть у деревенской девочки?
— Очень приятно Иоланта Певерелл. Святозар Змиев! — что и требовалось доказать. Девочка вздрогнула на том моменте, когда я встал из-за стола и сделав к ней навстречу несколько шагов, произнёс фамилию «ужасных некромантов» и её расширившиеся в удивление и страхе глаза говорят о том, что я попал в точку.
— Покиньте нас все. Мне нужно поговорить с Иолантой наедине. — только лишь Маркус немного запнулся на исполнении моего приказа, да только у него не было выбора и как бы он не хотел остаться здесь с нами, он не мог себе этого позволить. Если бы Иоланта была просто женой моего вассала, тогда да, я не мог просить его о подобном. Но так как она ведьмак и такой же мой личный вассал, как и её муж, то всё было строго в позволительных нашими узами сюзерен-вассал рамках.
Когда мы остались наедине, я приступил к её расспросу.
— Теперь, когда нас никто более не слышит, я хочу узнать, как так получилось, что дочь одного из самых древних магических родов Европы оказался в той самой деревне в Шотландии, где тебя нашли еле живой под завалом. — она же стояла передо мной прикусив губу и склонив голову, отчего челка прикрывала её глаза. Но вот она решилась и подняв на меня свои чёрные очи, в которых скапливалась влага, начала свой рассказ и эти воспоминания приносили ей боль.
Я просто не верил, какой подарок попал мне в руки. Когда Альфонсо вводил меня в курс дел, я узнал от него, что на Оловянных островах прервался герцогский род и один из столпов магической аристократии Альбиона — Певерелл.
Если бы Иоланта была просто женой моего вассала, тогда да, я не мог просить его о подобном. Но так как она ведьмак и такой же мой личный вассал, как и её муж, то всё было строго в позволительных нашими узами сюзерен-вассал рамках.
Когда мы остались наедине, я приступил к её расспросу.
— Теперь, когда нас никто более не слышит, я хочу узнать, как так получилось, что дочь одного из самых древних магических родов Европы оказался в той самой деревне в Шотландии, где тебя нашли еле живой под завалом. — она же стояла передо мной прикусив губу и склонив голову, отчего челка прикрывала её глаза. Но вот она решилась и подняв на меня свои чёрные очи, в которых скапливалась влага, начала свой рассказ и эти воспоминания приносили ей боль.
Я просто не верил, какой подарок попал мне в руки. Когда Альфонсо вводил меня в курс дел, я узнал от него, что на Оловянных островах прервался герцогский род и один из столпов магической аристократии Альбиона — Певерелл. А тут я узнаю, что оказывается у меня есть личный вассал, который несёт в себе их кровь и дары с магией. Раскрытый дар мага смерти у Певереллов означал принадлежность к главной ветви рода, хотя младших ветвей у него уже давно не осталось и все прервались ещё несколько веков назад.
— Когда мне было девять, умер мой отец и я осталась на попечении своего старшего и единственного брата. Он был старше меня на пятнадцать лет. Как только не стала отца и он стал главой рода, его будто бы подменили. Он постоянно где-то и с кем-то пропадал, кутил, сорил деньгами непомерно. Я пыталась увещевать ему о том, что это не достойно нашей фамилии, но он меня не слушал, не хотел слышать. А когда мне исполнилось десять, он заявился домой пьяный и завалившись в гостиной на полу, сквозь алкогольный дурман проговорился мне о том, что в скором времени я выйду замуж Лорда Флинта, которому он проиграл спор и ставкой в котором была моя рука. — окунувшись в свои воспоминания, которые приносили ей страдания, сделали её ещё бледнее.
А тут я узнаю, что оказывается у меня есть личный вассал, который несёт в себе их кровь и дары с магией. Раскрытый дар мага смерти у Певереллов означал принадлежность к главной ветви рода, хотя младших ветвей у него уже давно не осталось и все прервались ещё несколько веков назад.
— Когда мне было девять, умер мой отец и я осталась на попечении своего старшего и единственного брата. Он был старше меня на пятнадцать лет. Как только не стала отца и он стал главой рода, его будто бы подменили. Он постоянно где-то и с кем-то пропадал, кутил, сорил деньгами непомерно. Я пыталась увещевать ему о том, что это не достойно нашей фамилии, но он меня не слушал, не хотел слышать. А когда мне исполнилось десять, он заявился домой пьяный и завалившись в гостиной на полу, сквозь алкогольный дурман проговорился мне о том, что в скором времени я выйду замуж Лорда Флинта, которому он проиграл спор и ставкой в котором была моя рука. — окунувшись в свои воспоминания, которые приносили ей страдания, сделали её ещё бледнее. Но вот она встряхнуло головой и вспомнив, что она уже не беззащитная девочка, а сильная магиня и ведьмачка, со сталью в глазах продолжила свой рассказ.
— Ровно неделю я была подавлена и разбита горем, но проснувшись утром на восьмой день после того, как узнала о своём предполагаемом будущем, я стала искать способ избежать этого брака. Так как брат мог пропадать по несколько дней неизвестно где и я была предоставлена сама себе, то я зарылась в библиотеке, желая отыскать там способ, как мне отвертеться от нежеланного брака. Месяц трудов, сотни толстых, пыльных и плохо мне понятных в те годы талмудов по магии помогли мне отыскать один способ. «Вуаль Морены», так назывался этот ритуал, который накладывал на применившего его сокрытие от любого поиска по магии, крови, ауре, имени. Я собиралась бежать из дома! — я перебил её.
— Ритуал назывался именно «Вуаль Морены»? — как любопытно, неужели Певереллы родом с Руси? А ведь всем они декламировали о том, что берут своё начало из Скандинавии.
Но вот она встряхнуло головой и вспомнив, что она уже не беззащитная девочка, а сильная магиня и ведьмачка, со сталью в глазах продолжила свой рассказ.
— Ровно неделю я была подавлена и разбита горем, но проснувшись утром на восьмой день после того, как узнала о своём предполагаемом будущем, я стала искать способ избежать этого брака. Так как брат мог пропадать по несколько дней неизвестно где и я была предоставлена сама себе, то я зарылась в библиотеке, желая отыскать там способ, как мне отвертеться от нежеланного брака. Месяц трудов, сотни толстых, пыльных и плохо мне понятных в те годы талмудов по магии помогли мне отыскать один способ. «Вуаль Морены», так назывался этот ритуал, который накладывал на применившего его сокрытие от любого поиска по магии, крови, ауре, имени. Я собиралась бежать из дома! — я перебил её.
— Ритуал назывался именно «Вуаль Морены»? — как любопытно, неужели Певереллы родом с Руси? А ведь всем они декламировали о том, что берут своё начало из Скандинавии. Хотя, а почему нет? Вполне может быть, что из Руси они сперва добрались до Скандинавского полуострова, а уже оттуда, пожив там какое-то время, перебрались на Оловянные острова. Это ж сколько лет назад они покинули Русь, если история их рода в Англии насчитывает уже две с половиной тысячи лет. Они прибыли на Оловянные острова, когда туда ещё не добрались легионеры Рима. Любопытненько.
— Да, точно. Это разве так важно? — слегка удивилась она, что именно этот момент вызвал у меня вопрос. Мне было знакомо заклинание из магии смерти, спасибо Моргана, и оно называется «Саван Хель», с помощью которого некромаг может на недолгое время скрыть своё присутствие от любого обнаружения. А вот «Вуаль Морены», это видимо что-то из их родовых знаний, а если учитывать слухи о наличии в жилах Певереллов крови Аватара Смерти и их родство, то вполне может быть такое, что проведенный Иолантой ритуал скрыта, имел постоянное или как минимум очень длительное действие.
— В данный момент нет, вернёмся к этому моменту позже, а ты продолжай свой рассказ.
Хотя, а почему нет? Вполне может быть, что из Руси они сперва добрались до Скандинавского полуострова, а уже оттуда, пожив там какое-то время, перебрались на Оловянные острова. Это ж сколько лет назад они покинули Русь, если история их рода в Англии насчитывает уже две с половиной тысячи лет. Они прибыли на Оловянные острова, когда туда ещё не добрались легионеры Рима. Любопытненько.
— Да, точно. Это разве так важно? — слегка удивилась она, что именно этот момент вызвал у меня вопрос. Мне было знакомо заклинание из магии смерти, спасибо Моргана, и оно называется «Саван Хель», с помощью которого некромаг может на недолгое время скрыть своё присутствие от любого обнаружения. А вот «Вуаль Морены», это видимо что-то из их родовых знаний, а если учитывать слухи о наличии в жилах Певереллов крови Аватара Смерти и их родство, то вполне может быть такое, что проведенный Иолантой ритуал скрыта, имел постоянное или как минимум очень длительное действие.
— В данный момент нет, вернёмся к этому моменту позже, а ты продолжай свой рассказ. Я внимательно слушаю. — и располагающе ей улыбнулся, при этом излучая в ментале спокойствие и доброжелательность. И это подействовало. Хоть внешне она уже выглядела вновь собранной и стальной валькирией, как и полагается ведьмаку, но в душе у неё скреблись кошки, ей было больно вновь возвращаться в своё прошлое и теребить старую рану. Зато после моего лёгкого воздействие, она расслабилась и уже не была столь напряжена и депрессивна. Кивнув на моё желание услышать продолжение её истории, она вновь перенеслась в прошлое.
— Дождавшись очередного цикла, когда брат вернётся с попойки, отоспится, после приведёт себя в порядок и отправится на следующую, я в тот же час спустилась в ритуальный зал, где прошла ритуал «Вуаль Морены». Только я и не подозревала, что вместе с ним лишусь и магии. А как только морозное покрывало, которое проявилось на мне в процессе совершения ритуала, истаяло, появилась моя домовушка Тилли со слезами на глазах и постоянно каясь, взяла меня ослабленную за руку, переместила из поместья на перепутье, неподалеку от города Инвернесс.
Я внимательно слушаю. — и располагающе ей улыбнулся, при этом излучая в ментале спокойствие и доброжелательность. И это подействовало. Хоть внешне она уже выглядела вновь собранной и стальной валькирией, как и полагается ведьмаку, но в душе у неё скреблись кошки, ей было больно вновь возвращаться в своё прошлое и теребить старую рану. Зато после моего лёгкого воздействие, она расслабилась и уже не была столь напряжена и депрессивна. Кивнув на моё желание услышать продолжение её истории, она вновь перенеслась в прошлое.
— Дождавшись очередного цикла, когда брат вернётся с попойки, отоспится, после приведёт себя в порядок и отправится на следующую, я в тот же час спустилась в ритуальный зал, где прошла ритуал «Вуаль Морены». Только я и не подозревала, что вместе с ним лишусь и магии. А как только морозное покрывало, которое проявилось на мне в процессе совершения ритуала, истаяло, появилась моя домовушка Тилли со слезами на глазах и постоянно каясь, взяла меня ослабленную за руку, переместила из поместья на перепутье, неподалеку от города Инвернесс. — а что ты хотела девочка? Как ещё магия могла тебя скрыть, только закрыв доступ к твоей магии, крови и иным духовным оболочкам, дабы никто не имел возможности тебя найти. А как только она оказалась закрыта от мира, магия дома перестала видеть в ней ту, кто имеет право находиться на территории мэнора. Весь свой рассказ, она стояла напротив меня и сейчас я предложил нам присесть, а её откровение мне продолжилось.
— Оказавшись в незнакомом месте, в сгущающихся сумерках, в одной ритуальной мантии на осеннем холоде и обессиленная, я потеряла сознание. В себя я пришла только через неделю. Меня подобрала возвращающиеся из города к себе в село пожилая пара, ехавшая с торга в городе к себе домой. Оказалось я сильно простудилась, пока лёжа на шотландских камнях в одной тонкой льняной мантии и всё это время сердобольная семья отпаивала меня отварами и ухаживала за мной, пока я была в бреду. Я прожила у них пол года, а затем на деревню напали волколаки. Я в этот момент находилась в доме и даже не успела понять, как домик стал разваливаться от мощного удара и меня придавило бревном, сильно распоров ногу.
— а что ты хотела девочка? Как ещё магия могла тебя скрыть, только закрыв доступ к твоей магии, крови и иным духовным оболочкам, дабы никто не имел возможности тебя найти. А как только она оказалась закрыта от мира, магия дома перестала видеть в ней ту, кто имеет право находиться на территории мэнора. Весь свой рассказ, она стояла напротив меня и сейчас я предложил нам присесть, а её откровение мне продолжилось.
— Оказавшись в незнакомом месте, в сгущающихся сумерках, в одной ритуальной мантии на осеннем холоде и обессиленная, я потеряла сознание. В себя я пришла только через неделю. Меня подобрала возвращающиеся из города к себе в село пожилая пара, ехавшая с торга в городе к себе домой. Оказалось я сильно простудилась, пока лёжа на шотландских камнях в одной тонкой льняной мантии и всё это время сердобольная семья отпаивала меня отварами и ухаживала за мной, пока я была в бреду. Я прожила у них пол года, а затем на деревню напали волколаки. Я в этот момент находилась в доме и даже не успела понять, как домик стал разваливаться от мощного удара и меня придавило бревном, сильно распоров ногу. — Неужели? А на ку! Бааа. Как любопытно!!! Я ещё не смотрел на неё в духовном зрении, но сейчас глянув на неё им, я не увидел ровным счётом ничего. И это может быть проблемой.
— Скажи Иоланта, ты в курсе того, что Вуаль всё ещё на тебе? — и получив утвердительный кивок, задал ещё один вопрос, — А ты можешь её снять или отменить? — ведь если она вновь получила доступ к магии, значит она должна была разобраться с механизмом работы заклинания наложенного на неё при помощи ритуала.
— Когда меня спас из под завала Маркус и после того, как я оказалась уже в Цитадели и узнала здесь, что мой брат погиб, я прошла ритуал инициации ведьмака, больше не опасаясь того, что меня могут искать, — логично, ведь неизвестно как на неё подействует ритуал инициации и повлияет на «Вуаль Морены», — после становления ведьмаком и получения доступа к собственной магии, я смогла научиться контролировать её и по желанию включать или отключать. — и после этих слов она сняла с себя сокрытие и я чутка прифигел от того, какую синергию дали ритуал инициации ведьмака и «Вуаль Морены».
— Неужели? А на ку! Бааа. Как любопытно!!! Я ещё не смотрел на неё в духовном зрении, но сейчас глянув на неё им, я не увидел ровным счётом ничего. И это может быть проблемой.
— Скажи Иоланта, ты в курсе того, что Вуаль всё ещё на тебе? — и получив утвердительный кивок, задал ещё один вопрос, — А ты можешь её снять или отменить? — ведь если она вновь получила доступ к магии, значит она должна была разобраться с механизмом работы заклинания наложенного на неё при помощи ритуала.
— Когда меня спас из под завала Маркус и после того, как я оказалась уже в Цитадели и узнала здесь, что мой брат погиб, я прошла ритуал инициации ведьмака, больше не опасаясь того, что меня могут искать, — логично, ведь неизвестно как на неё подействует ритуал инициации и повлияет на «Вуаль Морены», — после становления ведьмаком и получения доступа к собственной магии, я смогла научиться контролировать её и по желанию включать или отключать. — и после этих слов она сняла с себя сокрытие и я чутка прифигел от того, какую синергию дали ритуал инициации ведьмака и «Вуаль Морены». Для начала стоит сказать, что передо мной сейчас стоит почти магистр по силе и знаниям, ведь её магический ноус очень структурирован и спокоен, а также обладающая очень сильным даром мага смерти и чуть послабее малефика и мага крови. Но то что меня удивило, было наличие у неё Ме, особой надстройки души (духовного артефакта), который крепиться к седьмой оболочке души, а так как у Иоланты после становления ведьмаков сразу же стала формироваться восьмая оболочка души, то сейчас её Ме находилось между восьмой и седьмой.
И если я всё правильно понимаю, хотя без ритуала познания тут точно и не скажешь, но полагаю, что «Вуаль Морены» теперь навсегда с Иолантой. А судя по её назначению, скорее всего именно этот ритуал был в основе создания мантии-невидимки, которая досталось роду Поттер. Определённо её нужно затащить в диагностирующий ритуальный круг и изучить структуру этой Ме, а вместе с этим разработать позже такую же плюшку для себя, которая сможет скрывать меня также.
Для начала стоит сказать, что передо мной сейчас стоит почти магистр по силе и знаниям, ведь её магический ноус очень структурирован и спокоен, а также обладающая очень сильным даром мага смерти и чуть послабее малефика и мага крови. Но то что меня удивило, было наличие у неё Ме, особой надстройки души (духовного артефакта), который крепиться к седьмой оболочке души, а так как у Иоланты после становления ведьмаков сразу же стала формироваться восьмая оболочка души, то сейчас её Ме находилось между восьмой и седьмой.
И если я всё правильно понимаю, хотя без ритуала познания тут точно и не скажешь, но полагаю, что «Вуаль Морены» теперь навсегда с Иолантой. А судя по её назначению, скорее всего именно этот ритуал был в основе создания мантии-невидимки, которая досталось роду Поттер. Определённо её нужно затащить в диагностирующий ритуальный круг и изучить структуру этой Ме, а вместе с этим разработать позже такую же плюшку для себя, которая сможет скрывать меня также. Однозначно Хочу!!!
— Иоланта. Готовься к тому, что в ближайшие дни мы с тобой отправимся в Англию и ты примешь управление родом и привяжешь к себе родовой алтарь. — и видя в её глазах нежелание, — я как твой сюзерен обязан защищать тебя, в том числе и от наказания самой Магией. Если ты не примешь главенство в роду в ближайший срок, то это может грозить тебе серьёзным наказанием от неё. И каким оно будет, я не примусь гадать. Это может быть и родовое проклятье, и даже становление тебя бесплодной. Поэтому не спорь! А то, что ты станешь главой рода, тебя это ни к чему не обязывает, кроме как дать ему потомков. Надеюсь против этого ты не возражаешь? — и грозная, сопротивляющейся моим хотелкам воительница превратилась в смущающееся дитя, которое стало смешно вертеть в стороны головой. Давая тем самым понять, как она сильно этого не хочет и милое покраснение щёчек на лице ‘ужасного’ мага смерти и повелителя армии умертвий, делало эту ситуацию ещё более смешной.
— Ну вот и прекрасно.
Однозначно Хочу!!!
— Иоланта. Готовься к тому, что в ближайшие дни мы с тобой отправимся в Англию и ты примешь управление родом и привяжешь к себе родовой алтарь. — и видя в её глазах нежелание, — я как твой сюзерен обязан защищать тебя, в том числе и от наказания самой Магией. Если ты не примешь главенство в роду в ближайший срок, то это может грозить тебе серьёзным наказанием от неё. И каким оно будет, я не примусь гадать. Это может быть и родовое проклятье, и даже становление тебя бесплодной. Поэтому не спорь! А то, что ты станешь главой рода, тебя это ни к чему не обязывает, кроме как дать ему потомков. Надеюсь против этого ты не возражаешь? — и грозная, сопротивляющейся моим хотелкам воительница превратилась в смущающееся дитя, которое стало смешно вертеть в стороны головой. Давая тем самым понять, как она сильно этого не хочет и милое покраснение щёчек на лице ‘ужасного’ мага смерти и повелителя армии умертвий, делало эту ситуацию ещё более смешной.
— Ну вот и прекрасно. Вы с Маркусом бракосочетались по древнему ритуалу? — ещё один кивок утвердительный, — Прекрасно. Тогда он тоже отправится с нами в Англию. Представишь его алтарю как собственного мужа, сделав консортом и ваши будущие дети будут законными Певереллами. -
Всё складывается просто замечательно, а вообще надо бы мне навестить ритуальный зал под цитаделью, где находятся установленные мною артефакты-алтари в количестве двадцати штук, которые обеспечивают инициацию ведьмаков. Так как в них находятся мои иллюзии и все инициации новых ведьмаков проходили через их руки, то они обладают точными данными по всем моим новым вассалам. Вдруг найдётся ещё кто-нибудь интересный. К слову именно им приносят клятву верности новоиспечённые ведьмаки и это возможно благодаря тому, что иллюзии эти являются частью моих духовных оболочек. Бытие фейри даёт множество плюсов!
И пока я думал над этим, у меня в голове стал зарождаться план! А почему бы и нет? Хм. Да, это определённо отличная идея!!!
Что же я придумал? Да всё ведь перед глазами.
Вы с Маркусом бракосочетались по древнему ритуалу? — ещё один кивок утвердительный, — Прекрасно. Тогда он тоже отправится с нами в Англию. Представишь его алтарю как собственного мужа, сделав консортом и ваши будущие дети будут законными Певереллами. -
Всё складывается просто замечательно, а вообще надо бы мне навестить ритуальный зал под цитаделью, где находятся установленные мною артефакты-алтари в количестве двадцати штук, которые обеспечивают инициацию ведьмаков. Так как в них находятся мои иллюзии и все инициации новых ведьмаков проходили через их руки, то они обладают точными данными по всем моим новым вассалам. Вдруг найдётся ещё кто-нибудь интересный. К слову именно им приносят клятву верности новоиспечённые ведьмаки и это возможно благодаря тому, что иллюзии эти являются частью моих духовных оболочек. Бытие фейри даёт множество плюсов!
И пока я думал над этим, у меня в голове стал зарождаться план! А почему бы и нет? Хм. Да, это определённо отличная идея!!!
Что же я придумал? Да всё ведь перед глазами. Неучтённая девочка, утерянная родом, после того, как последний его представитель умер, стала главным претендентом на наследие своей семьи. А ведь уже пошло хреновое веянье среди аристократических родов выгонять из семьи сквибов. Идиоты! Гнать родную кровь от себя и рода, явно не прибавит таким магам любви собственной родовой магии и если бы она имела полноценный разум, то обязательно бы объяснила этим баранам, что сквибы это не магические калеки. Они результат механизма попытки собственной родовой маги очиститься от вросших в неё проклятий. У сквибов неактивное ядро, но при этом они понемногу тянут из окружающего фона нейтральную ману, которая после прогоняется, циркулирует по наличествующим у них магическим канал и омывает их спящее ядро. Таким вот образом нейтральная мана медленно, но непреклонно вымывает из седьмой оболочки не инициированного мага его родовые проклятья и если это не удается сделать с ними в первом поколении, то процесс продолжается с их потомками и в конечном итоге у сквибов рождаются маги, которые несут в себя абсолютно чистую магию рода.
Неучтённая девочка, утерянная родом, после того, как последний его представитель умер, стала главным претендентом на наследие своей семьи. А ведь уже пошло хреновое веянье среди аристократических родов выгонять из семьи сквибов. Идиоты! Гнать родную кровь от себя и рода, явно не прибавит таким магам любви собственной родовой магии и если бы она имела полноценный разум, то обязательно бы объяснила этим баранам, что сквибы это не магические калеки. Они результат механизма попытки собственной родовой маги очиститься от вросших в неё проклятий. У сквибов неактивное ядро, но при этом они понемногу тянут из окружающего фона нейтральную ману, которая после прогоняется, циркулирует по наличествующим у них магическим канал и омывает их спящее ядро. Таким вот образом нейтральная мана медленно, но непреклонно вымывает из седьмой оболочки не инициированного мага его родовые проклятья и если это не удается сделать с ними в первом поколении, то процесс продолжается с их потомками и в конечном итоге у сквибов рождаются маги, которые несут в себя абсолютно чистую магию рода. Конечно они не обладают внушительной силой, так как из-за отсутствия работающего ядра у их родителей и остальных предков сквибов, они не развивали своего магического ноуса, соответственно и их ребёнок-маг не будет обладать высоким потенциалом, зато он несёт в себе очищенную от «грязи кровь» и подобрав ему правильную пару, у них родятся сильные маги с родовыми дарами отцовской династии и при этом без проклятий.
Это же как надо было извратить в недалёком будущем суть истины, что белое стало черным, а чёрное белым? Когда настоящие грязнокровки чистокровные, называли таковыми и всячески угнетали и издевались над теми, кто вернулся в волшебный мир с кристально чистым наследием своих предков. Да, они были магически слабее своих родственников, что не покидали род и имели/имеют связь с родовым источником, да, у них менее слабый ноус и их седьмая оболочка уступает их родне из магического мира, но они ведь реальный шанс на здоровье и сильное потомство для всего своего рода в целом.
Конечно они не обладают внушительной силой, так как из-за отсутствия работающего ядра у их родителей и остальных предков сквибов, они не развивали своего магического ноуса, соответственно и их ребёнок-маг не будет обладать высоким потенциалом, зато он несёт в себе очищенную от «грязи кровь» и подобрав ему правильную пару, у них родятся сильные маги с родовыми дарами отцовской династии и при этом без проклятий.
Это же как надо было извратить в недалёком будущем суть истины, что белое стало черным, а чёрное белым? Когда настоящие грязнокровки чистокровные, называли таковыми и всячески угнетали и издевались над теми, кто вернулся в волшебный мир с кристально чистым наследием своих предков. Да, они были магически слабее своих родственников, что не покидали род и имели/имеют связь с родовым источником, да, у них менее слабый ноус и их седьмая оболочка уступает их родне из магического мира, но они ведь реальный шанс на здоровье и сильное потомство для всего своего рода в целом. Ввести их сперва в младшую ветвь, подобрать благоприятную пару, а уже после рождения у них детей, обручить тех с наследниками рода и таким образом уже во втором поколении после принятия в род детей сквибов, они имеют высокие шансы скинуть проклятья уже с самого камня рода.
Необразованные идиоты!
Но как гласит американская мудрость, которую пока ещё не родила здешняя действительность: «Проблемы негров шерифа не ебут!». Вы выбрасываете, а мы подберём. А там глядишь и через лет двести — триста и среди моих вассалов окажутся половина глав родов имеющих законное место в Палатах Лордов Европы.
Очень, очень перспективная идея! Пусть Орден и без моих далеко идущих планов на будущее занят поиском сквибов по всей Европе, но делается это не очень уж усердно. Ведьмаков и без того уже много и мы полностью перекрыли потребность человечества в Европе в защитниках от угроз в виде монстров и иных проявлений мистики. Но так не только охотой и убийствами можно заниматься и открытия собственного производства и ферм тому подтверждение.
Ввести их сперва в младшую ветвь, подобрать благоприятную пару, а уже после рождения у них детей, обручить тех с наследниками рода и таким образом уже во втором поколении после принятия в род детей сквибов, они имеют высокие шансы скинуть проклятья уже с самого камня рода.
Необразованные идиоты!
Но как гласит американская мудрость, которую пока ещё не родила здешняя действительность: «Проблемы негров шерифа не ебут!». Вы выбрасываете, а мы подберём. А там глядишь и через лет двести — триста и среди моих вассалов окажутся половина глав родов имеющих законное место в Палатах Лордов Европы.
Очень, очень перспективная идея! Пусть Орден и без моих далеко идущих планов на будущее занят поиском сквибов по всей Европе, но делается это не очень уж усердно. Ведьмаков и без того уже много и мы полностью перекрыли потребность человечества в Европе в защитниках от угроз в виде монстров и иных проявлений мистики. Но так не только охотой и убийствами можно заниматься и открытия собственного производства и ферм тому подтверждение. Нужно озадачить своих головорезов, чтобы они целенаправленно собирали всех встречающихся на их пути детей-сквибов и забирали тех в орден. Не важно каким это будет сделано путём, ныне можно спокойно выкупить детей у их собственных родителей за пару монет и даже не золотых, на серебро будут согласны, ведь тут что не год, то война, голод, холод или ещё какая напасть к примеру в виде оборзевшего в край владетеля земли и завышенных налогов, которые не дают житья простым жителям. Города полны беспризорников и среди них я уверен бегает не мало таких вот деток, которых пинком под жопу выкинули во внешний мир их «благородные» и «чистокровные» родители. В общем простор для поисков огромный и инструментов для изъятия детей из той среды, где найдутся сквибы, предостаточно. Да даже то что ведьмаки ныне это меч и щит под стягами Ватикана, даёт возможность привлекать к отъёму детей к нам в Орден служителей церкви на местах, вплоть до кардиналов. Любой рыцарь моего ордена имеет право на беспрепятственную встречу с любым высокопоставленным иерархом церкви, если считает, что этого требует случай.
Нужно озадачить своих головорезов, чтобы они целенаправленно собирали всех встречающихся на их пути детей-сквибов и забирали тех в орден. Не важно каким это будет сделано путём, ныне можно спокойно выкупить детей у их собственных родителей за пару монет и даже не золотых, на серебро будут согласны, ведь тут что не год, то война, голод, холод или ещё какая напасть к примеру в виде оборзевшего в край владетеля земли и завышенных налогов, которые не дают житья простым жителям. Города полны беспризорников и среди них я уверен бегает не мало таких вот деток, которых пинком под жопу выкинули во внешний мир их «благородные» и «чистокровные» родители. В общем простор для поисков огромный и инструментов для изъятия детей из той среды, где найдутся сквибы, предостаточно. Да даже то что ведьмаки ныне это меч и щит под стягами Ватикана, даёт возможность привлекать к отъёму детей к нам в Орден служителей церкви на местах, вплоть до кардиналов. Любой рыцарь моего ордена имеет право на беспрепятственную встречу с любым высокопоставленным иерархом церкви, если считает, что этого требует случай. Только к Папе Римскому необходимо обращаться через Главу Ордена.
Необходимо лишь согласовать этот вопрос с инквизицией и Орденом Творца, ведь они так же набирают себе послушников из подобных детей и отроков. Но право слово, сейчас в мире столько сирот, что уверен особых сложностей с урегулированием этого момента с остальными заинтересованными сторонами не возникнет.
Так, пора выныривать из транса, во время которого я ускорил своё сознание, пока обдумывал свои планы и возвращаться к Иоланте и позвать остальных обратно в зал. Нужно сегодня же озадачить их этим вопросом.
— Ну раз мы пришли с тобой к пониманию, то давай позовём остальных. Мне ещё есть, что интересного им поведать и ты тоже остаёшься с нами на собрании. Отныне ты в ходишь в состав руководства Ордена! —
Только к Папе Римскому необходимо обращаться через Главу Ордена.
Необходимо лишь согласовать этот вопрос с инквизицией и Орденом Творца, ведь они так же набирают себе послушников из подобных детей и отроков. Но право слово, сейчас в мире столько сирот, что уверен особых сложностей с урегулированием этого момента с остальными заинтересованными сторонами не возникнет.
Так, пора выныривать из транса, во время которого я ускорил своё сознание, пока обдумывал свои планы и возвращаться к Иоланте и позвать остальных обратно в зал. Нужно сегодня же озадачить их этим вопросом.
— Ну раз мы пришли с тобой к пониманию, то давай позовём остальных. Мне ещё есть, что интересного им поведать и ты тоже остаёшься с нами на собрании. Отныне ты в ходишь в состав руководства Ордена! — Опять же, последовательность является ключевым моментом.
Опять же, последовательность является ключевым моментом.





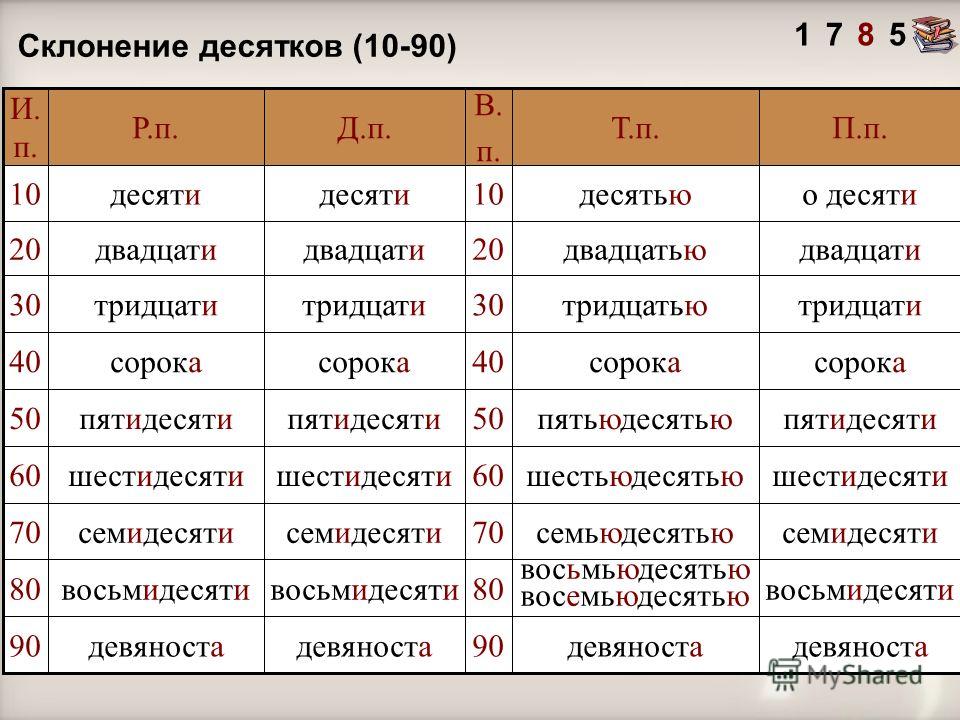


 In to
In to Вот лишь несколько примеров:
Вот лишь несколько примеров: Например, 28 000 000 можно записать как 28 миллионов. 3 700 000 000 можно сократить до 3,7 миллиарда.
Например, 28 000 000 можно записать как 28 миллионов. 3 700 000 000 можно сократить до 3,7 миллиарда.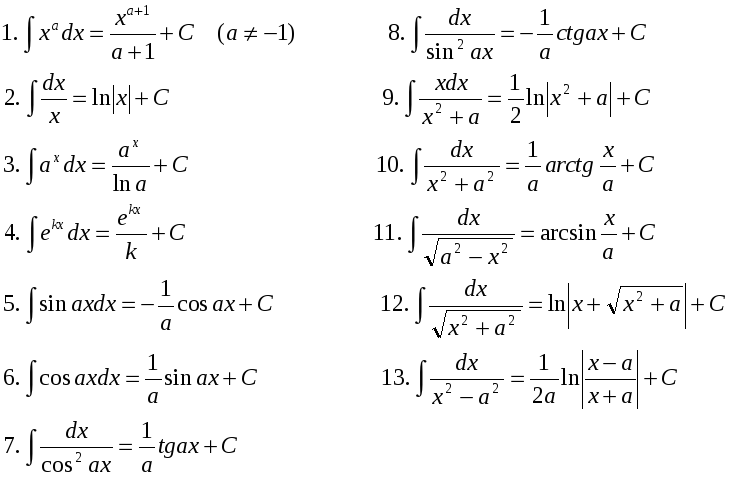

 {\prime}=-\sin x-\frac{1}{x}
\)
{\prime}=-\sin x-\frac{1}{x}
\) (C )’ = 1, (x )’ = 1
(C )’ = 1, (x )’ = 1

 (ax )’ = ax ln a ,
(ax )’ = ax ln a ,

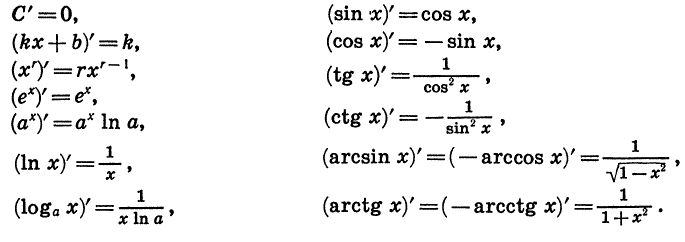


 (arcsin x )’ =
(arcsin x )’ = (arccos x )’ = −
(arccos x )’ = −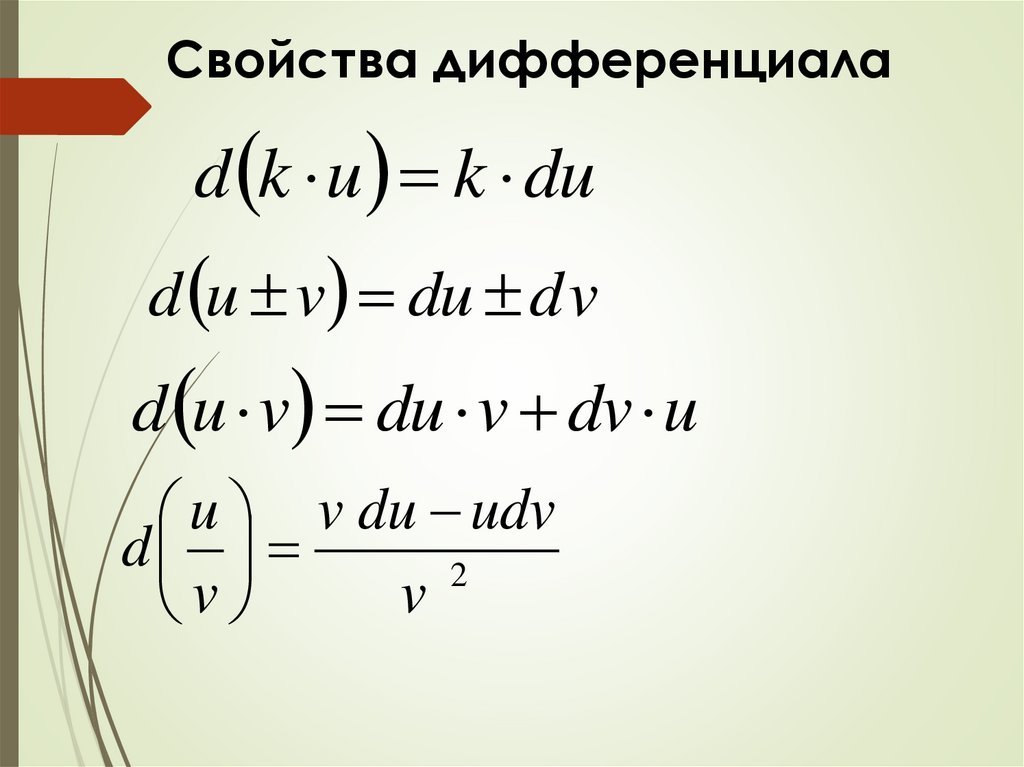 (arctgx )’ =
(arctgx )’ = (arcctgx )’ = −
(arcctgx )’ = − ∫
∫
 04.20151.47 Mб21стихи о лете.pdf
04.20151.47 Mб21стихи о лете.pdf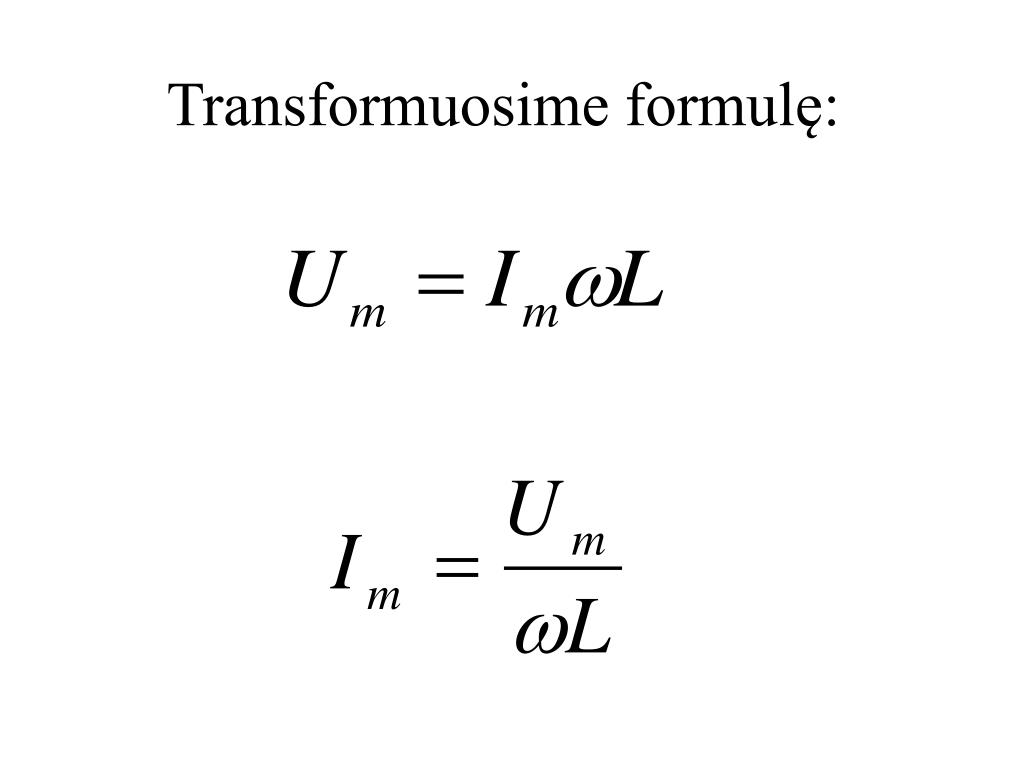 При вычислении определенного интеграла определяется площадь криволинейной трапеции, которая ограничивается сверху кривой (графиком заданной функции), снизу осью х, справа и слева вертикальными прямыми, которые параллельны оси y в заданных точках.
При вычислении определенного интеграла определяется площадь криволинейной трапеции, которая ограничивается сверху кривой (графиком заданной функции), снизу осью х, справа и слева вертикальными прямыми, которые параллельны оси y в заданных точках. 2}\right|\right.\right)+C\\\)
2}\right|\right.\right)+C\\\)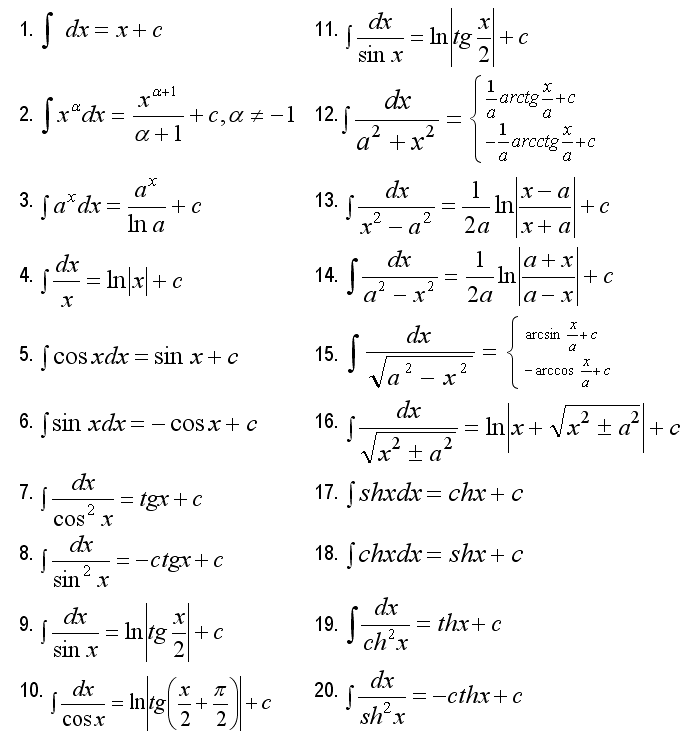 x\;+C\)
x\;+C\)
 Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
 Аналогично, (18) — частный случай (19).
Аналогично, (18) — частный случай (19).
 Получаем:
∫3x2dx+∫2sinxdx−∫7exdx+∫12dx
Получаем:
∫3x2dx+∫2sinxdx−∫7exdx+∫12dx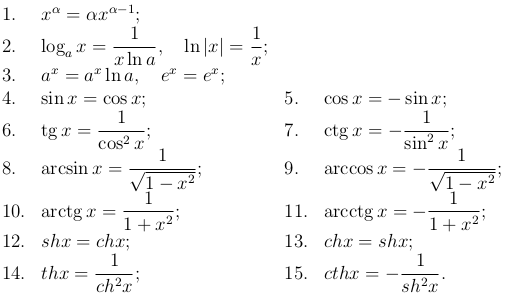 Будем решать Ваши проблемы вместе!
Будем решать Ваши проблемы вместе!
 В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
 Последние 2 цикла «for» использовались для отображения матрицы «z» в оболочке с помощью оператора объекта «cout». После всего этого последний оператор cout используется для добавления конечной строки. Теперь наша программа готова к компиляции в оболочке.
Последние 2 цикла «for» использовались для отображения матрицы «z» в оболочке с помощью оператора объекта «cout». После всего этого последний оператор cout используется для добавления конечной строки. Теперь наша программа готова к компиляции в оболочке. Для выполнения умножения значение первой строки матрицы должно быть равно значению второго столбца матрицы, т. е. r1=c2 или r2=c1. Мы обновили значение столбца «c» до 3. Теперь значения строк и столбцов для матриц «x» и «y» не совпадают. Произведение не будет рассчитано, так как матрица «х», а «у» будет иметь 2 строки и 3 столбца, т.е. r1 не равно c2, а r2 не равно c1. Остальной код останется без изменений и будет сохранен для компиляции через Ctrl+S.
Для выполнения умножения значение первой строки матрицы должно быть равно значению второго столбца матрицы, т. е. r1=c2 или r2=c1. Мы обновили значение столбца «c» до 3. Теперь значения строк и столбцов для матриц «x» и «y» не совпадают. Произведение не будет рассчитано, так как матрица «х», а «у» будет иметь 2 строки и 3 столбца, т.е. r1 не равно c2, а r2 не равно c1. Остальной код останется без изменений и будет сохранен для компиляции через Ctrl+S. Давайте сохраним этот обновленный код и скомпилируем его.
Давайте сохраним этот обновленный код и скомпилируем его.