Решение некоторых задач по теории множеств
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
, где
“” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если , то , где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):
(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
(рис.3)
Обозначим буквой Е основное или универсальное множество, где A С Е (“”- любо число), т.е. А Е = Е; АЕ =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕ или Ā (рис.4)
Е
(рис. 4)
4)
Примерами для понимания этих понятий являются свойства:
_
А Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
АВ = А∩В
________ _ _
АВ = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (AB) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (АВ)
m (ABC) = m (A) + m (В) + m (С)– m (А∩В) — m (А∩С) – m (В∩С) – m (А∩В∩С).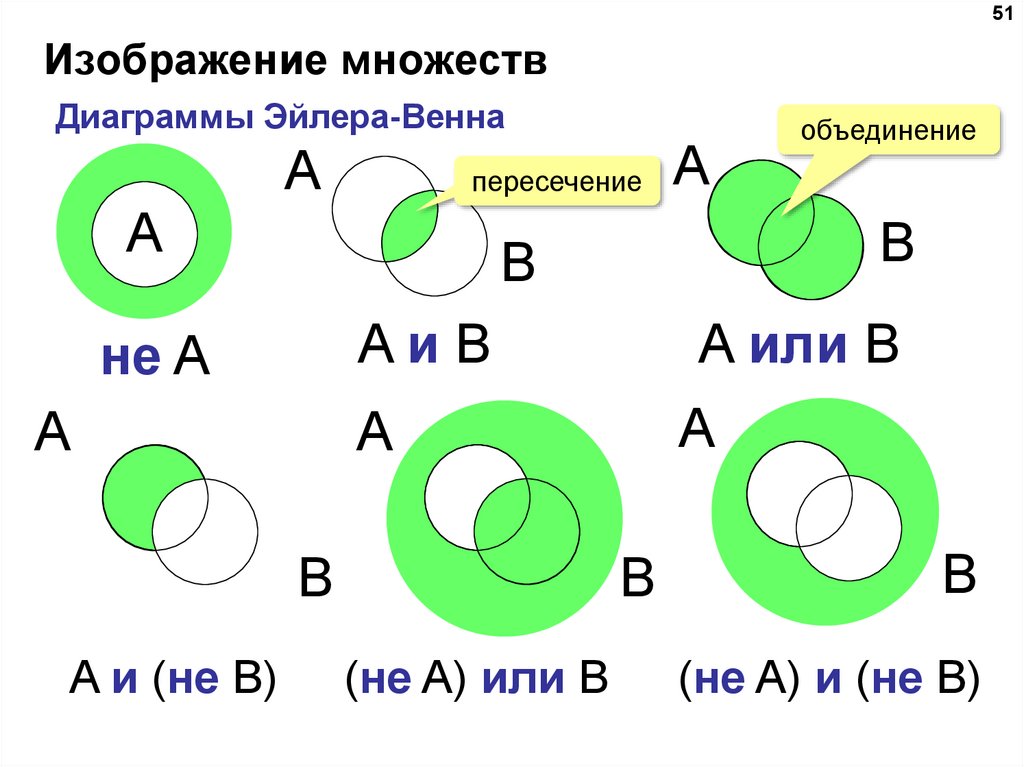
А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.
- Сколько учащихся решили все задачи?
- Сколько учащихся решили только две задачи?
- Сколько учащихся решили только одну задачу?
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
- m (Е) = 40
- m (А) = 20
- m (В) = 18
- m (С) = 18
- m (А∩В) = 7
- m (А∩С) = 8
- m (В∩С) = 9
___________
m (АВС) = 3 => m (АВС) = 40 – 3 = 37
Обозначим разбиение универсального множества Е множествами А, В, С (рис. 5).
5).
(рис.5)
К1 – множество учеников, решивших только одну задачу по алгебре;
К2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К3 – множество учеников, решивших только задачу по геометрии;
К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К5 – множество всех учеников, решивших все три задачи;
К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К7 – множество всех учеников, решивших только задачу по тригонометрии;
К8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
- m (К5) = m (А∩В∩С)= m (АВС) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
- m (К5) = 37-20-18-18+7+8+9=5
- m (К2) = m (А∩В) — m (К5) = 7-5=2
- m (К4) = m (А∩С) — m (К5) = 8-5=3
- m (К6) = m (В∩С) — m (К5) = 9-5=4
- m (К1) = m (А) — m (К2) — m (К4) — m (К5) = 20-2-3-5=10
- m (К3) = m (В) — m (К2) — m (К6) — m (К5) = 18-2-4-5=7
- m (К7) = m (С) — m (К4) — m (К6) — m (К5) = 18-3-4-5 =6
- m (К2) + m (К4) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
- m (К1) + m (К3) + m (К7) = 10+7+6=23 – число учеников решивших только одну задачу.

Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
- m (АВ) = 33
- m (АС) = 31
- m (ВС) = 32
- m (К2) + m (К4) + m (К6) + m (К5) = 20
Найти m (К1) + m (К3) + m (К7)
- m (АUВ) = m (К1) + m (К2) + m (К3) + m (К4) + m (К5) + m (К6) = m (К1) + m (К3) + 20 = 33 =>
- m (К1) + m (К3) = 33 – 20 = 13
- m (АUС) = m (К1) + m (К4) + m (К2) + m (К5) + m (К6) + m (К7) = m (К1) + m (К7) + 20 = 31 =>
- m (К1) + m (К7) = 31 – 20 = 11
- m (ВUС) = m (К3) + m (К2) + m (К5) + m (К6) + m (К7) + m (К4) = m (К3) + m (К7) + 20 = 32 =>
- m (К3) + m (К7) = 32 – 20 = 12
- 2m (К1) + m (К3) + m (К7) = 13+11=24
- 2m (К1) + 12 = 24
- m (К3)= 13-6=7
- m (К7)=12-7=5
- m (К1) + m (К3) + m (К7) = 6+7+5=18
Ответ:
Только одну контрольную работу решили 18 учеников.
Решение задачи № 3
- m (Е) = 35
- m (А∩В∩С)= m (К5) = 6
- m (А∩В)= 15
- m (А∩С)= 13
- m (В∩С)= 9
Найти m (К1) + m (К3) + m (К7)
- m (К2) = m (А∩В) — m (К5) = 15-6=9
- m (К4) = m (А∩С) — m (К5) = 13-6=7
- m (К6) = m (В∩С) — m (К5) = 9-6=3
- m (К1) + m (К3) + m (К7) = m (Е) — m (К4) — m (К2) — m (К6) — m (К5) = 35-7-9-3-6=10
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
Задачник по Python. Тема 7. Работа с множествами
Оглавление
Содержание
python / задачник
Тип данных: set
Контент: Вопросы (5шт) + задачи (5шт)
Предыдущая тема
Тема 6. Работа с кортежами
Работа с кортежами
Следующая тема
Тема 8. Работа со строками
Оглавление
Введение
Рассмотрим, что из себя представляют множества в Python, какими характеристиками они обладают, и какие темы нужно повторить для решения задач.
Перейти
Вопросы и ответы
5 вопросов по теме «Множества» + ответы
Перейти
Условия задач
5 задач по теме двух уровней сложности: Базовый и *Продвинутый
Перейти
Решения задач
Приводим код решений указанных выше задач
Перейти
Введение
Множества – неупорядоченный тип уникальных данных, включающий только хешируемые элементы. Их можно изменять, неизменяемый аналог – frozenset. Не имеют индексации. Поиск объекта внутри множества очень быстрый (по сравнению со списками и кортежами).
Для успешного решения заданий требуется повторить: особенности множеств, уникальные методы, основные операции, способы модификации.
Читайте также
Программирование на Python. Урок 2. Типы данных
Разбираем типы данных в Python: списки, кортежи, словари, множества и т. д. Рассматриваем часто используемые способы ввода-вывода данных. Решаем задачи.
Вопросы по теме «Работа с множествами»
Мощность множества показывает количество элементов в нем. По факту, это аналог функции len() для других коллекций. Более того, она же и применяется к множествам. Только правильно говорить мощность, а не длина множества.
Пример – Интерактивный режим
>>> st = {3, 4, 8, 89}
>>> lst = [1, 5, 4, 5, 5]
>>> len(st)
4
>>> len(lst)
5
Для удаления элемента из множества применяются 3 способа:
1 – pop() – удаляет случайный элемент и возвращает его, но вызовет ошибку, если множество пустое (нам для ответа не подходит)
2 – remove() – удаляет объект с конкретным значением, но вызовет ошибку, если его нет (опять же, не наш выбор)
3 – discard() – также удаляет определенный элемент, но не приводит к ошибке, если он отсутствует в данном множестве (как и требовалось ответить)
Пример – Интерактивный режим
>>> st = {3, 7, 8, 89}
>>> st. pop() # Просто удаляет какой-то выборочный элемент
pop() # Просто удаляет какой-то выборочный элемент
>>> st.remove(9) # Ошибка KeyError: 9
KeyError: 9
>>> st.discard(9) # Хоть элемента нет, ошибка не возникает
Объединение подразумевает формирование множества из всех элементов участников. Функционально оно осуществимо двумя способами:
1 – через метод union(). Сюда можно передать не только множество, но и другие итерабельные объекты (списки, кортежи, строки)
2 – через оператор |. По обе стороны от оператора обязаны быть множества.
Пример – Интерактивный режим
>>> st_1 = {3, 7, 8, 89}
>>> st_2 = {4, 100, 8}
>>> words = ‘string spring’
>>> lst = [4, 4, 3, 55, 2]
# Метод union()
>>> st_1.union(st_2)
{3, 100, 4, 7, 8, 89}
>>> st_1.union(words)
{‘g’, 3, ‘n’, 7, 8, ‘t’, ‘ ‘, ‘r’, ‘i’, ‘p’, ‘s’, 89}
>>> st_1. union(lst)
union(lst)
{2, 3, 4, 7, 8, 55, 89}
# Через оператор |
>>> st_1 | st_2
{3, 100, 4, 7, 8, 89}
>>> st_1 | words
Ошибка TypeError
Супермножество включает в себя все элементы другого множества и может быть равно с ним по мощности. Еще есть чистое супермножество, которое строго больше подмножества и содержит все его компоненты. Для проверки на супермножество можно использовать метод issuperset() или знак >=. Для чистого – только оператор >.
Пример – Интерактивный режим
>>> st_1 = {3, 7, 8, 89}
>>> st_2 = {7, 89}
>>> st_1.issuperset(st_2)
True
>>> st_1 >= st_2
True
>>> st_1 > st_2
True
>>> st_2.issuperset(st_1)
False
Так как элементы множества хешируются, их поиск осуществляется практически мгновенно. Чтобы найти объект списка, требуется его перебирать (в худшем случае полностью). Для оценки времени обнаружения конкретного значения проведем тест.
Чтобы найти объект списка, требуется его перебирать (в худшем случае полностью). Для оценки времени обнаружения конкретного значения проведем тест.
Пример – IDE
from time import perf_counter_ns
MAX_VALUE = 20_000_000
SEARCH_ITEM = 19_999_000
def measure_time(data):
____start = perf_counter_ns()
____SEARCH_ITEM in data
____return perf_counter_ns() — start
st = set(range(1, MAX_VALUE))
lst = list(range(1, MAX_VALUE))
print(f’Set search time: {measure_time(st)}ns’)
print(f’List search time: {measure_time(lst)}ns’)
Результат выполнения
Set search time: 4276ns
List search time: 299974854ns
Получается, в множестве элемент нашелся в тысячи раз быстрее.
Задачи по теме «Работа с множествами»
Решение
Решение
Решение
Решение
Решение
Решения
Задача 1.
 Базовый уровень
Базовый уровеньУсловие
На входе функция to_set() получает строку или список чисел. Преобразуйте их в множество. На выходе должно получиться множество и его мощность.
Список чисел или строка преобразуются в множество без возможных ошибок. Нужно просто обернуть их в конструктор и воспользоваться методом len() для получения ответа.
Решение – IDE
def to_set(element):
st = set(element)
return st, len(st)
# Тесты
print(to_set('я обычная строка'))
print(to_set([4, 5, 4, 6, 2, 9, 11, 3, 4, 2]))
Результат выполнения
({'к', 'б', 'я', 'ы', 'н', 'р', 'т', 'о', 'ч', ' ', 'с', 'а'}, 12)
({2, 3, 4, 5, 6, 9, 11}, 7)
Задача 2. Базовый уровень
Условие
Имеется список с произвольными данными. Поставлена задача преобразовать его в множество. Если какие-то элементы нельзя хешировать, то пропускаем их. Функция list_to_set() выводит на печать получившееся множество.
При решении придется проверять каждый элемент списка на хешируемость. Для этого воспользуемся классом Hashable из модуля collections.
Решение — IDE
from collections.abc import Hashable
def list_to_set(lst):
st = {item for item in lst if isinstance(item, Hashable)}
print(st)
# Тесты
list_to_set([1, [2]])
list_to_set([1, [2], 55, 55, {1, 2, 3}, (2, 2), 'string', 5.11])Результат выполнения
{1}
{1, 5.11, 'string', 55, (2, 2)}Читайте также
Программирование на Python. Урок 5. Модули и пакеты. Импорт.
Рассматриваем модули и пакеты из стандартной библиотеки Python и PyPI. Учимся использовать инструкции import и from..import и различать абсолютный и относительный импорт. Разбираемся с виртуальными пространствами venv. Создаем собственные модули.
Задача 3. Базовый уровень
Условие
На основании 3 исходных множеств (передаются в качестве аргументов функции diff()) требуется написать функцию, которая будет возвращать либо симметричную разность, либо просто разность (если дополнительный аргумент функции symmetric имеет значение False) приведенных объектов в порядке: 1-ое множество, 2-ое множество, 3-е множество.set_3 return set_1 - set_2 - set_3
Вариант 2. При помощи методов
Решение – IDE
def diff(set_1, set_2, set_3, symmetric=True):
if symmetric:
return set_1.symmetric_difference(set_2).symmetric_difference(set_3)
return set_1.difference(set_2, set_3)
# Тесты
set_1 = {3, 4, 5, 6, 20}
set_2 = {4, 6, 7, 8, 9}
set_3 = {5, 3, 8, 1}
print(diff(set_1, set_2, set_3))
print(diff(set_1, set_2, set_3, asymmetric=False))Результат выполнения
{1, 20, 7, 9}
{20}Задача 4. Базовый уровень
Условие
Напишите функцию superset(), которая принимает 2 множества. Результат работы функции: вывод в консоль одного из сообщений в зависимости от ситуации:
1 - «Супермножество не обнаружено»
2 – «Объект {X} является чистым супермножеством»
3 – «Множества равны»Для написания функции необходимо выявить подчиненность множеств, наличие чистого супермножества. При помощи print() вывести ответ по результатам оценки.
При помощи print() вывести ответ по результатам оценки.
Решение — IDE
def superset(set_1, set_2):
if set_1 > set_2:
print(f'Объект {set_1} является чистым супермножеством')
elif set_1 == set_2:
print(f'Множества равны')
elif set_1 < set_2:
print(f'Объект {set_2} является чистым супермножеством')
else:
print('Супермножество не обнаружено')
# Тесты
set_1 = {1, 8, 3, 5}
set_2 = {3, 5}
set_3 = {5, 3, 8, 1}
set_4 = {90, 100}
superset(set_1, set_2)
superset(set_1, set_3)
superset(set_2, set_3)
superset(set_4, set_2)
Результат выполнения
Объект {8, 1, 3, 5} является чистым супермножеством
Множества равны
Объект {8, 1, 3, 5} является чистым супермножеством
Супермножество не обнаруженоЗадача 5. * Продвинутый уровень
Условие
Предоставлен список натуральных чисел.Требуется сформировать из них множество. Если какое-либо число повторяется, то преобразовать его в строку по образцу: например, если число 4 повторяется 3 раза, то в множестве будет следующая запись: само число 4, строка «44» (второе повторение, т.е. число дублируется в строке), строка «444» (третье повторение, т.е. строка множится на 3). Реализуйте вывод множества через функцию set_gen().
Для решения удобно воспользоваться методом count().
Решение — IDE
def set_gen(lst):
index = 0
while index < len(lst):
cnt = lst.count(lst[index])
if cnt > 1:
lst[index] = str(lst[index]) * cnt
index += 1
return set(lst)
# Тесты
list_1 = [1, 1, 3, 3, 1]
list_2 = [5, 5, 5, 5, 5, 5, 5]
list_3 = [2, 2, 1, 2, 2, 5, 6, 7, 1, 3, 2, 2]
print(set_gen(list_1))
print(set_gen(list_2))
print(set_gen(list_3))
Результат выполнения
{1, 3, '111', '33', '11'}
{'5555555', 5, '55', '55555', '5555', '555555', '555'}
{1, 2, 3, 5, 6, 7, '22', '2222', '22222', '222', '11', '222222'}
Предыдущая тема
Тема 6. Работа с кортежами
Работа с кортежами
Следующая тема
Тема 8. Работа со строками
Как вам материал?
| ПОКАЗАТЬ КОММЕНТАРИИ |
Задачник. Программирование на Python.
Задачник по Python. Тема 1. Целые числа.
Задачник по Python. Тема 2. Числа с плавающей точкой
Задачник по Python. Тема 4. Работа со списками
Задачник по Python. Тема 6. Работа с кортежами
Set Designer Tasks — Драма 10 класса
ЗАДАЧА ДИЗАЙНЕРА A: исследование
Когда вы думаете о дизайне сцены, вашей отправной точкой должен быть сценарий или придуманная работа . Это должно быть в вашей голове все раз — вы разрабатываете набор для пьесы , и что вы делаете, должны поддерживать произведение. Ваш дизайн декораций также должен иметь непосредственное отношение к пьесе и периоду времени или концепции, которую вы используете. Обсудите с актерами, каковы важные элементы пьесы, чтобы ваш дизайн отражал их.
Обсудите с актерами, каковы важные элементы пьесы, чтобы ваш дизайн отражал их.
Когда вы думаете о дизайне сцены, вашей отправной точкой должен быть сценарий или придуманная работа . Это должно быть в вашей голове все раз — вы разрабатываете набор для пьесы , и что вы делаете, должны поддерживать произведение. Ваши эскизы реквизита также должны иметь непосредственное отношение к пьесе и должны поддерживать произведение.
Узнайте, что актеры, которых вы создаете, на самом деле делают в дораме. Где они ходят, сидят, стоят? Используют ли они отдельные участки сцены? Будут ли они использовать уровни? Обсудите как группа будет использовать сцену. Какой реквизит они будут использовать? Насколько надежными они должны быть?
Составьте базовый список того, что вам понадобится в спектакле, на основе сценария. Следуйте приложенному шаблону.
planning_my_production_concept. docx docx |
ЗАДАЧА СПЕЦИАЛИСТА b: размеры и линии обзора
Произвести точные измерения зоны производительности. Вам нужно будет сделать масштабный чертеж или модель окончательного дизайна, реализованного в пространстве для выступлений — будьте осторожны при уменьшении размеров! Попросите вашего учителя помочь, если вы не уверены в этом.
Поместите элементы набора , сделанные из раскрашенного картона, на большой лист бумаги или материала, отмеченный линиями сетки — это простой способ работы с дизайном вашего набора. Или используйте картонную коробку в качестве модели арки авансцены, установленной в качестве приблизительного руководства, прежде чем вы сделаете окончательную модель.
Учитывайте «линии обзора» , чтобы зрители могли видеть как можно больше. Остерегайтесь больших предметов декораций, размещенных внизу сцены — они могут мешать зрителям видеть сцену.
Цвет — помните, что разные цвета символизируют разные идеи — например, красный — опасность, белый — невинность. Если художник по свету использует цветные гели, выясните, как это повлияет на цвета вашего набора. Красный, например, при красном освещении имеет тенденцию выглядеть размытым, а при синем свете он начинает казаться темным, почти черным. Так что выбирайте цвет с осторожностью!
Освещение — выбор освещения сильно повлияет на ваш набор. Вы можете захотеть, чтобы на съемочной площадке были вырисовывающиеся тени, и вам нужно будет спланировать это с дизайнером по свету.
Смена сцены — если в спектакле требуется смена сцены, декорации нужно будет легко перемещать. Экономьте время, поворачивая элемент или выталкивая его за пределы сцены. Что бы вы ни делали, будьте проще.
Сохраняйте заметки и ранние наброски дизайна вашего набора в журнале процесса под заголовками выше. Они будут полезны, чтобы показать ваш прогресс вашему учителю, поскольку они оценивают вашу работу.
Они будут полезны, чтобы показать ваш прогресс вашему учителю, поскольку они оценивают вашу работу.
ЗАДАНИЕ ДЕКОРАТОРА c: дизайн
Набросок из всех сцен спектакля. Сделайте базовую раскадровку для основных изменений сцены и того, как сцена изменится, чтобы показать это. Добавьте их в свой рабочий журнал. Как только вы убедитесь, что весь ваш набор можно использовать в меру своих возможностей, проверьте их с вашим учителем, режиссером и постановщиком. Добавьте эти примечания и любые изменения в свой журнал процессов.
Масштабная модель . Вам потребуется создать масштабную модель окончательного проекта и масштабный план и/или масштабный чертеж любого проектируемого объекта. Используйте демонстрационную коробку, коробку для фотокопий или что-то вроде мусорной корзины, которая позволит вам легко измерить, чтобы создать 25:! макет зрительного зала
Зайдите на веб-сайт Дэвида Нита, чтобы узнать, как создать модель театрального дизайна. Есть также другие замечательные сайты и инструкции на Youtube, которым вы можете следовать, чтобы получить дополнительные советы.
Есть также другие замечательные сайты и инструкции на Youtube, которым вы можете следовать, чтобы получить дополнительные советы.
http://davidneat.wordpress.com/tag/theatre-set-design-model-making/
ЗАДАЧА ДЕКОРАТОРА d: изменения и компромиссы
Будьте готовы к компромиссу — другие группы будут использовать этап во время проведения оценки, и вам, возможно, придется пойти на некоторые компромиссы в своем наборе. Объясните это учителю и в своем журнале процесса, если это повлияет на ваш окончательный дизайн. Лента
После показа режиссеру, постановщику сцены и учителю запишите любые изменения в журнале процесса и их причины.
Прикрепите свои эскизы к сцене — это даст актерам общее представление о том, где находится декорация для репетиций. Это также позволит вам найти мебель для репетиций и настроить ее для использования, пока другие предметы находятся в поиске, или, если вы хотите, чтобы он не выглядел изношенным из-за чрезмерного использования.
Поиск и/или изготовление набора —
Есть несколько способов сделать это, и многое зависит от вашего бюджета.
. Найдите мебель из школы, вашего дома, друзей и т. д. Это хороший вариант, если он подходит для вашей игры и ничего не стоит. убедитесь, что вы проконсультировались с нужными людьми и спросили разрешения, прежде чем просто взять что-либо
— Конвертировать набор — Посмотрите, что уже доступно для вас в отделе драмы и перекраски, обоев и творчества
— Купите новые предметы. В зависимости от вашего бюджета вам, возможно, придется искать дешевые места в Интернете. Вы даже можете найти то, что вам нужно, и преобразовать его
— Сделай это. Проявите творческий подход с папье-маше, пенополистиролом, коробками, клейкой лентой, клеем, краской и т. д. Убедитесь, что ваш набор всегда в безопасности и достаточно надежен для ваших нужд, и посмотрите, на что вы способны. Вы ограничиваете только свое творчество.
– Использовать минимальный набор с черными ящиками. Черные ящики — это хорошее решение для быстрых изменений, замены сложных или дорогих элементов набора и хорошая основа для создания поверх них. Вы можете наслоить их цветным материалом, чтобы сделать холмы, троны, столы или кровати. Еще раз ваш творческий потенциал является вашим пределом здесь.
Черные ящики — это хорошее решение для быстрых изменений, замены сложных или дорогих элементов набора и хорошая основа для создания поверх них. Вы можете наслоить их цветным материалом, чтобы сделать холмы, троны, столы или кровати. Еще раз ваш творческий потенциал является вашим пределом здесь.
Репетиции
Уточните у директора, с каким видом они хотят репетировать. Вы отвечаете за подготовку сцены к каждой репетиции. Y9u может быть в состоянии переместить все самостоятельно, или вам может понадобиться нанять людей, которые помогут вам. Попросите своего режиссера и учителя помочь вам составить список людей, которые помогут перенести декорации и снова аккуратно упаковать их после каждой репетиции.
ЗАДАЧА СПЕЦИАЛИСТА e: техническая репетиция
Люди неизбежно захотят потрогать и использовать вашу декорацию во время репетиций. Тем не менее, вы отвечаете за то, чтобы убедиться, что нужный реквизит находится в нужном месте в нужное время. Убедитесь, что никто не прикасается к чужому реквизиту — обратитесь за помощью к режиссеру, постановщику сцены или учителю, если вам нужна поддержка.
Убедитесь, что никто не прикасается к чужому реквизиту — обратитесь за помощью к режиссеру, постановщику сцены или учителю, если вам нужна поддержка.
Репетиция
Перед любой репетицией, на которой режиссер просит использовать реквизит, убедитесь, что они готовы к сценам, над которыми им нужно работать, до начала репетиции. Это означает, что если репетиция начинается в 10:00, вам, возможно, придется прийти в 9:45, чтобы подготовить декорации. Вам также нужно будет уточнить у режиссера до его прибытия, какие сцены будут репетироваться. После репетиции убедитесь, что воровство упаковано и хранится в безопасности. Запишите любые повреждения, которые нужно исправить, или новый реквизит, который может понадобиться для следующей репетиции.
Сценические рабочие
Если в вашем сете много переходов, вам может понадобиться организация рабочих, которые помогут вам поднимать и убирать сцену. Поговорите со своим постановщиком сцены и учителем, чтобы они помогли вам составить список людей, которые будут помогать вам в классе во время репетиции. Возможно, вам придется попросить кого-нибудь из других людей на ночь выступления, чтобы актеров нельзя было увидеть во время репетиции.
Возможно, вам придется попросить кого-нибудь из других людей на ночь выступления, чтобы актеров нельзя было увидеть во время репетиции.
ЗАДАЧА ДЕКОРАТОРА f: окончательный дизайн
Сфотографируйте все ваши финальные декорации, размещенные на сцене для каждой сцены. В своем журнале процесса отметьте любые изменения, произошедшие с вашими окончательными проектами, и объясните, почему они изменились.
ЗАДАЧА ДЕКОРАТОРА g: время показа
Выполните все шаги, описанные выше для репетиции.
Слушайте указания и будьте открытыми.
ЗАДАЧА ДЕКОРАТОРА h: упаковать
После окончания представления вам нужно будет упаковать декорации. Уберите все декорации из помещения для представления и либо верните их законным владельцам, либо выбросьте, если они скоропортящиеся (проконсультируйтесь с учителем и утилизируйте столько, сколько сможете), либо пожертвуйте их на факультет драмы. Убедитесь, что ваша закулисная зона чистая и аккуратная, как когда вы начали этот процесс.
ЗАДАЧА СПЕЦИАЛИСТА i: размышление
В своем рабочем журнале запишите ответы на следующие вопросы:
1) Насколько хорошо вы выполняли свои индивидуальные обязанности? Приведите примеры того, как вы делали это для всего процесса, например, я соблюдал все сроки и своевременно вносил записи в журнал процесса и т. д.
2) Насколько успешным было производство в целом? Откуда вы знаете? Приведите конкретные примеры того, что сработало хорошо, что можно улучшить и как.
3) Насколько эффективно вы доносили свою роль до аудитории? Другими словами, насколько хорошо вы исполнили свою роль на шоу?
Как успешно ставить задачи команде разработчиков
Есть поговорка, которая гласит: «Иди не знаю куда и принеси не знаю что», и обычно, в основном по иронии судьбы, это описывает плохо поставленную задачу — то, что мы все тоже знаем ну и пришлось перетерпеть не раз. Но после более чем трех лет работы над проектами всех уровней сложности я развил некоторые специальные организаторские способности и глубокие ноу-хау работы в команде. И в результате команда разработчиков, с которой я работаю, готова работать эффективнее, чем когда-либо.
И в результате команда разработчиков, с которой я работаю, готова работать эффективнее, чем когда-либо.
Коммуникация внутри любой команды является одним из ее самых сильных столпов. Результаты совместных усилий членов команды зависят от того, насколько хорошо они могут обсуждать части процесса, идеи и предложения. Но самым важным является то, как сообщаются начальные задачи. Четкие, прозрачные задачи легче понять, а это значит, что команда может начать работу раньше и не тратить много времени на задавание вопросов в процессе. Также, если каждый поймет, какова его роль и какую часть продукта они разрабатывают, будет легче собрать эти части воедино, когда придет время. Кроме того, Немедленное информирование о ценности определенной задачи разработки или всего продукта улучшит командный дух и мотивацию.
Если вы думаете о команде разработчиков как о драгоценных часах, то каждый ее член является ценной частью. Для того чтобы часы функционировали должным образом, все детали должны находиться на своих местах, выполняя свои роли. С людьми немного сложнее, но принцип тот же. А общение — это то, что помогает смазать колеса в человеческом механизме. Если ты правильно поставишь задачи, если будешь говорить четко и логично, твои часы, то есть твоя команда будут служить тебе верой и правдой долгие годы.
С людьми немного сложнее, но принцип тот же. А общение — это то, что помогает смазать колеса в человеческом механизме. Если ты правильно поставишь задачи, если будешь говорить четко и логично, твои часы, то есть твоя команда будут служить тебе верой и правдой долгие годы.
Правда в том, что недопонимание при постановке задач — большая проблема, чем мы думали. По данным Project Management Institute, неудачная коммуникация приводит к провалу каждого пятого проекта.
К сожалению, есть бизнесмены , владельцы продукта или бизнес-аналитики , которые пишут задачи для команд разработчиков и даже не подозревают, что у них проблемы с коммуникацией. Даже опытные бизнесмены иногда становятся жертвами бюрократии и расширенной иерархии. Иногда Владельцы Продукта просто не выполняют свою роль в полной мере. Владельцы продукта должны быть связующим звеном между бизнес-стороной и командой разработчиков. Их основная задача — хранить все функции, запрашиваемые бизнес-стороной, в одном месте и сообщать разработчикам требования к продукту. Однако это не всегда происходит так, как должно.
Их основная задача — хранить все функции, запрашиваемые бизнес-стороной, в одном месте и сообщать разработчикам требования к продукту. Однако это не всегда происходит так, как должно.
В этом случае возможны два сценария. Либо Product Owner даже не подозревает о проблемах с доведением задач, либо этот сложный процесс является обычным способом ведения бизнеса.
Тем не менее, нам всем приходится сталкиваться с тем фактом, что неправильно поставленных целей могут привести к стрессу и напряжению в команде разработчиков, в то время как неправильно или иррационально поставленные задачи часто требуют больше усилий (и денег) для выполнения. Что приводит к превышению бюджета и нарушению сроков (что также может привести к штрафным санкциям). И, конечно же, мы тратим много времени, снова и снова объясняя требования.
Давайте внимательно посмотрим, что происходит. Каковы основные проблемы, которые могут вызвать недопонимание между командой разработчиков и клиентом? Большинство из них можно условно разделить на три подвопроса:
После того, как мы определили эти три направления, будет легче понять, что именно клиенты могут сделать, чтобы лучше ставить задачи командам разработчиков, с которыми они работают, экономя время, деньги и энергию. Самое главное, помните, что там, где есть проблема, всегда есть решение.
Самое главное, помните, что там, где есть проблема, всегда есть решение.
Итак, что делать, если команда разработчиков не знает тонкостей домена , с которым им приходится работать?
Перед запуском процесса разработки начните сотрудничество с презентации набора характеристик будущего продукта. Подробно опишите, какую проблему он собирается решить, а также его бизнес-ожидания. Приведите примеры конкурентов и установите сроки , если они есть. Это могут быть либо обещанные заинтересованным сторонам, либо связанные с профессиональной выставкой.*
*Например, если через шесть месяцев будет выставка стартапов, в которой вы обязательно хотите принять участие, сообщите об этом разработчикам, и заранее определите масштаб для команды разработчиков, чтобы у них было достаточно времени для работы.
Имея эту информацию, команда разработчиков может начать эффективную работу над архитектурными решениями уже на ранних стадиях, что может помочь им понять, сколько это займет времени и какие подходы они должны использовать, а также увидеть ценность своей работы для бизнеса.
Это поможет определить более разумный и согласованный подход к развитию. Самое главное, это поможет разработчикам понять порядок , в котором должны быть реализованы все функции, как все они работают вместе и каковы их зависимости — друг от друга, параллельное выполнение или важные контракты.*
* Если вы работаете над чем-то, что требует интеграции с банком , или платежной системой, например, имейте в виду, что банки довольно бюрократичны, поэтому не рассчитывайте на быстрое подписание всех необходимых контрактов. . А если вы работаете над комплексным решением для банковских услуг, бумажная работа может существенно повлиять на сроки.
Деловой и технический языки разные. Что вы можете сделать при сотрудничестве с командой разработчиков, чтобы это не испортило ваше общение?
Независимо от того, насколько хороши разработчики в своей области, им может быть сложно понять некоторые требования клиента. Особенно, если они используют очень специфическую терминологию из области, в которой будет использоваться продукт. Как клиент компании-разработчика или владелец продукта, работающий с ней, вы должны помнить об этом и не усложнять. Задания должны быть написаны понятным для всех языком. Или, если вы чувствуете, что обойти такие термины невозможно, обе стороны должны оговорить и договориться о том, какую лексику вы собираетесь использовать во время проекта.
Особенно, если они используют очень специфическую терминологию из области, в которой будет использоваться продукт. Как клиент компании-разработчика или владелец продукта, работающий с ней, вы должны помнить об этом и не усложнять. Задания должны быть написаны понятным для всех языком. Или, если вы чувствуете, что обойти такие термины невозможно, обе стороны должны оговорить и договориться о том, какую лексику вы собираетесь использовать во время проекта.
Если после всего этого остались неясные вопросы, команда разработчиков может направить свои запросы клиенту. Важно, чтобы они были четко сформулированы и профессионально , , а также использовались деловые термины и фразы типа «Правильно ли я/мы поняли, что…» или «…быть на одной волне». Ни при каких обстоятельствах клиент не должен чувствовать себя неполноценным из-за непонимания технического термина. Но если обе стороны найдут взаимопонимание, а команда разработчиков полностью понимает бизнес-потребности клиента, они могут даже предложить лучший подход к их реализации. Это, однако, может быть достигнуто только в условиях открытого и доверительного общения.
Это, однако, может быть достигнуто только в условиях открытого и доверительного общения.
В заключение этой части мы рекомендуем хранить все коммуникации в одном месте. Это поможет вам упорядочить все обсуждения и легко их найти, чтобы ничего не потерялось. Таким образом, если член команды, кто-то вне команды или, может быть, кто-то новый в проекте захочет покопаться, у них будет доступ ко всей информации, относящейся к проекту. Наконец, ведение одного источника информации по проекту предотвратит потерю вашей командой данных, если кто-то покинет проект и заберет с собой все их чаты и переписку.
Плохо объясненные задачи, вероятно, являются наиболее распространенной проблемой, которая ставит под угрозу успех не только в работе с (удаленными) командами разработчиков или управлении ими, но и в любом виде предприятия. В разработке программного обеспечения есть понятие Ready for Development. Это, по сути, описывает соглашение между командой разработчиков и владельцем продукта о том, что такое полное описание задачи, чтобы команда могла начать над ней работать.
Подробнее: Советы по созданию плана коммуникации Scrum
К этому моменту мы много говорили о том, чего нельзя делать, поэтому, вероятно, пришло время поговорить о том, что нужно делать при написании задач для разработчиков. Какова правильная структура? Как на самом деле выглядит хорошо объясненная и завершенная задача?
Задание, которое имеет структуру и фокусируется на важном, легче понять и реализовать. Вот почему, я думаю, команде важно заранее определиться с типами и содержанием задач, над которыми они будут работать.
На мой взгляд, есть три типа задач по разработке программного обеспечения: разработка новых функций, исправление ошибок и расследование. Все они имеют свои отличительные особенности. Чтобы поддерживать хорошую структуру задач, сосредоточьтесь на них и на том, что действительно важно.
Существует множество подходов к формулированию задач, но их общая цель состоит в том, чтобы подробно описать признаки и предоставить ценную информацию. Обычно они состоят из:
Обычно они состоят из:
- Заголовок – по существу, краткое описание задания, отвечающее на вопросы Что? Где? Когда?
- Описание — основная часть задачи и фактический набор целей, которые необходимо достичь.
- Бонус! – дополнения, помогающие разобраться в описании:
- Скриншот с пометками, относящимися к заданию
- Зависимости и влияние на другие части приложения
- Файл с сохраненными формулами (если это расчет)
- Интерактивный прототип, показывающий, как перемещаться между страницами
- Ссылка на конкурента
Если вы должны сообщить об ошибке , эти задачи в разработке программного обеспечения требуют немного другой информации. Вы должны четко указать, что пошло не так, где, когда и при каких обстоятельствах. Чтобы сделать его четким и прозрачным, используйте эти части:
- Заголовок – эта часть такая же, как и в (а) – в краткой форме вы говорите, что произошло, где и когда.

- Описание. Помимо шагов для воспроизведения, идеальное описание содержит
- Пользовательские данные о том, кто столкнулся с ошибкой, и о среде, в которой возникла ошибка;
- Время возникновения;
- Дополнительные условия, типичные для данного применения;
- Ожидаемый и фактический результат;
- Ссылки на исходные требования, скриншоты и т. д.
Не все клиенты осознают важность хорошо написанного отчета об ошибке. Следовательно, они не тратят время на то, чтобы записать шаги для воспроизведения. Иногда они просто не понимают ценности детальной задачи, но все же исправляют ошибку как можно быстрее. Однако это приводит только к обратному — недостаточно описанному багу, который в конечном итоге исследуется, воспроизводится и, наконец, исправляется годами.
Есть еще одна проблема, которая может возникнуть, когда клиенты не осознают важность среды или точного местоположения ошибки. Это когда клиенты могут сообщить о проблемной кнопке, просто отправив скриншот кнопки, но не всего экрана, показывающего URL-адрес, время на экране компьютера и т. д. Эти данные могут существенно увеличить время исправления. Чтобы сэкономить время, обе стороны должны обсудить и согласовать процесс сообщения об ошибках заранее.
д. Эти данные могут существенно увеличить время исправления. Чтобы сэкономить время, обе стороны должны обсудить и согласовать процесс сообщения об ошибках заранее.
Всплески — это задачи, которые необходимо исследовать. Результатом всплеска является получение ценной информации на основе проведенных исследований. Когда клиенту необходимо определиться, с какой системой интегрироваться, необходимо провести определенный анализ для принятия оптимального решения. Для этого и существуют следственные задачи — спайки. Результатом таких задач являются не строки кода, а данные, на основании которых клиент может принять взвешенное решение или подготовить следующую разработку.
Как и многие вещи в жизни, маленькие детали могут иметь большое значение. Точно так же есть функции, которые помогут сделать задачу более понятной для всех , а также обеспечить прозрачность и порядок всего процесса разработки.
- Правопреемник – лицо, которому поручено задание и которое отвечает за его выполнение.
 К кому-то, к кому клиент может обратиться с вопросами, касающимися этой конкретной части процесса.
К кому-то, к кому клиент может обратиться с вопросами, касающимися этой конкретной части процесса. - Priority — оптимизация процесса разработки за счет установки приоритета задач и минимизации ненужных коммуникаций. Клиенты должны решить, какая функция и какая задача для них важнее в данный момент.
- Срок выполнения — конечно, команда должна знать временные рамки, назначенные для задачи, особенно если это не было решено или согласовано заранее.
Чтобы помочь всем участникам видеть, где они находятся в любой момент времени, важно включать обновления состояния каждой задачи. Мы рекомендуем единое описание статуса – три этапа, которые при необходимости можно разделить на подэтапы. Это поможет сохранить прозрачность и даст общее представление о том, что происходит:
Этап 1. Разработка бизнес-требований.
Этап 2. Процесс разработки.
Этап 3. Принято клиентом и развернуто.
Принято клиентом и развернуто.
Если вы подробно изучите эти шаги, это будет выглядеть примерно так:
Когда вы начинаете проект, вам нужна информация о продукте. Как только все требования выполнены, задача готова к разработке. От задачи в списке дел вы можете перейти к задаче, которую проверяете. После тестирования он либо завершается и готов к развертыванию, либо повторно открывается для улучшения и только после завершения помечается как готовый к развертыванию.
Все это доказывает, что любой проект требует структурированного общения и четкого понимания между клиентом и исполнителем, владельцем проекта и поставщиком. Плохо объясненные задачи и расплывчато сформулированные требования могут затормозить любой проект, существенно задержать развертывание продукта и значительно увеличить затраты на разработку.
Чтобы избежать возможного недопонимания, обе стороны должны знать, какие болевые точки могут возникнуть в будущем, и обсудить их заранее.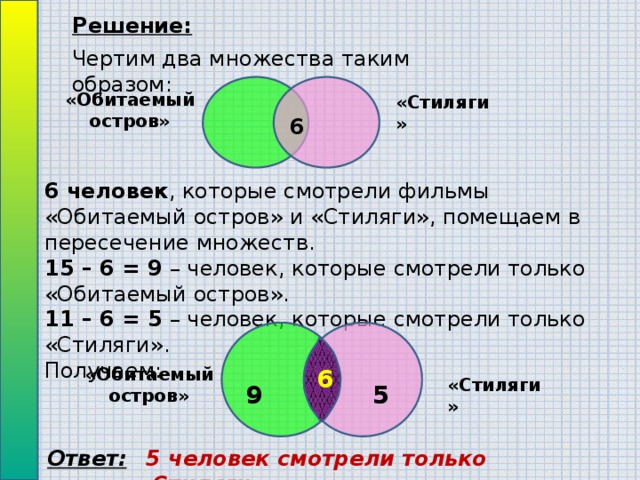
Остановившись на словаре, который будет использоваться в проекте, вы сможете прояснить любые термины, которые могут вызвать проблемы. Наконец, очень важно обсудить сроки и другие возможные ограничения. Вдобавок ко всему этому должна быть обсуждаемая эффективная структура задач, а также способ сообщать об ошибках в приложении. Это может показаться пустяком, но, в конце концов, это то, что сделает работу как для клиента, так и для команды разработчиков максимально гладкой.
Чтобы применить эти советы на практике, свяжитесь с нами и обсудите задачи для вашего проекта с командой Django Stars.
Часто задаваемые вопросы
- Как писать задачи для разработчиков?
- Сделать презентацию проекта
- Предоставить дорожную карту бизнеса
- Найти общий язык
- Организовать общение
- Как выглядят задачи по разработке ПО ?
- Существует три типа задач по разработке программного обеспечения: разработка новых функций, исправление ошибок и исследования.
 Все они имеют свои отличительные особенности. Чтобы поддерживать хорошую структуру задач, сосредоточьтесь на них и на том, что действительно важно.
Все они имеют свои отличительные особенности. Чтобы поддерживать хорошую структуру задач, сосредоточьтесь на них и на том, что действительно важно.
- Как правильно ставить задачи разработчикам?
- Существует множество подходов к формулированию задач, но их общая цель — подробное описание функций и предоставление ценной информации. Обычно они состоят из:
- Заголовка (краткий ответ на вопрос Что? Где? Когда?)
- Описание (основная часть задачи и собственно набор целей, которые необходимо достичь)
- Дополнения, помогающие понять описание (скриншоты, зависимости, формулы, кликабельный прототип или ссылка на конкурента)
- Как сообщить об ошибке?
- Вы должны четко указать, что пошло не так, где, когда и при каких обстоятельствах. Чтобы оно было ясным и прозрачным, используйте следующие части:
- Заголовок (что произошло, где и когда)
- Описание (помимо шагов по воспроизведению, идеальное описание содержит пользовательские данные о том, кто столкнулся с ошибкой, среда, в которой возникла ошибка, время возникновения, дополнительные условия, характерные для данного конкретного приложения, ожидаемый и фактический результат, а также ссылки на исходные требования, скриншоты и т.


 е. не содержащее ни одного элемента.
е. не содержащее ни одного элемента.


 set_3
return set_1 - set_2 - set_3
set_3
return set_1 - set_2 - set_3 Требуется сформировать из них множество. Если какое-либо число повторяется, то преобразовать его в строку по образцу: например, если число 4 повторяется 3 раза, то в множестве будет следующая запись: само число 4, строка «44» (второе повторение, т.е. число дублируется в строке), строка «444» (третье повторение, т.е. строка множится на 3). Реализуйте вывод множества через функцию set_gen().
Требуется сформировать из них множество. Если какое-либо число повторяется, то преобразовать его в строку по образцу: например, если число 4 повторяется 3 раза, то в множестве будет следующая запись: само число 4, строка «44» (второе повторение, т.е. число дублируется в строке), строка «444» (третье повторение, т.е. строка множится на 3). Реализуйте вывод множества через функцию set_gen().

 К кому-то, к кому клиент может обратиться с вопросами, касающимися этой конкретной части процесса.
К кому-то, к кому клиент может обратиться с вопросами, касающимися этой конкретной части процесса. Все они имеют свои отличительные особенности. Чтобы поддерживать хорошую структуру задач, сосредоточьтесь на них и на том, что действительно важно.
Все они имеют свои отличительные особенности. Чтобы поддерживать хорошую структуру задач, сосредоточьтесь на них и на том, что действительно важно.

 Если нет, посмотрите его первую десятичную дробь после k-й, и если она равна 5 или больше, отбросьте все десятичные знаки после k-й, и добавьте 1 к k-й десятичной дроби, чтобы получить round(x), а если первая десятичная дробь после k-й меньше 5, отбросьте все десятичные знаки после k-й, чтобы получить round(x)
Если нет, посмотрите его первую десятичную дробь после k-й, и если она равна 5 или больше, отбросьте все десятичные знаки после k-й, и добавьте 1 к k-й десятичной дроби, чтобы получить round(x), а если первая десятичная дробь после k-й меньше 5, отбросьте все десятичные знаки после k-й, чтобы получить round(x)

 Калькулятор будет делать это по умолчанию, если вы не укажете значение точности.
Калькулятор будет делать это по умолчанию, если вы не укажете значение точности.
 Например, если я попрошу вас получить десятичное разложение 1/3, вы можете написать что-то вроде 1/3 = 0.3333333333…… Эта последовательность не заканчивается, поэтому обычно при выражении на бумаге нужно округлять.
Например, если я попрошу вас получить десятичное разложение 1/3, вы можете написать что-то вроде 1/3 = 0.3333333333…… Эта последовательность не заканчивается, поэтому обычно при выражении на бумаге нужно округлять.
 4)», а для округления 3,48 до ближайшей десятой можно использовать «=ROUND(3.48, 1)».
4)», а для округления 3,48 до ближайшей десятой можно использовать «=ROUND(3.48, 1)».

 58\).
58\).

 Кроме того, еще один важный расчет, который может вас заинтересовать, заключается в следующем
перевести дробь в проценты
или также для преобразования
дробь до десятичной
.
Кроме того, еще один важный расчет, который может вас заинтересовать, заключается в следующем
перевести дробь в проценты
или также для преобразования
дробь до десятичной
.
 Независимо от того, какой тип округления вам необходим, этот онлайн-калькулятор справится с этой задачей!
Независимо от того, какой тип округления вам необходим, этот онлайн-калькулятор справится с этой задачей!
 В этом случае, введите 8491.5372.
В этом случае, введите 8491.5372.
 В общем случае, если цифра, которая стоит сразу после той, до которой мы округляем, меньше пяти, то предыдущая цифра не меняется. Если эта цифра больше или равна пяти, то предыдущая цифра увеличивается на единицу.
В общем случае, если цифра, которая стоит сразу после той, до которой мы округляем, меньше пяти, то предыдущая цифра не меняется. Если эта цифра больше или равна пяти, то предыдущая цифра увеличивается на единицу. 75 до ближайшего целого, то сначала мы округляем 1.75 до 2, а затем меняем знак и получаем -2. Если же число -1.25 округляется до ближайшего целого, то мы сначала округляем 1.25 до 1, а затем меняем знак и получаем -1.
75 до ближайшего целого, то сначала мы округляем 1.75 до 2, а затем меняем знак и получаем -2. Если же число -1.25 округляется до ближайшего целого, то мы сначала округляем 1.25 до 1, а затем меняем знак и получаем -1.
 Округление может быть выполнено в большую или меньшую сторону, в зависимости от выбранного метода округления.
Округление может быть выполнено в большую или меньшую сторону, в зависимости от выбранного метода округления.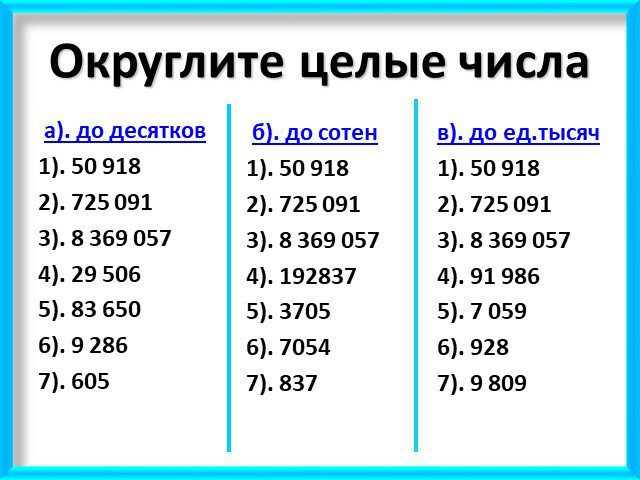 Например, если число должно быть округлено до двух знаков после запятой, то число 3,456 будет округлено до 3,46, а число 3,453 — до 3,45.
Например, если число должно быть округлено до двух знаков после запятой, то число 3,456 будет округлено до 3,46, а число 3,453 — до 3,45. n
n Если первая отброшенная цифра меньше 5, то целая часть не изменяется.
Если первая отброшенная цифра меньше 5, то целая часть не изменяется. Мы ценим ваше мнение и постараемся учесть все ваши замечания и предложения.
Мы ценим ваше мнение и постараемся учесть все ваши замечания и предложения.

 0456853
0456853


 На этой странице сможете точно определить сколько дней осталось до нужной вам даты, наш таймер покажет это онлайн и не потребует дополнительных вычислений. Всем часто нужно знать, сколько дней, часов, минут и секунд осталось до 1 января! Счётчик поможет подсчитать всего в один клик, через сколько дней наступит нужное вам событие – сейчас откройте сайт. Попробуйте сами и поймете, насколько это легко, с этим справится даже ребенок. Отсчет ведется автоматически, в реальном времени.
На этой странице сможете точно определить сколько дней осталось до нужной вам даты, наш таймер покажет это онлайн и не потребует дополнительных вычислений. Всем часто нужно знать, сколько дней, часов, минут и секунд осталось до 1 января! Счётчик поможет подсчитать всего в один клик, через сколько дней наступит нужное вам событие – сейчас откройте сайт. Попробуйте сами и поймете, насколько это легко, с этим справится даже ребенок. Отсчет ведется автоматически, в реальном времени. Используйте наш официальный информационный таймер, чтобы мгновенно рассчитать сколько дней ждать до 1 января.
Используйте наш официальный информационный таймер, чтобы мгновенно рассчитать сколько дней ждать до 1 января. 2425 суток, но календари измеряют дни в целых сутках. Поэтому каждый 4-й год мы добавляем високосный день. Чтобы дни равноденствия не убежали, ведь средняя продолжительность земного года оказывается равной 365,2425 суток. Юлий Цезарь в 45 г. до н. э., что римляне будет использовать новый календарь, – Юлианский календарь. Эта версия была не очень точной. Улучшенный календарь был введен Папой Римским Григорием XIII в 1582 году, он стал называться григорианский календарь. Счет дней был передвинут на 10 суток вперед, и следующий за четвергом – 4 октября 1582 г., день решили считать не 5, а пятница 15 октября с сохранением подсчета дней недели. Здесь вы увидите вечный календарь на любой год и получить полную информацию про каждый день года.
2425 суток, но календари измеряют дни в целых сутках. Поэтому каждый 4-й год мы добавляем високосный день. Чтобы дни равноденствия не убежали, ведь средняя продолжительность земного года оказывается равной 365,2425 суток. Юлий Цезарь в 45 г. до н. э., что римляне будет использовать новый календарь, – Юлианский календарь. Эта версия была не очень точной. Улучшенный календарь был введен Папой Римским Григорием XIII в 1582 году, он стал называться григорианский календарь. Счет дней был передвинут на 10 суток вперед, и следующий за четвергом – 4 октября 1582 г., день решили считать не 5, а пятница 15 октября с сохранением подсчета дней недели. Здесь вы увидите вечный календарь на любой год и получить полную информацию про каждый день года. Это означает, что до этого момента осталось 36,29 недель, 6096,0 часов и 9,07 месяцев. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 1 января имеет для вас особое значение, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
Это означает, что до этого момента осталось 36,29 недель, 6096,0 часов и 9,07 месяцев. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 1 января имеет для вас особое значение, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
 и 3,23% в январе.
и 3,23% в январе. : Козерог (козерог)
: Козерог (козерог)
 8 дней
8 дней



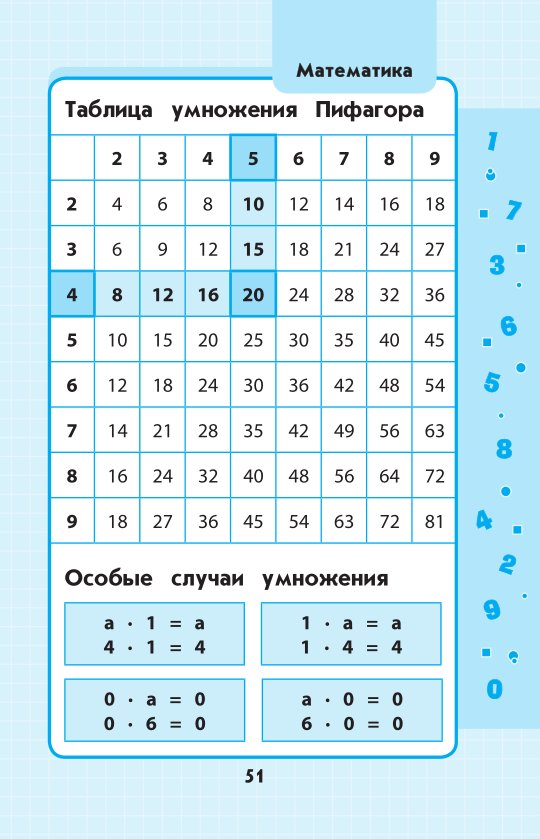 Они могут быть чрезвычайно полезны при решении математических задач и вычислений. В этом уроке давайте выучим таблицу умножения от 1 до 20 . Печатные таблицы умножения на 20 помогают сэкономить время и с легкостью решать вопросы.
Они могут быть чрезвычайно полезны при решении математических задач и вычислений. В этом уроке давайте выучим таблицу умножения от 1 до 20 . Печатные таблицы умножения на 20 помогают сэкономить время и с легкостью решать вопросы.

 Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.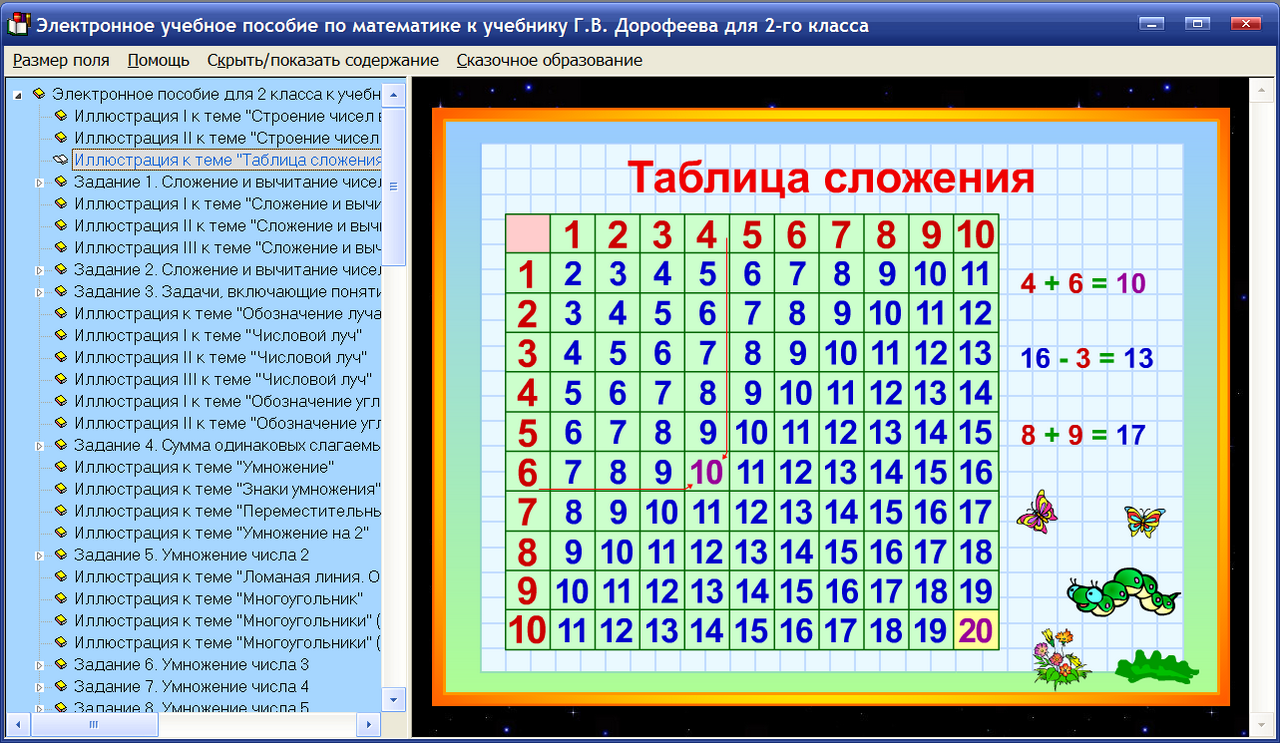

 Некоторые из них приведены ниже.
Некоторые из них приведены ниже. 
 Давайте посмотрим, как читать и писать таблицы 4.
Давайте посмотрим, как читать и писать таблицы 4.  Столы будут организованы по темам:
Столы будут организованы по темам: 
 При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить логические построения, аккуратность и внимательность для того, чтобы не потерять решение и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры.
При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить логические построения, аккуратность и внимательность для того, чтобы не потерять решение и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры.
 К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение и неравенство и т.д.
К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение и неравенство и т.д. Графики функций y = ax + 12 и y = (3 – a)x + a пересекаются в точке с абсциссой 2. Найдите ординату точки пересечения.
Графики функций y = ax + 12 и y = (3 – a)x + a пересекаются в точке с абсциссой 2. Найдите ординату точки пересечения.

 Виета =3
Виета =3
 В курсе 7-8 классов в основном рассматриваются две темы – Линейные уравнения и сводящиеся к ним и Квадратные уравнения и сводящиеся к ним. В дальнейшем я планирую разработать курс и для учащихся 9-х классов и применять в своей практике курс «Параметры» с 7-11 классы.
В курсе 7-8 классов в основном рассматриваются две темы – Линейные уравнения и сводящиеся к ним и Квадратные уравнения и сводящиеся к ним. В дальнейшем я планирую разработать курс и для учащихся 9-х классов и применять в своей практике курс «Параметры» с 7-11 классы. Минута». 2 класс. УМК «Школа России».» Математика
Минута». 2 класс. УМК «Школа России».» Математика Санкт-Петербурга
Санкт-Петербурга К концу учебного года 19/20 автор планирует создать методичку для подготовки к решению заданий с параметром из ЕГЭ.
К концу учебного года 19/20 автор планирует создать методичку для подготовки к решению заданий с параметром из ЕГЭ.
 Для тех, кто готовится к поступлению в высшие учебные заведения.
Для тех, кто готовится к поступлению в высшие учебные заведения. Ведь параметры встречаются гораздо чаще, чем мы себе представляем. Изучение многих процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Включая такое большое количество столкновений, пусть и косвенных, с параметром, я пришел к выводу, что необходимо изучать данную тему более детально. Также, решение уравнений с параметром способствует развитию логического и вариативного мышление человека, что позволит ему улучшить свои знания и умения. В моей работе рассмотрены часто встречающиеся типы уравнений, и я надеюсь, что знания, которые я получил в процессе работы, а также использовал при выполнении данной проектной работы, помогут мне и другим одиннадцатиклассникам при сдаче ЕГЭ. Выполняя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рациональных способов решения. На мой взгляд, графо-аналитический метод является самым удобным и наглядным способом решения уравнений с параметрами, так как при таком решении можно наглядно увидеть все корни и гораздо легче заметить ошибки.
Ведь параметры встречаются гораздо чаще, чем мы себе представляем. Изучение многих процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Включая такое большое количество столкновений, пусть и косвенных, с параметром, я пришел к выводу, что необходимо изучать данную тему более детально. Также, решение уравнений с параметром способствует развитию логического и вариативного мышление человека, что позволит ему улучшить свои знания и умения. В моей работе рассмотрены часто встречающиеся типы уравнений, и я надеюсь, что знания, которые я получил в процессе работы, а также использовал при выполнении данной проектной работы, помогут мне и другим одиннадцатиклассникам при сдаче ЕГЭ. Выполняя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рациональных способов решения. На мой взгляд, графо-аналитический метод является самым удобным и наглядным способом решения уравнений с параметрами, так как при таком решении можно наглядно увидеть все корни и гораздо легче заметить ошибки.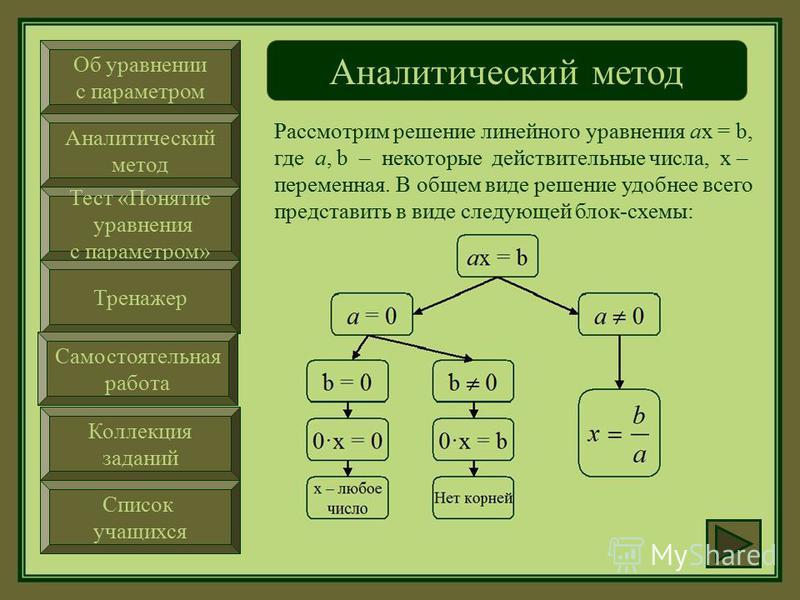
 Насколько я знаю, мне нужна форма эшелона, чтобы определить, сколько существует решений. Должен ли я просто подключить $k=-2$, чтобы уменьшить его еще больше? Если да, то что можно сказать о количестве решений, если $k \neq =2$?
Насколько я знаю, мне нужна форма эшелона, чтобы определить, сколько существует решений. Должен ли я просто подключить $k=-2$, чтобы уменьшить его еще больше? Если да, то что можно сказать о количестве решений, если $k \neq =2$? В любом другом случае $A$ необратима, поэтому $v \to A \cdot v$ не инъективна и, следовательно, существуют $v, w$ такие, что
В любом другом случае $A$ необратима, поэтому $v \to A \cdot v$ не инъективна и, следовательно, существуют $v, w$ такие, что 2.
2. Существует единственное решение для каждого значения z; переместите ползунок, чтобы изменить z.
Существует единственное решение для каждого значения z; переместите ползунок, чтобы изменить z. )
)

 33 (вы: не рейтинг)
33 (вы: не рейтинг) hofmann
hofmann
 12 баллов0004
12 баллов0004
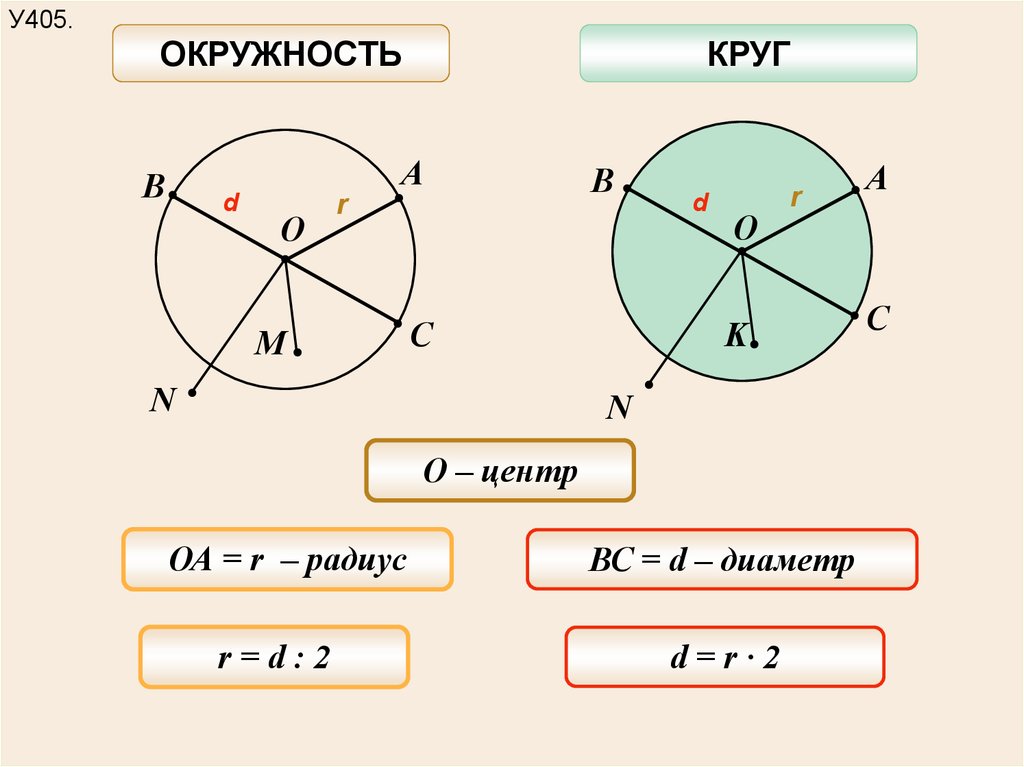
 Общая точка прямой и окружности называется точкой касания. В этом случае d=R.
Общая точка прямой и окружности называется точкой касания. В этом случае d=R.
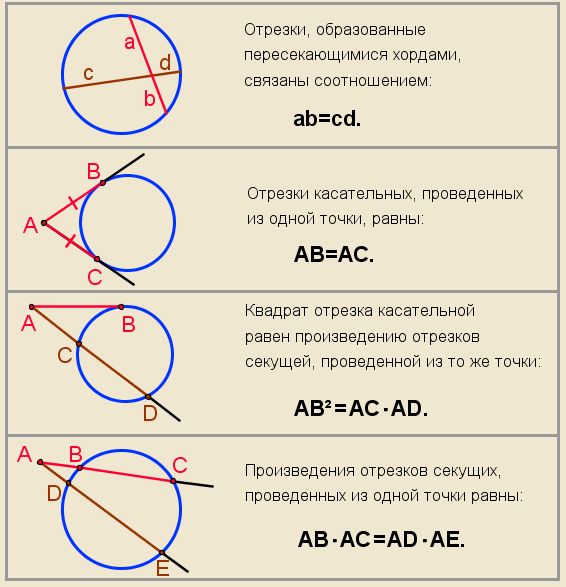
 На рисунке: CA⋅CA1=CB⋅CB1
На рисунке: CA⋅CA1=CB⋅CB1 Круг имеет 360°.
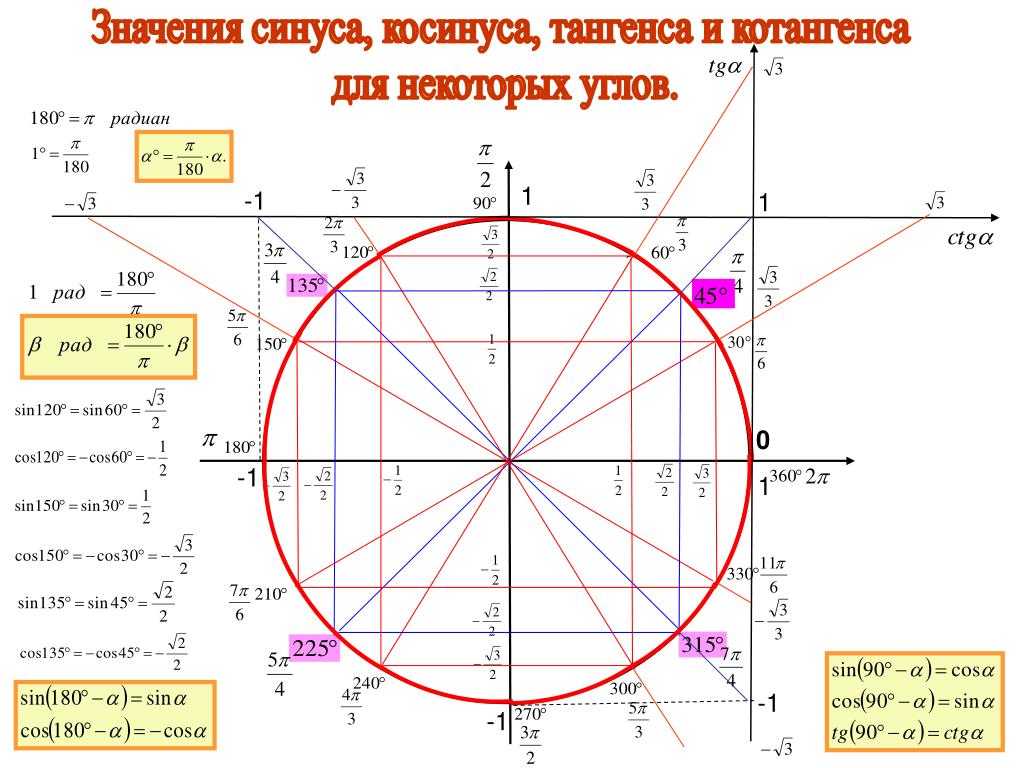
Круг имеет 360°. Используйте оценку только для 9 0012 π , если варианты ответов содержат числа вместо π .
Используйте оценку только для 9 0012 π , если варианты ответов содержат числа вместо π .

 Каково отношение расстояния, которое проходит точка M , к расстоянию, которое проходит точка H за 6 часов?
Каково отношение расстояния, которое проходит точка M , к расстоянию, которое проходит точка H за 6 часов? 
 Вставка в надписи имеет его вертеро. два аккорда.
Вставка в надписи имеет его вертеро. два аккорда.
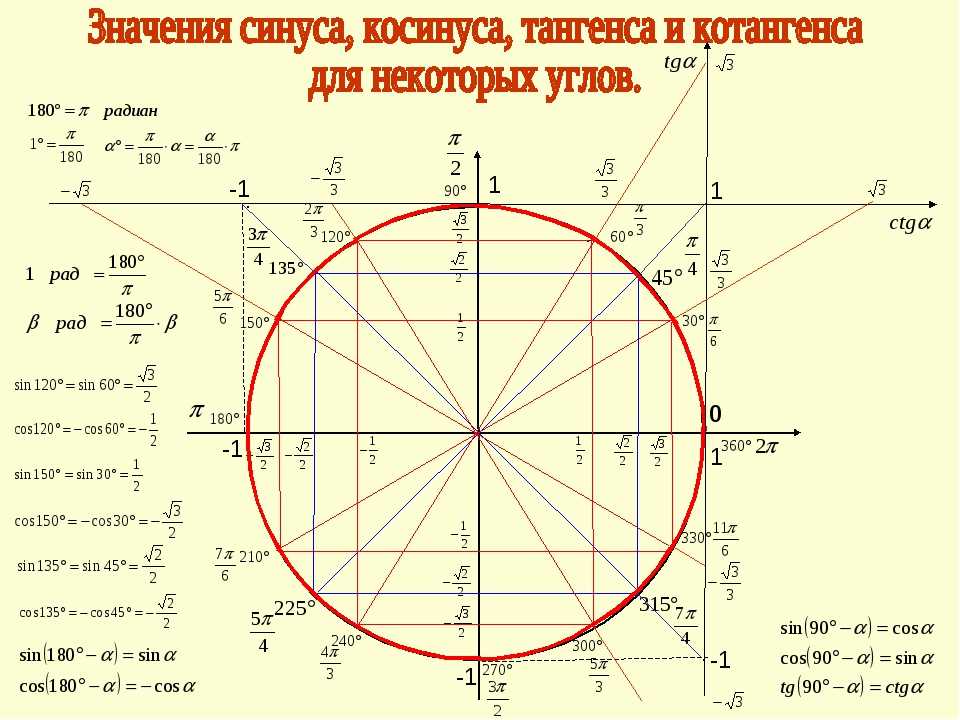
 Используйте 3,14 в качестве оценки для π .
Используйте 3,14 в качестве оценки для π . 




 Беннетт
Беннетт В гиперболической геометрии
В гиперболической геометрии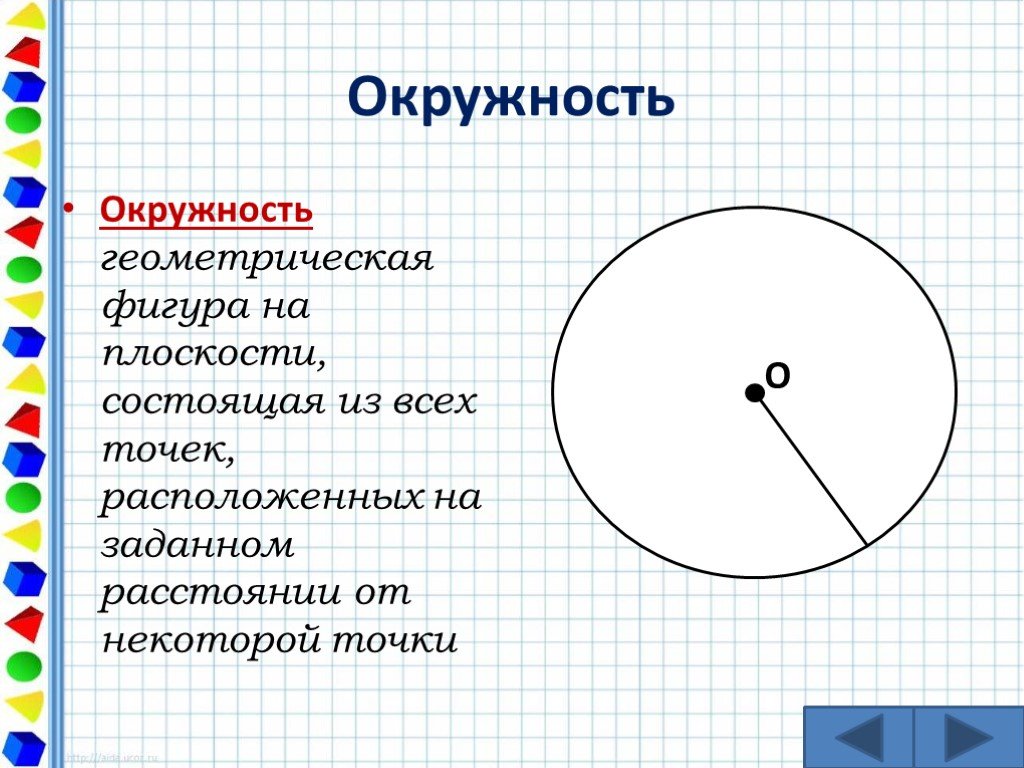 Щелкните мышью точку и перетащите ее (удерживая кнопку мыши нажатой), чтобы переместить точку. Радиус и окружность будут следовать за точкой. За краем полуплоскости (отмечено серым) вы увидите гиперболическое расстояние между красной и синей точками. ( Предупреждение об ошибке: Иногда, когда окно закрывается, а затем открывается другими окнами на мониторе вашего компьютера, апплет не перерисовывается полностью. Если щелкнуть точку и переместить ее или свернуть, а затем восстановить окно, апплет перерисуется правильно.)
Щелкните мышью точку и перетащите ее (удерживая кнопку мыши нажатой), чтобы переместить точку. Радиус и окружность будут следовать за точкой. За краем полуплоскости (отмечено серым) вы увидите гиперболическое расстояние между красной и синей точками. ( Предупреждение об ошибке: Иногда, когда окно закрывается, а затем открывается другими окнами на мониторе вашего компьютера, апплет не перерисовывается полностью. Если щелкнуть точку и переместить ее или свернуть, а затем восстановить окно, апплет перерисуется правильно.)

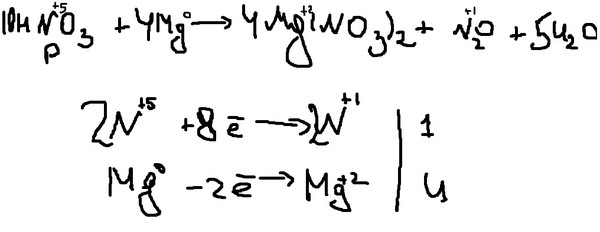 S. Не забывайте выбирать лучший ответ по мнению автора!
S. Не забывайте выбирать лучший ответ по мнению автора! 4K
4K По химической активности выделяют три группы металлов.
По химической активности выделяют три группы металлов.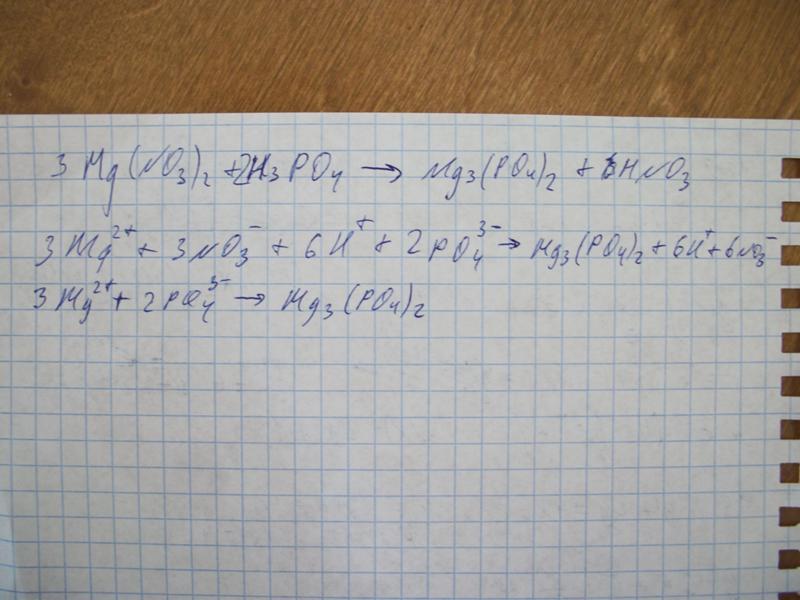 Например, так делает железо:
Например, так делает железо:
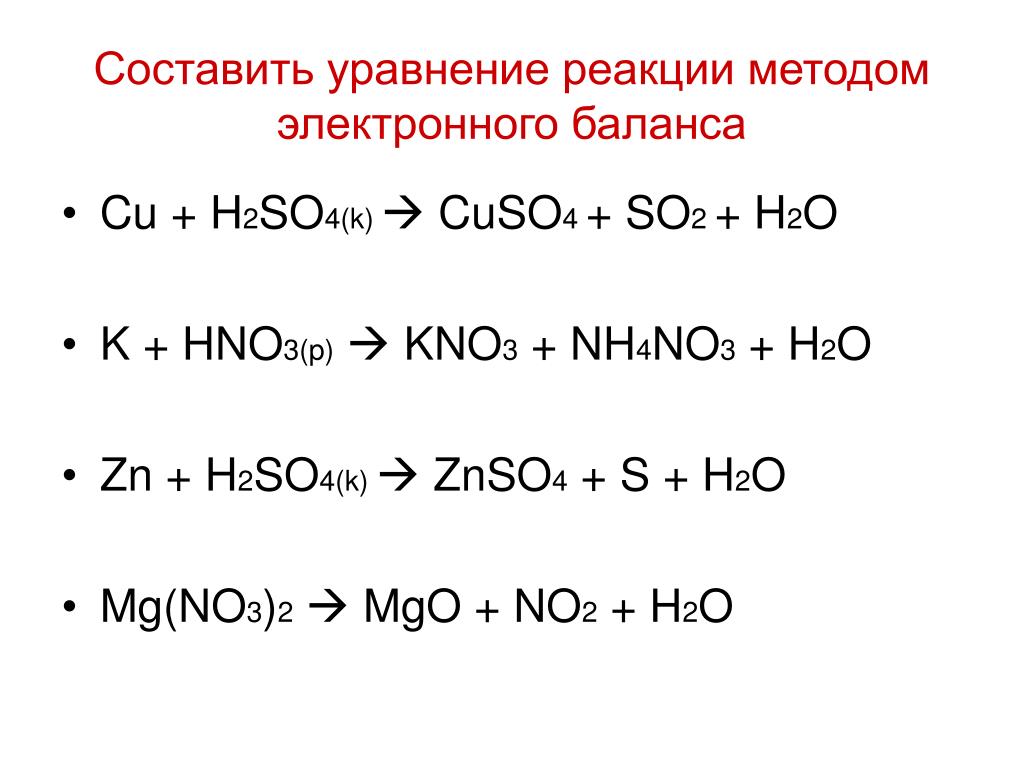 Результат данной реакции — образование оксида.
Результат данной реакции — образование оксида.

 Простые вещества — металлы в окислительно-восстановительных реакциях являются восстановителями. По положению металла в электрохимическом ряду можно судить о том, насколько активно он способен вступать в химические реакции (т. е. насколько сильно у металла проявляются восстановительные свойства).
Простые вещества — металлы в окислительно-восстановительных реакциях являются восстановителями. По положению металла в электрохимическом ряду можно судить о том, насколько активно он способен вступать в химические реакции (т. е. насколько сильно у металла проявляются восстановительные свойства). 5K
5K

 ..
.. 