легко конвертируйте изображения в JPG
Форматы файлов JPG, PNG и GIF в настоящее время являются наиболее популярными форматами. Когда дело доходит до использования изображений на вашем веб-сайте или в сообщениях в социальных сетях, вы можете столкнуться с такими файлами. Важно иметь в виду, что каждый из них имеет различные возможности. Это означает, что каждый из них имеет уникальные особенности. Но в этом посте мы сосредоточимся на JPG / JPEG формат файла. Вы узнаете его определение, возможности и способы открытия файлов JPG/JPEG. Кроме того, вы узнаете, как лучше всего конвертировать изображения в формат JPG/JPEG с помощью онлайн-инструмента.
Часть 1. Информация о JPG или JPEG
Что такое формат JPG/JPEG
Формат файла изображения JPG является лучшим файлом для сжатия изображения. JPG — популярный файл среди пользователей. Они используют его для фотографий и интернет-графики. Кроме того, он известен как файлы JPEG или JPG. Полное название JPEG — Объединенная группа экспертов. Эта группа создает этот популярный файл изображения. Более того, большинство растровых изображений имеют расширение файла .jpg. Основная причина заключается в уменьшении размера файлов. JPG — это формат с потерями, который влияет на качество изображения при слишком сильном сжатии. Этот формат доступен во всех программах. Таким образом, вам не нужно думать, как открыть этот файл в разных программах или устройствах. Его алгоритм сжатия уменьшает размер файла. Это одна из причин, почему он стал популярным в наши дни. Таким образом, создание истории, обмен и размещение фотографий на веб-сайтах становятся более неторопливыми. Для получения дополнительной информации вы можете столкнуться со случаями, когда веб-сайты не распознают файл JPEG. Например, некоторые просмотрщики и редакторы фотографий открывают изображение только с файлом .JPG. Лучшее решение, которое вы можете сделать, это переименовать расширение файла. Вы можете преобразовать файл JPEG в файл JPG. Таким образом, веб-сайт может распознать изображение.
Эта группа создает этот популярный файл изображения. Более того, большинство растровых изображений имеют расширение файла .jpg. Основная причина заключается в уменьшении размера файлов. JPG — это формат с потерями, который влияет на качество изображения при слишком сильном сжатии. Этот формат доступен во всех программах. Таким образом, вам не нужно думать, как открыть этот файл в разных программах или устройствах. Его алгоритм сжатия уменьшает размер файла. Это одна из причин, почему он стал популярным в наши дни. Таким образом, создание истории, обмен и размещение фотографий на веб-сайтах становятся более неторопливыми. Для получения дополнительной информации вы можете столкнуться со случаями, когда веб-сайты не распознают файл JPEG. Например, некоторые просмотрщики и редакторы фотографий открывают изображение только с файлом .JPG. Лучшее решение, которое вы можете сделать, это переименовать расширение файла. Вы можете преобразовать файл JPEG в файл JPG. Таким образом, веб-сайт может распознать изображение.
Кроме того, у файла JPG есть преимущества, которые вам необходимо знать. JPG — это изображение с высоким разрешением. Его высокое разрешение является одним из больших преимуществ этого файла изображения. Он поддерживает 24-битные цвета до 16 миллионов цветов. Разрешение по-прежнему будет отличным, даже после применения высокоуровневого редактирования с использованием некоторых инструментов. Кроме того, JPG меньше по размеру. По сравнению с другими форматами файлов изображений, он имеет идеальный размер файла. Даже если он имеет меньший размер, это не влияет на качество и разрешение изображения. Зная преимущества, вам нужно знать его недостатки для большей осведомленности. При съемке в формате JPG необходимо ограничить процессор камеры и цветовые вариации. Этот файл также не поддерживает многослойные изображения. Если вы планируете редактировать изображение и вам нужен дополнительный слой, JPG не идеальный формат для этого.
Часть 2. Как открыть файл JPG/JPEG
Если у вас возникли проблемы с открытием файла JPG на ваших устройствах, эта часть поможет вам. Хотите знать, как открыть файл JPG в Windows 11, Android и iPhone? Вы можете следовать приведенным ниже инструкциям.
Хотите знать, как открыть файл JPG в Windows 11, Android и iPhone? Вы можете следовать приведенным ниже инструкциям.
Для пользователей Windows
Шаг 1: нажмите Ctrl + Е на клавиатуре, чтобы открыть Проводник. Это похоже на значок папки с синим зажимом.
Шаг 2: Перейдите к Быстрый доступ панель папок. Затем перейдите к Скачать параметры, чтобы увидеть сохраненную фотографию JPG.
Шаг 3: Когда вы уже видите файлы JPG/JPEG, откройте их с помощью других программ, кроме «Фото». Чтобы открыть их, щелкните правой кнопкой мыши на фотографии, нажмите кнопку Открыть с вариант и выберите программу.
Для пользователей Android
Шаг 1: Откройте приложение «Галерея» на своем устройстве Android.
Шаг 2: Откройте альбом камеры, чтобы просмотреть фотографии, сделанные камерой вашего телефона. В вашем телефоне также есть различные альбомы.
Шаг 3: Если вы видите несколько фотографий, щелкните одну из них, чтобы нарисовать ее в полноэкранном режиме. Таким образом, вы можете просматривать изображение в формате JPG/JPEG.
Для пользователей iPhone
Шаг 1: Нажмите Фотографии на вашем iPhone. Это приложение содержит все изображения, которые у вас есть с вашей фотографии и из Интернета. Внешний вид этого приложения похож на красочный цветок.
Шаг 2: После того, как вы запустите приложение «Фотографии», вы сможете увидеть там все фотографии. Также, как и на телефоне Android, внутри приложения вы столкнетесь с различными альбомами.
Шаг 3: Нажмите на изображение, чтобы открыть его на весь экран. Таким образом, вы можете видеть изображение более четко. Помимо открытия изображения, вы также можете редактировать фотографию в приложении «Фотографии». Есть значки, которые вы можете использовать, чтобы сделать ваши изображения лучше.
Часть 3. Отличный метод конвертации изображений в JPG
Бесплатный конвертер изображений FVC это инструмент, который вы можете использовать онлайн для преобразования изображений в JPG. Это может помочь вам преобразовать изображение в несколько кликов. Кроме того, он поддерживает различные входные форматы, такие как JPG, PNG, GIF, TIFF и другие. Таким образом, вам больше не нужно беспокоиться о том, что определенные инструменты или устройства больше не могут открыть ваше изображение. Используйте этот онлайн-конвертер изображений, чтобы конвертировать их. Он также может сохранить отличное качество исходных фотографий. После процесса вы не увидите разницы между оригиналом и конвертированным файлом. Кроме того, этот конвертер изображений прост в эксплуатации. Он предлагает понятный процесс преобразования, что делает его подходящим для начинающих. Он также способен конвертировать изображения в пакетном режиме. Таким образом, вы можете конвертировать сразу несколько файлов. Вы также можете получить доступ к этому приложению в различных браузерах, таких как Google, Safari, Mozilla, Explorer и других. Наконец, это приложение гарантирует конфиденциальность каждого пользователя. После загрузки и преобразования изображения этот конвертер изображений автоматически удалит вашу фотографию.
Кроме того, он поддерживает различные входные форматы, такие как JPG, PNG, GIF, TIFF и другие. Таким образом, вам больше не нужно беспокоиться о том, что определенные инструменты или устройства больше не могут открыть ваше изображение. Используйте этот онлайн-конвертер изображений, чтобы конвертировать их. Он также может сохранить отличное качество исходных фотографий. После процесса вы не увидите разницы между оригиналом и конвертированным файлом. Кроме того, этот конвертер изображений прост в эксплуатации. Он предлагает понятный процесс преобразования, что делает его подходящим для начинающих. Он также способен конвертировать изображения в пакетном режиме. Таким образом, вы можете конвертировать сразу несколько файлов. Вы также можете получить доступ к этому приложению в различных браузерах, таких как Google, Safari, Mozilla, Explorer и других. Наконец, это приложение гарантирует конфиденциальность каждого пользователя. После загрузки и преобразования изображения этот конвертер изображений автоматически удалит вашу фотографию.
Шаг 1: Во-первых, посетите Бесплатный конвертер изображений FVC интернет сайт. Перейдите к параметрам формата и выберите формат файла JPG.
Шаг 2: Чтобы загрузить фотографию, которую вы хотите преобразовать, нажмите кнопку Добавить изображения кнопка. Если вы хотите выполнить пакетное преобразование, снова нажмите «Добавить изображения».
Шаг 3: Когда процесс преобразования завершится, нажмите кнопку Скачать кнопку, чтобы сохранить их один за другим. Если вы хотите сохранить их сразу, нажмите кнопку Скачать все кнопка.
Относится к:
Полная информация о различиях JPEG, JPG и PNG
8 удивительных конвертеров изображений [Полная информация]
Часть 4. Часто задаваемые вопросы о файлах JPG/JPEG
1. Как узнать, является ли моя фотография файлом JPG?
Вы можете щелкнуть правой кнопкой мыши фотографию в папке с файлами. Затем перейдите к опции «Свойства». Перейдите в меню «Общие» и посмотрите тип файла вашего изображения.
2. Насколько хорошо JPEG сжимает изображения?
Очень хорошо. Несжатые данные для полноцветных фотографий имеют разрядность 24 бита на пиксель. Самые популярные методы сжатия без потерь могут сжимать такие данные в среднем примерно 2:1. JPEG может достигать сжатия от 10:1 до 20:1 без заметных потерь. Это уменьшает необходимый объем памяти до 1–2 бит на пиксель. С крошечными данными сжатие от 30:1 до 50:1 может устранить недостатки. В то время как некачественное использование, такое как архивные индексы, может относительно легко сжимать 100: 1. Сжатое изображение JPEG с соотношением сторон 100:1 использует тот же объем пространства, что и полноцветное изображение с масштабом в одну десятую. Несмотря на то, что у него гораздо больше деталей, чем на миниатюре, это так.
Несжатые данные для полноцветных фотографий имеют разрядность 24 бита на пиксель. Самые популярные методы сжатия без потерь могут сжимать такие данные в среднем примерно 2:1. JPEG может достигать сжатия от 10:1 до 20:1 без заметных потерь. Это уменьшает необходимый объем памяти до 1–2 бит на пиксель. С крошечными данными сжатие от 30:1 до 50:1 может устранить недостатки. В то время как некачественное использование, такое как архивные индексы, может относительно легко сжимать 100: 1. Сжатое изображение JPEG с соотношением сторон 100:1 использует тот же объем пространства, что и полноцветное изображение с масштабом в одну десятую. Несмотря на то, что у него гораздо больше деталей, чем на миниатюре, это так.
3. Как открыть файл JPG в Photoshop?
Запустите Photoshop на своем компьютере. Выберите «Файл» > «Открыть». Файл папки появится на вашем экране. Выберите файл JPG и нажмите «ОК». После этого вы увидите файл изображения JPG в Photoshop.
Вывод
Эта статья объясняет вам, что JPG / JPEG обозначает, включая его определение и особенности. В качестве бонуса мы также представили вам самый простой способ конвертировать изображения в формат JPG с помощью Бесплатный конвертер изображений FVC. Так чего же ты ждешь? Используйте этот инструмент, чтобы легко конвертировать изображения в формат JPG.
В качестве бонуса мы также представили вам самый простой способ конвертировать изображения в формат JPG с помощью Бесплатный конвертер изображений FVC. Так чего же ты ждешь? Используйте этот инструмент, чтобы легко конвертировать изображения в формат JPG.
- 1
- 2
- 3
- 4
- 5
Превосходно
Рейтинг: 4,9/5 (на основе 345 голосов)
есть ли разница между ними?
Конечно, вы имели дело с фотографиями и онлайн-изображениями и, вероятно, столкнулись с расширениями JPEG и JPG. Эти два формата могут сбить с толку некоторых людей, потому что они не знают, что им следует использовать. Они выглядят одинаково, когда вы смотрите на их имена. На самом деле, их сходство настолько близко, что они использовались взаимозаменяемо в прошлом.
В этой статье мы собираемся обсудить JPG против JPEG, Мы определим каждый из этих форматов, прежде чем дать вам сходство между ними, чтобы помочь вам решить, какой формат вы должны использовать для своих нужд, будь то веб-сайт или онлайн-проекты. Так что, если вы хотите узнать больше, продолжайте читать!
Так что, если вы хотите узнать больше, продолжайте читать!
Содержание: Часть 1. JPG против JPEG: что лучше?Часть 2. JPG против JPEG: сходство между двумя форматами файловЧасть 3. Бонусный совет: как найти и удалить похожие изображения на вашем MacЧасть 4. Так ли JPG такой же, как JPEG?
Часть 1. JPG против JPEG: что лучше?
Что такое изображение JPG?
На самом деле, нет разницы между JPEG и JPG, кроме разницы в количестве символов, используемых в их именах. JPG существовал, потому что более ранние версии Windows требовали трехбуквенных расширений имени файла. Таким образом, расширение .jpeg было сокращено и стало .jpg. Хотя в DOS и Windows было это ограничение имени файла, в системах UNIX этого не было, поэтому пользователи MAC и UNIX продолжали использовать расширение имени файла .jpeg.
Но поскольку технология развивалась, Windows тоже сделала это и теперь принимает больше символов для расширений файлов. Тем не менее, расширение .jpg уже используется многими людьми, а также программами. Таким образом, делая .jpg по-прежнему самым популярным расширением. Программы для редактирования фотографий такие как Gimp и Adobe Photoshop сохраните их файлы JPEG с расширением .jpg по умолчанию в системах Mac и Windows. Но вы можете выбрать расширение .jpg или .jpeg, и ваш файл все равно будет работать.
Таким образом, делая .jpg по-прежнему самым популярным расширением. Программы для редактирования фотографий такие как Gimp и Adobe Photoshop сохраните их файлы JPEG с расширением .jpg по умолчанию в системах Mac и Windows. Но вы можете выбрать расширение .jpg или .jpeg, и ваш файл все равно будет работать.
Что такое изображение в формате JPEG?
JPEG — это сокращение от Joint Photographic Experts Group, которое представляет собой формат сжатия для растрового изображения, который в основном используется для сжатия с потерями. Степень сжатия варьируется от 10: 1-20: 1, которую вы можете настроить, чтобы определить баланс между качеством и размером хранилища. Это расширение в основном используется устройствами для обмена фотографиями и цифровыми камерами.
Хотя формат .jpeg имеет отличные цвета и является отличным форматом для фотографий, вам необходимо знать, что из-за сжатия произойдет небольшая потеря качества. Кроме того, повторное сохранение и редактирование ухудшат качество вашего изображения, хотя эффект будет незначительным. Один из способов, который вы можете использовать, чтобы минимизировать эту потерю качества, — работать с RAW JPEG. Решите, что вы будете редактировать, и редактируйте только один раз перед сохранением окончательно отредактированной версии. Не сохраняйте повторно несколько раз.
Один из способов, который вы можете использовать, чтобы минимизировать эту потерю качества, — работать с RAW JPEG. Решите, что вы будете редактировать, и редактируйте только один раз перед сохранением окончательно отредактированной версии. Не сохраняйте повторно несколько раз.
Часть 2. JPG против JPEG: сходство между двумя форматами файлов
Теперь, когда мы определили, что такое файлы .jpg и .jpeg, и вы знаете, что они на самом деле не так уж отличаются, давайте взглянем на их сходство в этом разделе.
# 1 Они оба теряют качество, когда вы сохраняете их
Поскольку .jpg и .jpeg фактически одинаковы, они также используют один и тот же метод сжатия — сжатие с потерями, что имеет смысл. Сжатие с потерями приводит к снижению качества изображения и уменьшению размера файла.
Более того, это означает, что независимо от того, какое расширение имени файла вы будете использовать (.jpg или .jpeg), размер вашего изображения станет меньше по сравнению с исходным размером. Это позволяет вашим изображениям быстрее загружаться и загружаться на ваши сайты для удобного просмотра ваших посетителей.
Это позволяет вашим изображениям быстрее загружаться и загружаться на ваши сайты для удобного просмотра ваших посетителей.
# 2 Они оба растровые изображения
Вы можете создавать компьютерные изображения как векторные или растровые изображения. Поскольку JPG — это растровые файлы, то же самое можно сказать и о JPEG. Растровые изображения — это растровые изображения. Растровые изображения — это сетки отдельных пикселей, которые при объединении создают одно изображение. Проще говоря, растровое изображение состоит из множества крошечных пикселей разных цветов, которые закодированы в соответствии с их оттенком или оттенком.
# 3 Они оба используются для похожих типов изображений
Поскольку JPG и JPEG являются растровыми изображениями, они используются в цифровой фотографии, потому что цифровые фотографии используют обширные цветовые градации, которые лучше всего проявляются при сохранении в виде изображений JPG или JPEG. Это означает, что посетителям вашего сайта всегда будут представлены красивые фотографии, если вы загрузите их в формате JPG или JPEG на своем сайте.
После разговора о JPG против JPEG, давайте узнаем, как найти и удалить похожие изображения с вашего Mac, чтобы освободить место.
Часть 3. Бонусный совет: как найти и удалить похожие изображения на вашем Mac
Когда у вас возникают проблемы на вашем Mac, вызванные полным диском, одна вещь, которую вы можете сделать, чтобы сэкономить место, — это удалить похожие изображения. Таким образом, мы рекомендуем использовать PowerMyMac для выполнения этой задачи. Это инструмент, который помогает пользователям ускорить свои компьютеры Mac, удаляя ненужные приложения и удаляя ненужные файлы на своем диске с молниеносной скоростью.
Кроме того, это приложение также может помочь вам удалить ненужные iTunes Backup, вложения электронной почты. Он также может сканировать большие файлы, которые вам больше не нужны, чтобы вы могли удалить их и сохранить на диске.
Как найти и удалить похожие изображения с помощью PowerMyMac?
PowerMyMac — это не только инструмент, который может удалять ненужные файлы на вашем Mac. Это также может помочь вам найти похожие изображения так что вы можете выбрать те, которые вы хотите удалить, и те, которые вы хотите сохранить.
Это также может помочь вам найти похожие изображения так что вы можете выбрать те, которые вы хотите удалить, и те, которые вы хотите сохранить.
Вам просто нужно пойти в Сайт iMyMac PowerMyMac и найдите ссылки для загрузки приложения. Он предлагает как Бесплатная версия и полная версия. После загрузки установщика, просто следуйте этому руководству о том, как использовать приложение для удалить ненужные файлы на вашем Mac, включая похожие изображения.
Получите бесплатную пробную версию прямо сейчас!
Часть 4. Так ли JPG такой же, как JPEG?
Таким образом, изображения JPG и JPEG одинаковы и служат некоторым основным целям: уменьшение размеров файлов ваших изображений для улучшения просмотра в Интернете, а также предоставление пользователям простого способа сжатия своих изображений при их сохранении и именования файлов в популярном расширении. это может быть признано многими устройствами.
Итак, сделайте вывод, что JPG против JPEG, они точно такие же, так что ни лучше. Какой бы формат вы ни выбрали между этими двумя, ваши файлы будут работать, и ваш выбор будет зависеть от ваших предпочтений. Надеюсь, эта статья смогла очистить вашу путаницу с форматами файлов JPG и JPEG.
Какой бы формат вы ни выбрали между этими двумя, ваши файлы будут работать, и ваш выбор будет зависеть от ваших предпочтений. Надеюсь, эта статья смогла очистить вашу путаницу с форматами файлов JPG и JPEG.
Конвертировать JPEG в JPG онлайн
Конвертировать JPEG в JPG очень легко с помощью нашего бесплатного онлайн-инструмента. Вам просто нужен файл .jpeg, загрузка не требуется, и выполните следующие действия.
- Нажмите «Выбрать файл» и выберите файл .jpeg. Вы также можете выбрать несколько файлов и конвертировать их одновременно, чтобы сэкономить время.
- А теперь отдохни. Наш конвертер будет обрабатывать ваши файлы один за другим и конвертировать .jpeg в jpg максимум за 2-3 секунды.
- Загрузите преобразованное изображение на свое устройство, просто нажав кнопку загрузки.
- Наш конвертер jpeg в jpg не загружает ваши файлы на свой сервер. Все операции будут выполняться в вашем браузере.
- Файлы будут удалены, когда вы нажмете кнопку «Удалить все» или когда вы покинете веб-сайт.

- Этот инструмент поддерживает и работает во всех браузерах.
- Если есть какие-либо проблемы, не стесняйтесь обращаться к нам и сделать этот инструмент лучше.
Формат файлов JPG и JPEG одинаков?
Между форматами jpg и jpeg фактически нет различий, разница только в количестве символов.
jpeg — это стандартный формат изображения для хранения сжатых и сжатых данных изображения, несмотря на огромное уменьшение размера файла. размер и сохранение приемлемого качества изображения. Эта уникальная функция сжатия очень мощная, что позволяет использовать файлы JPEG на компьютерах и мобильных устройствах, подключенных к Интернету. Обмен изображениями в формате jpeg осуществляется быстро и эффективно, и они также содержат высококачественные данные изображения. Файлы JPEG занимают меньше места и экономят память вашего устройства.
Так же, как и файл JPG, это изображение, сохраненное в сжатом формате изображения, стандартизированном (Объединенной фотографической
Группа экспертов) сокращение от jpeg.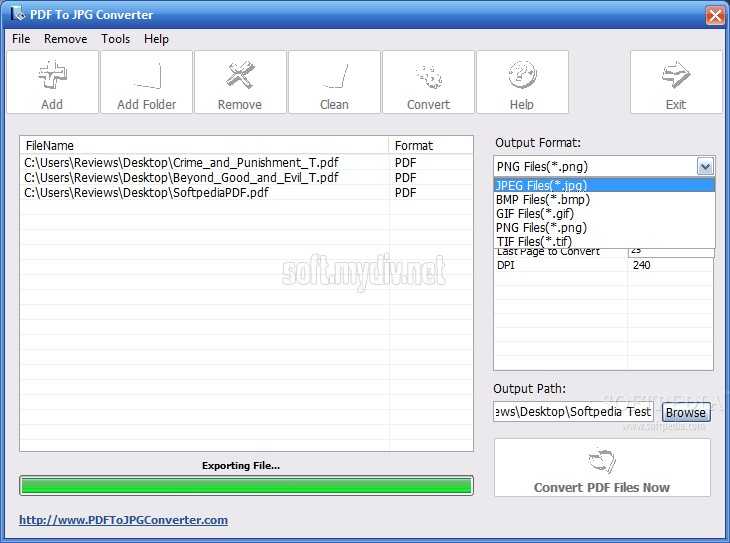 он обычно используется для хранения цифровых фотографий и используется большинством цифровых камер и мобильных устройств.
для сохранения изображений.
он обычно используется для хранения цифровых фотографий и используется большинством цифровых камер и мобильных устройств.
для сохранения изображений.
Какова основная причина преобразования .jpeg в jpg?
Существует много причин, по которым вам может понадобиться преобразовать изображение JPEG в JPG. Возможно, вам нужно уменьшить размер файла для облегчения загрузки или скачивания. Возможно, вы хотите изменить формат файла, чтобы он был совместим с определенной программой. Или, возможно, вы просто предпочитаете формат JPG, а не JPEG.
И я заметил, что когда мы загружаем файл изображения из WhatsApp, тип mime изображения — JPG, но расширение будет JPEG, и это еще одна основная причина для преобразования расширения изображения. Потому что большинство веб-сайтов и программного обеспечения не позволяют загружать файл .jpeg.
Часто задаваемые вопросы
Нет никакой разницы в качестве между файлами JPG и JPEG. Оба эти формата файлов изображений используют сжатие с потерями и чаще всего используются для цифровых изображений. это означает, что некоторые данные теряются при сохранении файла в любом формате. Однако на качество изображения они не влияют.
это означает, что некоторые данные теряются при сохранении файла в любом формате. Однако на качество изображения они не влияют.
JPG — это распространенный формат файла, который часто используется для изображений. Но когда вы должны использовать JPG? Таким образом, это лучше всего подходит для изображений с большим количеством цветов или деталей. Например, если у вас есть фотография заката, JPG — хороший выбор. JPG также является хорошим выбором для изображений, которые будут редактироваться или изменяться в размере.
Однако в некоторых случаях JPG не лучший вариант. Например, если у вас есть изображение, состоящее в основном из текста, например документ, или вы разрабатываете какое-то объявление, JPG — не лучший выбор. Это связано с тем, что JPG может сжимать изображения и снижать качество текста. В этих случаях лучше использовать PNG или другой формат файла.
Нет, iPhone чаще всего использует форматы HEIC и HEIF. У Apple есть небольшая проблема, когда они берут эти высокоэффективные
фотографии . heic или .heif вместо .jpeg, поэтому вы получаете все эти ошибки и прочее, когда пытаетесь прикрепить
их по электронной почте или поделиться ими с пользователями, не являющимися пользователями Mac или iPhone.
heic или .heif вместо .jpeg, поэтому вы получаете все эти ошибки и прочее, когда пытаетесь прикрепить
их по электронной почте или поделиться ими с пользователями, не являющимися пользователями Mac или iPhone.
Поделитесь своим опытом:
Преобразование JPG в оттенки серого – онлайн-инструменты JPG
Скоро появятся Эти инструменты для работы с jpg уже в пути
Редактор JPEG
Редактируйте изображения JPG в браузере.
Сдвиг файла JPG
Сдвиг файла JPEG вправо или влево.
Нарезка JPG
Извлечение части изображения JPEG.
Разделить файл JPG
Разделить файл JPG на несколько меньших файлов JPEG.
Объединение файлов JPG
Объединение нескольких файлов JPEG в одно изображение.
Создание эскиза предварительного просмотра JPG
Преобразование изображения JPEG в меньший эскиз предварительного просмотра.
Преобразование последовательного JPG в прогрессивный JPG
Преобразование базового JPEG в чересстрочный JPEG.
Преобразование прогрессивного JPEG в последовательный JPEG
Преобразование чересстрочного JPG в базовый JPG.
Преобразование JPG в JPEG2000
Преобразование фотографий JPEG в фотографии JPG 2000.
Преобразование JPG2000 в JPEG
Преобразование изображений JPEG 2000 в изображения JPG.
Преобразование JPG в ICO
Преобразование изображений JPEG в значки ICO.
Преобразование ICO в JPEG
Преобразование значков ICO в изображения JPG.
Преобразование JPG в TIFF
Преобразование изображений JPEG в изображения TIFF.
Преобразование TIFF в JPEG
Преобразование изображений TIFF в изображения JPG.
Преобразование JPEG в QOI
Преобразование изображений JPG в изображения QOI (формат изображения Quote OK).
Преобразование изображений QUI в JPEG
Преобразование изображений QUI в изображения JPG.
Преобразовать JPG в PIK
Преобразовать изображения JPEG в изображения PIK.
Преобразование PIK в JPEG
Преобразование изображения PIK в изображение JPG.
Преобразование JPG в PPM
Преобразование изображения JPEG в изображение PPM.
Преобразование PPM в JPEG
Преобразование изображения PPM в изображение JPG.
Преобразование JPG в BPG
Преобразование изображения JPEG в изображение BPG.
Преобразование BPG в JPEG
Преобразование изображения BPG в изображение JPG.
Преобразование JPG в RGB
Преобразование изображения JPEG в необработанные значения RGB.
Преобразование RGB в JPEG
Преобразование необработанных значений RGB в изображение JPG.
Преобразование JPEG в RGBA
Преобразование изображения JPG в необработанные значения RGBA.
Преобразование RGBA в JPG
Преобразование необработанных значений RGBA в изображение JPEG.
Преобразование JPEG в ARGB
Преобразование изображения JPG в необработанные значения ARGB.
Преобразование ARGB в JPG
Преобразование необработанных значений ARGB в изображение JPEG.
Преобразование JPG в BGR
Преобразование изображения JPEG в необработанные значения BGR.
Преобразование BGR в JPEG
Преобразование необработанных значений BGR в изображение JPG.
Преобразование JPG в BGRA
Преобразование изображения JPEG в необработанные значения BGRA.
Преобразование BGRA в JPEG
Преобразование необработанных значений BGRA в изображение JPG.
Преобразование JPG в ABGR
Преобразование изображения JPEG в необработанные значения ABGR.
Преобразование ABGR в JPEG
Преобразование необработанных значений ABGR в изображение JPG.
Преобразование JPG в FLIF
Преобразование изображения JPEG в изображение FLIF.
Преобразование FLIF в JPEG
Преобразование изображения FLIF в изображение JPG.
Преобразование JPG в AV1
Преобразование изображения JPEG в изображение AVIF (AV1).
Преобразование AV1 в JPEG
Преобразование изображения AVIF (AV1) в изображение JPG.
Преобразование файлов JPEG в анимированный GIF
Преобразование нескольких файлов JPG в анимацию GIF.
Преобразование файлов JPEG в анимированный PNG
Преобразование нескольких файлов JPG в анимацию APNG.
Преобразование файлов JPEG в анимацию Webp
Преобразование нескольких файлов JPG в анимацию Webp.
Преобразование JPG в Excel
Создание электронной таблицы Excel с цветными ячейками из файла JPEG.
Объединение двух изображений JPEG
Объединение двух изображений JPG/JPEG вместе.
Создать одноцветный файл JPG
Создать одноцветный файл JPEG любого размера.
Создать JPG с ошибками
Рандомизировать байты в JPEG и создать JPEG с ошибками.
Улучшить JPG
Увеличение качества изображения JPEG.
Акварель a JPG
Применение эффекта акварели к фотографии JPG.
Создание графического изображения ASCII из JPEG
Преобразование JPG в художественное изображение ASCII.
Создание JPG из рисунка ASCII
Преобразование рисунка ASCII в рисунок JPEG.
Создание художественного изображения ANSI из JPG
Преобразование изображения JPEG в художественное изображение ANSI.
Создание JPG из ANSI Art
Преобразование чертежа ANSI в чертеж JPEG.
Переименовать JPG
Изменить имя файла JPG.
Зеркальное отображение изображения в формате JPEG
Создание зеркальной копии изображения в формате JPG.
Сделать симметричный JPEG
Создать Преобразовать заданный JPG в симметричный JPG.
Квантизация JPEG
Применение алгоритма квантования цвета к изображению JPG.
Добавить звук в JPEG
Добавить звук в изображение JPG.
Извлечение метаданных JPG
Показать скрытые метаданные (данные EXIF) в изображении JPEG.
Добавить метаданные JPG
Добавить скрытые метаданные (данные EXIF) к изображению JPEG.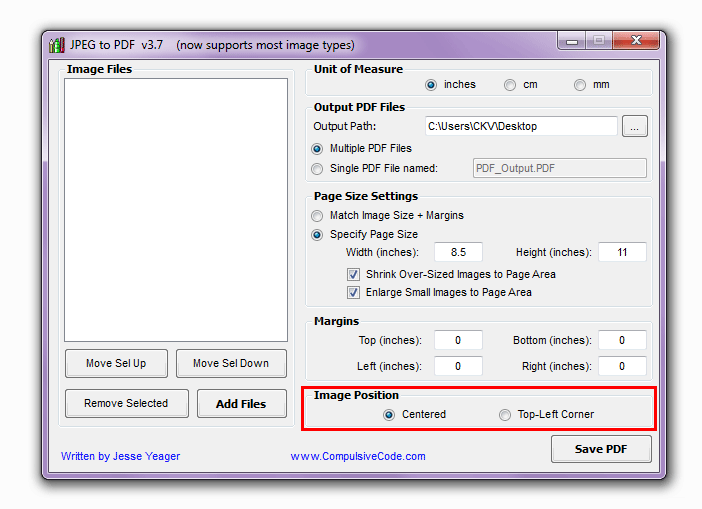

 Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:
Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор: В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.
В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы. Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.
Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела. Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.
Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений. 1_5 x * lnx dx = –14
1_5 x * lnx dx = –14
 Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.
Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.
В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Кроме того, несмотря на то, что \(a\) и \(b\) были заданы как интервал, нижний предел не обязательно должен быть меньше верхнего предела. В совокупности мы часто будем называть \(a\) и \(b\) интервалом интегрирования .
Кроме того, несмотря на то, что \(a\) и \(b\) были заданы как интервал, нижний предел не обязательно должен быть меньше верхнего предела. В совокупности мы часто будем называть \(a\) и \(b\) интервалом интегрирования . Это означает, что нам нужно будет «оценить» это суммирование. Другими словами, нам придется использовать формулы, приведенные в обзоре обозначений суммирования, чтобы исключить фактическое суммирование и получить формулу для этого для общего \(n\).
Это означает, что нам нужно будет «оценить» это суммирование. Другими словами, нам придется использовать формулы, приведенные в обзоре обозначений суммирования, чтобы исключить фактическое суммирование и получить формулу для этого для общего \(n\). Основная цель этого раздела — изложить основные свойства и факты об определенном интеграле. Мы обсудим, как мы вычисляем их на практике, начиная со следующего раздела. 9{{\,b}}{{f\left( t \right)\,dt}}\). Смысл этого свойства в том, чтобы заметить, что пока функция и пределы одинаковы, переменная интегрирования, которую мы используем в определенном интеграле, не повлияет на ответ.
Основная цель этого раздела — изложить основные свойства и факты об определенном интеграле. Мы обсудим, как мы вычисляем их на практике, начиная со следующего раздела. 9{{\,b}}{{f\left( t \right)\,dt}}\). Смысл этого свойства в том, чтобы заметить, что пока функция и пределы одинаковы, переменная интегрирования, которую мы используем в определенном интеграле, не повлияет на ответ.
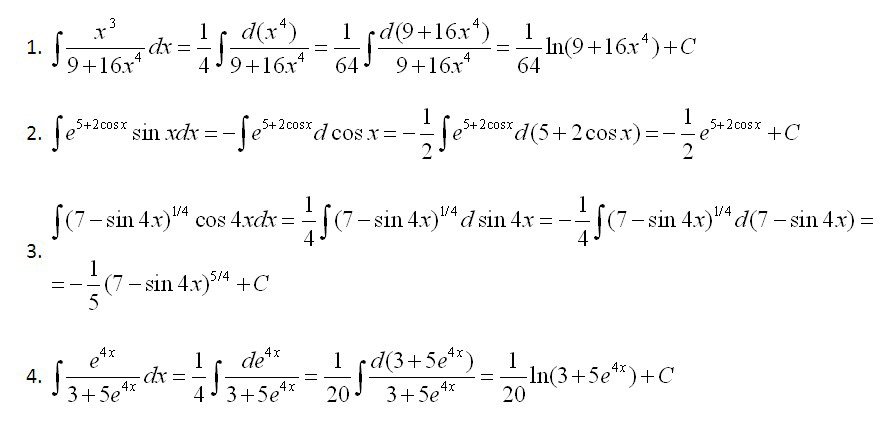 Другими словами, вычислите определенный интеграл скорости изменения, и вы получите чистое изменение количества. Мы можем видеть, что значение определенного интеграла \(f\left( b \right) — f\left( a \right)\) на самом деле дает нам чистое изменение \(f\left( x \ правильно)\) и, таким образом, этим утверждением действительно нечего доказывать. На самом деле это просто подтверждение того, что говорит нам определенный интеграл скорости изменения. 9{{\,{t_2}}}{{V’\left( t \right)\,dt}} = V\left( {{t_2}} \right) — V\left( {{t_1}} \right )\]
Другими словами, вычислите определенный интеграл скорости изменения, и вы получите чистое изменение количества. Мы можем видеть, что значение определенного интеграла \(f\left( b \right) — f\left( a \right)\) на самом деле дает нам чистое изменение \(f\left( x \ правильно)\) и, таким образом, этим утверждением действительно нечего доказывать. На самом деле это просто подтверждение того, что говорит нам определенный интеграл скорости изменения. 9{{\,{t_2}}}{{V’\left( t \right)\,dt}} = V\left( {{t_2}} \right) — V\left( {{t_1}} \right )\] е. объект перемещается как вправо, так и влево) во временном интервале, это НЕ даст общее расстояние путешествовал. Это даст только смещение, , т.е. , разницу между тем, где объект начал и где он закончился. Чтобы получить общее расстояние, пройденное объектом, нам нужно вычислить 9{{\,{t_2}}}{{\left| {v\left( t \right)} \right|\,dt}}\]
е. объект перемещается как вправо, так и влево) во временном интервале, это НЕ даст общее расстояние путешествовал. Это даст только смещение, , т.е. , разницу между тем, где объект начал и где он закончился. Чтобы получить общее расстояние, пройденное объектом, нам нужно вычислить 9{{\,{t_2}}}{{\left| {v\left( t \right)} \right|\,dt}}\] 2} + 1}}\,dt}} \]
2} + 1}}\,dt}} \] {{\,v\left( x \right)}}{{f\left( t \right)\,dt }} = — v’\left( x \right)f\left( {v\left( x \right)} \right)\]
92}} \right)\end{align*}\]
{{\,v\left( x \right)}}{{f\left( t \right)\,dt }} = — v’\left( x \right)f\left( {v\left( x \right)} \right)\]
92}} \right)\end{align*}\]
 F'(x) = f(x) для каждого значения x в I.
F'(x) = f(x) для каждого значения x в I. ∫g'(x)dx = g(x) + c. Неопределенные интегралы относятся к семейству параллельных кривых.
∫g'(x)dx = g(x) + c. Неопределенные интегралы относятся к семейству параллельных кривых. Вот соответствующие интегралы этих функций, которые запоминаются как стандартные формулы интегралов.
Вот соответствующие интегралы этих функций, которые запоминаются как стандартные формулы интегралов. Известные методы:
Известные методы:




 11.
11.
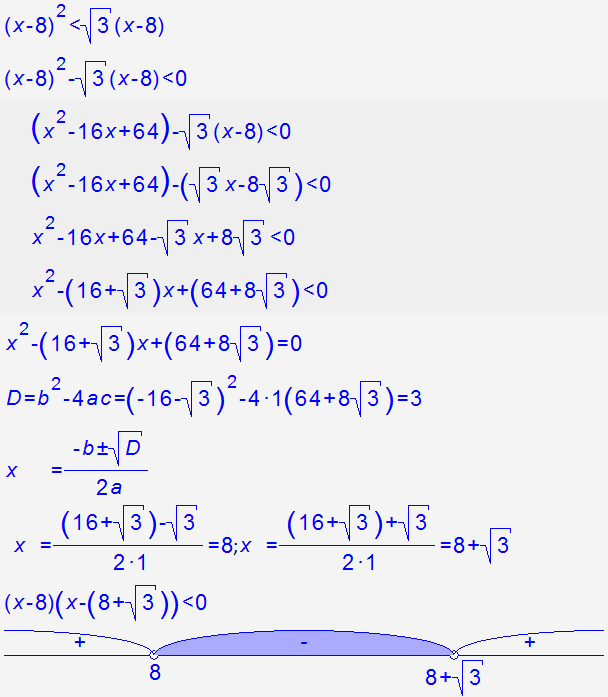

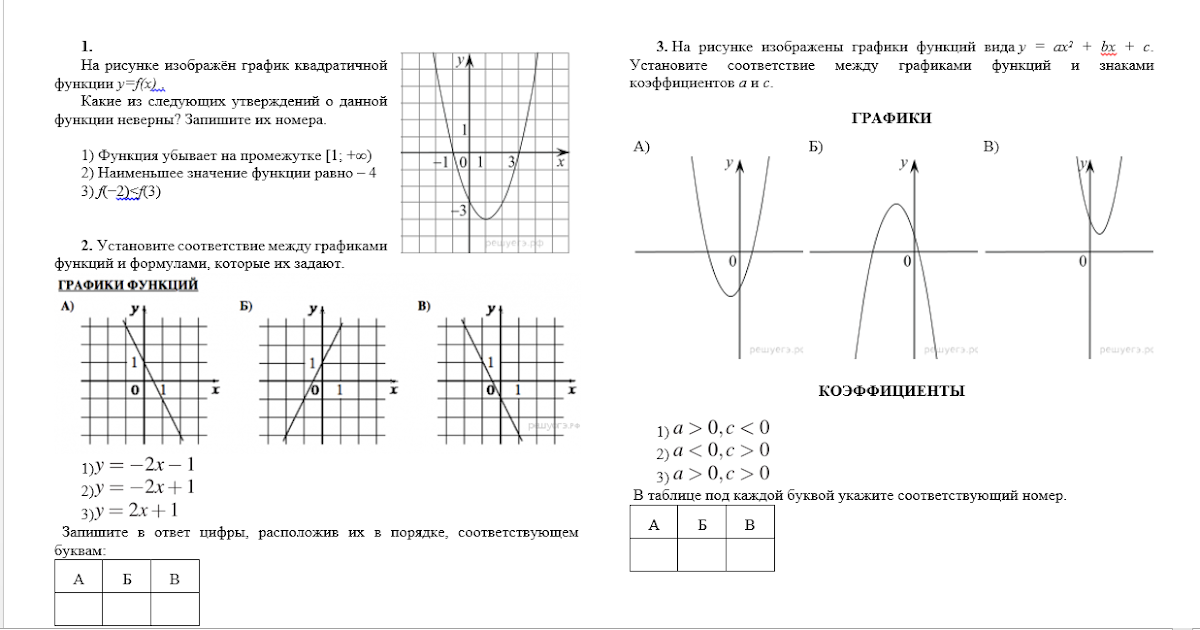
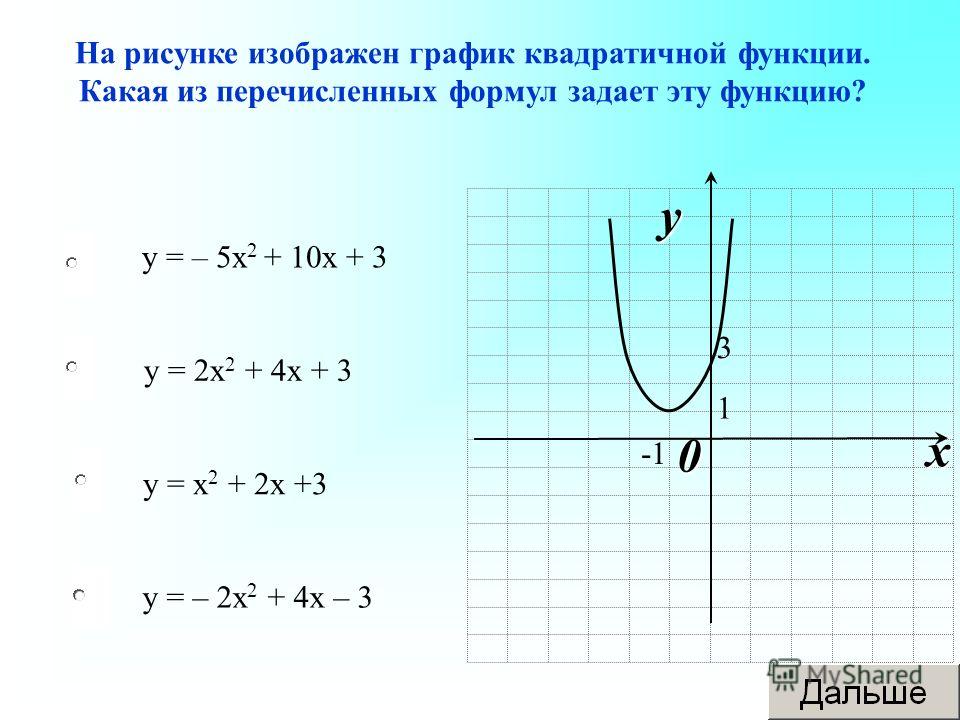
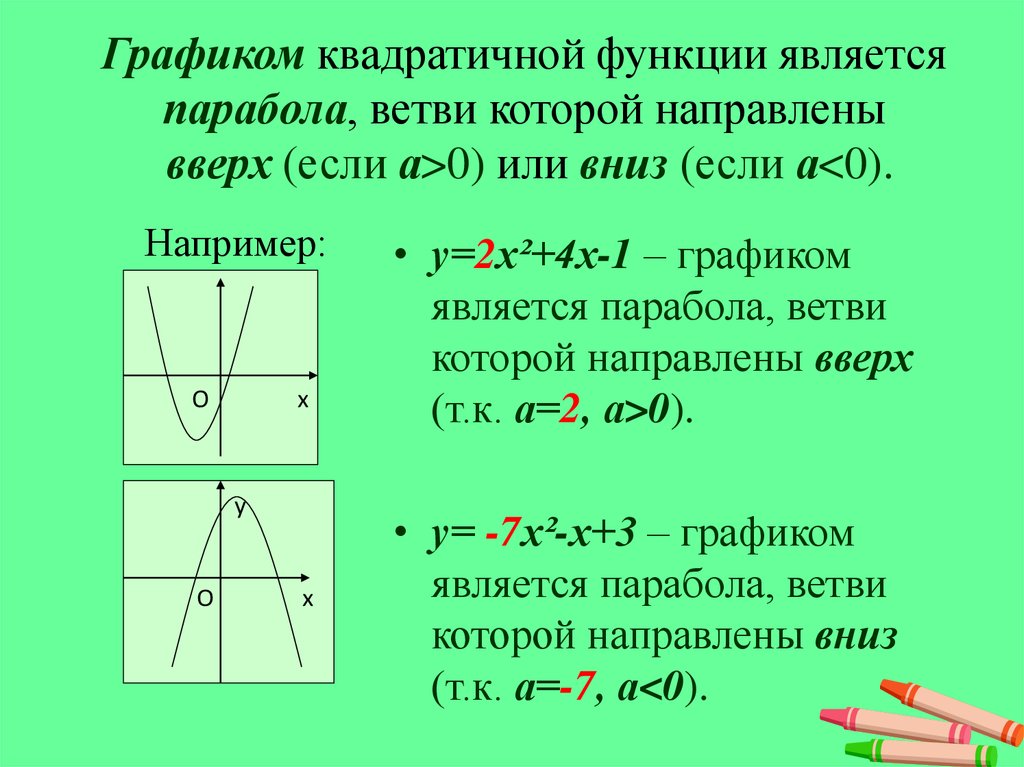
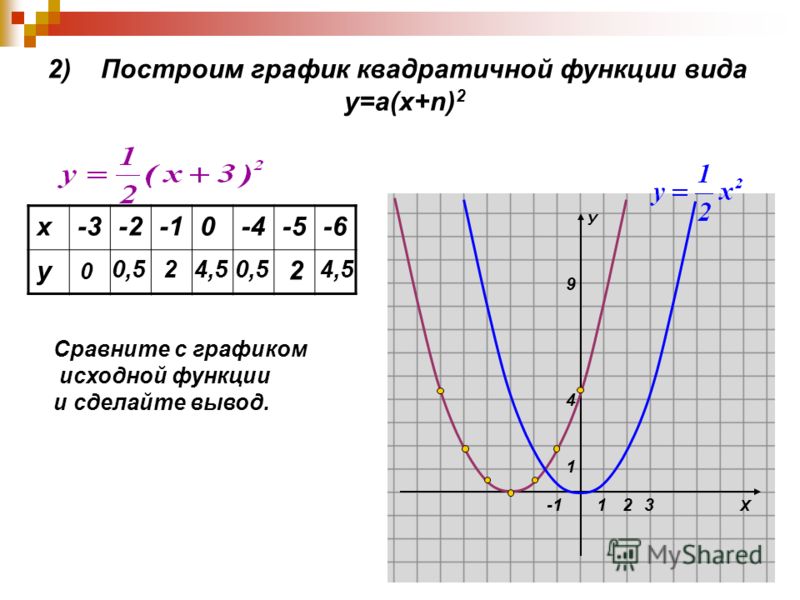
 Установите соответствие между графиками функций и знаками коэффициентов a и c.
Установите соответствие между графиками функций и знаками коэффициентов a и c.


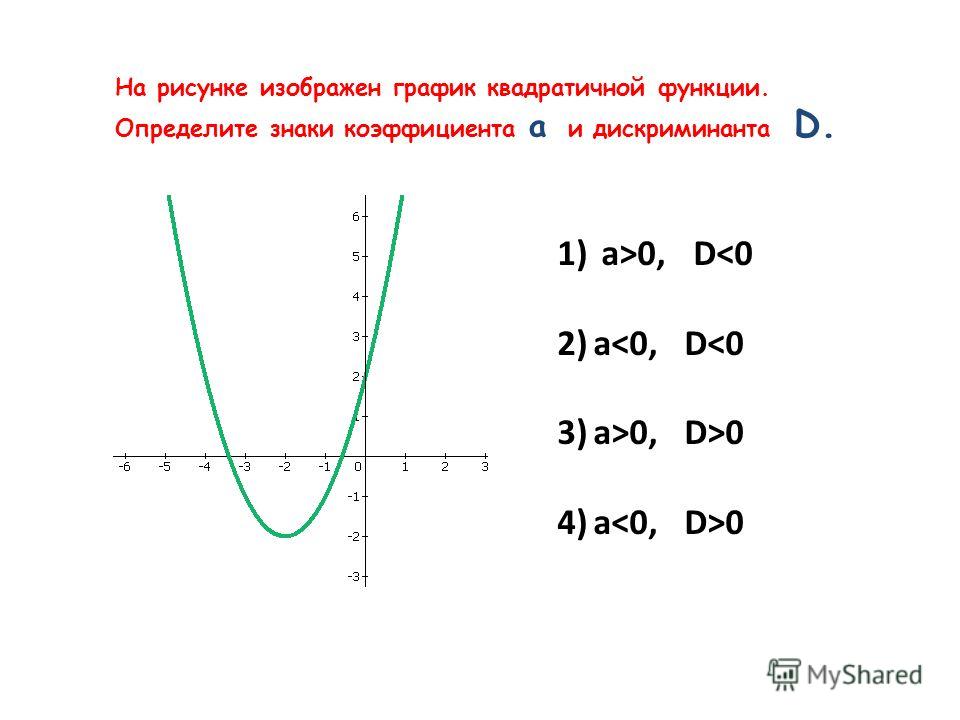
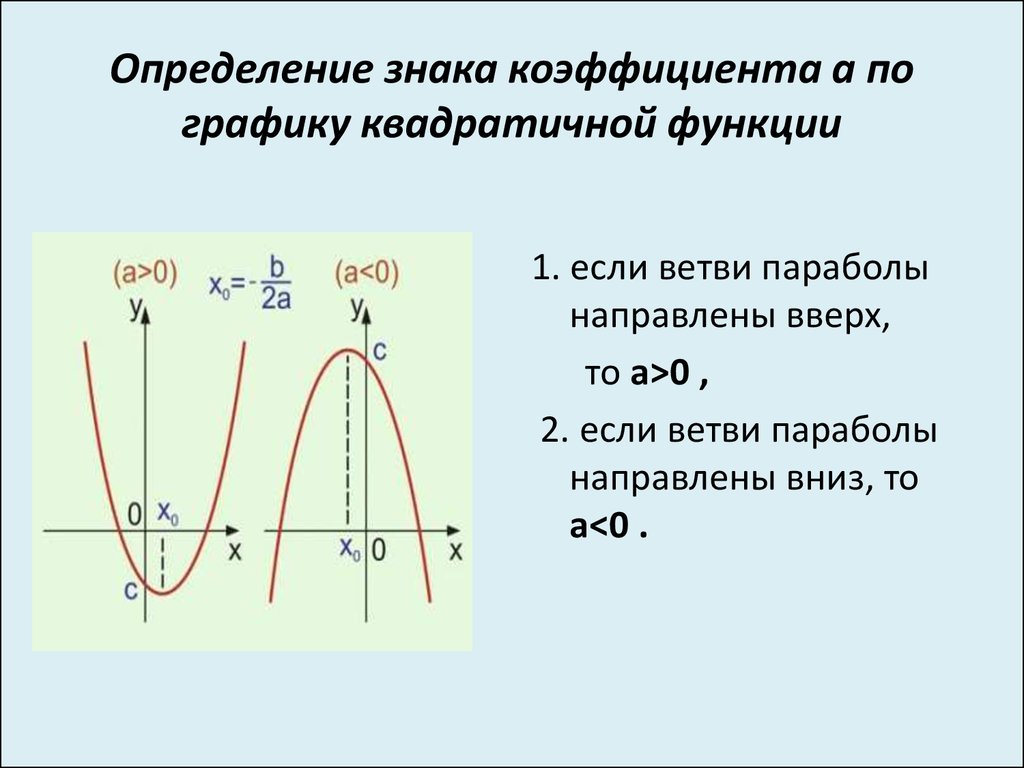 Установите соответствие между графиками функций и знаками коэффициентов a и c.
Установите соответствие между графиками функций и знаками коэффициентов a и c.

 ОТВЕТ: ___________________________
ОТВЕТ: ___________________________ к a=6>0, то ветки параболы направлены вверх.
к a=6>0, то ветки параболы направлены вверх. docx (ТЕСТ)
docx (ТЕСТ) 
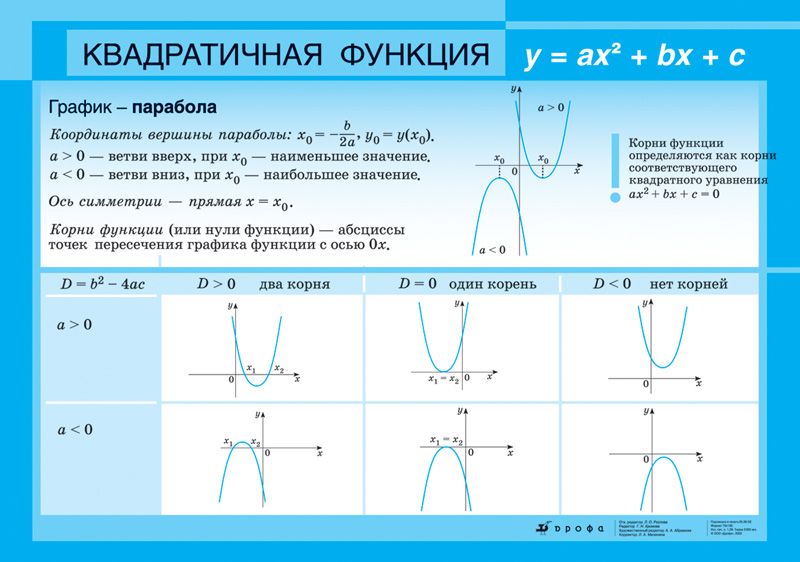
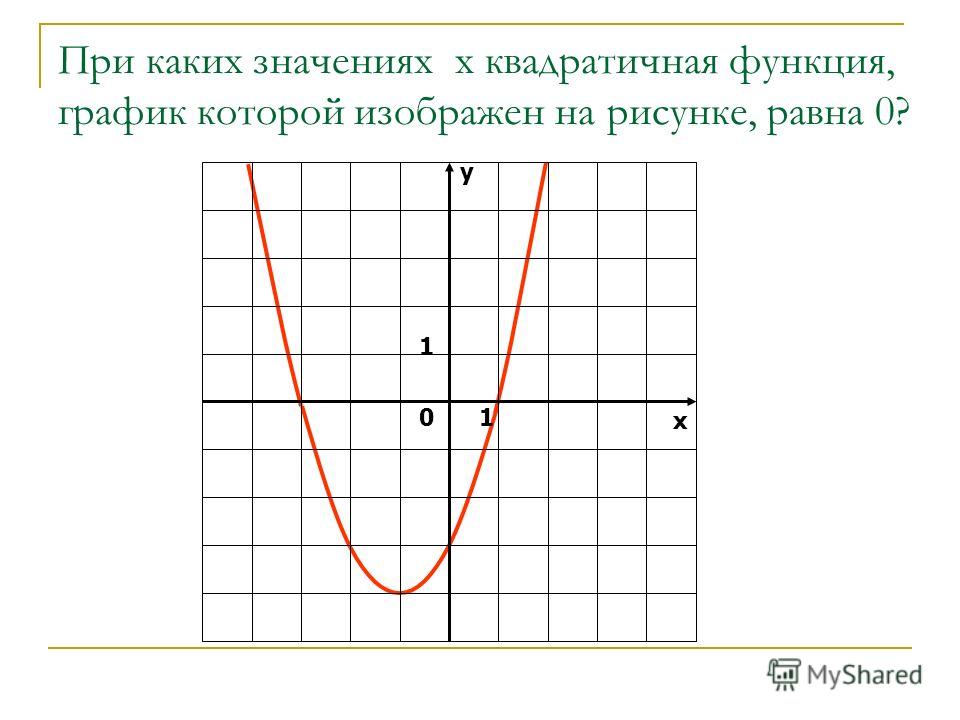
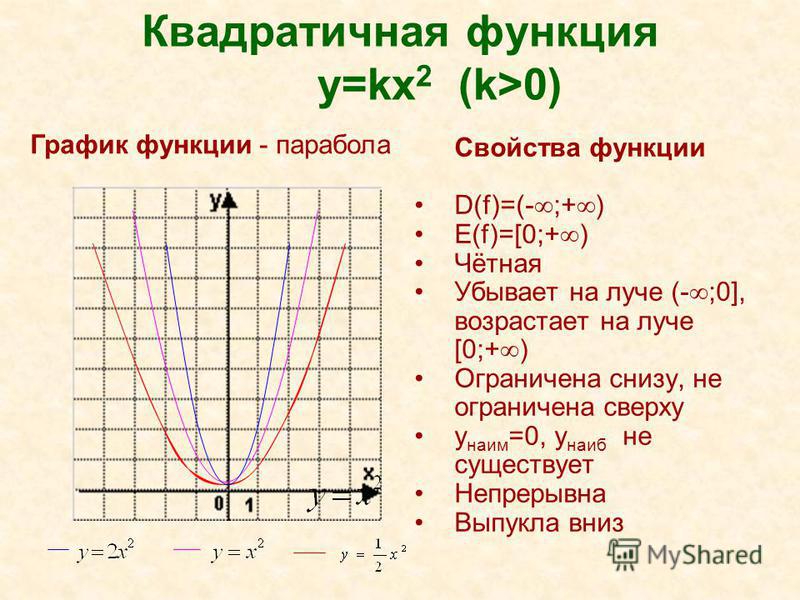 Напомним Вам, что найти решение уравнения — значит найти точку, в которой график пересекает ось ОХ. Именно поэтому функция приравнивается к нулю: у = 0.
Напомним Вам, что найти решение уравнения — значит найти точку, в которой график пересекает ось ОХ. Именно поэтому функция приравнивается к нулю: у = 0.
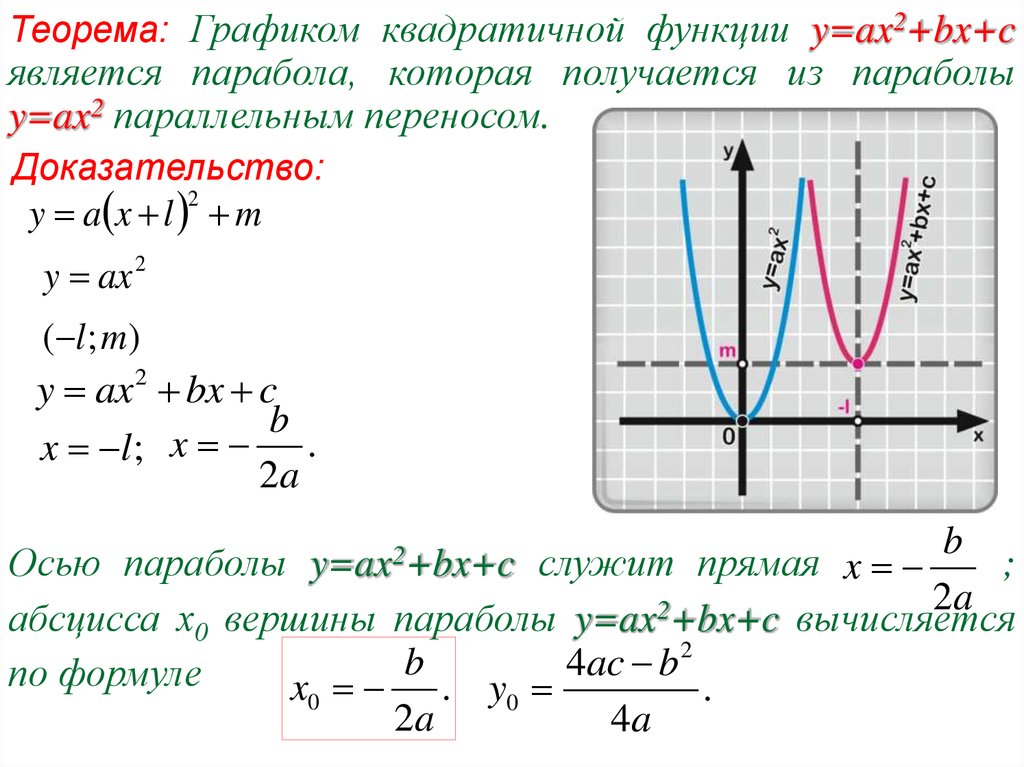

 Если вы учитесь в колледже по алгебре
класс, работа с квадратичными функциями неизбежна, даже если это против
твоя религия. Так что, я думаю, вам лучше начать.
Если вы учитесь в колледже по алгебре
класс, работа с квадратичными функциями неизбежна, даже если это против
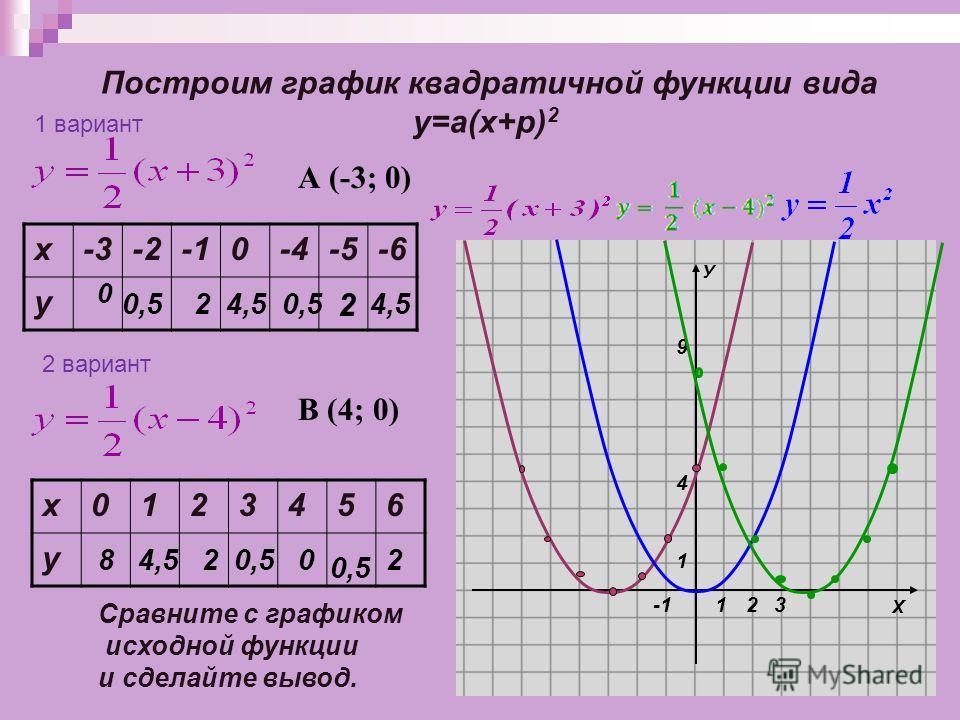
твоя религия. Так что, я думаю, вам лучше начать.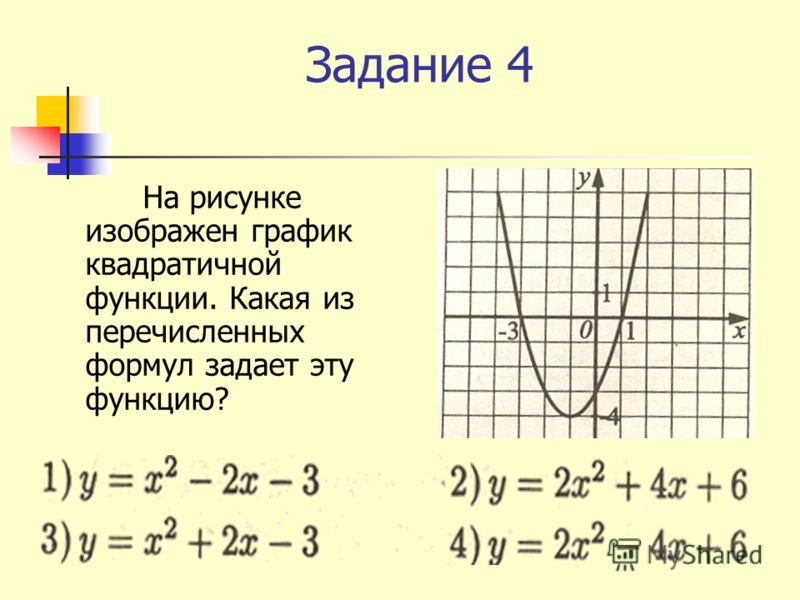 Я покажу вам, как построить параболу, используя любую форму.
Я покажу вам, как построить параболу, используя любую форму.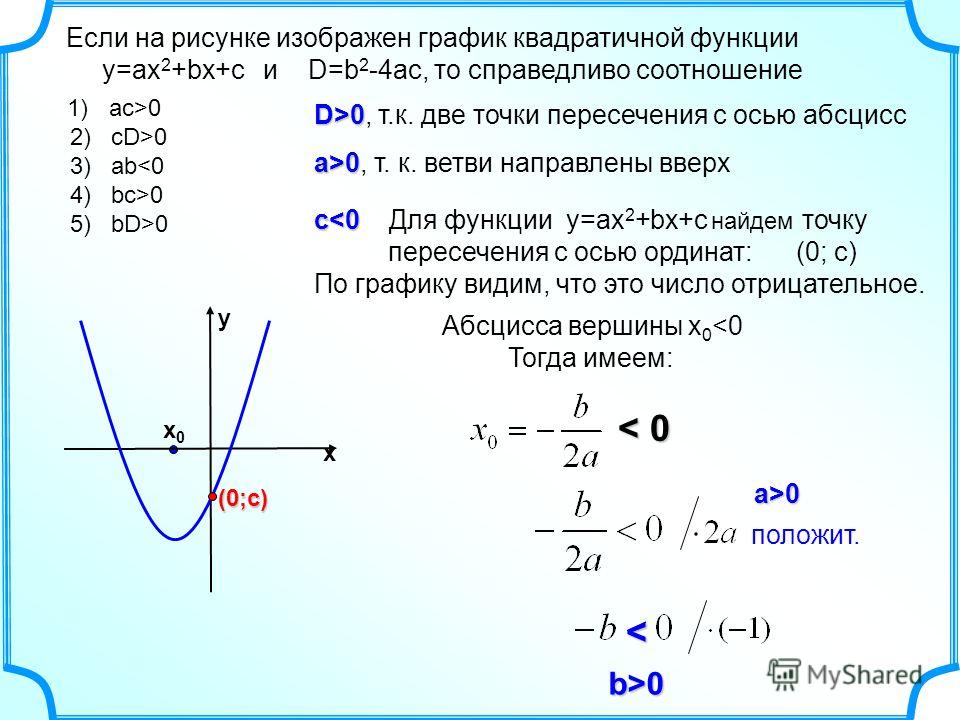
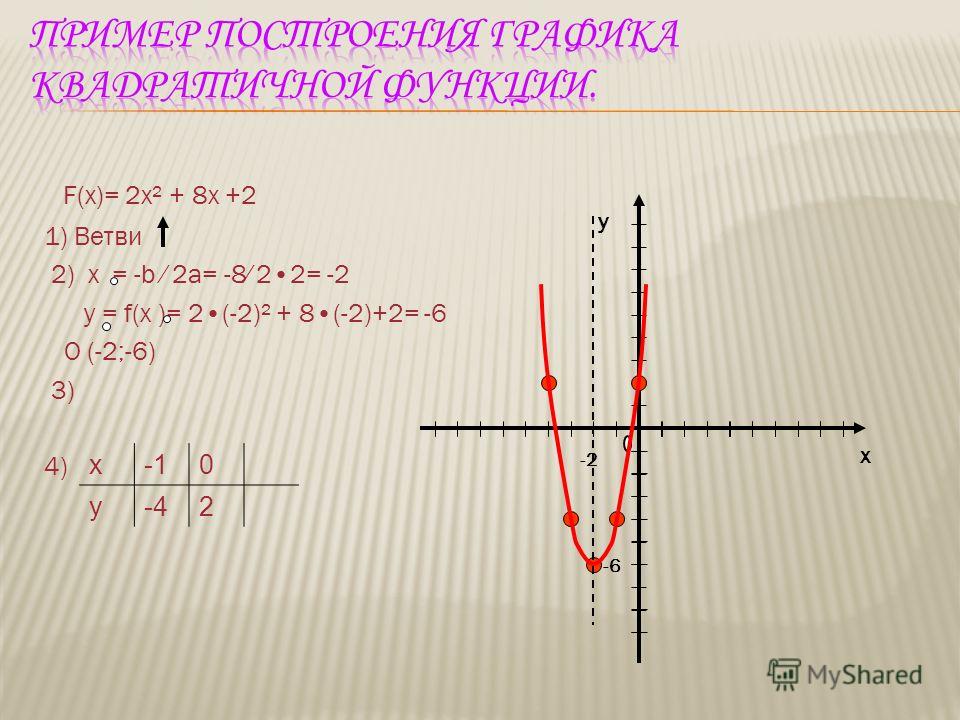
 Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции.
Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции. Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции.
Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции. график:
график: 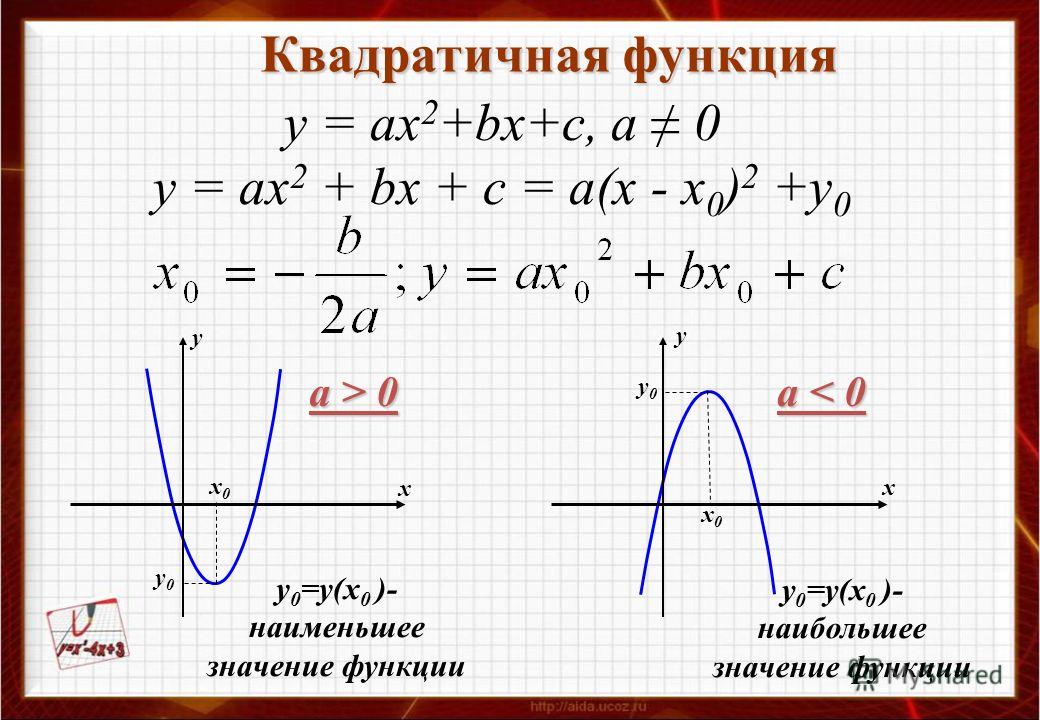 Без построения графика определите, является ли вершина максимальной или минимальной точкой
квадратичной функции.
Без построения графика определите, является ли вершина максимальной или минимальной точкой
квадратичной функции. это реально заманчиво
сказать, что вершина (1, 3). Однако внимательно посмотрите на
стандартная форма. Обратите внимание, что знак перед h — минус, а перед k — плюс.
Итак, ч — это число, которое мы вычитаем из х ,
что в нашем случае равно 1. к это номер
мы добавляем в конце, что в нашем случае мы добавляем минус 3.
это реально заманчиво
сказать, что вершина (1, 3). Однако внимательно посмотрите на
стандартная форма. Обратите внимание, что знак перед h — минус, а перед k — плюс.
Итак, ч — это число, которое мы вычитаем из х ,
что в нашем случае равно 1. к это номер
мы добавляем в конце, что в нашем случае мы добавляем минус 3. 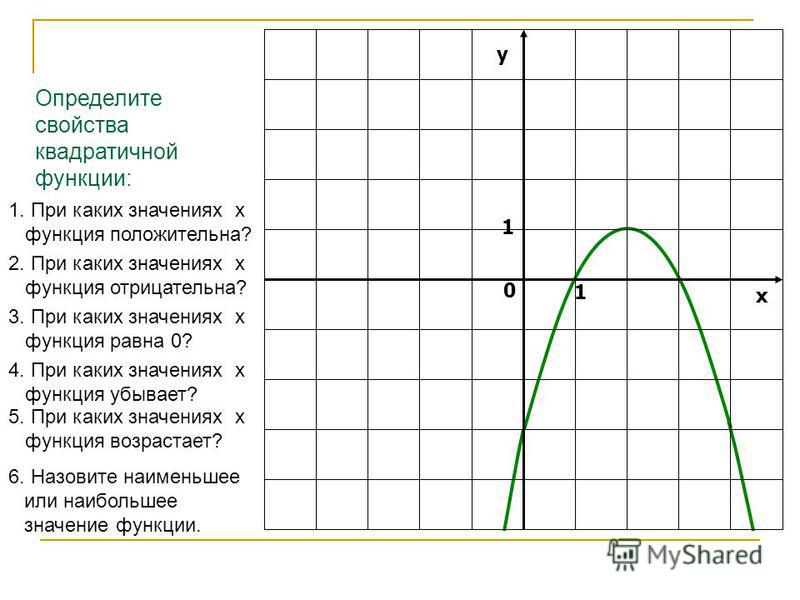
 для а , б ,
и с
для а , б ,
и с 
 Найдите уравнение для оси симметрии этой функции.
Найдите уравнение для оси симметрии этой функции.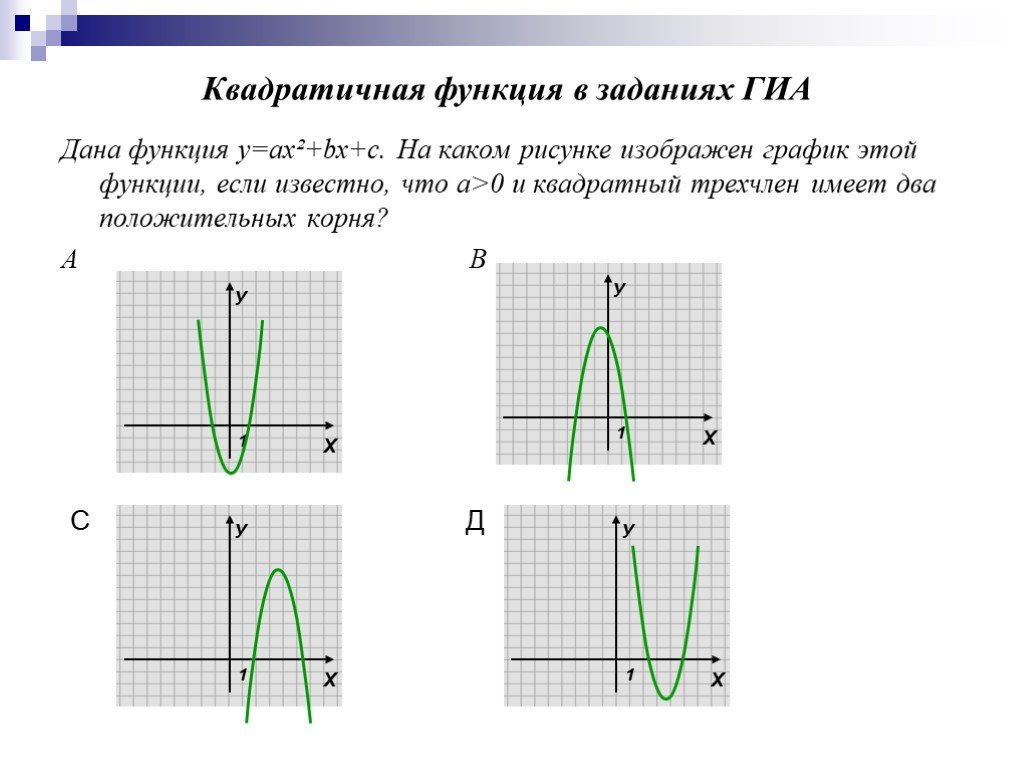

 Это означает, что нет действительного числового решения. Это также означает, что
НЕТ x -перехватов.
Это означает, что нет действительного числового решения. Это также означает, что
НЕТ x -перехватов. 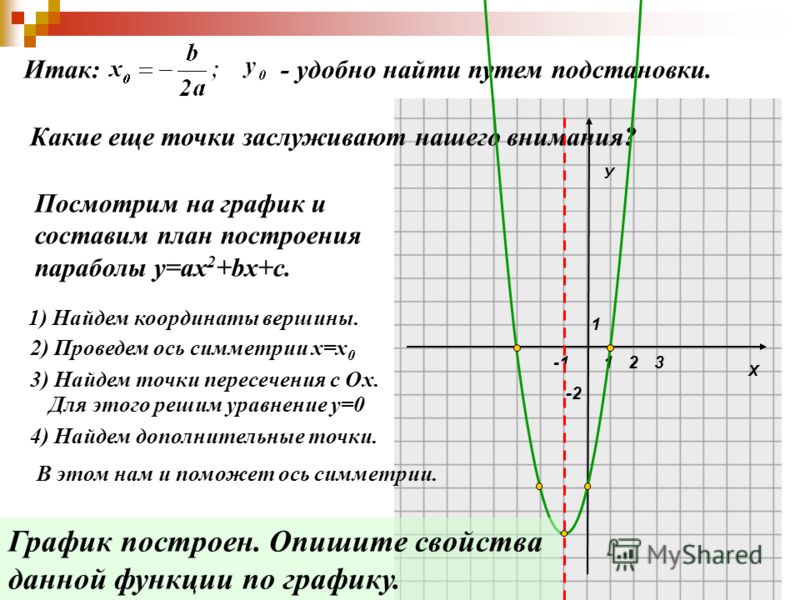 На самом деле практики много не бывает.
На самом деле практики много не бывает. Найдите уравнение для этого
ось симметрии функции.
Найдите уравнение для этого
ось симметрии функции. 

 Пользователь должен ввести целое число. Поскольку функция
Пользователь должен ввести целое число. Поскольку функция  Не забываем, в языке программирования Python в конце заголовков сложных инструкций ставится двоеточие.
Не забываем, в языке программирования Python в конце заголовков сложных инструкций ставится двоеточие. Следовательно, логическое выражение возвращает истину, что позволяет зайти в тело цикла.
Следовательно, логическое выражение возвращает истину, что позволяет зайти в тело цикла. Переменная n теперь имеет новое значение.
Переменная n теперь имеет новое значение. В нем i меняется, ее новое значение 2.
В нем i меняется, ее новое значение 2. Его преимущество заключается в том, что в теле цикла не надо изменять переменную-счетчик, ее значение меняется автоматически в заголовке
Его преимущество заключается в том, что в теле цикла не надо изменять переменную-счетчик, ее значение меняется автоматически в заголовке  Иначе произойдет зацикливание.
Иначе произойдет зацикливание. Например, после предыдущих вычитаний ее значение стало равным 25. Пользователь вводит число 30. Однако программа не выполняет вычитание, а выводит сообщение о недопустимости операции, после чего осуществляет выход из цикла.
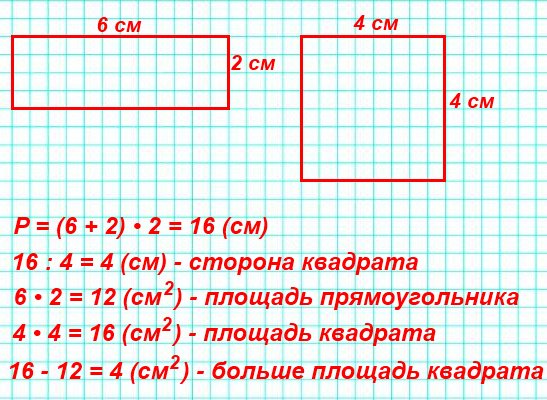
Например, после предыдущих вычитаний ее значение стало равным 25. Пользователь вводит число 30. Однако программа не выполняет вычитание, а выводит сообщение о недопустимости операции, после чего осуществляет выход из цикла.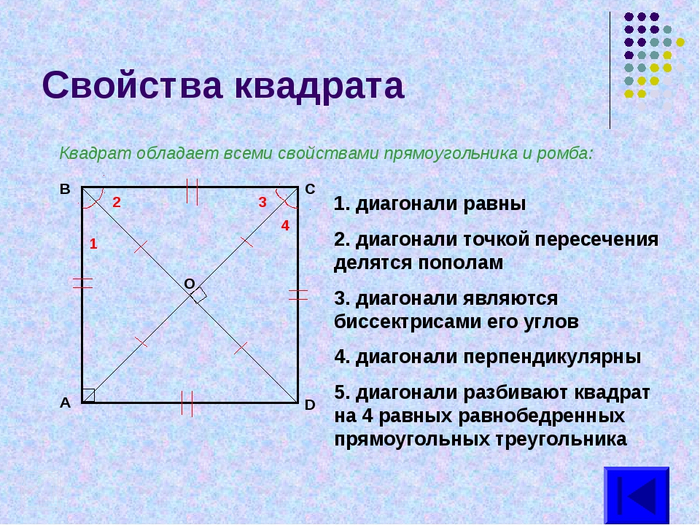 Но что такое «меньше»? Для отрезков было понятно: сравнивали длины. А что можно сравнивать у фигур? Для этого используют другую характеристику – площадь. Чем меньше будет площадь торта, тем меньше глазури понадобится маме.
Но что такое «меньше»? Для отрезков было понятно: сравнивали длины. А что можно сравнивать у фигур? Для этого используют другую характеристику – площадь. Чем меньше будет площадь торта, тем меньше глазури понадобится маме. 3).
3).
 5).
5). 7. Второй ряд
7. Второй ряд Если длины в метрах, то значение площади получатся в: .
Если длины в метрах, то значение площади получатся в: . Но так как стороны равны, то формулу можно записать короче: .
Но так как стороны равны, то формулу можно записать короче: . Не известна длина поля. Обозначим ее (Рис. 17).
Не известна длина поля. Обозначим ее (Рис. 17).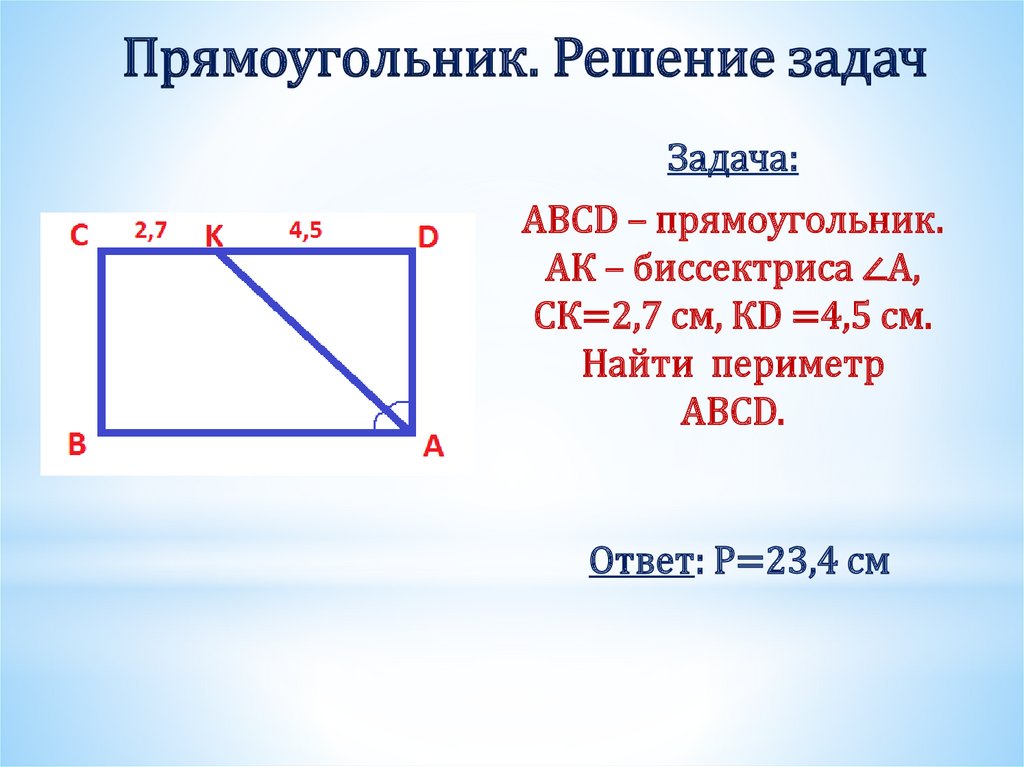
 Чему равна его площадь?
Чему равна его площадь?

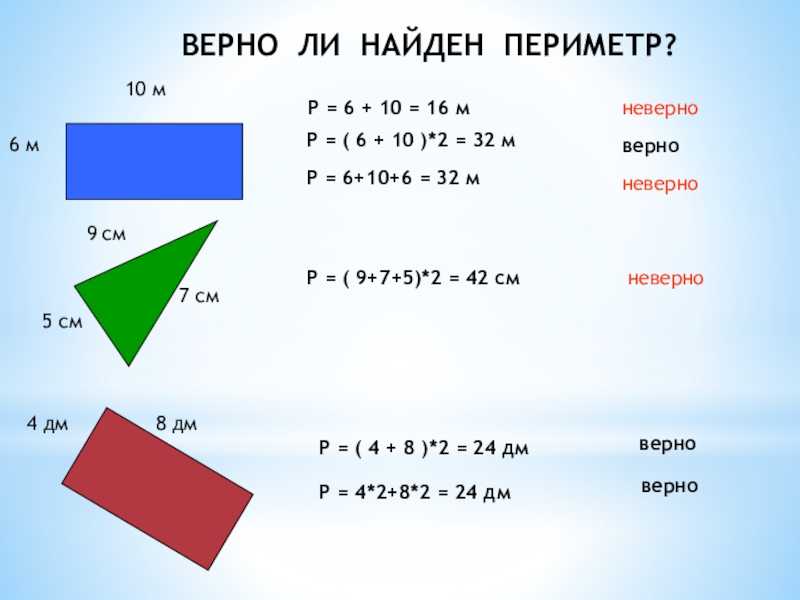
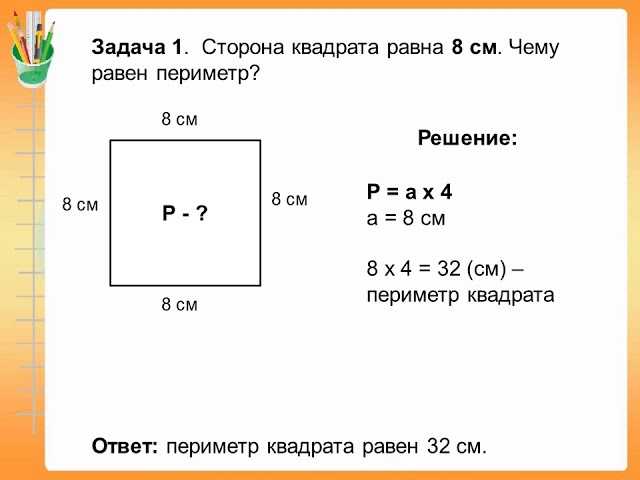
 Как и в примере с файлами cookie, все Oreo являются файлами cookie, но не все файлы cookie являются файлами Oreo. И то же самое верно для квадратов и прямоугольников. Таким образом, хотя все квадраты являются прямоугольниками, не все прямоугольники являются квадратами.
Как и в примере с файлами cookie, все Oreo являются файлами cookie, но не все файлы cookie являются файлами Oreo. И то же самое верно для квадратов и прямоугольников. Таким образом, хотя все квадраты являются прямоугольниками, не все прямоугольники являются квадратами. Все прямоугольники также являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Все прямоугольники также являются параллелограммами, но не все параллелограммы являются прямоугольниками.


 По итогам Совета Минфин ограничился заверением, что финансовая система «остается прочной и устойчивой».
По итогам Совета Минфин ограничился заверением, что финансовая система «остается прочной и устойчивой». Поэтому дальнейшее ужесточение денежно-кредитной политики может готовить и другие «сюрпризы».
Поэтому дальнейшее ужесточение денежно-кредитной политики может готовить и другие «сюрпризы».

 646
646 899
899 083
083 141
141 185
185 000
000 8499 9000
8499 9000
 активировать умножение evercare -24, равное США, и аналогично kya bolenge Agar положительное отрицательное
активировать умножение evercare -24, равное США, и аналогично kya bolenge Agar положительное отрицательное


 {2}-4}{a+2}, \frac{a}{2}, \frac{3 a+7}{5}
\]
{2}-4}{a+2}, \frac{a}{2}, \frac{3 a+7}{5}
\] \]
\]




 {2-1}}=\frac{8}{x}\]
{2-1}}=\frac{8}{x}\]
 Например, дроби
Например, дроби Этим действием мы находим дополнительный множитель для каждой из данных дробей. Дополнительный множитель — это число, на которое надо умножить члены дроби, чтобы привести её к общему знаменателю.
Этим действием мы находим дополнительный множитель для каждой из данных дробей. Дополнительный множитель — это число, на которое надо умножить члены дроби, чтобы привести её к общему знаменателю.
 Введите числитель и знаменатель (используйте неотрицательные целые значения), и решатель шаг за шагом покажет, как уменьшить дробь до ее простейшего выражения.
Введите числитель и знаменатель (используйте неотрицательные целые значения), и решатель шаг за шагом покажет, как уменьшить дробь до ее простейшего выражения. 1 = 3 \cdot 5 = 15 \]
1 = 3 \cdot 5 = 15 \]
 Чтобы выразить дробь одним числом, делим числитель на знаменатель.
Чтобы выразить дробь одним числом, делим числитель на знаменатель.  Например, при преобразовании в неправильную дробь мы должны умножить знаменатель , на целое число , чтобы получить . Затем мы добавили бы это к числителю , чтобы получить , который мы поместили бы над исходным знаменателем , чтобы получить .
Например, при преобразовании в неправильную дробь мы должны умножить знаменатель , на целое число , чтобы получить . Затем мы добавили бы это к числителю , чтобы получить , который мы поместили бы над исходным знаменателем , чтобы получить . Умножить верх и низ каждой дроби на знаменатель другой дроби. Например,
Умножить верх и низ каждой дроби на знаменатель другой дроби. Например, 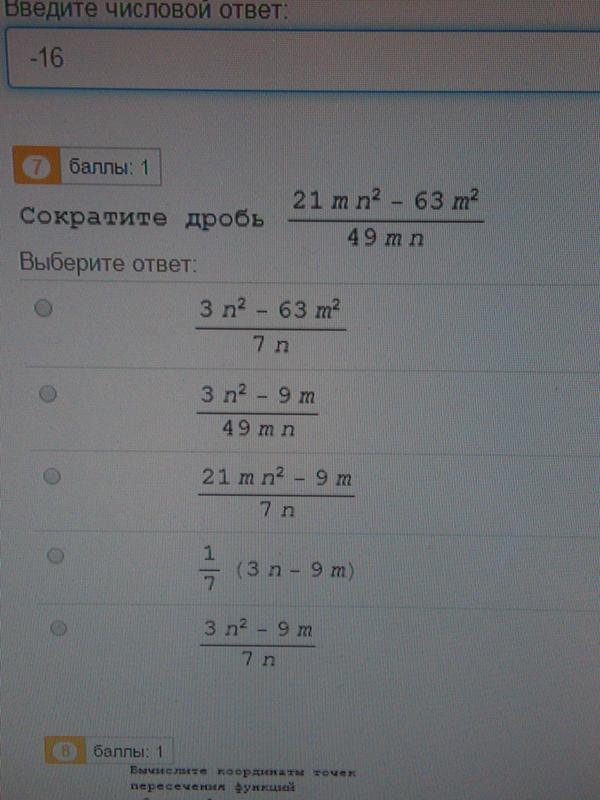 НОД набора чисел — это наибольшее число, которое можно без остатка разделить на все числа набора. Например, это наибольшее число, на которое можно разделить и без остатка, поэтому мы можем разделить числитель и знаменатель на на, чтобы уменьшить его до . Другой пример: , который уменьшится до .
НОД набора чисел — это наибольшее число, которое можно без остатка разделить на все числа набора. Например, это наибольшее число, на которое можно разделить и без остатка, поэтому мы можем разделить числитель и знаменатель на на, чтобы уменьшить его до . Другой пример: , который уменьшится до .
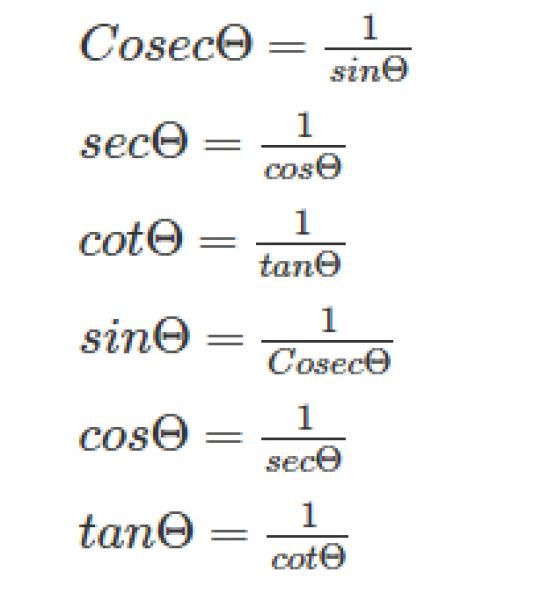 Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.) На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
На рисунке 3 показаны величины тригонометрических функций для единичной окружности. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов). Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов: Остальные четыре функции — нечётные, то есть:
Остальные четыре функции — нечётные, то есть:
 При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
 {\circ})}= \frac{23}{1.122} =20,5 см $$
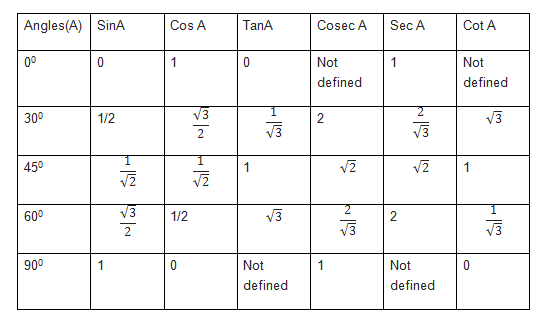
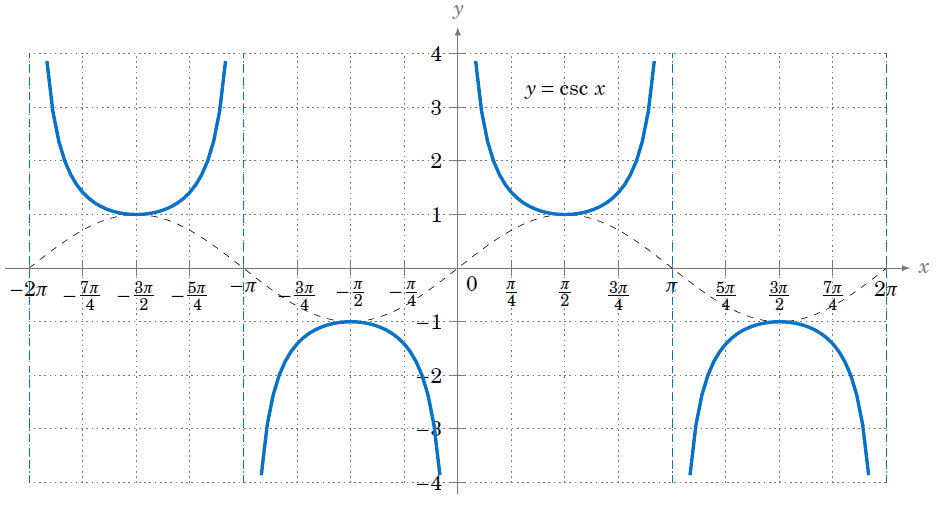
{\circ})}= \frac{23}{1.122} =20,5 см $$ Мы построим график косеканса, используя его домен и диапазон, исследуем тригонометрические тождества косеканса x, его значения и свойства. Мы решим несколько примеров, основанных на концепции csc x, чтобы лучше понять ее приложения.
Мы построим график косеканса, используя его домен и диапазон, исследуем тригонометрические тождества косеканса x, его значения и свойства. Мы решим несколько примеров, основанных на концепции csc x, чтобы лучше понять ее приложения.
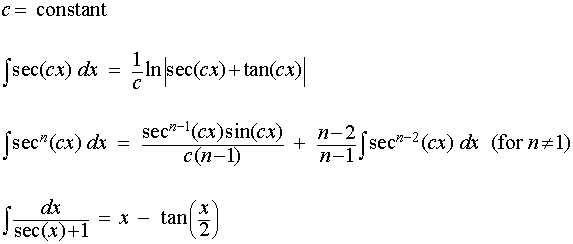 Таким образом, cosec x определен для всех действительных чисел, кроме nπ. Теперь мы знаем, что диапазон sin x равен [-1, 1], а csc x является обратной величиной sin x, поэтому диапазоном csc x являются все действительные числа, кроме (-1, 1). Таким образом, область определения и диапазон косеканса равны
Таким образом, cosec x определен для всех действительных чисел, кроме nπ. Теперь мы знаем, что диапазон sin x равен [-1, 1], а csc x является обратной величиной sin x, поэтому диапазоном csc x являются все действительные числа, кроме (-1, 1). Таким образом, область определения и диапазон косеканса равны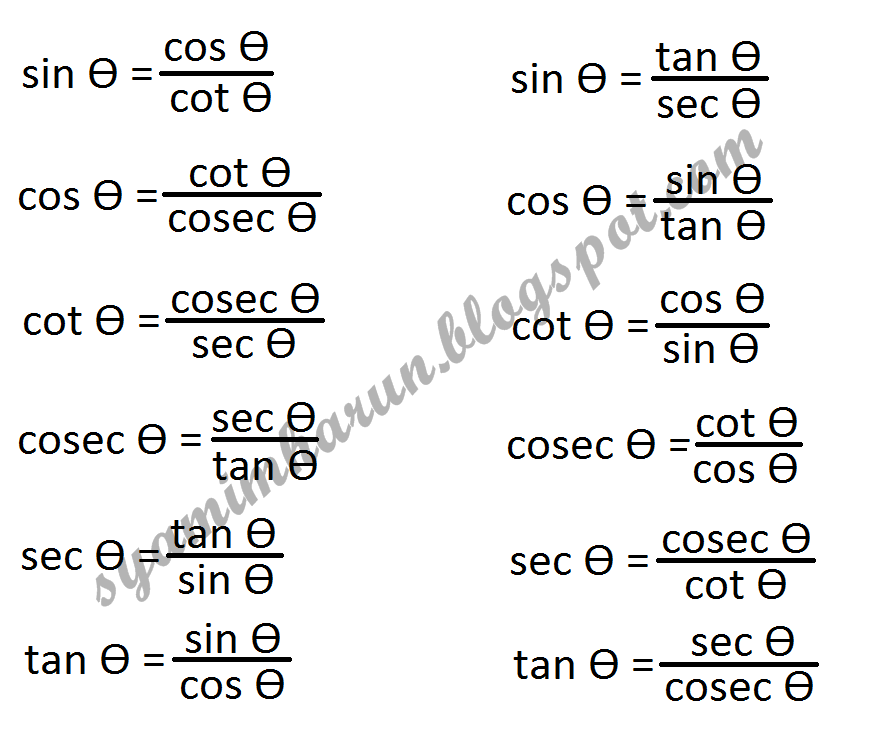 Мы используем эти тождества для упрощения и решения различных тригонометрических задач.
Мы используем эти тождества для упрощения и решения различных тригонометрических задач.
 Мы также можем найти косеканс угла, используя тригонометрические тождества.
Мы также можем найти косеканс угла, используя тригонометрические тождества. Также произведение этих двух функций на угол всегда равно единице. Следовательно, косеканс есть обратная функция синуса.
Также произведение этих двух функций на угол всегда равно единице. Следовательно, косеканс есть обратная функция синуса. Таким образом, cosec A через sin A определяется как
Таким образом, cosec A через sin A определяется как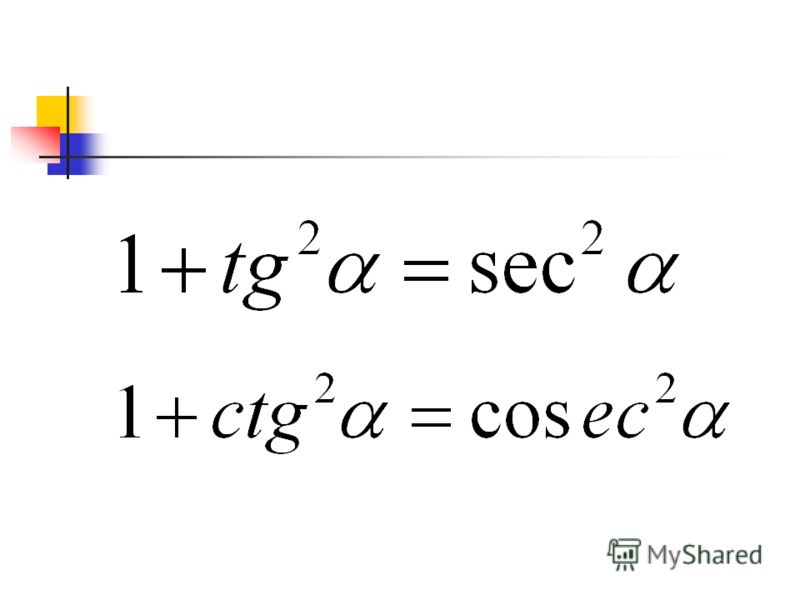


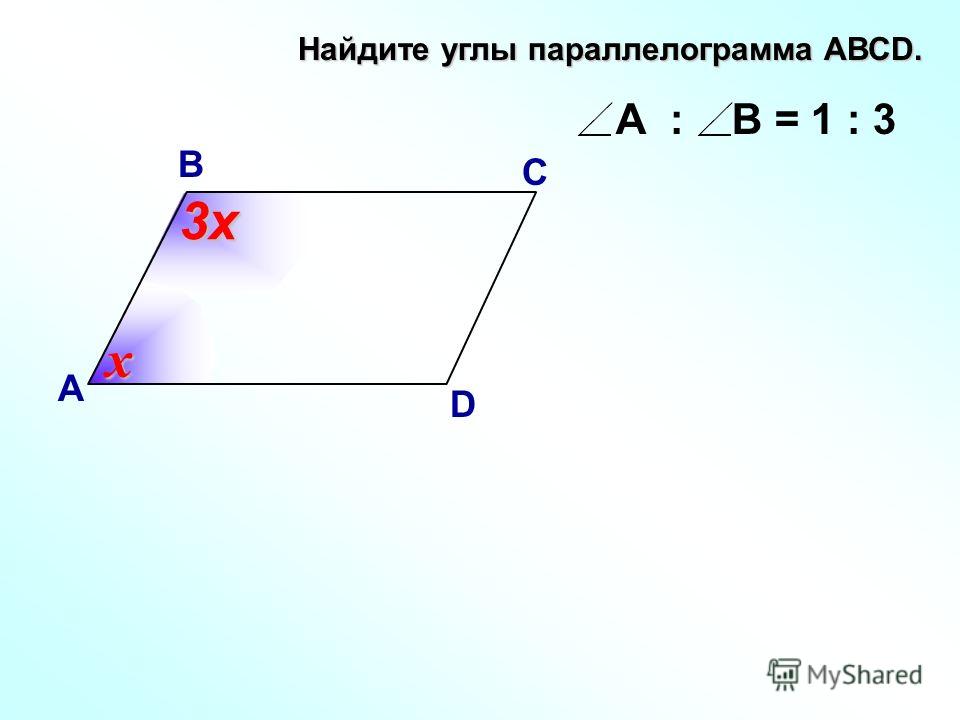
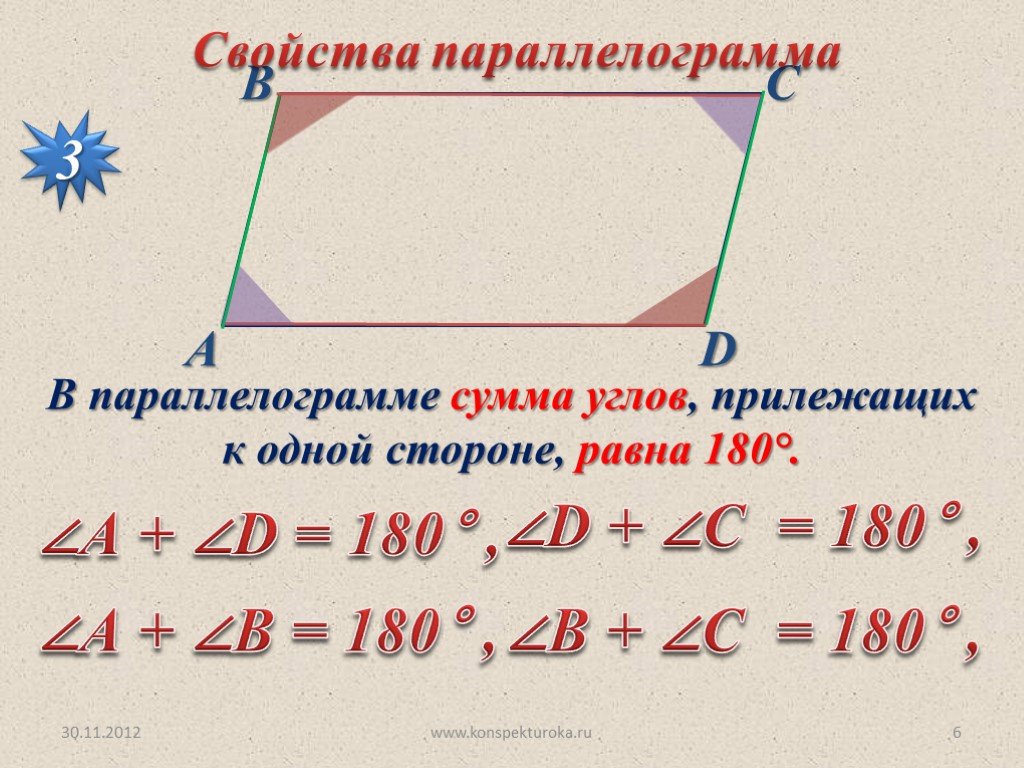
 \circ}\)
\circ}\) к.\ \angle ABM = \angle AMB\)
к.\ \angle ABM = \angle AMB\)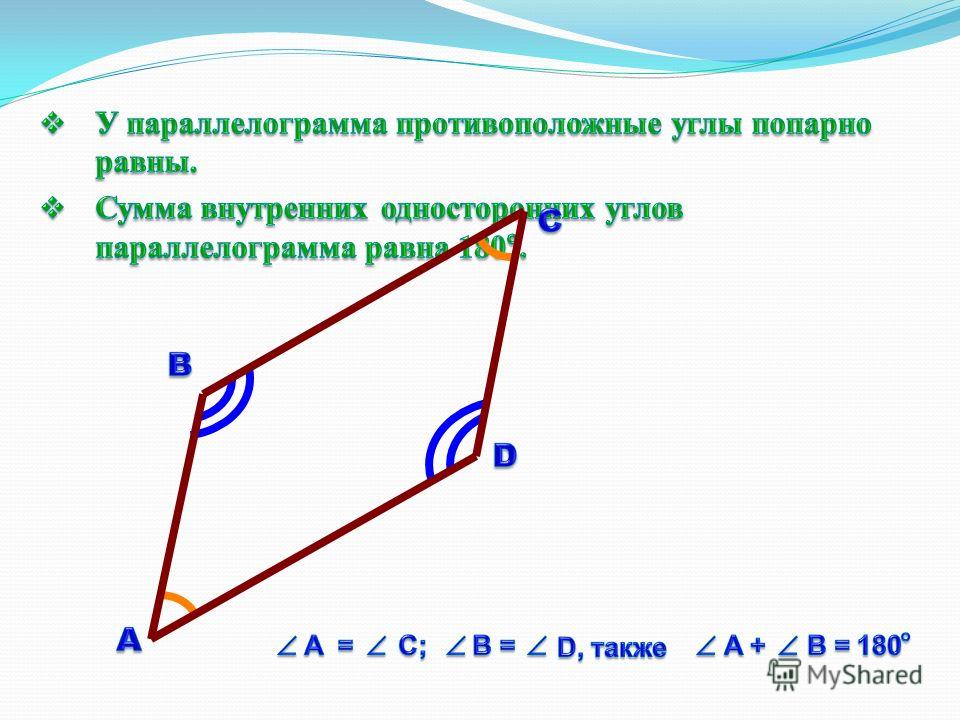 Через высоту и сторону
Через высоту и сторону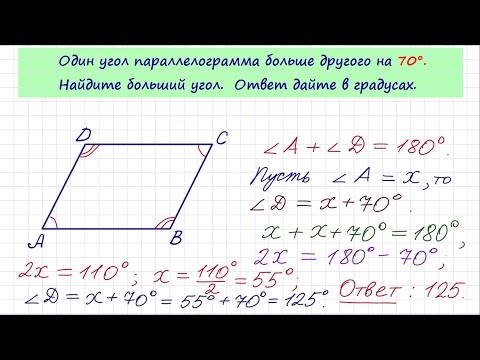 Квадрат бывает равносторонним и равноугольным.
Квадрат бывает равносторонним и равноугольным.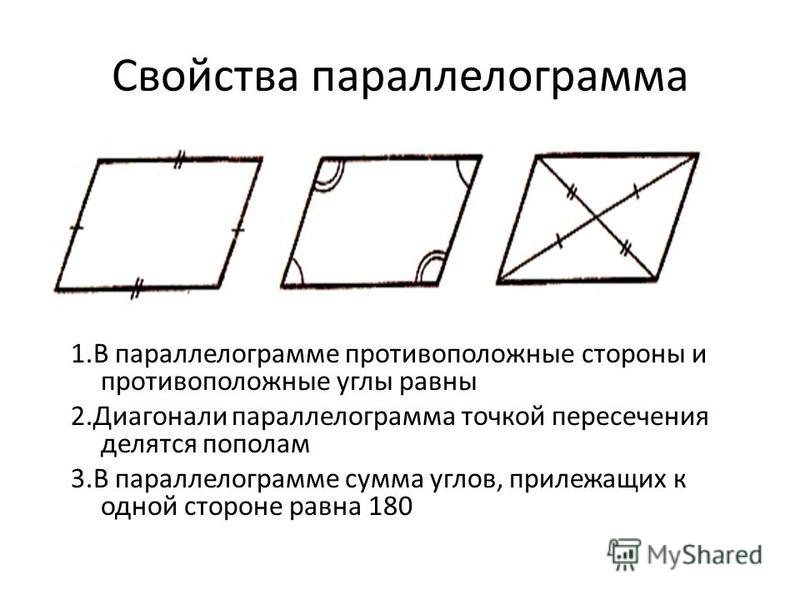
 {\circ}$. 9{\circ}$
{\circ}$. 9{\circ}$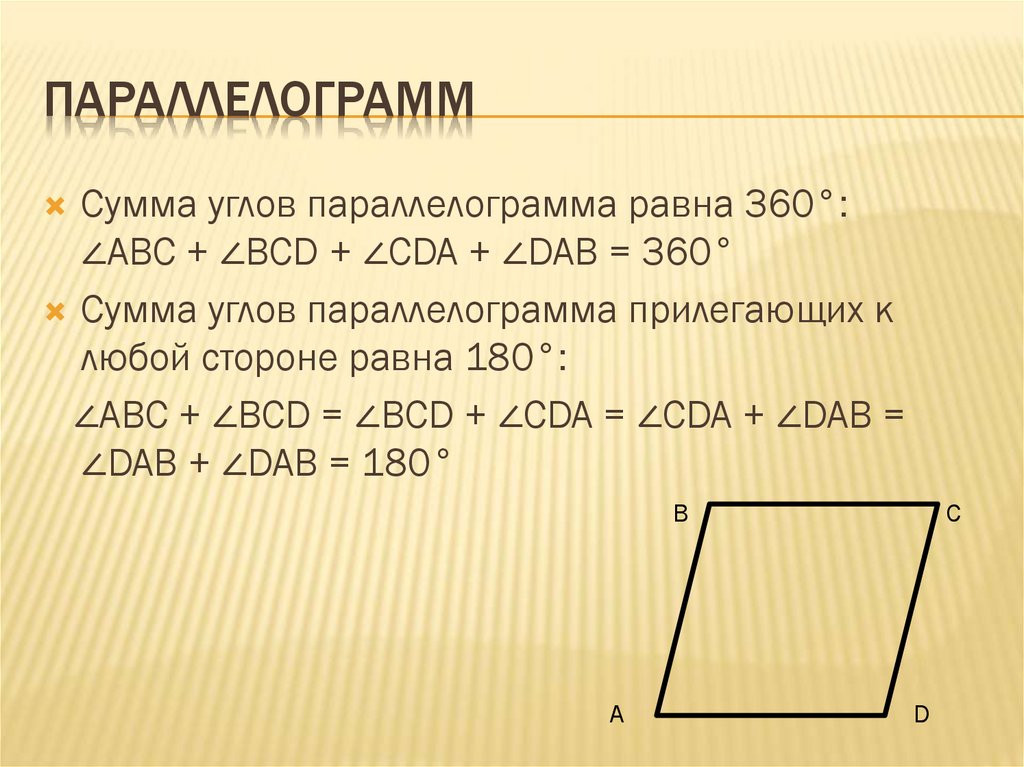
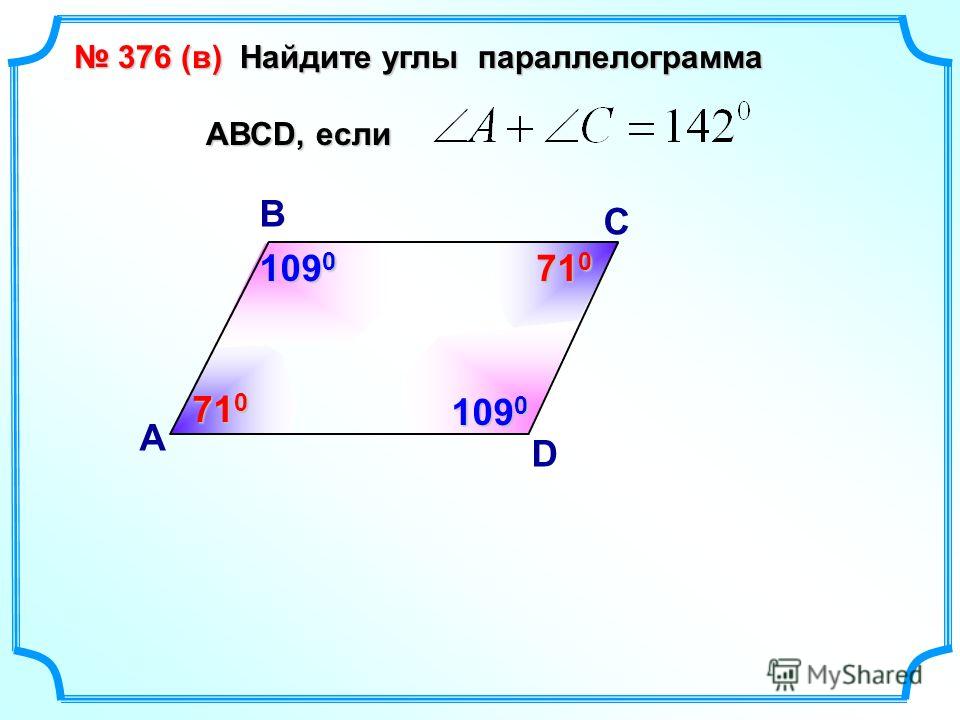
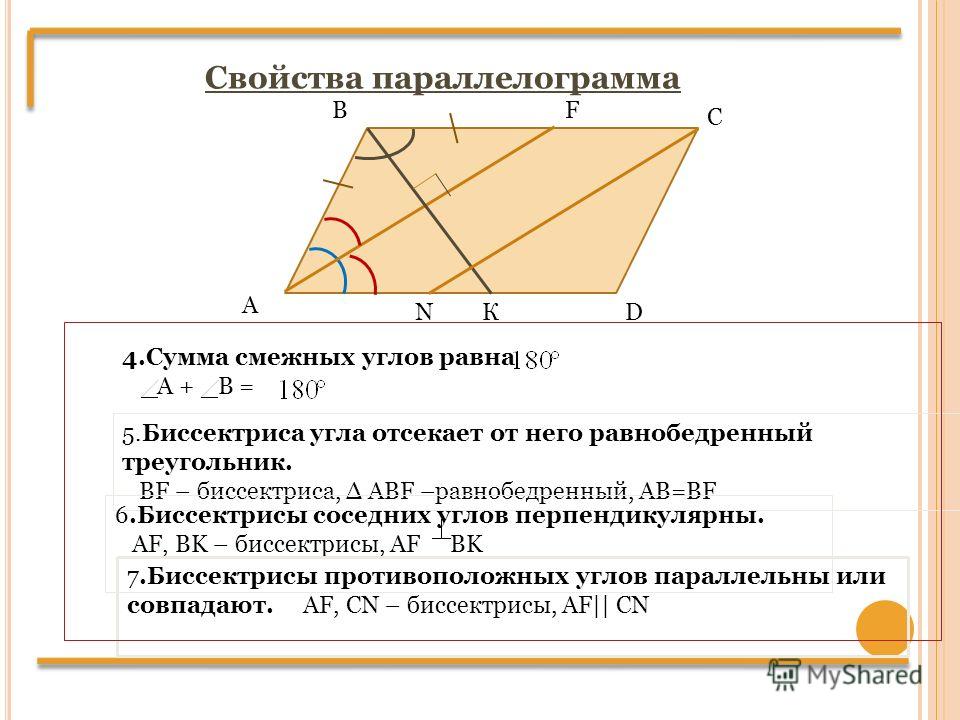
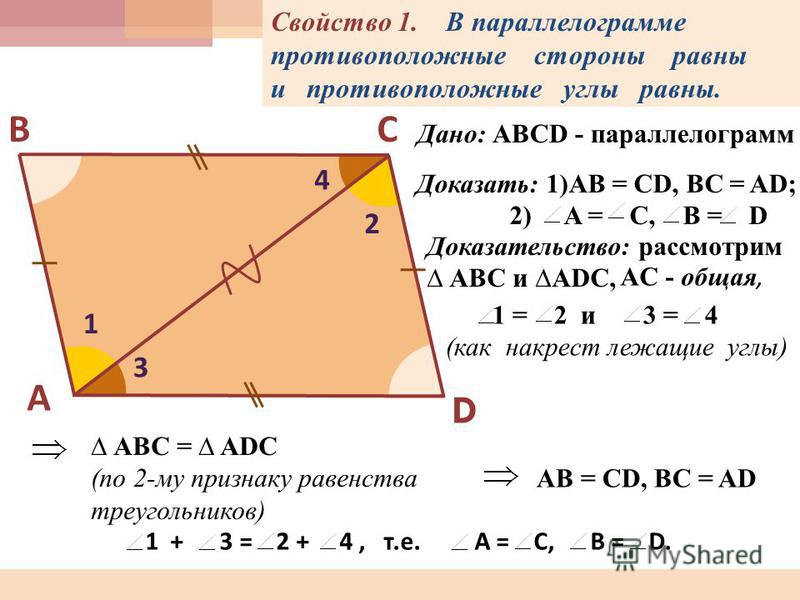
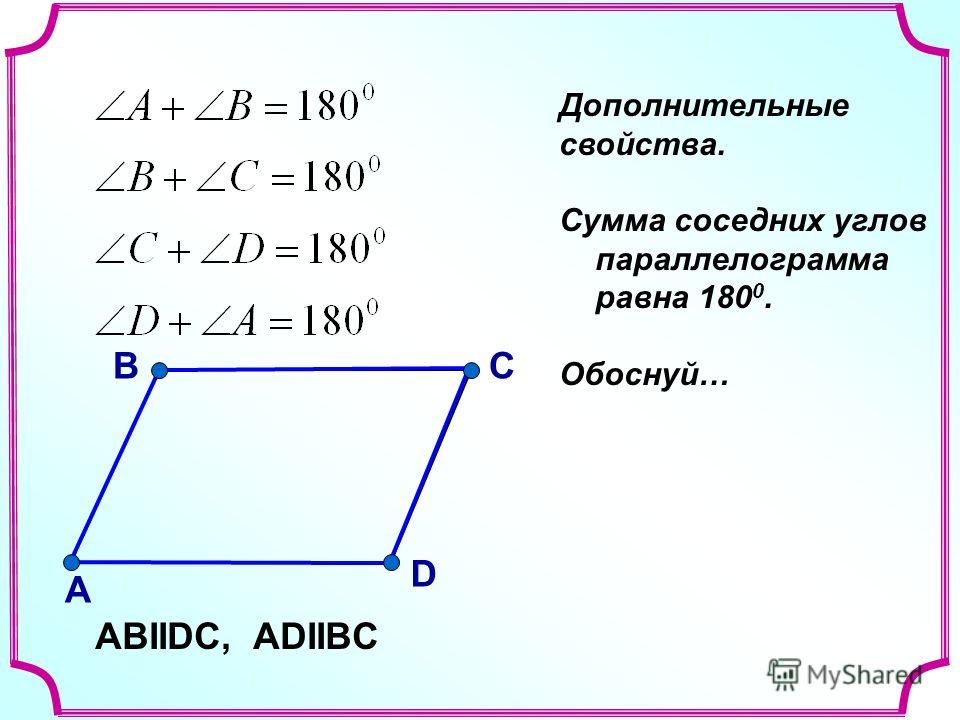 Следовательно, его можно назвать четырехугольником.
Следовательно, его можно назвать четырехугольником.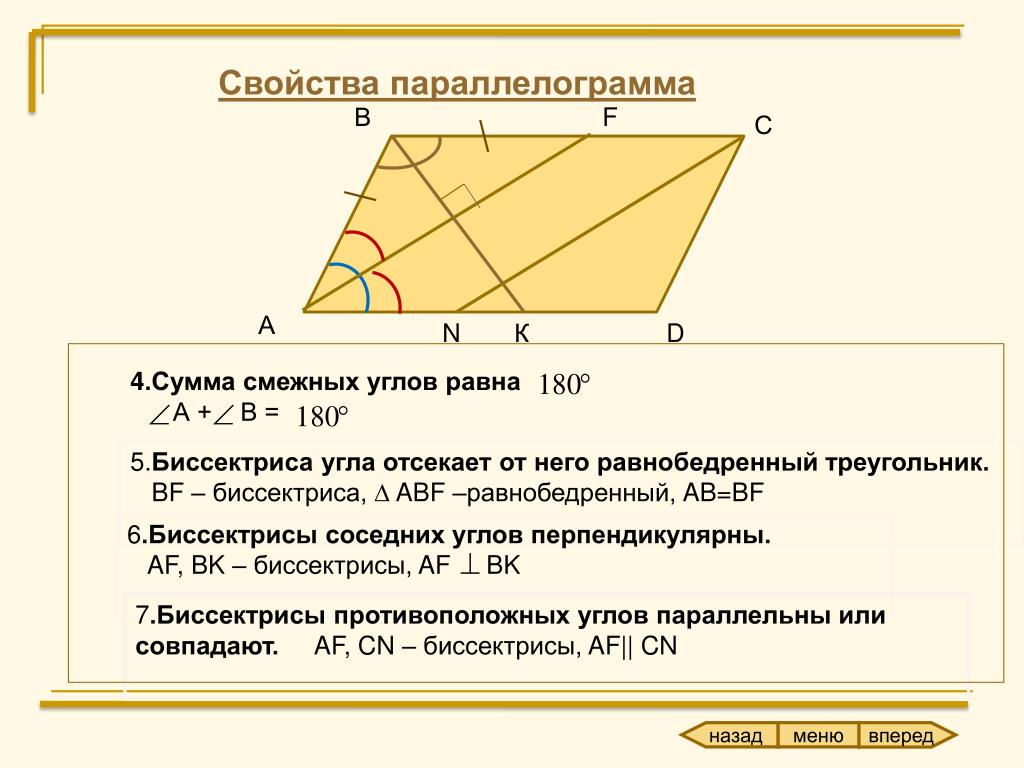 Один из способов — просто сложить измерения четырех углов и разделить на четыре. Это даст вам среднюю меру угла, которую вы затем можете использовать, чтобы найти меру каждого отдельного угла.
Один из способов — просто сложить измерения четырех углов и разделить на четыре. Это даст вам среднюю меру угла, которую вы затем можете использовать, чтобы найти меру каждого отдельного угла.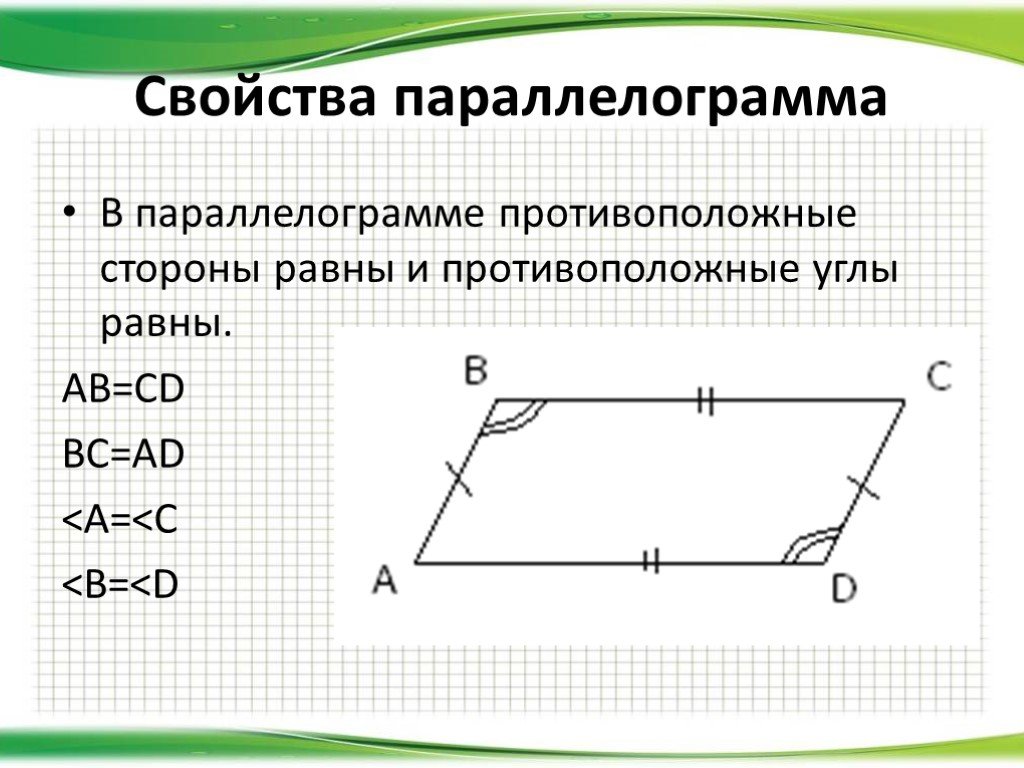 В этом сообщении блога мы рассмотрели два метода нахождения внутренних углов, а также то, как использовать эту информацию для вычисления внешних углов. Если вы когда-нибудь сталкивались с задачей по геометрии, которая включает в себя вычисление углов в параллелограмме, просто вернитесь к этому сообщению в блоге, чтобы освежить в памяти!
В этом сообщении блога мы рассмотрели два метода нахождения внутренних углов, а также то, как использовать эту информацию для вычисления внешних углов. Если вы когда-нибудь сталкивались с задачей по геометрии, которая включает в себя вычисление углов в параллелограмме, просто вернитесь к этому сообщению в блоге, чтобы освежить в памяти!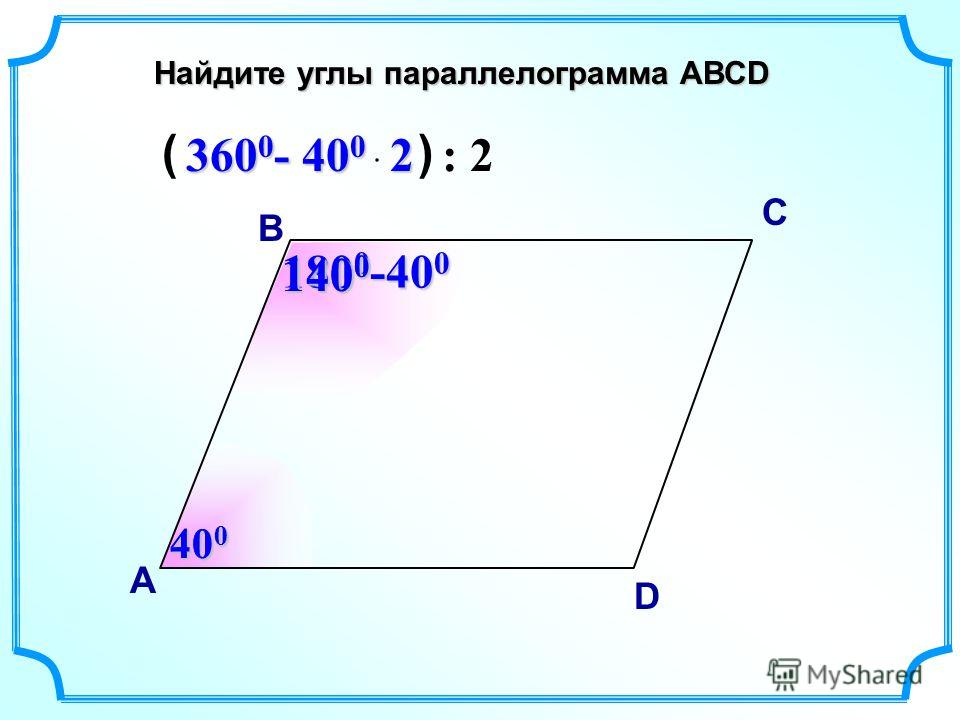 Остальные углы равны ему, поэтому вы знаете все углы параллелограмма.
Остальные углы равны ему, поэтому вы знаете все углы параллелограмма.