Автор: 
4.5. Разложение в ряд Фурье только по синусам или только по косинусам
Начнем с простого замечания: если заданная на отрезке интегрируемая функция является нечетной, то есть для всех выполняется равенство , то .
Для четной функции справедливо .
Напомним некоторые свойства четных и нечетных функций на :
Произведение двух четных или двух нечетных функций есть функция четная;
Произведение четной и нечетной функций есть нечетная функция.
Утверждение. Пусть определена и интегрируема на , а -ее коэффициенты Фурье. Тогда
если -нечетная, то
, а ряд Фурье имеет вид .
если — четная, то
,
а
ряд Фурье имеет вид
.
Допустим, что функция задана на отрезке . Если мы хотим найти разложение на этом отрезке в ряд Фурье, то сначала продолжим на симметричный промежуток произвольным образом, а потом воспользуемся формулами для коэффициентов Фурье.
Если продолжить функцию четным образом, то получим разложение только по косинусам, а если продолжить нечетным образом, то – только по синусам. При этом в первом случае продолженная функция будет иметь вид
,
а во втором случае
4.6. Разложение в ряд Фурье функции, заданной на произвольном промежутке
Пусть задана на отрезке , и на этом отрезке она кусочно-гладкая. Рассмотрим периодическую кусочно-гладкую функцию с периодом
,
которая совпадает с на , а -произвольная кусочно-гладкая функция.
Таким
образом,
была продолжена на симметричный отрезок.
Теперь для
существует разложение в ряд Фурье. Сумма
этого ряда совпадает с
во
всех точках непрерывности отрезка
,
то
есть функция
разложена
в ряд Фурье на
.
Алгоритм разложения функции в тригонометрический ряд Фурье:
выяснить формально ряд Фурье по заданию функции;
найти коэффициенты ряда Фурье;
используя теорему о достаточном условии сходимости ряда Фурье, найти сумму ряда, построить график и . Выяснить, в каких точках совпадает с .
4.7. Контрольные вопросы и задания.
Какая функция называется периодической? Является ли функция Дирихле периодической? Чему равен период? Имеет ли эта функция основной период?
Что такое тригонометрический ряд?
Какой тригонометрический ряд называется рядом Фурье?
Являются ли тригонометрические ряды и рядами Фурье?
Сформулировать достаточные условия поточечной сходимости ряда Фурье.
Записать равенство Парсеваля и неравенство Бесселя для тригонометрического ряда Фурье.
Какой вид имеет ряд Фурье для нечетной интегрируемой функции?
Какой вид имеет ряд Фурье для -периодической функции?
4.8. Образцы решения типовых задач
При нахождении коэффициентов Фурье полезно помнить:
.
Пример 1. Разложить функцию в ряд Фурье на интервале . Построить график суммы ряда Фурье. Вычислить суммы получающихся рядов, полагая .
Построим график данной функции:
Продолжим данную функцию периодически с периодом на всю прямую.
Построим график суммы ряда Фурье
Найдём коэффициенты ряда Фурье. Так как нечётная на
Итак, .
Используя полученное разложение с учётом вида графика суммы ряда Фурье, из которого видно, к чему сходится ряд в точках разрыва, найдём суммы некоторых числовых рядов.
При получим .
При получим
.
При получим
.
Пример 2. Разложить в ряд Фурье по косинусам функцию (полупериод функции равен )
Изобразим график заданной функции
Продолжим функцию чётным образом на промежутке , тогда коэффициенты .
Продолжим полученную функцию с периодом на всю прямую. Так как продолжение будет непрерывной функцией, то для график суммы ряда Фурье совпадает с графиком продолженной функции
Вычислим коэффициенты ряда Фурье
при .
Пример 3. Разложить в ряд Фурье по синусам функцию (полупериод функции равен )
Разложение функции в ряд по синусам — это ряд Фурье нечётного продолжения функции с промежутка на промежуток .
Изобразим график суммы ряда Фурье
Имеем .
КАТЕГОРИИ: Главная Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748) | Так как функция заданана отрезке , то ее можно доопределить на отрезок четным или нечетным образом. Если функция доопределена четным образом, то она, как четная функция может быть разложена по формулам для четной функции
, , . = (в точках непрерывности функции). Это – разложение в ряд Фурье по косинусам кратных дуг.
Если функция доопределена нечетным образом, то она, как нечетная функция может быть разложена по формулам для нечетной функции
, ,..
= (в точках непрерывности функции). Это – разложение в ряд Фурье по синусам кратных дуг.
Одну и ту же функцию, заданную на отрезке , можно разложить и по синусам, и по косинусам кратных дуг. Пример. Разложить по косинусам и синусам кратных дуг функцию , заданную на отрезке . Так как мы доопределяем функцию на отрезок при разложении по косинусам и синусам кратных дуг, то . Разложим функцию по косинусам кратных дуг. , , . ==1. Разложим функцию по синусам кратных дуг. , ,.. == , (теорема Дирихле).
Дата добавления: 2014-01-06; Просмотров: 10582; Нарушение авторских прав?; Мы поможем в написании вашей работы! Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет |
Дифференциальные уравнения. Косинусные ряды Фурье
Онлайн-заметки Пола
Главная
/
Дифференциальные уравнения
/
Краевые задачи и ряды Фурье
/ Косинусный ряд Фурье
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 8.5: Косинус Фурье, ряд
В этом разделе мы рассмотрим ряд косинусов Фурье. Мы начнем так же, как и в предыдущем разделе, где мы рассмотрели ряды синусов Фурье. Начнем с предположения, что функция \(f\left( x \right)\), с которой мы будем работать изначально, является четной функцией ( , т.е. \(f\left( { — x} \right) = f\left( x \right)\)) и что мы хотим написать представление этой функции в виде ряда на \( — L \le x \le L\) в терминах косинусов (которые также четны). Другими словами, мы собираемся искать следующее, 9\infty {{A_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \]
Этот ряд называется косинусным рядом Фурье и обратите внимание, что в этом случае (в отличие от синусоидального ряда Фурье) мы можем начать представление ряда с \(n = 0\), поскольку этот член не будет равен нулю, поскольку это было с синусом.
Кроме того, как и в случае ряда синусов Фурье, аргумент \(\frac{{n\pi x}}{L}\) в косинусах используется только потому, что это аргумент, с которым мы столкнемся в следующем глава. Единственное реальное требование здесь состоит в том, чтобы заданный набор функций, которые мы используем, был ортогонален на интервале, над которым мы работаем. 9{L} {\ cos \ left ( {\ frac {{n \ pi x}} {L}} \ right) \ cos \ left ( {\ frac {{m \ pi x}} {L}} \ right )\,dx}} = \left\{ {\begin{array}{*{20}{l}}{2L}&{{\mbox{if}}n = m = 0}\\L&{{\ mbox{if}}n = m \ne 0}\\0&{{\mbox{if}}n \ne m}\end{массив}} \right.\]
Мы получим формулу для коэффициентов почти точно так же, как в предыдущем разделе. Мы начнем с представления выше и умножим обе части на \(\cos\left({\frac{{m\pi x}}{L}} \right)\), где \(m\) — фиксированное целое число в диапазоне \(\left\{ {0,1,2,3, \ldots } \right\}\). Это дает 9{{\,L}}{{\cos \left({\frac{{n\,\pi x}}{L}} \right)\cos \left({\frac{{m\,\pi x }}{L}} \right)\,dx}}} \end{align*}\]
Теперь мы знаем, что все интегралы в правой части будут равны нулю, за исключением случая \(n = m\), потому что набор косинусов образует ортогональный набор на интервале \( — L \le x \le L\ ).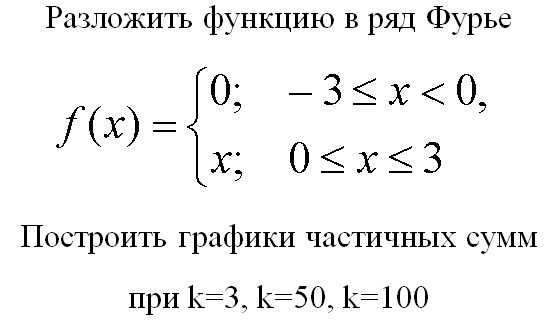
{{\,L}}{{f\left( x \right)\cos \left({\frac{{n\,\pi x}}{L}} \right) \,dx}}}&{\,\,\,\,\,n \ne 0}\end{массив}} \right.\]
92}}}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \]
Обратите внимание, что мы часто будем выбрасывать \(n = 0\) из ряда, как мы сделали здесь, потому что он почти всегда будет отличаться от других коэффициентов, и это позволяет нам фактически подставлять коэффициенты в ряд .
Теперь, как и в предыдущем разделе, давайте спросим, что нам нужно сделать, чтобы найти ряд косинусов Фурье нечетной функции. Как и в случае с рядом синусов Фурье, когда мы делаем это изменение, нам нужно будет перейти на интервал \(0 \le x \le L\) теперь вместо \( — L \le x \le L\), и снова мы будем предположим, что ряд будет сходиться к \(f\left( x \right)\) в этой точке, и оставим обсуждение сходимости этого ряда в следующем разделе.
Мы могли бы выполнить работу, чтобы найти коэффициенты здесь дважды, как мы это сделали с рядами синусов Фурье, однако в этом нет реальной причины.
Итак, хотя мы могли бы повторить всю работу выше, чтобы получить формулы для коэффициентов, давайте вместо этого сразу перейдем ко второму методу нахождения коэффициентов.
В этом случае, прежде чем мы на самом деле продолжим, нам нужно определить четное расширение функции \(f\left( x \right)\) на \( — L \le x \le L\) . Итак, для данной функции \(f\left( x \right)\) мы определим четное расширение функции как
\[g\left(x\right) = \left\{ {\begin{array}{*{20}{l}}{f\left(x\right)}&{\,\,\,\, {\mbox{if}}0 \le x \le L}\\{f\left( { — x} \right)}&{\,\,\,\,{\mbox{if}} — L \ le x \le 0}\end{массив}} \right.\]
Показать, что это четная функция, достаточно просто.
\[g\left(-x \right)=f\left(-\left(-x \right) \right)=f\left( x \right)=g\left( x \right) \hspace{0.25 in} \text{для}0 , и мы можем видеть, что \(g\left( x \right) = f\left( x \right)\) на \(0 \le x \le L\) и если \(f\left( x \ right)\) уже является четной функцией, мы получаем \(g\left( x \right) = f\left( x \right)\) на \( — L \le x \le L\). Показать все решения Скрыть все решения a \(f\left( x \right) = L — x\) на \(0 \le x \le L\) Показать решение Вот еще расширение этой функции. \[\ begin{align*}g\left(x\right) & = \left\{ {\begin{array}{*{20}{l}}{f\left(x\right)}&{\ ,\,\,\,{\mbox{if}}0 \le x \le L}\\{f\left( { — x} \right)}&{\,\,\,\,{\mbox {if}} — L \le x \le 0}\end{массив}} \right.\\ & = \left\{ {\begin{array}{*{20}{l}}{L — x} &{\,\,\,\,{\mbox{if}}0 \le x \le L}\\{L + x} &{\,\,\,\,{\mbox{if}} — L \le x \le 0}\end{массив}} \right.\end{align*}\]
93}}&{\,\,\,\,{\mbox{if}} — L \le x \le 0}\end{массив}} \right. Эскиз функции и четное расширение, c \ (f \ left ( x \ right) = \ left \ { {\ begin {array} {* {20} {l}} {\ frac {L} {2}} & {\, \, \, \ ,{\mbox{if}}0 \le x \le \frac{L}{2}}\\{x — \frac{L}{2}}&{\,\,\,\,{\mbox {if }}\frac{L}{2} \le x \le L}\end{array}} \right.\) Показать решение Вот четное расширение этой функции, \[\ begin{align*}g\left(x\right) & = \left\{ {\begin{array}{*{20}{l}}{f\left(x\right)}&{\ ,\,\,\,{\mbox{if}}0 \le x \le L}\\{f\left( { — x} \right)}&{\,\,\,\,{\mbox {if}} — L \le x \le 0}\end{массив}} \right.\\ & = \left\{ {\begin{array}{*{20}{l}}{x — \frac {L} {2}} & {\, \, \, \, {\ mbox {if}} \ frac {L} {2} \ le x \ le L} \\ {\ frac {L} {2} } & {\, \, \, \, {\ mbox {if}} 0 \ le x \ le \ frac {L} {2}} \\ {\ frac {L} {2}} & {\, \ ,\,\,{\mbox{if}} — \frac{L}{2} \le x \le 0}\\{ — x — \frac{L}{2}}&{\,\,\ ,\,{\mbox{if}} — L \le x \le — \frac{L}{2}}\end{array}} \right. Эскиз функции и четное расширение: Хорошо, давайте теперь подумаем о том, как мы можем использовать четное расширение функции, чтобы найти ряд косинусов Фурье любой функции \(f\left( x \right) \) на \(0 \le x \le L\). Итак, для функции \(f\left( x \right)\) пусть \(g\left( x \right)\) будет четным расширением, как определено выше. Теперь \(g\left( x \right)\) является четной функцией на \( — L \le x \le L\), поэтому мы можем записать ее ряд косинусов Фурье. Это, 9{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}}&{ \,\,\,\,\,n \ne 0}\end{массив}} \right.\] и обратите внимание, что мы будем использовать вторую форму интегралов для вычисления констант. Теперь, поскольку мы знаем, что на \(0 \le x \le L\) мы имеем \(f\left( x \right) = g\left( x \right)\) и, следовательно, ряд косинусов Фурье \(f\left( x \right)\) на \(0 \le x \le L\) также определяется как \[f\left( x \right) = \sum\limits_{n = 0}^\infty {{A_n}\cos \left( {\frac {{n\,\pi x}}{L}} \ справа)} \ hspace {0,25 дюйма} {A_n} = \ left \ { {\ begin {array} {* {20} {l}} {\ displaystyle \ frac {1} {L} \ int_ {{\, 0 }}^{{\,L}}{{f\left( x \right)\,dx}}}&{\,\,\,\,\,n = 0}\\{\displaystyle \frac{ 2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}} {L}} \right)\,dx}}}&{\,\,\,\,\,n \ne 0}\end{массив}} \right. Наконец, давайте кратко рассмотрим кусочную функцию. Пример 5. Найдите ряд косинусов Фурье для \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{L}{2}}&{ \,\,\,\,{\mbox{if}}0 \le x \le \frac{L}{2}}\\{x — \frac{L}{2}}&{\,\, \,\,{\mbox{if}}\frac{L}{2} \le x \le L}\end{array}} \right.\) на \(0 \le x \le L\). Показать решение
9{\pi/2} \cos(x)\,dx=\frac 4 \pi.$$
$$\tag{1}$$ График $\cos x$ (пунктирная линия) и $|\cos x|$ (сплошная линия) в интервале $[-\pi,\pi]$. Коэффициенты $b_n=0$ как вы заключили. Что касается коэффициентов $a_n$, то только нечетные равны $0$ (см. ниже). Функции $\cos(x)$ и $\cos(nx)$ ортогональны в интервале $[-\pi,\pi]$, но $|\cos(x)|$ и $\cos(nx) $ нет. Начиная с \begin{equation*}
\left\vert \cos (x)\right\vert =\left\{
\начать{массив}{с}
\cos (х) \\
-\cos (х)
\конец{массив}
\начать{массив}{с}
\текст{если} \\
\текст{если}
\конец{массив}
\начать{массив}{с}
0\leq х\leq \пи /2 \\
\pi /2\leq x\leq \pi,
\конец{массив}
\верно.
3}\) на \(0 \le x \le L\)
\end{align*}\]
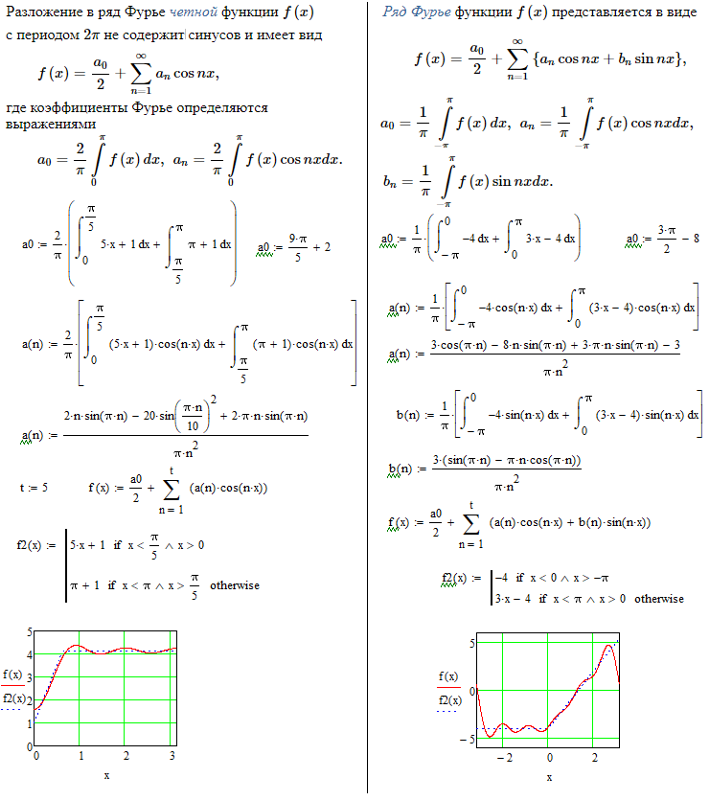\end{align*}\]
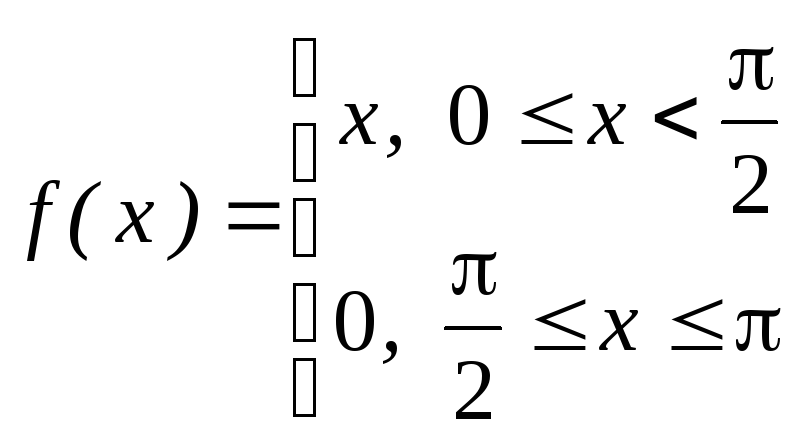3}\) на \(0 \le x \le L\).
9n}} \right)\cos \left( {\frac {{n\,\pi x}}{L}} \right)} \]
В ходе мероприятия был представлен основной ассортимент оборудования ZONT и рассмотрены особенности подбора конкретной модели. Подробно разобрали вопросы подключения термостатов и контролеров ZONT и ключевые моменты в настройке системы.
09.2020
руб
Они хранят информацию, которая помогает разработать конкретный профиль для показа рекламы, которая будет интересна именно вам.
Аналогичные технологии хранения информации могут использоваться для защиты данных вашей учетной записи или для выявления нестандартных действий при использовании браузера в целях предотвращения несанкционированного доступа к вашей учетной записи, а так же для оценки эффективности функционирования веб-сайтов, сервисов, приложений или иных инструментов.
1 Найти корни (нули) : F(x) = x 2 Калькулятор корней полиномов 5 представляет собой набор методов, направленных на нахождение значений x, для которых F(x)=0 
00
00
В нашем случае это означает, что 
(x) = x 4 +2x 3 +4x 2 +8x+16
00
00
)
)
)
)
)
)
)
)
09.17
2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
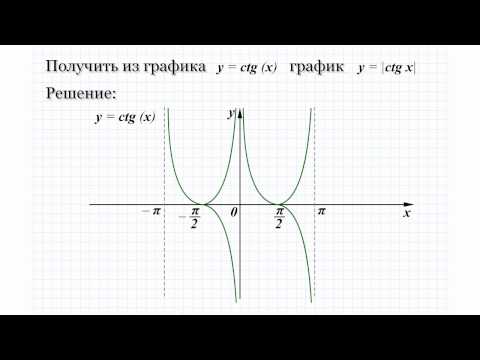
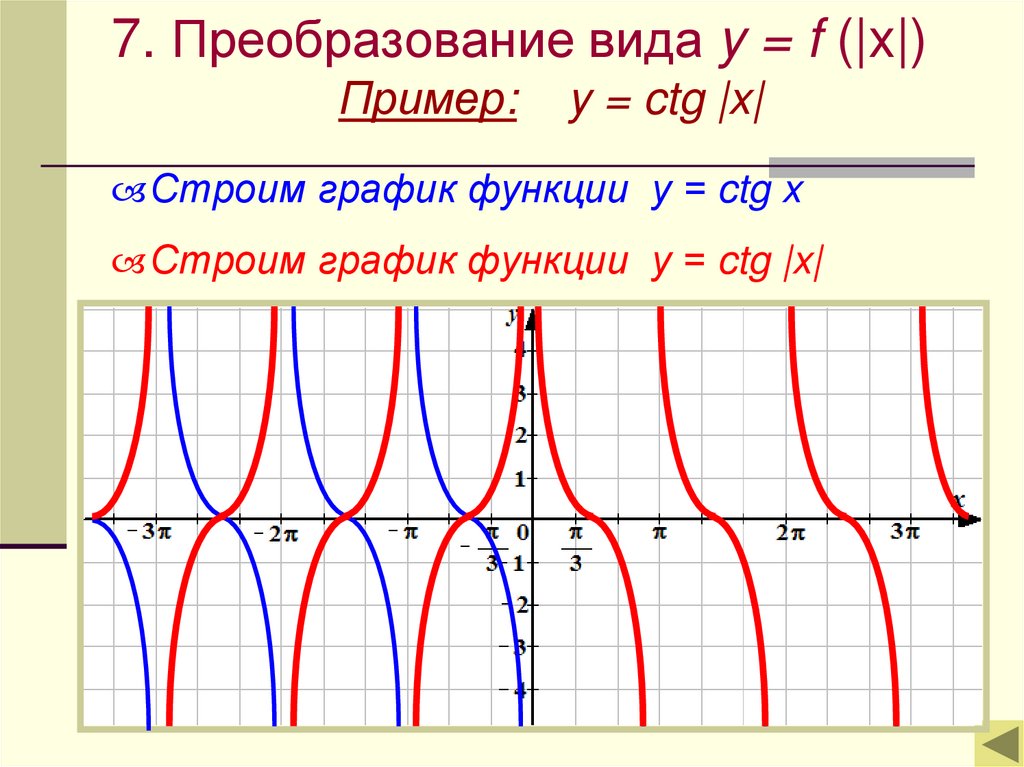
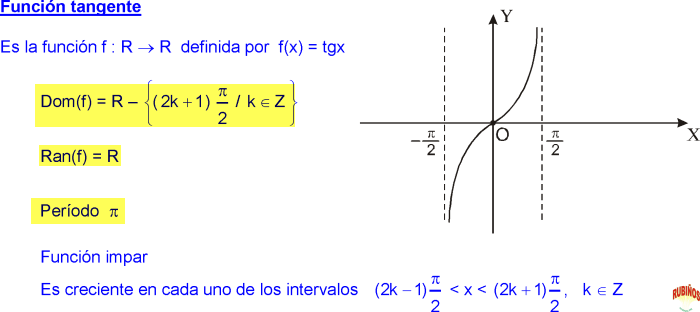
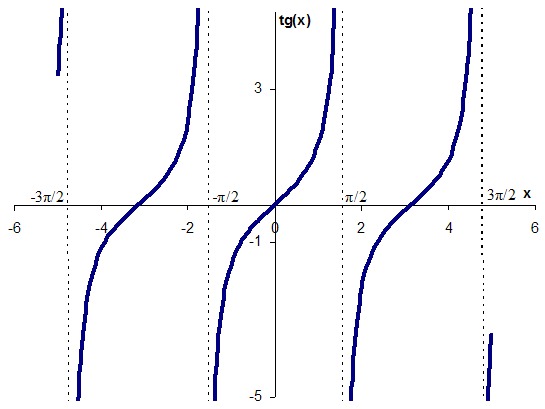
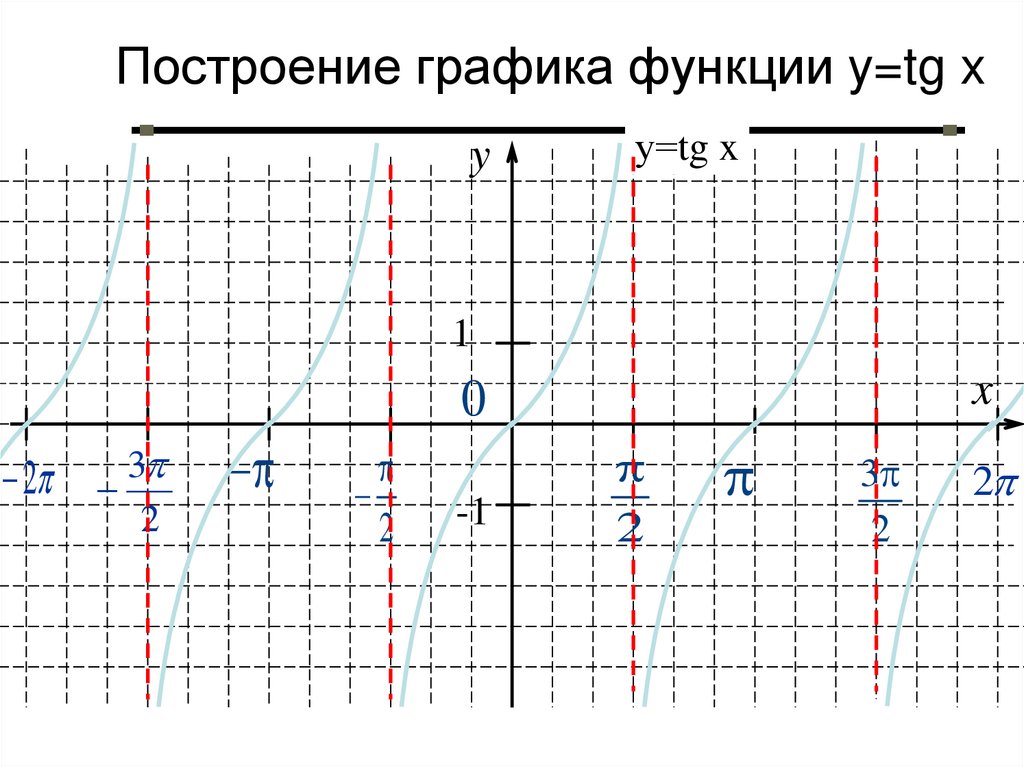
)/3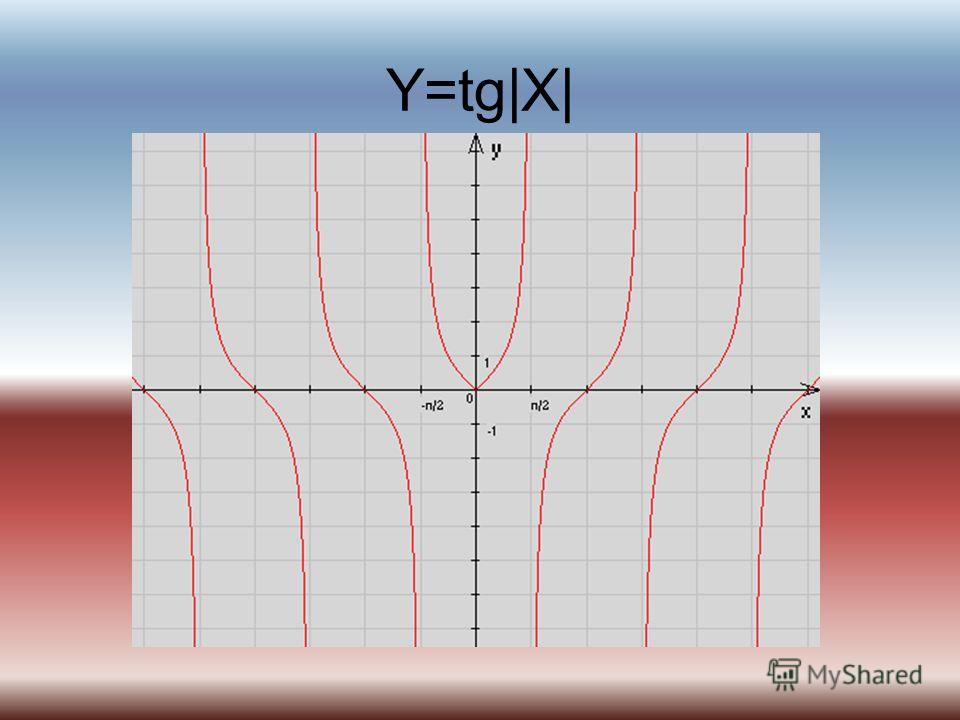
Следующее тригонометрическое соотношение, которое мы рассмотрим, — это отношение тангенса. Но значения касательной трудно отобразить на единичной окружности. Это связано с тем, что тангенс формируется путем деления значения единичного круга для синуса на его значение для косинуса, каждое из которых иногда равно нулю, а мы не можем делить на ноль.
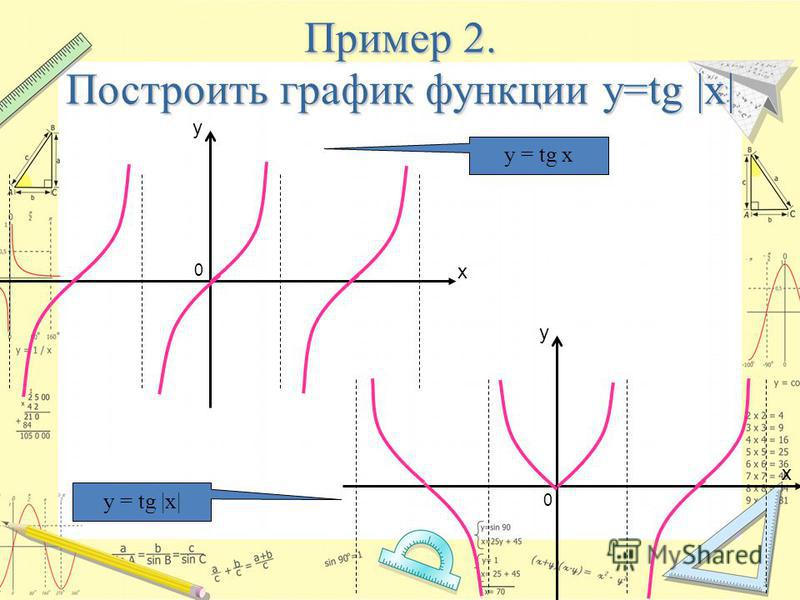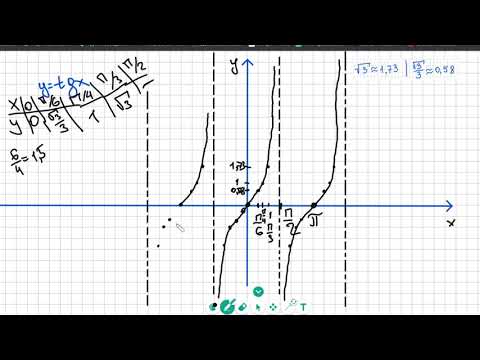
Таким образом, тангенс будет иметь вертикальные асимптоты везде, где косинус равен нулю. Придерживаясь того же интервала от -π до 2π, вертикальные асимптоты будут при -π/2, π/2 и 3π/2. Другими словами, между каждым числом, кратным π, будет вертикальная асимптота.
Рассмотрим интервал между нулем в точке 0π и асимптотой в точке ½π.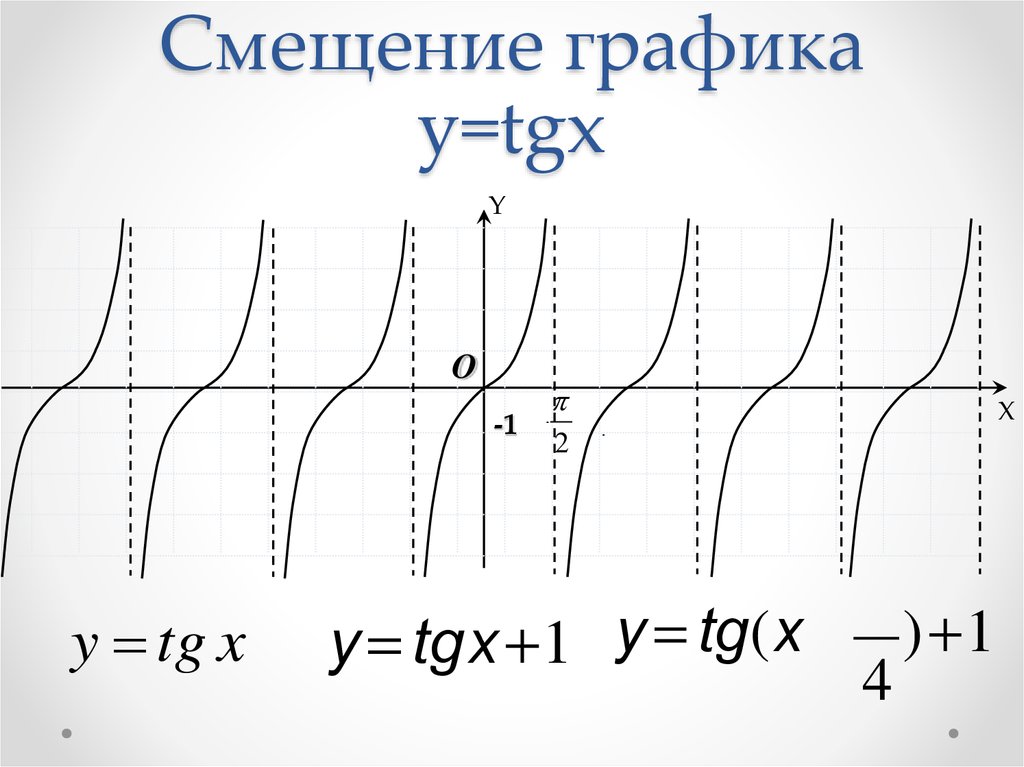
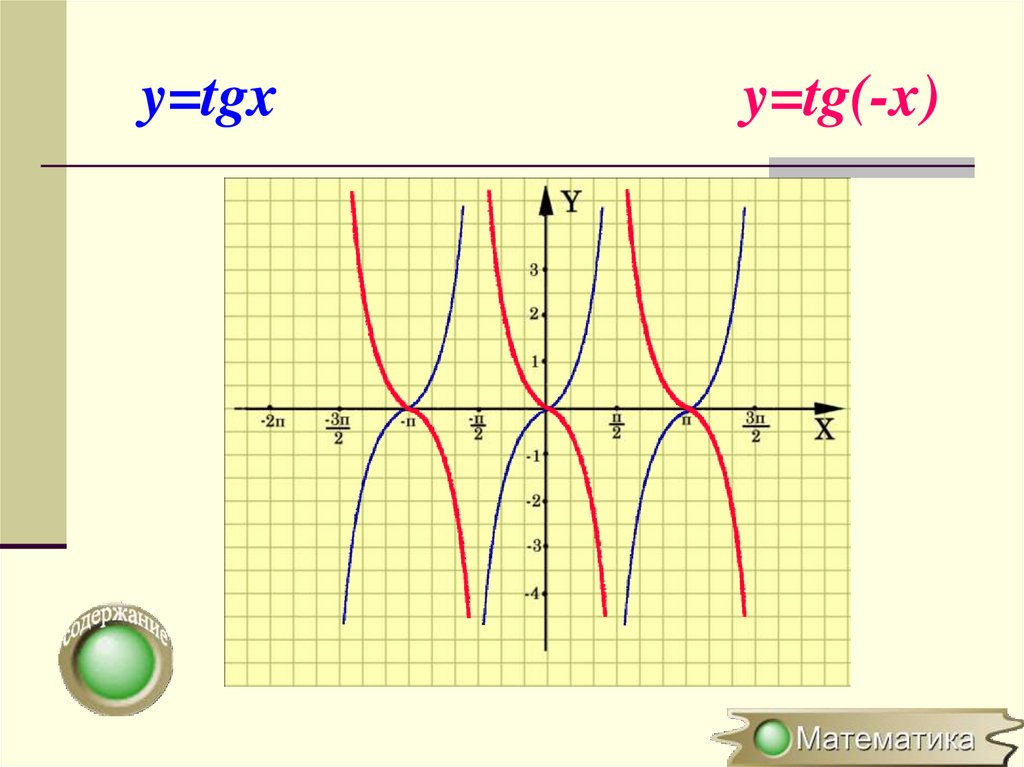
Давайте нарисуем этот бит: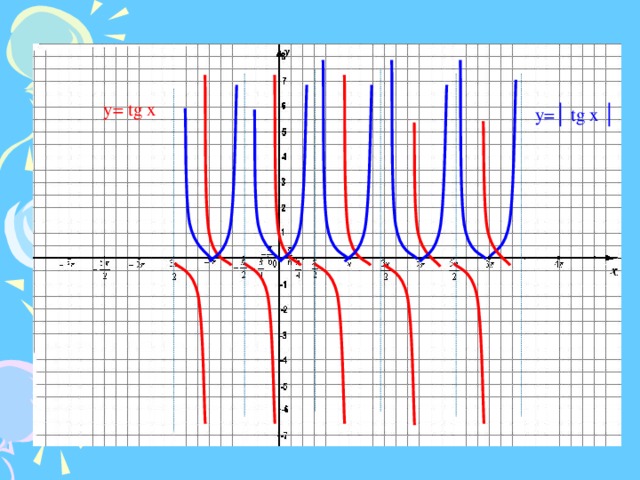
Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».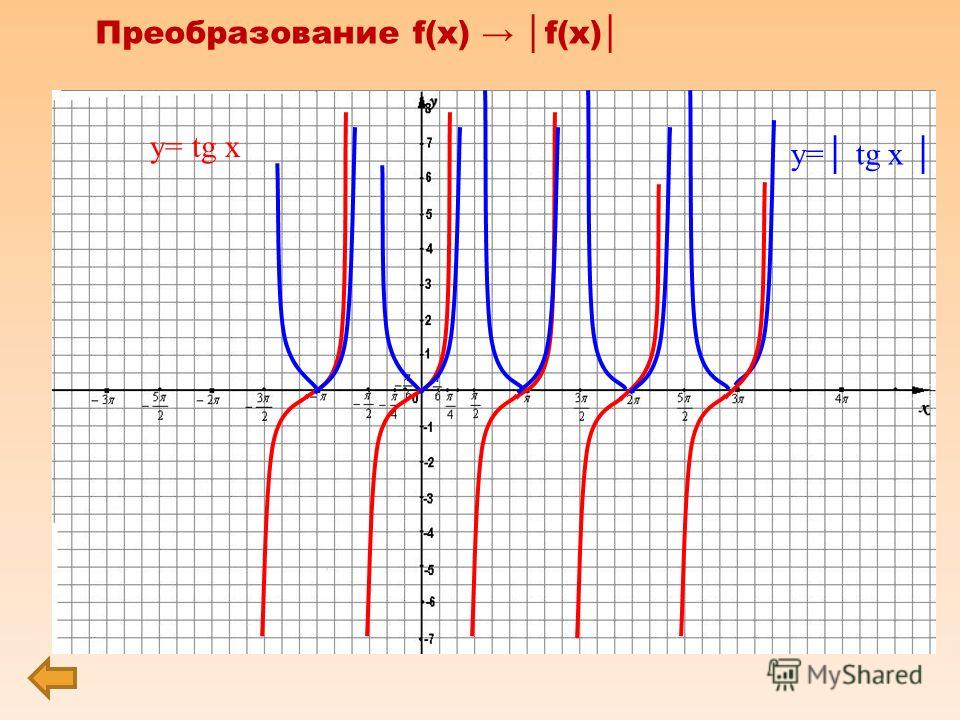
Целую часть вычитаем из целой части, а дробную часть из дробной.
2) Условие
Если дробная часть уменьшаемого меньше дробной части вычитаемого, сначала надо занять единицу у целой части, представить ее в виде дроби, у которой числитель равен знаменателю, и прибавить эту дробь к дробной части уменьшаемого.
Зубарева И.И.Параграф 43.Задание 760. – Рамблер/класс
Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
..
Книга 1: Великое ограбление хомяка
Проверьте веб-браузер
настройки, чтобы убедиться, что он включен.
На одном чертеже 1/4 дюйма может представлять собой 1 фут на фактическом здании, что соответствует масштабу 1/48. На другом чертеже 1/8 дюйма может представлять 1 фут, что составляет 1/9 дюйма.6 масштаб.
Цифры на шкале читаются в футах и дюймах в соответствии с соответствующей шкалой. Например, в масштабе 1/4 каждый фут, написанный на шкале, находится на расстоянии трех дюймов друг от друга.
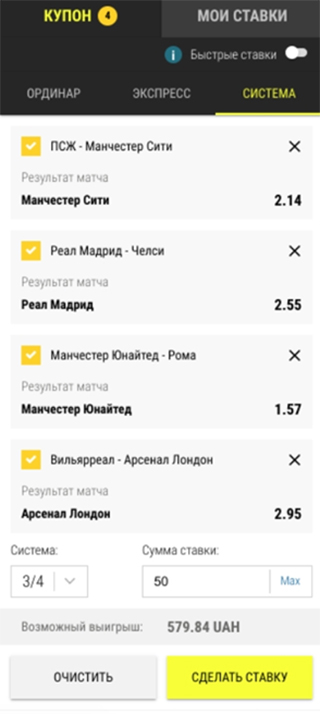
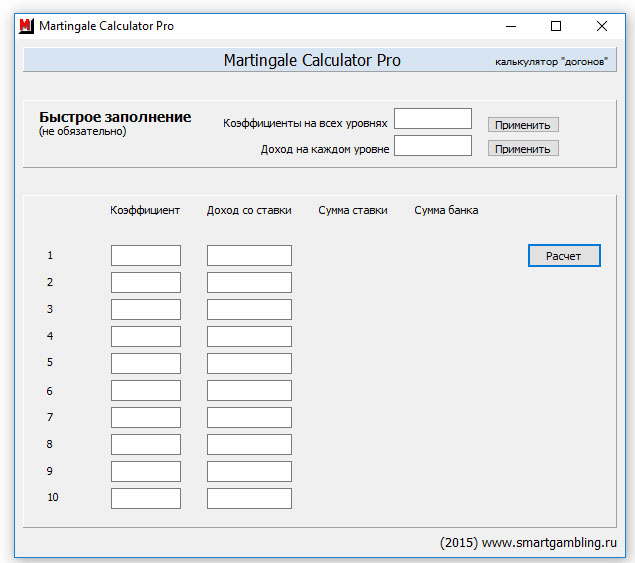Однако, более масштабные системы самостоятельно посчитать очень сложно, ввиду чего и рекомендуется воспользоваться специальным инструментом. При помощи калькулятора системы ставок вы сможете считать пари, содержащие до 12 исходов.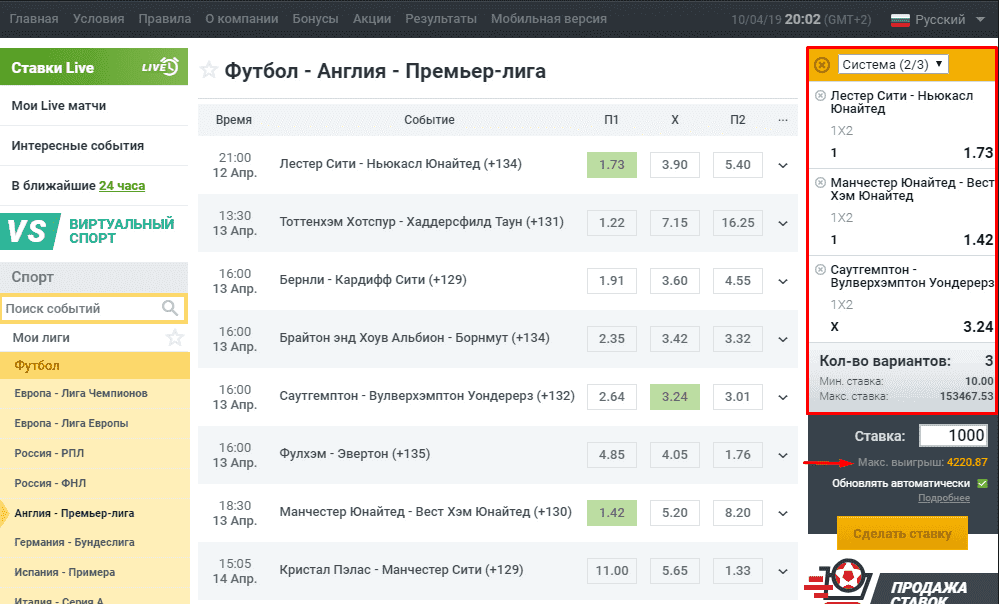
Следует внести информацию в три строки:
Ведь они в значительной степени упрощают жизнь всем любителям ставок. И если вы относитесь к их числу, то мы настоятельно рекомендуем их к использованию. А если вы лишь начинаете свой путь в сфере букмекерских контор, то просто посетите нашу школу ставок, чтобы полностью освоить все азы беттинга и начать заключать пари как профессионалы. На это пока нет времени? Тогда рекомендует перейти в раздел с бесплатными прогнозами на спорт от экспертов и заключать ставки на их основании, зарегистрировавшись на сайте одного из легальных российских букмекеров!
Совершенно нет смысла тратить время на проведение расчетов для более сложных систем.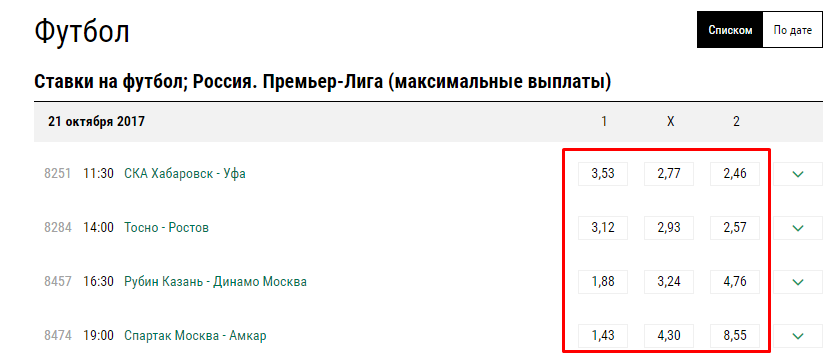
Вы узнаете нужные результаты за несколько секунд.
Результаты демонстрируются в специальной таблице, где показываются и промежуточные результаты, которые букмекеры зачастую скрывают.
– Краткая версия: выберите систему – введите коэффициенты – вычислите 
С системной ставкой катастрофа проигрыша вашей ставки не произошла бы если бы не удалась только одна нога. С помощью системной ставки в приведенном выше примере на аккумулятор с четырьмя ногами, например, вы выиграли бы денег или, по крайней мере, не проиграли бы так много в любом случае.
Поэтому ставка на две из трех систем сработала в вашу пользу.
Как правило, вы обнаружите, что вам следует поставить бонус бесплатной игры на огромных проигравших, а затем сделать хедж-ставку в другом месте, чтобы зафиксировать безрисковую прибыль. Этот калькулятор бесплатной игры поможет вам сориентироваться в сложном мире бонусов бесплатной игры.
Возможно, вам придется перевернуть его 5 раз, 10 раз, 12 раз или более, прежде чем эти деньги станут доступными для вывода. Затем вы можете использовать стратегии хеджирования или арбитража, чтобы обеспечить себе безрисковую прибыль после выполнения требования о пролонгации.
Вы должны ввести 200 долларов в поле «Размер бесплатной игры» и +200 в поле «Линия бесплатной игры». Если вы найдете -215 на Patriots в букмекерской конторе B, вы должны ввести это значение в поле Hedge Line. Затем нажмите «Рассчитать», и он быстро сообщит вам оптимальную сумму, которую вы должны поставить на Патриоты в букмекерской конторе B, чтобы максимизировать свою безрисковую прибыль. В этом случае вам нужно будет поставить 273,02 доллара на Патриотов в букмекерской конторе B, чтобы зафиксировать прибыль в размере 126,9 доллара.8, независимо от того, какая команда победит.
Например, десятичные коэффициенты 200,0000 будут введены как «d200» или «0200».
Это в равной степени относится и к новичкам, которые хотят зарегистрироваться в лучших онлайн-букмекерских конторах, и к опытным игрокам, которые хотят воспользоваться новыми интересными бонусами, и ко всем, кто находится между ними.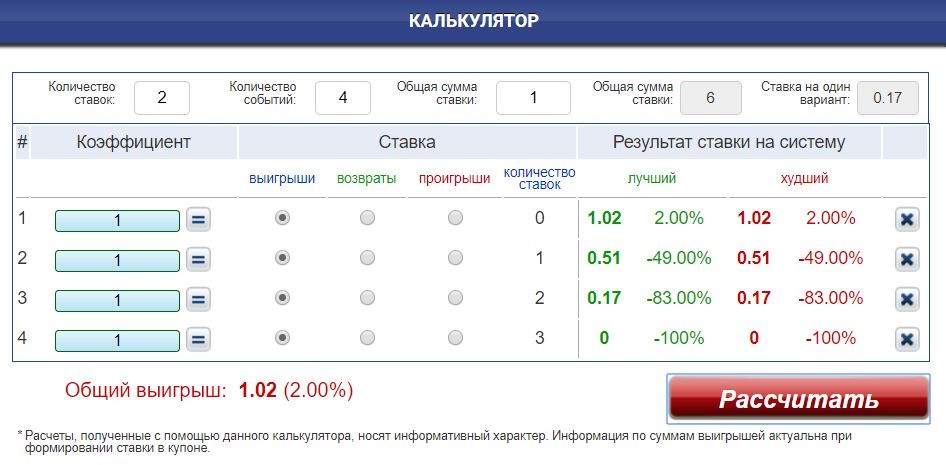
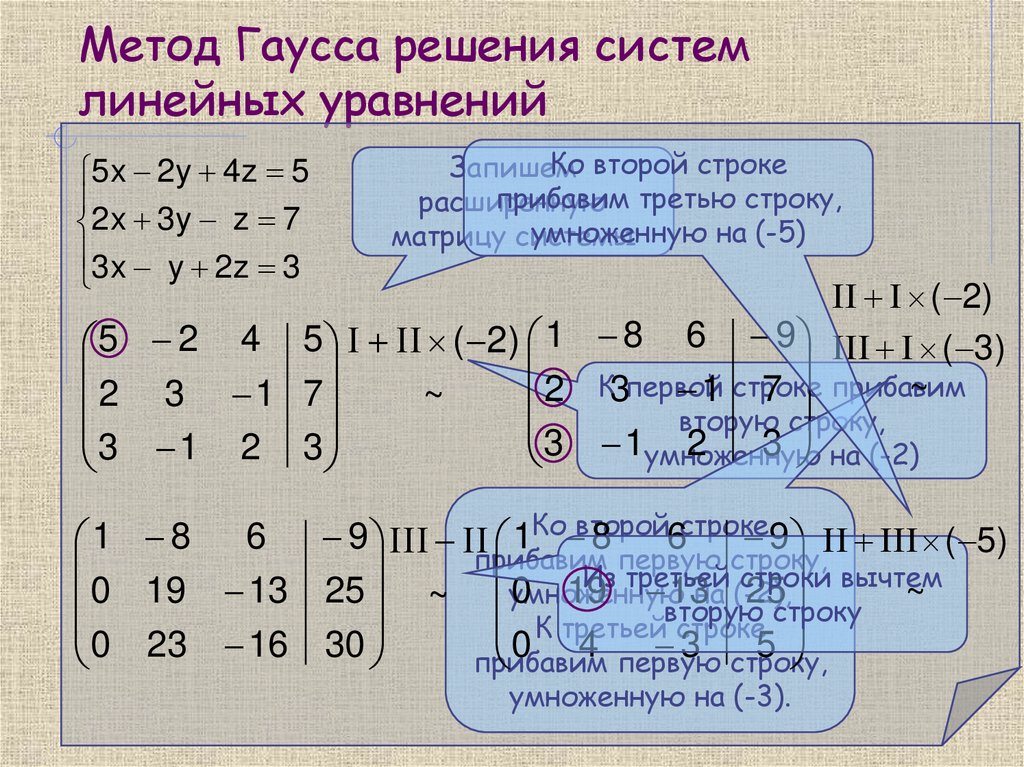
Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Добавим 4-ую строку к 3-ой:
Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя 5.1.с и к методу нахождения ранга матрицы (раздел 5.8). Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.
Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.
д.
В предыдущем примере , базисный минор расположен в строках с номерами 1, 2, столбцах с номерами 2, 5. 
Получим
При наличии в этом уравнении всех неизвестных эта подстановка почти всегда покажет наличие ошибки, если таковая была допущена. 
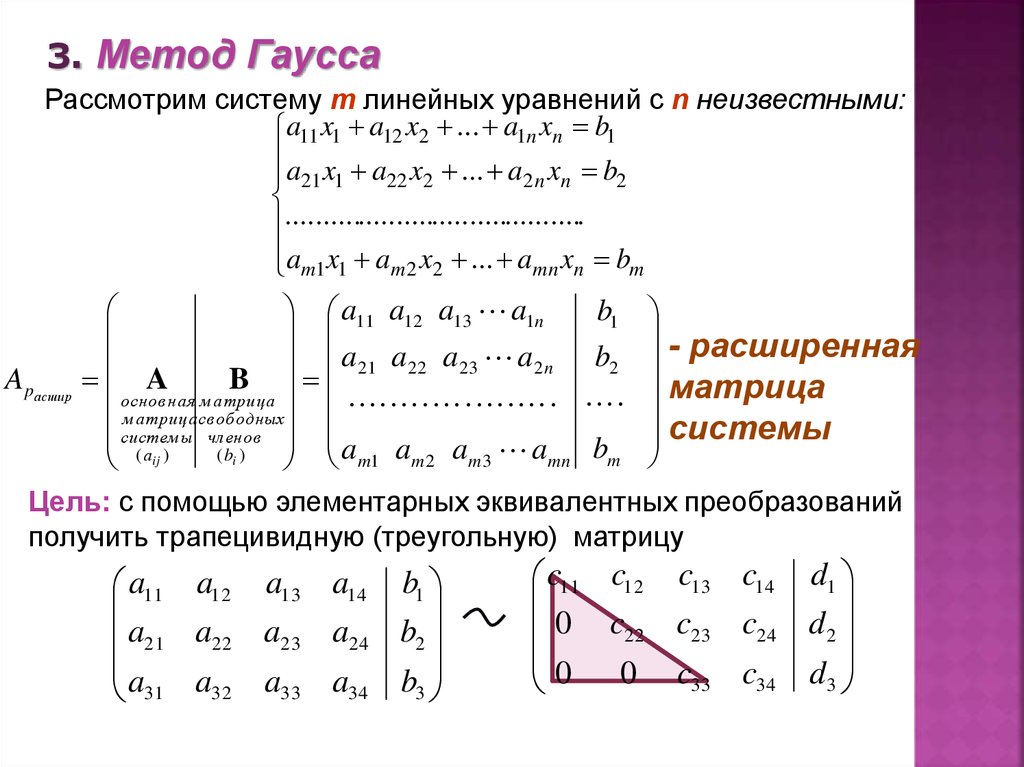
Эти два уравнения несовместимы, поэтому система не имеет решений. Вы можете видеть это при выполнении исключения Гаусса:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 &-2 &3 &2\\
2&-3&8&7\\
3 &-4 &13& 8\\
\end{массив}\right) &\stackrel{R_2-2R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
3 и -4 и 13 и 8
\end{массив}\right) \stackrel{R_3-3R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 2
\конец{массив}\справа)\\
&\stackrel{R_3-2R_2}{\longrightarrow} \left(\begin{array}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и -4
\end{массив}\right) \stackrel{-\frac{1}{4}R_3}{\longrightarrow}
\left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
И коэффициент, и расширенная матрица теперь имеют эшелонированную форму строк: первый ненулевой элемент каждой строки — это $1$, и $1$ в каждой строке появляется справа от $1$ в предыдущей строке, и все строки $0$ находятся внизу.
com/watch?v=Fp4n7Qk221U”
710
Этот универсальный онлайн-калькулятор дробей позволяет невероятно легко вводить, решать и показывать арифметические задачи из алгебры, дискретной математики, исчисления, линейной алгебры и исчисления с несколькими переменными. Вы даже можете вводить задачи с помощью камеры, что дает вам возможность быстро просмотреть свои задания.
Камера вашего мобильного устройства используется программой Photomath для быстрого сканирования и решения математических задач.
В знак признания высокой степени надежности в качестве справочного инструмента EAS присваивает калькулятору множественных дробей плюс 4 звезды.
06.2005 
07.2001 
Знаю, как бы странно это не звучало, но на самом деле Алгебратор мне очень помог.
Я никогда не был в школе с высоким рейтингом, но все из-за этого программного обеспечения мои навыки решения математических задач даже лучше, чем у студентов, обучающихся в одной из этих модных школ.
Но вопрос, где взять? Любой?
Я настоятельно рекомендую использовать его, чтобы помочь улучшить навыки решения проблем.
Мне конкретно нужно, чтобы так было. Поэтому, пожалуйста, не предлагайте мне изменить подпись. 😉
meshgrid(x, y)
Z = (XY)**2
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
plt.show()
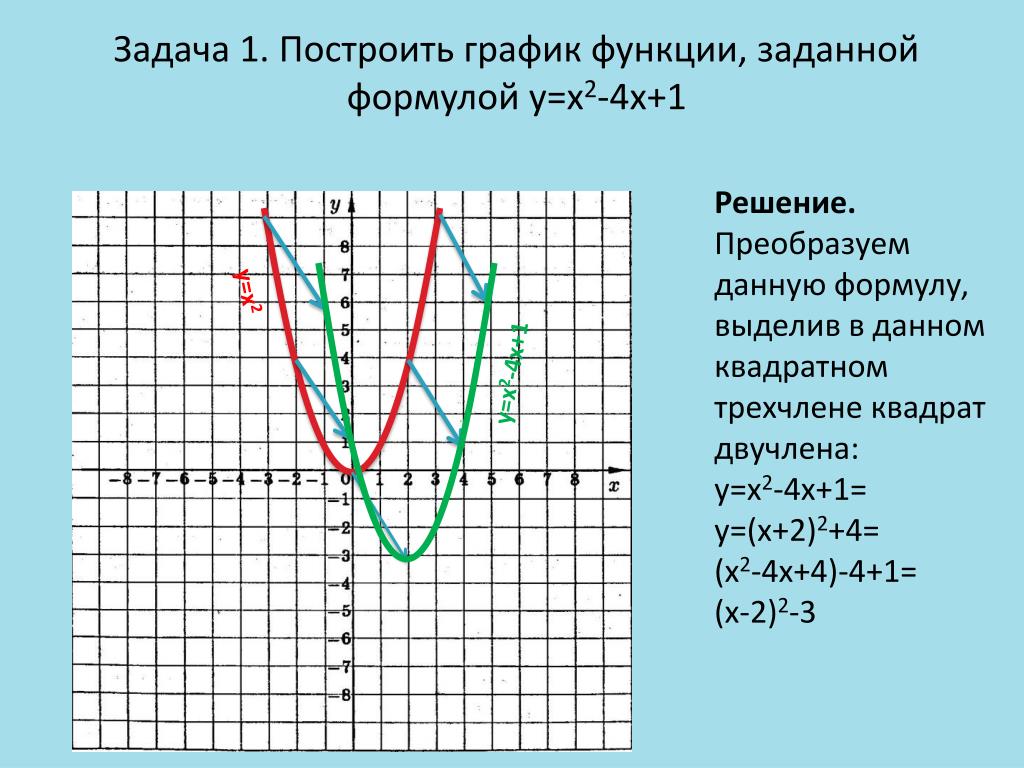
Аналогично найдётся такая точка x2, в которой значение функции
будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).
Для каждого значения аргумента xиз этого промежутка функция y=f(x) имеет
определенное значение.
Таким образом,
е. будет функцией времени.
Составим
отношение и заметим, что .
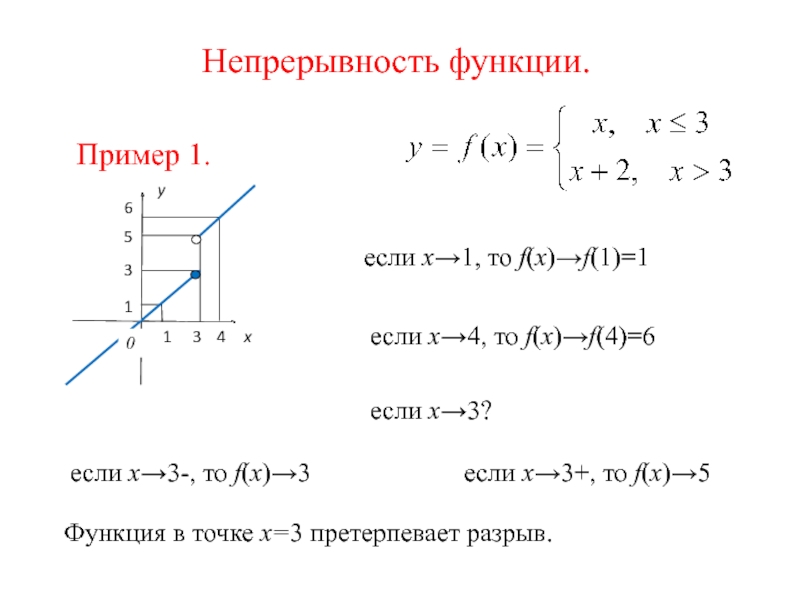
В точке A графика нет определенной
касательной, но есть две различные односторонние касательные с угловыми коэффициентами
к1
и к2. Такой тип точек
называют угловыми точками.
Следовательно, Δy = f(Δx) – f(0) = |Δx|
Поскольку два предела не согласуются, предел как \(z \to 0\) не существует!
\nonumber \]
Причина: это понятно, и именно по этой причине мы определили переходы для arg. Мы должны удалить отрицательную вещественную ось, потому что \(\text{Arg} (z)\) прыгает на \(2 \pi\), когда вы ее пересекаете. Мы также должны удалить \(z = 0\), потому что \(\text{Arg} (z)\) даже не определено в 0,
mit.edu/courses/mathematics/18-04-complex-variables-with-applications-spring-2018
