Конвертировать JPG в PDF онлайн
Преобразование JPG файлов в PDF
Выберите файлКак сконвертировать PDF в JPG?
Шаг 1
Выберите JPG файл или перетащите его на страницу.
Шаг 2
Выберите PDF или любой другой формат, в который вы хотите конвертировать файл (более 50 поддерживаемых форматов)
Шаг 3
Выберите ориентацию и размер страниц и другие параметры конвертации, если это необходимо.
Шаг 4
Подождите, пока ваш PDF файл сконвертируется и скачайте его или экспортируйте его в Dropbox или Google Drive.
О нашем сервисе
Как пользоваться 2pdf.com
Перетащите файл PDF на страницу и выберите действия, которые хотите с ним выполнить. Вы можете преобразовать PDF-файл в другие форматы, уменьшить размер PDF-файла, объединить несколько PDF-файлов в один или разделить на несколько отдельных файлов. Все сервисы бесплатны и работают онлайн, вам не нужно ничего устанавливать на свой компьютер.
Вам не нужно беспокоиться о безопасности файлов.
Ваши загруженные файлы будут удалены сразу после преобразования, а преобразованные файлы будут удалены через 24 часа. Все файлы защищены от доступа третьих лиц, никто кроме вас не может получить к ним доступ.
Конвертер PDF для всех платформ
2pdf.com работает во всех браузерах и на всех платформах. Вы можете конвертировать, соединять, вращать, разделять PDF-файлы без необходимости загружать и устанавливать программы.
Гарантия качества
Протестируйте и убедитесь сами! Для обеспечения наилучшего качества преобразования PDF — лучший поставщик решений на рынке.
Преобразование файлов PDF в различные форматы
Преобразуйте свои изображения, документы и электронные таблицы в PDF и наоборот. Мы поддерживаем более 120 направлений конвертации из PDF.
Доступ из любого места
Наш конвертер PDF можно использовать везде, где есть доступ в Интернет. Процесс конвертации происходит в облаке и не потребляет ресурсов вашего устройства.
Упорядочить PDF
Редактировать PDF
Редактировать метаданные PDF
Объединить PDF
Разделить PDF
Поворот страниц PDF
Улучшить PDF
Конвертировать из PDF
pdf в wmf
pdf в pcx
pdf в ps
pdf в pict
pdf в tif
pdf в gif
pdf в jpeg
pdf в pgm
pdf в tga
pdf в dwg
pdf в fax
pdf в palm
pdf в psd
pdf в tiff
pdf в bmp
pdf в ppm
pdf в ico
pdf в odg
pdf в jpg
pdf в svg
pdf в djvu
pdf в eps
pdf в dst
pdf в png
pdf в emf
pdf в ttf
pdf в dxf
pdf в vsd
pdf в ai
pdf в dwf
Более
Преобразовать в PDF
dxf в pdf
svg в pdf
webp в pdf
gif в pdf
pcx в pdf
dwg в pdf
xwd в pdf
mng в pdf
ppm в pdf
eps в pdf
jpg в pdf
wmf в pdf
fax в pdf
cr2 в pdf
pnm в pdf
dst в pdf
odg в pdf
pict в pdf
jpeg в pdf
tiff в pdf
sfw в pdf
bmp в pdf
cdr в pdf
png в pdf
tif в pdf
xcf в pdf
dcm в pdf
pwp в pdf
cgm в pdf
heic в pdf
raw в pdf
djvu в pdf
emf в pdf
psd в pdf
ai в pdf
dng в pdf
ps в pdf
vsd в pdf
jfif в pdf
Более
Преобразование JPG в PDF бесплатно онлайн
Перетащите файлы сюда или нажмите, чтобы загрузить.
Используйте Ctrl или Shift, чтобы добавить несколько файлов одновременно
Оцените нас из 5
4.1 / 5 (3903)
No votes so far! Be the first to rate this post.
We are sorry that our service was not useful for you!
Let us improve service!
Tell us what issue you are facing?
- Почему конвертировать JPG в PDF?
- Как конвертировать JPG в PDF онлайн?
- Почему наш онлайн инструмент является лучшим JPG в PDF конвертер?
- Вопросы и ответы
У вас есть важный файл образа, который нужно отправить в виде файла PDF для своего клиента, поставщика, университет, или применения к работе, интересно, как конвертировать JPG в PDF и запутать, что делать?
Не волнуйтесь !!
Вам не нужно тратить слишком много времени и рыть для быстрого решения.
У нас есть быстрое решение преобразования JPG в PDF; Pngtopdf.net лучший JPG в PDF конвертер , который позволяет превратить JPG изображений в PDF с самым передовым онлайным конвертером непринужденно.
Независимо от того, используете ли вы операционную систему Windows, или макинтош IOS, вы можете конвертировать JPG в PDF с одним щелчком мыши.
Кроме того, сайт позволяет конвертировать JPG в PDF файлы без ущерба для его качества; она выглядит так же, как и оригинальные изображения.
JPG является формат файла изображения и PDF является печать дружественный формат документа. Лучше всего в PDF, оно может держать оба изображения и текст, а также.
JPG и форматы PDF файлов очень компактные, более годные к употреблению форматов файлов в Интернете.
JPG стандартный формат файла, который наиболее часто используется для отображения графики на веб-сайтах, JPG, как правило, имеет меньшие размеры файлов и позволяет высокую степень сжатия изображений, но некоторые из фотографий потеряли свое качество при сжатии и сохраняется.
Он считает формат файла с потерями, что означает, что качество не может восстановиться, когда он сжат. Формат JPG основном используется в цифровых камер и сканеров.
В то время как PDF является печати формат файла, разработанный Adobe, и это также стандартный формат файла, который использует в Интернете.
Он является предшественником PostScript, который обеспечивает отличное качество, когда дело доходит до печати документа.
Почему конвертировать JPG в PDF?
Есть так много сайтов , которые принимают только формат , специфичный , чтобы они могли распечатать его и представить его как позже файл.
Она является наиболее распространенным для написания исследования, резюме, сопроводительные письма, и писать образцы.
Что делать, если вы потратили часы, созданные профессиональные резюме в Adobe InDesign, сохраненные в формате JPG, а теперь претендуют на работу, и они только позволяют загружать только файлы PDF.
Это происходит много раз, и тогда вы ищете быстрое решение , как конвертировать JPG в PDF?
PDF является универсальным форматом файлов , который является к печати и может легко прочитать на всех устройствах, включая смартфоны, персональные ноутбуки и планшеты.
Кроме того , так много возможностей, она выделяется своей безопасностью. Вы можете поставить безопасность пользователя и пароль на файл, так как шифрование PDF используется для защиты PDF – файлы файлов , так что вы можете быть отправлены надежно другими.
Иногда нам нужно сделать скриншот из основных документов в наших смартфонах, которые в основном сохраненные в формате JPG.
Так что теперь, вы также можете конвертировать любые картинки в формате PDF в pngtopdf.net с одним щелчком мыши.
Как конвертировать JPG в PDF онлайн?
Несмотря на то, что можно конвертировать изображения в PDF без использования какой – либо третьей стороной платформы, но почему нужно пройти через длительный процесс , когда вы можете конвертировать JPG в PDF с одним щелчком мыши?
Да, благодаря JPG в PDF конвертер , который позволяет конвертировать JPG в PDF очень легко? Это удобный онлайн – конвертер , который поставляется с функцией перетаскивания мышью.
Этот конвертер поддерживает все форматы файлов , такие как JPG, PNG, TIFF, GIF и файлов.
- Открыть JPG в PDF конвертер , загружать или использовать функцию перетаскивания мышью , чтобы загрузить изображение
- После загрузки изображения, нажмите на кнопку «Convert», чтобы начать процесс преобразования PDF.
- Нажмите кнопку преобразовать
- Скачать преобразованный PDF на свой компьютер или смартфон
- Вы можете загружать несколько файлов одновременно, используя Ctrl или клавишу Shift,
Вы можете конвертировать неограниченное JPG в PDF онлайн без входа в систему или зарегистрироваться.
Почему наш онлайн инструмент является лучшим JPG в PDF конвертер?
Лучший онлайн JPG в PDF конвертер
Наш онлайн JPG в PDF конвертер бесплатно , что позволяет превратить неограниченное количество изображений в формате PDF. Мы гарантируем , чтобы сохранить все ваши важные файлы и данные в безопасности. Наш интернет – конвертер PDF поддерживает почти все форматы изображений, включая JPG, PNG, GIF и TIFF. Преобразование вашего JPG в PDF теперь можно с помощью одного клика.
Мы не храним файлы
Лучшее особенность нашего онлайн JPG в PDF конвертер является автоматическое удаление файлов. Да, после преобразования изображений в PDF, у вас есть всего несколько часов , чтобы загрузить файлы. После этого файлы будут автоматически удалены с сервера. Мы не идти на компромисс в вашей личной жизни.
Безопасная загрузка и хранение:
Наш интернет – конвертер привержен сохраняет ваши данные и личные файлы безопасны. Для того, чтобы выполнить наши обязательства, мы зашифровать все файлы, загруженные на нашей платформе с помощью шифрования SSL.
Таким образом, неавторизованные третьи стороны не могут взломать шифрование SSL. Мы никогда не передаем ваши файлы, информацию третьих лиц.
Преобразование JPG в PDF из любой точки мира
Вы можете преобразовать свою фотографию в PDF из любого места, в любое время, если у вас есть доступ в Интернет.
Наш онлайн бесплатно JPG в PDF конвертер совместим со всеми устройствами, вы можете использовать и преобразовать файл в Windows, Linux, Mac, IOS, Android и т. д.
д.
Всегда жить до даты
JPG в PDF конвертер на облаке; Вы можете получить доступ к веб-сайт в любое время. Это всегда живет со 100% Провели конвертировать JPG в PDF с несколькими щелчками мыши, не регистрации, или загрузками программного обеспечения не требуется.
Вопросы и ответы
Как открыть файл PDF в окнах?
В окне, то EDGE браузер Microsoft, Chromes или Firefox, или браузер по умолчанию любой позволяет открывать и читать PDF – файлы изначально.
У вас также есть возможность открыть его с помощью Adobe Acrobat Reader; Вы можете скачать его бесплатно с Adobe Вебсайта .
Если вы используете Windows 10 или версию обновления , которая поддерживает Microsoft EDGE, вы можете дважды щелкнуть на файл PDF, и она будет открыта в браузере Microsoft EDGE.
Как открыть PDF – файлы в Linux?
Linux имеет в основном для чтения PDF, но если он отсутствует или вы не используете обновленную версию, вы можете установить его. Откройте терминал и введите «Sudo APT-получить установку Evince» установку в скором времени начнется, а затем вы можете открыть PDF – файлы в Linux.
Откройте терминал и введите «Sudo APT-получить установку Evince» установку в скором времени начнется, а затем вы можете открыть PDF – файлы в Linux.
Как открыть файл PDF в Mac Операционная система?
Вам необходимо установить Adobe Acrobat Reader от Adobe сайта , чтобы получить доступ к файлу PDF.
Как открыть JPG в Windows?
Дважды щелкните на файле JPG и изображение откроется в средстве просмотра фотографий Windows. У вас также есть возможность открыть JPEG в браузере.
Как открыть JPG в Linux?
Вы можете открыть JPG файлов в Linux с помощью GIMP.
Как открыть JPG в операционной системе Mac?
Операционная система Mac имеет встроенный Photo Viewer , которая будет автоматически открывать файлы JPG.
Резюме
Если у Вас есть JPG изображения и хотите конвертировать в PDF файлы, бесплатно и быстро JPG в PDF онлайн конвертер делает это очень просто.
Наш интернет – конвертер PDF бесплатно; Вы можете включить неограниченное JPG изображений в PDF файлы без каких – либо ограничений.
Этот конвертер поддерживает практически все форматы изображения, такие как JPG, TIFF, PNG, GIF, BMP, и т.д., так что теперь вы можете конвертировать ваши фотографии в PDF – файлы в считанные секунды с помощью одного клика.
Кроме того, наш онлайн конвертер не разделяет ваши данные или важные файлы в какой – либо третьей стороне; данные автоматически удалять с нашего сервера.
Три способа конвертировать JPG в PDF на Mac (включая macOS 11)
Одри Гудвин
27.04.2023 09:40:32 • Подано в: PDFelement for Mac How-Tos Articles • Проверенные решения
JPG формат изображения, который часто используется. Из-за их сжатого размера изображениями в формате JPG легче поделиться, прикрепив их к электронному письму или загрузив в Интернете, но время от времени вы можете также делиться ими в формате PDF. У вас может быть несколько изображений JPG, которые вы хотите преобразовать в PDF на Mac (включая macOS 11). В этой статье мы рассмотрим решения для преобразования JPG в PDF на Mac , если вам нужно преобразовать изображение JPG в PDF или объединить несколько JPG в один PDF.
- Часть 1. Как конвертировать JPG в PDF на Mac
- Часть 2. Как объединить файлы JPG в один PDF-файл на Mac
- Часть 3. Как преобразовать JPG в PDF онлайн на Mac
- Часть 4. Как преобразовать JPG в PDF на Mac с помощью Preview
- Часть 5: лучший конвертер JPG в PDF на Mac
Как конвертировать JPG в PDF на Mac
PDFelement для Mac — это мощное, но простое в использовании решение для работы с PDF. Он предлагает все функции, необходимые для преобразования JPG в PDF на Mac, например, массовое преобразование JPG в PDF для экономии вашего времени, объединение JPG в один PDF-файл, преобразование изображений JPG в редактируемые PDF-файлы.
Нажмите кнопку ниже, чтобы бесплатно загрузить PDFelement на свой Mac. Выполните следующие шаги, чтобы легко конвертировать JPG в PDF на macOS:
ПОПРОБУЙТЕ БЕСПЛАТНО ПОПРОБУЙТЕ БЕСПЛАТНОШаг 1. Конвертируйте JPG в PDF на Mac
Откройте программу на вашем Mac, и вы можете перейти к «Файл» в главном меню и нажмите «Создать», а затем опцию «PDF из файла», которая также позволит вам добавить файлы JPG, которые вы хотите преобразовать.
Вы можете добавить любое количество файлов JPG. PDFelement может конвертировать несколько JPG в PDF одновременно, чтобы сэкономить ваше время.
Шаг 2. Преобразование JPG в редактируемый PDF (необязательно)
Файлы JPG теперь будут отображаться в формате PDF. Программа автоматически обнаружит, что изображения отсканированы, и предложит выполнить OCR для редактирования текста. Если вам нужно отредактировать текст в формате JPG, нажмите для этого кнопку «Выполнить распознавание». После завершения OCR нажмите «Редактировать» и начните изменять файл PDF по мере необходимости. Узнайте больше о том, как редактировать отсканированные PDF-файлы на Mac.
ПОПРОБУЙТЕ БЕСПЛАТНО ПОПРОБУЙТЕ БЕСПЛАТНОШаг 3. Сохранение JPG в PDF на Mac
После редактирования PDF нажмите «Файл» в главном меню и выберите «Сохранить как». Переименуйте файл и сохраните его. Теперь вы конвертировали JPG в PDF на Mac.
Часть 2. Как объединить файлы JPG в один PDF-файл на Mac
Если у вас есть несколько файлов JPG и вам нужно объединить изображения в один PDF-файл на Mac, вы можете легко сделать это с помощью PDFelement.
После запуска PDFelement на Mac нажмите «Файл» > «Создать» > «PDF из изображений». Затем выберите все изображения JPG, которые нужно объединить в PDF.
После открытия изображений в PDFelement они объединяются в один файл PDF. Вы можете расположить изображения в правильном порядке, перетаскивая миниатюры вверх и вниз. Наконец, нажмите «Сохранить», чтобы сохранить файлы JPG в один файл PDF.
ПОПРОБУЙТЕ БЕСПЛАТНО ПОПРОБУЙТЕ БЕСПЛАТНОЧасть 3: Как преобразовать JPG в PDF онлайн на Mac
Онлайн-конвертер JPG в PDF также является отличным вариантом, когда вам просто нужно время от времени конвертировать JPG в PDF. HiPDF — это онлайн-инструмент PDF, который может конвертировать JPG, PNG, Word, Excel и другие файлы в PDF.
Шаг 1: Откройте этот конвертер JPG в PDF онлайн на вашем Mac.
Шаг 2: Нажмите «Выбрать файлы», чтобы загрузить изображения JPG.
Шаг 3: Нажмите Преобразовать. И изображение JPG будет преобразовано в файл PDF. Теперь вам просто нужно скачать преобразованный PDF-файл.
Теперь вам просто нужно скачать преобразованный PDF-файл.
Хотя онлайн-конвертер JPG в PDF очень удобен, он не может предложить расширенные функции, такие как объединение файлов JPG в один PDF-файл или преобразование JPG в редактируемый PDF-файл. Если вам нужны эти функции, загрузите профессиональную программу PDF, например PDFelement для Mac.
ПОПРОБУЙТЕ БЕСПЛАТНО ПОПРОБУЙТЕ БЕСПЛАТНОЧасть 4. Как преобразовать JPG в PDF на Mac с помощью предварительного просмотра
Программа предварительного просмотра также может помочь вам преобразовать JPG в PDF на Mac. Шаги описаны ниже:
Шаг 1. Откройте JPG с предварительным просмотром
Дважды щелкните файл JPG, чтобы открыть его с предварительным просмотром по умолчанию. Затем нажмите кнопку «Файл»> «Экспортировать как PDF» в верхнем меню.
Шаг 2. Сохранить JPG как PDF
В новом всплывающем окне переименуйте файл и выберите выходную папку для сохранения файла PDF в локальной папке.
Часть 5. Лучший конвертер JPG в PDF на Mac
Чтобы преобразовать JPG в PDF, вам понадобится подходящее программное обеспечение PDF, которое может создавать PDF-файлы из форматов изображений, включая файлы JPG. Одной из таких программ, которая может конвертировать изображения в PDF, является PDFelement для Mac. Это программное обеспечение также поддерживает несколько форматов изображений, таких как PNG, BMP, GIF и TIFF. Это многоязычное программное обеспечение работает в macOS 11, 10.15 и 10.14. Другие функции PDFelement для Mac включают:
ПОПРОБУЙТЕ БЕСПЛАТНО ПОПРОБУЙТЕ БЕСПЛАТНО- Преобразует PDF-файлы в RTF, TXT, DOC, DOCS, XLS, PPT, HTML, EPUB и изображения.
- Позволяет редактировать текст, изменять размер или цвет шрифта, добавлять изображения, а также удалять, добавлять, заменять или извлекать страницы.
- Позволяет комментировать, добавлять комментарии, рисовать пометки, добавлять водяные знаки, добавлять ссылки, а также подчеркивать и выделять текст.

- Позволяет с легкостью заполнять PDF-формы, а также создавать формы.
- Он оснащен плагином OCR, который делает отсканированные PDF-файлы доступными для редактирования, выбора и поиска.
- Подключаемый модуль OCR, который находится в купленной версии, поддерживает более 20 языков, включая испанский, французский, корейский и многие другие.
- Позволяет применить цифровую подпись к документу PDF.
Скачайте бесплатно или купите PDFelement прямо сейчас!
Скачайте бесплатно или купите PDFelement прямо сейчас!
Купите PDFelement прямо сейчас!
Купите PDFelement прямо сейчас!
JPG в PDF | Преобразование JPG в PDF онлайн бесплатно
Конвертируйте изображение JPG в файл PDF онлайн.
Перетащите файл сюда
Выберите файлЗагрузить файл ↓ Установите расширение для браузера
Пожалуйста, загрузите файл с правильным расширением.
Сервер сейчас занят. Пожалуйста, повторите попытку позже.
Разблокируйте файл и повторите попытку.
Максимально допустимый размер файла: 32 МБ.
Повторите попытку позже.
Выберите свой план
Веб-ежемесячник
5,95 долл. США в месяц
Подписаться
Текущий план
Онлайн-приложение
Неограниченное количество задач
19 конвертеров
- 9000 2 5 инструментов редактирования.
Подписаться
Текущий план
Веб-ежегодник Сэкономьте 60%
1,65 долл. США в месяц
Подписаться$71,519,95 долларов США ежегодноТекущий план
Онлайн-приложение
Неограниченное количество задач
19 конвертеров
- 9000 2 5 инструментов редактирования
Безопасность гарантирована
1,65 долл.
 США/месяц
США/месяц
Подписаться$71,519 долларов0,95 оплачивается ежегодноТекущий план
Ежегодный рабочий стол
2,50 долл. США в месяц
29,95 долл. США при ежегодной оплате
ПодписатьсяТекущий план
Настольное решение
Неограниченное пакетное преобразование
Дополнительные форматы преобразования
Подробнее инструменты редактирования
Редактирование текста
Электронные подписи
Заполняемые PDF-формы
Гарантия безопасности
2,50 $/месяц 90 005
29,95 долларов США ежегодно
ПодписатьсяТекущий тарифный план
Откройте для себя дополнительные возможности PDFChef для ПК
Загрузите PDFChef от Movavi для ПК или Mac и настройте PDF-файлы в соответствии с вашими потребностями.
 Получите бесплатный доступ к расширенным инструментам и различным режимам редактирования PDF.
Получите бесплатный доступ к расширенным инструментам и различным режимам редактирования PDF.Попробуйте бесплатно
Попробуйте бесплатно
Дополнительные функции
Как конвертировать JPG в PDF онлайн:
Шаг 1
Добавьте файл JPG с помощью кнопки Выберите файл или перетащите его в загрузку область.
Шаг 2
Подождите несколько секунд, приложение превратит файл в PDF.
Шаг 3
Нажмите Загрузить файл .
Почему выбирают нас?
Преобразование JPG в PDF бесплатно
PDFChef позволяет бесплатно преобразовывать файлы JPG в PDF с помощью любого браузера или устройства. Если вы много работаете с PDF-файлами и вам нужен доступ к неограниченным преобразованиям, рассмотрите возможность приобретения одного из наших планов.
Сохранение качества
Благодаря алгоритмам точного преобразования PDFChef легко преобразует файлы из формата JPG в PDF, сохраняя при этом высокое качество изображения.



 США/месяц
США/месяц Получите бесплатный доступ к расширенным инструментам и различным режимам редактирования PDF.
Получите бесплатный доступ к расширенным инструментам и различным режимам редактирования PDF.
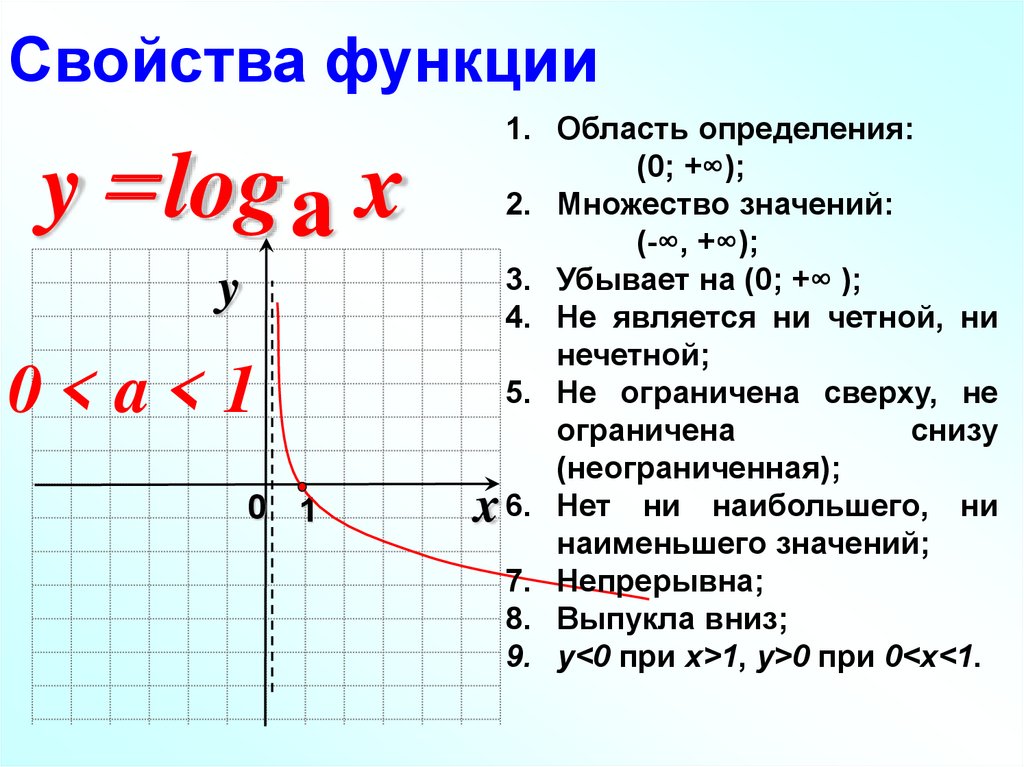
 Множество значений так же состоит из всех чисел E(y)=(-∞;+∞).
Множество значений так же состоит из всех чисел E(y)=(-∞;+∞).

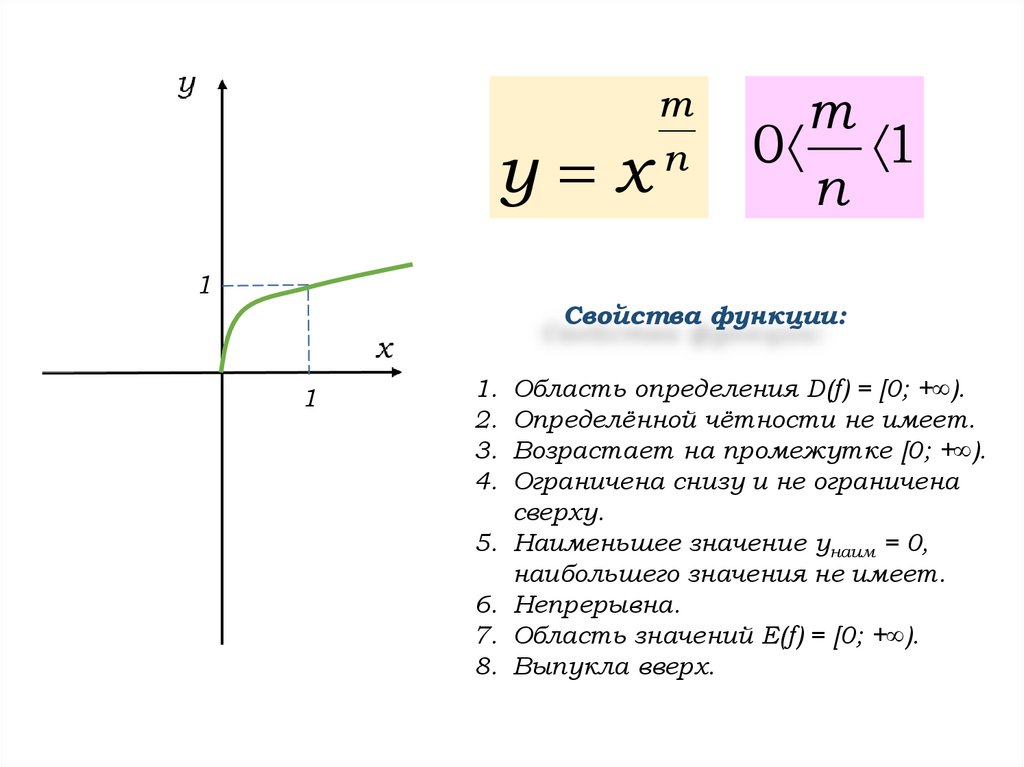
 Следовательно, y∈[0; +∞).
Следовательно, y∈[0; +∞).
 Поэтому попытка получить значение локальной переменной вне функции вызывает ошибку.
Поэтому попытка получить значение локальной переменной вне функции вызывает ошибку.



 Здесь вам не нужно указывать тип используемой переменной. В отличие от других языков программирования, у вас нет разных типов данных для разных типов значений.
Здесь вам не нужно указывать тип используемой переменной. В отличие от других языков программирования, у вас нет разных типов данных для разных типов значений.
 Если вы попытаетесь получить доступ к любой переменной, определенной внутри функции, извне или из другой функции, она выдаст ошибку.
Если вы попытаетесь получить доступ к любой переменной, определенной внутри функции, извне или из другой функции, она выдаст ошибку. Вы не можете получить доступ к переменным, определенным внутри функции, извне функции или из другой функции. Var, let и const работают одинаково при использовании внутри функции.
Вы не можете получить доступ к переменным, определенным внутри функции, извне функции или из другой функции. Var, let и const работают одинаково при использовании внутри функции. В противном случае вы также можете использовать строгий режим локально внутри функции.
В противном случае вы также можете использовать строгий режим локально внутри функции.

 Используйте любые доступные инструменты, если вы хотите редактировать и манипулировать файлом PDF. Нажмите на кнопку преобразования и дождитесь завершения преобразования. После этого загрузите преобразованный файл JPG.
Используйте любые доступные инструменты, если вы хотите редактировать и манипулировать файлом PDF. Нажмите на кнопку преобразования и дождитесь завершения преобразования. После этого загрузите преобразованный файл JPG.


 Осталось вычесть из целого числа дробное. Мы это уже делали:
Осталось вычесть из целого числа дробное. Мы это уже делали: Чтобы научиться ездить на велосипеде, не так важно смотреть, как ездят другие, а необходимо пробовать это делать самостоятельно.
Чтобы научиться ездить на велосипеде, не так важно смотреть, как ездят другие, а необходимо пробовать это делать самостоятельно. Сложение и вычитание смешанных чисел.
Сложение и вычитание смешанных чисел.

 Но это может помочь представить модель в уме, когда вы читаете шаги.
Но это может помочь представить модель в уме, когда вы читаете шаги.
 Мы должны записать ответ в том виде, в каком он был задан, поэтому, если нам даны смешанные числа для вычитания, мы запишем ответ как смешанное число.
Мы должны записать ответ в том виде, в каком он был задан, поэтому, если нам даны смешанные числа для вычитания, мы запишем ответ как смешанное число.



 Нарисуйте картинку, иллюстрирующую вашу модель.
Нарисуйте картинку, иллюстрирующую вашу модель.
 Согласно выкройкам, которые она будет использовать, ей потребуется \(2 \dfrac{3}{8}\) ярдов ткани для рубашки мужа и \(1 \dfrac{1}{8}\) ярдов ткани для рубашки сына. рубашка. Сколько ткани ей нужно, чтобы сшить обе рубашки?
Согласно выкройкам, которые она будет использовать, ей потребуется \(2 \dfrac{3}{8}\) ярдов ткани для рубашки мужа и \(1 \dfrac{1}{8}\) ярдов ткани для рубашки сына. рубашка. Сколько ткани ей нужно, чтобы сшить обе рубашки?

 Не так уж и страшно, согласитесь?
Не так уж и страшно, согласитесь?


 А. Г. Мордковича. –М.: Мнемозина, 2009.
А. Г. Мордковича. –М.: Мнемозина, 2009. учреждений).-М.: Просвещение, 2003.
учреждений).-М.: Просвещение, 2003. Просмотров 11.3k.
Просмотров 11.3k. Представим левую и правую части в виде степеней с основанием 2:
Представим левую и правую части в виде степеней с основанием 2:

 3 Решение квадратных уравнений
3 Решение квадратных уравнений Для линейных уравнений существует не более одного решения уравнения.
Для линейных уравнений существует не более одного решения уравнения.



 1 Введение
1 Введение
 В этом случае a,b, и c должны быть константами или действительными числами, такими как 2, 3, 4, и т. д. Коэффициенты х и у , которые в данном случае а и б, , не должны быть равны 0 . Здесь двумя неизвестными переменными будут x и y, поскольку a, b и c — действительные числа. Например, 4x+5y+3=12 можно рассматривать как линейное уравнение с двумя переменными.
В этом случае a,b, и c должны быть константами или действительными числами, такими как 2, 3, 4, и т. д. Коэффициенты х и у , которые в данном случае а и б, , не должны быть равны 0 . Здесь двумя неизвестными переменными будут x и y, поскольку a, b и c — действительные числа. Например, 4x+5y+3=12 можно рассматривать как линейное уравнение с двумя переменными. В этом случае x координата будет умножена на a, , чтобы получить первое значение, а координата будет умножена на b , чтобы предоставить второе значение . Сумма этих двух значений будет равна c . Таким образом, в линейных уравнениях с двумя переменными существует бесконечное множество значений и решений.
В этом случае x координата будет умножена на a, , чтобы получить первое значение, а координата будет умножена на b , чтобы предоставить второе значение . Сумма этих двух значений будет равна c . Таким образом, в линейных уравнениях с двумя переменными существует бесконечное множество значений и решений.
 Затем мы можем вычесть одно уравнение из другого и отменить эту конкретную переменную. Оставшееся уравнение будет иметь только одну оставшуюся переменную, что облегчит нам поиск ее значения. Затем в исходное уравнение мы можем подставить это значение и найти правильное значение другой переменной (той, которую мы исключили). Следовательно, используя этот метод из линейных уравнений с двумя переменными класса 10, мы можем построить оба уравнения на графике.
Затем мы можем вычесть одно уравнение из другого и отменить эту конкретную переменную. Оставшееся уравнение будет иметь только одну оставшуюся переменную, что облегчит нам поиск ее значения. Затем в исходное уравнение мы можем подставить это значение и найти правильное значение другой переменной (той, которую мы исключили). Следовательно, используя этот метод из линейных уравнений с двумя переменными класса 10, мы можем построить оба уравнения на графике. 14.
14.  Представьте эту ситуацию алгебраически и графически.
Представьте эту ситуацию алгебраически и графически.


 14159..
14159.. что она должна вернуть нам исходное значение:
что она должна вернуть нам исходное значение: Поместите «y» вместо «f(x)» и решите для x:
Поместите «y» вместо «f(x)» и решите для x: 
 )
)

 .. так что теперь f -1 (x) , а не f -1 (y) :
.. так что теперь f -1 (x) , а не f -1 (y) :
 7 (стр. 150) текста.
7 (стр. 150) текста. д.
д.

 То же самое можно сделать для всех точек на
графики f и f -1 .
То же самое можно сделать для всех точек на
графики f и f -1 . Следовательно, не существует функции, обратной f.
Следовательно, не существует функции, обратной f.



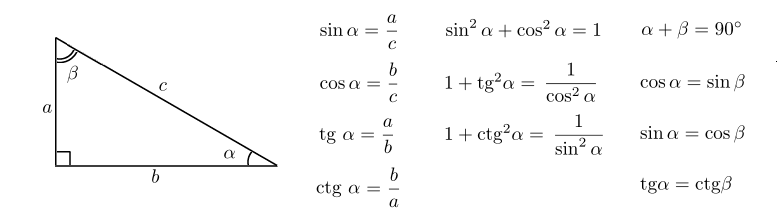 Найдите b5
Найдите b5
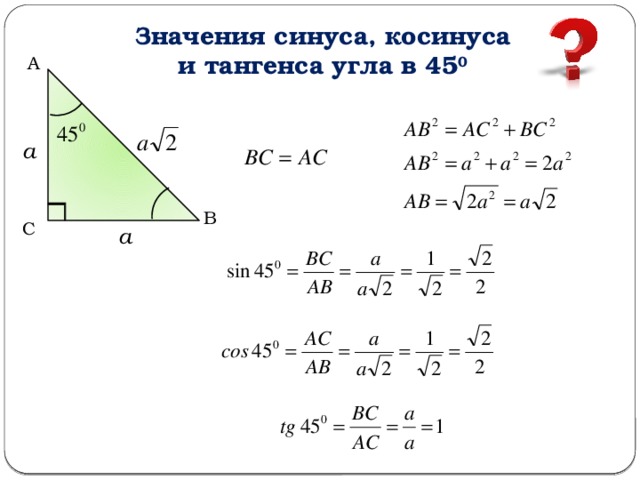 Из них мы можем получить тангенс, а также обратные секанс, косеканс и котангенс. В прошлом математики также использовали множество других тригонометрических функций. Некоторые из них проиллюстрированы ниже.
Из них мы можем получить тангенс, а также обратные секанс, косеканс и котангенс. В прошлом математики также использовали множество других тригонометрических функций. Некоторые из них проиллюстрированы ниже. \]
\]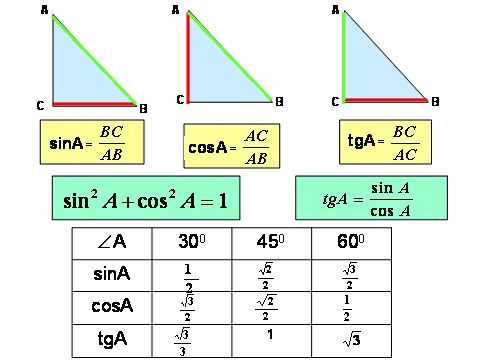 Итак, \[AG = \cot\theta \sin\theta = \cos\theta.\]
Итак, \[AG = \cot\theta \sin\theta = \cos\theta.\] \]
\]

 Для справки:
Для справки: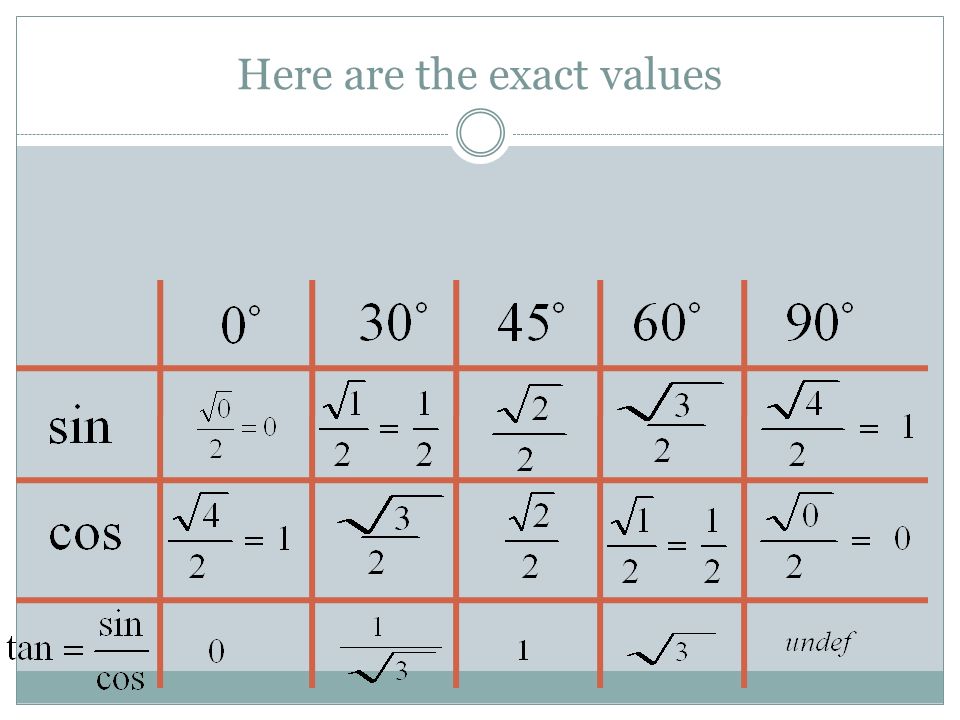

 angle1] $}
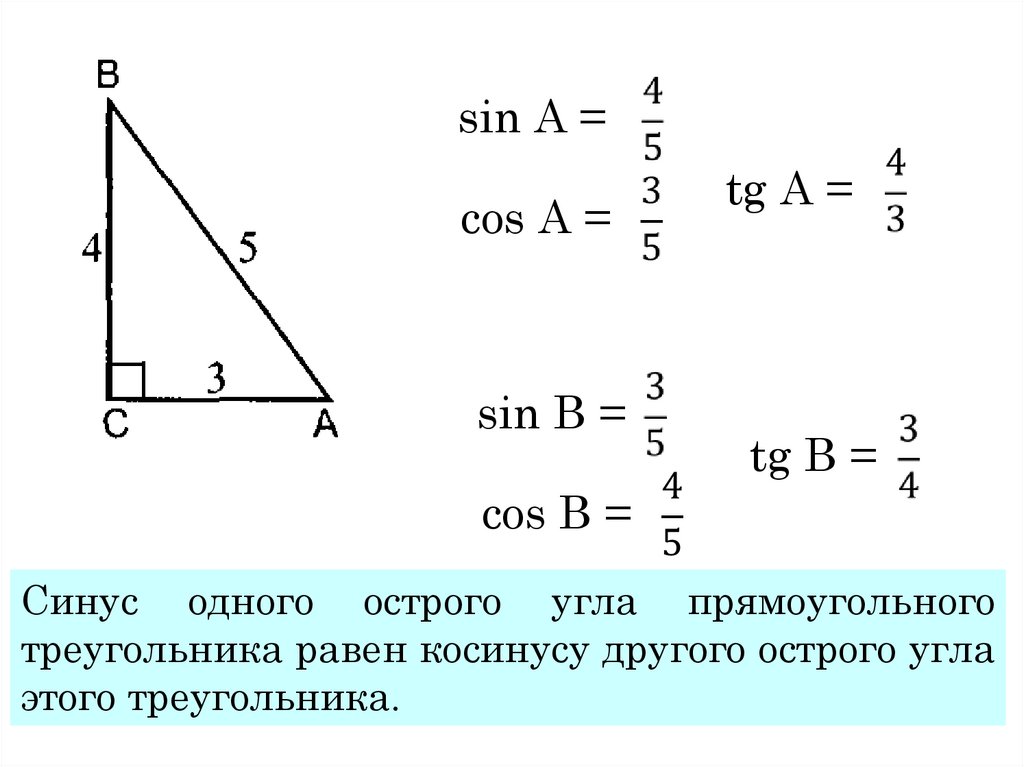
angle1] $} Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты. Изначально косинусы рассчитывались только для прямоугольных треугольников, однако с развитием математической науки косинусы прочно вошли в расчеты и сейчас используются для любых треугольников. Одним из таких примеров является теорема косинусов — теорема евклидовой геометрии, которая расширяет теорему Пифагора на любые плоские треугольники.
Изначально косинусы рассчитывались только для прямоугольных треугольников, однако с развитием математической науки косинусы прочно вошли в расчеты и сейчас используются для любых треугольников. Одним из таких примеров является теорема косинусов — теорема евклидовой геометрии, которая расширяет теорему Пифагора на любые плоские треугольники. Вся бытовая математика находится на уровне математических познаний древних греков, когда для простейших расчетов используются элементарные арифметические функции и рациональные соотношения. Однако большая часть современных технологий функционирует с использованием различных тригонометрических функций. К примеру, для определения мощности электротехнических приборов используется косинус фи — косинус угла между векторными значениями тока и напряжения. Еще пример: через тригонометрические функции легко перевести геодезические углы в привычные нам координаты на земной поверхности.
Вся бытовая математика находится на уровне математических познаний древних греков, когда для простейших расчетов используются элементарные арифметические функции и рациональные соотношения. Однако большая часть современных технологий функционирует с использованием различных тригонометрических функций. К примеру, для определения мощности электротехнических приборов используется косинус фи — косинус угла между векторными значениями тока и напряжения. Еще пример: через тригонометрические функции легко перевести геодезические углы в привычные нам координаты на земной поверхности. Программа мгновенно выдаст значение угла. Рассмотрим пару примеров использования калькулятора.
Программа мгновенно выдаст значение угла. Рассмотрим пару примеров использования калькулятора. Правильность решения легко проверить, сложив величины углов:
Правильность решения легко проверить, сложив величины углов:
 .
. Тангенс — это тригонометрическая функция угла. Он обозначается как tanθ, где θ – угол между двумя сторонами.
Тангенс — это тригонометрическая функция угла. Он обозначается как tanθ, где θ – угол между двумя сторонами.
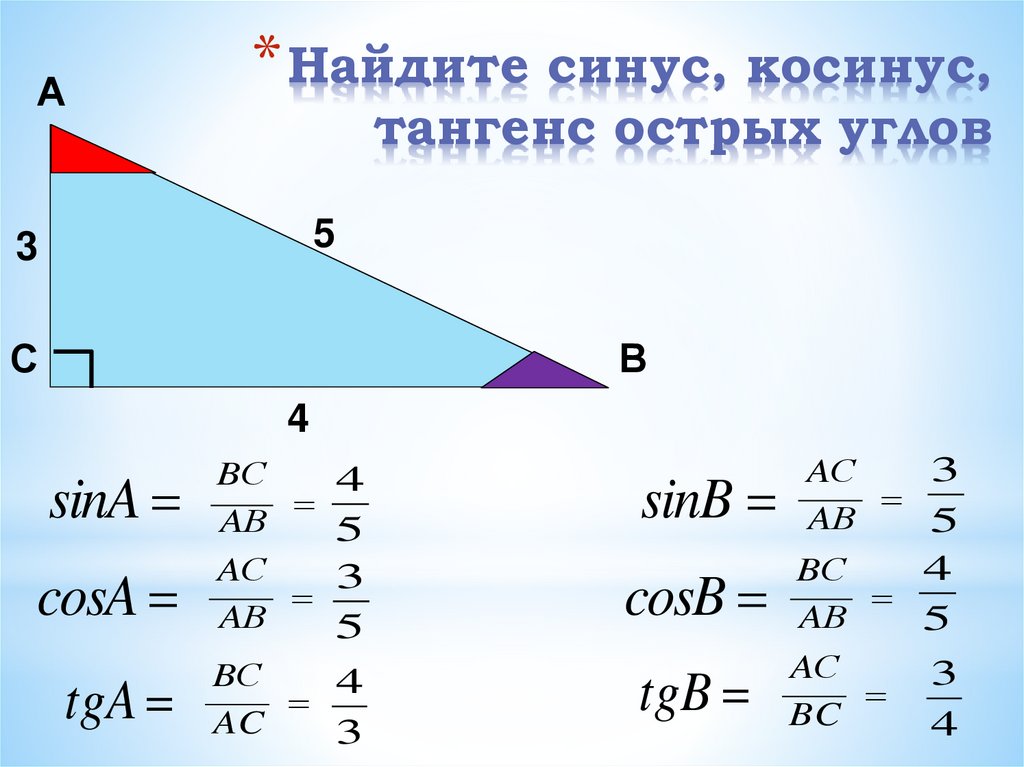


 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.