Чему равен квадратный корень из −1? (Математика, Оксфорд) . Вопрос на засыпку. Как заставить мозги шевелиться
Это, пожалуй, самый трудный вопрос в математике, над которым на протяжении тысячелетий бились практически все великие ученые. Впрочем, проблема заключается в поиске корня не только из –1, но и из любого отрицательного числа. Квадратный корень числа – это значение, которое при возведении в квадрат дает оригинальное число. Так, квадратный корень из 9 равен 3 (3 ? 3 = 9), квадратный корень из 4 равен 2 (2 ? 2 = 4), а квадратный корень из 1 равен 1 (1 ? 1 = 1). Но это неприменимо к отрицательным числам, поскольку два отрицательных числа при умножении дают положительное: так, ?2 ? ?2 = (+)4, а ?1 ? ?1 = (+)1.
И как же тогда найти корень из отрицательного числа, например из –1? Дело в том, что никак, и математики называют такие значения мнимыми числами. С тем же успехом их можно было бы назвать нереальными, абсурдными или просто дурацкими числами, поскольку они, по-видимому, не существуют. Однако сейчас мы едва ли можем представить нашу жизнь без них. Они необходимы для передовой квантовой физики, они важны для проектирования подвесных мостов и крыльев самолетов. Они мнимые, поскольку не обозначают какое-либо существующее число, но они реальны, поскольку являются частью реального мира. Поэтому, как ни парадоксально, они одновременно воображаемые и настоящие, невозможные и возможные.
Однако сейчас мы едва ли можем представить нашу жизнь без них. Они необходимы для передовой квантовой физики, они важны для проектирования подвесных мостов и крыльев самолетов. Они мнимые, поскольку не обозначают какое-либо существующее число, но они реальны, поскольку являются частью реального мира. Поэтому, как ни парадоксально, они одновременно воображаемые и настоящие, невозможные и возможные.
Данное противоречие обнаружили еще древние египтяне, а также один из величайших математиков Античности Герон Александрийский, который столкнулся с отрицательными числами около 2000 лет назад, когда пытался вычислить объем усеченной пирамиды. В расчетах ему понадобилось найти квадратный корень из 81–144 (то есть ??63). Поскольку получить корень из отрицательного числа не представлялось возможным, Герон просто поменял его на положительное и извлек корень из 63. Разумеется, античный ученый просто подогнал ответ под желаемый, но что ему оставалось делать? В те времена даже к отрицательным числам относились с крайней осторожностью, что там говорить о квадратных корнях из них!
Средневековые математики порой сталкивались с данной проблемой при решении кубических уравнений, но они просто рассматривали корни из отрицательных чисел как невозможные. Первым нарушил устоявшийся подход пользовавшийся (по-видимому) сомнительной репутацией у современников итальянский астролог Джероламо Кардано, и, пожалуй, именно такой человек идеально подходил для решения казавшихся невозможными задач. В конце жизни Кардано работал астрологом в Ватикане, но до этого, в 1545 году, он исследовал в своем трактате «Великое искусство» проблему корня из ?1. Он утверждал, что подобное число возможно, хотя и счел его абсолютно бесполезным.
Первым нарушил устоявшийся подход пользовавшийся (по-видимому) сомнительной репутацией у современников итальянский астролог Джероламо Кардано, и, пожалуй, именно такой человек идеально подходил для решения казавшихся невозможными задач. В конце жизни Кардано работал астрологом в Ватикане, но до этого, в 1545 году, он исследовал в своем трактате «Великое искусство» проблему корня из ?1. Он утверждал, что подобное число возможно, хотя и счел его абсолютно бесполезным.
Рафаэль Бомбелли в своем изданном в 1572 году труде «Алгебра» отнесся более положительно к отрицательным числам. Бомбелли доказал, что произведение двух отрицательных чисел дает действительное число. Поначалу он счел свои выводы несколько сомнительными. «Данная проблема относится скорее к области софистики, – писал он. – Но я изучал ее очень долго, и мне удалось доказать, что мои результаты верны».
На протяжении двух последующих столетий различные ученые высказывали свое мнение относительно корней из отрицательных чисел, признавая или отвергая их существование. В итоге проблему удалось решить гениальному швейцарскому математику Леонарду Эйлеру (1707–1783) в поздние годы жизни. Он ввел «мнимую единицу», символ i. Символ i обозначает мнимое число, квадрат которого равен ?1. Таким образом, i можно представить как ??1. Идея Эйлера предполагает, что квадратный корень любого отрицательного числа может использоваться в уравнении как число i, помноженное на квадратный корень числа. Он утверждал, что корни любых отрицательных чисел – ??1, ??2, ??3 и т. д. – являются мнимыми, но не бессмысленными: это просто их математическое наименование.
В итоге проблему удалось решить гениальному швейцарскому математику Леонарду Эйлеру (1707–1783) в поздние годы жизни. Он ввел «мнимую единицу», символ i. Символ i обозначает мнимое число, квадрат которого равен ?1. Таким образом, i можно представить как ??1. Идея Эйлера предполагает, что квадратный корень любого отрицательного числа может использоваться в уравнении как число i, помноженное на квадратный корень числа. Он утверждал, что корни любых отрицательных чисел – ??1, ??2, ??3 и т. д. – являются мнимыми, но не бессмысленными: это просто их математическое наименование.
Символ i представлял собой простое, но гениальное решение, позволившее математикам наконец-то использовать ??1 и квадратные корни из других отрицательных чисел в уравнениях, выражая их с использованием i. Это означает, что математикам больше не приходилось рассматривать природу мнимых чисел: они могли просто использовать их в практических целях.
Однако парадокс так и не был решен. Эйлер, несмотря на то что его изобретение сделало мнимые числа реальными, сам признавал их нереальность, говоря: «Мы можем считать, что они не больше, чем ничто, и не меньше, чем ничто, что неизбежно делает их мнимыми или невозможными». Множество скептических отзывов не смущало Эйлера. По его мнению, если мнимые числа применимы в математике, они реальны, как действительные числа.
Множество скептических отзывов не смущало Эйлера. По его мнению, если мнимые числа применимы в математике, они реальны, как действительные числа.
Идеи Эйлера дали понять, что нам не обязательно находить ответы на все вопросы для исследования тех или иных областей бытия. Мнимые числа могут быть окутаны тайной, равно как и квадратный корень из ?1, но это не означает, что мы не имеем права их использовать. С такой же смелостью Ньютон разработал теорию гравитации исключительно как математическую модель, даже не пытаясь представить, как она впишется в рамки дальнодействия и короткодействия. Мы до сих пор не представляем, как работает гравитация, но теория Ньютона остается одной из важнейших вех в истории науки. Аналогичным образом мнимые числа подтвердили свою практическую пользу и широко применяются передовыми математиками, хоть и по-прежнему остаются загадкой. Это доказывает, что воображение и математическая логика не противоречат друг другу.
Корень из числа: определения, примеры
В этой статье мы введем понятие корня из числа. Будем действовать последовательно: начнем с квадратного корня, от него перейдем к описанию кубического корня, после этого обобщим понятие корня, определив корень n-ой степени. При этом будем вводить определения, обозначения, приводить примеры корней и давать необходимые пояснения и комментарии.
Будем действовать последовательно: начнем с квадратного корня, от него перейдем к описанию кубического корня, после этого обобщим понятие корня, определив корень n-ой степени. При этом будем вводить определения, обозначения, приводить примеры корней и давать необходимые пояснения и комментарии.
Квадратный корень, арифметический квадратный корень
Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.
Начнем с определения квадратного корня.
Определение
Квадратный корень из числа a — это число, квадрат которого равен a.
Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (52=5·5=25, (−0,3)2=(−0,3)·(−0,3)=0,09, (0,3)2=0,3·0,3=0,09 и 02=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.
Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.
Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b2 невозможно для любого отрицательного a, так как b2 – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.
Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.
Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.
Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 02=0·0=0 и определения квадратного корня.
Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b2=0, что невозможно, так как при любом отличном от нуля b значение выражения b2 является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.
Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.
Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b2=a и c2=a, из них следует, что b2−c2=a−a=0, но так как b2−c2=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.
Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.
Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.
Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.
Определение
Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.
Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.
Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.
Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.
При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.
В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.
Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .
На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.
Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.
В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x2=a относительно переменной x.
К началу страницы
Кубический корень из числа
Определение кубического корня из числа a дается аналогично определению квадратного корня. Только оно базируется на понятии куба числа, а не квадрата.
Определение
Кубическим корнем из числа a называется число, куб которого равен a.
Приведем примеры кубических корней. Для этого возьмем несколько чисел, например, 7, 0, −2/3, и возведем их в куб: 73=7·7·7=343, 03=0·0·0=0, . Тогда, основываясь на определении кубического корня, можно утверждать, что число 7 – это кубический корень из 343, 0 есть кубический корень из нуля, а −2/3 является кубическим корнем из −8/27.
Можно показать, что кубический корень из числа a, в отличие от квадратного корня, всегда существует, причем не только для неотрицательных a, но и для любого действительного числа a. Для этого можно использовать тот же способ, о котором мы упоминали при изучении квадратного корня.
Более того, существует только единственный кубический корень из данного числа a. Докажем последнее утверждение. Для этого отдельно рассмотрим три случая: a – положительное число, a=0 и a – отрицательное число.
Легко показать, что при положительном a кубический корень из a не может быть ни отрицательным числом, ни нулем. Действительно, пусть b является кубическим корнем из a, тогда по определению мы можем записать равенство b3=a. Понятно, что это равенство не может быть верным при отрицательных b и при b=0, так как в этих случаях b3=b·b·b будет отрицательным числом либо нулем соответственно. Итак, кубический корень из положительного числа a является положительным числом.
Теперь предположим, что помимо числа b существует еще один кубический корень из числа a, обозначим его c. Тогда c3=a. Следовательно, b3−c3=a−a=0, но b3−c3=(b−c)·(b2+b·c+c2) (это формула сокращенного умножения разность кубов), откуда (b−c)·(b2+b·c+c2)=0. Полученное равенство возможно только когда b−c=0 или b2+b·c+c2=0. Из первого равенства имеем b=c, а второе равенство не имеет решений, так как левая его часть является положительным числом для любых положительных чисел b и c как сумма трех положительных слагаемых b2, b·c и c2. Этим доказана единственность кубического корня из положительного числа a.
При a=0 кубическим корнем из числа a является только число нуль. Действительно, если предположить, что существует число b, которое является отличным от нуля кубическим корнем из нуля, то должно выполняться равенство b3=0, которое возможно лишь при b=0.
Для отрицательных a можно привести рассуждения, аналогичные случаю для положительных a. Во-первых, показываем, что кубический корень из отрицательного числа не может быть равен ни положительному числу, ни нулю. Во-вторых, предполагаем, что существует второй кубический корень из отрицательного числа и показываем, что он обязательно будет совпадать с первым.
Итак, всегда существует кубический корень из любого данного действительного числа a, причем единственный.
Дадим определение арифметического кубического корня.
Определение
Арифметическим кубическим корнем из неотрицательного числа a называется неотрицательное число, куб которого равен a.
Арифметический кубический корень из неотрицательного числа a обозначается как , знак называется знаком арифметического кубического корня, число 3 в этой записи называется показателем корня. Число под знаком корня – это подкоренное число, выражение под знаком корня – это подкоренное выражение.
Число под знаком корня – это подкоренное число, выражение под знаком корня – это подкоренное выражение.
Хотя арифметический кубический корень определяется лишь для неотрицательных чисел a, но удобно также использовать записи, в которых под знаком арифметического кубического корня находятся отрицательные числа. Понимать их будем так: , где a – положительное число. Например, .
О свойствах кубических корней мы поговорим в общей статье свойства корней.
Вычисление значения кубического корня называется извлечением кубического корня, это действие разобрано в статье извлечение корней: способы, примеры, решения.
В заключение этого пункта скажем, что кубический корень из числа a является решением кубического уравнения вида x3=a.
К началу страницы
Корень n-ой степени, арифметический корень степени n
Обобщим понятие корня из числа – введем определение корня n-ой степени для натуральных чисел n.
Определение
Корень n-ой степени из числа a – это число, n-я степень которого равна a.
Из данного определения понятно, что корень первой степени из числа a есть само число a, так как при изучении степени с натуральным показателем мы приняли a1=a.
Выше мы рассмотрели частные случаи корня n-ой степени при n=2 и n=3 – квадратный корень и кубический корень. То есть, квадратный корень – это корень второй степени, а кубический корень – корень третьей степени. Для изучения корней n-ой степени при n=4, 5, 6, … их удобно разделить на две группы: первая группа – корни четных степеней (то есть, при n=4, 6, 8, …), вторая группа – корни нечетных степеней (то есть, при n=5, 7, 9, …). Это связано с тем, что корни четных степеней аналогичны квадратному корню, а корни нечетных степеней – кубическому. Разберемся с ними по очереди.
Начнем с корней, степенями которых являются четные числа 4, 6, 8, … Как мы уже сказали, они аналогичны квадратному корню из числа a. То есть, корень любой четной степени из числа a существует лишь для неотрицательного a. Причем, если a=0, то корень из a единственный и равен нулю, а если a>0, то существует два корня четной степени из числа a, причем они являются противоположными числами.
То есть, корень любой четной степени из числа a существует лишь для неотрицательного a. Причем, если a=0, то корень из a единственный и равен нулю, а если a>0, то существует два корня четной степени из числа a, причем они являются противоположными числами.
Обоснуем последнее утверждение. Пусть b – корень четной степени (обозначим ее как 2·m, где m – некоторое натуральное число) из числа a. Предположим, что существует число c – еще один корень степени 2·m из числа a. Тогда b2·m−c2·m=a−a=0. Но мы знаем формулу сокращенного умножения вида b2·m−c2·m=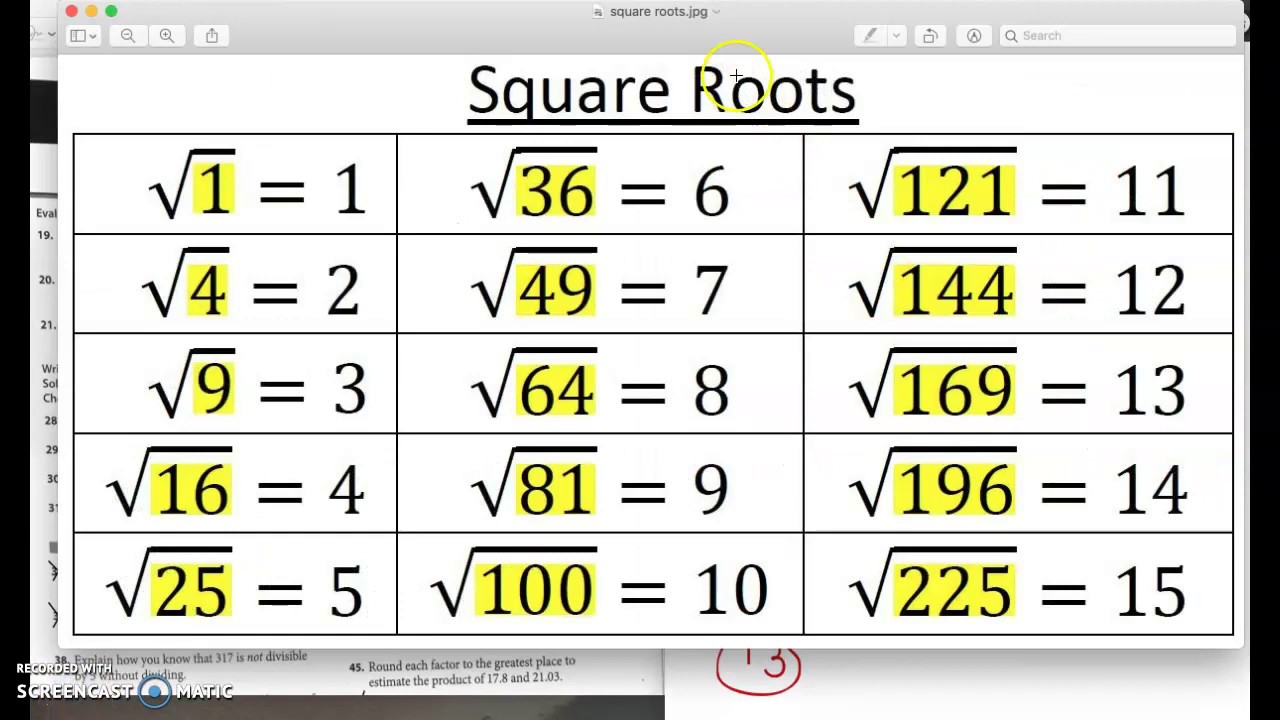 Первые два равенства означают, что числа b и c равны или b и c – противоположны. А последнее равенство справедливо лишь при b=c=0, так как в его левой части находится выражение, которое неотрицательно при любых b и c как сумма неотрицательных чисел.
Первые два равенства означают, что числа b и c равны или b и c – противоположны. А последнее равенство справедливо лишь при b=c=0, так как в его левой части находится выражение, которое неотрицательно при любых b и c как сумма неотрицательных чисел.
Что касается корней n-ой степени при нечетных n, то они аналогичны кубическому корню. То есть, корень любой нечетной степени из числа a существует для любого действительного числа a, причем для данного числа a он является единственным.
Единственность корня нечетной степени 2·m+1 из числа a доказывается по аналогии с доказательством единственности кубического корня из a. Только здесь вместо равенства a3−b3=(a−b)·(a2+a·b+c2) используется равенство вида b2·m+1−c2·m+1=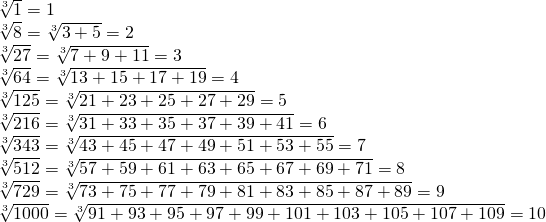 Например, при m=2 имеем b5−c5=(b−c)·(b4+b3·c+b2·c2+b·c3+c4)=
Например, при m=2 имеем b5−c5=(b−c)·(b4+b3·c+b2·c2+b·c3+c4)=
Пришло время разобраться с обозначениями корней n-ой степени. Для этого дается определение арифметического корня n-ой степени.
Для этого дается определение арифметического корня n-ой степени.
Определение
Арифметическим корнем n-ой степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Арифметический корень n-ой степени из неотрицательного числа a обозначается как . Число a называют подкоренным числом, а число n – показателем корня. Для примера рассмотрим запись , здесь подкоренным числом является 125,36, а показатель корня равен 5.
Заметим, что при n=2 мы имеем дело с квадратным корнем из числа, в этом случае показатель корня принято не записывать, то есть, записи и означают одно и то же число.
Несмотря на то, что определение арифметического корня n-ой степени, а также его обозначение введены для неотрицательных подкоренных чисел, мы в целях удобства для нечетных показателей корня и отрицательных подкоренных чисел будем использовать записи вида , которые будем понимать как . Например, и .
Например, и .
Корням же четной степени с отрицательными подкоренными числами мы не будем придавать никакого смысла (до начала изучения комплексных чисел). К примеру, выражения и не имеют смысла.
Вычисление корней n-ой степени подробно разобрано в статье извлечение корней.
На основании данного выше определения обосновываются свойства корней n-ой степени, которые имеют широкое практическое применение.
В заключение стоит сказать, что корни n-ой степени являются корнями уравнений вида xn=a.
К началу страницы
Практически важные результаты
Первый практически важный результат: .
Этот результат по сути отражает определение корня четной степени. Знак ⇔ означает равносильность. То есть, приведенную запись стоит понимать так: если , то , и если , то . А теперь то же самое, но словами: если b есть корень четной степени 2·k из числа a, то b – это неотрицательное число, удовлетворяющее равенству b2·k=a, и обратно, если b – неотрицательное число, удовлетворяющее равенству b2·k=a, то b есть корень четной степени 2·k из числа a.
А теперь то же самое, но словами: если b есть корень четной степени 2·k из числа a, то b – это неотрицательное число, удовлетворяющее равенству b2·k=a, и обратно, если b – неотрицательное число, удовлетворяющее равенству b2·k=a, то b есть корень четной степени 2·k из числа a.
Из первого равенства системы понятно, что число a – неотрицательное, так как оно равно неотрицательному числу b, возведенному в четную степень 2·k.
Таким образом, в школе рассматривают корни четных степеней только из неотрицательных чисел, понимают их как , а корням четных степеней из отрицательных чисел не придают никакого смысла.
Второй практически важный результат: .
Он по сути объединяет определение арифметического корня нечетной степени и определение корня нечетной степени из отрицательного числа. Поясним это.
Из определений, данных в предыдущих пунктах, понятно, что придают смысл корням нечетных степеней из любых действительных чисел, не только неотрицательных, но и отрицательных. Для неотрицательных чисел b считают, что . Из последней системы вытекает условие a≥0. Для отрицательных чисел −a (при этом a – положительное число) принимают . Понятно, что при таком определении — отрицательное число, так как оно равно , а есть положительное число. Также понятно, что возведение в степень 2·k+1 корня дает подкоренное число –a. Действительно, учитывая такое определение и свойства степеней, имеем
Для неотрицательных чисел b считают, что . Из последней системы вытекает условие a≥0. Для отрицательных чисел −a (при этом a – положительное число) принимают . Понятно, что при таком определении — отрицательное число, так как оно равно , а есть положительное число. Также понятно, что возведение в степень 2·k+1 корня дает подкоренное число –a. Действительно, учитывая такое определение и свойства степеней, имеем
Из этого заключаем, что корень нечетной степени 2·k+1 из отрицательного числа −a есть такое отрицательное число b, степень 2·k+1 которого равна −a, в буквенном виде . Объединяя результаты для a≥0 и для –a<0, приходим к следующему выводу: корень нечетной степени 2·k+1 из произвольного действительного числа a есть число b (оно может быть как неотрицательным, так и отрицательным), которое при возведении в степень 2·k+1 равно a, то есть .
Таким образом, в школе рассматривают корни нечетных степеней из любых действительных чисел и понимают их так: .
В заключение еще раз запишем два интересующих нас результата: и .
Корень | математика | Britannica
- Ключевые люди:
- Франсуа Виет, сеньор де ла Биготьер
- Связанные темы:
- собственное значение Итерационный метод Ньютона метод ложного положения Метод Хорнера решение
Просмотреть весь связанный контент →
корень , в математике решение уравнения, обычно выражаемое числом или алгебраической формулой.
В IX веке арабские писатели обычно называли один из равных множителей числа jadhr («корень»), а их средневековые европейские переводчики использовали латинское слово radix (от которого происходит прилагательное radix ). . Если a — положительное действительное число, а n — положительное целое число, то существует уникальное положительное действительное число x такое, что x n = a . Это число — (главное) n корень из a — записывается n Квадратный корень из √ a или a 1/ n . Целое число n называется индексом корня. Для n = 2 корень называется квадратным корнем и записывается Квадратный корень из √ a . Корень 3 Квадратный корень из √ из называется кубическим корнем из из . Если a является отрицательным, а n нечетным, уникальный отрицательный n -й корень из a называется основным. Например, главный кубический корень из –27 равен –3.
Это число — (главное) n корень из a — записывается n Квадратный корень из √ a или a 1/ n . Целое число n называется индексом корня. Для n = 2 корень называется квадратным корнем и записывается Квадратный корень из √ a . Корень 3 Квадратный корень из √ из называется кубическим корнем из из . Если a является отрицательным, а n нечетным, уникальный отрицательный n -й корень из a называется основным. Например, главный кубический корень из –27 равен –3.
Викторина «Британника»
Числа и математика
Если целое число (целое положительное) имеет рациональный n -й корень, т. е. такой, который можно записать в виде обыкновенной дроби, то этот корень должен быть целым числом. Таким образом, 5 не имеет рационального квадратного корня, потому что 2 2 меньше 5, а 3 2 больше 5. Ровно n комплексных чисел удовлетворяют уравнению x n = 1, и они называются комплексом n -го корня из единицы. Если правильный многоугольник из n сторон вписан в единичную окружность с центром в начале координат так, что одна вершина лежит на положительной половине оси x , радиусы вершин являются векторами, представляющими комплекс n н -й корни единства. Если корень, вектор которого составляет наименьший положительный угол с положительным направлением x -ось обозначается греческой буквой омега, ω, затем ω, ω 2 , ω 3 , …, ω n = 1 составляют все п -й корни единства. Например, ω = −1/2 + квадратный корень из √ −3/2, ω 2 = −1/2 − квадратный корень из √ −3/2 и ω 3 = 1 являются кубическими корнями. единства. Любой корень, обозначаемый греческой буквой эпсилон, ε, обладающий тем свойством, что ε, ε 2 , …, ε n = 1 дает все n -й корень из единицы называется примитивным.
Ровно n комплексных чисел удовлетворяют уравнению x n = 1, и они называются комплексом n -го корня из единицы. Если правильный многоугольник из n сторон вписан в единичную окружность с центром в начале координат так, что одна вершина лежит на положительной половине оси x , радиусы вершин являются векторами, представляющими комплекс n н -й корни единства. Если корень, вектор которого составляет наименьший положительный угол с положительным направлением x -ось обозначается греческой буквой омега, ω, затем ω, ω 2 , ω 3 , …, ω n = 1 составляют все п -й корни единства. Например, ω = −1/2 + квадратный корень из √ −3/2, ω 2 = −1/2 − квадратный корень из √ −3/2 и ω 3 = 1 являются кубическими корнями. единства. Любой корень, обозначаемый греческой буквой эпсилон, ε, обладающий тем свойством, что ε, ε 2 , …, ε n = 1 дает все n -й корень из единицы называется примитивным. Очевидно, задача нахождения n -го корня из единицы эквивалентна задаче вписания в окружность правильного многоугольника с n сторонами. Для каждого целого числа n n -й корень из единицы может быть определен в терминах рациональных чисел с помощью рациональных операций и радикалов; но они могут быть построены линейкой и циркулем (т. е. определены в терминах обычных операций арифметики и извлечения квадратных корней) только в том случае, если n является произведением различных простых чисел вида 2 h + 1, или 2 k , умноженных на такое произведение, или имеет вид 2 k . Если a является комплексным числом, отличным от 0, уравнение x n = a имеет ровно n корней, и все n -го корня 90 021 и являются продуктами любого из этих корней на n -й корней из единицы.
Очевидно, задача нахождения n -го корня из единицы эквивалентна задаче вписания в окружность правильного многоугольника с n сторонами. Для каждого целого числа n n -й корень из единицы может быть определен в терминах рациональных чисел с помощью рациональных операций и радикалов; но они могут быть построены линейкой и циркулем (т. е. определены в терминах обычных операций арифметики и извлечения квадратных корней) только в том случае, если n является произведением различных простых чисел вида 2 h + 1, или 2 k , умноженных на такое произведение, или имеет вид 2 k . Если a является комплексным числом, отличным от 0, уравнение x n = a имеет ровно n корней, и все n -го корня 90 021 и являются продуктами любого из этих корней на n -й корней из единицы.
Термин корень был перенесен из уравнения x n = a во все полиномиальные уравнения. Таким образом, решение уравнения f ( x ) = a 0 x n + a 1 x n − 1 + … + a n − 1 x + a n = 0, где a 0 ≠ 0, называется корнем уравнения. Если коэффициенты лежат в комплексном поле, уравнение n -й степени имеет ровно n (не обязательно различных) комплексных корней. Если коэффициенты вещественные, а n нечетное, то корень вещественный. Но уравнение не всегда имеет корень в поле коэффициентов. Таким образом, x 2 — 5 = 0 не имеет рационального корня, хотя его коэффициенты (1 и –5) являются рациональными числами.
Таким образом, решение уравнения f ( x ) = a 0 x n + a 1 x n − 1 + … + a n − 1 x + a n = 0, где a 0 ≠ 0, называется корнем уравнения. Если коэффициенты лежат в комплексном поле, уравнение n -й степени имеет ровно n (не обязательно различных) комплексных корней. Если коэффициенты вещественные, а n нечетное, то корень вещественный. Но уравнение не всегда имеет корень в поле коэффициентов. Таким образом, x 2 — 5 = 0 не имеет рационального корня, хотя его коэффициенты (1 и –5) являются рациональными числами.
В более общем смысле термин корень может применяться к любому числу, которое удовлетворяет любому заданному уравнению, будь то полиномиальное уравнение или нет. Таким образом, π является корнем уравнения x sin ( x ) = 0,
Эта статья была недавно пересмотрена и обновлена Уильямом Л. Хошем.
Хошем.
Квадратный корень | математика | Британика
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.



 )
) )
) )
) )
) )
) )
) )
) 2x=2 — вопрос №1847740 — Учеба и наука
2x=2 — вопрос №1847740 — Учеба и наука 02.16
02.16 .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30. )/3
)/3
 Как правило, когда два множителя умножаются вместе, чтобы получить 0, это означает, что по крайней мере один из двух множителей равен 0,9.0907
Как правило, когда два множителя умножаются вместе, чтобы получить 0, это означает, что по крайней мере один из двух множителей равен 0,9.0907 Вы можете найти этот угол, если отразите свой угол по оси x, что даст вам последний ответ, х=216,1。
Вы можете найти этот угол, если отразите свой угол по оси x, что даст вам последний ответ, х=216,1。  ответил 16.11.21
ответил 16.11.21
 Когда это сделано, отрицательное число используется как основание и многократно умножается.
Когда это сделано, отрицательное число используется как основание и многократно умножается.
 Массовая доля химического элемента: что означает и как высчитывается
Массовая доля химического элемента: что означает и как высчитывается
 Какова молекулярная формула углеводорода?
Какова молекулярная формула углеводорода?

 2. Как определить формулу органического соединения
2. Как определить формулу органического соединения

 После полного сжигания в кислороде арена, имевшего массу 0,92 г, выделился оксид углерода (IV). Пропуская газ через избыток раствора щелочи Ca(OH)2, получили 7 грамм осадка. Какова молекулярная формула арена?
После полного сжигания в кислороде арена, имевшего массу 0,92 г, выделился оксид углерода (IV). Пропуская газ через избыток раствора щелочи Ca(OH)2, получили 7 грамм осадка. Какова молекулярная формула арена?

 Номер строки определен предыдущей формулой и является числом 3. Поэтому мы только ссылаемся на ячейку AB2 с первой формулой. Далее с помощью функции ДВССЫЛ определяется ссылка на диапазон, который должен быть найден в соответствии с местом нахождения ошибок. Нет необходимости выполнять поиск по целой таблице нагружая таким образом процессор компьютера излишне отнимая вычислительные ресурсы программы Excel. Нас интересует только третья строка.
Номер строки определен предыдущей формулой и является числом 3. Поэтому мы только ссылаемся на ячейку AB2 с первой формулой. Далее с помощью функции ДВССЫЛ определяется ссылка на диапазон, который должен быть найден в соответствии с местом нахождения ошибок. Нет необходимости выполнять поиск по целой таблице нагружая таким образом процессор компьютера излишне отнимая вычислительные ресурсы программы Excel. Нас интересует только третья строка. После чего функция МИН выбирает наименьшее числовое значение первого массива, которое соответствует номеру столбца содержащего первую ошибку. Так как били вычислены номер строки и столбца завершается вычисление формулы функцией АДРЕС. Она уже возвращает текстовым значением готовый адрес ячейки на основе номера столбца и строки указанных в ее аргументах.
После чего функция МИН выбирает наименьшее числовое значение первого массива, которое соответствует номеру столбца содержащего первую ошибку. Так как били вычислены номер строки и столбца завершается вычисление формулы функцией АДРЕС. Она уже возвращает текстовым значением готовый адрес ячейки на основе номера столбца и строки указанных в ее аргументах.


 Оба имеют эмпирическую формулу \(\ce{CH_2O}\).
Оба имеют эмпирическую формулу \(\ce{CH_2O}\).
 Результат должен быть целым числом или очень близким к целому числу.
Результат должен быть целым числом или очень близким к целому числу.
 .. Меньше
.. Меньше

 Причина в том, что MindOnMap Free JPG Word Converter Online поддерживает множество популярных форматов, включая JPG/JPEG, PNG, BMP, GIF, TIFF, PDF, DOC, DOCX, XLS, XLSX, PPT, PPTX и т. д. Следовательно, если вы время от времени вводите эту страницу и другие файлы для конвертации, вы также можете использовать MindOnMap Free JPG Word Converter Online.
Причина в том, что MindOnMap Free JPG Word Converter Online поддерживает множество популярных форматов, включая JPG/JPEG, PNG, BMP, GIF, TIFF, PDF, DOC, DOCX, XLS, XLSX, PPT, PPTX и т. д. Следовательно, если вы время от времени вводите эту страницу и другие файлы для конвертации, вы также можете использовать MindOnMap Free JPG Word Converter Online.
 И это преимущество действительно экономит мне много времени.
И это преимущество действительно экономит мне много времени.


 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Вычисление двух последовательных интегралов позволяет вычислить площади функций с двумя переменными для интегрирования на заданном интервале.
Вычисление двух последовательных интегралов позволяет вычислить площади функций с двумя переменными для интегрирования на заданном интервале. также: Определенный интеграл — функции примитивов
также: Определенный интеграл — функции примитивов За исключением явной лицензии с открытым исходным кодом (указывается Creative Commons/бесплатно), алгоритма «Двойной интеграл», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, взломщик, транслятор) или «Двойной интеграл». «Интегральные» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Double Integral» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
За исключением явной лицензии с открытым исходным кодом (указывается Creative Commons/бесплатно), алгоритма «Двойной интеграл», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, взломщик, транслятор) или «Двойной интеграл». «Интегральные» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Double Integral» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!  csv или .txt можно выполнить бесплатно, щелкнув значок export . , https://www.dcode.fr/double-integral
csv или .txt можно выполнить бесплатно, щелкнув значок export . , https://www.dcode.fr/double-integral  Этот калькулятор использует двумерную функцию и предоставляет пошаговое решение для обеих переменных. Этот калькулятор двойного интегрирования легко решит двойные определенные и неопределенные задачи.
Этот калькулятор использует двумерную функцию и предоставляет пошаговое решение для обеих переменных. Этот калькулятор двойного интегрирования легко решит двойные определенные и неопределенные задачи.

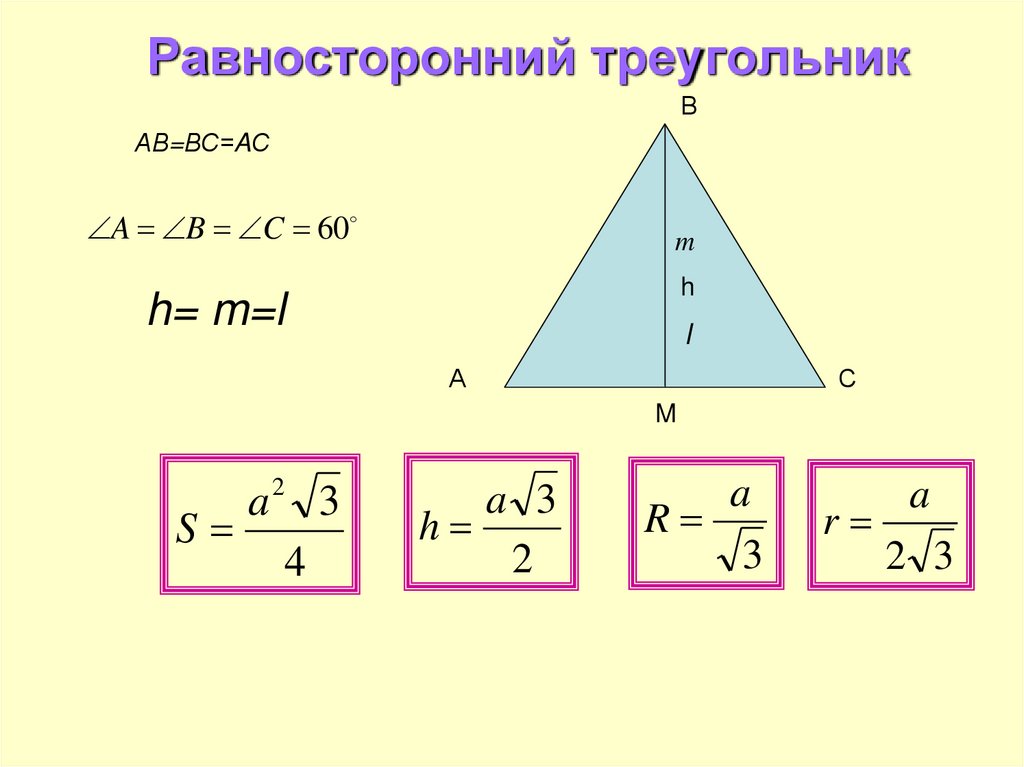
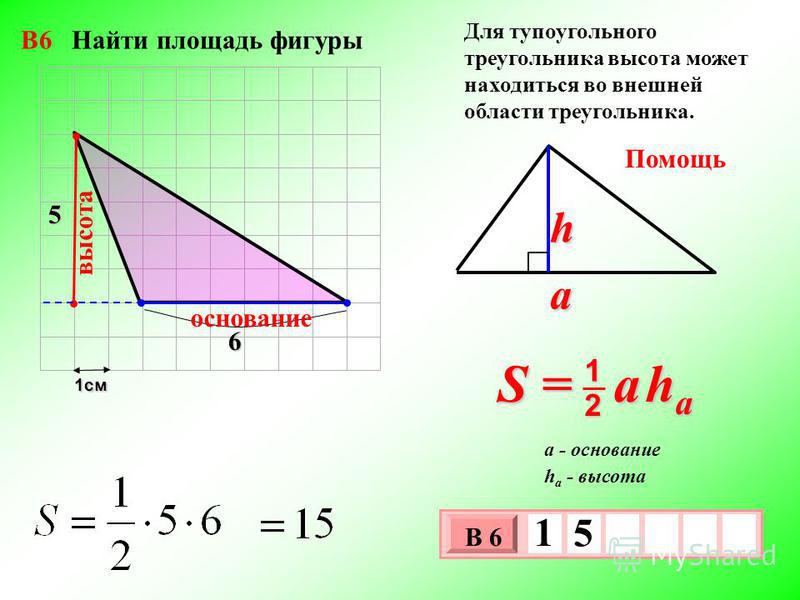
 Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из
вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см.
Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ:
5 см.
Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из
вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см.
Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ:
5 см. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике
ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол
АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС.
Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном
треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC,
значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту
(АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.
По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике
ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол
АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС.
Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном
треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC,
значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту
(АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.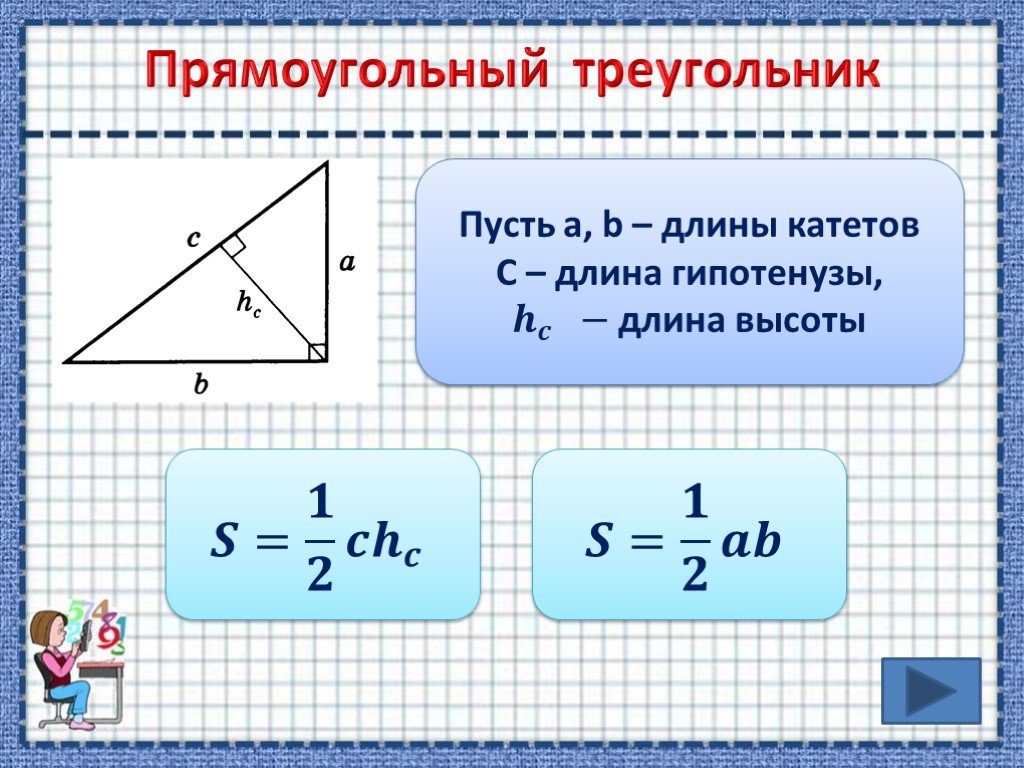 В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к
основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию
треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН,
является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По
формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см.
Ответ: 6 см.
В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к
основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию
треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН,
является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По
формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см.
Ответ: 6 см. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚.
Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике
найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то
треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем
высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим
полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ:
3√2 см
В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚.
Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике
найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то
треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем
высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим
полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ:
3√2 см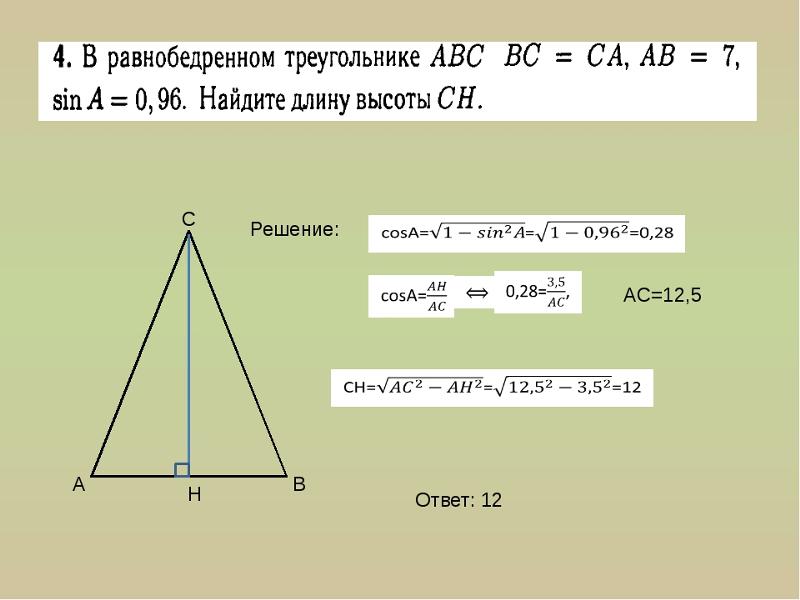 Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ:
6 см
Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ:
6 см
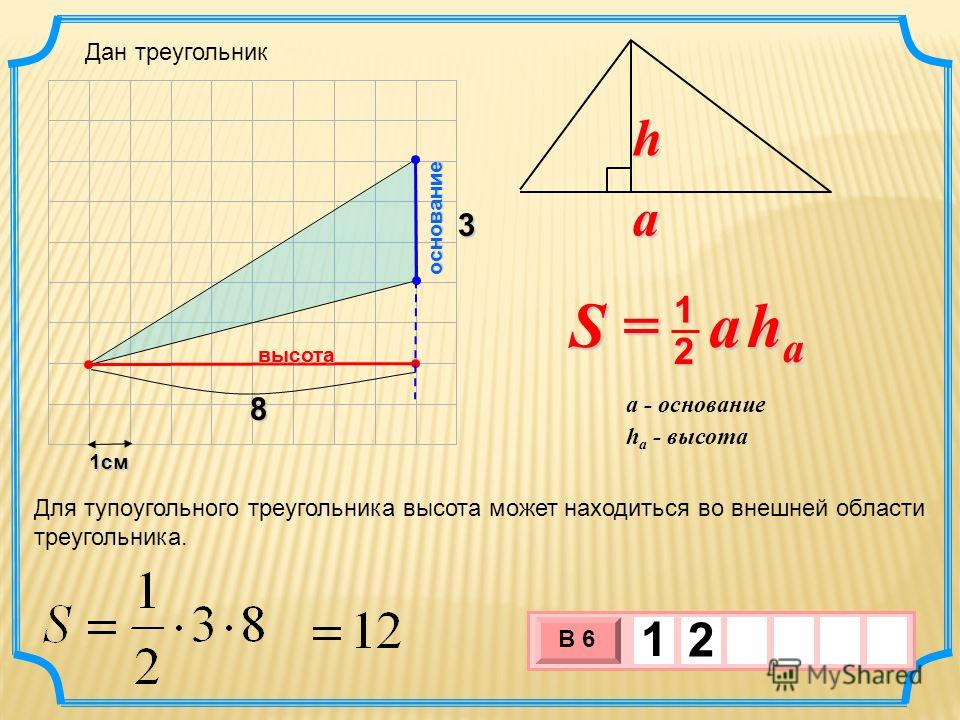
 Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.
Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.
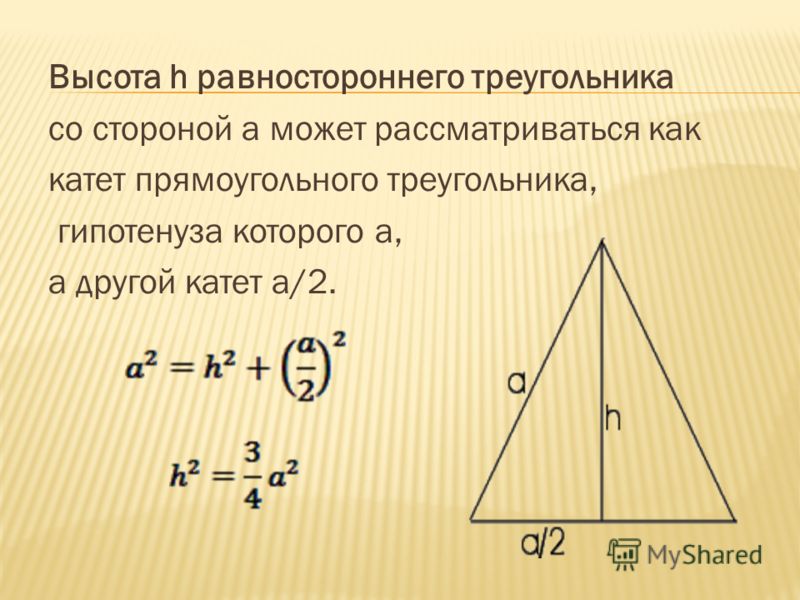
 В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.
В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.
 Мы уже знаем, что гипотенуза равна 24 см .
Мы уже знаем, что гипотенуза равна 24 см . Это не будет работать на разносторонних треугольниках!
Это не будет работать на разносторонних треугольниках!
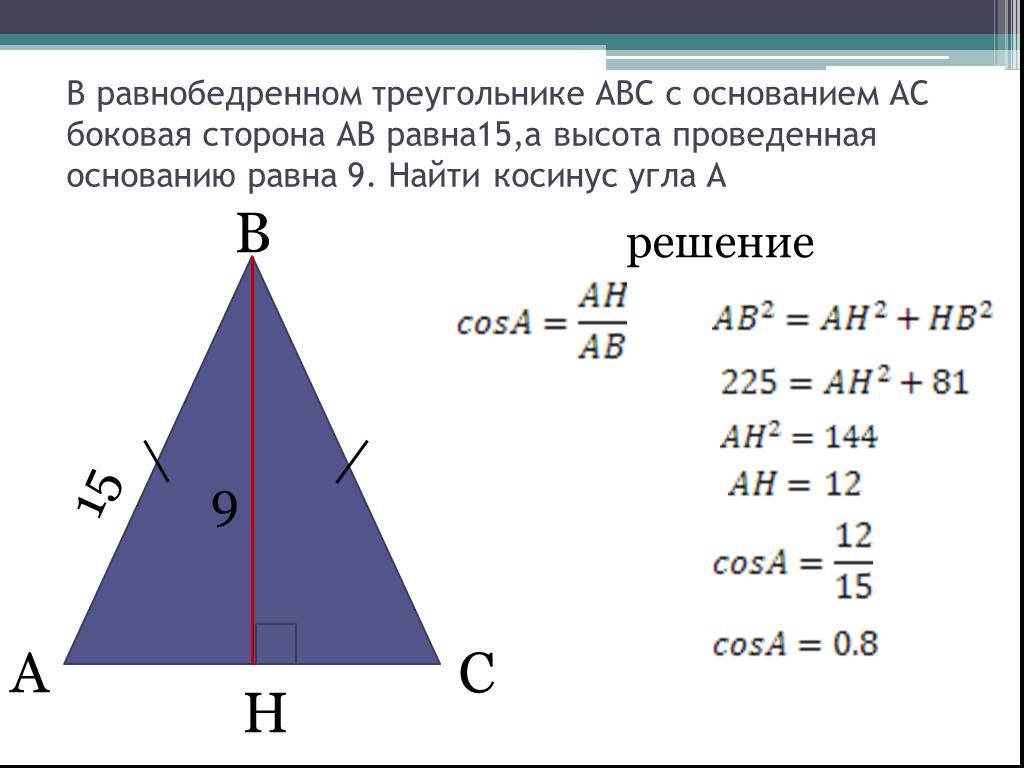 ед. Найдите длину высоты, если длина основания равна 9.0 единиц.
ед. Найдите длину высоты, если длина основания равна 9.0 единиц.
 Два калькуля разряда Пятёрок равны одному калькулю из разряда ДЕСЯТОК. То есть, при достижении в разряде Пятёрок количества в два калькуля – разряд Пятёрок обнуляется с одновременным увеличением разряда Десяток на один калькуль.
Два калькуля разряда Пятёрок равны одному калькулю из разряда ДЕСЯТОК. То есть, при достижении в разряде Пятёрок количества в два калькуля – разряд Пятёрок обнуляется с одновременным увеличением разряда Десяток на один калькуль.
 Знай себе вычитай из соответствующего разряда соответствующий разряд.
Знай себе вычитай из соответствующего разряда соответствующий разряд.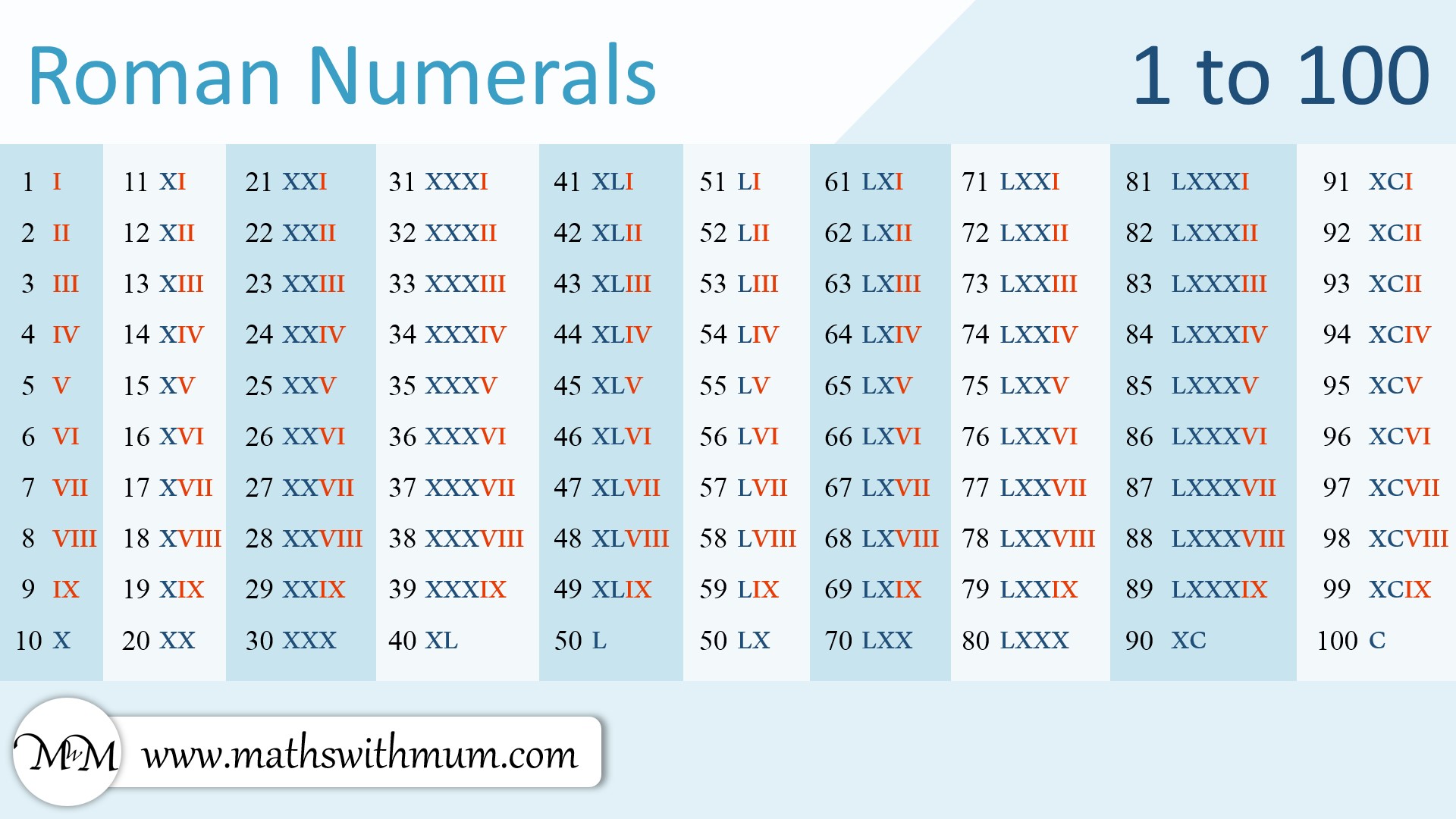
 д.
д.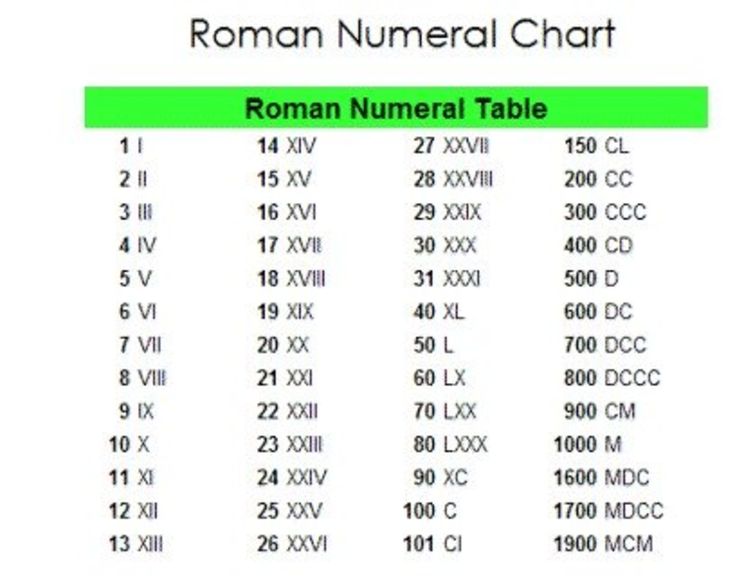

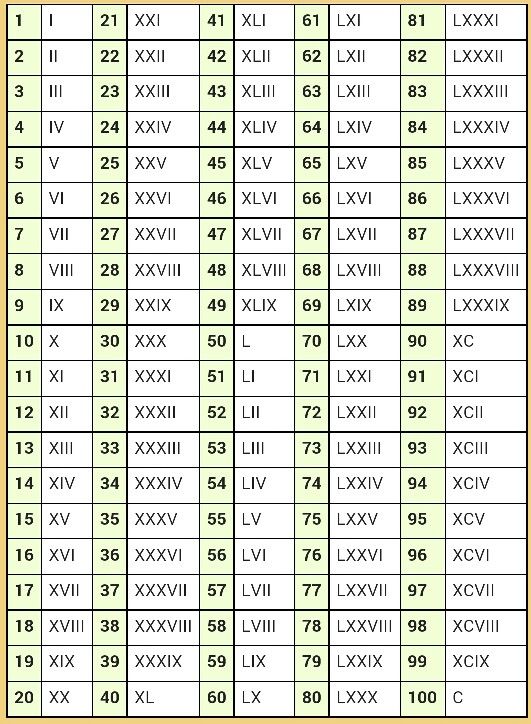 Кроме того, L, V, D не могут повторяться, иначе число считается недействительным.
Кроме того, L, V, D не могут повторяться, иначе число считается недействительным. Современное использование римских цифр включает буквы I, V, X, L, C, D и M.
Современное использование римских цифр включает буквы I, V, X, L, C, D и M.




 Вы можете использовать калькулятор римских цифр, чтобы проверить свои ответы.
Вы можете использовать калькулятор римских цифр, чтобы проверить свои ответы.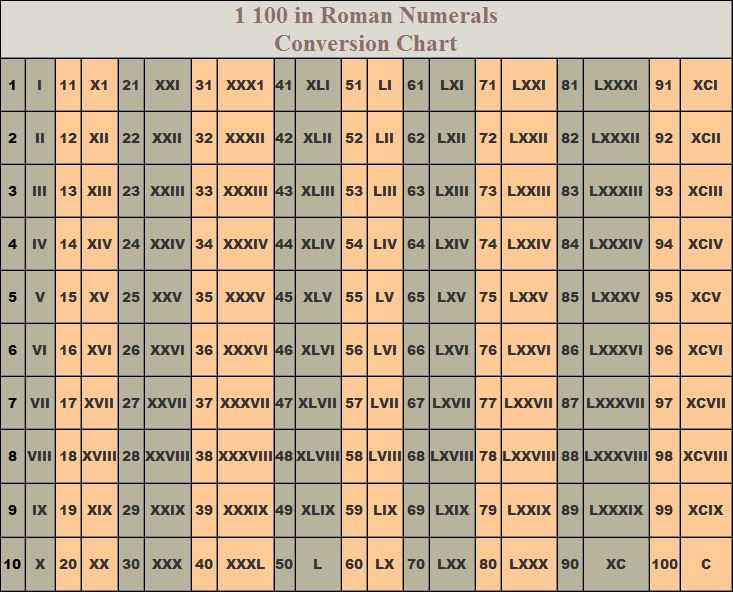 Например, VIII = 5 + 1 + 1 + 1 = 8 или XV = 10 + 5 = 15,
Например, VIII = 5 + 1 + 1 + 1 = 8 или XV = 10 + 5 = 15, Например, если у нас есть XVII, мы можем расширить и добавить их как X + V + I + I = 10 + 5 + 1 + 1 = 17,
Например, если у нас есть XVII, мы можем расширить и добавить их как X + V + I + I = 10 + 5 + 1 + 1 = 17,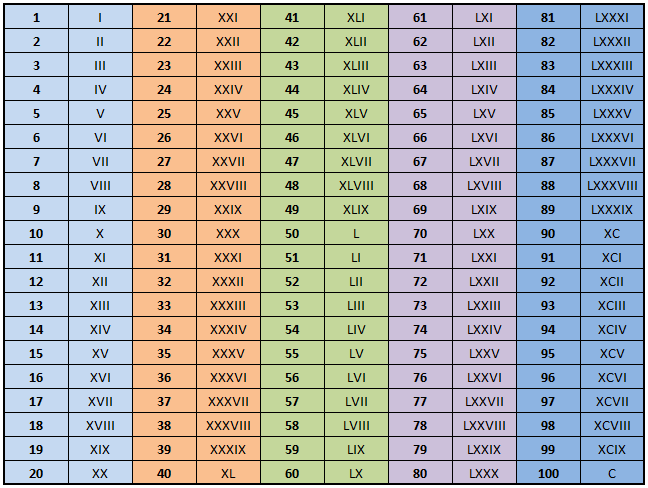 Если мы посмотрим на данную римскую цифру MCMXI, мы увидим, что C ставится перед M, которая имеет большее значение, поэтому мы вычтем их (M — C), и тогда расширение будет как M + (M — C) + Х + I = 1000 + (1000 — 100) + 10 + 1 = 1000 + 900 + 10 + 1 = 1911. Это означает, что римская цифра MCMXI равна 1911, а значение CLX = C + L + X = 100 + 50 + 10 равно 160.
Если мы посмотрим на данную римскую цифру MCMXI, мы увидим, что C ставится перед M, которая имеет большее значение, поэтому мы вычтем их (M — C), и тогда расширение будет как M + (M — C) + Х + I = 1000 + (1000 — 100) + 10 + 1 = 1000 + 900 + 10 + 1 = 1911. Это означает, что римская цифра MCMXI равна 1911, а значение CLX = C + L + X = 100 + 50 + 10 равно 160.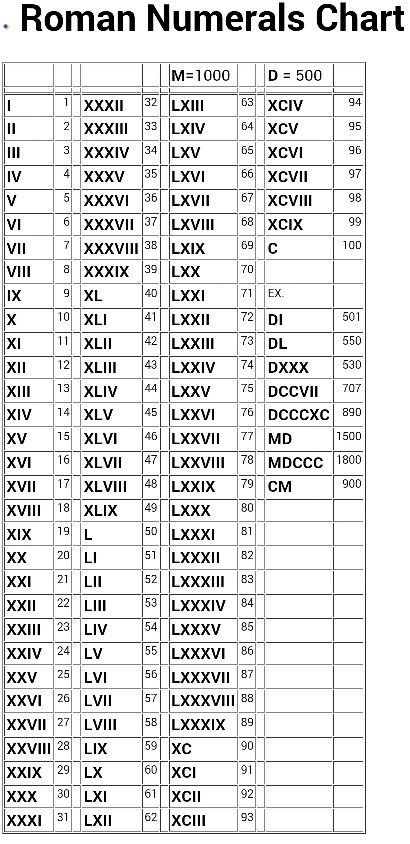 д. В следующем списке показано несколько страниц рабочих листов с римскими цифрами с загружаемыми PDF-файлами.
д. В следующем списке показано несколько страниц рабочих листов с римскими цифрами с загружаемыми PDF-файлами.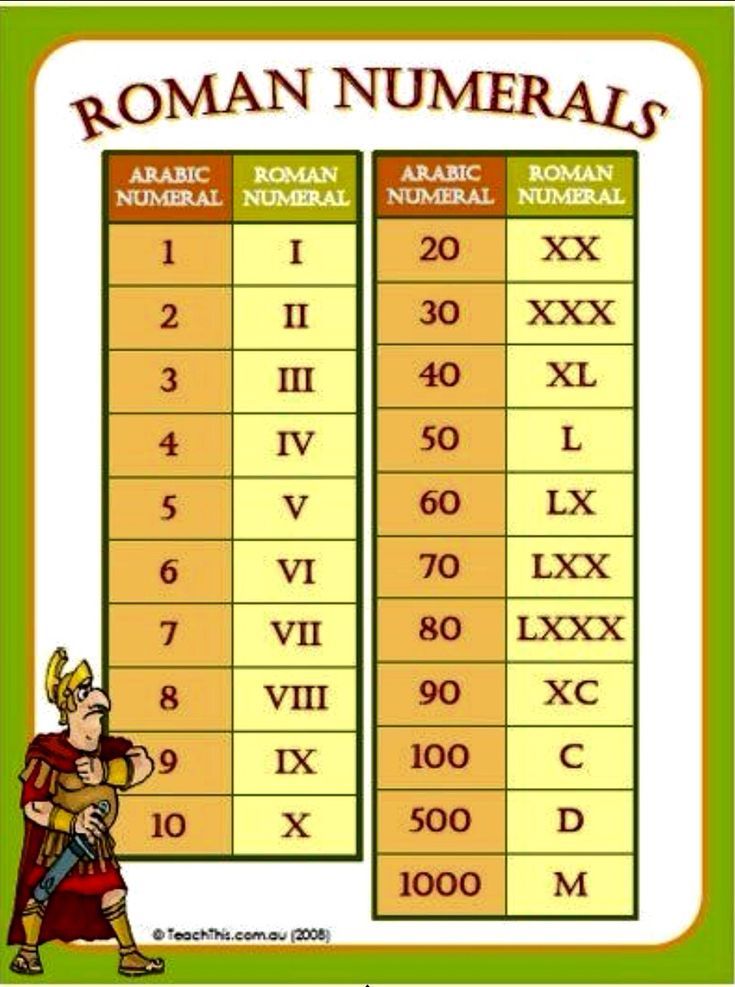 Здесь первые буквы, выделенные жирным шрифтом, показывают римские цифры в порядке убывания.
Здесь первые буквы, выделенные жирным шрифтом, показывают римские цифры в порядке убывания.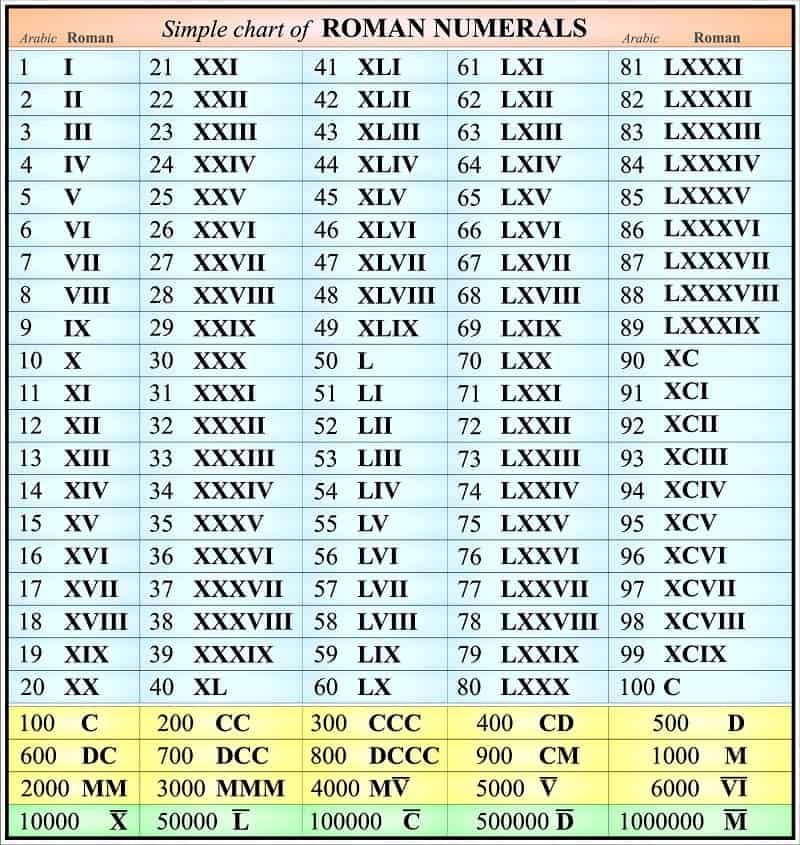 Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении. Если мы посмотрим на данную римскую цифру XIX, мы увидим, что I стоит перед X, что имеет большее значение, поэтому мы их вычтем. Это будет записано как X + (X — I) = 10 + (10 — 1) = 10 + 9.= 19
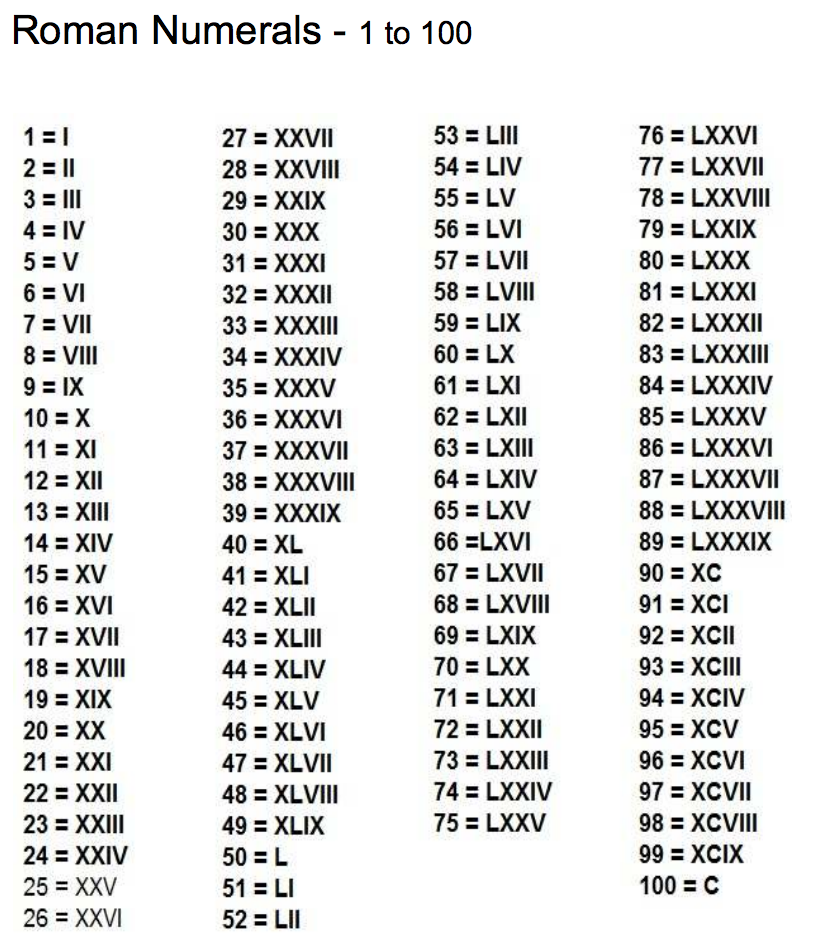
Если мы посмотрим на данную римскую цифру XIX, мы увидим, что I стоит перед X, что имеет большее значение, поэтому мы их вычтем. Это будет записано как X + (X — I) = 10 + (10 — 1) = 10 + 9.= 19 У них Латинские буквы I, V, X, L, C, D и M , обозначающие числа 1, 5, 10, 50, 100, 500 и 1000 соответственно. Каждое число может быть выражено как римская цифра, используя определенные правила, которые определяются римскими числами.
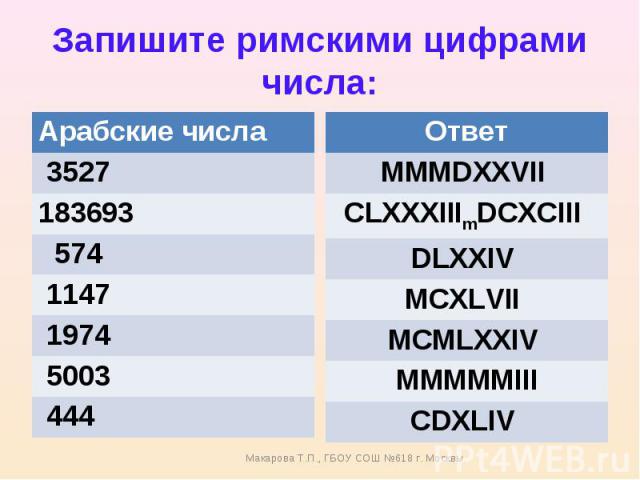
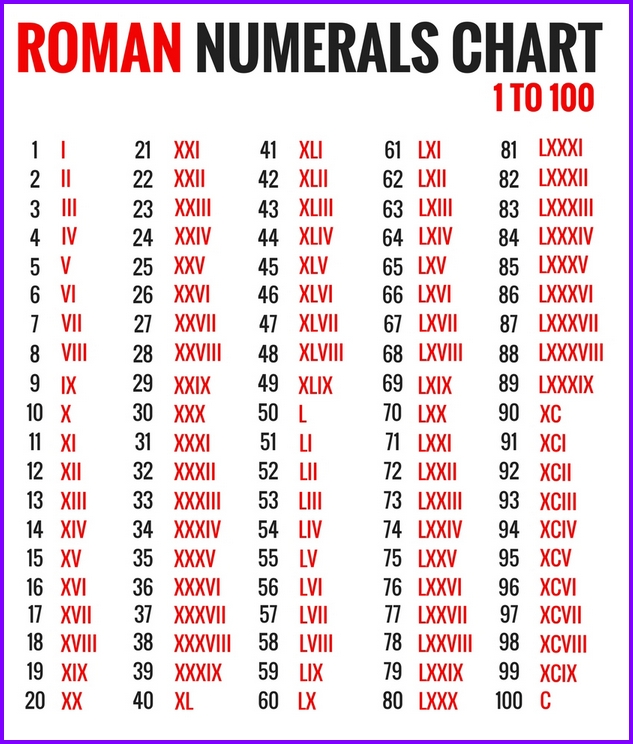
У них Латинские буквы I, V, X, L, C, D и M , обозначающие числа 1, 5, 10, 50, 100, 500 и 1000 соответственно. Каждое число может быть выражено как римская цифра, используя определенные правила, которые определяются римскими числами.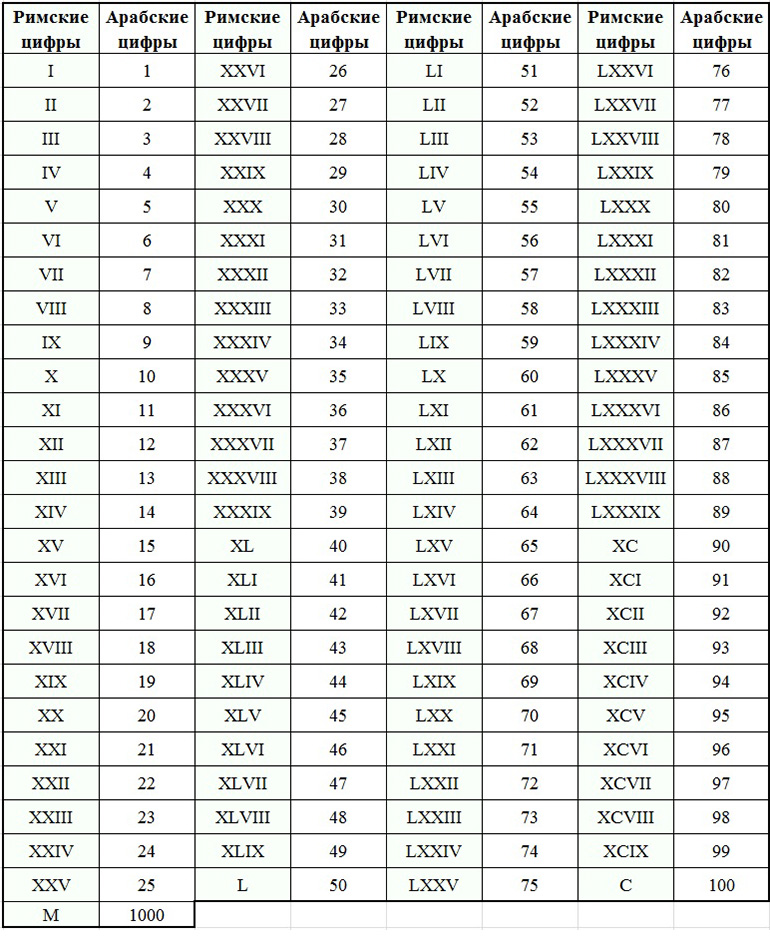 Соответственно, 2020 можно выразить как 2020 = 1000 + 1000 + 10 + 10 = M + M + X + X = MMXX. Следовательно, 2020 год можно записать как MMXX римскими цифрами.
Соответственно, 2020 можно выразить как 2020 = 1000 + 1000 + 10 + 10 = M + M + X + X = MMXX. Следовательно, 2020 год можно записать как MMXX римскими цифрами. Римское число М представляет 1000 или тысячу в десятичной системе счисления.
Римское число М представляет 1000 или тысячу в десятичной системе счисления. Число 100 представлено буквой С римскими цифрами.
Число 100 представлено буквой С римскими цифрами.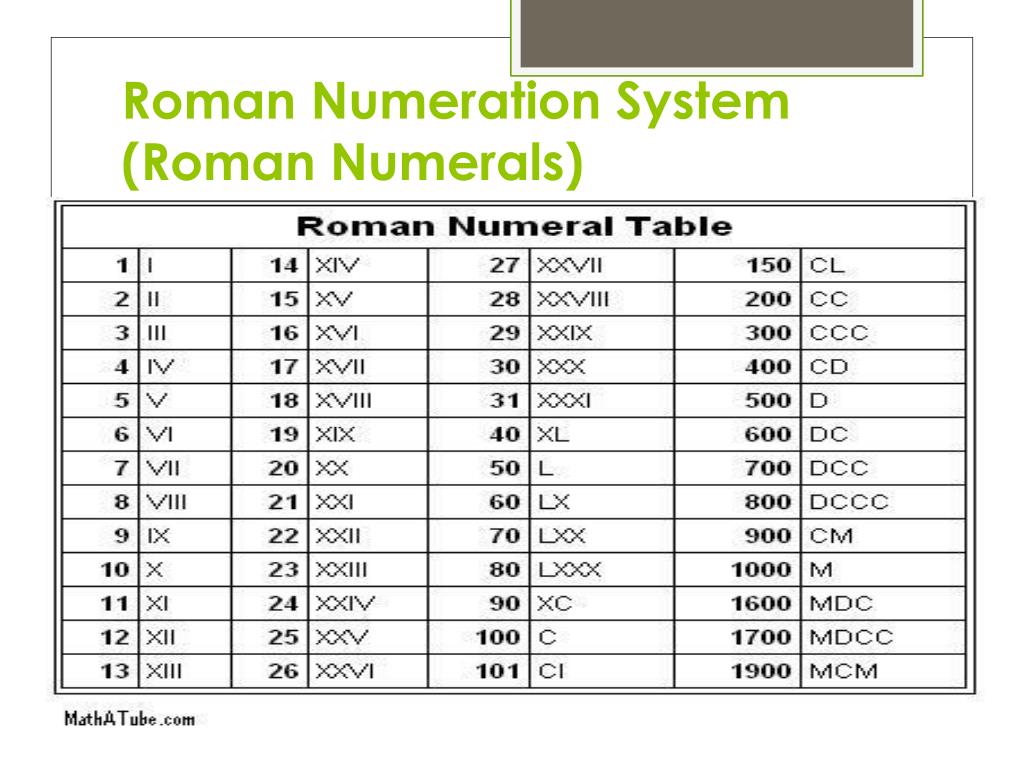
 Например, II = 1 + 1 = 2, или ХХ = 10 + 10 = 20, или ХХХ = 10 + 10 + 10 = 30,9.0078
Например, II = 1 + 1 = 2, или ХХ = 10 + 10 = 20, или ХХХ = 10 + 10 + 10 = 30,9.0078 Например, XIV = 10 + (5 — 1) = 14 или XIX = 10 + (10 — 1) = 19
Например, XIV = 10 + (5 — 1) = 14 или XIX = 10 + (10 — 1) = 19  После этого мы получаем V + I + I. После подстановки значений V = 5, I = 1 мы получаем 5 + 1 + 1 = 7.
После этого мы получаем V + I + I. После подстановки значений V = 5, I = 1 мы получаем 5 + 1 + 1 = 7.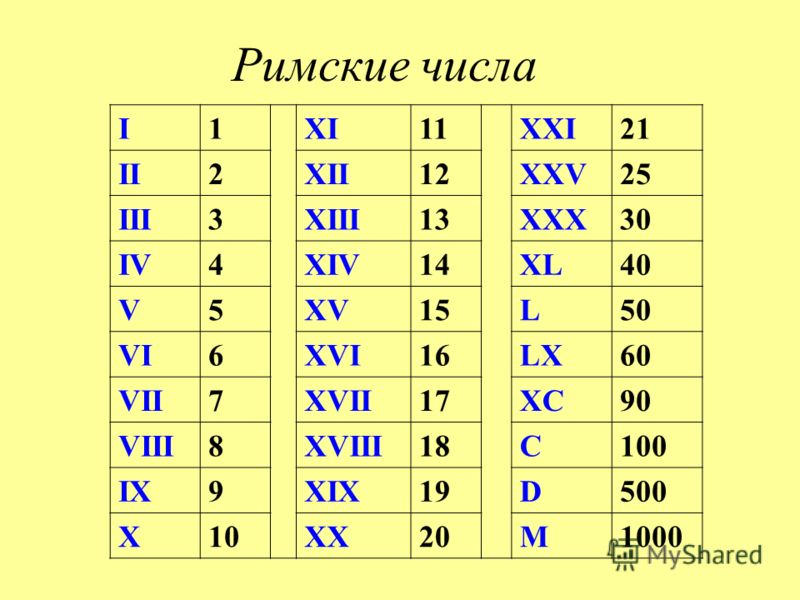 В этой статье мы объясним, как правильно преобразовать 2022 год римскими цифрами.
В этой статье мы объясним, как правильно преобразовать 2022 год римскими цифрами.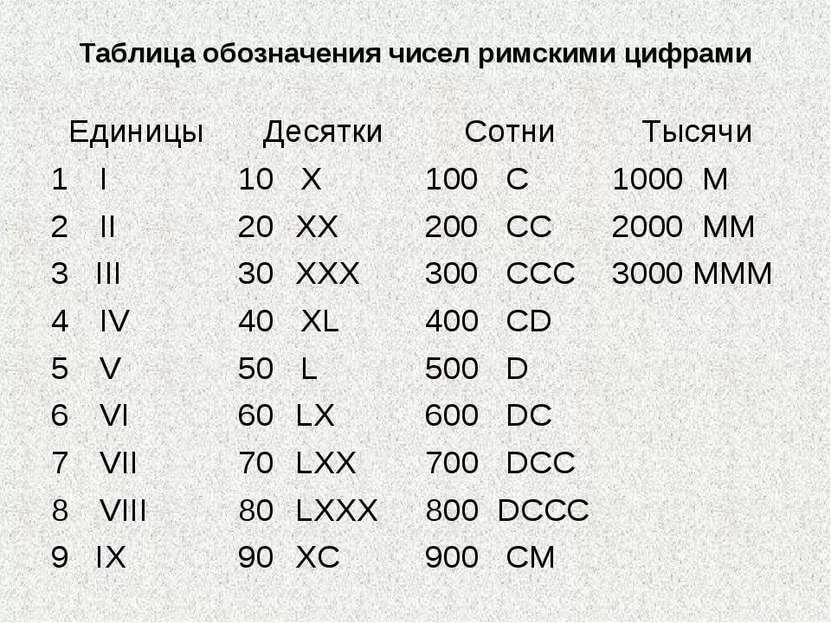

 Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.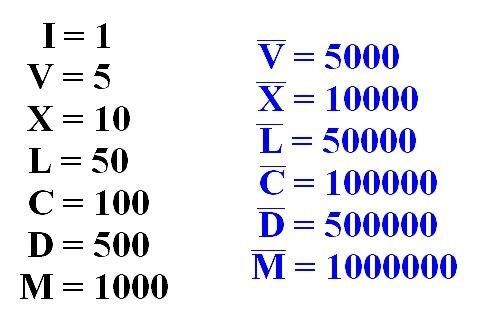

 Дополнительно в тело плиты закладывают рифленую арматуру диаметров 10 и 12 мм. Для удобства перемещения подножника имеется три монтажных петли из стали класса А-100 или А-200 с предварительным термическим упрочнением. Крепеж опоры со стойкой фундамента осуществляется посредством болтового соединения. Для этого внедряют закладные детали М55. Все стальные компоненты покрывают цинконаполненными составами, которые предотвращают развитие коррозионных процессов и продлевают срок службы всей бетонной конструкции.
Дополнительно в тело плиты закладывают рифленую арматуру диаметров 10 и 12 мм. Для удобства перемещения подножника имеется три монтажных петли из стали класса А-100 или А-200 с предварительным термическим упрочнением. Крепеж опоры со стойкой фундамента осуществляется посредством болтового соединения. Для этого внедряют закладные детали М55. Все стальные компоненты покрывают цинконаполненными составами, которые предотвращают развитие коррозионных процессов и продлевают срок службы всей бетонной конструкции. Складирование осуществляется на складах. Раскладка конструкций выполняется в один ряд, либо по схеме, которая имеет обоснование в сохранности продукции в пригодном для монтажа состоянии. Под железобетонные плиты кладут деревянные щиты.
Складирование осуществляется на складах. Раскладка конструкций выполняется в один ряд, либо по схеме, которая имеет обоснование в сохранности продукции в пригодном для монтажа состоянии. Под железобетонные плиты кладут деревянные щиты. .. и не только
.. и не только Первая неделя дала нам почти все. С учетом сказанного, давайте приступим к нашему первому раунду рейтинга силы! Первый рекорд – это СЕРИЙНЫЙ рекорд команды, второй – их ИГРОВОЙ рекорд.
Первая неделя дала нам почти все. С учетом сказанного, давайте приступим к нашему первому раунду рейтинга силы! Первый рекорд – это СЕРИЙНЫЙ рекорд команды, второй – их ИГРОВОЙ рекорд. Мы сомневались в том, что эта команда принимает решения в формате 5 на 5 все межсезонье, но кого это сейчас волнует. У них действительно хороший и чрезвычайно интересный состав 3 на 3. Jyden играл как человек, все еще злящийся из-за того, что его не удержали, как и DjayTooCold. Добавьте к этому отличный профессиональный дебют от LawRich, и вы получите команду, за которой нужно следить каждую неделю. Мне сказали, что группу кенгуру называют мафией, так что считайте меня частью мафии НБЛ до особого распоряжения.
Мы сомневались в том, что эта команда принимает решения в формате 5 на 5 все межсезонье, но кого это сейчас волнует. У них действительно хороший и чрезвычайно интересный состав 3 на 3. Jyden играл как человек, все еще злящийся из-за того, что его не удержали, как и DjayTooCold. Добавьте к этому отличный профессиональный дебют от LawRich, и вы получите команду, за которой нужно следить каждую неделю. Мне сказали, что группу кенгуру называют мафией, так что считайте меня частью мафии НБЛ до особого распоряжения. Мне тоже понравилось то, что я увидел в Хесе, его развитие очень важно для этой команды в будущем. Эта команда начала успешный прошлый сезон, прежде чем угаснуть, и, надеюсь, они смогут избежать ладдера в 2023 году.0003
Мне тоже понравилось то, что я увидел в Хесе, его развитие очень важно для этой команды в будущем. Эта команда начала успешный прошлый сезон, прежде чем угаснуть, и, надеюсь, они смогут избежать ладдера в 2023 году.0003 Его заменил Коннор, выбранный в первом раунде, и, хотя он до сих пор выступал превосходно, в этой команде чего-то не хватает. Может быть, мы просто возвращаемся к удаленной игре, но эта команда не кажется такой ужасающей, как в прошлом сезоне, они на самом деле чувствуют себя довольно смертными. Я определенно еще не списываю их со счетов, слишком рано делать это с командой 3 на 3 с Ant и BagMotion, но пакет Pistons GT просто не бьет то же самое прямо сейчас. Возможно, еще несколько игр с их новым составом сделают свое дело.
Его заменил Коннор, выбранный в первом раунде, и, хотя он до сих пор выступал превосходно, в этой команде чего-то не хватает. Может быть, мы просто возвращаемся к удаленной игре, но эта команда не кажется такой ужасающей, как в прошлом сезоне, они на самом деле чувствуют себя довольно смертными. Я определенно еще не списываю их со счетов, слишком рано делать это с командой 3 на 3 с Ant и BagMotion, но пакет Pistons GT просто не бьет то же самое прямо сейчас. Возможно, еще несколько игр с их новым составом сделают свое дело. На его IQ и чувство игры приятно смотреть, а наличие двух очень умных игроков в лице Каазе и Риа делает его жизнь еще проще. У них есть склонность время от времени терять фокус, отсюда и рекорд 2-2, но мне очень нравится, как эта команда находится в тренде. Очень сложно обыграть команду, у которой третьим лучшим игроком 3 на 3 является Каазе или Риа, глупо говорить вслух. Им потребуется некоторое время, чтобы добиться успеха. Я не удивлюсь, если они вылетят в начале этого турнира, но когда придет время чемпионата? Темная лошадка.
На его IQ и чувство игры приятно смотреть, а наличие двух очень умных игроков в лице Каазе и Риа делает его жизнь еще проще. У них есть склонность время от времени терять фокус, отсюда и рекорд 2-2, но мне очень нравится, как эта команда находится в тренде. Очень сложно обыграть команду, у которой третьим лучшим игроком 3 на 3 является Каазе или Риа, глупо говорить вслух. Им потребуется некоторое время, чтобы добиться успеха. Я не удивлюсь, если они вылетят в начале этого турнира, но когда придет время чемпионата? Темная лошадка. Мы видели много элитной двухсторонней игры, которая позволила им выиграть чемпионат STEAL OPEN и занять лидирующие позиции в чемпионатах, но этого было недостаточно последовательно. Мне также показалось, что Unguardable немного давит. Возможно, ему немного помешало быть «парнем», я видел кучу нехарактерных для него игр за всю неделю. Я уверен, что он и остальная часть команды во всем разберутся, но просто нужно следить за этим. Может быть, мы воздержимся от хардкорных мнений о них, пока групповая игра не закончится.
Мы видели много элитной двухсторонней игры, которая позволила им выиграть чемпионат STEAL OPEN и занять лидирующие позиции в чемпионатах, но этого было недостаточно последовательно. Мне также показалось, что Unguardable немного давит. Возможно, ему немного помешало быть «парнем», я видел кучу нехарактерных для него игр за всю неделю. Я уверен, что он и остальная часть команды во всем разберутся, но просто нужно следить за этим. Может быть, мы воздержимся от хардкорных мнений о них, пока групповая игра не закончится.
 0, туалетного — 1.8, мыльной стружки — 2.2.
0, туалетного — 1.8, мыльной стружки — 2.2. Соотношение данных цифр и даст нам рост производительности труда.
Соотношение данных цифр и даст нам рост производительности труда. S. Догадайтесь, откуда я знаю, что на производстве были заняты 8 человек?
S. Догадайтесь, откуда я знаю, что на производстве были заняты 8 человек? При этом планируется ряд мероприятий, которые позволят снизить трудоемкость на 9%, а также возможно увеличение производительности за счет организационных мероприятий на 7%.
При этом планируется ряд мероприятий, которые позволят снизить трудоемкость на 9%, а также возможно увеличение производительности за счет организационных мероприятий на 7%.

 В базовом году численность рабочих составляла 274 человека. Численность других категорий работающих не изменяется.
В базовом году численность рабочих составляла 274 человека. Численность других категорий работающих не изменяется. После внедрения организационно-технических мероприятий нормы времени начали выполняться на 125%. Как изменилась при этом производительность труда.
После внедрения организационно-технических мероприятий нормы времени начали выполняться на 125%. Как изменилась при этом производительность труда.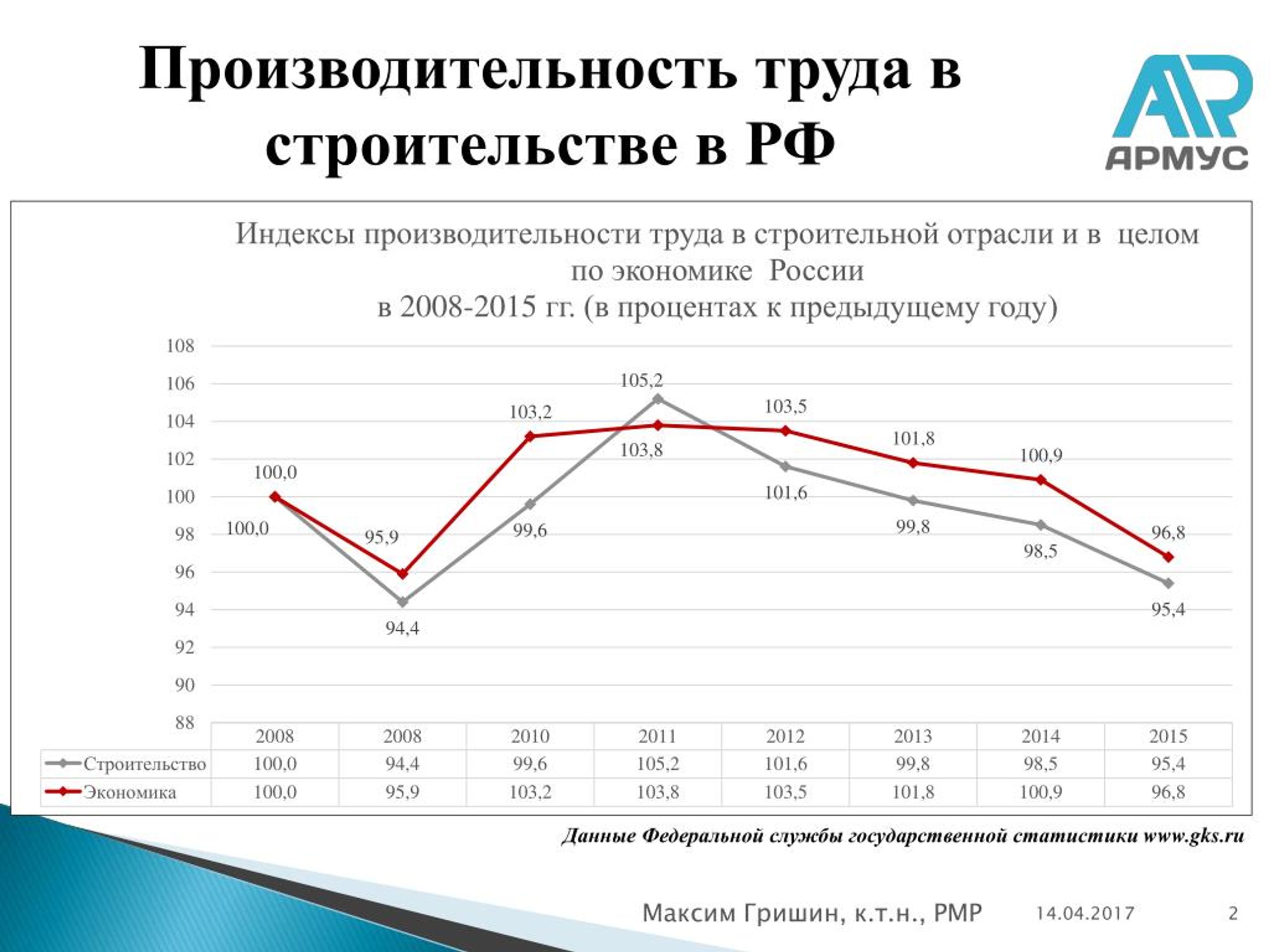 Изменение трудоемкости при изменении производительности труда
Изменение трудоемкости при изменении производительности труда
 Определите общее изменение производительности труда.
Определите общее изменение производительности труда.

 Насколько вырастет производительность труда в Государстве, примерно настолько же увеличится объем денег в кошельках населения. Это в теории. На практике — Россия более 100 лет борется за повышение производительности труда. Все руководители ставили эту задачу. Иногда это действительно получалось.
Насколько вырастет производительность труда в Государстве, примерно настолько же увеличится объем денег в кошельках населения. Это в теории. На практике — Россия более 100 лет борется за повышение производительности труда. Все руководители ставили эту задачу. Иногда это действительно получалось. То есть мы вкладываем много сил, времени, а на выходе результаты весьма средние». Почему так происходит? Одной из причин он назвал недостаточную конкуренцию в экономике, и следовательно, недостаточное количество стимулов к наращиванию производительности труда.
То есть мы вкладываем много сил, времени, а на выходе результаты весьма средние». Почему так происходит? Одной из причин он назвал недостаточную конкуренцию в экономике, и следовательно, недостаточное количество стимулов к наращиванию производительности труда.


 Корпоративная прибыль и доходы акционеров напрямую связаны с ростом производительности.
Корпоративная прибыль и доходы акционеров напрямую связаны с ростом производительности.
 Это основано на отношении ВВП к общему количеству часов, отработанных в экономике. Рост производительности труда происходит за счет увеличения объема капитала, доступного каждому работнику (углубление капитала), образования и опыта рабочей силы (состав рабочей силы), а также совершенствования технологий (многофакторный рост производительности).
Это основано на отношении ВВП к общему количеству часов, отработанных в экономике. Рост производительности труда происходит за счет увеличения объема капитала, доступного каждому работнику (углубление капитала), образования и опыта рабочей силы (состав рабочей силы), а также совершенствования технологий (многофакторный рост производительности). К таким вещам относятся инвестиции в заводы и оборудование, инновации, улучшение логистики цепочки поставок, образование, предпринимательство и конкуренция.
К таким вещам относятся инвестиции в заводы и оборудование, инновации, улучшение логистики цепочки поставок, образование, предпринимательство и конкуренция.
 Низкие нормы сбережений могут привести к снижению норм инвестиций и снижению темпов роста производительности труда и реальной заработной платы. Вот почему опасаются, что низкий уровень сбережений в США может повредить росту производительности в будущем.
Низкие нормы сбережений могут привести к снижению норм инвестиций и снижению темпов роста производительности труда и реальной заработной платы. Вот почему опасаются, что низкий уровень сбережений в США может повредить росту производительности в будущем.

 Его «производственная система Toyota» (TPS) является одной из основных причин этого.
Его «производственная система Toyota» (TPS) является одной из основных причин этого.

 com, участник Investopedia, а также основатель и менеджер Free Lances Ltd.
com, участник Investopedia, а также основатель и менеджер Free Lances Ltd. Она специализируется в личных финансах и инвестициях, а также в сфере недвижимости.
Она специализируется в личных финансах и инвестициях, а также в сфере недвижимости. Стандартный расчет дает нам выход в единицу времени, например, пять тонн в час труда. Увеличение физической производительности вызывает соответствующее увеличение стоимости труда, что повышает заработную плату. Вот почему работодатели ищут образование и обучение на рабочем месте. Знания и опыт увеличивают человеческий капитал работников и делают их более продуктивными.
Стандартный расчет дает нам выход в единицу времени, например, пять тонн в час труда. Увеличение физической производительности вызывает соответствующее увеличение стоимости труда, что повышает заработную плату. Вот почему работодатели ищут образование и обучение на рабочем месте. Знания и опыт увеличивают человеческий капитал работников и делают их более продуктивными. Если бы вместо этого у вас была лопата, вам потребовалось бы всего три часа, чтобы вырыть яму. Рыночная стоимость вашего труда только что выросла до 15 долларов в час. С достаточно большим экскаватором вы сможете выкопать его за 15 минут и заработать 180 долларов в час. На рынке совершенной конкуренции труд зарабатывает свой предельный продукт.
Если бы вместо этого у вас была лопата, вам потребовалось бы всего три часа, чтобы вырыть яму. Рыночная стоимость вашего труда только что выросла до 15 долларов в час. С достаточно большим экскаватором вы сможете выкопать его за 15 минут и заработать 180 долларов в час. На рынке совершенной конкуренции труд зарабатывает свой предельный продукт.
