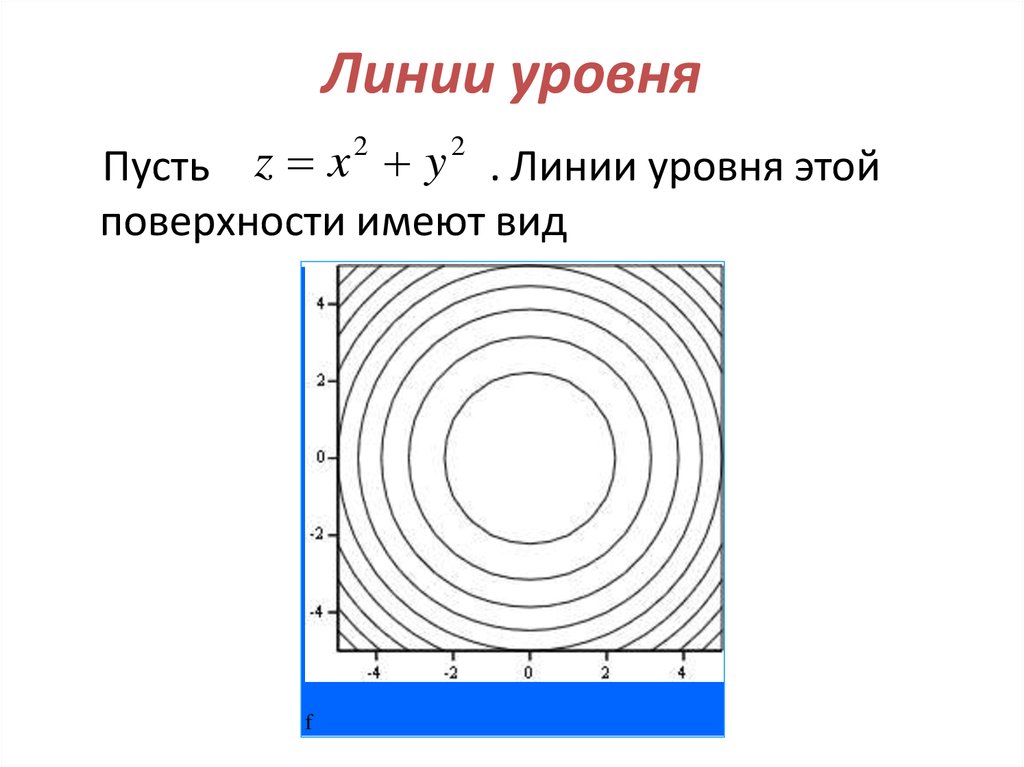
Формула нахождения середины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Теперь найдем координаты точки K:
Ответ : K = (0,5; 0; 1)
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .
Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:
Ответ : L = (0,5; 0,5; 1)
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как найти середину отрезка с помощью циркуля?Элементарная задачка о нахождении середины отрезка при помощи циркуля была сформулирована еще в античности. Часто ее приписывают древнегреческим мудрецам, однако, скорее всего, она присутствовала и в других культурах, в которых была развита математика и геометрия (например, в древнеегипетской). В древности эта задача имела и вполне практическое применение, ведь знание того, как найти середину отрезка при помощи простейших измерительных приборов, было полезно, например, в землемерстве, землеустройстве и строительстве. Сегодня, при наличии сложной измерительной техники, такое задание скорее представляет упражнение для развития интеллектуальных способностей и пространственной фантазии школьников.
Часто ее приписывают древнегреческим мудрецам, однако, скорее всего, она присутствовала и в других культурах, в которых была развита математика и геометрия (например, в древнеегипетской). В древности эта задача имела и вполне практическое применение, ведь знание того, как найти середину отрезка при помощи простейших измерительных приборов, было полезно, например, в землемерстве, землеустройстве и строительстве. Сегодня, при наличии сложной измерительной техники, такое задание скорее представляет упражнение для развития интеллектуальных способностей и пространственной фантазии школьников.
Как же на самом деле решается данная задача? Берем циркуль и открываем его таким образом, чтобы радиус предполагаемой окружности был очевидно больше половины заданного отрезка. Теперь, ставим основание (иглу) циркуля в одну из точек, ограничивающих отрезок, и рисуем окружность выбранного радиуса. В принципе, решая задачу о том, как построить середину отрезка, достаточно нарисовать и полукруг, располагающийся «внутри» отрезка. Затем устанавливаем иглу циркуля в другой конец отрезка и повторяем процедуру очерчивания полукруга.Проделав описанную процедуру, видим, что наши окружности пересекаются в двух точках. Берем линейку и соединяем эти две точки прямой линией. Получаем линию перпендикулярную исходному отрезку. Именно точка пересечения этой линии и отрезка и является серединой последнего.
Затем устанавливаем иглу циркуля в другой конец отрезка и повторяем процедуру очерчивания полукруга.Проделав описанную процедуру, видим, что наши окружности пересекаются в двух точках. Берем линейку и соединяем эти две точки прямой линией. Получаем линию перпендикулярную исходному отрезку. Именно точка пересечения этой линии и отрезка и является серединой последнего.
Конечно, здесь важно понять саму сущность данной задачи. Почему центр отрезка получится именно там, где пересекутся линии? Знание смысла данной задачи может, например пригодиться, при поиска ответа на вопрос о том, как найти середину треугольника, а также при решении других, более сложных геометрических задач.Итак, если соединить крайние точки исходного отрезка с точками пересечения наших окружностей, то получим четырехугольник. Но какой четырехугольник? Все его стороны являются радиусами наших окружностей, а значит равными по длине (ведь мы использовали одинаковый радиус). Любой четырехугольник с равными сторонами представляет собой ромб, диагонали которого всегда пересекаются под прямым углом и, что более важно для нашей задачи, делят друг друга пополам. Именно в этом и состоит логика подобного решения задачи о построении середины отрезка при помощи циркуля.
Именно в этом и состоит логика подобного решения задачи о построении середины отрезка при помощи циркуля.
Если же вопрос формулируется иначе, а именно о том, как найти координаты середины отрезка, то для его решения необходимо знать координаты его конечных точек. Координаты же середины будут равны полусуммам координат точек окончания отрезка. Конечно, здесь уже используется декартова система координат, в связи с чем данные задачи имеют разную сущность, хотя и решают одну проблему.
В любом случае, решение разных формулировок геометрических задач очень полезно для развития интеллекта и образного мышления ребенка. Поэтому не стоит пренебрегать этими инструментами личностного развития.
Инструкция
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте математические методы вычисления среднеарифметического значения. Минимальное значение (его начало) сложите с максимальным () и разделите результат пополам — это один из способов вычисления среднеарифметического значения. Например, это применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Например, это применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала . В этом варианте сначала определите ширину диапазона — отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя соответствует значению 47,15, а верхняя — 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий — если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал такую же . В противном случае вам надо определить динамику ширины интервалов, предшествующих открытому, и его условную ширину, исходя из полученной тенденции изменения.
Источники:
- что такое открытый интервал
При изучении вариации – различий индивидуальных значений признака у единиц изучаемой совокупности – рассчитывают ряд абсолютных и относительных показателей. На практике наибольшее применение среди относительных показателей нашел коэффициент вариации. 2/N. Иными словами дисперсия – это средний квадрат отклонения от среднего арифметического значения. определяет, насколько в среднем отклоняются конкретные показатели ряда от их среднего значения. Оно является абсолютной мерой колеблемости признака, а потому четко интерпретируется.
2/N. Иными словами дисперсия – это средний квадрат отклонения от среднего арифметического значения. определяет, насколько в среднем отклоняются конкретные показатели ряда от их среднего значения. Оно является абсолютной мерой колеблемости признака, а потому четко интерпретируется.
Координаты середины отрезка. Как найти координаты середины отрезка Формулы для вычисления середины отрезка
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A.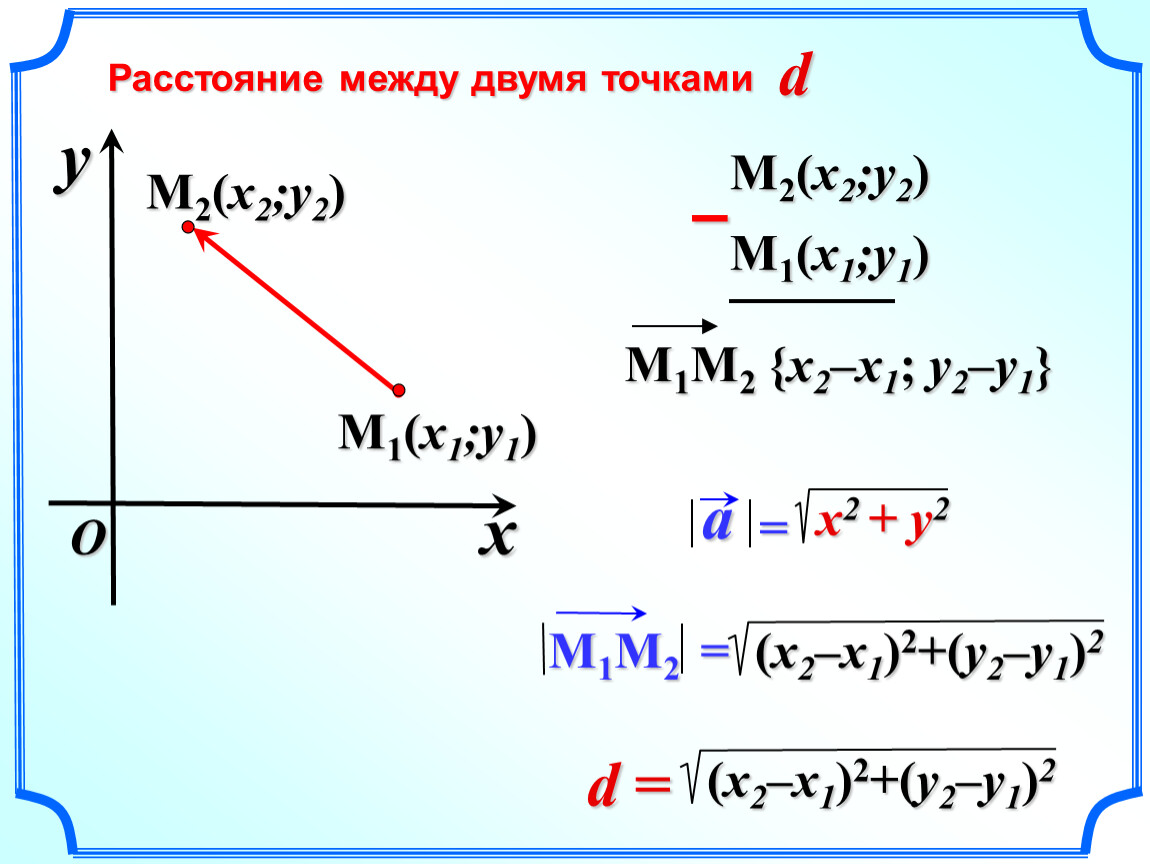 Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Ответ : K = (0,5; 0; 1)
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .
Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:
Ответ : L = (0,5; 0,5; 1)
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:
Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.
Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.
Решение.
Используем рассмотренную выше формулу:
Ответ . М (5; 14).
С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.
Рассмотрим пример.
Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.
Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:
Подставим известные координаты и вычислим отдельные координаты:
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.
Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пример.
Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).
Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:
Используем соответствующие формулы:
Следовательно, середина МО будет иметь координаты К (3,5; 5,5).
Ответ. К (3,5; 5,5).
Видео-вопрос: нахождение параметрического уравнения прямой, проходящей через середину между двумя точками и заданного вектора направления
Приведите параметрическое уравнение прямой, проходящей через середину между 𝑝₁ = (1, 2, 3) и 𝑝₂ = (3, 6, −5) с направляющим вектором 〈−1, 2, 5〉.
Стенограмма видео
Приведите параметрическое уравнение линия, проходящая через середину между 𝑝 один равен одному, два, три и 𝑝 два равно трем, шести, минус пяти с отрицательным вектором направления один, два, пять.
Нам дано, что линия проходит
через середину между двумя точками 𝑝 один и 𝑝 два и имеет направление
вектор с отрицательными компонентами один, два и пять.-16514864281403904547626faedcb85fd.jpg) Теперь мы знаем, что параметрический
уравнения прямой в пространстве представляют собой неединственную систему из трех уравнений: 𝑥 равно 𝑥
sub 𝐴 плюс 𝑡𝑙, 𝑦 равно 𝑦 sub 𝐴 плюс 𝑡𝑚 и 𝑧 равно 𝑧 sub 𝐴 плюс
𝑡𝑛. И вот где 𝐴 точка на
линия с координатами 𝑥 под 𝐴, 𝑦 под 𝐴 и 𝑧 под 𝐴; вектор с
компоненты 𝑙, 𝑚, 𝑛 — вектор направления прямой; а 𝑡 — действительный параметр
между отрицательным и положительным ∞.
Теперь мы знаем, что параметрический
уравнения прямой в пространстве представляют собой неединственную систему из трех уравнений: 𝑥 равно 𝑥
sub 𝐴 плюс 𝑡𝑙, 𝑦 равно 𝑦 sub 𝐴 плюс 𝑡𝑚 и 𝑧 равно 𝑧 sub 𝐴 плюс
𝑡𝑛. И вот где 𝐴 точка на
линия с координатами 𝑥 под 𝐴, 𝑦 под 𝐴 и 𝑧 под 𝐴; вектор с
компоненты 𝑙, 𝑚, 𝑛 — вектор направления прямой; а 𝑡 — действительный параметр
между отрицательным и положительным ∞.
Нам дали направление
вектор для линии. Так что мы можем сразу записать
компоненты 𝑙, 𝑚 и 𝑛. Это 𝑙 равно минус единице, 𝑚
равно двум, а 𝑛 равно пяти. И вычислить точку на
линии, мы можем использовать формулу средней точки для средней точки между 𝑝 единицей и 𝑝
два. Это как раз тот момент, чей
координаты представляют собой средние значения 𝑥-, 𝑦- и 𝑧-координат соответственно
две заданные точки. Итак, с 𝑝 один равен один, два,
три и 𝑝 два равно три, шесть, минус пять, наша середина имеет координаты один
плюс три на два, два плюс шесть на два и три плюс минус пять на
два. Это четыре больше двух, восемь больше
два, и минус два на два, что является точкой с координатами два, четыре и
отрицательный.
Итак, с 𝑝 один равен один, два,
три и 𝑝 два равно три, шесть, минус пять, наша середина имеет координаты один
плюс три на два, два плюс шесть на два и три плюс минус пять на
два. Это четыре больше двух, восемь больше
два, и минус два на два, что является точкой с координатами два, четыре и
отрицательный.
Итак, освободив место, у нас есть
наш вектор направления с отрицательными компонентами один, два и пять и точка на
линия с координатами 𝑥 sub 𝐴 равна двум, 𝑦 sub 𝐴 равна четырем, а 𝑧 sub 𝐴
равняется отрицательной единице. А теперь подставив их в
выражения для параметрических уравнений прямой имеем 𝑥 равно двум, что
это 𝑥 под 𝐴, плюс минус один, то есть 𝑙, умноженный на 𝑡. Это 𝑥 равно двум минус 𝑡. 𝑦 равно четырем, это 𝑦 под 𝐴,
плюс два, то есть 𝑚, умноженное на 𝑡. А 𝑧 равно минус единице, 𝑧 sub
𝐴 плюс пять, то есть 𝑛, умноженное на 𝑡.
Таким образом, параметрические уравнения линия, проходящая через середину 𝑝 одного и 𝑝 двух с направляющим вектором минус один, два, пять равно 𝑥 равно двум минус 𝑡, 𝑦 равно четырем плюс два 𝑡, и 𝑧 равно минус один плюс пять 𝑡.
r — Найти середины между значениями в векторе
Задавать вопрос
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 3к раз
Часть R Language Collective
Функция для расчета AUC с использованием правила средней точки. Используя R, как я могу определить вектор, который содержит средние точки между значениями предыдущего вектора? Или как я могу сместить значения вектора в их средние точки?
# определить h (или дельту x) ч <- (б - а)/н # определить вектор на основе пределов интегрирования, от a до b с шагом h xj <- seq.


 D(y)=
D(y)= (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)
(Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)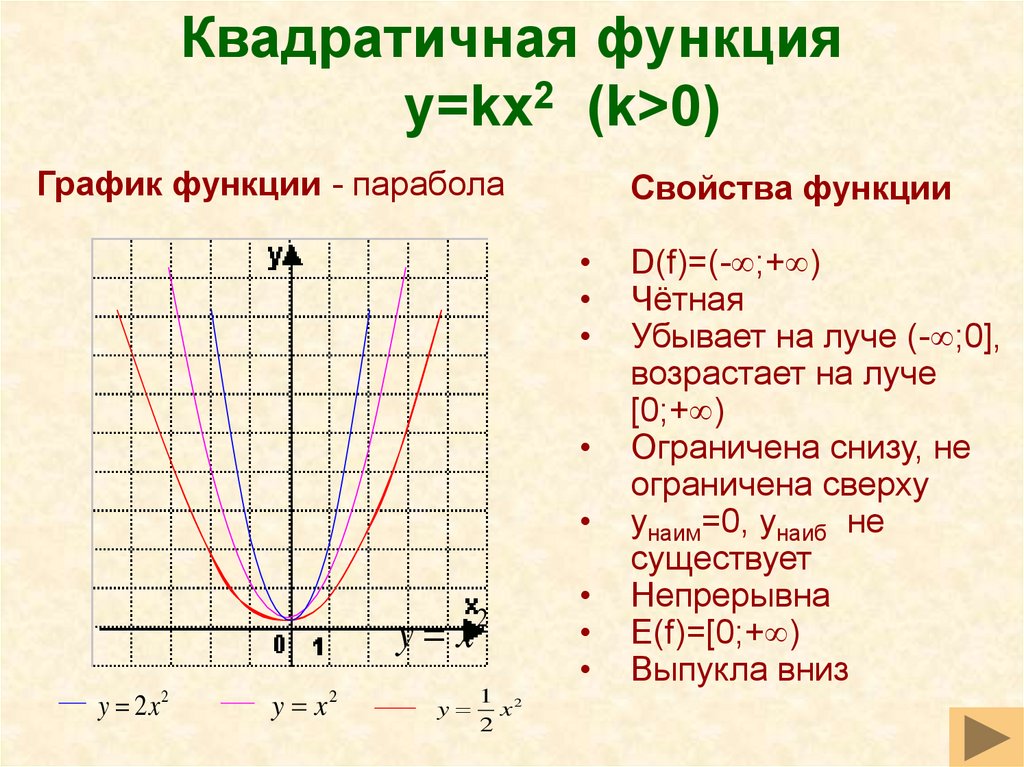 Противоположным значениям аргумента соответствуют равные значения функции.
Противоположным значениям аргумента соответствуют равные значения функции.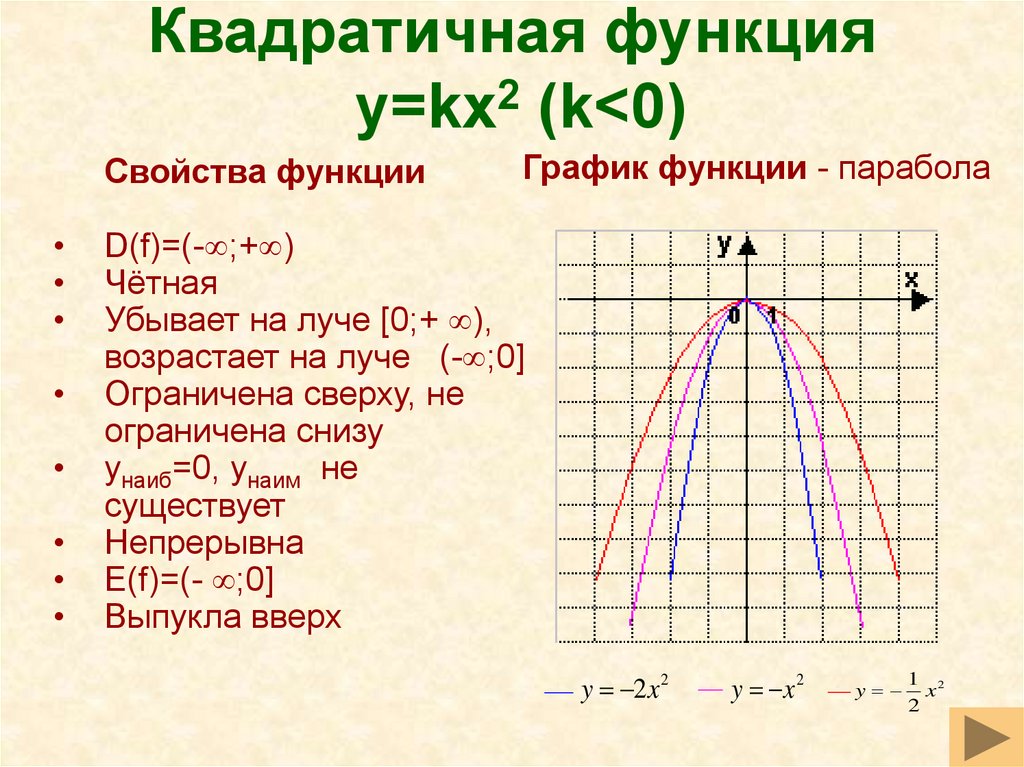
 Уравнение, представляющее параболическую функцию, является квадратным уравнением со второй степенью по x.
Уравнение, представляющее параболическую функцию, является квадратным уравнением со второй степенью по x. 


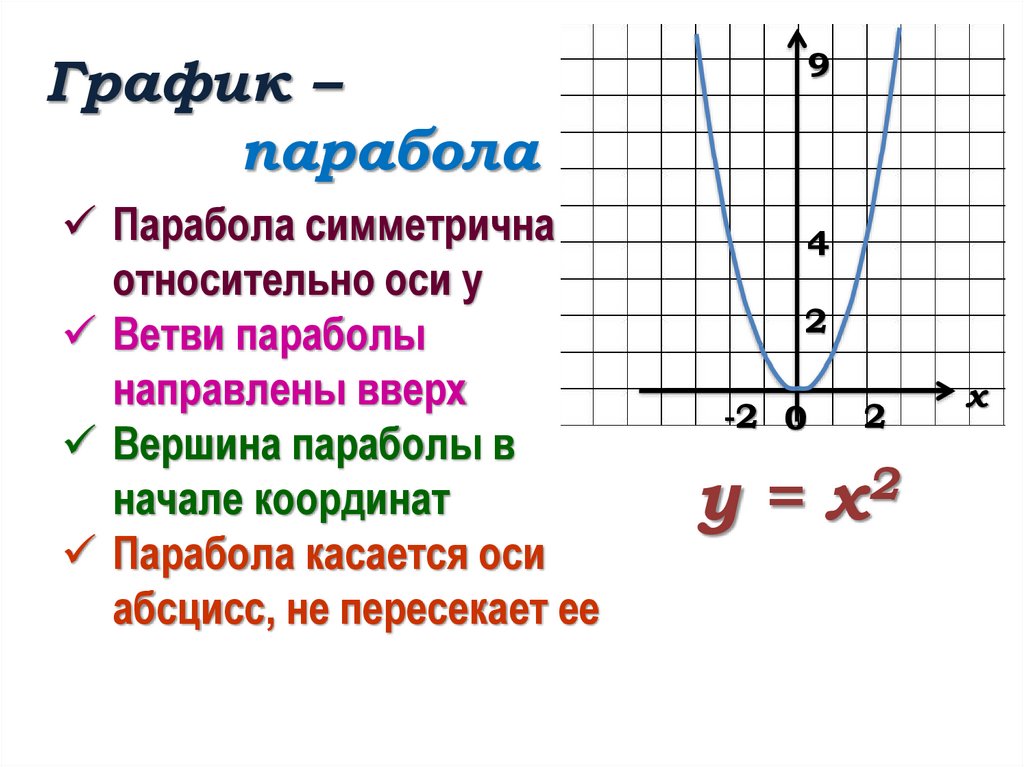 Диапазон параболической функции представлен на оси Y.
Диапазон параболической функции представлен на оси Y. 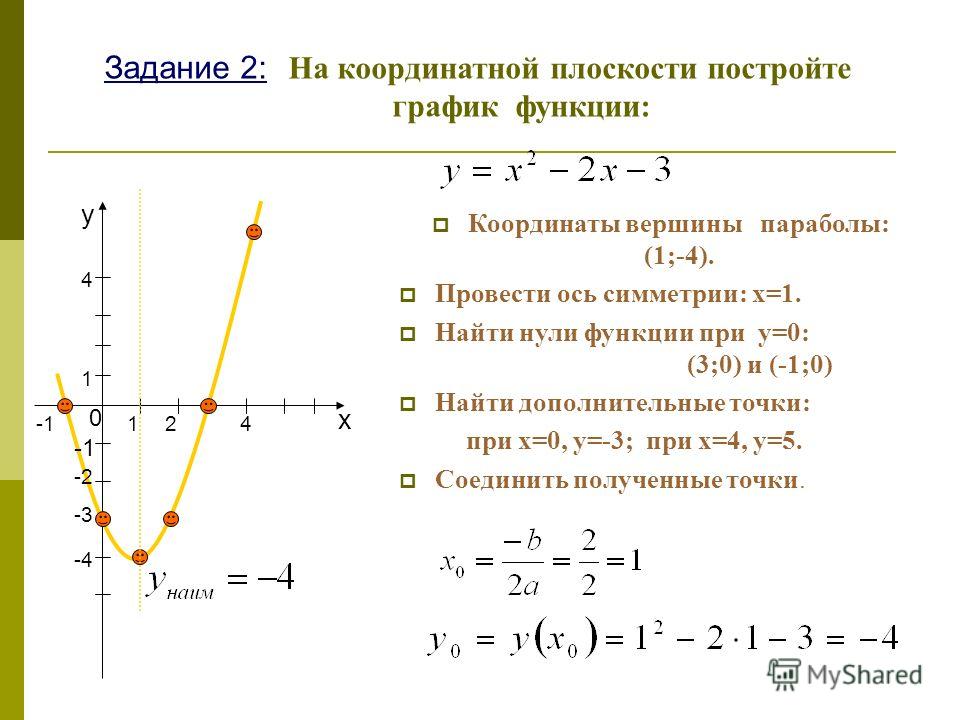
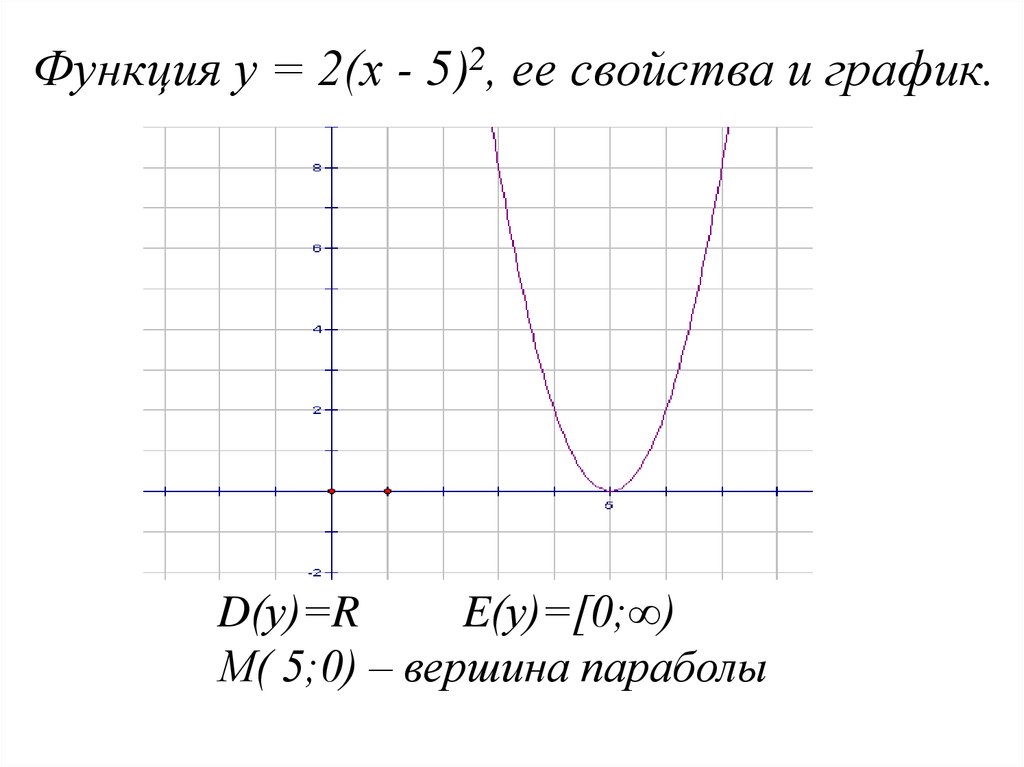
 В любом случае вершина является поворотной точкой на графе. График также симметричен, а вертикальная линия проходит через вершину, называемую 9.0103 ось симметрии .
В любом случае вершина является поворотной точкой на графе. График также симметричен, а вертикальная линия проходит через вершину, называемую 9.0103 ось симметрии .  Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]
Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex] 

 И они пробуют свои силы. Если в процессе этого появляется некий побочный продукт, полезный для общества, то хорошо. Например, создание электрических батарей стало возможным благодаря работе Джеймса Максвелла по изучению магнетизма и электричества, однако шотландский физик занимался наукой не ради батареек.
И они пробуют свои силы. Если в процессе этого появляется некий побочный продукт, полезный для общества, то хорошо. Например, создание электрических батарей стало возможным благодаря работе Джеймса Максвелла по изучению магнетизма и электричества, однако шотландский физик занимался наукой не ради батареек. д. Эти числа составляют значительную часть математических операций для проведения вычислений.
д. Эти числа составляют значительную часть математических операций для проведения вычислений.  Множество натуральных чисел задано N = 1, 2, 3, 4, 5, 6, 7,…
Множество натуральных чисел задано N = 1, 2, 3, 4, 5, 6, 7,…  Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q.
Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q. 

 Более высокие уровни ереси могут быть связаны с религией или наукой — не соглашайтесь с ортодоксальными предположениями здесь, и вас сочтут вполне возможно сумасшедшим. Высший уровень ереси в современном мире — математическая ересь . Несогласие с математической ортодоксией равносильно тому, чтобы «быть полноценным чудаком». Вам просто не позволено сомневаться в определенных идеях математики, не будучи осужденным как интеллектуальный прокаженный.
Более высокие уровни ереси могут быть связаны с религией или наукой — не соглашайтесь с ортодоксальными предположениями здесь, и вас сочтут вполне возможно сумасшедшим. Высший уровень ереси в современном мире — математическая ересь . Несогласие с математической ортодоксией равносильно тому, чтобы «быть полноценным чудаком». Вам просто не позволено сомневаться в определенных идеях математики, не будучи осужденным как интеллектуальный прокаженный. 
 )
)  Я, например, не думаю, что математики знают, что такое прямые. И поскольку их теории построены на их метафизических заявлениях о «линиях и точках», теории должны быть пересмотрены с нуля.
Я, например, не думаю, что математики знают, что такое прямые. И поскольку их теории построены на их метафизических заявлениях о «линиях и точках», теории должны быть пересмотрены с нуля. 
 Точки не могут иметь длину, ширину или глубину. И тем не менее, все формы якобы построены из них. Поэтому вы можете спросить: «Подождите, как фигуры, имеющие размеры, могут состоять из набора точек, не имеющих измерений?»
Точки не могут иметь длину, ширину или глубину. И тем не менее, все формы якобы построены из них. Поэтому вы можете спросить: «Подождите, как фигуры, имеющие размеры, могут состоять из набора точек, не имеющих измерений?»  Буквальное основание, на котором строится вся теоретическая структура современной геометрии, — «точка» — сомнительно. Ошибки на этом уровне могут иметь катастрофические последствия.
Буквальное основание, на котором строится вся теоретическая структура современной геометрии, — «точка» — сомнительно. Ошибки на этом уровне могут иметь катастрофические последствия.  Хотя неспециалисты могут назвать его «кругом», это всего лишь приближение к математическому кругу, который иногда называют «идеальным кругом».
Хотя неспециалисты могут назвать его «кругом», это всего лишь приближение к математическому кругу, который иногда называют «идеальным кругом». 
 Его «диаметр» тоже представляет собой простое целое число — количество пикселей, из которых он состоит. Поместите одно целое число в числитель и одно целое число в знаменатель, и вы получите рациональное число пи.
Его «диаметр» тоже представляет собой простое целое число — количество пикселей, из которых он состоит. Поместите одно целое число в числитель и одно целое число в знаменатель, и вы получите рациональное число пи.  Не существует «одного истинного отношения, называемого «пи», по той же причине, по которой не существует «единого истинного отношения высоты стола к длине». Каждая таблица и круг построены конечным числом единиц, расположенных по-разному, и поэтому их соотношения будут различаться.
Не существует «одного истинного отношения, называемого «пи», по той же причине, по которой не существует «единого истинного отношения высоты стола к длине». Каждая таблица и круг построены конечным числом единиц, расположенных по-разному, и поэтому их соотношения будут различаться. 



 Это только начало совершенно новой теории математики, которую я называю «математикой базовых единиц». Это основы базовой геометрии:
Это только начало совершенно новой теории математики, которую я называю «математикой базовых единиц». Это основы базовой геометрии: 
 И, как это бывает, пока круг не построен из крошечного количества основных единиц, отношение числа пи составит около 3,14159.(Хотя, если мы будем предельно точны, мы должны обозначать дроби, поскольку десятичное расширение может быть сомнительным в рамках базовых единиц. Но это будущая статья.). Не существует «общего» или «идеального» круга. Существуют конкретные реальные окружности, каждая из которых представляет собой составной объект, построенный конечным числом точек.
И, как это бывает, пока круг не построен из крошечного количества основных единиц, отношение числа пи составит около 3,14159.(Хотя, если мы будем предельно точны, мы должны обозначать дроби, поскольку десятичное расширение может быть сомнительным в рамках базовых единиц. Но это будущая статья.). Не существует «общего» или «идеального» круга. Существуют конкретные реальные окружности, каждая из которых представляет собой составной объект, построенный конечным числом точек.  В этой статье я не могу осветить все возражения против геометрии базовых единиц, но объясню еще несколько способов ее осмысления и поясню, почему она превосходит стандартную ортодоксальность.
В этой статье я не могу осветить все возражения против геометрии базовых единиц, но объясню еще несколько способов ее осмысления и поясню, почему она превосходит стандартную ортодоксальность.  Возможно, сейчас это не имеет большого значения, но по мере того, как технология приближается к базовым размерам физического пространства, это может иметь большое значение.
Возможно, сейчас это не имеет большого значения, но по мере того, как технология приближается к базовым размерам физического пространства, это может иметь большое значение.  Чем ровнее край круга, тем больше площадь круга.)
Чем ровнее край круга, тем больше площадь круга.)  Эти объекты просто не будут коррелировать с нашей вселенной. Кто знает, возможно, мы могли бы сказать правду о другой физической вселенной с меньшими базовыми единицами.
Эти объекты просто не будут коррелировать с нашей вселенной. Кто знает, возможно, мы могли бы сказать правду о другой физической вселенной с меньшими базовыми единицами.  Объект строится, пока вы наблюдаете за ним. То же самое происходит и в математике; объекты строятся так, как вы их себе представляете. Об этом еще много будет сказано в следующих статьях.
Объект строится, пока вы наблюдаете за ним. То же самое происходит и в математике; объекты строятся так, как вы их себе представляете. Об этом еще много будет сказано в следующих статьях.  Это неправильно. Окружности и многоугольники состоят из конечного числа точек , а не линий. Линии ничего не составляют; они сами являются составными объектами.
Это неправильно. Окружности и многоугольники состоят из конечного числа точек , а не линий. Линии ничего не составляют; они сами являются составными объектами. 
 Ященко И. В. Тренировочная работа 35 Вопрос 9 Найдите корень выражения
Ященко И. В. Тренировочная работа 35 Вопрос 9 Найдите корень выражения Найти главную линейную часть приращения площади этого квадрата и оценить относительную ошибку ( в процентах) при замене приращения его главной частью.
[46]
Найти главную линейную часть приращения площади этого квадрата и оценить относительную ошибку ( в процентах) при замене приращения его главной частью.
[46] Примем, что при смешении приращение площади поверхности раздела за отрезок времени dt прямо пропорционально разности между максимально возможным и текущим значением межфазной поверхности.
[51]
Примем, что при смешении приращение площади поверхности раздела за отрезок времени dt прямо пропорционально разности между максимально возможным и текущим значением межфазной поверхности.
[51] Подъем поплавка или поршня, линейно связанный с приращением площади отверстия, выражает непосредственно величину расхода.
[54]
Подъем поплавка или поршня, линейно связанный с приращением площади отверстия, выражает непосредственно величину расхода.
[54] [57]
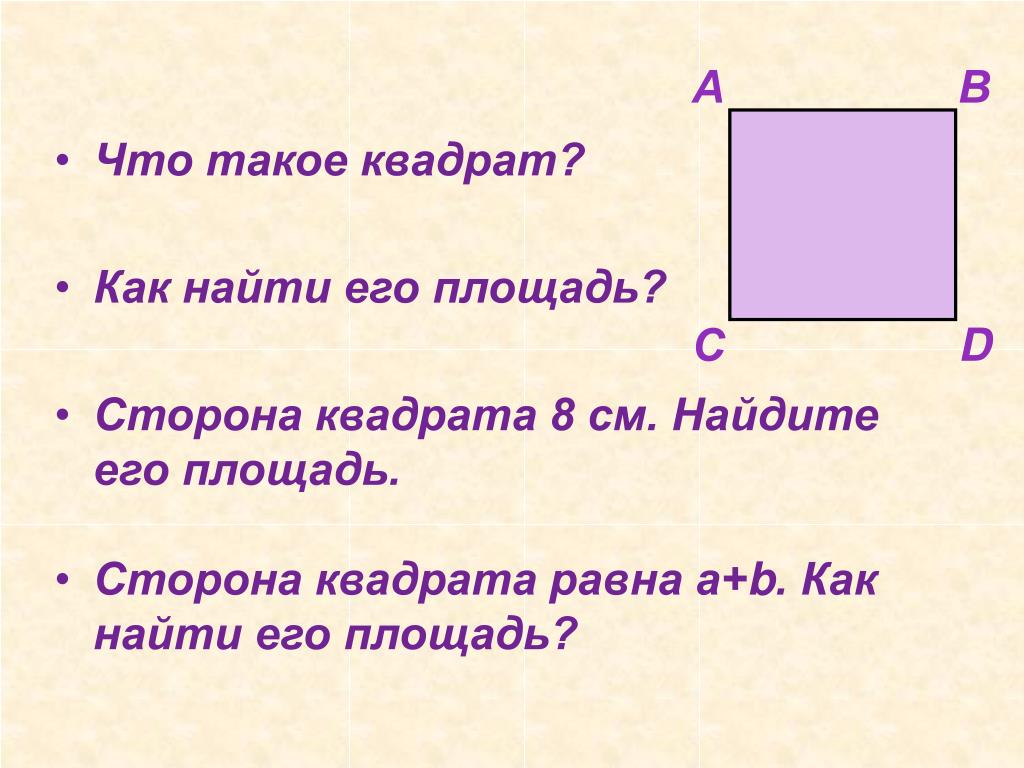
[57] Найдите площадь квадрата, проведенного по диагонали исходного квадрата (8 см Х 8 см)». eNotes Editorial , 28 января 2013 г., https://www.enotes.com/homework-help/side-square-8-cm-find-area-square-drown-diagonal-77955.
По состоянию на 28 апреля 2023 г.
Найдите площадь квадрата, проведенного по диагонали исходного квадрата (8 см Х 8 см)». eNotes Editorial , 28 января 2013 г., https://www.enotes.com/homework-help/side-square-8-cm-find-area-square-drown-diagonal-77955.
По состоянию на 28 апреля 2023 г.
 в 18:48:45.
в 18:48:45.
 2 cm है। वर्ग का क्षेत्रफल ज्ञात करें?
2 cm है। वर्ग का क्षेत्रफल ज्ञात करें? 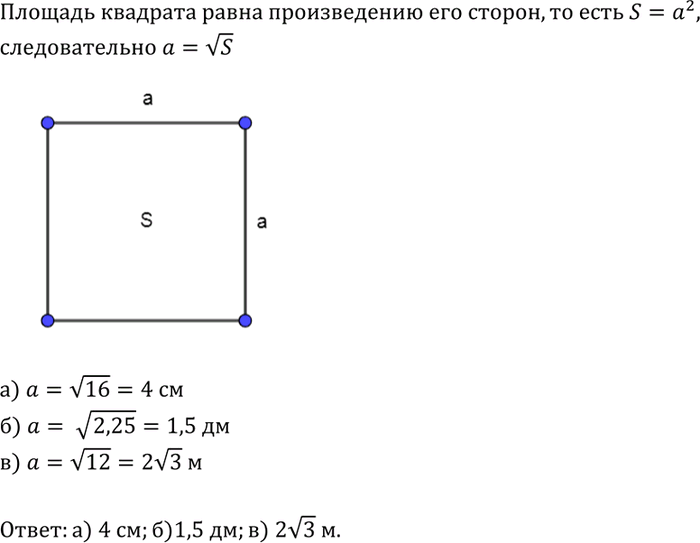 2, то найдите площадь треугольника ADB? 92, то найдите длину…
2, то найдите площадь треугольника ADB? 92, то найдите длину… 
 2
3-x-1=0 Tiger Algebra Solver
2
3-x-1=0 Tiger Algebra Solver  00
00  000000000 -1.000000000 2.000000000 5.000000000
0,000000000 -1,000000000 2,000000000 5,000000000
1.000000000 -1.000000000 2.000000000 5.000000000
1,000000000 -1,000000000 1,500000000 0,875000000
1,250000000 -0,296875000 1,500000000 0,875000000
1,250000000 -0,296875000 1,375000000 0,224609375
1,312500000 -0,051513672 1,375000000 0,224609375
1,312500000 -0,051513672 1,343750000 0,082611084
1,312500000 -0,051513672 1,328125000 0,014575958
1,320312500 -0,018710613 1,328125000 0,014575958
1,324218750 -0,002127945 1,328125000 0,014575958
1,324218750 -0,002127945 1,326171875 0,006208830
1,324218750 -0,002127945 1,325195312 0,002036651
1,324707031 -0,000046595 1,325195312 0,002036651
1,324707031 -0,000046595 1,324951172 0,000994791
1,324707031 -0,000046595 1,324829102 0,0004740391,324707031 -0,000046595 1,324768066 0,000213707
1,324707031 -0,000046595 1,324737549 0,000083552
1,324707031 -0,000046595 1,324722290 0,000018478
1,324714661 -0,000014059 1,324722290 0,000018478
1,324714661 -0,000014059 1,324718475 0,000002209
1.
000000000 -1.000000000 2.000000000 5.000000000
0,000000000 -1,000000000 2,000000000 5,000000000
1.000000000 -1.000000000 2.000000000 5.000000000
1,000000000 -1,000000000 1,500000000 0,875000000
1,250000000 -0,296875000 1,500000000 0,875000000
1,250000000 -0,296875000 1,375000000 0,224609375
1,312500000 -0,051513672 1,375000000 0,224609375
1,312500000 -0,051513672 1,343750000 0,082611084
1,312500000 -0,051513672 1,328125000 0,014575958
1,320312500 -0,018710613 1,328125000 0,014575958
1,324218750 -0,002127945 1,328125000 0,014575958
1,324218750 -0,002127945 1,326171875 0,006208830
1,324218750 -0,002127945 1,325195312 0,002036651
1,324707031 -0,000046595 1,325195312 0,002036651
1,324707031 -0,000046595 1,324951172 0,000994791
1,324707031 -0,000046595 1,324829102 0,0004740391,324707031 -0,000046595 1,324768066 0,000213707
1,324707031 -0,000046595 1,324737549 0,000083552
1,324707031 -0,000046595 1,324722290 0,000018478
1,324714661 -0,000014059 1,324722290 0,000018478
1,324714661 -0,000014059 1,324718475 0,000002209
1.

 е. областью определения данной функции является круг радиуса
е. областью определения данной функции является круг радиуса Найти области определения функции
Найти области определения функции Пусть min(/j — fj) достигается при / = /о. Так как ус-
[c.304]
Пусть min(/j — fj) достигается при / = /о. Так как ус-
[c.304]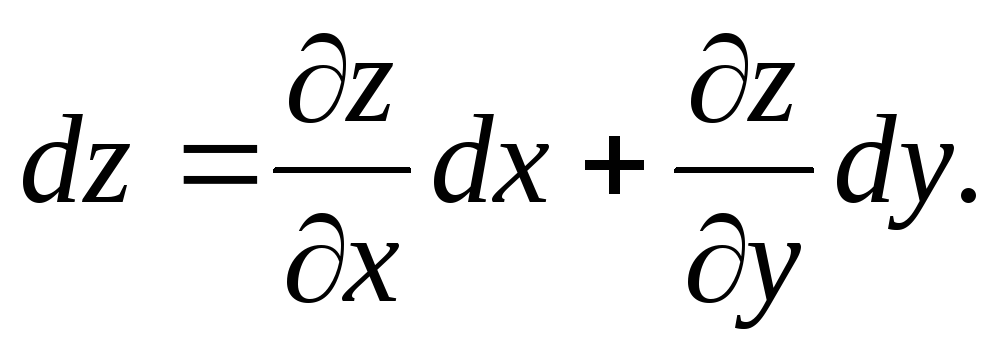 С тестированием трендовой линией уровня 1981, это было хорошее место для изменения тренда. Когда доходность, коротко проколола эту восемнадцати-с-лишним-летнюю трендовую линию и не смогла пойти выше, прозвенел звонок (для агрессивных трейдеров) с сигналом покупать облигации. (Одна из стратегий, используемых агрессивными трейдерами заключается в противоположной торговле, когда рынок оказывается не в состоянии производить «ожидаемое» поведение. Прорыв восемнадцатилетней трендовой линии должен был привести к большой распродаже. Когда это не произошло, были сделаны покупки.)
[c.200]
С тестированием трендовой линией уровня 1981, это было хорошее место для изменения тренда. Когда доходность, коротко проколола эту восемнадцати-с-лишним-летнюю трендовую линию и не смогла пойти выше, прозвенел звонок (для агрессивных трейдеров) с сигналом покупать облигации. (Одна из стратегий, используемых агрессивными трейдерами заключается в противоположной торговле, когда рынок оказывается не в состоянии производить «ожидаемое» поведение. Прорыв восемнадцатилетней трендовой линии должен был привести к большой распродаже. Когда это не произошло, были сделаны покупки.)
[c.200] Но требуется найти наиболее выгодное их сочетание. Пунктирные линии, как и в предыдущем примере, — линии уровня. Здесь они соединяют планы, при которых себестоимость смесей
[c.172]
Но требуется найти наиболее выгодное их сочетание. Пунктирные линии, как и в предыдущем примере, — линии уровня. Здесь они соединяют планы, при которых себестоимость смесей
[c.172] 1.2 это направление показано стрелкой. Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую прибыль (линию уровня целевой функции) в направлении вектора-
[c.442]
1.2 это направление показано стрелкой. Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую прибыль (линию уровня целевой функции) в направлении вектора-
[c.442]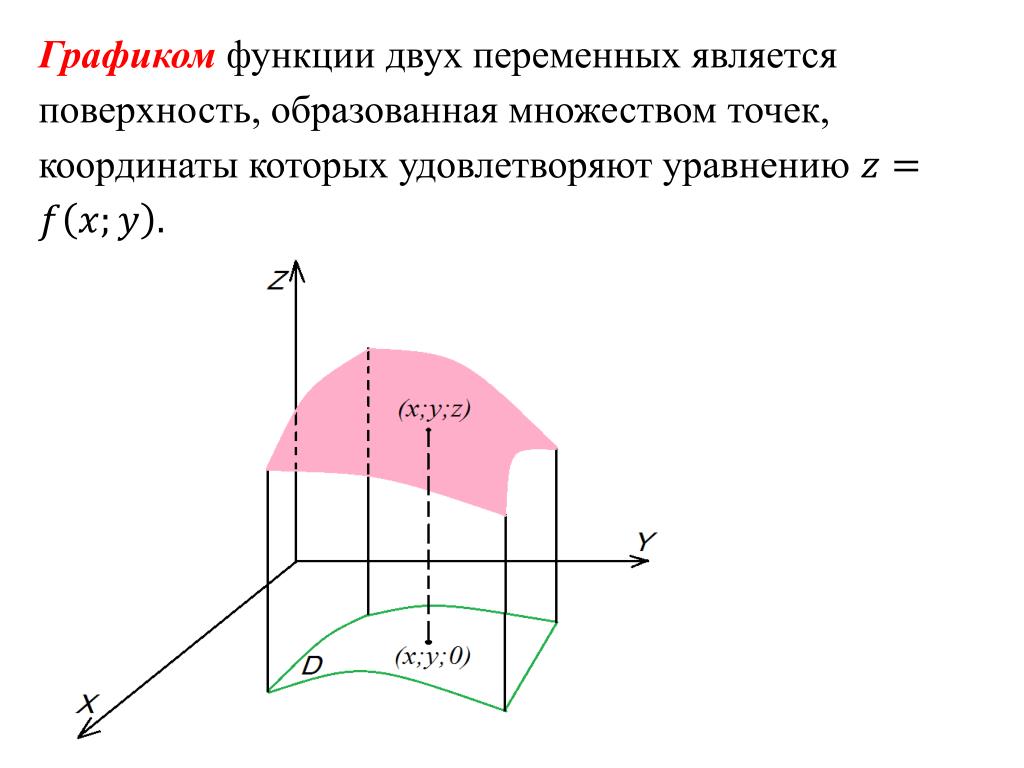 Применение соответствующей формы регистрации связано прежде всего с содержанием хозяйственной операции.
[c.327]
Применение соответствующей формы регистрации связано прежде всего с содержанием хозяйственной операции.
[c.327] 3. Здесь же мы рассмотрим их более подробно. Сторонники теханализа считают, что существующая тенденция должна проявлять себя внутри линий тренда. Эти линии, таким образом, служат чем-то вроде рельсов, по которым катится локомотив рынка. Если, скажем, происходит пробой линии, то это важный сигнал к смене тенденции. Например, если пробивается линия поддержки на восходящем тренде, то это веский аргумент в пользу того, что восходящий тренд сменится либо горизонтальной, либо нисходящей тенденцией (см. рис. 51) [116] [c.137]
3. Здесь же мы рассмотрим их более подробно. Сторонники теханализа считают, что существующая тенденция должна проявлять себя внутри линий тренда. Эти линии, таким образом, служат чем-то вроде рельсов, по которым катится локомотив рынка. Если, скажем, происходит пробой линии, то это важный сигнал к смене тенденции. Например, если пробивается линия поддержки на восходящем тренде, то это веский аргумент в пользу того, что восходящий тренд сменится либо горизонтальной, либо нисходящей тенденцией (см. рис. 51) [116] [c.137] [c.175]
[c.175]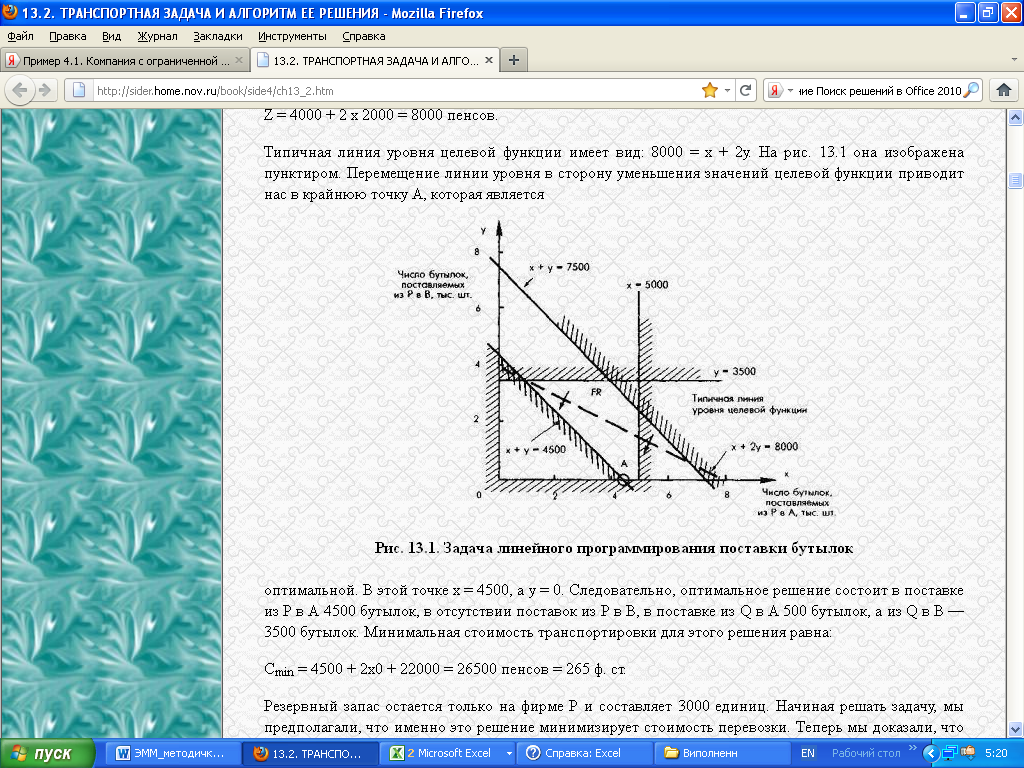 е. максимум целевой функции. Выбрав произвольно прямую с1х1 + с2х2 = П с произвольной константой П и обозначив ее ММ, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании х, и х2 (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи.) Точка М0 и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Мо-
[c.171]
е. максимум целевой функции. Выбрав произвольно прямую с1х1 + с2х2 = П с произвольной константой П и обозначив ее ММ, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании х, и х2 (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи.) Точка М0 и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Мо-
[c.171] На рис. 9.7, а показано расположение линий уровня, соответствующих задаче, изображенной на рис. 9.4. При замене равенства /1 = 0 на /1 = С поверхность Д перестанет касаться с плоскостью, соответствующей значению С . Если точка касания а при сколь угодно малом изменении С исчезнет, то произойдет скачок функции достижимости в сторону ее уменьшения (рис. 9.7, б).
[c.340]
На рис. 9.7, а показано расположение линий уровня, соответствующих задаче, изображенной на рис. 9.4. При замене равенства /1 = 0 на /1 = С поверхность Д перестанет касаться с плоскостью, соответствующей значению С . Если точка касания а при сколь угодно малом изменении С исчезнет, то произойдет скачок функции достижимости в сторону ее уменьшения (рис. 9.7, б).
[c.340] [c.46]
[c.46]
 Эта точка разделения гарантирует, что характерные линии пересекаются на одной и той же высоте.
Эта точка разделения гарантирует, что характерные линии пересекаются на одной и той же высоте. 

 В противном случае инструмент завершит работу с сообщением об ошибке, указывающим, что перед обработкой типы полей должны совпадать.
В противном случае инструмент завершит работу с сообщением об ошибке, указывающим, что перед обработкой типы полей должны совпадать. 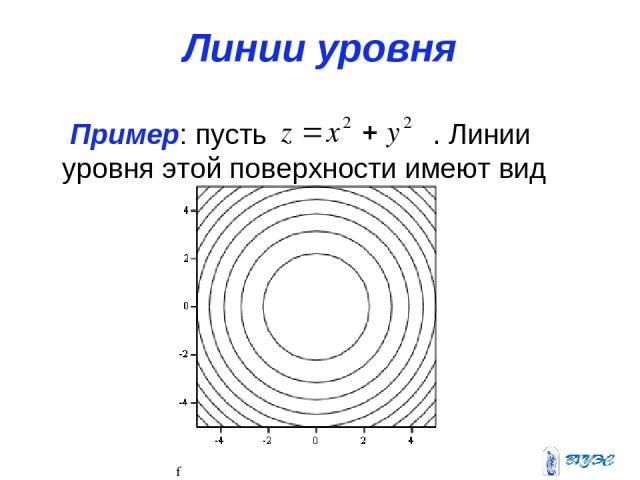 Доступные параметры зависят от записей, доступных в таблице метаданных.
Доступные параметры зависят от записей, доступных в таблице метаданных. 

 Варианты, которые доступны в этом раскрывающемся меню, зависят от выбранного уравнения.
Варианты, которые доступны в этом раскрывающемся меню, зависят от выбранного уравнения.
 Ниже приведены некоторые типы проблем, поддерживаемые в зависимости от формулы, которую вы пытаетесь решить.
Ниже приведены некоторые типы проблем, поддерживаемые в зависимости от формулы, которую вы пытаетесь решить.
 Системы могут быть написаны двумя разными способами:
Системы могут быть написаны двумя разными способами: 

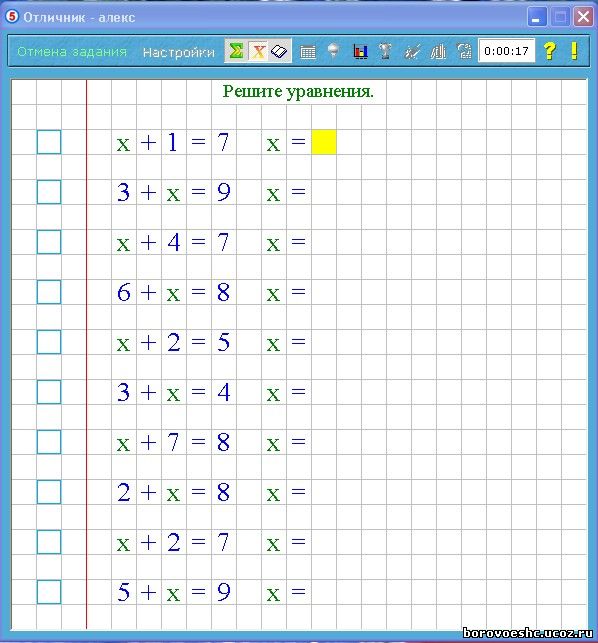 Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
 А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.) Внушает?)
Внушает?)

 Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась! А вот как вы получили этот ответ? Подобрали? Угадали?
А вот как вы получили этот ответ? Подобрали? Угадали?
 Так уж в математике повелось: ничего не написано — значит, плюс.)
Так уж в математике повелось: ничего не написано — значит, плюс.) Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит: ) Ладно, это эмоции…
) Ладно, это эмоции… Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается… А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
А двойка мешает. 🙂 Вот и делим на 2 всю левую часть: Тогда сразу числа попроще станут:
Тогда сразу числа попроще станут: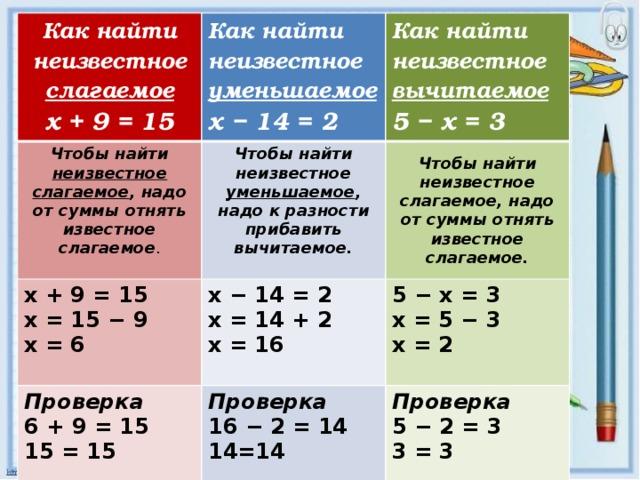 Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂 Следовательно, вычтите 8 с обеих сторон.
Следовательно, вычтите 8 с обеих сторон.




 Это особенно верно, когда вы приступаете к продвинутой курсовой математике. В большинстве случаев утомительное написание задач от руки не нужно, нежелательно для инструкторов и требует много времени.
Это особенно верно, когда вы приступаете к продвинутой курсовой математике. В большинстве случаев утомительное написание задач от руки не нужно, нежелательно для инструкторов и требует много времени. Вы можете использовать Microsoft Excel для некоторых математических вычислений, но для этого требуется много настроек, а интерфейс сильно отличается от других математических приложений и служб. Excel не предназначен для чистой математики, и это видно. Вы также не сможете экспортировать свои расчеты в формате, пригодном для исследовательских работ.
Вы можете использовать Microsoft Excel для некоторых математических вычислений, но для этого требуется много настроек, а интерфейс сильно отличается от других математических приложений и служб. Excel не предназначен для чистой математики, и это видно. Вы также не сможете экспортировать свои расчеты в формате, пригодном для исследовательских работ. Когда вы видите знак равенства, у вас есть уравнение. Но это еще не все, что есть в уравнении, особенно в алгебраической математике и не только.
Когда вы видите знак равенства, у вас есть уравнение. Но это еще не все, что есть в уравнении, особенно в алгебраической математике и не только.
 Если вы предпочитаете использовать свой iPhone или iPad, PocketCAS синхронизируется со своими приложениями для iOS и iPadOS через iCloud, чтобы вся ваша работа была в одном месте.
Если вы предпочитаете использовать свой iPhone или iPad, PocketCAS синхронизируется со своими приложениями для iOS и iPadOS через iCloud, чтобы вся ваша работа была в одном месте.

 Вы можете вводить математические вычисления, функции, даты и преобразования единиц измерения, которые легко читать и форматировать, и приложение даст вам результаты, которые вы можете использовать.
Вы можете вводить математические вычисления, функции, даты и преобразования единиц измерения, которые легко читать и форматировать, и приложение даст вам результаты, которые вы можете использовать.
 x5 = 3 · 5×5 · 5 = 3 · 5x = 15
x5 = 3 · 5×5 · 5 = 3 · 5x = 15






 Уравнение в этом случае станет справедливым равенством, если найденное значение х оправдает знак равенства. Тогда левая часть выражения станет равна правой части.
Уравнение в этом случае станет справедливым равенством, если найденное значение х оправдает знак равенства. Тогда левая часть выражения станет равна правой части.
 Преобразуем уравнение так, чтобы числовой коэффициент при х стал равным единице. Для этого нужно поделить обе части уравнения на число 4:
Преобразуем уравнение так, чтобы числовой коэффициент при х стал равным единице. Для этого нужно поделить обе части уравнения на число 4:



 Второй шаг – решение уравнения. Давайте посмотрим на некоторые примеры.
Второй шаг – решение уравнения. Давайте посмотрим на некоторые примеры.
 com. Все права защищены.
com. Все права защищены. 
 Это можно сделать разными способами. Например, линейное уравнение может быть выражено в стандартной форме, в форме точки пересечения или в форме точка-наклон. Теперь, если мы возьмем стандартную форму линейного уравнения, давайте узнаем, как оно выражается. Мы видим, что оно варьируется от случая к случаю в зависимости от количества переменных, и следует помнить, что наивысшая (и единственная) степень всех переменных в уравнении должна быть 1.
Это можно сделать разными способами. Например, линейное уравнение может быть выражено в стандартной форме, в форме точки пересечения или в форме точка-наклон. Теперь, если мы возьмем стандартную форму линейного уравнения, давайте узнаем, как оно выражается. Мы видим, что оно варьируется от случая к случаю в зависимости от количества переменных, и следует помнить, что наивысшая (и единственная) степень всех переменных в уравнении должна быть 1.

 Так линейное уравнение изображается на графике.
Так линейное уравнение изображается на графике. Наконец, значение x = 12/3 = 4.
Наконец, значение x = 12/3 = 4. Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется верным. Точно так же, если мы умножаем или делим одно и то же число в обеих частях уравнения, это правильно. Мы подносим переменные к одной стороне уравнения, а константу к другой стороне, а затем находим значение неизвестной переменной. Это способ решения линейного уравнения с одной переменной. Давайте разберемся в этом с помощью примера.
Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется верным. Точно так же, если мы умножаем или делим одно и то же число в обеих частях уравнения, это правильно. Мы подносим переменные к одной стороне уравнения, а константу к другой стороне, а затем находим значение неизвестной переменной. Это способ решения линейного уравнения с одной переменной. Давайте разберемся в этом с помощью примера.
 Это означает, что 2x = 44 — 10. Упрощая RHS, мы получаем 2x = 34, поэтому значение x равно 17. Это означает, что одно число равно 17, а другое число равно 17 + 10 = 27,
Это означает, что 2x = 44 — 10. Упрощая RHS, мы получаем 2x = 34, поэтому значение x равно 17. Это означает, что одно число равно 17, а другое число равно 17 + 10 = 27,
 д.
д. Следовательно, мы получаем x + 2x = 5 + 1. Таким образом, 3x = 6. Это дает x = 2,
Следовательно, мы получаем x + 2x = 5 + 1. Таким образом, 3x = 6. Это дает x = 2,

 Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?
Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?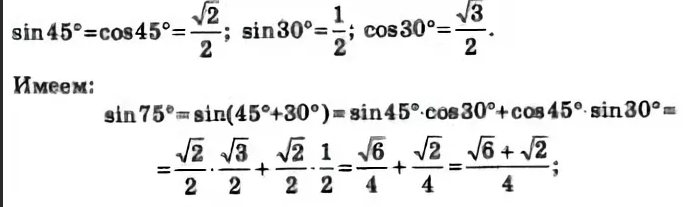 2 … …)на месте точек должны быть цифры или знаки + и —
2 … …)на месте точек должны быть цифры или знаки + и — )/3
)/3 . . . Cos 75 градусов в радианах записывается как cos (75° × π/180°), то есть cos (5π/12) или cos (1,308996…). В этой статье мы обсудим способы нахождения значения cos 75 градусов на примерах.
. . . Cos 75 градусов в радианах записывается как cos (75° × π/180°), то есть cos (5π/12) или cos (1,308996…). В этой статье мы обсудим способы нахождения значения cos 75 градусов на примерах. Поскольку функция косинуса положительна в первом квадранте, значение cos 75° = (√6 — √2)/4 или 0,2588190. . .
Поскольку функция косинуса положительна в первом квадранте, значение cos 75° = (√6 — √2)/4 или 0,2588190. . . 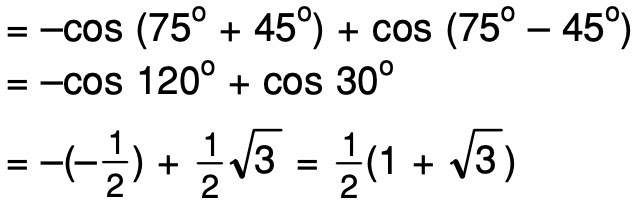 Поскольку 75° лежит в 1-м квадранте, окончательное значение cos 75° будет положительным.
Поскольку 75° лежит в 1-м квадранте, окончательное значение cos 75° будет положительным. [Подсказка: используйте cos 75° = 0,2588]
[Подсказка: используйте cos 75° = 0,2588]  Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.


 В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны). Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
 Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
 Эта особенность дает треугольнику определенные свойства.
Эта особенность дает треугольнику определенные свойства.
 Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
 Треугольники и прямоугольники являются многоугольниками.
Треугольники и прямоугольники являются многоугольниками. Вот краткая справка для вас:
Вот краткая справка для вас: .. начнем с самых простых фигур:
.. начнем с самых простых фигур: .. формы, которые можно нарисовать на листе бумаги
.. формы, которые можно нарисовать на листе бумаги  Треугольники и прямоугольники являются многоугольниками.
Треугольники и прямоугольники являются многоугольниками.