
Y x 2 x 3 график: Mathway | Популярные задачи


При управлении собственной и клиентскими позициями многие задачи по управлению рисками могут быть автоматизированы. Большинство из них связаны с расчетом и контролем маржинальных показателей, а также, с управлением лимитами. Платформа QORT обрабатывает информацию в режиме онлайн, и ее применение позволяет сочетать решение задач контроля рисков и учета собственных и клиентских операций в одном продукте. За решение задач управления рисками на фондовом и валютном рынках отвечает Модуль «Контроль рисков спот-рынков».

Модуль рассчитывает такие маржинальные показатели, как размер ГО, размер задолженности, размер собственных средств, оценка коротких и длинных позиций, уровень маржи, уровень достаточности средств, размер начальной маржи и другие в соответствии с выбранной для клиента схемой маржинального кредитования. Расчет показателей ведется в режиме онлайн.
По каждой сделке модуль позволяет в автоматическом режиме фиксировать признаки маржинальной и необеспеченной сделки, состояние основных показателей до и после операции.
Специальный калькулятор позволяет рассчитать значения будущих маржинальных показателей при планировании сделки или операции ввода/вывода средств. Этот же калькулятор позволяет решить обратную задачу – рассчитать параметры операций для приведения маржинальных показателей к заданным значениям. Расчет производится с учетом комиссий, которые будут списаны в будущем по ранее проведенным операциям.
Расчет производится с учетом комиссий, которые будут списаны в будущем по ранее проведенным операциям.
Существует возможность пересчитывать маржинальные показатели как в конце торгового дня, так и при изменениях в составе операций, в том числе, при прогнозировании изменений собственных дисконтов брокера.

При организации маржинального кредитования клиентов Модуль позволяет автоматизировать полный цикл задач по риск-менеджменту клиентских операций на фондовом и валютном рынках.
Модуль позволяет переносить длинные и короткие позиции на следующий день биржевыми операциями следующих видов:
Система готовит заявки на перенос позиций по запросу пользователя и выгружает их в QUIK. Кроме того, возможно формировать адресные заявки РЕПО на перенос коротких позиций из файла. Перенос позиций возможен с помощью регистрации внебиржевых сделок РЕПО непосредственно в QORT с терминала пользователя. В случае, когда брокер использует дисконты НКЦ, Модуль позволяет использовать их при оценке заявок переноса позиций. Кроме того, из QUIK импортируется Перечень ценных бумаг обеспечения.
Кроме того, из QUIK импортируется Перечень ценных бумаг обеспечения.
При переносе позиций возможен анализ нехватки средств. Таблица отображает активы, заявки переноса по которым были сформированы не полностью.
Система позволяет следить за состоянием портфеля и рассылать уведомления в случае снижения/повышения стоимости портфеля в сравнении с отслеживаемой величиной. Уведомления могут автоматически формироваться и рассылаться по электронной почте.
При снижении стоимости портфеля ниже уровня минимальной маржи система автоматически отправляет маржинальные требования (margin call) клиентам по электронной почте или сообщениями в системе QUIK. Существующая система шаблонов сообщений позволяет гибко настраивать текст этих уведомлений.
Для принудительного закрытия позиций Модуль автоматически готовит заявки, обновляя их параметры онлайн. Решение о принудительном закрытии позиции принимает риск-менеджер. Модуль позволяет выставлять заявки на закрытие позиции либо в определенной последовательности, либо в зависимости от количества или объема позиции. В Модуле можно настроить различные правила для принудительного закрытия маржинальных позиций по каждому счету или группе счетов:
Решение о принудительном закрытии позиции принимает риск-менеджер. Модуль позволяет выставлять заявки на закрытие позиции либо в определенной последовательности, либо в зависимости от количества или объема позиции. В Модуле можно настроить различные правила для принудительного закрытия маржинальных позиций по каждому счету или группе счетов:
Система позволяет готовить перед началом торговой сессии и загружать и корректировать лимиты по бумагам и денежным средствам в торговую систему QUIK, а так же устанавливать размер «плеча» при маржинальном кредитовании. Дальнейшие корректировки, с учетом всех сделок и неторговых операций, могут проводиться как по необходимости, так и в режиме онлайн.
Модуль позволяет готовить данные для регистров маржинальных и необеспеченных сделок, а также автоматизировать ведение реестра клиентов с повышенным уровнем риска, хранить копии и вести журнал направленных уведомлений.
Для организации риск-менеджмента по собственной позиции Модуль позволяет отслеживать различные виды внутренних лимитов. Внутренние лимиты устанавливаются и отслеживаются в QORT без выгрузки их значений во фронт-офисные системы.

Кроме того, есть возможность задавать лимиты потерь. Данный вид лимита может быть задан как для группы активов, так и для каждого актива в отдельности.
Все описанные лимиты контролируются в режиме post-trade. Для лимитов на размер открытой позиции в инструментах эмитента и на размер открытой позиции на контрагента предусмотрен также pre-trade контроль при регистрации внебиржевых сделок непосредственно в QORT.
Модуль позволяет осуществлять перенос собственной позиции аналогично переносу позиций клиентов.
Малому бизнесу
годовых в рублях
минимальная сумма
срок
ОткрытьПодробнее
Копилка с дополнительным доходомНакопительный счет — отличный способ копить и свободно пользоваться денежными средствами, получая проценты. Можно пополнять и снимать любую сумму в любое время без ограничений и без потери процентов — это главное отличие накопительного счета от вклада.
Удобно следить за счетами— Открыть вклад или накопительный счет можно в офисе банка или удаленно: онлайн на сайте или через приложение
— Пополнение и снятие без лимитов и ограничений
— Ежемесячная выплата процентов
Вопросы и ответы
Налогообложение
ParagraphWrapper» color=»brand-primary»>Собрали все вопросы по налогам на доходы по вкладам и счетам здесь.
+7 495 777-17-17Для звонков по Москве
8 800 700-91-00Для звонков из других регионов России
Следите за нами в соцсетях и в блоге
© 2003 – 2023 АО «Райффайзенбанк»
Генеральная лицензия Банка России № 3292 от 17.02.2015
119002, Москва, пл. Смоленская-Сенная, д. 28
Информация о процентных ставках по договорам банковского вклада с физическими лицами
Кодекс корпоративного поведения RBI Group
Центр раскрытия корпоративной информации
LinkList.P» color=»brand-primary»>Раскрытие информации в соответствии с Указанием Банка России от 28.12.2015 года № 3921-У
Продолжая пользование сайтом, я выражаю согласие на обработку моих персональных данных
Следите за нами в соцсетях и в блоге
+7 495 777-17-17Для звонков по Москве
8 800 700-91-00Для звонков из других регионов России
© 2003 – 2023 АО «Райффайзенбанк».
Генеральная лицензия Банка России № 3292 от 17.02.2015.
119002, Москва, пл. Смоленская-Сенная, д. 28.
Информация о процентных ставках по договорам банковского вклада с физическими лицами.
Дисперсия — средний квадрат отклонений индивидуальных значений признака от их средней величины.
Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю.
2. Уменьшение всех значений признака на одну и ту же величину А не меняет величины дисперсии. Значит средний квадрат отклонений можно вычислить не по заданным значениям признака, а по отклонениям их от какого-то постоянного числа.
3. Уменьшение всех значений признака в k раз уменьшает дисперсию в k2 раз, а среднее квадратическое отклонение — к раз. Значит, все значения признака можно разделить на какое-то постоянное число (скажем, на величину интервала ряда), исчислить среднее квадратическое отклонение, а затем умножить его на постоянное число.
4. Если исчислить
средний квадрат отклонений от любой
величины
А, то в той
или иной степени отличающейся от средней
арифметической (X~),
то он всегда будет больше среднего
квадрата отклонений, исчисленного от
средней арифметической. Средний квадрат
отклонений при этом будет больше на
вполне определенную величину — на квадрат
разности средней и этой условно взятой
величины.
Средний квадрат
отклонений при этом будет больше на
вполне определенную величину — на квадрат
разности средней и этой условно взятой
величины.
Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия s2 измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.
Межгрупповая дисперсия (s2x) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.
Внутригрупповая дисперсия (s2i) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.
Существует
закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из
внутригрупповых и межгрупповых дисперсий:
Общая дисперсия равна сумме средней из
внутригрупповых и межгрупповых дисперсий:
Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака.
Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.
Правило сложения дисперсий широко применяется при исчислении показателей тесноты связей, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев.
Многообразие взаимосвязей в которых находятся социально-экономические явления, рождают необходимость в их классификации.
По видам
различают функциональную и корреляционную
зависимость.
Функциональной называют такую зависимость, при которой одному значению факторного признака X соответствует одно строго определенное значение результативного признака Y.
В отличие от функциональной зависимости, корреляционная выражает такую связь между социально-экономическими явлениями, при которой одному значению факторного признака X могут соответствовать несколько значений результативного признака Y.
По направлению различают прямую и обратную зависимость.
Прямой называют такую зависимость, при которой значение факторного признака X и результативного признака Y изменяются в одном направлении. Т.о. при увеличении значения X, значения Y в среднем увеличиваются, а при уменьшении X — Y уменьшается.
Обратная зависимость между факторным и
результативным признаками, если они
изменяются в противоположных направлениях. n\mathsf DX_i+2\sum_{1\leqslant i<j\leqslant n}\mathop{\mathrm{cov}}(X_i,X_j),D(X1+…+Xn)=i=1∑nDXi+21⩽i<j⩽n∑cov(Xi,Xj),где
n\mathsf DX_i+2\sum_{1\leqslant i<j\leqslant n}\mathop{\mathrm{cov}}(X_i,X_j),D(X1+…+Xn)=i=1∑nDXi+21⩽i<j⩽n∑cov(Xi,Xj),где
cov(Xi,Xj)=E{(Xi−EXi)(Xj−EXj)}\mathop{\mathrm{cov}}(X_i,X_j)=\mathsf E\{(X_i-\mathsf EX_i)(X_j-\mathsf EX_j)\}cov(Xi,Xj)=E{(Xi−EXi)(Xj−EXj)}обозначает ковариацию случайных величин XiX_iXi иXj X_jXj. Если случайные величины X1,…,XnX_1,\ldots,X_nX1,…,Xn попарно независимы, то cov(Xi,Xj)=0\mathop{\mathrm{cov}}(X_i,X_j)=0cov(Xi,Xj)=0. Поэтому для попарно независимых случайных величин
D(X1+…+Xn)=DX1+…+DXn.(2)\tag{2} \mathsf D(X_1 +\ldots + X_n) = \mathsf DX_1 +\ldots + \mathsf DX_n.D(X1+…+Xn)=DX1+…+DXn.(2)Обратное утверждение неверно: из (2) не следует независимость. Однако, как правило, применение формулы (2) базируется на независимости случайных величин. Строго говоря, для справедливости (2) достаточно лишь, чтобы cov(Xi,Xj)=0\mathop{\mathrm{cov}}(X_i,X_j)=0cov(Xi,Xj)=0, т. е. чтобы случайные величины X1,…,XnX_1,\ldots,X_nX1,…,Xn были попарно некоррелированы.
Применения понятия дисперсии развиваются по следующим двум направлениям. Во-первых, применения в области предельных теорем теории вероятностей. Если последовательность случайных величин X1,X2…,Xn,…X_1,X_2\ldots,X_n,\ldotsX1,X2…,Xn,… обладает тем свойством, что DXn→0\mathsf DX_n\to 0DXn→0 при n→∞n\to\inftyn→∞, то для любого ε>0\varepsilon>0ε>0 при n→∞n\to\inftyn→∞
Р{∣Xn−EXn∣>ε}→0\mathsf Р \{|X_n-\mathsf EX_n|>\varepsilon\}\to 0Р{∣Xn−EXn∣>ε}→0(см. Неравенство Чебышёва), т. е. практически при больших nnn случайная величина XXX совпадает с неслучайной величиной EXn\mathsf EX_nEXn. Развитие этих соображений приводит к доказательству закона больших чисел, к доказательству состоятельности оценок в математической статистике, а также к иным применениям, в которых устанавливается сходимость по вероятности случайных величин. Другое применение в области предельных теорем связано с понятием нормировки. Нормировка случайной величины XXX производится путём вычитания математического ожидания и деления на среднее квадратичное отклонение DX\sqrt{\mathsf DX}DX, иными словами, рассматривается величина Y=(X−EX)/DXY=(X-\mathsf EX)/\sqrt{\mathsf DX}Y=(X−EX)/DX. 2DY=σ2. Поэтому параметры теоретического закона имеют следующий смысл: a=EYa=\mathsf EYa=EY и σ=DY\sigma=\sqrt{\mathsf DY}σ=DY. Отсюда вытекает способ определения этих параметров по выборке.
2DY=σ2. Поэтому параметры теоретического закона имеют следующий смысл: a=EYa=\mathsf EYa=EY и σ=DY\sigma=\sqrt{\mathsf DY}σ=DY. Отсюда вытекает способ определения этих параметров по выборке.
Дата публикации: 24 декабря 2022 г. в 21:21 (GMT+3)
Статистическая дисперсия описывает дисперсию чисел в наборе данных по сравнению со средним или средним значением. Он рассчитывается путем умножения стандартного отклонения на квадрат. Дисперсия может определять степень растяжения или сжатия распределения.
В этой статье мы рассмотрим свойства ожидания и дисперсии, свойства среднего и дисперсии и решим несколько примеров задач. Дисперсия имеет тот недостаток, что, в отличие от стандартного отклонения, ее единицы отличаются от случайной величины, поэтому после завершения расчета стандартное отклонение чаще сообщается как мера дисперсии.
Прогнозируемая вариация между значениями в наборе данных — это дисперсия. Он вычисляет разницу между каждой цифрой и средним значением. Трейдеры и рыночные аналитики часто используют дисперсию для прогнозирования волатильности рынка и постоянства определенного дохода от инвестиций с течением времени. Дисперсия обычно обозначается знаком σ², тогда как ее квадратный корень, т. е. стандартное отклонение, обозначается символом σ.
Под населением понимается все членство в группе. Дисперсия населения используется для определения того, как каждая точка данных колеблется или распределяется в определенной совокупности. Он вычисляет квадрат расстояния каждой точки данных от среднего значения генеральной совокупности.
Трудно рассмотреть каждую точку данных, если совокупность слишком велика. В этой ситуации берется выборка точек данных из совокупности для создания выборки, которую можно использовать для характеристики всей группы. В результате выборочная дисперсия равна среднему квадрату отклонения от среднего. Выборочное среднее всегда используется для определения дисперсии. 9
В результате выборочная дисперсия равна среднему квадрату отклонения от среднего. Выборочное среднее всегда используется для определения дисперсии. 9
S² = выборка дисперсии
н= количество наблюдений
Дисперсия может быть определена с помощью следующих шагов:
Вычислить среднее значение наблюдений. Разделите сумму всех наблюдений на количество наблюдений, чтобы получить этот результат.
Затем из каждого наблюдения следует вычесть среднее значение; после возведения в квадрат каждого из этих значений сложите все значения, полученные на предыдущем шаге, после вычитания. Затем разделите значение на n в случае дисперсии населения и n-1 в случае дисперсии выборки.
Ниже приведены некоторые свойства дисперсии, которые можно использовать для решения как простых, так и сложных задач на суммы.

Если X — дискретная случайная величина, то ожидаемое значение X (или среднее значение) представляет собой средневзвешенное значение всех возможных значений, которые может принять X, каждое из которых взвешивается в соответствии с вероятностью того, что оно произойдет . Обычно E(X) или m представляет ожидаемое значение X.
E(X) = S x P(X = x)
Другими словами, ожидаемое значение равно: [(каждый возможный результат) * (вероятность происходящего результата)].
Точнее, ожидание — это то, что вы ожидаете от результатов эксперимента в среднем.
Это были некоторые свойства ожидания и дисперсии.

После помня все эти теории и свойства, потренируйтесь на некоторых решенных примерах и вопросах. Ниже приведены некоторые ключевые моменты, которые вы должны помнить о свойствах ожидания и дисперсии и свойствах среднего и дисперсии.
Дисперсия измеряет изменчивость данных, отражающую распределение точек данных вокруг среднего значения. Выборочная дисперсия и дисперсия генеральной совокупности являются двумя формами дисперсии. Существует два типа данных: сгруппированные данные и разгруппированные данные. В результате возможны сгруппированная выборочная дисперсия, негруппированная выборочная дисперсия, сгруппированная дисперсия совокупности и негруппированная дисперсия совокупности.
Квадрат стандартного отклонения представляет собой дисперсию. Зависимая случайная величина и независимая случайная величина описываются ковариацией.
Дисперсия — это широко используемое понятие в вероятностной и описательной статистике для измерения изменчивости заданных данных. Дисперсия — это метод определения различных терминов в финансах. Это то же самое, что и стандартное отклонение, но измеряется в квадратах.
Дисперсия — это метод определения различных терминов в финансах. Это то же самое, что и стандартное отклонение, но измеряется в квадратах.
Давайте рассмотрим термин дисперсия.
Какая разница в статистике?Дисперсия может быть определена как статистическая мера отклонения между числами в наборе данных. Дисперсия набора измеряет, насколько далеко каждое число от ожидаемого значения (среднего), а также от других чисел.
Результатом дисперсии является квадрат стандартного отклонения. Термин стандартное отклонение — это еще один статистический метод, который измеряет среднее значение квадратов отклонений. Символически термин дисперсия может быть записан как s 2 , σ 2 или Var(x).
Набор данных в дисперсии может быть совокупностью или выборкой. Выборочные данные представляют собой набор выборочных значений, взятых из всей совокупности для измерения оценочного значения. Принимая во внимание, что набор данных о населении представляет собой набор целого ряда значений, таких как население, принимающее все данные.
Существует два основных вида дисперсии:
Формулы для дисперсии выборки и генеральной совокупности:
| 31 | σ 2 = [∑(x i – μ) 2 /N] | s 2 = [∑(x i – x̄) 2 /(N – 1)] |
| > 9010 3 σ 2 — обозначение дисперсии генеральной совокупности. > мк — среднее значение популяционных данных. > X i — набор заданных значений данных. > N — общее количество наблюдений. | > s 2 — обозначение выборочной дисперсии. > x̄ — среднее значение выборочных данных. > X i — набор заданных значений данных.  > N — общее количество наблюдений. |
Есть некоторые преимущества и недостатки дисперсии. Кратко обсудим их.
| Преимущества |
| Он используется для измерения взаимосвязи между числами и средними значениями, чтобы упростить работу статистиков, поскольку другой способ довольно сложен, например, распределение чисел по квартилям. |
| Отклонения от ожидаемых значений обрабатываются одинаково в дисперсии независимо от их направления. |
| В данных нет никакой изменчивости, так как сумма квадратов отклонений не может равняться нулю. |
Некоторые свойства дисперсии: 7 Вар(Х + С) = Var(X)
2) Произведение постоянного члена на дисперсию должно брать квадрат постоянного члена. например
например
Var(C * X) = C 2 * Var(X)
3) Аналогично, произведение и сумма постоянного члена с дисперсией должны брать квадрат постоянного члена. Например,
Var(aX + b) = a 2 * Var(X)
4) Дисперсия должна применяться к каждому члену отдельно, если случайные величины X 1 , X 2 , …, X n задаются, например,
Var(X 1 , X 2 , …, X n ) = Var(X 1 ) + Var(X 2 ) +……..+Var(X n )
Примеры отклоненийНиже приведены несколько примеров дисперсии.
Пример 1: Для выборочной дисперсии
Измерьте изменчивость данных данной выборки.
Данные выборки = 12, 15, 16, 20, 25, 24, 23, 30, 35, 36, 42
Решение –
Шаг 1: принимая частное суммы наблюдений и общего количества значений данных.
Сумма данных образца = 12 + 15 + 16 + 20 + 25 + 24 + 23 + 30 + 35 + 36 + 42
Сумма = 278
Общее количество наблюдения = n = 11
Среднее значение = 278 /11
Среднее значение выборки = 25,27
Шаг 2: Теперь найдите отклонение (отличие каждого значения данных от среднего).
9019 5| Данные | 12 – 25,27 = -13,27 |
| 15 | 15 – 25,27 = -10,27 |
| 16 | 16 – 25,27 = -9,27 |
| 20 | 20 – 25,27 = -5,27 |
| 25 | 25 – 25,27 = -0,27 |
| 24 | 24 – 25,27 = -1,27 |
| 23 | 23 – 25,27 = -2,27 |
| 30 | 30 – 25,27 = 4,73 |
| 35 | 35 – 25,27 = 9,73 |
| 36 | 36 – 25,27 = 10,73 |
| 42 | 42 – 25,27 = 16,73 |
Шаг 3: Теперь возьмем квадрат отклонений, чтобы все результаты были положительными.
| ( z i – z̄) 2 |
| (-13,27) 2 = 176,09 |
| (-10,27) 2 = 105,47 |
| (-9,27) 2 = 85,93 |
| (-5,27) 2 = 27,77 |
| (-0,27) 2 = 0,0 7 |
| (-1,27) 2 = 1,61 |
| (- 2,27) 2 = 5,15 |
| (4,73) 2 = 22,37 |
| (9,73) 2 = 94,67 |
| (10,73) 2 = 115,13 |
| (16,73) 2 = 279,89 |
Шаг 4: Теперь возьмите сумму квадратов отклонений.
∑(z i – z̄) 2 = 176,09 + 105,47 + 85,93 + 27,77 + 0,07 + 1,61 + 5,15 + 22,37 + 94,67 + 115,13 + 279,89
∑(z i – z̄) 2 = 914,15
Шаг 5: Используйте формулу выборочной дисперсии для оценки выборочной дисперсии.
∑(z i – z̄) 2 / (N – 1) = 914,15 / 11 – 1
∑(z i – z̄) 2 / (N – 1) = 914,15 / 10
∑(z i – z̄) 2 / (N – 1) = 91,415
Следовательно, выборочная дисперсия данных выборки равна 91.415.
Калькулятор дисперсии от calculates.tech можно использовать, чтобы избежать трудоемких вычислений дисперсии.
Пример 2: Для данных о населении
Оцените среднее квадратов отклонений от заданных данных о населении.
Данные о населении = 9, 11, 13, 15, 14, 16, 18, 23, 26, 28, 30
Решение –
Шаг 1: Прежде всего, найдите среднее значение генеральной совокупности, взяв частное суммы наблюдений и общего количества значений данных.
Сумма данных о населении = 9 + 11 + 13 + 15 + 14 + 16 + 18 + 23 + 26 + 28 + 30
Сумма = 203
Общее число наблюдений = N = 11 = 203/11
Среднее значение населения = µ = 18,455
Шаг 2: Теперь найдите отклонение (отличие каждого значения данных от среднего).
90 206 9 – 18,455 = -9,45 902 06 14 – 18,455 = -4,45| Значения данных | y i – µ |
| 9 | |
| 11 | 11 – 18,455 = -7,45 |
| 13 | 13 – 18,455 = -5,45 |
| 15 | 15 – 18,455 = -3,45 |
| 14 | |
| 16 | 16 – 18,455 = -2,45 |
| 18 | 18 – 18,455 = =0,45 |
| 23 | 23 – 18,455 = 4,55 |
| 26 9 0135 | 26 – 18,455 = 7,55 |
| 28 | 28 – 18,455 = 9,55 |
| 30 | 30 – 18,455 = 11,55 |
Шаг 3: Теперь возьмем квадрат отклонений, чтобы все результаты были положительными.
| ( y i – мк) 2 |
| (-9,45) 2 = 89,30 |
| (-7,45) 2 = 55,50 |
| (-5,45) 2 = 29,70 |
| (-3,45) 2 = 11,90 |
| (-4,45) 2 = 19,80 |
| (-2,45) 2 = 6,00 901 35 |
| (=0,45) 2 = 0,20 |
| (4,55) 2 = 20,70 |
| (7,55) 2 = 57,00 |
| (9,55) 2 = 91,20 |
| (11,55) 2 = 133. 40 |
Шаг 4: Теперь возьмите сумму квадратов отклонений.
После полученных начальных сведений о дробях перейдем к действиям с алгебраическими дробями. С ними можно выполнять любые действия вплоть до возведения в степень. При их выполнении мы в итоге получаем алгебраическую дробь. Все пункты необходимо разбирать последовательно.
Действия с алгебраическими дробями аналогичны действиям с обыкновенными дробями. Поэтому стоит отметить, что правила являются совпадающими при любых выполняемых с ними действиями.
Сложение может выполняться в двух случаях: при одинаковых знаменателях, при наличии разных знаменателей.
Если необходимо произвести сложение дробей с одинаковыми знаменателями, нужно сложить числители, а знаменатель оставить без изменения. Это правило позволяет воспользоваться сложением дробей и многочленов, которые находятся в числителях. Получим, что
a2+a·ba·b-5+2·a·b+3a·b-5+2·b4-4a·b-5=a2+a·b+2·a·b+3+2·b4-4a·b-5==a2+3·a·b-1+2·b4a·b-5
Если имеются числители дроби с разными числителями, тогда необходимо применить правило: воспользоваться приведением к общему знаменателю, выполнить сложение полученных дробей.
Нужно произвести сложение дробей xx2-1 и 3×2-x
Решение
Приводим к общему знаменателю вида x2x·x-1·x+1 и 3·x+3x·(x-1)·(x+1).
Выполним сложение и получим, что
x2x·(x-1)·(x+1)+3·x+3x·(x-1)·(x+1)=x2+3·x+3x·(x-1)·(x+1)=x2+3·x+3×3-x
Ответ: x2+3·x+3×3-x
Статья о сложении и вычитании таких дробей имеет подробную информацию, где подробно описано каждое действие, производимое над дробями. При выполнении сложения возможно появление сократимой дроби.
Вычитание выполняется аналогично сложению. При одинаковых знаменателях действия выполняются только в числителе, знаменатель остается неизменным. При различных знаменателях выполняется приведение к общему. Только после этого можно приступать к вычислениям.
Пример 2Перейдем к вычитанию дробей a+5a2+2 и 1-2·a2+aa2+2.
Решение
Видно, что знаменатели идентичны, что означает a+5a2+2-1-2·a2+aa2+2=a+5-(1-2·a2+a)a2+2=2·a2+4a2+2.
Произведем сокращение дроби 2·a2+4a2+2=2·a2+2a2+2=2.
Ответ: 2
Пример 3Выполним вычитание 45·x и 3x-1.
Решение
Знаменатели разные, поэтому приведем к общему 5·x·(x-1), получаем 45·x=4·x-15·x·(x-1)=4·x-45·x·(x-1) и 3x-1=3·5·x(x-1)·5·x=15·x5·x·(x-1).
Теперь выполним
45·x-3x-1=4·x-45·x·(x-1)-15·x5·x·(x-1)=4·x-4-15·x5·x·(x-1)==-4-11·x5·x·(x-1)=-4-11·x5·x2-5·x
Ответ: -4-11·x5·x2-5·x
Детальная информация указана в статье о сложении и вычитании алгебраических дробей.
С дробями можно производить умножение аналогичное умножению обыкновенных дробей: для того, чтобы умножить дроби, необходимо произвести умножение числителей и знаменателей отдельно.
Рассмотрим пример такого плана.
Пример 4При умножении 2x+2 на x-x·yy из правила получаем, что 2x+2·x-x·yy=2·(x-x·y)(x+2)·y.
Теперь необходимо выполнить преобразования, то есть умножить одночлен на многочлен. Получаем, что
Получаем, что
2·x-x·y(x+2)·y=2·x-2·x·yx·y+2·y
Предварительно следует произвести разложение дроби на многочлены для того, чтобы упростить дробь. После можно производить сокращение. Имеем, что
2·x3-8·x3·x·y-y·6·y5x2+2·x=2·x·(x-2)·(x+2)y·(3·x-1)·6·y5x·(x+2)==2·x·(x-2)·(x+2)·6·y5y·(3·x-1)·x·x+2=12·(x-2)·y43·x-1=12·x·y4-24·y43·x-1
Подробное рассмотрение данного действия можно найти в статье умножения и деления дробей.
Рассмотрим деление с алгебраическими дробями. Применим правило: для того, чтобы разделить дроби, необходимо первую умножить на обратную вторую.
Дробь, которая обратная данной считается дробь с поменянными местами числителем и знаменателем. То есть, эта дробь называется взаимообратной.
Рассмотрим пример.
Пример 5Выполнить деление x2-x·y9·y2: 2·x3·y.
Решение
Тогда обратная 2·x3·y дробь запишется как 3·y2·x. Значит, получим, что x2-x·y9·y2:2·x3·y=x2-x·y9·y2·3·y2·x=x·x-y·3·y9·y2·2·x=x-y6·y.
Ответ: x2-x·y9·y2: 2·x3·y=x-y6·y
Если имеется натуральная степень, тогда необходимо применять правило действий с возведением в натуральную степень. При таких вычислениях используем правило: при возведении в степень нужно числитель и знаменатель отдельно возводить в степени, после чего записать результат.
Пример 6Рассмотрим на примере дроби 2·xx-y. Если необходимо возвести ее в степень равную 2, тогда выполняем действия : 2·xx-y2=2·x2(x-y)2. После чего возводим в степень получившийся одночлен. Выполнив действия, получим, что дроби примет вид 4·x2x2-2·x·y+y2.
Детальное решение подобных примеров рассматривается в статье про возведение алгебраической дроби в степень.
При работе со степенью дроби необходимо помнить, что числитель и знаменатель отдельно возводятся в степень. Это заметно упрощает процесс решения и дальнейшего упрощения дроби. Стоит обращать внимание и на знак перед степенью. Если имеется знак «минус», то такую дробь следует переворачивать для простоты вычисления.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
спросил
Изменено 2 месяца назад
Просмотрено 42к раз
Например, когда я вычисляю 98/42 , я хочу получить 7/3 , а не 2.3333333 , есть ли функция для этого с использованием Python или Нампи ?
 7
7 Модуль фракций может сделать это 9000 5
>>> из фракций импорт Фракция >>> Дробь(98, 42) Дробь(7, 3)
Здесь есть рецепт для numpy gcd. Который вы затем могли бы использовать, чтобы разделить вашу дробь
>>> def numpy_gcd (a, b): ... а, б = np.broadcast_arrays (а, б) ... а = а.копировать() ... б = б.копировать () ... pos = np.nonzero(b)[0] ... пока len(pos) > 0: ... b2 = b[поз] ... a[pos], b[pos] = b2, a[pos] % b2 ... позиция = позиция[b[позиция]!=0] ... вернуть ... >>> numpy_gcd(np.array([98]), np.array([42])) массив([14]) >>> 98/14, 42/14 (7, 3)2
Дополнение к ответу Джона:
Чтобы получить упрощенную дробь из десятичного числа (скажем, 2,0372856077554062)
Использование дроби дает следующий результат:
Дробь (2,037285607) 7554062) #> Дробь(4587559351967261, 2251799813685248)
Чтобы получить упрощенный ответ :
Дробь (2.20372856077554062).limit_denominator() #> Дробь (2732, 1341)
Этот код Python использует только математический модуль «»»
импорт математики
def _fractions_(числитель, знаменатель):
если math.gcd(числитель, знаменатель) == знаменатель:
вернуть int(числитель/знаменатель)
elif math.gcd (числитель, знаменатель) == 1:
вернуть строку (числитель) + "/" + строку (знаменатель)
еще:
вершина = числитель / math.gcd (числитель, знаменатель)
внизу = знаменатель / math.gcd (числитель, знаменатель)
вернуть ул (сверху) + "/" + ул (снизу)
печать (_фракции_ (46,23))
печать (_фракции_ (34,25))
печать (_фракции_ (24, 28))
«»»
Есть ли в Python функция сокращения дробей?
Нет ни встроенной, ни внешней функции, но у вас есть два решения.
1. Использование модуля фракций
Вы можете использовать объекты фракций из модуля фракций . Из документации:
Из документации:
из импорта фракций Фракция Дробь(16, -10)
>>> Fraction(-8, 5)
В этом модуле неявно сокращается дробь, можно получить числитель и знаменатель:
а = 16
б = -10
q = дробь (а, б)
a = q.числитель
b = q.знаменатель
напечатать (f'{q} == {a}/{b}')
>>> -8/5 == -8/5
2. Сокращение с помощью НОД
Любую дробь можно сократить с помощью НОД, наибольшего общего делителя числителя и знаменателя: a/ b == (a/gcd)/(b/gcd) .
Функция GCD доступна как из модулей numpy , так и math :
импортировать numpy как np
а = 98
б = 42
НОД = np. НОД (а, б)
print(f'{a}/{b} == {int(a/gcd)}/{int(b/gcd)}')
`>>> 98/42 == 7/3
Существует альтернатива, но я не считаю ее подходящей для общих нужд: используйте символьную математику с модулем sympy.
Это позволяет работать с точными числами за счет потери эффективности.
sympy — это отдельный мир, и требуется некоторое время для обучения.
Требуется, но не отображается
Требуется, но не отображается
Приведите дроби к простейшей форме с помощью этого калькулятора Simplify Calculator.
Числитель дроби (верхнее число)
Знаменатель дроби
(нижний номер)
Вычислить простейшую форму дроби.
Пример: Для дроби 33 / 99 число 33 является числителем, а
99 — знаменателем.
Сначала найдите наибольший общий делитель двух чисел.
GCF = 33
Калькулятор GCF
Во-вторых, разделите и числитель, и знаменатель на GCF.
Числитель находится из 33/33 = 1
Знаменатель находится из 99/33 = 3
Дробь 33 / 99 , приведенная к простейшему виду, равна 1 / 3 .
Другой пример. На этот раз мы рассмотрим дробь 6 / 10 . Число 6 — числитель, а 10 — знаменатель.
Довольно легко увидеть, что и числитель, и знаменатель — четные числа. Итак, мы знаем, что они оба делятся на 2. Давайте разделим и числитель, и знаменатель на 2,
Это дает нам числитель 3 и знаменатель 10. Это была бы самая простая форма для того факта, что одно из чисел является простым числом и не делится дальше.
Дробь 6 / 10 приведенная к простейшей форме равна 3 / 5 .
Для следующего примера преобразуем дробь 12 / 20 в самой простой форме. В числителе 12, а в знаменателе 20.
Как и в предыдущем примере, числитель и знаменатель — четные числа. Как и в предыдущем случае, и числитель, и знаменатель четный и делится на 2. Но вы можете заметить, что они также делятся на 4. Поскольку 4 — больший множитель, давайте разделим оба на это число.
Наши новые числа 3 и 5.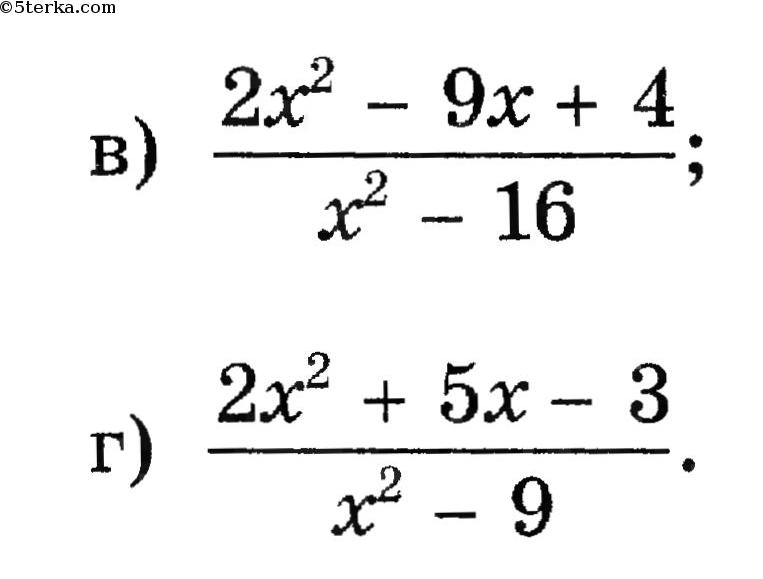
Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:
— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.
Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.
Уравнение прямой на координатной плоскости имеет вид:
где k – это и есть угловой коэффициент прямой.
Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.
Он лежит в пределах от 0 до 180 градусов.
То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.
Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:
Подробнее об этой формуле рассказано в этой статье!
Рассмотрим задачи (аналогичные задачам из открытого банка заданий):
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).
В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:
Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:
*Оба катета равны шести (это их длины).
Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.
Ответ: 1
Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (5;0) и (0;5). Значит,
Приведём формулу к виду y = kx + b
Получили, что угловой коэффициент k = – 1.
Ответ: –1
Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!
Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!
В данном случае, проще использовать свойство подобия треугольников.
Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.
Искомая абсцисса равна 40/3.
Ответ: 40/3
Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.
Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:
По условию точки имеют координаты (0;8) и (–12;0). Значит,
Значит,
Приведём к виду y = kx + b:
Получили, что угловой k = 2/3.
*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.
Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:
Найти величину b мы можем подставив абсциссу и ординату в уравнение:
Таким образом, прямая имеет вид:
Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:
Ответ: 18
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).
Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (0;0) и (10;24). Значит,
Значит,
Приведём к виду y = kx + b
Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значение b найдём подставив в это уравнение координаты точки В(10;12):
Получили уравнение прямой:
Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:
*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).
Искомая ордината равна –12.
Ответ: –12
Найдите ординату точки пересечения прямой, заданной уравнением
3х + 2у = 6, с осью Oy.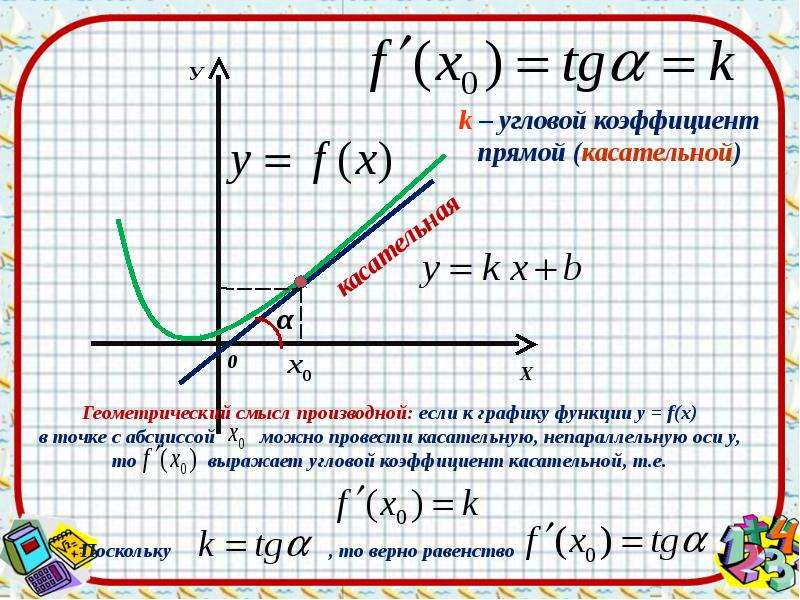
Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:
Ордината точки пересечения прямой с осью оу равна 3.
*Решается система:
Ответ: 3
Найдите ординату точки пересечения прямых, заданных уравнениями
3х + 2у = 6 и у = – х.
Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:
В первом уравнении подставляем – х вместо у:
Ордината равна минус шести.
Ответ: – 6
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).
Посмотреть решение
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).
Посмотреть решение
Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Посмотреть решение
Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Посмотреть решение
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).
Посмотреть решение
Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.
Посмотреть решение
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6 и у = х.
Посмотреть решение
Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению.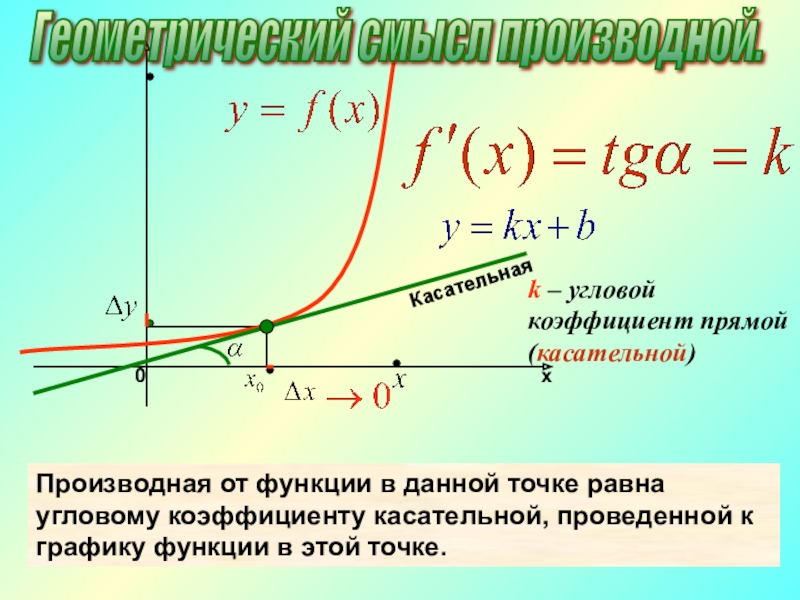 Надеюсь, это удалось.
Надеюсь, это удалось.
1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.
2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.
3. Помните о том, что угловые коэффициенты параллельных прямых равны.
4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.
5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.
6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике.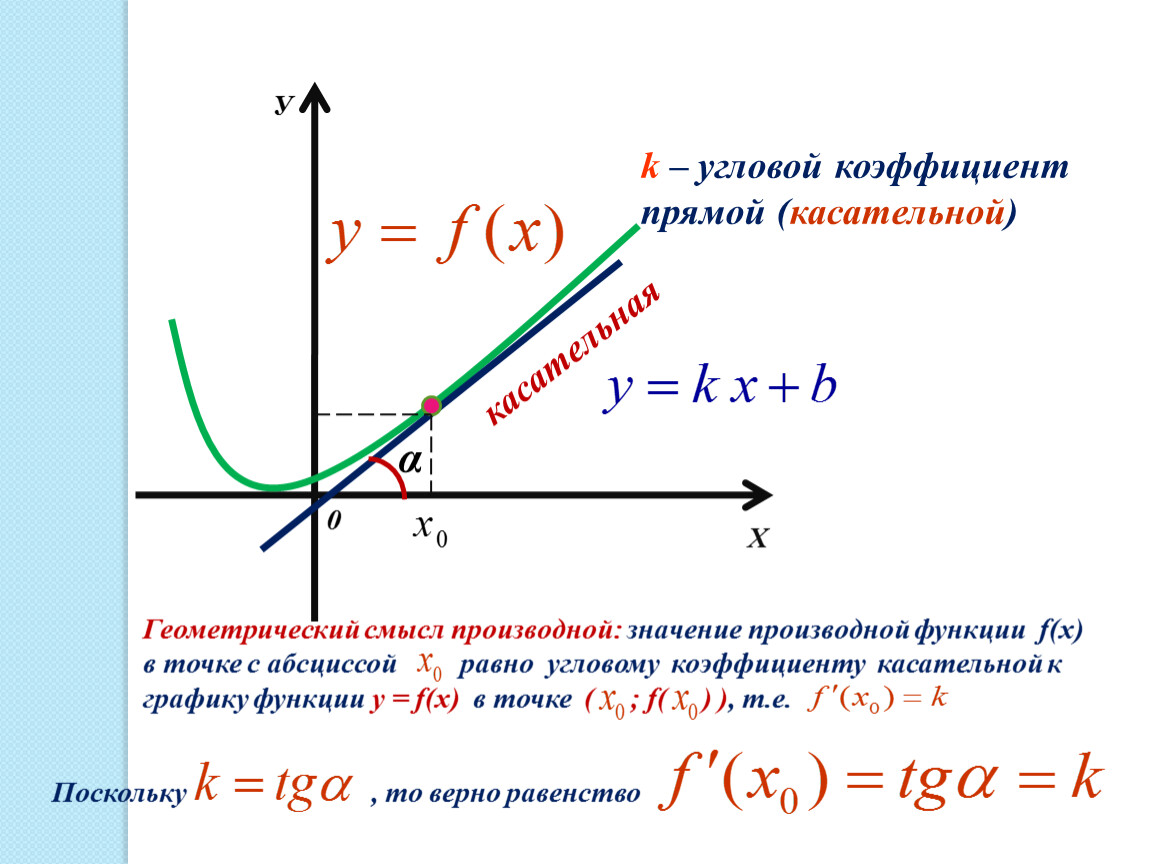 Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
>> Угол наклона прямой от 0 до 90 градусов <<
>> Угол наклона прямой от 90 до 180 градусов <<
В данных двух случаях, по свойству тангенса:
То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.
В данной рубрике продолжим рассматривать задачи, не пропустите!
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Наклон линии представляет собой ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как подъем относительно пробега. Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Наклон линии является мерой ее крутизны.
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор уклона показывает работу и дает следующие решения для уклона:
Вам также будет предоставлена настраиваемая ссылка на Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Рассчитать уклон, м , используя формулу для уклона:
Здесь вам нужно знать координаты 2-х точек на прямой, (x 1 , y 1 ) и (x 2 , y 2 ).
Δу = у 2 — у 1
Δх = х 2 — х 1
м = Δy/Δx
Допустим, вы знаете две точки на прямой, и их координаты (2, 5) и (9, 19). Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
Δу = у 2 — у 1
Δу = 19 — 5
Δy = 14
Δх = х 2 — х 1
Δx = 9 — 2
Δx = 7
\( m = \dfrac {14} {2} \)
\(m = 7 \)
Существует 3 распространенных способа записи уравнений линии с наклоном:
Точечный уклон формы записывается как
y — y 1 = м (x — x 1 )
Используя координаты одной из точек на линии, вставьте значения в x1 и y1 точек, чтобы получить уравнение линии в форме точечного наклона.
Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы вычислили как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
y — 5 = 7(x — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения уклона записывается как
y = м x + b
Возьмите уравнение формы уклона точки и умножьте его на 7 x и 7 на 2.
y — 5 = 7(x — 2) )
y — 5 = 7x — 14
Продолжайте работать над уравнением так, чтобы y было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме точки пересечения:
y = 7x — 9
Стандартная форма уравнения для линии записывается как
Ax + By = C
Вы также можете увидеть стандартную форму, записанную как Ax + By + C = 0 в некоторых ссылках.
Используйте либо формулу формы точки наклона, либо формулу пересечения наклона и выполните математические вычисления, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Наклон форма перехвата y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.
Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
 Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Наклон — это коэффициент x, поэтому в этом случае наклон = 3Точка пересечения с осью y представляет собой значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
y = 3(0) — 6
y = -6
Точка пересечения с осью y равна -6
Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
x = 2
Х-отрезок равен 2
Если известен наклон прямой, любая параллельная ей линия будет иметь одинаковый наклон, и эти линии никогда не пересекутся.
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикуляр означает, что линии образуют угол 90° при пересечении.
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
13 диагностических тестов 452 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 Следующая →
Справка по математике GRE » Геометрия » Координатная геометрия » Линии » Другие линии » Как найти наклон линии
См. следующий график:
следующий график:
Какой наклон изображенной линии?
Возможные ответы:–1
–1/3
1/3
3
–3
Правильный ответ :–3
Объяснение:Можно использовать либо формулу наклона m = (y 2 – y 1 )/(x 2 – x 1 ), либо стандартное линейное уравнение y = mx + b для решения уклон, м. Расчетом или наблюдением можно определить, что наклон равен –3.
Сообщить об ошибке
Каков наклон уравнения 4 x + 3 y = 7?
Возможные ответы:3/4
–3/4
–4/3
4/3
–7/3
Правильный ответ:–4/3
Объяснение:Мы должны представить это уравнение в виде y = м x + b , где м — уклон.
Начнем с 4 x + 3 y = 7.
Изолируем член y : 3 y = 7 – 4 x 9000 5
Разделить на 3: y = 7/3 – 4/3 * x
Переставьте члены: y = –4/3 * x + 7/3, поэтому наклон равен –4/3.
Сообщить об ошибке
Каков наклон уравнения?
Возможные ответы: Правильный ответ: Объяснение:Чтобы найти наклон линии, вы должны преобразовать уравнение в форму пересечения наклона. В этом случае уравнение будет , что означает, что наклон равен .
Сообщить об ошибке
Каков наклон линии?
Возможные ответы: Правильный ответ: Объяснение:Чтобы найти наклон, представим уравнение в форме пересечения наклона. В этом случае имеем , что указывает на то, что наклон равен .
Сообщить об ошибке
Каков наклон линии, проходящей через точку, если она определяется:
?
Возможные ответы: Правильный ответ: Объяснение: Поскольку уравнение определено как есть, вы знаете, что точка пересечения по оси Y равна . В этом суть. Чтобы найти наклон линии, вам просто нужно использовать две имеющиеся у вас точки и найти уравнение:
В этом суть. Чтобы найти наклон линии, вам просто нужно использовать две имеющиеся у вас точки и найти уравнение:
Сообщить об ошибке
Какое из следующего может быть уравнением для красной линии, изображенной выше?
Возможные ответы: Правильный ответ: Объяснение:Об этом чертеже необходимо отметить два ключевых факта. Во-первых, линия явно имеет отрицательный наклон, учитывая, что она идет «под гору», если смотреть на нее слева направо. Во-вторых, он имеет положительную точку пересечения по оси y. Таким образом, вы знаете, что коэффициент для термина должен быть отрицательным, а числовой коэффициент для точки пересечения оси Y должен быть положительным. Это происходит только в уравнении . Поэтому это единственный возможный вариант.
Сообщить об ошибке
Каков наклон линии, определяемой уравнением:
Возможные ответы: Правильный ответ:900 05 Объяснение:
Такой вопрос на самом деле довольно прост.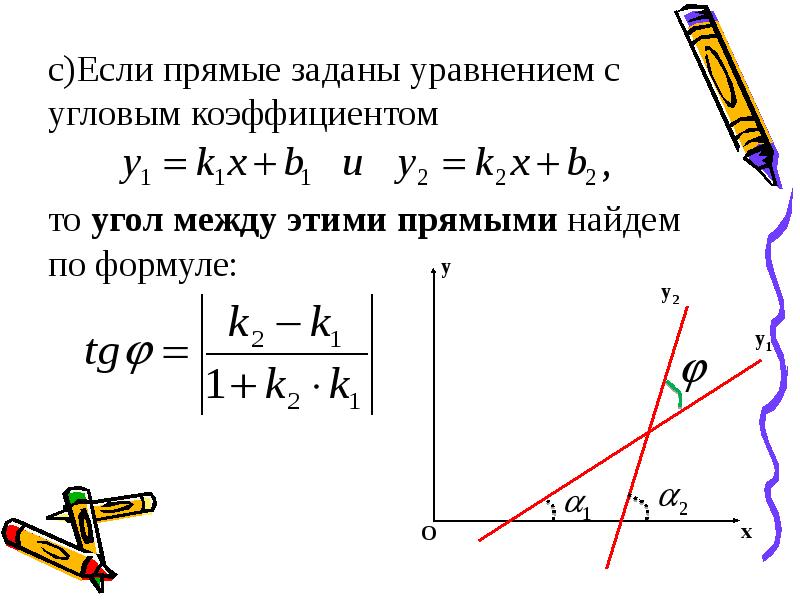 Все, что вам нужно сделать, это переписать уравнение в форме пересечения наклона, то есть:
Все, что вам нужно сделать, это переписать уравнение в форме пересечения наклона, то есть:
Следовательно, начнем упрощать:
Становится…
Затем…
Наконец, разделите обе стороны на :
Коэффициент для члена – это ваш наклон:
Сообщить об ошибке
Каков наклон линии 3 = 8y — 4x?
Возможные ответы:0,5
-2
2
-0,5
Правильный ответ:0,5
Объяснение:Решите уравнение для y. y=mx+b, где m — уклон
Сообщить об ошибке
Найти наклон линии 6X – 2Y = 14
Возможные ответы:
3
-6
12
-3
Правильный ответ:3
Объяснение:Представьте уравнение в форме точки пересечения наклона:
y = mx + b
-2y = -6x +14
y = 3x – 7
Наклон линии представлен буквой M; следовательно, наклон линии равен 3,9.
Статьи › Находится › Как находится область определения функции заданной формулой
Чтобы найти значение функции при заданном значении аргумента, надо значение аргумента подставить в уравнение функции вместо x и вычислить ее значение.
Если формула задана формулой вида y = f (x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.
Значение функции — значение, соответствующее заданному значению. Например: найдем область определения и область значений функции y = x 2 + 8. Решение. Поскольку выражение x 2 + 8 имеет смысл при всех значениях переменной, то x ∈ R.
А) Чтобы найти значение функции по заданному значению аргумента, необходимо значение аргумента (x) подставить в формулу и посчитать значение функции (y). Например, необходимо найти значение функции при x=3. Следовательно, при x=3 значение функции равно 30.
Ответы1. В математике: Аргумент — это независимая переменная, обычно ее обозначают «x».
Чтобы найти наибольшее или наименьшее значение функции необходимо:

Найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку; вычислить значения функции на концах отрезка и в выбранных критических точках; среди найденных значений выбрать наименьшее и наибольшее значения; Множество значений функции заключить между этими значениями.
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления. Все функции Excel можно найти на вкладке «формулы» на ленте.
Значения зависимой переменной называют значениями функции. Если зависимость переменной игрек от переменной икс является функцией, то коротко это записывают так: y = f(x) (читают: «игрек равен эф от икс»). Символ эф от икс также обозначает значение функции, соответствующее значению аргумента икс.
Символ эф от икс также обозначает значение функции, соответствующее значению аргумента икс.
Функция — это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют
Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞). Для нецелых действительных положительных показателей степени: D(f) = [0, +∞). Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой. Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой.
Термин «аргумент» подразумевает, что конкретно и какой конкретной функции было передано, а параметр — в каком качестве функция применила это принятое. То есть вызывающий код передает аргумент в параметр, который определен в члене спецификации функции.
Аргуме́нт (лат. argumentum — рассказ, довод, тема) — многозначный термин: Аргумент (переносное значение слова) — средство силового воздействия, давления на кого-либо или что-либо, используемое для достижения цели; способ убеждения.
Аргумент может принимать любое, ни от чего не зависящее значение из области определения функции, поэтому аргумент еще называют независимой переменной величиной, а функцию — зависимой переменной, так как ее значение зависит от того, какое значение принимает аргумент.
В любой функции есть 2 переменные: х и у, каждая из которых имеет свое название. х — это аргумент, значит значение, присваиваемое этой переменной называется значением аргумента.
х — это аргумент, значит значение, присваиваемое этой переменной называется значением аргумента.
Аргументом является независимая переменная, которая принимает любые допустимые значения. 2. Функция является выражением, с левой стороны которого зависимая переменная, а с правой — выражение с независимой переменной.
Аргумент (лат. argumentum) — суждение (или совокупность взаимосвязанных суждений), посредством которого обосновывается истинность другого суждения (или теории).
Свойства функции разберем на примере о графика произвольной функции y = f (x): Область определения функции — это множество всех значений переменной x, которые имеют соответствующие им значения функции. Обозначают: D(f).
Функция | y = sin x | y = cos x |
|---|---|---|
Монотонность | возрастает при убывает при | возрастает при убывает при |
Решение:

G-функция — название нескольких функций в математике: G-функция Барнса (Barnes G-function) — связана с гамма-функцией, расширяет понятие суперфакториала на поле комплексных чисел. G-функция Зигеля (Siegel G-function) — класс функций в теории трансцендентности.
Функция — это зависимая переменная величина. Аргумент — это независимая переменная.
Аргумент — это независимая переменная, обычно аргумент обозначают латинской строчной буквой «x». От значения аргумента зависит значение функции.
Нули функции это значения аргумента, при которых функция обращается в нуль. Промежутки знакопостоянства функции это промежутки из области определения, на которых функция сохраняет знак (либо положительна, либо отрицательна).
Промежутки знакопостоянства функции это промежутки из области определения, на которых функция сохраняет знак (либо положительна, либо отрицательна).
Чтобы задать функцию, надо описать, каким образом значению аргумента сопоставляется значение функции. Описывать это можно разными способами. Наиболее распространены аналитический (с помощью формулы), табличный и графический способы задания функции.
Функции и графики
Название функции | Формула функции | Название графика |
|---|---|---|
Линейная | y = kx + b | Прямая |
Квадратичная | y = x2 | Парабола |
Квадратичная | y = ax2 + bx + c | Парабола |
Степенная | y = x3 | Кубическая парабола |
Фу́нкция в математике — соответствие между элементами двух множеств — правило, по которому каждому элементу первого множества, называемого областью определения, соответствует один и только один элемент второго множества, называемого областью прибытия.
Y = f(x), где f (начальная буква слова function — функция) заменяет слово функция, y — это функция, а x — аргумент.
В программировании функции могут не только возвращать данные, но также принимать их, что реализуется с помощью так называемых параметров, которые указываются в скобках в заголовке функции.
Аргументы функции
Функция может принимать произвольное количество аргументов или не принимать их вовсе. Также распространены функции с произвольным числом аргументов, функции с позиционными и именованными аргументами, обязательными и необязательными.
Аргументы могут быть числами, текстом, логическими значениями, такими как Истина или ложь, массивами, значениями ошибок, например #N/a или ссылками на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
В качестве аргументов также используются константы, формулы и другие функции.
ОглавлениеПРЕДИСЛОВИЕАНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. Понятие о предмете аналитической геометрии § 2. Координаты § 3. Прямоугольная система координат § 4. Прямоугольные координаты § 5. Координатные углы § 6. Косоугольная система координат § 7.  Уравнение линии Уравнение линии§ 8. Взаимное расположение линии и точки § 9. Взаимное расположение двух линий § 10. Расстояние между двумя точками § 11. Деление отрезка в данном отношении § 11а. Деление отрезка пополам § 12. Определитель второго порядка § 13. Площадь треугольника § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом) § 15. Прямая, параллельная оси § 16. Общее уравнение прямой § 17. Построение прямой по ее уравнению § 18. Условие параллельности прямых § 19. Пересечение прямых § 20. Условие перпендикулярности двух прямых § 21. Угол между двумя прямыми § 22. Условие, при котором три точки лежат на одной прямой § 23. Уравнение прямой, проходящей через две точки § 24. Пучок прямых § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой § 27. Взаимное расположение прямой и пары точек § 28.  2+bx+c 2+bx+c§ 51. Директрисы эллипса и гиперболы § 52. Общее определение эллипса, гиперболы и параболы § 53. Конические сечения § 54. Диаметры конического сечения § 55. Диаметры эллипса § 56. Диаметры гиперболы § 57. Диаметры параболы § 58. Линии второго порядка § 59. Запись общего уравнения второй степени § 60. Упрощение уравнения второй степени; общие замечания § 61. Предварительное преобразование уравнения второй степени § 62. Завершающее преобразование уравнения второй степени § 63. О приемах, облегчающих упрощение уравнения второй степени § 64. Признак распадения линий второго порядка § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка § 66. Инварианты уравнения второй степени § 67. Три типа линий второго порядка § 68. Центральные и нецентральные линии второго порядка § 69. Нахождение центра центральной линии второго порядка § 70. Упрощение уравнения центральной линии второго порядка § 71.  Равносторонняя гипербола как график уравнения y=k/x Равносторонняя гипербола как график уравнения y=k/x§ 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q) § 73. Полярные координаты § 74. Связь между полярными и прямоугольными координатами § 75. Архимедова спираль § 76. Полярное уравнение прямой § 77. Полярное уравнение конического сечения АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 78. Понятие о векторах и скалярах § 79. Вектор в геометрии § 80. Векторная алгебра § 81. Коллинеарные векторы § 82. Нуль-вектор § 83. Равенство векторов § 84. Приведение векторов к общему началу § 85. Противоположные векторы § 86. Сложение векторов § 87. Сумма нескольких векторов § 88. Вычитание векторов § 89. Умножение и деление вектора на число § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор) § 91. Проекция точки на ось § 92. Проекция вектора на ось § 93. Основные теоремы о проекциях вектора § 94. Прямоугольная система координат в пространстве § 95.  Координаты точки Координаты точки§ 96. Координаты вектора § 97. Выражения вектора через компоненты и через координаты § 98. Действия над векторами, заданными своими координатами § 99. Выражение вектора через радиусы-векторы его начала и конца § 100. Длина вектора. Расстояние между двумя точками § 101. Угол между осью координат и вектором § 102. Признак коллинеарности (параллельности) векторов § 103. Деление отрезка в данном отношении § 104. Скалярное произведение двух векторов § 104а. Физический смысл скалярного произведения § 105. Свойства скалярного произведения § 106. Скалярные произведения основных векторов § 107. Выражение скалярного произведения через координаты сомножителей § 108. Условие перпендикулярности векторов § 109. Угол между векторами § 110. Правая и левая системы трех векторов § 111. Векторное произведение двух векторов § 112. Свойства векторного произведения § 113. Векторные произведения основных векторов § 114.  Выражение векторного произведения через координаты сомножителей Выражение векторного произведения через координаты сомножителей§ 115. Компланарные векторы § 116. Смешанное произведение § 117. Свойства смешанного произведения § 118. Определитель третьего порядка § 119. Выражение смешанного произведения через координаты сомножителей § 120. Признак компланарности в координатной форме § 121. Объем параллелепипеда § 122. Двойное векторное произведение § 123. Уравнение плоскости § 124. Особые случаи положения плоскости относительно системы координат § 125. Условие параллельности плоскостей § 126. Условие перпендикулярности плоскостей § 127. Угол между двумя плоскостями § 128. Плоскость, проходящая через данную точку параллельно данной плоскости § 129. Плоскость, проходящая через три точки § 130. Отрезки на осях § 131. Уравнение плоскости в отрезках § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям § 134.  Точка пересечения трех плоскостей Точка пересечения трех плоскостей§ 135. Взаимное расположение плоскости и пары точек § 136. Расстояние от точки до плоскости § 137. Полярные параметры плоскости § 138. Нормальное уравнение плоскости § 139. Приведение уравнения плоскости к нормальному виду § 140. Уравнения прямой в пространстве § 141. Условие, при котором два уравнения первой степени представляют прямую § 142. Пересечение прямой с плоскостью § 143. Направляющий вектор § 144. Углы между прямой и осями координат § 145. Угол между двумя прямыми § 146. Угол между прямой и плоскостью § 147. Условия параллельности и перпендикулярности прямой и плоскости § 148. Пучок плоскостей § 149. Проекции прямой на координатные плоскости § 150. Симметричные уравнения прямой § 151. Приведение уравнений прямой к симметричному виду § 152. Параметрические уравнения прямой § 153. Пересечение плоскости с прямой, заданной параметрически § 154. Уравнения прямой, проходящей через две данные точки § 155.  Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой§ 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости § 157. Уравнение плоскости, проходящей через данную точку и данную прямую § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости § 164. Уравнения общего перпендикуляра к двум данным прямым § 165. Кратчайшее расстояние между двумя прямыми § 165а. Правые и левые пары прямых § 166. Преобразование координат § 167. Уравнение поверхности § 168. 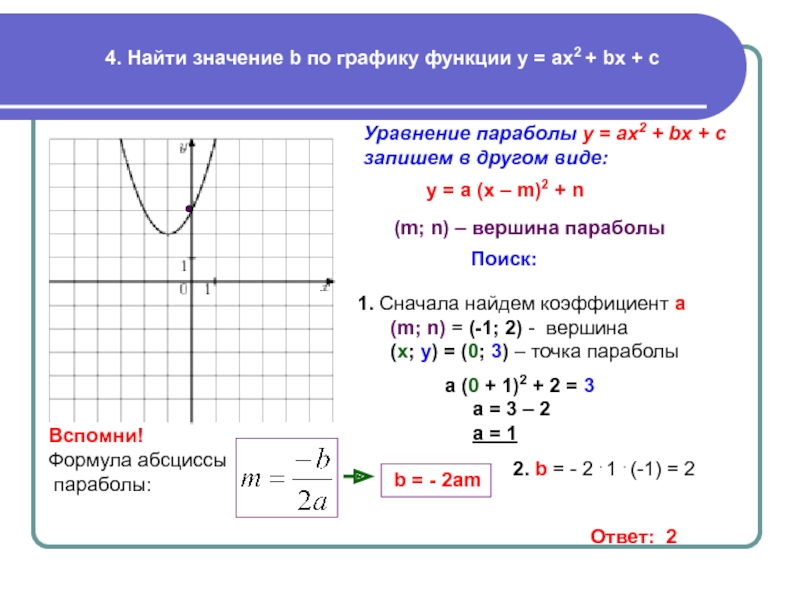 Цилиндрические поверхности, у которых образующие параллельны одной из осей координат Цилиндрические поверхности, у которых образующие параллельны одной из осей координат§ 169. Уравнения линии § 170. Проекция линии на координатную плоскость § 171. Алгебраические поверхности и их порядок § 172. Сфера § 173. Эллипсоид § 174. Однополостный гиперболоид § 175. Двуполостный гиперболоид § 176. Конус второго порядка § 177. Эллиптический параболоид § 178. Гиперболический параболоид § 179. Перечень поверхностей второго порядка § 180. Прямолинейные образующие поверхностей второго порядка § 181. Поверхности вращения § 182. Определители второго и третьего порядков § 183. Определители высших порядков § 184. Свойства определителей § 185. Практический прием вычисления определителей § 186. Применение определителей к исследованию и решению системы уравнений § 187. Два уравнения с двумя неизвестными § 188. Два уравнения с двумя неизвестными § 189. Однородная система двух уравнений с тремя неизвестными § 190.  Два уравнения с двумя неизвестными Два уравнения с двумя неизвестными§ 190а. Система n уравнений с n неизвестными ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 192. Рациональные числа § 193. Действительные (вещественные) числа § 194. Числовая ось § 195. Переменные и постоянные величины § 196. Функция § 197. Способы задания функции § 198. Область определения функции § 199. Промежуток § 200. Классификация функций § 201. Основные элементарные функции § 202. Обозначение функции § 203. Предел последовательности § 204. Предел функции § 205. Определение предела функции § 206. Предел постоянной величины § 207. Бесконечно малая величина § 208. Бесконечно большая величина § 209. Связь между бесконечно большими и бесконечно малыми величинами § 210. Ограниченные величины § 211. Расширение понятия предепа § 212. Основные свойства бесконечно малых величин § 213. Основные теоремы о пределах § 214. Число е § 215. Предел sinx/x при x стремящемся к 0 § 216.  Эквивалентные бесконечно малые величины Эквивалентные бесконечно малые величины§ 217. Сравнение бесконечно малых величин § 217а. Приращение переменной величины § 218. Непрерывность функции в точке § 219. Свойства функций, непрерывных в точке § 219а. Односторонний предел; скачок функции § 220. Непрерывность функции на замкнутом промежутке § 221. Свойства функций, непрерывных на замкнутом промежутке ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 223. Скорость § 224. Определение производной функции § 225. Касательная § 226. Производные некоторых простейших функций § 227. Свойства производной § 228. Дифференциал § 229. Механический смысл дифференциала § 230. Геометрический смысл дифференциала § 231. Дифференцируемые функции § 232. Дифференциалы некоторых простейших функций § 233. Свойства дифференциала § 234. Инвариантность выражения f'(x)dx § 235. Выражение производной через дифференциалы § 236. Функция от функции (сложная функция) § 237. Дифференциал сложной функции § 238.  Производная сложной функции Производная сложной функции§ 239. Дифференцирование произведения § 240. Дифференцирование частного (дроби) § 241. Обратная функция § 242. Натуральные логарифмы § 243. Дифференцирование логарифмической функции § 244. Логарифмическое дифференцирование § 245. Дифференцирование показательной функции § 246. Дифференцирование тригонометрических функций § 247. Дифференцирование обратных тригонометрических функций § 247а. Некоторые поучительные примеры § 248. Дифференциал в приближенных вычислениях § 249. Применение дифференциала к оценке погрешности формул § 250. Дифференцирование неявных функций § 251. Параметрическое задание линии § 252. Параметрическое задание функции § 253. Циклоида § 254. Уравнение касательной к плоской линии § 254а. Касательные к кривым второго порядка § 255. Уравнение нормали § 256. Производные высших порядков § 257. Механический смысл второй производной § 258. Дифференциалы высших порядков § 259.  Выражение высших производных через дифференциалы Выражение высших производных через дифференциалы§ 260. Высшие производные функций, заданных параметрически § 261. Высшие производные неявных функций § 262. Правило Лейбница § 263. Теорема Ролля § 264. Теорема Лагранжа о среднем значении § 265. Формула конечных приращений § 266. Обобщенная теорема о среднем значении (Коши) § 267. Раскрытие неопределенности вида 0/0 § 268. Раскрытие неопределенности вида бесконесность на бесконечность § 269. Неопределенные выражения других видов § 270. Исторические сведения о формуле Тейлора § 271. Формула Тейлора § 272. Применение формулы Тейлора к вычислению значений функции § 273. Возрастание и убывание функции § 274. Признаки возрастания и убывания функции в точке § 274а. Признаки возрастания и убывания функции в промежутке § 275. Максимум и минимум § 276. Необходимое условие максимума и минимума § 277. Первое достаточное условие максимума и минимума § 278. Правило нахождения максимумов и минимумов § 279.  Второе достаточное условие максимума и минимума Второе достаточное условие максимума и минимума§ 280. Нахождение наибольшего и наименьшего значений функции § 281. Выпуклость плоских кривых; точка перегиба § 282. Сторона вогнутости § 283. Правило для нахождения точек перегиба § 284. Асимптоты § 285. Нахождение асимптот, параллельных координатным осям § 286. Нахождение асимптот, не параллельных оси ординат § 287. Приемы построения графиков § 288. Решение уравнений. Общие замечания § 289. Решение уравнений. Способ хорд § 290. Решение уравнений. Способ касательных § 291. Комбинированный метод хорд и касательных ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ § 293. Первообразная функция § 294. Неопределенный интеграл § 295. Геометрический смысл интегрирования § 296. Вычисление постоянной интегрирования по начальным данным § 297. Свойства неопределенного интеграла § 298. Таблица интегралов § 299. Непосредственное интегрирование § 300. Способ подстановки (интегрирование через вспомогательную переменную) § 301.  Интегрирование по частям Интегрирование по частям§ 302. Интегрирование некоторых тригонометрических выражений § 303. Тригонометрические подстановки § 304. Рациональные функции § 304а. Исключение целой части § 305. О приемах интегрирования рациональных дробей § 306. Интегрирование простейших рациональных дробей § 307. Интегрирование рациональных функций (общий метод) § 308. О разложении многочлена на множители § 309. Об интегрируемости в элементарных функциях § 310. Некоторые интегралы, зависящие от радикалов § 311. Интеграл от биномиального дифференциала § 312. Интегралы вида … § 313. Интегралы вида S R(sinx, cosx)dx § 314. Определенный интеграл § 315. Свойства определенного интеграла § 316. Геометрический смысл определенного интеграла § 317. Механический смысл определенного интеграла § 318. Оценка определенного интеграла § 318а. Неравенство Буняковского § 319. Теорема о среднем интегрального исчисления § 320. Определенный интеграл как функция верхнего предела § 321.  Дифференциал интеграла Дифференциал интеграла§ 322. Интеграл дифференциала. Формула Ньютона — Лейбница § 323. Вычисление определенного интеграла с помощью неопределенного § 324. Определенное интегрирование по частям § 325. Способ подстановки в определенном интеграле § 326. О несобственных интегралах § 327. Интегралы с бесконечными пределами § 328. Интеграл функции, имеющей разрыв § 329. О приближенном вычислении интеграла § 330. Формулы прямоугольников § 331. Формула трапеций § 332. Формула Симпсона (параболических трапеций) § 333. Площади фигур, отнесенных к прямоугольным координатам § 334. Схема применения определенного интеграла § 335. Площади фигур, отнесенных к полярным координатам § 336. Объем тела по поперечным сечениям § 337. Объем тела вращения § 338. Длина дуги плоской линии § 339. Дифференциал дуги § 340. Длина дуги и ее дифференциал в полярных координатах § 341. Площадь поверхности вращения ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ § 342.  Кривизна Кривизна§ 343. Центр, радиус и круг кривизны плоской линии § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии § 345. Эволюта плоской линии § 346. Свойства эволюты плоской линии § 347. Развертка (эвольвента) плоской линии § 348. Параметрическое задание пространственной линии § 349. Винтовая линия § 350. Длина дуги пространственной линии § 351. Касательная к пространственной линии § 352. Нормальная плоскость § 353. Вектор-функция скалярного аргумента § 354. Предел вектор-функции § 355. Производная вектор-функции § 356. Дифференциал вектор-функции § 357. Свойства производной и дифференциала вектор-функции § 358. Соприкасающаяся плоскость § 359. Главная нормаль. Сопутствующий трехгранник § 360. Взаимное расположение линии и плоскости § 361. Основные векторы сопутствующего трехгранника § 362. Центр, ось и радиус кривизны пространственной линии § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии § 364. 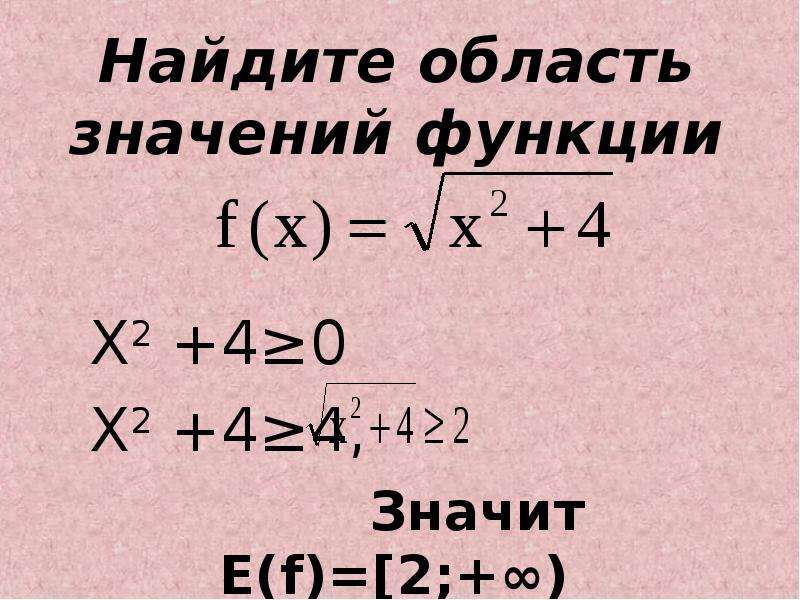 О знаке кривизны О знаке кривизны§ 365. Кручение РЯДЫ § 367. Определение ряда § 368. Сходящиеся и расходящиеся ряды § 369. Необходимое условие сходимости ряда § 370. Остаток ряда § 371. Простейшие действия над рядами § 372. Положительные ряды § 373. Сравнение положительных рядов § 374. Признак Даламбера для положительного ряда § 375. Интегральный признак сходимости § 376. Знакопеременный ряд. Признак Лейбница § 377. Абсолютная и условная сходимость § 378. Признак Даламбера для произвольного ряда § 379. Перестановка членов ряда § 380. Группировка членов ряда § 381. Умножение рядов § 382. Деление рядов § 383. Функциональный ряд § 384. Область сходимости функционального ряда § 385. О равномерной и неравномерной сходимости § 386. Определение равномерной и неравномерной сходимости § 387. Геометрический смысл равномерной и неравномерной сходимости § 388. Признак равномерной сходимости; правильные ряды § 389. Непрерывность суммы ряда § 390.  Интегрирование рядов Интегрирование рядов§ 391. Дифференцирование рядов § 392. Степенной ряд § 393. Промежуток и радиус сходимости степенного ряда § 394. Нахождение радиуса сходимости § 395. Область сходимости ряда, расположенного по степеням х – х0 § 396. Теорема Абеля § 397. Действия со степенными рядами § 398. Дифференцирование и интегрирование степенного ряда § 399. Ряд Тейлора § 400. Разложение функции в степенной ряд § 401. Разложение элементарных функций в степенные ряды § 402. Применение рядов к вычислению интегралов § 403. Гиперболические функции § 404. Обратные гиперболические функции § 405. Происхождение наименований гиперболических функций § 406. О комплексных числах § 407. Комплексная функция действительного аргумента § 408. Производная комплексной функции § 409. Возведение положительного числа в комплексную степень § 410. Формула Эйлера § 411. Тригонометрический ряд § 412. Исторические сведения о тригонометрических рядах § 413.  Ортогональность системы функций cos nx, sin nx Ортогональность системы функций cos nx, sin nx§ 414. Формулы Эйлера-Фурье § 415. Ряд Фурье § 416. Ряд Фурье для непрерывной функции § 417. Ряд Фурье для четной и нечетной функции § 418. Ряд Фурье для разрывной функции ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ § 420. Функция трех и большего числа аргументов § 421. Способы задания функций нескольких аргументов § 422. Предел функции нескольких аргументов § 424. Непрерывность функции нескольких аргументов § 425. Частные производные § 426. Геометрический смысл частных производных для случая двух аргументов § 427. Полное и частное приращения § 428. Частный дифференциал § 429. О выражении частной производной через дифференциал § 430. Полный дифференциал § 431. Геометрический смысл полного дифференциала (случай двух аргументов) § 432. Инвариантность выражения … полного дифференциала § 433. Техника дифференцирования § 434. Дифференцируемые функции § 435.  Касательная плоскость и нормаль к поверхности Касательная плоскость и нормаль к поверхности§ 436. Уравнение касательной плоскости § 437. Уравнения нормали § 438. Дифференцирование сложной функции § 439. Замена прямоугольных координат полярными § 440. Формулы для производных сложной функции § 441. Полная производная § 442. Дифференцирование неявной функции нескольких переменных § 443. Частные производные высших порядков § 444. Полные дифференциалы высших порядков § 445. Техника повторного дифференцирования § 446. Условное обозначение дифференциалов § 447. Формула Тейлора для функции нескольких аргументов § 448. Экстремум (максимум и минимум) функции нескольких аргументов § 449. Правило нахождения экстремума § 450. Достаточные условия экстремума (случай двух аргументов) § 451. Двойной интеграл § 452. Геометрический смысл двойного интеграла § 453. Свойства двойного интеграла § 454. Оценка двойного интеграла § 455. Вычисление двойного интеграла (простейший случай) § 456.  Вычисление двойного интеграла (общий случай) Вычисление двойного интеграла (общий случай)§ 457. Функция точки § 458. Выражение двойного интеграла через полярные координаты § 459. Площадь куска поверхности § 460. Тройной интеграл § 461. Вычисление тройного интеграла (простейший случай) § 462. Вычисление тройного интеграла (общий случай) § 463. Цилиндрические координаты § 464. Выражение тройного интеграла через цилиндрические координаты § 465. Сферические координаты § 466. Выражение тройного интеграла через сферические координаты § 467. Схема применения двойного и тройного интегралов § 468. Момент инерции § 471. Криволинейный интеграл § 472. Механический смысл криволинейного интеграла § 473. Вычисление криволинейного интеграла § 474. Формула Грина § 475. Условие, при котором криволинейный интеграл не зависит от пути § 476. Другая форма условия предыдущего параграфа ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 478. Уравнение первого порядка § 479. Геометрический смысл уравнения первого порядка § 480.  Изоклины Изоклины§ 481. Частное и общее решения уравнения первого порядка § 482. Уравнения с разделенными переменными § 483. Разделение переменных. Особое решение § 484. Уравнение в полных дифференциалах § 484а. Интегрирующий множитель § 485. Однородное уравнение § 486. Линейное уравнение первого порядка § 487. Уравнение Клеро § 488. Огибающая § 489. Об интегрируемости дифференциальных уравнений § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера § 491. Интегрирование дифференциальных уравнений с помощью рядов § 492. О составлении дифференциальных уравнений § 493. Уравнение второго порядка § 494. Уравнение n-го порядка § 495. Случаи понижения порядка § 496. Линейное уравнение второго порядка § 497. Линейное уравнение второго порядка с постоянными коэффициентами § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части § 498а. Связь между случаями 1 и 3 § 498 § 499.  Линейное уравнение второго порядка с постоянными коэффициентами с правой частью Линейное уравнение второго порядка с постоянными коэффициентами с правой частью§ 500. Линейные уравнения любого порядка § 501. Метод вариации постоянных § 502. Системы дифференциальных уравнений. Линейные системы НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ § 503. Строфоида § 504. Циссоида Диокла § 505. Декартов лист § 506. Верзьера Аньези § 507. Конхоида Никомеда § 508. Улитка Паскаля; кардиоида § 509. Линия Кассини § 510. Лемниската Бернулли § 511. Архимедова спираль § 512. Эвольвента (развертка) круга § 513. Логарифмическая спираль § 514. Циклоиды § 515. Эпициклоиды и гипоциклоиды § 516. Трактриса § 517. Цепная линия |
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Исчисление 2 Помощь » Интегралы » Интегральные приложения » Средние значения и длины функций
Какова длина дуги, если , от ?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу для длины дуги.
Вычислите производные.
Подставляем производные и оценки в интеграл.
Сообщить об ошибке
Каково среднее значение функции
от до ?
Возможные ответы:
Правильный ответ:
Пояснение:
Среднее значение функции p(t) от t=a до t=b находится с помощью интеграла
.
В этом случае мы должны вычислить значение интеграла
.
Замена делает этот интеграл более понятным. Позволять . Затем . Мы также должны переписать пределы интегрирования через u. Когда t = 0, u=1, а когда t = 2, u = 5. Выполнение этих замен приводит к интегралу
Вычисление этого интеграла с учетом того, что
дает
Сообщить об ошибке
Каково среднее значение функции на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
В общем случае среднее значение функции за интервал равно
Это означает, что среднее значение за интервал равно
.
Поскольку первообразная равна , интеграл равен
.
Сообщить об ошибке
Какова длина кривой на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
Общая формула для нахождения длины кривой на интервале:
В этом примере длину дуги можно найти, вычислив интеграл
.
Производную от можно найти с помощью правила степени, , что приводит к
.
На этом этапе замена будет полезна.
Пусть
.
Мы также можем выразить пределы интегрирования в терминах для упрощения вычислений. Когда и когда .
Выполнение этих замен приводит к
.
Теперь используйте правило степени, которое обычно используется , чтобы вычислить интеграл.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
90 014 Объяснение:Когда f интегрируемо на [a,b], среднее значение f(x) на [a,b] определяется как:
Для постановки задачи нам дано f( x) и интервалы [a,b]. Все, что нужно сделать, это решить интеграл по этому интервалу и разделить результат на разницу между двумя интервалами.
Все, что нужно сделать, это решить интеграл по этому интервалу и разделить результат на разницу между двумя интервалами.
Итак:
Чтобы решить этот интеграл, у нас есть два варианта. Мы можем ФОЛОСОВАТЬ термины и решить интеграл полученного полинома, или мы можем использовать простую u-подстановку. В любом случае результат всегда будет одинаковым. Мы попробуем оба способа, чтобы доказать, что это верно:
Метод FOIL:
9 0004 Это один из вариантов ответа!Метод U-подстановки:
Далее мы должны скорректировать границы нового интеграла, который будет выражаться в u .
Таким образом, новый интеграл становится:
Как видите, оба метода дают один и тот же ответ!
Сообщить об ошибке
Каково среднее значение между интервалами и ?
Возможные ответы:
Правильный ответ:
Объяснение:
При запросе среднего значения между интервалами формы и интеграл становится равным
, поэтому в этом случае мы можем переписать нашу задачу о среднем значении как
.
Интеграл оценивается как и , что упрощается до
(обратите внимание, что равно 1).
Однако, поскольку мы ищем среднее значение , мы должны разделить все это на b-a, что в данном случае равно 2, поэтому окончательный ответ – 9.0005
.
Сообщить об ошибке
Каково среднее значение функции на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции за интервал определяется как интеграл от функции, деленный на длину интервала.
Общее правило для этого типа интеграции следующее.
Получаем:
Сообщить об ошибке
Чему равно среднее значение функции
на интервале ?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции находится путем взятия интеграла функции по интервалу и деления на длину интервала.
Общее правило для этого типа интеграции следующее.
Итак, имеем:
Сообщить об ошибке
Каково среднее значение функции на интервале ?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции находится путем взятия интеграла функции по интервалу и деления на длину интервала.
Общее правило для этого типа интеграции следующее.
Итак, имеем:
Сообщить об ошибке
Каково среднее значение функции на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции находится путем взятия интеграла функции по интервалу и деления на длину интервала.
Общее правило для этого типа интеграции следующее.
Итак, у нас есть:
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Обучение по концепции
Давайте начнемМашина функцийСвязь между y = и обозначением функцийЗначения функцийПрактика учащихсяСловарный запасЗанятие в дневнике
Стандарты TEKS и ожидания учащихся
A(12) Численные и алгебраические методы. Студент применяет стандарты математического процесса и алгебраические методы для написания, решения, анализа и оценки уравнений, отношений и функций. Ожидается, что учащийся:
A(12)(B) оценивает функции, выраженные в виде функций, по одному или нескольким элементам в их предметных областях
Ресурсная цель(и) функцию, учащийся найдет определенные значения функции.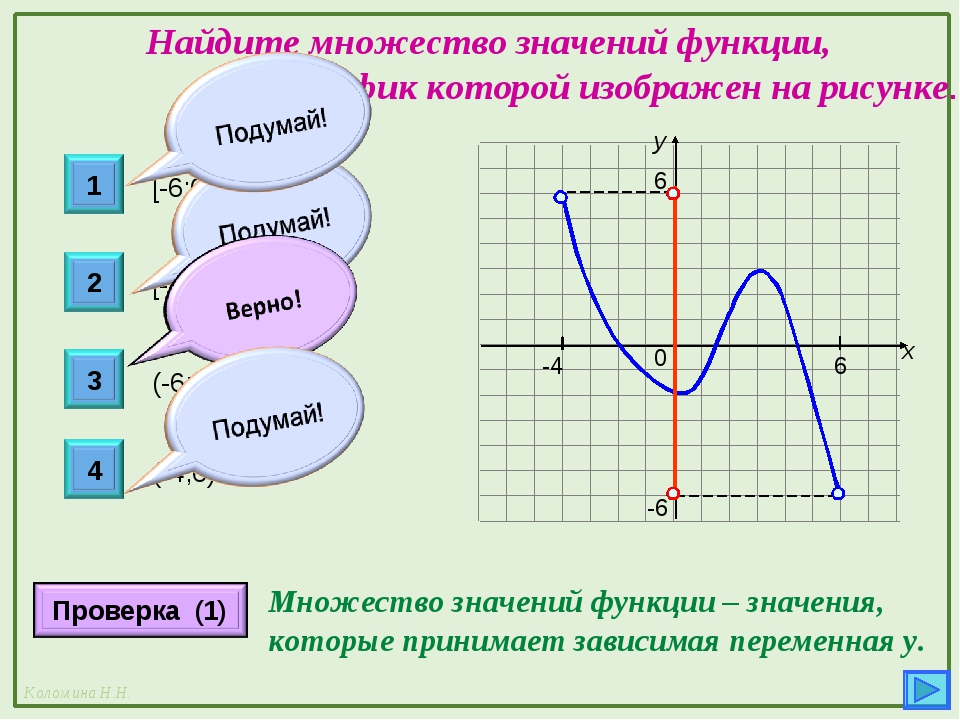
Основные вопросы
Каким методом можно найти значение функции?
Чем обозначение функции похоже на обозначение и ?
Чем обозначение функции отличается от обозначения и ?
Словарь
Мы собираемся использовать интерактивную функциональную машину и записать x -значение, y -значение и функция на вашей собственной бумаге.
Указания
Составьте на своем листе не менее трех таблиц, подобных приведенной ниже таблице.
 904:30
904:30Познакомившись с функциональной машиной, пришло время взглянуть на взаимосвязь между y= и функциональной нотацией, в том числе на то, как эти нотации можно использовать для разработки таблицы значений.
Перейдите по ссылке ниже, чтобы просмотреть видео, объясняющее эту взаимосвязь.
Таблицы из правил функций
Функции часто представляются с помощью обозначения функций. Как вы можете видеть в следующем видео, обозначения функций обычно записываются строчными или прописными буквами, такими как f, g или H, за которыми следует переменная в скобках. Функция «f( x )» читается как «f of x » и не подразумевает умножения между двумя переменными. Это просто математический способ задать правило, которое можно использовать для создания таблицы значений.
Извлечь word файлов из rar Powered by aspose.com and aspose.cloud
Перетащите или выберите файлы*
Выбрать файл
Выбрать из Google Drive Выбрать из Dropbox
Введите Url
* Загружая свои файлы или используя нашу службу, вы соглашаетесь с Условиями использования и Политикой конфиденциальности
Сохранить как DOCXFILEPDFMP2MPVOGGM4PM4VM4AFLACMP3WAVWMAJPGXMLZIPPNGPPTXDOCTEXTIFFTXTHTMLXLSXSVGCSVEPUBMHTMLXPSWEBPMHTLATEX7ZBMPGZMOBIDJVUEMFTARPSBZ2BASE64MP4AVIMOVWEBMFLVWMVMKVMPGMPEG
Ваши файлы обработаны успешно
СКАЧАТЬОтправить результат в:
ПОСМОТРЕТЬ РЕЗУЛЬТАТПОСМОТРЕТЬ РЕЗУЛЬТАТ
Отправить результат в:
1000 символов максимум
Обратная связь
Или оставьте, пожалуйста, отзыв в наших социальных сетях 👍
Попробуйте другие наши конвертеры:
PDFDOCWordXLSExcelEPUBMOBILaTeXPostScriptEPSXPSOXPSMHTMLMHTPCLMarkdownTextSVGSRTXMLBMPPNGTIFFJPGEMFDICOMPSDCDRDJVUWEBPZIPRAR7zipTARGZBZ2PPTPowerPointBase64MP4MOVMP3WAVIMAGESPHOTOGIFHEIC
Other apps
Конвертируйте RAR в Word файлы онлайн бесплатно. Мощный бесплатный онлайн RAR в Word конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мощный бесплатный онлайн RAR в Word конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
С точки зрения доступности вы можете использовать наши онлайн-инструменты преобразования RAR в Word для обработки различных форматов файлов и размеров файлов в любой операционной системе. Независимо от того, находитесь ли вы на MacBook, компьютере с Windows или даже на карманном мобильном устройстве, конвертер RAR в Word всегда доступен в Интернете для вашего удобства.
1
Откройте вебстраницу RAR и выберите приложение Конвертер.2
Кликните в области FileDrop для выбора RAR файлов или drag & drop RAR файлы.3
Вы можете одновременно отправить максимум 10 файлов.
4
Нажмите кнопку КОНВЕРТИРОВАТЬ. Ваши RAR файлы будут отправлены и преобразованы в нужный формат.5
Ссылка для скачивания результирующих файлов будет доступна сразу после конвертации.6
Вы так же можете отправить ссылку на скачивание полученных файлов на email себе или Вашим коллегам.7
Примечание: результирующие файлы будут удалены с нашего сервера через 24 часа и ссылка на скачивание будет не рабочей.1
Сначала Вам нужно добавить файл для преобразования: перетащите файл RAR или щелкните внутри белой области, чтобы выбрать файл. Затем нажмите кнопку «Конвертировать». Когда преобразование RAR в WORD завершено, вы можете загрузить файл WORD.
2
Этот конвертер работает быстро. Вы можете преобразовать RAR в WORD в течении нескольких секунд.
3
Конечно! Ссылка для скачивания файлов WORD будет доступна сразу после конвертации. Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать. Никто не имеет доступа к вашим файлам. Преобразование файлов (включая RAR в WORD) абсолютно безопасно.
Никто не имеет доступа к вашим файлам. Преобразование файлов (включая RAR в WORD) абсолютно безопасно.
4
Да, вы можете использовать RAR конвертер в любой операционной системе через веб-браузер. Наш конвертер RAR в WORD работает в режиме онлайн и не требует установки программного обеспечения.
5
Вы можете использовать любой современный браузер для преобразования RAR в WORD, например, Google Chrome, Firefox, Opera, Safari.
Загрузите документ, выберите тип сохраненного формата и нажмите кнопку «Конвертировать». Вы получите ссылку для скачивания, как только файл будет конвертирован.
Вы получите ссылку для скачивания, как только файл будет конвертирован.
Он работает со всех платформ, включая Windows, Mac, Android и iOS. Все файлы обрабатываются на наших серверах. Вам не требуется установка плагинов или программного обеспечения.
. Все файлы обрабатываются с использованием Aspose APIs, которое используются многими компаниями из списка Fortune 100 в 114 странах мира.
Вы можете также преобразовывать RAR во множество других форматов. Посмотрите список, приведенный ниже.
RAR в FILE
RAR в PDF
RAR в DOC
RAR в Word
RAR в Excel
RAR в CSV
RAR в PowerPoint
RAR в XML
RAR в PostScript
RAR в XPS
RAR в DJVU
RAR в EPUB
RAR в MOBI
RAR в LaTeX
RAR в HTML
RAR в MHTML
RAR в MHT
RAR в BMP
RAR в PNG
RAR в SVG
RAR в TIFF
RAR в JPG
RAR в EMF
RAR в Text
RAR в WEBP
RAR в ZIP
RAR в 7zip
RAR в TAR
RAR в GZ
RAR в BZ2
RAR в Base64
RAR в MP4
RAR в AVI
RAR в FLV
RAR в MKV
RAR в MOV
RAR в WMV
RAR в WEBM
RAR в MPG
RAR в MPEG
RAR в MP2
RAR в MPV
RAR в OGG
RAR в M4P
RAR в M4V
RAR в M4A
RAR в FLAC
RAR в MP3
RAR в WAV
RAR в WMA
Инструкции приводятся ниже
Вот шаги по преобразованию RAR-архива в файл DOC с помощью ezyZip.
Нажмите зеленую кнопку «Сохранить», чтобы сохранить отдельный файл doc на локальном диске.
Сначала следуйте инструкциям выше
Нажмите «Сохранить все». Если кнопка неактивна, значит ваш браузер не поддерживает эту функцию или она не включена.
В Chrome вы можете включить функцию, переключив этот параметр:
chrome://flags/#native-file-system-api
(скопируйте и вставьте в адресную строку браузера)
Выберите пустую папку, куда вы хотите извлечь файлы. Внимание: если там уже есть файлы с такими именами, ezyZip ПЕРЕЗАПИШЕТ ИХ.
После того, как вы выбрали папку, браузер запросит разрешение на доступ к ней. Кликните «Просмотреть файлы», а затем «Сохранить изменения».
Затем начнется сохранение файлов и подпапок в указанную вами.
Кликните на лого Dropbox () на кнопке выбора rar файла.
Появится окно выбора файла в Dropbox. При первом запуске будет необходимо подтвердить доступ к ezyZip.
Как только вы выберете rar файл, он сразу скачается в вашем браузере и откроется после скачивания.
Для сохранения doc файлов на Dropbox, кликните «Dropbox» выбрав данный пункт из появляющегося под кнопкой «Сохранить» или «Сохранить все». Необходимо будет авторизовать Dropbox для ezyZip при первом использовании.
Файлы будут сохранены в папке /Apps/ezyZip.
ezyZip поддерживает любую ОС, которая может работать с современным браузером. Мы протестировали его для работы с Windows, MacOS, Linux (например, Ubuntu, Mint, Debian), Android, ChromeOS (Chromebook), Android, iOS (iPhone, iPad и iPod Touch).
Убедитесь, что вы используете последнюю версию одного из популярных браузеров или их вариации (например, Chrome, Firefox, Safari, Opera).
ezyZip — это бесплатная онлайн-утилита для извлечения doc файлов из zip-архива . Нет необходимости устанавливать дополнительное программное обеспечение, так как оно работает в браузере. Он поддерживает множество других извлечения файлов и вариантов преобразования тоже.
Он поддерживает множество других извлечения файлов и вариантов преобразования тоже.
В отличие от других онлайн-утилит для конвертации zip-файлов, ezyZip не требует от вас загрузки файлов на сервер. Он работает локально как приложение для браузера, что делает его намного быстрее, чем другие аналогичные инструменты онлайн-преобразования. ограничений на размер файла нет! Это также гарантирует, ваша конфиденциальность будет защищена, так как никакие данные файла не будут покидать ваш браузер .
Извлечение файлов word из rar Работает на aspose.com и aspose.cloud
Перетащите или загрузите ваши файлы*
Выберите файл
Выберите с Google Диска Выберите из Dropbox
Введите URL-адрес
*Загружая файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности PSWEBPMHTLATEX7ZBMPGZMOBIDJVUEMFTARPSBZ2BASE64MP4AVIMOVWEBMFLVWMVMKVMPGMPEG
Ваши файлы успешно обработаны
СКАЧАТЬОтправить результат по адресу:
ПОСМОТРЕТЬ РЕЗУЛЬТАТЫПОСМОТРЕТЬ РЕЗУЛЬТАТЫ
Лучший бесплатный онлайн-конвертер RAR в Word
 Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.
Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.Быстро и просто
RAR to Word Converter — это онлайн-сервис для преобразования файлов из одного типа в другой. Мы поддерживаем множество популярных форматов для работы, все возможные форматы изображений, форматы мультимедийных файлов и т.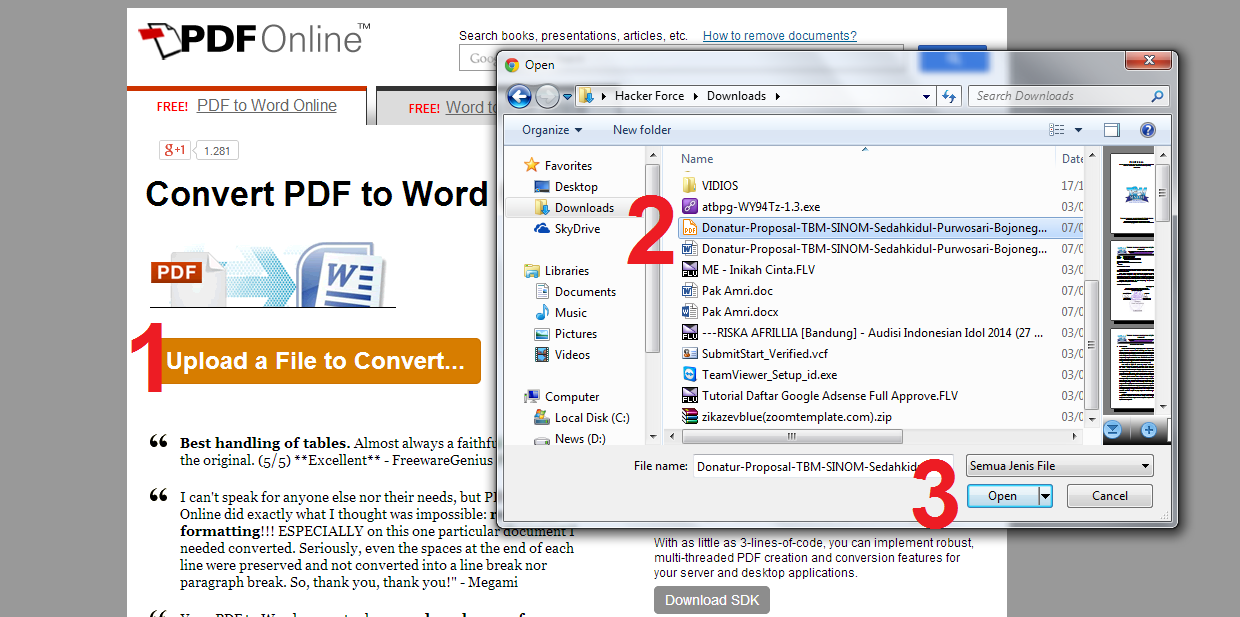 д. Наш инструмент преобразования RAR в Word прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
д. Наш инструмент преобразования RAR в Word прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
Безопасность гарантирована
Мы гарантируем безопасность и конфиденциальность. Мы не получаем права на ваш файл и ручной проверки не будет. Мы заботимся о вашей конфиденциальности и ваших файлах. В связи с этим мы также не будем передавать ваши данные другим сторонам. Крайне важно, чтобы у вас была возможность немедленно удалить загруженные вами файлы с нашего сервера. Если вы забудете это сделать, они будут автоматически удалены с нашего сервера через 24 часа. Мы полностью защищаем вашу информацию.
Универсальное преобразование
Вы можете конвертировать файлы из RAR в Word из любой ОС или устройства с подключением к Интернету. Наш сервис работает на любой ОС, включая Windows, Mac и Linux.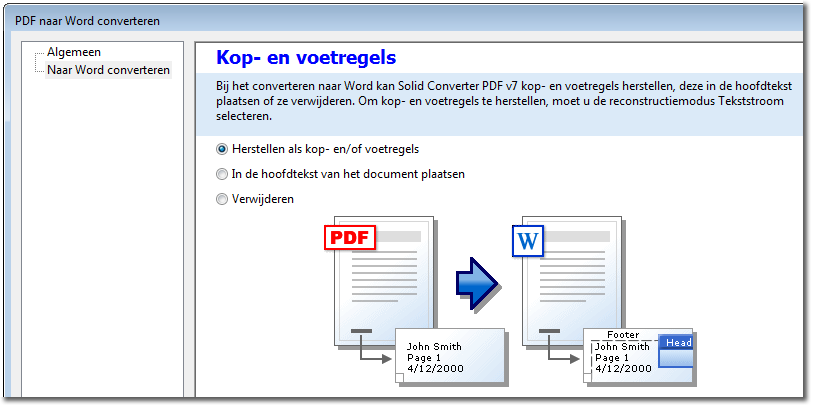
Самые популярные варианты конвертации
Мы поддерживаем самые распространенные варианты конвертации для работы и учебы. Используйте наше бесплатное приложение, чтобы уменьшить нагрузку при работе как с документами, так и с файлами изображений.
1
Откройте бесплатный веб-сайт RAR и выберите приложение Convert.2
Щелкните внутри области перетаскивания файлов, чтобы загрузить или перетащить файлы.3
Вы можете загрузить максимум 10 файлов для операции.4
Нажмите кнопку Преобразовать. Файлы будут загружены и преобразованы.5
Ссылка для скачивания файлов результатов будет доступна сразу после конвертации.6
Вы также можете отправить ссылку на файл на свой адрес электронной почты.
7
Обратите внимание, что файл будет удален с наших серверов через 24 часа, а ссылки для скачивания перестанут работать по истечении этого периода времени.1
Во-первых, вам нужно добавить файл для преобразования: перетащите или щелкните внутри белой области. Затем нажмите кнопку «Конвертировать». Когда преобразование завершено, вы можете загрузить свой результат.
2
Это приложение работает быстро. Вы можете получить результат в течение нескольких секунд.
3
Конечно! Ссылка для скачивания файлов результатов будет доступна сразу после конвертации. Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать по истечении этого периода времени. Никто не имеет доступа к вашим документам. Приложение абсолютно безопасно.
4
Да, вы можете использовать бесплатное приложение Converter в любой операционной системе с веб-браузером. Наше приложение работает онлайн и не требует установки какого-либо программного обеспечения.
5
Для конвертации можно использовать любой современный браузер. Например, Google Chrome, Firefox, Opera, Safari.
Например, Google Chrome, Firefox, Opera, Safari.
Загрузите документ, выберите формат сохранения и нажмите кнопку «Конвертировать». Вы получите ссылку для скачивания, как только файл будет конвертирован.
Работает на всех платформах, включая Windows, Mac, Android и iOS. Все файлы обрабатываются на наших серверах. Для вас не требуется установка плагинов или программного обеспечения.
. Все файлы обрабатываются с помощью API-интерфейсов Aspose, которые используются многими компаниями из списка Fortune 100 в 114 странах.
Инструкции ниже
В этом обучающем видео наш представитель Эзрия Ципперновски демонстрирует , как преобразовать файл rar в doc .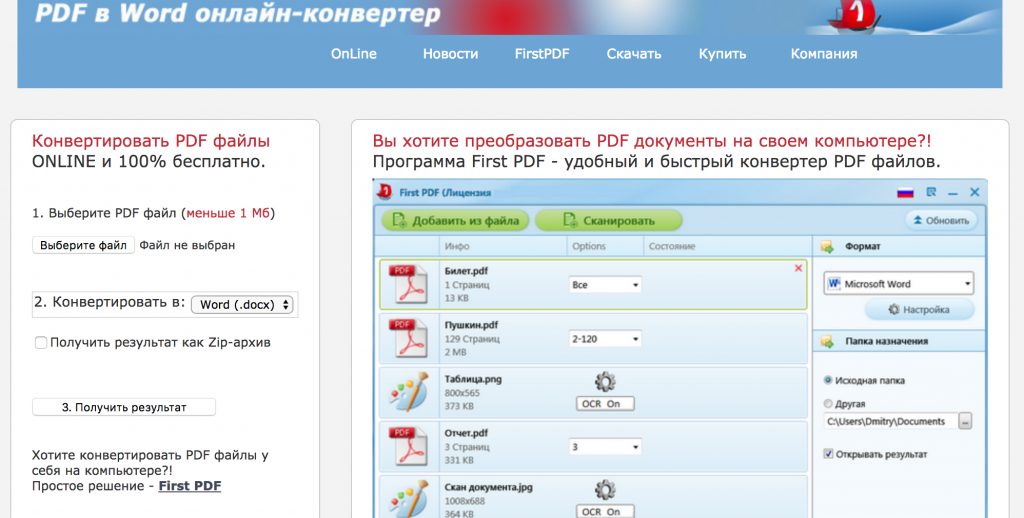 В этом примере используется файл png, но те же шаги применимы и к файлам doc.
В этом примере используется файл png, но те же шаги применимы и к файлам doc.
Вот шаги для преобразования архива в файл(ы) DOC с помощью ezyZip:
Нажмите зеленую кнопку «Сохранить», чтобы сохранить отдельный файл документа на локальном диске.
Сначала следуйте приведенным выше инструкциям
Нажмите «Сохранить все». Если кнопка отключена, это означает, что ваш браузер не поддерживает эту функцию или она не включена.
В Chrome вы можете включить его, переключив следующую настройку:
chrome://flags/#native-file-system-api
(скопируйте/вставьте его в адресную строку браузера)
Выберите пустую папку , куда вы хотите извлечь файлы. Обратите внимание: если у вас уже есть файлы с таким именем, ezyZip ПЕРЕЗАПИСЫВАЕТ ИХ .
После выбора папки браузер запросит разрешение на доступ к ней. Нажмите «Просмотреть файлы», а затем «Сохранить изменения».
Затем он начнет сохранять файлы и подпапки в указанную вами цель.
Появится окно выбора файлов Dropbox. Вам нужно будет авторизовать доступ к ezyZip в первый раз.
После того, как вы выбрали файл RAR, он загрузит его в ваш браузер и покажет содержимое.
Чтобы сохранить файлы документов в Dropbox, щелкните раскрывающийся список «Dropbox» под кнопками «Сохранить» или «Сохранить все». Вам нужно будет авторизовать Dropbox для ezyZip в первый раз, когда вы это сделаете.
Файлы будут сохранены в папке /Apps/ezyZip .
ezyZip поддерживает любую ОС, на которой можно запустить современный браузер. Мы протестировали его на совместимость с Windows, MacOS, Linux (например, Ubuntu, Mint, Debian), Android, ChromeOS (Chromebook), iOS (iPhone, iPad и iPod Touch).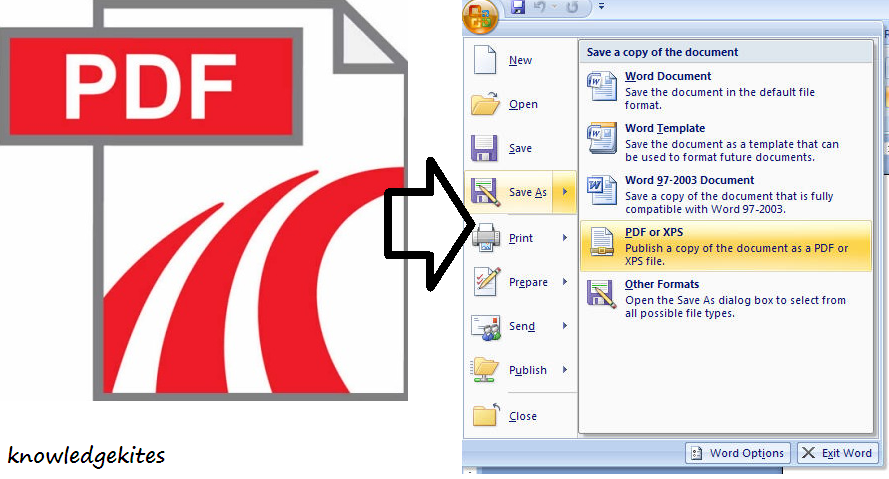
8. Таблица умножения и деления на 2 и 3
|
Организационный этап
Вы, ребята, отдыхали, Сегодня на уроке мы повторим таблицу умножения и деления на 2 и 3. Будем учиться решать задачи с использованием действий умножения и деления. Говорят, что математика – гимнастика для ума. Урок у нас будет немного спортивный, ведь на помощь к нам сегодня пришли символы зимней олимпиады 2014 в Сочи – Зайка, Леопард, Белый мишка.
|
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Чтобы работать быстро и ловко, Нас ждёт «Разминка перед стартом».
Устный счёт
Задание 1 Найдите и исправьте ошибки в примерах. 18 – 9 = 7 (9) 9 + 6 = 15 13 – 6 = 8 (7) 7 + 6 = 13 15 – 8 = 9 (7) 16 – 9 = 7 5 + 7 = 12 11 – 2 = 8 (9) Проверьте себя.
13 – 6 = 7 15 – 8 = 7 11 – 2 = 9
Задание 2 14 лыж у крылечка стоят. Проверьте себя.
Задание 3 Решите примеры, которые подготовил для вас Зайка. 4·2……8 3·3……9 16:2……8 19-8……11 12:3…..4 Найдите лишний пример.
Сегодня на уроке мы проверим и закрепим знание таблицы умножения и деления на 2 и на 3, будем решать задачи с использованием действий умножения и деления. |
|
|
Этап усвоения новых знаний
Что такое Умножение? Это умное сложение. Ведь умней — умножить раз, Давайте вспомним, как составляется таблица умножения. Два на два мы умножаем и 4 получаем и т. д. Два на 3 мы умножаем и 6 получаем Два на 4 мы умножаем и 8 получаем. Два на 5 мы умножаем и 10 получаем Два на 6 мы умножаем и 12 получаем. Два на 7 мы умножаем и 14 получаем Два на 8 мы умножаем и 16 получаем. Два на 9 мы умножаем и 18 получаем. Два на 10 мы умножаем и 20 получаем. Таблицу умножения читают так: дважды два – четыре, дважды три – шесть. Для того, чтобы каждый раз не заменять умножение сложением, таблицу умножения надо знать наизусть.
Точно также составляется таблица умножения и деления на 3. Выполним это. Проверьте с нашими олимпийцами запись у своего соседа по парте.
|
|
|
Этап закрепления новых знаний
Задание 1 Задание от Зайки. Запишите числа. 11, 12, 13, 14, 15, 16, 17, 18, 19, 20. Перед вами числа второго десятка. Ребята первого варианта, подчеркните числа, которые делятся на 2, а второго варианта – те числа, которые делятся на 3. Проверьте, так ли у вас получилось?
12, 14, 16, 18, 20 2 вариант 12, 15, 18.
|
|
|
Задание 2 от Леопарда Лыжники на соревнованиях бегут дистанцию в 18 км. Она разделена на 3 равных участка. Сколько км в одном участке? Проиллюстрируйте задачу схематическим чертежом. Линией обозначьте дистанцию, так как она разделена на три равных участка, то линию разделите на три равные части. Найдите, чему равна одна часть. Запишите решение. Проверьте себя и оцените свои успехи.
Ответ: в одном участке 6 км. Задание 3 от Белого мишки Начертите квадрат со стороной 2 см и найдите его периметр сначала при помощи сложения, а затем – умножения. Проверьте себя и оцените свои успехи.
Заменим сложение умножением: 2·4 =8 (см) Периметр квадрата равен 8 см.
|
|
|
Этап подведения итогов
Как называется действие, которым можно заменить сумму одинаковых слагаемых… умножение Чтобы быстро задания выполнять, заучите наизусть таблицу умножения и деления на 2 и на 3.
|
|
|
Рефлексия
Оцените свою работу на уроке. Выберите солнышко, которое соответствует вашему настроению. Юное тело свое закаляй, Спасибо за работу! |
|
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
⬑ Другие статьи
Итак, каждому родителю рано или поздно приходится столкнуться с необходимостью их ребёнка выучить таблицу умножения и деления. На сегодняшний момент существует большое множество различных способов, помогающих детям запомнить таблицу умножения (она же Таблица Пифагора) — это разнообразные онлайн тренажеры по математике, игры, картинки, видео, песни и даже стихи.
Однако далеко не все способы действительно эффективны и позволяют легко и быстро научить ребенка таблице умножения. Например, способ запоминания таблицы на пальцах довольно сложен в исполнении и затрате по времени. А вариант с применением стихов не желателен по той причине, что в школе ученику надо будет быстро решать примеры, а не «чистую» Пифагорову таблицу, поэтому времени на вспоминание не самых простых строк из стихотворений у ребёнка не будет.
Онлайн тренажердля изучения таблицы умножения за 20 минут |
Правильнее всего будет разбить процесс обучения на 2 этапа:
1. Объяснение принципов умножения и сути таблицы
2. Заучивание наизусть «сухих» чисел из таблицы
Почему это правильно? Если вы сможете максимально понятно донести до ребёнка суть и смысл умножения, он сможет применять полученные знания сам на других примерах из жизни. Понимая смысл все этого, ребёнок уже не будет «тупо» заучивать наизусть числа, а будет учить их с мыслью о том, что это наиболее простой способ дальнейшего применения таблицы умножения.
Понимая смысл все этого, ребёнок уже не будет «тупо» заучивать наизусть числа, а будет учить их с мыслью о том, что это наиболее простой способ дальнейшего применения таблицы умножения.
Одно из первых понятий умножения, которое нужно объяснить ребенку, что умножение — это повторение, быстрый способ складывания одинаковых чисел, и был он придуман исключительно для удобства.
Покажите ребенку примеры, например, 3+7 или 4+5, и для сравнения 2+2+2+2 или 4+4+4+4+4. Спросите у него, какой пример быстрее и проще посчитать? Конечно, который короче, там, где меньше слагаемых.
Объясните ребенку, что в случае, когда складываются несколько одинаковых чисел, используется умножение. Покажите ребёнку запись подобных примеров: , привидите примеры использования в жизни.
Плавно подведите ребёнка к теме таблицы умножения и деления. Покажите ему таблицу, но не список примеров с обратной стороны некоторых тетрадей – так ребёнку будет легче вникнуть в суть.
Поясните, для того чтобы не пересчитывать каждый раз элементарные примеры, и была придумана таблица умножения – набор чисел, характеризующих собой произведения пересечений значений столбцов и строк. Не забудьте при этом упомянуть о зеркальности в таблице (свойство коммутативности).
Не забудьте при этом упомянуть о зеркальности в таблице (свойство коммутативности).
Еще одним полезным действием будет наглядно показать ребёнку произведение на клеточках тетради, в дальнейшем это поможет ему понять суть площади фигуры.
Когда ребёнок до конца понял смысл умножения, ему необходимо запомнить всего лишь 36 комбинаций чисел (связки трех чисел).
Сегодня это проще всего сделать, используя Тренажер для изучения таблицы умножения. Во многих случаях это и удобнее, и быстрее, чем поиск стихов, наглядных инструкций по использованию пальцев, подготовка карточек и самостоятельный контроль ребёнка.
Однако учить важно тоже правильно! Некоторые источники утверждают, что ребёнку важно делать частые перерывы, а материал подавать крохотными порциями: по 1-2 колонки чисел в день. Это не совсем верно, так как наибольшую эффективность мозг показывает при нагрузке в течении интервалов обучения в 40-50 минут, с перерывами по 5-10 минут между ними (именно так и чередуются уроки в школах). Учить же надо сразу всю таблицу умножения (это всего лишь 36 комбинаций!), чтобы она была в его голове как единое целое. Поверьте, это по силам ученику 2-3 класса.
Учить же надо сразу всю таблицу умножения (это всего лишь 36 комбинаций!), чтобы она была в его голове как единое целое. Поверьте, это по силам ученику 2-3 класса.
Как показывает практика, всю таблицу умножения и деления можно запомнить легко и быстро всего лишь за 20-30 минут чистого времени. Однако не стоит полагать, что при этом информация останется в голове ребёнка навсегда – очень важны регулярные повторения на математических тренажерах устного счёта для большего эффекта.
Онлайн тренажердля изучения таблицы умножения за 20 минут |

Продукт:- Ответ, который мы получаем, когда мы умножаем два или более множителя.
Фактор:- Число, умноженное на другое число, чтобы получить продукт.
Если множитель, умноженный на множитель, равен произведению, а деление противоположно умножению, то мы можем сказать:
Например:
18 ÷ 3 = ?
Решение:
Подумайте, 3 × ? = 18
Три раза какое число равно 18?
3 × 6 = 18
Итак, 18 ÷ 3 = 6
Напишите уравнение с отсутствующими множителями, а затем используйте таблицу умножения, чтобы найти 15 ÷ 3.
Решение:
Шаг 1: Здесь один множитель равен 3, найдите 3 в первый столбец этой таблицы умножения.
Шаг 2: И продукт равен 15. Следуйте за строкой, в которой находится 3, пока не дойдете до 15.
Шаг 3: Посмотрите прямо вверх в этот столбец таблицы. Число в верхней части столбца равно 5. Таким образом, недостающий множитель равен 5,9.0035
3 × 5 = 15
15 ÷ 3 = 5
Пример:
Напишите уравнение с отсутствующими множителями и используйте таблицу умножения для решения задачи на деление.
12 ÷ 3 = ?
Решение:
Здесь один множитель равен 3
произведение равно 12
Находим 12 в строке 3
Итак, 12 точка пересечения 3 и 4 5
3 4 034 Другой множитель равен 34 3 × 4 = 12 12 ÷ 3 = 4Мы можем найти недостающие множители, используя умножение или деление
2 × 8 = 16
2 × 5 = 10
2 × 4 = 8
9 × 5 = 35 900 45 900 45
4 × 8 = 32
4 × 4 = 16
7 × 8 = 56
7 × 5 = 35
7 × 4 = 28
Используйте таблицу умножения, чтобы помочь.
24 ÷ 6 = ____
24 = 6 × ____
Решение:
Здесь один множитель равен 6
произведение равно 24
Используя таблицу, мы можем найти 6 в столбце таблицы.
Двигаемся вперед, пока не получим 24.
Смотрим в эту строку, мы находим, что другой множитель равен 4.
24 ÷ 6 = 4
6 × 4 = 24
Пример:
5 Найдите недостающее
фактор и продукты.Решение:
2 × 8 = 16
2 х 5 = 10
2 х 7 = 14
5 х 8 = 40
5 х 7 =35
6 х 5 = 30
3 6 х 8 = 459 0 90 3
Счетная таблицаСчетная таблица — это простой способ записи и подсчета частот. Каждое вхождение показано меткой подсчета.
Пример:
Давайте создадим итоговую диаграмму для вышеуказанных данных.
Это выглядит намного проще для чтения.
Семейство фактов
Факторы – перемножаемые числа.
3 × 7 = 21
Обратная операция – Противоположная операция, отменяющая другую.
3 × 7 = 21 21 ÷ 7 = 3
Пример: Каковы четыре 4 члена семейства фактов 8 из 4?
4 × 8 = 32
8 × 4 = 32
32 ÷ 8 = 4
32 ÷ 4 = 8

Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Приведенный выше ресурс умножения и деления соответствует (полностью или частично) стандарту 3OA07, взятому из Общего базового стандарта по математике (см. выдержку ниже). Различные ресурсы, перечисленные ниже, соответствуют одному стандарту.
Свободно умножайте и делите в пределах 100, используя такие стратегии, как отношение между умножением и делением (например, зная, что 8 x 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
 45 ÷ 5
45 ÷ 5
Объект: электрооборудование 110 кВ и выше
Результат: отчет с оценкой ХАРГ в масле и рекомендациями по дальнейшей эксплуатации электрооборудования
_______________________________________________________________________________________________________________________
ХАРГ это эффективный метод выявления дефектов оборудования на ранней стадии развития, не обнаруживаемых традиционными способами.
Хроматографический анализ газов растворенных в масле, является специальным методом, служащим для обнаружения повреждений и дефектов конструктивных узлов электрооборудования, но практически не информирующем о качестве и состоянии самого масла. Хроматографический анализ (ХАРГ) позволяет:

Для оценки состояния маслонаполненного оборудования используются газы: водород (Н2), метан (Ch5), этан (C2H6), этилен (C2h5), ацетилен (С2Н2), угарный газ (CO), углекислый газ (CO2). Кроме этого, всегда присутствуют кислород и азот, а их концентрация изменяется в зависимости от герметичности корпуса трансформатора и могут выделяться такие газы как пропан, бутан, бутен и другие, но их исследование в диагностических целях не получило широкого распространения.
Состояние оборудования оценивается сопоставлением полученных при анализе количественных данных с граничными значениями концентрации газов и по скорости роста концентрации газов в масле. Важно различать нормальные и чрезмерные объемы газа. Нормальное старение или газовая генерация изменяется в зависимости от конструкции трансформатора, нагрузки и типа изоляционных материалов.
Взаимосвязь основных газов и наиболее характерных видов дефектов.
| Водород (Н2) | Дефекты электрического характера: частичные разряды, искровые и дуговые разряды |
| Метан (Ch5) |
Дефекты термического характера: нагрев масла и бумажно-масляной изоляции в диапазоне температур (400-600)°С или нагрев масла и бумажно-масляной изоляции, сопровождающийся разрядами; |
| Этан (C2H6) | Дефекты термического характера: нагрев масла и бумажно-масляной изоляции в диапазоне температур (300-400)°С; |
| Этилен (C2h5) | Дефекты термического характера: нагрев масла и бумажно-масляной изоляции выше 600°С |
| Ацетилен (С2Н2) | Дефекты электрического характера: электрическая дуга, искрение |
| Угарный газ (CO) | Дефекты термического характера: старение и увлажнение масла и/или твердой изоляции; |
| Углекислый газ (CO2) |
Дефекты термического характера: старение и увлажнение масла и/или твердой изоляции; нагрев твердой изоляции |
Дефекты трансформаторов, определяемые с помощью хроматографического анализа:
|
Наименование дефектов |
Основные газы | Характерные газы |
| Перегревы токоведущих соединений |
С2Н4 — в случае нагрева масла |
Н2, СН4 и С2Н6 |
|
— нагрев и выгорание контактов переключающих устройств; — ослабление и нагрев места крепления электростатического экрана; — обрыв электростатического экрана; |
||
|
— ослабление винтов компенсаторов отводов НН; — ослабление и нагрев контактных соединений отвода НН и шпильки проходного изолятора; — лопнувшая пайка элементов обмотки: замыкание параллельных и элементарных проводников обмотки и др |
С2Н2 — в случае перегрева масла, |
|
| Перегревы элементов конструкции остова. | ||
|
— неудовлетворительная изоляция листов электротехнической стали; — нарушение изоляции стяжных шпилек или накладок, ярмовых балок с образованием короткозамкнутого контура; — общий нагрев и недопустимый местный нагрев от магнитных полей рассеяния в ярмовых балках, бандажах, рессующих кольцах и винтах; — неправильное заземление магнитопровода; — нарушение изоляции амортизаторов и шипов поддона реактора, домкратов и прессующих колец при распрессовке и др. |
||
| Частичные разряды | Н2 |
СН4 и С2Н2 с малым содержанием |
| Искровые и дуговые разряды | Н2 или С2Н2 |
СН4 и С2Н2 с любым содержанием |
| Ускоренное старении и/или увлажнение твердой изоляции | СО и СO2 | |
| Перегрев твердой изоляции | СO2 |
Для получения объективных результатов хроматографического анализа трансформаторного масла необходимо квалифицированно произвести отбор проб из маслонаполненного оборудования. Более подробные требования по отбору проб трансформаторного масла представлены в разделе Отбор проб масла
Более подробные требования по отбору проб трансформаторного масла представлены в разделе Отбор проб масла
Периодичность проведения ХАРГ трансформаторного масла
| Наименование оборудования | Периодичность |
| для трансформаторов 110 кВ и выше | не реже 1 раза в 6 месяцев |
|
для герметичных вводов, имеющих удовлетворительные результаты регламентных испытаний — для вводов 110-220 кВ — для вводов 330-750 кВ |
1 раз в 4 года 1 раз в 2 года |
Преимущество этого метода состоит в том, что образцы масла можно отобрать в любое время без вывода оборудования из работы.
Детальную информацию по проведению и использованию хроматографического анализа трансформаторного масла вы можете получить из руководящих документов:
 0-46.302-00 «Методические указания по диагностике развивающихся дефектов трансформаторного оборудования по результатам хроматографического анализа газов, растворенных в масле»
0-46.302-00 «Методические указания по диагностике развивающихся дефектов трансформаторного оборудования по результатам хроматографического анализа газов, растворенных в масле»
Если Вы хотите получить более подробную информацию, техническую консультацию, обсудить оптимальный вариант решения стоящей перед вами задачи, вы можете:
ПОЗВОНИТЬ: +7 (495) 315-68-02, +7 (495) 542-88-48 НАПИСАТЬ ПИСЬМО: diagnost@ntc-retec.ru ЗАПОЛНИТЬ на сайте ЗАЯВКУ
Аннотация: Основная функция трансформаторного масла заключается в обеспечении изоляции, охлаждения и гашении дуг в баке трансформатора. Из-за электрических и термических неисправностей, вызванных неблагоприятными условиями работы трансформаторов, происходит образование газа в трансформаторном масле. Наряду со старением при нормальных режимах работы трансформаторов, такие эксплуатационные факторы, как перегревы, сильные электрические поля, электрические разряды, механические напряжения, разрушение изоляции и загрязняющие вещества, увеличивают физический износ и риск необратимого повреждения активной части трансформаторов. Во всем мире электроэнергетические предприятия используют хорошо зарекомендовавшие себя и широко используемые методы для анализа растворенных в трансформаторном масле газов (DGA). Это обеспечивает своевременную и правильную диагностику электрических и термических неисправностей, возникающих в трансформаторах, чтобы сэкономить время, оборудование и расходы. Соотношения Дорненбурга, соотношения Роджерса, треугольники Дюваля, методы стандартов МЭК и предельные уровни ключевых газов являются одними из классических инструментов, используемых для определения неисправностей трансформатора.
Из-за электрических и термических неисправностей, вызванных неблагоприятными условиями работы трансформаторов, происходит образование газа в трансформаторном масле. Наряду со старением при нормальных режимах работы трансформаторов, такие эксплуатационные факторы, как перегревы, сильные электрические поля, электрические разряды, механические напряжения, разрушение изоляции и загрязняющие вещества, увеличивают физический износ и риск необратимого повреждения активной части трансформаторов. Во всем мире электроэнергетические предприятия используют хорошо зарекомендовавшие себя и широко используемые методы для анализа растворенных в трансформаторном масле газов (DGA). Это обеспечивает своевременную и правильную диагностику электрических и термических неисправностей, возникающих в трансформаторах, чтобы сэкономить время, оборудование и расходы. Соотношения Дорненбурга, соотношения Роджерса, треугольники Дюваля, методы стандартов МЭК и предельные уровни ключевых газов являются одними из классических инструментов, используемых для определения неисправностей трансформатора. Большинство указанных инструментов используют ручные вычисления для определения условий отказа, которые требуют больших усилий и времени. Основной целью данной статьи является получение результатов DGA с помощью различных методов, их сопоставление и оценка эффективности их применения в автоматизированном программном обеспечении.
Большинство указанных инструментов используют ручные вычисления для определения условий отказа, которые требуют больших усилий и времени. Основной целью данной статьи является получение результатов DGA с помощью различных методов, их сопоставление и оценка эффективности их применения в автоматизированном программном обеспечении.
А. Методы обнаружения растворенных газов
В этом методе газы в миллионных объемных долях (ppm) обнаруживаются в масле с использованием блока экстракции газа и газового хроматографа. Методика состоит из последовательных этапов:
Следующие два метода используются для обнаружения газов, растворенных в масле.
B. Типы неисправностей, обнаруживаемых DGA
Различные типы неисправностей, которые возникают в трансформаторе, могут быть обнаружены с помощью DGA.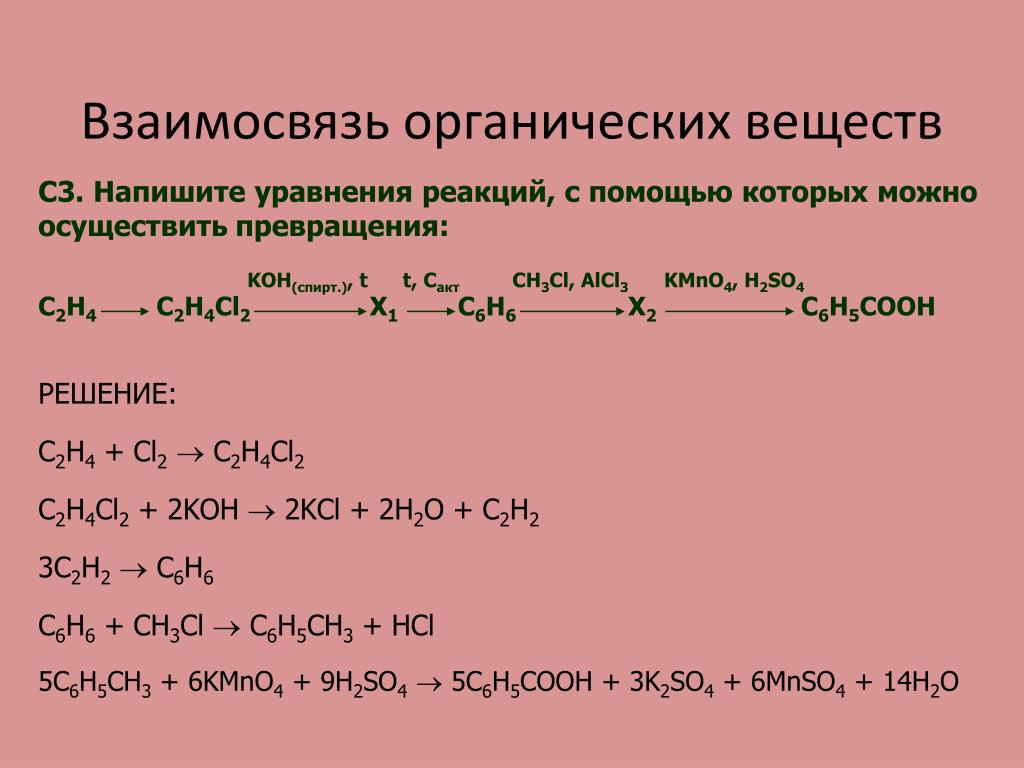 Основные недостатки, которые могут быть идентифицированы методами DGA:
Основные недостатки, которые могут быть идентифицированы методами DGA:
C. DGA Рекомендуемые значения уровней газов по DGA
Таблица 1 — Допустимые уровни растворенных газов в работающем трансформаторе
| Газ | Менее 4 лет в работе, (ppm) | Менее 10 лет в работе, (ppm) | Более 10 лет в работе, (ppm) |
| Водород (h3) | 150 | 300 | 300 |
| Метан (Ch5) | 70 | 150 | 300 |
| Ацетилен (C2h3) | 30 | 50 | 150 |
| Этилен (C2h5) | 150 | 200 | 400 |
| Этан (C2H6) | 50 | 150 | 1000 |
| Двуокись углерода (СО2) | 3500 | 5000 | 12000 |
| Монооксид углерода (СО) | 300 | 500 | 700 |
Приведенная выше таблица показывает нормальные безопасные уровни растворенных газов в масле трансформатора, основанные на статистических данных, накопленных за годы эксплуатации. Однако стоит онимать, что вышеупомянутые пределы не могут быть приняты в качестве предельно допустимых, а должны приниматься только как ориентировочные усреднённые значения. DGA — это скорее метод мониторинга тренда, чем определение предельных значениях. Нормальные значения растворенного газа в минеральном масле не указывают на зарождающуюся неисправность в трансформаторе. Однако, если в трансформаторе наблюдается значительное повышение уровня газа (между предыдущим отбором проб и последующим отбором проб), это может указывать на возникновение некоторой неисправности. Прежде чем неисправность станет критической и приобретет аварийный характер, необходимо предпринять восстановительные мероприятия, что позволит избежать внезапного отказа трансформатора. Регламент действий включает незамедлительный повторный анализ масла, постановку оборудования на учащенный контроль, определение периодичности последующих отборов, предложение других диагностических работ и т.д. Любой скачок уровней концентрации растворенных газов должен интерпретироваться для дальнейшего хода корректирующих действий, поэтому в таких случаях возникает потребность в непрерывном мониторинге параметров масла.
Однако стоит онимать, что вышеупомянутые пределы не могут быть приняты в качестве предельно допустимых, а должны приниматься только как ориентировочные усреднённые значения. DGA — это скорее метод мониторинга тренда, чем определение предельных значениях. Нормальные значения растворенного газа в минеральном масле не указывают на зарождающуюся неисправность в трансформаторе. Однако, если в трансформаторе наблюдается значительное повышение уровня газа (между предыдущим отбором проб и последующим отбором проб), это может указывать на возникновение некоторой неисправности. Прежде чем неисправность станет критической и приобретет аварийный характер, необходимо предпринять восстановительные мероприятия, что позволит избежать внезапного отказа трансформатора. Регламент действий включает незамедлительный повторный анализ масла, постановку оборудования на учащенный контроль, определение периодичности последующих отборов, предложение других диагностических работ и т.д. Любой скачок уровней концентрации растворенных газов должен интерпретироваться для дальнейшего хода корректирующих действий, поэтому в таких случаях возникает потребность в непрерывном мониторинге параметров масла.
Anderson, D. C., Nicely, J. M. , Вулф Г. М., Ханиско Т. Ф., Салавич Р. Дж., Канти Т. П., Дикерсон Р. Р., Апель Э. К., Байдар С., Баннан, Т. Дж., Блейк, Н. Дж., Чен, Д., Дикс, Б., Фернандес, Р. П., Холл, С. Р., Хорнбрук, Р. С., Грегори Хьюи, Л., Джоссе , Б., Йокель П., Киннисон Д. Э., Кениг Т. К., Ле Бретон М., Марекал В., Моргенштерн О., Оман Л. Д., Пан Л. Л., Персиваль К., Пламмер Д., Ревелл Л. Э., Розанов Э., Саиз-Лопес А., Стенке А., Судо К., Тилмес С., Ульманн К. ., Volkamer, R., Weinheimer, A. J., and Zeng, G.: Формальдегид в тропиках западной части Тихого океана: химические источники и поглотители, конвективный перенос и представление в моделях CAM-Chem и CCMI, J. Geophys. рез.-атмосфер., 122, 11201–11226, https://doi.org/10.1002/2016JD026121, 2017. a
Блюменшток Т., Хасе Ф., Киенс А., Чурлок Д. , Колебэтч О., Гарсия О., Гриффит Д. В. Т., Груттер М., Ханниган Дж. В., Хейккинен П., Джесек П., Джонс Н., Киви Р., Лутч Э., Макарова М., Имхасин Х.К., Мелквист Дж., Морино И., Нагахама Т., Нотхольт Дж., Ортега , И., Палм, М., Раффальски, У., Реттингер, М., Робинсон, Дж., Шнайдер, М., Серве, К., Смейл, Д., Стремме, В., Стронг, К., Суссманн , Р., Те, Ю., и Веласко, В.А.: Характеристика и потенциал для уменьшения оптических резонансов в инфракрасных спектрометрах с преобразованием Фурье Сети для обнаружения изменений состава атмосферы (NDACC), Atmos. Изм. Тех., 14, 1239–1252, https://doi.org/10.5194/amt-14-1239-2021, 2021. a
, Колебэтч О., Гарсия О., Гриффит Д. В. Т., Груттер М., Ханниган Дж. В., Хейккинен П., Джесек П., Джонс Н., Киви Р., Лутч Э., Макарова М., Имхасин Х.К., Мелквист Дж., Морино И., Нагахама Т., Нотхольт Дж., Ортега , И., Палм, М., Раффальски, У., Реттингер, М., Робинсон, Дж., Шнайдер, М., Серве, К., Смейл, Д., Стремме, В., Стронг, К., Суссманн , Р., Те, Ю., и Веласко, В.А.: Характеристика и потенциал для уменьшения оптических резонансов в инфракрасных спектрометрах с преобразованием Фурье Сети для обнаружения изменений состава атмосферы (NDACC), Atmos. Изм. Тех., 14, 1239–1252, https://doi.org/10.5194/amt-14-1239-2021, 2021. a
Борсдорф, Т., ан де Брюг, Дж., Шнайдер, А., Лоренте, А., Бирк, М., Вагнер Г., Киви Р., Хазе Ф., Файст Д. Г., Суссманн Р., Реттингер М., Вунч Д., Варнеке Т. и Ландграф Дж.: Улучшение Продукт данных TROPOMI CO: обновление спектроскопической базы данных и удаление одиночных орбит, Atmos. Изм. Tech., 12, 5443–5455, https://doi.org/10.5194/amt-12-5443-2019, 2019. a
a
Канти, Т. и Миншванер, К.: Изменчивость сезонного и солнечного цикла ОН в средняя атмосфера, J. Geophys. рез.-атм., 107, АЧ 1-1–АЧ 1-6, https://doi.org/10.1029/2002JD002278, 2002. a
Цао, К., Де Лючия, Ф. Дж., Сюн, X., Вулф, Р., и Венг, Ф.: Ранние эксплуатационные характеристики бортового радиометра с видимым инфракрасным изображением на орбите спутник Национального полярно-орбитального партнерства Суоми (S-NPP), IEEE Trans. Geosci. Remote Sens., 52, 1142–1156, https://doi.org/10.1109/TGRS.2013.2247768, 2014. a
Crippa, M., Guizzardi, D., Muntean, M., Schaaf, E., Dentener , Ф., ван Аарденне, Дж. А., Монни, С., Деринг, У., Оливье, Дж. Г. Дж., Пальяри, В., и Янссенс-Менхаут, Г.: Выбросы загрязнителей воздуха в координатной сетке за период 1970–2012 в рамках EDGAR v4.3.2, Earth Syst. науч. Data, 10, 1987–2013, https://doi.org/10.5194/essd-10-1987-2018, 2018. a
Де Мазьер М., Томпсон А. М., Курило М. Дж., Уайлд Д. Д., Бернхард Г., Блюменшток Т., Браатен Г.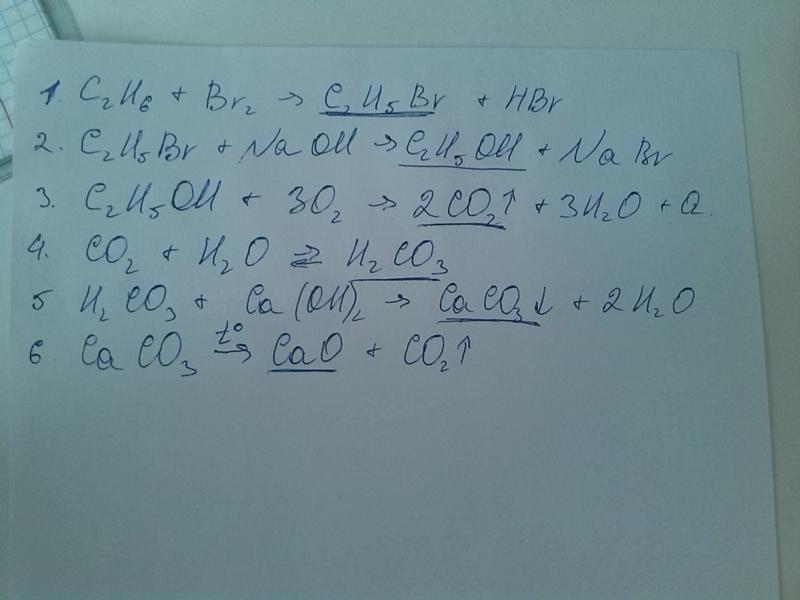 О., Ханниган Дж. У., Ламберт Ж.-К., Леблан Т., МакГи Т. Дж., Недолуха Г., Петропавловских И., Секмайер Г., Саймон , PC, Steinbrecht, W. и Strahan, SE: Сеть для обнаружения изменений состава атмосферы (NDACC): история, состояние и перспективы, Atmos. хим. физ., 18, 4935–4964, https://doi.org/10.5194/acp-18-4935-2018, 2018. a
О., Ханниган Дж. У., Ламберт Ж.-К., Леблан Т., МакГи Т. Дж., Недолуха Г., Петропавловских И., Секмайер Г., Саймон , PC, Steinbrecht, W. и Strahan, SE: Сеть для обнаружения изменений состава атмосферы (NDACC): история, состояние и перспективы, Atmos. хим. физ., 18, 4935–4964, https://doi.org/10.5194/acp-18-4935-2018, 2018. a
Дюфло, В., Дилс, Б., Барай, Ж. Л., Де Мазьер, М., Аттье, Дж. Л., Ванхэлевин, Г., Сентен, К., Вигуру, К., Клейн, Г., и Дельмас, Р.: Анализ происхождения распределения CO в субтропических южных Индийский океан в 2007 г., J. Geophys. рез.-атмосфер., 115, 1–16, https://doi.org/10.1029/2010JD013994, 2010. a
Дункан Б. Н., Логан Дж. А., Бей И., Мегрецкая И. А., Янтоска Р. М., Новелли, П. К., Джонс, Н. Б., и Ринсленд, К. П.: Глобальный бюджет CO, 1988–1997: Оценки источников и проверка с помощью глобальной модели, J. Geophys. Res.-Atmos., 112, D22301, https://doi.org/10.1029/2007JD008459, 2007. a
Finlayson-Pitts, B. and Pitts Jr, J. N.: Атмосферная химия образования тропосферного озона: Научные и нормативные последствия, воздух и отходы, 43, 1091–1100, https://doi. org/10.1080/1073161X.1993.10467187, 1993. a
org/10.1080/1073161X.1993.10467187, 1993. a
Fortems-Cheiney, A., Chevallier, F., Pison, I. , Bousquet, P., Saunois, M., Szopa, S., Cressot, C., Kurosu, T.P., Chance, K., and Fried, A.: Баланс формальдегида с точки зрения глобальных множественных ограничений и многокомпонентная инверсионная система, Atmos. хим. физ., 12, 6699–6721, https://doi.org/10.5194/acp-12-6699-2012, 2012. a, b
Гарсия Р. Р., Лопес-Пуэртас М., Функе Б., Марш, Д. Р., Киннисон Д. Э., Смит А. К. и Гонсалес-Галиндо Ф.: О распределении CO 2 и CO в мезосфере и нижней термосфере, J. Geophys. Res., 119, 5700–5718, https://doi.org/10.1002/2013JD021208, 2014. a
Goode, J. G., Yokelson, R. J., Ward, D. E., Susott, R. А., Бэббит Р. Э., Дэвис М. А. и Хао В. М.: Измерение избытка O 3 , CO 2 , CO, CH 4 , C 2 H 4 , C 2 H 2 , HCN, NO, NH 3 , HCOOH, CH 3 COOH , HCHO и Ch4OH в 1997 г. шлейфы горения биомассы на Аляске с помощью бортовой инфракрасной спектроскопии с преобразованием Фурье (AFTIR), J.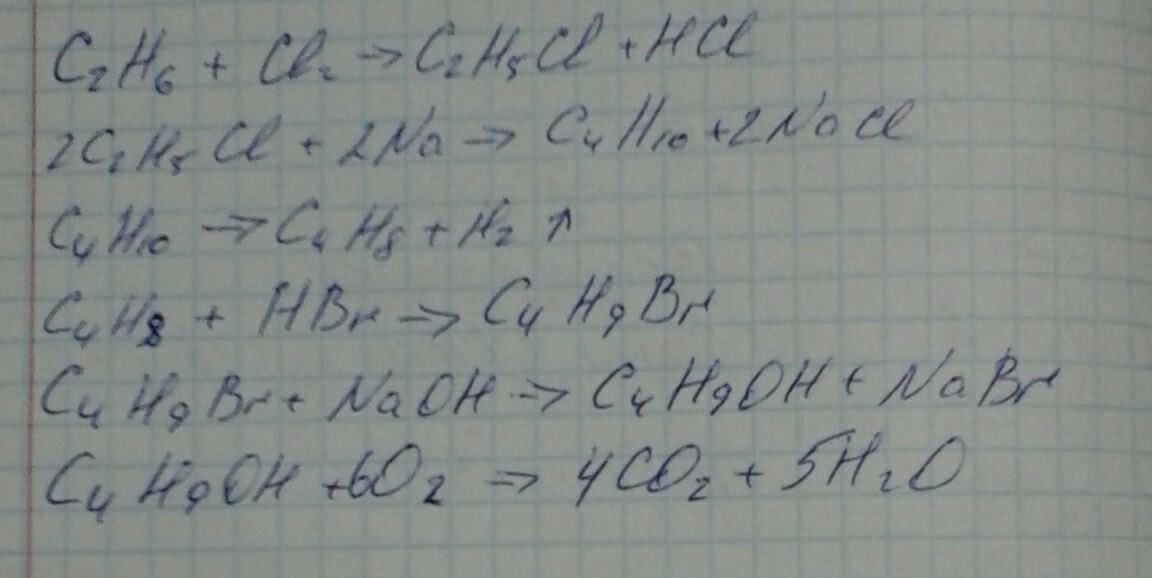 Geophys. Рез.-Атмос., 105, 22147–22166, https://doi.org/10.1029/2000JD
Geophys. Рез.-Атмос., 105, 22147–22166, https://doi.org/10.1029/2000JD
7, 2000. a
Гордон И. Э., Ротман Л. С., Хилл С., Кочанов, ул. Р. В., Тан Ю., Бернат, П. Ф., Бирк М., Будон В., Кампарг А., Шанс К. В., Друэн Б. Ж., Фло, Ж. М., Гамаш, Р. Р., Ходжес, Ж. Т., Жакмар, Д., Перевалов, В. И., Перрин А., Шайн К. П., Смит М. А., Теннисон Дж., Тун Г. К., Тран Х., Тютерев В. Г., Барбе А., Часар А. Г., Деви, В. М., Фуртенбахер Т., Харрисон Дж. Дж., Хартманн Дж. М., Джолли А., Джонсон Т. Дж., Карман Т., Кляйнер И., Кюберис А. А., Лоос Дж., Люлин, О. М., Масси С. Т., Михайленко С. Н., Моаззен-Ахмади Н., Мюллер, Х. С., Науменко О. В., Никитин А. В., Полянский О. Л., Рей М., Ротгер, М., Шарп С. В., Сунг К., Старикова Э., Ташкун С. А., Аувера Дж. В., Вагнер Г., Вильжевски Дж., Вцисло П., Ю С. и Зак Э. Дж.: База данных молекулярной спектроскопии HITRAN2016, J. Quant. Спектроск. Радиат. трансф., 203, 3–69, https://doi.org/10.1016/j.jqsrt.2017.06.038, 2017. a
Харрисон, Дж. Дж., Аллен, Н. Д., и Бернат, П. Ф.: Сечения инфракрасного поглощения для этана (C 2 H 6 ) в области 3 мкм, J. Quant. Спектроск. Радиат. Transf., 111, 357–363, https://doi.org/10.1016/J.JQSRT.2009.09.010, 2010. a
Д., и Бернат, П. Ф.: Сечения инфракрасного поглощения для этана (C 2 H 6 ) в области 3 мкм, J. Quant. Спектроск. Радиат. Transf., 111, 357–363, https://doi.org/10.1016/J.JQSRT.2009.09.010, 2010. a
Hase, F., Blumenstock, T., and Paton-Walsh, C.: Инструментальный анализ Форма линии ИК-Фурье-спектрометров высокого разрешения с газом Измерения клеток и новое программное обеспечение для поиска, Appl. Оптики, 38, 3417, https://doi.org/10.1364/AO.38.003417, 1999. a
Холлоуэй, Т., Леви II, Х., и Касибхатла, П.: Глобальное распределение углерода монооксид, J. Geophys. Рез.-Атм., 105, 12123–12147, https://doi.org/10.1029/1999JD
3, 2000. a, bХу, Б., Ван, Ю. и Лю, Г.: Вариационные характеристики ультрафиолета излучение, полученное в результате измерений и реконструкции в Пекине, Китай, Теллус Б Хим. физ. Метеорол., 62, 100–108, https://doi.org/10.1111/j.1600-0889.2010.00452.x, 2010. a
Хуанг, Г., Брук, Р., Криппа, М., Янссенс-Мэнхаут, Г. , Шиберле, К. ., Доре, К., Гиззарди, Д., Мунтин, М., Шааф, Э., и Фридрих, Р.: Видообразование антропогенных выбросов неметановых летучих органических соединений: глобальный набор данных с координатной привязкой для 1970–2012, Атмос. хим. Phys., 17, 7683–7701, https://doi.org/10.5194/acp-17-7683-2017, 2017 (данные доступны по адресу: https://edgar.jrc.ec.europa.eu/, последний доступ : 1 января 2023 г.). а
, Шиберле, К. ., Доре, К., Гиззарди, Д., Мунтин, М., Шааф, Э., и Фридрих, Р.: Видообразование антропогенных выбросов неметановых летучих органических соединений: глобальный набор данных с координатной привязкой для 1970–2012, Атмос. хим. Phys., 17, 7683–7701, https://doi.org/10.5194/acp-17-7683-2017, 2017 (данные доступны по адресу: https://edgar.jrc.ec.europa.eu/, последний доступ : 1 января 2023 г.). а
МГЭИК: Изменение климата, 2013 г.: Основы физических наук. Вклад Рабочей группы I в Пятый оценочный отчет Межправительственной группы экспертов по изменению климата, под редакцией: Стокер, Т. Ф., Цинь, Д., Платтнер, Г.-К., Тигнор, М., Аллен, С. К., Бошунг, Дж. ., Nauels, A., Xia, Y., Bex, V., and Midgley, P.M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013. a
Цзи, Д., Чжоу, М., Ван, П., Ян, Ю., Ван, Т., Сунь, X., Херманс, К., Яо, Б. и Ван, Г.: Получение темпорального и вертикальное распределение метана в
Xianghe использует наземный инфракрасный и газоанализатор с преобразованием Фурье
Измерения, доп. Атмос. наук, 37, 597–607,
https://doi.org/10.1007/s00376-020-9233-4, 2020. a, b
Атмос. наук, 37, 597–607,
https://doi.org/10.1007/s00376-020-9233-4, 2020. a, b
Халил, М. и Расмуссен, Р.: Глобальный цикл окиси углерода: тенденции и баланс массы, Хемосфера, 20, 227–242, https://doi.org/10.1016/0045-6535(90)-E, 1990. a
Курокава, Дж. и Охара, Т.: Долгосрочные исторические тенденции выбросов загрязнителей воздуха в Азии: Региональный кадастр выбросов в Азии (РЕАС), версия 3, Атмос. хим. Phys., 20, 12761–12793, https://doi.org/10.5194/acp-20-12761-2020, 2020. a
Курокава Дж., Охара Т., Морикава Т., Ханаяма С. ., Янссенс-Мэнхаут, Г., Фукуи, Т., Кавасима, К., и Акимото, Х.: Выбросы загрязнителей воздуха и парниковых газов над регионами Азии в 2000–2008 гг.: Региональный кадастр выбросов в Азии (REAS), версия 2 , Атмос. хим. Физ., 13, 11019–11058, https://doi.org/10.5194/acp-13-11019-2013, 2013 г. (данные доступны по адресу: https://www.nies.go.jp/REAS/, последний доступ: 1 января 2023 г.). a
Ли, М., Лю, Х., Гэн, Г., Хун, К., Лю, Ф. , Сун, Ю., Тонг, Д., Чжэн, Б., Цуй, Х., Ман, Х., Чжан К. и Хе К.: Инвентаризация антропогенных выбросов в Китае: обзор, Natl. науч. Rev., 4, 834–866, https://doi.org/10.1093/nsr/nwx150, 2017. a
, Сун, Ю., Тонг, Д., Чжэн, Б., Цуй, Х., Ман, Х., Чжан К. и Хе К.: Инвентаризация антропогенных выбросов в Китае: обзор, Natl. науч. Rev., 4, 834–866, https://doi.org/10.1093/nsr/nwx150, 2017. a
Li, M., Zhang, Q., Zheng, B., Tong, D., Lei, Ю., Лю Ф., Хун К., Канг С., Ян Л., Чжан Ю., Бо Ю., Су Х., Ченг Ю. и Хе К.: стойкие рост антропогенных выбросов неметановых летучих органических соединений (НМЛОС) в Китае в течение 1990–2017: движущие силы, видообразование и потенциал образования озона, Атмос. хим. Phys., 19, 8897–8913, https://doi.org/10.5194/acp-19-8897-2019, 2019 (данные доступны по адресу: http://meicmodel.org.cn/, последний доступ: 1 января 2023 г.). ). a
Ли, К., Джейкоб, Д. Дж., Бей, И., Янтоска, Р. М., Чжао, Ю., Кондо, Ю., и Нотхольт, Дж.: Атмосферный цианистый водород (HCN): источник сжигания биомассы, океанская раковина?, Geophys. Рез. Письма, 27, 357–360, https://doi.org/10.1029/1999GL010935, 2000. a, b
Ли, К., Джейкоб, Д. Дж., Янтоска, Р. М., Хилд, К. Л., Сингх, Х. Б. ., Койке М., Чжао Ю., Саксе Г. В. и Стритс Д. Г.: Глобальная трехмерная модель
анализ атмосферных балансов HCN и CH 3 CN: ограничения из
самолетные и наземные измерения // J. Geophys. Рез.-Атм., 108, 8827, г.
https://doi.org/10.1029/2002JD003075, 2003. a, b
Л., Сингх, Х. Б. ., Койке М., Чжао Ю., Саксе Г. В. и Стритс Д. Г.: Глобальная трехмерная модель
анализ атмосферных балансов HCN и CH 3 CN: ограничения из
самолетные и наземные измерения // J. Geophys. Рез.-Атм., 108, 8827, г.
https://doi.org/10.1029/2002JD003075, 2003. a, b
Liu, W.-T., Chen, S.-P., Chang, C.-C., Ou-Yang, C.- Ф., Ляо, В.-К., Су, Ю.-К., Ву, Ю.-К., Ван, К.-Х., и Ван, Дж.-Л.: Оценка угарного газа (СО ) скорректированные выбросы неметановых углеводородов (NMHC) автопарка – исследование длинного туннеля, Atmos. Окружающая среда, 89, 403–414, https://doi.org/10.1016/j.atmosenv.2014.01.002, 2014. a
Лутч, Э., Даммерс, Э., Конвей, С. и Стронг, К.: Транспортировка на большие расстояния NH 3 , CO, HCN и C 2 H 6 из Канадских лесных пожаров 2014 г. , Геофиз. Рез. Lett., 43, D12305, https://doi.org/10.1002/2016GL070114, 2016. a
Паркер Р.Дж., Ремедиос Дж.Дж., Мур Д.П. и Канаваде В.П.: Ацетилен C 2 H 90 025 2 извлечения из данных MIPAS и областей повышенных концентраций в верхней тропосфере в августе 2003 г. , Atmos. хим. Phys., 11, 10243–10257, https://doi.org/10.5194/acp-11-10243-2011, 2011. a
, Atmos. хим. Phys., 11, 10243–10257, https://doi.org/10.5194/acp-11-10243-2011, 2011. a
Писсо, И., Соллум, Э., Грит, Х., Кристиансен, Н.И., Кассиани, М., Экхардт, С., Арнольд, Д., Мортон Д., Томпсон Р.Л., Грут Зваафтинк С.Д., Евангелиу Н., Содеманн Х., Хаймбергер Л., Хенне С., Бруннер Д., Буркхарт Дж. Ф., Фуйу А., Бриуде Дж. ., Philipp, A., Seibert, P., and Stohl, A.: Лагранжева модель дисперсии частиц FLEXPART, версия 10.4, Geosci. Model Dev., 12, 4955–4997, https://doi.org/10.5194/gmd-12-4955-2019, 2019. a
Пугачев Н. С., Коннор Б. Дж. и Ринсланд С. П.: Инфракрасные измерения вертикального распределения озона над Китт-Пиком, J. Geophys. Рез., 100, 16689, https://doi.org/10.1029/95JD01296, 1995. a
Роджерс, К. Д.: Обратные методы зондирования атмосферы – теория и практика, Серия по физике атмосферы, океанов и планет, том. 2, мир Научное издательство Co. Pte. Ltd, Сингапур, https://doi.org/10.1142/9789812813718, 2000. a, b
Ротман, Л. С., Гордон, И. Э., Барбе, А. , Беннер, Д. К., Бернат, П. Ф., Бирк, М., Будон, В., Браун, Л. Р., Кампарг, А., Чемпион, Дж. П., Шанс, К., Кудер, Л. Х., Дана, В., Деви, В. М., Фалли, С., Флод, Ж. М., Гамаш Р. Р., Голдман А., Жакмар Д., Кляйнер И., Лакоме Н., Лафферти В. Дж.,
Мандин Дж. Ю., Мэсси С. Т., Михайленко С. Н., Миллер С. Э.,
Моаззен-Ахмади Н., Науменко О. В., Никитин А. В., Орфал Ю., Перевалов И.
В. И., Перрин А., Предой-Кросс А., Ринсланд С. П., Ротгер М.,
Шимечкова М., Смит М. А., Сун К., Ташкун С. А.,
Теннисон, Дж., Тот, Р. А., Вандаэле, А. С., и Вандер Ауэра, Дж.:
База данных молекулярной спектроскопии HITRAN 2008, J. Quant. Спектроск. Радиат.
перевод, 110, 533–572, https://doi.org/10.1016/j.jqsrt.2009.02.013, 2009. a
, Беннер, Д. К., Бернат, П. Ф., Бирк, М., Будон, В., Браун, Л. Р., Кампарг, А., Чемпион, Дж. П., Шанс, К., Кудер, Л. Х., Дана, В., Деви, В. М., Фалли, С., Флод, Ж. М., Гамаш Р. Р., Голдман А., Жакмар Д., Кляйнер И., Лакоме Н., Лафферти В. Дж.,
Мандин Дж. Ю., Мэсси С. Т., Михайленко С. Н., Миллер С. Э.,
Моаззен-Ахмади Н., Науменко О. В., Никитин А. В., Орфал Ю., Перевалов И.
В. И., Перрин А., Предой-Кросс А., Ринсланд С. П., Ротгер М.,
Шимечкова М., Смит М. А., Сун К., Ташкун С. А.,
Теннисон, Дж., Тот, Р. А., Вандаэле, А. С., и Вандер Ауэра, Дж.:
База данных молекулярной спектроскопии HITRAN 2008, J. Quant. Спектроск. Радиат.
перевод, 110, 533–572, https://doi.org/10.1016/j.jqsrt.2009.02.013, 2009. a
Рудольф, Дж.: Распределение тропосферы и бюджет этана, J. Geophys. Res.-Atmos., 100, 11369–11381, https://doi.org/10.1029/95JD00693, 1995. a
Саха С., Мурти С., Ву С., Ван Дж., Надига , С., Трипп, П., Берингер, Д., Хоу, Ю.-Т., Я Чуанг, Х., Иределл, М., Эк, М., Мэн, Дж., Ян, Р. , Мендес, М. П., ван ден Дул, Х., Чжан, К., Ван, В., Чен, М., и Беккер, Э.: Система прогнозирования климата NCEP, версия 2, J. Climate, 27, 2185–2208. ,
https://doi.org/10.1175/JCLI-D-12-00823.1, 2014. a
, Мендес, М. П., ван ден Дул, Х., Чжан, К., Ван, В., Чен, М., и Беккер, Э.: Система прогнозирования климата NCEP, версия 2, J. Climate, 27, 2185–2208. ,
https://doi.org/10.1175/JCLI-D-12-00823.1, 2014. a
Шредер, В., Олива, П., Гиглио, Л., и Чизар, И. А.: Новый информационный продукт для обнаружения активного пожара VIIRS 375 m: описание алгоритма и начальная оценка, Remote Sens. Environ., 143, 85–96 , https://doi.org/10.1016/j.rse.2013.12.008, 2014 г. (данные доступны по адресу: https://firms.modaps.eosdis.nasa.gov/, последний доступ: 13 января 2023 г.). a, b
Шен Л., Джейкоб Д. Дж., Чжу Л., Чжан К., Чжэн Б., Сульприцио М. П., Ли К., Де Смедт И., Гонсалес Абад, Г., Цао, Х., Фу, Т.-М., и Ляо, Х.: Тенденции столбцов формальдегида над Китаем, наблюдаемые со спутников в 2005–2016 гг.:
Увеличение антропогенных выбросов летучих органических соединений и
Снижение выбросов сельскохозяйственных пожаров // Геофиз. Рез. Lett., 46, 4468–4475, https://doi.org/10.1029/2019GL082172, 2019. a
a
Steck, T.: Методы определения регуляризации для поиска атмосферы проблемы, заявл. Optics, 41, 1788–1797, https://doi.org/10.1364/AO.41.001788, 2002. a
Sun, Y., Liu, C., Zhang, L., Palm, M., Notholt, J. ., Инь, Х., Вигуру, К., Луч, Э., Ван, В., Шан, К., Блюменшток, Т., Нагахама, Т., Морино, И., Махье, Э., Стронг, К. ., Ланжерок, Б., Де Мазьер, М., Ху, К., Чжан, Х., Петри, К. и Лю, Дж.: Преобразование Фурье инфракрасных временных рядов тропосферных HCN в восточном Китае: сезонность, межгодовая изменчивость , и указание источника, Atmos. хим. Phys., 20, 5437–5456, https://doi.org/10.5194/acp-20-5437-2020, 2020. a, b, c, d
Té, Y., Jeseck, P., Franco, B., Mahieu, E., Jones, N., Paton-Walsh, C., Griffith, D.W.T., Buchholz, R.R., Hadji-Lazaro, J., Hurtmans, D. и Janssen, C.: Сезонная изменчивость угарного газа на поверхности и в столбе над мегаполисом Парижем, высокогорным Юнгфрауйохом и южным полушарием Вуллонгонгом. станции, Атмос. хим. Phys., 16, 10911–10925, https://doi. org/10.5194/acp-16-10911-2016, 2016. a, b
org/10.5194/acp-16-10911-2016, 2016. a, b
Viatte, C., Strong, K., Walker, K.A., and Drummond , JR: Пять лет CO, HCN, C 2 H 6 , C 2 H 2 , CH 3 OH, HCOOH и H 2 Общие столбцы CO измерены в высоких широтах Канады, атм. Изм. Tech., 7, 1547–1570, https://doi.org/10.5194/amt-7-1547-2014, 2014. a, b
Vigouroux, C., Stavrakou, T., Whaley, C., Dils , Б., Дюфло, В., Херманс, К., Кампс, Н., Мецгер, Дж.-М., Сколас, Ф., Ванхэлюин, Г., Мюллер, Дж.-Ф., Джонс, Д. Б. А., Ли , Q., и De Mazière, M.: Временные ряды FTIR продуктов горения биомассы (HCN, C 2 H 6 , C 2 H 2 , CH 3 OH и HCOOH) на острове Реюньон (21 ∘ ю.ш., 55 901 47 ∘ E) и сравнение с модельными данными, Atmos. хим. Phys., 12, 10367–10385, https://doi.org/10.5194/acp-12-10367-2012, 2012. a, b
Vigouroux, C., Bauer Aquino, C.A., Bauwens, M., Becker , К., Блюменсток, Т. , Де Мазьер, М., Гарсия, О., Груттер, М., Гуарин, К., Ханниган, Дж., Хасэ, Ф., Джонс, Н., Киви, Р., Кошелев Д., Лангерок Б., Луч Э., Макарова М., Мецгер Ж.-М., Мюллер Ж.-Ф., Нотхолт Ж., Ортега И., Пальм М. , Патон-Уолш К., Поберовский А., Реттингер М., Робинсон Дж., Смейл Д., Ставраку Т., Стремме В., Стронг К., Суссманн Р., Те, Y. и Toon, G.: Согласованные NDACC временные ряды формальдегида по 21 ИК-Фурье станции, охватывающие широкий диапазон содержаний в колонке, Atmos. Изм. Тех., 11, 5049–5073, https://doi.org/10.5194/amt-11-5049-2018, 2018. a, b
, Де Мазьер, М., Гарсия, О., Груттер, М., Гуарин, К., Ханниган, Дж., Хасэ, Ф., Джонс, Н., Киви, Р., Кошелев Д., Лангерок Б., Луч Э., Макарова М., Мецгер Ж.-М., Мюллер Ж.-Ф., Нотхолт Ж., Ортега И., Пальм М. , Патон-Уолш К., Поберовский А., Реттингер М., Робинсон Дж., Смейл Д., Ставраку Т., Стремме В., Стронг К., Суссманн Р., Те, Y. и Toon, G.: Согласованные NDACC временные ряды формальдегида по 21 ИК-Фурье станции, охватывающие широкий диапазон содержаний в колонке, Atmos. Изм. Тех., 11, 5049–5073, https://doi.org/10.5194/amt-11-5049-2018, 2018. a, b
Волкамер Р., Циманн П. Дж. и Молина М. Дж.: Образование вторичного органического аэрозоля из ацетилена (C 2 H 2 ): влияние затравки на выход SOA из-за органической фотохимии в водной фазе аэрозоля, Atmos. хим. Phys., 9, 1907–1928, https://doi.org/10.5194/acp-9-1907-2009, 2009. a
Wang, T., Wong, C. H., Cheung, T. F. , Блейк Д. Р., Аримото Р., Бауманн К., Танг Дж., Дин Г. А., Ю, С. М., Ли Ю. С., Стритс, Д. Г. и Симпсон И. Дж.: Взаимосвязь следовых газов и аэрозолей с характеристиками выбросов в Линьане, сельской местности на востоке Китая, весной 2001 г.,
Дж. Геофиз. Рез.-Атм., 109, D19S05, https://doi.org/10.1029/2003JD004119, 2004. a
Г. и Симпсон И. Дж.: Взаимосвязь следовых газов и аэрозолей с характеристиками выбросов в Линьане, сельской местности на востоке Китая, весной 2001 г.,
Дж. Геофиз. Рез.-Атм., 109, D19S05, https://doi.org/10.1029/2003JD004119, 2004. a
Wetzel, G., Friedl-Vallon, F., Glatthor, N., Grooß, J.-U., Gulde, T., Хёпфнер М., Йоханссон С., Хосрави Ф., Кирнер О., Кляйнерт А., Кречмер Э., Маухер Г., Нордмейер Х., Эльхаф Х., Орфал Дж., Пиш, К., Зиннхубер, Б.-М., Унгерманн, Дж., и Фогель, Б.: Следовые газы загрязнения C 2 H 6 , C 2 H 2 , HCOOH и PAN в Североатлантический UTLS: наблюдения и моделирование, Atmos. хим. Phys., 21, 8213–8232, https://doi.org/10.5194/acp-21-8213-2021, 2021. a
Xiao, Y., Jacob, D. J., and Turquety, S.: Атмосферный ацетилен и его взаимосвязь с CO как индикатор возраста воздушной массы, J. Геофиз. Res.-Atmos., 112, D12305, https://doi.org/10.1029/2006JD008268, 2007. a, b, c, d, e, f
Xiao, Y., Logan, J. A., Jacob , Д. Дж., Хадман, Р. К., Янтоска, Р., и Блейк, Д. Р.: Глобальный бюджет этана и региональные ограничения на источники в США, J. Geophys. Рез.-Атм., 113, D21306, https://doi.org/10.1029/2007JD009415, 2008. a, b, c
A., Jacob , Д. Дж., Хадман, Р. К., Янтоска, Р., и Блейк, Д. Р.: Глобальный бюджет этана и региональные ограничения на источники в США, J. Geophys. Рез.-Атм., 113, D21306, https://doi.org/10.1029/2007JD009415, 2008. a, b, c
Yang, Y., Zhou, M., Langerock, B., Sha, M.K., Hermans, C., Wang, T., Ji, D., Vigouroux, C., Кампс, Н., Ван, Г., Де Мазьер, М., и Ван, П.: Новые наземные измерения поглощения Солнца в ближней инфракрасной области с преобразованием Фурье XCO 2 , XCH 4 и XCO в Xianghe, Китай, система Земли. науч. Data, 12, 1679–1696, https://doi.org/10.5194/essd-12-1679-2020, 2020. a, b, c, d
Зенг, Г., Вуд, С. В., Моргенштерн, О. , Джонс, Н.Б., Робинсон, Дж., и Смейл, Д.: Тенденции и изменения в CO, C 2 H 6 и HCN в Южном полушарии указывают на снижение антропогенных выбросов CO и C 2 H 6 , Atmos. хим. Phys., 12, 7543–7555, https://doi.org/10.5194/acp-12-7543-2012, 2012. a
Zhang, Q., Zheng, Y. , Tong, D., Shao, M. ., Ван С., Чжан Ю., Сюй С., Ван Дж., Хе Х., Лю В., Дин Ю., Лэй Ю., Ли Дж., Ван З. ., Чжан С., Ван Ю., Ченг Дж., Лю Ю., Ши К., Ян Л., Гэн Г., Хун С., Ли М., Лю Ф. ., Чжэн Б., Цао Дж., Дин А., Гао Дж., Фу Ц., Хо Дж., Лю Б., Лю З., Ян Ф., Хе К. ., и Хао, Дж.: Драйверы улучшенной БДМ 2.5 Качество воздуха в Китае с 2013 по 2017 гг., P. Natl. акад. науч. США, 116, 24463–24469,
https://doi.org/10.1073/pnas.1907956116, 2019. a
, Tong, D., Shao, M. ., Ван С., Чжан Ю., Сюй С., Ван Дж., Хе Х., Лю В., Дин Ю., Лэй Ю., Ли Дж., Ван З. ., Чжан С., Ван Ю., Ченг Дж., Лю Ю., Ши К., Ян Л., Гэн Г., Хун С., Ли М., Лю Ф. ., Чжэн Б., Цао Дж., Дин А., Гао Дж., Фу Ц., Хо Дж., Лю Б., Лю З., Ян Ф., Хе К. ., и Хао, Дж.: Драйверы улучшенной БДМ 2.5 Качество воздуха в Китае с 2013 по 2017 гг., P. Natl. акад. науч. США, 116, 24463–24469,
https://doi.org/10.1073/pnas.1907956116, 2019. a
Чжао Ю., Стронг К., Кондо Ю., Койке М., Мацуми Ю., Ирие Х., Ринсланд , C. P., Jones, N. B., Suzuki, K., Nakajima, H., Nakane, H. и Murata, I.: Спектроскопические измерения тропосферного CO, C 2 H 6 , C 2 H 2 и HCN в северной Японии, J. Geophys. Рез.-Атмос., 107, 4343, https://doi.org/10.1029/2001JD000748, 2002. a, b, c
Чжэн Б., Шевалье Ф., Сиаис П., Инь Ю., Дитер М. Н., Уорден Х. М.,
Ван Ю., Чжан К. и Хе К.: Быстрое снижение выбросов угарного газа
и экспорт из Восточной Азии в период с 2005 по 2016 год, Environ. Рез. лат.,
13, 044007, https://doi.org/10.1088/1748-9326/aab2b3, 2018. a
Рез. лат.,
13, 044007, https://doi.org/10.1088/1748-9326/aab2b3, 2018. a
Zhong, Q., Huang, Y., Shen, H., Chen, Y., Chen, H., Хуанг Т., Цзэн Э. Ю. и Тао С.: Глобальные оценки выбросов окиси углерода с 1960 по 2013 год, Environ. науч. Загрязн. Рез., 24, 864–873, https://doi.org/10.1007/s11356-016-7896-2, 2017 (данные доступны по адресу: http://inventory.pku.edu.cn/, последний доступ: 1 января 2023 г.). a, b
Zhou, M., Vigouroux, C., Langerock, B., Wang, P., Dutton, G., Hermans, C., Kumps, N., Metzger, J.-M., Toon, Г., и Де Мазьер, М.: CFC-11, CFC-12 и HCFC-22 наземные измерения дистанционного зондирования FTIR на острове Реюньон и сравнение с данными MIPAS/ENVISAT, Atmos. Изм. Tech., 9, 5621–5636, https://doi.org/10.5194/amt-9-5621-2016, 2016. a
Zhou, M., Langerock, B., Vigouroux, C., Sha, M.K. , Рамонет М., Дельмотт М., Махье Э., Бадер В., Херманс К., Кампс Н., Мецгер Ж.-М., Дюфло В., Ван З., Палм , М., и Де Мазьер, М.: Атмосферный CO и CH 4 Временные ряды и сезонные вариации на острове Реюньон по наземным измерениям in situ и FTIR (NDACC и TCCON), атмосферные явления. хим. Phys., 18, 13881–13901, https://doi.org/10.5194/acp-18-13881-2018, 2018. a, b
хим. Phys., 18, 13881–13901, https://doi.org/10.5194/acp-18-13881-2018, 2018. a, b
Zhou, M., Wang, P., Langerock, B., Vigouroux , C., Hermans, C., Kumps, N., Wang, T., Yang, Y., Ji, D., Ran, L., Zhang, J., Xuan, Y., Chen, H., Posny , Ф., Дюфло, В., Метцгер, Ж.-М., и Де Мазьер, М.: Наземное инфракрасное преобразование Фурье (FTIR) O 3 извлечений из 3040 см 9Спектральный диапазон 0147 −1 в Сянхэ, Китай, Атмос. Изм. Tech., 13, 5379–5394, https://doi.org/10.5194/amt-13-5379-2020, 2020. a
Zhou, M., Langerock, B., Vigouroux, C., Dils, B. ., Херманс, К., Кумпс, Н., Нан, В., Мецгер, Ж.-М., Махье, Э., Ван, Т., Ван, П. и Де Мазьер, М.: Тропосфера и стратосфера NO получено из наземных измерений с преобразованием Фурье в инфракрасном диапазоне (FTIR), Atmos. Изм. Тех., 14, 6233–6247, https://doi.org/10.5194/amt-14-6233-2021, 2021. а, б
27 страниц Опубликовано: 5 октября 2022 г.
Просмотреть все статьи Литао Лю
принадлежность к SSRN не указана0003
принадлежность к SSRN не указана
принадлежность к SSRN не указана РН
принадлежность не указана к SSRN
Эта работа была направлена на экспериментальное сравнение влияния смесевых топлив (C2H6, C2h5, CO и смесь h3 в различных пропорциях) на поведение давления взрыва метана и смесевых топлив в воздухе. Свойства взрывного давления смесей были испытаны в сферическом газовом баллоне емкостью 20 л при температуре окружающей среды. Для исследования воздействия каждого горючего газа на метан использовался анализ главных компонентов. На основе экспериментальных результатов были разработаны модели множественной регрессии для прогнозирования влияния основных компонентов на максимальное давление взрыва Ch5. Кроме того, программное обеспечение CHEMKIN использовалось для анализа и сравнения нормализованной чувствительности, вариации чувствительности и анализа нормализованной вариации чувствительности. Для обедненной топливовоздушной смеси Ch5 результаты показали, что P max смешанных газов увеличивалась по мере увеличения объемной доли смесевых топлив. Влияние других газов на коэффициент эквивалентности φ =0,72 следует порядку C2H6>C2h5>h3>CO. Значение (dP/dt)max, измеренное с добавлением смешанных газов, увеличилось на 162,75 %, 140,76 %, 80,97% и 108,99% соответственно. Для стехиометрических концентраций (φ=1) порядок степени влияния был h3>CO>C2H6>C2h5, а Pmax смешанных газов имеет тенденцию к незначительному уменьшению. Значение (dP/dt)max, измеренное после добавления смесевых топлив, уменьшилось на 46,07%, 39,05%, 26,59% и 8,9% соответственно. По мере увеличения объемной доли смесевых топлив до 2%, Pmax для Ch5 показал тенденцию к снижению для богатой топливом смеси Ch5-воздух. Влияние смесевых топлив на коэффициент эквивалентности φ = 1,1 следует порядку C2h5>h3>CO>C2H6. Значение (dP/dt)max, измеренное при добавлении смесевых топлив, уменьшилось на 88,55%, 81,45%, 790,4% и 70,46% соответственно.
Для обедненной топливовоздушной смеси Ch5 результаты показали, что P max смешанных газов увеличивалась по мере увеличения объемной доли смесевых топлив. Влияние других газов на коэффициент эквивалентности φ =0,72 следует порядку C2H6>C2h5>h3>CO. Значение (dP/dt)max, измеренное с добавлением смешанных газов, увеличилось на 162,75 %, 140,76 %, 80,97% и 108,99% соответственно. Для стехиометрических концентраций (φ=1) порядок степени влияния был h3>CO>C2H6>C2h5, а Pmax смешанных газов имеет тенденцию к незначительному уменьшению. Значение (dP/dt)max, измеренное после добавления смесевых топлив, уменьшилось на 46,07%, 39,05%, 26,59% и 8,9% соответственно. По мере увеличения объемной доли смесевых топлив до 2%, Pmax для Ch5 показал тенденцию к снижению для богатой топливом смеси Ch5-воздух. Влияние смесевых топлив на коэффициент эквивалентности φ = 1,1 следует порядку C2h5>h3>CO>C2H6. Значение (dP/dt)max, измеренное при добавлении смесевых топлив, уменьшилось на 88,55%, 81,45%, 790,4% и 70,46% соответственно. Анализ изменения чувствительности и анализ нормированного изменения чувствительности показали, что реакция разветвления цепи 2Ch4(+M)C2H6(+M) является наиболее чувствительной реакцией в различных условиях. Однако он не был очень чувствителен к изменениям соотношения топливных смесей. Большинство реакций были чувствительны к изменениям соотношения топливных смесей. 10 наиболее чувствительных реакций, как правило, были гораздо более чувствительны к изменениям соотношения топливных смесей в 2% смесевых топливах, чем в 0,4% смесевых топливах.
Анализ изменения чувствительности и анализ нормированного изменения чувствительности показали, что реакция разветвления цепи 2Ch4(+M)C2H6(+M) является наиболее чувствительной реакцией в различных условиях. Однако он не был очень чувствителен к изменениям соотношения топливных смесей. Большинство реакций были чувствительны к изменениям соотношения топливных смесей. 10 наиболее чувствительных реакций, как правило, были гораздо более чувствительны к изменениям соотношения топливных смесей в 2% смесевых топливах, чем в 0,4% смесевых топливах.
Ключевые слова: Топливные смеси, Характеристики давления взрыва, Анализ главных компонентов, Регрессионная модель, Анализ чувствительности
Рекомендуемое цитирование: Рекомендуемая ссылка
Лю, Литао и Луо, Чжэньминь и Эккарт, Свен и Краузе, Хартмут и Ван, Тао и Су, Бинь и Чжан, Чунянь, Исследование C2h6, C2h5, Co, h3 О поведении метана/смесевого топлива при давлении взрыва.