Математические задания в картинках для печати
Математические задания для 1 класса — это яркие красочные картинки с развивающими упражнениями по математике, включающие в себя разнообразные игровые задания для детей. Но не только первоклашки могут заниматься с помощью таких заданий, но и старшие дошкольники, которые учатся выполнять простейшие арифметические действия. С нашими увлекательными заданиями математика перестанет быть скучной и дети смогут сами убедиться в том, что обучение — это необыкновенно интересное занятие!
1. Математические задания для 1 класса — Посчитай и поставь знак
Представленные математические задания для 1 класса разработаны для тренировки счета от 1 до 10, а также умения подбирать нужный математический знак между двумя числами. Вооружайтесь ручкой и цветными карандашами, распечатывайте скачанную во вложениях картинку и приступайте к занятию, объяснив ребенку условия:
- В первом задании нужно подобрать к каждой картинке с овощами и фруктами соответствующее число (число нужно обвести и соединить с картинкой, используя карандаш того цвета, в который раскрашен кружок с данным числом).
 В конце задания пусть ребенок ответит, какие числа оказались лишними. Затем ребенок должен придумать примеры для каждой картинки. Например, в первой картинке пример звучит так: 3 красных яблока + 6 зеленых яблок = 9 яблок.
В конце задания пусть ребенок ответит, какие числа оказались лишними. Затем ребенок должен придумать примеры для каждой картинки. Например, в первой картинке пример звучит так: 3 красных яблока + 6 зеленых яблок = 9 яблок. - Во втором задании нужно посчитать количество насекомых в каждой картинке и записать числа-ответы в пустые клетки под ними. Клеточка посредине между числами — для математического знака (>=), который покажет сравнение этих чисел — больше или меньше одно число другого или числа равны.
Скачать математические задания для 1 класса с математическими знаками:
2. Сколько пар — Математические задания для первоклассников
Знает ли ваш ребенок, что такое пара? Пара — это когда чего-то или кого-то двое. Здесь ребенок сможет потренироваться в умении находить пары, выполняя интересные математические задания для первоклассников. Также ему понадобится свободное знание цветов, умение считать до 10, решать простые примеры и, конечно же, раскрашивать.
- В первом задании нужно внимательно посмотреть на прямоугольники, которые раскрашены по-разному. Прямоугольник состоит из четырех квадратиков, выстроенных в ряд. В каждом прямоугольнике квадратики раскрашены в красный цвет в определенной последовательности. Ребенку нужно найти пары одинаково раскрашенных прямоугольников и соединить их линиями между собой.
- Во втором задании сначала нужно решить примеры. Затем яблоки с одинаковыми ответами нужно раскрасить в один цвет. Например, два яблока (т.е. пару) с ответом 4 — раскрасить в красный цвет, пару яблок с другим ответом — в зеленый и т.д. После этого ребенку нужно посчитать, сколько получилось раскрашенных пар яблок.
- В третьем задании нужно раскрасить все цветы в таком же порядке, как и первый. То есть должна полностью сохраниться следующая последовательность цветов по кругу: голубой, розовый, серый, зеленый, оранжевый, желтый, коричневый, фиолетовый. Для усложнения задания остальные цветочки слегка повернуты по часовой стрелке.
 Поэтому расположение цветов не совпадает, но сама последовательность четко сохраняется. Затем нужно посчитать, сколько пар цветов, сколько пар лепестков в каждом цветке?
Поэтому расположение цветов не совпадает, но сама последовательность четко сохраняется. Затем нужно посчитать, сколько пар цветов, сколько пар лепестков в каждом цветке?
Скачать математическое задание «Сколько пар?»:
3. Выполни задания — Посчитай, соедини и зачеркни
Здесь ребенку нужно выполнить математические задания для 1 класса на умение считать, решать примеры и мыслить логически.
- В первом задании необходимо внимательно рассмотреть картинки с мультипликационными героями и подумать, какие примеры можно составить с ними. Например картинка с четырьмя огурцами и двумя грушами — это числа 4 и 2. Значит, пример может быть или 4 + 2, или 4 — 2. Таким образом ребенок должен размышлять и с остальными вариантами. Подходящий пример нужно выбрать среди четырех вариантов и соединить линиями с соответствующими картинками.
- Во втором задании нужно посчитать количество мультипликационных героев на каждой картинке. Под картинкой необходимо зачеркнуть все числа, которые не соответствуют этому количеству.
 В конце выполнения задания ребенка нужно спросить, на что он обратил внимание, считая героев (все картинки с героями расположены по порядку счета).
В конце выполнения задания ребенка нужно спросить, на что он обратил внимание, считая героев (все картинки с героями расположены по порядку счета).
Скачать задания — Посчитай, соедини и зачеркни:
4. Математическое задание — Обведи картинки по точкам с числами
Это математическое задание предназначено для учеников 1 класса и направлено на тренировку порядкового счета от 1 до 40. Такие задания дети обожают, поэтому не стоит пренебрегать таким чудесным способом запоминания чисел и порядкового счета.
Если ребенок еще не ходит в школу и не знает счета больше 10, то можно написать на отдельном листе бумаги числа от 1 до 40 по порядку и дать ребенку в качестве подсказки. Проводя линии от точки к точке, руководствуясь подсказкой, ребенок будет параллельно запоминать данный порядок чисел.
- В первом задании, если ребенок правильно соединит линиями все числа по порядку их счета, то увидит, от кого убегают малыши и мышонок Джерри.
- Во втором задании турист отправился в поход, не ожидая, что впереди надвигается гроза.
 Когда ребенок объединит точки, то увидит, что могло бы помочь туристу в этой ситуации.
Когда ребенок объединит точки, то увидит, что могло бы помочь туристу в этой ситуации.
Скачать математическое задание по обведению чисел:
5. Математическая настольная игра для 1 класса
Представленная настольная математическая игра для 1 класса является хорошим средством для тренировки разных математических действий. Здесь вы найдете и решение примеров на сложение и вычитание, и выполнение простых алгоритмов, и сравнение чисел друг с другом. Игра хорошо развивает логическое и математическое мышление. Очень эффективно проводить это занятие с группой детей.
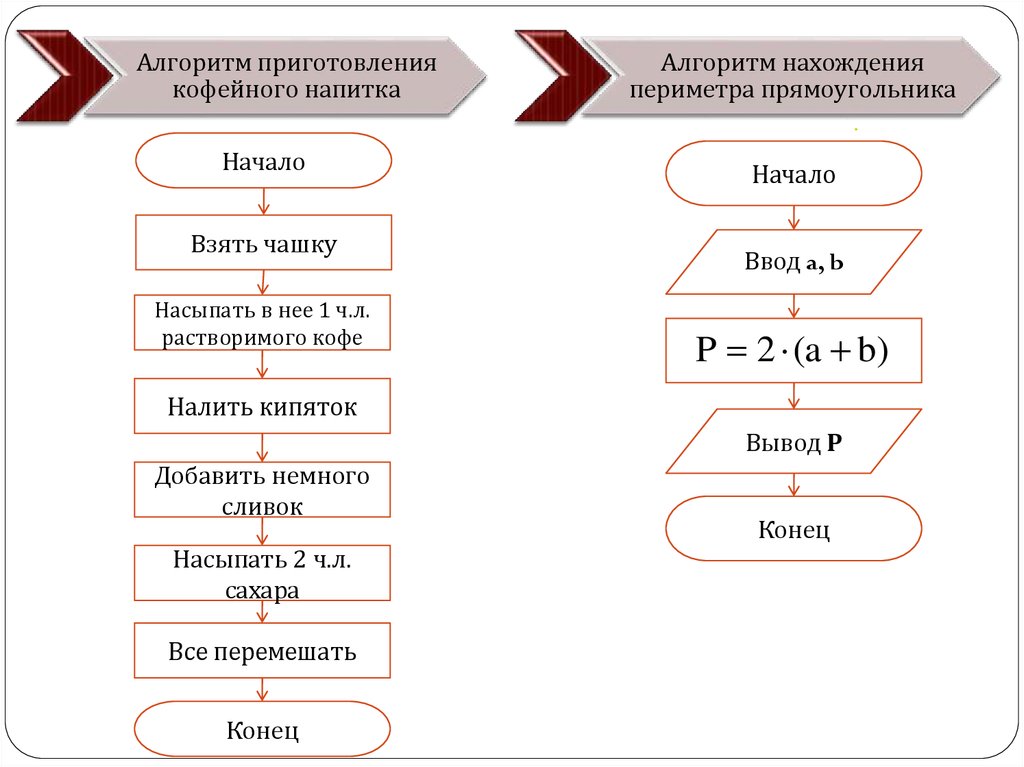
Задание №1. Тренируем умение составлять примеры в пределах 10. Здесь нужно заполнить пустые ячейки (круги и квадраты со знаком вопроса). В квадратах должны находится числа (ответы примеров), а в кружках — прибавление или отнимание какого либо числа (смотрите пример в кружке вверху картинки). Внимательно следите за стрелочками — именно в направлении стрелочек составляется и читается пример.
Задание №2. Учимся пользоваться знаками сравнения чисел. В этом задании нам нужно расселить по разным домикам все числа, стоящие в ряду. В каждом доме живет одно или два числа (не больше). Чтобы попасть в домик, числа должны идти по соответствующим дорожкам. На каждой дороге стоят дорожные знаки, которые и показывают, кто может пройти дальше, а кто нет. Например, по пути в верхний домик стоят знаки 3 и перечеркнутая 2 — это означает, что дальше может пройти только число, которое меньше 3 и не является 2. То есть в этом случае подходят только два числа — 0 и 1.
Правильные ответы:
Задание №3. Здесь принцип выполнения такой же, как и в задании с домиками. Только теперь нужно распределить по стоянкам города машинки с числами.
Правильные ответы:
Задание №4. Учимся выполнять простые алгоритмы. В самый верхний кружок нужно вписать любое число от 1 до 10. Затем ребенок должен выполнить все указанные в задании действия — сначала сравнить число, является ли оно меньше 5, как указано в ромбе со знаком вопроса. Если да — то следующее действие будет по стрелке «Да», если нет, то по стрелке «Нет». Дальше выполняется сложение или вычитание, и в нижний кружок вписывается ответ. Выполнять задание можно множество раз, меняя только число в верхнем кружке.
Затем ребенок должен выполнить все указанные в задании действия — сначала сравнить число, является ли оно меньше 5, как указано в ромбе со знаком вопроса. Если да — то следующее действие будет по стрелке «Да», если нет, то по стрелке «Нет». Дальше выполняется сложение или вычитание, и в нижний кружок вписывается ответ. Выполнять задание можно множество раз, меняя только число в верхнем кружке.
Задание №5. Выполняется аналогично предыдущему.
Такие задания можно составлять самостоятельно, рисуя такие же схемы на листе и меняя только числа и знаки.
Примеры в картинках, Обведи по точкам
- Просмотров: 1429
Добавить комментарий
Примеры по математике для 1 класса
Вы здесь
Главная » Задания для детей » Развивающие задания для детей » Задания по математике » Примеры по математике » Примеры по математике для 1 класса
Книги по математике для 1 класса
3000 примеров по математике с ответами и методическими рекомендациями.
 Столбики-цепочки. Все темы. Быстрый устный счёт. 1 класс — О. В. Узорова
Столбики-цепочки. Все темы. Быстрый устный счёт. 1 класс — О. В. УзороваМатематика. Мини-примеры на все темы. 1 класс — Е. А. Нефёдова
Математика. 1 класс — О. В. Савельева
Итоговые проверочные работы. Русский язык. Математика. Итоговая комплексная работа. 1 класс — О. Н. Журавлева
Математика. 1 класс — О. Д. Ушакова
3000 примеров по математике. Устный счет. Счет в пределах 10. 1 класс — О. В. Узорова
3000 примеров по математике и задания повышенной сложности. Счёт в пределах 10. 1 класс — О. В. Узорова
Поурочные разработки по математике. 1 класс (к УМК Л. Г. Петерсон) — Т. Н. Максимова
3000 новых примеров по математике. Счет в пределах десятка. 1 класс — О. В. Узорова
Повтори летом! Математика.
 Полезные и увлекательные задания. 1 класс — О. В. Узорова
Полезные и увлекательные задания. 1 класс — О. В. УзороваУчусь решать олимпиады по математике. Тренажёр. 1 класс — М. Н. Алимпиева
Тимсик и его друзья. Тренировочные задания по математике и естествознанию. 1 класс — О. П. Клементьева
Поурочные разработки по математике. 1 класс (К УМК Г.В. Дорофеева и др. («Перспектива»)) — Т. Н. Ситникова
Примеры по математике. 1 класс — И. О. Родин
3000 примеров по математике. Супертренинг. Цепочки примеров. Три уровня сложности. 1 класс — О. В. Узорова
3000 примеров по математике. Супертренинг. Три уровня сложности. Счет в пределах 20. 1 класс — О. В. Узорова
3000 примеров по математике. Самые простые примеры с картинками. 1 класс — О. В. Узорова
3000 примеров по математике.
 Нескучные задачи и нелегкие примеры. С ответами и пояснениями. 1 класс — О. В. Узорова
Нескучные задачи и нелегкие примеры. С ответами и пояснениями. 1 класс — О. В. Узорова300 задач по математике. 1 класс — О. В. Узорова
Тесты по математике для тематического и итогового контроля. 1 класс — О. В. Чистякова
Математика. Все задания для уроков и олимпиад. 1 класс — Т. А. Конобеева
3000 примеров по математике с ответами и методическими рекомендациями. Счёт в пределах десятка. 1 класс — О. В. Узорова
Полный курс математики. Все типы заданий, все виды задач, примеров, неравенств, все контрольные работы, все виды тестов. 1 класс — О. В. Узорова
Большой тренажёр по математике. 1 класс — О. В. Узорова
Учусь писать контрольные работы по математике. 1 класс — М. Н. Алимпиева
Тренажер по математике.
 Разрядный состав чисел до 10. 1 класс — Группа авторов
Разрядный состав чисел до 10. 1 класс — Группа авторовТренажер по математике. Задачи на сложение и вычитание в пределах 20. 1 класс — Группа авторов
Тренажёр по математике. Цифры и счёт. 1 класс — О. В. Узорова
Поурочные разработки по математике. 1 класс (к УМК М.И. Моро и др. («Школа России»)) — Т. Н. Ситникова
Поурочные разработки по математике. 1 класс (к УМК А. Л. Чекина «Перспективная начальная школа») — Е. Е. Ипатова
Быстро решаем задачи по математике. 1 класс — О. В. Узорова
Устный счёт. Математика. Разноуровневые задания. 1 класс — М. Н. Алимпиева
Математика. Сложение и вычитание. 1 класс — Т. С. Позднева
Математика. Научусь решать любые примеры. 1 класс — А. А. Кулаков
Математика.
 1 класс — И. Соловьева
1 класс — И. СоловьеваРабочая программа по математике. 1 класс — Группа авторов
Тренажер по математике. Сложение и вычитание в пределах 10. 1 класс — Группа авторов
3000 примеров по математике с ответами и методическими рекомендациями. Устный счёт. Сложение и вычитание в пределах 20. 1 класс — О. В. Узорова
Поурочные разработки по математике. 1 класс (к УМК И. И. Аргинской и др., система Л. В. Занкова) — В. В. Захарова
Объясняем трудную тему. Математика за 10 дней. 1 класс — О. В. Чистякова
3000 примеров по математике с ответами и методическими рекомендациями. Устный счёт. Сложение и вычитание в пределах 10. 1 класс — О. В. Узорова
Математика. Тетрадь для диагностики и самооценки универсальных учебных действий. 1 класс — Т. П. Хиленко
Математика.
 Числа и фигуры. 1 класс — С. В. Бахтина
Числа и фигуры. 1 класс — С. В. БахтинаПримеры и задачи по математике. 1 класс — О. Е. Васильева
Математика. Методические рекомендации. 1 класс — Г. В. Дорофеев
Математика в схемах и таблицах. Все темы школьного курса. Тесты с ответами. 1 класс — О. В. Узорова
Все комплексные тесты для начальной школы. Математика, окружающий мир, русский язык, литературное чтение (стартовый и текущий контроль). 1 класс — М. А. Танько
Математика. Итоговое тестирование. 1 класс — О. В. Узорова
Математика. 1 класс — В. А. Сазонова
22 занятия по математике для освоения учебной программы. 1 класс — О. Д. Ушакова
Летние задания по математике для повторения и закрепления учебного материала. 1 класс — О. В. Узорова
300 примеров по математике.
 Геометрические задания. 1 класс — О. В. Узорова
Геометрические задания. 1 класс — О. В. УзороваПодготовка к проверочным работам по математике. 1 класс — М. Н. Алимпиева
Считаем и решаем. Математика на «отлично». 1 класс — Г. В. Дорофеева
Тренажер по математике. Сравнение чисел в пределах 20. 1 класс — Группа авторов
Контрольно-измерительные материалы. Математика. 1 класс — Т. Н. Ситникова
Итоговое тестирование. Русский язык. Математика. 1 класс — О. В. Узорова
3000 примеров по математике. Вычисления по схемам в пределах 20. Сложение и вычитание с пятью числами. Ответы. 1 класс — О. В. Узорова
Сборник упражнений по математике. 1 класс — Т. В. Векшина
Тренажёр по математике. 1 класс — ВАКО
Тренажер по математике. Состав чисел до 10.
 1 класс — Д. В. Овчаров
1 класс — Д. В. Овчаров320 примеров по математике. Геометрические задания. 1 класс — О. В. Узорова
Математика. Тематические тесты. 1 класс — Группа авторов
3000 примеров по математике. Счёт от 6 до 10. 1 класс — О. В. Узорова
Математика. Классные задания для закрепления знаний. 1 класс — Ирина Исаева
Математика. Методические рекомендации. 1 класс — М. А. Бантова
Математика. Задачи. 1 класс — С. В. Бахтина
Математика. Устные упражнения. 1 класс — С. И. Волкова
Тренажер по математике. 1 класс — Л. А. Иляшенко
Задачи. Математика. 1 класс — И. О. Родин
Математика. Все приёмы устного счёта. 1 класс — Т. С. Позднева
Математика.
 Все примеры на все темы школьной программы. 1 класс — Т. С. Позднева
Все примеры на все темы школьной программы. 1 класс — Т. С. ПоздневаБыстро повторим – быстро проверим. Математика. 1 класс — О. В. Узорова
Математика. Устный счет. 1 класс — О. В. Узорова
Все основные вопросы по математике для итоговой аттестации. 1 класс — О. В. Узорова
Контрольно-измерительные материалы. Русский язык, литературное чтение, математика, окружающий мир. Стартовый, промежуточный и итоговый контроль знаний. 1 класс — Е. М. Плахута
Математика. Мини-тесты и примеры на все темы школьного курса. 1 класс — Е. А. Нефёдова
3000 примеров по математике. Считаем и объясняем. Сложение и вычитание. 1 класс — О. В. Узорова
Школьные олимпиады по математике. 1 класс — О. В. Узорова
Контрольные и проверочные работы по математике.
 1 класс — И. О. Родин
1 класс — И. О. РодинТренажер по математике. Сравнение чисел в пределах 20. 1 класс — Д. В. Овчаров
3000 примеров по математике. Счёт в пределах 20. Разные уровни сложности. 1 класс — О. В. Узорова
Математика. Учусь считать быстро. 1 класс — Т. С. Позднева
Русский язык. Математика. Повторение пройденного. 1 класс — О. Б. Калинина
Дидактический материал для занятий с детьми, испытывающими трудности в усвоении математики и чтения. 1 класс — Ю. А. Костенкова
Математика. Все цепочки примеров для устных и письменных работ. 1 класс — Алексей Кулаков
Счёт в пределах 20. Тренажер по математике, 1 класс — О. В. Узорова
Комплексный тренажёр по математике. 1 класс — Группа авторов
Задачи по математике для уроков и олимпиад.
 1 класс — О. В. Узорова
1 класс — О. В. УзороваЗанятия-пятиминутки по математике. 1 класс — М. Н. Алимпиева
Тренировочные упражнения в картинках. Русский язык, математика, литературное чтение. 1 класс — О. Д. Ушакова
Математические прописи. Учимся писать цифры. 1 класс — О. В. Узорова
Математика. 1 класс — Анна Горохова
Диагностические комплексные работы. Русский язык. Математика. Окружающий мир. Литературное чтение. 1 класс — О. В. Узорова
7 Единых базовых математических заданий для первоклассников
Для многих учителей и администраторов начало 2013-14 учебного года также означает полное внедрение Единых основных государственных стандартов. Поскольку CCSS — это руководство, а не национальная учебная программа, многие учителя начальных классов, желающие соответствовать новым математическим стандартам для своих детей, в течение лета усердно готовили новые планы уроков. Вот семь уникальных идей для увлекательных математических занятий в соответствии с CCSS для первого класса, которые помогут вам начать работу:
Вот семь уникальных идей для увлекательных математических занятий в соответствии с CCSS для первого класса, которые помогут вам начать работу:
1. Домино
CCSS требует, чтобы первоклассники знали, как представлять и решать задачи на сложение и вычитание. Чтобы сделать процесс немного более увлекательным, используйте домино для тренировки сложения. Положите стопку карточек с числами перед учащимися и переверните одну. Попросите их найти костяшки домино с таким же количеством точек, а затем пусть они запишут свои мыслительные процессы на листе бумаги в виде уравнения сложения.
2. Сборка поездов с помощью кубиков
Снэп-кубики — это манипулятор, открывающий бесконечные возможности для обучения математике в первом классе. В соответствии с CCSS первоклассники должны понимать, что 5 + 3 = 3 + 5. Предложите учащимся с помощью кубиков собрать поезд из двух цветов (они могут выбрать свои любимые оттенки). Попросите их построить поезд, используя менее 10 кубиков, и напишите числовое предложение, описывающее то, что они создали. Затем попросите учеников перевернуть поезд и написать новую последовательность. Это поможет им понять, что независимо от порядка чисел общая сумма одинакова.
Затем попросите учеников перевернуть поезд и написать новую последовательность. Это поможет им понять, что независимо от порядка чисел общая сумма одинакова.
3. Браслеты
Использование декоративно-прикладного искусства на уроках математики всегда делает их более увлекательными. Чтобы рассказать первоклассникам о разрядности (например, о том, как набор из 10 можно представить как 10), сделайте браслеты, используя ершик для труб и бусины. Попросите каждого ученика отсчитать по 10 бусин своего любимого цвета и нанизать их на ершик для чистки труб. После того, как они сделают браслеты, покажите им, как сдвигать бусины в разные стороны, чтобы продемонстрировать различные пары чисел, которые в сумме могут составлять 10.
4. Экскурсия в яблоневый сад
Всегда интересно заниматься математикой вне класса, так почему бы не пригласить первоклассников на экскурсию в яблоневый сад? Пусть они посчитают яблоки, пока каждый наполняет свою бочку. Затем вы можете использовать разноцветные яблоки, чтобы продемонстрировать задачу со словами. Например, показаны все различные комбинации красных и желтых яблок, которые можно использовать для создания коробки из 10 штук.
Затем вы можете использовать разноцветные яблоки, чтобы продемонстрировать задачу со словами. Например, показаны все различные комбинации красных и желтых яблок, которые можно использовать для создания коробки из 10 штук.
5. Празднование 100-дневного праздника
Достижение 100-го дня в школе всегда волнительно для учеников, так почему бы не направить всю эту энергию на урок математики? Это отличная практика — поддерживать Единые базовые государственные стандарты, которые требуют, чтобы первоклассники умели считать до 120. Пусть каждый учащийся принесет группу из 100 предметов, чтобы отпраздновать это событие, и прогуляйтесь по классу галереей.
6. Игра «Плюс один/минус один»
Почему бы не создавать математические задания с помощью кубиков? Чтобы помочь первоклассникам практиковать свои навыки сложения и вычитания, сделайте коврик, напоминающий доску для игры в бинго, на которой будут цифры от двух до семи. Разделите учащихся на пары и дайте каждому по 10 фишек (это может быть что угодно, от фигурок из плотной бумаги до кусочков шахматной доски). Затем каждый игрок по очереди бросает кубик и прибавляет один (или вычитает один, в зависимости от игры) и ставит свою фишку на соответствующее число. Игра заканчивается, когда учащиеся используют все свои фишки.
Затем каждый игрок по очереди бросает кубик и прибавляет один (или вычитает один, в зависимости от игры) и ставит свою фишку на соответствующее число. Игра заканчивается, когда учащиеся используют все свои фишки.
7. Увлекательные уроки DreamBox
Современные дети разбираются в технологиях — большинство из них не помнят мир без компьютеров. Чтобы поддерживать их интерес, используйте технологию интеллектуального адаптивного обучения DreamBox Learning, чтобы изучать новые концепции и улучшать понимание. Игровая учебная среда с уроками, согласованными с Common Core, делает обучение увлекательным благодаря темам, персонажам и системе вознаграждений.
Хотите больше советов по успешному планированию математики CCSS? Ознакомьтесь с бесплатным информационным документом от DreamBox.
13 лучших математических приложений для 1-го класса
Поддержите основные концепции вашего плана урока математики с помощью таких технологий, как лучшие математические приложения для 1-го класса. Существуют сотни игр и приложений, которые рекламируют развлечение и увлекательность, но как узнать, какое из них лучше всего подходит для ваших учеников?
Существуют сотни игр и приложений, которые рекламируют развлечение и увлекательность, но как узнать, какое из них лучше всего подходит для ваших учеников?
Ваш план урока для первого класса будет включать четыре критических сегмента. Учащиеся будут развивать свое понимание сложения, вычитания, отношений целых чисел и разряда, а также линейных измерений. В этих сегментах они будут работать над стратегиями сложения и вычитания с использованием чисел 1–20, измерения длины в единицах, а также составления и разложения геометрических фигур. Отличное математическое приложение может поддерживать эти важные области обучения за счет вовлечения и взаимодействия с концепциями в сценариях, которые относятся к первоклассникам. Математические приложения также являются отличными ресурсами для самостоятельной, групповой или партнерской работы.
Содержание
- Подходят ли математические приложения для детей?
- 13 лучших математических приложений для 1-го класса
- Ознакомьтесь с этими дополнительными ресурсами для 1-го класса
Математические приложения отлично подходят для детей и легко интегрируются в план урока без необходимости ИТ-поддержки. Когда вы ищете приложение, есть несколько особенностей, которые вы можете проверить, чтобы убедиться, что они соответствуют вашим потребностям.
Когда вы ищете приложение, есть несколько особенностей, которые вы можете проверить, чтобы убедиться, что они соответствуют вашим потребностям.
Лучшие приложения будут поддерживать разработку важнейших областей вашего плана урока математики, предлагать стратегии адаптивного обучения и постоянно обеспечивать оценку и анализ. Стоимость является фактором — она должна быть доступна для всего класса, независимо от социально-экономических факторов.
Они также должны соответствовать возрасту и быть рекомендованы преподавателями и школами. Наконец, математическое приложение должно способствовать обучению, способствуя творческому мышлению и стимулируя каскад вознаграждений за счет положительного подкрепления.
В партнерстве с Teach Simple, чья торговая площадка полна образовательных материалов, созданных настоящими учителями (плюс 50% всех доходов идут им), я собрал 13 веселых и увлекательных математических приложений для 1-го класса, которые будут развлекать ваших учеников во время учебы. развиваем математические способности!
развиваем математические способности!
13
Лучшие математические приложения для 1-го класса Minecraft для образования: математикаЕсли вы не знакомы с Minecraft, по сути, это игра с основанием из десяти. Игроки строят все, что хотят, используя строительные блоки в разных средах. С момента выхода в 2009 году он привлек внимание людей всех возрастов по всему миру.
Из-за такой популярности игра легко поддается игровым обучающим модулям. Они даже разработали образовательную лабораторию для учителей и школ с такими функциями, как элементы управления учебным залом, характерные для учебной среды. Например, в режиме «Классная комната» учителя могут наблюдать за учениками на карте мира и общаться с ними в одной группе. Если ученик выходит из группы, вы можете вернуть его аватар на урок.
Minecraft для образования: математический модуль помогает вашим учащимся развивать критические математические навыки с помощью интерактивной творческой игры, совместного решения задач и использования технологий в соответствии с возрастом. Этот продукт доступен учителям и школам, требует наличия учетной записи Office 365 и доступен для платформ Android и iOS.
Этот продукт доступен учителям и школам, требует наличия учетной записи Office 365 и доступен для платформ Android и iOS.
Найти здесь
Moose MathMoose Math — это простое приложение для детей, в котором используются творческие персонажи, чтобы увлечь учащихся уроками игры.
По мере того, как учащийся преодолевает уровень, сложность увеличивается, и их прогресс виден родителям и преподавателям на экране табеля успеваемости. Эта бесплатная игра согласуется с основными компетенциями учебной программы первого класса и представляет собой простое в использовании приложение, которое укрепляет основные математические концепции.
С помощью Moose Math дети изучают следующие базовые математические навыки:
- Понимание взаимосвязи между числами и количествами
- Решение текстовых задач и алгебраическое мышление
- Practice number pattern recognition
- Count by 1’s, 2’s, 5’s and 10’s
- Master counting to 100
- Add and subtract by 1’s, 2’s, 5’s and 10’s
- Add and subtract up to 20
- Научитесь складывать и вычитать с числами, кубиками и рекенреками
- Изучите геометрию в детском саду и первом классе
- Научитесь определять и узнавать фигуры
- Понимание и сравнение длин
Найти здесь
SplashLearn В SplashLearn есть несколько различных математических приложений и игр, которые охватывают все математические понятия, которые изучают учащиеся 1 класса. Игры на стратегии сложения и вычитания, разрядность, определение времени и многое другое доступны в категории первого класса. В то время как в веселых играх со счетом используются числовые линии и диаграммы сотен, группировка по десяткам использует наборы разноцветных объектов. Кроме того, SplashLearn охватывает принципы математики и чтения для разных классов, чтобы дети могли продолжать играть в новые игры по мере их взросления.
Игры на стратегии сложения и вычитания, разрядность, определение времени и многое другое доступны в категории первого класса. В то время как в веселых играх со счетом используются числовые линии и диаграммы сотен, группировка по десяткам использует наборы разноцветных объектов. Кроме того, SplashLearn охватывает принципы математики и чтения для разных классов, чтобы дети могли продолжать играть в новые игры по мере их взросления.
Найти здесь
Khan Academy KidsKhan Academy Kids — это бесплатный учебный ресурс для учащихся всех возрастов. Это приложение предлагает практику с различными базовыми навыками в математике и других областях обучения первого класса. Раздел математики поддерживает план урока для первого класса, который включает числа, простое сложение и логику.
Найти здесь
Monster Math Эта игра включает в себя все основные знания ранней математики в увлекательной сюжетной линии. Игры могут быть адаптированы к потребностям учащихся и предлагают практику с более чем 40 математическими навыками в сочетании с математическими занятиями в автономном режиме в виде печатных форм.
Игры могут быть адаптированы к потребностям учащихся и предлагают практику с более чем 40 математическими навыками в сочетании с математическими занятиями в автономном режиме в виде печатных форм.
Найти здесь
OsmoOsmo — это приложение для iPad, которое включает в себя элементы набора для манипулирования, которые вдохновляют на обучение с помощью цифровых и практических занятий. Продукт предлагает два основных модуля оплаты: один для домашнего обучения и один для школ. Для математики есть несколько вариантов приложений, включая Math Wizard Magical Workshop, Essential Math Bundle, Genius Numbers и Genius Tangram.
Найти здесь
Marble Math Marble Math предлагает детям интересный способ попрактиковаться в умственной арифметике. Он использует шарики в качестве награды. Учащиеся могут взять под контроль свое обучение, если даны неправильные ответы, попробовав еще раз или выбрав показ правильного ответа, прежде чем двигаться дальше. Создайте несколько учетных записей и адаптируйте игры к потребностям каждого игрока.
Создайте несколько учетных записей и адаптируйте игры к потребностям каждого игрока.
Найти здесь
Math Kids: Математические игры для детейТворческие и веселые персонажи занимаются с детьми простыми математическими задачами в этом приложении. Головоломки и викторины развивают математические навыки на уровнях от Pre-K до 1 класса. Math Kids — это бесплатная обучающая игра, которая поможет детям научиться определять числа и познакомит их с головоломками на сложение и вычитание. Они отлично проведут время, выполняя игры и зарабатывая наклейки, а вы прекрасно проведете время, наблюдая, как они растут и учатся.
Найти здесь
Todo Math Todo Math предлагает учащимся более 2000 математических заданий на 8 языках. Он всеобъемлющий, инклюзивный и доступный благодаря таким функциям, как игра для левшей и дислектический шрифт. Это бесплатно попробовать и не требует кредитной карты для регистрации.
Найти здесь
DoodleMathsПовысьте уверенность учащихся в математике с помощью этого простого в использовании персонализированного математического приложения. Он содержит разнообразный набор вопросов, предназначенных для поддержки каждого стиля обучения, и вознаграждает детей за их усилия, а не за их способности.
DoodleMath предлагает платформы для родителей и учителей, каждая из которых имеет свои особенности и преимущества. У них также есть версии приложений для разных стран и их учебных программ, в том числе для США.
Найти здесь
Operation MathЭто забавная математическая игра на шпионскую тему с карточками. Студенты выполняют миссии по всему миру, чтобы заработать шпионское снаряжение, отвечая на вопросы сложения, вычитания, умножения и деления. Это простое цифровое дополнение к существующему плану урока.
Найти здесь
Kahoot Numbers and Big Numbers от Dragon Box Kahoot Numbers и Big Numbers идеально подходят для первоклассников и могут быть приобретены как отдельное приложение или как часть Kahoot+ Family или Подписка на Премиум доступ. Игры по-разному помогают детям в освоении основ математики. Также доступны Kahoot Algebra и Geometry, чтобы охватить все основные математические концепции 1-го класса.
Игры по-разному помогают детям в освоении основ математики. Также доступны Kahoot Algebra и Geometry, чтобы охватить все основные математические концепции 1-го класса.
Найти здесь
Prodigy Math GameБесплатное, эффективное и увлекательное образовательное математическое содержание в одном приложении, где учащиеся могут зарабатывать награды, выполнять квесты и играть с друзьями. С новыми задачами на каждом углу учащиеся должны отвечать на адаптивные математические вопросы, чтобы побеждать в битвах и выполнять квесты. Кроме того, это интеллектуальное приложение позволяет учащимся учиться на нужном уровне с помощью адаптивного алгоритма, обеспечивающего эффективную практику.
Найдите здесь
Что должен знать первоклассник по математике?Основная учебная программа по математике для первого класса охватывает следующие четыре ключевых понятия:
- данные и измерения
- геометрия
- число и операции с основанием десять
- операции и алгебраическое мышление
В геометрии первоклассники будут учиться рассуждать с формами и их атрибутами.

 В конце задания пусть ребенок ответит, какие числа оказались лишними. Затем ребенок должен придумать примеры для каждой картинки. Например, в первой картинке пример звучит так: 3 красных яблока + 6 зеленых яблок = 9 яблок.
В конце задания пусть ребенок ответит, какие числа оказались лишними. Затем ребенок должен придумать примеры для каждой картинки. Например, в первой картинке пример звучит так: 3 красных яблока + 6 зеленых яблок = 9 яблок.  Поэтому расположение цветов не совпадает, но сама последовательность четко сохраняется. Затем нужно посчитать, сколько пар цветов, сколько пар лепестков в каждом цветке?
Поэтому расположение цветов не совпадает, но сама последовательность четко сохраняется. Затем нужно посчитать, сколько пар цветов, сколько пар лепестков в каждом цветке? В конце выполнения задания ребенка нужно спросить, на что он обратил внимание, считая героев (все картинки с героями расположены по порядку счета).
В конце выполнения задания ребенка нужно спросить, на что он обратил внимание, считая героев (все картинки с героями расположены по порядку счета). Когда ребенок объединит точки, то увидит, что могло бы помочь туристу в этой ситуации.
Когда ребенок объединит точки, то увидит, что могло бы помочь туристу в этой ситуации. Столбики-цепочки. Все темы. Быстрый устный счёт. 1 класс — О. В. Узорова
Столбики-цепочки. Все темы. Быстрый устный счёт. 1 класс — О. В. Узорова Полезные и увлекательные задания. 1 класс — О. В. Узорова
Полезные и увлекательные задания. 1 класс — О. В. Узорова Нескучные задачи и нелегкие примеры. С ответами и пояснениями. 1 класс — О. В. Узорова
Нескучные задачи и нелегкие примеры. С ответами и пояснениями. 1 класс — О. В. Узорова Разрядный состав чисел до 10. 1 класс — Группа авторов
Разрядный состав чисел до 10. 1 класс — Группа авторов 1 класс — И. Соловьева
1 класс — И. Соловьева Числа и фигуры. 1 класс — С. В. Бахтина
Числа и фигуры. 1 класс — С. В. Бахтина Геометрические задания. 1 класс — О. В. Узорова
Геометрические задания. 1 класс — О. В. Узорова 1 класс — Д. В. Овчаров
1 класс — Д. В. Овчаров Все примеры на все темы школьной программы. 1 класс — Т. С. Позднева
Все примеры на все темы школьной программы. 1 класс — Т. С. Позднева 1 класс — И. О. Родин
1 класс — И. О. Родин 1 класс — О. В. Узорова
1 класс — О. В. Узорова Исправим опечатки/ошибки или вернем оплату за проблемные задания (по статистике дорабатывается не более 3.2% заказов).
Исправим опечатки/ошибки или вернем оплату за проблемные задания (по статистике дорабатывается не более 3.2% заказов).

 Стоимость решения задачи зависит от предмета и сложности. Подав запрос на сайте и указав детали работы, вы сразу же получите компетентный ответ со всеми объяснениями.
Стоимость решения задачи зависит от предмета и сложности. Подав запрос на сайте и указав детали работы, вы сразу же получите компетентный ответ со всеми объяснениями.

 Ключевое слово здесь — практика: чем больше задач решают учащиеся, тем больше стратегий и методов они усваивают.
Ключевое слово здесь — практика: чем больше задач решают учащиеся, тем больше стратегий и методов они усваивают. Учащиеся должны угадывать, пока не найдут правильный ответ.
Учащиеся должны угадывать, пока не найдут правильный ответ. Дети должны понимать, что воссоздание математических задач пригодится для управления проектами и инженерной карьеры.
Дети должны понимать, что воссоздание математических задач пригодится для управления проектами и инженерной карьеры. Лучший способ обнаружить закономерности в математической задаче — научить учеников извлекать и перечислять важные детали. Они могут использовать эту стратегию при изучении форм и повторяющихся понятий, что делает этот подход одной из самых эффективных элементарных математических стратегий для решения задач.
Лучший способ обнаружить закономерности в математической задаче — научить учеников извлекать и перечислять важные детали. Они могут использовать эту стратегию при изучении форм и повторяющихся понятий, что делает этот подход одной из самых эффективных элементарных математических стратегий для решения задач. Используйте фигуры или числа для представления форм, чтобы не усложнять задачу. В зависимости от ситуации узоры и графики также могут быть полезны, и вы можете предложить детям использовать точки или буквы для обозначения предметов.
Используйте фигуры или числа для представления форм, чтобы не усложнять задачу. В зависимости от ситуации узоры и графики также могут быть полезны, и вы можете предложить детям использовать точки или буквы для обозначения предметов. Поэтому не спешите отговаривать детей от использования стратегии проб и ошибок.
Поэтому не спешите отговаривать детей от использования стратегии проб и ошибок. Имея степень бакалавра и магистра математики, ей нравится воспитывать математических гениев, независимо от их возраста, уровня и навыков. Помимо репетиторства, Джессика ведет блог в Brighterly. У нее также есть опыт работы в области детской психологии, домашнего обучения и консультирования по учебным программам для школ и веб-сайтов EdTech.
Имея степень бакалавра и магистра математики, ей нравится воспитывать математических гениев, независимо от их возраста, уровня и навыков. Помимо репетиторства, Джессика ведет блог в Brighterly. У нее также есть опыт работы в области детской психологии, домашнего обучения и консультирования по учебным программам для школ и веб-сайтов EdTech.


 Итак… в общем все. Возможно, поэтому я не мог придерживаться стратегии из года в год.
Итак… в общем все. Возможно, поэтому я не мог придерживаться стратегии из года в год.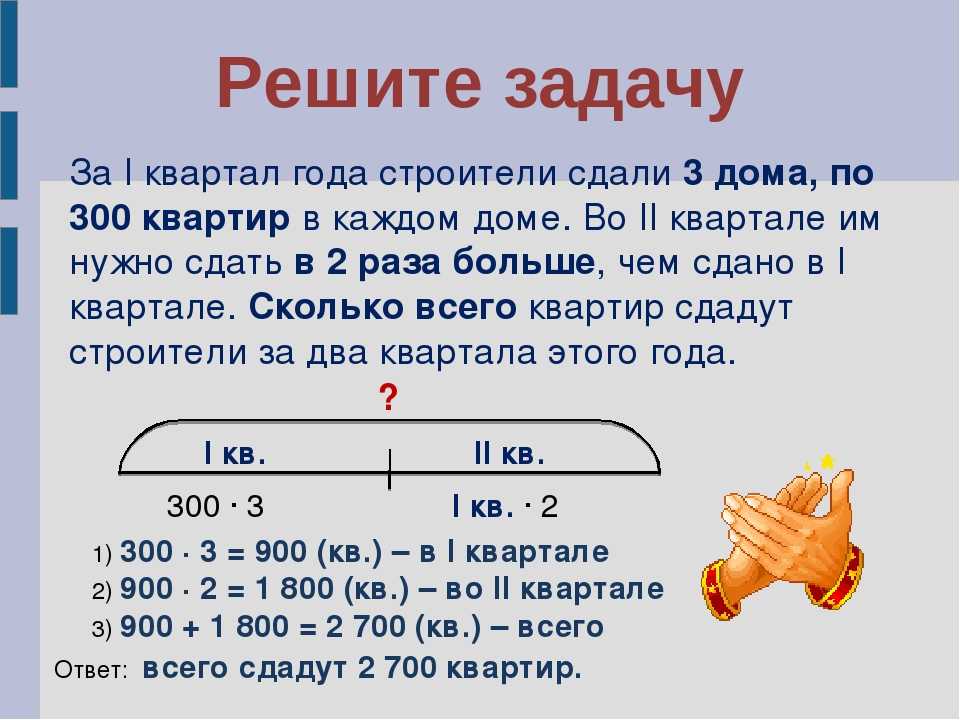
 Это означает, что вам нужно запомнить соответствующие формулы, чтобы вы могли быстро их вызывать по мере необходимости. Не паникуйте! Поскольку программа ACT очень специфична в отношении типов вопросов, на которые она ожидает от вас ответов, вы можете легко подготовиться к их решению.
Это означает, что вам нужно запомнить соответствующие формулы, чтобы вы могли быстро их вызывать по мере необходимости. Не паникуйте! Поскольку программа ACT очень специфична в отношении типов вопросов, на которые она ожидает от вас ответов, вы можете легко подготовиться к их решению. В нашей книге ACT Premium Prep, мы покажем вам, как решать проблемы на TI-83.
В нашей книге ACT Premium Prep, мы покажем вам, как решать проблемы на TI-83. Отличный признак того, что вы можете включить ответ. Проблема заключается в том, чтобы попросить самый большой, поэтому начните с выбора (E). Работает ли уравнение, если x = 5? 5 2 — 4(5) + 3 = 25 — 20 + 3 ≠ 0. Исключить вариант (E). Попробуйте вариант (D), 4 2 — 4(4) + 3 = 16 — 16 + 3 ≠ 0. Попробуйте вариант (С), 3 2 — 4 (3) + 3 = 9 — 12 + 3 = 0, Это работает, и потому что вы вставляете ответ, вы можете остановиться, как только найдете правильный ответ. Если вы выбрали вариант (A), будьте осторожны; это наименьшее значение x, которое решает уравнение.
Отличный признак того, что вы можете включить ответ. Проблема заключается в том, чтобы попросить самый большой, поэтому начните с выбора (E). Работает ли уравнение, если x = 5? 5 2 — 4(5) + 3 = 25 — 20 + 3 ≠ 0. Исключить вариант (E). Попробуйте вариант (D), 4 2 — 4(4) + 3 = 16 — 16 + 3 ≠ 0. Попробуйте вариант (С), 3 2 — 4 (3) + 3 = 9 — 12 + 3 = 0, Это работает, и потому что вы вставляете ответ, вы можете остановиться, как только найдете правильный ответ. Если вы выбрали вариант (A), будьте осторожны; это наименьшее значение x, которое решает уравнение.
 Он есть только у (D), поэтому это единственный правильный ответ. если вы do найдите неизвестную сторону, вспомните тройки Пифагора: это треугольник 5:12:13, поэтому неизвестная сторона должна быть 12.
Он есть только у (D), поэтому это единственный правильный ответ. если вы do найдите неизвестную сторону, вспомните тройки Пифагора: это треугольник 5:12:13, поэтому неизвестная сторона должна быть 12.

 Он может построить только 400-футовый забор из сосны. Если он захочет построить квадратную ограду из соснового леса, какова будет площадь в квадратных футах?»
Он может построить только 400-футовый забор из сосны. Если он захочет построить квадратную ограду из соснового леса, какова будет площадь в квадратных футах?»
 Как правило, существует множество способов решения проблемы. Если вы решите это во второй раз с другим подходом и получите тот же ответ, вы должны быть уверены в своем ответе. Это хороший способ не тратить время на перепроверку математики, прежде чем отвечать на все остальные вопросы.
Как правило, существует множество способов решения проблемы. Если вы решите это во второй раз с другим подходом и получите тот же ответ, вы должны быть уверены в своем ответе. Это хороший способ не тратить время на перепроверку математики, прежде чем отвечать на все остальные вопросы.

 После того, как репетитор по математике заметил ошибку, помарку или даже неточность, необходимо указать на нее и позаботится о предупреждении аналогичной ситуации в будущем. Существует множество способов акцентирования внимания к допущенным ошибкам:
После того, как репетитор по математике заметил ошибку, помарку или даже неточность, необходимо указать на нее и позаботится о предупреждении аналогичной ситуации в будущем. Существует множество способов акцентирования внимания к допущенным ошибкам: Чем больше радости и позитива принесет ученику урок репетитора по математике, тем дольше и прочнее изложенная информация будет храниться в его памяти.
Чем больше радости и позитива принесет ученику урок репетитора по математике, тем дольше и прочнее изложенная информация будет храниться в его памяти. Давайте представим себе, что знак равно – это дверь между квартирой и улицей, а процесс перемещения слагаемого – вход или выход из квартиры. Что мы делаем, когда мы входим или выходим из помещения? Правильно. Переобуваемся. Этот процесс можно сравнить со сменой знаков минус и плюс при переносе слагаемого. Если ученик пропустил смену, то репетитор по математике отреагирует на это таким образом: «Слагаемое вышло в тапках на улицу».
Давайте представим себе, что знак равно – это дверь между квартирой и улицей, а процесс перемещения слагаемого – вход или выход из квартиры. Что мы делаем, когда мы входим или выходим из помещения? Правильно. Переобуваемся. Этот процесс можно сравнить со сменой знаков минус и плюс при переносе слагаемого. Если ученик пропустил смену, то репетитор по математике отреагирует на это таким образом: «Слагаемое вышло в тапках на улицу».
 Имея перед глазами яркие примеры и сравнения, математика перестанет казаться ученику тяжелым и скучным предметом. Необходимая моторика работы с алгоритмами быстрее вырабатывается, а ошибки легче запоминаются.
Имея перед глазами яркие примеры и сравнения, математика перестанет казаться ученику тяжелым и скучным предметом. Необходимая моторика работы с алгоритмами быстрее вырабатывается, а ошибки легче запоминаются. Н, репетитор по математике, Колпаков А.Н. Москва, м.Строгино. м.Щукинская.
Н, репетитор по математике, Колпаков А.Н. Москва, м.Строгино. м.Щукинская. [а1]). Но Лефшец и Вейль имели в виду не только элементарные предложения. Вот почему Вейль работал с универсальными областями, т. е. с алгебраически замкнутыми полями бесконечной степени трансцендентности над их простым полем. Итак, гипотеза заключалась в том, что существует только одна алгебраическая геометрия над универсальными областями фиксированной характеристики. Удовлетворительная формализация и теоретико-модельное доказательство принадлежит П. Эклофу [a2]. Он использует бесконечный язык $L_{\infty\omega}$, который допускает бесконечное количество конъюнкций и дизъюнкций в одном предложении. С помощью такого предложения можно выразить тот факт, что поле имеет бесконечную степень трансцендентности над своим простым полем. Это невозможно сделать с помощью одного элементарного предложения. Действительно, алгебраически замкнутые поля элементарно эквивалентны алгебраическому замыканию своего простого поля, даже если они имеют бесконечную степень трансцендентности.
[а1]). Но Лефшец и Вейль имели в виду не только элементарные предложения. Вот почему Вейль работал с универсальными областями, т. е. с алгебраически замкнутыми полями бесконечной степени трансцендентности над их простым полем. Итак, гипотеза заключалась в том, что существует только одна алгебраическая геометрия над универсальными областями фиксированной характеристики. Удовлетворительная формализация и теоретико-модельное доказательство принадлежит П. Эклофу [a2]. Он использует бесконечный язык $L_{\infty\omega}$, который допускает бесконечное количество конъюнкций и дизъюнкций в одном предложении. С помощью такого предложения можно выразить тот факт, что поле имеет бесконечную степень трансцендентности над своим простым полем. Это невозможно сделать с помощью одного элементарного предложения. Действительно, алгебраически замкнутые поля элементарно эквивалентны алгебраическому замыканию своего простого поля, даже если они имеют бесконечную степень трансцендентности. Аналогичный принцип известен для $p$-адически замкнутых полей (см. $p$-адически замкнутое поле). Принципы Акса–Кохена–Ершова в теории моделей нормированных полей можно рассматривать как принципы условного переноса.
Аналогичный принцип известен для $p$-адически замкнутых полей (см. $p$-адически замкнутое поле). Принципы Акса–Кохена–Ершова в теории моделей нормированных полей можно рассматривать как принципы условного переноса. Ниже обсуждается зачет по математическим курсам, пройденным в учебных заведениях США, отличных от Duke, в то время как учащийся уже зачислен в Duke. Если вы заинтересованы в кредите за курс, который вы прошли до для зачисления в Duke, пожалуйста, см. кредит Duke Prematriculation. Если вы заинтересованы в получении кредита на курс математики, который будет проходить во время вашего обучения по программе обучения за рубежом в иностранном учебном заведении, см. «Изучение математики во время обучения за границей».
Ниже обсуждается зачет по математическим курсам, пройденным в учебных заведениях США, отличных от Duke, в то время как учащийся уже зачислен в Duke. Если вы заинтересованы в кредите за курс, который вы прошли до для зачисления в Duke, пожалуйста, см. кредит Duke Prematriculation. Если вы заинтересованы в получении кредита на курс математики, который будет проходить во время вашего обучения по программе обучения за рубежом в иностранном учебном заведении, см. «Изучение математики во время обучения за границей». 
 Вы можете избежать напрасной траты времени, самостоятельно сравнив учебные программы и описания курсов и выбрав другой курс, когда увидите очевидные различия.
Вы можете избежать напрасной траты времени, самостоятельно сравнив учебные программы и описания курсов и выбрав другой курс, когда увидите очевидные различия.
 Благодаря техническим упражнениям на абакусе увеличивается скорость мышления, усидчивость, развивается концентрация. На первом этапе обучения ребенок учится правильной технике выполнения счета на абакусе и осваивает все операции первоначально на абакусе.
Благодаря техническим упражнениям на абакусе увеличивается скорость мышления, усидчивость, развивается концентрация. На первом этапе обучения ребенок учится правильной технике выполнения счета на абакусе и осваивает все операции первоначально на абакусе. Благодаря разработанным возрастным программам обучения в Абакус центре дети с радостью приходят на занятия.
Благодаря разработанным возрастным программам обучения в Абакус центре дети с радостью приходят на занятия.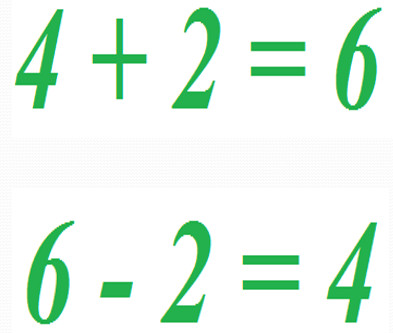 Особенно это если ребенок не справлялся со школьными математическими диктантами и испытывал постоянный стресс.
Особенно это если ребенок не справлялся со школьными математическими диктантами и испытывал постоянный стресс. Дети становятся увереннее в своих достижениях, снимают психологическое напряжение.
Дети становятся увереннее в своих достижениях, снимают психологическое напряжение. Дети не просто становятся увереннее в своих знаниях, они приобретают привычку быть успешными, что позволит в будущем добиться высоких результатов!
Дети не просто становятся увереннее в своих знаниях, они приобретают привычку быть успешными, что позволит в будущем добиться высоких результатов!

 Математике не научат.
Математике не научат.
 Дети которые занимаются ментальной арифметикой очень сильно отличаются от других детей в своих способностях.
Дети которые занимаются ментальной арифметикой очень сильно отличаются от других детей в своих способностях. А это очень важно.
А это очень важно.
 Другими словами, если в класс идут 4 мальчика и 2 девочки, но 2 девочки решают пойти на обед, сколько молодых людей пойдет в класс?
Другими словами, если в класс идут 4 мальчика и 2 девочки, но 2 девочки решают пойти на обед, сколько молодых людей пойдет в класс?
 Мы называем вычитаемое число вычитаемым, а число, из которого оно вычитается, — уменьшаемым. Ответ — разница.
Мы называем вычитаемое число вычитаемым, а число, из которого оно вычитается, — уменьшаемым. Ответ — разница. Факты сложения от одного до десяти в одном направлении (слева направо) и от одного до двадцати в другом направлении (сверху вниз). Используя ответы в таблице, мы можем вычесть число вверху (или слева), и ответом будет число слева (или вверху).
Факты сложения от одного до десяти в одном направлении (слева направо) и от одного до двадцати в другом направлении (сверху вниз). Используя ответы в таблице, мы можем вычесть число вверху (или слева), и ответом будет число слева (или вверху). Это также вычитающий элемент идентичности. Ноль плюс любое число — исходное число; исходное число минус ноль является исходным числом.
Это также вычитающий элемент идентичности. Ноль плюс любое число — исходное число; исходное число минус ноль является исходным числом. Следовательно, ответ 2 десятка и 1 единица или двадцать один.
Следовательно, ответ 2 десятка и 1 единица или двадцать один.


 2 Системы уравнений с исключением
2 Системы уравнений с исключением  Его прокачивают каждую среду. Способ предоставить лучший образовательный продукт, который этот папа нашел где угодно!
Его прокачивают каждую среду. Способ предоставить лучший образовательный продукт, который этот папа нашел где угодно! Наша комплексная учебная программа по математике охватывает как предалгебру, так и подготовку к соревнованиям по математике.
Наша комплексная учебная программа по математике охватывает как предалгебру, так и подготовку к соревнованиям по математике.

 Через некоторое время порт покинуло 17 кораблей. Сколько кораблей осталось в порту?
Через некоторое время порт покинуло 17 кораблей. Сколько кораблей осталось в порту? Сколько яблок у Дениса, если известно, что у него на 3 яблока меньше, чем у Вовы и Димы вместе?
Сколько яблок у Дениса, если известно, что у него на 3 яблока меньше, чем у Вовы и Димы вместе? Счет сотнями.
Счет сотнями. Мы, учителя второго класса, знаем эти стандарты как свои пять пальцев, потому что мы преподаем этот модуль месяцами за месяцами каждый год! Не знаю, как вы все, но я всегда ищу свежие, новые практические упражнения на сложение и вычитание для обучения этому разделу, потому что даже после того, как он закончится, нам нужно продолжать работу по спирали, чтобы поддерживать интерес наших учеников. навыки свежие!
Мы, учителя второго класса, знаем эти стандарты как свои пять пальцев, потому что мы преподаем этот модуль месяцами за месяцами каждый год! Не знаю, как вы все, но я всегда ищу свежие, новые практические упражнения на сложение и вычитание для обучения этому разделу, потому что даже после того, как он закончится, нам нужно продолжать работу по спирали, чтобы поддерживать интерес наших учеников. навыки свежие!
 Эти подсказки для журналов можно спроецировать или распечатать и вырезать, чтобы учащиеся могли вклеить их в тетради по математике. Они практикуют каждый из основных математических стандартов для этого модуля, гарантируя, что ваши ученики будут писать о своем мышлении на каждом уроке, который вы преподаете! Распечатайте и вырежьте их в начале нового блока и держите их наготове в качестве отличной разминки в начале каждого математического блока!
Эти подсказки для журналов можно спроецировать или распечатать и вырезать, чтобы учащиеся могли вклеить их в тетради по математике. Они практикуют каждый из основных математических стандартов для этого модуля, гарантируя, что ваши ученики будут писать о своем мышлении на каждом уроке, который вы преподаете! Распечатайте и вырежьте их в начале нового блока и держите их наготове в качестве отличной разминки в начале каждого математического блока! Пусть дети во 2-м классе посчитают блоки и стержни, вычислят слагаемые и сложит их.
Пусть дети во 2-м классе посчитают блоки и стержни, вычислят слагаемые и сложит их.
 Потренируйтесь определять время с точностью до минут, наблюдая за минутной и часовой стрелками на всех аналоговых часах.
Потренируйтесь определять время с точностью до минут, наблюдая за минутной и часовой стрелками на всех аналоговых часах.




 Рефлексия:
Рефлексия:


 Сложение. Знак плюс.
Сложение. Знак плюс.  NBT.1). Этот навык помогает им понимать значения больше или меньше. Навык второго класса также тесно связан с навыком первого класса понимания разрядных значений (единиц и десятков) в двузначных числах (1.NBT.2).
NBT.1). Этот навык помогает им понимать значения больше или меньше. Навык второго класса также тесно связан с навыком первого класса понимания разрядных значений (единиц и десятков) в двузначных числах (1.NBT.2).
 Если числа равны, они могут выполнять обе позы в течение 10 секунд.
Если числа равны, они могут выполнять обе позы в течение 10 секунд. Поскольку 7 больше 3, она заключает, что 738 больше 396.
Поскольку 7 больше 3, она заключает, что 738 больше 396.
 Больше или меньше стандарта Common Core стандарта , необходимого в первом и втором классе. Вот 9рабочие листы, проекты и больше или меньше, чем действия , чтобы помочь вам увеличить ваши планы уроков.
Больше или меньше стандарта Common Core стандарта , необходимого в первом и втором классе. Вот 9рабочие листы, проекты и больше или меньше, чем действия , чтобы помочь вам увеличить ваши планы уроков. С третьего по пятый класс.
С третьего по пятый класс.
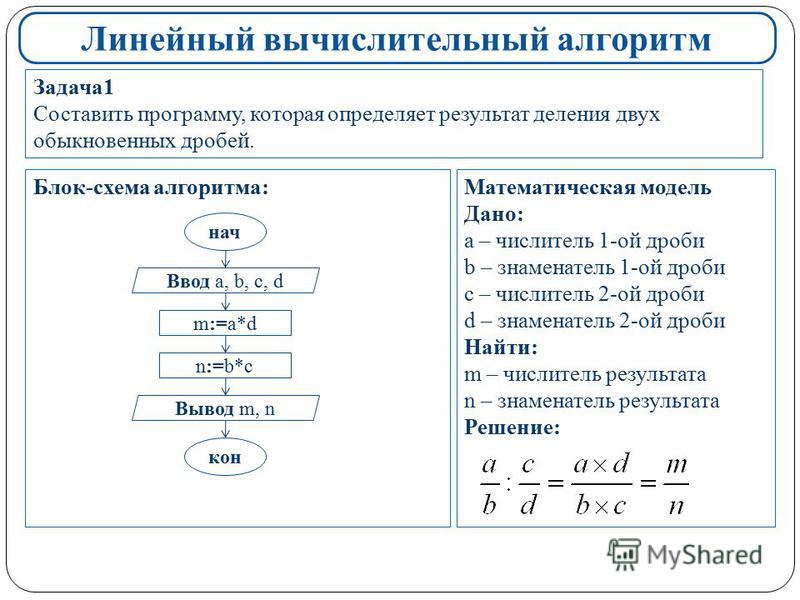
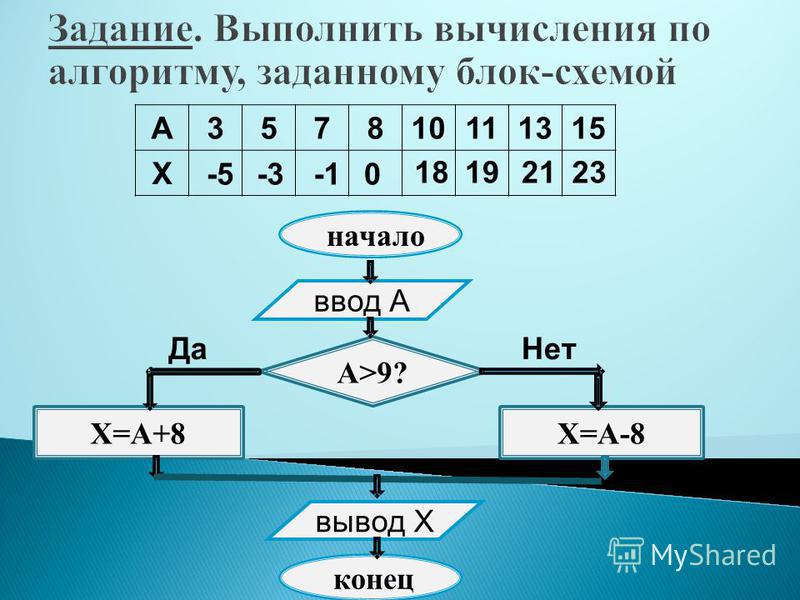
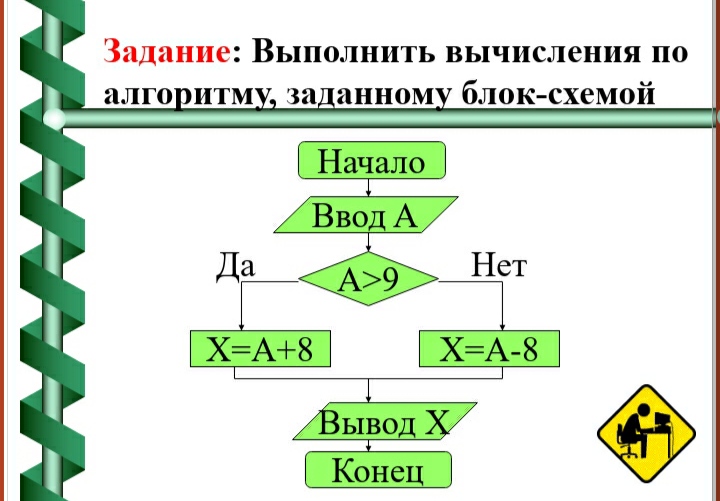 Выписать ответ.
Выписать ответ.
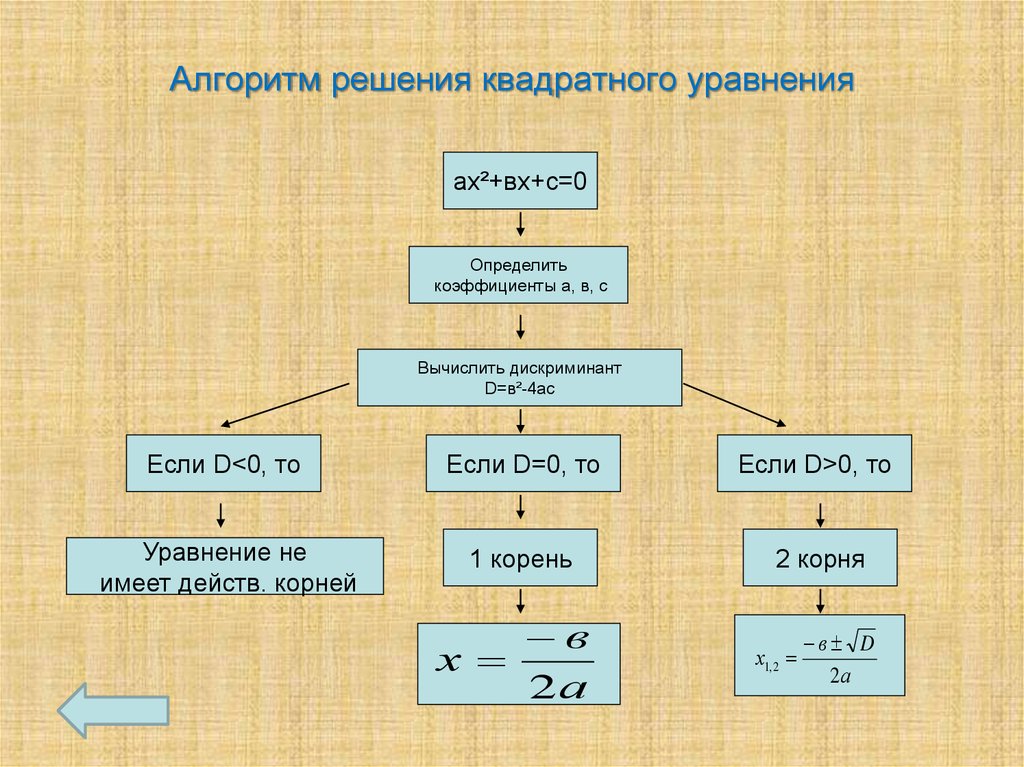
 выписать множители, входящие в разложение одного из чисел;
выписать множители, входящие в разложение одного из чисел; привести данные дроби к наименьшему общему знаменателю;
привести данные дроби к наименьшему общему знаменателю;
 провести умножение делимого и преобразованного делителя.
провести умножение делимого и преобразованного делителя.
 Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».
Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».
 В основном изготавливается из стали. Молоток — один из древнейших инструментов, используемых разумным человеком.
В основном изготавливается из стали. Молоток — один из древнейших инструментов, используемых разумным человеком. И это будет формальное «определение» для изготовления. Формальное «определение» для использования тоже потребуются, если этим молотком будет пользоваться не человек, а машина.
И это будет формальное «определение» для изготовления. Формальное «определение» для использования тоже потребуются, если этим молотком будет пользоваться не человек, а машина. И таких способов слишком много, и только самые важные появляются в статьях этой серии. И способ, которым является сама Математика, будет рассмотрен в текущей статье. Да, мы будем с помощью Математики описывать как работает Математика. Думаю, Льюис Кэрролл порадовался бы такому приключению для Алисы. С чего же нам начать? Ах, да…
И таких способов слишком много, и только самые важные появляются в статьях этой серии. И способ, которым является сама Математика, будет рассмотрен в текущей статье. Да, мы будем с помощью Математики описывать как работает Математика. Думаю, Льюис Кэрролл порадовался бы такому приключению для Алисы. С чего же нам начать? Ах, да… Что же это за близнецы Перенос и Трансляция? И почему необходимо их все же различать для продолжения разговора об Алгоритме?
Что же это за близнецы Перенос и Трансляция? И почему необходимо их все же различать для продолжения разговора об Алгоритме? – Я сбилась со счета.
– Я сбилась со счета. На основе этого знания попробуем запланировать количество труда «пастуха» (читай написать алгоритм вычисления трудозатрат). Для этого не нужно знать слово «количество» и даже знание «чисел» не является необходимым.
На основе этого знания попробуем запланировать количество труда «пастуха» (читай написать алгоритм вычисления трудозатрат). Для этого не нужно знать слово «количество» и даже знание «чисел» не является необходимым. Суровая сила эволюционного отбора. Не будем рассказывать это Алисе и оставим такие сведения для взрослых размышлений.
Суровая сила эволюционного отбора. Не будем рассказывать это Алисе и оставим такие сведения для взрослых размышлений.
 И что нужно с ними сделать? Правильно сопоставить! Палец сопоставим слову «один». А камешек сопоставим одной корове. Легко сказать «сопоставить». А каким алгоритмом это можно сделать?
И что нужно с ними сделать? Правильно сопоставить! Палец сопоставим слову «один». А камешек сопоставим одной корове. Легко сказать «сопоставить». А каким алгоритмом это можно сделать? С ними можно выполнить подсчет. С кучкой камней легко придумать алгоритм формирования запаса сена на зиму в отдельном от коровника хранилище. И можно выполнить много еще чего. Мы перенесли опору алгоритма запаса сеном на зиму с использования коров на использование камешков. И упростили жизнь «пастуху», сделав его уже немного «математиком».
С ними можно выполнить подсчет. С кучкой камней легко придумать алгоритм формирования запаса сена на зиму в отдельном от коровника хранилище. И можно выполнить много еще чего. Мы перенесли опору алгоритма запаса сеном на зиму с использования коров на использование камешков. И упростили жизнь «пастуху», сделав его уже немного «математиком». И эта область только поначалу была камешками, а в последствие дополнилась числами, интегралами, исчислением предикатов и много, много, много еще чем…
И эта область только поначалу была камешками, а в последствие дополнилась числами, интегралами, исчислением предикатов и много, много, много еще чем… Отказываться ли от этих «странных» отрицательных чисел? Или можно использовать их, но не переносить в коровы? Со знаниями, которыми обладает современный школьник старших классов, ответ тривиален. Конечно, использовать! И, видимо, Алисе придётся все же изучить и такое «странное» вычитание. Но «древним математикам» было не так легко. И только польза от алгоритмов, использующих отрицательные числа, помогла принять это сложное решение и ответить на заданный вопрос утвердительно. Да, нужно использовать отрицательные числа!
Отказываться ли от этих «странных» отрицательных чисел? Или можно использовать их, но не переносить в коровы? Со знаниями, которыми обладает современный школьник старших классов, ответ тривиален. Конечно, использовать! И, видимо, Алисе придётся все же изучить и такое «странное» вычитание. Но «древним математикам» было не так легко. И только польза от алгоритмов, использующих отрицательные числа, помогла принять это сложное решение и ответить на заданный вопрос утвердительно. Да, нужно использовать отрицательные числа! «Бесконечность», например, для нахождения значения предела сходящейся суммы бесконечного ряда (еще древнегреческий философ Зенона размышлял над этой странной задачей в парадоксе «Ахиллес и черепаха»). Парадоксов перед математиками было много. Некоторые все же исключались, потому что не было возможности использовать их в полезных алгоритмах. Так было, например, с парадоксом «Множество всех множеств». Но основой всех таких размышлений и решений было одно — наличие полезных алгоритмов, в которых использовались эти «странности». И тут «естественный отбор» тоже работал. И эволюционный способ формирования математических алгоритмов, медленным и в дополнение к нему быстрым накоплением привел к тому, что мы сейчас называем слово «Математика».
«Бесконечность», например, для нахождения значения предела сходящейся суммы бесконечного ряда (еще древнегреческий философ Зенона размышлял над этой странной задачей в парадоксе «Ахиллес и черепаха»). Парадоксов перед математиками было много. Некоторые все же исключались, потому что не было возможности использовать их в полезных алгоритмах. Так было, например, с парадоксом «Множество всех множеств». Но основой всех таких размышлений и решений было одно — наличие полезных алгоритмов, в которых использовались эти «странности». И тут «естественный отбор» тоже работал. И эволюционный способ формирования математических алгоритмов, медленным и в дополнение к нему быстрым накоплением привел к тому, что мы сейчас называем слово «Математика». Вне этого подмножества перенос невозможен. Как невозможна «минус одна корова». Эти ограничения необходимы в представленной модели с «отрицательными числами». Самой простой модели, которую удалось найти. Но такие же ограничения есть и для моделей с трансляцией куда более сложной. Все же здесь остановимся. Не будем всё сваливать в одну кучу — ведь перед нами нечто посложнее стада коров.
Вне этого подмножества перенос невозможен. Как невозможна «минус одна корова». Эти ограничения необходимы в представленной модели с «отрицательными числами». Самой простой модели, которую удалось найти. Но такие же ограничения есть и для моделей с трансляцией куда более сложной. Все же здесь остановимся. Не будем всё сваливать в одну кучу — ведь перед нами нечто посложнее стада коров. Пусть даже наградой будет лишь похвала и перечисление значимых свершений.
Пусть даже наградой будет лишь похвала и перечисление значимых свершений. Пожалуйста, не судите строго эту наивную публикацию «сверх-идеи» устаревшей версии 2019 года.
Пожалуйста, не судите строго эту наивную публикацию «сверх-идеи» устаревшей версии 2019 года. Если вы будете следовать инструкциям, вы сможете получить ответ в кратчайшие сроки!
Если вы будете следовать инструкциям, вы сможете получить ответ в кратчайшие сроки!
 Выровняйте числа по вертикали, сопоставив разряды.
Выровняйте числа по вертикали, сопоставив разряды. Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.
Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.
 Алгоритм здесь идентифицирует сообщения, с которыми вы взаимодействуете, и показывает вам больше таких сообщений, потому что считает, что вам нравятся такие сообщения.
Алгоритм здесь идентифицирует сообщения, с которыми вы взаимодействуете, и показывает вам больше таких сообщений, потому что считает, что вам нравятся такие сообщения. Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
 Налейте воду в пустую кастрюлю
Налейте воду в пустую кастрюлю
 Алгоритм получает ввод и производит вывод после выполнения конечного числа инструкций.
Алгоритм получает ввод и производит вывод после выполнения конечного числа инструкций. К сожалению, мы не можем сказать этого об операциях умножения и деления — они, как известно, сложны для понимания и выполнения даже для относительно небольших чисел. В частности, алгоритм деления, возможно, гораздо сложнее выполнить, чем умножение.
К сожалению, мы не можем сказать этого об операциях умножения и деления — они, как известно, сложны для понимания и выполнения даже для относительно небольших чисел. В частности, алгоритм деления, возможно, гораздо сложнее выполнить, чем умножение. Но это не относилось к ранним компьютерам, где у них были аппаратные блоки для выполнения только сложения и вычитания. Операции умножения и деления были построены с использованием программных подпрограмм сверху, с использованием повторяющихся сложений и вычитаний соответственно. Даже сегодня многие из крошечных маломощных процессоров по-прежнему не имеют встроенного аппаратного умножителя и/или делителя — просто потому, что эти две операции очень требовательны к ресурсам. Итак, в случае, если мы получим такие ограниченные процессоры, которые довольно распространены в крошечных гаджетах с низким энергопотреблением, таких как наручные часы (не умные часы) и дешевые карманные калькуляторы, нам потребуется программное решение.
Но это не относилось к ранним компьютерам, где у них были аппаратные блоки для выполнения только сложения и вычитания. Операции умножения и деления были построены с использованием программных подпрограмм сверху, с использованием повторяющихся сложений и вычитаний соответственно. Даже сегодня многие из крошечных маломощных процессоров по-прежнему не имеют встроенного аппаратного умножителя и/или делителя — просто потому, что эти две операции очень требовательны к ресурсам. Итак, в случае, если мы получим такие ограниченные процессоры, которые довольно распространены в крошечных гаджетах с низким энергопотреблением, таких как наручные часы (не умные часы) и дешевые карманные калькуляторы, нам потребуется программное решение. Если бы мы смогли найти эффективный алгоритм нахождения обратных величин, мы могли бы использовать гораздо более простую операцию умножения для решения задачи деления.
Если бы мы смогли найти эффективный алгоритм нахождения обратных величин, мы могли бы использовать гораздо более простую операцию умножения для решения задачи деления.
 Большинство наших математических методов основаны на желании не повторяться. Оказывается, это прямо противоположно тому, как компьютеры предназначены для работы. Компьютеры, как правило, превосходно справляются с повторяющимися задачами — на самом деле, они такие мощные, потому что очень эффективно выполняют простые повторяющиеся задачи. Вот почему очень трудно писать хорошие компьютерные алгоритмы, потому что мы должны отказаться от большинства методов, которые были оптимизированы для ручных вычислений, чтобы их выполняли люди.
Большинство наших математических методов основаны на желании не повторяться. Оказывается, это прямо противоположно тому, как компьютеры предназначены для работы. Компьютеры, как правило, превосходно справляются с повторяющимися задачами — на самом деле, они такие мощные, потому что очень эффективно выполняют простые повторяющиеся задачи. Вот почему очень трудно писать хорошие компьютерные алгоритмы, потому что мы должны отказаться от большинства методов, которые были оптимизированы для ручных вычислений, чтобы их выполняли люди. Теперь у нас может не быть точного результата, но мы можем сделать обоснованное предположение. Предположим, что наше первое предположение x ₁, которое может быть хорошим или нет, но мы можем написать следующее уравнение,
Теперь у нас может не быть точного результата, но мы можем сделать обоснованное предположение. Предположим, что наше первое предположение x ₁, которое может быть хорошим или нет, но мы можем написать следующее уравнение,
 Может показаться, что мы ходим по кругу, но есть простой выход. Если выберем, к = 1, тогда 1/ a отменяется, и у нас нет никаких проблем. Таким образом, при таком выборе k предыдущее уравнение может быть записано как
Может показаться, что мы ходим по кругу, но есть простой выход. Если выберем, к = 1, тогда 1/ a отменяется, и у нас нет никаких проблем. Таким образом, при таком выборе k предыдущее уравнение может быть записано как