Как сформулировать маркетинговые цели и задачи | by Transformator
Цели и задачи компании невероятно ценны для вашего бренда, они могут как укрепить, так и ослабить связь с потенциальными и нынешними клиентами.
Но разобраться в значении этих терминов не так просто, как кажется. Часто маркетологи считают цели и задачи синонимичными понятиями. Но это не так.
Бренды должны уметь формулировать цели и задачи, которые приведут их к успеху.
В маркетинге термины “цели” и “задачи” обычно не разграничиваются. Но между ними есть разница. Ее понимание может стать ключом к успеху бренда.
- Цели — общие направления, на основе которых составляется маркетинговая стратегия. Обычно это ожидаемый результат или выгода бизнеса.
- Задачи — конкретные действия, которые необходимо совершить для достижения поставленных целей.
Сначала бренд должен сформулировать цели или ожидаемые результаты маркетинговых усилий. Затем, ориентируясь на цели, необходимо составить список необходимых для их реализации действий и инициатив.
Затем, ориентируясь на цели, необходимо составить список необходимых для их реализации действий и инициатив.
Предположим, вы хотите улучшить показатели трафика и вовлеченности на сайте. В этом случае вашими целями будет увеличение трафика и вовлеченности посетителей. Конкретные стратегии, направленные на достижение этих целей, например, публикация SEO контента и его продвижение в соцсетях, — это ваши задачи.
При постановке целей используйте SMART подход, согласно которому они должны быть:
- Конкретными (Specific): ориентирующимися на конкретную метрику или показатель эффективности.
- Измеримыми (Measurable): поддающимися объективной оценке.
- Вдохновляющими (Aspirational): мотивирующими на действия.
- Реалистичными (Realistic): другими словами, достижимыми.
- Ограниченными во времени (Time-bound): эффективность которых оценивается спустя определенные промежутки времени.

Сформулировать цели вам также поможет следующий шаблон:
К ______ (время/дата) маркетинговая команда ______ (название компании) достигнет ______ (число/показатель) _____ (метрика).
Можно также использовать ориентир “каждый ______ (промежуток времени)”, чтобы формулировать для команды повторяющиеся цели.
Из всего вышесказанного понятно, что “привлечь больше трафика на сайт” — это не SMART цель. Вот как ее следует сформулировать:
“К концу второго квартала 2018 года маркетинговая команда JessWellsIncorporated будет привлекать на сайт 1 200 посетителей в месяц”.
Так намного лучше.
При формулировании целей важно помнить, что они должны быть конкретными.
Маркетинговые команды часто ставят перед собой следующие цели:
- Увеличить продажи
- Рассказать о новом продукте
- Повысить узнаваемость бренда
Подобные формулировки неэффективны. Их всегда следует дополнять конкретными метриками:
- Увеличить продажи на 5%
- Увеличить конверсию на посадочной странице нового продукта на 3%
- Привлекать 1 000 посетителей сайта и 10 новых клиентов каждый месяц
Чем конкретнее будут ваши цели, тем проще формулировать задачи.
Поставив перед собой конкретные и измеримые цели, ваша команда может начать формулировать задачи. При этом важно ориентироваться на данные о вашей аудитории.
Например, если вы обнаружили, что потребители активно реагируют на email-рассылку, этот прием, определенно, стоит включить в вашу маркетинговую стратегию.
Следующие тесты помогут вам избежать распространенных ошибок:
- Тест на понятность. Ваши цели и задачи четкие и ясные, нет ли в них двусмысленности (особенно в вопросе измерения результатов)?
- Тест на целесообразность. Ваши цели достаточно важны, они оправдывают связанные с их достижением расходы?
- Тест “И что из этого?”. Если вы не можете объяснить, почему ваша цель важна, что-то нужно менять.
Если вы затрудняетесь определить цели и задачи ваших маркетинговых усилий, используйте технику мозгового штурма SWOT.
Она подразумевает анализ внутренних и внешних факторов и определение элементов, выделяющих вас на фоне конкурентов, а также препятствий на пути к успеху.
SWOT расшифровывается следующим образом:
- Сильные стороны — Strengths (внутренние)
- Слабые стороны — Weaknesses (внутренние)
- Возможности — Opportunities (внешние)
- Угрозы — Threats (внешние)
Этот подход позволит убедиться, что ваши цели и задачи соотносятся с общими целями бизнеса. Для этого нужно учитывать следующие моменты:
- Какие у нашей компании сильные стороны? В чем наш маркетинг лучше, чем у конкурентов? Какие инструменты и ресурсы помогут нам в достижении целей?
- Какие у нашей компании слабые стороны? Как можно улучшить наши маркетинговые планы? Есть ли у нас ограничения в ресурсах, которое не позволит достичь поставленных целей?
- Какие возможности есть у нашего бренда? Можем ли мы создавать контент, интересный читателям? Можем ли мы извлечь выгоду из последних маркетинговых трендов?
- Какие угрозы могут повлиять на наш бренд? Что наши конкуренты делают лучше? Может ли ситуация на рынке или особенности аудитории помешать нам достичь поставленных целей?
После ответа на эти вопросы важно делать ставку на сильные стороны бренда и возможности, и при этом стараться максимально сократить влияние ваших слабостей и внешних угроз.
Когда вы и ваша маркетинговая команда, используя описанные выше приемы, поставит перед собой цели и сформулирует задачи, вы сможете сфокусироваться и действовать максимально уверенно и продуктивно.
Автор: Ия Пфанштиль
Источник
Основные цели, задачи и функции отдела маркетинга на предприятии — PowerBranding.ru
Основы → Основные элементы и принципы маркетинга → Чем занимается маркетинг?
В современной литературе существует множество определений термина «маркетинг», но не столько важно знать все определения, сколько важно понимать, что все они отражают единую суть маркетинговой деятельности: для получения прибыли кампания должна эффективно, на конкурентоспособном уровне продавать свои товары или услуги конечному покупателю.
В современной практике выделяют 6 основных функций и задач отдела маркетинга на предприятии. Но важно не знать все функции, а правильно использовать это знание на практике. Поэтому мы не просто разберем каждую функцию службы маркетинга, а по каждой рассмотренной задаче определим основную цель для маркетинга, по которой можно оценивать эффективность работы всего отдела.
Какие основные KPI менеджера по маркетингу?
Читайте в нашей подробной статье об основных индикаторах эффективности маркетинговой деятельности: «Основные KPI менеджера по маркетингу».
Задача маркетинга №1: Повышение воспринимаемой ценности продукта
Главная задача и цель всей маркетинговой деятельности: убедить покупателя заплатить больше за товар компани. Ценность товара для конечного покупателя определяется с помощью оценки «воспринимаемой ценности продукта» и формируется на основе представления о свойствах и пользе товара. Высокая воспринимаемая ценность продукта — результат эффективного брендинга и правильной рекламной кампании.
Выразить данную функцию маркетинга в виде конкретной цели можно через рентабельность единицы продукции (или рентабельность продаж), рост общего объема продаж и рост прибыли. Так как маркетолог управляет рекламным бюджетом, который тратиться на повышение воспринимаемой ценности товара, то цель по прибыли обычно устанавливается за вычетом рекламных расходов.
Задача маркетинга №2: Анализ рынка и выбор целевых рынков сбыта
Аналитическая (или исследовательская) функция маркетинга в компании выражается в необходимости проведения постоянного мониторинга рынка, в отслеживании ключевых рыночных тенденций, в поиске новых свободных рыночных ниш и рынков сбыта. Задачи службы маркетинга в данном направлении должны быть сосредоточены на построении регулярного сбора первичной информации о динамике рынка, конкурентах и ключевых драйверах рынка. Чем лучше компания понимает рынок, тем быстрее она может правильно войти в новые ниши, своевременно отреагировать на агрессивные действия конкурентов, закрыть бизнес в стагнирующих сегментах.
Отслеживать эффективность работы в данном направлении можно через установление целей для отдела маркетинга по росту продаж, опережающих темпы роста ключевых рынков, на которых работает предприятие.
Задача маркетинга №3: Работа с потребителями
Работа с потребителями — приоритетное направление любой службы маркетинга. Маркетолог должен говорить с потребителями на одном языке, понимать их потребности, ценности, модель совершения покупки, причины отказа от покупки и восприятие ключевых брендов в отрасли. Зная данную информацию, очень легко провести сегментирование рынка, определить целевую аудиторию компании, разработать эффективное рекламное сообщение и показать его в нужных каналах коммуникации. В задачу «работа с потребителями» входит работа с текущей потребительской базой с целью увеличения частоты и объема покупок (что проявляется через лояльность к компании).
Маркетолог должен говорить с потребителями на одном языке, понимать их потребности, ценности, модель совершения покупки, причины отказа от покупки и восприятие ключевых брендов в отрасли. Зная данную информацию, очень легко провести сегментирование рынка, определить целевую аудиторию компании, разработать эффективное рекламное сообщение и показать его в нужных каналах коммуникации. В задачу «работа с потребителями» входит работа с текущей потребительской базой с целью увеличения частоты и объема покупок (что проявляется через лояльность к компании).
Установив цель по росту клиентов (или потребительской базы) и повышению лояльности к компании, вы сможете всегда проследить качество работы вашего отдела маркетинга в данном направлении.
Задача маркетинга №4: Разработка стратегии и принципов конкуренции
Отдел маркетинга участвует в стратегическом планировании компании. Благодаря знанию рынка, конкурентов и особенностей потребления, служба маркетинга может разработать оптимальную стратегию роста продаж, повышения конкурентоспособности продукта, определить ключевые рынки сбыта и предложить эффективную стратегию продвижения товара компании. На основе утвержденной стратегии рождается план тактических мероприятий, расписанный на год.
На основе утвержденной стратегии рождается план тактических мероприятий, расписанный на год.
Задача маркетинга №5: Управление ассортиментом компании
Управление широтой ассортимента, установление цен на товары и контроль рентабельности каждого SKU компании — основные задачи товарной (производственной) функции маркетинга на предприятии. Служба маркетинга регулярно отслеживает спрос на каждый продукт, ведет проектную работу по вводу на рынок новых продуктов, определяет локомотивные товары компании и предлагает снять неликвидный ассортимент. Эффективное управление ассортиментом позволяет значимо снизить затраты компании на хранение товара, повышает рентабельность продаж и обеспечивает стабильный рост продаж каждой товарной группы в портфеле организации.
Задача маркетинга №6: Анализ результатов работ
Организационная, управленческая и контрольная функция — неотъемлемые задачи любой маркетинговой деятельности. Отдел маркетинга постоянно курирует множество проектов по разработке новых продуктов, по продвижению товара, по исследованию новых рынков; оценивает эффективность проведенных маркетинговых программ, отслеживает динамику индикаторов здоровья бренда и подводит анализ свой работы на ежегодной основе.
Please enable JavaScript to view the comments powered by Disqus.comments powered by Disqus
Роль отдела маркетинга в бизнесе
Отдел маркетинга играет жизненно важную роль в продвижении бизнеса и миссии организации. Он служит лицом вашей компании, координируя и производя все материалы, представляющие бизнес. Работа отдела маркетинга заключается в том, чтобы обратиться к потенциальным клиентам, клиентам, инвесторам и/или сообществу, создавая общий образ, который представляет вашу компанию в положительном свете.
В зависимости от вашей компании обязанности отдела маркетинга могут включать одно или несколько из следующих действий:
- Определение и управление вашим брендом. Это включает в себя определение того, кто вы, что вы отстаиваете, что вы говорите о себе, что вы делаете и как действует ваша компания. Это, в свою очередь, определяет опыт, который вы хотите получить от своих клиентов и партнеров при взаимодействии с вами.

- Управление кампаниями по маркетинговым инициативам. Маркетинг заблаговременно определяет продукты и услуги, на которых следует сосредоточиться в течение цикла продаж, а затем создает материалы и сообщения, которые доносят информацию.
- Производство маркетинговых и рекламных материалов. Ваш отдел маркетинга должен создавать материалы, описывающие и продвигающие ваши основные продукты и/или услуги. Их следует обновлять по мере развития этих продуктов и услуг.
- Создание контента, обеспечивающего поисковую оптимизацию вашего веб-сайта. Ваш веб-сайт часто является первым (и, возможно, единственным) местом, куда люди обращаются за информацией о вас. Ваш отдел маркетинга будет нести ответственность за актуальность веб-контента, а также следить за тем, чтобы ваш сайт быстро появлялся, когда кто-то ищет информацию о вашем бизнесе.
- Мониторинг и управление социальными сетями. Маркетинг должен способствовать, управлять и поддерживать ваши страницы в социальных сетях.
 Он также должен управлять учетными записями и внимательно следить за тем, что публикуется о вас в Интернете.
Он также должен управлять учетными записями и внимательно следить за тем, что публикуется о вас в Интернете. - Производство внутренних коммуникаций. Ваши сотрудники должны понимать вашу компанию, ее ценности, цели и приоритеты. Маркетинг часто отвечает за общение сотрудников через информационный бюллетень и/или интранет.
- Выступает в качестве представителя СМИ. Когда ваша компания цитируется в средствах массовой информации, сотрудник отдела маркетинга часто выступает в качестве представителя вашей компании или дает указания руководителям, как отвечать на запросы СМИ.
- Проведение исследований клиентов и рынка. Исследования помогают определить целевые рынки и возможности, а также помогают понять, как воспринимаются ваши продукты и услуги.
- Надзор за внешними поставщиками и агентствами. Маркетинг обычно отвечает за выбор и управление агентствами и поставщиками, которые производят маркетинговые материалы и/или предоставляют маркетинговую поддержку.
 К ним могут относиться рекламные агентства, поставщики полиграфии, PR-агентства или специалисты, веб-провайдеры и т. д.
К ним могут относиться рекламные агентства, поставщики полиграфии, PR-агентства или специалисты, веб-провайдеры и т. д.
Вот уже более 200 лет компании доверяют The Hartford. Мы можем помочь вам получить правильное покрытие с помощью онлайн-котировки.
Начальная котировка
задач управления маркетингом: 8 обязанностей, которые нужно освоить
Ожидается, что в течение следующего десятилетия перспективы работы для менеджеров по маркетингу вырастут на 10%, что быстрее, чем в среднем по стране среди всех должностей.
Почему?
Скорее всего потому, что это сложная работа, требующая не только лидерских качеств, но и творчества, дальновидности и глубокого понимания концепций маркетинга. Когда вы посмотрите на все, что делают эти менеджеры, вы обнаружите, что на них лежит так много обязанностей. Если вы хотите получить некоторое представление о том, что для этого требуется, мы обрисовали в общих чертах некоторые из наиболее важных задач управления маркетингом ниже.
Управление маркетингом или управление маркетинговыми проектами — это роль с широким кругом обязанностей. Менеджеры по маркетингу возглавляют маркетинговые команды, что означает, что они контролируют брендинг, стратегии, кампании, ход проекта, показатели, измеряющие успех и инвестиции, и многое другое.
Организация находится в центре управления маркетингом. Чтобы контролировать все эти вещи, оптимизируя кампании и выполняя проекты вовремя, менеджерам по маркетингу нужны организационные навыки высокого уровня, чтобы помочь со всем планированием, составлением графиков и отслеживанием, которые связаны с работой.
Программное обеспечение для планирования проектов также является огромным плюсом. Организационные навыки — это полдела, и вам понадобится платформа, которая даст вам место для всей организации. Щелкните здесь , чтобы узнать, как сделать планирование проектов простым, интуитивно понятным и эффективным с помощью Teamwork.
Как мы уже говорили, управление маркетингом — это обширная роль с множеством различных обязанностей. Хотя приведенный ниже список не является исчерпывающим, он охватывает основные элементы, которые помогут создать сильный бренд, достичь маркетинговых целей и обеспечить долгосрочный рост.
Хотя приведенный ниже список не является исчерпывающим, он охватывает основные элементы, которые помогут создать сильный бренд, достичь маркетинговых целей и обеспечить долгосрочный рост.
1. Разработка маркетинговых стратегий и кампаний
Наиболее важной задачей управления маркетингом является планирование и разработка стратегий и кампаний. Хотя менеджеры не выполняют всю эту работу самостоятельно (для этого и предназначена остальная маркетинговая команда), они играют ключевую роль в этом процессе.
Запускайте новые кампании, начиная с мозгового штурма и заканчивая работой над проектом.
Контролировать весь маркетинговый процесс, что означает, что одной из ключевых функций является обеспечение последовательного брендинга в стратегиях и кампаниях.
Организуйте задачи в рамках кампаний, чтобы убедиться, что маркетинговые усилия проходят гладко, а члены команды знают, что и когда делать.
Планировать очень много, и даже лучшие менеджеры по маркетингу не могут организовать все это без небольшой дополнительной помощи. Вот где Teamwork приходит на помощь: ознакомьтесь с нашим шаблоном маркетинговой кампании , чтобы упростить процесс планирования.
Вот где Teamwork приходит на помощь: ознакомьтесь с нашим шаблоном маркетинговой кампании , чтобы упростить процесс планирования.
2. Отслеживание и мониторинг маркетинговых кампаний
В управлении маркетингом существует три способа отслеживания и мониторинга кампаний: управление ресурсами, целей и ключевых результатов (OKR) и ключевых показателей эффективности (KPI).
Управление ресурсами означает отслеживание как бюджета, так и человеческих ресурсов, чтобы убедиться, что время и деньги распределяются надлежащим образом.
OKR — это измерения (например, достижение 1000 подписчиков в социальных сетях или увеличение посещаемости веб-сайта на 10%), которые вы устанавливаете в качестве вех для отслеживания прогресса на пути к более крупной цели.
Ключевые показатели эффективности измеряют эффективность маркетинговой программы, что делает их важными для оптимизации кампаний.
3.
 Сбор отзывов от клиентов
Сбор отзывов от клиентовВ прошлом маркетинг полагался почти исключительно на рекламу, но современные маркетологи должны предлагать больше с точки зрения потребительской ценности. Это означает связь с целевыми клиентами с помощью маркетинга в социальных сетях и других тактик, таких как сбор отзывов клиентов. Обратная связь является особенно эффективным маркетинговым приемом, поскольку она строится на отношениях с клиентами, поощряя лояльность к бренду и вовлеченность.
4. Создание сильного и надежного бренда
Понимание бренда организации является ключевой частью управления маркетингом, и менеджеры должны уметь использовать это понимание для создания более сильного бренда при одновременном повышении узнаваемости бренда.
Это означает смотреть на бренд так, как его видят покупатели. Каковы сильные и слабые стороны бренда? Собирая подобные маркетинговые идеи, менеджеры могут управлять брендингом, чтобы лучше доносить ценность до существующих и новых клиентов, чтобы лучше донести ценность.
5. Внедрение новых продуктов или услуг
Разработка новых продуктов означает запуск новых продуктов, перед которыми ставится собственный набор задач. Большая часть процесса управления будет заключаться в сборе маркетинговой информации о целевых рынках и о том, как новые продукты принесут пользу клиентам. Это поможет вашей команде проанализировать потенциал рынка и создать рекламные кампании, отвечающие потребностям клиентов.
6. Увеличение продаж компании
Целью каждого отдела маркетинга является увеличение продаж компании, и как руководители групп, менеджеры несут ответственность, когда продажи растут или падают. Эффективные менеджеры будут знать, как использовать маркетинговые возможности, проводить исследования рынка и использовать эту информацию, чтобы помочь своим командам разрабатывать кампании, которые приведут новых потенциальных клиентов и новых платежеспособных клиентов.
7. Обеспечение ценности для ваших клиентов и потенциальных клиентов
Один из основных принципов маркетинга заключается в том, что вам необходимо создавать ценность для клиентов и потенциальных клиентов, чтобы стимулировать продажи. На практике это означает тщательный анализ как клиентов, так и самого продукта. Начните с изучения болевых точек клиентов, чтобы вы могли решить их с помощью контент-маркетинга или других типов кампаний.
На практике это означает тщательный анализ как клиентов, так и самого продукта. Начните с изучения болевых точек клиентов, чтобы вы могли решить их с помощью контент-маркетинга или других типов кампаний.
Не забудьте также глубоко изучить сам продукт. Узнайте, чем он превосходит предложения конкурентов, определите, что делает его незаменимым, и узнайте, как он улучшит жизнь тех, кто его купит. Это ценная информация, которую можно добавить в маркетинговый комплекс, чтобы ваша команда могла разрабатывать кампании, которые продаются.
8. Обеспечение успешного маркетингового роста с течением времени
Существует большая разница между маркетинговыми кампаниями и маркетинговыми стратегиями . Думайте о кампании как о спринте: это краткосрочные усилия, направленные на увеличение продаж.
С другой стороны, маркетинговые стратегии ориентированы на долгосрочную перспективу и используют целостный маркетинговый подход, часто учитывающий сразу несколько кампаний.



 Он также должен управлять учетными записями и внимательно следить за тем, что публикуется о вас в Интернете.
Он также должен управлять учетными записями и внимательно следить за тем, что публикуется о вас в Интернете. К ним могут относиться рекламные агентства, поставщики полиграфии, PR-агентства или специалисты, веб-провайдеры и т. д.
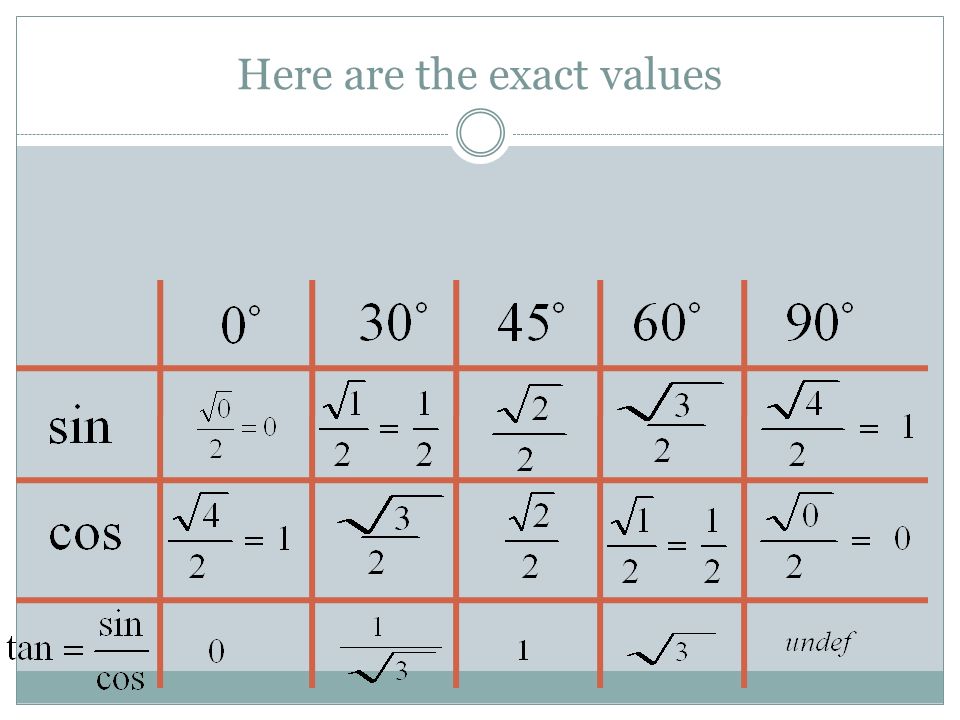
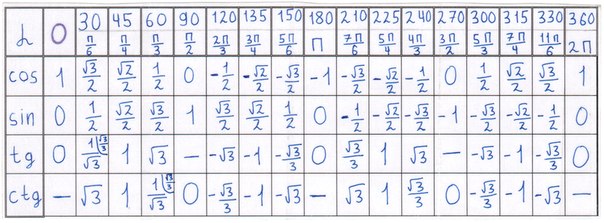
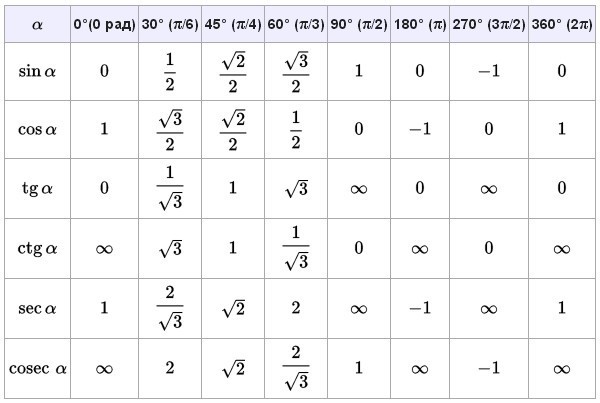
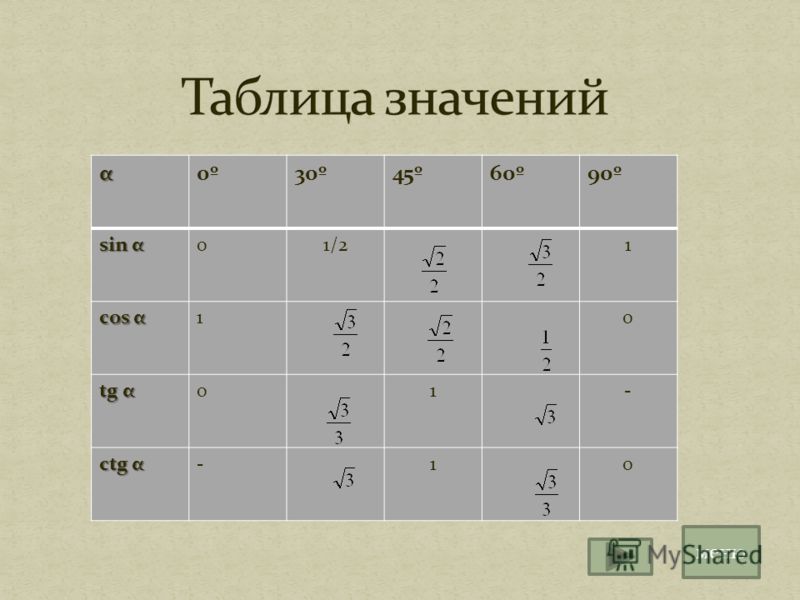
К ним могут относиться рекламные агентства, поставщики полиграфии, PR-агентства или специалисты, веб-провайдеры и т. д. Обычно любой тригонометрический расчет просто свести к вычислению нескольких заметных углов для
косинус
и
синус
.
Обычно любой тригонометрический расчет просто свести к вычислению нескольких заметных углов для
косинус
и
синус
.

 Те, которые не могут быть упрощены напрямую (если таковые имеются), оставляют как есть, или дают приближенное (
округлённое значение
) из них
Те, которые не могут быть упрощены напрямую (если таковые имеются), оставляют как есть, или дают приближенное (
округлённое значение
) из них
 Процесс прост: он заключается в следующем
упрощение выражений
в которых используются только числа, дроби и общие числовые выражения с прямой оценкой.
Процесс прост: он заключается в следующем
упрощение выражений
в которых используются только числа, дроби и общие числовые выражения с прямой оценкой.
 … Можете ли вы упростить это? Является ли это заметным углом?
… Можете ли вы упростить это? Является ли это заметным углом?

 7071\).
7071\).
 0125\).
0125\).
 8706\).
8706\).
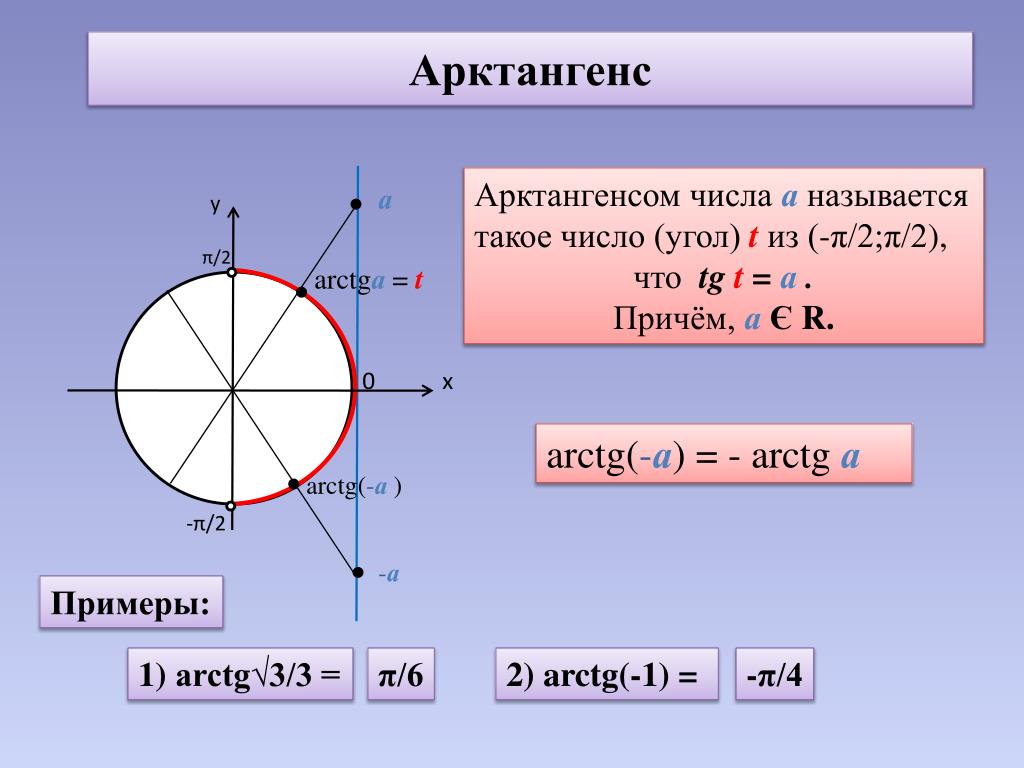
 Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).
Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).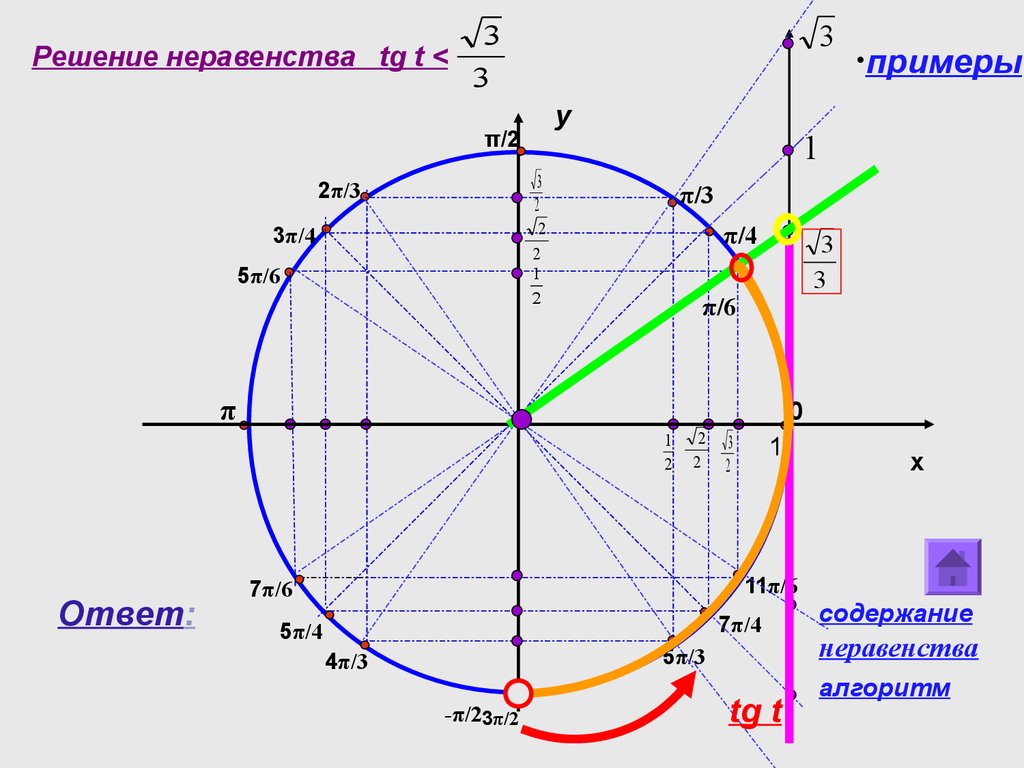 Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции.
Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции. Функции онлайн калькулятора >>
Функции онлайн калькулятора >>
 Онлайн-калькулятор и решатель простых тригонометрических уравнений с функцией тангенса вида tan x = a.
Онлайн-калькулятор и решатель простых тригонометрических уравнений с функцией тангенса вида tan x = a. Найдите квадрант угла в стандартном положении.
Найдите квадрант угла в стандартном положении.
 Вычислить обратную тригонометрическую функцию arccsc(x) в радианах и градусах.
Вычислить обратную тригонометрическую функцию arccsc(x) в радианах и градусах.
 Но вероятность точного припоминания каждый раз для нас все равно меркнет. Учитывая эту проблему, мы разработали калькулятор SOH CAH TOA, чтобы помочь вам определить правильное тригонометрическое соотношение.
Но вероятность точного припоминания каждый раз для нас все равно меркнет. Учитывая эту проблему, мы разработали калькулятор SOH CAH TOA, чтобы помочь вам определить правильное тригонометрическое соотношение. Они даны следующим образом:
Они даны следующим образом: Позвольте нам вести вас!
Позвольте нам вести вас!
 такжеСоздание графика и добавление уравнений с помощью Графического калькулятора на MacСтатья службы поддержки Apple: «Сочетания клавиш Mac»
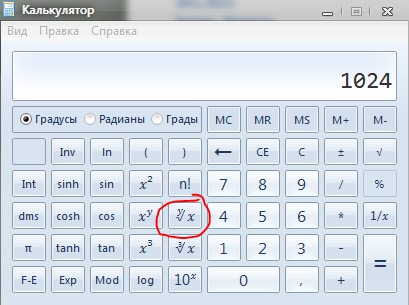
такжеСоздание графика и добавление уравнений с помощью Графического калькулятора на MacСтатья службы поддержки Apple: «Сочетания клавиш Mac» (1/3) 4 = 0, что может быть легче решить. 3) Кубический корень можно использовать в различных приложениях в науке, технике и других областях. Например, в физике кубический корень из объема используется для вычисления объема куба с заданной длиной стороны. В финансах кубический корень из цены акции используется для расчета отношения цены акции к прибыли.
(1/3) 4 = 0, что может быть легче решить. 3) Кубический корень можно использовать в различных приложениях в науке, технике и других областях. Например, в физике кубический корень из объема используется для вычисления объема куба с заданной длиной стороны. В финансах кубический корень из цены акции используется для расчета отношения цены акции к прибыли.
 Функциональная клавиша извлечения квадратного корня расположена над клавишей x -квадрат (x 2 ). Чтобы получить доступ к функции извлечения квадратного корня, нажмите вторую функциональную клавишу (2-ю) в верхнем левом углу клавиатуры. Затем нажмите клавишу x 2 и введите значение для оценки. Нажмите Enter, чтобы вычислить квадратный корень.
Функциональная клавиша извлечения квадратного корня расположена над клавишей x -квадрат (x 2 ). Чтобы получить доступ к функции извлечения квадратного корня, нажмите вторую функциональную клавишу (2-ю) в верхнем левом углу клавиатуры. Затем нажмите клавишу x 2 и введите значение для оценки. Нажмите Enter, чтобы вычислить квадратный корень. Если программирование калькулятора включает порядок операций, то последовательность будет правильно рассчитана как
Если программирование калькулятора включает порядок операций, то последовательность будет правильно рассчитана как Изучение клавиатуры показывает, что символ квадратного корня (√) находится над квадратной функцией (x 2 ), что указывает на то, что клавиша извлечения квадратного корня является второй функцией. Для доступа ко вторым функциональным клавишам используйте желтую клавишу с пометкой «2nd», расположенную в верхнем левом углу клавиатуры. Нажмите «2nd», а затем клавишу под символом нужной функции.
Изучение клавиатуры показывает, что символ квадратного корня (√) находится над квадратной функцией (x 2 ), что указывает на то, что клавиша извлечения квадратного корня является второй функцией. Для доступа ко вторым функциональным клавишам используйте желтую клавишу с пометкой «2nd», расположенную в верхнем левом углу клавиатуры. Нажмите «2nd», а затем клавишу под символом нужной функции. Итак, чтобы найти длину стороны квадрата с помощью ТИ-83 или ТИ-84, начните с желтой «2-й» клавиши, а затем нажмите х 2 ключ для доступа к функции извлечения квадратного корня. Введите площадь, 225, и нажмите Enter, чтобы найти квадратный корень. Длина каждой стороны квадрата равна 15 метрам.
Итак, чтобы найти длину стороны квадрата с помощью ТИ-83 или ТИ-84, начните с желтой «2-й» клавиши, а затем нажмите х 2 ключ для доступа к функции извлечения квадратного корня. Введите площадь, 225, и нажмите Enter, чтобы найти квадратный корень. Длина каждой стороны квадрата равна 15 метрам.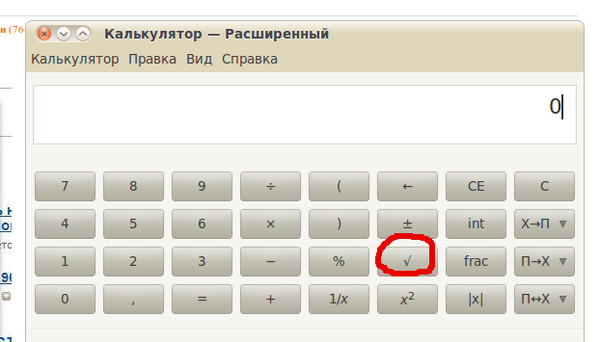 Чтобы найти значение квадратного корня, используйте ту же процедуру: нажмите клавишу «2», затем клавишу x 2 , число и Enter.
Чтобы найти значение квадратного корня, используйте ту же процедуру: нажмите клавишу «2», затем клавишу x 2 , число и Enter.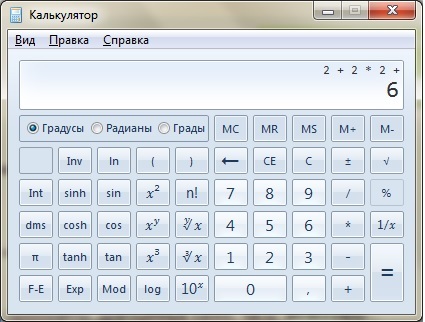

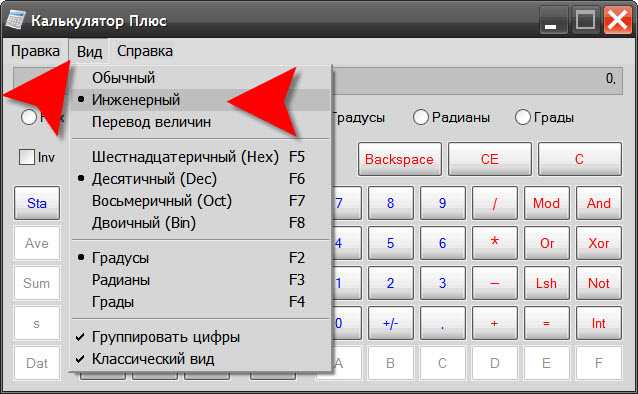
 MacOS позволяет вам вводить символ в любом приложении, которое позволяет печатать, включая ваш веб-браузер.
MacOS позволяет вам вводить символ в любом приложении, которое позволяет печатать, включая ваш веб-браузер.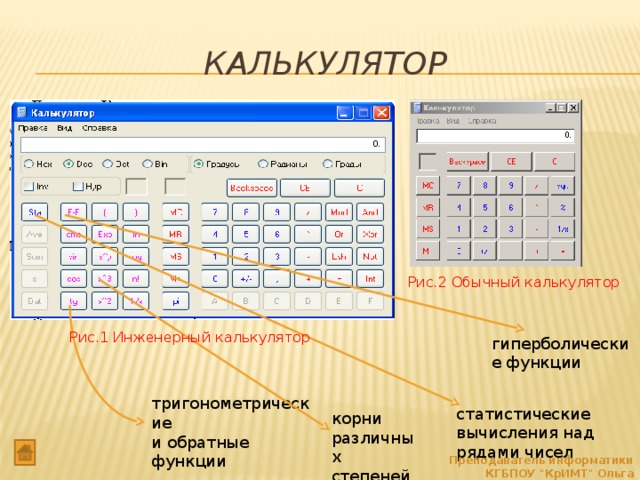 Должен появиться символ квадратного корня.
Должен появиться символ квадратного корня.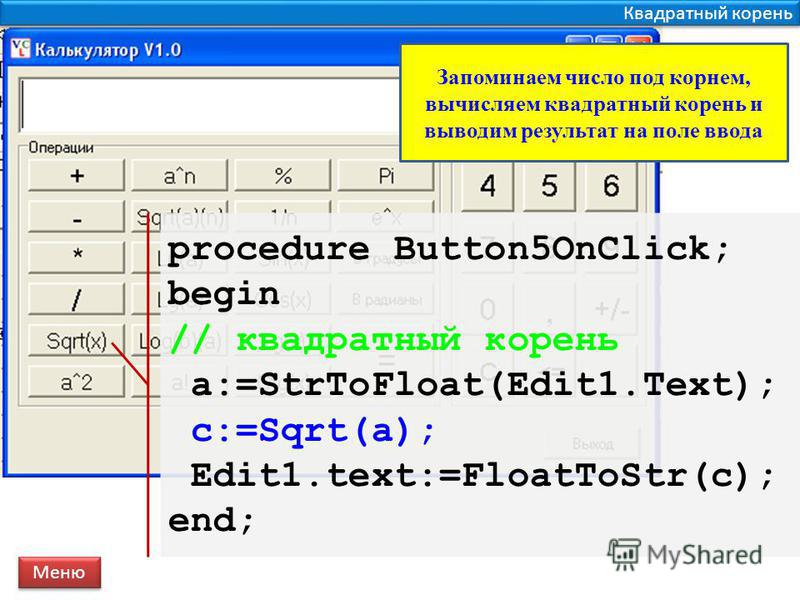
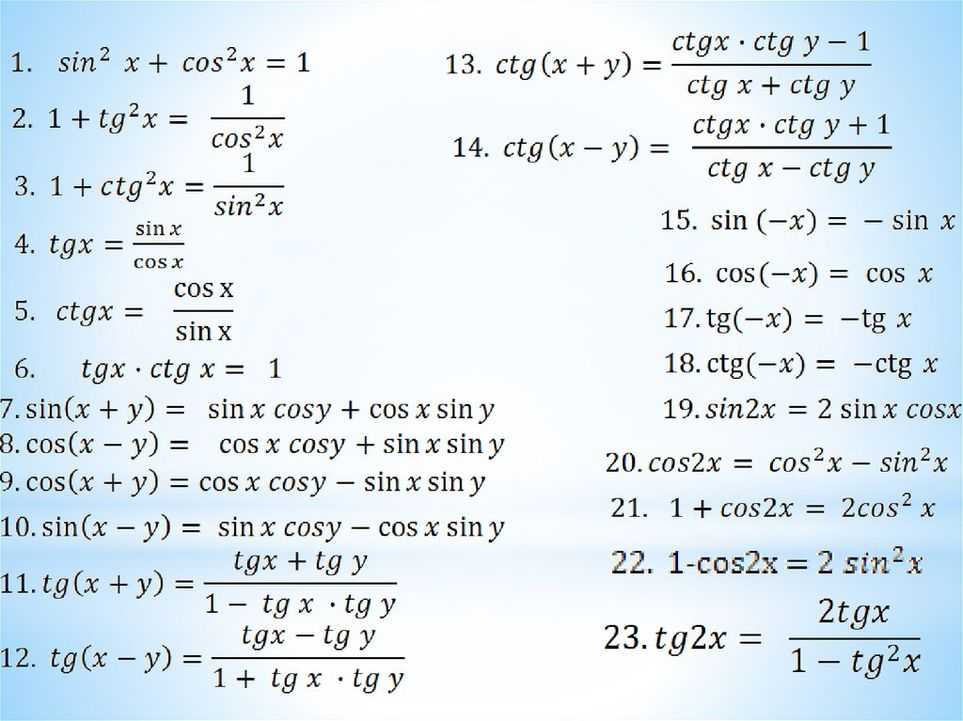





 0175
0175  0698
0698 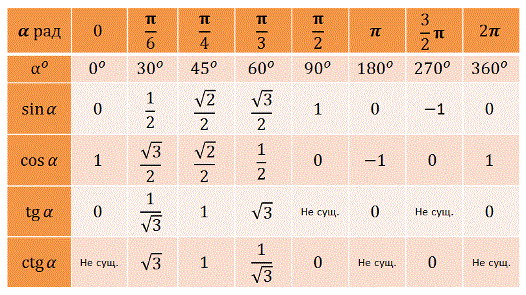 4137
4137 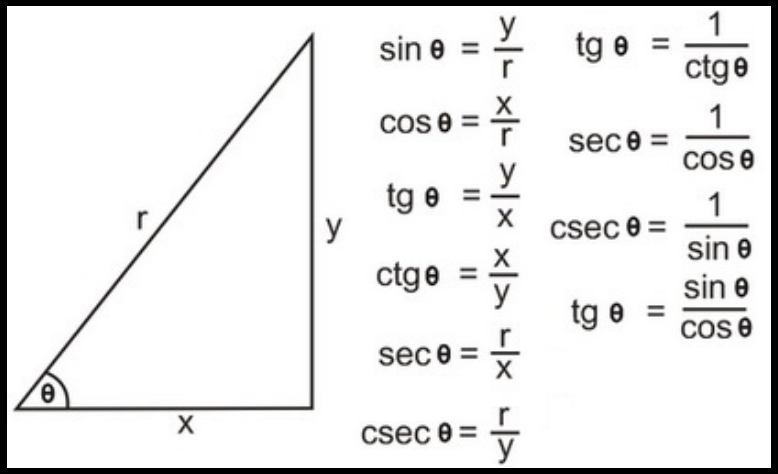 0223
0223 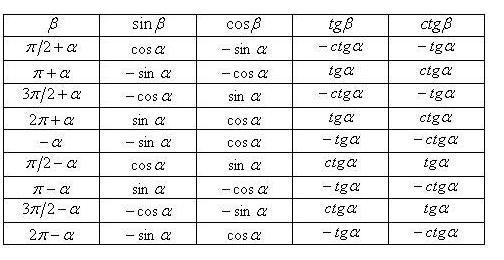 9659
9659  3142
3142 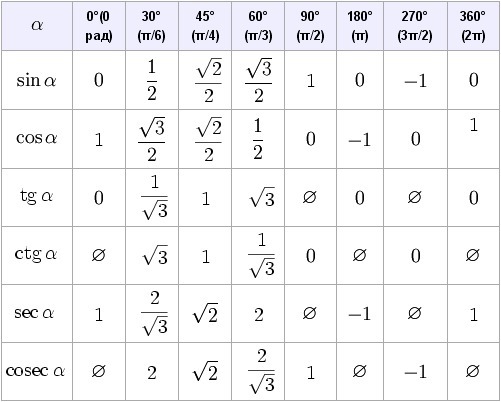 2217
2217 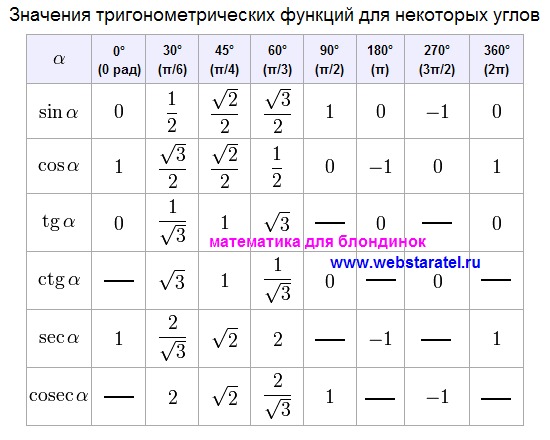 1694
1694 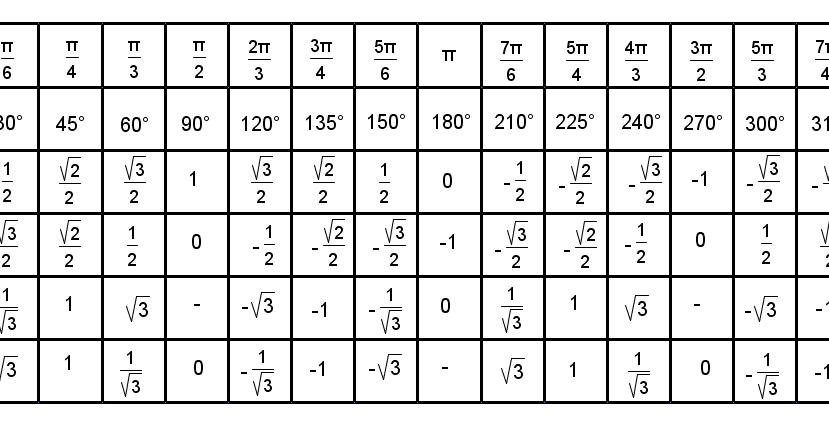 1126
1126 8746
8746  5585
5585  2521
2521 7660
7660 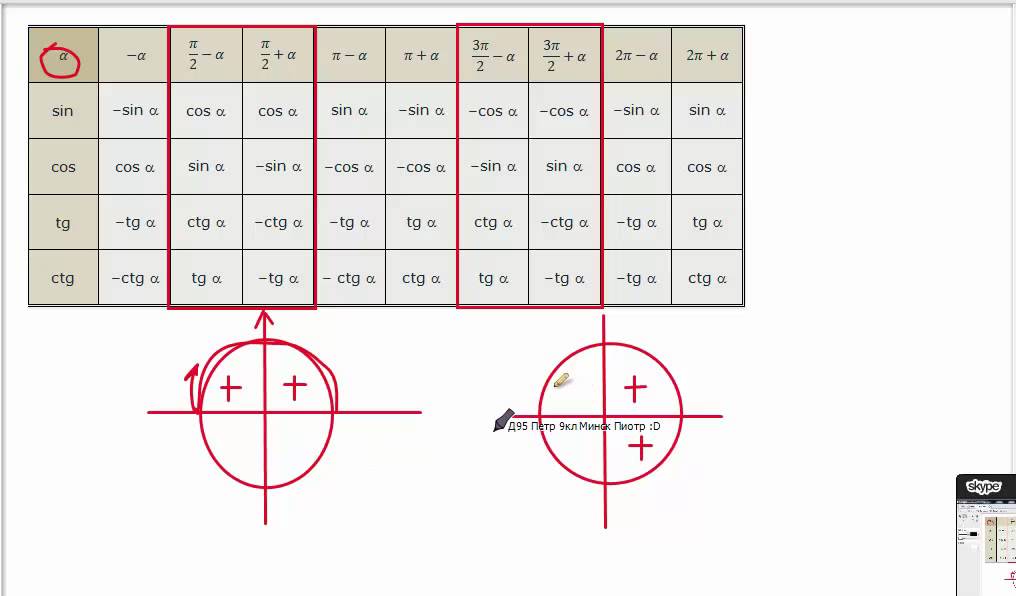 7505
7505  7854
7854 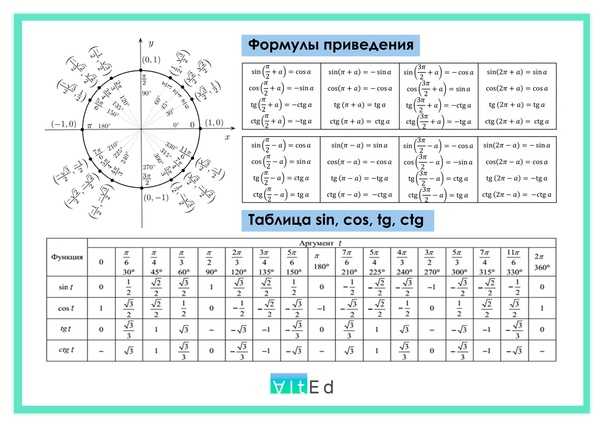 Они включены исключительно для демонстрации шаблона.
Они включены исключительно для демонстрации шаблона. Мы можем использовать приведенную ниже фразу, чтобы запомнить
Мы можем использовать приведенную ниже фразу, чтобы запомнить  $\sin 120 = \cos (180 -60) = \sin 60$. Здесь, поскольку sin положителен во II квадранте, мы ставим положительный знак
$\sin 120 = \cos (180 -60) = \sin 60$. Здесь, поскольку sin положителен во II квадранте, мы ставим положительный знак

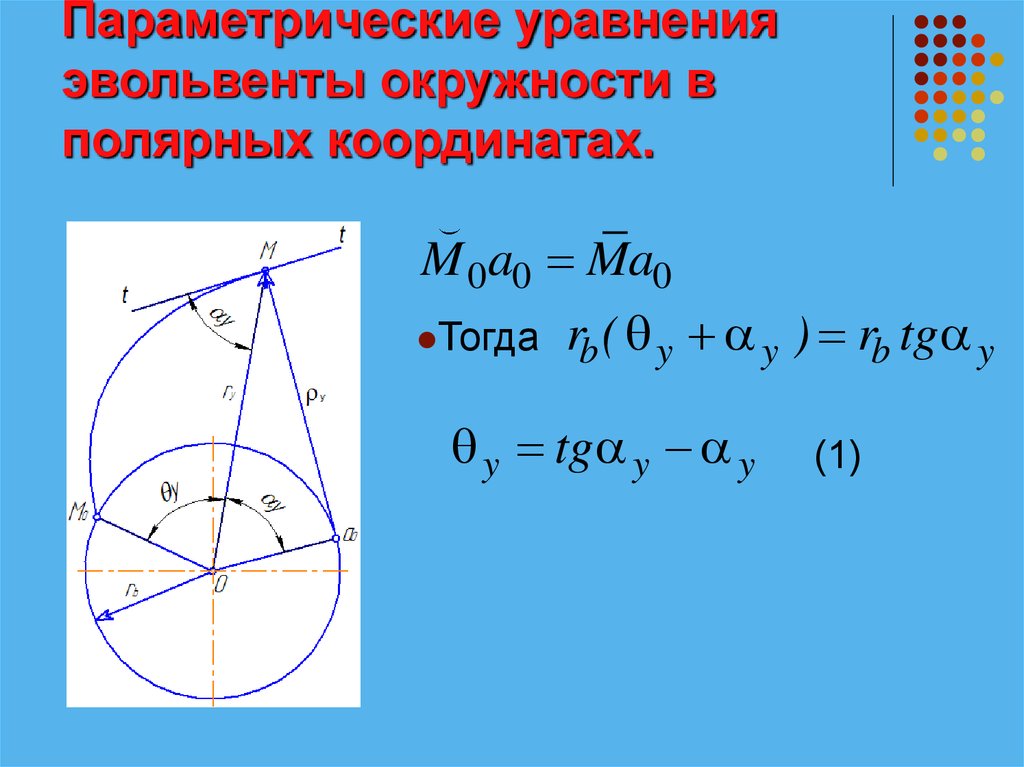
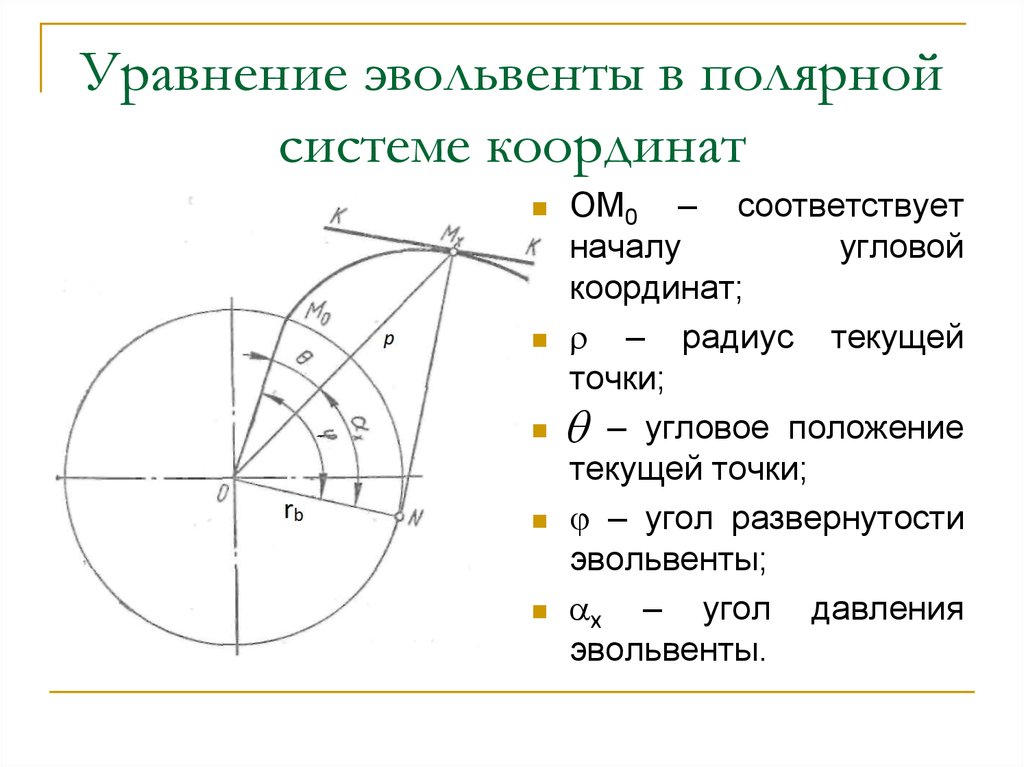
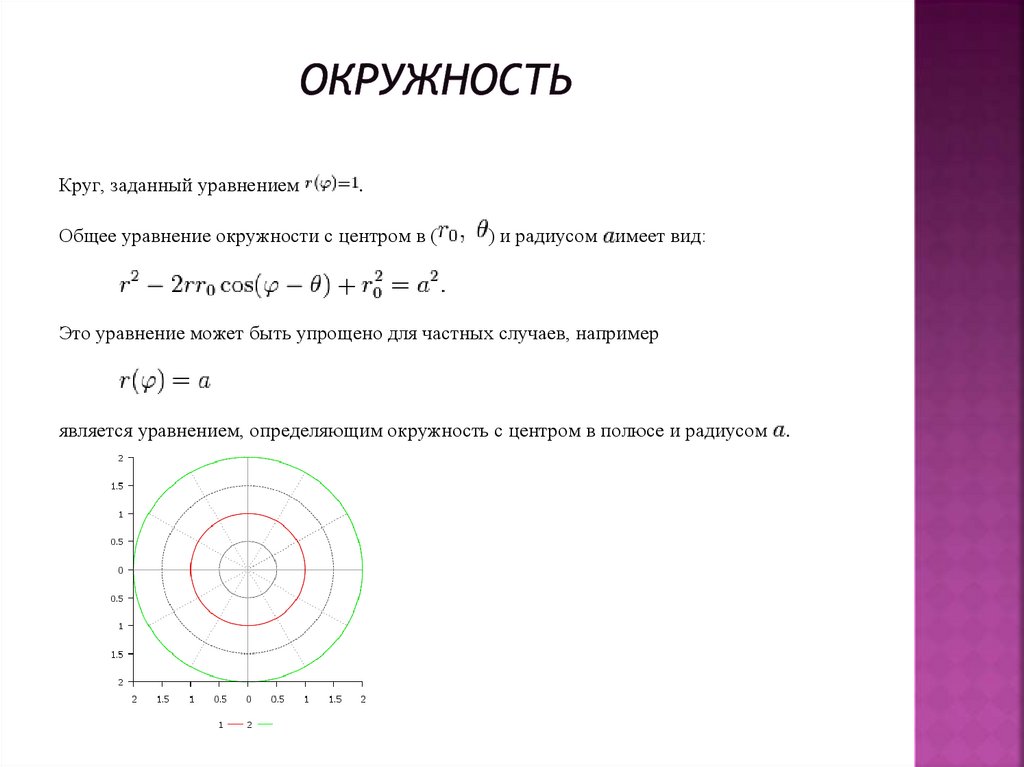 ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ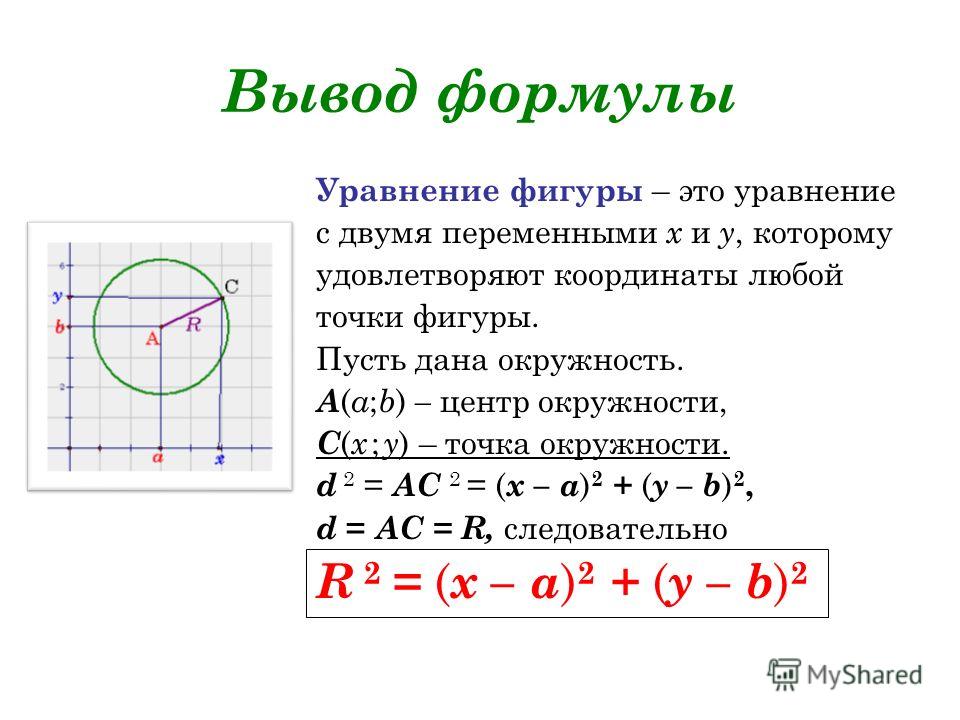 Общие уравнения прямой.
Общие уравнения прямой.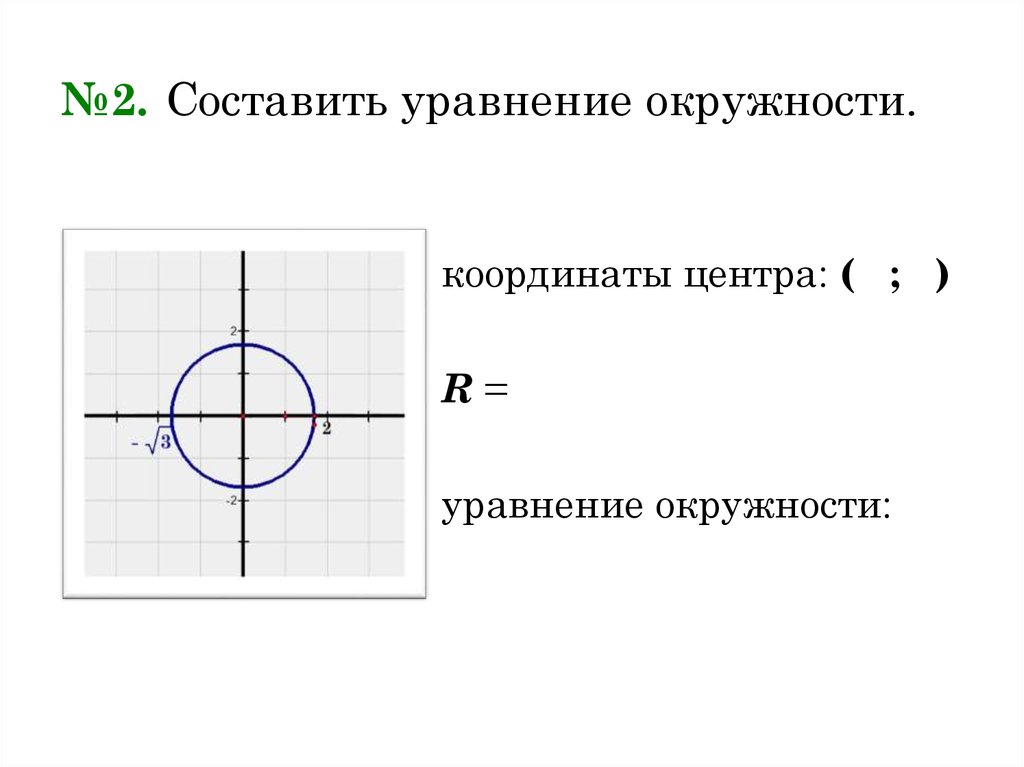 Конструкции В. Г. Шухова.
Конструкции В. Г. Шухова. На
следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до :
На
следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до : 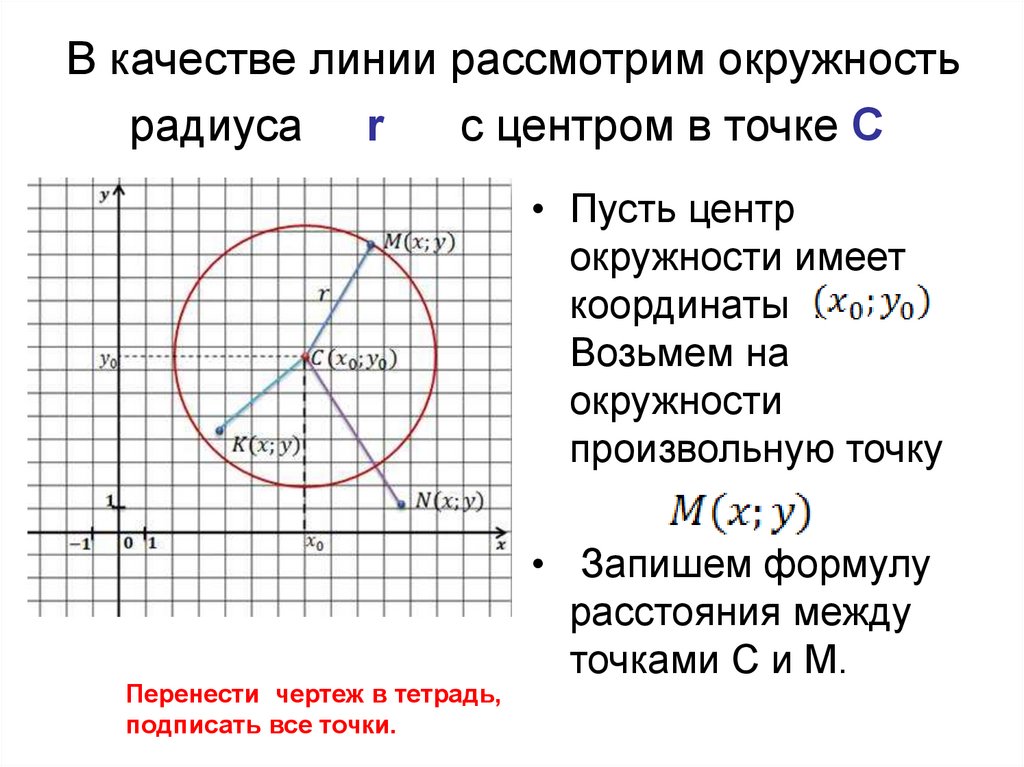

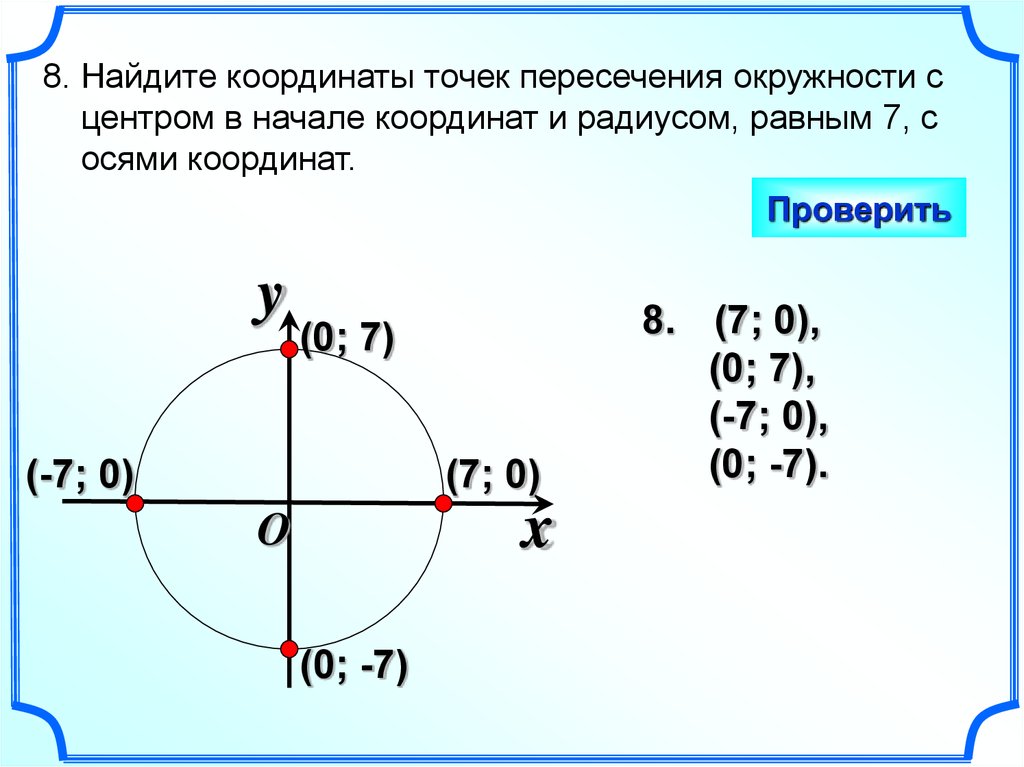
 Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.
Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему). 5. Полярная роза
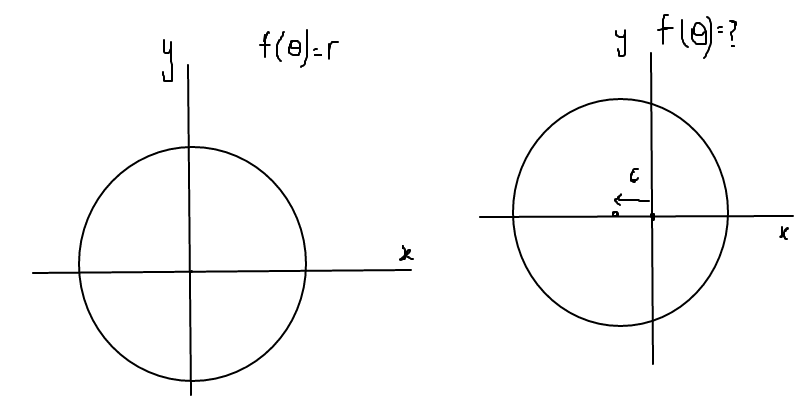
5. Полярная роза Иногда этот угол, наряду с расстоянием точки от начала координат, обеспечивает более полезный способ описания местоположения точки, чем обычные декартовы координаты.
Иногда этот угол, наряду с расстоянием точки от начала координат, обеспечивает более полезный способ описания местоположения точки, чем обычные декартовы координаты.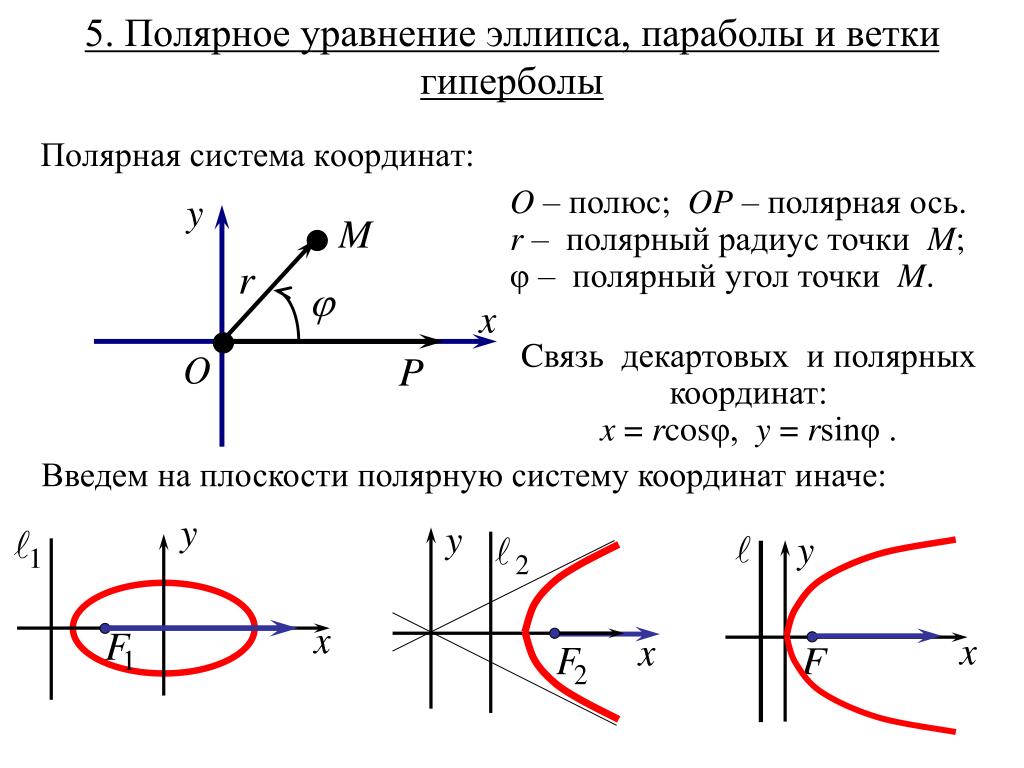 На обычной числовой прямой мы измеряем положительные значения справа и отрицательные значения слева. Аналогично нанесем эту точку. Для начала мы поворачиваем на угол \(\dfrac{\pi}{4}\).
На обычной числовой прямой мы измеряем положительные значения справа и отрицательные значения слева. Аналогично нанесем эту точку. Для начала мы поворачиваем на угол \(\dfrac{\pi}{4}\). 9{2}\]
9{2}\]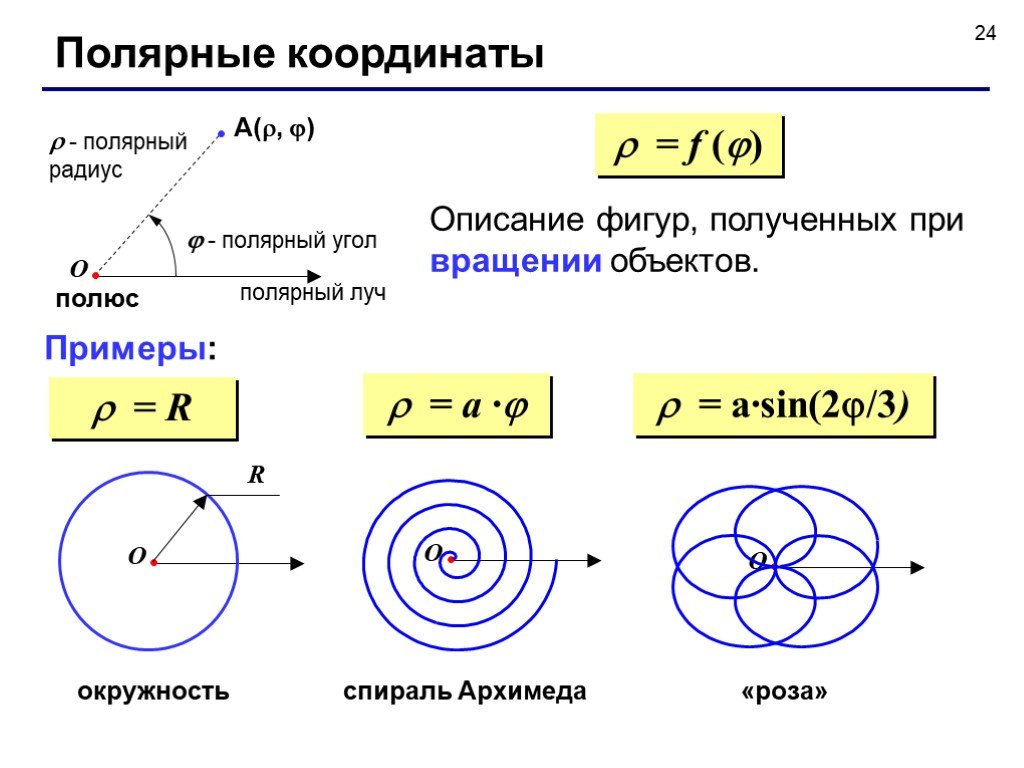 9{\text{rd}}\) квадранта, мы можем определить, что второй угол и есть тот, который нам нужен. Полярные координаты этой точки равны \((r, \theta) = (5, 4,069)\).
9{\text{rd}}\) квадранта, мы можем определить, что второй угол и есть тот, который нам нужен. Полярные координаты этой точки равны \((r, \theta) = (5, 4,069)\).


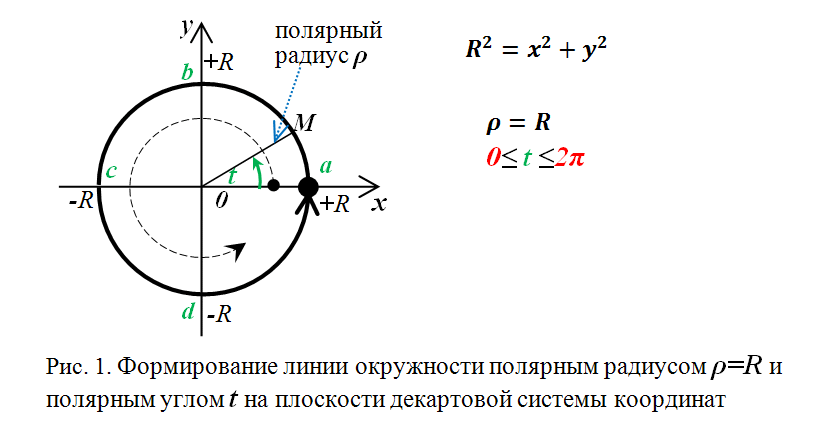 Решение для случая \(x = 4\) эквивалентно решению \(r\cos(\theta) = 4\). 9{2}(\theta)= 1\nonumber\]У этого есть решения, когда
Решение для случая \(x = 4\) эквивалентно решению \(r\cos(\theta) = 4\). 9{2}(\theta)= 1\nonumber\]У этого есть решения, когда 
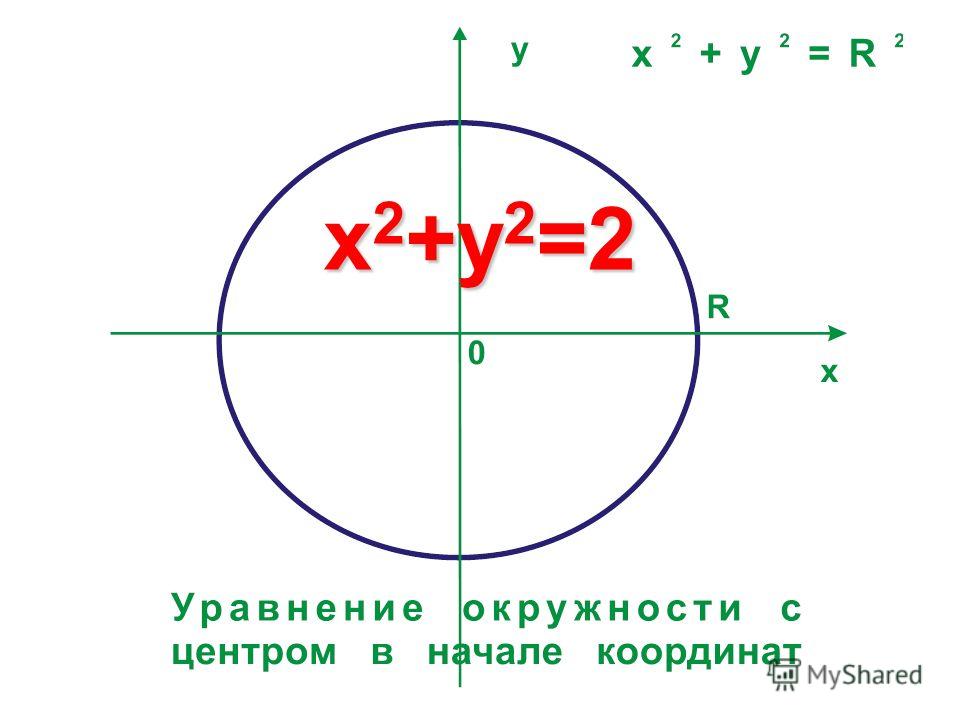 Вы бы назвали эту функцию limaçon 9?0049 или роза ?
Вы бы назвали эту функцию limaçon 9?0049 или роза ?

 opentextbookstore.com/details.php?id=30
opentextbookstore.com/details.php?id=30 Мы используем
калькулятор для построения графика
Мы используем
калькулятор для построения графика Затем
множество точек P на плоскости с
Затем
множество точек P на плоскости с
 50 вариантов ответов по русскому языку. Вариант 33 ч.2 Задание 3 ОГЭ Русский язык 9 класс Средство выразительности речи — эпитет
50 вариантов ответов по русскому языку. Вариант 33 ч.2 Задание 3 ОГЭ Русский язык 9 класс Средство выразительности речи — эпитет (Подробнее…)
(Подробнее…)
 В каждой такой
маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких
маленьких областей, а наибольший диаметр Δvi —
наоборот, уменьшать. Можем составить интегральную сумму вида
В каждой такой
маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких
маленьких областей, а наибольший диаметр Δvi —
наоборот, уменьшать. Можем составить интегральную сумму вида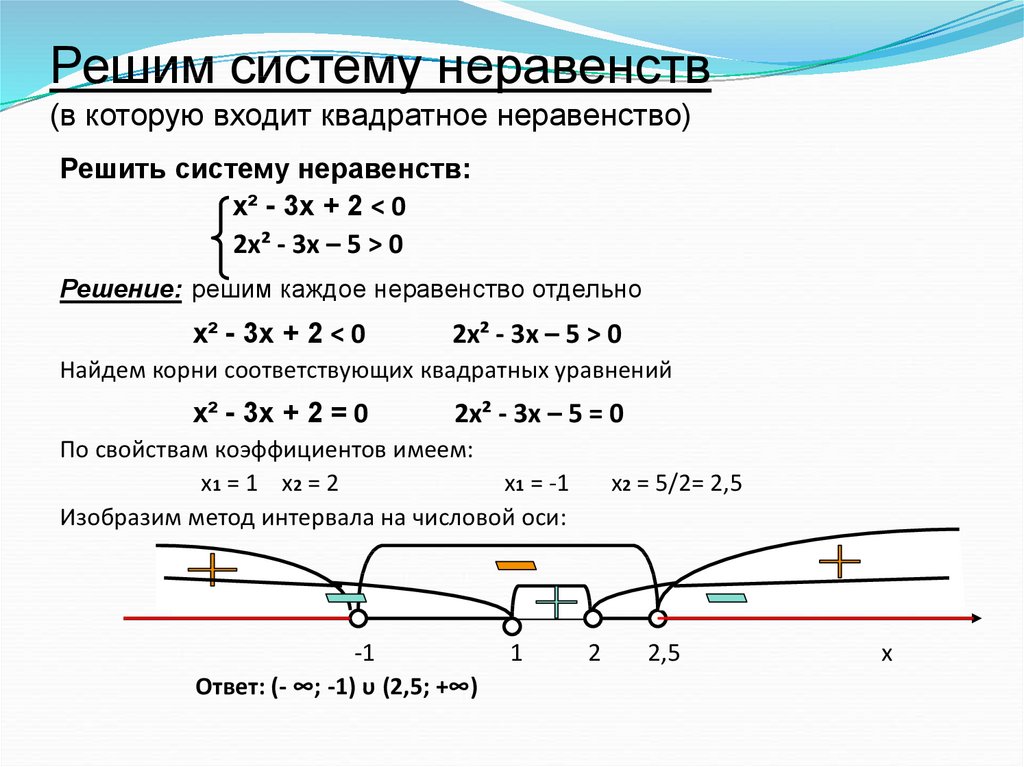




 Область V проецируется на плоскость xOy в треугольник D, как показано
на рисунке ниже.
Область V проецируется на плоскость xOy в треугольник D, как показано
на рисунке ниже.
 В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение
со знаком минус будет нижним пределом интегрирования по переменной z:
Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение
со знаком минус будет нижним пределом интегрирования по переменной z:
 Проверьте,
чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно
придётся.
Проверьте,
чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно
придётся. Можем найти пределы интегирования по «иксу»
чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго — верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
Можем найти пределы интегирования по «иксу»
чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго — верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов: Получаем:
Получаем: Получаем y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же
четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.
Получаем y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же
четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).
Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).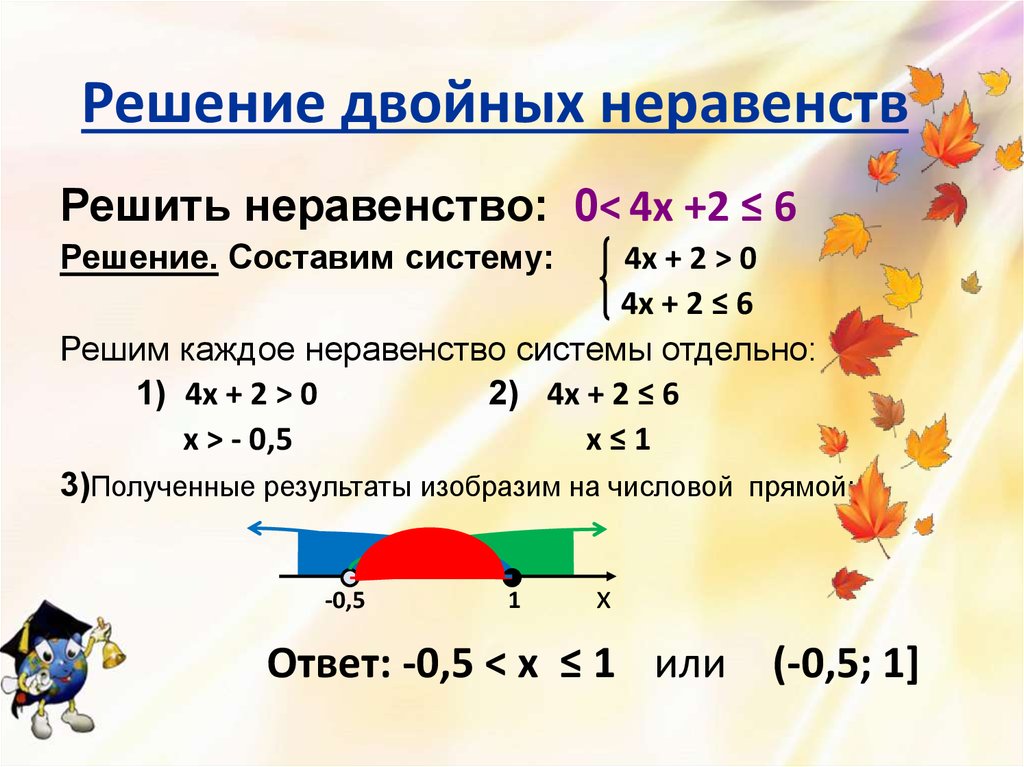
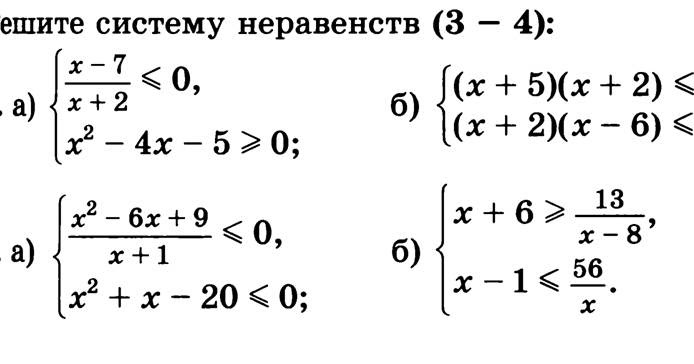 Переходим к цилиндрическим координатам и получаем:
Переходим к цилиндрическим координатам и получаем:
 Перепишем подынтегральную
функцию:
Перепишем подынтегральную
функцию: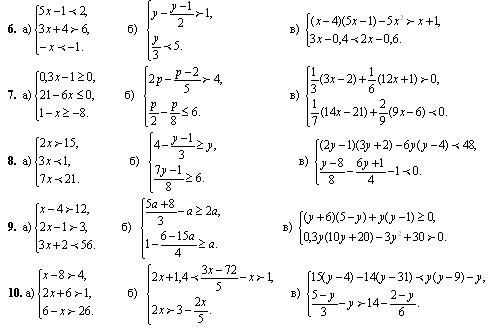 Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z)
можно вычислить по формулам:
Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z)
можно вычислить по формулам: Вычислить объём тела, ограниченного поверхностями
,
,
.
Вычислить объём тела, ограниченного поверхностями
,
,
. Это перекрытие или пересечение решений каждого неравенства. Когда два неравенства соединены словом или , решение составного неравенства происходит, когда или из неравенств верны. Решение представляет собой комбинацию или объединение двух отдельных решений.
Это перекрытие или пересечение решений каждого неравенства. Когда два неравенства соединены словом или , решение составного неравенства происходит, когда или из неравенств верны. Решение представляет собой комбинацию или объединение двух отдельных решений. Как бы мы интерпретировали, какими могут быть числа x , и как бы выглядел интервал?
Как бы мы интерпретировали, какими могут быть числа x , и как бы выглядел интервал? На следующей диаграмме Венна показаны две вещи, которые не имеют общих черт или элементов, но часто рассматриваются в одном и том же приложении, например онлайн-покупки или банковские операции.
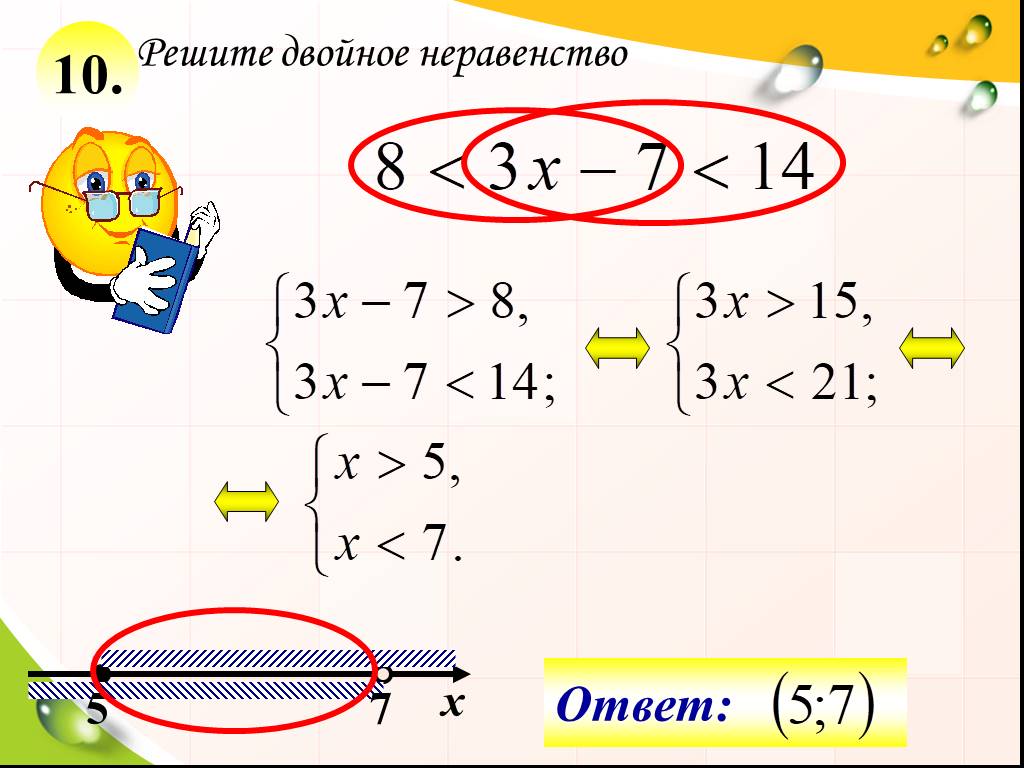
На следующей диаграмме Венна показаны две вещи, которые не имеют общих черт или элементов, но часто рассматриваются в одном и том же приложении, например онлайн-покупки или банковские операции. Это то, что мы называем союзом, как упоминалось выше. Обозначение интервала, связанное с объединением, представляет собой большую букву U, поэтому вместо записи или мы соединяем наши интервалы большой буквой U, например:
Это то, что мы называем союзом, как упоминалось выше. Обозначение интервала, связанное с объединением, представляет собой большую букву U, поэтому вместо записи или мы соединяем наши интервалы большой буквой U, например:
 0057 х .
0057 х .
 Какую бы операцию вы ни выполняли над средней частью неравенства, вы также должны выполнить ее с каждой из внешних частей. Обратите особое внимание на деление или умножение на отрицание.
Какую бы операцию вы ни выполняли над средней частью неравенства, вы также должны выполнить ее с каждой из внешних частей. Обратите особое внимание на деление или умножение на отрицание.
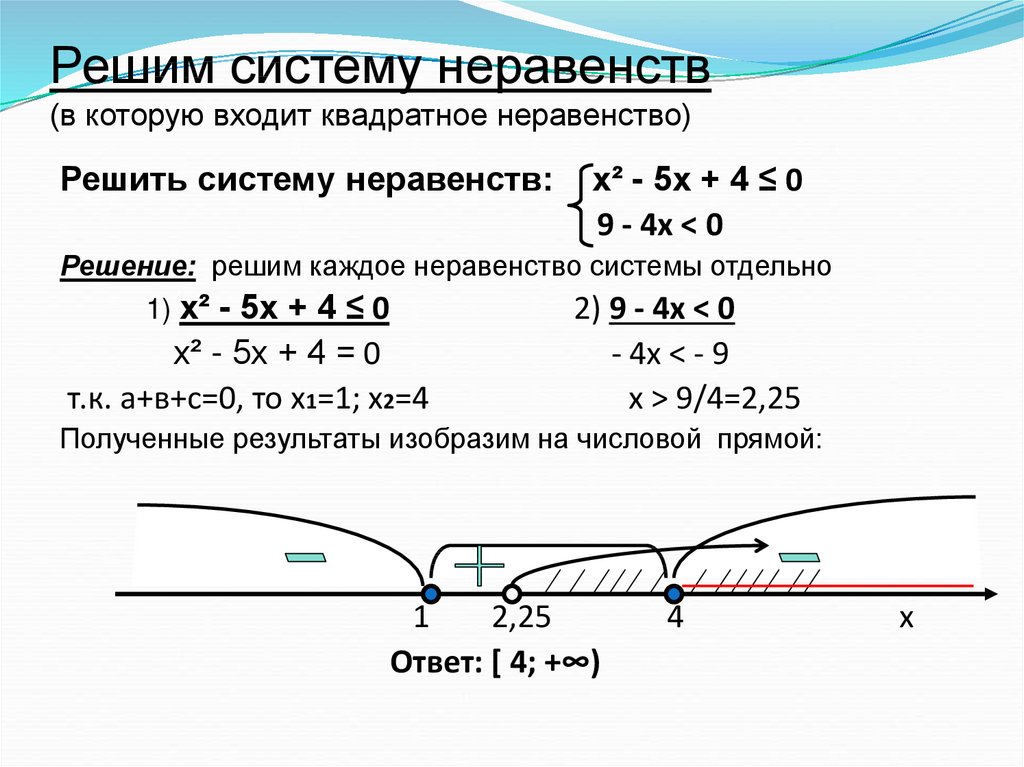
 Начнем с простого неравенства.
Начнем с простого неравенства.




 По условию задачи потенциал
цинкового электрода должен быть на
0,015 В меньше его стандартного электродного
потенциала, т.е.
-0,763 В — 0,015 В=
-778 В. По уравнению Нернста рассчитываем
концентрацию ионов Zn2+ (в моль/л).
По условию задачи потенциал
цинкового электрода должен быть на
0,015 В меньше его стандартного электродного
потенциала, т.е.
-0,763 В — 0,015 В=
-778 В. По уравнению Нернста рассчитываем
концентрацию ионов Zn2+ (в моль/л). у.). При этом образовалось
у.). При этом образовалось п. функцию восстановителя
выполняет кислород воды, окисляясь при
этом по схеме:
п. функцию восстановителя
выполняет кислород воды, окисляясь при
этом по схеме: Учитывая, что 1 моль эквивалентов воды
имеет массу 9 г. Рассчитываем количество
разложившейся воды:
Учитывая, что 1 моль эквивалентов воды
имеет массу 9 г. Рассчитываем количество
разложившейся воды: 4 Прочие реакции
4 Прочие реакции


 S → CuS
Просмотреть все уравнения с медью в качестве реагента
S → CuS
Просмотреть все уравнения с медью в качестве реагента 3 ) 2 Просмотреть все уравнения с Hg2(NO3)2 в качестве произведения
3 ) 2 Просмотреть все уравнения с Hg2(NO3)2 в качестве произведения (2+) = + 0,79(2+) = -2,37 В `
(2+) = + 0,79(2+) = -2,37 В `  0K 3,0K
0K 3,0K 0k VIEWS
0k VIEWS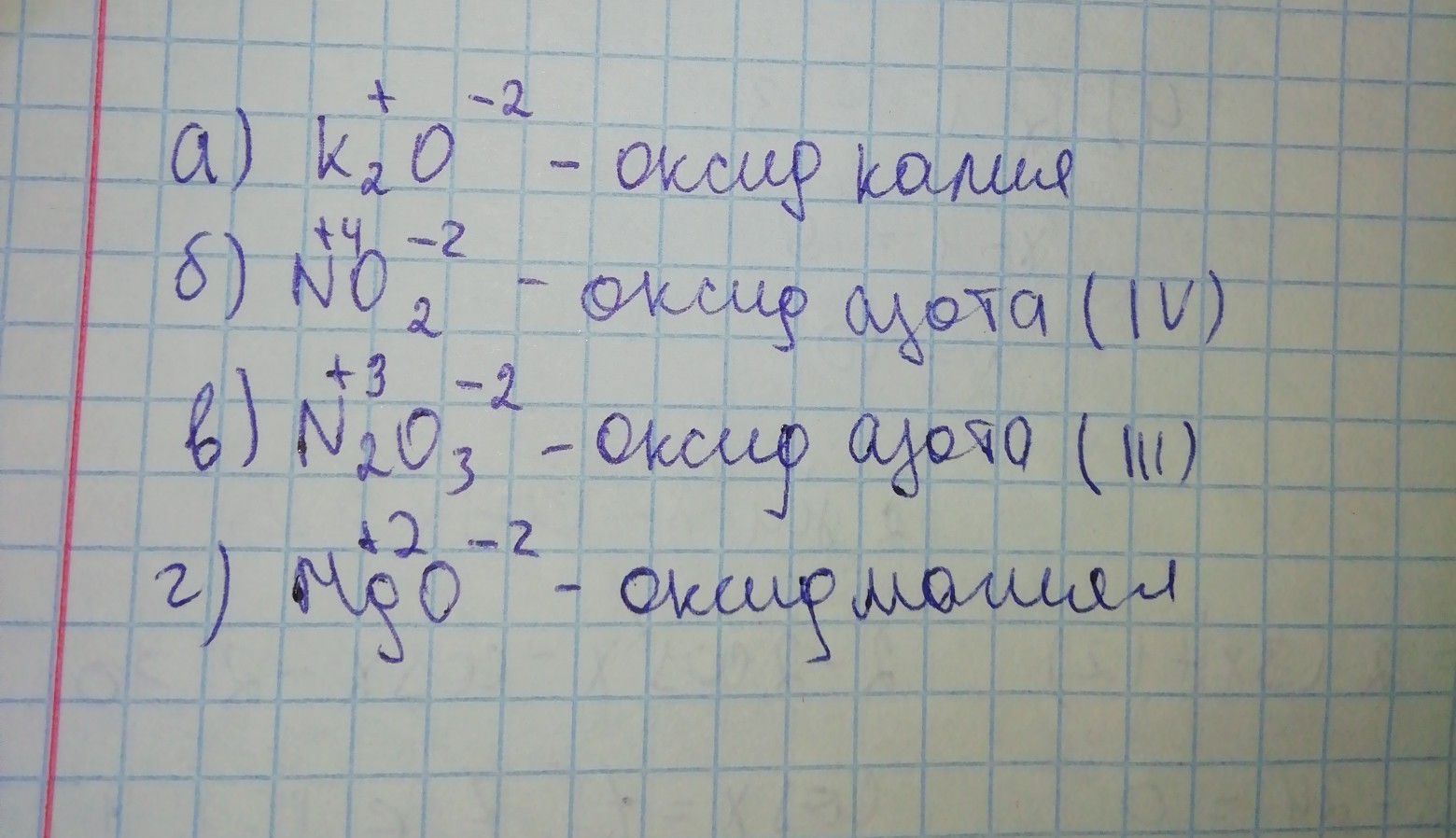 причина [ CBSE PMT 200…
причина [ CBSE PMT 200…
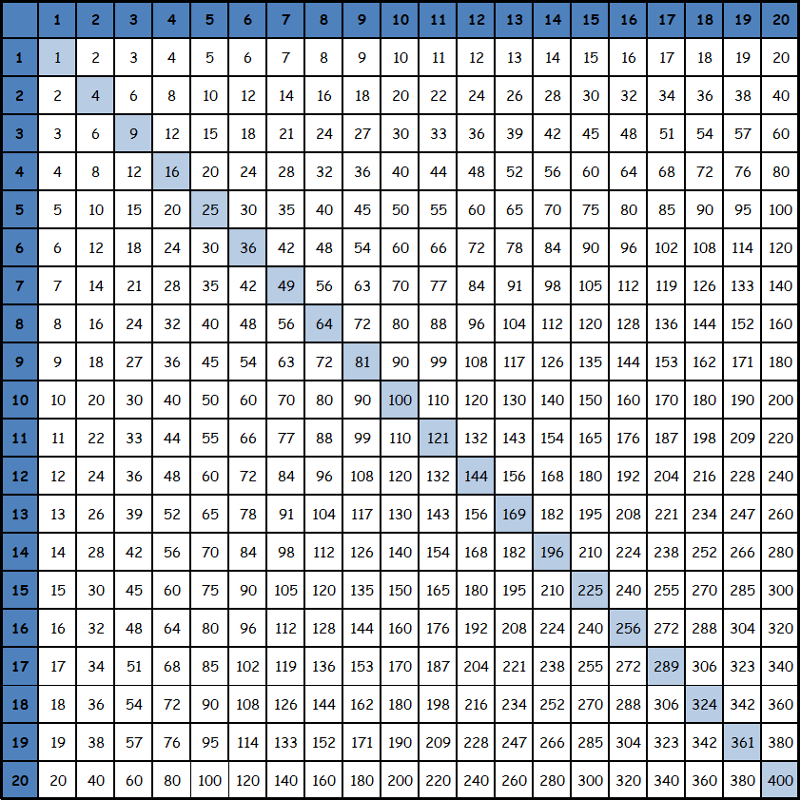
 В итоге вы получаете 27. Сгибайте пальцы дальше, и проверяйте, сколько получается.
В итоге вы получаете 27. Сгибайте пальцы дальше, и проверяйте, сколько получается. Делается это так:
Делается это так:
 Рифма – это своеобразный мнемонический приём. Вспомните, старую песню, которую вы наверняка слышали и не раз в школе: «дважды два — …, это всем известно в целом мире». Ответ приходит в голову мгновенно. Именно так работает эта мнемотехника.
Рифма – это своеобразный мнемонический приём. Вспомните, старую песню, которую вы наверняка слышали и не раз в школе: «дважды два — …, это всем известно в целом мире». Ответ приходит в голову мгновенно. Именно так работает эта мнемотехника.
 Математика. Никольский. Учебник. Ответы к стр. 36
Математика. Никольский. Учебник. Ответы к стр. 36 Поэтому 5 пишем под 3, а ноль приписываем справа.
Поэтому 5 пишем под 3, а ноль приписываем справа.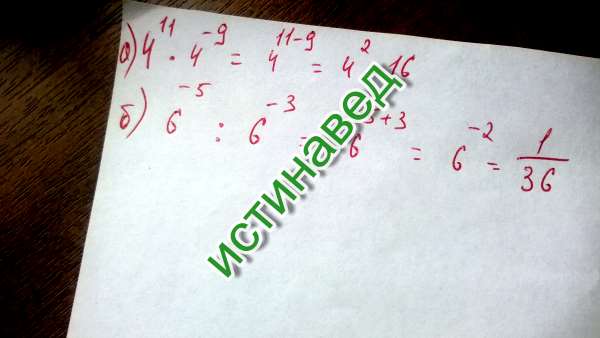


 Вычислите произведение чисел:
Вычислите произведение чисел: Вычислите наиболее простым способом:
Вычислите наиболее простым способом: 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Таким образом, чтобы найти и перечислить все делители числа 36, нужно перебрать все числа до и включая 36, и проверьте, какие числа дают четное частное (что означает отсутствие десятичного знака).
Таким образом, чтобы найти и перечислить все делители числа 36, нужно перебрать все числа до и включая 36, и проверьте, какие числа дают четное частное (что означает отсутствие десятичного знака).



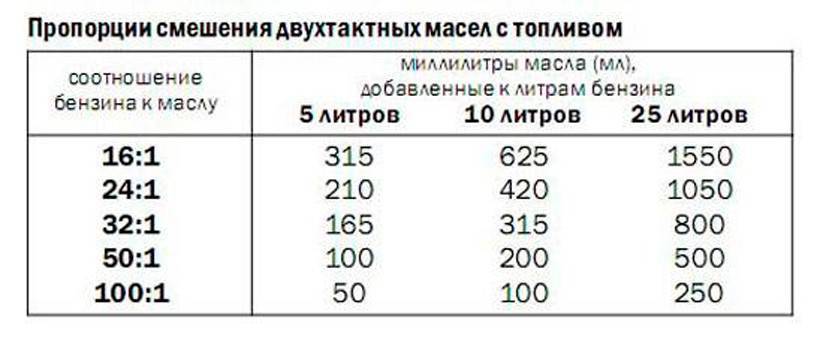
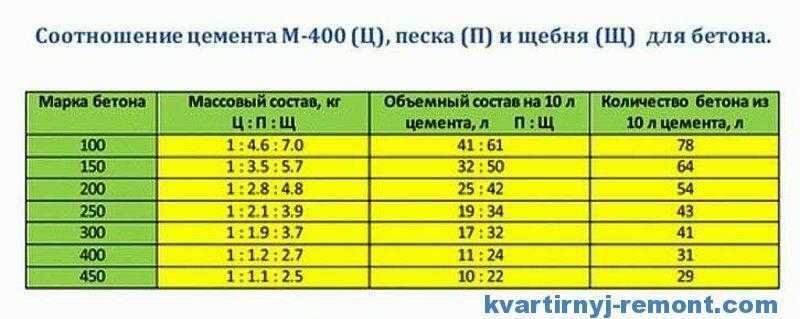
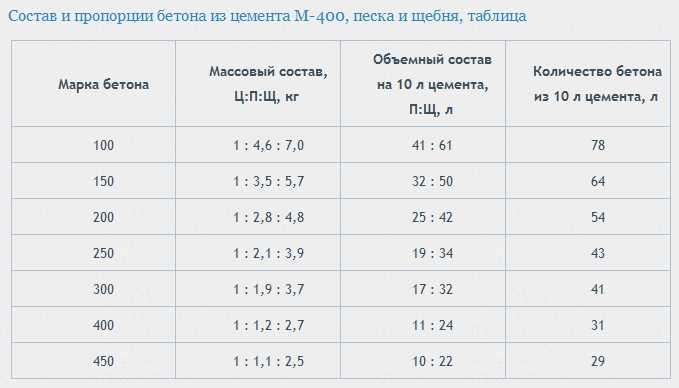 Автомобильное, а тем более, трансмиссионное масло использовать категорически запрещается. Производится двухтактное масло в трех видах:
Автомобильное, а тем более, трансмиссионное масло использовать категорически запрещается. Производится двухтактное масло в трех видах: д.
д. Покупайте бензин только на брендовых заправках, там риск купить А-80 вместо АИ-92 практически равна нулю.
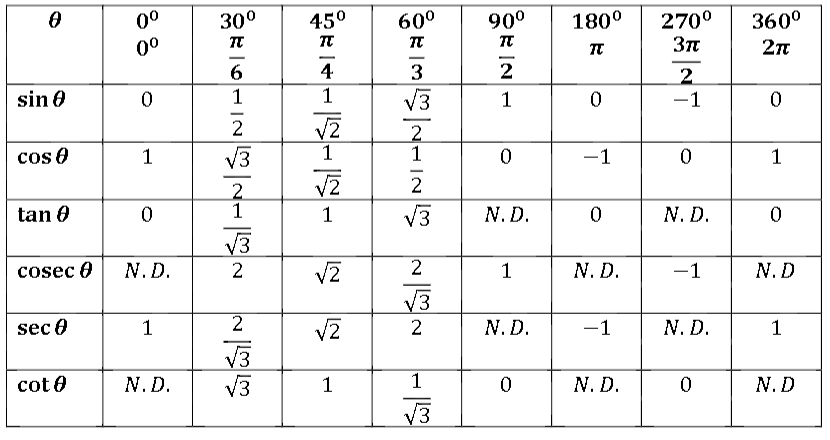
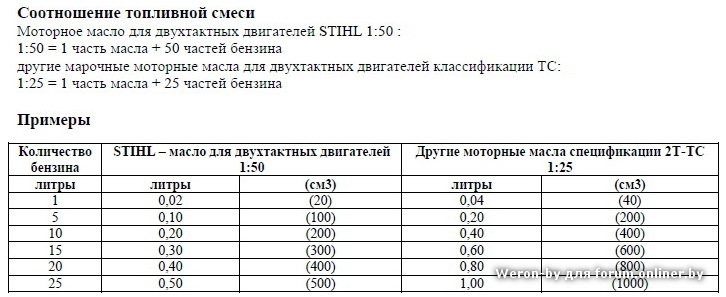
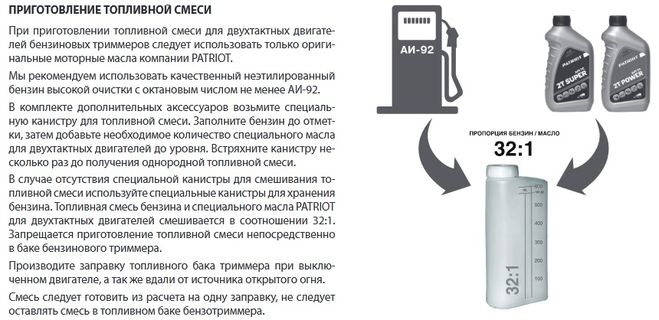
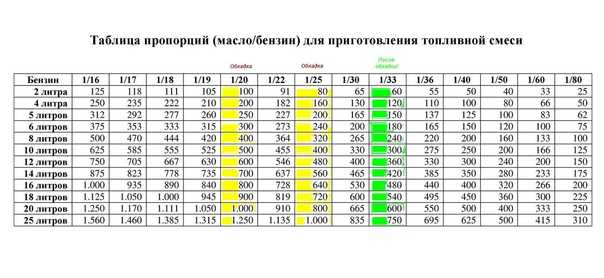
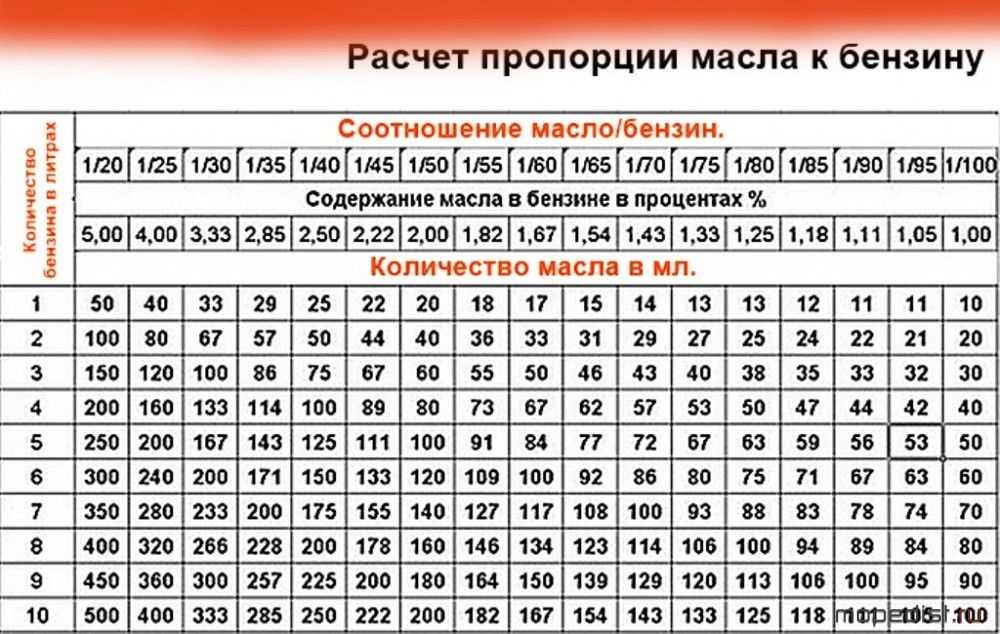
Покупайте бензин только на брендовых заправках, там риск купить А-80 вместо АИ-92 практически равна нулю.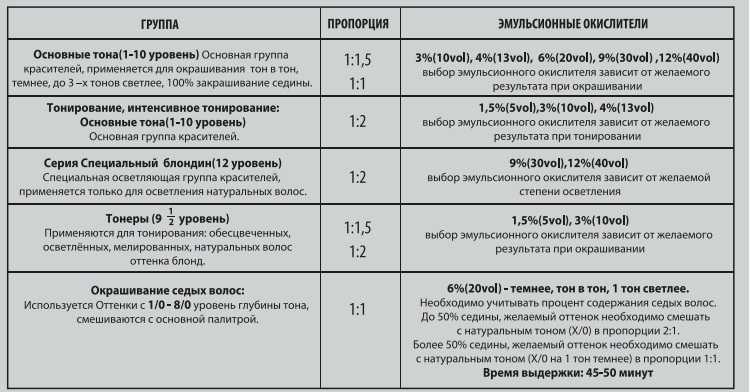 В каждой инструкции к триммеру приведены пропорции, как разбавлять топливную смесь. Обычно это 1:25. 1:40 или 1:50. На практике это выглядит так:
В каждой инструкции к триммеру приведены пропорции, как разбавлять топливную смесь. Обычно это 1:25. 1:40 или 1:50. На практике это выглядит так: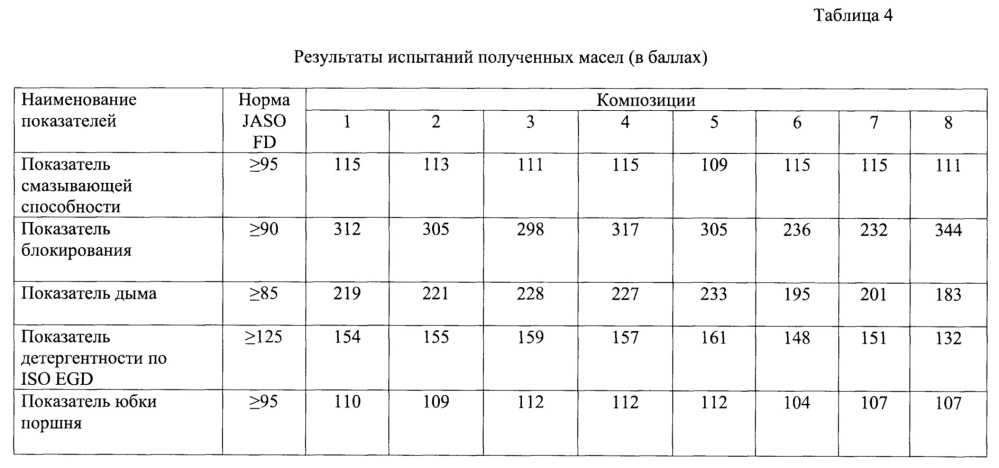 Лучше стеклянную или металлическую. Пластик тоже можно применить, но нужно выбирать бутылку с жесткими стенками.
Лучше стеклянную или металлическую. Пластик тоже можно применить, но нужно выбирать бутылку с жесткими стенками.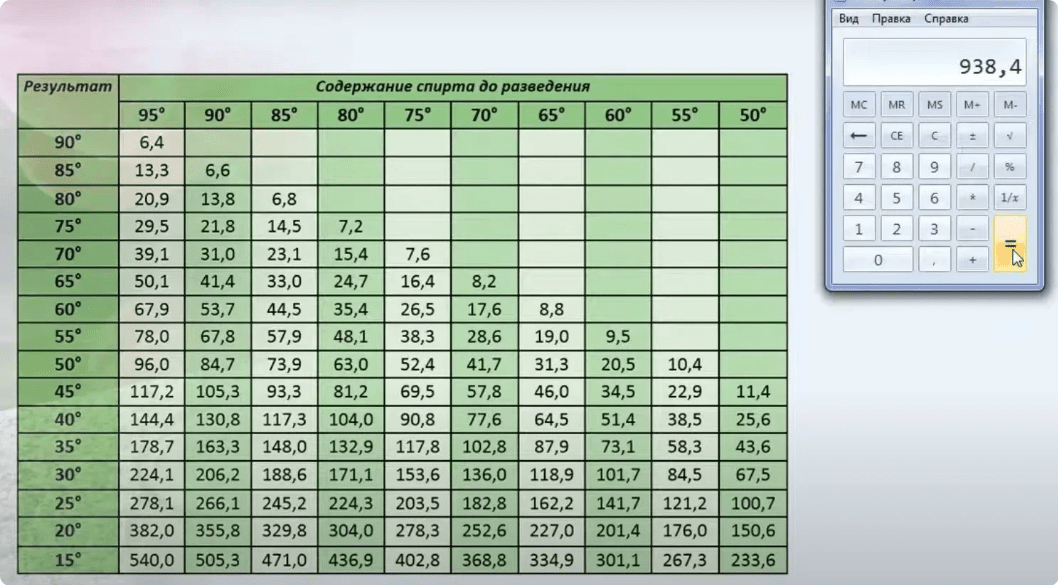 io, продукты и проекты группы
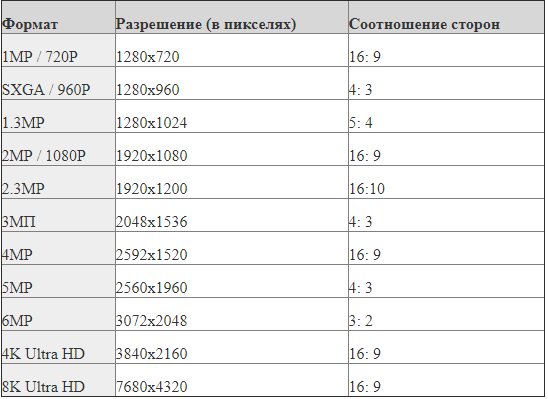
io, продукты и проекты группы Кадры видео и фотоснимков обладают пропорцией кадра (формат кадра), а пикселы, составляющие кадр, — попиксельной пропорцией (иногда называемой PAR). В различных стандартах видеозаписи используются разные пропорции. Например, видео для телевидения записывается с пропорцией кадра (форматом кадра) 4:3 или 16:9. Дополнительную информацию см. в разделе Пропорция кадра.
Кадры видео и фотоснимков обладают пропорцией кадра (формат кадра), а пикселы, составляющие кадр, — попиксельной пропорцией (иногда называемой PAR). В различных стандартах видеозаписи используются разные пропорции. Например, видео для телевидения записывается с пропорцией кадра (форматом кадра) 4:3 или 16:9. Дополнительную информацию см. в разделе Пропорция кадра.




 Изображение 4:3 с квадратными пикселами, неправильно интерпретированное для отображения на мониторе 4:3 (ТВ) с неквадратными пикселами
Изображение 4:3 с квадратными пикселами, неправильно интерпретированное для отображения на мониторе 4:3 (ТВ) с неквадратными пикселами  Можно исправить искажение отдельного клипа вручную, указав попиксельную пропорцию исходного клипа в диалоговом окне «Интерпретировать материал».
Можно исправить искажение отдельного клипа вручную, указав попиксельную пропорцию исходного клипа в диалоговом окне «Интерпретировать материал». 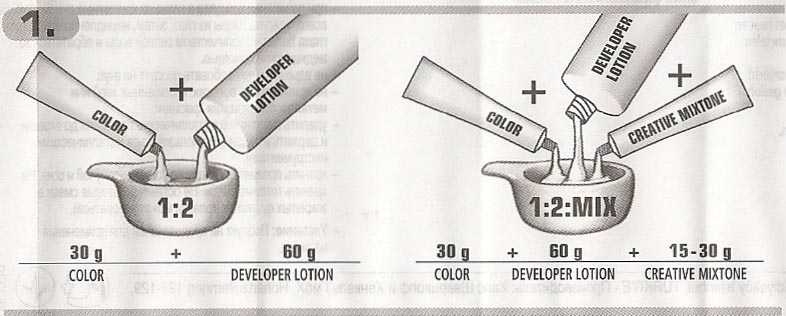

 Использование этого шаблона настроек гарантирует создание изображений с правильными пропорциями.
Использование этого шаблона настроек гарантирует создание изображений с правильными пропорциями.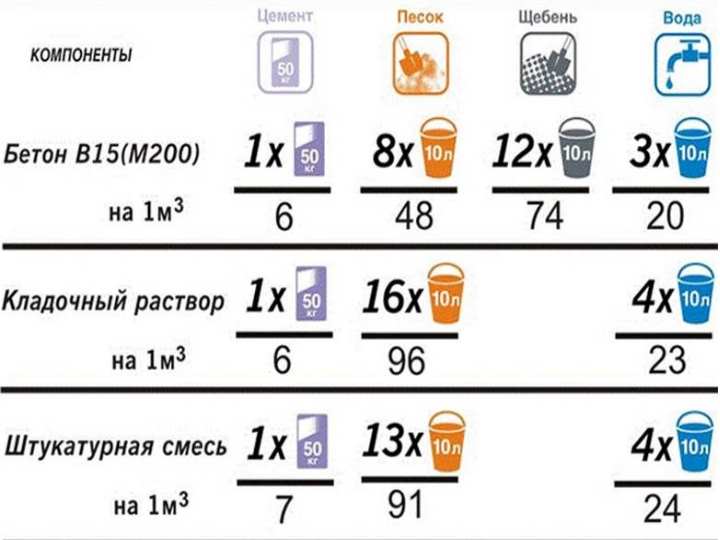 Этот параметр также подходит для материалов, которые были перенесены с пленки или предназначены для проектов с индивидуальной настройкой.
Этот параметр также подходит для материалов, которые были перенесены с пленки или предназначены для проектов с индивидуальной настройкой.


 (Этот вопрос и способ его решения подробно описаны ниже).
(Этот вопрос и способ его решения подробно описаны ниже).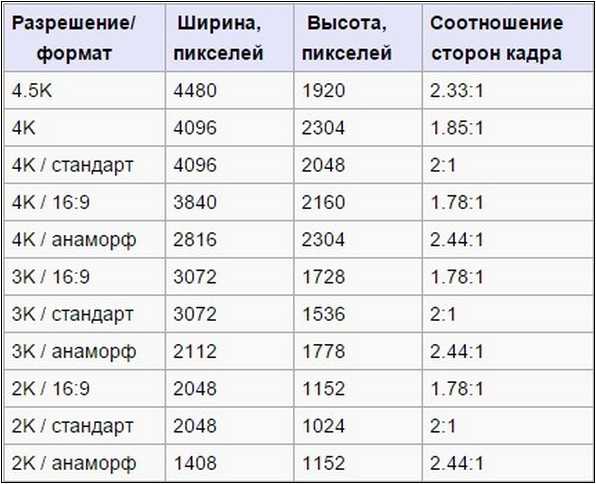 Итак, в отношении 3:1 антецедент равен 3, а консеквент равен 1.
Итак, в отношении 3:1 антецедент равен 3, а консеквент равен 1.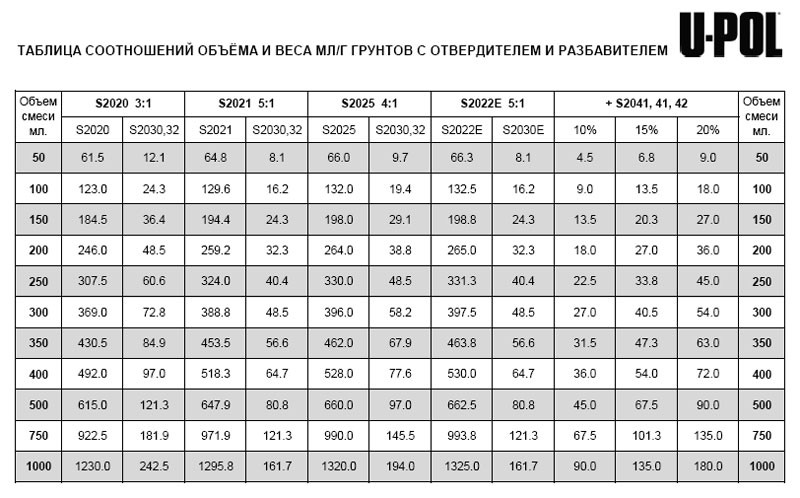 Это облегчает обучение решению задачи на соотношение.
Это облегчает обучение решению задачи на соотношение.
 Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей.
Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей. Одна часть равна 6
Одна часть равна 6
 Тем не менее, вы будете следовать тем же простым шагам, которые вы бы использовали, если бы вычисляли в уме:
Тем не менее, вы будете следовать тем же простым шагам, которые вы бы использовали, если бы вычисляли в уме:
 Например, исследователь может
говорят, что на каждые десять студентов общежития приходилось пять женщин.
Пять на десять (5/10) — это пропорция. Пропорции должны соответствовать всем
числа в одних и тех же единицах и часто записываются в виде дробей.
Например, исследователь может
говорят, что на каждые десять студентов общежития приходилось пять женщин.
Пять на десять (5/10) — это пропорция. Пропорции должны соответствовать всем
числа в одних и тех же единицах и часто записываются в виде дробей.