Число в первой и нулевой степени
Степень числа – это краткая запись произведения одинаковых сомножителей
Пример.
7 · 7 · 7 · 7 = 74.
В записи 74 число 7 — это основание степени, то есть число, повторяющееся сомножителем, а число 4 — показатель степени, то есть число, показывающее количество одинаковых сомножителей.
Первая степень числа
Любое число в первой степени равно самому себе, так как показатель степени 1 указывает что число берётся сомножителем всего один раз, то есть оно ни на что не умножается, а просто остаётся без изменений.
Примеры:
71 = 7,
1001 = 100,
-251 = -25.
Нулевая степень числа
Любое число в нулевой степени (за исключением 0) равно 1.
Примеры:
70 = 1,
1000 = 1,
-250 = 1.
Чтобы разобраться почему число в нулевой степени равно 1, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если разделить одинаковые степени с одинаковыми основаниями, то в результате получится основание в нулевой степени:
a3 : a3 = a3-3 = a0.
Так как два одинаковых числа, взятых в одной и той же степени, равны, по сути, они являются одним и тем же числом, то при их делении в частном получается единица. Значит:
a3 : a3 = 1.
Следовательно, любое число в нулевой степени равно единице. Это можно легко доказать, проведя проверку деления умножением, умножив частное на делитель:
a0 · a3 = a0+3 = a3
или
1 · a3 = a3.
Таблица степеней натуральных чисел — 2mb.ru
Ниже представлена таблица степеней от 2 до 10 натуральных чисел от 1 до 20.
Используя второй столбик вы получите таблицу квадратов чисел. Например берем в таблице число 11 и находим напротив во втором столбике квадрат числа 121.
Третий столбик таблицы представляет из себя значение кубов натуральных чисел.
Воспользовавшись таблицей вы можете узнать, что 2 в степени 10 равно 1024, а 20 в десятой степени равно 1 0240 000 000 000.
| Степень | |||||||||
| Число | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1 024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2 187 | 6 561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1 024 | 4 096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3 125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 1 296 | 7 776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7 | 49 | 343 | 2 401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4 096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6 561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
| 11 | 121 | 1 331 | 14 641 | 161 051 | 1 771 561 | 19 487 171 | 214 358 881 | 2 357 947 691 | 25 937 424 601 |
| 12 | 144 | 1 728 | 20 736 | 248 832 | 2 985 984 | 35 831 808 | 429 981 696 | 5 159 780 352 | 61 917 364 224 |
| 13 | 169 | 2 197 | 28 561 | 371 293 | 4 826 809 | 62 748 517 | 815 730 721 | 10 604 499 373 | 137 858 491 849 |
| 14 | 196 | 2 744 | 38 416 | 537 824 | 7 529 536 | 105 413 504 | 1 475 789 056 | 20 661 046 784 | 289 254 654 976 |
| 15 | 225 | 3 375 | 50 625 | 759 375 | 11 390 625 | 170 859 375 | 2 562 890 625 | 38 443 359 375 | 576 650 390 625 |
| 16 | 256 | 4 096 | 65 536 | 1 048 576 | 16 777 216 | 268 435 456 | 4 294 967 296 | 68 719 476 736 | 1 099 511 627 776 |
| 17 | 289 | 4 913 | 83 521 | 1 419 857 | 24 137 569 | 410 338 673 | 6 975 757 441 | 118 587 876 497 | 2 015 993 900 449 |
| 18 | 324 | 5 832 | 104 976 | 1 889 568 | 34 012 224 | 612 220 032 | 11 019 960 576 | 198 359 290 368 | 3 570 467 226 624 |
| 19 | 361 | 6 859 | 130 321 | 2 476 099 | 47 045 881 | 893 871 739 | 16 983 563 041 | 322 687 697 779 | 6 131 066 257 801 |
| 20 | 400 | 8 000 | 160 000 | 3 200 000 | 64 000 000 | 1 280 000 000 | 25 600 000 000 | 512 000 000 000 | 10 240 000 000 000 |
Виды и степени нарушений Слуха
Виды и степени нарушений Слуха
Около 10% всего населения Земного шара в той или иной степени имеют нарушения Слуха.
Тугоухость определяют как снижение Cлуха, при котором затруднено общение с окружающими людьми по причине недостаточного восприятия чужой речи. С нарушением восприятия звуков можно столкнуться в любом возрасте. Тугоухость может варьировать по степени тяжести — от легкой до глубокой.
Степень нарушения Слуха определяется в ходе специального исследования, называемого Аудиометрией. Суть исследования состоит в измерении порога Слухового восприятия человека почастотно.
Если человек слышит Звуки на всех Частотах до 25 Децибелл (дБ), то его Слух считается нормальным.
Если он слышит только Звуки громче, чем 25 дБ, говорят о снижении Слуха.
Чем большая громкость Звука требуется для того, чтобы человек услышал подаваемый в наушники сигнал, тем большая у него степень Тугоухости.
Согласно Международной классификации Тугоухости:
1. Слух в норме означает, что человек слышит Звуки на всех частотах от 0 до 25 дБ и не испытывает проблем с общением.
2. 1-я степень Тугоухости (слабая) означает, что человек слышит Звуки только громче 26-40 дБ. У него появляются трудности в восприятии тихой и отдаленной речи.
3. 2-я степень Тугоухости (средняя) означает, что человек слышит Звуки только громче 41-55 дБ. У него имеются трудности в восприятии тихой и отдаленной речи, диалога.
4. 3-я степень Тугоухости (средне-тяжелая) означает, что человек слышит Звуки только громче 56-70 дБ. Он воспринимает только громкую речь и испытывает затруднение при коллективном общении и разговоре по телефону.
5. 4-я степень Тугоухости (тяжелая) означает, что человек слышит Звуки только громче 71-90 дБ. Он с трудом воспринимает даже громкую речь. Понятен только крик или усиленная наушниками речь. Разговор по телефону не возможен.
6. Глухота (глубокая) означает, что человек может услышать звуки только громче 91 дБ и испытывает трудности в понимании даже усиленной наушниками речи.
Снижение Слуха может возникать в следствии различных причин.
Кондуктивная Тугоухость
Эта Тугоухость, вызываемая препятствиями на пути проведения звуковой волны. Такая Тугоухость хорошо лечится либо консервативным, либо хирургическим путем.
Основными причинами развития данного вида Тугоухости являются: скопления ушной серы, средний отит, отосклероз и др.
Нейросенсорная (сенсоневральная) Тугоухость.
Эта Тугоухость связана с нарушением преобразования механических колебаний в электрические импульсы. Причинами ее развития являются нарушения во внутреннем ухе или улитке. Поражение рецепторов звукового анализатора может быть вызвано акустическими травмами, ототоксическим действием антибиотиков, сосудистыми нарушениями кровоснабжения улитки и др. причинами, приводящими к гибели волосковых клеток внутреннего уха.
Данный вид Тугоухости очень тяжело поддается лечению и может быть компенсирован только Слухопротезированием.
Смешанная Тугоухость.
Эта Тугоухость представляет собой сочетание двух вышеупомянутых типов нарушения Слуха
Статья 19. Материальное обеспечение судей / КонсультантПлюс
КонсультантПлюс: примечание.
П. 1 ст. 19 (в ред. ФЗ от 06.03.2019 N 25-ФЗ) распространяется в том числе на судей, ставших инвалидами до 06.03.2019 вследствие причин, не связанных со служебной деятельностью.1. Ежемесячное денежное вознаграждение судьи состоит из месячного оклада в соответствии с замещаемой им должностью судьи (далее — должностной оклад), месячного оклада судьи в соответствии с присвоенным ему квалификационным классом (далее — оклад за квалификационный класс), ежемесячного денежного поощрения, ежемесячной доплаты за выслугу лет, ежемесячных доплат за ученую степень кандидата юридических наук, доктора юридических наук, за ученое звание доцента, профессора, за почетное звание «Заслуженный юрист Российской Федерации», а также в случаях, предусмотренных законодательством Российской Федерации, ежемесячной доплаты за знание иностранных языков и их использование при исполнении должностных обязанностей.
Размер должностного оклада Председателя Конституционного Суда Российской Федерации устанавливается указом Президента Российской Федерации.Установить размеры должностных окладов судей Конституционного Суда Российской Федерации в процентном отношении к должностному окладу Председателя Конституционного Суда Российской Федерации согласно приложению 6 к настоящему Закону.Установить размер должностного оклада Председателя Верховного Суда Российской Федерации в размере 98 процентов должностного оклада Председателя Конституционного Суда Российской Федерации.
(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
КонсультантПлюс: примечание.
Действие абз. 6 п. 1 ст. 19 приостановлено до 01.01.2022 (ФЗ от 30.12.2020 N 485-ФЗ).Размеры должностных окладов судей ежегодно увеличиваются (индексируются) в соответствии с федеральным законом о федеральном бюджете на соответствующий год и на плановый период с учетом уровня инфляции (потребительских цен).Решениеоб увеличении (индексации) размеров должностных окладов судей принимается Президентом Российской Федерации.
Установить размеры окладов за квалификационный класс судей в процентном отношении к должностным окладам судей:
девятый квалификационный класс — 30 процентов;
восьмой квалификационный класс — 40 процентов;
седьмой квалификационный класс — 50 процентов;
шестой квалификационный класс — 60 процентов;
пятый квалификационный класс — 75 процентов;
четвертый квалификационный класс — 90 процентов;
третий квалификационный класс — 105 процентов;
второй квалификационный класс — 120 процентов;
первый квалификационный класс — 135 процентов;
высший квалификационный класс — 150 процентов.
Установить размеры ежемесячного денежного поощрения Председателя Конституционного Суда Российской Федерации и судей Конституционного Суда Российской Федерации согласно приложению 6 к настоящему Закону.Установить размеры ежемесячного денежного поощрения судей согласно приложению 7 к настоящему Закону.Исчислять ежемесячное денежное поощрение судей, установленное приложениями 6 и 7 к настоящему Закону, исходя из должностных окладов судей.Установить размеры ежемесячной доплаты за выслугу лет судей в процентном отношении к должностным окладам судей:
от 2 до 5 лет — 15 процентов;
от 5 до 10 лет — 25 процентов;
от 10 до 15 лет — 30 процентов;
от 15 до 20 лет — 40 процентов;
свыше 20 лет — 50 процентов.
Порядок и условия определения выслуги лет судей утверждаются постановлением Совета судей Российской Федерации.Установить следующие размеры ежемесячной доплаты судьям:
имеющим ученую степень кандидата юридических наук или ученое звание доцента, — 5 процентов должностного оклада;
имеющим ученую степень доктора юридических наук или ученое звание профессора, — 10 процентов должностного оклада;
имеющим почетное звание «Заслуженный юрист Российской Федерации», — 10 процентов должностного оклада.
Установить размер ежемесячной доплаты судьям Конституционного Суда Российской Федерации за знание иностранных языков и их использование при исполнении должностных обязанностей — 20 процентов должностного оклада.
Судье выплачивается ежеквартальное денежное поощрение, которое не входит в состав ежемесячного денежного вознаграждения судьи.
Ежеквартальное денежное поощрение выплачивается в размере ежемесячного денежного поощрения по замещаемой должности.
Ежемесячное денежное вознаграждение судьи и ежеквартальное денежное поощрение судьи, замещающего соответствующую должность судьи, не могут быть уменьшены.
В соответствии с федеральными законами и иными нормативными правовыми актами Российской Федерации судьям производятся другие выплаты, которые не входят в состав ежемесячного денежного вознаграждения судьи.
В случаях, установленных законодательством Российской Федерации, к ежемесячному денежному вознаграждению судьи, ежеквартальному денежному поощрению судьи и другим выплатам, предусмотренным соответствующими федеральными законами и иными нормативными правовыми актами Российской Федерации, устанавливаются районный коэффициент, коэффициент за работу в пустынных и безводных местностях, коэффициент за работу в высокогорных районах и процентная надбавка за работу в районах Крайнего Севера и приравненных к ним местностях, в южных районах Восточной Сибири и Дальнего Востока в размерах, определяемых с учетом размеров коэффициентов и процентных надбавок, установленных соответствующими нормативными правовыми актами Российской Федерации.
В пределах установленного фонда оплаты труда судьям могут выплачиваться премии и оказываться материальная помощь.
Порядок выплаты премий и оказания материальной помощи судьям определяется актами Конституционного Суда Российской Федерации и Верховного Суда Российской Федерации для судей соответственно Конституционного Суда Российской Федерации и Верховного Суда Российской Федерации и актами Судебного департамента при Верховном Суде Российской Федерации по согласованию с Советом судей Российской Федерации для судей судов общей юрисдикции и арбитражных судов.(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
Судьям, проработавшим в районах Крайнего Севера и приравненных к ним местностях соответственно не менее 15 и 20 календарных лет и ушедшим (удаленным) в отставку, ежемесячное пожизненное содержание и ежемесячное денежное содержание по инвалидности назначаются и выплачиваются с учетом районного коэффициента к ежемесячному денежному вознаграждению независимо от их места жительства и времени обращения за указанным содержанием.
(в ред. Федерального закона от 06.03.2019 N 25-ФЗ)(см. текст в предыдущей редакции
)
Размеры ежемесячного пожизненного содержания судей, а также ежемесячного денежного содержания по инвалидности увеличиваются (индексируются) в размерах и сроки, которые предусмотрены для увеличения (индексации) размеров должностных окладов судей. Также производится пересчет размеров ежемесячного пожизненного содержания судей и ежемесячного денежного содержания по инвалидности в случае увеличения (индексации) размеров любых составляющих ежемесячного денежного вознаграждения судьи.
(в ред. Федеральных законов от 22.12.2014 N 435-ФЗ, от 06.03.2019 N 25-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
1.1. Фонд оплаты труда судей сверх суммы средств, направляемых для выплаты должностных окладов, формируется за счет средств для выплаты (в расчете на год):
1) оклада за квалификационный класс:
в Конституционном Суде Российской Федерации — в размере 18 должностных окладов;
в Верховном Суде Российской Федерации — в размере 17,6 должностного оклада;
(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
в кассационных судах общей юрисдикции, апелляционных судах общей юрисдикции, кассационном военном суде, апелляционном военном суде, верховных судах республик, краевых, областных судах, судах городов федерального значения, суде автономной области, судах автономных округов, окружных (флотских) военных судах, арбитражных судах округов, арбитражных апелляционных судах, арбитражных судах субъектов Российской Федерации и Суде по интеллектуальным правам — в размере 13,8 должностного оклада;
(в ред. Федерального закона от 29.07.2018 N 266-ФЗ)(см. текст в предыдущей редакции
)
в районных, городских, межрайонных и гарнизонных военных судах — в размере 8,4 должностного оклада;
мировым судьям — в размере 5,4 должностного оклада;
2) ежемесячного денежного поощрения:
в Конституционном Суде Российской Федерации — в размере 122,1 должностного оклада;
в Верховном Суде Российской Федерации — в размере 73,2 должностного оклада;
в кассационных судах общей юрисдикции, апелляционных судах общей юрисдикции, кассационном военном суде, апелляционном военном суде, верховных судах республик, краевых, областных судах, судах городов федерального значения, суде автономной области, судах автономных округов, окружных (флотских) военных судах, арбитражных судах округов, арбитражных апелляционных судах, арбитражных судах субъектов Российской Федерации и Суде по интеллектуальным правам — в размере 26,7 должностного оклада;
в районных, городских, межрайонных и гарнизонных военных судах — в размере 26,7 должностного оклада;
мировым судьям — в размере 26,4 должностного оклада;
(пп. 2 в ред. Федерального закона от 29.07.2018 N 266-ФЗ)(см. текст в предыдущей редакции
)
3) ежемесячной доплаты за выслугу лет:
в Конституционном Суде Российской Федерации — в размере 6 должностных окладов;
в Верховном Суде Российской Федерации — в размере 6 должностных окладов;
(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
в кассационных судах общей юрисдикции, апелляционных судах общей юрисдикции, кассационном военном суде, апелляционном военном суде, верховных судах республик, краевых, областных судах, судах городов федерального значения, суде автономной области, судах автономных округов, окружных (флотских) военных судах, арбитражных судах округов, арбитражных апелляционных судах, арбитражных судах субъектов Российской Федерации и Суде по интеллектуальным правам — в размере 6 должностных окладов;
(в ред. Федерального закона от 29.07.2018 N 266-ФЗ)(см. текст в предыдущей редакции
)
в районных, городских, межрайонных и гарнизонных военных судах — в размере 4,5 должностного оклада;
мировым судьям — в размере 3 должностных окладов;
4) доплат за ученую степень кандидата юридических наук, доктора юридических наук, за ученое звание доцента, профессора, за почетное звание «Заслуженный юрист Российской Федерации», за знание иностранных языков и их использование при исполнении должностных обязанностей:
в Конституционном Суде Российской Федерации — в размере 4,8 должностного оклада;
в Верховном Суде Российской Федерации — в размере 1,2 должностного оклада;
(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
5) ежеквартального денежного поощрения:
в Конституционном Суде Российской Федерации — в размере 40,7 должностного оклада;
в Верховном Суде Российской Федерации — в размере 24,4 должностного оклада;
в кассационных судах общей юрисдикции, апелляционных судах общей юрисдикции, кассационном военном суде, апелляционном военном суде, верховных судах республик, краевых, областных судах, судах городов федерального значения, суде автономной области, судах автономных округов, окружных (флотских) военных судах, арбитражных судах округов, арбитражных апелляционных судах, арбитражных судах субъектов Российской Федерации и Суде по интеллектуальным правам — в размере 8,9 должностного оклада;
в районных, городских, межрайонных и гарнизонных военных судах — в размере 8,9 должностного оклада;
мировым судьям — в размере 8,8 должностного оклада;
(пп. 5 в ред. Федерального закона от 29.07.2018 N 266-ФЗ)(см. текст в предыдущей редакции
)
6) других выплат, предусмотренных соответствующими федеральными законами и иными нормативными правовыми актами Российской Федерации:
в Конституционном Суде Российской Федерации — в размере 9 должностных окладов;
в Верховном Суде Российской Федерации — в размере от 6 до 9 должностных окладов исходя из установленных судьям размеров указанных выплат;
(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
в кассационных судах общей юрисдикции, апелляционных судах общей юрисдикции, кассационном военном суде, апелляционном военном суде, верховных судах республик, краевых, областных судах, судах городов федерального значения, суде автономной области, судах автономных округов, окружных (флотских) военных судах, арбитражных судах округов, арбитражных апелляционных судах, арбитражных судах субъектов Российской Федерации и Суде по интеллектуальным правам — в размере 3 должностных окладов;
(в ред. Федерального закона от 29.07.2018 N 266-ФЗ)(см. текст в предыдущей редакции
)
в районных, городских, межрайонных и гарнизонных военных судах — в размере 1 должностного оклада;
мировым судьям — в размере 0,1 должностного оклада.
В пределах средств, предусмотренных абзацами четвертым, пятым и шестым настоящего подпункта, Верховный Суд Российской Федерации и Судебный департамент при Верховном Суде Российской Федерации устанавливают конкретный размер средств для получателей бюджетных средств, определяя его исходя из количества судей, в отношении которых законодательством Российской Федерации предусмотрены другие выплаты;(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
7) районного коэффициента, коэффициента за работу в пустынных и безводных местностях, коэффициента за работу в высокогорных районах и процентной надбавки за работу в районах Крайнего Севера и приравненных к ним местностях, в южных районах Восточной Сибири и Дальнего Востока к ежемесячному денежному вознаграждению судьи, ежеквартальному денежному поощрению судьи и другим выплатам, предусмотренным соответствующими федеральными законами и иными нормативными правовыми актами Российской Федерации, — в размерах, определяемых с учетом размеров коэффициентов и процентных надбавок, установленных соответствующими нормативными правовыми актами Российской Федерации.
(п. 1.1 введен Федеральным законом от 25.12.2012 N 269-ФЗ)1.2. Конституционный Суд Российской Федерации, Верховный Суд Российской Федерации, Судебный департамент при Верховном Суде Российской Федерации вправе перераспределять средства фонда оплаты труда судей между выплатами, предусмотренными пунктом 1.1 настоящей статьи.(п. 1.2 в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
2. Судьям предоставляются ежегодные оплачиваемые отпуска продолжительностью 30 рабочих дней.
Судьям, работающим в районах Крайнего Севера, ежегодные оплачиваемые отпуска предоставляются продолжительностью 51 рабочий день, а в местностях, приравненных к районам Крайнего Севера, и в местностях с тяжелыми и неблагоприятными климатическими условиями, где установлены коэффициенты к заработной плате, — 45 рабочих дней.Судье предоставляется ежегодный дополнительный оплачиваемый отпуск с учетом стажа его работы в области юриспруденции:
(в ред. Федерального закона от 02.07.2013 N 185-ФЗ)(см. текст в предыдущей редакции
)
от 5 до 10 лет — 5 рабочих дней;
от 10 до 15 лет — 10 рабочих дней;
свыше 15 лет — 15 рабочих дней.
Время следования судьи к месту отдыха и обратно в срок отпуска не засчитывается. Стоимость проезда к месту отдыха и обратно подлежит оплате.
Порядок определения стажа работы для предоставления ежегодного дополнительного оплачиваемого отпуска устанавливается Верховным Судом Российской Федерации.(в ред. Федерального закона от 12.03.2014 N 29-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
В жилых помещениях, занимаемых судьями, во внеочередном порядке устанавливается телефон с оплатой по установленным тарифам.
В таком же порядке предоставляются места в дошкольных образовательных организациях, общеобразовательных организациях, имеющих интернат, летних оздоровительных учреждениях детям судей.
(в ред. Федерального закона от 02.07.2013 N 185-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
КонсультантПлюс: примечание.
Действие п. 5 распространено на судей, ушедших на пенсию с этой должности, независимо от времени ухода на пенсию (ФЗ от 21.06.1995 N 91-ФЗ).5. Судья и члены его семьи имеют право на получение медицинской помощи, включая обеспечение лекарственными препаратами для медицинского применения, которое оплачивается за счет средств федерального бюджета. Они также имеют право на санаторно-курортное лечение, которое судье, его супруге (супругу) и несовершеннолетним детям оплачивается за счет средств федерального бюджета. Эти права сохраняются за судьей и после ухода (удаления) его в отставку или на пенсию. При этом находящийся в отставке или на пенсии судья и члены его семьи получают медицинскую помощь за счет средств федерального бюджета в тех же медицинских организациях, в которых они состояли на учете.
(в ред. Федеральных законов от 21.06.1995 N 91-ФЗ, от 25.11.2013 N 317-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
В случае упразднения или реорганизации суда, а также если судья оказывается состоящим в близком родстве или свойстве (супруг (супруга), родители, дети, родные братья и сестры, дедушки, бабушки, внуки, а также родители, дети, родные братья и сестры супругов) с председателем или заместителем председателя того же суда, судья может быть с его согласия переведен в другой суд. За время, в течение которого оформляется перевод, за судьей сохраняется ежемесячное денежное вознаграждение. В случае отказа судьи от перевода он имеет право на выход в отставку на общих основаниях. В этом случае ему также выплачивается компенсация в размере 12 ежемесячных денежных вознаграждений по последней должности.
(в ред. Федеральных законов от 25.12.2008 N 274-ФЗ, от 25.12.2012 N 269-ФЗ)(см. текст в предыдущей редакции
)
(см. текст в предыдущей редакции
)
КонсультантПлюс: примечание.
Действие п. 7 распространено на судей, ушедших на пенсию с этой должности, независимо от времени ухода на пенсию (ФЗ от 21.06.1995 N 91-ФЗ).7. Судьи в служебных целях обеспечиваются проездными документами на проезд всеми видами транспорта общего пользования (кроме такси) в городском, пригородном и местном сообщении, приобретаемыми судами у соответствующих транспортных организаций в порядке, определяемом Правительством Российской Федерации.При направлении в служебные командировки судьи пользуются правом бронирования и получения вне очереди мест в гостиницах и приобретения проездных документов на все виды транспорта.
(п. 7 в ред. Федерального закона от 22.08.2004 N 122-ФЗ)(см. текст в предыдущей редакции
)
8. Судьи и имеющие классные чины работники судов обеспечиваются служебным обмундированием в порядке и по нормам
, которые устанавливаются Правительством Российской Федерации.
(см. текст в предыдущей редакции
)
Степени снижения слуха | «Центр Слухопротезирования «СЛУХ 66″» — г. Екатеринбург
Слух снижается постепенно, это может длиться годами. Чтобы определить степень потери слуха проводят различные исследования. Человек в ходе исследования должен различать звука на основных тонах в диапазоне от 125 Гц до 8.000 Гц.
Существует 4 степени нарушения слуха:
- Легкая потеря слуха (I степень тугоухости)
Нарушение слуха до 40 дБ. Шепотную речь человек слышит с расстояния 4-1,5 м, разговорную речь – с 5 м и больше. Возникает нарушение понимания спокойной речи или шёпота, либо речи в шумной обстановке.
- Умеренная — легкая потеря слуха (II степень тугоухости)
Нарушение слуха от 41 до 55 дБ. Шепотную речь человек воспринимает с расстояния 1,5-0,5 м, разговорную – с 3-5 м. Возникает нарушение понимания спокойной речи близко от источника звука, либо обычной речи в тихой ситуации, особенно при наличии фонового шума. Сложность понимания речи в повседневной жизни.
- Тяжелая потеря слуха (III степень тугоухости)
Нарушение слуха от 56 до 70 дБ. Шепотную речь человек не слышит, разговорную с расстояния 1-3 м. Человек имеет возможность слышать только громкие звуки: стук в дверь, громкую речь, крик, сигнал автомобиля. Большое количество звуков будет недоступна для слуха. Собеседник должен говорить очень громко с близкого расстояния.
- Глубокая потеря слуха (IV степень тугоухости)
Нарушение слуха от 71 до 90 дБ. Разговорная речь доступна с расстояния до 1 м или крик у ушной раковины. При этом нарушении очень трудно услышать звук очень громкой мощности – работающего вблизи двигателя, имеется возможность слышать некоторые очень громкие звуки. Общение без слухового аппарата невозможно.
Нарушение слуха более 91 дБ. Человек не слышит даже крик у ушной раковины.
В соответствии с исследованиями установлено, что срок до обращения к специалисту человека с потерей слуха составляет около 8 лет. Снижение слуха процесс длительный и медленный. Обнаружение проблемы со слухом на ранних стадиях дает большую вероятность того, что при проведенной коррекции слуха и лечении можно вернуться к жизни, привычной для человека.
Слуховой аппарат – это современное электронное техническое устройство, улучшающие качество жизни людям с нарушением слуха и компенсирующие ту или иную степень потери слуха. Но для того чтобы ощутить результат надо правильно выбрать слуховой аппарат, который будет настроен в соответствии с Вашей потери слуха.
Специалист нашего центра аудиолог-слухопротезист с образованием сурдолог (стаж работы более 25 лет) поможет вам с выбором слухового аппарат, соответствующего Вашему образу жизни и настроит его под Ваш слух.
Читайте так же: Снижение слуха. Первые признаки нарушения слуха
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| ax3 + bx2 + bx + a = 0, | (1) |
где a, b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
ax2 + (b – a) x + a = 0.
Пример 1. Решить уравнение
| 2x3 + 7x2 + 7x + 2 = 0. | (2) |
Решение. Разложим левую часть уравнения (2) на множители:
Ответ:.
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| ax4 + bx3 + cx2 + + bx + a = 0, | (3) |
а также уравнения вида
| ax4 + bx3 + cx2– – bx + a = 0, | (4) |
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение (3), разделим его на x2. В результате получится уравнение
| (5) |
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
| (6) |
Если теперь обозначить
| (7) |
то уравнение (6) станет квадратным уравнением:
| ay2 + by + c – 2a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x2. В результате получится уравнение
| (9) |
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
| (10) |
Если теперь обозначить
| (11) |
то уравнение (10) станет квадратным уравнением:
| ay2 + by + c + 2a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (4) завершено.
Пример 2. Решить уравнение
| 2x4 – 3x3 – x2 – – 3x + 2 = 0. | (13) |
Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на x2. В результате получится уравнение
| (14) |
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
| (15) |
Если теперь обозначить
| (16) |
то уравнение (15) станет квадратным уравнением:
| 2y2 – 3y – 5 = 0. | (17) |
Решим уравнение (17):
| (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ:
Пример 3. Решить уравнение
| 6x4 – 25x3 + 12x2 + + 25x + 6 = 0. | (19) |
Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на x2. В результате получится уравнение
| (20) |
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
| (21) |
Если теперь обозначить
| (22) |
то уравнение (21) станет квадратным уравнением:
| 6y2 – 25y + 24 = 0. | (23) |
Решим уравнение (23):
| (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ:
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
| (25) |
где a, b, c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x2. В результате получится уравнение
| (26) |
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
| (28) |
то уравнение (27) станет квадратным уравнением:
| (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (25) завершено.
Пример 4. Решить уравнение
| 2x4 – 15x3 + 35x2 – – 30 x + 8 = 0. | (30) |
Решение. Введем для коэффициентов уравнения (30) следующие обозначения
a = 2 , b =– 15,
c = 35, d = – 30,
и найдем значение выражения
Поскольку
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение
| (31) |
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
| (32) |
Если теперь обозначить
| (33) |
то уравнение (32) станет квадратным уравнением:
| 2y2 – 15y + 27 = 0. | (34) |
Решим уравнение (34):
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Банк России принял решение повысить ключевую ставку на 50 б.п., до 5,50% годовых
Совет директоров Банка России 11 июня 2021 года принял решение повысить ключевую ставку на 50 б.п., до 5,50% годовых. Российская и мировая экономика восстанавливаются быстрее, чем ожидалось ранее. Инфляция складывается выше прогноза Банка России. Вклад в инфляцию со стороны устойчивых факторов возрастает в связи с более быстрым расширением спроса по сравнению с возможностями наращивания выпуска. На краткосрочном горизонте это влияние усиливается ростом цен на мировых товарных рынках. C учетом высоких инфляционных ожиданий баланс рисков значимо сместился в сторону проинфляционных.
Повышенное инфляционное давление в условиях завершающегося восстановления экономики может привести к более значительному и продолжительному отклонению инфляции вверх от цели. Это формирует необходимость дальнейшего повышения ключевой ставки на ближайших заседаниях. Решения по ключевой ставке будут приниматься с учетом фактической и ожидаемой динамики инфляции относительно цели, развития экономики на прогнозном горизонте, а также оценки рисков со стороны внутренних и внешних условий и реакции на них финансовых рынков. В условиях проводимой денежно-кредитной политики годовая инфляция вернется к цели Банка России во втором полугодии 2022 года и будет находиться вблизи 4% в дальнейшем.
Динамика инфляции. Инфляция складывается выше прогноза Банка России. В мае месячные сезонно сглаженные темпы роста потребительских цен существенно ускорились, а годовая инфляция увеличилась до 6,0% (после 5,5% в апреле). По оценкам на 7 июня, годовая инфляция выросла до 6,15%. Показатели, отражающие наиболее устойчивые процессы ценовой динамики, по оценкам Банка России, в мае также повысились и находятся значимо выше 4% в годовом выражении.
Это является отражением того факта, что устойчивый рост внутреннего спроса опережает возможности расширения предложения по широкому кругу отраслей. На этом фоне предприятиям легче переносить в цены возросшие издержки.
Инфляционные ожидания населения уже несколько месяцев находятся вблизи максимальных значений за последние 4 года. Продолжают расти ценовые ожидания предприятий, оставаясь выше локальных максимумов 2019–2020 годов. Ожидания профессиональных аналитиков на среднесрочную перспективу заякорены вблизи 4%.
В условиях проводимой денежно-кредитной политики годовая инфляция вернется к цели Банка России во втором полугодии 2022 года и будет находиться вблизи 4% в дальнейшем.
Денежно-кредитные условия остаются мягкими с учетом повышенных инфляционных ожиданий и фактической инфляции. В этих условиях кредитование продолжает расти темпами, близкими к максимумам последних лет. Вместе с тем доходности краткосрочных ОФЗ увеличились, отражая ожидания более быстрого повышения Банком России ключевой ставки. Наметилась тенденция к росту депозитных ставок. Решения Банка России о повышении ключевой ставки и произошедшее с начала текущего года увеличение доходностей ОФЗ обусловят дальнейший рост кредитно-депозитных ставок. Это позволит повысить привлекательность банковских депозитов для населения, защитить покупательную способность сбережений и обеспечит сбалансированный рост кредитования.
Экономическая активность восстанавливается быстрее ожиданий Банка России. Оперативные индикаторы свидетельствуют об устойчивом росте потребительского и инвестиционного спроса. По оценкам Банка России, потребительская активность в целом достигла уровней до начала пандемии. Продолжается активное восстановление сектора услуг населению. Выпуск в большинстве отраслей экономики, по оценкам Банка России, превысил докризисные уровни. Спрос на рабочую силу растет по широкому кругу отраслей. При этом в некоторых секторах наблюдается ее дефицит.
Поддержку российской экономике также оказывает внешний спрос. На фоне постепенной нормализации эпидемической обстановки в мире улучшаются перспективы восстановления мировой экономики. Это, в свою очередь, усиливает рост цен на мировых товарных рынках.
В этих условиях, по оценкам Банка России, российская экономика вернется к докризисному уровню уже в II квартале 2021 года. На среднесрочную траекторию экономического роста значимое влияние будут оказывать факторы со стороны как внутренних, так и внешних условий. Динамика внутреннего спроса будет во многом определяться темпами дальнейшего расширения потребительского и инвестиционного спроса. Поддержку потребительскому спросу будет оказывать дальнейшее снижение склонности домашних хозяйств к сбережению наряду с ростом доходов и кредитования. Влияние на внутренний спрос также окажет процесс нормализации бюджетной политики с учетом объявленных дополнительных социальных и инфраструктурных мер. Динамика внешнего спроса будет в большей степени зависеть от мер бюджетной поддержки в отдельных развитых странах, а также темпов вакцинации в мире.
Инфляционные риски. Баланс рисков значимо сместился в сторону проинфляционных. Действие проинфляционных факторов может быть усилено повышенными инфляционными ожиданиями и сопутствующими вторичными эффектами.
Источником инфляционного давления может стать более существенное, чем ожидается, снижение склонности домашних хозяйств к сбережению под влиянием сочетания низких процентных ставок и роста цен. Дополнительное повышательное давление на цены могут продолжить оказывать сохраняющиеся затруднения в производственных и логистических цепочках. Проинфляционные риски также создает ценовая конъюнктура мировых товарных рынков под воздействием факторов как со стороны спроса, так и со стороны предложения. Это может влиять на внутренние цены соответствующих товаров. Вместе с тем дальнейшая динамика продовольственных цен будет во многом зависеть от перспектив урожая сельскохозяйственных культур как внутри страны, так и за рубежом.
Краткосрочные проинфляционные риски также связаны с усилением волатильности на глобальных рынках, в том числе под влиянием различных геополитических событий, что может отражаться на курсовых и инфляционных ожиданиях. В условиях более быстрого, чем ожидалось ранее, восстановления мировой экономики и, соответственно, исчерпания необходимости проведения беспрецедентно стимулирующей политики в развитых экономиках возможно более раннее начало нормализации денежно-кредитной политики центральными банками этих стран. Это может стать дополнительным фактором роста волатильности на мировых финансовых рынках.
Дезинфляционные риски для базового сценария остаются умеренными. Открытие границ по мере снятия ограничительных мер может восстановить потребление зарубежных услуг, а также ослабить ограничения со стороны предложения на рынке труда через приток иностранной рабочей силы. Замедлить дальнейший рост экономической активности могут, в частности, низкие темпы вакцинации и распространение новых штаммов вируса, а также связанное с этим ужесточение ограничительных мер.
На среднесрочную динамику инфляции значимо влияет бюджетная политика. В базовом сценарии Банк России исходит из заложенной в Основных направлениях бюджетной, налоговой и таможенно-тарифной политики на 2021 год и на плановый период 2022 и 2023 годов траектории нормализации бюджетной политики, предполагающей возвращение к параметрам бюджетного правила в 2022 году. Банк России также будет учитывать в прогнозе решения об инвестировании ликвидной части Фонда национального благосостояния сверх порогового уровня в 7% ВВП.
Повышенное инфляционное давление в условиях завершающегося восстановления экономики может привести к более значительному и продолжительному отклонению инфляции вверх от цели. Это формирует необходимость дальнейшего повышения ключевой ставки на ближайших заседаниях. Решения по ключевой ставке будут приниматься с учетом фактической и ожидаемой динамики инфляции относительно цели, развития экономики на прогнозном горизонте, а также оценки рисков со стороны внутренних и внешних условий и реакции на них финансовых рынков.
Следующее заседание Совета директоров Банка России, на котором будет рассматриваться вопрос об уровне ключевой ставки, запланировано на 23 июля 2021 года. Время публикации пресс-релиза о решении Совета директоров Банка России и среднесрочного прогноза Банка России — 13:30 по московскому времени.
Заявление Председателя Банка России Эльвиры Набиуллиной по итогам заседания Совета директоров 11 июня 2021 года
При использовании материала ссылка на Пресс-службу Банка России обязательна.
Цельсия в градусы Фаренгейта (° C в ° F)
Фаренгейта в Цельсия ►
Как преобразовать градусы Цельсия в градусы Фаренгейта
0 градусов Цельсия равно 32 градусам Фаренгейта:
0 ° C = 32 ° F
Температура T в градусах Фаренгейта (° F) равна температуре T в градусах Цельсия (° C), умноженной на 9/5 плюс 32:
T (° F) = T (° C) × 9/5 + 32
или
T (° F) = T (° C) × 1.8 + 32
Пример
Преобразование 20 градусов Цельсия в градусы Фаренгейта:
T (° F) = 20 ° C × 9/5 + 32 = 68 ° F
Таблица преобразованияградусов Цельсия в градусы Фаренгейта
| Цельсия (° C) | по Фаренгейту (° F) | Описание |
|---|---|---|
| -273,15 ° С | -459,67 ° F | температура абсолютного нуля |
| -50 ° С | -58.0 ° F | |
| -40 ° С | -40.0 ° F | |
| -30 ° С | -22,0 ° F | |
| -20 ° С | -4,0 ° F | |
| -10 ° С | 14,0 ° F | |
| -9 ° С | 15.8 ° F | |
| -8 ° С | 17,6 ° F | |
| -7 ° С | 19,4 ° F | |
| -6 ° С | 21.2 ° F | |
| -5 ° С | 23,0 ° F | |
| -4 ° С | 24,8 ° F | |
| -3 ° С | 26,6 ° F | |
| -2 ° С | 28,4 ° F | |
| -1 ° С | 30,2 ° F | |
| 0 ° С | 32,0 ° F | точка замерзания / плавления воды |
| 1 ° С | 33.8 ° F | |
| 2 ° С | 35,6 ° F | |
| 3 ° С | 37,4 ° F | |
| 4 ° С | 39,2 ° F | |
| 5 ° С | 41.0 ° F | |
| 6 ° С | 42,8 ° F | |
| 7 ° С | 44,6 ° F | |
| 8 ° С | 46,4 ° F | |
| 9 ° С | 48.2 ° F | |
| 10 ° С | 50,0 ° F | |
| 11 ° С | 51,8 ° F | |
| 12 ° С | 53,6 ° F | |
| 13 ° С | 55,4 ° F | |
| 14 ° С | 57,2 ° F | |
| 15 ° С | 59.0 ° F | |
| 16 ° С | 60.8 ° F | |
| 17 ° С | 62,6 ° F | |
| 18 ° С | 64,4 ° F | |
| 19 ° С | 66,2 ° F | |
| 20 ° С | 68.0 ° F | |
| 21 ° С | 69,8 ° F | Комнатная температура |
| 22 ° С | 71,6 ° F | |
| 23 ° С | 73.4 ° F | |
| 24 ° С | 75,2 ° F | |
| 25 ° С | 77.0 ° F | |
| 26 ° С | 78,8 ° F | |
| 27 ° С | 80,6 ° F | |
| 28 ° С | 82,4 ° F | |
| 29 ° С | 84,2 ° F | |
| 30 ° С | 86.0 ° F | |
| 31 ° С | 87,8 ° F | |
| 32 ° С | 89,6 ° F | |
| 33 ° С | 91,4 ° F | |
| 34 ° С | 93,2 ° F | |
| 35 ° С | 95.0 ° F | |
| 36 ° С | 96,8 ° F | |
| 37 ° С | 98.6 ° F | Средняя температура тела |
| 38 ° С | 100,4 ° F | |
| 39 ° С | 102,2 ° F | |
| 40 ° С | 104.0 ° F | |
| 50 ° С | 122.0 ° F | |
| 60 ° С | 140.0 ° F | |
| 70 ° С | 158.0 ° F | |
| 80 ° С | 176.0 ° F | |
| 90 ° С | 194.0 ° F | |
| 100 ° С | 212.0 ° F | температура кипения воды |
| 200 ° С | 392.0 ° F | |
| 300 ° С | 572,0 ° F | |
| 400 ° С | 752,0 ° F | |
| 500 ° С | 932.0 ° F | |
| 600 ° С | 1112.0 ° F | |
| 700 ° С | 1292.0 ° F | |
| 800 ° С | 1472.0 ° F | |
| 900 ° С | 1652.0 ° F | |
| 1000 ° С | 1832.0 ° F |
Фаренгейта в Цельсия ►
См. Также
Перевести Фаренгейты в Цельсия | Калькулятор ° F — ° C
Переход от градусов Фаренгейта к Цельсию? Наш преобразователь температуры поможет вам легко переключаться между ° F и ° C.Попробуйте сами!
Преобразование между градусами Цельсия и градусами Фаренгейта является обычным, когда дело доходит до преобразований температуры . Правительства хотели стандартизировать измерения температуры, поэтому использовали для этого градусы Цельсия. Сейчас шкала температуры Цельсия в основном используется в мире, за исключением США, где предпочтение отдается Фаренгейту. При чтении рецептов и приготовлении пищи, например, для шоколадных десертов, обычно требуется переключение между этими двумя температурами.Используйте этот конвертер по Фаренгейту — Цельсия для переключения между ними. Ознакомьтесь с другими нашими преобразователями температуры.
Как использовать конвертер градусов Фаренгейта в Цельсия?
В указанном выше калькуляторе по Фаренгейту — Цельсию введите количество градусов в Фаренгейте, которое вы хотите изменить, и нажмите «преобразовать», чтобы получить точный эквивалент в Цельсиях. Для обратного преобразования посмотрите, как преобразовать Цельсий в Фаренгейт.
Формула для перевода Фаренгейтов в Цельсия
Математическая формула, используемая преобразователем температуры f в c , показана ниже и полезна, если вам нужно знать, как выполняется онлайн-преобразование.Например, 10 ° F = -12 ° C = и 100 ° F = 37,7 ° C
(° F — 30) / 2 = ° C
Когда использовать по Фаренгейту?
В США предпочтение отдается температурной шкале по Фаренгейту . Шкала Фаренгейта, известная нам сегодня, основана на шкале, предложенной немецким физиком Даниэлем Фаренгейтом. Температура замерзания воды с использованием этой температурной шкалы составляет 32 ° F, а точка кипения — 212 ° F. Попробуйте наш инструмент для преобразования ° F — ° C .
Когда использовать градусы Цельсия?
градусов Цельсия — это наиболее распространенная форма измерения температуры, используемая в термометрах и в новостях при сообщении погоды.Ранее известная как градусы Цельсия, шкала Цельсия происходит от шкалы температур, предложенной шведским астрономом Андерсом Цельсием, где 0 означает кипящую воду, а 100 — замерзающую воду. Используйте преобразователь температуры F в C из выше.
Сколько это 1 градус Фаренгейта в градусах Цельсия?
1 градус Фаренгейта равен -17,222222222222 градусу Цельсия (1 ° F = -17.222222222222 ° С)
Сколько 2 градуса Фаренгейта и градуса Цельсия?
2 градуса по Фаренгейту равны -16.666666666667 градусов Цельсия (2 ° F = -16,666666666667 ° C)
Сколько 3 градуса Фаренгейта и градуса Цельсия?
3 градуса по Фаренгейту равны -16.111111111111 градусов Цельсия (3 ° F = -16,111111111111 ° С)
Сколько 4 градуса Фаренгейта и градуса Цельсия?
4 градуса по Фаренгейту равны -15.555555555556 градусов Цельсия (4 ° F = -15,555555555556 ° C)
Сколько 5 градусов по Фаренгейту и градусов Цельсия?
5 градусов по Фаренгейту равны -15 градусов Цельсия (5 ° F = -15 ° C)
Сколько 10 градусов по Фаренгейту в градусах Цельсия?
10 градусов по Фаренгейту равны -12.222222222222 градусов Цельсия (10 ° F = -12,222222222222 ° С)
Сколько 15 градусов по Фаренгейту в градусах Цельсия?
15 градусов по Фаренгейту равны -9,4444444444444 градусов Цельсия (15 ° F = -9,4444444444444 ° C)
Сколько 20 градусов по Фаренгейту в градусах Цельсия?
20 градусов по Фаренгейту равны -6.6666666666667 градусов Цельсия (20 ° F = -6,6666666666667 ° C)
Сколько 25 градусов по Фаренгейту в градусах Цельсия?
25 градусов по Фаренгейту равны -3,8888888888889 градусов Цельсия (25 ° F = -3,8888888888889 ° C)
Сколько 30 градусов по Фаренгейту в градусах Цельсия?
30 градусов по Фаренгейту равны -1.1111111111111 градусов Цельсия (30 ° F = -1,1111111111111 ° С)
Сколько 50 градусов по Фаренгейту в градусах Цельсия?
50 градусов по Фаренгейту равны 10 градусов Цельсия (50 ° F = 10 ° C)
Сколько 100 градусов по Фаренгейту в градусах Цельсия?
100 градусов по Фаренгейту равны 37.777777777778 градусов Цельсия (100 ° F = 37,777777777778 ° C)
Сколько 200 градусов по Фаренгейту в градусах Цельсия?
200 градусов по Фаренгейту равны 93,333333333333 градусов Цельсия (200 ° F = 93,333333333333 ° C)
Сколько 500 градусов по Фаренгейту в градусах Цельсия?
500 градусов по Фаренгейту равны 260 градусов Цельсия (500 ° F = 260 ° C)
Сколько 1000 градусов по Фаренгейту в градусах Цельсия?
1000 градусов по Фаренгейту равны 537.77777777778 градусов Цельсия (1000 ° F = 537,77777777778 ° C)
Pon este converor en tu web
Преобразование температуры из Цельсия в Фаренгейт
Быстрый градус Цельсия (
° C, ) / Фаренгейт ( ° F, ) Преобразование:measure / images / thermometer.js? mode = коробки
Введите значение в любое поле
Или используйте слайдер
Или интерактивный термометр
Или этот метод:
| ° C до ° F | Разделите на 5, затем умножьте на 9 и прибавьте 32 |
| ° F до ° C | Вычтите 32, затем умножьте на 5, затем разделите на 9 |
(объяснение ниже…)
Типичные температуры
(только полужирный, точно такие же)
| ° С | ° F | Описание | |
|---|---|---|---|
| 220 | 430 | Горячая печь | |
| 180 | 360 | Духовка среднего размера | |
| 100 | 212 | Вода закипает | |
| 40 | 104 | Горячая ванна | |
| 37 | 98.6 | Температура тела | |
| 30 | 86 | Погода на пляже | |
| 21 | 70 | Комнатная температура | |
| 10 | 50 | Прохладный день | |
| 0 | 32 | Температура замерзания воды | |
| −18 | 0 | Очень холодный день | |
| −40 | −40 | Extremely Cold Day (и столько же!) |
16 — около 61
28 — около 82
Пояснение
Существуют две основные температурные шкалы:
- ° C , шкала Цельсия (часть метрической Система, используемая в большинстве стран)
- ° F , шкала Фаренгейта (используется в США)
Они оба измеряют одно и то же (температуру!), Но используют разные номера:
- Кипящая вода (при нормальном давлении) измеряет 100 ° по Цельсию, но 212 ° по Фаренгейту
- И замерзание воды измеряет 0 ° по Цельсию, но 32 ° по Фаренгейту
Как это:
Глядя на схему, обратите внимание:
- Шкалы начинаются с другого числа (0 против 32), поэтому мы будем нужно добавить или вычесть 32
- Шкала увеличивается с разной скоростью (100 против 180), поэтому мы будем также нужно умножить
Итак, преобразовать:
от Цельсия до Фаренгейта: сначала умножьте на 180 100 , затем добавьте 32
от Фаренгейта до Цельсия: сначала вычтите 32, затем умножьте по 100 180
180 100 можно упростить до 9 5 ,
и 100 180 можно упростить до 5 9 , поэтому мы получаем
от ° C до ° F: Разделите на 5, затем умножьте на 9, затем добавьте 32
от ° F до ° C: Вычтите 32, затем умножьте на 5, затем разделите на 9
Пример: преобразовать 25 ° Цельсия
(хороший теплый день) в Фаренгейта. Сначала: 25 ° / 5 = 5
Затем: 5 × 9 = 45
Затем: 45 + 32 = 77 ° F
Пример: преобразовать 98.6 ° по Фаренгейту
(нормальная температура тела) от до по Цельсию Сначала: 98,6 ° — 32 = 66,6
Затем: 66,6 × 5 = 333
Затем: 333/9 = 37 ° C
Мы можем поменять местами порядок деления и умножения, если захотим, но не меняем сложение или вычитание. Так что это тоже нормально:
Пример: преобразовать 98,6 ° Фаренгейта в Цельсий (снова)
Сначала: 98,6 ° — 32 = 66,6
Затем: 66.6/9 = 7,4
Тогда: 7,4 × 5 = 37 ° C
(Тот же ответ, что и раньше, было легче или сложнее?)
Мы можем записать их в виде формул: по Цельсию по Фаренгейту: (° C × 9 5 ) + 32 = ° F
по Фаренгейту по Цельсию: (° F — 32) × 5 9 = ° C
Другие эффективные методы
Используйте 1.8 вместо 9/5
9/5 равно 1.8, поэтому мы также можем использовать этот метод:
по Цельсию по Фаренгейту: ° C × 1,8 + 32 = ° F
по Фаренгейту по Цельсию: (° F — 32) / 1,8 = ° C
Чтобы упростить «× 1,8», мы можем умножить на 2 и вычесть 10% , но это работает только от ° C до ° F:
Цельсия в Фаренгейта: (° C × 2) минус 10% + 32 = ° F
Пример: преобразовать 20 ° Цельсия
(хороший день) в градусы Фаренгейта- 20 x2 = 40
- минус 10% равно 40−4 = 36
- 36 + 32 = 68 ° F
Сложить 40, умножить, вычесть 40
Поскольку обе шкалы пересекаются под углом −40 ° (−40 ° C равняется −40 ° F), мы можем:
- доб 40,
- умножить на 5/9 (для ° F — ° C) или 9/5 (для ° C — ° F)
- вычесть 40
Как это:
градусов Цельсия в градусы Фаренгейта: прибавьте 40, умножьте на 9/5, затем вычтите 40
градусов по Фаренгейту в градусы Цельсия: прибавьте 40, умножьте на 5/9, затем вычтите 40
Пример: преобразовать 10 ° Цельсия
(прохладный день) в градусы Фаренгейта- 10 +40 = 50
- 50 × 9/5 = 90
- 90-40 = 50 ° F
Чтобы запомнить 9/5 для ° C — ° F, подумайте, что «F больше, чем C, поэтому существует больше ° F, чем ° C»
Быстро, но
Неточно градуса Цельсия в градусах Фаренгейта: удвоить, затем прибавить 30
градусов по Фаренгейту к градусам Цельсия: вычесть 30, затем уменьшить вдвое
Примеры ° C → ° F:
- 0 ° C → 0 + 30 → 30 ° F (меньше на 2 °)
- 10 ° C → 20 + 30 → 50 ° F (точно!)
- 30 ° C → 60 + 30 → 90 ° F (высокий на 4 °)
- 180 ° C → 360 + 30 → 390 ° F (высокий на 34 °, плохо)
Примеры ° F → ° C:
- 40 ° F → 10/2 → 5 ° C (почти справа)
- 80 ° F → 50/2 → 25 ° C (низкая примерно на 2 °)
- 120 ° F → 90/2 → 45 ° C (низкое примерно на 4 °)
- 450 ° F → 420/2 → 210 ° C (ниже примерно на 22 °, плохо)
Сноска: Температура — это мера того, насколько быстро движутся частицы объекта.
1041, 1042, 1043, 1044, 3724, 3725, 3726, 3727, 3728, 3729
Градус Символ °
° Копировать символ степени в буфер обмена
Градус обозначает ° . Иногда студентам или тем, кто занимается математикой, физикой или различными видами вычислений, может потребоваться ввести знак градуса , но у нас его нет прямо на нашей клавиатуре. Градус может использоваться в случае, если мы имеем дело с углами, или когда нам нужно работать с температурой и использовать градусы Цельсия.Это также общий знак градуса координат . На самом деле, есть несколько способов сделать символ градусов . Вы можете либо скопировать пасту, либо использовать код степени в своем документе. См. Несколько примеров ниже:
° & # 176;html десятичный градус
° & # xb0;html, шестнадцатеричный градус
° & deg;html степень имени
Как ввести символ степени на ПК с Microsoft Windows?
Нажмите и удерживайте клавишу ALT и введите 0 1 7 6 на цифровой клавиатуре вашей клавиатуры.Убедитесь, что NumLock включен, и введите 0176 с нулем в начале. Если нет цифровой клавиатуры, нажмите и удерживайте Fn , прежде чем вводить цифры 0176 из символа градусов .
Как ввести символ степени в Mac OS?
Нажмите и удерживайте SHIFT OPTION 8 клавиш на клавиатуре.
Символградуса в LaTeX
СимволDegree можно набрать в LaTeX с помощью пакетов.
textcomp
\ usepackage {textcomp}
\ begin {document}
Обозначение степени: 90 \ si {\ textdegree}
\ конец {документ}
gensymb
\ usepackage {gensymb}
\ begin {document}
Обозначение степени: 90 \ si {\ deg}
\ конец {документ}
siunitx
\ usepackage {siunitx}
\ begin {document}
Обозначение степени: 90 \ si {\ deg}
\ конец {документ}
Символ градуса Цельсия
℃ & # 8451;десятичный градус Цельсия
℃ & # x2103;шестнадцатеричный градус Цельсия
℃ \ u2103градуса Цельсия исходный код
градус Фаренгейта
℉ & # 8457;десятичный градус Фаренгейта
℉ & # x2109;шестнадцатеричный градус Фаренгейта
℉ \ u2109исходный код степени по Фаренгейту
Мужской порядковый индикаторный символ
º \ u00BAградусов исходный код
Кольцо над символом
˚ \ u02DAградусов исходный код
Кольцо под символом
̥ \ u0325градусов исходный код
Надстрочный нулевой символ
⁰ & # 8304;десятичный градус
⁰ \ u2070градусов исходный код
Символ оператора кольца
∘ & # 8728;десятичный градус
∘ \ u2218градусов исходный код
Примеры обозначения градусов
Градус по геометрии.
- Прямой угол составляет 90 °. (90 градусов)
- Прямой угол 180 °. (180 градусов)
- Острый угол менее 90 °. (<90 градусов)
- Тупой угол больше 90 ° и меньше 90 °. (> 90 градусов и <180 градусов)
- Угол отражения больше 180 °. (> 180 градусов)
Обозначение градуса в географической системе координат.
- Широта 32,344790 равна 32 ° 20 ‘41,244’ ‘северной широты (32 градуса северной широты)
- Долгота -64.6 равен 64 °° 41 ‘32,3052’ ‘з.д. (64 градуса з.д.)
Обозначение градуса при измерениях температуры.
- 2 ° C: 2 градуса Цельсия
- 20 ° C: 20 градусов Цельсия
- 23 ° C: 23 градуса Цельсия
- 10 ℃: 10 градусов Цельсия
- 15 ℃: 15 градусов Цельсия
- -21 ℃: -21 градус Цельсия
Копировать Вставить символ степени
° Копировать символ степени в буфер обмена
Также ознакомьтесь с другими вариантами использования символа градуса:
Полезные ресурсы
Расчет уклона и общего уклона в архитектуре
Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения.Например, крыши обозначаются градиентами, а поперечные уклоны тротуаров обычно обозначаются в градусах. Полезно понять, как рассчитать каждый метод.
Существует три различных способа указать наклон поверхности относительно горизонтальной плоскости: градусы, уклон и процент.
Расчет градиента уклона
Градиенты уклона записываются как Y: X, где Y — это единичная величина подъема, а X — это пробег. Оба числа должны использовать одни и те же единицы измерения.Например, если вы путешествуете на 3 дюйма по вертикали и 3 фута (36 дюймов) по горизонтали, наклон будет 3:36 или 1:12. Это читается как «наклон один из двенадцати».
Расчет процента уклона
Процент уклона рассчитывается так же, как и уклон. Преобразуйте приближение и бег в те же единицы, а затем разделите приближение на разбег. Умножьте это число на 100, и вы получите наклон в процентах. Например, подъем 3 дюйма, деленный на пробег 36 дюймов = 0,083 x 100 = 8.Уклон 3%.
Расчет уклона в градусах
Самый сложный способ вычисления наклона — в градусах, и для этого требуется немного математики средней школы. Тангенс данного угла (в градусах) равен подъему, деленному на пробег. Следовательно, величина, обратная тангенсации подъема, деленная на длину пробега, даст угол.
Таблица общих наклонов в архитектуре
В таблице ниже показаны некоторые распространенные уклоны. Для полов с уклоном 1:20 поручни не требуются, но все, что круче 1:20, считается пандусом и требует поручней.Пандусы с уклоном 1:12 — это максимальный уклон, разрешенный правилами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что чуть больше 2%. Однако мы видели некоторые юрисдикции, которые разрешают максимальный поперечный уклон 1:50.
| Градусы | Градиент | Процент |
|---|---|---|
| 0,6 ° | 1: 95,49 | 1,0% |
| 1 ° | 1: 57.29 | 1,7% |
| 1,15 ° | 1: 50 | 2% |
| 1,19 ° | 1: 48 | 2,08% |
| 2,86 ° | 1: 20 | 5% |
| 4,76 ° | 1: 12 | 8,3% |
| 7,13 ° | 1: 8 | 12,5% |
| 10 ° | 1: 5,67 | 17,6% |
| 14,04 ° | 1: 4 | 25% |
| 15 ° | 1: 3.73 | 26,8% |
| 26,57 ° | 1: 2 | 50% |
| 30 ° | 1: 1,73 | 57,7% |
| 45 ° | 1: 1 | 100% |
| 56,31 ° | 1: 0,67 | 150% |
| 60 ° | 1: 0,6 | 173,2% |
| 63,43 ° | 1: 0,5 | 200% |
| 78,69 ° | 1: 0.2 | 500% |
| 89,43 ° | 1: 0,1 | 1000% |
| 90 ° | 1: 0 | инф. |
Скаты крыши
Наклоны крыши идентифицируются с помощью метода градиента, описанного выше, где подъем меняется, но обычно высота подъема составляет 12. На некоторых очень крутых крышах вы можете увидеть, что уклон перевернут, так что подъем меняется, но подъем сохраняется как 12.
Кровля с малым уклоном
Крыши с низким уклоном имеют уклон 3:12 или меньше.У них должна быть мембранная кровельная система для обеспечения водонепроницаемости.
| Градиент крыши | Градусы | Процент |
|---|---|---|
| 1/4: 12 | 1,19 ° | 2,08% |
| 1/2: 12 | 2,39 ° | 4,17% |
| 1: 12 | 4,76 ° | 8,3% |
| 2: 12 | 9,46 ° | 16,67% |
| 3: 12 | 14.04 ° | 25% |
Крутые крыши
Все, что выше 3:12, считается крутой крышей и может быть покрыто металлическими панелями, черепицей или черепицей — эти крыши проливают воду и не считаются водонепроницаемыми.
| Градиент крыши | Градусов | Процент |
|---|---|---|
| 4: 12 | 18,43 ° | 33,33% |
| 5: 12 | 22,62 ° | 41,67% |
| 6: 12 | 26.57 ° | 50% |
| 7: 12 | 30,26 ° | 58,33% |
| 8: 12 | 33,69 ° | 66,67% |
| 9: 12 | 36,87 ° | 75 % |
| 10: 12 | 39,81 ° | 83,33% |
| 11: 12 | 42,51 ° | 91,67% |
| 12: 12 | 45 ° | 100% |
Измерение углов
Измерение угловПонятие угла
Понятие угла — одно из важнейших понятий в геометрии.Понятия равенства, сумм и разностей углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 дюймов. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равняется π /180 радиана также 1 радиан равен 180/ π градусовБольшинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая справка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге Elements of Algebra явно сказал, что углы измеряются длиной дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e iθ = cos θ + i sin θгде θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, тогда мера в радианах равна 1.5.Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов для измерения в градусах и радианах. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы дать десятичной дроби, но радианы часто появляются с коэффициентом π .| Уголок | Градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, подсказки для решения упражнений и в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину проходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). л = 0,16296, л = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан. .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус составляет r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
Преобразование 25 Цельсия в
ФаренгейтаЧто такое 25 градусов Цельсия в градусах Фаренгейта? Насколько жарко 25 градусов по Цельсию? Перевести 25 ° с C на F.
из
Цельсия, Фаренгейта, Кельвина
Спо
Цельсия, Фаренгейта, Кельвина
25 ° Цельсия =77 ° по Фаренгейту
(точный результат)
Около
Цельсия, или градус Цельсия, используется для измерения температуры в большинстве стран мира.Вода замерзает при 0 ° Цельсия и закипает при 100 ° Цельсия.
Фаренгейта — это шкала, обычно используемая для измерения температуры в Соединенных Штатах.
Обратное преобразование
Формула преобразования
| ° Фаренгейта = | 9 | * ° Цельсия + 32 |
| 5 |
Ближайшие значения
| ° Цельсия | ° по Фаренгейту |
|---|---|
| 25.00 | 77,000 |
| 25,01 | 77.018 |
| 25.02 | 77.036 |
| 25.03 | 77.054 |
| 25.04 | 77.072 |
| 25.05 | 77.090 |
| 25.06 | 77.108 |
| 25.07 | 77,126 |
| 25,08 | 77.144 |
| 25.09 | 77.162 |
| 25,10 | 77,180 |
| 25,11 | 77,198 |
| 25,12 | 77,216 |
| 25,13 | 77,234 |
| 25,14 | 77,252 |
| 25,15 | 77,270 |
| 25,16 | 77,288 |
| 25,17 | 77,306 |
| 25,18 | 77,324 |
| 25.19 | 77,342 |
| 25,20 | 77,360 |
| 25,21 | 77,378 |
| 25,22 | 77,396 |
| 25,23 | 77,414 |
| 25,24 | 77,432 |
| 25,25 | 77,450 |
| 25,26 | 77,468 |
| 25,27 | 77,486 |
| 25,28 | 77.504 |
| 25,29 | 77,522 |
| 25,30 | 77,540 |
| 25,31 | 77,558 |
| 25,32 | 77,576 |
| 25,33 | 77,594 |
| 25,34 | 77,612 |
| 25,35 | 77,630 |
| 25,36 | 77,648 |
| 25,37 | 77,666 |
| 25.38 | 77,684 |
| 25,39 | 77,702 |
| 25,40 | 77,720 |
| 25,41 | 77,738 |
| 25,42 | 77,756 |
| 25,43 | 77,774 |
| 25,44 | 77,792 |
| 25,45 | 77,810 |
| 25,46 | 77,828 |
| 25,47 | 77.846 |
| 25,48 | 77,864 |
| 25,49 | 77,882 |
| 25,50 | 77.900 |
| 25.51 | 77,918 |
| 25,52 | 77,936 |
| 25,53 | 77,954 |
| 25,54 | 77,972 |
| 25,55 | 77,990 |
| 25,56 | 78.008 |
| 25.57 | 78,026 |
| 25,58 | 78,044 |
| 25,59 | 78.062 |
| 25.60 | 78,080 |
| 25,61 | 78,098 |
| 25,62 | 78,116 |
| 25,63 | 78,134 |
| 25,64 | 78,152 |
| 25,65 | 78,170 |
| 25,66 | 78.188 |
| 25,67 | 78,206 |
| 25,68 | 78,224 |
| 25,69 | 78,242 |
| 25,70 | 78,260 |
| 25,71 | 78,278 |
| 25,72 | 78,296 |
| 25,73 | 78,314 |
| 25,74 | 78,332 |
| 25,75 | 78,350 |
| 25.76 | 78,368 |
| 25,77 | 78,386 |
| 25,78 | 78,404 |
| 25,79 | 78,422 |
| 25,80 | 78,440 |
| 25,81 | 78,458 |
| 25,82 | 78,476 |
| 25,83 | 78,494 |
| 25,84 | 78,512 |
| 25,85 | 78.530 |
| 25,86 | 78,548 |
| 25,87 | 78,566 |
| 25,88 | 78,584 |
| 25,89 | 78,602 |
| 25,90 | 78,620 |
| 25,91 | 78,638 |
| 25,92 | 78.656 |
| 25.93 | 78,674 |
| 25,94 | 78,692 |
| 25.95 | 78,710 |
| 25,96 | 78,728 |
| 25,97 | 78,746 |
| 25,98 | 78,764 |
| 25,99 | 78,782 |

 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.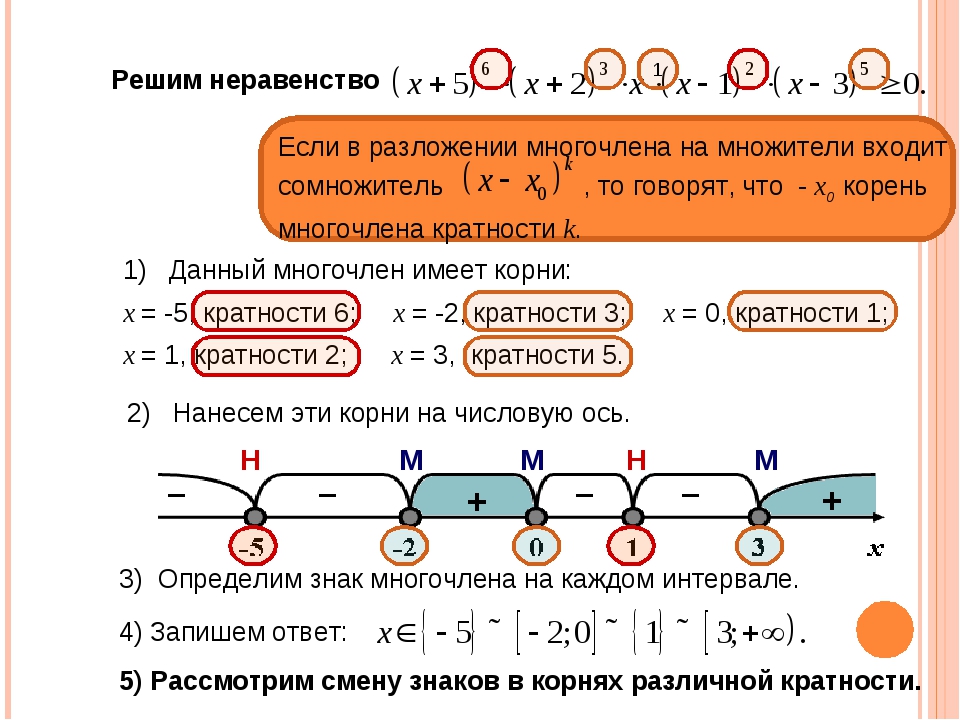
 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
2 есть отрицательное число -4, и свободный член -7 тоже отрицателен. 2 — 5x + 6 ≥ 0.
2 — 5x + 6 ≥ 0. Например: х = -1. Подставляем:
Например: х = -1. Подставляем: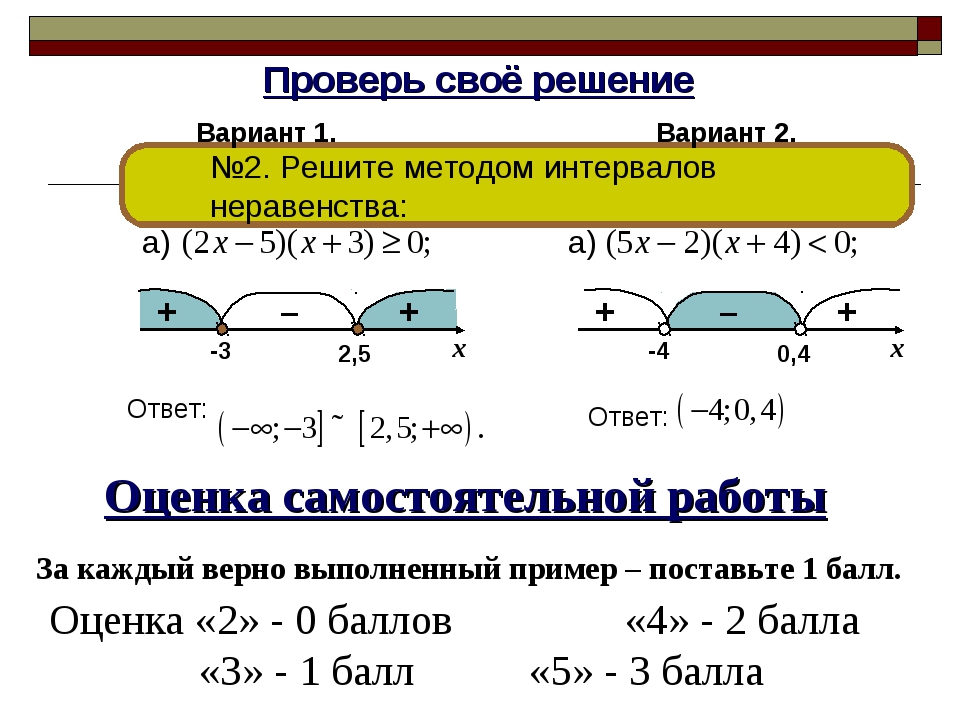
 Фиксируем знаки: −, −:
Фиксируем знаки: −, −: Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;
Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;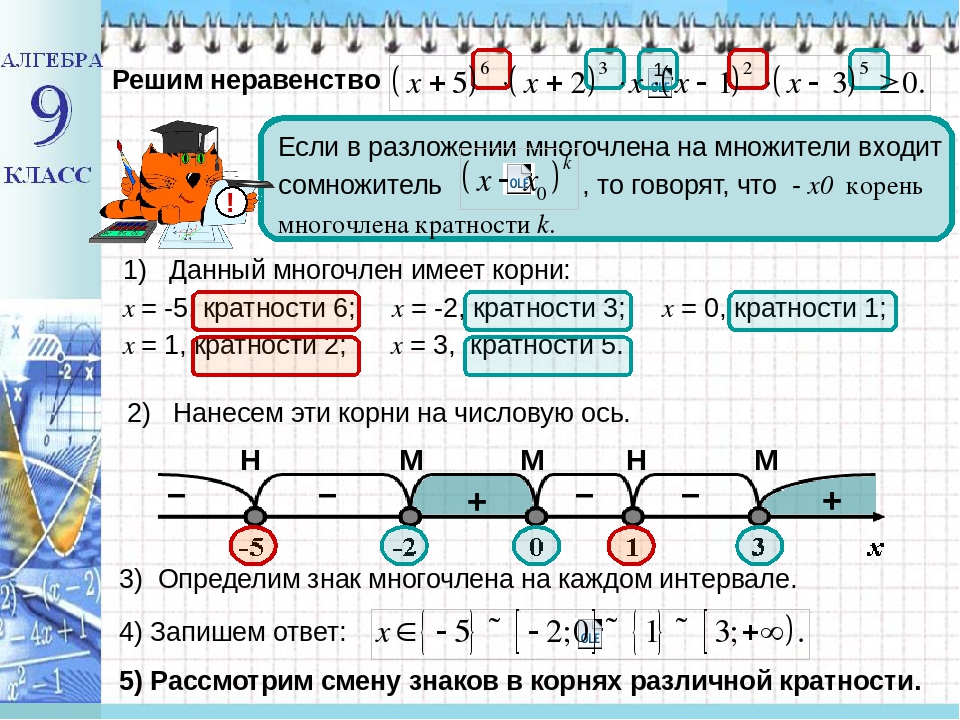 Имеем:
Имеем: Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ. к. знак нашего неравенства ≤.
к. знак нашего неравенства ≤.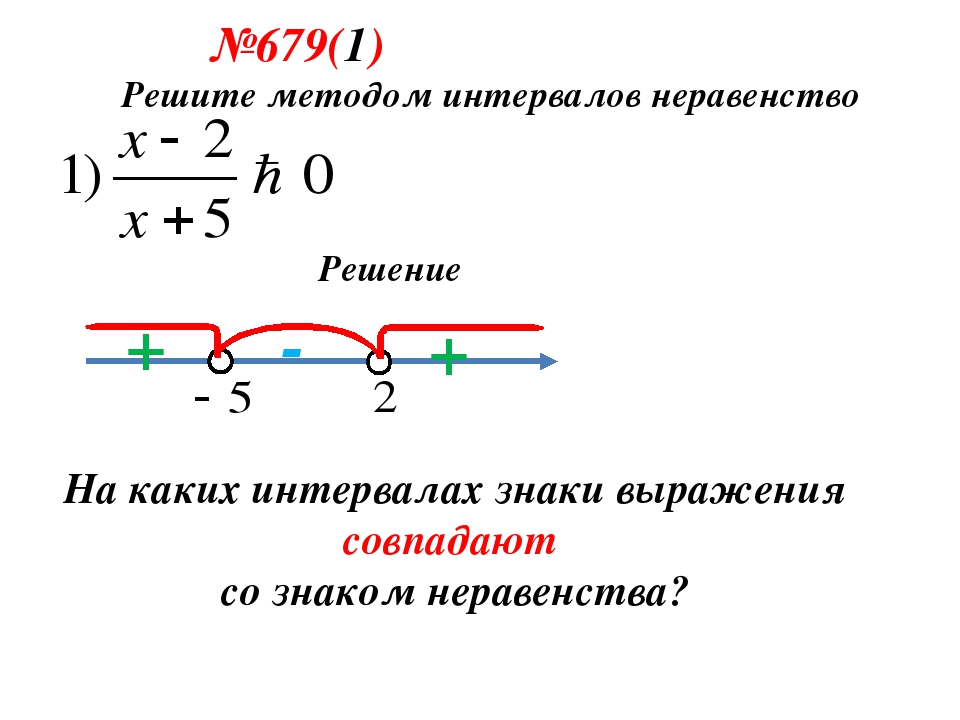 Соответственно, в данной точке на числовой прямой рисуем петлю.
Соответственно, в данной точке на числовой прямой рисуем петлю. Таким образом, в промежуток, из которого взяли нуль, ставим знак «-«, остальные знаки чередуем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.
Таким образом, в промежуток, из которого взяли нуль, ставим знак «-«, остальные знаки чередуем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ. Получает (-)/(-)=(+). Остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.
Получает (-)/(-)=(+). Остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.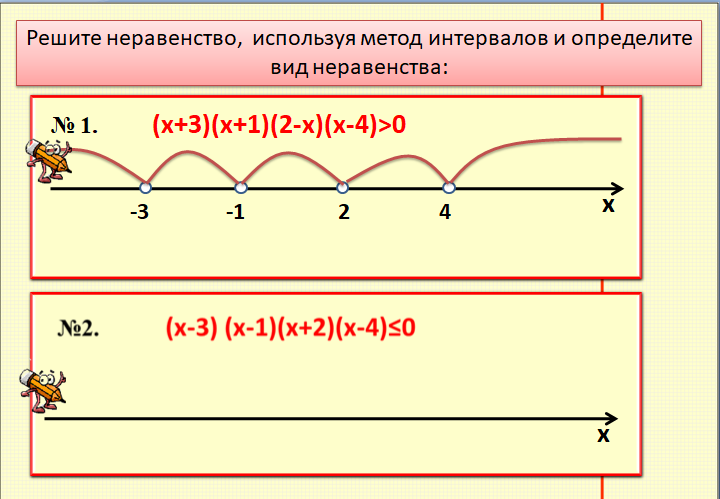

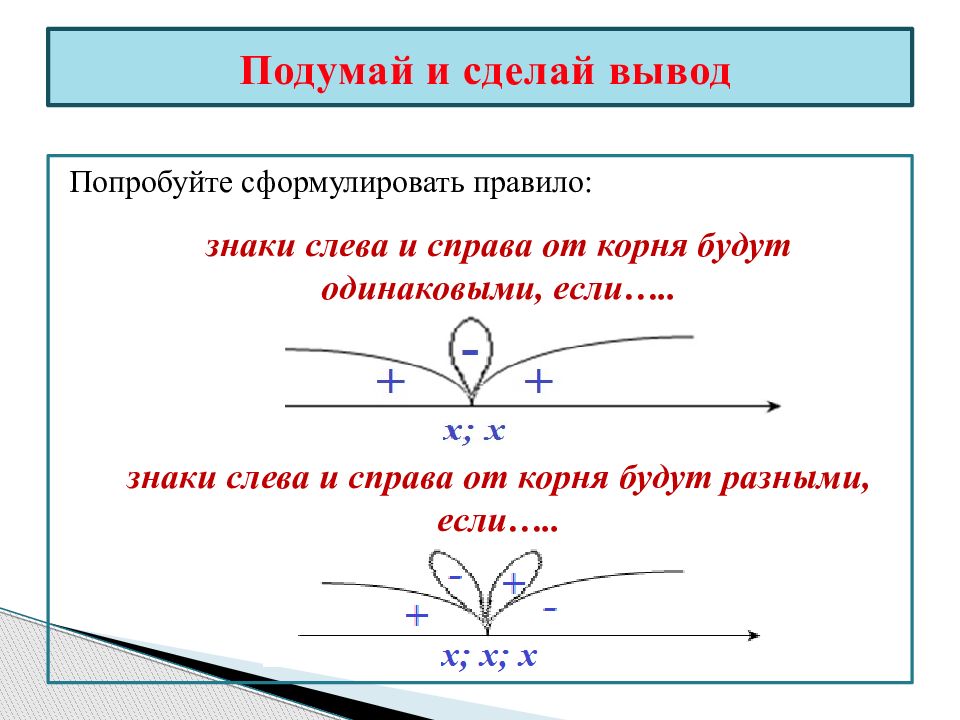 Другими словами, внутри каждого из полученных промежутков числовой оси значения функции (2) будут или положительными, или отрицательными.
Другими словами, внутри каждого из полученных промежутков числовой оси значения функции (2) будут или положительными, или отрицательными.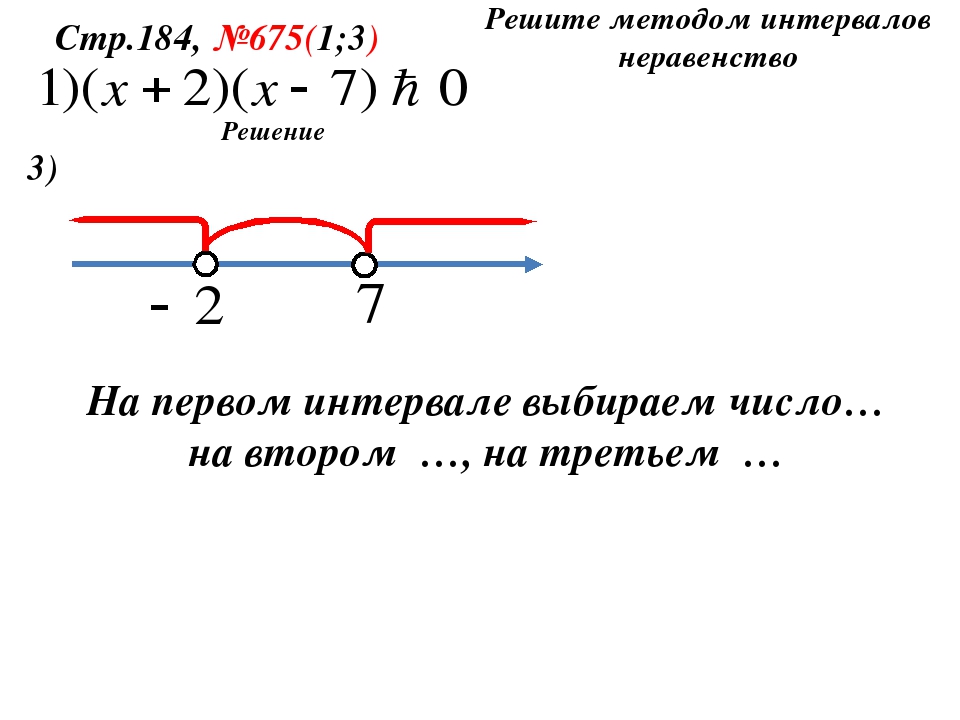

 Для завершения решения примера остаётся лишь добавить, что концы промежутков
Для завершения решения примера остаётся лишь добавить, что концы промежутков Концы промежутков в ответ не входят.
Концы промежутков в ответ не входят. 
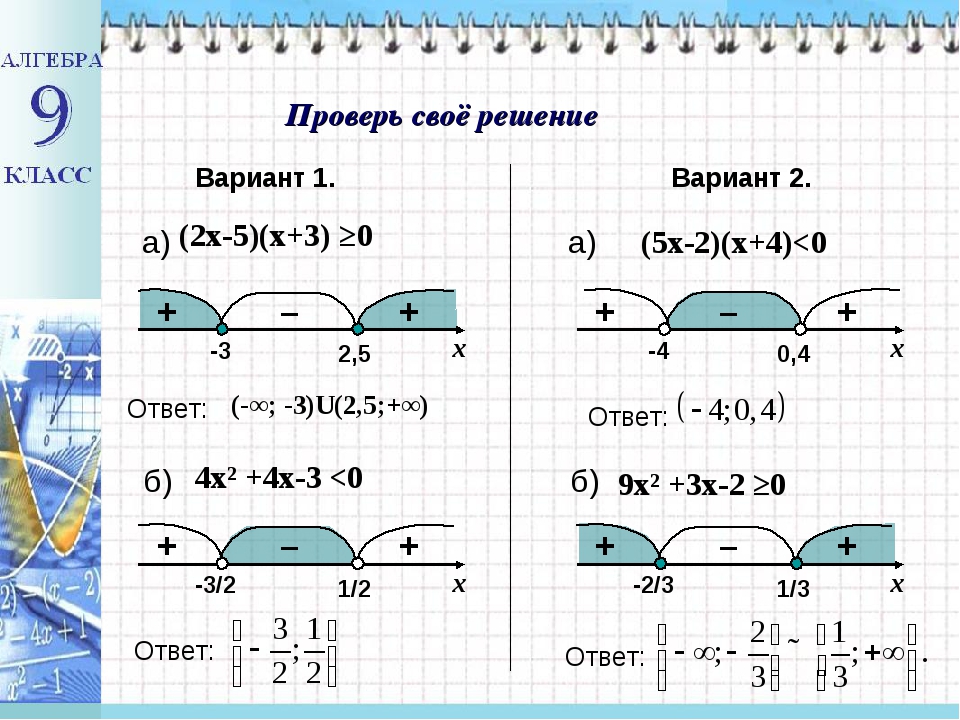 5, нарисуем «арки» над интервалами между отмеченными точками.
5, нарисуем «арки» над интервалами между отмеченными точками.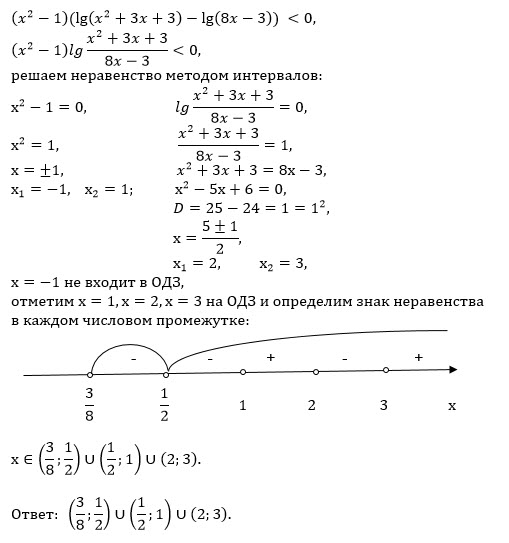 Если мы получим верное неравенство,
значит мы нашли ответ квадратного неравенства верно.
Если мы получим верное неравенство,
значит мы нашли ответ квадратного неравенства верно. Требуется решить квадратное неравенство:
Требуется решить квадратное неравенство: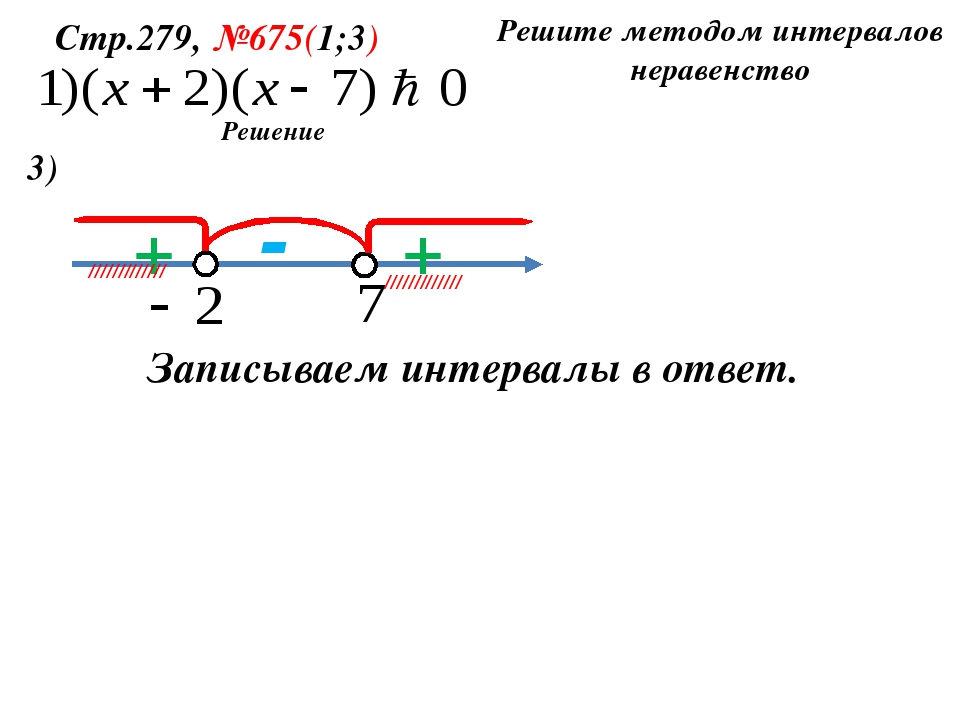


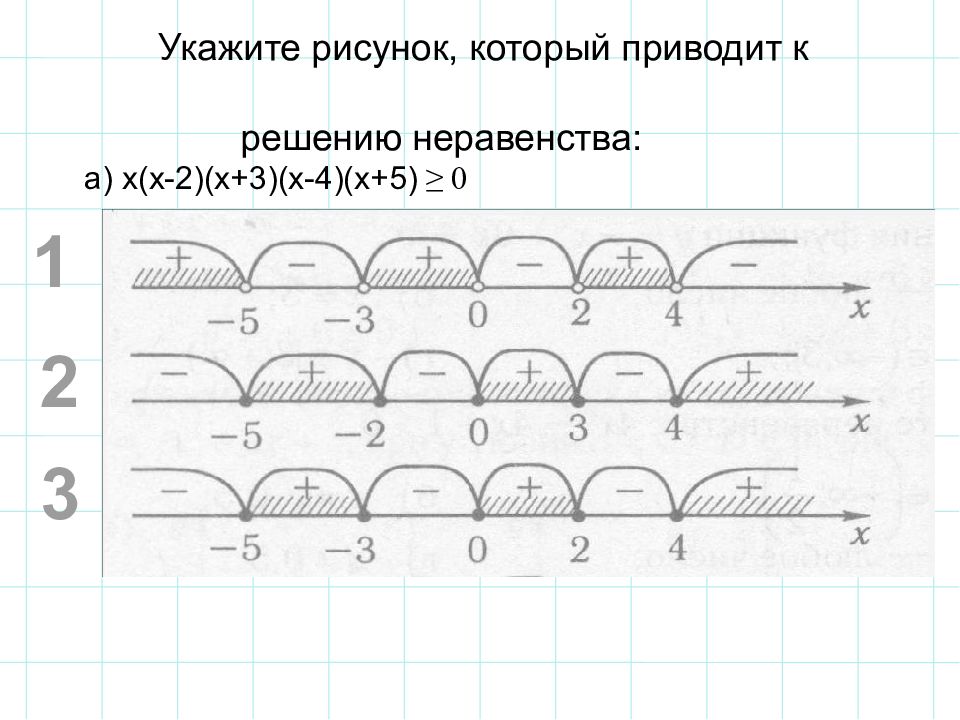 Для этого достаточно проанализировать, как расположен график функции y = ax2 + bx + c в координатной плоскости: куда направлены ветви параболы – вверх или вниз, пересекает ли парабола ось x и если пересекает, то в каких точках.
Для этого достаточно проанализировать, как расположен график функции y = ax2 + bx + c в координатной плоскости: куда направлены ветви параболы – вверх или вниз, пересекает ли парабола ось x и если пересекает, то в каких точках.
 Схематично изобразим эту параболу.
Схематично изобразим эту параболу.
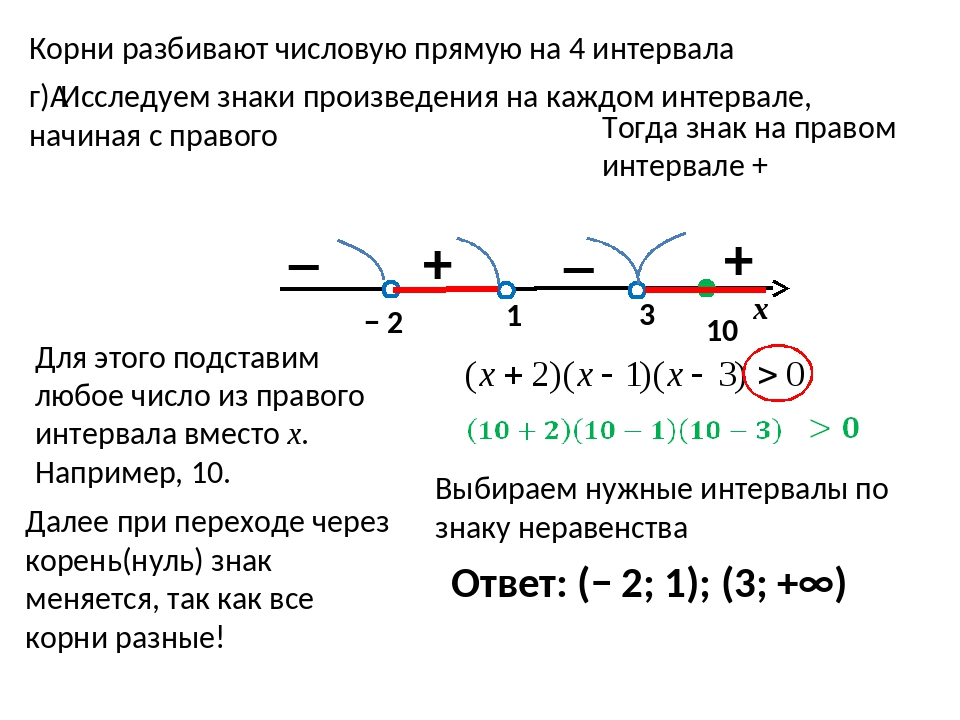 Выясним, как располагается эта парабола относительно оси x. Для этого решим квадратное уравнение:
Выясним, как располагается эта парабола относительно оси x. Для этого решим квадратное уравнение:
 Точки -3, -1 и 2 нули функции, которые разбивают область определения на промежутки -∞;-3,-3;-1,-1;2,2;+∞. Выясним знак функции в каждом из указанных промежутков.
Точки -3, -1 и 2 нули функции, которые разбивают область определения на промежутки -∞;-3,-3;-1,-1;2,2;+∞. Выясним знак функции в каждом из указанных промежутков.


 Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем. В этих утверждениях используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем. В этих утверждениях используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
 Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.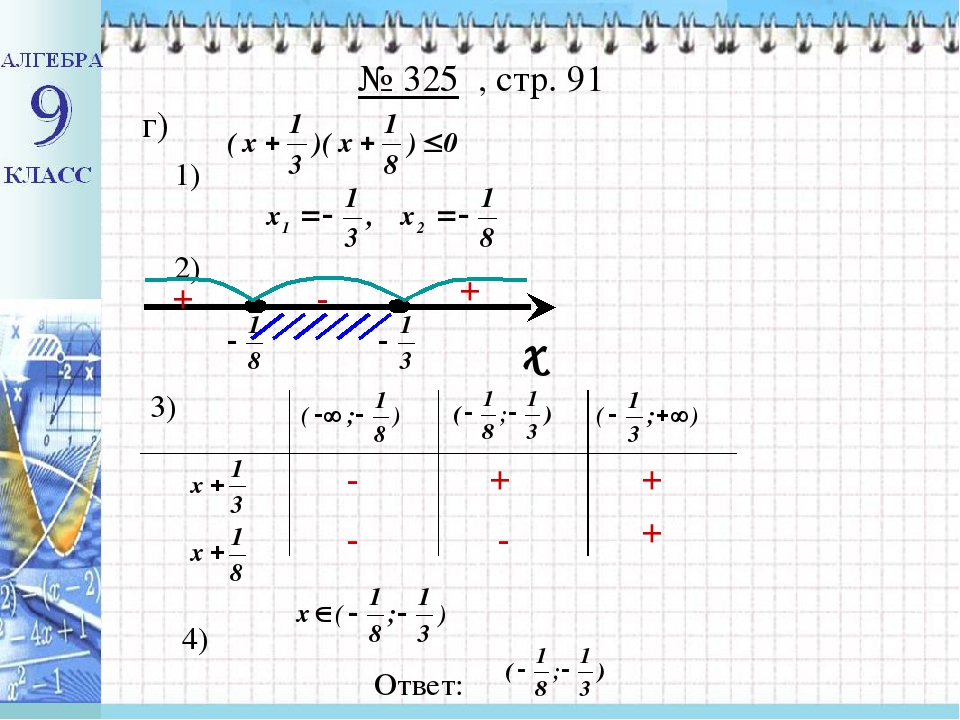 Стороны любого неравенства можно поменять местами, если символ неравенства между ними также перевернут.
Стороны любого неравенства можно поменять местами, если символ неравенства между ними также перевернут. \ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для больше (>) или меньше (<). Дело в , а не в части решения.
\ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для больше (>) или меньше (<). Дело в , а не в части решения.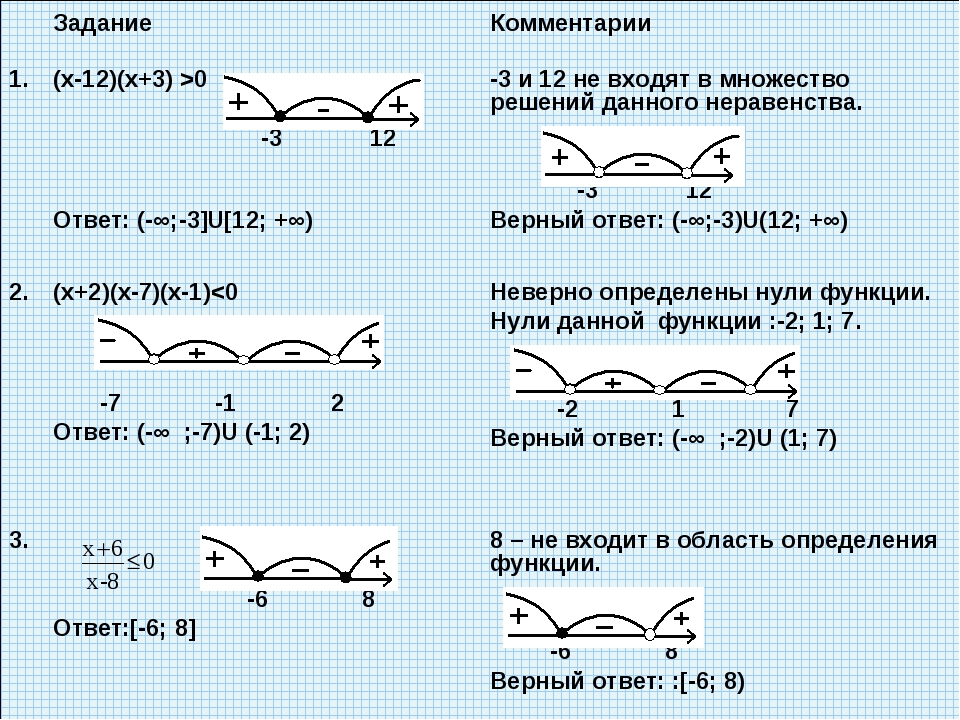
 Затем мы построим его график.
Затем мы построим его график.  Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [/ латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше, включая [latex] 1 [/ latex].В таблице ниже представлены возможные варианты. Не забывайте читать неравенства слева направо, как текст.
Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [/ латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше, включая [latex] 1 [/ latex].В таблице ниже представлены возможные варианты. Не забывайте читать неравенства слева направо, как текст.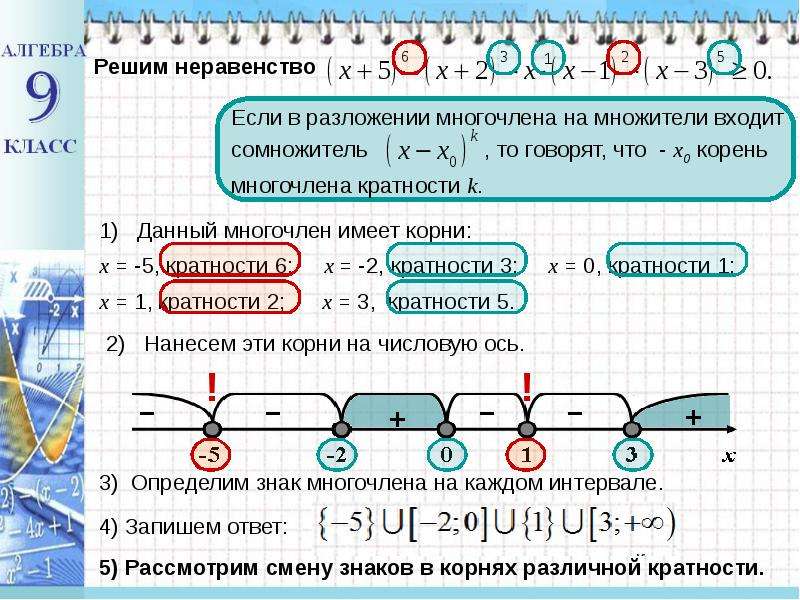 «>
«>
 [латекс] x <10 [/ латекс]
[латекс] x <10 [/ латекс]


 Синяя стрелка нарисована слева от точки [латекс] -2 [/ латекс], потому что это значения меньше, чем [латекс] -2 [/ латекс].
Синяя стрелка нарисована слева от точки [латекс] -2 [/ латекс], потому что это значения меньше, чем [латекс] -2 [/ латекс]. 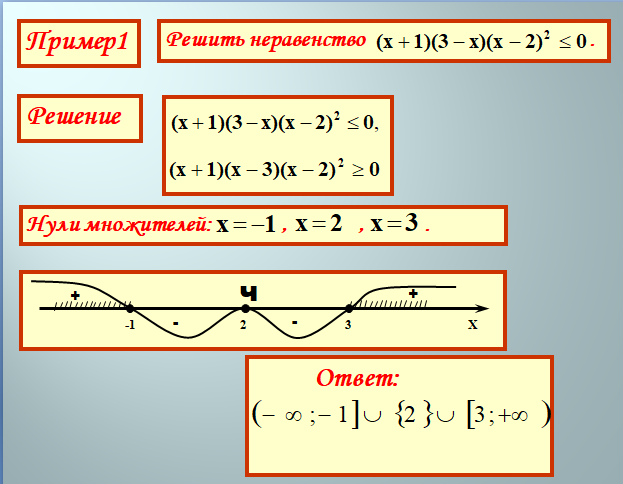 [латекс] a-17> -17 [/ латекс]
[латекс] a-17> -17 [/ латекс] (Это значение будет на затененной части графика.)
(Это значение будет на затененной части графика.)
 (Это значение будет на затененной части графика.)
(Это значение будет на затененной части графика.)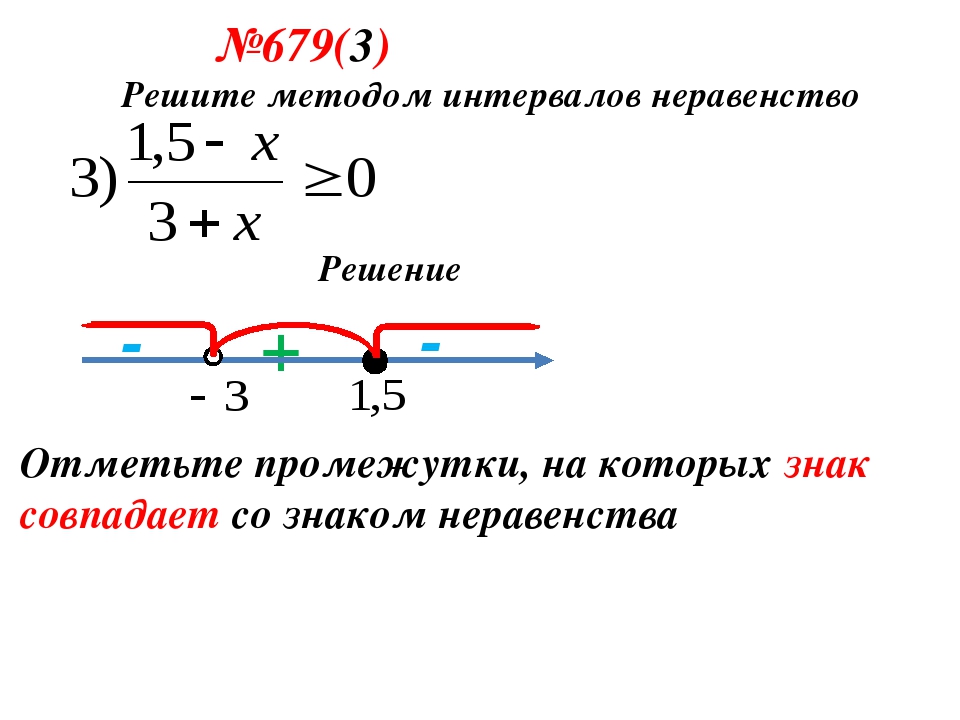
 Если сложить или вычесть на отрицательное число, неравенство останется прежним.
Если сложить или вычесть на отрицательное число, неравенство останется прежним.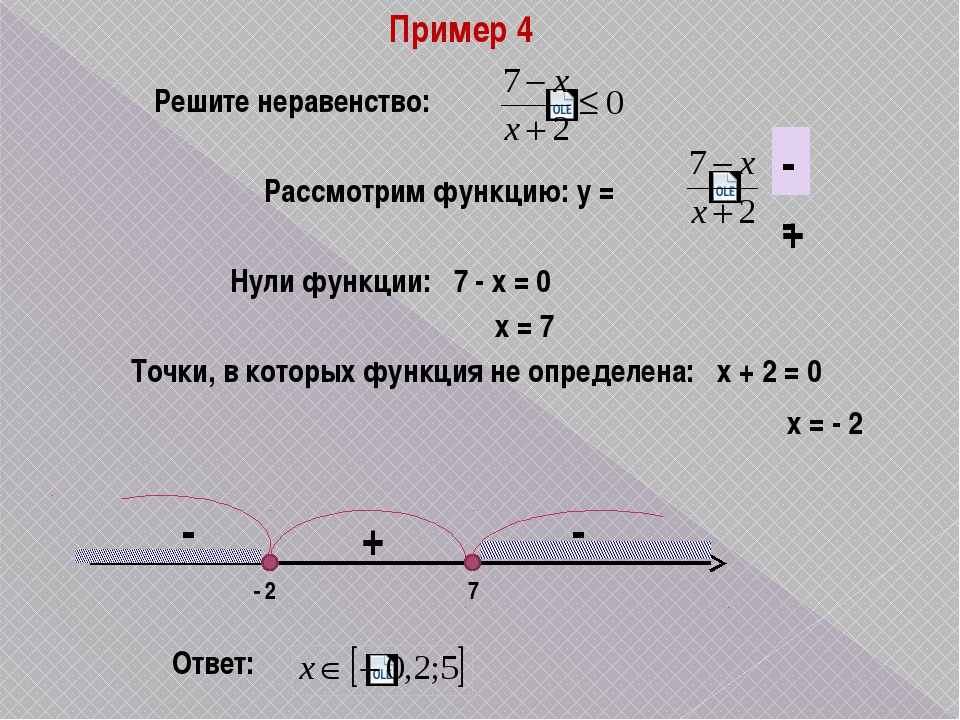 В следующем примере есть деление на отрицательное число, поэтому есть дополнительный шаг в решении!
В следующем примере есть деление на отрицательное число, поэтому есть дополнительный шаг в решении!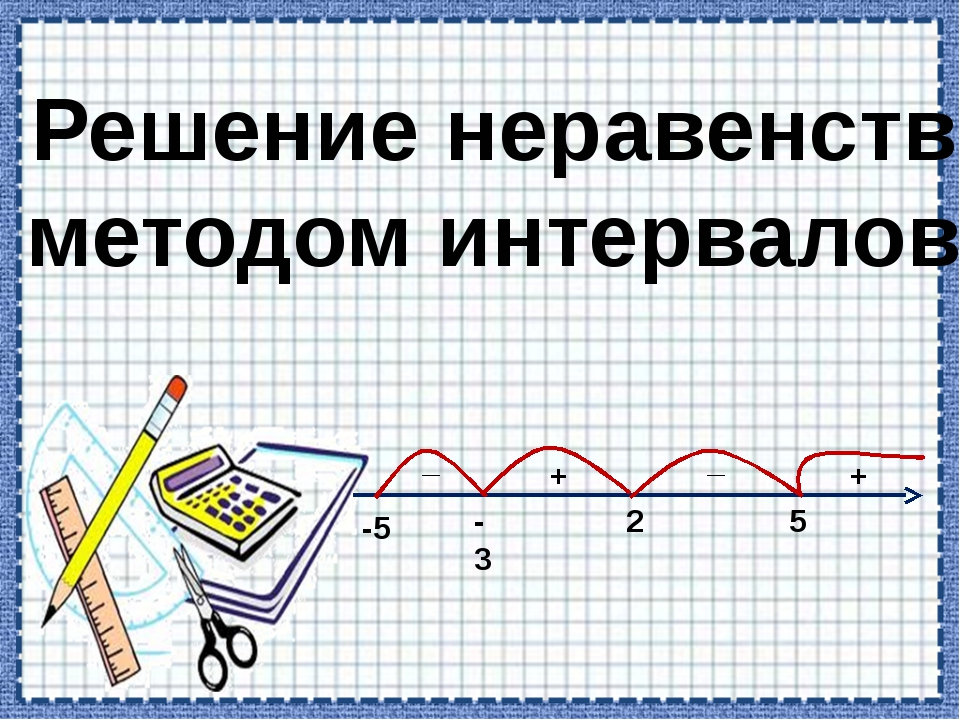
 Поскольку вы делите на отрицательное число, вам нужно изменить направление знака неравенства.
Поскольку вы делите на отрицательное число, вам нужно изменить направление знака неравенства.

 Давайте использовать [latex] p = 0 [/ latex].
Давайте использовать [latex] p = 0 [/ latex]. Линия продолжается вправо от 16, потому что все числа больше 16 также будут составлять неравенство [латекс] 3x – 7 \ ge 41 [/ латекс] верно.
Линия продолжается вправо от 16, потому что все числа больше 16 также будут составлять неравенство [латекс] 3x – 7 \ ge 41 [/ латекс] верно.



 Попробуйте 0.
Попробуйте 0.
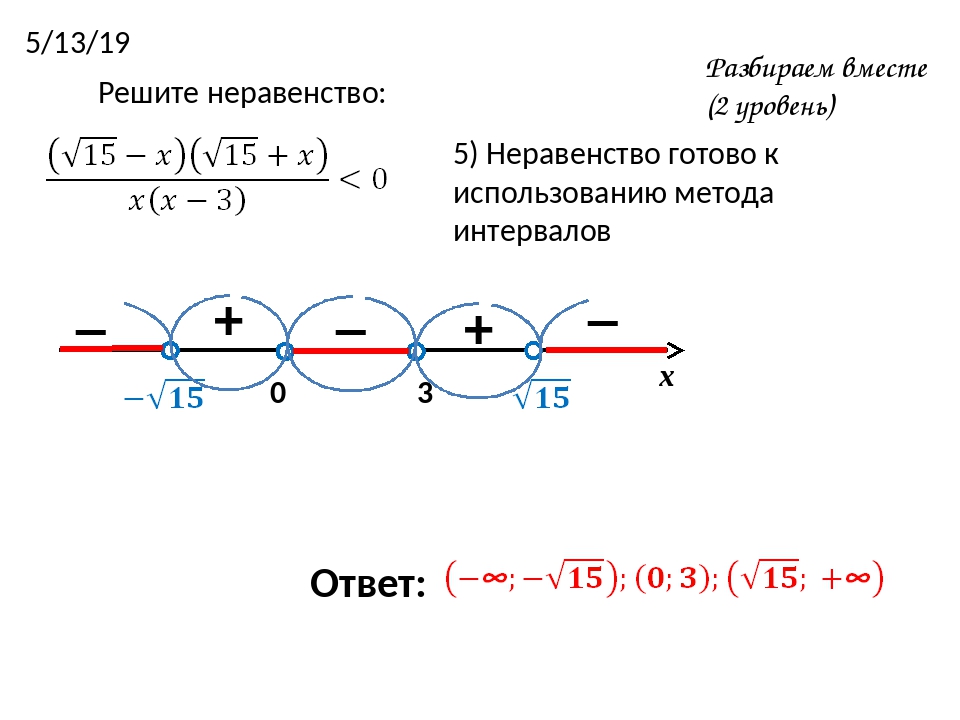 Линия продолжается влево, чтобы показать, что значения меньше 8 также включены в набор решений.
Линия продолжается влево, чтобы показать, что значения меньше 8 также включены в набор решений. Решения неравенств можно представить тремя способами: интервал, график и неравенство.Поскольку обычно существует более одного решения неравенства, когда вы проверяете свой ответ, вы должны проверить конечную точку и одно другое значение, чтобы проверить направление неравенства.
Решения неравенств можно представить тремя способами: интервал, график и неравенство.Поскольку обычно существует более одного решения неравенства, когда вы проверяете свой ответ, вы должны проверить конечную точку и одно другое значение, чтобы проверить направление неравенства. )
)
 Стоит помнить, что их суммарный вес не должен превышать 100 МБ.
Стоит помнить, что их суммарный вес не должен превышать 100 МБ.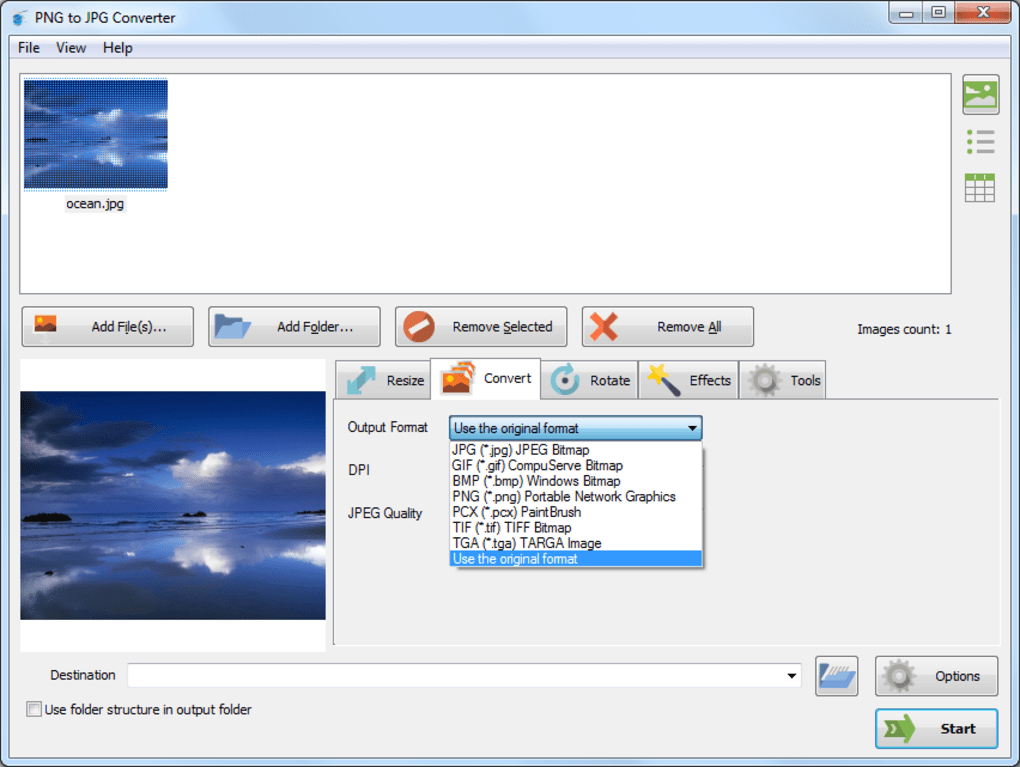 Например, если вы добавили картинку PNG, то она автоматически будет конвертирована в JPG, и наоборот.
Например, если вы добавили картинку PNG, то она автоматически будет конвертирована в JPG, и наоборот.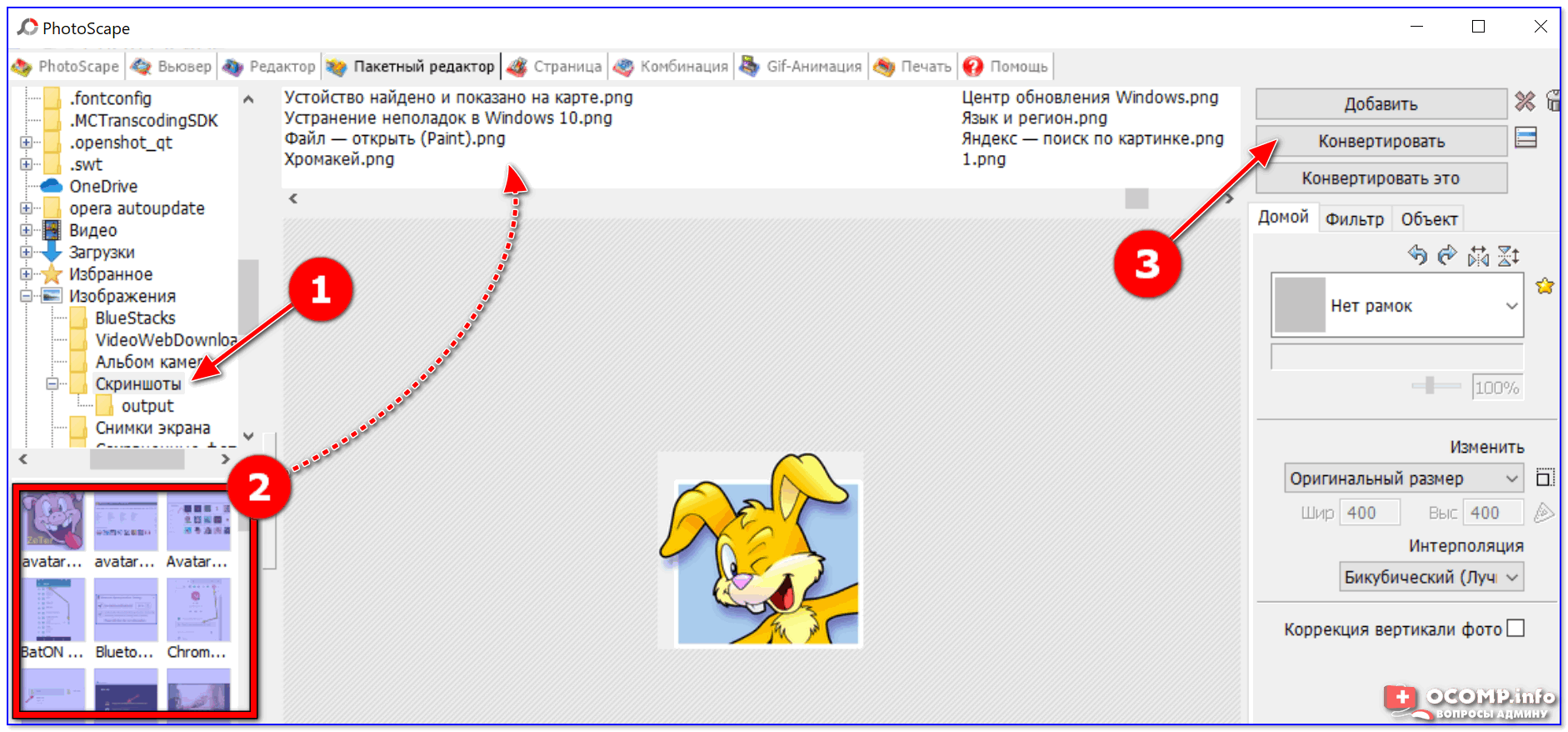
 .. Они являются наиболее распространенными, с которыми вы работаете. Но иногда вы обнаруживаете, что вам нужно преобразовать изображение JPG в PNG, Ты умеешь это делать?
.. Они являются наиболее распространенными, с которыми вы работаете. Но иногда вы обнаруживаете, что вам нужно преобразовать изображение JPG в PNG, Ты умеешь это делать? И что он делает? Хорошо сжимает изображения, как в оттенках серого, так и в цветных, с сохранением высокого качества (хотя есть потери, которые можно настроить).
И что он делает? Хорошо сжимает изображения, как в оттенках серого, так и в цветных, с сохранением высокого качества (хотя есть потери, которые можно настроить). Наиболее распространены обычно JPG, GIF и, да, PNG. Однако этот формат имеет некоторые характеристики, которые отличаются от других и могут иметь положительное или отрицательное влияние в зависимости от того, как вы хотите его использовать.
Наиболее распространены обычно JPG, GIF и, да, PNG. Однако этот формат имеет некоторые характеристики, которые отличаются от других и могут иметь положительное или отрицательное влияние в зависимости от того, как вы хотите его использовать. Вот почему это наиболее предпочтительный формат для сохранения логотипов, изображений очень высокого качества или когда они имеют градиенты или прозрачность.
Вот почему это наиболее предпочтительный формат для сохранения логотипов, изображений очень высокого качества или когда они имеют градиенты или прозрачность.

 ..
.. Название PNG – это аббревиатура от Portable Network Graphic. Этот формат изображений используется, прежде всего, в Интернете для размещения на веб-страницах, поскольку файлы PNG применяют сжатие по алгоритму Deflate, не теряя качества. Разработка данного формата была предпринята для того, чтобы заменить формат GIF, к которому было немало претензий. Качество изображения и характеристики у PNG оказались намного лучше, однако в отличие от GIF он не поддерживает анимацию и использует палитру CMYK.
Название PNG – это аббревиатура от Portable Network Graphic. Этот формат изображений используется, прежде всего, в Интернете для размещения на веб-страницах, поскольку файлы PNG применяют сжатие по алгоритму Deflate, не теряя качества. Разработка данного формата была предпринята для того, чтобы заменить формат GIF, к которому было немало претензий. Качество изображения и характеристики у PNG оказались намного лучше, однако в отличие от GIF он не поддерживает анимацию и использует палитру CMYK. Каким бы прекрасным и качественным не был файл, его придётся конвертировать в требуемое расширение. Однако несмотря на кажущуюся сложность, количество программных продуктов настолько велико, что каждый желающий может с лёгкостью решить такую компьютерную задачку.
Каким бы прекрасным и качественным не был файл, его придётся конвертировать в требуемое расширение. Однако несмотря на кажущуюся сложность, количество программных продуктов настолько велико, что каждый желающий может с лёгкостью решить такую компьютерную задачку. Однако, несмотря на различные области применения, у некоторых владельцев ПК периодически возникает необходимость преобразовать png в jpg. Тем не менее в ряде случаев возникает необходимость в конвертировании из одного формата в другой.
Однако, несмотря на различные области применения, у некоторых владельцев ПК периодически возникает необходимость преобразовать png в jpg. Тем не менее в ряде случаев возникает необходимость в конвертировании из одного формата в другой. Овладеть этим хитрым редактором пытается каждый, кто хочет в дальнейшем профессионально заниматься изображениями и, в частности, фотографиями. Посредством этой программы можно с лёгкостью конвертировать png в jpg.
Овладеть этим хитрым редактором пытается каждый, кто хочет в дальнейшем профессионально заниматься изображениями и, в частности, фотографиями. Посредством этой программы можно с лёгкостью конвертировать png в jpg.


 Фотоконвертер располагает множеством доступных форматов и удобным, интуитивно понятным интерфейсом. Однако, для того чтобы данный процесс совершенно точно не вызвал у вас затруднений, мы подготовили подробное пошаговое руководство:
Фотоконвертер располагает множеством доступных форматов и удобным, интуитивно понятным интерфейсом. Однако, для того чтобы данный процесс совершенно точно не вызвал у вас затруднений, мы подготовили подробное пошаговое руководство: Чтобы перейти к обработанным картинкам, нажмите на «Показать файлы».
Чтобы перейти к обработанным картинкам, нажмите на «Показать файлы».
 Кроме того, здесь же выставьте формат «JPG – JPEG/JFIF».
Кроме того, здесь же выставьте формат «JPG – JPEG/JFIF».
 Несмотря на то, что возможности большинства представленных на просторах интернета сайтов легко и быстро справляются с преобразованием файлов в формате PNG, полученные в результате модификаций изображения сильно искажаются.
Несмотря на то, что возможности большинства представленных на просторах интернета сайтов легко и быстро справляются с преобразованием файлов в формате PNG, полученные в результате модификаций изображения сильно искажаются.

 Состояние
Состояние  -iname '*.png' | while read i; do mogrify -format jpg "$i" && rm "$i"; fn="all/$((n++)).jpg"; mv "${i%.*}.jpg" "$fn"; echo "Moved $i to $fn"; done
-iname '*.png' | while read i; do mogrify -format jpg "$i" && rm "$i"; fn="all/$((n++)).jpg"; mv "${i%.*}.jpg" "$fn"; echo "Moved $i to $fn"; done

 Формат PNG сжимает данные не влияя при этом на качество изображения и поэтому широко используется для изображений в интернете и веб-дизайнерами.
Формат PNG сжимает данные не влияя при этом на качество изображения и поэтому широко используется для изображений в интернете и веб-дизайнерами. Но что происходит, когда вы хотите преобразовать что-то из одного типа файла в другой? Когда-то процесс преобразования был трудным, но теперь в Windows, macOS и даже в ваш веб-браузер есть встроенные функции, позволяющие это сделать. Не говоря уже о множестве (многих) онлайн-инструментов. Вот все, что вам нужно знать, чтобы легко преобразовывать эти типы файлов.
Но что происходит, когда вы хотите преобразовать что-то из одного типа файла в другой? Когда-то процесс преобразования был трудным, но теперь в Windows, macOS и даже в ваш веб-браузер есть встроенные функции, позволяющие это сделать. Не говоря уже о множестве (многих) онлайн-инструментов. Вот все, что вам нужно знать, чтобы легко преобразовывать эти типы файлов. Вы должны заметить, что ваш компьютер теперь обращается к файлу в новом формате.
Вы должны заметить, что ваш компьютер теперь обращается к файлу в новом формате. Вы увидите, что URL-адрес изображения содержит расширение файла или заканчивается им.Если у вас есть .jpg или .webp (-rw для изображений в Google Play), замените его на .png, чтобы преобразовать изображение в файл PNG при загрузке. В Chrome, Edge и Safari вы можете конвертировать в PNG только на поддерживаемых сайтах. Firefox преобразует только в .jpg.
Вы увидите, что URL-адрес изображения содержит расширение файла или заканчивается им.Если у вас есть .jpg или .webp (-rw для изображений в Google Play), замените его на .png, чтобы преобразовать изображение в файл PNG при загрузке. В Chrome, Edge и Safari вы можете конвертировать в PNG только на поддерживаемых сайтах. Firefox преобразует только в .jpg.
 Вы можете отказаться от подписки на информационные бюллетени в любое время.
Вы можете отказаться от подписки на информационные бюллетени в любое время. Обычно он используется, когда кому-то нужно загрузить или загрузить большое количество изображений.
Обычно он используется, когда кому-то нужно загрузить или загрузить большое количество изображений. Другие варианты — использовать программу преобразования. В Интернете есть множество бесплатных программ на выбор. Все зависит от того, хотите ли вы использовать систему на основе браузера или установленную программу.
Другие варианты — использовать программу преобразования. В Интернете есть множество бесплатных программ на выбор. Все зависит от того, хотите ли вы использовать систему на основе браузера или установленную программу.
 На мой взгляд, JPG и PNG были абсолютно одинаковыми.
На мой взгляд, JPG и PNG были абсолютно одинаковыми. Посетите один из бесплатных онлайн-конвертеров PNG в JPG, перечисленных в разделе ниже.
Посетите один из бесплатных онлайн-конвертеров PNG в JPG, перечисленных в разделе ниже.
 Постройте график функции y=
Постройте график функции y= Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|. Этот вариант нам не подходит.
Этот вариант нам не подходит.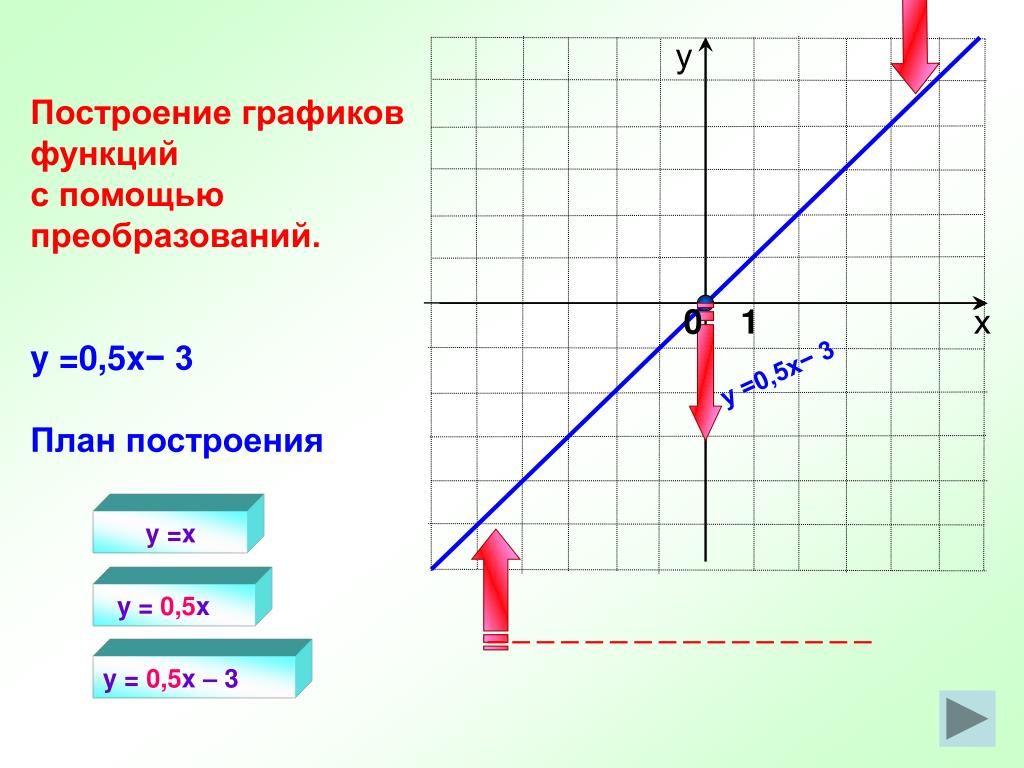
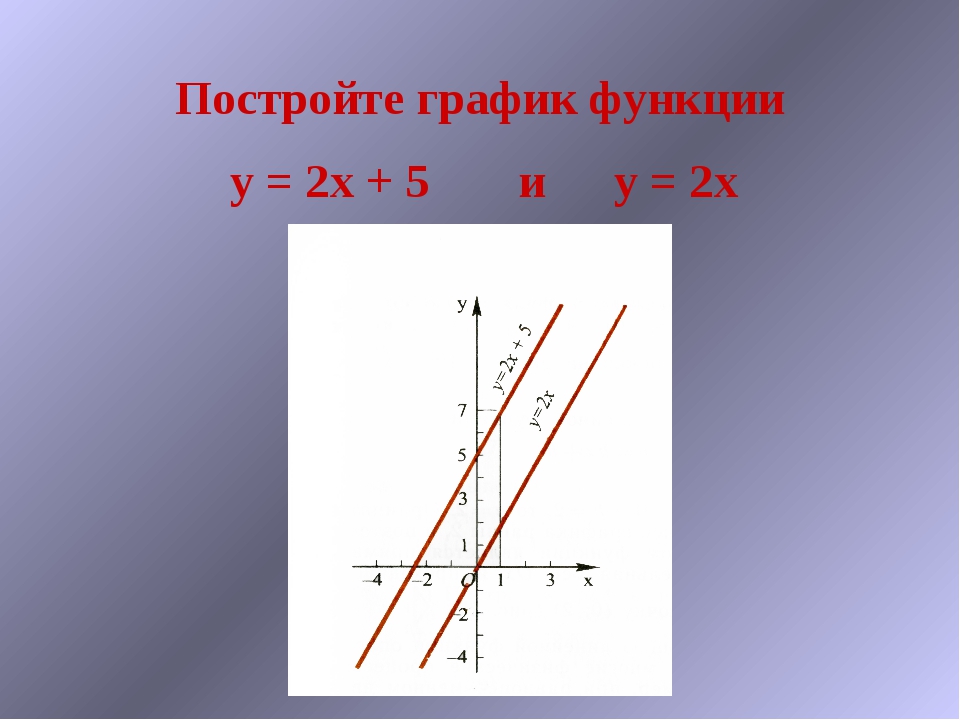 Сделать выводы..В одной координатной плоскости построить графики функций:
Сделать выводы..В одной координатной плоскости построить графики функций: е.
е. Создадим табличку
Создадим табличку 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.

 Настрой
учащихся на учебную деятельность.
Настрой
учащихся на учебную деятельность. Найдите значение
функции, соответствующее значению аргумента,
равному -3;0;5
Найдите значение
функции, соответствующее значению аргумента,
равному -3;0;5


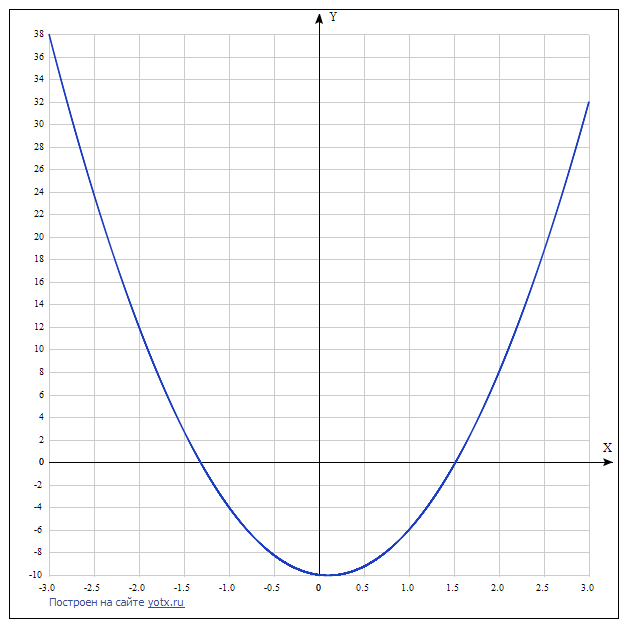

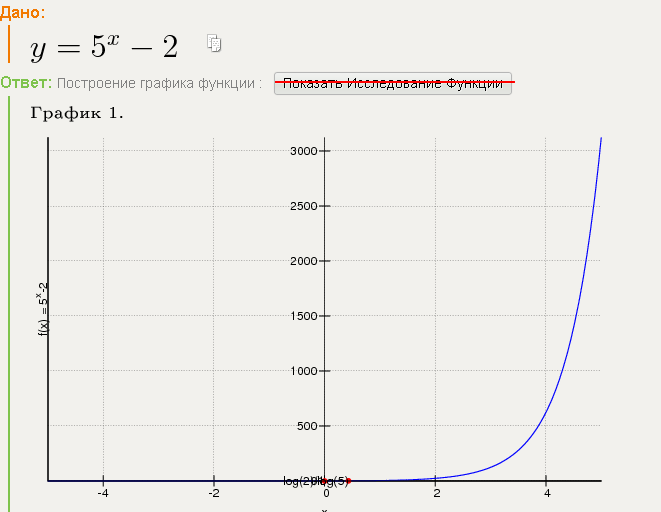 Постройте график
Постройте график
 Назовем ее базовой функцией.
Назовем ее базовой функцией.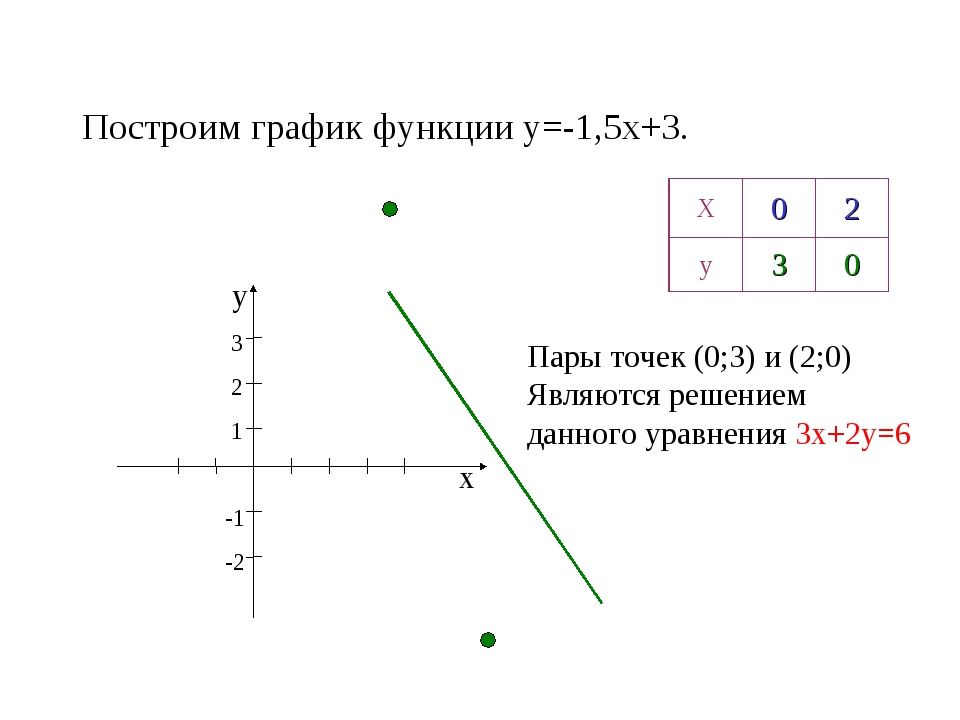 f(x) f(-x)
f(x) f(-x)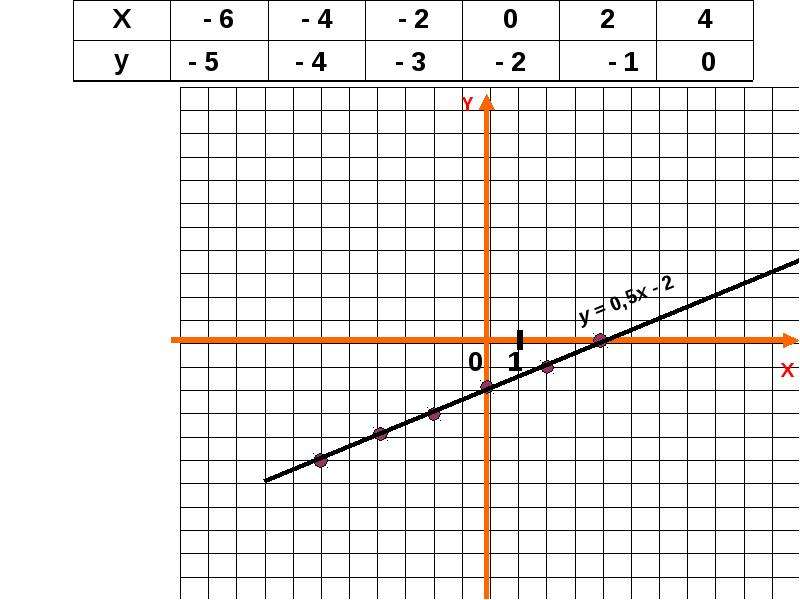 Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
Все преобразования аргумента совершаются «наоборот» и «в обратном порядке». Строим график функции
Строим график функции  Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси: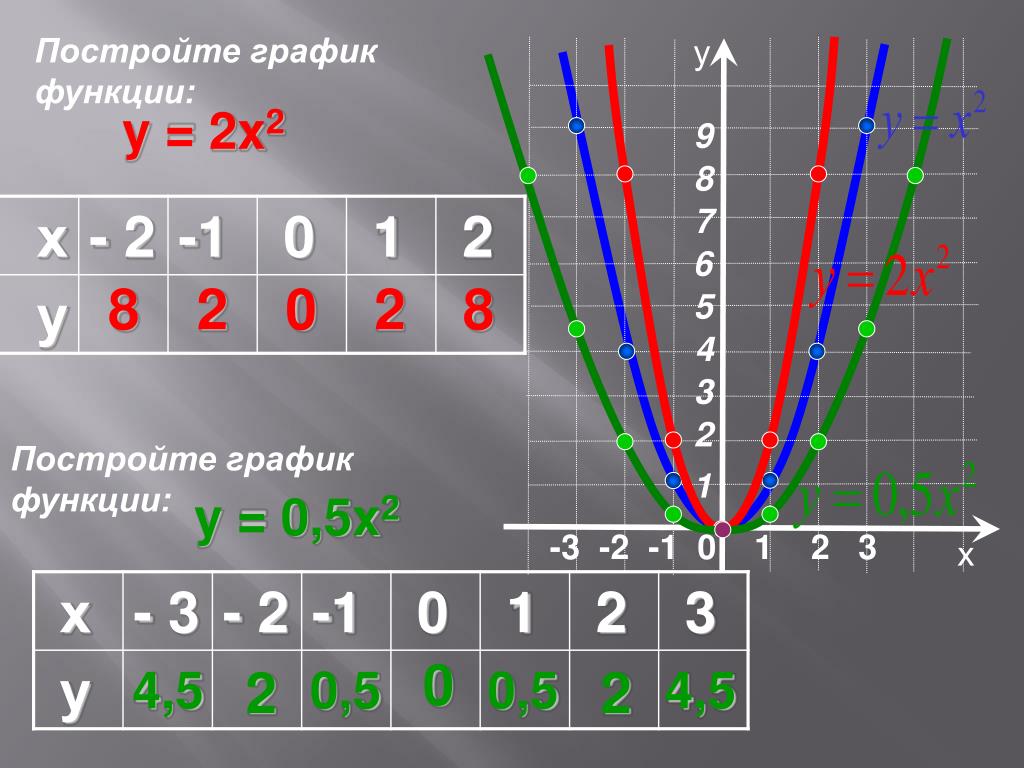 В. Фельдман, репетитор по математике.
В. Фельдман, репетитор по математике.
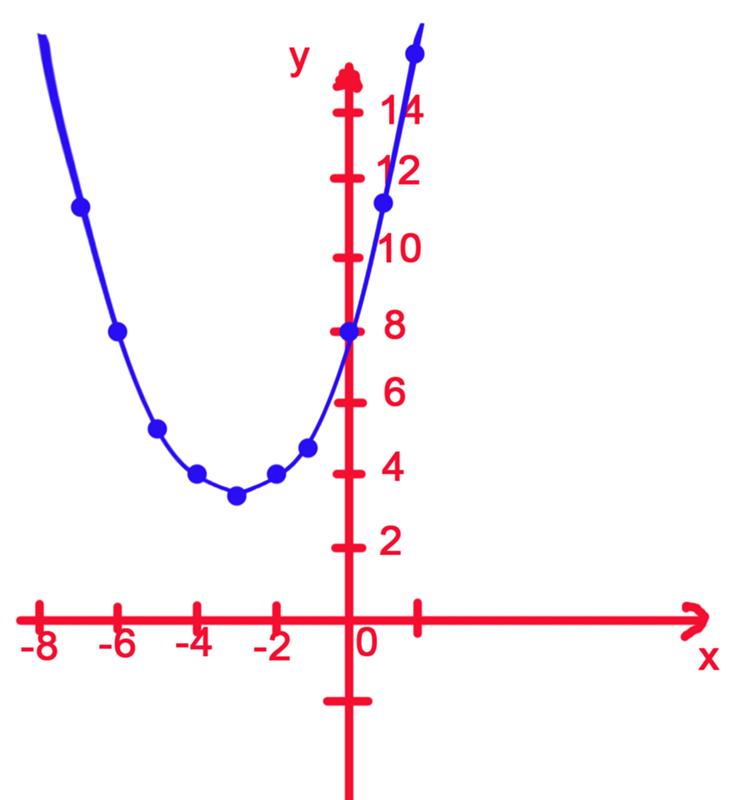
 Стрелки на каждом конце графика показывают, что линия бесконечно продолжается в обоих направлениях.Каждая точка в этой строке является решением линии
Стрелки на каждом конце графика показывают, что линия бесконечно продолжается в обоих направлениях.Каждая точка в этой строке является решением линии В этом уроке мы будем дополнять это, посмотрев
при построении графиков линейных уравнений путем нанесения точек, которые
решения.
По сути, когда вы строите график, вы строите решения и соединяете точки с
получать
ваш график. Конкретно,
когда вы построите график линейных уравнений, вы получите прямой
линия.
Посмотрим, что вы можете сделать с этими линейными уравнениями.
В этом уроке мы будем дополнять это, посмотрев
при построении графиков линейных уравнений путем нанесения точек, которые
решения.
По сути, когда вы строите график, вы строите решения и соединяете точки с
получать
ваш график. Конкретно,
когда вы построите график линейных уравнений, вы получите прямой
линия.
Посмотрим, что вы можете сделать с этими линейными уравнениями.






 ) Вы
хочу, чтобы это было как можно проще. Ниже приведена диаграмма
Я закончил после подключения значений, которые я упомянул для x .
) Вы
хочу, чтобы это было как можно проще. Ниже приведена диаграмма
Я закончил после подключения значений, которые я упомянул для x . Это позволит вам проверить и понять, понимаете ли вы
эти
типы проблем. Math работает так же, как
что-нибудь
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
Это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.
Это позволит вам проверить и понять, понимаете ли вы
эти
типы проблем. Math работает так же, как
что-нибудь
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
Это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.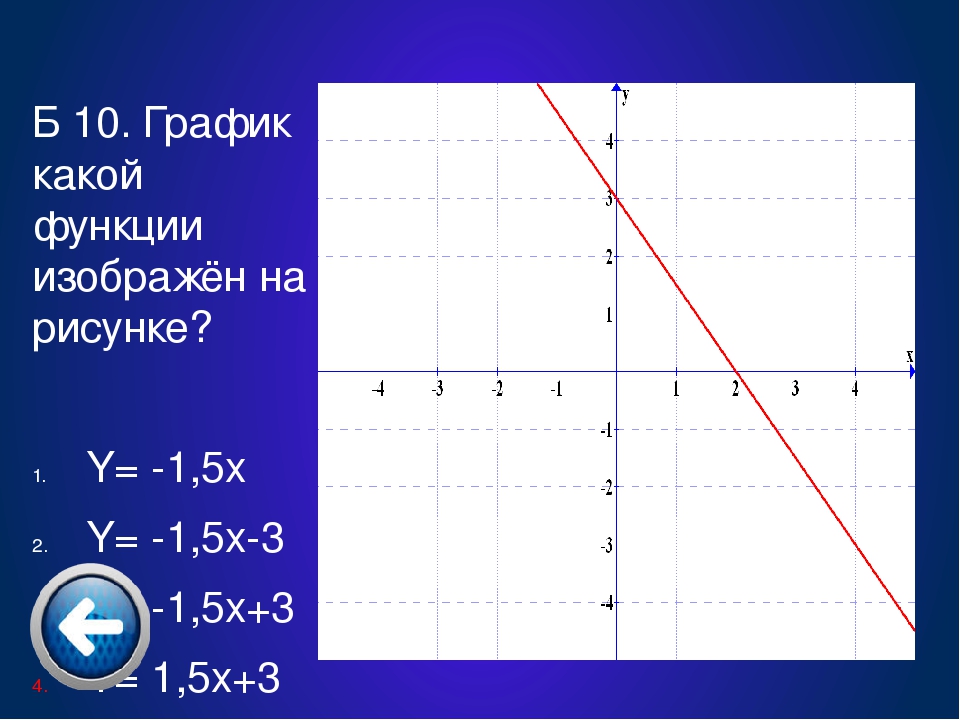
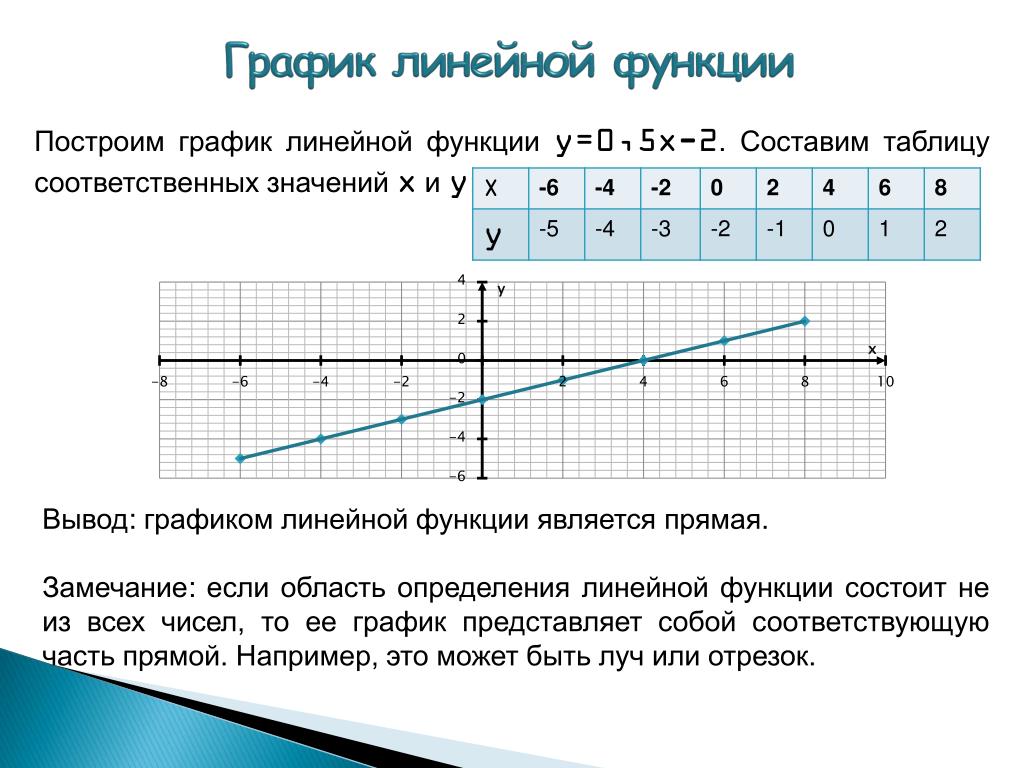 1 Решите y-5x + 25 = 0
1 Решите y-5x + 25 = 0 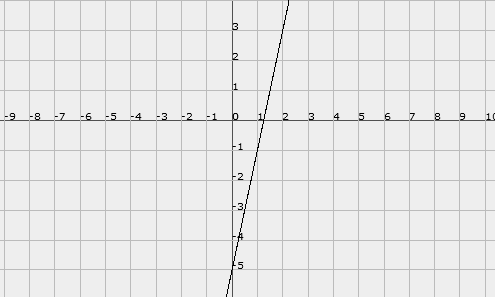 Отметим, что для x = 0 значение y равно -25,000, а для x = 2,000 значение y равно -15,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на -15.000 — (-25.000) = 10.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / ПЕРЕДАЧА)
Отметим, что для x = 0 значение y равно -25,000, а для x = 2,000 значение y равно -15,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на -15.000 — (-25.000) = 10.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / ПЕРЕДАЧА)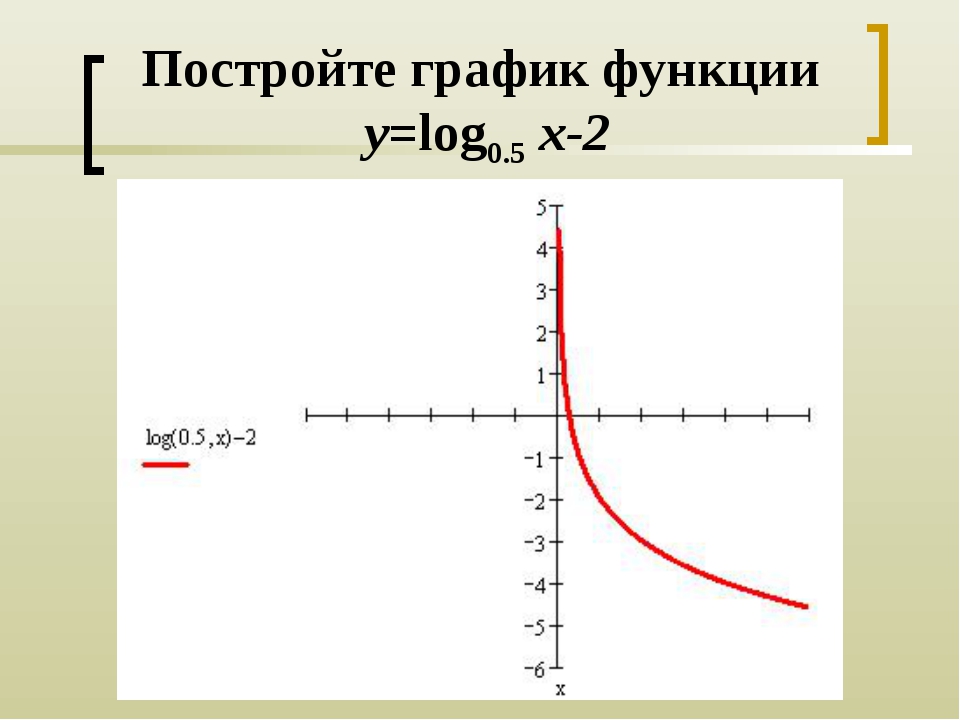
 Рассмотрим предыдущий пример, где x — количество произведенных товаров.
и продано, была независимой переменной в трех функциях: функции затрат,
функция дохода и функция прибыли.
Рассмотрим предыдущий пример, где x — количество произведенных товаров.
и продано, была независимой переменной в трех функциях: функции затрат,
функция дохода и функция прибыли.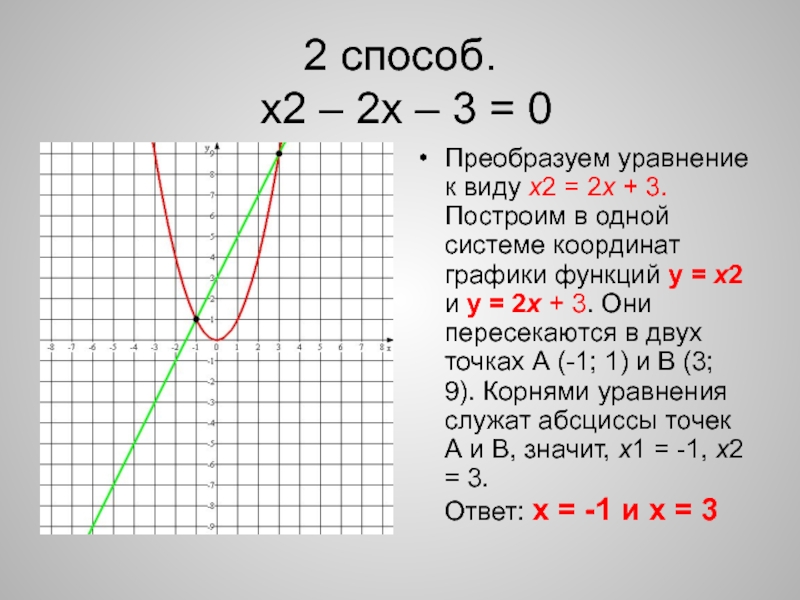 5 (0) = 1
5 (0) = 1 Установив
сначала x, а затем y равны нулю, можно найти точку пересечения y на
вертикальная ось и точка пересечения x на горизонтальной оси.
Установив
сначала x, а затем y равны нулю, можно найти точку пересечения y на
вертикальная ось и точка пересечения x на горизонтальной оси.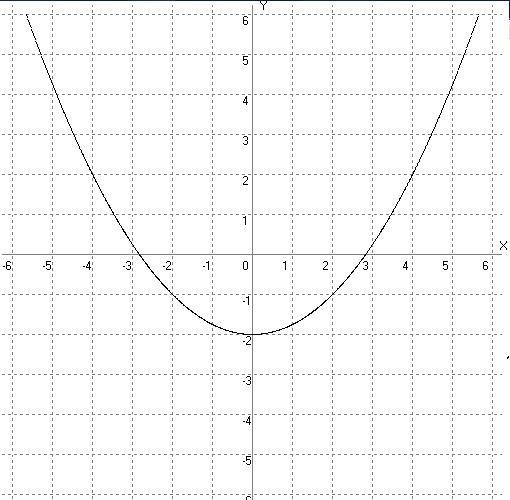
 Таким образом, цена — это
зависимая переменная.Было бы логичнее рассматривать количество как
зависимая переменная, и этот подход использовал великий французский экономист,
Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя
Анализ Маршалла, который называют крестом Маршалла.
Таким образом, цена — это
зависимая переменная.Было бы логичнее рассматривать количество как
зависимая переменная, и этот подход использовал великий французский экономист,
Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя
Анализ Маршалла, который называют крестом Маршалла.

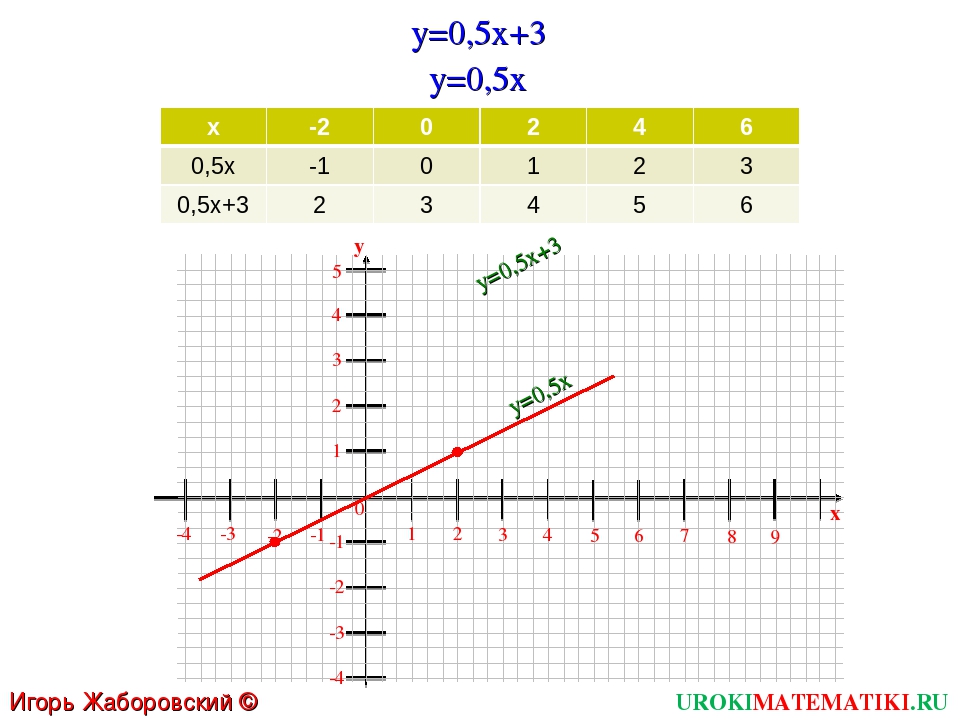 Это дает
Это дает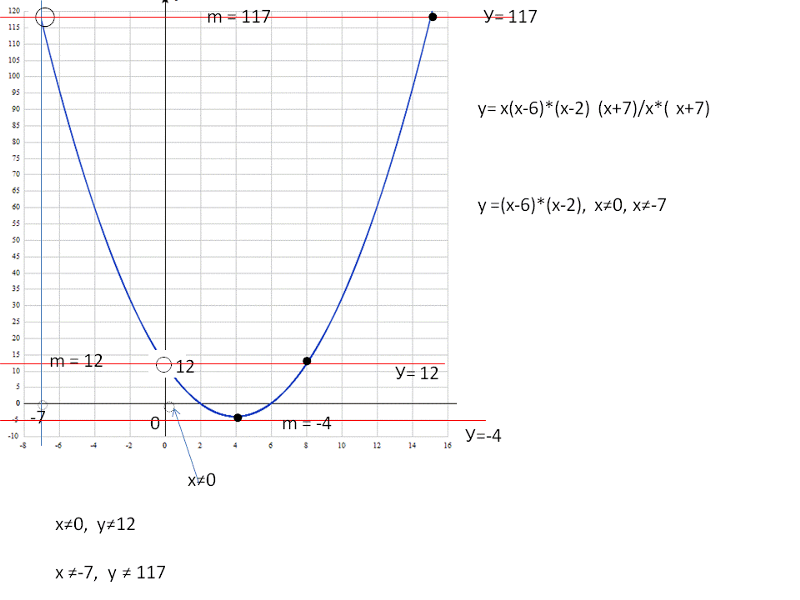 Значение, полученное для x 3 , используется для решения x 2 и
наконец, значения, полученные для x 3 и x 2 , используются для
решить относительно x 1 .
Значение, полученное для x 3 , используется для решения x 2 и
наконец, значения, полученные для x 3 и x 2 , используются для
решить относительно x 1 . Из Части А осталось два уравнения. Из этих двух уравнений исключить
x 2 .
Из Части А осталось два уравнения. Из этих двух уравнений исключить
x 2 .


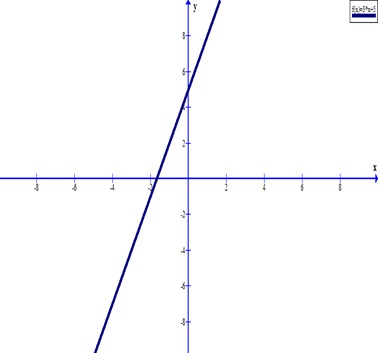
 Имеет переменную стоимость
25 долларов США за единицу и фиксированная стоимость 1600 долларов США.
Имеет переменную стоимость
25 долларов США за единицу и фиксированная стоимость 1600 долларов США.  Например, график ниже считается симметричным относительно оси y (линия x = 0), потому что четверть круга слева от оси y является зеркальным отображением четверти круга справа от оси y. ось. Фактически, если бы вы могли сложить эту страницу по оси Y, две четверти круга идеально совпали бы.
Например, график ниже считается симметричным относительно оси y (линия x = 0), потому что четверть круга слева от оси y является зеркальным отображением четверти круга справа от оси y. ось. Фактически, если бы вы могли сложить эту страницу по оси Y, две четверти круга идеально совпали бы. Это может быть особенно полезно, если вы работаете в трехмерном пространстве, как это делается в многомерном исчислении.
Это может быть особенно полезно, если вы работаете в трехмерном пространстве, как это делается в многомерном исчислении. Черная точка представляет исходную точку, а цветные точки демонстрируют четыре типа симметрии.
Черная точка представляет исходную точку, а цветные точки демонстрируют четыре типа симметрии.

 Вы можете думать о симметрии относительно начала координат как о отражении относительно оси y, а также оси x. Тест на симметрию относительно начала координат объединяет элементы из первых двух тестов.
Вы можете думать о симметрии относительно начала координат как о отражении относительно оси y, а также оси x. Тест на симметрию относительно начала координат объединяет элементы из первых двух тестов. Мы должны сначала решить для y (в терминах x), чтобы использовать графический калькулятор.
Мы должны сначала решить для y (в терминах x), чтобы использовать графический калькулятор.
 Приходя из университета домой, он продолжал учиться и вскоре понял, что не понимает, на что тратит своё время.
Приходя из университета домой, он продолжал учиться и вскоре понял, что не понимает, на что тратит своё время.

 В таком виде не получится отследить логические связи и закономерности. Есть более удобный для изучения способ — таблица Пифагора:
В таком виде не получится отследить логические связи и закономерности. Есть более удобный для изучения способ — таблица Пифагора:
 Еще один эффективный способ — учить таблицу умножения в игровой форме.
Еще один эффективный способ — учить таблицу умножения в игровой форме.
 Достаточно выучить, что цифры 3 и 4 в любом порядке при умножении друг на друга дают 12.
Достаточно выучить, что цифры 3 и 4 в любом порядке при умножении друг на друга дают 12.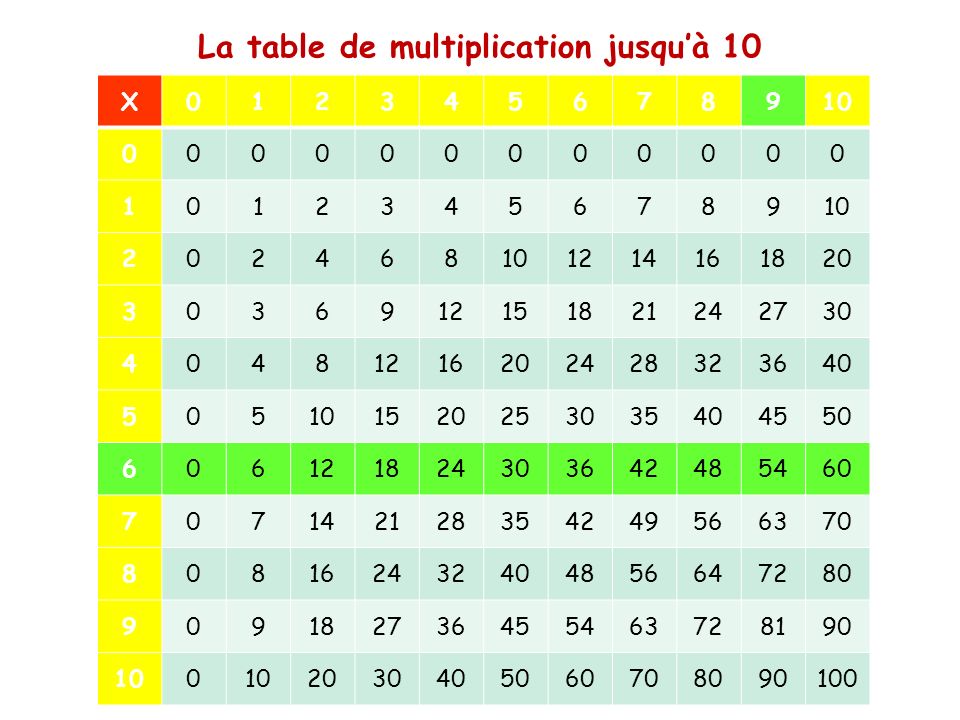


 Дальше действуйте так.
Дальше действуйте так. Или выяснит, сколько людей пойдёт на пикник, если вы собираетесь встретиться четырьмя семьями, в каждой из которых по три человека.
Или выяснит, сколько людей пойдёт на пикник, если вы собираетесь встретиться четырьмя семьями, в каждой из которых по три человека. Пусть школьник бросает два кубика или вытягивает две карты из колоды.
Пусть школьник бросает два кубика или вытягивает две карты из колоды. Это снизит стресс и вызовет стремление учиться дальше.
Это снизит стресс и вызовет стремление учиться дальше.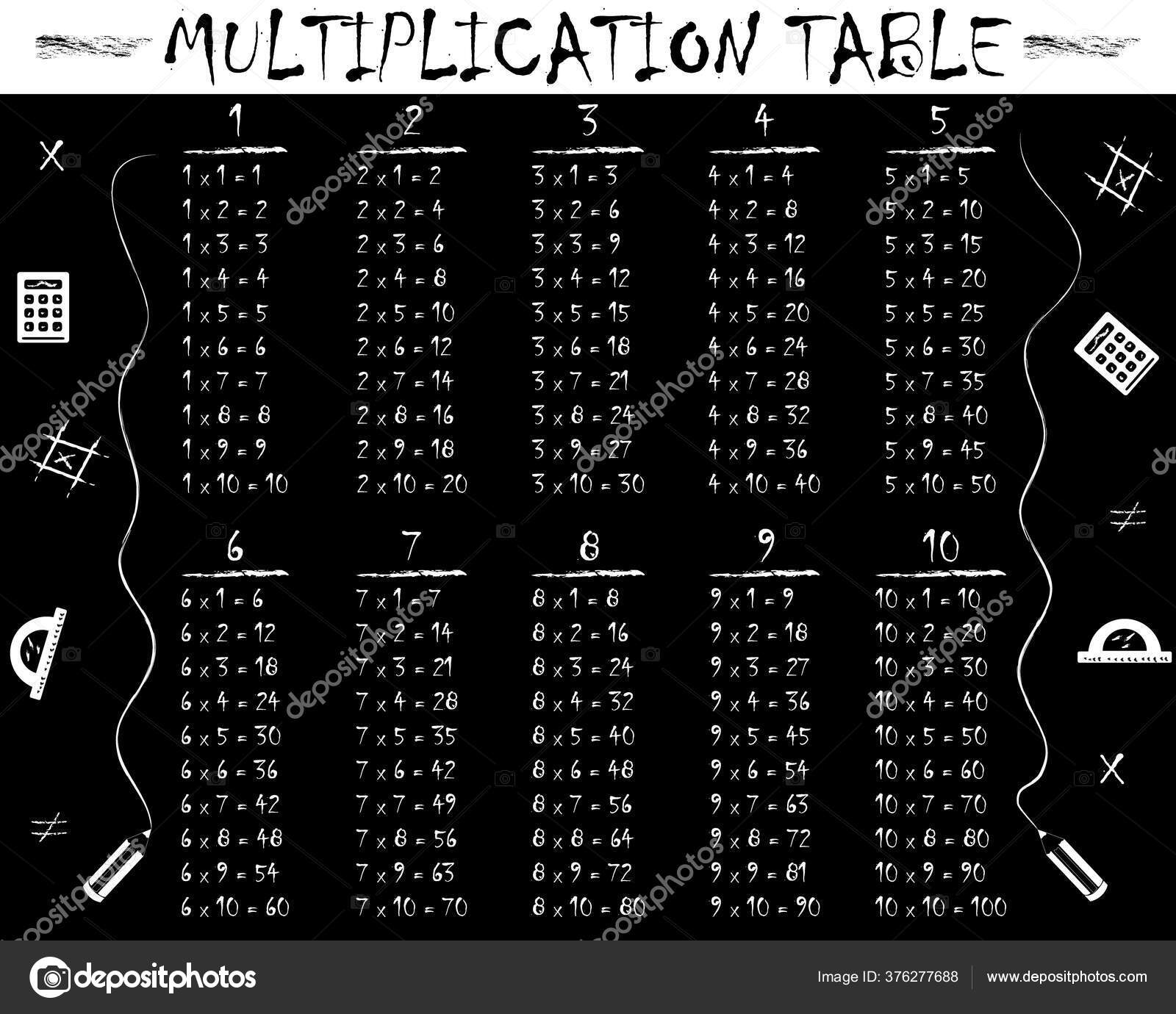 Лучше, если обучение будет проходить по таблице умножения Пифагора, потому как приведённая выше таблица это лишь столбик, в котором число 10 умножают на различные числа. В данном случае невозможно объяснить логические связи между цифрами и закономерности между ними, поэтому ребёнку придётся заучить данный столбик наизусть, как стихотворение. Мы же рекомендуем начинать изучение таблицы умножения по таблице Пифагора.
Лучше, если обучение будет проходить по таблице умножения Пифагора, потому как приведённая выше таблица это лишь столбик, в котором число 10 умножают на различные числа. В данном случае невозможно объяснить логические связи между цифрами и закономерности между ними, поэтому ребёнку придётся заучить данный столбик наизусть, как стихотворение. Мы же рекомендуем начинать изучение таблицы умножения по таблице Пифагора. В ней мы рассказываем, как научиться умножать числа до 10 друг на друга, запомнив всего 36 примеров вместо 100. А ещё показываем 5 полезных игр и пару лайфхаков, которые помогут выучить таблицу умножения не только быстро, но и весело.
В ней мы рассказываем, как научиться умножать числа до 10 друг на друга, запомнив всего 36 примеров вместо 100. А ещё показываем 5 полезных игр и пару лайфхаков, которые помогут выучить таблицу умножения не только быстро, но и весело.

 Это задание помогает наглядно увидеть, как работает умножение, и показывает, как устроена таблица Пифагора.
Это задание помогает наглядно увидеть, как работает умножение, и показывает, как устроена таблица Пифагора.
 А чтобы их получить, придётся подобрать правильные карточки.
А чтобы их получить, придётся подобрать правильные карточки. Игра построена на уникальной методике, которая помогает детям своими глазами увидеть, что такое умножение, и даже подержать его в руках. А это так важно для первых шагов в арифметике.
Игра построена на уникальной методике, которая помогает детям своими глазами увидеть, что такое умножение, и даже подержать его в руках. А это так важно для первых шагов в арифметике.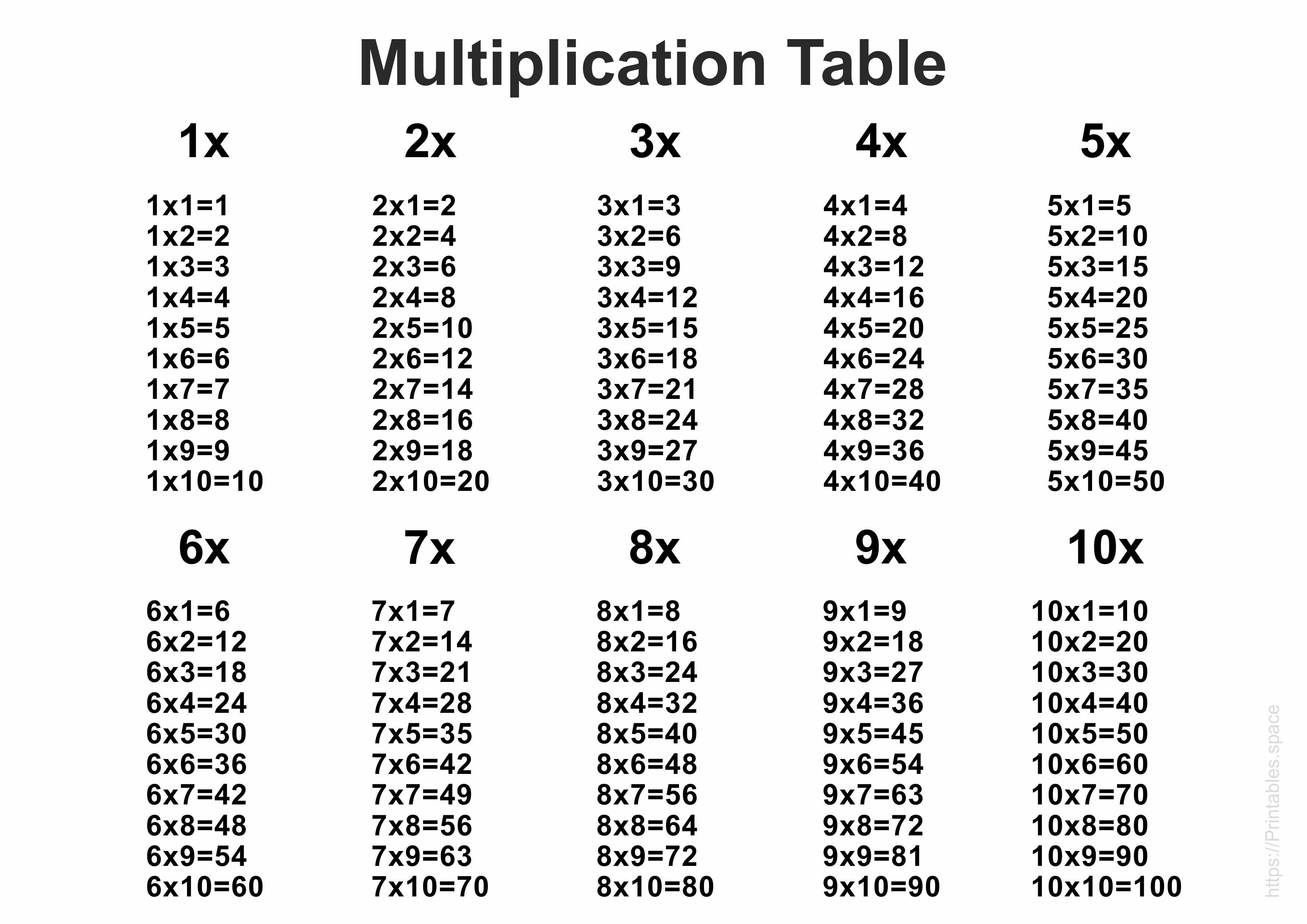


 Он основан на последовательности изучения отдельных таблиц для отдельных чисел и знания их некоторых закономерностей.
Он основан на последовательности изучения отдельных таблиц для отдельных чисел и знания их некоторых закономерностей.


 Вы можете посмотреть данную таблицу на нашем сайте в любое время, а также при необходимости можно сохранить ее себе на компьютер в виде картинки, чтобы иметь к ней доступ без подключения к интернету.
Вы можете посмотреть данную таблицу на нашем сайте в любое время, а также при необходимости можно сохранить ее себе на компьютер в виде картинки, чтобы иметь к ней доступ без подключения к интернету.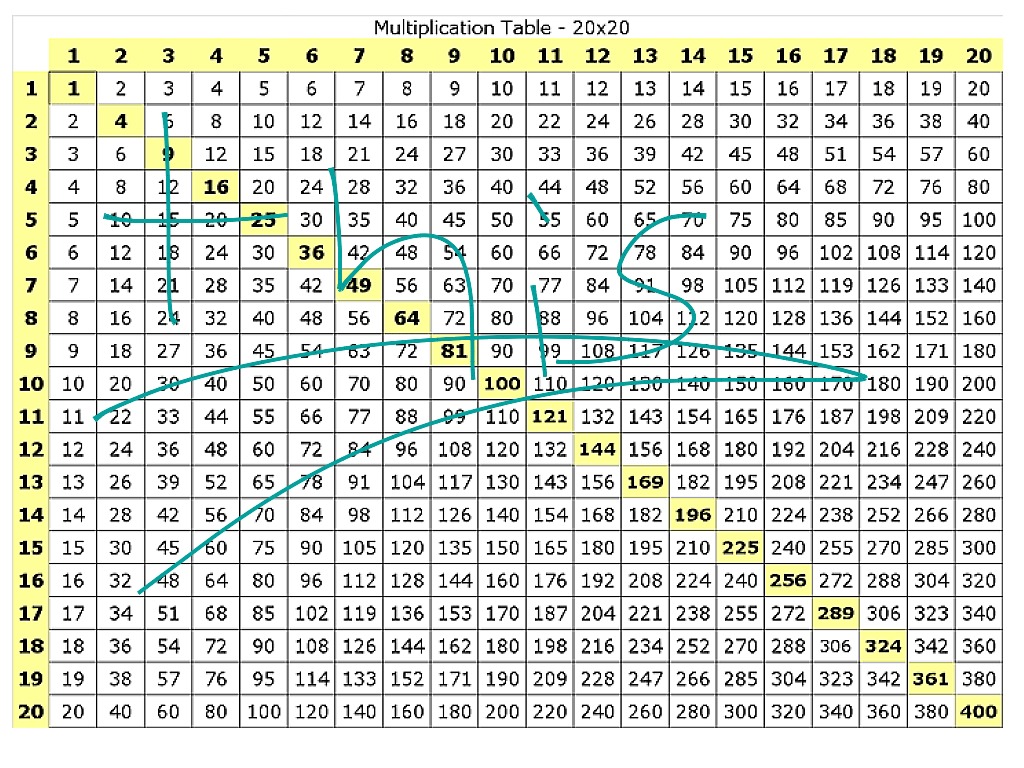
 Она выглядит вот так:
Она выглядит вот так: В игре с карточками работает и зрительная память, и слуховая (нужно озвучить уравнение). А также учащийся хочет поскорее «расправиться» со всеми карточками.
В игре с карточками работает и зрительная память, и слуховая (нужно озвучить уравнение). А также учащийся хочет поскорее «расправиться» со всеми карточками.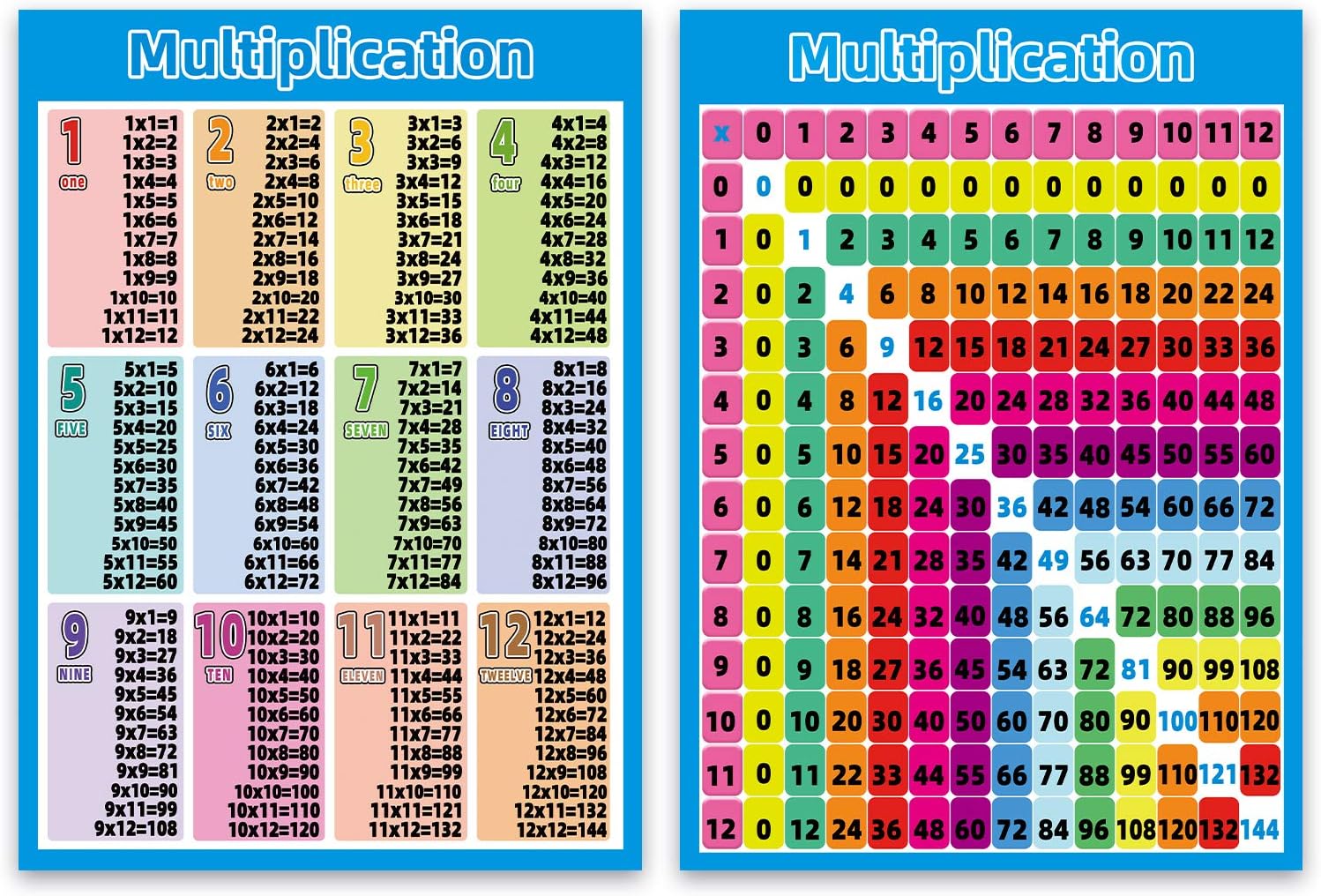
 Если ребенку показать наглядный пример умножения на каких либо предметах из его окружения, то он легче запомнит ответ, который у него будет ассоциироваться с каким-либо предметом.
Если ребенку показать наглядный пример умножения на каких либо предметах из его окружения, то он легче запомнит ответ, который у него будет ассоциироваться с каким-либо предметом.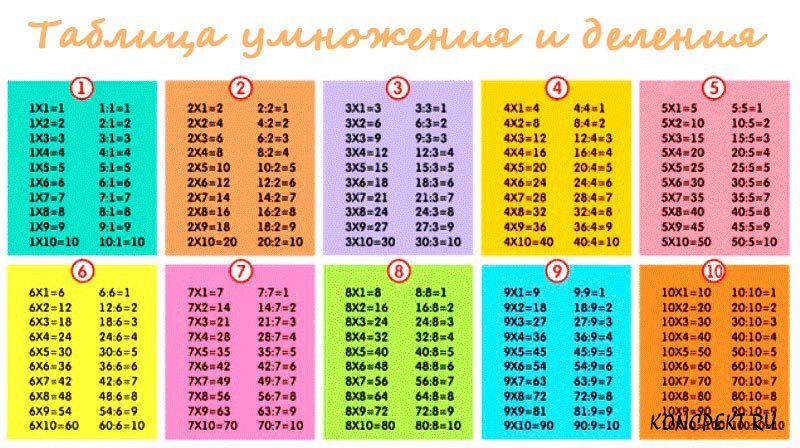 Выучить умножение на 9 можно с помощью пальцев!
Выучить умножение на 9 можно с помощью пальцев! Например, мимо вас пробежало 4 собаки. Спросите ребенка, сколько всего у собак лап, ушей, хвостов?
Например, мимо вас пробежало 4 собаки. Спросите ребенка, сколько всего у собак лап, ушей, хвостов? Родителям не нужно впадать в панику и не стоит ругать малыша.
Родителям не нужно впадать в панику и не стоит ругать малыша. Разложите на столе, например, 8, 9 или 10 пар счетных палочек. Пусть малыш самостоятельно составить действие на умножение. Вы увидите, с каким интересом он будет это делать
Разложите на столе, например, 8, 9 или 10 пар счетных палочек. Пусть малыш самостоятельно составить действие на умножение. Вы увидите, с каким интересом он будет это делать Помогите малышу своими подсказками и поддержкой в виде слов подбадривания и похвалы, и он обязательно все сможет.
Помогите малышу своими подсказками и поддержкой в виде слов подбадривания и похвалы, и он обязательно все сможет. Благодаря этому он уже сможет умножать на «5» моментально.
Благодаря этому он уже сможет умножать на «5» моментально. В нем есть пару сложных действий, которые нужно заучить.
В нем есть пару сложных действий, которые нужно заучить.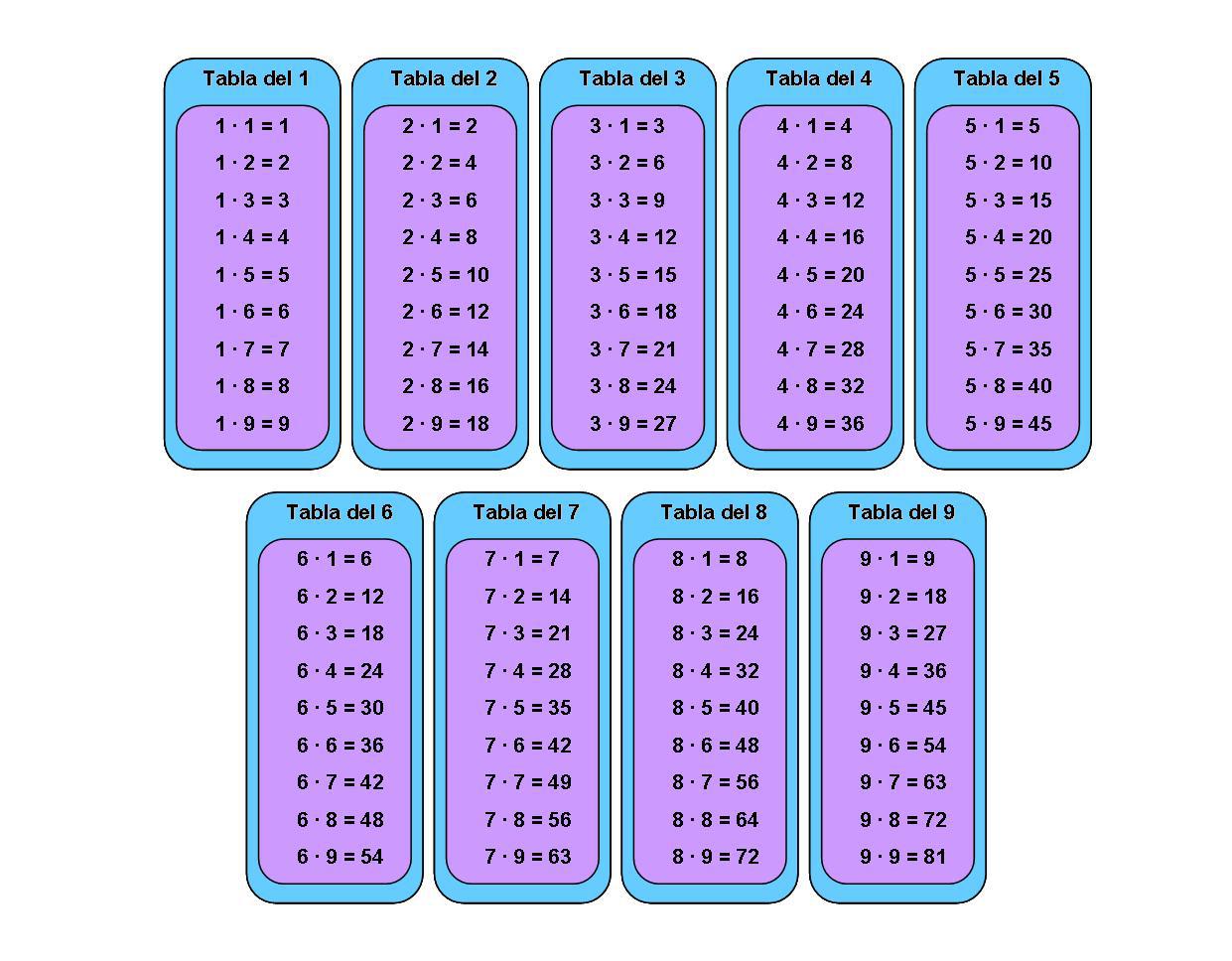
 Это интересно и увлекательно. Вот несколько стихов на действия таблицы умножения:
Это интересно и увлекательно. Вот несколько стихов на действия таблицы умножения:
 единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева Это явление называется релятивистским замедлением времени. Вышеописанная разница во времени значительна при скоростях, близких к скорости света, и была экспериментально доказана, например, в эксперименте Хафеле-Китинга. Ученые синхронизировали пять атомных часов и оставили одни неподвижным в лаборатории. Остальные часы дважды облетели вокруг Земли на пассажирских самолетах. Хафеле и Китинг обнаружили, что «часы-путешественники» отстают от стационарных часов, как и предсказывает теория относительности. Воздействие гравитации, так же, как и увеличение скорости, замедляет время.
Это явление называется релятивистским замедлением времени. Вышеописанная разница во времени значительна при скоростях, близких к скорости света, и была экспериментально доказана, например, в эксперименте Хафеле-Китинга. Ученые синхронизировали пять атомных часов и оставили одни неподвижным в лаборатории. Остальные часы дважды облетели вокруг Земли на пассажирских самолетах. Хафеле и Китинг обнаружили, что «часы-путешественники» отстают от стационарных часов, как и предсказывает теория относительности. Воздействие гравитации, так же, как и увеличение скорости, замедляет время.
 На момент написания статьи (январь 2013 года) строится опытный образец этих часов.
На момент написания статьи (январь 2013 года) строится опытный образец этих часов. Их погрешность составляет менее одной секунды за миллион лет. Водородные атомные часы примерно в десять раз более точны в течение более коротких отрезков времени, до недели.
Их погрешность составляет менее одной секунды за миллион лет. Водородные атомные часы примерно в десять раз более точны в течение более коротких отрезков времени, до недели. С 2012 года TAI на 35 секунд опережает UTC, потому что UTC, в отличие от TAI, использует средние солнечные сутки. Так как солнечный день немного длиннее 24 часов, для координации UTC с солнечным днем к UTC добавляются секунды координации. Иногда эти секунды координации вызывают различные проблемы, особенно в сферах, где используются компьютеры. Чтобы подобные проблемы не возникали, некоторые учреждения, такие как отдел серверов в компании Гугл, вместо секунд координации используют «високосное смазывание» — удлинение ряда секунд на миллисекунды, чтобы в сумме эти удлинения были равны одной секунде.
С 2012 года TAI на 35 секунд опережает UTC, потому что UTC, в отличие от TAI, использует средние солнечные сутки. Так как солнечный день немного длиннее 24 часов, для координации UTC с солнечным днем к UTC добавляются секунды координации. Иногда эти секунды координации вызывают различные проблемы, особенно в сферах, где используются компьютеры. Чтобы подобные проблемы не возникали, некоторые учреждения, такие как отдел серверов в компании Гугл, вместо секунд координации используют «високосное смазывание» — удлинение ряда секунд на миллисекунды, чтобы в сумме эти удлинения были равны одной секунде. Тропический год постепенно становится короче на 0,53 секунды каждые 100 тропических лет, поэтому в будущем, вероятно, нужна будет реформа, чтобы синхронизировать солнечные календари с тропическим годом.
Тропический год постепенно становится короче на 0,53 секунды каждые 100 тропических лет, поэтому в будущем, вероятно, нужна будет реформа, чтобы синхронизировать солнечные календари с тропическим годом. Это делается каждые четыре года, за исключением годов, которые делятся на 100, но не делятся на 400. Например, 2000 год был високосным, а 1900 — нет.
Это делается каждые четыре года, за исключением годов, которые делятся на 100, но не делятся на 400. Например, 2000 год был високосным, а 1900 — нет. Например, японское летоисчисление (年号 нэнго, буквально, название эры), используется в дополнение к григорианскому календарю. Название года соответствует названию периода, который также называется девизом императора, и году правления императора этого периода. При вступлении на престол, новый император утверждает свой девиз, и начинается отсчет нового периода. Девиз императора позже становится его посмертным именем. Согласно этой схеме, 2013 год называется Хэйсэй 25, то есть, 25-й год правления императора Акихито периода Хэйсэй.
Например, японское летоисчисление (年号 нэнго, буквально, название эры), используется в дополнение к григорианскому календарю. Название года соответствует названию периода, который также называется девизом императора, и году правления императора этого периода. При вступлении на престол, новый император утверждает свой девиз, и начинается отсчет нового периода. Девиз императора позже становится его посмертным именем. Согласно этой схеме, 2013 год называется Хэйсэй 25, то есть, 25-й год правления императора Акихито периода Хэйсэй. Сколько времени ваши часы показывают? – [Maí chisý atstayút (spishát, zabýl dóma, slamális′). Skól′ka vrémini váshi chisý pakázyvayut?] — My watch is falling behind (hurry, forgot at home, broke). What time does your clock show?
Сколько времени ваши часы показывают? – [Maí chisý atstayút (spishát, zabýl dóma, slamális′). Skól′ka vrémini váshi chisý pakázyvayut?] — My watch is falling behind (hurry, forgot at home, broke). What time does your clock show? 00 или 23.00 – Одиннадцать часов или двадцать три часа
00 или 23.00 – Одиннадцать часов или двадцать три часа
 15).
15). Petersburg.
Petersburg. It’s time to return to work after rest.
It’s time to return to work after rest.
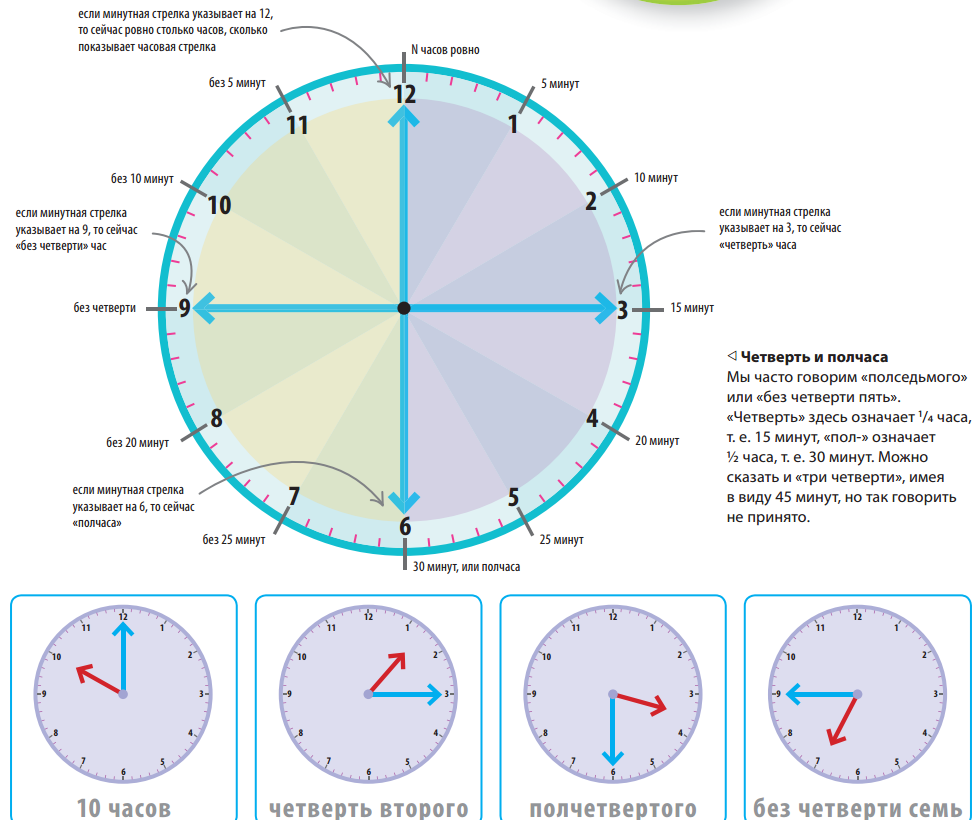 Потому что тогда не знали, к чему приведет длительное лишение сна — возможно, к смерти».
Потому что тогда не знали, к чему приведет длительное лишение сна — возможно, к смерти».
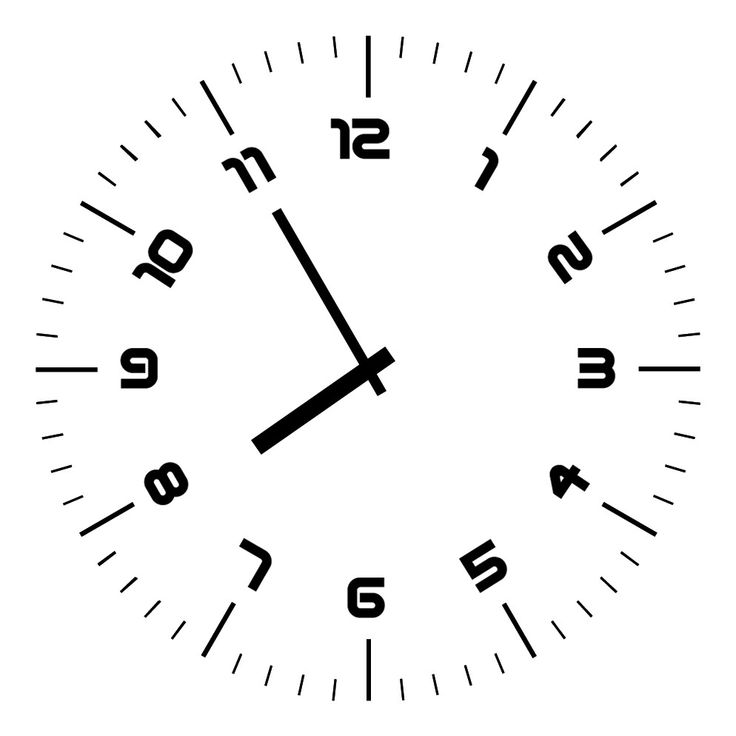
 Затем она стала уменьшаться и вскоре стала обычной».
Затем она стала уменьшаться и вскоре стала обычной».