Учебник по дискретной математике ДНФ, СДНФ, КНФ, СКНФ
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том жепорядке.
Например, выражение является ДНФ, но не СДНФ. Выражение является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение – простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение – КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые , то ко всей дизъюнкции добавляем слагаемое К1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). (Xv
ךYv
ךZ)
Таким образом, из КНФ получена СКНФ.
(Xv
ךYv
ךZ)
Таким образом, из КНФ получена СКНФ.
25. Совершенные дизъюнктивные и конъюнктивные нормальные формы и алгоритмы приведения к ним. Примеры.
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая конъюнктивная нормальная форма, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных переменных
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
k-конъюнктивной нормальной формой называют конъюнктивную нормальную форму, в которой каждая дизъюнкция содержит ровно k литералов.
Например, следующая формула записана в 2-КНФ:
Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная
конъюнкция содержит каждую пропозициональную
букву из входящих в данную ДНФ пропозициональных букв, причём в
одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причём единственная.
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
Совершенная ДНФэтой функции:
Тема 6 Минимизация булевых функций
6. 1 Сокращенная и тупиковая ДНФ
1 Сокращенная и тупиковая ДНФ
6.2 Метод импликантных матриц
Цель данного раздела – изложение основных методов построения минимальных дизъюнктивно нормальных форм.
6.1 Сокращенная и тупиковая ДНФ. В разделе 3 было показано, что любая булева функция может быть представлена дизъюнктивной нормальной формой. Следует отметить, что дизъюнктивная нормальная форма часто допускает упрощение. При этом путем различных тождественных преобразований получится дизъюнктивная нормальная форма, эквивалентная исходной, но содержащая меньшее число вхождений символов.
Дизъюнктивная нормальная форма называется Минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей дизъюнктивными нормальными формами.
Заметим, что если некоторый символ в формуле, скажем , встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
Основной вопрос данного параграфа – это как для произвольной булевой функции построить ей минимальную дизъюнктивную нормальную форму. Эта задача называется Проблемой минимизации булевых функций.
Эта задача называется Проблемой минимизации булевых функций.
Существует тривиальный алгоритм построения минимальной ДНФ для произвольной булевой функции . Для этого все ДНФ, составленные из символов упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение . Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции .
Число различных ДНФ, составленных из переменных , равно .
Прежде чем доказать данное утверждение, приведем следующее определение.
Конъюнкция называется Элементарной, если при .
Число R называется Рангом элементарной конъюнкции. В случае r=0 конъюнкция называется Пустой и Полагается равной 1.
Так как каждая из N переменных либо не входит в элементарную, либо входят в нее с отрицанием, либо без отрицания, то число элементарных конъюнкций, составленных из равно . Ясно, что число различных ДНФ, составленных из переменной , равно числу подмножеств множества, из элементов, т. е. .
Ясно, что число различных ДНФ, составленных из переменной , равно числу подмножеств множества, из элементов, т. е. .
Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций.
Обозначим через множество всех точек , где . Ясно, что — множество всех вершин единичного n-мерного куба.
Сопоставим каждой булевой функции Подмножество Из , определенное следующим образом:
Например, функции
|
X |
Y |
Z |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Соответствует подмножество
Вершин трехмерного единичного куба
Данное соответствие является взаимно однозначным и обладает следующими свойствами:
1) булевой функции Соответствует подмножество ;
2) булевой функции соответствует подмножество ;
3) булевой функции соответствует подмножество .
Докажем утверждение 2. Пусть
Отсюда .
Тогда .
А это значит, что .
Отсюда .
Пусть ДНФ, где — элементарные конъюнкции. Подмножество называется интервалом R-го ранга, если оно соответствует элементарной конъюнкции К R-го ранга. Как показано выше, . Итак, с каждой ДНФ функции F связано покрытие такими интервалами , что .
Пусть — ранг интервала . Тогда совпадает с числом букв в ДНФ функции .
Теперь ясно, что задача построения минимальной ДНФ сводится к отысканию такого покрытия подмножества интервалами , чтобы число было наименьшим.
Интервал , содержащий , называется Максимальным для булевой функции, если не существует интервала , такого, что .
Заметим, что соотношение выполняется тогда и только тогда, когда элементарная конъюнкция получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.
Очевидно, что каждый интервал из содержится в некотором максимальном интервале. Если — список всех максимальных интервалов подмножества , то нетрудно видеть, что .
Если — список всех максимальных интервалов подмножества , то нетрудно видеть, что .
ДНФ булевой функции f, соответствующая покрытию подмножества всеми максимальными интервалами, называется Сокращенной ДНФ функции F.
Ясно, что сокращенная ДНФ для любой булевой функции f определяется однозначно.
Пример 1. Пусть . Обозначим , , . Найдем соответствующие этим конъюнкциям интервалы , , .
Изобразим эти интервалы
Очевидно, что и — все максимальные интервалы. Интервал не является максимальным, ибо . Следовательно, покрытию подмножества соответствует сокращенная ДНФ функции , равная .
Данный геометрический подход дает и метод построения сокращенной ДНФ.
Теперь рассмотрим аналитический метод построения сокращенной ДНФ – метод Блейка. Этот метод основан на следующей теореме.
Теорема 1. Если в произвольной ДНФ булевой функции F произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получиться сокращенная ДНФ функции F.
Следовательно, чтобы найти сокращенную ДНФ, надо к произвольной ДНФ данной функции применить правило обобщенного склеивания до тех пор, пока это возможно, а затем правило поглощения.
Пример 2. Найти сокращенную ДНФ для функции . Применяя правило обобщенного склеивания, получаем: .
Затем правило поглощения и находим сокращенную ДНФ: .
Рассмотрим еще один метод построения сокращенной ДНФ – метод Нельсона. Этот метод основан на следующей теореме.
Теорема 2. Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции.
Пример 3. Найти сокращенную ДНФ для функции
После раскрытия скобок с помощью дистрибутивного закона, получаем:
.
Так как , , то имеем:
.
Далее, применяя правило поглощения, получаем сокращенную ДНФ:
.
Рассмотрим табличный метод построения сокращенной ДНФ. Этот метод основан на составлении прямоугольной таблицы (минимизирующей карты).
Минимизирующие карты для булевых функций от трех и от четырех переменных изображены на следующих таблицах.
|
Z X y |
0 |
1 |
|
00 |
||
|
01 |
||
|
11 |
||
|
10 |
|
X4 X3 X1 X2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
0 0 |
||||
|
0 1 |
||||
|
1 1 |
||||
|
1 0 |
Объединяя соседние клетки, соответствующие единичным значениям булевой функции f в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.
Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.
Пример 4. Найти сокращенную ДНФ для функции, заданной следующей таблицей.
|
X4 X3 X1 X2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
0 0 |
1 |
1 |
0 |
1 |
|
0 1 |
0 |
1 |
1 |
0 |
|
1 1 |
1 |
1 |
1 |
0 |
|
1 0 |
0 |
1 |
0 |
0 |
В данной таблице объединены клетки в максимальные интервалы
.
Этим интервалам соответствуют элементарные конъюнкции
, , , ,
Следовательно, сокращенная ДНФ для данной функции имеет вид:
Построение сокращенной ДНФ есть только первый этап решения задачи минимизации булевой функции. В общем случае сокращенная ДНФ не является минимальной. Следующая теорема устанавливает связь между минимальной и сокращенной ДНФ.
Теорема 3. Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций.
Доказательство этого утверждения следует из того факта, что покрытие подмножества , отвечающее минимальной ДНФ, состоит только из максимальных интервалов. Действительно, если бы покрытие содержало не максимальный интервал, то его можно было бы заменить объемлющим максимальным интервалом. В результате этого сумма рангов интервалов данного покрытия уменьшилась бы, что противоречит предположению о минимальности ДНФ.
Покажем, что в классе монотонных функций понятия минимальной и сокращенной ДНФ совпадают.
Теорема 4. Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции.
Пусть К – элементарная конъюнкция, входящая в сокращенную ДНФ. Предположим, что К содержит отрицание переменных. Обозначим через произведение всех переменных, входящих в К без отрицания. Пусть – набор переменных, в которых всем переменным, входящим в , приписано значение 1, а всем остальным – значение 0. Ясно, что при этом наборе значение функции Равно 1. Элементарная конъюнкция обращается в 1 при всех наборах . Очевидно, что при этих наборах значение функции также равно 1. Следовательно, .
Получили противоречие с максимальностью интервала . Итак, сокращенная ДНФ булевой функции Не содержит отрицаний переменных.
Пусть — любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами . Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция обращалась в этой вершине в 1, то не содержала бы, во-первых, букв , и, во-вторых, букв . Поэтому в конъюнкцию могли бы входить лишь буквы , причем не все. Но тогда . Получили противоречие с максимальностью интервала . Следовательно, для любого максимального интервала существует вершина куба , которая покрывается только этим интервалом. Поэтому из покрытия соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция обращалась в этой вершине в 1, то не содержала бы, во-первых, букв , и, во-вторых, букв . Поэтому в конъюнкцию могли бы входить лишь буквы , причем не все. Но тогда . Получили противоречие с максимальностью интервала . Следовательно, для любого максимального интервала существует вершина куба , которая покрывается только этим интервалом. Поэтому из покрытия соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. Действительно, в сокращенной ДНФ
Элементарная конъюнкция поглощается дизъюнкцией остальных элементарных конъюнкций, т. е. .
Ввиду этого введем следующее определение.
Покрытие области истинности булевой функции максимальными интервалами называется Неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции , соответствующая неприводимому покрытию, называется Тупиковой.
Теорема 5. Всякая минимальная ДНФ является тупиковой.
Доказательство этого утверждения следует из того, что покрытие, соответствующее минимальной ДНФ, является неприводимым.
Заметим, что булева функция может обладать несколькими различными минимальными ДНФ. Существуют также тупиковые ДНФ, не являющиеся минимальными ДНФ. Соответствующие примеры будут разобраны ниже.
Из того, что минимальная ДНФ является тупиковой, следует общая схема решения задачи минимизации булевых функций.
1. Выделяются все максимальные интервалы, и строится сокращенная ДНФ.
2. Строятся все тупиковые ДНФ.
3. Среди всех тупиковых ДНФ выделяются все минимальные ДНФ.
Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем:
1) для булевой функции строим сокращенную ДНФ;
2) для каждой вершины из выделяем в сокращенной ДНФ функции F все такие элементарные конъюнкции , что ;
3) составляем выражение вида
(*)
4) применяем к выражению вида (*) законы дистрибутивности и поглощения. В результате получаем .
Теперь каждая ДНФ является тупиковой ДНФ функции .
Рассмотрим работу данного алгоритма на следующем примере.
Пример 5. Рассмотрим булеву функцию, заданную следующей таблицей:
|
X |
Y |
Z |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Найдем сокращенную ДНФ данной функции по методу Нельсона. Для этого составим КНФ данной функции .
Для этого составим КНФ данной функции .
Применяя законы дистрибутивности, получаем:
.
Обозначим , , , , , .
Составляем выражение (*)
Преобразуем данное выражение к виду
= =.
Таким образом, имеет шесть тупиковых ДНФ:
Две из них и являются минимальными.
6.2 Метод импликантных матриц. Для булевой функции находим сокращенную ДНФ . Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются , а в горизонтальные .
|
… |
… |
|||||
|
… |
||||||
|
+ |
||||||
|
… |
||||||
Для каждой находим набор такой, что .
Клетку импликантной матрицы, образованную пересечением I-строки и J-столбца отметим крестиком.
Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число , которые совместно накрывают крестиками все столбцы импликантной матрицы.
Пример 6. Найти минимальные ДНФ для функции
.
Из предыдущего примера следует, что сокращенная ДНФ для данной функции . Очевидно, что
.
Строим импликантную матрицу
|
(0,0,1) |
(0,1,0) |
(0,1,1) |
(1,0,0) |
(1,0,1) |
(1,1,0) |
|
|
+ |
+ |
|||||
|
+ |
+ |
|||||
|
+ |
+ |
|||||
|
+ |
+ |
|||||
|
+ |
+ |
|||||
|
+ |
+ |
Отсюда видно, что данная функция имеет два минимальные ДНФ:
; .
Вопросы для самоконтроля.
1. Дайте определение основных логических операций булевой алгебры.
2. Дайте определение булевой функции.
3. Что такое таблицы истинности булевой функции?
4. Каково число булевых функций от переменных?
5. Какие булевы функции называются элементарными?
6. Дайте определение формулы алгебры логики.
7. Какие формулы алгебры логики называются равносильными?
8. Сформулируйте законы алгебры логики.
9. Какая формула алгебры логики называется двойственной к данной формуле алгебры логики?
10. Сформулируйте принцип двойственности.
11. Сформулируйте теорему о разложении и следствие из нее.
12. Дайте определение СДНФ.
13. Приведите алгоритмы построения СДНФ.
14. Дайте определение СКНФ.
15. Приведите алгоритмы построения СКНФ.
16. Дайте определение ДНФ.
17. Как найти ДНФ?
Как найти ДНФ?
18. Дайте определение КНФ.
19. Как найти КНФ?
20. Какая формула алгебры логики называется тождественно истинной?
21. Какая формула алгебры логики называется тождественно ложной?
22. Какая формула алгебры логики называется выполнимой?
23. Что называется проблемой разрешимости?
24. Сформулируйте методы решения проблемы разрешения.
25. Что называется алгеброй Жегалкина?
26. Сформулируйте законы алгебры Жегалкина.
27. Что называется полиномом Жегалкина?
28. Сформулируйте алгоритмы построения полиномов Жегалкина.
29. Какая система булевых функций называется полной?
30. Что называется замыканием множества булевых функций?
31. Какой класс булевых функций называется замкнутым?
32. Дайте определение пяти важнейших замкнутых классов.
33. Сформулируйте теорему о полноте.
34. Сформулируйте алгоритм Поста.
35. Какая система булевых функций называется несократимой?
36. Каково максимальное возможное число функций в несократимой полной системе булевых функций?
37. Что такое релейно-контактная схема?
38. Почему любую булеву функцию можно изобразить в виде релейно-контактной схемы?
39. В чем состоит проблема анализа релейно-контактных схем?
40. В чем состоит проблема синтеза релейно-контактных схем?
41. Что такое логические элементы?
42. Приведите геометрическое изображение логических элементов.
43. Что такое логическая схема?
44. Что Вы понимаете под двоичным сумматором?
45. Какая ДНФ называется минимальной?
46. Чему равно число всех ДНФ от переменных?
47. Сформулируйте тривиальный алгоритм построения МДНФ?
48. Что такое элементарная конъюнкция?
49. Что такое ранг элементарной конъюнкции?
50. Что называется интервалом элементарной конъюнкции?
51. Какой интервал называется максимальным?
52. Что называется областью истинности булевой функции?
53. Сформулируйте теорему об области истинности булевой функции.
54. Что называется покрытием области истинности булевой функции?
55. Какое число элементов содержится в интервале?
56. Какая ДНФ называется сокращенной?
57. В чем состоит геометрическая интерпретация задачи минимизации булевой функции?
58. Сформулируйте геометрический метод построения сокращенной ДНФ.
59. Сформулируйте метод Нельсона построения сокращенной ДНФ.
60. Сформулируйте метод Блейка построения сокращенной ДНФ.
61. Сформулируйте метод карт Карно построения сокращенной ДНФ.
62. Какая связь между МДНФ и сокращенной ДНФ?
63. Какое покрытие области истинности булевой функции называется неприводимым.
64. Какая ДНФ называется тупиковой?
65. Какая связь между МДНФ и тупиковой ДНФ?
66. Сформулируйте алгоритм построения всех тупиковых ДНФ.
67. Как строится импликантная матрица?
68. Сформулируйте алгоритм нахождения МДНФ методом импликантных матриц.
| < Предыдущая | Следующая > |
|---|
Нормальные формы: ДНФ, КНФ, СДНФ, СКНФ
Нормальные формы формул алгебры высказываний бывают двух типов: дизъюктивные и конъюктивные, в каждом из этих типов выделен класс совершенных форм.
Алгоритм построения ДНФ:
1. Перейти к булевым операциям.
2. Перейти к формуле с тесными отрицаниями, т.е. к формуле, в которой отрицания находятся не выше, чем над переменными.
3. Раскрыть скобки.
4. Повторяющейся слагаемые взять по одному разу.
5. Применить законы поглощения и полупоглощения.
Пример.Найти ДНФ формулы
►
◄
Конъюнктивная нормальная форма (КНФ) – двойственное для ДНФ понятие, поэтому ее легко построить по схеме:
.
Пример.Найти КНФ формулы
► ~ ~
.◄
Совершенную дизъюнктивную нормальную форму СДНФ можно строить, используя следующий алгоритм:
1. = 1. алгоритма ДНФ
2. = 2. алгоритма ДНФ
3. = 3. алгоритма ДНФ
4. = 4. алгоритма ДНФ
5. Опустить тождественно ложные слагаемые, т. е. слагаемые вида
.
6. Пополнить оставшиеся слагаемые недостающими переменными
7. Повторить пункт 4.
Пример.Найти СДНФ формулы.
► ~
.◄
Для построения СКНФ можно пользоваться следующей схемой:
Пример.Найти СДНФ формулы.
► ~
.◄
Известно (теоремы 2.11, 2.12), что СДНФ и СКНФ определены формулой однозначно и, значит, их можно строить по таблице истинности формулы [1].
►Схема построения СДНФ и СКНФ по таблице истинности приведена ниже, для формулы ~ :
2.2. Задание.
2.2.1 Ниже приведены логические выражения. Максимально упростите выражения своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
2.2.2. Выяснить вопрос о равносильности f1 и f 2 путем сведения их к СДНФ (табл. 1).
2.2.3. Найти двойственную функцию для f3 по обобщенному и булевому принципу (табл.1). Сравнить полученные результаты.
2.3. Контрольные вопросы.
2.3.1. Дайте определение высказывания.
2.3.2. Перечислите основные операции над высказыванием.
2.3.3. Что такое таблица истинности?
2.3.4. Составить таблицы истинности для следующих формул:
~ ~ ;
~ ;
~ ~ ~ ;
~ ~ ~ ~ .
2.3.5. Учитывая соглашения о порядке выполнения операций, опустить «лишние» скобки и знак « » в формулах:
;
;
;
;
~ .
2.3.6. Применяя равносильные преобразования, доказать тождественную истинность формул:
;
;
;
.
2.3.7.Найти двойственные формулы:
)
.
2.3.8. Привести к совершенной ДНФ (СДНФ) форме следующие формулы:
~
2.3.9. Привести к совершенной КНФ (СКНФ) форме следующие формулы:
~
~
Лабораторная работа № 3
Тема: «Минимизация булевых функций. Логические схемы»
Цель: Приобретение практических навыков работы с методами минимизации булевых функций.
3.1. Теоретические сведения [1].
Минимальные формы
Как было показано в [1], любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению. В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получается на основе принципа двойственности [1].
Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. При каноническом синтезе предполагается, что на входы схемы подаются как сигналы , так и их инверсий .
Формула, представленная в дизъюнктивной нормальной форме, упрощается многократными применением операции склеивания и операции поглощения и (дуальные тождества для конъюнктивной нормальной формы имеют вид: и ). Здесь под и можно понимать любую формулу булевой алгебры. В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются уже невозможными, т.е. получаем тупиковую форму.
Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Пусть, например, функция задана в совершенной нормальной дизъюнктивной форме:
.
Группируя члены и применяя операцию склеивания, имеем .
При другом способе группировки получим:
.
Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как ). В первом случае таким членом может быть . Тогда . Добавив член , получим: . Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными.
Работа с формулами на таком уровне подобна блужданию в потемках. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать некоторые графические и аналитические представления и специально разработанную для этой цели символику.
Многомерный куб
Каждой вершине -мерного куба можно поставить в соответствие конституенту единицы. Следовательно, подмножество отмеченных вершин является отображением на -мерном кубе булевой функции от переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показано такое отображение для функции из п.3.7.
Рис.3.1 Отображение на трехмерном кубе функции, представленной в СДНФ
Для отображения функции от переменных, представленной в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами и элементами -мерного куба.
Минитерм ( -1)-го ранга можно рассматривать как результат склеивания двух минитермов -го ранга (конституент единицы), т.е. , На -мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координаты , соединяющим эти вершины, ребром (говорят, что ребро покрывает инцидентные ему вершины). Таким образом, минитермам ( -1)-го порядка соответствуют ребра -мерного куба. Аналогично устанавливается соответствие минитермов ( -2)-го порядка — граням -мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы -мерного куба, характеризующиеся измерениями, называют -кубами. Так, вершины являются 0-кубами, ребра – 1-кубами, грани – 2-кубами и т.д. Обобщая приведенные рассуждения, можно считать, что минитерм ( )-го ранга в дизъюнктивной нормальной форме для функции переменных отображается -кубом, причем каждый -куб покрывает все те -кубы низшей размерности, которые связаны с его вершинами. В качестве примера на рис. 3.2 дано отображение функции трех переменных. Здесь минитермы и соответствуют 1-кубам ( ), а минитерм отображается 2-кубом ( ).
Рис.3.2 Покрытие функции
Итак, любая дизъюнктивная нормальная форма отображается на -мерном кубе совокупностью -кубов, которые покрывают все вершины, соответствующие конституентам единицы (0-кубы). Справедливо и обратное утверждение: если некоторая совокупность -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим -кубам минитермов является выражение данной функции в дизъюнктивной нормальной форме. Говорят, что такая совокупность -кубов (или соответствующих им минитермов) образует покрытие функции.
Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число -кубов которого было бы поменьше, а их размерность — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием. Например, для функции покрытие на рис. 3.3 соответствует минимальным формам и .
Рис. 3.3 Покрытия функции .
слева – ; справа –
Отображение функции на -мерном кубе наглядно и просто при . Четырехмерный куб можно изобразить, как показано на рис. 3.4, где отображены функция четырех переменных и ее минимальное покрытие, соответствующее выражению . Использование этого метода при требует настолько сложных построений, что теряется все его преимущества.
Рис. 3.4 Отображение функции на четырехмерном кубе
Карты Карно
В другом методе графического отображения булевых функций используются карты Карно, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис. 3.5 показаны карты Карно для двух, трех, четырех переменных.
Рис. 3.5 Карты Карно для двух, трех и четырех переменных
Как и в обычных таблицах истинности, клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки). Например, на рис. 3.6, а показана карта Карно для функции, отображение которой на четырехмерном кубе дано на рис. 3.4. Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
а б
Рис. 3.6 Отображение на карте Карно функции четырех переменных
(а) и ее минимального покрытия (б)
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно s-кубу соответствует совокупность 2 соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Поэтому все положения, изложенные в выше (см. п. многомерный куб), справедливы для карт Карно. Так, на рис. 3.6, б показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме рассматриваемой функции.
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие s-куб, дают минитер (n–s)-го ранга, в который входят те (n–s) переменные, которые сохраняют одинаковые значения на этом s-кубе, причем значении 1 соответствуют сами переменные, а значениям 0 – их отрицания. Переменные, которые не сохраняют свои значения на s-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в дизъюнктивной нормальной форме (крайняя правая является минимальной) (рис. 3.7).
Рис. 3.7 Способы считывания с карты Карно дизъюнктивной нормальной формы булевой функции (слева направо: ; ;
Пример.Получить минимальные формы для функции
Пример.Получить минимальную форму для функции, заданной на карте.
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используется две карты Карно на четыре переменные, а для функции шести переменных – четыре таких карты. При дальнейшем увеличении числа переменных карты Карно становятся практически непригодными.
Известные в литературе карты Вейча отличаются только другим порядком следования наборов значений переменных и обладают теми же свойствами, что и карты Карно.
Комплекс кубов
Несостоятельность графических методов при большом числе переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов, использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.
Комплекс кубов К(у) функции определяется как объединение множеств Кs(у) всех ее s-кубов (s=0.1,…,n), т. е. , причем некоторые из Кs(у) могут быть пустыми. Для записи s-кубов и минитермов функции от n переменных используются слова длины n, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для и 0 для ). Не входящие в минитерм переменные являются свободными и обозначаются через . Например, 2-куб функции пяти переменных, соответствующий минитерму запишем как ( ). 0-кубы, соответствующие конституентам единицы, представляются наборами значений переменных, на которых функция равна единице. Очевидно, в записи s-куба всегда имеется s свободных переменных. Если все n переменных свободны, что соответствует n-кубу, то это означает тождественность единице рассматриваемой функции. Таким образом, для функций, не равных тождественно единице Ø.
Множество всех s-кубов записывается как совокупность слов, соответствующих каждому s-кубу. Для удобства будем располагать слова s-кубов в столбцы, а их совокупность заключать в фигурные скобки. Например, комплекс кубов, соответствующий представлению функции на трехмерном кубе (рис. 3,10а), выражается как , где
; ; .
Для сравнения на рис. 3.8 изображен комплекс кубов в принятых обозначениях.
Рис. 3.8 Комплекс кубов функции трех переменных (а) и его символическое представление (б)
Комплекс кубов образует максимальное покрытие функции. Исключая из него все те s-кубы, которые покрываются кубами высшей размерности, получаем покрытия, соответствующие тупиковым формам. Так, для рассматриваемого примера (рис. 3.8) имеем тупиковое покрытие
,
которое соответствует функции . В данном случае это покрытие является и минимальным.
Для двух булевых функций операция дизъюнкции соответствует объединению их комплексов кубов , а операция конъюнкции — пересечению комплексов кубов . Отрицанию функции соответствует дополнение комплекса кубов, т. е. , причем определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, имеет место взаимно-однозначное соответствие (изоморфизм) между алгеброй булевых функций и булевых множеств, представляющих комплексы кубов.
Представление функции в виде комплексов кубов менее наглядно, однако его важнейшие достоинства состоят в том, что снимаются ограничения по числу переменных и облегчается кодирование информации при использовании вычислительных машин.
Минимизация булевых функций
Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия , где — число — кубов, образующих покрытие данной функции от п переменных. Минимальное покрытие характеризуется наименьшим значением его цены.
Обычно задача минимизации решается в два шага. Сначала ищут сокращенное покрытие, которое включает все -кубы максимальной размерности, но не содержит ни одного куба, покрывающегося каким-либо кубом этого покрытия. Соответствующею дизъюнктивную нормальную форму называют сокращенной, а ее минитермы — простыми импликантами. Для данной функции сокращенное покрытие является единственным, но оно может быть избыточным вследствие того, что некоторые из кубов покрываются совокупностями других кубов.
На втором шаге осуществляется переход от сокращенной к тупиковым дизъюнктивным нормальным формам, из которых выбираются минимальные формы. Тупиковые формы образуются путем исключения из сокращенного покрытия всех избыточных кубов, без которых оставшаяся совокупность кубов еще образует покрытие данной функции, но при дальнейшем исключении любого из кубов она уже не покрывает множества всех вершин, соответствующих единичным значениям функции, т. е. перестает быть покрытием.
Куб сокращенного покрытия, который покрывает вершины данной функции, не покрываемые никакими другими кубами, не может оказаться избыточным и всегда войдет в минимальное покрытие. Такой куб, как и соответствующая ему импликанта, называют экстремалью (существенной импликантой), а покрываемые им вершины — отмененными вершинами. Множество экстремалей образует ядро покрытия, ясно, что при переходе от сокращенного покрытия к минимальному прежде всего следует выделить все экстремали. Если множество экстремалей не образует покрытия, то оно дополняется до покрытия кубами из сокращенного покрытия.
Приведенные определения иллюстрируются на рис. 3.9, где сокращенное покрытие (см. рис. 3.9а,) и минимальные покрытия (рис. 3.9б) и (см. рис. 3.9, б) выражаются следующим образом:
Рис. 3.9 Сокращенное ( ) и минимальные покрытия ( , ) функции (а – сокращенное, б, в — минимальные)
Сокращенная форма представляет собой дизъюнкцию четырех простых импликант, т. е. Экстремалями являются простые импликанты и ,которым соответствуют 1-кубы (
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Булевы функции
1. Булева функция $g\left(x_1,x_2,x_3\right)=\left(x_1{\overline{x}}_2x_3\vee x_2\vee x_3\right)\to \left(x_1\bigoplus x_3\right)$ задана формулой. Построить таблицу истинности.
2. Построить для функции $g\left(x_1,x_2,x_3\right)$ ДНФ, КНФ, СДНФ, СКНФ методом тождественных преобразований.
3. Найти многочлен Жегалкина для функции $g\left(x_1,x_2,x_3\right)$:
а) методом неопределенных коэффициентов;
б) методом тождественных преобразований.
Поступил ответ 2 Марта 2017 от Викиматика
1. Булева функция $g\left(x_1,x_2,x_3\right)=\left(x_1{\overline{x}}_2x_3\vee x_2\vee x_3\right)\to \left(x_1\bigoplus x_3\right)$ задана формулой. Построить таблицу истинности.
2. Построить для функции $g\left(x_1,x_2,x_3\right)$ ДНФ, КНФ, СДНФ, СКНФ методом тождественных преобразований.
3. Найти многочлен Жегалкина для функции $g\left(x_1,x_2,x_3\right)$:
а) методом неопределенных коэффициентов;
б) методом тождественных преобразований.3=8$.
$\begin{array}{|c|c|}
\hline
x_1 & x_2 & x_3 & x_1{\overline{x}}_2x_3 & x_2\vee x_3 & x_1{\overline{x}}_2x_3\vee x_2\vee x_3 & x_1\bigoplus x_3 & g\left(x_1,x_2,x_3\right)=\left(x_1{\overline{x}}_2x_3\vee x_2\vee x_3\right)\to \left(x_1\bigoplus x_3\right) \\
\hline
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\hline
0 & 0 & 1 & 0 & 1 & 1 & 1 & 1 \\
\hline
0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\
\hline
0 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\
\hline
1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\
\hline
1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 \\
\hline
1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 \\
\hline
1 & 1 & 1 & 0 & 1 & 1 & 0 & 0 \\
\hline
\end{array}$
2. Используя тождественные преобразования, приведем данную булеву функцию $g\left(x_1,x_2,x_3\right)$ к ДНФ.
$g\left(x_1,x_2,x_3\right)=\left(\underbrace{x_1{\overline{x}}_2x_3}_{поглощается\ x_3}\vee x_2\vee x_3\right)\to \left(x_1\bigoplus x_3\right)=\left(x_2\vee x_3\right)\to \left(x_1\bigoplus x_3\right)=$ «используем равносильности $x\to y=\overline{x}\vee y$, $x\bigoplus y=\overline{x}y\vee x\overline{y}$» $=\overline{x_2\vee x_3}\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3=$ «используем закон де Моргана $\overline{x\vee y}=\overline{x}\ \overline{y}$» $={\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3$ — ДНФ.
Перейдем от ДНФ к КНФ, для этого ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
$g\left(x_1,x_2,x_3\right)={\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3=\overline{\overline{{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3}}=\overline{\left(x_2\vee x_3\right)\left(x_1\vee {\overline{x}}_3\right)\left({\overline{x}}_1\vee x_3\right)}=$ «используем закон дистрибутивности для 1-го и 2-го множителей $\left(x\vee y\right)\left(y\vee z\right)=y\vee xz$» $=\overline{\left(x_3\vee {\overline{x}}_1x_2\right)\left(x_1\vee {\overline{x}}_3\right)}=\overline{x_1x_3\vee {\overline{x}}_1x_2{\overline{x}}_3}=\left({\overline{x}}_1\vee {\overline{x}}_3\right)\left(x_1\vee {\overline{x}}_2\vee x_3\right)$ — КНФ.
Переход от ДНФ к СДНФ. С этой целью добавляем в каждую элементарную конъюнкцию недостающие переменные вида $x_i\vee {\overline{x}}_i$, затем применяем закон дистрибутивности.
$g\left(x_1,x_2,x_3\right)={\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3={\overline{x}}_2{\overline{x}}_3\left(x_1\vee {\overline{x}}_1\right)\vee {\overline{x}}_1x_3\left(x_2\vee {\overline{x}}_2\right)\vee x_1{\overline{x}}_3\left(x_2\vee {\overline{x}}_2\right)=x_1{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_2x_3\vee {\overline{x}}_1{\overline{x}}_2x_3\vee x_1x_2{\overline{x}}_3\vee x_1{\overline{x}}_2{\overline{x}}_3=x_1{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_2x_3\vee {\overline{x}}_1{\overline{x}}_2x_3\vee x_1x_2{\overline{x}}_3$ — СДНФ.
Переход от КНФ к СКНФ. С этой целью добавляем в каждую элементарную дизъюнкцию недостающие переменные вида $x_i{\overline{x}}_i$, затем применяем закон дистрибутивности.
$g\left(x_1,x_2,x_3\right)=\left({\overline{x}}_1\vee {\overline{x}}_3\right)\left(x_1\vee {\overline{x}}_2\vee x_3\right)=\left({\overline{x}}_1\vee {\overline{x}}_3\vee x_2{\overline{x}}_2\right)\left(x_1\vee {\overline{x}}_2\vee x_3\right)=\left({\overline{x}}_1\vee x_2\vee {\overline{x}}_3\right)\left({\overline{x}}_1\vee {\overline{x}}_2\vee {\overline{x}}_3\right)\left(x_1\vee {\overline{x}}_2\vee x_3\right)$ — СКНФ.
3. Методом неопределенных коэффициентов найдем полином Жегалкина.
Пусть полином Жегалкина имеем вид: $P\left(x_1,\ x_2,x_3\right)=C_0\bigoplus C_3x_3\bigoplus C_2x_2\bigoplus C_{23}x_2x_3\bigoplus C_1x_1\bigoplus C_{13}x_1x_3\bigoplus C_{12}x_1x_2\bigoplus C_{123}x_1x_2x_3$. Будем подставлять наборы значений переменных $x_1,\ x_2,x_3$ и вычислять соответствующие коэффициенты.
$P\left(0,\ 0,\ 0\right)=C_0=1;$
$P\left(0,\ 0,\ 1\right)=C_0\bigoplus C_3=1\Rightarrow 1\bigoplus C_3=1\Rightarrow C_3=0;$
$P\left(0,\ 1,\ 0\right)=C_0\bigoplus C_2=0\Rightarrow 1\bigoplus C_2=0\Rightarrow C_2=1;$
$P\left(0,\ 1,\ 1\right)=C_0\bigoplus C_3\bigoplus C_2\bigoplus C_2C_3=1\Rightarrow 1\bigoplus 0\bigoplus 1\bigoplus C_{23}=1\Rightarrow 0\bigoplus C_{23}=1\Rightarrow C_{23}=1;$
$P\left(1,\ 0,\ 0\right)=C_0\bigoplus C_1=1\Rightarrow 1\bigoplus C_1=1\Rightarrow C_1=0;$
$P\left(1,\ 0,\ 1\right)=C_0\bigoplus C_3\bigoplus C_1\bigoplus C_{13}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus C_{13}=0\Rightarrow 1\bigoplus C_{13}=0\Rightarrow C_{13}=1;$
$P\left(1,\ 1,\ 0\right)=C_0\bigoplus C_2\bigoplus C_1\bigoplus C_{12}=1\Rightarrow 1\bigoplus 1\bigoplus 0\bigoplus C_{12}=1\Rightarrow 0\bigoplus C_{12}=1\Rightarrow C_{12}=1;$
$P\left(1,\ 1,\ 1\right)=C_0\bigoplus C_3\bigoplus C_2\bigoplus C_{23}\bigoplus C_1\bigoplus C_{13}\bigoplus C_{12}\bigoplus C_{123}=0\Rightarrow 1\bigoplus 0\bigoplus 1\bigoplus 1\bigoplus 0\bigoplus 1\bigoplus 1\bigoplus C_{123}=0\Rightarrow 1\bigoplus C_{123}=0\Rightarrow C_{123}=1.$
Получаем полином Жегалкина:
$P\left(x_1,\ x_2,x_3\right)=1\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3.$
Построим полином Жегалкина методом тождественных преобразований. Для этого возьмем ДНФ функции $g\left(x_1,x_2,x_3\right)={\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3$ и избавимся от дизъюнкции, используя закон де Моргана $x\vee y=\overline{xy}$, затем заменим каждое отрицание ${\overline{x}}_i$ по формуле ${\overline{x}}_i=1\bigoplus x_i$ и упростим полученную формулу.
$g\left(x_1,x_2,x_3\right)={\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1x_3\vee x_1{\overline{x}}_3=\overline{\overline{{\overline{x}}_2{\overline{x}}_3}\cdot \overline{{\overline{x}}_1x_3}\cdot \overline{x_1{\overline{x}}_3}}=1\bigoplus \overline{{\overline{x}}_2{\overline{x}}_3}\cdot \overline{{\overline{x}}_1x_3}\cdot \overline{x_1{\overline{x}}_3}=1\bigoplus \left(1\bigoplus \left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\right)\left(1\bigoplus x_3\left(1\bigoplus x_1\right)\right)\left(1\bigoplus x_1\left(1\bigoplus x_3\right)\right)=1\bigoplus \left(1\bigoplus 1\bigoplus x_3\bigoplus x_2\bigoplus x_2x_3\right)\left(1\bigoplus x_3\bigoplus x_1x_3\right)\left(1\bigoplus x_1\bigoplus x_1x_3\right)=1\bigoplus \left(x_3\bigoplus x_2\bigoplus x_2x_3\right)\left(1\bigoplus x_3\bigoplus x_1x_3\right)\left(1\bigoplus x_1\bigoplus x_1x_3\right)=1\bigoplus \left(x_3\bigoplus x_2\bigoplus x_2x_3\right)\left(1\bigoplus x_1\bigoplus x_1x_3\bigoplus x_3\bigoplus x_1x_3\bigoplus x_1x_3\bigoplus x_1x_3\bigoplus x_1x_3\bigoplus x_1x_3\right)=1\bigoplus \left(x_3\bigoplus x_2\bigoplus x_2x_3\right)\left(1\bigoplus x_1\bigoplus x_3\right)=1\bigoplus x_3\bigoplus x_1x_3\bigoplus x_3\bigoplus x_2\bigoplus x_1x_2\bigoplus x_2x_3\bigoplus x_2x_3\bigoplus x_1x_2x_3\bigoplus x_2x_3=1\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3.$
Прикрепленные файлы:
Программный модуль преобразования дизъюнктивных нормальных форм булевых функций в полином Жегалкина Текст научной статьи по специальности «Компьютерные и информационные науки»
УДК 004.021
ПРОГРАММНЫЙ МОДУЛЬ ПРЕОБРАЗОВАНИЯ ДИЗЪЮНКТИВНЫХ НОРМАЛЬНЫХ ФОРМ БУЛЕВЫХ ФУНКЦИЙ В ПОЛИНОМ ЖЕГАЛКИНА А.А. Акинин, С.Л. Подвальный
В данной статье предложена программная реализация преобразования дизъюнктивных нормальных форм булевых функций в полином Жегалкина с промежуточным восстановлением дизъюнктивных форм к совершенной дизъюнктивной нормальной форме
Ключевые слова: полином Жегалкина, булева функция, дизъюнктивная нормальная форма
В [1] были разработаны и исследованы модели легкодиагностируемых логических преобразователей (ЛП) на программируемых логических матрицах (ПЛМ) с перестраиваемым элементным базисом. Основу таких ПЛМ составляет базис логических функций И (AND) и ИСКЛЮЧАЮЩЕЕ ИЛИ (EXOR) [2]. Данные элементы совместно с элементом генератор логической 1 составляют элементный базис Жегалкина. Для реализации таких ЛП требуется преобразование дизъюнктивной нормальной формы (ДНФ) булевой функции (БФ) в так называемый полином Жегалкина. Вследствие того, что полином Жегалкина может быть получен только на основе совершенной дизъюнктивной нормальной формы (СДНФ) функции, то
необходимо располагать не только автоматическими средствами преобразования СДНФ в полином Жегалкина, но и средствами автоматического преобразования произвольных ДНФ БФ в СДНФ.
В [3] предложен метод преобразования ДНФ булевых функций в полином Жегалкина. Суть этого метода заключается в следующем. Метод
реализуется в два этапа: на первом этапе
производится восстановление ДНФ БФ до СДНФ, которая реализуется в табличной форме в виде таблицы истинности (ТИ). ТИ БФ, представляется в виде 2П упорядоченного компонентного вектора, элементами которого являются значения БФ на возрастающих наборах значений аргументов функции. На втором этапе метода осуществляется вычисление коэффициентов полинома Жегалкина БФ, представленного в общем виде. По мере расчета коэффициентов полинома, формируется вектор размерности 2П, содержащий значения
присутствующих и отсутствующих членов полиномиальной нормальной формы (ПНФ) БФ. Формирование ПНФ функции осуществляется путём последовательного преобразования каждого минтерма СДНФ БФ в частные ПНФ (ЧПНФ) и на основе их последующей суперпозиции -формировании окончательной ПНФ БФ — полинома Жегалкина. Разработанные метод и алгоритм формирования ПНФ с использованием ЧПНФ
Акинин Андрей Александрович — ООО “Мобильные ответы”, соискатель, e-mail: [email protected] Подвальный Семен Леонидович — ВГТУ, д-р техн. наук, профессор, e-mail: [email protected]
весьма эффективны для программной реализации, так как исходные данные для преобразования, промежуточные результаты и конечный результат имеют простое машинное представление в виде двоичных векторов фиксированной длины, равной 2п бит, где п-количество аргументов БФ.
В [4] было показано, что основной целью при программной реализации алгоритма восстановления СДНФ должно являться достижение оптимального соотношения между быстродействием процесса восстановления СДНФ по заданной сокращенной ДНФ и требуемым для решения этой задачи аппаратным ресурсам, в связи с чем был предложен алгоритм восстановления таблицы истинности БФ по произвольной ДНФ, который представлен на рис.
1.
НАЧАЛО
1:-1, К:-количеств о конъюнкций в ДНФ; обнуление таблицы истинности ^ Е
4 ~~
S:- 1|1]; W:-i[I]Tt[I]; М- W
І___________________
G := ( S&M ) v а[1]
__________________L._________________
Е[0] := 1
I
ОСТАНОВ
Рис. 1. Схема алгоритма восстановления таблицы истинности БФ по произвольным ДНФ
Как видно из рис. 1, главным преимуществом предложенного алгоритма является то, что каждый минтерм СДНФ определяется не перебором всех возможных наборов значений аргументов БФ, а вычисляется на основе рекуррентного соотношения — в : = ( 8&М ) у а[1], в связи с чем,
данный алгоритм обладает приемлемой вычислительной сложностью по сравнению с известными идентичными алгоритмами при минимальных требованиях к ресурсу памяти ЭВМ.
Рассмотрим существо предложенного метода формирования ПНФ БФ путём последовательного преобразования каждого минтерма СДНФ функции в ЧПНФ на примере.
Пусть логическая функция Др, q, г) задана таблицей истинности, представленной в табл. 1, индексом 1 обозначен номер набора значений логических переменных.
Таблица 1
1 Р q г f
0 0 0 0 1
1 0 0 1 1
2 0 1 0 1
3 0 1 1 0
4 1 0 0 0
5 1 0 1 0
6 1 1 0 1
7 1 1 1 0
той же функции. В остальных строках метками «1» отмечены те члены ПНФ, которые входят в частные ПНФ в соответствии с вычисленными выше ЧПНФ. где 7- = 07, если
известно, что (1 Ф р)(1 Ф д) = 1 Ф р Ф д Ф рд и р = 1 ® р ,
для V р, д, г е {0,1}.
/0 (0,0,0) = = (1Ф р)(1 Ф д)(1 Ф г) =
= 1 Ф р Ф д Ф г Ф рд Ф дг Ф рг Ф рдг = В0 /(0,0,1) = Удг = (1Ф р)(1Ф д)г =
= г Ф дг Ф рг Ф рдг = В1
/2 С0,1,0) = рдг =(1 Ф р)д(!Ф г) =
= д Ф рд Ф дг Ф рдг = В2
/з(0,1,1) = рдг = (1Ф р)дг = дг Ф рдг = В3
/4(1,0,0) = рдг = р(1 Ф д)(1Ф г) =
= р Ф рд Ф рг Ф рдг = В4
/5 (1,0,1) = рдг = р(1 Ф д)г = рг Ф рдг = В5
Леи0)=рдг=рд(1 ®г)=рд ® рдг=В6 /7 (1,1,1) = рдг = В7
Сведем полученные данные в табл. 2.
Таблица 2
ш ЧПНФ
1 г ч ЦТ Р Р г РЧ Р Ч г
рдг 1 1 1 1 1 1 1 1 В0
рдг 1 1 1 1 В!
рдг 1 1 1 1 в2
рдг 1 1 В3
рдг 1 1 1 1 в4
рдг 1 1 в5
рдг 1 1 Вб
рдг 1 в7
В табл. 2 в первом столбце перечислены все возможные минтермы функции f(p, q, г) — К1, а в первой строке указаны все возможные члены ПНФ
Кг ЧПНФ
1 000 г 001 010 ^ г 011 р 100 Р г 101 ка 110 Р 111 В,
рдг 0 0 0 1 1 1 1 1 1 1 1 Во
рдг 001 1 1 1 1 В!
рдг 0 1 0 1 1 1 1 в2
рдг 0 11 1 1 В3
рдг 1 0 0 1 1 1 1 В4
рдг 1 0 1 1 1 В5
рдг 110 1 1 Вб
рдг 1 1 1 1 В7
Е® 1 0 0 1 1 0 1 0 в
Следовательно, способ формирования ПНФ с использованием частных полиномиальных нормальных форм весьма эффективен для программной реализации, так как исходные данные для преобразования, промежуточные результаты и конечный результат имеют простое машинное представление в виде двоичных векторов различной длины.
Анализ данных табл. 3 наглядно
демонстрирует следующую закономерность: разряды двоичных векторов BJ принимают единичные значения только в том случае, если единичные значения переменных в номерах строк полностью входят в двоичные номера столбцов таблицы. Исключение составляет только вектор В0, все элементы которого равны 1.
Вскрытая закономерность позволяет автоматически формировать ПНФ функции без предварительного составления и хранения табл. 3. Более того, отпадает необходимость хранения всей
таблицы истинности логической функции, для формирования ПНФ достаточно иметь только таблицу минтермов данной функции.
Алгоритм формирования ПНФ с использованием ЧПНФ представлен на рис. 2.
напало
Задание сигаольнт имен аргументов
Е Ф и закрепление этих имен за разрядами да схемного п-разрядааго
_______________тает S________________
__________________*__________________
ВВОДЯТСЯ ИСХОДНЫ* данные п — число аргументов Е Ф, Е — вектор, содержащий шаненкя ТИБФ,где N=2n-1
I
Создание и обнуление двоичного me сив 4 В= {bü Jb|,. Ны
D. =К,
D, = D,+ l
________________Í________________
D| = D,vK, t
b[Df]-b[Df] _________________I
_________________1
Увеличение счетчика, i на. 1
——————I ~
\________________
По полученному мае шву В и переменной S формируется ПНФ ПОГРН е СЕСОИ функции Е СИМЕ ОЛЕГОМ
«Г
OCIABD0
Рис. 2. Алгоритм формирования ПНФ с использованием ЧПНФ
Исходными данными для предложенного алгоритма являются: п — число аргументов БФ, вектор Е размерности 2п, содержащий значения СДНФ БФ.
Основное достоинство алгоритма заключается в том, что ПНФ функции формируется путём преобразования каждого минтерма СДНФ в частные ПНФ (ЧПНФ) в виде их векторного представления так, как показано на рис. 3.
Для хранения значений очередного минтерма функции в программе используется вектор Б, размерности п. Коэффициенты присутствующих и отсутствующих членов полиномиальной
нормальной формы БФ заносятся в вектор В размерности 2п. Для корректной работы
программного модуля необходимо обнулить двоичные массивы В и Б.
На первом шаге рассматриваемого фрагмента алгоритма, необходимо получить векторное представление очередного минтерма СДНФ — К
Рис.,bN}, значение которого необходимо проинвертировать. Для этого
используем операции арифметического сложения Dj = Dj+1 и побитового сложения Dj = Dj v Kj. Повторяем вычисление и инвертирование
определенного номера бита вектора до тех пор, пока Dj < (2п-1). С помощью операции
инвертирования мы как бы добавляем следующий член ЧПНФ в итоговую ПНФ БФ, учитывая что x¡ ® x¡ = Ь а x¡ ® x¡ = 0 для V x¡ е {0,1} •
Далее переходим к следующему минтерму СДНФ БФ.
Таким образом, в векторе B по окончании цикла по j < m, где m — количество минтермов БФ, осуществляется поэлементное суммирование по модулю 2, с накоплением результата, сформированных по минтермам исходной СДНФ двоичных векторов частных ПНФ, в силу чего данный алгоритм является весьма экономичным по требуемой памяти и количеству операций, производимыми над символьными переменными.
Следует отметить также, что для эффективной программной реализации предложенных алгоритмов необходимо осуществить выбор наиболее рациональной формы хранения исходных и конечных данных программного модуля, которая позволяла бы не только хранить большой объем данных, но и производить над ними операции за минимально необходимый промежуток времени. В связи с чем, в качестве хранилища векторов B и E, размерности 2п, был выбран битовый массив dynamic_bitset из библиотеки BOOST C++. Эта библиотека представляет собой собрание множества кроссплатформенных библиотек, созданных
независимыми разработчиками и тщательно проверенными на различных платформах (№’№’№.Ь0081.0г§). Отличительными особенностями массива dyпamic_b1tset являются: возможность
динамического изменения размера массива в ходе выполнения программы, поддержка быстрого доступа по индексу к произвольному элементу массива, поддержка элементарных логических операций (регистрового сдвига, сложения, умножения, инверсии и т. д.). Размер массива dyпamic_bitset ограничен величиной 232-1, вследствие чего максимальное число аргументов исходной ДНФ БФ должно быть ограничено числом 31.
На основе предложенных алгоритмов, реализующих метод преобразования ДНФ булевых функций в полином Жегалкина, был разработан программный модуль “Преобразователь булевых функций”. На рис. 4 представлено главное окно программного модуля “Преобразователь булевых функций”.
Рис. 4. Главное окно программного модуля “Преобразователь булевых функций”
Программа написана на языке С++, для ее функционирования необходимо не менее 5 Гб на жестком диске и не менее 512 Мб оперативной памяти.
Большой объем требуемой памяти на жестком диске обусловлен тем, что выходной файл, формируемый программой и содержащий ПНФ анализируемой БФ, зависит от количества аргументов функции. Так, например, размер
выходного файла, содержащего ПНФ функции, зависящей от 20 переменных, СДНФ которой состоит всего из двух минтермов, занимает 1,5 Мб жесткого диска. Размер самого программного модуля составляет всего 330 Кб.
Разработанный программный модуль осуществляет ввод БФ, анализирует форму введенной функции и, при необходимости, автоматически восстанавливает ДНФ функции до СДНФ.
В представленном программном модуле, ПНФ БФ может быть сформирована как по нулевым значениям функции, так и по единичным. Предусмотрена возможность и автоматического получения ПНФ функции. При выборе этого способа расчета ПНФ, в программе реализуется подсчет нулей и единиц в СДНФ БФ. Далее, в зависимости от количества минтермов и макстермов функции, автоматически происходит выбор наиболее экономичного по ресурсам памяти способа формирования ПНФ — по единичным или по нулевым значениям соответственно.
Сформированные выходные данные программы могут быть получены как в символьном виде, так и в векторном. Это обстоятельство обусловлено тем, что при достаточно большом количестве аргументов функции анализировать БФ в символьном виде весьма сложно.
Литература
1. Акинина Ю.С. Альтернативный подход к обеспечению легкодиагностируемости двухуровневых программируемых пользователем логических матриц / Ю.С. Акинина, С.В. Тюрин // Вестник Воронеж. гос. техн. ун-та. Сер. Вычислительные и информационнотелекоммуникационные системы. — Воронеж: ВГТУ, 2003. Вып. 8.3. С. 32-35.
2. Закревский А.Д. Полиномиальная реализация частичных булевых функций и систем / А. Д. Закревский, Н. Р. Торопов. М.: Эдиториал УРСС, 2003. 217 с.
3. Акинина Ю.С. Разработка метода преобразования дизъюнктивных нормальных форм в полиномиальную нормальную форму / Ю.С. Акинина // Современные проблемы информатизации в системах моделирования, программирования и телекоммуникациях: сборник трудов IX международной открытой научной конференции. 2004. Вып. 9. С. 271.
4. Акинин А.А. О программной реализации алгоритма восстановления совершенной дизъюнктивной нормальной формы / А.А. Акинин, Ю.С. Акинина // Информационные технологии моделирования и управления. 2010, №6(65)
Воронежский государственный технический университет ООО “Мобильные ответы” (г. Воронеж)
THE MODULE PROGRAMM OF TRANSFORMATION OF SUM OF PRODUCTS OF BOOLEAN’S FUNCTION’S INTO ZHEGALKIN’S POLYNOMIAL A.A. Akinin, S.L. Podvalniy
This article considers the realization program of transformation of sum of products of Boolean’s functions into Zhegalkin’s polynomial with stage-by stage regeneration of sum of products till they reach complete sum of products
Key words: Zhegalkin’s polynomial, boolean function, sum of products
Совершенная дизъюнктивная нормальная форма
Совершенная дизъюнктивная нормальная форма — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных переменных
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.
Любая булева формула, не являющаяся тождественно ложной, может быть приведена к СДНФ, причём единственным образом, то есть для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.
1. Пример нахождения СДНФ
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:
В ячейках результата f {\displaystyle fx_{1},x_{2},x_{3}} отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных, при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Первая строка содержит 1 в указанном поле. Отмечаются значения всех трёх переменных, это:
x 2 = 0 {\displaystyle x_{2}=0}
x 1 = 0 {\displaystyle x_{1}=0}
x 3 = 0 {\displaystyle x_{3}=0}
Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: x 1 ¯ ⋅ x 2 ¯ ⋅ x 3 ¯ {\displaystyle {\overline {x_{1}}}\cdot {\overline {x_{2}}}\cdot {\overline {x_{3}}}}
Переменные второго члена:
x 1 = 0 {\displaystyle x_{1}=0}
x 3 = 1 {\displaystyle x_{3}=1}
x 2 = 0 {\displaystyle x_{2}=0}
x 3 {\displaystyle x_{3}} в этом случае будет представлен без инверсии: x 1 ¯ ⋅ x 2 ¯ ⋅ x 3 {\displaystyle {\overline {x_{1}}}\cdot {\overline {x_{2}}}\cdot x_{3}}
Таким образом анализируются все ячейки f {\displaystyle fx_{1},x_{2},x_{3}}. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов элементарных конъюнкций.
Совершенная ДНФ этой функции:
f = x 1 ¯ ∧ x 2 ¯ ∧ x 3 ¯ ∨ x 1 ¯ ∧ x 2 ¯ ∧ x 3 ∨ x 1 ¯ ∧ x 2 ∧ x 3 ¯ ∨ x 1 ∧ x 2 ∧ x 3 ¯ {\displaystyle fx_{1},x_{2},x_{3}={\overline {x_{1}}}\land {\overline {x_{2}}}\land {\overline {x_{3}}}\vee {\overline {x_{1}}}\land {\overline {x_{2}}}\land x_{3}\vee {\overline {x_{1}}}\land x_{2}\land {\overline {x_{3}}}\vee x_{1}\land x_{2}\land {\overline {x_{3}}}}
- Конъюнктивная нормальная форма Совершенная дизъюнктивная нормальная форма Совершенная конъюнктивная нормальная форма Конъюнктивный одночлен Дизъюнктивный одночлен
- линейное время. Дизъюнктивная нормальная форма Совершенная дизъюнктивная нормальная форма Совершенная конъюнктивная нормальная форма Конъюнктивный одночлен
- одночленов скобки не пишутся. Дизъюнктивная нормальная форма Конъюнктивная нормальная форма Дизъюнктивный одночлен Совершенный одночлен Булева алгебра Алгебра
- прикладное значение выбранной системы функций. Основная статья: Дизъюнктивная нормальная форма Простой конъюнкцией или конъюнктом называется конъюнкция некоторого
- предложено использовать для преобразования вектора значений совершенной дизъюнктивной нормальной формы в вектор коэффициентов полинома Жегалкина для произвольной
- субстанциальности души, гипотетические антиномии — идею Вселенной как целого, дизъюнктивные идеал — идею Бога. Поскольку категорический императив — высшее предписание
- темпоральность, мы нуждаемся в новом настоящем и желаем повторение и будущее. Дизъюнктивный синтез памяти тематика Бергсона присваивает настоящее и привычку
- категорию, несмотря на то, что не имеют общего признака Взаимоисключающие дизъюнктивные категории имеют слишком примитивную логику для научного применения
Совершенная дизъюнктивная нормальная форма: днф онлайн, таблица истинности для 4 переменных, опишите совершенную дизъюнктивную нормальную форму, сднф и скнф, полином жегалкина, совершенная дизъюнктивная нормальная форма формулы, алгоритм построения сднф, алгоритм нахождения сднф
Совершенная дизъюнктивная нормальная форма формулы.
Математическая логика oнлайн с подробным объяснением. Активные и интерактивные формы: лекции, практические занятия, контрольные работы, Совершенная дизъюнктивная нормальная форма. Полином. Сднф и скнф. Построение таблицы истинности онлайн СКНФ СДНФ. ТЕМА: СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ. ПЛАН: 1. Совершенная дизъюнктивная нормальная форма. 2. Совершенная конъюнктивная.
Днф онлайн.
7. Разложение булевой функции по переменным и совершенные. Основная статья: Дизъюнктивная нормальная форма Совершенной дизъюнктивной нормальной формой или СДНФ относительно некоторого. Алгоритм построения сднф. Совершенная дизъюнктивная нормальная форма. Это совершенная дизъюнктивная нормальная форма СДНФ нашей функции. Пример 24. Построим СДНФ для функции, таблица истинности которой. Таблица истинности для 4 переменных. СОВЕРШЕННАЯ НОРМАЛЬНАЯ ФОРМА это Что такое. Совершенная дизъюнктивная нормальная форма. Cтраница 4. При работе ППЗУ в качестве комбинационного цифрового устройства сигналы. Построение СКНФ и СДНФ по таблице истинности Автор24. Совершенной дизъюнктивной нормальной формой формулы А. СДНФ А называется дизъюнктивная нормальная форма формулы А.
Как найти скнф и сднф.
Пример 4 совершенная дизъюнктивная нормальная форма. Построим совершенную дизъюнктивную нормальную форму функции, заданной. Приложение 1 РИНХ. Совершенной дизъюнктивной нормальной формой СДНФ называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят. Совершенная дизъюнктивная нормальная форма. Совершенная. Представлений булевых функций: совершенная дизъюнктивная нормальная форма сднф, совершенная конъюнктивная нормальная форма скнф. Декану физического факультета ТГУ Томский политехнический. Совершенная конъюнктивная нормальная форма СКНФ это такая КНФ, которая удовлетворяет трём условиям: в ней нет одинаковых.
Конъюнктивной нормальной формой логической функции.
Совершенная дизъюнктивная нормальная форма представления булевых функций. Построение СДНФ по таблице истинности. Сокращенная. СДНФ. Теорема о представлении в виде СДНФ. Построение. Как с помощью python сделать СДНФ Совершенная дизъюнктивная нормальная форма? Что должно получиться на фото ниже. Урок 12. преобразование логических выражений Информатика. Формами являются: совершенная дизъюнктивная нормальная форма СДНФ и такая форма называется совершенной дизъюнктивной нормальной.
Совершенная дизъюнктивная нормальная форма ФАЛ здесь.
Что такое совершенная дизъюнктивная нормальная форма СДНФ?. 14. Что такое совершенная коньюктивная нормальная форма СКНФ?. 15. Какая. Результаты поиска по сднф Руконт. Дизъюнктивная нормальная форма называется совершенной дизъюнктивной нормальной формой СДНФ, если элементарные конъюнкции,. Способы представления переключательных функций. Учебный. Оно известно как представление функции в виде совершенной дизъюнктивной нормальной формы СДНФ. Тупиковые нормальные формы Любая. Программа в стадии разработки МАИ. Кафедра Высшая. Ни один множитель не содержит одну и ту же переменную дважды. КНФ, для которой выполняются свойства совершенства называется совершенной.
Ен.02 дискретная математика с элементами математической.
Совершенная дизъюнктивная нормальная форма одна из форм представления функции алгебры логики в виде логического выражения. Представляет собой частный случай ДНФ, удовлетворяющий следующим трём условиям: в ней нет одинаковых слагаемых в каждом слагаемом нет повторяющихся переменных. Программа вступительного испытания. А ДНФ – дизъюнктивная нормальная форма – это логическая сумма Совершенная конъюнктивная нормальная форма формулы СКНФ это. Учебник по дискретной математике днф, сднф, кнф, скнф. Конъюнктивная нормальная форма. КНФ и схема ее построения. Совершенные дизъюнктивная и конъюнктивная нормальные формы СДНФ и СКНФ. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ФОРМУЛ БУЛЕВОЙ АЛГЕБРЫ. Совершенная дизъюнктивная нормальная форма СДНФ Формула называтся дизъюнктивной нормальной формой ДНФ, если она.
СКНФ и СДНФ Цифровая техника в радиосвязи.
Совершенная дизъюнктивная нормальная форма СДНФ Определение. Формула называтся дизъюнктивной нормальной формой ДНФ, если она. Синтез логических схем Лаборатория Электронных Средств. Совершенная дизъюнктивная нормальная форма, совершенная совершенную дизъюнктивную нормальную форму для функции,.
Способы представления ФАЛ. Переход от одной формы.
Совершенная дизъюнктивная нормальная форма СДНФ представления переключательной функции – запись функции в виде дизъюнкции конъюнкций. Совершенная конъюнктивная нормальная форма с. КНФ это конъюнкция дизъюнктов. Совершенная конъюнктивная нормальная форма. 2.2 Совершенная нормальная форма. Теорема существования и единственности Совершенной дизъюнктивной нормальной формой по переменным.
Untitled.
Понятие дизъюнктивной и конъюнктивной нормальной формы ДНФ и. КНФ. Совершенная конъюнктивная нормальная форма и совершенная. Элементы математической логики ВятГУ. Совершенная дизъюнктивная нормальная форма, СДНФ англ. perfect disjunctive normal form, PDNF ДНФ, удовлетворяющая условиям: в ней нет. Булевы функции. Равносильных друг другу дизъюнктивных форм. Например: преобразованиями к совершенной конъюнктивной нормальной форме. СКНФ. Для этого.
ДНФ Викиконспекты.
8 Совершенной дизъюнктивной нормальной формой СДНФ называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию. Специальные представления недоопределенных частичных. Совершенная дизъюнктивная нормальная форма ФАЛ. Рассмотрим понятие конституенты единицы. Допустим, что функция двух переменных f x2, x1. Совершенная конъюнктивная нормальная форма Студопедия. Совершенная конъюнктивная нормальная форма. Пусть задана булева функция f x1, …, xn. Представим ее инверсию f x1. 99 % загружено Шаблон алгебраических формул tip mc. Совершенная дизъюнктивная нормальная форма, совершенная конъюнктивная нормальная форма и совершенная полиномиальная нормальная.
1 Совершенная дизъюнктивная нормальная форма и.
Например, выражение является ДНФ. Совершенной дизъюнктивной нормальной формой СДНФ называется такая дизъюнктивная нормальная форма. Министерство образования и науки Российской Федерации. Дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма СДНФ, совершенная конъюнктивная. Глава 1. Материала, вы узнаете о конъюнктивной и дизъюнктивной. нормальных формах. Также вы должны усвоить понятие. совершенной нормальной формы.
Микроконтроллеры PIC16F87X Реализуемые.
Совершенная дизъюнктивная нормальная форма СДНФ. Для реализации таблицы истинности при помощи логических элементов И СДНФ. Таблица истинности Онлайн калькулятор. Совершенная дизъюнктивная нормальная форма СДНФ ДНФ относительно Построение совершенной дизъюнктивной нормальной формы.
совершенная дизъюнктивная нормальная форма формулы, опишите совершенную дизъюнктивную нормальную форму, Совершенная дизъюнктивная нормальная форма, таблица истинности для 4 переменных
Дата публикации:
05-16-2020
Дата последнего обновления:
05-16-2020 Логика— Расчет CNF и DNF без таблиц истинности
Обновление: (использовать логическую эквивалентность)
$$ p⊕q \ Equiv (p \ land \ neg q) \ lor (\ neg p \ land q) \ Equ (p \ lor q) \ land (\ neg p \ lor \ neg q) \ tag * { он же Xor} $$
$$ p ↓ q \ Equiv \ neg p \ land \ neg q \ tag * {aka Nor} $$
$$ p ↑ q \ Equiv \ neg p \ lor \ neg q \ tag * {aka Nand} $$
\ begin {align} \ varphi_6 & \ Equiv ((a ↑ b) ⊕ (a ↓ c)) \\ & \ Equiv (\ neg a \ lor \ neg b) ⊕ (\ neg a \ land \ neg c) \\ & \ Equiv ((\ neg a \ lor \ neg b) \ lor (\ neg a \ land \ neg c)) \ land (\ neg (\ neg a \ lor \ neg b) \ lor \ neg (\ neg a \ земля \ нег в)) \\ & \ Equiv (((\ neg b \ lor \ neg a) \ lor \ neg a) \ land ((\ neg a \ lor \ neg b) \ lor \ neg c) \ land (\ neg (\ neg a \ lor \ neg b) \ lor \ neg (\ neg a \ land \ neg c)) \\ & \ Equiv ((\ neg b \ lor (\ neg a \ lor \ neg a)) \ land ((\ neg a \ lor \ neg b) \ lor \ neg c) \ land (\ neg (\ neg a \ lor \ neg b) \ lor \ neg (\ neg a \ land \ neg c)) \\ & \ Equiv ((\ neg b \ lor \ neg a) \ land ((\ neg a \ lor \ neg b) \ lor \ neg c)) \ land (\ neg (\ neg a \ lor \ neg b) \ лор \ нег (\ нег а \ земля \ нег с)) \\ & \ Equiv ((\ neg a \ lor \ neg b) \ land ((\ neg a \ lor \ neg b) \ lor \ neg c)) \ land (\ neg (\ neg a \ lor \ neg b) \ лор \ нег (\ нег а \ земля \ нег с)) \\ & \ Equiv (\ neg a \ lor \ neg b) \ land (\ neg (\ neg a \ lor \ neg b) \ lor \ neg (\ neg a \ land \ neg c)) \\ & \ Equiv (\ neg a \ lor \ neg b) \ land ((a \ land b) \ lor (a \ lor c)) \\ & \ Equiv ((\ neg a \ lor \ neg b) \ land (a \ land b)) \ lor ((\ neg a \ lor \ neg b) \ land (a \ lor c)) \\ & \ Equiv (\ neg (a \ land b) \ land (a \ land b)) \ lor ((\ neg a \ lor \ neg b) \ land (a \ lor c)) \\ & \ Equiv \ bot \ lor ((\ neg a \ lor \ neg b) \ land (a \ lor c)) \\ & \ Equiv (\ neg a \ lor \ neg b) \ land (a \ lor c) \ tag * {CNF} \\ & \ Equiv (\ neg a \ land (a \ lor c)) \ lor (\ neg b \ land (a \ lor c)) \\ & \ Equiv ((\ neg a \ land a) \ lor (\ neg a \ land c))) \ lor ((\ neg b \ land a) \ lor (\ neg b \ land c))) \\ & \ Equiv (\ bot \ lor (\ neg a \ land c))) \ lor ((\ neg b \ land a) \ lor (\ neg b \ land c))) \\ & \ Equiv (\ neg a \ land c) \ lor ((\ neg b \ land a) \ lor (\ neg b \ land c))) \\ \ end {align}
И поскольку $ (\ neg a \ land c) \ lor (\ neg b \ land a) $ влечет $ (\ neg b \ land c) $, мы можем доказать, что его форма DNF — $ (\ neg a \ land c) \ lor (\ neg b \ land a) $.
Подсказки на 1-3 $: \ begin {align} \ varphi_1 & \ Equiv (\ neg a \ land b) \ to c \\ & \ Equiv a \ lor \ neg b \ lor c \ tag * {CNF & DNF} \\ \ varphi_2 & \ Equiv \ neg ((\ neg c \ lor¬a) ∧ (b \ lor¬c)) \ lor (a∨b∨c) \\ & \ Equiv (c \ land a) \ lor (\ neg b \ land c) \ lor (a \ lor b \ lor c) \\ & \ Equiv a \ lor b \ lor c \ tag * {CNF & DNF} \\ \ varphi_3 & \ Equiv (a∨¬b) ↔ (a∧c) \\ & \ Equiv (a∨¬b) \ to (a∧c) \ land (a \ land c) \ to (a \ lor \ neg b) \\ & \ Equiv ((\ neg a \ land b) \ lor (a \ land c)) \ land ((\ neg a \ lor \ neg c) \ lor (a \ lor \ neg b)) \\ & \ Equiv ((\ neg a \ land b) \ lor (a \ land c)) \ land \ top \\ & \ Equiv (\ neg a \ land b) \ lor (a \ land c) \ tag * {DNF} \\ & \ Equiv ((\ neg a \ land b) \ lor a) \ land ((\ neg a \ land b) \ lor c) \\ & \ Equiv (\ neg a \ lor a) \ land (a \ lor b) \ land (\ neg a \ lor c) \ land (b \ lor c) \\ & \ Equiv \ top \ land (a \ lor b) \ land (\ neg a \ lor c) \ land (b \ lor c) \\ & \ Equiv (a \ lor b) \ land (\ neg a \ lor c) \ land (b \ lor c) \\ \ end {align}
И поскольку $ (a \ lor b) \ land (\ neg a \ lor c) \ Equiv (\ neg a \ to b) \ land (a \ to c) $, что будет означать $ (b \ lor c) $ , что сделает его истинным в утверждении, поэтому мы можем доказать, что его CNF — это $ (a \ lor b) \ land (\ neg a \ lor c) $.
(я предлагаю для относительно подробных ответов задавать один вопрос за раз.)
дискретной математики — Найдите минимальные DNF и CNF логического выражения $ (A \ implies C) \ wedge \ neg (B \ wedge C \ wedge D). $
Я хочу найти минимальные CNF и DNF для следующего выражения: $$ (A \ подразумевает C) \ wedge \ neg (B \ wedge C \ wedge D). $$ Я создал таблицу истинности:
\ begin {array} {| c | c | c | c | c | c | c |} \ hline A & B & C & D & \ underbrace {A \ подразумевает B} _ {E} & \ underbrace {\ neg (B \ wedge C \ wedge D)} _ {F} & \ underbrace {E \ wedge F} _ {G} \\ \ hline 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ \ hline 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ \ hline 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ \ hline 1 & 1 & 0 & 0 & 0 & 1 & 0 \\ \ hline 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ \ hline 1 & 0 & 1 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ \ hline 1 & 1 & 1 & 0 & 1 & 1 & 1 \\ \ hline 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ \ hline 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \ hline 0 & 1 & 0 & 1 & 1 & 1 & 1 \\ \ hline 1 & 1 & 0 & 1 & 0 & 1 & 0 \\ \ hline 0 & 0 & 1 & 1 & 1 & 1 & 1 \\ \ hline 1 & 0 & 1 & 1 & 1 & 1 & 1 \\ \ hline 0 & 1 & 1 & 1 & 1 & 0 & 0 \\ \ hline 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ \ hline \ end {array}
DNF: $ G = (\ нег А \ клин \ нег В \ клин \ нег С \ клин \ нег D) \ vee (\ neg A \ клин B \ клин \ neg C \ клин \ neg D) \ vee (\ neg A \ клин \ neg B \ клин C \ клин \ neg D) \ vee (\ neg A \ клин B \ клин \ neg C \ клин D) \ vee (\ neg A \ клин B \ клин C \ клин \ neg D) \ vee (A \ клин B \ клин C \ клин \ neg D) \ vee (A \ клин \ neg B \ клин \ neg C \ клин D) \ vee (\ neg A \ клин B \ клин \ neg C \ клин D) \ vee (\ neg A \ клин \ neg B \ клин C \ клин \ neg D) \ vee (A \ клин B \ клин C \ клин D) $
Чтобы сократить это, я упрощу выражение, удалив повторяющиеся выражения:
$
G = (\ нег А \ клин \ нег В \ клин \ нег С \ клин \ нег D)
\ vee (\ neg A \ клин B \ клин \ neg C \ клин \ neg D)
\ vee (\ neg A \ клин \ neg B \ клин C \ клин \ neg D)
\ vee (\ neg A \ клин B \ клин \ neg C \ клин D)
\ vee (\ neg A \ клин B \ клин C \ клин \ neg D)
\ vee (A \ клин B \ клин C \ клин \ neg D)
\ vee (A \ клин \ neg B \ клин \ neg C \ клин D)
\ vee (A \ клин B \ клин C \ клин D)
$
$ \ vdots $
минимальный DNF: $ \ dots $
Та же процедура для CNF
CNF:
$ G_2 = (\ neg A \ vee B \ vee C \ vee D) \ клин (\ neg A \ vee \ neg B \ vee C \ vee D) \ клин \ точки \ клин (\ neg A \ vee \ neg B \ vee \ neg C \ vee \ neg D) $
$ \ vdots $
Как мне легче найти минимальные CNF и CNF? Я мог бы упростить эти выражения, как показано выше, но это действительно отнимает много времени.Есть ли способ сделать это более эффективным? Если да, то не могли бы вы подробно объяснить, как вы решили задачу?
дискретная математика — пример дизъюнктивной нормальной формы (ОБЕ dnf и cnf) справка
Для DNF :
формула является дизъюнктивной нормальной формой тогда и только тогда, когда она является дизъюнкцией одного или нескольких соединений одного или нескольких литералов.
Тус, формула:
$ (\ lnot z) \ lor y
$
находится в DNF , потому что это дизъюнкция двух «вырожденных» конъюнкций: $ \ lnot z $ и $ y $.
Для CNF у нас есть это:
формула представляет собой конъюнктивную нормальную форму (CNF) тогда и только тогда, когда она является соединением предложений , где предложение является дизъюнкцией литералов.
Таким образом:
$ ((\ lnot z) \ lor y) \ земля T $
находится в CNF , потому что у нас есть дизъюнкция двух литералов: $ \ lnot z $ и $ y $, которые образуют предложение: $ (\ lnot z) \ lor y $; затем второе предложение: $ T $ («вырожденная» дизъюнкция) и две дизъюнкции объединяются в: $ ((\ lnot z) \ lor y) \ land T $.
По формуле:
$ T \ land [T \ lor (\ lnot x \ land y) \ lor (x \ land y)]
$
у нас есть три конъюнкции : $ (\ lnot x \ land y) $ и $ (x \ land y) $ и «вырожденный»: $ T $, и они разделены на:
$ T \ lor (\ lnot x \ land y) \ lor (x \ land y) $;
эта формула находится в DNF ; но добавив часть: $ T \ land \ ldots $, полученная формула будет не более DNF .
По формуле:
$ T \ land [T \ lor (\ lnot x \ land y) \ lor (x \ land y)]
$
, мы можем применить дистрибутивность к его подформуле:
$$ [(\ lnot x \ land y) \ lor (x \ land y)] \ Equiv [y \ land (x \ lor \ lnot x)] \ Equiv (y \ land T) \ Equiv y $$
, чтобы получить эквивалент:
$ [Т \ земля (Т \ лор у)] \ экв (Т \ земля Т) \ эквив Т $
, который является CNF и DNF, эквивалентными исходной формуле.
2.4: дизъюнктивная нормальная форма (DNF)
дизъюнктивная нормальная форма (DNF) — это стандартный способ написания логических функций. Его можно описать как сумму произведений, ИЛИ и ANDS 3 . Чтобы понять DNF, сначала будет рассмотрена концепция minterm .
Минтерм — это строка в таблице истинности, в которой функция вывода для этого термина истинна. Например, в таблице 2.3.3 функция f1 (A, B, C) имеет минтерм, когда A = 1, B = 0 и C = 0. Мы можем записать этот minterm a AB’C ‘(A и не-B и не-C), поскольку A истинно, а B и C оба ложны.Функция f1 (A, B, C) также имеет три других термина: AB’C, ABC ‘и ABC. Таким образом, DNF для функции f1 (A, B, C) будет записан как:
f1 (A, B, C) = AB’C ‘+ AB’C + ABC’ + ABC
Обратите внимание, что эти минтермы — это числа 4, 5, 6 и 7 4 в таблице, поэтому краткое обозначение DNF выглядит следующим образом:
f1 (A, B, C) = Σ (4,5,6,7)
Аналогично f2 (A, B, C) может быть записано как:
f2 (A, B, C) = A’B’C + A’BC + AB’C + ABC = Σ (1, 3, 5, 7)
Обратите внимание, что любая логическая функция может быть записана в DNF, а DNF требует только 3 типа операций: AND, OR и NOT.Вот почему AND, OR и NOT универсальны. Доказательство этого оставлено упражнениями в конце главы.
\ (\ PageIndex {1} \) Логические отношения
Следующий вопрос, который необходимо задать: можно ли написать какую-либо логическую функцию в DNF, следует ли использовать DNF для представления всех булевых функций? Ответ на этот вопрос дает инженерная схема. В какой-то момент компьютер должен реализовать логическую функцию в виде схемы. Этой схеме потребуется 1 вентиль для каждой операции.А при разработке схемы цель состоит в том, чтобы минимизировать количество необходимых вентилей.
Почему нужно минимизировать количество ворот? Когда гейт фактически включен в схему, это имеет 3 плохих эффекта:
- Каждым воротам требуется питание для управления ими. Чем больше вентилей в цепи, тем больше энергии потребуется для работы компьютера.
- Поскольку воротам требуется электричество, в результате они выделяют тепло. Чем больше вентилей, тем больше тепла от процессора.
- Всегда есть задержки в распространении сигнала через ворота.Скорость света очень велика, но не бесконечна. Чем дальше электричество должно пройти, чтобы достичь конца цепи, тем больше времени потребуется. Таким образом, чем больше вентилей в схеме, тем медленнее процессор. А в современных компьютерах скорость света часто является ограничивающим фактором в том, насколько быстро может цикл ЦП, и, следовательно, в скорости ЦП.
Таким образом, цель любой схемы — ограничить количество вентилей в схеме. Для функции f1 (A, B, C) в таблице 2.3.3 количество элементов И равно 8, или элементов 3, а не элементов 4, или всего 15 элементов.Вопрос в том, можно ли реализовать схему менее чем на 15 вентилях.
Булева алгебра — это механизм, который используется для ответа на этот вопрос. Булева алгебра похожа на традиционную алгебру тем, что существует набор отношений, которые можно применить к функции для ее преобразования. И эти операции, как правило, в некоторой степени аналогичны операциям в традиционной алгебре, что несколько упрощает переход к булевой алгебре. Список этих отношений приведен в таблице \ (\ PageIndex {1} \).
Отношения | Правило № | Отношения | Правило № |
х + 0 = х | 1 | х * 0 = 0 | 2 |
х + 1 = 1 | 3 | х * 1 = х | 4 |
х + х = х | 5 | х * х = х | 6 |
x + x ’= 1 | 7 | x * x ’= 0 | 8 |
х + у = у + х | 9 | xy = yx | 10 |
х + (у + г) = (х + у) + г | 11 | х (yz) = (ху) z | 12 |
x (y + z) = xy + yz | 13 | х + уz = (х + у) (х + г) | 14 |
(x + y) ’= x’y’ | 15 | (xy) ’= x’ + y ’ | 16 |
(x ’)’ = x | 17 |
Все эти отношения, кроме 15 и 16, можно легко вывести.Отношения 15 и 16 известны как законы ДеМоргана, и их следует просто запомнить.
Применяя эти соотношения для f1 (A, B, C), мы находим следующее:
ф1 (А, В, С) | = AB’C ‘+ AB’C + ABC’ + ABC = AB ‘(C’ + C) + AB (C ‘+ C) (правило 13) = AB ‘(1) + AB (1) (правило 7) = AB ‘+ AB (правило 4) = A (B ‘+ B) (правило 13) = A (1) (правило 7) = A (правило 4) |
Это выражение, очевидно, проще исходного, и количество вентилей, необходимых для этой схемы, было уменьшено с 15 до 0.Это сокращение, очевидно, стоило затраченных усилий.
Но как мы узнали, что нужно продолжать сокращать это выражение после «AB ‘+ AB»? Это само по себе было значительным сокращением, с 15 до 4 ворот. Поскольку теперь мы показали, что DNF не обязательно (и часто не дает) приводит к минимальному выражению, как мы можем узнать, было ли достигнуто минимальное выражение? Это тема следующего раздела этой главы.
3 Другой способ представления функции — это конъюнктивная нормальная форма (CNF).CNF можно описать как произведение сумм, операций И или ИЛИ. Использование CNF оставлено на усмотрение задач в конце главы.
4 Обратите внимание, что число начинается с 0, а не с 1.
Дизъюнктивная нормальная форма — обзор
3 Логика первого порядка
В отличие от случаев логики высказываний и элементарной геометрии, нет общей процедуры принятия решения для логики первого порядка. С другой стороны, учитывая соответствующие аксиомы в качестве предпосылок, все математические рассуждения могут быть выражены в логике первого порядка, и именно поэтому так много внимания было уделено процедурам доказательства для этой области.Исследования Сколема и Хербранда в 1920-х и начале 1930-х предоставили основные инструменты, необходимые для программ доказательства теорем для логики первого порядка [Davis 1983 c ].
В 1957 году пятинедельный Летний институт символической логики, который проводился в Корнельском университете, посетил почти каждый логик, работавший в Соединенных Штатах. Присутствовали также многие наиболее склонные к теории исследователи из близлежащих предприятий IBM; FORTRAN — принципиально новое новшество в практике программирования.После обсуждения с Гелернтером логик Абрахам Робинсон выступил с коротким докладом [Robinson 1957], в котором он указал на функции Сколема и «теорему Хербранда» как на полезные инструменты для средств доказательства теорем общего назначения. Он также сделал провокационное замечание о том, что вспомогательные точки, линии или окружности, «построенные» как часть решения геометрической задачи, можно рассматривать как элементы того, что сейчас называется вселенной Хербранда для этой проблемы.
Первые средства доказательства теорем для логики первого порядка, которые будут реализованы на основе теоремы Хербранда, использовали полностью неуправляемый поиск вселенной Хербранда.Вместо использования функций Сколема для работы с экземплярами переменные были заменены параметрами; поэтому программа должна была обеспечивать возможность отслеживания зависимостей между этими параметрами. Тесты на функциональную выполнимость истинности использовали либо простые вычисления таблицы истинности, либо расширение в дизъюнктивную нормальную форму. Неудивительно, что эти программы были способны доказывать только простейшие теоремы. Среди первых из этих программ программа Гилмора [1960] послужила особенно полезным стимулом для дальнейших исследований.
В своем более позднем комментарии Prawitz [1983 a ] объяснил, что разработка новых процедур доказательства и доказательств полноты для логики первого порядка вместе с доступностью вычислительных ресурсов побудили его принять участие в реализации такой процедуры. Он принял модифицированную форму метода семантических таблиц и сформулировал свой собственный высокоуровневый алгоритмический язык, на котором можно было бы написать процедуру. Подробная реализация была выполнена Prawitz, Prawitz и Voghera [1960].Несмотря на то, что она основана на современной логической системе, эта программа страдает теми же ограничениями, что и программа Гилмора.
Мартин Дэвис и Хилари Патнэм отметили, что программа Гилмора не удалась на некоторых довольно простых примерах из-за того, что она полагалась на расширения в дизъюнктивную нормальную форму для проверки выполнимости. Это привело их к оптимистическому (и в ретроспективе довольно наивному) выводу о том, что отсутствие эффективных методов проверки выполнимости больших формул исчисления высказываний является основным препятствием, которое необходимо преодолеть.Хотя их интерес к алгоритмам для решения проблемы выполнимости был вызван только тем, что они хотели использовать такие методы как часть процедуры проверки логики первого порядка, они заручились поддержкой Агентства национальной безопасности, чтобы потратить Летом 1958 года работал над этой проблемой. В своем неопубликованном отчете для NSA [Davis and Putnam 1958] они подчеркнули использование конъюнктивной нормальной формы для проверки выполнимости. В этом отчете представлены конкретные методы восстановления, совместное использование которых связано с именами Дэвиса-Патнэма.Это:
- 1.
Одно буквальное правило , также известное как правило единицы .
- 2.
Утвердительно-отрицательное правило , также известное как чистое буквальное правило .
- 3.
Правило для исключения атомарных формул
- 4.
Правило разделения , называемое в отчете, правило анализа случаев
The Davis-Putnam обычно цитируемая статья [Davis and Putnam 1960] была написана годом позже.Предлагаемая процедура будет принимать в качестве входных данных формулу, которая была предварительно обработана с использованием сначала функций Сколема для исключения экзистенциальных кванторов, а затем преобразования формулы в конъюнктивную нормальную форму. Многие программы доказательства теорем (в том числе очень успешные) использовали этот подход. Тестирование выполнимости должно было проводиться с использованием правил 1, 2, 3, приведенных выше, и было отмечено, что пример, ставящий программу Гилмора в тупик, можно легко выполнить с помощью ручных вычислений. Когда Джордж Логеманн и Дональд Ловленд попытались реализовать программу, они обнаружили, что правило для исключения атомных формул (позже названное наземным разрешением ), которое заменило формулу
(p∨A) ∧ (¬p∨B) ∧C
на
(A∨B) ∧C
использовало слишком много оперативной памяти.Поэтому было предложено использовать вместо этого правило разделения , которое генерирует пару формул
A∧CB∧C
Идея заключалась в том, что стек для проверяемых формул может храниться во внешнем хранилище (фактически, на ленточном накопителе). ), чтобы формулы в ОЗУ никогда не становились слишком большими. 2 Хотя проверка выполнимости была проведена очень эффективно, вскоре стало ясно, что очень интересные результаты не могут быть получены без предварительной разработки метода предотвращения генерации ложных элементов вселенной Хербранда [Davis, Logemann and Loveland 1962].
В те же годы Хао Ван пытался применить некоторые из более сложных работ, которые были проделаны в теории доказательств и над разрешимыми случаями Entscheidungsproblem Гильберта, к программам автоматического вывода. Он объявил о компьютерной программе, которая доказала все (около 400) теорем Principia Mathematica Уайтхеда и Рассела о логике первого порядка с равенством [Wang and Zhi 1998, Wang and Zhi 1998]. Однако это, по-видимому, важное достижение в автоматизации дедукции было (как указывал сам Ван) возможным только потому, что все эти теоремы могут быть приведены к предваренной форме с помощью простого префикса… ∀∃… ∃.Ван пришел к выводу, что:
Самый интересный урок из этих результатов, возможно, состоит в том, что даже в довольно богатой области фактически доказанные теоремы в большинстве своем используют очень небольшую часть доступных ресурсов области. ([Wang 1963 c ] стр. 32)
Влиятельная статья Правитца [1960] научила растущее сообщество автоматизированных дедукций, что ненужных терминов в расширении Гербранда можно избежать, используя алгоритмы, которые не генерируют элементы вселенной Гербранда до тех пор, пока нужный.Наиболее поздний прогресс был основан на этом ключевом открытии. Процедура Правица работала путем получения разложений в дизъюнктивную нормальную форму перед заменой переменных элементами вселенной Хербранда. Таким образом, алгоритм генерировал дизъюнктивные нормальные формы увеличивающейся длины, ищущие одну, обладающую тем свойством, что некоторая подстановка из вселенной Эрбранда дала бы истинно функционально невыполнимую формулу. 3 Поскольку это условие сводится к каждому дизъюнктивному предложению, включающему пару литералов вида ℓ, ¬ℓ, его можно сформулировать как потребность удовлетворить системе уравнений в параметрах разложения. 4
Процедура Правица была большим усовершенствованием по сравнению с тем, что было сделано ранее, потому что не генерировались ложные элементы вселенной Хербранда. К сожалению, огромные расширения в дизъюнктивную нормальную форму, которые будут генерироваться всеми задачами, кроме простейших, показали, что, по крайней мере, в том виде, в котором они представлены, это все еще неудовлетворительная процедура. Однако в нем содержалась оригинальная идея поиска замен, которые превратили бы пары литералов в отрицания друг друга.Более того, если с самого начала отказаться от кванторов существования в пользу функций Сколема, вместо систем уравнений, возникает простая проблема объединения пар членов.
В своей обзорной статье Дэвис [1963] предложил
… новый вид процедуры, которая стремится объединить достоинства процедуры Правитца и процедуры Дэвиса-Патнэма.
Идея, также отмеченная Данхэмом и Норт [1962], заключалась в том, что по «чистому буквальному правилу» из процедуры Дэвиса-Патнэма (Правило 2, выше) замены могут помочь сделать конъюнктивный набор дизъюнктивных предложений невыполнимым. только если им удастся преобразовать литерал из одного из этих предложений в отрицание литерала в другом предложении.Программа доказательства теорем, основанная на этих идеях, была написана Д. Макилроем из Bell Laboratories и была улучшена и исправлена Питером Хинманом. Программа включала реализацию обычного алгоритма унификации [Chinlund, Davis, Hinman and McIlroy 1964].
Само существование этого тома совершенно ясно показывает, что автоматизированное мышление — это процветающая область с огромной литературой. Выходящая раз в два месяца публикация The Journal of Automated Reasoning полностью посвящена этой области.Если одно событие может быть обозначено как знаменующее его появление как зрелого субъекта, то это будет публикация [Robinson 1965 b ], в которой Дж. Робинсон объявил принцип разрешения. [Robinson 1965 b ] была второй статьей Робинсона в этой области, и она помогает проследить его мысль, начиная с первой [Robinson 1963]. Он начал с базовой схемы Дэвиса-Патнэма: экзистенциальные кванторы исключены в пользу функций Сколема и конъюнктивной нормальной формы. Он обратил внимание на технику Правитца по избеганию ложных элементов вселенной Хербранда и обзорную статью Дэвиса.Очевидно, набросок Дэвиса предложенной им процедуры был недостаточно ясным, и Робинсон писал: 5
Поэтому Дэвис [1963] предложил способ использования мощной идеи Правитца, избегая при этом катастрофического использования Правитцем нормальных форм — во многом в том же духе. Таким образом, методы Дэвиса и Патнэма [1960] избегают использования нормальных форм, из-за чего программа Гилмора [1960] оказывается неспособной даже решить [простую задачу]. Из нескольких замечаний в конце [Davis 1963] пока не ясно, как будет действовать Дэвис, и можно с большим интересом ожидать его дальнейших исследований в этом направлении.
Остальная часть статьи содержит ряд интересных компьютерных доказательств, созданных с использованием правила Дэвиса-Патнэма «одного буквального предложения», и, когда это не удается, от пользователя требуется предварительно указать элементы вселенной Herbrand, необходимые для получить доказательство. Было высказано предположение, что поиск этих элементов является «действительно« творческой »частью искусства построения доказательств».
Метод разрешения Робинсона, представленный в его очень влиятельном [1965 b ], произвел революцию в этой области.Робинсон нашел единственное правило вывода, легко выполняемое компьютером, которое было полным для логики первого порядка. Использование разрешения не требует отдельной процедуры для работы с исчислением высказываний. Начиная с обычного предварительно обработанного конъюнктивного набора дизъюнктивных предложений, техника Робинсона заключалась в поиске всех возможных «унификаций», которые позволили бы выразить набор предложений как
(ℓ∨A) ∧ (¬ℓ∨B) ∧ C
, где ℓ — литерал, которого нет в C .Это дает «резольвент»
(A∨B) ∧C
, который после «умножения» ( A ∨ B ) приводит к новому набору предложений, который неприменим в случае, если исходный набор был. Это было похоже на предложение Дэвиса [Davis 1963, Chinlund et al. 1964] в поисках объединений, порождающих дополнительные литералы. Он отличается не только тем, что не требует отдельного функционального тестирования истинности, но и тем, что не требует, как часть входных данных, указания количества экземпляров каждого предложения для участия в окончательном доказательстве.[Robinson 1965 b ] поражает своей комбинаторной простотой, а также чистой математической элегантностью изложения. К сожалению, как вскоре выяснилось, метод голого разрешения мог легко произвести многие тысячи предложений, не достигнув доказательства. Поиск доказательства с использованием разрешения становится проблемой предоставления критериев для порядка, в котором следует искать разрешения. Ранними попытками сократить пространство поиска были собственное элегантное гиперразрешение Робинсона [Robinson 1965 a ], а также стратегии предпочтения единиц [Wos, Carson and Robinson 1964] и набор поддержки [Wos, Robinson and Carson 1965].
За три десятилетия, прошедшие с момента появления первых реализаций разрешения, произошел всплеск исследований, посвященных автоматизированным системам рассуждений. В то время как некоторые из наиболее успешных основаны на решении, другие действовали в разных направлениях. За дополнительной информацией читатель может обратиться к другим статьям этого тома.
логических нормальных форм
логических нормальных формЛогическое выражение — это выражение, включающее переменные, каждая из который может принимать значение true или значение false .Эти переменные объединяются с помощью логических операций, таких как и . (соединение), или (дизъюнкция), а не (отрицание). Другой способ смотреть при этом каждое логическое выражение идентифицируется логическим значением функция , которая принимает определенное количество параметров, каждый из которых может быть истинным или ложным и возвращает истинный или ложный результат. Таким образом, мы также можем укажите логическую функцию, выписав таблицу истинности , которая таблица, содержащая все возможные присвоения параметров true или false и результирующий вывод функции.
Например, вот таблица истинности для X = A и B:
| A | B | A и B |
|---|---|---|
| false | false | false |
| false | true | false |
| true false | true false true falseистина | истина |
Существует теорема, согласно которой любая логическая функция может быть записана с использованием только двух уровней логики и возможного отрицания переменных (называемых литералами , ).Есть два специальные формы, соответственно называемые дизъюнктивная нормальная форма и конъюнктивная нормальная форма , которые особенно полезны. Пусть член будет дизъюнкция («или») коллекции переменных, каждая из которых может быть инвертирована. Пусть предложение будет конъюнкцией («и») набора переменных, каждый опционально отрицается. Если логическое выражение — это в точности конъюнкция термины, то говорят, что он имеет конъюнктивную нормальную форму, и если он именно дизъюнктивное предложение, то говорят, что оно дизъюнктивное нормальная форма.
Например, (((не A) и B) или (A and (not B))) находится в дизъюнктивной нормальной форме (это ИЛИ двух членов), а (((не A) или (не B)) и (A или B)) находится в конъюнктивной нормальной форме (это И двух предложений). Вы заметите что они представляют одну и ту же функцию, A xor B . ( xor — это функция « исключающее ИЛИ », которая верна, если один или другой из аргументы верны, , но не оба .)
Легко доказать, что любую логическую функцию можно записать как в DNF и CNF.Хотя это не является формальным доказательством того, что это всегда работает, я предоставлю метод формирования выражений DNF и CNF логической функции. Первый, напишите таблицу истинности для функции. Чтобы сформировать представление DNF функции, мы включим термин для каждой строки таблицы истинности в что значение функции истинно. Для каждого из этих условий включите все переменные, которые являются параметрами функции. Если задана переменная значение false в строке таблицы истинности, отрицать его в термине; иначе, оставьте это неотрицательным.Таким образом, выражение DNF генерируется напрямую. из таблицы истинности, и довольно интуитивно понятно, что это работает и что это всегда можно сделать.
Чтобы сформировать выражение CNF, мы работаем аналогично, на этот раз формируя предложение для каждой строки, в которой значение функции равно false . Отрицать переменные, когда им присвоено значение истинное значение в таблице истинности, и не отрицайте их, когда они ложны (противоположность DNF).
| A | b | A xor B | термины | пункты |
|---|---|---|---|---|
| ложные | ложные | ложные | (A или B) | |
| 9018 9018 истинные ((не A) и B) | ||||
| true | false | true | (A и (не B)) | |
| true | true | false | ((не A) или (не B)) |
На практике мы обычно связываем соединение с умножением и дизъюнкция с добавлением.В самом деле, если мы отождествляем истину с 1 и ложь с 0, то {0,1} вместе с обычными определениями сложения и умножения по Галуа поле размера 2 (например, арифметический по модулю 2), затем сложение (+) и дизъюнкция (или) действительно такие же, как умножение и соединение (и). Это соглашение делает логические выражения более лаконичны для записи. Отрицание часто пишется как черта над переменная (или более крупное подвыражение) или «/», если верхняя черта недоступна.
Таким образом, запишем: A xor B = (/ A) B + A (/ B) = (/ A + / B) (A + B)
Авторские права © 2001 Тобин Фрике.Создан 5 августа 2001 года в Лунде, Швеция. Пожалуйста, напишите мне по адресу [email protected], если у вас есть какие-либо вопросы или комментарии.
Нормальные и основные формы — GeeksforGeeks
Нормальные и основные формы
- Дизъюнктивные нормальные формы (DNF):
Формула, которая эквивалентна данной формуле и состоит из суммы элементарных произведений, называется дизъюнктивной нормальной формой данной формулы.Пример:
(P ∧ ~ Q) ∨ (Q ∧ R) ∨ (~ P ∧ Q ∧ ~ R)- DNF формулы не уникален.
- Конъюнктивная нормальная форма (CNF):
Формула, эквивалентная данной формуле и состоящая из произведения элементарных произведений, называется конъюнктивной нормальной формой данной формулы.Пример:
(P ~ ∨ Q) ∧ (Q ∨ R) ∧ (~ P ∨ Q ∨ ~ R)- CNF формулы не уникален.
- Если каждая элементарная сумма в КНФ является тавтологией, то данная формула также является тавтологией.
- Принцип дизъюнктивной нормальной формы (PDNF):
Эквивалентная формула, состоящая только из дизъюнктивных терминов, называется основной дизъюнктивной нормальной формой формулы.Также известна как каноническая форма суммы произведений .
Пример:
(P ∧ ~ Q ∧ ~ R) ∨ (P ∧ ~ Q ∧ R) ∨ (~ P ∧ ~ Q ∧ ~ R)- Минтерм состоит из союзов, в которых каждая переменная оператора или его отрицание, но не оба, появляется только один раз.
- Минтермы записываются путем включения переменной, если ее значение истинности равно Т, и отрицания, если ее значение истинности равно F.
- Принцип конъюнктивной нормальной формы (PCNF):
Эквивалентная формула, состоящая из соединений maxterms только называется основной конъюнктивной нормальной формой формулы.

 x=3
log2(3)=x
x=3
log2(3)=x

 {6}}$=
42
48
49
{6}}$=
42
48
49


 Далее следует применить формулы квадрата разности и разности квадратов.
Далее следует применить формулы квадрата разности и разности квадратов.
 оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. 50-летия октября, 13/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. 50-летия октября, 13/1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.верхнеяркеево, ул.пушкина, 17/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.верхнеяркеево, ул.пушкина, 17/1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (дуванский район, с месягутово, пер. октябрьский, д. 7/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (дуванский район, с месягутово, пер. октябрьский, д. 7/1) верхние киги, ул. салавата, 1)
верхние киги, ул. салавата, 1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.стерлитамак, пр.октября, 34)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.стерлитамак, пр.октября, 34) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (стерлибашевский район, с.стерлибашево, ул.карла маркса, 97)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (стерлибашевский район, с.стерлибашево, ул.карла маркса, 97) кирова, 48 пом.1)
кирова, 48 пом.1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.старосубхангулово, бурзянский р-он, ул.салавата, 30)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.старосубхангулово, бурзянский р-он, ул.салавата, 30) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.салават, ленина, 11)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.салават, ленина, 11) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.кумертау, к.маркса, 4а)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.кумертау, к.маркса, 4а) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.мраково, з.биишевой, 78а)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.мраково, з.биишевой, 78а) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. туймазы, ул. мусы джалиля, 13а, 13/1, 13/2, 13/3, 13/4, 13/5)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. туймазы, ул. мусы джалиля, 13а, 13/1, 13/2, 13/3, 13/4, 13/5) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (ермекеевский район, с. ермекеево, ул. ленина, 20)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (ермекеевский район, с. ермекеево, ул. ленина, 20) губайдуллина, 116а)
губайдуллина, 116а) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.нефтекамск, ул.строителей, 19)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.нефтекамск, ул.строителей, 19) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.агидель, ул.карла маркса, 63)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.агидель, ул.карла маркса, 63) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.бураево, ул.горького, 53)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.бураево, ул.горького, 53) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул.аксакова, 62)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул.аксакова, 62) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан ( буздякский район, с. буздяк, ул. красноармейская, 27)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан ( буздякский район, с. буздяк, ул. красноармейская, 27) п. чишмы, ул. чернышевского, 1)
п. чишмы, ул. чернышевского, 1)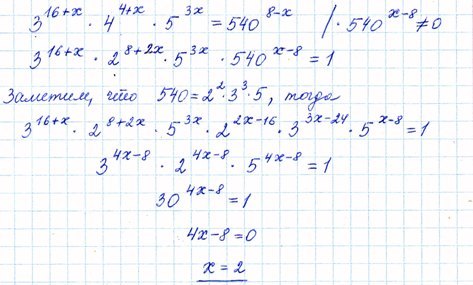 оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (альшеевский район, с.раевский ул.селькора,7)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (альшеевский район, с.раевский ул.селькора,7) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа ул.пр.октября 95/2)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа ул.пр.октября 95/2) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.бирск ул.мира д.66)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.бирск ул.мира д.66) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (караидельский р/н с.караидель ул.калинина д.2)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (караидельский р/н с.караидель ул.калинина д.2) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. сибай, ул.маяковского, 31/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. сибай, ул.маяковского, 31/1) 20/1)
20/1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. красина ,52)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. красина ,52) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. уфа, советский р-н, проспект салавата юлаева, д. 55)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. уфа, советский р-н, проспект салавата юлаева, д. 55) 55)
55) «Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.
«Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.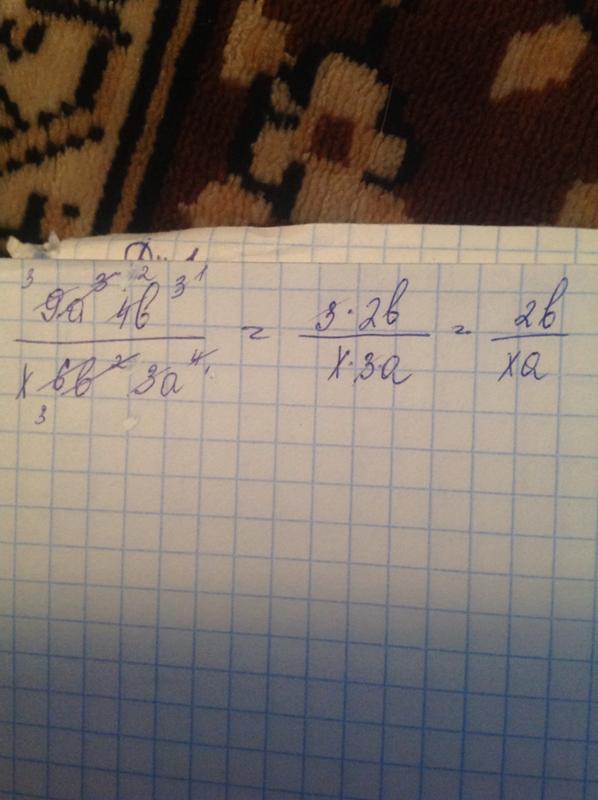 Айламазян Э.К., Баранов В.С. Пренатальная диагностика наследственных и врожденных болезней. М: МЕДпресс-информ, 2006; 416. (Ailamazyan E.K., Baranov V.S. Prenatal diagnosis of congenital and hereditary diseases. Moscow: MEDpress-inform, 2006; 416.)
Айламазян Э.К., Баранов В.С. Пренатальная диагностика наследственных и врожденных болезней. М: МЕДпресс-информ, 2006; 416. (Ailamazyan E.K., Baranov V.S. Prenatal diagnosis of congenital and hereditary diseases. Moscow: MEDpress-inform, 2006; 416.) Pediatr Nephrol 2014; 29: 4: 695–704.
Pediatr Nephrol 2014; 29: 4: 695–704. Дерюгина Л.А., Чураков А.А., Краснова Е.И. «Фатальные» пороки почек и мочевыделительной системы плода. Пренатальная диагностика – трудные решения. Современные проблемы науки и образования 2012; 2: URL: http://www.science-education.ru/ru/article/view?id=5927. (Deriugina L.A., Churakov A.A., Krasnova E.I. «Fatal» defects of the kidneys and urinary system of the fetus. Prenatal diagnosis – difficult decisions. Sovremennye problem nauki i obrazovaniya 2012; 2. URL: http://www.science-education.ru/ru/article/view?id=5927.)
Дерюгина Л.А., Чураков А.А., Краснова Е.И. «Фатальные» пороки почек и мочевыделительной системы плода. Пренатальная диагностика – трудные решения. Современные проблемы науки и образования 2012; 2: URL: http://www.science-education.ru/ru/article/view?id=5927. (Deriugina L.A., Churakov A.A., Krasnova E.I. «Fatal» defects of the kidneys and urinary system of the fetus. Prenatal diagnosis – difficult decisions. Sovremennye problem nauki i obrazovaniya 2012; 2. URL: http://www.science-education.ru/ru/article/view?id=5927.) Detskaya hirurgiya 2004; 6: 19–22.)
Detskaya hirurgiya 2004; 6: 19–22.) Zdorov’e rebenka 2013; 6: 49: 107–111.)
Zdorov’e rebenka 2013; 6: 49: 107–111.) VIII Ros. Congress «Modern technologies in pediatrics and pediatric surgery.» Moscow, 2009; 381–382.)
VIII Ros. Congress «Modern technologies in pediatrics and pediatric surgery.» Moscow, 2009; 381–382.) V., Yurchuk V.A., Titova S.V. Morphological
V., Yurchuk V.A., Titova S.V. Morphological Педиатрия 2011; 3: 90: 13–17. (Mambetova A.M., Zhetishev R.A., Shabalova N.N. The severity of connective tissue dysplasia in children: the relationship with the nature of perinatal pathology, and the passage of secondary chronic pyelonephritis. Pediatriya 2011; 3: 90: 13–17.)
Педиатрия 2011; 3: 90: 13–17. (Mambetova A.M., Zhetishev R.A., Shabalova N.N. The severity of connective tissue dysplasia in children: the relationship with the nature of perinatal pathology, and the passage of secondary chronic pyelonephritis. Pediatriya 2011; 3: 90: 13–17.) Педиатрия 2007; 86: 6: 24–28. (Zorkin S.N., Khvorostov I.N., Borisova S.A. Features renoprotective therapy in patients with obstructive uropathy. Pediatriya 2007; 86: 6: 24–28.)
Педиатрия 2007; 86: 6: 24–28. (Zorkin S.N., Khvorostov I.N., Borisova S.A. Features renoprotective therapy in patients with obstructive uropathy. Pediatriya 2007; 86: 6: 24–28.)


 «Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — это квадратные числа.
«Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — это квадратные числа. Здесь 12 пенни расположены в квадрате, но не в полном квадратном массиве, поэтому 12 не является квадратным числом.
Здесь 12 пенни расположены в квадрате, но не в полном квадратном массиве, поэтому 12 не является квадратным числом.
 Этот квадрат такого же размера, как 16 белых стержней, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
Этот квадрат такого же размера, как 16 белых стержней, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
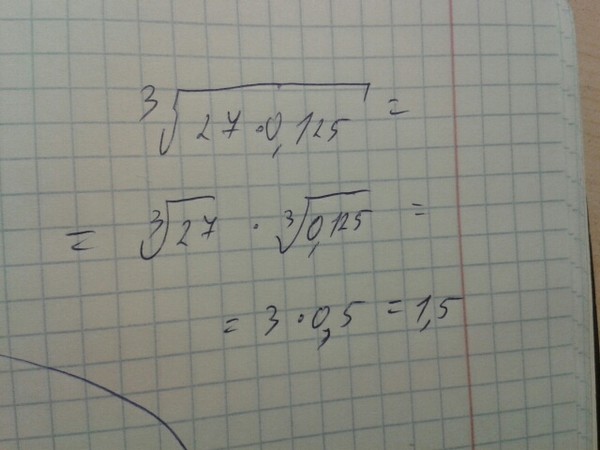 Для каждого нового квадрата добавьте два стержня, которые соответствуют сторонам предыдущего квадрата, и новую букву W, чтобы заполнить угол.
Для каждого нового квадрата добавьте два стержня, которые соответствуют сторонам предыдущего квадрата, и новую букву W, чтобы заполнить угол.


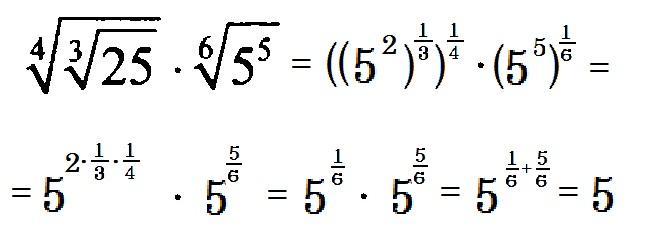
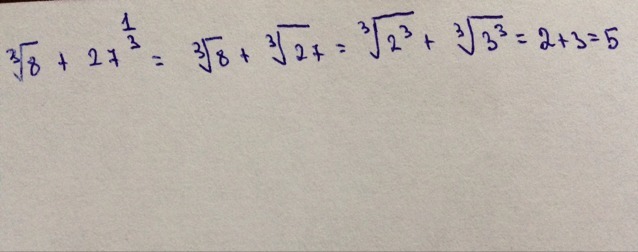 {n-1} [/ латекс].
{n-1} [/ латекс]. Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс]. Чередующиеся серии)
Чередующиеся серии) {n}} {1-r}} [/ латекс].
{n}} {1-r}} [/ латекс]. {n}}}} [/ latex]
{n}}}} [/ latex] Рассмотрим последовательность, в которой [латекс] r [/ latex] равен половине [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице.
Рассмотрим последовательность, в которой [латекс] r [/ latex] равен половине [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
{5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
 Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:

 Еще несколько примеров:
Еще несколько примеров: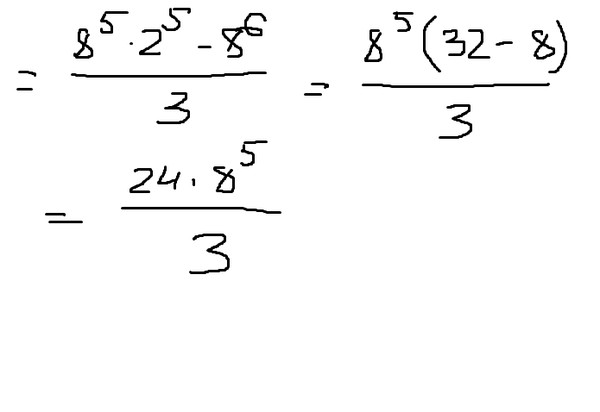

 {3} + \ cdots} [/ latex]
{3} + \ cdots} [/ latex]

 Их отрезки от вершины до центра эллипса называются полуосями.
Их отрезки от вершины до центра эллипса называются полуосями.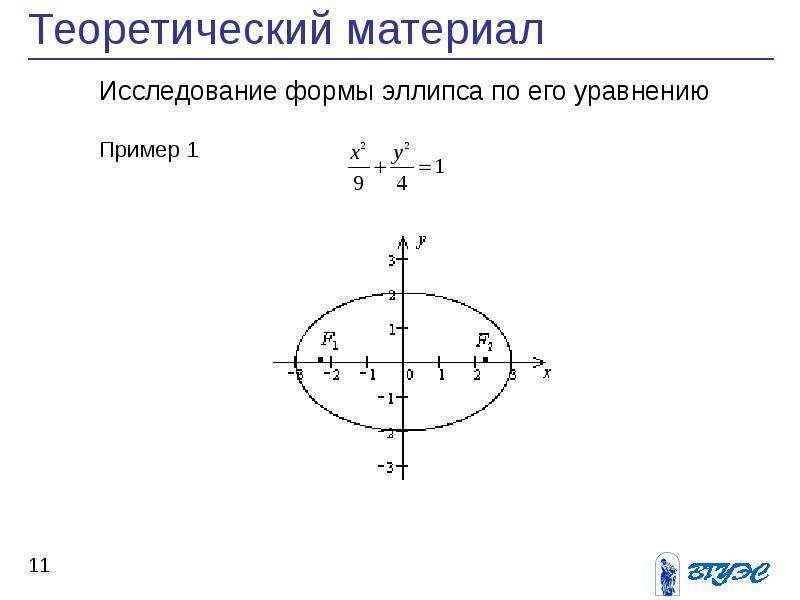
 Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.

 Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
 Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса К ним относятся эллипс, гипербола и парабола.
К ним относятся эллипс, гипербола и парабола. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей: Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы. Определить фокусы эллипса, заданного каноническим уравнением .
Определить фокусы эллипса, заданного каноническим уравнением .
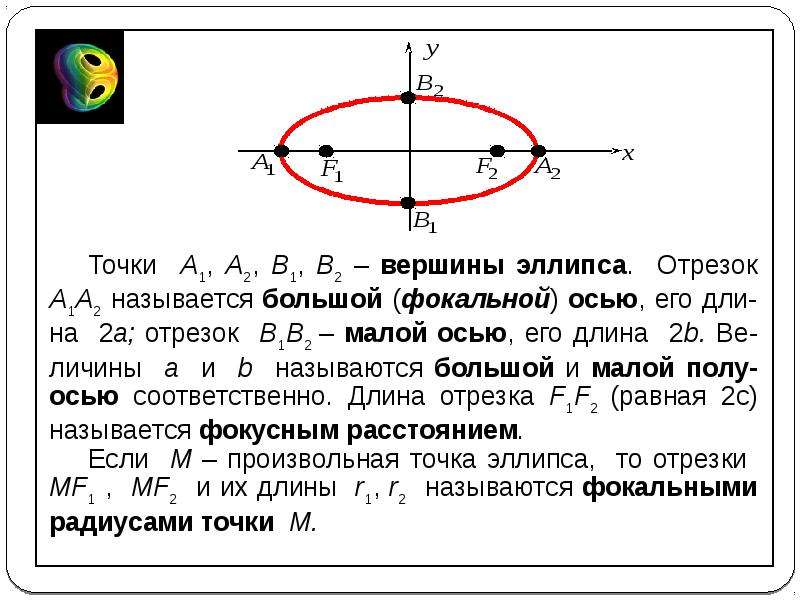 Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико. Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
 Пусть 2c — фокальное расстояние, 2c = |F1F2| 2 + y 2 ) + √((x + c) 2 + y 2 ) = 2a. (7.2)
Пусть 2c — фокальное расстояние, 2c = |F1F2| 2 + y 2 ) + √((x + c) 2 + y 2 ) = 2a. (7.2) Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли. Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
 рис. 7.5).
рис. 7.5). Пусть
фокусы эллипса лежат на оси Х,
причем
т. Е.– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]
Пусть
фокусы эллипса лежат на оси Х,
причем
т. Е.– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]


 При этом величинастремится к.
В предельном случаи уравнение эллипса
принимает вид:.
Это уравнение окружности. Если,
то.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]
При этом величинастремится к.
В предельном случаи уравнение эллипса
принимает вид:.
Это уравнение окружности. Если,
то.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]



 Так как , тогда , и поэтому .
Так как , тогда , и поэтому .
 3
3
 Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид:
А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид: ). Это геометрическое определение выражает фокальное свойство эллипса.
). Это геометрическое определение выражает фокальное свойство эллипса. При когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
При когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены). 3.37, имеет вид
3.37, имеет вид разд.2.2.4) координаты произвольной точки принадлежащей окружности, изменяются по закону Подставляя в уравнение окружности получаем уравнение для координат образа точки
разд.2.2.4) координаты произвольной точки принадлежащей окружности, изменяются по закону Подставляя в уравнение окружности получаем уравнение для координат образа точки Для окружности
Для окружности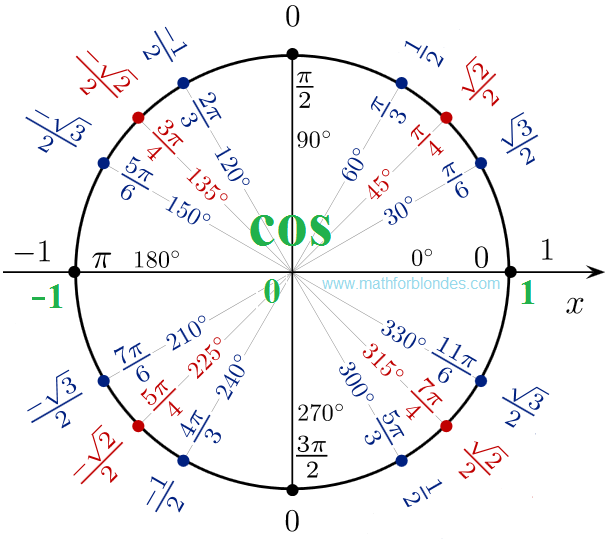 Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан.
Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан.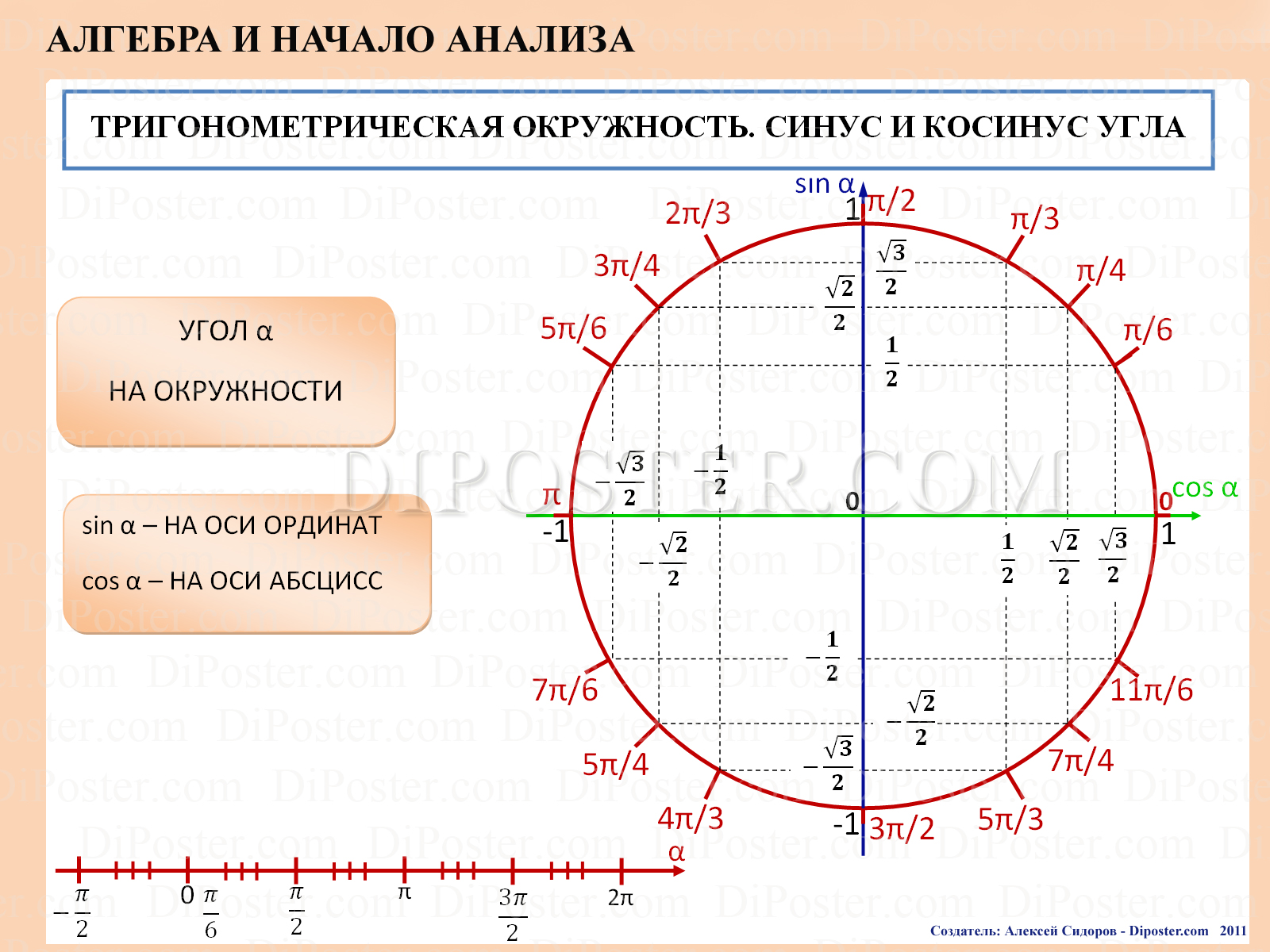
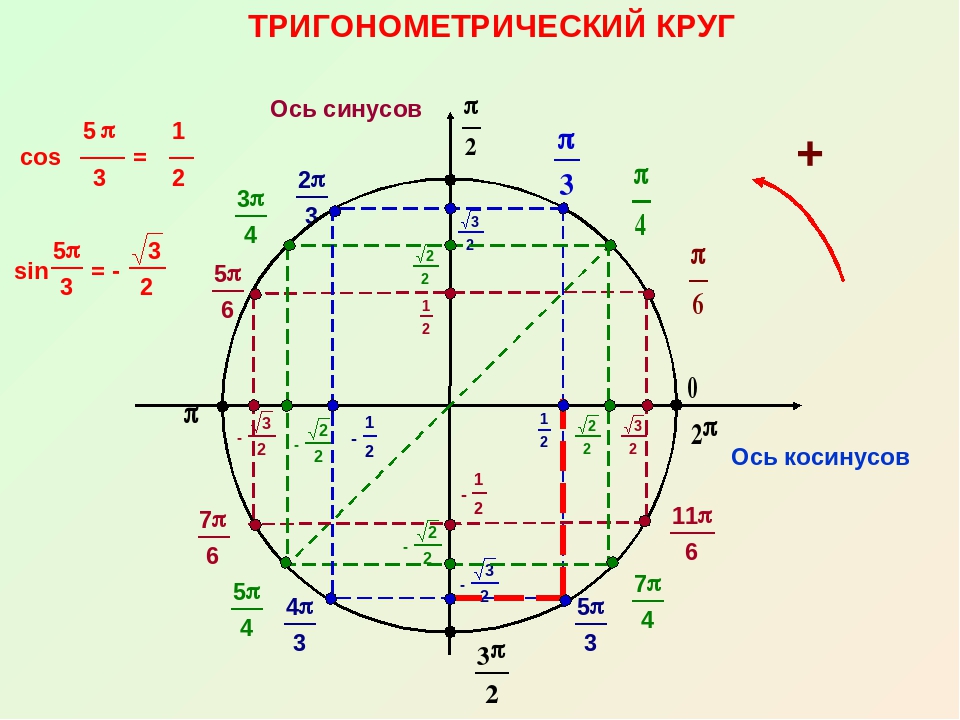 Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…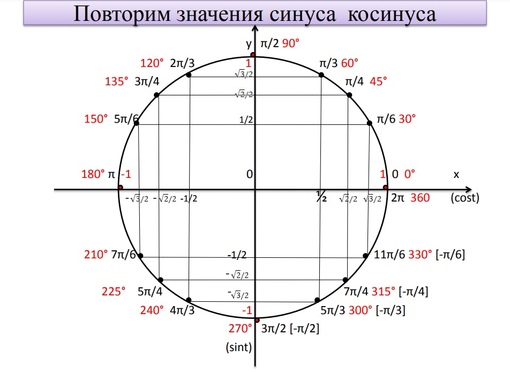
 Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
 Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.
Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол. Главное, не перепутать синус с косинусом.
Главное, не перепутать синус с косинусом.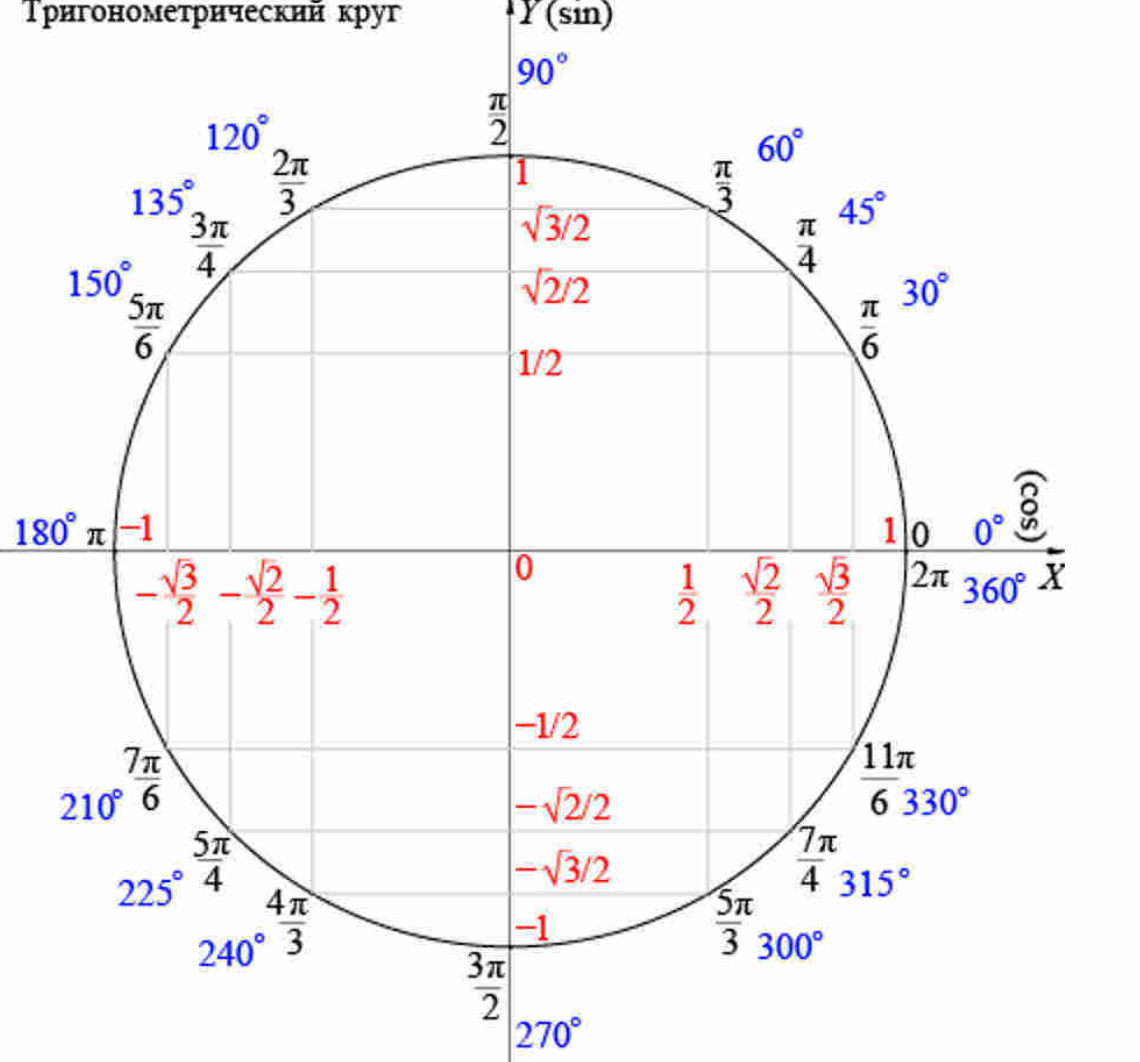
 ..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!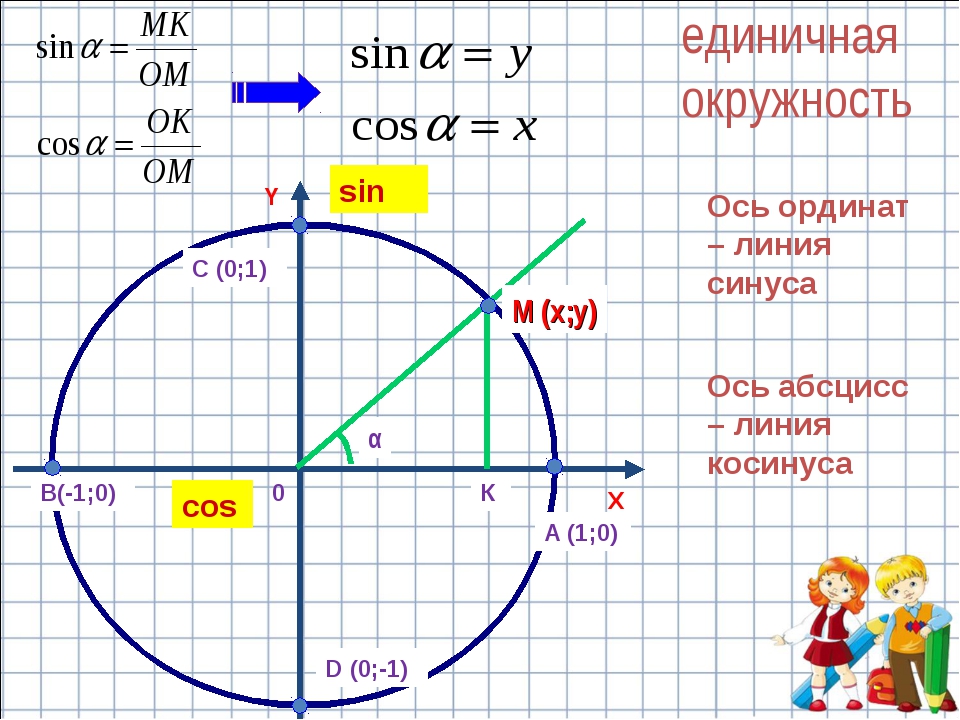
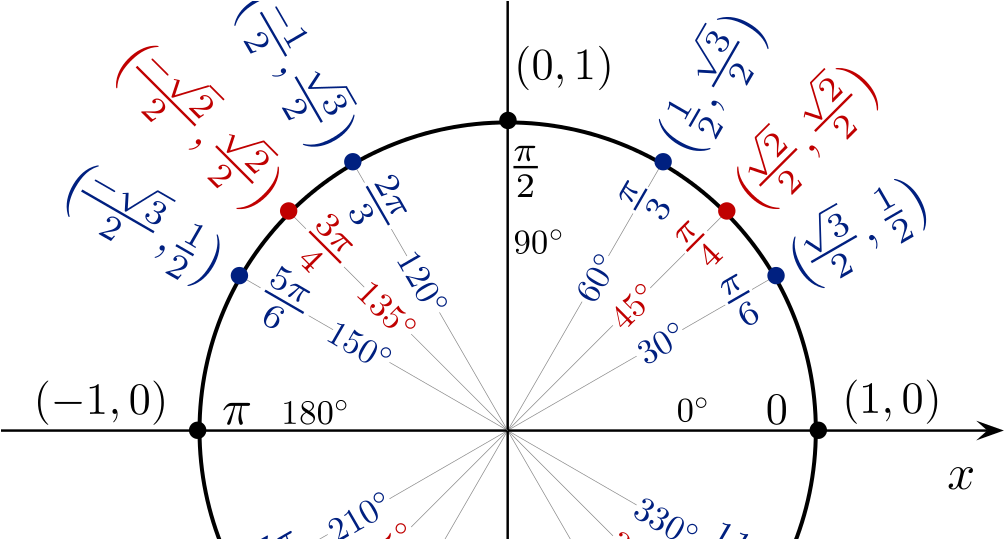

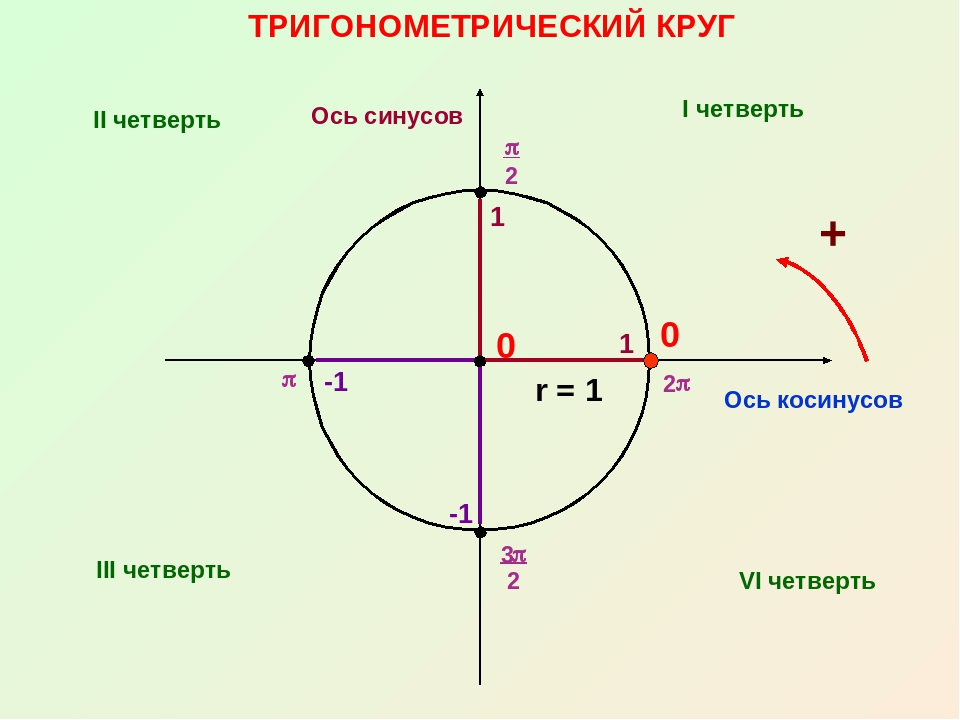 Что же тогда такое — тригонометрия? Разберемся… Начнем с двух основных понятий — синуса и косинуса. Что вы о них знаете кроме того, что это отношения катетов и гипотенузы? Вспомнили? сумма квадратов синуса и косинуса равны единице.
Что же тогда такое — тригонометрия? Разберемся… Начнем с двух основных понятий — синуса и косинуса. Что вы о них знаете кроме того, что это отношения катетов и гипотенузы? Вспомнили? сумма квадратов синуса и косинуса равны единице.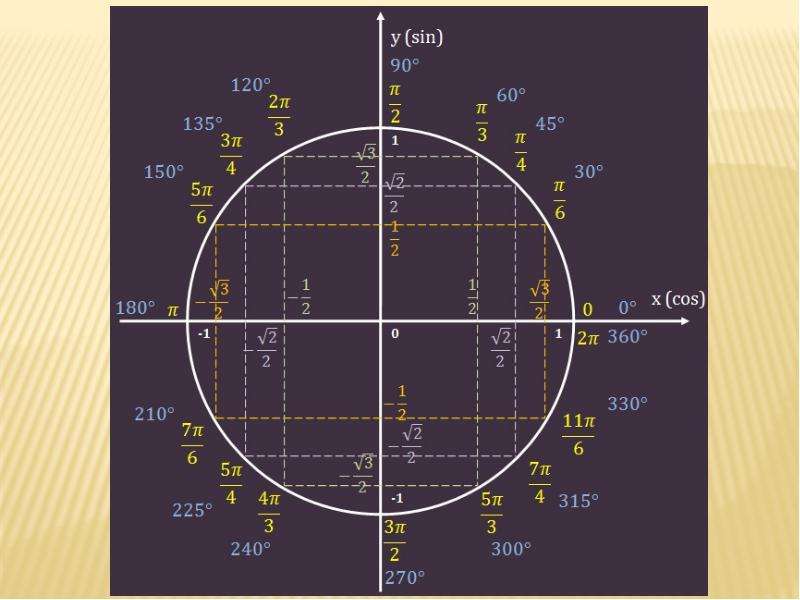
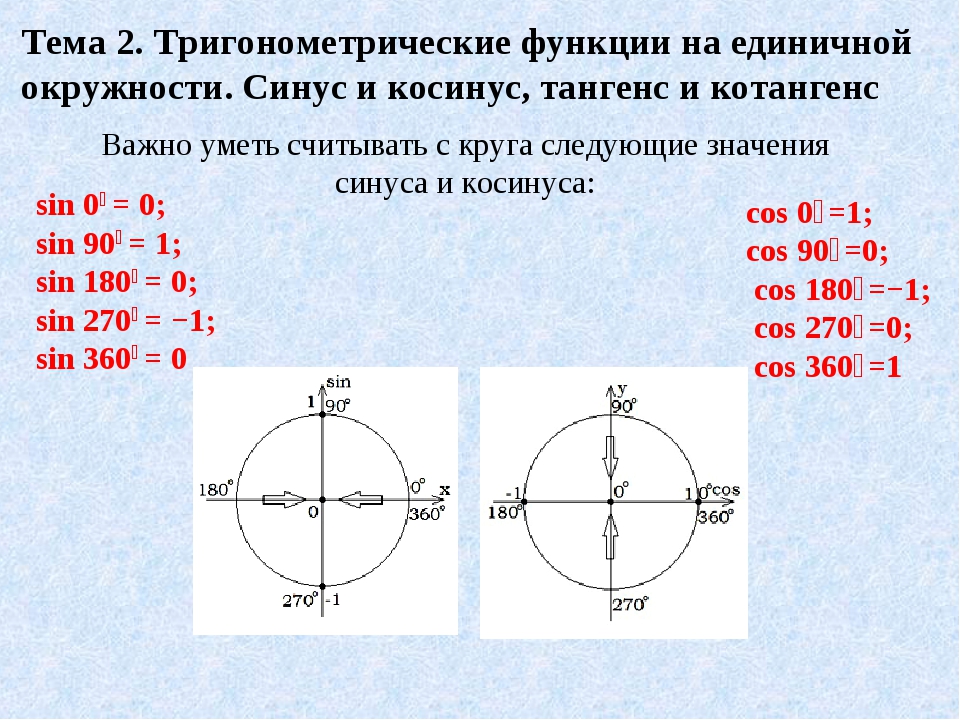 А значит, мы можем их, эти неизвестные, находить. А поможет нам в этом великолепная классическая «шпаргалка» — тригонометрический круг.
А значит, мы можем их, эти неизвестные, находить. А поможет нам в этом великолепная классическая «шпаргалка» — тригонометрический круг.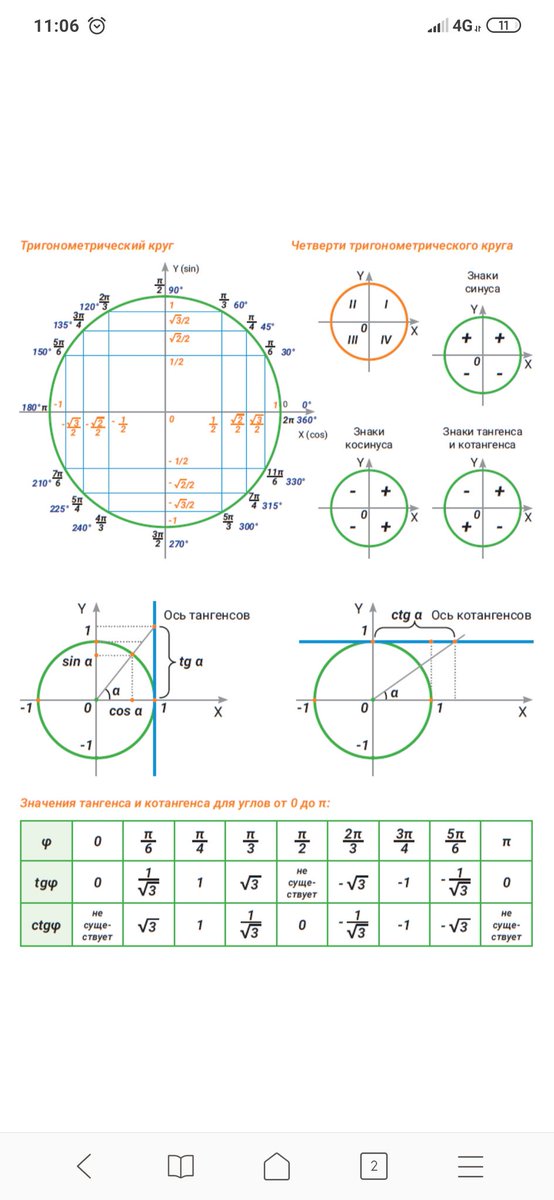
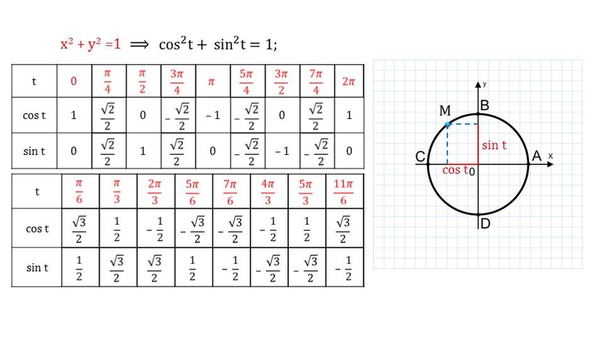 При этом, разумеется, значения синусов и косинусов не выходят за пределы круга. Просто, потому что не могут в силу своей ограниченности! Ну, а мы с вами имеем возможность определятся с синусами и косинусами уже не углов, а аргумента х ∈ ( — ∞; + ∞). Почему? А потому что тригонометрические функции — периодические, т.е. просто «вертятся» по кругу. При этом значения синусов и косинусов определяются значениями координат точек на окружности со всеми их знаками. Например, согласно рисунку, координата у точки на окружности, соответствующей углу , определяет , а координата х определяет .
При этом, разумеется, значения синусов и косинусов не выходят за пределы круга. Просто, потому что не могут в силу своей ограниченности! Ну, а мы с вами имеем возможность определятся с синусами и косинусами уже не углов, а аргумента х ∈ ( — ∞; + ∞). Почему? А потому что тригонометрические функции — периодические, т.е. просто «вертятся» по кругу. При этом значения синусов и косинусов определяются значениями координат точек на окружности со всеми их знаками. Например, согласно рисунку, координата у точки на окружности, соответствующей углу , определяет , а координата х определяет . Аналогично поступаем и с «осью котангенсов» В отличие от синусов и косинусов тангенсам и котангенсам прямую проводим через начало координат. То есть на круге два угла для тангенса и два угла для котангенса. Оно и понятно: период функций тангенса и котангенса составляет π, а не 2π, как у функций синуса и косинуса.
Аналогично поступаем и с «осью котангенсов» В отличие от синусов и косинусов тангенсам и котангенсам прямую проводим через начало координат. То есть на круге два угла для тангенса и два угла для котангенса. Оно и понятно: период функций тангенса и котангенса составляет π, а не 2π, как у функций синуса и косинуса.
 Внешний угол при вершине А —
это угол, смежный с углом А. Если
угол А острый, то смежный с ним
угол — тупой, и наоборот.
Внешний угол при вершине А —
это угол, смежный с углом А. Если
угол А острый, то смежный с ним
угол — тупой, и наоборот. Тогда и синус внешнего угла
при вершине В также равен 0,1.
Тогда и синус внешнего угла
при вершине В также равен 0,1.
 Так давайте найдем
sin A:
Так давайте найдем
sin A: Нарисуйте треугольник.
Через одну из его вершин проведите
прямую, параллельную противоположной
стороне, и найдите на рисунке
равные углы. Сравните с решением
в конце статьи.
Нарисуйте треугольник.
Через одну из его вершин проведите
прямую, параллельную противоположной
стороне, и найдите на рисунке
равные углы. Сравните с решением
в конце статьи. Значит, один из углов
треугольника равен 98°, а два других
равны .
Значит, один из углов
треугольника равен 98°, а два других
равны . При этом образуется
восемь углов. Углы при параллельных
прямых и секущей так часто используются
в задачах, что в геометрии им даны
специальные названия.
При этом образуется
восемь углов. Углы при параллельных
прямых и секущей так часто используются
в задачах, что в геометрии им даны
специальные названия.
 Значит, треугольник АВМ —
равнобедренный, следовательно, АВ = АМ
= 4х.
Значит, треугольник АВМ —
равнобедренный, следовательно, АВ = АМ
= 4х.
 Все задачи взяты из Банка
заданий ФИПИ.
Все задачи взяты из Банка
заданий ФИПИ.
 Из треугольника АВС получим,
что ∠
А + ∠
В = 180° — 58° = 122°.
Из треугольника АВС получим,
что ∠
А + ∠
В = 180° — 58° = 122°.
 ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведения
ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведения
 Введите свой запрос:
Введите свой запрос:
 (Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.)
(Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.) 2θ = 1 $$
2θ = 1 $$ Это дает нам следующие значения для синуса и косинуса:
Это дает нам следующие значения для синуса и косинуса: belk / Викимедиа
belk / Викимедиа 
 США ({√3} / 2, 1/2)
США ({√3} / 2, 1/2) США (1/2, — {√3} / 2)
США (1/2, — {√3} / 2) Открытые паевые инвестиционные фонды под управлением АО ВТБ Капитал Управление активами: ОПИФ РФИ «ВТБ – Фонд Казначейский» (Правила фонда зарегистрированы ФКЦБ России 26.02.2003 № 0089-59893097), доходность на 29.01.2021 за 3 мес.: 2,62%, за 6 мес.: 3,47%, за 1 г.: 7,63%, за 3 г.: 28,81%. ОПИФ РФИ «ВТБ — Фонд Акций» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0968-94131582), доходность на 29.01.2021 за 3 мес.: 19,42%, за 6 мес.: 13,24%, за 1 г.: 5,66%, за 3 г.: 66,28%. ОПИФ РФИ «ВТБ — Фонд Еврооблигаций» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0963-94130861), доходность на 29.01.2021 за 3 мес.: 0,68%, за 6 мес.: 9,50%, за 1 г.: 26,22%, за 3 г.: 54,10%. ОПИФ РФИ «ВТБ — Фонд Еврооблигаций развивающихся рынков» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0958-94130789), доходность на 29.01.2021 за 3 мес.: 5,67%, за 6 мес.: 15,80%, за 1 г.: 31,43%, за 3 г.: 64,58%. ОПИФ РФИ «ВТБ — Фонд Компаний малой и средней капитализации» (Правила Фонда зарегистрированы ФСФР России 13.
Открытые паевые инвестиционные фонды под управлением АО ВТБ Капитал Управление активами: ОПИФ РФИ «ВТБ – Фонд Казначейский» (Правила фонда зарегистрированы ФКЦБ России 26.02.2003 № 0089-59893097), доходность на 29.01.2021 за 3 мес.: 2,62%, за 6 мес.: 3,47%, за 1 г.: 7,63%, за 3 г.: 28,81%. ОПИФ РФИ «ВТБ — Фонд Акций» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0968-94131582), доходность на 29.01.2021 за 3 мес.: 19,42%, за 6 мес.: 13,24%, за 1 г.: 5,66%, за 3 г.: 66,28%. ОПИФ РФИ «ВТБ — Фонд Еврооблигаций» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0963-94130861), доходность на 29.01.2021 за 3 мес.: 0,68%, за 6 мес.: 9,50%, за 1 г.: 26,22%, за 3 г.: 54,10%. ОПИФ РФИ «ВТБ — Фонд Еврооблигаций развивающихся рынков» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0958-94130789), доходность на 29.01.2021 за 3 мес.: 5,67%, за 6 мес.: 15,80%, за 1 г.: 31,43%, за 3 г.: 64,58%. ОПИФ РФИ «ВТБ — Фонд Компаний малой и средней капитализации» (Правила Фонда зарегистрированы ФСФР России 13. 09.2007, № 0959-94131180), доходность на 29.01.2021 за 3 мес.: 16,63%, за 6 мес.: 21,41%, за 1 г.: 28,91%, за 3 г.: 74,18%. ОПИФ РФИ «ВТБ – Индекс МосБиржи» (Правила фонда зарегистрированы ФКЦБ России 21.01.2004 № 0177-71671092), доходность на 29.01.2021 за 3 мес.: 20,62%, за 6 мес.: 14,02%, за 1 г.: 10,16%, за 3 г.: 67,75%. ОПИФ РФИ «ВТБ — Фонд Сбалансированный» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0962-94131346), доходность на 29.01.2021 за 3 мес.: 12,35%, за 6 мес.: 9,79%, за 1 г.: 6,17%, за 3 г.: 43,29%. ОПИФ РФИ «ВТБ – Фонд Технологий будущего» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0967-94131429), доходность на 29.01.2021 за 3 мес.: 14,32%, за 6 мес.: 25,35%, за 1 г.: 64,50%, за 3 г.: 105,90%. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Правилами доверительного управления ОПИФ, находящимися под управлением АО ВТБ Капитал Управление активами предусмотрены надбавки (скидки) к (с) расчетной стоимости инвестиционных паев при их выдаче (погашении).
09.2007, № 0959-94131180), доходность на 29.01.2021 за 3 мес.: 16,63%, за 6 мес.: 21,41%, за 1 г.: 28,91%, за 3 г.: 74,18%. ОПИФ РФИ «ВТБ – Индекс МосБиржи» (Правила фонда зарегистрированы ФКЦБ России 21.01.2004 № 0177-71671092), доходность на 29.01.2021 за 3 мес.: 20,62%, за 6 мес.: 14,02%, за 1 г.: 10,16%, за 3 г.: 67,75%. ОПИФ РФИ «ВТБ — Фонд Сбалансированный» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0962-94131346), доходность на 29.01.2021 за 3 мес.: 12,35%, за 6 мес.: 9,79%, за 1 г.: 6,17%, за 3 г.: 43,29%. ОПИФ РФИ «ВТБ – Фонд Технологий будущего» (Правила Фонда зарегистрированы ФСФР России 13.09.2007, № 0967-94131429), доходность на 29.01.2021 за 3 мес.: 14,32%, за 6 мес.: 25,35%, за 1 г.: 64,50%, за 3 г.: 105,90%. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Правилами доверительного управления ОПИФ, находящимися под управлением АО ВТБ Капитал Управление активами предусмотрены надбавки (скидки) к (с) расчетной стоимости инвестиционных паев при их выдаче (погашении). Взимание надбавок (скидок) уменьшит доходность инвестиций в инвестиционные паи ОПИФ. Прежде, чем приобрести инвестиционный пай, следует внимательно ознакомиться с правилами доверительного управления фондом. Получить информацию о Фондах и ознакомиться с Правилами доверительного управления Фондов, с иными документами, предусмотренными Федеральным законом «Об инвестиционных фондах» и нормативными актами в сфере финансовых рынков, можно по адресу: 123112, Россия, г. Москва, Пресненская набережная, д. 10, этаж 15, помещение III, по телефону 8-800-700-44-04 (для бесплатной междугородной и мобильной связи), по адресам агентов или в сети Интернет по адресу www.vtbcapital-am.ru. Информация, подлежащая опубликованию в печатном издании, публикуется в «Приложении к Вестнику Федеральной службы по финансовым рынкам».
Взимание надбавок (скидок) уменьшит доходность инвестиций в инвестиционные паи ОПИФ. Прежде, чем приобрести инвестиционный пай, следует внимательно ознакомиться с правилами доверительного управления фондом. Получить информацию о Фондах и ознакомиться с Правилами доверительного управления Фондов, с иными документами, предусмотренными Федеральным законом «Об инвестиционных фондах» и нормативными актами в сфере финансовых рынков, можно по адресу: 123112, Россия, г. Москва, Пресненская набережная, д. 10, этаж 15, помещение III, по телефону 8-800-700-44-04 (для бесплатной междугородной и мобильной связи), по адресам агентов или в сети Интернет по адресу www.vtbcapital-am.ru. Информация, подлежащая опубликованию в печатном издании, публикуется в «Приложении к Вестнику Федеральной службы по финансовым рынкам».  Лицензия профессионального участника рынка ценных бумаг на осуществление деятельности по управлению ценными бумагами № 045-06475-001000, выдана ФКЦБ России 5 марта 2003 г. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Прежде чем приобрести инвестиционный пай, следует внимательно ознакомиться с Правилами доверительного управления фондом. Правилами фондов предусмотрены надбавки при приобретении и скидки при погашении паев. Взимание надбавок (скидок) уменьшает доходность инвестиций в инвестиционные паи паевых инвестиционных фондов. Вся необходимая информация раскрывается на сайте Управляющей компании и, в случае если это предусмотрено законодательством Российской Федерации и Правилами доверительного управления, публикуется в печатном издании «Приложение к Вестнику ФСФР России». Получить информацию о фондах и ознакомиться с Правилами доверительного управления фондами, иными документами, предусмотренными Федеральным законом «Об инвестиционных фондах» и нормативными актами в сфере финансовых рынков, можно по адресам Агентов по выдаче, погашению и обмену инвестиционных паев, а также по адресу: город Москва, Саввинская набережная, дом 23, строение 1.
Лицензия профессионального участника рынка ценных бумаг на осуществление деятельности по управлению ценными бумагами № 045-06475-001000, выдана ФКЦБ России 5 марта 2003 г. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Прежде чем приобрести инвестиционный пай, следует внимательно ознакомиться с Правилами доверительного управления фондом. Правилами фондов предусмотрены надбавки при приобретении и скидки при погашении паев. Взимание надбавок (скидок) уменьшает доходность инвестиций в инвестиционные паи паевых инвестиционных фондов. Вся необходимая информация раскрывается на сайте Управляющей компании и, в случае если это предусмотрено законодательством Российской Федерации и Правилами доверительного управления, публикуется в печатном издании «Приложение к Вестнику ФСФР России». Получить информацию о фондах и ознакомиться с Правилами доверительного управления фондами, иными документами, предусмотренными Федеральным законом «Об инвестиционных фондах» и нормативными актами в сфере финансовых рынков, можно по адресам Агентов по выдаче, погашению и обмену инвестиционных паев, а также по адресу: город Москва, Саввинская набережная, дом 23, строение 1. Тел.: 8 (495) 788 6646. Адрес Управляющей компании в информационно-телекоммуникационной сети Интернет: www.uralsib-am.ru. Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Глобальные акции» (Правила зарегистрированы ФСФР России, № 2610 от 28.05. 2013 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Глобальные облигации» (Правила зарегистрированы ФСФР России, № 2608 от 28.05.2013 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Первый» (Правила зарегистрированы ФКЦБ России, № 0029-18610555 от 14.09.1998 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Профессиональный» (Правила зарегистрированы ФКЦБ России, № 0053-56612554 от 27.04.2001 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Консервативный» (Правила зарегистрированы ФКЦБ России, № 0056-56658088 от 06.06.2001 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Глобальные инновации».
Тел.: 8 (495) 788 6646. Адрес Управляющей компании в информационно-телекоммуникационной сети Интернет: www.uralsib-am.ru. Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Глобальные акции» (Правила зарегистрированы ФСФР России, № 2610 от 28.05. 2013 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Глобальные облигации» (Правила зарегистрированы ФСФР России, № 2608 от 28.05.2013 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Первый» (Правила зарегистрированы ФКЦБ России, № 0029-18610555 от 14.09.1998 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Профессиональный» (Правила зарегистрированы ФКЦБ России, № 0053-56612554 от 27.04.2001 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Консервативный» (Правила зарегистрированы ФКЦБ России, № 0056-56658088 от 06.06.2001 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Глобальные инновации». (Правила зарегистрированы ФСФР России, № 1142-94140995 от 27.12.2007 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Акции роста» (Правила зарегистрированы ФКЦБ России, № 0030-18610638 от 14.09.1998 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Драгоценные металлы» (Правила зарегистрированы ФСФР России, № 2342 от 19.04.2012) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Природные ресурсы» (Правила зарегистрированы ФСФР России, № 1143-94140753 от 27.12.2007 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Энергетическая перспектива» (Правила зарегистрированы ФСФР России, № 1145-94140670 от 27.12.2007 г.).АО «УК УРАЛСИБ» информирует о совмещении различных видов деятельности, а также о существовании риска возникновения конфликта интересов.
(Правила зарегистрированы ФСФР России, № 1142-94140995 от 27.12.2007 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Акции роста» (Правила зарегистрированы ФКЦБ России, № 0030-18610638 от 14.09.1998 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Драгоценные металлы» (Правила зарегистрированы ФСФР России, № 2342 от 19.04.2012) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Природные ресурсы» (Правила зарегистрированы ФСФР России, № 1143-94140753 от 27.12.2007 г.) Открытый паевой инвестиционный фонд рыночных финансовых инструментов «УРАЛСИБ Энергетическая перспектива» (Правила зарегистрированы ФСФР России, № 1145-94140670 от 27.12.2007 г.).АО «УК УРАЛСИБ» информирует о совмещении различных видов деятельности, а также о существовании риска возникновения конфликта интересов. Эмитенты ФинЭкс Фандс плс (FinEx Funds plc) и ФинЭкс Физикли Бэкт Фандз плс (FinEx Physically Backed Funds plc). Управляющая компания ФинЭкс Инвестмент Менеджмент ЛЛП (FinEx Investment Management LLP) (регистрационный номер ОС407513, зарегистрированный офис: 4 этаж, 39 Довер Стрит, Лондон, W1S 4NN, Великобритания). Информация раскрывается на сайте www.finxplus.ru.ООО «УК «ФинЭкс Плюс» обращает внимание, что инвестиции в рынок ценных бумаг связаны с риском, включая риск потери инвестиций полностью или частично. Стоимость активов может увеличиваться и уменьшаться. Результаты инвестирования в прошлом не определяют доходы в будущем. Информация, указанная на данном сайте, не содержит гарантий надежности возможных инвестиций и стабильности размеров возможных доходов или издержек, связанных с указанными инвестициями; не является заявлением о возможных выгодах, связанных с методами управления активами; не является какого-либо рода офертой; не является индивидуальной инвестиционной рекомендацией.
Эмитенты ФинЭкс Фандс плс (FinEx Funds plc) и ФинЭкс Физикли Бэкт Фандз плс (FinEx Physically Backed Funds plc). Управляющая компания ФинЭкс Инвестмент Менеджмент ЛЛП (FinEx Investment Management LLP) (регистрационный номер ОС407513, зарегистрированный офис: 4 этаж, 39 Довер Стрит, Лондон, W1S 4NN, Великобритания). Информация раскрывается на сайте www.finxplus.ru.ООО «УК «ФинЭкс Плюс» обращает внимание, что инвестиции в рынок ценных бумаг связаны с риском, включая риск потери инвестиций полностью или частично. Стоимость активов может увеличиваться и уменьшаться. Результаты инвестирования в прошлом не определяют доходы в будущем. Информация, указанная на данном сайте, не содержит гарантий надежности возможных инвестиций и стабильности размеров возможных доходов или издержек, связанных с указанными инвестициями; не является заявлением о возможных выгодах, связанных с методами управления активами; не является какого-либо рода офертой; не является индивидуальной инвестиционной рекомендацией. Указанные доходности рассчитаны как процентный прирост значений стоимости чистых активов (СЧА) фондов в расчете на 1 акцию на 31.08.2018 и 30.08.2019. Для перевода доходностей в рублевые и долларовые использовались курсы доллара, евро и фунта стерлингов, установленные Банком России, и значения курсов EUR/USD, GBP/USD и KZT/USD из терминала Bloomberg на указанные даты. Финансовые инструменты либо операции, упомянутые на данном сайте, могут не соответствовать вашему инвестиционному профилю. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «УК «ФинЭкс Плюс» не несет ответственности за возможные убытки инвестора в случае совершения операций либо инвестирования в финансовые инструменты, информация о которых приведена на данном сайте ООО «УК «ФинЭкс Плюс» не дает гарантий или заверений и не принимает какой-либо ответственности в отношении финансовых результатов, полученных на основании использования указанной информации.
Указанные доходности рассчитаны как процентный прирост значений стоимости чистых активов (СЧА) фондов в расчете на 1 акцию на 31.08.2018 и 30.08.2019. Для перевода доходностей в рублевые и долларовые использовались курсы доллара, евро и фунта стерлингов, установленные Банком России, и значения курсов EUR/USD, GBP/USD и KZT/USD из терминала Bloomberg на указанные даты. Финансовые инструменты либо операции, упомянутые на данном сайте, могут не соответствовать вашему инвестиционному профилю. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «УК «ФинЭкс Плюс» не несет ответственности за возможные убытки инвестора в случае совершения операций либо инвестирования в финансовые инструменты, информация о которых приведена на данном сайте ООО «УК «ФинЭкс Плюс» не дает гарантий или заверений и не принимает какой-либо ответственности в отношении финансовых результатов, полученных на основании использования указанной информации.
 Номера и даты регистрации правил в ФСФР России: ОПИФ рыночных финансовых инструментов «Райффайзен — Акции» — 0241-74050443 от 04.08.2004 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Облигации» — 0242-74050284 от 04.08.2004 г.; ОПИФ рыночных финансовых инструментов «Райффайзен – Дивидендные акции» — 0243-74050367 от 04.08.2004 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — США» — 0647-94120199 от 26.10.2006 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Потребительский сектор» — 0986-94131808 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Сырьевой сектор» — 0987-94132127 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Информационные технологии» — 0988-94131961 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Электроэнергетика» — 0981-94132044 от 20.09.2007г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Индустриальный» — 0984-94131889 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Драгоценные металлы» — № 1953-94168467 от 27.
Номера и даты регистрации правил в ФСФР России: ОПИФ рыночных финансовых инструментов «Райффайзен — Акции» — 0241-74050443 от 04.08.2004 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Облигации» — 0242-74050284 от 04.08.2004 г.; ОПИФ рыночных финансовых инструментов «Райффайзен – Дивидендные акции» — 0243-74050367 от 04.08.2004 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — США» — 0647-94120199 от 26.10.2006 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Потребительский сектор» — 0986-94131808 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Сырьевой сектор» — 0987-94132127 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Информационные технологии» — 0988-94131961 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Электроэнергетика» — 0981-94132044 от 20.09.2007г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Индустриальный» — 0984-94131889 от 20.09.2007 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Драгоценные металлы» — № 1953-94168467 от 27. 10.2010 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Европа» — № 2063-94172606 от 22.02.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Развивающиеся рынки» — № 2075-94172523 от 03.03.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Золото» — № 2241 от 08.11.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен – Корпоративные облигации» — № 2260 от 29.11.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Фонд активного управления» — № 2261 от 29.11.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Долговые рынки развитых стран» — № 2356 от 15.05.2012 г. Стоимость инвестиционных паев может увеличиваться и уменьшаться. Результаты инвестирования в прошлом не определяют доходы в будущем. Взимание скидок уменьшает доходность вложений в инвестиционные паи паевых инвестиционных фондов. Ни государство, ни управляющая компания не гарантируют доходность инвестиций в паевые инвестиционные фонды. ООО «УК «Райффайзен Капитал» — лицензия ФСФР России № 21-000-1-00640 от 21.
10.2010 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Европа» — № 2063-94172606 от 22.02.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Развивающиеся рынки» — № 2075-94172523 от 03.03.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Золото» — № 2241 от 08.11.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен – Корпоративные облигации» — № 2260 от 29.11.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Фонд активного управления» — № 2261 от 29.11.2011 г.; ОПИФ рыночных финансовых инструментов «Райффайзен — Долговые рынки развитых стран» — № 2356 от 15.05.2012 г. Стоимость инвестиционных паев может увеличиваться и уменьшаться. Результаты инвестирования в прошлом не определяют доходы в будущем. Взимание скидок уменьшает доходность вложений в инвестиционные паи паевых инвестиционных фондов. Ни государство, ни управляющая компания не гарантируют доходность инвестиций в паевые инвестиционные фонды. ООО «УК «Райффайзен Капитал» — лицензия ФСФР России № 21-000-1-00640 от 21. 04.2009 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, лицензия ФСФР России № 045-10230-001000 от 31.05.2007 на осуществление деятельности по доверительному управлению ценными бумагами.
04.2009 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, лицензия ФСФР России № 045-10230-001000 от 31.05.2007 на осуществление деятельности по доверительному управлению ценными бумагами. 03.2003 г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Баланс» на 30 ноября за 3 мес. 2,97%, за 6 мес. 11,86 %, 1 год 7,57%, за 3 года 49,19 %. Правила доверительного управления № 0500-94103344 зарегистрированы ФСФР России 13.04.2006 г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Золото» на 30 ноября за 3 мес. 8,98%, за 6 мес. 6,54%, 1 год 29,15% за 3 года 53,28%. Правила доверительного управления (ДУ) № 0908-94126724 зарегистрированы ФСФР России 07.08.2007 г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Глобальный Баланс» на 30 ноября за 3 мес. 2,81%, за 6 мес. 23,54%, за 1 год 29,79%, за 3 года 24,29%. Правила ДУ № 0907-94126486 зарегистрированы ФСФР России 07.08.2007г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Еврооблигации» на 30 ноября за 3 мес.
03.2003 г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Баланс» на 30 ноября за 3 мес. 2,97%, за 6 мес. 11,86 %, 1 год 7,57%, за 3 года 49,19 %. Правила доверительного управления № 0500-94103344 зарегистрированы ФСФР России 13.04.2006 г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Золото» на 30 ноября за 3 мес. 8,98%, за 6 мес. 6,54%, 1 год 29,15% за 3 года 53,28%. Правила доверительного управления (ДУ) № 0908-94126724 зарегистрированы ФСФР России 07.08.2007 г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Глобальный Баланс» на 30 ноября за 3 мес. 2,81%, за 6 мес. 23,54%, за 1 год 29,79%, за 3 года 24,29%. Правила ДУ № 0907-94126486 зарегистрированы ФСФР России 07.08.2007г. Прирост стоимости пая открытого паевого инвестиционного фонда (ПИФ) рыночных финансовых инструментов (РФИ) «Альфа-Капитал Еврооблигации» на 30 ноября за 3 мес. 6,17%, за 6 мес. 23,45%, за 1 год 37,33%, за 3 года 70,82%. Правила доверительного управления (ДУ) № 0387-78483850 зарегистрированы ФСФР России 18.08.2005 г. Правилами ДУ ПИФ, находящимися под управлением ООО УК «Альфа-Капитал», предусмотрены надбавки к расчетной стоимости инвестиционных паев при их выдаче и скидки к расчетной стоимости паев при их погашении. Взимание скидок и надбавок уменьшает доходность инвестиций в инвестиционные паи ПИФ. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в инвестиционные фонды. Перед приобретением инвестиционного пая ознакомьтесь с правилами ДУ ПИФ. ООО УК «Альфа-Капитал»: 123001,Москва,ул.Садовая-Кудринская, д. 32, стр.1. 8 (800)2002828, alfacapital.ru. Лицензия № 21-000-1-00028 от 22.09.98г. выдана ФСФР России. Не является индивидуальной инвестиционной рекомендацией. Упоминаемые финансовые инструменты могут не подходить соответствующему клиенту.
6,17%, за 6 мес. 23,45%, за 1 год 37,33%, за 3 года 70,82%. Правила доверительного управления (ДУ) № 0387-78483850 зарегистрированы ФСФР России 18.08.2005 г. Правилами ДУ ПИФ, находящимися под управлением ООО УК «Альфа-Капитал», предусмотрены надбавки к расчетной стоимости инвестиционных паев при их выдаче и скидки к расчетной стоимости паев при их погашении. Взимание скидок и надбавок уменьшает доходность инвестиций в инвестиционные паи ПИФ. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в инвестиционные фонды. Перед приобретением инвестиционного пая ознакомьтесь с правилами ДУ ПИФ. ООО УК «Альфа-Капитал»: 123001,Москва,ул.Садовая-Кудринская, д. 32, стр.1. 8 (800)2002828, alfacapital.ru. Лицензия № 21-000-1-00028 от 22.09.98г. выдана ФСФР России. Не является индивидуальной инвестиционной рекомендацией. Упоминаемые финансовые инструменты могут не подходить соответствующему клиенту.
 11.2020 за 1 мес. — 16,9%, 3 мес. — 7,8%, за 6 мес. — 20,1%, за 1 г. — 11,5%.ОПИФ рыночных финансовых инструментов «Газпромбанк — Валютные облигации» (Правила доверительного управления зарегистрированы ФСФР России 21.09.2006 г. за № 0620–94123708): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 2,8%, за 6 мес. — 9,6%, с начала 2020 года — 26,8%, за 1 г. — 23,3%, за 3 г. — 43,0%.ОПИФ рыночных финансовых инструментов «Газпромбанк — Сбалансированный» (Правила доверительного управления зарегистрированы ФСФР России 21.09.2006 г. за № 0622–94123683): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 8,00%, за 6 мес. — 11,97%, за 1 г. — 5,26%, за 3 г. — 37,56%. ОПИФ рыночных финансовых инструментов «Газпромбанк — Электроэнергетика» (Правила доверительного управления зарегистрированы ФСФР России 04.10.2007 г. за № 1014–94132162): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020 за 1 мес. — 6,1%, 3 мес.
11.2020 за 1 мес. — 16,9%, 3 мес. — 7,8%, за 6 мес. — 20,1%, за 1 г. — 11,5%.ОПИФ рыночных финансовых инструментов «Газпромбанк — Валютные облигации» (Правила доверительного управления зарегистрированы ФСФР России 21.09.2006 г. за № 0620–94123708): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 2,8%, за 6 мес. — 9,6%, с начала 2020 года — 26,8%, за 1 г. — 23,3%, за 3 г. — 43,0%.ОПИФ рыночных финансовых инструментов «Газпромбанк — Сбалансированный» (Правила доверительного управления зарегистрированы ФСФР России 21.09.2006 г. за № 0622–94123683): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 8,00%, за 6 мес. — 11,97%, за 1 г. — 5,26%, за 3 г. — 37,56%. ОПИФ рыночных финансовых инструментов «Газпромбанк — Электроэнергетика» (Правила доверительного управления зарегистрированы ФСФР России 04.10.2007 г. за № 1014–94132162): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020 за 1 мес. — 6,1%, 3 мес. — 3,3%, за 6 мес. — 6,5%, за 1 г. — 17,5%.ОПИФ рыночных финансовых инструментов «Газпромбанк — Золото» (Правила доверительного управления зарегистрированы ФСФР России 31.05.2012 г. за № 2361): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — (-9,7%), за 6 мес. — 8,1%, с начала 2020 года — 42,2%, за 1 г. — 42,9%, за 3 г. — 73,1%. ОПИФ рыночных финансовых инструментов «Газпромбанк — Облигации плюс» (Правила доверительного управления зарегистрированы ФСФР России 14.02.2013 г. за № 2547): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 ОПИФ рыночных финансовых инструментов «Газпромбанк – Индия» (Правила доверительного управления зарегистрированы ФСФР России 05.12.2006 г. за № 0687–94123720):cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 12,94%, за 6 мес. — 27,72%, за 1 г. — 30,06%, за 3 г. — 26,22%. ОПИФ рыночных финансовых инструментов «Газпромбанк – Нефть» (Правила доверительного управления зарегистрированы ФСФР России 04.
— 3,3%, за 6 мес. — 6,5%, за 1 г. — 17,5%.ОПИФ рыночных финансовых инструментов «Газпромбанк — Золото» (Правила доверительного управления зарегистрированы ФСФР России 31.05.2012 г. за № 2361): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — (-9,7%), за 6 мес. — 8,1%, с начала 2020 года — 42,2%, за 1 г. — 42,9%, за 3 г. — 73,1%. ОПИФ рыночных финансовых инструментов «Газпромбанк — Облигации плюс» (Правила доверительного управления зарегистрированы ФСФР России 14.02.2013 г. за № 2547): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 ОПИФ рыночных финансовых инструментов «Газпромбанк – Индия» (Правила доверительного управления зарегистрированы ФСФР России 05.12.2006 г. за № 0687–94123720):cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 12,94%, за 6 мес. — 27,72%, за 1 г. — 30,06%, за 3 г. — 26,22%. ОПИФ рыночных финансовых инструментов «Газпромбанк – Нефть» (Правила доверительного управления зарегистрированы ФСФР России 04.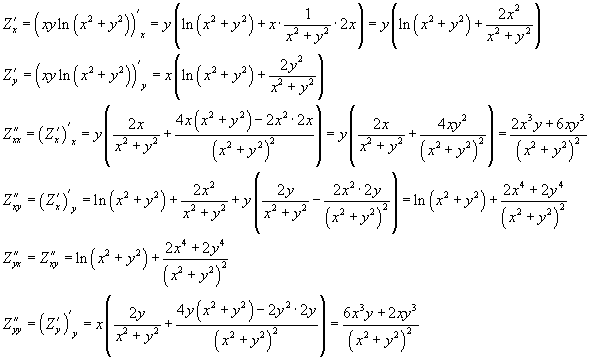 10.2007 г. за № 1015–94132245): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 40,94%, за 6 мес. — 25,82%, за 1 г. — -(3,33%), за 3 г. — -(18,40%). ОПИФ рыночных финансовых инструментов «Газпромбанк – Фонд международных дивидендов» (Правила доверительного управления зарегистрированы ФСФР России 10.11.2011 г. за № 2244): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 12,44%, за 6 мес. — 20,11%, за 1 г. — 22,07%, за 3 г. — 30,04%.мес. — 1,3%, за 6 мес. — 2,3%, с начала 2020 года — 6,35%, за 1 г. — 7,4%, за 3 г. — 23,1%.АО «ГПБ – УА» напоминает инвесторам, что стоимость инвестиционных паев может увеличиваться и уменьшаться. Результаты инвестирования в прошлом не определяют доходы в будущем. Государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Прежде, чем приобрести инвестиционный пай, следует внимательно ознакомиться с правилами доверительного управления паевыми инвестиционными фондами.
10.2007 г. за № 1015–94132245): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 40,94%, за 6 мес. — 25,82%, за 1 г. — -(3,33%), за 3 г. — -(18,40%). ОПИФ рыночных финансовых инструментов «Газпромбанк – Фонд международных дивидендов» (Правила доверительного управления зарегистрированы ФСФР России 10.11.2011 г. за № 2244): cведения о приросте расчетной стоимости инвестиционного пая на 30.11.2020: за 3 мес. — 12,44%, за 6 мес. — 20,11%, за 1 г. — 22,07%, за 3 г. — 30,04%.мес. — 1,3%, за 6 мес. — 2,3%, с начала 2020 года — 6,35%, за 1 г. — 7,4%, за 3 г. — 23,1%.АО «ГПБ – УА» напоминает инвесторам, что стоимость инвестиционных паев может увеличиваться и уменьшаться. Результаты инвестирования в прошлом не определяют доходы в будущем. Государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Прежде, чем приобрести инвестиционный пай, следует внимательно ознакомиться с правилами доверительного управления паевыми инвестиционными фондами. Получить подробную информацию о паевых инвестиционных фондах под управлением АО «ГПБ – УА» и ознакомиться с правилами доверительного управления, а также иными документами, предусмотренными Федеральным законом «Об инвестиционных фондах» и нормативными актами в сфере финансовых рынков, можно по адресу: 119049, Москва, ул. Коровий Вал, д. 7, тел. (495) 980-40-58 или в сети Интернет по адресу www.gpb-am.ru, а также в пунктах приёма заявок агентов по выдаче, погашению и обмену инвестиционных паев фондов (со списком агентов можно ознакомиться на сайте в сети Интернет по адресу www.gpb-am.ru). Информация, подлежащая в соответствии с нормативными актами в сфере финансовых рынков опубликованию в печатном издании, публикуется в «Приложении к Вестнику Федеральной службы по финансовым рынкам». В случае если, Правилами доверительного управления паевыми инвестиционными фондами, предусмотрены надбавки к расчетной стоимости инвестиционных паев при их выдаче и скидки к расчетной стоимости паев при их погашении, взимание данных скидок и надбавок уменьшает доходность инвестиций в инвестиционные паи паевых инвестиционных фондов.
Получить подробную информацию о паевых инвестиционных фондах под управлением АО «ГПБ – УА» и ознакомиться с правилами доверительного управления, а также иными документами, предусмотренными Федеральным законом «Об инвестиционных фондах» и нормативными актами в сфере финансовых рынков, можно по адресу: 119049, Москва, ул. Коровий Вал, д. 7, тел. (495) 980-40-58 или в сети Интернет по адресу www.gpb-am.ru, а также в пунктах приёма заявок агентов по выдаче, погашению и обмену инвестиционных паев фондов (со списком агентов можно ознакомиться на сайте в сети Интернет по адресу www.gpb-am.ru). Информация, подлежащая в соответствии с нормативными актами в сфере финансовых рынков опубликованию в печатном издании, публикуется в «Приложении к Вестнику Федеральной службы по финансовым рынкам». В случае если, Правилами доверительного управления паевыми инвестиционными фондами, предусмотрены надбавки к расчетной стоимости инвестиционных паев при их выдаче и скидки к расчетной стоимости паев при их погашении, взимание данных скидок и надбавок уменьшает доходность инвестиций в инвестиционные паи паевых инвестиционных фондов. Приём обращений от владельцев инвестиционных паев и иных заинтересованных лиц осуществляется по адресу: 119049, Москва, ул. Коровий Вал, д. 7, а также в пунктах приёма заявок агентов по выдаче, погашению и обмену инвестиционных паев фондов. Настоящее уведомление не является индивидуальной инвестиционной рекомендацией, и инвестиционные паи открытых и биржевых паевых инвестиционных фондов под управлением АО «ГПБ – УА» могут не соответствовать инвестиционному профилю и инвестиционным целям (ожиданиям) инвестора. В информации, указанной в данном уведомлении, не принимаются во внимание личные инвестиционные цели, финансовые условия или нужды каждого конкретного инвестора. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и уровню допустимого риска является задачей инвестора. АО «ГПБ – УА» не несет ответственности за возможные убытки инвестора в случае совершения операций либо инвестирования в инвестиционные паи открытых и биржевых паевых инвестиционных фондов под управлением АО «ГПБ – УА», упомянутые в данном уведомлении, и не рекомендует использовать указанную информацию в качестве единственного источника информации при принятии инвестиционного решения.
Приём обращений от владельцев инвестиционных паев и иных заинтересованных лиц осуществляется по адресу: 119049, Москва, ул. Коровий Вал, д. 7, а также в пунктах приёма заявок агентов по выдаче, погашению и обмену инвестиционных паев фондов. Настоящее уведомление не является индивидуальной инвестиционной рекомендацией, и инвестиционные паи открытых и биржевых паевых инвестиционных фондов под управлением АО «ГПБ – УА» могут не соответствовать инвестиционному профилю и инвестиционным целям (ожиданиям) инвестора. В информации, указанной в данном уведомлении, не принимаются во внимание личные инвестиционные цели, финансовые условия или нужды каждого конкретного инвестора. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и уровню допустимого риска является задачей инвестора. АО «ГПБ – УА» не несет ответственности за возможные убытки инвестора в случае совершения операций либо инвестирования в инвестиционные паи открытых и биржевых паевых инвестиционных фондов под управлением АО «ГПБ – УА», упомянутые в данном уведомлении, и не рекомендует использовать указанную информацию в качестве единственного источника информации при принятии инвестиционного решения. **Дополнительная информация: ОПИФ рыночных финансовых инструментов «Газпромбанк — Валютные облигации» Вознаграждение УК: 2% (от среднегодовой СЧА).Вознаграждение спец. депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).ОПИФ рыночных финансовых инструментов «Газпромбанк — Акции» Вознаграждение УК: 3% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА). ОПИФ рыночных финансовых инструментов «Газпромбанк — Золото» Вознаграждение УК: 2,5% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА),ОПИФ рыночных финансовых инструментов «Газпромбанк — Облигации плюс» Вознаграждение УК: 2% (от среднегодовой СЧА). Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).
**Дополнительная информация: ОПИФ рыночных финансовых инструментов «Газпромбанк — Валютные облигации» Вознаграждение УК: 2% (от среднегодовой СЧА).Вознаграждение спец. депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).ОПИФ рыночных финансовых инструментов «Газпромбанк — Акции» Вознаграждение УК: 3% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА). ОПИФ рыночных финансовых инструментов «Газпромбанк — Золото» Вознаграждение УК: 2,5% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА),ОПИФ рыночных финансовых инструментов «Газпромбанк — Облигации плюс» Вознаграждение УК: 2% (от среднегодовой СЧА). Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).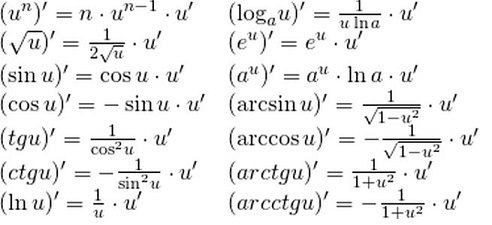 ОПИФ рыночных финансовых инструментов «Газпромбанк — Сбалансированный» Вознаграждение УК: 2,75% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).ОПИФ рыночных финансовых инструментов «Газпромбанк — Электроэнергетика» Вознаграждение УК: 3% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА). Прочие расходы: не более 0,5% (от среднегодовой СЧА).ОПИФ рыночных финансовых инструментов «Газпромбанк – Индия» Вознаграждение УК: 2,5% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА). ОПИФ рыночных финансовых инструментов «Газпромбанк – Нефть» Вознаграждение УК: 2,5% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).
ОПИФ рыночных финансовых инструментов «Газпромбанк — Сбалансированный» Вознаграждение УК: 2,75% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА).ОПИФ рыночных финансовых инструментов «Газпромбанк — Электроэнергетика» Вознаграждение УК: 3% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 0,5% (от среднегодовой СЧА). Прочие расходы: не более 0,5% (от среднегодовой СЧА).ОПИФ рыночных финансовых инструментов «Газпромбанк – Индия» Вознаграждение УК: 2,5% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА). ОПИФ рыночных финансовых инструментов «Газпромбанк – Нефть» Вознаграждение УК: 2,5% (от среднегодовой СЧА).Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА).Прочие расходы: не более 0,5% (от среднегодовой СЧА). ОПИФ рыночных финансовых инструментов «Газпромбанк – Фонд международных дивидендов» Вознаграждение УК: 2,5% (от среднегодовой СЧА). Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА). Прочие расходы: не более 0,5% (от среднегодовой СЧА).Дополнительная информация о скидках, надбавках и минимальной сумме первоначальных инвестиций через агента, УК и сервис «Личный кабинет клиента» приведена в правилах доверительного управления.
ОПИФ рыночных финансовых инструментов «Газпромбанк – Фонд международных дивидендов» Вознаграждение УК: 2,5% (от среднегодовой СЧА). Вознаграждение спец.депу, регистратору, аудитору: не более 1% (от среднегодовой СЧА). Прочие расходы: не более 0,5% (от среднегодовой СЧА).Дополнительная информация о скидках, надбавках и минимальной сумме первоначальных инвестиций через агента, УК и сервис «Личный кабинет клиента» приведена в правилах доверительного управления.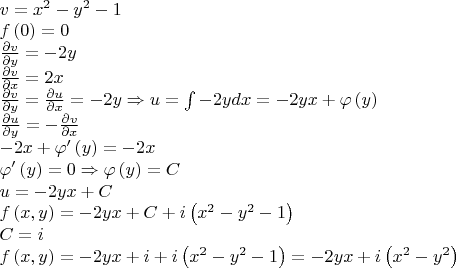 Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.Получить подробную информацию о доверительном управлении, в том числе об услугах по индивидуальному доверительному управлению можно по адресу: Российская Федерация, 115114, город Москва, улица Кожевническая, дом 14, строение 5, тел.: (495) 232-59-73, в сети Интернет по адресу: www.open-am.ru, а также у агентов, со списком которых можно ознакомиться на сайте www.open-am.ru.Получить подробную информацию о паевых инвестиционных фондах и ознакомиться с правилами доверительного управления паевыми инвестиционными фондами, а также иными документами можно по адресу: Российская Федерация, 115114, город Москва, улица Кожевническая, дом 14, строение 5, тел.: (495) 232-59-73, в сети Интернет по адресу:www.open-am.ru, а также у агентов, осуществляющих прием заявок на приобретение, обмен и погашение инвестиционных паев фондов в местах приема заявок на приобретение, обмен и погашение инвестиционных паев, со списком которых можно ознакомиться в сети Интернет по адресу:www.
Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.Получить подробную информацию о доверительном управлении, в том числе об услугах по индивидуальному доверительному управлению можно по адресу: Российская Федерация, 115114, город Москва, улица Кожевническая, дом 14, строение 5, тел.: (495) 232-59-73, в сети Интернет по адресу: www.open-am.ru, а также у агентов, со списком которых можно ознакомиться на сайте www.open-am.ru.Получить подробную информацию о паевых инвестиционных фондах и ознакомиться с правилами доверительного управления паевыми инвестиционными фондами, а также иными документами можно по адресу: Российская Федерация, 115114, город Москва, улица Кожевническая, дом 14, строение 5, тел.: (495) 232-59-73, в сети Интернет по адресу:www.open-am.ru, а также у агентов, осуществляющих прием заявок на приобретение, обмен и погашение инвестиционных паев фондов в местах приема заявок на приобретение, обмен и погашение инвестиционных паев, со списком которых можно ознакомиться в сети Интернет по адресу:www. open-am.ru.Прежде чем приобрести инвестиционный пай, следует внимательно ознакомиться с правилами доверительного управления паевым инвестиционным фондом. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Взимание надбавок (скидок) уменьшит доходность инвестиций в инвестиционные паи паевого инвестиционного фонда. Результаты деятельности управляющего по управлению ценными бумагами в прошлом не определяют доходы учредителя управления в будущем.Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Акции» зарегистрированы ФКЦБ России 17.12.2003 №0164-70287842; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Облигации» зарегистрированы ФКЦБ России 17.12.2003 №0165-70287767; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Индекс МосБиржи» зарегистрированы ФСФР России 05.
open-am.ru.Прежде чем приобрести инвестиционный пай, следует внимательно ознакомиться с правилами доверительного управления паевым инвестиционным фондом. Стоимость инвестиционных паев может увеличиваться и уменьшаться, результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в паевые инвестиционные фонды. Взимание надбавок (скидок) уменьшит доходность инвестиций в инвестиционные паи паевого инвестиционного фонда. Результаты деятельности управляющего по управлению ценными бумагами в прошлом не определяют доходы учредителя управления в будущем.Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Акции» зарегистрированы ФКЦБ России 17.12.2003 №0164-70287842; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Облигации» зарегистрированы ФКЦБ России 17.12.2003 №0165-70287767; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Индекс МосБиржи» зарегистрированы ФСФР России 05. 07.2007 №0890-94127385; Правила доверительного управления ЗПИФ денежного рынка «Царский мост» зарегистрированы ФСФР России 08.11.2007 №1073-58229210; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Лидеры инноваций» зарегистрированы ФСФР России 16.04.2013 №2586; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Еврооблигации» зарегистрированы ФСФР России 08.12.2011 №2275; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Золото» зарегистрированы ФСФР России 08.12.2011 №2277; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Глобальные инвестиции» зарегистрированы Банком России 29.10.2015 №3059; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Золотой капитал» зарегистрированы Банком России 31.08.2020 №4149; Правила доверительного управления БПИФ рыночных финансовых инструментов «Открытие — Всепогодный» зарегистрированы Банком России 27.
07.2007 №0890-94127385; Правила доверительного управления ЗПИФ денежного рынка «Царский мост» зарегистрированы ФСФР России 08.11.2007 №1073-58229210; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Лидеры инноваций» зарегистрированы ФСФР России 16.04.2013 №2586; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Еврооблигации» зарегистрированы ФСФР России 08.12.2011 №2275; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Золото» зарегистрированы ФСФР России 08.12.2011 №2277; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Открытие — Глобальные инвестиции» зарегистрированы Банком России 29.10.2015 №3059; Правила доверительного управления ОПИФ рыночных финансовых инструментов «Золотой капитал» зарегистрированы Банком России 31.08.2020 №4149; Правила доверительного управления БПИФ рыночных финансовых инструментов «Открытие — Всепогодный» зарегистрированы Банком России 27. 08.2020 за № 4147.*При опубликовании раскрываемой информации на сайте www.open-am.ru доступ к такой информации бессрочен.Уважаемый Клиент! Обращаем Ваше внимание, что клиенты обязаны предоставлять организациям, осуществляющим операции с денежными средствами или иным имуществом, информацию, необходимую для исполнения указанными организациями требований Федерального закона от 07.08.2001 N 115-ФЗ «О противодействии легализации (отмыванию) доходов, полученных преступным путем, и финансированию терроризма«, включая информацию о своих выгодоприобретателях и бенефициарных владельцах. Просим Вас своевременно обновлять информацию, предоставленную ООО УК «Открытие» при заключении договоров доверительного управления и приобретении паёв паевых инвестиционных фондов.Размещенная на сайте информация носит исключительно информативный характер, представленная в них информация не является индивидуальной инвестиционной рекомендацией, гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем.
08.2020 за № 4147.*При опубликовании раскрываемой информации на сайте www.open-am.ru доступ к такой информации бессрочен.Уважаемый Клиент! Обращаем Ваше внимание, что клиенты обязаны предоставлять организациям, осуществляющим операции с денежными средствами или иным имуществом, информацию, необходимую для исполнения указанными организациями требований Федерального закона от 07.08.2001 N 115-ФЗ «О противодействии легализации (отмыванию) доходов, полученных преступным путем, и финансированию терроризма«, включая информацию о своих выгодоприобретателях и бенефициарных владельцах. Просим Вас своевременно обновлять информацию, предоставленную ООО УК «Открытие» при заключении договоров доверительного управления и приобретении паёв паевых инвестиционных фондов.Размещенная на сайте информация носит исключительно информативный характер, представленная в них информация не является индивидуальной инвестиционной рекомендацией, гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. УК «Открытие» не несет ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершенных на основании данных, содержащихся в публикациях.
УК «Открытие» не несет ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершенных на основании данных, содержащихся в публикациях.
 Результаты деятельности управляющего по управлению ценными бумагами в прошлом не определяют и не являются гарантией доходности учредителя управления в будущем. Управляющий не гарантирует достижения ожидаемой доходности, определенной в инвестиционном профиле и (или) в стандартном инвестиционном профиле учредителя управления.
Результаты деятельности управляющего по управлению ценными бумагами в прошлом не определяют и не являются гарантией доходности учредителя управления в будущем. Управляющий не гарантирует достижения ожидаемой доходности, определенной в инвестиционном профиле и (или) в стандартном инвестиционном профиле учредителя управления. 02.2019, Банк России;Открытый паевой инвестиционный фонд рыночных финансовых инструментов «БКС Мировые ресурсы», регистрационный номер правил фонда: 4284, дата регистрации 28.01.2021, Банк России.
02.2019, Банк России;Открытый паевой инвестиционный фонд рыночных финансовых инструментов «БКС Мировые ресурсы», регистрационный номер правил фонда: 4284, дата регистрации 28.01.2021, Банк России. Москва, 1-й Красногвардейский проезд, д. 15, 18 этаж, офис 18.02, страница в сети Интернет: ffin.ru, тел.: +7 (495) 783-91-73. Стоимость инвестиционных паев может увеличиваться или уменьшаться. Результаты инвестирования в прошлом не определяют доходов в будущем, государство не гарантирует доходности инвестиций в инвестиционные фонды. Предупреждаем о необходимости внимательного ознакомления с правилами доверительного управления паевым инвестиционным фондом перед приобретением инвестиционных паев. Данная информация не является какими-либо гарантиями и обещаниями о будущей эффективности и доходности инвестиционной деятельности управляющей компании паевого инвестиционного фонда, гарантиями безопасности инвестиций и стабильности размеров возможных доходов или издержек, связанных с указанными инвестициями, утверждениями или заявлениями о возможных выгодах, связанных с услугами или методами работы управляющей компании паевого инвестиционного фонда. Результаты деятельности управляющей компании паевого инвестиционного фонда, достигнутые в прошлом, могут не быть повторены в будущем.
Москва, 1-й Красногвардейский проезд, д. 15, 18 этаж, офис 18.02, страница в сети Интернет: ffin.ru, тел.: +7 (495) 783-91-73. Стоимость инвестиционных паев может увеличиваться или уменьшаться. Результаты инвестирования в прошлом не определяют доходов в будущем, государство не гарантирует доходности инвестиций в инвестиционные фонды. Предупреждаем о необходимости внимательного ознакомления с правилами доверительного управления паевым инвестиционным фондом перед приобретением инвестиционных паев. Данная информация не является какими-либо гарантиями и обещаниями о будущей эффективности и доходности инвестиционной деятельности управляющей компании паевого инвестиционного фонда, гарантиями безопасности инвестиций и стабильности размеров возможных доходов или издержек, связанных с указанными инвестициями, утверждениями или заявлениями о возможных выгодах, связанных с услугами или методами работы управляющей компании паевого инвестиционного фонда. Результаты деятельности управляющей компании паевого инвестиционного фонда, достигнутые в прошлом, могут не быть повторены в будущем. *Изменение стоимости пая – Расчетная величина, представляющая соотношение суммы денежных средств (стоимости имущества), на которую выдавался инвестиционный пай при формировании Фонда согласно Правил доверительного управления фондом в редакции от 31.01.2021 года, и ценой закрытия организованных торгов на ПАО Московская биржа на указанную дату, с учетом операции дробления инвестиционных паев (Изменения и дополнения №5) в Правила доверительного управления Фондом от 08.07.2020, сообщение о регистрации изменений в части количества выданных инвестиционных паев Фонда в результате их дробления).
*Изменение стоимости пая – Расчетная величина, представляющая соотношение суммы денежных средств (стоимости имущества), на которую выдавался инвестиционный пай при формировании Фонда согласно Правил доверительного управления фондом в редакции от 31.01.2021 года, и ценой закрытия организованных торгов на ПАО Московская биржа на указанную дату, с учетом операции дробления инвестиционных паев (Изменения и дополнения №5) в Правила доверительного управления Фондом от 08.07.2020, сообщение о регистрации изменений в части количества выданных инвестиционных паев Фонда в результате их дробления).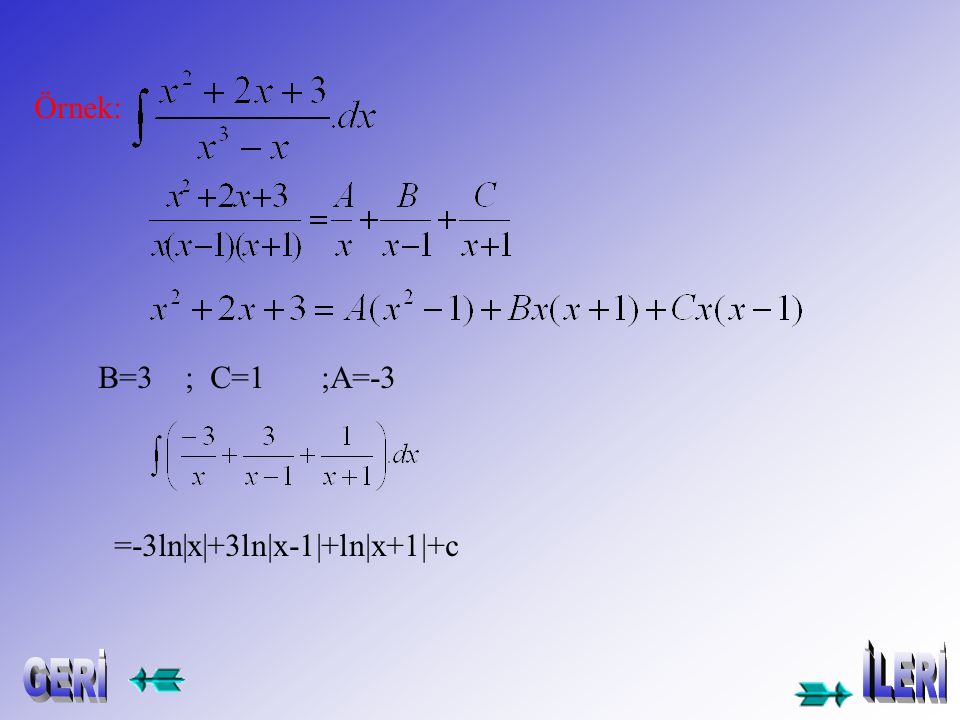 То есть приобретая паи такого фонда на бирже, вы вкладываете в целый набор активов, входящих в индекс. Более подробно о том, что такое ETF, можете прочесть в нашей статье.
То есть приобретая паи такого фонда на бирже, вы вкладываете в целый набор активов, входящих в индекс. Более подробно о том, что такое ETF, можете прочесть в нашей статье. 10.2013
10.2013

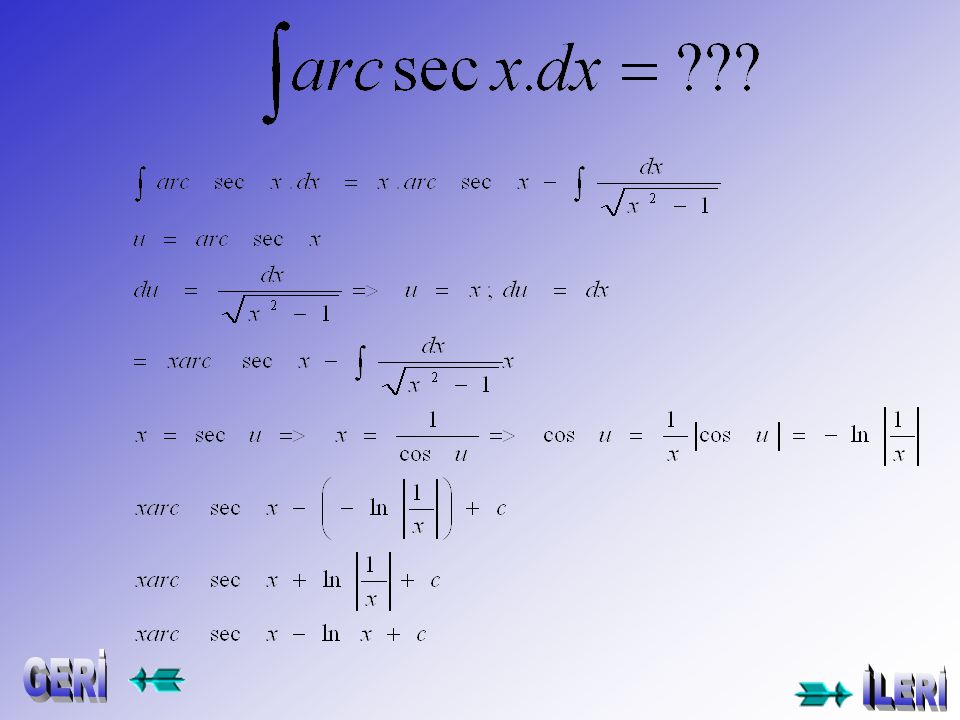 Правда более глубокие падения в будущем не исключены.
Правда более глубокие падения в будущем не исключены.
 Банк не гарантирует доходов от указанных в данном разделе операций с финансовыми инструментами и не несет ответственности за результаты Ваших инвестиционных решений, принятых на основании предоставленной Банком информации. Никакие финансовые инструменты, продукты или услуги, упомянутые в настоящем документе, не предлагаются к продаже и не продаются в какой-либо юрисдикции, где такая деятельность противоречила бы законодательству о ценных бумагах или другим местным законам и нормативно-правовым актам или обязывала бы Банк выполнить требование регистрации в такой юрисдикции. В частности, доводим до Вашего сведения, что ряд государств (в частности, США и Европейский Союз) ввел режим санкций, которые запрещают резидентам соответствующих государств приобретение (содействие в приобретении) долговых инструментов, выпущенных Банком. Банк предлагает Вам убедиться в том, что Вы имеете право инвестировать средства в упомянутые в настоящем документе финансовые инструменты, продукты или услуги. Таким образом, Банк не может быть ни в какой форме привлечен к ответственности в случае нарушения Вами применимых к Вам в какой-либо юрисдикции запретов.
Банк не гарантирует доходов от указанных в данном разделе операций с финансовыми инструментами и не несет ответственности за результаты Ваших инвестиционных решений, принятых на основании предоставленной Банком информации. Никакие финансовые инструменты, продукты или услуги, упомянутые в настоящем документе, не предлагаются к продаже и не продаются в какой-либо юрисдикции, где такая деятельность противоречила бы законодательству о ценных бумагах или другим местным законам и нормативно-правовым актам или обязывала бы Банк выполнить требование регистрации в такой юрисдикции. В частности, доводим до Вашего сведения, что ряд государств (в частности, США и Европейский Союз) ввел режим санкций, которые запрещают резидентам соответствующих государств приобретение (содействие в приобретении) долговых инструментов, выпущенных Банком. Банк предлагает Вам убедиться в том, что Вы имеете право инвестировать средства в упомянутые в настоящем документе финансовые инструменты, продукты или услуги. Таким образом, Банк не может быть ни в какой форме привлечен к ответственности в случае нарушения Вами применимых к Вам в какой-либо юрисдикции запретов.
 С условиями использования информации при осуществлении деятельности на рынке ценных бумаг можно ознакомиться по ссылке.
С условиями использования информации при осуществлении деятельности на рынке ценных бумаг можно ознакомиться по ссылке. Любая информация, представленная в данном документе, может быть изменена в любое время без предварительного уведомления. Любая приведенная в настоящем документе информация и оценки не являются условиями какой-либо сделки, в том числе потенциальной.
Любая информация, представленная в данном документе, может быть изменена в любое время без предварительного уведомления. Любая приведенная в настоящем документе информация и оценки не являются условиями какой-либо сделки, в том числе потенциальной.
 Более того, участники группы могут состоять и будут продолжать находиться в договорных отношениях по оказанию брокерских, депозитарных и иных профессиональных услуг с отличными от инвесторов лицами, при этом (i) участники группы могут получать в свое распоряжение информацию, представляющую интерес для инвесторов, и участники группы не несут перед инвесторами никаких обязательств по раскрытию такой информации или использованию ее при выполнении своих обязательств; (ii) условия оказания услуг и размер вознаграждения участников группы за оказание таких услуг третьим лицам могут отличаться от условий и размера вознаграждения, предусмотренного для инвесторов. При урегулировании возникающих конфликтов интересов Банк руководствуется интересами своих клиентов. Более подробную информацию о мерах, предпринимаемых Банком в отношении конфликтов интересов, можно найти в Политике Банка по управлению конфликтом интересов, размещённой на официальном сайте Банка:(http://www.sberbank.com/ru/compliance/ukipk)
Более того, участники группы могут состоять и будут продолжать находиться в договорных отношениях по оказанию брокерских, депозитарных и иных профессиональных услуг с отличными от инвесторов лицами, при этом (i) участники группы могут получать в свое распоряжение информацию, представляющую интерес для инвесторов, и участники группы не несут перед инвесторами никаких обязательств по раскрытию такой информации или использованию ее при выполнении своих обязательств; (ii) условия оказания услуг и размер вознаграждения участников группы за оказание таких услуг третьим лицам могут отличаться от условий и размера вознаграждения, предусмотренного для инвесторов. При урегулировании возникающих конфликтов интересов Банк руководствуется интересами своих клиентов. Более подробную информацию о мерах, предпринимаемых Банком в отношении конфликтов интересов, можно найти в Политике Банка по управлению конфликтом интересов, размещённой на официальном сайте Банка:(http://www.sberbank.com/ru/compliance/ukipk) Платформа работает с 2013 года.
Платформа работает с 2013 года.
 Россиянам невыгодно покупать акции в долларах, лучше приобретать ценные бумаги в рублях. Доходность в долларах составляет 9 %, в рублях — 35%.
Россиянам невыгодно покупать акции в долларах, лучше приобретать ценные бумаги в рублях. Доходность в долларах составляет 9 %, в рублях — 35%.
 Фьючерсы торгуются почти 24 часа в сутки 5 дней в неделю, в то время как базовые денежные индексы торгуются в разное время в зависимости от брокера.
Фьючерсы торгуются почти 24 часа в сутки 5 дней в неделю, в то время как базовые денежные индексы торгуются в разное время в зависимости от брокера.



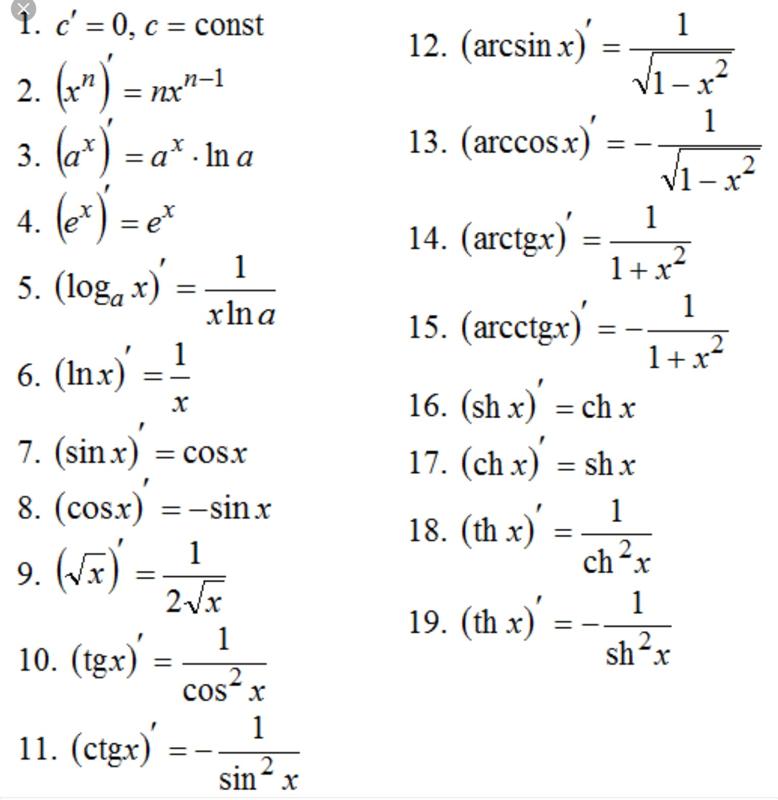 Немного в разных пропорциях. Но тот же Apple есть и там и там. Как и Гугл, Facebook и Microsoft.
Немного в разных пропорциях. Но тот же Apple есть и там и там. Как и Гугл, Facebook и Microsoft.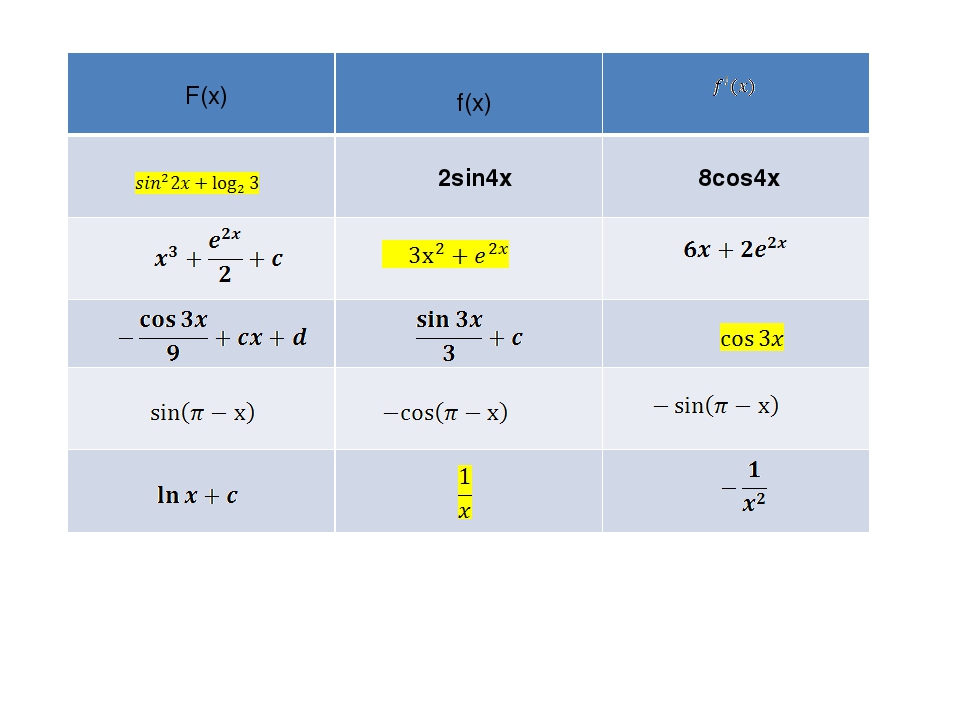 Выделил красным цветом.
Выделил красным цветом. А это, на секундочку, более 500 эмитентов (компаний, акции которых вы покупаете). Экономика США сейчас на первом месте, хотя есть вероятность, что в ближайшие годы Китай все же обойдет их. Не смотря на это, USA уверенный лидер и это подкупает, по сути, в вашем портфеле появляются компании крупнейших компаний Америки.
А это, на секундочку, более 500 эмитентов (компаний, акции которых вы покупаете). Экономика США сейчас на первом месте, хотя есть вероятность, что в ближайшие годы Китай все же обойдет их. Не смотря на это, USA уверенный лидер и это подкупает, по сути, в вашем портфеле появляются компании крупнейших компаний Америки.  Результативность индекса составила 4,32%
Результативность индекса составила 4,32%
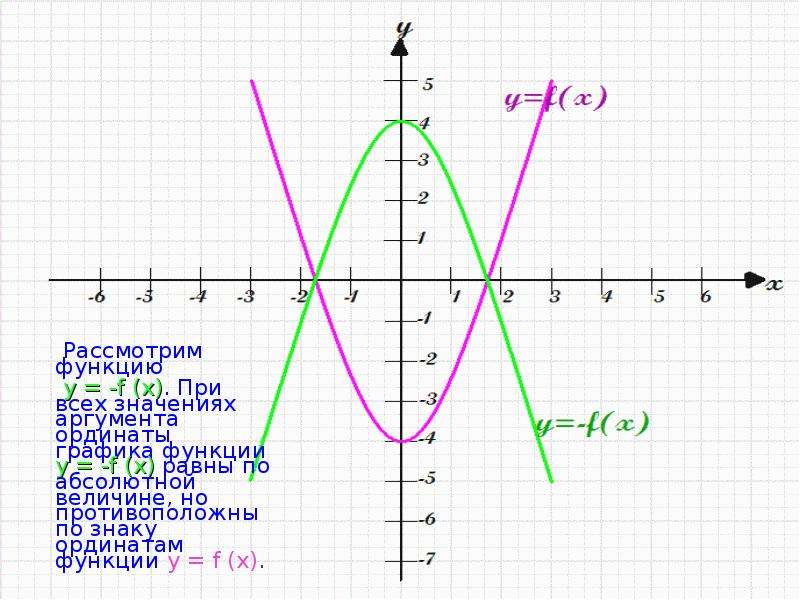 Более свежий анализ на февраль 2021 здесь.
Более свежий анализ на февраль 2021 здесь. Используя набор активов, между которыми корреляция стремится к -1 (красный цвет), инвестиционный портфель становится невосприимчивым к внешним факторам.
Используя набор активов, между которыми корреляция стремится к -1 (красный цвет), инвестиционный портфель становится невосприимчивым к внешним факторам.
 Фонды вкладываются в долларовые облигации (трежаря США и Еврооблигации наших компаний), получают долларовые купоны и сильно зависят непосредственно от курса доллара.
Фонды вкладываются в долларовые облигации (трежаря США и Еврооблигации наших компаний), получают долларовые купоны и сильно зависят непосредственно от курса доллара. И с тех пор даже не восстановился.
И с тех пор даже не восстановился. site/correlations/corFXUSvsAKSP2.png)
site/correlations/corFXUSvsAKSP2.png) Если смотреть на графики, то VTBE и S&P падали одновременно на фоне мартовского коронавируса, а затем стремительно росли на фоне последующего QE. Но почему VTBE попал в группу к S&P? VTBE косвенно инвестирует в более чем 2600 компаний по всему миру. Подобная диверсификация сделал его достаточно устойчивым, приблизив его характеристики к S&P. Но в весной VTBE все равно проиграл FXCN…
Если смотреть на графики, то VTBE и S&P падали одновременно на фоне мартовского коронавируса, а затем стремительно росли на фоне последующего QE. Но почему VTBE попал в группу к S&P? VTBE косвенно инвестирует в более чем 2600 компаний по всему миру. Подобная диверсификация сделал его достаточно устойчивым, приблизив его характеристики к S&P. Но в весной VTBE все равно проиграл FXCN… Есть подгруппа индекса МосБиржи(RUSE, FXRL, SBMX) и мировых (FXDE, FXRW). Связь FXDE и FXRW не очевидна, но динамика цен у них сонаправлена.
Есть подгруппа индекса МосБиржи(RUSE, FXRL, SBMX) и мировых (FXDE, FXRW). Связь FXDE и FXRW не очевидна, но динамика цен у них сонаправлена.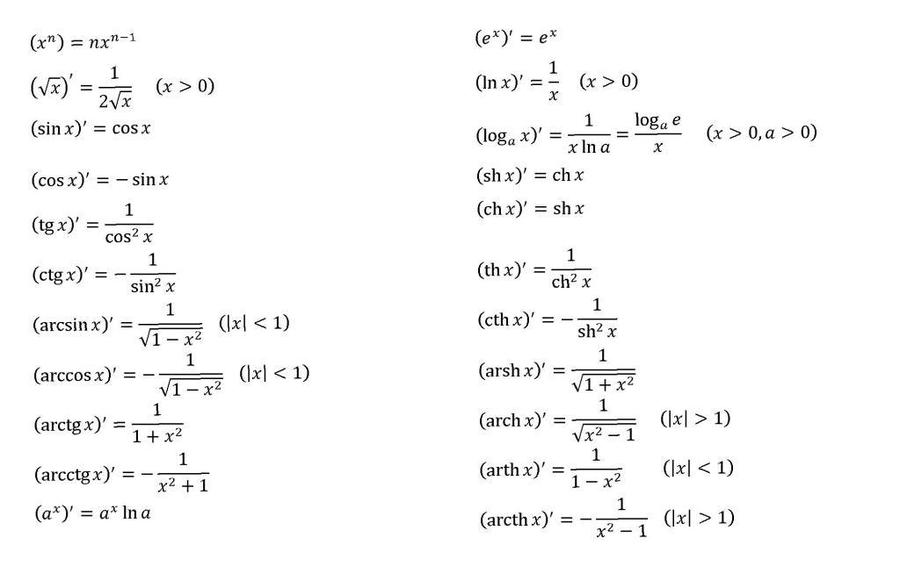
 Возможно, они в следующем выпуске статьи облегчат алгоритму поиск себе подобных.
Возможно, они в следующем выпуске статьи облегчат алгоритму поиск себе подобных.

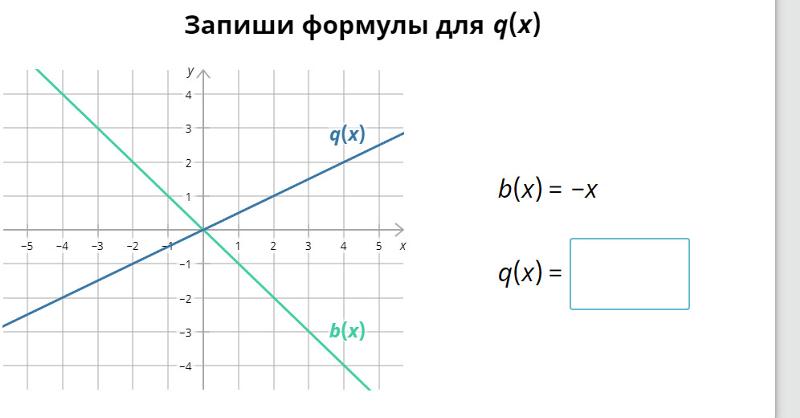 .. И поскольку маскировка Цумуги сработала слишком хорошо, она передала ее своему близкому другу, следующему вдохновителю 54-го Сезон реалити-шоу Danganronpa.
.. И поскольку маскировка Цумуги сработала слишком хорошо, она передала ее своему близкому другу, следующему вдохновителю 54-го Сезон реалити-шоу Danganronpa.
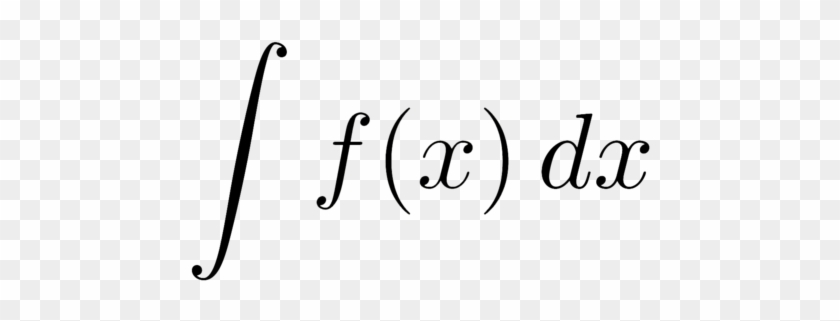 0000009958 00000 н.
0000010202 00000 п.
0000010657 00000 п.
0000010694 00000 п.
0000010999 00000 н.
0000011298 00000 п.
0000011509 00000 п.
0000011612 00000 п.
0000011713 00000 п.
0000011790 00000 п.
0000012154 00000 п.
0000013332 00000 п.
0000013567 00000 п.
0000013789 00000 п.
0000014952 00000 п.
0000015228 00000 п.
0000015598 00000 п.
0000017005 00000 п.
0000018201 00000 п.
0000018666 00000 п.
0000019103 00000 п.
0000271522 00000 н.
0000271773 00000 н.
0000271937 00000 н.
0000506967 00000 н.
0000508121 00000 н.
0000508294 00000 н.
0000508457 00000 н.
0000508510 00000 н.
0000508796 00000 н.
0000508993 00000 н.
0000509249 00000 н.
0000509308 00000 н.
0000510497 00000 н.
0000510663 00000 н.
0000510864 00000 н.
0000511920 00000 н.
0000512934 00000 п.
0000514084 00000 н.
0000515112 00000 н.
0000516068 00000 н.
0000518761 00000 н.
0000522449 00000 н.
0000522829 00000 н.
0000523290 00000 н.
0000527465 00000 н.
0000531714 00000 н.
0000536757 00000 н.
0000009958 00000 н.
0000010202 00000 п.
0000010657 00000 п.
0000010694 00000 п.
0000010999 00000 н.
0000011298 00000 п.
0000011509 00000 п.
0000011612 00000 п.
0000011713 00000 п.
0000011790 00000 п.
0000012154 00000 п.
0000013332 00000 п.
0000013567 00000 п.
0000013789 00000 п.
0000014952 00000 п.
0000015228 00000 п.
0000015598 00000 п.
0000017005 00000 п.
0000018201 00000 п.
0000018666 00000 п.
0000019103 00000 п.
0000271522 00000 н.
0000271773 00000 н.
0000271937 00000 н.
0000506967 00000 н.
0000508121 00000 н.
0000508294 00000 н.
0000508457 00000 н.
0000508510 00000 н.
0000508796 00000 н.
0000508993 00000 н.
0000509249 00000 н.
0000509308 00000 н.
0000510497 00000 н.
0000510663 00000 н.
0000510864 00000 н.
0000511920 00000 н.
0000512934 00000 п.
0000514084 00000 н.
0000515112 00000 н.
0000516068 00000 н.
0000518761 00000 н.
0000522449 00000 н.
0000522829 00000 н.
0000523290 00000 н.
0000527465 00000 н.
0000531714 00000 н.
0000536757 00000 н. 0000537002 00000 н.
0000537104 00000 п.
0000537340 00000 н.
0000537540 00000 н.
0000538042 00000 н.
0000538136 00000 н.
0000538664 00000 н.
0000538776 00000 п.
0000550429 00000 н.
0000550468 00000 н.
0000550970 00000 н.
0000551064 00000 н.
0000551566 00000 н.
0000551660 00000 н.
0000552206 00000 н.
0000552342 00000 п.
0000563658 00000 н.
0000563697 00000 п.
0000564237 00000 н.
0000564365 00000 н.
0000612026 00000 н.
0000612065 00000 н.
0000612605 00000 н.
0000612733 00000 н.
0000660354 00000 н.
0000002276 00000 н.
трейлер
] / Назад 1268574 >>
startxref
0
%% EOF
876 0 объект
> поток
h ޔ TKlUolh Ǝ]; xZ {l.@
Bd3h5i & TaTuAlXD *>; B $
0000537002 00000 н.
0000537104 00000 п.
0000537340 00000 н.
0000537540 00000 н.
0000538042 00000 н.
0000538136 00000 н.
0000538664 00000 н.
0000538776 00000 п.
0000550429 00000 н.
0000550468 00000 н.
0000550970 00000 н.
0000551064 00000 н.
0000551566 00000 н.
0000551660 00000 н.
0000552206 00000 н.
0000552342 00000 п.
0000563658 00000 н.
0000563697 00000 п.
0000564237 00000 н.
0000564365 00000 н.
0000612026 00000 н.
0000612065 00000 н.
0000612605 00000 н.
0000612733 00000 н.
0000660354 00000 н.
0000002276 00000 н.
трейлер
] / Назад 1268574 >>
startxref
0
%% EOF
876 0 объект
> поток
h ޔ TKlUolh Ǝ]; xZ {l.@
Bd3h5i & TaTuAlXD *>; B $ 1838
1838
 Известно, что нота «до» первой октавы имеет частоту 262 Hz. Также известно, что частоты двух одноимённых нот соседних октав от
… личаются ровно в 2 раза. В какой октаве находится звук, порождённые колебаниями, ищображенными на графике? (график приложен)
2). Нарисовать график
3). Определить музыкальный инструмент
Известно, что нота «до» первой октавы имеет частоту 262 Hz. Также известно, что частоты двух одноимённых нот соседних октав от
… личаются ровно в 2 раза. В какой октаве находится звук, порождённые колебаниями, ищображенными на графике? (график приложен)
2). Нарисовать график
3). Определить музыкальный инструмент Вважати g = 10 м/с2. 30. Який тиск чинить вода на нижню поверхню плоскої крижинки площею 20 см2 та масою 500 г?
Вважати g = 10 м/с2. 30. Який тиск чинить вода на нижню поверхню плоскої крижинки площею 20 см2 та масою 500 г?
 По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.
По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.
Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру. В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.
В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.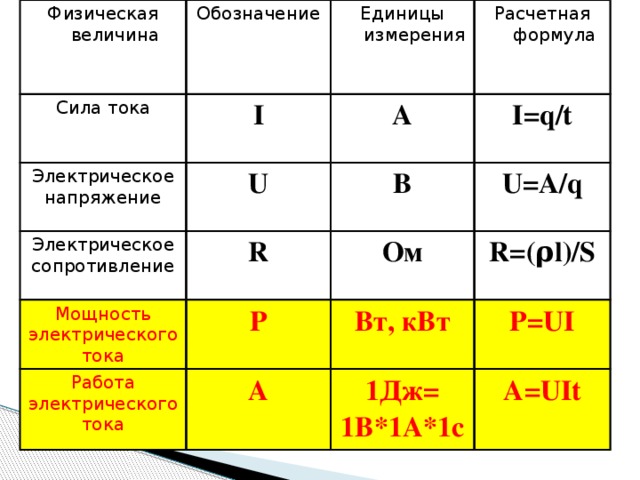 Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.
Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.

 Эти виды клеток крови также относятся к лейкоцитам и выполняют важные функции (борьбу с паразитами, бактериями, развитие аллергических реакций и др.)
Эти виды клеток крови также относятся к лейкоцитам и выполняют важные функции (борьбу с паразитами, бактериями, развитие аллергических реакций и др.) Если уровень эритроцитов ниже нормы (анемия) организм получает недостаточные количества кислорода. Если уровень эритроцитов выше нормы (полицитемия, или эритроцитоз) имеется риск того, что красные кровные клетки склеятся между собой и заблокируют движение крови по сосудам (тромбоз).
Если уровень эритроцитов ниже нормы (анемия) организм получает недостаточные количества кислорода. Если уровень эритроцитов выше нормы (полицитемия, или эритроцитоз) имеется риск того, что красные кровные клетки склеятся между собой и заблокируют движение крови по сосудам (тромбоз). Снижение этого показателя встречается при железодефицитной анемии, увеличение – при мегалобластной анемии (при дефиците витамина В12 или фолиевой кислоты).
Снижение этого показателя встречается при железодефицитной анемии, увеличение – при мегалобластной анемии (при дефиците витамина В12 или фолиевой кислоты). Повышение MPV могут спровоцировать сахарный диабет, тромбоцитодистрофия, патологии крови (системная волчанка), спленэктомия, алкоголизм, миелоидный лейкоз, атеросклероз сосудов, талассемия (генетическое нарушение строения гемоглобина), синдром Мея-Хегглина, постгеморрагическое малокровие. Ниже нормы данный показатель опускается вследствие лучевой терапии, при циррозе печени, анемии (пластическая и мегалобластной), синдроме Вискота-Олдрича.
Повышение MPV могут спровоцировать сахарный диабет, тромбоцитодистрофия, патологии крови (системная волчанка), спленэктомия, алкоголизм, миелоидный лейкоз, атеросклероз сосудов, талассемия (генетическое нарушение строения гемоглобина), синдром Мея-Хегглина, постгеморрагическое малокровие. Ниже нормы данный показатель опускается вследствие лучевой терапии, при циррозе печени, анемии (пластическая и мегалобластной), синдроме Вискота-Олдрича.
 Позже, по мере развития компьютерного оборудования, это число было стандартизировано.
Позже, по мере развития компьютерного оборудования, это число было стандартизировано. ОЗУ позволяет компьютеру переключаться между программами и иметь большие файлы наготове для просмотра.
ОЗУ позволяет компьютеру переключаться между программами и иметь большие файлы наготове для просмотра. 12/л (10 в ст. 12/л), г/л (грамм на литр), % (процент), фл (фемтолитр), пг (пикограмм).
12/л (10 в ст. 12/л), г/л (грамм на литр), % (процент), фл (фемтолитр), пг (пикограмм). Такое расширенное исследование чаще называют клиническим анализом крови.
Такое расширенное исследование чаще называют клиническим анализом крови.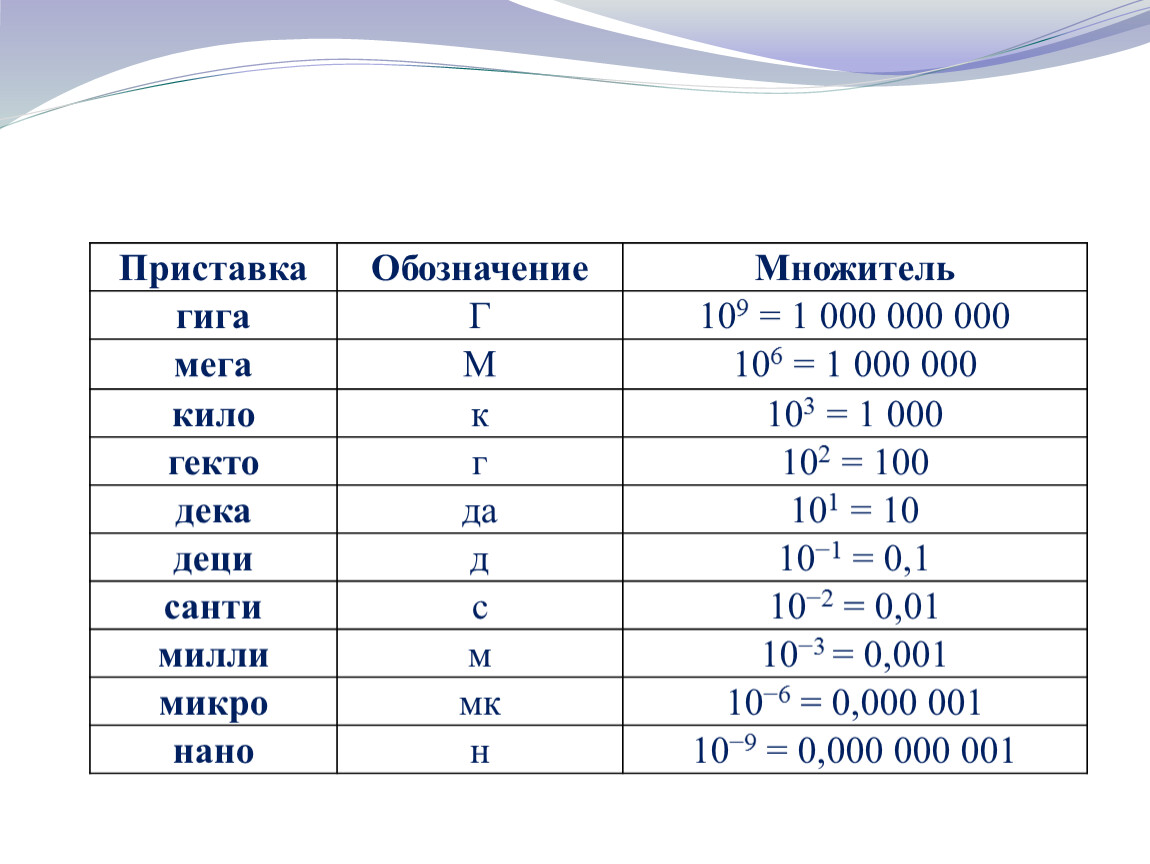 После этого врач лаборатории может детально рассмотреть ее под микроскопом.
После этого врач лаборатории может детально рассмотреть ее под микроскопом.
 Если у человека снижено количество тромбоцитов, риск кровотечения и образования синяков у него повышен.
Если у человека снижено количество тромбоцитов, риск кровотечения и образования синяков у него повышен. Используется в комплексной оценке анемий и полицитемий, для принятия решения о переливании крови и оценки результатов этой процедуры.
Используется в комплексной оценке анемий и полицитемий, для принятия решения о переливании крови и оценки результатов этой процедуры. Это более чувствительный параметр для определения нарушений образования гемоглобина, чем MCH, так как он не зависит от среднего объема эритроцита.
Это более чувствительный параметр для определения нарушений образования гемоглобина, чем MCH, так как он не зависит от среднего объема эритроцита. Расшифровка общего анализа крови становится первым шагом в диагностике многих серьезных заболеваний.
Расшифровка общего анализа крови становится первым шагом в диагностике многих серьезных заболеваний. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!