Ответ: 264,6 м/с
2.Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Измерение ускорения свободного падения на различных высотах при помощи математического маятника
- Участник: Мингалеев Артур Эдуардович
- Руководитель: Баскова Мария Аркадьевна
1. Введение
Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается. Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря. Для достижения поставленной цели были сформулированы следующие задачи исследования:
- Ознакомиться с историей открытия свободного падения тел;
- Изучить методы измерения ускорения свободного падения на поверхности Земли;
- Провести самостоятельные измерения ускорения свободного падения при помощи математического маятника;
- Провести измерения на различных высотах.

Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с2 и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.
Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.
Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли. Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.
2. Основная часть
2.1. Исторические сведения об открытии свободного падения и методах его измерения
Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно. Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами.
Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха.
Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с «постоянным ускорением»; темп увеличения скорости тела не меняется, т.е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
S1 : S2 : S3 : … = 1 : 2 : 3 : … (при V0 = 0)
Таким образом, можно предположить, что свободное падение есть равноускоренное движение. Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
S1 : S2 : S3 = t12 : t22 : t32 (2)
Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
2.2. Практическая значимость нахождения значения ускорения свободного падения
Я много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
2.3. Методы измерения ускорения свободного падения
На самом деле методов по измерению ускорения свободного падения достаточно много. Приведу только те, которые сам испробовал.
Приведу только те, которые сам испробовал.
1) Измерение ускорения свободного падения с помощью наклонной плоскости
Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка. Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
Записывая второй закон Ньютона в проекциях на оси координат:
Ох: – Fтр+ mgsinα = ma
Oy: N – mgcosα = 0
и учитывая, что N = mgcosα; Fтр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:
| g = | a |
| sinα – μcosα |
При этом ускорение a можно вычислить из формулы
так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:
Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.
Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:
Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.
При равномерном движении бруска эти силы будут попарно равны: Fтр = Fупр, Fтяж = N, т. е. Fупр = μFтяж, тогда коэффициент трения равен
Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.
2) Определение
g благодаря давлению жидкостиКак известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.
Если преобразовать формулу P = ρgh, получится формула нахождения g. Эта формула выглядит так g = P / ρh, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м3.
При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.
3) Измерение ускорения свободного падения с помощью математического маятника
Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Подготовка к проведению работы
В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника
Тогда период
и ускорения свободного падения может быть вычислено по формуле
Результаты измерений и вычислений представлены в разделе 2.5
2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах
Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
где G — гравитационная постоянная (G = 6,6743 · 10–11 (H ·м2)/кг2).
При вычислениях я применял такие значения:
R = 6370 · 103 м – радиус Земли на широте Казани;
M = 5,9722 · 1024 кг – масса Земли.
Таким образом теоретическое значение gт = 9,823386 м/с2.
Согласно формуле
естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.
Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.
Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:
|
В классе |
На станции метро Кремлевская |
На 36-м этаже небоскреба |
|
R = 6370 км, h = 0 |
R = 6370 км, h = –16 м |
R = 6370 км, h = +120 м |
|
9,8234 |
9,8231 |
9,8227 |
2.
 5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
5. Экспериментальное определение ускорения свободного падения с помощью математического маятникаКак уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Ход работы
Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.
- Я установил на краю стола штатив. У его верхнего конца укрепил с помощью муфты кольцо и подвесил к нему шарик на нити. Шарик должен висеть и свободно совершать колебания.
- Нить я взял метровой длины для удобства вычислений.
- Отклонив шарик на небольшое расстояние (5-8 см), я возбудил колебания маятника.
- Измерил в пяти экспериментах время t 20 колебаний маятника и вычислил tср:
| tср = | t1 + t2 + t3 + t4 + t5 |
| 5 |
- Затем вычислил среднюю абсолютную погрешность измерения времени:
| ∆tср = | │t1 – tср│ + │t2 – tср│+ │t3– tср│ + │t4– tср│ + │t5– tср│ |
| 5 |
- Вычислил ускорение свободного падения по формуле:
Таблица результатов измерений в классе
| n |
N |
t, c |
tср, с |
Δtср, с |
g, м/с2 |
|
1 |
20 |
40,26 |
39,94 |
0,36 |
9,88924 |
|
2 |
20 |
39,20 |
|||
|
3 |
20 |
40,30 |
|||
|
4 |
20 |
40,18 |
|||
|
5 |
20 |
39,78 |
- Я определил относительную погрешность измерения времени εt.

| ε = | ∆t | = | ∆tи + ∆tотсчета | = | 1 с + 1 с | = | 2 c | = | 2 с | = 0,05 = 5% |
| t | t | t | tсредн | 39,94 с |
- Определил относительную погрешность измерения длины маятника:
| εl = | ∆l | = | ∆lи + ∆lотсчета | = | половина цены деления + цена деления | = |
| l | l | длина маятника |
| = | 0,0005 м + 0,001 м | = | 0,0015 м | = | 0,0015 м | = 0,0015 = 0,15% |
| l | l | 1 м |
- Вычислил относительную погрешность измерения g:
εg = εl+ 2εt = 0,05 + 2 · 0,0015 = 0,053 = 5,3%
- Определил абсолютную погрешность вычисления ускорения свободного падения:
∆g = εggсредняя = 0,053 · 9,73971 м/с2 = 0,5162 м/с2 ≈ 0,520
Итог моих измерений и вычислений:
9,37 ≤ g ≤ 10,41
Такие действия я проделал в казанском метрополитене, на станции метро Кремлевская и на 36-м этаже единственного в Казани небоскреба «Лазурные небеса».
Таблица результатов измерений на станции метро Кремлевская
|
n |
N |
t, c |
tср, с |
Δtср, с |
g, м/с2 |
|
1 |
20 |
31,80 |
31,71 |
0,042 |
9,96232 |
|
2 |
20 |
31,72 |
|||
|
3 |
20 |
31,62 |
|||
|
4 |
20 |
31,69 |
|||
|
5 |
20 |
31,71 |
При измерениях в метро пришлось использовать длину нити 63,5 см.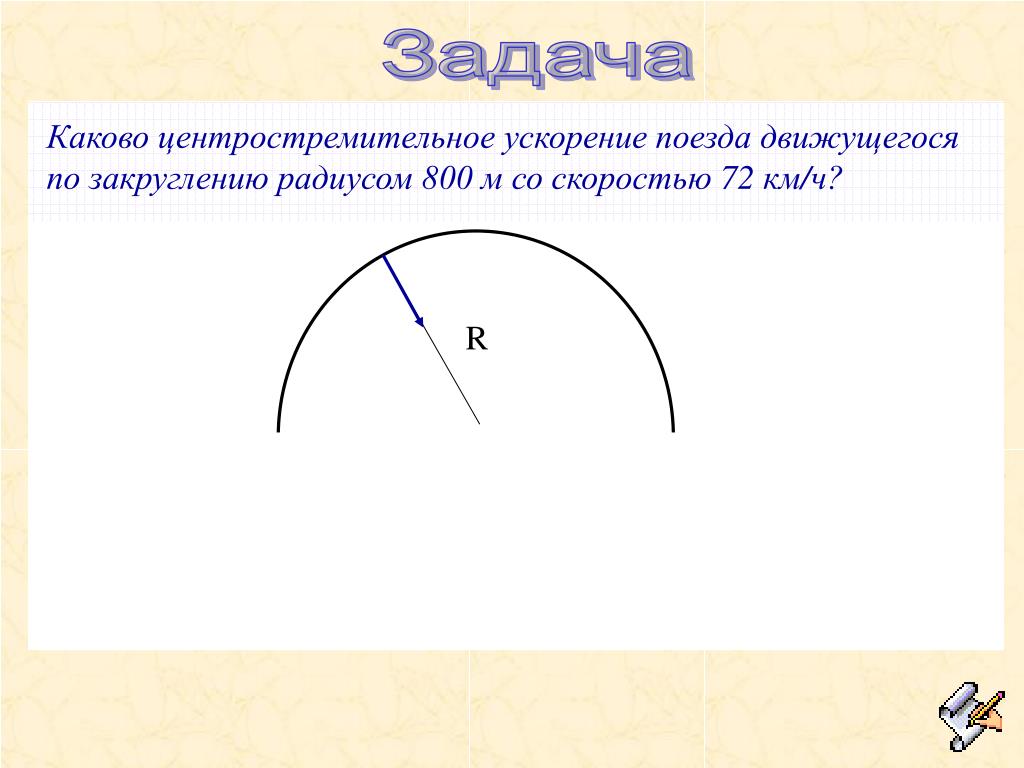
Относительная погрешность измерения времени εt = 0,063 = 6,3%.
Относительная погрешность измерения длины маятника: εl = 0,24%
Относительная погрешность измерения g: εg = 6,78%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,63 м/с2.
Итог моих измерений и вычислений:
9,33 ≤ g ≤ 10,59
Таблица результатов измерений на 36-м этаже небоскреба «Лазурные небеса»
| n |
N |
t, c |
tср, с |
Δtср, с |
g, м/с2 |
|
1 |
20 |
28,59 |
28,57 |
0,10 |
9,85664 |
|
2 |
20 |
28,56 |
|||
|
3 |
20 |
28,81 |
|||
|
4 |
20 |
28,52 |
|||
|
5 |
20 |
28,39 |
Здесь при измерениях пришлось длину нити еще сократить до 51 см.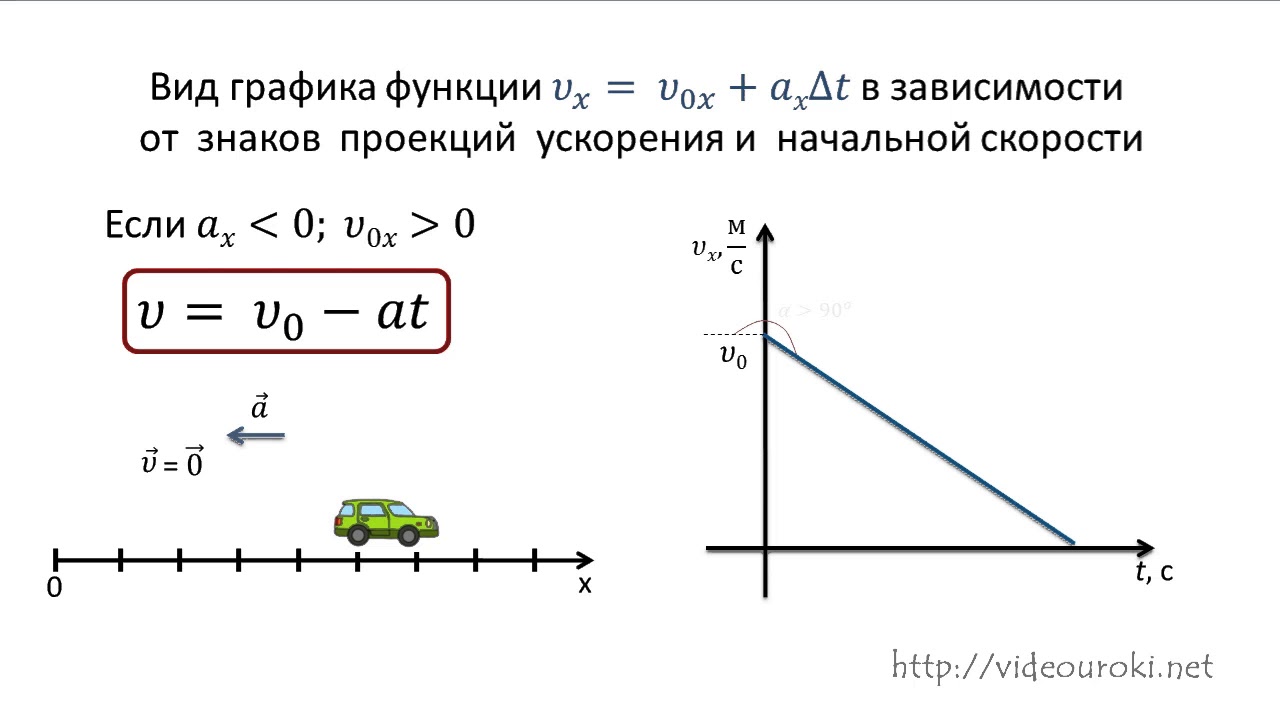
Относительная погрешность измерения времени εt = 7%.
Относительная погрешность измерения длины маятника: εl = 0,29%
Относительная погрешность измерения g: εg = 7,58%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,75 м/с2.
Итог моих измерений и вычислений:
9,11 ≤ g ≤ 10,61
Таблица сравнения теоретически полученных значений g (м/с2) и полученных экспериментально
|
|
В классе |
На станции метро Кремлевская |
На 36-м этаже небоскреба |
|
R = 6370 км, h = 0 |
R = 6370 км, h = –16 м |
R = 6370 км, h = +120 м |
|
|
Теория |
9,8234 |
9,8231 |
9,8227 |
|
Эксперимент |
9,8892 |
9,9623 |
9,8566 |
3.
 Заключение
ЗаключениеПри подготовке к защите данной работы и в результате теоретического исследования, чтения разных книг и статей я узнал многое об ускорении свободного падения. Как уже упоминал, для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
Также я узнал, что расчеты различия ускорения свободного падения в разных точках на поверхности Земли могут указывать на гравитационные аномалии.
Самое главное, я научился измерять g, различными способами, рассчитывать погрешности измерений, грамотно проводить эксперимент.
Считаю цель исследования достигнута. Средние значение ускорения свободного падения на различных высотах отличаются в зависимости от высоты над уровнем моря: при увеличении высоты значение g уменьшается, при углублении в недра Земли – увеличивается. Экспериментально полученные значения хорошо это показывают.
Экспериментально полученные значения хорошо это показывают.
Погрешность измерений достаточно велика, но не превышает 10%. Уменьшить погрешность возможно путем проведения большего числа измерений: ни 5, а 20; большего числа колебаний: не 20, а 100. Также при расчетах можно учесть, что Казань находится примерно на уровне 250-300 м над уровнем моря.
В дальнейшем хотелось бы усовершенствовать экспериментальные установки, чтобы измерять ускорение свободного падения с большей точностью.
Планирую самостоятельно исследовать значения ускорения свободного падения в различных уголках земного шара.
Взаимодействие тел, инертность, масса — ЗФТШ, МФТИ
Из наблюдений можно заметить, что тела изменяют свою скорость только при наличии не скомпенсированного действия. Т. к. быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.
Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.
Установились считать: чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.
Инертность – это свойство тела сохранять свою скорость постоянной (то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.
Например, движущийся по дороге автомобиль не может мгновенно остановиться, для уменьшения скорости требуется некоторое время, а за это время он успевает переместиться на довольно большое расстояние (десятки метров). (Осторожно переходите дорогу!!!)
Мерой инертности является инертная масса.
Масса (инертная) – мера инертности тела.
Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение: a∼1m\boxed{a\sim\frac 1m}.
Данная зависимость записана единственно правильным способом, т. к. форма m∼1am \sim \frac 1a не верна. Масса не может зависеть от ускорения, она является свойством тела, а ускорение является характеристикой состояния движения тела.
Данная зависимость подтверждается многочисленными опытными результатами.
Рис. 2 Измерение массы методом взаимодействия тел.
Два тела, скреплённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться не которое время с ускорением (рис. 1) . Опыт показывает, что при любых взаимодействиях данных двух тел отношение ускорений тел равно обратному отношению их масс:
\[\frac{a_1}{a_2} = \frac{m_2}{m_1};\]
если взять первую массу за эталонную (m1=mэтm_1 = m_\mathrm{эт}), то m2=mэтaэтa2m_2 = m_\mathrm{эт}\frac{a_\mathrm{эт}}{a_2}.
Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной.
Измерение массы методом взвешивания тел.
Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы (рис. 2).
Рис. 2
| Рис. 3 |
Масса, измеренная путём взвешивания, называется гравитационной.
В качестве эталона и той и другой массы принята масса тела, выполненного в форме цилиндра высотой 39 мм39\ \mathrm{мм} и диаметром 39 мм39\ \mathrm{мм}, изготовленного из сплава 10 % иридия и 90 % платины (рис.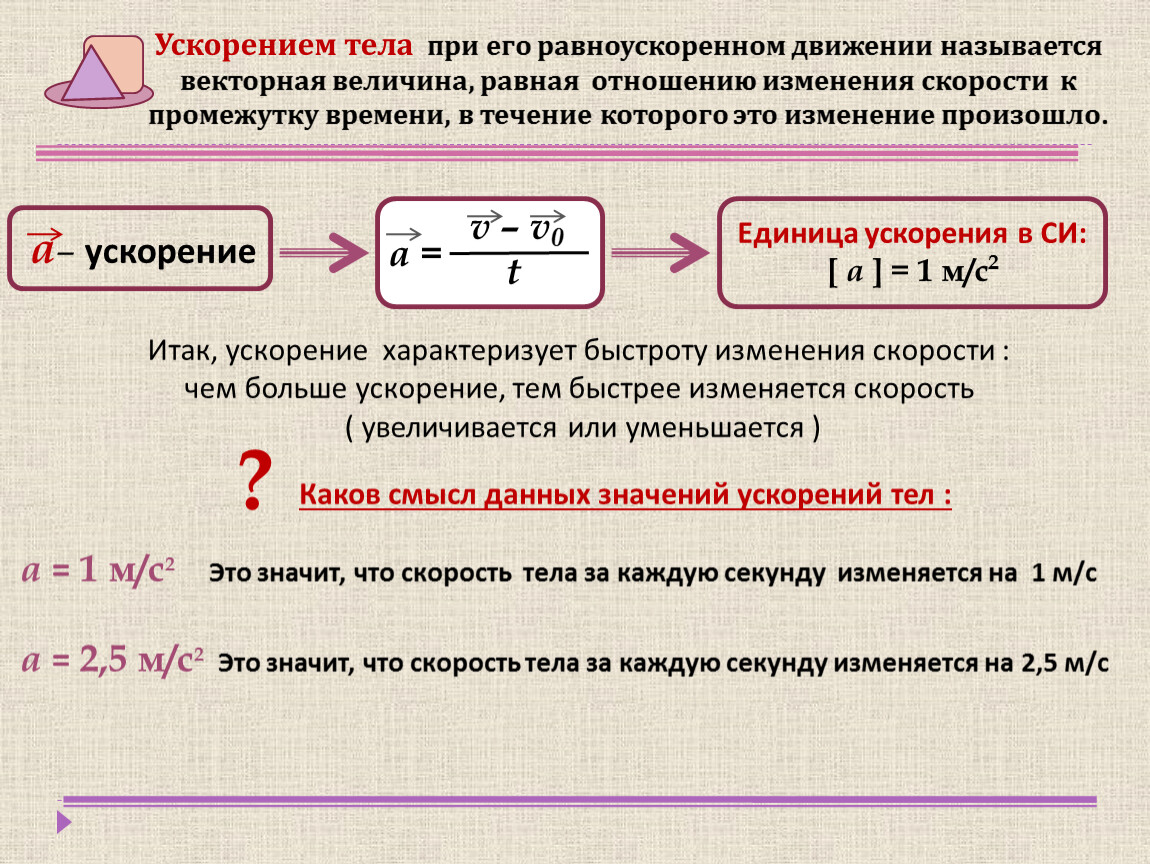 {-12} % эти массы равны.
{-12} % эти массы равны.
Данный факт известен был и ранее, и послужил основанием для формулировки Эйнштейном принципа эквивалентности.
Принцип эквивалентности утверждает, что
1) ускорение, вызванное гравитационным взаимодействием в малой области пространства, и за небольшой интервал времени, неотличимо от ускоренно движущейся системы отсчёта.
2) ускоренно движущееся тело эквивалентно неподвижному телу, находящемуся в гравитационном поле.
Пример 1.
Два тела массами 400 г400\ \mathrm{г} и 600 г600\ \mathrm{г} двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью 3 м/с3\ \mathrm{м}/\mathrm{с}?
Решение.
Сила, возникающая при взаимодействии тел, конечно же, не остаётся постоянной, и ускорения тоже. Мы будем считать, что и силы, и ускорения принимают некоторы е средние значения, причём одинаковые для любого момента времени. Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1\frac{a_1}{a_2} = \frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:
Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1\frac{a_1}{a_2} = \frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:
\[\frac{m_2}{m_1} = \frac{a_1}{a_2} = \frac{\frac{\Delta v_1}{\Delta t}}{\frac{\Delta v_2}{\Delta t}} = \frac{v_\mathrm{к1}-v_{01}}{v_\mathrm{к2}-v_{02}} = \frac{v_{01}}{v_{02}},\]
откуда получим искомую скорость: v02=m1m2·v01.v_{02} = \frac{m_1}{m_2}\cdot v_{01}.
Количественно ответ будет таким: v02=0,4 кг0,6 кг·3 мс=2 мсv_{02} = \frac{0,4\ \mathrm{кг}}{0,6\ \mathrm{кг}}\cdot 3\ \frac{\mathrm{м}}{\mathrm{с}} = 2\ \frac{\mathrm{м}}{\mathrm{с}}.
Прямолинейное равноускоренное движение. Ускорение, скорость, перемещение
1439. Мотоцикл в течение 5 с может увеличить скорость от 0 до 72 км/ч. Определите ускорение мотоцикла.
1440. Определите ускорение лифта в высотном здании, если он увеличивает свою скорость на 3,2 м/с в течение 2 с.
Определите ускорение лифта в высотном здании, если он увеличивает свою скорость на 3,2 м/с в течение 2 с.
1441. Автомобиль, двигавшийся со скоростью 72 км/ч, равномерно тормозит и через 10 с останавливается. Каково ускорение автомобиля?
1442. Как назвать движения, при которых ускорение постоянно? равно нулю?
Равноускоренное, равномерное.
1443. Санки, скатываясь с горы, движутся равноускоренно и в конце третьей секунды от начала движения имеют скорость 10,8 км/ч. Определите, с каким ускорением движутся санки.
1444. Скорость автомобиля за 1,5 мин движения возросла от 0 до 60 км/ч. Найдите ускорение автомобиля в м/с2 , в см/с2.
1445. Мотоцикл «Хонда», двигавшийся со скоростью 90 км/ч, начал равномерно тормозить и через 5 с сбросил скорость до 18 км/ч. Каково ускорение мотоцикла?
1446. Объект из состояния покоя начинает двигаться с постоянным ускорением, равным 6 • 10-3 м/с2.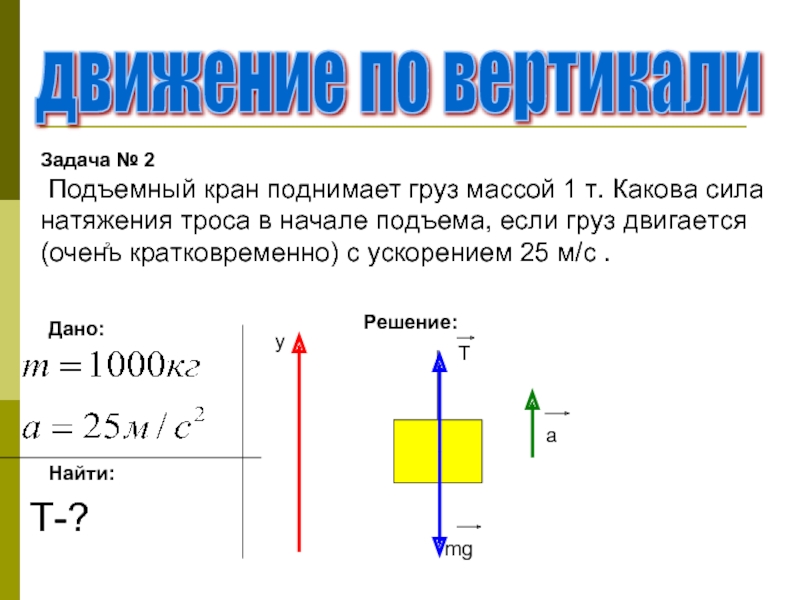 Определите скорость через 5 мин после начала движения. Какой путь прошел объект за это время?
Определите скорость через 5 мин после начала движения. Какой путь прошел объект за это время?
1447. Яхту спускают на воду по наклонным стапелям. Первые 80 см она прошла за 10 с. За какое время яхта прошла оставшиеся 30 м, если ее движение оставалось равноускоренным?
1448. Грузовик трогается с места с ускорением 0,6 м/с2. За какое время он пройдет путь в 30 м?
1449. Электричка отходит от станции, двигаясь равноускоренно в течение 1 мин 20 с. Каково ускорение электрички, если за это время ее скорость стала 57,6 км/ч? Какой путь она прошла за указанное время?
1450. Самолет для взлета равноускоренно разгоняется в течение 6 с до скорости 172,8 км/ч. Найдите ускорение самолета. Какое расстояние прошел самолет при разгоне?
1451. Товарный поезд, трогаясь с места, двигался с ускорением 0,5 м/с2 и разогнался до скорости 36 км/ч. Какой путь он при этом прошел?
1452. От станции равноускоренно тронулся скорый поезд и, пройдя 500 м, достиг скорости 72 км/ч. Каково ускорение поезда? Определите время его разгона.
Каково ускорение поезда? Определите время его разгона.
1453. При выходе из ствола пушки снаряд имеет скорость 1100 м/с. Длина ствола пушки равна 2,5 м. Внутри ствола снаряд двигался равноускоренно. Каково его ускорение? За какое время снаряд прошел всю длину ствола?
1454. Электричка, шедшая со скоростью 72 км/ч, начала тормозить с постоянным ускорением, равным по модулю 2 м/с2. Через какое время она остановится? Какое расстояние она пройдет до полной остановки?
1455. Городской автобус двигался равномерно со скоростью 6 м/с, а затем начал тормозить с ускорением, по модуля равным 0,6 м/с2. За какое время до остановки и на каком расстоянии от нее надо начать торможение?
1456. Санки скользят по ледяной дорожке с начальной скоростью 8 м/с, и за каждую секунду их скорость уменьшается на 0,25 м/с. Через какое время санки остановятся?
1457. Мотороллер, двигавшийся со скоростью 46,8 км/ч, останавливается при равномерном торможении в течение 2 с. Каково ускорение мотороллера? Каков его тормозной путь?
Каково ускорение мотороллера? Каков его тормозной путь?
1458. Теплоход, плывущий со скоростью 32,4 км/ч, стал равномерно тормозить и, подойдя к пристани через 36 с, полностью остановился. Чему равно ускорение теплохода? Какой путь он прошел за время торможения?
1459. Товарняк, проходя мимо шлагбаума, приступил к торможению. Спустя 3 мин он остановился на разъезде. Какова начальная скорость товарняка и модуль его ускорения, если шлагбаум находится на расстоянии 1,8 км от разъезда?
1460. Тормозной путь поезда 150 м, время торможения 30 с. Найдите начальную скорость поезда и его ускорение.
1461. Электричка, двигавшаяся со скоростью 64,8 км/ч, после начала торможения до полной остановки прошла 180 м. Определите ее ускорение и время торможения.
1462. Аэроплан летел равномерно со скоростью 360 км/ч, затем в течение 10 с он двигался равноускоренно: его скорость возрастала на 9 м/с за секунду. Определите, какую скорость приобрел аэроплан. Какое расстояние он пролетел при равноускоренном движении?
Какое расстояние он пролетел при равноускоренном движении?
1463. Мотоцикл, двигавшийся со скоростью 27 км/ч, начал равномерно ускоряться и через 10 с достиг скорости 63 км/ч. Определите среднюю скорость мотоцикла при равноускоренном движении. Какой путь он проехал за время равноускоренного движения?
1464. Прибор отсчитывает промежутки времени, равные 0,75 с. Шарик скатывается с наклонного желоба в течение трех таких промежутков времени. Скатившись с наклонного желоба, он продолжает двигаться по горизонтальному желобу и проходит в течение первого промежутка времени 45 см. Определите мгновенную скорость шарика в конце наклонного желоба и ускорение шарика при движении по этому желобу.
1465. Отходя от станции, поезд движется равноускоренно с ускорением 5 см/с2. По прошествии какого времени поезд приобретает скорость 36 км/ч?
1466. При отправлении поезда от станции его скорость в течение первых 4 с возросла до 0,2 м/с, в течение следующих 6 с еще на 30 см/с и за следующие 10 с на 1,8 км/ч. Как двигался поезд в течение этих 20 с?
Как двигался поезд в течение этих 20 с?
1467. Санки, скатываясь с горы, движутся равноускоренно. На некотором участке пути скорость санок в течение 4 с возросла от 0,8 м/с до 14,4 км/ч. Определите ускорение санок.
1468. Велосипедист начинает двигаться с ускорением 20 см/с2. По истечении какого времени скорость велосипедиста будет равна 7,2 км/ч?
1469. На рисунке 184 дан график скорости некоторого равноускоренного движения. Пользуясь масштабом, данным на рисунке, определите путь, проходимый в этом движении в течение 3,5 с.
1470. На рисунке 185 изображен график скорости некоторого переменного движения. Перечертите рисунок в тетрадь и обозначьте штриховкой площадь, численно равную пути, проходимому в течение 3 с. Чему примерно равен этот путь?
1471. В течение первого промежутка времени от начала равноускоренного движения шарик проходит по желобу 8 см. Какое расстояние пройдет шарик в течение трех таких же промежутков, прошедших от начала движения?
1472. В течение 10 равных промежутков времени от начала движения тело, двигаясь равноускоренно, прошло 75 см. Сколько сантиметров прошло это тело в течение двух первых таких же промежутков времени?
В течение 10 равных промежутков времени от начала движения тело, двигаясь равноускоренно, прошло 75 см. Сколько сантиметров прошло это тело в течение двух первых таких же промежутков времени?
1473. Поезд, отходя от станции, движется равноускоренно и в течение двух первых секунд проходит 12 см. Какое расстояние пройдет поезд в течение 1 мин, считая от начала движения?
1474. Поезд, отходя от станции, движется равноускоренно с ускорением 5 см/с2. Сколько времени потребуется для развития скорости 28,8 км/ч и какое расстояние пройдет поезд за это время?
1475. Паровоз по горизонтальному пути подходит к уклону со скоростью 8 м/с, затем движется вниз по уклону с ускорением 0,2 м/с. Определите длину уклона, если паровоз проходит его за 30 с.
1476. Начальная скорость тележки, движущейся вниз по наклонной доске, равна 10 см/с. Всю длину доски, равную 2 м, тележка прошла в течение 5 сек. Определите ускорение тележки.
1477. Пуля вылетает из ствола ружья со скоростью 800 м/с. Длина ствола 64 см. Предполагая движение пули внутри ствола равноускоренным, определите ускорение и время движения.
Пуля вылетает из ствола ружья со скоростью 800 м/с. Длина ствола 64 см. Предполагая движение пули внутри ствола равноускоренным, определите ускорение и время движения.
1478. Автобус, двигаясь со скоростью 4 м/с, начинает равномерно ускоряться на 1 м/с за секунду. Какой путь пройдет автобус за шестую секунду?
1479. Грузовик, имея некоторую начальную скорость, начал двигаться равноускоренно: за первые 5 с прошел 40 м, а за первые 10 с — 130 м. Найдите начальную скорость грузовика и его ускорение.
1480. Катер, отходя от пристани, начал равноускоренное движение. Пройдя некоторое расстояние, он достиг скорости 20 м/с. Какова была скорость катера в тот момент, когда он проплыл половину этого расстояния?
1481. Лыжник скатывается с горы с нулевой начальной скоростью. На середине горы его скорость была 5 м/с, через 2 с скорость стала 6 м/с. Считая, что она увеличивается равномерно, определите скорость лыжника через 8 с после начала движения.
1482. Автомобиль тронулся с места и двигается равноускоренно. За какую секунду от начала движения путь, пройденный автомобилем, вдвое больше пути, пройденного им в предыдущую секунду?
1483. Найдите путь, пройденный телом за восьмую секунду движения, если оно начинает двигаться равноускоренно без начальной скорости и за пятую секунду проходит путь 27 м.
1484. Провожающие стоят у начала головного вагона поезда. Поезд трогается и движется равноускоренно. За 3 с весь головной вагон проходит мимо провожающих. За какое время пройдет мимо провожающих весь поезд, состоящий из 9 вагонов?
1485. Материальная точка движется по закону x = 0,5t². Какое это движение? Каково ускорение точки? Постройте график зависимости от времени:
а) координаты точки;
б) скорости точки;
в) ускорения.
1486. Поезд остановился через 20 с после начала торможения, пройдя за это время 120 м. Определите первоначальную скорость поезда и ускорение поезда.
1487. Поезд, идущий со скоростью 18 м/с, начал тормозить, и через 15 с остановился. Считая движение поезда при торможении равнозамедленным, определите путь, пройденный поездом за эти 15 с.
1488. Постройте графики скорости равнозамедленного движения для случаев:
1) V0 = 10 м/с, а = — 1,5 м/с2;
2) V0 = 10 м/с; а = — 2 м/с2.
Масштаб в обоих случаях одинаков: 0,5 см – 1 м/с; о,5 см – 1 сек.
1489. Изобразите пройденный путь за время t на графике скорости равнозамедленного движения. Принять V0 = 10 м/с, а = 2 м/с2.
1490. Опишите движения, графики скоростей которых даны на рисунке 186, а и б.
а) движение будет равнозамедленным;
б) сначала тело будет двигаться равноускоренно, затем равномерно. На 3м участке движение будет равнозамедленное.
«Не до жиру, быть бы живу». Каково будущее квантового компьютера Google — Наука
ТАСС, 2 января. Специалисты компании Google, которые создали прототип квантового компьютера Sycamore, планируют использовать его для решения как теоретических, так и практических научных задач. Среди них – алгоритмы для автономного транспорта, изучение квантового хаоса и внутреннелго устройства черных дыр. Об этом ТАСС рассказал один из разработчиков этого компьютера Вадим Смелянский.
Среди них – алгоритмы для автономного транспорта, изучение квантового хаоса и внутреннелго устройства черных дыр. Об этом ТАСС рассказал один из разработчиков этого компьютера Вадим Смелянский.
Что такое квантовый компьютер?
Квантовыми компьютерами называют вычислительные устройства, в основе работы которых лежат принципы квантовой механики. В отличие от обычных компьютеров, в которых для передачи и обработки данных используются биты – единицы информации, которые содержат либо 1, либо 0, квантовые компьютеры оперируют кубитами – ячейками памяти и примитивными вычислительными модулями, которые могут хранить в себе одновременно и ноль, и единицу. Благодаря этому квантовые компьютеры могут обрабатывать большие объемы информации во много раз быстрее обычных – даже если это суперкомпьютеры с огромными вычислительными мощностями.
Существует два подхода к разработке подобных устройств – классический и адиабатический. В первом случае ученые пытаются создать так называемый универсальный квантовый компьютер, который по принципу работы похож на обычный современный компьютер. Адиабатический компьютер ближе к аналоговым компьютерам. Создавать их проще, но подобные устройства умеют решать лишь ограниченное количество задач.
Адиабатический компьютер ближе к аналоговым компьютерам. Создавать их проще, но подобные устройства умеют решать лишь ограниченное количество задач.
Инженеры и ученые Google почти пять лет разрабатывают устройство, которое должно объединить достоинства обоих подходов. Первая его версия состояла из девяти кубитов. Главная задача специалистов компании состояла в том, чтобы достичь так называемого квантового превосходства, то есть момента, когда ни один классический компьютер не может достичь тех же результатов, что и квантовый.
На эту тему
В ноябре прошлого года представители Google заявили, что достигли квантового превосходства в математической задаче, которая сводится к перебору набора псевдослучайных чисел. Для ее решения ученые использовали прототип квантового компьютера, Sycamore, который состоял из 53 сверхпроводящих кубитов. Несколько миллионов решений он нашел меньше чем за четыре минуты, тогда как у самого мощного суперкомпьютера на это ушло бы больше 10 тыс. лет.
лет.
В 2020 году об аналогичном достижении рассказали ученые из китайского Научно-технического университета. Их квантовый компьютер, «Цзю Чжан», создан на основе 73 фотонных кубитов. Он за 20 секунд решил еще одну задачу по выработке случайных чисел, которую обычный компьютер завершил бы за несколько миллиардов лет. Как и в случае с Sycamore, эти заявления вызвали множество споров о том, что можно считать нерешаемой задачей и как ее можно просчитывать на квантовом компьютере.
Революция в науке
Подобные достижения заставили ученых задуматься, какие практические задачи сможет решить квантовый компьютер. Одним из направлений, как считает Вадим Смелянский, может стать симуляция физических систем. «Уже сейчас, еще до появления систем коррекции ошибок, с помощью квантовых компьютеров можно изучать явления, связанные с квантовым хаосом и исчезновением информации. Другая команда Google будет использовать квантовые цепи для построения моделей квантовой гравитации», – пояснил ученый.
На эту тему
Также исследователи планируют использовать подобные системы, чтобы изучать, как некоторые полупроводники и металлы могут превращаться в изоляторы из-за взаимодействий электронов внутри них. Ученые недавно обнаружили, что аналогичные процессы, так называемые переходы Андерсона, могут возникать в самых разных условиях, в том числе и внутри кристаллов, электромагнитных волн или облаков из атомов.
Смелянский и его коллеги надеются, что квантовые компьютеры помогут понять природу этих переходов и выяснить, какую роль они играют в формировании свойств того или иного типа материи. По словам ученого, для этого необязательно использовать Sycamore и другие сверхпроводниковые квантовые компьютеры – достаточно будет и других машин с подходящим количеством кубитов и высоким уровнем их связанности.
«Все эти явления можно изучать в квантовых системах самых разных видов, в том числе и нейтральных атомов и ионов. Однако сверхпроводящие кубиты пока максимально приспособлены для решения этих задач. По сравнению с «конкурентами» они сильно связаны друг с другом и работают быстро. Это важно, к примеру, при изучении квантового хаоса и различных переходов между подобными состояниями», – продолжает физик.
По сравнению с «конкурентами» они сильно связаны друг с другом и работают быстро. Это важно, к примеру, при изучении квантового хаоса и различных переходов между подобными состояниями», – продолжает физик.
Ничейная полоса
В будущем, как отметил Смелянский, Google планирует применять квантовые компьютеры, чтобы создавать научные задачи, на которых будут обучаться системы искусственного интеллекта, а также для химических расчетов на уровне отдельных атомов. Однако это станет возможным только после того, как ученые решат еще одну важную задачу.
На эту тему
«Есть еще задачи квантовой химии, однако пока мы не понимаем, можно ли их будет решать без создания систем коррекции ошибок, в отличие от тех алгоритмов, о которых я уже говорил. По сути, мы перейдем в новое измерение, когда эта веха будет достигнута, так как мы сможем ставить перед собой совершенно иные, более амбициозные и сложные проблемы», – отметил физик.
С помощью алгоритмов коррекции ошибок физики и химики смогут просчитывать, как взаимодействуют между собой отдельные атомы и электроны внутри самых сложных молекул. Благодаря этому ученые смогут точно предсказывать, какие свойства есть у то или иного – даже пока не существующего – соединения, а также целенаправленно синтезировать вещества с конкретными свойствами.
Благодаря этому ученые смогут точно предсказывать, какие свойства есть у то или иного – даже пока не существующего – соединения, а также целенаправленно синтезировать вещества с конкретными свойствами.
По словам Смелянского, для этого пока не хватает двух вещей. С одной стороны, количество кубитов в квантовых компьютерах пока слишком невелико для того, чтобы на них могли работать уже существующие алгоритмы квантовой коррекции ошибок. С другой стороны кубиты во время простых вычислительных операций пока делают слишком много случайных ошибок.
Из-за этого ученые пока не могут создавать достаточно большие квантовые компьютеры, которые могли бы самостоятельно исправлять ошибки в своей работе. В результате квантовые компьютеры находятся в своеобразной «ничейной полосе». Их можно использовать для решения ограниченного числа сложных практических задач, однако пока нельзя превратить в универсальные вычислительные машины.
«Мы предполагаем, что той точности работы наших логических схем, которую сейчас можно достичь, скорее всего, не хватит для ведения квантово-химических расчетов. С другой стороны, пока этот вопрос открыт. Вполне возможно, что мы сможем реализовать какой-то более простой подход для коррекции ошибок, который не потребует кубитов, живущих бесконечно долго, подавления квантовых шумов и других сложных трюков. В течение нескольких лет мы будем этим заниматься», – отметил Смелянский.
Квантовое ускорение
При этом, по его словам, ученые должны фокусировать свои усилия не на увеличении точности работы кубитов, а на создании алгоритмов, которые смогли бы подавлять помехи, а также облегченных схем, с помощью которых можно было бы корректировать ошибки.
На эту тему
«Даже если мы в разы уменьшим уровень ошибок и повысим качество работы связанных цепочек кубитов, то этого все равно не хватит для того, чтобы решать задачи квантовой химии. Поэтому нам критически важен прогресс именно в области подавления ошибок. Без этого мы ничего не сможем сделать. И если мы достигнем всего вышеперечисленного, то все равно никакой гарантии успеха у нас нет», – подчеркнул физик.
По словам Смелянского, в дальнейшем ученые будут совершенствовать уже существующие и достаточно развитые подходы, в том числе сверхпроводящие цепи, полупроводниковые схемы, холодные атомы или ионы. Чтобы создавать принципиально иные системы для квантовых вычислений, в том числе на базе атомных ядер, нужны будут колоссальные усилия и время. Ученый пока не видит никаких перспективных, но пока не изученных направлений.
«Наши российские коллеги сейчас говорят о том, что они планируют развивать все четыре направления в рамках квантового проекта «Росатома». Однако в данном случае речь идет о том, что они будут изучать, что сделали другие. Это невозможно делать, просто читая журналы – для этого нужны лаборатории. Как я понимаю, они будут этим заниматься до тех пор, пока они не примут решение сосредоточиться на чем-то одном», – добавил Смелянский.
Далеко не все эти усилия, как считает специалист Google, принесут результат. В частности, он отметил, что считает адиабатический подход, которые набирает популярность среди ученых и инвесторов, гораздо менее перспективным и интересным, чем создание универсальных квантовых вычислительных систем.
«Вкладывание ресурсов в такие проекты – большая ошибка. Квантовые отжигатели (так называют прототипы адиабатических квантовых компьютеров, – прим. ТАСС) можно будет использовать для физических экспериментов, однако они вряд ли подойдут для решения оптимизационных задач. Недавно наша группа показала, что адиабатические подходы во всех реалистичных случаях приходят к ответу не быстрее, чем классический квантовый алгоритм Монте-Карло. По сути, квантового ускорения здесь не наблюдается», – пояснил исследователь.
Новые перспективы
Сам Google, по словам Смелянского, планирует использовать универсальные квантовые вычислительные машины не только для проверки фундаментальных законов физики, улучшения работы систем поиска информации, тренировки искусственного интеллекта и других абстрактных IT-задач, но и на практике.
На эту тему
В частности, ученые собираются применять квантовые компьютеры для создания алгоритмов, которые управляют работой автономного транспорта, а также для улучшения свойств компонентов литиевых батарей и других типов аккумуляторов.
«Наследников» Sycamore планируют привлечь для помощи биологам и биохимикам из Google, а также их партнерам в Гарварде и в других американских университетах, чтобы значительно ускорить поиски различных новых материалов и катализаторов, а также лекарств от рака и других болезней.
Однако когда и как все это будет реализовано, пока сказать сложно, так как ученые еще не решили сложные технические вопросы, связанные с созданием универсального квантового компьютера с тысячами логических кубитов.
«Сейчас мы работаем и смотрим на эти проблемы в формате «не до жиру, быть бы живу». Поэтому первоочередная наша цель – просто построить машину, которая смогла бы решать подобные задачи. Только потом мы будем думать о том, как все эти параметры будут влиять на ее работу и разрабатывать метрики, по которым можно оценивать эти изменения», – подытожил Смелянский.
Каково это — катапультироваться из самолета
КАПИТАН ДАРРЕН «БАМ-БАМ» УИЗ, 29 лет, пилот BBC:
«Катапультирование — лучший способ испытать свое тело на прочность. Иногда люди при этом гибнут. Или теряют конечности: руки-ноги отрываются или гнутся в дугу. Я лично стал меньше ростом: был 174 см, а стал на 2 см короче. Дело было в тренировочном полете в Виргинии. Я пилотировал F-15E (американский истребитель. — Esquire). На борту были я и мой стрелок Красти. Идем на бреющем, с высокой скоростью. И вдруг вижу: справа промелькнул стервятник. Тут же машину сильно встряхнуло, и раздался взрыв. Это птицу засосало в двигатель. Через пару секунд хвост и правый борт оказались в пламени. Начинаю набирать высоту, но машина не поддается и заваливается на правое крыло. Надо сваливать. Сообщаю по радио ведомому, чтобы держался подальше, и даю команду: «Покинуть самолет!»
С обеих сторон кресла по ручке. Дергаю за них. Механизм срабатывает — отстреливается стекло кабины. Теперь совсем шумно, ветер хлещет. Взлетает заднее кресло — Красти выбросился. Остаюсь в машине один — кажется, на целую вечность, хотя прошло меньше секунды. Стискиваю ручки. Глаза закрыл. Весь напрягся — знаю, сейчас такой луна-парк начнется! Слышу: ведомый радирует диспетчерам, что мы вынуждены катапультироваться. И вылетаю из кабины сам.
Даже не знаю, как это описать. Сидишь в кресле, к которому приделана ракета. И стартуешь из самолета, который летит со скоростью 480 км/час. Да, к креслу действительно приделан ракетный двигатель. Он выпихивает тебя из самолета и еще метров 60 проносит по воздуху на реактивной тяге. В общем, набираю высоту с ускорением в 22 g. Если сравнить с аттракционами, то там максимальное ускорение составляет 2 g. Чувствую себя так, словно во мне полторы тонны весу. Ноги, спина и задница отяжелели. Ускорение вжимает меня в спинку кресла, пытается согнуть в дугу — вынуждает уткнуться лбом в колени. Такое ощущение, будто на тебя навалилась куча врагов: бьют кулаками, тянут во все стороны сразу. Чувствую, ремешок шлема врезался в подбородок. Шлем прямо срывает с головы. Кожа на подбородке лопнула под давлением изнутри. Я аж застонал. И тут, как и полагается, кресло подбрасывает меня в воздух. Я впервые открываю глаза. Вижу: кресло улетает. Автоматически раскрывается парашют. Скорость падает. Стропы сильно дергают меня за плечи. Дальше лечу плавно. Весь процесс — с момента, когда я дернул за ручки, до раскрытия парашюта — продлился секунды три-четыре. Открыв глаза, поискал глазами Красти: вон он спускается на парашюте. Смотрю в другую сторону — горящий самолет втыкается в землю. Как назло, около единственного дома в этой дикой горной местности. К счастью, никто не пострадал».
Что такое парадантоз и каковы его последствия?
Парадантоз крайне неприятное заболевание, которое в первую очередь затрагивает десна. По — другому, в простонародье, парадантоз называют болезнью десен.
Первым признаком возникновения такой болезни может служить обильный кровоток десен при утренней чистке зубов. Это означает, что десна стали ослабевать и им необходимо комплексное и профилактическое лечение, которое должно назначаться как можно раньше. Ведь чем раньше будет обнаружено такое заболевание, тем больше становится вероятность спасти десна и привести их в нужное состояние.
Вторым признаком, довольно неприятным для человека, может служить возникновение специфического запаха из ротовой полости, что вызывает у многих людей, страдающих такой болезнью крайнее неудобство. Запущенная форма парадантоза способствует уменьшению площади десен, что ведет к потере зубов. Но, стоит рассмотреть причины, ведущие к заболеванию десен.
В первую очередь, риск возникновения такого заболевания как парадантоз вызывает курение и чрезмерное употребление кофе и чая. Курение сужает маленькие сосуды, расположенные в деснах, в связи с чем, кровообращение замедляется, или вовсе перестает функционировать. Это не может быть незамеченным или не нести никаких последствий. Как правило, происходит разрушение десен, а следом начинается выпадение зубов.
Чтобы предотвратить столь нежелательную болезнь, стоит как можно чаще посещать стоматолога клиники Санация, чистить зубы два раза в день – утром и вечером, обязательно использовать средства для полоскания, в состав которого должен входит хлоргексидин. Кроме того, стоматологи клиник Санация рекомендуют использовать зубную нить после каждого приема пищи. Таким образом, необходимо избавляться от остатков пищи, которые в свою очередь могут повлиять на ускорение процесс гниения зубов, если в них есть дырки.
Зубы и десны нуждаются в постоянном контроле и уходе, чтобы избежать таких неприятных болезней, как парадантоз, кариес и возникновение зубного камня. Главное не затягивать визит к врачу, если ощущается излишние количество налета, запах изо рта или уменьшение площади десен. Ведь здоровая улыбка – залог успеха во многих повседневных делах.
Полезная информация
Терапевтическая стоматологияРазгон
Последняя математическая величина, обсуждаемая в Уроке 1, — это ускорение. Часто путают, что ускорение имеет значение, сильно отличающееся от значения, которое ассоциируется с ним спортивными комментаторами и другими людьми. Определение ускорения:
- Ускорение — это векторная величина, которая определяется как скорость, с которой объект изменяет свою скорость. Объект ускоряется, если он меняет свою скорость.
Спортивные комментаторы иногда говорят, что человек ускоряется, если он / она быстро движется.И все же ускорение не имеет ничего общего с быстрым движением. Человек может двигаться очень быстро, но при этом не ускоряться. Ускорение связано с изменением скорости движения объекта. Если объект не меняет свою скорость, значит, объект не ускоряется. Данные справа представляют движущийся на север ускоряющийся объект. Скорость меняется с течением времени. Фактически, скорость изменяется на постоянную величину — 10 м / с — каждую секунду. Каждый раз, когда скорость объекта изменяется, объект считается ускоряющимся; у него есть ускорение.
Значение постоянного ускорения
Иногда ускоряющийся объект меняет свою скорость на одну и ту же величину каждую секунду. Как упоминалось в предыдущем абзаце, приведенная выше таблица данных показывает, что объект меняет свою скорость на 10 м / с каждую последующую секунду. Это называется постоянным ускорением, поскольку скорость изменяется на постоянную величину каждую секунду. Не следует путать объект с постоянным ускорением с объектом с постоянной скоростью.Не дайте себя обмануть! Если объект меняет свою скорость — на постоянную или переменную величину — то это ускоряющийся объект. И объект с постоянной скоростью не ускоряется. Приведенные ниже таблицы данных отображают движения объектов с постоянным ускорением и изменяющимся ускорением. Обратите внимание, что каждый объект имеет изменяющуюся скорость.
Поскольку ускоряющиеся объекты постоянно меняют свою скорость, можно сказать, что пройденное расстояние / время не является постоянной величиной.Например, падающий объект обычно ускоряется при падении. Если бы мы наблюдали движение свободно падающего объекта (движение свободного падения будет подробно обсуждено позже), мы бы заметили, что объект имеет среднюю скорость примерно 5 м / с в первую секунду, примерно 15 м / с. во второй секунде примерно 25 м / с в третью секунду, примерно 35 м / с в четвертую секунду и т. д. Наш свободно падающий объект будет постоянно ускоряться. Учитывая эти средние значения скорости в течение каждого последовательного временного интервала в 1 секунду, мы могли бы сказать, что объект упадет на 5 метров в первую секунду, 15 метров во вторую секунду (для общего расстояния 20 метров), 25 метров в третью. второй (для общей дистанции 45 метров), 35 метров в четвертой секунде (для общей дистанции 80 метров через четыре секунды).Эти числа приведены в таблице ниже.
| Время Интервал | Изменение скорости В течение интервала | пр. Скорость В течение интервала | Пройденное расстояние В течение интервала | Общее пройденное расстояние с От 0 с до конца интервала |
| 0 — 1.0 с | от 0 до ~ 10 м / с | ~ 5 м / с | ~ 5 м | ~ 5 м |
| 1,0 — 2,0 с | ~ 10-20 м / с | ~ 15 м / с | ~ 15 м | ~ 20 м |
| 2,0 — 3,0 с | ~ от 20 до 30 м / с | ~ 25 м / с | ~ 25 м | ~ 45 м |
| 3,0 — 4.0 с | ~ 30-40 м / с | ~ 35 м / с | ~ 35 м | ~ 80 м |
Примечание. Используемый здесь символ ~ означает приблизительно.
Это обсуждение показывает, что свободно падающий объект, который ускоряется с постоянной скоростью, будет преодолевать разные расстояния за каждую последующую секунду. Дальнейший анализ первого и последнего столбцов приведенных выше данных показывает, что существует квадратная зависимость между общим пройденным расстоянием и временем путешествия для объекта, начинающегося из состояния покоя и движущегося с постоянным ускорением.2) расстояние; расстояние, пройденное за четыре секунды, в 16 раз превышает расстояние, пройденное за одну секунду. Для объектов с постоянным ускорением расстояние перемещения прямо пропорционально квадрату времени перемещения.
Расчет среднего ускорения
Среднее ускорение (a) любого объекта за заданный интервал времени (t) можно рассчитать с помощью уравнения
Это уравнение можно использовать для расчета ускорения объекта, движение которого представлено приведенной выше таблицей данных скорость-время.Данные скорости-времени в таблице показывают, что объект имеет ускорение 10 м / с / с. Расчет показан ниже.
Значения ускорения выражаются в единицах скорости / времени. Типичные устройства ускорения включают в себя следующие:
м / с / с
миль / час / с
км / час / с
м / с 2
Эти устройства могут показаться немного неудобными для начинающего студента-физика. Тем не менее, это очень разумные единицы, когда вы начинаете рассматривать определение и уравнение ускорения.Причина появления единиц становится очевидной после изучения уравнения ускорения.
Поскольку ускорение — это изменение скорости с течением времени, единицы измерения ускорения — это единицы скорости, деленные на единицы времени, то есть (м / с) / с или (миль / час) / с. Единицу измерения (м / с) / с можно математически упростить до м / с 2 .
Направление вектора ускорения
Поскольку ускорение является векторной величиной, с ним связано направление.Направление вектора ускорения зависит от двух вещей:
- , ускоряется или замедляется объект
- , движется ли объект в + или — направлении
Общий принцип определения ускорения:
Если объект замедляется, то его ускорение происходит в направлении, противоположном его движению.
Этот общий принцип может применяться для определения того, является ли знак ускорения объекта положительным или отрицательным, вправо или влево, вверх или вниз и т. Д.Рассмотрим две таблицы данных ниже. В каждом случае ускорение объекта происходит в положительном направлении . В Примере A объект движется в положительном направлении (т. Е. Имеет положительную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект имеет положительное ускорение. В примере B объект движется в отрицательном направлении (т.е. имеет отрицательную скорость) и замедляется.Согласно нашему общему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект также имеет положительное ускорение.
Тот же самый общий принцип может быть применен к движению объектов, представленных в двух таблицах данных ниже. В каждом случае ускорение объекта происходит в отрицательном направлении . В примере C объект движется в положительном направлении (т.е.е., имеет положительную скорость ) и замедляется. Согласно нашему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект имеет отрицательное ускорение. В Примере D объект движется в отрицательном направлении (т.е. имеет отрицательную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект также имеет отрицательное ускорение.
Обратите внимание на использование положительных и отрицательных слов в приведенном выше обсуждении (Примеры A — D). В физике использование положительного и отрицательного всегда имеет физический смысл. Это больше, чем просто математический символ. Положительное и отрицательное, используемые здесь для описания скорости и ускорения движущегося объекта, описывают направление. И скорость, и ускорение являются векторными величинами, и полное описание величины требует использования прилагательного направленного действия.Север, юг, восток, запад, вправо, влево, вверх и вниз — все прилагательные направления. Физика часто заимствует из математики и использует символы + и — как направленные прилагательные. В соответствии с математическим соглашением, используемым в числовых линиях и графиках, положительное значение часто означает вправо или вверх, а отрицательное — влево или вниз. Таким образом, сказать, что объект имеет отрицательное ускорение, как в примерах C и D, означает просто сказать, что его ускорение идет влево или вниз (или в любом направлении, определенном как отрицательное).Отрицательные ускорения не относятся к значениям ускорения меньше 0. Ускорение -2 м / с / с — это ускорение с величиной 2 м / с / с, которое направлено в отрицательном направлении.
Чтобы проверить свое понимание концепции ускорения, рассмотрите следующие проблемы и соответствующие решения. Используйте уравнение для ускорения, чтобы определить ускорение для следующих двух движений.
разгон | Физика
Цели обучения
К концу этого раздела вы сможете:
- Определение и различие между мгновенным ускорением, средним ускорением и замедлением.
- Рассчитайте ускорение с учетом начального времени, начальной скорости, конечного времени и конечной скорости.
Рис. 1. Самолет замедляется или замедляется при посадке на острове Сен-Мартен. Его ускорение противоположно его скорости. (Источник: Стив Конри, Flickr)
В повседневном разговоре ускорять означает ускоряться. Фактически, ускоритель в автомобиле может заставить его разогнаться. Чем больше ускорение , тем больше изменение скорости за заданный промежуток времени.Формальное определение ускорения согласуется с этими понятиями, но является более всеобъемлющим.
Среднее ускорениеСреднее ускорение — это скорость, с которой изменяется скорость ,
[латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {f} — {v} _ {0}} {{t} _ {f} — {t} _ {0}} [/ latex]
, где [latex] \ bar {a} [/ latex] — среднее ускорение, v — скорость, а t — время.(Полоса над a означает среднее ускорение .)
Поскольку ускорение — это скорость в м / с, деленная на время в секундах, единицами измерения ускорения в системе СИ являются м / с 2 , квадратные метры в секунду или метры в секунду в секунду, что буквально означает, сколько метров в секунду скорость меняется каждую секунду.
Напомним, что скорость — это вектор, у нее есть величина и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение в направлении .Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение возникает, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по обоим направлениям.
Ускорение как векторУскорение — это вектор в том же направлении, что и изменение скорости на , Δ v . Поскольку скорость — это вектор, она может меняться по величине или по направлению.Таким образом, ускорение — это изменение скорости или направления, либо и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда происходит в направлении движения . Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .
Мгновенное ускорение
Мгновенное ускорение a , или ускорение в определенный момент времени , получается с помощью того же процесса, который обсуждался для мгновенной скорости во времени, скорости и скорости, то есть путем рассмотрения бесконечно малого интервала время.Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 6 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На Рисунке 6 (а) ускорение незначительно меняется, и среднее значение за весь интервал почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1.8 м / с 2 ). На рисунке 6 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы можем рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с 2 и –2,0 м / с 2 соответственно.
В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 7.В (а) волан движется вправо, а в (б) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые аргументы, которые используются при решении проблем.
Пример 2. Расчет смещения: поезд метро
Каковы величина и знак смещений при движении поезда метро, показанных в частях (а) и (b) рисунка 7?
СтратегияЧертеж с системой координат уже предоставлен, поэтому нам не нужно делать набросок, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает.Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение Δ x = x f — x 0 . Это просто, поскольку даны начальная и конечная позиции.
Решение1. Определите известные. На рисунке мы видим, что x f = 6,70 км и x 0 = 4,70 км для части (a), и x ′ f = 3,75 км и x ′ 0 = 5.25 км по части (б).
2. Найдите смещение в части (а).
[латекс] \ Delta x = {x} _ {f} — {x} _ {0} = 6,70 \ text {km} -4,70 \ text {km} = \ text {+} 2,00 \ text {km} [ / латекс]
3. Найдите смещение в части (b).
[латекс] \ Delta x ′ = {x ′} _ {f} — {x ′} _ {0} = \ text {3,75 км} — \ text {5,25 км} = — \ text {1,50 км} [/ латекс]
ОбсуждениеНаправление движения в (a) — вправо, поэтому его смещение имеет положительный знак, тогда как движение в (b) — влево и, следовательно, имеет отрицательный знак.
Пример 3. Сравнение пройденного расстояния и перемещения: поезд метро
Какие расстояния проходят за движения, показанные в частях (a) и (b) поезда метро на Рисунке 7?
СтратегияЧтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которая была найдена в Примере 1.Пройденное расстояние — это общая длина пути, пройденного между двумя позициями. (См. Смещение.) В случае поезда метро, показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Решение1. Смещение для части (а) составило +2,00 км. Таким образом, расстояние между начальной и конечной позициями составило 2,00 км, а пройденное расстояние — 2,00 км.
2. Смещение для части (b) было -1.5 км. Таким образом, расстояние между начальной и конечной позициями составляло 1,50 км, а пройденное расстояние — 1,50 км.
ОбсуждениеРасстояние — скаляр. У него есть величина, но нет знака, указывающего направление.
Пример 4. Расчет ускорения: поезд метро набирает скорость
Предположим, что поезд на рис. 7 (а) ускоряется из состояния покоя до 30,0 км / ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени?
СтратегияЗдесь стоит сделать простой набросок:
Решение1.Определите известные. v 0 = 0 (поезда запускаются в состоянии покоя), v f = 30,0 км / ч и Δ t = 20,0 с.
2. Вычислите Δ v . Поскольку поезд стартует из состояния покоя, его скорость изменяется на [latex] \ Delta v \ text {=} \ text {+} \ text {30,0 км / ч} [/ latex], где знак плюс означает скорость вправо. .
3. Подставьте известные значения и решите неизвестное, [latex] \ bar {a} [/ latex].
[латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {+ \ text {30.{2} [/ латекс]
ОбсуждениеЗнак плюс означает, что ускорение направо. Это разумно, потому что поезд стартует из состояния покоя и заканчивает со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости на , как всегда.
Пример 5. Расчет ускорения: замедление поезда метро
Теперь предположим, что в конце поездки поезд на Рисунке 7 (а) замедляется до остановки со скорости 30.0 км / ч за 8.00 с. Какое у него среднее ускорение при остановке?
Стратегия Решение1. Определите известные. v 0 = 30,0 км / ч, v f = 0 км / ч (поезд остановлен, поэтому его скорость равна 0), и Δ t = 8,00 с.
2. Найдите изменение скорости Δ v .
Δ v = v f — v 0 = 0-30.{2} \ text {.} [/ Latex]
ОбсуждениеЗнак минус указывает на то, что ускорение происходит влево. Этот знак разумен, потому что поезд изначально имеет положительную скорость в этой задаче, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , которое здесь отрицательно. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики положения, скорости и ускорения отВремя для поездов в Примере 4 и Примере 5 показано на рисунке 10. (Мы приняли скорость постоянной от 20 до 40 с, после чего поезд замедляется.)
Пример 6. Расчет средней скорости: поезд метро
Какова средняя скорость поезда в части b примера 2, снова показанной ниже, если поездка занимает 5,00 минут?
СтратегияСредняя скорость — это смещение, разделенное на время. Здесь он будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.
Решение1. Определите известные. x ′ f = 3,75 км, x ′ 0 = 5,25 км, Δ t = 5,00 мин.
2. Определите смещение Δ x ′. В примере 2 мы обнаружили, что Δ x ′ составляет −1,5 км.
3. Найдите среднюю скорость.
[латекс] \ bar {v} = \ frac {\ Delta x ′} {\ Delta t} = \ frac {- \ text {1,50 км}} {\ text {5,00 мин}} [/ latex]
4. Перевести единицы.
[латекс] \ bar {v} = \ frac {\ Delta x ′} {\ Delta t} = \ left (\ frac {-1 \ text {.} \ text {50 км}} {5 \ text {.} \ text {00 min}} \ right) \ left (\ frac {\ text {60 min}} {1 h} \ right) = — \ text { 18} \ text {.0 км / ч} [/ latex]
ОбсуждениеОтрицательная скорость указывает на движение влево.
Пример 7. Расчет замедления: поезд метро
Наконец, предположим, что поезд на Рисунке 2 замедляется до остановки со скорости 20,0 км / ч за 10,0 с. Какое у него среднее ускорение?
СтратегияЕще раз нарисуем набросок:
Как и раньше, мы должны найти изменение скорости и изменение во времени, чтобы вычислить среднее ускорение.
Решение1. Определите известные. v 0 = −20 км / ч, v f = 0 км / ч, Δ t = 10,0 с.
2. Вычислите Δ v . Изменение скорости здесь действительно положительное, так как
[латекс] \ Delta v = {v} _ {f} — {v} _ {0} = 0- \ left (- \ text {20 км / ч} \ right) \ text {=} \ phantom {\ правило {0.25} {0ex}} \ text {+} \ text {20 км / ч} [/ latex]
3. Решите для [латекс] \ bar {a} [/ latex].
[латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {+ \ text {20} \ text {.{2} [/ латекс]
ОбсуждениеЗнак плюс означает, что ускорение направо. Это разумно, потому что поезд изначально имеет отрицательную скорость (слева) в этой задаче, а положительное ускорение противодействует движению (то есть справа). Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь положительно. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.
Пожалуй, самое важное, что нужно отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус — слева. Это легко представить для смещения и скорости. Но для разгона это немного менее очевидно. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в Примере 2, где положительное ускорение замедляло отрицательную скорость. Ключевым отличием было то, что ускорение происходило в направлении, противоположном скорости.Фактически, отрицательное ускорение увеличит отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае и v , и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и изменение скорости, объект ускоряется. Если ускорение имеет знак, противоположный изменению скорости, объект замедляется.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток.Опишите его ускорение.
РешениеЕсли принять восток за положительное значение, то самолет имеет отрицательное ускорение, так как он ускоряется в сторону запада. Он также замедляется: его ускорение противоположно его скорости.
Исследования PhET: моделирование движущегося человека
Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка взад и вперед с помощью мыши и наметьте его движение. Задайте положение, скорость или ускорение и позвольте симуляции перемещать человека за вас.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
Концептуальные вопросы
1. Возможно ли, чтобы скорость оставалась постоянной при ненулевом ускорении? Приведите пример такой ситуации.
2. Возможно ли, чтобы скорость была постоянной, если ускорение не равно нулю? Объяснять.
3. Приведите пример, в котором скорость равна нулю, а ускорение — нет.
4. Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
5.Знаки плюс и минус используются в одномерном движении для обозначения направления. Каков знак ускорения, уменьшающего величину отрицательной скорости? Положительной скорости?
Задачи и упражнения
1. Гепард может разогнаться от состояния покоя до скорости 30,0 м / с за 7,00 с. Какое у него ускорение?
2. Профессиональное приложение. Доктор Джон Пол Стапп, офицер ВВС США, изучал влияние экстремального замедления на человеческое тело.10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с, и был резко остановлен всего за 1,40 с! Вычислите его (а) ускорение и (б) замедление. Выразите каждое значение кратным г (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
3. Пассажир выезжает на машине задним ходом из гаража с ускорением 1,40 м / с 2 . (A) Сколько времени ему нужно, чтобы набрать скорость 2.00 м / с? (b) Если она затем тормозит до остановки через 0,800 с, каково ее замедление?
4. Предположим, что межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6,50 км / с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в м / с 2 и кратное g (9,80 м / с 2 ).
Глоссарий
- ускорение:
- скорость изменения скорости; изменение скорости с течением времени
- среднее ускорение:
- изменение скорости, деленное на время, в течение которого оно изменяется
- мгновенное ускорение:
- ускорение в определенный момент времени
- замедление:
- ускорение в направлении, противоположном скорости; ускорение, которое приводит к уменьшению скорости
Избранные решения проблем и упражнения
1.4,29 м / с 2
3. (а) 1,43 с (б) -2,50 м / с 2
Acceleration
Оптимизация лазерного ускорения электронов
4 декабря 2020 г. — Исследователи рассмотрели характеристики ускорения электронов в вакууме, вызываемого лазерными импульсами максимальной мощности, достижимыми сегодня, в поисках ключа к максимальной чистой энергии …
Не так быстро! Контроль скорости световых пуль
Декабрь14, 2020 — Исследователи точно и произвольно контролируют скорость полета легких пуль, открывая новые возможности для оптических и физических …
Обеспечение более длительных космических полетов
20 августа 2019 г. — Подруливающее устройство Холла — это двигательная установка, которая часто используется космическими кораблями, выполняющими более длительные миссии. Недавнее исследование показало, как можно увеличить срок службы этих систем …
Методы пропуска камней могут улучшить возвращение космических аппаратов в атмосферу
Апр.20, 2021 — Ученые выявили несколько ключевых факторов, которые влияют на количество отскоков, которым прыгает камень при ударе о воду. Исследование включало теоретическое моделирование и экспериментальную установку …
Мировой рекорд: плазменный ускоритель работает круглосуточно
19 августа 2020 г. — Исследователи достигли важной вехи на пути к ускорителю элементарных частиц будущего. Впервые лазерно-плазменный ускоритель проработал более суток в непрерывном режиме…
Веха для экспериментов по ускорению нового поколения
30 апреля 2021 г. — Будущее ускорения частиц наступило. Пробуждение — многообещающая концепция совершенно нового метода, с помощью которого частицы можно ускорять даже на короткие расстояния. Основанием для этого служит …
Новый математический инструмент может выбрать лучшие датчики для работы
17 сентября 2020 г. — В результате авиакатастрофы Boeing 737 Max в 2019 году восстановленный черный ящик после аварии намекал, что отказавший датчик давления, возможно, привел к тому, что злополучный самолет нырнул в нос.Этот и другие инциденты имеют …
Методы количественной оценки острых ощущений и судороги игрока в гольф
19 июля 2018 г. — Почти каждому гольфисту знакомо это чувство. Через несколько минут после идеальной езды по фарватеру каскад необъяснимых пропущенных паттов приводит к разочаровывающему тройному результату …
Переносной датчик вибрации для точного распознавания голоса
24 июня 2019 г. — Ученые разработали гибкий и носимый чувствительный к вибрации датчик.Когда этот датчик прикреплен к шее, он может точно распознавать голос по вибрации кожи шеи и не …
«Оптическая ракета», созданная с помощью интенсивного лазерного излучения
14 сентября 2018 г. — Эксперимент продемонстрировал, как применение интенсивного света увеличивает количество электронов до максимально возможного …
Три формулы, которые вам нужны
«Ого, ты действительно прошел с нуля до шестидесяти!»
Вы когда-нибудь слышали, чтобы кто-то использовал идиому «от нуля до шестидесяти», как я в приведенном выше примере? Когда кто-то говорит, что что-то пошло с нуля до шестидесяти, на самом деле они говорят, что все ускорилось очень быстро. Ускорение — это величина, на которую скорость чего-либо изменяется в течение заданного периода времени.
В этой статье мы поговорим об ускорении: что это такое и как его рассчитать. Пристегнитесь!
Что такое ускорение?
Ускорение — это скорость изменения скорости за заданный период времени. Для расчета ускорения необходимы скорость и время.
Многие путают ускорение со скоростью (или скоростью).Прежде всего, скорость — это просто скорость с направлением, поэтому они часто используются как синонимы, даже если они имеют небольшие различия. Ускорение — это скорость изменения скорости, означающая, что что-то становится быстрее или медленнее.
Что такое формула ускорения?
Для расчета ускорения можно использовать уравнение ускорения. Вот наиболее распространенная формула ускорения:
$$ a = {Δv} / {Δt} $$
где $ Δv $ — изменение скорости, а $ Δt $ — изменение во времени.
Вы также можете написать уравнение ускорения следующим образом:
$$ a = {v (f) — v (i)} / {t (f) — t (i)} $$
В этом уравнении ускорения $ v (f) $ — это конечная скорость, а — начальная скорость $ v (i) $. $ T (f) $ — это конечное время, а $ t (i) $ — начальное время.
Еще о некоторых вещах, о которых следует помнить при использовании уравнения ускорения:
- Вам нужно вычесть начальную скорость из конечной скорости. Если вы перевернете их, вы получите неверное направление вашего ускорения.
- Если у вас нет времени начала, вы можете использовать «0».
- Если конечная скорость меньше начальной, ускорение будет отрицательным, что означает, что объект замедлился.
Теперь давайте разберем уравнение ускорения пошагово на реальном примере.
Как рассчитать ускорение: пошаговая разбивка
Теперь давайте разберем формулу ускорения пошагово на реальном примере. 2 $$
$$ A = 6.2 $$
Давайте попробуем другой пример.
Велосипедист, движущийся со скоростью 23,2 м / с, полностью останавливается за 1,5 $ с $. Какое у нее было замедление?
Сначала напишите уравнение ускорения.
$$ a = (v (f) — v (i)) ÷ (t (f) — t (i)) $$
Затем определите свои переменные.
a = то, что мы решаем для
$$ V (f) = 0 м / с $$
$$ V (i) = 23,2 м / с $$
$$ T (f) = 1,4 с $$
$$ T (i) = 0 с $$
Теперь подставьте переменные в уравнение и решите:
$$ A = {{(0 — 23.2} $$
2 Другие общие формулы ускорения
Не знаете, как рассчитать ускорение по другой формуле? Есть несколько других распространенных формул ускорения.
Формула углового ускорения
Угловое ускорение — это скорость, с которой угловое ускорение вращающегося объекта изменяется во времени.
Вот уравнение углового ускорения:
$$ a = {\ change \ in \ angular \ velocity} / {\ change \ in \ time} $$
Формула центростремительного ускорения
Центростремительное ускорение — это скорость движения объекта внутрь к центру круга.2} / r $$
$ a (c) $ = ускорение, центростремительное
$ v $ = скорость
$ r $ = радиус
Основные выводы
Ускорение — это скорость изменения скорости за заданный период времени.
Вы вычисляете ускорение, разделив изменение скорости на изменение во времени.
Что дальше?
Ищете другие научные объяснения? Мы разбиваем электрическую энергию и как определить различных типов облаков с помощью наших экспертных руководств.
Работаете над исследовательской работой, но не знаете, с чего начать? Тогда ознакомьтесь с нашим руководством, где мы собрали множество высококачественных тем для исследований, которые вы можете использовать бесплатно.
Нужна помощь с уроком английского языка — в частности, с определением литературных приемов в текстах, которые вы читаете? Тогда вы обязательно захотите взглянуть на наше исчерпывающее объяснение самых важных литературных устройств и того, как они используются.
Ускорение силы тяжести — Frega Physics
Ускорение силы тяжести — это скорость, с которой объект изменяет свою скорость под действием силы тяжести. Все объекты, падающие с одной и той же точки, ударяются о землю за одно и то же время, независимо от массы. На Земле среднее ускорение свободного падения составляет -9,81 м / с 2 *. Объекты, которые не ударяются о землю, испытывают сопротивление воздуха — силу трения, которая замедляет их движение. Этого можно добиться, уменьшив сопротивление воздуха за счет изменения формы объекта.
Ускорение свободного падения ВСЕГДА отрицательное. Любой объект, на который действует только сила тяжести (снаряд или объект в свободном падении), имеет ускорение -9.81 м / с 2 независимо от направления. Ускорение отрицательное при подъеме, потому что скорость уменьшается. Ускорение отрицательное при спуске, потому что он движется в отрицательном направлении, вниз. Даже в верхней части траектории, где мгновенная скорость равна 0 м / с, ускорение по-прежнему составляет -9,81 м / с 2 .
Когда в задаче упоминается, что объект «находится в свободном падении», «падает», «брошен», «подбрасывается» или какой-либо другой синоним, предполагается постоянное значение ускорения свободного падения.Если в уравнении есть a , например, v = v 0 + at , ускорение будет отрицательным . Если в уравнении g , например W = mg, подразумевается направление и ускорение положительное .
* -10 м / с 2 — приемлемое число для большинства вычислений в задачах, но -9,81 — более точное число.
| Обозначение переменной | Имя переменной | Единица СИ | Другие возможные единицы | Характеристики | метров в секунду в секунду (м / с / с) или метров в секунду в квадрате (м / с 2 ) | миль / с, км / ч / с | Ускорение — это скорость, в которой скорость изменения; это изменение скорости в единицу времени.На этом уровне Предположим, что ускорение равномерное или постоянное. Поскольку это вектор, принимается направление в учетную запись. Будьте осторожны со своими отрицательными и положительными моментами. Положительный ускорение может означать ускорение, движение вперед или замедление, движение назад. Отрицательное ускорение может означать замедление, движение вперед или ускорение, движение назад. | |
| g | ускорение свободного падения | метров в секунду в секунду (м / с / с) или метров в секунду в квадрате (м / с 2 ) | миль / ч / с, км / ч / с | При отсутствии сопротивления воздуха все предметы в свободном падении будут попадать в
земли одновременно при падении с одинаковой высоты, независимо от
масса.Ускорение свободного падения
— установленное число для определенного местоположения, обычно по планете (но это
число может незначительно отличаться на поверхности планеты в зависимости от расстояния
из ядра планеты). На Земле среднее ускорение за счет
гравитация составляет -9,81 м / с 2 (хотя -10 м / с 2 приемлемо для большинства расчетов). Когда в уравнении используется символ g , предполагается направление, а для вычислений используется абсолютное значение (+9.81 или +10). |
См. «Ускорение (комплексное)», чтобы узнать, как использовать ускорение свободного падения в задаче свободного падения.
2,4 Разгон | Texas Gateway
Мгновенное ускорение
Мгновенное ускорение a, a, или ускорение в определенный момент времени , получается с помощью того же процесса, который обсуждался для мгновенной скорости во Time, Velocity и Speed, то есть путем рассмотрения бесконечно малого интервала времени.Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 2.29 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На рис. 2.29 (а) ускорение немного меняется, а среднее значение за весь интервал почти такое же, как и мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему — в данном случае около 1.8 м / с 21,8 м / с2. На рис. 2.29 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы могли бы рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с2 + 3,0 м / с2 и –2,0 м / с2, –2,0 м / с2. , соответственно.
Рис. 2.29. Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений.(а) Здесь ускорение изменяется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается. В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 2.30. В (а) волан движется вправо, а в (б) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые аргументы, которые используются при решении проблем.
Рис. 2.30. Одномерное движение поезда метро, рассмотренное в Примере 2.2, Примере 2.3, Примере 2.4, Примере 2.5, Примере 2.6 и Примере 2.7. Здесь мы выбрали ось xx так, что + означает вправо, а −− означает влево для смещений, скоростей и ускорений.(a) Поезд метро движется вправо от x0x0 до xfxf. Его смещение ΔxΔx составляет +2,0 км. (b) Поезд движется налево от x′0x′0 до x′f.x′f. size 12 {{{x}} sup {‘} rSub {size 8 {f}}} {} Его водоизмещение Δx′Δx ′ размер 12 {Δx’} {} составляет -1,5 км. Обратите внимание, что основной символ [′] используется просто для того, чтобы различать смещение в двух разных ситуациях. Расстояния проезда и размеры машин указаны в разных масштабах, чтобы все уместилось на диаграмме.Пример 2.2 Расчет смещения: поезд метро
Каковы величина и знак смещений при движении поезда метро, показанных в частях (a) и (b) Рисунка 2.30?
Стратегия
Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает. Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение Δx = xf − x0.Δx = xf − x0. size 12 {Δx = x rSub {size 8 {f}} — x rSub {size 8 {0}}} {} Это просто, поскольку даны начальная и конечная позиции.
Решение
1.Определите известные. На рисунке мы видим, что xf = 6,70 км xf = 6,70 км и x0 = 4,70 км x0 = 4,70 км для части (a) и x′f = 3,75 км x′f = 3,75 км и x′0 = 5,25 км x′0 = 5,25 км для части (b).
2. Найдите смещение в части (a).
2,12 Δx = xf − x0 = 6,70 км − 4,70 км = + 2,00 км. Δx = xf − x0 = 6,70 км − 4,70 км = + 2,00 км. размер 12 {Δx = x rSub {размер 8 {f}} — x rSub {размер 8 {0}} = 6 «.» «70 км» — 4 дюйма ». «70 км» «= +» 2 «.» «00 км»} {}3. Найдите смещение в части (b).
2.13 Δx ′ = x′f − x′0 = 3.75 км − 5,25 км = −1,50 км. Δx ′ = x′f − x′0 = 3,75 км − 5,25 км = −1,50 км. размер 12 {Δx ‘= {{x}} sup {‘} rSub {size 8 {f}} — {{x}} sup {‘} rSub {size 8 {0}} = 3 «.» «75 км» — 5 ». «25 км» = — 1 «.» «50 км»} {}Обсуждение
Направление движения в (a) — вправо, и, следовательно, его смещение имеет положительный знак, тогда как движение в (b) — влево и, таким образом, имеет знак минус.
Пример 2.3 Сравнение пройденного расстояния и водоизмещения: поезд метро
Каковы расстояния, пройденные за движения, показанные в частях (a) и (b) поезда метро на Рисунке 2.30?
Стратегия
Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которая была найдена в Примере 2.2. Пройденное расстояние — это общая длина пути, пройденного между двумя позициями. См. Смещение. В случае поезда метро, показанного на рис. 2.30, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Решение
1. Смещение для части (а) составило +2,00 км. Таким образом, расстояние между начальной и конечной позициями составило 2,00 км, а пройденное расстояние — 2,00 км.
2. Смещение части (б) составило -1,5 км. Таким образом, расстояние между начальной и конечной позициями составляло 1,50 км, а пройденное расстояние — 1,50 км.
Обсуждение
Расстояние — скаляр.У него есть величина, но нет знака, указывающего направление.
Пример 2.4 Расчет ускорения: поезд метро набирает скорость
Предположим, что поезд на рис. 2.30 (a) ускоряется из состояния покоя до 30,0 км / ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени?
Стратегия
Здесь стоит сделать простой набросок
Эта проблема состоит из трех этапов.Сначала мы должны определить изменение скорости, затем мы должны определить изменение во времени и, наконец, мы должны использовать эти значения для расчета ускорения.
Решение
1. Определите известные. v0 = 0v0 = 0 размер 12 {v rSub {size 8 {0}} = 0} {} (поезда запускаются в состоянии покоя), vf = 30,0 км / ч, vf = 30,0 км / ч, размер 12 {v rSub { размер 8 {f}} = «30» «.» «0 км / ч»} {} и Δt = 20,0 с.Δt = 20,0 с. размер 12 {Δt = «20» «.» «0 с»} {}
2. Рассчитайте Δv.Δv. размер 12 {Δv} {} Поскольку поезд трогается с места, его скорость изменяется Δv = + 30.0 км / ч, Δv = + 30,0 км / ч, размер 12 {Δv «= +» «30» «.» 0` «km / h»} {} где знак плюс означает скорость вправо.
3. Подставьте известные значения и найдите неизвестное, размер a-a-12 {{bar {a}}} {}.
2.14 a- = ΔvΔt = + 30,0 км / ч 30,0 с.a- = ΔvΔt = + 30,0 км / ч 30,0 с. размер 12 {{bar {a}} = {{Δv} over {Δt}} = {{+ «30» «.» 0` «км / ч»} больше {«20» «.» 0`s}}} {}4. Поскольку единицы измерения смешанные (у нас есть часы и секунды для времени), нам нужно преобразовать все в единицы измерения СИ — метры и секунды.См. Дополнительные указания в разделе «Физические величины и единицы».
2,15 a — = + 30 км / ч 30,0 с103 м1 км1 h4,600 с = 0,417 м / с2a — = + 30 км / ч 30,0 с103 м1 км1 ч4,600 с = 0,417 м / с2 размер 12 {{bar {a}} = left ({{+ «30 км / ч»} больше {«20» «.» «0 s»}} справа) left ({{«10» rSup {size 8 {3}} «m «} более {» 1 км «}} справа) слева ({{» 1 ч «} более {» 3600 с «}} справа) = 0″. » «417 м / с» rSup {размер 8 {2}}} {}Обсуждение
Знак плюс означает, что ускорение направо.Это разумно, потому что поезд стартует из состояния покоя и заканчивает со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и , изменяя скорость на , как всегда.
Пример 2.5 Расчет ускорения: замедление поезда метро
Теперь предположим, что в конце поездки поезд на рис. 2.30 (a) замедляется до остановки со скорости 30,0 км / ч за 8,00 с. Какое у него среднее ускорение при остановке?
Стратегия
В этом случае поезд замедляется, а его ускорение отрицательное, потому что он направлен влево.Как и в предыдущем примере, мы должны найти изменение скорости и изменение во времени, а затем вычислить ускорение.
Решение
1. Определите известные. v0 = 30,0 км / ч, v0 = 30,0 км / ч, vf = 0 км / ч — vf = 0 км / ч — поезд остановлен, поэтому его скорость равна 0 — и Δt = 8,00 с.Δt = 8,00 с.
2. Найдите изменение скорости Δv.Δv. размер 12 {Δv} {}
2,16 Δv = vf-v0 = 0-30,0 км / ч = -30,0 км / ч. Δv = vf-v0 = 0-30,0 км / ч = -30,0 км / ч. размер 12 {Δv = v rSub {размер 8 {f}} — v rSub {размер 8 {0}} = 0 — «30» «.»» 0 км / ч «= -» 30 «». «» 0 км / ч «} {}3. Подключите известные значения ΔvΔv, размер 12 {Δv} {} и Δt, Δt, и решите для aa-
2,17 a- = ΔvΔt = −30,0 км / ч 8,00 sa- = ΔvΔt = −30,0 км / ч 8,00 с. Размер 12 {{bar {a}} = {{Δv} over {Δt}} = { {- «30» «.» «0 км / ч»} более {8 «.» «00 с»}}} {}4. Преобразование единиц в метры и секунды.
2,18 a- = ΔvΔt = −30,0 км / ч 8,00 с103 м1 км1 h4,600 с = −1,04 м / с2 .a- = ΔvΔt = −30,0 км / ч 8,00 с103 м1 км1 h4,600 с = −1,04 м / с2. размер 12 {{bar {a}} = {{Δv} over {Δt}} = left ({{- «30» «.»» 0 км / ч «} больше {8». «» 00 s «}} справа) слева ({{» 10 «rSup {size 8 {3}}» m «} больше {» 1 км «}} справа ) слева ({{«1 час»} больше {«3600 с»}} справа) = — 1 «.» «04 м / с» rSup {размер 8 {2}} «.»} {}Обсуждение
Знак минус указывает на то, что ускорение происходит влево. Этот знак разумен, потому что поезд изначально имеет положительную скорость в этой задаче, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь отрицательно.Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики положения, скорости и ускорения в зависимости от времени для поездов в Примере 2.4 и Примере 2.5 показаны на Рисунке 2.33. Мы приняли скорость постоянной от 20 до 40 с, после чего поезд замедляется.
Рис. 2.33 (a) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее, когда он набирает скорость.Затем его положение меняется медленнее по мере замедления в конце пути. В середине пути, когда скорость остается постоянной, положение меняется с постоянной скоростью. (б) Скорость поезда во времени. Скорость поезда увеличивается по мере его ускорения в начале пути. Он остается неизменным в середине пути, когда нет ускорения. Оно уменьшается по мере замедления поезда в конце пути. (c) Ускорение поезда с течением времени. Поезд имеет положительное ускорение, поскольку он ускоряется в начале пути.У него нет ускорения, поскольку он движется с постоянной скоростью в середине пути. Его ускорение отрицательное, так как он замедляется в конце пути.
Пример 2.6 Расчет средней скорости: поезд метро
Какова средняя скорость поезда в части b примера 2.2, которая снова показана ниже, если поездка занимает 5,00 минут?
Стратегия
Средняя скорость — это смещение, разделенное на время. Здесь он будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.
Решение
1. Определите известные. x′f = 3,75 км, x′f = 3,75 км, x′0 = 5,25 км, x′0 = 5,25 км, Δt = 5,00 мин. Δt = 5,00 мин.
2. Определите перемещение Δx′.Δx ′. В примере 2.2 мы обнаружили, что Δx′Δx ′ составляет −1,5 км.
3. Найдите среднюю скорость.
2,19 v- = Δx′Δt = −1,50 км 5,00 мин. V- = Δx′Δt = −1,50 км 5,00 мин. размер 12 {{bar {v}} = {{Δ {{x}} sup {‘}} над {Δt}} = {{- 1 «.» «50 км»} больше {5 «.» «00 мин»}}} {}4.Преобразование единиц.
2,20 v- = Δx′Δt = −1,50 км 5,00 мин 60 мин1 h = −18,0 км / ч. V- = Δx′Δt = −1,50 км 5,00 мин60 мин1 h = −18,0 км / ч. размер 12 {{bar {v}} = {{Δx ‘} больше {Δt}} = слева ({{- 1 «.» «» 50 «» «км»} больше {5 «.» «00» `» мин «}} right) left ({{» 60 «` «min»} больше {1`h}} right) = — «18» «.» 0` «км / ч»} {}Обсуждение
Отрицательная скорость указывает на движение влево.
Пример 2.7 Расчет замедления: поезд метро
Наконец, представьте поезд на Рисунке 2.34 замедляется до полной остановки со скорости 20,0 км / ч за 10,0 с. Какое у него среднее ускорение?
Стратегия
Еще раз нарисуем скетч:
Как и раньше, мы должны найти изменение скорости и изменение во времени, чтобы вычислить среднее ускорение.
Решение
1. Определите известные. v0 = -20 км / ч, v0 = -20 км / ч, vf = 0 км / ч, vf = 0 км / ч, Δt = 10,0 с. Δt = 10,0 с.
2.Рассчитайте ΔvΔv размер 12 {Δv} {}. Изменение скорости здесь фактически положительное, так как
2,21 Δv = vf − v0 = 0−−20 км / ч = + 20 км / час. Δv = vf − v0 = 0−−20 км / ч = + 20 км / ч. час размер 12 {Δv = v rSub {size 8 {f}} — v rSub {size 8 {0}} = 0 — left (- «20 км / ч» справа) «= +» «20 км / ч»} { }3. Найдите размер aa- 12 {{bar {a}}} {}.
2,22 a- = ΔvΔt = + 20,0 км / ч 20,0 с.a- = ΔvΔt = + 20,0 км / ч 20,0 с.4. Перевести единицы.
2,23 а — = + 20,0 км / ч 20,0 с103 м1 км1 ч 4600 с = + 0,556 м / с2, а — = + 20,0 км / ч 20,0 с103 м1 км1 ч 4600 с = + 0.556 м / с2,Обсуждение
Знак плюс означает, что ускорение направо. Это разумно, потому что у поезда изначально отрицательная скорость (слева) в этой задаче, а положительное ускорение противодействует движению, то есть справа. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь положительно. Как и в примере 2.5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.
Как определить ускорение
Ускорение — это скорость изменения скорости как функция времени. Это вектор, то есть он имеет как величину, так и направление. Он измеряется в метрах в секунду в квадрате или в метрах в секунду (скорость или скорость объекта) в секунду.
В терминах исчисления ускорение — это вторая производная положения относительно времени или, альтернативно, первая производная скорости относительно времени.
Ускорение — изменение скорости
Каждый день ускорение происходит в автомобиле.Вы нажимаете на педаль акселератора, и автомобиль ускоряется по мере того, как двигатель прикладывает все возрастающее усилие к трансмиссии. Но замедление — это тоже ускорение — скорость меняется. Если вы уберете ногу с педали акселератора, сила и скорость уменьшатся со временем. Как видно из рекламы, ускорение следует правилу изменения скорости (миль в час) с течением времени, например, от нуля до 60 миль в час за семь секунд.
Ед. Ускорения
Единицы измерения ускорения в системе СИ: м / с 2
(метры в секунду в квадрате или метра в секунду в секунду).
Гал или галилей (Gal) — это единица ускорения, используемая в гравиметрии, но не единица СИ. Он определяется как 1 сантиметр на секунду в квадрате. 1 см / с 2
Английские единицы измерения ускорения — футы в секунду в секунду, фут / с 2
Стандартное ускорение свободного падения или стандартное ускорение свободного падения g 0 — это ускорение свободного падения объекта в вакууме у поверхности земли. Он сочетает в себе действие силы тяжести и центробежного ускорения от вращения Земли.
Преобразование единиц ускорения
| Значение | м / с 2 |
|---|---|
| 1 галлон, или см / с 2 | 0,01 |
| 1 фут / с 2 | 0,304800 |
| 1 г 0 | 9,80665 |
Второй закон Ньютона — расчет ускорения
Уравнение классической механики для ускорения происходит из Второго закона Ньютона: сумма сил ( F ) на объекте постоянной массы ( м ) равна массе м , умноженной на ускорение объекта ( a ). .
F = a м
Следовательно, это можно изменить, чтобы определить ускорение как:
a = F / м
Результатом этого уравнения является то, что если на объект не действуют силы ( F = 0), он не будет ускоряться. Его скорость останется постоянной. Если к объекту добавить массу, ускорение будет меньше. Если убрать массу с объекта, его ускорение будет выше.
Второй закон Ньютона — один из трех законов движения, опубликованных Исааком Ньютоном в 1687 году в книге Philosophiæ Naturalis Principia Mathematica ( Mathematical Principles of Natural Philosophy ).
Ускорение и относительность
Хотя законы движения Ньютона применяются на скоростях, с которыми мы сталкиваемся в повседневной жизни, как только объекты движутся со скоростью, близкой к скорости света, правила меняются. Именно тогда специальная теория относительности Эйнштейна более точна.


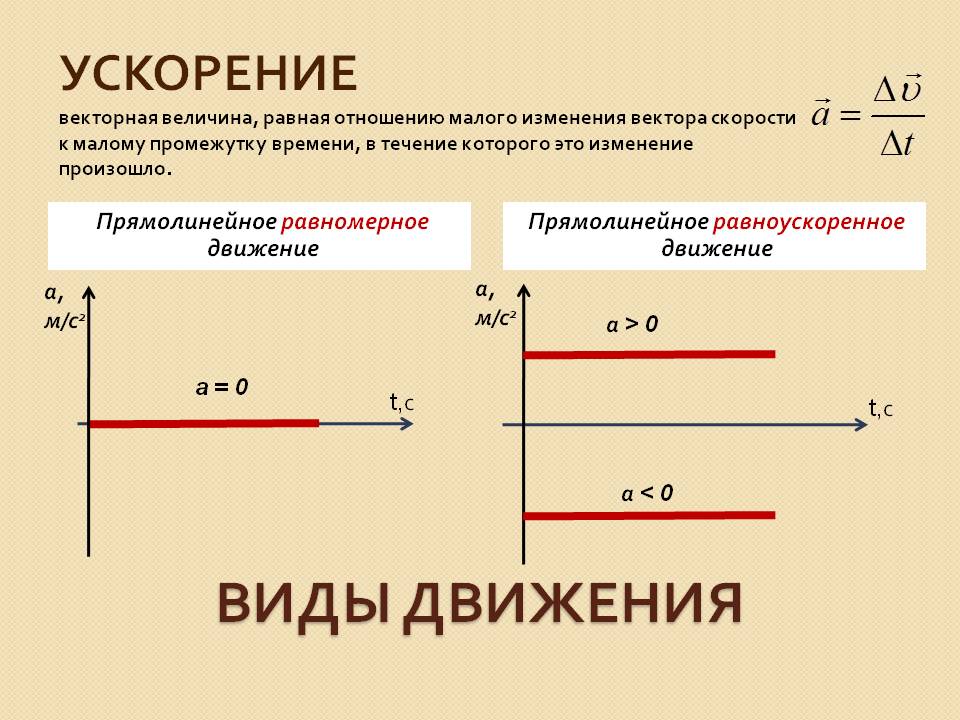
 Каждый квадратик создает пару с тремя остальными другими, естественно исключая вариант создания пары самим с собой. Для наглядности каждый квадратик со стрелками имеет свою цветовую маркировку.
Каждый квадратик создает пару с тремя остальными другими, естественно исключая вариант создания пары самим с собой. Для наглядности каждый квадратик со стрелками имеет свою цветовую маркировку.
 n
n combinations(range(1,10), 3)))
84
combinations(range(1,10), 3)))
84
 Еще один-два знака — и можно с точностью до атома рассчитать длину окружности с диаметром как у Вселенной.
Еще один-два знака — и можно с точностью до атома рассчитать длину окружности с диаметром как у Вселенной. Но вот с одинаковой ли частотой появляются цифры и их комбинации, неясно. Судя по всему, это так, но пока никто не привел строгого доказательства.
Но вот с одинаковой ли частотой появляются цифры и их комбинации, неясно. Судя по всему, это так, но пока никто не привел строгого доказательства.
 А советский математик Яков Перельман сочинил целый мнемонический диалог:
А советский математик Яков Перельман сочинил целый мнемонический диалог: Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание.
Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание. Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа.
Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.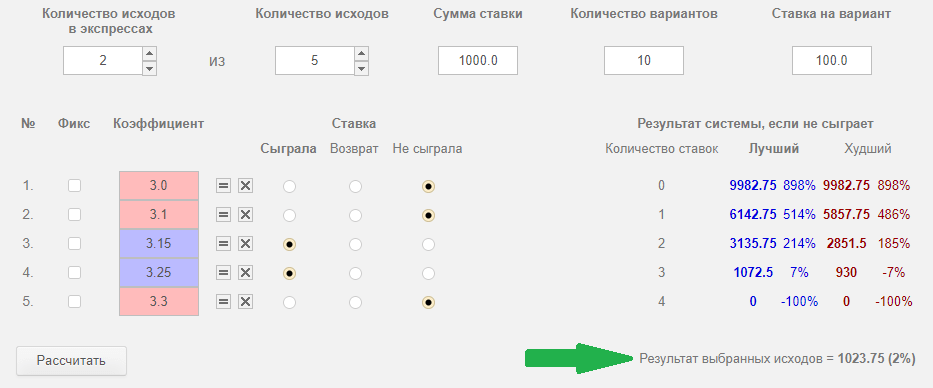
 Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?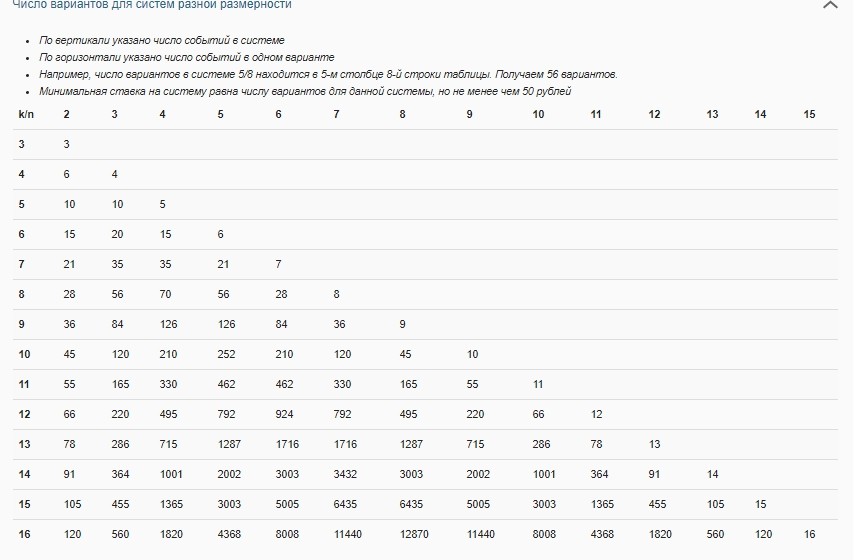 Перестановки, размещения, сочетания .
Перестановки, размещения, сочетания .

 Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).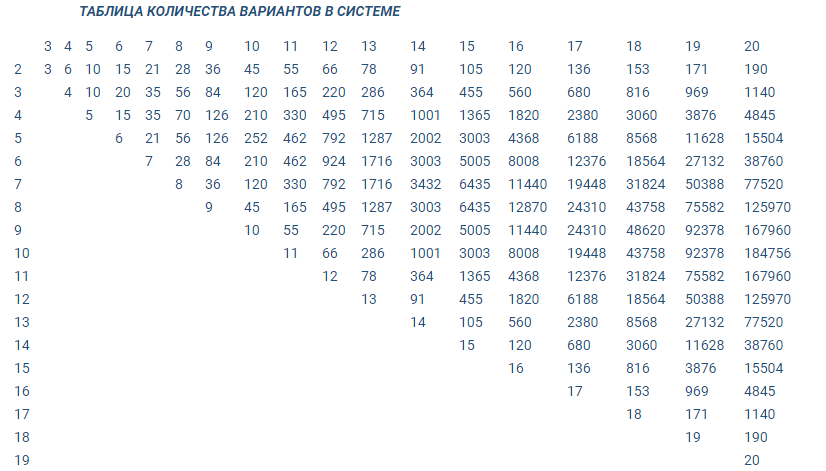
 06
06 40
40
 Чтобы найти сумму 5 последовательных чисел, можно:
Чтобы найти сумму 5 последовательных чисел, можно: проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60°, проведен из вершины А второй луч; получились три угла по 30°.
проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60°, проведен из вершины А второй луч; получились три угла по 30°. Простейший пример – подбрасывание монетки (экспериментатор не знает какая сторона монеты выпадет в каждом конкретном случае).
Простейший пример – подбрасывание монетки (экспериментатор не знает какая сторона монеты выпадет в каждом конкретном случае).
 Результаты эксперимента доказывают это на практике.
Результаты эксперимента доказывают это на практике.

 ). Если кратко, то по закону больших чисел в будущем должны получить примерно тот же результат.
). Если кратко, то по закону больших чисел в будущем должны получить примерно тот же результат. Расхождение с ожиданиями порядка 180-200%, на погрешность это списать нельзя.
Расхождение с ожиданиями порядка 180-200%, на погрешность это списать нельзя. Отличаются лишь инструменты анализа информации, сам принцип остается тем же.
Отличаются лишь инструменты анализа информации, сам принцип остается тем же. На основе этого рассчитывается норма для каждого менеджера;
На основе этого рассчитывается норма для каждого менеджера;
 Учитываются все составляющие – пол, сфера работы и должность, трудовой стаж, средний месячный доход, назначение займа, кредитная история, семейное положение.
Учитываются все составляющие – пол, сфера работы и должность, трудовой стаж, средний месячный доход, назначение займа, кредитная история, семейное положение.

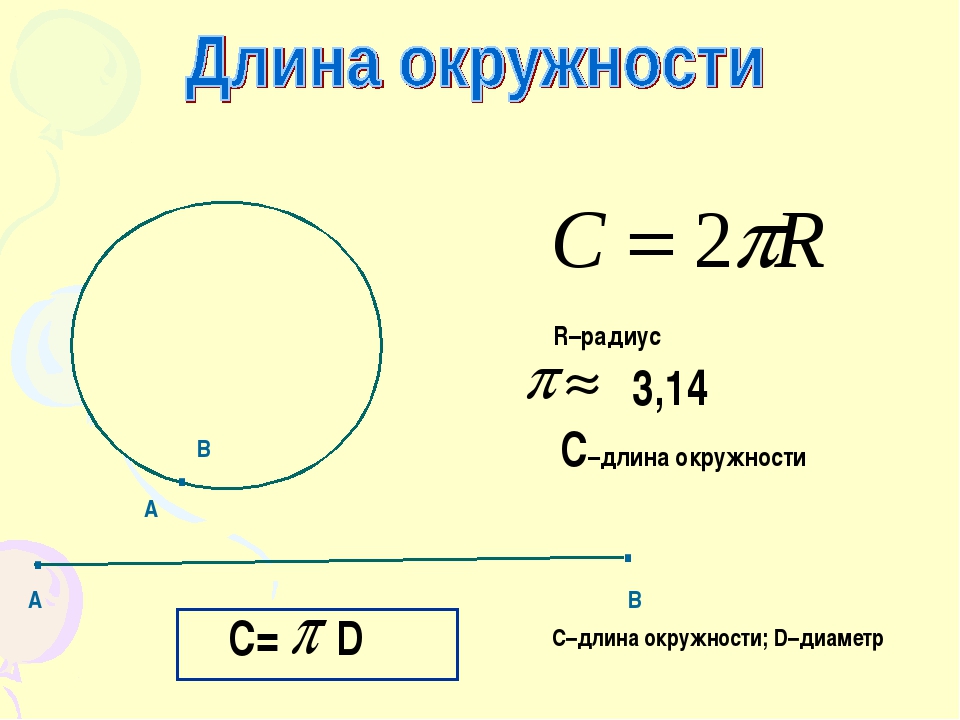 на данном луче от его начала отложить отрезок, равный данному.
на данном луче от его начала отложить отрезок, равный данному.


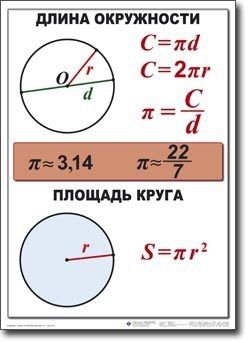 julij 2003, stran 20.
julij 2003, stran 20.
 (Apostolska dela 20:35)
(Apostolska dela 20:35) v3
v3
 Дуга окружности длиной S, опирающаяся на центральный угол ф, выражается зависимостью (рис. 14) s = / ф. Для радиуса кривизны имеем
[c.109]
Дуга окружности длиной S, опирающаяся на центральный угол ф, выражается зависимостью (рис. 14) s = / ф. Для радиуса кривизны имеем
[c.109] 111,6, закрепить звено АВ н повернуть звено D на угол Аф (рис. 111, а). Тогда центр шарнира С переместится в точку С по дуге окружности длиною сАф, а ползун по направляющей получит перемещение Ай =
[c.371]
111,6, закрепить звено АВ н повернуть звено D на угол Аф (рис. 111, а). Тогда центр шарнира С переместится в точку С по дуге окружности длиною сАф, а ползун по направляющей получит перемещение Ай =
[c.371] Среднее передаточное отношение зубчатой передачи, состоящей из колес / и 2, за полный цикл движения равно = 2. Величина передаточного отношения U]2 внутри цикла без учета знака меня-
[c.109]
Среднее передаточное отношение зубчатой передачи, состоящей из колес / и 2, за полный цикл движения равно = 2. Величина передаточного отношения U]2 внутри цикла без учета знака меня-
[c.109] 131
[c.405]
131
[c.405]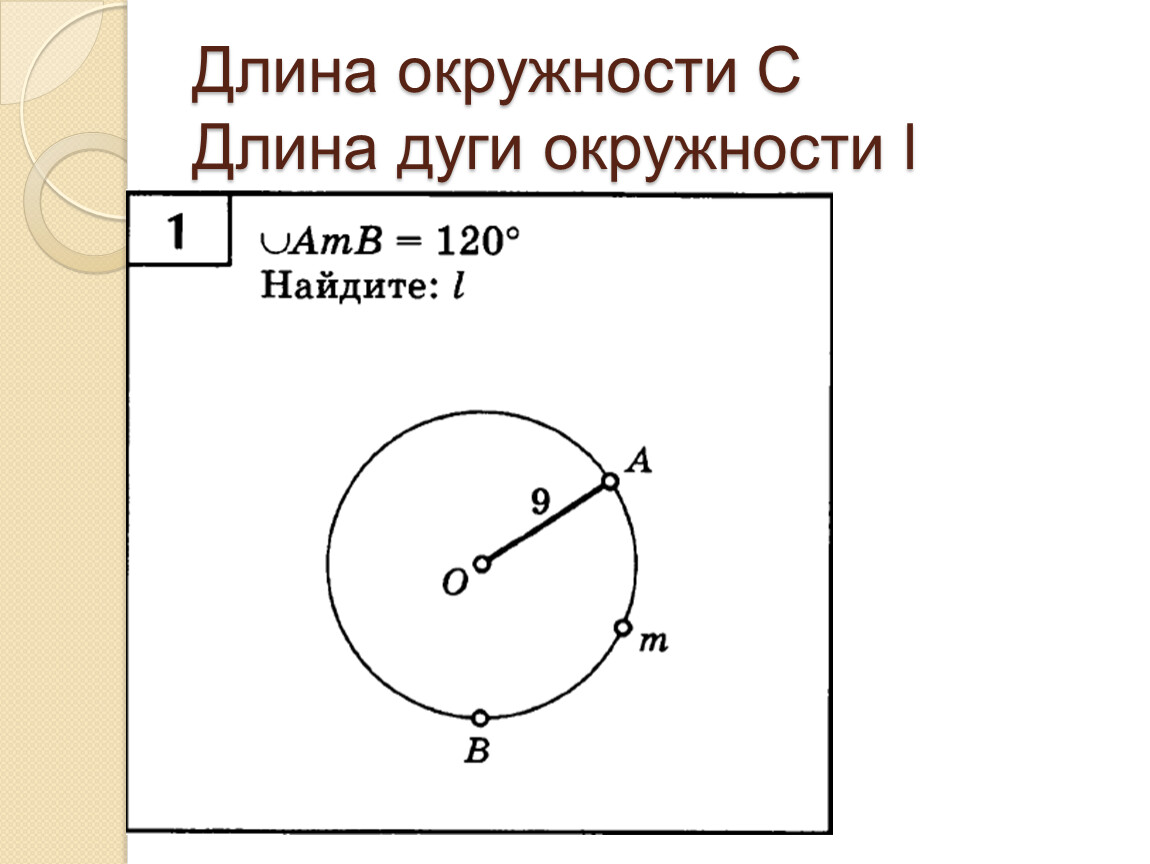 Длина зуба Ь ограничивается расстоянием между торцовыми поверхностями рабочей ширины зубчатого колеса.
[c.219]
Длина зуба Ь ограничивается расстоянием между торцовыми поверхностями рабочей ширины зубчатого колеса.
[c.219] 494]
494] Соединяют Лf с О, строят ОЫ 1 МО. Прямая МЫ — нормаль, — касательная. Архимедова спираль имеет две ветви. Вторая ветвь получится, если вращать прямую против движения часовой стрелки.
[c.60]
Соединяют Лf с О, строят ОЫ 1 МО. Прямая МЫ — нормаль, — касательная. Архимедова спираль имеет две ветви. Вторая ветвь получится, если вращать прямую против движения часовой стрелки.
[c.60] 70, б, закрепить звено АВ и повернуть звено СО на угол А,[, (рис. 70, в). Тогда центр шарнира С переместится в точку С1 по дуге окружности длиной сАф, а ползун по направляющей получит перемещение Аь = СхС1. При малом угле пово-
[c.157]
70, б, закрепить звено АВ и повернуть звено СО на угол А,[, (рис. 70, в). Тогда центр шарнира С переместится в точку С1 по дуге окружности длиной сАф, а ползун по направляющей получит перемещение Аь = СхС1. При малом угле пово-
[c.157] Масло оливковое Олнфа натуральная — Свойства 6 — 91 Олнфа-оксоль 6 — 91 Олово 1 (1-я) — 352
[c.178]
Масло оливковое Олнфа натуральная — Свойства 6 — 91 Олнфа-оксоль 6 — 91 Олово 1 (1-я) — 352
[c.178] Проекция траектории любой точки шайбы на плоскость, перпендикулярную к оси цилиндра, имеет вид окружности, и в случае расиоложения осей цилиндров в центре этих окружностей длина шатуна не будет оказывать влияния на закон движения поршня. При удержании качающейся шайбы от проворота с помощью плоских направляющих (рис. 2) точки, лежащие в удерживающей плоскости, движут-.3.36
[c.336]
Проекция траектории любой точки шайбы на плоскость, перпендикулярную к оси цилиндра, имеет вид окружности, и в случае расиоложения осей цилиндров в центре этих окружностей длина шатуна не будет оказывать влияния на закон движения поршня. При удержании качающейся шайбы от проворота с помощью плоских направляющих (рис. 2) точки, лежащие в удерживающей плоскости, движут-.3.36
[c.336] Если демпфирование слабое и близкие собственные частоты отсутствуют, то в 01фестнос-ти резонансной частоты эта характеристика представляет собой почти полную окружность, как для системы с одной степенью свободы.
[c.377]
Если демпфирование слабое и близкие собственные частоты отсутствуют, то в 01фестнос-ти резонансной частоты эта характеристика представляет собой почти полную окружность, как для системы с одной степенью свободы.
[c.377]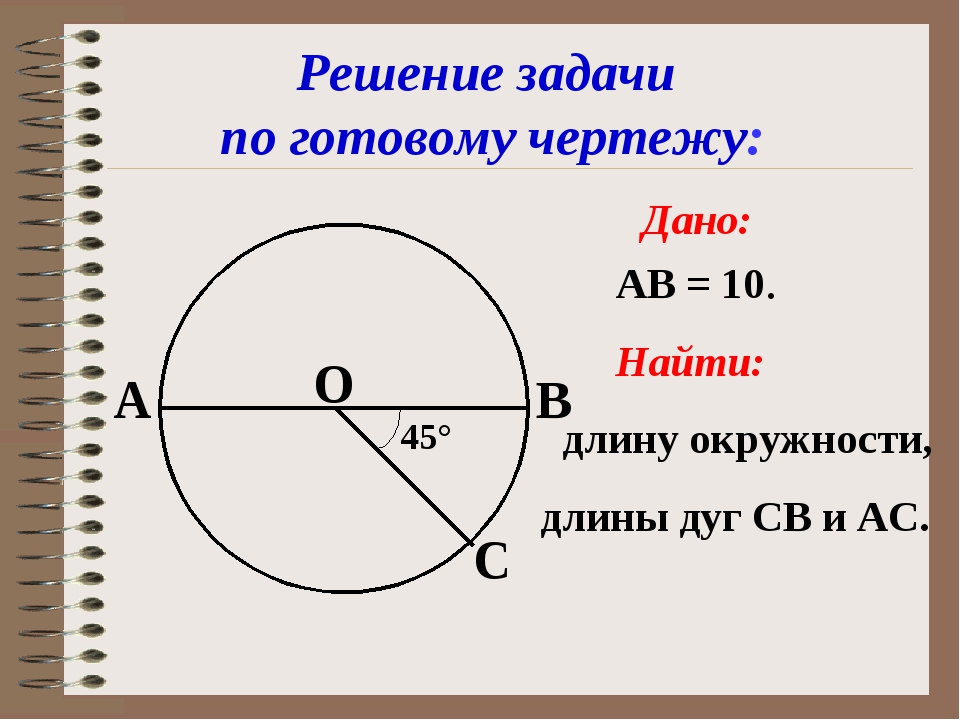 В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.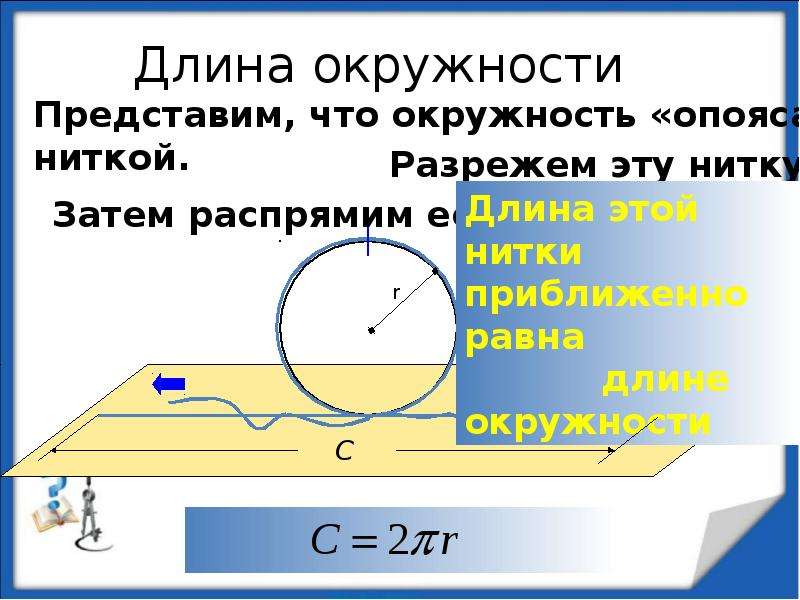 Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:

 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).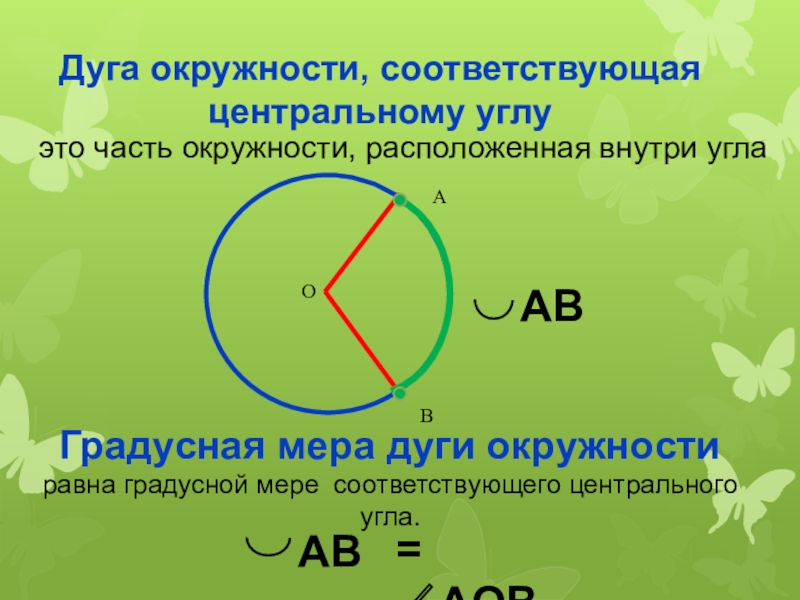 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.


 Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643… Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Это универсальный способ найти диаметр, когда у окружности известна ее длина. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
 Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи». Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
 Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника . Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.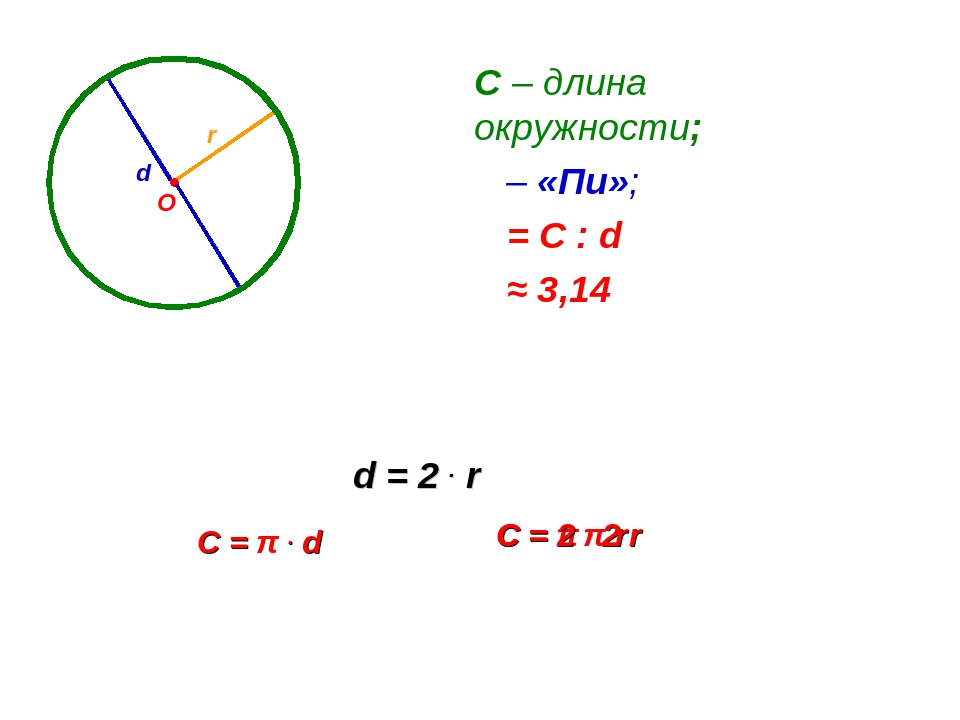 Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.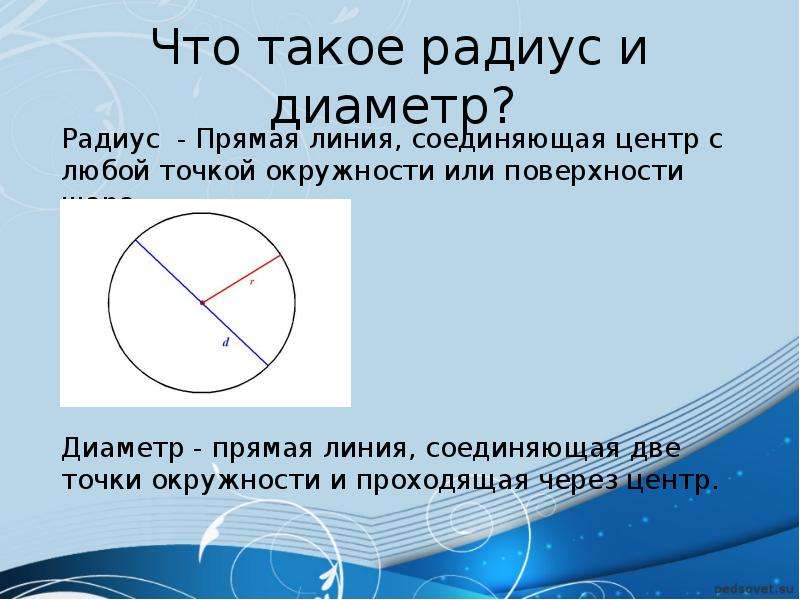 Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра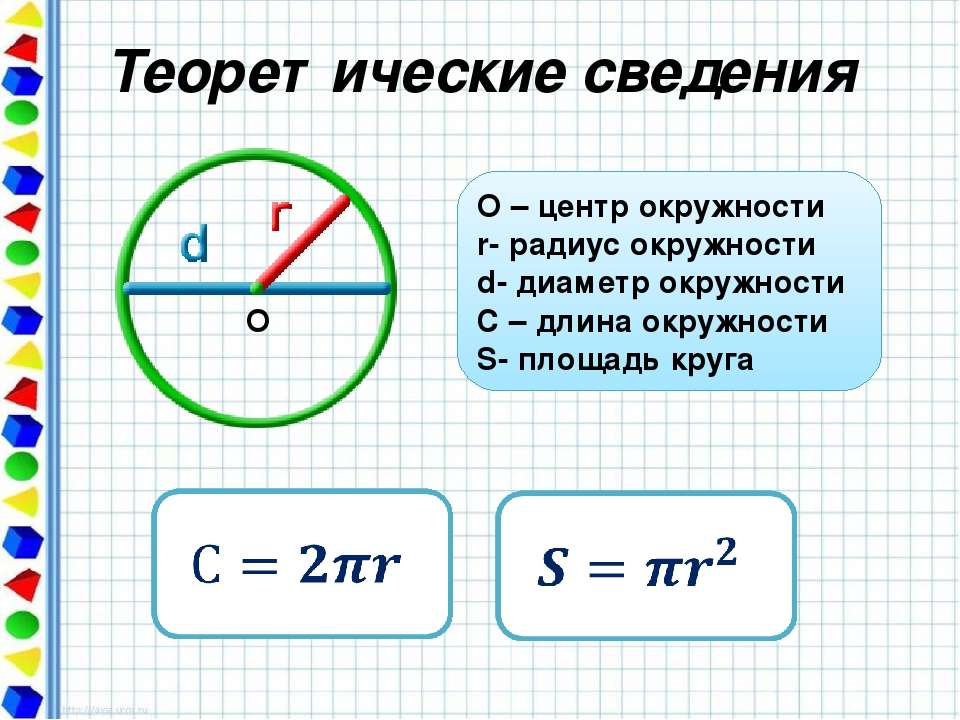 Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром. Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.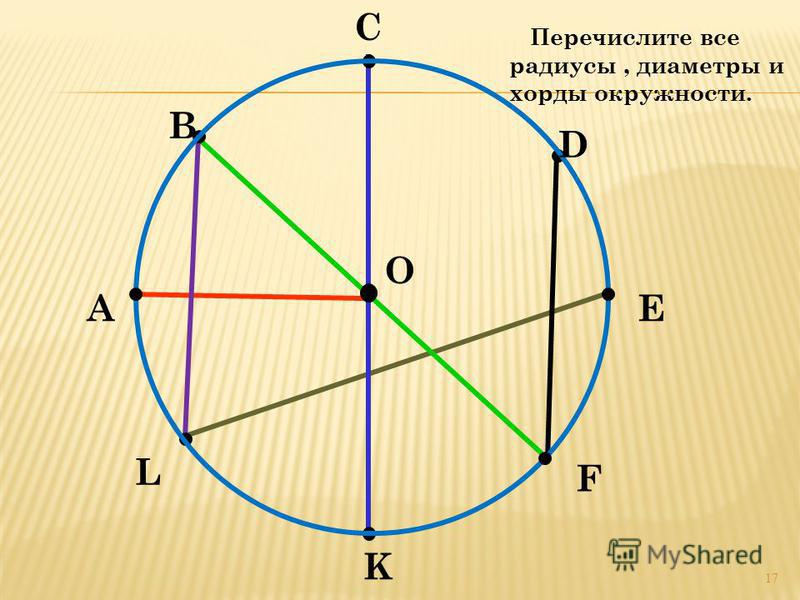
 В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
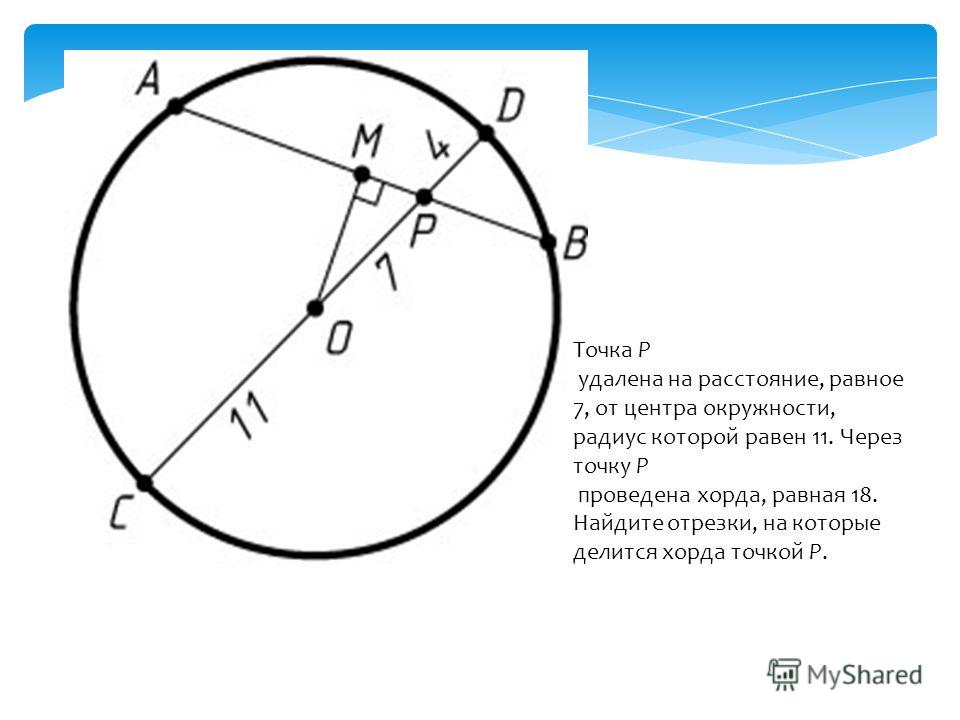 Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
 Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
 Радiани i градуси
Радiани i градуси Хорда может быть у дуги, окружности, эллипса и т.д.
Хорда может быть у дуги, окружности, эллипса и т.д. 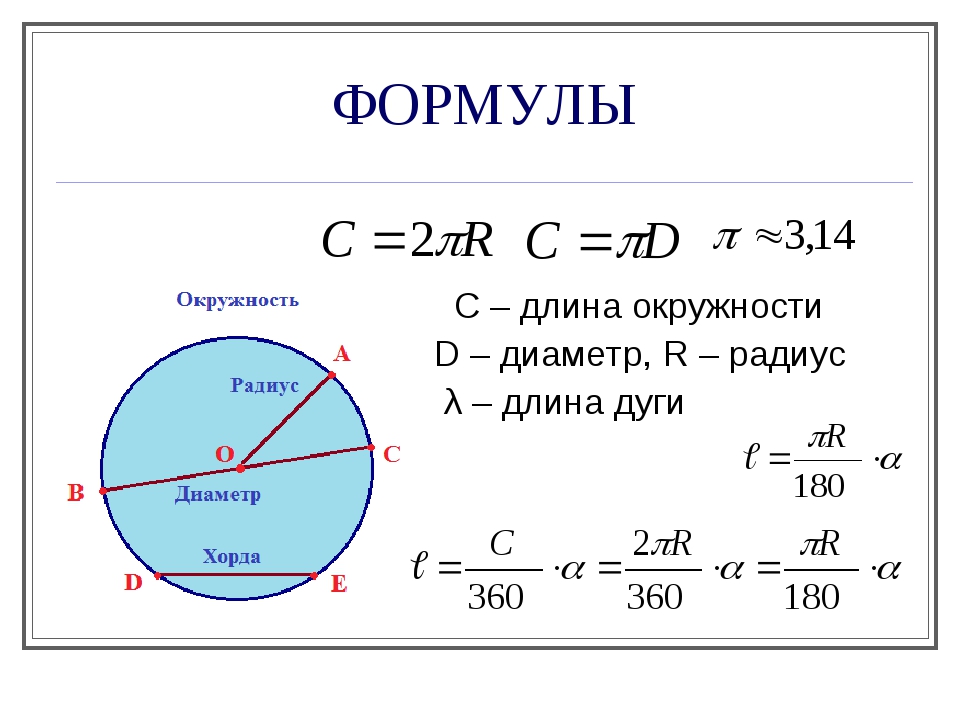 Верно и обратное
Верно и обратное ru содержит информацию о том, как внедрение среды MATLAB и Simulink может способствовать решению этой задачи, – отметил Сергей Сорокин, менеджер по маркетингу департамента MathWorks компании Softline. – Мы надеемся, что новый сайт станет привычным и удобным инструментом получения самой актуальной информации о продуктах MathWorks для русскоязычных пользователей. Добро пожаловать на www.sl-matlab.ru!»
ru содержит информацию о том, как внедрение среды MATLAB и Simulink может способствовать решению этой задачи, – отметил Сергей Сорокин, менеджер по маркетингу департамента MathWorks компании Softline. – Мы надеемся, что новый сайт станет привычным и удобным инструментом получения самой актуальной информации о продуктах MathWorks для русскоязычных пользователей. Добро пожаловать на www.sl-matlab.ru!»
 Программу MATLAB можно напрямую заказать в компании Keysight как опцию для большинства генераторов сигналов, анализаторов сигналов и анализаторов спектра. ПО MATLAB позволяет расширить возможности генераторов и анализаторов сигналов Keysight по проведению измерений, анализу и визуализации данных, формированию сигналов произвольной формы, управлению приборами и созданию испытательных систем. MATLAB включает наборы инструментов и функций командной строки для анализа данных, в том числе, обработки сигналов, модуляции, цифровой фильтрации и построения кривых. ПО MATLAB используют более 1 000 000 инженеров и научных работников во всем мире. Существует три конфигурации MATLAB: от базового пакета, позволяющего выполнять захват и анализ данных, до полного пакета, обеспечивающего обработку сигналов, разработку систем связи, создание фильтров, а также автоматизацию испытаний.
Программу MATLAB можно напрямую заказать в компании Keysight как опцию для большинства генераторов сигналов, анализаторов сигналов и анализаторов спектра. ПО MATLAB позволяет расширить возможности генераторов и анализаторов сигналов Keysight по проведению измерений, анализу и визуализации данных, формированию сигналов произвольной формы, управлению приборами и созданию испытательных систем. MATLAB включает наборы инструментов и функций командной строки для анализа данных, в том числе, обработки сигналов, модуляции, цифровой фильтрации и построения кривых. ПО MATLAB используют более 1 000 000 инженеров и научных работников во всем мире. Существует три конфигурации MATLAB: от базового пакета, позволяющего выполнять захват и анализ данных, до полного пакета, обеспечивающего обработку сигналов, разработку систем связи, создание фильтров, а также автоматизацию испытаний.
 Интегрированные приемопередатчики AD9361 и AD9364 имеют диапазон настройки частоты от 70 МГц до 6 ГГц и полосу канала от 200 кГц до 56 МГц. Во время презентации специалист компании Analog Devices расскажет об основных возможностях и устройстве этих микросхем, а затем будет рассмотрена системная модель передатчика и приемника AD9361 и AD9364, созданная в Simulink. Во время лабораторных испытаний данная модель была проверена компанией Analog Devices и полностью соответствует настоящему оборудованию. Модель может быть использована для тестирования РЧ тракта AD9361 и AD9364 (до полевых испытаний), проверки цифровых алгоритмов с реальными сигналами и искажениями, а также для программирования КИХ фильтров микросхем радиотрансиверов.
Интегрированные приемопередатчики AD9361 и AD9364 имеют диапазон настройки частоты от 70 МГц до 6 ГГц и полосу канала от 200 кГц до 56 МГц. Во время презентации специалист компании Analog Devices расскажет об основных возможностях и устройстве этих микросхем, а затем будет рассмотрена системная модель передатчика и приемника AD9361 и AD9364, созданная в Simulink. Во время лабораторных испытаний данная модель была проверена компанией Analog Devices и полностью соответствует настоящему оборудованию. Модель может быть использована для тестирования РЧ тракта AD9361 и AD9364 (до полевых испытаний), проверки цифровых алгоритмов с реальными сигналами и искажениями, а также для программирования КИХ фильтров микросхем радиотрансиверов.
 Web
Web 9
9 1
1 Обычно проприетарным называют любое несвободное ПО, включая полусвободное.
Обычно проприетарным называют любое несвободное ПО, включая полусвободное.
 Доступ к закрытому коду обычно имеют сотрудники компании-разработчика, но могут применяться и более гибкие условия ограничения доступа, в которых предоставление исходного кода разрешено партнёрам компании, техническим аудиторам или другим лицам в соответствии с политикой компании.
Доступ к закрытому коду обычно имеют сотрудники компании-разработчика, но могут применяться и более гибкие условия ограничения доступа, в которых предоставление исходного кода разрешено партнёрам компании, техническим аудиторам или другим лицам в соответствии с политикой компании. Такое программное обеспечение очень популярно и широко используется, а за счёт своей бесплатности имеет хорошую техническую поддержку со стороны специалистов, у которых отсутствует необходимость дополнительных затрат на обучение.
Такое программное обеспечение очень популярно и широко используется, а за счёт своей бесплатности имеет хорошую техническую поддержку со стороны специалистов, у которых отсутствует необходимость дополнительных затрат на обучение. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Могут помочь специальные фильтры, искусственное освещение и первоклассные подводные камеры, но между камерой и объектом на фотографии все еще остается много воды. Мы привыкли к сине-зеленому оттенку подводной фотографии. Как бы выглядел океан без воды? Каковы истинные цвета кораллового рифа? Благодаря новому алгоритму компьютерного зрения под названием Sea-thru, мы можем видеть, как будет выглядеть подводный мир, если ее сфотографировать в воздухе, а не в воде. Sea-thru устраняет визуальные искажения, возникающие при…
Могут помочь специальные фильтры, искусственное освещение и первоклассные подводные камеры, но между камерой и объектом на фотографии все еще остается много воды. Мы привыкли к сине-зеленому оттенку подводной фотографии. Как бы выглядел океан без воды? Каковы истинные цвета кораллового рифа? Благодаря новому алгоритму компьютерного зрения под названием Sea-thru, мы можем видеть, как будет выглядеть подводный мир, если ее сфотографировать в воздухе, а не в воде. Sea-thru устраняет визуальные искажения, возникающие при… 1. TensorFlow TensorFlow — это…
1. TensorFlow TensorFlow — это… Либо вы изучаете JavaScript заново, либо совершенствуете свои навыки программирования; Вы найдете эти десять самых популярных онлайн-курсов JavaScript, которые стоят вашего времени, усилий и денег. 1. Современный JavaScript c полного 0 Уровень — для начинающих Учебное пособие «Современный JavaScript с полного 0» посвящено созданию проектов без использования каких-либо JS-структур или библиотек. Он имеет…
Либо вы изучаете JavaScript заново, либо совершенствуете свои навыки программирования; Вы найдете эти десять самых популярных онлайн-курсов JavaScript, которые стоят вашего времени, усилий и денег. 1. Современный JavaScript c полного 0 Уровень — для начинающих Учебное пособие «Современный JavaScript с полного 0» посвящено созданию проектов без использования каких-либо JS-структур или библиотек. Он имеет… Для Back-End разработки у вас есть различные варианты: Python, Java, PHP, Ruby и многие другие. Но как выбрать правильный? Задача выбора между Ruby on Rails и другими средами упрощается, если вы знаете все за и против этой технологии и то, для чего используется Ruby on Rails. В этой статье мы…
Для Back-End разработки у вас есть различные варианты: Python, Java, PHP, Ruby и многие другие. Но как выбрать правильный? Задача выбора между Ruby on Rails и другими средами упрощается, если вы знаете все за и против этой технологии и то, для чего используется Ruby on Rails. В этой статье мы… Каждый из них выполняет разные, иногда одинаковые, но более эффективные функции. Здесь возникает вопрос — что лучше всего использовать? Что будет более эффективнее для конкретной задачи? Чтобы проанализировать, что лучше подходит вашей программе, вы должны понять, сопоставить и сравнить их, чтобы отфильтровать лучшее для вас. Поскольку компьютерное зрение стало одной из важных областей в технологической отрасли, можно ожидать появления множества рабочих…
Каждый из них выполняет разные, иногда одинаковые, но более эффективные функции. Здесь возникает вопрос — что лучше всего использовать? Что будет более эффективнее для конкретной задачи? Чтобы проанализировать, что лучше подходит вашей программе, вы должны понять, сопоставить и сравнить их, чтобы отфильтровать лучшее для вас. Поскольку компьютерное зрение стало одной из важных областей в технологической отрасли, можно ожидать появления множества рабочих… Теперь они могут использовать алгоритмы локализации и слежения, а также справочные примеры в…
Теперь они могут использовать алгоритмы локализации и слежения, а также справочные примеры в… MATLAB cодержит встроенные функции линейной алгебры (LAPACK, BLAS), быстрого преобразования Фурье (FFTW), функции для работы с полиномами, функции базовой статистики и численного решения дифференциальных уравнений; расширенные математические библиотеки для Intel MKL. Все встроенные функции ядра MATLAB разработаны и оптимизированы специалистами и работают быстрее или так же, как их эквивалент на C/C++.
MATLAB cодержит встроенные функции линейной алгебры (LAPACK, BLAS), быстрого преобразования Фурье (FFTW), функции для работы с полиномами, функции базовой статистики и численного решения дифференциальных уравнений; расширенные математические библиотеки для Intel MKL. Все встроенные функции ядра MATLAB разработаны и оптимизированы специалистами и работают быстрее или так же, как их эквивалент на C/C++. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и ln 0 5. Просто введите задачу в окошко и нажмите
«решить» здесь (например, ln калькулятор онлайн).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и ln 0 5. Просто введите задачу в окошко и нажмите
«решить» здесь (например, ln калькулятор онлайн). Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
 Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
 Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку logyx, она подставляет в строке ввода запись log(x x,y).
Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку logyx, она подставляет в строке ввода запись log(x x,y). Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.
Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.

 2-9) — YouTube
2-9) — YouTube
 Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную: е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.  е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. 
 Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой: Получаем:
Получаем: Найти производную функции
Найти производную функции Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию : 

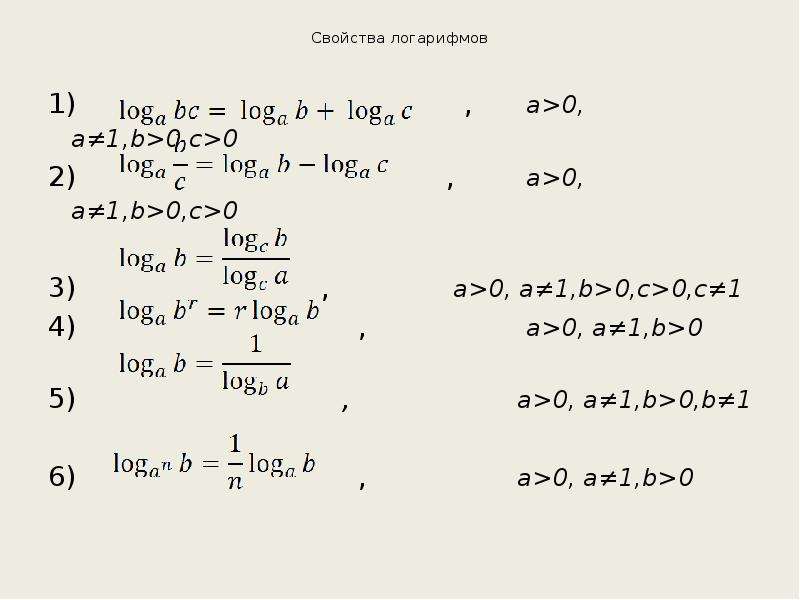
 Тогда по правилу дифференцирования суммы имеем:
Тогда по правилу дифференцирования суммы имеем: