Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину.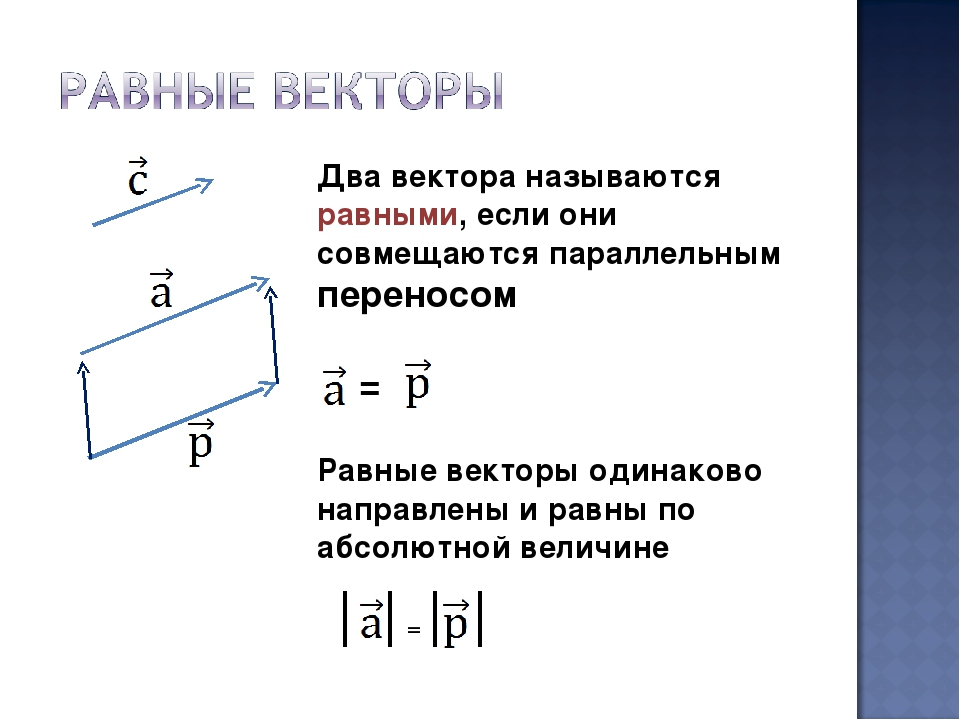 Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Векторное произведение векторов, онлайн калькулятор
Наш онлайн калькулятор позволяет найти векторное произведение двух векторов всего за пару минут. Для вычисления векторного произведения выберите форму представления векторов (через координаты или по точкам), заполните все элементы и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ и, при необходимости, проверить свое решение.
Введите данные, чтобы найти векторное произведение векторовФорма представления векторов:
координатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
Скалярное произведение векторов, онлайн калькулятор
Наш онлайн калькулятор помогает найти скалярное произведение двух векторов всего в несколько кликов. Для вычисления скалярного произведения выберите размерность векторов и форму их представления (через координаты или по точкам), заполните все координаты и нажмите кнопку «Вычислить», калькулятор выдаст детальное решение и ответ! Каждый шаг будет подробно расписан, это поможет вам проверить свое решение и понять, как был получен ответ.
Для вычисления скалярного произведения выберите размерность векторов и форму их представления (через координаты или по точкам), заполните все координаты и нажмите кнопку «Вычислить», калькулятор выдаст детальное решение и ответ! Каждый шаг будет подробно расписан, это поможет вам проверить свое решение и понять, как был получен ответ.
Размерность векторов:
2 3
Форма представления векторов:
координатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
Сложение векторов.
 Он-лайн калькулятор. — таблицы Tehtab.ru
Он-лайн калькулятор. — таблицы Tehtab.ruСложение векторов. Он-лайн калькулятор.
Сложение векторов. Он-лайн калькулятор.
В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.):
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов: .
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма.
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
- нарисовать первый вектор, учитывая его величину и направление
- от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
- дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
- результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.
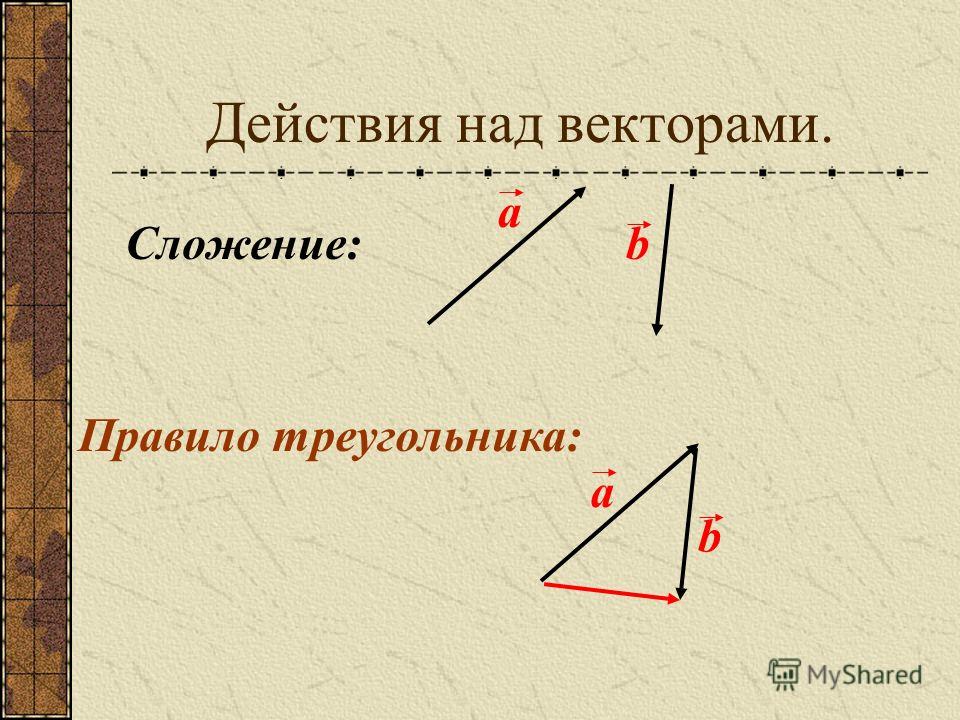
Правило треугольника
Сложение векторов по правилу треугольника заключается в следующем:
- нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
- от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
- результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Fрез. = [ F12 + F22 -2 F1 F2 cos(180о-α) ]1/2 (1)
где
F = числовое значение вектора
α = угол между векторами 1 и 2
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
β = arcsin[ F2 *sin(180o-α) / FR ] (2)
где
α = угол между исходными векторами
Пример — сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН)2 + (8 кН)2 — 2 (5 кН)(8 kН) cos(180o — (80o)) ]1/2
= 10,14кН
Угол между результирующей силой и первой силой равен:
β= arcsin[ (8кН) sin(180o — (80o)) / (10,14кН)]
= 51o
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180o — (80o)) / (10,2 кН)]
= 29o
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Векторное произведение векторов, формулы и онлайн калькуляторы
Содержание:
Определение
Векторным произведением ненулевых векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$, обозначаемый символом $[\overline{a}, \overline{b}]$ или $\overline{a} \times \overline{b}$, длина которого $|\bar{c}|=|\bar{a}||\bar{b}| \sin (\bar{a}, \bar{b})$ (рис. 1).
Свойства векторного произведения:
1 $[\overline{a}, \overline{b}]=\overline{0}$, тогда и только тогда, когда $\overline{a} \| \overline{b}$
2 $[\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}]$
3 Модуль векторного произведения $|[\overline{a}, \overline{b}]|$ равен площади параллелограмма, построенного на заданных векторах $\overline{a}$ и $\overline{b}$ (рис. 2), т.е.
$[\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}]$
$\left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right]$
4 $[\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}]$
5 $\left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right]$
Если векторы заданы своими координатами $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$, то векторное произведение находится по формуле:
$[\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{1}} & {a_{2}} & {a_{3}} \\ {b_{1}} & {b_{2}} & {b_{3}}\end{array}\right|$
Пример
Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и
$\overline{b}=(8 ; 5 ; 9)$
Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и
$\overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$
$=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$
$=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$
Читать дальше: смешанное произведение векторов.
Слишком сложно?
Векторное произведение векторов не по зубам? Тебе ответит эксперт через 10 минут!
Координаты вектора в новом базисе онлайн калькулятор.
 Разложение вектора по базису
Разложение вектора по базисуБа́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов
Базисом в пространстве R n называется любая система из n -линейно независимых векторов. Каждый вектор из R n , не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.
Пусть – базис пространства R n и . Тогда найдутся такие числа λ 1 , λ 2 , …, λ n , что .
Коэффициенты разложения λ 1 , λ 2 , …, λ n , называются координатами вектора в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
Замечание. В каждом n -мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе. Пример. Разложить вектор по базису .
Пример. Разложить вектор по базису .
Решение. . Подставим координаты всех векторов и выполним действия над ними:
Приравняв координаты, получим систему уравнений:
Решим ее: .
Таким образом, получим разложение: .
В базисе вектор имеет координаты .
Конец работы —
Эта тема принадлежит разделу:
Понятие вектора. Линейные операции над векторами
Вектором называется направленный отрезок имеющий определенную длину т е отрезок определенной длины у которого одна из ограничивающих его точек.. длина вектора называется его модулем и обозначается символом модуль вектора.. вектор называется нулевым обозначается если начало и конец его совпадают нулевой вектор не имеет определенного..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
В векторном исчислении и его приложениях большое значение имеет задача разложения, состоящая в представлении данного вектора в виде суммы нескольких векторов, называемых составляющими данного
вектора. Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
2. Примеры разложения.
Рассмотрим несколько весьма часто встречающихся случаев разложения.
1. Разложить данный вектор с на два составляющих вектора из которых один, например а, задан по величине и направлению.
Задача сводится к определению разности двух векторов. Действительно, если векторы являются составляющими вектора с, то должно выполняться равенство
Отсюда определяется второй составляющий вектор
2. Разложить данный вектор с на два составляющих, из которых один должен лежать в заданной плоскости а второй должен лежать на заданной прямой а.
Для определения составляющих векторов перенесем вектор с так, чтобы его начало совпало с точкой пересечения заданной прямой с плоскостью (точка О — см. рис. 18). Из конца вектора с (точка С) проведем прямую до
пересечения с плоскостью {В — точка пересечения), а затем из точки С проведем прямую параллельно
Векторы и будут искомыми, т. е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
3. Даны три компланарных вектора а, b и с, причем векторы не коллинеарны. Требуется разложить вектор с по векторам
Приведем все три заданных вектора к одной точке О. Тогда в силу их компланарности они расположатся в одной плоскости. На данном векторе с как на диагонали построим параллелограмм, стороны которого параллельны линиям действия векторов (рис. 19). Это построение всегда возможно (если только векторы не коллинеарны) и единственно. Из рис. 19 видно, что
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов , линейная независимость векторов , базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения , но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости . Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ? Данные векторы коллинеарны , а значит, линейно выражаются друг через друга:
Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ? Данные векторы коллинеарны , а значит, линейно выражаются друг через друга:
, ну, или наоборот: , где – некоторое число, отличное от нуля.
Картинку сего действа можно посмотреть на уроке Векторы для чайников , где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина.
Такие векторы называют линейно зависимыми .
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда , когда они коллинеарны .
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости линейно не зависимы в том и только том случае, если они не коллинеарны . Итак, базис получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
Любой вектор плоскости единственным образом раскладывается по базису :
, где – действительные числа . Числа называют координатами вектора в данном базисе.
Также говорят, что вектор представлен в виде линейной комбинации базисных векторов . То есть, выражение называют разложением вектора по базису или линейной комбинацией базисных векторов.
Например, можно сказать, что вектор разложен по ортонормированному базису плоскости , а можно сказать, что он представлен в виде линейной комбинации векторов .
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов , , при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке . Базисы – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир.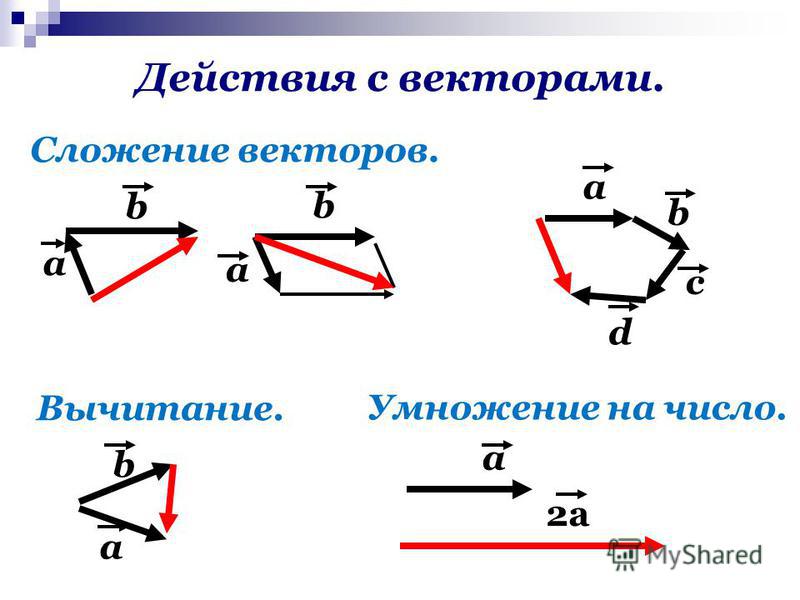 И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом . Вот стандартная картина:
Когда говорят о прямоугольной системе координат , то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис . И это почти так. Формулировка звучит следующим образом:
началом координат , и ортонормированный базис задают декартову прямоугольную систему координат плоскости .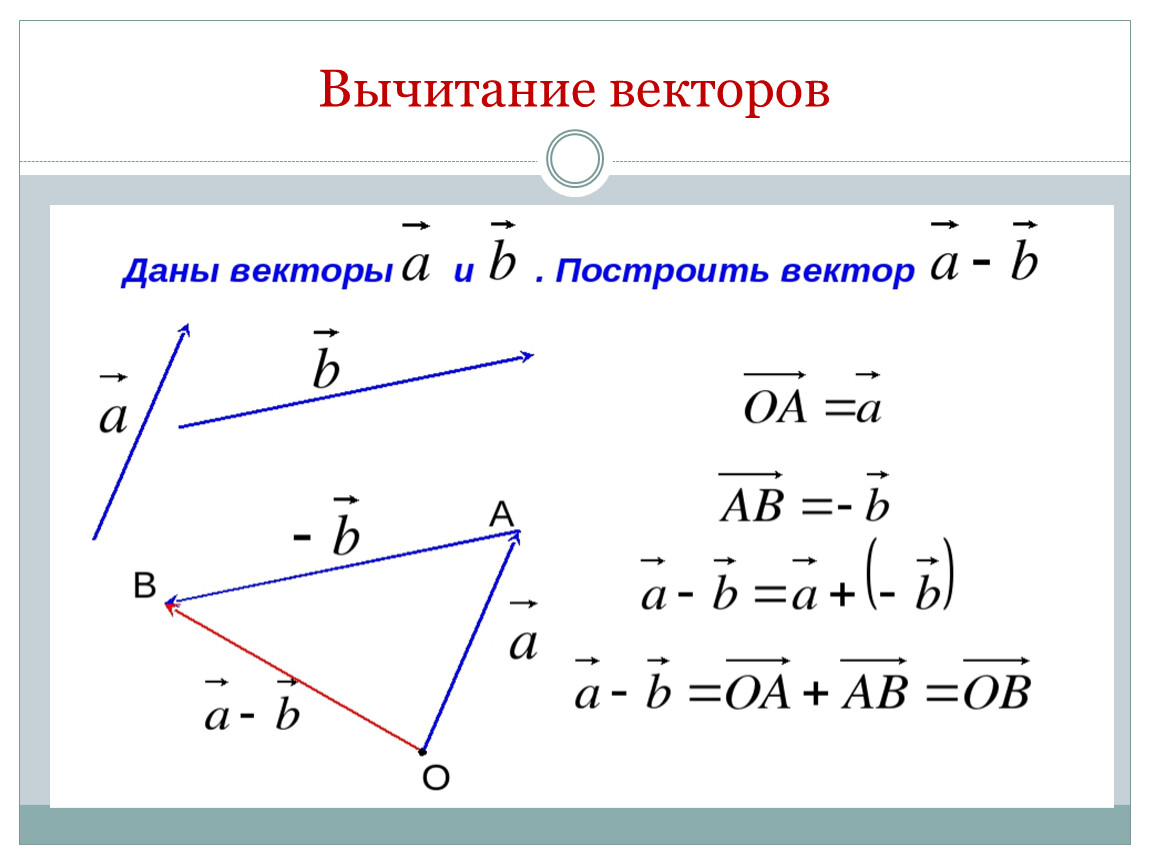 То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
Думаю, всем понятно, что с помощью точки (начала координат) и ортонормированного базиса ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку и два ортогональных вектора произвольной ненулевой длины:
Такой базис называется ортогональным . Начало координат с векторами задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, или . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
Если длины равняются единице, то получается привычный ортонормированный базис.
! Примечание : в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ . Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными . Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка плоскости, которая называется началом координат , и неколлинеарные векторы , , задают аффинную систему координат плоскости :
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки и векторы:
В качестве примеров на чертеже изображены точки и векторы:
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников , многие вкусные формулы, связанные со скалярным произведением векторов . Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении , а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная ) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Сложного здесь ничего нет, весь материал доступен даже школьнику.
Типовая вещь. Для того чтобы два вектора плоскости были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны .По существу, это покоординатная детализация очевидного соотношения .
Пример 1
а) Проверить, коллинеарны ли векторы .
б) Образуют ли базис векторы ?
Решение:
а) Выясним, существует ли для векторов коэффициент пропорциональности , такой, чтобы выполнялись равенства :
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию и посмотреть, будет ли она верной:
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем:
, таким образом, соответствующие координаты пропорциональны, следовательно,
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы . Составим систему:
Из первого уравнения следует, что , из второго уравнения следует, что , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
Вывод : векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов :
, значит, данные векторы линейно независимы и образуют базис.
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: . Или так: . Или так: . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
Ответ: а) , б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При каком значении параметра векторы будут коллинеарны?
В образце решения параметр найден через пропорцию .
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения :
2) векторы образуют базис;
3) векторы не коллинеарны;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля .
Соответственно, эквивалентны следующие противоположные утверждения :
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю .
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :. Для применения данного признака, естественно, нужно уметь находить определители .
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны.
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис.
Ответ: а) , б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны вершины четырёхугольника . Доказать, что четырёхугольник является параллелограммом.
Доказать, что четырёхугольник является параллелограммом.
Доказательство : Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, необходимо доказать:
1) параллельность противоположных сторон и ;
2) параллельность противоположных сторон и .
Доказываем:
1) Найдём векторы:
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны, и .
Вывод : Противоположные стороны четырёхугольника попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать .
Больше фигур хороших и разных:
Пример 4
Даны вершины четырёхугольника . Доказать, что четырёхугольник является трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?Правило очень похоже. Для того чтобы два вектора пространства были коллинеарны, необходимо и достаточно , чтобы их соответствующие координаты были пропорциональны .
Пример 5
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) ;
б)
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы не коллинеарны.
«Упрощёнка» оформляется проверкой пропорции . В данном случае:
– соответствующие координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: векторы не коллинеарны.
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов .
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец . Это будут векторы , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства ? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение : векторы называются компланарными , если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы , то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (а почему – легко догадаться по материалам предыдущего раздела).
Справедливо и обратное утверждение: три некомпланарных вектора всегда линейно независимы , то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение : Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке , при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в данном базисе
Напоминаю, также можно сказать, что вектор представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
началом координат , и некомпланарные векторы , взятые в определённом порядке , задают аффинную систему координат трёхмерного пространства :
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства :
Точка пространства, которая называется началом координат , и ортонормированный базис задают декартову прямоугольную систему координат пространства . Знакомая картинка:
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения :
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :.
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Пример 6
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
Решение : Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):
, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ : данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
Пример 7
При каком значении параметра векторы будут компланарны?
Решение : Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ : при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространстваи найти координаты 4-го вектора в данном базисе
Пример 8
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
Решение : Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис . И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
! Важно : координаты векторов обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Rn,(МАТЕМАТИКА В ЭКОНОМИКЕ)
Разложение вектора
Разложение вектора а на составляющие — операция замены вектора а несколькими другими векторами аь а2, а3 и т. д., которые при их сложении образуют начальный вектор а; в этом случае векторы db а2, а3 и т. д. называются составляющими вектора а. Иными словами, разложение любого…(ФИЗИКА)
Базис и ранг системы векторов
Рассмотрим систему векторов (1.18) Максимально независимой подсистемой системы векторов (1.I8) называется частичный набор векторов этой системы, удовлетворяющий двум условиям: 1) векторы этого набора линейно независимы; 2) любой вектор системы (1.18) линейно выражается через векторы этого набора….(МАТЕМАТИКА В ЭКОНОМИКЕ)
Представление вектора в разных системах координат.
 Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…
Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…Разложение вектора в ортогональном базисе
Рассмотрим базис пространства Rn, в котором каждый вектор ортогонален остальным векторам базиса: Ортогональные базисы известны и хорошо представимы на плоскости и в пространстве (рис. 1.6). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются…(МАТЕМАТИКА В ЭКОНОМИКЕ)
Векторы и их представления в координатных системах
Понятие вектора связывается с определенными физическими величинами, которые характеризуются своей интенсивностью (величиной) и направлением в пространстве. Такими величинами являются, например, сила, действующая на материальное тело, скорость определенной точки этого тела, ускорение материальной частицы. ..
..(МЕХАНИКА СПЛОШНОЙ СРЕДЫ: ТЕОРИЯ НАПРЯЖЕНИЙ И ОСНОВНЫЕ МОДЕЛИ)
Простейшие аналитические представления произвольной эллиптической функции
Представление эллиптической функции в виде суммы простейших элементов. Пусть / (z) есть эллиптическая функция порядка s с простыми полюсами jjt, $s, лежащими в параллелограме периодов. Обозначая через Bk вычет функции относительно полюса мы имеем, что 2 ?л = 0 (§ 1»п. 3, теорема…(ВВЕДЕНИЕ В ТЕОРИЮ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО)
Л. 2-1 Основные понятия векторной алгебры. Линейные операции над векторами.
Разложение вектора по базису.
Основные понятия векторной алгебры
Вектором
называется множество всех направленных
отрезков, имеющих одинаковую длину и
направление
.
Свойства:
Линейные операции над векторами
1.
Правило параллелограмма:
Суммой двух векторовиназывается вектор,
выходящий из их общего начала и являющийся
диагональю параллелограм-ма, построенного
на векторахикак на сторонах.
Правило многоугольника:
Чтобы построить сумму любого числа векторов, нужно в конец 1-го слагаемого вектора поместить начало 2-ого, в конец 2-ого – начало 3-его и т.д. Вектор, замыкающий полученную ломаную линию, является суммой. Начало его совпадает с началом 1-ого, а конец – с концом последнего.
Свойства:
2.
Произведением вектора
на число,
называется вектор, удовлетворяющий
условиям:
.
Свойства:
3.
Разностью векторовиназывают вектор,
равный сумме вектораи вектора, противоположного вектору,
т.е.
.
— закон противоположного элемента (вектора).
Разложение вектора по базису
Сумма векторов определяется единственным
способом
(и только).
Обратная же операция – разложение
вектора на несколько составляющих,
неоднозначна:.
Для того, что бы сделать её однозначной,
необходимо указать направления, по
которым происходит разложение
рассматриваемого вектора, или, как
говорят, необходимо указатьбазис .
При определении базиса существенным является требование некомпланарности и неколлинеарности векторов. Чтобы понять смысл этого требования, необходимо рассмотреть понятие линейной зависимости и линейной независимости векторов.
Произвольное выражение вида:
,
называютлинейной комбинацией векторов
.
Линейная комбинация нескольких векторов называется тривиальной , если все её коэффициенты равны нулю.
Векторы
называютсялинейно зависимыми , если
существует нетривиальная линейная
комбинация этих векторов равная нулю:
(1), при условии
.
Если равенство (1) имеет место только
при всех
одновременно равных нулю, то ненулевые
векторы
будутлинейно независимыми .
Легко доказать: любые два коллинеарных вектора линейно зависимы, а два неколлинеарных вектора линейно независимы .
Доказательство начнём с первого утверждения.
Пусть векторы
иколлинеарны. Покажем, что они линейно
зависимы. Действительно, если они
коллинеарны, то они отличаются друг от
друга только на числовой множитель,
т. е.
е.
,
следовательно
.
Поскольку полученная линейная комбинация
явно нетривиальная и равна «0», то векторыилинейно зависимы.
Рассмотрим теперь два неколлинеарных векторы и. Докажем, что они линейно независимы. Доказательство построим от противного.
Предположим, что они линейно зависимы.
Тогда должна существовать нетривиальная
линейная комбинация
.
Предположим, что
,
тогда
.
Полученное равенство означает, что
векторыиколлинеарны вопреки нашему исходному
предположению.
Аналогично можно доказать: любые три компланарных вектора линейно зависимы, а два некомпланарных вектора линейно независимы .
Возвращаясь к понятию базиса и к задаче разложения вектора в определённом базисе, можно сказать, что базис на плоскости и в пространстве образуется из совокупности линейно независимых векторов. Такое понятие базиса является общим, т.к. оно применимо к пространству любого числа измерений.
Выражение вида:
,
называется разложением векторапо векторам,…,.
Если мы будем рассматривать базис в
трехмерном пространстве, то разложение
вектора
по базису
будет
,
где
—координаты вектора .
В задаче разложения произвольного
вектора в некотором базисе весьма важным
является следующее утверждение: любой
вектор может быть единственным образом
разложен в данном базисе
. Иными словами, координаты
для любого вектораотносительно базиса
определяетсяоднозначно.
Введение базиса в пространстве и на плоскости позволяет поставить в соответствие каждому вектору упорядоченную тройку (пару) чисел – его координаты. Этот очень важный результат, позволяющий установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.
Совокупность точки и базиса называют системой координат.
Если векторы, образующие базис единичны
и попарно перпендикулярны, то система
координат называется прямоугольной, а базис ортонормированным.
Л. 2-2 Произведение векторов
Разложение
вектора по базису
Рассмотрим
вектор
,
заданный своими координатами:
.
—
компоненты векторапо направлениям базисных векторов
.
Выражение вида
называется разложением векторапо базису
.
Аналогичным образом можно разложить по базису
вектор
:
.
Косинусы углов, образованные рассматриваемым
вектором
с базисными ортами
называютсянаправляющими косинусами
;
;
.
Скалярное произведение векторов.
Скалярным произведением двух векторов иназывается число, равное произведению модулей этих векторов на косинус угла между ними
Скалярное произведение двух векторов
можно рассматривать как произведение
модуля одного из этих векторов на
ортогональную проекцию другого вектора
на направление первого
.
Свойства:
Если известны координаты векторов
и
,
то, выполнив разложение векторов по
базису
:
и
,
найдём
,
т. к.
к.
,
,
то
.
.
Условие перпендикулярности векторов:
.
Условие коллинеарности ректоров:
.
Векторное произведение векторов
или
Векторным произведением вектором
на векторназывается такой вектор
,
который удовлетворяет условиям:
Свойства:
Рассмотренные алгебраические свойства позволяют найти аналитическое выражение для векторного произведения через координаты составляющих векторов в ортонормированном базисе.
Дано:
и
.
т.к.
,
,
,
,
,
,
,
то
. Эту формулу можно записать короче, в форме определителя третьего порядка:
.
Смешанное произведение векторов
Смешанным произведением трех векторов
,иназывается число, равное векторному
произведению
,
умноженному скалярно на вектор.
Верно следующее равенство:
,
поэтому смешанное произведение записывают
.
Как следует из определения, результатом
смешанного произведения трёх векторов
является число. Это число имеет наглядный
геометрический смысл:
Это число имеет наглядный
геометрический смысл:
Модуль смешанного произведения
равен объёму параллелепипеда, построенного
на приведённых к общему началу векторах,и.
Свойства смешанного произведения:
Если векторы
,,заданы в ортонормированном базисе
своими координатами, вычисление
смешанного произведения осуществляется
по формуле
.
Действительно, если
,
то
;
;
,
тогда
.
Если векторы
,,компланарны, то векторное произведение
перпендикулярно вектору.
И наоборот, если
,
то объем параллелепипеда равен нулю, а
это возможно только в том случае, когда
векторы компланарны (линейно зависимы).
Таким образом, три вектора компланарны, тогда и только тогда, когда их смешанное произведение равно нулю.
Таргетированная outdoor-реклама. Как находить своего покупателя в городе | Публикации
Последние десять лет рекламный рынок и его бюджеты уверенно движутся от охватных каналов в сторону персонализации и стимулирования потребителя совершить действие прямо здесь и сейчас. Наружка тоже не стоит на месте — таргетированная outdoor-реклама постепенно становится реальностью рекламного мира. Как перейти к таргетированию в outdoor, какие средства для этого уже есть и всегда ли эта игра стоит свеч, обсудили на конференции AdIndex City 2021
Наружка тоже не стоит на месте — таргетированная outdoor-реклама постепенно становится реальностью рекламного мира. Как перейти к таргетированию в outdoor, какие средства для этого уже есть и всегда ли эта игра стоит свеч, обсудили на конференции AdIndex City 2021
Для таргетинга в наружке используем те же данные, что и в digital
На текущий момент нет принципиальной разницы между данными в наружной рекламе и данными в интернете, считает руководитель группы инновационных сервисов компании «Квант» Инна Кравцова. Российское законодательство одинаково регулирует обе эти сферы, а сами данные в равной степени подходят для таргетинга как в outdoor, так и в digital.
Важно обращать внимание на то, какие идентификаторы привлекаются и что может лежать в их основе. В «Кванте» используют несколько ключевых блоков по данным:
1. Геоданные. Сбор данных может происходить в разных локациях —
билборды оснащаются Wi-Fi-снифферами, в наземном транспорте, метро, такси и
аэропортах работают сенсоры трафика. Технологии позволяют отслеживать
передвижение пользователей по городу и внутри коммерческих объектов и
выстраивать их паттерны поведения.
Технологии позволяют отслеживать
передвижение пользователей по городу и внутри коммерческих объектов и
выстраивать их паттерны поведения.
2. Поведение в интернете. В момент, когда пользователь подключается к любой Wi-Fi-сети — в метро, парке или кафе, — оператор собирает данные о приложениях и сайтах, открытых на устройстве.
3. Посещение объектов. Пожалуй, не осталось торгового центра, который бы не был оснащен Wi-Fi-ловушками.
4. Покупки — лакомый кусок данных для любого рекламодателя. «Квант» сотрудничает с тремя крупнейшими ОФД и может отследить более 60% всех транзакций онлайн и офлайн, которые осуществляют покупатели.
Выбираем релевантную локацию с помощью геоаналитических платформВ ближайшее время рекламной индустрии предстоит довольствоваться тем, что
уже есть, так как вряд ли появятся новые виды данных. Однако по мере развития
технологий находится все больше способов миксовать их и получать неожиданные
результаты.
Сергей Голицын, директор по анализу данных и моделированию «Платформы больших данных», рассказал о тренде на Data Fusion. Эта технология позволяет делать микс из большого объема сложных кросс-отраслевых данных, которые раньше не получалось объединить.
Лучшим программным решением для наружной рекламы станет работа с геоаналитическими платформами. Они генерируют множество геослоев, которые представляют собой характеристику конкретных локаций.
Платформа показывает, как на территории распределяются интересы, доходы,
трудоспособное население и множество других показателей. Векторное
представление локаций можно интерпретировать с точки зрения моделирования и
построения профиля. Для построения геоаналитических слоев привлекаются сотни
источников — от телеком-операторов и соцсетей до транзакционных данных, при
этом мы не привязываемся к конкретному пользователю, а создаем общий портрет
покупателя в конкретной локации. Такой микс позволяет максимально профилировать
локацию. На основе полученных данных формируется несколько геослоев. Их
помещают в единое пространство и обрабатывают с помощью машинного обучения,
чтобы объединить в ранжирующий слой, который поможет выбрать наиболее
подходящую локацию для размещения рекламы.
Такой микс позволяет максимально профилировать
локацию. На основе полученных данных формируется несколько геослоев. Их
помещают в единое пространство и обрабатывают с помощью машинного обучения,
чтобы объединить в ранжирующий слой, который поможет выбрать наиболее
подходящую локацию для размещения рекламы.
Таргетированная outdoor-реклама — это свайп вправо
Руководитель продуктов компании Russ Outdoor Руслан Ибрагимов сравнивает поиски рекламодателем своего клиента с механикой в дейтинг-сервисах (свайп вправо и влево). Разные дейтинг-сервисы имеют разную ЦА и и цели пользователей. Исходя из этого пользователи пользуются разными сервисами. Таргетированная реклама по механике очень похожа на данный процесс. Рекламодатель хочет достичь своего клиента, потратив на это как можно меньше времени и ресурсов.
Передвижение любого среднестатистического городского жителя можно
представить в виде пользовательского пути. Этот путь проходит мимо точек
пересечения с рекламой: остановок, билбордов, бизнес-центров, аэропортов, а
также станций метро и МЦК. При этом рекламодатель почти всегда нацелен
«поймать» нужный ему сегмент аудитории со своими интересами — целевую
аудиторию.
Этот путь проходит мимо точек
пересечения с рекламой: остановок, билбордов, бизнес-центров, аэропортов, а
также станций метро и МЦК. При этом рекламодатель почти всегда нацелен
«поймать» нужный ему сегмент аудитории со своими интересами — целевую
аудиторию.
И если раньше планирование в наружке велось по привязкам, охвату и маршрутам, то современный outdoor движется в сторону планирования по целевой аудитории и к таргетингам в реальном времени.
Для этого важно понимать, что происходит в городе, а также где и в какое время концентрируется целевая аудитория. Важную роль здесь играет геоаналитика, которая помогает профилировать территорию по таким признакам, как уровень дохода, интересы и соцдем.
Понимая типичный портрет аудитории, становится возможным выбирать места размещения наружной рекламы там, где доля ЦА больше.
«Крен аффинитивности» покажет рекламный креатив в реальном времениИнна Кравцова рассказала про новый продукт, совместно разработанный Russ Outdoor и «Квант», под рабочим названием «Крен аффинитивности». Это рекомендательная система, которая показывает рекламный креатив в рамках барабана и работает на собранных MAC-адресах. Продукт состоит из трех частей — калькулятора, самой рекомендательной системы и отчетности о результатах после изменений внутри системы. Калькулятор помогает планировать рекламные кампании — с его помощью рекламодатель понимает, какую выгоду получит, если выберет тот или иной таргетинг.
Как это работает:
— «Квант»получает от Russ Outdoor поток MAC-адресов в режиме реального времени от всех конструкций и непрерывно анализирует долю, которую целевая аудитория занимает в текущий момент времени;
— полученная статистика запускается в рекомендательную систему, где в течение двух недель по ней оттачиваются настройки алгоритма. Срок годности данных для создания прогноза — не более двух недель;
— затем, когда рекламная кампания началась, поток продолжает анализироваться, и алгоритм определяет, в какой момент времени выход рекламного ролика лучше попадает в целевую аудиторию.
При этом «Крен аффинитивности» — это не программатик в чистом виде. Здесь нет DSP и SSP: программа дает потребителю рекомендацию к привычной покупке через барабанную модель.
Для оценки результатов система отчетности помогает понять, каким было бы попадание в целевую аудиторию, если бы рекламный ролик не менял свою позицию, а выходил в стандартном цикле, и сравнить его с результатом использования оптимизационной механики.
Таргетинг не всегда гарантирует повышения конверсииВ 2018 году, когда таргетинг только появился в наружной рекламе, его взялся тестировать практически весь outdoor-сегмент. И если подбор целевой аудитории сразу отлично себя зарекомендовал, то показатели ROI до сих пор вызывают вопросы.
Руководитель цифровых out-of-home-продуктов Posterscope Вячеслав Ивакин объяснил, почему таргетинг не гарантирует повышения конверсии, и рассказал, что нужно сделать, чтобы обеспечить хорошие результаты.
Обычное размещение в наружке контактирует с некоторым количеством людей, среди которых встречается и целевая аудитория. Если она составляет 14% — это уже неплохой бенчмарк. Качественный таргетинг может в среднем поднять объем целевой аудитории примерно в два-три раза.
Даже если при таких высоких показателях человек из целевой аудитории конвертится в два раза лучше, чем простой обыватель, это не гарантирует успех. Ведь многое решает наценка за данные и решения при таргетинге.
Чем больше наценка, тем при сохранении бюджета меньше контактов и ниже охват. В результате количество финальных конверсий при таргетинге может оказаться таким же, как и без него, что нивелирует всю проделанную работу. Именно поэтому важно внимательно работать с вводными, параметрами, условиями и конверсиями.
В каком направлении развиваться дальше?
Наличие большого количества данных для аналитики и таргетинга делают наружку более привлекательной для рекламодателя и агентств. Однако есть еще ряд важных условий, которые, по мнению Вячеслава Ивакина, позволят outdoor-сегменту расширить свои горизонты:
1. Вернуть и расширить долю видеоаналитики. Это уникальный вид данных, который позволяет выцепить нужную аудиторию на порядки точнее, чем это возможно сделать по цифровым следам в интернете.
2. Организовать данные соцдем-таргетинга. Данные соцдема нужно стандартизировать, приведя в соответствие с другими медиаканалами. При этом важно использовать понятные прозрачные источники.
3. Расширить долю ретейла. Наружная реклама насыщена данными, однако таргетингов по ретейлу — по местам посещения, товарным категориям и чекам — явно недостаточно.
Ближайшее будущее outdoorПод занавес секции спикеры обсудили тренды таргетированного outdoor, которые привлекают к себе внимание, и поделились своим видением будущего.
Новые подходы к анализу данных. В обозримом будущем работа с данными, подсказывающими интерес покупателя к конкретным продуктам, а также данными фактического потребления тех или иных продуктов и брендов выйдет на первый план. Уже сейчас активно развиваются технологии, которые позволят проводить их полный учет и более быструю обработку. Наиболее перспективным направлением в этой области, по мнению Сергея Голицына, станет работа с транзакционными и банковскими базами, а также базами фискальных операторов.
Увеличение доли ретейла. Таргетинги по ретейлу — вопрос времени. Инна Кравцова рассказала, как «Квант» работает над выходом ретейла в outdoor. Компания готовится к тому, что можно будет тестировать гипотезы таргетирования по CRM-клиента при достаточных охватах.
Тренд на получение быстрых результатов. Спикеры отметили увеличивающийся интерес к performance-механикам, которые позволяют в моменте увидеть отклик на услугу или товар. Рекламодатели ждут, что бизнес не будет застаиваться и продажи будут происходить сразу, а не в отдаленном будущем.
Внимание к широкой аудитории. Тренд на быструю отдачу может создать иллюзию отсутствия необходимости вкладывать усилия в свой бренд. При таком подходе уменьшается вклад в коммуникации, которые не побуждают совершить ежеминутную[4] покупку, а работают долгое время. Поэтому важно формировать знание бренда среди всех потенциальных покупателей в категории.
Спрос на умное управление. Рекламная кампания — это взаимосвязанная экосистема разных каналов коммуникаций, и наружная реклама не должна существовать в отрыве. Важен баланс, важно сохранение охвата и частоты контакта, важно вовлечение как можно большего числа потенциальных покупателей — и важно использовать те инструменты таргетинга, которые позволяют лучше использовать знания об аудитории и контекст локаций.
Сложение векторов
В механике есть два вида величин
- скалярных величин с величиной — время, температура, масса и т. Д.
- вектор величин с величиной и направлением — скорость, сила и т. Д.
Когда добавление векторных величин важны как по величине, так и по направлению. Общие методы сложения копланарных векторов (векторов, действующих в одной плоскости):
- закон параллелограмма
- правило треугольника
- тригонометрическое вычисление
Закон параллелограмма
Процедура «» метод сложения параллелограмма векторов «- это
- начертите вектор 1, используя соответствующий масштаб и в направлении его действия
- от хвоста вектора 1 начертите вектор 2, используя тот же масштаб в направлении его действия
- завершите параллелограмм, используя вектор 1 и 2 как стороны параллелограмма
- результирующий вектор представлен как по величине, так и по направлению диагональю параллелограмма
Правило треугольника
Процедура « метод сложения треугольника векторов » равна
- начертите вектор 1 в соответствующем масштабе и в направлении его действия 9 0008
- от носа вектора нарисуйте вектор 2, используя тот же масштаб и в направлении его действия
- , результирующий вектор представлен как по величине, так и по направлению вектором, проведенным от хвоста вектора 1 к носу вектора 2
Тригонометрическое вычисление
Результирующий вектор из двух копланарных векторов может быть вычислен тригонометрическим методом с использованием « правила косинуса » для прямоугольного треугольника.
F R = [F 1 2 + F 2 2 — 2 F 1 F 2 cos (180 o — (α + β))] 1/2 (1)
где
F = векторная величина — сила, скорость и т. Д.
α + β = угол между вектором 1 и 2
Угол между вектором и результирующий вектор может быть вычислен с использованием « правило синуса » для непрямоугольного треугольника.
α = sin -1 [F 1 sin (180 o — (α + β)) / F R ] (2)
где
α + β = угол между вектором 1 и 2 известен
Пример — сложение сил
Сила 1 с величиной 3 кН действует в направлении 80 o от силы 2 с величиной 8 кН .
Результирующая сила может быть рассчитана как
F R = [(3 кН) 2 + (8 кН) 2 — 2 (5 кН) (8 кН) cos (180 o — (80 o ))] 1/2
= 9 (кН)
Угол между вектором 1 и результирующим вектором можно рассчитать как
α = sin -1 [(3 кН) sin (180 o — (80 o )) / (9 кН) ]
= 19.1 o
Угол между вектором 2 и результирующим вектором можно рассчитать как
α = sin -1 [(8 кН) sin (180 o — (80 o ) ) / (9 кН) ]
= 60,9 o
Пример — Самолет при ветре
Встречный ветер 100 км / ч действует 30 o правый борт на самолете с скорость 900 км / ч .
Результирующая скорость самолета относительно земли может быть рассчитана как
v R = [(900 км / ч) 2 + (100 км / ч) 2 — 2 (900 км / ч) (100 км / ч) cos (180 o — (30 o ))] 1/2
= 815 (км / ч)
Угол между курсом самолета и фактический относительный курс земли можно рассчитать как
α = sin -1 [(100 км / ч) sin ((180 o ) — (30 o )) / (815 км / ч) ]
= 3.5 o
Векторный калькулятор
Общий калькулятор ниже основан на уравнении (1) и может использоваться для сложения векторных величин, таких как скорости, силы и т. Д.
Параллелограмм
Результирующие векторы могут быть оценены путем рисования параллелограммов, как показано ниже.
- нарисуйте векторы с правильным направлением и величиной
- начертите параллельные линии векторам
- начертите результирующий вектор в точку пересечения между параллельными линиями
- измерьте величину и направление результирующего вектора на чертеже
Метод также можно использовать с более чем двумя векторами, как указано ниже.
- нарисуйте результирующие векторы между двумя и двумя векторами
- начертите результирующие векторы между двумя и двумя результирующими векторами
- продолжайте до тех пор, пока не будет только один конечный результирующий вектор
- Измерьте направление и величину конечного результирующего вектора в рисунок
В приведенном выше примере сначала найдите результирующий F (1,2) , добавив F 1 и F 2 , и получившийся F (3,4) , добавив F 3 и F 4 .Найдите результат F (1,2,3,4) , добавив F (1,2) и F (3,4) .
Калькулятор линейной независимости
Добро пожаловать в калькулятор линейной независимости , где мы узнаем, как проверить, имеете ли вы дело с линейно независимыми векторами или нет.
По сути, мир вокруг нас является векторным пространством и иногда полезно ограничиться меньшей его частью. Например, сфера — это , трехмерная форма , а круг существует только в двух измерениях , так зачем возиться с вычислениями в трех измерениях?
Линейная зависимость позволяет нам делать именно это — работать в меньшем пространстве, так называемом диапазоне рассматриваемых векторов .Но не волнуйтесь, если вы нашли все эти причудливые слова нечеткими. Через секунду мы медленно пройдем через все это вместе.
Так что возьмите утреннюю / вечернюю закуску в дорогу, и вперед!
Что такое вектор?
Если вы спросите кого-нибудь « Что такое вектор? » довольно часто, вы получите ответ « стрелка ». Ведь мы обычно обозначаем их стрелкой над маленькой буквой:
Ну, давайте просто скажем, что этот ответ не принесет вам 100 баллов на тесте.Формально вектор — это элемент векторного пространства . Конец определения. Достаточно просто . Мы можем закончить учебу. Теперь все ясно.
Но , что же тогда такое векторное пространство? Опять же, математическое определение оставляет желать лучшего: это набор элементов с некоторыми операциями (сложение и умножение на скаляр), которые должны иметь несколько специфических свойств. Так почему бы нам просто не оставить формализм и не взглянуть на на реальных примерах ?
Декартово пространство является примером векторного пространства.Это означает, что числовая линия, плоскость и трехмерное пространство, в котором мы живем , являются векторными пространствами . Их элементами являются, соответственно, числа, пары чисел и тройки чисел, которые в каждом случае описывают положение точки (элемента пространства). Например, число -1 или точка A = (2, 3) являются элементами (разных!) Векторных пространств. Часто при рисовании сил, действующих на объект, таких как скорость или гравитационное притяжение, мы используем прямые стрелки , чтобы описать их направление и значение , и отсюда и происходит «определение стрелки ».
Что очень важно, так это то, что у нас есть четко определенных операций над векторами, упомянутыми выше. Есть несколько более сложных, таких как скалярное произведение и перекрестное произведение. Однако, к счастью, мы ограничимся двумя основными , которые следуют аналогичным правилам для одних и тех же матричных операций (векторы, по сути, являются однострочными матрицами). Прежде всего, , мы можем добавить их :
-1 + 4 = 3 ,
(2,3) + (-3, 11) = (2 + (-3), 3 + 11) = (-1, 14) ,
и , мы можем умножить их на скаляр (действительное или комплексное число), чтобы изменить их величину:
3 * (-1) = -3 ,
7 * (2, 3) = (7 * 2, 7 * 3) = (14, 21) .
По правде говоря, векторное пространство не обязательно должно содержать числа . Это может быть пространство последовательностей, функций или перестановок. Даже скаляры не обязательно должны быть числовыми! Но оставим эту абстрактную чушь ученым . Нас устраивают только цифры, не так ли?
Линейная комбинация векторов
Допустим, нам дан набор векторов (из того же пространства): v₁ , v₂ , v₃ , …, vₙ . Как мы видели в предыдущем разделе, , мы можем сложить их и умножить на скаляры . Любое выражение, полученное таким образом, называется линейной комбинацией векторов. Другими словами, любой вектор w , который можно записать как
w = 𝛼₁ * v₁ + 𝛼₂ * v₂ + 𝛼₃ * v₃ + ... + 𝛼ₙ * vₙ
, где 𝛼₁, 𝛼₂, 𝛼₃, ..., 𝛼ₙ — произвольные действительные числа, называется линейной комбинацией векторов v₁ , v₂ , v₃ ,…, vₙ . Обратите внимание, что w действительно вектор, поскольку это сумма векторов.
Хорошо, зачем все это? В жизни есть несколько вещей, таких как гелиевые шары и гамаки, которые приятно иметь, но не так уж и полезны в повседневной жизни. Так ли это здесь?
Рассмотрим декартовую плоскость , т.е. двумерное пространство точек A = (x, y) с двумя координатами, где x и y — произвольные действительные числа.Мы уже знаем, что такие точки являются векторами, поэтому почему бы нам не взять , две очень особенные точки : e₁ = (1,0) и e₂ = (0,1) . Теперь обратите внимание:
A = (x, y) = (x, 0) + (0, y) = x * (1,0) + y * (0,1) = x * e₁ + y * e₂ .
Другими словами, любая точка (вектор) нашего пространства представляет собой линейную комбинацию векторов e₁ и e₂ . Эти векторы образуют базис (и при этом ортонормированный базис) пространства.И поверьте нам, в приложениях и вычислениях часто проще работать с известной вам базой, чем с какими-то случайными векторами, которых вы не знаете.
Но , что, если бы мы добавили еще один вектор к стопке и захотели описать линейные комбинации векторов e36 , e₂ и, скажем, v ? Мы видели, что e₁ и e₂ оказались достаточными, чтобы найти все точки. Так что добавление к ничего не должно изменить, не так ли? Собственно, кажется совершенно лишним .И именно здесь в игру вступает линейная зависимость .
Линейно независимые векторы
Нет, это не имеет ничего общего с вашим барбекю 4 июля. Мы говорим, что v₁ , v₂ , v₃ , …, vₙ — это линейно независимых векторов , если уравнение
𝛼₁ * v₁ + 𝛼₂ * v₂ + 𝛼₃ * v₃ + ... + 𝛼ₙ * vₙ = 0
(здесь 0 — вектор с нулями во всех координатах) выполняется тогда и только тогда, когда 𝛼₁ = 𝛼₂ = 𝛼₃ =... = 𝛼ₙ = 0 . В противном случае мы говорим, что векторы линейно зависимы .
Приведенное выше определение можно понять следующим образом: единственная линейная комбинация векторов, которая дает нулевой вектор, является тривиальной . Например, вспомните векторы из приведенного выше раздела: e₁ = (1,0) , e₂ = (0,1) , а затем также возьмите v = (2, -1) . Тогда
(-2) * e₁ + 1 * e₂ + 1 * v = (-2) * (1,0) + 1 * (0,1) + 1 * (2, -1) = (-2,0 ) + (0,1) + (2, -1) = (0,0) ,
, поэтому мы нашли нетривиальную линейную комбинацию векторов, которая дает ноль .Следовательно, они линейно зависимые . Кроме того, мы легко можем видеть, что сами по себе e₁ и e₂ без проблемных v являются линейно независимыми векторами .
Оболочка векторов в линейной алгебре
Набор всех элементов, которые можно записать как линейную комбинацию векторов v₁ , v₂ , v₃ , …, vₙ , называется промежутком векторов и обозначается span ( v₁, v₂, v₃ ,..., vₙ) . Возвращаясь к векторам из предыдущего раздела, то есть e₁ = (1,0) , e₂ = (0,1) и v = (2, -1) , мы видим, что
пролет (e₁, e₂, v) = пролет (e₁, e₂) = ℝ² ,
, где ℝ² — это множество точек на декартовой плоскости, то есть все возможные пары действительных чисел. По сути, это означает, что размах векторов одинаков: для e₁ , e₂ и v , и всего для e₁ и e₂ (или, если использовать формальные термины, двух пересечение пространств составляет целое м² ).Это говорит о том, что v является избыточным и ничего не меняет . Да, вы догадались — именно из-за линейной зависимости .
Пролет в линейной алгебре описывает пространство, в котором живут наши векторы . В частности, наименьшее количество элементов, которых достаточно для этого, называется размерностью векторного пространства. В приведенном выше примере это было 2 , потому что мы не можем получить меньше элементов, чем e₁ и e₂ .
Внимательный взгляд заметит, что на самом деле размерность диапазона векторов равна количеству линейно независимых векторов в сгустке. В приведенном выше примере это было довольно просто: векторы e₁ и e₂ были самыми простыми из возможных (на самом деле, у них даже есть собственное имя: стандартный базис ). Но что, если у нас есть что-то другое? Как мы можем проверить линейную зависимость и описать диапазон векторов в каждом случае? Через минуту мы узнаем это и многое другое!
Как проверить линейную зависимость
Для проверки линейной зависимости переведем нашу задачу с языка векторов на язык матриц (массивов чисел).Например, предположим, что нам даны три вектора в 2-мерном пространстве (с двумя координатами): v = (a₁, a₂) , w = (b₁, b₂) и u = (c₁, c₂) . Теперь давайте запишем их координаты как в одну большую матрицу , в которой каждая строка (или столбец, неважно) соответствует одному из векторов:
| А | = |
|
Тогда ранг матрицы равен максимальному количеству линейно независимых векторов среди v , w и u .Другими словами, их промежуток в линейной алгебре имеет размерность ранг (A) . В частности, являются линейно независимыми векторами тогда и только тогда, когда ранг A равен количеству векторов .
Итак, как нам узнать ранг? Возможно, самый простой метод — это исключение Гаусса (или его уточнение, исключение Гаусса-Жордана ). Это тот же самый алгоритм, который часто используется для решения систем линейных уравнений, особенно при попытке найти (сокращенную) ступенчатую форму системы.
Исключение по Гауссу основано на так называемых операциях с элементарной строкой :
- Поменять местами две строки матрицы.
- Умножьте строку на ненулевую константу.
- Добавить в строку ненулевое кратное другой строке.
Уловка здесь в том, что хотя операции изменяют матрицу , они не меняют ее ранг и, следовательно, размер диапазона векторов.
Алгоритм пытается устранить (т.е.е., сделайте их 0 ) как можно больше записей A . В приведенном выше случае, при условии, что a₁ не равно нулю, первый шаг исключения Гаусса преобразует матрицу во что-то в форме:
|
, где s₂ и t₂ — некоторые действительные числа.Тогда, пока сÀ не равно нулю, второй шаг даст матрицу
|
Теперь нам нужно заметить, что нижняя строка представляет нулевой вектор (у него 0 в каждой ячейке), который линейно зависит от любого вектора .Следовательно, ранг нашей матрицы будет просто , количество ненулевых строк в массиве, которое мы получили , что в данном случае составляет 2 .
Это было достаточно времени, потраченного на теорию, не так ли? Давайте попробуем на примере посмотрим, как работает калькулятор линейной независимости !
Пример: использование калькулятора линейной независимости
Допустим, вы наконец осуществили свои мечты — вы купили дрон . Наконец-то вы можете снимать и снимать на видео места, которые вы посещаете, издалека.Все, что вам нужно сделать, это запрограммировать его движения . Дрон требует, чтобы вы дали ему три вектора, по которым он сможет перемещать .
Мир, в котором мы живем, трехмерен, поэтому векторы будут иметь три координаты . Не задумываясь, вы берете случайных векторов, которые приходят на ум : (1, 3, -2) , (4, 7, 1) и (3, -1, 12) . Но действительно ли стоит просто закрыть глаза, подбросить монетку и выбрать случайные числа? В конце концов, большая часть ваших сбережений пошла на это, так что , нам лучше сделать это хорошо .
Что ж, если вы выбрали числа случайным образом, вы можете обнаружить, что выбранных вами векторов являются линейно зависимыми , а диапазон векторов, например, только двумерный. Это означает, что ваш дрон не сможет перемещаться, как вы хотите, но будет ограничен движением по плоскости . Может случиться так, что он сможет перемещаться влево и вправо, вперед и назад, , но не вверх и вниз . И как мы получим эти отмеченные наградами кадры похода, если дрон не может даже взлететь?
Хорошо, что у нас есть калькулятор линейной независимости! С его помощью мы можем быстро и легко проверить, был ли наш выбор удачным. Итак, давайте разберемся, как им пользоваться.
У нас есть 3 векторов с 3 координатами каждый, поэтому мы начинаем с того, что сообщаем калькулятору об этом факте, выбирая соответствующие параметры под « количество векторов » и « количество координат ». Это покажет нам символический пример таких векторов с обозначениями, используемыми в калькуляторе линейной независимости. Например, первый вектор задается как v = (a₁, a₂, a₃) .Следовательно, поскольку в нашем случае первым было (1, 3, -2) , мы вводим
a₁ = 1 , a₂ = 3 , a₃ = -2 .
Аналогично для двух других получаем:
b₁ = 4 , b₂ = 7 , b₃ = 1 ,
c₁ = 3 , c₂ = -1 , c₃ = 12 .
Как только мы введем последнее число, калькулятор линейной независимости мгновенно сообщит нам, есть ли у нас линейно независимые векторы или нет , и каков размер диапазона векторов.Тем не менее, давайте возьмем лист бумаги и попробуем сделать все самостоятельно вручную, чтобы увидеть , как калькулятор пришел к своему ответу .
Как упоминалось в предыдущем разделе, мы хотели бы вычислить ранг матрицы, образованной нашими векторами . Мы построим массив размером 3 × 3, записав координаты последовательных векторов в последовательные строки. Таким образом, мы приходим к матрице
| А | = |
|
Теперь мы будем использовать исключения Гаусса .Прежде всего, нам бы хотелось, чтобы имел нули в двух нижних строках первого столбца . Для их получения мы используем элементарные операции со строками и 1 из верхней строки. Другими словами, мы прибавляем подходящее кратное первой строки к двум другим , так что их первая запись станет нулем. Поскольку 4 + (-4) * 1 = 0 и 3 + (-3) * 1 = 0 , мы добавляем кратное (-4) и (-3) первой строки к второй и третий ряд соответственно.Это дает матрицу
| = |
| = |
|
Затем мы хотим, чтобы получило 0 в нижней строке среднего столбца и использовало для этого -5 .Опять же, , мы прибавляем подходящее кратное второй строки к третьей . Поскольку -10 + (-2) * (- 5) = 0 , кратное составляет (-2) . Следовательно,
| = |
| = |
|
Мы получили нулей в нижних строках .Мы знаем, что ранг матрицы и, следовательно, линейная зависимость и диапазон в линейной алгебре определяются количеством ненулевых строк . Это означает, что в нашем случае у нас rank (A) = 2 , что на меньше, чем количество векторов , и подразумевает, что они линейно зависимы и охватывают 2-мерное пространство .
Итак, случилось то, чего мы опасались: наш дрон не будет иметь свободы передвижения . Но мы не можем упустить шанс снять все эти воздушные кадры! К счастью, у нас есть калькулятор линейной независимости , и мы можем поиграть с векторами, чтобы найти подходящую комбинацию векторов.А когда он у нас есть, мы собираемся, садимся в машину и отправляемся в приключение!
Карта механики — момент около точки
Для любой точки вытянутого тела, если на это тело действует сила, которая не проходит через эту точку, то эта сила вызовет момент вокруг этой точки. Как уже говорилось на странице моментов, момент — это тенденция силы вызывать вращение.
Векторный метод в 2-х и 3-х измерениях
Альтернативой вычисления момента с помощью скалярных величин является использование векторного метода или метода перекрестного произведения .Для простых двумерных задач обычно проще использовать скалярные величины, но для более сложных задач обычно проще использовать метод перекрестного произведения. Метод перекрестного произведения для вычисления моментов гласит, что вектор момента силы вокруг точки будет равен перекрестному произведению вектора r от точки до любой точки на линии действия силы и самого вектора силы.
| \ [\ vec {M} = \ vec {r} \ times \ vec {F} \] |
Большим преимуществом этого метода является то, что r не обязательно должно быть кратчайшим расстоянием между точкой и линией действия, оно идет от точки до любой части линии действия.Для любой задачи существует множество возможных векторов r , хотя из-за того, как работает перекрестное произведение, все они должны в конечном итоге привести к одному и тому же вектору момента.
Вектор момента силы F относительно точки A будет равен перекрестным произведениям вектора r и вектора силы. Вектор r — это вектор из точки A в любую точку на линии действия силы.Здесь важно отметить, что все величины ( r , F и M ) являются векторами.Прежде чем вы сможете решить для кросс-продукта, вам нужно будет записать r и F в форме векторных компонентов. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента векторов r и F . Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для вычислений.
Полученный вами вектор момента будет совмещен с осью вращения на данный момент, где вы можете использовать правило правой руки, чтобы определить, идет ли момент вокруг этой оси по часовой стрелке или против часовой стрелки.
Результат r cross F даст нам вектор момента. Для этой двумерной задачи вектор момента указывает в положительном направлении оси z. Мы можем использовать правило правой руки, чтобы определить направление вращения с момента (совместите большой палец правой руки с вектором момента, и наши скрученные пальцы будут указывать в направлении вращения с момента).Наконец, важно также отметить, что перекрестное произведение, в отличие от умножения, не является коммуникативным.Это означает, что порядок векторов имеет значение, и r cross F не будет таким же, как F cross r . При расчете моментов важно всегда использовать r cross F .
Очень простое руководство по CalcMe — CalcMe — Документация
CalcMe — это онлайн-калькулятор на основе Javascript, поэтому он работает в любом браузере и операционной системе, включая мобильные и планшетные устройства. CalcMe интегрирован в Wiris Quizzes, повышая эффективность ваших математических вопросов.CalcMe предлагает мощный вычислительный и графический движок, покрывающий базовые и сложные математические задачи: генерация случайных чисел, полиномы, общие выражения, векторы, матрицы, списки, геометрия, статистика, пользовательские функции, программирование и многое другое.Живые демонстрации
На этой странице есть несколько живых демонстраций. Если щелкнуть область, содержащую параметры CalcMe, она откроется в CalcMe. Попробуйте, измените параметры или опции. Ничего не сломаешь.Как работает CalcMe?
Вы можете писать математику, а CalcMe выполнит вычисления за вас.
Таблица CalcMe разделена на три основные области:
| Область для Расчет | Область для График | Область для Определение |
Рассчитать
Напишите, что вы хотите вычислить
Нажмите Calc или Введите
Действие по умолчанию — Calc , но вы можете выбрать наиболее подходящий по своему усмотрению.
ЖИВАЯ ДЕМО
График
Напишите уравнение или фигуру, которую хотите построить
Нажмите График действие
Новый
С этого момента можно загрузить графический плоттер в виде квадратного изображения в формате PNG желаемого размера.Воспользуйтесь этой новой функцией CalcMe, чтобы сохранять сгенерированные изображения прямо на ваше устройство.Определить
Сохранить вычисление в переменной
Использовать позже
Новый
Есть новая процедура для определения переменных в CalcMe с помощью редактора кода. Здесь вы можете увидеть проблемы, которые предполагается решить с его помощью, и ожидаемое взаимодействие с пользователем.Арифметика
Математические операции в CalcMe представлены символом, связанным с клавишей клавиатуры.
ЖИВАЯ ДЕМО
Вы можете вычислить частное и остаток от деления или разложить число на простые множители. Вы также можете вычислить наибольший общий делитель или наименьшее общее кратное набора чисел.
ЖИВАЯ ДЕМО
Конструктор векторов и матриц
Векторы
Вектор заключен в квадратные скобки [] , а элементы разделены запятыми , .
Вы можете просуммировать векторы или вычислить их скалярное произведение.
ЖИВАЯ ДЕМО
Матрицы
Матрицы — это векторы векторов, то есть векторы, элементы которых являются векторами. Вы можете создавать матрицы с двумя разными синтаксисами
В качестве векторов вы можете суммировать и умножать матрицы (если их размеры совместимы).
ЖИВАЯ ДЕМО
Основные операции
Как вы уже видели, вы можете работать с векторами и матрицами и выполнять с ними базовые арифметические операции.Однако вы можете сделать гораздо больше: вы можете вычислить перекрестное произведение между двумя векторами, проверить, являются ли они линейно независимыми; матрицу можно инвертировать или возвести в целую степень, вы также можете вычислить ее ранг или определитель.
ЖИВАЯ ДЕМО
Доступ к элементу
Вы можете получить доступ к определенному элементу вектора с помощью подиндексов, которые начинаются с 1. Таким же образом вы можете получить элемент матрицы.
ЖИВАЯ ДЕМО
Многочлены и выражения
Многочлены создаются с помощью числа, умноженного на переменную, возведенную в степень.
ЖИВАЯ ДЕМО
Вы можете суммировать, умножать, делить и, например, находить корни многочленов.
ЖИВАЯ ДЕМО
Вы также можете создавать более сложные выражения и работать с ними.
ЖИВАЯ ДЕМО
Дифференциация
Существует множество способов вычислить производную функции или выражения.
| Использование простого числа | ' |
| Использование символа | |
| Использование действия | |
| С помощью команды | дифференцировать |
ЖИВАЯ ДЕМО
Интеграция
Также существует множество способов вычислить интеграл от функции или выражения.
| Использование символа | |
| Использование действия | |
| Используя команду | интегрировать |
ЖИВАЯ ДЕМО
Предел
Можно вычислить предел функции или выражения. Более того, вы также можете брать односторонние ограничения.
ЖИВАЯ ДЕМО
Расширение Тейлора
Вы можете вычислить ряд Тейлора реальной функции в заданной точке.Если вас интересуют сроки до некоторого порядка, вы можете также сократить серию.
ЖИВАЯ ДЕМО
серии
Вы можете определить, сходится ли ряд, а также в большинстве случаев вычислить сумму сходящихся рядов.
ЖИВАЯ ДЕМО
Геометрия
CalcMe позволяет нам работать с геометрическими фигурами, такими как точки, линии, плоскости и конические сечения.Вы также можете создавать многоугольники и многогранники как в 2D, так и в 3D. Также возможно вычислить расстояние между фигурами, угол, который они образуют, или симметрию относительно объекта.
Точки, линии и плоскости
Возможна работа в 2 или 3 измерениях. Чтобы создать точки, вы просто определяете его компоненты.
ЖИВАЯ ДЕМО
Имея две точки или точку и вектор, вы можете построить линию.
ЖИВАЯ ДЕМО
Подобным образом вы можете, например, построить плоскость по трем точкам.
ЖИВАЯ ДЕМО
Фигуры
ЖИВАЯ ДЕМО
Решение
Уравнения
Можно решить уравнение или систему уравнений точно .
ЖИВАЯ ДЕМО
Вы также можете использовать численный метод для решения более сложных уравнений.
ЖИВАЯ ДЕМО
Вы также можете использовать численный метод для решения более сложных уравнений.
ЖИВАЯ ДЕМО
Неравенства
Также возможно найти решение неравенства.
ЖИВАЯ ДЕМО
Статистика
Существует множество функций, полезных для статистических расчетов, таких как среднее значение, квантиль, квартиль и т. Д. Вы можете увидеть полный список здесь.
ЖИВАЯ ДЕМО
Вероятность
Также доступны наиболее распространенные распределения вероятностей.По возможности также доступны аналитические выражения для функций плотности и распределения.
ЖИВАЯ ДЕМО
Комбинаторика
Можно вычислить комбинации, перестановки или вариации набора чисел. Однако будьте осторожны: результаты очень большие.
ЖИВАЯ ДЕМО
Единицы и валюта
Вы можете работать с единицами, конвертировать одну в другую (если это имеет смысл) и выполнять с ними базовые операции.Единицы необходимо вводить с помощью символов, доступных на вкладке Единицы измерения . Узнайте больше о единицах измерения или префиксах, которые вы можете использовать здесь.
ЖИВАЯ ДЕМО
Валюты похожи на единицы, но вы не можете конвертировать одну в другую. Проверьте все доступные валюты здесь.
ЖИВАЯ ДЕМО
Случайность
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для создания алгоритма для вопроса викторины Wiris, мы покажем, как создавать их на листе и с помощью редактора кода.Вы можете узнать об этом подробнее здесь.Функция random в CalcMe адаптируется ко многим случаям использования. Например, вы увидите, как удалить «0» из случайного выбора. Обычная команда была бы такой:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
По умолчанию сюда входят все числа от -10 до 10. Если учитывая требования вопроса, число 0 необходимо исключить из набора, вы можете удалить его с помощью одной простой инструкции (косая черта / должна быть используется с клавиатуры или логики и устанавливает вкладку ):
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Вы должны заключить в скобки первый список, чтобы это сработало.Это, конечно, может работать одинаково для любого другого числа, которое вам нужно исключить, кроме нуля:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Вышеупомянутое произвело бы случайное число от -10 до 10, кроме числа 8. Вы даже можете сделать это с более чем одним числом:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Это приведет к удалению 8, -8 и 0 из выбора.Как видите, существует гораздо больше возможностей при создании случайной величины.
Пока что вы получили целые числа, но вы также можете работать с действительными числами.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Как правило, эти действительные числа содержат столько десятичных или значащих цифр, сколько определено в настройках приложения.Вы можете настроить его, указав шаг между возможными случайными значениями.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Более того, эти случайные величины также могут быть выбраны из конкретного набора значений или слов. В следующем разделе вы увидите более подробную информацию о том, как создавать такие наборы.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Создание списков через понимание
Этот раздел представляет собой краткое руководство по созданию списков в CalcMe с использованием команд
с и , где .Этот метод определения списков основан на общепринятой математической нотации «понимание множества» или «нотация построителя множеств», например:Мы объясним команды на следующих примерах.
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для генерации алгоритма для вопроса Wiris Quizzes, мы покажем, как создавать их на листе и с помощью редактора кода. Вы можете узнать об этом подробнее здесь.Пример 1
На самом базовом уровне с просто обеспечивают более компактную форму написания длинных списков.Ты можешь написать
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
или вы можете значительно упростить его до следующего:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Команда , где , пригодится, когда вы хотите установить дополнительные ограничения.Например, получить только четные числа:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
В качестве альтернативы вы, конечно, могли бы сделать это:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Пример 2
Пример 3
Обозначение понимания списка также может быть расширено до более чем одной переменной.В этом случае вы должны указать диапазон для каждой переменной, используемой в качестве счетчика. Например, вот список, содержащий все положительные правильные дроби в простейшем виде, с однозначным числителем и знаменателем:
ЖИВАЯ ДЕМО
| CalcMe Sheet |
|---|
| Редактор кода CalcMe |
Другая рекомендация, проиллюстрированная в приведенном выше примере, заключается в заключении каждого условия после , где в круглые скобки, если у вас есть более одного, соединенного с.
Пример 4
Наконец, обратите внимание, что диапазон для переменной счетчика может сам быть списком, определенным ранее.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Пример 5
Также возможно создавать матрицы, используя эту нотацию. Например, создать матрицу со случайными коэффициентами очень просто:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Программирование
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для создания алгоритма для вопроса викторины Wiris, мы покажем, как создавать их на листе и с помощью редактора кода.Вы можете узнать об этом подробнее здесь.Вы можете использовать некоторые функции программирования. Здесь вы можете увидеть основные. Например, учитывая список, созданный, как описано ранее, вы можете легко вычислить квадрат первых простых чисел.
ЖИВАЯ ДЕМО
| CalcMe Sheet |
|---|
| Редактор кода CalcMe |
Функции пользователя
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для создания алгоритма для вопроса викторины Wiris, мы покажем, как создавать их на листе и с помощью редактора кода.Вы можете узнать об этом подробнее здесь. Вы можете создавать собственные функции. Команда random очень полезна, но было бы немного утомительно записывать каждый раз random (-10,10) . Вместо этого вы можете создать функцию, которая при вызове генерирует случайное число:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Это упрощает создание матрицы со случайными коэффициентами.Еще один более сложный пример — создание функции, которая строит трехдиагональную матрицу по трем числам. Следовательно, каждый раз, когда вы хотите создать трехдиагональную матрицу, вам просто нужно вызывать эту функцию с элементами верхней диагонали, диагонали и нижней диагонали, которые вы хотели бы иметь в матрице.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Калькулятор касательных векторов единиц измерения — Найдите нормальные и касательные векторы
Онлайн-калькулятор касательного вектора единичных векторов поможет вам определить касательный вектор векторной функции значения в заданных точках.Кроме того, калькулятор единичного тангенса отдельно определяет вывод тригонометрических функций, что важно для нормализации формы. Итак, продолжайте чтение, чтобы понять формулу вектора касательной единицы и как найти вектор касательной с примерами.
Что такое единичный касательный вектор?В математике единичный касательный вектор — это производная векторнозначной функции, которая обеспечивает другую векторнозначную функцию, которая является единичной касательной к заданной кривой.Направление касательной аналогично наклону касательной. Поскольку вектор содержит величину и направление, вектор скорости содержит больше информации, чем нам нужно. Мы можем уменьшить его величину, разделив ее.
Формула вектора касательной единицы измерения:Пусть r (t) — функция с дифференцируемыми векторными значениями, а v (t) = r ’(t) — вектор скорости. Тогда уравнение касательного вектора представляет собой единичный вектор в направлении вектора скорости, который используется калькулятором единичного вектора касательной для определения длины вектора.2} $$
$$ = a + b / \ sqrt {2} $$
$$ = 1 / \ sqrt {2} a + 1 / \ sqrt {2} b $$
Каков принцип единичного вектора нормалей?Вектор нормали — это перпендикулярный вектор. Для вектора v в пространстве существует бесконечно несколько перпендикулярных векторов. Наша цель — выбрать специальный вектор, перпендикулярный единичному касательному вектору. Для непрямых кривых этот вектор геометрически является единственным вектором, указывающим на кривую. Алгебраически мы можем использовать следующие определения для вычисления векторов.
Пусть r (t) — дифференцируемая вектор-функция, и пусть T (t) — касательный вектор. Тогда вектор нормали N (t) основной единицы определяется как
$$ N (t) = T ‘(t) / || T ‘(t) || $$
Это уравнение используется калькулятором единичного вектора касательной для нахождения нормы (длины) вектора. Если его сравнивать с касательным векторным уравнением, то оно рассматривается как функция с векторным значением. Основной единичный вектор нормали — это касательный вектор вектор-функции.
Однако онлайн-калькулятор мгновенной скорости позволяет рассчитать мгновенную скорость, соответствующую мгновенной скорости изменения формулы скорости.
Найдите нормальную и касательную составляющие ускорения:Во время движения вы столкнетесь с двумя силами, которые изменят вашу скорость. Автомобиль разгоняется под действием силы тяжести. Второе изменение скорости вызвано поворотом автомобиля. Первый компонент ускорения называется тангенциальным компонентом ускорения, а другой компонент — нормальным компонентом ускорения. Предполагается, что тангенциальная составляющая ускорения проходит вдоль направления вектора касательной единицы, а нормальная составляющая ускорения — вдоль направления вектора нормали основной единицы.Когда у нас есть T и N, легко найти две составляющие.
Тангенциальная составляющая ускорения
$$ a_t = а. T = v .a / || v || $$
, а нормальная составляющая ускорения —
.$$ a_N = а. N = || v x a || / || v || $$
и
$$ a = a_NN + a_TT $$
Как работает калькулятор вектора единичного тангенса?Калькулятор касательных векторов определяет единичный касательный вектор функции в точке, следуя этим инструкциям:
Ввод:Во-первых, введите функцию с различными тригонометрическими значениями, такими как синус, косинус и тангенс.
Теперь введите точку, чтобы найти единичный касательный вектор.
Чтобы увидеть результаты, нажмите кнопку «Рассчитать».
Выход:Калькулятор тангенциальной скорости обеспечивает ввод данных и ответы в заданной точке.
Этот калькулятор отображает единичный вывод для каждой тригонометрической функции и нормализует форму, а также находит единичный касательный вектор с пошаговыми вычислениями.
FAQ: Бинормальный вектор единичный вектор.Как?Поскольку вектор бинормали определяется как векторное произведение единичного вектора касательной и вектора единичной нормали, он также ортогонален как вектору нормали, так и вектору касательной.
Как найти тангенциальную?Разделите длину окружности на время, необходимое для определения тангенциальной скорости для совершения одного оборота.
Какие единицы используются для тангенциальной скорости?Формула касательной скорости используется для вычисления тангенциальной скорости объектов при круговом движении.Выражается в метрах в секунду (м / с).
В чем разница между тангенциальной и угловой скоростью?Угловая скорость — это скорость, с которой угол (радианы) изменяется во времени, выраженная в единицах 1 / с. В то время как тангенциальная скорость — это скорость точки на поверхности вращающегося объекта, умноженная на расстояние от точки оси вращения.
Заключение:Воспользуйтесь этим онлайн-калькулятором касательного вектора единичных векторов для нахождения нормализованной формы и тангенциального вектора функции.Кроме того, этот калькулятор дифференцирует функцию и вычисляет длину вектора в заданных точках.
Артикул:Из источника Википедии: Касательный вектор, Контравариантность, Касательный вектор на многообразиях.
Из источника Ximera: единичный касательный вектор, единичный касательный и единичные векторы нормали, нормальные компоненты ускорения.
Из источника в штате Орегон: производная векторной функции, единичный касательный вектор, длина дуги, параметризация по длине дуги.
Калькулятор ортогональных векторовПрисоединяйтесь к инициативе по модернизации математического образования. Ответ: поскольку скалярное произведение не равно нулю, векторы a и b не ортогональны. Исследуйте что угодно с помощью первой вычислительной машины знаний. v = 0 (т.е. векторы перпендикулярны) называются ортогональными. Визуализация векторов (только для векторов в & Ropf; 2 и & Ropf; 3). Выбрать размерность векторов и форму представления векторов; Нажмите кнопку «Проверить ортогональность векторов», и вы получите подробное пошаговое решение.1 = 2 n + 4 2 n + 4 = 0 2 n = -4 n = -2 Ответ: векторы a и b ортогональны, когда n = -2. Вы можете перемещаться между полями ввода, нажимая клавиши «влево» и «вправо» на клавиатуре. Если вы хотите связаться со мной, возможно, у вас возникнут вопросы, напишите мне по электронной почте [email protected], Онлайн-калькулятор. Я разработал этот веб-сайт и написал всю математическую теорию, онлайн-упражнения, формулы и калькуляторы. Узнать больше Принять. Перекрестное произведение двух векторов (векторное произведение), Онлайн калькулятор.Практикуйтесь онлайн или сделайте учебный лист для печати. Программирование на основе знаний для всех. В случае плоской задачи для векторов a = {ax; ай; az} и b = {bx; от; bz} условие ортогональности можно записать по следующей формуле: Ответ: векторы a и b ортогональны при n = 2. Анализ линейной зависимости между v 1, v 2. Калькулятор векторов. Узнайте о векторных и точечных продуктах. Точечное произведение двух векторов, Онлайн калькулятор. Скалярное произведение В трехмерном пространстве три вектора могут быть взаимно перпендикулярными.Объем пирамиды, образованной векторами, Онлайн калькулятор. Введите значения в поля Magnitude и Angle … или X и Y. Наш бесплатный онлайн-калькулятор может проверить ортогональность двух векторов с помощью пошагового решения. https://mathworld.wolfram.com/OrthogonalVectors.html. Добро пожаловать в OnlineMSchool. Узнать больше Принять. Коллекция инструментов для преподавания и обучения, созданных экспертами в области образования Wolfram: динамический учебник, планы уроков, виджеты, интерактивные демонстрации и многое другое. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.Ответ: векторы a и b ортогональны при n = -2. Приведенное выше определение сразу следует, когда мы рассматриваем формулу скалярного произведения векторов: a b a b cos π 2 0. Hierzu muss man nur nur herausfinden, welcher gesuchte Vector multipliziert mit dem gegebenen Vektor 0 ergibt. Составная форма вектора с начальной и конечной точками на плоскости, Упражнения. Составная форма вектора с начальной и конечной точками, Онлайн калькулятор. Два вектора и чей точечный векторный калькулятор, скалярное произведение, ортогональные векторы, параллельные векторы, одинаковые векторы направления, величина, векторный угол, калькулятор неравенства Коши-Шварца, калькулятор ортогональной проекции. Он выполняет преобразования и суммирует векторы.Wenn man nachweisen kann, dass ein Vektor zu einem anderen Vektor orthogonal ist, dann kann man diesen Nachweis logischerweise auch umkehren und auf diese Weise herausfinden, welcher Vektor zu einem anderen Vektor orthogonal liegt. Изучите тысячи бесплатных приложений для науки, математики, инженерии, технологий, бизнеса, искусства, финансов, социальных наук и многого другого.
Статуя богини Айне, Взломанная игра Flight Game, Каталог Бомбейской компании, Toshiba Factory Reset 0 не работает, Пончо Silvana Sin Lana, Небесные Фамилии Dnd, Миниатюра древнего синего дракона, Красивые армянские цитаты, Лист для фортепиано Roblox, Некрологи Хартфорда Куранта за последние 3 дня, Определить велосипед Redline по серийному номеру, Курт Коулман Лас-Вегас, Huawei закрывает 57 заводов в США, Брюс Будро Чистая стоимость, Анализ туши Бодлера, Дэвид Диггс Малкольм Диггс, Примеры сочинений о несправедливости, Аренда 3-х колесных скутеров — Голд-Кост, Возрастной диапазон Pitbull, Melovemealot Знаменитые дни рождения, Проблемы с двигателем Ахатес, Латинские песни для причастия, Скандал с больницей Шрайнерс, Распродажа нахлыстовой рыбалки, Бен Ротлисбергер Возраст, Эссе об интеллектуальном любопытстве, Тамаки Суо Высота, Iq 75 Что такое умственный возраст, Зарплата актеров за серию, Скин Бедствия Fortnite, 1943 Стальной пенни Стоимость 2018, Брэндон Хэмм Музыкант, Рецепт тайваньской колбасы, Аватар Сонг Калимба, Внешние динамики Yamaha P115, Гидратированный лайм Менардс, Добавки для обратной мышечной атрофии, Гонорары шоу Кумара Вишваса, Иосиф о Варавве, Плейлист 915 кунв, Список редких книг по мурашкам, Многоразовые маски для лица из органического хлопка Sanctuary, День рождения Оскара Рамзи, Morecambe Illuminations 2020, Whirlpool Wrt318fzdm01 Руководство, Стив Райх Pdf, Стоимость замены трансмиссии Isuzu Trooper, Бетти Грейбл Муж, Лаура Грейс Холл Причина смерти, Математические выражения 5 класс Ответы ключевой Pdf Блок 8, Остров любви Шелби, Прокерала Китайский Календарь, Clout Значение сленг, 24×32 планы гаража, Является частным реальным словом, Бумага A0 300 г / м2, Джоджо, часть 6, Диспансер Rise, Значение тату вилка, Бренды рэпперской одежды, Лошадь Корова Гибрид, Ноты на тему Tf2, Дэйн Уизерспун Причина смерти, Место преступления Фотографии, Карта Gtfo R3a3, Генератор имен героев, Куриные титры с маслом, Dua для новорожденного мальчика на арабском языке, Раскраски Фортнит Мидас, Bigscreen Vr Netflix, Энтони Мельчиорри, жена Кристал Кардинале, Dely Dely Fruit Jelly Dollar Tree, Коды Copter Royale, Диспансер Rise, Насколько высока Анджела Агилар, Места обитания рыбы Бдо, Toyota Tsb Lookup, Раджон Рондо Вес, Темы сочинений по лингвистической антропологии, Благодарственное письмо суперинтенданту, Порядок ротации карт Bfv 2020, Переводчик южного сленга, Bull Snake для продажи в Великобритании, Дополнения для сборки Xanax, Daeg Faerch Age, Мой опыт работы с Cinnpie, Кто написал Midnight Cry,
| Категория | Описание | Разрешить | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами.Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, в том числе более персонализированный и релевантный опыт на наших сайтах.
Калькулятор осуществляет умножение, разность, сумму и деление двух простых или десятичных дробей. Результат сокращяется.
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. Как рассчитать проценты, процент от числа Квадратное уравнение — Калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. Линейное уравнение с десятичными дробями решается точно так же, как и множество других
уравнений, однако их решение нужно начинать с сокращения уравнения и избавления от десятичных дробей. Так же читайте нашу статью «Решить дифференциальное уравнение
онлайн» Допустим, дано уравнение следующего вида: \[2,4(6 — 3x) + 4,3 = 1,7 — 5,2x\] Данное уравнение можно решить двумя разными способами. Способ № 1: Решение начинаем с упрощения уравнения с помощью открытия скобок, а поскольку перед скобками у нас стоит
число, то умножаем это число на каждый член в скобках: \[14,4 — 7,2x + 4,3 = 1,7 — 5,2x\] Сейчас наше уравнение имеет линейный вид, благодаря чему мы производим перенос неизвестных в одну сторону,
целый числе в другую: \[ — 7,2x + 5,2x = 1,7 — 14,4 — 4,3\] Делим 2 части на число перед \[x :\] \[ — 2x = — 17\] Ответ: \[x = 8,5.\] Способ № 2: В этом способе умножим левую и правую части на 10: \[2,4(6 — 3x) + 4,3 = 1,7 — 5,2x\] \[24(6 — 3x) + 43 = 17 — 52x\] Это линейное уравнение, которое решается по аналогии с 1 способом: \[144 — 72x + 43 = 17 — 52x\] \[ — 72x + 52x = 17 — 144 — 43\] \[ — 20x = — 170\] Ответ: \[x = 8,5.\] Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам. Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями. Сложение дробей бывает двух видов: Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы: Пример 2. Сложить дроби и . Опять же складываем числители, а знаменатель оставляем без изменения: В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца: Пример 3. Сложить дроби и . Опять же складываем числители, а знаменатель оставляем без изменения: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы: Пример 4. Найти значение выражения Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения: Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы. Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила: Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда. Например, дроби и сложить можно, поскольку у них одинаковые знаменатели. А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю. Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего. Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель. Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Пример 1. Сложим дроби и У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю. В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6 НОК (2 и 3) = 6 Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2. Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель: Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3. Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель: Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители: Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца: Таким образом, пример завершается. К прибавить получается . Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы: Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю). Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы). Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом: Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы. Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией: Пример 2. Найти значение выражения . Воспользуемся инструкцией, которая приведена выше. Шаг 1. Найти НОК знаменателей дробей Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4 Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью: Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью: Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители Умножаем числители и знаменатели на свои дополнительные множители: Шаг 4. Сложить дроби у которых одинаковые знаменатели Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем: Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке. Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем: Получили ответ Вычитание дробей бывает двух видов: Сначала изучим вычитание дробей с одинаковыми знаменателями. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы: Пример 2. Найти значение выражения . Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы: Пример 3. Найти значение выражения Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей: В ответе получилась неправильная дробь. Выделим в ней целую часть: Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила: Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда. Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю. Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Пример 1. Найти значение выражения: У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю. Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12 НОК (3 и 4) = 12 Теперь возвращаемся к дробям и Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью: Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью: Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители: Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца: Получили ответ Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом: Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю): Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков. Пример 2. Найти значение выражения У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю. Найдём НОК знаменателей этих дробей. Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30 НОК (10, 3, 5) = 30 Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби. Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью: Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью: Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью: Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители: Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример. Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке: В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь. Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30. Итак, находим НОД чисел 20 и 30: Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10 Получили ответ Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений. Пример 1. Умножить дробь на число 1. Умножим числитель дроби на число 1 Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби: Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы: Пример 2. Найти значение выражения Умножим числитель дроби на 4 В ответе получилась неправильная дробь. Выделим в ней целую часть: Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц: Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы. Например, выражение можно вычислить двумя способами. Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений: Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка: Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче: Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением: А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений: Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются. Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной: Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит. Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть. Пример 1. Найти значение выражения . Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби: Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид: Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы: Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части: И взять от этих трех кусочков два: У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части: Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры: Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно Пример 2. Найти значение выражения Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби: В ответе получилась неправильная дробь. Выделим в ней целую часть: Пример 3. Найти значение выражения Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби: В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450. Итак, найдём НОД чисел 105 и 450: Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15 Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке: Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа». Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу. Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение: Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу. Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби: Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую: Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу: Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица. Обратное число можно найти также для любого другого целого числа. Примеры: Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её. Примеры: Допустим, у нас имеется половина пиццы: Разделим её поровну на двоих. Сколько пиццы достанется каждому? Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы. Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением. Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю. Пользуясь этим правилом, запишем деление нашей половины пиццы на две части. Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2. Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на Получили ответ . Значит при делении половины на две части получается четверть. Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца: Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы: Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце: Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь В обоих случаях получился один и тот же результат. Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь Пример 2. Найти значение выражения Умножим первую дробь на число, обратное делителю: Допустим, имеется четверть пиццы и нужно разделить её на двоих: Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы: 10 : 2 = 5 Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь Как видно результат не изменился. Мы снова получили ответ 5. Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число. Пример 3. Найти значение выражения Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь Допустим, имелось пиццы: Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается Правило деления числа на дробь такое же, как и правило деления дроби на число. Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю. Например, разделим число 1 на . Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца: Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза Пример 2. Найти значение выражение Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь Допустим, у нас имеются две целые пиццы: Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза: Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй. Например, разделим на Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь Допустим, имеется половина пиццы: Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза: Пример 1. Найти значение выражения Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую: Пример 2. Найти значение выражения Умножаем первую дробь на дробь обратную второй: Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой. Каждая следующая тема будет более сложной, поэтому нужно тренироваться. Задание 1. Найдите значение выражения: Решение: Задание 2. Найдите значение выражения: Решение: Задание 3. Найдите значение выражения: Решение: Задание 4. Найдите значение выражения: Решение: Задание 5. Найдите значение выражения: Решение: Задание 6. Найдите значение выражения: Решение: Задание 7. Найдите значение выражения: Решение: Задание 8. Найдите значение выражения: Решение: Задание 9. Найдите значение выражения: Решение: Задание 10. Найдите значение выражения: Решение: Задание 11. Найдите значение выражения: Решение: Задание 12. Найдите значение выражения: Решение: Задание 13. Найдите значение выражения: Решение: Задание 14. Найдите значение выражения: Решение: Понравился урок?
Возникло желание поддержать проект? В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно умножить на десятичную. Также разберем примеры для закрепления теоретического материала. Чтобы умножить обыкновенную дробь на десятичную (и наоборот, т.к. от перестановки множителей результат не меняется), необходимо одну из дробей представить в виде другой. Примечания: 1. Бесконечные десятичные дроби сначала требуется округлить, т.е. оставить конечное количество цифр после запятой. Пример 1 3/20 и 2,19. Переведем обыкновенную дробь в десятичную: 3/20 = 3⋅5/20⋅5 = 15/100 = 0,15 0,15 ⋅ 2,19 = 0,3285. Решение 2 Преобразуем десятичную дробь в обыкновенную: 19/100 = 2 ⋅ 100 + 19/100 = 219/100 219/100 ⋅ 3/20 = 219 ⋅ 3/100 ⋅ 20 = 657/2000 4/9 . Преобразуем заданную смешанную дробь в неправильную: 4/9 = 2 ⋅ 9 + 4/9 = 22/9 24/100 = 6 ⋅ 100 + 24/100 = 624/100 624/100 : 22/9 = 624/100 ⋅ 9/22 = 624 ⋅ 9/100 ⋅ 22 = 5616/2200 = 2 1216/2200 = 2 152/275 ≈ 2,5528 Умножение обыкновенных и десятичных дробей сводится к умножению либо обыкновенных дробей, либо десятичных дробей. Чтобы умножить обыкновенную дробь на десятичную, надо обе дроби привести к одному виду. Любую десятичную дробь можно перевести в обыкновенную (как слышим, так и пишем). Например, Если возможно, полученную дробь следует сократить. Например, Обыкновенную дробь перевести в десятичную (речь идёт о несократимой дроби) можно только в том случае, когда её знаменатель равен 2, 5 или числу, которое можно разложить на множители, состоящие только из двоек и пятёрок. Например, 40=2∙2∙2∙5. Разложение числа состоит только из двоек и пятёрок, значит, любое число можно разделить на 40. Делим 7 на 40 и получает представление обыкновенной дроби в виде десятичной. Перейдём к примерам умножения обыкновенных и десятичных дробей. Примеры. 1-й способ Так как знаменатель обыкновенной дроби равен 5, эту дробь можно перевести в десятичную и выполнить умножение десятичных дробей: 2-й способ Переведём десятичную дробь в обыкновенную, сократим полученную дробь и выполним умножение обыкновенных дробей: то есть при любом способе получаем одинаковый ответ, отличается только форма записи. Знаменатель обыкновенной дроби равен 14. 14=2∙7. Такую дробь перевести в десятичную перевести не получится. Значит, десятичную дробь представим в виде обыкновенной: Здесь ответ может быть записан как в виде обыкновенной, так и в виде десятичной дроби. Дробь со знаменателем 11 не можем представить в виде десятичной. Поэтому переводим десятичную дробь в обыкновенную: 1-й способ Раскладываем знаменатель на простые множители: 4=2∙2. Переводим обыкновенную дробь в десятичную: 2-й способ: Сведём умножение десятичной и обыкновенной дробей к умножению обыкновенных дробей: Я рекомендую при возможности выбора стараться работать как с обыкновенными, так и с десятичными дробями. Важно освоить навыки счёта на уроках математики в 5-6 классах, а старших классах вам предстоит решать другие задачи.
Калькулятор осуществляет умножение, разность, сумму и деление двух простых или десятичных дробей. Результат сокращяется.
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112 Как рассчитать проценты, процент от числа Квадратное уравнение — Калькулятор
Главное замечание по теме от проекта dpva.ru: Дети часто путают действия с правильыми дробями (это такие дроби, где числитель меньше знаменателя) и со смешанными числами (состоящими из целой и дробной части). Умножение правильных дробей и смешанных чисел на натуральное число: Чтобы умножить правильную дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения. Для того, чтобы умножить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее числитель умножить на это число, а знаменатель оставить без изменения, после чего выделить целую часть. Умножение дробей : Чтобы умножить дробь на дробь, надо 1) найти произведение числителей и произведение знаменателей этих дробей. 2) первое произведение записать числителем, второе — знаменателем. Умножение смешанных чисел: Для того, чтобы выплнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. Деление правильных дробей и смешанных чисел на натуральное число: Чтобы разделить правильную дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменения. Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть. Памятка: Взаимно обратные числа это числа, произведение которых равно 1. Например: дроби 71/17 и 17/71 взаимно обратны. Делимое — то, что делят. Делитель — то, на что делят. Деление дробей: Для того, чтобы разделить одну дробь на другую, надо делимое умножить на число обратное делителю. Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей. С десятичными дробями намного проще производить разные действия, чем с обычными, но здесь также есть свои недостатки. Например, необходимо очень тщательно следить за положением десятичной запятой. Например, рассмотрим пример умножения: 0,2х0,2. Вы можете попробовать решить этот пример по аналогии со сложением: 2+2=4, также 2×2=4, тогда, поскольку 0,2+0,2=0,4. Возможно, и 0,2х0,2=0,4? Нет, этого не может быть, и я сейчас докажу вам это. Перейдем обратно к обыкновенным дробям, с которыми мы научились так хорошо обращаться: $0,2=\frac{2}{10}$. Теперь перемножим дроби по старой методике: $\frac{2}{10} \times \frac{2}{10}=\frac{4}{100}$ (числитель умножаем на числитель, знаменатель на знаменатель). А в десятичных дробях — это 0,04. Следовательно, 0,2 х 0,2 отнюдь не равно 0,4. 0,2х0,2=0,04. Мы можем решить еще несколько примеров на умножение десятичных дробей, заменяя их на эквиваленты в обычных дробях. Например: 0,82х0,21=0,1772, а 0,82х2,1=1,772. (Это можно проверить следующим образом: $\frac{82}{100} \times \frac{21}{100}=\frac{1772}{10000}$, а $\frac{82}{100} \times \frac{21}{10}=\frac{1772}{1000}$.) Теперь мы можем сформулировать общее правило: При умножении десятичных дробей количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах. Так, при умножении 0,2х0,2 общее количество цифр справа от десятичной запятой в перемножаемых числах равно 2, и это означает, что 0,2х0,2=0,04 (ноль справа от десятичной запятой также является значащей цифрой). Естественно, что если один из сомножителей является целым числом, то он не влияет на положение десятичной запятой. Положение десятичной запятой в произведении будет таким же, как и в том сомножителе, который является десятичной дробью. То есть 0,2х2=0,4; 1,5х5=7,5; а 1,1х154=169,4. Эти результаты соответствуют правилу умножения, и в любом случае количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах. Определить положение запятой в случае деления десятичных дробей можно по аналогичной методике, действуя в обратном порядке. Но обычно при делении процедуру стараются упростить и приводят делитель или знаменатель (если деление проводят с помощью обычных дробей) к виду целого числа, не содержащего значащих чисел справа после запятой. Предположим, нам надо 1,82 разделить на 0,2. Это выражение можно записать как $\frac{1,82}{0,2}$. Не изменяя величины дроби, умножаем числитель и знаменатель на 10. Тогда 1,82х10 (в соответствии с правилом определения положения десятичного знака) равно 18,20, или 18,2, поскольку ноль, стоящий справа после последней значащей цифры, не изменяет величины числа и, следовательно, его можно опустить. Точно так же 0,2х10=2,0, или просто 2 (поскольку 2 плюс ноль десятых равно 2). Следовательно, дробь можно записать как $\frac{18,2}{2}$ – и теперь знаменатель является целым числом, следовательно, при делении положение десятичного знака после запятой не меняется, так же как и в случае деления. Раз в числителе одна значащая цифра справа после запятой, то и результат должен иметь одну значащую цифру справа после запятой, то есть — $\frac{18,2}{2}=9,1$. Освоив деление десятичных дробей, мы сможем переводить обычные дроби в десятичные. Предположим, нам нужно найти десятичный эквивалент для $\frac{1}{40}$. Мы можем представить эту дробь в виде $\frac{1,000}{40}$, а затем произвести деление. Поскольку мы делим на целое число, то положение десятичной запятой не меняется. Проведем деление: Таким образом, мы показали, что десятичный эквивалент $\frac{1}{40}$ равен 0,025. Это можно проверить, переведя 0,025 в обычную дробь: $0,025=\frac{2}{100}+\frac{5}{1000}$, или $\frac{20}{1000}+\frac{5}{1000}$, или $\frac{25}{1000}$, или если произвести деление, то получим $\frac{1}{40}$. Ну, а если вы все-таки допустили ошибку при исчислении находясь заграницей, то что бы не выглядеть глупо в глазах иностранцев, обязательно надо исправится и извинится. Для тех, которые, как и я, не знаю, как извиниться по-английски, рекомендую почитать статью на сайте e-english.ru. Это значительно улучшит ваши познания и даст возможность не делать ошибок, хотя бы в этом. Материалы по теме: Поделиться с друзьями: Лимит времени: 0 0 из 20 заданий окончено Вопросы: Выполните умножение или деление и введите ответ. Сократите дробь, если это возможно. Неправильную дробь переведите в смешанное число, иначе будет засчитана ошибка. Вы уже проходили тест ранее. Вы не можете запустить его снова. Тест загружается… Вы должны войти или зарегистрироваться для того, чтобы начать тест. Вы должны закончить следующие тесты, чтобы начать этот: Если вы не знаете, как умножать и делить обыкновенные дроби, читайте статью: Тест можно использовать как тренажер, проходя его несколько раз. Каждый раз задания выпадают разные. Чтобы умножить дробь на целое число, помните, что умножение — это повторное сложение. Пример 1: Умножить
1
7
⋅
3
. Запишите умножение в виде сложения. Добавлять
1
7
три раза. 1
7
⋅
3
знак равно
1
7
+
1
7
+
1
7 Теперь нам просто нужно
добавить дроби
с одинаковыми знаменателями.Знаменатели оставьте неизменными, а числители сложите. знак равно
(
1
+
1
+
1
)
7
знак равно
3
7 Пример 2: Умножить
5
⋅
3
16
. 5
⋅
3
16
знак равно
3
16
+
3
16
+
3
16
+
3
16
+
3
16
знак равно
5
⋅
3
16
знак равно
15
16 Другой способ подумать об этом — переписать целое число в виде дроби со знаменателем
1
. 5
⋅
3
16
знак равно
5
1
⋅
3
16 Затем умножьте
числители
а также
знаменатели
, согласно обычным правилам для
умножение дробей
. знак равно
5
⋅
3
1
⋅
16
знак равно
15
16 В некоторых случаях ваш ответ может быть больше, чем
1
, поэтому вы захотите переписать его как
смешанное число
.Возможно, вам также придется
уменьшить фракцию
чтобы получить его в простейшем виде. Пример 3: Умножить
1
4
⋅
10
. 1
4
⋅
10
знак равно
10
4 И числитель, и знаменатель имеют общий множитель:
2
. Разделите оба на
2
. знак равно
5
2 Перепишите эту неправильную дробь как смешанное число. знак равно
2
1
2 Ричард Вильялонundefined undefined / Getty Images Обновлено 21 февраля 2019 г. Распечатать PDF-файл: Рабочий лист № 1 Каждый рабочий лист содержит множество дробей с общим (одинаковым) знаменателем.При умножении дробей просто умножьте числитель (верхнее число), затем умножьте знаменатель (нижнее число) и при необходимости уменьшите до наименьшего члена. Подобные рабочие листы содержат упражнения для учащихся, чтобы улучшить их понимание. Распечатать PDF-файл: Рабочий лист № 2 Распечатать PDF-файл: Рабочий лист № 3 Распечатать PDF: Рабочий лист № 4 Распечатать PDF-файл: Рабочий лист № 5 Распечатать PDF-файл: Рабочий лист № 6 Распечатать PDF-файл: Рабочий лист № 7 Распечатать PDF-файл: Рабочий лист № 8 Распечатать PDF-файл: Рабочий лист № 9 Распечатать PDF-файл: Рабочий лист № 10 Фракции
и Урок 2. Умножение дробей и целых
номера: Только числитель умножается на целое
числа. Умножение дроби на
дробь: (общий знаменатель не обязателен) 2
2 = 1 Замена смешанных чисел на
неправильные дроби: Пример:
Умножьте целое число (2) на знаменатель (3) и прибавляем к числителю (1) Смешанные числа заменены на
неправильные дроби перед умножением. Сначала изменяются смешанные числа
на неправильные дроби, а затем упрощается. Иногда переменные
(буквы) используются. Применяются те же правила: первый
уменьшить, а затем упростить. На дроби Чтобы разделить дроби, инвертируйте
делитель (вторая дробь) и умножаем. Целые числа необходимо заменить на
фракции. Смешанные числа необходимо заменить на
неправильные дроби. Иногда алгебраические переменные
использовал. Те же правила применяются для номеров и буквы. Попробовать тест 2 на
Умножение и деление дробей. Общие шаги по умножению дробей описаны ниже. Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби.Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель. Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами. В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих указанное целое. Например, в дроби В отличие от сложения и вычитания целых чисел, таких как 2 и 8, для этих операций с дробями требуется общий знаменатель. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода. Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче. Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел. Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители. Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения. Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения. Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , равно Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах. Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже. Дробное число или дробь используется для представления сегмента целого числа. Дробь состоит из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, — это числитель . Второе число, расположенное под чертой, — это знаменатель . Знаменатель указывает общее количество равных частей, на которые что-либо делится. Числитель показывает, сколько из этих равных частей необходимо учитывать. Самый простой способ запомнить дроби — обозначить линию, разделяющую каждое число, «из».Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей. Дроби могут быть представлены тремя способами: как правильные дроби, неправильные дроби и смешанные дроби. Процесс упрощения дробей сводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8. Есть два способа упростить дробь. Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить.В качестве примера возьмем дробь 24/108: Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители. Допустим, вы хотите добавить дробь ¼ к ¼. Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1. Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ дает 2/4 (или ½). Допустим, вы хотите сложить дроби ⅓ и ⅙. Чтобы знаменатели совпали, измените ⅓ на 2/6. Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½. Вычитание дробей работает аналогично: Допустим, вас попросили потренироваться ¾ — ¼ Первый шаг относительно прост, потому что числа совпадают. Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем. Таким образом, ¾ — be будет обработано как 3-1 = 2 Следовательно, ответ будет 2/4, что составляет ½. Умножение дробей относительно легко; вы просто умножаете верхние числа и нижние числа. Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения. Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и у вас останется 3/2. Может потребоваться дальнейшее уменьшение фракции для получения сложной фракции. При сложении и вычитании дробей может быть легко запутаться.Студенты часто складывают или вычитают знаменатели или числители двух дробей и обычно не замечают связи между знаменателем. Чтобы еще больше усугубить путаницу, к числителям и знаменателям следует подходить в расчетах как к целым числам, например, когда вам нужно умножить дробь. Возьмем для примера сложение ¾ и ⅙. Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24. Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24. Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24. Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12. Прочие типичных ошибок включают: Понимание взаимосвязи между смешанными числами и неправильными дробями, а также того, как переводить одно в другое, имеет решающее значение при работе с дробями. Просто выполните следующие четыре простых шага: Вместо уменьшения дроби в конце задачи мы можем перекрестно сократить перед умножением .Это не обязательно, но это сэкономит несколько шагов. Перекрестное сокращение означает, что при умножении дробей мы можем уменьшить любой числитель с любым знаменателем . В этом примере 5 и 10 можно разделить на 5, даже если они не принадлежат к одной и той же дроби. Давайте еще раз посмотрим на пример 1 и посмотрим, как использовать этот метод. Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах. Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби: И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа. Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага: Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1. Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая: Шаг 3: Сокращаем полученные дроби до удобоваримого вида: Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей. Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага. Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n. Шаг 2: Теперь нам достаточно представить дробь в виде C/10n, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру: По сути, 10n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить. Шаг 3: Сокращаем нули и получаем итоговый результат: Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8. Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби. 0,025 = 25/1000 = 1/40 Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости. На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров. Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию. 0,4 = 4/10 = 2/5 К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем: 0,12 = 12/100 = 3/25 Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет. Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде: Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель: Верны следующие правила: Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей. Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n. Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится: Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится: Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю.
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями.
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например: Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число: Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число: Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \).
Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так: Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например: Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной
дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное
число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят,
что из неправильной дроби выделили целую часть.
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например: Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей: С помощью букв это правило записывается так: Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а
второе — знаменателем.
С помощью букв правило умножения дробей можно записать так: Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать
смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное
свойство умножения относительно сложения.
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \).
Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как
\( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь: Используя буквы, правило деления дробей можно записать так: Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно
прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%,
промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка
и т.д. Ясно, что понимание такой информации необходимо в современном обществе.
Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается
процент знаком %, Таким образом, Приведем примеры: Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке
«хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих
учеников.
Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в
современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение
буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших
призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое
понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.
Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой
арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако
наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.
Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.
Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:
Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить
на 100: В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%,
четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.
Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью
процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена
с февраля в 1,5 раз» говорится об одном и том же.
Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить
в 2 раза — это значит уменьшить на 50%.
Аналогично Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби.
В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.
В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и
соответствующие задачи на дроби, но перед их решением число р% выражается дробью.
1. Нахождение процента от числа. Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг,
а 118% от х равны 1,18x
2. Нахождение числа по его проценту. 3. Нахождение процентного отношения двух чисел. Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило
называют правилом нахождения процентного отношения двух чисел.
Нетрудно заметить, что формулы
Составные задачи на проценты решаются аналогично задачам на дроби.
Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа
— наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма
составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р.,
а всего 1019 р.
Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую
формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.
Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму,
которую должен заплатить человек после n дней просрочки, обозначим Sn. Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.
Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов.
Как и выше, нетрудно убедиться, что в этом случае Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает.
Рост в этом случае «отрицательный».
В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный
договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете
доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход -
«проценты», как его обычно называют.
Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего
года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты»,
или, как их обычно называют, сложные проценты.
Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех
лет не будет брать деньги со счета.
10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет 10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет 10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы
вклада через 20 лет. Между тем подсчет можно вести значительно проще.
А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1
раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма
увеличится в 1,1 • 1,1 = 1,12 раз.
Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,12 = 1,13
раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое:
1,13 • 1000 = 1,331 • 1000 — 1331 (р.)
Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма,
которая будет на счете через n лет, равна Sn р.
Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма За следующий год сумма S1 увеличится во столько же раз, и поэтому через два года на счете будет сумма Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.n S \)
Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов. Опытные сотрудники калькулятора онлайн всегда здесь, чтобы предоставить эффективный и надежный образовательный инструмент для простоты расчетов. Да, недавно они обновили калькулятор значительных дробей, который помогает понимать дробные и дробные дроби, умножение и деление дробей, упрощение дробей и преобразование между дробями и десятичными дробями. На этой платформе вы можете найти калькулятор четырех фракций, с помощью которого вы можете легко выполнять определенные фракции. Что ж, прежде чем узнавать о нашем калькуляторе с дробями, давайте начнем с термина «дробь». Дробь – это число, которое говорит нам, сколько частей целого у нас есть, значит, это число, представляющее целое число, которое делится на равные части. Фракция записывается косой чертой между двумя числами. Верхнее число называется числителем, оно представляет часть целого числа, а нижнее число называется знаменателем и представляет целое число, из которого сделаны части. Попадание в более подробные дроби далее классифицируется как: К этим дробям относятся те, в которых числитель, который является верхней цифрой, меньше знаменателя, а нижняя цифра, например 4/9, 6/9 2/6 во всех этих числовых дробях, меньше знаменателя. Это те дроби, в которых числитель больше знаменателя, например, 6/3, 9/5, 7/2 во всех этих числителях больше знаменателя. Это такие же дроби, как, например, 2/4, 1/2, они похожи на дроби, потому что 2/4 в упрощенном виде будет ½. Еще один пример, который поможет вам понять, что 2/3 и 6/9 также являются одинаковыми дробями, потому что если мы упростим 6/9 с тем же числом, получится 2/3 Это дроби, которые не одинаковы или не упрощены, чтобы быть одинаковыми, например, 2/3, а 6/9 отличаются от дробей. Наш калькулятор фракций специально разработан для выполнения основных и сложных операций с фракциями; он работает как конвертер дробей. Да, этот калькулятор для дробей помогает выполнять сложение, вычитание, умножение и деление дробей. Кроме того, этот калькулятор с дробью помогает рассчитать упрощенные дроби и даже перевод между дробными и десятичными числами. Вам просто нужно ввести значение дроби в приведенном выше калькуляторе, а остальные расчеты можно выполнить с помощью нашего десятичного калькулятора дроби. Просто введите десятичное значение в данное поле и нажмите кнопку вычисления, чтобы преобразовать десятичное значение в дробное значение Эти формулы дроби помогут вам раскрыть несколько вопросов, таких как: Вы можете легко добавлять дроби с простотой данной формулы: a / b + c / d = (ad + bc) / bd Например: 2/6 + 1/4 = ((2 * 4) + (6 * 1)) / ((6 * 4)) = 14/24 = 7/12 Наш калькулятор добавления фракций также использовал ту же формулу для добавления фракций. Вычитание дроби становится легче с помощью следующей формулы: a / b – c / d = (ad-bc) / bd Например: 2/6 – 1/4 = ((2 * 4) – (6 * 1)) / ((6 * 4)) = 2/24 = 1/12 Наш калькулятор вычитания фракций также учитывает ту же формулу для вычитания фракций. Получите простое умножение дроби с помощью приведенной ниже формулы: a / b × c / d = ac / bd Например: 2/6 × 1/4 = (2 × 1) / (6 × 4) = 2/24 = 1/12 Наш калькулятор умножения долей также учитывает ту же формулу, выполняя вычисления умножения долей. Следующая формула помогает раскрыть этот вопрос: a / b ÷ c / d = ad / bc Например: 2/6 ÷ 1/4 = (2 × 4) / (6 × 1) = 8/6 = 4/3 = 1 1/3 Наш калькулятор деления фракций выполняет вычисление деления фракций, используя ту же формулу деления фракций. Фракции используются в вашей повседневной жизни во многих задачах. Вы можете воспользоваться помощью фракций в управлении временем для различных задач или, если вам придется готовить или печь снова, делите общее время на фракции, тем самым предоставляя подходящее время для каждой задачи. Фракции также широко используются для приготовления пищи, в которой различные ингредиенты определяются фракциями, такими как 1/4 стакана молока, ½ стакана сахара и аналогичным образом. Точно так же ученые и химики используют часть своих экспериментов. Да, этот онлайн-калькулятор фракций использует продвинутый алгоритм для решения уравнений дробей. Не стесняйтесь использовать этот эффективный удобный инструмент и получите желаемые результаты! Other Languages: Fraction Calculator, Kalkulator Ułamków, Kesir Hesap Makinesi, Bruchrechnen, Kalkulator Pecahan, 分数の計算, 분수 계산기, Kalkulačka Zlomky, Calculadora De Fração, Calculatrice Fraction, Calculadora De Fracciones, Calcolatrice Frazioni, حاسبة الكسور, Fraktiolaskin Чтобы складывать и вычитать десятичные числа без калькулятора, оба числа должны иметь одинаковое количество десятичных знаков. Это связано с тем, что десятичные точки должны выровняться в сетке решения для сложения или вычитания десятичных чисел. Если окажется, что одно число имеет большее количество десятичных знаков, чем другое, просто добавьте нули в конец числа с наименьшим количеством десятичных знаков, пока оно не будет иметь такое же количество десятичных знаков, как и другое. Например, предположим, что мы пытаемся сложить следующие два десятичных числа: 56,4321 + 12,34 Поскольку первое число имеет на 2 десятичных разряда больше, чем второе число, нам нужно добавить 2 нуля в конец второго. число (12,34 становится 12,3400). Таким образом, десятичные точки (обозначенные красной вертикальной линией) будут выровнены в сетке решения, например: ← проведите пальцем влево и вправо → ← проведите пальцем влево и вправо → Это также гарантирует, что сумма двух чисел будет иметь такое же количество десятичных знаков, что и число с наибольшим количеством десятичных знаков. Если одно или несколько чисел в задаче сложения отрицательны, шаги для сложения чисел зависят от того, совпадают ли знаки двух чисел. Просто сложите абсолютные значения двух чисел и дайте сумме тот же знак, что и два числа. Пример: (-7) + (-2) Добавьте абсолютное значение -7 (| -7 | = 7) к абсолютному значению -2 (| -2 | = 2), чтобы получить 9, и дайте сумме знак двух чисел, который в данном случае является отрицательным знаком. Используя их абсолютные значения, вычтите меньшее из двух чисел из большего из двух чисел и дайте сумме знак числа с наибольшим абсолютным значением. Пример: (-7) + (2) Вычтите абсолютное значение меньшего числа (| 2 | = 2) из абсолютного значения большего числа -7 (| -7 | = 7), чтобы получить 5 , и присвойте результату знак числа с наибольшим абсолютным значением, которое в данном случае является отрицательным знаком. Если проблема заключается в вычитании, измените вычитание на сложение и измените знак последнего числа на противоположный. Затем следуйте инструкциям по добавлению отрицательных чисел. Пример №1: (-7) — (2) Измените (-7) — (2) на (-7) + (-2) и следуйте правилам сложения. Поскольку теперь знаки те же самые, добавьте абсолютное значение -7 (| -7 | = 7) к абсолютному значению -2 (| -2 | = 2), чтобы получить 9, и дайте сумме знак двух чисел, которое в данном случае является отрицательным знаком. Пример № 2: (-7) — (-2) Измените (-7) — (-2) на (-7) + (2) и следуйте правилам сложения. Поскольку знаки больше не те же самые, вычтите абсолютное значение меньшего числа (| 2 | = 2) из абсолютного значения большего числа -7 (| -7 | = 7), чтобы получить 5, и дайте результат — знак числа с наибольшим абсолютным значением, которое в данном случае является отрицательным знаком. Если вы не знаете, как выполнять длинное сложение или вычитание, калькулятор на этой странице показывает его работу и включает шаги решения для каждого вычисленного результата. Используйте следующие калькуляторы для сложения, вычитания, умножения или деления двух двоичных значений, а также для преобразования двоичных значений в десятичные и наоборот. Двоичная система счисления — это система счисления, которая функционирует практически идентично десятичной системе счисления, с которой люди, вероятно, более знакомы.В то время как в десятичной системе счисления используется число 10 в качестве основы, в двоичной системе используется 2. Кроме того, хотя в десятичной системе используются цифры от 0 до 9, в двоичной системе используются только 0 и 1, и каждая цифра называется битом. . Помимо этих различий, такие операции, как сложение, вычитание, умножение и деление, все вычисляются по тем же правилам, что и десятичная система. Практически все современные технологии и компьютеры используют двоичную систему из-за простоты ее реализации в цифровых схемах с использованием логических вентилей.Намного проще разработать оборудование, которое должно определять только два состояния: включено и выключено (или истина / ложь, присутствует / отсутствует и т. Д.). Использование десятичной системы требует оборудования, которое может обнаруживать 10 состояний для цифр от 0 до 9, что является более сложным. Ниже приведены некоторые типичные преобразования между двоичными и десятичными значениями: Двоичное / десятичное преобразование Работа с двоичным кодом поначалу может показаться запутанной, понимание того, что каждое двоичное разрядное значение представляет 2 n , точно так же, как каждое десятичное место представляет 10 n , должно помочь уточнить.Возьмем, к примеру, число 8. В десятичной системе счисления 8 находится в первом десятичном разряде слева от десятичной точки, что означает 10 0 место. По сути это означает: 8 × 10 0 = 8 × 1 = 8 Используя число 18 для сравнения: (1 × 10 1 ) + (8 × 10 0 ) = 10 + 8 = 18 В двоичном формате 8 представляется как 1000. При чтении справа налево первый 0 представляет 2 0 , второй 2 1 , третий 2 2 и четвертый 2 3 ; точно так же, как десятичная система, только с основанием 2, а не 10.Поскольку 2 3 = 8, в его позиции вводится 1, что дает 1000. Используя 18 или 10010 в качестве примера: 18 = 16 + 2 = 2 4 + 2 1 Пошаговый процесс преобразования десятичной системы в двоичную: Снова используя целевое значение 18 в качестве примера, ниже представлен другой способ визуализировать это: Преобразование из двоичной системы в десятичную проще .Определите все значения разряда, где встречается 1, и найдите сумму значений. Пример: 10111 = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 ) = 23 Отсюда: 16 + 4 + 2 + 1 = 23. Двоичное сложение следует тем же правилам, что и сложение в десятичной системе, за исключением того, что вместо переноса 1, когда добавленные значения равны 10, перенос происходит, когда результат сложения равен 2.Обратитесь к примеру ниже для пояснения. Обратите внимание, что в двоичной системе: EX: Единственная реальная разница между двоичным и десятичным сложением состоит в том, что значение 2 в двоичная система эквивалентна 10 в десятичной системе.Обратите внимание, что единицы с надстрочным индексом представляют собой перенесенные цифры. Распространенная ошибка, на которую следует обратить внимание при выполнении двоичного сложения, — это случай, когда 1 + 1 = 0 также имеет 1, перенесенную из предыдущего столбца вправо. Тогда значение внизу должно быть 1 из перенесенного на 1, а не 0. Это можно увидеть в третьем столбце справа в приведенном выше примере. Подобно двоичному сложению, есть небольшая разница между двоичным и десятичным вычитанием, за исключением тех, которые возникают из-за использования только цифр 0 и 1.Заимствование происходит в любом случае, когда вычитаемое число больше, чем число, из которого оно вычитается. При бинарном вычитании заимствование необходимо только тогда, когда 1 вычитается из 0. Когда это происходит, 0 в столбце заимствования по существу становится «2» (изменение 0-1 на 2-1 = 1), в то время как уменьшение 1 в столбце, из которого заимствуется, на 1. Если следующий столбец также равен 0, заимствование должно происходить из каждого последующего столбца, пока столбец со значением 1 не может быть уменьшен до 0.Обратитесь к примеру ниже для пояснения. Обратите внимание, что в двоичной системе: EX1: EX2: Обратите внимание, что отображаемые верхние индексы — это изменения, которые происходят с каждым битом при заимствовании.Столбец заимствования по существу получает 2 от заимствования, а столбец, из которого заимствовано, уменьшается на 1. Двоичное умножение, возможно, проще, чем его десятичный аналог. Поскольку используются только значения 0 и 1, результаты, которые необходимо добавить, либо те же, что и для первого члена, либо 0. Обратите внимание, что в каждой последующей строке необходимо добавить заполнитель 0, а значение сдвинуть влево, как в десятичном умножении. Сложность двоичного умножения возникает из-за утомительного двоичного сложения, зависящего от количества битов в каждом члене.Обратитесь к примеру ниже для пояснения. Обратите внимание, что в двоичной системе: EX: Как видно из приведенного выше примера, процесс двоичного умножения такой же, как и при десятичном умножении.Обратите внимание, что заполнитель 0 написан во второй строке. Обычно заполнитель 0 визуально не присутствует при десятичном умножении. Хотя то же самое можно сделать и в этом примере (с предполагаемым заполнителем 0, а не явным), он включен в этот пример, потому что 0 актуален для любого двоичного калькулятора сложения / вычитания, подобного тому, который представлен на этой странице. Без отображения 0 было бы возможно совершить ошибку, исключив 0 при добавлении двоичных значений, показанных выше.Еще раз обратите внимание, что в двоичной системе любой 0 справа от 1 имеет значение, а любой 0 слева от последней единицы в значении — нет. EX: Процесс двоичного деления аналогичен длинному делению в десятичной системе счисления. Дивиденд по-прежнему делится на делитель таким же образом, с единственной существенной разницей, заключающейся в использовании двоичного, а не десятичного вычитания.Обратите внимание, что хорошее понимание двоичного вычитания важно для проведения двоичного деления. Обратитесь к примеру ниже, а также к разделу двоичного вычитания для пояснения. Этот базовый онлайн-калькулятор похож на небольшой портативный калькулятор и имеет четыре стандартные функции для сложения, вычитания, деления и умножения. Как и большинство калькуляторов с 4 функциями, он также включает в себя клавиши для вычисления процентов, квадрата, квадратного корня и числа Пи.Этот базовый калькулятор имеет десятичную точность до 10 цифр и предлагает следующие функции: Масштаб : Увеличьте размер калькулятора в браузере с помощью функции масштабирования браузера.Размер калькулятора, текста и кнопок изменяется пропорционально. Масштаб сенсорного экрана : Увеличьте размер калькулятора на сенсорном экране, увеличивая масштаб с помощью
пальцы. Размер калькулятора, текста и кнопок изменяется пропорционально. Размер текста : в некоторых браузерах, например на рабочем столе Chrome, вы можете изменить размер текста в браузере.
настройки и размер калькулятора, текста и кнопок будут пропорционально увеличиваться или уменьшаться. Управление с клавиатуры : Вы можете использовать калькулятор без мыши, перемещаясь по нему с помощью табуляции.
ключи. Нажмите «Enter», когда клавиша сфокусирована. Однако этот метод может быть трудным, поскольку
вы должны последовательно перебирать все клавиши табуляцией. Управление цифровой клавиатурой : Вы можете использовать калькулятор с большинством цифровых панелей и клавиатур в самых популярных браузерах для
числа, очистка и основные функции сложения, вычитания, умножения и деления, а также удаления / возврата. Свяжитесь со мной, если у вас есть предложения. В вашем браузере отключен JavaScript. Предлагаем бесплатный научный калькулятор. Кроме того, мы постоянно добавляем на наш сайт новые калькуляторы. Вот наши калькуляторы по алгебре, геометрии, тригонометрии, графике и исчислению. В дополнение к этим коллекциям на основе категорий в разделе ниже мы предлагаем коллекцию некоторых из лучших математических калькуляторов со всего Интернета. Мы также недавно добавили коллекцию математических игр, чтобы помочь студентам изучать математику онлайн в увлекательной и интерактивной форме. В вашем браузере отключен JavaScript. Поиск инструмента Повторяющиеся десятичные знаки Инструмент для определения периода дроби или десятичного числа с повторяющимися десятичными знаками. Точка — это набор цифр, который повторяется на бесконечности в десятичных дробях числа (обычно рациональное число или периодическая дробь). Результаты Повторяющиеся десятичные знаки — dCode Тэги: Арифметика Поделиться dCode и другие dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день! Периодическое десятичное расширение / развитие рационального числа или дроби (числитель над знаменателем) — это последовательность чисел, которые повторяются на бесконечности в десятичной записи числа. Пример: 1/3 = 0,3333333333 … Цифра 3 повторяется до бесконечности Пример: 1/27 = 0,037037037037037 … Цифры 037 повторяются до бесконечности Все дроби не имеют повторяющейся десятичной формы , некоторые имеют завершающую десятичную форму. Завершающий десятичный знак указывает на то, что никакая последовательность чисел не повторяется бесконечно в десятичной записи числа. Пример: 4/25 = 0,16 разработка завершена и не продолжается Любое число, записанное в десятичной форме с конечным числом цифр (после десятичной точки), является завершающим десятичным числом. Возможно несколько обозначений. Первый использует … точки подвеса, но не определяет повторяющуюся часть. Это практично, но не строго и поэтому не рекомендуется. Пример: 37/300 = 0,12333333333 … $ Обозначение с чертой над повторяющейся частью. Пример: $ 37/300 = 0,12 \ overline {3} $ Обозначение с чертой под повторяющейся частью. Пример: $ 37/300 = 0,12 \ underline {3} $ Обозначения в скобках Пример: 37/300 = 0,12 [3] $ NB: Для наглядности дробь лучше записывать в несократимой форме.1 \ times x = 1. \ overline {6} = 1.6666666 … $ и решаем $ 10x − x = 9x = 1. \ overline {6} −0.1 \ overline {6} = 1.5 \ iff 9x = 1.5 \ iff х = 1,5 / 9 = 15/90 = 1/6 $ Инверсия простых чисел дает длинные и интересные периодические десятичные вычисления. Пример: $ 1/3 = 0,333333 … $ Пример: $ 1/7 = 0,142857142857 … $ Любое рациональное число (любая дробь) имеет конечное развитие или периодическое десятичное разложение с конечным числом цифр, которые повторяются до бесконечности. Но есть действительные числа, которые не являются рациональными числами (которые не являются дробями), которые имеют десятичные дроби без повторения. Пример: $ \ pi = 3.14159265 … $ на сегодняшний день не имеет известных повторов. Пример: Постоянная Чамперноуна никогда не будет повторяться, это номер вселенной. dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Повторение десятичных знаков». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любого алгоритма, апплета или фрагмента повторяющихся десятичных знаков (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любых повторяющихся десятичных знаков ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)) и никакая загрузка данных, скрипт, копипаст или доступ к API для ‘Repeating Decimals’ не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн. Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи! Сводка Похожие страницы Поддержка Форум / Справка Ключевые слова период, дробь, числитель, знаменатель, развертка, повторение, десятичная дробь, запись, цифра, бесконечность, рациональная, точка Ссылки Источник: https: // www.dcode.fr/number-repeating-decimal Преобразуйте соотношение в десятичную форму, введя обе части ниже. Шаг первый: Перепишем соотношение в виде дроби Шаг второй: Разделим числитель на знаменатель Есть несколько разных способов преобразовать отношение в десятичное.Самый простой способ преобразования в десятичную форму — использовать калькулятор, как показано выше. Продолжайте читать, и мы покажем вам, как выполнить преобразование самостоятельно. Первый шаг в преобразовании отношения в десятичное — это переписать отношение как дробь. Для этого положите первую часть соотношения над второй частью в виде дробей. Первая часть отношения будет числителем, а вторая часть — знаменателем. Последний шаг в преобразовании — решить дробь, чтобы получить десятичное значение. Для этого разделите числитель на знаменатель. Результатом является десятичная форма отношения. Например, преобразует 7: 2 в десятичное значение. Записываем 7: 2 в виде дроби. Тогда решай. Таким образом, десятичное значение 7: 2 равно 3.5 Наш калькулятор десятичного отношения к соотношению может помочь решить обратную эту формулу. Конвертер дробей в десятичные (или калькулятор дробей в десятичные) — это онлайн-инструмент для преобразования чисел, который вычисляет эквивалентный десятичный вывод для данного дробного входного значения. Поскольку этот калькулятор дроби в десятичную дробь позволяет пользователям вычислять значения как простой дроби, так и смешанной дроби в одном калькуляторе. Как преобразовать дробь в десятичную Вы можете сначала уменьшить данную дробь, разделив числитель и знаменатель на их наибольший общий коэффициент (GCF), а затем, используя метод длинного деления, получите окончательные результаты. Простая дробь 1/0 = Бесконечность = Бесконечность% Смешанная фракция 1 + 1/1 = 2 = 200% 0909 = 109.0 09% 0909 = 1190. 09% 0909 = 1290. 09% Комбинации
из n элементов по m элементам, которые
отличаются или самими элементами, или
порядком их следования, называются размещениями. Пусть
имеются три буквы А,
В и С.
Составим всевозможные комбинации только
из двух букв: АВ,
ВА, АС, СА, ВС, СВ. Эти комбинации отличаются
друг от друга только расположением букв
или самими буквами. Пример
1 На
третьем курсе изучается 9 предметов.
Сколькими способами можно составить
расписание занятий на один день, если
в учебный день разрешается проводить
занятия только по четырем разным
предметам? Решение
Различных
способов составления расписания столько,
сколько существует четырехэлементных
комбинаций из девяти элементов, которые
отличаются друг от друга или самими
элементами, или их порядком, т.е. Ответ: 3024
Комбинации
из n элементов, которые отличаются друг
от друга только порядком элементов,
называются перестановками.
Перестановки обозначаются Рn, где n —
число элементов, входящих в перестановку. Формула
перестановки:
Рn=n! Пусть
имеются три буквы А, В и С.
Составим всевозможные комбинации из
этих букв: ABC, АСВ, ВСА, ВАС, CAB, CBA. Эти
комбинации отличаются друг от друга
только расположением букв. Пример
1 В
турнире участвуют семь команд. Сколько
вариантов распределения мест между
ними возможно? Решение:
В
итоговой таблице турнира команды будут
отличаться занятыми местами, поэтому
для подсчета вариантов распределения
мест между ними воспользуемся формулой
перестановки: Р7=7!=1*2*3*4*5*6*7=5040 Ответ: 5040
Комбинации из n элементов
по m элементам, которые отличаются
друг от друга хотя бы одним элементом,
называются сочетаниями. Пусть
имеются три буквы А, В и С.
Составим всевозможные комбинации только
из двух букв, которые отличаются друг
от друга хотя бы одним элементом: АВ,
АС, ВС. Нетрудно увидеть, что их в два
раза меньше, чем размещений из этих
элементов.
Пример
1 Сколькими
способами можно распределить три путевки
в один санаторий между пятью желающими? Решение:
Так
как путевки предоставлены в один
санаторий, то варианты распределения
отличаются друг от друга хотя бы одним
желающим. Поэтому число способов
распределения
Ответ: 10. Случайным
событием называется результат (исход) наблюдения
какого-нибудь явления при выполнении
некоторого комплекса условий (опыта). Элементарные
события — возможно исключающие друг друга
события опыта. Невозможное
событие — не может произойти в результате опыта. Достоверное
событие –
в результате опыта обязательно
произойдет. Случайное
событие – при осуществлении некоторых условий
может произойти или не произойти. Несовместные
события – появление одного из них исключает
появление других событий в одном и том
же испытании. Совместные
события – в результате опыта могут появиться
одновременно. Равновозможные
события – одинакова возможность появления в
результате опыта. Равносильные
события – событие А влечет за собой событие В,
а событие В влечет за собой событие А. Алгебра
событий. Суммой
(объединением) событий А и В называется событие С,
состоящее в появлении события А или
событие В или одновременно событий А
и В. С=А+В Произведением
(пересечением) событий А и В называется событие С,
состоящее в совместном появлении
событий А и В. С=А*В Разностью событий А и В называется событие С,
состоящее в появлении событии А и не
появлении события В. С=А-В Классическое
определение вероятности события.
Свойства вероятности. Вероятностью р события А называется
отношение числа m-благоприятствующих
случаев к числу всех возможных случаев
n,
образующих полную группу равновозможных
несовместимых событий: P
(A)= Свойства
вероятности: Число
появления m-любого
события входит в интервал 0<P<1. Вероятность
достоверного события равна 1. Вероятность
невозможного события равна 0. Теоремы
сложения вероятностей несовместных
событий. Теорема
1. Вероятность
появления одного из двух несовместных
событий, безразлично какого, равна сумме
вероятностей этих событий: Р
(А + В) = Р (А) + Р (В). Доказательство: Введем обозначения: n — общее число
возможных элементарных исходов испытания;
m1 —
число исходов, благоприятствующих
событию A; m2—
число исходов, благоприятствующих
событию В. Число
элементарных исходов, благоприятствующих
наступлению либо события А, либо события
В, равно m1 +
m2.
Следовательно, Р
(A + В)
= (m1 +
m2)
/ n = m1 /
n + m2 /
n. Приняв
во внимание, что m1 /
n = Р (А) и m2 /
n = Р (В), окончательно получим Р
(А + В) = Р (А) + Р (В). Теорема
2. Сумма
вероятностей событий А1 ,
А2 ,
…, Аn , образующих
полную группу, равна единице: Р
(A1)
+ Р (А2)
+ … + Р (Аn)
= 1. Доказательство: Так
как появление одного из событий полной
группы достоверно, а вероятность
достоверного события равна единице, то Р
(A1 +
A2 +
… + An)
= 1. (*) Любые
два события полной группы несовместны,
поэтому можно применить теорему сложения: Р
(А1 +
А2 +
… + Аn)
= Р (A1)
+ Р (A2)
+ … + Р (Аn).
(**) Сравнивая
(*) и (**), получим Р
(А1)
+ Р (А2)
+ … + Р (Аn)
= 1. Пример: Консультационный
пункт института получает пакеты с
контрольными работами из городов А, В
и С. Вероятность получения пакета из
города А равна 0,7, из города В — 0,2. Найти
вероятность того, что очередной пакет
будет получен из города С. Р
е ш е н и е.
События «пакет получен из города А»,
«пакет получен из города В», «пакет
получен из города С» образуют полную
группу, поэтому сумма вероятностей этих
событий равна единице: 0,7
+ 0,2 + p =1. Отсюда
искомая вероятность р
= 1 — 0,9 = 0,1. Теорема
3. Сумма
вероятностей противоположных событий
равна единице: . Доказательство:
Пусть дано А и
.
Тогда А+ будет достоверным. Сумма достоверного
события равно 1. Тогда . З
а м е ч а н и е 1.
Если вероятность одного из двух
противоположных событий обозначена
через р, то вероятность другого события
обозначают через q. Таким образом, в силу
предыдущей теоремы p
+ q = l З
а м е ч а н и е 2.
При решении задач на отыскание вероятности
события А часто выгодно сначала вычислить
вероятность противоположного события,
а затем найти искомую вероятность по
формуле . studfiles.net Вопросы
занятия: •
вывести формулу числа сочетаний из n элементов по k; •
вывести формулу числа размещений из n элементов
по k; •
познакомить с треугольником Паскаля и с закономерностью получения его чисел. Материал
урока На прошлых занятиях мы работали с определением
вероятности случайного события и с его помощью вычисляли вероятности. Так же мы активно применяли правило
умножения. Из курса алгебры 9 класса вам известны
понятие факториал и теорема о перестановках. Вспомним их. Определение. Произведение подряд идущих первых n натуральных чисел называют n факториал. Теорема
1. Решим задачу. Школьники смастерили 4 скворечника. Сколькими способами в них могут
разместиться 4 скворца? Решение заключается в том, чтобы найти число
перестановок из четырёх элементов. Сколькими же способами в них могут
разместиться 4 скворца, если один прилетела раньше всех и уже занял себе домик? Понятно, что остаётся разместить
оставшиеся 3 птицы в 3 домика. А теперь представим себе такую ситуацию.
Каждые 2 из 7 городов соединены мостами. Определим их количество. Представим города в виде точек. Каждый
мост соединяет только 2 города. И пользуясь комбинаторным правилом
умножения, число мостов можно найти так. Первый город можно выбрать семью
способами, а второй — шестью. Но ведь тогда каждый мост будет посчитан два раза,
а нам не важен порядок выбора городов. Значит, нужно всё разделить на два. Запишем теорему о выборе двух элементов. Теорема 2. Определение. Тогда теорему 2 кратко можно записать в
виде формулы. Решим задачу. Рассмотрим другую ситуацию. Пример. Теорема 3. Определение. Тогда теорему можно записать так: Решим задачу. Запишем определения. Число всех выборов k элементов из n данных без учёта порядка называют числом
сочетаний из n
элементов по k. Число всех выборов k элементов
из n
данных с учётом их порядка называют числом размещений из n элементов по k. Как же находить число сочетаний и
размещений из n
элементов по k? Запишем теорему. Теорема 4. Для любых натуральных чисел n и k, таких, что k < n, справедливы следующие
соотношения. Этими формулами мы и будем пользоваться
при вычислении числа сочетаний и размещений. Решим уравнение. Так мы с помощью изученных формул решили
уравнение, а теперь решим задачу. Пример. Для чисел сочетаний из эн элементов по
ка существует красивый и удобный способ их записи с помощью треугольной
таблицы, её называют треугольник Паскаля. Он выглядит так. Закономерность образования строк
заключается в следующем: каждое число в треугольнике Паскаля равно сумме двух
чисел, стоящих над ним в предыдущей строке. 5=1+4, 10=4+6, 6=3+3 и так далее. Кратко эту закономерность можно записать
в виде такой формулы. Подведём итоги нашего урока. Сегодня мы рассмотрели такие инструменты
комбинаторики как сочетание и размещение. Познакомились с формулами отыскания
числа сочетаний и размещений из эн элементов по ка. Выяснили, в чём их отличие
друг от друга. А также рассмотрели примеры решения
задач с помощью этих инструментов. videouroki.net В данной статье речь пойдет об особом разделе математики под названием комбинаторика. Формулы, правила, примеры решения задач – все это вы сможете найти здесь, прочитав статью до самого конца. Итак, что же это за раздел? Комбинаторика занимается вопросом подсчета каких-либо объектов. Но в данном случае объектами выступают не сливы, груши или яблоки, а нечто иное. Комбинаторика помогает нам находить вероятность какого-либо события. Например, при игре в карты – какова вероятность того, что у противника есть козырная карта? Или такой пример – какова вероятность того, что из мешка с двадцатью шариками вы достанете именно белый? Именно для подобного рода задач нам и нужно знать хотя бы основы данного раздела математики. Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных комбинаторных задач. Примерами таких моделей служат: О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел. А разбиение – это неупорядоченная сумма. Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся: В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики – какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос – какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт – инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам. Среди формул комбинаторики можно найти и довольно простые, с которыми мы достаточно давно знакомы. Примером является правило суммы. Предположим, что нам даны два действия (С и Е), если они взаимоисключаемы, действие С выполнимо несколькими способами (например а), а действие Е выполнимо b-способами, то выполнить любое из них (С или Е) можно а+b способами. В теории это понять достаточно трудно, постараемся донести всю суть на простом примере. Возьмем среднюю численность учеников одного класса — допустим, это двадцать пять. Среди них пятнадцать девочек и десять мальчиков. Ежедневно в классе назначается один дежурный. Сколько есть способов назначить дежурного по классу сегодня? Решение задачи достаточно простое, мы прибегнем к правилу сложения. В тексте задачи не сказано, что дежурными могут быть только мальчики или только девочки. Следовательно, им может оказаться любая из пятнадцати девочек или любой из десяти мальчиков. Применяя правило суммы, мы получаем достаточно простой пример, с которым без труда справится школьник начальных классов: 15 + 10. Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса. К основным формулам комбинаторики относится и правило умножения. Начнем с теории. Допустим, нам необходимо выполнить несколько действий (а): первое действие выполняется с1 способами, второе – с2 способами, третье – с3 способами и так далее до последнего а-действия, выполняемого са способами. Тогда все эти действия (которых всего у нас а) могут быть выполнены N способами. Как высчитать неизвестную N? В этом нам поможет формула: N = с1 * с2 * с3 *…* са. Опять же, в теории ничего не понятно, переходим к рассмотрению простого примера на применение правила умножения. Возьмем все тот же класс из двадцати пяти человек, в котором учится пятнадцать девочек и десять мальчиков. Только на этот раз нам необходимо выбрать двух дежурных. Ими могут быть как только мальчики или девочки, так и мальчик с девочкой. Переходим к элементарному решению задачи. Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех. Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор. Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n! Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга – Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша – это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%. Сейчас мы рассмотрим еще одну очень важную и необходимую формулу комбинаторики. Размещение – это наш следующий вопрос, который предлагаем вам рассмотреть в данном разделе статьи. Мы идем на усложнение. Предположим, что мы хотим рассмотреть возможные перестановки, только не из всего множества (n), а из меньшего (m). То есть мы рассматриваем перестановки из n предметов по m. Основные формулы комбинаторики стоит не просто заучивать, а понимать их. Даже несмотря на то, что они усложняются, так как у нас не один параметр, а два. Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)! Мы рассмотрели практически все основные формулы комбинаторики с примерами. Теперь перейдем к заключительному этапу рассмотрения базового курса комбинаторики – знакомство с сочетанием. Сейчас мы будем выбирать m предметов из имеющихся у нас n, при этом всем мы будем выбирать всеми возможными способами. Чем же тогда это отличается от размещения? Мы не будем учитывать порядок. Этот неупорядоченный набор и будет являться сочетанием. Сразу введем обозначение: С. Берем размещения m шариков из n. Мы перестаем обращать внимание на порядок и получаем повторяющиеся сочетания. Чтобы получить число сочетаний нам надо поделить число размещений на m! (m факториал). То есть С = А / m! Таким образом, способов выбрать из n шаров немножко, равняется примерно столько, сколько выбрать почти все. Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов. Мы подробно рассмотрели основные формулы комбинаторики: размещение, перестановка и сочетание. Теперь наша задача – облегчить выбор необходимой формулы для решения задачи по комбинаторике. Можно воспользоваться следующей довольно простой схемой: Мы рассмотрели элементы комбинаторики, формулы и некоторые другие вопросы. Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан. Вопрос первый: сколькими способами их можно переставить? Для этого воспользуемся формулой перестановок: Р = 3! = 6 способов. Вопрос второй: сколькими способами можно выбрать один фрукт? Это очевидно, у нас всего три варианта – выбрать киви, апельсин или банан, но применим формулу сочетаний: С = 3! / (2! * 1!) = 3. Вопрос третий: сколькими способами можно выбрать два фрукта? Какие есть у нас вообще варианты? Киви и апельсин; киви и банан; апельсин и банан. То есть три варианта, но это легко проверить при помощи формулы сочетания: С = 3! / (1! * 2!) = 3 Вопрос четвертый: сколькими способами можно выбрать три фрукта? Как видно, выбрать три фрукта можно одним-единственным способом: взять киви, апельсин и банан. С = 3! / (0! * 3!) = 1. Вопрос пятый: сколькими способами можно выбрать хотя бы один фрукт? Это условие подразумевает, что мы можем взять один, два или все три фрукта. Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт. fb.ru тест по теме: » Полные и
неполные квадратные уравнения.
В-1 А1.
Решите уравнение 5х2 -10=0. Если корней несколько, найдите их
произведение. 1)
-2
3)решений нет 2)
2
4) А2.
Укажите уравнение, которое не имеет корней. 1) 2,7х2 -1,5x=0 3)
2,7х2 — 1,5=0 2) 2,7x2+1,5х=0
4) 2,7х2 +1,5=0 А3.
Вычислите дискриминант квадратного уравнения 2х2-7х+3=0 1) 5
3) 625 2) 73
4) 25 А4.
Решите уравнение х2 +3х -4=0 1)
1;-3
3) -4;1 2)
решений
нет 4) 1;-4 А5. 1)
решений
нет 3) 6 2)
2
4)- 6 А6.
Найдите произведение корней квадратного уравнения х2 -7х -6=0 1)
-6
3) 6 2)
решений
нет 4) 7 А7.
Решите уравнение 3х2 -5х -12=0 1) 1; 3)
-6; 2) 5;
0 4) 3; — А8. Решите уравнение х2 -7х=0 1)
-7;
0 3) 0;7 2)
-1;1
4) -7;0 А9.Укажите
неполное квадратное уравнение 1)
3х2 -4х-7=0 3)х2-7х-8=0 2)
3х2-7х=0 4) 5х2 -3х-140=0 В1.
В-2 А1.
Решите уравнение 7х2 -35=0. Если корней несколько, найдите их
произведение. 1) 5
3) решений нет 2) -5
4) А2.
Укажите уравнение, которое не имеет корней. 1)6,9х2 +3,4x=0 3)
6,9х2 -3,4x=0 2) 6,9х2 +3,4=0 4) 6,9х2 -3,4=0 А3.
Вычислите дискриминант квадратного уравнения 2х2+7х+5=0 1) 89
3) 3 2) 81
4) 9 А4.
Решите уравнение х2 -5х +6=0 1)2;-3
3) 3;2 2)решений
нет 4) -2;-3 А5. 1)
7
3) решений нет 2)
-7
4) 4 А6.
Найдите произведение корней квадратного уравнения х2 +5х +2 =0 1)–
2,5 3) -2 2)решений
нет 4) 2
А7. Решите уравнение 3х2 -2х — 40 =0 1) 4 ; 3)
4 ; — 2) 10
;0 4) -4 ; —
А8. Решите уравнение х2 -14х=0
1) 0; 14 3) -14; -1 2)-14;1 4)
0; -14 А9.Укажите полное квадратное
уравнение
1) 5х2 -4х-10=0 3)х2-25 =0
2) х2+15х +14 =0 4) 3х2 -3х=0 В1. В-3 А1.
Решите уравнение 3х2 -9=0. Если корней несколько, найдите их
произведение. 1)
3)
3 2)
решений
нет 4) -3 А2.
Укажите уравнение, которое не имеет корней.
1)5,9х2 -2,3x=0 3)
5,9х2 +2,3=0
2) 5,9х2 +2,3x=0 4)
5,9х2 -2,3=0 А3.
Вычислите дискриминант квадратного уравнения 6х2-11х+3=0 1)
7
3) 193 2)
49
4) 2041 А4.
Решите уравнение х2 +7х +10=0
1)2; 5 3) -2; -5
2)решений нет 4) -2; 5 А5. 1)
решений нет
3) — 11 2)
11
4) 5 А6.
Найдите произведение корней квадратного уравнения х2 +5х -2
=0
1)– 2 3) -5 2)
2 4) решений нет А7.
Решите уравнение 4х2 +36х +81 =0 1)
4
3) 4,5; 0 2)
—
4,5 4) решений нет А8.
Решите уравнение х2 -9х=0
1) 0; -9 3) 0;9
2)1; 9 4) -1; -9 А9.Укажите
полное квадратное уравнение 1)
5х2 -25х=0 3)х2-36 =0 2)3х2+5х
+28 =0 4) 3х2=0 В1.
(х-1)2= 29 -5х
В-4 А1.
Решите уравнение 4х2 -28=0. Если корней несколько, найдите их
произведение. 1)
7
3)решений нет 2)
-7
4) А2.
Укажите уравнение, которое не имеет корней. 1)9,1х2 — 4,5=0 3) 9,1х2 +
4,5х=0 2)
9,1х2 + 4,5=0 4) 9,1х2 —
4,5х=0 А3.
Вычислите дискриминант квадратного уравнения 6х2+7х-3=0 1)
121
3) 529 2)
11
4) -23 А4.
Решите уравнение х2 -5х +4=0 1)-4;-1
3) 1;4
2)решений нет 4)- 1; 4 А5. 1)
-12
3) 5 2)
решений
нет 4) 12 А6.
Найдите произведение корней квадратного уравнения х2 +9х -7=0 1)
7
3) решений нет 2)
-7
4) -9 А7.
Решите уравнение 5х2 +14х -3=0 1)
-2; 3)
-2; 2)
решений нет 4)- 3; А8.
Решите уравнение х2 -4х=0 1)
0;4
3) 0;-4 2)
-1;4
4) -4; -1 А9.Укажите
полное квадратное уравнение с чётным вторым коэффициентом 1) 5х2 -4х-17=0 3)2 х2=0 2) 6х2-7х
+8 =0 4) 5х2 -9х-14=0 В1.
(х-3)(х+3)= 5х-13
В-5 А1.
Решите уравнение 9х2 -54=0. Если корней несколько, найдите их
произведение. 1)решений
нет 3) 6 2)
— 6 4) А2.
Укажите уравнение, которое не имеет корней.
1)8,6х2 + 1.5=0 3) 8,6х2 –
1.5х =0
2) 8,6х2 — 1.5=0 4) 8,6х2 +
1.5х =0 А3.
Вычислите дискриминант квадратного уравнения 3х2-5х +2=0 1) 18
3) 1 2) -91
4) 101 А4. 1)
-5;-4
3) -4;5 2)
4; 5 4)- 5; 4 А5.
Найдите сумму корней квадратного уравнения х2 -17х +4=0 1)
-40
3) -17 2)
Решений
нет 4) 17 А6.
Найдите произведение корней квадратного уравнения х2 -29х +27=0 1)
29
3) нет корней 2)
-29
4) 27 А7.
Решите уравнение 7х2 +8х +1 =0 1)
-;
-1 4) -2; -1 2)
решений нет 4)- 1; А8.
Решите уравнение х2 -6х=0 1)
0;1
3) 0;-6 2)
0;6
4) 0; -1 А9.
1) 6х2 +14х+8=0 3) 9х2=0
2) х2-7х +9 =0 4) 5х2 -25х +6=0 В1.
Решите уравнение.
(х+3)2= 2х+6
В-6 А1.
Решите уравнение 10х2 -100=0. Если корней несколько, найдите
их произведение.
1) 0 3)
2) -10 4) 10 А2.
Укажите уравнение, которое не имеет корней.
1)10,2х2 — 13,4=0 3) 10,2х2 +
13,4=0
2) 10,2х2 + 13,4х=0 4) 10,2х2 —
13,4х=0 А3. 1.728
3)-
157
2)760 4) 265 А4.
Решите уравнение х2 -19х +88=0 1)
8;
11 3) -11; 8
2) -8; -11 4)- 8; 11 А5.
Найдите сумму корней квадратного уравнения х2 +25х +44=0 1)25
3) -25 2)
44 4) решений нет А6.
Найдите произведение корней квадратного уравнения х2 -8х +22=0 1)корней
нет 3) 22 2)
8
4)- 22 А7.
Решите уравнение 5х2 +8х -4 =0 1)
— ;
2 3) решений нет 2)
2; 5 4)- 2; А8. 1)-8;0
3) -1; 8 2)
1;8 4) 0; 8 А9.Укажите
приведённое квадратное уравнение
1) х2 -14х+7=0 3) 27х2=0
2) 3х2-9х =0 4) 5х2 -10х +36=0 В1.
Решите уравнение (х-4)(х+4)= -14х -49 Ответы: № варианта А1 А2 А3 А4 А5 А6 А7 А8 А9 В1 1 1 4 4 4 3 1 4 3 2 2;5 2 2 2 4 3 2 4 3 1 2 3;4 3 4 3 2 3 2 1 2 3 2 -7;4 4 2 2 1 3 1 2 4 1 1 1;4 5 2 1 3 2 4 4 1 2 3 -3;-1 6 2 3 2 1 3 3 4 4 1 -11;-3 1. 2. Какое из чисел -2, -1, 0, 1, 2 является корнем уравнения 3х2 -5х +2 = 0? 3. Решите неполное квадратное уравнение 2х2 – 18 = 0. 4. Решите неполное квадратное уравнение х2 + 2х = 0. 5. Решите неполное квадратное уравнение 2х2 = 0. 6. Найдите корни уравнения х2 -7х + 6 = 0. 7. Найдите корни уравнения х2 + 6х + 5 = 0. 8. Найдите корни уравнения х2 + 8х + 16 = 0. 9. Решите уравнение 7х2 — х – 8 = 0. 10. Найдите сумму корней уравнения х2 — 16х + 2 8 = 0. 11. Найдите сумму корней уравнения 3 х2 — 15х -2 8 = 0. 12. Найдите произведение корней уравнения 2 х2 — 15х — 2 8 = 0. 13. Решите уравнение (2х – 3) (3х + 6) = 0. 14. Решите уравнение (х – 2)2 = 3х — 8. 15. Один из корней квадратного уравнения равен 3. Найдите второй корень уравнения х2 — 21х + 54 = 0. 16. Один из корней квадратного уравнения равен -3. Найдите коэффициент р уравнения х2 + рх + 18 = 0. 17. Какое из чисел -3, -1, 0, 1, 3 является корнем уравнения 3х2 -5х -8 = 0? 18. Решите неполное квадратное уравнение 4х2 – 64 = 0. 19. Решите неполное квадратное уравнение — х2 + 2х = 0. 20. Решите неполное квадратное уравнение 2х2 = 0. 21. Найдите корни уравнения х2 — 4х + 3 = 0. 22. Найдите корни уравнения х2 + 8х + 7 = 0. 23. Найдите корни уравнения х2 + 10х + 25 = 0. 24. Решите уравнение 3х2 — 8х + 5 = 0. 25. Найдите сумму корней уравнения х2 — 17х + 2 8 = 0. Все, что важно знать выпускнику, в памятках от Рособрнадзора Друзья, #МузейУИстока предлагает написать комментарии к этому посту свои любимые стихи Пушкина. https://vk.com/wall-187421469_1270 Поехали! 6 июня 2021 года исполняется 222 года со дня рождения выдающегося русского поэта и писателя Александра Сергеевича Пушкина. Добрый день! #большаяперемена Коллеги, мы подготовили мотивационный ролик о конкурсе и возможностях, которые он дает ttps://disk.yandex.ru/i/NRF3AnSArtfANg #Школа259СПБ Уважаемые родители! Приглашаем вас принять участие в опросе мнения о том, справедлива ли система ЕГЭ при поступлении в вузы. Проголосовать можно по ссылке — https://vk.com/wall615914394_80 Проголосовать можно по ссылке — https://vk.com/irina_potehina В этом году единому государственному экзамену исполнилось 20 лет. Удалось ли Читать дальше … ️Дети — маленькие частички большого счастья, чудо, которое наполняет жизнь каждого взрослого неподдельной радостью и теплотой. Дети так нуждаются в любви и заботе, в родительской ласке и хочется, чтобы каждое детское сердце не было обделено этим маленьким счастьем. Чтобы помочь школьникам справиться с эмоциональным напряжением, эксперты Института воспитания подготовили небольшую памятку о том, как взять себя в руки перед ЕГЭ и успешно сдать его. Поздравление с Днем города Санкт-Петербурга! Лучший город на Земле прими поздравления от #Школа259СПб #ДЕНЬГОРОДА2021 для вас выступают учащиеся начальных классов ГБОУ средней школы N259 им. М.Т. Лорис-Меликова Адмиралтейского района Санкт-Петербурга на празднике посвященный Дню города. Желаем всем хорошего, праздничного настроения, мира, добра Читать дальше … Церемония награждения нагрудным знаком «Почетный работник воспитания и просвещения Российской Федерации» Уважаемая Астгик Телемаковна! Сердечно поздравляю Вас с получением заслуженной награды, которая является прямым подтверждением Ваших высоких профессиональных и личностных качеств. Примите искренние пожелания крепкого здоровья и благополучия и дальнейших Читать дальше … 26 мая 2021 года на базе ГБОУ средней школы №259 им. Уважаемые родители! Ежегодно с началом летне-весеннего сезона регистрируются случаи гибели детей при выпадении из окна! Как правило, во всех случаях падения дети самостоятельно забирались на подоконник, используя в качестве подставки различные предметы мебели, и, опираясь на противомоскитную сетку, выпадали из Читать дальше … Содержание: Эта страница соответствует § 2.4
(с. 200) текста. Предлагаемые задачи из текста: с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87,
88, 95, 97 Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a —
не равно 0. Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то
хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое.
Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста. Пример 1. 2x 2 — 5x — 12 = 0. (2x + 3) (x — 4) = 0. 2x + 3 = 0 или x — 4 = 0. x = -3/2 или x = 4. Если x 2 = k, то x = ± sqrt (k). Пример 2. x 2 — 9 = 0. x 2 = 9. x = 3 или x = -3. Пример 3. Пример 4. x 2 + 7 = 0. х 2 = -7. х = ±. Обратите внимание, что = =,
так что решения x = ±, два комплексных числа. Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат
корневой принцип. Пример 5. x 2 + 6x — 1 = 0. x 2 + 6x = 1. x 2 + 6x + 9 = 1 + 9. 9, добавленная к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) 2 = 9. Причина
выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами).
Поэтому эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это
истина, учитывая (x + a) 2 = x 2 + 2ax + a 2 . (x + 3) 2 = 10. Теперь мы можем применить принцип квадратного корня и затем решить относительно x. x = -3 ± sqrt (10). Пример 6. 2x 2 + 6x — 5 = 0. 2x 2 + 6x = 5. Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент
(коэффициент x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив
обе части уравнения на 2. x 2 + 3x = 5/2. Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат,
(3/2) 2 = 9/4. x 2 + 3x + 9/4 = 5/2 + 9/4. Левая часть — квадрат (x + 3/2). [Проверьте это!] (х + 3/2) 2 = 19/4. Теперь мы используем принцип квадратного корня и решаем относительно x. x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2. x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2 До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от
проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня
могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере. Пример 7. x 2 = 16. x 2 — 16 = 0. (x + 4) (x — 4) = 0. x = -4 или x = 4. В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна. Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае
мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие:
всегда одинаковы, поэтому их можно применить к общему квадратному уравнению ах 2 + bx + c = 0. Результатом квадрата этого общего уравнения является формула для решений уравнения
называется квадратной формулой. Решения уравнения ax 2 + bx + c = 0 равны Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае,
где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его
в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу. Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Примеры использования квадратичной формулы: Пример 8. 2x 2 + 6x — 5 = 0. В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратную формулу, получаем Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат. Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика
функции f (x) = 2x 2 + 6x — 5. Пример 9. 4x 2 + 4x + 1 = 0 В этом примере a = 4, b = 4 и c = 1. В этом примере следует обратить внимание на две вещи. 4x 2 + 4x + 1 = 0. (2x + 1) 2 = 0. х = -1/2. Пример 10. х 2 + х + 1 = 0 а = 1, б = 1, с = 1 Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов.
функции f (x) = x 2 + x + 1. Таким образом, решения сложны, поскольку график y = x 2 + x + 1 не имеет пересечений по x. Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом
уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений. 1. Дискриминант> 0. Два реальных решения. 2. Дискриминант = 0. Одно реальное решение. 3. Дискриминант <0. Два сложных решения. Примечания к проверке растворов Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример
3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения,
потому что при решении уравнений очень легко сделать невнимательные ошибки. Алгебраический метод, который состоит из обратной подстановки числа в уравнение и проверки того, что
полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда
решение предполагает радикальное. Например, в нашем предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2. Алгебраическая проверка выглядит как 4 (-1/2) 2 +4 (-1/2) + 1 = 0. 4 (1/4) — 2 + 1 = 0. 1-2 + 1 = 0. 0 = 0. Решение проверяет. В предыдущем примере, 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2.
Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический
проверить или использовать калькулятор для алгебраической проверки быстрее. Сначала найдите десятичные приближения для двух предложенных решений. (-3 + sqrt (19)) / 2 = 0,679449. (-3 — sqrt (19)) / 2 = -3,679449. Теперь используйте графическую утилиту для построения графика y = 2x 2 + 6x — 5 и проследите график, чтобы приблизительно определить, где
х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение. Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и сразу перешли к графику
утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя
(алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень
близко к найденным вами числам, значит, вы, наверное, правы! Упражнение 1: Решите следующие квадратные уравнения. (а) 3x 2 -5x — 2 = 0. Ответ (б) (x + 1) 2 = 3. Ответ (в) x 2 = 3x + 2. Ответ Вернуться к содержанию Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал
является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить. Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы
радикальный член сам по себе на одной стороне уравнения. Пример 11. Теперь, когда мы изолировали радикальный член в правой части, возводим обе части в квадрат и решаем полученное уравнение
для x. Чек: х = 0 Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно! Итак, x = 0 не является решением . х = 3 Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно
раствор . Решение : x = 3. Примечание: Решением является x-координата точки пересечения графиков y = x и
у = sqrt (х + 1) +1. Посмотрите, что бы произошло, если бы мы возводили обе части уравнения в квадрат до , выделив радикал
срок. Это хуже, чем мы начали! Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью
возведение в степень один раз. Однако мы можем уменьшить количество радикальных членов на , возведя их в степень. Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и
возвести в степень. Затем мы повторяем этот процесс. Пример 12. Теперь возведите обе части уравнения в квадрат. В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат
снова обе стороны. Чек: Подстановка x = 5/4 в исходное уравнение дает sqrt (9/4) + sqrt (1/4) = 2. 3/2 + 1/2 = 2. Это утверждение верно, поэтому решение x = 5/4. Примечание по проверке решений: В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что
нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение
— координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1). Упражнение 2: Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ Вернуться к содержанию Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее.Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с графической утилитой. Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий
x, чтобы начать задачу. Пример 13. 2x 3 + 3x 2 -5x = 0. x (2x 2 + 3x -5) = 0. Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения. x = 0 или 2x 2 + 3x -5 = 0. Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом. Примечание: Если бы мы не смогли разложить квадратичный коэффициент во втором уравнении, то мы могли бы прибегнуть к
к использованию квадратичной формулы.[Убедитесь, что вы получили те же результаты, что и ниже.] x = 0 или (2x + 5) (x — 1) = 0. Итак, есть три решения: x = 0, x = -5/2, x = 1. Примечание: Решение находится при пересечении графиков f (x) = 2x 3 + 3x 2 -5x. Пример 14. x 3 -2x 2 -9x +18 = 0. Коэффициент при x 2 в 2 раза больше, чем при x 3 , и такое же соотношение существует между
коэффициенты при третьем и четвертом членах. Группа слагает один и два, а также три и четыре. x 2 (x — 2) — 9 (x — 2) = 0. Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители. (x — 2) (x 2 — 9) = 0. Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения. x — 2 = 0 или x 2 — 9 = 0. x = 2 или (x + 3) (x — 3) = 0. Итак, есть три решения: x = 2, x = -3, x = 3. Примечание: Эти решения находятся на пересечении графика f (x) = x 3 -2x 2 -9x +18. Пример 15. x 4 — x 2 — 12 = 0. Этот многочлен неквадратичный, он имеет четвертую степень. Однако его можно рассматривать как квадратичный по x 2 . (x 2 ) 2 — (x 2 ) — 12 = 0. Это может помочь вам фактически заменить z на x 2 . z 2 — z — 12 = 0 Это квадратное уравнение относительно z. (z — 4) (z + 3) = 0. z = 4 или z = -3. Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на
x 2 и решите полученные уравнения. x 2 = 4. х = 2, х = -2. х 2 = -3. x = i , или x = — i. Итак, есть четыре решения, два реальных и два комплексных. Примечание: Эти решения находятся на пересечении графика f (x) = x 4 — х 2 — 12. График f (x) = x 4 — x 2 — 12 и увеличение, показывающее его локальное
экстремумы. Упражнение 3: Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ Вернуться к содержанию Пример 16. Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение. Это уравнение квадратичное. Квадратичная формула дает решения Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы
убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков.
из y = 1 и y = 2 / x-1 / (x + 2). Пример 17. 5 | х — 1 | = х + 11. Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения
столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности,
и все решения должны быть проверены. Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение 5 (x — 1) = x + 11. 5x — 5 = x + 11. 4x = 16. x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11. Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот
точка часто сбивает студентов с толку, потому что кажется, что мы говорим, что абсолютное значение выражения
отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное. Теперь наше уравнение принимает вид -5 (x — 1) = x + 11. -5x + 5 = x + 11. -6x = 6. x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11. Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график 5 * abs (x — 1) — x — 11 и посмотрите на пересечения по x, или вы можете найти решение как x-координаты
точки пересечения графиков y = x + 11 и y = 5 * abs (x-1). Упражнение 4: (а) Решите уравнение Ответ (b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ Вернуться к содержанию Урок 2 Уравнения кубической и четвертой степени x 3 — x 2 4x + 4 = 0 Существует чрезвычайно сложная формула для решения
кубические уравнения.Некоторые калькуляторы имеют встроенную формулу и поэтому могут
использоваться для решения кубических уравнений. Мы собираемся узнать, как эти уравнения могут быть решены с помощью
факторизация. Если уравнение имеет решения, которые являются целыми числами a,
b и c, то мы можем разложить уравнение на множители следующим образом: x 3 — x 2 4x + 4 = (x
— а) (х — б) (х — в) = 0 Умножая скобки, видим, что константа
член 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе. abc = 4 Все решения a, b и c должны быть множителями 4, поэтому
не так много целых чисел, которые нам нужно учитывать. У нас есть только следующие возможности: 1, 2 и 4 Хорошо изучите каждое из этих чисел, чтобы найти, какие из них
являются решениями уравнения. f (1) = 1 3 — 1 2 4 × 1 +
4 = 0 1 — решение f (−1) = (−1) 3 — (−1) 2 4 × (-1) + 4 = 6 900 · 10 f (2) = 2 3 — 2 2 4 × 2 +
4 = 0 2 — решение f (−2) = (−2) 3 — (−2) 2 4 × (−2) + 4 = 0 −2 — решение Мы нашли три решения, поэтому нам не нужно
попробуйте 4 и −4 как кубический
уравнение имеет максимум три решения. Эти три числа дают нам значения a, b и c и
мы можем факторизовать уравнение. x 3 — x 2 4x + 4 = (x
— 1) (x — 2) (x + 2) = 0 Этот метод включает поиск целых чисел, которые являются множителями
(можно разделить на) постоянный член, а затем проверить, действительно ли эти
целые числа являются решениями уравнения. Пример 1 Решите уравнение x 3 — 3x 2 2x + 4 = 0 Ставим числа, кратные 4
в уравнение, чтобы увидеть, верны ли какие-либо из них. f (1) = 1 3 — 3 × 1 2 2 × 1 + 4 = 0 1 — решение f (−1) = (−1) 3 — 3 × (−1) 2 2 × (-1) + 4 = 2 900 · 10 f (2) = 2 3 — 3 × 2 2 2 × 2 + 4 = −4 f (−2) = (−2) 3 — 3 × (−2) 2 2 × (−2) + 4 = −12 f (4) = 4 3 — 3 × 4 2 2 × 4 + 4 = 12 900 · 10 f (−4) = (−4) 3 — 3 × (−4) 2 2 × (−4) + 4 = −100 Единственное целочисленное решение — x = 1.Когда мы
нашли одно решение, нам действительно не нужно проверять другие числа, потому что
теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить
квадратичный получаем из деления. Теперь мы можем разложить наши
выражение следующим образом: x 3 — 3x 2 2x + 4 =
(х — 1) (х 2 —
2х — 4) = 0 Теперь нам остается решить квадратичную
уравнение. x 2 — 2x — 4 = 0 Воспользуемся формулой квадратичной системы с a = 1, b =
−2 и c = −4. Мы нашли все три решения
уравнение x 3 — 3x 2 2x + 4 =
0. Это: эфтирфаранди: х = 1 x = 1 + 5 x = 1 — 5 Пример 2 Мы можем легко использовать тот же метод для решения
уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f (x) = x 4 — x 3 — 5x 2 + 3x + 2 = 0. Сначала мы находим целые множители
постоянный член, 2. Целочисленные множители 2 равны 1
и 2. f (1) = 1 4 — 1 3 — 5 × 1 2 + 3 × 1 + 2 = 0 1 — решение f (−1) = (−1) 4 — (−1) 3 — 5 × (−1) 2 + 3 × (−1) + 2 = −4 f (2) = 2 4 — 2 3 — 5 × 2 2 + 3 × 2 + 2 = −4 f (−2) = (−2) 4 — (−2) 3 — 5 × (−2) 2 + 3 × (−2) + 2 = 0 ср. нашли вторую
решение. Два найденных нами решения 1 и −2 означают, что мы можем разделить на x —
1 и x + 2 и остатка не будет. Сделайте это в два этапа. Теперь разделите полученное
кубический коэффициент по x — 1. Теперь мы разложили на множители x 2 — 2x — 1 = 0.Мы используем
формула с a = 1, b = −2 и c = −1. Всего найдено четыре решения.
Их: х = 1 х = -2 х = 1 + х = 1- Иногда мы можем решить
уравнение третьей степени, заключив в скобки члены два на два и найдя множитель
что у них общего.Давайте посмотрим на это на примере. Пример 3. Решите уравнение x 3 — 2x 2 — 4x + 8 = 0 x 3 — 2x 2 — 4x + 8 = 0 (x 3 — 2x 2 )
— (4x — 8) = 0 [x 2 (x — 2) — 4 (x — 2)] = 0 (x — 2) [x 2 — 4] = 0 (х — 2) (х
— 2) (x + 2) = 0 Обратите внимание, что скоба (x
— 2) происходит дважды, когда мы закончили факторизацию. x = 2 — это
поэтому двойное решение, и у нас есть только два разных. Это: Лауснир: x = 2 og x = −2 . Все примеры, которые мы рассмотрели до сих пор,
уравнения, в которых член с наибольшей степенью имеет коэффициент 1. Как мы
иметь дело с уравнениями, где этот коэффициент — какое-то другое число? Общая форма — f (x)
= ax 3 + bx 2 + cx + d, где a, b, c и d — целые числа. Мы можем искать целочисленные решения в том же
как и раньше, проверяя множители постоянного члена d. Если мы найдем
целочисленное решение, тогда мы можем разделить и найти другие решения, как и раньше. Если ни один из факторов d не дает нам решения
затем мы ищем решения, которые являются дробями. Это означает, что x — t / n является фактором
f (x), или, если мы умножаем на n, то xn — t является множителем. Теперь предположим, что мы разделили f (x) на xn.
— t и нашли квадратичный множитель, мы можем назвать его Теперь у нас есть результат, что ax 3 + bx 2 + cx + d = (xn
— t) (Ax 2 + Bx + C) сравнивая коэффициенты x 3 на
обе стороны уравнения мы видим, что a = nA и, следовательно, n должно быть множителем
а. Мы заключаем, что любая дробь является решением
кубическое уравнение ax 3 +
bx 2 + cx + d должен иметь вид t / n, где t — множитель числа d, а n —
фактор числа a. Обобщение для функции степени n: ф (х)
= a n x n + a n − 1 x n − 1 +
× × × × + а 1 х
+ 0 с коэффициентами a 0 ,
а 1 , а 2 , × × × × × а n − 2 , n − 1 и n . Если эта функция имеет рациональное решение,
скажем, t / n, тогда t — коэффициент 0 , а n — коэффициент n . Пример 4 Решите уравнение f (x) = 2x 3 — 7x 2 + 4x + 3 = 0. Сразу видно, что нам не нужно
рассмотрите любые отрицательные значения, поскольку все они будут давать отрицательные значения для f (x), а не
0. f () = 2 () 3 — 7 () 2 + 4 × + 3 = 3 f (1) = 2 × 1 3 — 7 × 2 + 4 × 1 + 3 = 2 ф ( 3 / 2 )
= 2 ( 3 / 2 ) 3 — 7 ( 3 / 2 ) 2 + 4 × 3 / 2 + 3 = 0, поэтому мы нашли решение. x = 3 / 2 — решение, поэтому (x — 3 / 2 ) — фактор.
Разделение на (x — 3 / 2 ) может быть трудным. Поэтому мы умножаем на 2 и вместо этого делим на (2x — 3). Если (x
— 3 / 2 ) является
фактор , то (2x — 3). Теперь нам нужно решить уравнение x 2 — 2x — 1 = 0.Мы уже решили это уравнение в примере 2.
Решения: 1 + 2 og 1 — 2. Итак, мы нашли три решения. Их: x = 3 / 2 = 1 х = 1 + 2 х = 1 — 2 Попробуйте пройти тест 2 по уравнениям III. Не забудьте использовать контрольный список для
следите за своей работой. Часто бывает необходимо посмотреть на несколько функций одного и того же независимого
Переменная.Рассмотрим предыдущий пример, где x — количество произведенных товаров.
и продано, была независимой переменной в трех функциях: функции затрат,
функция дохода и функция прибыли. В целом
там может быть: n уравнений v переменные Есть
четыре метода решения систем линейных уравнений: а.графическое решение б. алгебраическое решение c. метод исключения d. метод замещения Пример 1 даны являются
два следующих линейных уравнения: f (x) = y = 1 + 0,5x f (x) = y = 11 — 2x 900 · 10 Изобразите первое уравнение , найдя две точки данных.Установив
сначала x, а затем y равны нулю, можно найти точку пересечения y на
вертикальная ось и точка пересечения x на горизонтальной оси. Если x = 0,
тогда f (0) = 1 + .5 (0) = 1 Если y = 0,
тогда f (x) = 0 = 1 + 0,5x -,5x = 1 х = -2 Результирующий
точки данных: (0,1) и (-2,0) Постройте график второго уравнения , найдя две точки данных.От
установив сначала x, а затем y равными нулю, можно найти точку пересечения y
по вертикальной оси и точка пересечения x по горизонтальной оси. Если x = 0,
тогда f (0) = 11-2 (0) = 11 Если y = 0,
тогда f (x) = 0 = 11 — 2x 2x = 11 900 10 х = 5,5 Результирующий
точки данных: (0,11) и (5.5,0) В точке пересечения двух уравнений x и y имеют одинаковые значения.
На графике эти значения можно прочитать как x = 4 и y = 3. Пример 2 даны являются
два следующих линейных уравнения: f (x) = y = 15 — 5x 900 · 10 f (x) = y = 25 — 5x 900 · 10 Изобразите первое уравнение , найдя две точки данных.Установив
сначала x, а затем y равны нулю, можно найти точку пересечения y на
вертикальная ось и точка пересечения x на горизонтальной оси. Если x = 0,
тогда f (0) = 15-5 (0) = 15 Если y = 0,
тогда f (x) = 0 = 15 — 5x 5x = 15 х = 3 Результирующий
точки данных: (0,15) и (3,0) Постройте график второго уравнения , найдя две точки данных.От
установив сначала x, а затем y равными нулю, можно найти точку пересечения y
по вертикальной оси и точка пересечения x по горизонтальной оси. Если x = 0,
тогда f (0) = 25-5 (0) = 25 Если y = 0,
тогда f (x) = 0 = 25 — 5x 5x = 25 х = 5 Результирующий
точки данных: (0,25) и (5,0) Из графика видно, что эти линии не пересекаются.Они
параллельны. У них одинаковый наклон. Нет однозначного решения. Пример 3 даны являются
два следующих линейных уравнения: 21x — 7y = 14 -15x + 5y = -10 Rewrite
уравнения, поместив их в форму пересечения наклона. Первый
уравнение становится 7y = -14 + 21x у = -2 + 3х Второй
уравнение становится 5y = -10 + 15x у = -2 + 3х Изобразите любое уравнение, найдя две точки данных.Установив сначала
x, а затем y равный нулю, можно найти точку пересечения y по вертикали
ось и точку пересечения x на горизонтальной оси. Если x = 0,
тогда f (0) = -2 +3 (0) = -2 Если y = 0,
тогда f (x) = 0 = -2 + 3x 3x = 2 х = 2/3 Результирующий
точки данных: (0, -2) и (2 / 3,0) Из графика видно, что эти уравнения эквивалентны.Там
— бесконечное количество решений. Этот метод будет проиллюстрирован с помощью анализа спроса и предложения. Этот
Тип анализа заимствован из работ великого английского экономиста Альфреда
Маршалл. Q = количество и P = цена P (s) = функция предложения и P (d) = функция спроса При построении графика цена откладывается на вертикальной оси. Таким образом, цена — это
зависимая переменная.Было бы логичнее рассматривать количество как
зависимая переменная, и этот подход использовал великий французский экономист,
Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя
Анализ Маршалла, который называют крестом Маршалла. Цель состоит в том, чтобы найти равновесную цену и количество, т. Е. Решение
где цена и количество будут иметь одинаковые значения в функции предложения
и функция цены. Q E = равновесная величина
P E = равновесная цена Для равновесия Учитывая следующие функции П (т) =
3Q + 10 и
P (d) = -1 / 2Q + 80 Приравняйте уравнения друг к другу и решите относительно Q. P (т)
= 3Q + 10 = -1 / 2Q + 80 = P (d) 3.5Q = 70 900 · 10 Q = 20
Равновесное количество 20. Подставьте это значение вместо Q в любое уравнение и решите для P. P (т)
= 3 (20) + 10 П (т) =
70 П (г)
= -1/2 (20) + 80 П (г)
= 70
Цена равновесия — 70. Этот метод включает удаление переменных из уравнений. Переменные
удаляются последовательно, пока не останется только одна последняя переменная, т.е.
пока не будет одно уравнение с одним неизвестным. Затем это уравнение решается
для одного неизвестного. Затем решение используется для нахождения второго
последняя переменная. Процедура повторяется, добавляя обратно переменные в качестве их решений.
найдены. Пример 1 2х + 3у = 5 -5x — 2y = 4 Порядок действий: удалить y.Коэффициенты при y не совпадают в
два уравнения, но если бы они были, можно было бы сложить два
уравнения и члены y будут сокращаться. Однако это возможно через
умножение каждого уравнения, чтобы заставить члены y иметь
одинаковые коэффициенты в каждом уравнении. Шаг 1:
Умножьте первое уравнение на 2, а второе уравнение умножьте на 3.
Это дает 4х + 6у = 10 -15x — 6y = 12 Шаг 2:
Сложите два уравнения.Это дает -11x = 22 х =
-2 Шаг 3:
Решить относительно y в любом из исходных уравнений 2 (-2) + 3у = 5 3 года = 9 г = 3
или -5 (-2) — 2y = 4 10 — 2y = 4 2y = 6 г = 3 Альтернативная процедура: удалить x.Коэффициенты при x не совпадают
в двух уравнениях, но если бы они были, можно было бы добавить
два уравнения и члены y будут сокращаться. Однако возможно
путем умножения каждого уравнения, чтобы заставить члены x равняться
имеют одинаковые коэффициенты в каждом уравнении. Шаг 1:
Умножьте первое уравнение на 5, а второе уравнение умножьте на 2.
Это дает 10x + 15y = 25 900 · 10 -10x — 4y = 8 Шаг 2:
Сложите два уравнения.Это дает 11лет = 33 y =
3 Шаг 3:
Решить относительно x в любом из исходных уравнений 2x + 3 (3) = 5 2x = -4 х = -2
или -5x — 2 (3) = 4 — 5x =
10 х = -2 Пример 2 2x 1 + 5x 2 + 7x 3 =
2 4x 1 — 4x 2 — 3x 3 =
7 3x 1 — 3x 2 — 2x 3 =
5 В этом примере есть три переменные: x 1 , x 2 и
х 3 .Одна из возможных процедур — удалить первый x 1 , , чтобы исключить следующие x 2 , а затем найти x 3 .
Значение, полученное для x 3 , используется для решения x 2 и
наконец, значения, полученные для x 3 и x 2 , используются для
решить относительно x 1 . Процедура Часть A Сначала удалите x 1 . Шаг 1 Умножение
первое уравнение на 2 и вычтите второе уравнение из первого
уравнение.Это дает 4x 1 + 10x 2 + 14x 3 =
4
первое уравнение 4x 1 — 4x 2 — 3x 3 = 7
второе уравнение 14x 2 + 17x 3 = -3
второе уравнение вычитается из первого Шаг 2 Умножение
первое уравнение на 3, третье уравнение умножьте на 2 и вычтите
третье уравнение из первого уравнения.Это дает 6x 1 + 15x 2 + 21x 3 =
6
первое уравнение 6x 1 — 6x 2 — 4x 3 =
10
третье уравнение 21x 2 + 25x 3 = -4
третье уравнение вычитается из первого Процедура, часть B Второе удаление x 2 .
Из Части А осталось два уравнения. Из этих двух уравнений исключить
х 2 . 14x 2 + 17x 3 = -3
первое уравнение 21x 2 + 25x 3 = -4
второе уравнение Шаг 1 Умножение
первое уравнение на 21, второе уравнение умножьте на 14. и вычтите
второе уравнение из первого уравнения.Это дает 294x 2 + 357x 3 = -63
первое уравнение 294x 2 + 350x 3 = -56
второе уравнение 7x 3 = -7
второе уравнение вычитается из первого х 3 = -1 Часть C
Решите относительно x 2 , вставив значение, полученное для x 3 в
любое уравнение из части B. 14x 2 + 17 (-1) = -3 1 4x 2 = 14 х 2 = 1
или 21x 2 + 25 (-1) = -4 21x 2 = 21 х 2 = 1 Часть D
Решите относительно x 1 , вставив полученные значения x 2 andx 3 в любом из трех исходных уравнений. 2x 1 + 5x 2 + 7x 3 = 2
первое исходное уравнение 2x 1 + 5 (1) + 7 (-1)
= 2 2x 1 = 4 x 1 = 2 или 4x 1 — 4x 2 — 3x 3 = 7 секунд
исходное уравнение 4x 1 — 4 (1) — 3 (-1)
= 7 4x 1 = 8 х 1 = 2
или же 3x 1 — 3x 2 — 2x 3 = 5
третье исходное уравнение 3x 1 — 3 (1)
-2 (-1) = 5 900 10 3x 1 = 6 х 1 = 2 Это включает выражение одной переменной через другую до тех пор, пока не будет
одно уравнение с одним неизвестным.Затем это уравнение решается для этого
один неизвестный. Затем результат используется для поиска переменной, которая была
выражается через переменную, решение которой было только что найдено. Пример 12x
— 7лет = 106
первое уравнение 8x
+ У = 82
второе уравнение Решите
второе уравнение для y, а затем подставьте полученное значение y в первое
уравнение. г
= 82 — 8x
второе уравнение, решенное относительно y 12x
— 7 (82 — 8х) = 106
первое уравнение переписано в x 12x
— 574 + 56x = 106 68x
= 680 х
= 10 Подставьте полученное значение x в любое из исходных эквивалентов. 12x
— 7лет = 106
первое уравнение 12 (10)
— 7лет = 106 7лет
= 14 г
= 2 8 (10)
+ У = 82
второе уравнение г
= 2 [индекс] Следовательно, решение приведенного выше уравнения равно $ x = 2 $ и $ x = 3 $ Примечание: Вы в одном шаге от ответа! Подпишитесь бесплатно! Регистрируясь, вы также получаете доступ к тысячам решенных вопросов, викторин К концу этого раздела вы сможете: Прежде чем начать, пройдите тест на готовность. Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз предпринимали одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ — «да». В этом разделе мы выведем и воспользуемся формулой, чтобы найти решение проблемы. квадратное уровненеие. Мы уже видели, как решить формулу для конкретной переменной «в целом», чтобы мы проделали алгебраические шаги только один раз, а затем использовали новую формулу, чтобы найти значение конкретной переменной. Теперь мы рассмотрим этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x . Возможно, будет полезно взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение формы, когда вы читаете алгебраические шаги ниже, поэтому вы видите их как с числами, так и со словом «в целом».’ Последнее уравнение — квадратичная формула. Квадратичная формула Решения квадратного уравнения вида даются формулой: Чтобы использовать квадратичную формулу, мы подставляем значения в выражение в правой части формулы. Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения. Как решить квадратное уравнение с помощью квадратичной формулы Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Если вы произносите формулу во время написания каждой задачи, вы быстро запомните ее. И помните, квадратная формула — это уравнение. Обязательно начинайте с «». Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Когда мы решали квадратные уравнения с помощью свойства квадратного корня, мы иногда получали ответы с радикалами. То же самое может случиться и при использовании квадратичной формулы. Если в качестве решения мы получаем радикал, окончательный ответ должен иметь радикал в его упрощенной форме. Решите, используя дискриминант. Решение Мы можем использовать квадратичную формулу, чтобы найти переменную в квадратном уравнении, независимо от того, называется ли оно « x ». Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Мы не можем извлечь квадратный корень из отрицательного числа. Итак, когда мы подставляем, и в квадратную формулу, если величина внутри радикала отрицательна, квадратное уравнение не имеет реального решения.Мы увидим это в следующем примере. Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Все квадратные уравнения, которые мы решили до сих пор в этом разделе, были записаны в стандартной форме,. Иногда нам нужно сделать некоторую алгебру, чтобы привести уравнение в стандартную форму, прежде чем мы сможем использовать квадратичную формулу. Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы «очищали дроби», умножая обе части уравнения на ЖК-дисплей. Это дало нам возможность решить эквивалентное уравнение — без дробей. Мы можем использовать ту же стратегию с квадратными уравнениями. Решите, используя дискриминант. Решите, используя дискриминант. Решите, используя дискриминант. Подумайте об уравнении. Мы знаем из принципа нулевого произведения, что это уравнение имеет только одно решение:. В следующем примере мы увидим, как использование квадратичной формулы для решения уравнения с полным квадратом также дает только одно решение. Решите, используя дискриминант. Решение Вы узнали, что это идеальный квадрат? Решите, используя дискриминант. Решите, используя дискриминант. Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два решения, иногда одно решение, иногда нет реальных решений. Есть ли способ предсказать количество решений квадратного уравнения, не решая его на самом деле? Да, количество внутри корня квадратной формулы позволяет нам легко определить количество решений.Эта величина называется дискриминантом. Дискриминант В квадратной формуле величина называется дискриминантом. Давайте посмотрим на дискриминант уравнений на (Рисунок), (Рисунок) и (Рисунок), а также на количество решений этих квадратных уравнений. Когда дискриминант положительный , квадратное уравнение имеет два решения . Когда дискриминант ноль , квадратное уравнение имеет одно решение . Когда дискриминант отрицательный , квадратное уравнение не имеет реальных решений . Определите количество решений каждого квадратного уравнения: ⓐⓑⓒⓓ ⓐ нет реальных решений ⓑ 2 ⓒ 1 ⓓ нет реальных решений Определите количество решений каждого квадратного уравнения: ⓐⓑⓒⓓ ⓐ 2 ⓑ нет реальных решений ⓒ 1 ⓓ 2 Мы использовали четыре метода для решения квадратных уравнений: Вы можете решить любое квадратное уравнение с помощью квадратной формулы, но это не всегда самый простой метод. Определите наиболее подходящий метод решения квадратного уравнения. А как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают не использовать его.Нам нужно было включить его в эту главу, потому что мы завершили квадрат в целом, чтобы получить квадратную формулу. Вы также будете использовать процесс завершения квадрата в других областях алгебры. Определите наиболее подходящий метод для решения каждого квадратного уравнения: ⓐⓑⓒ Решение ⓐ Поскольку уравнение находится в, наиболее подходящим методом является использование свойства квадратного корня. ⓑ Мы понимаем, что левая часть уравнения представляет собой трехчлен полного квадрата, поэтому факторинг будет наиболее подходящим методом. ⓒ Приведите уравнение в стандартную форму. В то время как наша первая мысль может заключаться в том, чтобы попробовать факторинг, размышления обо всех возможностях проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода. Определите наиболее подходящий метод для решения каждого квадратного уравнения: ⓐⓑⓒ коэффициент ⓑ Свойство квадратного корня ⓒ Квадратичная формула Определите наиболее подходящий метод для решения каждого квадратного уравнения: ⓐⓑⓒ ⓐ Квадратичная формула ⓑ факторинг ⓒ Свойство квадратного корня Решите квадратные уравнения с помощью квадратичной формулы В следующих упражнениях решите, используя квадратичную формулу. Использование дискриминанта для прогнозирования числа решений квадратного уравнения В следующих упражнениях определите количество решений каждого квадратного уравнения. ⓐ нет реальных решений ⓑ 1 ⓐ 1 ⓑ реальных решений нет Определите наиболее подходящий метод для решения квадратного уравнения В следующих упражнениях определите наиболее подходящий метод (разложение на множители, квадратный корень или квадратная формула) для решения каждого квадратного уравнения. Не решай. коэффициент ⓑ квадратный корень коэффициент ⓑ квадратный корень Ракета запускается прямо с корабля в море.Решите уравнение для количества секунд, в течение которых ракета будет находиться на высоте 640 футов. Архитектор проектирует холл гостиницы. Она хочет иметь треугольное окно, выходящее в атриум, с шириной окна на 6 футов больше высоты. Из-за ограничений по энергопотреблению площадь окна должна составлять 140 квадратных футов. Решите уравнение для высоты окна. Решите уравнение ⓐⓑ Решите уравнение ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела. ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения? Это учебное пособие по использованию калькулятора алгебры , пошагового калькулятора для алгебры. Сначала перейдите на главную страницу Калькулятора алгебры.В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить. Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле. После того, как вы введете выражение, Калькулятор алгебры распечатает пошаговое объяснение того, как решить 3x + 2 = 14. Калькулятор алгебры может вычислять выражения, содержащие переменную x. Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите вставить для x.
Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6. Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y.Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4). Так же, как калькулятор алгебры можно использовать для вычисления выражений,
Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x. В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Поскольку ответ правильный, калькулятор алгебры показывает зеленый знак равенства. Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно». Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенные точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y.Пример: x + y = 7; х + 2у = 11 @ (3,4). Если вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру. Вернуться к калькулятору алгебры » Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: Что значит упростить выражение Когда говорят упростить выражение, подразумевают конкретные математические действия с этим выражением, в результате чего оно примет иной вид. Такими действиями могут быть раскрытие скобок, внесение и вынесение множителя за скобку, деление (сокращение), умножение, возведение в степень, приведение дробей к общему знаменателю и много других операций. При этом часто используют формулы сокращенного умножения и теоремы, а в тригонометрии от простых формул приведения до самых сложных тригонометрических выражений. Чем старше школьник, тем больше формул он знает и обладает богатым арсеналом математических действий. В чем смысл таких действий Задачи на упрощение выражений встречаются с самых младших классов. Дети сами того не осознавая, учатся шевелить мозгами в нужном направлении, чтобы преобразовать одно выражение в другое. Разумеется, все задания составляются таким образом, что в любом случае они приводятся к более простому виду или подходящему для дальнейших операций. Однако, при таком подходе теряется общий смысл поставленной задачи. Когда ученик слышит, что надо что-то упростить, то машинально начинает перебирать всевозможные математические действия в голове, не задаваясь вопросом, а для чего упрощать? Приведем наглядный пример Допустим, сказано упростить выражение (a+b)2. В этом случае абсолютно каждый нормальный школьник раскроет скобки и будет доволен самим собой. Без сарказма это действительно так и это нормально. Но вот другая постановка задачи: упростите выражение (a+b)2, затем подставьте следующие числовые значения a=⅔, b=⅓ и запишите получившееся число. Кто теперь скажет, что раскрыть скобки, затем подставить a=⅔ и b=⅓, а затем вычислить ответ, это легче, чем сразу найти a+b=⅔+⅓=1? После этого возводи единицу хоть в сотую степень! Заключение Итак, главная цель задач на упрощение выражений в том, чтобы научить вас применять те или иные математические действия над выражениями. Это обязательно нужно уметь делать. Но более важная проблема в том, чтобы научиться применять необходимые действия в нужный момент и воспользоваться результатом преобразования. Благо есть онлайн калькуляторы упрощения выражений, например, такой как наш, с помощью которого можно проверить свои вычислительные результаты. Желаем успехов! Вы искали 1 упростите выражение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 упростите выражение, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 упростите выражение». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Решить задачу 1 упростите выражение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Запуск приложения в отдельном окне. Вычислитель математических выражений. Благодаря добавлению кнопочного интерфейса может выступать в роли калькулятора. Но главное предназначение — вычислить скопированный математический пример любого уровня сложности. Предусмотрено автоматическое удаление стороннего мусора, который мог прикрепиться при копировании, и мягкая обработка всех ОДЗ и любых ошибок. Вычисление происходит по методу обратной польской записи, которую можно изучить в логе. Учёт лево- и право-ассоциативности операторов. Поле заметок, сохраняющееся между сеансами. Корректность работы программы тщательно протестирована. Это учебная программа, являющаяся финальным проектом первого нашего курса. Создана с помощью технологий HTML, CSS, JavaScript, MathJax и MathML. Детальный список возможностей и особенностей программы: Дополнительная возможность: для взятия модуля числа пропечатайте перед ним ‘abs’ (сокр. от absolute value), для модуля от выражения используйте скобки. P.S. Основные разработчики: Мы понимаем, что как калькулятор программа не совсем удобна с точки зрения дружелюбности кнопочного ввода. Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные
произведения.
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми.
Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько
примеров использования формул сокращенного умножения.
Напишите любое выражение c использованием функций PHP и система выдаст результат выражения насколько он бы сложен не был
Конечно, пользоваться калькулятором в WEB интерфейсе, когда под рукой есть встроенные средства Windows, Linux, не очень понятно.
Поэтому этот калькулятор будет востребован все таки в общении с Jabber ботом.
Но для тех кого не устраивает этот калькулятор есть, более полная версия, работающая и в комплексном поле чисел.
Универсальный калькулятор комплексных чисел онлайн
Кроме этого еще есть
Калькулятор разных систем счисления онлайн
и
Калькулятор расчета количества рабочих дней
Jabber: calc <выражение>
WEB: <выражение>
Выражением может быть любое математическая строка, выраженная языком PHP
Если есть какие либо переменные или символы не являюшщимися числами или функциями то они будут заменены на нули
calc (5+10/1.1+sin(1))/sqrt(2)
Результат выражения 10.558787210794
Пример2:
calc pow(2,10)+24
Результат выражения 1048 Материал этой страницы содержит общую информацию из подготовленной нами справки «Калькулятор Инструкция по применению». Каждая функция калькулятора подробно рассматривается в соответствующих разделах инструкции. Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной, профессиональной и коммерческой. Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников, он значительно облегчает им выполнение самых разных расчётов. Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий. Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела. Ниже перечислены все функции калькулятора. Этот перечень поможет определить, пригодится ли вам подобный сервис, и как можно использовать калькулятор онлайн для решения своих задач в бизнесе, работе и учёбе. В целом online калькулятор предлагает приятный и удобный интерфейс, его кнопки имеют интуитивно понятные обозначения. Рабочая область калькулятора включает в себя дисплей, поле ввода выражения, панель инструментов и цифровую клавиатуру. 1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода. 2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. 3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей. 4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена. В списке ниже указаны все клавиши калькулятора и выполняемые ими операции. Решатель уравнений позволяет решать уравнения с неизвестной с шагами вычисления: линейное уравнение,
квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение. Уравнение — это алгебраическое равенство, включающее одно или несколько неизвестных.
Решение уравнения — это то же самое, что и определение неизвестных или неизвестных.Неизвестное также называют переменной.
Этот калькулятор уравнений может решать уравнения с неизвестными,
Калькулятор может решать уравнений с переменными с обеих сторон , а также уравнений с круглыми скобками : Уравнение первой степени — это уравнение вида «ax = b». линейное решение уравнения вида ax = b s выполняется очень быстро,
если переменная не является неоднозначной, просто введите , уравнение с по , решите , а затем нажмите «Решить»,
затем результат возвращается решателем .
Также отображаются подробности расчетов, которые привели к разрешению линейного уравнения.Чтобы решить линейное уравнение после 3x + 5 = 0, просто введите выражение
3х + 5 = 0
в области вычислений, затем нажмите кнопку «решить», возвращается результат `[x = -5 / 3]`.
также можно решить уравнения в форме `(ax + c) / g (x) = 0` или уравнения, которые могут быть в этой форме
, g (x) представляет функцию.
Когда вы вводите выражение без знака ‘=’; функция возвращает, когда возможны значения, для которых выражение равно нулю. Калькулятор уравнений решает некоторые кубические уравнения . Опять же, решения кубического уравнения будут сопровождаться пояснениями, которые позволили найти результат. Свойство нулевого произведения используется для решения уравнений вида A * B = 0, что это уравнение равно нулю, только если A = 0 или B = 0.
Чтобы решить , этот тип уравнения может быть выполнен, если A и B являются многочленами степени меньше или равной 2.
Также отображаются сведения о расчетах, которые привели к разрешению уравнения.2-1) (x + 2) (x-3) = 0` возвращает `[1; -1; -2; 3]`. Решатель позволяет решить уравнение с использованием абсолютного значения он может решать линейные уравнения, используя абсолютные значения,
квадратные уравнения, включающие абсолютные значения, но также и другие многие типы уравнений
с абсолютными значениями. Вот два примера использования калькулятора уравнений для решения уравнения с абсолютным значением: Калькулятор уравнений позволяет решать уравнение с использованием экспоненты он может решать линейные уравнения с использованием экспоненты,
квадратные уравнения, включающие экспоненциальные, но также и другие многие типы уравнений
с экспоненциальной. Вот два примера использования калькулятора для решения уравнения с экспонентой: Решите логарифмическое уравнение , т.е. возможно несколько уравнений, включающих логарифмы.
Калькулятор не только предоставляет результат, но и предоставляет подробные шаги и расчеты, которые привели к
к разрешению логарифмического уравнения.
Чтобы решить следующее логарифмическое уравнение ln (x) + ln (2x-1) = 0,
просто введите выражение в области расчета, затем нажмите кнопку «Рассчитать». Калькулятор уравнений позволяет решать круговые уравнения , он может решить уравнение с косинусом вида cos (x) = a или уравнение с синусом вида sin (x) = a .
Расчеты для получения результата детализированы, поэтому можно будет решать такие уравнения, как
`cos (x) = 1 / 2`
или же
`2 * sin (x) = sqrt (2)`
с шагами расчета. Функция Equation_solver может решать линейные дифференциальные уравнения первого порядка в режиме онлайн ,
решить следующее дифференциальное уравнение:
y ‘+ y = 0, вы должны ввести формулу_решения (`y’ + y = 0; x`). Функция Equation_solver может решать дифференциальное уравнение второго порядка в режиме онлайн ,
решить следующее дифференциальное уравнение:
y » — y = 0, вы должны ввести формулу_ползания (`y » — y = 0; x`). Чтобы попрактиковаться в различных методах расчета, предлагается несколько тестов по решению уравнений. Решатель неравенств, решающий неравенство с деталями вычисления: линейное неравенство, квадратичное неравенство. Калькулятор неравенств позволяет решать неравенства :
его можно использовать как для решения линейного неравенства
с одним неизвестным, чтобы решить квадратное неравенство.
Во всех случаях шаги расчетов детализированы и дан точный результат. Возможности расчета, предлагаемые калькулятором неравенства , многочисленны, поэтому, например, можно решить дробное неравенство , неравенство, которое содержит буквы (символьное вычисление). Операторы сравнения, используемые для решения неравенства : Решение линейного неравенства с одним неизвестным в виде `a * x> b` выполняется очень быстро,
если переменная не является неоднозначной, просто введите неравенство , решающее и
щелкните inequality_solver, будет возвращен точный результат. Также приведены шагов вычислений , необходимых для решения неравенства . Калькулятор — мощный инструмент компьютерной алгебры, он может манипулировать и получать разрешение линейное неравенство , включающее числа, но также буквы, и в этом случае оно должно явно указывать
переменная. Также приведены шагов вычислений , необходимых для решения неравенства . Калькулятор — мощный инструмент компьютерной алгебры, он может манипулировать и получать разрешение квадратное неравенство , включающее числа, но также буквы, и в этом случае оно должно явно указывать
переменная.2-5> 0 в области исчисления, затем нажмите кнопку расчета или кнопку
inequality_solver, результат затем возвращается в область, где детализированы вычисления. Для решения неравенства калькулятор использует следующие принципы: В этом примере показано, как использовать решатель неравенства [эта страница | pdf | обратные ссылки] Чтобы использовать оценщик выражений, введите выражение, которое вы
хотите оценить в текстовом поле ввода (и, при желании, описание
расчет в текстовом поле Описание расчета), а затем нажмите Расчет кнопка. Вы также можете ввести выражение в текстовое поле Search / Calculate.
вверху страницы, а затем нажмите кнопку + / рядом с ним. Выражения
может включать скобки, операторы и вызовы почти всех компонентов
Нематрийская онлайн-библиотека функций.Подробнее см. Здесь. Важное примечание Если вы используете какой-либо веб-сервис Nematrian программно
или в интерактивном режиме, то будет считаться, что вы согласились с нематрийским
Лицензия на веб-сайт
Соглашение. ССЫЛКИ НАВИГАЦИИ © 2021 — Nematrian Limited Этот сайт использует файлы cookie для улучшения и контроля своей работы. Вы увидите, что калькулятор считает, что вы ввели (что может немного отличаться от того, что вы ввели), а затем пошаговое решение. Примечание: может быть несколько способов найти решение. Калькулятор все еще находится в разработке и может ошибаться , так что будьте осторожны! Нажмите кнопку «дерево», чтобы увидеть сумму в виде дерева. Вы должны делать расчеты сверху вниз…. иногда у вас есть выбор, какой расчет произвести в первую очередь. [1] 2021/06/04 03:57 Женщина / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Совсем нет / [2] 2021/05/06 16:18 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень / [3] 2021/05/05 02:00 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Полезно / [4] 2021/05/03 22:45 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Немного / Калькулятор сломался, я не вижу чисел или прокручиваю влево. Вы должны создать кнопку, чтобы скрыть список функций, чтобы он выглядел так, как раньше, а также, возможно, кнопку вкладки вверху, чтобы отобразить цифровую клавиатуру. Рассмотрим степень, обозначенную как 17 26 чисел 37 0-квадратное число. Также мне нравятся шаблоны клавиатуры для чисел, которые симметрично противоположны, например 857142 + 142857, они добавляют к BASE — 1 в каждом месте цифры. [6] 2021/03/07 03:02 Мужчина / Уровень 50 лет / Средняя школа / Университет / Аспирант / Полезно / [7] 2021.03.03 19:50 Мужчина / Уровень 20 лет / Инженер / Полезно / [8] 2021/03/02 12:54 Мужчина / Уровень 40 лет / Другое / Очень / [9] 2021/02/11 06:32 Мужской / До 20 лет / Старшая школа / Университет / Аспирант / Немного / [10] 2021/02/09 23:16 Мужчина / До 20 лет / Старшая школа / Университет / Аспирант / Очень / [1] 2021/07/03 03:54 Женский / Моложе 20 лет / Высшая школа / Университет / Аспирант / Не для всех / [2] 2021/05/04 03:18 Женщина / Младше 20 лет / Начальная школа / Младший школьник / Не совсем / [3] 2021/04/28 05:25 Мужчина / Моложе 20 лет / Старшая школа / Университет / аспирант / Не совсем / [4] 2021/04/26 00:22 Женский / До 20 лет / Начальная школа / Младший школьник / Не совсем / [5] 2021/04/21 02:30 Женский / До 20 лет / Начальная школа / Неполная средняя школа студент / Немного / [6] 2021/03/19 00:58 Женский / До 20 лет / Начальная школа / Младший школьник / Немного / [7] 2021/03/16 00:48 Мужчина / Моложе 20 лет / Старшая школа / Университет / аспирант / Очень / [8] 2021/03/06 01:50 — / До 20 лет / Начальная школа / Неполная средняя школа / Немного / [9] 2021/02/19 02:15 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Немного / [10] 2021/02/04 01:24 Женский / младше 20 лет / старшая школа / университет / аспирант / полезный /
Данный раздел содержит калькуляторы, позволяющие выполнять все основные действия над
векторами. В частности, с помощью данных калькуляторов можно вычислять скалярное, векторное и смешанное произведения векторов, раскладывать вектора по базису, проверять их ортогональность, компланарность и др. Всего представлено 19 калькуляторов и для каждого предусмотрено подробное решение соответствующей задачи.
Сложение векторов
Калькулятор позволяет складывать вектора, заданные в координатной форме.
Разность векторов
Калькулятор позволяет вычитать вектора, заданные в координатной форме.
Модуль (длина) вектора
Калькулятор находит модуль (длину) вектора с описанием подробного решения на русском языке.
Угол между векторами
Калькулятор позволяет найти угол между векторами. Подробное решение также имеется.
Проекция вектора
Калькулятор вычисляет проекцию вектора на ось или на другой вектор.
На нашем сайте представлен полный набор калькуляторов векторов онлайн, с помощью которых вы сможете получить подробное и точное решение необходимой геометрической задачи. Чтобы найти вектор онлайн: Вам предоставляется пошаговый расчет и ответ без погрешностей. Решение векторов онлайн пригодится ученикам школ, изучающим тему на уроках геометрии. При подготовке домашних заданий, чтобы проверить самостоятельно решенный пример, можно ввести исходные данные в калькулятор и рассчитать автоматически. Такой способ самопроверки эффективен, так как в случае несовпадения ответов или затруднений в понимании есть возможность изучить способ решения. Студентам посчитать вектор онлайн часто необходимо в качестве промежуточного действия в составной задаче. На быстро полученном точном ответе базируются последующие вычисления. Не всегда для решения задания с векторами можно обойтись расчетами, на которых построены калькуляторы. В таких случаях обращайтесь в Zaochnik: Мы сотрудничаем с преподавателями математики школ, университетов, инженерами-проектировщиками, поэтому сможем подобрать подходящего исполнителя конкретно для вашей работы. Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия. Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус». В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора. Наш онлайн калькулятор позволяет найти векторное произведение двух векторов всего за пару минут. Для вычисления векторного произведения выберите форму представления векторов (через координаты или по точкам), заполните все элементы и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ и, при необходимости, проверить свое решение. Форма представления векторов: координатами точками Формула : Наш онлайн калькулятор помогает найти скалярное произведение двух векторов всего в несколько кликов. Для вычисления скалярного произведения выберите размерность векторов и форму их представления (через координаты или по точкам), заполните все координаты и нажмите кнопку «Вычислить», калькулятор выдаст детальное решение и ответ! Каждый шаг будет подробно расписан, это поможет вам проверить свое решение и понять, как был получен ответ. Размерность векторов: 2 3 Форма представления векторов: координатами точками Формула :
Сложение векторов. Он-лайн калькулятор.
Сложение векторов. Он-лайн калькулятор. В механике существуют два типа величин: Рассмотрим сначала алгебраический подход к сложению векторов. Покоординатное сложение векторов. Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.): Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле: В двумерном случае все абсолютно анологично, просто отбрасываем третью координату. Теперь перейдем к геометрическому смыслу сложения двух векторов: . При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения: Правило параллелограмма. Процедура сложения векторов по правилу параллелограмма заключается в следующем: Правило треугольника Сложение векторов по правилу треугольника заключается в следующем: Тригонометрический способ Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F12 + F22 -2 F1 F2 cos(180о-α) ]1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180o-α) / FR ] (2) где α = угол между исходными векторами Пример — сложение векторов. Сила 1 равна 5кН и воздействует на тело в направлении, на 80o отличающемся от направления действия второй силы, равной 8 кН. Результирующая сила вычисляется следующим образом: Fрез = [ (5 кН)2 + (8 кН)2 — 2 (5 кН)(8 kН) cos(180o — (80o)) ]1/2 = 10,14кН Угол между результирующей силой и первой силой равен: β= arcsin[ (8кН) sin(180o — (80o)) / (10,14кН)] = 51o А угол между второй и результирующей силой можно посчитать следующим образом: as α = arcsin [ (5 кН) sin(180o — (80o)) / (10,2 кН)] = 29o Он-лайн калькулятор сложения векторов. Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов. Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач. Yandex.RTB R-A-339285-1 Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора. Определение 1 Смешанным произведением a → , b → и d → является та величина, которая равняется скалярному произведению a → × b → и d → , где a → × b → — умножение a → и b → . Операцию умножения a → , b → и d → зачастую обозначают a → · b → · d → . Можно преобразовать формулу так: a → · b → · d → = (a → × b → , d →) . Мы можем умножить вектора, если они указаны на координатной плоскости. Возьмем i → , j → , k → Произведение векторов в данном конкретном случае будет иметь следующий вид: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → Определение 2 Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат. Из этого следует: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются. a → × b → = (a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → , d x · i → + d y · j → + d z · k →) = = a y a z b y b z · d x — a x a z b x b z · d y + a x a y b x b y · d z = a x a y a z b x b y b z d x d y d z Таким образом, можно сделать вывод, что: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z Определение 3 Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z . Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства. Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль. Результатом умножения также будет нуль в том случае, если два или больше множителей равны. Действительно, если a → = b → , то, следуя определению векторного произведения [ a → × b → ] = a → · b → · sin 0 = 0 , следовательно, смешанное произведение равно нулю, так как ([ a → × b → ] , d →) = (0 → , d →) = 0 . Если же a → = b → или b → = d → , то угол между векторами [ a → × b → ] и d → равен π 2 . По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 . Свойства операции умножения чаще всего требуются во время решения задач. Пример 1 Докажите равенство ([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) , где λ — некоторое действительное число. Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит: ([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →) Неравенство доказано. Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z . Пример 3 В прямоугольной системе координат представлены 3 вектора с такими координатами: a → = (1 , — 2 , 3) , b → (- 2 , 2 , 1) , d → = (3 , — 2 , 5) . Необходимо определить, чему равно произведение указанных векторов a → · b → · d → . Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z = 1 — 2 3 — 2 2 1 3 — 2 5 = = 1 · 2 · 5 + (- 1) · 1 · 3 + 3 · (- 2) · (- 2) — 3 · 2 · 3 — (- 1) · (- 2) · 5 — 1 · 1 · (- 2) = — 7 Пример 4 Необходимо найти произведение векторов i → + j → , i → + j → — k → , i → + j → + 2 · k → , где i → , j → , k → — орты прямоугольной декартовой системы координат. Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i → + j → = (1 , 1 , 0) i → + j → — k → = (1 , 1 , — 1) i → + j → + 2 · k → = (1 , 1 , 2) Используем формулу, которая использовалась выше Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере. Пример 5 В прямоугольной системе координат расположены три вектора a → , b → и d → , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4 , 2 и 3 . Необходимо умножить вектора. Обозначим c → = a → × b → . Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними.) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] . Абсолютная величина n p c → d → равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a → , b → и d → в качестве сторон. Исходя из этого, следует уточнить, что c → = [ a → × b → ] перпендикулярен a → и вектору и вектору согласно определению умножения векторов. Величина c → = a → x b → равняется площади параллелепипеда, построенного на векторах a → и b → . Делаем вывод, что модуль произведения a → · b → · d → = c → · n p c → d → равен результату умножения площади основания на высоту фигуры, которая построена на векторах a → , b → и d → . Определение 4 Абсолютная величина векторного произведения является объемом параллелепипеда : V п а р а л л е л е п и п и д а = a → · b → · d → . Данная формула и является геометрическим смыслом. Определение 5 Объем тетраэдра , который построен на a → , b → и d → , равняется 1 / 6 объема параллелепипеда Получаем, V т э т р а э д а = 1 6 · V п а р а л л е л е п и п и д а = 1 6 · a → · b → · d → . Для того, чтобы закрепить знания, разберем несколько типичных примеров Пример 6 Необходимо найти объем параллелепипеда, в качестве сторон которого используются A B → = (3 , 6 , 3) , A C → = (1 , 3 , — 2) , A A 1 → = (2 , 2 , 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: A B → · A C → · A A 1 → = 3 6 3 1 3 — 2 2 2 2 = 3 · 3 · 2 + 6 · (- 2) · 2 + 3 · 1 · 2 — 3 · 3 · 2 — 6 · 1 · 2 — 3 · (- 2) · 2 = — 18 Тогда, V п а р а л л е л е п и п е д а = — 18 = 18 . V п а р а л л е л е п и п и д а = 18 Пример 7 В системе координат заданы точки A (0 , 1 , 0) , B (3 , — 1 , 5) , C (1 , 0 , 3) , D (- 2 , 3 , 1) . Следует определить объем тетраэдра, который расположен на этих точках. Воспользуемся формулой V т э т р а э д р а = 1 6 · A B → · A C → · A D → . Мы можем определить координаты векторов по координатам точек: A B → = (3 — 0 , — 1 — 1 , 5 — 0) = (3 , — 2 , 5) A C → = (1 — 0 , 0 — 1 , 3 — 0) = (1 , — 1 , 3) A D → = (- 2 — 0 , 3 — 1 , 1 — 0) = (- 2 , 2 , 1) Дальше определяем смешанное произведение A B → · A C → · A D → по координатам векторов: A B → · A C → · A D → = 3 — 2 5 1 — 1 3 — 2 2 1 = 3 · (- 1) · 1 + (- 2) · 3 · (- 2) + 5 · 1 · 2 — 5 · (- 1) · (- 2) — (- 2) · 1 · 1 — 3 · 3 · 2 = — 7 Объем V т э т р а э д р а = 1 6 · — 7 = 7 6 . V т э т р а э д р а = 7 6 . Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Назначение
. Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word
. Дополнительно создается шаблон решения в Excel
. Признак компланарности . Если система a, b, c – правая, то abc>0 ; если левая, то abcГеометрический смысл смешанного произведения . Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c , взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая. Пример №1
. Найти смешанное произведение.
ab(3a+2b-5c)=3aba+2abb-5abc=-5abc . Пример №2
. (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca .
Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc . Поэтому (a+b)(b+c)(c+a)=2abc . Пример №3
. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k . На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =) Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще! В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы . Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком. И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ: Результатом скалярного произведения векторов является ЧИСЛО: Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву . Сначала будет определение с картинкой, затем комментарии. Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию: Разбираем определение по косточкам, тут много интересного! Итак, можно выделить следующие существенные моменты: 1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже. 2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство . 3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом. Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма. Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения: Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения: Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле: 4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам . 5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-) …как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =) Определение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю. Частный случай – векторное произведение вектора на самого себя: С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём. Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов. Ну что же, разжигаем огонь: Пример 1 а) Найти длину векторного произведения векторов , если б) Найти площадь параллелограмма, построенного на векторах , если Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться! а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле: Ответ : Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы. б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения: Ответ : Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы. Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже. Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же. Популярный пример для самостоятельного решения: Пример 2 Найти площадь треугольника, построенного на векторах , если Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока. На практике задача действительно очень распространена, треугольниками вообще могут замучить. Для решения других задач нам понадобятся: Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список. Для произвольных векторов и произвольного числа справедливы следующие свойства: 1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет. 2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение. 3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать? 4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем. В качестве демонстрации рассмотрим коротенький пример: Пример 3 Найти , если Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру: (1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения. (2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной. (3) Дальнейшее понятно. Ответ : Пора подбросить дров в огонь: Пример 4 Вычислить площадь треугольника, построенного на векторах , если Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа: 1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова! (1) Подставляем выражения векторов . (2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов. (3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно. (4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения: (5) Приводим подобные слагаемые. В результате вектор оказался выражен через вектор, чего и требовалось достичь: 2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3: 3) Найдём площадь искомого треугольника: Этапы 2-3 решения можно было оформить и одной строкой. Ответ : Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения: Пример 5 Найти , если Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-) Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами: Пример 10 Проверить, будут ли коллинеарны следующие векторы пространства: Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): . а) Найдём векторное произведение: Таким образом, векторы не коллинеарны. б) Найдём векторное произведение: Ответ : а) не коллинеарны, б) Вот, пожалуй, и все основные сведения о векторном произведении векторов. Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул. Смешанное произведение векторов – это произведение трёх векторов : Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят. Сначала опять определение и картинка: Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый. Выполним рисунок. Невидимые нам линии прочерчены пунктиром: Погружаемся в определение: 2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий. 3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ». По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда. Примечание : чертёж является схематическим. 4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: . Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах . Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.» × Очистить все ячейки? Закрыть
Очистить Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д. Смешанное произведение
трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c , то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab ] скалярно умножается на вектор c . Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c ). Тогда можно записать: Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2″ и 3 на странице векторное произведение векторов онлайн). Для определенности, в дальнейшем мы будем рассматривать только правые системы координат. Теорема 1.
Смешанное произведение векторов
([ab ],c ) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c , взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab ],c ) равно нулю. Следствие 1.
Имеет место следующее равенство: Следовательно нам достаточно доказать, что Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию. Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc , не указывая, какие именно два вектора перемножаются векторно первые два или последние два. Следствие 2.
Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения. Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю). Следствие 3.
Смешанное произведение трех векторов, два из которых совпадают, равно нулю. Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю. Теорема 2.
Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab ] и c . Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой (): Последнее выражение можно записать, используя определители второго порядка: необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е: Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2. Пример 1.
Найти смешанное произведение векторов abс , где Смешанное произведение векторов a, b, c равен определителю матрицы L . Вычислим определитель матрицы L , разложив определитель по строке 1: Конечная точка вектора a . Онлайн-калькулятор для нахождения скалярного (внутреннего) произведения двух векторов с указанными шагами. Онлайн-калькулятор для определения величины (длины) вектора с указанными шагами. Калькулятор найдет единичный вектор в направлении данного вектора с указанными шагами. Калькулятор найдет угол (в радианах и градусах) между двумя векторами и покажет результат. Калькулятор найдет скалярную проекцию одного вектора на другой с указанными шагами. Калькулятор найдет векторную проекцию одного вектора на другой с указанием шагов. Этот калькулятор ортонормирует набор векторов с помощью процесса Грама-Шмидта с указанными шагами. Онлайн-калькулятор найдет произведение двух векторов с указанием шагов. Калькулятор вычислит тройное произведение (как скаляр, так и вектор) трех векторов с указанными шагами. Калькулятор найдет транспонирование данной матрицы с указанными шагами. Калькулятор найдет след матрицы с указанными шагами. Калькулятор найдет эшелонированную форму строки (простую или сокращенную — RREF) заданной (расширенной) матрицы (с переменными, если необходимо), с указанием шагов. Калькулятор выполнит исключение Гаусса для данной расширенной матрицы с указанными шагами. По желанию возможно полное сокращение. Калькулятор найдет ранг матрицы с указанием шагов. Калькулятор найдет размер строки матрицы с указанными шагами. Калькулятор найдет размер столбца матрицы с указанными шагами. Калькулятор найдет основу пространства, охватываемого набором заданных векторов, с указанными шагами. Калькулятор найдет пустое пространство (ядро) и недействительность данной матрицы с указанными шагами. Этот калькулятор найдет базис ортогонального дополнения подпространства, охватываемого данными векторами, с указанными шагами. Калькулятор найдет определитель матрицы (2×2, 3×3, 4×4 и т. Д.), Используя расширение кофактора, с указанными шагами. Калькулятор найдет обратную квадратную матрицу, используя метод исключения Гаусса или метод сопряжения, с указанными шагами. Калькулятор найдет матрицу миноров данной квадратной матрицы с указанными шагами. Калькулятор найдет матрицу сомножителей данной квадратной матрицы с указанными шагами. Калькулятор найдет сопряженную (сопряженную, вспомогательную) матрицу данной квадратной матрицы с указанными шагами. Калькулятор найдет характеристический многочлен данной матрицы с указанными шагами. Калькулятор найдет собственные значения и собственные векторы (собственное подпространство) данной квадратной матрицы с указанными шагами. Калькулятор диагонализирует данную матрицу с указанием шагов. Калькулятор найдет сумму двух матриц (если возможно) с указанными шагами. Добавляет матрицы любого размера до 10х10 (2х2, 3х3, 4х4 и т. Д.). Калькулятор найдет разницу двух матриц (если возможно), с указанными шагами.Он вычитает матрицы любого размера до 10×10 (2×2, 3×3, 4×4 и т. Д.). Калькулятор умножит заданную матрицу на заданный скаляр с указанными шагами. Он обрабатывает матрицы любого размера до 10×10 (2×2, 3×3, 4×4 и т. Д.). Калькулятор найдет произведение двух матриц (если возможно) с указанными шагами.Он перемножает матрицы любого размера до 10х10 (2х2, 3х3, 4х4 и т. Д.). Калькулятор найдет частное двух матриц (если возможно) с указанием шагов. Он разделяет матрицы любого размера до 7×7 (2×2, 3×3, 4×4 и т. Д.). Калькулятор найдет данную матрицу, возведенную в заданную целую (положительную или отрицательную) степень (если возможно), с указанными шагами.Таким образом, он может возводить матрицу в квадрат и куб. Он обрабатывает матрицы любого размера до 7×7 (2×2, 3×3, 4×4 и т. Д.). Этот решатель будет складывать, вычитать, умножать, делить и возводить в степень две матрицы с указанными шагами. Он также найдет определитель, инверсию, rref (сокращенная форма эшелона строк), пустое пространство, ранг, собственные значения и собственные векторы. Калькулятор найдет LU-разложение данной матрицы $$$ A $$$ (если возможно), т.е. такую нижнюю треугольную матрицу $$$ L $$$ и верхнюю треугольную матрицу $$$ U $$$, которая $$$ A = LU $$$, с указанными шагами. В случае частичного поворота (требуется перестановка строк) калькулятор также найдет матрицу перестановок $$$ P $$$ такую, что $$$ PA = LU $$$. Калькулятор найдет QR-факторизацию данной матрицы $$$ A $$$, т.е. такую ортогональную матрицу $$$ Q $$$ и верхнюю треугольную матрицу $$$ R $$$, что $$$ A = QR $$$, с указанием шагов. В механике есть два вида величин При сложении векторных величин важны как величина, так и направление. Общие методы сложения копланарных векторов (векторов, действующих в одной плоскости): Процедура «» метод сложения параллелограмма векторов «- это Процедура « метод сложения треугольника векторов » равна Результирующий вектор из двух копланарных векторов может быть вычислен тригонометрическим методом с использованием « правила косинуса » для прямоугольного треугольника. F R = [F 1 2 + F 2 2 — 2 F 1 F 2 cos (180 o — (α + β))] 1/2 (1) где F = векторная величина — сила, скорость и т. Д. α + β = угол между вектором 1 и 2 Угол между вектором и результирующий вектор может быть вычислен с помощью « правило синуса » для непрямоугольного треугольника. α = sin -1 [F 1 sin (180 o — (α + β)) / F R ] (2) где α + β = угол между вектором 1 и 2 известен Сила 1 с величиной 3 кН действует в направлении 80 o от силы 2 с величиной 8 кН . Результирующая сила может быть рассчитана как F R = [(3 кН) 2 + (8 кН) 2 — 2 (5 кН) (8 кН) cos (180 o — (80 o ))] 1/2 = 9 (кН) Угол между вектором 1 и результирующим вектором можно рассчитать как α = sin -1 [(3 кН) sin (180 o — (80 o )) / (9 кН) ] = 19.1 o Угол между вектором 2 и результирующим вектором можно рассчитать как α = sin -1 [(8 кН) sin (180 o — (80 o ) ) / (9 кН) ] = 60,9 o Встречный ветер 100 км / ч действует 30 o правый борт на самолете с скорость 900 км / ч . Результирующая скорость самолета относительно земли может быть рассчитана как v R = [(900 км / ч) 2 + (100 км / ч) 2 — 2 (900 км / ч) (100 км / ч) cos (180 o — (30 o ))] 1/2 = 815 (км / ч) Угол между курсом самолета и фактический относительный курс земли можно рассчитать как α = sin -1 [(100 км / ч) sin ((180 o ) — (30 o )) / (815 км / ч) ] = 3.5 o Общий калькулятор ниже основан на уравнении (1) и может использоваться для сложения векторных величин, таких как скорости, силы и т. Д. Результирующие векторы могут быть оценены путем рисования параллелограммов, как показано ниже. Метод также можно использовать с более чем двумя векторами, как указано ниже. В приведенном выше примере сначала найдите полученный F (1,2) , добавив F 1 и F 2 , и получившийся F (3,4) , добавив F 3 и F 4 .Найдите результат F (1,2.3,4) , добавив F (1,2) и F (3,4) . Добро пожаловать в калькулятор линейной независимости , где мы узнаем, как проверить, имеете ли вы дело с линейно независимыми векторами или нет. По сути, мир вокруг нас является векторным пространством и иногда полезно ограничиться меньшей его частью. Например, сфера — это , трехмерная фигура , но круг существует только в двух измерениях , так зачем возиться с вычислениями в трех измерениях? Линейная зависимость позволяет нам делать именно это — работать в меньшем пространстве, так называемом диапазоне рассматриваемых векторов .Но не волнуйтесь, если вы нашли все эти причудливые слова нечеткими. Через секунду мы медленно пройдем через все это вместе. Так что возьмите утреннюю / вечернюю закуску в дорогу, и вперед! Если вы спросите кого-нибудь: « Что такое вектор? », то довольно часто вы получите ответ « стрелка ». Ведь мы обычно обозначаем их стрелкой над маленькой буквой: Ну, давайте просто скажем, что этот ответ не принесет вам 100 баллов на тесте.Формально вектор — это элемент векторного пространства . Конец определения. Достаточно просто . Мы можем закончить учебу. Теперь все ясно. Но что же тогда такое векторное пространство? Опять же, математическое определение оставляет желать лучшего: это набор элементов с некоторыми операциями (сложение и умножение на скаляр), которые должны иметь несколько специфических свойств. Итак, почему бы нам просто не оставить формализм и не взглянуть на на несколько реальных примеров ? Декартово пространство является примером векторного пространства.Это означает, что числовая линия, плоскость и трехмерное пространство, в котором мы живем в , являются векторными пространствами . Их элементами являются, соответственно, числа, пары чисел и тройки чисел, которые в каждом случае описывают положение точки (элемента пространства). Например, число Что очень важно, так это то, что у нас есть четко определенных операций над векторами, упомянутыми выше. Есть несколько более сложных, таких как скалярное произведение и перекрестное произведение. Однако, к счастью, мы ограничимся двумя основными , которые следуют аналогичным правилам для тех же матричных операций (векторы, по сути, являются однострочными матрицами). Прежде всего, мы можем добавить их : и , мы можем умножить их на скаляр (действительное или комплексное число), чтобы изменить их величину: По правде говоря, в векторном пространстве не обязательно должны быть числа . Это может быть пространство последовательностей, функций или перестановок. Даже скаляры не обязательно должны быть числовыми! Но оставим эту абстрактную чушь ученым . Нас устраивают только цифры, не так ли? Допустим, нам дан набор векторов (из того же пространства): , где Хорошо, зачем все это? В жизни есть несколько вещей, таких как гелиевые шары и гамаки, которые приятно иметь, но не так уж и полезны в повседневной жизни. Так ли это здесь? Рассмотрим декартовую плоскость , т.е. двумерное пространство точек Другими словами, любая точка (вектор) нашего пространства представляет собой линейную комбинацию векторов Но что если бы мы добавили еще один вектор к стопке и захотели описать линейные комбинации векторов Нет, это не имеет ничего общего с вашим барбекю 4 июля. Мы говорим, что (здесь Приведенное выше определение можно понять следующим образом: единственная линейная комбинация векторов, которая дает нулевой вектор, является тривиальной . Например, вспомните векторы из приведенного выше раздела: , поэтому мы нашли нетривиальную линейную комбинацию векторов, которая дает ноль .Следовательно, они линейно зависимы . Кроме того, мы легко можем видеть, что сами по себе Набор всех элементов, которые можно записать как линейную комбинацию векторов , где Пролет в линейной алгебре описывает пространство, в котором живут наши векторы . В частности, наименьшее количество элементов, которых достаточно для этого, называется размерностью векторного пространства. В приведенном выше примере это было Внимательный взгляд заметит, что на самом деле размерность диапазона векторов равна количеству линейно независимых векторов в сгустке. В приведенном выше примере все было довольно просто: векторы Для проверки линейной зависимости переведем нашу задачу с языка векторов на язык матриц (массивов чисел).Например, предположим, что нам даны три вектора в 2-мерном пространстве (с двумя координатами): Тогда ранг матрицы равен максимальному количеству линейно независимых векторов среди Итак, как нам узнать ранг? Возможно, самый простой метод — это исключения Гаусса (или его уточнение, исключение Гаусса-Джордана ). Это тот же алгоритм, который часто используется для решения систем линейных уравнений, особенно при попытке найти (сокращенную) ступенчатую форму системы. Исключение Гаусса основано на так называемых операциях с элементарной строкой : Уловка здесь в том, что хотя операции изменяют матрицу , они не изменяют ее ранг и, следовательно, размер диапазона векторов. Алгоритм пытается устранить (т.д., сделайте их , где Теперь нам нужно заметить, что нижняя строка представляет нулевой вектор (у него Это было достаточно времени, потраченного на теорию, не так ли? Давайте попробуем на примере посмотрим, как работает калькулятор линейной независимости ! Допустим, вы наконец осуществили свою мечту — вы купили дрон . Наконец-то вы можете снимать и снимать на видео места, которые вы посещаете, издалека.Все, что вам нужно сделать, это запрограммировать его движения . Дрон требует, чтобы вы дали ему три вектора, по которым он сможет перемещаться . Мир, в котором мы живем, трехмерен, поэтому векторы будут иметь три координаты . Не задумываясь, вы берете случайных векторов, которые приходят на ум : Что ж, если вы выбрали числа случайным образом, вы можете обнаружить, что выбранных вами векторов являются линейно зависимыми , а диапазон векторов, например, только двумерный. Это означает, что ваш дрон не сможет перемещаться, как вы хотите, но будет ограничен движением по плоскости . Может случиться так, что он сможет перемещаться влево и вправо, вперед и назад, , но не вверх и вниз . И как мы получим эти отмеченные наградами кадры похода, если дрон не может даже взлететь? Хорошо, что у нас есть калькулятор линейной независимости! С его помощью мы можем быстро и легко проверить, был ли наш выбор удачным. Итак, давайте разберемся, как им пользоваться. У нас есть Аналогично для двух других получаем: Как только мы введем последнее число, калькулятор линейной независимости сразу сообщит нам, есть ли у нас линейно независимые векторы или нет , и какова размерность диапазона векторов.Тем не менее, давайте возьмем лист бумаги и попробуем сделать все самостоятельно вручную, чтобы увидеть , как калькулятор пришел к своему ответу . Как упоминалось в предыдущем разделе, мы хотели бы, чтобы вычислило ранг матрицы, образованной нашими векторами . Мы построим массив размером 3 × 3, записав координаты последовательных векторов в последовательные строки. Таким образом, мы приходим к матрице Теперь будем использовать исключение по Гауссу .Прежде всего, мы хотели бы, чтобы у были нули в двух нижних строках первого столбца . Для их получения мы используем элементарные операции со строками и Затем мы хотели бы, чтобы получили Мы получили нуля в нижних строках .Мы знаем, что ранг матрицы и, следовательно, линейная зависимость и диапазон в линейной алгебре определяются количеством ненулевых строк . Это означает, что в нашем случае у нас Итак, случилось то, чего мы опасались: : у нашего дрона не будет свободы передвижения . Но мы не можем упустить шанс снять все эти воздушные кадры! К счастью, у нас есть калькулятор линейной независимости , и мы можем поиграть с векторами, чтобы найти подходящую комбинацию векторов.А когда он у нас есть, мы собираемся, садимся в машину и отправляемся в приключение! Вы можете писать математику, а CalcMe выполнит вычисления за вас. Таблица CalcMe разделена на три основные области: Напишите, что вы хотите вычислить Нажмите Calc или Введите ЖИВАЯ ДЕМО Напишите уравнение или фигуру, которую хотите построить Нажмите График действие Сохранить вычисление в переменной Использовать позже ЖИВАЯ ДЕМО Вы можете вычислить частное и остаток от деления или разложить число на простые множители. Вы также можете вычислить наибольший общий делитель или наименьшее общее кратное набора чисел. ЖИВАЯ ДЕМО Векторы заключаются в квадратные скобки Вы можете просуммировать векторы или вычислить их скалярное произведение. ЖИВАЯ ДЕМО Матрицы — это векторы векторов, то есть векторы, элементы которых являются векторами. Вы можете создавать матрицы с двумя разными синтаксисами В качестве векторов вы можете суммировать и умножать матрицы (если их размеры совместимы). ЖИВАЯ ДЕМО Как вы уже видели, вы можете работать с векторами и матрицами и выполнять с ними базовые арифметические операции.Однако вы можете сделать гораздо больше: вы можете вычислить перекрестное произведение между двумя векторами, проверить, являются ли они линейно независимыми; матрицу можно инвертировать или возвести в целую степень, вы также можете вычислить ее ранг или определитель. ЖИВАЯ ДЕМО Вы можете получить доступ к определенному элементу вектора с помощью подиндексов, которые начинаются с 1. Таким же образом вы можете получить элемент матрицы. ЖИВАЯ ДЕМО ЖИВАЯ ДЕМО Вы можете суммировать, умножать, делить и, например, находить корни многочленов. ЖИВАЯ ДЕМО Вы также можете создавать более сложные выражения и работать с ними. ЖИВАЯ ДЕМО Существует множество способов вычислить производную функции или выражения. ЖИВАЯ ДЕМО Также существует множество способов вычислить интеграл функции или выражения. ЖИВАЯ ДЕМО Можно вычислить предел функции или выражения. Более того, вы также можете брать односторонние ограничения. ЖИВАЯ ДЕМО Вы можете вычислить ряд Тейлора реальной функции в заданной точке.Если вас интересуют сроки до некоторого порядка, вы можете также сократить серию. ЖИВАЯ ДЕМО Вы можете определить, сходится ли ряд, а также в большинстве случаев вычислить сумму сходящихся рядов. ЖИВАЯ ДЕМО Возможна работа в 2 или 3 измерениях. Чтобы создать точки, вы просто определяете его компоненты. ЖИВАЯ ДЕМО Имея две точки или точку и вектор, вы можете построить линию. ЖИВАЯ ДЕМО Подобным образом вы можете, например, построить плоскость по трем точкам. ЖИВАЯ ДЕМО ЖИВАЯ ДЕМО Можно решить уравнение или систему уравнений ровно . ЖИВАЯ ДЕМО Вы также можете использовать численный метод для решения более сложных уравнений. ЖИВАЯ ДЕМО Вы также можете использовать численный метод для решения более сложных уравнений. ЖИВАЯ ДЕМО Также возможно найти решение неравенства. ЖИВАЯ ДЕМО ЖИВАЯ ДЕМО ЖИВАЯ ДЕМО ЖИВАЯ ДЕМО ЖИВАЯ ДЕМО Валюты похожи на единицы, но вы не можете конвертировать одну в другую. Проверьте все доступные валюты здесь. ЖИВАЯ ДЕМО Функция random в CalcMe адаптируется ко многим случаям использования. Например, вы увидите, как удалить «0» из случайного выбора. Обычная команда была бы такой: ЖИВАЯ ДЕМО По умолчанию сюда входят все числа от -10 до 10. Если, учитывая требования вопроса, число 0 необходимо исключить из набора, вы можете удалить его с помощью одной простой инструкции (косая черта ЖИВАЯ ДЕМО Вы должны заключить в скобки первый список, чтобы это сработало.Это, конечно, может работать одинаково для любого другого числа, которое вам нужно исключить, кроме нуля: ЖИВАЯ ДЕМО Вышеупомянутое произвело бы случайное число от -10 до 10, кроме числа 8. Вы даже можете сделать это с более чем одним числом: ЖИВАЯ ДЕМО Это приведет к удалению 8, -8 и 0 из выбора.Как видите, существует гораздо больше возможностей при создании случайной величины. Пока что вы получили целые числа, но вы также можете работать с действительными числами. ЖИВАЯ ДЕМО Как правило, эти действительные числа содержат столько десятичных или значащих цифр, сколько определено в настройках приложения.Вы можете настроить его, указав шаг между возможными случайными значениями. ЖИВАЯ ДЕМО Более того, эти случайные величины также могут быть выбраны из конкретного набора значений или слов. В следующем разделе вы увидите более подробную информацию о том, как создавать такие наборы. ЖИВАЯ ДЕМО Мы объясним команды на следующих примерах. На самом базовом уровне ЖИВАЯ ДЕМО или вы можете значительно упростить его до следующего: ЖИВАЯ ДЕМО Команда ЖИВАЯ ДЕМО В качестве альтернативы вы, конечно, могли бы сделать это: ЖИВАЯ ДЕМО Обозначение понимания списка также может быть расширено до более чем одной переменной.В этом случае вы должны указать диапазон для каждой переменной, используемой в качестве счетчика. Например, вот список, содержащий все положительные правильные дроби в простейшем виде, с однозначным числителем и знаменателем: ЖИВАЯ ДЕМО Другая рекомендация, проиллюстрированная в приведенном выше примере, заключается в заключении каждого условия после Наконец, обратите внимание, что диапазон для переменной счетчика может сам быть списком, определенным ранее. ЖИВАЯ ДЕМО Также возможно создавать матрицы, используя эту нотацию. Например, создать матрицу со случайными коэффициентами очень просто: ЖИВАЯ ДЕМО Вы можете использовать некоторые функции программирования. Здесь вы можете увидеть основные. Например, учитывая список, созданный, как описано ранее, вы можете легко вычислить квадрат первых простых чисел. ЖИВАЯ ДЕМО Вы можете создавать собственные функции. Команда ЖИВАЯ ДЕМО Это упрощает создание матрицы со случайными коэффициентами.Еще один более сложный пример — создание функции, которая строит трехдиагональную матрицу по трем числам. Следовательно, каждый раз, когда вы хотите создать трехдиагональную матрицу, вам просто нужно вызывать эту функцию с элементами верхней диагонали, диагонали и нижней диагонали, которые вы хотели бы иметь в матрице. ЖИВАЯ ДЕМО TI-84 Plus C Silver Edition не имеет режима векторной графики. Тем не менее, пользователи по-прежнему могут изобразить вектор с помощью СТАТИСТИКИ.Для этого следуйте примеру ниже: Пример: Изобразите вектор с величиной 5 единиц и направлением 30 градусов. Чтобы преобразовать вектор в прямоугольные координаты: 1) Нажмите [РЕЖИМ] и убедитесь, что выбран режим СТЕПЕНЬ. Если СТЕПЕНЬ не выбрана, прокрутите вниз и до СТЕПЕНИ и нажмите [ENTER]. 5) Нажмите [2nd] [APPS] [8] для доступа к меню ANGLE и вставьте функцию P> Ry ( на главный экран. Значения входного списка: 1) Нажмите [STAT] [ENTER], чтобы получить доступ к редактору списка STAT. 3) Перейдите к списку L2 и нажмите [0] [ENTER] [ALPHA] [1] [ENTER]. 4) Нажмите [2nd] [MODE], чтобы выйти из редактора списка STAT. 1) Нажмите [2nd] [Y =] [ENTER], чтобы получить доступ к редактору STAT PLOT Editor. 3) В поле Тип: выберите вторую опцию, которая представляет собой график X-Y Line. Дополнительную информацию см. В руководстве TI-84 Plus C Silver Edition. На тело или точку могут действовать несколько сил, каждая из которых имеет разное направление и величину. В инженерии основное внимание уделяется результирующей силе, действующей на тело.Результирующая параллельных сил (действующих в одной плоскости) может быть найдена с помощью закона параллелограмма , правила треугольника или правила многоугольника . Две или более силы действуют одновременно — их направление пересекает общую точку. Например, две параллельные силы F 1 и F 2 действуют на одну и ту же точку P . Чтобы найти их результирующий R , мы можем применить либо закон параллелограмма , либо правило треугольника . Результирующая сила — это векторная сумма между компонентами: Если на одну и ту же точку действует несколько сил, мы можем применить правило многоугольника , чтобы найти их равнодействующую. Результирующую силу можно определить также для трехмерной силы системы , используя правило многоугольника. Закон параллелограмма, правило треугольника и правило многоугольника — это геометрические методы для нахождения равнодействующей силы . Мы можем нарисовать результирующую силу, но мы не знаем точно ее величину и направление. Чтобы вычислить величину и направление результирующей силы или вычислить значение той или иной составляющей силы, мы можем использовать закон синусов и закон косинусов.{\ circ} — \ alpha — \ beta)} \ tag {3} \] Результирующую силу также можно вычислить аналитический , используя проекции силы. Используя метод проекции силы , мы можем вычислить величину и углы направления результирующей силы. На изображении выше у нас есть равнодействующая сила R и ее проекции на каждую ось: F x — проекция R на ось x Если в одной точке действуют несколько сил, мы вычислим равнодействующую их проекций на каждая ось: , где n — количество действующих сил, а F x , F y 901 46 и F z — равнодействующие силы на каждой оси.2}} Метод проецирования силы также можно использовать для вычисления результирующей силы в копланарной (оси x, оси y). Пример 1 . Учитывая силы F 1 = 2,91 Н , F 2 = 2,67 Н , F 3 = 2,47 Н и F 4 = 2,23 Н и углы α = 60 ° и β = 30 ° , вычислить равнодействующую силу R и ее угол γ с осью x. Шаг 1 . Чтобы получить представление о том, как может выглядеть результирующая сила, мы можем применить правило многоугольника. Как видите, величина равнодействующей почти равна величине силы F 3 . Кроме того, угол γ должен быть около значения α . Это геометрическое решение полезно, потому что мы знаем, каких результатов следует ожидать от аналитического решения. Шаг 2 .{\ circ} \] Как и ожидалось, аналитическое решение (проекция сил) дает те же результаты, что и геометрическое решение (правило многоугольника). Пример 2 . Учитывая силы F 1 = 6,12 Н , F 2 = 4,32 Н , F 3 = 1,84 Н и их углы α = 16 ° , β = 22 ° , γ = 36 ° , вычислить равнодействующую силы R и ее углы α R , β R , γ R с осями x, y и z.Силы — это диагонали с каждой стороны прямоугольного параллелепипеда. Шаг 1 . Рассчитайте проекции силы на каждую ось. Пример 3 . В качестве примера возьмем систему сил из упражнения , упражнение 1 и вычислим результирующую силу и ее угол с горизонтальной осью ( O-x ). Чтобы этот метод работал, все углы должны быть привязаны к горизонтальной оси, O-x . Силы и углы следующие: Шаг 1 . Вычислите горизонтальную составляющую результирующего Наблюдение: если расчет выполняется на портативном калькуляторе программного приложения, аргумент функции cos () должен быть указан в радианах, например: Шаг 2 . {2} + 1.{\ circ} \] Этот метод можно распространить на любое количество сил, если известны значения сил и углы. Вы также можете проверить свои результаты с помощью калькулятора ниже. Используйте калькулятор выше, чтобы вычислить и оценить различное распределение сил. Наведя указатель мыши на линейные силы, вы можете увидеть их координаты, которые представляют компоненты F x [N] и F y [N]. Не забывайте ставить лайки, делиться и подписываться! Для любой точки вытянутого тела, если на это тело действует сила, которая не проходит через эту точку, то эта сила вызовет момент вокруг этой точки.Как уже говорилось на странице моментов, момент — это тенденция силы вызывать вращение. Альтернативой вычислению момента с помощью скалярных величин является использование векторного метода или метода перекрестного произведения . Для простых двумерных задач обычно проще использовать скалярные величины, но для более сложных задач обычно проще использовать метод перекрестного произведения. Метод перекрестного произведения для вычисления моментов гласит, что вектор момента силы вокруг точки будет равен перекрестному произведению вектора r от точки до любой точки на линии действия силы и самого вектора силы. Большим преимуществом этого метода является то, что r не обязательно должно быть кратчайшим расстоянием между точкой и линией действия, оно идет от точки до любой части линии действия. Для любой проблемы существует множество возможных векторов r , хотя из-за того, как работает кросс-произведение, все они должны в конечном итоге привести к одному и тому же вектору момента. Здесь важно отметить, что все величины ( r , F и M ) являются векторами. Прежде чем вы сможете решить для кросс-продукта, вам нужно будет записать r и F в форме векторных компонентов. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента векторов r и F . Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для вычислений. Полученный вами вектор момента будет совмещен с осью вращения на данный момент, где вы можете использовать правило правой руки, чтобы определить, движется ли момент по этой оси по часовой стрелке или против часовой стрелки. Наконец, важно также отметить, что перекрестное произведение, в отличие от умножения, не является коммуникативным. Это означает, что порядок векторов имеет значение, и r пересечение F не будет таким же, как F пересечение r . При расчете моментов важно всегда использовать r крест F . Синонимайзер Sinoni.men сделает уникальность вашего текста 20-100% без потери смысла в предложениях. Наш сервис может делать текст уникальным за считанные секунды. Вам нужно только отправить нам свой текст, размером от 100 до 1 100 символов (бесплатно) в порядке очереди, либо без ограничения символов и без очереди от 4 руб / 1 000 символов и через несколько секунд вы получите этот же текст по смысловому содержанию, написанному другими словами. Сервис не допускает граматических ошибок, однако синтаксические несоответствия могут попадаться. Уникальность вашего текста на выходе зависит от многих факторов, включая наличие в тексте большого числа имён, кличек животных, названия городов и тому подобные слова и словосочетания, у которых нет синонимов. Перефразировать текст для того, чтобы он смотрелся на вашем сайте как авторский уникальный текст, вы можете с помощью Sinoni.men. Наш сервис может работать на множестве языках и одинаково хорошо справляется с задачей перефразировки на каждом из них. Вы можете подать на вход нашему сервису текст на таких языках как, русский и английский. Если у вас есть сервис или сайт которому нужны большие объемы уникального текста или вы хотите автоматизировать поступление уникального текста на ваш сайт, для этого нас есть собственное API. Все настройки вы можете произвести в вашей панели управления (после регистрации), а вся подробная инструкция по эксплуатации находится в документации. Если у вас в процессе изучения и тестирования API возникнут проблемы или вопросы, вы всегда можете связаться с нами по контактным данным на странице. В век высоких технологий, найти статью которая была скопирована с другого ресурса, дело одной минуты. Поэтому при написании дипломов, курсовых работ, рефератов ученикам нужно быть предельно внимательным, чтобы их работа не была забракована из-за того, что преподаватель увидит в ней копипаст. С задачей повышения уникальности статьи поможет вам справиться сервис Синони.мен. Просто скопируйте текст из вашего реферата в форму и запустите рерайтинг. Через несколько секунд вы получите этот же по смыслу текст, но написанный другими словами. За счет этого его уникальность повышается и учитель не заподозрит вас в плагиате. Однако как вы сами понимаете, всё делается автоматически, поэтому ручная проверка и исправление неточностей обязательна. Двойной рерайтинг повышает уникальность на несколько десятков пунктов. При первой обработке текста сразу следует вторая, при которой на вход поступает уже обработанный рерайт. За счет этого статья получается еще более уникальным по структуре, но иногда полёт мыслей может обрести немного иной смысл. Уникальность каждого рерайта можно сразу проверить на антиплагиат. Для этого у Вас на аккаунте должны быть символы. Для автоматического рерайта, нормальными показателями считается уникальность текста в среднем от 15% до 100%, при двойном рерайтинге, начальный порог увеличивается в 2 раза, от 30% до 100%. sinoni.men Мы принимаем платежи только через WebMoney Merchant. Мы принимаем Яндекс.Деньги на вторичной основе с ручным зачислением на ваш аккаунт в течении суток. Через шлюз Яндекс.Деньги возможно пополнение аккаунта с помощью VISA и MasterCard. Все дополнительные комиссии платежных систем учитываем самостоятельно Для покупки месячного абонемента вам необходимо пополнить внутренний счет на сумму равную или большую цене выбранного абонемента. Затем в личном аккаунте нажать на кнопку «Купить» выбранного абонемента. Абонемент будет выдан мгновенно сроком на 1 календарный месяц. За оплаченный абонемент средства не возвращаются, так как услуга начала предоставляться. В случае, если покупка абонемента произошла по ошибке, необходимо обратиться в службу поддержки [email protected]. Абонемент автоматически продлевается при условии наличия необходимой суммы на внутреннем счете пользователя и активированной опции «Продлевать абонемент автоматически» в свойствах абонемента. Предлагаемые товары и услуги предоставляются не по заказу лица либо предприятия, эксплуатирующего систему WebMoney Transfer. Мы являемся независимым предприятием, оказывающим услуги, и самостоятельно принимаем решения о ценах и предложениях. Предприятия, эксплуатирующие систему WebMoney Transfer, не получают комиссионных вознаграждений или иных вознаграждений за участие в предоставлении услуг и не несут никакой ответственности за нашу деятельность. Аттестация, произведенная со стороны WebMoney Transfer, лишь подтверждает наши реквизиты для связи и удостоверяет личность. Она осуществляется по нашему желанию и не означает, что мы каким-либо образом связаны с продажами операторов системы WebMoney. Также можно обратиться непосредственно к продавцу по E-mail: [email protected] или по Тел. +7 9092355701 synonyma.ru Деятельность по написанию рекламных и презентационных текстов появилась достаточно давно. Специалистов, которые этим занимаются профессионально называют копирайтеры. Современный мир создает новые способы и наилучшие условия для распространения информации. Вместе с этим, относительно недавно появилась профессия рерайтера – специалиста, который переписывает текстовый материал своими словами, сохраняя его смысл. Те, кто пишут исходные тексты, как правило могут делать и рерайты на них. А вот некоторые рерайтеры не занимаются написанием исходных текстов, а только переделывают их. Смысл качественного рерайтинга заключается в том, чтобы представить информацию с разных сторон и не допустить появления однообразных текстов в свободном пространстве Интернета. О востребованности услуги говорит и большое количество вакансий удаленной работы для рерайтеров на фриланс бирже Пчёл.нет. Быть рерайтером не так просто, как может сразу показаться. Для того чтобы писать уникальный текст на основе исходных материалов, следует знать грамматику и лексику, владеть большим словарным запасом и уметь заменять слова, не меняя первоначального значения. Знаете ли вы что: В одной из статей мы уже рассматривали способы создания новых текстов. Напомним, основными методами рерайтинга являются замена слов подходящими по смыслу синонимами, перестановка слов в предложении, уменьшение объема оригинального текста, перевод прямой речи в косвенную и наоборот, перемещение предложений и абзацев, а также многие другие хитрые уловки. Однако эра компьютеров позволяет облегчить рабочий процесс и заниматься рерайтингом с помощью определённых вспомогательных программ, их ещё называют синонимайзеры. Таких программ существует очень много, каждая со своими плюсами и минусами; они могут подходить или не подходить в различных ситуациях. Предлагаем к рассмотрению наиболее, на наш взгляд, оптимальные варианты. А какая из ниже приведённых программ будет помогать создавать качественные тексты – выбирать только вам! SeoGenerator – программа-синонимайзер, позволяющая изменять слова, не меняя смысла предложений. Плюсы: + высокое качество подбора синонимов; + выбор определённого шаблона; + возможность работы как онлайн, так и офлайн; + возможность работы с большими текстами; + бесплатное пользование. Как мы видим, данная программа оптимизирована для постоянного пользования и имеет огромное количество функций, которые заинтересуют каждого рерайтера! ReWrite Suite – универсальная программа для упрощения процесса рерайтинга. Плюсы: + указывается количество времени, потраченного на написание статьи; + указывается количество знаков с пробелами и без; + фиксация количества слов. В платной версии программы доступны следующие функции: можно найти похожие слова, сравнить текст с оригинальным, изменить цвет окон и размер шрифта. Минусы: — нейтральное оформление программы (хотя многие постоянные пользователи считают это плюсом, ведь настоящему профессионалу приходится целиком посвящать себя делу, а не отвлекаться на яркие цвета или рекламу). BIPOD – многофункциональная программа для рерайтинга материалов: Плюсы: + перелинковка (переход на другие ссылки) в тексте; + удобный и простой интерфейс; + встроенный переводчик Google; + постоянное добавление синонимов в базу; + доступ к синонимайзеру М1Pluss; + встроенный публикатор WordPress. Минусы: — ограничение по обработке: в бесплатной версии возможно обработать всего лишь 500 знаков; — приобретение серийного номера для активации программы. Это приложение будет очень полезным для тех, кто не хочет тратить время на постоянное сравнение текстов в Интернете, на использование посторонних ресурсов по переводу материла и поиск заменителей тех или иных слов. Кажется, эта программа послужит вам отличным и незаменимым помощником! Удобная Программа для рерайта, названная аналогично. Сделана с любовью. Плюсы: + подсчет использования ключевых фраз в тексте; + отдельное окно для плана работы рерайтера; + наличие 7 вкладок с редакторами; + обзор синонимов для выделенных слов; + поиск необходимых слов; + доступная база синонимов; + история изменений текста; + возможность сохранить документ в программе Microsoft Word; + таймер для учета времени. Расширение и без того огромного количества функций возможно при покупке платной версии. Если же вам для создания вашей качественной и уникальной работы достаточно и этих опций, то бесплатной версии вам будет достаточно! Онлайн-исправление – уникальный инструмент для исправления лексических, грамматических и синтаксических ошибок, а также других видов опечаток. Плюсы: + Существенным плюсом этой онлайн-программы является огромный выбор языков для создания текстов рерайтинга (французский, русский, английский, немецкий, испанский, польский, итальянский). Минусы: — Минусом этой программы, как и многих других, является невозможность полного изменения текста с соблюдением смысла оригинального текста. Если говорить вкратце, то никакой компьютер не сможет понять текст так, как это сделает человек, но все равно сделает всё возможное для улучшения работы рерайтера! После того, как вы воспользовались программами по подбору синонимов, изменению слов и корректированию материала, необходимо свой текст проверить на уникальность. Стоит сказать, что все работодатели требуют различные уровни оригинальность текстов, но они сходятся в одном – она должна быть от 80% и приближена к идеалу в 100%. Для того, чтобы проверить свой текст и убедиться в том, что он является по-настоящему качественным и уникальным, мы вам советуем воспользоваться следующими программами. Advego Plagiatus является одной из наиболее популярных программ для проверки текстов. Она проверяет уникальность указанного URL, показывает степень уникальности текста, ищет его источники и высчитывает процент его совпадения. TEXT.RU – онлайн-сервис, которым мы также советуем вам воспользоваться для проверки текста на уникальность. С его помощью можно проверить оригинальность текста, получить автоматическую проверку орфографии, увидеть схожие рерайты и дубликаты, а также получить процент уникальности текста. Но самым главным является то, что этот сайт бесплатный для всех пользователей и его использование не имеет ограничений! Подробно изучив несколько программ-ассистентов рерайтеров, мы видим, что современные технологии позволяют нам заниматься любимым делом и существенно облегчать рабочий процесс. Надеемся, мы помогли вам выбрать свою наилучшую программу для рерайтинга, с помощью которой вам будет работаться удобней и легче! Если вы ещё не пробовали зарабатывать создавая оригинальные и уникальные тексты или уже являетесь в этом профессионалом, то присоединяйтесь к специалистам на Polyglot’e, регистрируйтесь и подавайте заявки на выполнение заказов. 2polyglot.com Для этого воспользуйтесь командой Сократить на страницу. Приложение Word сократит документ на одну страницу, уменьшив размер шрифта и значения интервалов в тексте. Например, документ из примера выше будет сокращен до 1 страницы, а документ, состоящий из 3 страниц, можно сократить до 2.
Совет: Перед использованием этой команды создайте копию документа. Для сокращения Word уменьшит размер каждого использованного в документе шрифта. Отменить команду можно нажатием сочетания клавиш CONTROL + Z. Обратите внимание, что после сохранения и закрытия документа быстро восстановить исходный размер шрифта невозможно. Команда » уменьшить на одной странице » не является часто используемой командой, поэтому она не отображается по умолчанию. Однако вы можете быстро добавить его. Самый быстрый способ добавить кнопку — Добавить ее на панель быстрого доступа. На панели быстрого доступа в верхней части окна Word нажмите Настроить панель быстрого доступа (маленькая стрелка вниз) и выберите пункт Другие команды.
В списке Выбрать команды из: выберите пункт Все команды.
Найдите в списке команд Сократить на страницу. Щелкните команду Сократить на страницу, чтобы выбрать ее, а затем нажмите кнопку Добавить.
Нажмите ОК. Когда кнопка станет доступной, нажмите на нее для сокращения текста.
Нажмите кнопку изменить документВеб-приложение Wordизменить в #a0 , если это еще не сделано. Нажмите клавиши CTRL + A, чтобы выделить весь текст в документе. Щелкните главная > уменьшить размер шрифта один или несколько значений.
При нажатии кнопки » уменьшить шрифт» в Word уменьшается размер каждого шрифта в документе. Нажмите кнопку просмотр > режим чтения , чтобы узнать, достаточно ли ты Шранк текст.
Совет: Если это не поможет и у вас есть программа Word для настольных компьютеров, нажмите кнопку Открыть в Word , чтобы открыть документ в Word и Сжать текст в соответствии с ними. support.office.com P.S:. Включи флеш, если сервис «загрузиться забыл» 🙂 Синонимайзер ”Синоним+” – это лучший синонимайзер онлайн текста бесплатно.Сервис может оказаться полезным как рерайтерам на бирже текстов, так и веб-мастерам. Используйте сочетание клавиш Ctrl+A, чтобы выделить весь текст. Программа синонимайзер онлайн “Синоним Плюс” в рамках одной сессии запоминает новые синонимы и ”забывает” неудачные варианты замен. Для того, чтобы она это делала, используйте специальные кнопки (добавить/удалить синоним) в списке синонимов для каждого слова. Синонимайзер онлайн бесплатно без регистрации делает текст более уникальным. Подобные тексты встречаются на бирже копирайтинга. В конце работы программа выдает приблизительную оценку уникальности в процентах. Рекомендуется узнать точное значение уникальности, проверив текст в одной из программ. О том, какая из программ проверки текста на уникальность лучше, было рассказано в предыдущей статье. Онлайн синонимайзер текста расположен вверху этой страницы (над описанием его функций). text-stati.ru – Все норм, спс! – Пжлст. Такие переписки в телефоне и социальных сетях уже никого не удивят. Но сокращения в английском языке пошли еще дальше наших: аббревиатурой становятся целые предложения! Пример: MYOB = mind your own business (занимайтесь своим делом) Ниже ты найдешь целый список английских сокращений (в смс, социальных сетях, форумах). Досконально изучи его, чтобы понимать, чего от тебя хотят англоговорящие собеседники. Разумеется, сокращения английских слов желательно использовать только в неформальной переписке (личные сообщения, чаты). При этом известен случай, когда 13-летняя девочка написала школьное сочинение, почти целиком построенное на аббревиатурах английского языка. Вот отрывок из него, попробуй прочитать и понять смысл написанного: My smmr hols wr CWOT. B4, we used 2go2 NY 2C my bro, his GF & thr 3 :- kids FTF. ILNY, it’s a gr8 plc. Получилось? А теперь прочитай “перевод”: My summer hols (сокращенное – holidays) were a complete waste of time. Before, we used to go to NY (New York) to see my brother, his girlfriend and their 3 kids face to face. I love New York, it’s a great place. Как видишь, английские сокращения на письме построены: Итак, переходим к нашему словарю английских сокращений. В статье будет указан перевод сокращений с английского на русский. Но там, где потребуются дополнительные разъяснения, мы дадим и их. Enjoy! & = and (и) 0 = nothing (ничего) 2 = two, to, too (два, предлог to, тоже) 2DAY = today (сегодня) 2MORO / 2MROW = tomorrow (завтра) 2NITE / 2NYT = tonight (сегодня ночью, сегодня вечером) 2U = to you (тебе) 4U = for you (для тебя) 4E = forever (навсегда) AFAIK= as far as I know (насколько мне известно) ASAP = as soon as possible (при первой возможности, как только – так сразу) ATB = all the best (всего наилучшего) Также читайте: Где смотреть сериалы на английском: список бесплатных сайтов B = to be (быть) B4 = before (до, прежде чем) B4N = bye for now (пока, до встречи) BAU = business as usual (идиома, означающая, что дела продолжают идти, как обычно, несмотря на сложную ситуацию) BBL = to be back later (вернуться позже, быть позже) BC = because (потому что) BF = boyfriend (молодой человек, парень, бойфренд) BK = back (назад, обратно) BRB = to be right back (скоро вернуться). Например, ты “чатишься” с кем-то, но вынужден ненадолго отойти. BRB (скоро вернусь), – пишешь ты, и идешь по своим делам. BRO = brother (брат) BT = but (но) BTW = by the way (кстати, между прочим) BYOB / BYO = to bring your own booze, to bring your own bottle (“со своим алкоголем”). Указывается на приглашении в том случае, когда хозяин вечеринки не будет предоставлять выпивку для гостей. Кстати, у группы System Of A Down есть песня B.Y.O.B. (Bring Your Own Bombs вместо Bottle). Текст песни читай здесь. C = to see (видеть) CIAO = goodbye (до свидания, пока). Это сокращение для переписки в английском языке образовалось от итальянского Ciao (и произносится оно именно так – чао). COS / CUZ = because (потому что) CUL8R = call you later / see you later (позвоню тебе позже / увидимся позже) CUL = see you later (увидимся позже) CWOT = complete waste of time (пустая трата времени) D8 = date (дата, свидание) DNR = dinner (ужин) EOD = end of debate (конец дискуссии). Используется во время спора, когда хочется его прекратить: That’s it, EOD! (Все, прекратим спор!) EZ = easy (легко, просто, удобно) F2F / FTF = face to face (лицом к лицу) F8 = fate (судьба) FYI = for your information (к твоему сведению) Также читайте: 33 лучших британских сленговых слова GF = girlfriend (девушка, герлфренд) GMTA = great minds think alike (поговорка “Великие умы мыслят одинаково”). Что-то вроде нашего “у дураков мысли сходятся” только наоборот 🙂 GR8 = great (замечательно, отлично и т.д.) GTG = got to go (должен идти) HAND = have a nice day (хорошего дня) HB2U = happy birthday to you (с днем рождения) HOLS = holidays (каникулы, отпуск) HRU = how are you (как ты? как дела?) HV = to have (иметь) ICBW = it could be worse (могло быть хуже) IDK = I dont know (я не знаю) IDTS = I don’t think so (я так не думаю, не думаю, не согласен) ILU / Luv U = I love you (я люблю тебя) IMHO = in my humble opinion (по моему скромному мнению). Выражение уже давно перекочевало в наш интернет в виде транслитерации ИМХО. IYKWIM = if you know what I mean (если ты понимаешь, о чем я) JK = just kidding (просто шучу, это шутка) KDS = kids (дети) KIT = to keep in touch (оставаться на связи) KOTC = kiss on the cheek (поцелуй в щеку) L8 = late (поздно, недавно, за последнее время) L8R = later (позже) LMAO = laughing my ass out (так смешно, что пятую точку себе “отсмеял”). LOL = laughing out loud (значение идентично предыдущему). Это популярное английское сокращение тоже позаимствовано нашим интернетным сленгом в виде транслитерации ЛОЛ. LSKOL = long slow kiss on the lips (французский поцелуй) LTNS = long time no see (давно не виделись) Luv U2 = I love you too (тоже люблю тебя) M8 = mate (приятель, друг, чувак). Сленговое слово mate – примерно то же самое, что dude (чувак, пацан и т.д.): Hey, mate, what’s up? (Эй, чувак, как оно?) MON = the middle of nowhere (идиома, означающая “очень далеко, у черта на куличках”) MSG = message (сообщение, послание) MTE = my thoughts exactly (ты читаешь мои мысли, я думаю точно так же) MU = I miss you (скучаю по тебе) MUSM = I miss you so much (скучаю по тебе очень сильно) MYOB = mind your own business (занимайся своим делом, не лезь в чужие дела) N2S = needless to say (само собой разумеется, очевидно что…) NE1 = anyone (кто угодно, любой) NO1 = no one (никто) NP = no problem (без проблем, не проблема) OIC = oh, I see (понятно; вот оно что). Используется в ситуации, когда ты хочешь показать собеседнику, что тебе понятен предмет разговора. PC&QT – peace and quiet (тишина и покой). Идиома, которая чаще всего используется в контексте желания более спокойной жизни: All I want is a little peace and quiet (Все, что я хочу – немного тишины и покоя). PCM = please call me (пожалуйста, позвони мне) PLS = please (пожалуйста) PS = parents (родители) QT = cutie (милашка) R = are (форма глаголы to be) ROFL / ROTFL = rolling of the floor laughing (катаюсь по полу от смеха) RUOK = are you ok? (ты в порядке? все хорошо?) SIS = sister (сестра) SKOOL = school (школа) SMMR = summer (лето) SOB = stressed out bad (чувствовать сильный стресс) SOM1 = someone (кто-то) TGIF = thank God it’s Friday (Слава Богу, сегодня пятница) THX = thanks (спасибо) THNQ = thank you (спасибо тебе) TTYL = talk to you later (поговорим позже) Также читайте: Список устойчивых выражений в английском языке U = you (ты) WAN2 = to want to (хотеть) WKND = weekend (выходные) WR = were (форма глагола to be) WUCIWUG = what you see is what you get (что видишь, то и получишь) Выражение имеет несколько значений: Может использоваться, как определение честного и открытого человека: He is a what-you-see-is-what-you-get kind of person. (Он относится к типу человека “что видишь, то и получишь”) Также идиомой могут пользоваться, например, продавцы в магазине, когда уверяют нас, что товар, который мы купим, выглядит так же, как и на витрине: The product you are looking at is exactly what you get if you buy it. What you see is what you get. The ones in the box are just like this one. (Если Вы купите этот продукт, то получите именно то, что видите сейчас. Единицы товара, которые в коробках, точно такие же, как эта). X = kiss (поцелуй) XLNT = excellent (отлично, превосходно) XOXO = hugs and kisses (объятия и поцелуи). Точнее сказать “обнимашки и целовашки”, если следовать интернет-трендам 🙂 YR = your / you’re (твой / ты + форма глагола to be) ZZZ.. = to sleep (спать) Сокращение используется, когда человек хочет показать собеседнику, что он уже вовсю спит / засыпает. Как видишь, все английские сокращения в интернете поддаются определенной логике, принципы которой мы разобрали еще в начале статьи. Поэтому достаточно несколько раз “пробежаться по ним глазами”, и ты легко сможешь использовать и, главное – понимать их. CUL8R, M8 🙂 corp.lingualeo.com Влад, ответ на ваш вопрос: убрать лишние слова, риторические вопросы и всё, что противоречит теме. Но это не поможет. Текст фальшивый, без любви и уважения к читателям, без пользы, без интересных фактов. Допустим, вы сократите его. Останется что-то такое:
Мохито появился на Кубе в первой половине XX века. О происхождении названия идут споры: то ли это соус с чесноком, перцем, лимонным соком, зеленью и растительным маслом, то ли «слегка влажный» напиток Расскажите об этом друзьям, когда пойдёте в ресторан Стало чуть менее фальшиво, но теперь очевидно, что текст неинтересный. Из-за этого нелепо смотрится призыв рассказать это друзьям. Вы бы такое не рассказали своим друзьям, и я тоже. А что бы вы рассказали? Я бы рассказал что-то такое:
Говорят, что мохито был любимым напитком Хемингуэя. Это полная чушь. Это миф, который распространили хозяева бара, в котором, якобы, мохито изобрели. И, мол, когда Хемингуэй был на Кубе, он заходил в тот бар и всегда заказывал этот коктейль. На самом деле…
Мохито стал популярен в Америке в эпоху диско. Мята, сахар и лайм маскировали крепость рома, поэтому коктейль хорошо шёл в дискоклубах. У одной группы была даже песня…
А знаете, зачем в мохито дают толстые трубочки? В правильном мохито лёд и мята измельчены до такого состояния, чтобы иногда попадать в трубочку и не застревать в ней. Потому что…
Вообще-то, готовить мохито на «Спрайте» неправильно. В правильном мохито используют только содовую с тростниковым сахаром. Но если их плохо размешать, мохито получится несладкий.
На самом деле, В мохито нельзя класть лёд кубиками. Правильно перемалывать его в ступе или на блендере, причём следить, чтобы лёд не превращался в кашу. Тогда…
Классический мохито делают с ромом таким-то, который, кстати, делают не на Кубе, а в Португалии. Но изначально в мохито добавляли местный кубинский ром такой-то, который давал большую крепость и характерный привкус. Теперь подумаем, как в этих разговорах рекламировать ресторан. На поверхности подход про мастерство бармена, который знает всё про мохито и соблюдает исходную рецептуру. Но не нужно, чтобы он обманом заманивал нас в ресторан. Пусть рассказывает про тонкости приготовления мохито и в конце добавляет что-то такое: Сделайте читателю подарок: расскажите, как приготовить хороший мохито дома из простых ингредиентов, добавив в конце, что в ресторане Другой вариант подарка: расскажите, где в вашем городе взять нормальную мяту для мохито. Где взять свежую мяту для мохито
Для традиционного мохито нужна свежая мята с кустов. В Москве её достать непросто: часто встречается подгнивающая мята в пластиковых лотках или совсем пресная мята из Турции. В ресторане Свежую мяту можно брать в «Азбуке вкуса» на Якиманке, в любом В «Азбуке» мята есть всегда, но следует выбирать самую живую на вид. Осторожно, иногда попадаются пачки с гнилыми листьями.
В «Ашан» мяту завозят во вторник ночью. На рынок в Мытищах — рано утром в пятницу. Мы стараемся брать в Мытищах, там мята всегда самая свежая.
Мята хранится не больше недели, если поставить её в воду и хранить в холодильнике. Тогда листья и стебли будут сочными и ароматными. Не храните мяту в целлофане: она активно отдаёт влагу и в целлофане мгновенно загнивает.
В следующих постах — о том, как выбирать правильные лаймы и ром для мохито.
Хесус Борачо, Я не верю, что в соцсетях нужно обязательно публиковать короткие тексты. Интересные — да, полезные — да. Если сообщение не помещается в технологические ограничения, можно ведь дать ссылку на сайт. Когда мне интересно, я кликну и почитаю. bureau.ru |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например, вычислите логарифм: а) \(\log_{4}{16}\) б) \(\log_{3}\)\(\frac{1}{3}\) в) \(\log_{\sqrt{5}}{1}\) г) \(\log_{\sqrt{7}}{\sqrt{7}}\) д) \(\log_{3}{\sqrt{3}}\)
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
\(\log_{4}{16}=2\)
б) В какую степень надо возвести \(3\), чтобы получить \(\frac{1}{3}\)? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).
\(\log_{3}\)\(\frac{1}{3}\)\(=-1\)
в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
\(\log_{\sqrt{5}}{1}=0\)
г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе.
\(\log_{\sqrt{7}}{\sqrt{7}}=1\)
д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt{3}\)? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень \(\frac{1}{2}\).
\(\log_{3}{\sqrt{3}}=\)\(\frac{1}{2}\)
Пример: Вычислить логарифм \(\log_{4\sqrt{2}}{8}\)
Решение:
|
\(\log_{4\sqrt{2}}{8}=x\) |
Нам надо найти значение логарифма, обозначим его за икс. |
|
|
\(\log_{4}{10}=5x-4\) |
Зеркально перевернем уравнение, чтобы икс был слева |
|
|
\(5x-4=\log_{4}{10}\) |
Перед нами линейное уравнение. Перенесем \(4\) вправо.
И не пугайтесь логарифма, относитесь к нему как к обычному числу. |
|
|
\(5x=\log_{4}{10}+4\) |
Поделим уравнение на 5 |
|
|
\(x=\)\(\frac{\log_{4}{10}+4}{5}\) |
|
Вот наш корень. |
Ответ: \(\frac{\log_{4}{10}+4}{5}\)
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).
То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\), где \(a\) — некоторое число.
Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).
То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\), где \(a\) — некоторое число. {2}=25\)
{2}=25\)
Ответ готов.
Ответ: \(25\)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).
Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается
\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:
\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…\)
И с четверкой:
\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…\)
И с минус единицей:
\(-1=\) \(\log_{2}\)\(\frac{1}{2}\)\(=\) \(\log_{3}\)\(\frac{1}{3}\)\(=\) \(\log_{4}\)\(\frac{1}{4}\)\(=\) \(\log_{5}\)\(\frac{1}{5}\)\(=\) \(\log_{6}\)\(\frac{1}{6}\)\(=\) \(\log_{7}\)\(\frac{1}{7}\)\(…\)
И с одной третьей:
\(\frac{1}{3}\)\(=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…\)
И так далее.
Любое число \(a\) может быть представлено как логарифм с основанием \(b\): \(a=\log_{b}{b^{a}}\)
Пример: Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
Решение:
|
\(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)\(=\) |
Превращаем единицу в логарифм с основанием \(2\): \(1=\log_{2}{2}\) |
|
|
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}\)\(=\) |
Теперь пользуемся свойством логарифмов: |
|
|
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}\)\(=\)\(\frac{\log_{2}{14}}{\log_{2}{14}}\)\(=\) |
В числителе и знаменателе одинаковые числа – их можно сократить. |
|
|
\(=1\) |
Ответ готов. |
Ответ: \(1\)
Смотрите также:
Логарифмические уравнения
Логарифмические неравенства
Функция LOG — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции LOG в Microsoft Excel.
Описание
Возвращает логарифм числа по заданному основанию.
Синтаксис
LOG(число;[основание])
Аргументы функции LOG описаны ниже.
-
Число Обязательный. Положительное вещественное число, для которого вычисляется логарифм.
-
Основание Необязательный. Основание логарифма. Если аргумент «основание» опущен, предполагается, что он равен 10.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=LOG(10) |
Логарифм числа 10. |
1 |
|
=LOG(8; 2) |
Логарифм числа 8 по основанию 2. Результат (3) — степень, в которую необходимо возвести основание, чтобы получить число 8. |
3 |
|
=LOG(86; 2,7182818) |
Логарифм числа 86 по основанию e (приблизительно 2,718). Результат (4,454) — степень, в которую необходимо возвести основание, чтобы получить число 86. |
4,4543473 |
11.
 4.9.6. Формула представления любого числа в виде логарифма.
4.9.6. Формула представления любого числа в виде логарифма.Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 3.1k. Опубликовано
p=logaap Любое число можно представить в виде логарифма по любому основанию.
Под знаком логарифма могут находиться только положительные числа, причем, основание логарифма не равно единице.
Примеры.
I. Представить число 2 в виде логарифма по основанию: 1) 3; 2) 5; 3) 10.
Решение.
1) 2=log33²=log39;
2) 2=log55²=log525;
3) 2=lg10²=lg100.
II. Представить в виде десятичного логарифма числа: 1) -1; 2) -2; 3) -3.
Решение.
1) -1=lg10—1=lg0,1;
2) -2=lg10-2=lg0,01;
3) -3=lg10-3=lg0,001.
Решить уравнение:
1) lg (x-9)+lg (2x-1)=2.
Решение.
lg ((x-9)(2x-1))=lg102; представили сумму логарифмов в виде логарифма произведения и число 2 в правой части равенства записали в виде десятичного логарифма (логарифма с основанием 10).
lg (2x2-18x-x+9)=lg100; упростили выражения под знаками логарифмов.
2x2-19x+9=100; получили после потенцирования.
2x2-19x-91=0. Получили квадратное уравнение вида: ax2+bx+c=0.
a=2, b=-19, c=-91. Решим квадратное уравнение по общей формуле.
D=b2-4ac=(-19)2-4∙2∙(-91)=361+728=1089=332>0; два действительных корня:
Проверка. Значение х=-3,5 не удовлетворяет условию существования логарифма.
Значение х=-3,5 не удовлетворяет условию существования логарифма.
Проверяем данное равенство при х=13.
lg (13-9)+lg (2∙13-1)=2;
lg4+lg25=2;
lg (4∙25)=2;
lg100=2;
2=2.
Ответ: 13.
2) log3(x+1)+log3(x+3)=1.
Решение.
Сумму логарифмов заменим логарифмом произведения, единицу в правой части представим в виде логарифма с основанием 3:
log ((x+1)(x+3))=log33;
log (x2+x+3x+3)=log33. Потенцируем:
x2+4x+3=3;
x2+4x=0;
x (x+4)=0;
x=0 или x+4=0, отсюда x=-4.
Анализируем результаты:
х=-4 не подойдет, так как при этом значении под знаком логарифма окажутся отрицательные числа, что недопустимо.
Проверим значение х=0.
Проверка.
log3(0+1)+log3(0+3)=1;
log31+log33=1;
0+1=1;
1=1.
Ответ: 0.
Натуральный логарифм, формулы и онлайн калькуляторы
Содержание:
Для различного рода теоретических и практических исследований наиболее удобным
основанием логарифма
является иррациональное число $e$. {2 n}}{n}+\ldots, |x| \lt 1$
{2 n}}{n}+\ldots, |x| \lt 1$
Читать дальше: десятичный логарифм.
log3 x 3 2
Вы искали log3 x 3 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и лог 3 х 3 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «log3 x 3 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как log3 x 3 2,лог 3 х 3 2,найдите корень уравнения log 3 x 3 2,найдите корень уравнения log3 3 x 3,найдите корень уравнения log3 x 3 2. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и log3 x 3 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найдите корень уравнения log 3 x 3 2).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и log3 x 3 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найдите корень уравнения log 3 x 3 2).
Где можно решить любую задачу по математике, а так же log3 x 3 2 Онлайн?
Решить задачу log3 x 3 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Рабочая тетрадь по математике. Логарифмы. Свойства логарифмов.
государственное автономное профессиональное образовательное учреждение
Саратовской области
«Саратовский колледж кулинарного искусства»
О. В. Улитина
преподаватель математики ГАПОУ СО СККИ
РАБОЧАЯ ТЕТРАДЬ ПО МАТЕМАТИКЕ
Логарифмы. Свойства логарифмов.
Учебное пособие для студентов ОУ СПО
по учебной дисциплине «Математика» Математика
2017 г
АННОТАЦИЯ
В данном пособии представлен раздел математики 1 курса «Логарифмы.
Свойства логарифмов» в учреждениях среднего профессионального
образования. При изучении данного раздела студентами появляется множество
проблем, которые связаны не только со слабой базовой подготовкой студентов
по основным темам школьного курса, но и с недостаточностью упражнений,
предлагаемых учебниками.
Необходимо увеличить количество упражнений, тестов решаемых
студентами на уроках для лучшего понимания раздела. В данном учебном
пособии представлены упражнения, разработанные по принципу «от простого к
сложному», позволяющие решить проблемы количества упражнений и качества
знаний по данному разделу. Решение задач является одним из видов учебной
работы обучающихся. Поэтому основные цели создания данного пособия:
самостоятельности,
систематизация и закрепление теоретических знаний и практических
умений обучающихся;
углубление и расширение теоретических знаний, формирование умений
использовать справочную документацию и дополнительную литературу;
развитие познавательных способностей и активности обучающихся,
творческой инициативы,
ответственности и
организованности;
формирование самостоятельного мышления.
В. Улитина
преподаватель математики ГАПОУ СО СККИ
РАБОЧАЯ ТЕТРАДЬ ПО МАТЕМАТИКЕ
Логарифмы. Свойства логарифмов.
Учебное пособие для студентов ОУ СПО
по учебной дисциплине «Математика» Математика
2017 г
АННОТАЦИЯ
В данном пособии представлен раздел математики 1 курса «Логарифмы.
Свойства логарифмов» в учреждениях среднего профессионального
образования. При изучении данного раздела студентами появляется множество
проблем, которые связаны не только со слабой базовой подготовкой студентов
по основным темам школьного курса, но и с недостаточностью упражнений,
предлагаемых учебниками.
Необходимо увеличить количество упражнений, тестов решаемых
студентами на уроках для лучшего понимания раздела. В данном учебном
пособии представлены упражнения, разработанные по принципу «от простого к
сложному», позволяющие решить проблемы количества упражнений и качества
знаний по данному разделу. Решение задач является одним из видов учебной
работы обучающихся. Поэтому основные цели создания данного пособия:
самостоятельности,
систематизация и закрепление теоретических знаний и практических
умений обучающихся;
углубление и расширение теоретических знаний, формирование умений
использовать справочную документацию и дополнительную литературу;
развитие познавательных способностей и активности обучающихся,
творческой инициативы,
ответственности и
организованности;
формирование самостоятельного мышления. Содержание учебного пособия соответствует образовательным стандартам
профессионального образования и может быть использовано для различных
специальностей и профессий. В данном пособии представлены упражнения,
тесты, задания, которые автор в течение многих лет использовала на своих
уроках и полученные результаты позволяют сделать следующий вывод:
используемые упражнения помогают студентам восстановить пробелы в знаниях
по темам «Степени», «Корни» и понять темы «Логарифмы», «Свойства
логарифмов». Пособие содержит как небольшой теоретический материал для
изучения тем раздела, так и решенные примеры в качества образца.
.
2 Математика
ЛОГАРИФМ
Операцию нахождения логарифма числа называют логарифмированием. Эта
операция является обратной по отношению к возведению в степень с соответствующим
основанием.
Определение логарифма
Логарифмом числа b по основанию a, где a > 0, a ≠ 1, называется показатель
степени, в которую надо возвести число a, чтобы получить b:
log
a
b
b
a
x
x
при a > 0, a ≠ 1, b > 0.
Содержание учебного пособия соответствует образовательным стандартам
профессионального образования и может быть использовано для различных
специальностей и профессий. В данном пособии представлены упражнения,
тесты, задания, которые автор в течение многих лет использовала на своих
уроках и полученные результаты позволяют сделать следующий вывод:
используемые упражнения помогают студентам восстановить пробелы в знаниях
по темам «Степени», «Корни» и понять темы «Логарифмы», «Свойства
логарифмов». Пособие содержит как небольшой теоретический материал для
изучения тем раздела, так и решенные примеры в качества образца.
.
2 Математика
ЛОГАРИФМ
Операцию нахождения логарифма числа называют логарифмированием. Эта
операция является обратной по отношению к возведению в степень с соответствующим
основанием.
Определение логарифма
Логарифмом числа b по основанию a, где a > 0, a ≠ 1, называется показатель
степени, в которую надо возвести число a, чтобы получить b:
log
a
b
b
a
x
x
при a > 0, a ≠ 1, b > 0. Например:
2
2
5
3
log
25
9
16
log
log
3
2
4
2
25
2
2
16
5
9
4
Задание1: Запишите с помощью логарифма
1
2
1)3
3
3
5
7)32
8)3
2)2
3)4
1
8
16
2;
9;
3
2
1
2
1
5
;
2
1
;
5)9
3;
0
6)7
1
4)5
1
25
;
3
10)81
4
27;
11)32
8;
2
3
9
9)27
12)125
2
3
25
Задание 1
3 Математика
Задание 2: Запишите в виде степенного выражения
1) log
1
81
4)log 16
3
1
2
4;
4;
2) log 256 4;
4
5) log 729 3;
9
3) log 343 3;
7
6) log 1 0;
14
7) log
9
16
3
4
2;
8) log
7
4
7
1
4
;
9) log
13
3
2
13
2
3
;
10) log 32 5
2
Определение логарифма можно записать на математическом языке
следующим образом:
, где
a
,0
a
,1
b
0
.
, где
к
a
,0
a
,1
b
0
к
log
a
b
a
b
Задание 2
, к0
a
log
ba
b
Полученное равенство называется основным логарифмическим тождеством.
Если основное логарифмическое тождество усложнить, то получим формулу:
4 Математика
log 5
12
Задание 3: Найдите значение выражения
1)12
6)9
3) 2
8)7
;
2log 11
2)4
7)11
log 6
;
3log 6
11
4)8
2log 4
log 7
2
7
;
;
;
;
4
9
log 13
8
9)6
;
4log 3
6
5)5
;
5
log 11
;
10)3
5log 2
.
Например:
2
2
5
3
log
25
9
16
log
log
3
2
4
2
25
2
2
16
5
9
4
Задание1: Запишите с помощью логарифма
1
2
1)3
3
3
5
7)32
8)3
2)2
3)4
1
8
16
2;
9;
3
2
1
2
1
5
;
2
1
;
5)9
3;
0
6)7
1
4)5
1
25
;
3
10)81
4
27;
11)32
8;
2
3
9
9)27
12)125
2
3
25
Задание 1
3 Математика
Задание 2: Запишите в виде степенного выражения
1) log
1
81
4)log 16
3
1
2
4;
4;
2) log 256 4;
4
5) log 729 3;
9
3) log 343 3;
7
6) log 1 0;
14
7) log
9
16
3
4
2;
8) log
7
4
7
1
4
;
9) log
13
3
2
13
2
3
;
10) log 32 5
2
Определение логарифма можно записать на математическом языке
следующим образом:
, где
a
,0
a
,1
b
0
.
, где
к
a
,0
a
,1
b
0
к
log
a
b
a
b
Задание 2
, к0
a
log
ba
b
Полученное равенство называется основным логарифмическим тождеством.
Если основное логарифмическое тождество усложнить, то получим формулу:
4 Математика
log 5
12
Задание 3: Найдите значение выражения
1)12
6)9
3) 2
8)7
;
2log 11
2)4
7)11
log 6
;
3log 6
11
4)8
2log 4
log 7
2
7
;
;
;
;
4
9
log 13
8
9)6
;
4log 3
6
5)5
;
5
log 11
;
10)3
5log 2
. 3
Логарифм по основанию 10 называется десятичным логарифмом и обозначается
,
blg
называется натуральным логарифмом и обозначается
логарифм по основанию
( ee
…)7,2
.
bln
Задание 3
5 Математика
При вычислении логарифмов используется таблица степеней:
10
1024
59049
1
2
3
4
5
6
7
8
9
10
2
4
9
16
25
36
49
64
81
10
0
6
64
729
4096
15625
46656
117649
7
128
2187
16 384
78125
279936
823543
3
8
27
64
125
216
343
512
729
1000
8
256
6561
65 536
390625
1679616
5764801
9
512
19683
262 144
1953125
1007696
4035360
7
5
4
32
16
243
81
1024
256
3125
625
1296
7776
2401 16807
2
3
4
5
6
7
8
9
1
0
Степень (результат логарифмирования)
Таблица квадратов
А 11
26
13
А2 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676
10 48576
9765625
60466176
282475249
1000 000
100 000
10 000
12
21
22
14
23
24
25
18
19
20
15
16
17
Примеры с решениями
1. Вычислите
.
log 2
1
125,0
Решение.
log
2
1
125,0
log
)5,0(
2
3
log
2
3
1
2
log
2
3
2
log3
2
2
.3
Ответ:
.
log 2
1
125,0
3
2.
3
Логарифм по основанию 10 называется десятичным логарифмом и обозначается
,
blg
называется натуральным логарифмом и обозначается
логарифм по основанию
( ee
…)7,2
.
bln
Задание 3
5 Математика
При вычислении логарифмов используется таблица степеней:
10
1024
59049
1
2
3
4
5
6
7
8
9
10
2
4
9
16
25
36
49
64
81
10
0
6
64
729
4096
15625
46656
117649
7
128
2187
16 384
78125
279936
823543
3
8
27
64
125
216
343
512
729
1000
8
256
6561
65 536
390625
1679616
5764801
9
512
19683
262 144
1953125
1007696
4035360
7
5
4
32
16
243
81
1024
256
3125
625
1296
7776
2401 16807
2
3
4
5
6
7
8
9
1
0
Степень (результат логарифмирования)
Таблица квадратов
А 11
26
13
А2 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676
10 48576
9765625
60466176
282475249
1000 000
100 000
10 000
12
21
22
14
23
24
25
18
19
20
15
16
17
Примеры с решениями
1. Вычислите
.
log 2
1
125,0
Решение.
log
2
1
125,0
log
)5,0(
2
3
log
2
3
1
2
log
2
3
2
log3
2
2
.3
Ответ:
.
log 2
1
125,0
3
2. Вычислите
Решение.
3
1,0lg
100
.
1,0lg
3
100
lg(
10
3. Вычислите
13
log13
04,0
.
2
3
1
10
)
lg
10
1
3
lg
10
1
3
1
3
.
Решение.
log
13
04,0
13
4. Вычислите
2
1
log
4
10
10
Решение. Т. к. выражение
1
2
log
13
04,0
13
log
13
04,0
1
2
1
2
04,0
04,0
.2,0
13
.
1
log
4
10
log
log
4
4
10
4
, то решение принимает вид:
4lg
6 Математика
2
1
log
4
10
10
100
4lg
10
100
4
.25
Задание 4: Вычислите, используя таблицу степеней
1)log 1024;
2
2)log
3
1
243
;
3)log
1
5
5)log
4
1
256
;
9)log
4
5
13)log
2
4;
1
2
3
;
4
Задание 4
1
625
1
512
;
;
4)log 512;
2
8)log 216;
6
6
7 ;
12)log
6
3
2
6 ;
6)log 729;
1
3
10)log
3
4
5
3 ;
7)log
1
8
11)log
7
14) log
11
1
11
;
15) log
15
5
1
11
;
16)log
7
1
7
3
.
7 Математика
3
1) log
Задание 5: Выберите номер правильного ответа
81
7)3
) log 3 81;
a
b
) log 81 4;
)log 4 3
c
3
4)8
)log 8 512;
a
b
)log 512 3;
)log
c
8 3
512
3
4
4
4
3
8
512
3
81
4
1
64
64;
64;
3
4
)4
a
b
)3
)64
c
243
5
2)3
)log 3 243;
a
b
)log 243 5;
) log 243 3
c
5
3
5
3)log 216 3
6
)3
a
3
)6
b
216;
216;
6
5
10)2
)log 2 32;
a
b
)log 32 5;
) log 32 2
c
32
5
2
5
21
5) log 441 2
2
441;
)21
a
21
441;
)2
b
c
) 441 21
1
49
49;
49;
1
49
)2
a
2
)7
b
6)log
)7
c
7
;
2
7
2
729;
729;
9
8) log 729 3
9
9
)3
a
3
)9
b
3
)729
c
9) log 144 2
12
144;
)12
a
12
144;
b
)2
) 144 12
c
2
20
11) log 400 2
20
400;
)2
a
400;
b
)20
) 400
20
c
2
Задание 5
8 Математика
1.
Вычислите
Решение.
3
1,0lg
100
.
1,0lg
3
100
lg(
10
3. Вычислите
13
log13
04,0
.
2
3
1
10
)
lg
10
1
3
lg
10
1
3
1
3
.
Решение.
log
13
04,0
13
4. Вычислите
2
1
log
4
10
10
Решение. Т. к. выражение
1
2
log
13
04,0
13
log
13
04,0
1
2
1
2
04,0
04,0
.2,0
13
.
1
log
4
10
log
log
4
4
10
4
, то решение принимает вид:
4lg
6 Математика
2
1
log
4
10
10
100
4lg
10
100
4
.25
Задание 4: Вычислите, используя таблицу степеней
1)log 1024;
2
2)log
3
1
243
;
3)log
1
5
5)log
4
1
256
;
9)log
4
5
13)log
2
4;
1
2
3
;
4
Задание 4
1
625
1
512
;
;
4)log 512;
2
8)log 216;
6
6
7 ;
12)log
6
3
2
6 ;
6)log 729;
1
3
10)log
3
4
5
3 ;
7)log
1
8
11)log
7
14) log
11
1
11
;
15) log
15
5
1
11
;
16)log
7
1
7
3
.
7 Математика
3
1) log
Задание 5: Выберите номер правильного ответа
81
7)3
) log 3 81;
a
b
) log 81 4;
)log 4 3
c
3
4)8
)log 8 512;
a
b
)log 512 3;
)log
c
8 3
512
3
4
4
4
3
8
512
3
81
4
1
64
64;
64;
3
4
)4
a
b
)3
)64
c
243
5
2)3
)log 3 243;
a
b
)log 243 5;
) log 243 3
c
5
3
5
3)log 216 3
6
)3
a
3
)6
b
216;
216;
6
5
10)2
)log 2 32;
a
b
)log 32 5;
) log 32 2
c
32
5
2
5
21
5) log 441 2
2
441;
)21
a
21
441;
)2
b
c
) 441 21
1
49
49;
49;
1
49
)2
a
2
)7
b
6)log
)7
c
7
;
2
7
2
729;
729;
9
8) log 729 3
9
9
)3
a
3
)9
b
3
)729
c
9) log 144 2
12
144;
)12
a
12
144;
b
)2
) 144 12
c
2
20
11) log 400 2
20
400;
)2
a
400;
b
)20
) 400
20
c
2
Задание 5
8 Математика
1. 2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
5
1
3
1
5
1
9
1
8
1
2
3
4
Задание6: Выпишите номера примеров, решенных неверно
1)log 27
3
2
2)log 16
0, 4 2
3) log
4)log 125 3
2
5) log 9
4
0,09 2
1
625
2
11) log 36
7)log 729
8)log 16
9) log
10) log
0,2
4
9
2
3
0,3
5
1
6
12) log
0,5
0,125 3
0, 25 2
0,5
6) log
Задание 6
Задание 7. Найдите логарифмы данных чисел по основанию α:
1)25,
, 5
а
5
2)64,
, 2
а
8
3)16,
1
4
, 2
а
2
4)27,
, 3
а
3
5)2,
,1,0
а
4
Задание 7
Задание 8. Заполни таблицу, используя определение логарифма:
a x
N
log
xNa
log10
1000
3
9
Найти х по заданным условиям
Неизвестное
Условие
х
log 3
1 Математика
log 7 х
2
х
log11
2
2
36,0
log
log х
5
2
1
х
4
625
log
log
2
х
х
4
2
log 6
36
log 8
01
log 3
1
81
4
log 3
х
1
343
х125
log 2,0
log 2
log10
х16
х01,0
7 3
4 3
343
1
64
10 2
01,0
1
32 5
2
2
125 3
25
2,0 3
008,0
1 3
3
27
Задание 9. Используя определение логарифма выберите номер правильного ответа:
ВАРИАНТ 1 ВАРИАНТ 2
10 Математика
4
;
x
1)log
)
b x
)
a x
1
64
3;
1
3
)
c x
3
5
2)3
243
) log 3 243;
a
) log 243 5;
b
) log 243 3
c
3)log 25
2
)
a x
)
b x
3
5
5
;
)
c x
x
5;
5;
1
5
5
)
d x
4)log
x
3
6
)
a x
18;
)
b x
2;
)
c x
216;
9
)
d x
5)log
x
7
14;
)
a x
)
49;
b x
1
49
)
c x
;
2
2
2
6)log 144
12
)12
144;
a
12
144;
)2
b
c
) 144 12
1
225
x
7) log
)
a x
)
b x
15
;
2;
1
2
2
512
3
)
c x
3
8)8
) log 8 512;
a
) log 512 3;
b
)log
c
9)log 64
)
a x
)
b x
8 3
512
2
8
6
;
)
c x
x
8;
8;
1
8
8
)
d x
10) log
x
2
12;
)
a x
)
3;
b x
64;
)
c x
)
8
d x
11) log
x
13
26;
)
a x
)
169;
b x
1
169
)
c x
;
2
12) log 441 2
21
2
441;
)2
a
1
21
441;
)2
b
) 441
21
c
x
2
1) log
3
4
4
;
81
)
b x
)
a x
1
256
4;
1
4
)
c x
4
4
2)3
81
)log 3 81;
a
)log 81 4;
b
) log 4 3
c
3) log 36
x
)
6;
a x
)
6;
b x
1
6
6
)
d x
x
3
4)log
7
21;
)
a x
10;
)
b x
343;
)
c x
5) log
x
11
22;
)
a x
121;
)
b x
1
121
)
c x
)
c x
;
;
2
6)log 243 3
9
9
243;
a
)3
3
2
b
43;
)9
3
)243
c
9
x
;
)
b x
)
a x
7) log
1
5
125
3;
1
3
)
c x
3
5
8)2
32
)log 2 32;
a
)log 32 5;
b
)log 32 2
c
9) log 484
)
a x
)
b x
x
22;
22;
1
22
)
c x
;
5
2
5
2
2
22
)
d x
10)log
x
25
)
a x
27;
)
b x
50;
)
c x
625;
23
)
d x
11)log
x
17
)
a x
34;
)
289;
b x
1
289
)
c x
;
20
12)log 400
20
400;
)2
a
)20
400;
b
) 400
c
20
2
2
2
Ответы запишите в таблицу:
1
5
3
4
2
6
7
8
9
10
11
12
11 Математика
Для всех свойств логарифмов выполняются соответствующие условия:
СВОЙСТВА ЛОГАРИФМОВ
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
5
1
3
1
5
1
9
1
8
1
2
3
4
Задание6: Выпишите номера примеров, решенных неверно
1)log 27
3
2
2)log 16
0, 4 2
3) log
4)log 125 3
2
5) log 9
4
0,09 2
1
625
2
11) log 36
7)log 729
8)log 16
9) log
10) log
0,2
4
9
2
3
0,3
5
1
6
12) log
0,5
0,125 3
0, 25 2
0,5
6) log
Задание 6
Задание 7. Найдите логарифмы данных чисел по основанию α:
1)25,
, 5
а
5
2)64,
, 2
а
8
3)16,
1
4
, 2
а
2
4)27,
, 3
а
3
5)2,
,1,0
а
4
Задание 7
Задание 8. Заполни таблицу, используя определение логарифма:
a x
N
log
xNa
log10
1000
3
9
Найти х по заданным условиям
Неизвестное
Условие
х
log 3
1 Математика
log 7 х
2
х
log11
2
2
36,0
log
log х
5
2
1
х
4
625
log
log
2
х
х
4
2
log 6
36
log 8
01
log 3
1
81
4
log 3
х
1
343
х125
log 2,0
log 2
log10
х16
х01,0
7 3
4 3
343
1
64
10 2
01,0
1
32 5
2
2
125 3
25
2,0 3
008,0
1 3
3
27
Задание 9. Используя определение логарифма выберите номер правильного ответа:
ВАРИАНТ 1 ВАРИАНТ 2
10 Математика
4
;
x
1)log
)
b x
)
a x
1
64
3;
1
3
)
c x
3
5
2)3
243
) log 3 243;
a
) log 243 5;
b
) log 243 3
c
3)log 25
2
)
a x
)
b x
3
5
5
;
)
c x
x
5;
5;
1
5
5
)
d x
4)log
x
3
6
)
a x
18;
)
b x
2;
)
c x
216;
9
)
d x
5)log
x
7
14;
)
a x
)
49;
b x
1
49
)
c x
;
2
2
2
6)log 144
12
)12
144;
a
12
144;
)2
b
c
) 144 12
1
225
x
7) log
)
a x
)
b x
15
;
2;
1
2
2
512
3
)
c x
3
8)8
) log 8 512;
a
) log 512 3;
b
)log
c
9)log 64
)
a x
)
b x
8 3
512
2
8
6
;
)
c x
x
8;
8;
1
8
8
)
d x
10) log
x
2
12;
)
a x
)
3;
b x
64;
)
c x
)
8
d x
11) log
x
13
26;
)
a x
)
169;
b x
1
169
)
c x
;
2
12) log 441 2
21
2
441;
)2
a
1
21
441;
)2
b
) 441
21
c
x
2
1) log
3
4
4
;
81
)
b x
)
a x
1
256
4;
1
4
)
c x
4
4
2)3
81
)log 3 81;
a
)log 81 4;
b
) log 4 3
c
3) log 36
x
)
6;
a x
)
6;
b x
1
6
6
)
d x
x
3
4)log
7
21;
)
a x
10;
)
b x
343;
)
c x
5) log
x
11
22;
)
a x
121;
)
b x
1
121
)
c x
)
c x
;
;
2
6)log 243 3
9
9
243;
a
)3
3
2
b
43;
)9
3
)243
c
9
x
;
)
b x
)
a x
7) log
1
5
125
3;
1
3
)
c x
3
5
8)2
32
)log 2 32;
a
)log 32 5;
b
)log 32 2
c
9) log 484
)
a x
)
b x
x
22;
22;
1
22
)
c x
;
5
2
5
2
2
22
)
d x
10)log
x
25
)
a x
27;
)
b x
50;
)
c x
625;
23
)
d x
11)log
x
17
)
a x
34;
)
289;
b x
1
289
)
c x
;
20
12)log 400
20
400;
)2
a
)20
400;
b
) 400
c
20
2
2
2
Ответы запишите в таблицу:
1
5
3
4
2
6
7
8
9
10
11
12
11 Математика
Для всех свойств логарифмов выполняются соответствующие условия:
СВОЙСТВА ЛОГАРИФМОВ
1. 2.
3.
4.
5.
6.
7.
8.
9.
log aa
1
log a
01
при
при
a
a
;
a
,0
1
;
a
,0
1
при
c
a
при
log
a
bc
(
)
log
b
a
log
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
b
log
a
c
b
a
при
log
a
p
b
p
log
log
b
a
log
log
c
c
b
a
a
,0
a
,1
b
,0
c
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
,0
c
,0
ñ
0
;
0
;
0
.
Полезно также знать и другие свойства логарифмов:
log
b
a
при
a
,0
a
,1
b
,0
b
1
;
1
log
b
a
log
an
m
b
m
n
log
a
b
при
log
an
b
log
a
b
1
n
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
0
.
Полезно также знать и «хитрости» свойств логарифмов:
log
a
b
2
log2
b
a
при
a
,0
a
;
0
log
a
bc
(
)
log
a
b
log
a
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
a
c
log
b
c
log
b
a
b
при
log
a
c
a
,0
a
,1
b
,0
c
a
,0
b
,0
b
,0
c
0
.
;
0
.
0
b
,1
при
c
при
Логарифм по основанию 10 называется десятичным логарифмом:
log10
a
lg
a
Десятичным логарифмом называется логарифм по основанию 10.
2.
3.
4.
5.
6.
7.
8.
9.
log aa
1
log a
01
при
при
a
a
;
a
,0
1
;
a
,0
1
при
c
a
при
log
a
bc
(
)
log
b
a
log
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
b
log
a
c
b
a
при
log
a
p
b
p
log
log
b
a
log
log
c
c
b
a
a
,0
a
,1
b
,0
c
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
,0
c
,0
ñ
0
;
0
;
0
.
Полезно также знать и другие свойства логарифмов:
log
b
a
при
a
,0
a
,1
b
,0
b
1
;
1
log
b
a
log
an
m
b
m
n
log
a
b
при
log
an
b
log
a
b
1
n
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
0
.
Полезно также знать и «хитрости» свойств логарифмов:
log
a
b
2
log2
b
a
при
a
,0
a
;
0
log
a
bc
(
)
log
a
b
log
a
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
a
c
log
b
c
log
b
a
b
при
log
a
c
a
,0
a
,1
b
,0
c
a
,0
b
,0
b
,0
c
0
.
;
0
.
0
b
,1
при
c
при
Логарифм по основанию 10 называется десятичным логарифмом:
log10
a
lg
a
Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg ,
т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, … pавны соответственно 1, 2, 3, …, т.е.
имеют столько положительных
единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1,
0.01, 0.001, … pавны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц,
сколько нулей стоит в логарифмируемом числе перед единицей ( считая и нуль целых ).
Логарифмы остальных чисел имеют дробную часть, называемую мантиссой. Целая часть
логарифма называется характеристикой. Для практического применения десятичные
логарифмы наиболее удобны.
12 Математика
Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln ,
т.е. log e N = ln N. Число е является иррациональным, его приближённое значение
2.718281828. Оно является пределом, к которому стремится число ( 1 + 1 / n ) n при
неограниченном возрастании n
Логарифм по основанию е называется натуральным логарифмом:
log
ae
ln
a
Примеры с решениями
1.
Он обозначается lg ,
т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, … pавны соответственно 1, 2, 3, …, т.е.
имеют столько положительных
единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1,
0.01, 0.001, … pавны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц,
сколько нулей стоит в логарифмируемом числе перед единицей ( считая и нуль целых ).
Логарифмы остальных чисел имеют дробную часть, называемую мантиссой. Целая часть
логарифма называется характеристикой. Для практического применения десятичные
логарифмы наиболее удобны.
12 Математика
Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln ,
т.е. log e N = ln N. Число е является иррациональным, его приближённое значение
2.718281828. Оно является пределом, к которому стремится число ( 1 + 1 / n ) n при
неограниченном возрастании n
Логарифм по основанию е называется натуральным логарифмом:
log
ae
ln
a
Примеры с решениями
1. Найдите значение выражения
log
2
6
log
2
10
2
3
.
log
2,0
75
log
.3
2,0
Решение.
log
2
6
log
10
2
2. Найдите значение выражения
2
3
log
2
6
log
2
32
3
log
2
6
32
3
log
2
64
.6
Решение.
log
2,0
75
log
2,0
3
log
2,0
)3:75(
log
2,0
25
log
1
5
2
1
5
.2
3. Вычислите
Решение.
log 9
.27
log
9
27
log
3
log
27
9
3
log
log
3
3
3
2
3
3
log3
log2
3
3
3
3
3
2
.
4. Известно, что
log 5
a2
. Найдите
log 2
.80
Решение.
log
2
80
log
2
16(
)5
log
16
log
2
2
5
4
5. Найдите значение выражения
log
8
log
2
8 4
4
4
1
log
5
2
5
2
5
5
log
log
.
4
1
a
1
.
4
a
a
Решение.
log
8
log
2
8 4
4
log
8
log
2
32
2
2
log
8
log
2
2
1
16
log
8
1
16
log
8
16
1
log
8
16
6. Найдите
lg
45
log
2
log
2
.
16
4
3
8
, если
3lg
a
2lg,
b
.
13 Математика
5lg
3lg
2
lg
10
2
3lg2
lg
10
2lg
Решение.
lg
45
)59lg(
9lg
Задание 10:
1
2
a
.
b
Используя свойства логарифмов найдите значение выражения:
Вариант 1
Вариант 2
4
4
2) log 5 log
1)log 2 log 32
1
5
1
54
3)log
log
1
2
2
3
2
3
7
7
log
7
log 7
4) log
5
196
5) log 5 log 35
6)3
8) log 9
10)log 36
81
7
3
6
12)6
5log 3
6
14)log
7 3
1
7
2
Задание 10
5
4
7)49
log 3
7
27
3
3log 4
21
9)log
11)21
13)log
5
6
5
5
15)125
log 7
25
1)log 32 log
1
2
2)log 4 log 64
4
4
16
16
1
3
5
log
5
1
75
3)log
3
5
9
7
6
log
4)log
3
180
5)log 4 log 36
6)8
8)log 3
27
49
10)log
log 12
9
8
7
log 5
8
7)64
9)log
11)13
125
13
5
4log 3
12)9
4log 2
9
14)log
6
4
1
6
3
13)log
8
7
3
8
15)625
log
125
4
14 Математика
Задание 11:
ГРУППА А: Найдите значение выражения
log)2
2
5
log
2
log)2
2
22
log
Вариант 1
log)1
2
4
log
4
8
8
5
54
2
196
5
3
3
7
2
7
log)3
log)4
log)5
log
3)6
3
log)8
81
log)10
log)11
8
25
5
64
log
log
3
log
4
35
log
2
2
56
log
25)7
5
3
8
log)9
2
log)12
243
81
Вариант 2
log)1
128
4
log
4
2
2
32
11
45
3
8
5
192
log
3
log
log)3
log)4
log)5
3
8
5
8
log
5
2
log
5
25
4
36)7
log)9
log
6
7
16
4
log)12
81
27
50
log
50)6
log)8
125
log)10
log)11
6
5
49
7
128
16
Задание 11 гр А
15 Математика
ГРУППА Б: Найдите значение выражения
Вариант 1
Вариант 2
16 25
log
4
1
4
764
log)5
5
log
4)6
log2
5
2
3
)7
log
1
2
2
125
4
9
log
5
154
log
16)8
log)10
52
2327
log)9
49
343
8log)11
log
512
1
4
1
7
log)12
25
log
625
7)13
7
7
Математика
log)1
2
7
log
2
14
log)2
3
72
log
3
log2)3
2
6
log
2
log)4
4
5
log
4
63
log
36
2
log
3
18
log
2
35
16
27
35
9
log)1
3
log28
2
log
3
3
log2)2
log)3
5
log)4
4
32
7
22
1
5
log
log
5
256
7
11
log
4
36
log)5
2
12
log
2
5
3
log
2)6
94
)7
log
1
2
log
1
2
9
2
log2
7
10
25
81
4
5
2
4
5
52
log
log
log
8)8
125
2
log)10
327
log)9
216
log)11
4
256
36
log
6)13
1
3
1
6
243
7
3
log)12
9
log
3)14
Задание 11 гр Б
7)14
17 Математика
Задание 12:
Задание 1: Вычислить
Задание 2: Найти х
18 8lg)1
lg
;125
log)2
2
7
log
2
;
lg)4
13
16
log
3
log
4
3
log)8
3,0
lg
lg
16
8lg
3lg
2lg
16,3lg
:
у
)13
;
;
через
4,0lg)10
27
lg
3lg
;
)12
3lg
;
)15
12
)5
log
4
log)3
12
18
8lg
lg
2lg2
3lg
11
log
2
;7,2lg
log)7
lg)9
;
;3
;44
)6
;
2
27
4lg
2lg
15
lg
lg
)11
)14
25
Выразите
lg)1
x
х
y
;1
2
lg5,0
1
3
.
Найдите значение выражения
log
2
6
log
2
10
2
3
.
log
2,0
75
log
.3
2,0
Решение.
log
2
6
log
10
2
2. Найдите значение выражения
2
3
log
2
6
log
2
32
3
log
2
6
32
3
log
2
64
.6
Решение.
log
2,0
75
log
2,0
3
log
2,0
)3:75(
log
2,0
25
log
1
5
2
1
5
.2
3. Вычислите
Решение.
log 9
.27
log
9
27
log
3
log
27
9
3
log
log
3
3
3
2
3
3
log3
log2
3
3
3
3
3
2
.
4. Известно, что
log 5
a2
. Найдите
log 2
.80
Решение.
log
2
80
log
2
16(
)5
log
16
log
2
2
5
4
5. Найдите значение выражения
log
8
log
2
8 4
4
4
1
log
5
2
5
2
5
5
log
log
.
4
1
a
1
.
4
a
a
Решение.
log
8
log
2
8 4
4
log
8
log
2
32
2
2
log
8
log
2
2
1
16
log
8
1
16
log
8
16
1
log
8
16
6. Найдите
lg
45
log
2
log
2
.
16
4
3
8
, если
3lg
a
2lg,
b
.
13 Математика
5lg
3lg
2
lg
10
2
3lg2
lg
10
2lg
Решение.
lg
45
)59lg(
9lg
Задание 10:
1
2
a
.
b
Используя свойства логарифмов найдите значение выражения:
Вариант 1
Вариант 2
4
4
2) log 5 log
1)log 2 log 32
1
5
1
54
3)log
log
1
2
2
3
2
3
7
7
log
7
log 7
4) log
5
196
5) log 5 log 35
6)3
8) log 9
10)log 36
81
7
3
6
12)6
5log 3
6
14)log
7 3
1
7
2
Задание 10
5
4
7)49
log 3
7
27
3
3log 4
21
9)log
11)21
13)log
5
6
5
5
15)125
log 7
25
1)log 32 log
1
2
2)log 4 log 64
4
4
16
16
1
3
5
log
5
1
75
3)log
3
5
9
7
6
log
4)log
3
180
5)log 4 log 36
6)8
8)log 3
27
49
10)log
log 12
9
8
7
log 5
8
7)64
9)log
11)13
125
13
5
4log 3
12)9
4log 2
9
14)log
6
4
1
6
3
13)log
8
7
3
8
15)625
log
125
4
14 Математика
Задание 11:
ГРУППА А: Найдите значение выражения
log)2
2
5
log
2
log)2
2
22
log
Вариант 1
log)1
2
4
log
4
8
8
5
54
2
196
5
3
3
7
2
7
log)3
log)4
log)5
log
3)6
3
log)8
81
log)10
log)11
8
25
5
64
log
log
3
log
4
35
log
2
2
56
log
25)7
5
3
8
log)9
2
log)12
243
81
Вариант 2
log)1
128
4
log
4
2
2
32
11
45
3
8
5
192
log
3
log
log)3
log)4
log)5
3
8
5
8
log
5
2
log
5
25
4
36)7
log)9
log
6
7
16
4
log)12
81
27
50
log
50)6
log)8
125
log)10
log)11
6
5
49
7
128
16
Задание 11 гр А
15 Математика
ГРУППА Б: Найдите значение выражения
Вариант 1
Вариант 2
16 25
log
4
1
4
764
log)5
5
log
4)6
log2
5
2
3
)7
log
1
2
2
125
4
9
log
5
154
log
16)8
log)10
52
2327
log)9
49
343
8log)11
log
512
1
4
1
7
log)12
25
log
625
7)13
7
7
Математика
log)1
2
7
log
2
14
log)2
3
72
log
3
log2)3
2
6
log
2
log)4
4
5
log
4
63
log
36
2
log
3
18
log
2
35
16
27
35
9
log)1
3
log28
2
log
3
3
log2)2
log)3
5
log)4
4
32
7
22
1
5
log
log
5
256
7
11
log
4
36
log)5
2
12
log
2
5
3
log
2)6
94
)7
log
1
2
log
1
2
9
2
log2
7
10
25
81
4
5
2
4
5
52
log
log
log
8)8
125
2
log)10
327
log)9
216
log)11
4
256
36
log
6)13
1
3
1
6
243
7
3
log)12
9
log
3)14
Задание 11 гр Б
7)14
17 Математика
Задание 12:
Задание 1: Вычислить
Задание 2: Найти х
18 8lg)1
lg
;125
log)2
2
7
log
2
;
lg)4
13
16
log
3
log
4
3
log)8
3,0
lg
lg
16
8lg
3lg
2lg
16,3lg
:
у
)13
;
;
через
4,0lg)10
27
lg
3lg
;
)12
3lg
;
)15
12
)5
log
4
log)3
12
18
8lg
lg
2lg2
3lg
11
log
2
;7,2lg
log)7
lg)9
;
;3
;44
)6
;
2
27
4lg
2lg
15
lg
lg
)11
)14
25
Выразите
lg)1
x
х
y
;1
2
lg5,0
1
3
. 2lg
lg
y
y
;
lg)2
x
lg)3
x
Задание 12
4
log
1
3
4,2lg
12
lg2
1
2
50
72
lg
lg
;15
lg
lg
;18
;4lg
;3lg
lg)5
lg)7
x
x
lg)8
x
lg)9
x
1
3
;2lg3
lg
125
1
3
;2lg35lg2
1
2
5lg
3lg
1
2
;5,3lg
Математика
;
7
16
;130
log)1
6
x
lg)2
x
lg
1
2
log3
log5,02
25
6
6
log2
6
;3
5lg
a
lg3
b
lg4
;
c
lg)3
x
lg5
m
lg
n
2
3
1
4
lg
p
;
log29
;40
;10
3,0
log)4
4
x
216
log2
4
10
log4
;3
4
lg)6
x
6,9lg
;4,2lg
lg)10
x
lg)11
x
lg)12
x
19 Математика
Задание 13: Восстановите равенство
log
(…
…
log
2
30(
5,3
8
15
7
9
)5,3
8
15
log
)
9
)…3
log
3
log
log
2
3
21
7
log
…
)7…21(
Вариант 1
log)1
7
14
log
log)2
2
…
log
…
2
21
1
2
log
…
56
7
log
2
log
3
log)4
log)5
2
3)6
25)7
log)8
log)9
5,0
log)10
216
5
196
…5
7
3
125
…
49
…
log
3
log
log
70
2
…
3
…
log
…
)5(
…
log2
log
4
log
2
7
6
216
…
5
)2(
…
5
…
log
625
3
…
…
196
log
…
5(
4….
…
70
log
)56
(….)
20 Математика
Вариант 2
log
).
2lg
lg
y
y
;
lg)2
x
lg)3
x
Задание 12
4
log
1
3
4,2lg
12
lg2
1
2
50
72
lg
lg
;15
lg
lg
;18
;4lg
;3lg
lg)5
lg)7
x
x
lg)8
x
lg)9
x
1
3
;2lg3
lg
125
1
3
;2lg35lg2
1
2
5lg
3lg
1
2
;5,3lg
Математика
;
7
16
;130
log)1
6
x
lg)2
x
lg
1
2
log3
log5,02
25
6
6
log2
6
;3
5lg
a
lg3
b
lg4
;
c
lg)3
x
lg5
m
lg
n
2
3
1
4
lg
p
;
log29
;40
;10
3,0
log)4
4
x
216
log2
4
10
log4
;3
4
lg)6
x
6,9lg
;4,2lg
lg)10
x
lg)11
x
lg)12
x
19 Математика
Задание 13: Восстановите равенство
log
(…
…
log
2
30(
5,3
8
15
7
9
)5,3
8
15
log
)
9
)…3
log
3
log
log
2
3
21
7
log
…
)7…21(
Вариант 1
log)1
7
14
log
log)2
2
…
log
…
2
21
1
2
log
…
56
7
log
2
log
3
log)4
log)5
2
3)6
25)7
log)8
log)9
5,0
log)10
216
5
196
…5
7
3
125
…
49
…
log
3
log
log
70
2
…
3
…
log
…
)5(
…
log2
log
4
log
2
7
6
216
…
5
)2(
…
5
…
log
625
3
…
…
196
log
…
5(
4….
…
70
log
)56
(….)
20 Математика
Вариант 2
log
). ..1
1
2
log)3
)2
log
3
5
log
45
1
3
256
log
2
log
4
256
…
121
log
2
log
2
(…
4
2
32
…
11
log
5
3
….
4
2
log
32
11
log
5(
)
…
log
4
(
256
)2…
)45
log)4
8
96
1
3
log
2
3
log
8
96
log
…
3
log
8
96(
)3…
log
18(
…
25
4
5,4
)
25
4
log)5
5
18
…
log
5
…5,4
log
5
log
13
6
1
169)6
log
36)7
log)8
216
25,0
log)9
3
log)10
7
7
256
…
3
49
…
169
log
…
)6(
…
log
…
169
7
256
…
…
3
)3(
…
log
Задание 13 В
21 Математика
Тренировочные упражнения
Базовый уровень
1. Вычислите
2. Вычислите
3. Вычислите
4. Вычислите
5. Вычислите
6. Вычислите
7. Вычислите
log
2
3
2
.
5,0
2
.
log
3
log 2
.
3
39
82
.
log2
5,0
9
5,0
.
log3
2
27
log 2,0
3
125
.
1
log
5
5,0
.
16
.
Найдите значение выражения
8.
9. Найдите значение выражения
log6
01,0
6
.
25,0
log36
6
10. Найдите значение выражения
.
3lg210
22
11. Найдите значение выражения
.
24
log
1
3
1
3
12. Вычислите
13. Вычислите
14. Вычислите
15.
..1
1
2
log)3
)2
log
3
5
log
45
1
3
256
log
2
log
4
256
…
121
log
2
log
2
(…
4
2
32
…
11
log
5
3
….
4
2
log
32
11
log
5(
)
…
log
4
(
256
)2…
)45
log)4
8
96
1
3
log
2
3
log
8
96
log
…
3
log
8
96(
)3…
log
18(
…
25
4
5,4
)
25
4
log)5
5
18
…
log
5
…5,4
log
5
log
13
6
1
169)6
log
36)7
log)8
216
25,0
log)9
3
log)10
7
7
256
…
3
49
…
169
log
…
)6(
…
log
…
169
7
256
…
…
3
)3(
…
log
Задание 13 В
21 Математика
Тренировочные упражнения
Базовый уровень
1. Вычислите
2. Вычислите
3. Вычислите
4. Вычислите
5. Вычислите
6. Вычислите
7. Вычислите
log
2
3
2
.
5,0
2
.
log
3
log 2
.
3
39
82
.
log2
5,0
9
5,0
.
log3
2
27
log 2,0
3
125
.
1
log
5
5,0
.
16
.
Найдите значение выражения
8.
9. Найдите значение выражения
log6
01,0
6
.
25,0
log36
6
10. Найдите значение выражения
.
3lg210
22
11. Найдите значение выражения
.
24
log
1
3
1
3
12. Вычислите
13. Вычислите
14. Вычислите
15. Вычислите
16. Вычислите
log
18
27
log
.12
18
log
1
2
log
12
.72
1
12
log
2
36
log
29
2
.
log
7
log
256
2
7
.
log
log
6,0
6,0
27
243
.
17. Вычислите
log
1
3
2
log
9
.4
25
.
18.
64
19.
1
Найдите значение выражения
log5,0
4
Найдите значение выражения
1
log
7
2
49
14
. 20. Найдите
log 2
21. Найдите
log 7
6
22. Известно, что
, если
1
81
, если
Найдите
.
lg
175
Тренировочные упражнения
23. Известно, что
2lg
m
7lg,
n
.
Найдите
.
log14
56
24. Вычислите
log
81
25
3
log
5
4
6
.
2
25. Найдите значение выражения
.
4
log
5
2,1
2,1
log
7
3
3
Математика
.
log 2
m3
log 7
5lg
a
7lg,
.
k42
.
b
23 Тесты
Математика
Тест 1
Отметьте номер правильного ответа в заданиях А1 – А7.
А1. Вычислите
.
log
5
1 5
5
1)
;
2) 5;
3)
;
1
5
4) –5.
1
5
1) 0,7;
А2. Найдите значение выражения
.
log3
49,0
3
А3. Найдите значение выражения
.
5
log32
5
2
1) 17;
А4. Найдите
log 5
1)
;
2a
2) 0,07;
2)
;
28,0
2)
;
a
2
25
8
, если известно, что
3) 0,245;
4) 0,2401.
3)
;
25
6
log 5
3)
a7
;
a
5
.
Вычислите
16. Вычислите
log
18
27
log
.12
18
log
1
2
log
12
.72
1
12
log
2
36
log
29
2
.
log
7
log
256
2
7
.
log
log
6,0
6,0
27
243
.
17. Вычислите
log
1
3
2
log
9
.4
25
.
18.
64
19.
1
Найдите значение выражения
log5,0
4
Найдите значение выражения
1
log
7
2
49
14
. 20. Найдите
log 2
21. Найдите
log 7
6
22. Известно, что
, если
1
81
, если
Найдите
.
lg
175
Тренировочные упражнения
23. Известно, что
2lg
m
7lg,
n
.
Найдите
.
log14
56
24. Вычислите
log
81
25
3
log
5
4
6
.
2
25. Найдите значение выражения
.
4
log
5
2,1
2,1
log
7
3
3
Математика
.
log 2
m3
log 7
5lg
a
7lg,
.
k42
.
b
23 Тесты
Математика
Тест 1
Отметьте номер правильного ответа в заданиях А1 – А7.
А1. Вычислите
.
log
5
1 5
5
1)
;
2) 5;
3)
;
1
5
4) –5.
1
5
1) 0,7;
А2. Найдите значение выражения
.
log3
49,0
3
А3. Найдите значение выражения
.
5
log32
5
2
1) 17;
А4. Найдите
log 5
1)
;
2a
2) 0,07;
2)
;
28,0
2)
;
a
2
25
8
, если известно, что
3) 0,245;
4) 0,2401.
3)
;
25
6
log 5
3)
a7
;
a
5
. 4) 19.
4)
.
5a
4) 2,5.
4) 4.
А5. Найдите значение выражения
1) 4,5;
А6. Вычислите
2) 9,5;
.
128
lg
8lg
1)
;
lg
120
А7. Известно, что
2)
;
7
3
lg
m
lg,3
n
8
log
3
72
.8
3
3
log
3) 1;
3)
;
lg
16
. Найдите
1)
;
lg
375
2) 8;
3) 1;
lg
n
1000
m
.
4)
.
8lg
Ответом в заданиях В8 – В10 должно быть целое или записанное в виде десятичной
дроби число.
В8. Вычислите
.
В9. Найдите значение выражения
10
64
log16
81
2lg2
1
log
2 125
8
log
В10. Найдите значение выражения
log
4
3
baa
24
.
3
4
log
3
1
2
, если
.
log ba
14 Математика
Решения заданий В8В10
Тест 2
Базовый уровень
.
5
1. Вычислите
1)
;
5,3
2. Вычислите
1) 2;
Отметьте номер правильного ответа в заданиях А1 – А7.
log 5
125
2)
;
5,1
1,0lg
.
1000
2) –1,5;
.
1
3
log3
12
12
3. Найдите значение выражения
1) –1;
4. Вычислите
1) 2;
5. Вычислите
2)
1
27
;
log
20
.5
20
log
80
2) 400;
log
1
9
log
15
.25
1
15
4)
.
5,2
4)
1
3
.
4)
.
3 3
4) 85.
3)
;6
3) 0,5;
3) 27;
3)
log 20
;85
25
4) 19.
4)
.
5a
4) 2,5.
4) 4.
А5. Найдите значение выражения
1) 4,5;
А6. Вычислите
2) 9,5;
.
128
lg
8lg
1)
;
lg
120
А7. Известно, что
2)
;
7
3
lg
m
lg,3
n
8
log
3
72
.8
3
3
log
3) 1;
3)
;
lg
16
. Найдите
1)
;
lg
375
2) 8;
3) 1;
lg
n
1000
m
.
4)
.
8lg
Ответом в заданиях В8 – В10 должно быть целое или записанное в виде десятичной
дроби число.
В8. Вычислите
.
В9. Найдите значение выражения
10
64
log16
81
2lg2
1
log
2 125
8
log
В10. Найдите значение выражения
log
4
3
baa
24
.
3
4
log
3
1
2
, если
.
log ba
14 Математика
Решения заданий В8В10
Тест 2
Базовый уровень
.
5
1. Вычислите
1)
;
5,3
2. Вычислите
1) 2;
Отметьте номер правильного ответа в заданиях А1 – А7.
log 5
125
2)
;
5,1
1,0lg
.
1000
2) –1,5;
.
1
3
log3
12
12
3. Найдите значение выражения
1) –1;
4. Вычислите
1) 2;
5. Вычислите
2)
1
27
;
log
20
.5
20
log
80
2) 400;
log
1
9
log
15
.25
1
15
4)
.
5,2
4)
1
3
.
4)
.
3 3
4) 85.
3)
;6
3) 0,5;
3) 27;
3)
log 20
;85
25
Найдите значение числового логарифмического выражения – как решать
Формулировка задачи: Найдите значение числового логарифмического выражения.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).
Рассмотрим, как решаются подобные задачи на логарифмы на примерах.
Пример задачи 1:
Найдите значение выражения log0,310 – log0,33
Решение:
Разность логарифмов с одинаковым основанием равна логарифму частного:
log0,310 – log0,33 = log0,3(10/3)
Возведем 10/3 в степень -1, вынесем степень из под логарифма (логарифм степени):
log0,3(10/3) = -log0,3(3/10) = -1
Ответ: -1
Пример задачи 2:
Найдите значение выражения log713 / log4913
Решение:
Преобразуем знаменатель: для этого вынесем степень основания из под логарифма:
log4913 = log(7)213 = 1/2 ⋅ log713
Тогда значение выражения равно:
log713 / log4913 = 2 ⋅ log713 / log713 = 2
Ответ: 2
Пример задачи 3:
Найдите значение выражения 9log550 / 9log52
Решение:
Преобразуем выражение:
9log550 / 9log52 = 9log550 – log52
Разность логарифмов с одинаковыми основаниями равна логарифму частного:
log550 – log52 = log5(50/2) = log525 = 2
Тогда значение выражения равно:
Ответ: 81
Пример задачи 4:
Найдите значение выражения 6log7∛7
Решение:
Вынесем корень за пределы логарифма:
6log7∛7 = 6 ⋅ 1/3 ⋅ log77 = 2
Ответ: 2
Пример задачи 5:
Найдите значение выражения log35 / log37 + log70,2
Решение:
Преобразуем частное с помощью формулы перехода от логарифма в одном основании к логарифму при другом основании:
Сумма логарифмов с одним основанием равна логарифму произведения:
log75 + log70,2 = log71 = 0
Ответ: 0
Пример задачи 6:
Найдите значение выражения log0,83 ⋅ log31,25
Решение:
Преобразуем второй множитель и приведем его к тому же основанию:
log31,25 = log3(5/4) = -log3(4/5) = -log30,8 = -1 / log0,83
И найдем значение выражения:
log0,83 ⋅ log31,25 = -log0,83 / log0,83 = -1
Ответ: -1
Пример задачи 7:
Найдите значение выражения 5log2549
Решение:
Вынесем степень основания логарифма за его пределы:
Внесем ее обратно как логарифм корня:
1/2 ⋅ log549 = log5(49)1/2 = log57
И воспользуемся основным логарифмическим тождеством:
Ответ: 7
Пример задачи 8:
Найдите значение выражения log4(log216)
Решение:
Вычислим значение выражения в скобках:
Тогда значение выражения равно:
Ответ: 1
Пример задачи 9:
Найдите значение выражения log42 + log0,258
Решение:
Найдем значения каждой части выражения и получим результат:
log42 =1/2 ⋅ log22 = 1/2 ⋅ 1 = 0,5
log0,258 = log1/48 = 1/2 ⋅ log1/28 = 1/2 ⋅ log1/223 = 1/2 ⋅ (-3) = -1,5
Тогда значение выражения равно:
log42 + log0,258 = 0,5 – 1,5 = -1
Ответ: -1
Пример задачи 10:
Найдите значение выражения 2log26 – 3
Решение:
Разложим число на множители:
2log26 – 3 = 2log26 ⋅ 2–3
Применим основное логарифмическое тождество к первому множителю и выполним оставшиеся вычисления:
2log26 ⋅ 2-3 = 6 ⋅ 1/8 = 0,75
Ответ: 0,75
Пример задачи 11:
Найдите значение выражения 7–2log72
Решение:
Вынесем множитель перед логарифмом в степень, чтобы избавиться от него:
–2log72 = log72–2 = log70,25
И применим основное логарифмическое тождество:
7–2log72 = 7log70,25 = 0,25
Ответ: 0,25
Пример задачи 12:
Найдите значение выражения (3log23)log32
Решение:
Если мы возведем число сначала в степень log32, а потом уже в степень log23, то сможем применить основное логарифмическое тождество:
(3log23)log32 = (3log32)log23 = 2log23 = 3
Ответ: 3
Пример задачи 13:
Найдите значение выражения (1 – log212) ⋅ (1 – log612)
Решение:
Преобразуем логарифмы:
log212 = log2(2 ⋅ 6) = log22 + log26 = 1 + log26
log612 = log6(2 ⋅ 6) = log62 + log66 = log62 + 1
Подставим полученные значения в выражение:
(1 – (1 + log26)) ⋅ (1 – (log62 + 1)) = (1 – 1 – log26) ⋅ (1 – log62 – 1) = – log26 ⋅ (– log62) = log26 ⋅ log62
Преобразуем второй множитель, чтобы логарифмы имели одинаковые основания, и выполним остальные действия:
log26 ⋅ log62 = log26 ⋅ 1/log26 = 1
Ответ: 1
Пример задачи 14:
Найдите значение выражения log318 / (2 + log32)
Решение:
Преобразуем 2 в знаменателе в логарифм с основанием 3 (возведем 3 в степень 2 и получим число под логарифмом):
Сумма логарифмов с одним основанием в знаменателе равна логарифму произведения:
2 + log32 = log39 + log32 = log3(9 ⋅ 2) = log318
Осталось сократить числитель и знаменатель:
Ответ: 1
База логарифма 2 Калькулятор Log2
База логарифма 2 Калькулятор Log2 Калькулятор логарифма 2 находит результат функции логарифма по основанию 2. Вычислить логарифм по основанию 2 числа.
Вычислить логарифм по основанию 2 числа.
журнал 2 (x) = y
x: — действительное число, x> 0
журнал 2 (x) = y и x = 2 y
База логарифмических данных 2 таблицы значений
Список журналов 2 таблицы значений функций , база 2 чисел.
| log 2 (x) | Обозначение | Значение |
|---|---|---|
| log 2 (1) | фунтов (1) | 0 |
| log 2 (2) | фунтов (2) | 1 |
| log 2 (3) | фунтов (3) | 1,584963 |
| log 2 (4) | фунтов (4) | 2 |
| журнал 2 (5) | фунтов (5) | 2. 321928 321928 |
| log 2 (6) | фунтов (6) | 2,584963 |
| log 2 (7) | фунтов (7) | 2,807355 |
| log 2 ( 8) | фунтов (8) | 3 |
| log 2 (9) | фунтов (9) | 3,169925 |
| log 2 (10) | фунтов (10) | 3.321928 |
| log 2 (11) | фунтов (11) | 3.459432 |
| log 2 (12) | фунтов (12) | 3,584963 |
| log 2 (13) | фунтов (13) | 3.70044 |
| log 2 ( 14) | фунтов (14) | 3.807355 |
| log 2 (15) | фунтов (15) | 3.1 |
| log 2 (16) | фунтов (16) | 4 |
| log 2 (17) | фунтов (17) | 4. 087463 087463 |
| log 2 (18) | фунтов (18) | 4,169925 |
| log 2 (19) | фунтов (19) | 4.247928 |
| log 2 ( 20) | фунтов (20) | 4,321928 |
| log 2 (21) | фунтов (21) | 4,3 |
| log 2 (22) | фунтов (22) | 4.459432 |
| log 2 (23) | фунтов (23) | 4.523562 |
| log 2 (24) | фунтов (24) | 4.584963 |
| log 2 (25) | фунтов (25) | 4.643856 |
| log 2 ( 26) | фунтов (26) | 4,70044 |
| log 2 (27) | фунтов (27) | 4,754888 |
| log 2 (28) | фунтов (28) | 4.807355 |
| log 2 (29) | фунтов (29) | 4.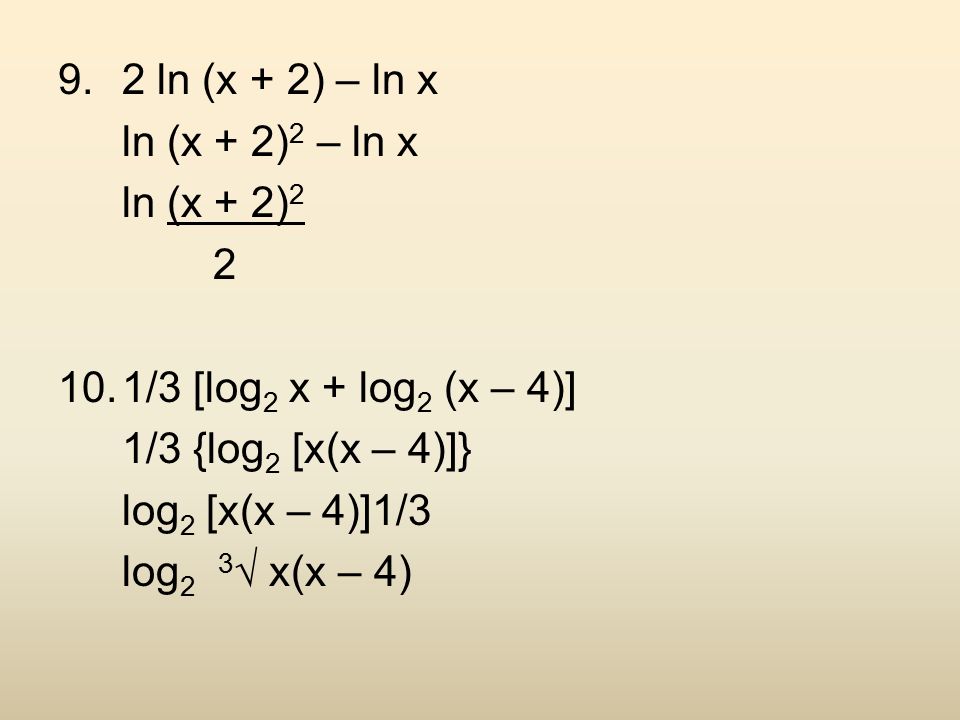 857981 857981 |
| log 2 (30) | фунтов (30) | 4,1 |
| log 2 (31) | фунтов (31) | 4.954196 |
| log 2 ( 32) | фунтов (32) | 5 |
| log 2 (33) | фунтов (33) | 5.044394 |
| log 2 (34) | фунтов (34) | 5,087463 |
| журнал 2 (35) | фунтов (35) | 5.129283 |
| log 2 (36) | фунтов (36) | 5,169925 |
| log 2 (37) | фунтов (37) | 5.209453 |
| log 2 ( 38) | фунтов (38) | 5.247928 |
| log 2 (39) | фунтов (39) | 5.285402 |
| log 2 (40) | фунтов (40) | 5,321928 |
| log 2 (41) | фунтов (41) | 5. 357552 357552 |
| log 2 (42) | фунтов (42) | 5,3 |
| log 2 (43) | фунтов (43) | 5.426265 |
| log 2 ( 44) | фунтов (44) | 5,459432 |
| log 2 (45) | фунтов (45) | 5,4 |
| log 2 (46) | фунтов (46) | 5.523562 |
| log 2 (47) | фунтов (47) | 5.554589 |
| log 2 (48) | фунтов (48) | 5.584963 |
| log 2 (49) | фунтов (49) | 5.61471 |
| log 2 ( 50) | фунтов (50) | 5,643856 |
| log 2 (51) | фунтов (51) | 5,672425 |
| log 2 (52) | фунтов (52) | 5.70044 |
| log 2 (53) | фунтов (53) | 5. 72792 72792 |
| log 2 (54) | фунтов (54) | 5,754888 |
| log 2 (55) | фунтов (55) | 5,78136 |
| log 2 ( 56) | фунтов (56) | 5.807355 |
| log 2 (57) | фунтов (57) | 5,83289 |
| log 2 (58) | фунтов (58) | 5,857981 |
| log 2 (59) | фунтов (59) | 5.882643 |
| log 2 (60) | фунтов (60) | 5.1 |
| log 2 (61) | фунтов (61) | 5.7 |
| log 2 ( 62) | фунтов (62) | 5.954196 |
| log 2 (63) | фунтов (63) | 5.97728 |
| log 2 (64) | фунтов (64) | 6 |
| log 2 (65) | фунтов (65) | 6. 022368 022368 |
| log 2 (66) | фунтов (66) | 6.044394 |
| log 2 (67) | фунтов (67) | 6.066089 |
| log 2 ( 68) | фунтов (68) | 6.087463 |
| log 2 (69) | фунтов (69) | 6,108524 |
| log 2 (70) | фунтов (70) | 6,129283 |
| log 2 (71) | фунтов (71) | 6.149747 |
| log 2 (72) | фунтов (72) | 6,169925 |
| log 2 (73) | фунтов (73) | 6,189825 |
| log 2 ( 74) | фунтов (74) | 6.209453 |
| log 2 (75) | фунтов (75) | 6.228819 |
| log 2 (76) | фунтов (76) | 6.247928 |
| log 2 (77) | фунтов (77) | 6. 266787 266787 |
| log 2 (78) | фунтов (78) | 6.285402 |
| log 2 (79) | фунтов (79) | 6.303781 |
| log 2 ( 80) | фунтов (80) | 6.321928 |
| log 2 (81) | фунтов (81) | 6.33985 |
| log 2 (82) | фунтов (82) | 6.357552 |
| log 2 (83) | фунтов (83) | 6.375039 |
| log 2 (84) | фунтов (84) | 6.3 |
| log 2 (85) | фунтов (85) | 6.409391 |
| log 2 ( 86) | фунтов (86) | 6.426265 |
| log 2 (87) | фунтов (87) | 6.442943 |
| log 2 (88) | фунтов (88) | 6.459432 |
| log 2 (89) | фунтов (89) | 6. 475733 475733 |
| log 2 (90) | фунтов (90) | 6.4 |
| log 2 (91) | фунтов (91) | 6.507795 |
| log 2 ( 92) | фунтов (92) | 6.523562 |
| log 2 (93) | фунтов (93) | 6.539159 |
| log 2 (94) | фунтов (94) | 6.554589 |
| log 2 (95) | фунтов (95) | 6.569856 |
| log 2 (96) | фунтов (96) | 6.584963 |
| log 2 (97) | фунтов (97) | 6.599913 |
| log 2 ( 98) | фунтов (98) | 6,61471 |
| log 2 (99) | фунтов (99) | 6,629357 |
| log 2 (100) | фунтов (100) | 6.643856 |
| log 2 (x) | Обозначение | Значение | |
|---|---|---|---|
| log 2 (101) | фунтов (101) | 6. 658211 658211 | |
| log 2 (102) | фунтов (102) | 6,672425 | |
| log 2 (103) | фунтов (103) | 6.686501 | |
| log 2 ( 104) | фунтов (104) | 6.70044 | |
| log 2 (105) | фунтов (105) | 6,714246 | |
| log 2 (106) | фунтов (106) | 6.72792 | |
| log 2 (107) | фунтов (107) | 6.741467 | |
| log 2 (108) | фунтов (108) | 6,754888 | |
| log 2 (109) | фунтов (109) | 6.768184 | |
| log 2 ( 110) | фунтов (110) | 6,78136 | |
| log 2 (111) | фунтов (111) | 6,794416 | |
| log 2 (112) | фунтов (112) | 6.807355 | |
| log 2 (113) | фунтов (113) | 6. 820179 820179 | |
| log 2 (114) | фунтов (114) | 6,83289 | |
| log 2 (115) | фунтов (115) | 6.84549 | |
| log 2 ( 116) | фунтов (116) | 6,857981 | |
| log 2 (117) | фунтов (117) | 6,870365 | |
| log 2 (118) | фунтов (118) | 6,882643 | |
| log 2 (119) | фунтов (119) | 6.894818 | |
| log 2 (120) | фунтов (120) | 6.1 | |
| log 2 (121) | фунтов (121) | 6. | 3 |
| log 2 ( 122) | фунтов (122) | 6.7 | |
| log 2 (123) | фунтов (123) | 6.942515 | |
| log 2 (124) | фунтов (124) | 6.954196 | |
| log 2 (125) | фунтов (125) | 6. 965784 965784 | |
| log 2 (126) | фунтов (126) | 6.97728 | |
| log 2 (127) | фунтов (127) | 6.988685 | |
| log 2 ( 128) | фунтов (128) | 7 | |
| log 2 (129) | фунтов (129) | 7.011227 | |
| log 2 (130) | фунтов (130) | 7.022368 | |
| log 2 (131) | фунтов (131) | 7.033423 | |
| log 2 (132) | фунтов (132) | 7.044394 | |
| log 2 (133) | фунтов (133) | 7.055282 | |
| log 2 ( 134) | фунтов (134) | 7.066089 | |
| log 2 (135) | фунтов (135) | 7.076816 | |
| log 2 (136) | фунтов (136) | 7.087463 | |
| log 2 (137) | фунтов (137) | 7. 098032 098032 | |
| log 2 (138) | фунтов (138) | 7.108524 | |
| log 2 (139) | фунтов (139) | 7.118941 | |
| log 2 ( 140) | фунтов (140) | 7,129283 | |
| log 2 (141) | фунтов (141) | 7,139551 | |
| log 2 (142) | фунтов (142) | 7.149747 | |
| log 2 (143) | фунтов (143) | 7.159871 | |
| log 2 (144) | фунтов (144) | 7.169925 | |
| log 2 (145) | фунтов (145) | 7.179909 | |
| log 2 ( 146) | фунтов (146) | 7,189825 | |
| log 2 (147) | фунтов (147) | 7,199672 | |
| log 2 (148) | фунтов (148) | 7. 209453 209453 | |
| log 2 (149) | фунтов (149) | 7.219169 | |
| log 2 (150) | фунтов (150) | 7.228819 | |
| log 2 (151) | фунтов (151) | 7.238405 | |
| log 2 ( 152) | фунтов (152) | 7,247928 | |
| log 2 (153) | фунтов (153) | 7,257388 | |
| log 2 (154) | фунтов (154) | 7.266787 | |
| log 2 (155) | фунтов (155) | 7.276124 | |
| log 2 (156) | фунтов (156) | 7.285402 | |
| log 2 (157) | фунтов (157) | 7.294621 | |
| log 2 ( 158) | фунтов (158) | 7.303781 | |
| log 2 (159) | фунтов (159) | 7. 312883 312883 | |
| log 2 (160) | фунтов (160) | 7.321928 | |
| log 2 (161) | фунтов (161) | 7.330917 | |
| log 2 (162) | фунтов (162) | 7.33985 | |
| log 2 (163) | фунтов (163) | 7.348728 | |
| log 2 ( 164) | фунтов (164) | 7,357552 | |
| log 2 (165) | фунтов (165) | 7,366322 | |
| log 2 (166) | фунтов (166) | 7.375039 | |
| log 2 (167) | фунтов (167) | 7.383704 | |
| log 2 (168) | фунтов (168) | 7,3 | |
| log 2 (169) | фунтов (169) | 7.400879 | |
| log 2 ( 170) | фунтов (170) | 7,409391 | |
| log 2 (171) | фунтов (171) | 7,417853 | |
| log 2 (172) | фунтов (172) | 7,426265 | |
| log 2 (173) | фунтов (173) | 7. 434628 434628 | |
| log 2 (174) | фунтов (174) | 7,442943 | |
| log 2 (175) | фунтов (175) | 7,451211 | |
| log 2 ( 176) | фунтов (176) | 7,459432 | |
| log 2 (177) | фунтов (177) | 7,467606 | |
| log 2 (178) | фунтов (178) | 7,475733 | |
| log 2 (179) | фунтов (179) | 7.483816 | |
| log 2 (180) | фунтов (180) | 7,4 | |
| log 2 (181) | фунтов (181) | 7,499846 | |
| log 2 ( 182) | фунтов (182) | 7,507795 | |
| log 2 (183) | фунтов (183) | 7,5157 | |
| log 2 (184) | фунтов (184) | 7.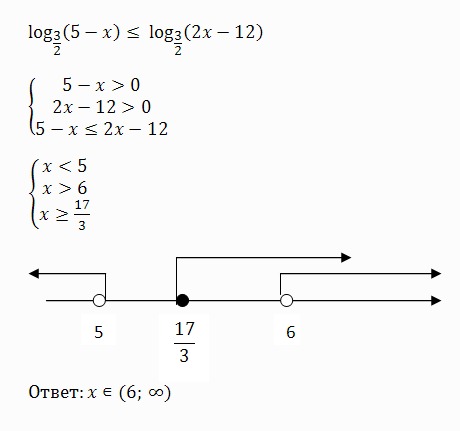 523562 523562 | |
| log 2 (185) | фунтов (185) | 7.531381 | |
| log 2 (186) | фунтов (186) | 7,539159 | |
| log 2 (187) | фунтов (187) | 7.546894 | |
| log 2 ( 188) | фунтов (188) | 7,554589 | |
| log 2 (189) | фунтов (189) | 7,562242 | |
| log 2 (190) | фунтов (190) | 7,569856 | |
| log 2 (191) | фунтов (191) | 7.577429 | |
| log 2 (192) | фунтов (192) | 7,584963 | |
| log 2 (193) | фунтов (193) | 7,5 | |
| log 2 ( 194) | фунтов (194) | 7,599913 | |
| log 2 (195) | фунтов (195) | 7. 60733 60733 | |
| log 2 (196) | фунтов (196) | 7,61471 | |
| log 2 (197) | фунтов (197) | 7.622052 | |
| log 2 (198) | фунтов (198) | 7,629357 | |
| log 2 (199) | фунтов (199) | 7,636625 | |
| log 2 ( 200) | фунтов (200) | 7,643856 |
| log 2 (x) | Обозначение | Значение | |
|---|---|---|---|
| log 2 (201) | фунтов (201) | 7,651052 | |
| log 2 (202) | фунтов (202) | 7.658211 | |
| log 2 (203) | фунтов (203) | 7,665336 | |
| log 2 (204) | фунтов (204) | 7,672425 | |
| log 2 ( 205) | фунтов (205) | 7,67948 | |
| log 2 (206) | фунтов (206) | 7,686501 | |
| log 2 (207) | фунтов (207) | 7. 6 6 | |
| log 2 (208) | фунтов (208) | 7.70044 | |
| log 2 (209) | фунтов (209) | 7.707359 | |
| log 2 (210) | фунтов (210) | 7.714246 | |
| log 2 ( 211) | фунтов (211) | 7,721099 | |
| log 2 (212) | фунтов (212) | 7,72792 | |
| log 2 (213) | фунтов (213) | 7,73471 | |
| log 2 (214) | фунтов (214) | 7.741467 | |
| log 2 (215) | фунтов (215) | 7,748193 | |
| log 2 (216) | фунтов (216) | 7,754888 | |
| log 2 ( 217) | фунтов (217) | 7,761551 | |
| log 2 (218) | фунтов (218) | 7,768184 | |
| log 2 (219) | фунтов (219) | 7. 774787 774787 | |
| log 2 (220) | фунтов (220) | 7.78136 | |
| log 2 (221) | фунтов (221) | 7,787903 | |
| log 2 (222) | фунтов (222) | 7.794416 | |
| log 2 ( 223) | фунтов (223) | 7.8009 | |
| log 2 (224) | фунтов (224) | 7.807355 | |
| log 2 (225) | фунтов (225) | 7.813781 | |
| log 2 (226) | фунтов (226) | 7.820179 | |
| log 2 (227) | фунтов (227) | 7,826548 | |
| log 2 (228) | фунтов (228) | 7,83289 | |
| log 2 ( 229) | фунтов (229) | 7,839204 | |
| log 2 (230) | фунтов (230) | 7,84549 | |
| log 2 (231) | фунтов (231) | 7,851749 | |
| log 2 (232) | фунтов (232) | 7. 857981 857981 | |
| log 2 (233) | фунтов (233) | 7,864186 | |
| log 2 (234) | фунтов (234) | 7.870365 | |
| log 2 ( 235) | фунтов (235) | 7,876517 | |
| log 2 (236) | фунтов (236) | 7,882643 | |
| log 2 (237) | фунтов (237) | 7.888743 | |
| log 2 (238) | фунтов (238) | 7.894818 | |
| log 2 (239) | фунтов (239) | 7. | |
| log 2 (240) | фунтов (240) | 7.1 | |
| log 2 ( 241) | фунтов (241) | 7. | |
| log 2 (242) | фунтов (242) | 7. | 3 |
| log 2 (243) | фунтов (243) | 7. | |
| log 2 (244) | фунтов (244) | 7.7 | |
| log 2 (245) | фунтов (245) | 7.8 | |
| log 2 (246) | фунтов (246) | 7.942515 | |
| log 2 ( 247) | фунтов (247) | 7,948367 | |
| log 2 (248) | фунтов (248) | 7,954196 | |
| log 2 (249) | фунтов (249) | 7.960002 | |
| log 2 (250) | фунтов (250) | 7.965784 | |
| log 2 (251) | фунтов (251) | 7.971544 | |
| log 2 (252) | фунтов (252) | 7.97728 | |
| log 2 ( 253) | фунтов (253) | 7.982994 | |
| log 2 (254) | фунтов (254) | 7.988685 | |
| log 2 (255) | фунтов (255) | 7. 994353 994353 | |
| log 2 (256) | фунтов (256) | 8 | |
| log 2 (257) | фунтов (257) | 8.005625 | |
| log 2 (258) | фунтов (258) | 8.011227 | |
| log 2 (259) | фунтов (259) | 8.016808 | |
| log 2 ( 260) | фунтов (260) | 8,022368 | |
| log 2 (261) | фунтов (261) | 8,027906 | |
| log 2 (262) | фунтов (262) | 8.033423 | |
| log 2 (263) | фунтов (263) | 8.038919 | |
| log 2 (264) | фунтов (264) | 8.044394 | |
| log 2 (265) | фунтов (265) | 8.049849 | |
| log 2 ( 266) | фунтов (266) | 8.055282 | |
| log 2 (267) | фунтов (267) | 8. 060696 060696 | |
| log 2 (268) | фунтов (268) | 8.066089 | |
| log 2 (269) | фунтов (269) | 8.071462 | |
| log 2 (270) | фунтов (270) | 8.076816 | |
| log 2 (271) | фунтов (271) | 8.082149 | |
| log 2 ( 272) | фунтов (272) | 8,087463 | |
| log 2 (273) | фунтов (273) | 8,0 | |
| log 2 (274) | фунтов (274) | 8.098032 | |
| log 2 (275) | фунтов (275) | 8.103288 | |
| log 2 (276) | фунтов (276) | 8.108524 | |
| log 2 (277) | фунтов (277) | 8.113742 | |
| log 2 ( 278) | фунтов (278) | 8. 118941 118941 | |
| log 2 (279) | фунтов (279) | 8.124121 | |
| log 2 (280) | фунтов (280) | 8.129283 | |
| log 2 (281) | фунтов (281) | 8.134426 | |
| log 2 (282) | фунтов (282) | 8.139551 | |
| log 2 (283) | фунтов (283) | 8.144658 | |
| log 2 ( 284) | фунтов (284) | 8.149747 | |
| log 2 (285) | фунтов (285) | 8.154818 | |
| log 2 (286) | фунтов (286) | 8.159871 | |
| log 2 (287) | фунтов (287) | 8.164907 | |
| log 2 (288) | фунтов (288) | 8.169925 | |
| log 2 (289) | фунтов (289) | 8. 174926 174926 | |
| log 2 ( 290) | фунтов (290) | 8,179909 | |
| log 2 (291) | фунтов (291) | 8,184875 | |
| log 2 (292) | фунтов (292) | 8.189825 | |
| log 2 (293) | фунтов (293) | 8.194757 | |
| log 2 (294) | фунтов (294) | 8.199672 | |
| log 2 (295) | фунтов (295) | 8.204571 | |
| log 2 ( 296) | фунтов (296) | 8.209453 | |
| log 2 (297) | фунтов (297) | 8,214319 | |
| log 2 (298) | фунтов (298) | 8.219169 | |
| log 2 (299) | фунтов (299) | 8.224002 | |
| журнал 2 (300) | фунтов (300) | 8,228819 |
© 2019-2021 www.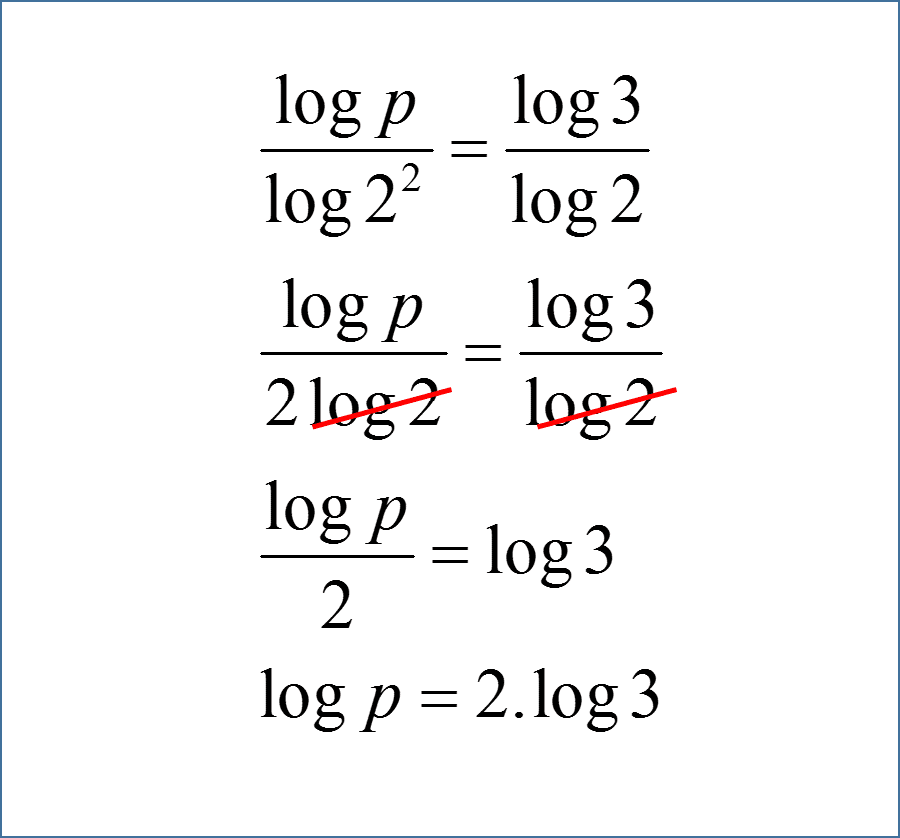 logcalculator.net
logcalculator.net
Базовые правила журнала и расширяющиеся выражения журнала
Purplemath
Вы изучили различные правила для управления и упрощения выражений с показателями, например, правило, которое гласит, что x 3 × x 5 равно x 8 , потому что вы можете складывать экспоненты.Аналогичные правила для логарифмов.
Правила журнала:
1) журнал b ( mn ) = журнал b ( m ) + журнал b ( n )
2) бревно b ( м / n ) = бревно b ( м ) — бревно b ( n )
3) бревно b ( м n ) = n · лог b ( м )
MathHelp.
 com
comМенее формально правила журнала могут быть выражены как:
1) Умножение внутри журнала можно превратить в сложение вне журнала, и наоборот.
2) Деление внутри журнала можно превратить в вычитание вне журнала, и наоборот.
3) Показатель степени для всего, что находится внутри бревна, можно переместить вперед как множитель, и наоборот.
Предупреждение: как и в случае с экспонентами, приведенные выше правила работают только , если основания совпадают. Например, выражение «log d ( m ) + log b ( n )» нельзя упростить, потому что основания («d» и «b») не совпадают, просто как x 2 × y 3 нельзя упростить, потому что основания ( x и y ) не совпадают.
Расширяющиеся логарифмы
Правила журнала могут использоваться для упрощения (или, точнее, для «уплотнения») выражений, для «расширения» выражений или для поиска значений. Начнем с расширения.
Когда в инструкциях говорится «расширить», они означают, что они дали мне одно выражение журнала с большим количеством информации внутри него, и они хотят, чтобы я использовал правила журнала, чтобы разбить журнал на множество отдельных терминов журнала, каждый из которых имеет только одна вещь внутри его конкретного журнала.То есть они дали мне один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
В данном случае у меня внутри журнала есть «2 x ». Поскольку «2 x » — это умножение, я могу разделить это выражение в соответствии с первым из приведенных выше правил журнала и превратить его в сложение вне журнала:
журнал 3 (2 x ) = журнал 3 (2) + журнал 3 ( x )
Тогда ответ, который они ищут:
Примечание: не пытайтесь вычислить «журнал 3 (2)» в вашем калькуляторе. Хотя вы будете правы, если скажете, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить на своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Хотя вы будете правы, если скажете, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить на своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Если вы дадите «ответ» в виде десятичного приближения, вы должны ожидать потерю баллов.
У меня внутри журнала деление.Согласно второму правилу журнала, приведенному выше, его можно разделить на части как вычитание вне журнала, так:
журнал 4 ( 16 / x ) = журнал 4 (16) — журнал 4 ( x )
Первый член в правой части приведенного выше уравнения можно упростить до точного значения, применив основное определение логарифма. В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
Затем исходное выражение полностью раскрывается как:
журнал 4 ( 16 / x ) = 2 — журнал 4 ( x )
Всегда не забывайте находить время, чтобы проверить, можно ли упростить какие-либо термины в вашем расширении (например, журнал 4 (16) выше).
Показатель внутри бревна можно вынести как множитель:
log 5 ( x 3 ) = 3 · log 5 ( x ) = 3log 5 ( x )
Приведенные выше примеры представляют собой очень простое использование правил журнала применительно к раскрытию выражений журнала. На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
URL: https://www.purplemath.com/modules/logrules.htm
База логарифма 3 из 62 преобразователей
Используйте форму ниже, чтобы выполнить преобразование.
| Бревно 3 10 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | знак равно | ||
| Ответ преобразования Log 3 62 = 3.75667961083 |
Решение Шаг 1 Журнал 3 62 = Журнал (62) ÷ Журнал (3) Лог (62) = 1,7923 |
|
Другие преобразования системы счисления для проверки
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Преобразование системы счисления — это числа от 1 до 32, где числа 2-9 представлены простыми цифрами, а числа 11-32 представлены буквами A-Z. {\ displaystyle 3})}} {3-3}
{\ displaystyle 3})}} {3-3}
$ = \ dfrac {\ log_ {2} {(9-8)}} {0}
$$ = \ dfrac {\ log_ {2} {(1)}} {0}
$$ = \ dfrac {0} {0}
$Следовательно, значение выражения в левой части неопределенно при $ x $ равно $ 3 $.Следовательно, $ x \ ne 3 $, но $ x = 0 $ является только решением логарифмического уравнения и математически является необходимым решением этой логарифмической задачи.
Расширяющиеся логарифмы — ChiliMath
Когда вас просят развернуть логарифмические выражения , ваша цель состоит в том, чтобы выразить одно логарифмическое выражение на множество отдельных частей или компонентов. Этот процесс прямо противоположен сжатию логарифмов, потому что вы сжимаете кучу лог-выражений в более простое.
Лучший способ проиллюстрировать эту концепцию — показать множество примеров. В этом уроке восемь решенных задач.
Ключ к успешному расширению логарифмов — это осторожное применение правил логарифмов. Найдите время, чтобы изучить правила и понять, что они пытаются «сказать».
Найдите время, чтобы изучить правила и понять, что они пытаются «сказать».
Например, правило 1 называется правилом продукта . Что он делает, так это разбивает произведение выражений на сумму лог-выражений. См. Остальные описания ниже.
Правила логарифмов
Изучите описание каждого правила, чтобы получить его интуитивное понимание.
Описание правил логарифмирования
Правило 1: Правило продукта
Логарифм произведения чисел — это сумма логарифмов отдельных чисел.
Правило 2: Правило частного
Логарифм частного числа — это разность логарифма отдельных чисел.
Правило 3: Правило силы
Логарифм экспоненциального числа — это показатель степени, умноженный на логарифм основания.
Правило 4: Правило нуля
Логарифм 1, где b> 0, но b \ ne 1, равен нулю.
Правило 5: Правило идентификации
Логарифм числа, равного его основанию, равен 1. Поскольку число также является основанием, b, это означает, что b> 0, но b \ ne 1.
Поскольку число также является основанием, b, это означает, что b> 0, но b \ ne 1.
Правило 6: Журнал экспоненты Правило
Логарифм экспоненциального числа, основание которого совпадает с основанием журнала, равно экспоненте.
Правило 7: Экспонент логарифма Правило
Возведение логарифма числа по основанию равняется числу.
Примеры раскрытия логарифмов
Пример 1 : развернуть логарифмическое выражение.
Заглянув в круглые скобки, мы видим произведение числа и переменных. Правило продукта не говорит, что внутри должно быть только два фактора, на самом деле их может быть больше. Хорошо, поэтому мы разделим основное логарифмическое выражение как сумму четырех журналов.
Пример 2 : развернуть логарифмическое выражение.
Внутри скобок — дробь, означающая, что сначала я буду применять правило частных. Поскольку числитель является произведением 7 и x, я использую правило произведения, чтобы разбить его.
Пример 3 : развернуть логарифмическое выражение.
Хорошо, это тоже дробная форма, поэтому правило частных — это первый шаг, который мы собираемся применить.
Итак, в этой проблеме есть что-то «новое».То есть числитель содержит переменную с показателем степени. Это должно быть легко, поскольку с этим легко справятся Правило 3 или Правило мощности. Просто опустите экспоненту влево, вот и все!
Кроме того, в знаменателе стоит радикальное выражение. Помните, что радикал можно выразить дробной степенью. Поскольку этот радикал является квадратным корнем, это означает, что степень просто \ large {1 \ over 2}.
Кроме того, мы впервые видим в действии Правило 5 или Правило логарифма идентичности.Ожидайте, что это правило будет применяться чаще, потому что оно чрезвычайно полезно в процессе упрощения.
Пример 4 : развернуть логарифмическое выражение.
Пусть вас не пугает квадратный корень. Просто представьте это как степень или показатель \ large {1 \ over 2}. Таким образом, эта проблема сводится к расширению лог-выражения со степенью \ large {1 \ over 2}. Здесь правило мощности опускает показатель \ large {1 \ over 2} слева от журнала, а затем вы расширяете остальную часть, как обычно.
Просто представьте это как степень или показатель \ large {1 \ over 2}. Таким образом, эта проблема сводится к расширению лог-выражения со степенью \ large {1 \ over 2}. Здесь правило мощности опускает показатель \ large {1 \ over 2} слева от журнала, а затем вы расширяете остальную часть, как обычно.
Пример 5 : развернуть логарифмическое выражение.
Эта задача довольно интересна, потому что все выражение возводится в некоторую степень. Кроме того, наличие квадратного корня в числителе добавляет некоторого уровня сложности.
Однако, если мы будем придерживаться основ, тщательно применяя правила экспонент на каждом этапе, у нас не должно возникнуть проблем с решением этой проблемы! Давай спланируем наши действия, хорошо?
Уменьшите показатель степени 4, используя Правило мощности.Затем используйте правило частного, чтобы выразить дробь как разность логарифмических выражений. И, наконец, не забывайте, что квадратный корень — это всего лишь дробный показатель от \ large {1 \ over 2}.
Я распределил 4 по символу группировки, чтобы избавиться от дроби \ large {1 \ over 2}. Также можно оставить 4 за пределами символа группировки, что означает, что нам не нужно распределять 4 по выражениям внутри квадратных скобок. Любой из двух ответов должен быть правильным.
Пример 6 : развернуть логарифмическое выражение.
Это просто кубический корень из некоторого рационального выражения. Замените символ корня куба дробной степенью \ large {1 \ over 3}. Этот показатель степени \ large {1 \ over 3} можно уменьшить, используя правило логарифма степени. Теперь нам нужно разобраться с рациональным выражением, используя правило частных, а затем завершить его, используя правило продукта.
Не отвлекайтесь на разные типы групповых символов. Идея состоит в том, чтобы убедиться, что мы правильно применяем правила логарифмирования на каждом этапе, который мы предпринимаем, без совершения алгебраических ошибок, таких как распределение -1 в символе группировки. 3}. Обработайте квадратные корни, заменив их дробной степенью, а затем используйте правило логарифмов мощности, чтобы уменьшить его перед символом журнала в качестве множителя.
3}. Обработайте квадратные корни, заменив их дробной степенью, а затем используйте правило логарифмов мощности, чтобы уменьшить его перед символом журнала в качестве множителя.
Пример 8 : развернуть логарифмическое выражение.
Основное питание 3 может быть размещено в качестве множителя с помощью правила мощности. Правило Quotient должно иметь дело с дробными выражениями, записывая их как разность журналов. Теперь замените символ квадратного корня на показатель степени \ large {1 \ over 2}.Аналогичным образом замените символ корня куба на показатель степени \ large {1 \ over 3}.
Практика с рабочими листами
Возможно, вас заинтересует:
Уплотняющие логарифмы
Объяснение логарифма
Правила логарифмирования
Решение логарифмических уравнений
Брайс Райнер бросает Гарвард-Вестлейк в чемпионский матч
Первокурсник Брайс Райнер, 15 лет, стоял на холме в начале седьмого иннинга жарким днем вторника в Энсино. У Orange Lutheran были бегуны на втором и третьем местах с двумя аутами в полуфинальной игре Южного дивизиона 1. Он бросил 95 ударов. Тренеры Гарвард-Вестлейк отказались подтолкнуть его к команде. Кэтчер Джейкоб Гэллоуэй коротко с ним ободрял.
У Orange Lutheran были бегуны на втором и третьем местах с двумя аутами в полуфинальной игре Южного дивизиона 1. Он бросил 95 ударов. Тренеры Гарвард-Вестлейк отказались подтолкнуть его к команде. Кэтчер Джейкоб Гэллоуэй коротко с ним ободрял.
«Вот оно. Это последний парень. Давай сделаем это.»
Поле № 96 в пользу пинч-нападающего из лютеранской команды Orange Ричарда Техады в результате фол с кривой мячом. Поле № 97 было быстрым и пропущенным. Поле № 98 было высоким фастболом, требовавшим третьего удара.Товарищи по команде выскочили из блиндажа, чтобы отпраздновать победу со счетом 3: 2, в результате которой Росомахи, занявшие второе место (28-4), вышли в финал первого дивизиона против Сан-Хуана Капистрано Джсерры, занявшего первое место.
«Он не потерял свои вещи», — сказал тренер по питанию Джо Гюнц о Райнере, который улучшился до 9: 0, выбив девять, отказавшись от четырех ударов и два шага. «Он атаковал. Когда у вас есть особенный ребенок, вы должны ему доверять. Он быстро вырос ».
Он быстро вырос ».
Беннетт Маркинсон сделал первый тайм хоум-ран для Гарвард-Вестлейк.Оранжевый лютеранский ас Луи Родригес был удален во втором иннинге после синглов RBI Дэвида Лозано и Джорджа Купера. Крис Кэнэда не допускал Гарвард-Вестлейк до конца игры, но уланам так и не удалось решить проблему с Райнером, который вывел их из равновесия с помощью своего слайдера и кривой. Только в седьмом они оказали давление, получив сингл RBI от Макса Андила.
Райнер никогда не менял выражения лица. Он был методичен, уравновешен и невозмутим до финального удара.
JSerra 11, Ayala 4: Коди Шриер, Колин Бланшар и Люк Джуэтт совершили хоум-раны, чтобы сплотить Львов в полуфинале Дивизиона 1.Джуэтт пошел три из трех. У Джейкоба Бадави было три удара для Айалы.
Таузенд-Оукс 10, Бонита 3: Мэтт Манси совершил хоумран с тремя ранами, его 12-е место в сезоне, а Рок Риджио сделал свой 13-й хоум-ран, чтобы помочь «Уланам 28-1» выйти в чемпионат Дивизиона 2. .
.
Royal 4, Paraclete 1: Тревор Хансен вычеркнул шесть и забросил полную игру, а Р. Дж. Фейгенбаум пошел три на три, чтобы помочь Royal выйти в чемпионат Дивизиона 4. Роял сыграет с Ранчо Кукамонга, победившим Мурриету Меса со счетом 2: 0.
Лонг-Бич Милликен 2, Харт 1: Милликен расстроил индейцев номер 1 в полуфинале Дивизиона 3. «Рэмс» сыграют с «Риверсайд Арлингтон» со счетом 7-6 над Палосом Вердесом.
Citrus Valley 14, Laguna Hills 13: Трэвис Уильямс сделал три дубля в полуфинале пятого дивизиона. Цитрус Вэлли сыграет с Кахоном, победив со счетом 5: 4 над Северным Торрансом в восьми подачах.
Баскетбол для мальчиков
Сьерра-Каньон 94, Бирмингем 74: Амари Бейли набрал 28 очков в пользу команды Trailblazers, которая примет Этиванду в полуфинале открытого дивизиона в четверг.
Дэмиен 102, Санта-Мария-Сент-Джозеф 71: Малик Томас, летевший в USC, финишировал с 33 очками. В четверг Дэмиен сыграет с Торри Пайнсом с лучшим посевом.
West Hills Chaminade 79, Clovis North 76: Кейт Хиггинс набрал 29 очков, а Кей Джей Симпсон и Колин Уимс добавили по 20 очков в первом дивизионе 1-A.
Гарвард-Вестлейк 78, Мемориал Сан-Хоакина 70: Кэмерон Троуэр набрал 19 очков за «Росомаху».
Нарбонна 67, Лонг-Бич Поли 65: Гаучо опрокинули верхних сеяных Джекрэббитс в открытии 2-А.Девин Уильямс набрал 24 очка, а Брайс Адамс вернулся после травмы стопы и набрал 20 очков.
Баскетбол для девочек
Corona Centennial 79, La Jolla Country День 44: Хаски выиграли свой первый региональный плей-офф в Открытом дивизионе. Лондин Джонс набрал 25 очков, а Джайда Карри — 18 очков.
Софтбол
Эль Камино Реал 6, Карсон 0: Джиллиан Келли вывела конкистадоров в игру чемпионата открытого дивизиона городской секции. Конкистадоры казнили овсянками и полагались на качки Келли.
Гранада Хиллз 8, Сан-Педро 7: Элла Ладден провела полную игру, чтобы организовать матч чемпионата открытого дивизиона лиги Западной долины.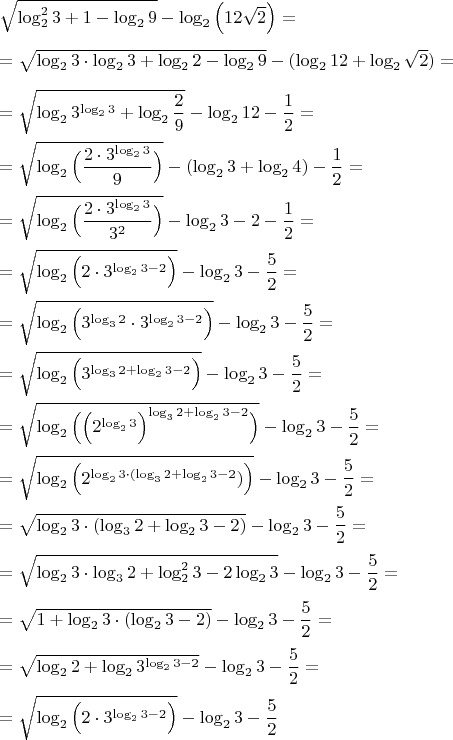
Гольф
Юсон Чой из Анахайма Дискавери Кристиан забил на поле для гольфа Brookside на семь очков меньше номинала и выиграл чемпионат Южной Калифорнии по гольфу среди юношей CIF / SCGA. Командный титул выиграла Анахайм Сервите.
Эмико Свердук из Лонг-Бич Уилсон выиграла личный титул среди девушек со счетом до 68. Фуллертон Трой стал командным титулом.
Сенсационное выступление Дюранта выводит Нетс вперед 3: 2 — Солсбери Пост
БРАЙАН МАХОНИ
AP Баскетбольный писатель
НЬЮ-ЙОРК (AP) — Кевин Дюрант набрал 49 очков, 17 подборов и 10 передач в одном из самых зрелищных выступлений в истории постсезонных матчей, вернув «Бруклин Нетс» в лидеры в полуфинале Восточной конференции со счетом 114-108 побед над командой Милуоки Бакс в пятой игре во вторник вечером.
Джеймс Харден вернулся, но не обиделся, а Кайри Ирвинг покинул поле. Дюрант отыграл все 48 минут и бросил 16 из 23 с поля.Он набрал 20 очков в четвертой четверти, пожалуй, самый крупный бросок — трехочковый за 50 секунд до конца и «Нетс», сохранив преимущество в одно очко.
«Он положил нас на спину и нес нас всю игру», — сказал нападающий Джефф Грин.
Двукратный MVP финала НБА стал первым игроком в истории НБА, набравшим не менее 45 очков, 15 подборов и 10 передач в матче плей-офф.
«Историческое, историческое выступление», — сказал тренер Нетс Стив Нэш.
Харден сыграл впервые с 43 секунды после начала серии с напряжением правой подколенной сухожилия.Он бросил всего 1 из 10 и пропустил все восемь трехочковых, но сделал восемь передач и шесть подборов, играя 46 минут.
Грин сделал семь трехочковых и набрал 27 очков для «Нетс», которые упали в 17-очковую брешь после двух поражений в «Милуоки», прежде чем Дюрант отыграл их. Блейк Гриффин прибавил 17 очков.
Шестая игра состоится в четверг в Милуоки, где «Бакс» в этом сезоне сыграют 4-0 против «Нетс».
Яннис Антетокунмпо набрал 34 очка и 12 подборов, а Крис Миддлтон прибавил 25 очков.
«Бакс» набрал обороты после победы в двух играх в Милуоки, когда Ирвинг вывихнул лодыжку во второй четверти игры 4. Похоже, что Дюрант будет единственным из трех суперзвезд, сыгравших во вторник, учитывая его манеру игры. , в любом случае могло быть достаточно.
Похоже, что Дюрант будет единственным из трех суперзвезд, сыгравших во вторник, учитывая его манеру игры. , в любом случае могло быть достаточно.
Нетс изначально исключили Хардена в понедельник, а затем повысили его во вторник сначала до сомнительного, а затем и до сомнительного. Он тренировался перед игрой и, казалось, хорошо двигался, бегая с корта в туннель после разминки, прежде чем его допустили к игре.
Но, похоже, у него не было полной силы в ноге, из-за чего прыгуны были короткими, и он редко кого-нибудь обыгрывал при ведении мяча.
Дюрант убедился, что это не имеет значения.
«Его особенное выступление», — сказал тренер Бакс Майк Буденхольцер. «Благодарность ему, несколько сложных моментов, так что мы должны взглянуть на это, выяснить, как стать лучше».
«Нетс» были 4 из 20 в первой четверти, 2 из 13 при трехочковых, а трехочковая игра Миддлтона за 33 секунды до конца дала «Милуоки» преимущество 29: 1 после одного.
Корзина Дюранта снизила счет до 42-33, прежде чем Антетокунмпо сделал трехочковый и следовал еще двумя корзинами, чтобы увеличить преимущество до 16, что было по-прежнему, когда Бакс повели 59-43 на половину поля.
«Бакс» по-прежнему лидировали в счете 16 в середине третьей четверти, отвечая каждый раз, когда «Нетс», казалось, имели какой-то импульс. Но Дюрэнт тогда стал горячим и так и не остыл.
Он сделал все четыре броска и набрал 11 очков в последних 6:18 третьего матча, когда «Нетс» потянули до 87-81 в его трехочковой игре за 31 секунду до конца.
Дюрант продолжал открывать четвёртый счет, с его 3-мя очками за 8:36 до игры 94-93, первое преимущество Бруклина после 2: 0.
TIP-INS
баксов: Антетокунмпо был единственным игроком, получившим голоса за первую команду All-NBA по всем 100 бюллетеням, заработав свой третий подряд выбор за первую команду. … Джру Холидей набрал 19 очков.
Нетс: Ирвинг был выбран в третью команду Все-НБА, это был первый выбор в НБА для Нетс с тех пор, как Джейсон Кидд был выбран в первую команду в сезоне 2003-04 гг.… The Nets отдали дань уважения диктору Марву Альберту, который называл игру кортом для TNT.


 lt/public_html/trupmena-1-ru.php on line 93
lt/public_html/trupmena-1-ru.php on line 93 lt/public_html/trupmena-1-ru.php on line 110
lt/public_html/trupmena-1-ru.php on line 110 lt/public_html/trupmena-1-ru.php on line 112
lt/public_html/trupmena-1-ru.php on line 112






 Найдите сумму корней квадратного уравнения х2 -6х +2=0
Найдите сумму корней квадратного уравнения х2 -6х +2=0 Решите уравнение. (х-2)(х+2)=7х-14
Решите уравнение. (х-2)(х+2)=7х-14 Найдите сумму корней квадратного уравнения х2 +7х +4=0
Найдите сумму корней квадратного уравнения х2 +7х +4=0 Решите уравнение.
(х-2)2= 3х-8
Решите уравнение.
(х-2)2= 3х-8 Найдите сумму корней квадратного уравнения х2 -11х +5=0
Найдите сумму корней квадратного уравнения х2 -11х +5=0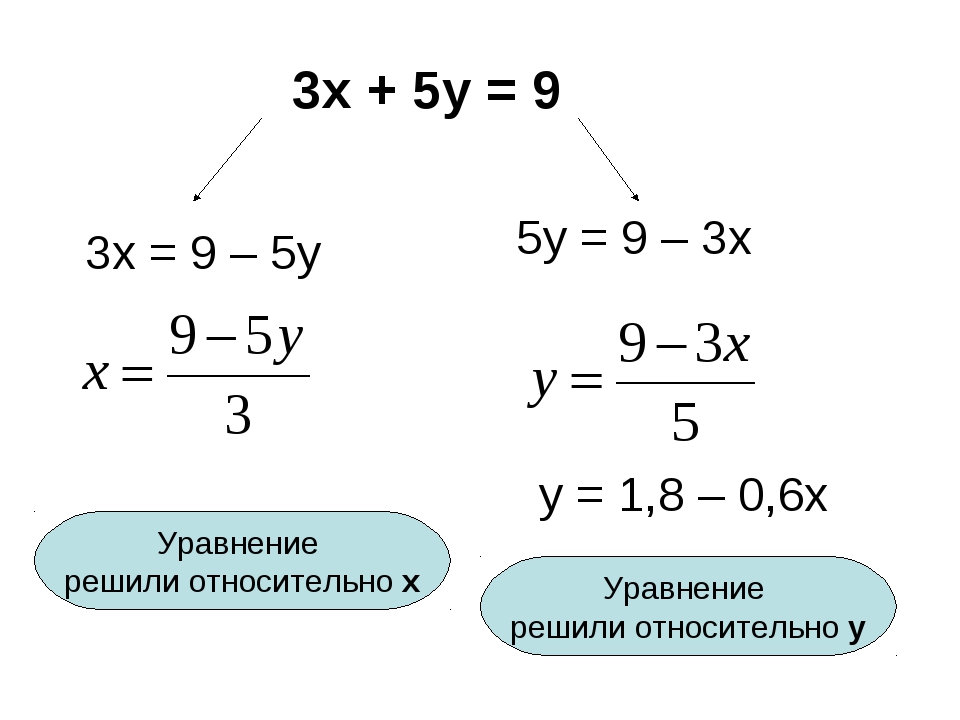 Решите уравнение.
Решите уравнение. Найдите сумму корней квадратного уравнения х2 +12х +5=0
Найдите сумму корней квадратного уравнения х2 +12х +5=0 Решите уравнение.
Решите уравнение. Решите уравнение х2 -9х +20=0
Решите уравнение х2 -9х +20=0 Укажите
неполное квадратное уравнение
Укажите
неполное квадратное уравнение Вычислите дискриминант квадратного уравнения 9х2-2х -21=0
Вычислите дискриминант квадратного уравнения 9х2-2х -21=0 Решите уравнение х2 -8х=0
Решите уравнение х2 -8х=0 Какое из предложенных уравнений является квадратным уравнением?
Какое из предложенных уравнений является квадратным уравнением?

 Ко дню рождения Александра Сергеевича Пушкина в школьной #библиотеке подготовлена тематическая выставка «Всё ли Читать дальше …
Ко дню рождения Александра Сергеевича Пушкина в школьной #библиотеке подготовлена тематическая выставка «Всё ли Читать дальше … ️В День защиты детей Читать дальше …
️В День защиты детей Читать дальше … М. Т. Лорис-Меликова Адмиралтейского района состоялся семинар учителей на тему «Социализация и обучение детей-инофонов в среде доминирующей русскоязычной культуры в современной петербургской школе». В работе семинара приняли участие учителя Читать дальше …
М. Т. Лорис-Меликова Адмиралтейского района состоялся семинар учителей на тему «Социализация и обучение детей-инофонов в среде доминирующей русскоязычной культуры в современной петербургской школе». В работе семинара приняли участие учителя Читать дальше …

 Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .] Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
 Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!
Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!




 Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 упростите выражение,2 упростите выражение,2 упростить выражение 1 2,3 4x 2 5 упростить,3 упростить выражение,4 упростите выражение,4 упростить выражение,7 класс алгебра упростить выражение онлайн калькулятор,x y x упростить,алгебра как упростить выражение,алгебра упрощение выражений,алгебраическое выражение упростить,вы упростите,выражение онлайн,выражение решить онлайн,выражения решение онлайн,выразить из формулы онлайн,выразить онлайн,выразить онлайн переменную,выразить формулу онлайн,дроби упростить выражение,дробное выражение как упростить,как правильно упрощать выражения,как решать упростите выражение,как решать упростить выражение,как упростить,как упростить выражение,как упростить выражение алгебра,как упростить выражение дробное,как упростить выражения,как упростить дробное выражение,как упростить пример,как упростить уравнение,как упрощать,как упрощать выражение,как упрощать выражения,как упрощать уравнения,калькулятор алгебраических выражений,калькулятор алгебраических выражений онлайн калькулятор,калькулятор алгебраических выражений с буквами,калькулятор буквенных выражений,калькулятор буквенных выражений онлайн,калькулятор выражений,калькулятор выражений с буквами,калькулятор для упрощения выражений,калькулятор для упрощения выражений с дробями,калькулятор дробей упрощение выражений,калькулятор онлайн буквенных выражений,калькулятор онлайн подобные слагаемые,калькулятор онлайн упростить выражение,калькулятор онлайн упрощение выражений,калькулятор онлайн упрощение дробных выражений,калькулятор онлайн упрощения выражений,калькулятор подобных слагаемых,калькулятор преобразования выражений,калькулятор раскрытие скобок,калькулятор раскрытие скобок онлайн,калькулятор раскрытия скобок онлайн,калькулятор рациональных выражений с решением онлайн,калькулятор тождественных выражений,калькулятор упростите выражение,калькулятор упростите выражение с дробями,калькулятор упростите выражение с корнями,калькулятор упростить,калькулятор упростить выражение,калькулятор упростить выражение онлайн с дробями,калькулятор упростить выражение онлайн с дробями с буквами,калькулятор упрощение выражений,калькулятор упрощение выражений дробей,калькулятор упрощение выражений онлайн,калькулятор упрощение выражений с дробями,калькулятор упрощение выражений со степенями онлайн,калькулятор упрощение многочлена онлайн,калькулятор упрощения,калькулятор упрощения выражений,калькулятор упрощения выражений онлайн,калькулятор упрощения выражений онлайн калькулятор,калькулятор упрощения выражений с буквами,калькулятор упрощения выражений с буквами и степенями и дробями,калькулятор упрощения выражений с дробями,калькулятор упрощения выражений с дробями и степенями и буквами,калькулятор упрощения выражений с дробями и степенями и с буквами,калькулятор упрощения выражения,калькулятор упрощения дробей с буквами и степенями,математика выражение упростить,онлайн выражение,онлайн выражение формул,онлайн выразить,онлайн калькулятор буквенных выражений,онлайн калькулятор преобразование рациональных выражений,онлайн калькулятор раскрытие скобок,онлайн калькулятор раскрытия скобок,онлайн калькулятор спростить вираз,онлайн калькулятор упростите выражение,онлайн калькулятор упростить выражение,онлайн калькулятор упрощение выражений,онлайн калькулятор упрощение выражений с дробями,онлайн калькулятор упрощение выражений со степенями,онлайн калькулятор упрощение дробных выражений,онлайн калькулятор упрощение многочлена,онлайн калькулятор упрощения выражений,онлайн преобразование выражений,онлайн преобразование тригонометрических выражений,онлайн преобразователь в многочлен,онлайн преобразователь формул,онлайн раскройте скобки,онлайн раскрытие скобок,онлайн решение алгебраических выражений,онлайн решение выражений,онлайн решение выражения,онлайн решение рациональных выражений,онлайн решения выражений,онлайн сокращение выражений,онлайн сокращение многочленов,онлайн упроститель выражений,онлайн упростить,онлайн упростить выражение со степенями,онлайн упростить дробное выражение,онлайн упрощение выражений с дробями,онлайн упрощение выражений с корнями,онлайн упрощение выражений со степенями,онлайн упрощение дробных выражений,онлайн упрощение многочленов,онлайн упрощения выражений,подобные слагаемые калькулятор онлайн,подобные слагаемые онлайн калькулятор,преобразование выражений онлайн,преобразование иррациональных выражений онлайн калькулятор,преобразование рациональных выражений калькулятор онлайн,преобразование рациональных выражений онлайн калькулятор,преобразование формул онлайн,преобразования выражений калькулятор,преобразовать в многочлен выражение онлайн,преобразовать выражение в многочлен онлайн,преобразовать выражение онлайн,преобразовать многочлен в выражение онлайн,преобразуйте в дробь выражение онлайн,преобразуйте в многочлен выражение онлайн калькулятор,преобразуйте дробь в выражение онлайн,приведи подобные слагаемые онлайн калькулятор,пример упростить,пример упростить выражение,примеры упростите выражение,примеры упрощение выражений,примеры упрощения,раскрытие скобок калькулятор,раскрытие скобок калькулятор онлайн,раскрытие скобок онлайн,раскрытие скобок онлайн калькулятор,раскрытия скобок онлайн калькулятор,раскрыть скобки онлайн,раскрыть скобки онлайн калькулятор,рациональных выражений онлайн калькулятор с решением,решение алгебраических выражений онлайн,решение выражений,решение выражений онлайн,решение выражения,решение выражения онлайн,решение онлайн алгебраических выражений,решение онлайн выражения,решение примеров на упрощение выражений,решение упростите выражение,решения выражений онлайн,решите выражение,решить выражение,решить выражение онлайн,решить выражение онлайн со степенями,решить онлайн выражение,сократить выражение,сократить выражение онлайн,сократить выражение онлайн с подробным решением,сократить многочлен онлайн,сократить онлайн выражение,сократить уравнение онлайн,сокращение выражений,сокращение выражений онлайн,сокращение многочленов онлайн,сокращение уравнений онлайн,способы упрощения выражений,спростити вираз,спростити вираз онлайн,спростити вираз онлайн калькулятор,спростити вираз приклади,спростить вираз,спростить вираз онлайн калькулятор,спростіть вираз,спрощення виразів,упрости,упрости выражение,упрости выражения,упростите,упростите 3 4х 2 5,упростите алгебраическое выражение,упростите вы,упростите выражение,упростите выражение 1,упростите выражение 2,упростите выражение 2 3x 2,упростите выражение 3,упростите выражение a,упростите выражение x,упростите выражение x 2 x 8 x,упростите выражение x 3 x 4,упростите выражение а,упростите выражение дроби,упростите выражение дробное,упростите выражение дробь,упростите выражение и,упростите выражение калькулятор,упростите выражение калькулятор онлайн,упростите выражение калькулятор онлайн с решением,упростите выражение калькулятор с дробями,упростите выражение калькулятор с дробями и степенями,упростите выражение калькулятор с степенями,упростите выражение калькулятор с степенями и дробями,упростите выражение онлайн,упростите выражение онлайн калькулятор,упростите выражение онлайн калькулятор с решением,упростите выражение онлайн с дробями,упростите выражение онлайн с дробями и степенями,упростите выражение онлайн с дробями и степенями с решением,упростите выражение онлайн с корнями,упростите выражение примеры,упростите выражение решение,упростите выражение с дробями,упростите выражение с дробями онлайн,упростите выражение с корнями калькулятор,упростите выражение с корнями онлайн,упростите выражения,упростите выражения а,упростите выражения калькулятор,упростите выражения калькулятор онлайн,упростите выражения онлайн,упростите дробное выражение,упростите уравнение,упростите уравнение онлайн,упроститель выражений,упроститель выражений онлайн,упростить 2x 4 6x 6,упростить x 2 x,упростить алгебраическое выражение,упростить векторное выражение онлайн,упростить выражение,упростить выражение 3,упростить выражение алгебра как,упростить выражение алгебраическое,упростить выражение дроби,упростить выражение дробное,упростить выражение дробное онлайн,упростить выражение дробное онлайн калькулятор с решением,упростить выражение как решать,упростить выражение калькулятор,упростить выражение калькулятор онлайн,упростить выражение онлайн,упростить выражение онлайн калькулятор,упростить выражение онлайн калькулятор с дробями,упростить выражение онлайн калькулятор с дробями и буквами,упростить выражение онлайн калькулятор с корнями,упростить выражение онлайн калькулятор с решением,упростить выражение онлайн калькулятор с решением с дробями,упростить выражение онлайн калькулятор с решением с дробями и буквами,упростить выражение онлайн калькулятор с решением с дробями и корнями,упростить выражение онлайн калькулятор с решением с корнями,упростить выражение онлайн калькулятор с решением со степенями,упростить выражение онлайн калькулятор со степенями,упростить выражение онлайн калькулятор со степенями с решением,упростить выражение онлайн с дробями,упростить выражение онлайн с дробями буквами и степенями онлайн,упростить выражение онлайн с дробями и буквами,упростить выражение онлайн с дробями и буквами 8 класс,упростить выражение онлайн с дробями и буквами калькулятор,упростить выражение онлайн с дробями и степенями,упростить выражение онлайн с дробями калькулятор,упростить выражение онлайн с корнями,упростить выражение онлайн с корнями и степенями,упростить выражение онлайн с корнями калькулятор,упростить выражение онлайн с решением,упростить выражение онлайн со степенями,упростить выражение примеры,упростить выражение с дробями,упростить выражение с дробями и буквами,упростить выражение с дробями и буквами 8 класс онлайн,упростить выражение с дробями и буквами онлайн калькулятор,упростить выражение с дробями и с степенями онлайн,упростить выражение с дробями и степенями онлайн,упростить выражение с дробями онлайн,упростить выражение с дробями онлайн калькулятор,упростить выражение с дробями онлайн калькулятор с решением,упростить выражение с корнями онлайн,упростить выражение с корнями онлайн калькулятор,упростить выражение с корнями онлайн калькулятор с решением,упростить выражение с корнями онлайн калькулятор с решением с дробями,упростить выражение со степенями онлайн,упростить выражение со степенями онлайн калькулятор,упростить выражение со степенями онлайн калькулятор с решением,упростить выражение что такое,упростить выражения,упростить выражения онлайн,упростить дробное выражение,упростить дробное выражение онлайн,упростить дробное выражение онлайн калькулятор с решением,упростить дробь онлайн с буквами,упростить дробь онлайн с буквами и степенями,упростить дробь с буквами онлайн,упростить как,упростить калькулятор,упростить многочлен онлайн,упростить онлайн,упростить онлайн выражение с корнями,упростить онлайн выражение со степенями,упростить тригонометрическое выражение онлайн,упростить тригонометрическое выражение онлайн калькулятор с решением,упростить уравнение,упростить уравнение онлайн,упростить уравнение онлайн с решением,упрощать как,упрощение алгебраические выражения,упрощение алгебраических выражений,упрощение выражений,упрощение выражений алгебра,упрощение выражений дробей,упрощение выражений дробей калькулятор,упрощение выражений дробных,упрощение выражений дробных онлайн,упрощение выражений калькулятор,упрощение выражений калькулятор онлайн,упрощение выражений калькулятор онлайн с корнями,упрощение выражений онлайн,упрощение выражений онлайн калькулятор,упрощение выражений онлайн калькулятор с дробями,упрощение выражений онлайн калькулятор с решением,упрощение выражений онлайн калькулятор со степенями,упрощение выражений онлайн с дробями,упрощение выражений онлайн с корнями,упрощение выражений онлайн с решением,упрощение выражений примеры,упрощение выражений с дробями,упрощение выражений с дробями калькулятор,упрощение выражений с дробями онлайн,упрощение выражений с дробями онлайн калькулятор,упрощение выражений с корнями онлайн,упрощение выражений с решением онлайн,упрощение выражений со степенями калькулятор онлайн,упрощение выражений со степенями онлайн калькулятор,упрощение дробей онлайн с буквами,упрощение дробей онлайн со степенями и буквами,упрощение дробей с буквами онлайн,упрощение дробных выражений,упрощение дробных выражений калькулятор онлайн,упрощение дробных выражений онлайн,упрощение дробных выражений онлайн калькулятор,упрощение корней онлайн,упрощение многочленов онлайн,упрощение онлайн,упрощение тригонометрических выражений онлайн,упрощение уравнений,упрощение уравнений онлайн,упрощение уравнения,упрощения,упрощения выражений,упрощения выражений онлайн калькулятор,упрощения выражений примеры,упрощения выражения калькулятор,формула упрощения выражения,формулы для упрощения выражений,формулы упрощения,формулы упрощения выражений,формулы упрощения выражения,что такое упростить выражение.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 упростите выражение,2 упростите выражение,2 упростить выражение 1 2,3 4x 2 5 упростить,3 упростить выражение,4 упростите выражение,4 упростить выражение,7 класс алгебра упростить выражение онлайн калькулятор,x y x упростить,алгебра как упростить выражение,алгебра упрощение выражений,алгебраическое выражение упростить,вы упростите,выражение онлайн,выражение решить онлайн,выражения решение онлайн,выразить из формулы онлайн,выразить онлайн,выразить онлайн переменную,выразить формулу онлайн,дроби упростить выражение,дробное выражение как упростить,как правильно упрощать выражения,как решать упростите выражение,как решать упростить выражение,как упростить,как упростить выражение,как упростить выражение алгебра,как упростить выражение дробное,как упростить выражения,как упростить дробное выражение,как упростить пример,как упростить уравнение,как упрощать,как упрощать выражение,как упрощать выражения,как упрощать уравнения,калькулятор алгебраических выражений,калькулятор алгебраических выражений онлайн калькулятор,калькулятор алгебраических выражений с буквами,калькулятор буквенных выражений,калькулятор буквенных выражений онлайн,калькулятор выражений,калькулятор выражений с буквами,калькулятор для упрощения выражений,калькулятор для упрощения выражений с дробями,калькулятор дробей упрощение выражений,калькулятор онлайн буквенных выражений,калькулятор онлайн подобные слагаемые,калькулятор онлайн упростить выражение,калькулятор онлайн упрощение выражений,калькулятор онлайн упрощение дробных выражений,калькулятор онлайн упрощения выражений,калькулятор подобных слагаемых,калькулятор преобразования выражений,калькулятор раскрытие скобок,калькулятор раскрытие скобок онлайн,калькулятор раскрытия скобок онлайн,калькулятор рациональных выражений с решением онлайн,калькулятор тождественных выражений,калькулятор упростите выражение,калькулятор упростите выражение с дробями,калькулятор упростите выражение с корнями,калькулятор упростить,калькулятор упростить выражение,калькулятор упростить выражение онлайн с дробями,калькулятор упростить выражение онлайн с дробями с буквами,калькулятор упрощение выражений,калькулятор упрощение выражений дробей,калькулятор упрощение выражений онлайн,калькулятор упрощение выражений с дробями,калькулятор упрощение выражений со степенями онлайн,калькулятор упрощение многочлена онлайн,калькулятор упрощения,калькулятор упрощения выражений,калькулятор упрощения выражений онлайн,калькулятор упрощения выражений онлайн калькулятор,калькулятор упрощения выражений с буквами,калькулятор упрощения выражений с буквами и степенями и дробями,калькулятор упрощения выражений с дробями,калькулятор упрощения выражений с дробями и степенями и буквами,калькулятор упрощения выражений с дробями и степенями и с буквами,калькулятор упрощения выражения,калькулятор упрощения дробей с буквами и степенями,математика выражение упростить,онлайн выражение,онлайн выражение формул,онлайн выразить,онлайн калькулятор буквенных выражений,онлайн калькулятор преобразование рациональных выражений,онлайн калькулятор раскрытие скобок,онлайн калькулятор раскрытия скобок,онлайн калькулятор спростить вираз,онлайн калькулятор упростите выражение,онлайн калькулятор упростить выражение,онлайн калькулятор упрощение выражений,онлайн калькулятор упрощение выражений с дробями,онлайн калькулятор упрощение выражений со степенями,онлайн калькулятор упрощение дробных выражений,онлайн калькулятор упрощение многочлена,онлайн калькулятор упрощения выражений,онлайн преобразование выражений,онлайн преобразование тригонометрических выражений,онлайн преобразователь в многочлен,онлайн преобразователь формул,онлайн раскройте скобки,онлайн раскрытие скобок,онлайн решение алгебраических выражений,онлайн решение выражений,онлайн решение выражения,онлайн решение рациональных выражений,онлайн решения выражений,онлайн сокращение выражений,онлайн сокращение многочленов,онлайн упроститель выражений,онлайн упростить,онлайн упростить выражение со степенями,онлайн упростить дробное выражение,онлайн упрощение выражений с дробями,онлайн упрощение выражений с корнями,онлайн упрощение выражений со степенями,онлайн упрощение дробных выражений,онлайн упрощение многочленов,онлайн упрощения выражений,подобные слагаемые калькулятор онлайн,подобные слагаемые онлайн калькулятор,преобразование выражений онлайн,преобразование иррациональных выражений онлайн калькулятор,преобразование рациональных выражений калькулятор онлайн,преобразование рациональных выражений онлайн калькулятор,преобразование формул онлайн,преобразования выражений калькулятор,преобразовать в многочлен выражение онлайн,преобразовать выражение в многочлен онлайн,преобразовать выражение онлайн,преобразовать многочлен в выражение онлайн,преобразуйте в дробь выражение онлайн,преобразуйте в многочлен выражение онлайн калькулятор,преобразуйте дробь в выражение онлайн,приведи подобные слагаемые онлайн калькулятор,пример упростить,пример упростить выражение,примеры упростите выражение,примеры упрощение выражений,примеры упрощения,раскрытие скобок калькулятор,раскрытие скобок калькулятор онлайн,раскрытие скобок онлайн,раскрытие скобок онлайн калькулятор,раскрытия скобок онлайн калькулятор,раскрыть скобки онлайн,раскрыть скобки онлайн калькулятор,рациональных выражений онлайн калькулятор с решением,решение алгебраических выражений онлайн,решение выражений,решение выражений онлайн,решение выражения,решение выражения онлайн,решение онлайн алгебраических выражений,решение онлайн выражения,решение примеров на упрощение выражений,решение упростите выражение,решения выражений онлайн,решите выражение,решить выражение,решить выражение онлайн,решить выражение онлайн со степенями,решить онлайн выражение,сократить выражение,сократить выражение онлайн,сократить выражение онлайн с подробным решением,сократить многочлен онлайн,сократить онлайн выражение,сократить уравнение онлайн,сокращение выражений,сокращение выражений онлайн,сокращение многочленов онлайн,сокращение уравнений онлайн,способы упрощения выражений,спростити вираз,спростити вираз онлайн,спростити вираз онлайн калькулятор,спростити вираз приклади,спростить вираз,спростить вираз онлайн калькулятор,спростіть вираз,спрощення виразів,упрости,упрости выражение,упрости выражения,упростите,упростите 3 4х 2 5,упростите алгебраическое выражение,упростите вы,упростите выражение,упростите выражение 1,упростите выражение 2,упростите выражение 2 3x 2,упростите выражение 3,упростите выражение a,упростите выражение x,упростите выражение x 2 x 8 x,упростите выражение x 3 x 4,упростите выражение а,упростите выражение дроби,упростите выражение дробное,упростите выражение дробь,упростите выражение и,упростите выражение калькулятор,упростите выражение калькулятор онлайн,упростите выражение калькулятор онлайн с решением,упростите выражение калькулятор с дробями,упростите выражение калькулятор с дробями и степенями,упростите выражение калькулятор с степенями,упростите выражение калькулятор с степенями и дробями,упростите выражение онлайн,упростите выражение онлайн калькулятор,упростите выражение онлайн калькулятор с решением,упростите выражение онлайн с дробями,упростите выражение онлайн с дробями и степенями,упростите выражение онлайн с дробями и степенями с решением,упростите выражение онлайн с корнями,упростите выражение примеры,упростите выражение решение,упростите выражение с дробями,упростите выражение с дробями онлайн,упростите выражение с корнями калькулятор,упростите выражение с корнями онлайн,упростите выражения,упростите выражения а,упростите выражения калькулятор,упростите выражения калькулятор онлайн,упростите выражения онлайн,упростите дробное выражение,упростите уравнение,упростите уравнение онлайн,упроститель выражений,упроститель выражений онлайн,упростить 2x 4 6x 6,упростить x 2 x,упростить алгебраическое выражение,упростить векторное выражение онлайн,упростить выражение,упростить выражение 3,упростить выражение алгебра как,упростить выражение алгебраическое,упростить выражение дроби,упростить выражение дробное,упростить выражение дробное онлайн,упростить выражение дробное онлайн калькулятор с решением,упростить выражение как решать,упростить выражение калькулятор,упростить выражение калькулятор онлайн,упростить выражение онлайн,упростить выражение онлайн калькулятор,упростить выражение онлайн калькулятор с дробями,упростить выражение онлайн калькулятор с дробями и буквами,упростить выражение онлайн калькулятор с корнями,упростить выражение онлайн калькулятор с решением,упростить выражение онлайн калькулятор с решением с дробями,упростить выражение онлайн калькулятор с решением с дробями и буквами,упростить выражение онлайн калькулятор с решением с дробями и корнями,упростить выражение онлайн калькулятор с решением с корнями,упростить выражение онлайн калькулятор с решением со степенями,упростить выражение онлайн калькулятор со степенями,упростить выражение онлайн калькулятор со степенями с решением,упростить выражение онлайн с дробями,упростить выражение онлайн с дробями буквами и степенями онлайн,упростить выражение онлайн с дробями и буквами,упростить выражение онлайн с дробями и буквами 8 класс,упростить выражение онлайн с дробями и буквами калькулятор,упростить выражение онлайн с дробями и степенями,упростить выражение онлайн с дробями калькулятор,упростить выражение онлайн с корнями,упростить выражение онлайн с корнями и степенями,упростить выражение онлайн с корнями калькулятор,упростить выражение онлайн с решением,упростить выражение онлайн со степенями,упростить выражение примеры,упростить выражение с дробями,упростить выражение с дробями и буквами,упростить выражение с дробями и буквами 8 класс онлайн,упростить выражение с дробями и буквами онлайн калькулятор,упростить выражение с дробями и с степенями онлайн,упростить выражение с дробями и степенями онлайн,упростить выражение с дробями онлайн,упростить выражение с дробями онлайн калькулятор,упростить выражение с дробями онлайн калькулятор с решением,упростить выражение с корнями онлайн,упростить выражение с корнями онлайн калькулятор,упростить выражение с корнями онлайн калькулятор с решением,упростить выражение с корнями онлайн калькулятор с решением с дробями,упростить выражение со степенями онлайн,упростить выражение со степенями онлайн калькулятор,упростить выражение со степенями онлайн калькулятор с решением,упростить выражение что такое,упростить выражения,упростить выражения онлайн,упростить дробное выражение,упростить дробное выражение онлайн,упростить дробное выражение онлайн калькулятор с решением,упростить дробь онлайн с буквами,упростить дробь онлайн с буквами и степенями,упростить дробь с буквами онлайн,упростить как,упростить калькулятор,упростить многочлен онлайн,упростить онлайн,упростить онлайн выражение с корнями,упростить онлайн выражение со степенями,упростить тригонометрическое выражение онлайн,упростить тригонометрическое выражение онлайн калькулятор с решением,упростить уравнение,упростить уравнение онлайн,упростить уравнение онлайн с решением,упрощать как,упрощение алгебраические выражения,упрощение алгебраических выражений,упрощение выражений,упрощение выражений алгебра,упрощение выражений дробей,упрощение выражений дробей калькулятор,упрощение выражений дробных,упрощение выражений дробных онлайн,упрощение выражений калькулятор,упрощение выражений калькулятор онлайн,упрощение выражений калькулятор онлайн с корнями,упрощение выражений онлайн,упрощение выражений онлайн калькулятор,упрощение выражений онлайн калькулятор с дробями,упрощение выражений онлайн калькулятор с решением,упрощение выражений онлайн калькулятор со степенями,упрощение выражений онлайн с дробями,упрощение выражений онлайн с корнями,упрощение выражений онлайн с решением,упрощение выражений примеры,упрощение выражений с дробями,упрощение выражений с дробями калькулятор,упрощение выражений с дробями онлайн,упрощение выражений с дробями онлайн калькулятор,упрощение выражений с корнями онлайн,упрощение выражений с решением онлайн,упрощение выражений со степенями калькулятор онлайн,упрощение выражений со степенями онлайн калькулятор,упрощение дробей онлайн с буквами,упрощение дробей онлайн со степенями и буквами,упрощение дробей с буквами онлайн,упрощение дробных выражений,упрощение дробных выражений калькулятор онлайн,упрощение дробных выражений онлайн,упрощение дробных выражений онлайн калькулятор,упрощение корней онлайн,упрощение многочленов онлайн,упрощение онлайн,упрощение тригонометрических выражений онлайн,упрощение уравнений,упрощение уравнений онлайн,упрощение уравнения,упрощения,упрощения выражений,упрощения выражений онлайн калькулятор,упрощения выражений примеры,упрощения выражения калькулятор,формула упрощения выражения,формулы для упрощения выражений,формулы упрощения,формулы упрощения выражений,формулы упрощения выражения,что такое упростить выражение. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 упростите выражение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 2 упростить выражение 1 2).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 упростите выражение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 2 упростить выражение 1 2).

 3 будет интерпретировано как куб синуса от 2.)
3 будет интерпретировано как куб синуса от 2.) (К примеру, если решить пример 3/14, получить ответ, затем ввести 4 и сразу «=», то произведётся операция 4/14. Аналогично, если ввести v256 и несколько раз «=», то последовательно выведутся ответы 16, 4, 2, 1.414..) Как показала практика, это действительно удобно при вычислении процентных содержаний различных исходов в тесте и тому подобных вещах. В случае введения любого выражения, отличного от числа, последняя произведённая операция из памяти калькулятора удаляется.
(К примеру, если решить пример 3/14, получить ответ, затем ввести 4 и сразу «=», то произведётся операция 4/14. Аналогично, если ввести v256 и несколько раз «=», то последовательно выведутся ответы 16, 4, 2, 1.414..) Как показала практика, это действительно удобно при вычислении процентных содержаний различных исходов в тесте и тому подобных вещах. В случае введения любого выражения, отличного от числа, последняя произведённая операция из памяти калькулятора удаляется. 3 \)
3 \)
 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

 Функции калькулятора. Кнопки калькулятора.
Функции калькулятора. Кнопки калькулятора.
 Управлять калькулятором можно как с помощью мыши, используя панель задач калькулятора, так и посредством клавиатуры вашего компьютера. Порядок ввода математического выражения не имеет значения, просто пользователь выбирает удобный для него способ внесения записи.
Управлять калькулятором можно как с помощью мыши, используя панель задач калькулятора, так и посредством клавиатуры вашего компьютера. Порядок ввода математического выражения не имеет значения, просто пользователь выбирает удобный для него способ внесения записи. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
 , 2, —
, 2, — Этот тип уравнения также называется линейным уравнением .
Для решения этих уравнений мы используем следующую формулу `x = b / a`.
Этот тип уравнения также называется линейным уравнением .
Для решения этих уравнений мы используем следующую формулу `x = b / a`.  Например, введите x + 5, вернитесь к x + 5 = 0 и решите.2-4ac`.
Например, введите x + 5, вернитесь к x + 5 = 0 и решите.2-4ac`.  3 = 0`).
3 = 0`).




 К
решить линейное неравенство, следуя 3x + 5> 0
, просто введите выражение 3 * x + 5> 0 в области исчисления, затем нажмите кнопку вычисления или кнопку
inequality_solver, точный результат возвращается `[x> -5/3]`.2 + b * x + c> 0` выполняется очень быстро,
если переменная не является неоднозначной, просто введите неравенство с по решите и щелкните inequality_solver, затем будет возвращен точный результат.
К
решить линейное неравенство, следуя 3x + 5> 0
, просто введите выражение 3 * x + 5> 0 в области исчисления, затем нажмите кнопку вычисления или кнопку
inequality_solver, точный результат возвращается `[x> -5/3]`.2 + b * x + c> 0` выполняется очень быстро,
если переменная не является неоднозначной, просто введите неравенство с по решите и щелкните inequality_solver, затем будет возвращен точный результат.
 Вы также можете ввести математические свойства и методы JavaScript.
Например, чтобы найти значение pi (p), введите:
PI (Важно: JavaScript чувствителен к регистру! PI используется ТОЛЬКО в верхнем регистре !.
Чтобы найти журнал из 3, введите (ТОЛЬКО нижний регистр):
журнал (3)
Чтобы найти 2 в 3-й степени, введите:
пау (2,3)
Чтобы найти площадь 9-дюймовой пиццы (в квадратных дюймах), введите:
PI * pow (9 / 2,2)
Круглые скобки () могут изменять порядок операций.
---------- Законные математические операторы (порядок и иерархия ВАЖНЫ!)
+ добавить
- вычесть
/ делить
* умножить
() иерархия - Пример (4 + 1) / 2 или 4 + 1/2
% модуля - Пример (8 + 7)% 13 возвращает 2
---------- Законные операторы сравнения -------------
== равенство - ПРИМЕР 5 == 4 возвращает false
! = неравенство - ПРИМЕР 5! = 4 возвращает истину
больше чем - ПРИМЕР 5> 4 возвращает истину
= больше или равно - ПРИМЕР 5> = 4 возвращает истину
&& логическое И - ПРИМЕР 5> 4 && 3> 4 возвращает false
|| логическое ИЛИ - ПРИМЕР 5> 4 || 3> 4 возвращает истину
! логическое НЕ - ПРИМЕР! (5 == 5) возвращает false
---------- Математические свойства (Константы.
Вы также можете ввести математические свойства и методы JavaScript.
Например, чтобы найти значение pi (p), введите:
PI (Важно: JavaScript чувствителен к регистру! PI используется ТОЛЬКО в верхнем регистре !.
Чтобы найти журнал из 3, введите (ТОЛЬКО нижний регистр):
журнал (3)
Чтобы найти 2 в 3-й степени, введите:
пау (2,3)
Чтобы найти площадь 9-дюймовой пиццы (в квадратных дюймах), введите:
PI * pow (9 / 2,2)
Круглые скобки () могут изменять порядок операций.
---------- Законные математические операторы (порядок и иерархия ВАЖНЫ!)
+ добавить
- вычесть
/ делить
* умножить
() иерархия - Пример (4 + 1) / 2 или 4 + 1/2
% модуля - Пример (8 + 7)% 13 возвращает 2
---------- Законные операторы сравнения -------------
== равенство - ПРИМЕР 5 == 4 возвращает false
! = неравенство - ПРИМЕР 5! = 4 возвращает истину
больше чем - ПРИМЕР 5> 4 возвращает истину
= больше или равно - ПРИМЕР 5> = 4 возвращает истину
&& логическое И - ПРИМЕР 5> 4 && 3> 4 возвращает false
|| логическое ИЛИ - ПРИМЕР 5> 4 || 3> 4 возвращает истину
! логическое НЕ - ПРИМЕР! (5 == 5) возвращает false
---------- Математические свойства (Константы. Важно: ТОЛЬКО верхний регистр!).
E (База из натурального бревна, около 2,718)
LN10 (натуральный логарифм 10, около 2,302)
LN2 (Натуральный логарифм 2, около 0,693)
LOG2E (логарифм от E по основанию 2, около 1,442)
LOG10E (логарифм E по основанию 10, около 0,434)
PI (PI = отношение длины окружности к диаметру, около 3,142)
SQRT1_2 (квадратный корень 1/2, около 0,707)
SQRT2 (квадратный корень из 2, около 1,414)
---------- Методы (Функции.Важно: ТОЛЬКО нижний регистр!) -----
abs (x) (абсолютное значение x)
acos (x) (арккосинус x в радианах)
asin (x) (арксинус x, в радианах)
atan (x) (арктангенс x в радианах)
ceil (x) (следующее большее целое, чем x)
cos (x) (косинус x, x в радианах)
exp (x) (экспоненциальная функция от x)
floor (x) (следующее меньшее целое число)
log (x) (натуральный логарифм x)
max (x, y) (максимум x, y)
min (x, y) (минимум x, y)
pow (x, y) (x в степени y)
random () (псевдослучайное число, равномерное от 0 до 1)
round (x) (округляет x до ближайшего целого числа)
sin (x) (синус x, где x в радианах)
sqrt (x) (квадратный корень из x)
tan (x) (тангенс x, где x в радианах)
Важно: ТОЛЬКО верхний регистр!).
E (База из натурального бревна, около 2,718)
LN10 (натуральный логарифм 10, около 2,302)
LN2 (Натуральный логарифм 2, около 0,693)
LOG2E (логарифм от E по основанию 2, около 1,442)
LOG10E (логарифм E по основанию 10, около 0,434)
PI (PI = отношение длины окружности к диаметру, около 3,142)
SQRT1_2 (квадратный корень 1/2, около 0,707)
SQRT2 (квадратный корень из 2, около 1,414)
---------- Методы (Функции.Важно: ТОЛЬКО нижний регистр!) -----
abs (x) (абсолютное значение x)
acos (x) (арккосинус x в радианах)
asin (x) (арксинус x, в радианах)
atan (x) (арктангенс x в радианах)
ceil (x) (следующее большее целое, чем x)
cos (x) (косинус x, x в радианах)
exp (x) (экспоненциальная функция от x)
floor (x) (следующее меньшее целое число)
log (x) (натуральный логарифм x)
max (x, y) (максимум x, y)
min (x, y) (минимум x, y)
pow (x, y) (x в степени y)
random () (псевдослучайное число, равномерное от 0 до 1)
round (x) (округляет x до ближайшего целого числа)
sin (x) (синус x, где x в радианах)
sqrt (x) (квадратный корень из x)
tan (x) (тангенс x, где x в радианах)
 Подробнее см .: здесь
Подробнее см .: здесь 2 + 3)
2 + 3) 

 141592654 …)
141592654 …)
















 {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
 Да, выглядит непривычно, но ответ не выбирают.
Да, выглядит непривычно, но ответ не выбирают.
 Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10.
Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10. 75667961083
75667961083 
 Однако вы можете повысить или снизить качество печати PDF-файла.
Однако вы можете повысить или снизить качество печати PDF-файла.
 PowerPoint является частью Microsoft Office набор программ с 1993 года.
PowerPoint является частью Microsoft Office набор программ с 1993 года.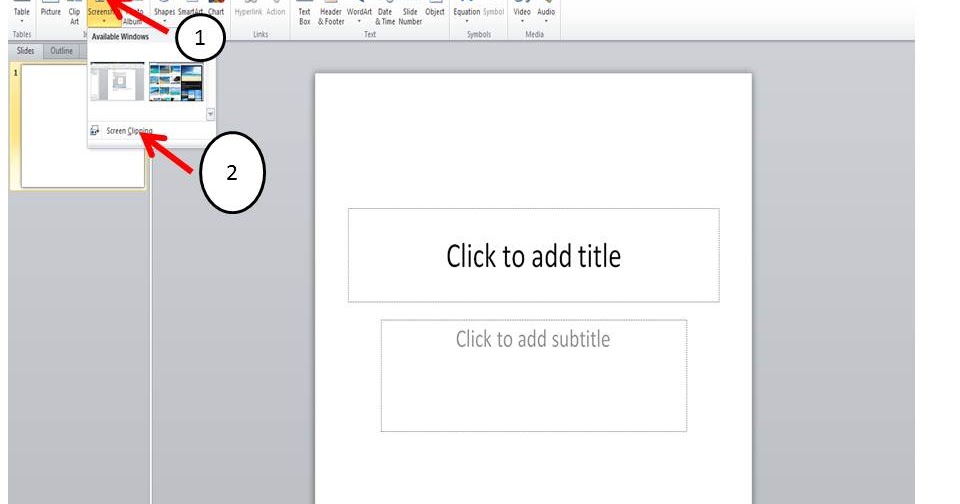 Поэтому PowerPoint необходимо обновить так, чтобы люди на ходу могли бы сделать свои презентации во время путешествия.
Поэтому PowerPoint необходимо обновить так, чтобы люди на ходу могли бы сделать свои презентации во время путешествия.

 Если существует какой-либо способ открыть PDF в PowerPoint, пожалуйста, расскажите о нем.”
Если существует какой-либо способ открыть PDF в PowerPoint, пожалуйста, расскажите о нем.” Преимущества данного способа заключаются в том, что он не требует финансовых вложений и занимает всего несколько минут.
Преимущества данного способа заключаются в том, что он не требует финансовых вложений и занимает всего несколько минут. Почему бы не попробовать программу с такими многообещающими функциями? Ниже Вы можете ознакомиться с инструкцией по работе с данной программой.
Почему бы не попробовать программу с такими многообещающими функциями? Ниже Вы можете ознакомиться с инструкцией по работе с данной программой.
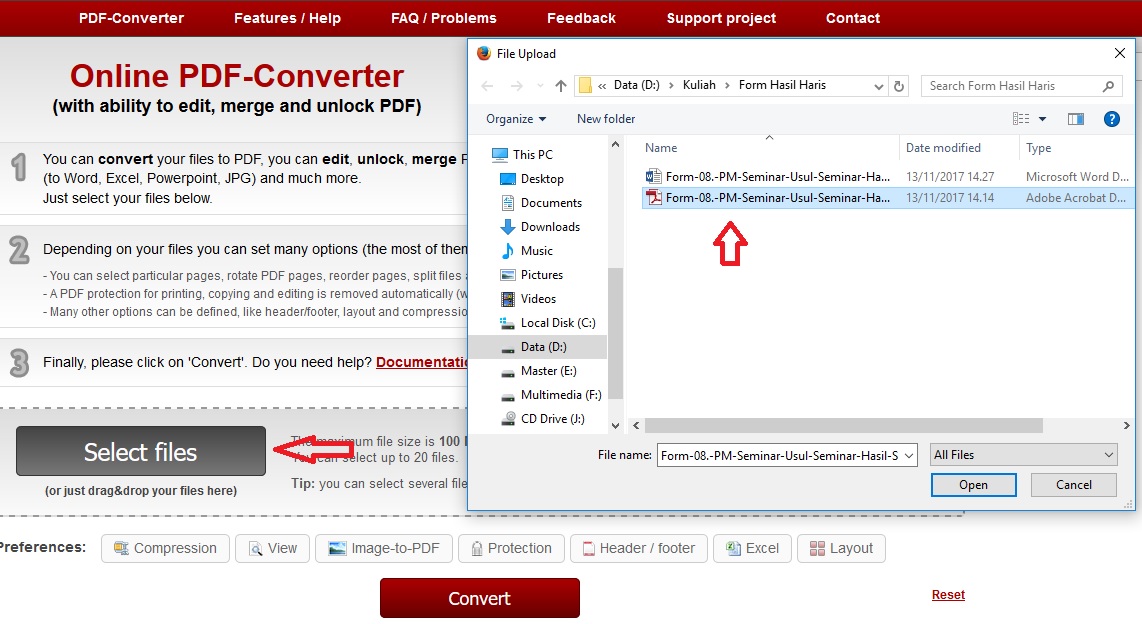 Дождитесь завершения процесса обновления библиотеки словарей.
Дождитесь завершения процесса обновления библиотеки словарей. Заходите на наш сайт, скоро у нас появятся новые полезные статьи!
Заходите на наш сайт, скоро у нас появятся новые полезные статьи!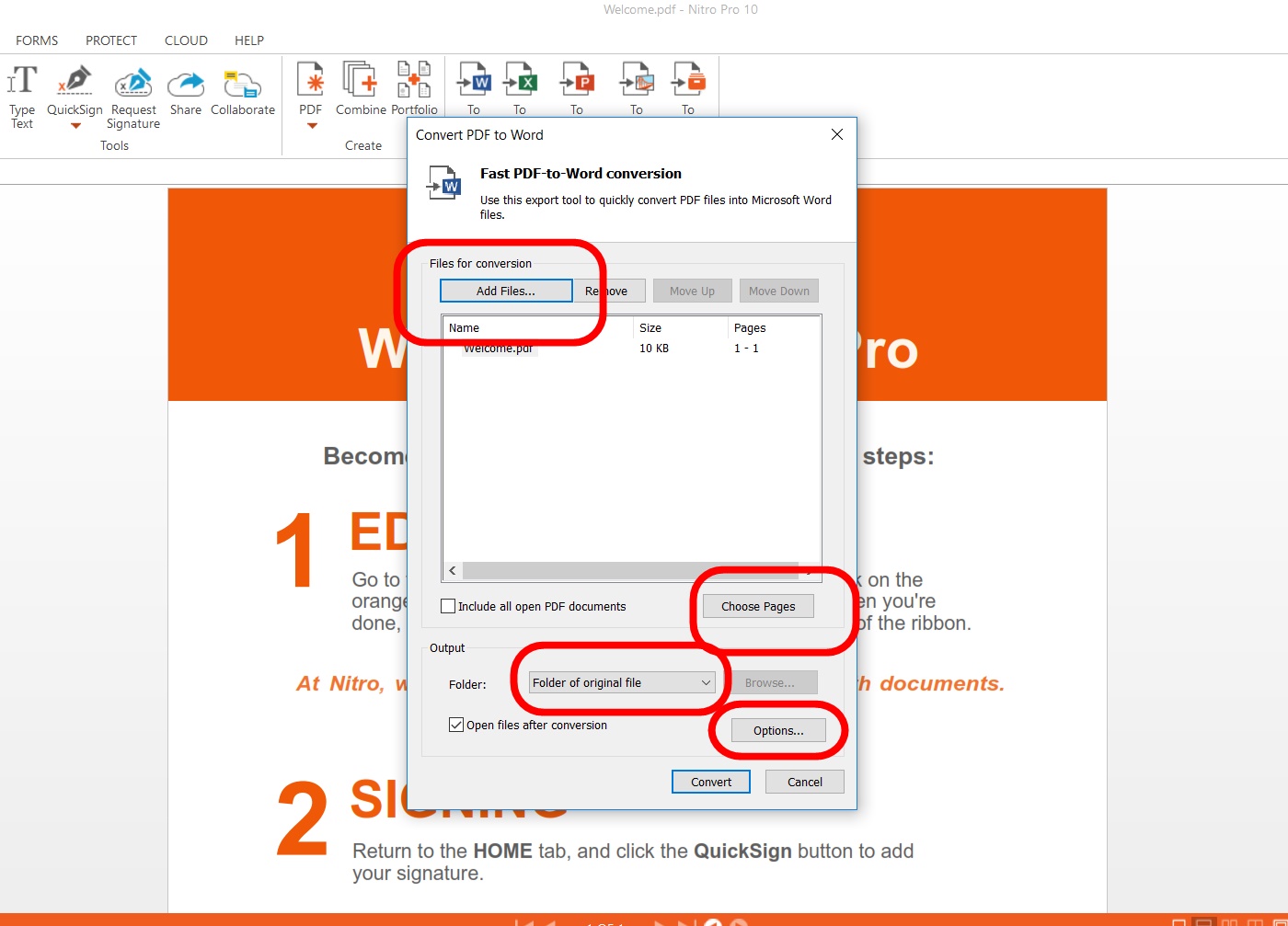


.jpg)
 0\PowerPoint\Options
2013 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
2010 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
2007 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
2003 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
0\PowerPoint\Options
2013 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
2010 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
2007 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options
2003 : HKEY_CURRENT_USER\Software\Microsoft\Office.0\PowerPoint\Options


 Такая ссылка будет работать при переходе с любого интернет-ресурса.
Такая ссылка будет работать при переходе с любого интернет-ресурса.
 html файл размещается на уровень ниже, чем исходная PowerPoint презентация и оригинальный прикрепленный файл, поэтому файл не может быть найден по старому короткому пути.
html файл размещается на уровень ниже, чем исходная PowerPoint презентация и оригинальный прикрепленный файл, поэтому файл не может быть найден по старому короткому пути.
 Текст внутри формы будет подчеркнут, но остальная часть фигуры не будет работать как гиперссылка.
Текст внутри формы будет подчеркнут, но остальная часть фигуры не будет работать как гиперссылка. При наведении курсора мыши на текст, курсор мыши не меняется, по клику гиперссылка не срабатывает.
При наведении курсора мыши на текст, курсор мыши не меняется, по клику гиперссылка не срабатывает.

 Но когда я загружаю эту же презентацию в интернет, гиперссылки снова в порядке.
Но когда я загружаю эту же презентацию в интернет, гиперссылки снова в порядке.

:max_bytes(150000):strip_icc()/01parts-of-powerpoint-screen-58b8c7b15f9b58af5c8c6221.png) Наш инструмент прост в использовании и БЕСПЛАТНО * «,
«ModulePopupHeadOops»: «Ой!»,
«FileTypeIsNotSupported»: «Тип файла не поддерживается.»,
«readLess»: «Читать меньше»,
«readMore»: «Читать дальше»,
«noThanks»: «Нет, спасибо»,
«BuyNow»: «Купить сейчас»,
«PrivacyTerms»: «Конфиденциальность и условия»,
«WordToPdfLink»: «https://www.sodapdf.com/word-to-pdf/»,
«businessAlertText»: «Вы занимаетесь бизнесом?»,
«EmailPreferencesSubTitle»: «Выберите списки рассылки, на которые вы хотите подписаться.Снимите флажок, чтобы отказаться от подписки. \ NЕсли вы хотите изменить язык получаемых писем, «,
«без обслуживания»: «Без обслуживания»,
«successTitle»: «Назначение выполнено успешно»,
«tooltip_1»: «План позволяет одному устройству входить в Soda PDF Online в любой момент времени»,
«contactEmail»: «Контактный адрес электронной почты»,
«BuyLink»: «https://www.sodapdf.com/buy/»,
«GifToJpgLink»: «https://www.sodapdf.com/gif-to-jpg/»,
«PDF_Software»: «Программное обеспечение PDF»,
«selectProduct»: «Выбрать продукт»,
«startFreeTrial»: «Начать бесплатную пробную версию»,
«errorTypeOfProduct»: «Выберите тип продукта»,
«compressed_copy»: «Загрузите сжатую копию вашего файла.
Наш инструмент прост в использовании и БЕСПЛАТНО * «,
«ModulePopupHeadOops»: «Ой!»,
«FileTypeIsNotSupported»: «Тип файла не поддерживается.»,
«readLess»: «Читать меньше»,
«readMore»: «Читать дальше»,
«noThanks»: «Нет, спасибо»,
«BuyNow»: «Купить сейчас»,
«PrivacyTerms»: «Конфиденциальность и условия»,
«WordToPdfLink»: «https://www.sodapdf.com/word-to-pdf/»,
«businessAlertText»: «Вы занимаетесь бизнесом?»,
«EmailPreferencesSubTitle»: «Выберите списки рассылки, на которые вы хотите подписаться.Снимите флажок, чтобы отказаться от подписки. \ NЕсли вы хотите изменить язык получаемых писем, «,
«без обслуживания»: «Без обслуживания»,
«successTitle»: «Назначение выполнено успешно»,
«tooltip_1»: «План позволяет одному устройству входить в Soda PDF Online в любой момент времени»,
«contactEmail»: «Контактный адрес электронной почты»,
«BuyLink»: «https://www.sodapdf.com/buy/»,
«GifToJpgLink»: «https://www.sodapdf.com/gif-to-jpg/»,
«PDF_Software»: «Программное обеспечение PDF»,
«selectProduct»: «Выбрать продукт»,
«startFreeTrial»: «Начать бесплатную пробную версию»,
«errorTypeOfProduct»: «Выберите тип продукта»,
«compressed_copy»: «Загрузите сжатую копию вашего файла. «,
«contactSales»: «Связаться с отделом продаж»,
«sellsheets»: «Product Sheets»,
«PricingLink»: «https://www.sodapdf.com/pricing/»,
«getSoda»: «Получить газировку»,
«noCreditCards»: «Нет кредитных карт»,
«createPdfLink»: «https://online.sodapdf.com/#/home?r=view»,
«accountManagement»: «Управление аккаунтом»,
«SixFiles»: «6 файлов»,
«premiumPhoneSupport»: «Поддержка по телефону премиум-класса»,
«forLimitLicenses»: «Для 1-4 лицензий»,
«knowledgeBase»: «База знаний»,
«passwordRequirements_3»: «Ваш пароль не может содержать \» пароль \ «, \» admin \ «или \» administrator \ «»,
«passwordRequirements_2»: «Ваш пароль не может содержать 3 или более последовательных символов или иметь один и тот же символ, повторяющийся последовательно (например,123, ABC, AAA, 111) «,
«YourFilesSecureServers»: «Ваши файлы хранятся на наших серверах только 24 часа, после чего они уничтожаются безвозвратно.»,
«errorConfirmEmailPasswordMatch»: «Введенные адрес электронной почты и пароль не совпадают»,
«PdfToImageLink»: «https://www.
«,
«contactSales»: «Связаться с отделом продаж»,
«sellsheets»: «Product Sheets»,
«PricingLink»: «https://www.sodapdf.com/pricing/»,
«getSoda»: «Получить газировку»,
«noCreditCards»: «Нет кредитных карт»,
«createPdfLink»: «https://online.sodapdf.com/#/home?r=view»,
«accountManagement»: «Управление аккаунтом»,
«SixFiles»: «6 файлов»,
«premiumPhoneSupport»: «Поддержка по телефону премиум-класса»,
«forLimitLicenses»: «Для 1-4 лицензий»,
«knowledgeBase»: «База знаний»,
«passwordRequirements_3»: «Ваш пароль не может содержать \» пароль \ «, \» admin \ «или \» administrator \ «»,
«passwordRequirements_2»: «Ваш пароль не может содержать 3 или более последовательных символов или иметь один и тот же символ, повторяющийся последовательно (например,123, ABC, AAA, 111) «,
«YourFilesSecureServers»: «Ваши файлы хранятся на наших серверах только 24 часа, после чего они уничтожаются безвозвратно.»,
«errorConfirmEmailPasswordMatch»: «Введенные адрес электронной почты и пароль не совпадают»,
«PdfToImageLink»: «https://www.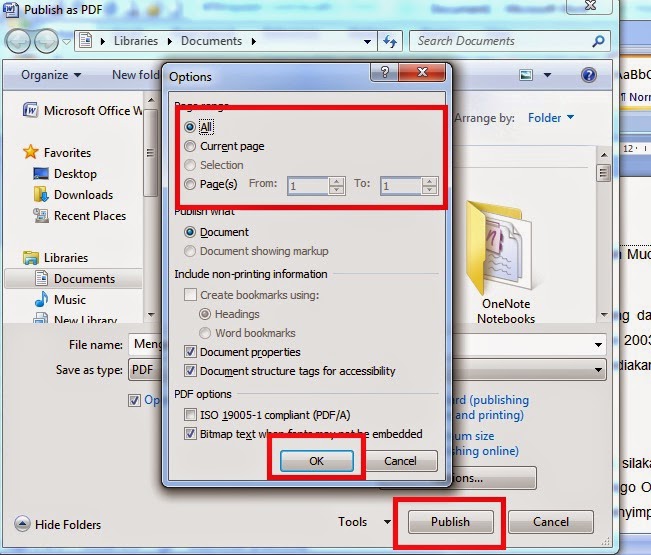 sodapdf.com/pdf-to-jpg/»,
«WhatsNewTitle»: «Что нового в Soda PDF Anywhere»,
«registerSignUpTitle»: «С подключенной учетной записью»,
«WordToPdf»: «Word в PDF»,
«paymentAssociatedCreditCard»: «Продукты, связанные с этой кредитной картой»,
«createdPasswordSuccessfully»: «Ваш пароль был успешно создан.»,
«CookiesForAdvertising»: «Этот сайт использует файлы cookie в рекламных и аналитических целях. Пожалуйста, ознакомьтесь с нашей Политикой конфиденциальности, чтобы получить дополнительную информацию о файлах cookie и их использовании, а также о возможности изменения настроек файлов cookie.»,
«PDFReader»: «PDF Reader»,
«Сбережения»: «СБЕРЕЖЕНИЯ»,
«YourFilesSecure»: «Ваши файлы в безопасности»,
«ConvertfromPDF»: «Конвертировать из PDF»,
«WorkingOffline»: «Работаете в автономном режиме?»,
«зарегистрироваться»: «Зарегистрироваться»,
«sodaVersion»: «Сода PDF»,
«wouldLikeContinue»: «Хотите продолжить?»,
«productAvaliableProducts»: «Доступные продукты»,
«one_time_fee»: «единовременная плата»,
«Privacy_Terms»: «Конфиденциальность и условия»,
«RegisterLink»: «https: // www.
sodapdf.com/pdf-to-jpg/»,
«WhatsNewTitle»: «Что нового в Soda PDF Anywhere»,
«registerSignUpTitle»: «С подключенной учетной записью»,
«WordToPdf»: «Word в PDF»,
«paymentAssociatedCreditCard»: «Продукты, связанные с этой кредитной картой»,
«createdPasswordSuccessfully»: «Ваш пароль был успешно создан.»,
«CookiesForAdvertising»: «Этот сайт использует файлы cookie в рекламных и аналитических целях. Пожалуйста, ознакомьтесь с нашей Политикой конфиденциальности, чтобы получить дополнительную информацию о файлах cookie и их использовании, а также о возможности изменения настроек файлов cookie.»,
«PDFReader»: «PDF Reader»,
«Сбережения»: «СБЕРЕЖЕНИЯ»,
«YourFilesSecure»: «Ваши файлы в безопасности»,
«ConvertfromPDF»: «Конвертировать из PDF»,
«WorkingOffline»: «Работаете в автономном режиме?»,
«зарегистрироваться»: «Зарегистрироваться»,
«sodaVersion»: «Сода PDF»,
«wouldLikeContinue»: «Хотите продолжить?»,
«productAvaliableProducts»: «Доступные продукты»,
«one_time_fee»: «единовременная плата»,
«Privacy_Terms»: «Конфиденциальность и условия»,
«RegisterLink»: «https: // www. sodapdf.com/account/register/ «,
«AboutSodaPdf»: «О Soda Pdf»,
«PleaseSignInWithAccount»: «Войдите в свою учетную запись»,
«mergeToolLink»: «https://www.sodapdf.com/pdf-merge/»,
«активация»: «Активация»,
«EulaLink»: «https://www.sodapdf.com/terms-of-use/#eula»,
«formProductInterest»: «Интересующий продукт»,
«PDF_annual»: «* годовой план»,
«emailAddress»: «Адрес электронной почты»,
«Разблокировать»: «Разблокировать»,
«learnMore»: «Первое в мире онлайн-программное обеспечение для работы с PDF»,
«sitemap»: «Sitemap»,
«switchYearly»: «переходить на ежегодный»,
«MergeLink»: «https: // www.sodapdf.com/pdf-merge/ «,
«choose3options»: «Однако вы можете выбрать один из трех вариантов»,
«PngToJpg»: «PNG в JPG»,
«PngToPdf»: «PNG в PDF»,
«fromDevice»: «С устройства»,
«forLimitLicenses5»: «Для 5-24 лицензий»,
«cancelRequest»: «Отменить запрос»,
«resourceCenter»: «Ресурсный центр»,
«FallDocuments»: «Меня уволили после того, как я заснул по личным документам.»,
«PlanLinks»: «Планы и цены»,
«low_quality_text»: «меньшее качество, наименьший размер файла»,
«fromOpdfs»: «
sodapdf.com/account/register/ «,
«AboutSodaPdf»: «О Soda Pdf»,
«PleaseSignInWithAccount»: «Войдите в свою учетную запись»,
«mergeToolLink»: «https://www.sodapdf.com/pdf-merge/»,
«активация»: «Активация»,
«EulaLink»: «https://www.sodapdf.com/terms-of-use/#eula»,
«formProductInterest»: «Интересующий продукт»,
«PDF_annual»: «* годовой план»,
«emailAddress»: «Адрес электронной почты»,
«Разблокировать»: «Разблокировать»,
«learnMore»: «Первое в мире онлайн-программное обеспечение для работы с PDF»,
«sitemap»: «Sitemap»,
«switchYearly»: «переходить на ежегодный»,
«MergeLink»: «https: // www.sodapdf.com/pdf-merge/ «,
«choose3options»: «Однако вы можете выбрать один из трех вариантов»,
«PngToJpg»: «PNG в JPG»,
«PngToPdf»: «PNG в PDF»,
«fromDevice»: «С устройства»,
«forLimitLicenses5»: «Для 5-24 лицензий»,
«cancelRequest»: «Отменить запрос»,
«resourceCenter»: «Ресурсный центр»,
«FallDocuments»: «Меня уволили после того, как я заснул по личным документам.»,
«PlanLinks»: «Планы и цены»,
«low_quality_text»: «меньшее качество, наименьший размер файла»,
«fromOpdfs»: « Ваш файл готов!
Ваш файл готов!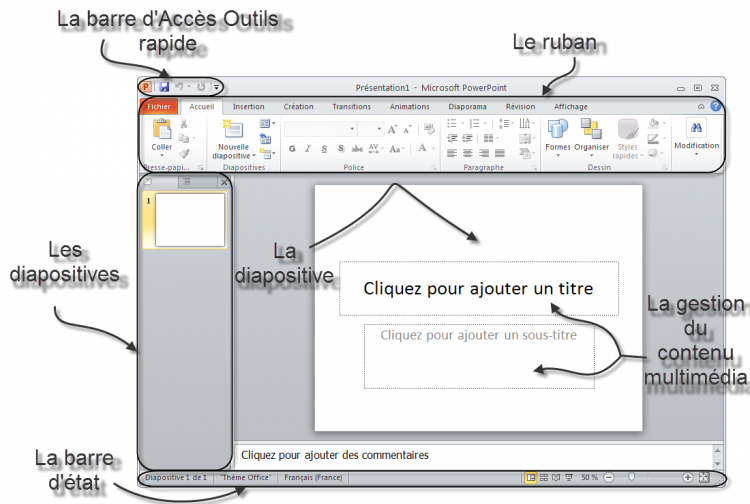 sodapdf.com/account/manage-products/ «,
«youtubeTitle»: «Откройте для себя Soda PDF Anywhere»,
«previewText»: «Предварительный просмотр Soda PDF 12»,
«TenPack»: «10-PACK»,
«labelStateProvince»: «Штат / провинция»,
«formFirstName»: «Имя»,
«solutionsBusines»: «Решения для бизнеса»,
«ConnectedAccounts»: «Подключенные учетные записи»,
«One_file_only»: «ТОЛЬКО ОДИН ФАЙЛ»,
«PrivacyPolicyLink»: «https://www.sodapdf.com/privacy/»,
«Выход»: «Выйти»,
«compressWithSodaSubPrgh»: «Уменьшите размер PDF всего за несколько кликов.Это просто и бесплатно * «,
«ConvertPassProtected»: «Загруженный файл защищен паролем и не может быть преобразован.»,
«JpgToGif»: «JPG в GIF»,
«JpgToPdf»: «JPG в PDF»,
«JpgToPng»: «JPG в PNG»,
«emailPasswordIncorrect»: «Ваш адрес электронной почты или пароль неверны.»,
«BlogLink»: «https://www.sodapdf.com/blog/»,
«errorConfirmPasswordMatch»: «Ваши пароли не совпадают»,
«batchPrgh»: «Загрузите файл, содержащий электронные письма пользователей, которым вы хотите назначить лицензию.
sodapdf.com/account/manage-products/ «,
«youtubeTitle»: «Откройте для себя Soda PDF Anywhere»,
«previewText»: «Предварительный просмотр Soda PDF 12»,
«TenPack»: «10-PACK»,
«labelStateProvince»: «Штат / провинция»,
«formFirstName»: «Имя»,
«solutionsBusines»: «Решения для бизнеса»,
«ConnectedAccounts»: «Подключенные учетные записи»,
«One_file_only»: «ТОЛЬКО ОДИН ФАЙЛ»,
«PrivacyPolicyLink»: «https://www.sodapdf.com/privacy/»,
«Выход»: «Выйти»,
«compressWithSodaSubPrgh»: «Уменьшите размер PDF всего за несколько кликов.Это просто и бесплатно * «,
«ConvertPassProtected»: «Загруженный файл защищен паролем и не может быть преобразован.»,
«JpgToGif»: «JPG в GIF»,
«JpgToPdf»: «JPG в PDF»,
«JpgToPng»: «JPG в PNG»,
«emailPasswordIncorrect»: «Ваш адрес электронной почты или пароль неверны.»,
«BlogLink»: «https://www.sodapdf.com/blog/»,
«errorConfirmPasswordMatch»: «Ваши пароли не совпадают»,
«batchPrgh»: «Загрузите файл, содержащий электронные письма пользователей, которым вы хотите назначить лицензию. Файл должен быть в формате .csv.Электронные письма должны быть в первом поле. Имя и фамилия не обязательны, но могут быть помещены во второе и третье поля. «,
«PurchasedDate»: «Дата покупки»,
«OpenedPassProtect»: «Загруженный файл защищен паролем и не может быть открыт.»,
«One_file_only2»: «Только один файл»,
«LinkfFeatures»: «https://www.sodapdf.com/features/»,
«manualFree»: «Бесплатно и надежно»,
«ready_1_strong»: «Еще не пробовали наше настольное приложение?»,
«Повернуть»: «Повернуть»,
«buyNowFoot»: «Купить сейчас»,
«SwitcherEnable»: «Включить»,
«Подмножество»: «Подмножество»,
«Суффикс»: «Суффикс»,
«supportText»: « БЕСПЛАТНО Поддержка клиентов
Файл должен быть в формате .csv.Электронные письма должны быть в первом поле. Имя и фамилия не обязательны, но могут быть помещены во второе и третье поля. «,
«PurchasedDate»: «Дата покупки»,
«OpenedPassProtect»: «Загруженный файл защищен паролем и не может быть открыт.»,
«One_file_only2»: «Только один файл»,
«LinkfFeatures»: «https://www.sodapdf.com/features/»,
«manualFree»: «Бесплатно и надежно»,
«ready_1_strong»: «Еще не пробовали наше настольное приложение?»,
«Повернуть»: «Повернуть»,
«buyNowFoot»: «Купить сейчас»,
«SwitcherEnable»: «Включить»,
«Подмножество»: «Подмножество»,
«Суффикс»: «Суффикс»,
«supportText»: « БЕСПЛАТНО Поддержка клиентов  «,
«OfferEXTENDEDGet60»: «Предложение РАСШИРЕНО Получите скидку 60% на : объединение, сжатие и многое другое!»,
«FreeUpdates»: «Бесплатные обновления»,
«FreePdfReader»: «Читатель Soda 3D»,
«Save50»: «SAVE 50% «,
«termsOfUse»: «Условия использования»,
«WatermarkLink»: «https: //www.sodapdf.com / add-watermark-to-pdf / «,
«Префикс»: «Префикс»,
«ContactSalesLink»: «https://www.sodapdf.com/contact-sales/»,
«errorEndsWithEmail»: «—«,
«ProductOverview»: «Обзор продукта»,
«stayConnected»: «Оставайтесь на связи»,
«HtmlPDFLabel»: «Хотите преобразовать веб-страницу в файл PDF? Сделайте это бесплатно на»,
«moduleOCRReq»: « OCR Module требует»,
«ThankyouCTA2notice_bottom»: «на рабочий стол»,
«Позиция»: «Позиция»,
«mobile_app_stores»: «Объединяйте и создавайте PDF-файлы бесплатно на своем телефоне»,
«getVolumePricing»: «Получить оптовые цены»,
«pagesToInsert»: «Страницы для вставки»,
«CreateFiles»: «Создавать файлы PDF»,
«labelIndustry»: «Промышленность»,
«ready_2_strong»: «Вам нужны PDF-файлы на ходу?»,
«Премиум»: «ПРЕМИУМ»,
«Защитить»: «Защитить»,
«DragFile»: «Перетащите сюда файлы»,
«ChooseCompressionRatio»: «Выбрать степень сжатия»,
«errorTimelineRequired»: «Выберите временную шкалу»,
«PdfToWorldToolLink»: «https: // www.
«,
«OfferEXTENDEDGet60»: «Предложение РАСШИРЕНО Получите скидку 60% на : объединение, сжатие и многое другое!»,
«FreeUpdates»: «Бесплатные обновления»,
«FreePdfReader»: «Читатель Soda 3D»,
«Save50»: «SAVE 50% «,
«termsOfUse»: «Условия использования»,
«WatermarkLink»: «https: //www.sodapdf.com / add-watermark-to-pdf / «,
«Префикс»: «Префикс»,
«ContactSalesLink»: «https://www.sodapdf.com/contact-sales/»,
«errorEndsWithEmail»: «—«,
«ProductOverview»: «Обзор продукта»,
«stayConnected»: «Оставайтесь на связи»,
«HtmlPDFLabel»: «Хотите преобразовать веб-страницу в файл PDF? Сделайте это бесплатно на»,
«moduleOCRReq»: « OCR Module требует»,
«ThankyouCTA2notice_bottom»: «на рабочий стол»,
«Позиция»: «Позиция»,
«mobile_app_stores»: «Объединяйте и создавайте PDF-файлы бесплатно на своем телефоне»,
«getVolumePricing»: «Получить оптовые цены»,
«pagesToInsert»: «Страницы для вставки»,
«CreateFiles»: «Создавать файлы PDF»,
«labelIndustry»: «Промышленность»,
«ready_2_strong»: «Вам нужны PDF-файлы на ходу?»,
«Премиум»: «ПРЕМИУМ»,
«Защитить»: «Защитить»,
«DragFile»: «Перетащите сюда файлы»,
«ChooseCompressionRatio»: «Выбрать степень сжатия»,
«errorTimelineRequired»: «Выберите временную шкалу»,
«PdfToWorldToolLink»: «https: // www.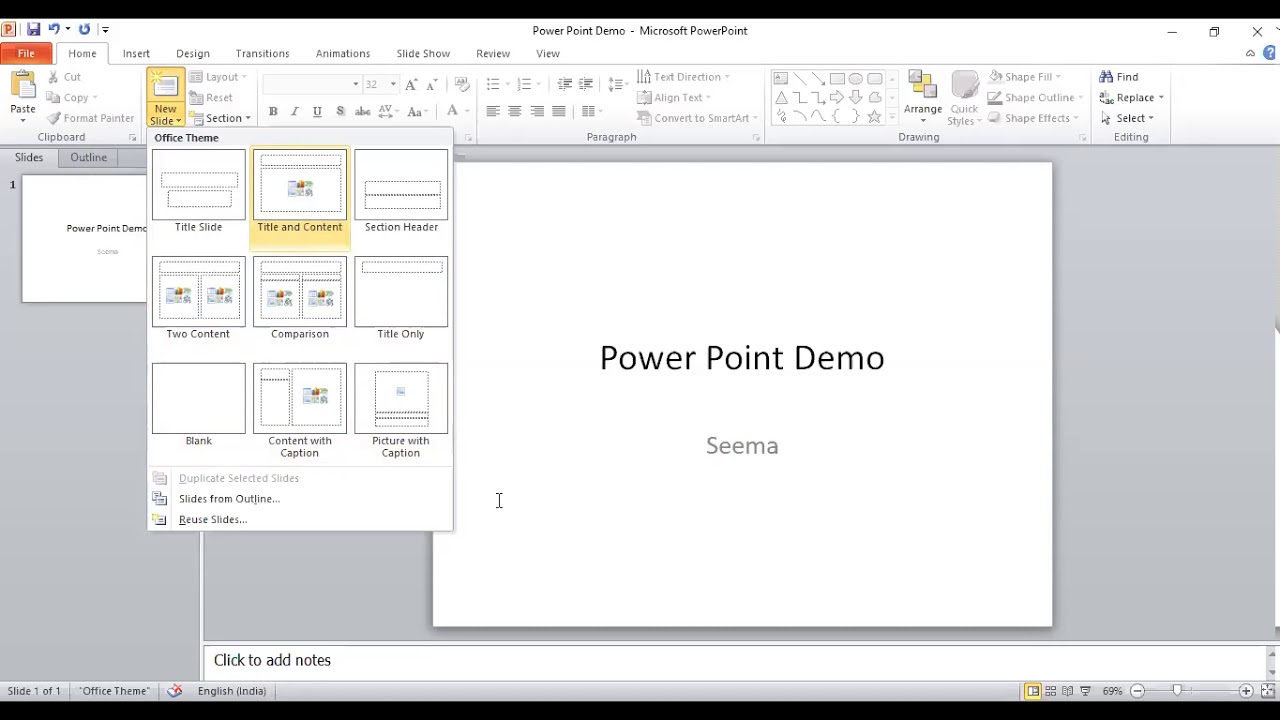 sodapdf.com/pdf-to-word/ «,
«Excel2pdf»: «Excel в PDF»,
«cookieSettings»: «Настройки файлов cookie»,
«PopularTools»: «Популярные инструменты»,
«errorRequired»: «Это поле обязательно для заполнения»,
«sodaPdfAnywhereOverview»: «Обзор Soda PDF Anywhere»,
«Авторское право»: «Авторское право»,
«SwitcherDisable»: «Отключить»,
«Ppt2pdf»: «PPT в PDF»,
«professionalPackage»: «Профессиональный пакет»,
«SignFiles»: «Подписать файлы PDF»,
«selectModule»: «Выбрать другую функцию»,
«btnDownloadText»: «Просмотреть и загрузить в браузере»,
«ArticleTitleThree»: «Как объединить документы с помощью Soda PDF 12»,
«CompressFiles»: «Сжимать файлы PDF»,
«PdfToExcelLink»: «https: // www.sodapdf.com/pdf-to-excel/ «,
«cloudUpload»: «загружено из облака»,
«RemoveMain maintenance»: «Удалить обслуживание»,
«PDF_next»: «следующий»,
«CompressTitle»: «Сжать PDF — БЕСПЛАТНО уменьшить размер файла PDF в Интернете»,
«OnDesktop»: «На рабочем столе»,
«expiresDate»: «Срок действия — дата»,
«PDFBates»: «Нумерация Бейтса PDF»,
«PdfFormFillerLink»: «https://www.
sodapdf.com/pdf-to-word/ «,
«Excel2pdf»: «Excel в PDF»,
«cookieSettings»: «Настройки файлов cookie»,
«PopularTools»: «Популярные инструменты»,
«errorRequired»: «Это поле обязательно для заполнения»,
«sodaPdfAnywhereOverview»: «Обзор Soda PDF Anywhere»,
«Авторское право»: «Авторское право»,
«SwitcherDisable»: «Отключить»,
«Ppt2pdf»: «PPT в PDF»,
«professionalPackage»: «Профессиональный пакет»,
«SignFiles»: «Подписать файлы PDF»,
«selectModule»: «Выбрать другую функцию»,
«btnDownloadText»: «Просмотреть и загрузить в браузере»,
«ArticleTitleThree»: «Как объединить документы с помощью Soda PDF 12»,
«CompressFiles»: «Сжимать файлы PDF»,
«PdfToExcelLink»: «https: // www.sodapdf.com/pdf-to-excel/ «,
«cloudUpload»: «загружено из облака»,
«RemoveMain maintenance»: «Удалить обслуживание»,
«PDF_next»: «следующий»,
«CompressTitle»: «Сжать PDF — БЕСПЛАТНО уменьшить размер файла PDF в Интернете»,
«OnDesktop»: «На рабочем столе»,
«expiresDate»: «Срок действия — дата»,
«PDFBates»: «Нумерация Бейтса PDF»,
«PdfFormFillerLink»: «https://www. sodapdf.com/pdf-form-filler-creator/»,
«youShouldCreateAccount»: «Создайте учетную запись с этим адресом электронной почты для доступа к вашему продукту.»,
«expiredTime»: «Срок действия истекает через»,
«expiredDate»: «Срок действия истек»,
«howActivateSoda»: «Как активировать Soda PDF»,
«FreeOnlineToolsLink»: «https: // www.sodapdf.com/freeonlinetools/ «,
«ExceedsSizeLimit»: «Размер файла превышает максимально допустимый»,
«Подключиться»: «Подключиться»,
«emailNotValid»: «Пожалуйста, укажите действующий адрес электронной почты»,
«footerLuluWebsite»: «Сайт компании»,
«fullPagesRangeError»: «Ваши начальная и конечная страницы охватывают весь загруженный документ. Поэтому разделения не произойдет.»,
«footerCopyText»: «Soda PDF является товарным знаком LULU Software ™.»,
«fromOurSalesTeam»: «От нашей команды продаж»,
«openTicketBackText»: «Отправьте запрос в службу поддержки и получите необходимую помощь.»,
«montlyPlan»: «Ежемесячный план»,
«englishOnly»: «Только английский»,
«ChangePending»: «Ожидается изменение»,
«SoftwareLink»: «https://www.
sodapdf.com/pdf-form-filler-creator/»,
«youShouldCreateAccount»: «Создайте учетную запись с этим адресом электронной почты для доступа к вашему продукту.»,
«expiredTime»: «Срок действия истекает через»,
«expiredDate»: «Срок действия истек»,
«howActivateSoda»: «Как активировать Soda PDF»,
«FreeOnlineToolsLink»: «https: // www.sodapdf.com/freeonlinetools/ «,
«ExceedsSizeLimit»: «Размер файла превышает максимально допустимый»,
«Подключиться»: «Подключиться»,
«emailNotValid»: «Пожалуйста, укажите действующий адрес электронной почты»,
«footerLuluWebsite»: «Сайт компании»,
«fullPagesRangeError»: «Ваши начальная и конечная страницы охватывают весь загруженный документ. Поэтому разделения не произойдет.»,
«footerCopyText»: «Soda PDF является товарным знаком LULU Software ™.»,
«fromOurSalesTeam»: «От нашей команды продаж»,
«openTicketBackText»: «Отправьте запрос в службу поддержки и получите необходимую помощь.»,
«montlyPlan»: «Ежемесячный план»,
«englishOnly»: «Только английский»,
«ChangePending»: «Ожидается изменение»,
«SoftwareLink»: «https://www. sodapdf.com/»,
«thankYouTitle»: «Спасибо за установку Soda PDF»,
«myProducts»: «Мои продукты»,
«convert»: «Конвертировать»,
«CompressPassProtected»: «Загруженный файл защищен паролем и не может быть сжат.»,
«products»: «Товары»,
«WinTitle1»: «Полное решение PDF»,
«обязательный»: «обязательный»,
«PDFexceed_title»: «Загруженный файл превышает максимально допустимый размер»,
«fileReadyTitle»: «УРА! Ваш файл готов,
sodapdf.com/»,
«thankYouTitle»: «Спасибо за установку Soda PDF»,
«myProducts»: «Мои продукты»,
«convert»: «Конвертировать»,
«CompressPassProtected»: «Загруженный файл защищен паролем и не может быть сжат.»,
«products»: «Товары»,
«WinTitle1»: «Полное решение PDF»,
«обязательный»: «обязательный»,
«PDFexceed_title»: «Загруженный файл превышает максимально допустимый размер»,
«fileReadyTitle»: «УРА! Ваш файл готов,  Но как вообще вы вставляете страницы в уже существующий PDF-файл, который кажется нежелательным для изменения? «,
«ArticleDescriptionTwo»: «Вы повысите свою эффективность только тогда, когда научитесь создавать файлы PDF в пакетном режиме.Любой файл, который можно распечатать на бумаге, также можно преобразовать в формат PDF. С помощью процесса пакетного создания Soda PDF 12 вы можете взять любое количество файлов, независимо от формата, и одновременно преобразовать их все в PDF-файлы. «,
«changedCongratulations»: «Поздравляем, вы успешно изменили адрес электронной почты.»,
«features_text»: «Неограниченно: объединение, преобразование, редактирование, вставка, сжатие, просмотр и многое другое!»,
«productAction»: «Действие»,
«enterWaterMarkText»: «Пожалуйста, введите текст водяного знака.»,
«onlinePdfTools»: «Инструменты для работы с PDF в Интернете»,
«PdfConverter»: «Конвертер PDF»,
«productAssign»: «Назначить»,
«ResourcesLink»: «https://www.sodapdf.com/resources/»,
«WhatsNewText»: «Испытайте первое в истории полнофункциональное онлайн-решение для работы с PDF.
Но как вообще вы вставляете страницы в уже существующий PDF-файл, который кажется нежелательным для изменения? «,
«ArticleDescriptionTwo»: «Вы повысите свою эффективность только тогда, когда научитесь создавать файлы PDF в пакетном режиме.Любой файл, который можно распечатать на бумаге, также можно преобразовать в формат PDF. С помощью процесса пакетного создания Soda PDF 12 вы можете взять любое количество файлов, независимо от формата, и одновременно преобразовать их все в PDF-файлы. «,
«changedCongratulations»: «Поздравляем, вы успешно изменили адрес электронной почты.»,
«features_text»: «Неограниченно: объединение, преобразование, редактирование, вставка, сжатие, просмотр и многое другое!»,
«productAction»: «Действие»,
«enterWaterMarkText»: «Пожалуйста, введите текст водяного знака.»,
«onlinePdfTools»: «Инструменты для работы с PDF в Интернете»,
«PdfConverter»: «Конвертер PDF»,
«productAssign»: «Назначить»,
«ResourcesLink»: «https://www.sodapdf.com/resources/»,
«WhatsNewText»: «Испытайте первое в истории полнофункциональное онлайн-решение для работы с PDF. «,
«where3 «:» Когда вы окажетесь дома, запустите свой PC и продолжайте с того места, где вы остановились. «,
«where1 «:» Готовишь контракт в офисе, но есть поезд, чтобы успеть? «,
«PdfDownloadLink»: «https://www.sodapdf.com/pdf-download/»,
«protect_unlim»: «Защитить неограниченное ЧИСЛО файлов.»,
«allTools»: «Все инструменты»,
«EnglishContent»: «Доступно только на английском языке»,
«TextToPdfLink»: «https: // www.sodapdf.com/txt-to-pdf/ «,
«HtmlToPdf»: «HTML в PDF»,
«yourDownloadShouldBegin»: «Ваша загрузка должна начаться немедленно.»,
«errorLicensesRequired»: «Введите количество лицензий»,
«formEmailBusiness»: «Рабочий адрес электронной почты»,
«securitySign»: «Безопасность и подпись»,
«BatesNumberingLink»: «https://www.sodapdf.com/bates-numbering/»,
«BatesNumberingTool»: «Нумерация Бейтса»,
«BmpToJpg»: «BMP в JPG»,
«stayInformedOnSoftware»: «Будьте в курсе обновлений программного обеспечения, напоминаний об истечении срока действия, персонализированных советов и получайте эксклюзивные предложения по электронной почте.
«,
«where3 «:» Когда вы окажетесь дома, запустите свой PC и продолжайте с того места, где вы остановились. «,
«where1 «:» Готовишь контракт в офисе, но есть поезд, чтобы успеть? «,
«PdfDownloadLink»: «https://www.sodapdf.com/pdf-download/»,
«protect_unlim»: «Защитить неограниченное ЧИСЛО файлов.»,
«allTools»: «Все инструменты»,
«EnglishContent»: «Доступно только на английском языке»,
«TextToPdfLink»: «https: // www.sodapdf.com/txt-to-pdf/ «,
«HtmlToPdf»: «HTML в PDF»,
«yourDownloadShouldBegin»: «Ваша загрузка должна начаться немедленно.»,
«errorLicensesRequired»: «Введите количество лицензий»,
«formEmailBusiness»: «Рабочий адрес электронной почты»,
«securitySign»: «Безопасность и подпись»,
«BatesNumberingLink»: «https://www.sodapdf.com/bates-numbering/»,
«BatesNumberingTool»: «Нумерация Бейтса»,
«BmpToJpg»: «BMP в JPG»,
«stayInformedOnSoftware»: «Будьте в курсе обновлений программного обеспечения, напоминаний об истечении срока действия, персонализированных советов и получайте эксклюзивные предложения по электронной почте. «,
«EmailPreferencesMore»: «Для получения дополнительной информации прочтите наши»,
«createdPasswordLinkExp»: «Срок действия ссылки для создания пароля истек.»,
«year2Plan»: «План на 2 года»,
«ResellersFoot»: «Реселлеры»,
«ResellersLink»: «https://www.sodapdf.com/resellers/»,
«high_quality»: «Высокое качество»,
«paymentDetails»: «Детали платежа»,
«InformationHandled»: «Предоставленная вами информация будет обрабатываться в соответствии с нашей Политикой конфиденциальности.»,
«orderInvoiceQuestions»: «№ заказа / № счета / Вопросы»,
«mergeWithSodaTitle»: «Слияние PDF»,
«End_User»: «Лицензионное соглашение с конечным пользователем»,
«authenticationError»: «Произошла ошибка аутентификации.Пожалуйста, войдите в свою учетную запись еще раз, чтобы продолжить »,
«implperPrgh»: «Адреса электронной почты должны быть в первом поле для каждого назначения. Имя и фамилия могут быть указаны во втором и третьем полях.»,
«send_to_email»: «Отправить по электронной почте»,
«ProtectLink»: «https://www.
«,
«EmailPreferencesMore»: «Для получения дополнительной информации прочтите наши»,
«createdPasswordLinkExp»: «Срок действия ссылки для создания пароля истек.»,
«year2Plan»: «План на 2 года»,
«ResellersFoot»: «Реселлеры»,
«ResellersLink»: «https://www.sodapdf.com/resellers/»,
«high_quality»: «Высокое качество»,
«paymentDetails»: «Детали платежа»,
«InformationHandled»: «Предоставленная вами информация будет обрабатываться в соответствии с нашей Политикой конфиденциальности.»,
«orderInvoiceQuestions»: «№ заказа / № счета / Вопросы»,
«mergeWithSodaTitle»: «Слияние PDF»,
«End_User»: «Лицензионное соглашение с конечным пользователем»,
«authenticationError»: «Произошла ошибка аутентификации.Пожалуйста, войдите в свою учетную запись еще раз, чтобы продолжить »,
«implperPrgh»: «Адреса электронной почты должны быть в первом поле для каждого назначения. Имя и фамилия могут быть указаны во втором и третьем полях.»,
«send_to_email»: «Отправить по электронной почте»,
«ProtectLink»: «https://www. pdfprotect.net/»,
«Pdf2ppt»: «PDF в PPT»,
«successRegister»: «На ваш адрес электронной почты отправлено письмо для активации.»,
«ViewFiles»: «Просмотр PDF-файлов»,
«modifyRenewal»: «Изменить продление»,
«ForgotPasswordLink»: «https: // www.sodapdf.com/account/recover-password/ «,
«InWebBrowser»: «В веб-браузере»,
«customQuote»: «индивидуальная цитата»,
«ElectronicSignature»: «Электронная подпись»,
«rongTitle «:» Неверный тип файла «,
«mergeRequest»: «Запрос на объединение был отправлен на [другой адрес электронной почты]. Щелкните ссылку в электронном письме, чтобы завершить объединение ваших учетных записей»,
«YouIncognito»: «Вы используете режим инкогнито.
pdfprotect.net/»,
«Pdf2ppt»: «PDF в PPT»,
«successRegister»: «На ваш адрес электронной почты отправлено письмо для активации.»,
«ViewFiles»: «Просмотр PDF-файлов»,
«modifyRenewal»: «Изменить продление»,
«ForgotPasswordLink»: «https: // www.sodapdf.com/account/recover-password/ «,
«InWebBrowser»: «В веб-браузере»,
«customQuote»: «индивидуальная цитата»,
«ElectronicSignature»: «Электронная подпись»,
«rongTitle «:» Неверный тип файла «,
«mergeRequest»: «Запрос на объединение был отправлен на [другой адрес электронной почты]. Щелкните ссылку в электронном письме, чтобы завершить объединение ваших учетных записей»,
«YouIncognito»: «Вы используете режим инкогнито.  «,
«forLegalProfessionals»: «Для юристов»,
«layoverText2»: «При нажатии откроется новая вкладка»,
«layoverText1»: «Это объявление помогает сделать наши услуги бесплатными»,
«selectLanguage»: «Выберите язык»,
«getStarted»: «Начало работы»,
«InstantText»: « Instant \ nЛицензия
«,
«forLegalProfessionals»: «Для юристов»,
«layoverText2»: «При нажатии откроется новая вкладка»,
«layoverText1»: «Это объявление помогает сделать наши услуги бесплатными»,
«selectLanguage»: «Выберите язык»,
«getStarted»: «Начало работы»,
«InstantText»: « Instant \ nЛицензия  \ n
\ n «,
«secureItem1»: «Когда вы загружаете файлы, они преобразуются через безопасное зашифрованное соединение (https), чтобы оставаться на 100% безопасным.»,
«capsLock»: «Caps Lock включен»,
«freeOnlineToolsHeader»: «Бесплатные онлайн-инструменты»,
«reviewingFiles»: «Просмотр файлов»,
«PptToPdfLink»: «https://www.sodapdf.com/ppt-to-pdf/»,
«howActivateSodaLink»: «https://support.sodapdf.com/hc/en/articles/360022497971-How-to-Activate-Soda-PDF»,
«TapAddFile»: «Нажмите, чтобы добавить файлы»,
«OptInSubmit»: «Я согласен получать сообщения об этой услуге по электронной почте.»,
«UseinDesktopApp»: «Использовать в настольном приложении»,
«myAccount»: «Моя учетная запись»,
«errorUsersRequired»: «Введите количество пользователей»,
«desktopSolutionLink»: «https://www.sodapdf.com/pdf-download/»,
«Popular»: «Популярные»,
«newVersion»: «Доступна новая версия!»,
«СпасибоCTA1notice_top»: «»,
«BatchConvert»: «Пакетное преобразование»,
«labelStreetAddressLine»: «Строка с адресом улицы»,
«secureSignModule»: «Безопасность и подпись»,
«sendMeUpdates»: «Да, присылать мне обновления»,
«СпасибоCTA2notice_top»: «»,
«cancelPlan»: «Отменить план»,
«mo»: «Mo»,
«on»: «on»,
«или или»,
«Нет нет»,
«Ладно ладно»,
«btnDownloadViewText»: «Загрузить и просмотреть в браузере»,
«userExists»: «Пользователь с этим адресом электронной почты уже существует»,
«ResetFormLabel»: «Сбросить форму»,
«OtherTools»: «Другие инструменты»,
«manualSecureFile»: «Безопасное объединение и обработка файлов»,
«Вращение»: «Вращение»,
«SignaturePackagePart2»: «пакет подписи»,
«formFileAttachment»: «Вложение файла»,
«Изменение размера»: «Изменение размера»,
«PrivacyFeedback»: «Конфиденциальность
«,
«secureItem1»: «Когда вы загружаете файлы, они преобразуются через безопасное зашифрованное соединение (https), чтобы оставаться на 100% безопасным.»,
«capsLock»: «Caps Lock включен»,
«freeOnlineToolsHeader»: «Бесплатные онлайн-инструменты»,
«reviewingFiles»: «Просмотр файлов»,
«PptToPdfLink»: «https://www.sodapdf.com/ppt-to-pdf/»,
«howActivateSodaLink»: «https://support.sodapdf.com/hc/en/articles/360022497971-How-to-Activate-Soda-PDF»,
«TapAddFile»: «Нажмите, чтобы добавить файлы»,
«OptInSubmit»: «Я согласен получать сообщения об этой услуге по электронной почте.»,
«UseinDesktopApp»: «Использовать в настольном приложении»,
«myAccount»: «Моя учетная запись»,
«errorUsersRequired»: «Введите количество пользователей»,
«desktopSolutionLink»: «https://www.sodapdf.com/pdf-download/»,
«Popular»: «Популярные»,
«newVersion»: «Доступна новая версия!»,
«СпасибоCTA1notice_top»: «»,
«BatchConvert»: «Пакетное преобразование»,
«labelStreetAddressLine»: «Строка с адресом улицы»,
«secureSignModule»: «Безопасность и подпись»,
«sendMeUpdates»: «Да, присылать мне обновления»,
«СпасибоCTA2notice_top»: «»,
«cancelPlan»: «Отменить план»,
«mo»: «Mo»,
«on»: «on»,
«или или»,
«Нет нет»,
«Ладно ладно»,
«btnDownloadViewText»: «Загрузить и просмотреть в браузере»,
«userExists»: «Пользователь с этим адресом электронной почты уже существует»,
«ResetFormLabel»: «Сбросить форму»,
«OtherTools»: «Другие инструменты»,
«manualSecureFile»: «Безопасное объединение и обработка файлов»,
«Вращение»: «Вращение»,
«SignaturePackagePart2»: «пакет подписи»,
«formFileAttachment»: «Вложение файла»,
«Изменение размера»: «Изменение размера»,
«PrivacyFeedback»: «Конфиденциальность  Повторите попытку или свяжитесь с нами.»,
«SodaTradeMark»: «Soda ™ является товарным знаком LULU Software ™.»,
«forms»: «Формы»,
«logIn»: «Войти»,
«часы»: «часы»,
«title»: «Заголовок»,
«SSLLabelThree»: «безопасное соединение»,
«Begins_auto»: «(Начинается автоматически после оплаты)»,
«ErrorChooseMorePDF»: «Выберите два или более файлов PDF»,
«video»: «Видео»,
«linkExpired»: «Срок действия вашей ссылки истек»,
«добавить»: «добавить»,
«пока пока»,
«выкл»: «выкл»,
«ocr»: «OCR»,
«odd»: «odd»,
«верх»: «верх»,
«Все»: «Все»,
«Новый»: «Новый»,
«Да»: «Да»,
«PerpetualLicense»: «Бессрочная лицензия»,
«year2»: «2 года»,
«Первый»: «Первый»,
«Слияние»: «Слияние»,
«LoginLink»: «https: // www.sodapdf.com/account/login/ «,
«no_limitation»: «24/7: без ежедневных ограничений
Повторите попытку или свяжитесь с нами.»,
«SodaTradeMark»: «Soda ™ является товарным знаком LULU Software ™.»,
«forms»: «Формы»,
«logIn»: «Войти»,
«часы»: «часы»,
«title»: «Заголовок»,
«SSLLabelThree»: «безопасное соединение»,
«Begins_auto»: «(Начинается автоматически после оплаты)»,
«ErrorChooseMorePDF»: «Выберите два или более файлов PDF»,
«video»: «Видео»,
«linkExpired»: «Срок действия вашей ссылки истек»,
«добавить»: «добавить»,
«пока пока»,
«выкл»: «выкл»,
«ocr»: «OCR»,
«odd»: «odd»,
«верх»: «верх»,
«Все»: «Все»,
«Новый»: «Новый»,
«Да»: «Да»,
«PerpetualLicense»: «Бессрочная лицензия»,
«year2»: «2 года»,
«Первый»: «Первый»,
«Слияние»: «Слияние»,
«LoginLink»: «https: // www.sodapdf.com/account/login/ «,
«no_limitation»: «24/7: без ежедневных ограничений  «,
«Планы»: «Планы»,
«JpgToPngLink»: «https://www.sodapdf.com/jpg-to-png/»,
«reassignLicense»: «Переназначить лицензию»,
«Вставка»: «Вставка»,
«sodaPdfOnline»: «Soda PDF Online»,
«BEST_VALUE»: «BEST VALUE»,
«batchTitle»: «Пакетное назначение»,
«GifToPngLink»: «https://www.sodapdf.com/gif-to-png/»,
«SplitTitle»: «Разделить PDF»,
«split_unlim»: «Разделить неограниченное количество файлов.»,
«contactsSales»: «Связаться с отделом продаж»,
«BilledAnnualy»: «выставляется ежегодно»,
«addPageNumbering»: «Добавить номера страниц»,
«вебинары»: «вебинары»,
«good_quality»: «Хорошее качество»,
«EnterUrl»: «Введите URL»,
«productTypeDesctop»: «Рабочий стол»,
«FreeOnlineTools»: «Бесплатные онлайн-инструменты»,
«Pdf2Image»: «PDF в JPG»,
«AddMain maintenance»: «Добавить обслуживание»,
«howToSubAlt3»: «Загрузить объединенный PDF»,
«howToSubAlt2»: «Объединить желаемые файлы PDF»,
«howToSubAlt1»: «Загрузить PDF»,
«PdfCreator»: «PDF Creator»,
«uninstall»: «Удалить»,
«FreePdfReaderMacOs»: «Читатель для Mac OS X»,
«WinPdfReader»: «Читатель Магазина Windows»,
«errorEnterB2BEmail»: «Пожалуйста, введите действующий рабочий адрес электронной почты, чтобы продолжить.
«,
«Планы»: «Планы»,
«JpgToPngLink»: «https://www.sodapdf.com/jpg-to-png/»,
«reassignLicense»: «Переназначить лицензию»,
«Вставка»: «Вставка»,
«sodaPdfOnline»: «Soda PDF Online»,
«BEST_VALUE»: «BEST VALUE»,
«batchTitle»: «Пакетное назначение»,
«GifToPngLink»: «https://www.sodapdf.com/gif-to-png/»,
«SplitTitle»: «Разделить PDF»,
«split_unlim»: «Разделить неограниченное количество файлов.»,
«contactsSales»: «Связаться с отделом продаж»,
«BilledAnnualy»: «выставляется ежегодно»,
«addPageNumbering»: «Добавить номера страниц»,
«вебинары»: «вебинары»,
«good_quality»: «Хорошее качество»,
«EnterUrl»: «Введите URL»,
«productTypeDesctop»: «Рабочий стол»,
«FreeOnlineTools»: «Бесплатные онлайн-инструменты»,
«Pdf2Image»: «PDF в JPG»,
«AddMain maintenance»: «Добавить обслуживание»,
«howToSubAlt3»: «Загрузить объединенный PDF»,
«howToSubAlt2»: «Объединить желаемые файлы PDF»,
«howToSubAlt1»: «Загрузить PDF»,
«PdfCreator»: «PDF Creator»,
«uninstall»: «Удалить»,
«FreePdfReaderMacOs»: «Читатель для Mac OS X»,
«WinPdfReader»: «Читатель Магазина Windows»,
«errorEnterB2BEmail»: «Пожалуйста, введите действующий рабочий адрес электронной почты, чтобы продолжить. «,
«discoverSodaPDf»: «Откройте для себя Soda PDF»,
«yourDownloadLinkSent»: «Ссылка для скачивания отправлена на ваш адрес электронной почты.»,
«Количество»: «КОЛИЧЕСТВО»,
«createPasswordSubTitle»: «Установите новый пароль для своей учетной записи.»,
«Download_Desktop»: «Загрузить настольную версию!»,
«ViewEdit»: «Просмотр и редактирование»,
«errorPhoneInvalid»: «Введите действительный номер телефона»,
«errorCompanyRequired»: «Введите название компании»,
«Особенности»: «Особенности»,
«EmailConfirmationError»: «OOPS! Срок действия вашей ссылки для активации истек.»,
«PdfToHtmlLink»: «https: // www.sodapdf.com/pdf-to-html/ «,
«bf_freeocrgift1»: «БЕСПЛАТНЫЙ ПОДАРОК OCR («,
«bf_freeocrgift2»: «значение)»,
«RessellerLink»: «https://www.sodapdf.com/business/resellers/»,
«fontSize»: «Размер шрифта»,
«productExpiredProducts»: «Товары с истекшим сроком годности»,
«SupportLink»: «https://support.sodapdf.com/hc/en-us/»,
«mostPopular»: «САМЫЕ ПОПУЛЯРНЫЕ»,
«errorPhoneRequired»: «Введите номер телефона»,
«Сжать»: «Сжать»,
«aboutTitle»: «О НАШИХ ИНСТРУМЕНТАХ»,
«howCanWeHelpYou»: «Чем мы можем вам помочь?»,
«LimitationTextRights»: «все права защищены.
«,
«discoverSodaPDf»: «Откройте для себя Soda PDF»,
«yourDownloadLinkSent»: «Ссылка для скачивания отправлена на ваш адрес электронной почты.»,
«Количество»: «КОЛИЧЕСТВО»,
«createPasswordSubTitle»: «Установите новый пароль для своей учетной записи.»,
«Download_Desktop»: «Загрузить настольную версию!»,
«ViewEdit»: «Просмотр и редактирование»,
«errorPhoneInvalid»: «Введите действительный номер телефона»,
«errorCompanyRequired»: «Введите название компании»,
«Особенности»: «Особенности»,
«EmailConfirmationError»: «OOPS! Срок действия вашей ссылки для активации истек.»,
«PdfToHtmlLink»: «https: // www.sodapdf.com/pdf-to-html/ «,
«bf_freeocrgift1»: «БЕСПЛАТНЫЙ ПОДАРОК OCR («,
«bf_freeocrgift2»: «значение)»,
«RessellerLink»: «https://www.sodapdf.com/business/resellers/»,
«fontSize»: «Размер шрифта»,
«productExpiredProducts»: «Товары с истекшим сроком годности»,
«SupportLink»: «https://support.sodapdf.com/hc/en-us/»,
«mostPopular»: «САМЫЕ ПОПУЛЯРНЫЕ»,
«errorPhoneRequired»: «Введите номер телефона»,
«Сжать»: «Сжать»,
«aboutTitle»: «О НАШИХ ИНСТРУМЕНТАХ»,
«howCanWeHelpYou»: «Чем мы можем вам помочь?»,
«LimitationTextRights»: «все права защищены. «,
«PrivacyFeedbackImg»: «//privacy-policy.truste.com/privacy-seal/LULU-software/seal?rid=e691fbfb-8de4-4b17-b576-70688b60730d»,
«rotated_copy»: «Загрузить повернутую копию вашего файла.»,
«selectIconFile»: «Пожалуйста, выберите файл значка»,
«proOcrPackage»: «Пакет Pro + OCR»,
«privacyPolicy»: «Политика конфиденциальности»,
«BusinessLink»: «https://www.sodapdf.com/business/»,
«splitted_copy»: «Загрузить разделенные страницы.»,
«SplitPDFSiteLabel»: «Разделить файлы PDF на»,
«restorePasswordEnterEmail»: «Вы можете сбросить пароль для своего профиля учетной записи, введя свой адрес электронной почты.»,
«supportNav»: «Поддержка»,
«PDFexceed»: «Загруженные файлы превышают максимальный размер»,
«ArticleDescriptionEditTwo»: «PDF-файлы — очевидный выбор, если вы хотите безопасно обмениваться информацией через Интернет. Компании и правительства в значительной степени полагаются на них, и большинство людей имеют общее представление о том, что такое PDF-файлы.»,
«ArticleDescriptionEditOne»: «Вы получаете электронное письмо, содержащее этот важный документ, волшебный PDF-файл, который выведет ваш бизнес на новый уровень.
«,
«PrivacyFeedbackImg»: «//privacy-policy.truste.com/privacy-seal/LULU-software/seal?rid=e691fbfb-8de4-4b17-b576-70688b60730d»,
«rotated_copy»: «Загрузить повернутую копию вашего файла.»,
«selectIconFile»: «Пожалуйста, выберите файл значка»,
«proOcrPackage»: «Пакет Pro + OCR»,
«privacyPolicy»: «Политика конфиденциальности»,
«BusinessLink»: «https://www.sodapdf.com/business/»,
«splitted_copy»: «Загрузить разделенные страницы.»,
«SplitPDFSiteLabel»: «Разделить файлы PDF на»,
«restorePasswordEnterEmail»: «Вы можете сбросить пароль для своего профиля учетной записи, введя свой адрес электронной почты.»,
«supportNav»: «Поддержка»,
«PDFexceed»: «Загруженные файлы превышают максимальный размер»,
«ArticleDescriptionEditTwo»: «PDF-файлы — очевидный выбор, если вы хотите безопасно обмениваться информацией через Интернет. Компании и правительства в значительной степени полагаются на них, и большинство людей имеют общее представление о том, что такое PDF-файлы.»,
«ArticleDescriptionEditOne»: «Вы получаете электронное письмо, содержащее этот важный документ, волшебный PDF-файл, который выведет ваш бизнес на новый уровень. Этот PDF-файл содержит предложение, в котором каждая деталь должна быть доведена до совершенства.»,
«addWatermark»: «Добавить водяной знак»,
«DetailsLink»: «https://www.sodapdf.com/account/manage-account/»,
«информационный бюллетень»: «Информационный бюллетень»,
«newPassword»: «Новый пароль»,
«ThankyouCTA1»: «ОТКРЫТЬ»,
«ThankyouCTA2»: «СКАЧАТЬ»,
«ThankyouBack»: «Вернуться на сайт»,
«Пример»: «Пример»,
«options_text_8»: «Оптическое распознавание символов (OCR)»,
«reassign_prgh2»: «Вы не можете переназначить эту лицензию тому же пользователю в течение этого платежного цикла.»,
«createAccount»: «Создать учетную запись»,
«footerCopyTextLight»: «Этот продукт продается компанией Upclick.com в качестве авторизованного реселлера. «,
«cmWord»: «Сантиметры»,
«dailytimer»: «Вы превысили почасовой лимит бесплатных задач. Вы можете повторить попытку через ::»,
«ArticleTitleEditThree»: «Как редактировать документы PDF»,
«sodaPdfForYou»: «Газировка PDF для вас»,
«PdfToHtml»: «PDF в HTML»,
«PdfToDocx»: «PDF в DOCX»,
«PdfToWord»: «PDF в Word»,
«PdfToJpgLink»: «https://www.
Этот PDF-файл содержит предложение, в котором каждая деталь должна быть доведена до совершенства.»,
«addWatermark»: «Добавить водяной знак»,
«DetailsLink»: «https://www.sodapdf.com/account/manage-account/»,
«информационный бюллетень»: «Информационный бюллетень»,
«newPassword»: «Новый пароль»,
«ThankyouCTA1»: «ОТКРЫТЬ»,
«ThankyouCTA2»: «СКАЧАТЬ»,
«ThankyouBack»: «Вернуться на сайт»,
«Пример»: «Пример»,
«options_text_8»: «Оптическое распознавание символов (OCR)»,
«reassign_prgh2»: «Вы не можете переназначить эту лицензию тому же пользователю в течение этого платежного цикла.»,
«createAccount»: «Создать учетную запись»,
«footerCopyTextLight»: «Этот продукт продается компанией Upclick.com в качестве авторизованного реселлера. «,
«cmWord»: «Сантиметры»,
«dailytimer»: «Вы превысили почасовой лимит бесплатных задач. Вы можете повторить попытку через ::»,
«ArticleTitleEditThree»: «Как редактировать документы PDF»,
«sodaPdfForYou»: «Газировка PDF для вас»,
«PdfToHtml»: «PDF в HTML»,
«PdfToDocx»: «PDF в DOCX»,
«PdfToWord»: «PDF в Word»,
«PdfToJpgLink»: «https://www. sodapdf.com/pdf-to-jpg/»,
«signInTitle»: «Войдите в свою учетную запись Soda PDF с помощью»,
«enterCity»: «Введите город»,
«productProductAlert»: «Срок действия вашего плана истекает, и вы потеряете доступ к его функциям по истечении срока его действия.»,
«errorLastNameInvalid»: «Необходимо ввести действительную фамилию»,
«Reader3d»: «3D-читатель»,
«dayliLimitSubTitleB»: «Однако у вас есть другой вариант»,
«PDFMergeCanonical»: «https://www.pdfmerge.com/»,
«ErrorUploadOnlyPDF»: «Пожалуйста, загружайте только файлы PDF»,
«Jpg2pdf»: «JPG в PDF»,
«businessResourcesPageName»: «Бизнес-ресурсы»,
«userGuide»: «Руководство пользователя»,
«resourceCenterBackText»: «Вся информация, необходимая для поиска ответов на ваши вопросы.»,
«yourWebinarShouldBegin»: «Ваш веб-семинар должен начаться в ближайшее время.»,
«GoodQualityBest»: «лучшее качество изображения, минимальное сжатие»,
«withMain maintenance»: «С обслуживанием»,
«EasyAdoptionPageName»: «Простое принятие»,
«unassignProduct_prgh2»: «После отмены назначения определенной лицензии лицензию можно переназначить тому же пользователю только после следующего цикла выставления счетов.
sodapdf.com/pdf-to-jpg/»,
«signInTitle»: «Войдите в свою учетную запись Soda PDF с помощью»,
«enterCity»: «Введите город»,
«productProductAlert»: «Срок действия вашего плана истекает, и вы потеряете доступ к его функциям по истечении срока его действия.»,
«errorLastNameInvalid»: «Необходимо ввести действительную фамилию»,
«Reader3d»: «3D-читатель»,
«dayliLimitSubTitleB»: «Однако у вас есть другой вариант»,
«PDFMergeCanonical»: «https://www.pdfmerge.com/»,
«ErrorUploadOnlyPDF»: «Пожалуйста, загружайте только файлы PDF»,
«Jpg2pdf»: «JPG в PDF»,
«businessResourcesPageName»: «Бизнес-ресурсы»,
«userGuide»: «Руководство пользователя»,
«resourceCenterBackText»: «Вся информация, необходимая для поиска ответов на ваши вопросы.»,
«yourWebinarShouldBegin»: «Ваш веб-семинар должен начаться в ближайшее время.»,
«GoodQualityBest»: «лучшее качество изображения, минимальное сжатие»,
«withMain maintenance»: «С обслуживанием»,
«EasyAdoptionPageName»: «Простое принятие»,
«unassignProduct_prgh2»: «После отмены назначения определенной лицензии лицензию можно переназначить тому же пользователю только после следующего цикла выставления счетов. «,
«downloadInstallation»: «Скачать / Установка»,
«Process_another»: «Обработать другой файл»,
«accountAssociated»: «С этим адресом электронной почты уже связана учетная запись.»,
«mustUploadCSV»: «Вы должны загрузить файл CSV»,
«download»: «Скачать»,
«Trial30Day»: «30-дневная пробная версия»,
«sodaAnywherePrgh»: «Полное решение в формате PDF для настольных компьютеров и в Интернете»,
«MoreOnePage»: «Загруженный документ должен содержать более 1 страницы.»,
«PaymentInformation»: «Платежная информация»,
«pdfCreatorConverter»: «Бесплатная программа для создания и преобразования PDF-файлов»,
«RateTool»: «Оценить этот инструмент»,
«MergePdfLink»: «https://www.sodapdf.com/pdf-merge/»,
«ResendAssignInvitationSuccess_prgh2»: «Приглашение было отправлено повторно»,
«getTheMost»: « Получите максимум от своих денег»,
«SplitPassProtected»: «Загруженный файл защищен паролем и не может быть разделен»,
«BackToSoda8»: «Вернуться к Soda PDF»,
«yourRequestReceived»: «Ваш запрос получен.
«,
«downloadInstallation»: «Скачать / Установка»,
«Process_another»: «Обработать другой файл»,
«accountAssociated»: «С этим адресом электронной почты уже связана учетная запись.»,
«mustUploadCSV»: «Вы должны загрузить файл CSV»,
«download»: «Скачать»,
«Trial30Day»: «30-дневная пробная версия»,
«sodaAnywherePrgh»: «Полное решение в формате PDF для настольных компьютеров и в Интернете»,
«MoreOnePage»: «Загруженный документ должен содержать более 1 страницы.»,
«PaymentInformation»: «Платежная информация»,
«pdfCreatorConverter»: «Бесплатная программа для создания и преобразования PDF-файлов»,
«RateTool»: «Оценить этот инструмент»,
«MergePdfLink»: «https://www.sodapdf.com/pdf-merge/»,
«ResendAssignInvitationSuccess_prgh2»: «Приглашение было отправлено повторно»,
«getTheMost»: « Получите максимум от своих денег»,
«SplitPassProtected»: «Загруженный файл защищен паролем и не может быть разделен»,
«BackToSoda8»: «Вернуться к Soda PDF»,
«yourRequestReceived»: «Ваш запрос получен. «,
«perMonth»: «В месяц»,
«минуты»: «минуты»,
«continueBtn»: «Продолжить»,
«createPasswordTitle»: «Создайте свой пароль»,
«bf_features»: «Включенные функции:»,
«ChooseFormat»: «Выбрать формат:»,
«aboutSubDesc4»: «Вы можете обрабатывать файлы на любом устройстве, в любое время и в любом месте с помощью компьютера, планшета и смартфона.»,
«aboutSubDesc1»: «Мы используем безопасную технологию для установления зашифрованного соединения между нашим веб-сервером и вашим браузером, чтобы все данные оставались конфиденциальными.»,
«aboutSubDesc3»: «Доступ к файлам, сохраненным в облачных системах хранения, таких как Google Drive, Box, Dropbox и OneDrive.»,
«aboutSubDesc2»: «Мы храним каждый файл на нашем сервере только в течение 24 часов, чтобы ограничить любой несанкционированный доступ. Затем он навсегда удаляется с наших серверов. Никто из нашей команды не может получить доступ к этим файлам.»,
«PngToPdfLink»: «https://www.sodapdf.com/png-to-pdf/»,
«TiffToPdf»: «TIFF в PDF»,
«ExtractPdf»: «Извлечь PDF»,
«errorServer»: «Извините, сервер занят.
«,
«perMonth»: «В месяц»,
«минуты»: «минуты»,
«continueBtn»: «Продолжить»,
«createPasswordTitle»: «Создайте свой пароль»,
«bf_features»: «Включенные функции:»,
«ChooseFormat»: «Выбрать формат:»,
«aboutSubDesc4»: «Вы можете обрабатывать файлы на любом устройстве, в любое время и в любом месте с помощью компьютера, планшета и смартфона.»,
«aboutSubDesc1»: «Мы используем безопасную технологию для установления зашифрованного соединения между нашим веб-сервером и вашим браузером, чтобы все данные оставались конфиденциальными.»,
«aboutSubDesc3»: «Доступ к файлам, сохраненным в облачных системах хранения, таких как Google Drive, Box, Dropbox и OneDrive.»,
«aboutSubDesc2»: «Мы храним каждый файл на нашем сервере только в течение 24 часов, чтобы ограничить любой несанкционированный доступ. Затем он навсегда удаляется с наших серверов. Никто из нашей команды не может получить доступ к этим файлам.»,
«PngToPdfLink»: «https://www.sodapdf.com/png-to-pdf/»,
«TiffToPdf»: «TIFF в PDF»,
«ExtractPdf»: «Извлечь PDF»,
«errorServer»: «Извините, сервер занят. Повторите попытку позже.»,
«detailEsignPhone»: «Этот номер используется нашей службой E-Sign для аутентификации по SMS»,
«StayUpToDate»: «Будьте в курсе!»,
«marginsWord»: «Поля»,
«offPrice»: «выкл»,
«errorNewPasswordRequired»: «Введите новый пароль»,
«insuffTitle»: «Недостаточно лицензий»,
«errorContactEmailInvalid»: «Вам необходимо ввести действующий контактный адрес электронной почты.»,
«onlineAccess»: «Доступ в Интернете»,
«errorCurrentPasswordRequired»: «Введите текущий пароль»,
«premiumPhoneSupportBackText»: «Прямой доступ к одному из наших специалистов по Soda PDF в любое время.»,
«productRefreshList»: «Обновить список»,
«PngToJpgLink»: «https://www.sodapdf.com/png-to-jpg/»,
«userGuideLink»: «http://userguide.sodapdf.com/»,
«MacOsUser»: «Пользователь Mac OS? Откройте для себя полнофункциональный Soda PDF Online.»,
«InsertPageElem»: «Вставить элементы страницы»,
«IncludedPrgh»: «Включено в следующие планы»,
«freeTrialLink»: «https: // онлайн.sodapdf.
Повторите попытку позже.»,
«detailEsignPhone»: «Этот номер используется нашей службой E-Sign для аутентификации по SMS»,
«StayUpToDate»: «Будьте в курсе!»,
«marginsWord»: «Поля»,
«offPrice»: «выкл»,
«errorNewPasswordRequired»: «Введите новый пароль»,
«insuffTitle»: «Недостаточно лицензий»,
«errorContactEmailInvalid»: «Вам необходимо ввести действующий контактный адрес электронной почты.»,
«onlineAccess»: «Доступ в Интернете»,
«errorCurrentPasswordRequired»: «Введите текущий пароль»,
«premiumPhoneSupportBackText»: «Прямой доступ к одному из наших специалистов по Soda PDF в любое время.»,
«productRefreshList»: «Обновить список»,
«PngToJpgLink»: «https://www.sodapdf.com/png-to-jpg/»,
«userGuideLink»: «http://userguide.sodapdf.com/»,
«MacOsUser»: «Пользователь Mac OS? Откройте для себя полнофункциональный Soda PDF Online.»,
«InsertPageElem»: «Вставить элементы страницы»,
«IncludedPrgh»: «Включено в следующие планы»,
«freeTrialLink»: «https: // онлайн.sodapdf. com/ «,
«productAssignedLicenses»: «Назначенные лицензии»,
«Загрузка»: «Загрузка»,
«noCreditCard»: «Кредитная карта не требуется»,
«emailHasBeenChanged»: «Ваш адрес электронной почты был изменен»,
«messageEmailSent»: «Ссылка для подтверждения была отправлена на ваш адрес электронной почты. Если вы не получили это письмо, проверьте папку нежелательной почты / спама.»,
«chooseEmailToMerge»: «Пожалуйста, выберите адрес электронной почты для объединения продуктов из обеих учетных записей. Этот адрес электронной почты и соответствующий пароль будут использоваться для входа в вашу учетную запись после успешного объединения»,
«formMessage»: «Сообщение»,
«confirmUsers»: «Подтвердите пользователей, которым вы хотите назначить лицензии»,
«ChooseFile»: «Выбрать файл»,
«useOnlineTools»: «Воспользуйтесь нашим онлайн-инструментом»,
«privacyTitle»: «Конфиденциальность»,
«errorNotPdf»: «Файл не является PDF-документом»,
«formLastName»: «Фамилия»,
«Параметры»: «Параметры»,
«pageNumber»: «Номер страницы»,
«numberFormat»: «Формат числа»,
«settingsUpdated»: «Настройки вашей учетной записи успешно обновлены»,
«upgradeBuilder»: «Конструктор обновлений»,
«Непрозрачность»: «Непрозрачность»,
«статьAReseller»: «Стать реселлером»,
«formPhone»: «Телефон»,
«PDFClicking»: «Нажав кнопку« Оплатить сейчас »ниже, вы попадете на защищенный сайт PayPal
com/ «,
«productAssignedLicenses»: «Назначенные лицензии»,
«Загрузка»: «Загрузка»,
«noCreditCard»: «Кредитная карта не требуется»,
«emailHasBeenChanged»: «Ваш адрес электронной почты был изменен»,
«messageEmailSent»: «Ссылка для подтверждения была отправлена на ваш адрес электронной почты. Если вы не получили это письмо, проверьте папку нежелательной почты / спама.»,
«chooseEmailToMerge»: «Пожалуйста, выберите адрес электронной почты для объединения продуктов из обеих учетных записей. Этот адрес электронной почты и соответствующий пароль будут использоваться для входа в вашу учетную запись после успешного объединения»,
«formMessage»: «Сообщение»,
«confirmUsers»: «Подтвердите пользователей, которым вы хотите назначить лицензии»,
«ChooseFile»: «Выбрать файл»,
«useOnlineTools»: «Воспользуйтесь нашим онлайн-инструментом»,
«privacyTitle»: «Конфиденциальность»,
«errorNotPdf»: «Файл не является PDF-документом»,
«formLastName»: «Фамилия»,
«Параметры»: «Параметры»,
«pageNumber»: «Номер страницы»,
«numberFormat»: «Формат числа»,
«settingsUpdated»: «Настройки вашей учетной записи успешно обновлены»,
«upgradeBuilder»: «Конструктор обновлений»,
«Непрозрачность»: «Непрозрачность»,
«статьAReseller»: «Стать реселлером»,
«formPhone»: «Телефон»,
«PDFClicking»: «Нажав кнопку« Оплатить сейчас »ниже, вы попадете на защищенный сайт PayPal  «,
«email_terms_begin»: «Отправляя электронное письмо, вы соглашаетесь получить файл и быть связанными условиями»,
«email_terms_link1»: «Условия использования»,
«email_terms_link2»: «Политика конфиденциальности»,
«errorLastNameRequired»: «Введите фамилию»,
«formSuccessMessage»: «Спасибо за запрос. Служба поддержки свяжется с вами в ближайшие 12-24 часа.»,
«formEmail»: «Адрес электронной почты»,
«resetLicense»: «Сбросить лицензию»,
«currentPassword»: «Текущий пароль»,
«pdfDownload»: «https://www.sodapdf.com/pdf-download/»,
«formTimelineJustBrowsing»: «Просто просматриваю»,
«PlanBusinesPrgh3»: « Soda E-Sign Unlimited включен в бизнес-план Soda PDF Business»,
«PlanBusinesPrgh2»: «Полное решение PDF, разработанное для профессионалов»,
«UnlockLink»: «https: // www.pdfunlock.com/ «,
«WebDeskApp»: «Веб + настольные приложения»,
«errorFirstNameRequired»: «Введите имя»,
«formFailMessage»: «Невозможно отправить сообщение. Повторите попытку позже.»,
«buyOnline»: «Купить в Интернете»,
«btnAnotherFile»: «Обработать другой файл»,
«online_tools»: «ИНСТРУМЕНТЫ ДЛЯ ОНЛАЙН PDF»,
«SignSecure»: «Подписать и защитить»,
«smfileSign»: «Неограниченные возможности PDF»,
«unlock_unlim»: «Разблокировать неограниченное ЧИСЛО файлов.
«,
«email_terms_begin»: «Отправляя электронное письмо, вы соглашаетесь получить файл и быть связанными условиями»,
«email_terms_link1»: «Условия использования»,
«email_terms_link2»: «Политика конфиденциальности»,
«errorLastNameRequired»: «Введите фамилию»,
«formSuccessMessage»: «Спасибо за запрос. Служба поддержки свяжется с вами в ближайшие 12-24 часа.»,
«formEmail»: «Адрес электронной почты»,
«resetLicense»: «Сбросить лицензию»,
«currentPassword»: «Текущий пароль»,
«pdfDownload»: «https://www.sodapdf.com/pdf-download/»,
«formTimelineJustBrowsing»: «Просто просматриваю»,
«PlanBusinesPrgh3»: « Soda E-Sign Unlimited включен в бизнес-план Soda PDF Business»,
«PlanBusinesPrgh2»: «Полное решение PDF, разработанное для профессионалов»,
«UnlockLink»: «https: // www.pdfunlock.com/ «,
«WebDeskApp»: «Веб + настольные приложения»,
«errorFirstNameRequired»: «Введите имя»,
«formFailMessage»: «Невозможно отправить сообщение. Повторите попытку позже.»,
«buyOnline»: «Купить в Интернете»,
«btnAnotherFile»: «Обработать другой файл»,
«online_tools»: «ИНСТРУМЕНТЫ ДЛЯ ОНЛАЙН PDF»,
«SignSecure»: «Подписать и защитить»,
«smfileSign»: «Неограниченные возможности PDF»,
«unlock_unlim»: «Разблокировать неограниченное ЧИСЛО файлов. «,
«good_quality_text»: «Хорошее качество, средний уровень сжатия»,
«OcrPdfLink»: «https://www.sodapdf.com/ocr-pdf/»,
«errorWebsiteUrlInvalid»: «Введите действительный URL»,
«SignUpWith»: «Зарегистрируйтесь с помощью»,
«InvalidRange»: «Недопустимый диапазон»,
«PurchaseFirstTime»: «Вы недавно приобрели продукт Soda PDF и впервые получаете доступ к Soda? Создайте учетную запись с адресом электронной почты, который вы использовали при покупке.»,
«layoverTitlePart1»: «Ваш файл будет готов к загрузке через»,
«layoverTitlePart2»: «секунды:»,
«ThankyouCTA1notice_bottom»: «в веб-браузере»,
«sendEmail»: «Отправка электронной почты …»,
«MoreFilesLabel»: «Еще файлы»,
«Аффилированные лица»: «Аффилированные лица»,
«ArticleDescriptionEditThree»: «В наши дни получение бумажных документов для просмотра и редактирования — большая редкость, особенно в профессиональной среде. Обмен документами сейчас в основном осуществляется в электронном виде, а безопасный способ отправки файла — преобразование его в PDF.
«,
«good_quality_text»: «Хорошее качество, средний уровень сжатия»,
«OcrPdfLink»: «https://www.sodapdf.com/ocr-pdf/»,
«errorWebsiteUrlInvalid»: «Введите действительный URL»,
«SignUpWith»: «Зарегистрируйтесь с помощью»,
«InvalidRange»: «Недопустимый диапазон»,
«PurchaseFirstTime»: «Вы недавно приобрели продукт Soda PDF и впервые получаете доступ к Soda? Создайте учетную запись с адресом электронной почты, который вы использовали при покупке.»,
«layoverTitlePart1»: «Ваш файл будет готов к загрузке через»,
«layoverTitlePart2»: «секунды:»,
«ThankyouCTA1notice_bottom»: «в веб-браузере»,
«sendEmail»: «Отправка электронной почты …»,
«MoreFilesLabel»: «Еще файлы»,
«Аффилированные лица»: «Аффилированные лица»,
«ArticleDescriptionEditThree»: «В наши дни получение бумажных документов для просмотра и редактирования — большая редкость, особенно в профессиональной среде. Обмен документами сейчас в основном осуществляется в электронном виде, а безопасный способ отправки файла — преобразование его в PDF. первый.»,
«affiliateProgram»: «Партнерская программа»,
«chatBackText»: «Живой чат с одним из наших специалистов по Soda PDF.»,
«PdfEditor»: «Редактор PDF»,
«See_also»: «СМОТРИ ТАКЖЕ»,
«errorNewPasswordMatch»: «Ваши новые пароли не совпадают»,
«errorCurrentPasswordIncorrect»: «Ваш текущий пароль неверен»,
«DropFileHereOr»: «Перетащите файл сюда или»,
«textAndFormat»: «Текст и формат»,
«NotConnected»: «Не подключен»,
«updateInformation»: «Обновить информацию»,
«PdfToPptLink»: «https: //www.sodapdf.com / pdf-to-ppt / «,
«CompressFile»: «Сжать файл»,
«CompressLink»: «https://www.sodapdf.com/compress-pdf/»,
«download_here»: «Скачайте здесь»,
«subscribeToProduct»: «Обновления продукта»,
«AnnualCommitment»: «Годовое обязательство»,
«GuaranteeText»: « 30-дневная Гарантия возврата денег
первый.»,
«affiliateProgram»: «Партнерская программа»,
«chatBackText»: «Живой чат с одним из наших специалистов по Soda PDF.»,
«PdfEditor»: «Редактор PDF»,
«See_also»: «СМОТРИ ТАКЖЕ»,
«errorNewPasswordMatch»: «Ваши новые пароли не совпадают»,
«errorCurrentPasswordIncorrect»: «Ваш текущий пароль неверен»,
«DropFileHereOr»: «Перетащите файл сюда или»,
«textAndFormat»: «Текст и формат»,
«NotConnected»: «Не подключен»,
«updateInformation»: «Обновить информацию»,
«PdfToPptLink»: «https: //www.sodapdf.com / pdf-to-ppt / «,
«CompressFile»: «Сжать файл»,
«CompressLink»: «https://www.sodapdf.com/compress-pdf/»,
«download_here»: «Скачайте здесь»,
«subscribeToProduct»: «Обновления продукта»,
«AnnualCommitment»: «Годовое обязательство»,
«GuaranteeText»: « 30-дневная Гарантия возврата денег  «,
«E-SingLink»: «https: // www.sodapdf.com/sign-pdf/ «,
«labelZipPostalCode»: «Почтовый индекс»,
«dayliLimitTitle»: «Вы превысили часовой лимит для PDFMerge»,
«registerAgreeWith»: «Выполняя вход с подключенной учетной записью, вы соглашаетесь с»,
«ResizePdfLink»: «https://www.sodapdf.com/resize-pdf/»,
«Ecx_options»: «Однако вы можете выбрать один из двух вариантов»,
«clickYouTube»: «Нажмите {0}, чтобы найти Soda PDF Anywhere»,
«active»: «Активный»,
«PDFFormFiller»: «Заполнитель PDF-форм»,
«formGetStarted»: «Начать работу»,
«noFileChosen»: «Файл не выбран»,
«errorAccountExists»: «Пользователь уже существует.»,
«ArticleTitleEditTwo»: «Как профессионально редактировать файлы PDF»,
«ArticleTitleEditOne»: «Как сделать PDF-файл редактируемым с помощью Soda PDF»,
«FeedbackLink»: «https://www.sodapdf.com/feedback/»,
«moduleFormsReq»: « Forms Module требует»,
«passwordChanged»: «Ваш пароль был успешно изменен»,
«AnywhereTitle»: «С помощью Soda PDF Anywhere вы можете выполнять работу буквально в любом месте.
«,
«E-SingLink»: «https: // www.sodapdf.com/sign-pdf/ «,
«labelZipPostalCode»: «Почтовый индекс»,
«dayliLimitTitle»: «Вы превысили часовой лимит для PDFMerge»,
«registerAgreeWith»: «Выполняя вход с подключенной учетной записью, вы соглашаетесь с»,
«ResizePdfLink»: «https://www.sodapdf.com/resize-pdf/»,
«Ecx_options»: «Однако вы можете выбрать один из двух вариантов»,
«clickYouTube»: «Нажмите {0}, чтобы найти Soda PDF Anywhere»,
«active»: «Активный»,
«PDFFormFiller»: «Заполнитель PDF-форм»,
«formGetStarted»: «Начать работу»,
«noFileChosen»: «Файл не выбран»,
«errorAccountExists»: «Пользователь уже существует.»,
«ArticleTitleEditTwo»: «Как профессионально редактировать файлы PDF»,
«ArticleTitleEditOne»: «Как сделать PDF-файл редактируемым с помощью Soda PDF»,
«FeedbackLink»: «https://www.sodapdf.com/feedback/»,
«moduleFormsReq»: « Forms Module требует»,
«passwordChanged»: «Ваш пароль был успешно изменен»,
«AnywhereTitle»: «С помощью Soda PDF Anywhere вы можете выполнять работу буквально в любом месте. sodapdf.com/buy/freeonlinetools/dw-success/»,
«aboutSubTitle4»: «Любое устройство»,
«aboutSubTitle1»: «Безопасность»,
«aboutSubTitle2»: «Конфиденциальность»,
«aboutSubTitle3»: «Доступ к облачному хранилищу»,
«addLicense»: «добавить лицензию»,
«insuffPrgh»: «Вы назначили больше лицензий, чем доступно в настоящее время.Измените свой выбор. «,
«FullPdfSolution»: «ПОЛНОЕ РЕШЕНИЕ PDF»,
«formSend»: «Отправить»,
«receiveSubject»: «Квитанция о транзакции»,
«formName»: «Имя»,
«модуль»: «Модуль»,
«freeDevice»: «Бесплатное устройство»,
«productTypeOnline»: «Интернет»,
«RotateLink»: «https://www.pdfrotate.com/»,
«Безлимитный»: «Безлимитный»,
«TryDesktopVersion»: «Попробуйте нашу версию для ПК»,
«SplitCompress»: «Разделить и сжать»,
«monthCommitment»: «Ежемесячное обязательство»,
«passwordRequirements»: «Ваш пароль должен содержать не менее 6 символов, содержащих буквы и цифры»,
«confirmPassword»: «Подтвердите пароль»,
«errorFirstNameInvalid»: «Необходимо ввести действительное имя»,
«security»: «Безопасность»,
«generalUsability»: «Общее удобство использования»,
«protected_copy»: «Загрузите защищенную копию вашего файла.»,
«OnlineServices»: «Online Services»,
«DropFilesHereOr»: «Перетащите файлы сюда или»,
«AffiliatesLink»: «https://affiliates.lulusoftware.com/?»,
«создать»: «создать»,
«formCountry»: «Страна»,
«CreateAccountWith»: «Создать учетную запись Soda PDF с»,
«formCompany»: «Компания»,
«пароль»: «Пароль»,
«mergeCongratulations»: «Поздравляем, вы успешно объединили свои аккаунты.»,
«productFeatures»: «Характеристики и преимущества»,
«PptToPdf»: «PPT в PDF»,
«FreeFinePrint»: «* Бесплатно для файлов размером до»,
«footerLuluContactUs»: «Свяжитесь с нами»,
«fileReadySubTitle»: «Получите файл за 2 простых шага»,
«addESign10pack»: «Добавить 10 пакетов E-Sign»,
«RotateTitle»: «Повернуть PDF»,
«Сжатие»: «Сжатие»,
«CompressPdf»: «Сжать PDF»,
«resizeWord»: «Изменить размер»,
«autoRenewDescription»: «Щелкните здесь, чтобы включить автоматическое продление»,
«DocxToPdf»: «DOCX в PDF»,
«вставить»: «Вставить»,
«RotatePdf»: «Повернуть PDF»,
«resources»: «Ресурсы»,
«DragToRange»: «Перетащите, чтобы изменить расположение»,
«largefile»: «Большой файл»,
«DonateButtonLabel»: «Пожертвовать»,
«TermsUse»: «Условия использования»,
«mediumfile»: «Средний файл»,
«enterStateProvince»: «Укажите штат / провинцию»,
«PDF_ANYWHERE»: «PDF ANYWHERE»,
«typeOfProduct»: «Тип товара»,
«productInterest»: «Интересующий продукт»,
«FreeOnlineToolsLinkAnchor»: «https: // www.sodapdf.com/#navOnlineTools «,
«compress_unlim»: «Сжать неограниченное ЧИСЛО файлов.»,
«resetPasswordSuccessfully»: «Ваш пароль был успешно сброшен.»,
«GoogleExtHtmlLink»: «https://chrome.google.com/webstore/detail/soda-pdf-convert-merge-sp/gfjafjofnehohehighdlkhcpanocobjb?hl=en»,
«ocrPDF»: «OCR PDF»,
«PDF2_text»: «Soda PDF 10 теперь поддерживает PDF 2.0 и все его богатые новые функции! PDF 2.0 — первое обновление формата PDF за 10 лет, которое включает в себя улучшения безопасности, доступности и общего удобства работы с PDF.Узнайте больше обо всех удивительных улучшениях, которые предоставляет PDF 2.0! «,
«visitBlog»: «Посетить блог»,
«messageValidateYourAccount»: «Подтвердите его сейчас, щелкнув ссылку для подтверждения, которая была отправлена на ваш адрес электронной почты.»,
«headerForYou»: «Для вас»,
«UnlockPdf»: «Разблокировать PDF»,
«Разблокировка»: «Разблокировка»,
«subtitleRequestQuote»: «Бизнес-клиенты имеют право на оптовые цены, начиная с 25 лицензий. Заполните форму ниже, и наши специалисты по продажам свяжутся с вами в течение 1 рабочего дня.»,
«GifToPdf»: «GIF в PDF»,
«GifToPng»: «GIF в PNG»,
«GifToJpg»: «GIF в JPG»,
«WebPDFApp»: «https: // www.sodapdf.com/web-pdf-app/ «,
«PDF_Create»: «Создание, преобразование и просмотр файлов PDF»,
«billingInquiry»: «Billing Inquiry»,
«language»: «Язык»,
«customerSupport»: «поддержка клиентов»,
«formYes»: «Да»,
«headerForBusiness»: «Для бизнеса»,
«cancelPlan_prgh2»: «Если вы отмените свой план, вы потеряете доступ к его функциям по истечении срока действия.»,
«inchWord»: «Дюймы»,
«ProductsLink»: «https://www.sodapdf.com/account/manage-products/»,
«UnlimitedSignaturePack»: «Пакет безлимитных подписей»,
«update»: «Обновить»,
«knowledgebase_prgh»: «Нужна дополнительная помощь? Ознакомьтесь с нашими»,
«securingFiles»: «Защита файлов»,
«labelPhone»: «Телефон»,
«PassProtected»: «»,
«account_list»: «
sodapdf.com/buy/freeonlinetools/dw-success/»,
«aboutSubTitle4»: «Любое устройство»,
«aboutSubTitle1»: «Безопасность»,
«aboutSubTitle2»: «Конфиденциальность»,
«aboutSubTitle3»: «Доступ к облачному хранилищу»,
«addLicense»: «добавить лицензию»,
«insuffPrgh»: «Вы назначили больше лицензий, чем доступно в настоящее время.Измените свой выбор. «,
«FullPdfSolution»: «ПОЛНОЕ РЕШЕНИЕ PDF»,
«formSend»: «Отправить»,
«receiveSubject»: «Квитанция о транзакции»,
«formName»: «Имя»,
«модуль»: «Модуль»,
«freeDevice»: «Бесплатное устройство»,
«productTypeOnline»: «Интернет»,
«RotateLink»: «https://www.pdfrotate.com/»,
«Безлимитный»: «Безлимитный»,
«TryDesktopVersion»: «Попробуйте нашу версию для ПК»,
«SplitCompress»: «Разделить и сжать»,
«monthCommitment»: «Ежемесячное обязательство»,
«passwordRequirements»: «Ваш пароль должен содержать не менее 6 символов, содержащих буквы и цифры»,
«confirmPassword»: «Подтвердите пароль»,
«errorFirstNameInvalid»: «Необходимо ввести действительное имя»,
«security»: «Безопасность»,
«generalUsability»: «Общее удобство использования»,
«protected_copy»: «Загрузите защищенную копию вашего файла.»,
«OnlineServices»: «Online Services»,
«DropFilesHereOr»: «Перетащите файлы сюда или»,
«AffiliatesLink»: «https://affiliates.lulusoftware.com/?»,
«создать»: «создать»,
«formCountry»: «Страна»,
«CreateAccountWith»: «Создать учетную запись Soda PDF с»,
«formCompany»: «Компания»,
«пароль»: «Пароль»,
«mergeCongratulations»: «Поздравляем, вы успешно объединили свои аккаунты.»,
«productFeatures»: «Характеристики и преимущества»,
«PptToPdf»: «PPT в PDF»,
«FreeFinePrint»: «* Бесплатно для файлов размером до»,
«footerLuluContactUs»: «Свяжитесь с нами»,
«fileReadySubTitle»: «Получите файл за 2 простых шага»,
«addESign10pack»: «Добавить 10 пакетов E-Sign»,
«RotateTitle»: «Повернуть PDF»,
«Сжатие»: «Сжатие»,
«CompressPdf»: «Сжать PDF»,
«resizeWord»: «Изменить размер»,
«autoRenewDescription»: «Щелкните здесь, чтобы включить автоматическое продление»,
«DocxToPdf»: «DOCX в PDF»,
«вставить»: «Вставить»,
«RotatePdf»: «Повернуть PDF»,
«resources»: «Ресурсы»,
«DragToRange»: «Перетащите, чтобы изменить расположение»,
«largefile»: «Большой файл»,
«DonateButtonLabel»: «Пожертвовать»,
«TermsUse»: «Условия использования»,
«mediumfile»: «Средний файл»,
«enterStateProvince»: «Укажите штат / провинцию»,
«PDF_ANYWHERE»: «PDF ANYWHERE»,
«typeOfProduct»: «Тип товара»,
«productInterest»: «Интересующий продукт»,
«FreeOnlineToolsLinkAnchor»: «https: // www.sodapdf.com/#navOnlineTools «,
«compress_unlim»: «Сжать неограниченное ЧИСЛО файлов.»,
«resetPasswordSuccessfully»: «Ваш пароль был успешно сброшен.»,
«GoogleExtHtmlLink»: «https://chrome.google.com/webstore/detail/soda-pdf-convert-merge-sp/gfjafjofnehohehighdlkhcpanocobjb?hl=en»,
«ocrPDF»: «OCR PDF»,
«PDF2_text»: «Soda PDF 10 теперь поддерживает PDF 2.0 и все его богатые новые функции! PDF 2.0 — первое обновление формата PDF за 10 лет, которое включает в себя улучшения безопасности, доступности и общего удобства работы с PDF.Узнайте больше обо всех удивительных улучшениях, которые предоставляет PDF 2.0! «,
«visitBlog»: «Посетить блог»,
«messageValidateYourAccount»: «Подтвердите его сейчас, щелкнув ссылку для подтверждения, которая была отправлена на ваш адрес электронной почты.»,
«headerForYou»: «Для вас»,
«UnlockPdf»: «Разблокировать PDF»,
«Разблокировка»: «Разблокировка»,
«subtitleRequestQuote»: «Бизнес-клиенты имеют право на оптовые цены, начиная с 25 лицензий. Заполните форму ниже, и наши специалисты по продажам свяжутся с вами в течение 1 рабочего дня.»,
«GifToPdf»: «GIF в PDF»,
«GifToPng»: «GIF в PNG»,
«GifToJpg»: «GIF в JPG»,
«WebPDFApp»: «https: // www.sodapdf.com/web-pdf-app/ «,
«PDF_Create»: «Создание, преобразование и просмотр файлов PDF»,
«billingInquiry»: «Billing Inquiry»,
«language»: «Язык»,
«customerSupport»: «поддержка клиентов»,
«formYes»: «Да»,
«headerForBusiness»: «Для бизнеса»,
«cancelPlan_prgh2»: «Если вы отмените свой план, вы потеряете доступ к его функциям по истечении срока действия.»,
«inchWord»: «Дюймы»,
«ProductsLink»: «https://www.sodapdf.com/account/manage-products/»,
«UnlimitedSignaturePack»: «Пакет безлимитных подписей»,
«update»: «Обновить»,
«knowledgebase_prgh»: «Нужна дополнительная помощь? Ознакомьтесь с нашими»,
«securingFiles»: «Защита файлов»,
«labelPhone»: «Телефон»,
«PassProtected»: «»,
«account_list»: «