Римская цифра IIII на циферблатах часов
Римские цифры – классический элемент дизайна циферблата часов. Практически все исторические модели содержали на своих циферблатах римские цифры. Однако владельцы часов с римскими цифрами могли заметить что-то необычное. В то время как цифра 4 обычно имеет вид «IV» в римской цифровой системе, большинство часов отображают на месте четверки «IIII». Как всегда, нет единого ответа на этот вопрос, но все же есть некоторые возможные объяснения этого абсурдно важного вопроса.
Римская цифровая система больше не имеет широкого применения. Большинство западных стран используют арабские цифры, азиатские страны имеют собственную цифровую систему, а арабская культура использует свою систему, отличную от классических арабских цифр. Однако в часовом деле римские цифры использовались и все еще продолжают использоваться при оформлении циферблатов.
Владельцы антикварных карманных часов или современных часов Glashütte Original, Lange, Ulysse Nardin, Blancpain, Cartier или даже Rolex могли заметить, что 4-я цифра на циферблате, обозначающая 4 часа, не написана в традиционном римском стиле. В большинстве случаев изображен символ «IIII». Конечно, есть исключения из правила, как, например, Биг Бен в Лондоне. Однако на большинстве циферблатов 4 часа изображено с «IIII».
Интересно понять, почему мир часового искусства почти единодушно решил переключиться на число IIII вместо привычного числа IV. Обычно римские цифры записываются следующим образом: I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII и т. д. Римские цифры возникли в древнем Риме, примерно в 1000 г. до н.э., и оставались обычным способом записи цифр по всей Европе в позднем Средневековье, задолго до упадка Римской Империи. Только в 14 веке римские цифры стали заменяться современными и более удобными арабскими цифрами. Числа в римской системе представлены комбинациями букв латинского алфавита. Упадок римских цифр совпадает с упадком латыни и появлением Ренессанса.
Однако, хотя в настоящее время широко признано, что число 4 должно быть написано в виде IV, оригинальный и самый древний образец римских цифр был не таким, каким мы знаем его сегодня. Самые ранние модели фактически использовали VIIII для 9 (вместо IX) и IIII для 4 (вместо IV). Однако эти две цифры оказались проблематичными, их легко путали с III и VIII. Вместо оригинальной добавочной нотации римская цифровая система изменилась на более привычную субтрактивную нотацию.
Первые механические часы были созданы в Европе в 13 веке в то время, когда все еще использовались римские цифры. Большинство часов были установлены на церквях, а латынь была официальным католическим языком. Таким образом, для большинства древних часов характерны римские цифры на их циферблатах. Тем не менее, причина, по которой часовые мастера решили использовать IIII вместо IV, когда это уже стало неактуальным, остается неясным.
Пока римляне не изобрели механические часы, они использовали концепцию солнечных часов, основанных на теневых часах в древней вавилонской астрономии (около 1500 г. до н.э.). Не стоит забывать, что часовое дело – наследие астрономии. В Риме были найдены античные солнечные часы с выгравированными римскими цифрами: и с IV, и с IIII.
Одной из причин, по которым в то время использовалась IIII, является римская мифология. Тогда самым почитаемым божеством Рима был Юпитер, бог неба и грома, царь среди богов в древнеримской религии. На латыни Юпитер был записан IVPPITER. Римляне, возможно, не решались выгравировать часть имени своего высшего божества на солнечных часах или напечатать в книгах. Вот почему число IIII, хотя и неудобное, возможно, было предпочтительнее IV. Хотя солнечные часы устарели с появлением часового дела, число IIII могло быть использовано только ради традиции.
Хотя субтрактивная нотация теперь широко применяется для римских цифр, ее использование наступало постепенно, и у ранних часовщиков все еще был выбор: использовать или не использовать IV.
Как уже упоминалось, ранние часы устанавливались на башнях церквей, где каждый житель города мог узнать время. В Древние времена и Средневековье только небольшая часть населения умела писать, читать и вычислять. Поэтому использование IIII вместо IV казалось более простым к пониманию. В то время как для IV требуется математика, базовая, но все же. Цифра IIII была куда более простой и понятной для значительной части необразованного европейского населения. Кроме того, могла возникнуть путаницу между IV и VI, а также между IX и XI. Вот почему на некоторых часах число девять написано в виде VIIII.
Также можно выдвинуть гипотезу о «ленивом часовщике». В часах, где применялся способ отливки цифр, IIII вместо IV и VIIII вместо IX могло бы существенно облегчить задачу мастеру. Таким образом, получаются цифры: I, II, III, IIII, V, VI, VII, VIII, VIIII, X, XI, XII. Это означает, что можно создать меньше форм, так как будет использоваться одна и та же основная форма для четырех первых цифр и одна и та же основная форма для чисел от VI до VIIII. Требуется только три формы: первая форма в виде IIII, которая была частично заполнена для создания чисел I, II, III и IIII, вторая — в форме VIIII, используемая для создания чисел V, VI, VII, VIII и VIIII и последняя, в виде XII, используемая для обозначения числа X, XI и XII. Хотя это не самая убедительная теория.
Более современная теория описывает французского короля Луи XIV. Этот французский монарх получил прозвище Луи Ле Гранд (Луи Великий) или Ле Рой Солейль (Солнечный король). Один из самых могущественных французских монархов, он объединил систему абсолютного монархического правления во Франции со всей политической и религиозной системой, вращающейся вокруг его фигуры — концепции божественного права королей, создающей централизованное государство, которое позже приведет к французской революция (при Людовике XVI). По тем же причинам, что и латинское написание имени Юпитер включало IV, король Людовик XIV предпочел IIII в оформлении часов. Будучи представителем Бога на Земле, часть его имени не могла быть напечатана на циферблате простых часов. Однако эта теория кажется весьма неправдоподобной. Использование IIII существовало в других землях с разными монархами, чьи имена не содержали букв IV. Это, по-видимому, не является достаточным объяснением, чтобы отказаться от субтрактивной нотации.
Последнее возможное объяснение является наиболее рациональным из всех и наиболее правдоподобным. Одной из причин использования IIII вместо IV может быть установление большего визуального баланса. IIII может обеспечить лучший визуальный баланс для цифры VIII, находящейся на другой стороне циферблата. Как в современных, так и в старинных часах присутствует как аддитивная, так и субтрактивная нотация (где 4 — IIII, а 9 — IX). Таким образом, циферблат имеет следующие цифры: I, II, III, IIII, V, VI, VII, VIII, IX, X, XI, XII. С помощью этой комбинации вы получаете три области на циферблате, в каждой из которых используются одинаковые цифры. Первая треть использует только I, вторая — использует V, и, наконец, последняя третья, которая показывает цифры с X. Таким образом, происходит балансировка циферблата с тремя отдельными областями. Современные часовые мануфактуры также используют IIII и IV на свое усмотрение и в наши дни.
Римские цифры — это… Что такое Римские цифры?
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этрусская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления.
Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.
Римские цифры появились за 500 лет до нашей эры у этрусков.
Цифры
римские цифры
В русском языке для закрепления в памяти буквенных обозначений цифр в порядке убывания существуют мнемонические правила:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх.
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
Соответственно M, D, C, L, X, V, I
Примеры
| Число | Римское обозначение | Примечание |
|---|---|---|
| 0 | — | |
| 4 | IV | до XIX века — IIII |
| 8 | VIII | |
| 9 | IX | |
| 31 | XXXI | |
| 46 | XLVI | |
| 99 | XCIX | |
| 583 | DLXXXIII | |
| 888 | DCCCLXXXVIII | от 1 до 1000 — самое длинное |
| 1668 | MDCLXVIII | |
| 1989 | MCMLXXXIX | |
| 2010 | MMX | |
| 2011 | MMXI | |
| 2012 | MMXII | |
| 3999 | MMMCMXCIX | |
| 5000 | ↁ | |
| 10 000 | ↂ |
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трёх раз; таким образом, с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000[источник не указан 683 дня] (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.
Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.
Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту: LXIV. Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: VM = 6000.
Часы марки Tissot с традиционным написанием «IIII»Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII».
Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. В этом случае повторения меньшей цифры не допускаются. По-римски число 94 будет XCIV=100-10+5-1=94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX). Существует шесть вариантов использования «правила вычитания»:
- IV = 4
- IX = 9
- XL = 40
- XC = 90
- CD = 400
- CM = 900
Необходимо отметить, что другие способы «вычитания» не допустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощенного (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:
- 999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX
- 95. Сто (C), вычтем 5 (V), получим 95 (VC) вместо XCV
- 1950: Тысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML
С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:
CXXIIICXXIII
А миллион как I, но только не с одной, а с двумя чертами во главе: I
Применение
В русском языке римские цифры используются в следующих случаях:
- Номер века или тысячелетия: XIX век, II тысячелетие до н. э.
- Порядковый номер монарха: Карл V, Екатерина II.
- Номер тома в многотомной книге (иногда — номера частей книги, разделов или глав).
- В некоторых изданиях — номера листов с предисловием к книге, чтобы не исправлять ссылки внутри основного текста при изменении предисловия.
- Маркировка циферблатов часов «под старину».
- Иные важные события или пункты списка, например: V постулат Евклида, II мировая война, XX съезд КПСС, Игры XXII Олимпиады и т. п.
- Валентность химических элементов.
- Порядковый номер ступени в звукоряде.
Римские цифры широко употреблялись в СССР при указании даты для обозначения месяца года: 11/III-85 или 9.XI.89. Для указания дат жизни и смерти на надгробиях часто использовался особый формат, где месяц года также обозначался римскими цифрами. С переходом на компьютерную обработку информации форматы даты, основанные на римских цифрах, практически вышли из употребления.
В других языках сфера применения римских цифр может иметь особенности, например, в западных странах римскими цифрами иногда записывается номер года.
Если разложить цифры графически, то получается следующее:
| № | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | L | I | I | I | I | V | I | I | I | I | X | |
| 1 | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | I | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | V | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | V | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | V | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | I | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | X | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | X | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | X | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | X | I | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | X | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | X | V | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | X | V | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | X | V | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | X | I | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | X | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | X | X | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | X | X | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | X | X | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | X | X | I | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | X | X | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | X | X | V | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | X | X | V | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | X | X | V | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | X | X | I | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | X | X | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | X | X | X | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | X | X | X | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | X | X | X | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | X | X | X | I | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | X | X | X | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | X | X | X | V | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | X | X | X | V | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | X | X | X | V | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | X | X | X | I | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | X | L | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | X | L | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | X | L | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | X | L | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | X | L | I | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | X | L | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | X | L | V | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | X | L | V | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | X | L | V | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | X | L | I | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | L | и т. д. до MMMCMXCIX (3999) |
Юникод
Стандарт Юникода рекомендует использовать для представления римских цифр обычные латинские буквы.[1] Тем не менее стандарт включает также специальные символы для римских цифр как часть Числовых форм (англ. Number Forms)[2] в области знаков с кодами с U+2160 по U+2188. Например, MCMLXXXVIII может быть представлено в форме ⅯⅭⅯⅬⅩⅩⅩⅧ. Этот диапазон включает как строчные, так и прописные цифры от 1 (Ⅰ или I) до 12 (Ⅻ или XII), в том числе и комбинированные глифы для составных чисел, таких как 8 (Ⅷ или VIII), главным образом для обеспечения совместимости с восточноазиатскими наборами символов в таких промышленных стандартах, как JIS X 0213, где эти символы определены. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ вместо его представления как Ⅹ и Ⅱ). В дополнение к этому, глифы существуют для архаичных[2] форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ), поздней формы записи 6 (ↅ, похожей на греческую стигму: Ϛ), ранней формы записи числа 50 (ↆ, похожей на стрелку, указывающую вниз Шаблон:Вмвауыаируфктр5ке4фуиUnicode[3]), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ.
| Код | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение[4] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 50 | 100 | 500 | 1 000 |
| U+2160 | Ⅰ 2160 | Ⅱ 2161 | Ⅲ 2162 | Ⅳ 2163 | Ⅴ 2164 | Ⅵ 2165 | Ⅶ 2166 | Ⅷ 2167 | Ⅸ 2168 | Ⅹ 2169 | Ⅺ 216A | Ⅻ 216B | Ⅼ 216C | Ⅽ 216D | Ⅾ 216E | Ⅿ 216F |
| U+2170 | ⅰ 2170 | ⅱ 2171 | ⅲ 2172 | ⅳ 2173 | ⅴ 2174 | ⅵ 2175 | ⅶ 2176 | ⅷ 2177 | ⅸ 2178 | ⅹ 2179 | ⅺ 217A | ⅻ 217B | ⅼ 217C | ⅽ 217D | ⅾ 217E | ⅿ 217F |
| Значение | 1 000 | 5 000 | 10 000 | — | — | 6 | 50 | 50 000 | 100 000 | |||||||
| U+2160! U+2180 | ↀ 2180 | ↁ 2181 | ↂ 2182 | Ↄ | ↄ | ↄ | ↄ | ↄ | ↄ | |||||||
Отображение всех этих символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.(?i)M{0,3}(D?C{0,3}|C[DM])(L?X{0,3}|X[LC])(V?I{0,3}|I[VX])$’. В языке Perl для поиска римских цифр в строке можно использовать регулярное выражение ‘m/((?i)M{0,3}(D?C{0,3}|C[DM])(L?X{0,3}|X[LC])(I[VX]|V?I{0,3}))/g’.
Преобразование
Для преобразования чисел, записанных арабскими цифрами, в римские, используются специальные функции. Например, в русской версии Microsoft Excel для этого существует функция РИМСКОЕ(аргумент), в английской версии Microsoft Excel и в любой версии OpenOffice.org Calc эта функция называется ROMAN(аргумент).
Функции преобразования на JavaScript
var arab = [1, 4, 5, 9, 10, 40, 50, 90, 100, 400, 500, 900, 1000];
var roman = ['I','IV','V','IX','X','XL','L','XC','C','CD','D','CM','M'];
function arabToRoman(number)
{
if(!number) return '';
var ret = '';
var i = arab.length - 1;
while(number > 0)
{
if(number >= arab[i])
{
ret += roman[i];
number -= arab[i];
}
else
{
i--;
}
}
return ret;
}
function romanToArab(str)
{
str = str.toUpperCase();
var ret = 0;
var i = arab.length - 1;
var pos = 0;
while(i >= 0 && pos < str.length )
{
if(str.substr(pos, roman[i].length) == roman[i])
{
ret += arab[i];
pos += roman[i].length;
}
else
{
i--;
}
}
return ret;
}
Аналогичные функции на Си (C89):
#include <string.h>
const int arabar[] = { 1, 4, 5, 9, 10, 40, 50, 90, 100, 400, 500, 900, 1000};
const char *romanar[] = { "I", "IV", "V", "IX", "X", "XL", "L", "XC", "C", "CD", "D", "CM", "M"};
char *arab2roman(unsigned short int arab) {
static char roman[80];
const int m = sizeof(arabar)/sizeof(int)-1, arabmax=arabar[m];
const char romanmax=romanar[m][0];
int i, n;
if(!arab) {
*roman=0;
return roman;
}
i=0;
while(arab>arabmax) {
roman[i++] = romanmax;
arab -= arabmax;
}
n=m;
while(arab > 0) {
if(arab >= arabar[n]) {
roman[i++] = romanar[n][0];
if(n&1)
roman[i++] = romanar[n][1];
arab -= arabar[n];
} else
n--;
}
roman[i]=0;
return roman;
}
unsigned short int roman2arab(char *roman) {
const int m = sizeof(arabar)/sizeof(int)-1;
unsigned short int arab;
int len, n, i, pir;
len=strlen(roman);
arab=0;
n=m;
i=0;
while(n >= 0 && i < len) {
pir=n&1;
if(roman[i] == romanar[n][0] && (!pir || roman[i+1] == romanar[n][1])) {
arab += arabar[n];
i += 1+pir;
} else
n--;
}
return arab;
}
Программа перевода арабских цифр в римские и наоборот[5]
type str2 = string[2];
const
Rims : array[1..14] of str2 = ('M','CM','D','CD','C','XC','L','XL','X','IX','V','IV','I',' ');
Arab : array[1..14] of integer = (1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1, 0);
var
N, NI, I, J : integer;
S : string;
function Arab2Rim(N : integer) : string;
var S : string;
I : integer;
begin
S := ''; I:=1;
while N > 0 do begin
while Arab[I]<=N do begin
S := S + Rims[I];
N := N - Arab[I]
end;
I:=I+1
end;
Arab2Rim := S
end;
function Rim2Arab (S:string) : integer;
var I, N : integer;
begin
I:=1; N := 0;
while S<>'' do begin
while Rims[I] = Copy(S, 1, Length(Rims[I]) ) do begin
S := Copy( S, 1+Length(Rims[I]), 255);
N := N + Arab[I]
end;
I:=I+1
end;
Rim2Arab := N
end;
begin
WriteLn('Перевод из арабских цифр в римские. 1999 B_SA');
{ Write('Введите число для преобразования:'); ReadLn(N);}
for NI := 26 to 46 do
WriteLn(NI,' = ',Arab2Rim(NI),' обратно ', Rim2Arab( Arab2Rim(NI) ));
end.
Функция преобразования арабского числа в римское на Pascal[6]
function Arab2Roman(arab:integer):string;
var
i:integer;
d:integer;
arab_str:string;
arab_len:integer;
begin
Result := '';
arab_str := IntToStr(arab);
arab_len := Length(arab_str);
for i := 0 to arab_len-1 do begin
d := StrToInt(String(arab_str[arab_len-i]));
if (d+1) mod 5 = 0 then
Result := Copy('IXCM', 1+i, 1) + Copy('VXLCDM', i*2 + (d+1) div 5, 1) + Result
else
Result := Copy('VLD', 1+i, d div 5) + Copy('IIIXXXCCCMMM', 1+i*3, d mod 5) + Result;
end;
end;
Отличительной особенностью данного алгоритма является то, что в нём не используются массивы (если, конечно, не считать строку массивом символов).
Функция преобразования арабского числа в римское на BASIC (самый краткий код)[7]
10 INPUT "АРАБСКОЕ ЧИСЛО: "; А$
20 FOR I=0 TO LEN(A$)-1
30 X=VAL(MID$(A$,LEN(A$)-I,1))
40 IF X=4 OR X=9 THEN B$=MID$("IXCM",I+1,1)+MID$("VXLCDM",I*2+(X+1)/5,1)+B$
50 IF X<4 THEN B$=MID$("IIIXXXCCCMMM",1+I*3,X)+B$
ELSE IF X>4 AND X<9 THEN B$=MID$("VLD",I+1,1)+MID$("IIIXXXCCCMMM",1+I*3,X-5)+B$
60 NEXT I
70 PRINT "РИМСКОЕ ЧИСЛО: "; B$
Функция преобразования арабского числа (в данном случае 1999) в римское на XPath
string-join(
for $num in (1999)
return (
('','M','MM','MMM')[($num idiv 1000) mod 10+1],
('','C','CC','CCC','CD','D','DC','DCC','DCCC','CM')[($num idiv 100) mod 10+1],
('','X','XX','XXX','XL','L','LX','LXX','LXXX','XC')[($num idiv 10) mod 10+1],
('','I','II','III','IV','V','VI','VII','VIII','IX')[$num mod 10+1]
),
'')
Функция преобразования арабского числа (в данном случае 1999) в римское на Perluse strict; use warnings; my $n = 1999; my $nums = [ ['', qw(I II III IV V VI VII VIII IX) ], ['', qw(X XX XXX XL L LX LXX LXXX XC) ], ['', qw(C CC CCC CD D DC DCC DCCC CM) ], ['', qw(M MM MMM) ] ]; my $i = 0; my @res = (); push @res, ($nums->[$i++][ ($n % 10, $n = int($n / 10))[0] ]) for 0 .. 3; print reverse @res;Класс для преобразования арабского числа (от 1 до 3999) в римское на Java
class ArabRome {
private int[] arabBase = {1000, 500, 100, 50, 10, 5, 1};
private String[] romeBase = {"M", "D", "C", "L", "X", "V", "I"};
public String ArabToRome(int arab) {
int result = 0;
int remainder = 0;
String resultRome = "";
for(short i = 0; i<arabBase.length; i+=2) {
result = arab/arabBase[i];
remainder = arab%arabBase[i];
if(result>0 && result<4) {
for(short j = 0; j<result; j++) {
resultRome += romeBase[i];
}
}
else if(result>=4 && result<9) {
for(short j=(short)result; j<5; j++) {
resultRome += romeBase[i];
}
resultRome += romeBase[i-1];
for(short j=5; j<result; j++) {
resultRome += romeBase[i];
}
}
else if(result == 9) {
resultRome += romeBase[i] + romeBase[i-2];
}
if(remainder==0) break;
arab = remainder;
}
return resultRome;
}
}
Extension class для преобразования римского числа в арабское и обратно, на CSharp
/// <summary>
/// Класс предназначен для преобразований арабских чисел в римские и обратно
/// </summary>
/// <remarks>
/// <para>Класс изначально содержит алфавит римских чисел, способных определять арабские числа от 1 до 39999</para>
/// <para>Если необходимо расширить диапазон, то можно определить дополнительные обозначения для римских чисел, используя
/// поле <see cref="БазовыеРимскиеЧисла"/>БазовыеРимскиеЧисла</remarks>
public static class РимскоеЧисло
{
/// <summary>
/// Алфавит базовых римских чисел
/// <para>Алфавит построен в виде словаря. Ключем словаря является арабское число (int), значением - соответствующее ему
/// римское число (string)</para>
/// </summary>
/// <remarks>
/// <para>Содержит римское обозначения арабских чисел 1*,4*,5*,9* - где "*"представляет собой 0...N нулей</para>
/// <para>При создании содержит в себе обозначение чисел от 1 до 10000 (I...ↂ) Так как в римском числе один символ не может
/// встречаться более трех раз, то изначально можно преобразовать в римский формат числа от 1 до 39999.</para>
/// <para>Если Вы хотите иметь возможность работать с большим количеством римских чисел, то вы должны добавить в список
/// дополнительные обозначения начиная с 40000 не пропуская элементы 1*,4*,5*,9*.</para>
/// </remarks>
public static SortedList<int, string> БазовыеРимскиеЧисла { get; set; }
static РимскоеЧисло()
{
БазовыеРимскиеЧисла = new SortedList<int, string>(17);
БазовыеРимскиеЧисла.Add(1, "I");
БазовыеРимскиеЧисла.Add(4, "IV");
БазовыеРимскиеЧисла.Add(5, "V");
БазовыеРимскиеЧисла.Add(9, "IX");
БазовыеРимскиеЧисла.Add(10, "X");
БазовыеРимскиеЧисла.Add(40, "XL");
БазовыеРимскиеЧисла.Add(50, "L");
БазовыеРимскиеЧисла.Add(90, "XC");
БазовыеРимскиеЧисла.Add(100, "C");
БазовыеРимскиеЧисла.Add(400, "CD");
БазовыеРимскиеЧисла.Add(500, "D");
БазовыеРимскиеЧисла.Add(900, "CM");
БазовыеРимскиеЧисла.Add(1000, "M");
БазовыеРимскиеЧисла.Add(4000, "Mↁ");
БазовыеРимскиеЧисла.Add(5000, "ↁ");
БазовыеРимскиеЧисла.Add(9000, "Mↂ");
БазовыеРимскиеЧисла.Add(10000, "ↂ");
}
/// <summary>
/// Рассчитывает максимально возможное римское число для текущего алфавита римских чисел.
/// </summary>
/// <returns>Максимально возможное римское число</returns>
public static uint МаксимальноеРимскоеЧисло()
{
int последнееЧисло = БазовыеРимскиеЧисла.Keys.Last();
int числоБезНулей = int.Parse(последнееЧисло.ToString().Replace('0','\0'));
int предварительное=0;
switch (числоБезНулей)
{
case 1:
предварительное = последнееЧисло * 4 - 1;
break;
case 4:
case 9:
предварительное = последнееЧисло;
break;
case 5:
предварительное = последнееЧисло + последнееЧисло / 5 * 3;
break;
default:
break;
}
return uint.Parse(предварительное.ToString().Replace('0', '9'));;
}
/// <summary>
/// Конвентирует целое число в римское число
/// </summary>
/// <param name="числоАраб">Арабское число, которое необходимо преобразовать в римскую запись</param>
/// <exception cref="ArgumentOutOfRangeException">Генерируется когда в качестве параметра передано число равное "0"
/// или число большее чем максимальная римское число.</exception>
/// <returns>Строку, представляющую собой римской число</returns>
public static string АрабскоеВРимское(this int числоАраб)
{
StringBuilder числоРимское = new StringBuilder();
//Исключаем знак "-" из арабского числа и делаем его первым символом римского числа
if (числоАраб < 0)
{
числоРимское.Append("-");
числоАраб = -числоАраб;
}
if (числоАраб == 0)
throw new ArgumentOutOfRangeException("числоАраб", числоАраб,
"Недопустимое значение аргумента: римские числа не могут быть равными\"0\"");
else if (числоАраб > МаксимальноеРимскоеЧисло())
throw new ArgumentOutOfRangeException("числоАраб", числоАраб,
string.Format("Недопустимое значение аргумента: невозможно задать римское число большее чем {0}",
МаксимальноеРимскоеЧисло()));
//Раскладываем арабское число на составляющие его римские числа и объединяем их в одну строку
var необходимыеБазовыеРимскиеЧисла =
from к in БазовыеРимскиеЧисла.Keys
where к <= числоАраб
orderby к descending
select к;
foreach (int тек in необходимыеБазовыеРимскиеЧисла)
{
while ((числоАраб / тек) >= 1)
{
числоАраб -= тек;
числоРимское.Append(БазовыеРимскиеЧисла[тек]);
}
}
return числоРимское.ToString();
}
/// <summary>
/// Конвентирует римское число в арабское
/// </summary>
/// <param name="числоРимское">Римское число, которое необходимо преобразовать в тип int</param>
/// <exception cref="FormatException">Генерируется когда в качестве параметра передано число не являющееся римским</exception>
/// <returns>Целое число, представляющее собой арабскую запись римского числа</returns>
public static int РимскоеВАрабское(this string числоРимское)
{
int числоАраб = 0;
sbyte отрицательное = 1;
string рим = числоРимское.");
//Соответствие должно обнаруживаться в конце строки
шаблонРимскогоНомера.Append("$");
//Упрощенная проверка. Не проверяет таких ошибок как IVII
if (!Regex.IsMatch(рим, шаблонРимскогоНомера.ToString()))
throw new FormatException(string.Format("Текст \"{0}\" не является римским числом",числоРимское));
Match число = Regex.Match(рим, шаблонРимскогоНомера.ToString());
foreach (int к in БазовыеРимскиеЧисла.Keys)
{
числоАраб += число.Groups[к.ToString()].Length / БазовыеРимскиеЧисла[к].Length * к;
}
return числоАраб * отрицательное;
}
}
Примечания
См. также
Как читать римские цифры | Прогулки по Риму
Даже если вы никогда не были в Вечном городе, римские цифры сопровождают вас всю жизнь. Любой из нас может с легкостью определить время на циферблате, номер главы в книге, век, в котором произошло событие. Сложности возникают, когда мы приезжаем в Рим, видим на каком-нибудь античном памятнике или надгробном камне дату и понимаем, что не можем ее прочитать, т. к. знаний цифр на часах недостаточно. Давайте разбираться вместе.
В современном варианте римская система счета представлена семи буквами латинского алфавита (обратите внимание: алфавит латинский, но цифры правильно называть «римскими»)
I -1
V -5
X -10
L -50
C -100
D -500
M -1000
Легче всего запомнить обозначения в обратном порядке, если выучить одну из мнемонических фраз: «Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам» или «Мы Dарим Сочные Lимоны, Хватит Vсем Iх».
Правила записи римскими цифрами:
- Цифры от 1 до 3 пишутся путем повторения I: I-1, II-2, III-3.
- Если меньшая цифра стоит перед большей — она вычитается из большей. Например, IV (5-1=4).
- Если большая цифра стоит перед меньшей — они складываются. Например, VI (5+1=6) или LXV (50+10+5=65).
- Цифры V, L, D не повторяются; цифры I, X, C, M могут повторяться не больше трех раз.
- Чтобы не было повторения цифры больше трех раз применяется следующий порядок написания: IX (10-1=9), XC (100-10=90), CM (1000-100=900), IV (5-1=4), XL (50-10=40), CD (500-100=400).
- Если над цифрой стоит горизонтальная черта, она увеличивается в 1000 раз.
- Если над цифрой стоят две горизонтальные черты, она становится миллионом. Два последних правила могут не действовать в русском рукописном тексте, т. к. у нас было принято выделять римские цифры подчеркиванием сверху или снизу.
Исключения из правил:
- 99 исторически пишется как XCIX (XC+IX, т. е. 90+9), а не IС (100-1).
- Иногда, если меньшая цифра стоит перед большей, это означает не вычитание, а умножение. В таких случаях, как правило, большая цифра написана чуть ниже. VIM — это 6×1000 = 6000.
- Умножение может обозначаться «.». Например VI.C — это 6х100 = 600.
- В некоторых печатных книгах на конце числа можно встретить вместо i или I соответственно j или J. Например xviii и xviij — оба = 18.
- В редких случаях I на конце числа обозначает не 1, а 2.
- В старых текстах большие числа иногда обозначались с использованием знака «)» и читались следующим образом: CI) как M, I) как D. В этом же правиле, если к таким цифрам дополнялся знак «( )», они умножались на 10. Например: I)= 500, (I)) = 5 000, а ((I))) = 50 000.
На что следует обратить внимание:
- Запрет на повторение одной и той же цифры более трех раз появился в XIX веке, поэтому в некоторых более ранних текстах можно увидеть XXXX вместо XL, IIIII вместо V и т. д.,
- Цифра «0» появилась только в Средние века, обозначалась буквой N (от лат. nulla — ноль),
- Для следующих цифр раньше использовались специальные знаки: 1000 — ↀ (или C|Ɔ), 5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ),
- Современные западные размеры одежды S, M, L, XL и т. д. никакого отношения к римским цифрам не имеют. Это аббревиатуры английских слов Small (маленький), Medium (средний), Large (большой), eXtraLarge (очень большой).
Таблица в помощь:
Давайте попробуем прочитать:
Год MMXVIII — считаем 1000+1000+10+5+3=2018.
Число DCCCLXXXVIII — считаем 500+100+100+100+50+10+10+10+5+1+1+1 = 888.
Год MCMLIV — сначала делим цифры на сегменты, определив позиции, где меньшая цифра стоит перед большей: M+CM+L+IV, считаем 1000+(1000-100)+50+(5-1)=1954.
Теории происхождения римских цифр:
— Согласно самой популярной гипотезе, древние римляне заимствовали цифры у этрусков, которые в своей системе счета использовали зарубки «I»: после четырех «IIII» каждую пятую отмечали скосом V, десятую перечеркивали X. По другой теории, X произошла из удвоенной V (у этрусков 5 обозначалась как нижняя половина X, у римлян как вехняя). Со временем зарубки приобрели самостоятельные значения, а еще позже стали идентифицироваться с буквами латинского алфавита.
— Еще одна теория принадлежит Альфреду Куперу, который соотнес обозначения цифр с пальцевым счетом. Купер считает, что I, II, III, IIII – это количество пальцев правой руки, V образовалась с помощью оттопыренного в сторону большого пальца и ладони, а X путем перекрещивания пальцев или рук. На левой руке показывали десятки: большой палец имел значение 50, остальные пальцы по 10.
Ваша Наталия Мархинина
Другие записи
Римские цифры или как правильно написать дату римскими цифрами для тату?
Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх (соответственно M, D, C, L, X, V, I).
Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно:
VI — 6, т.е. 5 + 1
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 + 1 + 1.
Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20).
Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
I (1) — unus (унус)
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decern (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V (5000) — quinque milla (квинквэ милиа)
X (10 000) — decem milia (дэцем милиа)
XX (20000) — viginti milia (вигинти милиа)
C (100000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа).
Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки.
Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10).
%d1%80%d0%b8%d0%bc%d1%81%d0%ba%d0%b8%d0%b5 %d1%86%d0%b8%d1%84%d1%80%d1%8b 18 0 0 1 пнг образ | Векторы и PSD-файлы
дым летать искры и частицы огня 1
3000*3000
1 juni hari lahir pancasila с garuda design
2000*2000
золотой номер 1
1200*1200
во имя аллаха 1 вт
1200*1200
twitch live streaming overlay facecam экран панели панели neon style 1
2301*2301
Социальные медиа кадр Хари Лахир Панкасила 1 Джуни с Гаруда Оранжевый цвет
2000*2000
memperingati hari kesaktian pancasila 1 октября
2000*2000
светящиеся линзы блики 1
3000*3000
День Панкасила с индонезийским красным и белым флагом
2000*2000
ปกเรียบหรู 4 в 1 обложки книги
1200*1200
купить 1 получить 1 бесплатная продажа речи пузырь баннер скидка тег значок дизайн шаблона
1500*1500
розовое золото № 1 с букетом
1200*1200
Золотое событие черный золотой шар номер 1
5000*5000
Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов
4167*4167
продажа и специальное предложение теги ценники продажа этикетки векторная иллюстрация купить 1 получить 1
8750*8750
1 одно число вектор золотисто желтый металлический буква цифра цифра 1 числовой символ алфавит типография элемент дизайна партия фольга символ цифра яркий металлик 3d реалистичная иллюстрация
5000*5000
3d top trophy номер 1 золотой цвет
2200*2200
золотая медаль вектор золотой 1 е место соревнование вызов награда падение яркий конфетти красная лента изолированный оливковая ветвь реалистичная иллюстрация
5000*5000
огонь пламя номер 1 прозрачный элемент png
3000*3000
один два три в реалистичной золотой серебряной бронзовой награде победителя лаврового венка изолированных иллюстрация
5000*5000
аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс
5000*5000
банановое дерево 1 реальный png
2000*2000
Празднование 1 й годовщины
2500*2500
youtbe 1 миллион просмотров эскиз оригами баннер
1200*1200
золотая медаль за 1 место вектор металлический реалистичный значок с достижением за первое место круглая этикетка с красным лавровым венком победитель звезды почетный приз соревнование игра золотой победитель
5000*5000
1 день идти с будильник
6250*6250
1 я награда вектор первое золотое размещение достижение цифра 1 один в реалистичном золотом лавровом венке красная лента изолированная иллюстрация
5000*5000
Трофей награда набор векторных фигур 1 2 3 один два три в реалистичной золотой серебряной бронзовой лавровый венок и красной лентой конкурс игры концепции изолированных на черном иллюстрации
5000*5000
уменьшенное изображение youtube 1 миллион просмотров
1200*1200
свет линзы блики 1
3000*3000
купите 1 промо уведомление по акции снижение цены продажи
1200*1200
День труда Хари Буруру Международный 1 й Мэй
5000*5000
1 палочка для еды
2000*2000
Воздушный шар обратного отсчета золотого открытия номер 0
5000*5000
глюк номер 1 вектор на прозрачном фоне
1200*1200
Граница рамка memperingati hari lahir pancasila 1 juni с красной белой лентой
2000*2000
номер 1 3d золотой
5000*5000
фоторамка 1
2778*2779
selamat memperingati hari lahirnya pancasila 1 Джуни с Гаруда Темно красный цвет
2000*2000
Приветствие Хари Рая Идул Фитри 1442 ч
1200*1200
3d как значок instagram желтый 1
2000*2000
3d номер 1 один круг
5000*5000
Награды Векторный набор достижений за 1 е 2 е и 3 е места на церемонии награждения на подиуме золотое серебро бронзовое достижение звание чемпиона лавровый венок с золотым щитом
5000*5000
Хари Лахир Панкасила Индонезия с блестящей иллюстрацией Гардуда
2500*2500
порванный рулон бумаги 1
3000*3000
синий номер 1 3d
3000*3000
pancasila gold logo
3000*3000
Черный красочный номер 1
1200*1200
Дым прозрачные облака 1
3000*3000
бумбокс с разноцветными музыкальными нотами
1200*1200
Конвертер римских чисел | Преобразование чисел
Введите римскую цифру или число и нажмите кнопку Конвертировать :
Римские цифры ►
Таблица преобразования римских цифр
| номер | Римская цифра | Расчет |
|---|---|---|
| 0 | не определен | |
| 1 | Я | 1 |
| 2 | II | 1 + 1 |
| 3 | III | 1 + 1 + 1 |
| 4 | IV | 5-1 |
| 5 | V | 5 |
| 6 | VI | 5 + 1 |
| 7 | VII | 5 + 1 + 1 |
| 8 | VIII | 5 + 1 + 1 + 1 |
| 9 | IX | 10-1 |
| 10 | X | 10 |
| 11 | XI | 10 + 1 |
| 12 | XII | 10 + 1 + 1 |
| 13 | XIII | 10 + 1 + 1 + 1 |
| 14 | XIV | 10-1 + 5 |
| 15 | XV | 10 + 5 |
| 16 | XVI | 10 + 5 + 1 |
| 17 | XVII | 10 + 5 + 1 + 1 |
| 18 | XVIII | 10 + 5 + 1 + 1 + 1 |
| 19 | XIX | 10-1 + 10 |
| 20 | XX | 10 + 10 |
| 21 | XXI | 10 + 10 + 1 |
| 22 | XXII | 10 + 10 + 1 + 1 |
| 23 | XXIII | 10 + 10 + 1 + 1 + 1 |
| 24 | XXIV | 10 + 10-1 + 5 |
| 25 | XXV | 10 + 10 + 5 |
| 26 | XXVI | 10 + 10 + 5 + 1 |
| 27 | XXVII | 10 + 10 + 5 + 1 + 1 |
| 28 | XXVIII | 10 + 10 + 5 + 1 + 1 + 1 |
| 29 | XXIX | 10 + 10-1 + 10 |
| 30 | XXX | 10 + 10 + 10 |
| 31 | XXXI | 10 + 10 + 10 + 1 |
| 32 | XXXII | 10 + 10 + 10 + 1 + 1 |
| 33 | XXXIII | 10 + 10 + 10 + 1 + 1 + 1 |
| 34 | XXXIV | 10 + 10 + 10-1 + 5 |
| 35 | XXXV | 10 + 10 + 10 + 5 |
| 36 | XXXVI | 10 + 10 + 10 + 5 + 1 |
| 37 | XXXVII | 10 + 10 + 10 + 5 + 1 + 1 |
| 38 | XXXVIII | 10 + 10 + 10 + 5 + 1 + 1 + 1 |
| 39 | XXXIX | 10 + 10 + 10-1 + 10 |
| 40 | XL | -10 + 50 |
| 41 | XLI | -10 + 50 + 1 |
| 42 | XLII | -10 + 50 + 1 + 1 |
| 43 | XLIII | -10 + 50 + 1 + 1 + 1 |
| 44 | XLIV | -10 + 50-1 + 5 |
| 45 | XLV | -10 + 50 + 5 |
| 46 | XLVI | -10 + 50 + 5 + 1 |
| 47 | XLVII | -10 + 50 + 5 + 5 + 1 |
| 48 | XLVIII | -10 + 50 + 5 + 1 + 1 + 1 |
| 49 | XLIX | -10 + 50-1 + 10 |
| 50 | L | 50 |
| 51 | LI | 50 + 1 |
| 52 | LII | 50 + 1 + 1 |
| 53 | LIII | 50 + 1 + 1 + 1 |
| 54 | LIV | 50-1 + 5 |
| 55 | LV | 50 + 5 |
| 56 | LVI | 50 + 5 + 1 |
| 57 | LVII | 50 + 5 + 1 + 1 |
| 58 | LVIII | 50 + 5 + 1 + 1 + 1 |
| 59 | LIX | 50-1 + 10 |
| 60 | LX | 50 + 10 |
| 61 | LXI | 50 + 10 + 1 |
| 62 | LXII | 50 + 10 + 1 + 1 |
| 63 | LXIII | 50 + 10 + 1 + 1 + 1 |
| 64 | LXIV | 50 + 10-1 + 5 |
| 65 | LXV | 50 + 10 + 5 |
| 66 | LXVI | 50 + 10 + 5 + 1 |
| 67 | LXVII | 50 + 10 + 5 + 1 + 1 |
| 68 | LXVIII | 50 + 10 + 5 + 1 + 1 + 1 |
| 69 | LXIX | 50 + 10-1 + 10 |
| 70 | LXX | 50 + 10 + 10 |
| 71 | LXXI | 50 + 10 + 10 + 1 |
| 72 | LXXII | 50 + 10 + 10 + 1 + 1 |
| 73 | LXXIII | 50 + 10 + 10 + 1 + 1 + 1 |
| 74 | LXXIV | 50 + 10 + 10-1 + 5 |
| 75 | LXXV | 50 + 10 + 10 + 5 |
| 76 | LXXVI | 50 + 10 + 10 + 5 + 1 |
| 77 | LXXVII | 50 + 10 + 10 + 5 + 1 + 1 |
| 78 | LXXVIII | 50 + 10 + 10 + 5 + 1 + 1 + 1 |
| 79 | LXXIX | 50 + 10 + 10-1 + 5 |
| 80 | LXXX | 50 + 10 + 10 + 10 |
| 81 | LXXXI | 50 + 10 + 10 + 10 + 1 |
| 82 | LXXXII | 50 + 10 + 10 + 10 + 1 + 1 |
| 83 | LXXXIII | 50 + 10 + 10 + 10 + 1 + 1 + 1 |
| 84 | LXXXIV | 50 + 10 + 10 + 10-1 + 5 |
| 85 | LXXXV | 50 + 10 + 10 + 10 + 5 |
| 86 | LXXXVI | 50 + 10 + 10 + 10 + 5 + 1 |
| 87 | LXXXVII | 50 + 10 + 10 + 10 + 5 + 1 + 1 |
| 88 | LXXXVIII | 50 + 10 + 10 + 10 + 5 + 1 + 1 + 1 |
| 89 | LXXXIX | 50 + 10 + 10 + 10-1 + 10 |
| 90 | XC | 100-10 |
| 91 | XCI | 100-10 + 1 |
| 92 | XCII | 100-10 + 1 + 1 |
| 93 | XCIII | 100-10 + 1 + 1 + 1 |
| 94 | XCIV | 100-10-1 + 5 |
| 95 | XCV | 100-10 + 5 |
| 96 | XCVI | 100-10 + 5 + 1 |
| 97 | XCVII | 100-10 + 5 + 1 + 1 |
| 98 | XCVIII | 100-10 + 5 + 1 + 1 + 1 |
| 99 | XCIX | 100-10-1 + 10 |
| 100 | C | 100 |
| 200 | CC | 100 + 100 |
| 300 | CCC | 100 + 100 + 100 |
| 400 | CD | 500–100 |
| 500 | D | 500 |
| 600 | DC | 500 + 100 |
| 700 | DCC | 500 + 100 + 100 |
| 800 | DCCC | 500 + 100 + 100 + 100 |
| 900 | CM | 1000–100 |
| 1000 | M | 1000 |
| 5000 | V | |
| 10000 | X | |
| 50000 | L | |
| 100000 | C | |
| 500000 | D | |
| 1000000 | M |
Конвертер даты в римские числа ►
Смотрите также
как пишутся века, годы, клавиши на клавиатуре
Римские цифры использовались в непозиционной системе счисления древних римлян. Однако в наше время в большинстве стран используется десятичная система, состоящая из более привычных нам арабских цифр.
В данной статье мы перечислим обозначения римских цифр, рассмотрим, как их напечатать, используя клавиши клавиатуры, приведем таблицу соответствия римских и арабских чисел от 1 до 1000. Также мы разберем, что из себя представляют и зачем нужны винкулум и система “Apostrophus”, и как записать годы и века римскими цифрами.
Обозначения римских цифр
| Число | Обозначение | Лат. |
| 1 | I | unus, unum |
| 5 | V | quinque |
| 10 | X | decem |
| 50 | L | quinquaginta |
| 100 | C | centum |
| 500 | D | quingenti |
| 1000 | M | mille |
microexcel.ru
Римские цифры на клавиатуре
Для набора римских цифр используются прописные буквы в английской раскладке.
Таблица соответствия римских и арабских чисел
| Число | Число римскими цифрами | Калькуляция |
| 0 | не задано | |
| 1 | I | 1 |
| 2 | II | 1+1 |
| 3 | III | 1+1+1 |
| 4 | IV | 5-1 |
| 5 | V | 5 |
| 6 | VI | 5+1 |
| 7 | VII | 5+1+1 |
| 8 | VIII | 5+1+1+1 |
| 9 | IX | 10-1 |
| 10 | X | 10 |
| 11 | XI | 10+1 |
| 12 | XII | 10+1+1 |
| 13 | XIII | 10+1+1+1 |
| 14 | XIV | 10-1+5 |
| 15 | XV | 10+5 |
| 16 | XVI | 10+5+1 |
| 17 | XVII | 10+5+1+1 |
| 18 | XVIII | 10+5+1+1+1 |
| 19 | XIX | 10-1+10 |
| 20 | XX | 10+10 |
| 21 | XXI | 10+10+1 |
| 22 | XXII | 10+10+1+1 |
| 23 | XXIII | 10+10+1+1+1 |
| 24 | XXIV | 10+10-1+5 |
| 25 | XXV | 10+10+5 |
| 26 | XXVI | 10+10+5+1 |
| 27 | XXVII | 10+10+5+1+1 |
| 28 | XXVIII | 10+10+5+1+1+1 |
| 29 | XXIX | 10+10-1+10 |
| 30 | XXX | 10+10+10 |
| 31 | XXXI | 10+10+10+1 |
| 32 | XXXII | 10+10+10+1+1 |
| 33 | XXXIII | 10+10+10+1+1+1 |
| 34 | XXXIV | 10+10+10-1+5 |
| 35 | XXXV | 10+10+10+5 |
| 36 | XXXVI | 10+10+10+5+1 |
| 37 | XXXVII | 10+10+10+5+1+1 |
| 38 | XXXVIII | 10+10+10+5+1+1+1 |
| 39 | XXXIX | 10+10+10-1+10 |
| 40 | XL | 50-10 |
| 41 | XLI | 50-10+1 |
| 42 | XLII | 50-10+1+1 |
| 43 | XLIII | 50-10+1+1+1 |
| 44 | XLIV | 50-10-1+5 |
| 45 | XLV | 50-10+5 |
| 46 | XLVI | 50-10+5+1 |
| 47 | XLVII | 50-10+5+1+1 |
| 48 | XLVIII | 50-10+5+1+1+1 |
| 49 | XLIX | 50-10-1+10 |
| 50 | L | 50 |
| 51 | LI | 50+1 |
| 52 | LII | 50+1+1 |
| 53 | LIII | 50+1+1+1 |
| 54 | LIV | 50-1+5 |
| 55 | LV | 50+5 |
| 56 | LVI | 50+5+1 |
| 57 | LVII | 50+5+1+1 |
| 58 | LVIII | 50+5+1+1+1 |
| 59 | LIX | 50-1+10 |
| 60 | LX | 50+10 |
| 61 | LXI | 50+10+1 |
| 62 | LXII | 50+10+1+1 |
| 63 | LXIII | 50+10+1+1+1 |
| 64 | LXIV | 50+10-1+5 |
| 65 | LXV | 50+10+5 |
| 66 | LXVI | 50+10+5+1 |
| 67 | LXVII | 50+10+5+1+1 |
| 68 | LXVIII | 50+10+5+1+1+1 |
| 69 | LXIX | 50+10-1+10 |
| 70 | LXX | 50+10+10 |
| 71 | LXXI | 50+10+10+1 |
| 72 | LXXII | 50+10+10+1+1 |
| 73 | LXXIII | 50+10+10+1+1+1 |
| 74 | LXXIV | 50+10+10-1+5 |
| 75 | LXXV | 50+10+10+5 |
| 76 | LXXVI | 50+10+10+5+1 |
| 77 | LXXVII | 50+10+10+5+1+1 |
| 78 | LXXVIII | 50+10+10+5+1+1+1 |
| 79 | LXXIX | 50+10+10-1+10 |
| 80 | LXXX | 50+10+10+10 |
| 81 | LXXXI | 50+10+10+10+1 |
| 82 | LXXXII | 50+10+10+10+1+1 |
| 83 | LXXXIII | 50+10+10+10+1+1+1 |
| 84 | LXXXIV | 50+10+10+10-1+5 |
| 85 | LXXXV | 50+10+10+10+5 |
| 86 | LXXXVI | 50+10+10+10+5+1 |
| 87 | LXXXVII | 50+10+10+10+5+1+1 |
| 88 | LXXXVIII | 50+10+10+10+5+1+1+1 |
| 89 | LXXXIX | 50+10+10+10-1+10 |
| 90 | XC | 100-10 |
| 91 | XCI | 100-10+1 |
| 92 | XCII | 100-10+1+1 |
| 93 | XCIII | 100-10+1+1+1 |
| 94 | XCIV | 100-10-1+5 |
| 95 | XCV | 100-10+5 |
| 96 | XCVI | 100-10+5+1 |
| 97 | XCVII | 100-10+5+1+1 |
| 98 | XCVIII | 100-10+5+1+1+1 |
| 99 | XCIX | 100-10-1+10 |
| 100 | C | 100 |
| 200 | CC | 100+100 |
| 300 | CCC | 100+100+100 |
| 400 | CD | 500-100 |
| 500 | D | 500 |
| 600 | DC | 500+100 |
| 700 | DCC | 500+100+100 |
| 800 | DCCC | 500+100+100+100 |
| 900 | CM | 1000-100 |
| 1000 | M | 1000 |
microexcel.ru
Примечание: римские цифры довольно часто используются для обозначения веков (столетий) или, например, на циферблатах часов. Зная и используя таблицу выше, трудностей с восприятием информации в таком виде быть не должно.
Винкулум (уздечка)
Горизонтальная линия (черточка) над римской цифрой, обозначающая, что она умножена на 1000.
| Число | Число римскими цифрами | Калькуляция |
| 5000 | V | 5 * 1000 |
| 10000 | X | 10 * 1000 |
| 50000 | L | 50 * 1000 |
| 100000 | C | 100 * 1000 |
| 500000 | D | 500 * 1000 |
| 1000000 | M | 1000 * 1000 |
microexcel.ru
Система “Apostrophus”
Позволяет выражать большие числа, т.к. с помощью 7 обычных буквенных обозначений сделать это затруднительно.
| Число | Обозначение |
| 500 | IƆ или D |
| 1000 | CIƆ или ↀ |
| 5000 | IƆƆ или ↁ |
| 10000 | CCIƆƆ или ↂ |
| 50000 | IƆƆƆ или ↇ |
| 100000 | CCCIƆƆƆ или ↈ |
microexcel.ru
Годы римскими цифрами
| Год | Год римскими цифрами |
| 1000 | M |
| 1100 | MC |
| 1200 | MCC |
| 1300 | MCCC |
| 1400 | MCD |
| 1500 | MD |
| 1600 | MDC |
| 1700 | MDCC |
| 1800 | MDCCC |
| 1900 | MCM |
| 1990 | MCMXC |
| 1991 | MCMXCI |
| 1992 | MCMXCII |
| 1993 | MCMXCIII |
| 1994 | MCMXCIV |
| 1995 | MCMXCV |
| 1996 | MCMXCVI |
| 1997 | MCMXCVII |
| 1998 | MCMXCVIII |
| 1999 | MCMXCIX |
| 2000 | MM |
| 2001 | MMI |
| 2002 | MMII |
| 2003 | MMIII |
| 2004 | MMIV |
| 2005 | MMV |
| 2006 | MMVI |
| 2007 | MMVII |
| 2008 | MMVIII |
| 2009 | MMIX |
| 2010 | MMX |
| 2011 | MMXI |
| 2012 | MMXII |
| 2013 | MMXIII |
| 2014 | MMXIV |
| 2015 | MMXV |
| 2016 | MMXVI |
| 2017 | MMXVII |
| 2018 | MMXVIII |
| 2019 | MMXIX |
| 2020 | MMXX |
| 2021 | MMXXI |
| 2022 | MMXXII |
| 2023 | MMXXIII |
| 2024 | MMXXIV |
| 2025 | MMXXV |
microexcel.ru
римских цифр: 18 = XVIII
.Текущая дата и время римскими цифрами
| 2021-06-14 | 19:47:51 |
| MMXXI-VI-XIV | XIX: XLVII: LI |
Вот текущая дата и время, написанные римскими цифрами.Поскольку в римской системе счисления нет нуля, час, минута и секунда в метках времени иногда становятся пустыми.
О римских цифрах
Римские цифры произошли, как следует из названия, из Древней Римской империи. В отличие от нашей системы координат с основанием 10, римская система основана на сложении (а иногда и вычитании) семи различных значений. Эти символы используются для обозначения этих значений:
Например, чтобы выразить число 737 римскими цифрами, вы пишете DCCXXXVII, то есть 500 + 100 + 100 + 10 + 10 + 10 + 5 + 1 + 1.Однако для чисел 4 и 9 вместо сложения используется вычитание, и меньшее число записывается перед большим числом: например, 14 записывается как XIV, то есть 10 + 5 — 1, а 199 выражается как CXCIX, т.е. 100 + 100 — 10 + 10 — 1. Можно утверждать, что 199 было бы легче записать как CIC, но согласно наиболее распространенному По определению, вы можете вычесть только число, которое на порядок меньше, чем числа, из которых вы вычитаете, а это означает, что IC для 99 неверно.
Римские цифры часто используются в пронумерованных списках, на зданиях, чтобы указать год, когда они были построены, и в именах регентов, таких как Людовик XVI из Франции.
Не стесняйтесь ссылаться на этот сайт, если найдете его полезным. Также можно напрямую ссылаться на определенные числа, такие как roman-numerals.info/XXXVII или roman-numerals.info/37. Вы также можете ссылаться на интервалы, например, roman-numerals.info/1-100 или римские цифры.info / 1980-2020, чтобы увидеть числа в формате списка.
римских цифр | Словарь | Английский Клуб
Обычно используемые числа (1, 2, 3 и т. Д.) Называются «арабскими цифрами». Но иногда мы используем другую систему записи чисел — « римские цифры, ». Римляне использовали буквы алфавита для обозначения чисел, и вы иногда будете видеть эту систему, используемую для номеров страниц, циферблатов, дат фильмов и т. Д.
Изображение: На циферблате вы видите римские цифры для часов и арабские цифры для минут.
В римских цифрах используются следующие буквы:
- I = 1
- В = 5
- Х = 10
- L = 50
- С = 100
- D = 500
- M = 1000
При написании римских цифр можно использовать прописные буквы (заглавные) или строчные (строчные). Таким образом, следующие числа точно такие же: XVIII = xviii = 18
Как правило, буквы располагаются в порядке убывания значения, например.грамм. XVI = 16 (10 + 5 + 1). Буквы можно повторять один или два раза для увеличения значения, например XX = 20, XXX = 30. Буквы не могут повторяться три раза, поэтому XXXX не используется для 40. В этом случае XL = 40 (50 минус 10).
Не дайте себя обмануть словом , повторять , что означает «повторить снова». Если мы напишем X, а затем повторим, у нас будет XX. Если мы повторим X два раза, мы получим XXX. Таким образом, XXX — это X, повторенный два раза, а не три раза!
Посмотрите на эти примеры используемых римских цифр:
- Введение находится на странице vii (= Введение находится на странице 7)
- © MMXVI EnglishClub (= © 2016 EnglishClub)
Значимые числа от единицы до тысячи
| Римские цифры | арабский цифры | |
|---|---|---|
| верхний регистр | строчная | |
| I | и | 1 |
| II | ii | 2 |
| III | iii | 3 |
| IV | iv | 4 |
| В | v | 5 |
| VI | vi | 6 |
| VII | vii | 7 |
| VIII | viii | 8 |
| IX | ix | 9 |
| х | х | 10 |
| XI | xi | 11 |
| XII | xii | 12 |
| XIII | xiii | 13 |
| XIV | xiv | 14 |
| XV | xv | 15 |
| XVI | xvi | 16 |
| XVII | xvii | 17 |
| XVIII | xviii | 18 |
| XIX | xix | 19 |
| XX | х х | 20 |
| XXI | xxi | 21 |
| XXII | xxii | 22 |
| XXIII | xxiii | 23 |
| XXX | ххх | 30 |
| XL | xl | 40 |
| л | л | 50 |
| LX | лк | 60 |
| LXX | lxx | 70 |
| LXXX | lxxx | 80 |
| XC | xc | 90 |
| К | с | 100 |
| CC | куб.см | 200 |
| CCC | куб.см | 300 |
| CD | кд | 400 |
| D | д | 500 |
| м | кв.м | 1000 |
Татуировка с 20 римскими цифрами для мужчин в 2021 году
У всех нас есть связь с числами.Может быть, это особая дата, например, день вашей свадьбы или рождение ребенка, или, возможно, это счастливое число. Привлекательно то, что это уникально для каждого человека, поэтому они делают глубоко личные и визуально интересные татуировки. В отличие от повседневной арабской системы счисления, римские цифры встречаются реже. Эти различные схемы можно использовать для обозначения моментов в вашей жизни, которые имеют большое значение. Сентиментальные мужчины часто предпочитают включать в свой боди-арт другие элементы, такие как перо, имя любимого человека или розу, каждый из которых только усиливает мощный символизм их чернил.Расположение вашего украшения также важно, и вы можете сделать небольшую татуировку с обручальным кольцом или выбрать что-то детализированное на спине. Если вы хотите узнать больше об этих классных чернилах, продолжайте читать.
1. Татуировка с римской цифрой и датой
У всех нас есть конкретная дата или время, которые имеют для нас значение, и вы можете отдать дань уважения выбранному вами дню татуировкой с римскими цифрами. Вы можете записать дату свадьбы, начало отношений или даже смерть любимого человека.Многие люди находят эту систему нумерации немного более абстрактной и интересной, чем арабские цифры, которые мы используем каждый день. Это также может быть более особенным, потому что не все сразу узнают дату.
2. Римские цифры + тату с часами
Многих мужчин привлекают татуировки с часами, потому что они очень символичны. Часы популярны среди тех, кто задумывается о своей смертности, и часто ассоциируются с жизнью и смертью.Ваше решение о том, где остановить стрелки, также имеет значение. Это может быть способ отметить рождение ребенка или почтить память умершего близкого человека. Эти конструкции обычно сложные и детализированные, что создает красивый законченный эффект. Тем не менее, они также вызовут более значительный дискомфорт и будут более дорогостоящими, поскольку отнимают много времени.
3. Римские цифры + тату с розой
Римские цифры— отличный способ написать важные даты или счастливые числа.Самое лучшее в этих татуировках — это то, что они имеют такое большое значение для владельца. Чтобы сделать свой предмет более индивидуальным и значимым, многие мужчины предпочитают добавлять в свой дизайн другие элементы, например перо или розу. Цветок — один из самых популярных символов для нанесения чернил, потому что он имеет большое символическое значение. Он представляет собой баланс между удовольствием и болью; Какой бы красивой ни была роза, шипы тоже могут причинить вред. Выбранный вами цвет также влияет на значение. Например, красный цвет ассоциируется со страстью и любовью, а черный — с горем и смертью.
СВЯЗАННЫЕ: 18 памятных татуировок роз для мужчин
4. Римские цифры + тату с крестом
Вы глубоко религиозный человек? Если это так, то фантастический способ почтить свою веру — это татуировка с крестом и римскими цифрами. Крест имеет большое значение в христианстве и рассматривается как символ жертвы, которую Иисус Христос принес человечеству. Ваше решение указать дату может означать момент, когда вы обрели свою веру, или это может означать смерть любимого человека.Красота этих чернил в том, что они открыты для интерпретации и уникальны для каждого владельца.
5. Римские цифры + тату перо
Римские цифры— это способ отметить даты или время, которые повлияли на нашу жизнь. Другие элементы, которые вы решите включить в свой боди-арт, могут добавить к общему значению, а перо является символом многих вещей. Это часто ассоциируется со свободой, мудростью, властью и силой. Многие любят добавлять перья к памятным чернилам.Оперение разных птиц также имеет разную интерпретацию; например, орел ассоциируется с храбростью, а сова — со знанием и переходом.
6. Римские цифры + татуировка с птицей
Выбирая следующий боди-арт, вы можете захотеть чего-то значительного, а что может быть лучше римских цифр и тату с птицами? Цифровые символы помогают отметить важные даты, а наши пернатые друзья ассоциируются со свободой и связью между небом и землей.Тем не менее, есть много птиц на выбор, и значение вашей татуировки будет меняться в зависимости от вашего решения. Например, ласточка может символизировать любовь, преданность и преданность вашей семье. С другой стороны, сова может символизировать знания, тайну или перемены.
7. Тату римские цифры + имя
Если вы хотите сделать татуировку сугубо личную, это может быть отличным выбором для нанесения имени любимого человека. Вы также можете добавить знаменательные даты, используя римские цифры, что сделает произведение еще более значимым.Это может быть прекрасный способ почтить память тех, кого вы любите, будь то мать, дедушка, ребенок или брат или сестра. Некоторых людей также может заинтересовать идея подписать их именем или инициалами своего романтического партнера, но перед этим убедитесь, что отношения будут длиться вечно. Вы не хотите возвращаться в тату-студию через несколько недель для сокрытия, потому что все закончилось плохо.
8. Татуировка с римскими цифрами со смыслом
Даты и имена часто используются, чтобы почтить память близких или вспомнить тех, кто умер.Решив сделать татуировку в память о потерянном человеке, вы можете сделать это осмысленно; путем нанесения римских цифр значимых дат, таких как их рождение или смерть. Существует множество вариаций этого дизайна, каждая из которых является индивидуальной для владельца, но наиболее популярными элементами, которые нужно включить, будут перо или крылья ангела.
9. Татуировка с римскими цифрами на запястье
При выборе татуировки часто так же важно ее расположение, как и выбранный дизайн.Если у вас есть особо значимый предмет, на который вы хотите нанести татуировку, то это может быть отличным выбором, если вы выберете место на теле, где вы можете видеть его каждый день, например, запястье. Вы можете напомнить себе о важных датах и о том, почему вы решили сделать им татуировку. Однако у этого места есть некоторые недостатки; это имеет тенденцию быть немного более болезненным из-за тонкой кожи и недостатка мышц. Детали запястья также быстрее выгорают из-за воздействия элементов.
10.Тату римские цифры на руке
Пожалуй, самое популярное место для татуировки — это рука, и на то есть веские причины. Во-первых, это место не считается высоким по шкале боли. Это также замечательно, если вы хотите показать свои чернила или если вы предпочитаете, чтобы они были скрыты. Другие части вашего тела отлично подходят для татуировок, но вы не всегда можете их увидеть, тогда как на руке вы сможете смотреть и ценить свой дизайн каждый день. По этой причине лучше убедиться, что это произведение, которое вам нравится.
11. Татуировка с римскими цифрами на груди
Ваша грудь — достаточно большая область, чтобы на ней можно было нанести детальную татуировку, но это также одно из самых значимых мест. В конце концов, это способ создать для вас дизайн, близкий вашему сердцу. Это фантастическое место для тех, кто хочет скрыть свой боди-арт, но если вы решите снять рубашку, это сделает заявление. Есть много плюсов, но вы испытаете некоторую боль.Проблема с татуировкой на груди заключается в том, что у большинства людей мало жира и мышц.
12. Татуировка на бицепсе с римскими цифрами
Мужчины, которые хотят выставить напоказ свои мускулы и одну из самых мужских частей своего тела, будут привлечены к татуировке на бицепсе. Место отлично смотрится с чернилами, потому что они могут улучшить форму, и это место, которым вы можете похвастаться, если хотите. Его также легко скрыть, если вы не хотите гнуться. Есть много плюсов в использовании дизайна в этом месте, но это вызовет некоторый дискомфорт из-за нервных окончаний, расположенных на нижней стороне руки.
13. Татуировка на ребре с римскими цифрами
Если вы мужчина, который не боится сильного дискомфорта, тогда татуировка на ребре — отличное место для дизайна римских цифр. Вероятно, это не лучшее место для ваших первых чернил, так как оно считается высоко оцененным по шкале боли. Это из-за близости к кости и тонкой кожи в этой области. Тем не менее, татуировкам в виде ребер требуется примерно столько же времени, чтобы зажить, как и большинству других мест, и они выглядят супер круто!
14.Татуировка на груди с римскими цифрами
Ключица — это место, которое одновременно видно и незаметно. Если вы не хотите снимать рубашку, никто не узнает, что у вас есть татуировка, и это особенно привлекательно для тех, кто более частный или имеет корпоративную работу. Форма области также хорошо сочетается с чем-то длинным и простым, например с римскими цифрами. Вы можете испытывать некоторый дискомфорт из-за близости к кости, но вы, вероятно, обнаружите, что оно того стоит.
15. Татуировка с римскими цифрами на спине
Ваша спина похожа на большой холст, и на нее можно нанести красивые значимые татуировки. Независимо от того, решите ли вы включить татуировку с римскими цифрами в замысловатый дизайн с различными другими элементами, такими как роза или часы, или оставите их сами по себе, это место сделает заявление. Вам не нужно хвастаться своим боди-артом, если вы этого не хотите, и хотя вы не сможете смотреть на него все время, символизм вашего решения останется прежним.Это смелый, но отличный вариант.
16. Татуировка на предплечье с римскими цифрами
Что может быть лучше для нанесения татуировок чем-то значимым для вас, чем ваше предплечье? Местоположение одновременно универсально и не слишком высоко по шкале боли. Это может быть отличное место для вашей первой или десятой татуировки, и поэтому тушь здесь так популярна. На предплечье будет хорошо смотреться несколько рисунков, в том числе татуировка с римскими цифрами. Он также достаточно большой, чтобы добавить к вашему изделию различные элементы, что сделает его еще более значимым и уникальным.
17. Татуировка на шее с римскими цифрами
Татуировки на шее не для слабонервных. Они смелы, требуют внимания и причиняют боль. Эта область заполнена нервными окончаниями и имеет тонкую кожу, что делает это место одним из самых болезненных для нанесения татуировки. Также здесь практически невозможно спрятать кусок, чтобы вас заметили, а это то, что вам нужно. Если вы можете терпеть боль, это одно из самых крутых мест для боди-арта, и хотя тату на шее когда-то предназначались для головорезов и правонарушителей, современный человек теперь использует это место для своих чернил.
18. Татуировка на перстне с римскими цифрами
Татуировки на пальцах стали невероятно популярными как у мужчин, так и у женщин. Они могут делать заявления, но могут быть и простыми. Один из множества вариантов этого размещения — татуировка на безымянном пальце, прекрасный способ показать свою приверженность тому, кого вы любите. Это гораздо более надежный вариант, чем украшение, которое можно снять, и сентиментальные люди будут привлечены этим прекрасным способом отметить свои отношения.Вам также не нужно беспокоиться о том, что ваше кольцо потеряно или украдено.
19. Татуировка с маленькими римскими цифрами
Боди-арт привлекает огромным разнообразием. Вы можете получить большой и подробный дизайн или что-то маленькое и простое, и оба они имеют значение. Некоторым предметам нужно больше места, чтобы отдать должное, но римские цифры выглядят так же хорошо, когда вы решите их уменьшить. Маленькие татуировки не требуют столько времени для завершения и доставляют меньше дискомфорта.Кроме того, их изготовление намного дешевле. Вы также не ограничены в плане размещения и можете нанести татуировку где угодно, в том числе на палец или шею.
20. Прикрытие татуировки римскими цифрами
Вы можете как можно больше обдумать дизайн татуировки, но все меняется, и иногда вы пожалеете о своем решении. Может случиться так, что человек, которого вы выбрали, или число, которое вы считали счастливым, больше к вам не относится.Прелесть татуировки в том, что всегда есть возможность скрыть ее или выбрать лазерное удаление. Тем не менее, боди-арт — это не то решение, которое следует принимать поспешно, но приятно осознавать, что если ваши обстоятельства изменятся, вам не придется нервничать.
Часто задаваемые вопросы
Что означают римские цифры в татуировках?
Римские цифры— это способ отметить число или знаменательную дату, которая имеет важное значение в вашей жизни.Они невероятно важны для владельца.
Сколько стоит татуировка с римскими цифрами?
При принятии решения приобрести боди-арт некоторые вещи влияют на стоимость. К ним относятся размер, детализация и цвет, которые использовались для создания выбранного вами предмета. Татуировка с римскими цифрами обычно довольно проста и понятна и обычно стоит от 50 до 100 долларов. Если у вас есть более сложные чернила, то они, несомненно, будут стоить дороже.
Как скрыть татуировку с римскими цифрами?
Размер вашего рисунка определит, насколько легко его скрыть.Тем не менее, опытный татуировщик может превратить ненужный предмет во что-то, что вам понравится.
Как лучше всего сделать татуировку с римскими цифрами?
Расположение татуировки с римскими цифрами зависит от размера, но, как правило, ее можно нанести на любом участке тела. Вы можете выбрать безымянный палец или большой узор на спине. Тем не менее, одними из самых популярных мест являются рука, предплечье и запястье.
ПОДПИСАТЬСЯ НА НАШИ НОВОСТИ
Подпишитесь на наш список рассылки и получайте интересные материалы и обновления на свой почтовый ящик.
Спасибо за подписку.
Что-то пошло не так.
Мы уважаем вашу конфиденциальность и серьезно относимся к ее защите.
Римские цифры [Диаграмма и конвертер]
Хотите знать, как читать или писать любые числа, используя римские цифры? Или, может быть, вы просто хотите перевести какое-то конкретное число, которое вам интересно?
Здесь вы можете получить и то, и другое! Переведите любое число с помощью этого интерактивного конвертера или узнайте все, что нужно знать о римских цифрах, в статье ниже.Читать дальше.
Преобразователь
Диаграмма
| 1 | I |
| 2 | II |
| 3 | III |
| 4 | IV |
| 5 | 000 VI |
| 7 | VII |
| 8 | VIII |
| 9 | IX |
| 10 | X |
| 11 | 06000 900 900 13XIII |
| 14 | XIV |
| 15 | XV |
| 16 | XVI |
| 17 | XVII |
| XIX | |
| 20 | XX |
| 21 | XXI |
| 22 | XXII |
| 23 | XXIII |
| 24 | XXIV |
| 25 | XXV | XXV | XXV |
| 28 | XXVIII |
| 29 | XXIX |
| 30 | XXX |
| 50 | L |
| 900 | 900 |
| 1000 | M |
| 1 — 50… | |
| 1 — 100… | |
| 1 — 1000… | |
| 1 — 10000… | |
Как работают римские цифры
В отличие от современной (индуистско-арабской) системы счисления, у римлян не было цифр (0–9) для обозначения чисел, поэтому они использовали буквы для их кодирования.Это семь букв, используемых для написания римских цифр, и их соответствующее значение арабскими цифрами:
- я
- 1
- В
- 5
- Х
- 10
- L
- 50
- С
- 100
- D
- 500
- M
- 1000
Читать и писать римские цифры несложно. Вам просто нужно знать значение каждой буквы и пару простых правил.
Основное правило таково: чтобы прочитать римское число, просто сложите значения его букв:
- III
- 1 + 1 + 1 = 3
- VI
- 5 + 1 = 6
- XVII
- 10 + 5 + 1 + 1 = 17
- ХХ
- 10 + 10 = 20
Вычитающее обозначение : В качестве исключения из приведенного выше правила, когда буква предшествует другой, имеющей большее значение, она не складывает, а вычитает. Некоторые примеры:
- IV
- 5 — 1 = 4
- IX
- 10 — 1 = 9
- XIX
- 10 + (10 — 1) = 19
- XL
- 50-10 = 40
- СМ
- 1000–100 = 900
Чтобы написать любое число, просто переводите каждый десятичный знак отдельно слева направо: тысячи, сотни, десятки и единицы.
- 39
- 30 + 9 → XXX + IX → XXXIX
- 140
- 100 + 40 → C + XL → CXL
- 2018
- 2000 + 10 + 8 → MM + X + VIII → MMXVIII
Принцип краткости : Вы всегда должны использовать минимальное количество букв, необходимое для каждого десятичного разряда отдельно (но не для всего числа). Например:
- 5
-
IIIII→ V - 9
-
VIIII→ IX - 44
-
XXXXIIII→ XLIV - 95
-
VC→ XCV - 999
-
IM→ CMXCIX
Теперь вы готовы принять участие в любой из наших викторин по римским цифрам.Вы можете выбрать один из трех уровней сложности:
Альтернативные формы
Хотя приведенные выше правила являются «стандартными» в настоящее время, в прошлом они не применялись последовательно. Например, можно найти древние документы и надписи с использованием нестандартных римских цифр, таких как IIII (4), IC (99), IIXX (18) или MDCCCCX (1910).
Миллионы римскими цифрами
Хотя римляне обычно не нуждались в большом количестве людей, они приняли для этого множество соглашений.Одной из самых популярных (по крайней мере, в средние века) была горизонтальная линия, или vinculum , умноженная на тысячу.
- В
- 5000
- Х
- 10 000
- L
- 50 000
- С
- 100 000
- D
- 500 000
- M
- 1 000 000
Некоторые авторы предполагают, что двойная линия, таким образом, представляет собой умножение на один миллион, хотя нет никаких доказательств того, что она когда-либо использовалась на практике.Однако для удобства наш конвертер римских цифр следует этому соглашению (на случай, если вам действительно нужно переводить такие большие числа!).
А как насчет нуля?
В римской системе счисления не было конкретной римской цифры для нуля. Для этого они просто использовали слово nulla (нет), nihil (ничего) или просто букву N .
Как сегодня используются римские цифры?
Римские цифры использовались до высокого и позднего средневековья, когда арабские цифры постепенно вошли в западный мир.
В настоящее время римские цифры используются только в определенных контекстах, например:
- Из одноименной серии пап, императоров или монархов ( Елизавета II, ). Они называются королевскими номерами .
- Назвать династии в определенных культурах ( Династия XVIII Египта ).
- На памятниках или мемориальных досках для обозначения года.
- Для обозначения часов на циферблатах.
- Для перечисления книг, томов, глав и т. Д., в литературных произведениях.
- Для нумерации страниц в предварительных главах книг (например, в прологе).
- Для повторяющихся мероприятий, таких как конгрессы, фестивали или чемпионаты ( Super Bowl LIII ).
- Некоторая серия названий продуктов или названий фильмов ( Mac OS X , Rocky IV ).
- В качестве суффиксов поколений (например, Patrick II вместо Patrick Jr. ).
- За год в авторских правах на некоторые фильмы или телешоу (например.г., © mmxviii).
В испанском языке есть два дополнительных использования:
- Века всегда записываются римскими цифрами ( 21 век → siglo xxi ).
- В сокращенных числах месяц можно записать римскими цифрами ( 25.12.2018 → 25 / XII / 2018 ).
Список литературы
Преобразователь римских цифрПреобразователь римских цифр
Преобразователь римских цифрО преобразователе римских цифр
Конвертер римских цифр используется для преобразования римских цифр в индусско-арабские цифры и наоборот.
Римские цифры
Римские цифры произошли от системы счисления Древнего Рима. Например, римскими цифрами 2021 будет MMXXI, а римскими цифрами 2020 — MMXX.
Первые десять римских цифр — это I, II, III, IV, V, VI, VII, VIII, IX и X.
Таблица с римскими цифрами
Ниже приводится список римских цифр от 1 до 1000:
| Индийско-арабские цифры | Римские цифры | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | I | |||||||||||
| 2 | II | |||||||||||
| 3 | III | |||||||||||
| 4 9000 V | ||||||||||||
| 6 | VI | |||||||||||
| 7 | VII | |||||||||||
| 8 | VIII | |||||||||||
| 9 | IX | |||||||||||
| 10 | 0006 | |||||||||||
| 12 | XII | |||||||||||
| 13 | XIII | |||||||||||
| 14 | XIV | |||||||||||
| 15 | XV | |||||||||||
| 16 | 0006 170007||||||||||||
| 16 | 106 XVI10618 | XVIII | ||||||||||
| 19 | XIX | |||||||||||
| 20 | XX | |||||||||||
| 21 | XXI | |||||||||||
| 22 | XXII | |||||||||||
| 23 | XXIII | |||||||||||
| 24 | XXIV | |||||||||||
| 25 | XXV | XXV | XXV | 27 | XXVII | |||||||
| 28 | XXVIII | |||||||||||
| 29 | XXIX | |||||||||||
| 30 | XXX | |||||||||||
| 31 | XXXI | XXXIII | ||||||||||
| 34 | XXXIV | |||||||||||
| 35 | XXXV | |||||||||||
| 36 | XXXVI | |||||||||||
| 37 | XXXVII | XXXVII | XXXVII | |||||||||
| 40 | XL | |||||||||||
| 41 | XLI | |||||||||||
| 42 | XLII | |||||||||||
| 43 | XLIII | |||||||||||
| 44 | XLIV | |||||||||||
| 45 | XLV | |||||||||||
| 48 | XLVIII | |||||||||||
| 49 | XLIX | |||||||||||
| 50 | L. | |||||||||||
| 54 | LIV | |||||||||||
| 55 | LV | |||||||||||
| 56 | LVI | |||||||||||
| 57 | LVII | |||||||||||
| 58 | ||||||||||||
| LX | ||||||||||||
| 61 | LXI | |||||||||||
| 62 | 900 06 LXII||||||||||||
| 63 | LXIII | |||||||||||
| 64 | LXIV | |||||||||||
| 65 | LXV | |||||||||||
| 66 | LXVI10 | |||||||||||
| 69 | LXIX | |||||||||||
| 70 | LXX | |||||||||||
| 71 | LXXI | |||||||||||
| 72 | LXXII | LXXII | 000||||||||||
| 75 | LXXV | |||||||||||
| 76 | LXXVI | |||||||||||
| 77 | LXXVII | |||||||||||
| 78 | LXXVIII | 000 | 81 | LXXXI | ||||||||
| 82 | LXXXII | 83 | LXXXIII | |||||||||
| 84 | LXXXIV | |||||||||||
| 85 | LXXXV | |||||||||||
| 86 | LXXXVI | 00060000007 89 | LXXXIX | |||||||||
| 90 | XC | |||||||||||
| 91 | XCI | |||||||||||
| 92 | XCII | |||||||||||
| 93 | ||||||||||||
| 93 | 0006 XCIII 9000000 9000000000000XCV | |||||||||||
| 96 | XCVI | |||||||||||
| 97 | XCVII | |||||||||||
| 98 | XCVIII | |||||||||||
| 99 | 1006 | |||||||||||
| 102 | CII | |||||||||||
| 103 | 9000 6 CIII||||||||||||
| 104 | CIV | |||||||||||
| 105 | CV | |||||||||||
| 106 | CVI | |||||||||||
| 107 | CVII | |||||||||||
| 10 | CVII | |||||||||||
| 109000 CIV | 109000 | |||||||||||
| 110 | CX | |||||||||||
| 111 | CXI | |||||||||||
| 112 | CXII | |||||||||||
| 113 | CXIII | 114 | 07114 | |||||||||
| 116 | CXVI | |||||||||||
| 117 | CXVII | |||||||||||
| 118 | CXVIII | |||||||||||
| 119 | CXIX | |||||||||||
| 120 9000 | ||||||||||||
| 120 9000 122 | CXXII | |||||||||||
| 123 | CXXIII | 124 | CXXIV | |||||||||
| 125 | CXXV | |||||||||||
| 126 | CXXVI | |||||||||||
| 127 | CXXVII | 07 | 07 | 130 | CXXX | |||||||
| 131 | CXXXI | |||||||||||
| 132 | CXXXII | |||||||||||
| 133 | CXXXIII | |||||||||||
| 1347000 | ||||||||||||
| 1347000 | ||||||||||||
| 1347000 | CXXXVI | |||||||||||
| 137 | CXXXVII | |||||||||||
| 138 | CXXXVIII | |||||||||||
| 139 | CXXXIX | 140 | ||||||||||
| 140 | 140 | |||||||||||
| 143 | CXLIII | |||||||||||
| 144 | CXLIV | |||||||||||
| 145 | CXLV | |||||||||||
| 146 | CXLVI | |||||||||||
| 147 | CXLVII | 150 | Класс | |||||||||
| 151 | Класс CLI | |||||||||||
| 152 | Класс II | |||||||||||
| 153 | Класс III | |||||||||||
| 154 | ||||||||||||
| CLVI | ||||||||||||
| 157 | CLVII | |||||||||||
| 158 | CLVIII | |||||||||||
| 159 | CLIX | |||||||||||
| 160 | ||||||||||||
| 163 | CLXIII | 164 | CLXIV | |||||||||
| 165 | CLXV | |||||||||||
| 166 | CLXVI | |||||||||||
| 167 | CLXVII | CLXVII | 06CLXVII | |||||||||
| 160009 170 | CLXX | |||||||||||
| 171 | CLXXI | |||||||||||
| 172 | CLXXII | |||||||||||
| 173 | CLXXIII | |||||||||||
| 174 | CLXXIII | |||||||||||
| 174 | CLXXVI | |||||||||||
| 177 | CLXXVII | |||||||||||
| 178 | CLXXVIII | |||||||||||
| 179 | CLXXIX | |||||||||||
| 180 | CLXXX | |||||||||||
| 181 | CLXXXI | |||||||||||
| 182 | CLXXXII | |||||||||||
| 183 | CLXXXI II | |||||||||||
| 184 | CLXXXIV | |||||||||||
| 185 | CLXXXV | |||||||||||
| 186 | CLXXXVI | |||||||||||
| 187 | CLXXXVII | |||||||||||
| 188 | CLXXXVIII | |||||||||||
| 189 | CLXXXIX | |||||||||||
| 190 | CXC | |||||||||||
| 191 | CXCI | |||||||||||
| 192 | CXCII | |||||||||||
| 193 | CXCIII | 9000 CXCIII | 9000 C | 196 | CXCVI | |||||||
| 197 | CXCVII | |||||||||||
| 198 | CXCVIII | |||||||||||
| 199 | CXCIX | 200 CC | 200 CC | 200 CC | CCII | |||||||
| 203 | 9 0006 CCIII||||||||||||
| 204 | CCIV | |||||||||||
| 205 | CCV | |||||||||||
| 206 | CCVI | |||||||||||
| 207 | CCVII | 207 | CCVII | 9000 | CCVII | |||||||
| 210 | CCX | |||||||||||
| 211 | CCXI | |||||||||||
| 212 | CCXII | |||||||||||
| 213 | CCXIII | CCXIII | 9000 CCXIII | 9000 CCXIII | 9000 CC7 | 9000 | ||||||
| 216 | CCXVI | |||||||||||
| 217 | CCXVII | |||||||||||
| 218 | CCXVIII | |||||||||||
| 219 | CCXIX | CCXIX CCXIX | ||||||||||
| CCXXII | ||||||||||||
| 223 | CCXXIII | |||||||||||
| 224 | CCXXIV | |||||||||||
| 225 | CCXXV | |||||||||||
| 226 | CCXXVI | |||||||||||
| 227 | 9000 CCXV9 | CCXV9 | CCXV9 | CCXV9 | ||||||||
| 230 | CCXXX | |||||||||||
| 231 | CCXXXI | |||||||||||
| 232 | CCXXXII | |||||||||||
| 233 | CCXXXIII | CCXXXIII | 9006236 | CCXXXVI | ||||||||
| 237 | CCXXXVII | |||||||||||
| 238 | CCXXXVIII | |||||||||||
| 239 | CCXXX10 | CCXXXIX | CCXXXIX | CCXLII | ||||||||
| 243 | CCXLIII | |||||||||||
| 244 | CCXLIV | |||||||||||
| 245 | CCXLV | |||||||||||
| 246 | CCXLVI | 246 | CCXLVI | 9000 CCXLVI | 9000 9000 CCXLVI | 9000 9000 249 | CCXLIX | |||||
| 250 | CCL | |||||||||||
| 251 | CCLI | |||||||||||
| 252 | CCLII | |||||||||||
| 253 | CCLII | |||||||||||
| 253 | CCL | CCLV | ||||||||||
| 256 | CCLVI | |||||||||||
| 257 | CCLVII | |||||||||||
| 258 | CCLVIII | |||||||||||
| 259 | CCL | CCL | CCL | |||||||||
| 262 | CCLXII 900 07 | |||||||||||
| 263 | CCLXIII | |||||||||||
| 264 | CCLXIV | |||||||||||
| 265 | CCLXV | |||||||||||
| 266 | CCLXVI | |||||||||||
| 266 | CCLXVI | |||||||||||
| CCLXVI | 000000000 CCLXVI000 900||||||||||||
| 269 | CCLXIX | |||||||||||
| 270 | CCLXX | |||||||||||
| 271 | CCLXXI | |||||||||||
| 272 | CCLXXII | 9006 272CCLXXII | 9006 27000 CC500027000 CCLXXII | 9006 27000 CC5 275CCLXXV | ||||||||
| 276 | CCLXXVI | |||||||||||
| 277 | CCLXXVII | |||||||||||
| 278 | CCLXXVIII | |||||||||||
| 279 | CCLXXIX | |||||||||||
| 280 | CCLXXX | |||||||||||
| 281 | CCLXXXI | |||||||||||
| 282 | CCLXXXII | |||||||||||
| 283 | CCLXXXIII | |||||||||||
| 284 | CCLXXXIV | |||||||||||
| 285 | CCLXXXV | |||||||||||
| 286 | CCLXXXVI | |||||||||||
| 287 | CCLXXXVII | |||||||||||
| 288 | CCLXXXVIII | |||||||||||
| 289 | CCLXXXIX | |||||||||||
| 290 | CCXC | |||||||||||
| 291 | CCXCI | |||||||||||
| 29000 CCXCI | ||||||||||||
| 29000 | CCXCIV | |||||||||||
| 295 | CCXCV | |||||||||||
| 296 | CCXCVI | |||||||||||
| 297 | CCXCVII | |||||||||||
| 29807 | CC7000 | CC7000 CC7 | CC7 | |||||||||
| 301 9000 7 | CCCI | |||||||||||
| 302 | CCCII | |||||||||||
| 303 | CCCIII | |||||||||||
| 304 | CCCIV | |||||||||||
| 305 | 10CV | |||||||||||
| CCCV | ||||||||||||
| 10CV | ||||||||||||
| 10CV 9000 CCCVII | ||||||||||||
| 308 | CCCVIII | |||||||||||
| 309 | CCCIX | |||||||||||
| 310 | CCCX | |||||||||||
| 311 | CCC106 | |||||||||||
| CCC106 9000 CCC7 | ||||||||||||
| 314 | CCCXIV | |||||||||||
| 315 | CCCXV | |||||||||||
| 316 | CCCXVI | |||||||||||
| 317 | CCCXVII | 9006CCCXVII | 90099000 CCCXVII | 320 | CCCXX | |||||||
| CCCXXI | ||||||||||||
| 322 | CCCXXII | |||||||||||
| 323 | CCCXXIII | |||||||||||
| 324 | 9000X||||||||||||
| 324 | 9000X CCCXVIV 9006||||||||||||
| CCCXXVII | ||||||||||||
| 328 | CCCXXVIII | |||||||||||
| 329 | CCCXXIX | |||||||||||
| 330 | CCCXXX | |||||||||||
| 331 | CCCXXXI | |||||||||||
| 332 | CCCXXXII | |||||||||||
| 333 | CCCXXXIII | |||||||||||
| 334 | CCCXXXIV | |||||||||||
| 335 | CCCXXXV | |||||||||||
| 336 | CCCXXXVI | |||||||||||
| 337 | CCCXXXVII | |||||||||||
| 338 | CCCXXXVIII | |||||||||||
| 339 | CCCXXXIX | |||||||||||
| CCCXL | ||||||||||||
| 341 | CCCXLI | |||||||||||
| 342 | CCCXLII | |||||||||||
| 343 | CCCXLIII | CCCIVLIII | CCCIVLIII | |||||||||
| CCCXLVI | ||||||||||||
| 347 | CCCXLVII | |||||||||||
| 348 | CCCXLVIII | |||||||||||
| 349 | CCCXLIX | CCCXLIX | CCCXLIX | CCCXLIX | 9000 9000 CC CCCLII||||||||
| 353 | CCCLIII | |||||||||||
| 354 | CCCLIV | |||||||||||
| 355 | CCCLV | |||||||||||
| 356 | CC107 | |||||||||||
| CC107 | ||||||||||||
| CC107 | CCCLV7||||||||||||
| 359 | CCCLIX | |||||||||||
| 360 | CCCLX | |||||||||||
| 361 | CCCLXI | |||||||||||
| 362 | CCCLXII | |||||||||||
| 363 | CC10X40006 | CCCLX7 | CC10X4 | CC0007CC10X4 | CC0007CC10X4 | CC0007CC10X4 9000 | ||||||
| 366 | CCCLXVI | |||||||||||
| 367 | CCCLXVII | |||||||||||
| 368 | CCCLXVIII | |||||||||||
| 369 | CCCLXIX | CCCLX7 CCCLX7 CCCLX7 | CCCLX7 | 372 | CCCLXXII | |||||||
| 373 | CCCLXXIII | |||||||||||
| 374 | CCCLXXIV | |||||||||||
| 375 | CCCLXXV | |||||||||||
| 376 | CCCLXXVI | |||||||||||
| 377 | CCCLXXVII | |||||||||||
| 378 | CCCLXXV III | |||||||||||
| 379 | CCCLXXIX | |||||||||||
| 380 | CCCLXXX | |||||||||||
| 381 | CCCLXXXI | |||||||||||
| 382 | CCCLXXXII | |||||||||||
| 383 | CCCLXXXIII | |||||||||||
| 384 | CCCLXXXIV | |||||||||||
| 385 | CCCLXXXV | |||||||||||
| 386 | CCCLXXXVI | |||||||||||
| 387 | CCCLXXXVII | |||||||||||
| 388 | CCCLXXXVIII | |||||||||||
| 389 | CCCLXXXIX | |||||||||||
| 390 | CCCXC | |||||||||||
| 391 | CCCXCI | |||||||||||
| 392 | CCCXCII | |||||||||||
| 393 | CCCXCIII | |||||||||||
| 394 | CCCXCIV | |||||||||||
| 395 | CCCXCV | |||||||||||
| 396 | CCCXCVI | |||||||||||
| 397 | 9000 6 CCCXCVII||||||||||||
| 398 | CCCXCVIII | |||||||||||
| 399 | CCCXCIX | |||||||||||
| 400 | CD | |||||||||||
| 401 | 402 | CDI | CDI | CDI | CDI | |||||||
| 404 | CDIV | |||||||||||
| 405 | CDV | |||||||||||
| 406 | CDVI | |||||||||||
| 407 | CDVII | |||||||||||
| CDVII | ||||||||||||
| 410 | CDX | |||||||||||
| 411 | CDXI | |||||||||||
| 412 | CDXII | |||||||||||
| 413 | CDXIII | |||||||||||
| 416 | CDXVI | |||||||||||
| 417 | CD XVII | |||||||||||
| 418 | CDXVIII | |||||||||||
| 419 | CDXIX | |||||||||||
| 420 | CDXX | |||||||||||
| 421 | CDXXI | 0000007 | ||||||||||
| 424 | CDXXIV | |||||||||||
| 425 | CDXXV | |||||||||||
| 426 | CDXXVI | |||||||||||
| 427 | CDXXVII | 430 | CDXXX | |||||||||
| 431 | CDXXXI | |||||||||||
| 432 | CDXXXII | |||||||||||
| 433 | CDXXXIII | CDXXXIII | 6||||||||||
| CDXXXVI | ||||||||||||
| CDXXXVII | ||||||||||||
| 438 | CDXXXVIII | |||||||||||
| 439 | CDXXXIX | |||||||||||
| 440 | CDXL | 440006 | CDXLIII | |||||||||
| 444 | CDXLIV | |||||||||||
| 445 | CDXLV | |||||||||||
| 446 | CDXLVI | |||||||||||
| 447 | 447 | |||||||||||
| 447 | CDXLIX||||||||||||
| 450 | CDL | |||||||||||
| 451 | CDLI | |||||||||||
| 452 | CDLII | |||||||||||
| 453 | CDLIII | 9006CDLIII | 9006CDLIII | 9006|||||||||
| 456 | CDLVI | |||||||||||
| 457 | CDLVII | |||||||||||
| 458 | CDLVIII | |||||||||||
| 459 | CDLIX | |||||||||||
| 460 | CDLX | 463 | CDLXIII | |||||||||
| 464 | CDLXIV | |||||||||||
| 465 | CDLXV | |||||||||||
| 466 | CDLXVI | CDLXIX | ||||||||||
| 470 | CDLXX | |||||||||||
| 471 | CDLXXI | |||||||||||
| 472 | CDLXII | |||||||||||
| 473 | ||||||||||||
| 473 | CDLXXV||||||||||||
| 476 900 07 | CDLXXVI | |||||||||||
| 477 | CDLXXVII | |||||||||||
| 478 | CDLXXVIII | |||||||||||
| 479 | CDLXXIX | |||||||||||
| 480 | CDLXXX | |||||||||||
| 481 | CDLXXXI | |||||||||||
| 482 | CDLXXXII | |||||||||||
| 483 | CDLXXXIII | |||||||||||
| 484 | CDLXXXIV | |||||||||||
| 485 | CDLXXXV | |||||||||||
| 486 | CDLXXXVI | |||||||||||
| 487 | CDLXXXVII | |||||||||||
| 488 | CDLXXXVIII | |||||||||||
| 489 | CDLXXXIX | |||||||||||
| 490 | CDXC | |||||||||||
| 491 | CDXCI | |||||||||||
| 492 | CDXCII000 | 9006495 | 90 006 CDXCV||||||||||
| 496 | CDXCVI | |||||||||||
| 497 | CDXCVII | |||||||||||
| 498 | CDXCVIII | |||||||||||
| 499 | ||||||||||||
| 502 | DII | |||||||||||
| 503 | DIII | |||||||||||
| 504 | DIV | |||||||||||
| 505 | DV | DV | ||||||||||
| 508 | DVIII | |||||||||||
| 509 | DIX | |||||||||||
| 510 | DX | |||||||||||
| 511 | DXI | |||||||||||
| 106 | 0009000II7 514 | DXIV | ||||||||||
| 515 | DXV | |||||||||||
| 516 | DXVI | |||||||||||
| 517 | DXVII | |||||||||||
| 518 | DXVIII | |||||||||||
| 519 | DXIX | DXXII | ||||||||||
| 523 | DXXIII | |||||||||||
| 524 | DXXIV | |||||||||||
| 525 | DXXV | |||||||||||
| 526 DXXV | ||||||||||||
| 526 DXXV | ||||||||||||
| 526 | DXXVIII | |||||||||||
| 529 | DXXIX | |||||||||||
| 530 | Dxxx | |||||||||||
| 531 | DXXXI | |||||||||||
| 532 | DXXXII | |||||||||||
| 533 | DXXXIII | |||||||||||
| 534 | DXXXIV | |||||||||||
| 535 | DXXXV | 900 10|||||||||||
| 536 | DXXXVI | |||||||||||
| 537 | DXXXVII | |||||||||||
| 538 | DXXXVIII | |||||||||||
| 539 | 000000 DX106X 9000000000000000000000000000000542 | DXLII | ||||||||||
| 543 | DXLIII | |||||||||||
| 544 | DXLIV | |||||||||||
| 545 | DXLV | DXLVIII | ||||||||||
| 549 | DXLIX | |||||||||||
| 550 | DL | |||||||||||
| 551 | DLI | |||||||||||
| 552 | 0006||||||||||||
| 552 | 0006 DLII||||||||||||
| 552 | 0006 DLII||||||||||||
| 552 | 0006 DLII DLIV||||||||||||
| 555 | DLV | |||||||||||
| 556 | DLVI | |||||||||||
| 557 | DLVII | |||||||||||
| 558 | DLVIII | |||||||||||
| 559 | DLIX | |||||||||||
| DLIX | ||||||||||||
| DLIX | ||||||||||||
| 562 | DLXII | |||||||||||
| 563 | DLXIII | |||||||||||
| 564 | DLXIV | |||||||||||
| 565 | DLXV | |||||||||||
| 566 | 0006 | DLXVIII | ||||||||||
| 569 | DLXIX | |||||||||||
| 570 | DLXX | |||||||||||
| 571 | DLXXI | |||||||||||
| 572 | 000 DLXXI | |||||||||||
| 572 | DLXX | DLXX | DLXX | DLXX | ||||||||
| 575 | DLXXV | 900 10|||||||||||
| 576 | DLXXVI | |||||||||||
| 577 | DLXXVII | |||||||||||
| 578 | DLXXVIII | |||||||||||
| 579 | DLXXIX | 000 | 900 DLXXIX000||||||||||
| 582 | DLXXXII | |||||||||||
| 583 | DLXXXIII | |||||||||||
| 584 | DLXXXIV | |||||||||||
| 585 | DLXXXV | |||||||||||
| 586 | DLXXXVI | |||||||||||
| 587 | DLXXXVII | |||||||||||
| 588 | DLXXXVIII | |||||||||||
| 589 | DLXXXIX | |||||||||||
| 590 | DXC | |||||||||||
| 591 | DXCI | |||||||||||
| 592 | 000000592 | |||||||||||
| 592 DXCI | ||||||||||||
| 592 | DXCIV||||||||||||
| 595 9000 7 | DXCV | |||||||||||
| 596 | DXCVI | |||||||||||
| 597 | DXCVII | |||||||||||
| 598 | DXCVIII | |||||||||||
| 5996 DXCVIII | ||||||||||||
| 5996 DXCVIII | ||||||||||||
| 5996 | DCI||||||||||||
| 602 | DCII | |||||||||||
| 603 | DCIII | |||||||||||
| 604 | DCIV | |||||||||||
| 605 | DCV | DCV | DCV | |||||||||
| 608 | DCVIII | |||||||||||
| 609 | DCIX | |||||||||||
| 10 | DCX | |||||||||||
| 611 | DCXI | 614 | DCXIV | |||||||||
| 615 | D CXV | |||||||||||
| 616 | DCXVI | |||||||||||
| 617 | DCXVII | |||||||||||
| 618 | DCXVIII | |||||||||||
| 619 | 10X6000 | |||||||||||
| 622 | DCXXII | |||||||||||
| 623 | DCXXIII | |||||||||||
| 624 | DCXXIV | |||||||||||
| 625 | DCXXV | 0006000000 | 000 | 0005628 | DCXXVIII | |||||||
| 629 | DCXXIX | |||||||||||
| 630 | DCXXX | |||||||||||
| 631 | DCXXXI | DCXXXIV | ||||||||||
| DCXXXV | ||||||||||||
| 636 | DCXXXVI | |||||||||||
| 637 | DCXXXVII | |||||||||||
| 638 | DCXXXVIII | DCXLI | ||||||||||
| 642 | DCXLII | |||||||||||
| 643 | DCXLIII | |||||||||||
| 644 | DCXLIV | |||||||||||
| 645 | ||||||||||||
| 645 | ||||||||||||
| 645 | DCXLVII||||||||||||
| 648 | DCXLVIII | |||||||||||
| 649 | DCXLIX | |||||||||||
| 650 | DCL | |||||||||||
| 651 | 106 | |||||||||||
| 654 | DCLIV | |||||||||||
| 655 | DCLV | |||||||||||
| 656 | DCLVI | |||||||||||
| 657 | DCLVII | |||||||||||
| 658 | DCLVIII | 9000 | ||||||||||
| 661 | DCLXI | |||||||||||
| 662 | DCLXII | |||||||||||
| 663 | DCLXIII | |||||||||||
| 664 | DCLXIV | DCLXIV | DC106000DCLXVII | |||||||||
| 668 | DCLXVIII | |||||||||||
| 669 | DCLXIX | |||||||||||
| 670 | DCLXX | |||||||||||
| 67000 | 0007000700070007 DCLXXIII||||||||||||
| 674 | DCLXXIV | |||||||||||
| 675 | DCLXXV | |||||||||||
| 676 | DCLXXVI | |||||||||||
| 677 | DCLXXVII | |||||||||||
| 678 | DCLXXVIII | |||||||||||
| 679 | DCLXXIX | |||||||||||
| 680 | DCLXXX | |||||||||||
| 681 | DCLXXXI | |||||||||||
| 682 | DCLXXXII | |||||||||||
| 683 | DCLXXXIII | |||||||||||
| 684 | DCLXXXIV | |||||||||||
| 685 | DCLXXXV | |||||||||||
| 686 | DCLXXXVI | |||||||||||
| 687 | DCLXXXVII | |||||||||||
| 688 | DCLXXXVIII | |||||||||||
| 689 | DCLXXXIX | |||||||||||
| 690 | DCXC | |||||||||||
| 691 | DCXCI | |||||||||||
| 692 | DCXCII | |||||||||||
| 693 | DCXCIII | |||||||||||
| 694 | DCXCIV | |||||||||||
| 695 | DCXCV | |||||||||||
| 696 | DCXCVI | |||||||||||
| 697 | 000 | |||||||||||
| 700 | DCC | |||||||||||
| 701 | DCCI | |||||||||||
| 702 | DCCII | |||||||||||
| 703 | DCCIII | 704 | 704 | 704 | 706 | DCCVI | ||||||
| 707 | DCCVII | |||||||||||
| 708 | DCCVIII | |||||||||||
| 709 | DCCIX | 00070007 | DCCXII | |||||||||
| 713 90 007 | DCCXIII | |||||||||||
| 714 | DCCXIV | |||||||||||
| 715 | DCCXV | |||||||||||
| 716 | DCCXVI | |||||||||||
| 000 | 000 | 000 DCCXIX | ||||||||||
| 720 | DCCXX | |||||||||||
| 721 | DCCXXI | |||||||||||
| 722 | DCCXXII | |||||||||||
| 723 | DCCXXIII | |||||||||||
| 724 | DCCXXIV | |||||||||||
| 725 | DCCXXV | |||||||||||
| 726 | DCCXXVI | |||||||||||
| 727 | DCCXXVII | |||||||||||
| 728 | DCCXXVIII | |||||||||||
| 729 | DCCXXIX | |||||||||||
| 730 | DCCXXX | |||||||||||
| 731 | DCCXXXI | |||||||||||
| 732 | DCCXXX II | |||||||||||
| 733 | DCCXXXIII | |||||||||||
| 734 | DCCXXXIV | |||||||||||
| 735 | DCCXXXV | |||||||||||
| 736 | DCCXXXVI | |||||||||||
| 737 | DCCXXXVII | |||||||||||
| 738 | DCCXXXVIII | |||||||||||
| 739 | DCCXXXIX | |||||||||||
| 740 | DCCXL | |||||||||||
| 741 | DCCXLI | |||||||||||
| 742 | DCCXLII | |||||||||||
| 743 | DCCXLIII | |||||||||||
| 744 | DCCXLIV | |||||||||||
| 745 | DCCXLV | |||||||||||
| 746 | DCCXLVI | |||||||||||
| 747 | DCCXLVII | |||||||||||
| 748 | DCCXLVIII | 000000000000000000000000000000000000000000000DCCLI 9000 7 | ||||||||||
| 752 | DCCLII | |||||||||||
| 753 | DCCLIII | |||||||||||
| 754 | DCCLIV | |||||||||||
| 755 | DCCLV | DCCLV | 6755DCCLV | 0007 DCCLV0007|||||||||
| 758 | DCCLVIII | |||||||||||
| 759 | DCCLIX | |||||||||||
| 760 | DCCLX | |||||||||||
| 761 | DCCLXI | 6000 | 000000000 | 0007000000 700070007000700070007 764DCCLXIV | ||||||||
| 765 | DCCLXV | |||||||||||
| 766 | DCCLXVI | |||||||||||
| 767 | DCCLXVII | |||||||||||
| 000 | 000 | 000 | 000 | 000 | DCIX7000000 | 000000000 | DCCLXX | |||||
| DCCLXXI | ||||||||||||
| 772 | DCCLXXII | |||||||||||
| 773 | DCCLXXIII | |||||||||||
| 774 | DCCLXXIV | |||||||||||
| 775 | DCCLXXV | |||||||||||
| 776 | DCCLXXVI | |||||||||||
| 777 | DCCLXXVII | |||||||||||
| 778 | DCCLXXVIII | |||||||||||
| 779 | DCCLXXIX | |||||||||||
| 780 | DCCLXXX | |||||||||||
| 781 | DCCLXXXI | |||||||||||
| 782 | DCCLXXXII | |||||||||||
| 783 | DCCLXXXIII | |||||||||||
| 784 | DCCLXXXIV | |||||||||||
| 785 | DCCLXXXV | |||||||||||
| 786 | DCCLXXXVI | |||||||||||
| 787 | DCCLXXXVII | |||||||||||
| 788 | DCCLXXXVIII | |||||||||||
| 789 | DCCLXXXIX 900 07 | |||||||||||
| 790 | DCCXC | |||||||||||
| 791 | DCCXCI | |||||||||||
| 792 | DCCXCII | |||||||||||
| 793 | DCCX106 | DCCX106 | ||||||||||
| 796 | DCCXCVI | |||||||||||
| 797 | DCCXCVII | |||||||||||
| 798 | DCCXCVIII | |||||||||||
| 799 | ||||||||||||
| 799 | 9000 9000 802 | DCCCII | ||||||||||
| 803 | DCCCIII | |||||||||||
| 804 | DCCCIV | |||||||||||
| 805 | DCCCV | |||||||||||
| 806 DC107 | ||||||||||||
| DCCCVIII | ||||||||||||
| DCCCIX | ||||||||||||
| 810 | DCCCX | |||||||||||
| 811 | DCCCXI | |||||||||||
| 812 | DCCCXII | |||||||||||
| DCCCXV | ||||||||||||
| 816 | DCCCXVI | |||||||||||
| 817 | DCCCXVII | |||||||||||
| 818 | DCCCXVIII | |||||||||||
| 000 | 000 | 000000000 9CCXVIII | ||||||||||
| 000 | 000000000000DCCCXXI | |||||||||||
| 822 | DCCCXXII | |||||||||||
| 823 | DCCCXXIII | |||||||||||
| 824 | DCCCXXIV | |||||||||||
| 825 | DCCCXXV | |||||||||||
| 826 | DCCCXXVI | |||||||||||
| 827 | DCCCXXVII | |||||||||||
| 828 | DCCCXXVIII | |||||||||||
| 829 | DCCCXXIX | |||||||||||
| 830 | DCCCXXX | |||||||||||
| 831 | DCCCXXXI | |||||||||||
| 832 | DCCCXXXII | |||||||||||
| 833 | DCCCXXXIII | |||||||||||
| 834 | DCCCXXXIV | |||||||||||
| 835 | DCCCXXXV | |||||||||||
| 836 | DCCCXXXVI | |||||||||||
| 837 | DCCCXXXVII | |||||||||||
| 838 | DCCCXXXVIII | |||||||||||
| 839 | DCCCXXXIX | |||||||||||
| 840 | DCCCXL | |||||||||||
| 841 | DCCCXLI | |||||||||||
| 842 | DCCCXLII | |||||||||||
| 843 | DCCCXLIII | |||||||||||
| 844 | DCCC106000 | DCCCXLIV | ||||||||||
| DCCCXLIV | DCCCXLIV | 0005847 | DCCCXLVII | |||||||||
| 848 | DCCCXLVIII | |||||||||||
| 849 | DCCCXLIX | |||||||||||
| 850 | DCCCL DCCCL | 9006853 | DCCCLIII | |||||||||
| 854 | DCCCLIV | |||||||||||
| 855 | DCCCLV | |||||||||||
| 856 | DCCCLVI | |||||||||||
| 0007 | 850007 | DCCCLIX | ||||||||||
| 860 | DCCCLX | |||||||||||
| 861 | DCCCLXI | |||||||||||
| 862 | DCCCLXII | |||||||||||
| 863 | DCCCLXIII | |||||||||||
| 864 | DCCCLXIV | |||||||||||
| 865 | DCCCLXV | 866 | DCCCLXVI | |||||||||
| 867 | DCCCLXVII | |||||||||||
| 868 | DCCCLXVIII | |||||||||||
| 869 | DCCCLXIX | |||||||||||
| 870 | DCCCLXX | |||||||||||
| 871 | DCCCLXXI | |||||||||||
| 872 | DCCCLXXII | |||||||||||
| 873 | DCCCLXXIII | |||||||||||
| 874 | DCCCLXXIV | |||||||||||
| 875 | DCCCLXXV | |||||||||||
| 876 | DCCCLXXVI | |||||||||||
| 877 | DCCCLXXVII | |||||||||||
| 878 | DCCCLXXVIII | |||||||||||
| 879 | DCCCLXXIX | |||||||||||
| 880 | DCCCLXXX | |||||||||||
| 881 | DCCCLXXXI | |||||||||||
| 882 | DCCCLXXXII | |||||||||||
| 883 | DCCCLXXXIII | |||||||||||
| 884 | D CCCLXXXIV | |||||||||||
| 885 | DCCCLXXXV | |||||||||||
| 886 | DCCCLXXXVI | |||||||||||
| 887 | DCCCLXXXVII | |||||||||||
| 888 | DCCCLXXXVIII | |||||||||||
| 889 | DCCCLXXXIX | |||||||||||
| 890 | DCCCXC | |||||||||||
| 891 | DCCCXCI | |||||||||||
| 892 | DCCCXCII | |||||||||||
| 893 | DCCCXCIII | |||||||||||
| 894 | DCCCXCIV | |||||||||||
| 895 | DCCCXCV | |||||||||||
| 896 | DCCCXCVI | |||||||||||
| 897 | DCCCXCVII | |||||||||||
| 898 | DCCCXCVIII | |||||||||||
| 899 | DCCCXCIX | |||||||||||
| 900 | CM | 900 | ||||||||||
| 904 | CMIV | |||||||||||
| 905 | CMV | |||||||||||
| 906 | CMVI | |||||||||||
| 907 | 904 | 9006 907 CMVICMVII 9006 | ||||||||||
| 910 | CMX | |||||||||||
| 911 | CMXI | |||||||||||
| 912 | CMXII | |||||||||||
| 913 | CMXIII | 9007CMXIII 9007 | ||||||||||
| 916 | CMXVI | |||||||||||
| 917 | CMXVII | |||||||||||
| 918 | CMXVIII | |||||||||||
| 919 | CMXIX | 9000 9000 | 9000 9000 9000 922CMXXII | |||||||||
| 923 | CMXXIII | |||||||||||
| 924 | CMXXIV | |||||||||||
| 925 | CMXXV | |||||||||||
| 926 | CMXXVI | |||||||||||
| 000 | CMX6 | 000000CMXV | ||||||||||
| 930 | CMXXX | |||||||||||
| 931 | CMXXXI | |||||||||||
| 932 | CMXXXII | |||||||||||
| CMXXXII | ||||||||||||
| 933 | 936 | CMXXXVI | ||||||||||
| 937 | CMXXXVII | |||||||||||
| 938 | CMXXXVIII | |||||||||||
| 939 | CMXXXIX | |||||||||||
| 940 | CMXL | |||||||||||
| 941 | CMXLI | |||||||||||
| 942 | CMXLII | |||||||||||
| 943 | CMXLIII | |||||||||||
| 944 | CMXLIV | |||||||||||
| 945 | CMXLV | |||||||||||
| 946 | CMXLVI | |||||||||||
| CMXLIX | ||||||||||||
| 950 | CML | |||||||||||
| 951 | CMLI | |||||||||||
| 952 | CMLII | |||||||||||
| 953 | 0007953 | 0007CMLV | ||||||||||
| 956 | CMLVI | |||||||||||
| 957 | CMLVII | |||||||||||
| 958 | CMLVIII | |||||||||||
| 95906 | CML | CML | CML | |||||||||
| 962 | CMLXII 900 07 | |||||||||||
| 963 | CMLXIII | |||||||||||
| 964 | CMLXIV | |||||||||||
| 965 | CMLXV | |||||||||||
| 966 | CMLXVI | 000000000000000000000000000000000000000|||||||||||
| 969 | CMLXIX | |||||||||||
| 970 | CMLXX | |||||||||||
| 971 | CMLXXI | |||||||||||
| 972 | CMLXXII | CMLXXV | ||||||||||
| 976 | CMLXXVI | |||||||||||
| 977 | CMLXXVII | |||||||||||
| 978 | CMLXXVIII | |||||||||||
| 979 | CMLXXIX | |||||||||||
| 980 | CMLXXX | |||||||||||
| 981 | CMLXXXI | |||||||||||
| 982 | CMLXXXII | |||||||||||
| 983 | CMLXXXIII | |||||||||||
| 984 | CMLXXXIV | |||||||||||
| 985 | CMLXXXV | |||||||||||
| 986 | CMLXXXVI | |||||||||||
| 987 | CMLXXXVII | |||||||||||
| 988 | CMLXXXVIII | |||||||||||
| 989 | CMLXXXIX | |||||||||||
| 990 | CMXC | |||||||||||
| 991 | CMXCI | 991 | CMXCI | |||||||||
| 995 | CMXCV | |||||||||||
| 996 | CMXCVI | |||||||||||
| 997 | CMXCVII | |||||||||||
| 99807 | CMXC | CMXC |
Часто используемые Miniwebtools:
Все минивеб-инструменты (отсортировано по названию):
Инструменты PWA (прогрессивное веб-приложение) (17) Финансовые калькуляторы (121) Здоровье и фитнес (31) Математика (161) Случайность (17) Спорт (8) Текстовые инструменты (30) Время и Дата (27) Инструменты для веб-мастеров (10) Хеш и контрольная сумма (8) Разное (108)Преобразование римских цифр в арабские числа
Каковы правила написания римских цифр?
- В римской системе счисления основными «цифрами» являются буквы I , V , X , L , C , D и M , которые представляют одни и те же числа независимо от их позиции.
- Символы располагаются в порядке значений, начиная с наибольших значений.
- Когда старшая цифра ставится перед младшей, добавляются значения каждой римской цифры.
- Когда меньшие значения предшествуют большим значениям, меньшие значения вычитаются из больших значений, а результат добавляется к общей сумме.
- Не повторяйте I , X и C более трех раз подряд. (Число 4 на часах с римскими цифрами обычно пишется как IIII .)
- Символы V , L и D не могут появляться более одного раза подряд.
- Не вычитайте число, превышающее более чем в 10 раз: I может предшествовать только V и X , X может предшествовать только L и C , а C может только предшествуют D и M .
| I | 1 | XI | 11 |
| II | 2 | XII | 12 |
| III | 3 | XIII | 13 |
| IV | 4 | XIV | 14 |
| В | 5 | XV | 15 |
| VI | 6 | XVI | 16 |
| VII | 7 | XVII | 17 |
| VIII | 8 | XVIII | 18 |
| IX | 9 | XIX | 19 |
| х | 10 | ХХ | 20 |
| XXX | 30 | класс | 150 |
| XL | 40 | CLIX | 159 |
| XLIX | 49 | CXC | 190 |
| л | 50 | CC | 200 |
| LX | 60 | CCC | 300 |
| LXX | 70 | CD | 400 |
| LXXX | 80 | Д | 500 |
| XC | 90 | постоянного тока | 600 |
| XCIX | 99 | CM | 900 |
| К | 100 | М | 1000 |
Когда им нужно было работать с большими числами (4000 и выше), римляне часто писали черту над цифрой или помещали ее в круглые скобки, чтобы обозначить умножение на 1000.
| МММ | 3 000 000 | XLILXII | 41 062 |
| XMXVII | 19 007 | XMCXI | 11 111 |
Согласно старой рекомендации ИЮПАК до 1985 года, римские цифры использовались для обозначения группы в периодической таблице элементов. Когда металл имеет более одного возможного ионного заряда или степени окисления, степень окисления (такая же, как заряд) иона металла представлена римской цифрой в скобках сразу после названия иона металла.Например, FeO — это оксид железа (II), а Fe 2 O 3 — оксид железа (III).
Индус — арабская система счисления и римские цифры
Цели обучения
- Ознакомьтесь с эволюцией системы подсчета, которую мы используем каждый день
- Запись чисел римскими цифрами
- Преобразование между индуистско-арабскими и римскими цифрами
Эволюция системы
Наша собственная система счисления, состоящая из десяти символов {0,1,2,3,4,5,6,7,8,9}, называется Hindu — арабская система .Это десятичная (десятичная) система счисления, поскольку разряды увеличиваются в степени десяти. Кроме того, эта система является позиционной, что означает, что положение символа влияет на значение этого символа в числе. Например, позиция символа 3 в числе 435 681 дает ему значение, намного превышающее значение символа 8 в том же числе. Позже мы рассмотрим базовые системы более подробно. Разработка этих десяти символов и их использование в позиционной системе пришла к нам в первую очередь из Индии.
Рис. 10. Аль-Бируни
Только в пятнадцатом веке символы, с которыми мы знакомы сегодня, впервые обрели форму в Европе. Однако история этих чисел и их развития насчитывает сотни лет. Одним из важных источников информации по этой теме является писатель аль-Бируни, фотография которого показана на рисунке 10. Аль-Бируни, который родился в современном Узбекистане, несколько раз посещал Индию и делал комментарии по индийской системе счисления.Когда мы смотрим на происхождение чисел, с которыми столкнулся аль-Бируни, мы должны вернуться к третьему веку до нашей эры, чтобы исследовать их происхождение. Именно тогда и использовались цифры Брахми.
Цифры Брахми были более сложными, чем те, которые используются в нашей современной системе. У них были отдельные символы для чисел от 1 до 9, а также отдельные символы для 10, 100, 1000,…, а также для 20, 30, 40,… и другие символы для 200, 300, 400,…, 900. Брахми символы для 1, 2 и 3 показаны ниже.
Эти цифры использовались вплоть до четвертого века нашей эры, с вариациями в зависимости от времени и географического положения. Например, в первом веке нашей эры один конкретный набор цифр Брахми принял следующую форму:
Начиная с четвертого века, вы фактически можете проследить несколько различных путей, по которым числа Брахми шли к разным точкам и воплощениям. Один из этих путей привел к нашей нынешней системе счисления и прошел через так называемые числа Гупта.Цифры Гупта были заметны во времена правления династии Гуптов и были распространены по всей этой империи, когда они завоевывали земли в течение четвертого-шестого веков. Они имеют следующий вид:
Вопрос о том, как числа пришли в форму Гупты, является предметом серьезных споров. Было предложено множество возможных гипотез, большинство из которых сводятся к двум основным типам. Гипотеза первого типа утверждает, что цифры произошли от начальных букв названий чисел. Это не редкость.. . греческие цифры развивались таким образом. Второй тип гипотез утверждает, что они произошли от какой-то более ранней системы счисления. Однако есть и другие гипотезы, одна из которых принадлежит исследователю Ифрах. Его теория состоит в том, что изначально было девять цифр, каждая из которых была представлена соответствующим количеством вертикальных линий. Одна из возможностей такова:
Поскольку для написания этих символов потребовалось бы много времени, они в конечном итоге превратились в курсивные символы, которые можно было писать быстрее.Если мы сравним их с числами Гупта, указанными выше, мы можем попытаться увидеть, как мог происходить этот эволюционный процесс, но наше воображение было бы практически всем, на что нам пришлось бы полагаться, поскольку мы не знаем точно, как этот процесс разворачивался.
Цифры Гупта в конечном итоге превратились в другую форму цифр, названную цифрами Нагари, и они продолжали развиваться до одиннадцатого века, когда они выглядели так:
Обратите внимание, что к этому времени появился символ 0! Однако у майя в Америке задолго до этого был символ нуля, как мы увидим позже в этой главе.
Эти цифры были приняты арабами, скорее всего, в восьмом веке во время вторжений ислама в северную часть Индии. Считается, что арабы способствовали их распространению в других частях мира, включая Испанию (см. Ниже).
Другие примеры вариаций до одиннадцатого века включают:
Рис. 11. Девангари, восьмой век
Рисунок 12. Западноарабский Гобар, X век
Рисунок 13. Испания, 976 г. до н.э.
Наконец, на рис. 14 показаны различные формы этих цифр по мере их развития и в конечном итоге схождения в Европе в пятнадцатом веке.
Рисунок 14.
Римские цифры
Числовая система, представленная римскими цифрами , возникла в Древнем Риме ( 753 г. до н.э. — 476 г. н.э.), и оставалась обычным способом записи чисел по всей Европе вплоть до позднего средневековья (обычно включающего 14-15 вв. 1301–1500)). Числа в этой системе представлены комбинациями букв латинского алфавита. Римские цифры, используемые сегодня, основаны на семи символах:
| Обозначение | я | В | Х | л | С | D | м |
| Значение | 1 | 5 | 10 | 50 | 100 | 500 | 1 000 |
Использование римских цифр продолжалось еще долгое время после упадка Римской империи.Начиная с XIV века римские цифры в большинстве случаев стали заменяться более удобными индо-арабскими цифрами; однако этот процесс был постепенным, и римские цифры до сих пор используются в некоторых второстепенных приложениях.
Цифры от 1 до 10 обычно выражаются римскими цифрами следующим образом:
- I, II, III, IV, V, VI, VII, VIII, IX, X .
Числа образуются путем комбинирования символов и сложения значений, поэтому II равно двум (две единицы), а XIII — тринадцати (десять и три единицы).Поскольку каждая цифра имеет фиксированное значение, а не представляет собой число, кратное десяти, сотне и так далее, в соответствии с позицией , нет необходимости в нулях «с сохранением места», как в числах типа 207 или 1066; эти числа записываются как CCVII (две сотни, пять и две единицы) и MLXVI (тысяча, пятьдесят, десять, пять и один).
Символы располагаются слева направо в порядке значений, начиная с самого большого. Однако в некоторых конкретных случаях, чтобы избежать последовательного повторения четырех символов (например, IIII или XXXX), используется вычитающая запись: как в этой таблице:
| Номер | 4 | 9 | 40 | 90 | 400 | 900 |
| Римская цифра | IV | IX | XL | XC | CD | CM |
Итого:
- Я поставил перед V или X означает на единицу меньше, поэтому четыре — это IV (один меньше пяти), а девять — IX (один меньше десяти)
- X, помещенный перед L или C, означает на десять меньше, поэтому сорок — это XL (десять меньше, чем пятьдесят), а девяносто — это XC (десять меньше, чем сто)
- C, помещенная перед D или M, означает на сто меньше, поэтому четыреста — это CD (сто меньше пятисот), а девятьсот — это CM (сто меньше тысячи).
Пример
Напишите индо-арабскую цифру для MCMIV.
Показать решениеОдна тысяча девятьсот четыре, 1904 г. (M — тысяча, CM — девятьсот, IV — четыре)
Современное применение
К XI веку индуистско-арабские цифры были завезены в Европу из Аль-Андалуса через арабских торговцев и арифметические трактаты. Римские цифры, однако, оказались очень стойкими, оставаясь обычным явлением на Западе даже в 14-15 веках, даже в бухгалтерских и других деловых записях (где фактические расчеты производились бы с использованием счётов).Замена их более удобными «арабскими» эквивалентами была довольно постепенной, и римские цифры все еще используются сегодня в определенных контекстах. Вот несколько примеров их текущего использования:
Испанский реал с использованием «IIII» вместо IV
- Имена монархов и пап, например Елизавета II Соединенного Королевства, Папа Бенедикт XVI. Они называются королевскими числами; например II произносится как «второй». Эта традиция спорадически зародилась в Европе в средние века и получила широкое распространение в Англии только во время правления Генриха VIII.Раньше монарх был известен не по цифрам, а по эпитету, например, Эдуард Исповедник. Некоторые монархи (например, Карл IV в Испании и Людовик XIV во Франции), кажется, предпочитали использовать IIII вместо IV на своих монетах (см. Иллюстрацию).
- Суффиксы поколений, особенно в США, для людей, носящих одно и то же имя из поколения в поколение, например William Howard Taft IV.
- Во французском республиканском календаре, инициированном во время Французской революции, годы были пронумерованы римскими цифрами — от года I (1792 г.), когда этот календарь был введен, до года XIV (1805 г.), когда он был заброшен.
- Год производства фильмов, телешоу и других произведений искусства в рамках самого произведения. BBC News предположили, возможно, шутливо, что это было первоначально сделано «в попытке скрыть век фильмов или телевизионных программ». [23] За пределами ссылки на работу будут использоваться обычные индусско-арабские цифры.
- Часовые метки на часах. В этом контексте 4 обычно пишется как IIII.
- Год постройки фасадов и краеугольных камней зданий.
- Нумерация страниц предисловий и вступлений к книгам, а иногда и приложений.
- Номера томов и глав книги, а также несколько актов в пьесе (например, Акт III, Сцена 2).
- Продолжение некоторых фильмов, видеоигр и других произведений (как в Rocky II ).
- Контуры, в которых используются числа для отображения иерархических отношений.
- Возникновение повторяющегося грандиозного события, например:
- Летние и зимние Олимпийские игры (e.грамм. XXI зимние Олимпийские игры; Игры ХХХ Олимпиады)
- Суперкубок, ежегодный чемпионат Национальной футбольной лиги (например, Суперкубок XXXVII; Суперкубок 50 — единовременное исключение [24] )
- WrestleMania, ежегодное мероприятие по профессиональному рестлингу для WWE (например, WrestleMania XXX).




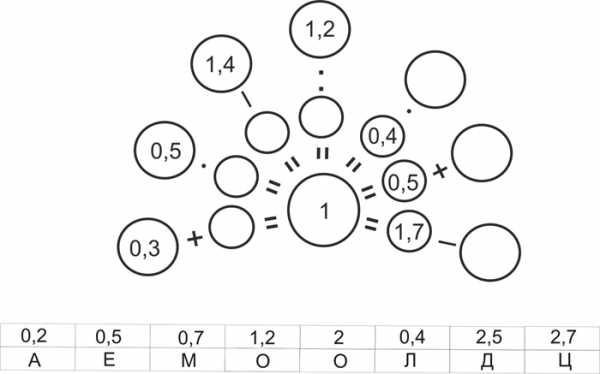
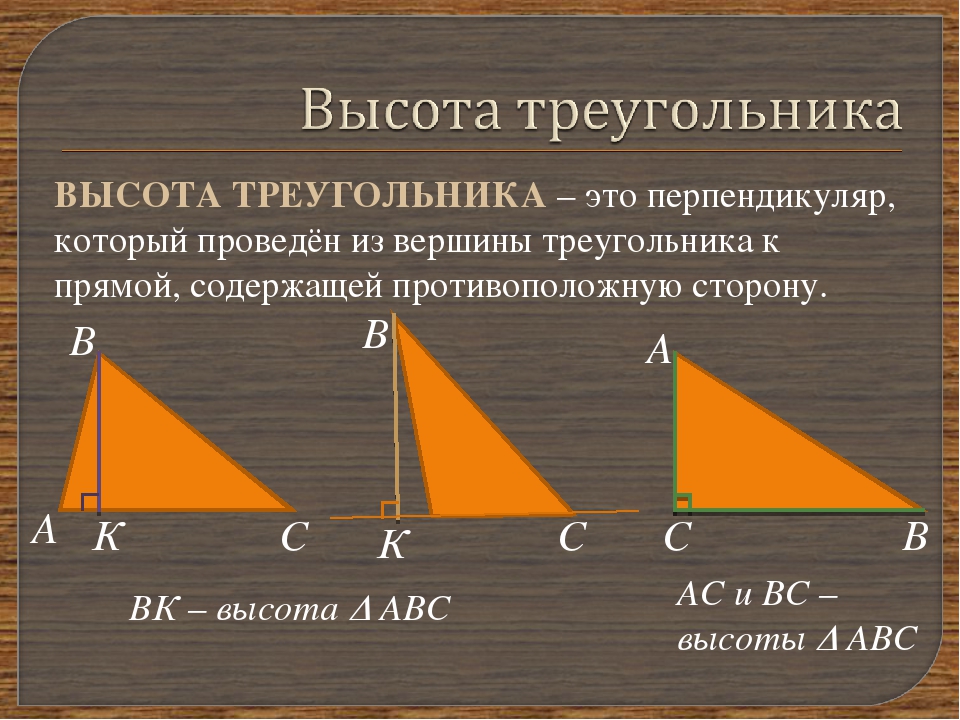 \circ -\angle ~B\).
\circ -\angle ~B\).




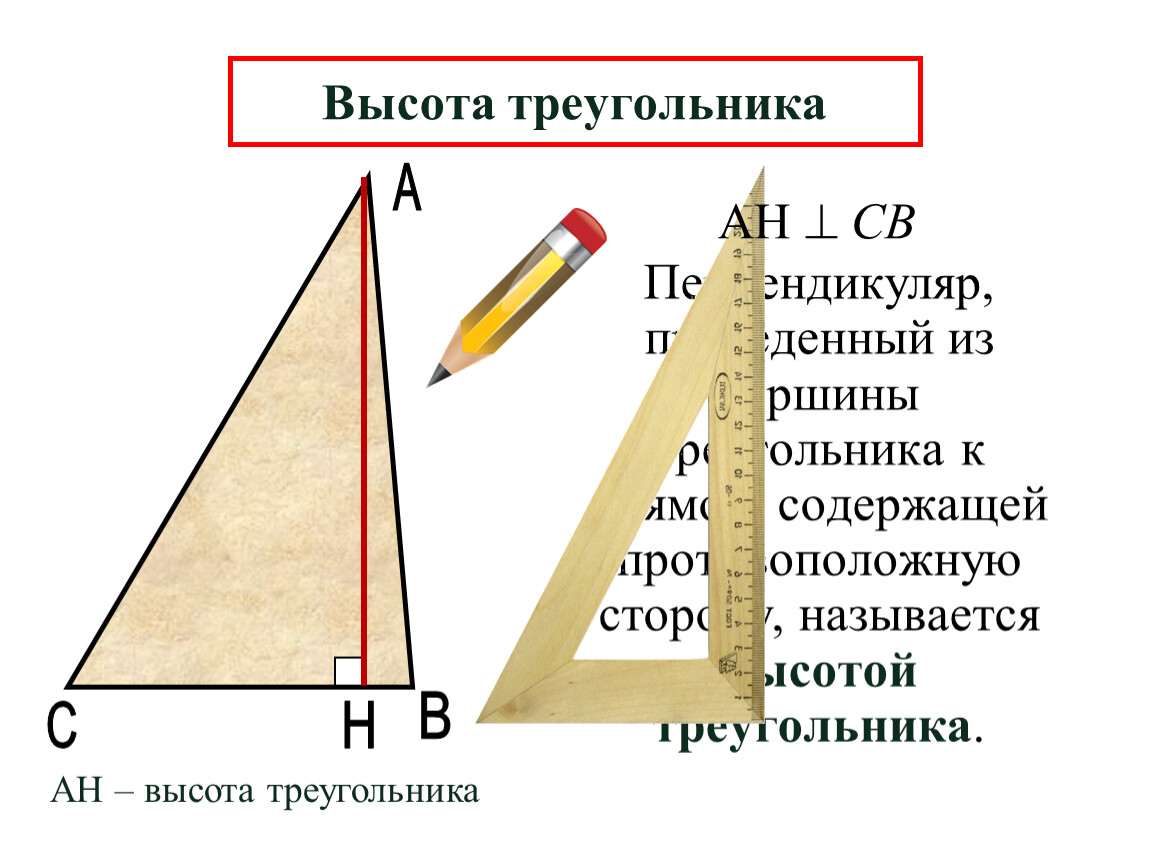

 Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6). Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC.
Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC. 9).
9). Для этого воспользуемся следующей леммой.
Для этого воспользуемся следующей леммой.
 Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться:
Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: 
 Эти три отрезка пересекаются в одной точке — ортоцентре (точка H на рисунке) треугольника.
Для тупого треугольника (имеющего один угол, больше чем 90°), ортоцентр находится за пределами треугольника.
Эти три отрезка пересекаются в одной точке — ортоцентре (точка H на рисунке) треугольника.
Для тупого треугольника (имеющего один угол, больше чем 90°), ортоцентр находится за пределами треугольника. Свойства, Признаки, Высота
Свойства, Признаки, Высота Давайте приступим.
Давайте приступим.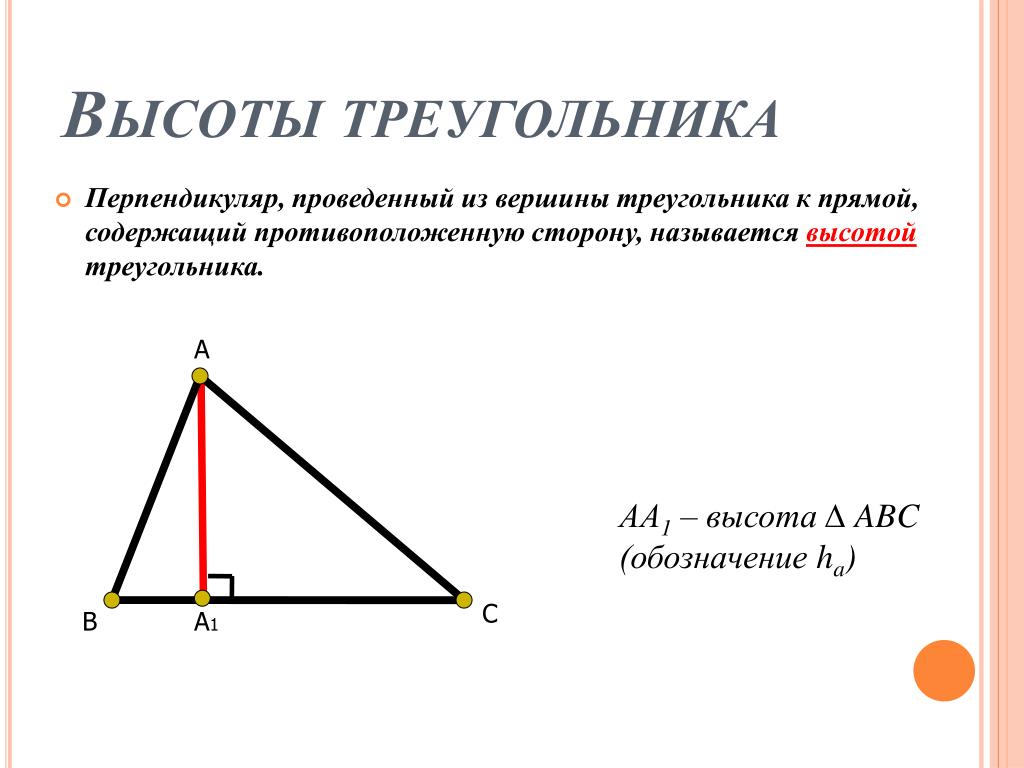

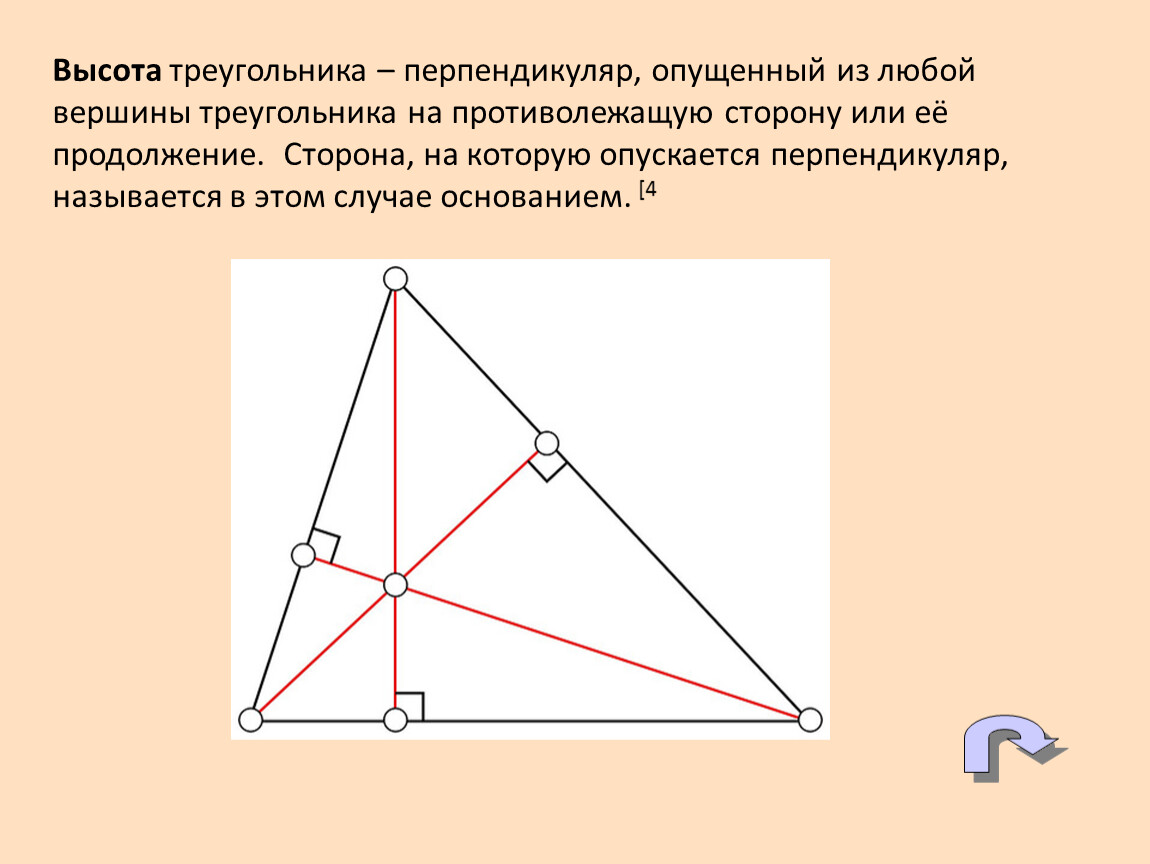

 Ну… почти ничего.
Ну… почти ничего.
 В тупоугольном треугольнике высоты из вершин острых углов проводятся на продолжение сторон и находятся за пределами площади, но тем не менее это именно высоты треугольника со всеми их свойствами.
В тупоугольном треугольнике высоты из вершин острых углов проводятся на продолжение сторон и находятся за пределами площади, но тем не менее это именно высоты треугольника со всеми их свойствами.
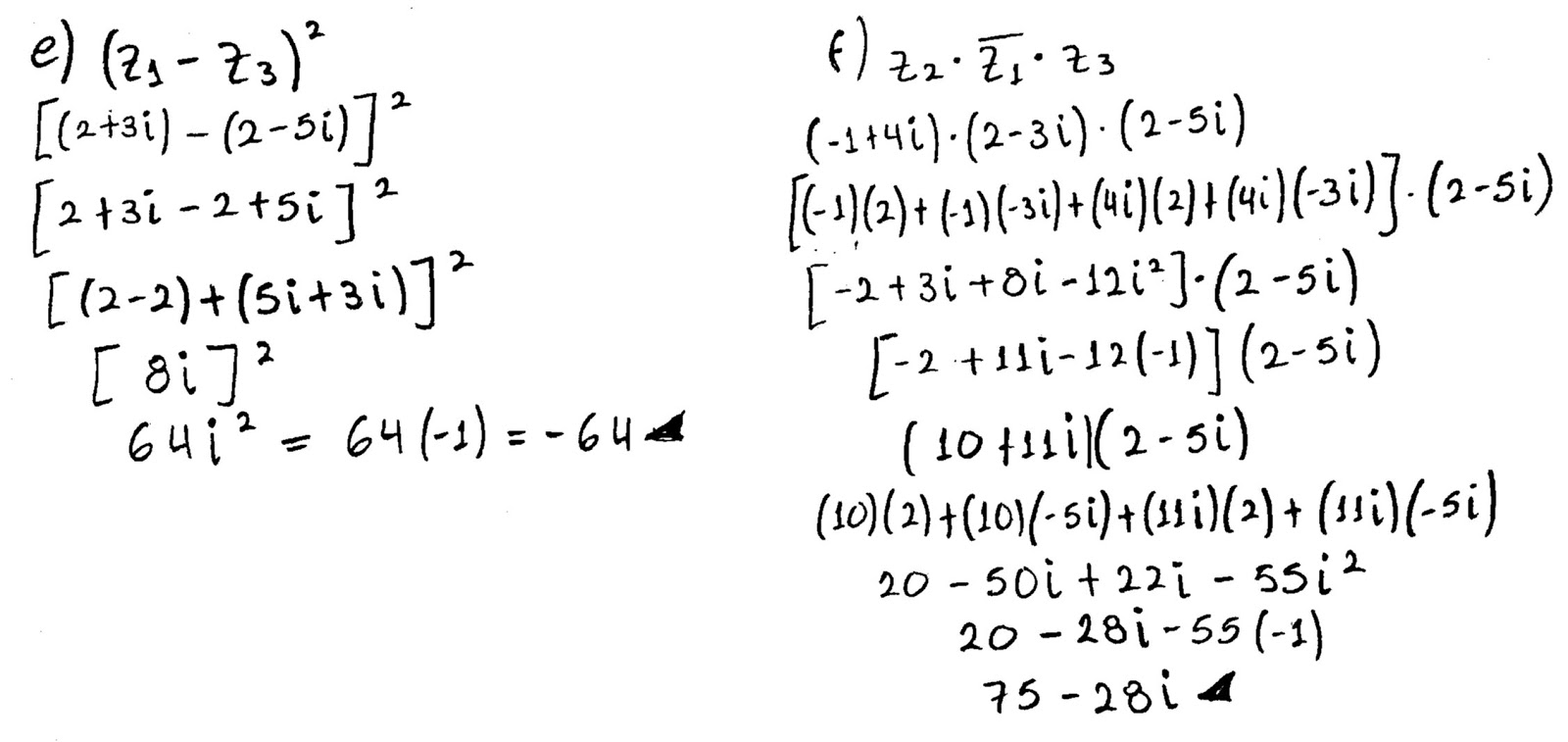
 В результате обработки таких снимков КНР запланировало создать базы данных для создания карт масштаба 1:50 000 и крупнее. «Цзыюань 3-02» — представитель семейства китайских спутников, создаваемых в рамках этого проекта.
В результате обработки таких снимков КНР запланировало создать базы данных для создания карт масштаба 1:50 000 и крупнее. «Цзыюань 3-02» — представитель семейства китайских спутников, создаваемых в рамках этого проекта.
 05.2016
05.2016
 В то же самое время, надирная панхроматическая камера имеет разрешение 2,1 метра и полосу захвата 51,1 км. Инфракрасная камера имеет спектральное разрешение 6 метров и полосу захвата около 51 км.
В то же самое время, надирная панхроматическая камера имеет разрешение 2,1 метра и полосу захвата 51,1 км. Инфракрасная камера имеет спектральное разрешение 6 метров и полосу захвата около 51 км.

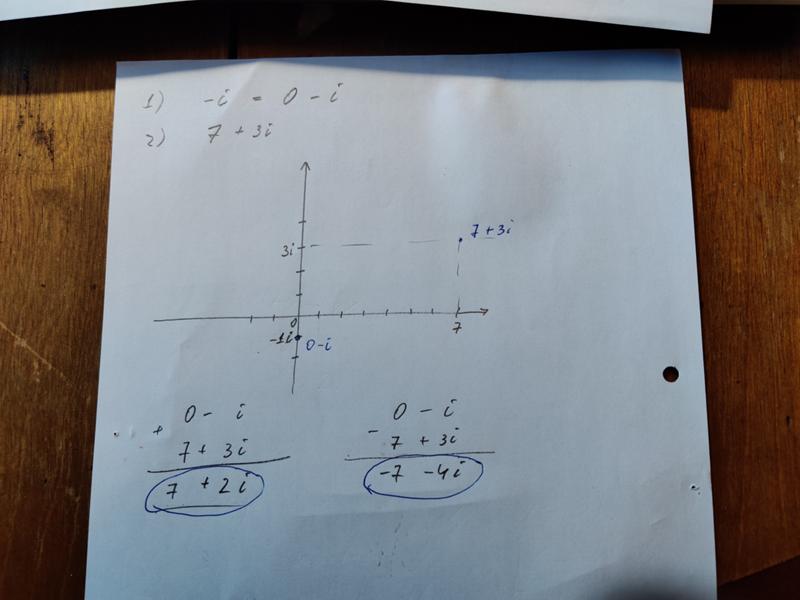
 Пришло на удивление очень быстро, за 12 дней
Пришло на удивление очень быстро, за 12 дней Еще не тестировали. Правая-оригинальная, левая-покупается на AliExpress
Еще не тестировали. Правая-оригинальная, левая-покупается на AliExpress )
)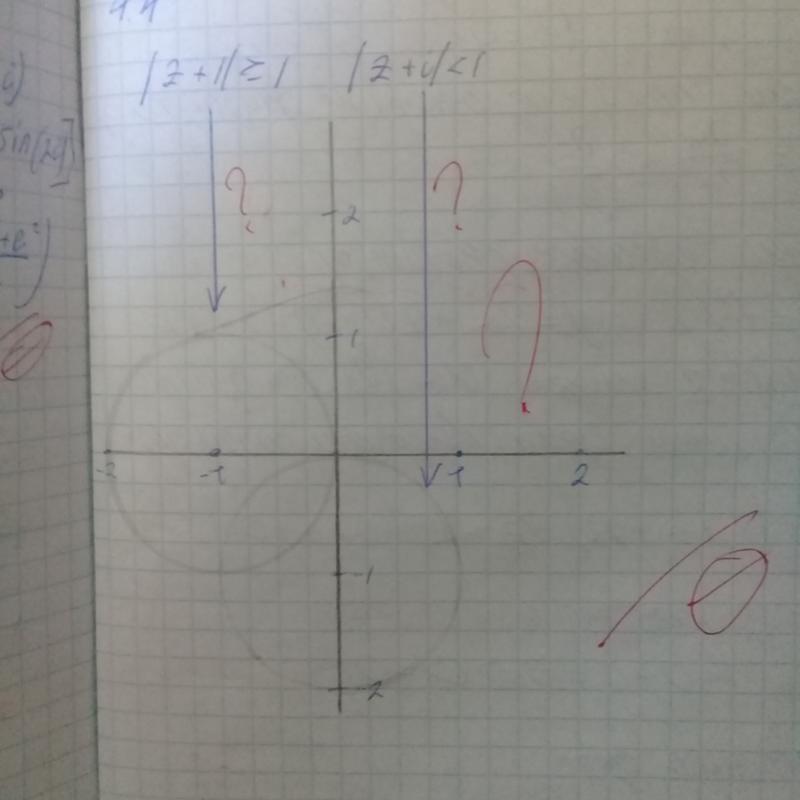 )
) )
) )
) )
) )
) )
)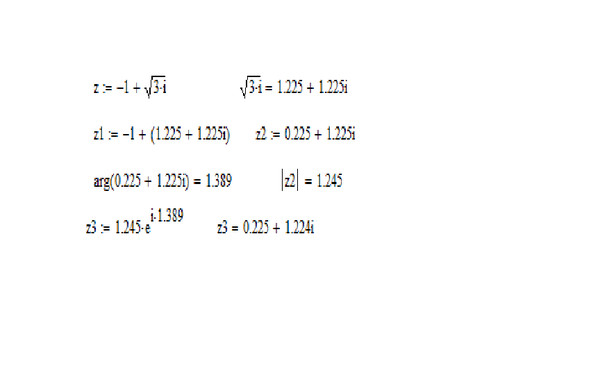 )
) )
) )
)
 По сути, это мой первый день, когда я занимаюсь комплексными числами, поэтому я совершенно потерялся здесь.
Я читал, что форма модуля-аргумент
$$ z = r (\ cos \ theta + i \ sin \ theta) $$
Теперь, в этом случае, я попытался расширить данное уравнение (сейчас я только часть i) и получил:
По сути, это мой первый день, когда я занимаюсь комплексными числами, поэтому я совершенно потерялся здесь.
Я читал, что форма модуля-аргумент
$$ z = r (\ cos \ theta + i \ sin \ theta) $$
Теперь, в этом случае, я попытался расширить данное уравнение (сейчас я только часть i) и получил: 2 \ theta = 1 $.
2 \ theta = 1 $.  2 $ в кольце $ 0 <| z-i | <2 $
2 $ в кольце $ 0 <| z-i | <2 $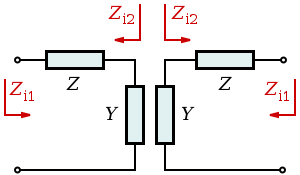 Регистрация займет всего минуту.
Регистрация займет всего минуту. 2} $.2} $.
2} $.2} $. 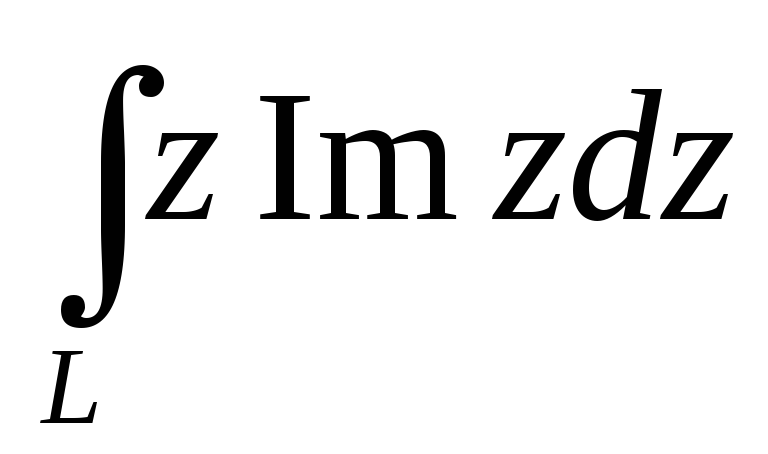
 Возможны три способа доставки, различающиеся составными частями, входящими в комплект:
Возможны три способа доставки, различающиеся составными частями, входящими в комплект:
 В комплект входит подробная спецификация на английском языке. Есть видеоинструкция, доступная для просмотра по ссылке.
В комплект входит подробная спецификация на английском языке. Есть видеоинструкция, доступная для просмотра по ссылке.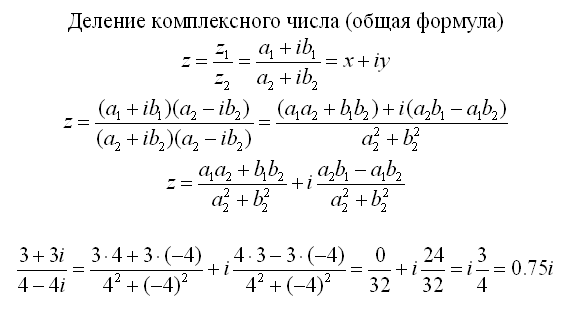 2 :
2 : Использовали метод аффинной ультрафильтрации-ультраэффективной жидкостной хроматографии-масс-спектрометрии (UPLC-MS). Кроме того, для дальнейшей валидации использовались in vitro анализ ингибирования СОХ-2 и метод молекулярного докинга in silico.
Использовали метод аффинной ультрафильтрации-ультраэффективной жидкостной хроматографии-масс-спектрометрии (UPLC-MS). Кроме того, для дальнейшей валидации использовались in vitro анализ ингибирования СОХ-2 и метод молекулярного докинга in silico.

 Сделать тесто не сложнее, чем собрать тесто для пиццы. Но вот вам совет: мы знали кого-то — не менее женщину из Китая — которая раньше делала баоцзы из купленного в магазине теста для печенья Pillsbury.
Сделать тесто не сложнее, чем собрать тесто для пиццы. Но вот вам совет: мы знали кого-то — не менее женщину из Китая — которая раньше делала баоцзы из купленного в магазине теста для печенья Pillsbury.
 Месите в течение 2 минут, чтобы избавиться от воздушных карманов. Скатайте тесто в длинную трубку и оторвите куски теста, чтобы получились отдельные шарики. Они должны быть размером с мяч для гольфа для больших булочек и примерно вдвое меньше для маленьких.
Месите в течение 2 минут, чтобы избавиться от воздушных карманов. Скатайте тесто в длинную трубку и оторвите куски теста, чтобы получились отдельные шарики. Они должны быть размером с мяч для гольфа для больших булочек и примерно вдвое меньше для маленьких. У вас получится примерно 10-15 складок. Это оно!
У вас получится примерно 10-15 складок. Это оно! Чтобы приготовить, просто следуйте инструкциям ниже, как если бы вы готовили их в свежем виде. Время приготовления просто немного увеличится!
Чтобы приготовить, просто следуйте инструкциям ниже, как если бы вы готовили их в свежем виде. Время приготовления просто немного увеличится! В нашем случае мы использовали кукурузную шелуху, нарезанную квадратиками.Также подойдут тонкие листья капусты напа. Если вы используете бамбуковую пароварку, смажьте ее стороны маслом, так как булочки расширятся и могут прилипнуть к бокам.
В нашем случае мы использовали кукурузную шелуху, нарезанную квадратиками.Также подойдут тонкие листья капусты напа. Если вы используете бамбуковую пароварку, смажьте ее стороны маслом, так как булочки расширятся и могут прилипнуть к бокам. То есть!
То есть!
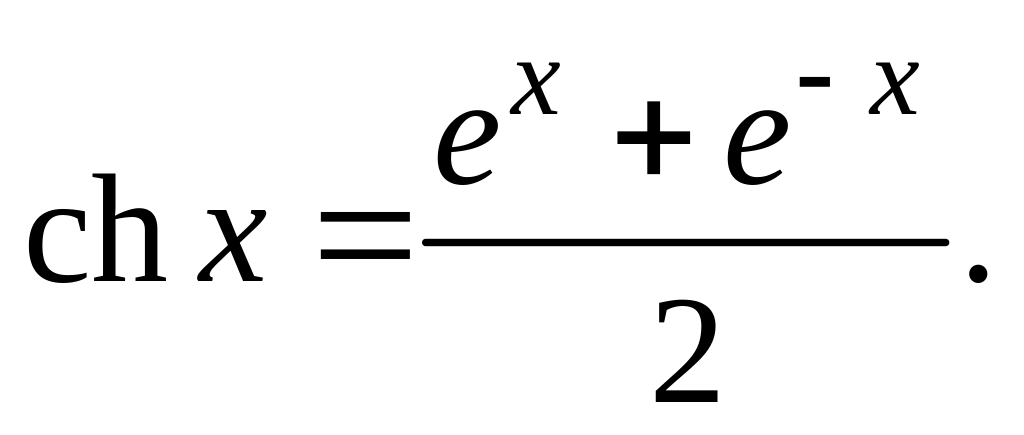


 Вы можете использовать любой аппарат для отпаривания, который вы обычно используете, но помните: 1) Кипящая вода не должна напрямую касаться булочки во время приготовления на пару. 2) Избегайте прилипания, нанося масло на поверхность, на которой находится булочка, или кладя какую-нибудь естественную антипригарную поверхность. В нашем случае мы использовали кукурузную лузгу.Также подойдут тонкие листья капусты напа. Если вы используете бамбуковую пароварку, смажьте ее стороны маслом, так как булочки расширятся и могут прилипнуть к бокам. 3) Поверхность, на которой сидят булочки, не должна быть твердой, как тарелка. Это задержит влагу и сделает булочки намокшими. Должна быть какая-то аэрация. 4) Убедитесь, что крышка плотно закрыта, чтобы не терять пар.
Вы можете использовать любой аппарат для отпаривания, который вы обычно используете, но помните: 1) Кипящая вода не должна напрямую касаться булочки во время приготовления на пару. 2) Избегайте прилипания, нанося масло на поверхность, на которой находится булочка, или кладя какую-нибудь естественную антипригарную поверхность. В нашем случае мы использовали кукурузную лузгу.Также подойдут тонкие листья капусты напа. Если вы используете бамбуковую пароварку, смажьте ее стороны маслом, так как булочки расширятся и могут прилипнуть к бокам. 3) Поверхность, на которой сидят булочки, не должна быть твердой, как тарелка. Это задержит влагу и сделает булочки намокшими. Должна быть какая-то аэрация. 4) Убедитесь, что крышка плотно закрыта, чтобы не терять пар.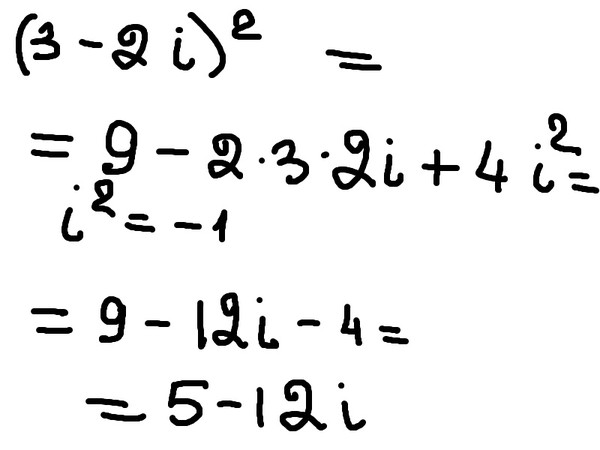 Если поверхность теста отскакивает, значит, все готово. Внимательно следите за ними. Избыточное приготовление на пару приведет к разрушению булочек, поэтому время приготовления очень важно.
Если поверхность теста отскакивает, значит, все готово. Внимательно следите за ними. Избыточное приготовление на пару приведет к разрушению булочек, поэтому время приготовления очень важно.


 Он был бывшим владельцем бара / ресторана Les Enfants de Boheme с 2003 по 2012 год.Les Enfants представила первый и единственный парклет Street Seat
Он был бывшим владельцем бара / ресторана Les Enfants de Boheme с 2003 по 2012 год.Les Enfants представила первый и единственный парклет Street Seat 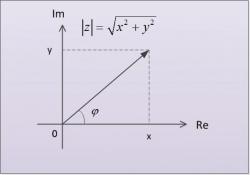
 Мы можем найти расстояние | z | с помощью теоремы Пифагора. Рассмотрим прямоугольный треугольник с одной вершиной в 0, другой в z и третьим в x на действительной оси непосредственно под z (или выше z , если z оказывается ниже действительной оси).Горизонтальная сторона треугольника имеет длину | | x |, вертикальная сторона имеет длину | y |, а диагональная сторона имеет длину | z |. Следовательно,
Мы можем найти расстояние | z | с помощью теоремы Пифагора. Рассмотрим прямоугольный треугольник с одной вершиной в 0, другой в z и третьим в x на действительной оси непосредственно под z (или выше z , если z оказывается ниже действительной оси).Горизонтальная сторона треугольника имеет длину | | x |, вертикальная сторона имеет длину | y |, а диагональная сторона имеет длину | z |. Следовательно, Единичный круг — это круг радиуса 1 с центром в 0. Он включает в себя все комплексные числа с абсолютным значением 1, поэтому он имеет уравнение | z | = 1.
Единичный круг — это круг радиуса 1 с центром в 0. Он включает в себя все комплексные числа с абсолютным значением 1, поэтому он имеет уравнение | z | = 1. Это означает, что a / c + i b / c — это комплексное число, которое лежит в блоке круг.Самая известная тройка Пифагора — 3: 4: 5. Эта тройка дает нам комплексное число 3/5 + i 4/5 на единичной окружности. Некоторые другие пифагорейские тройки: 5:12:13, 15: 8: 17, 7:24:25, 21:20:29, 9:40:41, 35:12:27 и 11:60:61. Как и следовало ожидать, их бесконечно много. (Для
немного больше о троек Пифагора см. в конце страницы по адресу http://www.clarku.edu/~djoyce/trig/right.html.)
Это означает, что a / c + i b / c — это комплексное число, которое лежит в блоке круг.Самая известная тройка Пифагора — 3: 4: 5. Эта тройка дает нам комплексное число 3/5 + i 4/5 на единичной окружности. Некоторые другие пифагорейские тройки: 5:12:13, 15: 8: 17, 7:24:25, 21:20:29, 9:40:41, 35:12:27 и 11:60:61. Как и следовало ожидать, их бесконечно много. (Для
немного больше о троек Пифагора см. в конце страницы по адресу http://www.clarku.edu/~djoyce/trig/right.html.)
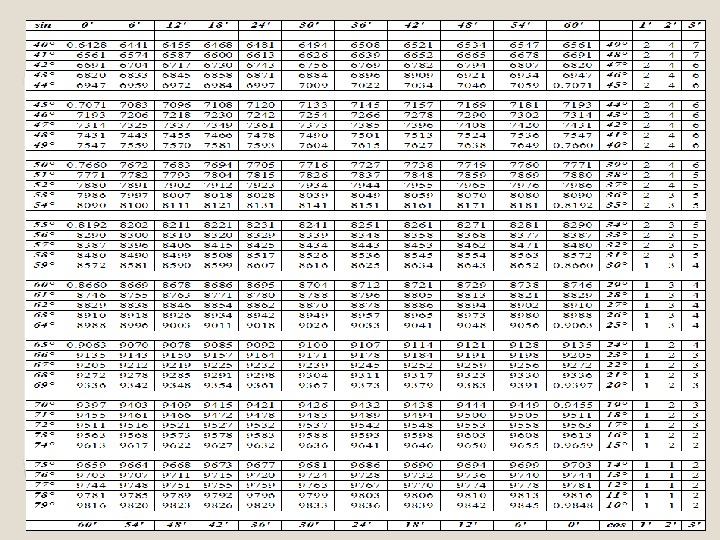
 0872
0872 1736
1736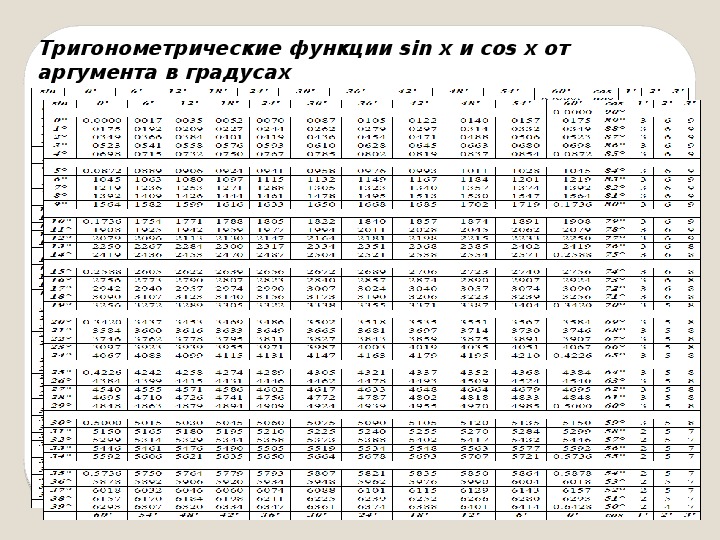 2588
2588 3420
3420 4226
4226 5000
5000 5736
5736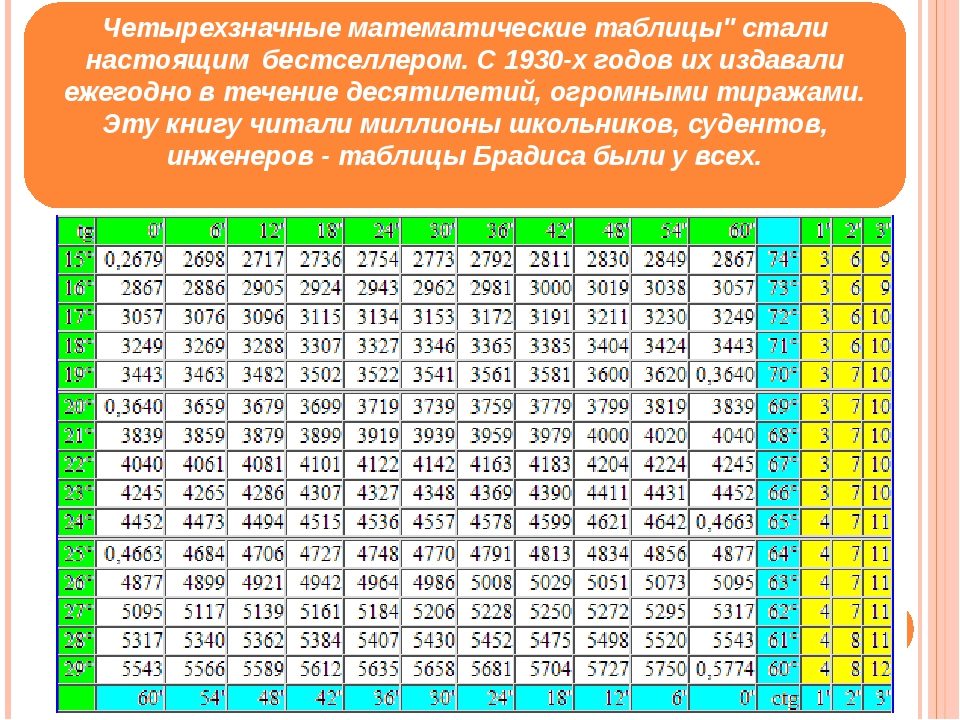 6428
6428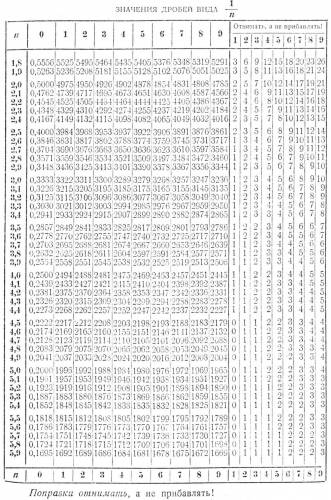 7071
7071 7660
7660 8192
8192 8660
8660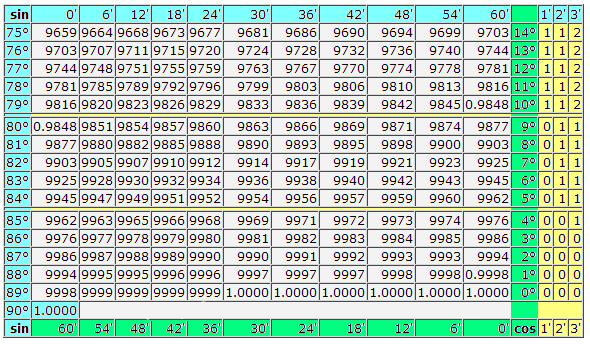 9063
9063 9397
9397 9659
9659 9848
9848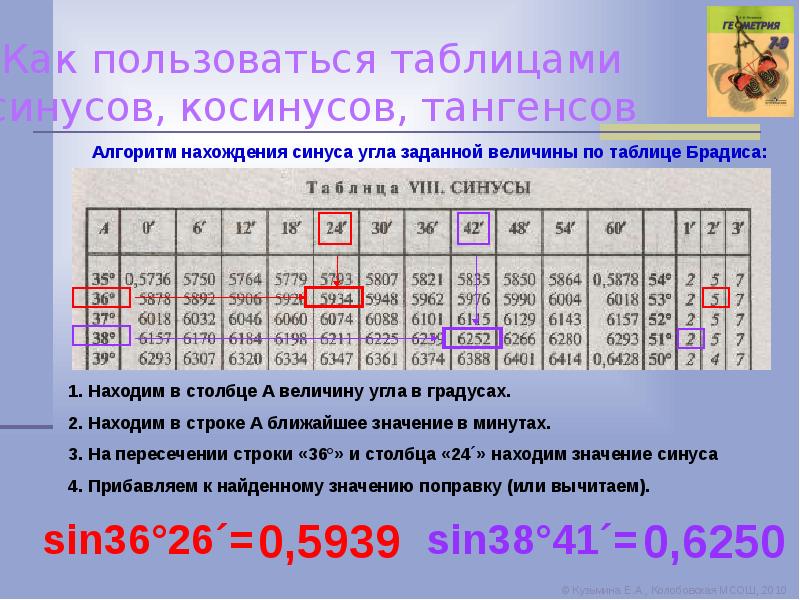 9998
9998
 0
0 Та же таблица синусов и косинусов служит для
разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать,
что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами
дополнительных углов.
Та же таблица синусов и косинусов служит для
разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать,
что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами
дополнительных углов.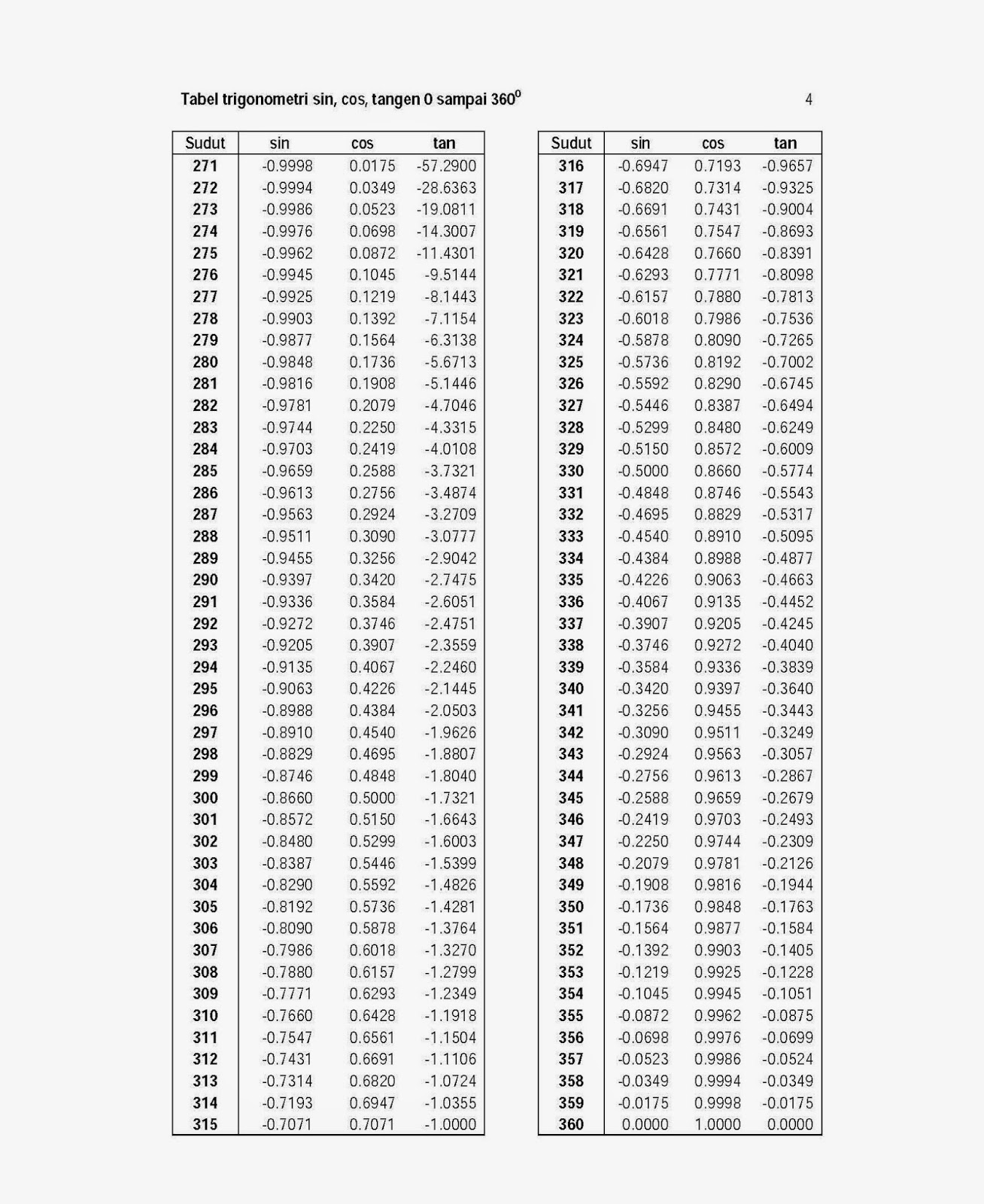 0
0 1544
1544 3613
3613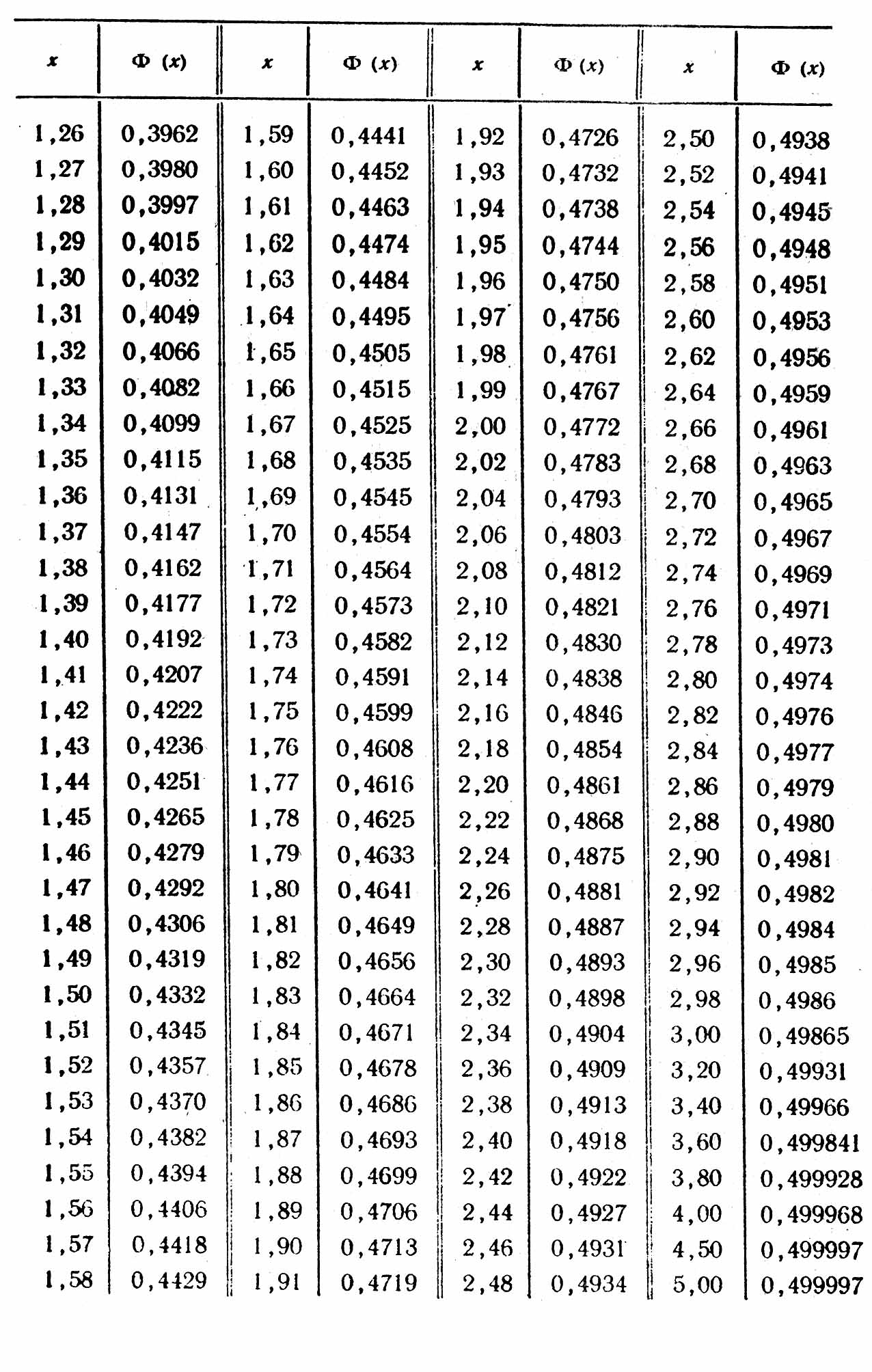 6003
6003 9292
9292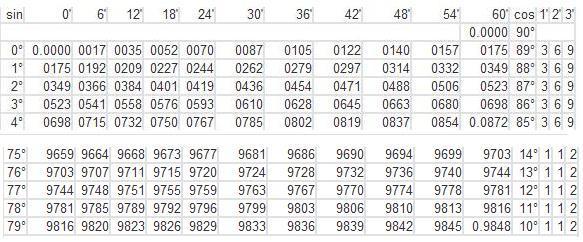 3559
3559 0108
0108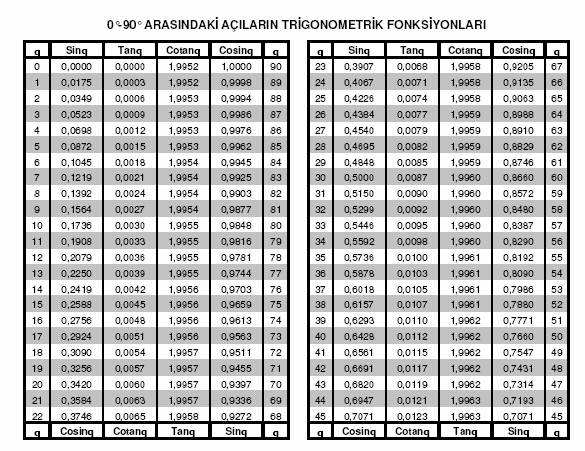 3138
3138 3007
3007
 Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.
Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828. Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926.
Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926. 0000
0000 0872
0872 1736
1736 3420
3420 4226
4226 5000
5000 5736
5736 6428
6428 7071
7071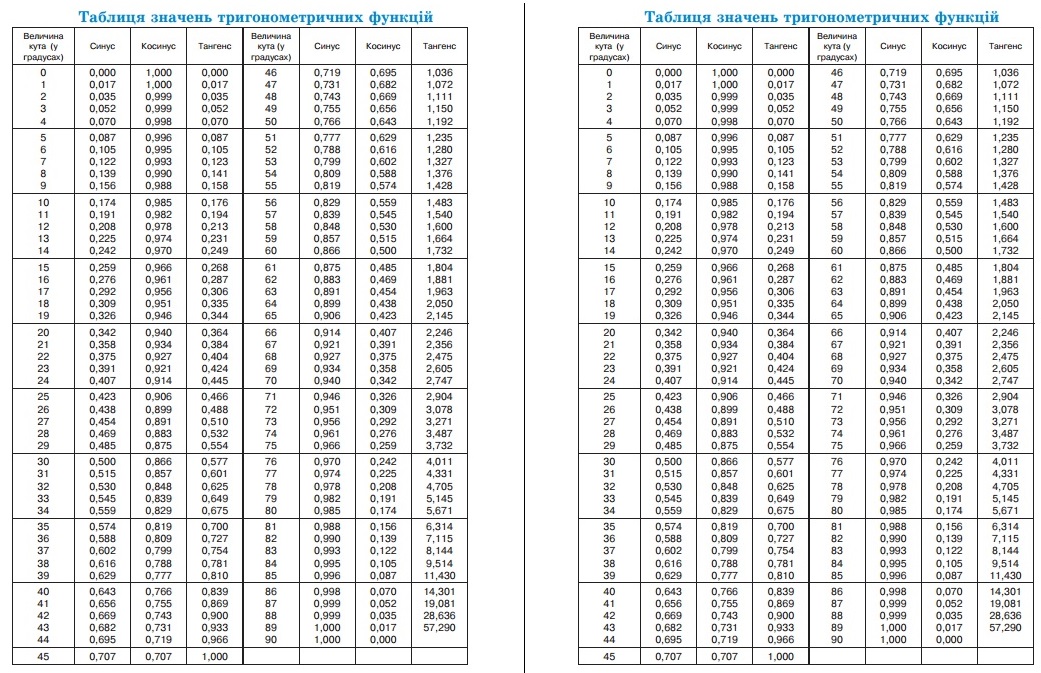 7660
7660 8192
8192 3. Механизм рыночного ценообразования
3. Механизм рыночного ценообразования
 Экономическая школа, считавшая источником богатства землю и труд, получила название — физиократии — меркантилизма — маржинализма — институционализма 2. Какое из приведенных ниже
Экономическая школа, считавшая источником богатства землю и труд, получила название — физиократии — меркантилизма — маржинализма — институционализма 2. Какое из приведенных ниже Тесты 1 (по 1 баллу):
Тесты 1 (по 1 баллу):
 Если при росте цен на товар с 10 до 20 ден. ед., объем спроса сократился с 400 до 100 штук, то спрос на данный товар является…
Если при росте цен на товар с 10 до 20 ден. ед., объем спроса сократился с 400 до 100 штук, то спрос на данный товар является… Кривая спроса характеризует …
Кривая спроса характеризует … Альтернативная стоимость 25 пар обуви равна _ вертолету(ам)
Альтернативная стоимость 25 пар обуви равна _ вертолету(ам) Может быть, прошлые акции не показывали роста продаж; может быть, в соседних магазинах тоже не особо-то готовятся надувать черные шары. И все же весь крупный онлайн-ритейл уже отчитался о продажах 11.11 и заряжает ядра в рекламные пушки на тему скидок в «Черную пятницу».
Может быть, прошлые акции не показывали роста продаж; может быть, в соседних магазинах тоже не особо-то готовятся надувать черные шары. И все же весь крупный онлайн-ритейл уже отчитался о продажах 11.11 и заряжает ядра в рекламные пушки на тему скидок в «Черную пятницу». Поэтому нанимаем витринистов на проект, либо сами жонглируем черным акрилом, подарочными упаковками, шарами и гематитом.
Поэтому нанимаем витринистов на проект, либо сами жонглируем черным акрилом, подарочными упаковками, шарами и гематитом.
 Главное, сделайте планку, при которой победит каждый, а также дополнительно наградите лучших продавцов и лучшие магазины
Главное, сделайте планку, при которой победит каждый, а также дополнительно наградите лучших продавцов и лучшие магазины
 По мере роста цены на апельсиновый сок спрос будет уменьшаться.
По мере роста цены на апельсиновый сок спрос будет уменьшаться. Например, если цена вырастет, продавец захочет продать больше товара по новой более высокой цене. Изменение предложения означает, что продавцы будут готовы продать больше (меньше) товара по всем возможным ценам. Например, до увеличения предложения продавцы были готовы продать 10 кусочков пиццы по цене 1 доллар США за ломтик. Теперь они готовы продать 15 кусочков пиццы по той же цене. Изменение объема предложения иллюстрируется движением кривой предложения, а изменение предложения — сдвигом кривой предложения.
Например, если цена вырастет, продавец захочет продать больше товара по новой более высокой цене. Изменение предложения означает, что продавцы будут готовы продать больше (меньше) товара по всем возможным ценам. Например, до увеличения предложения продавцы были готовы продать 10 кусочков пиццы по цене 1 доллар США за ломтик. Теперь они готовы продать 15 кусочков пиццы по той же цене. Изменение объема предложения иллюстрируется движением кривой предложения, а изменение предложения — сдвигом кривой предложения. Люди часто едут на Карибы из Новой Англии, чтобы спастись от холода.
погода, поэтому зимой спрос на карибские гостиничные номера высок. в
летом меньше людей едут на Карибы, так как северные страны более
приятный. Результатом, как показано на рис. 4-7, является сдвиг влево в
кривая спроса. Таким образом, равновесная цена карибских гостиничных номеров ниже в
летом, чем зимой, как показано на рисунке.
Люди часто едут на Карибы из Новой Англии, чтобы спастись от холода.
погода, поэтому зимой спрос на карибские гостиничные номера высок. в
летом меньше людей едут на Карибы, так как северные страны более
приятный. Результатом, как показано на рис. 4-7, является сдвиг влево в
кривая спроса. Таким образом, равновесная цена карибских гостиничных номеров ниже в
летом, чем зимой, как показано на рисунке. Кроме того, некоторые люди, которые
уже владеющие кадиллаками попробую их продать. В результате кривая спроса
для подержанных Кадиллаков сдвигается влево, а кривая предложения сдвигается в
справа, как показано на Рисунке 4-9. Результат — снижение равновесной цены.
подержанных кадиллаков.
Кроме того, некоторые люди, которые
уже владеющие кадиллаками попробую их продать. В результате кривая спроса
для подержанных Кадиллаков сдвигается влево, а кривая предложения сдвигается в
справа, как показано на Рисунке 4-9. Результат — снижение равновесной цены.
подержанных кадиллаков. Если забастовка металлургов приведет к повышению цен на сталь, затраты на производство
рост минивэнов (рост входных цен), поэтому предложение минивэнов уменьшается.
Спрос не пострадает. Результат — удорожание минивэнов и
снижение количества, как показано на Рисунке 4-13.
Если забастовка металлургов приведет к повышению цен на сталь, затраты на производство
рост минивэнов (рост входных цен), поэтому предложение минивэнов уменьшается.
Спрос не пострадает. Результат — удорожание минивэнов и
снижение количества, как показано на Рисунке 4-13. Рост цен на универсалы влияет на спрос на минивэны, потому что
универсалы заменяют минивэны (то есть
цена сопутствующего товара). В результате растет спрос на минивэны.
Предложение не затронуто. В равновесии цена и количество минивэнов
подниматься, как показано на Рисунке 4-12.
Рост цен на универсалы влияет на спрос на минивэны, потому что
универсалы заменяют минивэны (то есть
цена сопутствующего товара). В результате растет спрос на минивэны.
Предложение не затронуто. В равновесии цена и количество минивэнов
подниматься, как показано на Рисунке 4-12.
 4-22, результатом является снижение равновесия.
цена и увеличение равновесного количества толстовок.
4-22, результатом является снижение равновесия.
цена и увеличение равновесного количества толстовок. Я всегда ожидаю
графики!
Я всегда ожидаю
графики! Но если бы стоимость необходимых учебников была
Поднимитесь, у студентов не будет иного выбора, кроме как заплатить более высокую цену. Таким образом
количество требуемых учебников меньше зависит от цены, чем
количество востребованных детективных романов.
Но если бы стоимость необходимых учебников была
Поднимитесь, у студентов не будет иного выбора, кроме как заплатить более высокую цену. Таким образом
количество требуемых учебников меньше зависит от цены, чем
количество востребованных детективных романов. Товары имеют более эластичный спрос, чем
более длинные временные горизонты. Если цена на мазут временно повысится,
потребители не могли переключиться на другие источники топлива без больших затрат. Но
если бы цена на мазут долгое время оставалась высокой, люди бы
постепенно переходите на газовое или электрическое отопление.В результате объем спроса на
мазут в течение следующих шести месяцев менее чувствителен к цене, чем
количество потребляемого мазута в течение следующих пяти лет.
Товары имеют более эластичный спрос, чем
более длинные временные горизонты. Если цена на мазут временно повысится,
потребители не могли переключиться на другие источники топлива без больших затрат. Но
если бы цена на мазут долгое время оставалась высокой, люди бы
постепенно переходите на газовое или электрическое отопление.В результате объем спроса на
мазут в течение следующих шести месяцев менее чувствителен к цене, чем
количество потребляемого мазута в течение следующих пяти лет.
 Какое из следующих утверждений о кривых спроса ВЕРНО?
Какое из следующих утверждений о кривых спроса ВЕРНО?





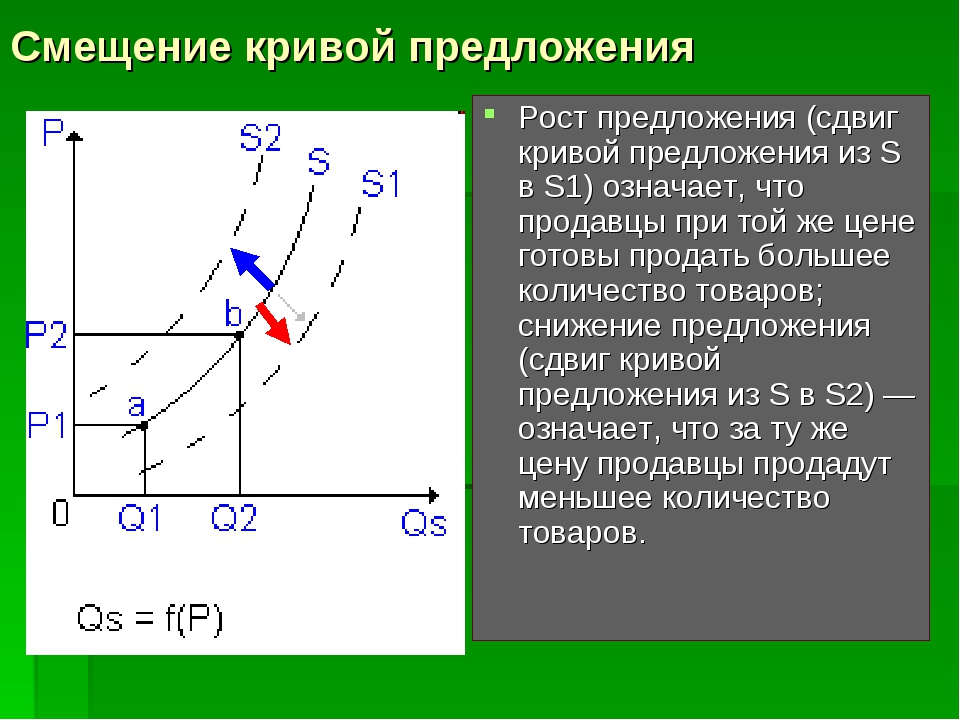





 Стоимость доставки 700 $. Избыток производителя от продажи его альта равен _____.
Стоимость доставки 700 $. Избыток производителя от продажи его альта равен _____. По какой из следующих причин?
По какой из следующих причин? По цене 8 $ есть:
По цене 8 $ есть:

 Обратите внимание, что две кривые спроса параллельны. Какие из следующих утверждений является верным?
Обратите внимание, что две кривые спроса параллельны. Какие из следующих утверждений является верным?
 Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая. 
 Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:



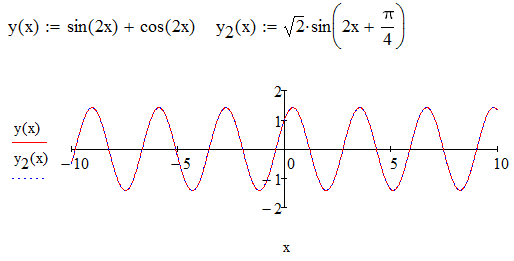
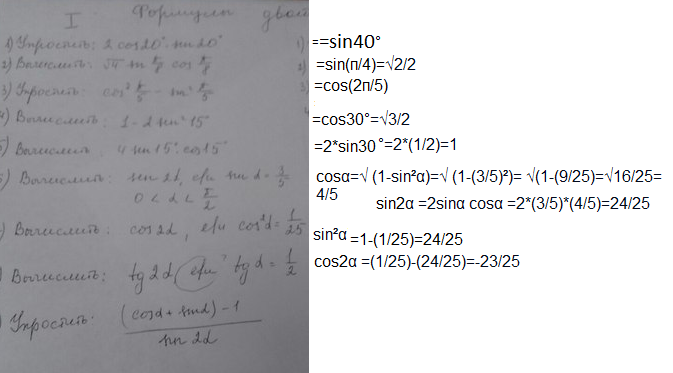



 Способов определения корней, которые принадлежат отрезку несколько.
Способов определения корней, которые принадлежат отрезку несколько.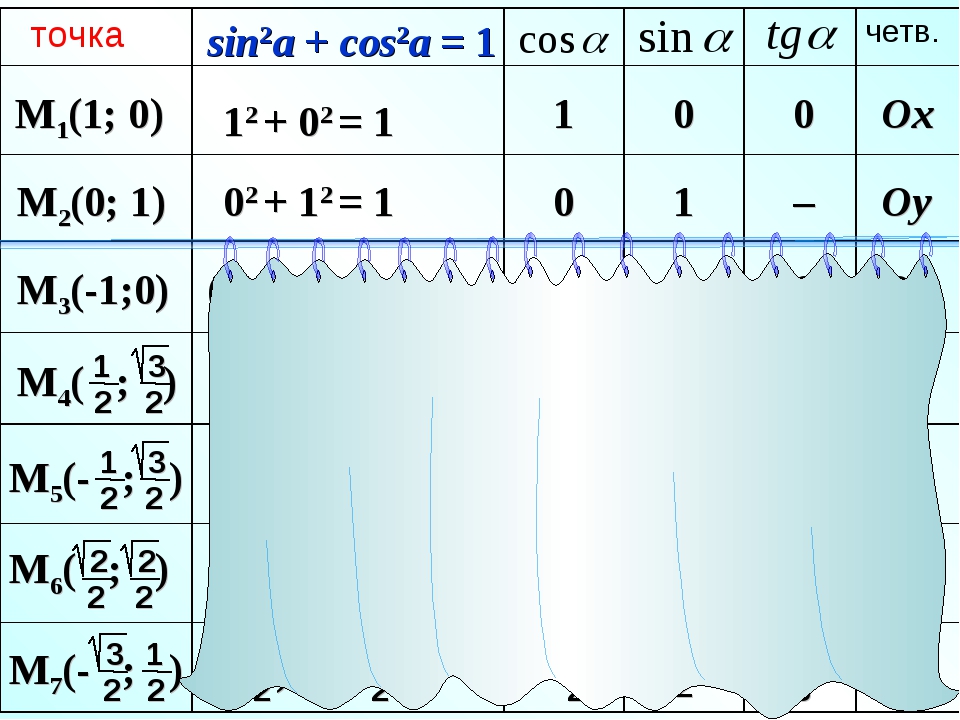

 У студента не будет лучшего способа практиковать алгебру, чем доказывать их. Ссылки на доказательства приведены ниже.
У студента не будет лучшего способа практиковать алгебру, чем доказывать их. Ссылки на доказательства приведены ниже.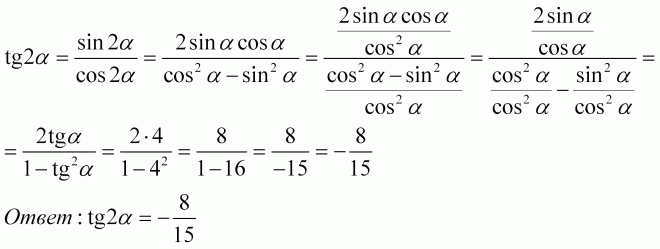
 Покажите: tan θ cos θ = sin θ.
Покажите: tan θ cos θ = sin θ.

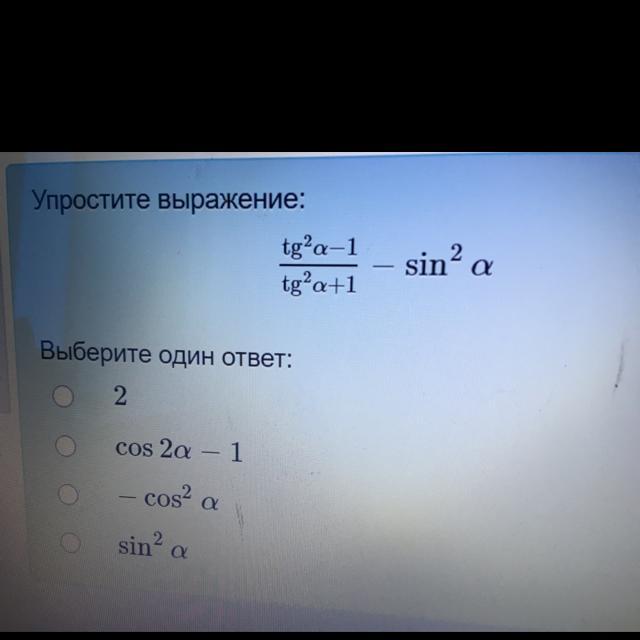 Оценить sin 15 °.
Оценить sin 15 °. Кривые рас-пре/.еления по своей форме напоминают нормальную кривую, но [c.41]
Кривые рас-пре/.еления по своей форме напоминают нормальную кривую, но [c.41] в. [c.292]
в. [c.292]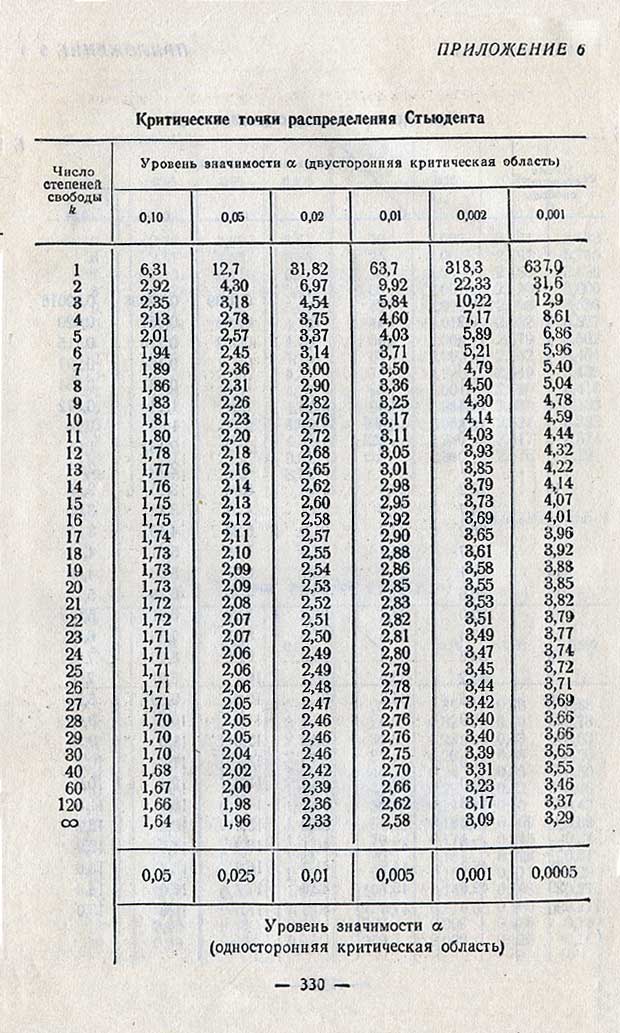 Затем, если т==4, для каждого отобранного значения по формуле (П. 131) вычисляется т, если тфА, по формуле (П. 134) т). После перехода к величинам т и т) для проверки гипотезы равномерного распределение т илп распределения Стьюдента т] (и, следовательно, нормальности исходного распределения) может быть применен любой из ра смотренных ранее критериев согласия. [c.68]
Затем, если т==4, для каждого отобранного значения по формуле (П. 131) вычисляется т, если тфА, по формуле (П. 134) т). После перехода к величинам т и т) для проверки гипотезы равномерного распределение т илп распределения Стьюдента т] (и, следовательно, нормальности исходного распределения) может быть применен любой из ра смотренных ранее критериев согласия. [c.68] Неучет этого приводит к необъективному, заниженному значению погрешности. Эта ненадежность, связанная с числом определений (параллельных проб), учитывается /-распределением Стьюдента, в котором предусматривается большая вероятность появления больших погрешностей, а малых меньше, чем в нормальном распределении. [c.129]
Неучет этого приводит к необъективному, заниженному значению погрешности. Эта ненадежность, связанная с числом определений (параллельных проб), учитывается /-распределением Стьюдента, в котором предусматривается большая вероятность появления больших погрешностей, а малых меньше, чем в нормальном распределении. [c.129] Рассмотрим случайную величину tn = % /n Xn Распределение этой случайной величины называется распределением Стьюдента с п степенями свободы. Его плотность имеет следующий вид [c.82]
Рассмотрим случайную величину tn = % /n Xn Распределение этой случайной величины называется распределением Стьюдента с п степенями свободы. Его плотность имеет следующий вид [c.82]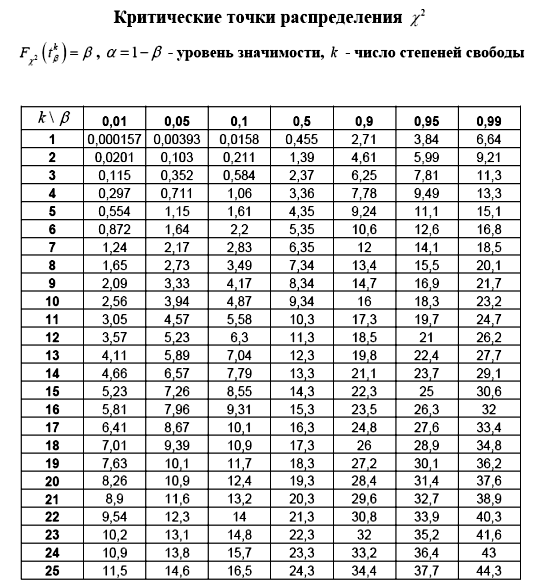 426]
426] Среднее значение трех параллельных измерений равно х = 97,8%. Ошибка воспроизводимости (выбороч-пьн 1 стандарт) х равна 0,52. Число степеней свободы ошибки воспроизводимости [ = 2. В качестве нулевой гипотезы рассмотрим гипотезу Яо пг = 99% следовательно, исследуемый реактив доброкачествен. Альтернативная гипотеза Н . гпхф =7 99. Используя распределение Стьюдента, определим вначале критическую область при двустороннем критерии. При р = 0,95 р = 0,05 и квантиль pj2 =4,30 [c.43]
Среднее значение трех параллельных измерений равно х = 97,8%. Ошибка воспроизводимости (выбороч-пьн 1 стандарт) х равна 0,52. Число степеней свободы ошибки воспроизводимости [ = 2. В качестве нулевой гипотезы рассмотрим гипотезу Яо пг = 99% следовательно, исследуемый реактив доброкачествен. Альтернативная гипотеза Н . гпхф =7 99. Используя распределение Стьюдента, определим вначале критическую область при двустороннем критерии. При р = 0,95 р = 0,05 и квантиль pj2 =4,30 [c.43]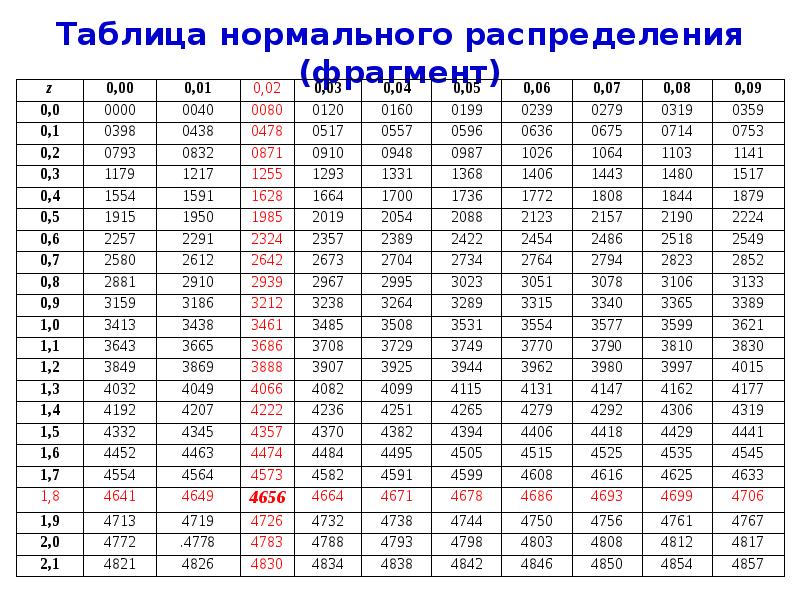 -коэффициент Стьюдента, учитывающий разницу в нормальном и /-распределении и при данной Р, зависящей от числа степеней свободы. Индекс Р у t указывает на фиксированную вероятность, f — число степеней свободы. Численные значения коэффициента tp, при различных Р и f приведены в табл. 7.1. Как видно, при Р = 95 % и f = 20 коэффициент ip,f = 2,09, т. е. близок к 2, характерному для нормального распределения. [c.130]
-коэффициент Стьюдента, учитывающий разницу в нормальном и /-распределении и при данной Р, зависящей от числа степеней свободы. Индекс Р у t указывает на фиксированную вероятность, f — число степеней свободы. Численные значения коэффициента tp, при различных Р и f приведены в табл. 7.1. Как видно, при Р = 95 % и f = 20 коэффициент ip,f = 2,09, т. е. близок к 2, характерному для нормального распределения. [c.130] Вычислим соответствующие выборочные параметры j и 5 и составим дробь t — х — р,) /5. Эта Дробь имеет рас- пределение Стьюдента с = п—1 числом степеней свободы. Сравним величину I с аргументом функции Лапласа и. Если ыл — мера отклонения среднего результата анализа от математического чэжидания р, в единицах генерального стандартного отклонения [c.92]
Вычислим соответствующие выборочные параметры j и 5 и составим дробь t — х — р,) /5. Эта Дробь имеет рас- пределение Стьюдента с = п—1 числом степеней свободы. Сравним величину I с аргументом функции Лапласа и. Если ыл — мера отклонения среднего результата анализа от математического чэжидания р, в единицах генерального стандартного отклонения [c.92]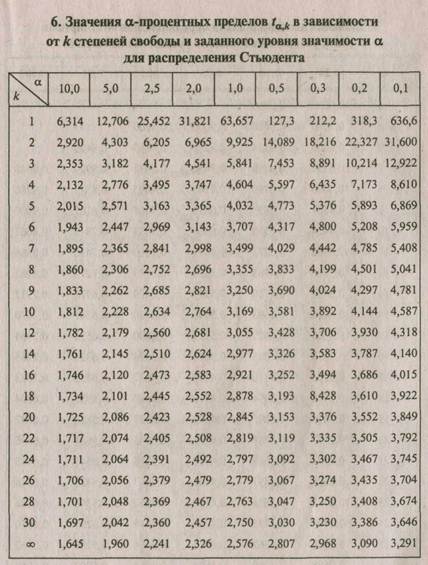 108]
108]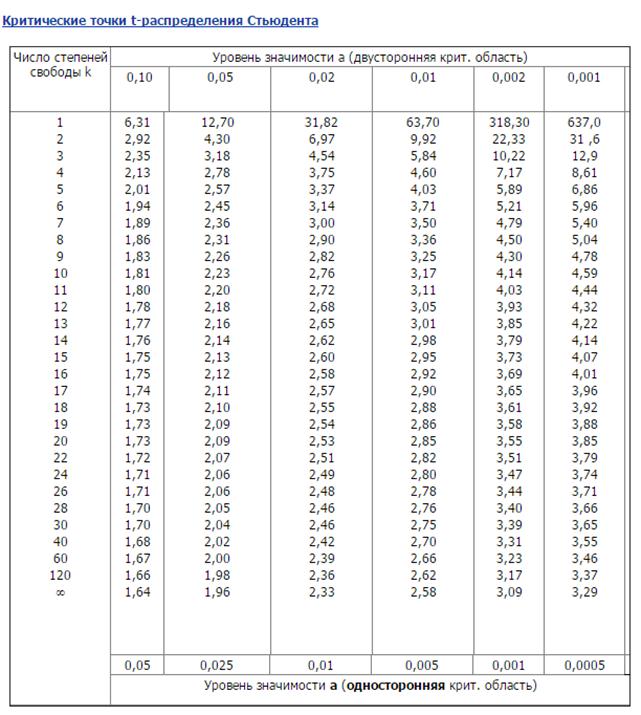
 Число степеней свободы, характеризующее распределение.
Число степеней свободы, характеризующее распределение. Для вероятности 0,05 и 10 степеней свободы двустороннее значение вычисляется по формуле СТЬЮДРАСПОБР(0,05;10) и равно 2,28139. Одностороннее значение для той же вероятности и числа степеней свободы может быть вычислено по формуле СТЬЮДРАСПОБР(2*0,05;10), возвращающей значение 1,812462.
Для вероятности 0,05 и 10 степеней свободы двустороннее значение вычисляется по формуле СТЬЮДРАСПОБР(0,05;10) и равно 2,28139. Одностороннее значение для той же вероятности и числа степеней свободы может быть вычислено по формуле СТЬЮДРАСПОБР(2*0,05;10), возвращающей значение 1,812462. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные. {n-k}$$
{n-k}$$ {–1}(P|N)$.
{–1}(P|N)$. {–1}(X)$$
{–1}(X)$$
 Значение t зависит от объема выборки, т. е. от величины N—1. Пользуясь этими таблицами, можно получить, например, что при 7V=20 и надежности 90% коэффициент i=l,73 при том же значении N и надежности 95%, 99%и 99,9% величина t будет соответственно равна 2,09, 2,86 и 3,88.
[c.72]
Значение t зависит от объема выборки, т. е. от величины N—1. Пользуясь этими таблицами, можно получить, например, что при 7V=20 и надежности 90% коэффициент i=l,73 при том же значении N и надежности 95%, 99%и 99,9% величина t будет соответственно равна 2,09, 2,86 и 3,88.
[c.72] 18—8.21. Более подробные таблицы можно найти в [7, 22, 46].
[c.460]
18—8.21. Более подробные таблицы можно найти в [7, 22, 46].
[c.460] Доверительный интервал выражается через среднее квадратическое отклонение, доверительная вероятность определяется по таблицам интеграла Лапласа (для закона нормального распределения) или, задаваясь доверительной вероятностью, определяют доверительные границы. Так, например, задаваясь 95%-ной вероятностью, считают доверительный интервал равным 4а, где а — среднее квадратическое отклонение результата измерения. При небольшом числе измерений доверительные интервалы и доверительную вероятность определяют, пользуясь распределением Стьюдента.
[c.131]
Доверительный интервал выражается через среднее квадратическое отклонение, доверительная вероятность определяется по таблицам интеграла Лапласа (для закона нормального распределения) или, задаваясь доверительной вероятностью, определяют доверительные границы. Так, например, задаваясь 95%-ной вероятностью, считают доверительный интервал равным 4а, где а — среднее квадратическое отклонение результата измерения. При небольшом числе измерений доверительные интервалы и доверительную вероятность определяют, пользуясь распределением Стьюдента.
[c.131] Если полученное значение /-статистики больше критического ( > то гипотезах значимости коэффициента fx xJ генеральной совокупности не отвергается.
[c.108]
Если полученное значение /-статистики больше критического ( > то гипотезах значимости коэффициента fx xJ генеральной совокупности не отвергается.
[c.108] 351]
351]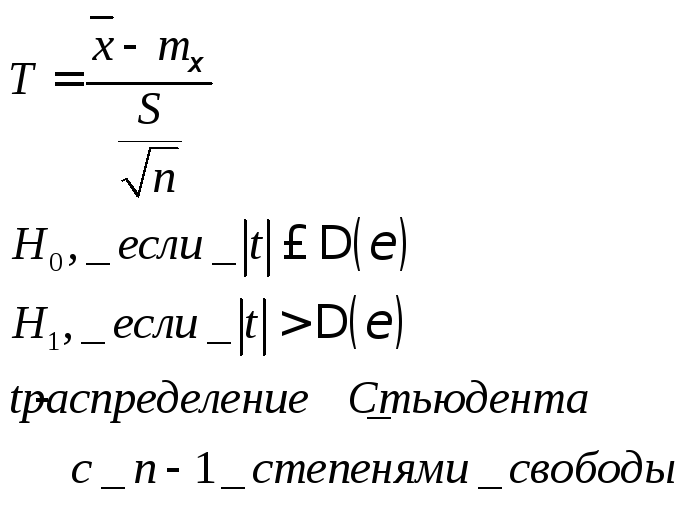 Таблицы распределения Стьюдента приведены, например, в [2, 4].
[c.534]
Таблицы распределения Стьюдента приведены, например, в [2, 4].
[c.534] 2.2).
[c.10]
2.2).
[c.10] Значения этих вероятностей при различных и приводятся в специальных таблицах (таблицы вероятностей по распределению Стьюдента). Так, например, вероятность того, что предельная ошибка малой выборки не превзойдет кpaтнyю среднюю ее ошибку равна (табл. 9).
[c.160]
Значения этих вероятностей при различных и приводятся в специальных таблицах (таблицы вероятностей по распределению Стьюдента). Так, например, вероятность того, что предельная ошибка малой выборки не превзойдет кpaтнyю среднюю ее ошибку равна (табл. 9).
[c.160]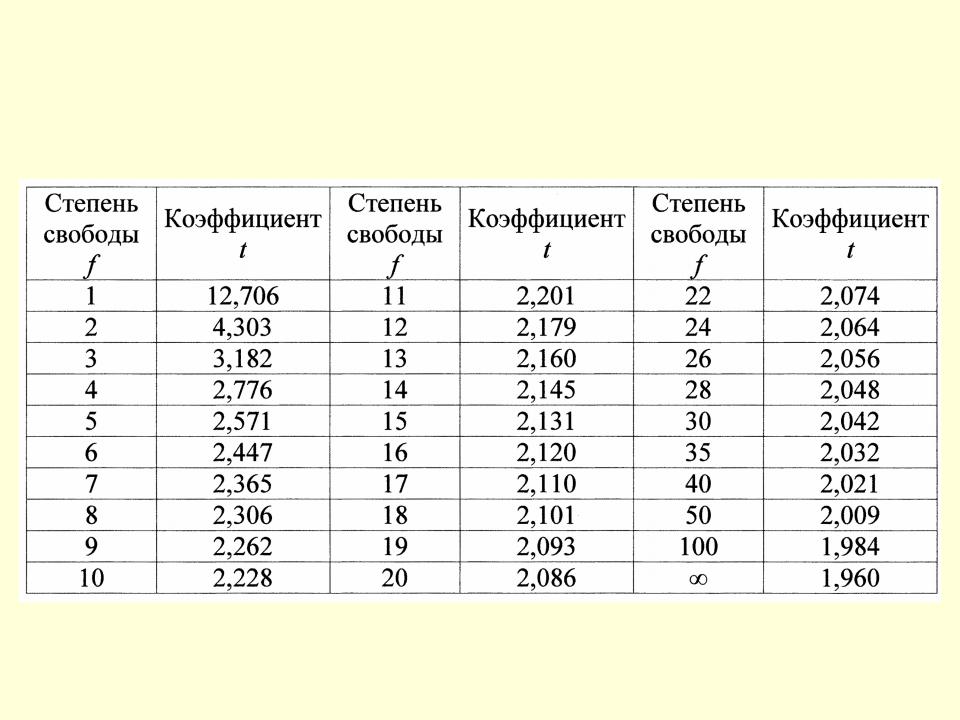 В частности, если резуль-паты наблюдений лишены систематич. ошибок, то х, = = О, и, значит, закону Стьюдента должны подчиняться отношения X, /si и iXal/sj. С помощью таблиц распределения Стьюдента с 1 — m = 8 степенями свободы можно убедиться, что если действительно х, = Хг = О, то с вероятностью 0,999 каждое пз этих отношений в отдельности не должно превосходить
[c.352]
В частности, если резуль-паты наблюдений лишены систематич. ошибок, то х, = = О, и, значит, закону Стьюдента должны подчиняться отношения X, /si и iXal/sj. С помощью таблиц распределения Стьюдента с 1 — m = 8 степенями свободы можно убедиться, что если действительно х, = Хг = О, то с вероятностью 0,999 каждое пз этих отношений в отдельности не должно превосходить
[c.352] 2.1 определяем вероятность нахождения случайной погрешности в заданном интервале. Таблица 2.1 предусматривает нормальный закон распредмения и бесконечно большое число измерений. Таблицей 2.1 можно пользоваться, как правило, когда число измерений более 30. При меньшем числе измерений следует пользоваться табл. 2.2, составленной для распределения Стьюдента.
[c.11]
2.1 определяем вероятность нахождения случайной погрешности в заданном интервале. Таблица 2.1 предусматривает нормальный закон распредмения и бесконечно большое число измерений. Таблицей 2.1 можно пользоваться, как правило, когда число измерений более 30. При меньшем числе измерений следует пользоваться табл. 2.2, составленной для распределения Стьюдента.
[c.11]





 Мы бы назвали t-статистику t 0.05
Мы бы назвали t-статистику t 0.05  Калькулятор.Оба подхода представлены ниже. Решение А - традиционное
подход. Это требует, чтобы вы вычислили статистику t на основе данных, представленных в
описание проблемы. Затем вы используете Калькулятор Т-распределения, чтобы найти
вероятность. Решение B проще. Вы просто вводите данные о проблеме в
Калькулятор Т-распределения. Калькулятор вычисляет t-статистику "за
сцены "и отображает вероятность. Оба подхода дают точную
тот же ответ.
Калькулятор.Оба подхода представлены ниже. Решение А - традиционное
подход. Это требует, чтобы вы вычислили статистику t на основе данных, представленных в
описание проблемы. Затем вы используете Калькулятор Т-распределения, чтобы найти
вероятность. Решение B проще. Вы просто вводите данные о проблеме в
Калькулятор Т-распределения. Калькулятор вычисляет t-статистику "за
сцены "и отображает вероятность. Оба подхода дают точную
тот же ответ. Затем вводим следующие данные:
Затем вводим следующие данные: Предположим, случайным образом выбраны и протестированы 20 человек. Стандартное отклонение в
группа выборки - 15. Какова вероятность того, что средний результат теста в
группа выборки будет максимум 110?
Предположим, случайным образом выбраны и протестированы 20 человек. Стандартное отклонение в
группа выборки - 15. Какова вероятность того, что средний результат теста в
группа выборки будет максимум 110?

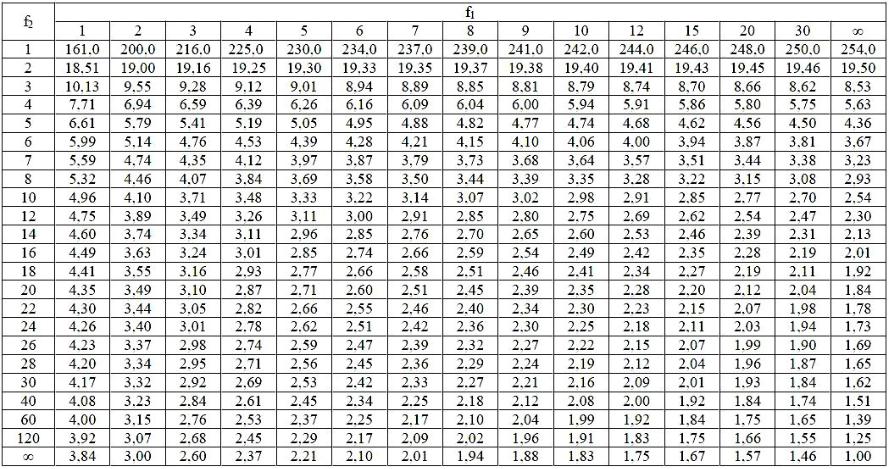 Кривые с большим количеством степеней свободы выше и имеют более тонкие хвосты. Все три дистрибутива t- имеют «более тяжелые хвосты», чем z-распределение.
Кривые с большим количеством степеней свободы выше и имеют более тонкие хвосты. Все три дистрибутива t- имеют «более тяжелые хвосты», чем z-распределение.
 Кривая снова представляет собой распределение t- с 21 степенью свободы. Для одностороннего теста значение из распределения t- с α = 0,05 составляет 1,721. Вы отклоняете нулевую гипотезу, если тестовая статистика превышает контрольное значение. Если статистика теста ниже контрольной линии, значит, вы не можете отклонить нулевую гипотезу.
Кривая снова представляет собой распределение t- с 21 степенью свободы. Для одностороннего теста значение из распределения t- с α = 0,05 составляет 1,721. Вы отклоняете нулевую гипотезу, если тестовая статистика превышает контрольное значение. Если статистика теста ниже контрольной линии, значит, вы не можете отклонить нулевую гипотезу. Если вы установите α = 0.05 для двустороннего теста и иметь только одностороннюю таблицу, затем используйте столбец для α = 0,025.
Если вы установите α = 0.05 для двустороннего теста и иметь только одностороннюю таблицу, затем используйте столбец для α = 0,025. Что означает «свободно варьироваться»? Вот пример с использованием среднего (среднего):
Что означает «свободно варьироваться»? Вот пример с использованием среднего (среднего):  Степеней свободы в этом случае:
Степеней свободы в этом случае:
 Поскольку степени свободы определены выше как n-1, вы могли бы подумать, что критическое значение t тоже должно увеличиться, но это не так: они становятся меньше . Это кажется нелогичным.
Поскольку степени свободы определены выше как n-1, вы могли бы подумать, что критическое значение t тоже должно увеличиться, но это не так: они становятся меньше . Это кажется нелогичным. Вы измеряете их вес, вычисляете среднюю разницу между парами образцов и повторяете этот процесс снова и снова.Крошечный размер выборки 4 приведет к t-распределению с жирными хвостами. Жирные хвосты говорят о том, что в вашей выборке вероятнее всего будут экстремальные значения. Вы проверяете свою гипотезу на уровне альфа 5%, который отсекает последние 5% вашего распределения . На графике ниже показано t-распределение с отсечкой 5%. Это дает критическое значение 2,6. ( Примечание : я использую здесь гипотетическое t-распределение в качестве примера - CV не является точным).
Вы измеряете их вес, вычисляете среднюю разницу между парами образцов и повторяете этот процесс снова и снова.Крошечный размер выборки 4 приведет к t-распределению с жирными хвостами. Жирные хвосты говорят о том, что в вашей выборке вероятнее всего будут экстремальные значения. Вы проверяете свою гипотезу на уровне альфа 5%, который отсекает последние 5% вашего распределения . На графике ниже показано t-распределение с отсечкой 5%. Это дает критическое значение 2,6. ( Примечание : я использую здесь гипотетическое t-распределение в качестве примера - CV не является точным).
 3: Доверительный интервал для совокупности Стандартное отклонение неизвестно, случай малой выборки
3: Доверительный интервал для совокупности Стандартное отклонение неизвестно, случай малой выборки