Уравнения математической физики, с примерами
Дифференциальные уравнения математической физики
Математические модели естественнонаучных явлений и процессов зачастую представляют собой задачи, содержащие дифференциальные уравнения с частными производными первого и второго порядков. Дифференциальные уравнения существенные для физики, механики техники называют дифференциальными уравнениями математической физики.
Каждое уравнение математической физики описывает бесконечное множество качественно аналогичных явлений или процессов, так как дифференциальные уравнения, которыми занимается математическая физика, имеют бесконечное множество частных решений. Конкретное решение, описывающее рассматриваемое физическое явление, выделяется из множества частных решений с помощью начальных и граничных условий.
Общий вид дифференциального уравнения в частных производных первого порядка относительно неизвестной искомой функции таков:
Если F является линейной функцией относительно старших производных, то есть:
данное уравнение называется квазилинейным дифференциальным уравнением.
Если функции не зависят от u, а зависимость P от u линейна, то есть , тогда уравнение (2) называется линейным. Если , то уравнение (2) называется однородным линейным дифференциальным уравнением в частных производных первого порядка.
Решений уравнений математической физики
Рассмотрим квазилинейное дифференциальное уравнение в частных производных первого порядка:
Для получения общего решения уравнения (3) рассматривают характеристическую систему обыкновенных дифференциальных уравнений:
Если с=0, то система сводится к одному уравнению .
Если общий интеграл уравнения, тогда – общее решение.
Само дифференциальное уравнение содержит в себе только самую общую информацию об описываемом процессе. Необходимо задание начальных и граничных условий, для конкретизации.
Дифференциальные уравнения математической физики второго порядка
Большое количество процессов и явлений в физике описывается с помощью дифференциальных уравнений второго порядка в частных производных, это связано с тем, что фундаментальные законы физики – законы сохранения – записываются в терминах вторых производных. Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов.
Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов.
Рассмотрим линейное уравнение с частными производными второго порядка с двумя независимыми переменными:
где a, b, c некоторые функции от x, y, имеющие непрерывные производные до второго порядка включительно.
Уравнение (5) принадлежит в точке (x, y)
- параболическому типу, если Канонический вид такого уравнения:
где — независимые переменные. Кроме того — дважды дифференцируемая функция в рассматриваемой области. Уравнение (6) так же как и уравнение теплопроводности имеет только один член высшей производной.
- гиперболическому типу, если Канонический вид такого уравнения:
первая каноническая форма:
где — независимые переменные,
вторая каноническая форма:
где .
 Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.
Левая часть уравнения (8) полностью совпадает с частью волнового уравнения. - эллиптическому типу, если Канонический вид такого уравнения:
где — независимые переменные. Левая часть этого уравнения совпадает с левой частью уравнения Лапласа.
Для того чтобы привести уравнение (5) к каноническому виду, надо записать так называемое характеристическое уравнение (10):
которое распадается на два уравнения:
и найти их общие интегралы.
В общем случае линейное уравнение с частными производными второго порядка параболического типа с n независимыми переменными можно записать так:
где
Уравнения параболического типа описывают неустановившиеся тепловые, диффузионные процессы, которые зависят от времени.
Уравнение (13) называют однородным, если =0.
Довольно часто при решении уравнения (13) ставят так называемую задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию:
В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию:
В общем случае — линейный дифференциальный оператор первого порядка по пространственным переменным, коэффициенты которого зависят от x и t.
Начальное условие называют однородным, если f(x)=0. Граничное условие называют однородным, если .
В общем случае линейное уравнение с частными производными второго порядка гиперболического типа с n независимыми переменными можно записать так:
где линейный дифференциальный оператор определен формулам (14). Уравнениями гиперболического типа описываются неустановившиеся волновые процессы, зависящие от времени.
При решении уравнения (15) ставят задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (15) (при и начальным условиям:
Граничные условия задаются (14).
Уравнения эллиптического типа
В общем случае линейное уравнение с частными производными второго порядка эллиптического типа с n независимыми переменными можно записать в виде:
где
Уравнения эллиптического типа описывают установившиеся тепловые, диффузионные и другие процессы, которые не зависят от времени. Уравнение (18) называется однородным, если
Уравнение (18) называется однородным, если
Граничные условия для эллиптического уравнения записывают так:
В общем случае — линейный дифференциальный оператор первого порядка.
Наиболее часто в прикладных примерах при описании различных процессов, происходящих в изотропных средах коэффициенты
таковыми и мы будем считать коэффициенты .
Для любых уравнений в частных производных второго порядка в зависимости от вида граничных условий принято выделять четыре типа краевых задач.
Первая краевая задача. На границе области S функция w(x,t) принимает заданные значения:
Вторая краевая задача. На границе области S задается производная по (внешней) нормали:
Третья краевая задача. На границе области S задана линейная связь между искомой функцией и ее производной по нормали:
Чаще всего В задачах массопереноса, где w – концентрация, граничное условие (22) при описывает поверхностную химическую реакцию.
Смешанные краевые задачи. В этом случае на различных участках границы S задают различные граничные условия.
Методы решения уравнений математической физики
Все методы решения уравнений математической физики можно разделить на две большие группы:
- аналитические методы решения уравнений, которые основаны на сведении уравнения в частных производных к обыкновенному или системе обыкновенных уравнений;
- численные методы решения (с помощью ЭВМ).
Среди аналитических методов решения уравнений следует выделить:
- Метод характеристик.
- Метод разделения переменных.
- Метод Фурье.
- Метод Деламбера.
- Метод интегральных преобразований.
- Преобразование Лапласа.
- Представление решений через функцию Грина.
Среди численных методов решения уравнений математической физики следует выделить:
- метод сеток;
- метод конечных разностей;
- методы расщепления: метод переменных направлений, метод дробных шагов;
- методы Эйлера;
- методы Рунге-Кутта;
- метод Адамса;
- символьно-численный метод.

Примеры решения задач
Уравнения и формулы физики — макеты
Физика заполнена уравнениями и формулами, которые имеют дело с угловым движением, двигателями Карно, жидкостями, силами, моментами инерции, линейным движением, простым гармоническим движением, термодинамикой, работой и энергией.
Вот список некоторых важных физических формул и уравнений, которые следует держать под рукой, упорядоченных по темам, чтобы вам не приходилось искать их.
Угловое движение
Уравнения углового движения применимы везде, где есть вращательные движения вокруг оси. Когда объект повернулся на угол θ с угловой скоростью ω и угловым ускорением α , то вы можете использовать эти уравнения, чтобы связать эти значения вместе.
Для измерения угла необходимо использовать радианы. Кроме того, если вы знаете, что расстояние от оси равно r, , то вы можете вычислить пройденное линейное расстояние, с , скорость, v , центростремительное ускорение, a c и силу , Ф с . Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.
Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.
Двигатели Карно
Тепловая машина берет тепло Q h от высокотемпературного источника при температуре T h и перемещает его к низкотемпературному стоку (температура T 9 0 ) по курсу Q c и при этом выполняет механическую работу, W . (Этот процесс можно обратить вспять, так что можно выполнить работу по перемещению тепла в противоположном направлении — тепловой насос.) Количество выполненной работы пропорционально количеству тепла, извлеченного из источника тепла, является КПД двигателя. Двигатель Карно является обратимым и имеет максимально возможный КПД, определяемый следующими уравнениями. Эквивалентом эффективности теплового насоса является коэффициент полезного действия.
Жидкости
Объем А, В , жидкости с массой, м , имеет плотность, ρ . Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт вода вытесненные , создают направленную вверх выталкивающую силу, F плавучесть . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости.
Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт вода вытесненные , создают направленную вверх выталкивающую силу, F плавучесть . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости.
Сил
Масса А, м , ускоряется со скоростью, a , из-за силы, F , действующей. Силы трения, F F , пропорциональны нормальной силе между материалами, F Н , с коэффициентом трения мк. Две массы, M 1 и M 2 , разделенные на расстояние, R , притягивает друг друга гравитационной силой, приведенным следующим уравнением, в продовольственных гравитационная постоянная Г :
Две массы, M 1 и M 2 , разделенные на расстояние, R , притягивает друг друга гравитационной силой, приведенным следующим уравнением, в продовольственных гравитационная постоянная Г :
Моменты инерции
Вращательный эквивалент массы — это инерция, I , , которая зависит от того, как масса объекта распределена в пространстве. Здесь показаны моменты инерции для различных форм:
Диск, вращающийся вокруг своего центра:
Полый цилиндр, вращающийся вокруг своего центра: I = mr 2
Полая сфера, вращающаяся с осью, проходящей через ее центр:
Обруч, вращающийся вокруг своего центра: I = mr 2
Точечная масса, вращающаяся на радиусе r: I = mr 2
Прямоугольник, вращающийся вокруг оси вдоль одного края, где другой край имеет длину r :
Прямоугольник, вращающийся вокруг оси, параллельной одному краю и проходящей через центр, где длина другого края равна г :
Стержень, вращающийся вокруг оси, перпендикулярной ему и проходящей через его центр:
Стержень, вращающийся вокруг оси, перпендикулярной ей и через один конец:
Сплошной цилиндр, вращающийся вокруг оси вдоль ее центральной линии:
Кинетическая энергия вращающегося тела с моментом инерции I и угловой скоростью ω :
Угловой момент вращающегося тела с моментом инерции, I , а угловая скорость ω :
Линейное движение
Когда объект в положении x движется со скоростью v , и ускорением a, в результате перемещения s , каждый из этих компонентов связан следующими уравнениями:
Простое гармоническое движение
Определенные виды силы приводят к периодическому движению, когда объект повторяет свое движение с периодом, T , с угловой частотой ω, и амплитудой A . Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.
Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.
Термодинамика
Беспорядочные колебательные и вращательные движения молекул, составляющих объект вещества, обладают энергией; эта энергия называется тепловая энергия. Когда тепловая энергия перемещается из одного места в другое, она называется теплотой, Q . Когда объект получает некоторое количество тепла, его температура T , повышается.
Кельвина ( K ), Цельсия ( C ) и Фаренгейта (F ) — это температурные шкалы. Вы можете использовать эти формулы для преобразования одной температурной шкалы в другую:
Теплота, необходимая для изменения температуры массы, m , увеличивается с константой пропорциональности, c , называется удельной теплоемкостью. В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:
В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:
Давление, P , и объем, V , из n молей идеального газа при температуре T определяется по этой формуле, где R — газовая постоянная:
В идеальном газе средняя энергия каждой молекулы KE avg пропорциональна температуре с постоянной Больцмана k :
Работа и энергия
Когда сила, F , перемещает объект на расстояние с , которое находится под углом Θ ,затем работа, W , выполнена. Импульс p является произведением массы m , и скорости v . Энергия, которой объект обладает благодаря своему движению, называется KE .
часто используемых уравнений – Гиперучебник по физике
[закрыть]
Механика
| уравнения движения |
|---|
| v = v 0 + at s = s 0 + v 0 t + 1 9 2 | 5 at
| работа | |||
|---|---|---|---|
| Вт = F ∆ с cos θ | |||
|
| питание | |||
|---|---|---|---|
| |||
|
| уравнения вращения |
|---|
| θ = θ 0 + ω 0 t + ½α t 2 ω 2 = ω 0 2 + 2α(θ − θ 0 ) ω = 1/2 (ω 6 6 0 900) 8 |
| крутящий момент |
|---|
| τ = rF sin θ |
| τ = r × F |
Теплофизика
| КПД | 9 | 9 904 0519 η реальный = 1 − | Q C |
|---|
| Q H |
| ? 15 Т С |
| T H |
c. Периметр треугольника 5 класс: Как найти периметр треугольника 🔺 формула нахожденияМерзляк 5 класс — § 14. Треугольник и его виды
Вопросы к параграфу1. Какие бывают виды треугольников в зависимости от вида их углов?
2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?
3. Какие бывают виды треугольников в зависимости от количества равных сторон?
4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?
5. Как называют стороны равнобедренного треугольника?
6. По какой формуле вычисляют периметр равностороннего треугольника? — Периметр равностороннего треугольника равен произведению числа 3 и длины его стороны : P = 3a. Решаем устно1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см? 8 • 4 = 32 (см) — периметр восьмиугольника. Ответ: 32 см. 2. Вычислите сумму 27 + 16 + 33 + 24. 27 + 16 + 33 + 24 = (27 + 33) = (16 + 24) = 60 + 40 = 100 Ответ: 100. 3. Каких чисел не хватает в цепочке вычислений? 4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале? 1) Мы знаем, что вначале на всех кустах было 15 роз, но потом на одной розе распустилось ещё 3 цветка: 15 + 3 = 18 (цветов) — стало на всех кустах в конце. 2) Мы знаем, что в конце на каждом из трёх кустов роз было поровну: 18 : 3 = 6 (цветов) — было на каждом кусте в конце. 3) Мы знаем, что на одном из кустов роз вначале было на 3 меньше: 6 — 3 = 3 (цветка) — было на одном из кустов вначале. 4) Мы знаем, что количество роз на остальных кустах не изменилось, то есть было и осталось по 6 цветков. Ответ: 6, 6 и 3 розы. Упражнения338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.
339. Начертите:
340. Начертите:
341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см. Периметр треугольника равен сумме длин все его сторон. P = 16 + 22 + 28 = 66 (см) Ответ: P = 66 см. 342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см. Периметр треугольника равен сумме длин все его сторон. P = 14 + 17 + 17 = 48 (см) Ответ: P = 48 см. 343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника. Начертим произвольный треугольник ABC. При помощи линейки измерим длины его сторон:
При помощи транспортира измерим его углы:
Найдём периметр треугольника ABC: P = AB + BC + AC =4,2 + 3,2 + 4,6 = 12 (см) ∠A + ∠B + ∠C = 42º + 74º + 64º = 180º Ответ: в треугольнике ABC: AB = 4,2 см, BC = 3,2 см, AC = 4,6 см, ∠A = 42º, ∠B = 74º, ∠C = 64º, периметр P = 12 см, сумма углов равна 180º. 344. Одна сторона треугольника равна 24 см, вторая сторона — на 18 см больше первой, а третья сторона — в 2 раза меньше второй. Найдите периметр треугольника. 1) 24 + 18 = 42 (см) — длина второй стороны треугольника. 2) 42 : 2 = 21 (см) — длина третьей стороны треугольника. 3) 24 + 42 + 21 = 87 (см) — периметр треугольника. Ответ: P = 87 см. 345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья — на 8 см меньше второй. Найдите периметр треугольника. 1) 12 • 3 = 36 (см) — длина второй стороны треугольника. 2) 36 — 8 = 28 (см) — длина третьей стороны треугольника. 3) 12 + 36 + 28 = 78 (см) — периметр треугольника. Ответ: P = 78 см. 346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона — 8 см. У равнобедренного треугольника боковые стороны равны. Значит у данного треугольника дву стороны по 8 см и одна сторона (основание) — 13 см. 8 + 8 + 13 = 29 (см) — периметр треугольника. Ответ: 29 см. 2) Периметр равнобедренного треугольника равен 39 см, а основание — 15 см. Найдите боковые стороны треугольника. Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину боковой стороны: (39 — 15) : 2 = 24 : 2 = 12 (см) — длина боковой стороны. Ответ: Каждая из двух боковых сторон этого равнобедренного треугольника равна 12 см. 347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона — 10 см. Найдите основание треугольника. Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину основания: 28 — 10 • 2 = 28 — 20 = 8 (см) — длина основания. Ответ: 8 см. 348. Периметр треугольника равен p см, одна сторона — 22 см, вторая сторона — b см. Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника: с = p — 22 — b (см) При р = 72, b = 26: с = 72 — 22 — 26 = 50 — 26 = 24 (см). Ответ: с = p — 22 — b, с = 24 см. 349. Периметр треугольника равен 97 см, одна сторона — а см, вторая — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26. Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника: с = 97 — а — b (см) При а = 32, b = 26: с = 97 — 32 — 26 = 65 — 26 = 39 (см). Ответ: с = 97 — а — b, с = 39 см. 350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если: 1) две стороны равны 3 см и 6 см, а угол между ними — 40° — разносторонний тупоугольный треугольник (тупым является угол B). 2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130° — разносторонний тупоугольный треугольник (тупым является угол А). 3) две стороны равны по 3 см 5 мм, а угол между ними — 54° — равнобедренный остроугольный треугольник 4) сторона АВ равна 4 см, а углы САВ и СВА соответственно равны 30° и 70° — разносторонний остроугольный треугольник. 5) сторона АВ равна 2 см 5 мм, а углы САВ и СВА соответственно равны 100° и 20° — разносторонний тупоугольный треугольник. 6) сторона ВС равна 5 см, а углы ABC и ВСА соответственно равны 30° и 60° — разносторонний прямоугольный треугольник. 7) сторона ВС равна 5 см 5 мм, а углы ABC и ВСА равны по 45° — равнобедренный прямоугольный треугольник. 8) сторона АС равна 5 см 5 мм, а углы ВАС и ВСА равны по 60° 351. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если: 1) две стороны равны 3 см и 4 см, а угол между ними — 90° — разносторонний прямоугольный треугольник. 2) две стороны равны по 4 см 5 мм, а угол между ними — 60° — равносторонний остроугольный треугольник. 3) сторона АС равна 6 см, а углы ВАС и ВСА соответственно равны 90° и 45° — равнобедренный прямоугольный треугольник. 4) сторона АВ равна 4 см 5 мм, а углы САВ и СВА соответственно равны 35° — равнобедренный тупоугольный треугольник. 352. Постройте треугольник, стороны которого содержат четыре точки, изображённые на рисунке 122. 353. Сколько треугольников изображено на рисунке 123?
Упражнения для повторения354. Запишите все углы, изображённые на рисунке 124, и укажите вид каждого угла.
355. 1) 17 ч 16 мин — 16 ч 48 мин = 16 ч 76 мин — 16 ч 48 мин = 28 мин — делал задание Миша. 2) 18 ч 20 мин — 17 ч 53 мин = 17 ч 80 мин — 17 ч 53 мин = 27 мин — делал задание Дима. 3) 28 мин — 27 мин = 1 мин — делал дольше Миша, чем Дима. Ответ: Миа делал домашнее задание на 1 минуту дольше, чем Дима. 356. Решите уравнение: 357. Вместо звёздочек поставьте цифры так, чтобы действие было выполнено правильно: Задача от мудрой совы358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык — 246 учеников, а английский и французский одновременно — 109 учеников. Сколько всего учеников учится в гимназии? 1) 328 — 109 = 219 (учеников) — изучает только английский язык. 2) 246 — 109 = 137 (учеников) — изучает только французский язык. 3) 219 + 109 + 137 = 465 (учеников) — всего в гимназии. Ответ: 465 учеников.
урок по теме «Треугольники и их виды» 5 класс | План-конспект урока по математике (5 класс):Слайд 1 Девиз урока: «Учиться можно весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Анатоль ФрансСлайд 2 Метапредмет – Изменение и развитие Знаешь ли ты? В истории математики известен такой случай. Однажды в Германии в конце XVIII в., для того чтобы заставить учеников поработать, учитель дал им задание – сложить все числа от 1 до 100. К аково же было его удивление, когда уже через несколько минут один из учеников сказал ответ: сумма равна 5050. Э тот ученик, Карл Фридрих Гаусс, впоследствии стал великим математиком. ИНТЕРЕСНО! Прозвенел звонок! Начинается урок! Слайд 4 Задание на внимание целеполагание На рисунке изображены равносторонние треугольники. Слайд 5 ТРЕУГОЛЬНИКИ И ИХ ВИДЫ Тема урока: 18.01 Целеполагание. Вхождение в тему Слайд 6 Треугольники и их виды Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника Периметр треугольника Узнать … … Освоить……. Закрепить……. Проверить……. Оценить…… Цели и задачи урока Слайд 7 Ключевое слово урока целеполагание Слайд 8 Выбрать среди геометрических фигур треугольники. Сколько углов имеет треугольник? Сколько сторон имеет треугольник? Как найти периметр треугольника? 1 2 3 4 5 6 Слайд 12 Анализ результатов проверочной работы Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Слайд 13 Классификация треугольников по сторонам равнобедренный разносторонний равносторонний Слайд 14 Классификация треугольников по сторонам Организация и самоорганизация учащихся. Организация обратной связи Слайд 15 Классификация треугольников по углам тупоугольный прямоугольный остроугольный Слайд 16 Классификация треугольников по углам Организация и самоорганизация учащихся. Организация обратной связи Слайд 17 Определить вид треугольника по градусной мере его углов Задание: соединить стрелочкой левый и правый столбики а) 45 0 , 45 0 , 90 0 б) 25 0 , 75 0 , 80 0 в) 120 0 , 30 0 , 30 0 г) 60 0 , 60 0 , 60 0 Слайд 18 Классификация треугольников по углам Организация и самоорганизация учащихся. Организация обратной связи Примеры треугольников Слайд 19 Виды треугольников Практикум Определите вид треугольника, углы которого равны: УЧЕБНИК № 4 06 ? тупоугольный а) 24 о , 137 о , 19 о ; ? прямоугольный б) 40 о , 50 о , 90 о ; ? остроугольный в) 35 о , 60 о , 85 о ; Слайд 20 Чертим треугольники Практикум а) Начертите на нелинованной бумаге прямоугольный треугольник, у которого стороны, образующие прямой угол, равны 3 см и 4 см. Слайд 21 Периметр треугольника Практикум а) Проволоку длиной 15 см согнули так, что получился равносторонний треугольник. Чему равен периметр этого треугольника? Чему равна его сторона? УЧЕБНИК № 528 периметр 15 см сторона 15 : 3 = 5 (см) Слайд 22 Периметр треугольника Практикум Вычислите периметр: УЧЕБНИК № 41 7 периметр 25 + 45 + 45 = 115 (мм) б) равнобедренного треугольника с основанием 25 мм и боковыми сторонами, равными 45 мм. Слайд 23 Периметр треугольника Проверка полученных результатов. Коррекция. В равнобедренном треугольнике периметр равен 36 см, а основание равно 10 см. найдите длину боковой стороны. УЧЕБНИК № 41 8 решение (36 – 10) : 2 = 13 (см) Слайд 24 Обсуждаем домашнее задание Вхождение в тему урока и создание условий для осознанного восприятия нового материала. б) Взяли проволоку длиной 17 см и из нее согнули треугольник, две стороны которого равны 5 см и 6 см. Слайд 25 Египетская цивилизация Подведение итогов, рефлексия, домашнее задание. Египетские пирамиды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес света» — пирамида Хеопса. Что представляют собой боковые грани этих пирамид? Где в жизни вы встречали подобные фигуры? Слайд 26 Подведем итоги Подведение итогов, рефлексия сегодня я узнал… было интересно… было трудно… я выполнял задания… я понял, что… теперь я могу… я почувствовал, что … я приобрел… я научился… у меня получилось … я смог… я попробую… меня удивило… урок дал мне для жизни… мне захотелось… Слайд 27 Подведение итогов, рефлексия, домашнее задание. Слайд 28 Существует ли треугольник с углами: а) 30 о , 60 о , 90 о ; б) 46 о , 160 о , 4 о ? 2) Найдите периметр треугольника, имеющего стороны 2 см 5 мм, 3 см, 4 см 7мм. 3) Может ли в треугольнике быть: а) два тупых угла; б) тупой и прямой углы? 4) Определите вид треугольника, а) если углы равны 40 0 , 50 0 , 90 0 ; б) если стороны равны 3 см, 5см, 3см? 5) В каком треугольнике сумма углов больше: в остроугольном или тупоугольном треугольнике? Проверка: а) да; б) нет. 2) 10 см 2 мм. а) нет; б) нет. 4) а) прямоугольный; б) равнобедренный. 5) Одинакова. Оценка: 8 верных ответов – 5 7,6 верных ответов – 4 4, 5 верных ответа — 3 Периметр треугольника: определение, формула, примеры, часто задаваемые вопросыЧто такое периметр треугольника? Периметр треугольника равен сумме всех его сторон. Другими словами, периметр треугольника — это общая длина его границы. Треугольник — это многоугольник, замкнутая двумерная фигура с тремя сторонами, тремя углами и тремя вершинами. Его периметр вычисляется путем сложения длин всех сторон. Периметр двумерной формы измеряется в линейных единицах измерения, таких как дюймы, футы, ярды и т. д. Родственные игрыПериметр треугольника: определениеПериметр треугольника можно определить как сумму всех сторон треугольника. Треугольник имеет три стороны. Периметр треугольника $=$ Сумма трех сторон треугольника. Давай выясним. Пусть a, b и c — длины трех сторон треугольника. Периметр треугольника $= a + b + c$ Как найти периметр треугольникаШаг 1: Запишите длины всех трех сторон данного треугольника. Убедитесь, что длины указаны в одних и тех же единицах измерения. Шаг 2: Добавьте длины трех сторон. Шаг 3: Сумма представляет собой периметр данного треугольника. Присвойте периметру ту же единицу, что и длину сторон. 9\circ)$ известен как равносторонний треугольник. Рассмотрим равносторонний треугольник ABC, длина каждой стороны которого равна a единиц. Периметр равностороннего треугольника $= a + a + a = 3a$ Итак, как найти периметр треугольника с тремя равными сторонами? Просто умножьте длину стороны на 3! Периметр равнобедренного треугольникаТреугольник с двумя равными сторонами известен как равнобедренный треугольник. Так как две стороны треугольника равны, мы имеем $a = b$ 92}$ Периметр равнобедренного прямоугольного треугольникаПрямоугольный треугольник, в котором основание и высота (два катета) имеют одинаковую длину, называется равнобедренным прямоугольным треугольником. Применение периметра треугольника Взгляните на треугольный парк. Предположим, нам нужно обнести его забором по внешней границе, нам нужно найти длину забора, необходимого для покрытия парка. Решенные примеры на периметр треугольника1. Найдите периметр равностороннего треугольника со стороной 6 дюймов. Решение: Сторона равностороннего треугольника $= a = 6$ дюймов Периметр равностороннего треугольника $= 3a$ $=3 \times 6$ $= 1 8$ дюймов 2. Чему равен периметр равнобедренного треугольника, равные стороны которого равны 4 футам каждая, а неравная сторона равна 6 футам? Решение: Пусть равные стороны равны $a = 4$ футам, а неравные стороны равны $b = 6$ футам Периметр заданного равнобедренного треугольника $= 2a+b$ $=(2 \ раз 4)+ 6$ $= 14$ футов 3. Если периметр данного треугольника равен 34 футам, какова длина недостающей стороны? Решение: В $\Delta XYZ$ имеем $XY = 9$ футов $XZ = 12$ футов Периметр $= 34$ футов … задано Периметр треугольника $= XY + YZ + XZ$ $34 = 9 + 12 + YZ$ $34 = YZ + 21$ $YZ = 13$ футов 4. Решение: Периметр треугольника $PQR = PQ + QR + PR$ $40 = x + x + 4 + x + 6$ 92} = \sqrt{36+36} = \sqrt{72} = 6\sqrt{2}$ дюймов Периметр прямоугольного треугольника$ = b + p + h = 6 + 6 + 6\sqrt{2} = (12 + 6\sqrt{2})$ дюймов Практические задачи на периметр треугольника1Каков периметр $\Delta ABC$?12 единиц 10 единиц 8 единиц 7 единиц Правильный ответ: 10 единиц Периметр равностороннего треугольника равен 45 дюймам. Чему равна сторона треугольника?22,5 дюйма 25 дюймов 15 дюймов 9 дюймов Правильный ответ: 15 дюймов Если периметр разностороннего треугольника равен 32 футам. Если две стороны равны 12 футам и 7 футам, то чему равна третья сторона? Если две стороны равны 12 футам и 7 футам, то чему равна третья сторона?13 футов 10 футов 27 футов 20 футов Правильный ответ: 13 футов Найдите периметр прямоугольного равнобедренного треугольника, две стороны которого равны 4 дюймам каждая.$(4 + 4\sqrt{2})$ дюймов $32\sqrt{2}$ дюймов $12\sqrt{2}$ дюймов 92} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2}$ дюймов Часто задаваемые вопросы о периметре треугольникаВ чем разница между площадью и периметром? Площадь — это область, ограниченная сторонами 2D-фигуры, тогда как периметр — это общая длина границы фигуры. По какой формуле находится площадь треугольника? Площадь треугольника $= \frac{1}{2} \× основание \× высота$ Чему равен полупериметр треугольника? Полупериметр — это половина периметра треугольника. Если стороны треугольника равны a, b и c, то полупериметр $= \frac{a + b + c}{2}$ Периметр треугольника ⭐ Формула, определение, примеры, факты
Добро пожаловать в Brighterly, где наша миссия состоит в том, чтобы сделать математику увлекательной и увлекательной для детей всех возрастов! Сегодня мы исследуем увлекательный мир геометрии, сосредоточившись на периметре треугольника. Каков периметр треугольника?Периметр любой формы относится к общей длине ее внешних краев. В случае треугольника периметр равен сумме длин трех его сторон. Треугольники бывают разных типов, включая разносторонние, равнобедренные, равносторонние и прямоугольные треугольники. В зависимости от типа треугольника способ вычисления его периметра может незначительно отличаться. Продолжайте читать, чтобы узнать, как найти периметр треугольника и формулы для каждого типа треугольника! Как найти периметр треугольника? Найти периметр треугольника очень просто! Все, что вам нужно сделать, это сложить длины его трех сторон. Формула периметра треугольникаОбщая формула для нахождения периметра треугольника: где ‘a’, ‘b’ и ‘c’ представляют длины из сторон треугольника. Эта формула применима ко всем типам треугольников, но некоторые определенные типы треугольников обладают уникальными свойствами, которые могут упростить вычисления. Давайте изучим формулы для каждого типа треугольника! Периметр разностороннего треугольникаРазносторонний треугольник имеет три стороны разной длины. Чтобы найти периметр разностороннего треугольника, просто используйте общую формулу: Периметр равнобедренного треугольника У равнобедренного треугольника две стороны одинаковой длины. , где «a» — длина равных сторон, а «b» — длина оставшейся стороны. Периметр равностороннего треугольникаУ равностороннего треугольника три стороны одинаковой длины. Следовательно, формула для его периметра: , где «а» — длина каждой стороны. Периметр прямоугольного треугольникаВ прямоугольном треугольнике один угол равен 90 градусов. Чтобы найти его периметр, вы можете использовать общую формулу: Однако, если у вас есть только длины двух катетов (сторон, прилегающих к прямому углу), вы можете использовать по теореме Пифагора найти длину гипотенузы (стороны, противоположной прямому углу): Затем можно рассчитать периметр по общей формуле. Периметр равнобедренного прямоугольного треугольника Равнобедренный прямоугольный треугольник имеет один угол в 90 градусов и две равные стороны. Затем вычислить периметр по общей формуле. Периметр равнобедренного, равностороннего и разностороннего треугольникаВ качестве резюме, вот формулы для нахождения периметра равнобедренного, равностороннего и разностороннего треугольника:
Помните об этих формулах, когда мы рассмотрим несколько примеров ниже! Примеры периметра треугольникаДавайте рассмотрим несколько примеров, которые помогут вам понять, как найти периметр треугольника:
Практические вопросы по периметру треугольника
ЗаключениеМы надеемся, что это подробное руководство по периметру треугольника не только помогло вам понять концепцию, но и вдохновило на новое понимание геометрии. В Brighterly мы считаем, что практика — это ключ к раскрытию вашего полного потенциала. Поэтому не стесняйтесь решать другие задачи и применять формулы для каждого типа треугольника. Продолжая оттачивать свои навыки, вы скоро станете мастером вычисления периметров треугольников и будете готовы решать еще более сложные математические задачи! Помните, обучение должно быть радостным путешествием, и мы в Brighterly стремимся сделать это путешествие как можно более приятным и увлекательным. Продолжайте исследовать, оставайтесь любопытными и, самое главное, получайте удовольствие! Часто задаваемые вопросы о периметре треугольникаЧто такое периметр треугольника? Периметр треугольника представляет собой общую длину его внешних сторон или сумму длин трех его сторон. Как найти периметр треугольника?Чтобы найти периметр треугольника, нужно сложить длины трех его сторон. Способ вычисления периметра может незначительно различаться в зависимости от типа треугольника (разносторонний, равнобедренный, равносторонний или прямоугольный). Для каждого типа треугольника существует определенная формула, по которой можно вычислить периметр:
Какова формула периметра треугольника? Общая формула для периметра треугольника: Задачник по алгебре: ГДЗ по алгебре 7 класс Мордкович (Решебник задачника)Алгебра. Задачник-тренажёр. 7 класс Бунимович и др.
Линия УМК: Алгебра. «Сферы» (7-9) Серия: Сферы Автор: Бунимович и др. 340,00 ₽ Количество: Аннотация Задачник-тренажёр является составной частью УМК Алгебра. «Сферы» (7-9) для 7 класса. Издание подготовлено в соответствии с Федеральным государственным образовательным стандартом основного общего образования.
Главной особенностью тетради является распределение заданий по видам деятельности внутри каждой главы, что позволяет учителю эффективно формировать требуемые умения и навыки, а также развивать познавательную деятельность учащихся.
Оставьте отзыв первым Алгебра 8 Мордкович ЗАДАЧНИК 2020Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями. Ознакомительная версия с цитатами из учебника для принятия решения о покупке книги: Алгебра. 8 класс. Учебник для учащихся общеобразовательных организаций. В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). В учебных целях представлены цитаты из второй части учебника, который содержит практический материал. Подбор и последовательность разноуровневых упражнений и их значительный объём позволяют школьнику освоить предмет, а учителю построить индивидуальную образовательную траекторию обучения для каждого учащегося. Во всех параграфах упражнения сгруппированы по двум блокам. Первый — до черты — содержит задания двух базовых уровней: устные (полу-устные) и задания среднего уровня сложности (слева от номеров таких заданий поставлен специальный значок). Второй блок — после черты — содержит задания выше среднего уровня и задания повышенной сложности. Задачи на повторение Упр. 1 — 34 Упр. 35 — 68 ГЛАВА 1. АЛГЕБРАИЧЕСКИЕ ДРОБИ§ 1. Основные понятия. Упр. 1.1 — 1.41 § 2. § 3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Упр. 3.1 — 3.29 § 4. Сложение и вычитание алгебраических дробей с разными знаменателями. Упр. 4.1 — 4.23 Упр. 4.24 — 4.56 § 5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Упр. 5.1 — 5.46 § 6. Преобразование рациональных выражений. Упр. 6.1 — 6.24 § 7. Первые представления о рациональных уравнениях. Упр. 7.1 — 7.40 § 8. Степень с отрицательным целым показателем. Упр. 8.1 — 8.32 § 9. Комбинаторные и вероятностные задачи. Дерево вариантов и правило нахождения вероятности. Упр. 9.1 — 9.7 Домашняя контрольная работа № 1 (с решениями) ГЛАВА 2. ФУНКЦИЯ у = √x.  СВОЙСТВА КВАДРАТНОГО КОРНЯ СВОЙСТВА КВАДРАТНОГО КОРНЯ§ 10. Рациональные числа. Упр. 10.1 — 10.29 § 11. Понятие квадратного корня из неотрицательного числа. Упр. 11.1 — 11.43 § 12. Иррациональные числа. Упр. 12.1 — 12.17 § 13. Множество действительных чисел. Упр. 13.1 — 13.22 § 14. Функция у = √x, её свойства и график. Упр. 14.1 — 14.32 § 15. Свойства квадратных корней. Упр. 15.1 — 15.36 § 16. Преобразование выражений содержащих операцию извлечения квадратного корня. Упр. 16.1 — 16.50 Упр. 16.51 — 16.99 § 17. Модуль действительного числа. Упр. 17.1 — 17.44 § 18. Комбинаторные и вероятностные задачи. Правило умножения. Упр. 18.1 — 18.7 Домашняя контрольная работа № 2 (с решениями) ГЛАВА 3. КВАДРАТИЧНАЯ ФУНКЦИЯ.  2 + bх + с, её свойства и график. Упр. 24.1 — 24.55 2 + bх + с, её свойства и график. Упр. 24.1 — 24.55 § 25. Графическое решение квадратных уравнений. Упр. 25.1 — 25.24 § 26. Комбинаторные и вероятностные задачи к главе 3. Упр. 26.1 — 26.7 Домашняя контрольная работа № 3 (с решениями). ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ § 27. Основные понятия. Упр. 27.1 — 27.39 § 28. Формулы корней квадратных уравнений. Упр. 28.1 — 28.48 § 29. Рациональные уравнения. Упр. 29.1 — 29.28 § 30. Рациональные уравнения как математические модели реальных ситуаций. Упр. 30.1 — 30.45 § 31. Ещё одна формула корней квадратного уравнения. Упр. 31.1 — 31.28 § 32. Теорема Виета и её применения. Упр. 32.1 — 32.55 § 33. Иррациональные уравнения. Упр. 33.1 — 33. § 34. Комбинаторные и вероятностные задачи к главе 4. Упр. 34.1 — 34.7 Домашняя контрольная работа № 4 (с решениями). ГЛАВА 5. НЕРАВЕНСТВА § 35. Числовые неравенства. Упр. 35.1 — 35.65 § 36. Решение линейных неравенств. Упр. 36.1 — 36.37 § 37. Решение квадратных неравенств. Упр. 37.1 — 37.46 § 38. Приближённые значения действительных чисел. Упр. 38.1 — 38.11 § 39. Стандартный вид числа. Упр. 39.1 — 39.19 § 40. Комбинаторные и вероятностные задачи к главе 5. Упр. 40.1 — 40.7 Домашняя контрольная работа № 5 (с решениями). ИТОГОВОЕ ПОВТОРЕНИЕ
Вы смотрели: Ознакомительную версию с цитатами из учебника для принятия решения о покупке книги: Алгебра. 8 класс. Учебник для учащихся общеобразовательных организаций. Просмотров: 1 254 458 Искусство решения проблемЭти учебника по математике рекомендованы администраторами Искусства решения проблем и членами сообщества AoPS. Уровни чтения и математических способностей в общих чертах определяются следующим образом:
Более сложные темы часто остаются без назначенных выше уровней. Прежде чем добавлять какие-либо книги на эту страницу, просмотрите страницу AoPSWiki:Связывание книг. Содержание
Книги по предметамОбщее введение / несколько темНачало работы
АлгебраНачало работы
Промежуточный
Абстрактная алгебраУниверситетская
ИсчислениеНачало работы
Одиночная переменная (средний уровень)
Многомерное (коллегиальное)
АнализКоллегиальный
КомбинаторикаПриступая к работе
Промежуточный уровень
Олимпиада
Коллегиальный
ГеометрияНачало работы
Средний уровень
Олимпиада
Collegiate
ТопологияКоллегиальная
НеравенстваПромежуточный уровень
Олимпиада
Collegiate
Теория чиселНачало работы
Олимпиада
Collegiate
ТригонометрияНачало работы
Промежуточный
Олимпиада
Решение задачНачало работы
Средний уровень
Олимпиада
Общий интерес
Сборники задач для соревнований по математикеНачальная школа
Начало работы
Средний уровень
Олимпиада
Collegiate
См. также
© 2023 ООО «АоПС Инкорпорейтед» Неверное имя пользователя Войти в АоПС Имя пользователя: Пароль: Оставаться в системе Огромная книга задач по алгебре У. Майкла КеллиУ. Майкл Келли Оцените эту книгу Когда числа просто не складываются… По стопам успешного The Humongous Books of Calculus Problems , автор бестселлеров Майкл Келли взял типичную рабочую тетрадь по алгебре и сделал пометки на полях, добавив недостающие шаги и упростив концепции и решения. • Аннотации по всему тексту поясняют каждую задачу и заполняют пропущенные шаги, необходимые для достижения решения, что делает эту книгу непохожей ни на одну другую рабочую тетрадь по алгебре на рынке. Об автореАвтор написал множество книг по математике (например, «Полное руководство идиота по предварительному исчислению», «Полное руководство идиота по исчислению» (второе издание) и «Огромная книга задач по исчислению»).Его веб-сайт www.calculus-help.com посещает более тысячи уникальных посетителей в день, несмотря на то, что на нем есть нелестная анимация, на которой он танцует на своей свадьбе. (с обложки одной из его книг) Что вы думаете? Оцените эту книгу Поиск по тексту рецензии Показано 1–6 из 6 рецензий 7 ноября 2008 г. Я знаю, о чем вы думаете…. Я знаю, о чем вы думаете…. «»что за умник!! вы действительно читаете эту книгу?!?!?!!»» хорошо, я говорю «да, я» эта книга, как следует из названия, ОГРОМНАЯ книга об алгебре I и II. В ней рассказывается об основных понятиях по обоим предметам и о том, как решать содержащиеся в ней задачи…. не волнуйтесь, эти книги облегчат жизнь людям, которые НЕ «ГОВОРЯТ» по математике.. лол эта книга специально создана за ВАС !!! Если вы любите математику и хотите расширить свои знания и углубить свой маленький ум, попробуйте эту книгу… 🙂 *****
22 января 2013 г. Для меня эта книга стала хорошим освежением давно утраченных навыков алгебры. Я не использовал его для сдачи каких-либо экзаменов, а скорее для самообучения в попытке в конечном итоге добраться до исчисления и дифференциальных уравнений. Я не могу поставить отзыв на 5 звезд, потому что в нем около десятка ошибок, которые читателю в большинстве своем легко уловить.
Lisa 794 отзыва17 подписчиков 1 апреля 2012 г. Определенно огромное количество задач по алгебре, но все же не содержит всех типов задач, которые вы могли видеть в алгебре 1 или 2. Наиболее примечательно не хватает словесных задач.
30 июля 2013 г. Эта книга действительно огромна, но она немного вводит в заблуждение. Он имеет много письменного содержания. То, что я искал, было просто набором практических задач. Как сделать из пнг джипег: Конвертировать PNG в JPEG онлайн — ConvertioPNG в JPG – Конвертация PNG-изображений в JPEGЗАГРУЗИТЬ Перетащите файлы сюда. Файлы PNG и JPG — это форматы изображений. Они очень похожи тем, что содержат данные изображения, например, фотографии. Однако каждый из них имеет свою индивидуальность. Файлы с окончанием .PNG — это файлы изображений, специально разработанные для передачи без потерь через Интернет. Файлы PNG лишены некоторых атрибутов, которые делают их пригодными для печати, в частности, они не поддерживают цветовые пространства CMYK. По сути, файлы PNG предназначены для того, чтобы отлично выглядеть на мониторах компьютеров и смартфонов, а не на бумаге. Между тем, файлы с окончанием .JPG или .JPEG немного отличаются. Файлы JPG, в отличие от файлов PNG, сжимаются, что приводит к некоторой потере качества изображения. Вы можете выбрать, насколько сильно вы хотите снизить качество изображения, что, в свою очередь, уменьшает его размер. Почему вы должны конвертировать PNG в JPG?Если у вас есть файл PNG, вы не сможете сделать с ним некоторые вещи. Например, вы не сможете напечатать его профессионально. Поскольку файлы PNG не содержат информации о цвете CMYK, профессиональная типография не примет их. Кроме того, файлы PNG содержат прозрачность, что позволяет пикселям внутри изображения быть абсолютно пустыми. Если вы попытаетесь распечатать PNG или загрузить его в определенные места в Интернете, эти пустые места могут быть заполнены черными или белыми пикселями, в результате чего изображение будет выглядеть совсем не так, как вы ожидаете. Именно поэтому преобразование PNG в JPG может быть очень полезным. Файлы JPG не поддерживают прозрачность, поэтому вы будете точно знать, как будет выглядеть загруженное изображение до того, как вы его загрузите. Кроме того, JPG поддерживают цвета CMYK, поэтому вы можете печатать их с высокой точностью. Как конвертировать файлы PNG в JPG бесплатно?Чтобы бесплатно конвертировать PNG в JPG, вам нужно загрузить PNG с помощью нашего инструмента выше. Нажмите кнопку “ЗАГРУЗИТЬ”. Перейдите к файлу (файлам), который вы хотите конвертировать. Вы также можете перетащить файлы, которые вы хотите загрузить. Вы можете загрузить до 20 файлов за один раз. Загрузив файл(ы), вы можете наблюдать, как наш инструмент конвертирует их в режиме реального времени. После конвертации вы можете нажать кнопку “СКАЧАТЬ” под каждым изображением, чтобы сохранить их. Однако если вы загрузили много файлов, вы можете загрузить их все сразу в формате ZIP, нажав кнопку “СКАЧАТЬ ВСЕ”. Если вам нужно конвертировать более 20 файлов, ничего страшного. Вы можете нажать кнопку “ОЧИСТИТЬ” и повторить шаги для следующей партии. Вы можете делать это сколько угодно раз, но не более 20 файлов. Обратите внимание, что конвертированные файлы должны быть загружены в течение часа. Если вы будете ждать загрузки файлов дольше часа, наш сервер их удалит. Безопасно ли конвертировать PNG в JPG?Когда вы используете наш инструмент для конвертации файлов, мы создаем копию вашего оригинала. Исходный файл на вашем компьютере, телефоне или планшете остается нетронутым. Поэтому использование этого инструмента абсолютно безопасно, так как ваш исходный файл не изменится. Кроме того, мы никогда не храним скопированные файлы дольше часа. Через час после загрузки файла мы все стираем. Поэтому вы можете быть спокойны, зная, что мы никогда не храним ваши конфиденциальные данные. PNG в JPG — online-convert.comПеретащите файлы сюда Максимальное качество Самый маленький файл Максимальное сжатие Качество: Выберите подходящее качество изображения. Максимальное сжатиеНаилучшее качество 0% 20% 40% 60% 80% 100% Изменить размер: Ширина: px Высота: px Применить цветной фильтр: без измененийГрадации серогоМонохромноеИнвертировать цветаРетроСепия Улучшить «/> Повысить резкость Сглаживание Сглаживание контраста Выровнять Нормализовать Устранить искажения Без многослойности Точек на дюйм: dpi Обрезать пиксели: Наверх: px Вниз: px Влево: px Вправо: px Настроить порог преобразования в ч/б: Обычно порог определяется автоматически, но его можно настроить и вручную. Допускаются значения от 0 до 255.»/> Укажите единицу разрешения для DPI: нетДюймыCM Set the chroma sub-sampling method to use: без изменений4:4:44:4:04:2:24:2:04:1:14:1:0 Информация: Включите поддержку JavaScript, чтобы обеспечить нормальную работу сайта.
Вы можете преобразовать файлы в обратную сторону из JPG в PNG: Конвертер JPG в PNG PNG в JPG — преобразование изображений PNG в JPEGЗАГРУЗИТЬ ФАЙЛЫ Перетащите сюда свои файлы Файлы PNG и JPG являются форматами изображений. Файлы, оканчивающиеся на .PNG, представляют собой файлы изображений, специально предназначенные для передачи без потерь через Интернет. В файлах PNG отсутствуют определенные атрибуты, которые сделали бы их удобными для печати, в частности, отсутствует поддержка цветовых пространств CMYK. По сути, файлы PNG созданы для того, чтобы отлично смотреться на мониторах компьютеров и смартфонах, а не на бумаге. Между тем, файлы, оканчивающиеся на .JPG или .JPEG, немного отличаются. Файлы JPG, в отличие от файлов PNG, сжаты, что приводит к некоторой потере качества изображения. Вы можете выбрать, насколько вы хотите понизить качество изображения, что, в свою очередь, уменьшит размер файла изображения. JPG хорошо работают как в цифровом, так и в печатном формате, но они не без потерь, как PNG. Зачем нужно конвертировать PNG в JPG? Если у вас есть файл PNG, некоторые вещи вы не сможете с ним сделать. Кроме того, файлы PNG содержат пробелы прозрачности. Это позволяет пикселям внутри изображения быть полностью пустыми. Если вы попытаетесь распечатать PNG или загрузить его в определенные места в Интернете, эти пустые места могут быть заполнены черными или белыми пикселями, из-за чего изображение будет выглядеть совсем иначе, чем вы ожидаете. Вот почему преобразование PNG в JPG может быть очень полезным. Файлы JPG не поддерживают прозрачность, поэтому вы будете точно знать, как будет выглядеть загрузка, прежде чем загружать ее. Кроме того, файлы JPG поддерживают цвета CMYK, поэтому вы можете печатать их с высокой точностью. Как бесплатно конвертировать файлы PNG в JPG? Чтобы бесплатно преобразовать PNG в JPG, вам нужно загрузить PNG с помощью нашего инструмента выше. Нажмите кнопку с надписью «ЗАГРУЗИТЬ ФАЙЛЫ». Загрузив файлы, вы можете наблюдать, как наш инструмент преобразует их в режиме реального времени. После преобразования вы можете нажать кнопку «СКАЧАТЬ» под каждым изображением, чтобы сохранить их. Однако, если вы загрузили много файлов, вы можете загрузить их все сразу в формате ZIP, нажав кнопку «СКАЧАТЬ ВСЕ». Если вам нужно преобразовать более 20 файлов, ничего страшного. Вы можете нажать кнопку «ОЧИСТИТЬ ОЧЕРЕДЬ» и повторить шаги для следующей партии. Вы можете делать это столько раз, сколько пожелаете, но вы можете делать это не более чем 20 файлами. Обратите внимание, однако, что вы должны загрузить преобразованные файлы в течение одного часа. Если вы будете ждать загрузки файлов более одного часа, наш сервер удалит их. Если это произойдет, вам нужно будет снова выполнить преобразование. Безопасно ли конвертировать PNG в JPG?Когда вы используете наш инструмент для преобразования файлов, мы создаем копию вашего оригинала. Оригинальный исходный файл на вашем компьютере, телефоне или планшете остается нетронутым. Так что использовать этот инструмент совершенно безопасно, так как исходный файл не изменится. Точно так же мы никогда не храним ваши скопированные файлы более часа. Через час после загрузки файла мы все стираем. Поэтому вы можете быть довольны тем, что мы никогда не храним ваши конфиденциальные данные. JPG в PNG — конвертировать JPEG в PNGЗАГРУЗИТЬ ФАЙЛЫ Перетащите сюда свои файлы Файлы, оканчивающиеся на .JPG и .PNG, являются файлами изображений. Они содержат визуальную информацию, обычно фотографии, рисунки, скриншоты или другие типы медиа. Однако файлы JPG (или иногда JPEG) отличаются от PNG. С JPG у вас есть файл с качеством с потерями. Между тем, файлы PNG не имеют потерь, что означает, что они не сжаты. PNG также поддерживают прозрачность, чего нет в JPG. Прозрачность позволяет сделать определенные пиксели изображения пустыми, что может быть полезно при размещении одного изображения поверх другого. PNG, к сожалению, не поддерживают цветовые пространства CMYK, что делает их не такими эффективными для печати. Зачем конвертировать JPG в PNG? Основной причиной преобразования файлов JPG в PNG является создание поддержки прозрачности. Если у вас есть изображение с большим количеством пустого пространства, которое вы хотите удалить в программном обеспечении для редактирования, вы не сможете это сделать. PNG также не сжимаются. Поэтому, если вы загружаете PNG в службу, которая сжимает изображения, ваша загрузка PNG будет выглядеть так же, как на вашем компьютере. Это может быть полезно, если у вас есть очень особенное или специфическое изображение, которое вы хотите сохранить. Однако вам следует опасаться преобразования JPG в PNG, если вы хотите в конечном итоге напечатать изображение. Поскольку файлы PNG не содержат информации CMYK, распечатать их сложно. Мы советуем сохранить исходный JPG, если вы думаете, что захотите распечатать его в будущем. Как бесплатно конвертировать файлы PNG в JPG? Во-первых, вам нужно загрузить файл JPG в наш инструмент выше. Нажмите кнопку «ЗАГРУЗИТЬ ФАЙЛЫ» и найдите файлы JPG, чтобы начать. Вы также можете перетащить файлы в поле с надписью «Перетащите файлы сюда». Однако имейте в виду, что вы можете загружать не более 20 файлов одновременно. После загрузки вы увидите, как наш инструмент преобразует файлы в режиме реального времени. Когда закончите, вы можете загрузить каждый из них один за другим, нажав кнопку «СКАЧАТЬ» под каждым изображением. Если у вас их много, вы можете сэкономить время, скачав их все сразу в формате ZIP. Просто нажмите кнопку «СКАЧАТЬ ВСЕ», чтобы сделать это. Если после загрузки файлов вы все еще хотите сделать больше преобразований, это нормально! Вы можете повторить этот процесс столько раз, сколько вам нужно. Просто имейте в виду, что вы можете конвертировать не более 20 пакетов. После преобразования файлов у вас есть один час на их загрузку. Обязательно загрузите свои файлы до истечения этого срока, так как вам нужно будет снова выполнить преобразование, если вы будете ждать слишком долго. Безопасно ли конвертировать JPG в PNG? Использование нашего инструмента для преобразования файлов абсолютно безопасно. Ваш исходный файл остается нетронутым на вашем телефоне, планшете или компьютере, поэтому вы всегда можете вернуться к оригиналу, если преобразованный файл вам не подходит. Nh3 o2 no h2o метод электронного баланса: электронный баланс NH3+O2=NO+H2O — вопрос №55248 — Учеба и наукаМетод электронного баланса для уравнивания окислительно-восстановительных реакцийПохожие презентации: Окислительно-восстановительные реакции (ОВР) Окислительно-восстановительные реакции (лекция 6) Окислительно-восстановительные реакции (ОВР) Окислительно-восстановительные реакции Электрохимия. Окислительно-восстановительные реакции Методы составления уравнений окислительно-восстановительных реакций. Лекция №20 Окислительно-восстановительные реакции Окислительно-восстановительные реакции Окислительно-восстановительные реакции. (лекция №10) Окислительно-восстановительные реакции 1. Метод электронного баланса для уравнивания окислительно-восстановительных реакцийМетод электронногобаланса для уравнивания окислительновосстановительных реакций 2. Вспомним!Степень окисления – это условныйзаряд, который приобрел бы атом в молекуле, если бы все электронные пары его химических связей сместились в сторону более электроотрицательных атомов.  1. Степень окисления атомов в простых веществах равна нулю: 0 0 0 h3, Cl2, Na . 2. В сложных веществах О-2. 3. В сложных веществах Н+1. 4. С.О. металлов всегда положительна, максимальное значение С.О. металлов главных подгрупп обычно совпадает с номером группы, в которой расположен металл. Алгебраическая сумма степеней окисления всех атомов в соединении всегда равна нулю: +1 -2 h3SO4 (+1)·2 + (+6)·1 + (–2)·4 = 0 В реакциях ионного обмена составные части веществ переходили в состав других веществ без изменений, степени окисления элементов и заряды ионов не менялись: +1 +5 -2 +1 -1 +1 -1 +1 +5 -2 AgNO3 + HCl = AgCl + HNO3 Однако существует огромное множество реакций, в ходе которых меняются степени окисления элементов: 0 0 +2 -2 Fe + S = FeS Химические реакции, в результате которых происходит изменение степеней окисления атомов химических элементов или ионов, образующих реагирующие вещества, называют окислительновосстановительными реакциями (ОВР).  Элемент, отдающий электроны, называется восстановителем, а принимающий электроны окислителем. Процесс отдачи электронов называется окислением, а принятия восстановлением. В процессе окисления степень окисления повышается, в процессе восстановления — понижается. Эти процессы неразрывно связаны между собой, число принятых окислителем электронов должно быть равно числу отданных восстановителем электронов. На этом основании составляется электронный баланс и расставляются коэффициенты. 10. Чтобы составить схему о-в процесса, необходимо:1. Определить степень окисления элементов.2. Определить элементы, изменившие степень окисления. 3. Составить схему: определить элемент, теряющий, и элемент, принимающий электроны. 4. Составить электронный баланс (число отданных электронов всегда должно равняться числу электронов, принятых). 5. Расставить коэффициенты в уравнении по электронному балансу, определить окислитель и восстановитель.  11. 0 0 +3 -202 в — ль 0 -2 Al +3 S = Al2S3 окисление Al0 — 3ē → Al+3 восстановление ок — ль +3 S0 + 2ē → S-2 6 2 2Al0–6ē→2Al+3 3 3S0 +6ē →3S-2 0 0 +2 -2 2 Mg + O2 = 2MgO в — ль окисление Mg0 — 2ē → Mg+2 восстановление ок — ль O20 + 4 ē → 2 O-2 4 2 2Mg0-4ē→2Mg+2 1 O20 +4ē → 2O-2 13. Окислительно-восстановительные реакции в природе и технике:Окислительновосстановительные реакции вприроде и технике: 14. Задание 1.Определите степени окисления всеххимических элементов, входящих в состав веществ: NaOH, MgCl2, K2CO3, AlCl3, h4PO4, K2SO4, HNO3, CuSO4, Fe, Zn(NO3)2. 15. Задание 2.Расставьте коэффициенты методомэлектронного баланса в следующих уравнениях реакций: 1) 2) 3) 4) 5) HgO = Hg + O2 h3S + O2 = SO2 + h3O KClO3 = KCl + O2 CuS + O2 = CuO + SO2 N2 + h3 = Nh4 16. Домашнее задание:Расставьте коэффициенты в Домашнее задание:Расставьте коэффициенты вуравнениях методом электронного баланса: 1) 2) 3) 4) 5) Fe + Cl2 → FeCl3 Zn + HCl → ZnCl2 HBr + O2 → h3O + Br2 Nh4 + O2 → NO + h3O Zn + HNO3 → Zn(NO3)2 + N2 + h3O English Русский Правила Задачи к разделу Окислительно-восстановительные реакцииВ данном разделе собраны задачи по теме Окислительно-восстановительные реакции. Приведены примеры задач на составление уравнений реакций, нахождение окислительно-восстановительного потенциал, и константы равновесия ОВР и другие. Задача 1. Какие соединения и простые вещества могут проявлять только окислительные свойства? Выберите такие вещества из предложенного перечня: NH3, CO, SO2, K2MnO4, Сl2, HNO2. Составьте уравнение электронного баланса, расставьте коэффициенты в уравнении реакции: HNO3 + H2S = H2SO4 + NO + H2O. Показать решение » Решение. Простые вещества, атомы которых не могут отдать электрон, а могут только присоединить его в реакциях являются только окислителями. Из простых веществ только окислителем может быть фтор F2, атомы которого имеют наивысшую электроотрицательность. В сложных соединениях – если атом, входящий в состав этого соединения (и меняющий степень окисления) находится в своей наивысшей степени окисления, то данное соединение будет обладать только окислительными свойствами. Из предложенного списка соединений, нет веществ, которые обладали бы только окислительными свойствами, т.к. все они находятся в промежуточной степени окисления. Наиболее сильный окислитель из них – Cl2, но в реакциях с более электроотрицательными атомами будет проявлять восстановительные свойства. N-3H3, C+2O, S+4O2, K2Mn+6O4, Сl02, HN+3O2 HNO3 + H2S = H2SO4 + NO + H2O. Составим электронные уравнения: N+5 +3e— = N+2 | 8 окислитель S-2 — 8e— = S+6 | 3 восстановитель Сложим два уравнения 8N+5 +3S-2— = 8N+2 + 3S+6 Подставим коэффициенты в молекулярное уравнение: 8HNO3 +3H2S = 3H2SO4 + 8NO + 4H2O. Задача 2. Почему азотистая кислота может проявлять как окислительные, так и восстановительные свойства? Составьте уравнения реакций HNO2: а) с бромной водой; б) с HI; в) с KMnO4. Какую функцию выполняет азотистая кислота в этих реакциях? Показать решение » Решение. HN+3O2 — Степень окисления азота в азотистой кислоте равна +3 (промежуточная степень окисления). а) HNO2 + Br2 + H2O = 2HBr + HNO3 N+3 – 2 e = N+5 | 1 восстановитель Br20 + 2 e = 2Br— | 1 окислитель N+3 + Br2 = N+5 + 2Br— б) HNO2 + 2HI = I2 + 2NO + 2H2O N+3 + e = N+2 | 1 окислитель 2I— — 2 e = I2 | 1 восстановитель N+3 + 2I— = N+2 + I2 в) 5HNO2 + 2KMnO4 + 3H2SO4 = 2MnSO4 + 5HNO3 + K2SO4 + 3H2O N+3 – 2 e = N+5 | 5 восстановитель Mn+7 + 5 e = Mn+2 | 2 окислитель 5N+3 + 2Mn+7 = 5N+5 + 2Mn+2 Задача 3. КСlO3 → КС1 + КСlO4. Укажите окислитель и восстановитель. Показать решение » Решение. Хлор может проявлять степени окисления от -1 до +7. Соединения, содержащие хлор в его высшей степени окисления, могут быть только окислителями, т.е. могут только принимать электроны. Соединения, содержащие хлор в его низшей степени окисления, могут быть только восстановителями, т.е. могут только отдавать электроны. Соединения, содержащие хлор в его промежуточной степени окисления, могут быть как восстановителями, так и окислителями, т. H+1Сl-1, Cl02, H+1Cl+3O2-2 , H+1Cl+5O3-2 , Cl2+7O7-2 Таким образом, в данном ряду Только окислитель — Cl2O7 Только восстановитель – HСl Могут быть как окислителем, так и восстановителем — Cl2, HClO2 , HClO3 КСlO3 → КС1 + КСlO4. Составим электронные уравнения Cl+5 +6e— = Cl— | 2 | 1 окислитель Cl+5 -2e— = Cl+7 | 6 | 3 восстановитель Расставим коэффициенты 4Cl+5 = Cl— + 3Cl+7 4КСlO3 → КС1 + 3КСlO4. Задача 4. Какие из приведенных реакций являются внутримолекулярными? Расставьте коэффициенты в уравнениях реакций. Укажите восстановитель, окислитель. а) KNO3 = KNO2 + O2; б) Mq+ N2 = Mq3N2; в) KClO3 = KCl + O2. Показать решение » Решение. В реакциях внутримолекулярного окисления-восстановления перемещение электронов происходит внутри одного соединения, т.е. и окислитель и восстановитель входят в состав одного и того же сложного вещества (молекулы) а) 2KNO3 = 2KNO2 + O2 — внутримолекулярная ОВР N+5 +2e— = N+3 | 2 окислитель 2O-2 -4e— = O20 | 1 восстановитель 2N+5 + 2O-2 = 2N+3 + O20 б) 3Mq + N2 = Mq3N2 — межмолекулярная ОВР N2 +6e— = 2N-3 | 2 | 1 окислитель Mg0 -2e— = Mg+2 | 6 | 3 восстановитель N2 + 3Mg0 = 2N-3 + 3Mg+2 в) 2KClO3 = 2KCl + 3O2 — внутримолекулярная ОВР Cl+5 +6e— = Cl— | 4 | 2 окислитель 2O-2 -4e— = O20 | 6 | 3 восстановитель 2Cl+5+ 6O-2 = 2Cl— + 3O20 Задача 5. а) Cl2 + KOH = KCl + KClO3 + H2O; б) KClO3 = KCl + KClO4 . Показать решение » Решение. В реакциях диспропорционирования окислителем и восстановителем являются атомы одного и того же элемента в одинаковой степени окисления (обязательно промежуточной). В результате образуются новые соединения, в которых атомы этого элемента обладают различной степенью окисления. а) 3Cl2 + 6KOH = 5KCl + KClO3 + 3H2O; Cl20 +2e— = 2Cl— | 10| 5 окислитель Cl20 -10e— = 2Cl+5 | 2 | 1 восстановитель 5Cl20 + Cl20 = 10Cl— + 2Cl+5 3Cl20 = 5Cl— + Cl+5 б) 4KClO3 = KCl + 3KClO4 Cl+5 +6e— = Cl— | 2 | 1 окислитель Cl+5 -2e— = Cl+7 | 6 | 3 восстановитель 4Cl+5 = Cl— + 3Cl+7 Задача 6. KMnO4 + KNO2 + H2SO4 = K2SO4 + MnSO4 + KNO3 + H2O Показать решение » Решение. Составим полуреакции: MnO4— + 8H+ +5e— = Mn2+ + 4H2O | 2 окислитель NO2— + H2O — 2e— = NO3— + 2H+ | 5 восстановитель Сложим две полуреакции, умножив каждую на соответствующий коэффициент: 2MnO4— + 16H+ + 5NO2—+ 5H2O = 2Mn2+ + 8H2O + 5NO3— + 10H+ После сокращения идентичных членов, получаем ионное уравнение: 2MnO4— + 6H+ + 5NO2— = 2Mn2+ + 3H2O + 5NO3— Подставим коэффициенты в молекулярное уравнение и уравняем его правую и левую части: 2KMnO4 + 5KNO2 + 3H2SO4 = K2SO4 + 2MnSO4 + 5KNO3 + 3H2O Задача 7. Zn + HNO3 = Zn(NO3)2 + NH4NO3 + H2O Zn + H2SO4(конц) = ZnSO4 + SO2 + H2O Показать решение » Решение. 4Zn + 10HNO3 = 4Zn(NO3)2 + NH4NO3 + 3H2O Составим электронные уравнения Zn0 – 2 e = Zn2+ | 8 | 4 | восстановитель N+5 + 8 e = N3- | 2 | 1 | окислитель 4Zn0 + N+5 = 4Zn2+ + N3- Zn + 2H2SO4(конц) = ZnSO4 + SO2 + 2H2O Составим электронные уравнения Zn0 – 2 e = Zn2+ | 2 | 1 восстановитель S+6 + 2 e = S+4 | 2 | 1 окислитель Zn0 + S+6 = Zn2+ + S+4 Задача 8. а) 2F— -2e— = F2, E0 = 2,85 В б) 2Сl— -2e— = Cl2, E0 = 1,36 В в) 2Br— -2e— = Br2, E0 = 1,06 В г) 2I— -2e— = I2, E0 = 0,54 В Стандартный окислительно-восстановительный потенциал системы Cr2O72- + 14H+ + 6e— = 2Cr3+ + 7H2O равен E0 =1,33 В Показать решение » Решение. Для определения возможности протекания ОВР в прямом направлении необходимо найти ЭДС гальванического элемента: ЭДС = Е0ок — Е0восст Если найденная величина ЭДС > 0, то данная реакция возможна. Итак, определим, можно ли K2Cr2O7 использовать в качестве окислителя в следующих гальванических элементах: F2|F— || Cr2O72-|Cr3+ E = 1,33 – 2,85 = -1,52 В Cl2|Cl— || Cr2O72-|Cr3+ E = 1,33 – 1,36 = -0,03 В Br2|Br— || Cr2O72-|Cr3+ E = 1,33 – 1,06 = +0,27 В I2|I— || Cr2O72-|Cr3+ E = 1,33 – 0,54 = +0,79 В Таким образом, в качестве окислителя дихромат калия можно использовать только для процессов: 2Br— -2e— = Br2 и 2I— -2e— = I Задача 9. Вычислите окислительно-восстановительный потенциал для системы MnO4— + 8H+ +5e— = Mn2+ + 4H2O Если С(MnO4—)=10-5 М, С(Mn2+)=10-2 М, С(H+)=0,2 М. Показать решение » Решение. Окислительно-восстановительный потенциал рассчитывают по уравнению Нернста: E = E° + (0,059/n)lg(Cок/Cвос) В приведенной системе в окисленной форме находятся MnO4— и H+, а в восстановленной форме — Mn2+, поэтому: E = 1,51 + (0,059/5)lg(10-5*0,2/10-2) = 1,46 В Задача 10. Рассчитайте для стандартных условий константу равновесия окислительно-восстановительной реакции: 2KMnO4 + 5HBr + 3H2SO4 = 2MnSO4 + 5HBrO + K2SO4 + 3H2O Показать решение » Решение. Константа равновесия K окислительно-восстановительной реакции связана с окислительно-восстановительными потенциалами соотношением: lgK = (E10 -E20 )n/0,059 Определим, какие ионы в данной реакции являются окислителем и восстановителем: MnO4— + 8H+ +5e— = Mn2+ + 4H2O | 2 окислитель Br— + H2O — 2e— = HBrO + H+ | 5 восстановитель Общее число электронов, принимающих участие в ОВР n = 10 E10 (окислителя) = 1,51 В E20 (восстановителя) = 1,33 В Подставим данные в соотношение для К: lgK = (1,51 — 1,33 )10/0,059 lgK = 30,51 K = 3,22*1030 Примеры ОВР с ответами приведены также в разделе тест Окислительно-восстановительные реакции Категории ОБЩАЯ ХИМИЯ, Окислительно-восстановительные реакцииNh4 + O2 в NO + h3O
Вопрос Обновлено: 26/04/2023 КИСЛОРОД-УРОВЕНЬ-3 11 видеоРЕКЛАМА Ab Padhai каро бина объявления ке Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке! Похожие видео స్థిరాంకం సమాసం కింది విధంగా ఉంది. 423823856 01:22 Напишите сбалансированное химическое уравнение для равновесной реакции, константа равновесия которой определяется выражением ? 96) Напишите сбалансированное химическое уравнение, соответствующее этому выражению. 642780622 Text Solution समीकरणों को संतुलित करें : 9015 2 Nh4+O2→N2+h3O 643055954 01:16 को संतुलित करें- 643056005 01:53 Сбалансируйте химическое уравнение 643261773 02:45 Завершите и сбалансируйте следующее уравнение: 643439666 01:40 निम्न रासायनिक समी करणों को संतुलित करें- 643530481 01:58 निम्न रासायनिक समीकरणों को संतुलित करें- 643530492 01:41 निम्न रासायनिक समी करणों को संतुलित करें- 643530502 01:58 901 31 Баланс химических уравнений PbO +NH_3 в Pb + H_2O + N_2 643924773 01:25 Баланс уравнения: h3O2→h3O+O2 644242421 01:45 Баланс химических уравнений : C_3 H_(8) + O_2 до CO_2 + H_2O 645952289 01:29 Сбалансируйте химические уравнения: CO_2 + H_2O до C_6 H_(12) O_6 + O_2 645952290 02:09 Сбалансируйте химические уравнения: 645952294 01:52 РЕКЛАМА
‘Хоть кислород и является сторонником жизни на земля, присутствие нитр. 04:49
Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления! Слушаем… Уравновешивание окислительно-восстановительных реакций – примеры
Окислительно-восстановительные или «окислительно-восстановительные» реакции происходят, когда элементы в химической реакции приобретают или теряют электроны, вызывая увеличение или уменьшение степени окисления. В окислительно-восстановительной реакции один или несколько элементов окисляются, а один или несколько элементов восстанавливаются. Окисление — это потеря электронов, тогда как восстановление — это приобретение электронов. Простой способ запомнить это — подумать о зарядах: заряд элемента уменьшается, если он получает электроны (аббревиатура для запоминания разницы: LEO = Lose Electron Oxidation и GER = Gain Electron Reduction). Окислительно-восстановительные реакции обычно происходят в одной из двух сред: кислой или щелочной. Чтобы сбалансировать окислительно-восстановительные уравнения, необходимо понимание степеней окисления. Некоторые моменты, которые следует помнить при балансировке окислительно-восстановительных реакций:
Далее эти шаги будут показаны в другом примере: Пример \(\PageIndex{1A}\): в кислом водном растворе 9{-}}\) ион с зарядом -1. Если мы сложим эти два заряда, то сможем вычислить, что в левой части уравнения общий заряд равен +7. В правой части есть атом \(\ce{Mn}\) с зарядом +2, а затем 4 молекулы воды с зарядом 0. Таким образом, общий заряд правой части равен +2. Мы должны добавить 5 электронов в левую часть уравнения, чтобы убедиться, что обе части уравнения имеют одинаковые заряды +2. Шаг 5: Умножьте обе стороны обеих реакций на наименьшее общее кратное, что позволит полуреакциям иметь одинаковое количество электронов и компенсировать друг друга. 9{2+} + 8 H_2O} \nonumber\] В этой задаче в обеих частях уравнения нет ничего, что можно было бы сократить, кроме электронов. Наконец, дважды проверьте свою работу, чтобы убедиться, что масса и заряд сбалансированы. Чтобы еще раз проверить это уравнение, вы можете заметить, что все сбалансировано, потому что обе части уравнения имеют общий заряд +4. Ранги матрицы онлайн с решением: Онлайн калькулятор. Ранг матрицы Калькулятор производных — Google Калькулятор производныхAlleBilderVideosShoppingMapsNewsBücherКалькулятор производных • С шагами! www.derivative-calculator.net Решите производные с помощью этого бесплатного онлайн-калькулятора. Пошаговое решение и графики прилагаются! Переменная дифференцирования: ax_____abcdfghjklmnopqrstuvwxyz Калькулятор производных — Symbolab www.symbolab.com › Step-by-Step › Исчисление Бесплатный калькулятор производных — дифференцирование функций со всеми шагами. Введите любую производную функции, чтобы получить решение, шаги и график. Первое производное · производное в точечном калькуляторе · Частичный производный · Третий производный Проивочный калькулятор — Wolfram | Alpha Www.wolframalpha.com ›Калькаляторы› Проверенный -C … Free Online Derivative Calculator позволяет вам разрешено. Калькулятор производных — Mathway www.mathway.com › Калькулятор › производный-калькулятор Калькулятор производных поддерживает вычисление первой, второй…., четвертой производной, а также неявное дифференцирование и нахождение нулей/корней . Калькулятор производных с шагами | Калькулятор дифференцирования calculate-derivative.com Калькулятор производных — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Инструмент позволяет пользователям вводить данные в форме … Калькулятор производных — MathPapa www.mathpapa.com › Калькулятор производных Калькулятор производных дает пошаговую помощь в нахождении производных. Этот калькулятор находится в стадии бета-тестирования. Мы ценим ваши отзывы, чтобы помочь нам улучшить его. Калькулятор производных — eMathHelp www.emathhelp.net › калькуляторы › исчисление-1 › производ… , цепное правило и т. д.) Калькулятор производных с шагами — Open Omnia openomnia.com › Калькулятор производных Вычисление производной функции. Получите пошаговые решения. Попробуйте Open Omnia сегодня. Калькулятор производных и решение — SnapXam www.snapxam.com › калькуляторы › расчет производных… Калькулятор производных онлайн с решением и шагами. Подробные пошаговые решения ваших задач с производными с помощью нашего математического решателя и онлайн … 92 Значение производной Формула производной Правила производной Калькулятор антипроизводной ESG Investing: ESG Ratings — MSCIESG Investing: ESG Ratings — MSCI Инвестирование в ESG: Рейтинги ESGИзмерение устойчивости компании к долгосрочным финансово значимым рискам ESG Что такое рейтинг MSCI ESG? Рейтинги MSCI ESG Ratings предназначены для оценки управления компанией финансово значимыми рисками и возможностями ESG. Загрузка видео с рейтингами ESG… Рейтинги ESGКак работают рейтинги MSCI ESG? Каковы существенные риски ESG? Как выглядит плохой рейтинг? Как вы можете их использовать? Загрузить стенограмму (PDF, 120 КБ) (откроется в новой вкладке) Загрузить брошюру Как работают рейтинги MSCI ESG?
Риски и возможности ESG могут различаться в зависимости от отрасли и компании. Ознакомьтесь с нашей структурой ключевых вопросов | Методологии ESG (откроется в новой вкладке) | Чем являются и чем не являются рейтинги MSCI ESG
Связаться с отделом продаж Ознакомьтесь с нашими инструментами прозрачности ESGРейтинги ESG и инструмент поиска климата Узнайте о предполагаемом повышении температуры, целях декарбонизации, рейтинге MSCI ESG и ключевых проблемах ESG более 2900 компаний. Изучите ключевые проблемы E, S и G по подотраслям или секторам GICS® и их вклад в рейтинги ESG компаний. Что входит в рейтинг MSCI ESG?Пример. Изучите показатели и источники данных, используемые для определения рейтинга MSCI ESG для американского производителя бумажной продукции. Инструмент поиска рейтингов фондов ESG Рейтинги фондов ESG предназначены для измерения устойчивости взаимных фондов и ETF к долгосрочным рискам и возможностям. Ознакомьтесь с показателями ESG и климатическими показателями для всех фондовых, фиксированных и смешанных индексов MSCI, регулируемых ЕС. Основные характеристики продукта:Мы оцениваем более 8 500 компаний (14 000 эмитентов, включая дочерние компании) и более 680 000 акций и ценных бумаг с фиксированным доходом по всему миру (по состоянию на октябрь 2020 г.), собирая тысячи точек данных для каждой компании.
MSCI Опыт исследований в области ESG и лидерство
MSCI ESG Research LLC. Уведомление MIFID2/MIFIR: MSCI ESG Research LLC не распространяет и не действует в качестве посредника в отношении финансовых инструментов или структурированных депозитов, а также не осуществляет сделки от своего собственного имени, не предоставляет услуги по исполнению для других и не управляет клиентскими счетами. Никакие продукты или услуги MSCI ESG Research не поддерживают, не продвигают и не предназначены для поддержки или продвижения любой такой деятельности. MSCI ESG Research — независимый поставщик данных, отчетов и рейтингов ESG, основанных на опубликованных методологиях и доступных клиентам по подписке. ESG ADV 2A (PDF, 354 КБ) (открывается в новой вкладке)
1 GICS®, глобальный стандарт отраслевой классификации, разработанный совместно MSCI Inc. Сколько двузначных трехзначных четырехзначных чисел: Сколько двузначных, трехзначных; четырехзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5 с повторением?6 класс. Математика. Никольский. Учебник. Ответы к стр. 34Отношения, пропорции, процентыЗадачи на перебор всех возможных вариантов Ответы к стр. 34 144. Запишите все двузначные числа, в записи которых используются цифры: а) На первое место можно поставить любую из трёх цифр, на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 3 • 2 = 6 возможных вариантов записи двузначного числа: 13, 19, 31, 39, 91, 93; б) На первое место можно поставить любую из трёх цифр, на второе место можно поставить также одну из трёх цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 11, 13, 19, 31, 33, 39, 91, 93, 99; в) На первое место можно поставить любую из трёх цифр, на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 3 • 2 = 6 возможных вариантов записи двузначного числа: 24, 26, 42, 46, 62, 64; 145. Запишите все двузначные числа, в записи которых используются цифры 0, 1, 5: а) без повторения; б) с повторением. а) На первое место можно поставить любую из трёх цифр, кроме нуля (то есть любую из двух цифр), на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 2 • 2 = 4 возможных вариантов записи двузначного числа: 10, 15, 50, 51; б) На первое место можно поставить любую из трёх цифр, кроме нуля (то есть любую из двух цифр), на второе место можно поставить также одну из трёх цифр, то есть имеется 2 • 3 = 6 возможных вариантов записи двузначного числа: 10, 11, 15, 50, 51, 55. 146. Сколько двузначных чисел можно записать цифрами 9, 8, 7: а) с повторением цифр; б) без повторения цифр? а) На первое место можно поставить любую из трёх цифр, на второе место можно поставить также одну из трёх цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 77, 78, 79, 87, 88, 89, 97, 98, 99. б) На первое место можно поставить любую из трёх цифр, на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 3 • 2 = 6 возможных вариантов записи двузначного числа: 78, 79, 87, 89, 97, 98. 147. Сколько двузначных чисел можно записать цифрами 0, 2, 4, 6: а) с повторением цифр; б) без повторения цифр? а) На первое место можно поставить любую из четырёх цифр, кроме нуля (то есть любую из трёх цифр), на второе место можно поставить также одну из четырёх цифр, то есть имеется 3 • 4 = 12 возможных вариантов записи двузначного числа: 20, 22, 24, 26, 40, 42, 44, 46, 60, 62, 64, 66; б) На первое место можно поставить любую из четырёх цифр, кроме нуля (то есть любую из трёх цифр), на второе место можно поставить только одну из трёх оставшихся цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 20, 24, 26, 40, 42, 46, 60, 62, 64. 148. Четыре подружки купили 4 билета в кино. Первая девочка может сесть на одно из четырёх мест, вторая девочка может выбрать себе одно из трёх оставшихся мест, третья девочка может выбрать себе одно из двух оставшихся мест, четвертая девочка может выбрать себе одно оставшееся место, то есть 4 • 3 • 2 • 1 = 24 способа занять места. 149. Сколько двузначных; трёхзначных; четырёхзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5 без повторения? На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, то есть имеется 5 • 4 = 20 возможных вариантов записи двузначного числа. На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, то есть имеется 5 • 4 • 3 = 60 возможных вариантов записи трёхзначного числа. На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, на четвёртое место можно поставить только одну из двух оставшихся цифр, то есть имеется 5 • 4 • 3 • 2 = 120 возможных вариантов записи четырёхзначного числа. 150. Сколько двузначных; трёхзначных; четырёхзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5 с повторением? На первое место можно поставить любую из пяти цифр, на второе место можно поставить также любую из пяти цифр, то есть имеется 5 • 5 = 25 возможных вариантов записи двузначного числа. На первое место можно поставить любую из пяти цифр, на второе и третье место можно поставить также любую из пяти цифр, то есть имеется 5 • 5 • 5 = 125 возможных вариантов записи трёхзначного числа. На первое место можно поставить любую из пяти цифр, на второе, третье и четвёртое место можно поставить также любую из пяти цифр, то есть имеется 5 • 5 • 5 • 5 = 625 возможных вариантов записи четырёхзначного числа. 151. а) Все четырёхзначные числа, записанные цифрами 1, 2, 3, 4 без повторения, занумеровали в порядке возрастания чисел. Какой номер имеет число 4312? а) На первое место можно поставить любую из четырёх цифр, на второе место можно поставить только одну из трёх оставшихся цифр, на третье место можно поставить только одну из двух оставшихся цифр, на четвёртое место можно поставить только одну последнюю оставшеюся цифру, то есть имеется 4 • 3 • 2 • 1 = 24 возможных вариантов записи четырёхзначного числа. Число 4321 является наибольшим, а значит имеет 24 порядковый номер. Число 4312 идёт перед ним, следовательно, оно имеет 23 порядковый номер. б) На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, на четвёртое место можно поставить только одну из двух оставшихся цифр, на пятое место можно поставить только одну последнюю оставшеюся цифру, то есть имеется 5 • 4 • 3 • 2 • 1 = 120 возможных вариантов записи пятизначного числа. Число 54 321 является наибольшим, а значит имеет 120 порядковый номер. Число 54 312 идёт перед ним, следовательно, оно имеет 119 порядковый номер. в) На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, на четвёртое место можно поставить только одну из двух оставшихся цифр, на пятое место можно поставить только одну последнюю оставшеюся цифру, то есть имеется 5 • 4 • 3 • 2 • 1 = 120 возможных вариантов записи пятизначного числа. Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика. 6 класс Таблица разрядов и классов чисел в математикеНаучим называть и записывать многозначные числа без ошибок Начать учиться Хорошо, когда все на своих местах: кастрюли в шкафу, зубная щетка — в ванной. У цифр при записи чисел тоже есть свое место. В этой статье раскроем тему разрядов и классов. Числа и цифрыЧисла — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины. Для записи чисел используются специальные знаки — цифры. Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название. Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9. Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99. Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Каждая цифра в записи многозначного числа занимает определенное место — позицию. Реши домашку по математике на 5. Подробные решения помогут разобраться в самой сложной теме. Классы чиселЦифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса. Таблица классов: Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Когда читаем класс единиц, добавлять слово «единиц» в конце не нужно. Разряды чиселОт позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч. Проясним, что такое разряд в математике. У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу. Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко. Низший (младший) разряд многозначного натурального числа — разряд единиц. Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе. Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
ПотренируемсяПример 1.
Ответ:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами. Пример 2. Сколько сотен содержится в числе 6284? Как рассуждаем: В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни. Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Значит, в данном числе содержится 62 сотни. Цифра 0 в любом разряде означает отсутствие единиц в данном разряде. Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Шпаргалки для родителей по математике Все формулы по математике под рукой Лидия Казанцева Автор Skysmart К предыдущей статье Многочлен стандартного вида К следующей статье 148.4K Теорема синусов Получите план обучения, который поможет понять и полюбить математикуПремиумНа вводном уроке с методистом
Математическая задача: двузначное число 7410 — практическая математическая задача, комбинаторика Сколько двузначных чисел можно записать, используя число 0,2,6? Мы также можем повторять цифры в числе. Правильный ответ:Нашли ошибку или неточность? Не стесняйтесь пишите нам. Спасибо! Советы по использованию связанных онлайн-калькуляторов Хотите подсчитать количество комбинаций? Чтобы решить эту математическую задачу со словами, вам необходимо знать следующие знания: 9арифметика 0019 числаУровень словесной задачи:
Числа до 3 цифр — определение, разрядное значение, расширенная форма 3-значные числа начинаются с 100 и заканчиваются на 999. Эти номера состоят из 3 цифр, в которых первая цифра должна быть 1 или больше 1 а оставшиеся 3 цифры могут быть любым числом от 0 до 9. Изучение трехзначных чисел является строительным блоком для более высоких цифр. Давайте узнаем больше о важности, формировании и значении чисел до 3 цифр.
Что такое трехзначные числа?Трехзначные числа — это те числа, которые состоят только из трех цифр. Они начинаются со 100 и продолжаются до 999. Например, 673, 104, 985 — трехзначные числа. Следует отметить, что первая цифра трехзначного числа не может быть нулем, потому что в этом случае оно становится двузначным числом. Например, 045 становится 45. Разрядное значение трехзначных чисел Значение каждого трехзначного числа можно найти, проверив разрядное значение каждой цифры. Разложение трехзначного числа : В трехзначном числе используются три разряда – сотни, десятки и единицы. Давайте возьмем один пример, чтобы понять это лучше. Здесь 465 — это трехзначное число и оно раскладывается в виде суммы трех чисел. Так как 5 на разряде единиц, 60 на разряде десятков и 400 на разряде сотен. Значение нуля в трехзначных числах: Число ноль не вносит никакого вклада в трехзначное число, если оно расположено в позиции, где слева от него нет других ненулевых чисел. Расширенная форма трехзначных чиселРасширенная форма трехзначного числа может быть выражена и записана тремя различными способами. Рассмотрим трехзначное число 457. Число 457 можно записать в одной форме как 457 = (4 × сотни) + (5 × десятки) + (7 × единицы). Вторым способом число 457 можно записать как 457 = (4 × 100) + (5 × 10) + (7 × 1). И, наконец, число 457 можно разложить в виде 457 = 400 + 50 + 7. Все три способа записи чисел в развернутом виде верны. Запись трехзначного числа в развернутой форме помогает узнать составные части числа. В основном разделение или расширение трехзначного числа помогает нам лучше понять трехзначное число. Важные примечания о трехзначных числах
Общие ошибки чисел до 3 цифр Некоторые распространенные ошибки наблюдаются при записи или чтении трехзначного числа. Эти ошибки в чтении и интерпретации трехзначного числа часто понимаются как какое-то другое число.
Операции с числами до 3 цифр Четыре арифметические операции сложения, вычитания, умножения и деления удобно выполнять над трехзначными числами. В процессе выполнения этих арифметических действий должно правильно совпадать разрядное значение соответствующего числа. Ошибка в сопоставлении разрядного значения может привести к неправильным ответам. Здесь мы рассмотрим простое упражнение с использованием трехзначных чисел, чтобы помочь нам понять закономерность изменения каждой из цифр сотого разряда, разряда десятков и разряда единиц. Эта деятельность должна помочь в лучшем понимании обучения, необходимого для трехзначных чисел.
Наименьшее трехзначное числоНаименьшее трехзначное число — 100, потому что предшествующее ему число — 99, двузначное число. Трехзначные числа начинаются со 100 и заканчиваются на 999. Наибольшее трехзначное числоНаибольшее трехзначное число — 999, потому что за ним следует 1000, четырехзначное число. Трехзначные числа начинаются со 100 и заканчиваются на 999. Пример 1: Сколько существует трехзначных чисел? Решение: Всего 900 трехзначных чисел. Пример 2: Решите головоломку: сложите наименьшее двузначное число с наименьшим однозначным числом. Вычтите сумму из на единицу меньше, чем наибольшее трехзначное число. Решение: Наименьшее двузначное число = 10. Наименьшее однозначное число = 1. Сумма этих двух чисел равна 10 + 1 = 11. На единицу меньше, чем наибольшее трехзначное число, равно 998. Вычтя 11 из 998, получим. 998 — 11 = 987. Пример 3: Найдите наибольшее трехзначное число, которое является полным квадратом. Решение: Наибольшее трехзначное число, являющееся полным квадратом, равно 961, потому что 31 2 = 961. перейти к слайдуперейти к слайдуперейти к слайду Помогите ребенку наглядно представить, как работают числа! Наша методология основана на визуальном обучении. Почувствуйте разницу, которую создают более 5000 визуализаций. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду Сколько существует трехзначных чисел?Всего имеется 900 трехзначных чисел. К ним относятся от наименьшего трехзначного числа — 100 до самого большого трехзначного числа — 999. Числа за пределами этих трехзначных чисел являются четырехзначными числами, а числа меньше трехзначных чисел являются двузначными числами. Какое самое большое трехзначное число? Самое большое трехзначное число — 999. Какова сумма трех самых больших трехзначных чисел?Три самых больших трехзначных числа — это 997, 998, 999. Их сумма равна 2994, т. е. 997 + 998 + 999 = 2994. Какое самое маленькое трехзначное число?Число 100 — наименьшее трехзначное число. Если из него вычесть 1, получится двузначное число. Всего существует 900 трехзначных чисел, из которых число 100 является наименьшим трехзначным числом. Сколько существует четных трехзначных чисел?Всего имеется 900 трехзначных чисел. Из них половина — четные числа, а оставшаяся половина — нечетные числа. Следовательно, есть 900/2 = 450 четных трехзначных чисел. Может ли трехзначное число иметь два нуля? В трехзначном числе может быть два нуля. Два нуля должны быть в разряде десятков и разряде единиц. Некоторыми примерами трехзначных чисел с двумя нулями являются 100, 200, 300 и 400. Следует отметить, что разряд сотен в трехзначном числе не может иметь число 0, потому что это сделает его двузначным. Тангенс пи на 5 умножить на котангенс пи на 5: 1)tg п/5 * ctg п/5=? 2)3tg 2,3 * ctg 2,3=? 3)tg п/7 * ctg п/7=? 4)7tg п/12 * ctg п/12=? или хатябы скажите какие числа подставить? — Знания.siteСинус 30 градусов, sin 30Автор Admin На чтение 4 мин Просмотров 10 Опубликовано Синус 30 градусов равняется одной второй или ноль целых пять десятых. sin 30° = 1/2 или sin 30° = 0,5 В радианной мере измерения углов синусу 30 градусов соответствует синус π/6: sin 30° = sin π/6 Как это ни странно, но справедливо и обратное равенство, которое утверждает, что синус π/6 (синус пи на 6) равняется синусу 30 градусов: sin π/6 .sin 30° Равняется синус пи / 6 так же одной второй или ноль целых пять десятых. sin π/6 = 1/2 или sin π/6 = 0,5 Это было для блондинок. Для брюнеток и лысых академиков математических наук можно записать всё это в общем виде, пусть распутывают: sin 30° = sinπ/6 = 1/2 = 0,5 Для полного счастья здесь явно не хватает картинки синуса 30 градусов.
Надеюсь, первую часть задачи я решил и мне удалось объяснить блондинкам, чему равен синус тридцати градусов. Теперь нужно решить вторую половину задачи, с которой не в состоянии справиться даже вся академия математических наук, вместе взятая. Нужно в Интернете найти блондинок, которые ищут синус 30 градусов. Попробую вооружиться логикой блондинок и перечислю ниже поисковые запросы, которые блондинки могут вводить в поисковые системы при поиске ответа на вопрос: чему равен синус 30 градусов? И так, поисковые запросы, разбавленные моими комментариями, дабы поисковые системы не отлучили мое творение от блондинок. Синус — это математики сверяют свои знания с Интернетом. Сколько синус 30 — ноль целых пять десятых. Кто может объяснить, почему синус 30 градусов равен 1/2? — ну, вундеркинды, блондинка задала вопрос. Кто осмелится ответить?
Коэффициент деления — Изучайте и решайте вопросы
Введение• Дата последнего обновления: 20 апреля 010 Всего просмотров: 46.8k • Просмотров сегодня : 1.16k Любое целое число, которое делит одно число на другое число поровну, считается множителем. Например, в задаче на деление \[10 \div 5 = 2\],10 имеет множители 1, 2, 5 и 10. Все эти множители можно разделить на равные группы, например две группы по пять, две группы из двух человек и одна группа из десяти человек, что соответствует двум группам из пяти человек, двум группам из двух человек, одной группе из десяти человек и одной группе из десяти человек соответственно. Коэффициент деления Числа, на которые можно точно разделить число, называются множителями. Делитель и множительЛюбое число, на которое делится другое число, называется делителем. Однако множитель — это делитель, который полностью делит целое число и не оставляет остатка. Следовательно, любой делитель числа является также и его делителем. Но не все множители являются делителями; делителями числа являются все его делители. На предыдущем рисунке компоненты числа 20 — это 4 и 5. Однако деление 20 на 3 не дает точного деления числа. Как разделить коэффициенты?Какие множители числа 18 (метод деления)?Шаги для нахождения множителей числа 18: ШАГ 1: Используя законы деления, мы определяем наименьший точный простой делитель числа (множитель). Здесь число 18 четное. Его можно разделить на 2. ШАГ 2: Нужно разделить полученное число (18) на его наименьший простой делитель, равный 9. ШАГ 3: Затем мы определяем простые множители производного частного. Повторяйте шаги 1 и 2, пока частное не станет простым числом. Здесь частное равно 9, поэтому \[9 = 3 \times 3\]. Здесь мы останавливаем операцию, потому что 3 — это частное. Следовательно, \[18 = 2 \times 3 \times 3\]. Таким образом, множители числа 18 равны 1,2, 3, 6, 9,18. Пары для множителей числа 18 Решенные примерыПример 1. Перечислите множители числа 18 и соответствующие им пары множителей в примере 1. Ответ: \[\begin{array}{l}1 \times 18 = 18\\2 \times 9 = 18\\3 \times 6 = 18\end{array}\] Следовательно, множители числа 18 равны 1, 2, 3, 6, 9 и 18. Пары множителей числа 18 равны (1,18), (2,9) и (3,6) Пример 2: Найти общие делители чисел 25 и 24. Ответ: Делители числа 25 следующие: 1, 5 и 25. Делители числа 24 следующие: 1, 2, 3, 4, 6, 8, 12 , и 24. Таким образом, общий делитель 25 и 24 равен 1, Пример 3: Найдите делители числа 72. Ответ: 72 представлено как произведение следующих дополнительных чисел: \[\begin{array}{l}1 \times 72 = 72\\2 \times 36 = 72\\3 \times 24 = 72\\4 \times 18 = 72\\6 \times 12 = 72\\8 \times 9 = 72\\9 \times 8 = 72\end{массив}\] Поскольку умножение в данный момент повторяется, его необходимо остановить. Заключение Множители и множители с использованием фактов деления, например, используются при работе с деньгами, сортировке предметов по коробкам, поиске закономерностей в числах, решении отношений, расширении или сокращении дробей. В математике множитель — это целое число, которое делит другое число на себя без остатка. Мы часто сталкиваемся с множителями и множителями. Недавно обновленные страницы Числа на английском языке — произношение, чтение и примеры Числа от 1 до 10 для печати — изучение с примерами для детей Расширенная форма десятичных знаков и система разрядов — определение, примеры и использование Половинки? — Изучите определение и примеры Nonagon: изучите определение, типы, свойства и формулы Unit Cubes: изучите определение, факты и примеры Числа на английском языке — произношение, чтение и примеры Числа от 1 до 10, которые можно распечатать, — обучение на примерах для детей Расширенная форма десятичных знаков и разрядная система — определение, примеры и использование Что такое половинки? — Изучите определение и примеры Nonagon: изучите определение, типы, свойства и формулы Единицы измерения кубов: изучите определение, факты и примеры Актуальные темы Фактор – Элементарная математика Фактор и множитель кратны иногда путают между собой. ЗначениеFactor может использоваться как глагол или существительное.
Итак, например, 3 — это делитель 12, потому что 3 — счетное число, и его можно умножить на 4, чтобы получить 12. Опять же, 3 — это делитель 12, потому что 3 делит 12 без остатка. Делителями 12 являются 1, 2, 3, 4, 6 и 12, потому что каждый из них делит 12 без остатка (или, альтернативно, каждый из них является счетным числом, которое можно умножить на другое счетное число, чтобы получить 12). Некоторые тонкости
Дополнительные сведения о математикеПростой множитель числа — это просто множитель этого числа, который также является простым. Итак, число 12 имеет шесть делителей — 1, 2, 3, 4, 6 и 12, — но только два из них (2 и 3) простые, поэтому оно имеет только два простых делителя. Разложение числа на простые множители — это факторизация — способ представления этого числа в виде произведения — состоящая только из простых чисел. Таким образом, число 12 может быть выражено в виде произведения многими способами — 1 × 2 × 2 × 3, или 3 × 4, 2 × 2 × 3 или 2 × 6, — но только один из них состоит исключительно из простых чисел: 2 × 2 × 3. (Число 1 не является простым. Углы образованные при пересечении двух прямых секущей: Углы при пересечении двух прямых«Свойства углов, образованных при пересечении двух параллельных прямых секущей»
Тема урока:
« Свойства углов, образованных при пересечении двух параллельных прямых секущей»
Подготовила: Н.И. Натальченко
г. Лиман
Донецкая область
Тема: « Свойства углов, образованных при пересечении двух параллельных прямых секущей»
Зашифрованное название темы.
(19,3,16,11,19,20,3,1 21,4,13,16,3 16,2,18,1,9,16,3,1,15,15,29,23 17,18,10 17,6,18,6,19,6,25,6,15,10,10 5,3,21,23 17,1,18,1,13,13,6,13,30,15,29,23 17,18,33,14,29,23 19,612,21,27,6,11)
Цель: закрепить и обобщить знания учащихся о свойствах углов образованных при пересечении параллельных прямых и секущей
Задачи:
Обучающие: повторить понятие, свойство смежных и вертикальных углов, параллельных прямых; отработать навыки нахождения накрест лежащих, односторонних и соответственных углов; Развивающие: активизировать познавательную деятельность учащихся; развивать логическое мышление, умения анализировать, сравнивать, обобщать, выделять главное, делать выводы; развивать быстроту реакции, развивать память; развивать умения и навыки применять математические знания к решению практических задач; Воспитательные: воспитывать у учащихся интерес к познанию геометрии; воспитывать аккуратность построений геометрических рисунков; культуру речи и культуру общения; воспитывать самостоятельность, волю и настойчивость, уверенность в своих силах, стремление к достижению результата. Тип урока: урок обобщения и систематизации знаний, умений, навыков.
Оборудование: Компьютер, мультимедийный проектор, экран, презентация в программе Power Point, индивидуальный раздаточный материал для учащихся (карточки с заданиями) и для работы в парах.
ХОД УРОКА I. Организационный момент Эпиграфом нашего сегодняшнего урока хотелось бы взять такое четверостишье:
Да, путь познания не гладок!
Но знаем мы со школьных лет
Загадок больше чем отгадок
И поискам предела нет!
На сегодняшнем уроке, мы с вами должны вспомнить ранее пройденный материал и продолжить решать задания на нахождение углов при параллельных прямых.
II. Проверка домашнего задания Домашнее задание проверяем устно. Из ответов полученных при решении домашних заданий с помощью алфавита ищем зашифрованное слово. 1.Какой угол образует с углом ∟11 внутренние накрестлежащие углы? (14) 2. Какой угол соответственный углу ∟12?(16) 3. Какой угол вертикален углу ∟16? (13) 4. ∟14 =… (16) 5. Угол ∟4 и ∟? — называются внутренние односторонние углы. (5) 6. (∟15 — ∟8)*8 =…(24) 7. ∟2+∟10=…(29)
14,16,13,16,5,24,29 слово – МОЛОДЦЫ
III. Актуализация опорных знаний
ПАЗЛЫ
Глядя на рисунок, заполните таблицу.
Физкульт.
Знают угол все, все, все на этой планете. Кто не знает, показать можем людям этим. Раз- прямой, (присели) Два- тупой, (наклон влево, вправо) Третий – острый, вот такой. (наклон вперед до колен) А четвертый угол класс! Мы покажем вам сейчас. ( стали на пальчики подняв руки вверх) Это угол 60ͦ, все выходит у ребят. Вот такие вот углы на уроке нам нужны. Подровнялись, тихо сели. Все на доску посмотрели.
IV. Закрепление знаний, умений, навыков
Решение задач 1. По данным рисунка найдите угол x
V. Самостоятельная работа.
Карточка №1 (низкий, средний уровни) Дано: аІІв, с – секущая ∟2 = 138 ͦ Найти : ∟6 — ?
Карточка №2 (низкий, средний уровни) Дано: аІІв, с – секущая ∟5 = 40 ͦ Найти : ∟3, ∟4 — ?
Карточка №3 (достаточный уровень) Дано: аІІв, с – секущая ∟2>∟1 в 2 раза Найти : ∟6 — ?
Карточка №4 (достаточный уровень) Дано: аІІв, с – секущая ∟4+∟5 =68 ͦ Найти : ∟5,∟6 — ?
Карточка №5 (достаточный уровень) Дано: аІІв, с – секущая ∟3>∟5в 4 раза Найти : ∟2 , ∟5- ?
VІ. Начальный уровень
1. Разница двух с восьми углов, образовавшихся при пересечении двух параллельных прямых секущей, равен 54° . Найдите каждый из восьми углов.
Средний уровень
2. Секущая пересекает две данные прямые; при этом образовались внутренние односторонние углы, разность которых равен 108°, а отношение — 4 : 1. Докажите, что данные прямые параллельны.
Достаточный уровень
3. Отрезки AB и CD есть параллельными и ровными. Докажите, что Δ ABC = Δ DCB, если отрезки AD и BC пересекаются
Высокий уровень
4. Через точки A и B, что лежат на сторонах тупого угла AOB, проведены прямые, параллельные сторонам данного угла и пересекающиеся в точке C. Найдите угол AOB, если прямые AC и BC пересекаются под углом 40°.
VІІ. Итог урока Я предлагаю поиграть в игру «Верю – не верю» и проверить хорошо ли вы усвоили, какими свойствами наделены углы
1. 2. Если мне надо доказать, что прямые параллельны – я вспоминаю свойства углов образованных при пересечении параллельных прямых и секущей. 3. Через точку, которая не належит прямой, можно провести множество параллельних ей прямых. 4.Если в результате пересечения параллельных прямых с секущей образовались два угла по 80º. Могут ли они быть: соответственными; внутренними односторонними; мне нужно доказать, что две прямые параллельны – я вспоминаю признаки параллельности прямых. 5. Если один из соответственных углов острый, то другой тупой. 6. Если один из внутренних односторонних углов острый, то другой тупой. 7. Если сумма внутренних накрестлежащих углов140º, то один из них 70º.
VІІІ. Рефлексия
У вас на партах лежат наборы смайликов. Какой из них подходит вашему настроению тот и бросьте при выходе из класса в почтовый ящик на двери.
Углы при пересечении двух прямых третьей прямой (секущей). Виды углов урок 5. Геометрия 7 класс12+ 6 месяцев назад Математика от Баканчиковой300 подписчиков Геометрия 7 класс. Сколько углов получается при пересечении 2-х прямых третьей (секущей)? Как называются эти углы, как их запомнить находить на разных рисунках? Сегодня на 5 уроке про виды углов мы ответим на эти вопросы. А чтобы Вы лучше и быстрее запомнили новый материал, сначала мы поясним Вам, что такое секущая, и как она расположена. Затем напомним Вам об углах, которые получаются при пересечении двух прямых или углов «в паре»: вертикальных и смежных. Подробно мы остановимся на 5 видах углов: внутренние односторонние, внешние односторонние, внутренние накрест лежащие, внешние накрест лежащие и соответственные. Объясним, почему они так называются, и дадим подсказки, как их находить. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео. Пересекающиеся линии и углы — SAT MathematicsВсе ресурсы SAT по математике137 Практические тесты Вопрос дня Карточки Learn by Concept SAT Mathematics Help » Треугольники, линии и углы » Пересекающиеся линии и углы На приведенном выше рисунке линия a параллельна линии b , а линия d параллельна линии e . Возможные ответы: 25 10 15 30 Правильный ответ: 15 Пояснение: Пересекающиеся и параллельные линии встречаются во множестве различных геометрических фигур: параллелограммах, трапециях, квадратах и т. д. Всякий раз, когда вы видите их в вопросе, вы должны правильно использовать основные свойства дополнительных и вертикальных углов. В этой задаче самый быстрый способ найти y — понять, что 5x в левом нижнем углу является дополнительным к 2x + 5 в правом нижнем углу (из-за пересечения двух параллельных прямых). Следовательно, 5x + 2x + 5 = 180 и x = 25. Получив эту информацию, вы можете использовать тот факт, что сумма внутренних углов треугольника равна 180, и увидеть, что x + 5x + 2y = 180. Подставляя вместо x 25, вы видите, что 25+125+2y = 180 и 2y = 30. Сообщить об ошибке На рисунке выше . Что из следующего должно быть правдой?
I. II. Две горизонтальные линии параллельны. III. Возможные ответы: Только I и II Только II и III I, II и III Только I и III Правильный ответ: Только I и II Объяснение: Здесь SAT дает вам пару прямых с секущей, но не говорит вам, что прямые параллельны — он просит вас это доказать. Вам это говорят. Поскольку угол и угол являются вертикальными углами, а углы и являются вертикальными углами, вы знаете, что и . Это означает, что вы можете написать уравнение как: , или Если это означает и это. Прямая линия содержит 180 градусов, так что вы это знаете . И так как , вы можете заключить, что также. Чтобы горизонтальные линии были параллельны, необходимо знать, что либо альтернативные внешние углы, либо альтернативные внутренние углы равны. Поскольку вы это уже доказали, вы знаете и это. Поскольку у вас есть пара альтернативных внешних углов, две прямые должны быть параллельны. Утверждение II также верно. Утверждение III, однако, не обязательно верно. Если тогда все углы были бы равны 90. Однако без этого знания вы не можете прийти к каким-либо выводам о взаимосвязи между и . Утверждение III не обязательно верно, поэтому правильным ответом будет только I и II. Сообщить об ошибке Две пересекающиеся прямые образуют углы, указанные выше. Если мера угла x в три раза больше угла y, то какова мера угла z? Возможные ответы: 60 45 120 135 Правильный ответ: 135 9 0005 Объяснение: Поскольку линии x и y в сумме дают 180 градусов, у вас есть два уравнения для работы: x + y = 180 x = 3y Это означает, что вы можете заменить 3y на x в порядке найти у: 3у + у = 180 4у = 180 у = 45 А так как z также в сумме с y дает 180, то z должно быть 180 — 45 = 135 градусов. Сообщить об ошибке Если на рисунке выше прямые g и k параллельны, а угол h равен 121 градусу, каково значение p? Возможные ответы: 59 71 49 61 Правильный ответ: 59 Объяснение: Если h равно 121, то угол непосредственно под h должен быть равен 59, так как это дополнительный угол, образованный диагональной линией. Поскольку g и k параллельны, этот угол в 59 градусов должен точно соответствовать p, поскольку они являются альтернативными внутренними углами. Сообщить об ошибке На приведенном выше рисунке прямые AD и BE пересекаются в точке C. Чему равен угол ACE? Возможные ответы: 145 115 125 135 Правильный ответ: 90 005 125 Объяснение: Два правила углов очень важны для этого вопроса: 1) Сумма внутренних углов треугольника всегда равна 180. 2) Дополнительные углы, смежные углы при пересечении двух прямых, должны в сумме давать 180 градусов. Если вы знаете, что ECD равно 55, то ACE как дополнительный угол должен образовывать остальные 125 градусов, чтобы сумма этих двух углов составила 180. Следовательно, правильный ответ — 125. Сообщить об ошибке Что такое a + b + c + d? Возможные ответы: 110 130 120 150 Правильный ответ: 90 005 150 Объяснение: В этой задаче важно понимать, что вы имеете дело с двумя пересекающимися треугольниками, которые образуют внешние дополнительные углы вдоль прямой линии внизу. Чтобы убедиться в этом, рассмотрите приведенную ниже диаграмму, для которой добавлены углы x и y: Угол y является внешним дополнительным углом к треугольнику рядом с ним, поэтому y = a + c. Используя ту же логику, вы можете увидеть, что x = b + d в другом пересекающемся треугольнике. Поскольку проблема заключается в том, чтобы задать a + b + c + d, вы должны признать, что этот вопрос на самом деле такой же, как и вопрос о том, что такое x + y. Почему? Вы можете заменить x на b + d и y на a + c в основе вопроса. Так как x + y = 180 — 30 на прямой внизу, правильный ответ 150. Обратите внимание, что еще один способ решить эту задачу состоит в том, чтобы увидеть два больших тупоугольных треугольника: один с углами a, c и (x+30), а другой с углами b, d и (y+30). Если вы сделаете это, у вас будет:
a+c+x+30=180, поэтому a+c+x=150 b+d+y+30=180, поэтому b+d+y= 150 И вы знаете, что x+y+30=180, потому что x, 30 и y — это все углы, которые составляют прямую линию в 180 градусов, проходящую через нижнюю часть рисунка. Затем можно суммировать уравнения треугольника: a+c+x+b+d+y=150+150=300 А затем подставьте x+y = 150, и у вас останется a+b+c+d=150. Сообщить об ошибке На изображении выше . Каково значение Возможные ответы: 70 60 80 50 Правильный ответ: 60 Пояснение: Эта задача основана на двух важных правилах геометрии: 1) Сумма всех внутренних углов треугольника равна 180. Здесь вы знаете, что в верхнем треугольнике углы равны 30 и 80, а это означает, что угол при точка пересечения линий должна быть равна 70, так как 30+80=110, а сумма последнего угла должна равняться 180. 2) Вертикальные углы — углы, противоположные друг другу при пересечении двух прямых — равны. Поскольку вы определили, что угол в основании треугольника наверху равен 70°, это также означает, что верхний, непомеченный угол нижнего треугольника равен 70°. Сообщить об ошибке
ПРИМЕЧАНИЕ. Рисунок выполнен не в масштабе. Какое значение на рисунке выше? Возможные ответы: 115 135 150 125 Правильный ответ: 90 005 135 Объяснение: В этой задаче сильно используются два правила: 1) Сумма углов треугольника равна 180. 2) Дополнительные углы — смежные углы, образующиеся при пересечении одной прямой другой — должны в сумме давать 180. Здесь вы можете сначала использовать угол в 140 градусов, чтобы указать, что его соседний сосед — его дополнительный партнер — должен быть равен 40. Это дает вам два из трех углов в самом верхнем треугольнике: 20 и 40. Отсюда вы должны увидеть, что угол в 120 градусов является вертикальным углом, а это означает, что его противоположность также будет равна 120. И это дает вам второй угол в нижний правый треугольник. Знание того, что у вас есть углы 15 и 120, означает, что третий угол этого треугольника должен быть равен 45. А поскольку этот угол является дополнительным к углу x, тогда x должен быть равен 135.
Сообщить об ошибке На рисунке выше линии и параллельны. Какова ценность ? Возможные ответы: 95 125 105 115 Правильный ответ: 900 05 125 Объяснение: Эта задача сильно зависит от двух важных правил для прямых и углов: 1) Сумма трех внутренних углов треугольника всегда равна 180. 2) Дополнительные углы — углы рядом друг с другом, образованные двумя пересекающимися линиями — также должны в сумме давать 180. нижний правый угол маленького треугольника вверху, вы можете закрыть этот треугольник. Для углов 40° и 85° это означает, что нижний левый угол должен быть равен 55°. Отсюда вы можете использовать тот факт, что параллельные линии приведут к конгруэнтным углам. Поскольку прямые и параллельны, угол рядом с будет равен 55 градусам, а это означает, что будет равен 125. Сообщить об ошибке На диаграмме выше линии и все пересекаются в точке A. Если и , каково значение ? Возможные ответы: 20 50 30 40 Правильный ответ: 30 Объяснение: Эта задача проверяет два важных правила. Во-первых, угловая мера прямой линии равна 180. Далее, знайте, что когда линии пересекаются, образуя углы в определенной точке, противоположные (вертикальные) углы конгруэнтны. Угол измерения прямо противоположен углу, который вы только что рассчитали в градусах, поэтому должен быть таким же. Сообщить об ошибке Уведомление об авторских правах Все ресурсы по математике SAT137 Практические тесты Вопрос дня Карточки Learn by Concept Угол между двумя линиями — Infinity Learn Угол, образованный двумя линиями Полезно понимать взаимосвязь между двумя линиями. Это будет угол наклона между двумя линиями. Есть два угла, образованных двумя пересекающимися прямыми: острый угол и тупой угол. Также стоит отметить, что угол, образованный пересечением двух прямых, не может быть рассчитан, если одна из прямых параллельна оси y, потому что наклон линии, параллельной оси y, не определен. Зарегистрируйтесь, чтобы получить индивидуальный план обучения, который поможет вам улучшить свои результаты! Класс Целевой экзамен +91 Проверка OTP-кода (обязательно) Я согласен с условиями и политикой конфиденциальности. Формула угла между двумя прямымиЕсли θ — угол, образованный двумя пересекающимися линиями, определяемыми y 1 = m 1 x 1 +c 1 9042 1 и у 2 = м 2 x 2 +c 2, угол будет: tanθ = ±(m 2 -m 1 ) / (1+m 1 904 21 м 2 ) Угол между двумя прямыми Вывод Линии L 1 и линия L 2 пересекаются в точке на рисунке выше. Теперь измерение уклона выглядит следующим образом: tan a 1 = m 1 и tan a 2 = m 2 Тогда, исходя из рисунка, мы можем если θ = a 2 -a 1 Итак, tan θ = tan (a 2 -a 1 ) = (tan a 2 – tan a 1 ) / (1- загар 1 tan a 2 ) При подстановке значений tan a 1 и tan a 2 как m 1 и m 2 соответственно имеем , tanθ= (м 2 – m 1 ) / (1+m 1 m 2 ) Следует отметить, что в этом уравнении значение тангенса θ будет положительным, если θ острое, и отрицательным, если θ тупым. Угол между двумя линиями Координатная геометрияЕсли в аналитической геометрии действительно заданы координаты трех точек A, B и C, то угол между линиями AB и BC можно вычислить следующим образом: Наклон линии с конечными точками (x 1 , y 1 ) и (x 2 , y 2 ) определяется уравнением: 9000 4 Всякий раз, когда известен наклон каждой линии из уравнения угол между двумя линиями можно рассчитать, вычислив наклон каждой линии, а затем используя его в формуле для определения угла между двумя линиями. |
|---|

 Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.
Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.




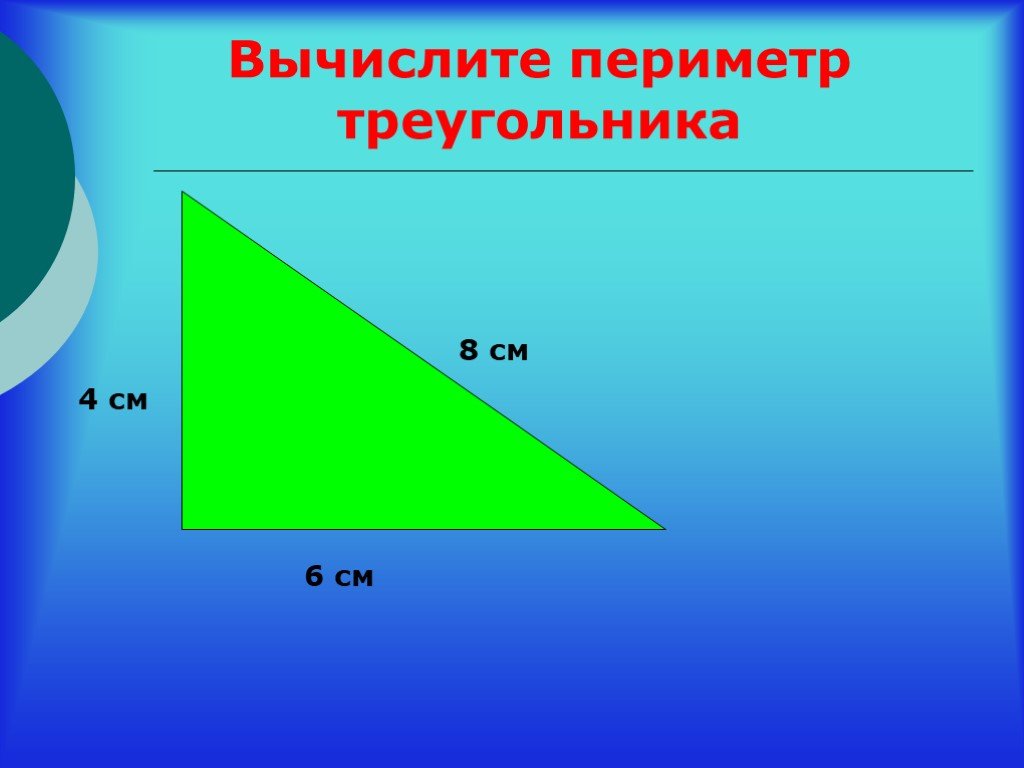 Найдём периметр:
Найдём периметр: Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.
Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.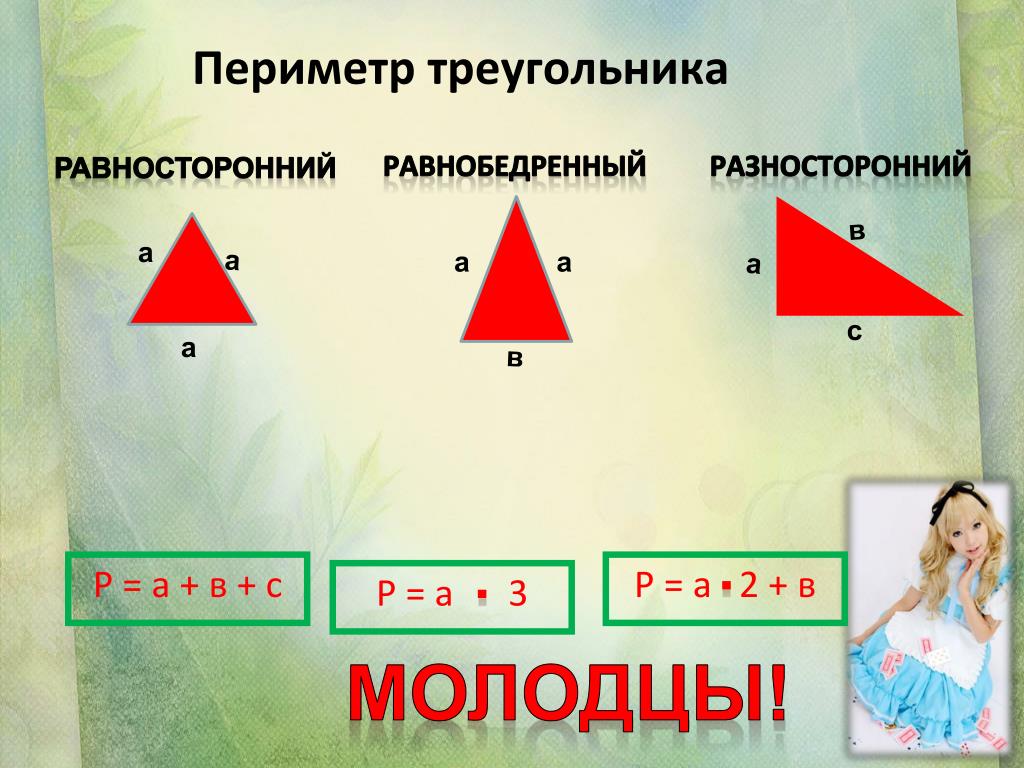

 Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
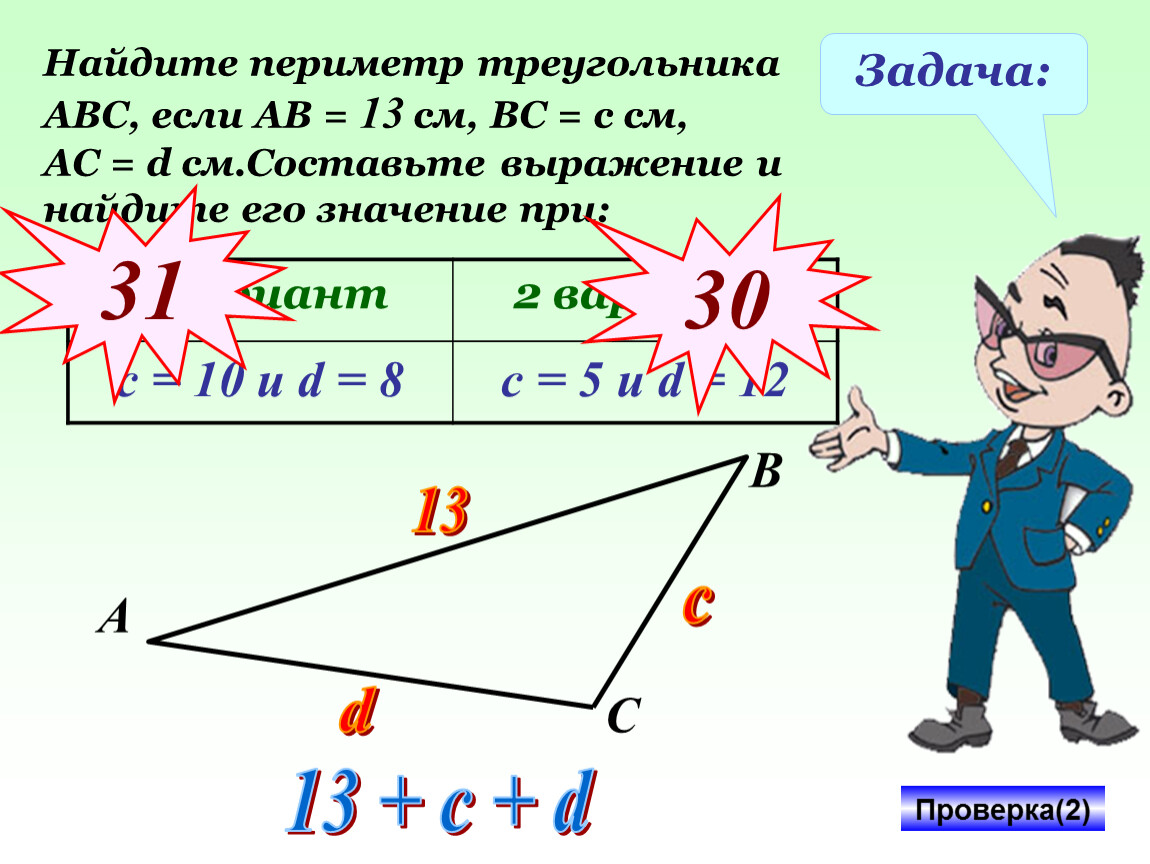 Сколько треугольников вы видите? устно № 1 Часто знает и дошкольник, Что такое треугольник, А уж вам-то как не знать! Но совсем другое дело – Быстро, точно и умело Треугольники считать. Например, на картинке этой Сколько разных? Рассмотри! Все внимательно исследуй И по краю, и внутри! На рисунке изображено 13 треугольников .
Сколько треугольников вы видите? устно № 1 Часто знает и дошкольник, Что такое треугольник, А уж вам-то как не знать! Но совсем другое дело – Быстро, точно и умело Треугольники считать. Например, на картинке этой Сколько разных? Рассмотри! Все внимательно исследуй И по краю, и внутри! На рисунке изображено 13 треугольников . Наши итоги 1 2 3 3 12 4 6 5 Характерные ошибки… Как исправить… Над чем поработать дома с родителями…
Наши итоги 1 2 3 3 12 4 6 5 Характерные ошибки… Как исправить… Над чем поработать дома с родителями…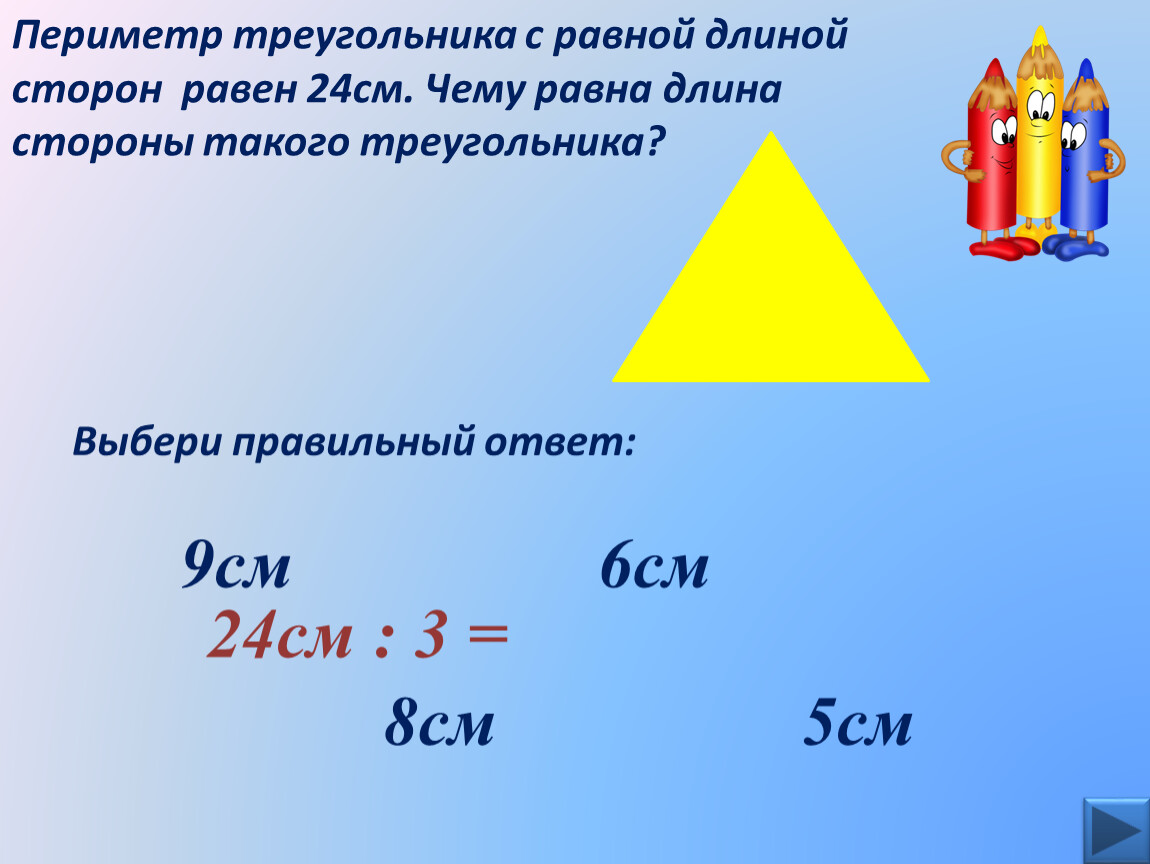 Обозначьте его. Измерьте сторону, противолежащую прямому углу. УЧЕБНИК № 4 10 построение АВ = 5 см А В С 4 см 3 см 5 см
Обозначьте его. Измерьте сторону, противолежащую прямому углу. УЧЕБНИК № 4 10 построение АВ = 5 см А В С 4 см 3 см 5 см Ч то вы можете сказать об этом треугольнике? УЧЕБНИК № 4 16 ? Равнобедренный, т.к. 17 – (5 + 6) = 6 (см). Вычислите периметр равностороннего треугольника со стороной 8 см. УЧЕБНИК № 4 1 7 ? Р = 8 + 8 + 8 = 24 (см) б) В равнобедренном треугольнике периметр равен 21 см, а боковая сторона равна 6 см. найдите длину основания. УЧЕБНИК № 4 1 8 ? 2 ∙ 6 = 12 (см) 21 – 12= 9(см)
Ч то вы можете сказать об этом треугольнике? УЧЕБНИК № 4 16 ? Равнобедренный, т.к. 17 – (5 + 6) = 6 (см). Вычислите периметр равностороннего треугольника со стороной 8 см. УЧЕБНИК № 4 1 7 ? Р = 8 + 8 + 8 = 24 (см) б) В равнобедренном треугольнике периметр равен 21 см, а боковая сторона равна 6 см. найдите длину основания. УЧЕБНИК № 4 1 8 ? 2 ∙ 6 = 12 (см) 21 – 12= 9(см)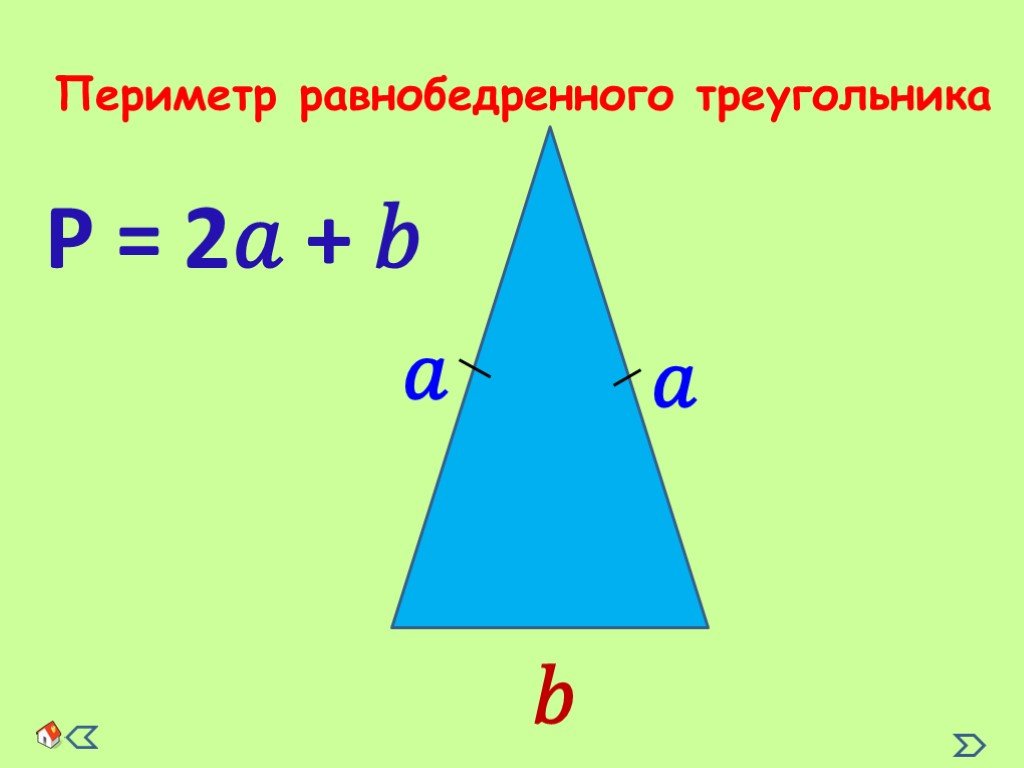 Задачное множество Домашнее задание п.7.1, №п.7.1, №523, 534, выполнить задания на сайте » Учи.ру » — ГЕОМЕТРИЯ. Треугольники
Задачное множество Домашнее задание п.7.1, №п.7.1, №523, 534, выполнить задания на сайте » Учи.ру » — ГЕОМЕТРИЯ. Треугольники
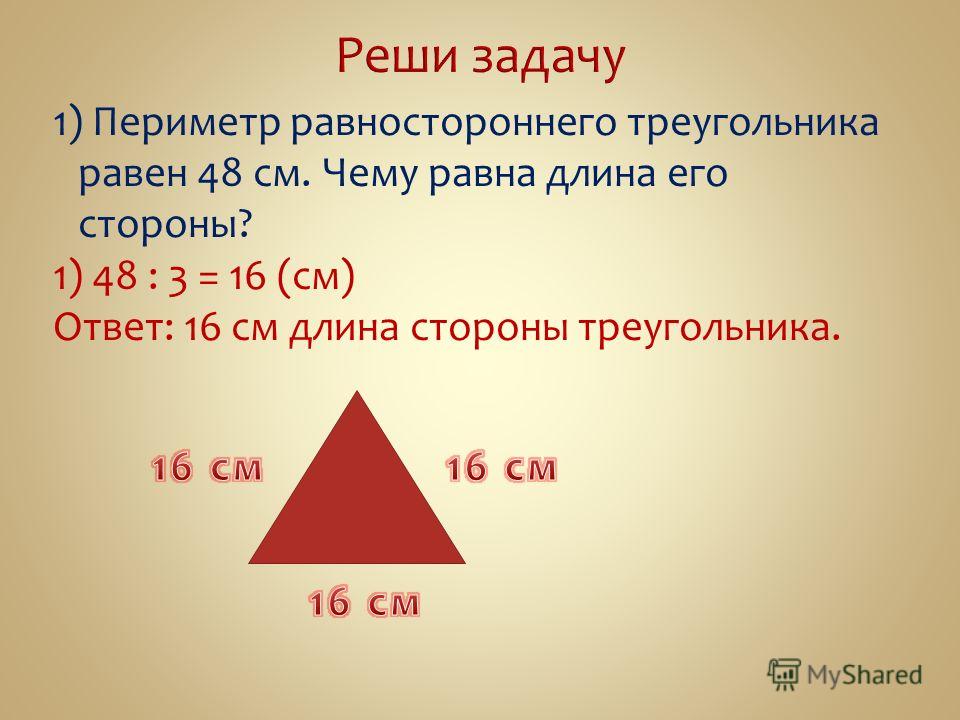
 Как мы это делаем? Необходимую длину забора можно рассчитать, найдя общую длину границы (периметра) треугольника.
Как мы это делаем? Необходимую длину забора можно рассчитать, найдя общую длину границы (периметра) треугольника. Каково значение x, если периметр треугольника PQR равен 40 единицам? Также найдите длину трех сторон.
Каково значение x, если периметр треугольника PQR равен 40 единицам? Также найдите длину трех сторон. 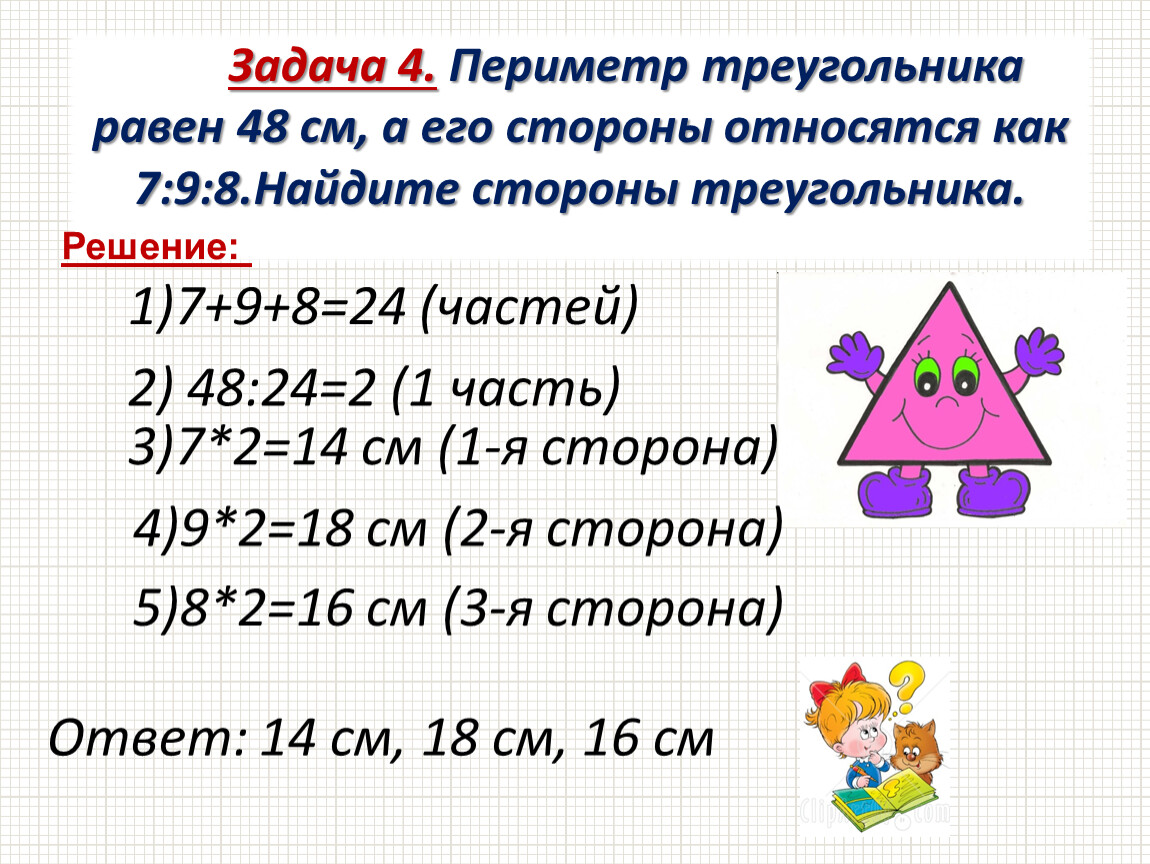
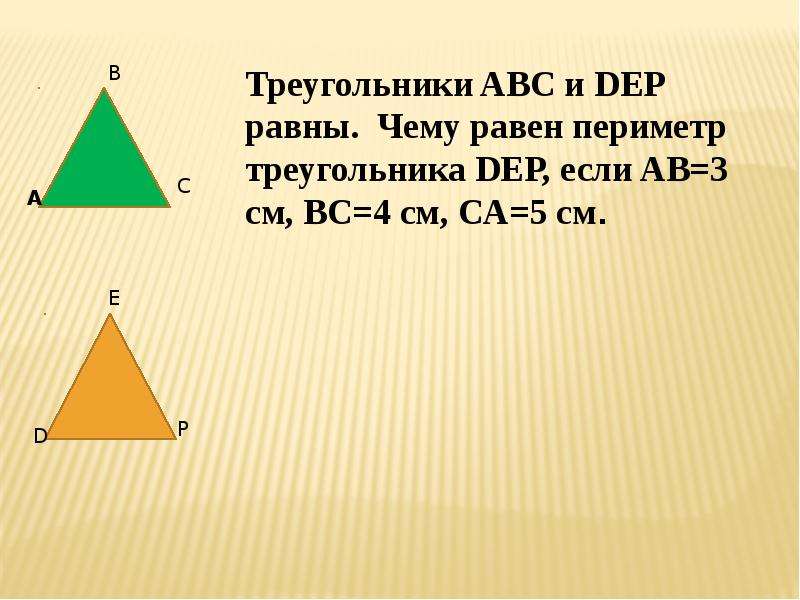 Эта фундаментальная концепция важна для понимания учащимися, поскольку она закладывает основу для более сложных математических тем. Итак, без лишних слов, давайте отправимся в приключение в царство периметров треугольников и откроем секреты этого геометрического чуда!
Эта фундаментальная концепция важна для понимания учащимися, поскольку она закладывает основу для более сложных математических тем. Итак, без лишних слов, давайте отправимся в приключение в царство периметров треугольников и откроем секреты этого геометрического чуда!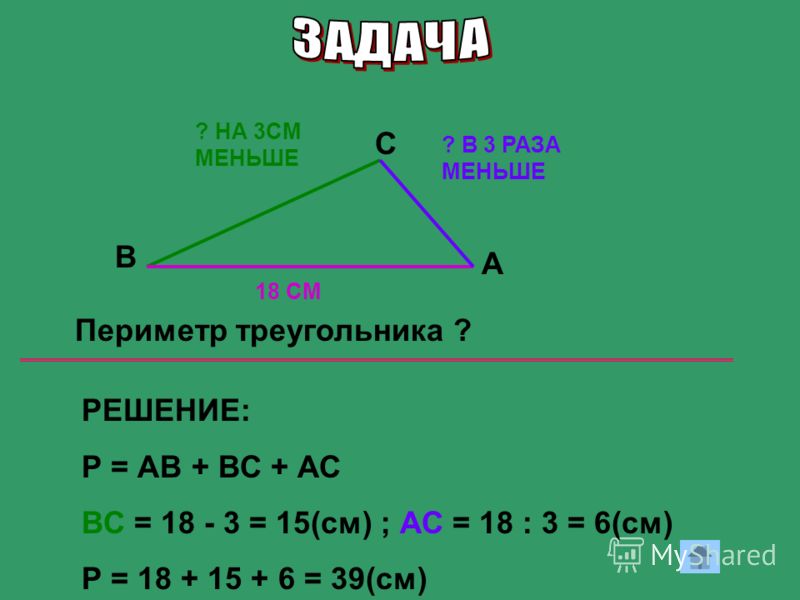 Однако, если вам не хватает некоторых длин сторон, вам может понадобиться использовать другую информацию о треугольнике, чтобы найти недостающие значения. Например, вы можете использовать теорему Пифагора для прямоугольных треугольников или применить свойства равнобедренных и равносторонних треугольников. Ниже мы обсудим формулы для нахождения периметра различных типов треугольников.
Однако, если вам не хватает некоторых длин сторон, вам может понадобиться использовать другую информацию о треугольнике, чтобы найти недостающие значения. Например, вы можете использовать теорему Пифагора для прямоугольных треугольников или применить свойства равнобедренных и равносторонних треугольников. Ниже мы обсудим формулы для нахождения периметра различных типов треугольников. Поскольку две стороны равны, формула для его периметра:
Поскольку две стороны равны, формула для его периметра: Поскольку к прямому углу примыкают равные стороны, можно воспользоваться теоремой Пифагора, чтобы найти гипотенузу:
Поскольку к прямому углу примыкают равные стороны, можно воспользоваться теоремой Пифагора, чтобы найти гипотенузу: Каков его периметр?
Каков его периметр? Периметр является важным понятием в геометрии и используется для измерения границ любой формы. В случае треугольников периметр помогает нам понять размер и масштаб треугольника на основе длин его сторон.
Периметр является важным понятием в геометрии и используется для измерения границ любой формы. В случае треугольников периметр помогает нам понять размер и масштаб треугольника на основе длин его сторон.
 В пособие собрана большая подборка заданий по темам курса алгебры 7 класса для отработки навыка решения тематических задач.
В пособие собрана большая подборка заданий по темам курса алгебры 7 класса для отработки навыка решения тематических задач.
 Часть 1-я — теоретический материал (учебник). Часть 2-я — практический материал (задачник).
Часть 1-я — теоретический материал (учебник). Часть 2-я — практический материал (задачник). Основное свойство алгебраической дроби. Упр. 2.1 — 2.48
Основное свойство алгебраической дроби. Упр. 2.1 — 2.48  24
24  В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями
В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями
 7.2 Промежуточный уровень
7.2 Промежуточный уровень Это написано членом сообщества AoPS cargeek9., в настоящее время младший в средней школе. Он охватывает основы алгебры, геометрии, комбинаторики и теории чисел, а также наборы сопутствующих практических задач в конце каждого раздела.
Это написано членом сообщества AoPS cargeek9., в настоящее время младший в средней школе. Он охватывает основы алгебры, геометрии, комбинаторики и теории чисел, а также наборы сопутствующих практических задач в конце каждого раздела.





 М. Гельфанда и Марка Сола.
М. Гельфанда и Марка Сола.


 Учащиеся узнают, как интерпретировать и решать задачи в том виде, в каком они обычно представлены на курсах алгебры, и подготовятся к решению тех задач, которые никогда не обсуждались в классе, но всегда появляются на экзаменах.
Учащиеся узнают, как интерпретировать и решать задачи в том виде, в каком они обычно представлены на курсах алгебры, и подготовятся к решению тех задач, которые никогда не обсуждались в классе, но всегда появляются на экзаменах. Тем не менее, весьма озадачивает, почему автор (имеющий довольно много книг по математике) не предоставил для них опечатки. Тем более, что у него есть веб-страница, посвященная этим книгам.
Тем не менее, весьма озадачивает, почему автор (имеющий довольно много книг по математике) не предоставил для них опечатки. Тем более, что у него есть веб-страница, посвященная этим книгам.

 В этом случае вам придется выполнить конвертацию заново.
В этом случае вам придется выполнить конвертацию заново. Чем выше качество, тем больше весит файл. И наоборот, чем ниже качество, тем меньше размер файла.
Чем выше качество, тем больше весит файл. И наоборот, чем ниже качество, тем меньше размер файла. Они очень похожи тем, что оба содержат данные изображений, например фотографии. Однако каждый из них имеет свою индивидуальность.
Они очень похожи тем, что оба содержат данные изображений, например фотографии. Однако каждый из них имеет свою индивидуальность. Например, вы не можете напечатать его профессионально. Поскольку файлы PNG не содержат информацию о цвете CMYK, профессиональная полиграфическая компания не примет их.
Например, вы не можете напечатать его профессионально. Поскольку файлы PNG не содержат информацию о цвете CMYK, профессиональная полиграфическая компания не примет их. Перейдите к файлам, которые вы хотите преобразовать. И наоборот, вы также можете перетаскивать файлы, которые хотите загрузить. Вы можете загрузить до 20 одновременно.
Перейдите к файлам, которые вы хотите преобразовать. И наоборот, вы также можете перетаскивать файлы, которые хотите загрузить. Вы можете загрузить до 20 одновременно. Это означает, что сжатие изображения несколько снизило его общее качество. Когда вы создаете JPG, вы можете выбрать, насколько он будет с потерями. Как правило, чем выше качество изображения, тем больше его размер, поэтому сжатие изображения может помочь ему занимать меньше места на жестком диске.
Это означает, что сжатие изображения несколько снизило его общее качество. Когда вы создаете JPG, вы можете выбрать, насколько он будет с потерями. Как правило, чем выше качество изображения, тем больше его размер, поэтому сжатие изображения может помочь ему занимать меньше места на жестком диске. JPG должны иметь информацию о цвете в каждом пикселе, поэтому пустые пиксели обычно заполняются черным или белым цветом.
JPG должны иметь информацию о цвете в каждом пикселе, поэтому пустые пиксели обычно заполняются черным или белым цветом.



 Азот в этой степени окисления может как принимать, так и отдавать электроны, т.е. может являться как окислителем, так восстановителем.
Азот в этой степени окисления может как принимать, так и отдавать электроны, т.е. может являться как окислителем, так восстановителем. Определите степени окисления всех компонентов, входящих в состав следующих соединений: HСl, Cl2, HClO2 , HClO3 , Cl2O7 . Какие из веществ являются только окислителями, только восстановителями, и окислителями и восстановителями? Расставьте коэффициенты в уравнении реакции:
Определите степени окисления всех компонентов, входящих в состав следующих соединений: HСl, Cl2, HClO2 , HClO3 , Cl2O7 . Какие из веществ являются только окислителями, только восстановителями, и окислителями и восстановителями? Расставьте коэффициенты в уравнении реакции: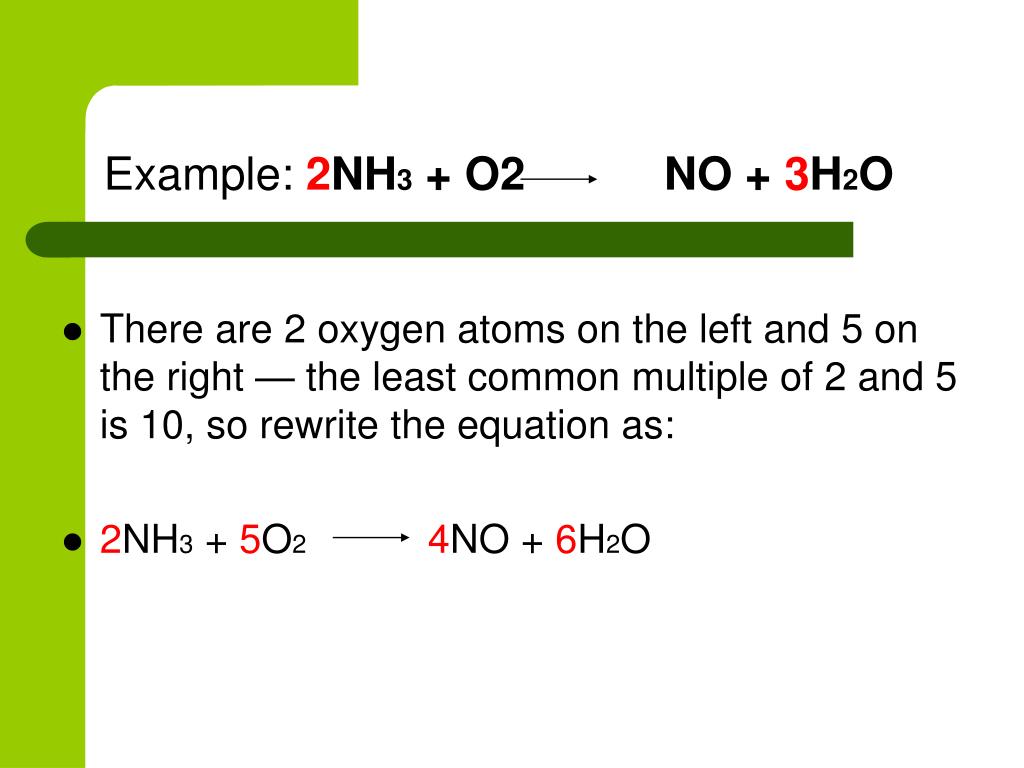 е. могут отдавать, так и принимать электроны.
е. могут отдавать, так и принимать электроны.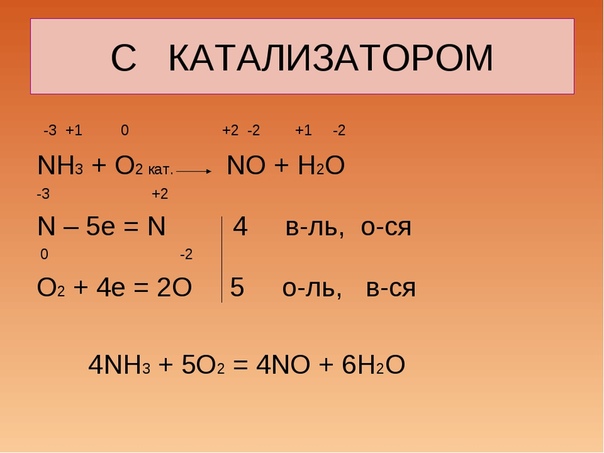
 Какие ОВР относятся к реакциям диспропорционирования? Расставьте коэффициенты в реакциях:
Какие ОВР относятся к реакциям диспропорционирования? Расставьте коэффициенты в реакциях: Составьте электронные уравнения и подберите коэффициенты ионно-электронным методом в реакции
Составьте электронные уравнения и подберите коэффициенты ионно-электронным методом в реакции Определите методом электронного баланса коэффициенты в уравнениях окислительно-восстановительных реакций:
Определите методом электронного баланса коэффициенты в уравнениях окислительно-восстановительных реакций: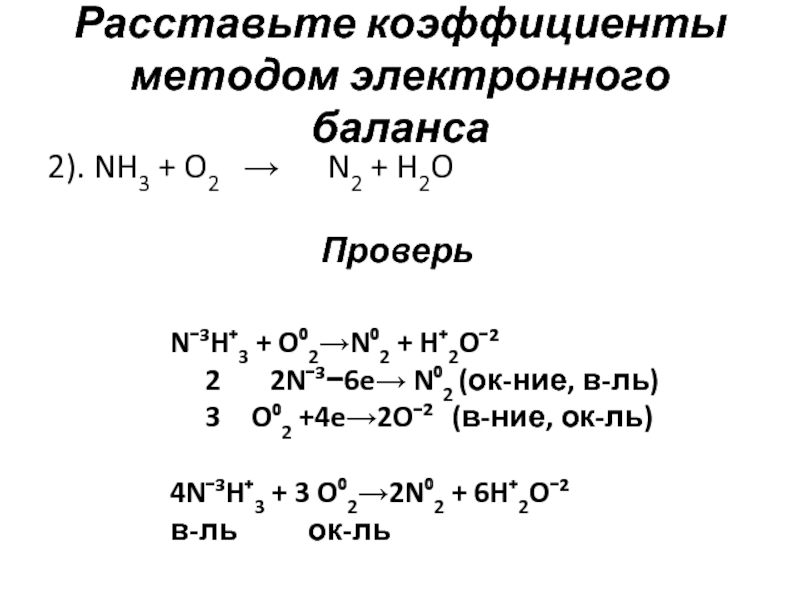 Можно ли в качестве окислителя в кислой среде использовать K2Cr2O7 в следующих процессах при стандартных условиях:
Можно ли в качестве окислителя в кислой среде использовать K2Cr2O7 в следующих процессах при стандартных условиях: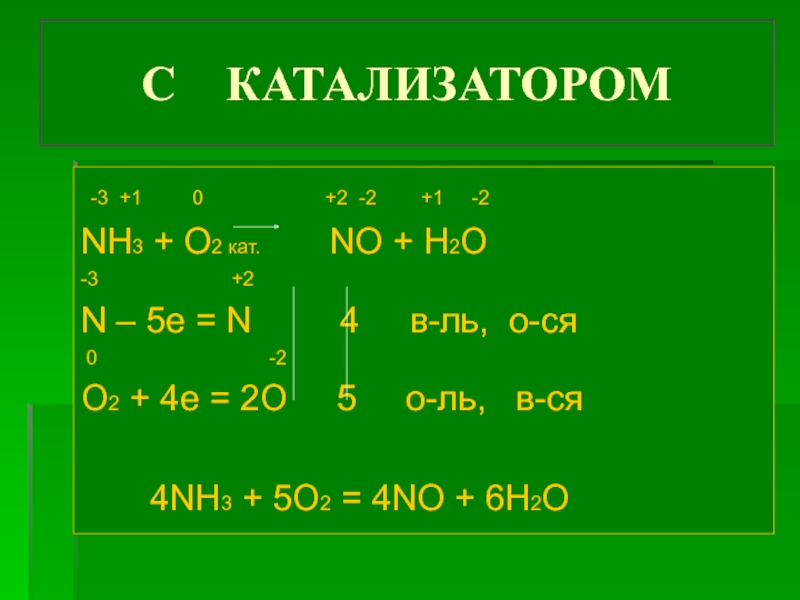

 Kc=[Nh4]4[O2]5[NO]4[h3O]6 న రసాయన సమీకరణం రాయండి.
Kc=[Nh4]4[O2]5[NO]4[h3O]6 న రసాయన సమీకరణం రాయండి. ..
.. Для балансировки этих реакций используется метод полууравнения.
Для балансировки этих реакций используется метод полууравнения.



 Мы используем методологию, основанную на правилах, для выявления лидеров отрасли и отстающих в зависимости от их подверженности рискам ESG и того, насколько хорошо они управляют этими рисками по сравнению с аналогами. Наши рейтинги ESG варьируются от лидера (AAA, AA), среднего (A, BBB, BB) до отстающего (B, CCC). Мы также оцениваем акции и ценные бумаги с фиксированным доходом, кредиты, взаимные фонды, ETF и страны.
Мы используем методологию, основанную на правилах, для выявления лидеров отрасли и отстающих в зависимости от их подверженности рискам ESG и того, насколько хорошо они управляют этими рисками по сравнению с аналогами. Наши рейтинги ESG варьируются от лидера (AAA, AA), среднего (A, BBB, BB) до отстающего (B, CCC). Мы также оцениваем акции и ценные бумаги с фиксированным доходом, кредиты, взаимные фонды, ETF и страны. Наша модель рейтингов MSCI ESG определяет риски ESG (то, что мы называем ключевыми проблемами), которые наиболее существенны для подотрасли или сектора GICS®. Имея более чем 13-летнюю историю отслеживания, мы смогли изучить и уточнить нашу модель, чтобы определить ключевые проблемы E, S и G, которые наиболее важны для отрасли.
Наша модель рейтингов MSCI ESG определяет риски ESG (то, что мы называем ключевыми проблемами), которые наиболее существенны для подотрасли или сектора GICS®. Имея более чем 13-летнюю историю отслеживания, мы смогли изучить и уточнить нашу модель, чтобы определить ключевые проблемы E, S и G, которые наиболее важны для отрасли.


 Мы ежегодно пересматриваем и корректируем модель ESG Ratings и запрашиваем отзывы наших клиентов о возможных изменениях и улучшениях посредством ежегодного процесса консультаций. Над
за последние семь лет MSCI ESG Research провела консультации с более чем 55 крупнейшими инвесторами по всему миру, чтобы усовершенствовать нашу методологию рейтингов ESG и расширить охват.
Мы ежегодно пересматриваем и корректируем модель ESG Ratings и запрашиваем отзывы наших клиентов о возможных изменениях и улучшениях посредством ежегодного процесса консультаций. Над
за последние семь лет MSCI ESG Research провела консультации с более чем 55 крупнейшими инвесторами по всему миру, чтобы усовершенствовать нашу методологию рейтингов ESG и расширить охват. является зарегистрированным инвестиционным консультантом в соответствии с Законом об инвестиционном консультанте от 1940. Самая последняя форма ADV SEC, включая часть 2A формы ADV, доступна на веб-сайте SEC США по адресу www.adviserinfo.sec.gov (открывается в новой вкладке).
является зарегистрированным инвестиционным консультантом в соответствии с Законом об инвестиционном консультанте от 1940. Самая последняя форма ADV SEC, включая часть 2A формы ADV, доступна на веб-сайте SEC США по адресу www.adviserinfo.sec.gov (открывается в новой вкладке). 

 Сколькими различными способами они могут занять свои места в зрительном зале?
Сколькими различными способами они могут занять свои места в зрительном зале?


 Число 54 321 является наибольшим, а значит имеет 120 порядковый номер. Число 54 312 идёт перед ним, следовательно, оно имеет 119 порядковый номер. А затем идёт число 54 231 под 118 порядковым номером.
Число 54 321 является наибольшим, а значит имеет 120 порядковый номер. Число 54 312 идёт перед ним, следовательно, оно имеет 119 порядковый номер. А затем идёт число 54 231 под 118 порядковым номером. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Наименьшее трехзначное — 100, наибольшее — 999.
Наименьшее трехзначное — 100, наибольшее — 999.
 Разряд — это позиция или место расположения цифры в записи натурального числа.
Разряд — это позиция или место расположения цифры в записи натурального числа.
 Записать цифрами число, в котором содержится:
Записать цифрами число, в котором содержится:



 А) Сколько таких чисел? Вы решаете, используя древовидную диаграмму. Б) Какой процент из них четные?
А) Сколько таких чисел? Вы решаете, используя древовидную диаграмму. Б) Какой процент из них четные?
 Рассмотрим число 243. Говорят, что первая крайняя правая цифра стоит на месте единиц, поэтому она будет умножена на 1. Следовательно, произведение равно 3 × 1 = 3. Тогда второе число равно 4, а поскольку оно стоит на разряде десятков, оно умножается на 10. Следовательно, значение равно 4 × 10 = 40. Третье число 2 стоит на разряде сотен. Таким образом, 2 умножается на 100, и его значение равно 2 × 100 = 200. Следовательно, число равно 200 + 40 + 3 = 243, 9.0003
Рассмотрим число 243. Говорят, что первая крайняя правая цифра стоит на месте единиц, поэтому она будет умножена на 1. Следовательно, произведение равно 3 × 1 = 3. Тогда второе число равно 4, а поскольку оно стоит на разряде десятков, оно умножается на 10. Следовательно, значение равно 4 × 10 = 40. Третье число 2 стоит на разряде сотен. Таким образом, 2 умножается на 100, и его значение равно 2 × 100 = 200. Следовательно, число равно 200 + 40 + 3 = 243, 9.0003 Так чем же 303 отличается от 033 или даже 003? В 033 значения равны (0 × 100) + (3 × 10) + (3 × 1) = 0 + 30 + 3 = 33, что означает, что число на самом деле становится двузначным числом, т. е. 33, или в в случае 003 оно становится однозначным числом, т. е. 3. В этих двух примерах ноль не вносит никакого вклада в число, поэтому числа также могут быть выражены как 33 или 3.
Так чем же 303 отличается от 033 или даже 003? В 033 значения равны (0 × 100) + (3 × 10) + (3 × 1) = 0 + 30 + 3 = 33, что означает, что число на самом деле становится двузначным числом, т. е. 33, или в в случае 003 оно становится однозначным числом, т. е. 3. В этих двух примерах ноль не вносит никакого вклада в число, поэтому числа также могут быть выражены как 33 или 3. Разделив, мы узнаем количество сотен, десятков и единиц, доступных в трехзначном числе.
Разделив, мы узнаем количество сотен, десятков и единиц, доступных в трехзначном числе.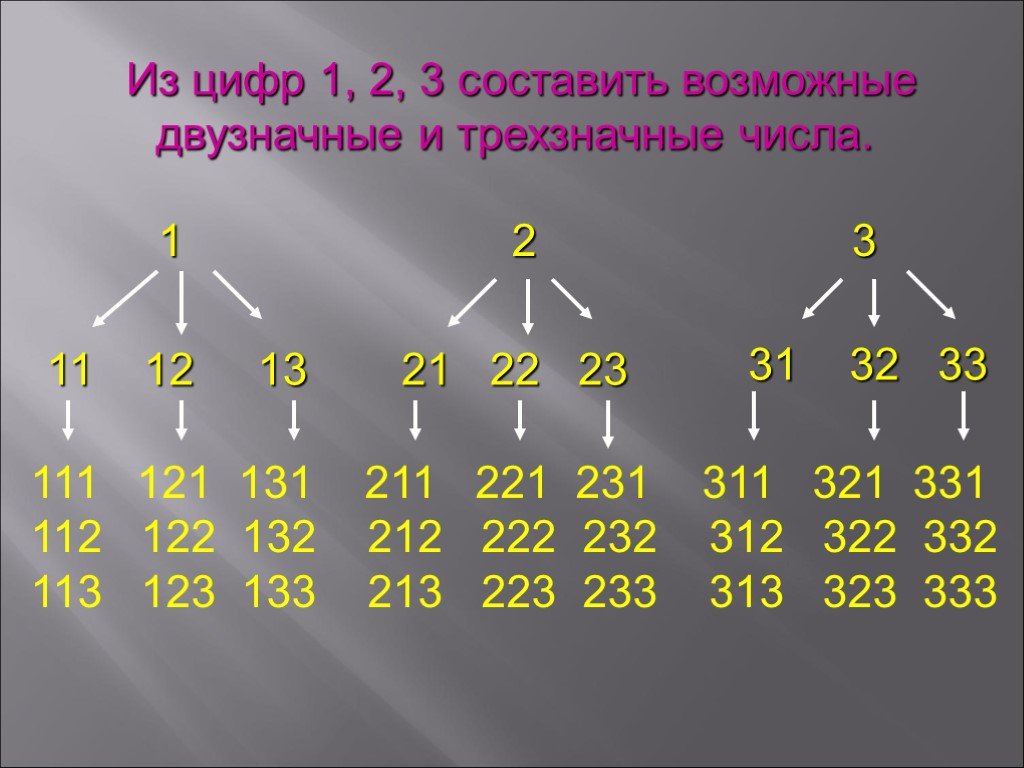 В процессе чтения, записи и интерпретации трехзначного числа необходимо правильно интерпретировать разрядное значение цифр. Ниже мы перечислили три распространенные ошибки, которые часто допускают дети при написании трехзначных чисел.
В процессе чтения, записи и интерпретации трехзначного числа необходимо правильно интерпретировать разрядное значение цифр. Ниже мы перечислили три распространенные ошибки, которые часто допускают дети при написании трехзначных чисел.
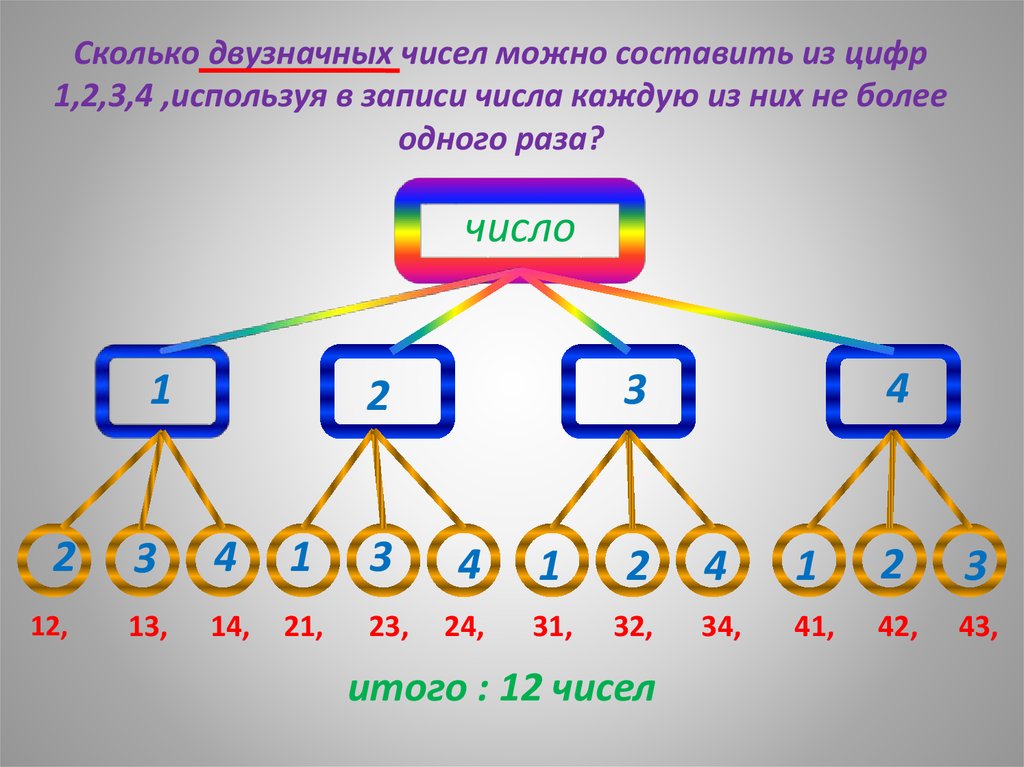
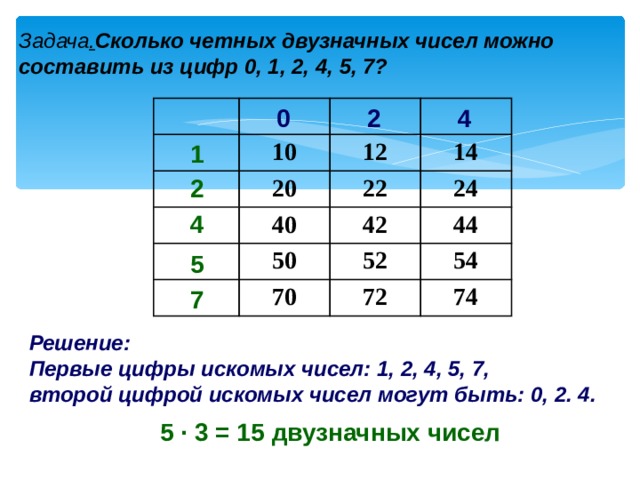
 Это можно рассчитать, используя следующий метод.
Это можно рассчитать, используя следующий метод.
 Если к нему добавить еще 1, оно станет четырехзначным, то есть 1000.
Если к нему добавить еще 1, оно станет четырехзначным, то есть 1000.

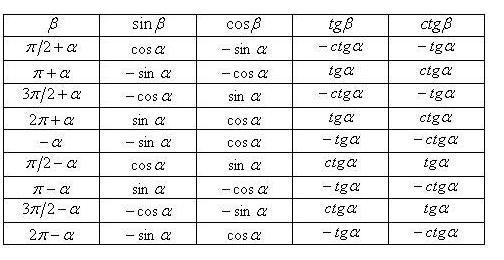

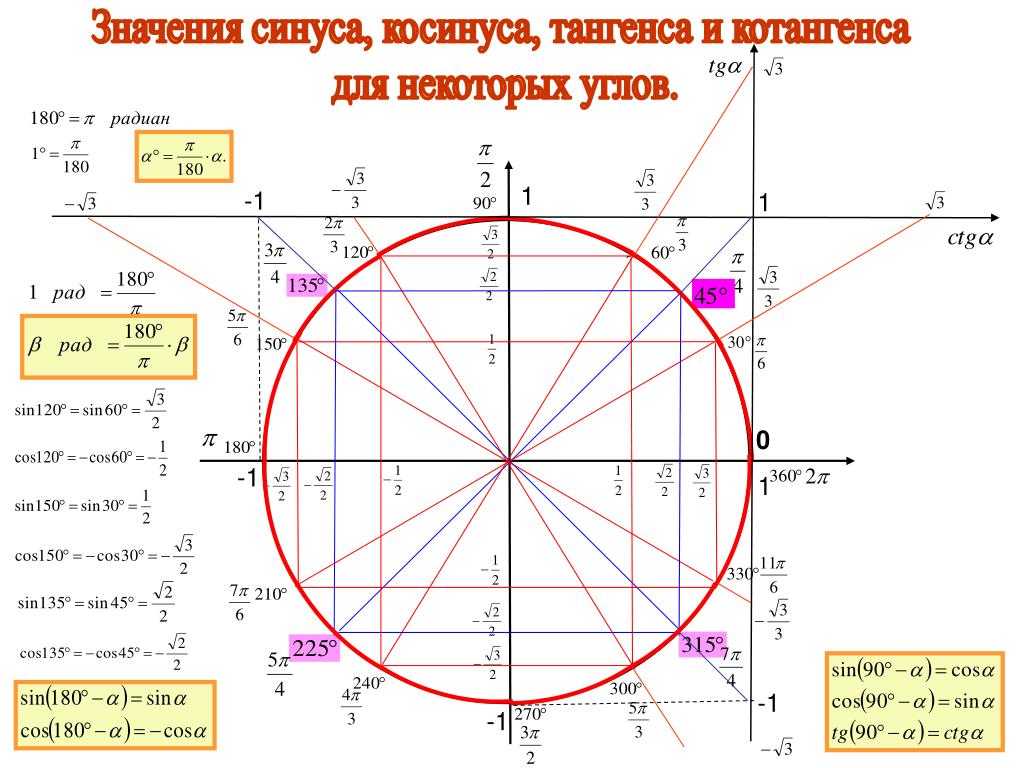 )/3
)/3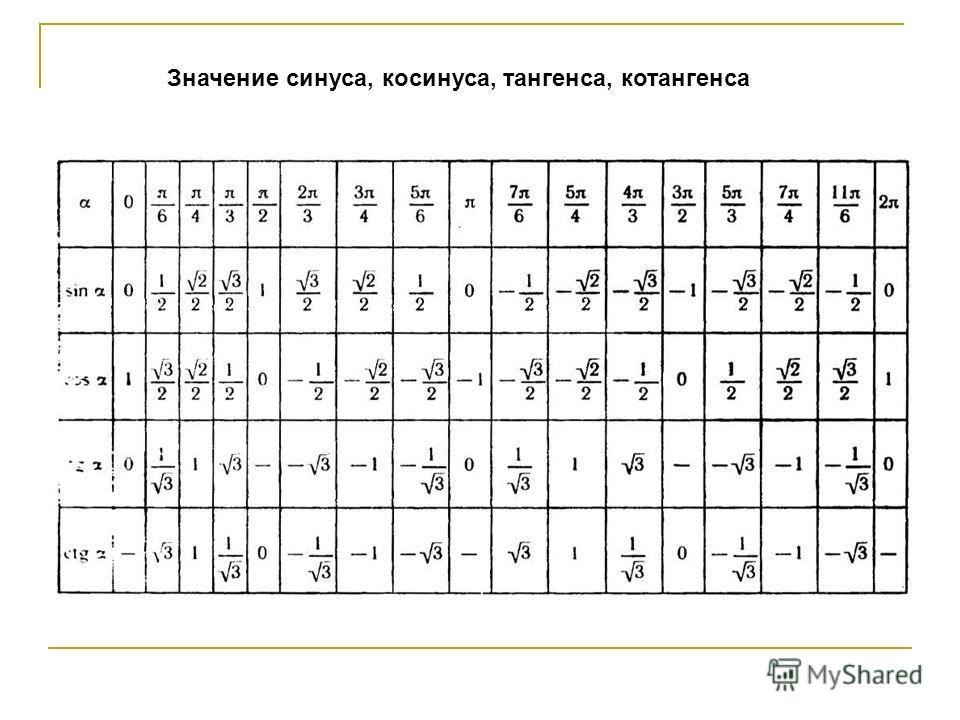
 При помощи канонического разложения можно найти все делители числа и их количество.
При помощи канонического разложения можно найти все делители числа и их количество. Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
 Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297.
Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах. 2
2 Следовательно, после деления не остается остатка. Числа, которые вы перемножаете, чтобы получить другое число, называются факторами. Таким образом, множитель является делителем другого числа.
Следовательно, после деления не остается остатка. Числа, которые вы перемножаете, чтобы получить другое число, называются факторами. Таким образом, множитель является делителем другого числа. Следовательно, 2 делит 18 без остатка. Таким образом, наименьший простой делитель числа 18 равен 2.
Следовательно, 2 делит 18 без остатка. Таким образом, наименьший простой делитель числа 18 равен 2.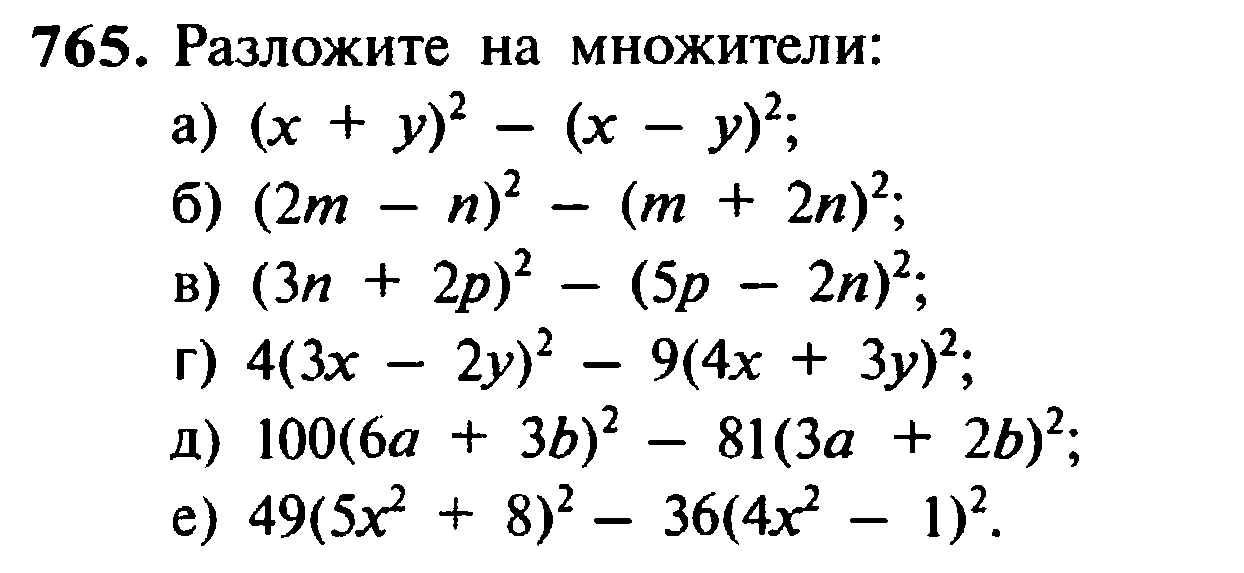

 Факторы 15 включают 3 и 5; числа, кратные 15, включают 30, 45, 60 (и более). Подробнее см. ниже и в нескольких местах.
Факторы 15 включают 3 и 5; числа, кратные 15, включают 30, 45, 60 (и более). Подробнее см. ниже и в нескольких местах.
 Например, 12 можно разложить как 3 × 4, или как 2 × 6, или как 2 × 2 × 3. Однако не все составные числа можно разложить более чем одним способом. Например, 25 можно разложить только как 5 × 5.
Например, 12 можно разложить как 3 × 4, или как 2 × 6, или как 2 × 2 × 3. Однако не все составные числа можно разложить более чем одним способом. Например, 25 можно разложить только как 5 × 5.

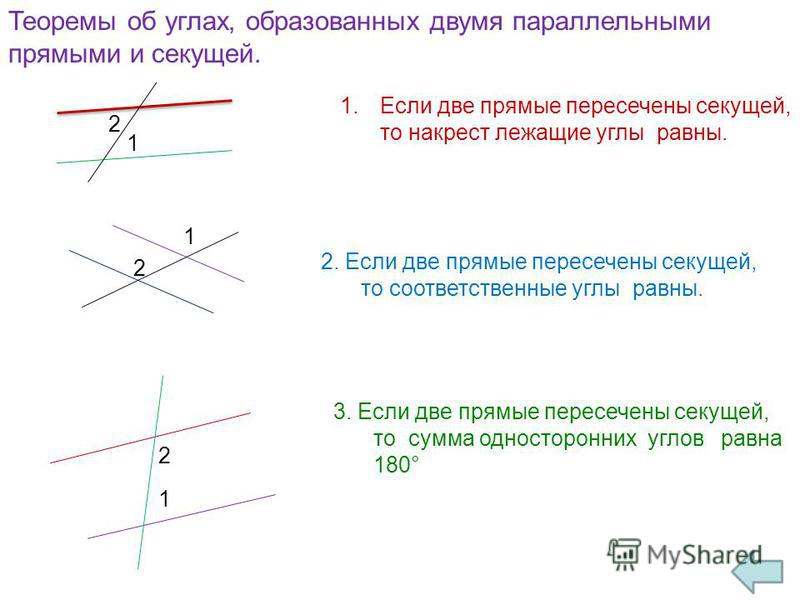
 Минутка
Минутка Домашнее задание Повторить п.4-8 решить задание на листочках.
Домашнее задание Повторить п.4-8 решить задание на листочках. Параллельные прямые на плоскости – это прямые, которые не пересекаются.
Параллельные прямые на плоскости – это прямые, которые не пересекаются.
 00:00 Начало видео.
00:32 Что такое секущая?
02:31 Сколько углов получается при пересечении 2-х прямых третьей?
03:29 Вспомним углы, получающиеся при пересечении 2-х прямых.
04:27 Внутренние односторонние углы.
05:59 Внешние односторонние углы.
06:53 Внутренние накрест лежащие углы.
07:52 Внешние накрест лежащие углы.
08:45 Соответственные углы.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки по геометрии, то рекомендуем Вам посмотреть следующие видео:
Геометрия 7 класс. Основные понятия и фигуры геометрии. Их компоненты. https://rutube.ru/video/321ccc54b501c6dbc235d9b52b266abb/
Геометрия 7 класс. Взаимное расположение прямых на плоскости. Перпендикулярные прямые. Примеры построения перпендикулярных прямых. https://rutube.ru/video/c46955ce83ccef0dee45f4c72fc2583e/
Свойства биссектрисы равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника. Геометрия 7 класс. https://rutube.ru/video/2a2b7dfc5b44830f209dc9cc4e28d2f7/
Геометрия 7 класс.
00:00 Начало видео.
00:32 Что такое секущая?
02:31 Сколько углов получается при пересечении 2-х прямых третьей?
03:29 Вспомним углы, получающиеся при пересечении 2-х прямых.
04:27 Внутренние односторонние углы.
05:59 Внешние односторонние углы.
06:53 Внутренние накрест лежащие углы.
07:52 Внешние накрест лежащие углы.
08:45 Соответственные углы.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки по геометрии, то рекомендуем Вам посмотреть следующие видео:
Геометрия 7 класс. Основные понятия и фигуры геометрии. Их компоненты. https://rutube.ru/video/321ccc54b501c6dbc235d9b52b266abb/
Геометрия 7 класс. Взаимное расположение прямых на плоскости. Перпендикулярные прямые. Примеры построения перпендикулярных прямых. https://rutube.ru/video/c46955ce83ccef0dee45f4c72fc2583e/
Свойства биссектрисы равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника. Геометрия 7 класс. https://rutube.ru/video/2a2b7dfc5b44830f209dc9cc4e28d2f7/
Геометрия 7 класс. Треугольники. Признаки равенства треугольников. Урок 3. https://rutube.ru/video/0339e0588490b1b5ca732547aac3ec06/
Геометрия 7 класс. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач на свойства медианы и биссектрисы. Урок 5.
https://rutube.ru/video/3c88c497ce7a312249ea9e2b770fb8b1/
Геометрия 7 класс. Треугольники. Высота треугольника. Определение, свойства, точки пересечения высот. Примеры построения. Урок 6. https://rutube.ru/video/575bead43e6717ec773788d15e7380c1/
Геометрия 7 класс. Вертикальные углы. Определение. Доказательство теоремы о свойстве вертикальных углов. Виды углов урок 3. https://rutube.ru/video/10ca7111475a4f1a6dbe6b67fd71588c/
Геометрия 7 класс. Смежные углы. Определение. Свойства. Примеры задач на свойство смежных углов. Виды углов урок 2. https://rutube.ru/video/f12d3379fb0751e037c1f1bede88805f/
Что такое обратная и прямая теоремы. Примеры обратных и прямых теорем. Геометрия 7 класс. https://rutube.ru/video/f72250e5edd8eeed8948bd0664a23692/
Доказательство теорем методом «от противного».
Треугольники. Признаки равенства треугольников. Урок 3. https://rutube.ru/video/0339e0588490b1b5ca732547aac3ec06/
Геометрия 7 класс. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач на свойства медианы и биссектрисы. Урок 5.
https://rutube.ru/video/3c88c497ce7a312249ea9e2b770fb8b1/
Геометрия 7 класс. Треугольники. Высота треугольника. Определение, свойства, точки пересечения высот. Примеры построения. Урок 6. https://rutube.ru/video/575bead43e6717ec773788d15e7380c1/
Геометрия 7 класс. Вертикальные углы. Определение. Доказательство теоремы о свойстве вертикальных углов. Виды углов урок 3. https://rutube.ru/video/10ca7111475a4f1a6dbe6b67fd71588c/
Геометрия 7 класс. Смежные углы. Определение. Свойства. Примеры задач на свойство смежных углов. Виды углов урок 2. https://rutube.ru/video/f12d3379fb0751e037c1f1bede88805f/
Что такое обратная и прямая теоремы. Примеры обратных и прямых теорем. Геометрия 7 класс. https://rutube.ru/video/f72250e5edd8eeed8948bd0664a23692/
Доказательство теорем методом «от противного». Параллельность прямых на плоскости. Геометрия 7 класс. https://rutube.ru/video/d4f7b6c064dd143c73b738ebe92373dd/
#Геометрия7класс #углыприпересечениидвухпараллельныхпрямых #углыприпересечениидвухпрямыхтретьей #углыприпересечениидвухпрямыхсекущей #углыприпересечениидвухпараллельныхпрямыхсекущей #углыприпересечениидвухпараллельныхпрямыхтретьей #соответственныеуглыприпересечениидвухпрямых #найдитеуглыобразованныеприпересечениидвухпрямых #углыобразованныеприпересечениидвухпрямыхсекущей #накрестлежащиеодносторонниеисоответственныеуглы #внутренниеодносторонниеуглы #внешниеодносторонниеуглы #внутренниенакрестлежащиеуглы #внешниенакрестлежащиеуглы #соответственныеуглы #секущаянакрестлежащиеуглы #односторонниеуглыприпараллельных #односторонниеуглырисунок #соответственныеуглыприпересечениипрямых #соответственныеуглырисунок #накрестлежащиеуглырисунок #МатематикаОтБаканчиковой
Геометрия 7 класс, углы при пересечении двух параллельных прямых, углы при пересечении двух прямых третьей, углы при пересечении двух прямых секущей, углы при пересечении двух параллельных прямых третьей, соответственные углы при пересечении двух прямых, углы образованные при пересечении двух прямых секущей, накрест лежащие односторонние и соответственные углы, внутренние односторонние углы, внешние односторонние углы, внутренние накрест лежащие углы, внешние накрест лежащие углы, соответственные углы, секущая накрест лежащие углы, односторонние углы при параллельных, односторонние углы рисунок, соответственные углы при пересечении прямых, соответственные углы рисунок, накрест лежащие углы рисунок
Параллельность прямых на плоскости. Геометрия 7 класс. https://rutube.ru/video/d4f7b6c064dd143c73b738ebe92373dd/
#Геометрия7класс #углыприпересечениидвухпараллельныхпрямых #углыприпересечениидвухпрямыхтретьей #углыприпересечениидвухпрямыхсекущей #углыприпересечениидвухпараллельныхпрямыхсекущей #углыприпересечениидвухпараллельныхпрямыхтретьей #соответственныеуглыприпересечениидвухпрямых #найдитеуглыобразованныеприпересечениидвухпрямых #углыобразованныеприпересечениидвухпрямыхсекущей #накрестлежащиеодносторонниеисоответственныеуглы #внутренниеодносторонниеуглы #внешниеодносторонниеуглы #внутренниенакрестлежащиеуглы #внешниенакрестлежащиеуглы #соответственныеуглы #секущаянакрестлежащиеуглы #односторонниеуглыприпараллельных #односторонниеуглырисунок #соответственныеуглыприпересечениипрямых #соответственныеуглырисунок #накрестлежащиеуглырисунок #МатематикаОтБаканчиковой
Геометрия 7 класс, углы при пересечении двух параллельных прямых, углы при пересечении двух прямых третьей, углы при пересечении двух прямых секущей, углы при пересечении двух параллельных прямых третьей, соответственные углы при пересечении двух прямых, углы образованные при пересечении двух прямых секущей, накрест лежащие односторонние и соответственные углы, внутренние односторонние углы, внешние односторонние углы, внутренние накрест лежащие углы, внешние накрест лежащие углы, соответственные углы, секущая накрест лежащие углы, односторонние углы при параллельных, односторонние углы рисунок, соответственные углы при пересечении прямых, соответственные углы рисунок, накрест лежащие углы рисунок Сколько стоит и , в градусах?
Сколько стоит и , в градусах? Правильный ответ 15.
Правильный ответ 15. Отсюда вы можете реконструировать то же самое уравнение, которое вы решили с первым набором углов. Если и и являются вертикальными углами, а и являются вертикальными углами, вы можете заключить, что . Оттуда вы можете настроить уравнение . Утверждение I верно.
Отсюда вы можете реконструировать то же самое уравнение, которое вы решили с первым набором углов. Если и и являются вертикальными углами, а и являются вертикальными углами, вы можете заключить, что . Оттуда вы можете настроить уравнение . Утверждение I верно.
 Здесь, поскольку у вас есть угол 90 градусов (CED) и угол 35 градусов (EDC) в нижнем треугольнике, тогда можно заключить, что угол ECD должен быть равен 55.
Здесь, поскольку у вас есть угол 90 градусов (CED) и угол 35 градусов (EDC) в нижнем треугольнике, тогда можно заключить, что угол ECD должен быть равен 55. Почему? Помните, что y является дополнительным к углу рядом с ним (x + 30), а (a + c) является дополнительным к тому же самому углу (сумма внутренних углов треугольника = 180). Следовательно, y и (a + c) идентичны. . Всякий раз, когда у вас есть прямая линия, проведенная из треугольника, вы должны понимать, что внешний дополнительный угол равен сумме двух противоположных углов.
Почему? Помните, что y является дополнительным к углу рядом с ним (x + 30), а (a + c) является дополнительным к тому же самому углу (сумма внутренних углов треугольника = 180). Следовательно, y и (a + c) идентичны. . Всякий раз, когда у вас есть прямая линия, проведенная из треугольника, вы должны понимать, что внешний дополнительный угол равен сумме двух противоположных углов. Итак, х+у=150.
Итак, х+у=150. Это позволяет добавить 70+50+ в качестве трех углов в нижний треугольник, а так как их сумма должна равняться 180, это означает, что .
Это позволяет добавить 70+50+ в качестве трех углов в нижний треугольник, а так как их сумма должна равняться 180, это означает, что . Вы можете использовать чтобы определить, что третий угол должен быть равен 120.
Вы можете использовать чтобы определить, что третий угол должен быть равен 120.
 Здесь, если вы проследите за линией, вы увидите, что ее угол разбит на три сегмента: и пустой угол между ними. Сумма этих трех углов должна равняться 180, поэтому, если вы уже знаете, что и , тогда неотмеченный угол между ними должен быть равен так что .
Здесь, если вы проследите за линией, вы увидите, что ее угол разбит на три сегмента: и пустой угол между ними. Сумма этих трех углов должна равняться 180, поэтому, если вы уже знаете, что и , тогда неотмеченный угол между ними должен быть равен так что .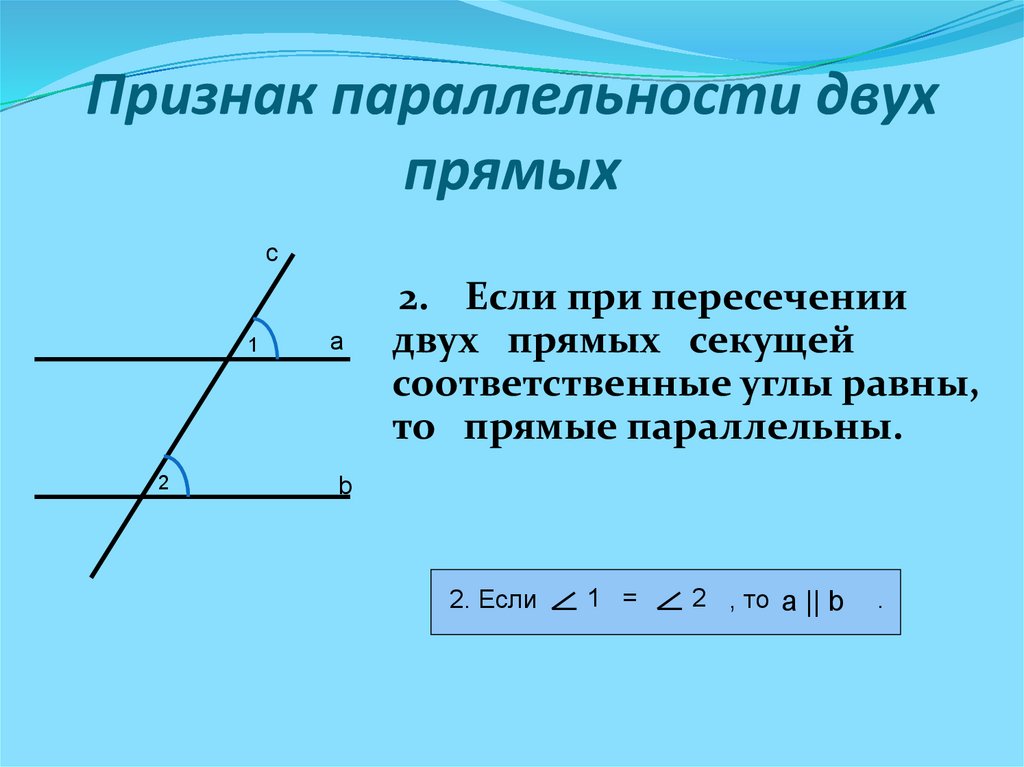 При пересечении двух прямых образуются два набора углов. Пересечение образует два острых и два тупых угла. Абсолютные значения образующихся углов определяются наклонами пересекающихся линий. Мы учитываем острый угол между двумя линиями при вычислении угла между ними. Мы могли бы использовать угол, образованный двумя линиями, для вычисления угла, образованного двумя сторонами замкнутого многоугольника.
При пересечении двух прямых образуются два набора углов. Пересечение образует два острых и два тупых угла. Абсолютные значения образующихся углов определяются наклонами пересекающихся линий. Мы учитываем острый угол между двумя линиями при вычислении угла между ними. Мы могли бы использовать угол, образованный двумя линиями, для вычисления угла, образованного двумя сторонами замкнутого многоугольника.