Число 24
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители…
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…
Сейчас изучают числа:
8 и 6 2011 2022 24742000 277353 31 8743 6929 5713 339 2247 110010100101 1043 1027 1019 1003 320 1543 36 и 45 444888 20449 594 и 60 500 391
Двадцать четыре
Описание числа 24
Неотрицательное рациональное
двузначное
число 24
является составным числом. Произведение цифр числа: 8.
Число имеет следующие делители: 1, 2, 3, 4, 6, 8, 12, 24.
Сумма делителей: 60.
Обратным числом является 0.041666666666666664.
Произведение цифр числа: 8.
Число имеет следующие делители: 1, 2, 3, 4, 6, 8, 12, 24.
Сумма делителей: 60.
Обратным числом является 0.041666666666666664.
Данное число представляется произведением: 2 * 2 * 2 * 3.
Другие представления числа 24: двоичная система: 11000, троичная система: 220, восьмеричная система: 30, шестнадцатеричная система: 18. 24 байта представляет из себя число байт 24.
В виде кода азбуки Морзе: ..— ….-
Косинус 24: 0.4242, синус 24: -0.9056, тангенс 24: -2.1349. Натуральный логарифм числа равен 3.1781. У числа 24 есть десятичный логарифм: 1.3802. Квадратный корень числа: 4.8990, а кубический: 2.8845. Возведение в квадрат: 576.00.
24 в секундах это 24 секунды .
В нумерологии число 24 означает цифру 6.
- ← 23
- 25 →
Вычисление наименьшего общего кратного
Введите цифры
- Три автобуса
Три автобуса общественного транспорта отправляются вместе с автовокзала утром. Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты. Как долго снова будем вместе на вокзале? Пожалуйста, экспресс - Портниха
Портниха оставила кусок холста короче 5 метров. Она решает, сшить ли ей юбку или платье. Холста было ровно столько, сколько они израсходовали, разрезав юбку до 120 см, или 180 сантиметров. Какой кусок холста оставил ей? - LCM двух чисел
Найдите наименьшее кратное 63 и 147 - Различные 6975
Три разных автобусных маршрута, 80, 81 и 82, отправляются с конечной станции в 5 ч 20 мин. Маршрут 80 отправляется каждые 30 минут, маршрут 81 — каждые 20 минут, а маршрут 82 — каждые 40 минут. Во сколько они снова уйдут? - Напоминание и частное
Даны числа A = 135, B = 315. Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1.
Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1. - Бакалейная лавка
Сьюзен решила сделать продуктовые наборы для своего магазина. Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество - Вокруг клумбы
Вокруг прямоугольной клумбы размерами 5,25 м и 3,5 м нужно посадить розы через равные промежутки так, чтобы розы находились в каждом углу клумбы и потреблять как можно меньше. а) На каком расстоянии посажены розы? б) Сколько роз - Автобусы
На остановке в 10 часов встретились автобусы №2 и №9. Автобус №2 ходит с интервалом 4 минуты, а автобус №9 с интервалом 9 минут. Сколько раз автобус встречается в 18:00 по местному времени? - Зубчатая передача
Зубчатая передача состоит из двух колес. У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?
Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо? - Автобусы 4
Интервалы: 1-й автобус 40 мин. 2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее? - Четыре класса
Учащиеся всех 7, 8 и 9 классов одной школы могут занимать 4, 5, 6 и 7 ряд подряд, и никого не останется. Сколько в среднем учеников в одном классе, если в каждом классе всегда четыре класса? - Gcd и lcm
Вычислить наибольший общий делитель и наименьшее общее кратное чисел. a) 16 и 18 b) 24 и 22 c) 45 и 60 d) 36 и 30 - Вычислить 2976
Вычислить наименьшее общее кратное чисел 120, 660 и 210. - Уточните: 4001
Укажите: a = D (240,320) b = n (40,64) - Pardubická 4651
Йирка решил разделить выигрыш от пари в Velká Pardubická между собой и тремя своими младшими братьями по возрасту в соотношении 2:3:5:7. Каждую сумму они платили целыми кронами. Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш?
Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш? - Веревка
Пол может разрезать веревку на равные части, не оставив ни одной веревки. Длина может быть 15 см, 18 см или 25 см. Какова наименьшая возможная длина веревки?
другие математические задачи »
Что такое наибольший общий делитель и наименьшее общее кратное?
Привет! Добро пожаловать в это видео, посвященное наименьшему общему кратному и наибольшему общему делителю!
Как вы знаете, бывают случаи, когда нам приходится алгебраически «настраивать» то, как выглядит число или уравнение, чтобы продолжить нашу математическую работу. Для этого мы можем использовать наибольший общий делитель и наименьшее общее кратное. Наибольший общий делитель (GCF) — это наибольшее число, которое является множителем двух или более чисел, а наименьшее общее кратное (НОК) — это наименьшее число, кратное двум или более числам.
Чтобы понять, насколько полезны эти понятия, давайте рассмотрим сложение дробей. Прежде чем мы сможем складывать дроби, мы должны убедиться, что знаменатели совпадают, создав эквивалентную дробь:
Прежде чем мы сможем складывать дроби, мы должны убедиться, что знаменатели совпадают, создав эквивалентную дробь:
\(\frac{2}{3}+\frac{1}{6} \rightarrow \frac{2 }{3} \times \frac{2}{2}\)\(+\frac{1}{6} \rightarrow \frac{4}{6} +\frac{1}{6}=\frac{ 5}{6}\)
В этом примере необходимо определить наименьшее общее кратное 3 и 6. Другими словами, «Каково наименьшее число, на которое можно разделить без остатка и 3, и 6?» Немного подумав, мы понимаем, что 6 является наименьшим общим кратным, потому что 6, деленное на 3, равно 2, а 6, деленное на 6, равно 1. Затем дробь \(\frac{2}{3}\) приводится к эквиваленту дробь \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2. Теперь можно сложить две дроби с общими знаменателями, чтобы получить окончательное значение \(\frac{5}{6}\) .
Найдите наименьшее общее кратное
В контексте сложения или вычитания дробей наименьшее общее кратное называется наименьшим общим знаменателем .
Как правило, вам нужно определить число, большее или равное двум или более числам, чтобы найти их наименьшее общее кратное.
Важно отметить, что существует несколько способов определения наименьшего общего кратного. Один из способов — просто перечислить все кратные рассматриваемых значений и выбрать наименьшее общее значение, как показано здесь:
Наименьшее общее кратное 8, 4, 6
\(8\rightarrow 8,16,24,32,40,48\)
\(4\rightarrow 4,8,12,16,20,24, 28,32\)
\(6\стрелка вправо 6,12,18,24,30,36\)
Это показывает, что наименьшее общее кратное чисел 8, 4 и 6 равно 24, поскольку оно является наименьшим число, на которое можно поровну разделить 8, 4 и 6.
Другой распространенный метод включает первичную факторизацию каждого значения. Помните, что простое число делится только на 1 и само на себя.
После определения простых множителей перечислите общие множители один раз, а затем умножьте их на остальные оставшиеся простые множители. Результатом является наименьшее общее кратное:
Результатом является наименьшее общее кратное:
\(30=2\умножить на 2\умножить на 3\умножить на 3\)
\(90=2\умножить на 3\умножить на 3\умножить на 5\)\(\text {НОК}=2\умножить на 3\умножить на 3\умножить на 2\умножить на 5\)
Наименьшее общее кратное также можно найти путем общего (или повторного) деления. Этот метод иногда считают более быстрым и эффективным, чем листинг 9.0062 умножить на и найти простые множители. Вот пример нахождения наименьшего общего кратного чисел 3, 6 и 9 с помощью этого метода:
Разделите числа на множители любого из трех чисел. 6 имеет коэффициент 2, поэтому давайте использовать 2. Девять и 3 не могут делиться на 2, поэтому мы просто перепишем здесь 9 и 3. Повторяйте этот процесс, пока все числа не будут уменьшены до 1. Затем перемножьте все множители вместе, чтобы получить наименьшее общее кратное.
| 2 | 3 | 6 | 9 |
| 3 | 3 | 3 | 9 |
| 3 | 1 | 1 | 3 |
| 1 | 1 | 1 |
НОК \(=2\умножить на 3\умножить на 3=18\)
Теперь, когда были введены методы нахождения наименьших общих кратных, нам нужно изменить свое мышление, чтобы найти наибольший общий множитель двух или более числа. Мы будем определять значение, меньшее или равное рассматриваемым числам. Другими словами, спросите себя: «Какое наибольшее число делит оба этих числа?» Понимание этой концепции необходимо для деления и факторизации многочленов.
Мы будем определять значение, меньшее или равное рассматриваемым числам. Другими словами, спросите себя: «Какое наибольшее число делит оба этих числа?» Понимание этой концепции необходимо для деления и факторизации многочленов.
Какой наибольший общий делитель?
Разложение на простые множители также можно использовать для определения наибольшего общего делителя. Однако вместо того, чтобы умножать все простые множители, как мы это делали для наименьшего общего кратного, мы будем умножать только те простые множители, которые являются общими для чисел. Полученное произведение является наибольшим общим множителем.
Обзор
Давайте завершим парой правильных или неверных вопросов:
1. Наименьшее общее кратное 45 и 60 равно 15.
2. Наименьшим общим кратным является число, большее или равное рассматриваемым числам.
Спасибо за просмотр и приятного изучения!
Часто задаваемые вопросы
Q
Как найти LCM и GCF?
A
Существует множество методов определения LCM и GCF. Две наиболее распространенные стратегии включают составление списка или использование простой факторизации.
Две наиболее распространенные стратегии включают составление списка или использование простой факторизации.
Например, НОК 5 и 6 можно найти, просто перечислив кратные \(5\) и \(6\), а затем указав наименьшее кратное, общее для обоих чисел.
\(5, 10, 15, 20, 25, \mathbf{30}, 35…\)
\(6, 12, 18, 24, \mathbf{30}, 36…\)
\(\mathbf{ 30}\) — LCM.
Аналогичным образом, GCF можно найти, перечислив факторы каждого числа, а затем указав наибольший общий фактор. Например, GCF для \(40\) и \(32\) можно найти, перечислив множители каждого числа.
\(40\): \(1, 2, 4, 5, \mathbf8, 10, 20, 40\)
\(32\): \(1, 2, 4, \mathbf8, 16, 32\ )
\(\mathbf8\) — это GCF.
Для больших чисел будет нереально составить список факторов или множителей для определения GCF или LCM. Для больших чисел наиболее эффективно использовать метод простой факторизации.
Например, при нахождении НОК начните с нахождения разложения каждого числа на простые множители (это можно сделать, создав дерево факторов). Простая факторизация \(20\) равна \(2\times2\times5\), а простая факторизация \(32\) — это \(2\times2\times2\times2\times2\). Обведите общие факторы и посчитайте эти только один раз .
Простая факторизация \(20\) равна \(2\times2\times5\), а простая факторизация \(32\) — это \(2\times2\times2\times2\times2\). Обведите общие факторы и посчитайте эти только один раз .
Теперь умножьте все множители (помните, что не нужно дважды считать обведенные \(2\)). Это становится \(2\times2\times5\times2\times2\times2\), что равняется \(160\). LCM \(20\) и \(32\) равен \(160\).
Находя GCF, начните с перечисления простой факторизации каждого числа (это можно сделать, создав дерево факторов). Например, простая факторизация \(45\) равна \(5\times3\times3\), а простая факторизация \(120\) равна \(5\times3\times2\times2\times2\). Теперь просто умножьте все факторы, которые являются общими для обоих чисел. В этом случае мы умножим \(5\times3\), что равно \(15\). GCF \(45\) и \(120\) равен \(15\).
Подход с простой факторизацией может показаться довольно длительным процессом, но при работе с большими числами он гарантированно сэкономит время.
Q
Как найти GCF?
A
Существуют две основные стратегии нахождения GCF: перечисление факторов или использование простой факторизации.
Первая стратегия состоит в том, чтобы просто перечислить множители каждого числа, а затем найти наибольший множитель, общий для обоих чисел. Например, если мы ищем GCF для \(36\) и \(45\), мы можем перечислить множители обоих чисел и определить наибольшее общее число.
\(36\): \(1,2,3,4,6,\mathbf9,12,18,36\)
\(45\): \(1,3,5,\mathbf9,15,45 \)
GCF для \(36\) и \(45\) равен \(\mathbf9\).
Составление списка множителей каждого числа с последующим определением наибольшего общего множителя хорошо работает для небольших чисел. Однако при нахождении GCF очень больших чисел более эффективно использовать метод простой факторизации.
Например, при нахождении GCF чисел \(180\) и \(162\) мы начинаем с перечисления простой факторизации каждого числа (это можно сделать, создав дерево факторов). Простая факторизация \(180\) равна \(2\times2\times3\times3\times5\), а простая факторизация \(162\) — это \(2\times3\times3\times3\times3\). Теперь найдите факторы, которые являются общими для обоих чисел. В этом случае оба числа имеют одну общую \(2\) и две \(3\)s, или \(2\times3\times3\). Результатом \(2\times3\times3\) является \(18\), что является GCF! Эта стратегия часто более эффективна при нахождении GCF действительно больших чисел.
В этом случае оба числа имеют одну общую \(2\) и две \(3\)s, или \(2\times3\times3\). Результатом \(2\times3\times3\) является \(18\), что является GCF! Эта стратегия часто более эффективна при нахождении GCF действительно больших чисел.
Q
Что означает GCF?
A
GCF означает «наибольший общий делитель». GCF определяется как наибольшее число, являющееся множителем двух или более чисел. Например, GCF для \(24\) и \(36\) равен \(12\), потому что наибольший делитель, общий для \(24\) и \(36\), равен \(12\). \(24\) и \(36\) имеют другие общие факторы, но \(12\) является самым большим.
Q
Как найти наименьшее общее кратное?
A
Существует множество методов нахождения наименьшего общего кратного. Двумя распространенными подходами являются перечисление кратных и использование простой факторизации. Список кратных так же, как это звучит, просто перечислите кратные каждого числа, а затем найдите наименьшее кратное, общее для обоих чисел. Например, при нахождении наименьшего общего кратного чисел \(3\) и \(4\) перечислите кратные:
Например, при нахождении наименьшего общего кратного чисел \(3\) и \(4\) перечислите кратные:
\(3\): \(3,6,9,\mathbf{12},15,18 …\)
\(4\): \(4,8,\mathbf{12},16,20…\)
\(\mathbf{12}\) — это наименьшее кратное, общее для \(3\) и \(4\).
Список кратных — отличная стратегия, когда числа довольно малы. Когда числа большие, такие как \(38\) и \(42\), мы должны использовать метод простой факторизации. Начните с перечисления простой факторизации каждого числа (это можно сделать с помощью факторного дерева).
\(38\): \(2\times19\)
\(42\): \(2\times3\times7\)
Теперь обведите общие множители (считайте эти только один раз ).
Теперь умножьте все множители (не забудьте подсчитать \(2\) только один раз). Это становится \(2\times19\times3\times7\), что равняется \(798\). LCM \(38\) и \(42\) равен \(798\).
Q
Как вынуть LCM?
A
Извлечение НОК полезно при сложении или вычитании дробей. При определении наименьшего общего кратного получается знаменатель, одинаковый для обеих дробей. Например, общий знаменатель для \(\frac{2}{7}+\frac{3}{5}\) будет равен \(35\), потому что \(35\) является НОК для \(7\ ) и \(5\). Новые дроби становятся \(\frac{10}{35}+\frac{21}{35}\), что равняется \(\frac{31}{35}\).
Например, общий знаменатель для \(\frac{2}{7}+\frac{3}{5}\) будет равен \(35\), потому что \(35\) является НОК для \(7\ ) и \(5\). Новые дроби становятся \(\frac{10}{35}+\frac{21}{35}\), что равняется \(\frac{31}{35}\).
Практические вопросы
Вопрос №1:
Каков наибольший общий делитель чисел 16 и 42? Используйте его, чтобы уменьшить дробь \(\frac{16}{42}\).
GCF равно 8, и мы уменьшаем его до \(\frac{2}{5}\).
GCF равен 1, и мы не можем больше уменьшать.
GCF равно 4, и мы уменьшаем его до \(\frac{4}{11}\).
GCF равен 2, и мы уменьшаем его до \(\frac{8}{21}\).
Показать ответ
Ответ:
Правильный ответ D: GCF равен 2, и мы уменьшаем до \(\frac{8}{21}\).
Давайте подойдем к этой проблеме, перечислив простые множители как числителя, так и знаменателя.
\(16=2×2×2×2\)
\(42=2×3×7\)
Здесь мы видим, что 2 — единственный общий делитель чисел 16 и 42 и, следовательно, их наибольший общий делитель. Затем мы можем разделить оба числа на 2, чтобы уменьшить дробь:
Затем мы можем разделить оба числа на 2, чтобы уменьшить дробь:
\(\frac{16\div2}{42\div2}=\frac{8}{21}\)
Скрыть ответ
Вопрос № 2:
Найдите наименьшее общее кратное 2, 6 и 8.
16
18
24
48
Показать ответ
Ответ:
Правильный ответ C: 24,
2 простых чисел.
\(2=2\) (обратите внимание, что мы могли написать \(2\times1\), но 1 понимается или подразумевается, и обычно писать не нужно)
\(6=2\times3\)
\( 8=2\times2\times2\)
Помните, что при вычислении НОК двух или более чисел мы перечисляем каждый простой множитель один раз, который является общим для всех чисел. Поскольку каждое из наших чисел имеет 2 в качестве простого множителя, наш LCM также будет иметь 2 в качестве одного из своих простых множителей.
LCM \(=2\times\) _______
Теперь из 6 у нас осталась 3, а из 8 осталось две двойки. Мы умножаем их, чтобы получить
Мы умножаем их, чтобы получить
LCM \(=2\times3\times2\times2=24\)
Обратите внимание, что хотя 2, 6 и 8 являются делителями 48, решение не D, потому что 48 не является наименьшее общее кратное.
Скрыть ответ
Вопрос № 3:
Перечислите первые несколько чисел, кратных 3, 5 и 6, чтобы найти наименьшее общее кратное.
LCM IS 15
LCM — 30
LCM — 18
LCM — 75
Показать ответ
Ответ:
Правильный ответ B: LCM — 30.
. : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, …
Первые несколько кратных 5: 5, 10, 15, 20, 25, 30, 35, 40 , 45, 50, …
Первые несколько кратных 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
Как мы видели выше, 30 — это первое (наименьшее) число, которое является общим среди кратных чисел 3, 5 и 6, поэтому наименьшее общее кратное равно 30.
Скрыть ответ
У Кортни 54 конфеты, а у Триш 36. Они хотят приготовить мешочки с конфетами на день рождения своей подруги Ким, но в каждом мешочке должно быть одинаковое количество конфет. Чтобы в каждом пакете было как можно больше конфет, когда Кортни и Триш работают отдельно, сколько пакетов они могут сделать и сколько конфет будет в каждом пакете?
10 пакетов по 9 конфет
9 пакетов по 10 конфет
15 пакетов по 6 конфет
5 пакетов по 18 конфет
Показать Ответ
Ответ:
Правильный ответ D: 5 пакетов по 18 конфет в каждом.
Для начала перечислите простые множители чисел 54 и 36:
\(54=2\times3\times3\times3\)
\(36=2\times2\times3\times3\)
Обратите внимание, что они оба разделяют двойка и две тройки. Произведение этих общих простых множителей равно \(2\times3\times3=18\).

 Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1.
Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?
Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо? Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш?
Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш?
 Просто воспользуйтесь этим бесплатным онлайн конвертер JPG в PDF, который обеспечивает точное качество преобразования, он эффективно преобразует один или несколько файлов конвертировать джипег в пдф.
Просто воспользуйтесь этим бесплатным онлайн конвертер JPG в PDF, который обеспечивает точное качество преобразования, он эффективно преобразует один или несколько файлов конвертировать джипег в пдф.
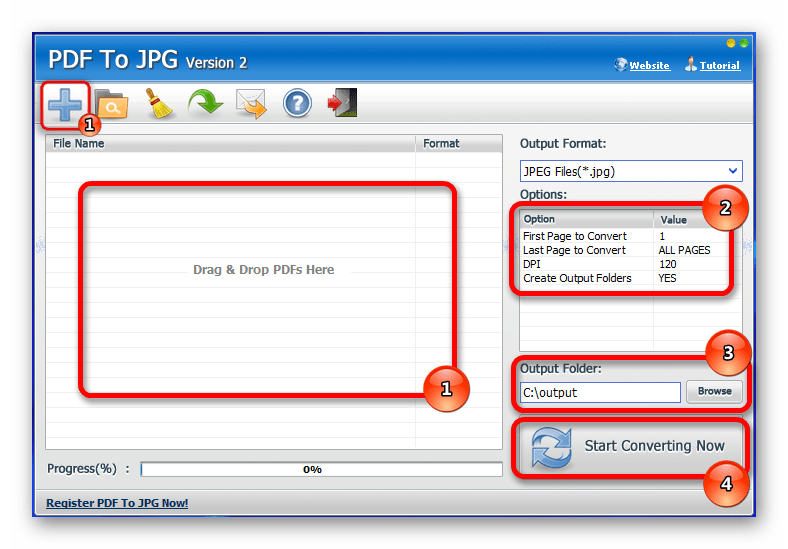 Затем добавьте дополнительные PDF и снова объедините их. Вы можете делать это столько раз, сколько захотите.
Затем добавьте дополнительные PDF и снова объедините их. Вы можете делать это столько раз, сколько захотите. +
+ PDF-файлы будут выглядеть одинаково, независимо от того, открываете ли вы их на Mac, Microsoft или на смартфонах.
PDF-файлы будут выглядеть одинаково, независимо от того, открываете ли вы их на Mac, Microsoft или на смартфонах. Добавляйте и редактируйте визуальный контент. Изменить порядок страниц формы. Добавьте заполняемые поля и отправьте на подпись. Сотрудничайте с другими, чтобы заполнить поля. Когда документ будет готов, загрузите его на свое устройство или сохраните в облаке.
Добавляйте и редактируйте визуальный контент. Изменить порядок страниц формы. Добавьте заполняемые поля и отправьте на подпись. Сотрудничайте с другими, чтобы заполнить поля. Когда документ будет готов, загрузите его на свое устройство или сохраните в облаке. Это все равно, что сказать, что если вы используете инструмент CDR только для преобразования одного видеоизображения в одно видео MP4, это все равно отличный инструмент для преобразования видео MP4 в видео H.264. В ближайшем будущем у нас есть действительно замечательные вещи. Получите доступ к огромному архиву изображений в формате JPEG.
Скачивайте файлы JPEG быстро и легко
Экономьте время с удобным интерфейсом приложения
Скачивайте изображения в формате JPEG на рабочий стол, компьютер или куда угодно
Переходите непосредственно к папкам с изображениями или копируйте папки с изображениями в другие папки.
Скачивайте файлы JPEG онлайн, включая фото и видео
Копируйте изображения на другие компьютеры или мобильные устройства
Экономьте время с удобным интерфейсом приложения
Форматы файлов PDF могут быть сложными в управлении по разным причинам, таким как нехватка места для хранения или трудности с поддержанием правильного межстрочного интервала между документами (как отображается на вашем мониторе).
Это все равно, что сказать, что если вы используете инструмент CDR только для преобразования одного видеоизображения в одно видео MP4, это все равно отличный инструмент для преобразования видео MP4 в видео H.264. В ближайшем будущем у нас есть действительно замечательные вещи. Получите доступ к огромному архиву изображений в формате JPEG.
Скачивайте файлы JPEG быстро и легко
Экономьте время с удобным интерфейсом приложения
Скачивайте изображения в формате JPEG на рабочий стол, компьютер или куда угодно
Переходите непосредственно к папкам с изображениями или копируйте папки с изображениями в другие папки.
Скачивайте файлы JPEG онлайн, включая фото и видео
Копируйте изображения на другие компьютеры или мобильные устройства
Экономьте время с удобным интерфейсом приложения
Форматы файлов PDF могут быть сложными в управлении по разным причинам, таким как нехватка места для хранения или трудности с поддержанием правильного межстрочного интервала между документами (как отображается на вашем мониторе). Рисунок 1-4a: Использование сенсорной панели для удаления или объединения страниц Страницы этой записной книжки пусты, но с каждой стороны есть по одной странице. Страницы сгруппированы по годам, и мы видим, что они были подписаны «Джоном Доу». Страницы с номерами от 1 до 4 находятся на разных сторонах дневника, поэтому, когда мы объединяем страницы 1 и 2 для создания новой страницы, мы делаем ее первой страницей, подписанной Джоном Доу..
Рисунок 1-4a: Использование сенсорной панели для удаления или объединения страниц Страницы этой записной книжки пусты, но с каждой стороны есть по одной странице. Страницы сгруппированы по годам, и мы видим, что они были подписаны «Джоном Доу». Страницы с номерами от 1 до 4 находятся на разных сторонах дневника, поэтому, когда мы объединяем страницы 1 и 2 для создания новой страницы, мы делаем ее первой страницей, подписанной Джоном Доу..
 Нажмите кнопку «Преобразовать файл(ы)», чтобы преобразовать изображения JPG в PDF. Сохраните преобразованный файл, нажав кнопку «Загрузить PDF-файл».
Нажмите кнопку «Преобразовать файл(ы)», чтобы преобразовать изображения JPG в PDF. Сохраните преобразованный файл, нажав кнопку «Загрузить PDF-файл». На боковой панели предварительного просмотра перетащите изображения в том порядке, в котором они должны отображаться в вашем PDF-файле. Выберите/выделите все изображения, которые необходимо включить в документ PDF. В противном случае только одно изображение может оказаться в документе PDF.
На боковой панели предварительного просмотра перетащите изображения в том порядке, в котором они должны отображаться в вашем PDF-файле. Выберите/выделите все изображения, которые необходимо включить в документ PDF. В противном случае только одно изображение может оказаться в документе PDF. В раскрывающемся меню «Принтер» в левом верхнем углу выберите Microsoft Print to PDF.
В раскрывающемся меню «Принтер» в левом верхнем углу выберите Microsoft Print to PDF.
 Мы часто используем PDF для загрузки документа, но иногда веб-сайт или программное обеспечение не имеют формата файла для поддержки формата PDF. Вы можете преобразовать PDF в JPG, если ваш файл PDF не поддерживает его. Mac имеет несколько различных функций для преобразования pdf в jpg. Пользователи внимательно читают статью, потому что я показываю, как мы конвертируем PDF-файл в JPG на Mac. Используйте WPS Office для преобразования PDF в JPG WPS Office широко распространен…
Мы часто используем PDF для загрузки документа, но иногда веб-сайт или программное обеспечение не имеют формата файла для поддержки формата PDF. Вы можете преобразовать PDF в JPG, если ваш файл PDF не поддерживает его. Mac имеет несколько различных функций для преобразования pdf в jpg. Пользователи внимательно читают статью, потому что я показываю, как мы конвертируем PDF-файл в JPG на Mac. Используйте WPS Office для преобразования PDF в JPG WPS Office широко распространен…
 01.2012, 14:58
01.2012, 14:58  01.2012, 15:00
01.2012, 15:00  01.2012, 15:02
01.2012, 15:02  01.2012, 15:08
01.2012, 15:08  01.2012, 15:16
01.2012, 15:16 

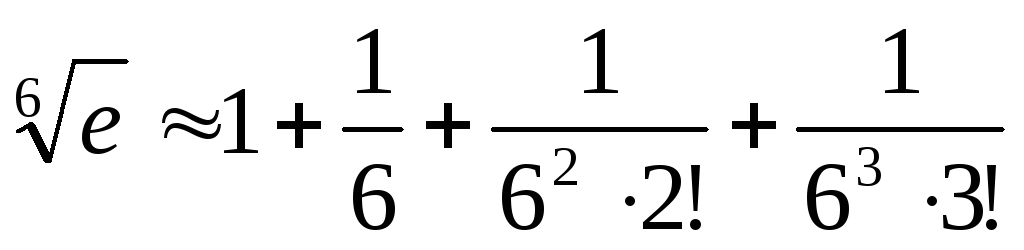 В ряде тейлора вроде как нет отрицательных степеней…видимо поэтому это разложение и нельзя назвать рядом тейлора.
В ряде тейлора вроде как нет отрицательных степеней…видимо поэтому это разложение и нельзя назвать рядом тейлора. 10.2021, 17:56
10.2021, 17:56  10.2021, 18:56
10.2021, 18:56  10.2021, 21:48
10.2021, 21:48  Да и при , так что все оценки валидны.
Да и при , так что все оценки валидны.
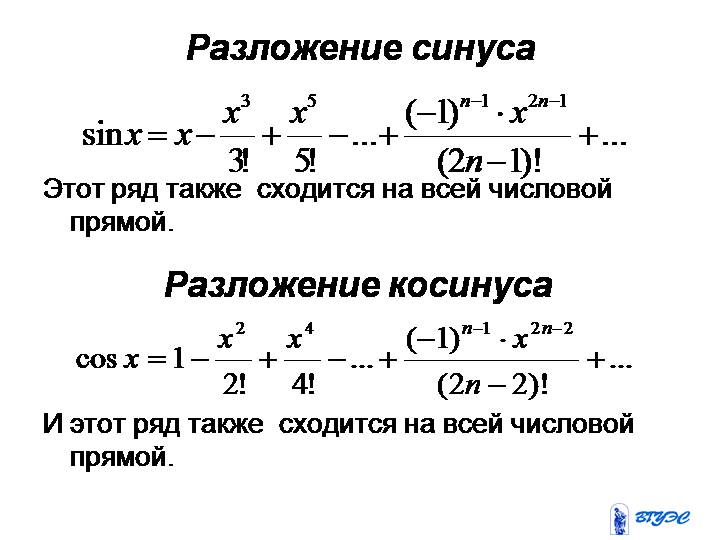
 Далее, замечаем, что выражение в какой-то окрестности нуля меньше единицы (ибо вообще стремится к нулю), так что подстановка оправдана. Ну а возможность перегруппировки слагаемых вытекает из абсолютной сходимости и теорем о повторных рядах. Не понятно только, причём тут о-малые, когда речь о рядах
Далее, замечаем, что выражение в какой-то окрестности нуля меньше единицы (ибо вообще стремится к нулю), так что подстановка оправдана. Ну а возможность перегруппировки слагаемых вытекает из абсолютной сходимости и теорем о повторных рядах. Не понятно только, причём тут о-малые, когда речь о рядах 7)
\end{выравнивание}
Отсюда можно вывести линейную систему
\начать{выравнивать}
\begin{pматрица}
1 и 0 и 0 и 0 и 0 и 0&0\\
0 и 1 и 0 и 0 и 0 и 0 &0\\
-1/2 &0 &1 & 0& 0& 0&0\\
0 и -1/2 и 0 и 1 и 0 и 0&0 \\
1/24 и 0 и -1/2 и 0 и 1 и 0&0\\
0 и 1/24 и 0 и -1/2 и 0 и 1 и 0\\
1/720 и 0 и 1/24 и 0 и -1/2 и 0 и 1
\end{pматрица}
\begin{pматрица}
а\\б\\в\\г\\е\\е\\г
\end{pматрица}
«=»
\begin{pmatrix}
0\1\0\-1/6\0\1/120\0
\end{pматрица}
\end{выравнивание}
Что имеет решение
\начать{выравнивать}
\begin{pматрица}
а\\б\\в\\г\\е\\е\\г
\end{pматрица}
= \begin{pmatrix}
0\1\0\1/3\0\2/15
\end{pматрица}
\end{выравнивание}
[Обратите внимание, что вы можете извлечь две линейные системы из приведенной выше. Затем вам нужно найти только нечетные степени $x$, поскольку $\tan(x)$ нечетно.] 97)
\end{выравнивание}
Что (на удивление) правильно, поскольку мы можем сравнить наше решение с WolframAlpha.
7)
\end{выравнивание}
Отсюда можно вывести линейную систему
\начать{выравнивать}
\begin{pматрица}
1 и 0 и 0 и 0 и 0 и 0&0\\
0 и 1 и 0 и 0 и 0 и 0 &0\\
-1/2 &0 &1 & 0& 0& 0&0\\
0 и -1/2 и 0 и 1 и 0 и 0&0 \\
1/24 и 0 и -1/2 и 0 и 1 и 0&0\\
0 и 1/24 и 0 и -1/2 и 0 и 1 и 0\\
1/720 и 0 и 1/24 и 0 и -1/2 и 0 и 1
\end{pматрица}
\begin{pматрица}
а\\б\\в\\г\\е\\е\\г
\end{pматрица}
«=»
\begin{pmatrix}
0\1\0\-1/6\0\1/120\0
\end{pматрица}
\end{выравнивание}
Что имеет решение
\начать{выравнивать}
\begin{pматрица}
а\\б\\в\\г\\е\\е\\г
\end{pматрица}
= \begin{pmatrix}
0\1\0\1/3\0\2/15
\end{pматрица}
\end{выравнивание}
[Обратите внимание, что вы можете извлечь две линейные системы из приведенной выше. Затем вам нужно найти только нечетные степени $x$, поскольку $\tan(x)$ нечетно.] 97)
\end{выравнивание}
Что (на удивление) правильно, поскольку мы можем сравнить наше решение с WolframAlpha.

 При обследовании необходимо учитывать генотип вируса, наличие и степень цитологических и гистологических изменений в тканях, увеличение или снижение вирусной нагрузки через несколько месяцев (6 месяцев и более) после предыдущего обследования.
При обследовании необходимо учитывать генотип вируса, наличие и степень цитологических и гистологических изменений в тканях, увеличение или снижение вирусной нагрузки через несколько месяцев (6 месяцев и более) после предыдущего обследования. Выявление области Е6 при отсутствии области Е1/Е2 позволяет косвенно судить о возможности интеграции вируса в геном человека. В случае обнаружения возможности интеграции вируса в геном в бланк ответа выводится соответствующая информация.
Выявление области Е6 при отсутствии области Е1/Е2 позволяет косвенно судить о возможности интеграции вируса в геном человека. В случае обнаружения возможности интеграции вируса в геном в бланк ответа выводится соответствующая информация.


 Нет точной статистики, сколько людей в мире заражены ВПЧ, потому что у большинства заражённых вирус никак себя не проявляет.
Нет точной статистики, сколько людей в мире заражены ВПЧ, потому что у большинства заражённых вирус никак себя не проявляет.
 Так, можно вылечить предраковое состояние шейки матки. Другие онкологии, связанные с ВПЧ, лучше поддаются лечению, если оно начинается на ранней стадии заболевания и контролируется периодическими исследованиями на снижение/повышение вирусной нагрузки.
Так, можно вылечить предраковое состояние шейки матки. Другие онкологии, связанные с ВПЧ, лучше поддаются лечению, если оно начинается на ранней стадии заболевания и контролируется периодическими исследованиями на снижение/повышение вирусной нагрузки.


 Потому проходить исследование нужно в диагностических центрах и лабораториях, персонал которых постоянно подтверждает свой профессионализм.
Потому проходить исследование нужно в диагностических центрах и лабораториях, персонал которых постоянно подтверждает свой профессионализм.
 ПЦР тест-системы используют также для обнаружения штаммов ВПЧ 6 и 11.
ПЦР тест-системы используют также для обнаружения штаммов ВПЧ 6 и 11.


 Знак вставки полезен в ситуациях, когда вы не хотите или не нуждаетесь в использовании надстрочного индекса.
Знак вставки полезен в ситуациях, когда вы не хотите или не нуждаетесь в использовании надстрочного индекса. Теперь, когда вы знаете, что такое 5 в 7-й степени, вы можете продолжить свой веселый путь.
Теперь, когда вы знаете, что такое 5 в 7-й степени, вы можете продолжить свой веселый путь. com/calculator/exponent/what-is-5-to-the-7th-power/. По состоянию на 27 апреля 2023 г.
com/calculator/exponent/what-is-5-to-the-7th-power/. По состоянию на 27 апреля 2023 г. Представление этих типов чисел непросто.
Представление этих типов чисел непросто.
 Аналогично 10 100 = 1000….0 представляют 100 нулей. Это очень большое число, и его нелегко прочитать, поэтому с помощью научных обозначений представление очень большого числа становится легким.
Аналогично 10 100 = 1000….0 представляют 100 нулей. Это очень большое число, и его нелегко прочитать, поэтому с помощью научных обозначений представление очень большого числа становится легким. Давайте посмотрим, как мы можем использовать этот метод для сложения чисел.
Давайте посмотрим, как мы можем использовать этот метод для сложения чисел. Вычесть экспоненциальное представление: (6,67 × 10 8 ) – (8,4 × 10 6 )
Вычесть экспоненциальное представление: (6,67 × 10 8 ) – (8,4 × 10 6 ) 
 )
) )
)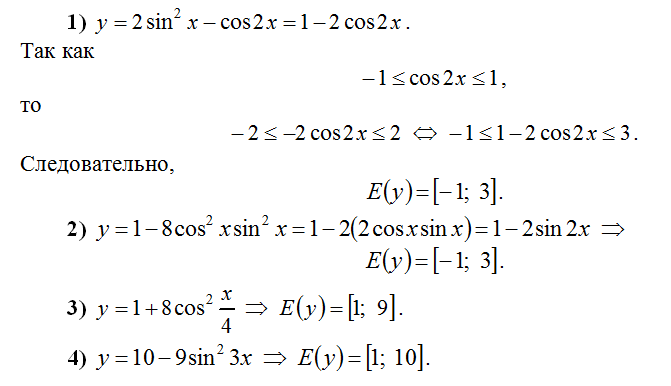 )
)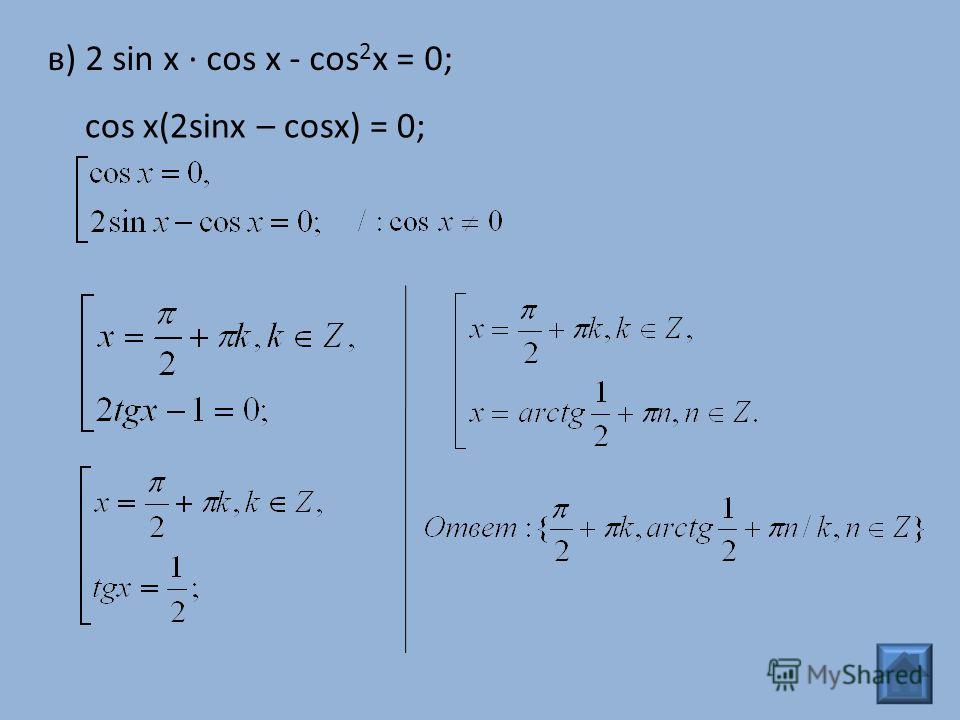 )
) )
) )
) )
) )
)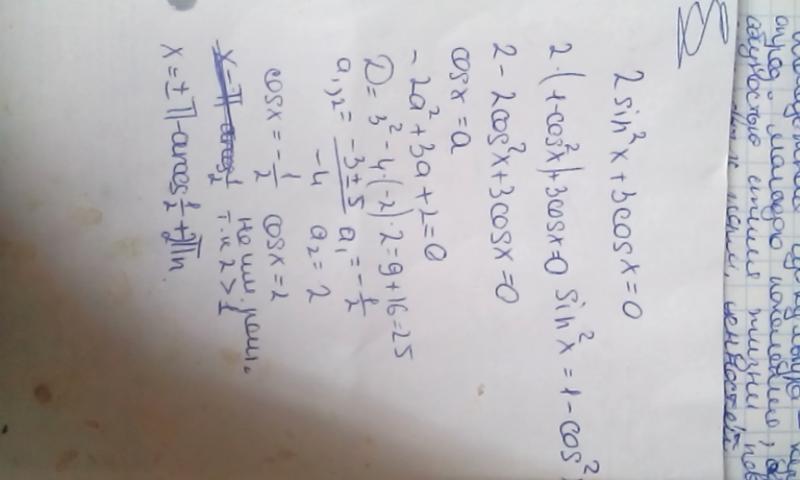 )
)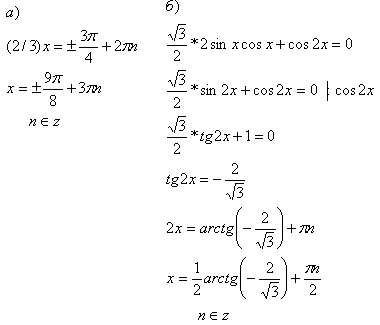 )
)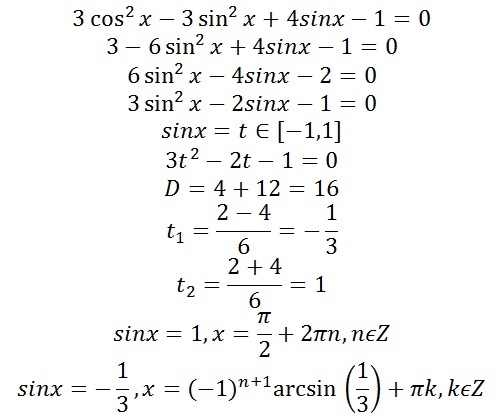 )
)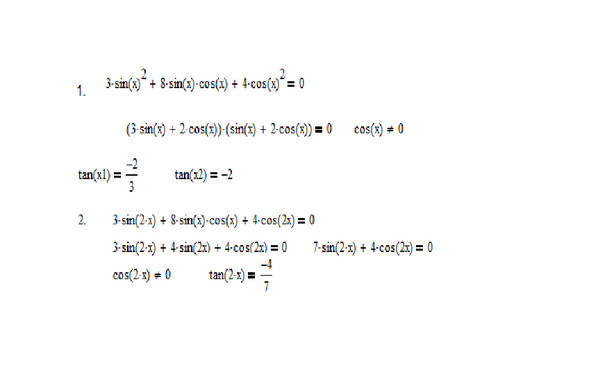 )
) )
) )
) )
) )
) )
)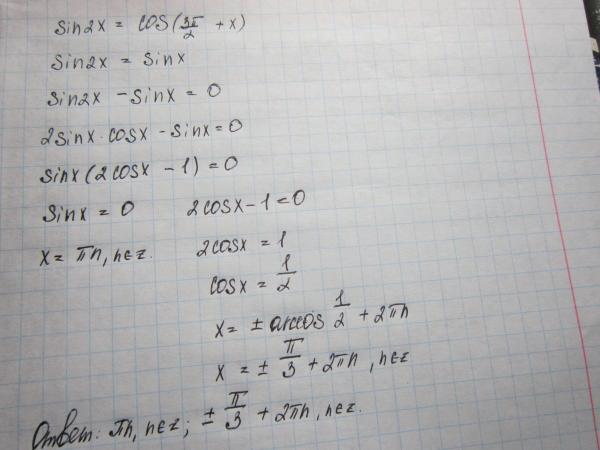
 …
…
 Когда у меня возникли проблемы с написанием бакалаврской работы, мне сразу нашли автора, который был со мной на связи все время, даже после сдачи работы. Считаю, что профессионалам FastFine можно доверять написание любых работ, здесь «своих» не бросают.
Когда у меня возникли проблемы с написанием бакалаврской работы, мне сразу нашли автора, который был со мной на связи все время, даже после сдачи работы. Считаю, что профессионалам FastFine можно доверять написание любых работ, здесь «своих» не бросают. Цены и сроки меня устроили, решила попробовать. Если честно, даже не ожидала, что можно переписать уже готовый текст своими словами и получить такой высокий процент уникальности. Видно, что это авторская работа, даже стиль написания немного отличается от исходника. На мой взгляд, статьи получились намного лучше оригинальных, такие не стыдно выкладывать. Автору ставлю отличную оценку! Тем, кого интересует рерайт высокого качества, рекомендую сайт fastfine.ru.
Цены и сроки меня устроили, решила попробовать. Если честно, даже не ожидала, что можно переписать уже готовый текст своими словами и получить такой высокий процент уникальности. Видно, что это авторская работа, даже стиль написания немного отличается от исходника. На мой взгляд, статьи получились намного лучше оригинальных, такие не стыдно выкладывать. Автору ставлю отличную оценку! Тем, кого интересует рерайт высокого качества, рекомендую сайт fastfine.ru. Чтобы не рисковать успеваемостью, лучше купить тест онлайн.
Чтобы не рисковать успеваемостью, лучше купить тест онлайн.
 М. Горького
М. Горького Здесь мы представляем результаты продолжающихся USGS испытаний бесконтактного георадара (GPR) для гидрологических и гидрогеофизических исследований.
Здесь мы представляем результаты продолжающихся USGS испытаний бесконтактного георадара (GPR) для гидрологических и гидрогеофизических исследований. Тестирование также показало, что необходимо решить определенные проблемы сбора и обработки данных, а также системные ограничения, прежде чем Геологическая служба США сможет внедрить широкое оперативное использование бесконтактного георадара. Геологическая служба США также разрабатывает инструменты поддержки принятия решений, чтобы информировать негеофизиков о понимании гидрологических и геологических условий, подходящих для бесконтактного развертывания георадара, и связанных с этим ограничений метода, основанных на опыте батиметрического картирования, приповерхностного изображения и глубины снежного покрова. опросы.
Тестирование также показало, что необходимо решить определенные проблемы сбора и обработки данных, а также системные ограничения, прежде чем Геологическая служба США сможет внедрить широкое оперативное использование бесконтактного георадара. Геологическая служба США также разрабатывает инструменты поддержки принятия решений, чтобы информировать негеофизиков о понимании гидрологических и геологических условий, подходящих для бесконтактного развертывания георадара, и связанных с этим ограничений метода, основанных на опыте батиметрического картирования, приповерхностного изображения и глубины снежного покрова. опросы. 
 Обратите внимание, что в исследовании изучались только уровни мышьяка и урана природного происхождения, а не уровни мышьяка и урана, возникающие в результате выбросов этих химических веществ в результате промышленных или других искусственных процессов.
Обратите внимание, что в исследовании изучались только уровни мышьяка и урана природного происхождения, а не уровни мышьяка и урана, возникающие в результате выбросов этих химических веществ в результате промышленных или других искусственных процессов.
 исследования Геологической службы США. За дополнительной информацией обращайтесь в MDPH по телефону 617-624-5757 или 800-240-4266.
исследования Геологической службы США. За дополнительной информацией обращайтесь в MDPH по телефону 617-624-5757 или 800-240-4266. Тем не менее, мы рекомендуем вам проверить вашу воду. Проживание в районе, где испытания USGS показывают, что грунтовые воды имеют больше шансов превысить стандарты питьевой воды по мышьяку и урану, не обязательно означает, что у вашего колодца будут проблемы. На самом деле мы ожидаем, что большинство частных скважин на этих участках не превышают нормы. Таким образом, вполне вероятно, но не обязательно, что ваша вода будет ниже стандартов. Единственный способ узнать наверняка, это хорошо проверить. Тем временем, если вы обеспокоены, вы можете использовать воду в бутылках, пока не получите результаты теста.
Тем не менее, мы рекомендуем вам проверить вашу воду. Проживание в районе, где испытания USGS показывают, что грунтовые воды имеют больше шансов превысить стандарты питьевой воды по мышьяку и урану, не обязательно означает, что у вашего колодца будут проблемы. На самом деле мы ожидаем, что большинство частных скважин на этих участках не превышают нормы. Таким образом, вполне вероятно, но не обязательно, что ваша вода будет ниже стандартов. Единственный способ узнать наверняка, это хорошо проверить. Тем временем, если вы обеспокоены, вы можете использовать воду в бутылках, пока не получите результаты теста. Фактические риски для здоровья зависят от трех ключевых факторов: уровня мышьяка и урана в питьевой воде; количество воды, фактически потребленной из вашей частной скважины; и сколько лет расходуется вода. Риски снижаются, если вы выпиваете менее 2 литров в день или потребляете воду меньше, чем всю жизнь.
Фактические риски для здоровья зависят от трех ключевых факторов: уровня мышьяка и урана в питьевой воде; количество воды, фактически потребленной из вашей частной скважины; и сколько лет расходуется вода. Риски снижаются, если вы выпиваете менее 2 литров в день или потребляете воду меньше, чем всю жизнь. Если скальный колодец установлен в месте, которое перехватывает подземные воды, содержащие относительно высокие концентрации мышьяка и/или урана, то содержание мышьяка и/или урана, извлекаемого из колодца, может превышать общедоступные стандарты питьевой воды.
Если скальный колодец установлен в месте, которое перехватывает подземные воды, содержащие относительно высокие концентрации мышьяка и/или урана, то содержание мышьяка и/или урана, извлекаемого из колодца, может превышать общедоступные стандарты питьевой воды. Результаты показали корреляцию между вероятностью превышения общественного стандарта питьевой воды по мышьяку и типом коренных пород. Исследование также показало сильную корреляцию между концентрациями мышьяка и близостью скважины к зоне разлома Клинтон-Ньюбери. Зона разлома Клинтон-Ньюбери простирается от восточной оконечности границы Массачусетса и Коннектикута на юге до долины реки Мерримак на северо-востоке.
Результаты показали корреляцию между вероятностью превышения общественного стандарта питьевой воды по мышьяку и типом коренных пород. Исследование также показало сильную корреляцию между концентрациями мышьяка и близостью скважины к зоне разлома Клинтон-Ньюбери. Зона разлома Клинтон-Ньюбери простирается от восточной оконечности границы Массачусетса и Коннектикута на юге до долины реки Мерримак на северо-востоке. Результаты 478 проб, отобранных для исследования, показали корреляцию между вероятностью превышения общедоступного стандарта питьевой воды по урану и типом коренных пород. В целом скважины, пройденные в гранитных (гранитного типа) коренных породах, имели наибольшую вероятность превышения норматива.
Результаты 478 проб, отобранных для исследования, показали корреляцию между вероятностью превышения общедоступного стандарта питьевой воды по урану и типом коренных пород. В целом скважины, пройденные в гранитных (гранитного типа) коренных породах, имели наибольшую вероятность превышения норматива.
 Тем не менее, большинство эффектов, наблюдаемых у людей, были вызваны сильными кратковременными воздействиями, а некоторые профессиональные исследования показали обратное воздействие на почки после прекращения воздействия. Хроническое воздействие также может привести к почечным последствиям. Воздействие на здоровье природного урана в питьевой воде связано с химической токсичностью урана. Агентство по охране окружающей среды США установило свой стандарт питьевой воды для урана в первую очередь из-за его химической токсичности, но в качестве меры предосторожности также рассмотрело возможность урана вызывать рак после продолжительного воздействия питьевой воды, исходя из предположения, что любой компонент, обладающий радиоактивными свойствами, может вызвать рак.
Тем не менее, большинство эффектов, наблюдаемых у людей, были вызваны сильными кратковременными воздействиями, а некоторые профессиональные исследования показали обратное воздействие на почки после прекращения воздействия. Хроническое воздействие также может привести к почечным последствиям. Воздействие на здоровье природного урана в питьевой воде связано с химической токсичностью урана. Агентство по охране окружающей среды США установило свой стандарт питьевой воды для урана в первую очередь из-за его химической токсичности, но в качестве меры предосторожности также рассмотрело возможность урана вызывать рак после продолжительного воздействия питьевой воды, исходя из предположения, что любой компонент, обладающий радиоактивными свойствами, может вызвать рак. Другие встречающиеся в природе радионуклиды, такие как газ радон и радий, обычно встречаются в тех же типах коренных пород, что и уран. Таким образом, несмотря на отсутствие данных о вероятности для газообразного радона и радия, районы с повышенной вероятностью повышенных концентраций урана, как правило, будут иметь повышенную вероятность повышенных концентраций радона и радия. Дополнительную информацию о стандартах общественной питьевой воды по радону и радию, воздействии на здоровье и вариантах лечения см. в разделе «Вопросы и ответы по радионуклидам».
Другие встречающиеся в природе радионуклиды, такие как газ радон и радий, обычно встречаются в тех же типах коренных пород, что и уран. Таким образом, несмотря на отсутствие данных о вероятности для газообразного радона и радия, районы с повышенной вероятностью повышенных концентраций урана, как правило, будут иметь повышенную вероятность повышенных концентраций радона и радия. Дополнительную информацию о стандартах общественной питьевой воды по радону и радию, воздействии на здоровье и вариантах лечения см. в разделе «Вопросы и ответы по радионуклидам».

 Хотя статистические данные о вероятности появления урана для этих конкретных гранитных или пегматитовых единиц отсутствуют, колодцы коренных пород в этих типах горных пород обычно имеют повышенную вероятность содержания природного радона, радия и урана в концентрациях, превышающих пределы питьевой воды.
Хотя статистические данные о вероятности появления урана для этих конкретных гранитных или пегматитовых единиц отсутствуют, колодцы коренных пород в этих типах горных пород обычно имеют повышенную вероятность содержания природного радона, радия и урана в концентрациях, превышающих пределы питьевой воды. мышьяк 3» до «мышьяк 5», что может потребоваться, а может и не потребоваться).
мышьяк 3» до «мышьяк 5», что может потребоваться, а может и не потребоваться).
 Системы обработки питьевой воды в точке входа (POE) (т. Е. Обработка всей воды, поступающей в дом) не могут сбрасываться в септическую систему Раздела 5. Сточные воды из системы очистки питьевой воды, которые нельзя сбрасывать в септическую систему Раздела 5, должны сбрасываться либо в муниципальную систему очистки сточных вод, либо в сухой колодец. Для сброса в сухой колодец требуется подача заявки на регистрацию MassDEP Underground Injection Control (UIC), за исключением объектов, которые используются только для проживания одной семьи.
Системы обработки питьевой воды в точке входа (POE) (т. Е. Обработка всей воды, поступающей в дом) не могут сбрасываться в септическую систему Раздела 5. Сточные воды из системы очистки питьевой воды, которые нельзя сбрасывать в септическую систему Раздела 5, должны сбрасываться либо в муниципальную систему очистки сточных вод, либо в сухой колодец. Для сброса в сухой колодец требуется подача заявки на регистрацию MassDEP Underground Injection Control (UIC), за исключением объектов, которые используются только для проживания одной семьи. Из-за эффектов разбавления MassDEP может одобрить сбросы в сухой колодец, которые превышают общедоступные стандарты питьевой воды, но не существует установленного предела, и каждое заявление рассматривается в каждом конкретном случае. MassDEP не может одобрить любые сбросы воды, в которых содержание мышьяка превышает федеральный порог содержания опасных отходов (характеристика токсичности) в 5 миллиграммов на литр (мг/л) или 5 частей на миллион (ppm), или в которых содержание урана превышает 0,600 мг/л или 600 частей на миллиард (ppb). Свяжитесь с Джо Черутти или Стивом Халлемом (контактная информация указана в конце этой страницы) для получения информации о допустимых концентрациях урана в сбросе в скважину UIC.
Из-за эффектов разбавления MassDEP может одобрить сбросы в сухой колодец, которые превышают общедоступные стандарты питьевой воды, но не существует установленного предела, и каждое заявление рассматривается в каждом конкретном случае. MassDEP не может одобрить любые сбросы воды, в которых содержание мышьяка превышает федеральный порог содержания опасных отходов (характеристика токсичности) в 5 миллиграммов на литр (мг/л) или 5 частей на миллион (ppm), или в которых содержание урана превышает 0,600 мг/л или 600 частей на миллиард (ppb). Свяжитесь с Джо Черутти или Стивом Халлемом (контактная информация указана в конце этой страницы) для получения информации о допустимых концентрациях урана в сбросе в скважину UIC. Эти ссуды или гранты могут быть использованы домовладельцами для проведения общего ремонта с целью улучшения или модернизации, защиты от погодных условий и/или устранения нарушений кодекса. безопасное и санитарное состояние жилого помещения. Эта программа доступна в сельских населенных пунктах и малых городах с населением до 10 000 человек. Некоторые сообщества с населением от 10 000 до 20 000 человек могут иметь право на участие. Домовладельцам следует посетить веб-сайт USDA Rural Development, чтобы узнать о требованиях и о том, как подать заявку, на веб-сайте USDA Rural Development: https://www.rd.usda.gov/ma.
Эти ссуды или гранты могут быть использованы домовладельцами для проведения общего ремонта с целью улучшения или модернизации, защиты от погодных условий и/или устранения нарушений кодекса. безопасное и санитарное состояние жилого помещения. Эта программа доступна в сельских населенных пунктах и малых городах с населением до 10 000 человек. Некоторые сообщества с населением от 10 000 до 20 000 человек могут иметь право на участие. Домовладельцам следует посетить веб-сайт USDA Rural Development, чтобы узнать о требованиях и о том, как подать заявку, на веб-сайте USDA Rural Development: https://www.rd.usda.gov/ma.

 Тем не менее, рекомендуется давать домашним животным питьевую воду, соответствующую тем же стандартам/рекомендациям, которые установлены для людей.
Тем не менее, рекомендуется давать домашним животным питьевую воду, соответствующую тем же стандартам/рекомендациям, которые установлены для людей.

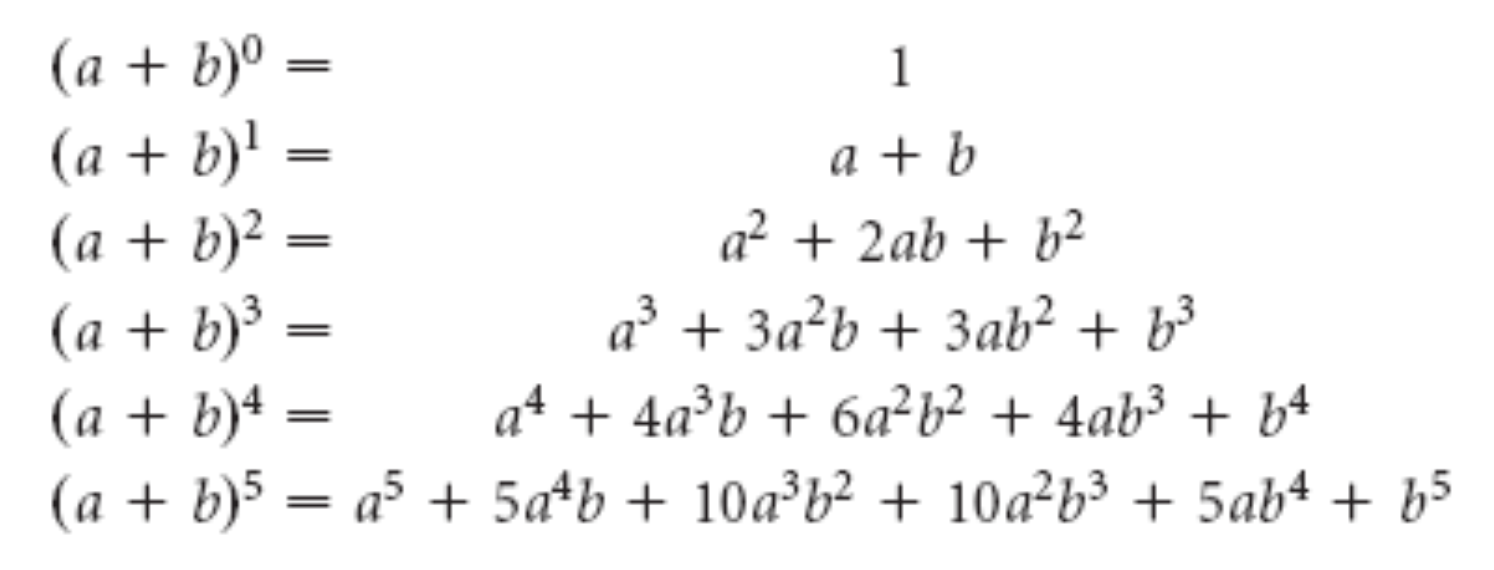 Частные приемы решения уравнений высших степеней
Частные приемы решения уравнений высших степеней СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ
СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ
 Теоретические основы решения показательных и логарифмических уравнений
Теоретические основы решения показательных и логарифмических уравнений Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.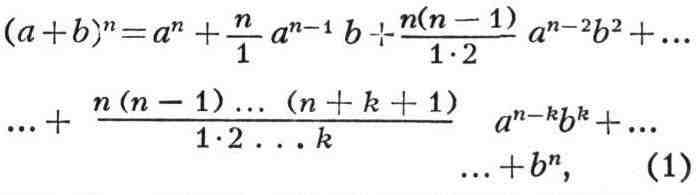 Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Сумма чисел в пятой степени
Сумма чисел в пятой степени

 На самом деле, пять выбирают один и пять выбирают четыре равно пяти, а пять выбирают два и пять выбирают три равны 10. Итак, у нас есть следующая формула, которая поможет нам распределить скобки cos 𝜃 плюс 𝑖 sin 𝜃 в пятой степени. Первый член — это просто cos 𝜃 в пятой степени, а второй — пять cos 𝜃 в четвертой степени, умноженные на 𝑖 sin 𝜃.
На самом деле, пять выбирают один и пять выбирают четыре равно пяти, а пять выбирают два и пять выбирают три равны 10. Итак, у нас есть следующая формула, которая поможет нам распределить скобки cos 𝜃 плюс 𝑖 sin 𝜃 в пятой степени. Первый член — это просто cos 𝜃 в пятой степени, а второй — пять cos 𝜃 в четвертой степени, умноженные на 𝑖 sin 𝜃. Тогда у нас есть пять cos 𝜃 умноженных на 𝑖 sin 𝜃 в четвертой степени. А так как 𝑖 в четвертой степени равно 𝑖 в квадрате, это отрицательная единица в квадрате, то есть просто единица. И этот термин становится пятью cos 𝜃 sin 𝜃 в четвертой степени.
Тогда у нас есть пять cos 𝜃 умноженных на 𝑖 sin 𝜃 в четвертой степени. А так как 𝑖 в четвертой степени равно 𝑖 в квадрате, это отрицательная единица в квадрате, то есть просто единица. И этот термин становится пятью cos 𝜃 sin 𝜃 в четвертой степени. И мы могли бы оставить это так. Но мы могли бы также вспомнить, что квадрат греха 𝜃 плюс квадрат квадрата 𝜃 равен единице. А затем, написав, что грех в квадрате 𝜃 равен единице минус косинус в квадрате 𝜃, мы находим косинус пять 𝜃 равно косинусу 𝜃 в пятой степени минус 10 косинус в кубе 𝜃 умноженный на один минус косинус в квадрате 𝜃 плюс пять косинусов 𝜃 умноженный на один минус косинус в квадрате 𝜃 в квадрате .
И мы могли бы оставить это так. Но мы могли бы также вспомнить, что квадрат греха 𝜃 плюс квадрат квадрата 𝜃 равен единице. А затем, написав, что грех в квадрате 𝜃 равен единице минус косинус в квадрате 𝜃, мы находим косинус пять 𝜃 равно косинусу 𝜃 в пятой степени минус 10 косинус в кубе 𝜃 умноженный на один минус косинус в квадрате 𝜃 плюс пять косинусов 𝜃 умноженный на один минус косинус в квадрате 𝜃 в квадрате .
 0 /Программа для обучения и тестирования детей/
0 /Программа для обучения и тестирования детей/ Табличное умножение»; 2-4 классы
Табличное умножение»; 2-4 классы Определение частей речи» /2-3 классы/
Определение частей речи» /2-3 классы/ Словарная работа»; 2-3 классы
Словарная работа»; 2-3 классы С.Пушкина», 3 — 5 класс
С.Пушкина», 3 — 5 класс










 Даже в алгебре вам все равно нужно будет уметь упрощать рациональные выражения и многочлены множителей, возможно, даже перемножать матрицы.
Даже в алгебре вам все равно нужно будет уметь упрощать рациональные выражения и многочлены множителей, возможно, даже перемножать матрицы. Потратьте на это 1-2 месяца. Это может окупиться!
Потратьте на это 1-2 месяца. Это может окупиться! Так же, как ваш ребенок, вероятно, уже запомнил ваш адрес и телефон
число, теперь она или он собирается запомнить некоторые математические факты. Вы должны ожидать, что ребенок ответит немедленно, когда вы тренируете. Если он или она не знает ответ наизусть (по памяти), то скажите ему или ей правильный ответ.
Так же, как ваш ребенок, вероятно, уже запомнил ваш адрес и телефон
число, теперь она или он собирается запомнить некоторые математические факты. Вы должны ожидать, что ребенок ответит немедленно, когда вы тренируете. Если он или она не знает ответ наизусть (по памяти), то скажите ему или ей правильный ответ. Правильная дрель требует затрат времени от
инструктор. Если можете, привлекайте старших братьев и сестер к выполнению задания по сверлению.
Правильная дрель требует затрат времени от
инструктор. Если можете, привлекайте старших братьев и сестер к выполнению задания по сверлению.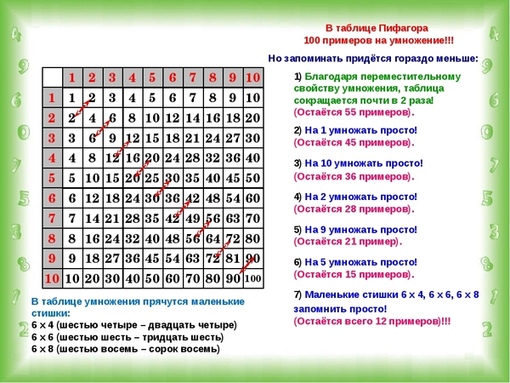 Эта техника использует чувства зрения,
слышать и осязать одновременно, чтобы зафиксировать информацию в мозгу. После
он просмотрел список несколько раз, попросите его повторить его по памяти.
Эта техника использует чувства зрения,
слышать и осязать одновременно, чтобы зафиксировать информацию в мозгу. После
он просмотрел список несколько раз, попросите его повторить его по памяти. Эти шаги
может хватить на один день. Но обязательно просмотрите позже в
день.
Эти шаги
может хватить на один день. Но обязательно просмотрите позже в
день. Держите таблицу видимой, скрывайте проблемы (но не ответы) и указывайте на
ответы в произвольном порядке. Эта техника может работать и по-другому.
вокруг, где студент говорит ответы, а вы создаете проблемы.
Иногда давайте неправильные ответы, чтобы проверить их.
Держите таблицу видимой, скрывайте проблемы (но не ответы) и указывайте на
ответы в произвольном порядке. Эта техника может работать и по-другому.
вокруг, где студент говорит ответы, а вы создаете проблемы.
Иногда давайте неправильные ответы, чтобы проверить их.
 Я взял в своих книгах и видео таблицы умножения. Практиковать их в обоих направлениях так здорово, потому что это позволяет учащимся осваивать «замаскированные» факты деления одновременно.
Я взял в своих книгах и видео таблицы умножения. Практиковать их в обоих направлениях так здорово, потому что это позволяет учащимся осваивать «замаскированные» факты деления одновременно. Напоминайте ребенку смотреть на нее несколько раз в день. Это может творить чудеса для визуалов!
Напоминайте ребенку смотреть на нее несколько раз в день. Это может творить чудеса для визуалов! Существует ряд компьютерных игр на время, которые очень хорошо подходят для
факты бурения. Вот некоторые онлайн:
Существует ряд компьютерных игр на время, которые очень хорошо подходят для
факты бурения. Вот некоторые онлайн: Доказательство в пудинге: просто попробуйте и посмотрите, что из этого выйдет.
Доказательство в пудинге: просто попробуйте и посмотрите, что из этого выйдет.
 Обходя свой «ментальный блок», они могут без труда выучить таблицы — они воспринимают это как забаву, а «математические триггеры», которые мозг использует для «блокировки» мозга и создания «реакции страха», никогда не стимулируются.
Кроме того, младшие братья и сестры часто разучивают песни (и их следует поощрять к разучиванию) в одно и то же время.
Обходя свой «ментальный блок», они могут без труда выучить таблицы — они воспринимают это как забаву, а «математические триггеры», которые мозг использует для «блокировки» мозга и создания «реакции страха», никогда не стимулируются.
Кроме того, младшие братья и сестры часто разучивают песни (и их следует поощрять к разучиванию) в одно и то же время. Например, если ребенок выучит 8 × 7 с помощью Times Tales, он запомнит дурацкую картинку с изображением «девушки восемь» и символа «семь» за рулем автомобиля, а также запомнит фразу «Сейчас 56». Это не слишком отличается от использования такой рифмы, как «5, 6, 7, 8, пятьдесят шесть семь раз по 8». Такая программа также может повысить уверенность в себе.
Например, если ребенок выучит 8 × 7 с помощью Times Tales, он запомнит дурацкую картинку с изображением «девушки восемь» и символа «семь» за рулем автомобиля, а также запомнит фразу «Сейчас 56». Это не слишком отличается от использования такой рифмы, как «5, 6, 7, 8, пятьдесят шесть семь раз по 8». Такая программа также может повысить уверенность в себе. Вы можете отступить и повторить попытку позже. Некоторые дают своим ученикам «костыль» — выписанные таблицы — и в конце концов ребенок замечает, как медленно ему/ей приходится проверять ответы в таблице вместо того, чтобы знать их, и решает запомнить их.
Вы можете отступить и повторить попытку позже. Некоторые дают своим ученикам «костыль» — выписанные таблицы — и в конце концов ребенок замечает, как медленно ему/ей приходится проверять ответы в таблице вместо того, чтобы знать их, и решает запомнить их.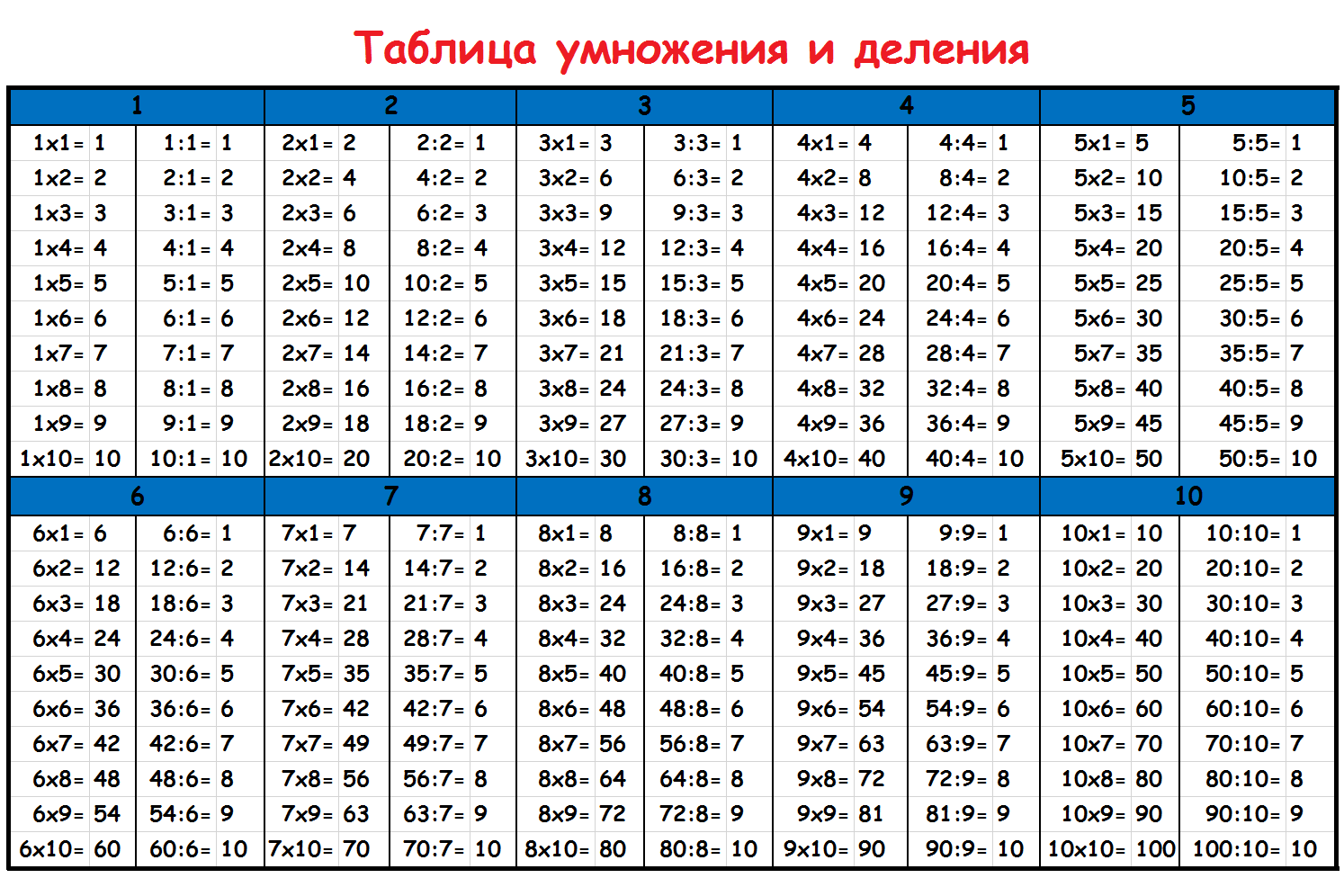 Моя дочь начала медленно, и я не был уверен, что это правильный продукт для нее. Потом я понял, что она недостаточно хорошо знает математические факты, чтобы двигаться дальше. Так что я просто вернулся к главам с фактами о математике в младших классах, и она поработает над ними. Ваши листы умножения потрясающие! Ваш способ преподавания настолько великолепен, что она действительно быстро схватывает их, и мы скоро сможем перейти к учебной программе 4-го класса. Вы действительно учите концепциям, а не только решению проблем. В отличие от многих домашних школьников, мне никогда не придется тратить больше денег на математическую программу за математической программой, пытаясь найти ту, которая работает. Спасибо!!
Моя дочь начала медленно, и я не был уверен, что это правильный продукт для нее. Потом я понял, что она недостаточно хорошо знает математические факты, чтобы двигаться дальше. Так что я просто вернулся к главам с фактами о математике в младших классах, и она поработает над ними. Ваши листы умножения потрясающие! Ваш способ преподавания настолько великолепен, что она действительно быстро схватывает их, и мы скоро сможем перейти к учебной программе 4-го класса. Вы действительно учите концепциям, а не только решению проблем. В отличие от многих домашних школьников, мне никогда не придется тратить больше денег на математическую программу за математической программой, пытаясь найти ту, которая работает. Спасибо!!  После пяти лет борьбы с математикой мой шестиклассник вырос как на дрожжах. Сейчас она действительно любит математику. Прежде чем получить математику, она провела три года, работая над таблицей умножения, используя карточки, упражнения, компьютерные игры, мнемонические устройства и программы с рифмованными историями в сочетании со своими учебниками. Все безрезультатно. После 5 месяцев использования ваших продуктов и методов она запомнила все свои факты умножения и перешла к делению в длинное число. Мой 5-летний ребенок слушает и действительно умеет считать двойки, тройки, четверки и пятерки без пропусков. Видимо ваши методы работают. БОЛЬШОЕ ВАМ СПАСИБО за всю вашу работу.
После пяти лет борьбы с математикой мой шестиклассник вырос как на дрожжах. Сейчас она действительно любит математику. Прежде чем получить математику, она провела три года, работая над таблицей умножения, используя карточки, упражнения, компьютерные игры, мнемонические устройства и программы с рифмованными историями в сочетании со своими учебниками. Все безрезультатно. После 5 месяцев использования ваших продуктов и методов она запомнила все свои факты умножения и перешла к делению в длинное число. Мой 5-летний ребенок слушает и действительно умеет считать двойки, тройки, четверки и пятерки без пропусков. Видимо ваши методы работают. БОЛЬШОЕ ВАМ СПАСИБО за всю вашу работу. Она делает это сама летом, потому что ей это нравится! Никогда не думал, что увижу это. Она действительно боролась с умножением, и она говорит, что это облегчает ей понимание. Мне нравится возможность использовать синюю серию, чтобы заполнить пробелы в том, что они не «получают» с первого раза. Это так настраивается для разных детей. Я тоже люблю формат pdf. Я могу собрать книгу в любом порядке. Мне нравится, когда нет учебника для учителя. С тремя детьми трудно тасовать 3 книги. Это намного лучше, потому что, когда у каждого ребенка есть вопросы, у них уже все есть с собой, когда они приносят их мне. Я был так взволнован, чтобы найти это. Желание
Я нашел его пару лет назад! Спасибо за этот учебный план и спасибо за то, что сделали его доступным. Я купил все 6 уровней сразу. Я никогда не мог позволить себе сделать это с любой другой учебной программой. На этом борьба (по большей части) с моей дочерью закончилась. Спасибо, что сделали обучение моих детей математике доступным, легким и даже приятным!
Она делает это сама летом, потому что ей это нравится! Никогда не думал, что увижу это. Она действительно боролась с умножением, и она говорит, что это облегчает ей понимание. Мне нравится возможность использовать синюю серию, чтобы заполнить пробелы в том, что они не «получают» с первого раза. Это так настраивается для разных детей. Я тоже люблю формат pdf. Я могу собрать книгу в любом порядке. Мне нравится, когда нет учебника для учителя. С тремя детьми трудно тасовать 3 книги. Это намного лучше, потому что, когда у каждого ребенка есть вопросы, у них уже все есть с собой, когда они приносят их мне. Я был так взволнован, чтобы найти это. Желание
Я нашел его пару лет назад! Спасибо за этот учебный план и спасибо за то, что сделали его доступным. Я купил все 6 уровней сразу. Я никогда не мог позволить себе сделать это с любой другой учебной программой. На этом борьба (по большей части) с моей дочерью закончилась. Спасибо, что сделали обучение моих детей математике доступным, легким и даже приятным! Для меня это первые дни с материалами Math Mammoth, так как я только что заказал светло-голубые тексты 1A и 3A/B в Rainbow Resource (нашел их по рекомендации одного из их специалистов по вопросам и ответам).
Для меня это первые дни с материалами Math Mammoth, так как я только что заказал светло-голубые тексты 1A и 3A/B в Rainbow Resource (нашел их по рекомендации одного из их специалистов по вопросам и ответам). Большое спасибо! Я бы хотел, чтобы все учителя государственных школ имели доступ к таким замечательным материалам, которые вы предоставляете (хорошо, если у них есть подключение к Интернету, но вы знаете, что школьная система предлагает им так много всего другого). Я надеюсь, что вы получите много положительных отзывов от многих людей за ваши усилия, потому что я уверен, что ваши усилия приносят пользу многим. Спасибо, что поделились своими знаниями!!!
Большое спасибо! Я бы хотел, чтобы все учителя государственных школ имели доступ к таким замечательным материалам, которые вы предоставляете (хорошо, если у них есть подключение к Интернету, но вы знаете, что школьная система предлагает им так много всего другого). Я надеюсь, что вы получите много положительных отзывов от многих людей за ваши усилия, потому что я уверен, что ваши усилия приносят пользу многим. Спасибо, что поделились своими знаниями!!! (Узнай отличия между всеми этими разноцветными сериями!)
(Узнай отличия между всеми этими разноцветными сериями!)
 05.13
05.13  by 2013-2016
by 2013-2016 6KB
6KB 07KB
07KB 05KB
05KB 75KB
75KB 87KB
87KB 01KB
01KB 78KB
78KB 41KB
41KB 32KB
32KB
 Это означает, что в стандартной форме
у
«=»
а
Икс
2
+
б
Икс
+
с
, выражение
Это означает, что в стандартной форме
у
«=»
а
Икс
2
+
б
Икс
+
с
, выражение
 Если уравнение находится в стандартной форме, то вы можете просто взять
с
как
у
-перехват. Например, в приведенном выше примере:
Если уравнение находится в стандартной форме, то вы можете просто взять
с
как
у
-перехват. Например, в приведенном выше примере: Диапазон ограничен теми точками, которые больше или равны
у
-координата вершины (или меньше или равна, в зависимости от того, открывается парабола вверх или вниз).
Диапазон ограничен теми точками, которые больше или равны
у
-координата вершины (или меньше или равна, в зависимости от того, открывается парабола вверх или вниз). Мы также будем решать примеры на основе концепции для лучшего понимания.
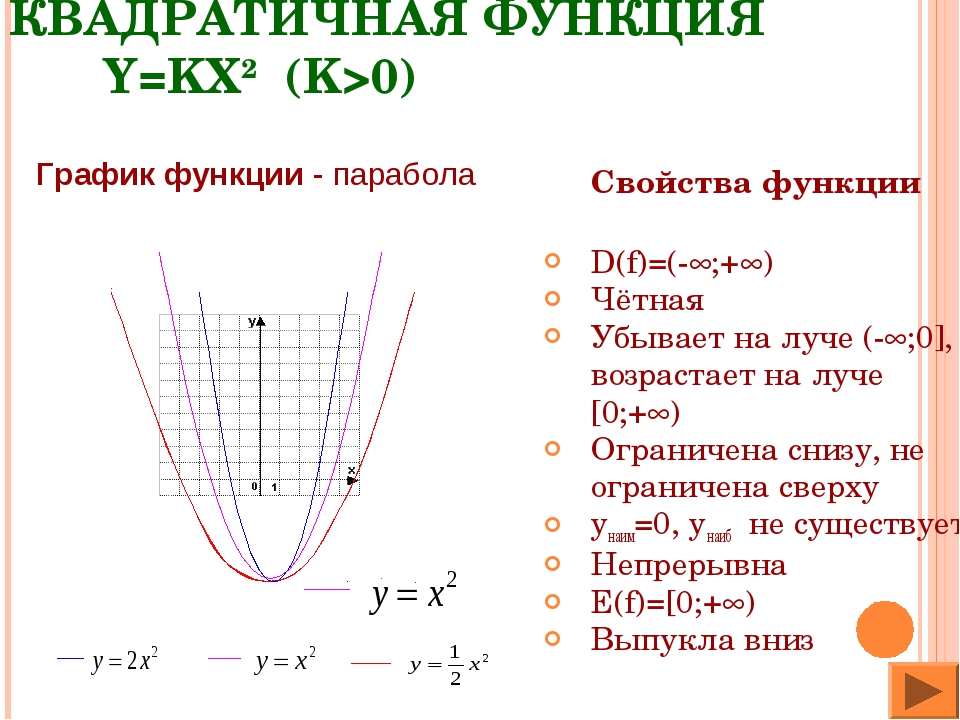
Мы также будем решать примеры на основе концепции для лучшего понимания. Квадратичная функция имеет минимум одного члена второй степени. Это алгебраическая функция.
Квадратичная функция имеет минимум одного члена второй степени. Это алгебраическая функция.
 Вот общие формы каждого из них:
Вот общие формы каждого из них: Вот пример.
Вот пример.
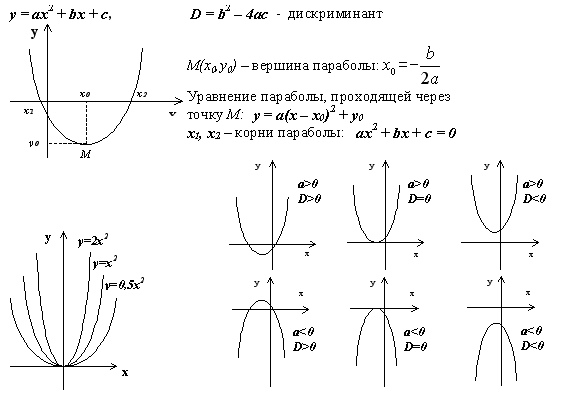


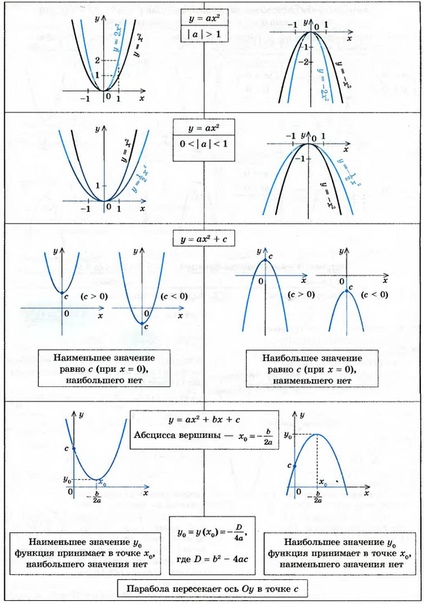 Следовательно, используя дифференцирование, мы можем найти минимум или максимум квадратичной функции.
Следовательно, используя дифференцирование, мы можем найти минимум или максимум квадратичной функции.


 Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y, таким образом получая координаты графика. После нанесения координат на график, свободной рукой соединяем точки, чтобы получить график квадратичных функций. Нахождение вершины помогает в построении квадратичного графа.
Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y, таким образом получая координаты графика. После нанесения координат на график, свободной рукой соединяем точки, чтобы получить график квадратичных функций. Нахождение вершины помогает в построении квадратичного графа.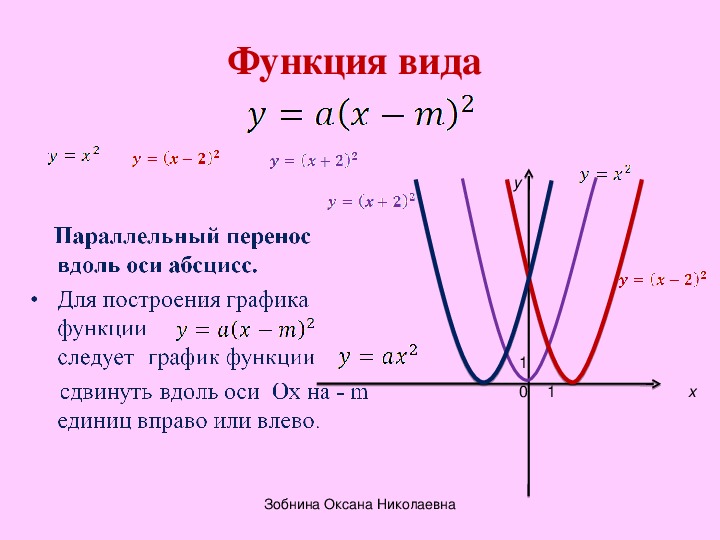
 Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение:
Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение: Поменяем местами 1 и косинус и вынесем минус за лимит.
Поменяем местами 1 и косинус и вынесем минус за лимит.
 5 / 5. Количество оценок: 6
5 / 5. Количество оценок: 6 Отсюда получим, что в точке x0=5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что
Отсюда получим, что в точке x0=5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.
Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности. .., то
.., то
 5)1×2=limx→02.51×22.5+∞=+∞
5)1×2=limx→02.51×22.5+∞=+∞




 Один из способов сделать это — нарисовать график 𝑦=𝑥𝑥sin.
Один из способов сделать это — нарисовать график 𝑦=𝑥𝑥sin. Это дает нам следующий результат.
Это дает нам следующий результат.
 Рассмотрим следующие наброски tan𝑥𝑥 и 1−𝑥𝑥cos, где 𝑥 измеряется в радианах.
Рассмотрим следующие наброски tan𝑥𝑥 и 1−𝑥𝑥cos, где 𝑥 измеряется в радианах.


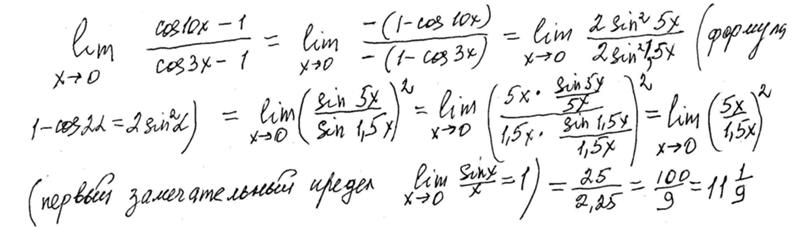 Это дает нам limsinlimsin→→1−𝑥2𝑥−=1−𝜃+2𝜃.
Это дает нам limsinlimsin→→1−𝑥2𝑥−=1−𝜃+2𝜃.
