Как найти время, скорость и расстояние
Поможем понять и полюбить математику
Начать учиться
411.5K
Каждый день мы смотрим на часы, спидометр, фитнес-браслет и анализируем расстояние, скорость и время. Рассмотрим математические формулы, чтобы решать задачи на поиск времени, скорости и расстояния из учебников и реальной жизни.
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: s = v × t |
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: v = s : t |
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: t = s : v |
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
v = 50 м/мин
t = 15 мин
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.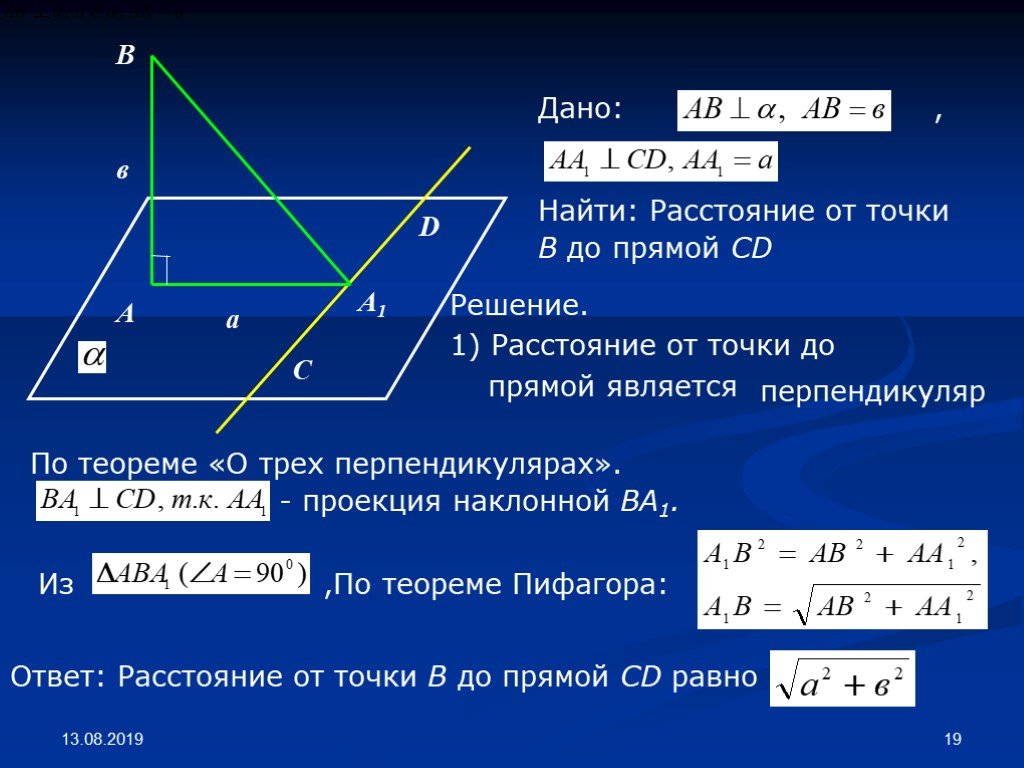
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
s = 500 м
v = 100 м/мин
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Сложение чисел с разными знаками
К следующей статье
314. 8K
8K
Объем параллелепипеда
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Расстояние, скорость, время
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Как далеко между
Этот инструмент можно использовать для определения расстояния между двумя точками. Введите названия двух мест и узнайте расстояние между ними. Отображаются прямое расстояние и расстояние вождения. Чтобы начать, введите названия мест ниже и нажмите кнопку «Показать».
Введите названия двух мест и узнайте расстояние между ними. Отображаются прямое расстояние и расстояние вождения. Чтобы начать, введите названия мест ниже и нажмите кнопку «Показать».
Как использовать
Введите название двух мест в текстовые поля и нажмите кнопку Показать.
Рекомендуемый формат для использования: [Город, Страна], т.е. [Город(запятая)(пробел)Страна].
Когда результат возвращен, вы можете скопировать ссылку для использования в качестве постоянной ссылки обратно на результат или отправить другим.
Примечание : Для почтовых индексов используйте расстояние между почтовыми индексами. Для почтовых индексов Великобритании используйте инструмент расстояния для почтовых индексов Великобритании. Кроме того, чтобы найти расстояние между точками, которые не имеют имени, вы можете использовать инструмент Измерить расстояние.
Информация о расстоянии между
Этот инструмент можно использовать для определения расстояния между двумя точками.
Вывод двух расстояний:
- As the Crow Flies — Прямое расстояние между точками
- Расстояние наземным транспортом (По возможности) — Расчетное расстояние при путешествии автомобильным и морским транспортом.
Расстояния могут быть выведены в следующих единицах измерения:
- км (километры)
- мили
Выход осуществляется через измерение расстояния, а также карту, которая показывает, что две локации и путь между ними по прямой и маршрут наземным транспортом.
Вы можете использовать элементы управления на карте для:
- панорамирования карты
- Увеличить карту
- Переключение между картой и видом со спутника
Некоторые примеры расстояний
Некоторые расстояния между городами, которые можно найти с помощью системы. Нажмите на один из них, чтобы увидеть его, или введите свои собственные места выше в текстовые поля.
- Расстояние между Венецией, Италия и Ноттингемом, Англия
- Расстояние между Белфастом, Северная Ирландия и Кабо-Сан-Лукас, Мексика
- Расстояние между Портсмутом, Англия и Инвернессом, Шотландия
- Расстояние между Лос-Анджелесом, Калифорния, США и Дели, Индия
- Расстояние между Редингом, Беркшир и Филадельфией, Пенсильвания, США
Известные проблемы
- Красная линия не пересекает международную линию перемены дат
- Автоматический зум не работает, когда кратчайшее расстояние проходит через международную линию перемены дат
- Разрешить запрос точек на удаление из базы данных, чтобы информация была аккуратной
Если вы обнаружите что-либо, требующее решения, свяжитесь с Free Map Tools.
История версий
- 15 октября 2018 г.: Исправление ошибки, неправильное расстояние при пересечении маршрута с IDL
- 30 сентября 2018 г.: исправление ошибки, неправильное поведение при расчете 2-го, 3-го и т. д. маршрута
- 28 сентября 2018 г.: Исправлена ошибка, при вычислении второго расстояния возникала ошибка .
- 21 сентября 2018 г.: исправлена проблема с форматом времени в пути .
- 19 сентября 2018 г.: переход на карты листовок
- 14 ноября 2016 г.: продолжительность поездки теперь выводится, если применимо.
- 28 июня 2016 г.: вывод URL теперь содержит информацию о единицах измерения (км)
- 22 июня 2016 г.: настройка км / миль теперь будет сохранять и запоминать свое состояние между сеансами .
- 28 мая 2015 г.: теперь использует Google Places.Autocomplete
- 15 марта 2015 г.: Новая возможность избегать автомагистралей/автомагистралей
- 27 января 2015 г.: добавлена кнопка полноэкранного режима
- 8 января 2014 г.
 : устранена незначительная проблема. Когда направления проезда не найдены, в поле теперь написано N/A. Ранее он не обновлялся и иногда сохранял значение предыдущего поискового расстояния .
: устранена незначительная проблема. Когда направления проезда не найдены, в поле теперь написано N/A. Ранее он не обновлялся и иногда сохранял значение предыдущего поискового расстояния . - 7 января 2014 г.: Решена незначительная проблема, из-за которой маршрут проезда из старого измерения все еще отображался, когда был выполнен другой поиск
- 13 ноября 2013 г.: реализован API Google Maps V3 .
- 7 марта 2010: Добавлен новый вид транспорта… Пассажирский Самолет
- 2 декабря 2009 г.: Теперь предложенные города и страны отображаются намного быстрее. Также показывает самые популярные места вверху списка
- 20 января 2008 г. Улучшено автоматическое масштабирование для получения более точных результатов.
- 15 декабря 2007 г.: добавлена опция сохранения данных .
- 29 ноября 2007 г.: добавлена опция измерения наземного транспорта .
- 4 ноября 2007 г.: динамический URL для сохранения расстояния между X и Y
- 21 октября 2007 г.
 : Добавлен поиск GlocalSearch для автоматического поиска большего количества мест
: Добавлен поиск GlocalSearch для автоматического поиска большего количества мест - 18 июля 2007 г. Исправлены выпадающие списки, чтобы они попадали на все содержимое ниже .
- 1 июля 2007 г.: Проделана работа, позволяющая пользователям добавлять новые местоположения, если они не находятся в системе .
- 30 июня 2007 г.: Страница создана с базовой функциональностью
Соответствующие ссылки
Листовка — библиотека JavaScript для интерактивных карт
Измерение расстояния на карте
Инструмент измерения расстояния — это простой способ определения расстояния между двумя или более точками на карте.
Как пользоваться инструментом «Измерить расстояние»
Просто нажмите один раз на одну точку, затем нажмите еще раз на вторую точку. Расстояние должно отображаться. Вы можете щелкнуть более двух точек, чтобы построить непрерывный маршрут.
Используйте переключатель миль/км/морских миль/ярдов для измерения расстояний в км, милях или морских милях. Опция Autopan будет перемещать карту по мере того, как вы нажимаете на точки.
Опция Autopan будет перемещать карту по мере того, как вы нажимаете на точки.
Текстовое поле «Поиск местоположения» позволяет быстро добраться до нужной области, не тратя время на масштабирование и панорамирование, чтобы найти ее. Например, если вы хотите найти город Рим в Италии, введите «Рим, Италия» и нажмите «Поиск». Затем карта отправится прямо в Рим. Обратите внимание на формат «[город][запятая][пробел][район]»
Маркеры-переключатели будут отображать или скрывать маркеры, если они мешают
Удалить последнюю удалит последнюю точку с карты максимально увеличить масштаб
Очистить карту — это кнопка сброса, которая удалит все точки и позволит вам снова начать измерение расстояния
Вы можете редактировать положение любых существующих точек, перетаскивая маркер (когда они отображаются) и маркер в новой позиции
Вы также можете отрегулировать высоту карты, чтобы сделать ее большой, средней или маленькой по размеру
Вы можете удалить точку, щелкнув узел
Будущие идеи и улучшения
- проблема продавца)
- Есть другие скорости, такие как оптоволоконный кабель (~ 0,6 c) и число Маха
- Возможность добавить заголовок к маркеру, который затем появляется при наведении указателя мыши и экспорте данных
- Добавить байдарку в список видов транспорта
История версий
- 20 апреля 2022 г.
 — Улучшено поведение при нажатии кнопки «Маленький/Средний/Большой»
— Улучшено поведение при нажатии кнопки «Маленький/Средний/Большой» - 21 февраля 2021 г. — выбранные единицы измерения расстояния сохраняются и вызываются при следующем посещении .
- 6 июля 2020 г. — Новая опция для экспорта ссылки на маршрут. Найдено в разделе «Параметры экспорта» .
- 2 июня 2019 г. — исправлена ошибка с неработающим выходом счетчиков
- 29 мая 2019 г. – Внедрение листовок-карт
- 20 мая 2019 г. — исправлена ошибка в браузере IE 9.0024
- 9 мая 2019 г. — исправлена проблема, из-за которой расстояние не сбрасывалось до нуля при нажатии кнопки «Очистить карту»
- 14 сентября 2017 г. Расстояние теперь отображается на карте в полноэкранном режиме
- 4 августа 2017 г. — Обновлен селектор юнитов. Добавлены единицы футов
- 24 июля 2017 г. — Полноэкранный режим перемещен на карту. Теперь находится в правом верхнем углу
- 4 июля 2017 г. — Исправлена проблема с экспортом CSV и XLSX
- 29 января 2017 г.
 — Возможность отображения диаграммы высот и экспорта файла CSV с данными высот вдоль маршрута 9.0024
— Возможность отображения диаграммы высот и экспорта файла CSV с данными высот вдоль маршрута 9.0024 - 25 ноября 2016 г. — экспорт KML для отображения контактов на каждом узле маршрута
- 23 ноября 2016 г. — Добавлена опция загрузки KML, CSV и XLSX .
- 19 июля 2016 г. — Исправлены ошибки, связанные с изменением вида транспорта и расчетного времени в пути при изменении единиц измерения
- 5 июля 2016 г. — Добавлены метры в качестве единицы измерения расстояния
- 25 июня 2016 г. — Единицы скорости движения меняются в зависимости от единиц расстояния
- 20 июня 2016 г. — исправлена ошибка, из-за которой при измерении количества дней в два раза отображалось фактическое значение
- 24 марта 2016 г. — точки маршрута теперь можно добавлять в середине пути. Точки также можно удалить, щелкнув правой кнопкой мыши .
- 25 января 2016 г. — Скорость теперь можно вводить вручную
- 28 декабря 2015 г. — добавлена возможность переключения между минутами, часами и днями для оценки времени в пути
- 24 июня 2014 г.


 : устранена незначительная проблема. Когда направления проезда не найдены, в поле теперь написано N/A. Ранее он не обновлялся и иногда сохранял значение предыдущего поискового расстояния
: устранена незначительная проблема. Когда направления проезда не найдены, в поле теперь написано N/A. Ранее он не обновлялся и иногда сохранял значение предыдущего поискового расстояния : Добавлен поиск GlocalSearch для автоматического поиска большего количества мест
: Добавлен поиск GlocalSearch для автоматического поиска большего количества мест — Улучшено поведение при нажатии кнопки «Маленький/Средний/Большой»
— Улучшено поведение при нажатии кнопки «Маленький/Средний/Большой» — Возможность отображения диаграммы высот и экспорта файла CSV с данными высот вдоль маршрута 9.0024
— Возможность отображения диаграммы высот и экспорта файла CSV с данными высот вдоль маршрута 9.0024
 )
) )
) )
) )
) )
) )
) )
) )
) 02.16
02.16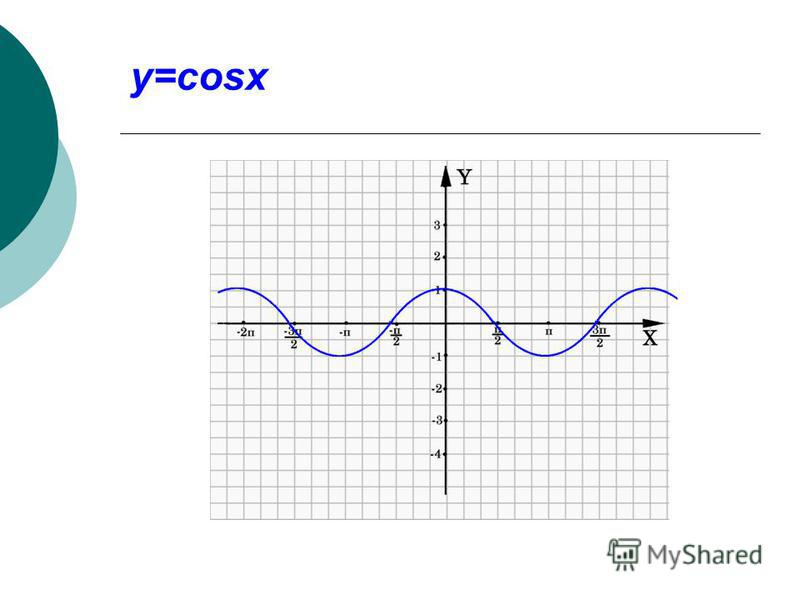 .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
 3 .
3.3.56. EMBED Equation.3 .
3.3.57. EMBED Equation.3 .
3.3.58. 0.
3.3.59. EMBED Equation.3 .
3.3.60. EMBED Equation.3 .
3 .
3.3.56. EMBED Equation.3 .
3.3.57. EMBED Equation.3 .
3.3.58. 0.
3.3.59. EMBED Equation.3 .
3.3.60. EMBED Equation.3 . П., 2006» для чтения, скачивания и покупки
П., 2006» для чтения, скачивания и покупки Для студентов высших технических учебных заведений.
Для студентов высших технических учебных заведений.
 2016 | Менеджмент)
2016 | Менеджмент) Подобраны и методически распределены задачи по аналитической геометрии и математическому анализу. В начале каждого параграфа приведены формулы, определения и другие краткие пояснения теории, необходимые для решения последующих задач. Сборник может быть использован при всех формах обучения. Для студентов высших технических учебных заведений.
Подобраны и методически распределены задачи по аналитической геометрии и математическому анализу. В начале каждого параграфа приведены формулы, определения и другие краткие пояснения теории, необходимые для решения последующих задач. Сборник может быть использован при всех формах обучения. Для студентов высших технических учебных заведений.
 ..
.. В начале каждой темы представлены формулы и краткое пояснение теории, которые нужны для решения задач. В конце каждой темы приведены задачи для повторения и закрепления полученной информации. Учебное пособие может использоваться для самостоятельного изучения, поскольку к задачам даны указания по их решению.
В начале каждой темы представлены формулы и краткое пояснение теории, которые нужны для решения задач. В конце каждой темы приведены задачи для повторения и закрепления полученной информации. Учебное пособие может использоваться для самостоятельного изучения, поскольку к задачам даны указания по их решению. сотрудниками кафедры математики Института инженеров путей сообщения, во главе которой стоял Н. М. Гюнтер.
сотрудниками кафедры математики Института инженеров путей сообщения, во главе которой стоял Н. М. Гюнтер. П. Минорский
П. Минорский
 ru
ru
 П. «Сборник задач по высшей математике» 2006г.
П. «Сборник задач по высшей математике» 2006г. gdz-online.ws
gdz-online.ws П. Сборник задач по высшей…
П. Сборник задач по высшей… П., 2006»
П., 2006»
 Удобный доступ к необходимой информации и данным в больших объемах текста и таблиц. Мы поможем вам быстро найти новости, документы, исследования рынка акций, стенограммы, презентации для инвесторов и многое другое. Углубите свои исследования с помощью оценок тональности, поиска по ключевым фразам и экспорта в Excel.
Удобный доступ к необходимой информации и данным в больших объемах текста и таблиц. Мы поможем вам быстро найти новости, документы, исследования рынка акций, стенограммы, презентации для инвесторов и многое другое. Углубите свои исследования с помощью оценок тональности, поиска по ключевым фразам и экспорта в Excel.



 информация. Сделайте еще один шаг вперед, создав собственные настраиваемые экраны кредитных рейтингов, которые необходимо отслеживать. Настройте оповещения, чтобы всегда быть в курсе изменений рейтинга и перспектив.
информация. Сделайте еще один шаг вперед, создав собственные настраиваемые экраны кредитных рейтингов, которые необходимо отслеживать. Настройте оповещения, чтобы всегда быть в курсе изменений рейтинга и перспектив.
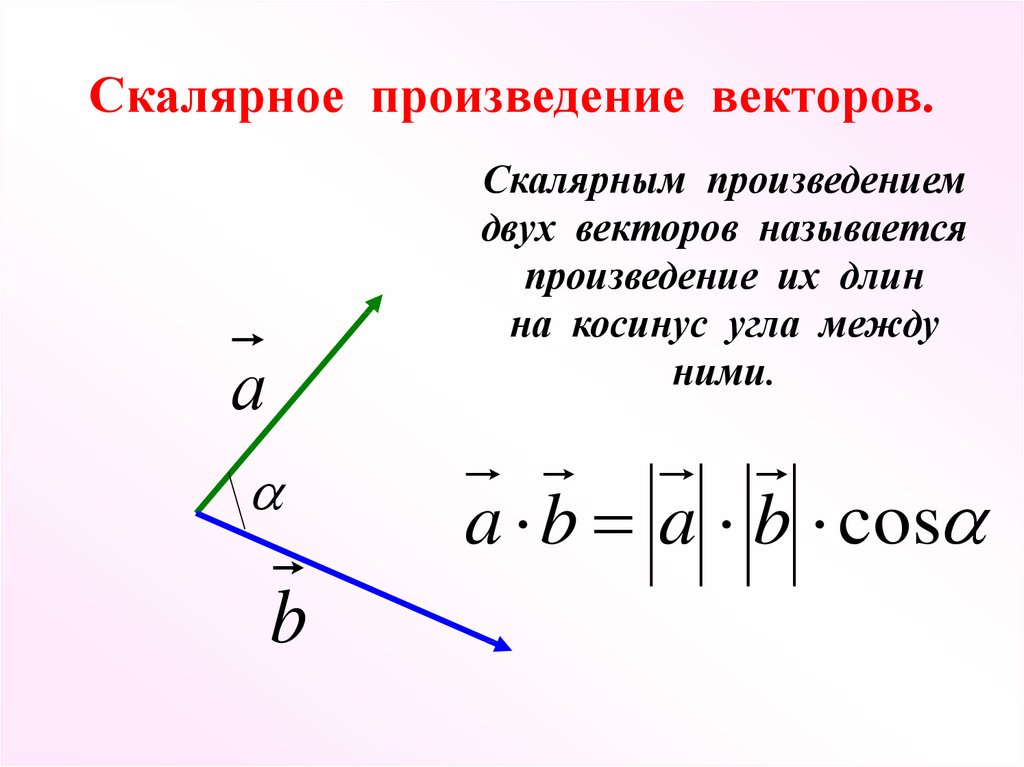
 .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой: Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
 Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
 {2}$ и называется скалярный квадрат.
{2}$ и называется скалярный квадрат. {\circ}$$
{\circ}$$ Затем щелкните символ скалярного произведения или угла. Векторы A и B не могут быть однозначно вычислены из скалярного произведения и угла. Если угол изменить, то B будет размещен вдоль оси x, а A — в плоскости xy.
Затем щелкните символ скалярного произведения или угла. Векторы A и B не могут быть однозначно вычислены из скалярного произведения и угла. Если угол изменить, то B будет размещен вдоль оси x, а A — в плоскости xy.
 Затем это число является скалярным произведением двух векторов.
Затем это число является скалярным произведением двух векторов. Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.
Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.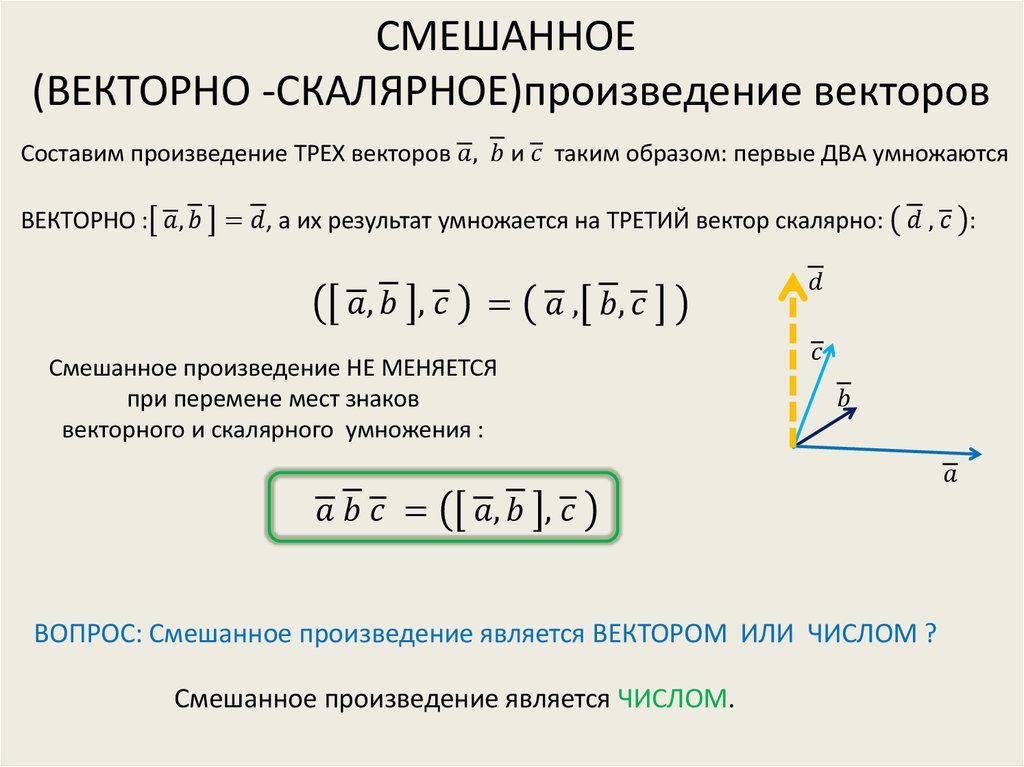 Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае a и b , как показано в следующей формуле:
Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае a и b , как показано в следующей формуле:

 Например, скалярное произведение можно использовать при установке солнечной панели на крыше. Сравнивая угол наклона солнца с углом панели, инженеры могут рассчитать наилучшее положение панели, чтобы максимизировать количество солнечной энергии, поглощаемой в течение дня.
Например, скалярное произведение можно использовать при установке солнечной панели на крыше. Сравнивая угол наклона солнца с углом панели, инженеры могут рассчитать наилучшее положение панели, чтобы максимизировать количество солнечной энергии, поглощаемой в течение дня.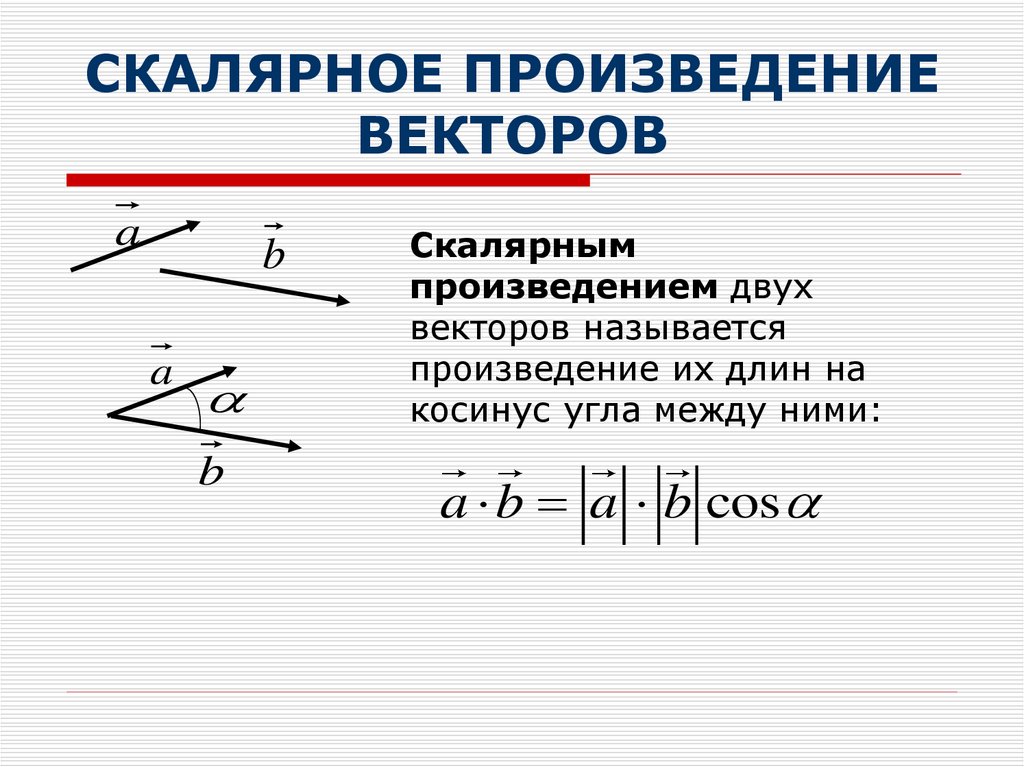
 Проверяет входящий и исходящий трафик…
Проверяет входящий и исходящий трафик… ..
..
 Введите свой запрос:
Введите свой запрос: Free xml sitemap generator
Free xml sitemap generator n\)
n\) 623\)
623\) 3}{3}\)
3}{3}\) Это не то, что было задумано. Базовая формула
Это не то, что было задумано. Базовая формула
 Отлично; Я включу:
Отлично; Я включу:
 е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график:
е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график:
 }\hfill \\ \hfill & \приблизительно 2,2266\text{ }\hfill & \text{ Используйте калькулятор для расчета до 4 знаков после запятой}\text{.}\hfill \end{array}[/latex]
}\hfill \\ \hfill & \приблизительно 2,2266\text{ }\hfill & \text{ Используйте калькулятор для расчета до 4 знаков после запятой}\text{.}\hfill \end{array}[/latex]

 Откуда: u’=1/x2 или du/dx=1/x2 или u = int(dx/x2) = -1/x+c1
Откуда: u’=1/x2 или du/dx=1/x2 или u = int(dx/x2) = -1/x+c1 Подставляя в уравнение, получаем Разделяя переменные, при p≠0, имеем Интегрируя, получаем или, что то же самое, . Тогда
или . Интегрируя последнее равенство, окончательно получаем При разделении переменных мы могли потерять решение y=C, которое получается при p=0, или, что то же самое, при y’=0, но оно содержится в полученном выше.
Подставляя в уравнение, получаем Разделяя переменные, при p≠0, имеем Интегрируя, получаем или, что то же самое, . Тогда
или . Интегрируя последнее равенство, окончательно получаем При разделении переменных мы могли потерять решение y=C, которое получается при p=0, или, что то же самое, при y’=0, но оно содержится в полученном выше.
 Разделяя переменные и интегрируя, получаем, ln(C1y-1) = C1x+C2
Разделяя переменные и интегрируя, получаем, ln(C1y-1) = C1x+C2 Если
в
этом интервале, то уравнение принимает вид:
Если
в
этом интервале, то уравнение принимает вид: Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая:
Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая: Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет. Для нахождения общего решения такого
дифференциального уравнения необходимо знать общее решение соответствующего
однородного дифференциального уравнения
и частное
решение
. Рассмотрим
некоторые случаи:
Для нахождения общего решения такого
дифференциального уравнения необходимо знать общее решение соответствующего
однородного дифференциального уравнения
и частное
решение
. Рассмотрим
некоторые случаи:

 \]
\] s},\) где \(s\) — порядок корня \(\alpha\) в характеристическом уравнении.
s},\) где \(s\) — порядок корня \(\alpha\) в характеристическом уравнении. 3}x + {A_1},\] 9{\простое\простое}_1} = 0.\]
3}x + {A_1},\] 9{\простое\простое}_1} = 0.\]


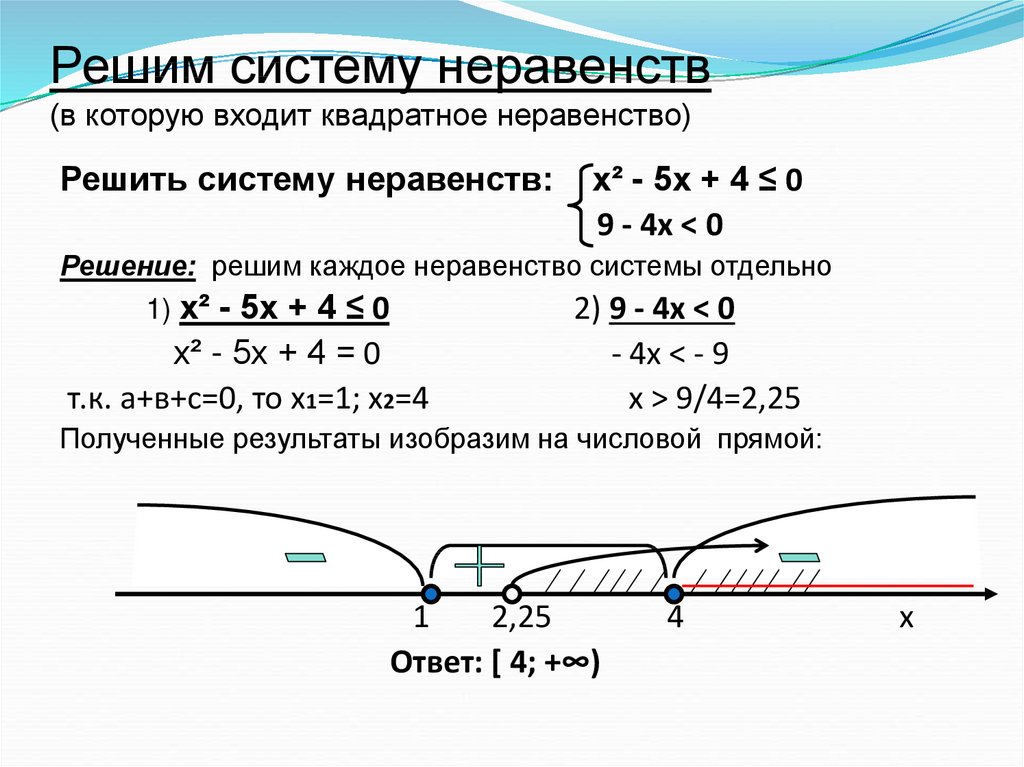 И также если а < b и b < c, то а < c.
И также если а < b и b < c, то а < c.
 На множестве положительных чисел обе части можно возвести в квадрат.
На множестве положительных чисел обе части можно возвести в квадрат. Знак неравенства при этом не меняется.
Знак неравенства при этом не меняется. А на месте x может быть обычное число.
А на месте x может быть обычное число.
 Неверно тогда, когда исходное не имеет решений.
Неверно тогда, когда исходное не имеет решений.


 6K
6K
 Это означает, что число входит в область решения.
Это означает, что число входит в область решения.





 Велоспорт
Велоспорт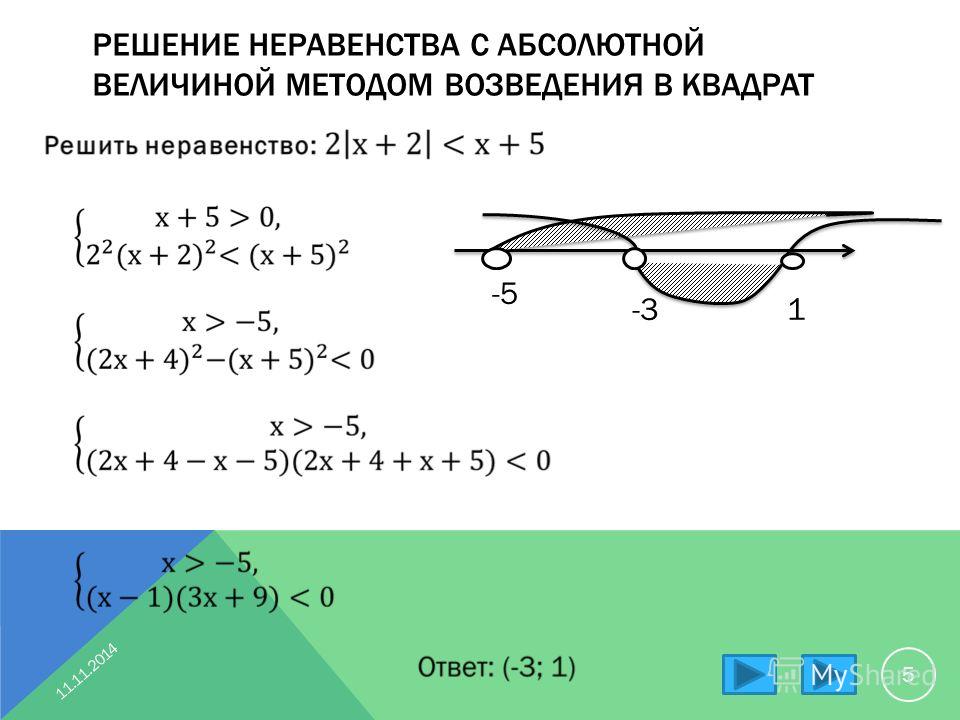
 Периметр комнаты 16 м.
Периметр комнаты 16 м. 
 com
com
 Метод решения точно такой же.
Метод решения точно такой же. Я решу это неравенство таким же образом. Однако, поскольку я буду делить обе части неравенства на минус, я должен не забыть перевернуть символ неравенства.
Я решу это неравенство таким же образом. Однако, поскольку я буду делить обе части неравенства на минус, я должен не забыть перевернуть символ неравенства.
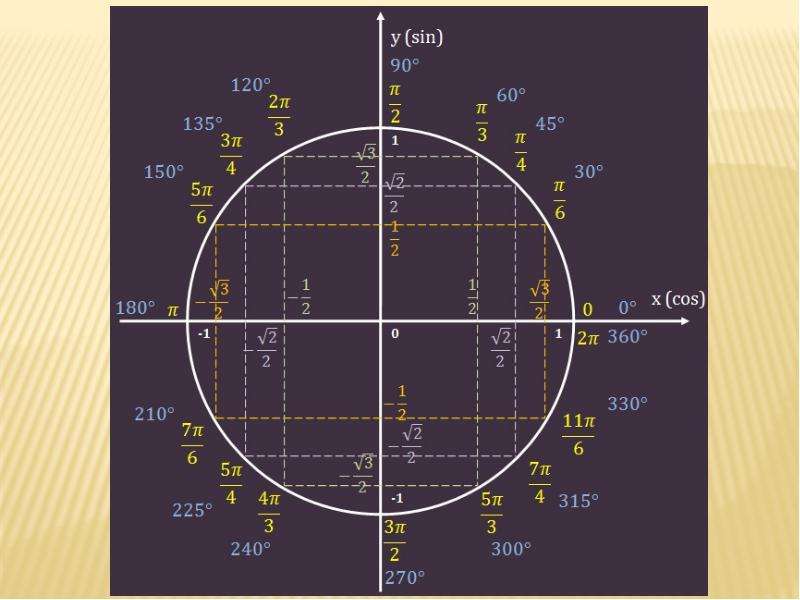
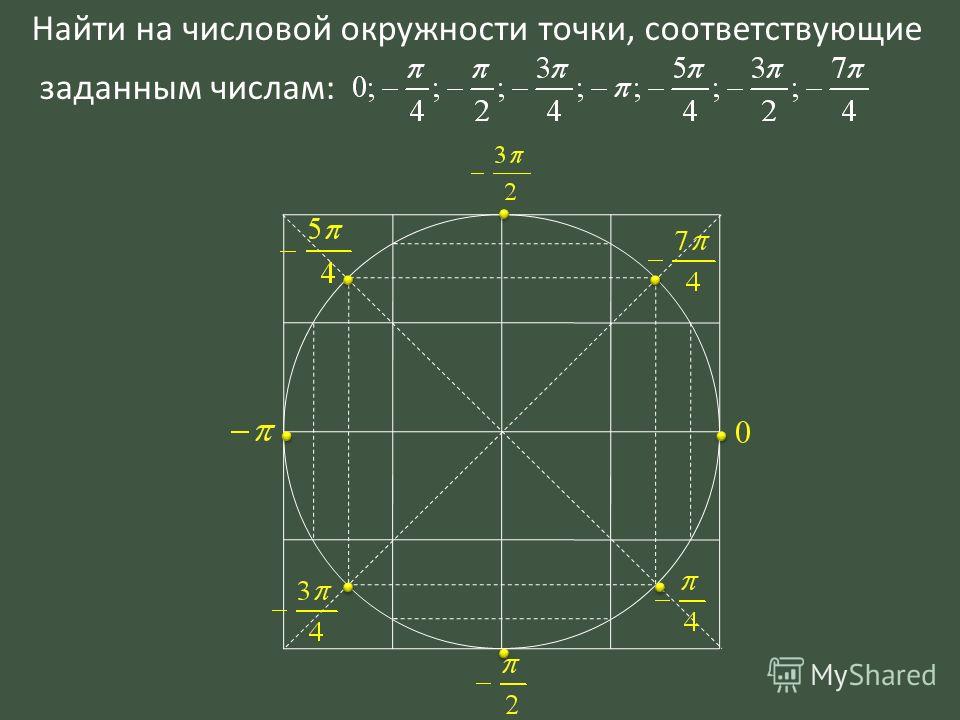
 е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

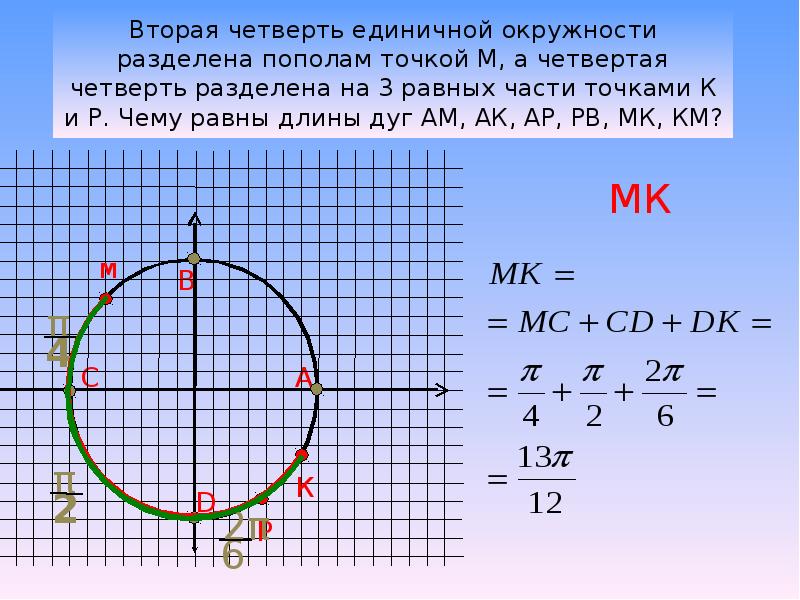 Отсюда видно, что от нуля в положительную сторону надо пройти расстояние \(π\), а потом еще \(\frac{π}{6}\).
Отсюда видно, что от нуля в положительную сторону надо пройти расстояние \(π\), а потом еще \(\frac{π}{6}\).

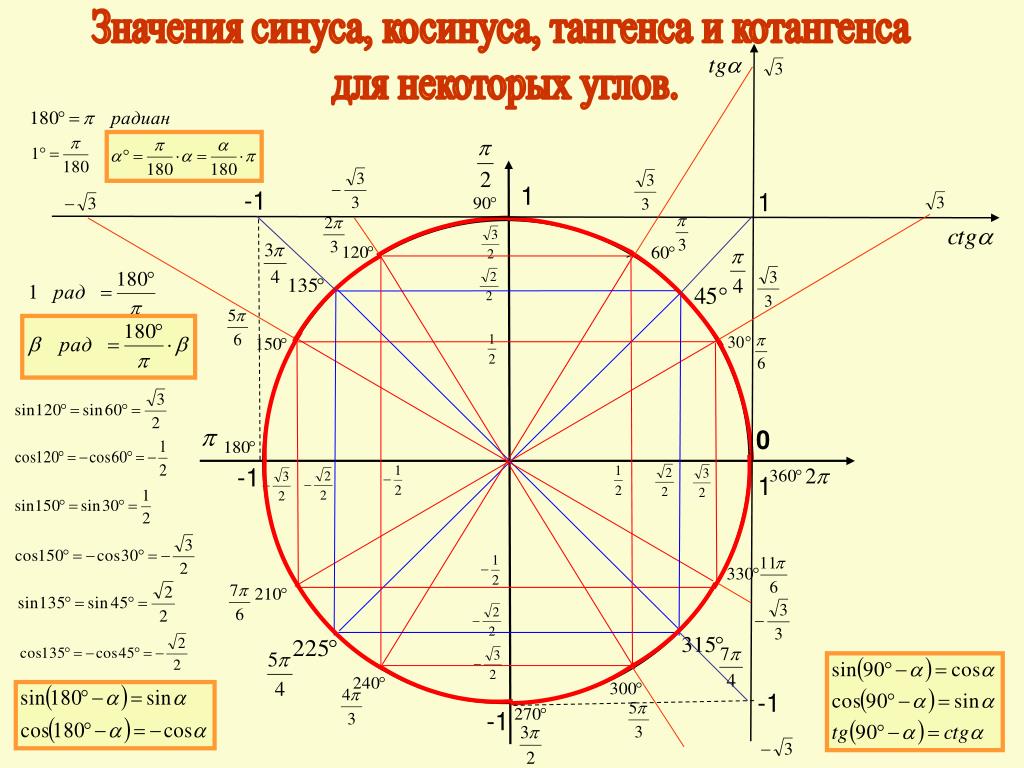
 Ясно, что от нуля надо пройти расстояние равное \(π+\)\(\frac{π}{3}\) – и мы найдем место точки \(\frac{16π}{3}\).
Ясно, что от нуля надо пройти расстояние равное \(π+\)\(\frac{π}{3}\) – и мы найдем место точки \(\frac{16π}{3}\).
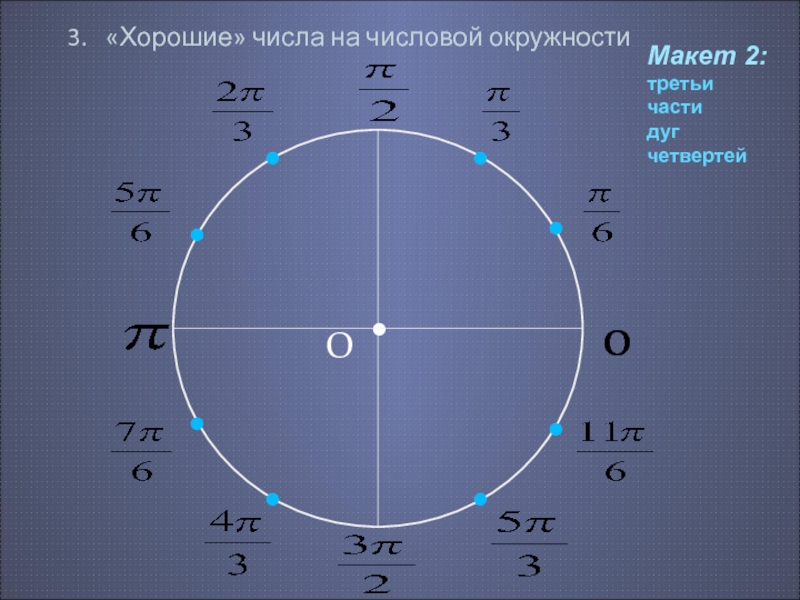 Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
 2a=0,64\)
2a=0,64\)
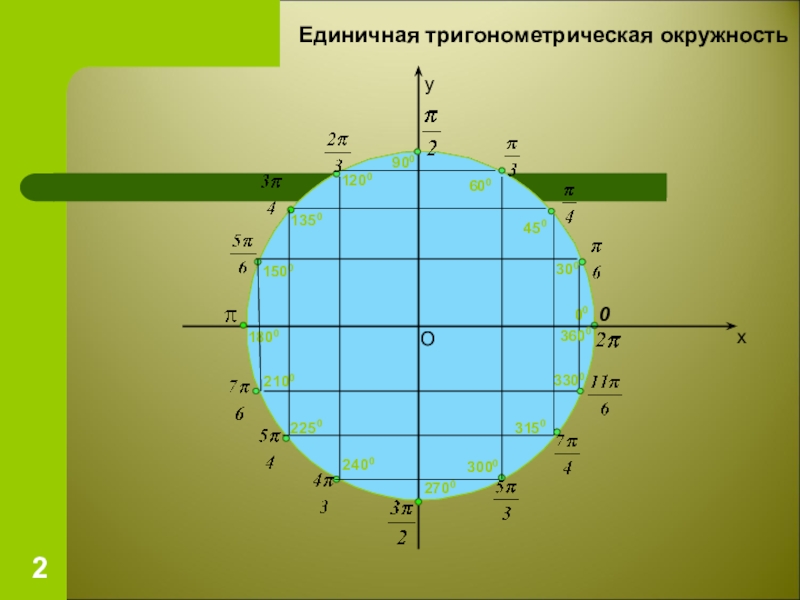 Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

 Итак, воображаемый — это просто
Итак, воображаемый — это просто  out=n+1)
политочки <- политочки[-длина(многоточечные)]
circx <- r * sin(многоточечный)
circy <- r * cos(polypoints)
data.frame(x=circx, y=circy)
}
eq_spacing (4)
х у
1 0,000000e+00 1,000000e+00
2 1.000000e+00 6.123032e-17
3 1.224606э-16 -1.000000э+00
4 -1.000000e+00 -1.836910е-16
график (eq_spacing (20), asp = 1)
out=n+1)
политочки <- политочки[-длина(многоточечные)]
circx <- r * sin(многоточечный)
circy <- r * cos(polypoints)
data.frame(x=circx, y=circy)
}
eq_spacing (4)
х у
1 0,000000e+00 1,000000e+00
2 1.000000e+00 6.123032e-17
3 1.224606э-16 -1.000000э+00
4 -1.000000e+00 -1.836910е-16
график (eq_spacing (20), asp = 1)
 Все, что нам нужно было знать, это место, где расположить центр круга, и меру радиуса, которую нужно установить на компасе. Затем мы удерживали циркуль в центре и вращали карандашную часть по кругу, чтобы нарисовать круг. Если бы мы нарисовали его на миллиметровой бумаге и внимательно посмотрели, мы, вероятно, смогли бы найти несколько определенных точек на нашем круге. 9{2}\)
Все, что нам нужно было знать, это место, где расположить центр круга, и меру радиуса, которую нужно установить на компасе. Затем мы удерживали циркуль в центре и вращали карандашную часть по кругу, чтобы нарисовать круг. Если бы мы нарисовали его на миллиметровой бумаге и внимательно посмотрели, мы, вероятно, смогли бы найти несколько определенных точек на нашем круге. 9{2}\)
 Таким образом, я могу нарисовать L-формы из центра, которые перемещаются на 4 единицы влево или вправо, а затем на 3 единицы вверх и вниз, чтобы найти больше точек.
Таким образом, я могу нарисовать L-формы из центра, которые перемещаются на 4 единицы влево или вправо, а затем на 3 единицы вверх и вниз, чтобы найти больше точек. Да, множественное число, потому что их будет 2.
Да, множественное число, потому что их будет 2.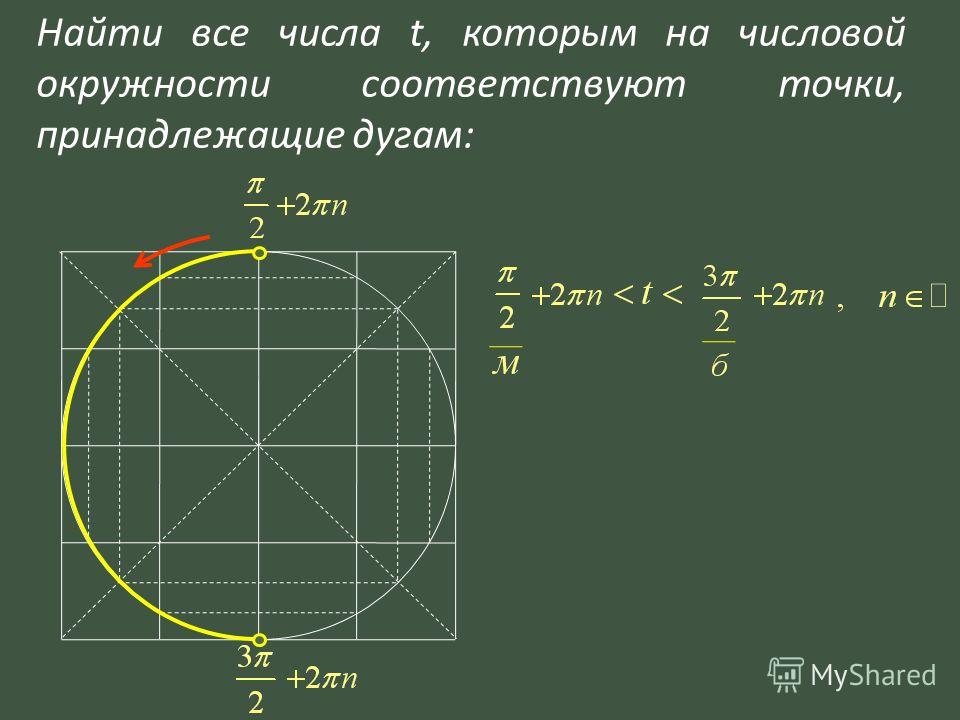 Так что мы можем изобразить их тоже!
Так что мы можем изобразить их тоже!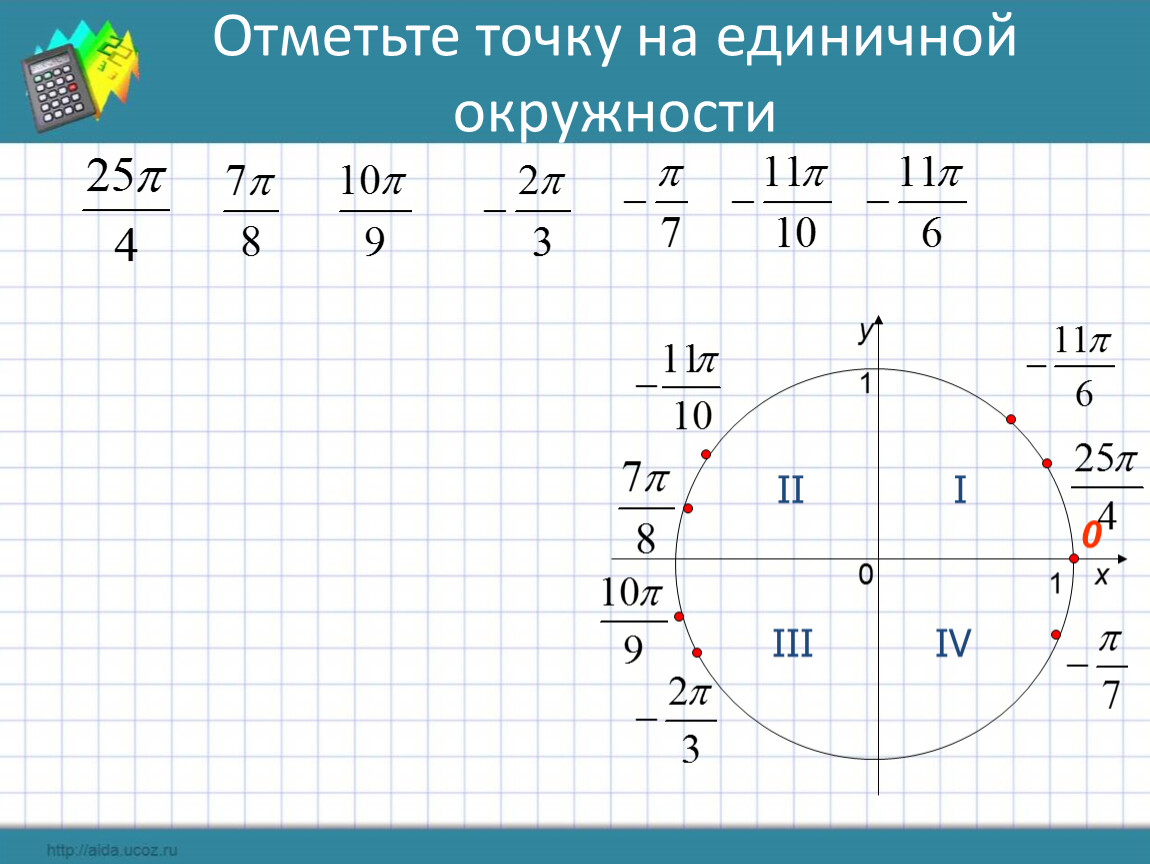









 К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1): Отсюда следует, что ранг исходной матрицы также равен двум.
Отсюда следует, что ранг исходной матрицы также равен двум.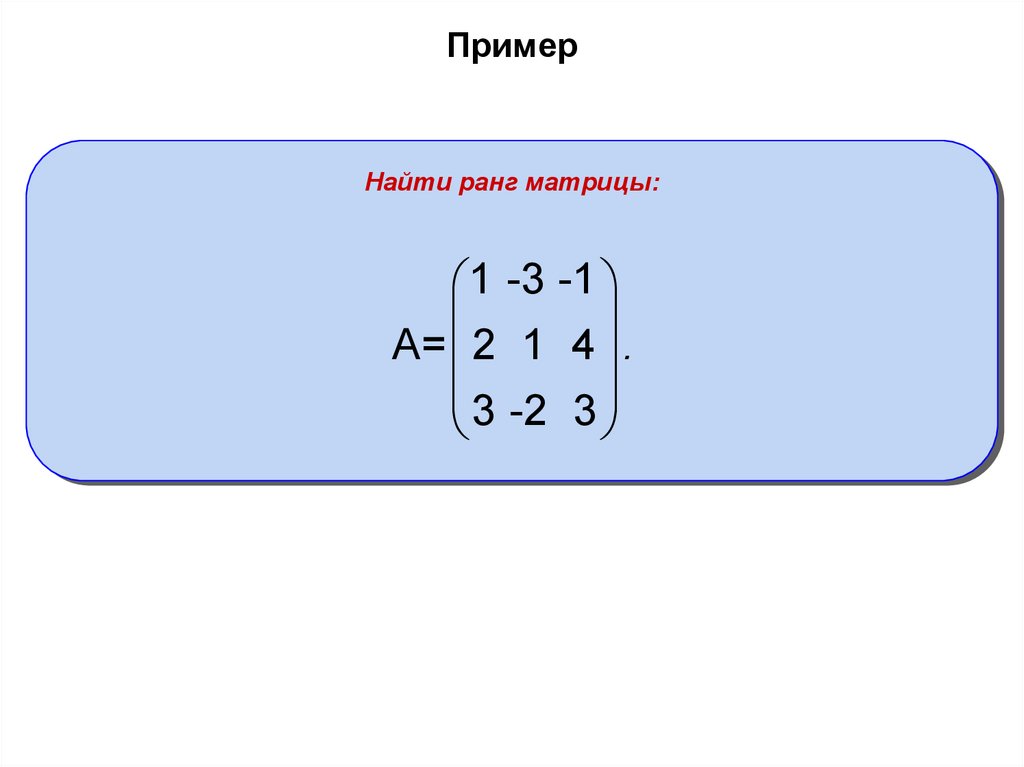 Посмотрим матрицы низших порядков.
Посмотрим матрицы низших порядков.


 Ранг её не должен превышать четырёх. Видно, что среди миноров
Ранг её не должен превышать четырёх. Видно, что среди миноров Решение
Решение Если все они нулевые, то ранг нашей матрицы будет равным 2. Если найдётся хотя бы один отличный от нуля, то ранг матрицы будет больше или равен 3.
Если все они нулевые, то ранг нашей матрицы будет равным 2. Если найдётся хотя бы один отличный от нуля, то ранг матрицы будет больше или равен 3. Берём следующий за добавленным столбец и получаем
Берём следующий за добавленным столбец и получаем Берём ещё один \[\begin{array}{ccc}2 & 0 & 4 \\3 & 6 & -2 \\-2 & -4 & 2\end{array}\].
Берём ещё один \[\begin{array}{ccc}2 & 0 & 4 \\3 & 6 & -2 \\-2 & -4 & 2\end{array}\].
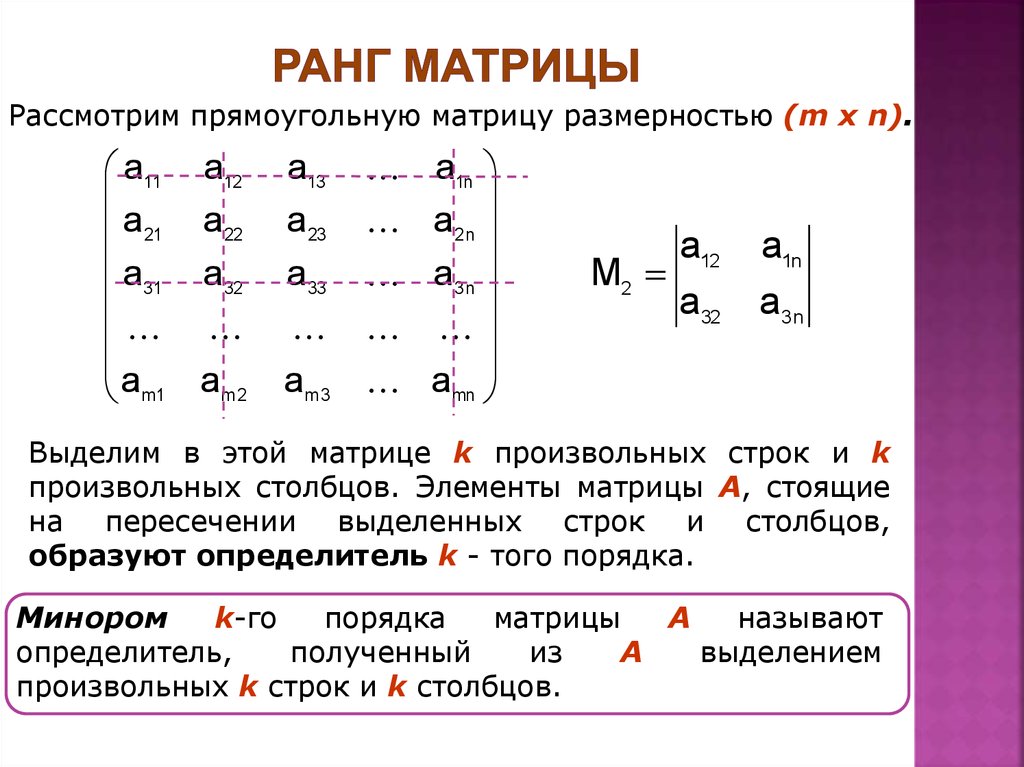 Решение найдено.
Решение найдено. $$
$$ Если вы хотите использовать определители, воспользуйтесь определением: «Ранг матрицы $A$ равен наибольшему $n$ такому, что $A$ содержит подматрицу $n \times n$, определитель которой отличен от нуля». Поскольку ваша матрица содержит подматрицы 2×2 с ненулевым определителем, ранг должен быть 2 или 3. Посмотрите на все подматрицы 3×3. Если вы можете найти $x$ такое, что все 4 из этих подматриц имеют определитель 0, то для этого значения $x$ ранг вашей матрицы равен 2. Если таких $x$ нет, ранг равен 3. 92-4} \end{bmatrix}
$$
Ранг 2 требует, чтобы последняя строка была нулевой, что невозможно. Обратите внимание на
Если вы хотите использовать определители, воспользуйтесь определением: «Ранг матрицы $A$ равен наибольшему $n$ такому, что $A$ содержит подматрицу $n \times n$, определитель которой отличен от нуля». Поскольку ваша матрица содержит подматрицы 2×2 с ненулевым определителем, ранг должен быть 2 или 3. Посмотрите на все подматрицы 3×3. Если вы можете найти $x$ такое, что все 4 из этих подматриц имеют определитель 0, то для этого значения $x$ ранг вашей матрицы равен 2. Если таких $x$ нет, ранг равен 3. 92-4} \end{bmatrix}
$$
Ранг 2 требует, чтобы последняя строка была нулевой, что невозможно. Обратите внимание на  Например, если мы рассмотрим единичную матрицу порядка 3 × 3, все ее строки (или столбцы) линейно независимы, и, следовательно, ее ранг равен 3.
Например, если мы рассмотрим единичную матрицу порядка 3 × 3, все ее строки (или столбцы) линейно независимы, и, следовательно, ее ранг равен 3. Рассмотрим ненулевую матрицу A. Говорят, что действительное число r является рангом матрицы A, если оно удовлетворяет следующим условиям:
Рассмотрим ненулевую матрицу A. Говорят, что действительное число r является рангом матрицы A, если оно удовлетворяет следующим условиям: Если det (A) ≠ 0, то ранг A = порядок A.
Если det (A) ≠ 0, то ранг A = порядок A.
 5543
5543 327
327 3315
3315 1446
1446 5399
5399 6745
6745 1944
1944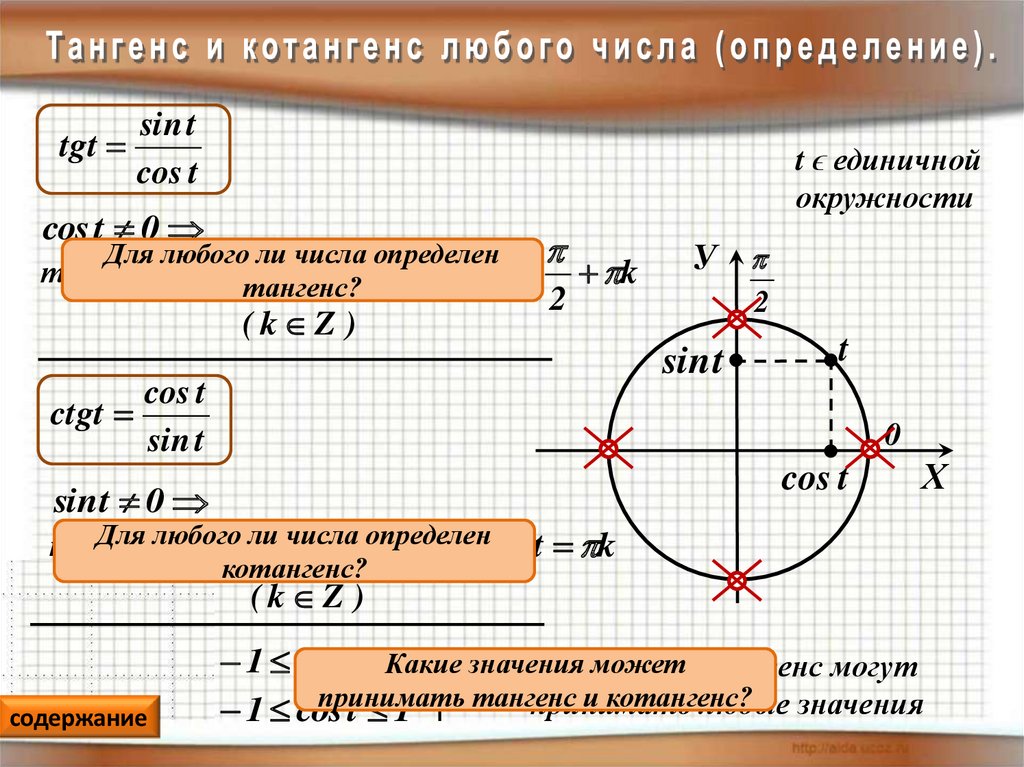 1763
1763 6745
6745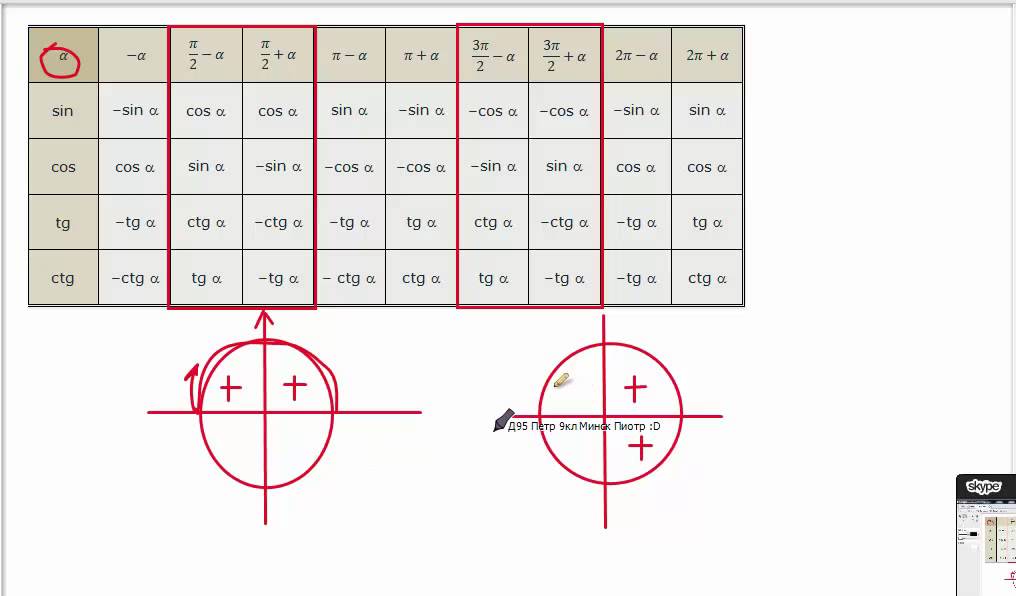 6003
6003 3138
3138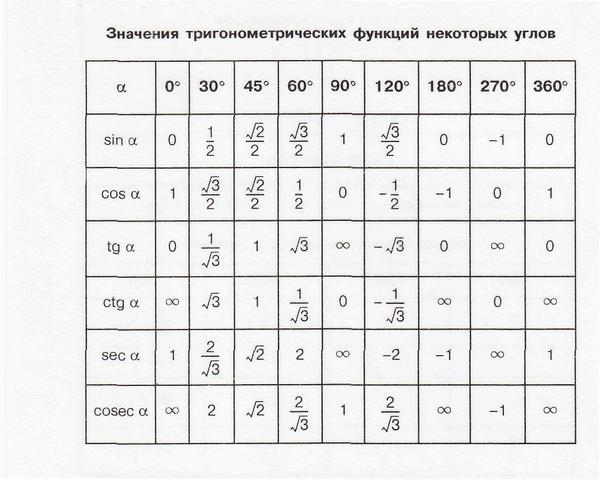 0108
0108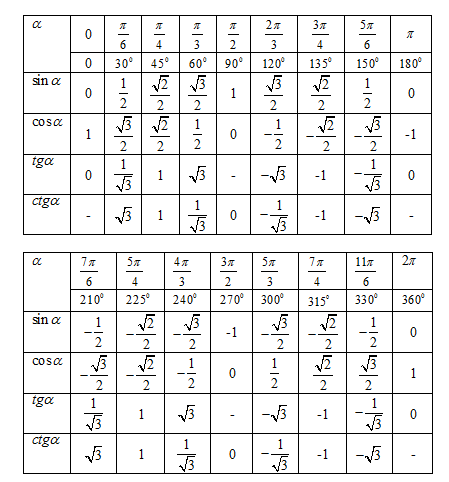 3764
3764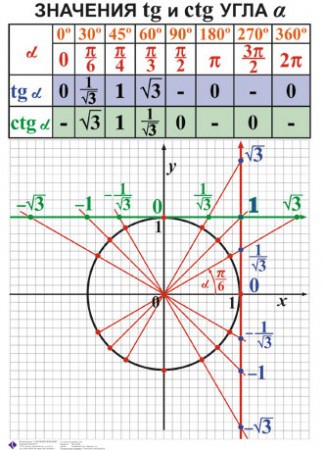 6009
6009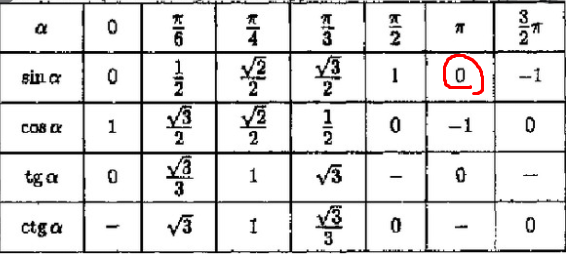 1405
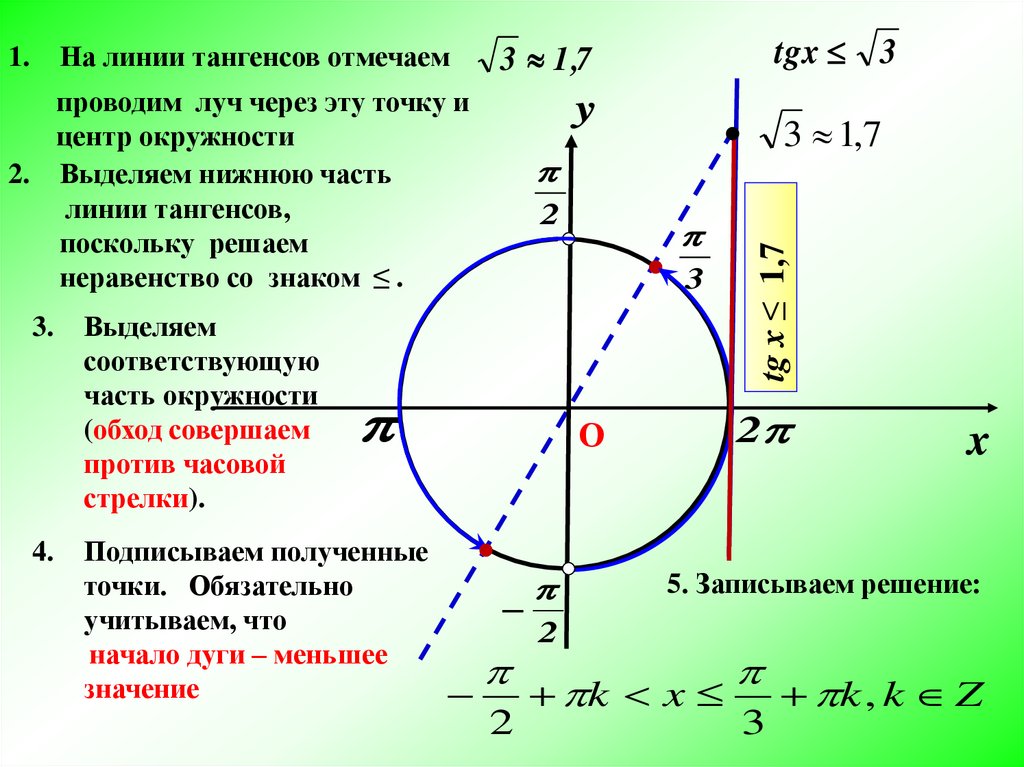
1405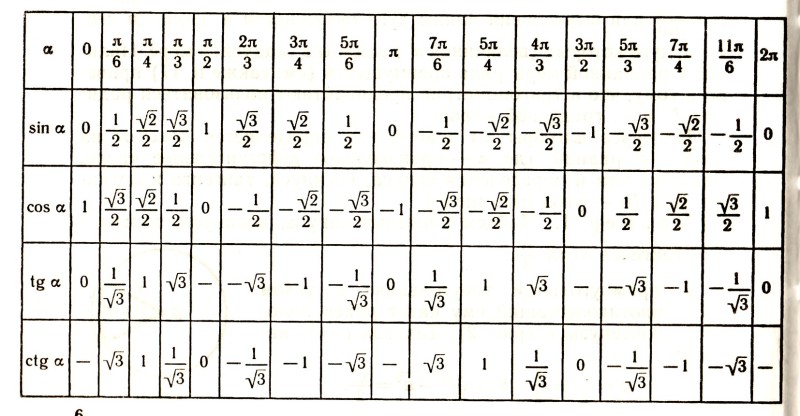 Попробуем приблизительно вычислить тангенс 30-ти градусов. Для этого нам нужно начерить прямоугольный треугольник (т.е. такой треугольник, в котором один угол будет 90°), пусть прямым углом будет угол C. В нашем треугольнике АВС угол А=30°, сторона ВС=5,8 см (катет противолежащий углу А), а сторона АС=10 см (катет прилежащий углу А).
Попробуем приблизительно вычислить тангенс 30-ти градусов. Для этого нам нужно начерить прямоугольный треугольник (т.е. такой треугольник, в котором один угол будет 90°), пусть прямым углом будет угол C. В нашем треугольнике АВС угол А=30°, сторона ВС=5,8 см (катет противолежащий углу А), а сторона АС=10 см (катет прилежащий углу А).
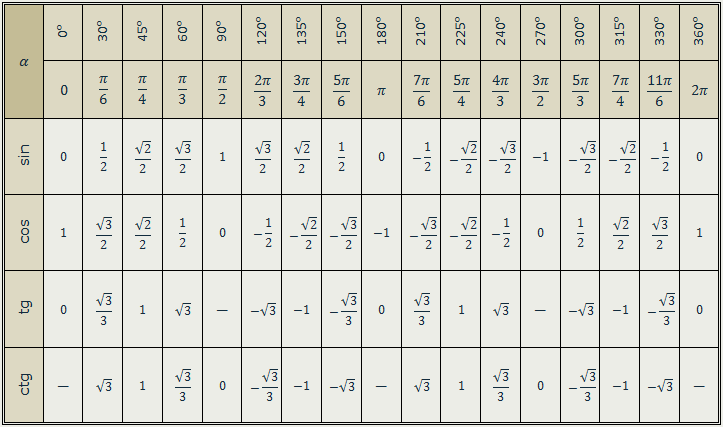
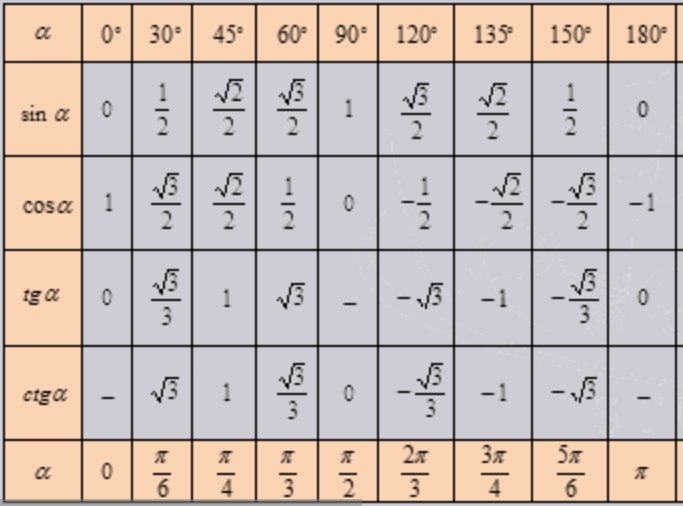 Таблица с точными значениями тангенса и котангенса этих углов будет дана ниже.
Таблица с точными значениями тангенса и котангенса этих углов будет дана ниже.


 При этой температуре полимеры переходят из стеклообразного состояния в каучукоподобное. Tg является важной характеристикой поведения полимера. Он знаменует собой область резкого изменения физико-механических свойств.
При этой температуре полимеры переходят из стеклообразного состояния в каучукоподобное. Tg является важной характеристикой поведения полимера. Он знаменует собой область резкого изменения физико-механических свойств.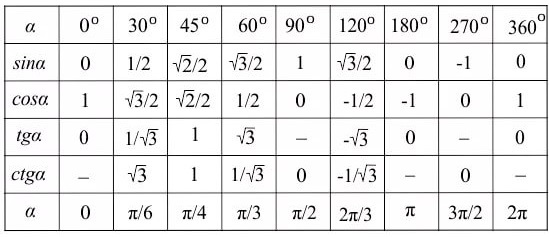 Tg зависит от химической структуры полимера, определяемой его кристалличностью. Они могут быть аморфными, кристаллическими или полукристаллическими.
Tg зависит от химической структуры полимера, определяемой его кристалличностью. Они могут быть аморфными, кристаллическими или полукристаллическими.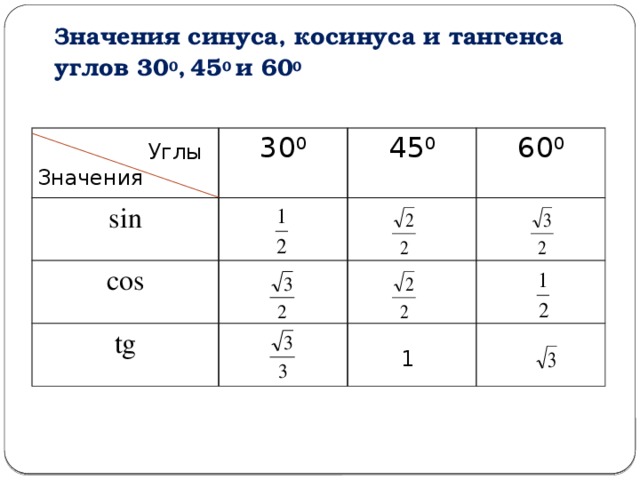
 Их Tg выше комнатной температуры. Узнайте больше о температуре хрупкого перехода »
Их Tg выше комнатной температуры. Узнайте больше о температуре хрупкого перехода » Чем более неподвижна цепь, тем выше значение Tg.
Чем более неподвижна цепь, тем выше значение Tg.
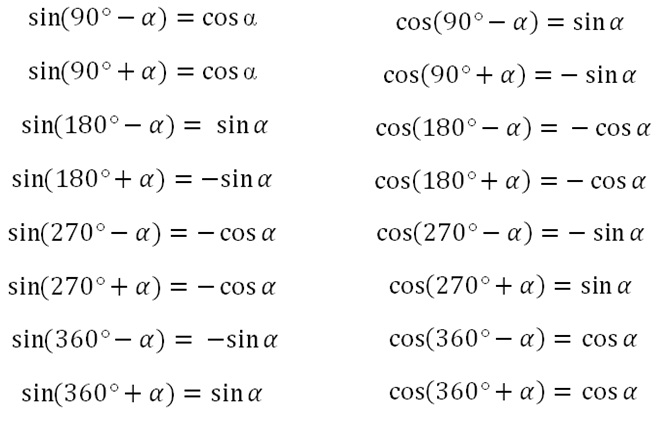 Полимерные цепи скользят относительно друг друга при более низких температурах, что приводит к снижению Tg.
Полимерные цепи скользят относительно друг друга при более низких температурах, что приводит к снижению Tg.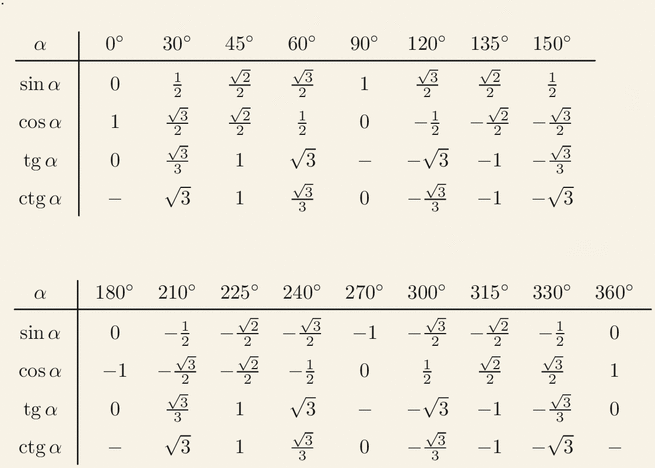 д.
д. Дифференциальная сканирующая калориметрия (ДСК)
Дифференциальная сканирующая калориметрия (ДСК)
 0
0 0
0 0
0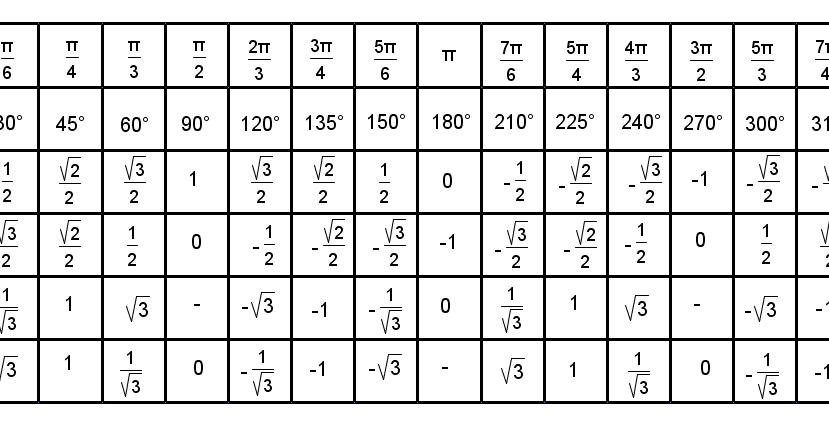 0
0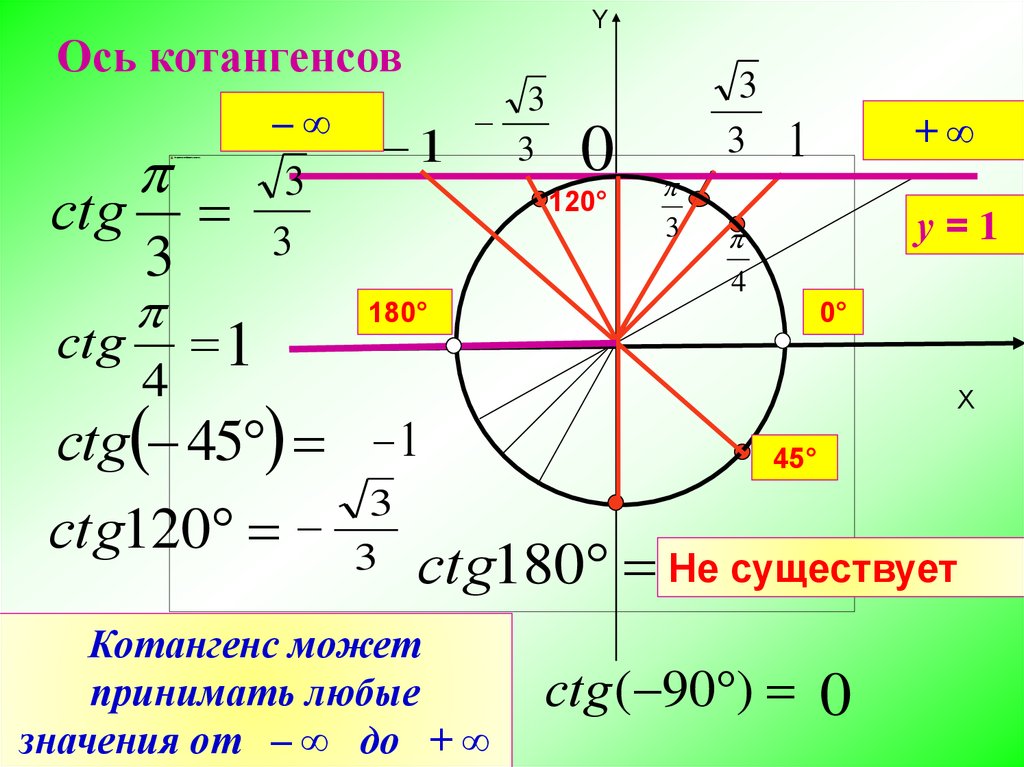 0
0 0
0 0
0 Это температура, при которой углеродные цепи начинают двигаться. На этом этапе аморфная область испытывает переход от жесткого состояния к гибкому состоянию с изменением температуры на границе твердого состояния на более вязкоупругое (резинообразное). При этой температуре свободный объем, или зазор между молекулярными цепями, увеличивается в 2,5 раза.
Это температура, при которой углеродные цепи начинают двигаться. На этом этапе аморфная область испытывает переход от жесткого состояния к гибкому состоянию с изменением температуры на границе твердого состояния на более вязкоупругое (резинообразное). При этой температуре свободный объем, или зазор между молекулярными цепями, увеличивается в 2,5 раза.