24. Дискретная случайная величина х имеет закон распределения
28
Чему равна вероятность p 4Построить многоугольник и диаграмму рас-
пределения.
25. Подбрасываются два игральных кубика, подсчитывается число
очков, выпавших на обеих верхних гранях. Найти закон распределения
дискретной случайной величины Х — суммы выпавших очков на двух иг-
ральных кубиках.
26. Вероятность изготовления нестандартного изделия при некото-
ром технологическом процессе равна 0,06. Контролер берет из партии из-
делие и сразу проверяет его на качество. Если оно оказывается нестан-
дартным, дальнейшие испытания прекращаются, а партия задерживается.
Если же изделие оказывается стандартным, контролер берет следующее и
т.
д.,
но всего проверяет не более пяти изделий.
Найти закон распределения
дискретной случайной величины Х — числа проверяемых изделий.
27. Дана функция
Показать, что эта функция является функцией распределения некоторой
случайной величины X. Найти вероятность того, что эта случайная вели-
чина принимает значения из интервала .
28. Дана функция
Является ли эта функция функцией распределения некоторой случайной
величины?
29. Является ли функцией распределения случайной величины функция
30. Плотность распределения случайной величины Х задана функцией
31. Плотность вероятности случайной величины Х задается функцией
29
Найти вероятность того, что в результате испытания величина Х примет
значение
из интервала (1;2).
32. Найти математическое ожидание дискретной случайной величи-
ны, закон распределения которой задан таблицей
33. Плотность распределения вероятности случайной величины Х
задана функцией
Найти математическое ожидание случайной величины Х.
34. Найти математическое ожидание случайной величины X, если
известна функция распределения этой величины
Найти дисперсию и среднее квадратичное отклонение случайной величи-
ны X.
36. Найти числовые характеристики М(Х), D{Х), (Х) непрерывной
случайной величины X, заданной плотностью распределения вероятности
37. В энергетической системе имеется группа из четырех одинако-
вых
агрегатов,
находящихся в одинаковых условиях.
Вероятности исправ-
ного состояния агрегатов в течение времени Т равны 0,6 и независимы.
Рассматривается случайная величина Х — число агрегатов, находящихся в
исправном состоянии в течение времени т. Построить ряд и функцию рас-
пределения случайной величины X.
38. Доля изделий высшего сорта на данном предприятии составляет
30 %. Чему равно наивероятнейшее число изделий высшего сорта в слу-
чайно отобранной партии из 75 изделий.
30
39. Радиоаппаратура состоит из 1000 элементов. Вероятность отказа
одного элемента в течение одного года работы равна 0,001 и не зависит от
состояния других элементов. Какова вероятность отказа двух элементов?
Какова вероятность отказа не менее двух элементов за год?
40. Телефонная станция обслуживает 400 абонентов. Для каждого
абонента вероятность того, что в течение часа он позвонит на станцию,
равна
0,01.
Найти вероятности следующих событий:
«в течение часа 5 або-
нентов позвонят на станцию»; «в течение часа не более 4 абонентов позво-
нят на станцию»; «в течение часа не менее 3 абонентов позвонят на стан-
цию».
41. Определить закон распределения случайной величины X, если ее
плотность вероятности задана функцией:
Найти математическое ожидание, дисперсию и функцию распреде-
ления случайной величины X.
42. При измерении детали получаются случайные ошибки, подчи-
ненные нормальному закону распределения с параметром =10 мм . Най-
ти вероятность того, что измерение произведено с ошибкой, не превосхо-
дящей 15 мм.
43. Линия связи обслуживает 1000 абонентов. Каждый абонент раз-
говаривает в среднем 6 минут в час. Сколько каналов должна иметь линия
связи, чтобы с практической достоверностью можно было утверждать, что
не произойдет ни одной потери вызова?
44.
Сколько следует произвести независимых
испытаний, чтобы ве-
роятность выполнения неравенства <0,05 превысила 0,75, если
I» 1
вероятность появления данного события в отдельном испытании р = 0,8?
45. Пусть двумерная случайная величина (Х,У) задана законом рас-
пределения (табл.1).
а) Найти законы распределения величин Х и У.
б) Найти условное распределение У при условии Х = 30.
в) Найти условное распределение Х при условии У =3.
г) Выяснить, будут ли случайные величины Х и У независимыми.
31 ‘ • .
46. Пусть распределение двумерной случайной величины (х,у) за-
дано табл. 2.
Требуется: 1) найти распределения ее компонент Л’ и У; 2) найти
распределения суммы Х-У, разности Х-У и произведения Х-У, 3) вы-
числить
математические ожидания М(Х), М(У), М(Х+7), М(Х—У).
и
М(Х—У); 4) вычислить ковариацию со\(Х,У); 5) вычислить М(Х,У) и
0(Х,У); 6) вычислить двумя способами дисперсии 0(Х+У) и 0(Х-У);
7) проверить независимость величин Х и У; 8) найти коэффициент корре-
ляции между случайными величинами X и У.
47. Имеется выборка, содержащая 45 числовых значений некоторого
признака случайной величины Х:
39,41,40, 42, 41, 40,42.44,40, 43,42,41,43,39,42,
41,42,39, 41, 37, 43, 41,38, 43, 42, 41,40,41, 38, 44,
40,39,41,40,42, 40,41,42, 40, 43, 38, 39,41, 41, 42.
Построить дискретный вариационный ряд, полигон, кумуляту и эмпириче-
скую
функцию распределения.
48. Результаты измерений отклонений от номинала диаметров 50
подшипников дали численные значения (в мкм), приведенные в табл. 3.
Для данной выборки построить интервальный вариационный ряд,
построить полигон, гистограмму, графики эмпирической функции распре-
деления и эмпирической плотности распределения. Построить кумуляту.
49. Имеется выборка (табл. 4), содержащая 100 числовых значений
некоторого признака случайной величины Х.
32
По приведенным данным требуется:
1) сгруппировать варианты значений признака по нескольким интер-
валам и получить таблицу статистического распределения выборки;
2) построить гистограмму частот;
3) считая уs, равными значению середины каждого интервала, по-
строить полигон частот, найти выборочную среднюю и выборочную дис-
персию.
33
Рекомендуемая литература
а) основная литература:
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное
исчисление. М. «Наука» 1988 г.
2. Бугров Я.С., Никольский С.М. Дифференциальные уравнения.
Кратные интегралы. Ряды. ФКП. М. «Наука» 1985 г.
3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и ана-
литической геометрии. М. «Наука» 1984 г.
4. Бугров Я.С., Никольский С.М. Высшая математика. Задачник… М.
«Наука» 1982 г.
5. Шипачее В.С. Высшая математика. М. «Высшая школа» 1998 г.
6. Пискунов Н. С. Дифференциальное и интегральное исчисление. Т.
1 и 2. М. «Наука» 1985 г.
7. Гмурман В.Е. Теория вероятностей и математическая статистика.
М. «Высшая школа» 1998 г.
8. Гмурман В.Е. Руководство к решению задач по теории вероятно-
стей
и математической статистике.
М. «Высшая
школа» 1997 г.
9. Кпетеник Д.В. Сборник задач по аналитической геометрии. М.
«Высшая школа» 1998 г.
10. Берман Г.Н. Сборник задач по курсу математического анализа. С-
П.2000 г.
11. Шипачее В.С. Задачи по высшей математике. М. «Высшая шко-
ла» 1998 г.
12. Шнейдер В.И., Слуцкий А.И., Шумов А.С. Краткий курс высшей
математики. Т. 1 и 2. М. «Высшая школа» 1978 г.
13. Мироненко Е.С. Высшая математика: Методические указания и
контрольные задания для студентов-заочников инженерных специально-
стей вузов. М. «Высшая школа» 1998 г. и последующие издания.
б) дополнительная литература:
14. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
упражнениях
и задачах. Т. 1 и 2. М. «Высшая школа» 1996
г.
15. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М. «Наука»
1999 г.
16. Кудрявцев Л. Д. Курс математического анализа. М. «Высшая шко-
ла» Т. 1 и 2 1998 г., Т. 3 1999 г.
17. Бутузов В.Ф., Крутицкий Н. Ч., Медведев Г.Н., Шишкин А.А. Ма-
тематический анализ в вопросах и задачах. М. «Наука», Физматлит 2000 г.
34
18. Корниенко В. С. Методика изучения математики на агроинженер-
ных специальностях с помощью системы Майгсаа: Монография. В 2-х ч.
Ч. 1 /Волгогр. гос. с.-х. акад.- Волгоград, 2002.- 248 с.
19. Корниенко В.С. Методика изучения математики на агроинженер-
ных специальностях с помощью системы МайсасЬ Монография. В 2-х ч.
Ч. 2 /Волгогр. гос. с.-х. акад.- Волгоград, 2002.- 252 с.
20. Корниенко
В.С. Практические занятия по математике
/Волгогр.
гос. с.-х. акад. — Волгоград, 2005. — 200 с. (СО)
21. Корниенко В.С. Приложения производной /Волгогр. гос. с.-х.
акад.- Волгоград, 2004. — 40 с.
22. Корниенко В.С. Представление гармонических колебаний в ком-
плексной форме. /Волгогр. гос. с.-х. акад.- Волгоград, 2004.-16 с.
23. Корниенко В.С., Горкоеенко Л.Г, Вычислительная математика в
электротехнических расчетах. /Волгогр. гос. с.-х. акад.- Волгоград, 2005. —
20 с.
24. Мильченко Н.Ю., Корниенко В.С. Введение в линейную алгебру и
аналитическую геометрию: Методические разработки /Волгогр. гос. с.-х.
акад. — Волгоград, 2005. -72с.
25. Корниенко В.С. Использование калькулятора АЬОЕВКА в реше-
ний задач по математике. Волгоград, 2005.-136 с. (СВ)
26. Корниенко В.С. Математика. Волгоград, 2005.- 744 с. (СО)
27. Гурский Д.А.
Вычисления в МайсаД
/Д.А.
Гурский.-
Мн.:
Новое
знание, 2003.-814 с.
28. Ивановский Р.И. Компьютерные технологии в науке и образова-
нии. Практика применения систем МайСАВ Рго: Учеб. пособие /Р.И. Ива-
новский. — М.: «Высшая школа», 2003. — 431 с.
29. Семененко М.Г. Математическое моделирование в МаШсаД.- М.:
Альтекс-А, 2003. — 208 с.
30. Макаров Е. Г. Инженерные расчеты в Майюаа. Учебный курс. —
СПб.: Питер, 2005. — 448 с.
31. Корниенко В.С. Анализ и обработка экспериментальных данных.
Волгоград, 2004.-356 с. (СП)
32. Кирьянов Д.В. Майсаа 12. — СПб.: БХВ-Петербург. 2005. — 576 с.
33. Гурский Д., Турбина Е. Ма1Ьсас1 для студентов и школьников. По-
пулярный самоучитель. — СПб.: Питер, 2005. — 400 с.
35
7.2. Распределения дискретной случайной величины
Биномиальный закон распределения
Если вероятность появления события А в каждом испытании постоянна и равна Р, то число появлений события А — дискретная случайная величина Х, принимающая значения 0, 1, 2, …, с вероятностями (формула Бернулли), где , , .
Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляется по формулам:
,
.
Распределение Пуассона
Если число испытаний велико, а вероятность появления события Р в каждом испытании очень мала, то вместо формулы Бернулли пользуются приближенной формулой Пуассона
,
Где Число появлений события в N независимых испытаниях; M принимает значения . (среднее число появлений события в N испытаниях).
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру , который определяет этот закон, т. е.
.
Геометрическое распределение
Дискретная случайная величина имеет геометрическое распределение, если она принимает значения 1, 2, …, M, …(бесконечное, но счетное множество значений) с вероятностями
,
Где .
Определение геометрического распределения корректно, так как сумма вероятностей
Случайная величина , имеющая геометрическое распределение, представляет собой число M испытаний, проведенных по схеме Бернулли, с вероятностью Р наступления события в каждом испытании до первого положительного исхода.
Математическое ожидание и дисперсия случайной величины Х , имеющей геометрическое распределение с параметром Р вычисляются по формулам:
Где
Гипергеометрическое распределение
Пусть имеется N элементов, из которых М элементов обладают некоторым признаком А. Извлекаются случайным образом без возвращения N элементов. Х — дискретная случайная величина, число элементов обладающих признаком А, среди отобранных N элементов. Вероятность, что Х = M определяется по формуле
.
Математическое ожидание и дисперсия случайной величины, распределенной по гипергеометрическому закону, определяются формулами:
,
.
Пример 7.2. В аккредитации участвуют 4 коммерческих вуза. Вероятности пройти аккредитацию и получить сертификат для этих вузов, соответственно равны 0,5; 0,4; 0,3; 0,2. Составить закон распределения числа коммерческих вузов, не прошедших аккредитацию. Найти числовые характеристики этого распределения.
Решение. В качестве случайной величины Х выступает число коммерческих вузов, не прошедших аккредитацию. Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3, 4.
Для составления закона распределения необходимо рассчитать соответствующие вероятности. Обозначим через событие — первый вуз прошел аккредитацию, — второй, — третий, — четвертый. Тогда ; ; ; . Вероятности для вузов не пройти аккредитацию соответственно равны ; ; ; .
Тогда имеем:
.
Запишем закон распределения в виде таблицы
Х | 0 | 1 | 2 | 3 | 4 |
Р | 0,012 | 0,106 | 0,320 | 0,394 | 0,168 |
Проверка: 0,012 + 0,106 + 0,32 + 0,394 + 0,168 = 1.
Вычислим
.
Вычислим :
,
. .
Пример 7.3. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые последовательно посетит студент, чтобы взять необходимую книгу, если в городе 3 библиотеки.
Решение. В качестве случайной величины Х выступает число библиотек, которые посетит студент, чтобы получить необходимую книгу. Возможные значения, которые примет случайная величина Х: 1, 2, 3.
Обозначим через событие — книга свободна в первой библиотеке, — во второй, — в третьей. Тогда . Вероятность противоположного события, что книга занята
.
Для составления закона распределения рассчитаем соответствующие вероятности:
,
,
Запишем закон распределения в виде таблицы.
Х | 1 | 2 | 3 |
Р | 0,3 | 0,21 | 0,49 |
Проверка: 0,3 + 0,21 + 0,49 = 1.
Пример 7.4. Из поступающих в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Составить закон распределения числа просмотренных часов. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. В качестве случайной величины Х выступает число просмотренных часов. Возможные значения, которые примет случайная величина Х: 1, 2, 3, 4. Все значения случайной величины зависимы.
Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Для расчета вероятностей будем использовать формулу классической вероятности и теорему умножения для зависимых событий.
Пусть событие — первые, взятые наугад, часы, нуждающиеся в чистке, — вторые, — третьи, — четвертые. Тогда имеем:
,
,
,
Запишем закон распределения в виде таблицы
Х | 1 | 2 | 3 | 4 |
Р |
Проверим, что :
.
Вычислим математическое ожидание случайной величины по формуле
.
Вычислим дисперсию случайной величины по формуле
.
Вычислим ,
.
Пример 7.5. Известно, что в определенном городе 20 % горожан добираются на работу личным автотранспортом. Случайно выбраны 4 человека. Составить закон распределения числа людей, добирающихся на работу личным автотранспортом. Найти числовые характеристики этого распределения. Написать функцию распределения и построить ее график.
Решение. В качестве случайной величины Х выступает число людей в выборке, которые добираются на работу личным автотранспортом. Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3, 4.
Вероятность того, что каждый из отобранных людей, которые добираются на работу личным автотранспортом, постоянна и равна . Вероятность противоположного события, т. е. того, что каждый из отобранных людей добирается на работу не личным автотранспортом, равна .
Все 4 испытания независимы. Случайная величина Подчиняется биномиальному закону распределения вероятностей с параметрами ; ; . Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений.
Расчет искомых вероятностей осуществляется по формуле Бернулли:
.
,
,
,
,
.
Запишем закон распределения в виде таблицы
Х | 0 | 1 | 2 | 3 | 4 |
Р | 0,4096 | 0,4096 | 0,1536 | 0,0256 | 0,0016 |
Так как все возможные значения случайной величины образуют полную группу событий, то сумма их вероятностей должна быть равна 1.
Проверка: 0,4096 + 0,4096 + 0,1536 + 0,0256 + 0,0016 = 1.
Найдем числовые характеристики дискретной случайной величины: математическое ожидание, дисперсию и среднее квадратическое отклонение.
Математическое ожидание может быть рассчитано по формуле
.
Так как случайная величина подчиняется биноминальному закону, то для расчета математического ожидания можно воспользоваться формулой
.
Дисперсия случайной величины может быть рассчитана по формуле :
,
.
В данном случае дисперсию можно рассчитать по формуле
.
Рассчитаем среднее квадратическое отклонение случайной величины по формуле
.
Составим функцию распределения случайной величины Х по формуле
.
1. .
2. .
3. .
4. .
5. .
6. .
Запишем функцию распределения
График функции распределения вероятностей имеет ступенчатый вид (рис. 7.3). Скачки равны вероятностям, с которыми случайная величина принимает возможные значения.
Рис. 7.3
Пример 7.6. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1.
Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Решение. В качестве случайной величины Х выступает число кредитов, возвращенных клиентами в срок. Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3, 4, 5.
Вероятность того, что каждый клиент возвратит кредит в срок, постоянна и равна . Вероятность того, что кредит не будет возвращен в срок, равна . Все 5 испытаний независимы. Случайная величина подчиняется биномиальному распределению с параметрами ; ; ; . Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Расчет искомых вероятностей осуществляется по формуле Бернулли
,
,
,
,
,
,
.
Запишем закон распределения в виде таблицы
Х | 0 | 1 | 2 | 3 | 4 | 5 |
Р | 0,00001 | 0,00045 | 0,0081 | 0,0729 | 0,32805 | 0,59049 |
Математическое ожидание вычислим по формуле
.
Дисперсию вычислим по формуле
.
Пример 7.7. Из 10 телевизоров на выставке оказались 4 телевизора фирмы «Сони». Наудачу для осмотра выбраны 3 телевизора. Составить закон распределения числа телевизоров фирмы «Сони» среди 3 отобранных.
Решение. В качестве случайной величины Х выступает число телевизоров фирмы «Сони». Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3. Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Эти вероятности можно рассчитать по формуле классической вероятности :
;
.
Запишем закон распределения
Х | 0 | 1 | 2 | 3 |
Р |
Убедимся, что .
Пример 7.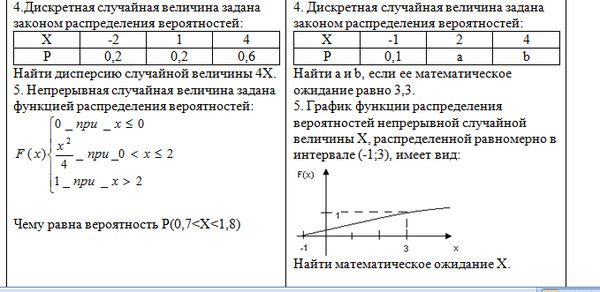
8. На двух автоматических станках производятся одинаковые изделия. Даны законы распределения числа бракованных изделий, производимых в течение смены на каждом из них:
Х: для первого
Х | 0 | 1 | 2 | 3 |
Р | 0,1 | 0,6 | 0,2 | 0,1 |
Y: для второго
Y | 0 | 1 | 2 | |
Р | 0,5 | 0,3 | 0,2 |
Составить закон распределения числа производимых в течение смены бракованных изделий обоими станками. Проверить свойство математического ожидания суммы случайных величин.
Решение. Для того чтобы составить закон распределения Х + Y необходимо складывать , а соответствующие им вероятности умножить :
; ,
; ,
; ,
; ,
; ,
; ,
,
,
,
,
,
.
Закон распределения запишем в виде таблицы
Х + Y | 0 | 1 | 2 | 3 | 4 | 5 |
P | 0,05 | 0,33 | 0,3 | 0,23 | 0,07 | 0,02 |
Проверим свойство математического ожидания :
,
,
,
.
Пример 7.9. Дискретная случайная величина Х имеет только два возможных значения: И , причем . Вероятность того, что Х примет значение , равна 0,6. Найти закон распределения величины Х, если математическое ожидание ; .
Решение. Сумма вероятностей всех возможных значений случайной величины равна единице, поэтому вероятность того, что Х примет значение . Напишем закон распределения Х
X | ||
P | 0,6 | 0,4 |
Для того чтобы отыскать И необходимо составить два уравнения.
Из условия задачи следует, что , .
Составим систему уравнений
Решив эту систему, имеем ; и ; .
По условию , поэтому задаче удовлетворяет лишь первое решение, т. е. ; . Тогда закон распределения имеет вид
X | 1 | 2 |
P | 0,6 | 0,4 |
Пример 7.10. Случайные величины И Независимы. Найти дисперсию случайной величины , если известно, что , .
Решение. Так как имеют место свойства дисперсии
и , то получим
.
| < Предыдущая | Следующая > |
|---|
Дискретная случайная величина X имеет следующее распределение вероятностей:\n \n \n \n \n Найдите значение k.
Ответ
Проверено
220,6 тыс.+ просмотров
Подсказка: в распределении вероятностей сумма всех вероятностей равна 1.
Четыре значения даны в P(X). Итак, мы просто суммируем все значения P(X), а затем приравниваем ее к 1. Используя это, мы находим значение k.
Полный пошаговый ответ:
Если значение X равно 0,5, то вероятность P(X) равна k.
\[P(0,5)=k\].
Когда значение X равно 1, то вероятность этого 2k.
$P(1)=2k$.
Когда значение Х равно 1,5, то вероятность этого 3к.
$P(1.5)=3k$.
Когда значение X равно 2, то вероятность этого k.
$P(2)=k$.
Теперь нам нужно найти значение k.
«Сумма вероятностей всех исходов должна быть равна 1».
$\therefore $ Если два события не имеют общих исходов, вероятность того, что одно или другое произойдет, равна сумме их индивидуальных вероятностей. Вероятность того, что событие не произойдет, равна 1 минус вероятность того, что событие произойдет.
Сумма распределения всех вероятностей равна 1.
Теперь
Сложите все значения P(X) и приравняйте их к 1.
$\begin{align}
& \Rightarrow k+2k+3k +k=1 \\
& \Rightarrow 7k=1 \\
& \therefore k=\dfrac{1}{7} \\
\end{align}$
Следовательно, значение k в распределении вероятностей равно $\dfrac{1}{7}$.
Примечание: Ключевым шагом для решения этой задачи является основное свойство суммы распределения вероятностей для дискретной случайной величины X. Согласно этому свойству сумма вероятностей всех событий равна единице. Это даст нам необходимое уравнение для решения и оценки значения k.
Дата последнего обновления: 05 мая 2023 г.
•
Всего просмотров: 220,6 тыс.
•
Просмотров сегодня: 5,85 тыс. 03
Расчет изменения энтропии при преобразовании химии класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Химический класс 11 JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg знаки химического класса 11 JEE_Main
Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main
Рассчитать изменение энтропии, связанное с преобразованием химического класса 11 JEE_Main
900 02 Закон, сформулированный Д-р Нернст — это Первый закон термодинамики.
Химический класс 11 JEE_MainДля реакции при rm0rm0rmC и нормальном давлении.0003
Для реакции rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main
Изменение энтальпии перехода жидкой воды 11 класса химии JEE_Main
Актуальные сомнения 9000 3
Дискретная случайная величина: значение и типы
Есть Вы когда-нибудь играли в стрельбу из лука и пытались узнать, сколько раз вы можете бросить стрелу, прежде чем поразите конкретную цель? Делая это, вы проверяете вероятности и исходы случайных событий. Мы можем выразить и описать результаты случайных событий с помощью случайных величин.
Дискретные случайные величины — это тип случайных величин, значения которых конечны.
Другими словами, значения являются счетными и имеют ограниченное число результатов. Примерами дискретных случайных величин являются, среди прочего, количество книг в пачке, количество кубиков сахара в коробке, количество коз в загоне и размер обуви человека.
В этом уроке мы подробно узнаем о дискретных случайных величинах и их вероятностных распределениях.
А дискретная случайная величина — это переменная, которая может принимать только ограниченное число определенных счетных значений. Все значения в области определения случайной величины имеют связанные с ними вероятности. Эти вероятности должны суммироваться до \(1\), когда рассматриваются все возможные значения.
Дискретные случайные величины: Типы распределения
Прежде всего, давайте вспомним понятие распределения. Распределение вероятностей для дискретной случайной величины X представляет собой исчерпывающий набор каждого потенциального значения \(X\) вместе с вероятностью того, что \(X\) примет это значение в одном испытании эксперимента. Другими словами, дискретные распределения вероятностей используются для описания вероятностей, связанных со значениями дискретной случайной величины. Двумя распространенными типами дискретных случайных величин являются биномиальные случайные величины (с биномиальное распределение вероятностей) и геометрические случайные величины (с геометрическим распределением вероятностей ) .
В этой статье мы рассматриваем только биномиальные и геометрические случайные величины, которые имеют отношение к курсу AP Statistics. Другие типы, которые не будут рассмотрены в этой статье, включают распределения Бернулли, мультиномиальное, гипергеометрическое и распределение Пуассона.
Биномиальные и геометрические распределения вероятностей дискретных случайных величин
Распределение вероятностей дискретной случайной величины относится к каталогу потенциальных значений этой дискретной случайной величины вместе с вероятностью того, что она примет это значение при одной попытке эксперимента.
Распределения дискретных случайных величин должны удовлетворять следующим двум условиям для данной дискретной случайной величины \(X\):
Давайте рассмотрим пример того, что подразумевается под распределением вероятностей дискретной случайной величины.
Пусть \(X\) будет числом выпадений орла при двукратном подбрасывании правильной монеты.
Сначала постройте распределение вероятностей \(X\). Во-вторых, найти вероятность того, что выпадет хотя бы один орёл.
Решение:
Для этого выборочного пространства возможные значения \(X\) равны \(0\), \(1\) и \(2\). Потенциальные результаты имеют равные шансы на появление и следуют как:
\(S = {hh, ht, th, tt}\).
То есть «\(hh\)» относится к результату двух орлов,
«\(ht\)» относится к результату одной решки и одной решки и так далее.
Поскольку количество наблюдаемых головок представлено \(X = 0\):
\(X = 0\) соответствует \({tt}\), без наблюдаемых головок
\(X = 1\ ) соответствует \({ht, th}\), с \(1\) наблюдаемыми головками
\(X = 2\) соответствует \({hh}\), с \(2\) наблюдаемыми головками
Путем простого подсчета мы получаем вероятность каждого из этих трех событий, представленную дискретной переменной \(X\).
Таким образом:
Таблица 1: Распределение вероятности двукратного подбрасывания правильной монеты 49
математическое выражение: \(X \geq 1\). Вероятность этого конкретного события (по крайней мере, одна голова) рассчитывается путем сложения двух взаимоисключающих событий \(X = 1\) и \(X = 2\). Следовательно, \(P (X \geq 1) = P (1) + P (2) = 0,50 + 0,25 = 0,75\). Другими словами, существует вероятность \(75\%\) того, что хотя бы один орел выпадет при двойном подбрасывании монеты.
Биномиальные случайные величины
Биномиальная случайная величина — это тип дискретной случайной величины, которую мы используем для выражения частоты определенного исхода (или события) на протяжении фиксированного числа экспериментальных испытаний. Биномиальная случайная величина выражается в рамках биномиального распределения.
Чтобы дискретная случайная величина также была биномиальной случайной величиной, должны применяться следующие характеристики:
Число испытаний заранее определено или исправлено .
Испытания независимы. (Результаты испытаний не влияют друг на друга.)
В каждом испытании могут быть только два исхода: «успех» или «неудача». Другими словами, конкретное интересующее событие либо произойдет, либо не произойдет. Этот тип результата также можно назвать «бинарным».
Любое данное испытание имеет такую же вероятность «успеха», как и другие в эксперименте.
Если дискретная случайная величина \((X)\) классифицируется как биномиальная, ее можно использовать для подсчета количества успехов в n испытаниях. Отсюда следует, что \(X\) имеет биномиальное распределение со следующими двумя параметрами:
«\(n\)», который измеряет количество испытаний, и
«\(p\)», который измеряет вероятность успеха определенного события.
Например, давайте рассмотрим случайную выборку из 125 медсестер, выбранных из крупной больницы, в которой доля медсестер женского пола составляет 57%. Предположим, что X обозначает количество женщин-медсестер в выборке. В этом эксперименте есть 125 (n = 125) идентичных и независимых испытаний общей процедуры: выбор медсестры наугад. Для каждого испытания есть ровно два возможных исхода: «успех» (рассчитываемое нами событие, что медсестра — женщина) и «неудача» (не женщина). Наконец, вероятность успеха в любом испытании равна одному и тому же числу (p = 0,57). Поскольку доля медсестер составляет 57% женщин, случайный отбор, таким образом, дает 57%-ную вероятность выбора медсестры-женщины. Таким образом, X является биномиальной случайной величиной с параметрами n = 125 и p = 0,57. 9{n-x}}\]
где,
\(P\) = биномиальная вероятность
\(x\) = частота конкретного исхода в пределах определенного числа испытаний
\(\begin{pmatrix} n \\ X \end {pmatrix} \)= количество комбинаций
\(p\) = вероятность успеха в одном испытании
\(q\) = вероятность неудачи в одном испытании
\(n\) = число попыток
Предположим, что правильная монета подбрасывается \(10\) раз, какова вероятность того, что выпадет \(6\) решка?
Решение
В эксперименте с подбрасыванием монеты можно получить два результата: орёл или решка.
Следовательно:
Вероятность выпадения решки равна \(50\%\) (или \(0,5\)) при данном броске.
Количество испытаний, \(n = 10\).
Частота исхода, \(x = 6\).
- Вероятность успеха в одном испытании, \(p = 0,5\)
- Вероятность неудачи в одном испытании, \(q = 0,5\). 9{n-x}}\]
\[P(X=x)=0,205\]
Геометрические случайные величины
Геометрические случайные величины — это дискретные случайные величины, которые образуют геометрическое распределение . Эта концепция используется в нескольких сферах жизни, таких как анализ затрат и результатов в финансовых отраслях.
Экспериментальные условия, необходимые для геометрических случайных величин, очень похожи на условия для биномиальных случайных величин: и те, и другие классифицируют испытания как успешные или неудачные, и испытания должны быть независимыми, с одинаковой вероятностью возникновения для каждого из них.
Однако, в отличие от биномиальных случайных величин, количество испытаний для геометрических случайных величин заранее не фиксируется. Скорее, это зависит от количества последовательных неудач, которые происходят до достижения успеха.Например, рассмотрим геометрическую случайную величину \(X = 3\), которая представляет получение числа \(3\) в результате броска игральной кости.
В этом геометрическом эксперименте со случайной величиной мы должны подсчитать, сколько раз игральная кость бросается до достижения значения \(3 (X = 3)\) раз .
Испытание, в котором выпало \(3\), помечается как «успех», а любое испытание, в котором не выпало \(3\), помечается как «неудача». Поскольку это эксперимент с геометрическими случайными величинами, нам нужно получить только один успех, чтобы закончить его.
Поскольку наблюдения независимы друг от друга, вероятность того, что \(X = 3\) (\(3\) выпадет в результате броска игральной кости) будет равна \(1/6\) для каждого броска.
{х-1}р\]где \(0
Представитель отдела маркетинга Национального театра случайным образом выбирает людей на случайной улице в Вашингтоне, округ Колумбия, пока не найдет человек, посетивший последний киносеанс.
Пусть \(p\), вероятность того, что ему удастся найти такого человека, равна \(0,20\). И пусть \(X\) обозначает количество людей, которых он выбирает, пока не добьется своего первого успеха.
а. Какова вероятность того, что специалист по маркетингу должен выбрать 4 человека, прежде чем он найдет одного из пришедших на кинопоказ? 9{4-1}0,2=0,1024\]
Таким образом, существует примерно \(10\%\) вероятность того, что представителю отдела маркетинга придется выбрать \(4\) человек, прежде чем он найдет того, кто посетит последний фильм показывать.
Среднее значение, дисперсия и стандартное отклонение дискретных случайных величин
В этом разделе мы обсудим среднее значение, дисперсию и стандартное отклонение применительно к дискретным случайным величинам.
Затем мы применяем эти концепции к примерной задаче.Среднее
Среднее также известно как ожидаемое значение и относится к среднее значений. Для дискретных случайных величин среднее значение относится к среднему значению всех значений, присвоенных событиям, которые происходят в повторяющихся испытаниях эксперимента. Среднее значение дискретной случайной величины определяется следующим выражением:
\[\mu= E(x)=\sum x \cdot P(x)\]
Таким образом, среднее значение получается путем умножения каждого значения на вероятность его возникновения. Затем эти значения суммируются, чтобы получить среднее значение эксперимента.
Найдите среднее значение дискретного распределения вероятностей ниже:
\(х\)
\(-2\)
\(1\)
9000 2 \(2\) \(3,5\)
\(P(x)\)
\(0,21\)
\(0,34\)
\( 0,54\)
\(0,31\)
Решение:
Следуя формуле:
\[\mu= E(x)=\sum x \cdot P(x)\] 92P(x)}\]
Дискретная случайная величина X имеет следующее распределение вероятностей: \)
\(4\) \(P(x)\) \(0,2\) \(0,5\) \(α\) \(0. 1\)Определяем следующее: (Х ≥ 0)\)
5. Среднее \(\mu\) от \(X\)
6. Дисперсия \(X\)
7. Стандартное отклонение \(X\)
Решение
1. Поскольку все вероятности должны составлять в сумме \(1\),\( α = 1 – (0,2 + 0,5 + 0,1) = 0,2\)
2. Ссылаясь на таблицу, \(P (0) = 0,5 \)
3. Из таблицы еще раз, \(P (X > 0) = P (1) + P (4) = 0,2 + 0,1 = 0,3\)
4. Из таблицы, \(P ( X ≥ 0) = P (0) + P (1) + P (4) = 0,5 + 0,2 + 0,1 = 0,8\) 92P(x)}\]
\[\sigma= \sqrt{1,84}=1,3565\]
Дискретная случайная величина — ключевые выводы
- Дискретные случайные величины — это случайные величины, которые принимают заданные или конечные значения в интервале.
- Дискретные случайные величины — это случайные величины, которые принимают заданные или конечные значения в интервале.
Однако, в отличие от биномиальных случайных величин, количество испытаний для геометрических случайных величин заранее не фиксируется. Скорее, это зависит от количества последовательных неудач, которые происходят до достижения успеха.
{х-1}р\]
Затем мы применяем эти концепции к примерной задаче.
1\)
В
этом примере число уравнений совпадает
с числом неизвестных. Это обстоятельство
несколько облегчает рассуждения.
Обратимся к замечанию из предыдущего
пункта: система л.у. с числом уравнений,
совпадающем с числом неизвестных, как
правило,
совместна. Тогда попробуем установить
условия, обеспечивающие противоположное
свойство — несовместность. Оно,
фактически, единственно: за все отвечает
определитель системы
.
Если он отличен от нуля — система
совместна.
Выберем произвольным
образом в рассматриваемой системе
какую-то подсистему, состоящую
из
уравнений.
Она, как правило, будет иметь единственное
решение. Теперь составим другую
подсистему, хотя бы одним уравнением
отличающуюся от предыдущей (поскольку
такое
всегда можно сделать). Новая подсистема
снова, как правило, будет иметь единственное
решение. Однако решения этих двух
подсистем будут, как правило, различными
и, следовательно, сама основная система
не будет иметь решения. В этом последнем
случае переопределенной системы имеется,
однако, важный исключительный, который
рассмотрим ☞ НИЖЕ.
Л.Додсону,
оно было напечатано им в 1867 г. в книге
k\) миноров k-го порядка.
Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.
\)
{(1)} = \triangle_r.\)
\)
Но
Итак, р(А) = 3.
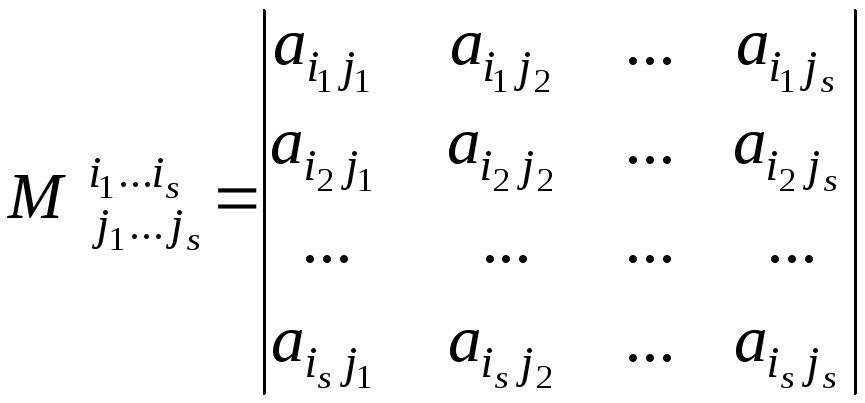Элементы матрицы расположены в строках и столбцах. Порядок матрицы — это представление количества ее строк и столбцов в виде MxN, где m — количество строк, а n — количество столбцов. Две матрицы называются равными, если они имеют одинаковый порядок и их элементы одинаковы. Существует разница между терминами «равные матрицы» и «эквивалентные матрицы». Эквивалентность двух матриц обозначается символом «~». Две матрицы называются эквивалентными, если одну матрицу можно изменить элементарным преобразованием матрицы, чтобы получить другую матрицу.
Он также используется для нахождения обратных матриц, определителей матриц и решения системы линейных уравнений. Для выполнения элементарных преобразований между любыми двумя матрицами порядок двух матриц должен быть одинаковым.
Он символически представлен как Ci → k Ci, что указывает на то, что каждый элемент столбца умножается на коэффициент масштабирования «k».
Вы можете создавать различные таблицы с несколькими рабочими книгами, формулами и различными источниками данных. Файлы можно сохранить в формате XLSX, который основан на открытом формате XML и использует сжатие ZIP для более маленького размера файлов.
Таким образом, данные могут проходить через корпоративные шлюзы безопасности беспрепятственно.
xml
XML содержат базовую структуру, в рамках которой пользователи могут определять свои собственные тэги. Каждый файл начинается с того, что называется декларацией XML. Это определяет версию и кодировку внутри самого файла. Затем файл должен определить корневой элемент, известный также как родительский элемент. Затем, корневой элемент получает дочерний элемент (ы). Все тэги в XML-файла должны иметь соответствующий закрывающий тэг. XML-файлы могут содержать комментарии, ссылки на объекты и атрибуты. Затем могут быть разработаны приложения для извлечения значений внутри файла и их представления по желанию.
Пожалуйста, смотрите полный список ниже.
Выберите файлы для конвертации
Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов.
И обслуживание клиентов отличное. Только что возникла проблема, когда мне предъявили обвинение, и я не согласился с обвинением, и они позаботились об этом, хотя в этом не было необходимости.
Я могу сделать несколько больших файлов за короткий промежуток времени.
Преобразователь Замзара был идеальным.
Какой инструмент вы используете, зависит от вас!
Выберите файл XLSX, который вы хотите преобразовать.
ZIP в XLSX
ODS в XLSX
PDF в XLSX
WKS в XLSX
XLR в XLSX
XLS в XLSX
com
&
aspose.cloud 
09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.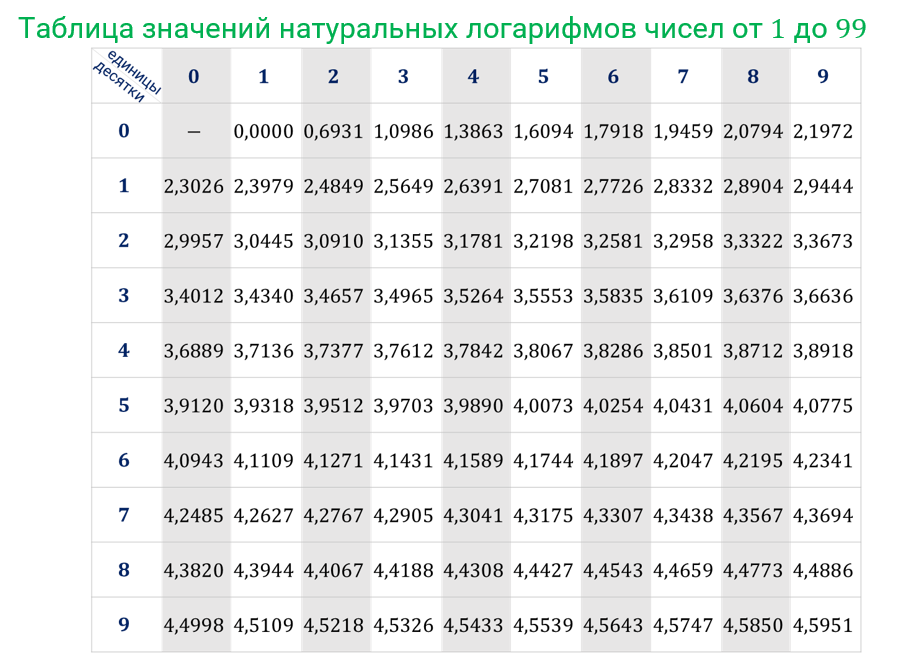
Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
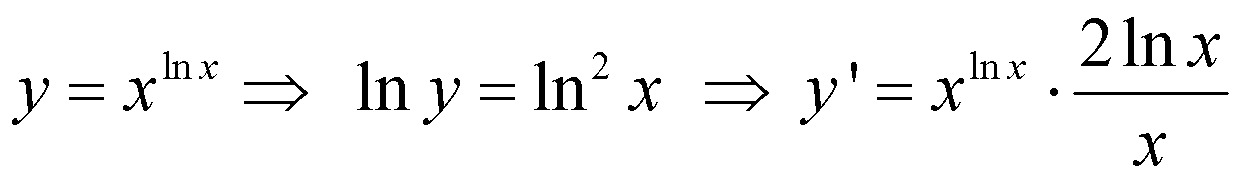В общем получается
Мы можем записать это уравнение в таком виде:
Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
693 / ставка
Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.
Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
е. как интеграл :
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.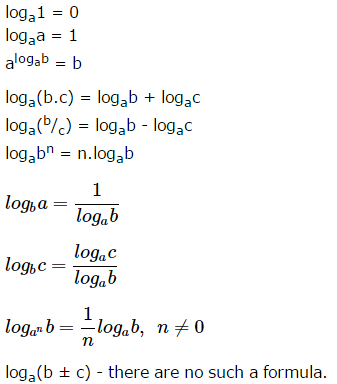
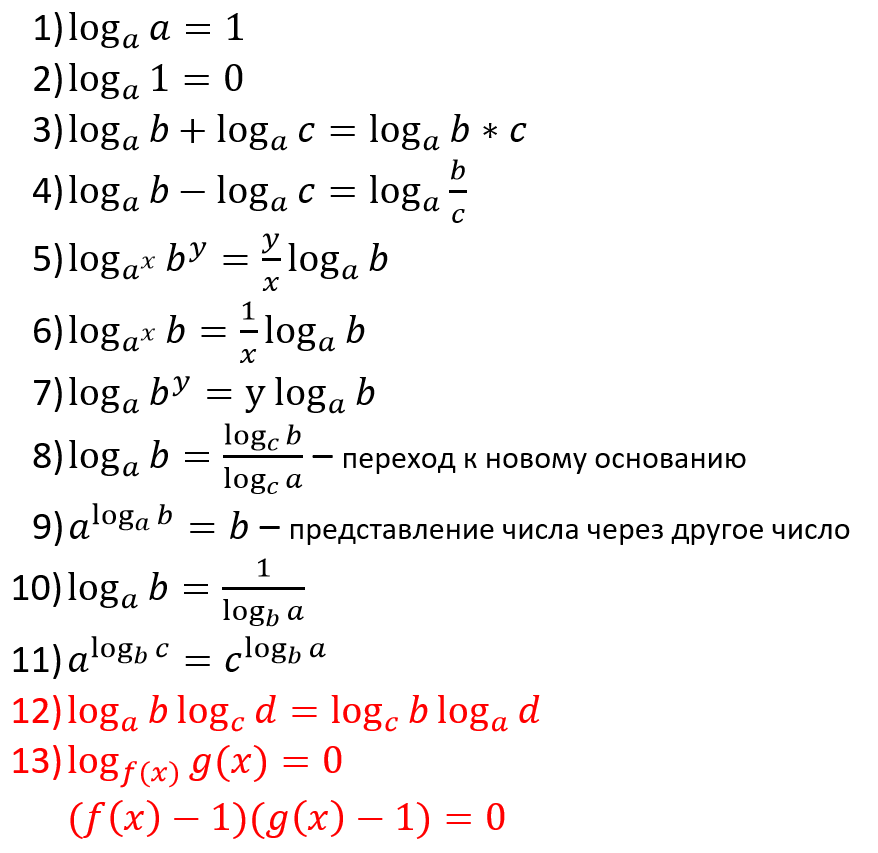Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
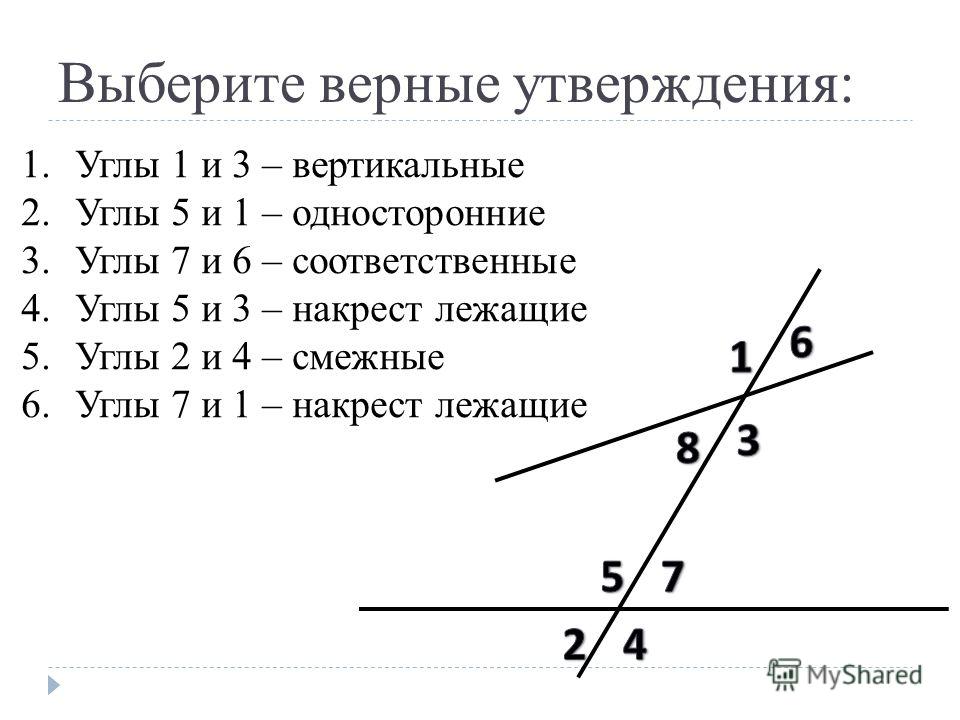
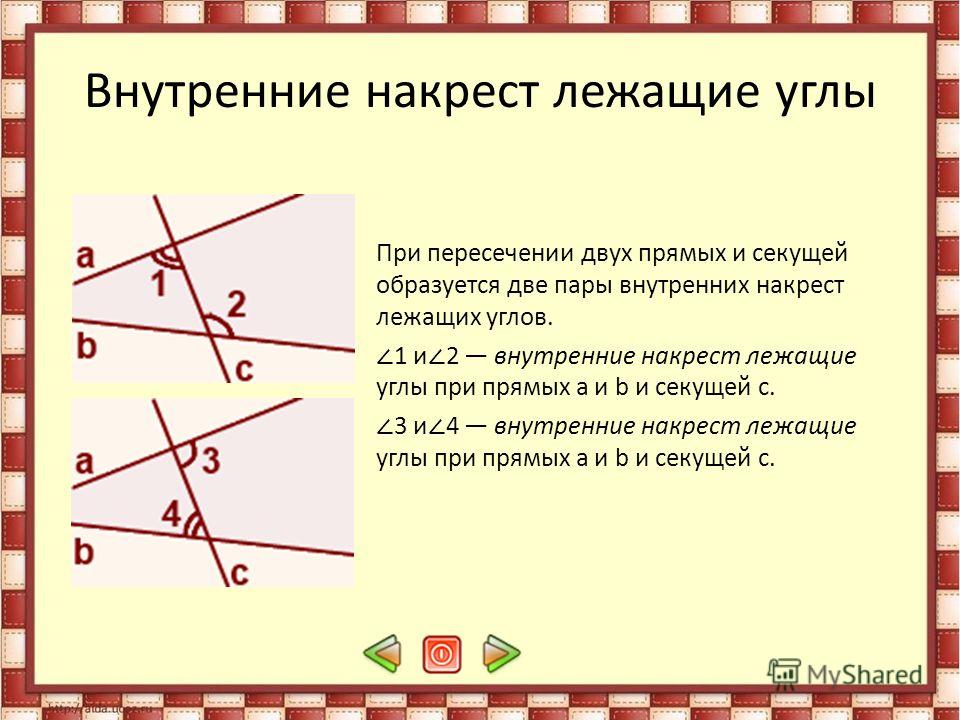
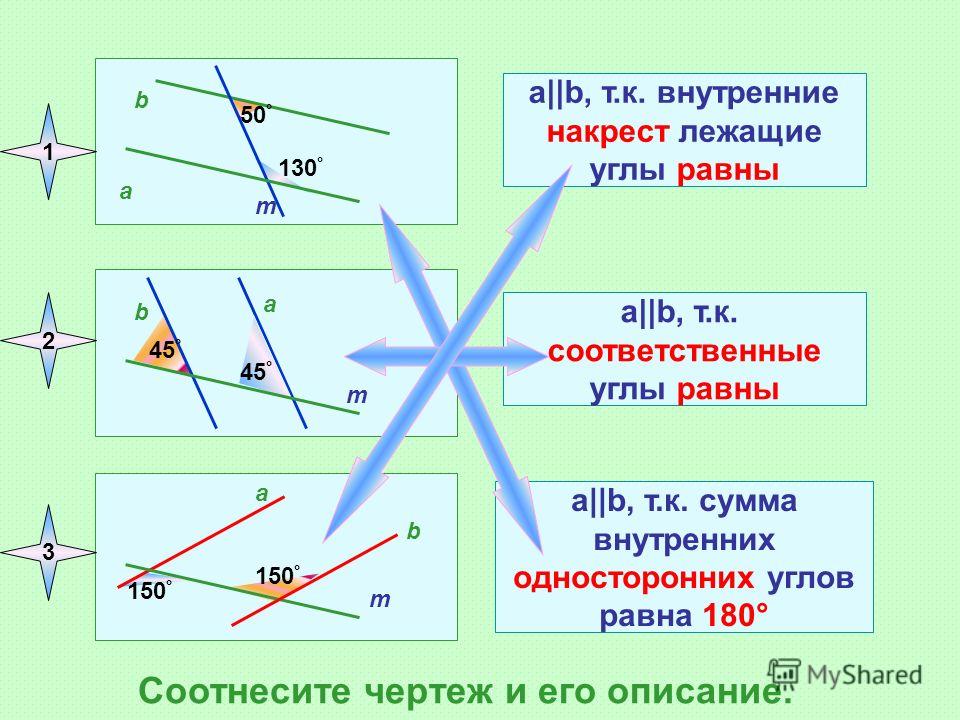
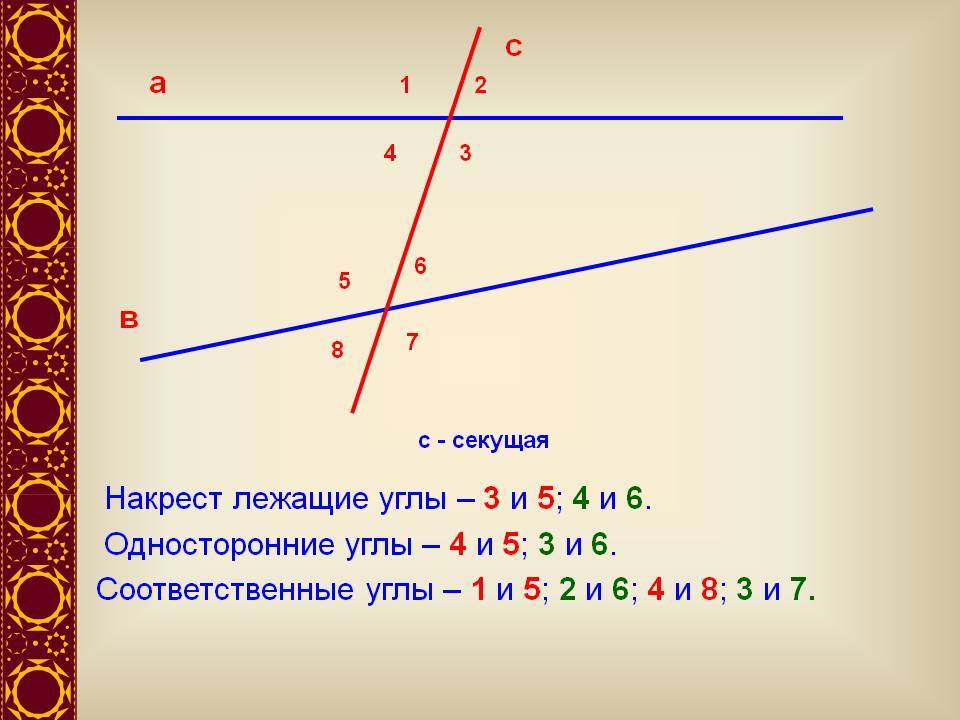
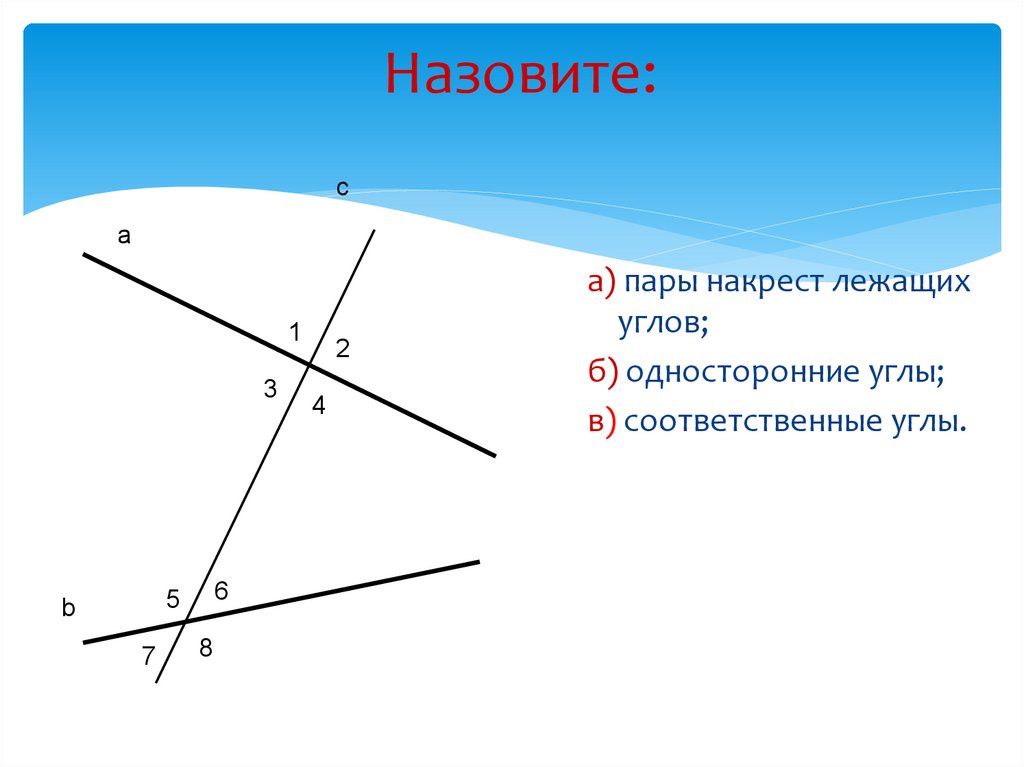Так как такие углы являются равными, то величина 8 = 53°. 
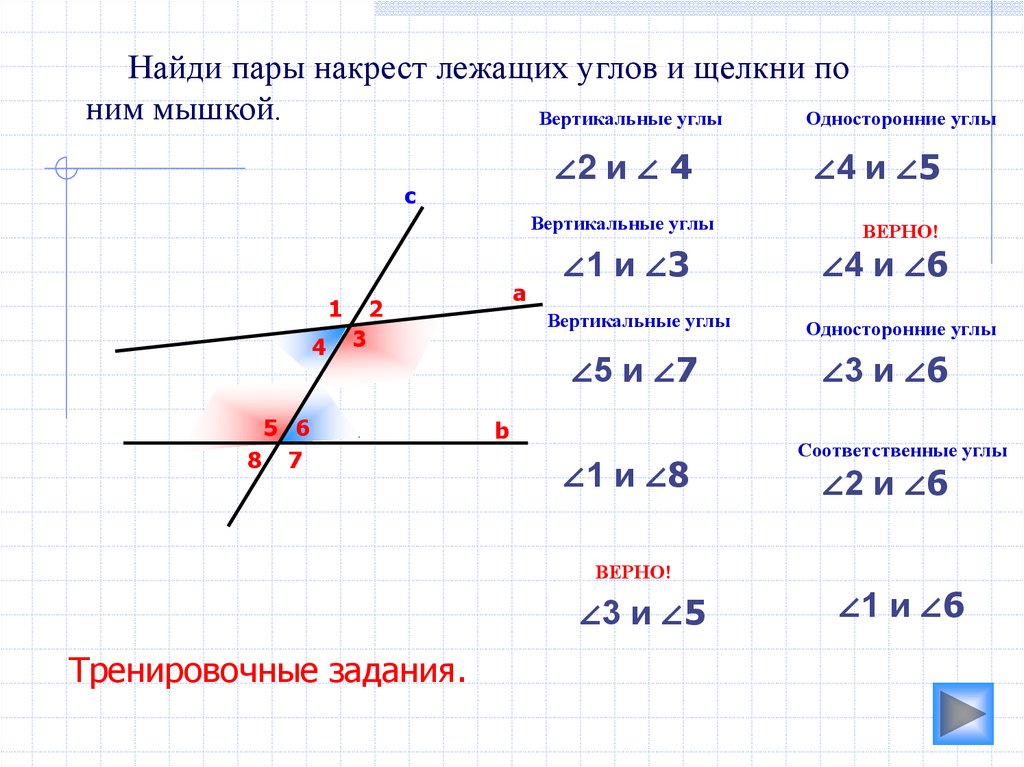Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.
То, что мы обнаружили, было шокирующим по своим масштабам.
Когда люди чувствуют связь с землей, они с большей вероятностью будут ее защищать. Прочтите отчет onX Corner-Locked ниже, чтобы получить представление о проблеме и о том, что делается для решения этой сложной проблемы.
Но при этом их тела также пересекли воздушное пространство двух других посылок, встречающихся в этой точке, которые были частными. Их суд, назначенный на середину апреля, решит, нарушили ли они границу, когда пролетали через это частное воздушное пространство.
По мере того как земля распределялась среди поселенцев и вновь образованных штатов, предназначалась для парков, лесов и резерваций, а федеральное правительство сохраняло за собой или рекультивировало их, сформировалась сложная лоскутная мозаика собственности. Свойства объединялись, разделялись и трансформировались во все мыслимые формы, но основная единица — скромный квадратный участок площадью 640 акров — все еще можно найти по всему Западу.
Но никто, в том числе и сами федеральные агентства по управлению земельными ресурсами, точно не знал, сколько государственной земли находится вне досягаемости населения. Так в 2018 и 2019 гг., onX и Партнерство по охране природы Теодора Рузвельта совместно открыли 15,8 млн акров федеральных земель и земель штата, не имеющих выхода к морю, по всему Западу.
Это называется прыганием за угол, пересечением угла или нарушением угла, в зависимости от того, кого вы спросите. За пределами мира охоты и за пределами Запада это ограничение редко обсуждается. На самом деле, в книгах нет закона, в котором прямо говорится, что переход через угол собственности с общественной земли на общественную землю является незаконным. Несмотря на различные попытки законодательных собраний штатов сделать пересечение поворотов законным или незаконным, ни один штат еще не принял такой закон. Это оставило решение о судебном преследовании «угловых прыгунов» в руках местных правоохранительных органов и местных судов.
За этими углами лежат 8,3 миллиона акров федеральных земель и земель штата, которые недоступны для широкой публики, поскольку законность пересечения углов остается неясной. Другими словами, более половины всех не имеющих выхода к морю общественных земель на западе США были бы разблокированы, если пересечение углов было бы легализовано. Эти акры запрещены не только для охоты, но и для рыбалки, пеших прогулок, наблюдения за дикой природой, катания на беговых лыжах и всех других форм наслаждения на открытом воздухе.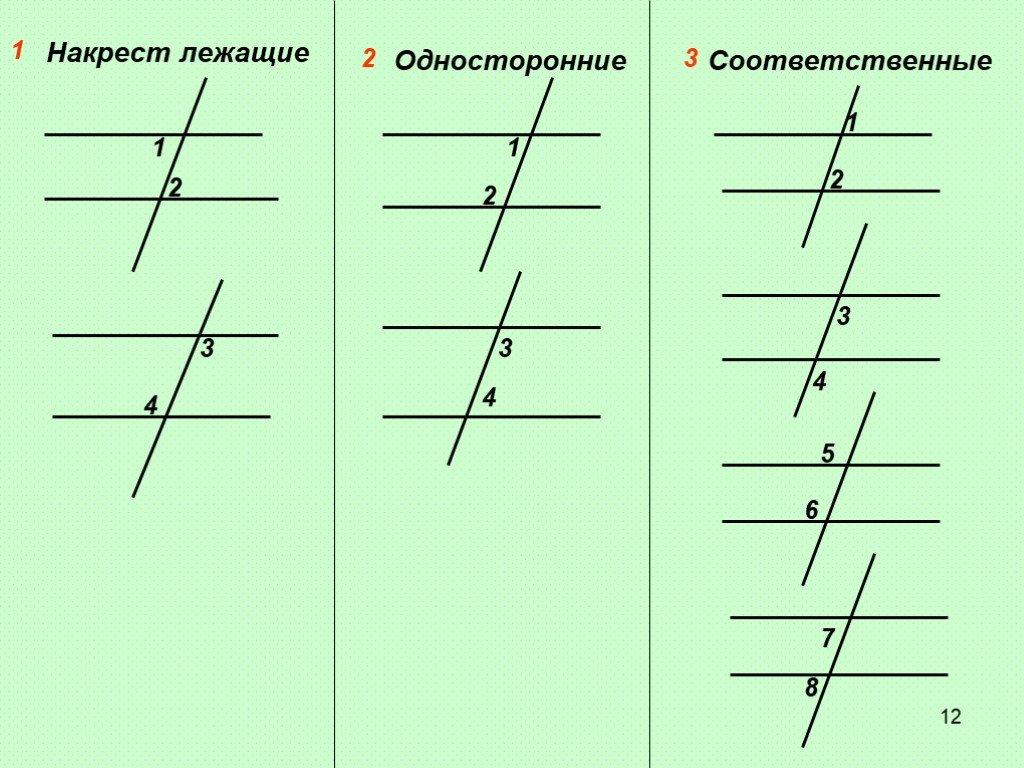
Поскольку большая часть невостребованных и мелиорированных земель на Западе оказалась в руках агентства, которое стало Бюро по управлению земельными ресурсами, неудивительно, что 70% всех выявленных нами запертых акров находятся в ведении этого агентства.
В Неваде 1,93 миллиона акров земли, в Аризоне — 1,33 миллиона акров, а в Монтане — 871 000 акров.
Поскольку земля не была бы очень полезной, если бы права собственности были ограничены поверхностью — скажем, уровнем, который волнует червей и муравьев, — существует понимание того, что воздушное пространство до определенной высоты также принадлежит землевладельцу. Это понимание облегчает строительство конструкций и заборов и используется для обеспечения того, чтобы вертолеты и дроны не могли без приглашения парить над чьим-то домом. Кроме того, углы собственности считаются бесконечно малыми точками в пространстве. Таким образом, перешагнуть через угол, где встречаются два государственных земельных участка и два частных земельных участка, человек автоматически попадает в воздушное пространство частной земли, поскольку мы не можем уменьшить наши тела до бесконечно малых размеров.
Он был свидетелем того, как люди стреляли в оленей на его территории с прилегающей общественной земли, и он видел, как люди стреляли в оленей в пределах его собственности. Он слышал выстрелы с того же направления, откуда его дети чинили заборы, вызывая панику. Были времена, когда он пытался приблизиться к нарушителям, но они скрылись с места происшествия, оставив мертвых или раненых оленей. Правоохранительные органы в его районе слишком напряжены, чтобы реагировать на все звонки.
Но нам нужно взять правоприменение под контроль».
Другими словами, все и ничего не было выяснено.
Этот законопроект также не был принят Палатой представителей.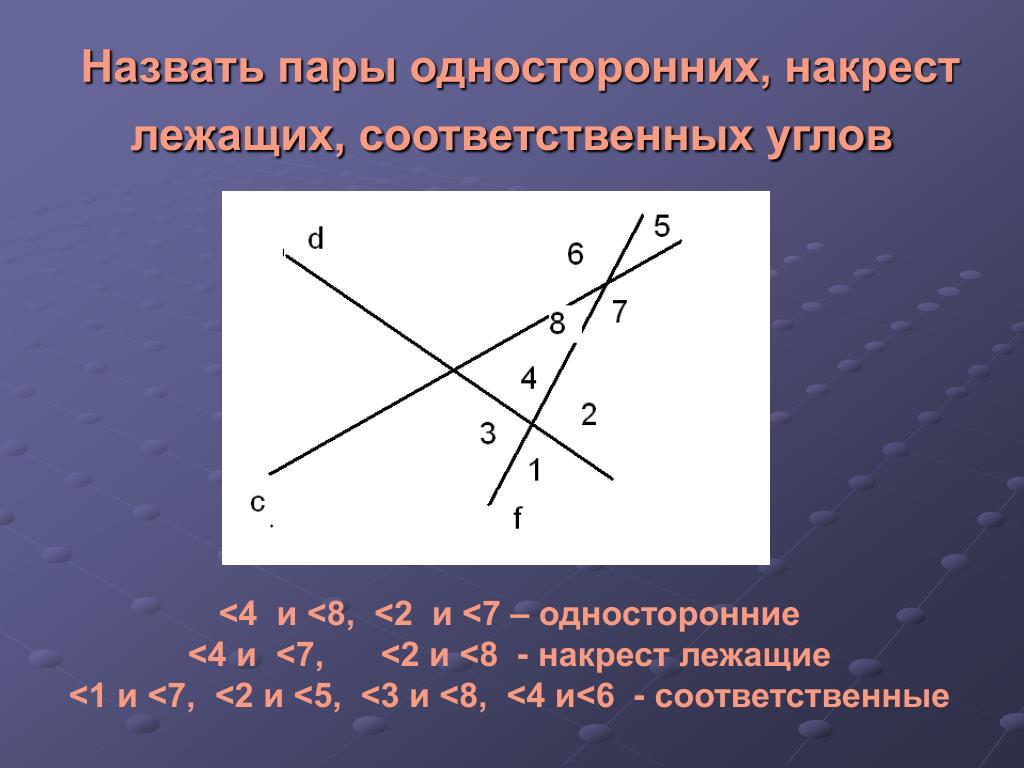
Неудивительно, что дебаты бушуют.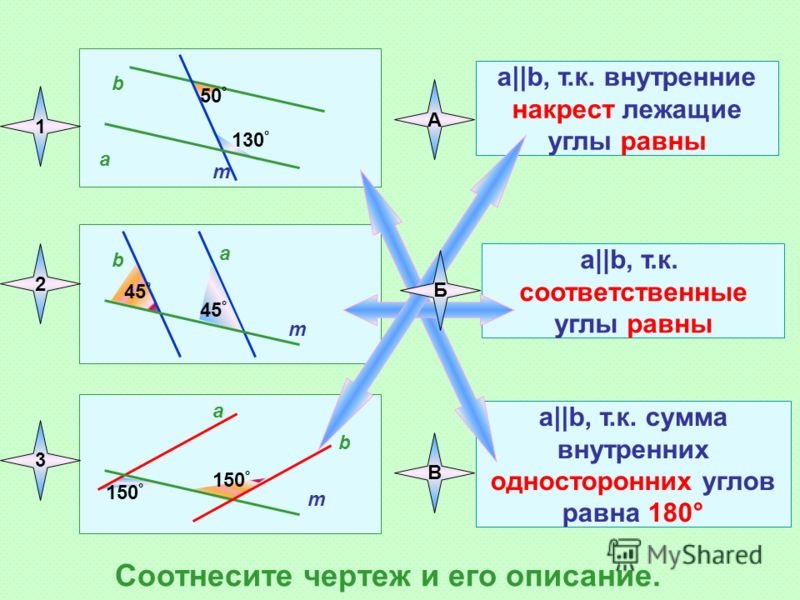
Кроме того, эти соглашения с отдельными землевладельцами заключаются на ежегодной основе, что оставляет неопределенность в отношении долгосрочного доступа, поскольку землевладельцы могут передумать об участии в программе или могут продать свою собственность.
Сервитуты — это законное право использовать чужое имущество для определенной цели. Сервитуты доступа и права проезда конкретно предоставляют владельцу право путешествовать по чужой собственности. Многие государственные сервитуты предоставляют широкой публике право их использовать. Часто сервитуты такого типа создаются в процессе продажи земли или обмена землей, но они также могут быть приобретены агентством по управлению земельными ресурсами или партнером по охране природы без смены владельца земли. В местах, где сервитут пересекает или огибает угол собственности, сервитут должен быть всего несколько футов в ширину и несколько футов в длину. Преимущества этого решения заключаются в том, что сервитуты действуют вечно, даже если земля продана, а узкий путь сервитута означает, что представители общественности должны придерживаться назначенного маршрута — они не могут блуждать по остальной части частной земли. .
Одним из таких последствий является то, что теперь миллионы акров государственной земли считаются запрещенными.
Что бы ни случилось дальше, эта юридическая серая зона вполне может оставаться ясной как туман на десятилетия вперед.
0
свойство real trRadius: 15.0
свойство real brRadius: 0.0
свойство реальное blRadius: 0.0
Путь формы {
strokeColor: "прозрачный"
fillColor: "красный"
стартX: 0; startY: расширенныйShape.tlRadius
Дуга Пути {
х: расширенныйShape.tlRadius; г: 0
радиусX: advancedShape.tlRadius; радиусY: advancedShape.tlRadius
useLargeArc: ложь
}
Линия пути {
x: advancedShape.width - advancedShape.trRadius; г: 0
}
Дуга Пути {
х: расширенныйShape.width; у: расширенныйShape.trRadius
радиусX: advancedShape.trRadius; радиусY: advancedShape.trRadius
useLargeArc: ложь
}
Линия пути {
х: расширенныйShape.width; у: advancedShape.height - advancedShape.brRadius
}
Дуга Пути {
x: advancedShape.width - advancedShape.brRadius; у: расширенныйShape.height
радиусX: advancedShape.brRadius; радиусY: advancedShape.
brRadius
useLargeArc: ложь
}
Линия пути {
х: расширенныйShape.blRadius; у: расширенныйShape.height
}
Дуга Пути {
х: 0; y: advancedShape.height - advancedShape.blRadius
радиусX: advancedShape.blRadius; радиусY: advancedShape.blRadius
useLargeArc: ложь
}
Линия пути {
х: 0; у: расширенныйShape.tlRadius
}
}
}
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.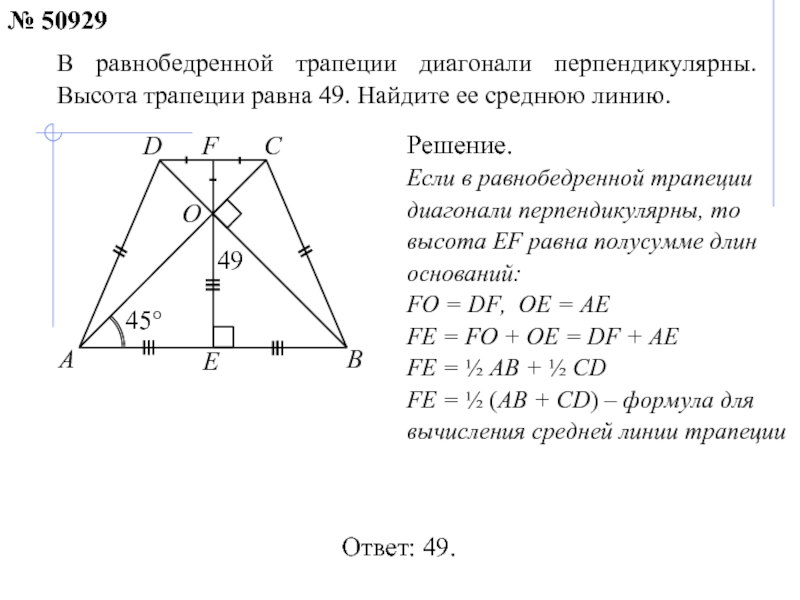
По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
\circ\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Докажем, что \(M\)
– середина \(AD\)
.
Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
И ее свойства проистекают из этого обстоятельства.
А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
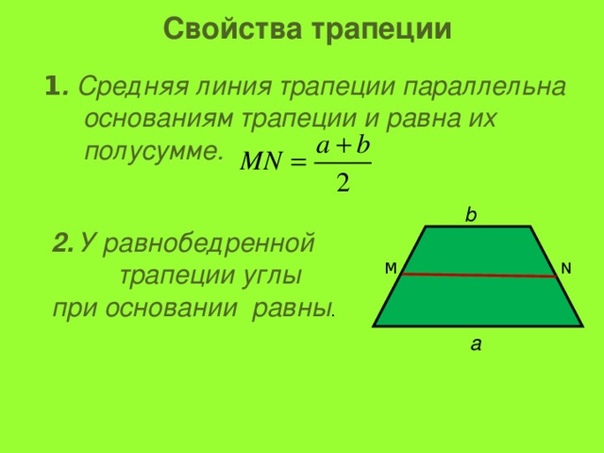{2}
.
Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
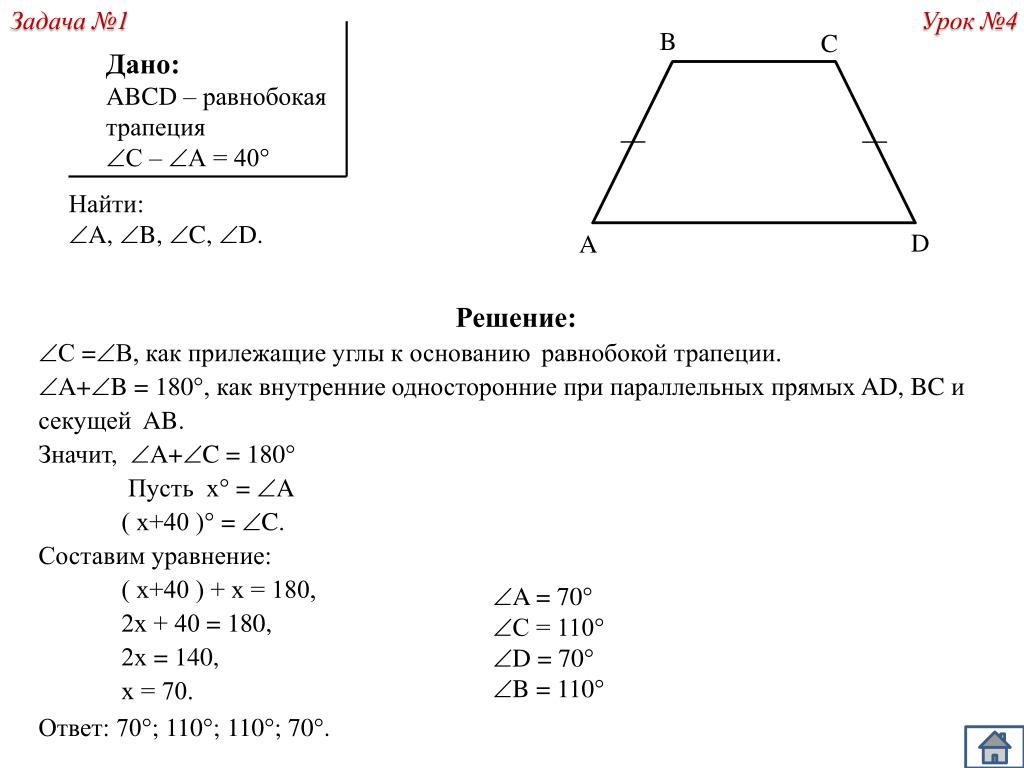
Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.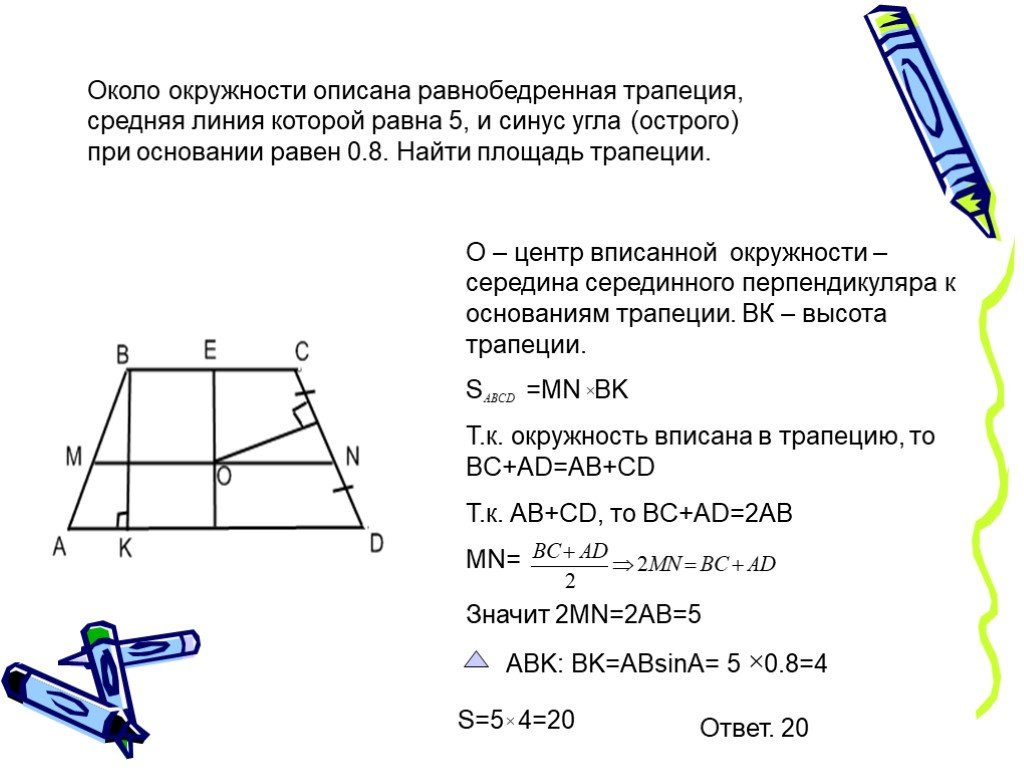
Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
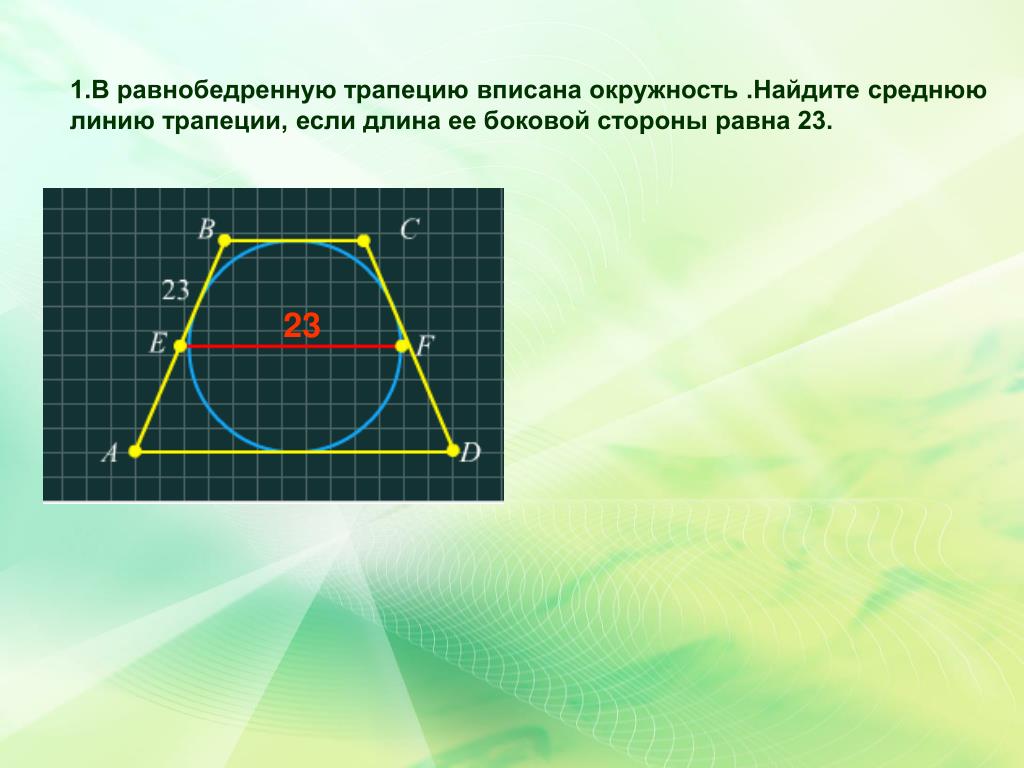
Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.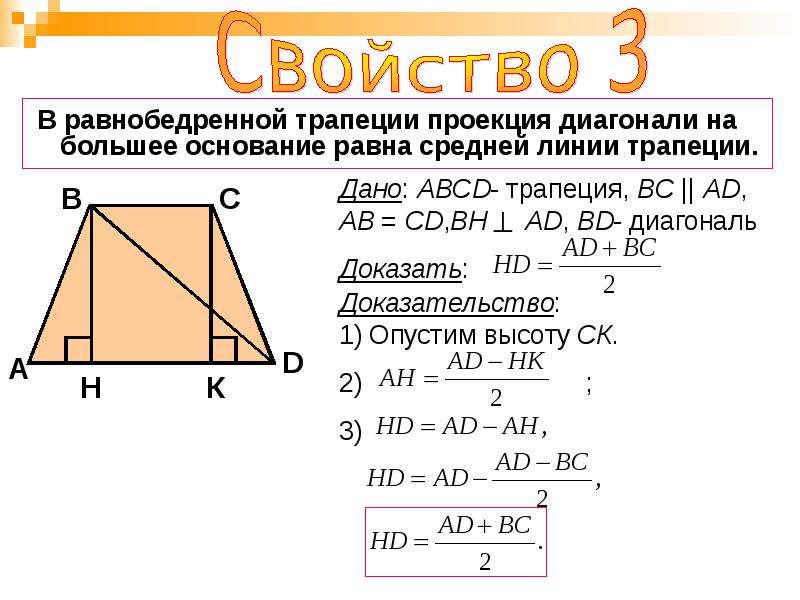
Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.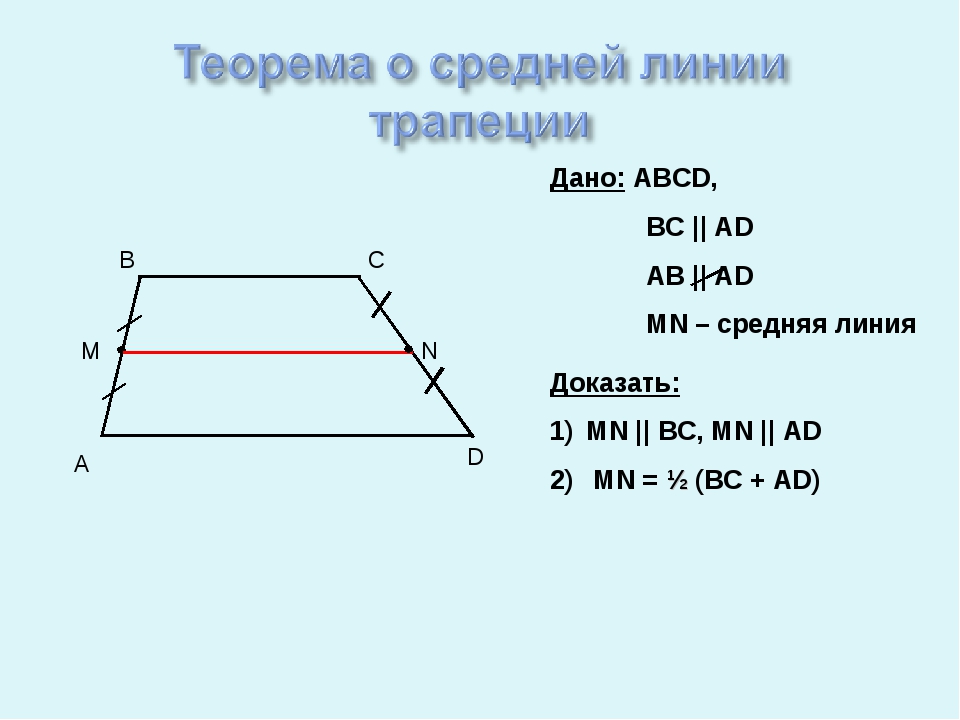
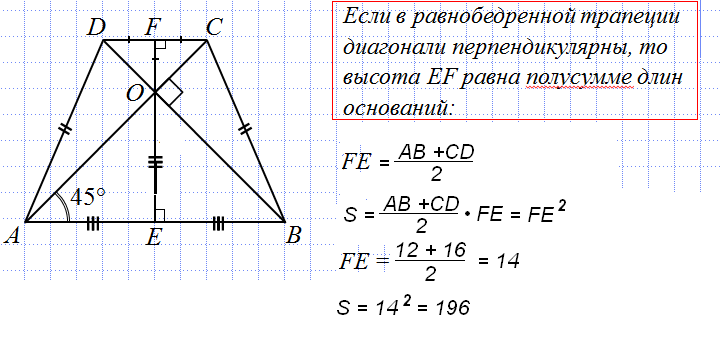
Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Если таких пар две, то получится параллелограмм. Две параллельные стороны называются основания , а две другие стороны называются ножками .
Нам необходимо дополнительно знать, что два основания рассматриваемой равнобедренной трапеции имеют одинаковую длину..jpg)
ниже)
Следовательно, нормальный вектор плоскости BCD будет являться направляющим вектором для прямой.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
Сделать чертеж пирамиды в системе
координат.
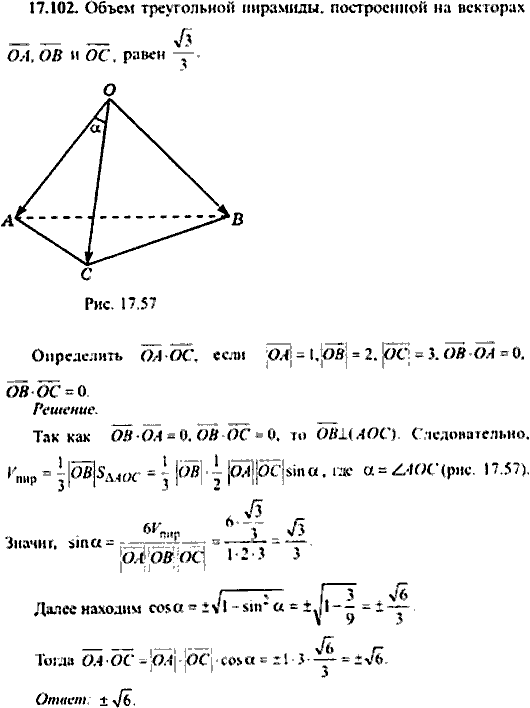
Одна вершина расположена над прямоугольным основанием пирамиды. Остальные четыре вершины лежат в четырех углах основания.
Все боковые грани пирамиды представляют собой треугольники, где одна сторона каждого треугольника сливается со стороной основания. Давайте узнаем больше об объеме пирамиды, а также о ее формуле, доказательстве и нескольких решенных примерах.
Название пирамиды происходит от ее основания. Например, пирамида с квадратным основанием называется квадратной пирамидой. Таким образом, площадь основания играет главную роль в определении объема пирамиды. Объем пирамиды есть не что иное, как одна треть произведения площади основания на ее высоту.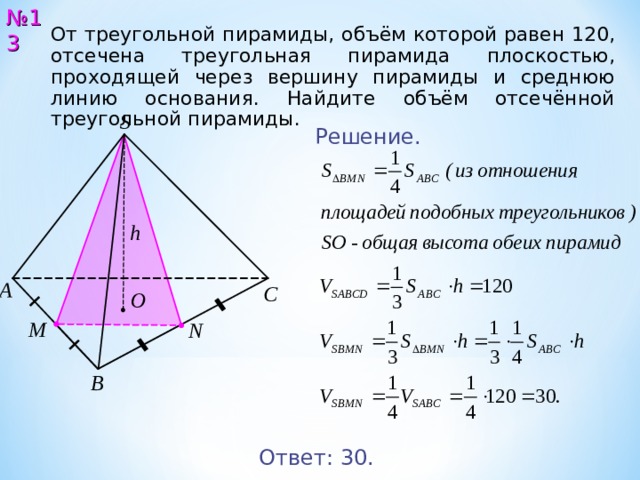
Таким образом, (x/2) 2 + h 2 = s 2 . Мы можем использовать это при решении задач нахождения объема пирамиды по ее наклонной высоте.
Вычислите ее объем.
Объем пирамиды, площадь основания которой равна «B», а высота — «h», составляет (1/3) (Bh) кубических единиц.
Его базовая площадь «B» находится путем применения формулы площади прямоугольника. т. е. если «l» и «w» — размеры основания (прямоугольника), то его площадь равна B = lw. Если «h» — высота пирамиды, то ее объем равен V = (1/3) (Bh) = (1/3) lwh кубических единиц.
В результате математических операций получим
Таким образом, вы можете познакомиться с каждым процессом решения математических функций от производных исчисления с помощью этого калькулятора.
Этот производный калькулятор дает вам ответы за доли секунды.
Математически,
Или можете загрузить пример из выпадающего списка.
4. Плотность распределения
Системы случайных величин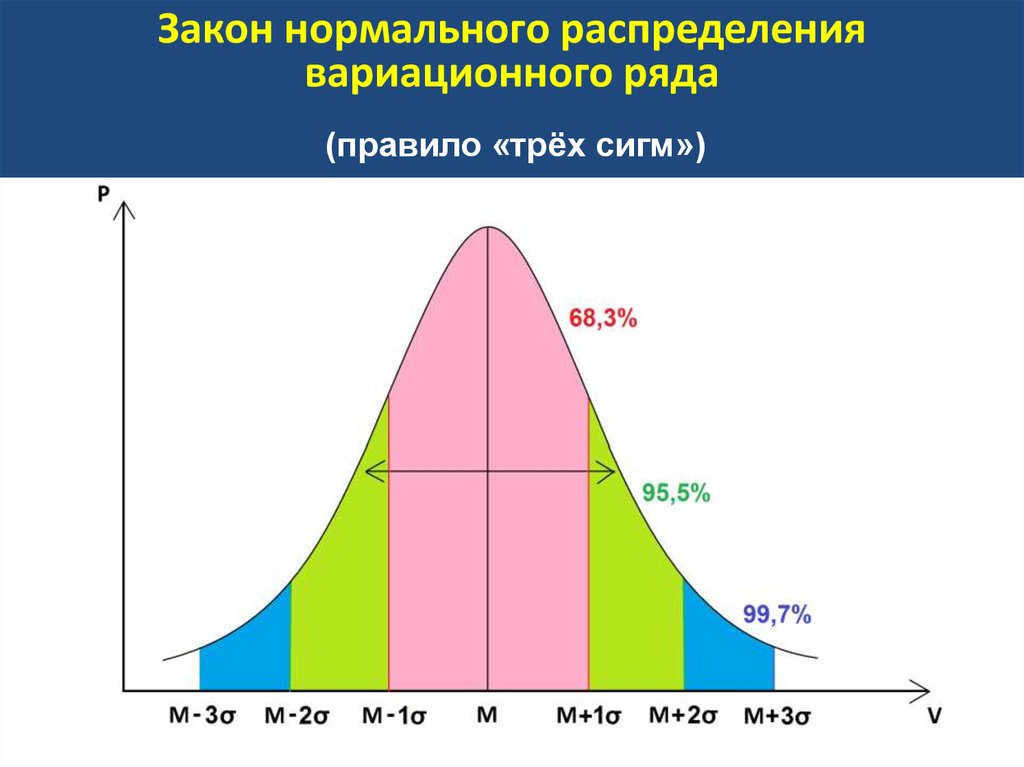
Общая запись нормального закона для системы произвольного числа случайных величин
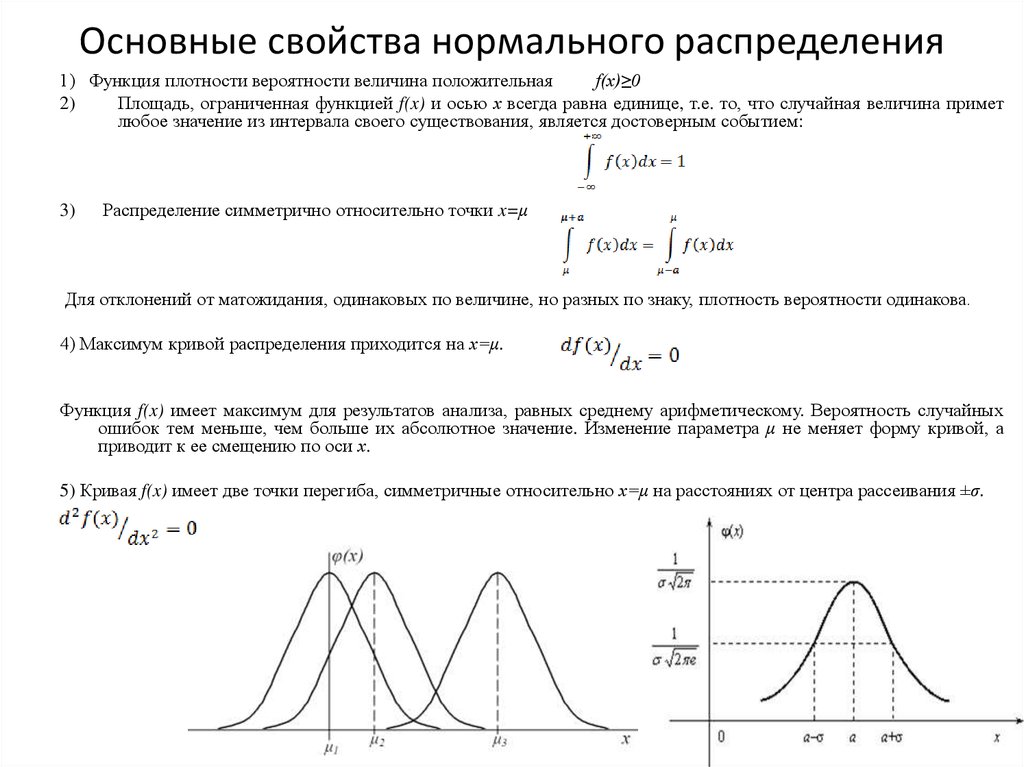Композиция законов распределения
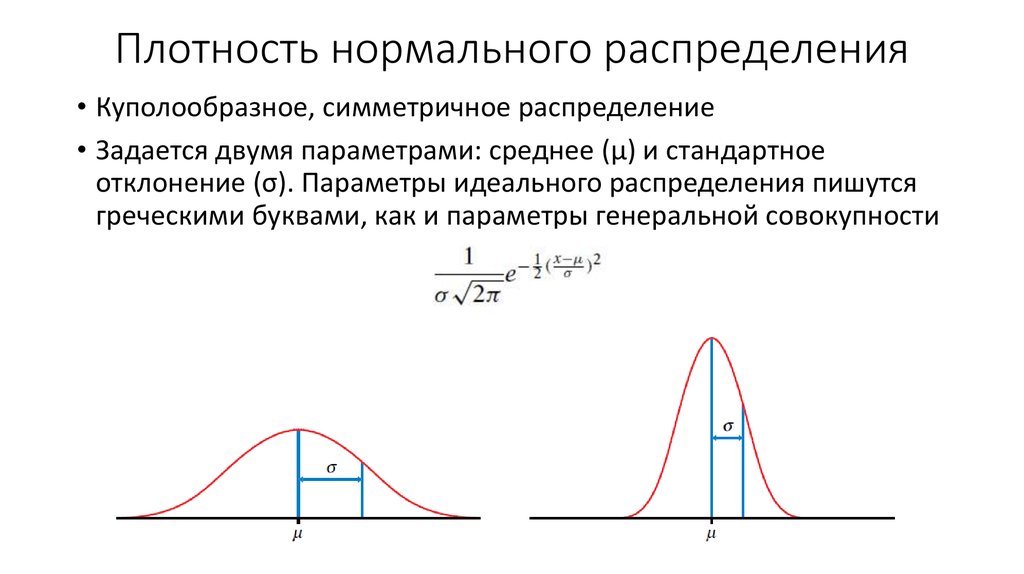3. Доверительный интервал. Доверительная вероятность
7.2. Производная от случайной функции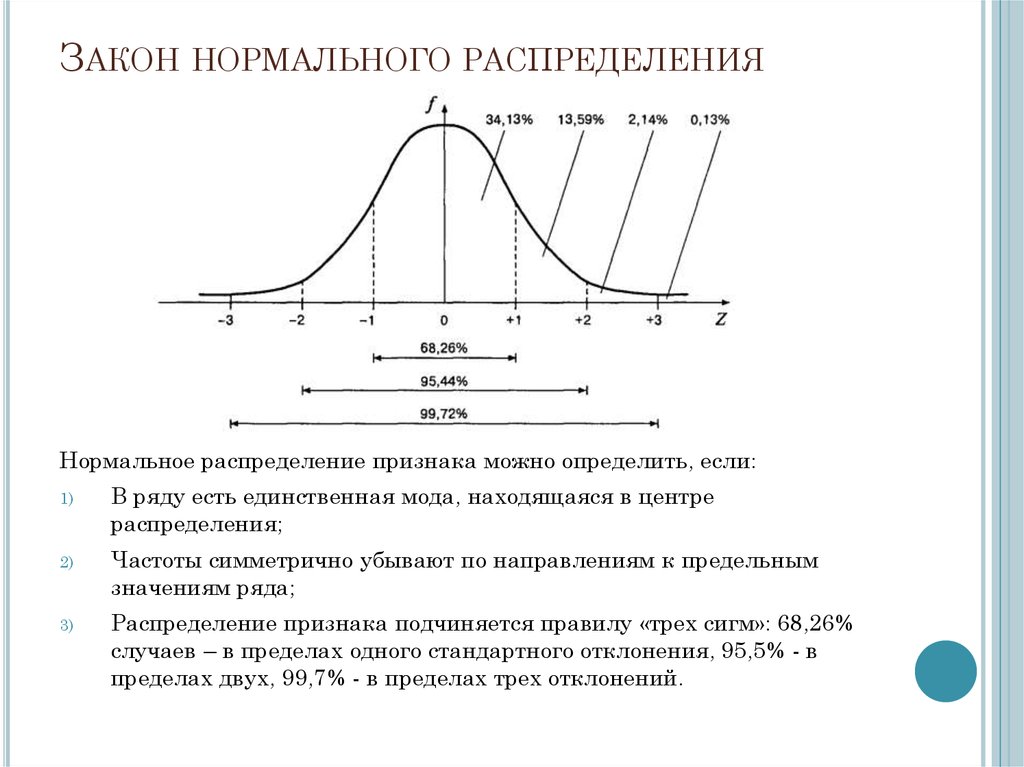
7. Эргодическое свойство стационарных случайных функций
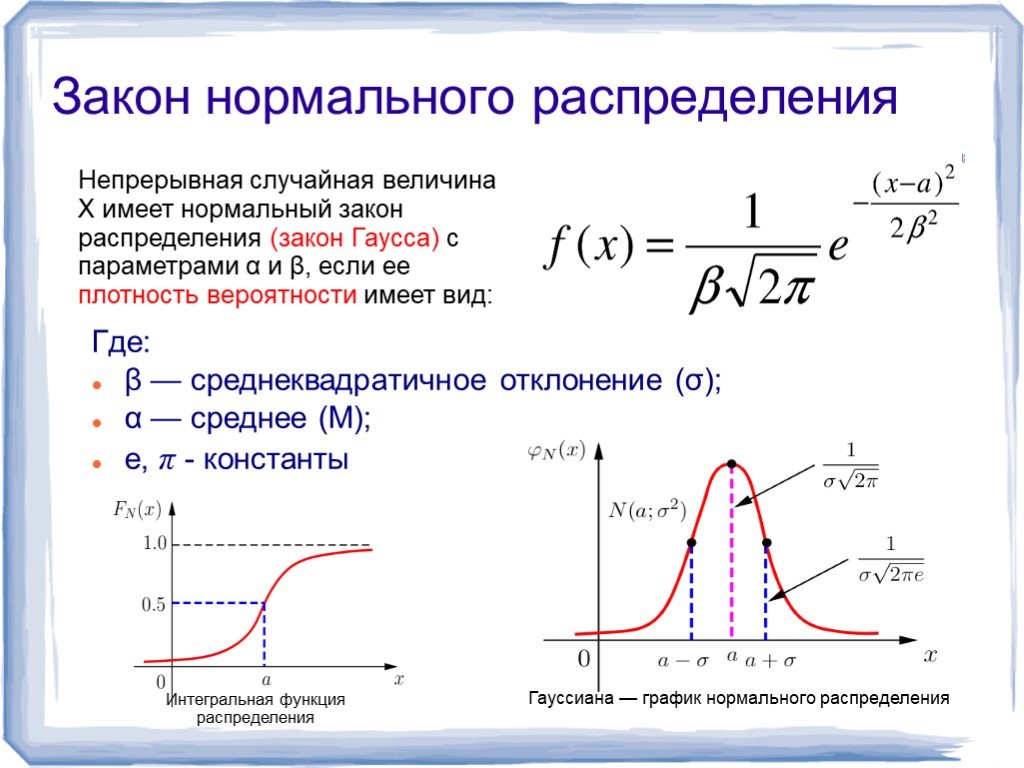3. Поток событий. Простейший поток и его свойства
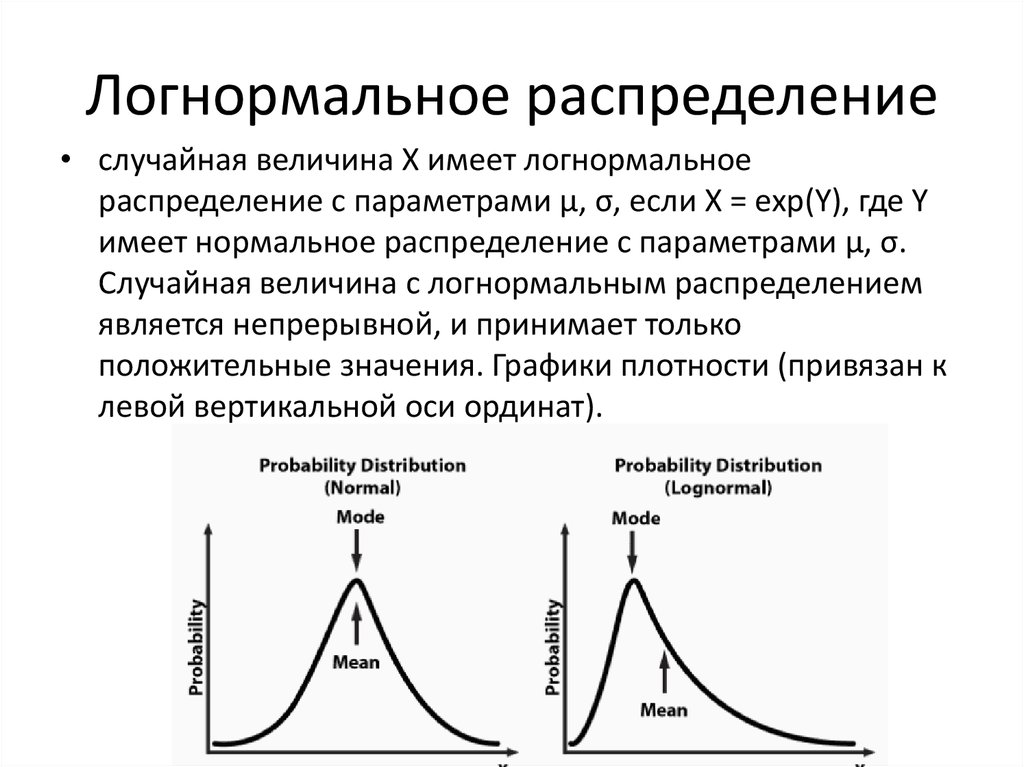Причинами это являются:
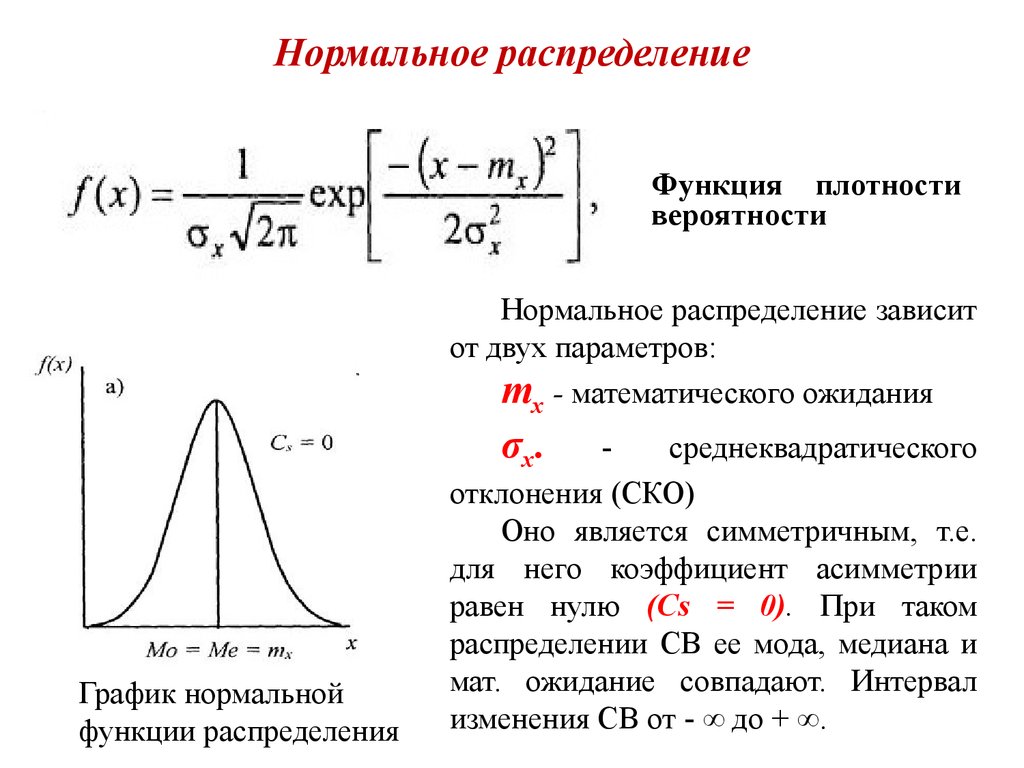В 1713 году была опубликована книга швейцарского математика Якоба Бернулли «Искусство предположений». В этой книге был рассмотрен ряд вопросов теории вероятностей. Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).
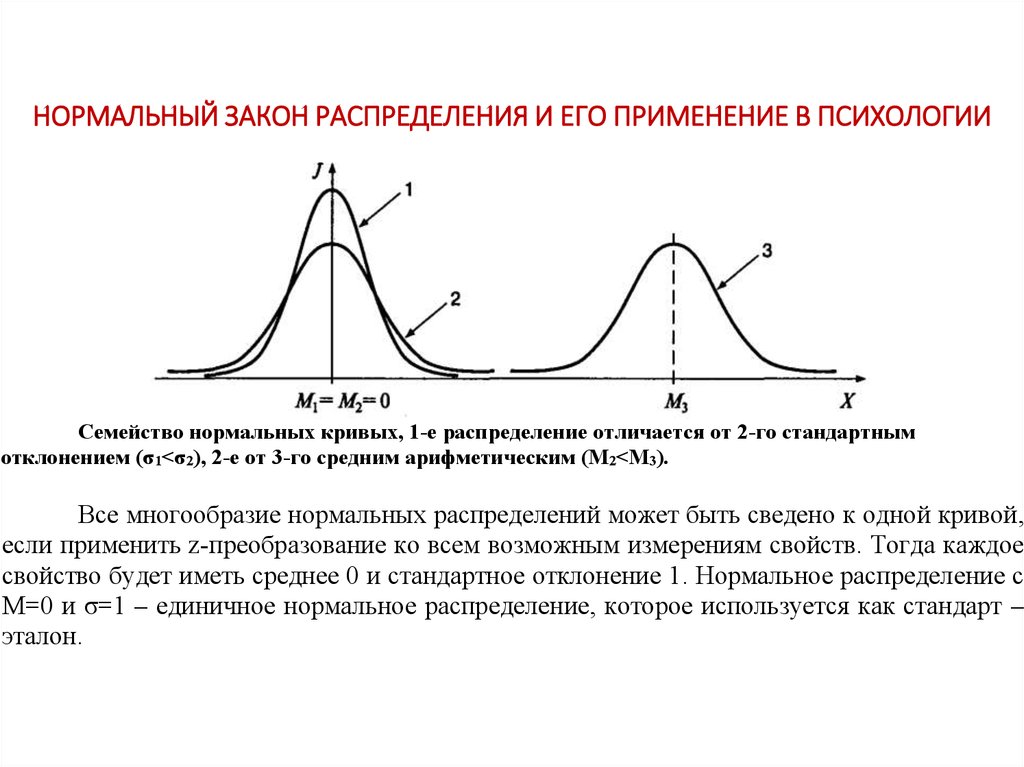1). То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление формулы нормального распределения значительно упростило расчеты вероятностей событий.
4).
Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.
1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле: U= (X-μ)/σ.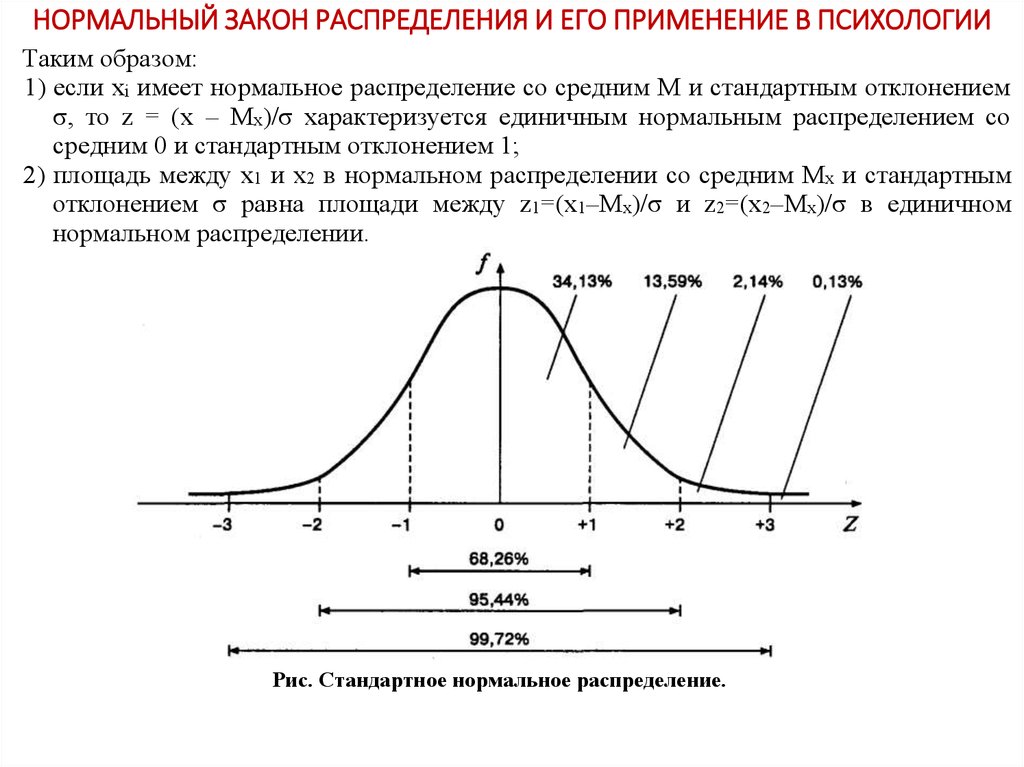
ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.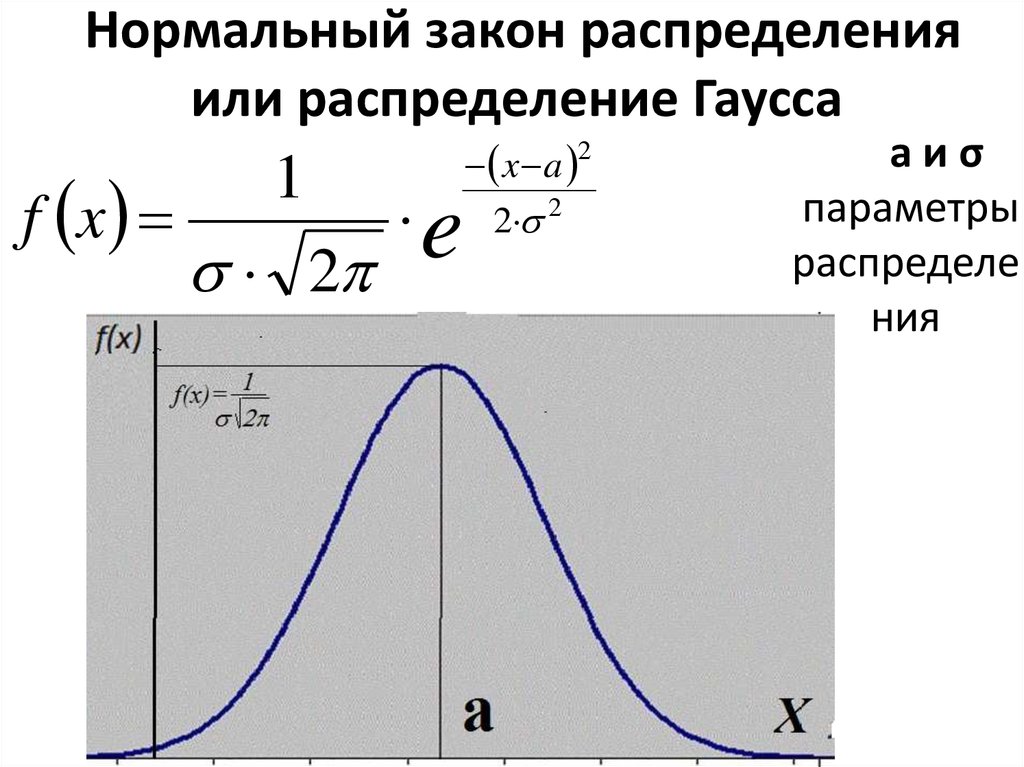
Середина диапазона также известна как 9.0023 означает дистрибутива.
Однако обратное не всегда верно; то есть не все симметричные распределения являются нормальными. На кривой нормального распределения пик всегда находится посередине, а среднее значение, мода и медиана одинаковы.
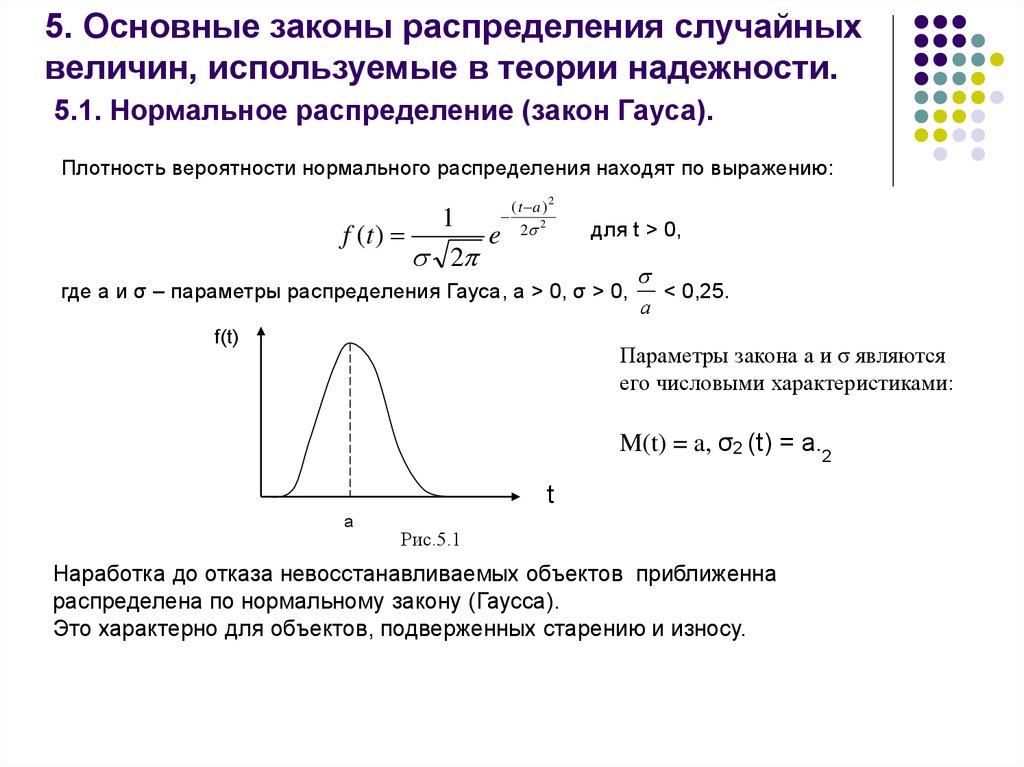
Однако его симметричность все равно будет сохраняться.
techtarget.com» type=»text/html» frameborder=»0″> Асимметрия и эксцесс в нормальном распределении
также: статистический анализ, гистограмма, зависимая переменная, данные, специалист по данным, большие данные, классификация данных, интеллектуальный анализ данных, контекст данных и анализ временных рядов в ИТ-средах. 
..
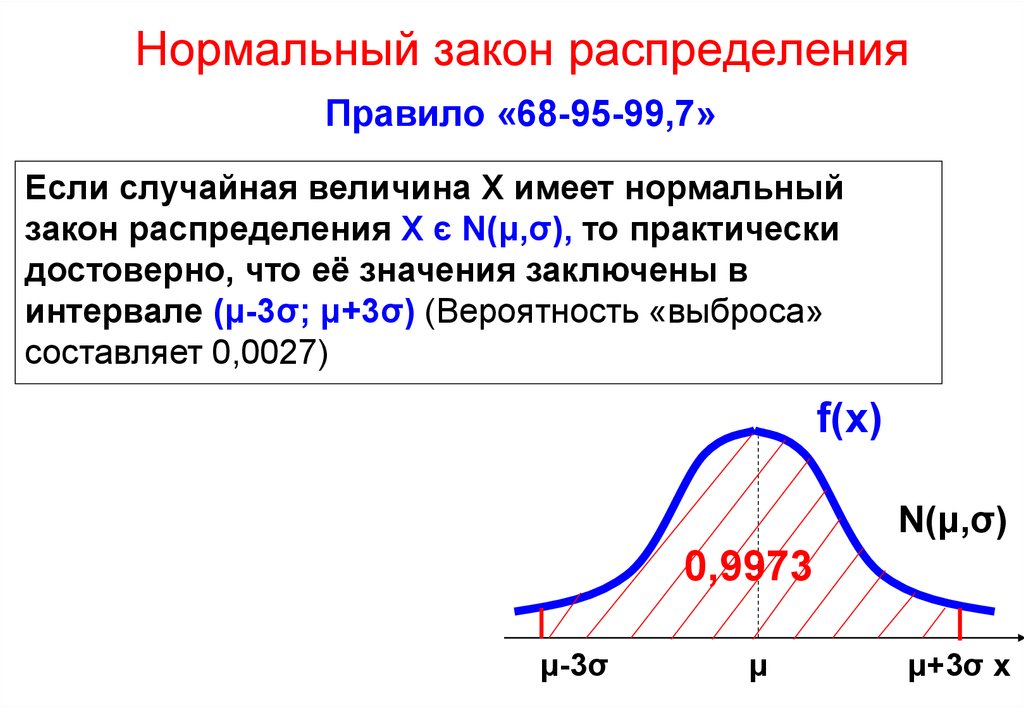Проверяет входящий и исходящий трафик…
..
..
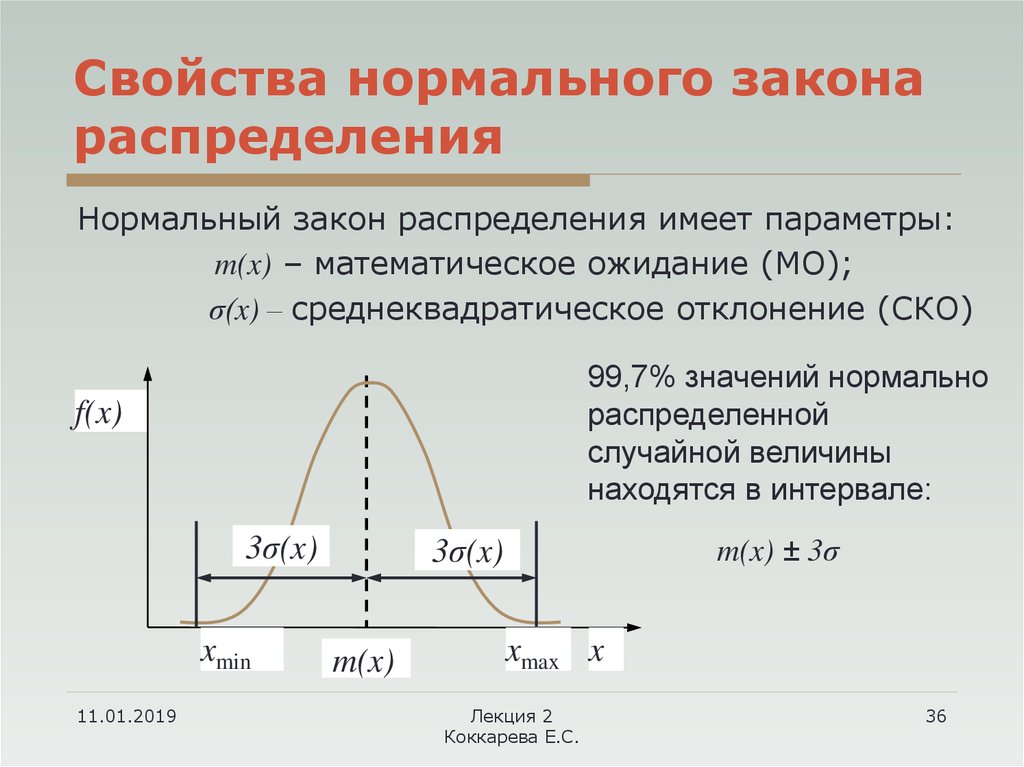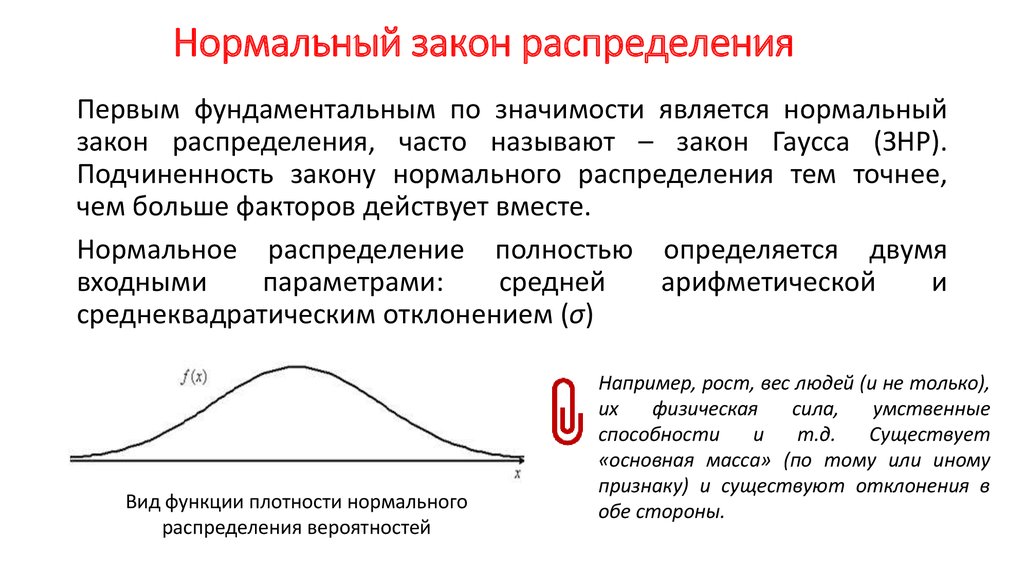Кривая применяется к оси Y (цена), поскольку она является переменной, тогда как время в течение всего периода просто линейно. Таким образом, область в пределах одного стандартного отклонения от среднего значения — это область стоимости, в которой цена и фактическая стоимость актива наиболее точно совпадают.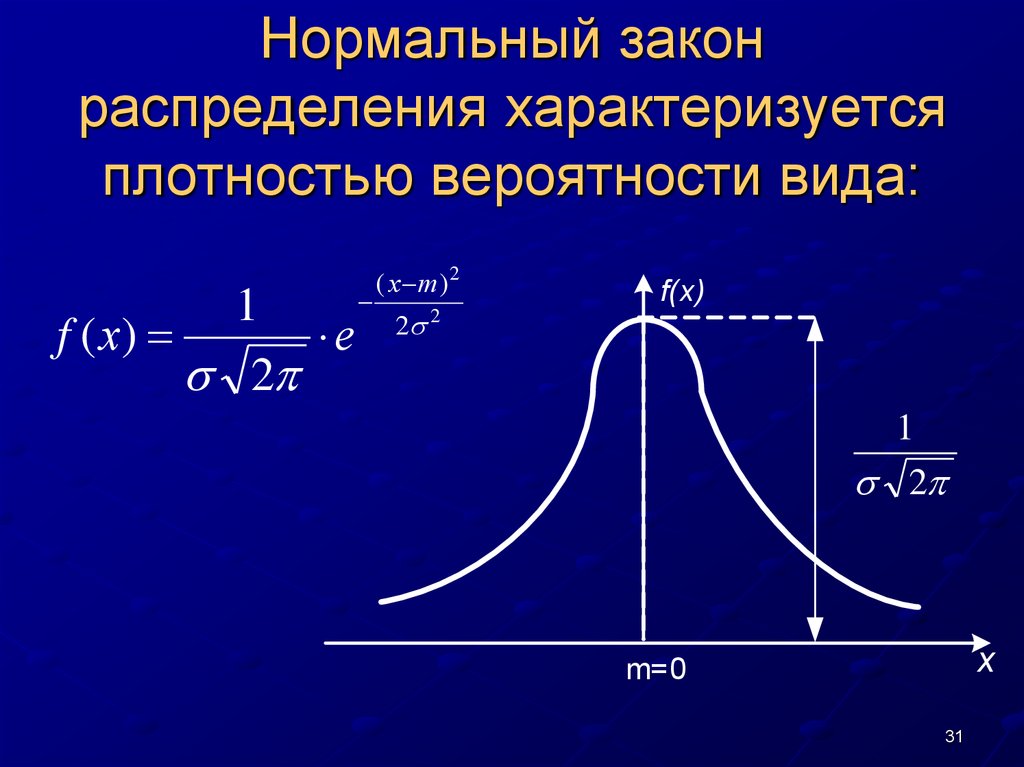
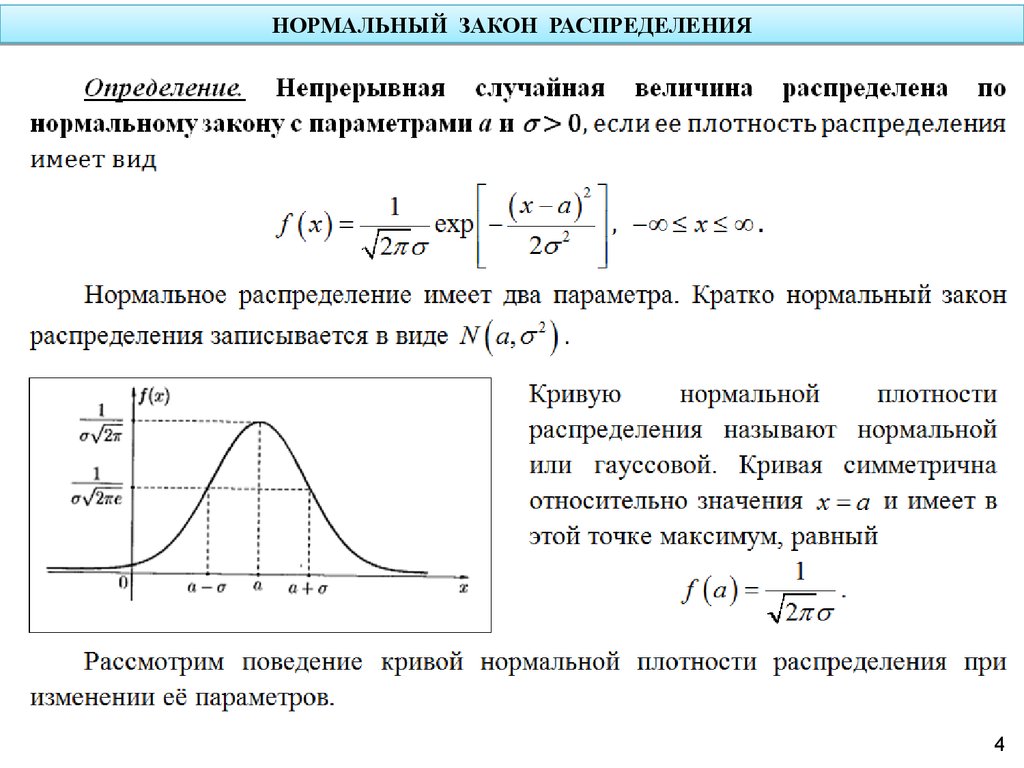Асимметричное распределение либо смещено влево, либо смещено вправо. Распределение с асимметрией влево, известное как отрицательное распределение, имеет более длинный левый хвост. Распределение с асимметрией вправо или распределение с асимметрией в положительном направлении имеет более длинный правый хвост. Определение того, является ли среднее значение положительным или отрицательным, важно при анализе асимметрии набора данных, поскольку это влияет на анализ распределения данных. Логарифмически нормальное распределение — это обычно цитируемое асимметричное распределение с асимметрией вправо.
