Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.
В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.
Содержание темы:
- Минор $M_{ij}$ элемента $a_{ij}$.
- Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$.
- Минор k-го порядка матрицы $A_{m\times n}$. Главный минор, базисный минор, окаймляющий минор.
- Минор k-го порядка матрицы $A_{n\times n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Минор $M_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{n\times n}$ (т.е. квадратная матрица n-го порядка).
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A_{n\times n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).
Для примера рассмотрим квадратную матрицу четвёртого порядка: $A=\left( \begin{array} {ccc} 1 & 0 & -3 & 9\\ 2 & -7 & 11 & 5 \\ -9 & 4 & 25 & 84\\ 3 & 12 & -5 & 58 \end{array} \right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:
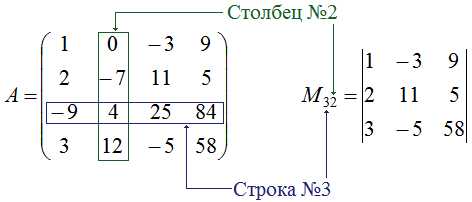
Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$ M_{32}=\left| \begin{array} {ccc} 1 & -3 & 9\\ 2 & 11 & 5 \\ 3 & -5 & 58 \end{array} \right|= 1\cdot 11\cdot 58+(-3)\cdot 5\cdot 3+2\cdot (-5)\cdot 9-9\cdot 11\cdot 3-(-3)\cdot 2\cdot 58-5\cdot (-5)\cdot 1=579. $$Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.
Часто вместо словосочетания «минор элемента матрицы» в литературе встречается «минор элемента определителя». Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя $\left| \begin{array} {ccc} -1 & 3 & 2\\ 9 & 0 & -5 \\ 4 & -3 & 7 \end{array} \right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:
Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:
$$ M_{12}=\left| \begin{array} {ccc} 9 & -5\\ 4 & 7 \end{array} \right|=9\cdot 7-(-5)\cdot 4=83. $$Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.
Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{n\times n}$ (т.е. квадратная матрица n-го порядка).
Алгебраическое дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A_{n\times n}$ находится по следующей формуле: $$ A_{ij}=(-1)^{i+j}\cdot M_{ij}, $$где $M_{ij}$ – минор элемента $a_{ij}$.
Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=\left( \begin{array} {ccc} 1 & 0 & -3 & 9\\ 2 & -7 & 11 & 5 \\ -9 & 4 & 25 & 84\\ 3 & 12 & -5 & 58 \end{array} \right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:
Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=\left( \begin{array} {ccc} -5 & 10 & 2\\ 6 & 9 & -4 \\ 4 & -3 & 1 \end{array} \right)$. Согласно формуле $A_{12}=(-1)^{1+2}\cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:
Минор k-го порядка матрицы $A_{m\times n}$
Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_{m\times n}$, т.е. матрица, содержащая m строк и n столбцов.
Минором k-го порядка матрицы $A_{m\times n}$ называется определитель, элементы которого расположены на пересечении k строк и k столбцов матрицы $A$ (при этом предполагается, что $k≤ m$ и $k≤ n$).
Например, рассмотрим матрицу $A=\left( \begin{array} {ccc} -1 & 0 & -3 & 9\\ 2 & 7 & 14 & 6 \\ 15 & -27 & 18 & 31\\ 0 & 1 & 19 & 8\\ 0 & -12 & 20 & 14\\ 5 & 3 & -21 & 9\\ 23 & -10 & -5 & 58 \end{array} \right)$ и запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки с номерами 2, 4, 6 и столбцы с номерами 1, 2, 4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:
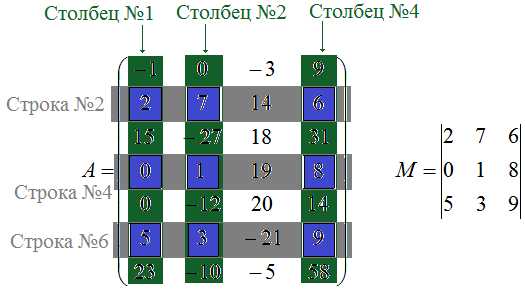
Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.
Минор k-го порядка матрицы $A_{m\times n}=(a_{ij})$ называется главным, если на главной диагонали данного минора находятся только главные диагональные элементы матрицы $A$.
Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_{11}$, $a_{22}$, $a_{33}$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_{11}=-1$, $a_{22}=7$, $a_{33}=18$, $a_{44}=8$. На рисунке они выделены розовым цветом:
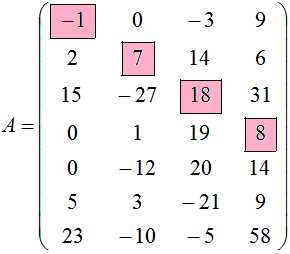
Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_{11}=-1$ и $a_{33}=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:
Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.
Пусть некий минор $M$ k-го порядка матрицы $A_{m\times n}$ не равен нулю, т.е. $M\neq 0$. При этом все миноры, порядок которых выше k, равны нулю. Тогда минор $M$ называют базисным, а строки и столбцы, на которых расположены элементы базисного минора, именуют базисными строками и базисными столбцами.
Для примера рассмотрим матрицу $A=\left( \begin{array} {ccc} -1 & 0 & 3 & 0 & 0 \\ 2 & 0 & 4 & 1 & 0\\ 1 & 0 & -2 & -1 & 0\\ 0 & 0 & 0 & 0 & 0 \end{array} \right)$. Звапишем минор этой матрицы, элементы которого расположены на пересечении строк с номерами 1, 2, 3 и столбцов с номерами 1, 3, 4. Мы получим минор третьего порядка:
Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$ M=\left| \begin{array} {ccc} -1 & 3 & 0\\ 2 & 4 & 1 \\ 1 & -2 & -1 \end{array} \right|=4+3+6-2=11. $$Итак, $M=11\neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.
Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.
Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.
Введём ещё одно понятие – окаймляющий минор.
Пусть некий минор k-го порядка $M$ матрицы $A_{m\times n}$ расположен на пересечении k строк и k столбцов. Добавим к набору этих строк и столбцов ещё одну строку и столбец. Полученный минор (k+1)-го порядка именуют окаймляющим минором для минора $M$.
Для примера обратимся к матрице $A=\left( \begin{array} {ccc} -1 & 2 & 0 & -2 & -14\\ 3 & -17 & -3 & 19 & 29\\ 5 & -6 & 8 & -9 & 41\\ -5 & 11 & 19 & -20 & -98\\ 6 & 12 & 20 & 21 & 54\\ -7 & 10 & 14 & -36 & 79 \end{array} \right)$. Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4.
Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены розовым цветом, а элементы, которые мы добавляем к минору $M$ – зелёным:
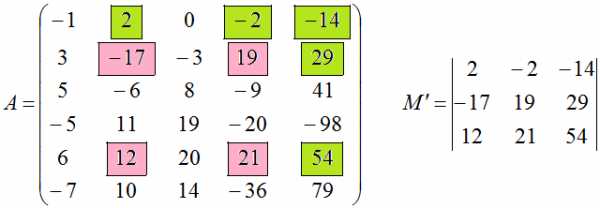
Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):
Минор $M»$ также является окаймляющим минором для минора $M$.
Минор k-го порядка матрицы $A_{n\times n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.
Пусть задан некий минор $M$ k-го порядка матрицы $A_{n\times n}$. Определитель (n-k)-го порядка, элементы которого получены из матрицы $A$ после вычеркивания строк и столбцов, содержащих минор $M$, называется минором, дополнительным к минору $M$.
Для примера рассмотрим квадратную матрицу пятого порядка: $A=\left( \begin{array} {ccc} -1 & 2 & 0 & -2 & -14\\ 3 & -17 & -3 & 19 & 29\\ 5 & -6 & 8 & -9 & 41\\ -5 & 11 & 16 & -20 & -98\\ -7 & 10 & 14 & -36 & 79 \end{array} \right)$. Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка:
Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (убираемые строки и столбцы показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:
Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.
Алгебраическим дополнением к минору $M$ квадратной матрицы $A_{n\times n}$ называется выражение $(-1)^{\alpha}\cdot M’$, где $\alpha$ – сумма номеров строк и столбцов матрицы $A$, на которых расположены элементы минора $M$, а $M’$ – минор, дополнительный к минору $M$.
Словосочетание «алгебраическое дополнение к минору $M$» часто заменяют словосочетанием «алгебраическое дополнение минора $M$».
Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка $ M=\left| \begin{array} {ccc} 2 & -14 \\ -6 & 41 \end{array} \right| $ и дополнительный к нему минор третьего порядка: $M’=\left| \begin{array} {ccc} 3 & -3 & 19\\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array} \right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:
$$ M^*=(-1)^\alpha\cdot M’. $$Параметр $\alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $\alpha=1+3+2+5=11$. Итак:
$$ M^*=(-1)^{11}\cdot M’=-\left| \begin{array} {ccc} 3 & -3 & 19\\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array} \right|. $$В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:
$$ M^*=-\left| \begin{array} {ccc} 3 & -3 & 19\\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array} \right|=-30. $$math1.ru
Минор k-го порядка
Минором порядка k заданной матрицы называется определитель любой квадратной матрицы k-го порядка, которая находится на пересечении произвольных kстолбцов и kстрочек прямоугольной матрицы.
k столбцов
• •• *• *
• •• *
• •
•• *•
••
•*
•*
••
•*
••
•*
••
••
•*
•*
••
•*
••
•*
••
• | • | • | • |
• | • | * |
|
• | |||
• | • | * | • |
• | • | • |
|
• | |||
• | • | * | • |
• | • | • |
|
• | |||
• | • | * |
|
• | |||
• | • | • |
|
• |
* * * *
* * * *
* * * *
* * * *

Пример. В данной матрице выписать миноры всех возможных порядков
| 1 | 5 | 2 |
|
| 3 | 1 | 2 |
|
|
| |||
| −2 | 0 | 5 |
|
|
|
Решение
Миноры первого порядка
|
| 1 |
| =1 |
| 5 |
| =5 |
| 2 |
| = 2 | ||||||
|
|
|
|
|
| |||||||||||||
|
| 3 |
| =3 |
| −2 |
| = −2 |
| 0 |
|
| = 0 | |||||
|
|
|
|
|
|
| ||||||||||||

Рангом матрицы A называется максимальный порядок отличного от нуля минора этой матрицы.
Обозначение: r(A) илиrang(A)
r(Am×n)≤min(m,n)

Базисным минором называется любой из отличных от нуля миноров матрицыА, порядок которого равенr(A).
Замечание. Базисных миноров может быть несколько.
studfiles.net
Определитель 4 порядка. Калькулятор
Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.
Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.
Пример 1. Вычислить определитель методом разложения.
Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются — выделено красным)
В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников
Найденные значения подставляем в выходной детерминант
Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.
Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных

Результаты совпадают, следовательно вычисления проведены верно.
Пример 2. Вычислить определитель матрицы четвертого порядка.
Решение.
Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде
Далее переходим к отысканию определителей по правилу треугольников
Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем
Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком

Метод возведения определителя к треугольному виду
Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.
Пример 3. Найти определитель матрицы сведением к треугольному виду
Решение.
Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим
Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем
Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид
Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе
По свойству, определитель треугольной матрицы равен произведению диагональных элементов.
По желанию можно проверить результат матричным калькулятором.

В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.
Рассмотрим более сложный.
Пример 4.
Найти определитель матрицы 4-го порядка
Решение.
Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант
Для удобства вычислений, меняем третью строчку со вторым местами..
По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.
От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим
Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.
Результат будет следующим
От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.
Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления
Проверка матричным калькулятором подтверждает правильность производимых вычислений.

Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.
yukhym.com
Вычисление дополнительного минора матрицы онлайн
Минором Δij элемента аij квадратной матрицы Аn×n (матрицы n-го порядка) будет определитель матрицы А (n-1) -го порядка, который находим способом вычеркивания i-й строки и j-го столбца из матрицы А (вычеркиваем строку и столбец, на пересечении которых расположен элемент аij).
Рассмотрим квадратную матрицу А
Пусть
Для любого элемента аij матрицы можно найти дополнительный минор Δij посредством вычеркивания строки i и столбца j.
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка является его минор, знак которого состоит из номеров строки и столбца:
Aij = (-1)i+j х Δij,
Mij — обозначение минора элемента аij.
Представим матрицу
Тогда каждому ее элементу будет соответствовать алгебраическое дополнение
(-1)i+j × Δij
Алгебраическое дополнение и минор будут одинаковыми при четной сумме номеров строки и столбца. Если сумма номеров является нечетным числом, то они будут различаться знаком.
В прямоугольных матрицах количество строк не равно количеству столбцов. В этом случае минором k-го порядка матрицы A, состоящей из m строк и n столбцов, является определитель с элементами, находящимися на пересечении k строк и k столбцов матрицы. При этом, k ≤ m и k ≤ n
С помощью онлайн калькулятора вы сможете быстро рассчитать значение минора.
infofaq.ru
Минор и алгебраическое дополнение матрицы.
Определение.
Минором Mij к элементу aij определителя n-го порядка называется определитель (n — 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.Пример 1.
Найти миноры матрицы AA = 571-410203
Решение:
| M11 = | = 1·3 — 0·0 = 3 — 0 = 3 |
| M12 = | = -4·3 — 0·2 = -12 -0 = -12 |
| M13 = | = -4·0 — 1·2 = 0 — 2 = -2 |
| M21 = | = 7·3 — 1·0 = 21 — 0 = 21 |
| M22 = | = 5·3 — 1·2 = 15 — 2 = 13 |
| M23 = | = 5·0 — 7·2 = 0 — 14 = -14 |
| M31 = | = 7·0 — 1·1 = 0 — 1 = -1 |
| M32 = | = 5·0 — 1·(-4) = 0 + 4 = 4 |
| M33 = | = 5·1 — 7·(-4) = 5 + 28 = 33 |
Определение.
Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется числоAij = (-1)i + j · Mij
Пример 2.
Найти алгебраические дополнения матрицы AA11 = 571-410203
Решение:
A11 = (-1)1 + 1·M11 = (-1)2·1003 = 1·3 — 0·0 = 3 — 0 = 3
A12 = (-1)1 + 2·M12 = (-1)3·-4023 = -(-4·3 — 0·2) = -(-12 -0) = 12
A13 = (-1)1 + 3·M13 = (-1)4·-4120 = -4·0 — 1·2 = 0 — 2 = -2
A21 = (-1)2 + 1·M21 = (-1)3·7103 = -(7·3 — 1·0) = -(21 — 0) = -21
A22 = (-1)2 + 2·M22 = (-1)4·5123 = 5·3 — 1·2 = 15 — 2 = 13
A23 = (-1)2 + 3·M23 = (-1)5·5720 = -(5·0 — 7·2) = -(0 — 14) = 14
A31 = (-1)3 + 1·M31 = (-1)4·7110 = 7·0 — 1·1 = 0 — 1 = -1
A32 = (-1)3 + 2·M32 = (-1)5·51-40 = -(5·0 — 1·(-4)) = -(0 + 4) = -4
A33 = (-1)3 + 3·M33 = (-1)6·57-41 = 5·1 — 7·(-4) = 5 + 28 = 33
ru.onlinemschool.com
Вычисление минора и алгебраического дополнения
Понятия минора и алгебраического дополнения изложены в уроке «Определители, свойства определителей, вычисление». А на этой странице тренируемся в решении задач на вычисление миноров и алгебраических дополнений.
Пример 1. Записать и вычислить миноры второго порядка, содержащиеся в первой и третьей строках определителя
Решение. Перебираем все комбинации столбцов определителя и получаем 10 миноров второго порядка:
,
,
,
,
,
,
,
,
,
.
Пример 2. Записать и вычислить алгебраические дополнения к минорам и определителя из предыдущего примера.
Решение. Умножаем минус единицу в степени, которую составляет сумма номеров строк и столбцов, в которых находятся миноры, на дополнительный минор к данному минору. Дополнительный минор получается вычёркиванием из определителя тех строк и столбцов, на пересечении которых находится данный минор. Получаем:
,
.
Пример 3. Найти алгебраические дополнения для элементов и определителя
Решение. Аналогично действиям в предыдущем примере получаем:
,
.
Пример 4. Найти миноры третьего порядка, содержащиеся в первой, третьей и четвёртой строках определителя
Решение. Перебираем все комбинации столбцов определителя и получаем 4 минора третьего порядка:
,
,
,
.
Пример 5. Вычислить алгебраические дополнения для миноров, полученных в предыдущем примере.
Решение. Последовательно вычёркиваем из исходного определителя 4-го порядка строки и столбцы, в которых находятся полученные миноры. Получаем дополнительные миноры к полученным. Эти дополнительные миноры являются определителями первого порядка, то есть, состоят из одного элемента. Вычисляем и получаем:
,
,
,
.
Пример 6. Найти алгебраические дополнения для элементов второй строки определителя
Решение. Вычёркиваем последовательно из определителя элементы второй строки и получаем миноры третьего порядка — дополнительные миноры к этим элементам. На них умножаем минус единицу в степени, определяемой суммой номеров строки и столбца, в которых находятся элементы. Вычисляем и получаем:
Начало темы «Определители»
Продолжение темы «Линейная алгебра»
Поделиться с друзьями
function-x.ru
Определение ранга матрицы. Вычисление ранга матрицы по определению.
Для работы с понятием ранга матрицы нам понадобятся сведения из темы «Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений». В первую очередь это касается термина «минор матрицы», так как ранг матрицы станем определять именно через миноры.
Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.
Эквивалентные матрицы – матрицы, ранги которых равны между собой.
Поясним подробнее. Допустим, среди миноров второго порядка есть хотя бы один, отличный от нуля. А все миноры, порядок которых выше двух, равны нулю. Вывод: ранг матрицы равен 2. Или, к примеру, среди миноров десятого порядка есть хоть один, не равный нулю. А все миноры, порядок которых выше 10, равны нулю. Вывод: ранг матрицы равен 10.
Обозначается ранг матрицы $A$ так: $\rang A$ или $r(A)$. Ранг нулевой матрицы $O$ полагают равным нулю, $\rang O=0$. Напомню, что для образования минора матрицы требуется вычёркивать строки и столбцы, – однако вычеркнуть строк и столбцов более, чем содержит сама матрица, невозможно. Например, если матрица $F$ имеет размер $5\times 4$ (т.е. содержит 5 строк и 4 столбца), то максимальный порядок её миноров равен четырём. Миноры пятого порядка образовать уже не удастся, так как для них потребуется 5 столбцов (а у нас всего 4). Это означает, что ранг матрицы $F$ не может быть больше четырёх, т.е. $\rang F≤4$.
В более общей форме вышеизложенное означает, что если матрица содержит $m$ строк и $n$ столбцов, то её ранг не может превышать наименьшего из чисел $m$ и $n$, т.е. $\rang A≤\min(m,n)$.
В принципе, из самого определения ранга следует метод его нахождения. Процесс нахождения ранга матрицы по определению можно схематически представить так:
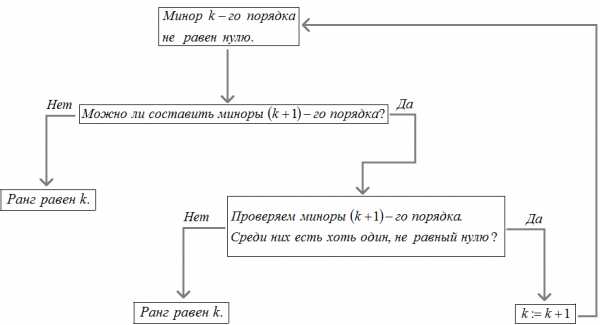
Поясню эту схему более подробно. Начнём рассуждать с самого начала, т.е. с миноров первого порядка некоторой матрицы $A$.
- Если все миноры первого порядка (т.е. элементы матрицы $A$) равны нулю, то $\rang A=0$. Если среди миноров первого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 1$. Переходим к проверке миноров второго порядка.
- Если все миноры второго порядка равны нулю, то $\rang A=1$. Если среди миноров второго порядка есть хотя бы один, не равный нулю, то $\rang A≥ 2$. Переходим к проверке миноров третьего порядка.
- Если все миноры третьего порядка равны нулю, то $\rang A=2$. Если среди миноров третьего порядка есть хотя бы один, не равный нулю, то $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.
- Если все миноры четвёртого порядка равны нулю, то $\rang A=3$. Если среди миноров четвёртого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 4$. Переходим к проверке миноров пятого порядка и так далее.
Что ждёт нас в конце этой процедуры? Возможно, что среди миноров k-го порядка найдётся хоть один, отличный от нуля, а все миноры (k+1)-го порядка будут равны нулю. Это значит, что k – максимальный порядок миноров, среди которых есть хотя бы один, не равный нулю, т.е. ранг будет равен k. Может быть иная ситуация: среди миноров k-го порядка будет хоть один не равный нулю, а миноры (k+1)-го порядка образовать уже не удастся. В этом случае ранг матрицы также равен k. Короче говоря, порядок последнего составленного ненулевого минора и будет равен рангу матрицы.
Перейдём к примерам, в которых процесс нахождения ранга матрицы по определению будет проиллюстрирован наглядно. Ещё раз подчеркну, что в примерах данной темы мы станем находить ранг матриц, используя лишь определение ранга. Иные методы (вычисление ранга матрицы методом окаймляющих миноров, вычисление ранга матрицы методом элементарных преобразований) рассмотрены в следующих темах.
Кстати, вовсе не обязательно начинать процедуру нахождения ранга с миноров самого малого порядка, как это сделано в примерах №1 и №2. Можно сразу перейти к минорам более высоких порядков (см. пример №3).
Пример №1
Найти ранг матрицы $A=\left(\begin{array}{ccccc} 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end{array} \right)$.
Решение
Данная матрица имеет размер $3\times 5$, т.е. содержит три строки и пять столбцов. Из чисел 3 и 5 минимальным является 3, посему ранг матрицы $A$ не больше 3, т.е. $\rang A≤ 3$. И это неравенство очевидно, так как миноры четвёртого порядка образовать мы уже не сможем, – для них нужно 4 строки, а у нас всего 3. Перейдём непосредственно к процессу нахождения ранга заданной матрицы.
Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть ненулевые. Например, 5, -3, 2, 7. Вообще, нас не интересует общее количество ненулевых элементов. Есть хотя бы один не равный нулю элемент – и этого достаточно. Так как среди миноров первого порядка есть хотя бы один, отличный от нуля, то делаем вывод, что $\rang A≥ 1$ и переходим к проверке миноров второго порядка.
Начнём исследовать миноры второго порядка. Например, на пересечении строк №1, №2 и столбцов №1, №4 расположены элементы такого минора: $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|$. У этого определителя все элементы второго столбца равны нулю, поэтому и сам определитель равен нулю, т.е. $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=0$ (см. свойство №3 в теме свойства определителей). Или же можно банально вычислить сей определитель, используя формулу №1 из раздела по вычислению определителей второго и третьего порядков:
$$ \left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=5\cdot 0-0\cdot 7=0. $$Первый проверенный нами минор второго порядка оказался равен нулю. О чём это говорит? О том, что нужно дальше проверять миноры второго порядка. Либо они все окажутся нулевыми (и тогда ранг будет равен 1), либо среди них найдётся хотя бы один минор, отличный от нуля. Попробуем осуществить более удачный выбор, записав минор второго порядка, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №5: $\left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|$. Найдём значение этого минора второго порядка:
$$ \left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|=5\cdot 3-2\cdot 7=1. $$Данный минор не равен нулю. Вывод: среди миноров второго порядка есть хотя бы один, отличный от нуля. Следовательно $\rang A≥ 2$. Нужно переходить к исследованию миноров третьего порядка.
Если для формирования миноров третьего порядка мы станем выбирать столбец №2 или столбец №4, то такие миноры будут равными нулю (ибо они будут содержать нулевой столбец). Остаётся проверить лишь один минор третьего порядка, элементы которого расположены на пересечении столбцов №1, №3, №5 и строк №1, №2, №3. Запишем этот минор и найдём его значение:
$$ \left|\begin{array}{ccc} 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end{array} \right|=-20-18-14+16+21+15=0. $$Итак, все миноры третьего порядка равны нулю. Последний составленный нами ненулевой минор был второго порядка. Вывод: максимальный порядок миноров, среди которых есть хотя бы один, отличный от нуля, равен 2. Следовательно, $\rang A=2$.
Ответ: $\rang A=2$.
Пример №2
Найти ранг матрицы $A=\left( \begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right)$.
Решение
Имеем квадратную матрицу четвёртого порядка. Сразу отметим, что ранг данной матрицы не превышает 4, т.е. $\rang A≤ 4$. Приступим к нахождению ранга матрицы.
Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть хотя бы один, не равный нулю, поэтому $\rang A≥ 1$. Переходим к проверке миноров второго порядка. Например, на пересечении строк №2, №3 и столбцов №1 и №2 получим такой минор второго порядка: $\left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|$. Вычислим его:
$$ \left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|=0-10=-10. $$Среди миноров второго порядка есть хотя бы один, не равный нулю, поэтому $\rang A≥ 2$.
Перейдём к минорам третьего порядка. Найдём, к примеру, минор, элементы которого расположены на пересечении строк №1, №3, №4 и столбцов №1, №2, №4:
$$ \left | \begin{array} {cccc} -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end{array} \right|=105-105=0. $$Так как данный минор третьего порядка оказался равным нулю, то нужно исследовать иной минор третьего порядка. Либо все они окажутся равными нулю (тогда ранг будет равен 2), либо среди них найдётся хоть один, не равный нулю (тогда станем исследовать миноры четвёртого порядка). Рассмотрим минор третьего порядка, элементы которого расположены на пересечении строк №2, №3, №4 и столбцов №2, №3, №4:
$$ \left| \begin{array} {ccc} -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end{array} \right|=-28. $$Среди миноров третьего порядка есть хотя бы один, отличный от нуля, поэтому $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.
Любой минор четвёртого порядка располагается на пересечении четырёх строк и четырёх столбцов матрицы $A$. Иными словами, минор четвёртого порядка – это определитель матрицы $A$, так как данная матрица как раз и содержит 4 строки и 4 столбца. Определитель этой матрицы был вычислен в примере №2 темы «Понижение порядка определителя. Разложение определителя по строке (столбцу)», поэтому просто возьмём готовый результат:
$$ \left| \begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right|=86. $$Итак, минор четвертого порядка не равен нулю. Миноров пятого порядка образовать мы уже не можем. Вывод: наивысший порядок миноров, среди которых есть хотя бы один отличный от нуля, равен 4. Итог: $\rang A=4$.
Ответ: $\rang A=4$.
Пример №3
Найти ранг матрицы $A=\left( \begin{array} {cccc} -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end{array} \right)$.
Решение
Сразу отметим, что данная матрица содержит 3 строки и 4 столбца, поэтому $\rang A≤ 3$. В предыдущих примерах мы начинали процесс нахождения ранга с рассмотрения миноров наименьшего (первого) порядка. Здесь же попробуем сразу проверить миноры максимально возможного порядка. Для матрицы $A$ такими являются миноры третьего порядка. Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №4:
$$ \left| \begin{array} {ccc} 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end{array} \right|=-8-60-20=-88. $$Итак, наивысший порядок миноров, среди которых есть хоть один, не равный нулю, равен 3. Поэтому ранг матрицы равен 3, т.е. $\rang A=3$.
Ответ: $\rang A=3$.
Вообще, нахождение ранга матрицы по определению – в общем случае задача довольно-таки трудоёмкая. Например у матрицы сравнительно небольшого размера $5\times 4$ имеется 60 миноров второго порядка. И если даже 59 из них будут равны нулю, то 60й минор может оказаться ненулевым. Тогда придётся исследовать миноры третьего порядка, которых у данной матрицы 40 штук. Обычно стараются использовать менее громоздкие способы, такие как метод окаймляющих миноров или метод эквивалентных преобразований.
math1.ru


 ОПРЕДЕЛЕНИЕ
ОПРЕДЕЛЕНИЕ

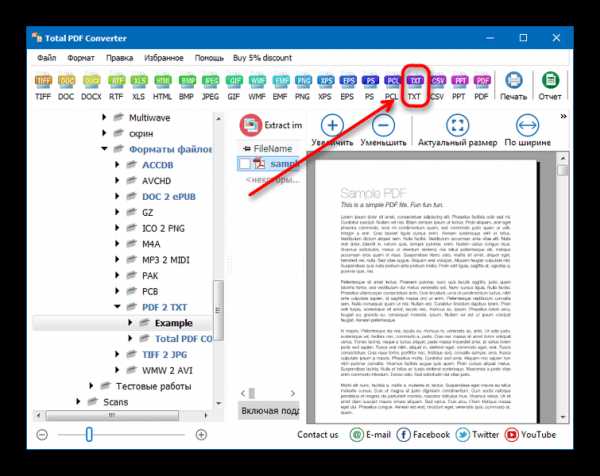
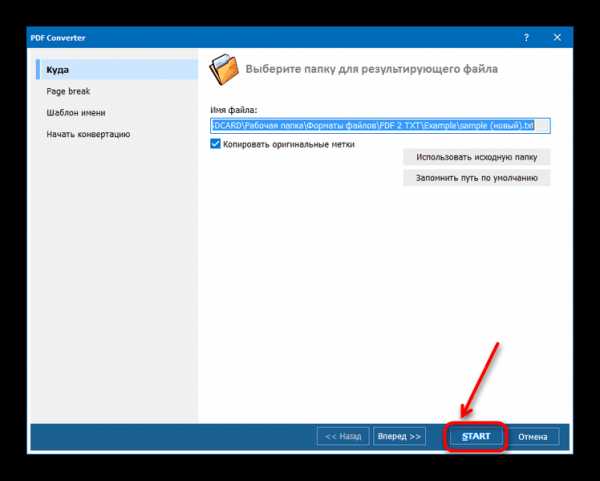


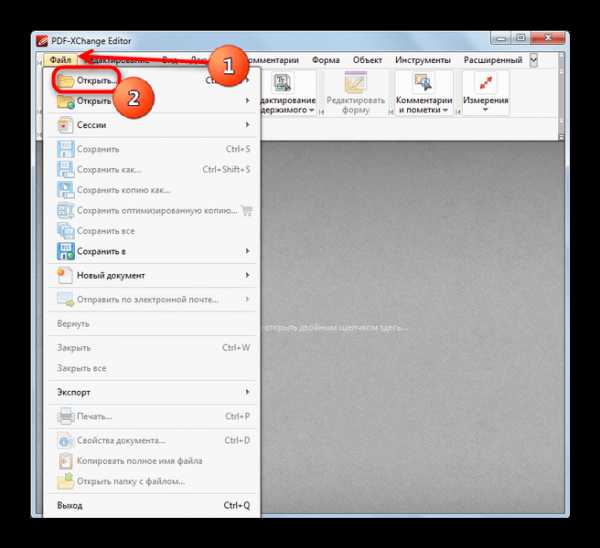
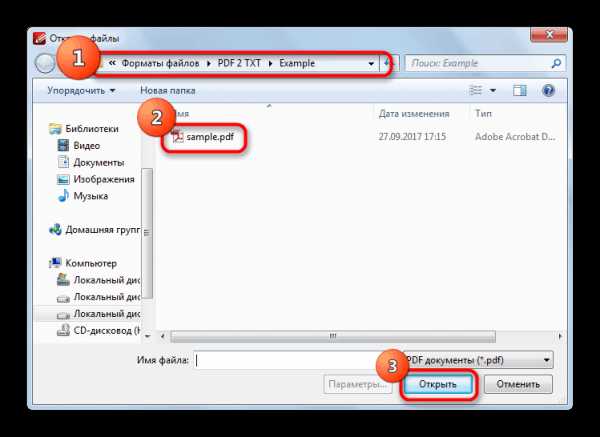
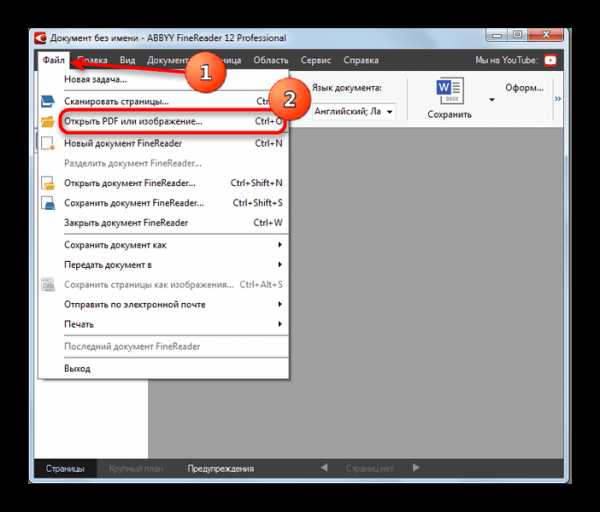
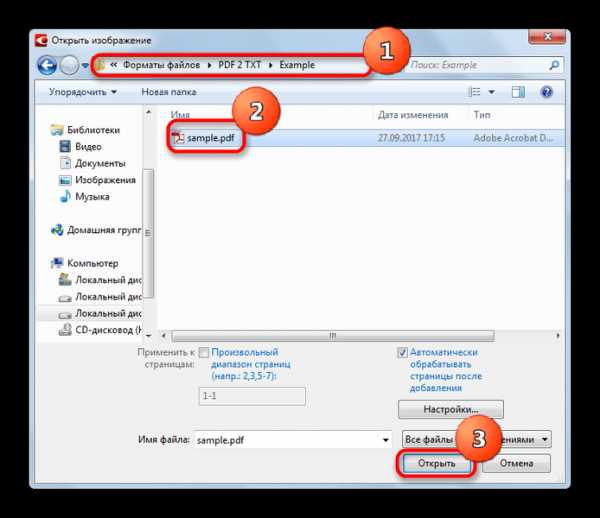

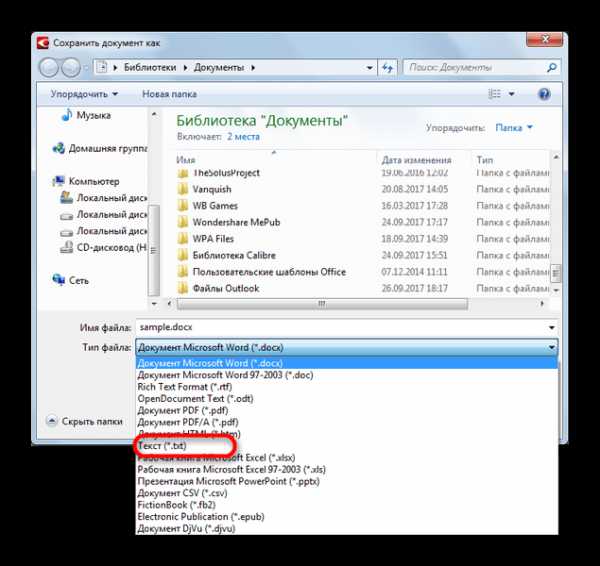
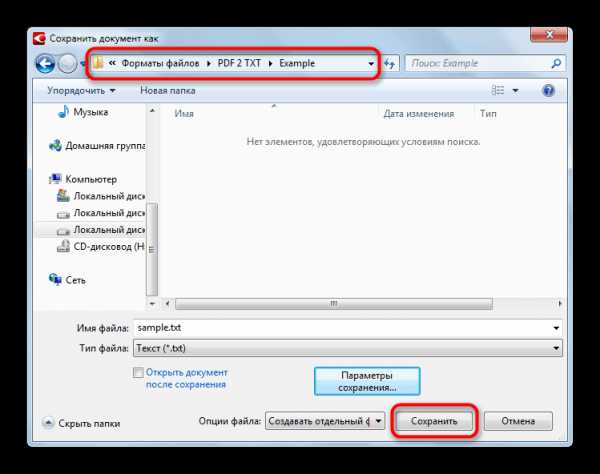
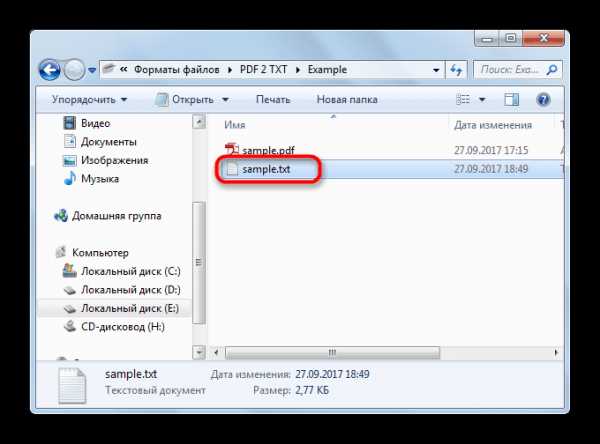
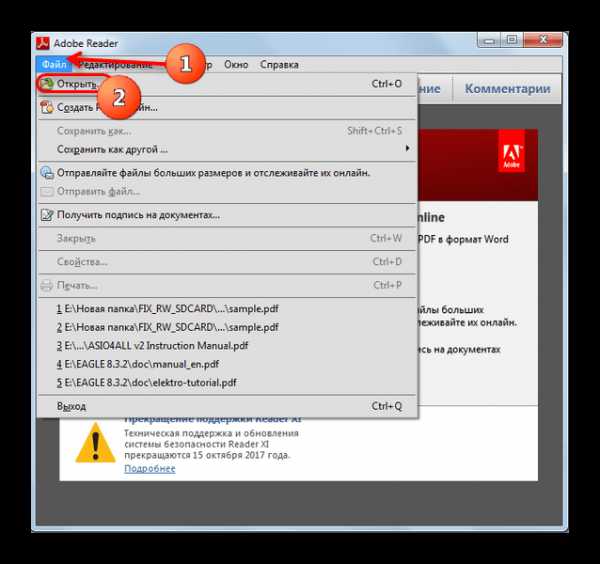
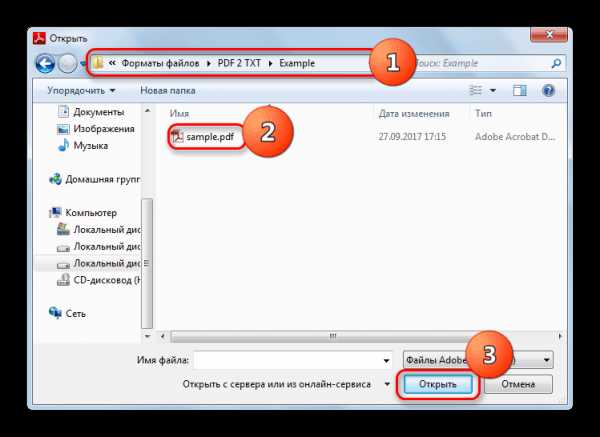

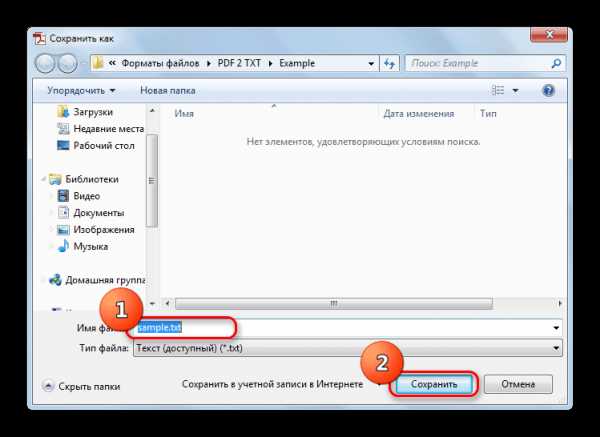

 ,
, 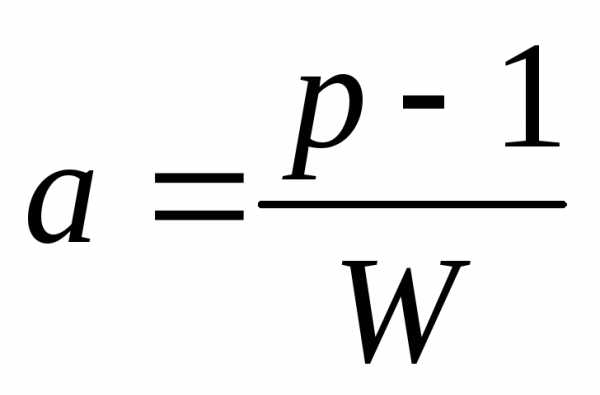 , W =
, W = 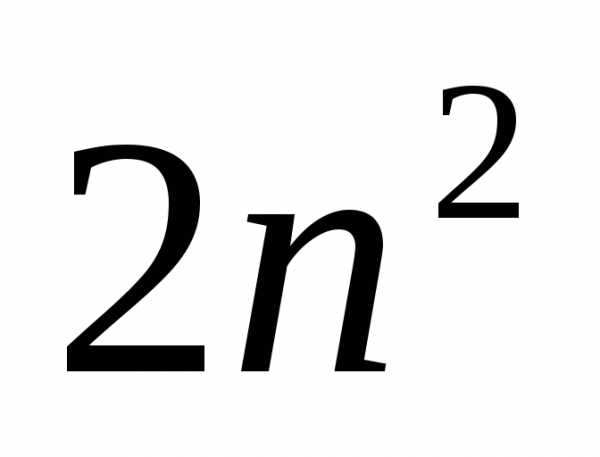 .
.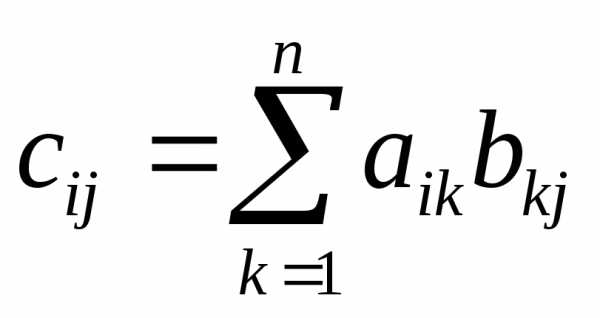 ,
.
,
.

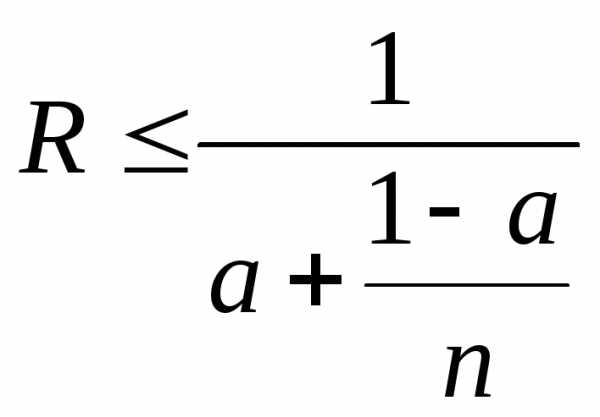 ,
, 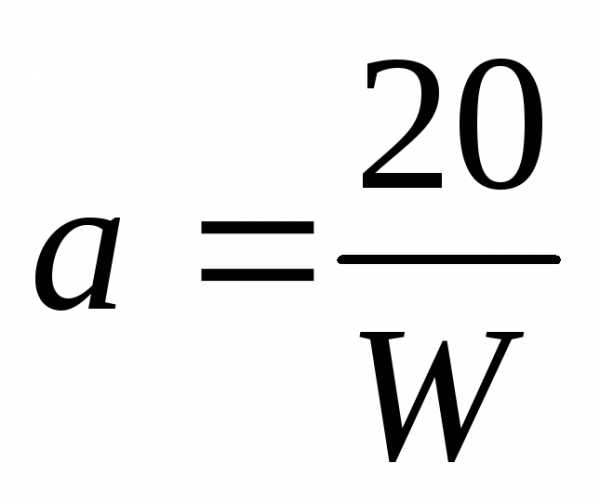 , W= .
, W= .
 Часы марки Tissot с традиционным написанием «IIII»
Часы марки Tissot с традиционным написанием «IIII» Римские цифры, обозначающие день недели, на витрине одного из магазинов в Вильнюсе
Римские цифры, обозначающие день недели, на витрине одного из магазинов в Вильнюсе



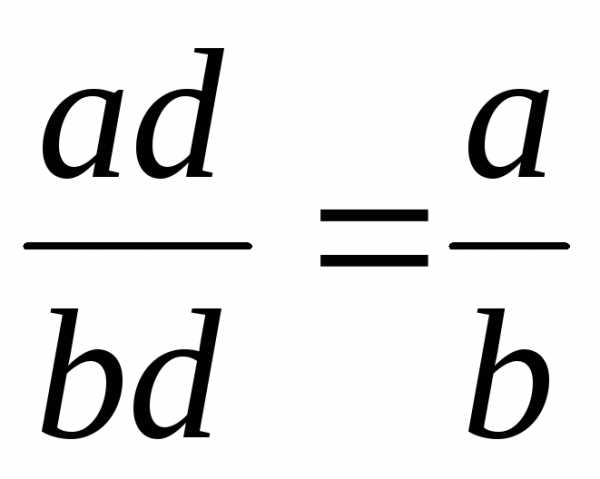 .
Например,
.
Например,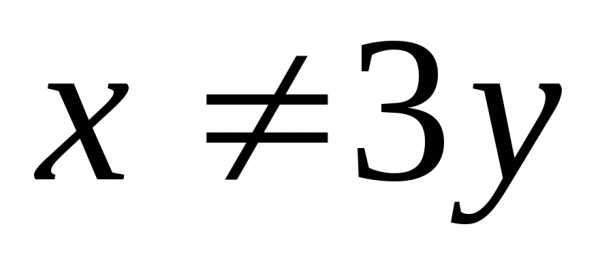 ).
).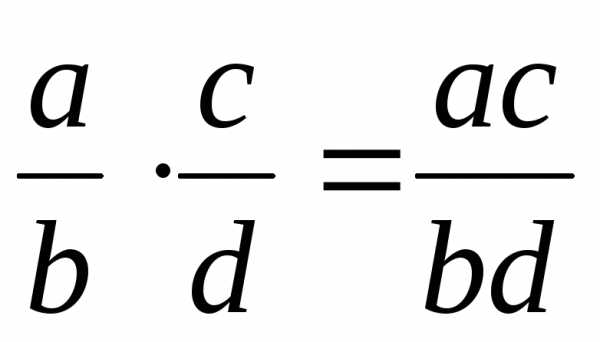 ,
, 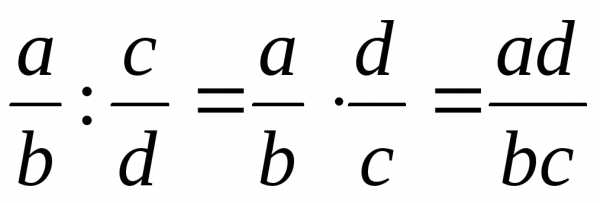 ,
,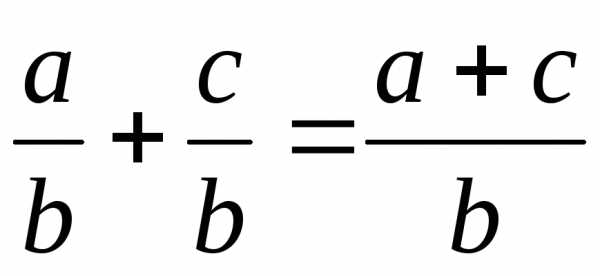 .
.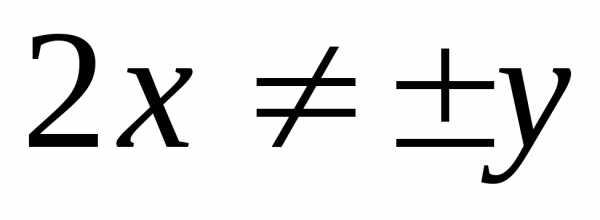 ).
). , (
, (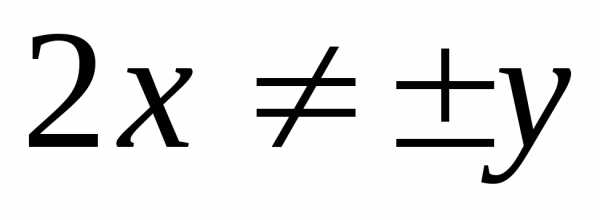 ).
).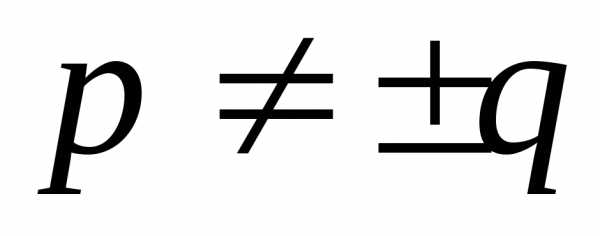 ).
).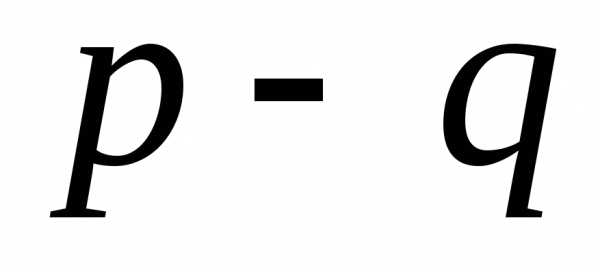 , (,
, (,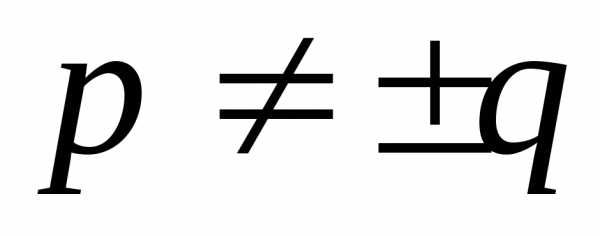 ).
).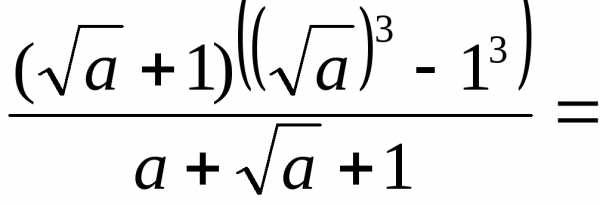
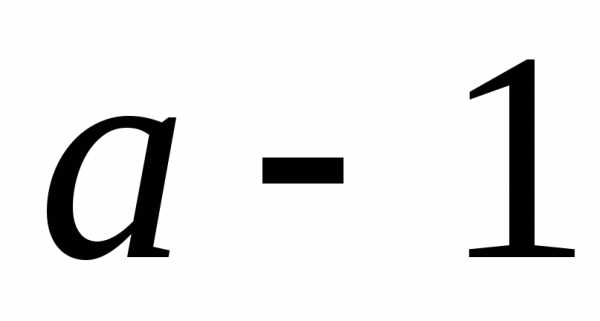 .
.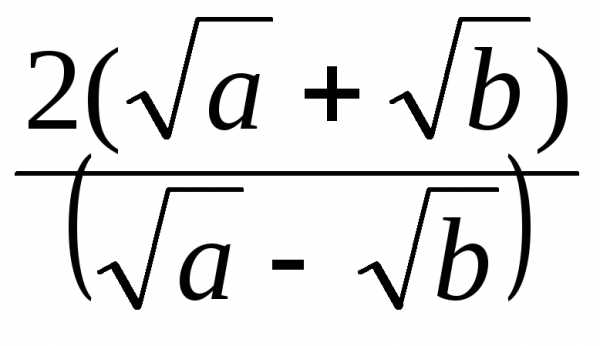 .
.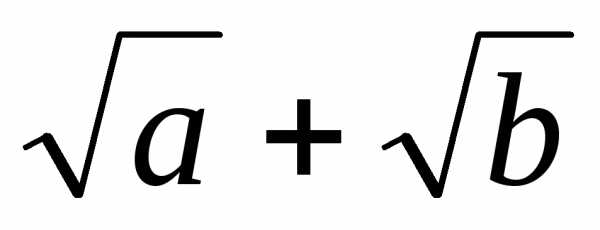 .
Получим
.
Получим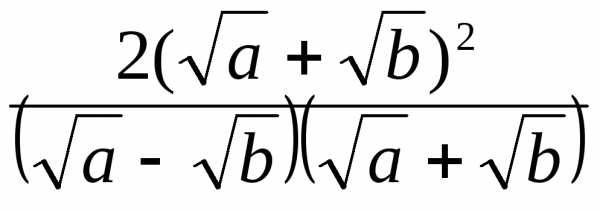
 .
.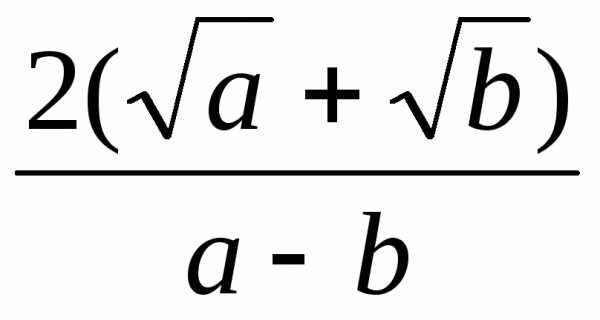 .
.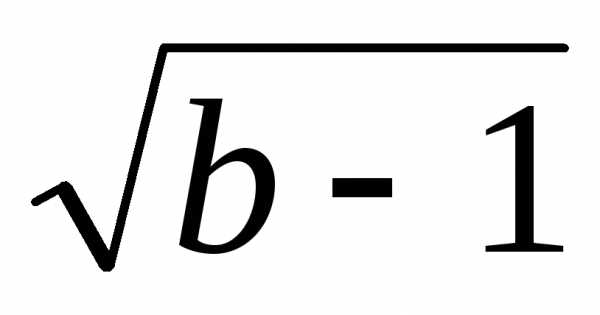 .
. .
.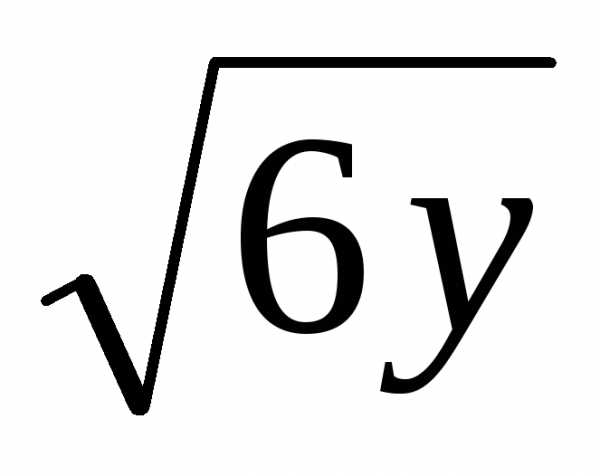 .
.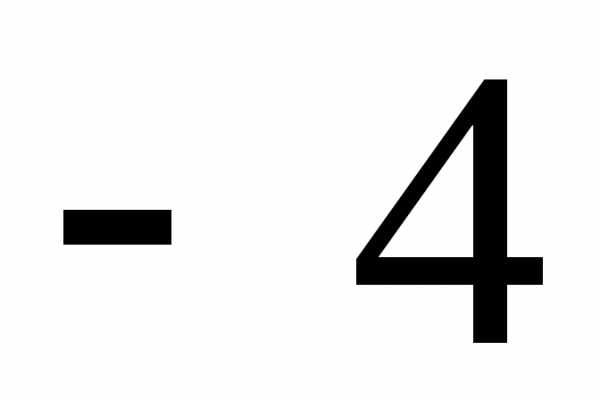 .
.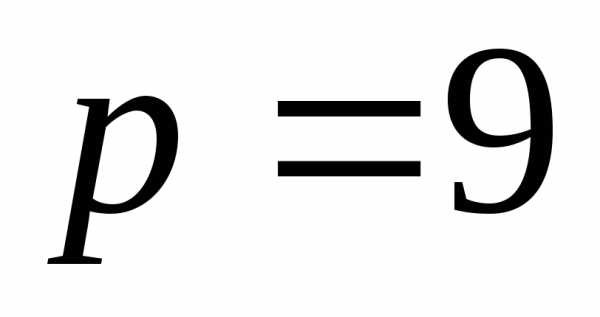 .
.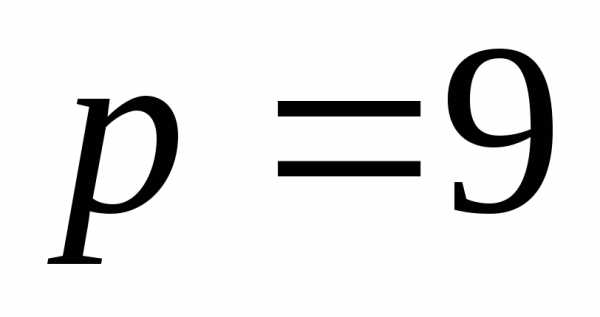 получим .
получим .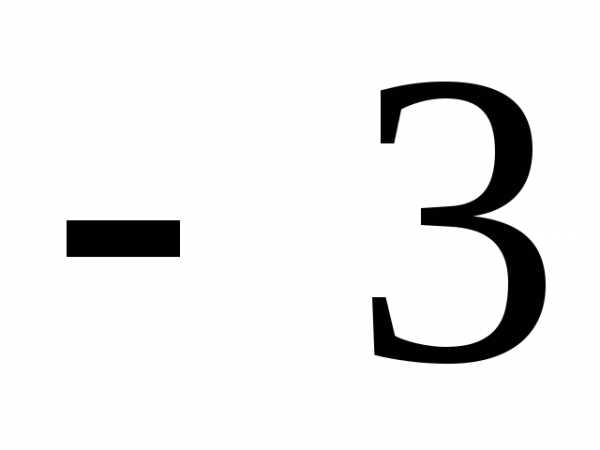 ;
б) 4; в) 3.
;
б) 4; в) 3.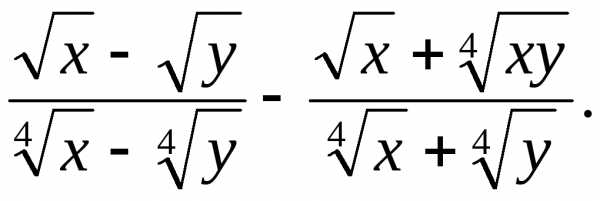
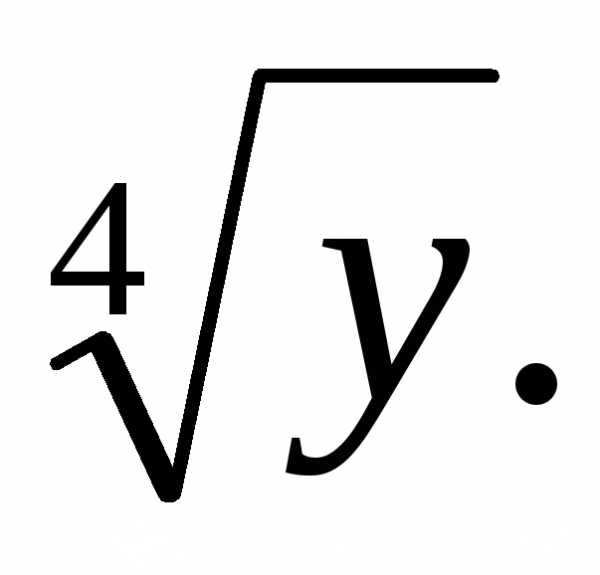
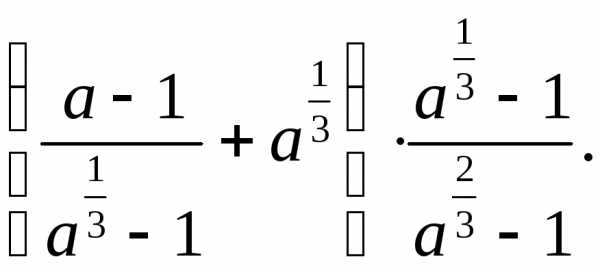
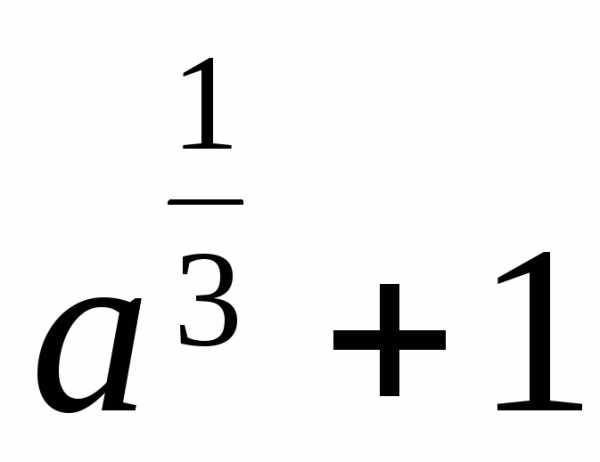 , .
, . .
.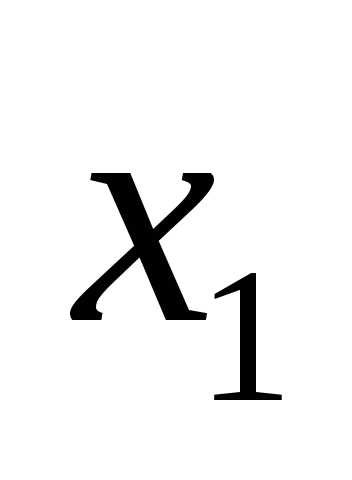 и
и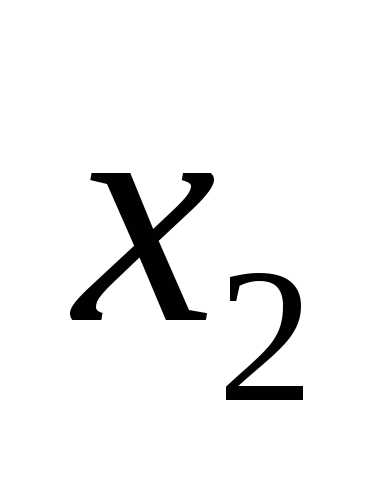
 (1)
(1)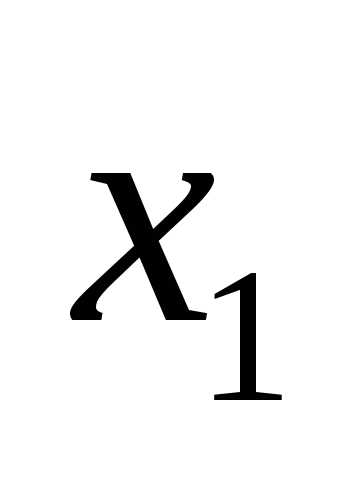 и
и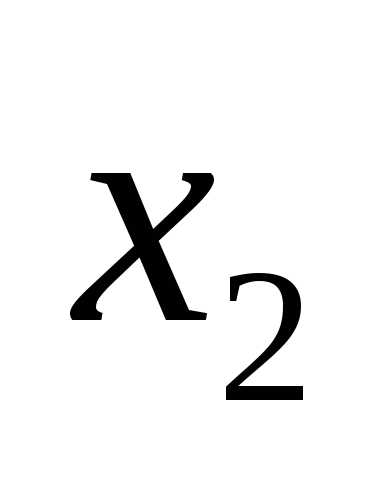 рассматривать как координаты точки
плоскости, то совокупность точек
плоскости, координаты которых удовлетворяют
неравенству (1), называется областью
решений данного неравенства. Следовательно,
областью решений неравенства (1) является
полуплоскость с граничной прямой линией.
рассматривать как координаты точки
плоскости, то совокупность точек
плоскости, координаты которых удовлетворяют
неравенству (1), называется областью
решений данного неравенства. Следовательно,
областью решений неравенства (1) является
полуплоскость с граничной прямой линией.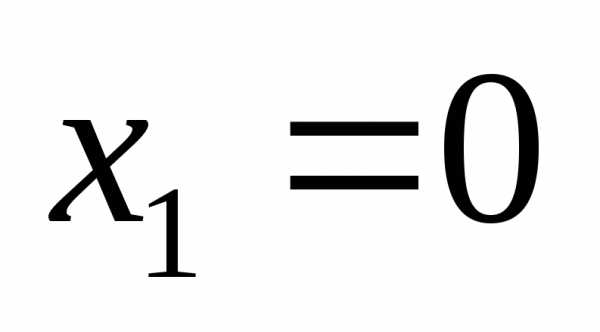 и
и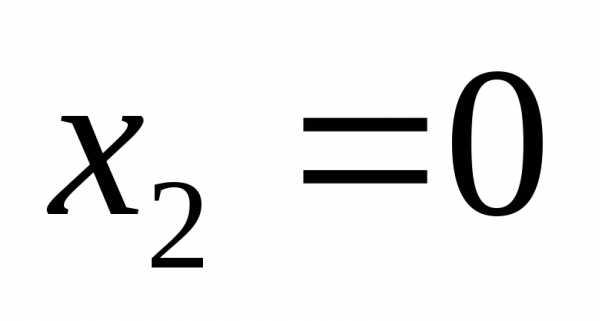 в заданное неравенство. Получим
в заданное неравенство. Получим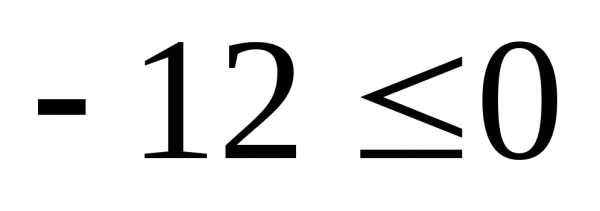 .
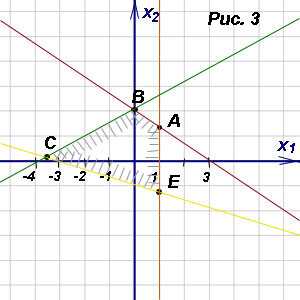
Следовательно, полуплоскость «к нулю»
является областью решений данного
неравенства (заштрихованная часть
рис. 1).
.
Следовательно, полуплоскость «к нулю»
является областью решений данного
неравенства (заштрихованная часть
рис. 1).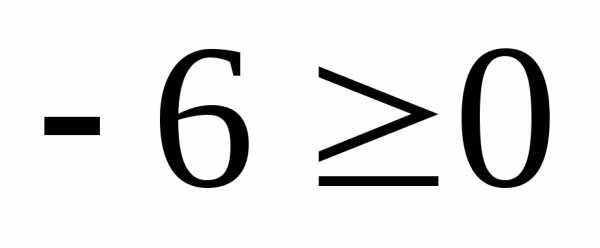 .
Это неверно. Значит, областью решений
данного неравенства будет та полуплоскость,
которой не принадлежит контрольная
точка (заштрихованная часть рис. 2).
.
Это неверно. Значит, областью решений
данного неравенства будет та полуплоскость,
которой не принадлежит контрольная
точка (заштрихованная часть рис. 2).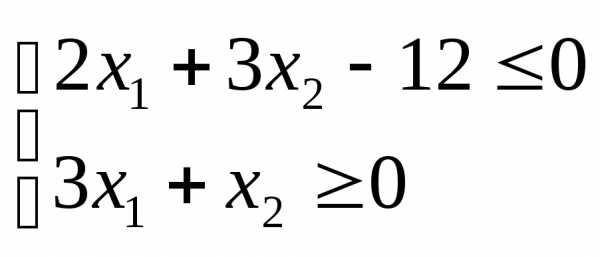
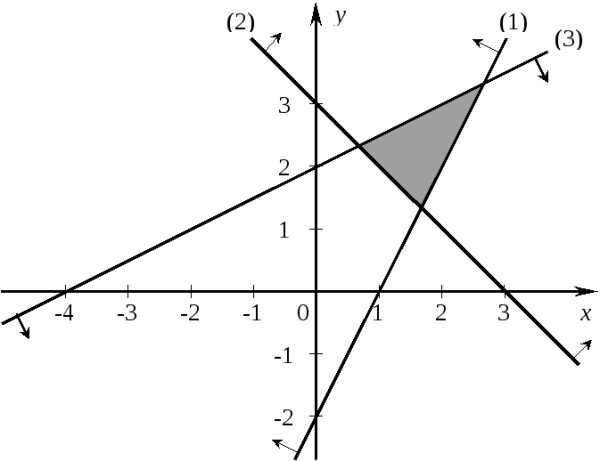
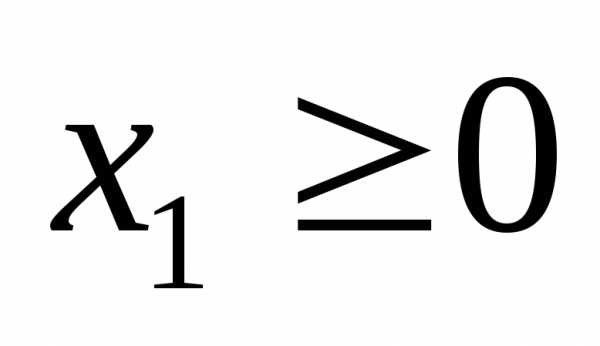 и
и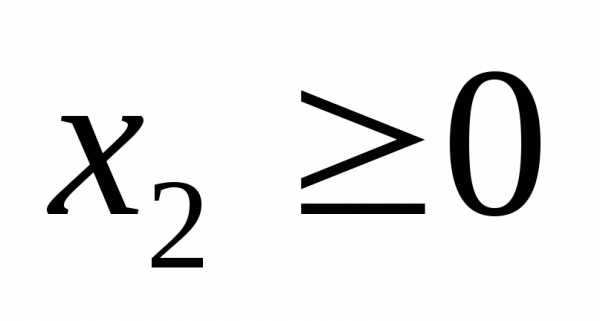 ,
то область решений системы неравенств
,
то область решений системы неравенств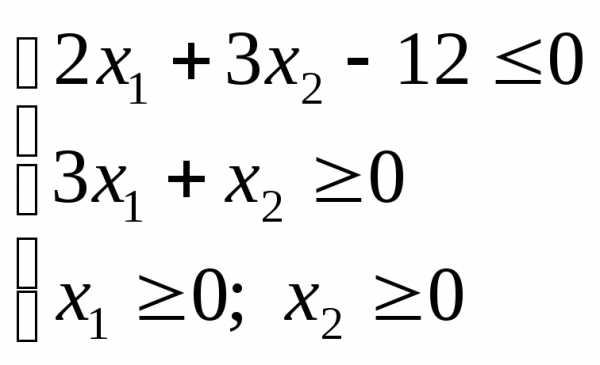 будет находиться только вI
координатной четверти (рис. 4).
будет находиться только вI
координатной четверти (рис. 4).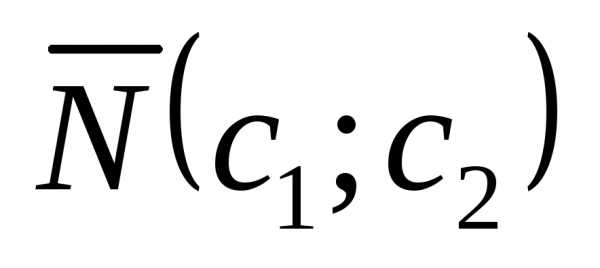 ,
выходящий из начала координат, где
,
выходящий из начала координат, где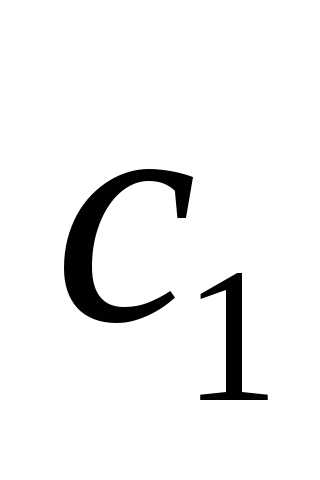 и
и – это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции.
– это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции. проводим так называемую линию уровня
проводим так называемую линию уровня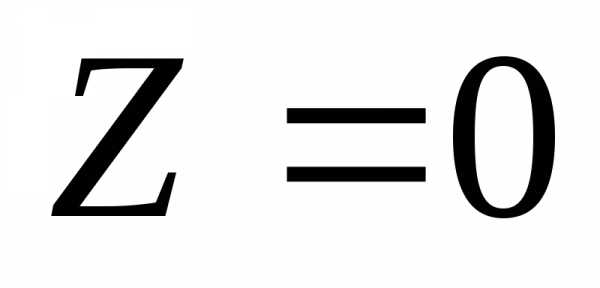 (т.е. прямую,
проходящую через начало координат).
(т.е. прямую,
проходящую через начало координат).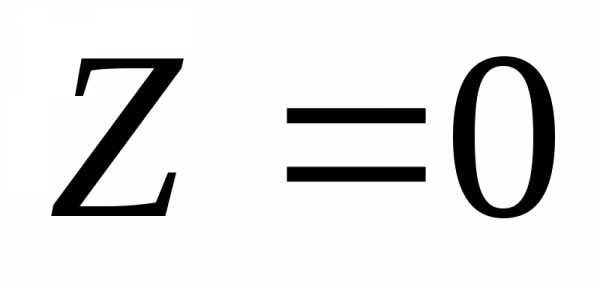 параллельно самой себе в направлении
вектора
параллельно самой себе в направлении
вектора (если задача на максимум (max))
или в противоположном направлении
(если задача на минимум (min))
до тех пор, пока линия уровня имеет хотя
бы одну общую точку с ОДР.
(если задача на максимум (max))
или в противоположном направлении
(если задача на минимум (min))
до тех пор, пока линия уровня имеет хотя
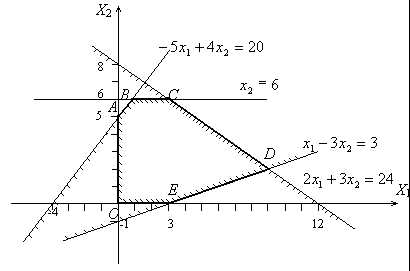
бы одну общую точку с ОДР.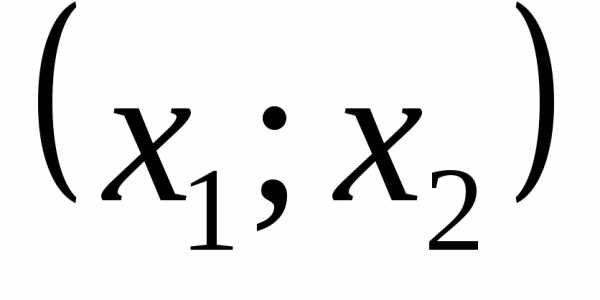 этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится.
этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится.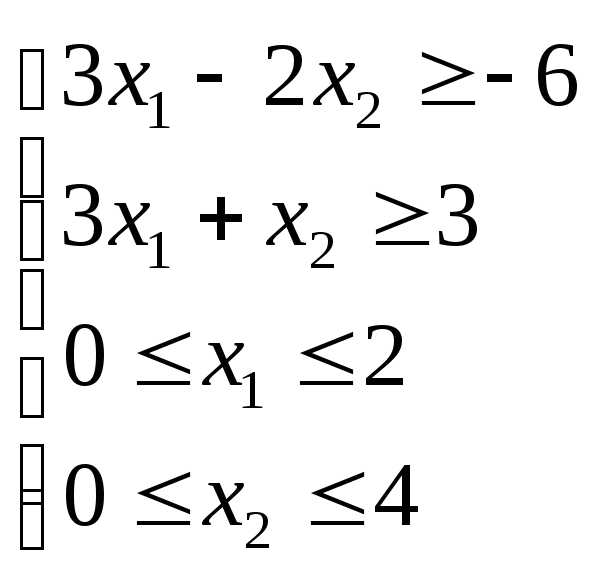
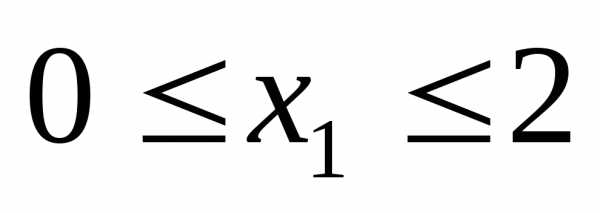 ,
это
,
это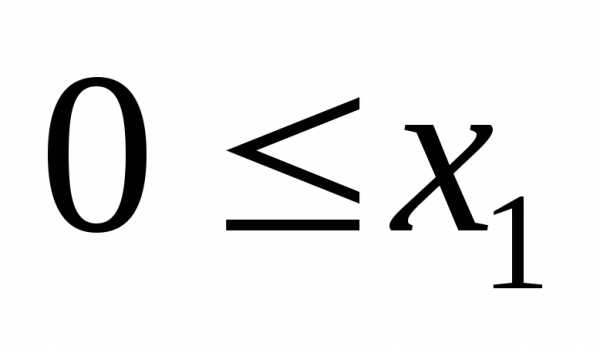 и
и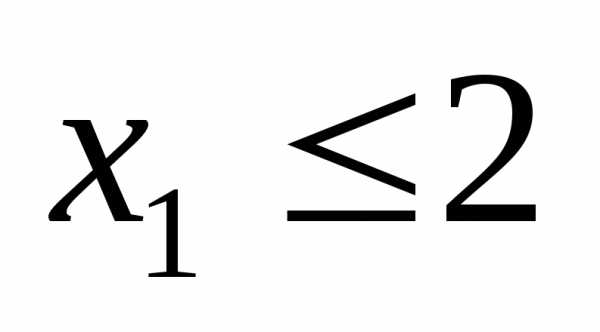 ,
т.о. первое из полученных неравенств
,
т.о. первое из полученных неравенств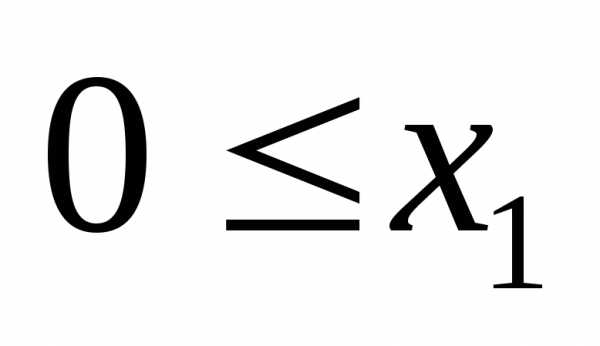 (или
(или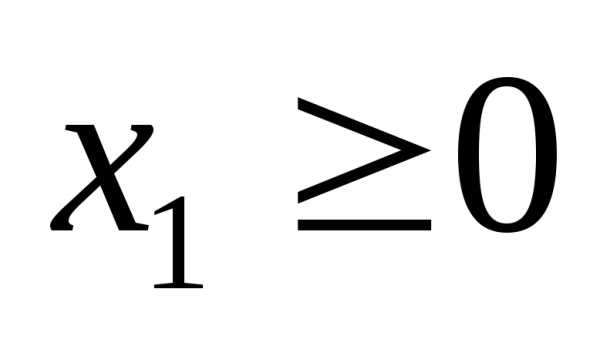 )
относится к условию неотрицательности,
а второе
)
относится к условию неотрицательности,
а второе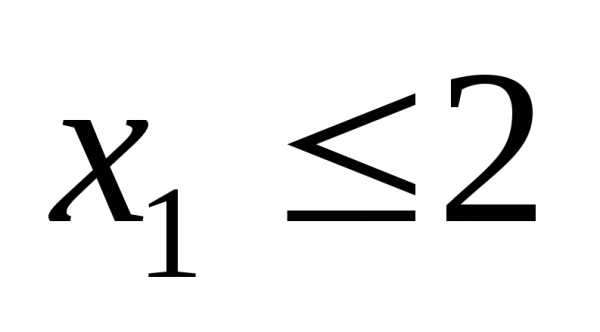 к системе ограничений. Аналогично,
к системе ограничений. Аналогично,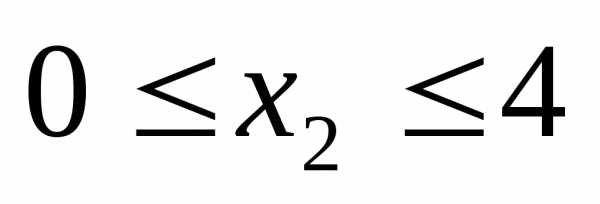 это
это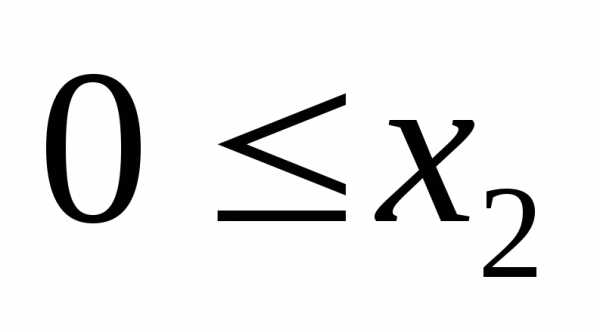 и
и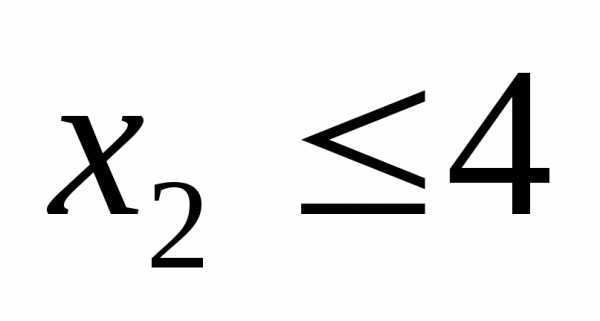 .
.
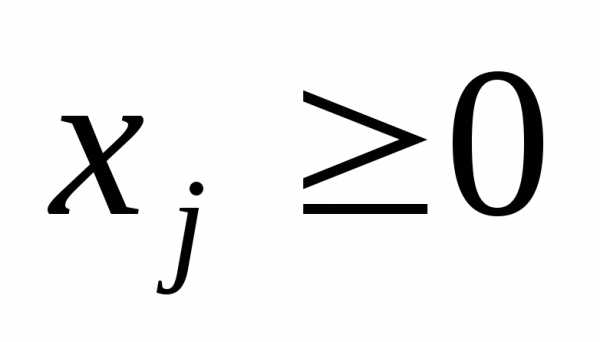 ,
, 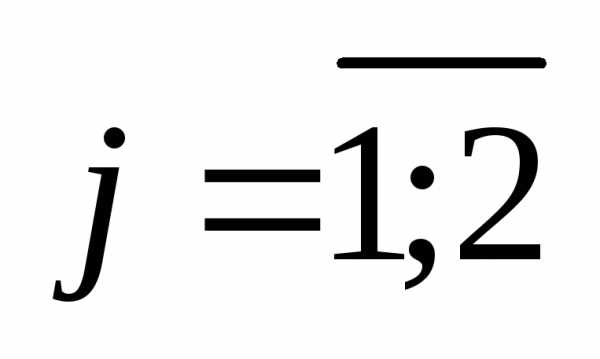
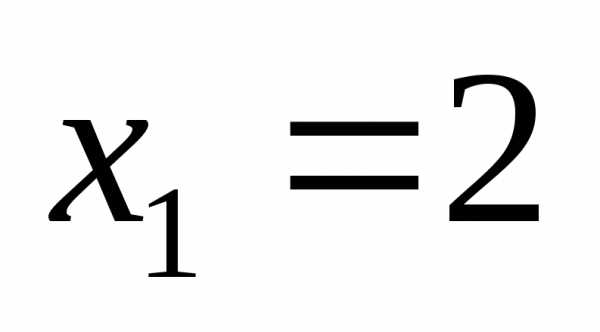 ;
;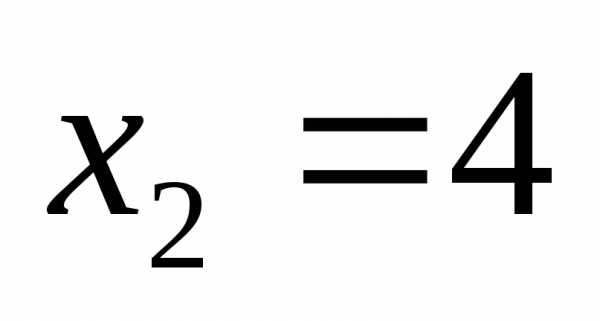 .
.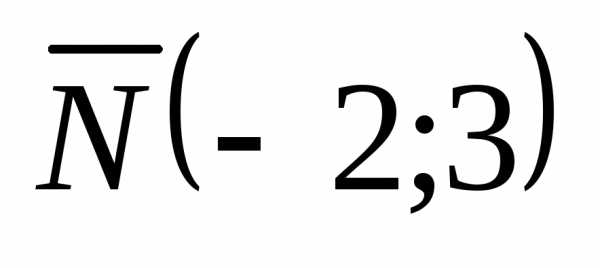 . Через
начало координат перпендикулярно
вектору
. Через
начало координат перпендикулярно
вектору  проведем линию уровня
проведем линию уровня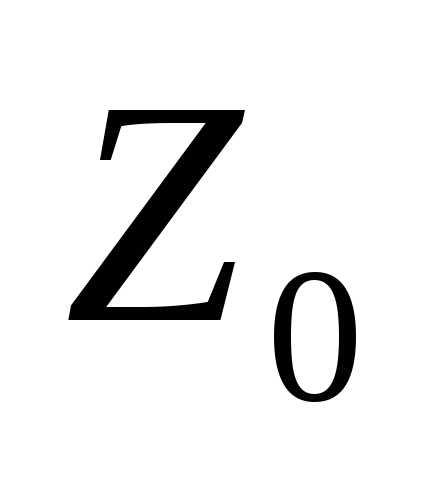 .
И затем будем перемещать ее параллельно
самой себе в направлении вектора
.
И затем будем перемещать ее параллельно
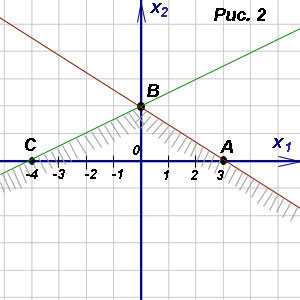
самой себе в направлении вектора до точки выхода из области допустимых
решений. Это будет точкаС.
Найдем координаты этой точки, решив
систему, состоящую из уравнений первой
и четвертой прямых:
до точки выхода из области допустимых
решений. Это будет точкаС.
Найдем координаты этой точки, решив
систему, состоящую из уравнений первой
и четвертой прямых: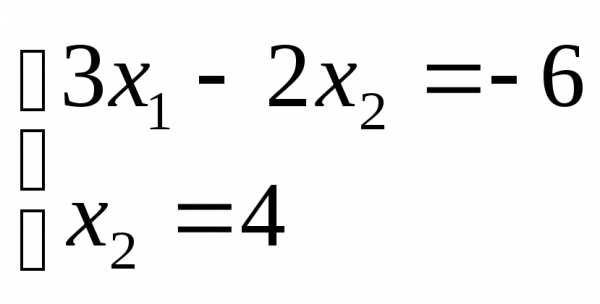

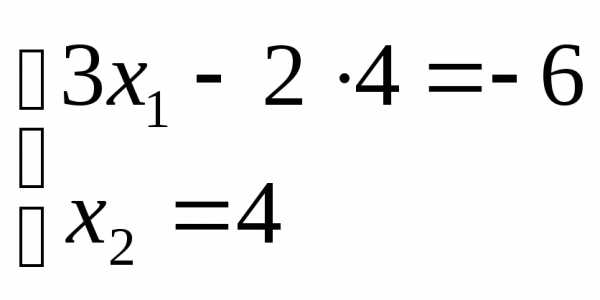

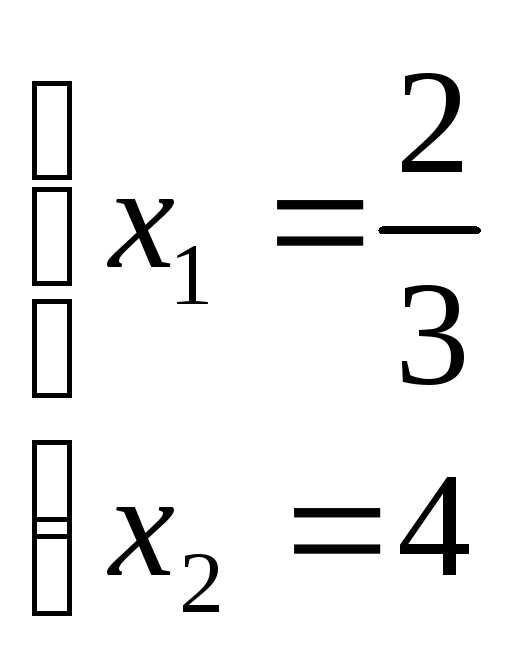

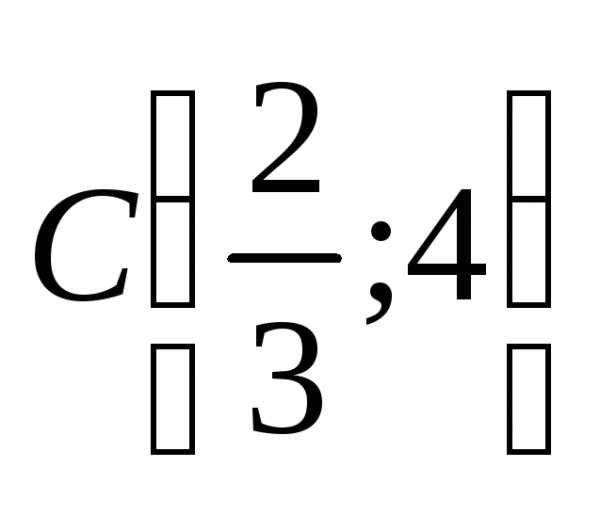 .
.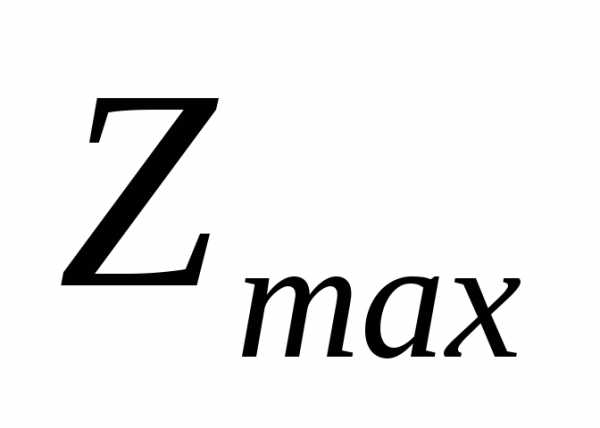 и
и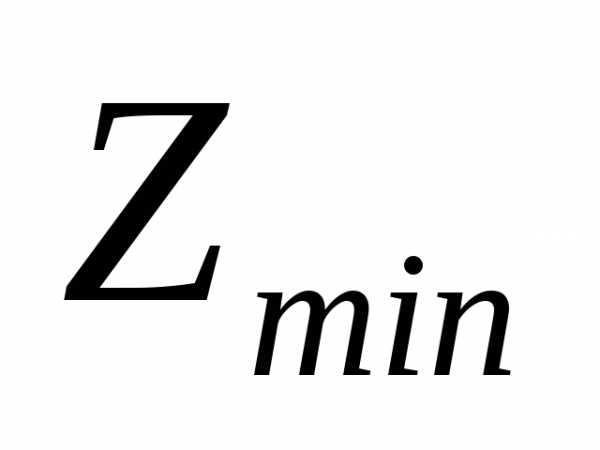 для задачи линейного программирования:
для задачи линейного программирования: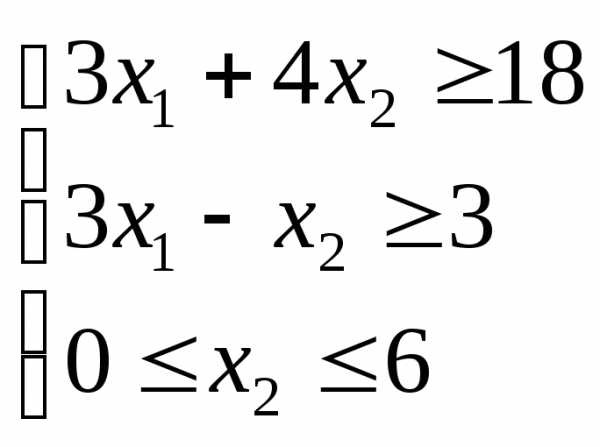
 проходит через точкуВ.
Функция Z имеет минимум в этой точке. Линию уровня
проходит через точкуВ.
Функция Z имеет минимум в этой точке. Линию уровня 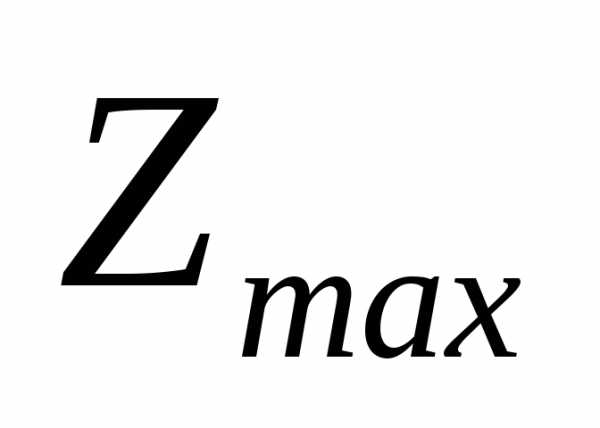 построить нельзя, так как нет точки
выхода из области допустимых решений,
это значит, что
построить нельзя, так как нет точки
выхода из области допустимых решений,
это значит, что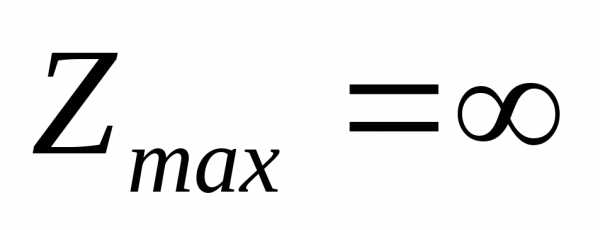 .
.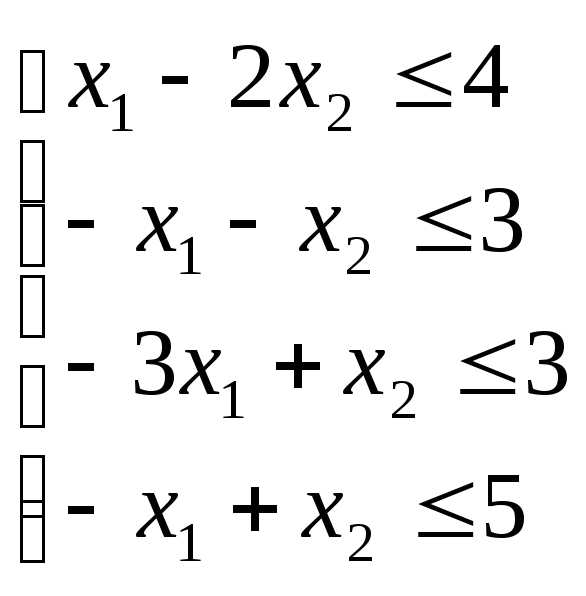 б)
б)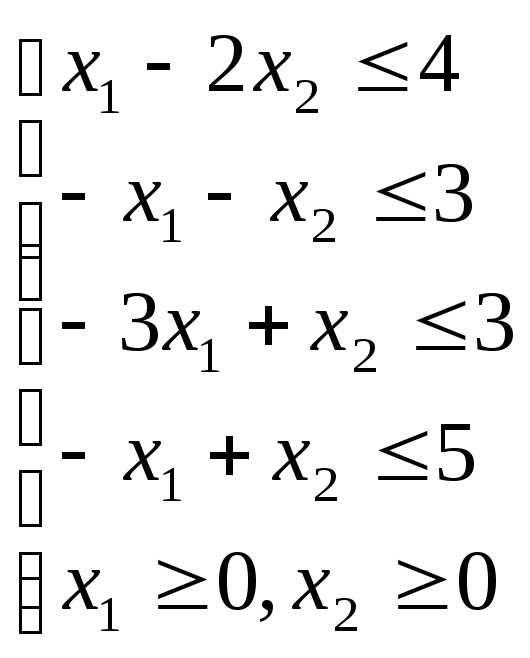
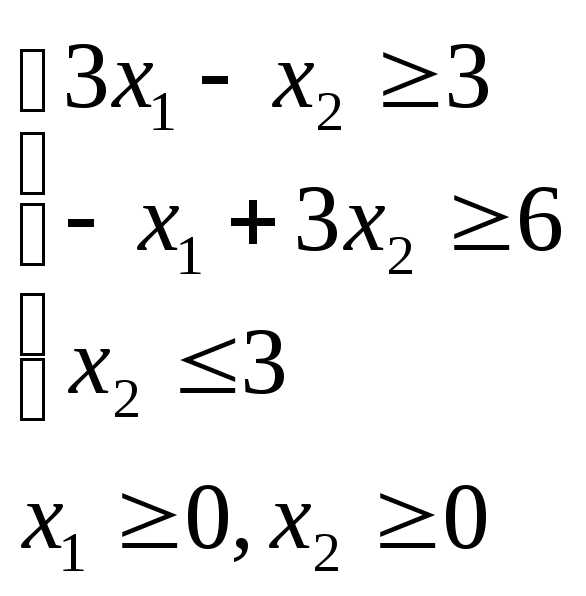
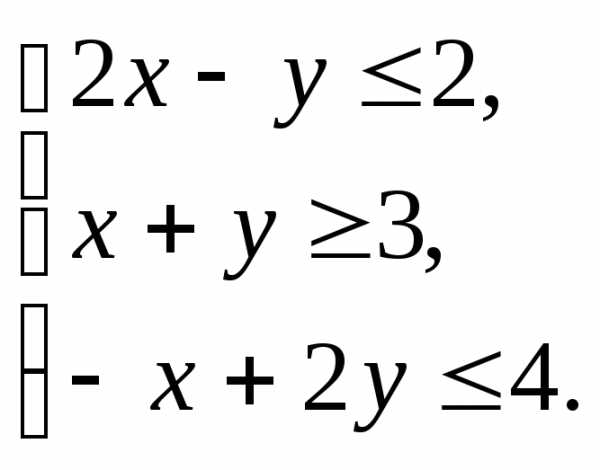
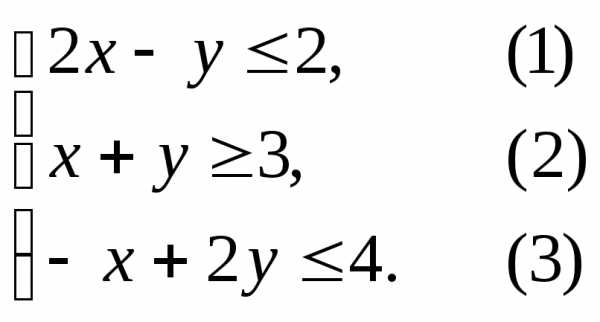
 ;
;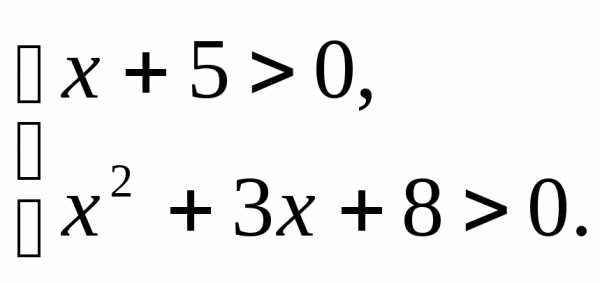
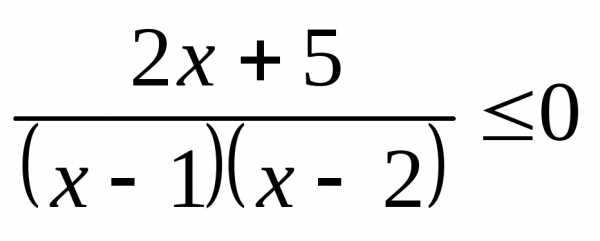 ;
;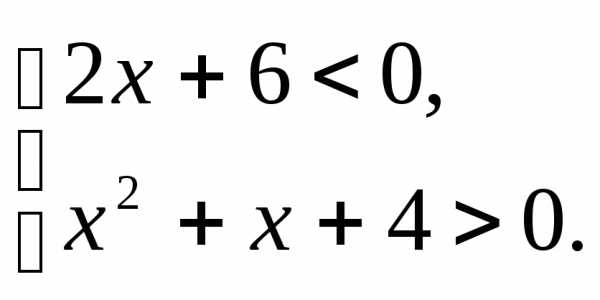
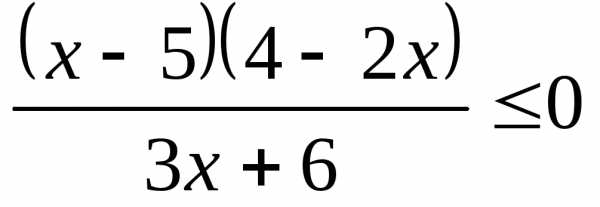 ;
;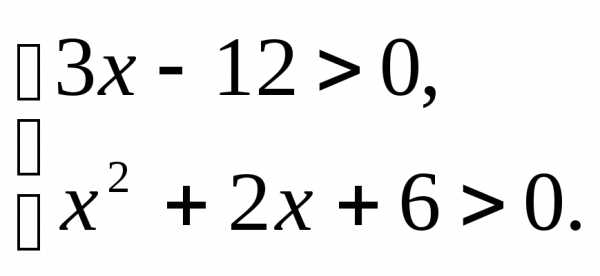
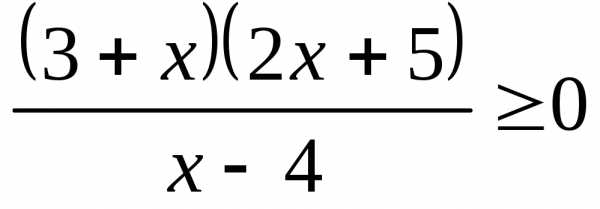 ;
;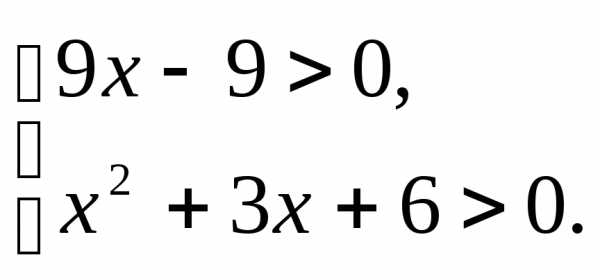
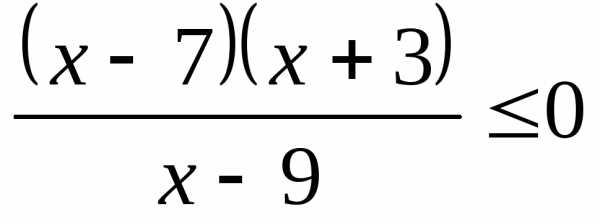 ;
;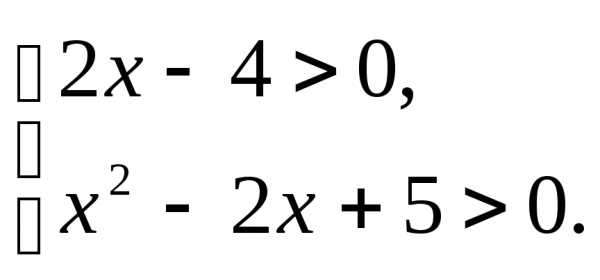
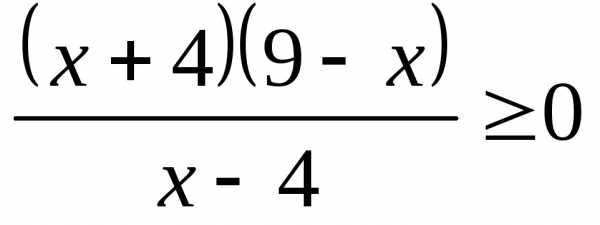 ;
;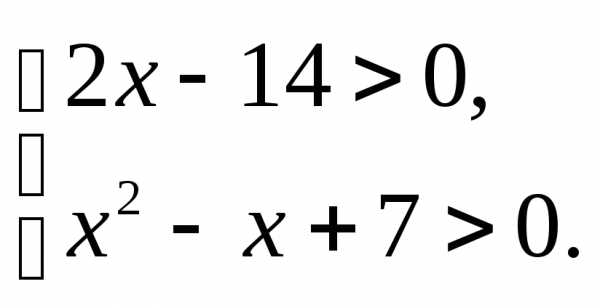
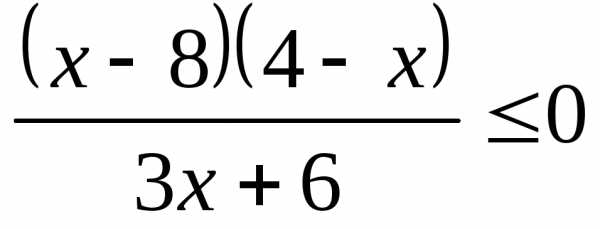 ;
;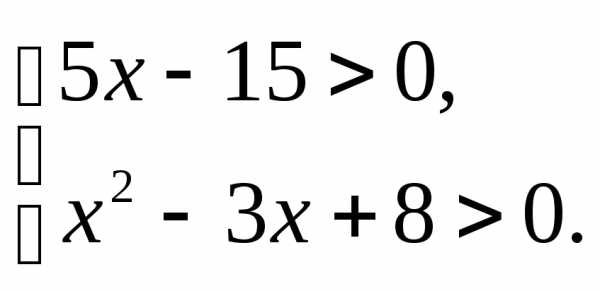
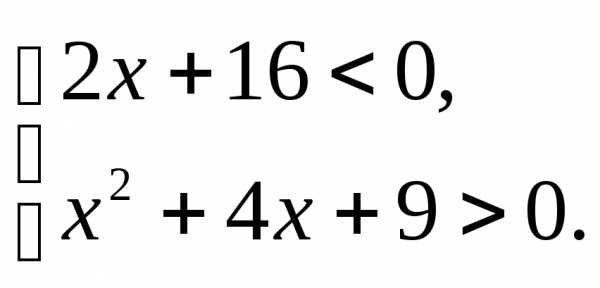
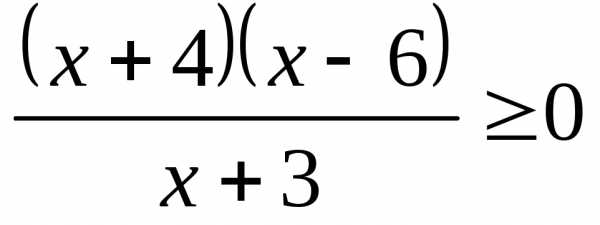 ;
;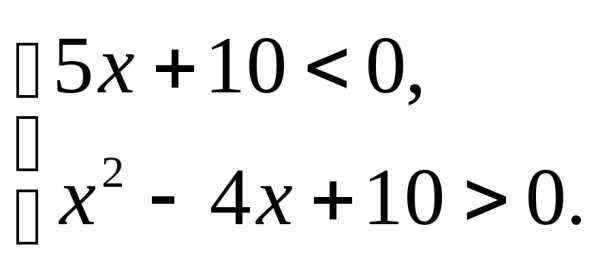
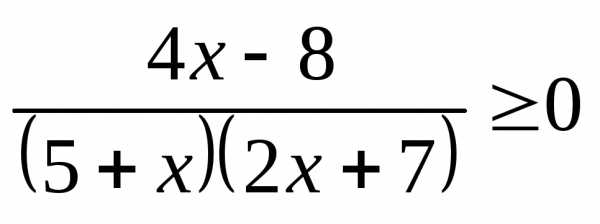 ;
;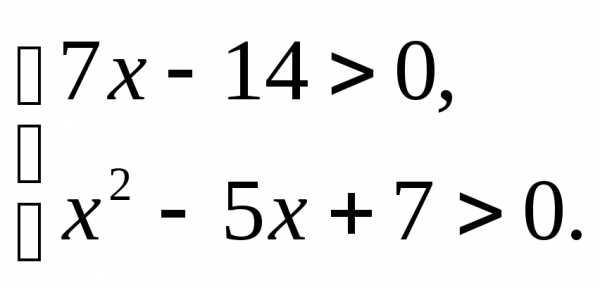
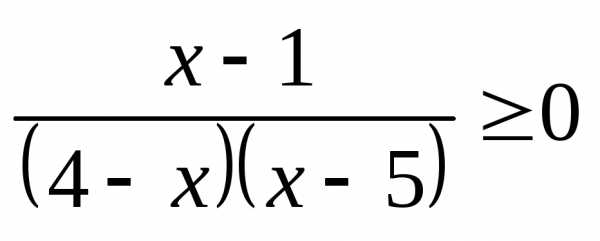 ;
;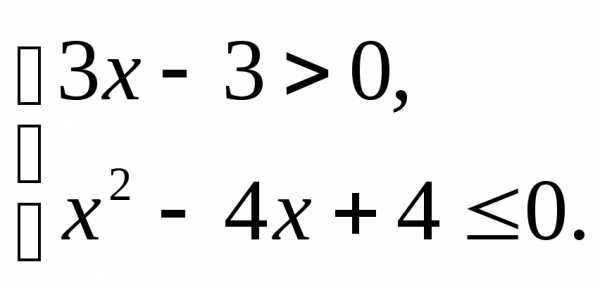
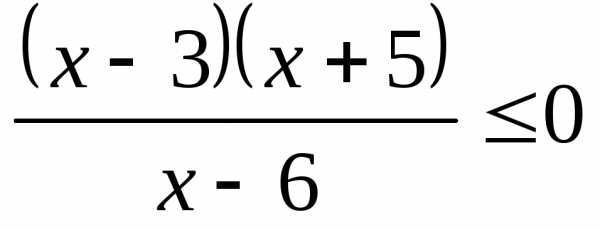 ;
;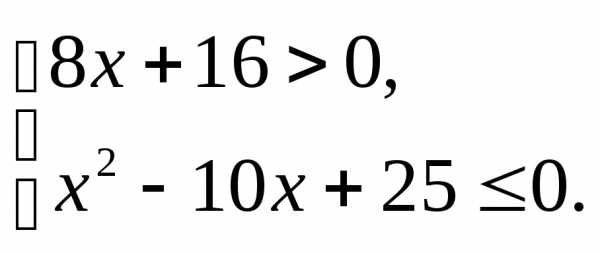
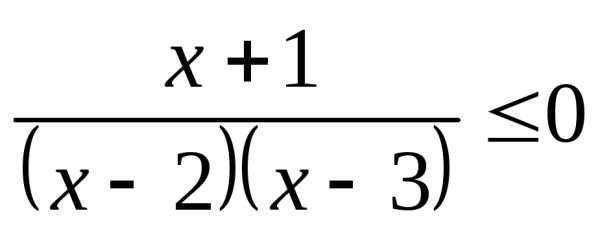 ;
;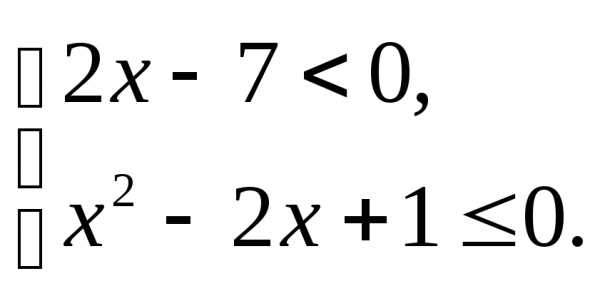
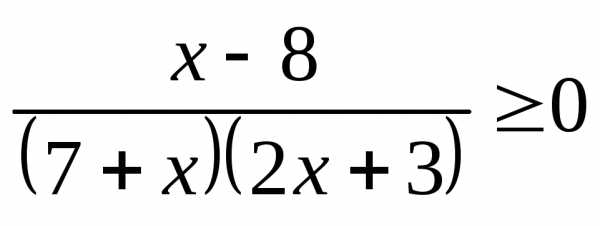 ;
;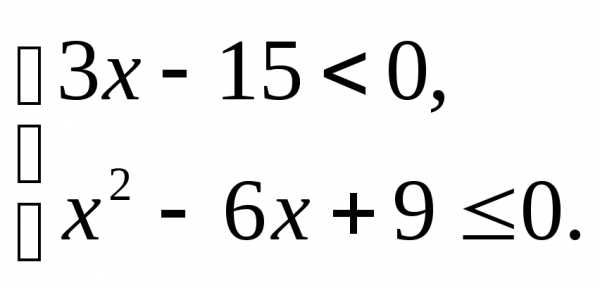
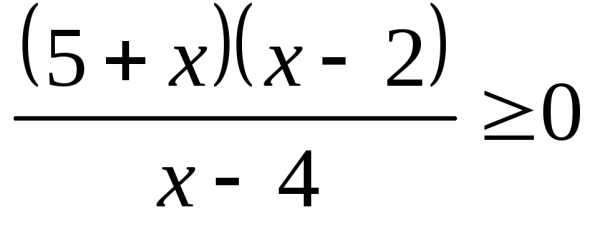 ;
;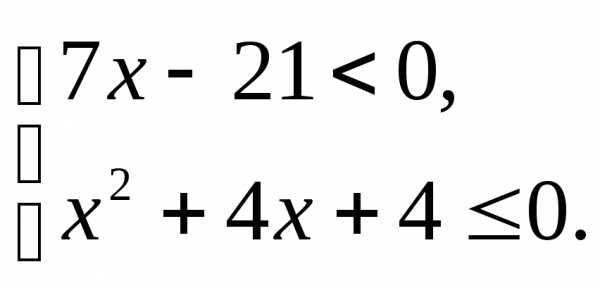
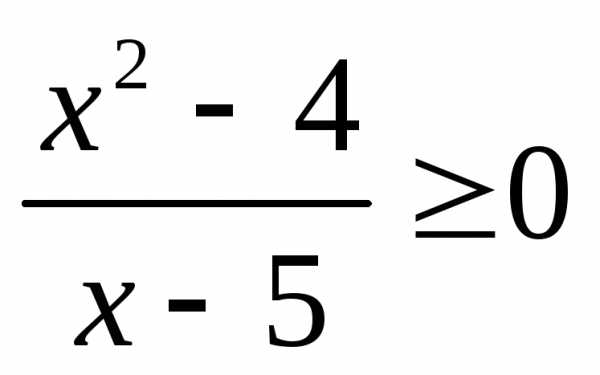 ;
;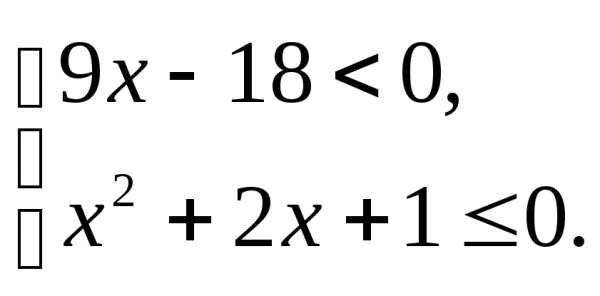
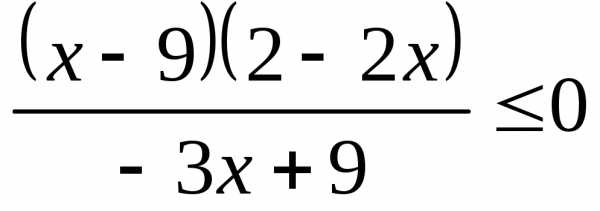 ;
;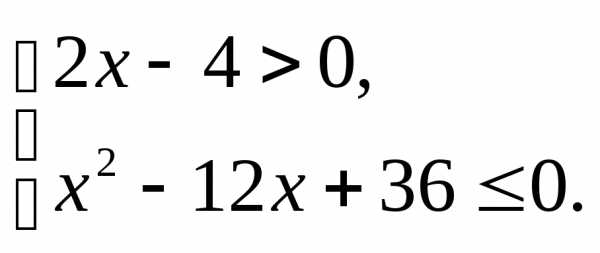
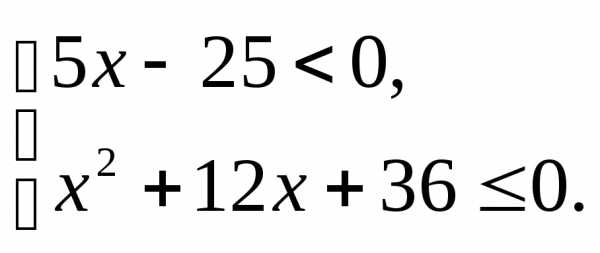
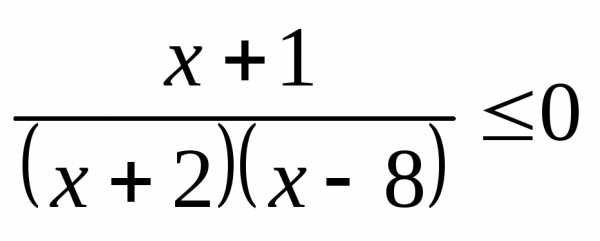 ;
;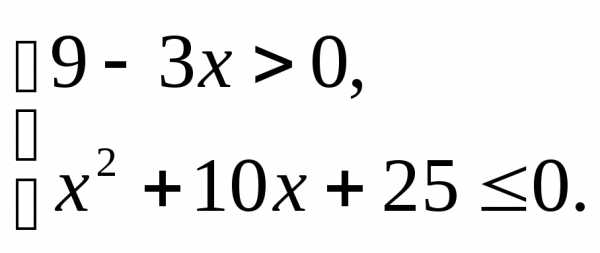
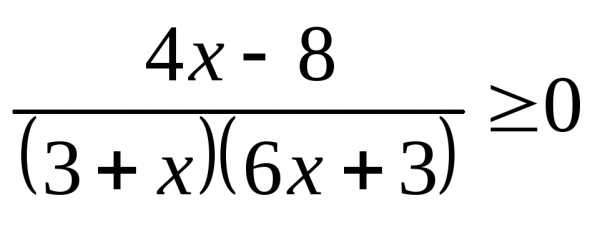 ;
;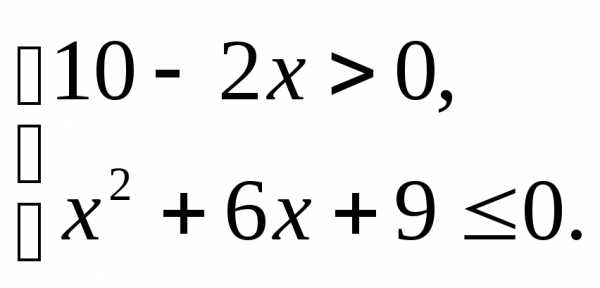
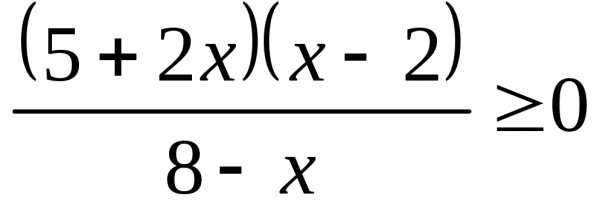 ;
;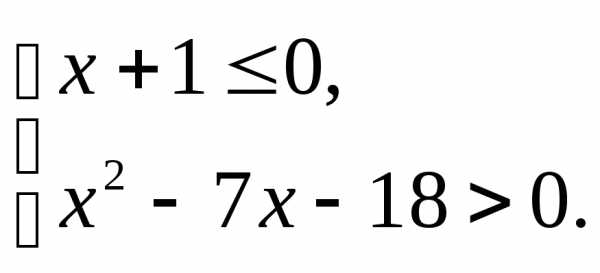
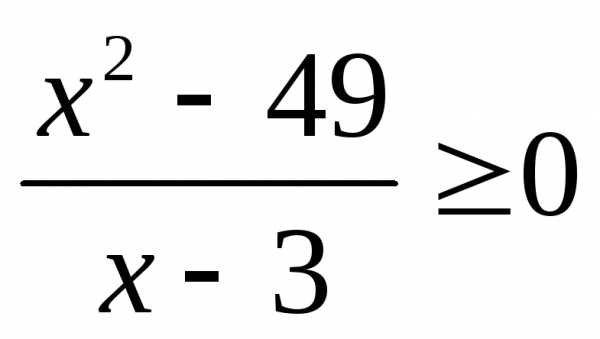 ;
;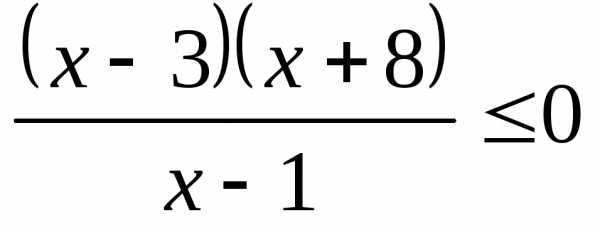 ;
;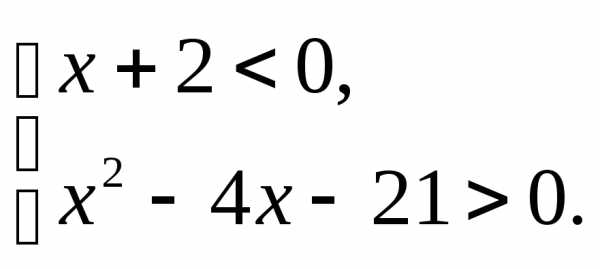
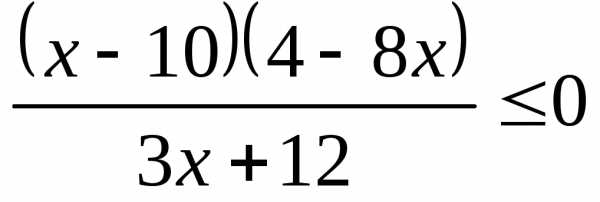 ;
;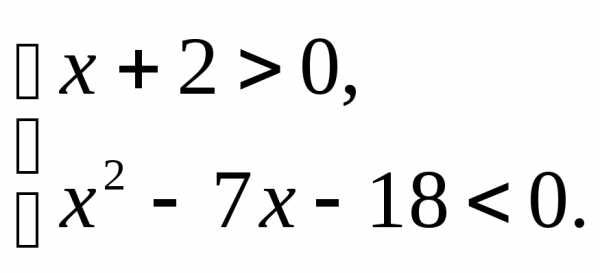
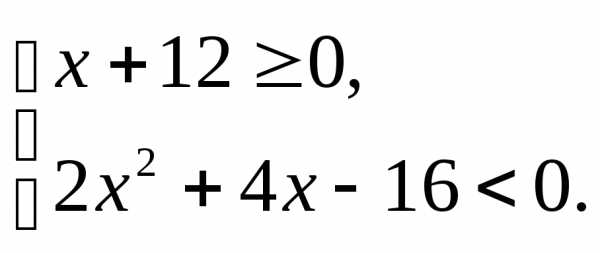
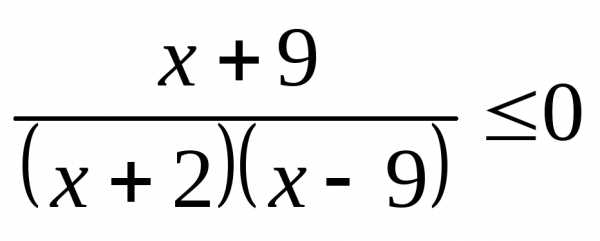 ;
;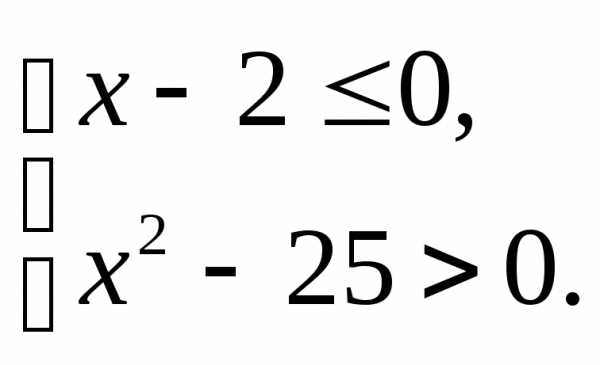
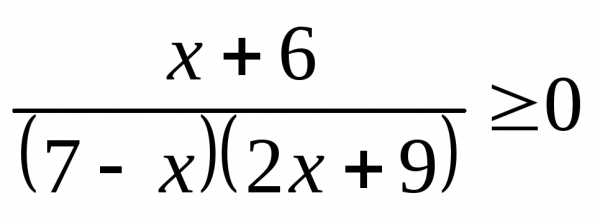 ;
;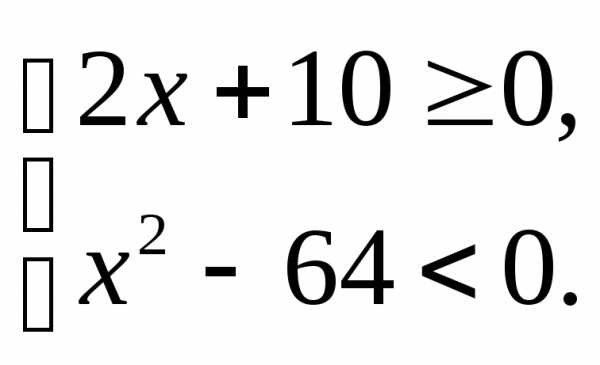
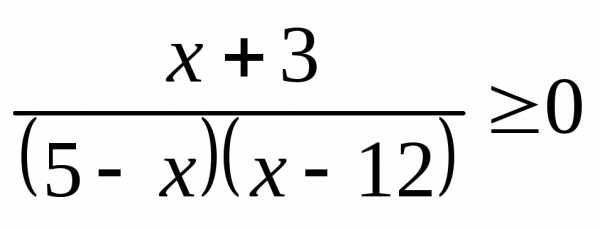 ;
;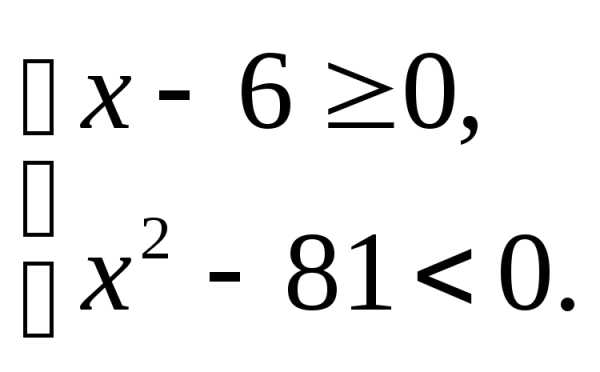
 ;
;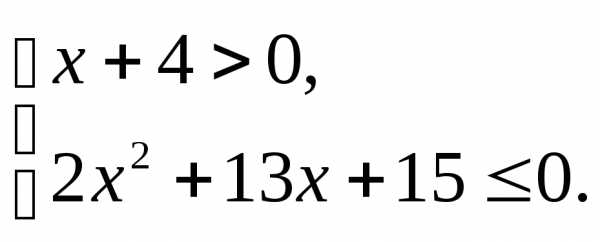
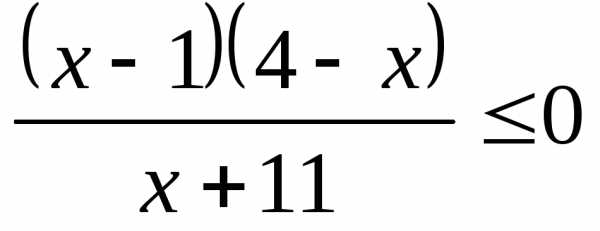 ;
;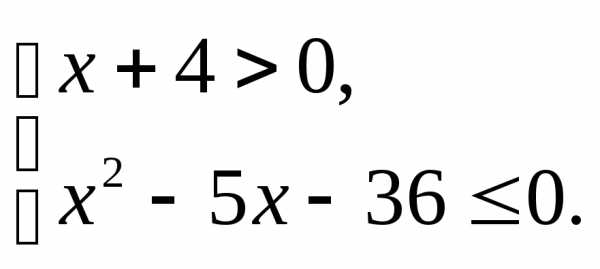
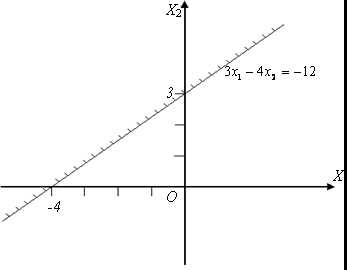
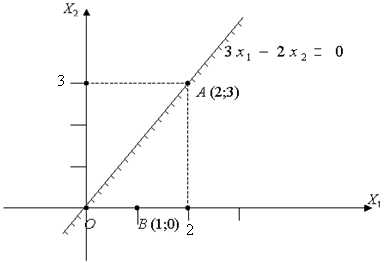
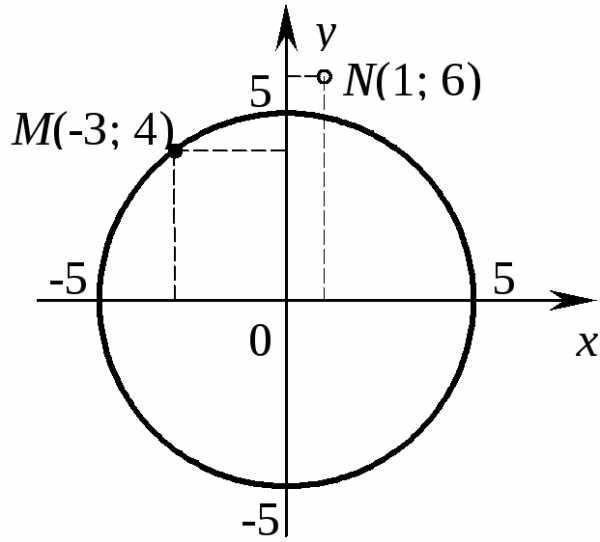
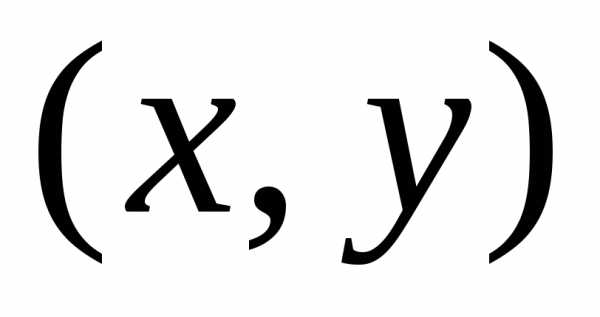 ,
которые удовлетворяют неравенству. Геометрически
решением линейного неравенства являетсяполуплоскость,
границей которой является прямая
.
,
которые удовлетворяют неравенству. Геометрически
решением линейного неравенства являетсяполуплоскость,
границей которой является прямая
.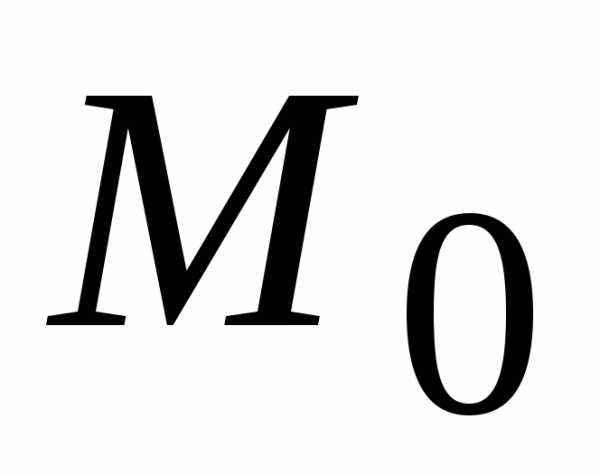 (в противном случае берется другая
полуплоскость). Плоскость выделяется
штриховкой.
(в противном случае берется другая
полуплоскость). Плоскость выделяется
штриховкой.

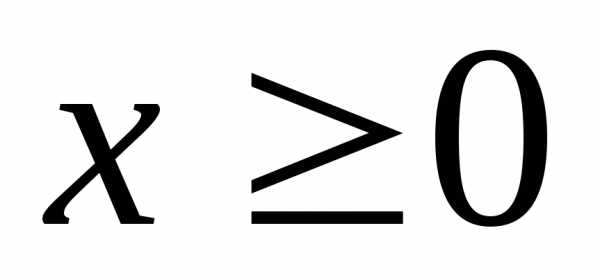 определяетправую
координатную полуплоскость (от оси
определяетправую
координатную полуплоскость (от оси 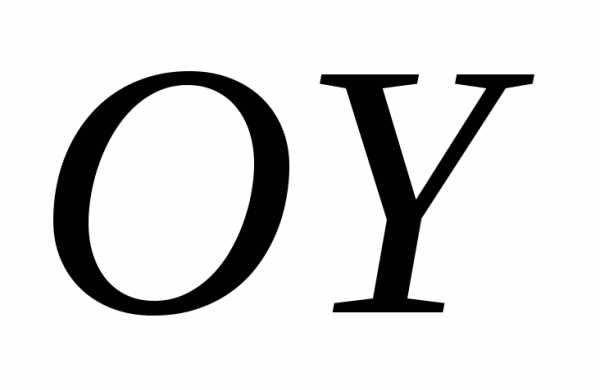 ),
а неравенство
),
а неравенство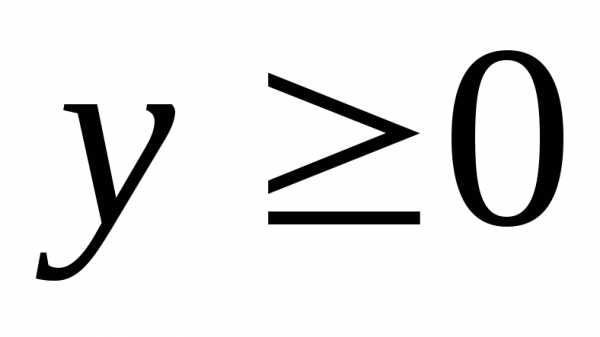 —верхнюю
координатную полуплоскость (от
оси
—верхнюю
координатную полуплоскость (от
оси  ).
).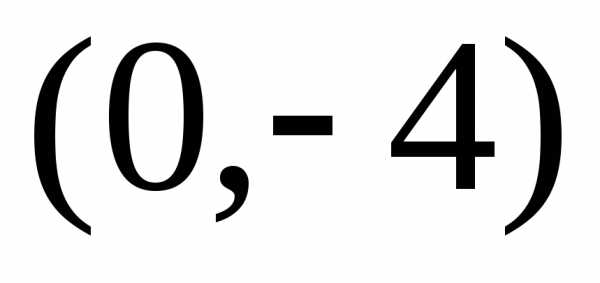 и
и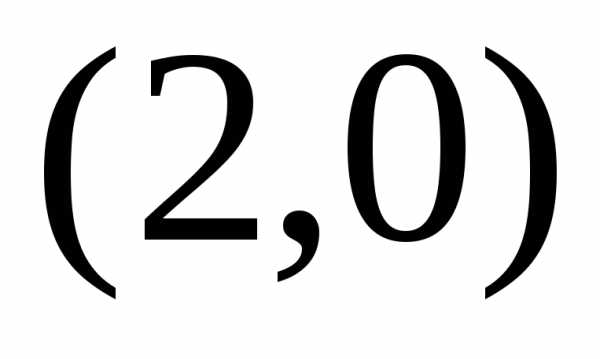 .
Прямая делит плоскость на две полуплоскости.
.
Прямая делит плоскость на две полуплоскости.
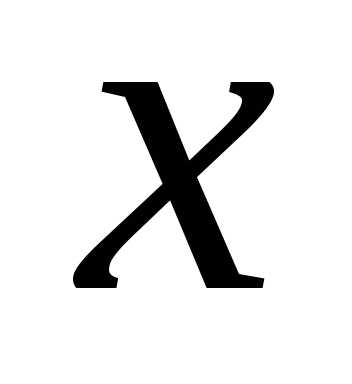
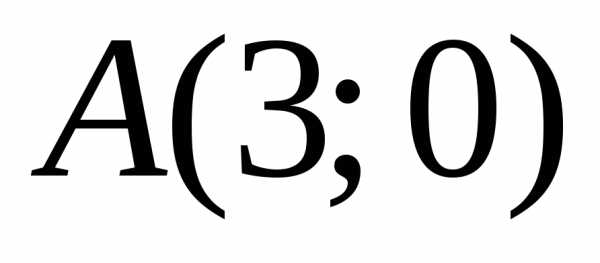 удовлетворяют неравенству(
удовлетворяют неравенству(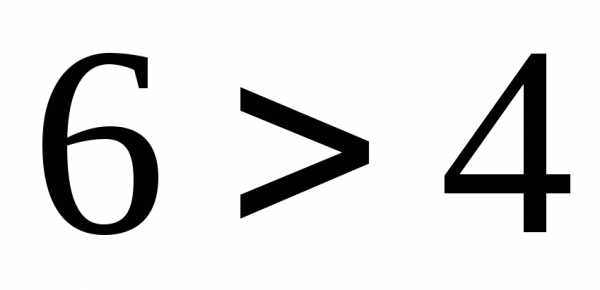 – верно), значит, и координаты всех точек
полуплоскости, содержащей точку
– верно), значит, и координаты всех точек
полуплоскости, содержащей точку 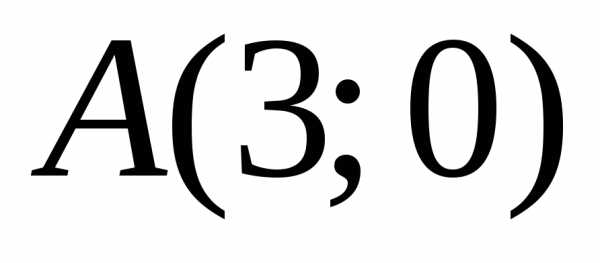 ,
удовлетворяют неравенству. Решением
неравенства будут координаты точек
полуплоскости, расположенной справа
от граничной прямой,
включая точки на границе. Искомая
полуплоскость на рисунке выделена.
,
удовлетворяют неравенству. Решением
неравенства будут координаты точек
полуплоскости, расположенной справа
от граничной прямой,
включая точки на границе. Искомая
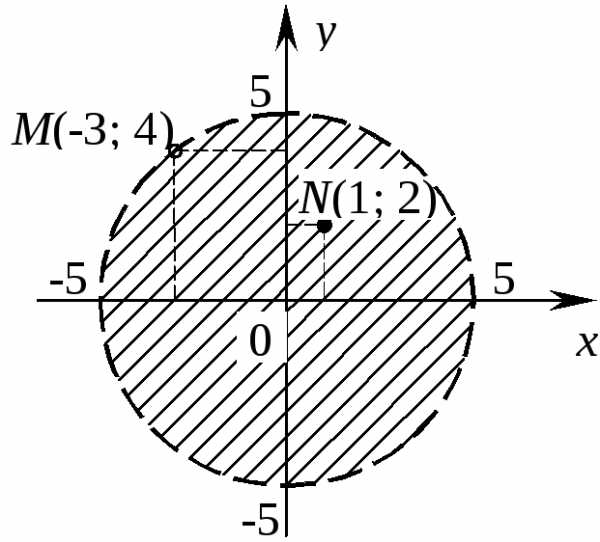
полуплоскость на рисунке выделена.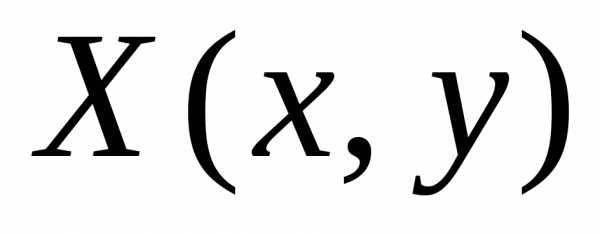 системы неравенств называетсядопустимым,
если его координаты неотрицательны
системы неравенств называетсядопустимым,
если его координаты неотрицательны 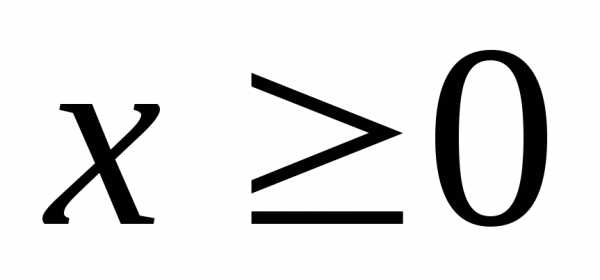 ,
,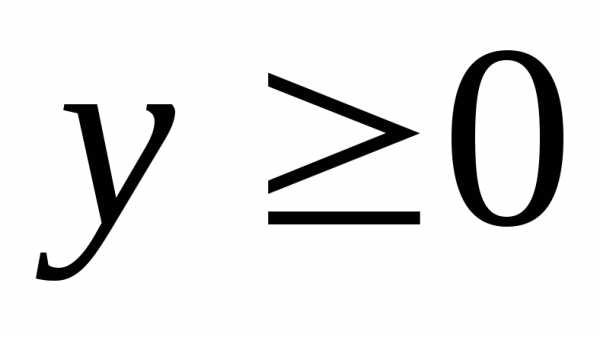 .
Множество допустимых решений системы
неравенств образует область, которая
расположена в первой
четверти координатной плоскости.
.
Множество допустимых решений системы
неравенств образует область, которая
расположена в первой
четверти координатной плоскости.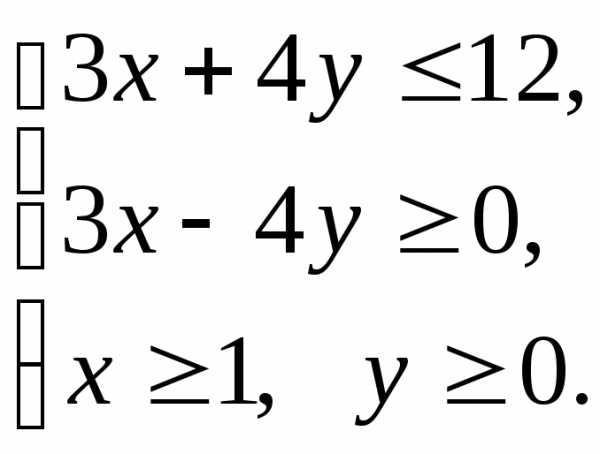
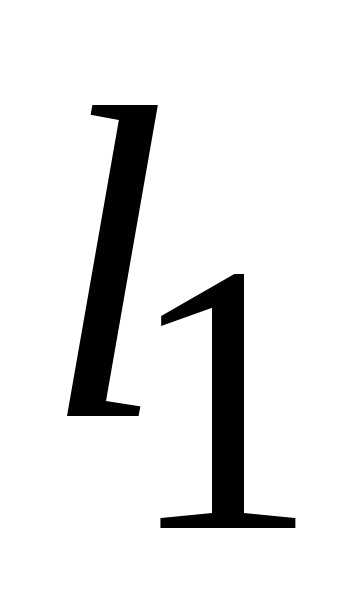 );
); );
); — полуплоскость, расположенная правее
прямой (
— полуплоскость, расположенная правее
прямой (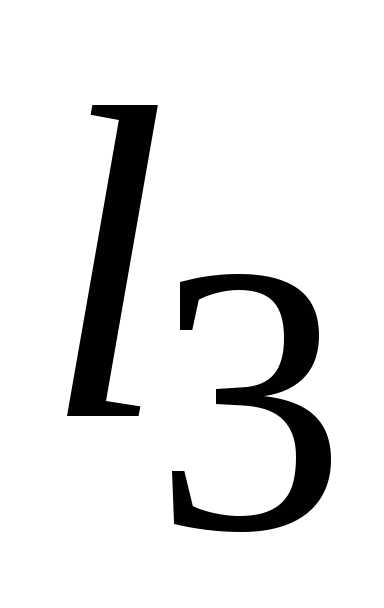 )
)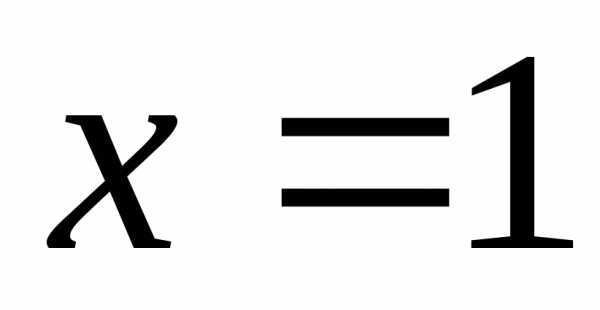 ;
;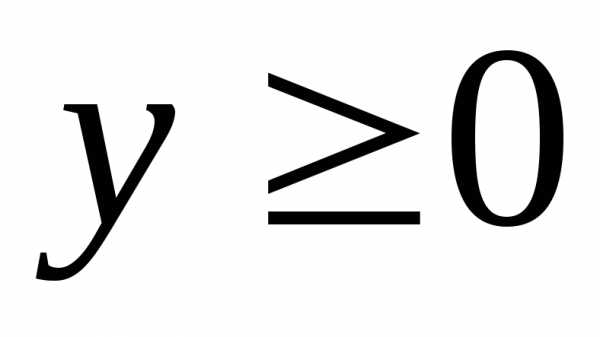 — полуплоскость выше оси абсцисс, то
есть прямой (
— полуплоскость выше оси абсцисс, то
есть прямой ( )
) 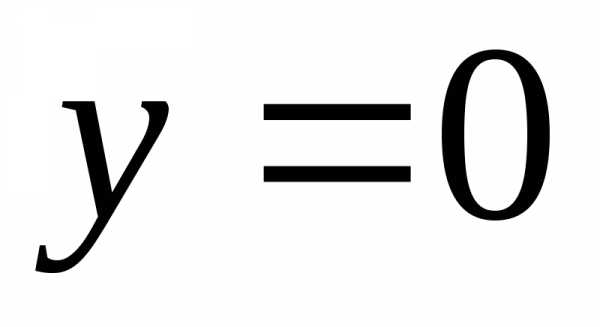 .
.
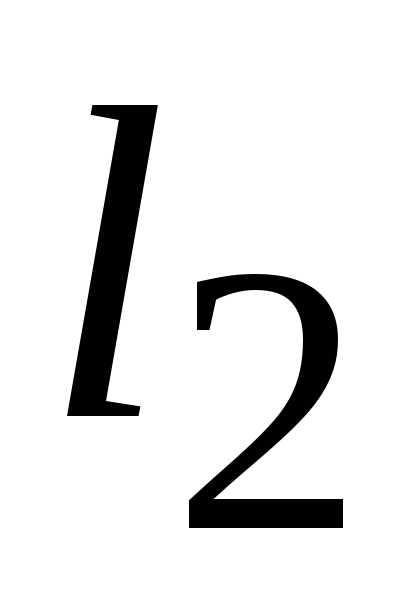

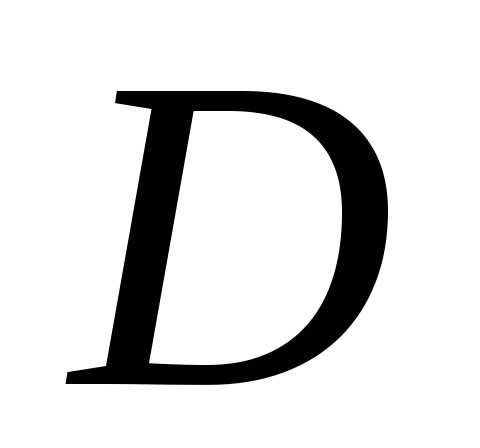
 0
0 
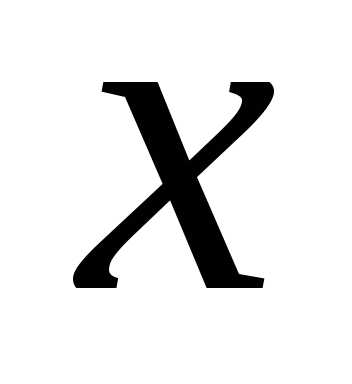
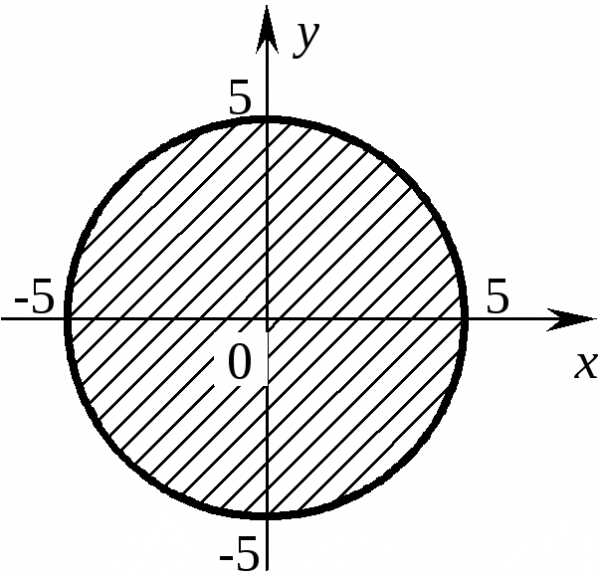
 ,
являющегосяпересечением четырех полуплоскостей.
,
являющегосяпересечением четырех полуплоскостей.