Таблица умножения для 2 класса
Таблица умножения на 2
1 × 2 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10
2 × 6 = 12
2 × 7 = 14
2 × 8 = 16
2 × 9 = 18
2 × 10 = 20
Таблица умножения на 3
3 × 1 = 3
3 × 2 = 6
3 × 3 = 9
3 × 4 = 12
3 × 5 = 15
3 × 6 = 18
3 × 7 = 21
3 × 8 = 24
3 × 9 = 27
3 × 10 = 30
Таблица умножения на 4
4 × 1 = 4
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
4 × 6 = 24
4 × 7 = 28
4 × 8 = 32
4 × 9 = 36
4 × 10 = 40
Таблица умножения на 5
5 × 1 = 5
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
5 × 5 = 25
5 × 6 = 30
5 × 7 = 35
5 × 8 = 40
5 × 9 = 45
5 × 10 = 50
Таблица умножения на 6
6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
6 × 5 = 30
6 × 6 = 36
6 × 7 = 42
6 × 8 = 48
6 × 9 = 54
6 × 10 = 60
Таблица умножения на 7
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35
7 × 6 = 42
7 × 7 = 49
7 × 8 = 56
7 × 9 = 63
7 × 10 = 70
Таблица умножения на 8
8 × 1 = 8
8 × 2 = 16
8 × 3 = 24
8 × 4 = 32
8 × 5 = 40
8 × 6 = 48
8 × 7 = 56
8 × 8 = 64
8 × 9 = 72
8 × 10 = 80
Таблица умножения на 9
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45
9 × 6 = 54
9 × 7 = 63
9 × 8 = 72
9 × 9 = 81
9 × 10 = 90
Таблица умножения на 10
10 × 1 = 10
10 × 2 = 20
10 × 3 = 30
10 × 4 = 40
10 × 5 = 50
10 × 6 = 60
10 × 7 = 70
10 × 8 = 80
10 × 9 = 80
10 × 10 = 100
Таблица умножения на 0
0 × 1 = 0
0 × 2 = 0
0 × 3 = 0
0 × 4 = 0
0 × 5 = 0
0 × 6 = 0
0 × 7 = 0
0 × 8 = 0
0 × 9 = 0
0 × 10 = 0
Таблица умножения на 1
1 × 1 = 1
1 × 2 = 2
1 × 3 = 3
1 × 4 = 4
1 × 5 = 5
1 × 6 = 6
1 × 7 = 7
1 × 8 = 8
1 × 9 = 9
1 × 10 = 10
Умножение до: 3456
www.math10.com
Таблиця множення | Cubens
Таблиця множення чисел від 1 до 10
Таблиця множення на 2
(5 помножити на 2 дорівнюватиме 10)
Таблиця множення на 3
(2 помножити на 3 дорівнюватиме 6)
Таблиця множення на 4
(6 помножити на 4 дорівнюватиме 24)
Таблиця множення на 5
(6 помножити на 5 дорівнюватиме 30)
Таблиця множення на 6
(2 помножити на 6 дорівнюватиме 12)
Таблиця множення на 7
(3 помножити на 7 дорівнюватиме 27)
Таблиця множення на 8
(5 помножити на 8 дорівнюватиме 40)
Таблиця множення на 9
(5 помножити на 9 дорівнюватиме 45)
Таблиця Піфагора
Таблиця множення чисел від 1 до 20
Таблиця множення до 20 також називається таблиця Піфагора
Для знаходження результатів множення двох чисел потрібно одне число, взяти у верхньому рядку таблиці множення, друге число — по першому вертикальному стовпчику. На перетині шпальти і рядки знаходиться результат їх множення.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 74 | 80 | 86 | 92 | 98 | 104 | 110 | 116 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 210 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Приклади знаходження по таблиці множення:
Таблиця множення десяткових чисел вивчається як складова частина елементарної арифметики по всьому світу, оскільки вона закладає фундамент для арифметичних операцій з десятковими числами. Необхідно вивчити таблицю до 9 * 9 , або до 12 * 12 аби бути вправним у традиційній математиці.
cubens.com
Як швидко вивчити таблицю ділення? Таблиця ділення і множення – тренажер. Гра: таблиця ділення
 Таблиця ділення
Таблиця ділення
Таблицю розподілу вивчити просто. Батькам потрібно запастися терпінням і тактом по відношенню до дитини.
- Математика – це складний предмет для багатьох школярів. Тема на розподіл викладається в третьому класі. На неї відводиться один або два уроки. Дитина за цей час повинен встигнути освоїти матеріал
- Хтось пропускає уроки через хворобу, а іншим просто складно запам’ятати таблицю розподілу за один день. Тому необхідно з такими дітьми займатися вдома – це допоможе надолужити згаяне і наздогнати однолітків
Як швидко вивчити таблицю ділення?
 Як швидко вивчити таблицю ділення?
Як швидко вивчити таблицю ділення?
Важливо: Намагайтеся займатися з дитиною в ігровій формі. Йому буде цікаво, а значить, заняття пройдуть захоплююче і без особливих зусиль.
Порада: Щоб дитині було легко вчити таблицю розподілу, він повинен досконало знати таблицю множення. Тому перевірте навички множення і якщо є прогалини, повторіть пройдений матеріал.
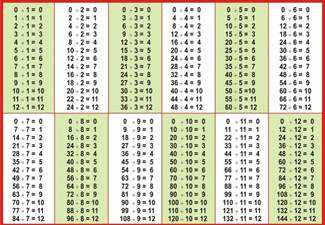 Таблиця ділення
Таблиця ділення
Отже, як швидко вивчити таблицю ділення :
- Не потрібно змушувати малюка « зубрити » дії. Він повинен зрозуміти алгоритм
- Використовуйте для пояснення монети або рахункові палички. За допомогою цих предметів дитина зможе не тільки засвоїти поділ, а й розвинути дрібну моторику рук, що добре позначається на мозкової діяльності
- Почніть вчити таблицю розподілу з 9. Коли ви дійдете до 5, складна половина таблиці буде вивчена – інше запам’ятається легко
- Хваліть малюка і заохочуйте його улюбленими солодощами, адже він намагається
- Заняття проводите щодня. Це допоможе розвинути зорову пам’ять
- Спочатку дитині буде складно запам’ятовувати дії, але з часом він буде давати правильну відповідь
- Тренуйте пам’ять малюка навіть під час прогулянки. Наприклад, нехай він вважатиме, по скільки цукерок було куплено для кожного члена сім’ї
Таблиця ділення і множення – тренажер
 Таблиця ділення і множення – тренажер
Таблиця ділення і множення – тренажер
Важливо: Спеціальні програми допомагають вивчати таблицю ділення і множення. Можна на стіну повісити плакат з великими надрукованими цифрами в цих діях.
Такий тренажер – це наочний приклад. Дитина зможе до нього звертатися за допомогою завжди, коли це буде необхідно.
Існують різні програми, які допомагають здобути навички усного рахунку і ділення.
Відео: Золота арифметика – сама класна програма для тренування усного рахунку !!!
Відео: поділ 2 клас презентація
Таблиця ділення на 2

Таблиця ділення на 2
Порада: Не проводьте додаткові заняття з дитиною вдома, якщо він себе погано почуває або просто вередує. Зачекайте пару днів, а потім продовжите займатися.
Таблиця ділення на 2:
0: 2=0 (0 розділити на 2, виходить 0)
2: 2=1 (2 розділити на 2, виходить 1)
4: 2=2 (4 розділити на 2, виходить 2)
6: 2=3 (6 розділити на 2, виходить 3)
8: 2=4 (8 розділити на 2, виходить 4)
10: 2=5 (10 розділити на 2, виходить 5)
12: 2=6 (12 розділити на 2, виходить 6)
14: 2=7 (14 розділити на 2, виходить 7)
16: 2=8 (16 розділити на 2, виходить 8)
18: 2=9 (18 розділити на 2, виходить 9)
20: 2=10 (20 розділити на 2, виходить 10)
Таблиця ділення на 3
 Таблиця ділення на 3
Таблиця ділення на 3
Важливо: Поясніть дитині , що при розподілі нуля на будь-яке число, результат буде дорівнює нулю. На нуль ділити не можна!
Розподіл трохи складніше, ніж множення, але без цього дії також не обходиться жодна математична задача. Тому малюк повинен вивчити тему « Розподіл » ;, щоб потім йому було легко вирішувати будь-які приклади і завдання в математиці.
Таблиця ділення на 3:
0: 3=0 (0 розділити на 3, виходить 0)
3: 3=1 (3 розділити на 3, виходить 1)
6: 3=2 (6 розділити на 3, виходить 2)
9: 3=3 ( 9 розділити на 3, виходить 3)
12: 3=4 (12 розділити на 3, виходить 4)
15: 3=5 (15 розділити на 3, виходить 5)
18: 3=6 (18 розділити на 3, виходить 6)
21: 3=7 (21 розділити на 3, виходить 7)
24: 3=8 (24 розділити на 3, виходить 8)
27: 3=9 (27 розділити на 3, виходить 9)
30: 3=10 (30 розділити на 3 , виходить 10)
Таблиця ділення на 4

Таблиця ділення на 4
Розподіл на чотири – це легке дію для школяра, який добре знає таблицю множення і таблицю ділення на 2 і 3. Дитина може навіть порахувати результат в розумі, якщо у немає настрою заучувати дії.
Таблиця ділення на 4:
0: 4=0 (0 розділити на 4, виходить 0)
4: 4=1 (4 розділити на 4, виходить 1)
8: 4=2 (8 розділити на 4, виходить 2)
12: 4=3 (12 розділити на 4, виходить 3)
16: 4=4 (16 розділити на 4 , виходить 4)
20: 4=5 (20 розділити на 4, виходить 5)
24: 4=6 (24 розділити на 4, виходить 6)
28: 4=7 (28 розділити на 4, виходить 7)
32: 4=8 (32 розділити на 4, виходить 8)
36: 4=9 (36 розділити на 4, виходить 9)
40: 4=10 (40 розділити на 4, виходить 10)
Таблиця ділення на 5
 Таблиця ділення на 5
Таблиця ділення на 5
Розподіл на 5 – просто і легко. Запам’ятовується легко, як і таблиця множення на 5.
Таблиця ділення на 5:
0: 5=0 (0 розділити на 5, виходить 0)
5: 5=1 (5 розділити на 5, виходить 1)
10: 5=2 (10 розділити на 5, виходить 2)
15: 5=3 (15 розділити на 5, виходить 3)
20: 5=4 (20 розділити на 5, виходить 4)
25: 5=5 (25 розділити на 5, виходить 5)
30: 5=6 (30 розділити на 5, виходить 6)
35: 5=7 (35 розділити на 5, виходить 7)
40: 5=8 (40 розділити на 5, виходить 8)
45: 5=9 (45 розділити на 5, виходить 9)
50: 5=10 (50 розділити на 5, виходить 10)
Таблиця ділення на 6
Таблиця ділення на 6
Якщо розподіл на 6 дитині ще важко дається, тоді нехай він спробує ділити стовпчиком. Чим більше він буде займатися з розподілом в стовпчик, тим швидше маля зрозуміє алгоритм розподілу.
Таблиця ділення на 6:
0: 6=0 (0 розділити на 6, виходить 0)
6: 6=1 (6 розділити на 6, виходить 1)
12: 6=2 (12 розділити на 6, виходить 2)
18: 6=3 (18 розділити на 6, виходить 3)
24: 6=4 (24 розділити на 6, виходить 4)
30: 6=5 (30 розділити на 6 , виходить 5)
36: 6=6 (36 розділити на 6, виходить 6)
42: 6=7 (42 розділити на 6, виходить 7)
48: 6=8 (48 розділити на 6, виходить 8)
54: 6=9 (54 розділити на 6, виходить 9)
60: 6=10 (60 розділити на 6, виходить 10)
Таблиця ділення на 7
Починається найскладніший процес – заучування ділення на 7.
Рада: Поясніть дитині, що йому залишилося вивчити тільки розподіл на 7, 8 і 9, а розподіл на 10 є простим дією для запам’ятовування.
Таблиця ділення на 7:
0: 7=0 (0 розділити на 7, виходить 0)
7: 7=1 (7 розділити на 7, виходить 1)
14: 7=2 (14 розділити на 7, виходить 2)
21: 7=3 (21 розділити на 7 , виходить 3)
28: 7=4 (28 розділити на 7, виходить 4)
35: 7=5 (35 розділити на 7, виходить 5)
42: 7=6 (42 розділити на 7, виходить 6)
49: 7=7 (49 розділити на 7, виходить 7)
56: 7=8 (56 розділити на 7, виходить 8)
63: 7=9 (63 розділити на 7, виходить 9)
70: 7=10 (70 розділити на 7, виходить 10)
Таблиця ділення на 8
 Таблиця ділення на 8
Таблиця ділення на 8
Важливо: Виділіть пару днів на запам’ятовування ділення на 8. Це допоможе дитині зрозуміти алгоритм дії і вивчити матеріал.
Таблиця ділення на 8:
0: 8=0 (0 розділити на 8, виходить 0)
8: 8=1 (8 розділити на 8, виходить 1)
16: 8=2 (16 розділити на 8, виходить 2)
24: 8=3 (24 розділити на 8, виходить 3)
32: 8=4 (32 розділити на 8, виходить 4)
40: 8=5 (40 розділити на 8, виходить 5)
48: 8=6 (48 розділити на 8, виходить 6)
56: 8=7 (56 розділити на 8, виходить 7)
64: 8=8 (64 розділити на 8, виходить 8)
72: 8=9 (72 розділити на 8, виходить 9)
80: 8=10 ( 80 розділити на 8, виходить 10)
Таблиця ділення на 9
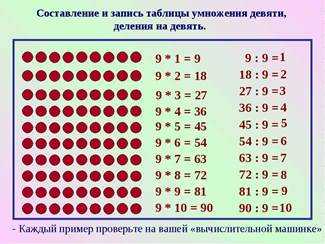 Таблиця ділення на 9
Таблиця ділення на 9
Одне з найскладніших дій в таблиці розподілу – це розподіл на 9. Багато дітей швидко розуміють ці приклади, а іншим потрібен час.
Важливо: Запасіться терпінням і у вас все вийде.
Таблиця ділення на 9:
0: 9=0 ( 0 розділити на 9, виходить 0)
9: 9=1 (9 розділити на 9, виходить 1)
18: 9=2 (18 розділити на 9, виходить 2)
27: 9=3 (27 розділити на 9, виходить 3)
36: 9=4 (36 розділити на 9, виходить 4)
45: 9=5 (45 розділити на 9, виходить 5)
54: 9=6 (54 розділити на 9, виходить 6)
63: 9=7 (63 розділити на 9 , виходить 7)
72: 9=8 (72 розділити на 9, виходить 8)
81: 9=9 (81 розділити на 9, виходить 9)
90: 9=10 (90 розділити на 9, виходить 10)
Гра – таблиця розподілу
 Гра – таблиця розподілу
Гра – таблиця розподілу
в даний час в спеціалізованих шкільних магазинах можна купити не тільки звичайні паперові плакати з таблицею ділення і множення, але і розмальовки для кращого запам’ятовування, електронні плакати « говорить таблиця ».
Також добре дитині допомагають гри таблиці розподілу або просто відео-пояснення.
Відео: Ментальна арифметика. Розподіл. Урок №13
Відео: Розвиваючий мультфільм Математика Вивчення напам’ять таблиці множення і ділення на 2
Відео: Математика 6 клас. Множення І РОЗПОДІЛ ПОЗИТИВНИХ І НЕГАТИВНИХ ЧИСЕЛ.
Часто буває так, що дитина не може зрозуміти, що хочуть від нього батьки. Якщо включити відео з поясненнями таблиці розподілу від дітей або інших дорослих людей, думки відразу прояснюються і стає все зрозуміло.
Відео: Розподіл в стовпчик
Відео: Математика 3 клас. Два способи поділу
bezlichporad.in.ua
Тренажер Таблица деления в мультиках

Наш обучающий тренажер Таблица деления в мультиках рассчитан на учащихся 2 класса, 3 класса, 4 класса школы, разработан на основании уникальной методики изучения деления двузначных чисел на однозначные числа, создан с целью помощи детям в овладении приемами деления с использованием красочных картинок и мелодий из известных мультипликационных фильмов.
С помощью игры Таблицы деления в мультиках можно быстро выучить ребенку таблицу деления на 2, 3, 4, 5, 6, 7, 8, 9 и другие числа, при этом занятие по математике будет интересным, смешным и увлекательным, учащийся твердо закрепит свои знания на деление чисел и прекрасно проведет время, рассматривая персонажей любимых мультфильмов. Деление чисел в тренажере сопровождается просмотром героев мультфильмов и прослушиванием музыки.
Игра Таблица деления в мультиках
Данный обучающий тренажер на таблицу деления разработан для учеников, которые испытывают трудности с математикой и хотели бы улучшить свои знания в умножении и делении в более игровой форме, хотели бы закрепить знания, при этом играя, просматривая картинки и слушая веселую музыку из отечественных и зарубежных мультипликационных фильмов.
Настоящая игра на таблицу деления поможет ученикам лучше разбираться с подобными примерами уже через 5 минут использования тренажера, при этом закрепить как таблицу деления, так и таблицу умножения в игре. Отличникам по математике не помешает дополнительная тренировка знаний по математике перед самостоятельной или контрольной работой по данному предмету в общеобразовательной школе.
В программе-тренажёре школьник может выбрать язык интерфейса: русский, украинский или английский. Игра создана в среде программирования Borland Delphi.
On this page it is possible to download division table program.
В каждом этапе Таблицы деления предлагается 9 примеров и 9 вариантов ответа, с каждым выполненным примером скрытая картинка из мультфильма частично открывается, а при отсутствии ошибок на деление в игре она откроется полностью и будет проигран фрагмент мелодии из соответствующего мультфильма. При наличии ошибок деления в тренажере происходит переход на повторное прохождение тура, картинка мультипликационного фильма при этом генерируется новая.
Тренажер Таблица деления в мультиках
Последний финальный тур тренажера таблицы умножения и деления в мультиках состоит из 25 примеров на деление и соответствующего количества ответов, при этом картинки с мелодиями и примеры выводятся случайным образом в разброс, таким образом усложняя деление и умножение в игровом тренажере. Тренажер-игру можно бесплатно скачать ниже на этой странице.
Правильные ответы в Таблице деления в мультиках отмечаются зеленым цветом, их количество отображается на эквалайзере справа (вертикальная полоска), неправильные ответы отмечаются красным цветом и их количество отображается на эквалайзере слева — вертикальной полоске игрового тренажера на деление чисел.
Обучающий игровой тренажер по таблице деления подходит для учеников 3 класса, содержит множество примеров на деление и умножение чисел, хранит 27 скрытых кадров мультфильмов и столько же мелодий из лучших мультипликационных фильмов России, Украины и зарубежья. Цель занятия с тренажером — не допуская ошибок в примерах на деление, пройти все этапы игры, открыть изображения, прослушать музыку из любимых мультфильмов и прийти к победе.
Операционная система: Windows 98/ME/2000/XP/2003/Vista/7/8
Язык интерфейса: Русский, Украинский, Английский
Автор: директор школы, учитель информатики и математики Андрейчук Николай Васильевич.
Дата создания: 14.12.2012.
Скачать: Таблица деления в мультиках 1.0
Размер: 17.71 Мb
Наша обучающая игра и тренажер «Таблица деления в мультиках» предназначена для бесплатного скачивания. При размещении тренажера таблицы деления или ее описания на других сайтах, наличие прямой ссылки на данную авторскую страницу является обязательным условием разработчика!
Код ссылки на эту страницу: <a href=»http://obuchonok.ru/node/207″ target=»_blank»>Таблица деления в мультиках</a>
Код баннера на сайт Обучонок:
<a href=»http://obuchonok.ru/»target=»_blank»>
<img src=»http://obuchonok.ruhttp://obuchonok.ru//banners/banob2.gif» title=»Обучающие программы и исследовательские проекты детей» alt=»Обучонок»></a>
Код ссылки на форум: [URL=http://obuchonok.ru/node/207]Таблица деления в мультиках[/URL]
obuchonok.ru
Таблиця ділення 2:2=1 3:3=1 4:4=1 5:5=1 4:2=2 6:3=2 8:4
Таблиця ділення
2:2=1 | 3:3=1 | 4:4=1 | 5:5=1 |
4:2=2 | 6:3=2 | 8:4=2 | 10:5=2 |
6:2=3 | 9:3=3 | 12:4=3 | 15:5=3 |
8:2=4 | 12:3=4 | 16:4=4 | 20:5=4 |
10:2=5 | 15:3=5 | 20:4=5 | 25:5=5 |
12:2=6 | 18:3=6 | 24:4=6 | 30:5=6 |
14:2=7 | 21:3=7 | 28:4=7 | 35:5=7 |
16:2=8 | 24:3=8 | 32:4=8 | 40:5=8 |
18:2=9 | 27:3=9 | 36:4=9 | 45:5=9 |
20:2=10 | 30:3=10 | 40:4=10 | 50:5=10 |
6:6=1 | 7:7=1 | 8:8=1 | 9:9=1 |
12:6=2 | 14:7=2 | 16:8=2 | 18:9=2 |
18:6=3 | 21:7=3 | 24:8=3 | 27:9=3 |
24:6=4 | 28:7=4 | 32:8=4 | 36:9=4 |
30:6=5 | 35:7=5 | 40:8=5 | 45:9=5 |
36:6=6 | 42:7=6 | 48:8=6 | 54:9=6 |
42:6=7 | 49:7=7 | 56:8=7 | 63:9=7 |
48:6=8 | 56:7=8 | 64:8=8 | 72:9=8 |
54:6=9 | 63:7=9 | 72:8=9 | 81:9=9 |
60:6=10 | 70:7=10 | 80:8=10 | 90:9=10 |
30
3 КЛАС
Круг і коло
На малюнку зображено круг. Лінія, яка є межею круга, називається колом. Коло креслять за допомогою циркуля. Точка О, в якій розміщується голка циркуля – центр кола. Відрізок ОА – радіус кола.
А
О
Збільшення та зменшення числа в кіька разів
Щоб збільшити число в 4 рази, його необхідно помножити на 4.
Наприклад: 5х4=20.
Щоб зменшити число в 4 рази, його необхідно поділити на 3.
Наприклад: 15:3=5.
31
Порядок дій
1) Якщо у виразі без дужок є тільки додавання і віднімання, їх виконують у тому порядку, в якому вони записані.
Наприклад: 40-12+8=36
57-9-20=28
2) Якщо у виразі без дужок є тільки множення і ділення, їх виконують у тому порядку, в якому вони записані.
Наприклад: 24 : 4 : 3=2 12 : 3 х 8=32
Ід. ІІд. Ід. ІІд.
3) Якщо у виразі немає дужок, то спочатку виконують по порядку множення і ділення, а потім додавання і віднімання.
Наприклад: 24 – 8 : 4 = 22 4 х 3 + 2 х 6 = 24
ІІд. Ід. Ід. ІІІд. ІІд.
4) Якщо у виразі є дужки, тоді спочатку виконують дії в дужках.
Наприклад: 35 – (41 – 24) = 18 36 : (13 – 9) = 9
ІІд. Ід. ІІд. Ід.
32
Одиниці вимірювання величин
Час
Доба (д)
Година (год)
Хвилина (хв)
Секунда (с)
В 1 добі 24 години
В 1 годині 60 хвилин
В 1 хвилині 60 секунд
1 год = 60 хв
1 хв = 60с
Довжина
Метр – основна одиниця довжини
Дециметр – десята частина метра
Сантиметр – десята частина дециметра, або сота частина метра
Міліметр – десята частина сантиметра
10 дм = 1 м
10 см = 1 дм
100 см = 1м
10 см = 10 мм
Маса
Кілограм (кг)
Грам (г)
1 кг = 100 г
33
Задача, яка містить буквене дане
З однієї грядки зібрали R гарбузів, а з другої – в 3 рази більше. Усі гарбузи склали в 2 ящики порівну в кожний. Скільки гарбузів клали в один ящик?
1) R х 3 – зібрали гарбузів з другої грядки
2) R + R х 3 – зібрали гарбузів з двох грядок
3) (R + R х 3) : 2 – клали гарбузів в один ящик
Відповідь: (R + R х 3) : 2 гарбузів.
Якщо умова задачі містить буквене дане, то відповідь записують у вигляді виразу.
Трицифрові числа
Сотні | Десятки | Одиниці |
3 | 4 | 5 |
5 | 0 | 6 |
ІІІ розряд | ІІ розряд | Ірозряд |
Говорять: розряд одиниць, розряд десятків, розряд сотень
Розряд одиниць – І розряд
Розряд десятків – ІІ розряд
Розряд сотень – ІІІ розряд
34
Складання і віднімання трицифрових чисел без переходу через десяток
Додаючи трицифрові числа, сотні додають до сотен, десятки до десятків.
Наприклад: 520 + 340 = (500+300)+(20+40)=800+60=860
500+20 300+40
Віднімаючи трицифрові числа, сотні віднімають від сотень, десятки віднімають від десятків.
Наприклад: 470 – 320 = (400-300)+(70-20)=100+50=150
400+70 300+20
Письмове додавання і віднімання трицифрових чисел
При додаванні трицифрових чисел одиниці додають до одиниць, десятки до десятків і сотні до сотень.
Наприклад: 325
+413
738
35
Усне множення і ділення
Множення і ділення з числами 0, 1, 10, 100
№1
Формула а х 1 = а
У результаті множення будь-якого числа на одиницю в добутку маємо те саме число. Наприклад: 5х1=5.
№2
Формула а х 0 = 0
При множенні будь-якого числа на 0 у добутку дістаємо 0. Наприклад: 15х0=0.
№3
Формула а : 1 = а
При діленні будь-якого числа на 1 у частці буде те саме число. Наприклад: 23:1=23.
№4
Формула а : a = 1
При діленні будь-якого числа на це саме число у частці маємо те саме число. Наприклад: 9:9=1
№5
Формула 1 х а = а
При множенні одиниці на будь-яке число в добутку маємо те саме число. Наприклад: 1х40=40
№6
Формула 0 : а = 0
При діленні нуля на будь-яке число у частці маємо нуль. Наприклад: 0:52=0.
№7
Ділити на нуль не можна!
Наприклад: 4:0.
36
Множення і ділення на 10, 100
№1
Щоб помножити число на 10, треба до нього справа приписати один нуль. Наприклад: 4х10=40.
№2
Щоб помножити число на 100 треба до нього справа приписати два нулі. Наприклад: 4х100=400.
№3
Щоб поділити число, яке закінчується нулями, на 10 треба в ньому відкинути справа один нуль. Наприклад: 40:10=4.
№4
Щоб поділити число, яке закінчується нулями на 100, треба в ньому відкинути справа два нулі. Наприклад: 400:100=4.
1. Ділення числа на добуток
Поділити число на добуток можна так: поділити число на один з множників, а потім – результат поділити на другий множник.
Наприклад: 18: (2х3)=18:2:3=3.
Формула: А: (ВхС)=А:В:С
2. Множення суми на число
Щоб помножити суму на число, можна помножити на це число кожний доданок і знайдені добутки додати.
Наприклад: (20+8)х8=20х8+8х8=160+64=224.
Формула: (А+В)хС=АхС+ВхС
37
3. Множення числа на суму
Щоб помножити число на суму, можна помножити число на кожний доданок і здобуті результати додати.
Наприклад:7х(20+5)=7х20+7х5=140+35=175.
Формула: Ах(В+С)=АхВ+АхС
4. Множення одноцифрового числа на двоцифрове
Якщо другий множник – двоцифрове число, то його можна розкласти на десятки й одиниці, а потім перший множник помножити окремо на десятки та одиниці і результати додати.
Наприклад: 3х24=3х20+3х4=60+12=72.
20 4
5. Ділення суми на число
Щоб поділити суму на число, можна поділити на це число кожний доданок і знайдені частки додати.
Наприклад: (24+12):4=24:4+12:4=6+3=9.
Формула: (А+В):С=А:С+В:С
6. Ділення різниці на число
Щоб поділити різницю на число, можна поділити на це число зменшуване і від’ємник, а потім результати відняти.
Наприклад: (90-21):3=90:3-21:3=30-7=23.
Формула: (А-В):С=А:С-В:С
38
4 КЛАС
Багатоцифрові числа
Чотирицифрові числа
Тисячі | Сотні | Десятки | Одиниці |
1 | 5 | 6 | 3 |
8 | 6 | 3 | 0 |
П’ятицифрові числа
Десятки тисяч | Одиниці тисяч | Сотні | Десятки | Одиниці |
1 | 0 | 5 | 6 | 4 |
8 | 9 | 6 | 3 | 1 |
Шестицифрові числа
Сотні Тисяч | Десятки тисяч | Одиниці тисяч | Сотні | Десятки | Оди-ниці |
5 | 2 | 0 | 8 | 3 | 9 |
9 | 9 | 9 | 0 | 6 | 5 |
Клас тисяч | Клас одиниць | ||||
Тисяча тисяч – це мільйон
1000000
39
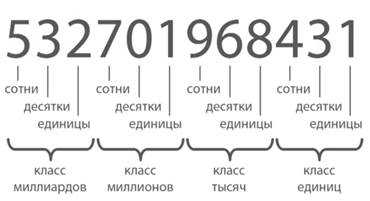
Кількість десятків, сотень, тисяч у числі
1) Щоб дізнатися, скільки всього десятків у числі, достатньо відкинути останню цифру справа. Число, що залишилося, покаже, скільки повних десятків у числі.
Наприклад: 4563. В числі 456 десятків.
2) Щоб дізнатися, скільки всього сотень у числі, достатньо відкинути дві останніх цифри справа. Число, що залишилося, покаже, скільки повних сотень у числі.
Наприклад: число 4563. В ньому 45 сотень.
3) Щоб дізнатися, скільки всього тисяч у числі, достатньо відкинути три останніх цифри справа. Число, що залишилося, покаже, скільки повних тисяч у числі.
Наприклад: число 4563. В ньому 4 тисячі.
Десяткова система числення
Перелічуючи будь-які предмети, називають числа: один, два, три, чотири, п’ять, шість, сім і т.д.
Це натуральні чисел. Якщо їх записати так, що за кожним натуральним числом буде йти число, на одиницю більше від нього, то дістанемо натуральний ряд чисел. У ньому найменше число одиниця, а найбільшого числа не існує.
Спочатку люди кожному новому числу давали окрему назву. Але поступово стали застосовувати спеціальні способи для називання й позначення чисел. Яким би
великим не було число, його можна записати за
40
допомогою тільки десяти числових знаків – цифр: 1, 2, 3,
4, 5, 6, 7, 8, 9, 0. Записуючи й читаючи числа використовуємо групування по 10: десять одиниць – десяток; десять десятків – сотня; десять сотень – тисяча; десять, десять тисяч – десяток тисяч і т. д. Такий спосіб лічби групами по 10 характерний для десяткової системи числення або десяткової нумерації.
Десяткове групування чисел зумовило появу поняття про розряд, розрядні числа, розрядні одиниці.
В усній нумерології, крім розрядної лічби застосовують ще спосіб групування розрядів у класи. Щоб прочитати багатоцифрове число, його запис розбивають на групи, по три цифри у кожній. Три перші цифри справа утворюють клас тисяч.
Так само утворюють класи для чисел, які більші за мільйон.
У кожному класі своя лічильна одиниця. Одиницею першого класу є одиниця. У другому класі лічильною одиницею є тисяча. Читаючи числа, називають число одиниць, кожного класу, назву класу. Письмова нумерація ґрунтується на помісцевому значенні цифр (позиційний принцип), тобто значення цифри в запису числа залежить від того, яке місце (позицію) вона займає. Якщо цифру переставити на одне місце вліво, її значення збільшується в 10 раз, а якщо на одне місце вправо, то її значення зменшується в 10 раз. Можна сказати, що нумерація ґрунтується ще на принципі додавання, оскільки число є не що інше, як запис суми його розрядних доданків. Наприклад: 34415=30000+4000+400+10+5.
41
Система назв величезних чисел з позначкою кількості нулів після одиниці
Назва класа | Кількість нулів | Ступінь |
Мільйон | 6 | 106 |
Більон | 9 | 109 |
Трільон | 12 | 1012 |
Квадрільон | 15 | 1015 |
Квінтільон | 18 | 1018 |
Секстільон | 21 | 1021 |
Септільон | 24 | 1024 |
Октальон | 27 | 1027 |
Нональон | 30 | 1030 |
Декальон | 33 | 1033 |
Ендікальон | 36 | 1036 |
Додекальон | 39 | 1039 |
42
Одиниці вимірювання величин
1. Одиниці вимірювання довжини
1 м = 10 дм 1 км = 1000м
1 м = 100 см 1дм = 10 см
1 м = 1000 мм 1 см = 10 мм
2. Одиниці вимірювання маси
1 т = 1000 кг 1ц = 100 кг
1 кг = 1000г 1т = 10ц
3. Одиниці вимірювання часу
1 хв = 60 с 1 доба = 24 г
1 год = 60 хв 1 рік = 24 міс
1 рік = 365 днів 1 вік = 100 років
4. Одиниці вимірювання площі
1 см2 = 100 мм2 1 ар = 100м2
1 дм2 = 100 см2 1 га = 100 арів
1 м2 = 1000 дм2 1 км2 = 1000000 м2
43
Закони додавання
№1
Переставній закон додавання
Від переставляння доданків сума не змінюється.
Наприклад: 50+60=60+50
Формула: а+b=b+a
№2
Сполучний закон додавання
Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого і третього.
Наприклад: (50+20)+5=50+(20+5)
Формула: (a+b)+c=a+(b+c)
№3
Властивість переставного і сполучного закону
дії додавання
У сумі кількох доданків можна переставляти доданки і брати їх у дужки будь-яким чином.
Віднімання суми із числа
Щоб від числа відняти суму двох чисел, достатньо послідовно відняти кожний доданок окремо.
Наприклад: 28-(8+9)=(28-8)-9=20-9=11
Додавання і віднімання іменованих чисел
53 м 08 см – 9 м 73 см = 43 м 35 см
5308 53 м 08 см
973 9 м 73 см
4335 (см) 43 м 35 см
44
Коло і круг
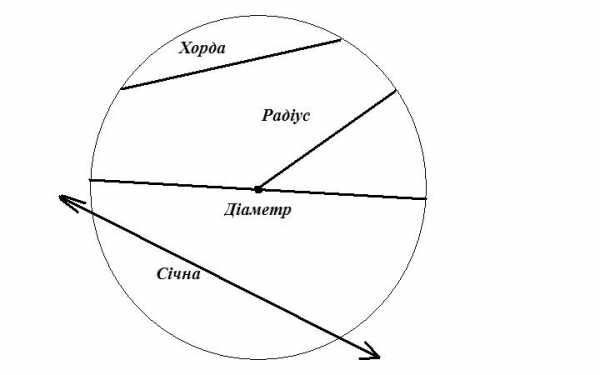
Круг і його елементі. Хорда круга, діаметр круга, радіус, сектор круга, сегмент круга.
Види трикутників
За кутами трикутники поділяють на гострокутні, прямокутні й тупокутні. Якщо всі кути трикутника гострі, то він називається гострокутним, а якщо один з його кутів тупий, то тупокутним. Трикутник, який має прямий кут, називається прямокутним. Залежно від довжин сторін трикутники поділяються на різносторонні (всі сторони за довжиною різні), рівнобедрені (дві сторони рівні) і рівносторонні (всі сторони рівні).
Гострокутний Тупокутний Прямокутний
45
Різносторонній Рівнобедрений Рівносторонній
Круглі числа
Числа, що закінчуються нулем або кількома нулями, називають круглими числами.
Наприклад: 40, 100, 250, 1000 – круглі числа.
Швидкість. Час. Відстань
v t s
1. Щоб знайти швидкість, треба відстань поділити на час.
Формула: s = v : t
2. Щоб знайти відстань, треба швидкість помножити на час.
Формула: s = v х t
3. Щоб знайти час, треба відстань поділити на швидкість.
Формула: t = s : v
46
Геометричні фігури
Геометричні фігури діляться на геометричні тіла і плоскі фігури. Циліндр, куб, куля, конус, зрізаний конус, паралелепіпед, піраміда, зрізана піраміда, призма – це геометричні тіла. Круг, коло, кільце, квадрат, прямокутник, трикутник – це плоскі фігури.
Геометричні тіла
Круглі тіла

куля циліндр конус зрізаний конус
Призми та піраміди

призма паралелепіпед піраміда
куб зрізана піраміда
47
Плоскі тіла
круг коло кільце
квадрат прямокутник трикутник
трапеція ромб овал
48
Закони множення
1. Переставний закон множення
Від переставляння множників добуток не змінюється.
Формула: a x b = b x a
Наприклад: 5 х 6 = 6 х 5
2. Сполучний закон множення
Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого і третього чисел.
Формула: (a x b) x c = a x (b x c)
Наприклад: (5 х 6) х 3 = 5 х (6 х 3)
Властивість переставного і сполучного
законів дії множення
У добутку кількох множників можна переставляти множники і брати їх у дужки будь-яким чином.
Формула: a x b x c x d = (a x b) x (c x d)
Наприклад: 3 х 4 х 25 х 30 = (3 х 4) х (25 х 30)
3 х 4 х 25 х 30 = (3 х 30) х (4 х 25)
a x b x c x d = (a x d) x (b x c)
3. Розподільний закон множення
Добуток суми двох чисел на будь-яке число дорівнює сумі добутків кожного доданка на це число.
Формула: (a + b) x c = a x c + b x c
Наприклад: (3 + 5) х 4 = 3 х 4 + 5 х 4
49
Площа фігури
Площа квадрата і прямокутника
Квадратний сантиметр – це площа квадрата зі стороною 1 см.
1 см2
Щоб обчислити площу прямокутника, треба визначити його довжину і ширину і знайти добуток цих чисел.
В 4 см С
2 см
А Д
SАВСД = 4 х 2 = 8 (см2)
Відповідь: SАВСД = 8 см2
Одиниці вимірювання площі
Площа – одна з математичних величин. Для її вимірювання користуються не тільки квадратним сантиметром, а й іншими одиницями. У таблиці подано одиниці вимірювання площі, які найчастіше застосовують у практичній діяльності.
1 мм2 – площа квадрата, сторона якого 1 мм
1 см2 – площа квадрата, сторона якого 1 см
1 дм2 – площа квадрата, сторона якого 1 дм
1 м2 – площа квадрата, сторона якого 1 см
Ар (сотка) – площа квадрата, сторона якого 10 м
Гектар (га) – площа квадрата, сторона якого 100 м
1 км2 – площа квадрата, сторона якого 1 км
50
Одиниці площі
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 1000 дм2
1 ар = 100 м2
1 км2 = 1000000 м2

1 см2
1 дм2
51
refdb.ru
Таблица умножения без ответов распечатать. Таблица умножения, карточки. — Наши дети — Полезные советы — Каталог статей
Таблица умножения без ответов распечатать. Таблица умножения, карточки.
Ниже дана таблица умножения без ответов. Такая таблица умножения хорошо подходит, когда нужно проконтролировать, как ребенок ее учит.
Таблицу умножения можно распечатать. Таблицу можно разрезать по числам и сделать карточки. Карточки давать ребенку проверяя знание умножения определенного числа.
Давайте заучивать ребенку таблицу умножения постепенно, по одному столбику в день.
Чтобы проще было выучить таблицу умножения с ней нужно решать примеры, так ребенок визуально быстрей запомнит ее.
Таблица умножения без ответов
2 х 1= 3 х 1= 4 х 1= 5 х 1=
2 х 2= 3 х 2= 4 х 2= 5 х 2=
2 х 3= 3 х 3= 4 х 3= 5 х 3=
2 х 4= 3 х 4= 4 х 4= 5 х 4=
2 х 5= 3 х 5= 4 х 5= 5 х 5=
2 х 6= 3 х 6= 4 х 6= 5 х 6=
2 х 7= 3 х 7= 4 х 7= 5 х 7=
2 х 8= 3 х 8= 4 х 8= 5 х 8=
2 х 9= 3 х 9= 4 х 9= 5 х 9=
2 х 10= 3 х 10= 4 х 10= 5 х 10=
Таблица умножения без ответов
6 х 1= 7 х 1= 8 х 1= 9 х 1=
6 х 2= 7 х 2= 8 х 2= 9 х 2=
6 х 3= 7 х 3= 8 х 3= 9 х 3=
6 х 4= 7 х 4= 8 х 4= 9 х 4=
6 х 5= 7 х 5= 8 х 5= 9 х 5=
6 х 6= 7 х 6= 8 х 6= 9 х 6=
6 х 7= 7 х 7= 8 х 7= 9 х 7=
6 х 8= 7 х 8= 8 х 8= 9 х 8=
6 х 9= 7 х 9= 8 х 9= 9 х 9=
6 х 10= 7 х 10= 8 х 10= 9 х 10=
Ниже дана ссылка по которой можно распечатать таблицу умножения.
Таблица умножения без ответов распечатать
Вам понравилась статья, поделитесь с друзьями в вашей социальной сети, нажав на кнопку:
optim-z.ru

 Слово «цифра» происходит от арабского «сыфр», что в переводе означает «ноль». Люди привыкли называть цифры арабскими, но на самом деле было бы правильнее именовать их индийскими. Первые цифры появились в Индии, оттуда перешли к арабам, а затем начали появляться и в Европе.
Слово «цифра» происходит от арабского «сыфр», что в переводе означает «ноль». Люди привыкли называть цифры арабскими, но на самом деле было бы правильнее именовать их индийскими. Первые цифры появились в Индии, оттуда перешли к арабам, а затем начали появляться и в Европе.





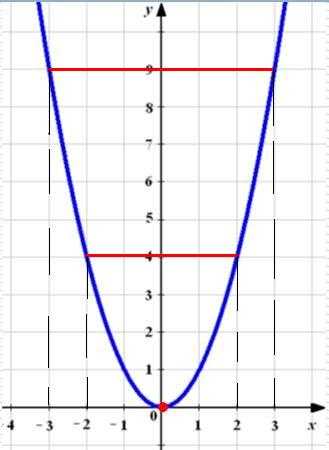
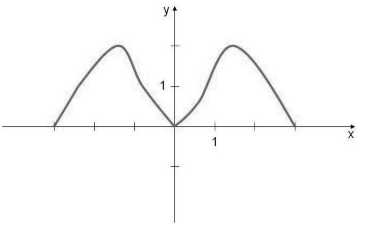
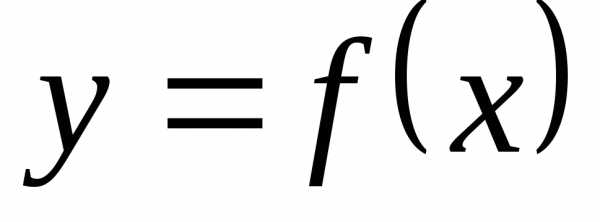 называетсячетной, если она не
изменяет своего значения при изменении
знака аргумента, т.е..
называетсячетной, если она не
изменяет своего значения при изменении
знака аргумента, т.е..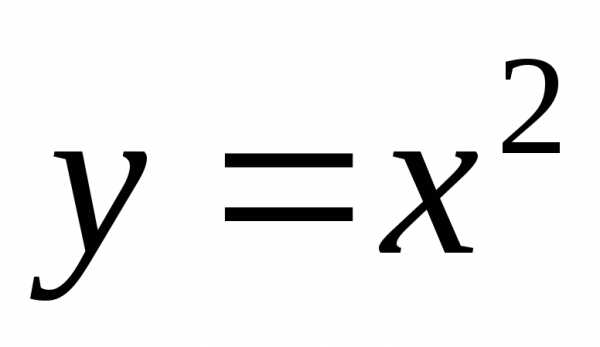 ;
;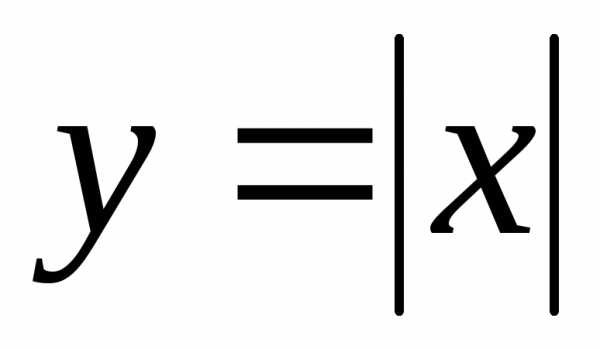 – четные функции.
– четные функции.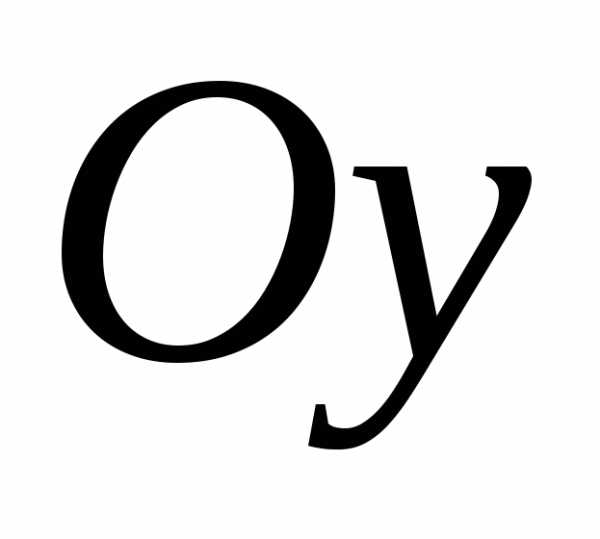 (рис.1.4).
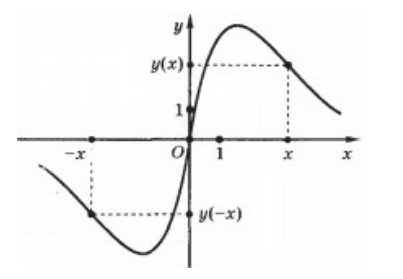
(рис.1.4).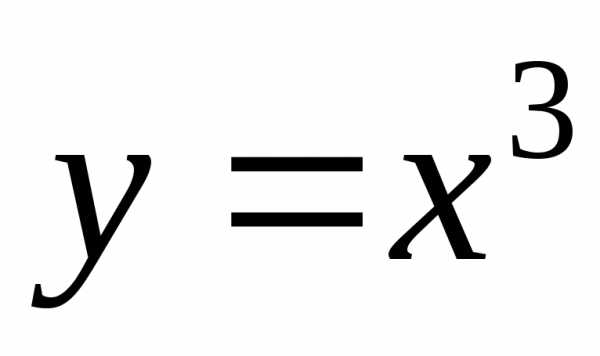 – нечетные функции.
– нечетные функции.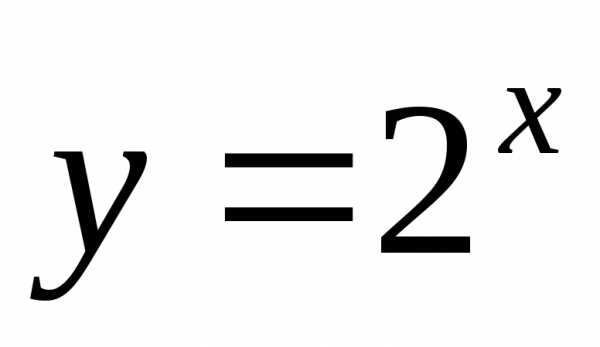 ;
;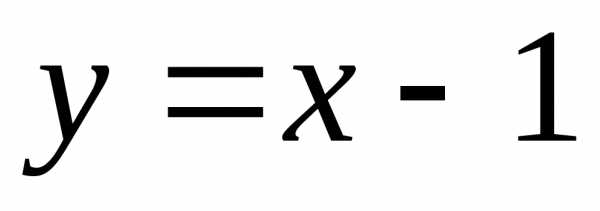 ;
;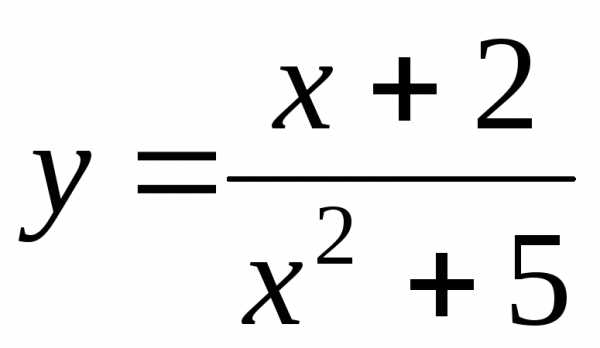 .
.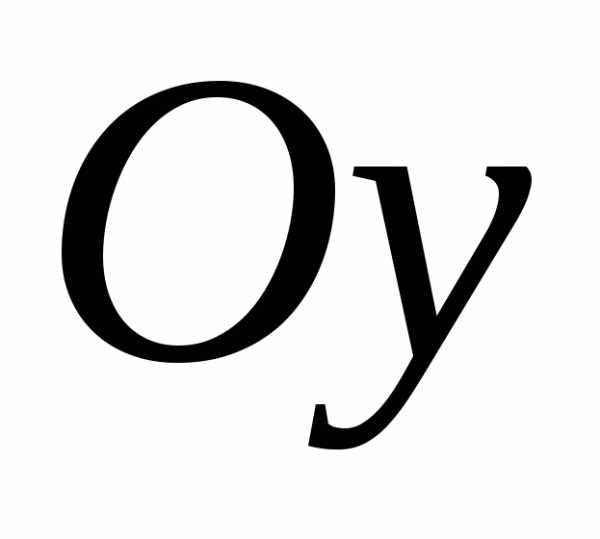 ,
ни относительно начала координат.
,
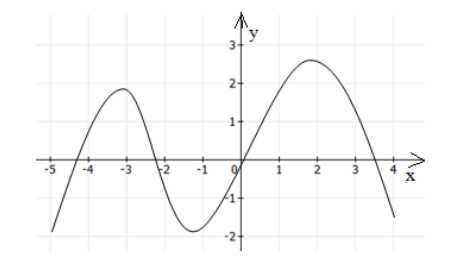
ни относительно начала координат.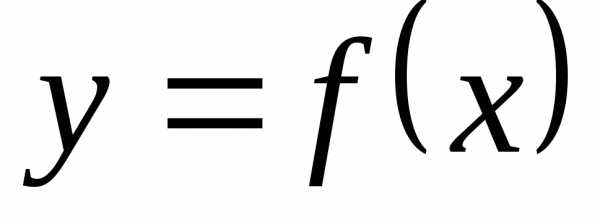 называется периодической, если существует
такое положительное число
называется периодической, если существует
такое положительное число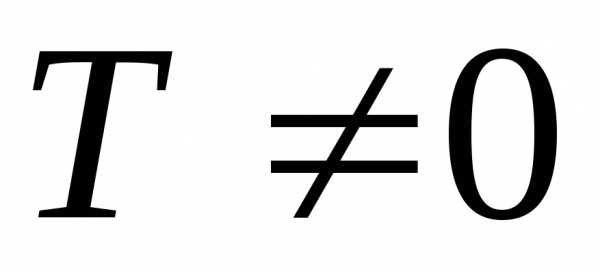 ,
чтов
области определения функции.
,
чтов
области определения функции.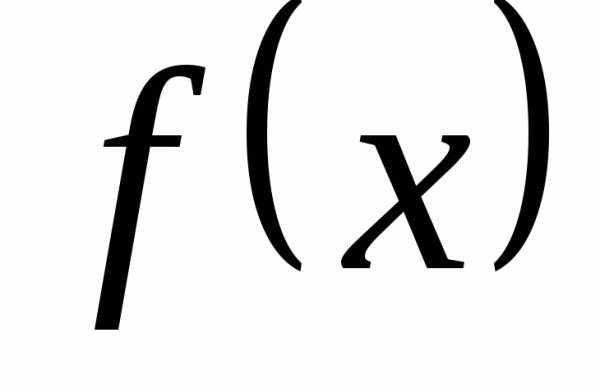 .
.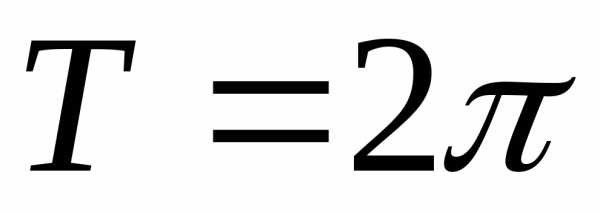 .
.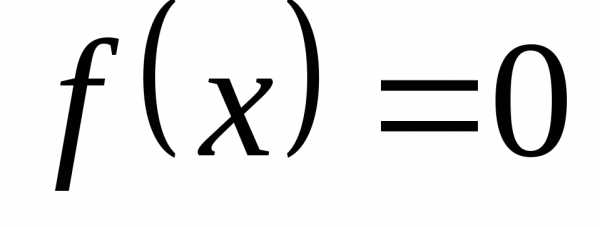 ,
называетсянулем функции.
,
называетсянулем функции.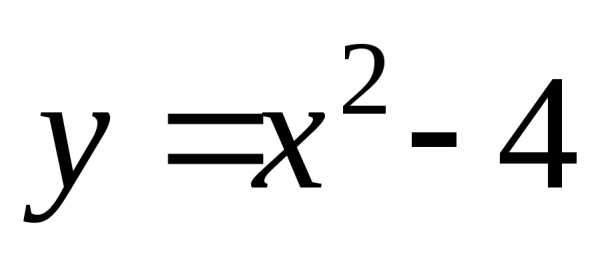 являются значения
являются значения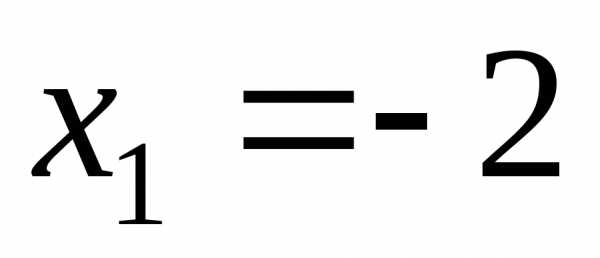 и
и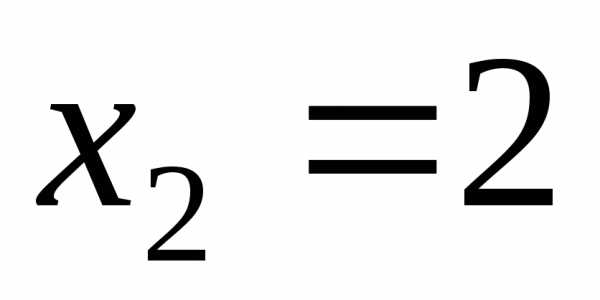 .
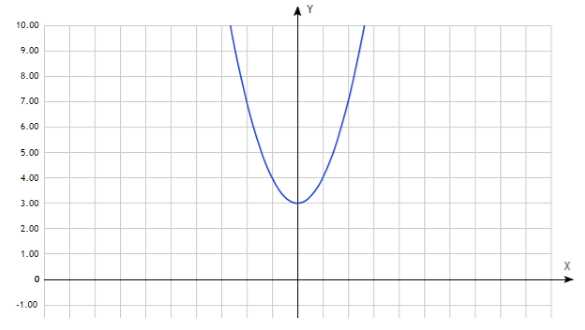
.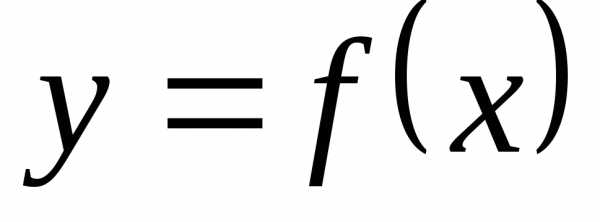 называетсяограниченнойна множествеХ, если существует такое число
называетсяограниченнойна множествеХ, если существует такое число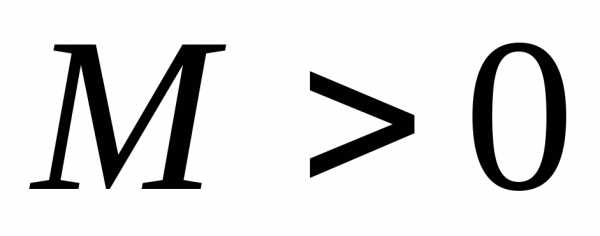 ,
что для всех
,
что для всех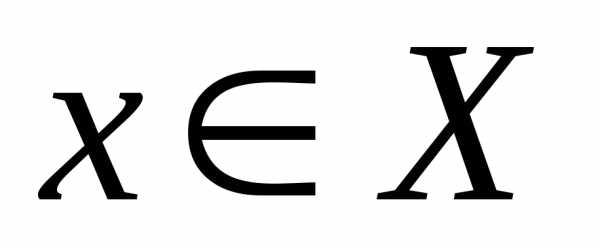 выполняется неравенство
выполняется неравенство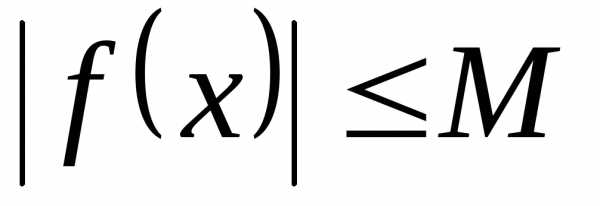 .
.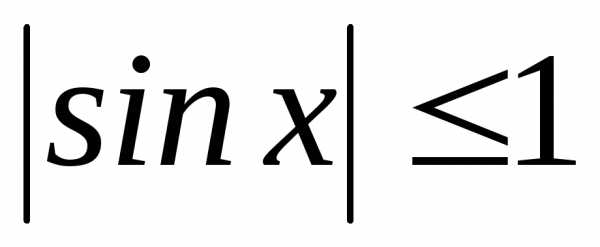 и
и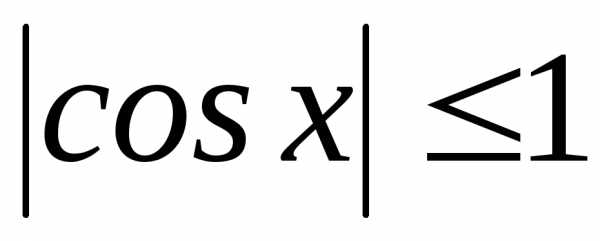 для.
для.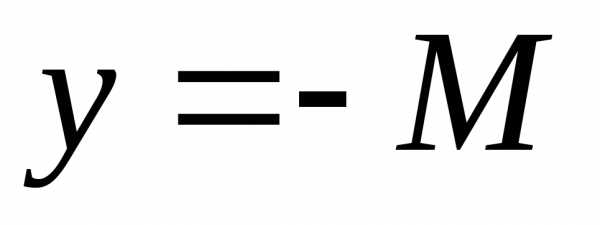 и
и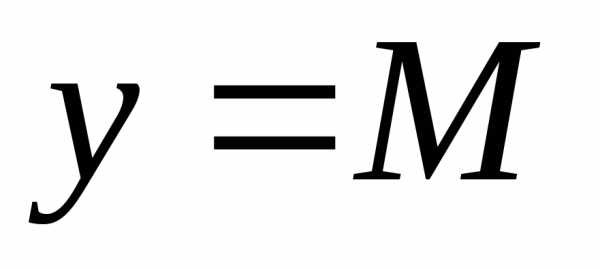 (рис.1.8).
(рис.1.8).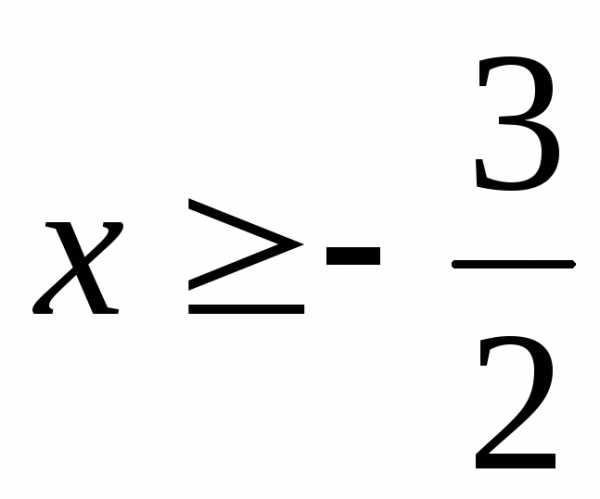 ;
;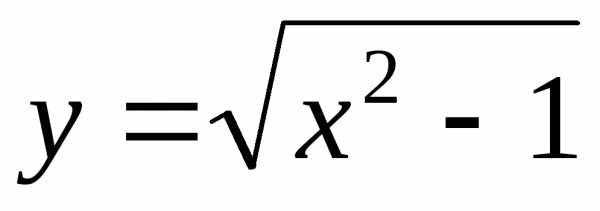 ; Ответ:
; Ответ: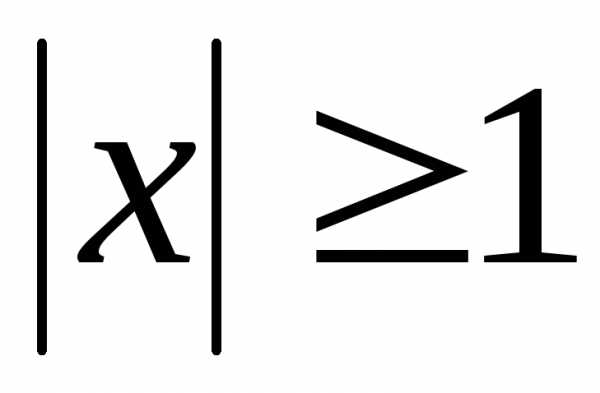 ;
;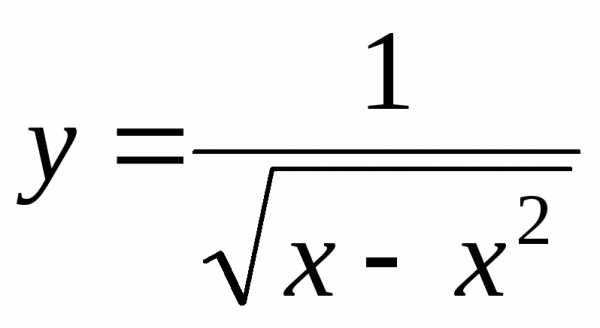 ; Ответ:;
; Ответ:;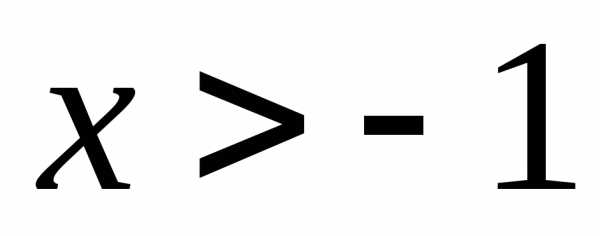 .
.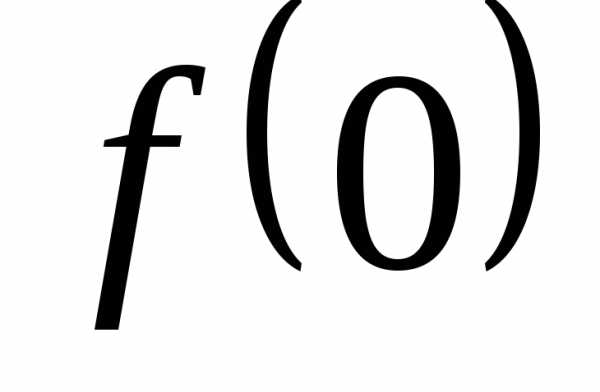 ,
,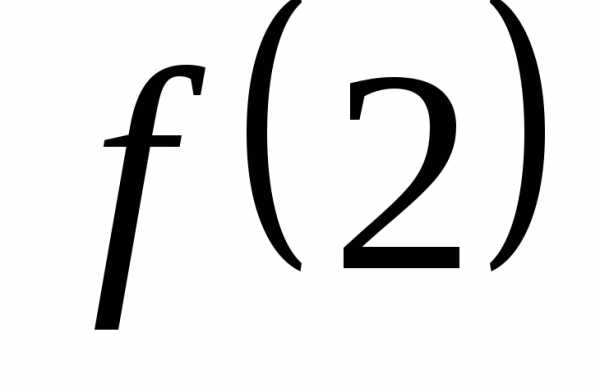 ,
,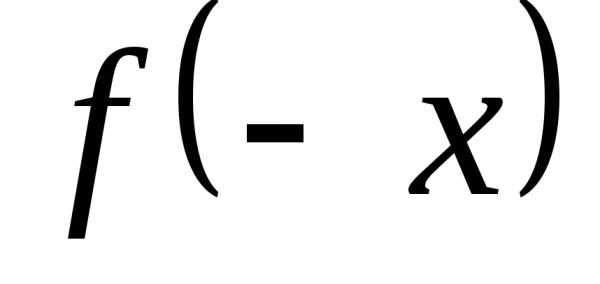 ,
,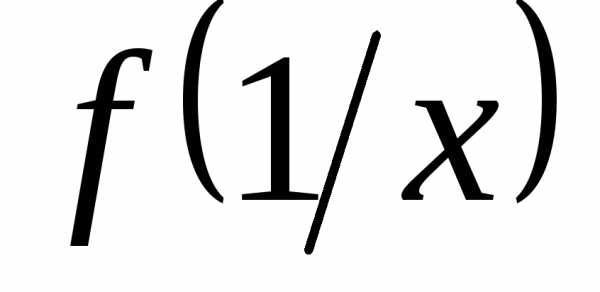 ,
если.
,
если.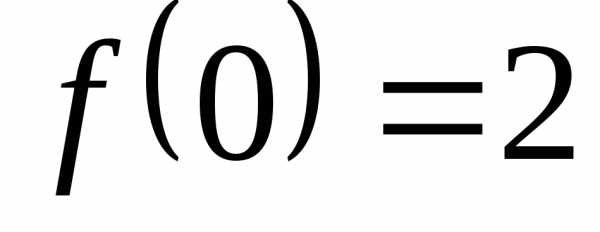 ;
; ;;.
;;.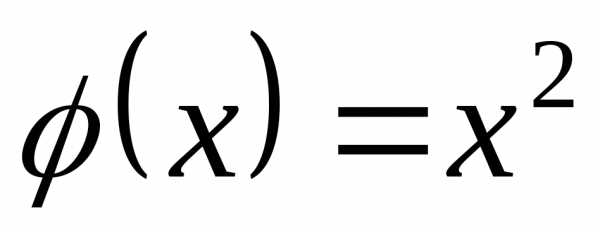 и
и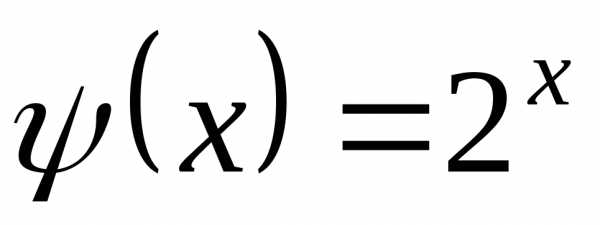 .
Найти
.
Найти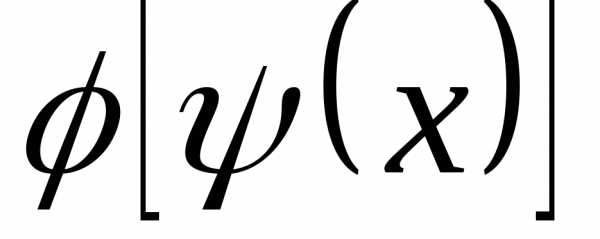 и
и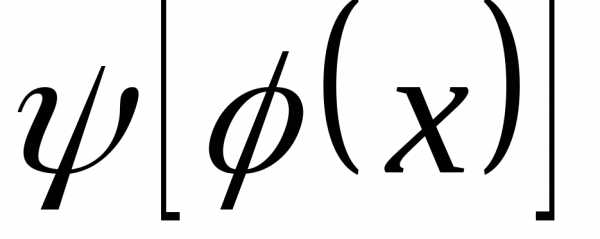 .
.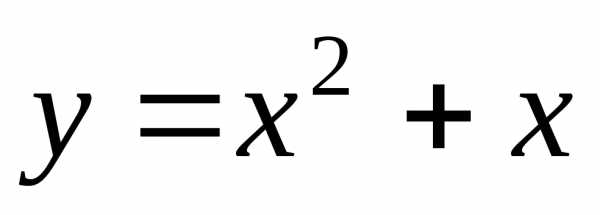 ; Ответ:
общего вида;
; Ответ:
общего вида;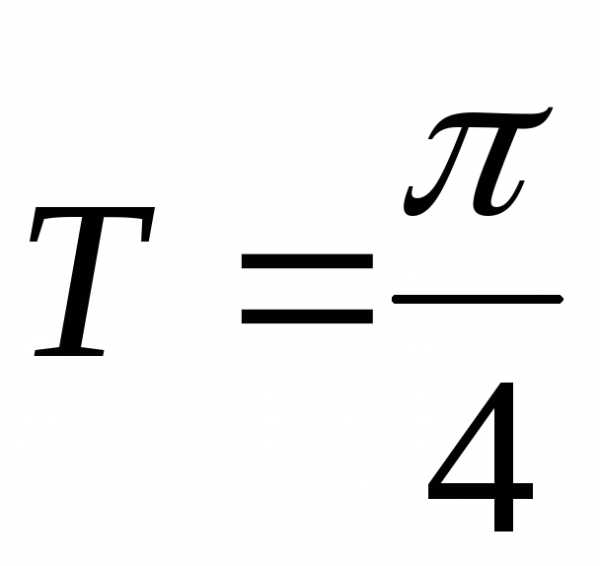 ;
;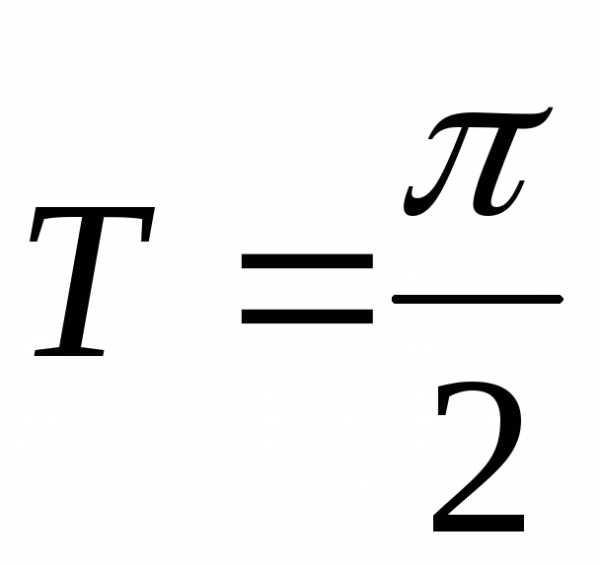 ;
;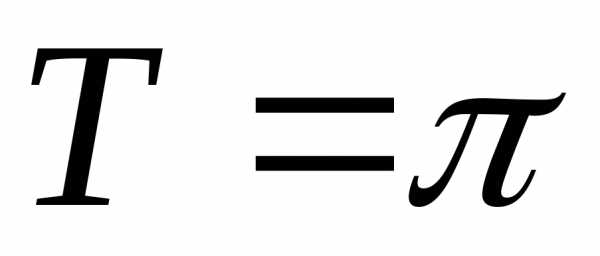 .
.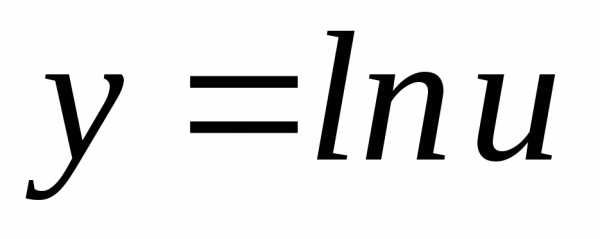 ;
;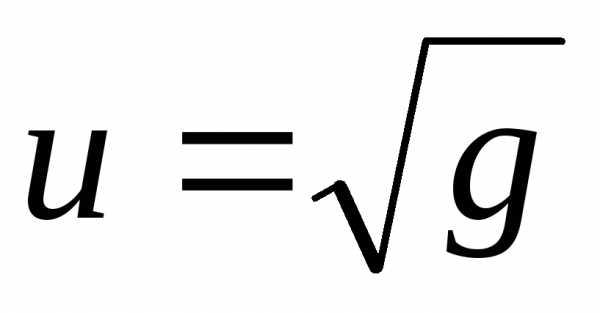 ;;
;;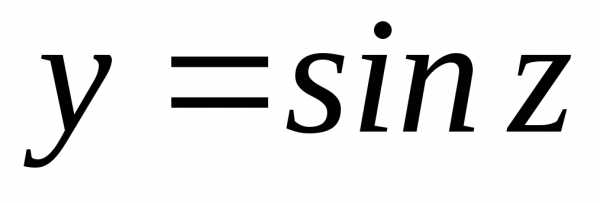 ;
;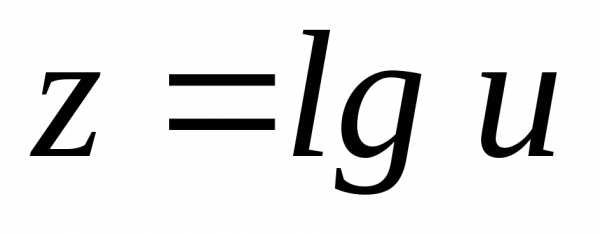 ;;
;;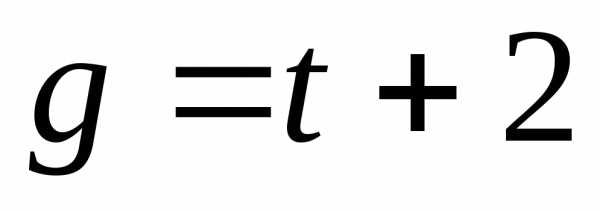 ;
;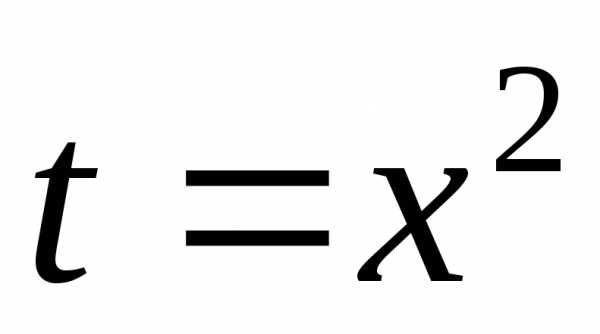 .
.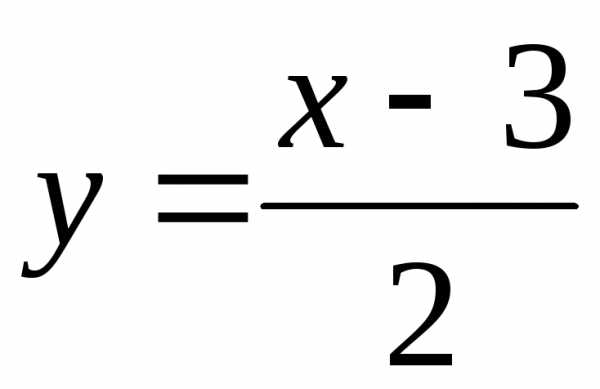 ;
;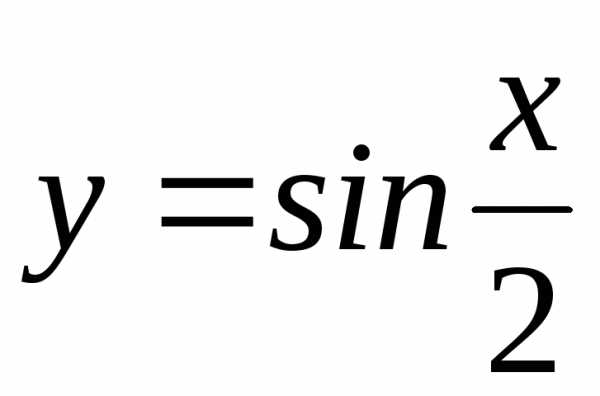 ; Ответ:;
; Ответ:;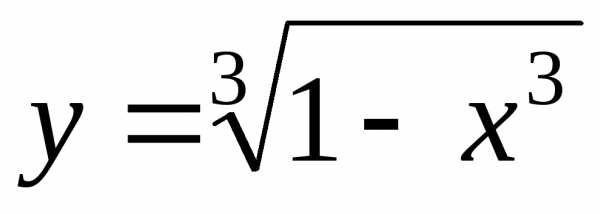 ; Ответ:
; Ответ: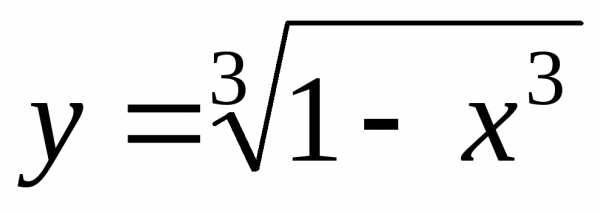 .
.
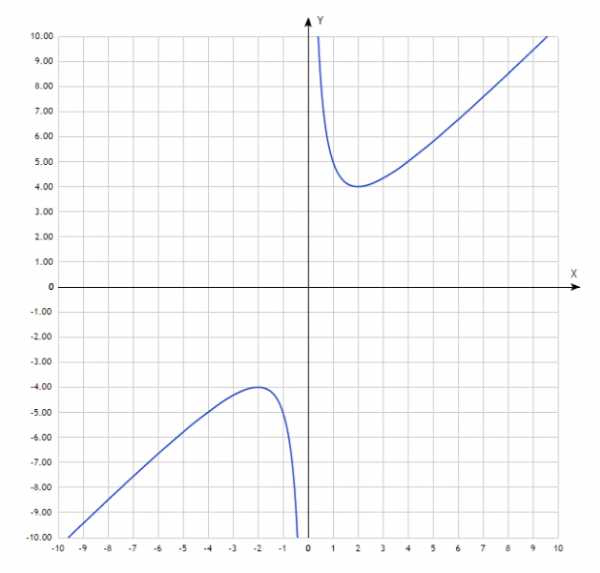
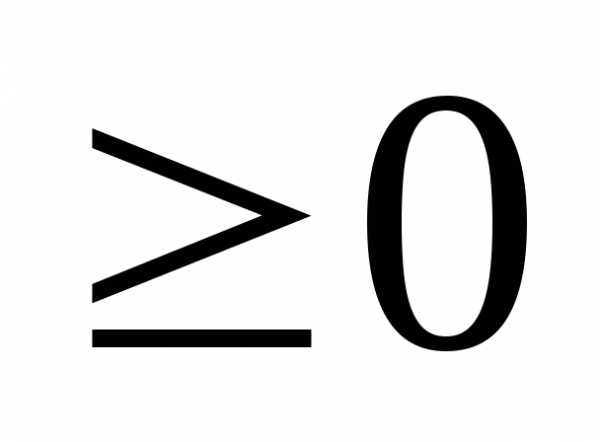 .
График функции y=f(x)
в области отрицательных значений
аргумента симметричен построенной
ветви относительно оси ординат и
получается отражением её относительно
этой оси.
.
График функции y=f(x)
в области отрицательных значений
аргумента симметричен построенной
ветви относительно оси ординат и
получается отражением её относительно
этой оси.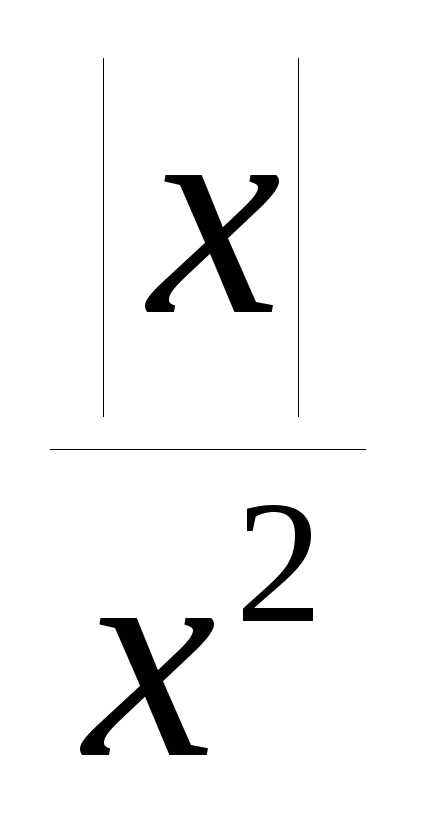 .
. .
График функцииy=
.
График функцииy=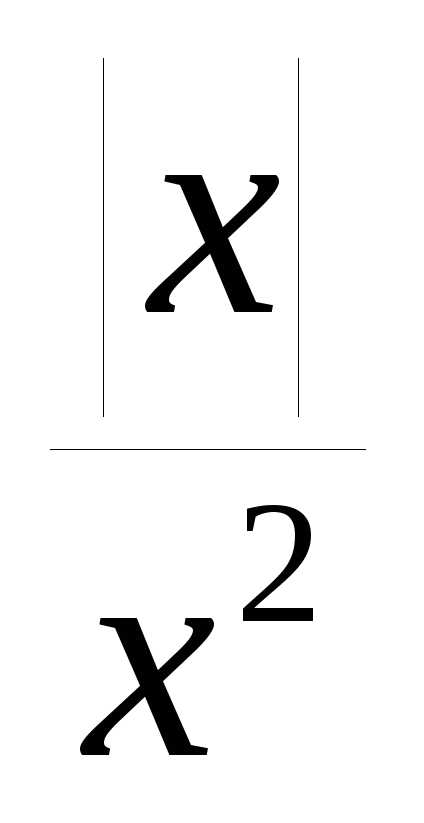 в области отрицательных значенийx
получаем отражением относительно оси
ординат (рис.11).
в области отрицательных значенийx
получаем отражением относительно оси
ординат (рис.11).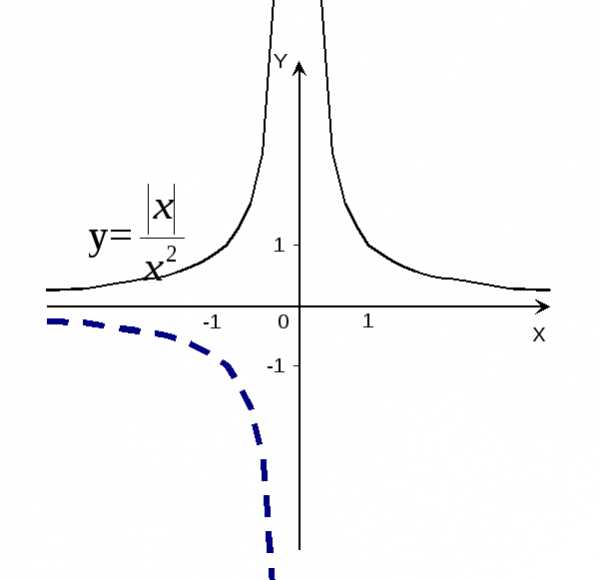
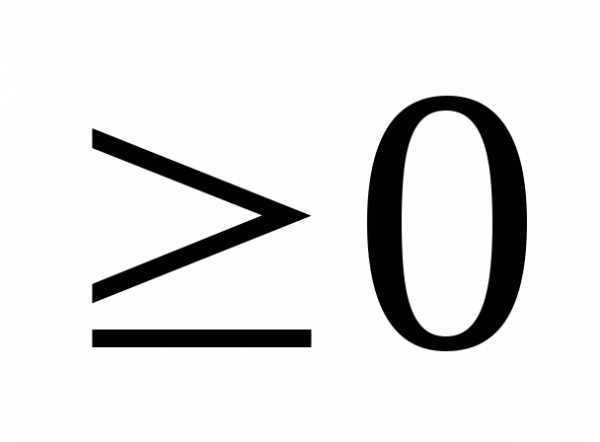 ).
). .
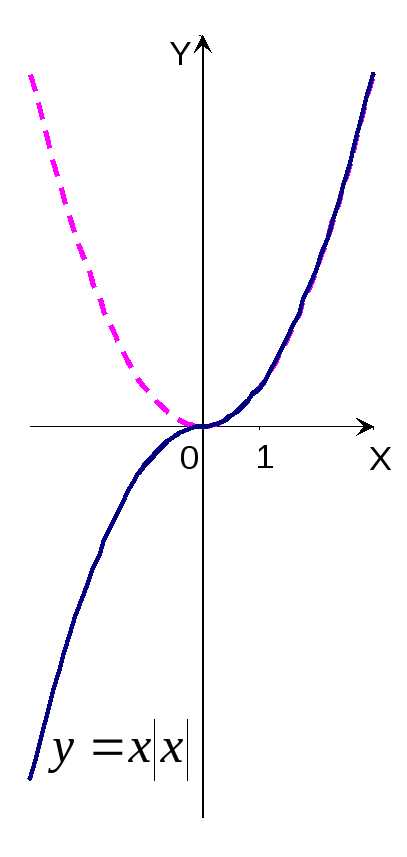
.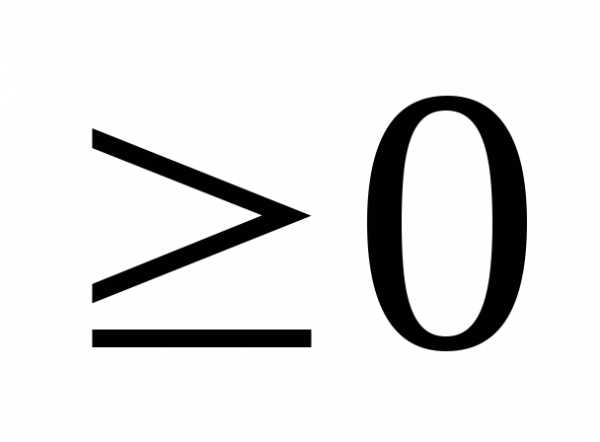 ),
где она имеет вид y=x2.
График функции y=x
),
где она имеет вид y=x2.
График функции y=x в области отрицательных значений
аргумента получаем отражением
построенной ветви относительно начала
координат (рис.12).
в области отрицательных значений
аргумента получаем отражением
построенной ветви относительно начала
координат (рис.12).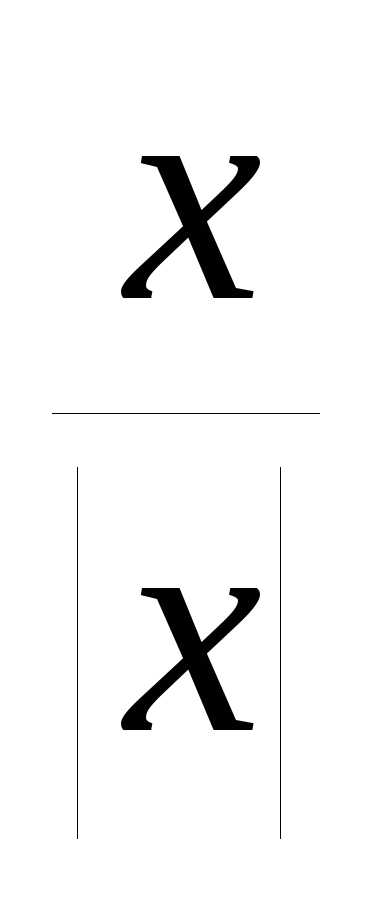 .
. I
и III
координатных углов, т.е. относительно
прямой y=x.
Таким образом, получаем следующее
правило.
I
и III
координатных углов, т.е. относительно
прямой y=x.
Таким образом, получаем следующее
правило.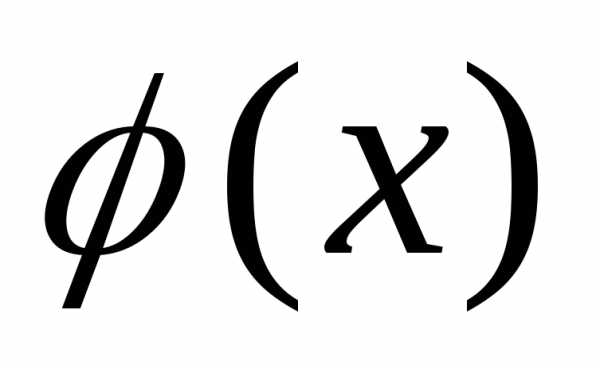 ,
обратной по отношению к функцииy=f(x),
следует построить график y=f(x)
и отразить его относительно прямой y=x.
,
обратной по отношению к функцииy=f(x),
следует построить график y=f(x)
и отразить его относительно прямой y=x. .
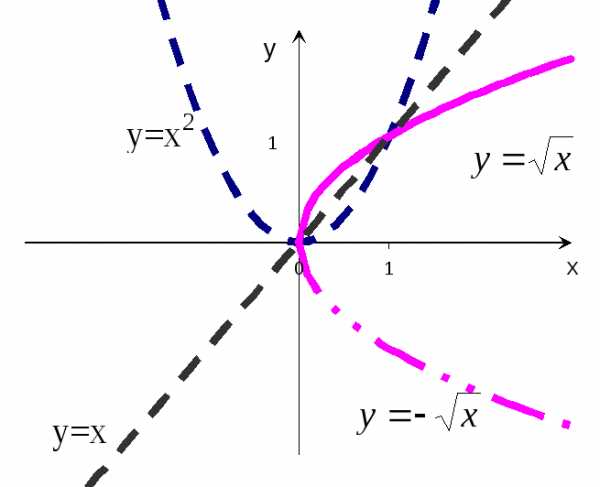
.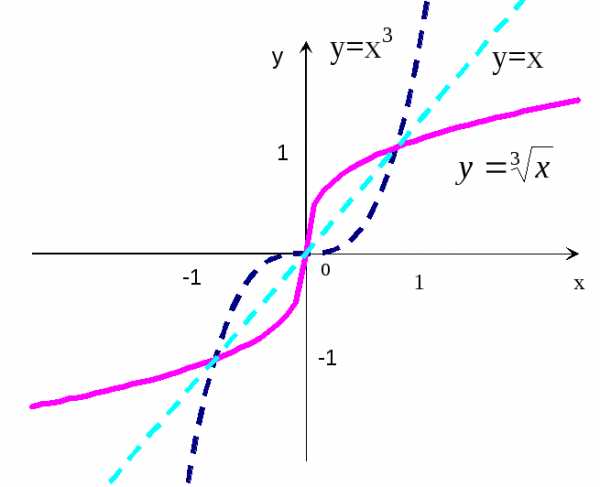 тобы
построить график данной функции,
рассмотрим график параболыy=x2 (рис.14 – пунктирная кривая) и график
обратной к ней функции y=
тобы
построить график данной функции,
рассмотрим график параболыy=x2 (рис.14 – пунктирная кривая) и график
обратной к ней функции y=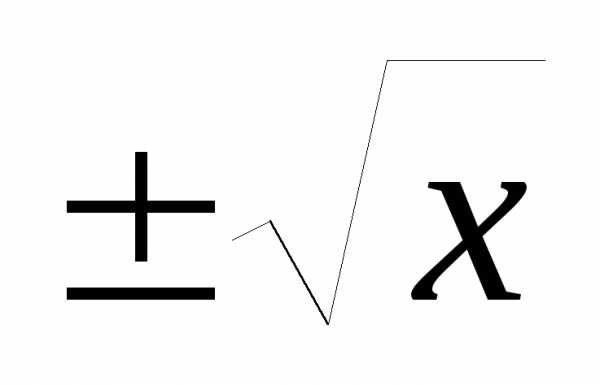 ,
получаемый отражением параболы
относительно прямой y=x.
Обратная функция является двузначной.
В силу того, что исходная функция y=
,
получаемый отражением параболы
относительно прямой y=x.
Обратная функция является двузначной.
В силу того, что исходная функция y= однозначна и область её изменения есть
полуинтервал 0
однозначна и область её изменения есть
полуинтервал 0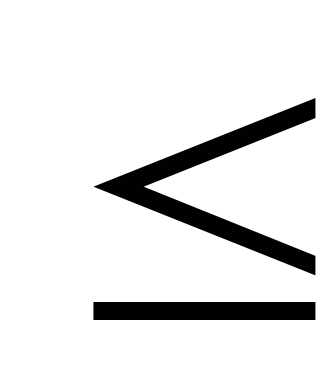 y<
y< ,
графиком функцииy=
,
графиком функцииy= является верхняя ветвь отражённой
параболы (сплошная кривая). Нижняя же
ветвь (штрих-пунктир) представляет
собой график функцииy=
—
является верхняя ветвь отражённой
параболы (сплошная кривая). Нижняя же
ветвь (штрих-пунктир) представляет
собой график функцииy=
— .
.
 .
.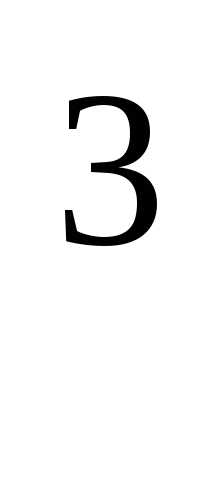 ,
поэтому строим график функции
,
поэтому строим график функции  y=x
y=x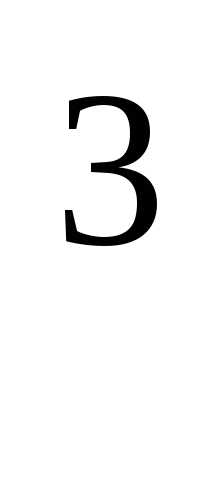 и отражаем его относительно прямой y=x
(рис.15).
и отражаем его относительно прямой y=x
(рис.15).























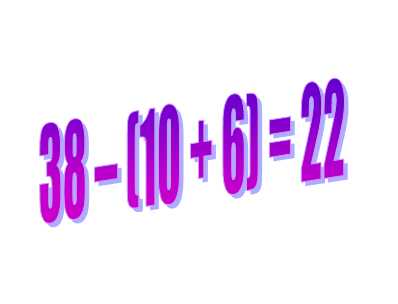 Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.