Задачи В6. Теория вероятностей. | Подготовка к ЕГЭ по математике
Предлагаю рассмотреть решение Задач №4 из открытого банка задач ЕГЭ по математике.
Часть 1.
(Смотрите часть 2 здесь)
При решении задач мы будем опираться на классическое определение вероятности события.
Задача 1. На экзамене 40 вопросов, Коля не выучил 4 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Решение: + показать
Задача 2. В фирме такси в данный момент свободно 35 машин: 11 красных, 17 фиолетовых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Решение: + показатьВероятность того, что к заказчице приедет зеленое такси равна
Ответ: 0,2.
Задача 3. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение: + показатьВ сумме выпадет 7 очков в следующих вариантах:
5+1+1 (3 комбинации)
1+2+4 (6 комбинаций)
1+3+3 (3 комбинации)
2+2+3 (3 комбинации)
Всего вариантов.
Каждый из трех кубиков может выпасть шестью гранями, поэтому общее число исходов равно .
Следовательно, вероятность того, что в сумме выпадет 7 очков, равна
Ответ: 0,07.
Задача 4. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка не выпадет ни разу.
Решение: + показатьБлагоприятный исход: орел-орел-орел-орел.
Всего исходов –
Значит, вероятность того, что решка не выпадет ни разу – есть
Ответ: 0,0625.
Задача 5. Научная конференция проводится в 3 дня. Всего запланировано 75 докладов — в первый день 27 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: + показатьВсего запланировано 75 докладов, и так как в первый день запланировано 27, то на оставшиеся два дня остается 75-27=48 докладов, при этом во второй и третий дни будет прочитано по 48:2=24 доклада.
Значит вероятность, что доклад профессора М. окажется запланированным на третий день есть
Ответ: 0,32.
Задача 6. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России?
Решение: + показатьВ первом туре Василий Лукин может сыграть с 26 − 1 = 25 шашистом, из которых 3 − 1 = 2 из России.
Значит, вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России, есть
Ответ: 0,08.
Задача 7. В чемпионате мира учавствуют 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Китая окажется в первой группе?
Решение: + показатьКоличество карточек с номером «1» – 4 штуки. Всего карточек (команд) – 20.
Значит, вероятность того, что команда Китая окажется в первой группе равна
Ответ: 0,2.
Задача 8. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет меньше 4?
Решение: + показатьНа клавиатуре телефона цифр меньше 4-х – 4 штуки (0; 1; 2; 3). Всего цифр 10.
Значит, вероятность того, что случайно нажатая цифра будет меньше 4 равна
Ответ: 0,4.
Задача 9. Какова вероятность того, что случайно выбранное натуральное число от 41 до 56 делится на 2?
Решение: + показатьОт 41 до 56 ровно 16 чисел. Среди них четных 8 штук (42; 44; 46; 48; 50; 52; 54; 56).
Значит, вероятность того, что случайно выбранное натуральное число от 41 до 56 делится на 2 равна
Ответ: 0,5.
Задача 10. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А=«сумма очков равна 10»?
Решение: + показатьСумма очков равна 10 в следующих трех случаях:
4+6; 6+4; 5+5.
Ответ: 3.
Задача 11. В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
Решение: + показатьПусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг окажется среди этих 6 человек, равна 6 : 20 = 0,3.
Ответ: 0,3.
Задача 12. Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,096. В некотором городе из 1000 проданных блендеров в течение года в гарантийную мастерскую поступило 102 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: + показатьЧастота события «гарантийный ремонт» составляет
Вероятность же, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,096.
Разница между частотой события и вероятностью составляет
Ответ: 0,006.
Задача 13. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов.
Решение: + показатьНа циферблате между 6 часами и 9 располагаются три часовых деления.
Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Ответ: 0,25.
Задача 14. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Решение: + показать«Фиксируем» одну из девочек на одном из стульев. Благоприятной ситуацией для нас будет посадка второй девочки на один из двух стульев, стоящих рядом со стулом, занятым первой девочкой. Всего свободных стульев для второй девочки – .
Итак, вероятность того, что обе девочки будут сидеть рядом есть , то есть
Ответ:
Часть 2
Вы можете пройти тест по Задачам №4.
egemaximum.ru
Теория вероятностей и математическая статистика
В разделе размещены подробно разобранные задачи по теории вероятностей и математической статистике, перед решением которых излагается теория в сжатом виде, где содержаться основные формулы разбираемой темы. Примеры упорядочены в соответствии с содержанием курса теории вероятностей в ВУЗах. Задачи будут полезны для студентов экономических и технических специальностей.
Случайные события
Комбинаторика — основные формулыВ краткой форме раскрыты основные понятия — перестановки,
размещения, сочетания, и приведены основные формулы комбинаторики. После каждой формулы приводится пример решения задачи.
Классическая вероятностьВ краткой форме рассмотрено понятие вероятности случайного события и
дано классическое определение вероятности. На подробном примере решения задач о бросании игральных костей и извлечении шаров из урны раскрыто одно из важнейших
определений теории вероятностей.
Геометрическое определение вероятностиИзложено геометрическое определение вероятности и приведен пример решения
широко известной задачи о встрече.
Формула полной вероятности и формула БайесаНа примере решения задачи рассмотрены формула полной вероятности и формула
Байеса, а также рассказывается, что такое гипотезы и условные вероятности.
Повторение испытаний
Формула БернуллиСтраница содержит краткое изложение теории повторных независимых
испытаний и приведен пример решения задачи на формулу Бернулли.
Локальная теорема Муавра — ЛапласаИзложены краткие теоретические сведения по локальной
теореме Муавра — Лапласа, рассмотрены условия ее применимости, а также приведен пример решения задачи.
Интегральная теорема ЛапласаВ краткой форме раскрыто содержание интегральной теоремы
Муавра — Лапласа, рассматриваются условия ее применимости. Приводится образец задачи с подробным решением.
Отклонение относительной частоты от постоянной вероятностиРассматривается на подробном примере решения задачи отклонение
относительной частоты от постоянной вероятности в независимых испытаниях.
Наивероятнейшее числоРассматривается на подробном примере решения задачи понятие наивероятнейшего
числа и как найти вероятность появления наивероятнейшего числа.
Формула ПуассонаРассматривается формула Пуассона и условие ее
применимости, а также закон распределения Пуассона. Приведен пример решения задачи теории вероятностей на формулу Пуассона.
Дискретная случайная величина
На странице рассмотрен закон распределения дискретной случайной
величины, изложена схема вычислений математического ожидания и дисперсии одномерной дискретной случайной величины. Приведен пример решения задачи с построением
функции распределения.
Математическое ожидание и его свойстваРассматривается математическое ожидание случайной величины — одно из важнейших
понятий теории вероятностей. Приведены примеры решения задач. Кратко излагается что такое математическое ожидание и каковы его свойства.
Математическое ожидание суммы и произведения случайных величин.
Дисперсия и ее свойстваИзлагается определение дисперсии случайной величины и
среднего квадратического отклонения, которые являются важными понятиями в курсе теории вероятностей и математической статистики. Описываются свойства дисперсии —
дисперсия суммы случайных величин, дисперсия постоянной величины.
Биномиальное распределениеСтраница содержит определение биномиального закона
распределения, формулу для вычисления математического ожидания и дисперсии случайной величины, распределенной по биномиальному закону.
Приведен пример решения задачи.
Геометрическое распределениеИзлагается понятие геометрического закона распределения
дискретной случайной величины и рассматривается пример решения задачи. Приведены формулы математического ожидания и дисперсии случайной величины, распределенной по
геометрическому закону.
Гипергеометрическое распределениеРассматривается гипергеометрическое распределение, моделирующее количество
удачных выборок без возвращения из конечной совокупности. Страница содержит определение гипергеометрического закона распределения, формулы для вычисления математического
ожидания и дисперсии случайной величины, распределенной по гипергеометрическому закону, а также образец решения задачи.
Неравенство ЧебышеваРассмотрен пример решения задачи
на закон больших чисел (неравенство Чебышева).
Непрерывная случайная величина
На странице рассматривается непрерывная случайная величина,
ее функция распределения и плотность распределения. Перечислены свойства плотности вероятности, приведены формулы для вычисления
математического ожидания и дисперсии НСВ. Даны образцы решения задач на расчет характеристик и построение графиков функции распределения
и плотности распределения непрерывной случайной величины.
Нормальный закон распределенияРассматривается нормальное распределение случайной величины —
его плотность и функция распределения, а также правило трех сигм. Приведены необходимые теоретические сведения и
образцы решения задач на нормальный закон распределения.
Показательный закон распределенияРассмотрен экспоненциальный (показательный) закон распределения
случайной величины, приведены необходимые теоретические сведения и примеры решения задач. Излагаются понятия математического ожидания, дисперсии и параметра
показательного закона распределения.
Равномерное распределениеИзлагается понятие закона равномерного распределения случайной величины.
Приведены необходимые теоретические сведения, рассмотрены математическое ожидание и дисперсия случайной величины, распределенной равномерно и
приведен пример решения задачи на эту тему.
Двумерная дискретная случайная величинаПриведен подробный пример решения задачи — рассматривается
двумерная дискретная случайная величина и ее числовые характеристики — математическое ожидание, дисперсия, среднее квадратическое отклонение,
а также условные законы распределения, коэффициенты ковариации и корреляции.
Выборочный метод
Интервальный вариационный рядРассмотрена выборка, заданная интервальным вариационным рядом,
дан расчет характеристик распределения — выборочной средней и исправленной дисперсии и среднеквадратического отклонения.
Построены графики распределения выборки — полигон и гистограмма. А также вычислены теоретические частоты нормального распределения и
осуществлена проверка гипотезы о нормальном распределении СВ с помощью критерия Пирсона.
Полигон, гистограмма, кумулята, огиваРассматривается подробно построение полигона и гистограммы частот и
относительных частот — графиков статистического ряда распределения.
Также затронута тема построения графиков накопленных частот — кумуляты и огивы с примерами задач.
Несмещенная оценка дисперсии — исправленная выборочная дисперсияВ задаче, приведенной на странице, вычисляется несмещенная оценка дисперсии (исправленная выборочная дисперсия)
Показатели асимметрии и эксцессаПриведены необходимые теоретические сведения на тему
показателей асимметрии и эксцесса, и образцы решения задач, где показан подробный расчет коэффициента асимметрии и эксцесса распределения.
Доверительные интервалы для среднего и дисперсииПостроение доверительного интервала для математического ожидания
(среднего) и дисперсии — рассмотрена краткая теория, приведен подробный пример решения задачи.
Линейная регрессия и корреляцияДан образец решения задачи на построение выборочной линейной
регрессии методом наименьших квадратов и расчет коэффициентов корреляции и детерминации. Пример содержит построение корреляционного поля.
Статистическая проверка статистических гипотез
Проверка гипотезы о равенстве среднихНа примере решения задачи подробно рассматривается проверка гипотезы о
равенстве средних значений, понятия нулевой и конкурирующей гипотезы.
Проверка гипотезы о распределении по закону ПуассонаРассматривается проверка гипотезы о распределении генеральной совокупности
по закону Пуассона. Показано вычисление теоретических частот и применение критерия Пирсона на примере решения задачи.
Однофакторный дисперсионный анализДаны краткие теоретические сведения о дисперсионном анализе.
Рассмотрен пример решения задачи на однофакторный дисперсионный анализ с вычислениями факторной и случайной дисперсии.
Статистические таблицы
Таблица значений функции ЛапласаПриведена таблица значений функции Лапласа и образцы решения задач.
Таблица критических точек СтьюдентаПриведена таблица критических точек t-критерия Стьюдента и образцы решения
задач.
Таблица критических точек «Хи-квадрат»Приведена таблица критических точек распределения χ2 (хи-квадрат) критерия
Пирсона и образцы решения задач.
Таблица критических точек Фишера-СнедекораПриведена таблица критических точек
распределения F Фишера-Снедекора и образцы решения задач.
Задачи с решением по другим предметам100task.ru
Задачи по теории вероятностей с решениями
Задачи по теории вероятностей с решениями
- Классическое и статистическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
- Вероятность появления хотя бы одного события
- Формула полной вероятности
- Формула Байеса
- Формула Бернулли
- Локальная и интегральная теоремы Лапласа
- Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
- Наивероятнейшее число появлений события в независимых испытаниях
- Производящая функция
- Закон распределения вероятностей дискретной случайной величины. Закон биномиальный и Пуассона
- Простейший поток событий
- Числовые характеристики дискретных случайных величин
- Теоретические моменты
- Неравенство Чебышева
- Теорема Чебышева
- Функции распределения вероятностей случайной величины
- Плотность распределения вероятностей непрерывной случайной величины
- Числовые характеристики непрерывных случайных величин
- Равномерное распределение
- Нормальное распределение
- Показательное распределение и его числовые характеристики
- Функция надежности
- Функция одного случайного аргумента
- Функция двух случайных аргументов
- Закон распределения двумерной случайной величины
- Условные законы распределения вероятностей составляющих дискретной двумерной случайной величины
- Отыскание плоскостей и условных законов распределения составляющих непрерывной двумерной случайной величины
- Числовые характеристики непрерывной системы двух случайных величин
Метки задачи, теория вероятностей. Смотреть запись.
www.itmathrepetitor.ru
Примеры решения задач теории вероятностей
Задачи по теории вероятноти
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместимых событий, которые могут произойти в результате одного испытания или наблюдения:
Р =
Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2k.
Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6k.
Свойства вероятностей
Свойство 1. Вероятность достоверного события равна единице: Р(А) = 1.
Свойство 2. Вероятность невозможного события равна нулю: Р(А) = 0.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 0 ≤ Р(А) ≤ 1.
Задача №1
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение.
Игральные кости – это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике.
Т.е. всего различных вариантов 6×6 = 36.
Варианты (исходы эксперимента) будут такие:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
и т.д. …………………………
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Всего 5 вариантов.
Найдем вероятность: 5/36 = 0,138 ≈ 0,14.
Задача №2
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Всего 4 варианта: о; о о; р р; р р; о.
Благоприятных 2: о; р и р; о.
Вероятность равна 2/4 = 1/2 = 0,5.
Задача №3
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные − из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение.
Всего участвует 20 спортсменок,
из которых 20 – 8 – 7 = 5 спортсменок из Китая.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25.
Задача №4
В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение:
1000 – 5 = 995 – насосов не подтекают.
Вероятность того, что один случайно выбранный для контроля насос не подтекает, равна 995/1000 = 0,995.
Задача №5
Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение:
100 + 8 = 108 – сумок всего (качественных и со скрытыми дефектами).
Вероятность того, что купленная сумка окажется качественной, равна 100/108 = 0,(925) ≈ 0,93.
Задача №6
В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 − из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение:
Всего участвует 4 + 7 + 9 + 5 = 25 спортсменов. Вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна
9/25 = 36/100 = 0,36.
Задача №7
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение:
В последний день конференции запланировано
(75 – 17 × 3) : 2 = 12 докладов.
Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.
Задача №8
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений − по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Решение:
В третий день конкурса запланировано
(80 – 8) : 4 = 18 выступлений.
Вероятность того, что выступление представителя России состоится в третий день конкурса, равна
18/80 = 9/40 = 225/1000 = 0,225.
Задача №9
На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Решение:
Всего участвует 3 + 3 + 4 = 10 ученых.
Вероятность того, что восьмым окажется доклад ученого из России, равна 3/10 = 0,3.
Задача №10
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение:
Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России.
Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.
Задача №11
В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
Решение:
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна 11/55 =1/5 = 0,2.
Задача №12
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение:
25 – 10 = 15 – билетов не содержат вопрос по неравенствам.
Вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна
15/25 = 3/5 = 0,6.
Задача №13
На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая.
Решение:
Всего участвует 25 спортсменов.
Вероятность того, что шестым будет выступать прыгун из Парагвая, равна 9/25 = 36/100 = 0,36.
Задача №14
Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Меркурий» по очереди играет с командами «Марс», «Юпитер», «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда «Меркурий»?
Решение: Обозначим право владения первой мячом команды «Меркурий» в матче с одной из других трех команд как «Решка». Тогда право владения второй мячом этой команды – «Орел». Итак, напишем все возможные исходы бросания монеты три раза.
«О» – орел, «Р» – решка.
Итак, всего исходов получилось 8, нужных нам – 1, следовательно,
вероятность выпадения нужного исхода 1/8 = 0,125.
Задача №15
Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при первом броске выпало 2 очка.
Решение.
В сумме на двух кубиках должно выпасть 8 очков. Это возможно, если будут следующие комбинации:
2 и 6
6 и 2
3 и 5
5 и 3
4 и 4
Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.
Такой вариант 1.
Найдем вероятность: 1/5 = 0,2.
Задача №16
Тоша и Гоша играют в кости. Они бросают кубик по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. Первым бросил Тоша, у него выпало 3 очка. Найдите вероятность того, что Гоша не выиграет.
Решение.
При условии, что у Тоши выпало 3 очка, возможны следующие варианты:
3 и 1
3 и 2
3 и 3
3 и 4
3 и 5
3 и 6
Всего 6 вариантов. Подсчитаем количество исходов, в которых Гоша не выиграет, т.е. наберет 1, 2 или 3 очка.
Таких вариантов 3.
Найдем вероятность: 3/6 = 0,5.
Задача №17
В чемпионате мира участвует 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе.
Решение:
Всего команд 20, групп – 5.
В каждой группе – 4 команды.
Итак, всего исходов получилось 20, нужных нам – 4, значит, вероятность выпадения нужного исхода 4/20 = 0,2.
Задача №18
Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение:
Вероятность того, что игру должен будет начинать любой из мальчиков равна
1/4 = 0,25.
В том числе и для Пети.
Задача №19
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
Решение:
Количество четных цифр на клавиатуре равно 5:
infourok.ru
Задачи ЕГЭ по теории вероятностей (с решениями)
Задачи ЕГЭ по теории вероятностей с решениями
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 спортсменов, среди которых 10 участников из России, в том числе Григорий Поддубный. Найдите вероятность того, что в первом туре Григорий Поддубный будет играть с каким-либо спортсменом из России?
Решение. Пусть Поддубный попал в одну из групп, тогда для остальных 9 россиян осталось 75 мест.
Ответ: 0,12.
2. В группе иностранных туристов51 человек, среди них два француза. Для посещения маленького музея группу случайным образом делят на три подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.
Решение. В каждой подгруппе 17 человек. Будем считать, что один француз уже занял место в какой-то подгруппе. Надо найти вероятность того, что второй француз окажется в той же подгруппе. Для второго француза осталось 50 мест , а в подгруппе -16 мест. Размещения туристов случайны, значит события равновозможны. Поэтому вероятность того, что второй француз попадёт в ту же подгруппу : Р
Ответ: 0,32.
3. Петя подкинул три монеты. С какой вероятностью они выпали одной стороной?
Решение:
Орёл-О, решка-Р. Все возможные случаи:
ООО, ООР, ОРО, ОРР, РРР, РОР, РРО, РОО. Их восемь. Благоприятных исходов два.
Р=
Ответ: 0, 25
4. Какова вероятность того, что случайно выбранное число будет делиться нацело на 195? Ответ округлить до тысячных.
Решение. Количество трёхзначных чисел: 999-99=900. Количество чисел, делящихся на 195: 5 (195, 195∙2, 195∙3, 195∙4. 195∙5=985).
Р=
Ответ.0,006.
5.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение.
Закрасим ячейки, где сумма равна 7, их шесть.
Р=.
Ответ. 0,17.
6.Двое военнослужащих на учениях независимо друг от друга проходят полосу препятствий. Для первого вероятность пройти ее равна 0,8, а для второго 0,5. Найдите вероятность того, что они оба не пройдут это испытание.
Решение:
Вероятность того, что первый не пройдёт препятствие: 1-0,8=0,2, а второго : 1-0,5= 0,5. Так как эти события независимы друг от друга, то
Р= 0,2∙0,5=0,1.
Ответ: 0,1.
7.Стрелок стреляет в мишень три раза. Вероятность попадания при каждом выстреле равна 0,9.Найдите вероятность того, что стрелок промахнётся все три раза.
Решение. Вероятность того, что стрелок промахнётся: 1-0,9 =0,1.Так как три выстрела─ независимые друг от друга события, то Р = 0,1∙0,1∙0,1= 0,001.
Ответ. 0,001.
8.Вероятность того, что Андрей сдаст экзамен по математике равна 0,99, а вероятность того, что он сдаст экзамен по русскому языку . равна 0,98. Найдите вероятность того, что он сдаст оба эти экзамена.
Решение. Так как эти события независимы друг от друга, то Р=0,99∙0,98=0,9702.
Ответ.0,9702.
9. Вероятность того, что телевизор прослужит больше 5 лет равна 0,92.Вероятность того, что телевизор прослужит больше 10 лет равна 0,39. Найдите вероятность того, что он прослужит больше 5, но меньше 10 лет.
Решение.
0,92- 0,39=0,53.
Ответ.0,53.
10.Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Найдите вероятность того, что мишень будет поражена (одним из выстрелов).
Решение.
Р(Á) = 1 — Р(А) = 1 — 0,6= 0,4 — вероятность того, что в первый раз стрелок промахнется.
Заметим, что вероятность события С, что стрелок попадет в цель 2-й раз равна 0,6 (так как она не зависит, первый раз стрелок стреляет или второй), то есть Р(С) = 0,6.
Получим Р(В) = Р(Á*С) = 0,4*0,6 = 0,24.
Значит, Р(А+В) = 0,6+0,24 = 0,84.
Ответ: 0,84.
11. Две фабрики выпускают одинаковые лампочки. Первая фабрика выпускает 60% лампочек, вторая — 40%. Среди продукции первой фабрики 3% лампочек дефектные, среди продукции второй фабрики — 2%. Найдите вероятность того, что случайно купленная в магазине лампочка окажется дефектной.
Решение.
По условию задачи первая фабрика выпускает 60% лампочек из 100%. Другими словами она выпускает 60/100 = 6/10 доли от общего производства двух фабрик. Вторая фабрика аналогично выпускает 40% = 40/100 = 4/10 доли от общего числа лампочек. Среди этих 6/10 по условию 3% брака, что значит 3/100 от 6/10, это равно: 3/100 * 6/10 = 18/1000. То есть от всего объема выпущенных лампочек 18/1000 окажутся дефектными с первой фабрики. Аналогично найдем долю дефектных лампочек со второй фабрики: 2/100 * 4/10 = 8/1000. Всего бракованных лампочек с обеих фабрик будет: 18/1000 + 8/1000 = 26/1000 = 0,026. Это и будет равно вероятности того, что случайно выбранная в магазине лампочка окажется дефектной.
Ответ: 0,026.
12. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Решение.
«Фиксируем» одну из девочек на одном из стульев. Благоприятной ситуацией для нас будет посадка второй девочки на один из двух стульев, стоящих рядом со стулом, занятым первой девочкой. Всего свободных стульев для второй девочки – 4.Итак, вероятность того, что обе девочки будут сидеть рядом есть , то есть 0,5.
Ответ: 0,5
13. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
А = {кофе закончится в первом автомате}
В = {кофе закончится во втором автомате}
С = A U B = {кофе закончится хотя бы в одном автомате}
По условию: Р(А) = Р(В) = 0,2, Р(А ∩ В) = 0,16
По смыслу задачи события А и В являются
совместными. Имеем:
Р(С) = Р(A U B) = Р(А) + Р(В) – Р(А ∩ В) =
= 0,2 + 0,2 – 0,16 = 0,24.
Р( A U B) = 1 – 0,24 = 0,76.
Ответ: 0,76
14.В магазине три продавца. Каждый из них занят с клиентом с вероятностью 30%. Найдите вероятность того, что в случайный момент все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга)
Решение.
Р = Р(А+В+С)= Р(А)+Р(В)+Р(С)= 0,3+0,3+0,3=0,9
Ответ.0,9.
15. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства – яйца высшей категории, а во втором хозяйстве – 30% яиц высшей категории. Всего высшей категории получается 54% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из второго хозяйства. Решение.
Составим уравнение: 0,6·(1-х) + 0,3·х = 0,54
0,6-0,6х+0,3х=0,54
-0,3х= -0,06
х=0,2
Ответ: 0,2
16. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов.
Решение.
На циферблате между шестью и девятью часами располагаются три часовых деления.
Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Ответ: 0,25.
17. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение.
Джон хватает пристрелянный револьвер (вероятность этого 0,4) и промахивается (вероятность 1-0.9=0,1). Вероятность этого события 0,4*0,1=0,04
Джон хватает непристрелянный револьвер (вероятность этого 0,6) и промахивается (вероятность 1-0,3=0,7). Вероятность этого события 0,6*0,7=0,42
Искомая вероятность есть:
0,04+0,42=0,46
Ответ: 0,46.
18. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 3 августа погода в Волшебной стране хорошая. Найдите вероятность того, что 6 августа в Волшебной стране будет отличная погода.
Решение.
Возможны следующие события (при условии, что 3 августа хорошая погода):
А) ХХХХ E) ХООХ
В) ХОХХ F) ХХОО
С) ХХОХ J) ХООО
D) ХХХО H) ХОХО
(«X» – «хорошая погода», «O» – «отличная погода»)
Интересующие нас события (6 августа – отличная погода): D, F, J, H.
Событие D: XХXO произойдет с вероятностью 0,8*0,8*0,2=0,128
Событие F: ХХОО произойдет с вероятностью 0,8*0,2*0,8=0,128
Событие J: ХOОО произойдет с вероятностью 0,2*0,8*0,8=0,128
Событие H: ХОXО произойдет с вероятностью 0,2*0,2*0,2=0,008
Тогда вероятность того, что 6 августа в Волшебной стране будет отличная погода есть 3*0,128+0,08=0.392
Ответ: 0,392.
19. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение. Переформулируем вопрос задачи:
Сколько выстрелов потребуется для того, чтобы вероятность промаха была бы меньше 0,02?
При одном выстреле вероятность промаха – 0,6.
При двух выстрелах вероятность промаха –0,6*0,4=0,24 (первый выстрел – промах и второй выстрел – промах).
При трех выстрелах вероятность промаха –0,6*0,4*0,4=0,096
При четырех выстрелах вероятность промаха –0,6*0,4*0,4*0,4=0,0384
При пяти выстрелах вероятность промаха –0,6*0,4*0,4*0,4*0,4=0,01536
Замечаем, что . 0,01536<0,02
Итак, пяти выстрелов достаточно, чтобы вероятность уничтожения цели была не менее 0,98.
Ответ: 5.
20. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ дает положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что у 6% пациентов с подозрением на гепатит анализ дает положительный результат. Найдите вероятность того, что пациент, поступивший с подозрением на гепатит, действительно болен гепатитом. Ответ округлите до тысячных.
Решение.
Пусть р – вероятность того, что пациент, поступивший с подозрением на гепатит, действительно болен гепатитом.
Тогда (1-р) – вероятность того, что пациент, поступивший с подозрением на гепатит, не болен гепатитом.
Так как по условию задачи у 6% пациентов с подозрением на гепатит анализ дает положительный результат, то Р*0,9+(1-р)*0,01=0,06
0,9р-0,01р=0,05
0,89р=0,05
Ответ: 0,056.
infourok.ru
теория и примеры решения задач
Формула полной вероятности позволяет найти вероятность события
A, которое может наступить только с каждым из
n исключающих друг друга событий ,
образующих полную систему, если известны их вероятности , а
условные вероятности события A относительно
каждого из событий системы равны .
События
также называются гипотезами, они являются исключающими друг друга. Поэтому в литературе
можно также встретить их обозначение не буквой B, а буквой H (hypothesis).
Для решения задач с такими условиями необходимо рассмотреть 3, 4, 5
или в общем случае n возможностей наступления события A
— с каждым событий .
По теоремам сложения и умножения вероятностей получаем сумму произведений вероятности
каждого из событий системы на условную вероятность события A относительно
каждого из событий системы. То есть, вероятность события A может быть вычислена по
формуле
или в общем виде
,
которая и называется формулой полной вероятности.
Пример 1. Имеются три одинаковых на вид урны:
в первой 2 белых шара и 3 чёрных, во второй — 4 белых и один чёрный, в третьей — три
белых шара. Некто подходит наугад к одной из урн и вынимает из неё один шар. Пользуясь
формулой полной вероятности, найти вероятность того, что этот шар будет белым.
Решение. Событие A — появление
белого шара. Выдвигаем три гипотезы:
— выбрана первая урна;
— выбрана вторая урна;
— выбрана третья урна.
Вероятности этих гипотез (событий):
.
Условные вероятности события A относительно
каждой из гипотез:
,
,
.
Применяем формулу полной вероятности, в результате — требуемая вероятность:
.
Пример 2. На первом заводе из каждых 100 лампочек
производится в среднем 90 стандартных, на втором — 95, на третьем — 85, а продукция этих
заводов составляет соответственно 50%, 30% и 20% всех электролампочек, поставляемых
в магазины некоторого района. Найти вероятность приобретения стандартной электролампочки.
Решение. Обозначим вероятность приобретения стандартной электролампочки
через A, а события, заключающиеся в том, что
приобретённая лампочка изготовлена соответственно на первом, втором и третьем заводах,
через .
По условию известны вероятности этих событий: ,
,
и
условные вероятности события A относительно
каждого из них: ,
,
.
Это вероятности приобретения стандартной лампочки при условии её изготовления
соответственно на первом, втором, третьем заводах.
Событие A наступит,
если произойдут или событие K — лампочка изготовлена на первом заводе и стандартна,
или событие L — лампочка изготовлена на втором заводе и стандартна, или
событие M — лампочка изготовлена на третьем заводе и стандартна. Других
возможностей наступления события A нет.
Следовательно, событие A является суммой
событий K, L и M, которые являются несовместимыми.
Применяя теорему сложения вероятностей, представим вероятность события
A в виде
а по теореме умножения вероятностей получим
то есть, частный случай формулы полной вероятности.
Подставив в левую часть формулы значения вероятностей, получаем
вероятность события A:
Пример 3. Производится посадка самолёта на
аэродром. Если позволяет погода, лётчик сажает самолёт, пользуясь, помимо приборов,
ещё и визуальным наблюдением. В этом случае вероятность благополучной посадки равна
.
Если аэродром затянут низкой облачностью, то лётчик сажает самолёт, ориентируясь
только по приборам. В этом случае вероятность благополучной посадки равна
;
.
Приборы, обеспечивающие слепую посадку, имеют надёжность (вероятность безотказной
работы) P. При наличии низкой облачности и
отказавших приборах слепой посадки вероятность благополучной посадки равна
;
.
Статистика показывает, что в k% случаев
посадки аэродром затянут низкой облачностью. Найти полную вероятность события
A — благополучной посадки самолёта.
Решение. Гипотезы:
— низкой облачности нет;
— низкая облачность есть.
Вероятности этих гипотез (событий):
;
.
Условная вероятность .
Условную вероятность
снова найдём по формуле полной вероятности с гипотезами
— приборы слепой посадки действуют;
— приборы слепой посадки отказали.
Вероятности этих гипотез:
;
.
По формуле полной вероятности
.
Отсюда
.
Пример 5. По объекту производится три одиночных
(независимых) выстрела. Вероятность попадания при первом выстреле равна 0,4, при
втором 0,5, при третьем 0,7. Для вывода объекта из строя заведомо достаточно
трёх попаданий. При двух попаданиях он выходит из строя с вероятностью 0,6, при
одном — с вероятностью 0,2. Найти вероятность того, что в результате трёх выстрелов
объект будет выведен из строя.
Решение. Обозначаем вероятность вывода объекта из строя
через A.
Гипотезы:
— в объект попал один снаряд;
— в объект попали два снаряда;
— в объект попали три снаряда.
Находим вероятность гипотез. Событие
представим в виде суммы трёх несовместных вариантов:
=
{первый выстрел попал, второй и третий не попали}+
{второй выстрел попал, первый и третий не попали}+{третий выстрел попал, второй и первый
не попали}.
Применяем правила сложения и умножения вероятностей:
Аналогично
.
Условные вероятности события A
при этих гипотезах равны
;
;
.
По формуле полной вероятности находим:
function-x.ru
Примеры решения типовых задач по теории вероятностей
Задача 47. В отделении 10 стрелков, из них 3 отличных, 5 хороших и 2 посредственных. Известно, что вероятность попадания в цель отличным стрелком — 0,9, хорошим — 0,8, и стреляющим удовлетворительно — 0,6. Из строя наугад вызывается один стрелок для производства выстрела по цели. Какова вероятность попадания в цель этим стрелком?
Решение. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий H1, H2, …, Hn, образующих полную группу (гипотез), в соответствии с Формулой полной вероятности, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А, т. е. P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn)=.
Пусть событие А – стрелок попал в цель. Гипотезы: H1 – стрелок отличный; H2 – стрелок хороший; H3 – стрелок посредственный. Вероятности этих гипотез следующие: ; ; .
Условные вероятности поражения цели по этим гипотезам даны:
P(A/H1)=0,9; P(A/H2)=0,8; P(A/H3)=0,6
Тогда, согласно формуле полной вероятности, искомая вероятность попадания в цель будет равна
P(A)=0,3×0,9+0,5×0,8+0,2×0,6=0,79.
Задача 48. В условиях предыдущей задачи 47 будем считать, что вызванный наугад стрелок произвел выстрел и попал в цель. Требуется определить вероятности, характеризующие его принадлежность к различным категориям стрелков.
Решение. В соответствии с Формулами Байеса, вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на условную вероятность события по этой гипотезе, деленному на полную вероятность события:
В нашей задаче событие А – стрелок попал в цель; гипотезы Н1 – стрелял отличный стрелок; Н2 – стрелял хороший стрелок; Н3 – стрелял посредственный стрелок.
Априорные[1] (доопытные) вероятности гипотез нам известны: Р(Н1)=0,3; Р(Н2)=0,5; Р(Н3)=0,2. Условные вероятности попадания в цель по этим гипотезам даны: Р(А/Н1)=0,9; Р(А/Н2)=0,8; Р(А/Н3)=0,6. Полная вероятность попадания в цель Р(А)=0,79.
Тогда апостериорные[2] (послеопытные) вероятности гипотез будут равны
;
;
Заметим, что сумма вероятностей гипотез после испытания всегда равна единице. Для нашего примера .
Задача 49. Всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.
Решение. Воспользуемся Формулой Бернулли. Если производится П независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна Р, а вероятность противоположного события равна Q=1-P, то вероятность Рп(т) того, что при этом событие А осуществляется ровно Т раз, вычисляется по формуле
(1)
Где есть число сочетаний из П элементов по Т.
А) По условию задачи вероятность всхожести семян Р=0,9; тогда Q=0,1; в данном случае П=5 и Т=4. Подставляя эти данные в формулу Бернулли (1), получим
Б) Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом, Р(А)=Р5(4)+Р5(5). Первое слагаемое уже найдено. Для вычисления второго снова применяем формулу (1):
Следовательно, Р(А)=0,328+0,591=0,919.
Задача 50. Вероятность появления события А в каждом из 625 испытаний равна 0,64. Найти вероятность того, что событие А в этих испытаниях появиться ровно 415 раз.
Решение. Если число испытаний П велико, то применение формулы Бернулли приводит к громоздким вычислениям. Использование этой формулы становиться практически невозможным. В таких случаях применяют приближенную формулу, которая выражает суть локальной теоремы Лапласа.
Если вероятность наступления события А в каждом из П независимых испытаний постоянна и равна Р (Р отлично от нуля и единицы), а число П достаточно велико, то вероятность Рп(т) того, что в этих испытаниях событие А наступит Т раз (безразлично, в какой последовательности) вычисляется приближенно по формуле
(2)
Где
Имеются готовые таблицы значений функции J(х) (см. табл. 1 Приложения).
Для Х>5 считают, что J(х)»0. Так как функция J(х) четная, то J(-х)=J(х). По условию задачи П=625, Т=415, Р=0,64. Находим Q=1-0,64=036. Определяем значение Х при этих данных:
По табл. 1 находим, что J(1,25)=0,1826. Подставив это значение в (2), получим
Задача 51. Среди семян ржи 0,04 % сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?
Решение. Применение асимптотической формулы (2) для случая, когда вероятность Р близка к нулю, приводит к значительному отклонению от точного значения Рп(т). При малых значениях Р (и при малых значениях Q) применяют асимптотическую формулу Пуассона.
Если вероятность появления события А в каждом из П независимых испытаний мала, а число испытаний П достаточно велико, то вероятность того, что событие А наступит Т раз, вычисляется приближенно по формуле
(3)
Где L=Пр.
Формулу (3) применяют в тех случаях, когда L£10. При этом чем больше число П И меньше число Р, тем точнее результат по этой формуле. По условию задачи П=5000, Т=5, Р=0,0004. Тогда L=5000.0,0004=2. Применяя (3), получим
Задача 52. Вероятность попадания в цель при отдельном выстреле равна 0,6. Найти вероятность того, что число попаданий при 600 выстрелах будет заключено в пределах от 330 до 375.
Решение. Формулы Бернулли, Пуассона, асимптотическая формула (2), выражающая суть локальной теоремы Лапласа, позволяют найти вероятность появления события А ровно Т раз при П независимых испытаниях. На практике часто требуется определить вероятность того, что событие А наступит не менее Т1 раз и не более Т2 раз, т. е. число Т Определено неравенствами Т1£Т£Т2. В таких случаях применяют интегральную теорему Лапласа.
Если вероятность наступления события А в каждом из П независимых испытаний постоянна и равна Р (Р отлична от нуля и единицы), а число П достаточно велико, то вероятность того, что событие А в таких испытаниях наступит не менее Т1 раз и не более Т2 раз, вычисляется приближенно по формуле
(4)
Где
Имеются таблицы значений функции (см. табл. 2 Приложения). Ф(х) называется функцией Лапласа. Эта функция является нечетной, т. е. Ф(-х)=-Ф(х). Поэтому таблица значений дается только для положительных чисел. Функция Ф(х) является монотонно возрастающей. При неограниченном возрастании Х функция Ф(х) стремиться к 0,5. Если воспользоваться готовыми значениями функции Лапласа, то формулу (4) можно записать так:
(5)
По условию П=600, Р=0,6, Т1=330, Т2=375. Находим A И B:
По таблице 2 находим Ф(1,25)=0,3944; Ф(-2,5)=-Ф(2,5)=-0,4938. Подставив эти значения в (5), получим искомую вероятность:
Задача 53. Случайная величина Х распределена по нормальному закону. Математическое ожидание М(Х)=5; дисперсия D(X)=0,64. Найти вероятность того, что в результате испытания Х примет значение в интервале (4,7).
Решение. Если случайная величина Х задана дифференциальной функцией F(X), то вероятность того, что Х примет значение, принадлежащее интервалу (A,B), вычисляется по формуле
Если величина Х распределена по нормальному закону, то
(6)
Где А=М(Х) и . По условию S=5, , A=4 и B=7. Подставив эти данные в (6), получим
Задача 54. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Стандартная длина (математическое ожидание) A=40 см, среднее квадратическое отклонение S=0,4 см. Найти вероятность того, что отклонение длины от стандартной составит по абсолютной величине не более 0,6 см.
Решение. Если Х – длина детали, то по условию задачи эта величина должна быть в интервале (А-D, а+D), где А=40 и D=0,6. Подставив в формулу (6) A=а-D И B=а+D, получим
Таким образом,
(7)
Подставляя в (7) имеющиеся данные, получим
Итак, вероятность того, что изготовление детали по длине будут в пределах от 39,4 до 40,6 см, составляет 0,8664.
matica.org.ua










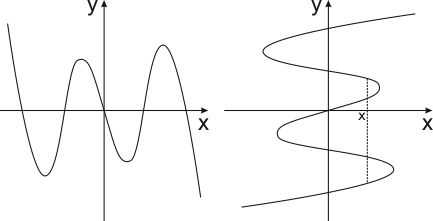
 Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:
Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру: Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.
Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x. Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.
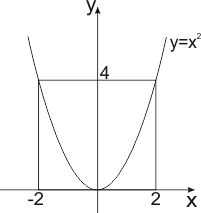
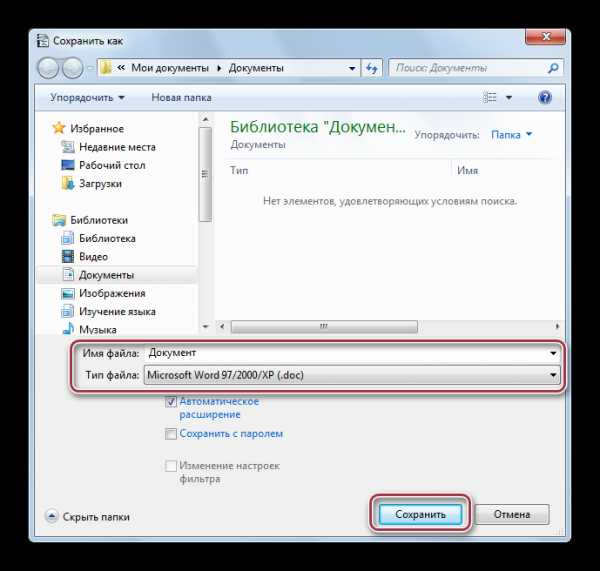
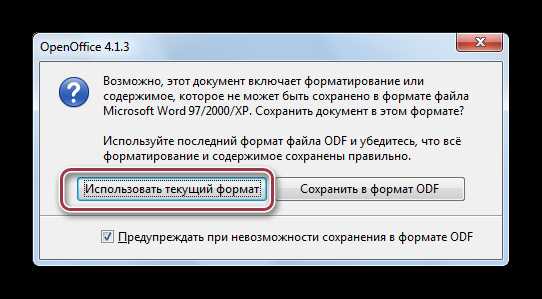
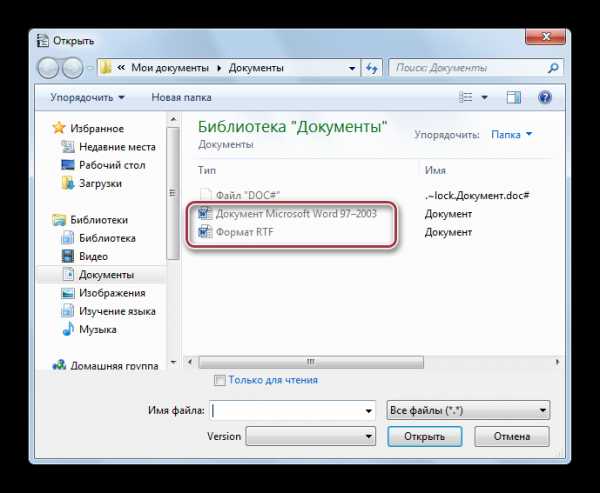
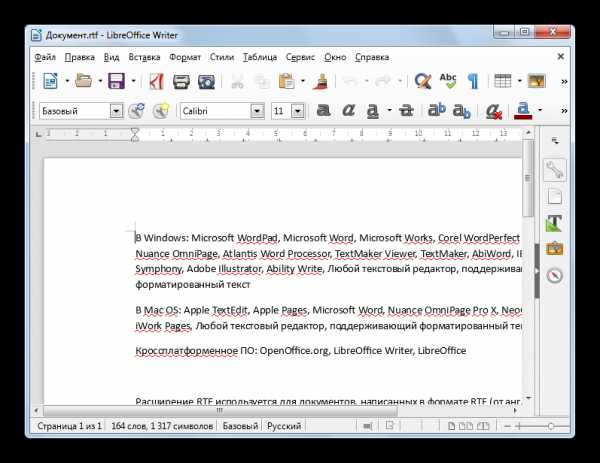
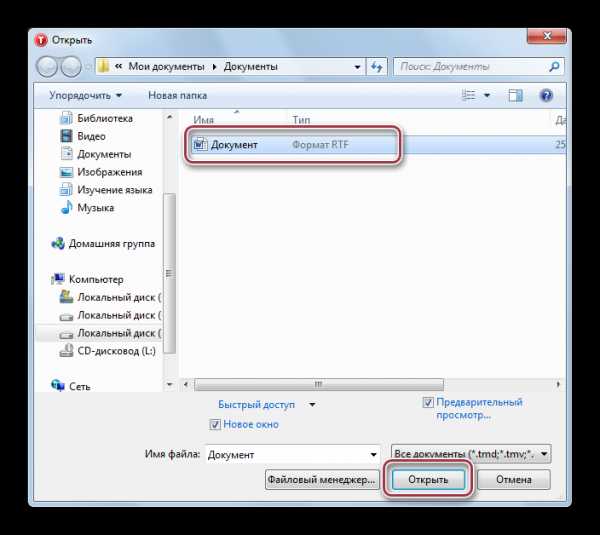
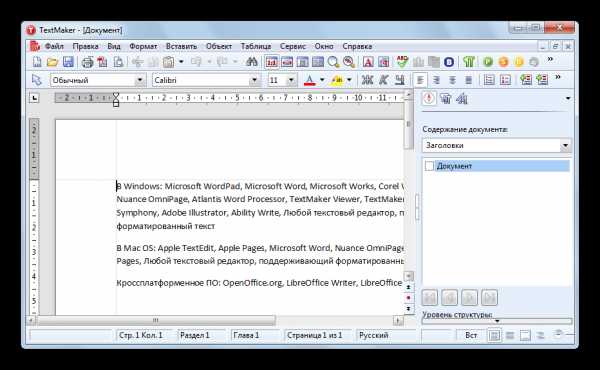
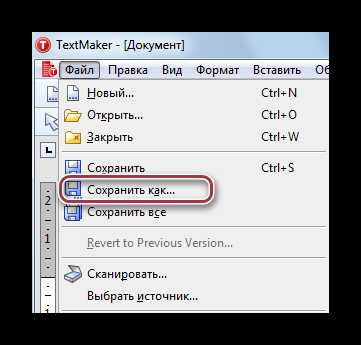
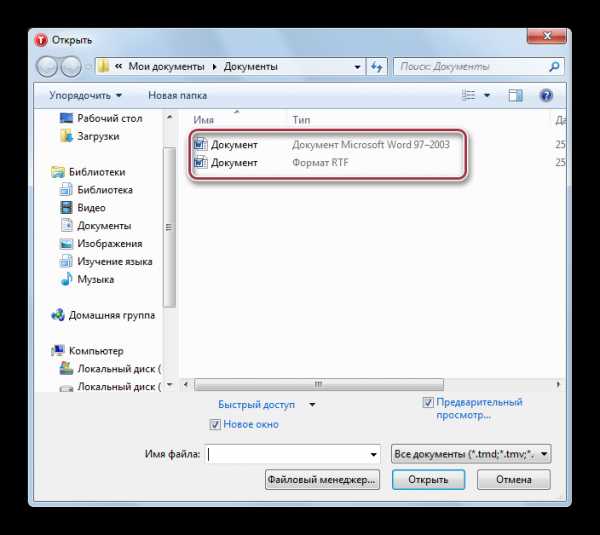
Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.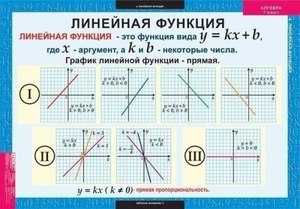 «Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.
«Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.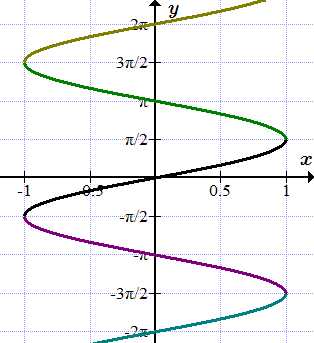
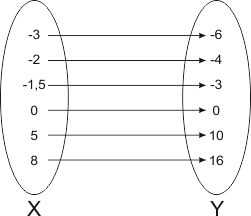
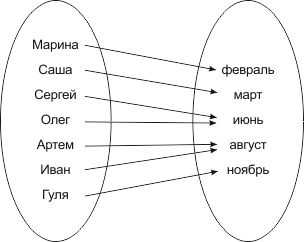



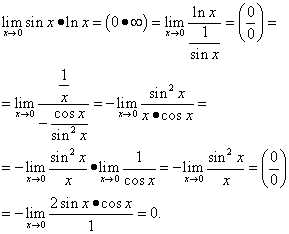 .
.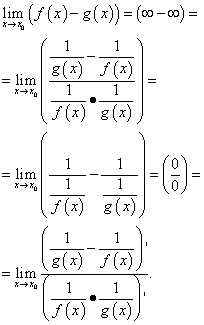
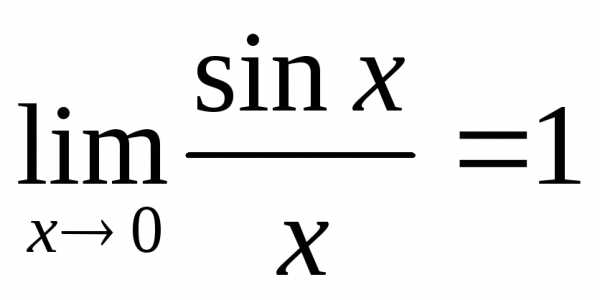
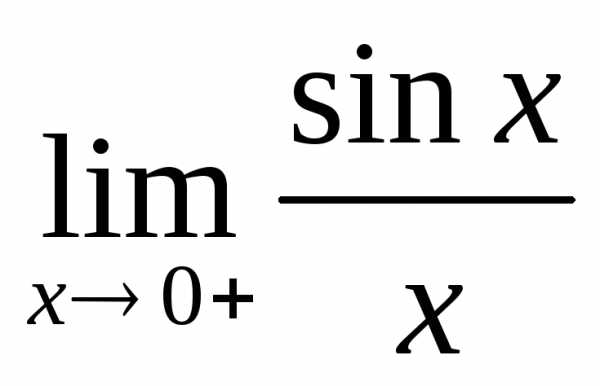 x(0,
x(0,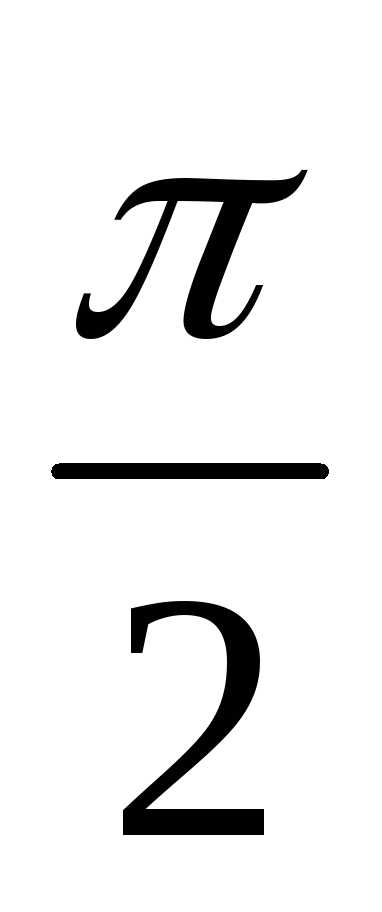 )
)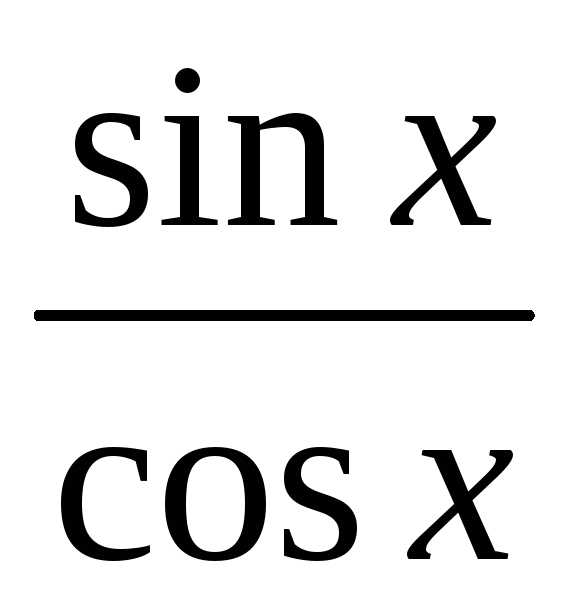
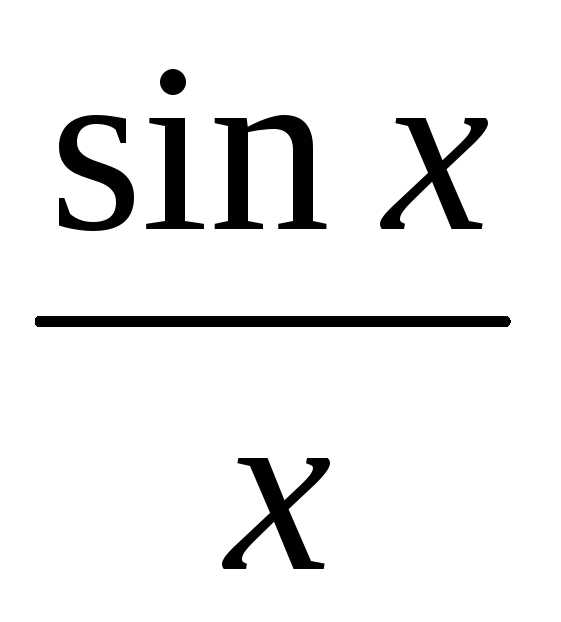 <1<
<1<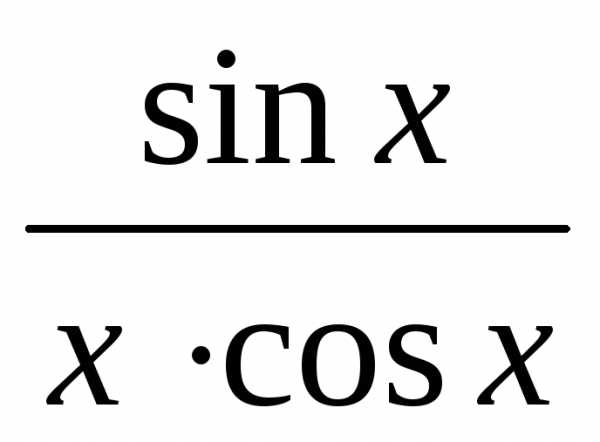
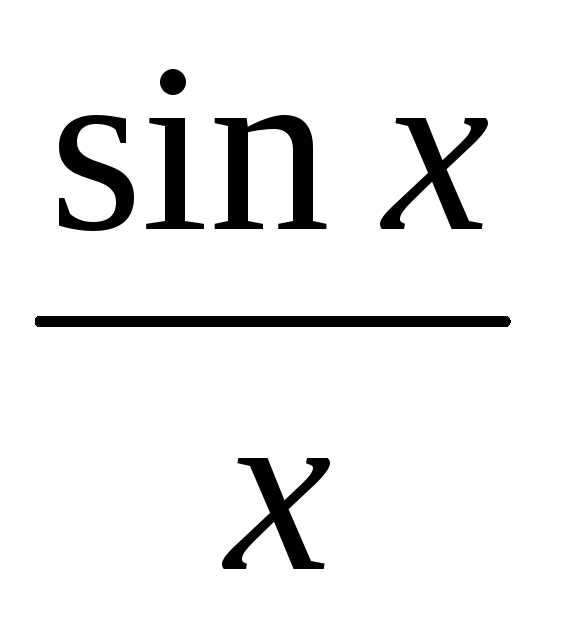 <1
<1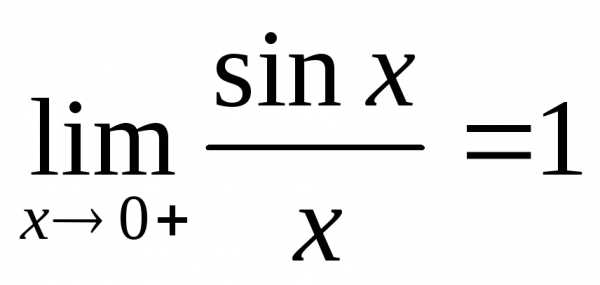
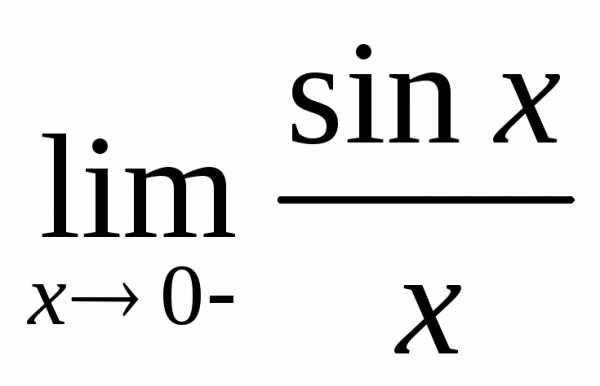 x(-
x(-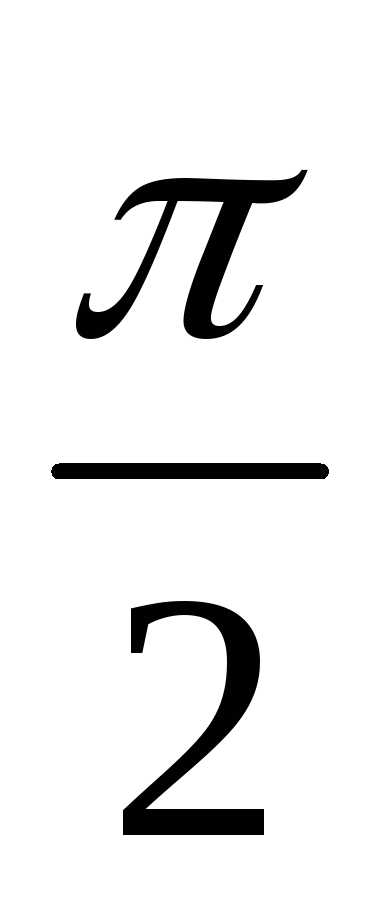 ,0)
,0)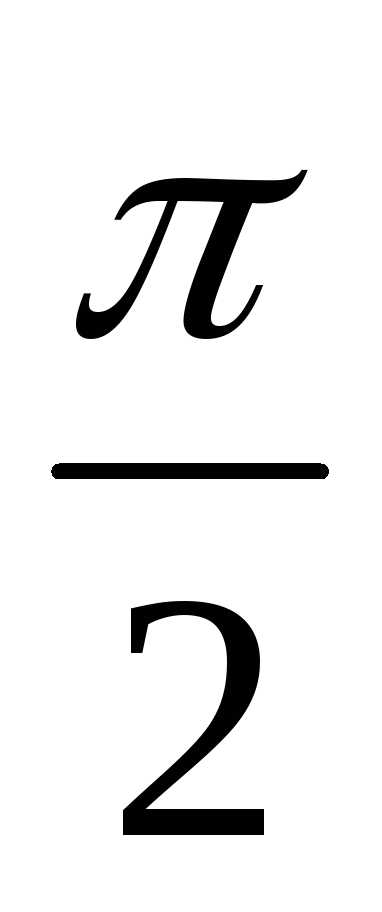 )
)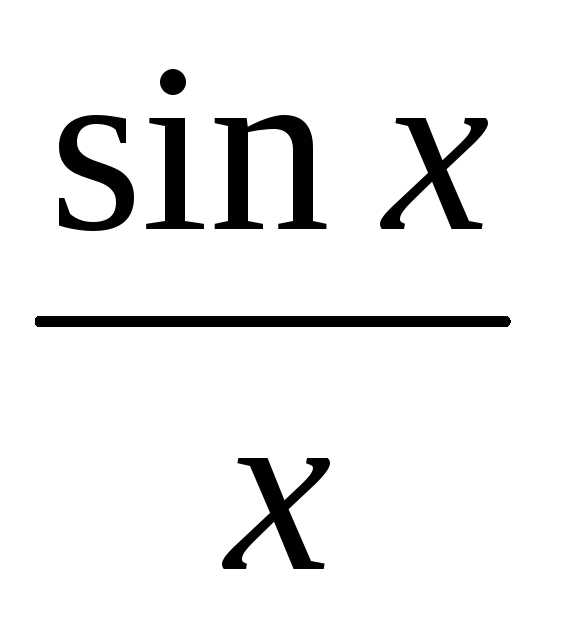 =
=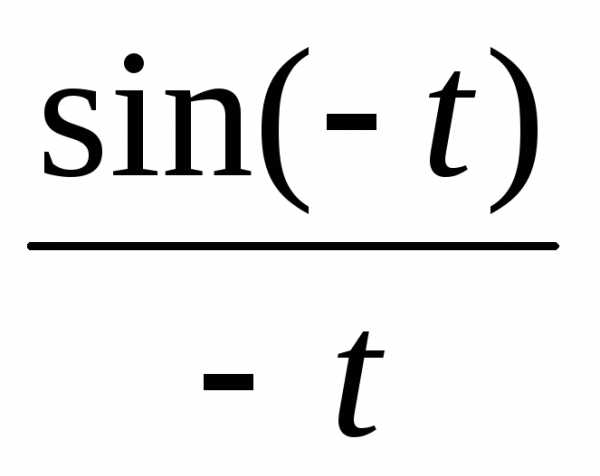 =
=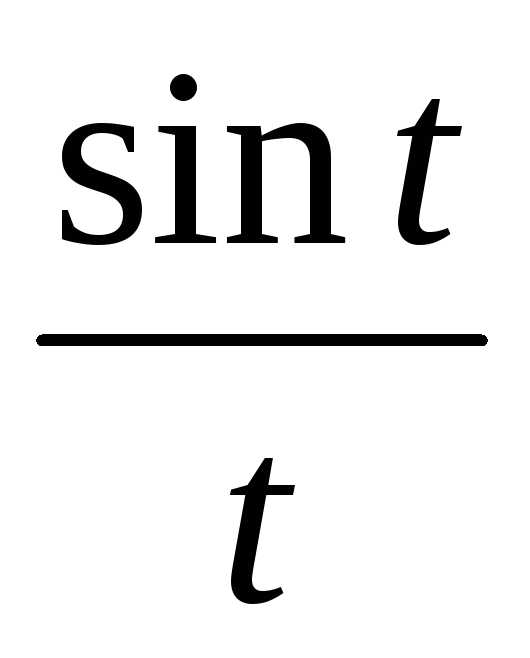
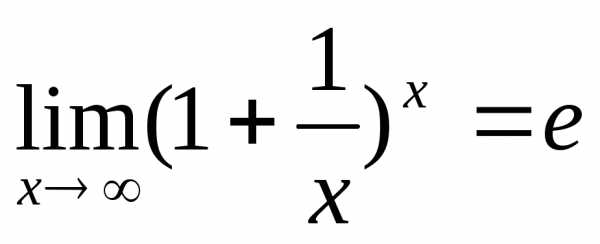
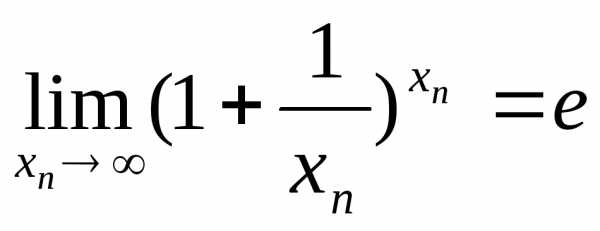
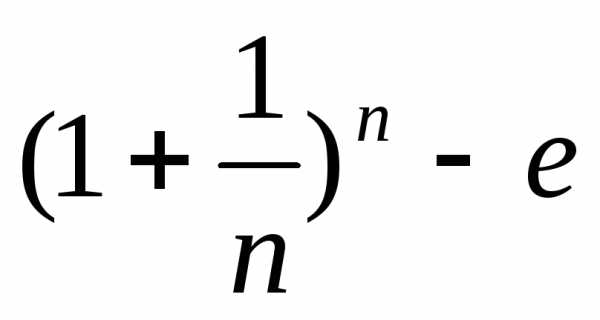 |<
|<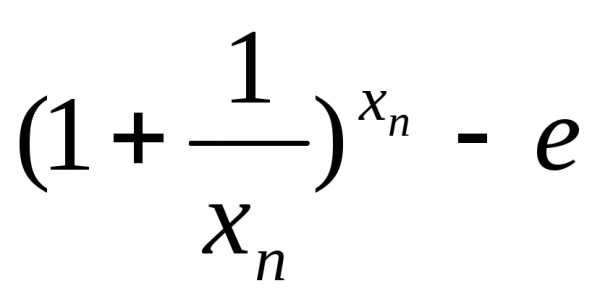 |<
|<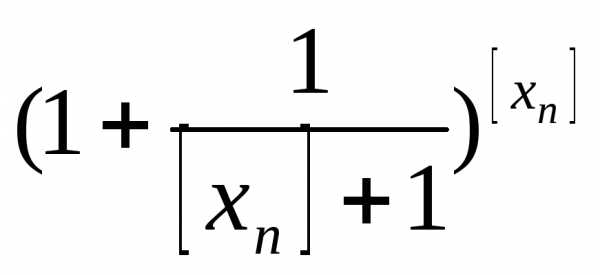 ≤
≤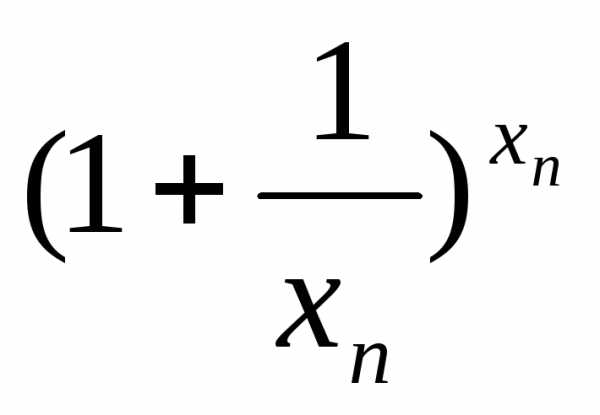 ≤
≤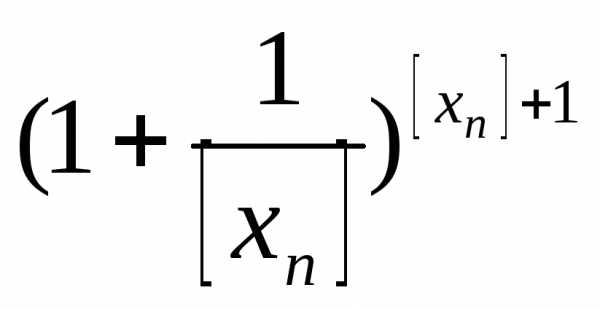
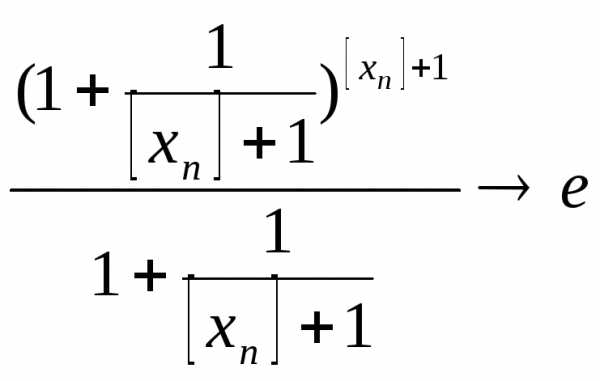
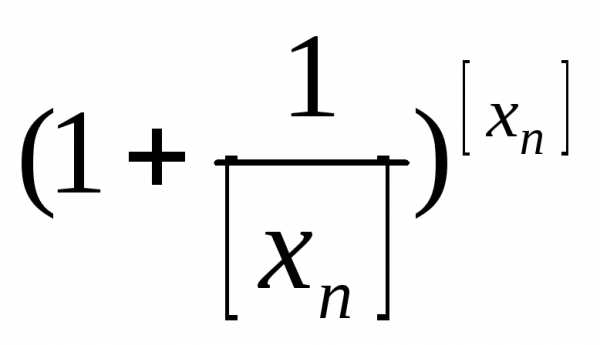 ∙
∙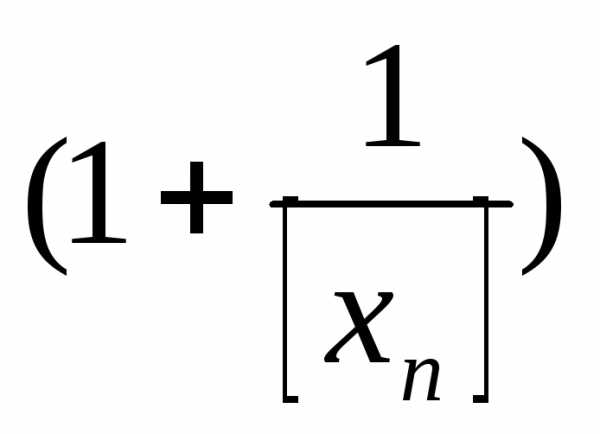
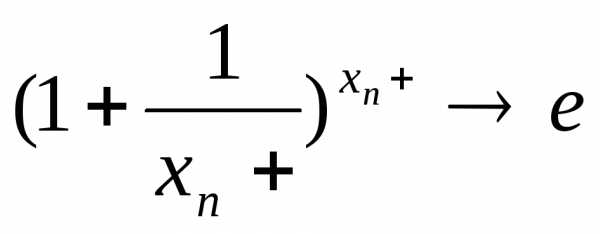
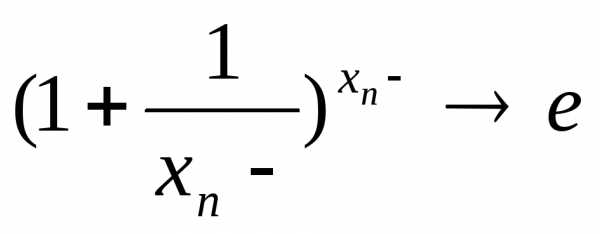
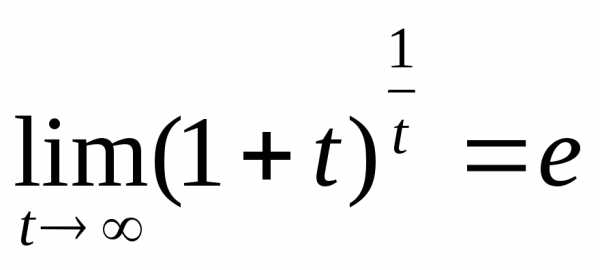
 (β(x))
в т.а
(β(x))
в т.а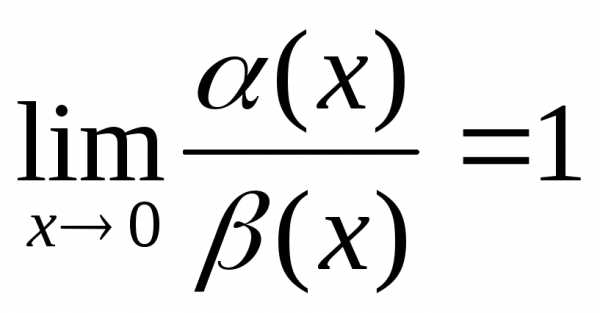 =>
они эквивалентны
=>
они эквивалентны (α(x))
(α(x))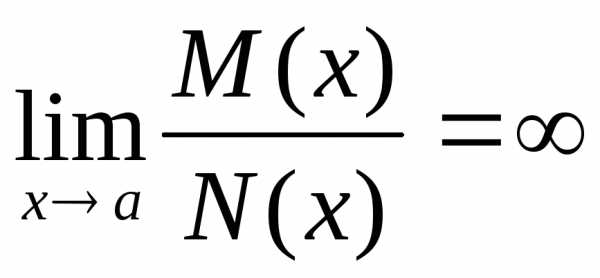



 Литература (настоящая) представляет собой подлинное мастерство создания текстов, сотворение нового объекта при посредстве слов. Как и в любом сложном ремесле, в литературе существуют свои специальные приёмы. Один из них ─ «сравнение». При его помощи для большей выразительности или иронического контраста сличаются те или иные объекты, их качества, люди, черты их характера.
Литература (настоящая) представляет собой подлинное мастерство создания текстов, сотворение нового объекта при посредстве слов. Как и в любом сложном ремесле, в литературе существуют свои специальные приёмы. Один из них ─ «сравнение». При его помощи для большей выразительности или иронического контраста сличаются те или иные объекты, их качества, люди, черты их характера. Художественный приём, придающий тексту большую выразительность, яркость и позволяющий более полно и образно показать свойства явления или предмета (или его качеств) путём изучения различия или сходства с иными явлениями или предметами (или их качествами).
Художественный приём, придающий тексту большую выразительность, яркость и позволяющий более полно и образно показать свойства явления или предмета (или его качеств) путём изучения различия или сходства с иными явлениями или предметами (или их качествами). Отрицательное. Не гром гремит, Илья Муромец палицей по щиту гвоздит.
Отрицательное. Не гром гремит, Илья Муромец палицей по щиту гвоздит. Почти.
Почти. Сравнение в литературном произведении — это средство художественной выразительности, помогающее усилить значение действия, предмета или события.
Сравнение в литературном произведении — это средство художественной выразительности, помогающее усилить значение действия, предмета или события.  Приведем примеры сравнений из произведений, написанных в стихах.
Приведем примеры сравнений из произведений, написанных в стихах.
 Журчание реки успокаивает, хочется слушать бесконечно. Подобным сравнением А.С. Пушкин подчеркивает красивую и складную речь, которой можно заслушаться.
Журчание реки успокаивает, хочется слушать бесконечно. Подобным сравнением А.С. Пушкин подчеркивает красивую и складную речь, которой можно заслушаться. Так Лев Николаевич демонстрирует Александра – мужа Анны, представляя образного персонажа. Он не смотрит по сторонам, он углублен в себя и отказывается понимать, что с ним происходит, игнорируя происходящее.
Так Лев Николаевич демонстрирует Александра – мужа Анны, представляя образного персонажа. Он не смотрит по сторонам, он углублен в себя и отказывается понимать, что с ним происходит, игнорируя происходящее.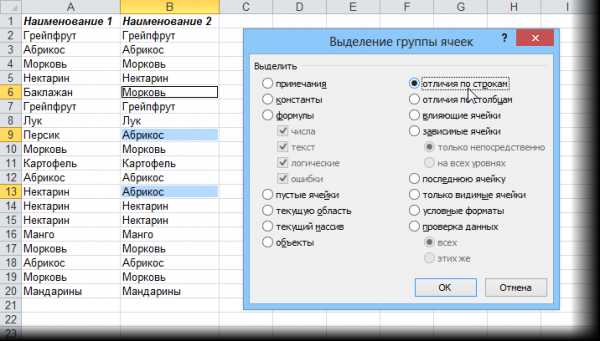
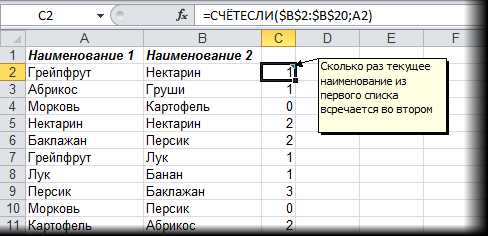

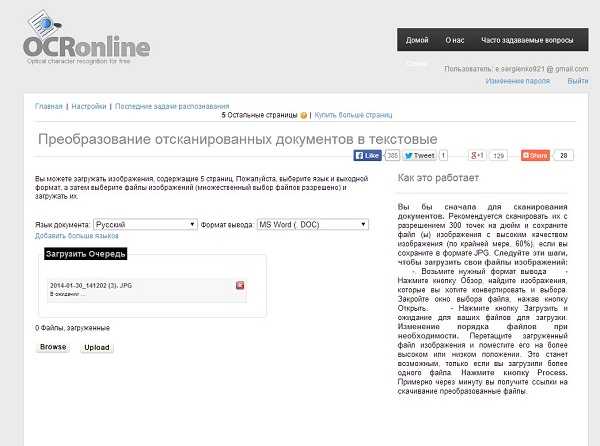
 Результат распознавания Finereader. (ФИО и город распознаны, но стерты вручную)
Результат распознавания Finereader. (ФИО и город распознаны, но стерты вручную)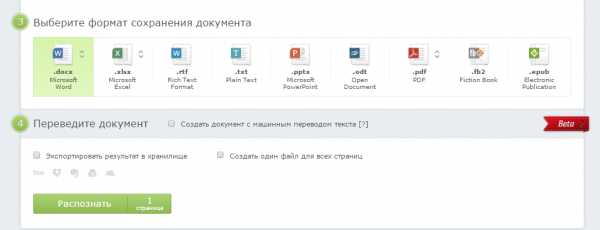
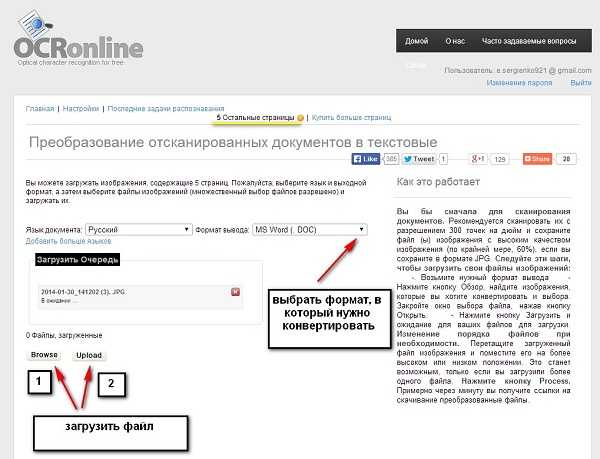
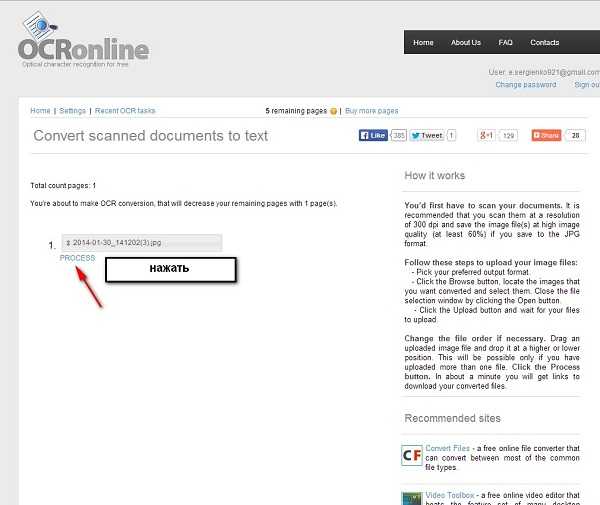
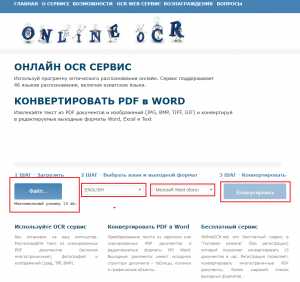
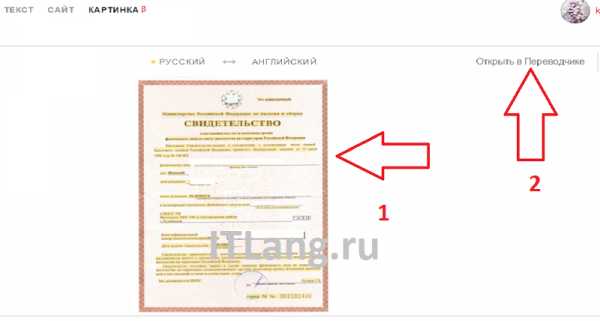
 Результат распознавания в Online OCR (ФИО и дата распознаны, но стерты вручную)
Результат распознавания в Online OCR (ФИО и дата распознаны, но стерты вручную)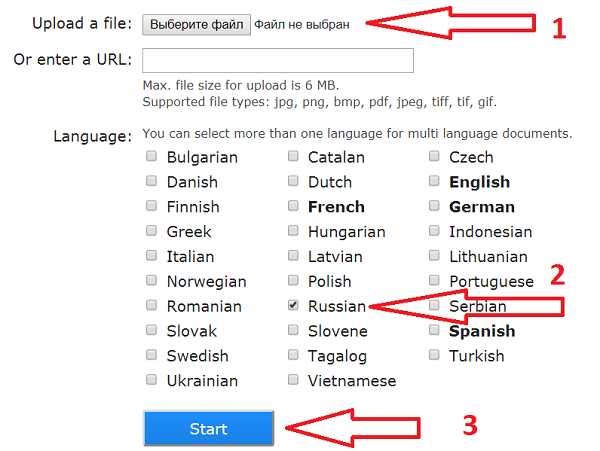 Не забудьте правильно указать язык.
Не забудьте правильно указать язык.
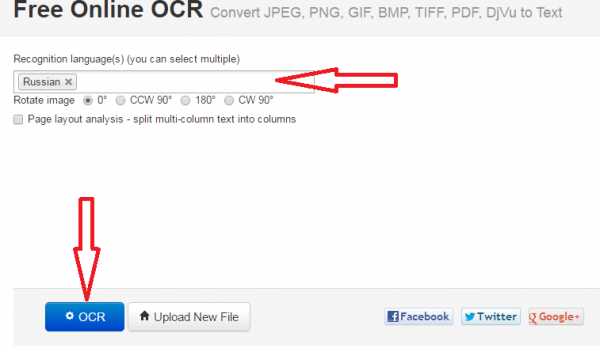
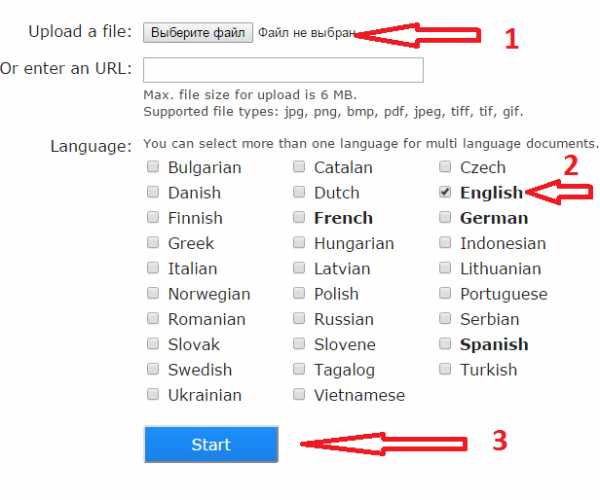
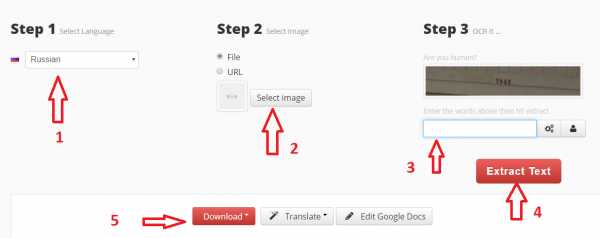
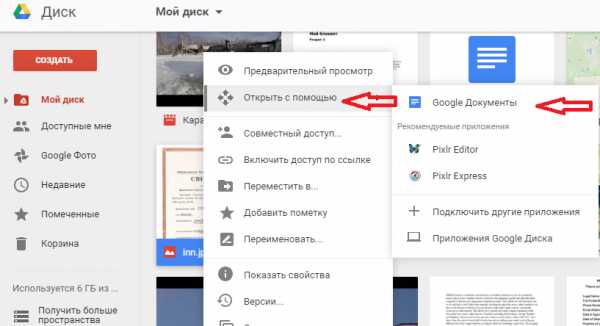
 Перетащите картинку
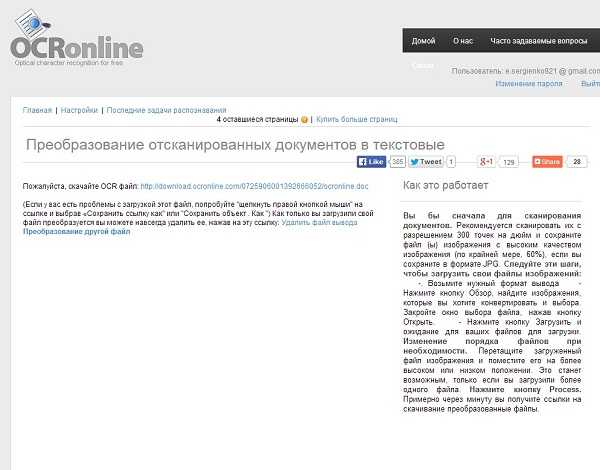
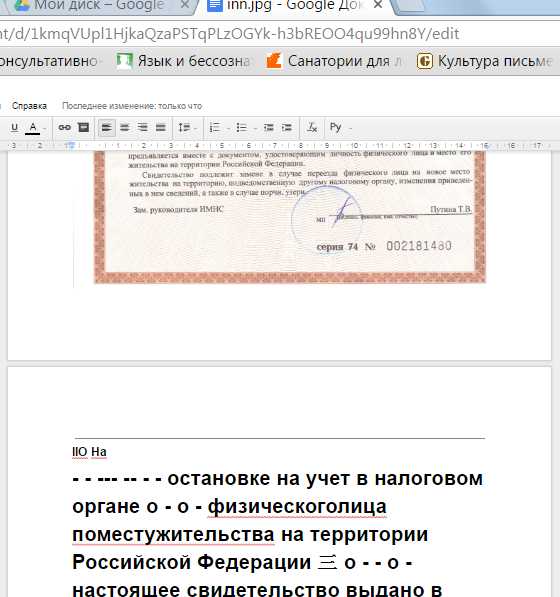
Перетащите картинку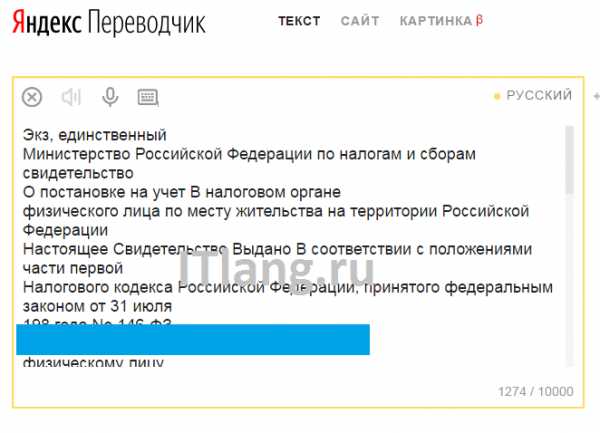 Результат распознавания
Результат распознавания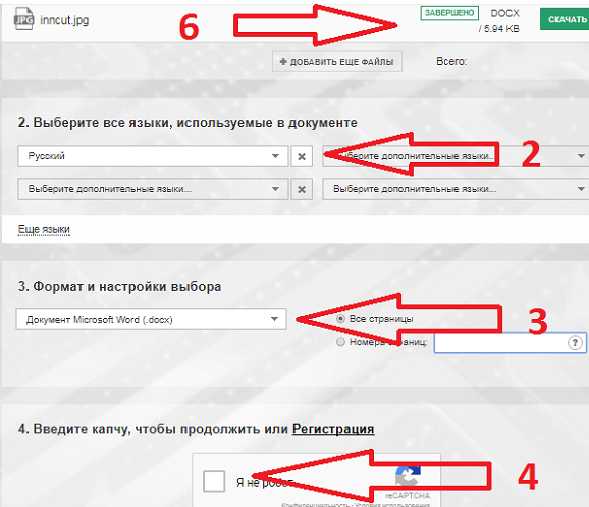 Интерфейс Convertio
Интерфейс Convertio Результат работы Convertio
Результат работы Convertio