Примеры функций и их графиков — Функции — Математика — Алгебра
Примеры функций и их графиков
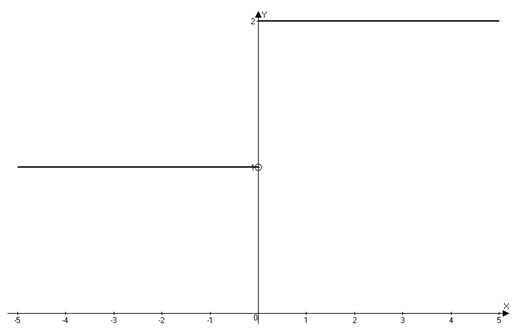
Линейная функция
Линейной называется функция, которую можно задать формулой , где х — аргумент, а k и b — данные числа.График линейной функции — прямая. k называется угловым коэффициентом прямой, которая является графиком линейной функции. Каждая прямая на координатной плоскости, которая является перпендикулярной к оси абсцисс,- график некоторой линейной функции.
Через две точки можно провести одну и только одну прямую, поэтому для построения графика линейной функции достаточно знать координаты двух точек (очень хорошо, если это будут точки пересечения графика с осями). Точка пересечения графика с осью абсцисс имеет ординату 0, а точка пересечения графика с осью ординат имеет абсцису 0.
Пример
Постройте график функции .
, ; , , , .
Построим график (см. рисунок).
Если в линейной функции , то график функции пересекает ось абсцисс;
если , то график функции — прямая, параллельная оси абсцисс;
если , , график функции совпадает с осью абсцисс.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Можно найти координаты точки пересечения прямых, не выполняя построения графиков функций. Так, если прямые заданы уравнениями и , то достаточно решить систему уравнений:
Линейную функцию, которая задается формулой , где , называют прямой пропорциональностью.
График прямой пропорциональности — прямая, проходящая через начало координат. Если , график лежит в I и III координатных четвертях, а если — то во II и IV координатных четвертях.
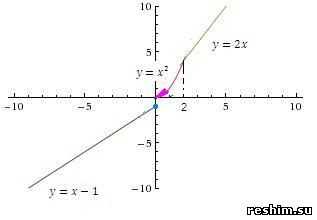
Примеры
1) , , .
2) , , .
Построим в одной системе координат графики функций и (см. рисунок).
Обратная пропорциональность
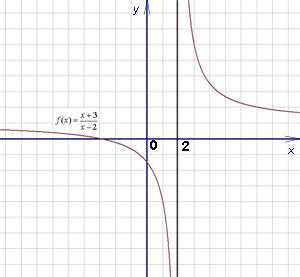
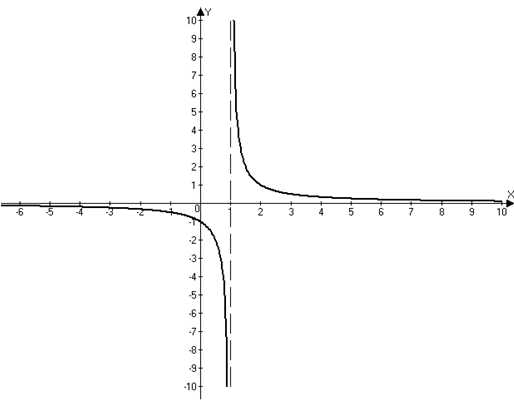
Функцию, заданную формулой , где х — независимая переменная, — данное число, называют обратной пропорциональностью.Область определения функции — множество всех чисел, кроме 0.
График функции — гипербола, симметричная относительно начала координат. Когда , ветки такой гиперболы расположены в I и III координатных углах, когда — в II и IV.
В качестве примера построим график функции . Заполним таблицу (значение x задаем, y — вычисляем по формуле :
Нанесем полученные точки на координатную плоскость. Соединив эти точки плавной линией, получим график (см. рисунок):
Обратите внимание на поведение графика вблизи осей координат. График до них бесконечно приближается, но не пересекает. Действительно, не входит в область определения, следовательно, точки пересечения с осью Oy нет. ни при каком значении х, значит, если , точки пересечения с осью Ox нет.
Функция
Заполним таблицу (значение x задаем, y — вычисляем по формуле y = x2).Нанесем найденные точки на координатную плоскость. Соединив эти точки, получим график функции (см. рисунок ниже).
Область определения этой функции — множество всех действительных чисел.
. График проходит через начало координат .
при всех значениях х. Все точки графика расположены ниже оси Ох.
Противоположным значениям аргумента соответствуют равные значения функции, то есть график симметричен относительно оси ординат.
Функция
Область определения — множество всех неотрицательных действительных чисел.График — одна ветвь параболы, которая расположена в I координатном углу (см. рисунок).
na-uroke.in.ua
Примеры сложных функций | Математика
Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная.
А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.
1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом:
y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u.
y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.
y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u.
2) y=cos x — «простая» функция. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом:
y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u.
y=cos (7x³ -4x²). Внутренняя функция u=7x³ -4x², внешняя — y=cos u.
3) y=tg x — «простая» функция. y = tg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — тангенс:
y=tg(17+5x²). Внутренняя функция u=17+5x², внешняя — y=tg u.
y=tg(9-x). Внутренняя u=9-x, внешняя — y=tg u.
4) y=ctg x — «простая» функция. y=ctg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — котангенс:
y=ctg(2x+6). Внутренняя функция u=2x+6, внешняя — y=ctg u.
y=ctg(√x). u=√x, f=ctg u.
5) y=√x — «простая» функция. y=√u — сложная, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — квадратный корень:
Здесь внутренняя функция y=sin x, а внешняя — f=√u.
Здесь u=9x³-12x+5, f=√u.
6) y=xⁿ — «простая» функция. y=uⁿ — сложная, если u=u(x). Примеры сложных функция для случая, когда внешняя функция — степенная.
y=sin³x. Внутренняя функция y=sin x (так как sin³x=(sin x)³), внешняя — у=u³.
7) y=arcsin x — «простая» функция. y=arcsin u — сложная, когда u=u(x).
Например, y=arcsin (3x-9) — сложная функция. Внутренняя функция u=3x-9, внешняя — f=arcsin u.
y=arcsin (17-5x³). u=17-5x³, f=arcsin u.
8) y=arccos x — «простая» функция. y=arccos u — сложная, при u=u(x).
Например, y=arccos (34x+5) — сложная функция. Внутренняя функция u=34x+5, внешняя — f=arccos u.
9) y=arctg x — «простая» функция. y=arctg u — сложная, при u=u(x).
Например, y= arctg (6x+2x³-7). Внутренняя функция u =6x+2x³-7, внешняя — f=arctg u.
10) y=arcctg x — «простая функция. При u=u(x) функция y=arcctg u — сложная.
Например, y= arcctg(2-11x+x²) — сложная функция. u=2-11x+x², f= arcctg u.
11) y=ln x — «простая» функция. y= ln u — сложная, при u=u(x).
Например, y=ln(4+32x-2x³). Внутренняя функция y=4+32x-2x³, внешняя — f=ln u.
Это — «простая» функция. А вот при u=u(x) получаем логарифм сложной функции:
Например,
Эта функция — «простая» (называется экспонента). А вот если в показателе стоит не x, а некоторая функция от икса: u=u(x), то это — уже экспонента сложной функции:
Например,
Эта функция — «простая». А вот если в показателе стоит не x, а некоторое выражение с x — функция u=u(x), то это уже степень сложной функции:
Например,
Эта функция — сложная. Внутренняя функция u=8x³+5x, а внешняя — степень сложной функции
Следует добавить, что внутренняя функция u, в свою очередь, может быть сложной функцией. И таких «вложенных» функций может быть несколько (теоретически — сколько угодно).
Например,
1) y=cos³(3x-12). Здесь внутренняя функция u =cos(3x-12), а внешняя функция f=u³. Но внутренняя функция y=cos(3x-12), в свою очередь, тоже является сложной функцией. Для нее внутренняя функция u=3x-12, а внешняя f=cos x.
Сначала рассмотрим эту функцию, как логарифм сложной функции. Тогда внутренняя функция
внешняя — логарифм:
В свою очередь, функция
— тоже сложная. Это — синус сложной функции, то есть
Но u — снова сложная функция. Здесь уже внутренняя функция u=2x²+5x, а внешняя f=√u.
www.matematika.uznateshe.ru
Свойства функции: разбираем на примере
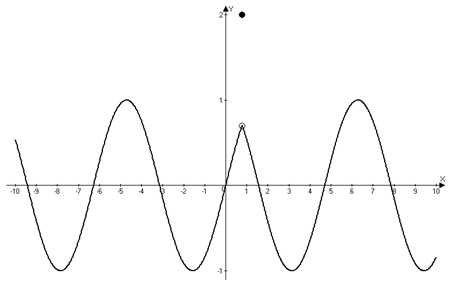
Для понимая данной темы, рассмотрим функцию , изображенную на графике // Покажем, как график функции позволяет определить ее свойства.
Разбираем свойства функции на примере
Областью определения функции явл. промежуток [ 3,5; 5,5].
Областью значений функции явл. промежуток [ 1; 3].
1. При x = -3, x =- 1, x = 1,5, х=4,5 значение функции равно нулю.
Значение аргумента, при котором значение функции равно нулю, называют нулем функции.
//т.е. для данной функции числа -3;-1;1,5; 4,5 являются нулями.
2. На промежутках [ 4,5; 3) и (1; 1,5) и (4,5;5,5] график функции f расположен над осью абсцисс, а на промежутках (-3; -1) и (1,5; 4,5) под осью абсцисс, это объясняется так -на промежутках [ 4,5; 3) и (1; 1,5) и (4,5;5,5] функция принимает положительные значения, а на промежутках (-3; -1) и (1,5; 4,5) отрицательные.
Каждый из указанных промежутков (там где функция принимает значения одного и того же знака) называют промежутком знакопостоянства функции f.//т.е. например, если взять промежуток (0; 3), то он не является промежутком знакопостоянства данной функции.
В математике принято при поиске промежутков знакопостоянства функции указывать промежутки максимальной длины. //Т.е. промежуток ( 2; 3) является промежутком знакопостоянства функции f, но в ответ следует включить промежуток [ 4,5; 3), содержащий промежуток ( 2; 3).
3. Если перемещаться по оси абсцисс от 4,5 до 2, то можно заметить, что график функции идет вниз, то есть значения функции уменьшаются. //В математике принято говорить, что на промежутке [ 4,5; 2] функция убывает.
С увеличением x от 2 до 0 график функции идет вверх, т.е. значения функции увеличиваются. //В математике принято говорить, что на промежутке [ 2; 0] функция возрастает.
Функцию f называют возрастающей на некотором промежутке, если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f (x2) > f (x1). // или Функцию называют возрастающей на некотором промежутке, если для любых значений аргумента из этого промежутка большему значению аргумента соответствует большее значение функции.//т.е. чем больше х, тем больше у.
Функцию f называют убывающей на некотором промежутке, если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f(x2)убывающей на некотором промежутке, если для любых значений аргумента из этого промежутка большему значению аргумента соответствует меньшее значение функции. //т.е. чем больше х, тем меньше у.
Если функция возрастает на всей области определения, то ее называют возрастающей.
Если функция убывает на всей области определения, то ее называют убывающей.
Пример 1. график возрастающей и убывающей функций соотвественно.
Пример 2.
Определить явл. ли линейная функция f (x) = 3x + 5 возрастающей или убывающей?
Доказательство. Воспрользуемся определениями. Пусть х1 и x2 произвольные значения аргумента, причем x1 < x2., например х1=1, х2=7
Получаем при подстановке
f (x1) f (x2) = (3*х1 + 5) (3*x2 + 5) = 3*x1+ 5 3*x2- 5 = 3*х1-3*х2=3*1-3*7=3-21=-19<0
Получаем, что f (x1) f (x2) < 0,а значит f (x1) < f (x2) т.е.данная функция является возрастающей.// т.е. чем больше х, тем больше у.
Нужна помощь в учебе?
Предыдущая тема: Функция: область определения и область значений функций + ПРИМЕРЫ
Следующая тема:   Квадратный трехчлен и его корни: как их найти, 2 способа решения
Все неприличные комментарии будут удаляться.
www.nado5.ru
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции — это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
19. Основные элементарные функции, их свойства и графики. Применение функ-ций в экономике.
Основные элементарные функции. Их свойства и графики
1. Линейная функция.
Линейной функцией называется функция вида , где х — переменная, а и b — действительные числа.
Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.
Свойства линейной функции
1. Область определения — множество всех действительных чисел: Д(y)=R
2. Множество значений — множество всех действительных чисел: Е(у)=R
3. Функция принимает нулевое значение при или.
4. Функция возрастает (убывает) на всей области определения.
5. Линейная функция непрерывная на всей области определения, дифференцируемая и .
2. Квадратичная функция.
Функция вида , где х — переменная, коэффициенты а, b, с — действительные числа, называетсяквадратичной.
Коэффициенты а, b, с определяют расположение графика на координатной плоскости
Коэффициент а определяет направление ветвей. График квадратичной функции — парабола. Координаты вершины параболы находятся по формулам:
Свойства функции:
1. D(у)=R.
2. Множество значений одного из промежутков: или.
3. Функция принимает нулевые значения при , где дискриминант вычисляется по формуле:.
4. Функция непрерывна на всей области определения и производная функции равна .
studfiles.net
Функции
Автор: Sepehr HassannejadВ каждой функции две переменных, таких как $x$ и $y$. Одна из них является независимой переменной — выбирается произвольно (в этой книге это $x$), тогда как другая является зависимой переменной. Когда меняется независимая переменная, то зависимая принимает значение согласно условиям функции.
Определение:
Пусть $A$ и $B$ два множества, а $f$ — подмножество Декартова произведения $A \times B$. $f$ является функцией тогда и только тогда, если
$(x,y_1) \in f \,\,,\,\, (x,y_2) \in f \longrightarrow y_1=y_2$
Другими словами $f$ является подмножеством пар $A \times B$, так, что не существует двух различных пар с одинаковым первым компонентом.Пример:
Пусть $A= \lbrace 1,3,7 \rbrace$ and $B=\lbrace -2,0 \rbrace$. Декартово произведение $A\times B$ равно
$A \times B = \lbrace (1,-2),(1,0),(3,-2),(3,0),(7,-2),(7,0) \rbrace$
Также пусть $f=\lbrace (1,0),(3,-2),(7,-2) \rbrace$.$f$ является подмножеством $A \times B$, а также является функцией, ведь не существует двух различных пар с одинаковым первым компонентом.
Пример:
На картинке ниже $f$ функция $A$ от $B$.
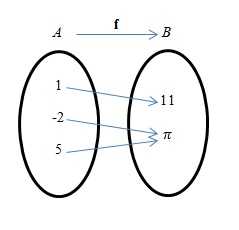 Обратите внимание, что $f=\lbrace (1,11),(-2,\pi),(5,\pi) \rbrace$
Обратите внимание, что $f=\lbrace (1,11),(-2,\pi),(5,\pi) \rbrace$Пример:
На картинке ниже $g$ НЕ является функцией $A$ от $B$.
 Обратите внимание, что $g=\lbrace (-1,\dfrac{1}{7}),(-1,\sqrt{2}),(0,\dfrac{1}{7}),(4,\sqrt{2}) \rbrace$
Обратите внимание, что $g=\lbrace (-1,\dfrac{1}{7}),(-1,\sqrt{2}),(0,\dfrac{1}{7}),(4,\sqrt{2}) \rbrace$Пример:
Является ли $R=\lbrace (\sqrt{2}-1,4),(\dfrac{1}{\sqrt{2}+1},5),(3,6),(\dfrac{1}{2-\sqrt{3}},1),(2+\sqrt{3},1)\rbrace$ функцией? Если нет, то найти подмножества $R$, которые являются функциями и каждое из которых состоит из трех пар.
Решение:
Прежде всего отметим, что
$\dfrac{1}{\sqrt{2}+1}=\dfrac{1}{\sqrt{2}+1} \times \dfrac{\sqrt{2}-1}{\sqrt{2}-1}=\dfrac{\sqrt{2}-1}{2-1}=\sqrt{2}-1$
$\dfrac{1}{2-\sqrt{3}}=\dfrac{1}{2-\sqrt{3}} \times \dfrac{2+\sqrt{3}}{2+\sqrt{3}}=\dfrac{2+\sqrt{3}}{4-3}=2+\sqrt{3}$
Значит $R$ можно переписать ввиде$R=\lbrace(\sqrt{2}-1,4),(\sqrt{2}-1,5),(3,6),(2+\sqrt{3},1) \rbrace$
что не является функцией.Теперь подставим
$f_1=\lbrace (\sqrt{2}-1,4),(3,6),(2+\sqrt{3},1) \rbrace$
$f_2= \lbrace (\sqrt{2}-1,5),(3,6),(2+\sqrt{3},1) \rbrace$
Очевидно, что $f_1$ и $f_2$ — это два подмножества $R$, которые являются функциями.Пример:
Если $R=\lbrace (3,m-5),(-1,m),(2,m^2),(3,8) \rbrace$ яляется функцией, то каково значение $m$?
Решение:
$(3,m-5)=(3,8) \rightarrow m-5=8 \rightarrow m=13$
Ясно, что$R=\lbrace (3,8),(-1,13),(2,169) \rbrace$
Пример:
Если $f=\lbrace(a^2-2a,3),(3,3),(-1,4),(a,3) \rbrace$ яляется функцией, то каково значение $a$?
Решение:
$(a^2-2a,3)=(3,3) \rightarrow a^2-2a=3 \rightarrow a^2-2a-3=0 \rightarrow a=-1 \,\,,\,\, a=3$
Отметим, что если $a=-1$ , то $f=\lbrace(3,3),(-1,4),(-1,3) \rbrace$, что не является функцией.Следовательно, $a=-1$ не подходит. Значит $a=3$ и $f=\lbrace (3,3),(-1,4) \rbrace$
Пример:
Доказать, что $f(x)=x^3-2$ является функцией.
Решение:
Согласно определению функции, нам нужно доказать, что если $x_1=x_2$, то $y_1=y_2$. Значит
$x_1=x_2 \rightarrow x_1 ^3=x_2 ^3 \rightarrow x_1 ^3 -2 =x_2 ^3 -2 \rightarrow y_1=y_2$
Следовательно, $f$ является функцией.Пример:
Доказать, что $x^2+y^2=4$ НЕ является функцией.
Решение:
$x^2+y^2=4 \rightarrow y^2=4-x^2$
Теперь$x_1=x_2 \rightarrow x_1 ^2= x_2 ^2 \rightarrow -x_1 ^2=-x_2 ^2 \rightarrow 4-x_1 ^2=4-x_2 ^2 \rightarrow y_1 ^2= y_2 ^2 \rightarrow y_1 = \pm y_2$
Таким образом не является функцией.Совет:
$(x — \alpha)^2 + (y — \beta)^2 = R^2$
является стандартной формой уравнения окружности. Отметим, что $(\alpha,\beta)$ является центром окружности, а $R$ — ее радиусом.Упражнения
1.На каком рисунке изображена функция?
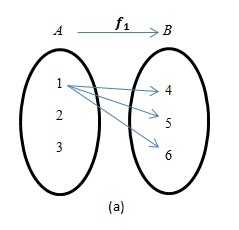
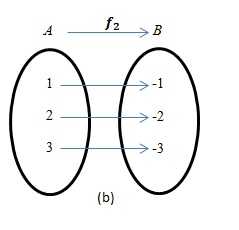
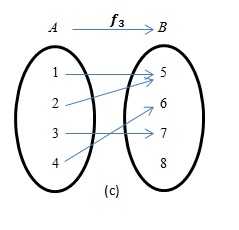
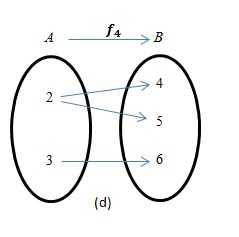 2. Если $f=\lbrace (a,3),(1,-3),(2a+4,3) \rbrace$ является функцией, то каково значение $a$?
2. Если $f=\lbrace (a,3),(1,-3),(2a+4,3) \rbrace$ является функцией, то каково значение $a$?3. Если $f=\lbrace (a+b,2),(a^2-2,3),(a^2-2a,3),(3,2) \rbrace$ является функцией, то каково значение $a+b$?
4. Если $f=\lbrace (7,11),(a^-6a,11),(a,4) \rbrace $ является функцией, то каково значение $a$?
5. Если $f=\lbrace (3,2),(a-b,2),(2a+b,4),(2b,4),(1,\sqrt{2}),(-2,3) \rbrace$ является функцией, то каково значение $(f(a))^2+f(b)$?
6. Доказать, что $y=2|x|+3x-4$ является функцией.
7. Доказать, что $|y|+|x|=1$ НЕ является функцией.
8. Добавив дополнительнон ограничение к $(x-3)^2+(y-4)^2=11$, это была функция. Найти это ограничение.
Область определения и множество значений функции
www.math10.com
Свойства функции
В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.
Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.
Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.
Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.
Множество Х называется областью определения функции.
Множество Y называется множеством значений значений функции.
Равенство называется уравнением функции. В этом уравнении — независимая переменная, или аргумент функции. — зависимая переменная.
Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.
Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения .
Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
3. Нули функции.
Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.
Чтобы найти нули функции , нужно решить уравнение . Корни этого уравнения и будут нулями функции .
Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть или .
Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .
Чтобы найти промежутки знакопостоянства функции по ее графику, нужно
- найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента ,
- найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента .
5. Промежутки монотонности функции.
Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.
Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение:.
Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.
Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .
Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.
6. Точки максимума и минимума функции.
Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
.
Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция называется четной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.
Другими словами, область определения четной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Функция называется нечетной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.
Другими словами, область определения нечетной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции , и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.
Если область определения функции — симметричное множество, то проверяем п. б)
б). В уравнение функции нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду или .
Если , то функция четная.
Если , то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция называется периодической, если существует такое положительное число Т, что
- для любого значения х из области определения функции, х+Т также принадлежит D(x)
В программе средней школы из числа периодических функций изучают только тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции, график которой изображен на рисунке:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Функции и формулы в Excel с примерами
Описание функций в Excel с картинками и готовыми примерами их применения на практике.Функции для эффективных расчетов
Функция ОСПЛТ для расчета регулярного платежа по кредиту в Excel.Примеры как рассчитать регулярные расходы на погашение платежей по кредитам с помощью финансовой функции ОСПЛТ. Формула аннуитетной схемы регулярных платежей. Функция ЧИСТНЗ для расчета приведенной стоимости в Excel .
Примеры использования функции ЧИСТНЗ при вычислении приведенной стоимости проекта и денежного потока. Формула и алгоритм работы ЧИСТНЗ с описанием всех аргументов. Функции распределения ПУАССОН и ПУАССОН.РАСП в Excel.
Примеры расчета распределения вероятностей разной плотности случайной величины по закону Пуассона. Как рассчитать биномиальное распределение Пуассона? Как сделать комментарий в формуле Excel пример функции Ч.
Примеры использования функции Ч для преобразования всех типов значений в число. Способ добавления комментариев к формулам. Суммирование логических значений. Примеры формул с функцией ЕЧИСЛО в Excel для проверки на число.
Как работать с функцией ЕЧИСЛО для формул проверки является ли строка числом. Проверка типов данных значений таблицы в строках и столбцах. Примеры функция БИЗВЛЕЧЬ в Excel для выборки данных из таблицы.
Создание запросов для извлечения значений из базы данных используя поисковую функцию БИЗВЛЕЧЬ в формулах массива. Как сделать базу данных в Excel? НОРМСТРАСП функция стандартного нормального распределения в Excel.
Описание алгоритма, параметров и принципа действия функции НОРМСТРАСП. Расчет вероятности нормальным стандартным распределением. Таблица нормального закона. Функция ТИП.ОШИБКИ для определения типа ошибки в ячейках Excel.
Как определить какую ошибку возвращает формула в результатах своих вычислений? Как получить код типа для всех возможных ошибок формул? Список всех типов ошибок в ячейках Excel. Функция МОПРЕД для нахождения детерминанта матрицы в Excel.
Примеры как находить детерминант матрицы с использованием специальной функции МОПРЕД. Проверка решений систем линейных уравнений методом Крамера. Функция СРЗНАЧЕСЛИМН среднее значение в Excel по условию.
Пример использования и применения функции СРЗНАЧЕСЛИМН для расчета среднего чека выбранных категорий товаров по условию пользователя. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
exceltable.com

 Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!», — но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!», — но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность. Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой. Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.  Правило, согласно которому умножать на ноль нельзя, порождает массу споров между преподавателями и их учащимися. Важно понимать, что умножение на ноль является спорным аспектом ввиду своей неоднозначности.
Правило, согласно которому умножать на ноль нельзя, порождает массу споров между преподавателями и их учащимися. Важно понимать, что умножение на ноль является спорным аспектом ввиду своей неоднозначности. В результате отсутствия знаний по теме преподаватель и нерадивый ученик оказываются по противоположные стороны противоречивой ситуации.
В результате отсутствия знаний по теме преподаватель и нерадивый ученик оказываются по противоположные стороны противоречивой ситуации. Изучение алгоритма действий при умножении на ноль целесообразно начинать с обозначения сути арифметического действия.
Изучение алгоритма действий при умножении на ноль целесообразно начинать с обозначения сути арифметического действия. Следует отметить, что подобное мнение в современном мировом научном обществе отличается от точки зрения древних восточных ученых. Согласно теории, которой они придерживались, ноль приравнивался к бесконечности.
Следует отметить, что подобное мнение в современном мировом научном обществе отличается от точки зрения древних восточных ученых. Согласно теории, которой они придерживались, ноль приравнивался к бесконечности. Среди учеников довольно часто на первых порах освоения учебного материала встречаются попытки число умножить на 0. Подобное действие является грубейшей ошибкой.
Среди учеников довольно часто на первых порах освоения учебного материала встречаются попытки число умножить на 0. Подобное действие является грубейшей ошибкой. Рассмотрим пример умножения на ноль целого числа. Сколько будет, если 2 (два) умножить на 0 (ноль)? Любое число, умноженное на ноль, равняется нулю. И не важно, известно нам это число, или не известно.
Рассмотрим пример умножения на ноль целого числа. Сколько будет, если 2 (два) умножить на 0 (ноль)? Любое число, умноженное на ноль, равняется нулю. И не важно, известно нам это число, или не известно.



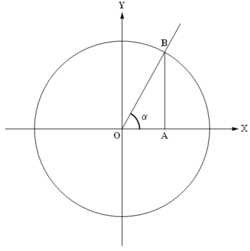 Рис. 2
Рис. 2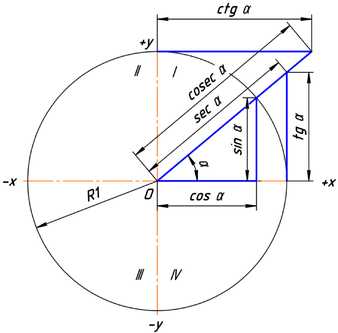 Рис. 3
Рис. 3 Значения косинуса и синуса на окружности.
Значения косинуса и синуса на окружности.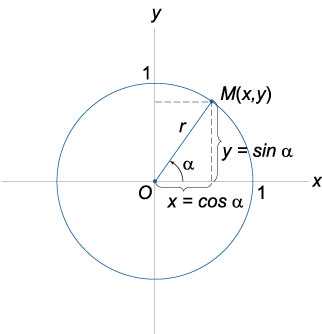
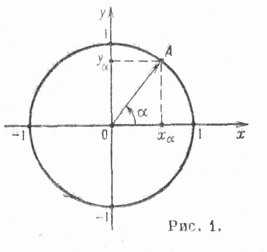
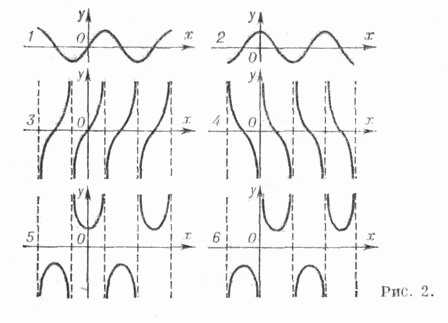 Основные свойства Т.
ф.: область определения, множество значений, четность и участки монотонности приведены в табл.
Основные свойства Т.
ф.: область определения, множество значений, четность и участки монотонности приведены в табл. 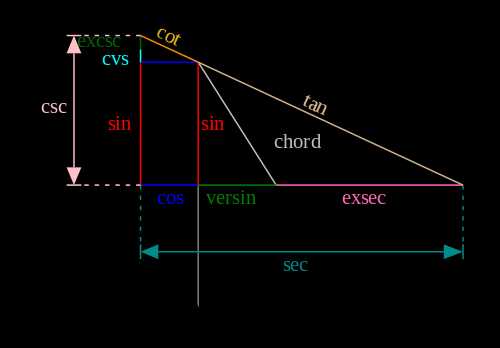
 Первые тригонометрические таблицы видимо были составлены Гиппархом, который сейчас известен как «отец тригонометрии»[2].
Первые тригонометрические таблицы видимо были составлены Гиппархом, который сейчас известен как «отец тригонометрии»[2].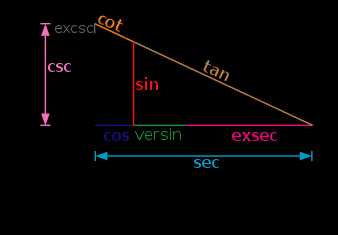
 Секстант — навигационный измерительный инструмент, используемый для измерения высоты светила над горизонтом с целью определения географических координат той местности, в которой производится измерение.
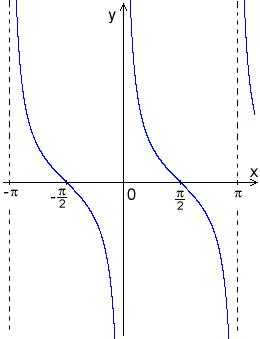
Секстант — навигационный измерительный инструмент, используемый для измерения высоты светила над горизонтом с целью определения географических координат той местности, в которой производится измерение.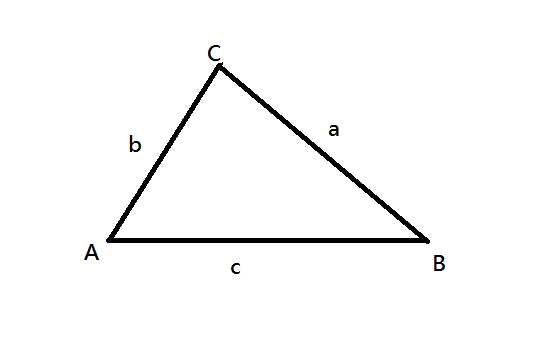 Треугольник со сторонами a, b, c и соответственно противоположными углами A, B, C
Треугольник со сторонами a, b, c и соответственно противоположными углами A, B, C