Практическая работа по теме «Текстовый редактор — 7»
Практические работы «Текстовый редактор»
7 класс
Задание 1. Ввод символов
1. Запустите текстовый процессор, установленный на вашем компьютере.
2. Введите с помощью клавиатуры:
Аа Бб Вв Гг Дд Ее Ёё Жж Зз Ии Йй Кк Лл Мм Нн Оо Пп Рр Сс Тт Уу Фф Хх Цц Чч Шш Щщ Ъъ Ыы Ьь Ээ Юю Яя Аа Bb Сс Dd Ее Ff Gg Hh Ii Jj Kk Ll Mm Nn Oo Pp Qq Rr Ss Tt Uu Vv Ww Xx Yy Zz 0123456789 I(1) V(5) Х(10) L(50) С( 100) D(500) М(1000) ! » № ; % : ? * () _ + / — = \ ! @ # $ % А & * () _ + | — = \ |
3. Сохраните файл в личной папке под именем Символы.rtf.
Задание 2. Правила ввода текста
1. Запустите текстовый процессор, установленный на вашем компьютере.
2. Введите текст:
При вводе текста соседние слова отделяются одним пробелом. Знаки препинания (запятая, двоеточие, точка, восклицательный и вопросительный знаки) пишутся слитно с предшествующим словом и отделяются пробелом от следующего слова. Кавычки и скобки пишутся слитно с соответствующими словами (группой слов). Тире выделяется пробелами с двух сторон. Дефис пишется слитно с соединяемыми им словами. |
3. Введите текст, обращая внимание на соблюдение соответствующих правил:
Тема «Правила ввода текста», гостиница «Малахит», шоколад «Алёнка», роман «Война и мир». Этапы создания текстового документа: ввод, редактирование, форматирование. Информация во Всемирной паутине организована в виде страниц (web-страниц). Всё-таки, Мамин-Сибиряк, Жар-птица, северо-восток, Ростов- на-Дону, Нью-Йорк. Пришлось волей-неволей остаться здесь на ночь. Горя бояться — счастья не видать. Москва — огромный город, город-страна. Конец XVII века — первая половина XIX века. |
4. Сохраните файл в личной папке под именем Правила_ввода.rtf.
Задание 3. Вставка символов
1. В текстовом процессоре откройте файл Bставкa.rtf:
Прснльнй кмпьютр: сстмнй блк (мтрнск плт, цнтрльнй прцсср, пртвн пмть, жсткй дек), вншн стрств, клвтр, мшь, мнтр, прнтр, кстчск клнк). |
2. В нужные места вставьте буквы, обозначающие гласные звуки, так, чтобы получились названия устройств персонального компьютера.
3. Сохраните файл в личной папке под именем Устройства.rtf.
Задание 4. Замена символов
1. В текстовом процессоре откройте файл Замена.rtf:
К*литка, к*морка, к*вычки, к*блук, б*гровый, п*гром, с*тира, ур*ган, *кв*ланг, н*в*ждение, ср*жение. |
2. Замените символы «*» на буквы «а» или «о», чтобы слова были написаны правильно.
3. Сохраните файл в личной папке под именем Cлова.rtf.
Задание 5. Поиск и замена
1. При вводе текста неопытные пользователи очень часто допускают ошибки, расставляя лишние пробелы и «вручную» переходя на новую строку в рамках одного абзаца. Вам предлагается отредактировать такой документ.
2. В текстовом процессоре откройте файл Поиск_и_3аменa.rtf.
3. Удалите лишние пробелы перед точками и запятыми, заменяя встречающиеся подряд пробел и знак препинания на один этот знак.
4. Уберите в тексте лишние символы конца абзаца, заменяя встречающиеся подряд пробел и символ конца абзаца на один пробел.
5. Удалите лишние пробелы, заменяя два идущих подряд пробела на один.
6. Удалите лишние пустые строки, заменяя два идущих подряд символа конца абзаца на один.
7. Сохраните документ с изменениями в личной папке под тем же именем.
Задание 6. Удаление фрагментов
1. В текстовом процессоре откройте файл Удаление.rtf:
|
2. В каждой группе найдите лишнее слово (словосочетание) и удалите его.
3. Сохраните файл в личной папке под именем Нет_лишнего.rtf.
Задание 7. Перемещение фрагментов
1. В текстовом процессоре откройте файл Перемещение.rtf:
CPU — RAM — |
2. Создайте пары, поместив рядом с каждым англоязычным термином его русский аналог.
3. Сохраните файл в личной папке под именем Пары.rtf.
Задание 8. Копирование фрагментов
1. В текстовом процессоре создайте новый документ.
2. Используя операции копирования и вставки, наберите текст стихотворения на английском языке:
Meet me in the morning. |
3. Сохраните файл в личной папке под именем Стих.rtf.
Задание 9. Склеивание и разрезание строк1. В текстовом процессоре откройте файл Строки.rtf:
Я не трус, но я боюсь! Да нам, царям, молоко нужно выдавать за вредность! |
2. Отредактируйте содержимое файла так, чтобы каждая фраза и название соответствующего ей фильма занимали ровно один абзац.
3. Сохраните файл в личной папке под именем Афоризмы.rtf.
Задание 10. Изменение свойств символов1. В текстовом процессоре откройте файл Цвет.rtf:
Воздействие цвета на человека |
2. Выполните форматирование текста согласно следующему описанию:
для заголовка задайте размер шрифта 16 пунктов, цвет шрифта красный;
для названий цветов задайте соответствующий им цвет шрифта, начертание — полужирное, размер — 14 пунктов;
для описаний цветов задайте начертание курсив и размер шрифта 12 пунктов.
3. Сохраните файл с изменениями в личной папке и закройте его.
Задание 11. Индексы1. В текстовом процессоре создайте новый файл и сохраните его в личной папке под именем Индексы.rtf.
2. Выберите тип шрифта Arial, размер шрифта 14, начертание курсив.
3. Наберите следующий текст:
Единицы измерения количества информации: 1 байт = 8 битов |
4. Сохраните изменения в файле и закройте его.
Задание 12. Варианты форматирования символов1. В текстовом процессоре откройте файл Эффекты.rtf.
2. Измените формат символов по образцу:

3. Сохраните файл с изменениями в личной папке и закройте его.
Задание 13. Варианты подчёркивания1. В текстовом процессоре создайте новый документ.
2. Шрифтом Times New Roman в 14 пунктов наберите текст и выполните форматирование символов по образцу:
3. Сохраните файл в личной папке под именем Подчеркивание.rtf и закройте его.
Задание 14. Форматирование абзацев1. В текстовом процессоре создайте новый документ.
2. Наберите черновик документа (Times New Roman, 14 пунктов, выравнивание по левому краю) со следующим текстом:

3. Выполните форматирование в соответствии со следующими требованиями:
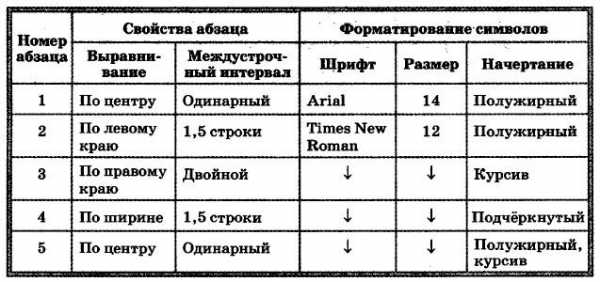
4. Сохраните файл в личной папке под именем Принтерны.rtf и закройте его.
Задание 15. Форматирование абзацев1. В текстовом процессоре создайте новый документ.
2. Наберите черновик документа (Times New Roman, 14 пунктов, выравнивание по левому краю) с информацией о своей школе, себе и своём учителе:

3. Выполните форматирование абзацев в соответствии со следующими требованиями:
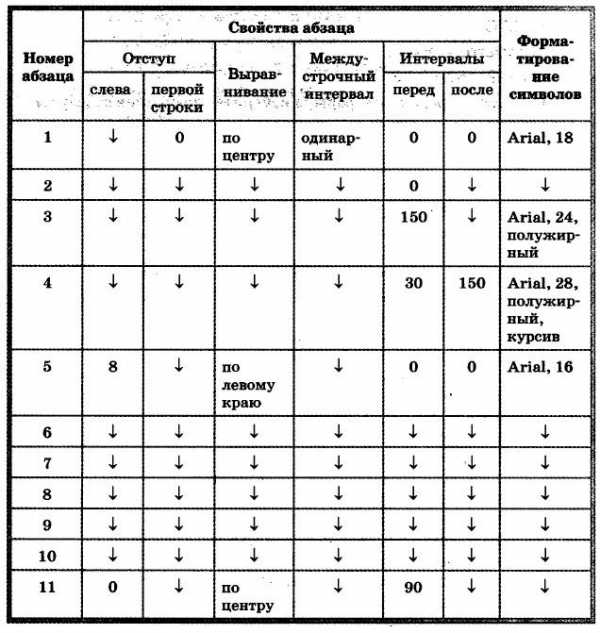
4. Сохраните файл в личной папке под именем Титул.rtf и закройте его.
kopilkaurokov.ru
7 класс_ФГОС_Практическая работа_Графические изображения
Просмотр содержимого документа
«7 класс_ФГОС_Практическая работа_Графические изображения»
Текстовый редактор MS Word 2010.
Графические изображения
Работу выполнил | |
Фамилия Имя | |
Класс | |
Текущая дата и время | |
Примечание: текущую дату и время введите через меню Вставка.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ- Вставка картинки из галереи клипов
Вставка Картинка в правой части окна Word (в области задач) появляется окно коллекции клипов. Необходимо щелкнуть по кнопке Начать, чтобы коллекция клипов сформировалась. Затем выбрать интересующую картинку и щелкнуть по ней – картинка будет вставлена в позицию текстового курсора как символ текста.  Выделите картинку щелчком по ней – картинка имеет рамку, на которой располагаются квадратики-маркеры, позволяющие изменять размеры по горизонтали, по вертикали и по диагонали. Пропорции картинки не искажаются, если увеличивать или уменьшать изображение за диагональные направляющие.
Выделите картинку щелчком по ней – картинка имеет рамку, на которой располагаются квадратики-маркеры, позволяющие изменять размеры по горизонтали, по вертикали и по диагонали. Пропорции картинки не искажаются, если увеличивать или уменьшать изображение за диагональные направляющие.
Чтобы картинка стала перемещаемой необходимо изменить её обтекание: выделить картинку, вкладка Формат (или вызвать контекстное меню), выполнить Обтекание текстом, задать обтекание Вокруг рамки или По контуру. Теперь картинку можно перемещать по тексту.
2. Вставка рисунка из внешнего файлаВставка Рисунок появляется окно Вставка рисунка выберите интересующий рисунок из любой папки, нажмите кнопку Вставить.
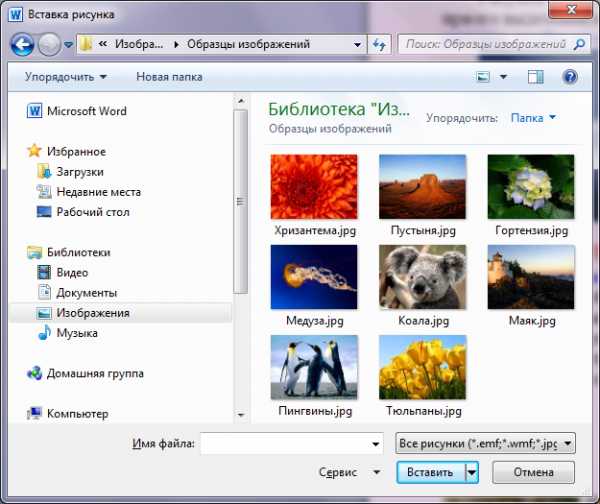
Рисунок будет вставлен в позицию текстового курсора как символ текста, при его выделении появляются квадратики-маркеры. Измените обтекание рисунка, чтобы он стал перемещаемым: выделить рисунок, вкладка Формат (или вызвать контекстное меню), выполнить Обтекание текстом, задать обтекание Вокруг рамки или По контуру. Теперь рисунок можно перемещать по тексту.

В каждом задании вы найдете ОБРАЗЕЦ (представлен в виде скриншота), а после слова РЕЗУЛЬТАТ – место для выполнения задания.
ЗАДАНИЕ 1. Вставка картинок из галереи клипов.
Создайте таблицу, состоящую из 3-х столбцов и 2-х строк. Вставьте в каждую ячейку таблицы картинку из галереи клипов. Выполните горизонтальное и вертикальное выравнивание содержимого ячеек по Центру (вкладка Макет группа Выравнивание).
ОБРАЗЕЦ:
РЕЗУЛЬТАТ:
ЗАДАНИЕ 2. Создание диаграммы.
Установите курсор после слова РЕЗУЛЬТАТ и выполните цепочку команд: Вставка SmartArt Иерархия Организационная диаграмма Оk. Выделите и удалите лишние блоки, введите текст по предложенному образцу. Через вкладку Конструктор измените однотонный цвет диаграммы на любой цветной, а также выберите любой стиль. Измените размер диаграммы, чтобы она поместилась на одной странице с образцом.
ОБРАЗЕЦ:
РЕЗУЛЬТАТ:
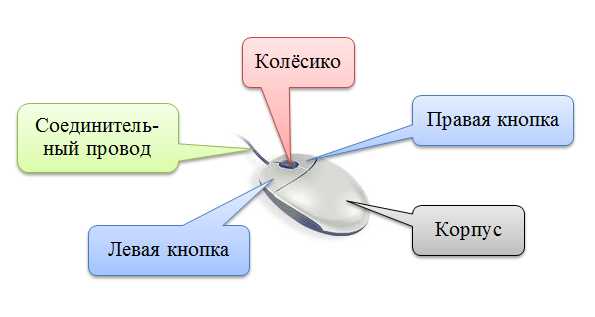
ЗАДАНИЕ 3. Вставка рисунка из внешнего файла.
Установите курсор после слова РЕЗУЛЬТАТ и выполните цепочку команд: Вставка Рисунок укажите расположение файла Мышь.jpg (Общая папка\7 класс_Материалы\Заготовки\…). Разместите изображение по центру строки. Сделайте выноски с надписями основных частей мыши (Вставка Фигуры Выноски). Измените стиль каждой выноски (выделить выноску Формат Стили фигур).
ОБРАЗЕЦ:
РЕЗУЛЬТАТ:
ЗАДАНИЕ 4. Создание буквицы.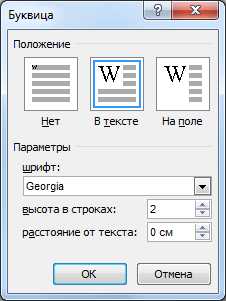
Установите курсор в начале абзаца и выполните цепочку команд: Вставка Буквица Параметры буквицы. Параметры задайте согласно представленному скриншоту. Щёлкните по контуру буквицы и через вкладку Главная установите полужирное начертание и цвет.
ОБРАЗЕЦ:
РЕЗУЛЬТАТ:
Дело мастера боится.
Семь раз отмерь, один раз отрежь.
Без труда не выловишь рыбку из пруда.
ЗАДАНИЕ 5. Декоративный заголовок WordArt.
Установите курсор после слова РЕЗУЛЬТАТ и выполните цепочку команд:
Вставка WordArt.
В открывшемся меню выберите один из 30 экспресс-стилей.
В области редактирования содержимого объекта WordArt введите нужный текст (вместо Поместите здесь ваш текст).
Щелчком мыши выделите рамку декоративного текста.
Через вкладку Формат задайте обтекание В тексте (в результате WordArt не будет перемещаться). Здесь же задайте изгиб тексту (Анимация Преобразовать Волна).
Через вкладку Главная измените размер шрифта.
Картинки вставьте из галереи клипов (Вставка Картинка).
ОБРАЗЕЦ:
РЕЗУЛЬТАТ:
Сохраните результат работы в личной папке под прежним именем.
8
multiurok.ru
Практическая работа по информатике 7 класс по теме «Редактирование и форматирование текста»
Практическая работа «Форматирование и редактирование текста» (урок 14, класс 7)
Задание 1.
1. Создайте текстовый документ: Пуск → Все программы → Microsoft Office → Microsoft Office Word.
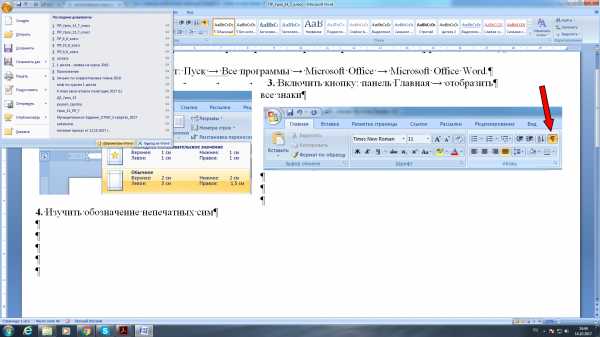
2. Установить поля: 3. Включить кнопку: панель Главная → отобразить
все знаки
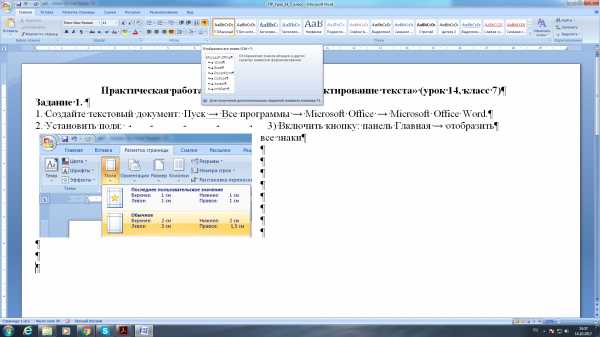

4. Изучить обозначение непечатных знаков
Задание 2. Переписать в тетрадь правила набора текста.
1. В тексте не может быть нескольких пробелов подряд.
2. После любого разделительного знака идет пробел (исключение – открывающиеся скобка или кавычки).
3. Перед любым разделительным знаком не должно быть пробела (исключение – закрывающиеся скобка или кавычки).
4. Если подряд идут два разделительных знака, пробел между ними не ставится.
5. Тире отделяется пробелами с обеих сторон, дефис не отделяется.
Задание 3. Произвести форматирование абзаца
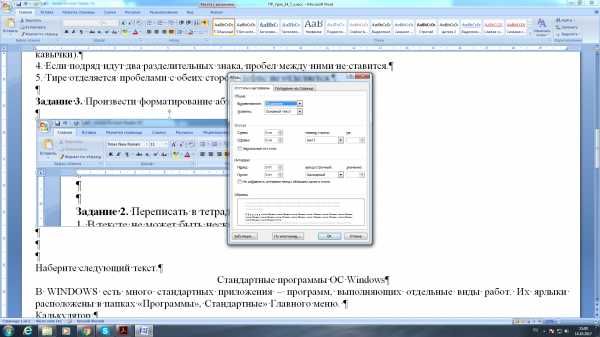
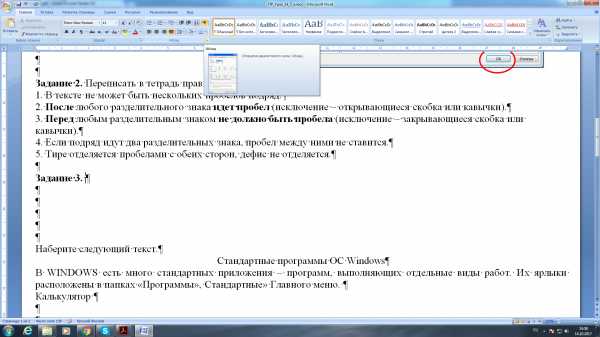
Задание 4. Наберите следующий текст.
Стандартные программы ОС Windows
В Windows есть много стандартных приложений – программ, выполняющих отдельные виды работ. Их ярлыки расположены в папках «Программы», Стандартные» Главного меню.
Калькулятор. Позволяет произвести вычисления высокой степени сложности. Имеет два вида: обычный (для простейших арифметических действий) и инженерный (для более сложных расчетов с возможностью использования двоичной, восьмеричной и шестнадцатеричной систем счисления).
Блокнот. Это простейший текстовый редактор. Используется в случае, если нужно просто записать несколько слов или предложений (аналог записной книжки).
Графический редактор Paint. Позволяет создавать несложные рисунки в растровом формате с использованием набора базовых инструментов.
При наборе текста использовать приведенные ниже параметры форматирования и шрифты.
— Заголовок. Абзацные отступы: красная строка – 0, левая граница – 0, правая граница – 2, центрирование. Шрифт Comic Sans MS, размер 14, полужирное начертание, курсив, цвет – красный.
— Первый абзац. Абзацные отступы: красная строка – 1, левая граница – 0, правая граница – 5, выравнивание по ширине. Шрифт Times New Roman, размер 12, цвет – черный. Для выделения слов использовать полужирное начертание (темно-синий цвет), курсив (темно-синий цвет).
— Второй абзац. Абзацные отступы: красная строка – 0,5, левая граница – 5, правая граница – 0, выравнивание по ширине. Шрифт Arial, размер 12, цвет – черный. Для выделения слова «Калькулятор» использовать полужирное начертание (темно-голубой цвет), для остальных слов – полужирное начертание (черный цвет).
— Третий абзац. Абзацные отступы: красная строка – 2,5, левая граница – 0, правая граница – 3, выравнивание по ширине. Шрифт Arial, размер 12, цвет – черный. Для выделения слова «Блокнот» использовать полужирное начертание (темно-голубой цвет), для остальных слов – полужирное начертание (черный цвет).
— Четвертый абзац. Абзацные отступы: красная строка – 0,5, левая граница – 5, правая граница – 0, выравнивание по ширине. Шрифт Arial, размер 12, цвет – черный. Для выделения слов «Графический редактор Paint» использовать полужирное начертание (малиновый цвет).
Задание 5. Сохранить текст под своей фамилией
infourok.ru
Лабораторно-практическая работа «Создание гипертекстовых ссылок в таблицах Microsoft Word» 7 класс
Тема: Практическая работа «Создание гипертекстовых ссылок в таблицах Microsoft Word»
Предмет: Информатика
Класс: 7 (углубленное изучение)
Литература:
Семакин И.Г. «Базовый курс. 7-9», Москва, «Просвещение» , 2006г.
Житкова О.А., Жаркова В.Б., Кудрявцева Е.К. «Редактор WORD 2000», Москва, «ИНТЕЛЛЕКТ-ЦЕНТР», 2003г.
Босова Л.Л., Чомова Т.Н., Савельева В.С. «Обработка текстовой информации. Дидактические материалы», Москва, «БИНОМ. Лаборатория знаний», 2002г.
Аннотация:
Данные задания позволяют учащимся повторить все основные моменты, изученных тем в текстовом редакторе Microsoft Word и научиться создавать гиперссылки для перехода между страницами документа.
Гипертекстовые ссылки
Гипертекст – это способ организации текстовой информации, внутри которой установлены смысловые связи между её различными фрагментами (т.е. гиперсвязи).
Гипертекстовую информацию можно читать в обычном порядке «листая страницы» на экране, можно перемещаясь по смысловым связям в произвольном порядке.
Задание:
В текстовом редакторе Microsoft Word, создайте 5 страниц документа со следующим содержанием:
1 страница
2 страница
3 страница
4 страница
5 страница
Устройство компьютера
1. Схема
2. Память
3. Процессор
4. Устройства ввода/вывода
Схема
Память
Внутренняя
Внешняя
Процессор
1. АЛУ
2. УУ
3. Набор регистров
Устройства
Ввода
Вывода
мышь
монитор
клавиатура
принтер
сканер
колонки
Сделайте закладки на ключевые слова на всех страницах, кроме первой (т.е. схема, память, процессор, устройства):
Выделите необходимое слово/Вставка/Закладка/Напишите это слово /Добавить.
Сделайте гиперссылки с 1 страницы на эти закладки:
Выделите нужное слово /Вставка/Гиперссылка/Связать с…/местом в документе/выберите место в документе/выберите нужную закладку.
Сделайте гиперссылки со 2 — 4 страниц с этих закладок на 1 страницу:
Выделите нужное слово/Вставка/Гиперссылка/Связать с…/местом в документе/выберите место в документе/Начало документа/Ок.
www.metod-kopilka.ru
Практическая работа по информатике «Создание списков и таблиц в Word» 7 класс
Практическая работа «Создание списков и таблиц»
Цели практической работы:
— изучить создание таблицы, заполнение ячеек таблицы;
— научиться составлять нумерованный и маркированный списки.
Задание №1.
1. Запустите текстовый процессор MS Word (Пуск-Все программы-Microsoft Office—Microsoft Word).
2. Создать таблицу по образцу. Для этого использовать команду Вставка-Таблица. В диалоговом окне Вставить таблицу установить параметры Размера таблицы: число столбцов: 6, число строк: 5 .
3. Текст в таблице должен быть Times New Roman, кегль 14.
4. Выполнить оформление таблицы. Ячейки, в которых находятся названия дней недели закрасить в темно-синий цвет (1.Выделяем нужные ячейки, 2. Нажимаем команду Конструктор-Заливка, в появившемся диалоговом окне выбираем темно-синий цвет.)
5. Сохраните документ под именем Расписание уроков.doc.
6. Закрыть документ.
Понедельник
Вторник
Среда
Четверг
Пятница
1.
Математика
Литература
Математика
Русский язык
Физкультура
2.
Физика
Информатика
Литература
Этика
Математика
3.
Литература
Русский язык
Русский язык
Математика
Литература
4.
Физкультура
Математика
Физика
Информатика
Информатика
Задание №2 (а).
1. Запустите текстовый процессор MS Word (Пуск-Все программы-Microsoft Office—Microsoft Word).
2. Наберите предложенный текст по образцу. Создайте нумерованный список (выделите весь текст, который должен быть выполнен в виде списка, нажмите команду Главная-Абзац-Нумерация, в появившемся диалоговом окне выберите номера.). Текст должен быть Times New Roman, кегль 14, заголовок полужирный.
3. Сохраните документ под именем Нумерованный список.doc.
4. Закрыть документ.
Есть такие деревья.
Хлебное дерево из семейства тутовых.
Ландышевое дерево, растение рода клетра.
Индийский миндаль.
Ландышевое дерево, растение рода клетра.
Задание №2 (b)
1. Запустите текстовый процессор MS Word (Пуск—Все программы-Microsoft Office-Microsoft Word).
2. Наберите предложенный текст по образцу. Создайте маркированный список (1 абзац – выделите весь текст, который должен быть выполнен в виде списка, нажмите команду Главная-Абзац-Нумерация, в появившемся диалоговом окне выберите номера.). Текст должен быть Times New Roman, кегль 14, заголовок полужирный, выравнивание заголовка по центру, выравнивание основного текста по левому краю. Проведение нижней черты – одновременно нажать кнопку Schift и клавишу со знаком «-».
2 абзац – красная строка 1.25, список маркированный (выделите весь текст, который должен быть выполнен в виде списка, нажмите команду Главная-Абзац-Маркеры, в появившемся диалоговом окне выберите маркер-галочка, выравнивание текста по левому краю, начертание – полужирное, курсив).
3. Сохраните документ под именем Списки.doc.
4. Закрыть документ.
Предметы
______________________________________________________________
В комплект поставки операционной системы Windows входят стандартные приложения прикладного назначения:
графический редактор Paint;
текстовые редакторы WordPad и Блокнот;
калькулятор;
программа работы с изображением Imaging;
комплекс программ Связь для связи по телефонной сети;
комплекс программ мультимедиа Развлечения.
infourok.ru
План-конспект урока по информатике и икт (7 класс) по теме: Урок в 7 классе по теме «Вычисления в таблицах MS Word»
Фамилия, имя, класс ____________________________ Тест по теме «ТЕКСТОВЫЙ РЕДАКТОР»
Метка на экране монитора, указывающая позицию, в которой будет отображен вводимый с клавиатуры символ
Приложение 3 Документы Word часто содержат данные, оформленные в виде таблицы. Таблица состоит из столбцов и строк, на пересечении которых находятся ячейки. В ячейках таблиц размещается информация произвольного типа: текст, числа, графика, рисунки, формулы. Одной из возможностей текстового процессора MS Word и непосредственно работой с таблицами являются расчеты в таблицах. В редакторе Microsoft Office Word принята система адресации ячеек, такая же, как и в Microsoft Office Excel – столбцы именуются буквами латинского алфавита, а строки – цифрами. Обычно таблицы используются для более удобного расположения информации документа. Word предоставляет возможность использования таблиц произвольной конфигурации с различным числом строк, столбцов даже на уровне отдельной строки таблицы. Таблица Word может содержать максимум 31 столбец и произвольное число строк. Высота строк — произвольная, но ячейки одной строки имеют одинаковую высоту. Ширина ячеек одной строки и даже одного столбца — произвольная, в том числе и одинаковая. Первоначально указанное при создании таблицы число строк и столбцов можно изменять, добавляя новые или удаляя существующие строки и столбцы. |
|
Приложение 4
Категория | Функиция | Назначение |
Статистические | AVERAGE() | Вычисление среднего значения для диапазона ячеек, например: = AVERAGE(A1:C20; B25; A30) |
COUNT() | Подсчет числа значений в указанном диапазоне ячеек, например: = COUNT(A1:C20; B25; A30) | |
MAX() | Нахождение максимального значения в указанном блоке ячеек, например: = MAX(A1:C20; B25; A30) | |
MIN() | Нахождение минимального значения в указанном блоке ячеек, например: = MIN(A1:C20; B25; A30) | |
SUM() | Нахождение суммы чисел в указанном блоке ячеек, например: = SUM(A1:C20; B25; A30) | |
Математические | ABS(x) | Абсолютное значение вычисляемого выражения, например: =ABS(A1*B12-C25+100) |
MOD(x,y) | Остаток от деления первого числа на второе, например: =MOD(A1,C12) | |
INT(x) | Целая часть числа, например: =INT(2345.45) | |
PRODUCT() | Произведение чисел в указанном диапазоне ячеек, например: PRODUCT(A1:C20; B25; A30) | |
ROUND(x,y) | Округление значения до указанного числа знаков, например, округлить до сотен: =Round(2345.45, -2) | |
SIGN(x) | Определение знака числа, например (-1 для отрицательных и 1 для положительных чисел): =SIGN(-2345.45) | |
AND(x,y) | Вычисляет значение 1, если заданы истинные значения логических аргументов, иначе — 0,Например: =AND(A4>3; B2 |
Категория | Функиция | Назначение |
Статистические | AVERAGE() | Вычисление среднего значения для диапазона ячеек, например: = AVERAGE(A1:C20; B25; A30) |
COUNT() | Подсчет числа значений в указанном диапазоне ячеек, например: = COUNT(A1:C20; B25; A30) | |
MAX() | Нахождение максимального значения в указанном блоке ячеек, например: = MAX(A1:C20; B25; A30) | |
MIN() | Нахождение минимального значения в указанном блоке ячеек, например: = MIN(A1:C20; B25; A30) | |
SUM() | Нахождение суммы чисел в указанном блоке ячеек, например: = SUM(A1:C20; B25; A30) | |
Математические | ABS(x) | Абсолютное значение вычисляемого выражения, например: =ABS(A1*B12-C25+100) |
MOD(x,y) | Остаток от деления первого числа на второе, например: =MOD(A1,C12) | |
INT(x) | Целая часть числа, например: =INT(2345.45) | |
PRODUCT() | Произведение чисел в указанном диапазоне ячеек, например: PRODUCT(A1:C20; B25; A30) | |
ROUND(x,y) | Округление значения до указанного числа знаков, например, округлить до сотен: =Round(2345.45, -2) | |
SIGN(x) | Определение знака числа, например (-1 для отрицательных и 1 для положительных чисел): =SIGN(-2345.45) | |
AND(x,y) | Вычисляет значение 1, если заданы истинные значения логических аргументов, иначе — 0,Например: =AND(A4>3; B2 |
Приложение 5
Ввод формул
Формулы служат для выполнения математических вычислений с числами и вставки результатов вычислений в виде поля.
Поле — последовательность кодов, указывающих Word вставить текст, графику, номера страниц и другие материалы в документ автоматически. В MS Word можно вставить в текст таблицу с автоматически вычисляемыми значениями ячеек, т.е. электронную таблицу. Иногда некоторые простейшие вычисления можно производить самим, например, подсчитать сумму по строкам или столбцам созданной таблицы. При работе с таблицей поле с результатом вычислений вставляется в ячейку, на которую указывает курсор. Ячейки характеризуются своим адресом и обозначаются как А1, А2, В1, В2 и т.д., где буква (A, B, C ,D…) представляет столбец, а число (1, 2, 3, 4…) указывает номер строки, в которой расположены данные. Если не указывается другая операция, Word производит сложение и выполняет суммирование, руководствуясь следующими правилами:
· если в числах, с которыми производится вычисление, имеется форматирование, например, присутствует денежный знак, результат также получает это форматирование;
· если ячейка, на которую указывает курсор, находится на пересечении строки и столбца, которые имеют в своем составе цифры, то суммируются столбцы;
· если ячейка, на которую указывает курсор, содержит текст или числа, то они игнорируются.
Таким образом, формула – это выражение, содержащее допустимое сочетание чисел, полей, значением которых являются числа, операторов и функций. Выражение может ссылаться на содержимое ячеек таблиц и значения, возвращаемые функциями. В поле Формула (команда Таблица4Формула) можно использовать значения, возвращаемые перечисленными ниже функциями.
Каждая формула в Word должна начинаться со знака равенства (=). Для этого необходимо ввести имя функции после знака равенства (=) или выбрать его из списка Вставить функцию (Таблица / Формула), затем ввести диапазон ячеек, который следует использовать в вычислениях. Для функций с пустыми скобками допустимо любое число аргументов, разделенных точками с запятыми (;). Аргументами функций могут быть числа или формулы. При этом ссылки на ячейки таблицы допустимы в качестве аргументов следующих функций: AVERAGE(), COUNT(), MAX(), MIN(), PRODUCT() и SUM().
Приложение 6
Приложение 7
Морской бой
Если участник выбрал ячейку “поле боя”, в котором нет корабля, то ход передается сле-дующему. Ход передается и в том случае, если ответ был неверным. На «поле боя» на экране отме-чаются удары, и если цель уничтожена, то она закрашивается цветным мелом. Сами участники на своих листках с “полем боя” отмечает подбитые ими корабли ручкой (желательно цветной), а кораб-ли потопленные соперником карандашом.
Вопросы
Б2 Текстовый редактор — программа, предназначенная для создания, редактирования и форма-тирования текстовой информации
Б3 С помощью компьютера текстовую информацию можно Хранить, получать и обрабатывать
Б4 Символ, вводимый с клавиатуры при наборе текста, отображается на экране монитора в пози-ции Положением курсора
Б8 Для переключения режимов при наборе прописных и строчных букв в текстовых редакторах служи клавиша Caps Lock, Shift
Б10 Минимальным объектом, используемым в текстовом редакторе, является символ
В10 В текстовом редакторе выполнение операции Копирование становится возможным после выделения фрагмента текста
Г2 Чтобы удалить строку (столбец) таблицы, нужно
В6 Форматирование – это…
Г6 Редактирование – это…
Е10 Курсор – это Отметка на экране монитора, указывающая позицию, в которой будет ото-бражен вводимый с клавиатуры символ.
Ж1 При редактировании теста для удаления неверно набранного символа используется клавиша Delete
Ж2 Что является основным элементом таблицы: ячейка
И4 В текстовом редакторе выполнение операции Удаление фрагмента текста становится возмож-ным после выделения фрагмента текста
К4 Какую информацию можно занести в таблицу?
К7 Для объединения ячеек в таблице нужно:
И10 Назовите 3 этапа форматирования
К10 Гипертекст — это структурированный текст, в котором могут осуществляться переходы по выделенным меткам
Ж6 При открытии документа с диска пользователь должен указать имя файла
Ж7 Что относится к форматированию символов?
Ж8 Для изменения оформления границ таблицы надо …
nsportal.ru
Практические работы «Параметры страницы, текста в текстовом редакторе MS Word» (7 класс)
Жаравина А.Г. МБОУ «Хибинская гимназия» г.Кировск
Изменение параметров страницы, текста
Изменение шрифта: выделить текст – выбрать необходимый шрифт из списка
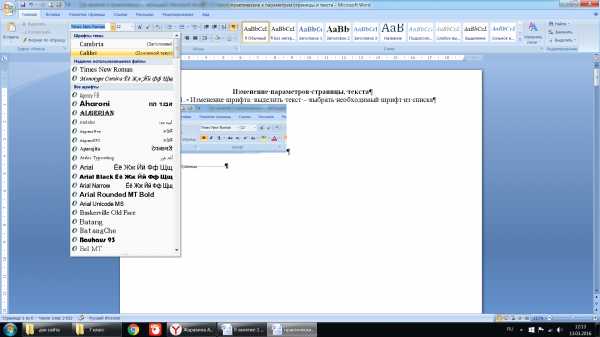
Изменение размера текста: выделить текст – выбрать необходимый размер из списка
Для подбора размера шрифта можно воспользоваться кнопками увеличения/уменьшения размера

изменение начертания текста. Выделить текст, выбрать необходимое начертание: полужирное, курсив, подчеркнутое, зачеркнутое
 . Для удаления начертания необходимо выделить текст и нажать подсвеченную кнопку еще раз
. Для удаления начертания необходимо выделить текст и нажать подсвеченную кнопку еще разИзменение цвета текста,
 . Выделить текст, выбрать нужный цвет текста, раскрыв список цветов (нажать на чёрный треугольник справа от буквы А)
. Выделить текст, выбрать нужный цвет текста, раскрыв список цветов (нажать на чёрный треугольник справа от буквы А)Изменение регистра. Выделить текст, выбрать нужный регистр из списка


Изменение выравнивания текста. Выделить текст, применить необходимое выравнивание

 выравнивание по левому краю
выравнивание по левому краю выравнивание по центру
выравнивание по центру выравнивание по правому краю
выравнивание по правому краю выравнивание по ширине
выравнивание по ширинеИзменение расстояния между строчками (межстрочный интервал). Выделить текст, выбрать необходимый параметр или задать свой
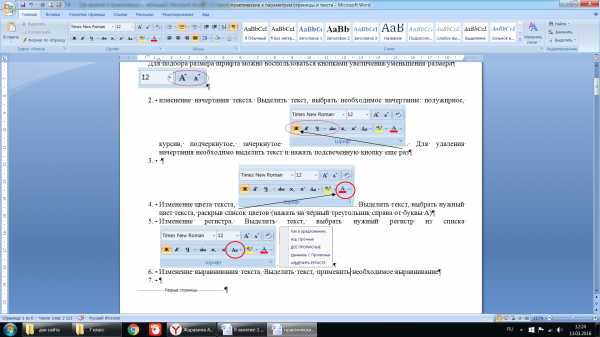
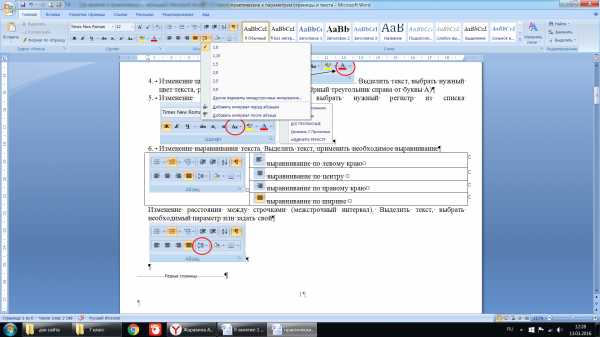
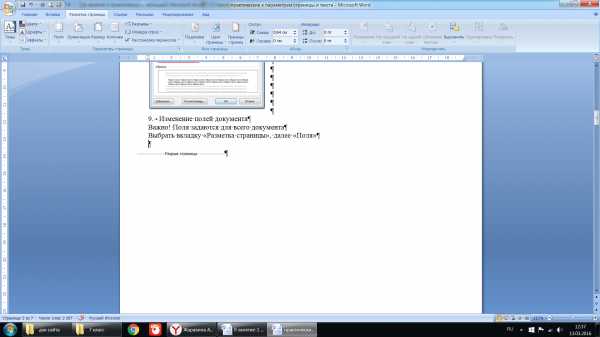
Изменение параметров абзаца. Отрыть список параметров:

В открывшемся диалоговом окне задать необходимые параметры: 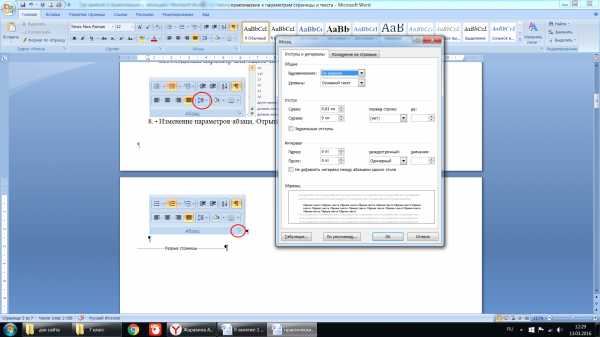
отступ абзаца, интервал перед и после абзаца.
Значение для первой строки: нет, отступ (первая строка смещена вправо относительно основного текста), выступ (первая строка смещена влево относительно основного текста)
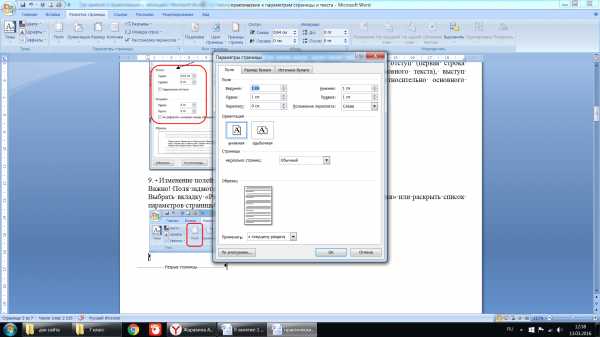
Изменение полей документа
Важно! Поля задаются для всего документа
Выбрать вкладку «Разметка страницы», далее «Поля» — «Настраиваемы поля» или раскрыть список параметров страницы
Задать необходимые размеры полей
Задание №1
Создать новый документ MS Office Word
Установить следующие параметры:
Поля: левое – 1,7, правое – 2,3, верхнее и нижнее – 1
Первая строка выступ на 0,5
Выравнивание текста по центру
Межстрочный интервал – 2
Интервал после абзаца – 5 пт
Отступ абзаца слева на 1
Шрифт текста – Times New Roman
Размер шрифта – 10 пт
Регистр – все прописные
Начертание текста – курсив
Цвет текста – черный
Набрать следующий текст:
Вырос и возмужал прекрасный и могучий бог Зевс. Он восстал против своего отца и заставил его вернуть опять на свет поглощенных им детей. Одного за другим изверг из уст Крон своих детей-богов, прекрасных и светлых. Они начали борьбу с Кроном и титанами за власть над миром.
Зевс метал одну за другой пламенные молнии и оглушительно рокочущие громы. Огонь охватил всю землю, моря кипели, дым и смрад заволокли все густой пеленой.
Наконец, могучие титаны дрогнули. Их сила была сломлена, они были побеждены. Олимпийцы сковали их и низвергли в мрачный Тартар, в вековечную тьму. У медных несокрушимых врат Тартара на стражу стали сторукие гекатонхейры, и стерегут они, чтобы не вырвались опять на свободу из Тартара могучие титаны. Власть титанов в мире миновала.
Сохранить текст в своей папке.
Задание №2
Создать новый документ MS Office Word
Установить следующие параметры:
Поля: левое – 2,7, верхнее – 0,5, нижнее – 0,5, правое -0,87
Первая строка отступ на 0,8
Отступ абзаца вправо на 2,3
Выравнивание текста по правому краю
Межстрочный интервал – 1,3
Интервал перед абзацем – 8 пт
Интервал после абзаца – 5 пт
Шрифт текста – Arial
Размер шрифта – 9 пт
Начертание текста – курсив, подчеркивание
Цвет текста – красный
Набрать следующий текст:
Высоко на светлом Олимпе царит Зевс, окруженный сонмом богов. Здесь и супруга его Гера, и златокудрый Аполлон с сестрой своей Артемидой, и златая Афродита, и могучая дочь Зевса Афина, и много других богов. Три прекрасные Оры охраняют вход на высокий Олимп и подымают закрывающее врата густое облако, когда боги нисходят на землю или возносятся в светлые чертоги Зевса.
Высоко над Олимпом широко раскинулось голубое, бездонное небо, и льется с него золотой свет. Ни дождя, ни снега не бывает в царстве Зевса; вечно там светлое, радостное лето. А ниже клубятся облака, порой закрывают они далекую землю. Там, на земле, весну и лето сменяют осень и зима, радость и веселье сменяются несчастьем и горем. Правда, и боги знают печали, но они скоро проходят, и снова водворяется радость на Олимпе.
Сохранить текст в своей папке
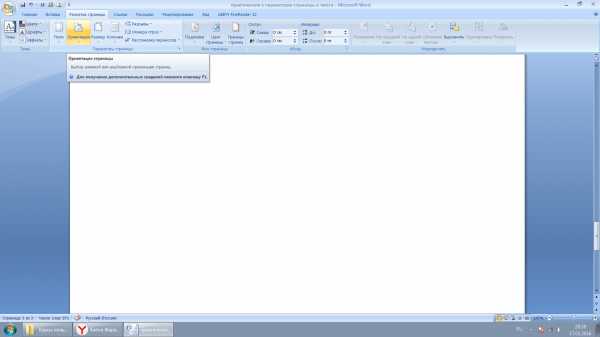
Изменение ориентации страницы:
Выбрать вкладку «Разметка страницы» — «Ориентация» — «Альбомная»/ «Книжная»
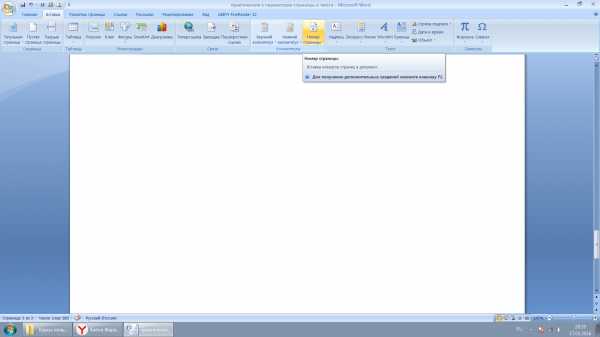
Вставка номера страницы
Выбрать вкладку «Вставка» — «Номер страницы» — Выбрать необходимое расположение номера
Задание начального номера страницы (ЕСЛИ НУМЕРАЦИЯ НАЧИНАЕТСЯ НЕ С 1)
Выбрать вкладку «Вставка» — «Номер страницы» — «Формат номеров страницы» — «начать с» — задать начальное значение
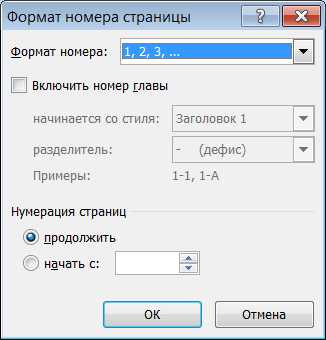
Не печать номер на первой странице
Вставить номер – по номеру страницы щелкнуть два раза левой кнопкой мыши. Поставить галочку «Особый колонтитул для первой страницы», нажать «Закрыть окно колонтитулов»
Справка: колонтитул — Заголовочные данные (название произведения, части, главы и т. п.), помещаемые над текстом каждой страницы
Вставка разрыва страницы
Набрать текст, в месте, где необходимо вставить разрыв страницы выбрать вкладку «Вставка» — «Разрыв страницы» или нажать Ctrl+Enter, поле этого текст будет печататься на новом листе.
Задание №3
Создать новый документ MS Office Word
Набрать текст:
Пируют боги в своих золотых чертогах, построенных сыном Зевса Гефестом. Царь Зевс сидит на высоком золотом троне. Величием и гордо-спокойным сознанием власти и могущества дышит мужественное, божественно прекрасное лицо Зевса. У трона его – богиня мира Эйрена и постоянная спутница Зевса крылатая богиня победы Никэ. Вот входит прекрасная, величественная богиня Гера, жена Зевса. Зевс чтит свою жену: почетом окружают Геру, покровительницу брака, все боги Олимпа. Когда, блистая своей красотой, в пышном наряде, великая Гера входит в пиршественный зал, все боги встают и склоняются перед женой громовержца Зевса. А она, гордая своим могуществом, идет к золотому трону и садится рядом с царем богов и людей – Зевсом. Около трона Геры стоит ее посланница, богиня радуги, легкокрылая Ирида, всегда готовая быстро нестись на радужных крыльях исполнять повеления Геры в самые дальние края земли.
Установить следующие параметры:
Ориентация страницы: альбомная
Поля: левое 3, правое 1, верхнее и нижнее 1,25
Вставить номер страницы внизу от центра
Первая строка отступ на 0,5
Отступ абзаца слева 3; справа 2
Выравнивание текста по ширине
Межстрочный интервал – 1,1
Интервал после абзаца – 10 пт
Регистр – все прописные
Шрифт текста – Courier New
Размер шрифта – 9 пт
Цвет текста – темно-синий
Сохранить текст в своей папке под именем Задание 3.
Задание №4
Создать новый документ MS Office Word
Набрать следующий текст:
Пируют боги. Дочь Зевса, юная Геба, и сын царя Трои, Ганимед, любимец Зевса, получивший от него бессмертие, подносят им амврозию и нектар – пищу и напиток богов. Прекрасные хариты и музы услаждают их пением и танцами. Взявшись за руки, водят они хороводы, а боги любуются их легкими движениями и дивной, вечно юной красотой. Веселее становится пир олимпийцев. На этих пирах решают боги все дела, на них определяют они судьбу мира и людей.
С Олимпа рассылает людям Зевс свои дары и утверждает на земле порядок и законы. В руках Зевса судьба людей; счастье и несчастье, добро и зло, жизнь и смерть – все в его руках. Два больших сосуда стоят у врат дворца Зевса. В одном сосуде дары добра, в другом – зла. Зевс черпает в них добро и зло и посылает людям.
Установить следующие параметры:
Поля: левое 1,5, правое 1, верхнее и нижнее 0,5
Вставить номер страницы – сверху слева
Начать нумерацию с 7
Первая строка – нет
Выравнивание текста по центру
Межстрочный интервал – 1,73
Интервал после абзаца – 12 пт
Интервал перед абзацем – 12 пт
Отступ абзаца справа 1,4
Шрифт текста – Monotype Corsiva
Размер шрифта – 14 пт
Цвет текста – оранжевый
Начертание шрифта — подчеркнутый
Сохранить текст в своей папке под именем Задание 4.
Задание №5
Создать новый документ MS Office Word
Набрать следующий текст:
Зевс. Самый великий и могущественный из греческих богов, громовержец, сын Реи (Земли) и Кроноса (Времени). Кронос безжалостно пожирал всех своих детей, опасаясь, что они восстанут против него. Рея спасла Зевса, своего шестого ребенка, дав Кроносу проглотить вместо младенца камень, завернутый в пеленки. Возмужавший Зевс заставил отца вернуть проглоченных им детей и вместе с ними вступил в борьбу с Кроносом и титанами за власть над миром. (Вставить разрыв страницы) Зевс освободил из Тартара циклопов и сторуких великанов — гека-тонхейров и с их помощью низверг туда титанов. Ему помогал титан Прометей, который перешел на его сторону. Свергнув Кроноса, Зевс и его братья разделили свои владения. Зевс оставил себе небо, Посейдону досталось море, а Аиду — подземное царство душ умерших. И стал Зевс царить на Олимпе в окружении сонма богов. Рядом с Зевсом на троне сидит его жена, величественная богиня Гера.
Установить следующие параметры:
Поля: левое 1, правое 2, верхнее и нижнее 2,5
Вставить номер страницы – внизу от цетра
Начать нумерацию с 5, установить особый колонтитул для первой страницы
Первая строка – отступ на 1
Выравнивание текста по ширине
Межстрочный интервал – 1,5
Интервал после абзаца – 12 пт
Интервал перед абзацем – 12 пт
Отступ абзаца справа 1,4
Шрифт текста – Comic Sans MS
Размер шрифта – 16 пт
Цвет текста – темно-зеленый
Начертание шрифта – подчеркнутый волнистой линией
Сохранить текст в своей папке под именем Задание 5.
Вставка рамки страницы
Выбрать вкладку «Разметка страницы» — «Границы страниц»
В появившемся окне можно выбрать рамку для документа и тип линии
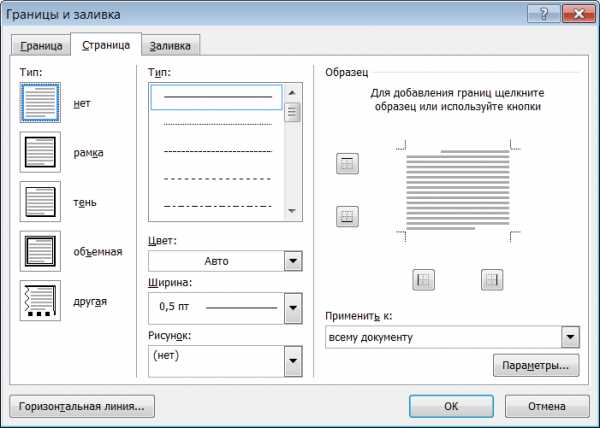
Можно выбрать рисунок, который будет отображаться как рамка документа
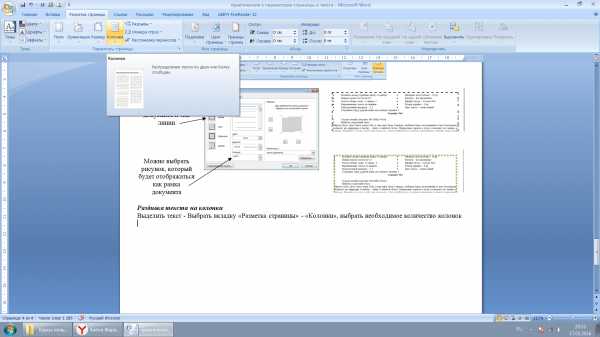
Разбивка текста на колонки
Выделить текст — Выбрать вкладку «Разметка страницы» — «Колонки», выбрать необходимое количество колонок
Задание №6
Создать новый документ MS Office Word
Набрать следующий текст:
Зевс – главное божество древнегреческой мифологии, царь всех других богов, олицетворение беспредельного неба, повелитель молний. В римской религии ему соответствовал Юпитер.
Посейдон – бог морей, у древних греков – второе божество по значению после Зевса. Как олицетворение изменчивой и бурной водной стихии
Аид – владыка мрачного подземного царства мёртвых, населённого бесплотными тенями умерших и ужасными существами-демонами. Аид (Гадес), Зевс и Посейдон составляли триаду самых могущественных богов Древней Эллады. В качестве повелителя глубин земли Аид имел отношение и к сельскохозяйственным культам, с которыми тесно связывалась его жена, Персефона. У римлян именовался Плутоном.
Гера – сестра и жена Зевса, главная женская богиня греков. Покровительница брака и супружеской любви. Ревнивая Гера сурово карает за нарушение брачных уз. У римлян ей соответствовала Юнона.
Аполлон – первоначально бог солнечного света, чей культ затем получил более широкое значение и связь с идеями душевной чистоты, художественной красоты, врачебного целительства, воздаяния за грехи.
Артемида – сестра Аполлона, девственная богиня лесов и охоты. Подобно культу Аполлона, почитание Артемиды было занесено в Грецию с Востока (малоазиатская богиня Ртемис).
Афина – богиня душевной гармонии и мудрости. Считалась изобретательницей и покровительницей большинства наук, искусств, духовных занятий, земледелия, ремесёл. С благословения Афины Паллады строятся города и идёт государственная жизнь.
Гермес – древнейший догреческий бог дорог и полевых межей, всех границ, отделяющих одно от другого. Из-за своей исконной связи с дорогами Гермес позднее почитался как посланник богов с крыльями на пятках, покровитель путешествий, купцов и торговли.
Афродита – древнегреческая богиня чувственной любви и красоты. Её тип очень близок к семитско-египетскому почитанию производительных сил природы в образе Астарты (Иштар) и Исиды.
Деметра – в Древней Греции олицетворяла производительную силу природы, но не дикую, как некогда Артемида, а «упорядоченную», «цивилизованную», ту, что проявляется в закономерных ритмах. Деметра считалась богиней земледелия, которая управляет ежегодным природным циклом обновления и увядания. Она же руководила и круговоротом человеческой жизни – от рождения к смерти.
Установить следующие параметры:
Поля: левое 2, правое 1,5 верхнее и нижнее 1
Вставить номер страницы – сверху слева
Первая строка – отступ на 1,5
Выравнивание текста по ширине
Межстрочный интервал – 1,5
Интервал перед абзацем – 12 пт
Отступ абзаца справа 1,4
Шрифт текста – Times New Roman
Размер шрифта – 18 пт
Цвет текста – черный
Рассказ о каждом боге древней Греции начинать с новой страницы
Оформить границы страницы с помощью рисунков
Сохранить текст в своей папке под именем Задание 6.
Задание №7
Создать новый документ MS Office Word
Набрать следующий текст:
Титаны
Титаны – второе поколение богов Древней Греции, порождённое природными стихиями. Первыми титанами были шесть сыновей и шесть дочерей, произошедших от связи Геи-Земли с Ураном-Небом. Шесть сыновей: Крон (Время), Океан, Гиперион, Кей, Крий, Япет. Шесть дочерей: Тефида (Вода), Тейя (Блеск), Рея (Мать-Гора?), Фемида (Справедливость), Мнемосина (Память), Феба.
Уран и Гея. Древнеримская мозаика 200-250 по Р. Х.
Кроме титанов Гея родила от брака с Ураном циклопов и гекатонхейров.
Циклопы – три великана с большим, круглым, огненным глазом посредине лба. В глубокой древности – олицетворения туч, из которых сверкает молния
Гекатонхейры – «сторукие» великаны, против ужасной силы которых ничто не может устоять. Воплощения страшных землетрясений и потопов.
Установить следующие параметры:
Поля: левое 2, правое 1,5 верхнее и нижнее 1
Ориентация страницы — альбомная
Вставить номер страницы – внизу в центре
Первая строка – выступ на 1,5
Выравнивание текста по ширине
Межстрочный интервал – 2
Интервал перед абзацем – 12 пт
Отступ абзаца справа 1,4
Шрифт текста – Times New Roman
Размер шрифта – 18пт
Цвет текста – черный
Разбить текст на две колонки
Сохранить текст в своей папке под именем Задание 7.
infourok.ru

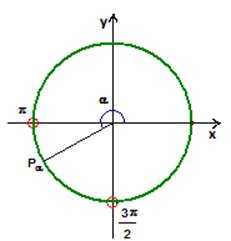
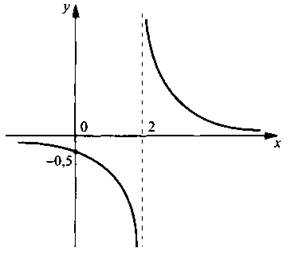
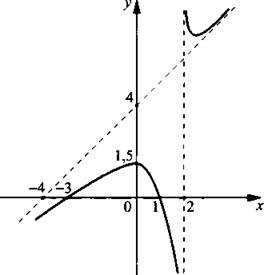
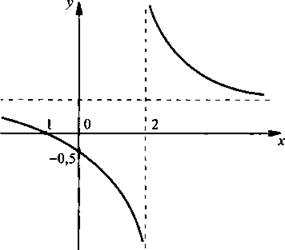
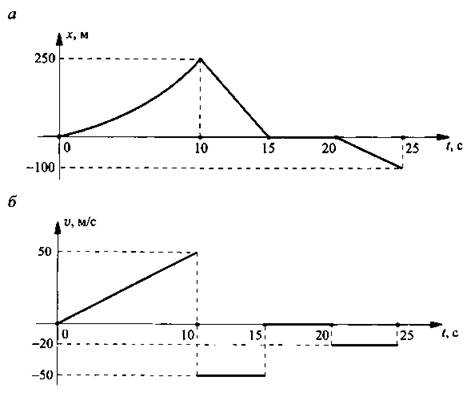
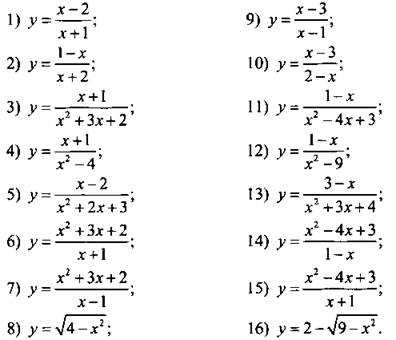
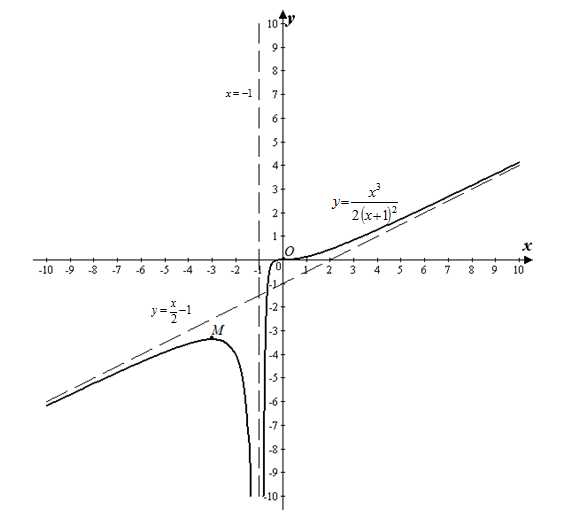

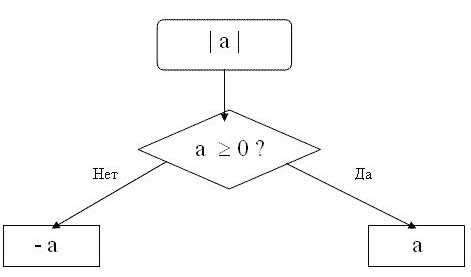

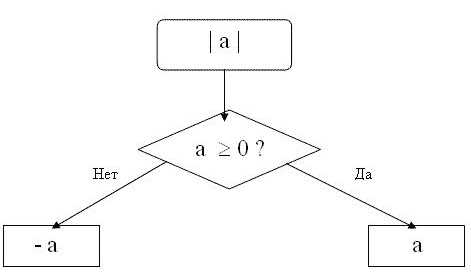





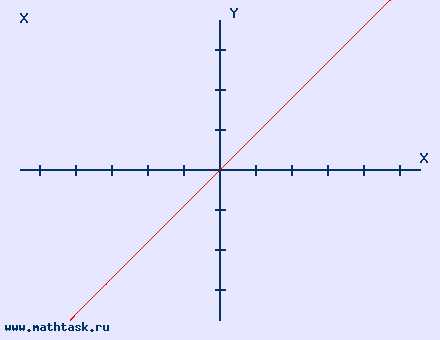
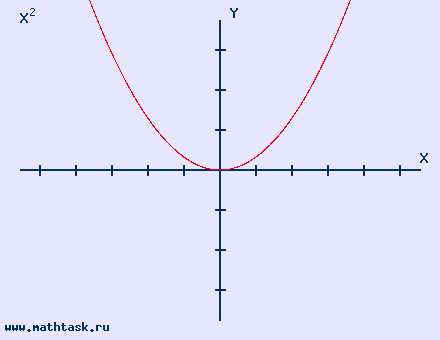
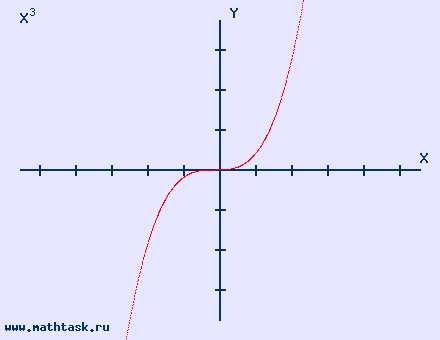
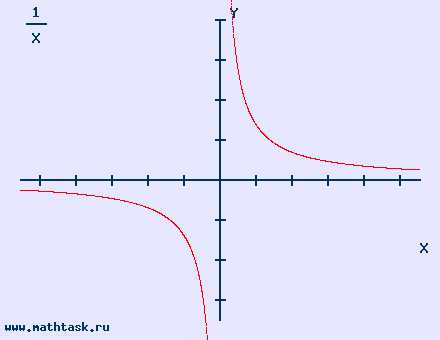
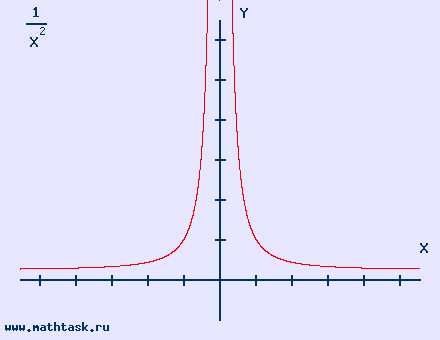
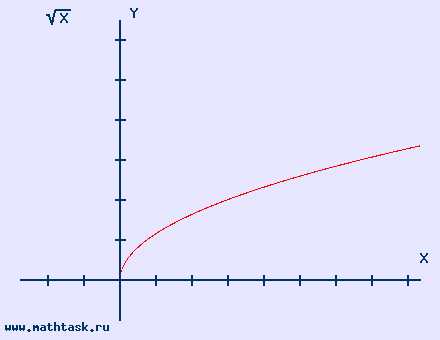
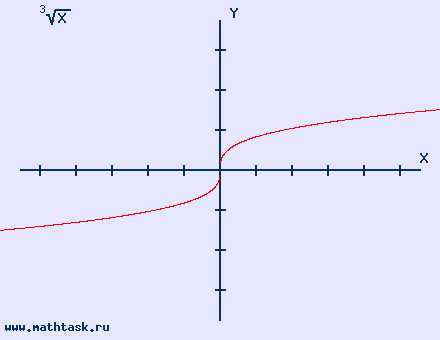
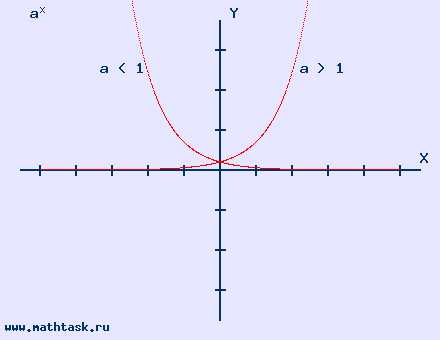
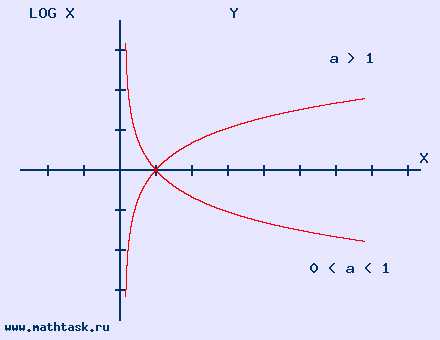
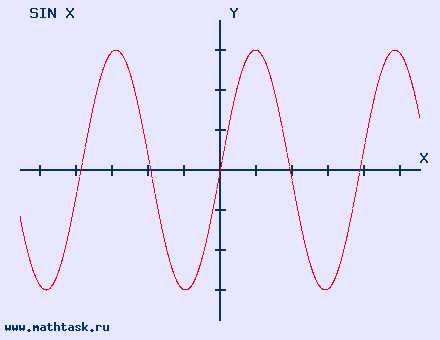
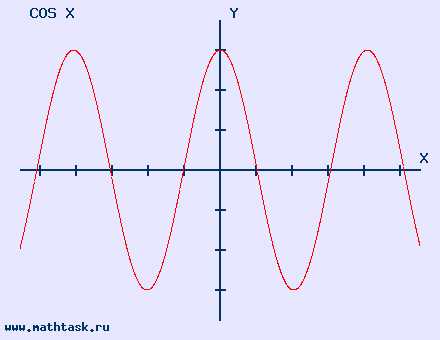
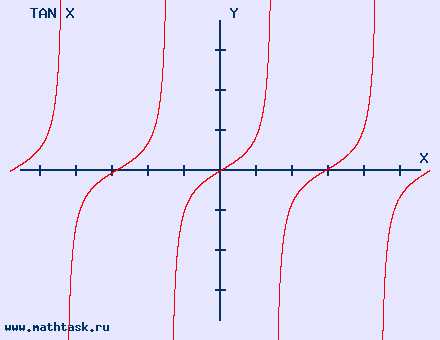
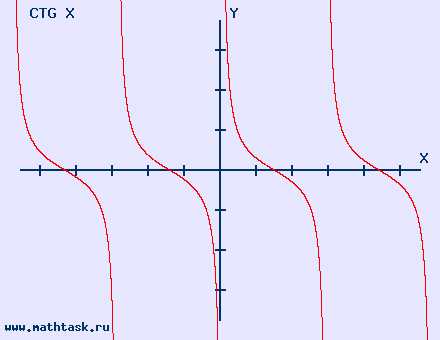
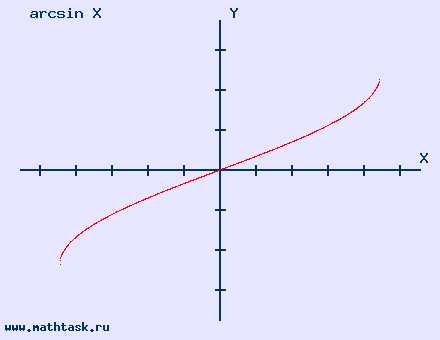
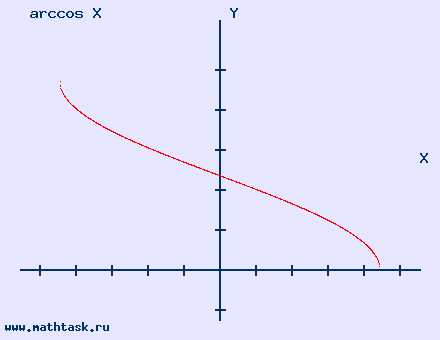
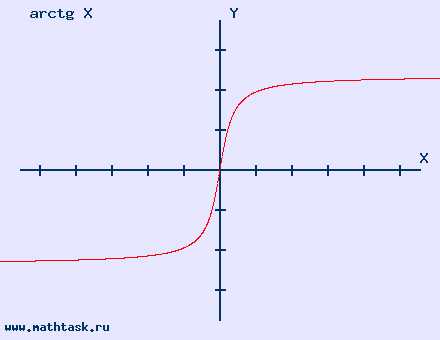
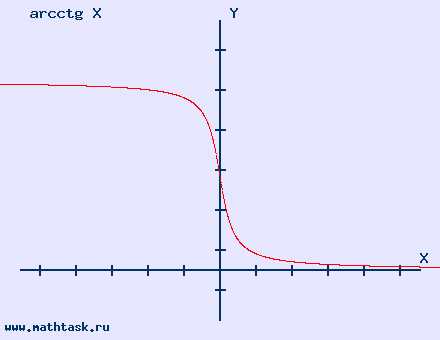



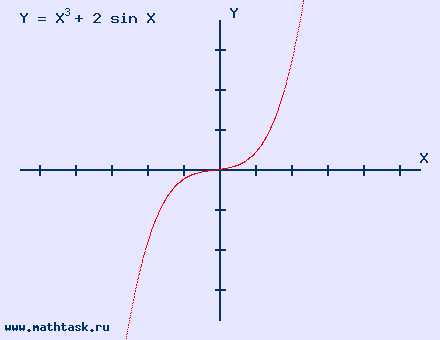
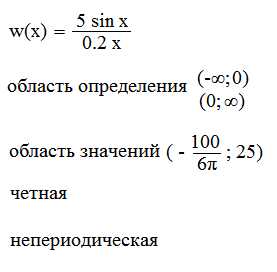
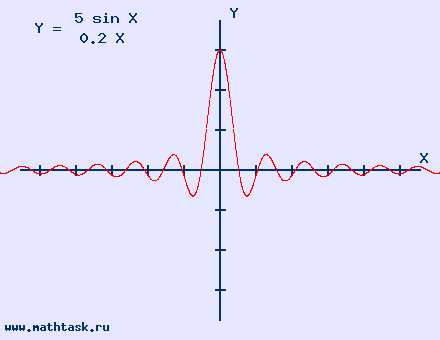
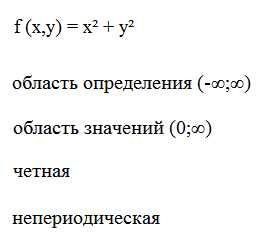
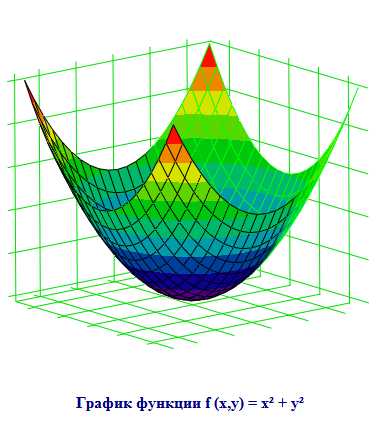
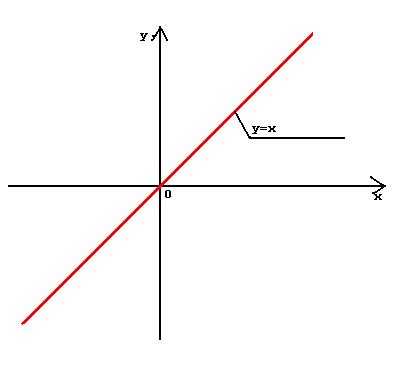
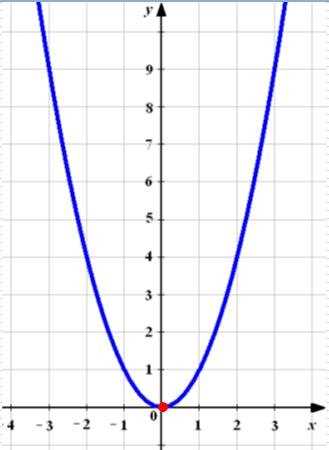
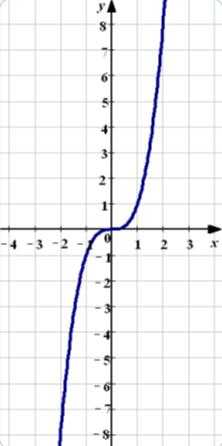
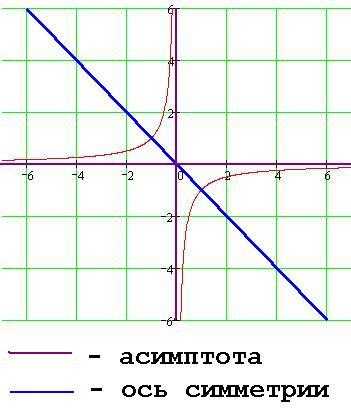
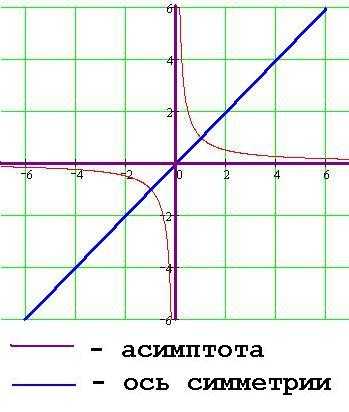
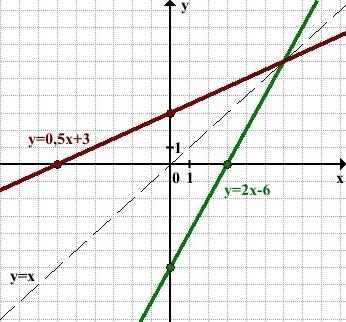 Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).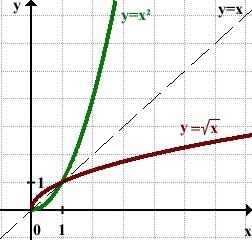























 Модели солдатиков в масштабе 1/6, или как их принято еще называть – коллекционные фигуры, а так же Military action figures 1/6 , у нас, в России в силу ряда причин пока незаслуженно обойдены широким вниманием и являются в основном уделом небольшого числа любителей-коллекционеров.
Модели солдатиков в масштабе 1/6, или как их принято еще называть – коллекционные фигуры, а так же Military action figures 1/6 , у нас, в России в силу ряда причин пока незаслуженно обойдены широким вниманием и являются в основном уделом небольшого числа любителей-коллекционеров.
 Или, допустим, игрушечные резиновые ботинки горного егеря. Которые для одной из своих работ при помощи обычной эмали постарался превратить в настоящие кожаные, повидавшие уже не один десяток горных километров.
Или, допустим, игрушечные резиновые ботинки горного егеря. Которые для одной из своих работ при помощи обычной эмали постарался превратить в настоящие кожаные, повидавшие уже не один десяток горных километров.

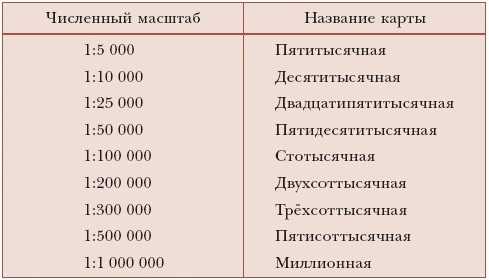
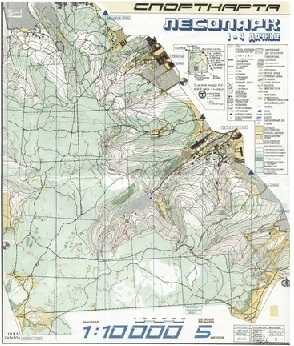 На десятитысячной карте, т.е. карте с масштабом 1:10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.
На десятитысячной карте, т.е. карте с масштабом 1:10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.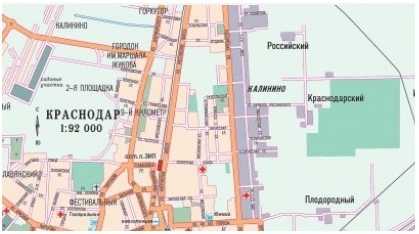
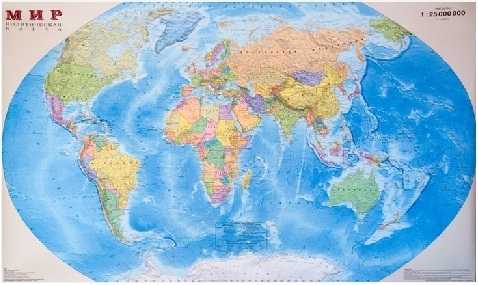
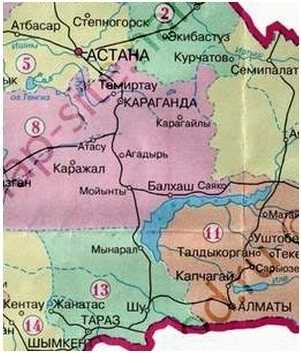 Задача 1. Пользуясь картой масштабом 1:12 250 000, найдите расстояние (по прямой) между Астаной и Таразом на местности.
Задача 1. Пользуясь картой масштабом 1:12 250 000, найдите расстояние (по прямой) между Астаной и Таразом на местности.