ТЕМА 1.1 ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ.
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒
Краткие теоретические сведения:
Матрицей размера n x m, где n – это число строк, m – число столбцов, называется таблица чисел, расположенных в определенном порядке. Элементы матрицы обозначаются aij, где i – номер строки, j – номер столбца.
Матрица может состоять как из одной строки, так и из одного столбца и из одного элемента. Матрица, состоящая только из одной строки (только из одного столбца) называется матрицей-строкой или вектор-строкой (вектор-столбцом).
Если n=m, то матрица называется квадратной.
Матрица вида = Е, называется единичной.
Если anm=amn, то матрица называется симметрической.
Квадратная матрица вида называется диагональной.
Матрица, все элементы которой выше или ниже главной диагонали равны нулю, называется треугольной.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Данные операции определены только для матриц одинакового размера.
Операции умножения (деления) матрицы на произвольное число (≠0) число сводятся к умножению (делению) каждого элемента матрицы на это число.
Произведением матрицы называется матрица, элементы которой могут быть вычислены как сумма произведений элементов i-той строки первой матрицы на элементы j-ого столбца второй матрицы.
Умножение матриц не коммутативно, т.е. АВ≠ВА. Но, если для каких либо матриц АВ≠ВА, то матрицами называются перестановочными.
Умножение матриц справедливо, если число столбцов первой матрицы равно числу строк второй матрицы.
Матрицу В называют транспонированной матрице А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
Определителем квадратной матрицы называется число, которое может быть вычислено по элементам матрицы с помощью миноров и алгебраических дополнений по теореме: «Определитель матрицы равен произведению элементов какой-либо строки или какого-либо столбца на соответствующие алгебраические дополнения этих элементов».
Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Определитель единичной матрицы равен 1.
Определитель матрицы второго порядка равен разности произведений элементов главной и побочной диагоналей.
Определитель треугольной матрицы равен произведению элементов главной диагонали.
Минор произвольного элемента квадратной матрицы равен определителю матрицы, полученному из исходного вычеркиванием i – ой строки и j – го столбца.
Алгебраическим дополнением называется минор матрицы, умноженный на (-1) в степени, равной сумме номеров строк и столбцов минора матрицы.
Определитель матрицы обладает следующими свойствами:
- Определитель не меняется при транспонировании матрицы.
- Определитель суммы матриц равен сумме определителей матриц.
- Определитель произведения матриц равен произведению определителей матриц.
- При перестановке двух строк или двух столбцов матрицы определитель поменяет знак, не изменившись по абсолютной величине.
- Если какую-либо строку или столбец матрицы умножить на отличное от нуля число, то и определитель умножится на это число.
- Определитель, содержащий две пропорциональных строки или два пропорциональных столбца равен нулю.
- Определитель, содержащий две одинаковых строки или два одинаковых столбца равен нулю.
8. Определитель, содержащий нулевую строку или нулевой столбец равен нулю.
9. Определитель не изменится, если к элементам какой-либо строки или столбца прибавить элементы другой строки или столбца, умноженные на одно и то же, отличное от нуля число.
Задача 1.Вычислите определитель матицы A=
Решение:
Det=
Элементарными преобразованиями матрицы называют следующие преобразования:
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другой строки;
- перестановка строк;
- вычеркивание одной из одинаковых строк;
- транспонирование.
Данные операции применимы и для столбцов.
Если существуют квадратные матицы Х иА, удовлетворяющие условию: ХА=АХ=Е, гдеЕ – единичная матрица того же самого порядка, то матрица Х называется обратнойк матрице А и обозначается , причем .
Задача 2.Найдите обратную матрицу для матрицы
Решение:
detA=4-6=-2
A11=4, A12=-3, A21=-2, A22=1
Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы Аобозначается через r(A).
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
Самостоятельная работа №1.
Вид работы: подготовка доклада на тему «История численности и таблиц».
Форма организации работы: индивидуальная.
Порядок выполнения работы:
- Подготовьте устный доклад по теме.
Указание: выступление с докладом по времени не должно занимать более 10 минут; доклад должен сопровождаться соответствующими иллюстрациями, картинками, оформленными в виде слайд-шоу.
Самостоятельная работа №2.
Вид работы: подготовка к практической работе №1 на тему «Выполнение простейших операций над матрицами».
Форма организации работы: коллективная.
Порядок выполнения работы:
- Повторите теоретический материал по теме работы (с.5).
- Ответьте на вопросы:
— Что называется матрицей?
— Какие виды матриц вы знаете? Охарактеризуйте их.
— Какие операции можно выполнять над матрицами?
— Перечислите свойства этих операций?
— В каком случае операция умножения матриц невыполнима?
Самостоятельная работа №3.
Вид работы: подготовка к практической работе №2 на тему «Вычисление определителей матриц».
Форма организации работы: коллективная.
Порядок выполнения работы:
- Повторите теоретический материал по теме работы (с.5-6).
- Ответьте на вопросы:
— Что называется определителем матрицы?
— Сформулируйте правила для вычисления определителей второго и третьего порядка.
— Какими свойствами обладает определитель?
— Что называется алгебраическим дополнением? Минором матрицы?
— Сформулируйте правило для вычисления определителя высшего порядка.
Самостоятельная работа №4.
Вид работы: подготовка к практической работе №3 на тему «Нахождение обратной матрицы».
Форма организации работы: коллективная.
Порядок выполнения работы:
- Повторите теоретический материал по теме работы (с.5-7).
- Ответьте на вопросы:
— Какая матрица называется обратной по отношению к данной?
— В каком случае матрица не имеет обратную?
— Сформулируйте алгоритм обращения матрицы.
Самостоятельная работа №5.
Вид работы: подготовка к практической работе №4 на тему «Вычисление ранга матрицы».
Форма организации работы: коллективная.
Порядок выполнения работы:
- Повторите теоретический материал по теме работы (с.5-7).
- Ответьте на вопросы:
— Что называется рангом матрицы?
— Что называется дефектом матрицы? Как найти дефект матрицы?
— Как вычислить ранг матрицы методом окаймления?
— Какие преобразования называют элементарными преобразованиями матрицы?
— В чем заключается суть метода вычисления ранга матрицы с помощью элементарных преобразований?
Самостоятельная работа №6.
Вид работы: решение задач по образцу.
Форма организации работы: коллективная.
Порядок выполнения работы:
- Решите задачи:
1.1
Найдите 2А2 +В
Вычислите определитель матрицы В.
Найдите ранг матрицы, обратной к матрице А.
Рекомендуемые страницы:
lektsia.com
Матрицы и определители 3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН
Рудненский индустриальный институт
ДИСТАНЦИОННОЕ ОБРАЗОВАНИЕ
МАТЕМАТИКА
ЮНИТА № 1
Матрицы и определители.
Рудный 2005
ББК 22.1я73
Рецензент: Т.А.Калдыбиев
Рекомендовано к изданию УМС РИИ
Курс: Математика. Базовый курс.
Юнита 1. Матрицы и определители
Юнита 2 Системы линейных уравнений
Юнита 3 Векторная алгебра
Юнита 4 Аналитическая геометрия на плоскости
Юнита 5 Аналитическая геометрия в пространстве
Юнита 6 Предел функции и непрерывность
Юнита 7 Дифференцирование
Юнита 8 Исследование функций и построение графиков
Юнита 9 Неопределенный интеграл.
Юнита 10 Определенный интеграл
Юнита 11 Дифференциальное исчисление функции многих переменных.
Юнита 12 Диффференциальные уравнения (1 и высших порядков) Юнита 13 Дифференциальные уравнения с постоянными коэффициентами.
Юнита 14 Числовые и функциональные ряды
Юнита 15 Ряды Фурье
Юнита 16 Кратные интегралы
Юнита 17 Криволинейные интегралы
Юнита 18 Линейное программирование
Юнита 19 Теория вероятностей
Юнита 20 Математическая статистика
ЮНИТА 1
В данном учебном пособии содержится материал, включающий понятия матриц, определителей, их основных свойств, понятие обратной матрицы. Комплектуется файлом материалов.
Для студентов технических специальностей: 050707, 050709, 050726, 050730, 050729, 050724, 050713, 050718, 050702, 050731, 050901, 050703.
Для студентов экономических специальностей: 050506, 050511
Юнита соответствует типовой образовательной программе
Для внутривузовского использования
© Рудненский индустриальный институт 2005
Содержание
Тематический план………………………………………………………..4
Литература…………………………………………………………………5
Тематический обзор……………………………………………………….6
Глава 1. Матрицы………………………………………………………….7
§1. Основные определения………………………………………………..7
§2. Линейные операции над матрицами…………………………………..8
§3. Умножение матриц………….…………………………………………8
Глава 2. Определители……………………………………………………10
§1. Определители второго и более высоких порядков……………………………………………………………………10
§2. Свойства определителей………………………………………………12
Глава 3. Обратная матрица. Существование и структура обратной матрицы…………………………………………………………………….13
Файл материалов….………………………………………………………16
Перечень умений……………………………………………………………21
Тренинг умений…………………………………………………………….23
Задания для самостоятельной работы……………………………………………………………………….30
Глоссарий
Тематический план
Матрицы, действия над матрицами (сложение, умножение на число, умножение матриц).
Определители 2го и 3го порядков.
Правило Саррюса (треугольника).
Свойства определителей. Обратная матрица.
Литература
Основная
- И.В. Виленкин, В.М. Гробер Высшая математика. Ростон-на-Дону, 2002
- В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов Краткий курс высшей математики. Т. 1, М. 1978
Дополнительная
3. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Ч. 1. М. 1980
Тематический обзор
Широкое применение математических методов в самых различных областях науки, техники, экономики и практической деятельности инженеров предъявляет повышенные требования к изучению математических приемов. Особенно важны методы и приемы линейной алгебры, наиболее простые и важные из которых рассматриваются в этом курсе.
В задачи нашего курса входит ознакомление с действиями над матрицами, изучение вычисления определителей, нахождения обратной матрицы.
Глава 1. Матрицы
§1. Основные определения.
МАТРИЦЕЙ размера m. n называется прямоугольная таблица чисел
,содержащая m строк и n столбцов. Каждый элемент матрицы а ik имеет два индекса: i – номер строки и k – номер столбца. Краткая форма записи матрицы:
А = (а ik )m,n
Матрица называется КВАДРАТНОЙ порядка n , если она состоит из n строк, и n столбцов.
Матрица размера 1 . n называется МАТРИЦЕЙ-СТРОКОЙ , а матрица размера m. 1 — МАТРИЦЕЙ-СТОЛБЦОМ .
НУЛЕВОЙ матрицей заданного размера называется матрица, все элементы которой равны нулю.
ТРЕУГОЛЬНОЙ матрицей n-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:
.ЕДИНИЧНОЙ называется квадратная матрицаn-го порядка, у которой элементы главной диагонали равны единице, а в се остальные элементы – нули:
.Матрицы А = (а ik )m,n и В = (в ik )m,n называются РАВНЫМИ , если а ik = в ik i = 1,…,m
k = 1,…,n.
§2. Линейные операции над матрицами.
СУММОЙ матриц А = (а ik )m,n и В = (в ik )m,n называются матрица А + В = (а ik + в ik )m,n .
ПРОИЗВЕДЕНИЕМ матрицы А = (а ik )m,n на число l называется матрица lА = (lа ik )m,n .
Для любых матриц одинакового размера и любых чисел l и m выполняются свойства:
1) А + В = В +А 2) А + (В + С) = (А + В) + С
3) А + 0 = А 4) l(mА) = (lm)А
5) l(А + В) = lА + lВ 6) (l + m)А = lА + mА
Докажем свойство 5):
l(А + В) = (l(а ik + в ik ))m,n = (lа ik + lв ik )m,n = (lа ik )m,n + lв ik )m,n = lА + lВ
Доказательство Остальных свойств читатель проведет самостоятельно.
ТРАНСПОНИРОВАННОЙ для матрицы А называется матрица АТ , строки которой являются столбцами матрицы А, а столбцы – строками матрицы А.
ПРИМЕР 1. Даны матрицы
иПостроить матрицу С = 2А – 3В + АТ .
РЕШЕНИЕ .
-++
=.§3. Умножение матриц.
ПРОИЗВЕДЕНИЕМ матрицы А = (а ik )m,р на матрицу В = (в ik )р,n называется матрица D размера m. n с элементами
Иными словами, для получения элемента, стоящего в i -ой строке результирующей матрицы и в k -ом ее столбце, следует вычислить сумму попарных произведений элементовi -ой строки матрицы А на k -ый столбец матрицы В.
ПРИМЕР 2. Найти произведение матрицы
на матрицу .РЕШЕНИЕ.
т.е.
.В самом определении произведения матриц заложено, что число столбцов первой матрицы равно числу строк второй. Это – условие согласования матриц при умножении. Если оно нарушено, матрицы перемножить нельзя. Поэтому возможна ситуация, когда произведение А*В существует, а произведение В*А – нет. Кроме того, когда существуют оба произведения, то чаще всего они не совпадают, т.е. в большинстве случаев произведение матриц некоммутативно: А*В¹В*А. Если А, В, С – квадратные матрицы одинакового порядка и Е – единичная матрица того же размера, то справедливы тождества:
Свойство 1) оставим без доказательства ввиду его громоздкости.
Докажем 2):
Свойство 3) доказывается аналогично, а 4) следует из определения умножения матриц.
Глава 2. Определители
§1. Определители второго и более высоких порядков.
Пусть
— квадратная матрица 2-го порядка.Определителем 2-го порядка (матрицы а) называется число
D(А) =
.Пример . Вычислить определитель матрицы
.РЕШЕНИЕ . D(А) =
.Пусть
— матрица 3-го порядка.Определителем 3-го порядка (матрицы А) называется число
D(А) =
mirznanii.com
03. Пример решения Заданий из раздела №1
Задание 1. Для данного определителя найти миноры и алгебраические дополнения элементов . Вычислить определитель : а) разложив его по элементам I-ой строки; б) разложив его по элементам J-го столбца; в) получив предварительно нули в I-ой строки.
I = 1, J = 2
Решение: 1. Находим миноры к элементам :
Алгебраические дополнения элементов соответственно равны:
2. а). Вычислим определитель, разложив его по элементам первой строки:
Б) Вычислим определитель, разложив его по элементам второго столбца:
В) Вычисли определитель , Получив предварительно нули в первой строке. Используем свойство определителей: определитель Не ИЗмеНиТся, ЕСлИ ко всЕМ эЛеМентам кАКой-либо строки (столбца) прибавить СоотВЕтстВУющие эЛеМЕНтЫ другой строки (столбца), умноженНЫе на одно И то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому, затем умножим на (-2) и прибавим ко второму. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом опредЕЛитель по элемЕНтам первой строки и вычислим его:
В опрЕДЕЛитЕЛе трЕТьЕГо порядка получили нули в ПеРвом столбце по свойству тому же свойству определителей.
Задание 2.
Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г) .
Решение: а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле . ИмеЕМ:
Б) Вычислим
ОчЕВидНО, что ;
В) Обратная матрица матрицы А имеет виД
,
Где — алгебраическое дополнение, -минор, т. е. определитель полученный из основного определителя вычёркивание i-строки, j-столбца.
,
Т. е. матрица A — Невырожденная, и, значит, существуЕТ матрица . Находим:
Тогда
;
Г) Проверка
;
Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее а) по формулам Крамера б) методом Гаусса.
Решение: Совместность данной системы проверим по теореме Кронекера — Капелли. С помощью элементарных преобразований найдем ранг матрицы
Данной системы и ранг расширенной матрицы
Для этого умножим первую строку матрицы В на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей, поменяем местами второй и третий столбцы. Получим
.
Следовательно, (т. е. числу неизвестных). Значит, исходная система совместна и имеет единственное решение.
А) По формулам Крамера
,
Где -главный определитель, который мы посчитаем, например, по правилу треугольника
,
Аналогично найдем
,
,
,
Находим: .
Б) Решим систему методом Гаусса. Исключим из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:
Из полученной системы находим .
Задание 4
Решить матричное уравнение
Пусть ,
решение матричного уравнения находим по формуле
Х=А -1В, где А -1 обратная матрица
— алгебраическое дополнение, где
— определитель, полученный из основного вычеркивание i-строки, j-столбца, — определитель матрицы.
Найдем обратную матрицу.
(-1)1+14=4
А12=(-1)1+23=-3
А21= (-1)2+12=-2
А22=(-1)2+21=1
DetA==1*4-2*3=4-6=-2
Итак,
Задание 5
Предприятие выпускает три вида продукции, используя сырье трёх видов: . Необходимые характеристики указаны в таблице .
Вид сырья | Нормы расхода сырья на изготовление одного вида продукции, усл. ед. | Расход сырья за один день, усл. ед. | ||
Сапог | Кроссовок | Ботинок | ||
S1 S2 S3 | 5 2 3 | 3 1 2 | 4 1 2 | 2700 900 1600 |
Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно фабрика выпускает x1 – единиц продукции первого вида, x2 — единиц продукции второго вида, x3 — единиц продукции третьего вида. Тогда в соответствии с расходом сырья каждого вида имеем систему.
Решаем систему линейных уравнений любым способом. Решим данную систему, например, методом Гаусса. Составим матрицу из коэффициентов стоящих перед неизвестными и из свободных членов.
Обнуляем первый столбец, кроме первого элемента
1. Первую строчку оставляем без изменения
2. Вместо второй записываем сумму первой, умноженной на -2 и второй, умноженной на 5
3. Вместо третьей записываем сумму первой, умноженной на -3 и третьей, умноженной на 5
Аналогично обнуляем второй столбец под элементом второй строки второго столбца
˜˜
Вернемся к системе
Т. е. фабрика выпускает 200- единиц продукции первого вида, 300- единиц продукции второго вида и 200- единиц продукции третьего вида.
Задание 6. Решить однородную систему линейных алгебраических
Уравнений.
Решение: Так как определитель системы
,
То система ИМЕЕт бЕСчисленное множество решений. Поскольку , , возьмем любые два уравнения системы (наПРИМЕР, ПЕрвое И второе) и найдем ее рЕШение. ИмЕеМ:
Так как определитель из коэффициентов при неизвестных и не равен нулю, то в качестве базисных нЕИзвестных ВОзьмЕМ и (хотя можно брать и другие пары нЕИзвЕСтных) И ПеРЕМЕСтим члЕНы с в правые частИ УравнЕНИЙ:
РЕШаЕМ пОСлЕдНюю систЕМу по формулам КрамЕРа :
Где
,
,
.
Отсюда находим, что Полагая , где K—Произвольный коэффициент пропорциональности (произвольная постоянная), получаем решение исходной сИСтЕМы: .
| < Предыдущая | Следующая > |
|---|
matica.org.ua





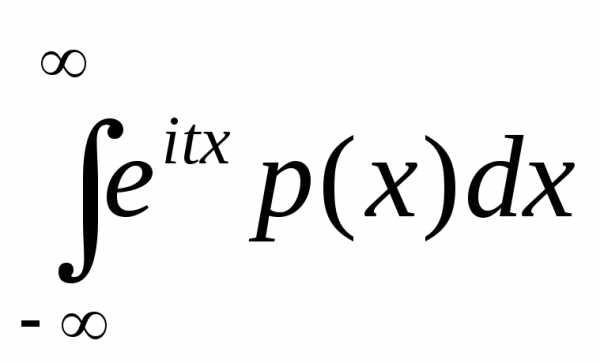

 ,
сходится равномерно, если интеграл по
множеству, гдеx>A
или x<-A
стремится к 0, когда A.
,
сходится равномерно, если интеграл по
множеству, гдеx>A
или x<-A
стремится к 0, когда A.
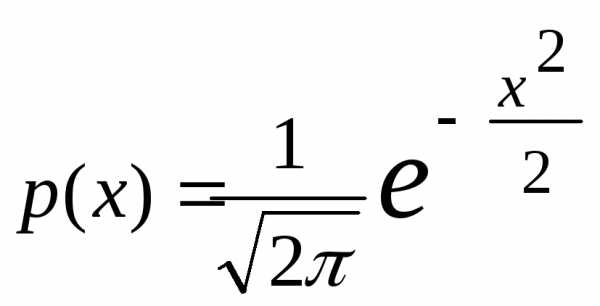 , тогда характеристическая функция
, тогда характеристическая функция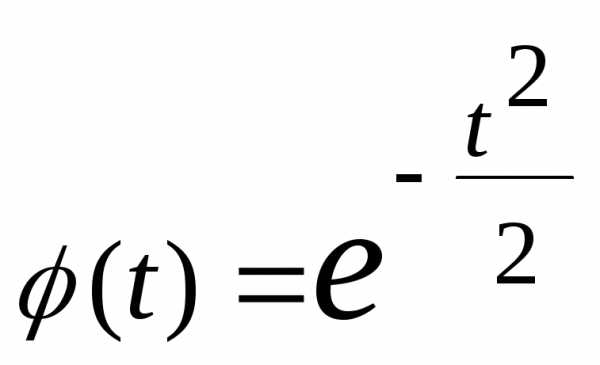
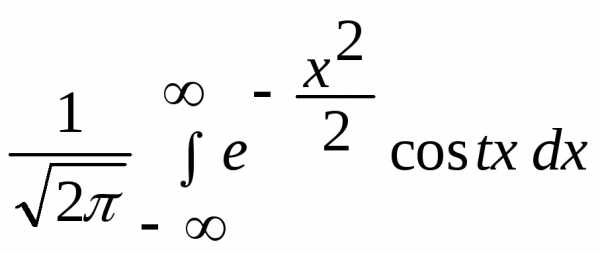 =
=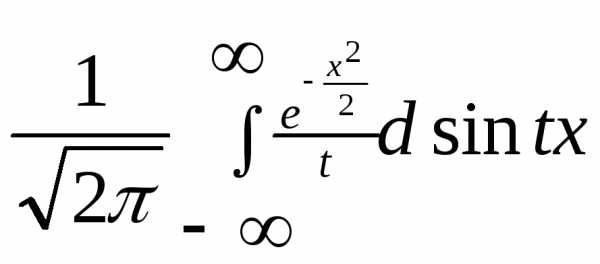 =
=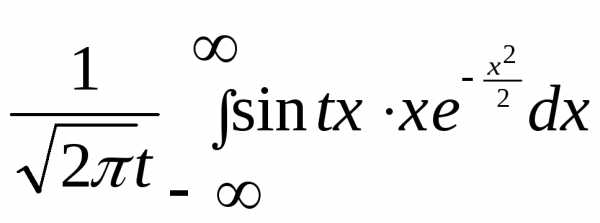
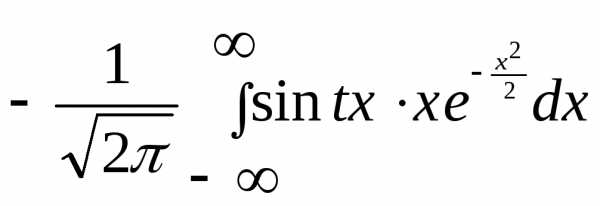
 =-t
Проинтегрируем
=-t
Проинтегрируем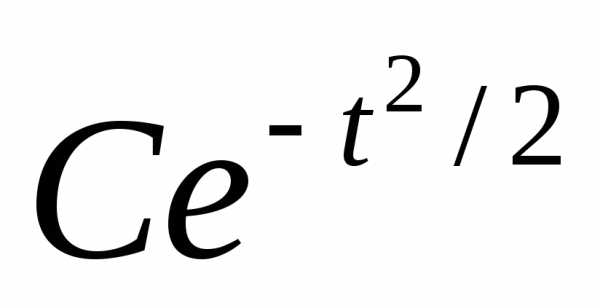 C-
какая-то постоянная
C-
какая-то постоянная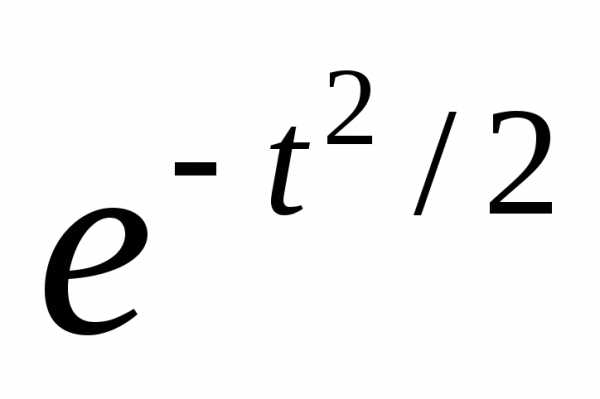 , ч.т.д.
, ч.т.д.




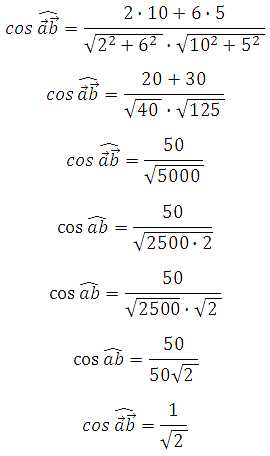








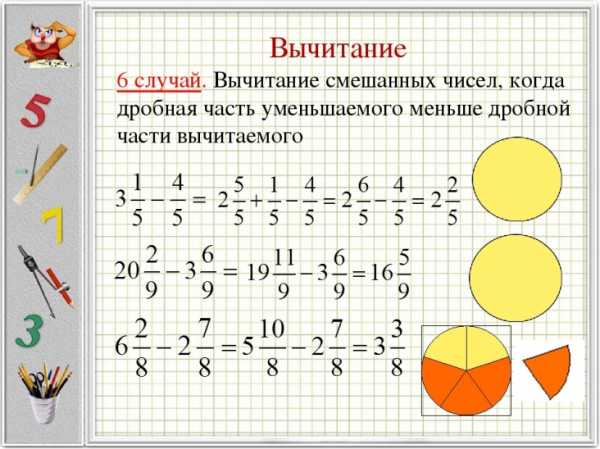



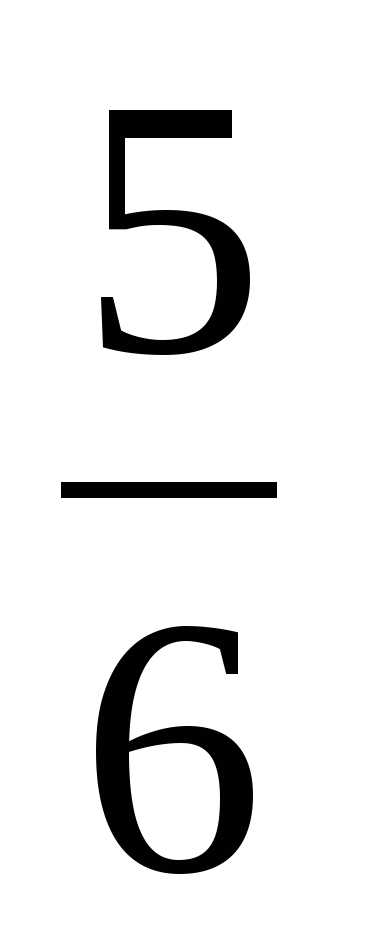 ;
;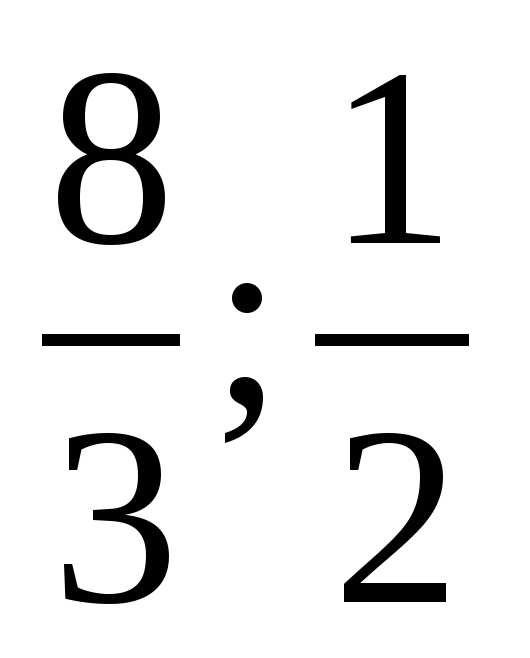 лишняя 8/3 т.к она неправильная
лишняя 8/3 т.к она неправильная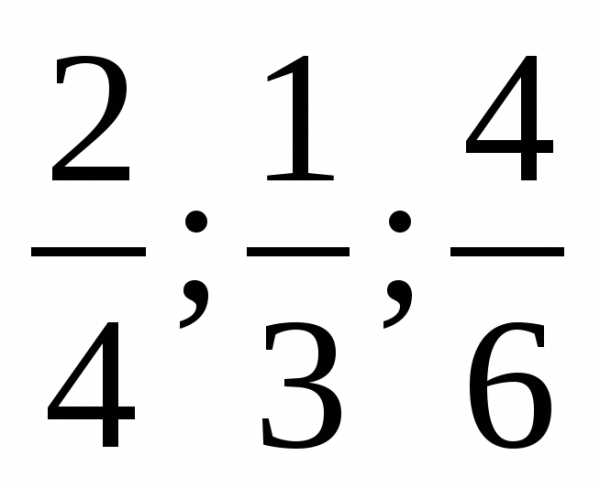 лишняя 1/3 т.к она несократима.
лишняя 1/3 т.к она несократима.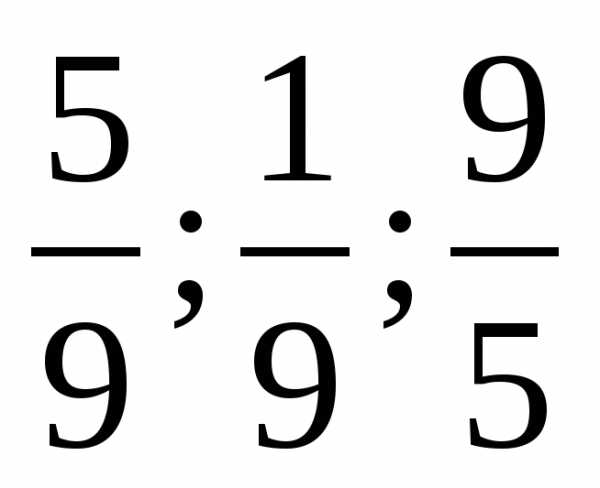 лишняя 1/9 т.к 5/9 и 9/5 взаимообратные
лишняя 1/9 т.к 5/9 и 9/5 взаимообратные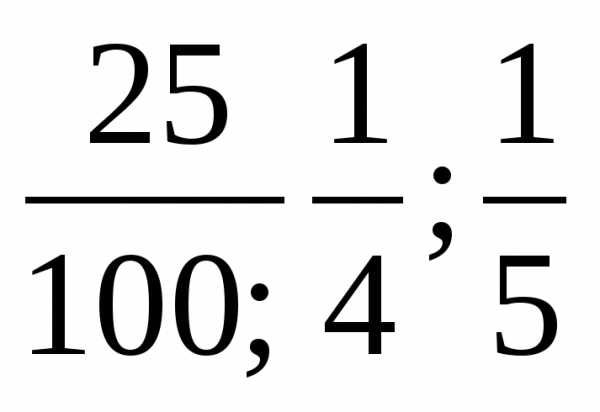 лишняя 1/5 т.к 25/100 и ¼ это равные дроби
лишняя 1/5 т.к 25/100 и ¼ это равные дроби

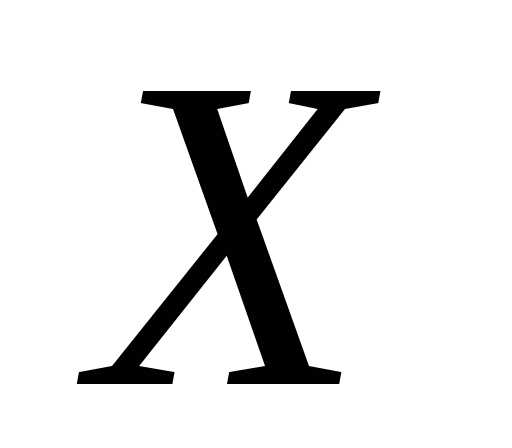 примет значение
примет значение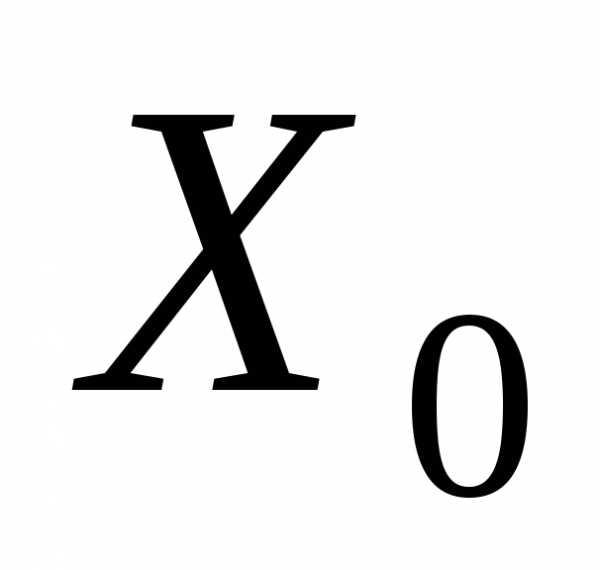 ,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина
,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина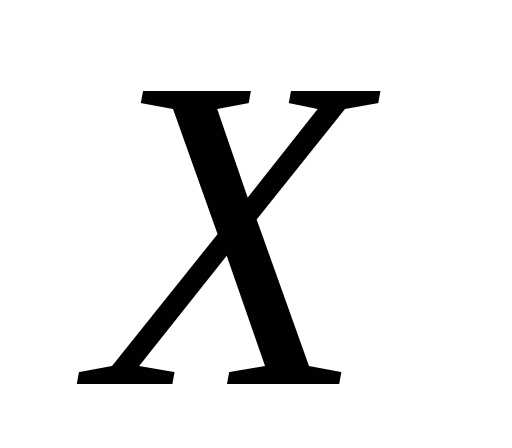 примет значение, меньшее некоторой
текущей переменной
примет значение, меньшее некоторой
текущей переменной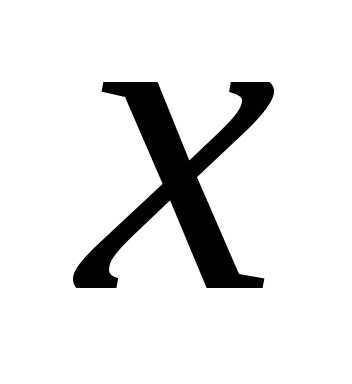 .
Вероятность этого события зависит от
значения
.
Вероятность этого события зависит от
значения ,
т.е. является функцией
от
,
т.е. является функцией
от 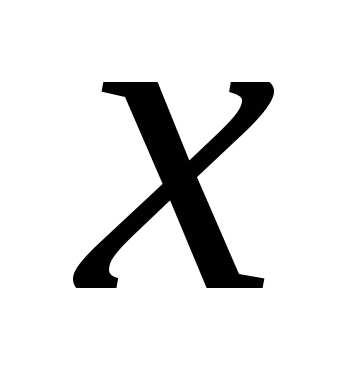 .
Эта функция называется функцией
распределения
.
Эта функция называется функцией
распределения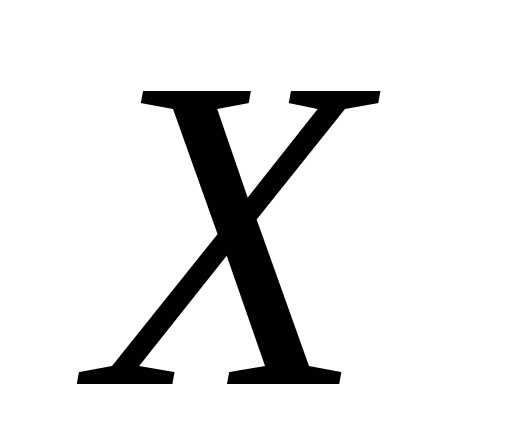 и обозначается
и обозначается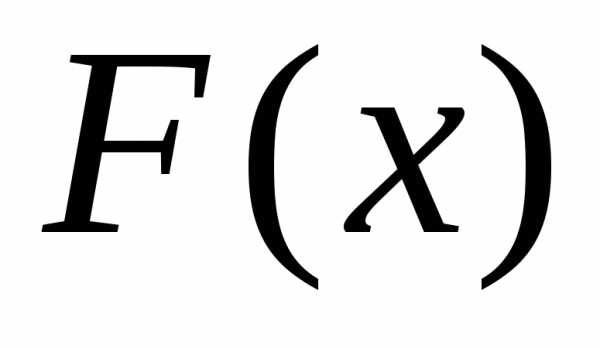 :
: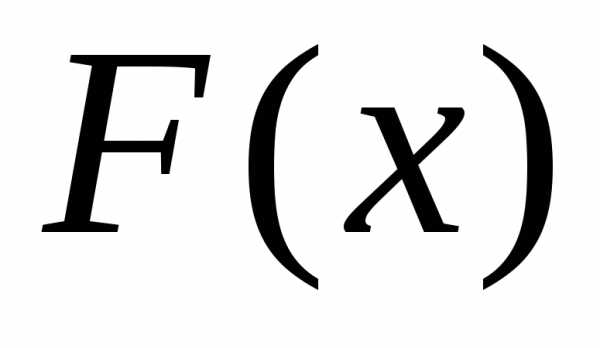 есть неубывающая функция сво-его
аргумента, т.е. при
есть неубывающая функция сво-его
аргумента, т.е. при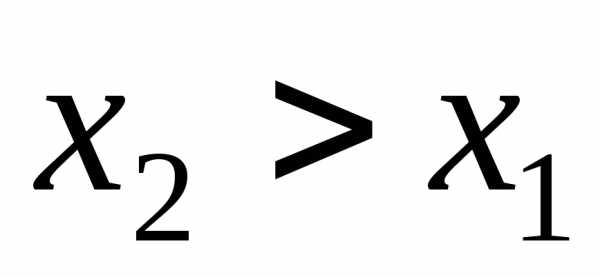 выполняется.
выполняется.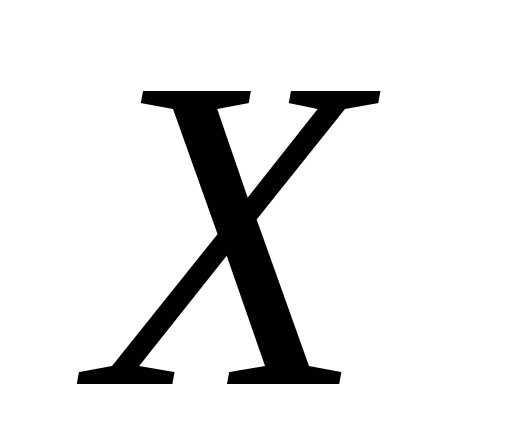 с функцией распределения
с функцией распределения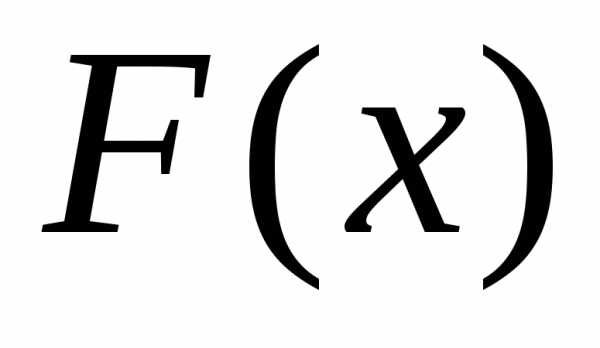 ,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой
,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой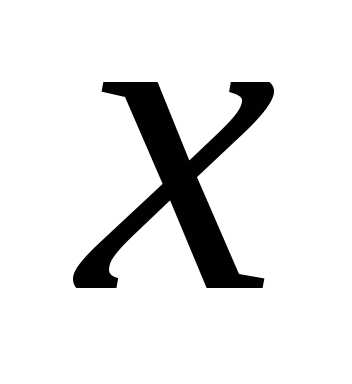 до
до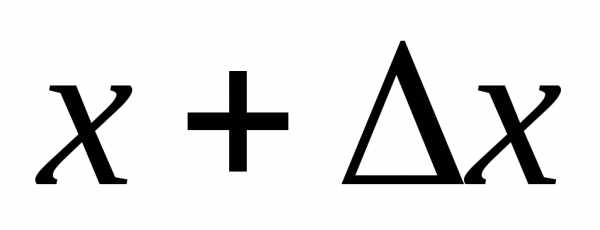 :
: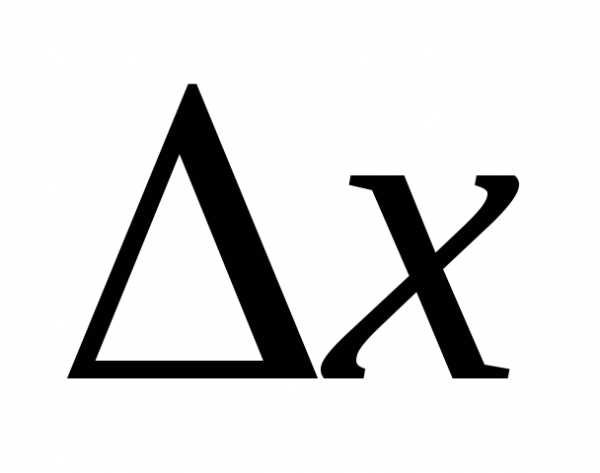 к нулю. В пределе получим производ-ную
от функции распределения:
к нулю. В пределе получим производ-ную
от функции распределения: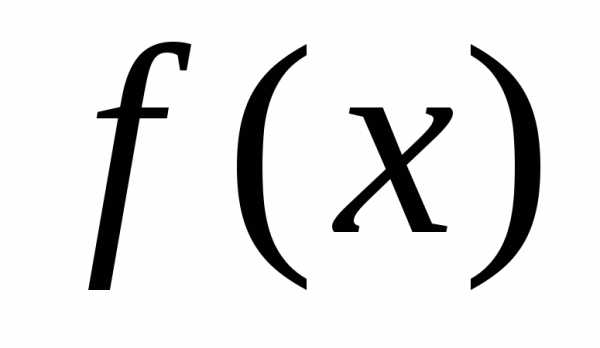 характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция
характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция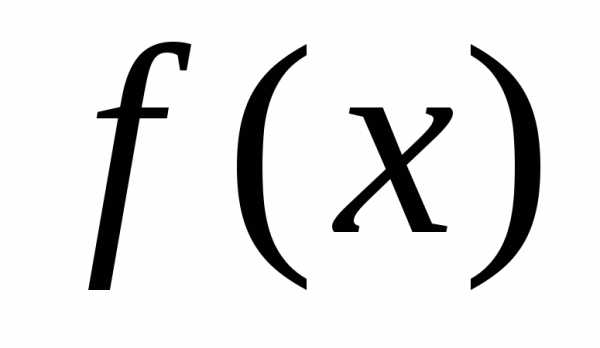 называется плотностью распределения
(или плотностью вероятности) непрерывной
случайной величины
называется плотностью распределения
(или плотностью вероятности) непрерывной
случайной величины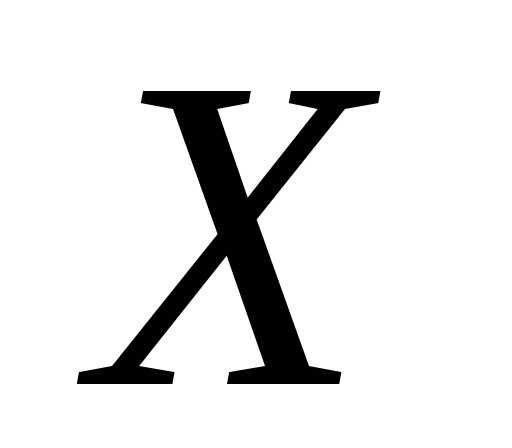 .
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
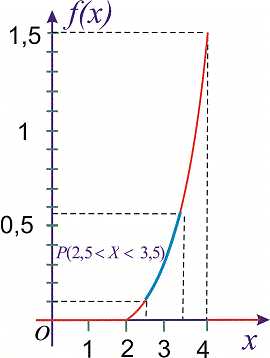
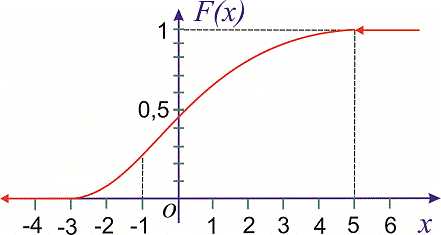
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2).
.
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
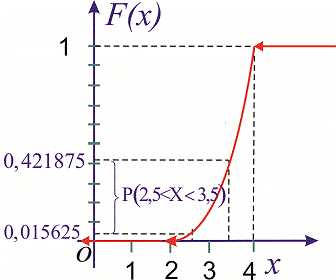
называется кривой распределения (рис.2). в участок
в участок равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения
равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения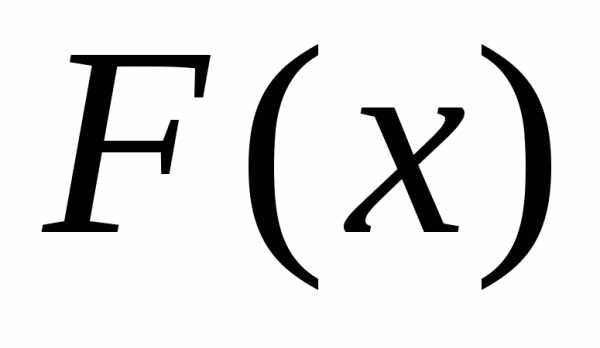 есть не что иное,как
площадь кривой распределения, лежащей
левее точки
есть не что иное,как
площадь кривой распределения, лежащей
левее точки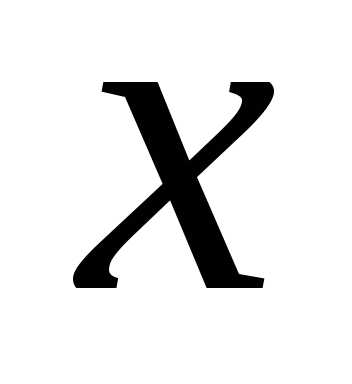 .
.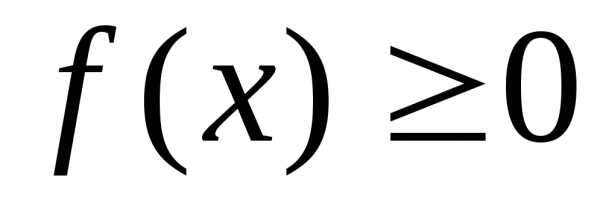 .
Это свойство вытекает непосредственно
из того, что
.
Это свойство вытекает непосредственно
из того, что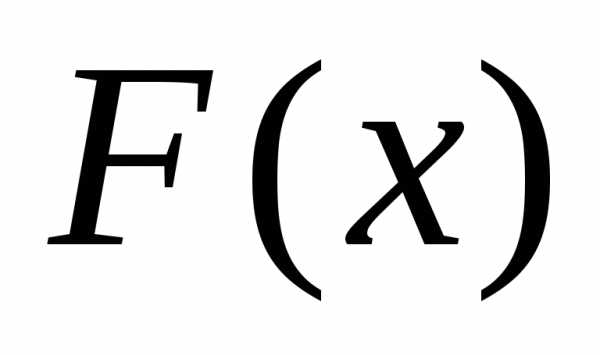 есть функция неубывающая.
есть функция неубывающая.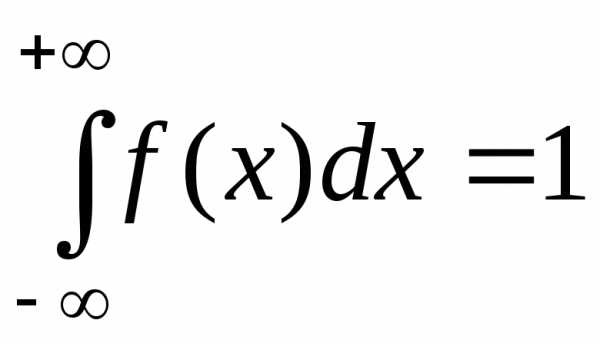 (условие
нормировки).
Условие говорит о том, что вероятность
принятия случайной величиной какого–ли-бо
значения равна единице.
(условие
нормировки).
Условие говорит о том, что вероятность
принятия случайной величиной какого–ли-бо
значения равна единице.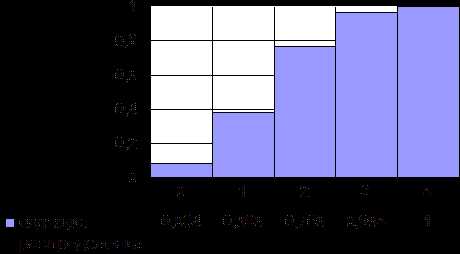
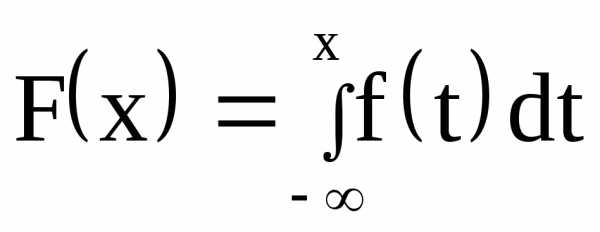
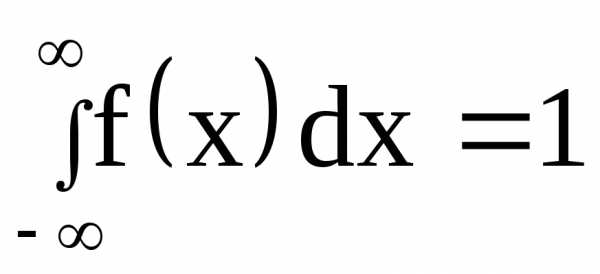
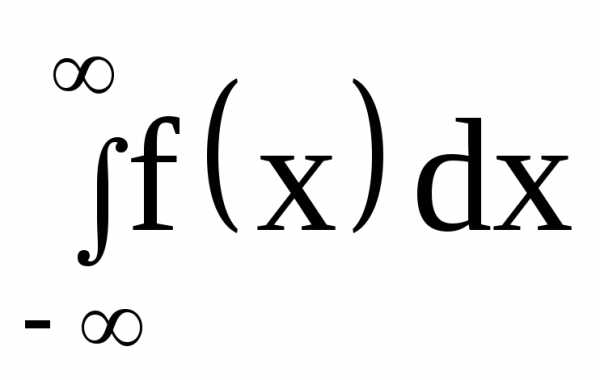 выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащая интервалу (-∞,
∞). Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.
выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащая интервалу (-∞,
∞). Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.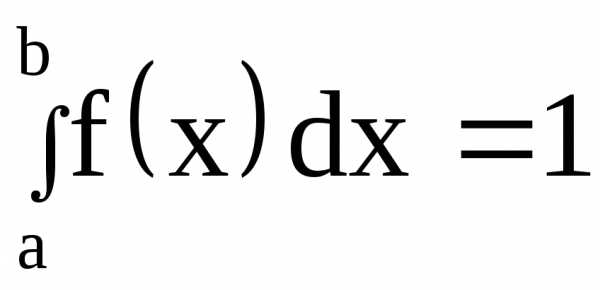 .
.
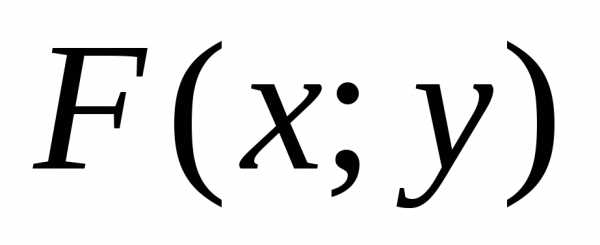 означает
вероятность попадания случайной точки
(x;y)
в заштрихованную область, расположенную
левее и ниже точки M(x;y).
означает
вероятность попадания случайной точки
(x;y)
в заштрихованную область, расположенную
левее и ниже точки M(x;y).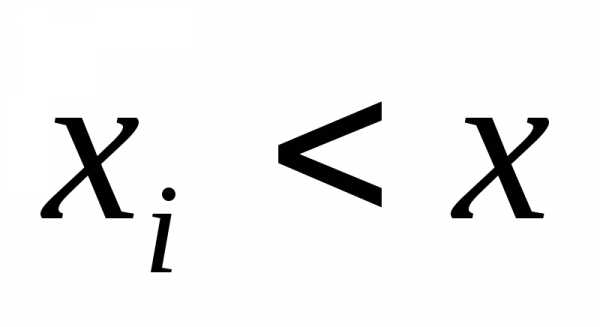 ,
и всеj,
для которых
,
и всеj,
для которых 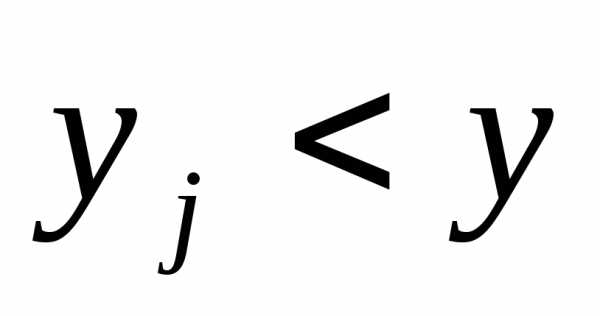
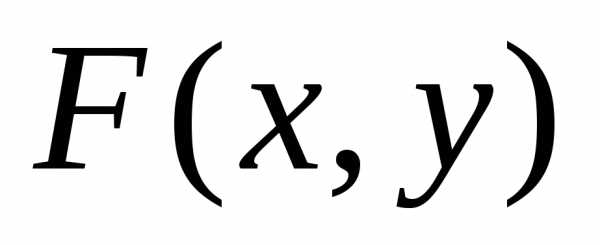 есть
неотрицательная функция, заключенная
между нулем и единицей, т.е.
есть
неотрицательная функция, заключенная
между нулем и единицей, т.е.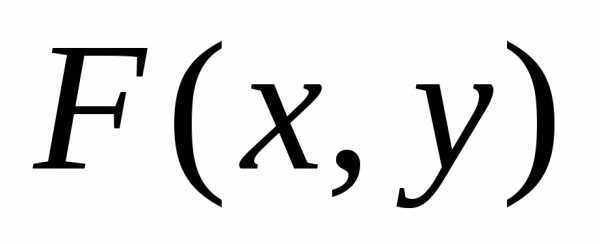 есть
неубывающая функция по каждому из
аргументов, т.е.
есть
неубывающая функция по каждому из
аргументов, т.е.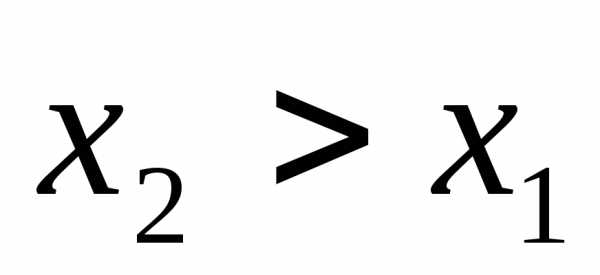
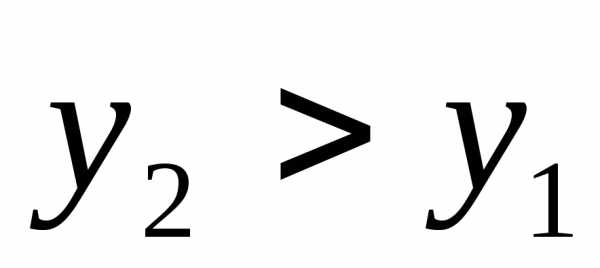
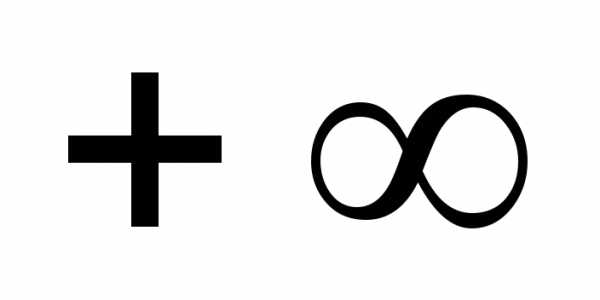 ,
функция распределения
,
функция распределения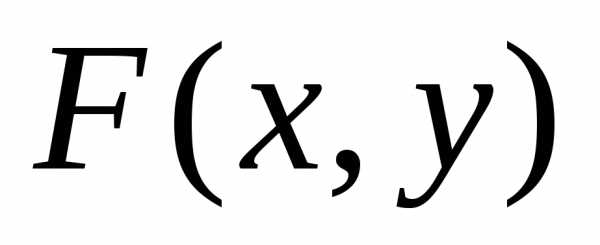 становится
равной функции распределения случайной
величины, соответствующей другому
аргументу:
становится
равной функции распределения случайной
величины, соответствующей другому
аргументу: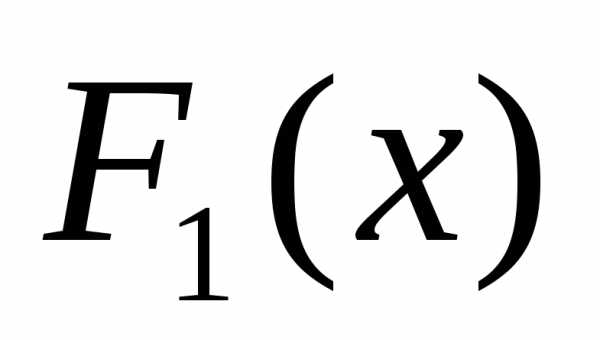 и
и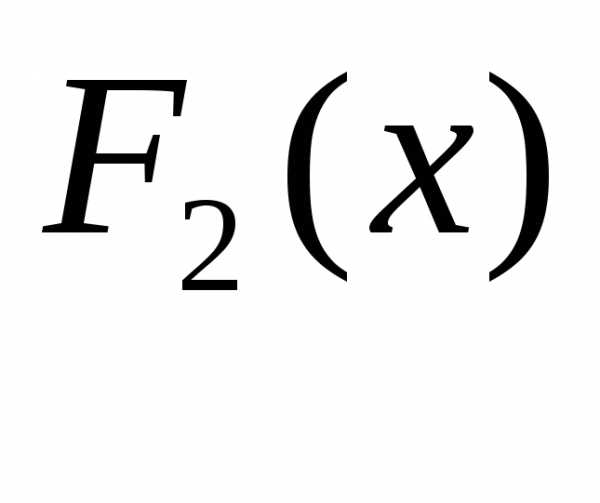 —
функции распределения случайных величинX и Y,
т.е.
—
функции распределения случайных величинX и Y,
т.е. ,
то функция распределения равна единице:
,
то функция распределения равна единице:
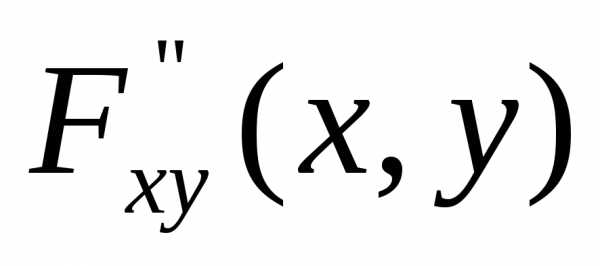 .
.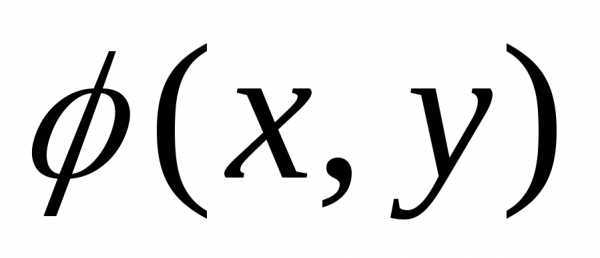 обладает свойствами аналогичными
свойствам плотности вероятности
одномерной случайной величины.
обладает свойствами аналогичными
свойствам плотности вероятности
одномерной случайной величины.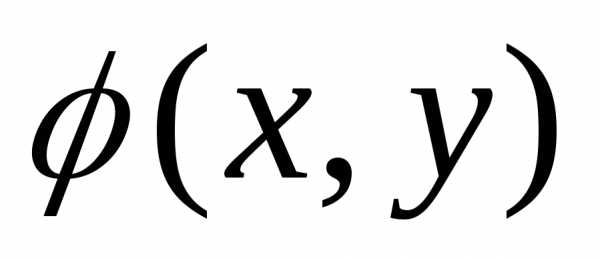 по формуле:
по формуле: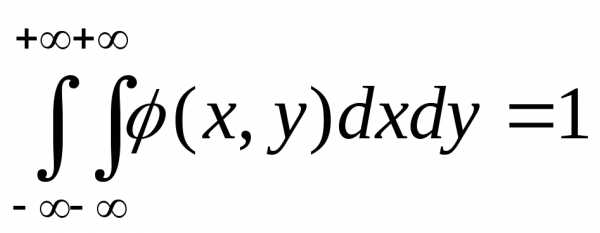
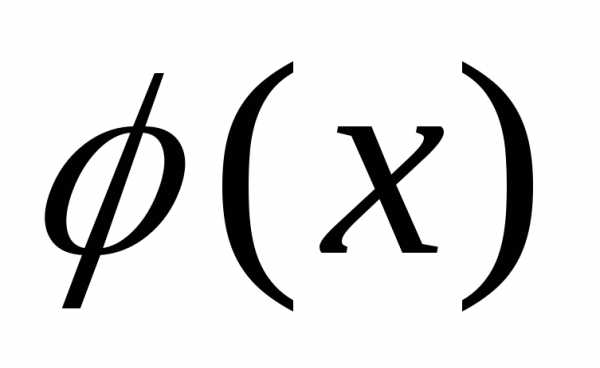 одномерной случайной величины, то
конкретное значение ее плотности
вероятности в данной точкеX
определяется ординатой кривой
одномерной случайной величины, то
конкретное значение ее плотности
вероятности в данной точкеX
определяется ординатой кривой 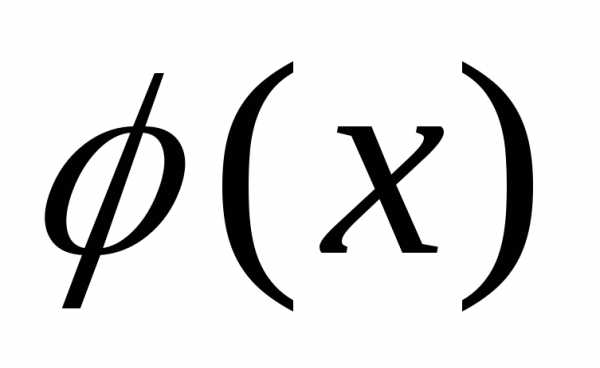
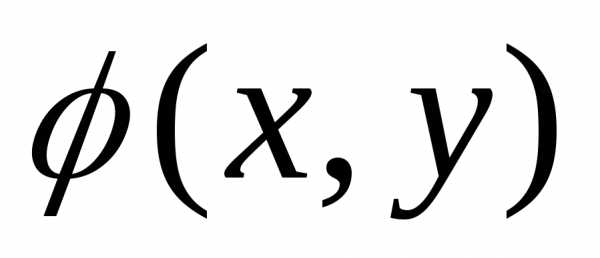 двухмерной
случайной величины, то конкретное
значение ее совместной плотности в
данной точке (x,y)
определяется геометрически аппликатой
поверхности
двухмерной
случайной величины, то конкретное
значение ее совместной плотности в
данной точке (x,y)
определяется геометрически аппликатой
поверхности 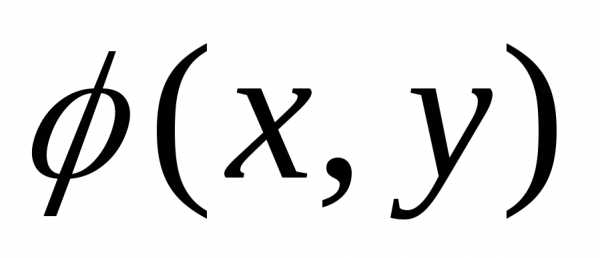 ,
а конкретное значение плотности
вероятности
,
а конкретное значение плотности
вероятности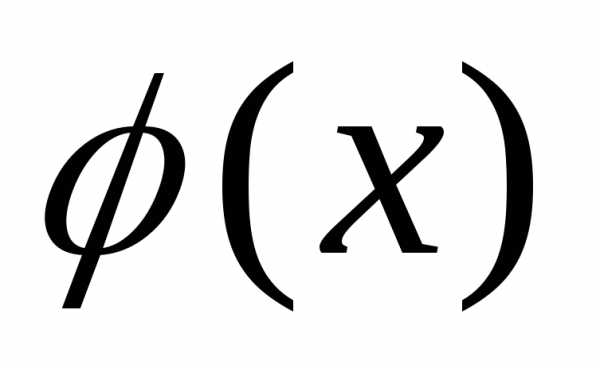 определится
геометрически площадью сечения
поверхности
определится
геометрически площадью сечения
поверхности .
Плоскость параллельна плоскостиOyz
и отсекает на оси OX
отрезок x.
.
Плоскость параллельна плоскостиOyz
и отсекает на оси OX
отрезок x.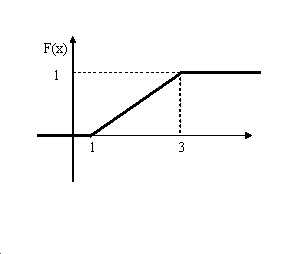
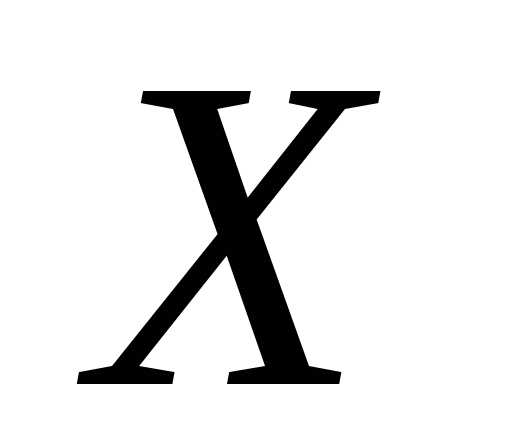 примет значение
примет значение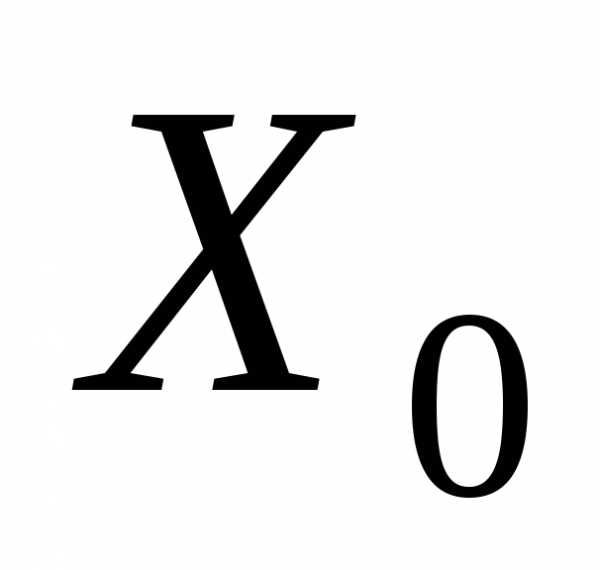 ,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина
,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина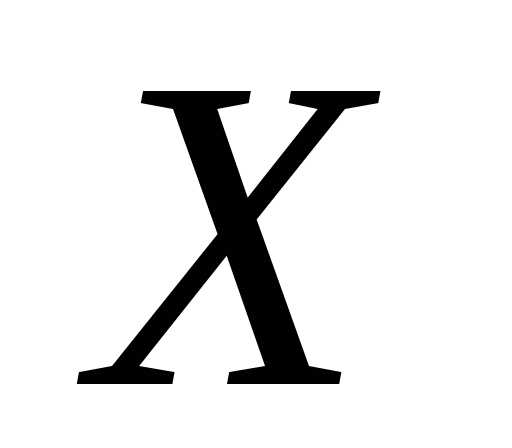 примет значение, меньшее некоторой
текущей переменной
примет значение, меньшее некоторой
текущей переменной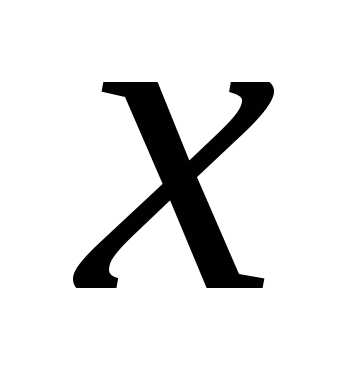 .
Вероятность этого события зависит от
значения
.
Вероятность этого события зависит от
значения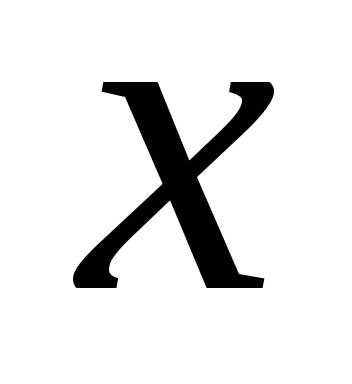 ,
т.е. является функцией
от
,
т.е. является функцией
от 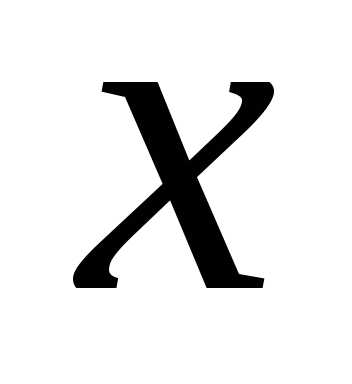 .
Эта функция называется функцией
распределения
.
Эта функция называется функцией
распределения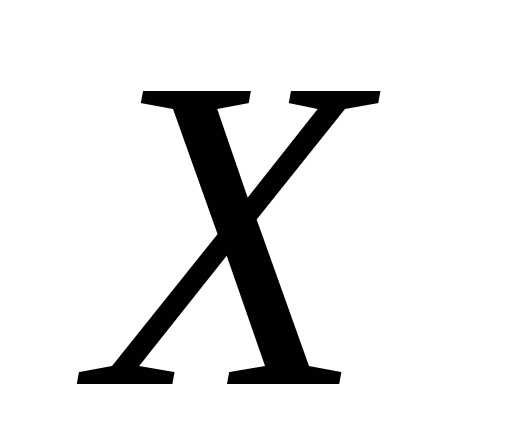 и обозначается
и обозначается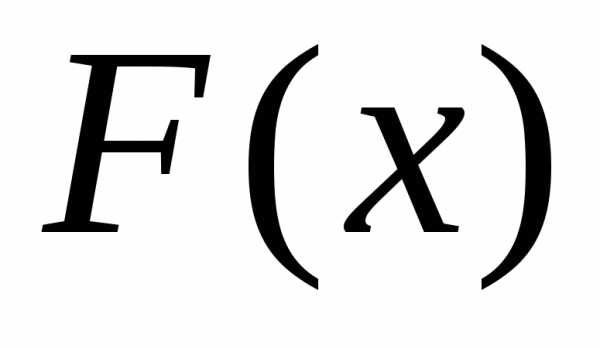 :
: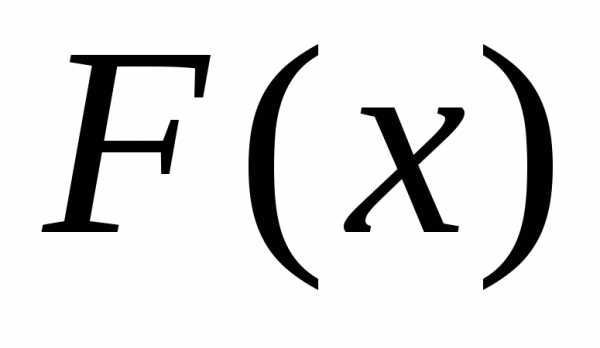 есть неубывающая функция сво-его
аргумента, т.е. при
есть неубывающая функция сво-его
аргумента, т.е. при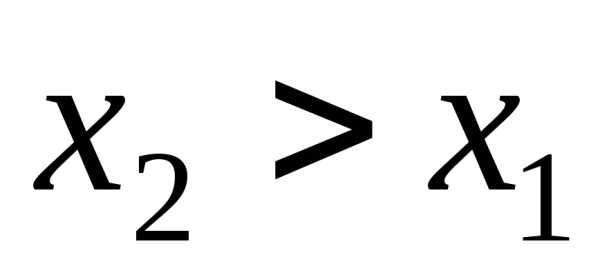 выполняется.
выполняется.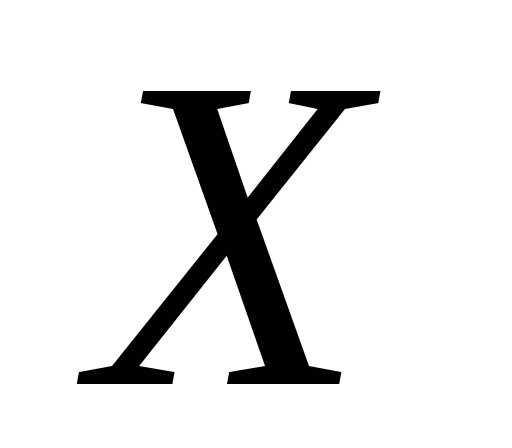 с функцией распределения
с функцией распределения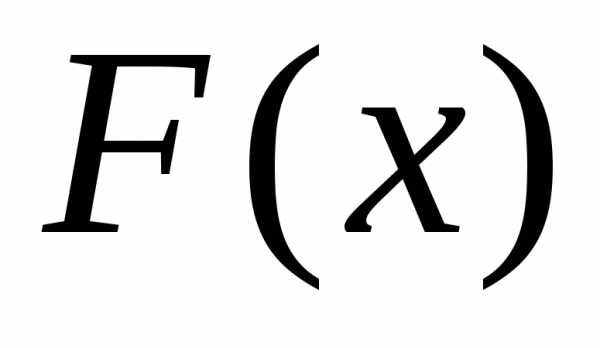 ,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой
,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой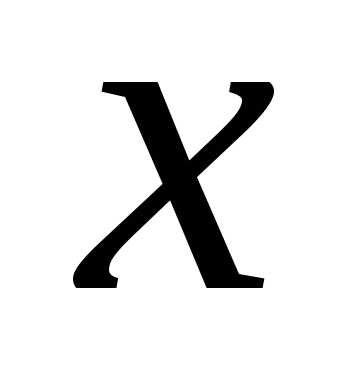 до
до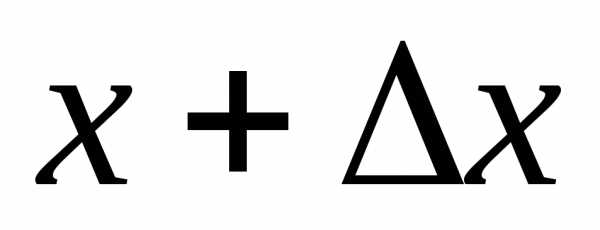 :
: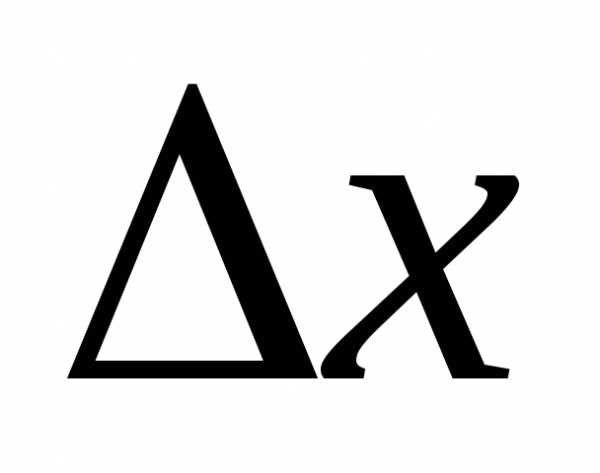 к нулю. В пределе получим производ-ную
от функции распределения:
к нулю. В пределе получим производ-ную
от функции распределения: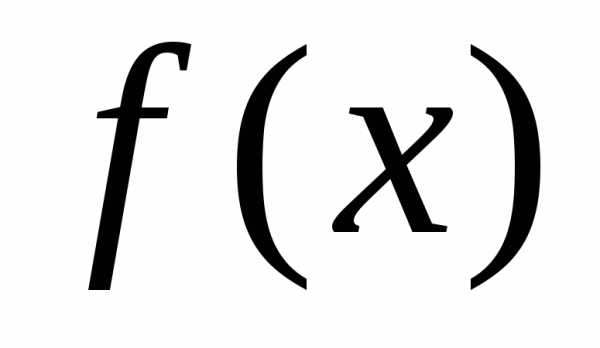 характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция
характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция называется плотностью распределения
(или плотностью вероятности) непрерывной
случайной величины
называется плотностью распределения
(или плотностью вероятности) непрерывной
случайной величины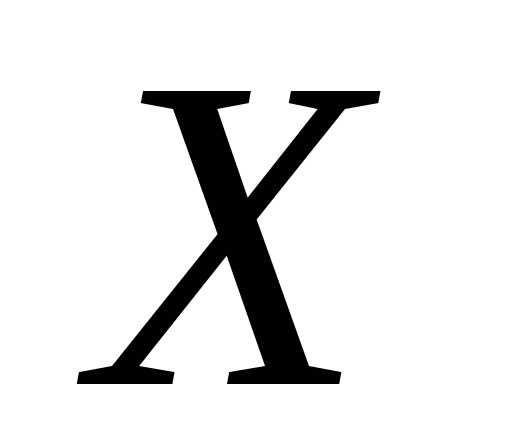 .
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2).
.
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2).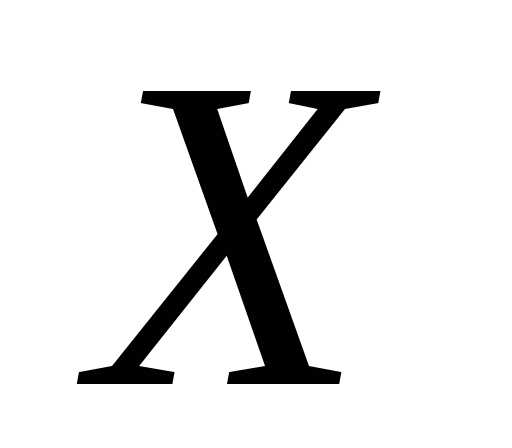 в участок
в участок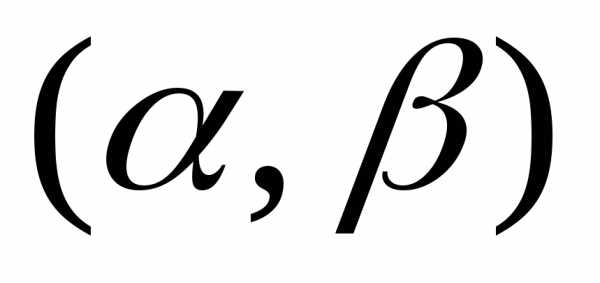 равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения
равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения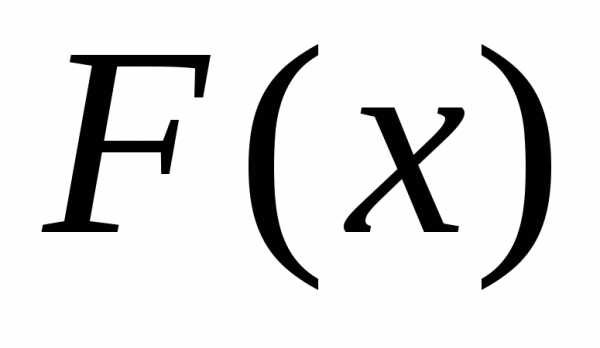 есть не что иное,как
площадь кривой распределения, лежащей
левее точки
есть не что иное,как
площадь кривой распределения, лежащей
левее точки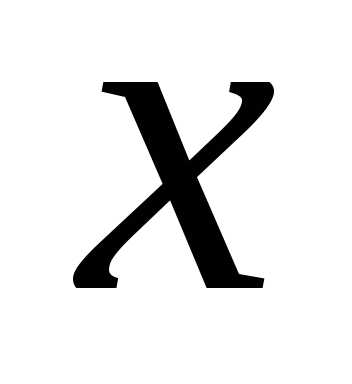 .
.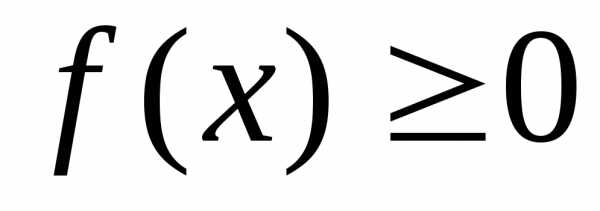 .
Это свойство вытекает непосредственно
из того, что
.
Это свойство вытекает непосредственно
из того, что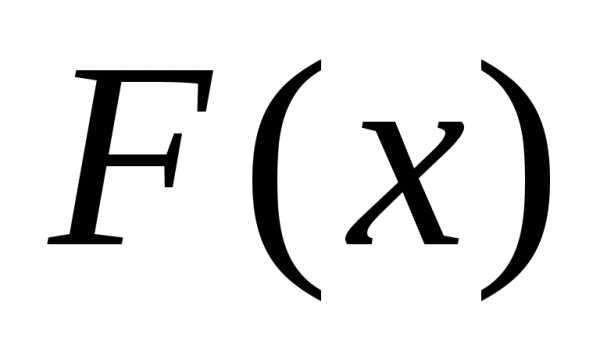 есть функция неубывающая.
есть функция неубывающая.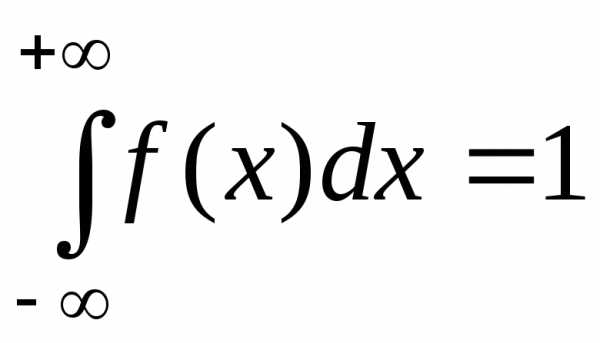 (условие
нормировки).
Условие говорит о том, что вероятность
принятия случайной величиной какого–ли-бо
значения равна единице.
(условие
нормировки).
Условие говорит о том, что вероятность
принятия случайной величиной какого–ли-бо
значения равна единице.