Точки экстремума функции. Как найти точки экстремума. Сумма точек экстремума
Важным понятием в математике является функция. С её помощью можно наглядно представить многие процессы, происходящие в природе, отразить с использованием формул, таблиц и изображений на графике взаимосвязь между определёнными величинами. Примером может служить зависимость давления слоя жидкости на тело от глубины погружения, ускорения — от действия на объект определённой силы, увеличения температуры — от передаваемой энергии и многие другие процессы. Исследование функции предполагает построение графика, выяснение её свойств, области определения и значений, промежутков возрастания и убывания. Важным моментом в данном процессе является нахождение точек экстремума. О том, как правильно это делать, и пойдёт разговор далее.

О самом понятии на конкретном примере
В медицине построение графика функции может рассказать о ходе развития болезни в организме пациента, наглядно отражая его состояние. Предположим, по оси ОХ откладывается время в сутках, а по оси ОУ — температура тела человека. На рисунке хорошо видно, как этот показатель резко поднимается, а потом падает. Нетрудно заметить также особые точки, отражающие моменты, когда функция, ранее возрастая, начинает убывать, и наоборот. Это точки экстремума, то есть критические значения (максимальные и минимальные) в данном случае температуры больного, после которых наступают изменения в его состоянии.

Угол наклона
Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.
Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.
Движение
Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.
Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.
На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.
Физический смысл производной
Описанное ранее наглядно показало, что производная по сути является скоростью изменения функции. В данном уточнении и заключён её физический смысл. Точки экстремума – это критические области на графике. Их возможно выяснить и обнаружить, вычислив значение производной, которая оказывается равной нулю.
Существует и другой признак, который является достаточным условием экстремума. Производная в таких местах перегиба меняет свой знак: с «+» на «-» в области максимума и с «-» на «+» в районе минимума.

Движение под влиянием силы притяжения
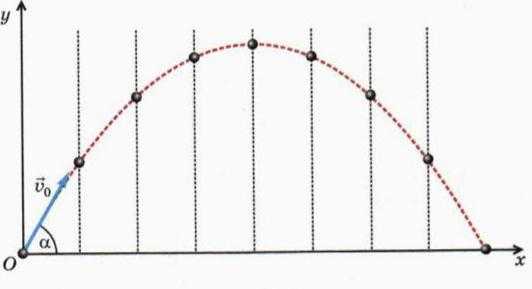
Представим ещё одну ситуацию. Дети, играя в мяч, бросили его таким образом, что он начал двигаться под углом к горизонту. В начальный момент скорость данного объекта являлась самой большой, но под действием силы тяжести начала уменьшаться, причём с каждой секундой на одну и ту же величину, равную приблизительно 9,8 м/с2. Это значение ускорения, возникающего под влиянием земной гравитации при свободном падении. На Луне оно бы было примерно в шесть раз меньше.
Графиком, описывающим перемещение тела, является парабола с ветвями, направленными вниз. Как найти точки экстремума? В данном случае это вершина функции, где скорость тела (мяча) принимает нулевое значение. Производная функции становится равной нулю. При этом направление, а следовательно, и значение скорости, меняется на противоположное. Тело летит вниз с каждой секундой всё быстрее, причём ускоряется на ту же величину — 9,8 м/с2.
Вторая производная
В предыдущем случае график модуля скорости рисуется как прямая. Данная линия оказывается сначала направлена вниз, так как значение этой величины постоянно убывает. Достигнув нуля в один из моментов времени, далее показатели этой величины начинают возрастать, а направление графического изображения модуля скорости кардинально меняется. Теперь линия направлена вверх.
Скорость, являясь производной от координаты по времени, тоже имеет критическую точку. В этой области функция, вначале убывая, начинает возрастать. Это место точки экстремума производной функции. В данном случае угол наклона касательной становится равным нулю. А ускорение, являясь второй производной от координаты по времени, меняет знак с «-» на «+». И движение из равнозамедленного становится равноускоренным.
График ускорения
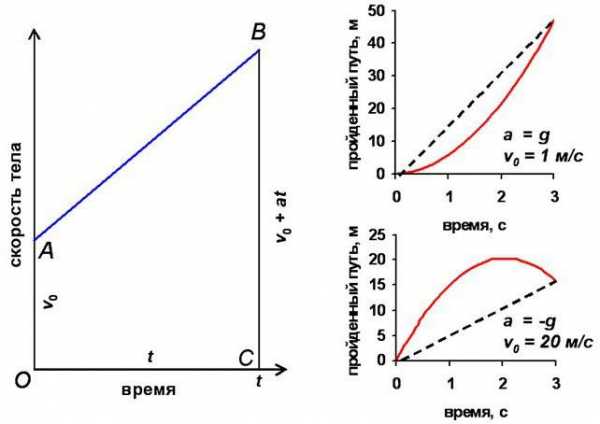
Теперь рассмотрим четыре рисунка. На каждом из них отображён график изменения с течением времени такой физической величины, как ускорение. В случае «А» значение его остаётся положительным и постоянным. Это означает, что скорость тела, как и его координата, постоянно увеличивается. Если представить, что объект будет двигаться таким образом бесконечно долго, функция, отражающая зависимость координаты от времени, окажется постоянно возрастающей. Из этого следует, что она не имеет критических областей. Точки экстремума на графике производной, то есть линейно изменяющейся скорости, также отсутствуют.
То же касается и случая «Б» с положительным и постоянно увеличивающимся ускорением. Правда, графики для координаты и скорости здесь будут несколько сложнее.
Когда ускорение стремится к нулю
Рассматривая рисунок «В», можно наблюдать совсем другую картину, характеризующую движение тела. Скорость его графически будет изображаться параболой с ветвями, направленными вниз. Если продолжить линию, описывающую изменение ускорения до пересечения её с осью ОХ, и дальше, то можно представить, что до этого критического значения, где ускорение окажется равным нулю, скорость объекта будет увеличиваться всё медленнее. Точка экстремума производной от функции координаты окажется как раз в вершине параболы, после чего тело кардинально поменяет характер движения и начнёт двигаться в другом направлении.
В последнем случае, «Г», характер движения точно определить невозможно. Здесь известно только, что ускорение за некоторый рассматриваемый период отсутствует. Значит, объект может оставаться на месте или движение происходит с постоянной скоростью.
Задача на сложение координат
Перейдём к заданиям, которые часто встречаются при изучении алгебры в школе и предлагаются для подготовки к ЕГЭ. На рисунке, который представлен ниже, изображён график функции. Требуется вычислить сумму точек экстремума.
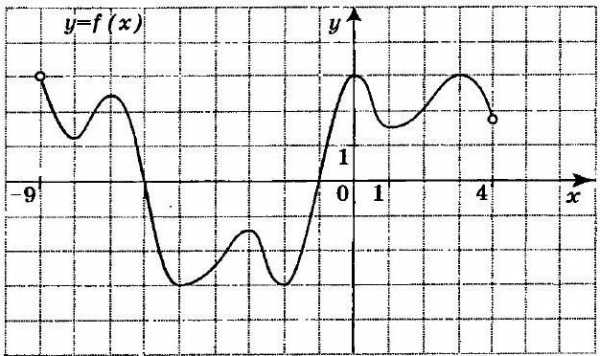
Сделаем это для оси ординат, определив координаты критических областей, где наблюдается изменение характеристик функции. Проще говоря, найдём значения по оси ОХ для точек перегиба, а затем перейдём к сложению полученных членов. По графику очевидно, что они принимают следующие значения: -8; -7 ; -5; -3; -2; 1; 3. В сумме это составляет -21, что и является ответом.
Оптимальное решение
Не стоит объяснять, насколько может оказаться важным в выполнении практических заданий выбор оптимального решения. Ведь путей достижения цели бывает много, а наилучший выход, как правило, — всего один. Это бывает крайне необходимо, к примеру, при конструировании судов, космических кораблей и самолётов, архитектурных сооружений для нахождения оптимальной формы данных рукотворных объектов.
Быстроходность средств передвижения во многом зависит от грамотного сведения к минимуму сопротивления, которое они испытывают при перемещении по воде и воздуху, от перегрузок, возникающих под действием гравитационных сил и многих других показателей. Кораблю на море необходимы такие качества, как устойчивость во время шторма, для речного судна важна минимальная осадка. При расчётах оптимальной конструкции точки экстремума на графике наглядно могут дать представление о наилучшем решении сложной проблемы. Задачи такого плана часто решаются в экономике, в хозяйственных областях, во множестве других жизненных ситуаций.
Из античной истории
Задачи на экстремум занимали даже древних мудрецов. Греческие учёные с успехом разгадали тайну площадей и объёмов путём математических вычислений. Это они первыми поняли, что на плоскости из разнообразных фигур, обладающих одним и тем же периметром, наибольшую площадь всегда имеет круг. Аналогичным образом шар наделён максимальным объёмом среди остальных предметов в пространстве с одинаковой величиной поверхности. Решению подобных задач посвятили себя такие известнейшие личности, как Архимед, Евклид, Аристотель, Аполлоний. Найти точки экстремума прекрасно удавалось Герону, который, прибегнув к расчётам, сооружал хитроумные устройства. К ним относились автоматы, перемещающиеся посредством пара, работающие по тому же принципу насосы и турбины.

Строительство Карфагена
Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.
Истоки математического анализа
А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.
Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона — Лейбница.
Задача на нахождение максимальной площади
Представим, что мы имеем проволоку, длина которой равна 50 см. Как составить из неё прямоугольник, обладающий наибольшей площадью?
Начиная решение, следует исходить из простых и известных любому истин. Понятно, что периметр нашей фигуры будет составлять 50 см. Он же складывается из удвоенных длин обеих сторон. Это значит, что, обозначив за «Х» одну из них, другую возможно выразить как (25 – Х).
Отсюда получаем площадь, равную Х(25 – Х). Данное выражение можно представить как функцию, принимающую множество значений. Решение задачи требует найти максимальное из них, а значит, следует узнать точки экстремума.
Для этого находим первую производную и приравниваем её нулю. В результате получается простое уравнение: 25 – 2Х = 0.
Из него мы узнаём, что одна из сторон Х = 12,5.
Следовательно, другая: 25 – 12,5 = 12,5.
Получается, что решением задачи будет квадрат со стороной 12,5 см.
Как найти максимальную скорость
Рассмотрим ещё один пример. Представим, что существует тело, прямолинейное движение которого описывается уравнением S = — t3 + 9t2 – 24t – 8, где пройденное расстояние выражается в метрах, а время в секундах. Требуется найти максимальную скорость. Как это сделать? Скачала находим скорость, то есть первую производную.
Получаем уравнение: V = — 3t2 + 18t – 24. Теперь для решения задачи снова нужно найти точки экстремума. Сделать это необходимо тем же способом, что и в предыдущей задаче. Находим первую производную от скорости и приравниваем её к нулю.
Получаем: — 6t + 18 = 0. Отсюда t = 3 с. Это время, когда скорость тела принимает критическое значение. Подставляем полученное данное в уравнение скорости и получаем: V = 3 м/с.
Но как понять, что это именно максимальная скорость, ведь критическими точками функции могут быть наибольшие или наименьшие её значения? Для проверки необходимо найти вторую производную от скорости. Она выражается числом 6 со знаком минус. Это значит, что найденная точка является максимумом. А в случае положительного значения второй производной был бы минимум. Значит, найденное решение оказалось правильным.
Приведённые в качестве примера задачи являются лишь частью из тех, которые возможно решить, умея находить точки экстремума функции. На самом деле их гораздо больше. А подобные знания открывают перед человеческой цивилизацией неограниченные возможности.
fb.ru
Найти сумму точек экстремума функции
Область определения функции:
Вычислим производную функции
Найдем точки экстремума, приравняв к нулю производную функции
Дробь равен нулю, когда числитель обращается в нуль.
___-___(-1)____+___(5)___-____
В точке х=-1 производная функции меняет знак с (-) на (+), следовательно, точка х = -1 — точка минимума. В точке х =5 производная функции меняет знак с (+) на (-), значит х = 5 — точка максимума.
Сумма точек экстремума: -1 + 5 = 4
Окончательный ответ: 4.
dvoechka.com
Найти сумму точек экстремума функции
Область определения функции:
Вычислим производную функции
Найдем точки экстремума, приравняв к нулю производную функции
Дробь равен нулю, когда числитель обращается в нуль.
___-___(-1)____+___(5)___-____
В точке х=-1 производная функции меняет знак с (-) на (+), следовательно, точка х = -1 — точка минимума. В точке х =5 производная функции меняет знак с (+) на (-), значит х = 5 — точка максимума.
Сумма точек экстремума: -1 + 5 = 4
Окончательный ответ: 4.
Оцени ответ
napyaterku.com
сумма ординат точек экстремума
Записи с меткой «сумма ординат точек экстремума»
По вашим просьбам!
4. Найти наибольшее целое решение неравенства:
Умножим обе части неравенства на 15 — наименьший общий знаменатель данных дробей. Получаем равносильное неравенство:
3·(x-2)-5·(2x+3)>15. Раскрываем скобки: 3x-6-10x-15>15 и упрощаем:
3x-10x>15+6+15. Получаем -7x>36. Делим обе части неравенство на отрицательный коэффициент при х, поэтому знак неравенства меняем на противоположный:
x<-36/7. Выделим целую часть и покажем решения неравенства на числовой прямой.
Наибольшее целое число из заштрихованного промежутка — это число -6.
5. Определите верное решение неравенства: log2(x-4)≤3.
Представим число 3 в виде логарифма с основанием 2.
log2(x-4)≤ log223 ; отсюда log2(x-4)≤log28. Так как логарифмическая функция по основанию 2 является возрастающей на множестве всех положительных чисел, то последнее неравенство будет выполняться при условии, что х-4≤8, но в то же время: х-4>0. Из первого условия следует: х≤12, а из второго, что х>4. Общим будет значение х∈(4; 12].
7. Укажите функцию, график которой изображен на рисунке.
На рисунке мы видим параболу, которую можно задать уравнением вида: y=a(x-m)2+n, где (m; n) — координаты вершины параболы. На рисунке вершина параболы — точка (2; 1). Следовательно, m=2; n=1. А что по поводу значения коэффициента а? Смотрим на ответы: везде коэффициент перед скобкой равен единице. Ну и прекрасно — меньше забот! Получили формулу: y=(x-2)2+1.
11. Длина прямоугольного участка 120 м, а ширина составляет 75% длины. Вспахано 35% этого участка, тогда не вспахано:
По условию ширина составляет 75% от 120 метров — длины участка. Это 3/4 от длины, т.е. 120:4·3=90 метров. Площадь прямоугольного участка равна произведению длины участка на его ширину, значит, составляет 120 м·90 м= 10800 м2. Вспахано 35%, следовательно не вспахано 100%-35%=65%. Нам осталось найти 65% от 10800. Обращаем проценты в десятичную дробь: 65%=0,65 и умножаем эту дробь на 10800.
0,65·10800=7020. Отвечаем на вопрос задачи: не вспахано 7020 м2.
12. Решите уравнение:
К правой части равенства применим основное логарифмическое тождество:
Мы получили равные степени по основанию 2, следовательно, и показатели этих степеней будут равны. Получается квадратное уравнение: x2+x=2 или x2+x-2=0. По теореме Виета подбираем корни: x1=-2; x2=1.
14. Решите уравнение: sin2x-cos2x=cos(x/2).
По формуле косинуса двойного угла: cos2α=cos2α-sin2α, тогда данное равенство преобразуется к виду:
-cos2х=cos(x/2) ⇒ -cos2х-cos(x/2)=0 ⇒ cos2х+cos(x/2)=0. Сумму косинусов преобразуем в произведение, используя формулу:
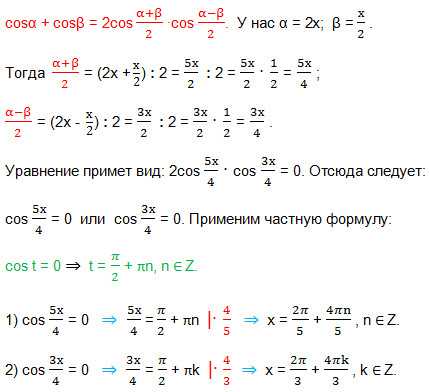
17. Найдите сумму ординат точек экстремума функции f(x)=x3/(x2-3).
Вы, конечно, знаете, что экстремумы — это минимумы и максимумы функции, возможные только в критических точках. Классическое решение этого задания: 1) найти производную данной функции; 2) найти критические точки и отметить их на числовой прямой; 3) определить знаки производной на промежутках, определенных критическими точками; 4) выяснить, какие из критических точек являются точками минимума и какие точками максимума; 5) найти значения самой функции в этих точках минимума и максимума — это и будут ординаты точек экстремума; 6) сложить эти значения ординат. Но в этом конкретном задании все гораздо проще! Функция нам дана нечетная, т.е. для всех возможных значений х выполняется равенство: f(-x)=f(x). График нечетной функции симметричен относительно начала координат. Что это значит, и чем это нам поможет? Рассуждаем: если эта функция имеет максимум в точке с абсциссой а, то в симметричной ей точке с абсциссой (-а) она будет иметь минимум. Опять же значения функции в этих точках а и -а также будут являться противоположными числами. А чему равна сумма противоположных чисел? Правильно: нулю. Вывод: если вам нужно найти сумму ординат точек экстремума нечетной функции, то ответ: 0.
21. Найдите сумму корней уравнения: x-2-16x-1-80=0.
Сделаем замену: x-1=y. Получим уравнение: y2-16y-80=0. Находим корни: y1=-4 и y2=20.
Тогда x-1=-4 или x-1=20.
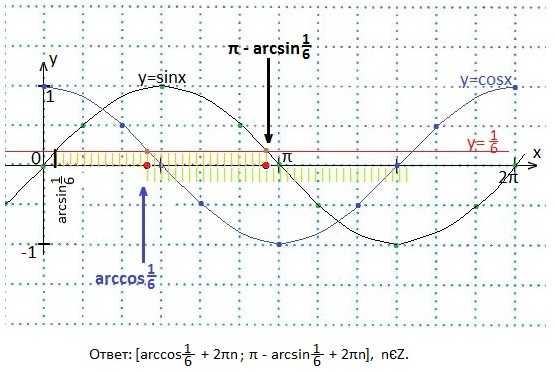
22. Решить систему неравенств:
В одной системе координат построим графики функций y=sinx, y=cosx и y= 1/6. Определим промежуток значений х, при которых график синуса лежит выше, а график косинуса ниже прямой y= 1/6.
24. Найдите площадь параллелограмма ABCD, если А(5; 4), В(0; 3), С(4; 7), D(9; 8).
Площадь параллелограмма найдем по формуле: S=absinA, где a=АD и b=AB — стороны параллелограмма, А — угол между этими сторонами. Используем векторы: найдем координаты и модули векторов, выражающих стороны АD и AB параллелограмма, косинус угла между этими векторами. Затем найдем синус этого угла, и в формулу площади параллелограмма подставим все нужные значения.

25. Электронные часы показывают время в часах и минутах (от 00:00 до 23:59). Сколько раз за сутки можно увидеть на табло 4 цифры 2, 0, 1, 9 (в любом порядке). Так как нет, например 91 минуты или 29 часов, то комбинаторика нам не поможет. Просто будем перечислять все возможные в реальности показания времени.
1) 01:29; 2) 02:19; 3) 09:12; 4) 09:21; 5) 10:29; 6) 12:09; 7) 19:02; 8) 19:20; 9) 20:19; 10) 21:09. Других значений из этих 4-х цифр быть не может.
Друзья, повторяйте формулы. Желаю успехов!
test-training.ru
Точки экстремума функции. Как найти точки экстремума. Сумма точек экстремума
Важным понятием в математике является функция. С её помощью можно наглядно представить многие процессы, происходящие в природе, отразить с использованием формул, таблиц и изображений на графике взаимосвязь между определёнными величинами. Примером может служить зависимость давления слоя жидкости на тело от глубины погружения, ускорения — от действия на объект определённой силы, увеличения температуры — от передаваемой энергии и многие другие процессы. Исследование функции предполагает построение графика, выяснение её свойств, области определения и значений, промежутков возрастания и убывания. Важным моментом в данном процессе является нахождение точек экстремума. О том, как правильно это делать, и пойдёт разговор далее.

О самом понятии на конкретном примере
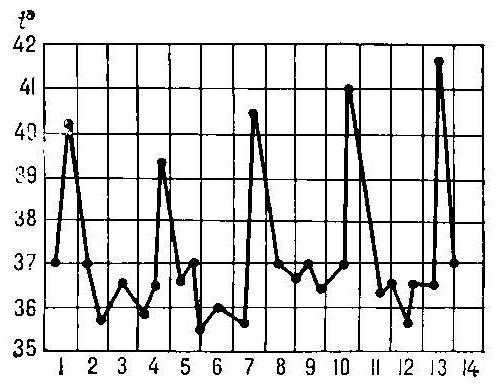
В медицине построение графика функции может рассказать о ходе развития болезни в организме пациента, наглядно отражая его состояние. Предположим, по оси ОХ откладывается время в сутках, а по оси ОУ — температура тела человека. На рисунке хорошо видно, как этот показатель резко поднимается, а потом падает. Нетрудно заметить также особые точки, отражающие моменты, когда функция, ранее возрастая, начинает убывать, и наоборот. Это точки экстремума, то есть критические значения (максимальные и минимальные) в данном случае температуры больного, после которых наступают изменения в его состоянии.
Угол наклона
Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.
Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.
Движение
Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.
Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.
На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.
Физический смысл производной
Описанное ранее наглядно показало, что производная по сути является скоростью изменения функции. В данном уточнении и заключён её физический смысл. Точки экстремума – это критические области на графике. Их возможно выяснить и обнаружить, вычислив значение производной, которая оказывается равной нулю.
Существует и другой признак, который является достаточным условием экстремума. Производная в таких местах перегиба меняет свой знак: с «+» на «-» в области максимума и с «-» на «+» в районе минимума.

Движение под влиянием силы притяжения
Представим ещё одну ситуацию. Дети, играя в мяч, бросили его таким образом, что он начал двигаться под углом к горизонту. В начальный момент скорость данного объекта являлась самой большой, но под действием силы тяжести начала уменьшаться, причём с каждой секундой на одну и ту же величину, равную приблизительно 9,8 м/с2. Это значение ускорения, возникающего под влиянием земной гравитации при свободном падении. На Луне оно бы было примерно в шесть раз меньше.
Графиком, описывающим перемещение тела, является парабола с ветвями, направленными вниз. Как найти точки экстремума? В данном случае это вершина функции, где скорость тела (мяча) принимает нулевое значение. Производная функции становится равной нулю. При этом направление, а следовательно, и значение скорости, меняется на противоположное. Тело летит вниз с каждой секундой всё быстрее, причём ускоряется на ту же величину — 9,8 м/с2.
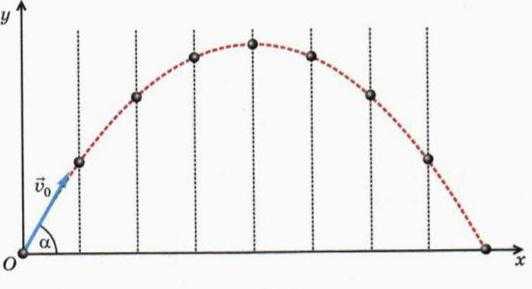
Вторая производная
В предыдущем случае график модуля скорости рисуется как прямая. Данная линия оказывается сначала направлена вниз, так как значение этой величины постоянно убывает. Достигнув нуля в один из моментов времени, далее показатели этой величины начинают возрастать, а направление графического изображения модуля скорости кардинально меняется. Теперь линия направлена вверх.
Скорость, являясь производной от координаты по времени, тоже имеет критическую точку. В этой области функция, вначале убывая, начинает возрастать. Это место точки экстремума производной функции. В данном случае угол наклона касательной становится равным нулю. А ускорение, являясь второй производной от координаты по времени, меняет знак с «-» на «+». И движение из равнозамедленного становится равноускоренным.
График ускорения
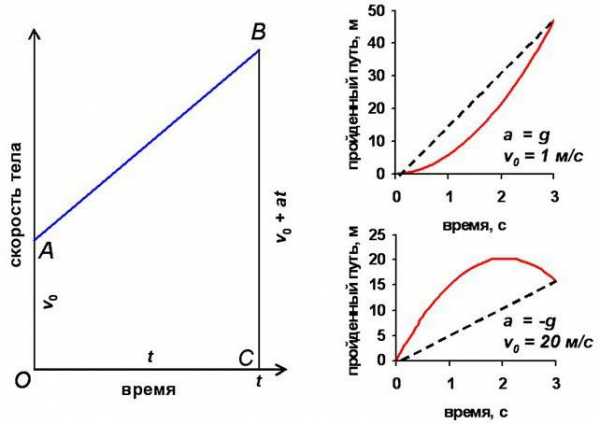
Теперь рассмотрим четыре рисунка. На каждом из них отображён график изменения с течением времени такой физической величины, как ускорение. В случае «А» значение его остаётся положительным и постоянным. Это означает, что скорость тела, как и его координата, постоянно увеличивается. Если представить, что объект будет двигаться таким образом бесконечно долго, функция, отражающая зависимость координаты от времени, окажется постоянно возрастающей. Из этого следует, что она не имеет критических областей. Точки экстремума на графике производной, то есть линейно изменяющейся скорости, также отсутствуют.
То же касается и случая «Б» с положительным и постоянно увеличивающимся ускорением. Правда, графики для координаты и скорости здесь будут несколько сложнее.
Когда ускорение стремится к нулю
Рассматривая рисунок «В», можно наблюдать совсем другую картину, характеризующую движение тела. Скорость его графически будет изображаться параболой с ветвями, направленными вниз. Если продолжить линию, описывающую изменение ускорения до пересечения её с осью ОХ, и дальше, то можно представить, что до этого критического значения, где ускорение окажется равным нулю, скорость объекта будет увеличиваться всё медленнее. Точка экстремума производной от функции координаты окажется как раз в вершине параболы, после чего тело кардинально поменяет характер движения и начнёт двигаться в другом направлении.
В последнем случае, «Г», характер движения точно определить невозможно. Здесь известно только, что ускорение за некоторый рассматриваемый период отсутствует. Значит, объект может оставаться на месте или движение происходит с постоянной скоростью.
Задача на сложение координат
Перейдём к заданиям, которые часто встречаются при изучении алгебры в школе и предлагаются для подготовки к ЕГЭ. На рисунке, который представлен ниже, изображён график функции. Требуется вычислить сумму точек экстремума.
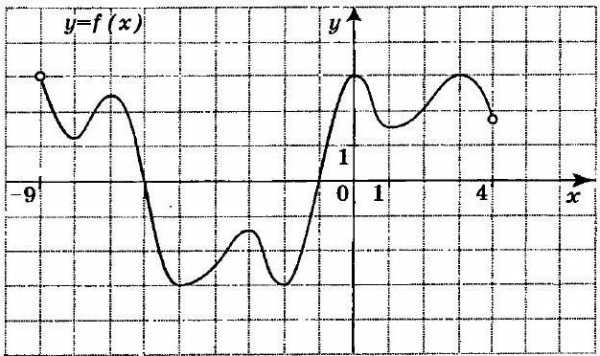
Сделаем это для оси ординат, определив координаты критических областей, где наблюдается изменение характеристик функции. Проще говоря, найдём значения по оси ОХ для точек перегиба, а затем перейдём к сложению полученных членов. По графику очевидно, что они принимают следующие значения: -8; -7 ; -5; -3; -2; 1; 3. В сумме это составляет -21, что и является ответом.
Оптимальное решение
Не стоит объяснять, насколько может оказаться важным в выполнении практических заданий выбор оптимального решения. Ведь путей достижения цели бывает много, а наилучший выход, как правило, — всего один. Это бывает крайне необходимо, к примеру, при конструировании судов, космических кораблей и самолётов, архитектурных сооружений для нахождения оптимальной формы данных рукотворных объектов.
Быстроходность средств передвижения во многом зависит от грамотного сведения к минимуму сопротивления, которое они испытывают при перемещении по воде и воздуху, от перегрузок, возникающих под действием гравитационных сил и многих других показателей. Кораблю на море необходимы такие качества, как устойчивость во время шторма, для речного судна важна минимальная осадка. При расчётах оптимальной конструкции точки экстремума на графике наглядно могут дать представление о наилучшем решении сложной проблемы. Задачи такого плана часто решаются в экономике, в хозяйственных областях, во множестве других жизненных ситуаций.
Из античной истории
Задачи на экстремум занимали даже древних мудрецов. Греческие учёные с успехом разгадали тайну площадей и объёмов путём математических вычислений. Это они первыми поняли, что на плоскости из разнообразных фигур, обладающих одним и тем же периметром, наибольшую площадь всегда имеет круг. Аналогичным образом шар наделён максимальным объёмом среди остальных предметов в пространстве с одинаковой величиной поверхности. Решению подобных задач посвятили себя такие известнейшие личности, как Архимед, Евклид, Аристотель, Аполлоний. Найти точки экстремума прекрасно удавалось Герону, который, прибегнув к расчётам, сооружал хитроумные устройства. К ним относились автоматы, перемещающиеся посредством пара, работающие по тому же принципу насосы и турбины.

Строительство Карфагена
Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.
Истоки математического анализа
А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.
Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона — Лейбница.
Задача на нахождение максимальной площади
Представим, что мы имеем проволоку, длина которой равна 50 см. Как составить из неё прямоугольник, обладающий наибольшей площадью?
Начиная решение, следует исходить из простых и известных любому истин. Понятно, что периметр нашей фигуры будет составлять 50 см. Он же складывается из удвоенных длин обеих сторон. Это значит, что, обозначив за «Х» одну из них, другую возможно выразить как (25 – Х).
Отсюда получаем площадь, равную Х(25 – Х). Данное выражение можно представить как функцию, принимающую множество значений. Решение задачи требует найти максимальное из них, а значит, следует узнать точки экстремума.
Для этого находим первую производную и приравниваем её нулю. В результате получается простое уравнение: 25 – 2Х = 0.
Из него мы узнаём, что одна из сторон Х = 12,5.
Следовательно, другая: 25 – 12,5 = 12,5.
Получается, что решением задачи будет квадрат со стороной 12,5 см.
Как найти максимальную скорость
Рассмотрим ещё один пример. Представим, что существует тело, прямолинейное движение которого описывается уравнением S = — t3 + 9t2 – 24t – 8, где пройденное расстояние выражается в метрах, а время в секундах. Требуется найти максимальную скорость. Как это сделать? Скачала находим скорость, то есть первую производную.
Получаем уравнение: V = — 3t2 + 18t – 24. Теперь для решения задачи снова нужно найти точки экстремума. Сделать это необходимо тем же способом, что и в предыдущей задаче. Находим первую производную от скорости и приравниваем её к нулю.
Получаем: — 6t + 18 = 0. Отсюда t = 3 с. Это время, когда скорость тела принимает критическое значение. Подставляем полученное данное в уравнение скорости и получаем: V = 3 м/с.
Но как понять, что это именно максимальная скорость, ведь критическими точками функции могут быть наибольшие или наименьшие её значения? Для проверки необходимо найти вторую производную от скорости. Она выражается числом 6 со знаком минус. Это значит, что найденная точка является максимумом. А в случае положительного значения второй производной был бы минимум. Значит, найденное решение оказалось правильным.
Приведённые в качестве примера задачи являются лишь частью из тех, которые возможно решить, умея находить точки экстремума функции. На самом деле их гораздо больше. А подобные знания открывают перед человеческой цивилизацией неограниченные возможности.
autogear.ru
Точки экстремума функции. Как найти? :: SYL.ru
Математический анализ — это довольно-таки занятный раздел математики, с которым сталкиваются абсолютно все ученики выпускных классов и студенты. Тем не менее далеко не каждому нравится матан. Некоторые не могут понять даже элементарных вещей наподобие, казалось бы, стандартного исследования функции. Данная статья призвана исправить подобную оплошность. Хотите поподробнее узнать об анализе функции? Желаете узнать, что такое точки экстремума и как их найти? Тогда данная статья для вас.
Исследование графика функции
Для начала стоит понять, зачем вообще необходимо анализировать график. Существуют простые функции, начертить которые не составит труда. Ярким примером подобной функции может служить парабола. Начертить ее график не составит труда. Все что необходимо, так это с помощью простого преобразования найти числа, при которых функция принимает значение 0. И в принципе это все что знать для того, чтобы начертить график параболы.
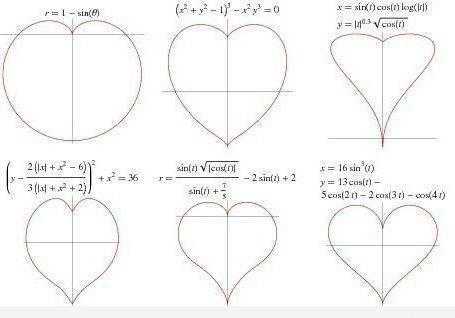
Но что делать, если функция, график которой нам нужно начертить, намного сложнее? Поскольку свойства сложных функций довольно-таки неочевидны, необходимо проводить целый анализ. Только после этого можно изобразить функцию графически. Как же это сделать? Ответ на этот вопрос вы сможете найти в данной статье.
План анализа функции
Первое, что необходимо сделать, так это провести поверхностное исследование функции, в ходе которого мы найдем область определения. Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х3 + х2 — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х2 — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.
Далее необходимо найти так называемые нули функции. Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.
Точки экстремума на графике функции
Во время исследования графика функции многие сталкиваются с проблемой в виде точек экстремума. И это странно. Ведь экстремумы — это довольно-таки простая тема. Не верите? Убедитесь сами, прочитав данную часть статьи, в которой мы поговорим о точках минимума и максимума.
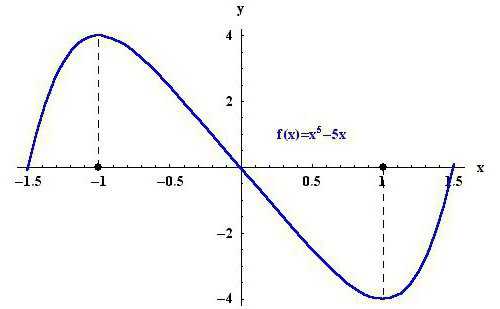
Для начала стоит разобраться в том, что собой представляет экстремум. Экстремум — это предельное значений, которое достигает функция на графике. Отсюда получается, что существует два крайних значения — максимум и минимум. Для наглядности можно посмотреть на картинку, что расположена выше. На исследованной области точка -1 является максимумом функции у (х) = х5 — 5х, а точка 1, соответственно, минимумом.
Также не стоит путать между собой понятия. Точки экстремума функции — это те аргументы, при которых заданная функция приобретает крайние значения. В свою очередь, экстремумом называют значение минимумов и максимумов функции. К примеру, вновь рассмотрим рисунок выше. -1 и 1 — это точки экстремума функции, а 4 и -4 — это сами экстремумы.
Нахождение точек экстремума
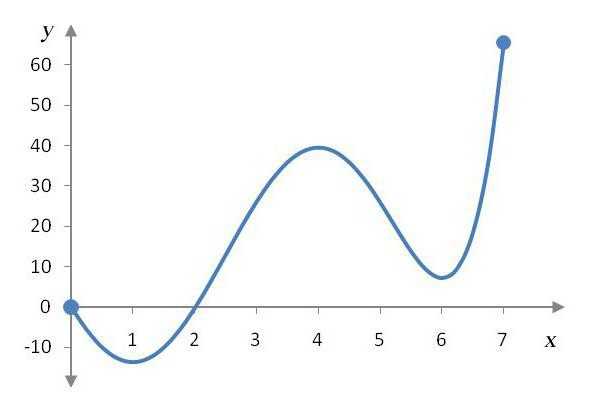
Но как все-таки найти точки экстремума функции? Все довольно-таки просто. Первое, что необходимо сделать — найти производную уравнения. Допустим, мы получили задание: «Найдите точки экстремума функции y (x), x — аргумент. Для наглядности возьмем функцию у (х) = х3 + 2х2 + х + 54. Проведем дифференцирование и получим следующее уравнение: 3х2 + 4х + 1. В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.
Сумма точек экстремума функции

Также стоит отметить, что на ЕГЭ требуют не просто найти точки экстремума, Но и провести с ними какую-то операцию (прибавить, умножить и т.д.). Именно по этой причине стоит обратить особое внимание на условия задачи. Ведь из-за невнимательности можно потерять баллы.
www.syl.ru
Точки экстремума функции. Как найти точки экстремума. Сумма точек экстремума
Образование 26 сентября 2017Важным понятием в математике является функция. С её помощью можно наглядно представить многие процессы, происходящие в природе, отразить с использованием формул, таблиц и изображений на графике взаимосвязь между определёнными величинами. Примером может служить зависимость давления слоя жидкости на тело от глубины погружения, ускорения — от действия на объект определённой силы, увеличения температуры — от передаваемой энергии и многие другие процессы. Исследование функции предполагает построение графика, выяснение её свойств, области определения и значений, промежутков возрастания и убывания. Важным моментом в данном процессе является нахождение точек экстремума. О том, как правильно это делать, и пойдёт разговор далее.

О самом понятии на конкретном примере
В медицине построение графика функции может рассказать о ходе развития болезни в организме пациента, наглядно отражая его состояние. Предположим, по оси ОХ откладывается время в сутках, а по оси ОУ — температура тела человека. На рисунке хорошо видно, как этот показатель резко поднимается, а потом падает. Нетрудно заметить также особые точки, отражающие моменты, когда функция, ранее возрастая, начинает убывать, и наоборот. Это точки экстремума, то есть критические значения (максимальные и минимальные) в данном случае температуры больного, после которых наступают изменения в его состоянии.
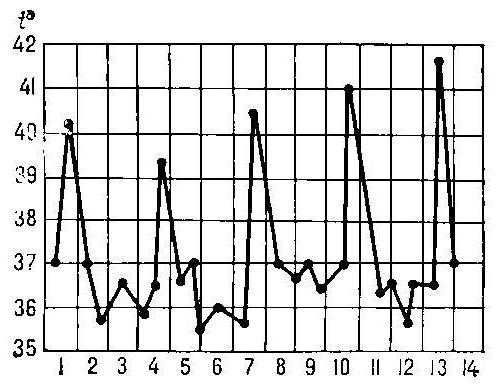
Угол наклона
Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.
Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.
Движение
Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.
Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.
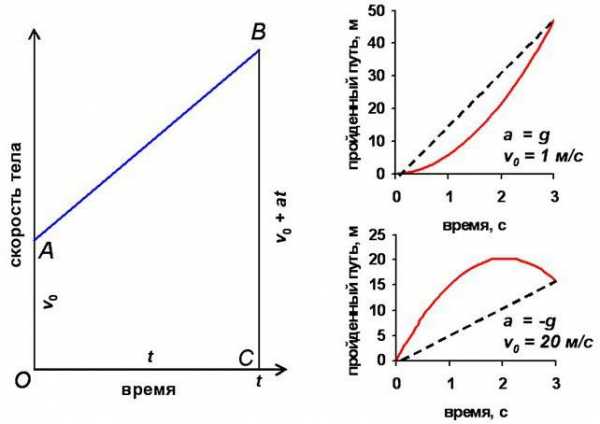
На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.
Физический смысл производной
Описанное ранее наглядно показало, что производная по сути является скоростью изменения функции. В данном уточнении и заключён её физический смысл. Точки экстремума – это критические области на графике. Их возможно выяснить и обнаружить, вычислив значение производной, которая оказывается равной нулю.
Существует и другой признак, который является достаточным условием экстремума. Производная в таких местах перегиба меняет свой знак: с «+» на «-» в области максимума и с «-» на «+» в районе минимума.

Движение под влиянием силы притяжения
Представим ещё одну ситуацию. Дети, играя в мяч, бросили его таким образом, что он начал двигаться под углом к горизонту. В начальный момент скорость данного объекта являлась самой большой, но под действием силы тяжести начала уменьшаться, причём с каждой секундой на одну и ту же величину, равную приблизительно 9,8 м/с2. Это значение ускорения, возникающего под влиянием земной гравитации при свободном падении. На Луне оно бы было примерно в шесть раз меньше.
Графиком, описывающим перемещение тела, является парабола с ветвями, направленными вниз. Как найти точки экстремума? В данном случае это вершина функции, где скорость тела (мяча) принимает нулевое значение. Производная функции становится равной нулю. При этом направление, а следовательно, и значение скорости, меняется на противоположное. Тело летит вниз с каждой секундой всё быстрее, причём ускоряется на ту же величину — 9,8 м/с2.
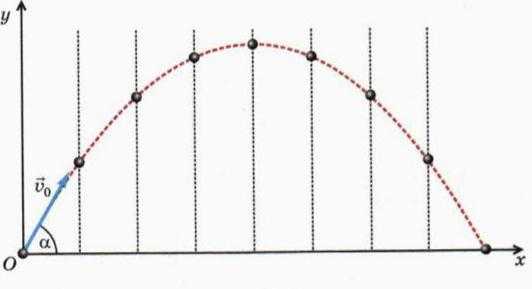
Вторая производная
В предыдущем случае график модуля скорости рисуется как прямая. Данная линия оказывается сначала направлена вниз, так как значение этой величины постоянно убывает. Достигнув нуля в один из моментов времени, далее показатели этой величины начинают возрастать, а направление графического изображения модуля скорости кардинально меняется. Теперь линия направлена вверх.
Скорость, являясь производной от координаты по времени, тоже имеет критическую точку. В этой области функция, вначале убывая, начинает возрастать. Это место точки экстремума производной функции. В данном случае угол наклона касательной становится равным нулю. А ускорение, являясь второй производной от координаты по времени, меняет знак с «-» на «+». И движение из равнозамедленного становится равноускоренным.
График ускорения
Теперь рассмотрим четыре рисунка. На каждом из них отображён график изменения с течением времени такой физической величины, как ускорение. В случае «А» значение его остаётся положительным и постоянным. Это означает, что скорость тела, как и его координата, постоянно увеличивается. Если представить, что объект будет двигаться таким образом бесконечно долго, функция, отражающая зависимость координаты от времени, окажется постоянно возрастающей. Из этого следует, что она не имеет критических областей. Точки экстремума на графике производной, то есть линейно изменяющейся скорости, также отсутствуют.
То же касается и случая «Б» с положительным и постоянно увеличивающимся ускорением. Правда, графики для координаты и скорости здесь будут несколько сложнее.
Когда ускорение стремится к нулю
Рассматривая рисунок «В», можно наблюдать совсем другую картину, характеризующую движение тела. Скорость его графически будет изображаться параболой с ветвями, направленными вниз. Если продолжить линию, описывающую изменение ускорения до пересечения её с осью ОХ, и дальше, то можно представить, что до этого критического значения, где ускорение окажется равным нулю, скорость объекта будет увеличиваться всё медленнее. Точка экстремума производной от функции координаты окажется как раз в вершине параболы, после чего тело кардинально поменяет характер движения и начнёт двигаться в другом направлении.
В последнем случае, «Г», характер движения точно определить невозможно. Здесь известно только, что ускорение за некоторый рассматриваемый период отсутствует. Значит, объект может оставаться на месте или движение происходит с постоянной скоростью.
Задача на сложение координат
Перейдём к заданиям, которые часто встречаются при изучении алгебры в школе и предлагаются для подготовки к ЕГЭ. На рисунке, который представлен ниже, изображён график функции. Требуется вычислить сумму точек экстремума.
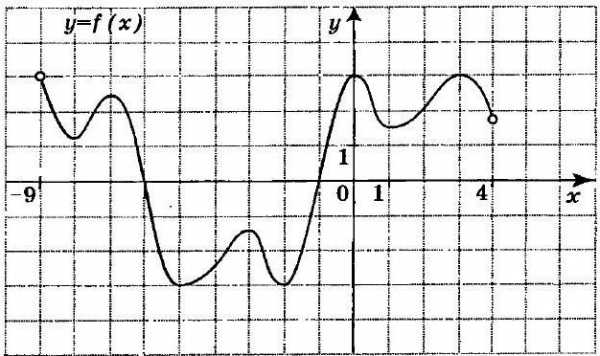
Сделаем это для оси ординат, определив координаты критических областей, где наблюдается изменение характеристик функции. Проще говоря, найдём значения по оси ОХ для точек перегиба, а затем перейдём к сложению полученных членов. По графику очевидно, что они принимают следующие значения: -8; -7 ; -5; -3; -2; 1; 3. В сумме это составляет -21, что и является ответом.
Оптимальное решение
Не стоит объяснять, насколько может оказаться важным в выполнении практических заданий выбор оптимального решения. Ведь путей достижения цели бывает много, а наилучший выход, как правило, — всего один. Это бывает крайне необходимо, к примеру, при конструировании судов, космических кораблей и самолётов, архитектурных сооружений для нахождения оптимальной формы данных рукотворных объектов.
Быстроходность средств передвижения во многом зависит от грамотного сведения к минимуму сопротивления, которое они испытывают при перемещении по воде и воздуху, от перегрузок, возникающих под действием гравитационных сил и многих других показателей. Кораблю на море необходимы такие качества, как устойчивость во время шторма, для речного судна важна минимальная осадка. При расчётах оптимальной конструкции точки экстремума на графике наглядно могут дать представление о наилучшем решении сложной проблемы. Задачи такого плана часто решаются в экономике, в хозяйственных областях, во множестве других жизненных ситуаций.
Из античной истории
Задачи на экстремум занимали даже древних мудрецов. Греческие учёные с успехом разгадали тайну площадей и объёмов путём математических вычислений. Это они первыми поняли, что на плоскости из разнообразных фигур, обладающих одним и тем же периметром, наибольшую площадь всегда имеет круг. Аналогичным образом шар наделён максимальным объёмом среди остальных предметов в пространстве с одинаковой величиной поверхности. Решению подобных задач посвятили себя такие известнейшие личности, как Архимед, Евклид, Аристотель, Аполлоний. Найти точки экстремума прекрасно удавалось Герону, который, прибегнув к расчётам, сооружал хитроумные устройства. К ним относились автоматы, перемещающиеся посредством пара, работающие по тому же принципу насосы и турбины.

Строительство Карфагена
Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.
Истоки математического анализа
А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.
Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона — Лейбница.
Задача на нахождение максимальной площади
Представим, что мы имеем проволоку, длина которой равна 50 см. Как составить из неё прямоугольник, обладающий наибольшей площадью?
Начиная решение, следует исходить из простых и известных любому истин. Понятно, что периметр нашей фигуры будет составлять 50 см. Он же складывается из удвоенных длин обеих сторон. Это значит, что, обозначив за «Х» одну из них, другую возможно выразить как (25 – Х).
Отсюда получаем площадь, равную Х(25 – Х). Данное выражение можно представить как функцию, принимающую множество значений. Решение задачи требует найти максимальное из них, а значит, следует узнать точки экстремума.
Для этого находим первую производную и приравниваем её нулю. В результате получается простое уравнение: 25 – 2Х = 0.
Из него мы узнаём, что одна из сторон Х = 12,5.
Следовательно, другая: 25 – 12,5 = 12,5.
Получается, что решением задачи будет квадрат со стороной 12,5 см.
Как найти максимальную скорость
Рассмотрим ещё один пример. Представим, что существует тело, прямолинейное движение которого описывается уравнением S = — t3 + 9t2 – 24t – 8, где пройденное расстояние выражается в метрах, а время в секундах. Требуется найти максимальную скорость. Как это сделать? Скачала находим скорость, то есть первую производную.
Получаем уравнение: V = — 3t2 + 18t – 24. Теперь для решения задачи снова нужно найти точки экстремума. Сделать это необходимо тем же способом, что и в предыдущей задаче. Находим первую производную от скорости и приравниваем её к нулю.
Получаем: — 6t + 18 = 0. Отсюда t = 3 с. Это время, когда скорость тела принимает критическое значение. Подставляем полученное данное в уравнение скорости и получаем: V = 3 м/с.
Но как понять, что это именно максимальная скорость, ведь критическими точками функции могут быть наибольшие или наименьшие её значения? Для проверки необходимо найти вторую производную от скорости. Она выражается числом 6 со знаком минус. Это значит, что найденная точка является максимумом. А в случае положительного значения второй производной был бы минимум. Значит, найденное решение оказалось правильным.
Приведённые в качестве примера задачи являются лишь частью из тех, которые возможно решить, умея находить точки экстремума функции. На самом деле их гораздо больше. А подобные знания открывают перед человеческой цивилизацией неограниченные возможности.
Источник: fb.rumonateka.com


 1. Какие из указанных выражений характеризуют РЕЧЬ?
1. Какие из указанных выражений характеризуют РЕЧЬ?
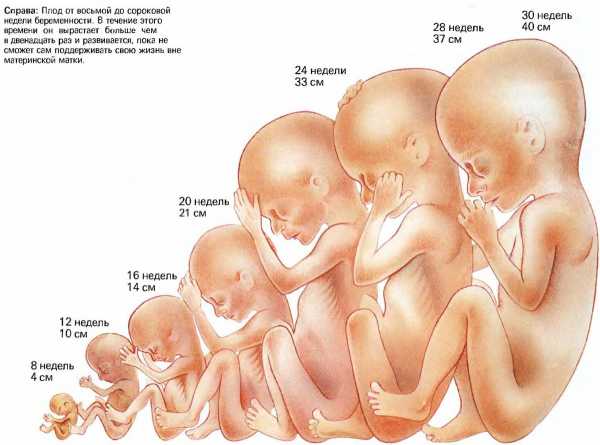
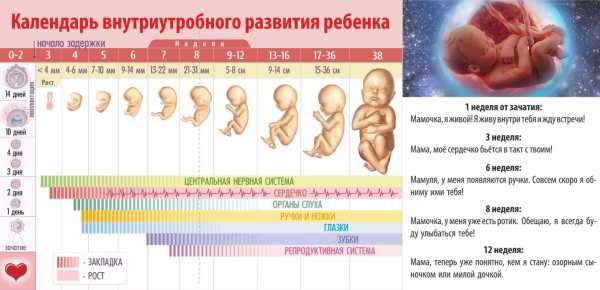
 Как известно, принято считать, что нормальная беременность длится ровно 9 месяцев. Однако, в виду того, что акушеры при подсчете срока отталкиваются от первого дня последней менструации, а для упрощения расчетов месяц принимают за 4 недели, продолжительность гестационного срока в таком случае увеличивается до 10 месяцев. Давайте попробуем разобраться в данной ситуации и ответить на вопрос женщин, который касается того, 9 месяцев беременности, — сколько это недель.
Как известно, принято считать, что нормальная беременность длится ровно 9 месяцев. Однако, в виду того, что акушеры при подсчете срока отталкиваются от первого дня последней менструации, а для упрощения расчетов месяц принимают за 4 недели, продолжительность гестационного срока в таком случае увеличивается до 10 месяцев. Давайте попробуем разобраться в данной ситуации и ответить на вопрос женщин, который касается того, 9 месяцев беременности, — сколько это недель. Сроки протекания беременности будут напрямую зависеть от многих факторов. Состояние беременной как эмоциональное, так и физическое, а также имеющиеся болезни могут способствовать негативному влиянию на плод и его преждевременному рождению, а в худшем случае и вовсе к смерти. Нормой развития плода в утробе матери является 42 недели, за это время ребенок полностью разовьется и получит все необходимые силы для жизни вне материнского организма.
Сроки протекания беременности будут напрямую зависеть от многих факторов. Состояние беременной как эмоциональное, так и физическое, а также имеющиеся болезни могут способствовать негативному влиянию на плод и его преждевременному рождению, а в худшем случае и вовсе к смерти. Нормой развития плода в утробе матери является 42 недели, за это время ребенок полностью разовьется и получит все необходимые силы для жизни вне материнского организма.