Вычислить сумму ряда
Выберите переменную: x y z n k m
Выберите нижний предел Ввести самому + Бесконечность — Бесконечность 0 и верхний предел Ввести самому + Бесконечность — Бесконечность
| x | y | π | e | 1 | 2 | 3 | ÷ | триг. функции | |||
| a2 | ab | ab | exp | 4 | 5 | 6 | × | стереть |
|||
| ( | ) | |a| | ln | 7 | 8 | 9 | — | ↑ | ↓ | ||
| √ | 3√ | C | loga | 0 | . | ↵ | + | ← | → | ||
| TRIG: | sin | cos | tan | cot | csc | sec | назад | |||
| INVERSE: | arcsin | arccos | arctan | acot | acsc | asec | стереть |
|||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| OTHER: | ‘ | , | y | = | < | > | ← | → | ||
Данный калькулятор по вычислению суммы ряда построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Нахождение суммы ряда онлайн
Сумма ряда
Matematikam.ru позволяет найти сумму ряда онлайн числовой последовательности. Помимо нахождения суммы ряда онлайн числовой последовательности, сервер в режиме онлайн найдет частичную сумму ряда. Это полезно для аналитических выкладок, когда сумму ряда онлайн необходимо представить и найти как решение предела последовательности частичных сумм ряда. По сравнению с другими сайтами, matematikam.ru обладает неоспоримым преимуществом, так как позволяет найти сумму ряда онлайн не только числового, но и функционального ряда, что позволит определить область сходимости исходного ряда, применяя наиболее известные методы. Согласно теории рядов, необходимым условием сходимости числовой последовательности является равенство нулю предела от общего члена числового ряда при стремлении переменной к бесконечности. Однако, это условие не является достаточным для определения сходимости числового ряда онлайн. Если ряд не сходится, то matematikam.ru укажет на это, выдав соответствующее сообщение. Для определения сходимости рядов онлайн найдены разнообразные достаточные признаки сходимости или расходимости ряда. Наиболее известные и часто применяемые из них — это признаки Д’Аламбера, Коши, Раабе, сравнения числовых рядов, а также интегральный признак сходимости числового ряда. Особое место среди числовых рядов занимают такие, в которых знаки слагаемых строго чередуются, а абсолютные величины числовых рядов монотонно убывают. Оказывается, для таких числовых рядов необходимый признак сходимости ряда онлайн является одновременно и достаточным, то есть равенство нулю предела от общего члена числового ряда при стремлении переменной к бесконечности. Существует множество различных сайтов, на которых представлены серверы для вычисления суммы ряда онлайн, а также разложения функций вряд в режиме онлайн в некоторой точке из области определения этой функции. Если разложить функцию в ряд онлайн не представляет на этих серверах особого труда, то вычислить сумму функционального ряда онлайн, каждым членом которого, в отличие от числового ряда, является не число, а функция, представляется практически невозможным в силу отсутствия необходимых технических ресурсов. Для www.matematikam.ru такой проблемы не существует.
Похожие сервисы:
Решение интегралов, производных, пределов онлайнSum of series online
matematikam.ru
Сумма ряда онлайн
www.matcabi.net позволяет найти сумму ряда онлайн числовой последовательности. Помимо нахождения суммы ряда онлайн числовой последовательности, сервер в режиме онлайн найдет частичную сумму ряда. Это полезно для аналитических выкладок, когда сумму ряда онлайн необходимо представить и найти как решение предела последовательности частичных сумм ряда. По сравнению с другими сайтами, www.matcabi.net обладает неоспоримым преимуществом, так как позволяет найти сумму ряда онлайн не только числового, но и функционального ряда, что позволит определить область сходимости исходного ряда, применяя наиболее известные методы. Согласно теории рядов, необходимым условием сходимости числовой последовательности является равенство нулю предела от общего члена числового ряда при стремлении переменной к бесконечности. Однако, это условие не является достаточным для определения сходимости числового ряда онлайн. Если числовой ряд онлайн не сходится, то www.matcabi.net укажет на это, выдав соответствующее сообщение. Для определения сходимости рядов онлайн найдены разнообразные достаточные признаки сходимости или расходимости ряда. Наиболее известные и часто применяемые из них — это признаки Д’Аламбера, Коши, Раабе, сравнения числовых рядов, а также интегральный признак сходимости числового ряда. Особое место среди числовых рядов занимают такие, в которых знаки слагаемых строго чередуются, а абсолютные величины числовых рядов монотонно убывают. Оказывается, для таких числовых рядов необходимый признак сходимости ряда онлайн является одновременно и достаточным, то есть равенство нулю предела от общего члена числового ряда при стремлении переменной к бесконечности. Существует множество различных сайтов, на которых представлены серверы для вычисления суммы ряда онлайн, а также разложения функций вряд в режиме онлайн в некоторой точке из области определения этой функции. Если разложить функцию в ряд онлайн не представляет на этих серверах особого труда, то вычислить сумму функционального ряда онлайн, каждым членом которого, в отличие от числового ряда, является не число, а функция, представляется практически невозможным в силу отсутствия необходимых технических ресурсов. Для www.matcabi.net такой проблемы не существует.
www.matcabi.net
Числовые ряды онлайн калькулятор с решением: последовательность формулы
Сумма ряда
С помощью данного онлайн калькулятора можно находить суммы рядов, определять их сходимость, абсолютную и условную. Ряд — это последовательность чисел (либо функций — для функциональных рядов), которые связаны между собой определенным законом. Сумма членов ряда это и есть сумма ряда. Для доказательства того, что такая сумма существует (то есть она не равна бесконечности) можно использовать принципы сходимости числовых рядов — принцип Коши, принцип Доламбера и т.д. После доказательства того, что ряд сходится вычислить сумму числового ряда уже необходимо индивидуально. Для геометрической прогрессии, например, сумма вычисляется по формуле:
Найти сумму ряда онлайн
На нашем сайте вы можете вычислить сумму ряда онлайн. Всегда быстро, надежно, бесплатно. Удобный интерфейс для ввода рядов, задание начального и конечного значения элементов. Возможность находить сумму функционального ряда, использование буквенных констант. На практике студенты имеют дело с числовыми рядами довольно часто. Они широко используются в приближенных вычислениях (вычисление интегралов не имеющих аналитического решения, выполнение математических действий, решение дифференциальных уравнений и т.д.). А про функциональные ряды наподобие ряда Тейлора или ряда Фурье и говорить не приходится. С помощью нашего калькулятора определить сумму ряда теперь не проблема.
Определение числовой последовательности
Определения
Численная последовательность Вызывается серия номеров.
свойство
Код числовой последовательности: (an), (bn), (xn) и т. Д.
(an) = {1, 2, 3, 4, …, n, …} = N. Здесь a1 = 1, a2 = 2, a100 = 100.
(bn) = {-18, 23, 11, -4, 35, …}.
Здесь b1 = -18, b5 = 35.
Серия компьютеров
правила
Окончательная последовательность — содержит ограниченное количество терминов.
Бесконечная последовательность — Он содержит бесконечное число членов.
Примеры решений
(an) = {1, 5, 8} — конечная последовательность (3 выражения).
(bn) = {10, -10. 10.-10, 10, …} — бесконечная последовательность.
правило
Восходящая последовательность — a + 1> a для каждого n N, m, e, каждый из следующих членов больше предыдущего.
Входящая последовательность — a + 1 N, например.
каждый последующий термин меньше предыдущего.
Примеры решений
1) -12; 14,5; 18; 40; … является восходящей последовательностью;
2) 4; 2; -1; -7; -11; … последовательность уменьшается;
3) -3; 2; -1; -4; 5; 3; -9 — не растет и не уменьшается;
4) 6; 6; 6; 6; 6; — стационарная (постоянная) последовательность.
правило
! Увеличение и уменьшение строго однообразный последовательность.
Рассчитать количество онлайн-сериалов
Функция ограничения
Введите функцию и точку, для которой вы хотите вычислить предел
Сайт предлагает подробное решение для поиска ограничений по функциям.
Мы будем вычислять границы функций в точке.
Указанная функция f (x). Мы вычисляем ваш предел по точке x0
Правила ввода терминов и функций
Выражения могут состоять из функций (запись в алфавитном порядке):
абсолютный (x) Абсолютное значение х
(модуль х или | x |) arccos (x) Функция — аркоксин из хarccosh (x) Арксозин является гиперболическим из хarcsin (x) Отдельный сын хarcsinh (x) HyperX гиперболический хarctg (x) Функция — арктангенс из хarctgh (x) Арктангенс является гиперболическим хее число — около 2,7 exp (x) Функция — показатель х (как е^х) log (x) или ln (x) Естественный логарифм х
(Да log7 (x), Необходимо ввести log (x) / log (7) (или, например, для log10 (x)= log (x) / log (10)) пи Число «Pi», которое составляет около 3,14 sin (x) Функция — Синус хcos (x) Функция — Конус от хsinh (x) Функция — Синус гиперболический хcosh (x) Функция — косинус-гиперболический хsqrt (x) Функция представляет собой квадратный корень из хsqr (x) или x ^ 2 Функция — квадрат хtg (x) Функция — Тангенс от хtgh (x) Функция — касательная гиперболическая от хcbrt (x) Функция представляет собой кубический корень хпочва (х) Функция округления х на нижней стороне (пример почвы (4.5) == 4.0) символ (x) Функция — символ хerf (x) Функция ошибки (Лаплас или интеграл вероятности)
Следующие операции можно использовать в терминах:
Реальные числа введите в форму 7,5, не 7,52 * x — умножение 3 / x — разделение x ^ 3 — eksponentiacija x + 7 — Кроме того, x — 6 — обратный отсчет
Сумма ряда
Введите данные для расчета суммы партии
Найдем сумму многих чисел.
Найдите сумму серии в Интернете
Если это не найдено, система рассчитывает сумму партии с определенной точностью.
Серия сходимости
Этот калькулятор может определить, сходится ли партия, он также показывает, какие критерии сходимости работают, а какие нет.
Он также знает, как определить сходимость степенных рядов.
Она также написала серию, где вы можете увидеть степень сходимости ряда (или расхождения).
Правила ввода терминов и функций
Выражения могут состоять из функций (запись в алфавитном порядке):
абсолютный (x) Абсолютное значение х
(модуль х или | x |) arccos (x) Функция — аркоксин из хarccosh (x) Арксозин является гиперболическим из хarcsin (x) Отдельный сын хarcsinh (x) HyperX гиперболический хarctg (x) Функция — арктангенс из хarctgh (x) Арктангенс является гиперболическим хее число — около 2,7 exp (x) Функция — показатель х (как е^х) log (x) или ln (x) Естественный логарифм х
(Да log7 (x), Необходимо ввести log (x) / log (7) (или, например, для log10 (x)= log (x) / log (10)) пи Число «Pi», которое составляет около 3,14 sin (x) Функция — Синус хcos (x) Функция — Конус от хsinh (x) Функция — Синус гиперболический хcosh (x) Функция — косинус-гиперболический хsqrt (x) Функция представляет собой квадратный корень из хsqr (x) или x ^ 2 Функция — квадрат хtg (x) Функция — Тангенс от хtgh (x) Функция — касательная гиперболическая от хcbrt (x) Функция представляет собой кубический корень хпочва (х) Функция округления х на нижней стороне (пример почвы (4.5) == 4.0) символ (x) Функция — символ хerf (x) Функция ошибки (Лаплас или интеграл вероятности)
Следующие операции можно использовать в терминах:
Реальные числа введите в форму 7,5, не 7,52 * x — умножение 3 / x — разделение x ^ 3 — eksponentiacija x + 7 — Кроме того, x — 6 — обратный отсчет
Серия сходимости
Общий член ряда является рациональной частью. Фракцию разлагают на антитело с использованием метода неопределенных коэффициентов:
Выберите счетчик счетчиков счетчика для первой части:
Развернуть скобки:
Теперь мы находим, что находим неизвестные коэффициенты:
После продолжения общий член ряда записывается следующим образом:
Затем мы составим частичную сумму ряда:
| NB: |
Часто читатели присылают нам запросы на поиск сумм их видов, потому что они не понимают, откуда они взялись. Имейте в виду, что вы должны скомпилировать его, замените термин для письма. После распространения скобок. |
Вместе мы получаем:
Для кадров мы страдаем одной секундой:
Заметим, что в скобках есть похожие выражения, которые взаимно уничтожают друг друга. Только два:
По-прежнему необходимо рассчитать предел частичной суммы. Если есть и закончено, то сумма ряда и сама серия сходится:
Сходимость ряда чисел
Забронированная сумма
Рассчитанная сумма для отпуска и длинных услуг на счетах потребителей не распространяется, но вычитается полностью на счет созданного резерва. [1]
Начисленные суммы представляют собой неоплаченные расходы, которые компания включила в отчет о прибылях и убытках.
Обычно это суммы, выплачиваемые через определенные промежутки времени, такие как заработная плата, заработная плата, государственные услуги и вычет подоходного налога с доходов. Например, если баланс находится в середине периода оплаты, платеж в эту дату отображается как сумма, начисленная. [2]
Рассчитанная сумма для отпуска и длинных услуг на счетах потребителей не распространяется, но вычитается полностью на счет созданного резерва.
[3]
Предварительно выставленные суммы пенсии, которые пенсионер не требует в установленные сроки, уплачиваются за последние три года до подачи пенсионного требования. [4]
Оплаченная страховая сумма должна распределяться среди сотрудников самозанятых бригад в соответствии с установленной тарифной ставкой и временем работы. [6]
Расчетная сумма выручки облагается НДС.
[7]
Предварительно выставленные суммы пенсии, которые не требуются пенсионерам своевременно, выплачиваются в прошлом не более чем за 3 года до подачи пенсионного требования. [8]
Предварительно выставленные суммы пенсии, которые пенсионер не требует в срок, уплачиваются за последние 3 года до подачи требования о выплате пенсии.
[9]
Уплаченная пенсия — это сумма, которую пенсионер не выплачивает своевременно, в течение последнего времени, но не более 3 лет (пенсионеры, получающие пенсию в соответствии с Законом о пенсиях и дополнениях для членов колхозов, 15 июля 1964 года — не более 1 года), прежде чем обращаться за пенсией.
Суммы пенсий, которые не были получены в установленный срок по вине органа, назначающего или выплачивающего пенсию, выдается без ограничений в прошлом.
[10]
Рассчитанные суммы выплат за отпуск облагаются налогом так же, как и предоплаченные зарплаты. [11]
Начисленные суммы пособий и средств для возмещения дополнительных затрат, которые не были получены процессором своевременно, оплачиваются просроченными, но не более одного года. [12]
Начисленные суммы пособий и средств на возмещение дополнительных расходов, которые они не получили в результате ошибки органа, назначенного и оплаченного ими, выплачиваются на протяжении всего прошедшего периода.
[13]
Уплаченная пенсия — это сумма, которую пенсионер не выплачивает своевременно, в течение последнего времени, но не более 3 лет (пенсионеры, получающие пенсию в соответствии с Законом о пенсиях и дополнениях для членов колхозов, 15 июля 1964 года — не более 1 года), прежде чем обращаться за пенсией. Размер пенсии не получает своевременно органом, назначается или выплачивается пенсия, он выдается недавно без каких-либо ограничений.
[14]
Платные пенсионные суммы, которые не требуются пенсионерам своевременно, подлежат оплате в течение периода, не превышающего одного года до подачи заявки на получение пенсии. [15]
Страницы: 1 2 3
vipstylelife.ru
Сумма математического ряда произвольного выражения онлайн
Данный сервис позволяет Вам легко оценить к чему стремится тот или иной ряд, заданный определенной функцией.
Функцией может быть любое математическое выражение написаное так, как это используется в универсальном калькуляторе комплексных чисел.
Не секрет, что все ряды можно разделить по признаку сходимости, то есть есть ряды сходящиеся к какому то значению, и есть расходящиеся, которые такого предела не имеют.
Например, любой степенной ряд всегда сходится.
Записав в исходное поле корректное математическое выражение с переменной x, где x — меняется от 1 до бесконечности, калькулятор высчитывает промежуточные значения на первых ста членах рядах, потом 500, потом 1000 и так далее.
Сумма ряда выше 10 тысяч не производится, так как связано с большим объемом вычислений, а альтернатива — интегрирование, пока не входит в функционал онлайн сервиса этого сайта.
Несмотря на это промежуточные вычисления в общих чертах позволят оценить стремление к тому или иному значению.
Калькулятор доработан для расчетов суммы ряда, в том числе и для комплексных выражений. На примерах это будет видно
Чему равна сумма ряда
Пишем 1/x/x
Ответ
Для проверки правильный ответ: PI^2/6=1.6449340668482
Внимание:
Учитывайте что первый элемент ряда равен 1.
То есть система начинает считать схождение ряда от единицы, а не от нуля как это могут предполагать.
Пример сумма от 0 до бесконечности ряда заданная формулой равна двум
Но если мы считаем здесь и задаем эту формулу в виде 1/2^x то в результате мы получим 1 так как суммирование идет с 1 элемента, а не с нулевого.
Еще один пример с комплексными числами
К чему стремится сумма ряда состяощая из элементов
Как видите ряд расходящийся.
Но если элемент ряда равен то сумма ряда стремится к числу
Удачных расчетов!!
- Транспозиция двух множеств онлайн >>
abakbot.ru
Числовые ряды. Сумма ряда.
Задача суммирования множества слагаемых решается в теории рядов.
где u1,u2,u3…., un…–члены бесконечной числовой последовательности, называется числовым рядом.
Числа u1,u2,u3…., un… называют членами ряда, а un– общий член ряда.
Сумма конечного числа n первых членов ряда называется n–й частичной суммой ряда.
Sn= u1 + u2 +… + un,
т.е. S1= u1; S2= u1+ u2
Sn= u1+ u2+…+ un
Ряд называется сходящимся, если существует конечный предел частичной суммы Snпри n, то есть
Число S называется суммой ряда.
В противном случае:
Тогда ряд называется расходящимся.
Эталонные ряды.
1. Геометрический ряд (геометрическая прогрессия)
.
.
Пример.
2. Гармонический ряд.
3. Обобщенный гармонический ряд.
Пример.
.
Признаки сходимости знакоположительных рядов
Теорема 1. Необходимый признак сходимости.
C помощью этого признака можно установить расходимость ряда.
Пример.
Достаточные признаки
Теорема 1.Признак сравнения рядов.
Пусть даны два знакоположительных ряда:
и
Причем тогда, если ряд (2) сходится, то сходится и ряд (1).
Если ряд (1) расходится, то расходится и ряд (2).
Пример. Исследовать ряд на сходимость:
Сравним этот ряд с геометрическим рядом:
Сравним ряды:
и так далее.
Следовательно, по признаку сравнения искомый ряд сходится.
Теорема 2. Признак Даламбера.
при
при
при вопрос о сходимости остается открытым.
Пример. Исследовать на сходимость ряд:
по признаку Даламберу ряд сходится.
Теорема 3.Радикальный признак Коши.
1) при
2) при
3) при вопрос о сходимости остается открытым.
Пример: исследовать на сходимость числовой ряд:
Решение:
Следовательно, ряд сходится по Коши.
Теорема 4. Интегральный признак Коши.
Пусть члены ряда
положительны и не возрастают, то есть и являются значениями непрерывной невозрастающей функцииf(x) при x= 1, 2, …, n.
Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл:
Пример.
Решение:
Следовательно, ряд расходится, так как расходится несобственный интеграл.
Знакопеременные ряды. Понятие абсолютной и условной сходимости знакопеременого ряда.
Ряд называется знакопеременным, если любой его член может быть, как положительным, так и отрицательным.
Рассмотрим знакочередующиеся ряды:
Теорема 1. Признак Лейбница (достаточный признак).
Если у знакочередующегося ряда
члены убывают по абсолютной величине, то есть и
то ряд сходится, и его сумма не превосходит первого члена, то есть S ≤.
Пример.
Решение:
Применим признак Лейбница:
.
Следовательно, ряд сходится по Лейбницу.
Теорема 2. Достаточный признак сходимости знакопеременного ряда.
Если для знакопеременного ряда сходится ряд, составленный из абсолютных величин его членов , то данный знакопеременный ряд сходится.
Пример: исследовать ряд на сходимость:
Решение:
из абсолютных величин членов исходного ряда сходится, как обобщенный гармонический ряд при .
Следовательно, исходный ряд сходится.
Этот признак является достаточным, но не необходимым, то есть существуют знакопеременные ряды, которые сходятся, хотя ряды, составленные из абсолютных величин, расходятся.
Определение 1. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Определение 2.Знакопеременный ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Отличие между ними в том, что абсолютно сходящийся ряд сходится из-за того, что его члены быстро убывают, а условно сходящийся ряд сходится из-за того, что положительные и отрицательные члены уничтожают друг друга.
Пример.
Решение:
Применим признак Лейбница:
Следовательно, ряд сходится по Лейбницу. Но ряд составленный из абсолютных величин его членов расходится, как гармонический.
Значит, исходный ряд сходится условно.
studfiles.net
Как исследовать сходимость числового ряда в Wolfram|Alpha
Для исследования сходимости числовых рядов Wolfram|Alpha предлагает несколько возможностей.Например, чтобы просто узнать сходится или расходится данный числовой ряд, можно обратится к Wolfram|Alpha на «естественном языке» — одним из следующих способов:
Во всех этих случаях Wolfram|Alpha интерпретирует запрос одинаково, и выводит следующий результат:
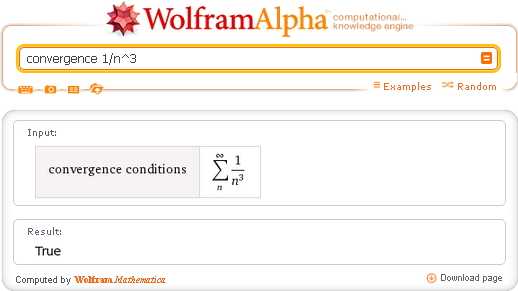
Результат «True» означает, что данный ряд сходится. Результат «False» будет означать, что ряд расходится:
convergence ((n+1)!*7^n)/n^2
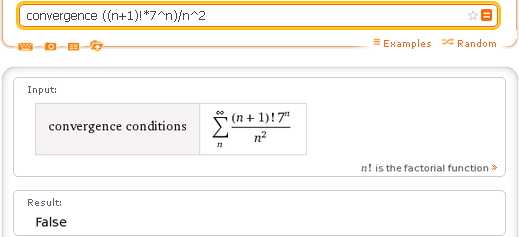
Однако, Вы, конечно, помните, что числовой ряд, это — сумма членов бесконечной числовой последовательности. Значит, для исследования числового ряда можно использовать запрос Sum , который дает больше информации:
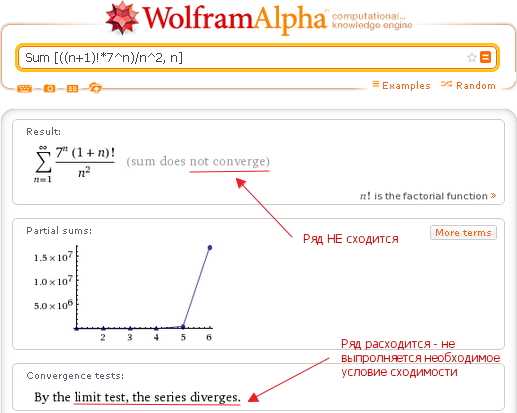
При использовании запроса Sum Wolfram|Alpha последовательно применяет доступные алгоритмы проверки признаков сходимости, пока не будет получен ответ. Это хорошо видно на следующем примере (гармонический ряд):
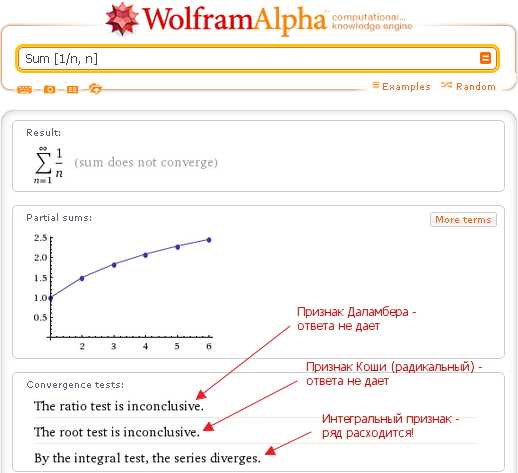
В том случае, когда числовой ряд сходится (а, это значит, что существует его сумма), Wolfram|Alpha по запросу Sum выводит также и сумму данного ряда:
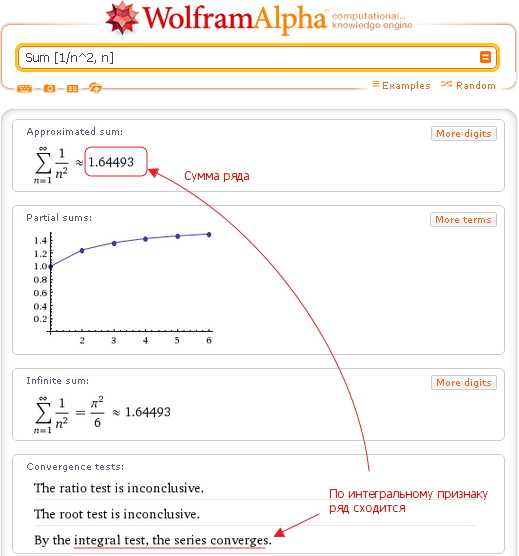
В рассмотренных выше примерах исследовались числовые ряды с положительными членами.
Теперь рассмотрим знакочередующийся ряд:
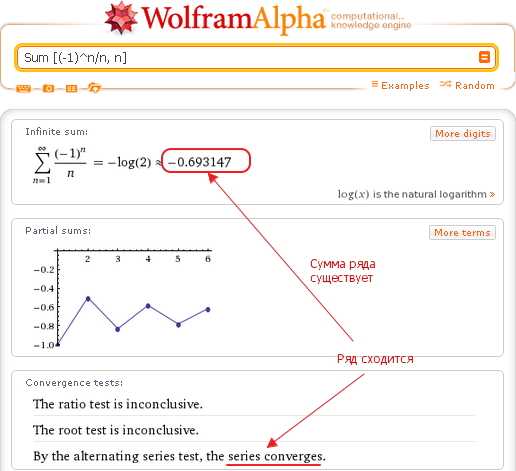
P.S.
Обратите внимание, что Wolfram|Alpha не всегда хватает отведенного лимита времени, чтобы вывести полный результат. Поэтому, в отдельных случаях (для уверенности) стоит повторить исследование сходимости ряда несколько раз подряд.
www.wolframalpha-ru.com

 m+n d
m+n d








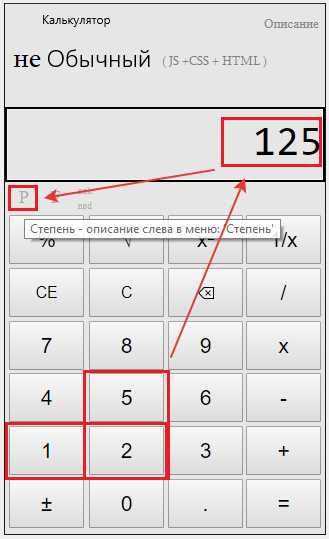 2.
Далее нажимаем кнопку степени – это буква Р.
2.
Далее нажимаем кнопку степени – это буква Р.  3.
Набираем дробь, 1/3 это и будет корень третьей степени!
3.
Набираем дробь, 1/3 это и будет корень третьей степени!  3.
И последним действием нажимаем равно – как видим корень третьей степени из 125 на калькуляторе будет равно 5.
3.
И последним действием нажимаем равно – как видим корень третьей степени из 125 на калькуляторе будет равно 5. 
 Пишем корень на компьютере
Пишем корень на компьютере Таблица символов
Таблица символов
 =
=
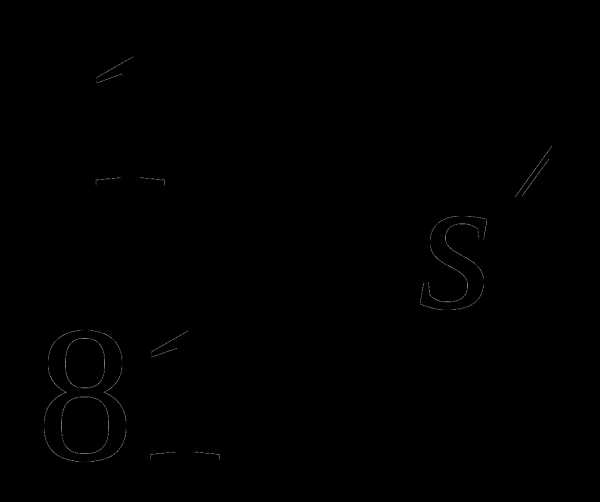 =
=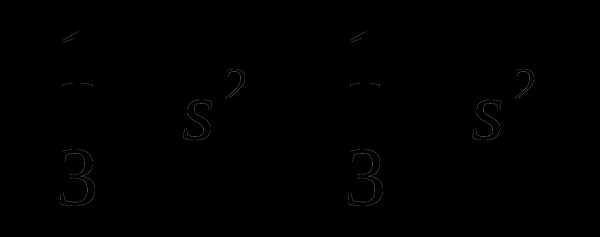
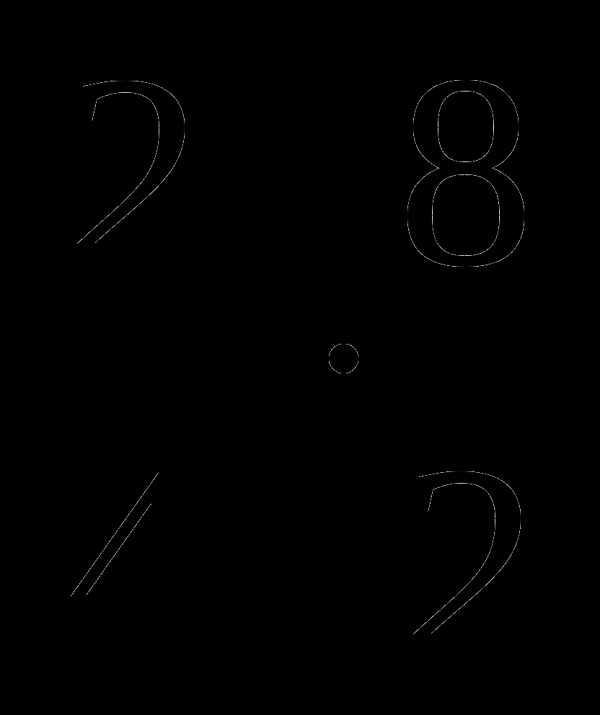

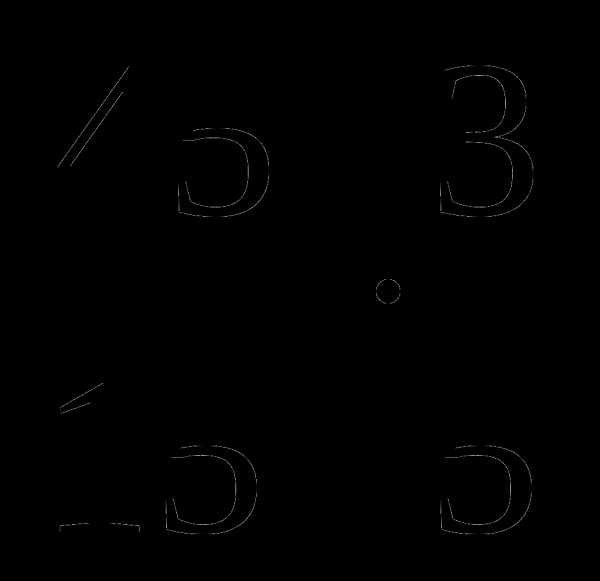




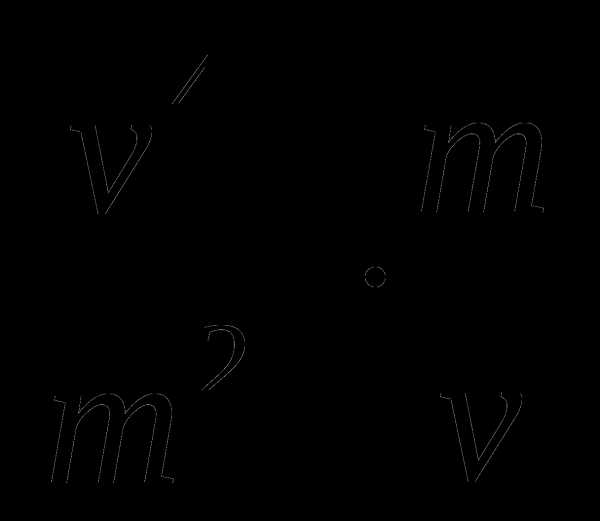
 Сферический треугольник.
Сферический треугольник.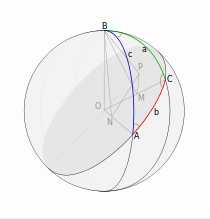 Рисунок к доказательству теоремы косинусов с помощью проекций.
Рисунок к доказательству теоремы косинусов с помощью проекций.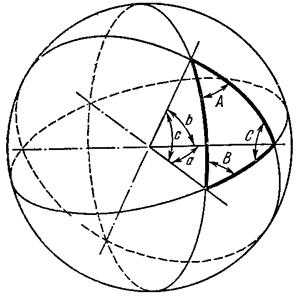
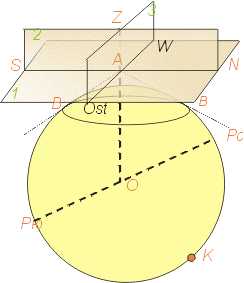
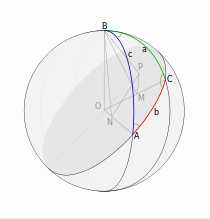 Рисунок к доказательству теоремы косинусов с помощью проекций.
Рисунок к доказательству теоремы косинусов с помощью проекций.