| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
www.mathway.com



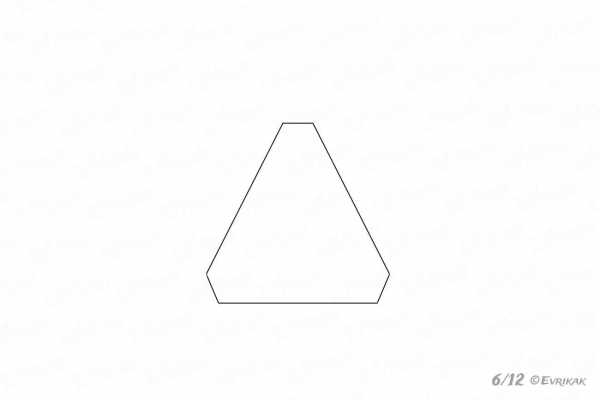
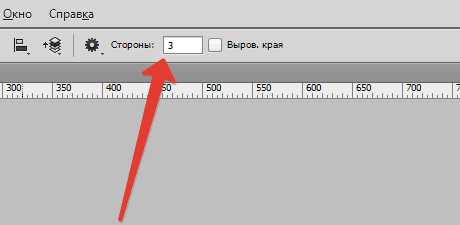
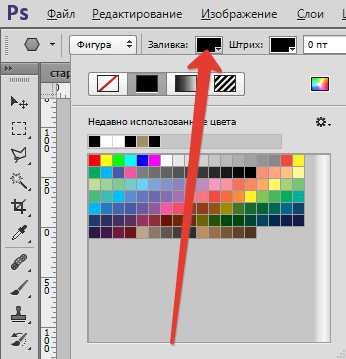
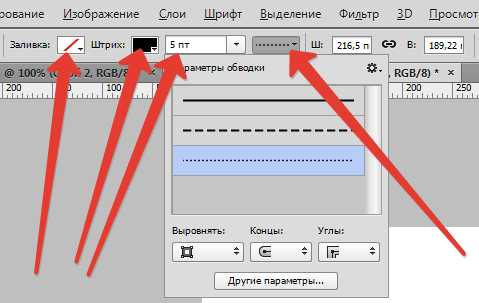
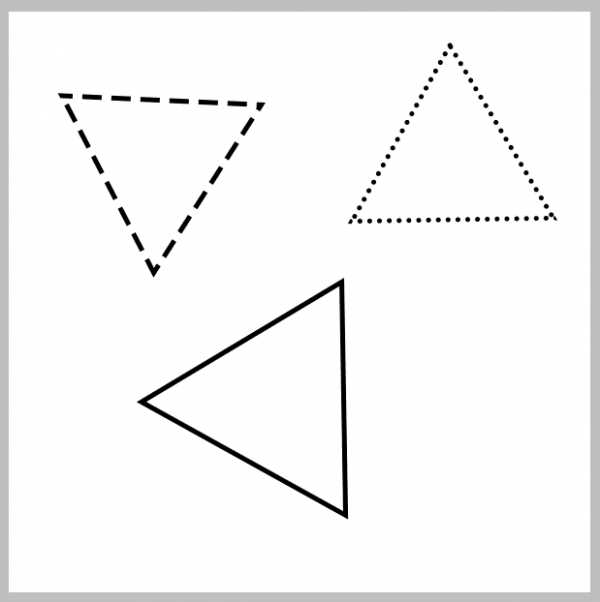
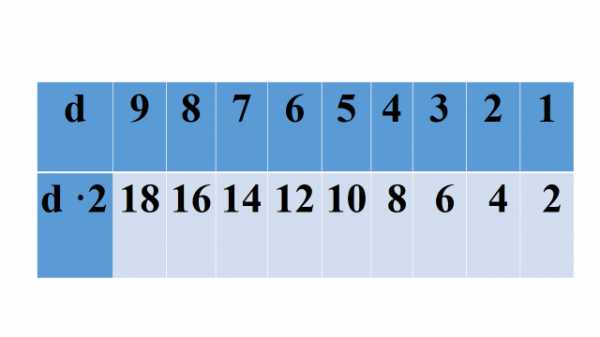
 Прямоугольник сверху стираем, срезая угол. Такие же фигуры изобразите внизу. Они должны быть слегка перевернуты.
Прямоугольник сверху стираем, срезая угол. Такие же фигуры изобразите внизу. Они должны быть слегка перевернуты.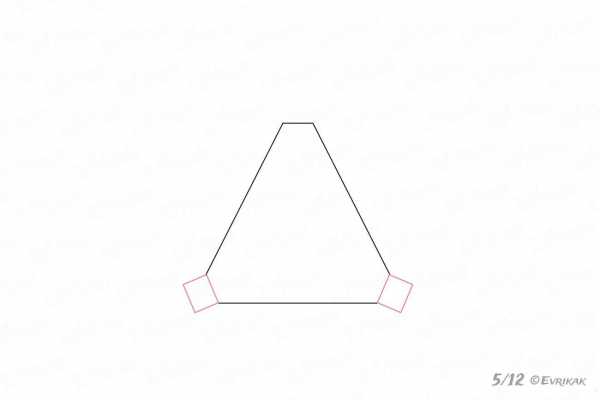





















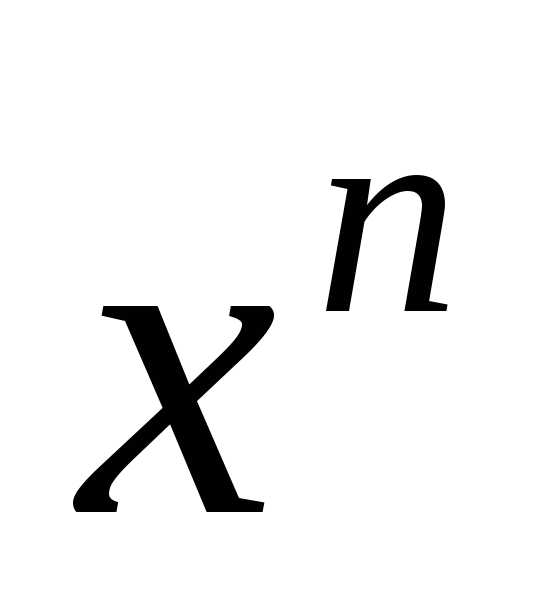
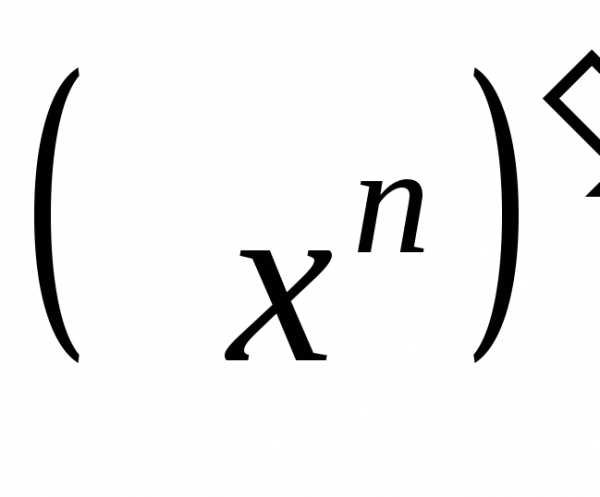 =
=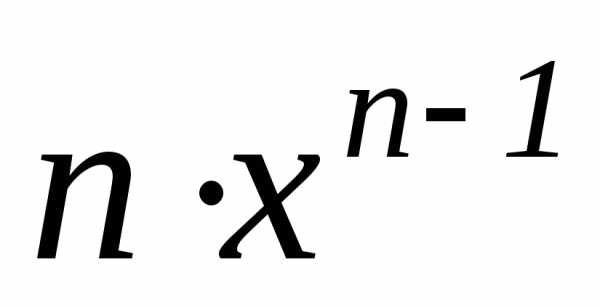
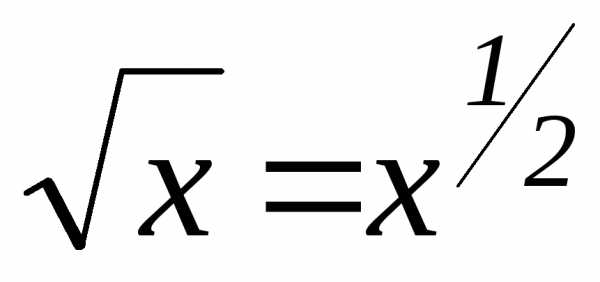
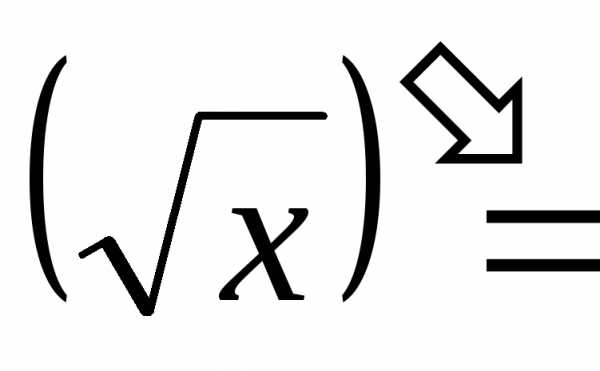
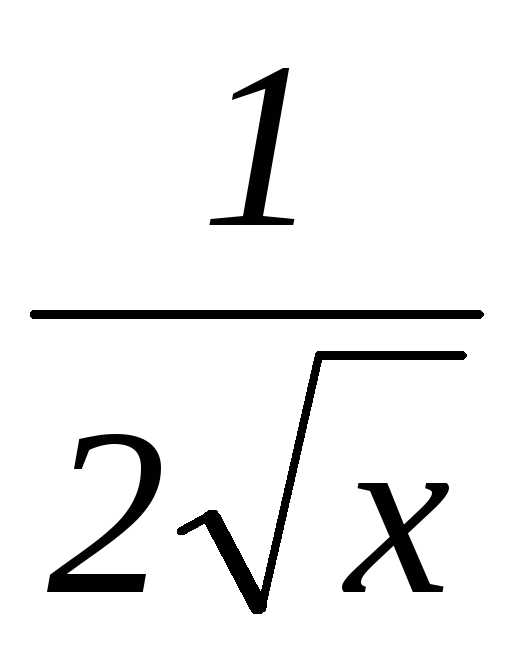
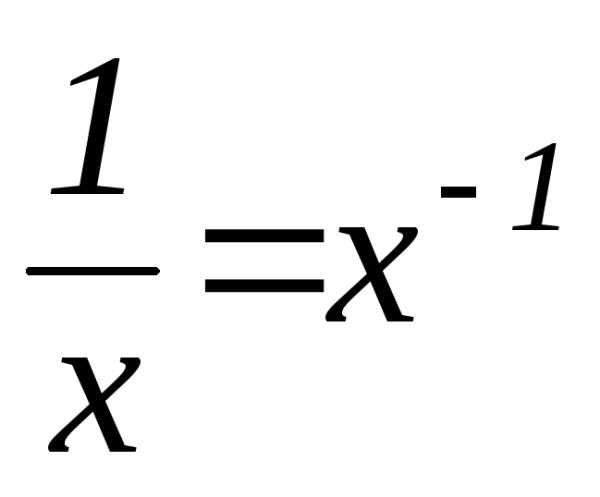
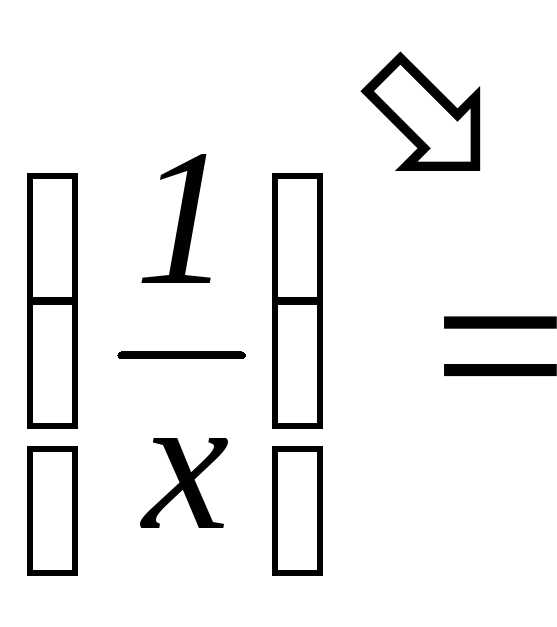
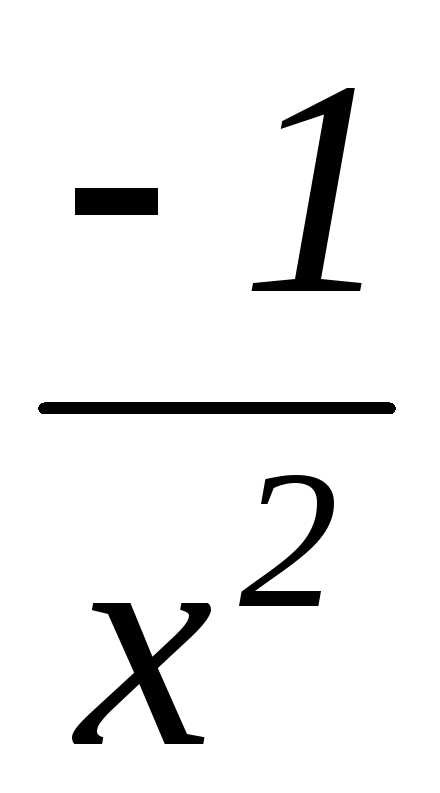
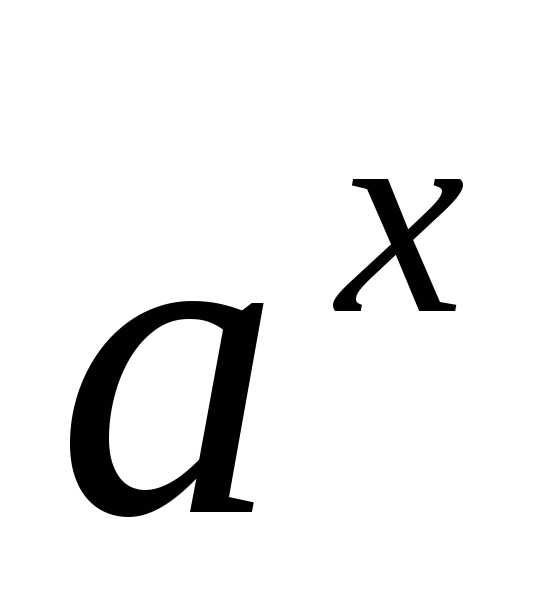
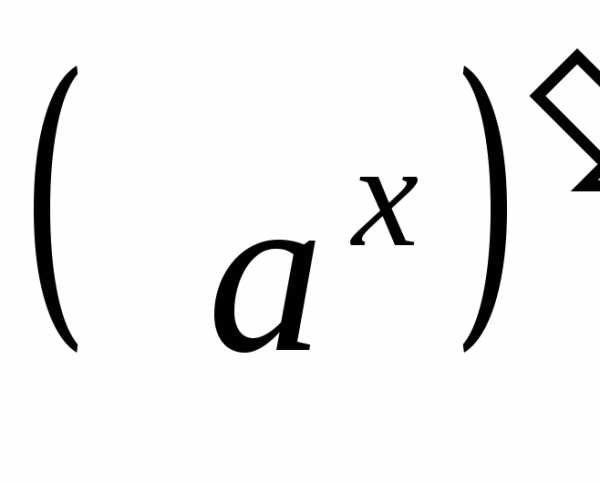 =
=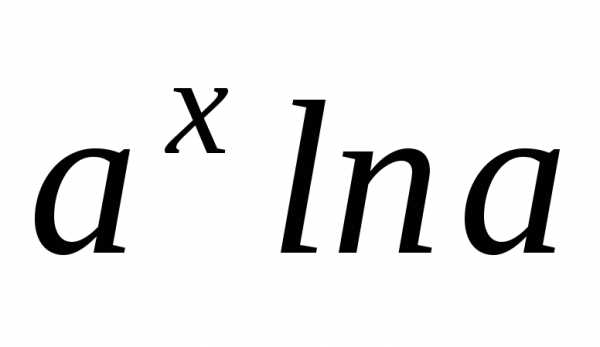
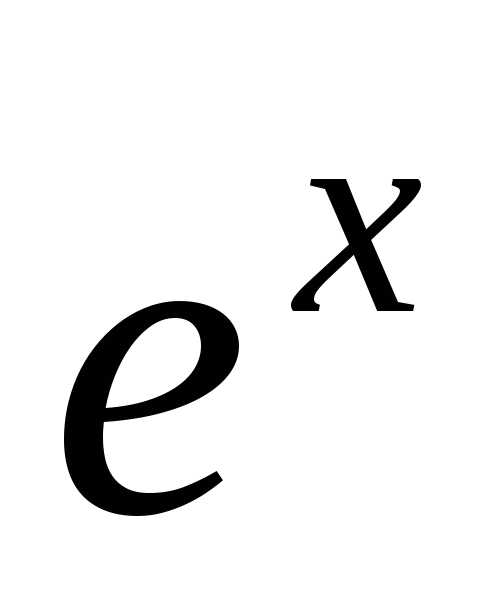
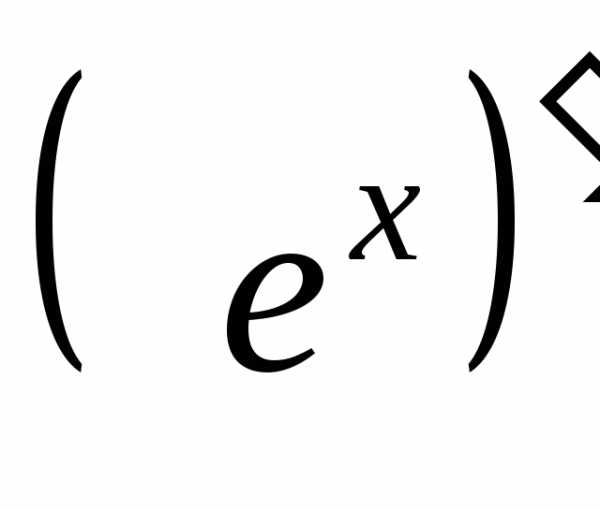 =
=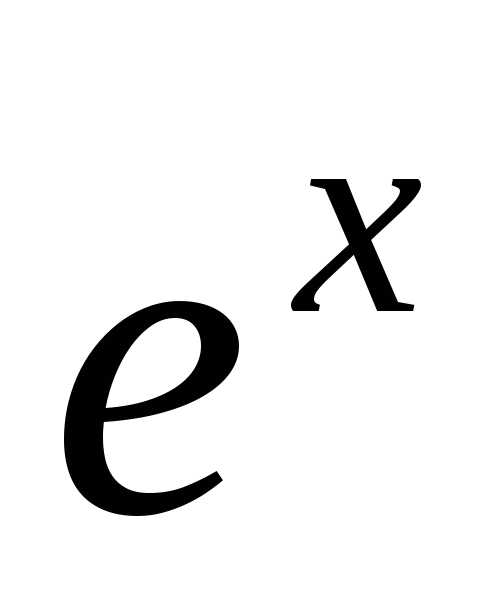
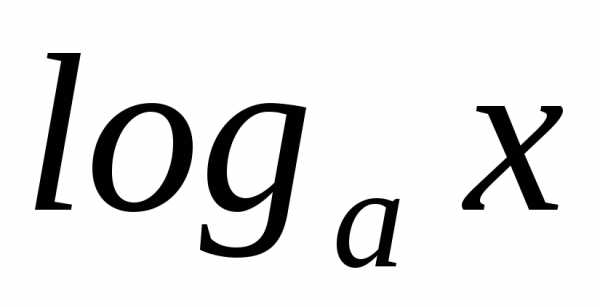
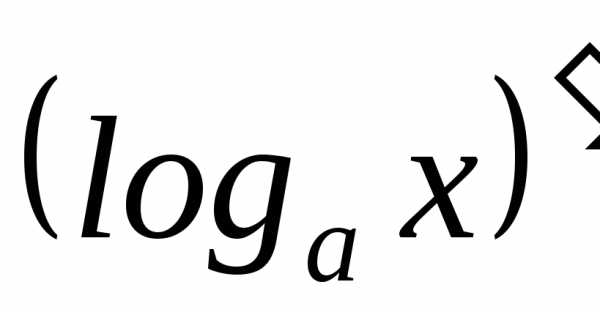 =
=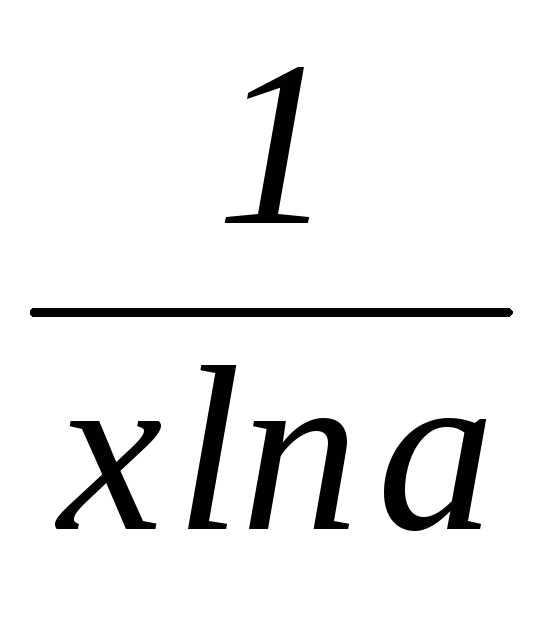
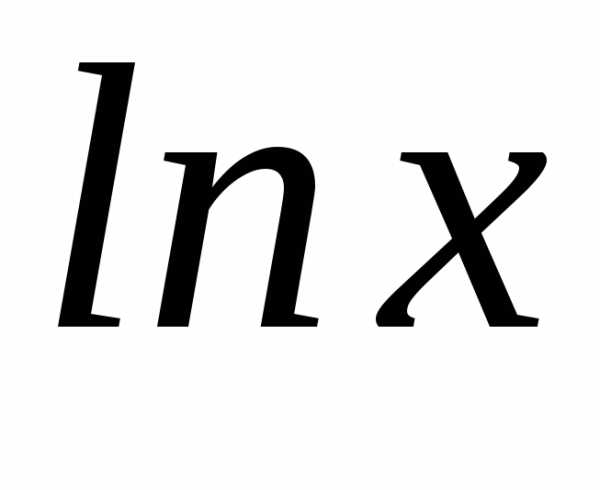
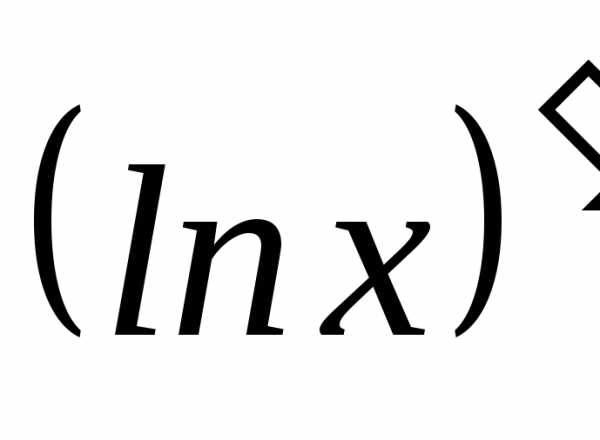 =
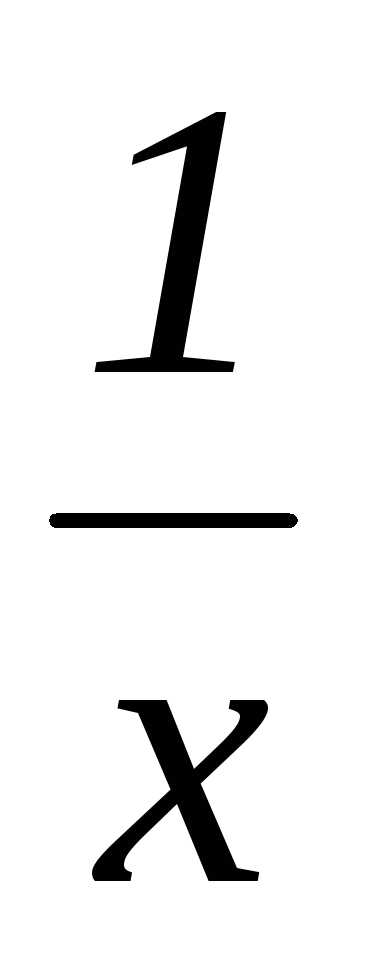
=
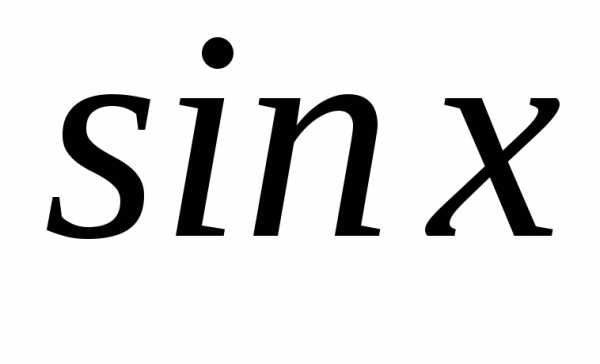
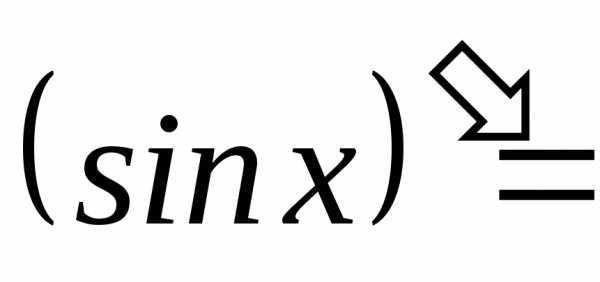
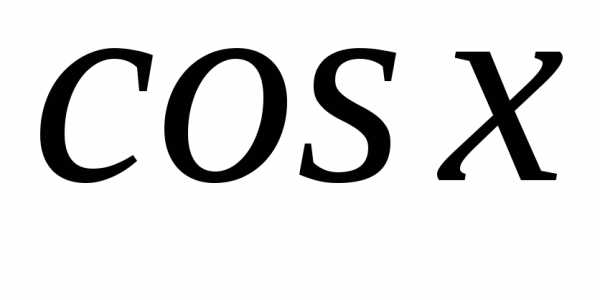
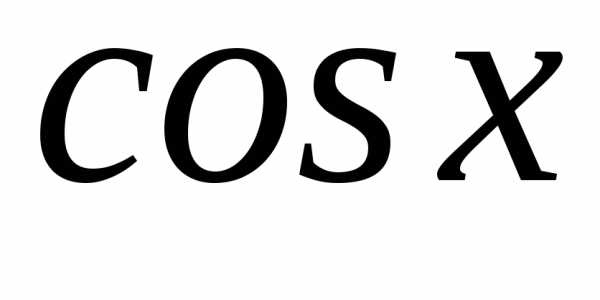
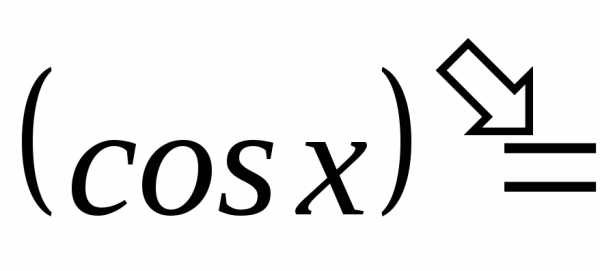
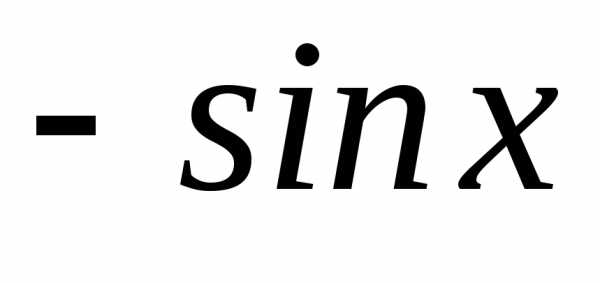
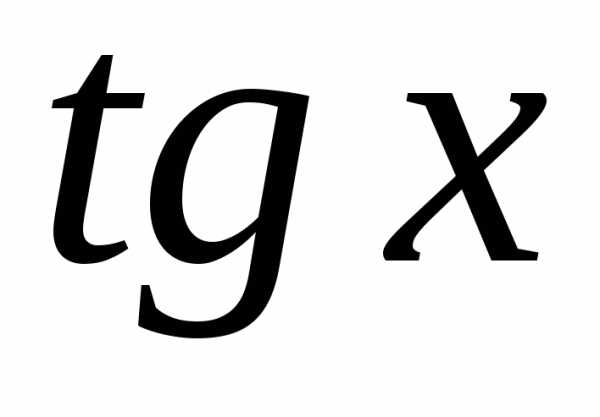
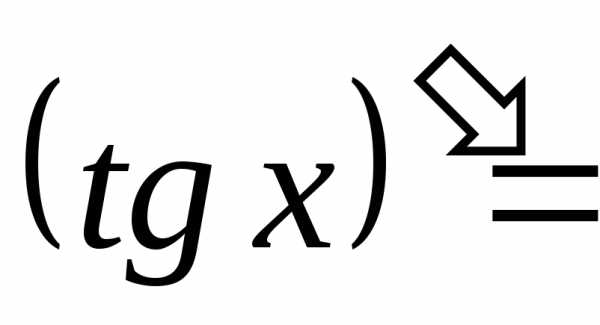
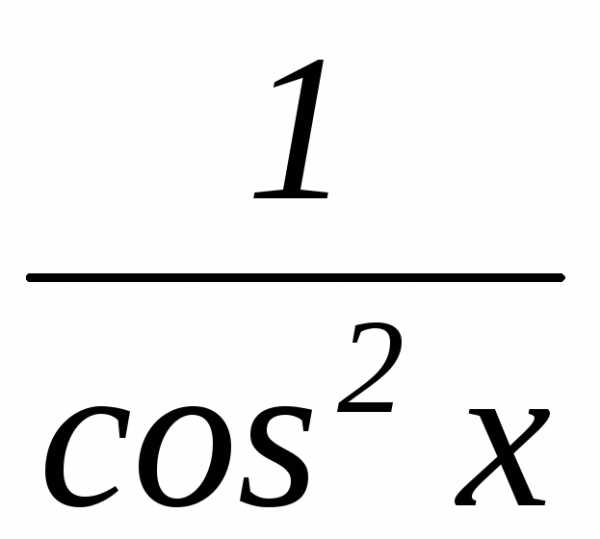
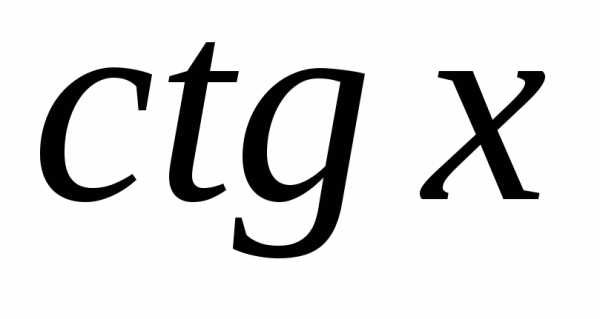
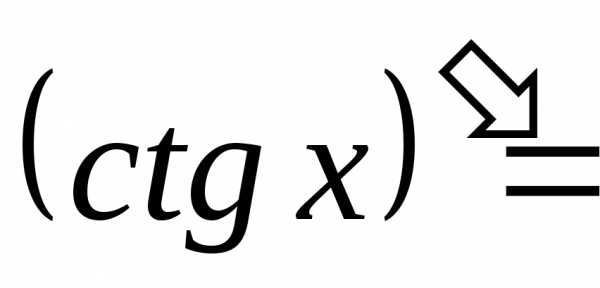
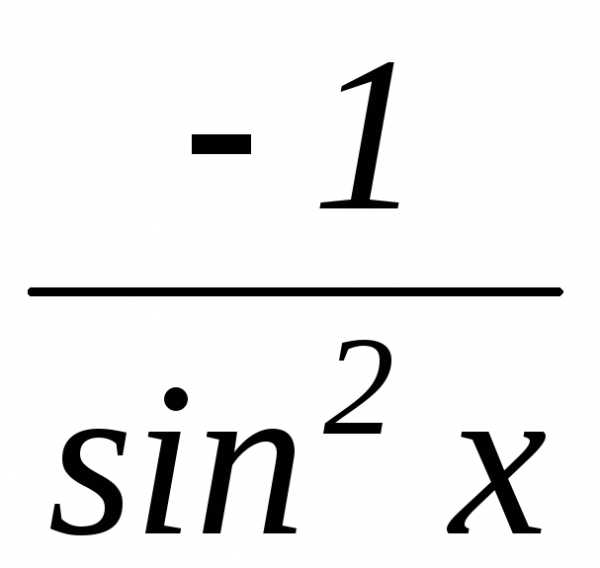
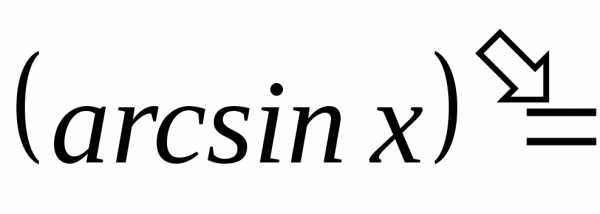
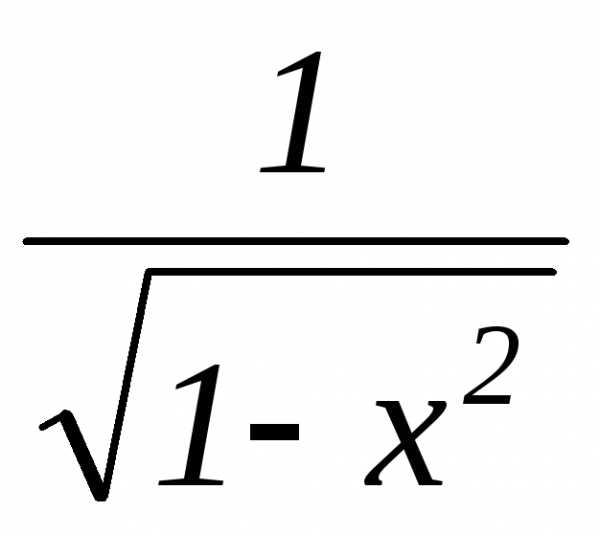
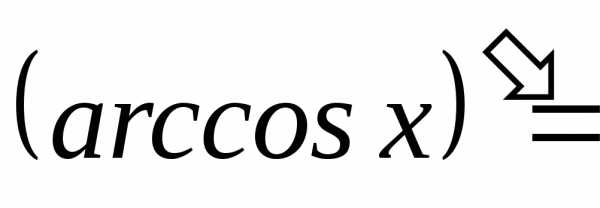
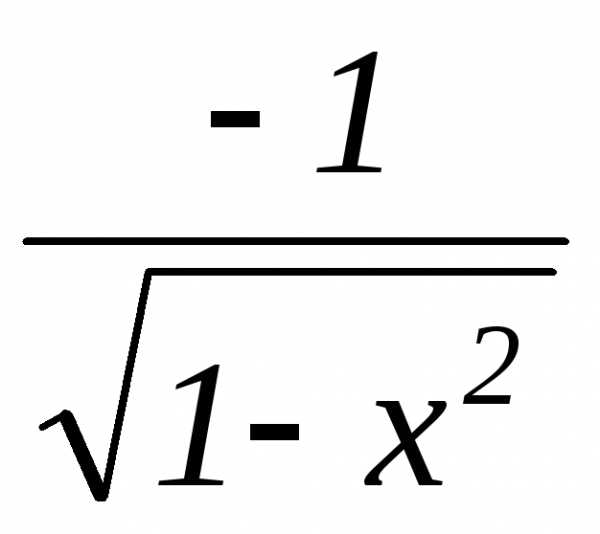
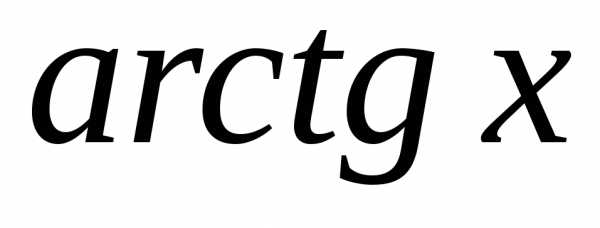
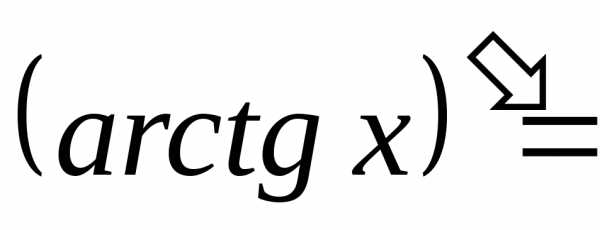
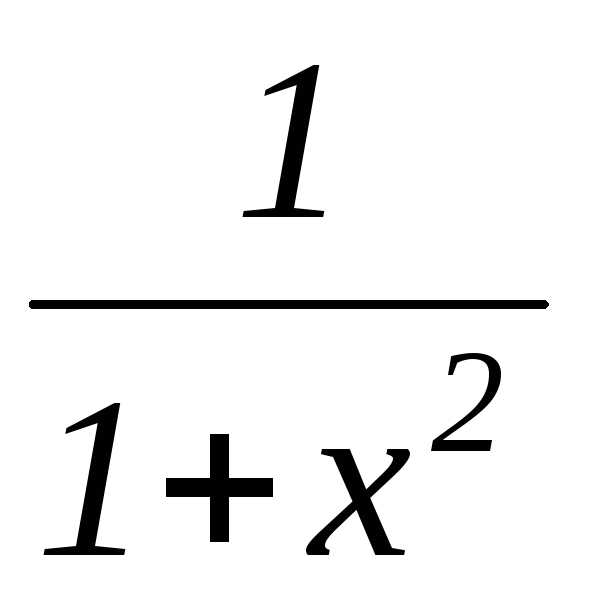
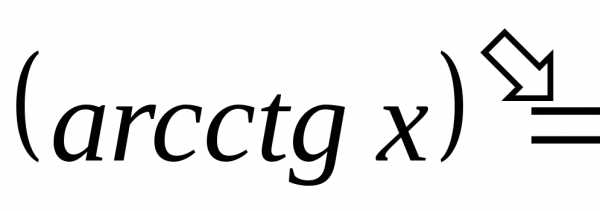
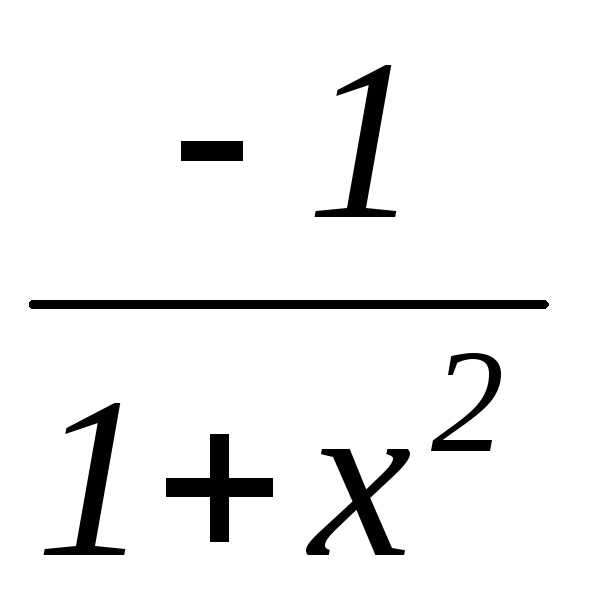
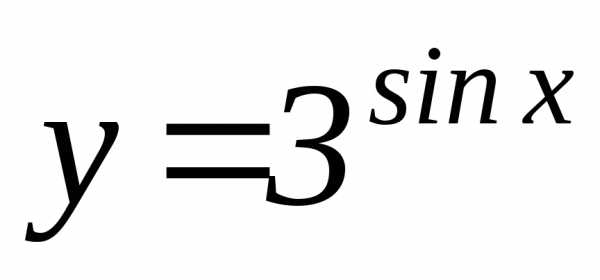 ;
;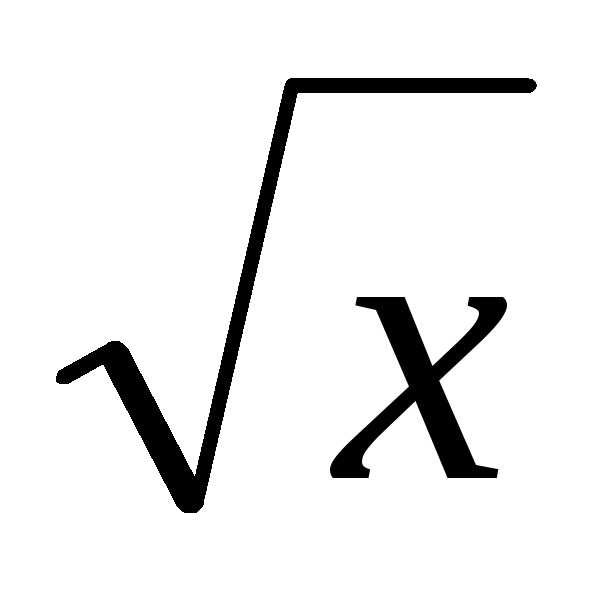 и линейной функции (2х-1).
и линейной функции (2х-1).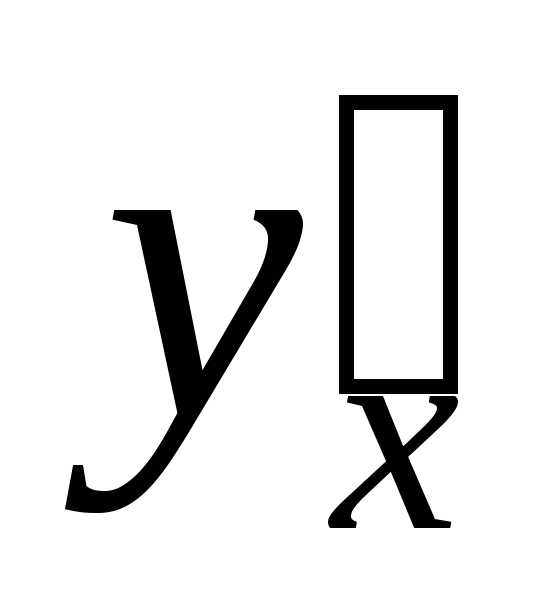 ,
функции, заданной неявно, надо найти
производную по переменнойх обеих частей выражения, задающего
функцию.
,
функции, заданной неявно, надо найти
производную по переменнойх обеих частей выражения, задающего
функцию.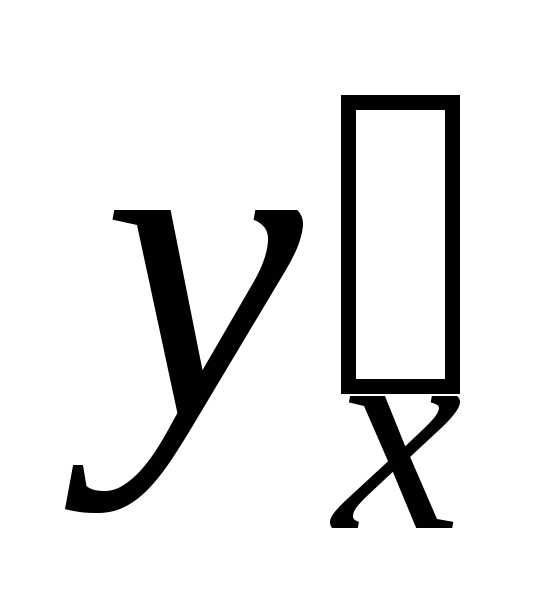 .
.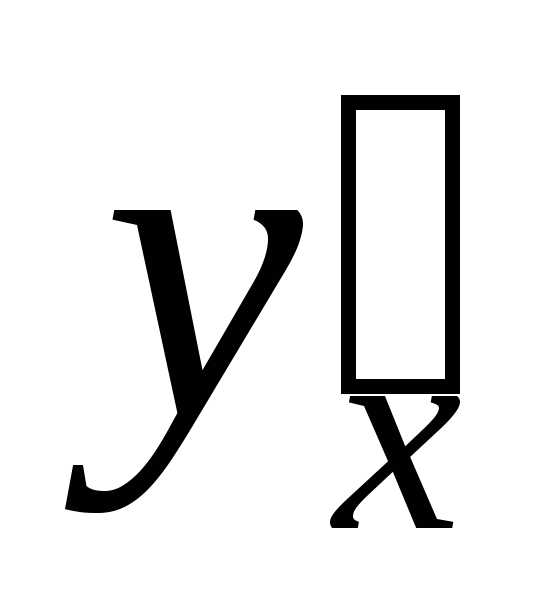 неявно заданной функции:
неявно заданной функции: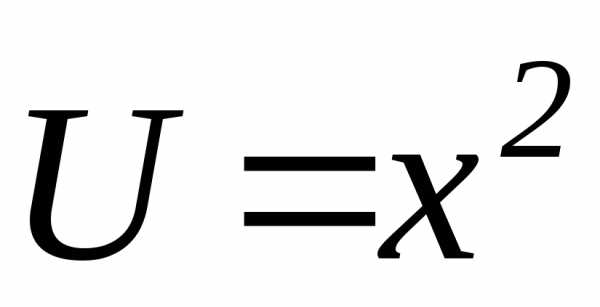 и
и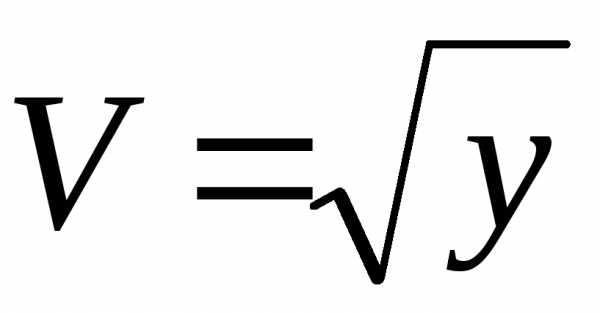




 Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
 Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.


 Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.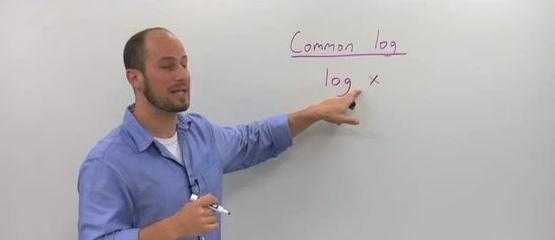
 Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
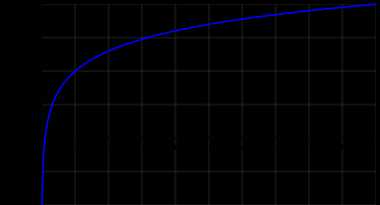 График десятичного логарифма
График десятичного логарифма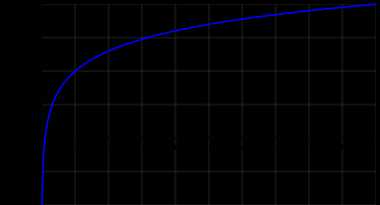 График десятичного логарифма
График десятичного логарифма