Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
А затем напряжение
Зная напряжения, найдем токи, протекающие через резисторы
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи
Отсюда мощность, выделяемая на R1
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
Таким образом производится расчет простых цепей постоянного тока.
electroandi.ru
правила расчета для определения силы тока
На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.
Пример сложных электрических цепей
Пути вычисления электрических схем
Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.
Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.
Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.
Все элементы и устройства подразделяются на три категории:
- Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
- Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
- Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.
Также к основным понятиям электрической схемы относятся:
- Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
- Узел электрической схемы – точка соединения трех и более ветвей схемы;
- Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.
Обозначение ветвей, узлов и контуров на схеме
Метод расчета по законам Ома и Кирхгофа
Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.
Закон Ома для участка цепи
По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:
UR=RI.
Исходя из этой формулы, найти силу тока можно по выражению:
I=UR/R, где:
- UR – напряжение или падение напряжения на резисторе;
- I – ток в резисторе.
Закон Ома для полной цепи
В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:
I=E/Rэ = E/r0+R, где:
- E – ЭДС источника питания;
- rо – внутреннее сопротивление источника питания.
Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.
Первый закон Кирхгофа
Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:
∑mIk=0, где m – число ветвей, подведенных к узлу.
Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».
Второй закон Кирхгофа
Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:
∑nEk=∑mRkIk=∑mUk, где:
- n – число источников ЭДС в контуре;
- m – число элементов с сопротивлением Rk в контуре;
- Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.
Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:
- Указать относительно положительные направления ЭДС, токов и напряжений;
- Указать направление обхода контура, описываемого уравнением;
- Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.
Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:
∑EI=∑RI2.
Метод преобразования электрической цепи
Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.
Последовательное и параллельное соединение элементов
Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.
Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:
- R1=R12R31/R12+R31+R23,
- R2=R12R23/R12+R31+R23,
- R3=R31R23/R12+R31+R23.
Треугольник и звезда соединений
Дополнительные методы расчета цепей
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
- Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.
Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Видео
Оцените статью:elquanta.ru
Закон Ома для полной цепи
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС
Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:
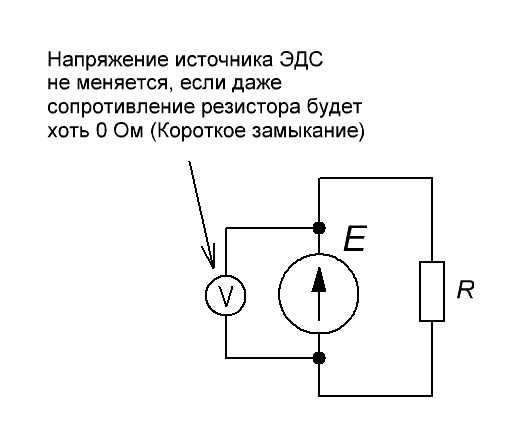
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.
Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?
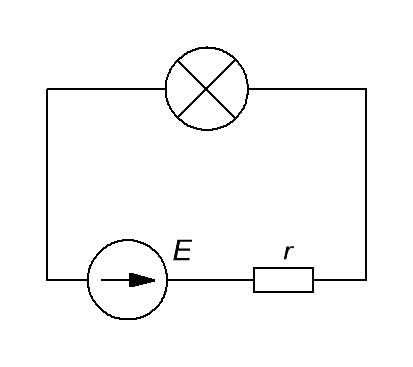
Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
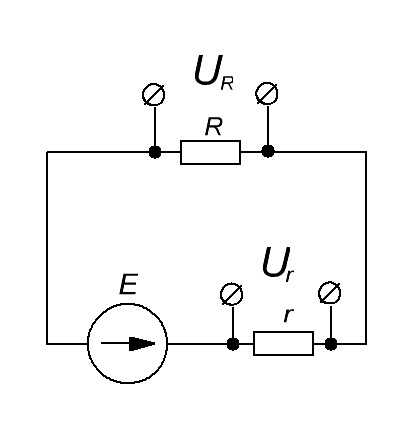
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что
Далее

Закон Ома для полной цепи
Итак, последнее выражение носит название “закон Ома для полной цепи”
где
Е – ЭДС источника питания, В
R – сопротивление всех внешних элементов в цепи, Ом
I – сила ток в цепи, А
r – внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
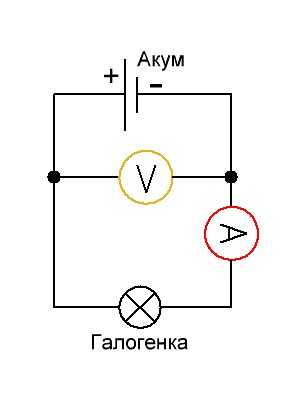
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r
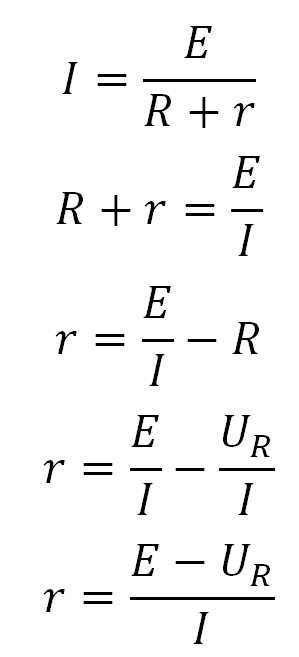
Резюме
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
www.ruselectronic.com
Формула напряжения тока. Как найти, вычислить электрическое напряжение.
Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.
Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.
Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).
Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.
Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.
Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт». Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.
Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».
В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.
P.S. Формула закона Ома является фундаментальной, и именно по ней всегда можно найти одну неизвестную величину из двух известных (ток, напряжение, сопротивление). На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.
electrohobby.ru
чему равен общий ток цепи и напряжение на участке при последовательном соединение???
Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3… Ток через все сопротивления протекает один ( I ). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм. I=U/Rсумм Мощность P=U*I или P=I*I*R (так как U=I*R). тогда, P1=I*I*R1 P2=I*I*R2 P3=I*I*R3
исходные данные где?
1) сумма 2)напряжение на участке цепи умножить на ток. При том ток, при последовательном соединении одиноковй в любой точке цепи
Сумма токов в узле равна нулю. Выход равен входу. 1) сложить. 2)сумме мощностей элементов цепи.
При последовательном соединении узлов нет. Ток цепи определяется делением приложенного напряжения в вольтах (V) на сопротивление цепи в омах (R). I=V : R. Падение напряжения на участке будет равнятся сопротивлению участка помноженному на ток. Общее сопротивление равно сумме всех сопротивлений. Мощность участка равняется падению напряжения на участке помноженному на ток. Это Закон Ома. А вообще-то это все в школьном учебнике физики в разделе-Электричество.
touch.otvet.mail.ru
Напряжение цепи переменного тока | Электрикам
Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).
u = Umsin(2πt + Ψ ) = Umsin(ωt + Ψ )
Где u = u(t) — мгновенное значение переменного напряжения [В].
Um — максимальное значение напряжения (амплитудное значение) [В].
f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1)
ω — угловая частота (омега) (единица угловой частоты — рад/с или с-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
U — Действующее значение напряжения [В]:
Рассмотрим параметры напряжения в бытовой электросети.
Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).
Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.
- Действующее значение напряжения U = 220 В.
- Амплитудное значение напряжения цепи переменного тока Um = U*√2 = 220 *√2 = 311 В.
- Угловая частота ω = 2πf = 3,14*2*50 = 314 рад/с.
- Начальная фаза Ψ = 0 град.
- Мгновенное значение u = 311sin(314t) В.
electrikam.com
Напряжение на участке цепи
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 1-13 изображен участок цепи, на котором есть резистор сопротивлением и нет ЭДС. Крайние точки этого участка обозначены буквами a и b. Пусть ток течет от точки a к точке b.
Рис. 1-13. Участок электрической цепи
На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал точки a выше потенциала точки b на величину, равную произведению тока на сопротивление :
.
В соответствии с определением, напряжение между точками a и b
. (1-8)
Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.
В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.
Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.
На рис. 1-14 а и б показаны участки некоторых цепей, по которым протекает ток .. Найдем напряжение между точками a и c для этих участков.
а) б)
Рис. 1-14. Участки электрической цепи
По определению
. (1-9)
Выразим потенциал точки a через потенциал точки c. При перемещении от точки c к точке b (рис. 1-14,а) идем встречно ЭДС , поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС , т.е.
. (1-10)
На рис. 1-14,б при перемещении от точки c к точке b идем согласно ЭДС и потому потенциал точки b оказывается больше, чем потенциал точки c на величину ЭДС , т.е.
. (1-11)
Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 1-14 потенциал точки a выше, чем потенциал точки b на величину падения напряжения на резисторе сопротивлением :
. (1-12)
Таким образом, для рис. 1-14,а имеем
, или
. (1-13)
И для рис. 1-14, б имеем
, или
. (1-14)
Положительное направление напряжения указывают на схемах стрелкой. Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения изобразится стрелкой, направленной от a к c.
Из самого определения напряжения следует также, что . Поэтому . Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.
Закон ома для участка цепи, не содержащего эдс
Закон Ома устанавливает связь между током и напряжением на некотором участке цепи. Так, применительно к участку цепи, изображенному на рис. 1-13 имеем
или
. (1-15)
studfiles.net

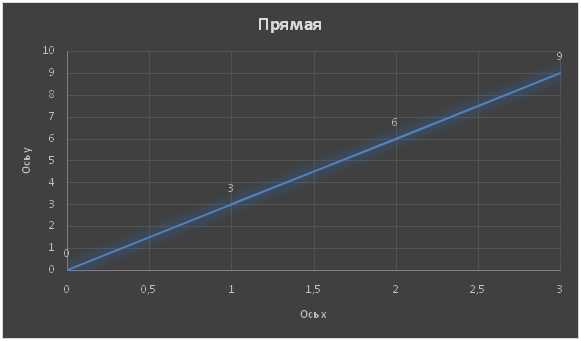
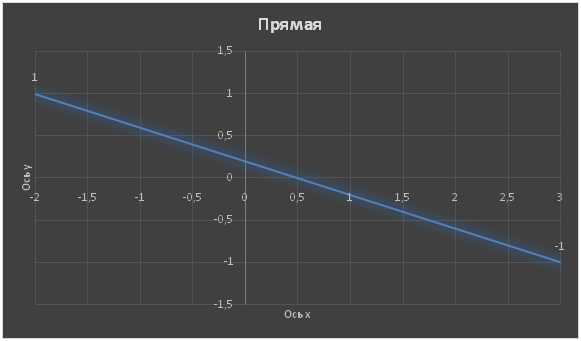
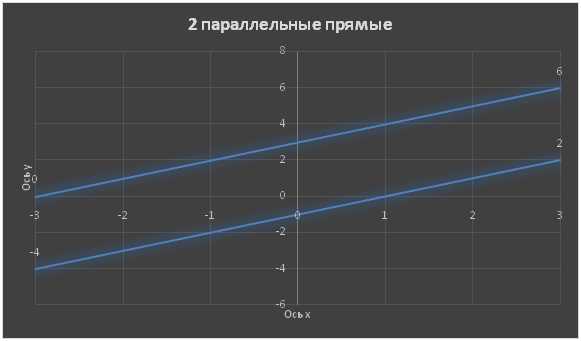
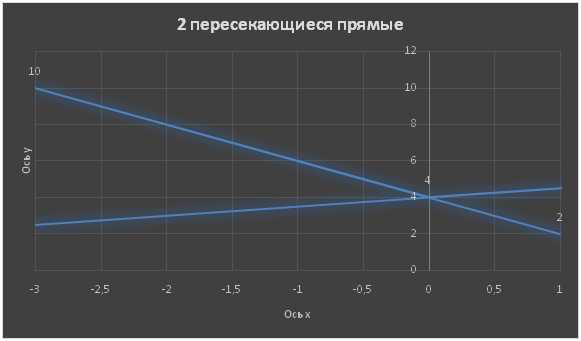
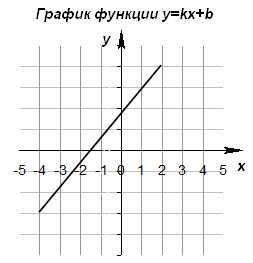
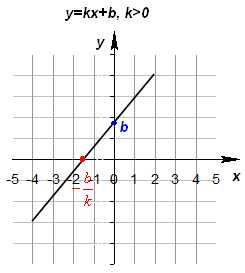

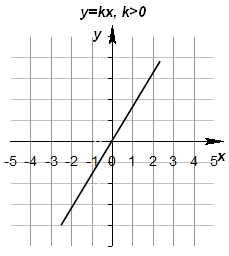
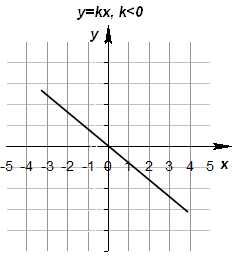

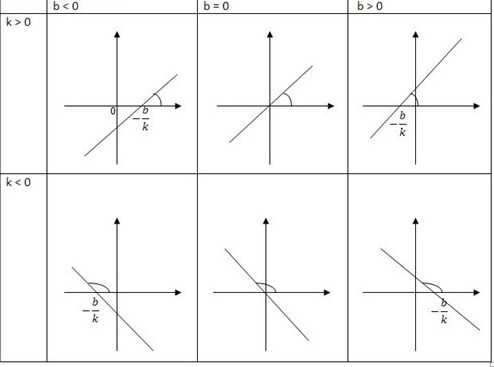
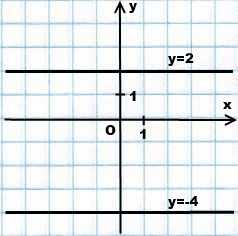
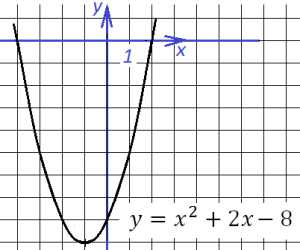
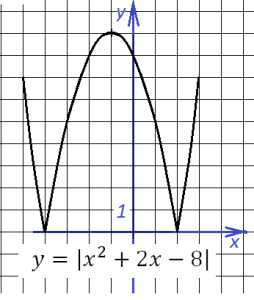
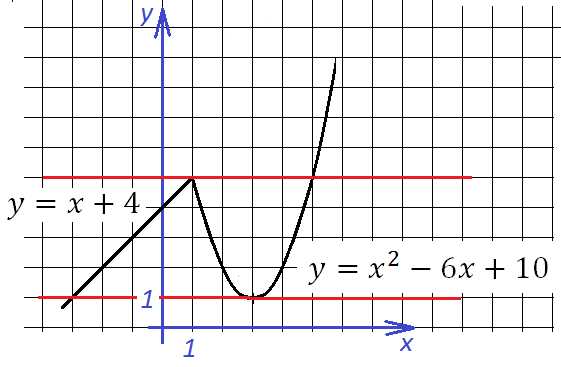
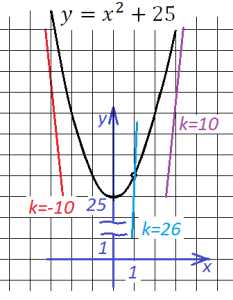
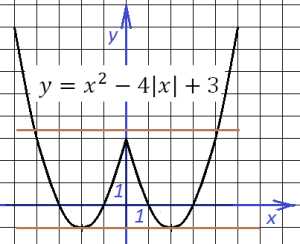
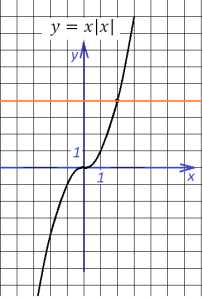

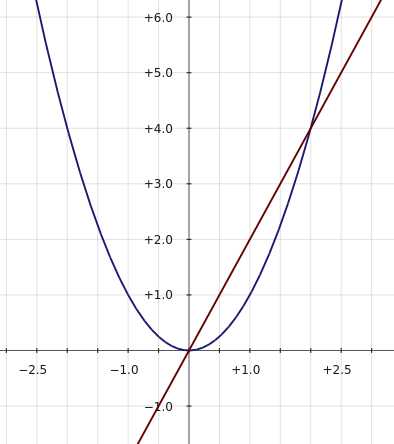
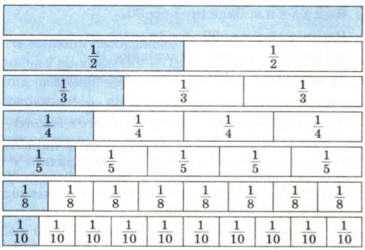 Используя рисунки, сравните части: 1/2 и 1/8; 1/8 и 1/10; 1/3 и 1/2; 1/4 и 1/5. Решение:
Используя рисунки, сравните части: 1/2 и 1/8; 1/8 и 1/10; 1/3 и 1/2; 1/4 и 1/5. Решение:





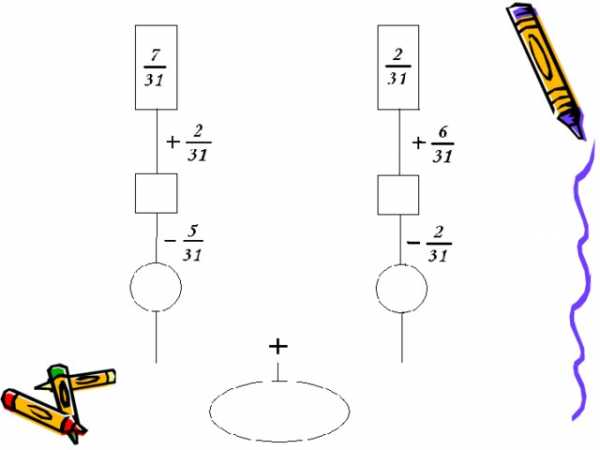





 Изображения в TIF формате позволяют сохранить его максимальное качество, так как они имеют несколько слоев и показывают большую глубину цвета. И, как правило, фотографии не сжаты, в виде многостраничного документа. Иногда их сжимают с помощью JPEG, ZIP, LZW.
Изображения в TIF формате позволяют сохранить его максимальное качество, так как они имеют несколько слоев и показывают большую глубину цвета. И, как правило, фотографии не сжаты, в виде многостраничного документа. Иногда их сжимают с помощью JPEG, ZIP, LZW. Просмотр фотографий Виндовс
Просмотр фотографий Виндовс