дата — это… Что такое дата?
Дата + — Дата+ Год основания 1992 Основатели Институт географии РАН, Ключевые фигуры Ушаков, Алексей Иванович; Орлов Андрей Владиславович Тип ООО Расположение Россия … Википедия
Дата+ — Тип ООО Деятельность геоинформационные системы Год основания 1992 Основатели Институт геогра … Википедия
ДАТА — месяц и число на разного рода документах, бумагах и письмах; указывает на время написания. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. ДАТА числовые данные. День и число на документах; датировать… … Словарь иностранных слов русского языка
дата — ы, ж. date f., нем. Datum, пол. data. 1. Помета на документе, письме и т. п. о времени (год, месяц, число) выдачи документа, написания письма и т. п. БАС 2. Я пишу тебе.. вести из различных мест, и потому, признаюсь, что мне хотелось подражать… … Исторический словарь галлицизмов русского языка
ДАТА — ДАТА, даты, жен. (франц. date) (книжн.). Точное календарное время какого нибудь события. Дата смерти. || Пометка на документе, письме о времени его написания. Вексель без даты не действителен. Дата почтового штемпеля. Ставить дату на документе.… … Толковый словарь Ушакова
дата — число, день; датировка, срок, годовщина, помета Словарь русских синонимов. дата число Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011 … Словарь синонимов
дата — ДАТА, день … Словарь-тезаурус синонимов русской речи
ДАТА — ВЕКСЕЛЬ вексель, срок платежа по которому устанавливается не на какой то определенный день, а через известный промежуток времени (несколько дней, недель или месяцев) с момента его выдачи … Юридический словарь
Дата — проставленное на документе обозначение числа, месяца и года, когда был составлен документ или совершена сделка, операция. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ДАТА — указание числа, месяца и года составления и подписания документа, его вступления в силу. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М.: ИНФРА М. 479 с.. 1999 … Экономический словарь
ДАТА — ДАТА, ы, жен. 1. Календарное время какого н. события. Исторические даты. Знаменательная д. Круглая д. (о дне рождения, юбилее, исчисляемом только десятками. У него сегодня круглая д. сорок лет). 2. Помета, указывающая время (год, месяц, число)… … Толковый словарь Ожегова
dic.academic.ru
ДАТА (функция ДАТА) — Служба поддержки Office
Функция ДАТА возвращает порядковый номер определенной даты.
Синтаксис: ДАТА(год;месяц;день)
Аргументы функции ДАТА описаны ниже.
-
Год — обязательный аргумент. Значение аргумента год может содержать от одной до четырех цифр. Excel интерпретирует аргумент год в соответствии с используемой системой дат, используемой на вашем компьютере. По умолчанию в Microsoft Excel для Windows используется система дат 1900, то есть первой датой считается 1 января 1900 г.
Совет: Во избежание непредвиденных результатов используйте в качестве значения аргумента год четыре цифры. Например, значение «07» может интерпретироваться как «1907» или «2007». Четырехзначное обозначение года предотвращает возникновение путаницы.
-
Если аргумент год находится в диапазоне от 0 (нуль) до 1899 (включительно), Excel для вычисления года прибавляет это значение к числу 1900. Например, функция ДАТА(108;1;2) возвращает 2 января 2008 (1900+108) года.
-
Если аргумент год находится в диапазоне от 1900 до 9999 (включительно), Excel использует это значение как год. Например, функция ДАТА(2008;1;2) возвращает 2 января 2008 года.
-
Если значение аргумента год меньше 0 или больше 9999, Excel возвращает значение ошибки #ЧИСЛО!.
-
-
Месяц — обязательный аргумент. Положительное или отрицательное целое число в диапазоне от 1 (январь) до 12 (декабрь), представляющее месяц года.
-
Если значение аргумента месяц больше 12, аргумент месяц добавляет число месяцев к первому месяцу указанного года. Например, функция ДАТА(2008;14;2) возвращает число, соответствующее 2 февраля 2009 года.
-
Если значение аргумента месяц меньше 1, аргумент месяц вычитает значение этого числа месяцев, увеличенное на 1, из первого месяца указанного года. Например, функция ДАТА(2008;-3;2) возвращает число, соответствующее 2 сентября 2007 года.
-
-
День — обязательный аргумент. Положительное или отрицательное целое число в диапазоне от 1 до 31, представляющее день месяца.
-
Если значение аргумента день больше числа дней в указанном месяце, аргумент день добавляет это число дней к первому дню месяца. Например, функция ДАТА(2008;1;35) возвращает число, соответствующее 4 февраля 2008 года.
-
Если значение аргумента день меньше 1, аргумент день вычитает значение этого числа дней, увеличенное на 1, из первого дня указанного месяца. Например, функция ДАТА(2008;1;-15) возвращает число, соответствующее 16 декабря 2007 года.
-
Примечание: В Excel даты хранятся в виде порядковых номеров, что позволяет использовать их в вычислениях. Дате 1 января 1900 года соответствует номер 1, а 1 января 2008 года — 39448, так как интервал между этими датами составляет 39 447 дней. Чтобы вывести правильную дату, нужно изменить формат ячейки.
Синтаксис: ДАТА(год;месяц;день)
Например, =ДАТА(C2;A2;B2) объединяет значение года из ячейки C2, месяца из ячейки A2 и дня из ячейки B2 и помещает их в одну ячейку в виде даты. В примере ниже показан результат в ячейке D2.
Нужно вставить даты, не используя формулу? Никаких проблем! Вы можете вставить в ячейку текущую дату и время или обновляемую дату. Вы также можете автоматически заполнить ячейки листа данными.
support.office.com
какая дата — Перевод на английский — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
В зависимости от того, какая дата бюджет выбрана, оба бюджета, возможно, можно было бы представлять одновременно каждый второй год.
Depending on what date was chosen, the two budgets possibly could be presented simultaneously every second year.Да, какая дата?
Какая дата на этом мосту?
Какая дата там стоит? — Дата?
Знаешь, какая дата на этой монете?
В этой связи участники совещания пожелали выяснить, какая дата на этапе изготовления цистерн должна считаться контрольной датой для целей применения вступающих в силу новых правил.
The question thus arose as to which date during the construction phase of tanks should be considered to be the application date for new rules that came into force.Кроме того, он хотелось бы узнать, на каком этапе находится процесс принятия нового законопроекта об иностранцах и какая дата предусмотрена для его вступления в силу.
He would also be glad to know what stage the process for the adoption of the new Aliens Bill had reached and the date on which the law was expected to enter into force.Многосторонний фонд имеет срок отсечения 25 июля 1995 года для всех секторов и химических веществ, однако он не принимал решения о том, какая дата отсечения могла бы применяться в случае проектов ГХФУ после приятия Сторонами решения ускорить отказ от ГФХУ.
The Multilateral Fund has had a cut off date of 25 July 1995 for all sectors and chemicals, but has not taken a decision on what cut-off date might apply to HCFC projects in the aftermath of the Parties decision to accelerate the HCFC phase-out.Третьим является вопрос интертемпоральности: какая дата имеет решающее значение для учета норм — дата заключения договора или дата на момент его применения?
The third is the question of inter-temporality: what is the critical date for the rules to be taken into account — the date of the conclusion of the treaty or the law in force at the moment of its application?Какая дата рождения в его паспорте?
Посмотри, какая дата на чеке об оплате хранилища, где мы нашли украденные вещи.
Check out the date on this receipt from the storage locker with the stolen art.4 45% для транспортных средств, зарегистрированных после 1988 года или с даты, указанной в требованиях, в зависимости от того, какая дата наступает позднее.
4 45 % for vehicles registered after 1988 or from the date specified in requirements whichever is the later.После обсуждений в Рабочей группе резолюцией 2054 (2012) Совет Безопасности продлил срок полномочий трех судей, участвующих в рассмотрении дела Нгирабатваре, до 31 декабря 2012 или до даты завершения рассмотрения этого дела в зависимости от того, какая дата наступит раньше.
Following the discussions in the Working Group, the Security Council, by resolution 2054 (2012), extended the terms of office of three trial judges until 31 December 2012 or the completion of the Ngirabatware case, whichever was sooner.ФМПООН объяснил задержку тем, что партнерам предоставляется выбор: представить отчет либо 30 января после завершения проекта, что совпадает с датой представления годовой отчетности, либо через 90 дней после окончания проекта, в зависимости от того, какая дата наступает позднее.
UNFIP attributed the delay to the option given to partners to submit the report either on 30 January following the completion of the project, to coincide with the date of submission of annual reports, or 90 days from the end of the project, whichever was later.постановляет также считать авансы и взносы подлежащими уплате в полном объеме в 30-дневный срок после получения от Генерального секретаря уведомления с предложением произвести платеж или же с 1 января 2000 года — в зависимости от того, какая дата наступит позднее;
Decides also that advances and contributions shall be due and payable in full within 30 days of the receipt of the communication of the Secretary-General requesting payment, or as of 1 January 2000, whichever is the later;context.reverso.net
Калькулятор дней онлайн, или Сколько дней между двумя датами
Расчеты времени постоянно встречаются в повседневной жизни: от вычисления дней до значимой даты до подсчета времени отпуска или периода выплат по банковскому кредиту. Сборник онлайн-калькуляторов поможет вам легко оперировать таким сложным параметром как время.
Время
Управление временем – это не название магического заклинания из компьютерной игры, а вполне себе реальная способность, снискавшая огромную популярность у бизнесменов и инвесторов. Управление временем или тайм-менеджмент – это техника расчета временных отрезков для эффективного выполнения определенного объема работ. Благодаря грамотному планированию рабочего времени и периодов отдыха люди, использующую технику мани-менеджмента, успевают сделать намного больше тех, кто не следит за временем и страдает от прокрастинации.
Естественно, тайм-менеджмент – это наука не только о распределении времени. К наиболее важным навыкам, позволяющим грамотно организовать работу, относятся:
Делегирование – это перепоручение работы подчиненным или коллегам. Многие неэффективные руководители полагают, что никто не сделает лучше, чем они сами. Естественно, что заваленные кучей незначимой работы они не успевают выполнять приоритетные задачи, в результате чего и становятся неэффективными.
Поиск приоритетов – не менее важная вещь. Принцип Парето гласит, что 80 % результата обеспечивают 20 % усилий. На практике это означает, что важно вовремя выполнять только те задачи, от которых зависит 80 % успеха. Как правило, таких задач немного, не строго 20 % как обещает принцип Парето, но обычно в диапазоне от 20 до 40 %. Именно умение отделять зерна от плевел и создают продуктивных руководителей и бизнесменов.
Наиболее известной, эффективной и в тоже время самой простой техникой считается «Помодоро». Это прием тайм-менеджмента, согласно которому работа выполняется через строго отведенные промежутки времени (обычно 20 минут), каждый из которых сопровождается пятиминутным отдыхом. Свое название техника «Помодоро» получила потому, что ее создатель отмерял промежутки времени при помощи кухонного таймера в виде помидора. С тех пор модернизированные версии тайм-менеджмента легли в основу успеха видных представителей бизнеса.
Расчет времени
Использовать принципы мани-менеджмента можно не только при решении ежедневных задач, но и при планировании крупных проектов, выполнение которых занимает недели или месяцы. Прежде всего следует выяснить, к какому сроку необходимо сдать проект или какое количество времени на него выделено. Рассмотрим подробнее.
Количество дней между двумя датами
Данный инструмент позволяет определить количество дней, укладываемых между двумя датами. К примеру, 20 октября 2017 года вам задали проект, который необходимо закончить к 18 января 2018 года. Идти к календарю и считать время не слишком удобно и проще воспользоваться калькулятором: достаточно выбрать тип программы и вбить обе даты. В ответе видим, что на выполнение плана у вас есть 2 месяца и 29 дней. Не слишком информативно при планировании. Программа выражает это время так же в днях, неделях или месяцах. Смотрим. У вас есть ровно 90 дней или 12 рабочих недель. С этим уже можно построить эффективную систему тайм-менеджмента и не допустить дедлайна.
Какая дата будет через n дней
Еще один удобный инструмент для эффективной работы. Крупный проект на работе могут поручить с пометкой «выполнить в течение 50 дней после принятия заказа». Это большое количество времени, но вновь бежать к календарю и высчитывать его не слишком удобно. Используем калькулятор. Допустим, заказ был принят в работу 28 апреля 2017 года. До какого дня его требуется сдать заказчику? Поменяем тип калькулятора и вычислим дату дедлайна. Это будет 17 июня 2017, суббота. Имея под рукой общее количество дней и дату икс, вы можете легко распределить силы для своевременного выполнения работы.
Какая дата была n дней назад
Данный калькулятор не пригодится вам в работе, но наверняка придет на помощь в личной жизни. Представьте, что вы получили смс-сообщение, в котором ваша пассия поздравляет вас с 100 днем совместной жизни. Это важная дата, которую забывать не стоит, поэтому лучше воспользоваться программой и узнать ее. Вы получили смску 4 июля 2017 года, теперь легко узнать, когда же вы съехались со своей пассией. Итак, выбираем тип калькулятора, вводим дату и юбилейные 100 дней. Ваша памятная дата – 26 марта 2017, воскресенье. Стоит обвести эту дату в календаре.
Временные величины
Данный калькулятор позволяет перевести одни временные величины в другие. При помощи программы можно выразить минуты в дни, недели в года или века в тысячелетия. На практике это может пригодиться при расчете рабочих часов для фрилансеров и свободных художников. Например, у вас есть 28 рабочих дней на выполнение очередного заказа. Это 672 часа. Отнимем время на сон 28 × 8 = 224, время на перерывы и отдых 28 × 4 = 112 и получим, что у вас есть 336 часов на эффективную работу. С этим уже можно работать и использовать техники тайм-менеджмента для продуктивного труда.
Сумма/разница во времени
Данная программа дарит возможность сложить часы или дни и вычислить общее время в месяцах, неделях, днях, минутах, секундах и даже в миллисекундах. Это занимательный калькулятор, который на практике можно использовать для подсчета времени, необходимого на выполнение нескольких видов работ или для вычисления свободного времени, оставшегося после завершения работы.
bbf.ru
Какая дата на упаковке
Мы привыкли к тому,как маркируются товары отечественного производства, а вот импортные товары иногда вызывают вопросы. Сегодня мы поговорим только о датах, которые присутствуют в маркировке импортных товаров.
Для еды и напитков наиболее законными считаются два типа маркировочные даты: «Use by» – использовать по указанную дату и «Best before» – годен до указанной даты.
«Use by» означает, что розничный торговец должен обеспечить, чтобы продукт после этой даты не предлагался покупателям. То есть, после даты «Use by» продукт не должен продаваться.
«Best before» означает, что продукт имеет наилучшее качество до указанной даты. После этой даты, качество будет постепенно ухудшается. В отличие от «Use by» закон позволяет продавать продукты после даты «Best before». Эта маркировка используется на продуктах, которые являются менее скоропортящимися.
Иногда можно встретить следующие маркировки: «display until» (показывать, предлагать до) и «sell by» (продавать по). Чаще всего, «display until» и «sell by» указывают на даты, предшествующие на два или три дня до «Use by» или «Best before. Эти альтернативные маркировки не имеют правового значения. Они — изобретение продавцов, предназначенное для удобства и ускорения продаж.
 На непродовольственных товарах можно встретить следующие типы дат: «Date of manufacture/production» (дата изготовления или производства), «Expiry date» (дата истечения срока годности), «Recommended life once the product has been opened or put into use» (рекомендованный срок службы после открытия товара или начала эксплуатации). Чаще всего эти даты используются на таких непродовольственных товарах, как зубная паста, косметика, батарейки и т.д. Следует отметить, что при маркировке возможны сокращения. Например, пишется EXP SEP 93 вместо EXPIRY DATE: SEP 93, MFD 7/91 вместо MANUFACTURED 7/91 или PROD 08/95 вместо PRODUCTED 08/95.
На непродовольственных товарах можно встретить следующие типы дат: «Date of manufacture/production» (дата изготовления или производства), «Expiry date» (дата истечения срока годности), «Recommended life once the product has been opened or put into use» (рекомендованный срок службы после открытия товара или начала эксплуатации). Чаще всего эти даты используются на таких непродовольственных товарах, как зубная паста, косметика, батарейки и т.д. Следует отметить, что при маркировке возможны сокращения. Например, пишется EXP SEP 93 вместо EXPIRY DATE: SEP 93, MFD 7/91 вместо MANUFACTURED 7/91 или PROD 08/95 вместо PRODUCTED 08/95.
Теперь, встретив на упаковке надпись из букв PROD и цифр 03 2017, вы будете знать, что она обозначает дату производства (изготовления) товара, а следующая надпись EXP 09/00 означает дату истечения срока годности.
x-prod.ru
Какая дата будет через 100 дней?
| Вы ввели следующее выражение |
| Полученный результат вычислений |
Когда мы наконец то научились получать по нашей (григорианской) дате — полную юлианскую дату Юлианская дата и григорианский календарь, становится прозаичной задача по вычислению разницы в днях(сутках) между двумя произвольными(!) датами.
Надо лишь вычесть из большей даты(в формате юлианского дня) меньшую и мы получим количество суток прошедших между этими датами.
Измерение времени, как и все другие измерения, заключается в сравнении измеряемого интервала времени с промежутком времени, принятым в качестве единицы. Основной единицей времени когда-то были приняты сутки. Это не случайно, ибо человек ежедневно убеждался в регулярности смены дня и ночи. Люди всегда соразмеряли и сообразовывали свою деятельность со сменой ночи и дня. Сутки — это промежуток времени, соответствующий полному периоду
вращения Земли вокруг своей оси относительно направления на некоторую точку в межпланетном пространстве.
На практике мы пользуемся более мелкими единицами времени. Это — часу минута, секунда которые являются производными от основной единицы — суток. Час равен 1 : 24, минута — 1 : 1440 и секунда — 1 : 86 400 части суток.
Заметим, что если сутки соответствуют времени поворота Земли вокруг своей оси на угол в 360 , то час, минута и секунда соответственно — на угол 15°, 15′ , 15″
Хотелось бы заметить, что вычитая из 31 декабря 2013 года, 1 января 2013 года вы получите 364 дня, а не 365 дней, как некоторым хотелось думать.
Все дело в том, что 1 секунда от полночи 1 января это Новый Год плюс одна секунда, а вот 1 секунда от полночи 31 января 2013 года, это совсем не Новый Год. До него еще осталось 23 часа 59 минут и 59 секунд.
Вот именно поэтому и получается 364 дня.
Программа не учитывает праздники РФ. Для этого появился новый сервис Калькулятор расчета количества рабочих дней. Универсальный, пригоден для всех стран, выходные можно ставить любые в пределах недели. Вообщем не калькулятор, а мечта! 🙂
Что же еще может этот бот?
Если Вы введете просто дату в формате день/месяц/год, то бот ответит вам днем недели, который приходится на эту дату.
Ели вы напишите разницу между двумя датами, то бот рассчитает количество суток, а также часов,минут и секунд разделяющие эти даты.
Если вы напишите дату и прибавите или отнимите число то получите дату которая наступит (или прошло) через указанное Вами число.
Если же вопрос имеет вид » определить количество месяцев между датами», то такой банальный ответ( зная, что в году 12 месяцев) боту не под силу 🙂
Бот конечно же универсален и легок в использовании, но даже он рассчитывает на какое то присутствие ума и знания устного счета у пользователя.
Еще немного информации о времени для любознательных:
Путешествуя на речных и морских судах, мы, хоть и слышим, как отбивают «склянки», но не осознаем их смысл.
Попробуем разобраться в этой традиции мореходов. Склянка — получасовой промежуток времени.
Само название этой единицы времени связано с известными нам песочными часами — стеклянной колбой с узким горлышком.
На парусном флоте использовали такие часы на 0,5 и 4 ч. Переворачивая получасовую «склянку» вахтенный матрос бил в судовой колокол. Причем, отсчет времени на корабле идет не с полуночи, а с полудня, т.е. с 12 часов, когда бьют рынду (троекратный бой в судовой колокол, последний и следует называть колоколом, а не рындой). В 12 часов 30 минут бьют один раз, в 13 часов — два раза (две склянки) и т.д. до 4 часов пополудни, когда в старое время били 8 склянок и переворачивали одновременно четырехчасовую и получасовую склянки. В 4 часа 30 минут бьют опять 1 склянку — начинают отсчет сначала. Особый шик при отбитии склянок — маленькая пауза после каждого четного удара.
На современных судах и кораблях песочные часы есть разве в медпункте, но вахтенные «бьют склянки» исправно, глядя на вполне современные часы.
Часы, точно идущие на полюсе Земли, при переносе на экватор будут отставать на 3 мин 12 с. Речь идет о маятниковых часах, на которые оказывает
влияние ускорение силы тяжести, а оно на экваторе меньше, чем на полюсе на 0,052 м/с2.
Примеры
Рассчитать разницу между двумя датами
22 июля 2013 года и 28 февраля 2010 года
так и пишем
dat 22/07/2013-28/02/2010
Разница между датами составляет
суток — 1240 часов — 0 минут — 0 секунд — 0
Очень просто, не правда ли?
Рассчитать разницу между двумя датами
23 февраля 2014 года 13 часов 37 минут 19 секунд и 8 марта 2015 года 23 часа 41 минута и 49 секунд
считаем
dat 23/02/2014/13/37/19-08/03/2015/23/41/49
Разница между датами составляет
суток — 378
часов — 10
минут — 4
секунд — 30
Какая дата будет если к 15 октября 2013 года прибавить 200 дней
пишем
dat 15/10/2013+200
По результатам вычислений получили что ответ содержит дату
год — 2014
месяц — 5
день — 3
час — 0
минута — 0
секунда — 0.00
3 мая 2014 года
Чудесно!
А если отнять 10 тысяч суток от 31 января 2014 года, какую получим дату?
пишем dat 31/12/2014-10000
По результатам вычислений получили что ответ содержит дату
год — 1987
месяц — 8
день — 15
час — 0
минута — 0
секунда — 0.00
15 августа 1987 года!
- Калькулятор расчета количества рабочих дней >>
abakbot.ru





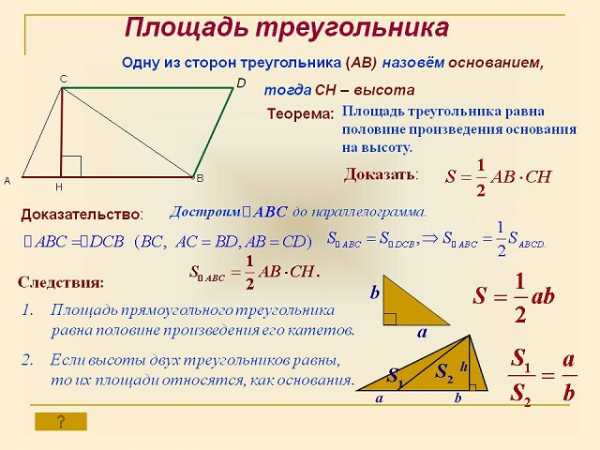

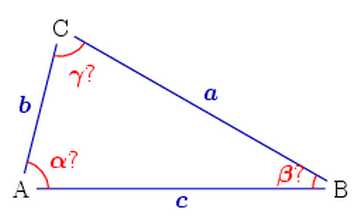 Точки называются вершинами, а отрезки сторонами. Для расчета треугольника существует множество формул, которые помогают найти как длины сторон, радиусы углов и прочие составляющие фигуры, так и площадь треугольника.
Точки называются вершинами, а отрезки сторонами. Для расчета треугольника существует множество формул, которые помогают найти как длины сторон, радиусы углов и прочие составляющие фигуры, так и площадь треугольника.




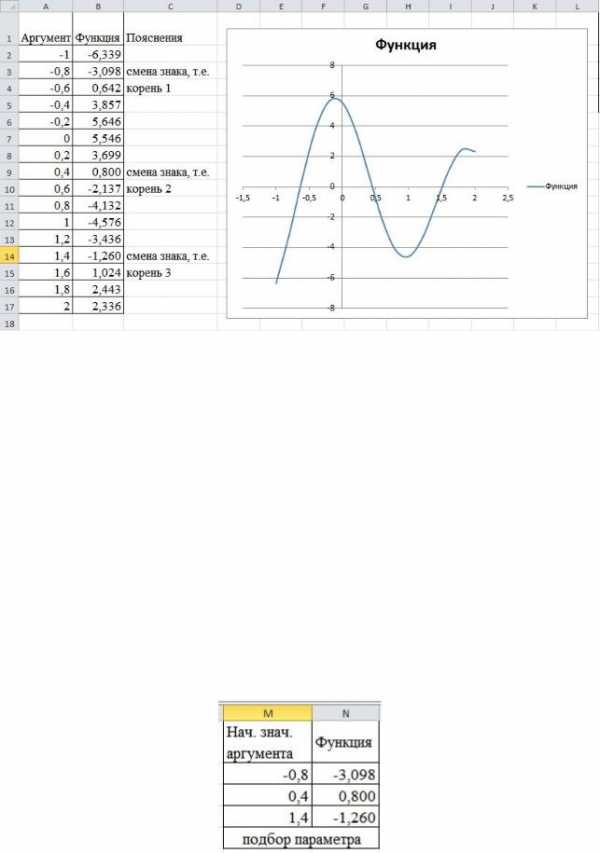
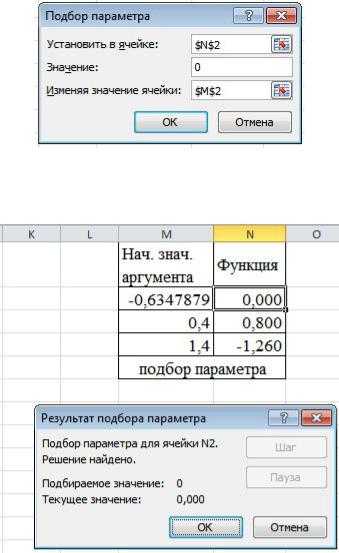
 с координатами
стремится к точке
сгущения некоторого множества
с координатами
стремится к точке
сгущения некоторого множества  ,
если
,
если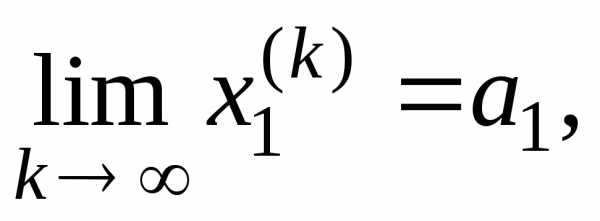
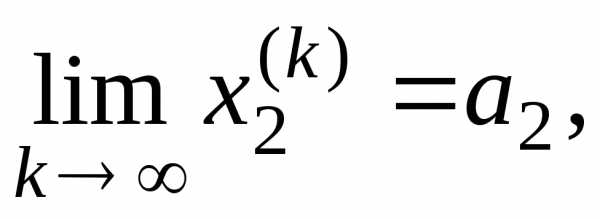 …,
…,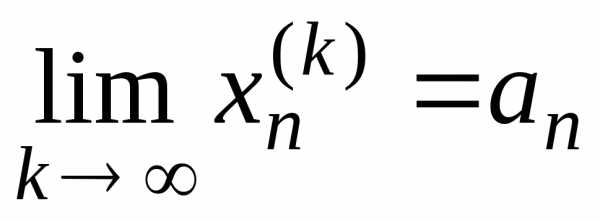 .
.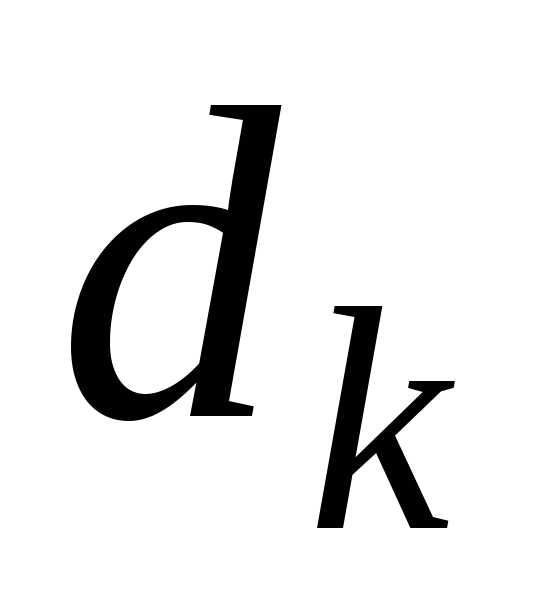 между точкамипоследовательности
и точкой
,
когданеограниченно возрастает, стремится
к нулю, т.е.
между точкамипоследовательности
и точкой
,
когданеограниченно возрастает, стремится
к нулю, т.е.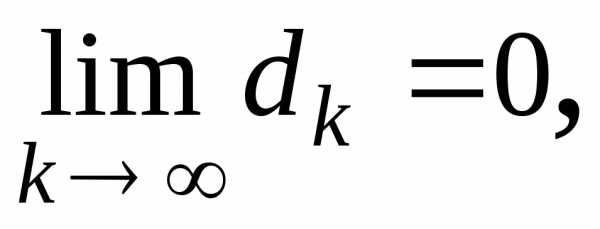
 =
= 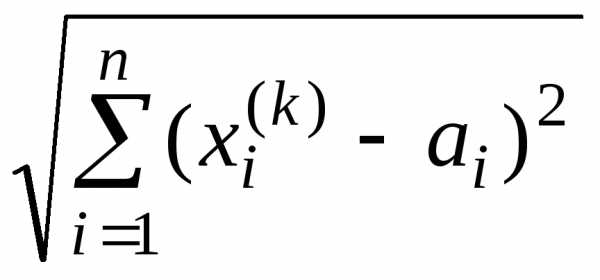 =
.
=
.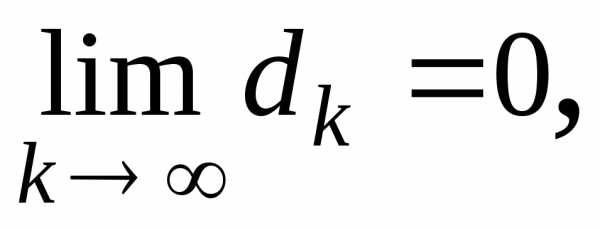 то последовательность точекстремится к точке.
то последовательность точекстремится к точке. ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки 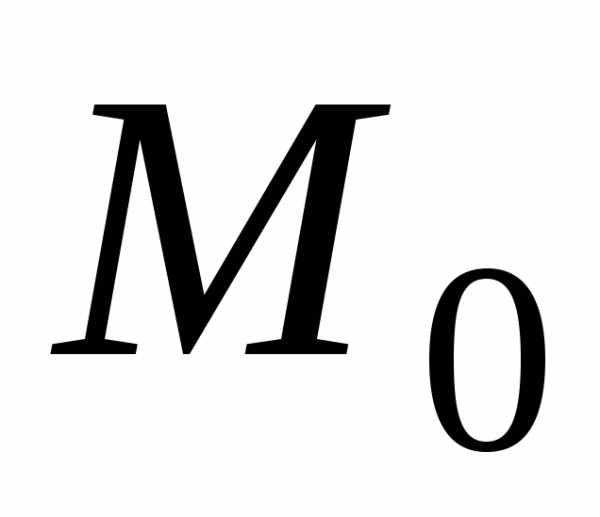 .
. при стремлении
переменных
,соответственно,
к
,если для каждого
сколь угодно малого наперед заданного
положительного числа
при стремлении
переменных
,соответственно,
к
,если для каждого
сколь угодно малого наперед заданного
положительного числа  (эпсилон) существует такое число
(эпсилон) существует такое число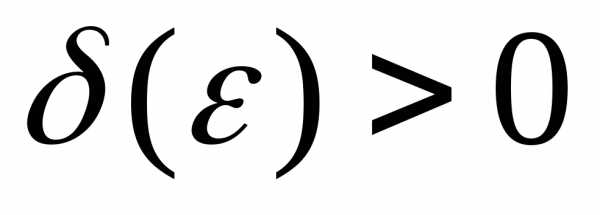 ,
что
,
что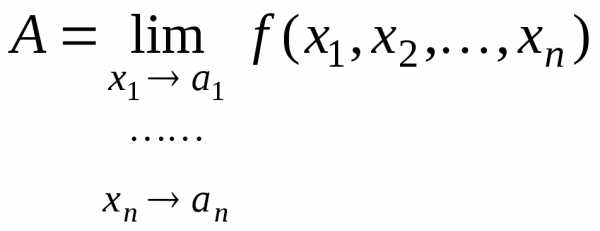 .
. являетсяпределом
функции
являетсяпределом
функции 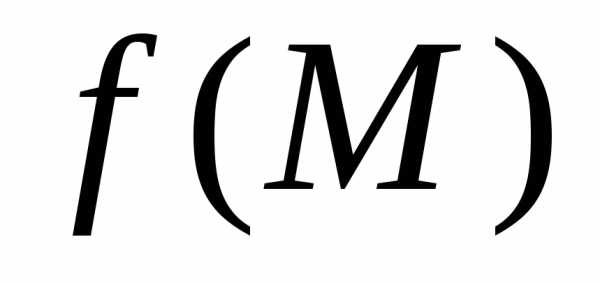 при стремлении
точки
при стремлении
точки  к точке
к точке (или – пределом функции
(или – пределом функции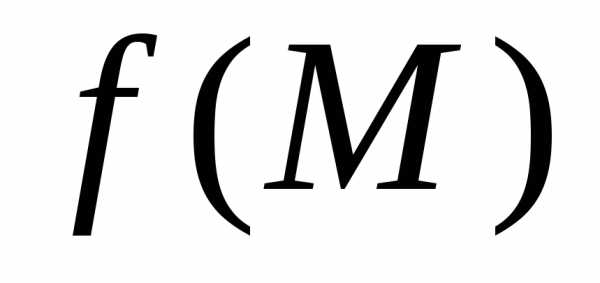 в точке
в точке 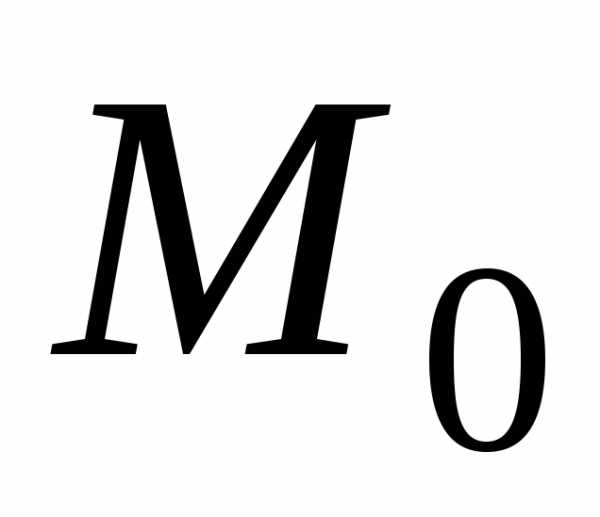 ),
если для каждого сколь угодно малого
наперед заданного положительного числа
),
если для каждого сколь угодно малого
наперед заданного положительного числа  существует такое число
существует такое число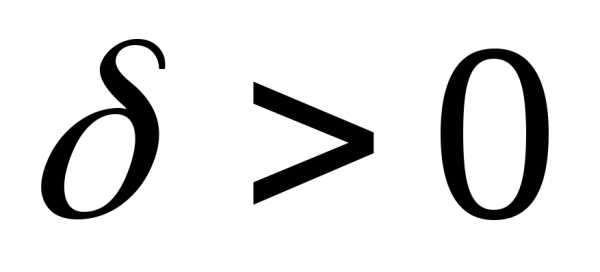 ,
что
,
что )
) предполагается взятой изD и отличной
от
предполагается взятой изD и отличной
от  ,
а неравенство для функции должно
выполняться во всех точках множества D,
лежащих в достаточно малой сферической окрестности точки
,
а неравенство для функции должно
выполняться во всех точках множества D,
лежащих в достаточно малой сферической окрестности точки 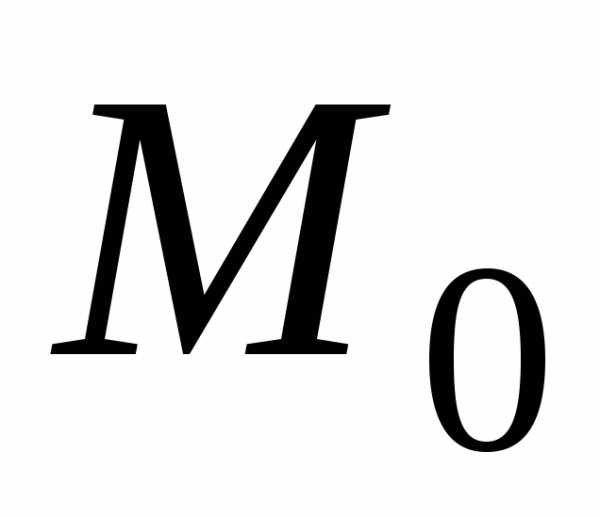 ,
за исключением самой этой точки.
,
за исключением самой этой точки. ,
и
,
и – произвольное наперед заданное сколь
угодно большое положительное число.
– произвольное наперед заданное сколь
угодно большое положительное число. при стремлении
переменных к
при стремлении
переменных к 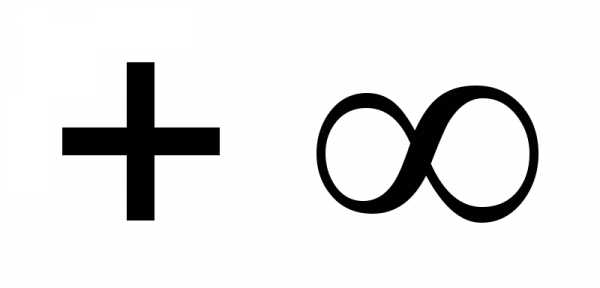 ,
если для каждого сколь угодно малого
наперед заданного положительного числа
,
если для каждого сколь угодно малого
наперед заданного положительного числа существует такое число
существует такое число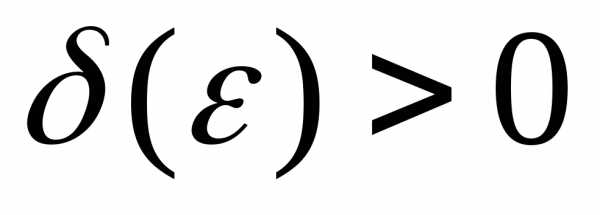 ,
что
,
что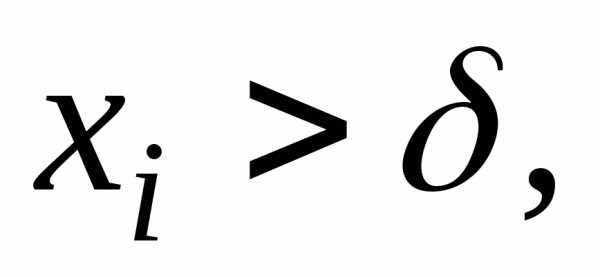
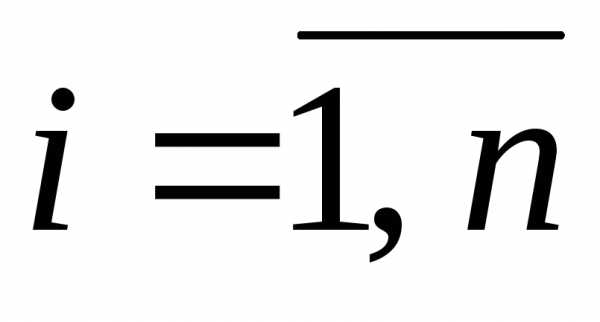 .
.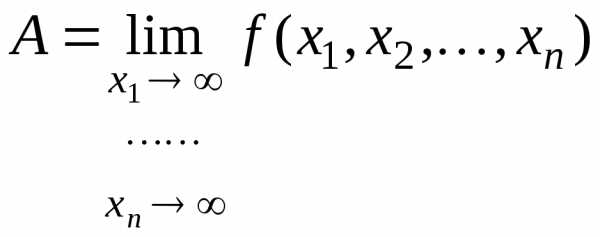 .
.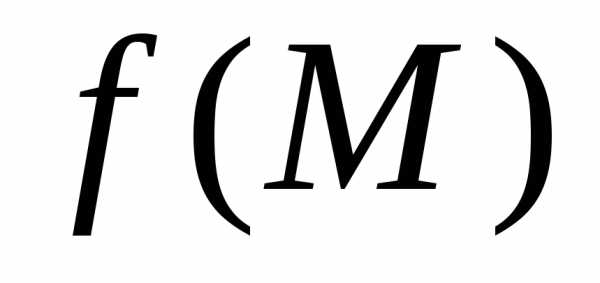 в точке
в точке формулирует следующая теорема.
формулирует следующая теорема.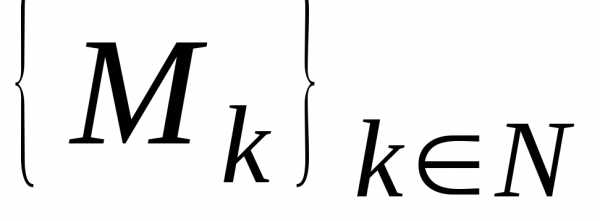 отличных от
отличных от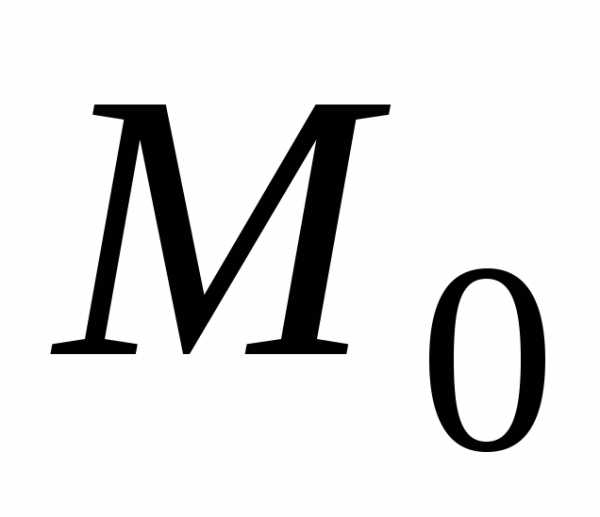 точек, сходящуюся к
точек, сходящуюся к ,
то числовая последовательность,
состоящая из соответствующих значений
функции, всегда сходится к.
,
то числовая последовательность,
состоящая из соответствующих значений
функции, всегда сходится к.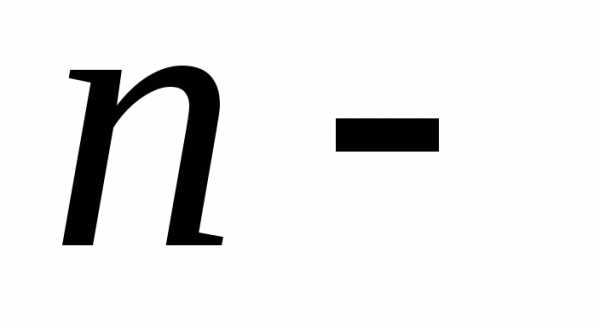 кратным(илидвойным, тройным и т.д. –
при,
соответственно).
кратным(илидвойным, тройным и т.д. –
при,
соответственно).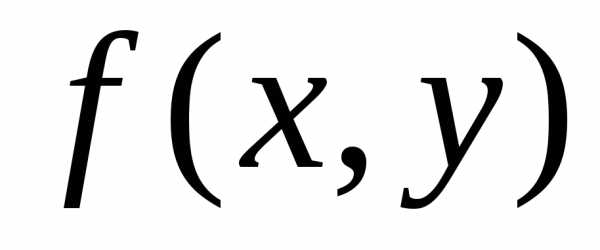 .
Пусть областьDизменения переменных
.
Пусть областьDизменения переменных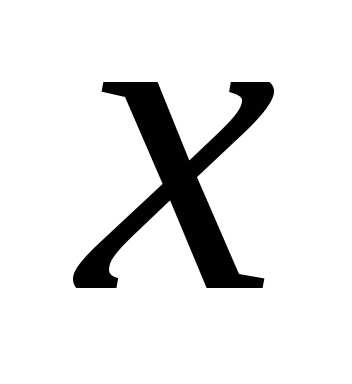 и
и такова, что
такова, что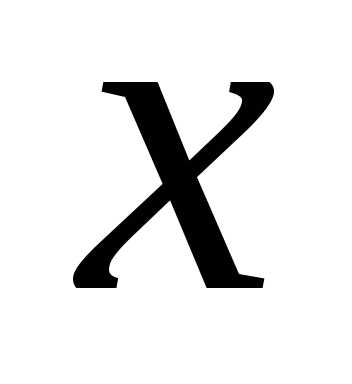 независимо от
независимо от  может принимать любое значение из
некоторого множества
может принимать любое значение из
некоторого множества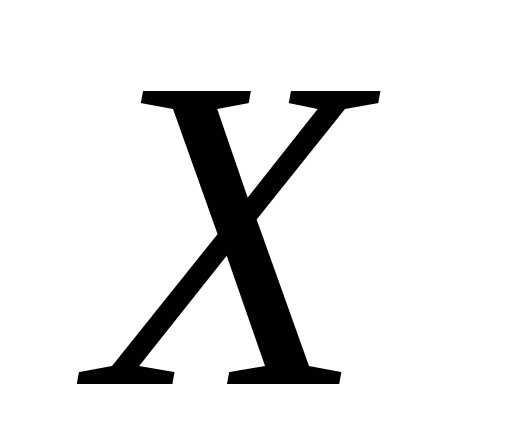 ,
для которого
,
для которого служит точкой сгущения, но не принадлежит
ему, а переменная
служит точкой сгущения, но не принадлежит
ему, а переменная ,
тоженезависимо от
,
тоженезависимо от  ,
– любое значение из множества
,
– любое значение из множества с не принадлежащей ему точкой сгущения
с не принадлежащей ему точкой сгущения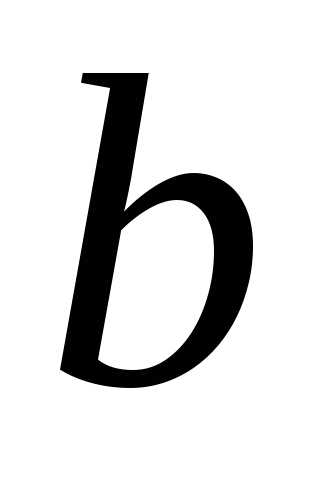 .
Тогда областьD.
.
Тогда областьD.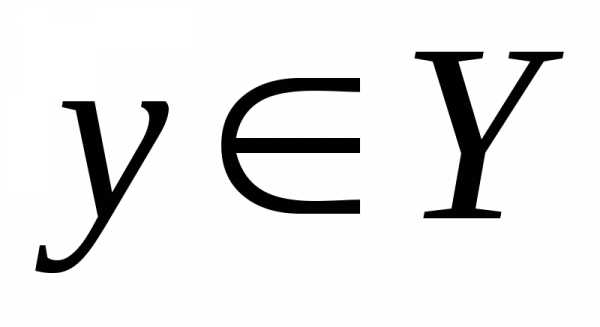 для функции
для функции (которая при фиксированном
(которая при фиксированном будет функцией одной переменной
будет функцией одной переменной )
существует предел при,
то он, этот предел, вообще говоря, будет
зависеть от зафиксированного
)
существует предел при,
то он, этот предел, вообще говоря, будет
зависеть от зафиксированного :
: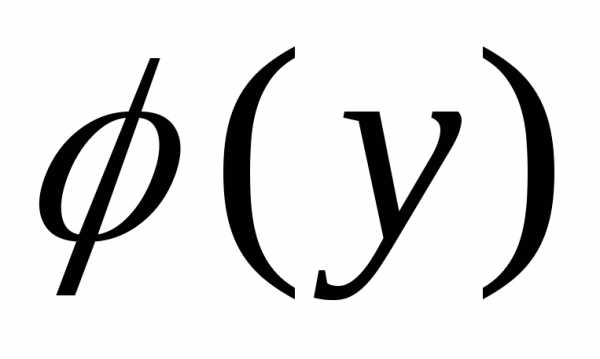 при
при ,
,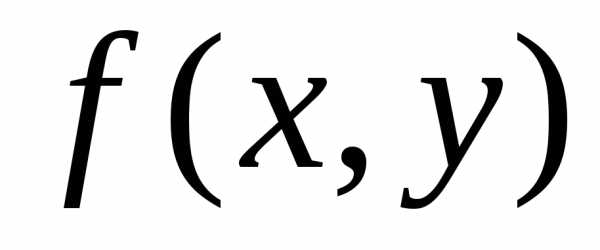 .
. 3.
3. .
.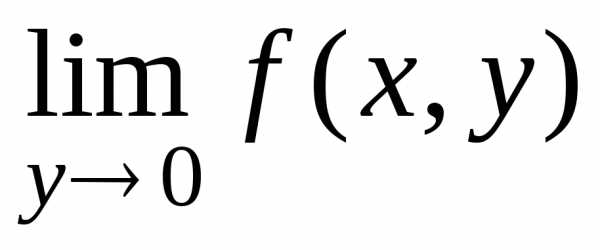 .Проверьте!
.Проверьте! и
и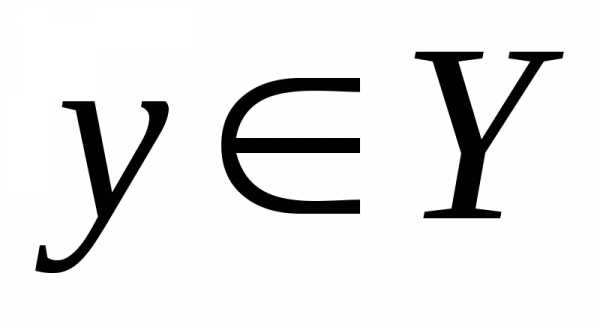 существуетконечный простой предел
по
существуетконечный простой предел
по 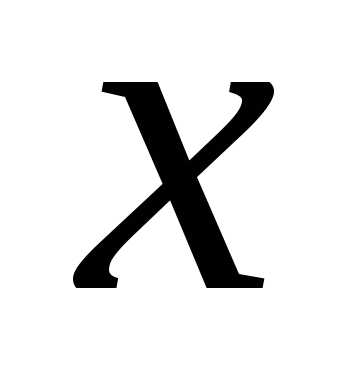
 .
.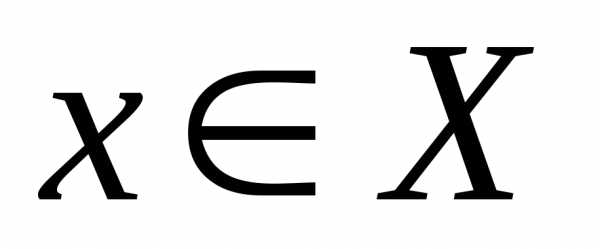 существуетконечный простой предел
по
существуетконечный простой предел
по 
 определена на всей плоскости
определена на всей плоскости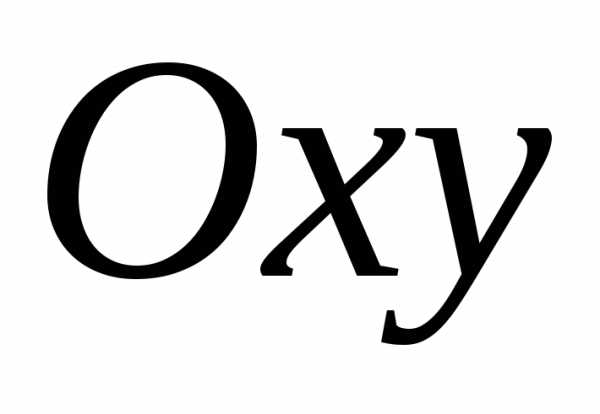 за исключением точки
за исключением точки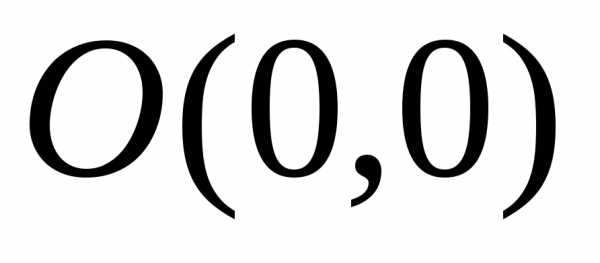 .
.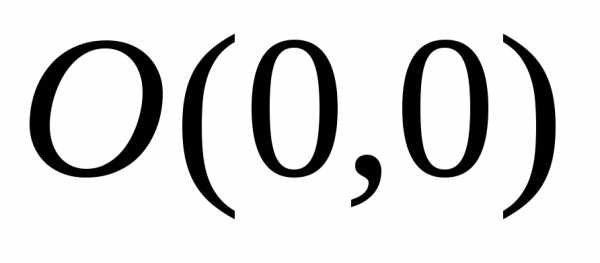 последовательности точек из области
последовательности точек из области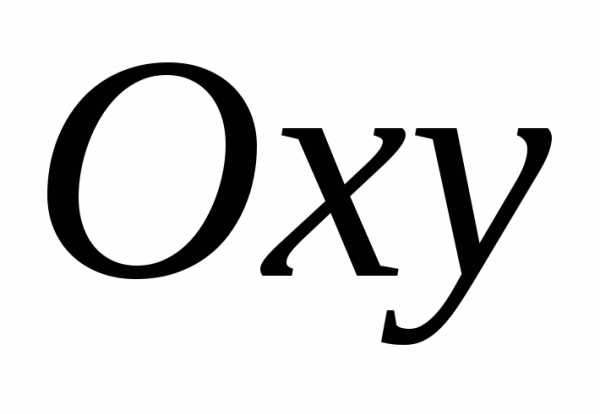 :
: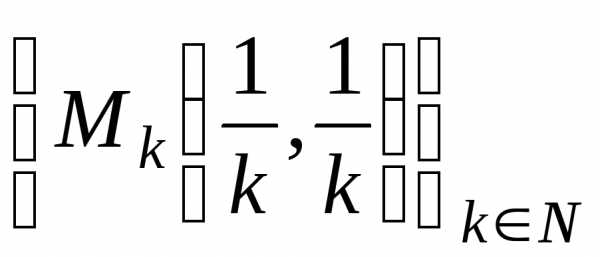 и
и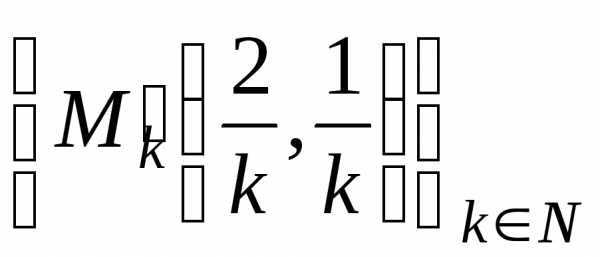 .
. не существует.
не существует.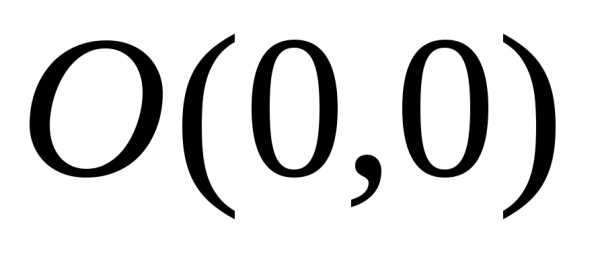 существуют и оба равны 0, хотя двойного
предела данная функция в данной точке
не имеет.
существуют и оба равны 0, хотя двойного
предела данная функция в данной точке
не имеет. ,.
,.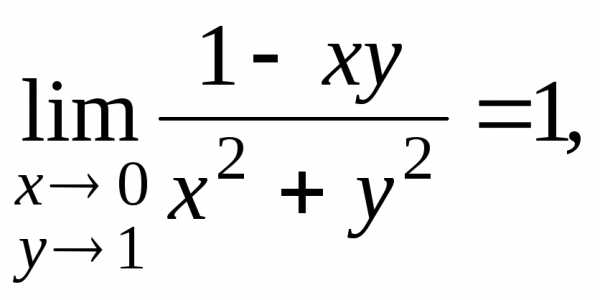 ,.
,.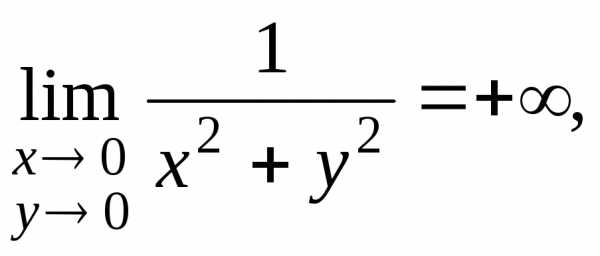 ,.
,.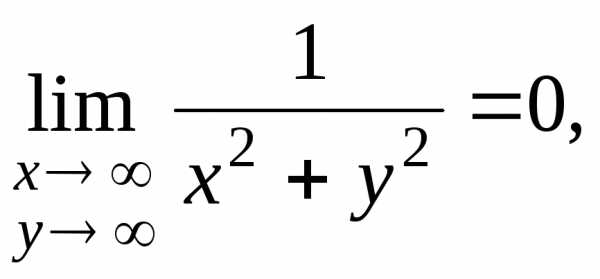 .
.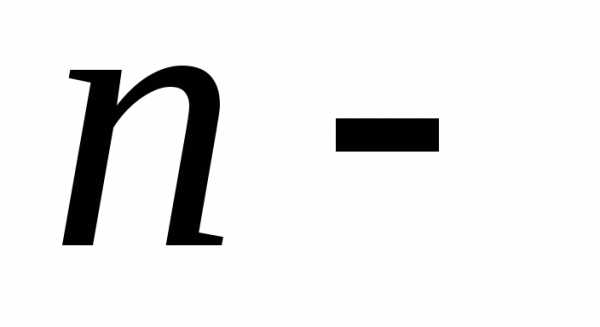 мерного пространства, и– точка сгущения этого множества,принадлежащая самому множеству,
т.е.
мерного пространства, и– точка сгущения этого множества,принадлежащая самому множеству,
т.е.  D.
D. найдется такое число
найдется такое число ,
что
,
что ,
или
,
или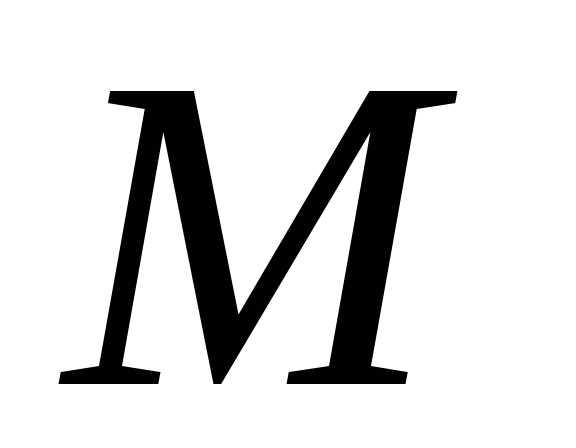 не совпадалаc
не совпадалаc  становится лишним.
становится лишним. функций есть непрерывная в этой точке
функция, если, конечно, в случае частного,
функция, стоящая в знаменателе, в точке
функций есть непрерывная в этой точке
функция, если, конечно, в случае частного,
функция, стоящая в знаменателе, в точке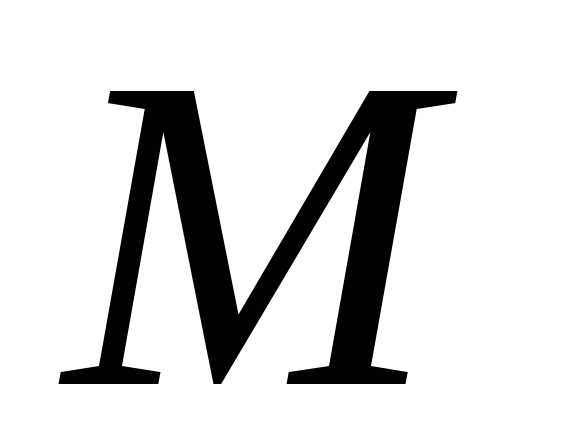 не обращается в ноль.
не обращается в ноль. переменных, если она может быть получена
из этих переменных и констант при помощи
конечного числа алгебраических операций.
переменных, если она может быть получена
из этих переменных и констант при помощи
конечного числа алгебраических операций. .
.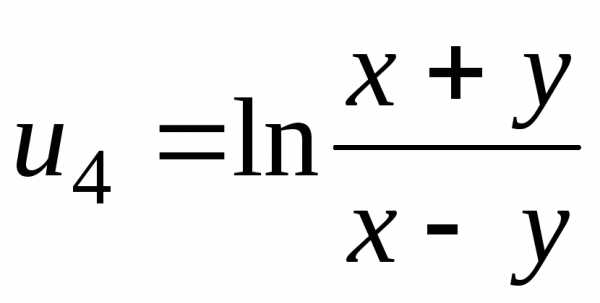 определена и непрерывна только в тех
точках, в которых дробь
определена и непрерывна только в тех
точках, в которых дробь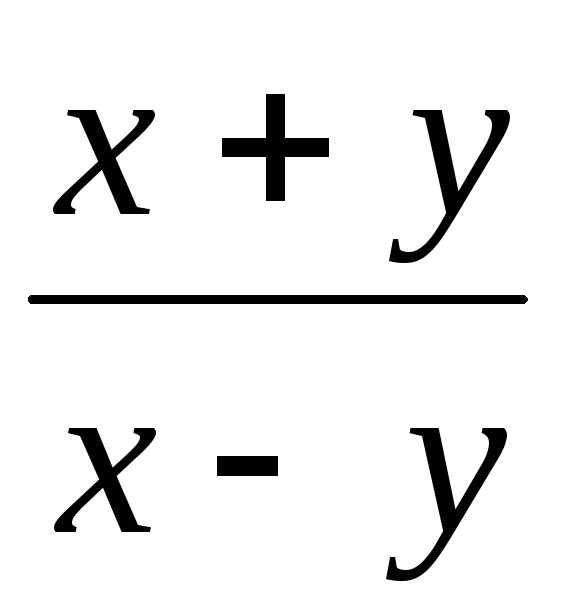 неотрицательна, а знаменатель этой
дроби не равен нулю.
неотрицательна, а знаменатель этой
дроби не равен нулю.