Пайонер калькулятор — вся информация по блокчейну, криптовалютам и майнингу
В наше время слова «Майнинг», «Блокчейн», «Биткоины» раздаются буквально отовсюду: от пассажиров трамвая до серьёзных бизнесменов и депутатов Госдумы. Разобраться во всех тонкостях и подводных камнях этих и смежных понятий сложно, однако в базе данных на нашем сайте Вы быстро найдёте исчерпывающую информацию, касающуюся всех аспектов.
Пайонер калькуляторВкратце же все необходимые знания будут изложены в этой статье.
Итак, начать стоит с блокчейна. Суть его в том, что компьютеры объединяются в единую сеть через совокупность блоков, содержащую автоматически зашифрованную информацию, попавшую туда. Вместе эти блоки образуют базу данных. Допустим, Вы хотите продать дом. Оформив документы, необходимо идти к нотариусу, затем в присутствии его, заверив передачу своей подписью, Вам отдадут деньги. Это долго, да и к тому же нужно платить пошлину.
Благодаря технологии блокчейна достаточно:
- Договориться.
- Узнать счёт получателя.
- Перевести деньги на счёт получателя.
…и не только деньги. Можно оформить электронную подпись и отправлять документы, любую другую информацию, в том числе и конфиденциальную. Опять же, не нужны нотариусы и другие чиновники: достаточно идентифицироваться Вам и получателю (будь то частное лицо или госучреждение) в своём компьютере.
Транзакция проходит по защищённому каналу связи, никто не видит (в том числе банки и государство), кто, что и кому перевёл.
Возможность взломать исключена из-за огромного количества блоков, описанных выше. Для хакера нужно подобрать шифр для каждого блока, что физически нереально.
Другие возможности использования блокчейна:
- Страхование;
- Логистика;
- Оплата штрафов
- Регистрация браков и многое другое.
С блокчейном тесно связано понятие криптовалюта. Криптовалюта — это новое поколение децентрализованной цифровой валюты, созданной и работающей только в сети интернет. Никто не контролирует ее, эмиссия валюты происходит посредством работы миллионов компьютеров по всему миру, используя программу для вычисления математических алгоритмов.
Вкратце это выглядит так:
1. Вы намереваетесь перевести кому-то деньги.
2. Генерируется математический код, проходящий через уже известные Вам блоки.
3. Множество компьютеров (часто представляющих собой совокупность их, с мощными процессорами и как следствие большей пропускной способностью) обрабатывают цифровую информацию, передавая их на следующие блоки, получая за это вознаграждение (некоторые транзакции можно совершать бесплатно)
4. Математический код доходит до электронного кошелька получателя, на его балансе появляются деньги.
Опять же, как это в случае с блокчейном, переводы криптовалют никем не контролируются.
Хотя база данных открыта, со всеми адресами переводящих и получающих деньги, но владельца того или иного адреса, с которого осуществляется перевод, никто не знает, если только хозяин сам не захочет рассказать.
Пайонер калькуляторРаботающих по подобному принципу валют много. Самой знаменитой является, конечно, биткоин. Также популярны эфириум, ритл, лайткоины, нумитсы, неймкоины и многие другие. Разница у них в разном типе шифрования, обработки и некоторых других параметрах.
Зарабатывают на технологии передачи денег майнеры.
Это люди, создавшие упомянутую выше совокупность компьютерных видеокарт, которая генерирует новые блоки, передающие цифровую информацию — биткоины (или ритлы, или любую другую криптовалюту). За это они получают вознаграждение в виде той же самой криптовалюты.
Существует конкуренция между майнерами, т.к. технология с каждой транзакции запрограммировано усложняется. Сначала можно было майнить с одного компьютера (2008 год), сейчас же такую валюту как биткоин физическим лицам уже просто невыгодно: нужно очень много видеокарт (их все вместе называют фермами), с огромными вычислительными мощностями. Для этого снимаются отдельные помещения, затраты электроэнергии для работы сравнимы с затратами промышленных предприятий.
Зато можно заработать на других, менее популярных, но развивающихся криптовалютах. Также различают соло майнинг и пул майнинг. Соло — это создание своей собственной фермы, прибыль забирается себе. Пул же объединяет других людей с такими же целями. Заработать можно гораздо больше, но придётся уже делиться со всеми.
Перспективами использования технологии блокчейна вообще и криптовалют в частности заинтересовались как и физические лица, так и целые государства.
В Японии криптовалюта узаконена. В России в следующем году собираются принять нормативно-правовые акты о легализации блокчейна, переводов криптовалюты и майнинга. Планируется перевод некоторых операций в рамки блокчейна. Имеет смысл изучить это подробнее, и, при желании, начать зарабатывать. Очевидно, что сейчас информационные технологии будут развиваться и входить в нашу жизнь всё больше и больше.
safe-crypto.me
Карта payoneer тарифы и регистрация в сервисе
Приветствую вас, дорогие друзья! Если кто-либо из вас знаком с электронной коммерцией или работает во фрилансе с заказчиками из других стран, то вопрос вывода заработанных средств стоит для вас крайне остро. Будучи жителем России или Украины, или Беларуси, или любого другого государства постсоветского пространства, вы, так или иначе, да сталкиваетесь с проблемой получения средств из-за рубежа. Обычные банковские переводы использоваться в качестве платежного инструмента не могут по причине огромных комиссий. Прибегая к этому способу оплаты вашего труда или товаров, которые вы продали зарубеж, ваша деятельность тут же превращается в убыточную. Здесь нужен совершенно другой подход. Идеально, конечно, если бы можно было получить деньги прямо на карточку или же вывести на электронный кошелек. Сегодня мы с вами можем перестать мечтать об этом, ведь теперь каждому доступна для заказа карта payoneer, предназначенная как раз-таки для получения платежей от иностранных компаний.
Небольшой экскурс в историю платежной системы
Итак, для начала предлагаю выяснить, что это за ягодка такая – платежная система Payoneer? Для этого имеется смысл отойти к истокам истории. Так, американская компания Пайонер появилась на рынке в 2005 году. Находится главный офис корпорации в Нью-Йорке. Payoneer входит в топ-100 компаний, предоставляющих финансовые услуги, по результатам рейтинга INC. Среди услуг, которые предлагает своим клиентам компания, можно найти множество зарплатных проектов. Но я хочу остановиться именно на тех услугах, которые могут быть полезны для нас с вами.
По состоянию на сегодняшний день держателями пластиковой карты этой платежной системы являются свыше трех миллионов людей на всем земном шаре. Разумеется, большая их часть – это фрилансы, в числе которых, несомненно, найдется немало тех, кто проживает в России. Доступна для заказа карта и в Беларуси, и в Казахстане, и в Украине. Всего компания обслуживает клиентов из более, чем 200 стран, поддерживая тем самым работу с примерно таким же числом национальных валют.

Главным достоинством карты Payoneer, безусловно, является моментальный вывод средств, полученных от иностранных плательщиков из Европы и Америки. Нужно отметить и то, что если сравнить тарифы этой компании с другими способами вывода денег, то вы просто поразитесь, насколько ниже будут ставки в случае с Пайонер. Основным инструментом платежной системы является самая обыкновенная дебетовая карта Пайонер MasterCard. С ее помощью вы можете рассчитаться за любые услуги в сети интернет, перевести деньги в электронную валюту, оплатить покупки в магазине или же обналичить средства в ближайшем банкомате.
Поскольку Payoneer расположена в Соединенных Штатах, деятельность компании регулируется строгими американскими и международными законами и ограничениями, среди которых Know Your Customers, Bank Secrecy Act и Anti-Money Laundering. Если у кого-то из вас возникают сомнения относительно надежности данной компании, настоятельно советую вам изучить перечень компаний, которые сотрудничают с Пайонер, и все ваши сомнения развеются как пыль.
к содержанию ↑
Достоинства системы
Чтобы вы окончательно убедились в эксклюзивности и необходимости карты Пайонер, предлагаю вам ознакомиться с перечнем ее достоинств:
- Payoneer – это простейший и удобнейший способ для вывода средств, полученных от иностранных компаний.
- Чтобы получить деньги из-за рубежа, не нужно будет открывать свой личный счет в западном банке.
- Вести карточный счет можно как в долларах, так и в евро, конвертируя тем самым валюту при выводе по текущему курсу.
- Для вывода денег нужно всего два часа времени.
- Снять деньги можно в любом терминале как долларах, так и в евро, и даже в местной валюте.
- Картой можно рассчитаться за любые покупки в интернете или в режиме оффлайн.
- Снимая деньги с карты в банкомате, у вас будет возможность самостоятельно определиться с тарифом конвертации: выбрать курс банка или вывести деньги по курсу системы MasterCard.
- Денежный счет будет доступен вам в любой точке мира. Для того, чтобы воспользоваться им, достаточно будет найти рабочую сеть Интернет.
- Управлять счетом вы можете из личного кабинета в системе Payoneer. Сервис хорош своей простотой и функциональностью.
- Имея карту Пайонер, вы сможете обменивать валюту, обналичивать электронные деньги и осуществлять переводы средств частным лицам.
- В любое время дня и ночи консультанты компании готовы прийти вам на помощь, оказать техническую поддержку в режиме онлайн.
Если мне удалось убедить вас в том, что пластик payoneer – это удобный и очень полезный инструмент для получения платежей из-за рубежа для тех, кто привык работать удаленно и относит себя к числу фрилансеров, то давайте разберемся, как нам получить этот продукт и начать пользоваться всеми его возможностями.
к содержанию ↑
Как зарегистрироваться в сервисе?
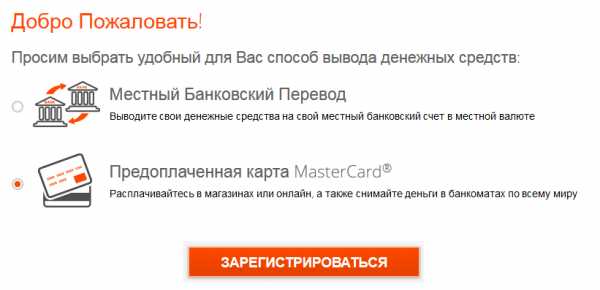 Процесс регистрации в системе Пайонер не займет у вас много времени. Для того, чтобы заказать карту, вам нужно будет всего лишь поочередно выполнить каждый пункт инструкции:
Процесс регистрации в системе Пайонер не займет у вас много времени. Для того, чтобы заказать карту, вам нужно будет всего лишь поочередно выполнить каждый пункт инструкции:
- Переходим на официальный сайт компании.

- Задаем в системе логин, который будет использоваться всякий раз, как вы захотите войти в свой аккаунт. После этого заполняем предоставленную сайтом регистрационную форму, указываем свои паспортные данные и отправляем их системе.
- Прописываем почтовый адрес, на который вы хотите получить карту.
 Обязательно указываете индекс, страну, город, улицу, номер дома и квартиры, имя получателя пластика.
Обязательно указываете индекс, страну, город, улицу, номер дома и квартиры, имя получателя пластика.  Учитывая то, что сайт англоязычный, вам нужно будет ввести адрес латиницей. Жителям России нужно ждать карту примерно 1-2 недели.
Учитывая то, что сайт англоязычный, вам нужно будет ввести адрес латиницей. Жителям России нужно ждать карту примерно 1-2 недели. - Теперь вам необходимо будет подтвердить вашу личность, чтобы сервис был уверен в том, что именно вы снимаете деньги со счета. Кроме того, эти данные могут понадобиться в том случае, если вы вдруг случайно потеряете свою карту.
 Просто введите в соответствующие поля регистрационной формы номер своего загранпаспорта и все, на этом регистрацию можно считать успешно оконченной. Теперь нам остается только ждать, когда нам доставят карту, и мы сможем начать выводить свой заработок.
Просто введите в соответствующие поля регистрационной формы номер своего загранпаспорта и все, на этом регистрацию можно считать успешно оконченной. Теперь нам остается только ждать, когда нам доставят карту, и мы сможем начать выводить свой заработок.
- Когда вы наконец-то получите долгожданный пластик, вам необходимо будет его активировать.
 Для этого потребуется специальный активационный код, который вы найдете в конверте со своей картой. Теперь, когда Payoneer MasterCadr активна и готова к использованию, вам достаточно просто перейти в личный кабинет сервиса и приступить к выводу денег.
Для этого потребуется специальный активационный код, который вы найдете в конверте со своей картой. Теперь, когда Payoneer MasterCadr активна и готова к использованию, вам достаточно просто перейти в личный кабинет сервиса и приступить к выводу денег.
к содержанию ↑
Повторный заказ карты
Если в оговоренный срок ваша карта не пришла, советую вам проверить статус вашей заявки в личном аккаунте сервиса. В случае, если карта уже была вам выслана, то в самом верху профиля вам высветится ориентировочная дата ее доставки. Если этот срок уже давно истек, имеет смысл повторить заказ пластика. Для этого:
- Нажмите в личном кабинете на ссылку «Не получили карту?», расположенную в верхнем углу экрана.
- Укажите свой почтовый адрес и кликните по кнопке «Заказать».
- После этого пройдите процесс верификации, указав свою дату рождения и пароль от личного кабинета.
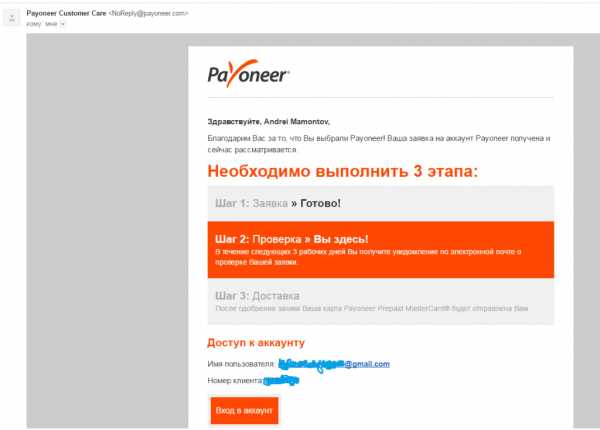
- Получите на email письмо, сообщающее о том, что ваша заявка была получена.
Перейти к регистрации
к содержанию ↑
Безопасность Payoneer
Практически каждого фрилансера волнует вопрос его финансовой безопасности. Если рассматривать с этой точки зрения продукт Пайонер, то я просто не могу не выделить такие его преимущества:
- Поскольку компания зарегистрирована в Соединенных Штатах Америки, то это значит, что работает она на базе американского законодательства. Как известно, законы США, контролирующие сферу личных финансов, отличаются особой строгостью. Именно поэтому вы можете не беспокоиться о том, что сведения о ваших личных счетах будут переданы третьей стороне, то есть налоговой. Абсолютно вся информация о денежных передвижениях хранится в строжайшей секретности.
- Так как Payoneer не является банковской структурой, а позиционирует себя как финансовый сервис, это позволяет ей «обходить» довольно многие законы в государствах, где гражданам не позволено иметь денежные сбережения заграницей. В случае с деньгами, которые хранятся на счетах Пайонер, этой проблемы нет, ведь денежные средства лежат не в банке, а значит, закон не нарушается.
к содержанию ↑
О тарифах и размерах комиссии
Обо всех тарифах вы сможете узнать в своем личном кабинете, перейдя в раздел «Помощь» и выбрав вкладку «Тарифы». 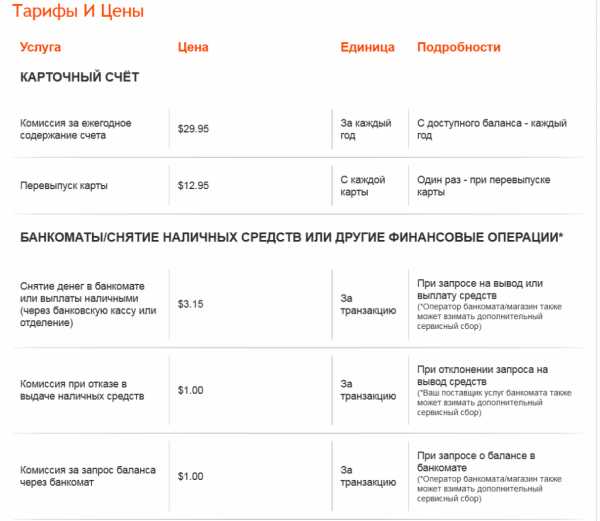 Всего в системе предусматриваются комиссии трех видов:
Всего в системе предусматриваются комиссии трех видов:
- за вывод и обналичивание средств в банкоматах – 3,15 доллара;
- за проверку баланса счета в банкомате – 1 доллар;
- за отказ вывода средств, если вы запросили наличку в банкомате – 1 доллар.
Для того, чтобы минимизировать потери денег при снятии наличных с карты Payoneer, нам нужно знать, какую комиссию с нас удержит система. Сразу хочу вас предупредить, что эта информация постоянно меняется по причине того, что банки периодически меняют размеры комиссионных и устанавливают новые ограничения на суммы снятия. По последним данным комиссия за снятие состоит из:
- Фиксированной суммы комиссии за снятие денег в банкомате или получение налички в банковской кассе. Размер этой суммы будет колебаться в зависимости от того, к какому партнеру сервиса вы подключены. Чаще всего она составляет 3,15 долларов, о чем я уже упоминал ранее.
- Фиксированного сбора за снятие денег. Если вы снимаете средства в национальной валюте, то вам придется заплатить до 3,5% от суммы снятия. Если же вы обналичиваете счет в долларах, то заплатить нужно будет всего 1,8%.
- %, который установлен в кассе банка, в которой вы снимаете деньги.
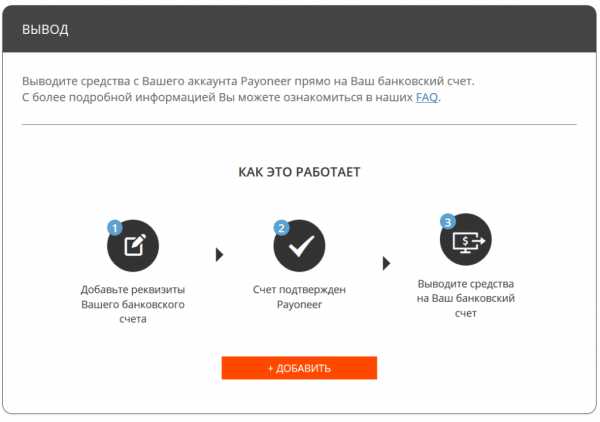
Для того, чтобы вы не ломали голову над тем, как снять деньги с карты с минимальными потерями, посоветую вам выводить максимально большие суммы за одну операцию. Таким образом вам не придется оплачивать одни и те же комиссии при каждом снятии денег.
к содержанию ↑
Лимиты
Что же касается ограничений по лимитам снятия денег в банкоматах в долларах, то здесь вам нужно знать следующее:
- Самую большую сумму для снятия – 400 долларов – вам предложат Юникредит и Ситибанк.
- Чуть меньше – 300 долларов – можно будет получить в Росбанке, Райффазен Банке, КредитЕвропе и в Банке Русский Стандарт.
- Самая маленькая сумма, доступная для разового снятия, составляет 200 долларов, и предлагают ее в АльфаБанке.
Если в банкомате вам предложат выбрать тип счета, то знайте, что по вашей карте уместен выбор вариантов «Текущий» и «Расчетный».
к содержанию ↑
Снятие в кассах банков
 Если вы решите снять деньги с карты в операционной кассе банка, то здесь вам придется заплатить дополнительные проценты за снятие денег с карты, выпущенной сторонним банком:
Если вы решите снять деньги с карты в операционной кассе банка, то здесь вам придется заплатить дополнительные проценты за снятие денег с карты, выпущенной сторонним банком:- В банках Россельхозбанк, Авангарде и Мособлбанке комиссия составит 2%.
- В Росбанке и Райфайзене за эту же услугу придется отдать уже 3%.
- В Банке Москвы за операцию по снятию суммы до 60 000 вам придется отдать 5%, если же вы снимаете сумму больше указанной, то процентная ставка снизится до 2%.
Ежегодно вам, как держателю карты, нужно платить за содержание пластика. В зависимости от того, через какого партера вы заказываете карту, будет изменяться и сумма годового обслуживания. К примеру, если вы оформили карту по моей пригласительной ссылке, то стоимость обслуживания составит для вас 29,95 долларов, и активация карты для жителей России будет бесплатная.
Если же вы заказали продукт через DepositPhotos или 123RF, то за пользование картой за год вам придется заплатить, как минимум, 35 долларов, то есть 3 доллара в месяц. Сразу хочу сказать, что если в месяц вы будете проводить от 5 платежей, комиссия снизится до 1 доллара. Кроме того, за активацию карты в первый год эксплуатации с вас будет удержано 12,95 долларов.
Воспользоваться услугами payoneer
к содержанию ↑
Payoneer Global Payment Service
После активации карты на ваш e-mail должно будет прийти письмо, в котором вам оповестят о том, что вы получили доступ к особым реквизитам для получения платежей из-за границы. Эти реквизиты необходимы для того, чтобы вы могли получать денежные переводы, например, от платежной системы skrill или вебмани.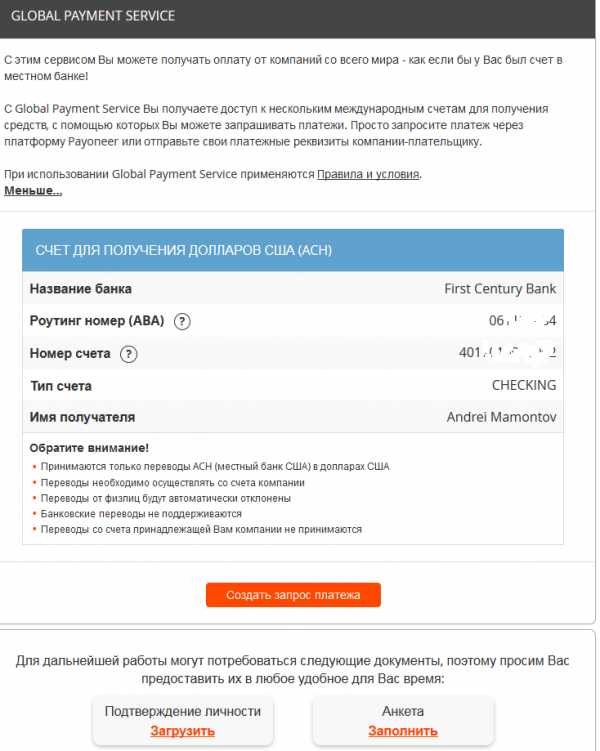
Global Payment Service поддерживает работу с платежами в долларах, евро и британских фунтах стерлингов. Система предоставляет всем держателям карты Пайонер реквизиты, по которым они могут получить денежные платежи во всех перечисленных валютах.
К огромному сожалению, в сентябре 2013 года стала невозможной привязка банковского счета GPS к имеющемуся у держателя карты счету PayPal. Именно поэтому вывод средств с PayPal возможен сегодня только на карты и банковские счета российских банков.
Для всех же прочих случаев вы можете попросить систему выслать вам данное письмо с реквизитами сразу же после того, как получите и активируете карту. Получить доступ к регистрации этого сервиса можно в личном кабинете во вкладке «Получение».
к содержанию ↑
Payoneer и Paypal
Довольно часто у держателей карты Пайонер возникают вопросы, связанные с совместимостью пластика и платежной системы PayPal. Я думаю, что имеет смысл отметить основные тезисы по данной теме, чтобы ни у кого из вас не было путаницы:
- Система PayPal беспрепятственно принимает карты Пайонер для проведения оплат в любых сервисах и за любые товары. Единственное, что от вас потребуется – указать четырехзначный код в системе PayPal, который вы найдете в выписке в личном кабинете Payoneer. Это мероприятие необходимо для успешной верификации карты.
- Вывести средства, хранящиеся на счету в paypal на карту Паойнер тоже реально без каких-либо сложностей. Единственное ограничение в этом пункте – геолокация. Все дело в том, что система разрешает выводить деньги на банковские счета в США или Европейском союзе, только пользователям данных стран. Мы с вами, будучи жителями постсоветского пространства, воспользоваться данной услугой не сможем. Что же касается жителей Казахстана, Грузии и Молдовы, то они смогут вывести деньги с Paypal исключительно на карту типа Visa, в то время, как пайонер выпускает мастеркард.
- Тщательно проверяйте свои данные, которые вы указываете во время регистрации в paypal. Любые несостыковки обнаруживаются системой на раз-два, а потому вы можете заплатить за свой обман потерей средств, которые останутся на балансе вашего замороженного аккаунта.
к содержанию ↑
Payoneer и Webmoney
Среди огромного множества всевозможных услуг, которые система электронных платежей Вебмани предоставляет свои пользователям, есть еще и возможность прикрепления специальной дебетовой карты к wmz счету, которая упрощает обмен и вывод средств. Одной из таких дебеток, может являться, именно Payoneer Mastercard. Будучи обладателем такой связки, вы навсегда забудете о каких-либо процедурах вывода средств с кошелька вебмани.
Чтобы обзавестись таким полезным платежным инструментом, вам достаточно оформить заказ на прикрепление карты через сервис Webmoney Cards, расположенный в одном из разделов официального сайта компании. Если кто-то из вас уже задумался над тем, как пополнить карту Пайонер, то сделать это вы сможете за счет средств, хранящихся на WMZ-кошельке. Прикрепить пластик может любой зарегистрированный в системе Вебмани участник, имеющий, как минимум, формальный аттестат.
к содержанию ↑
Партнерка Payoneer: кому 25 долларов?
Те, кто заинтересовался, как получить бонус от сервиса payoneer, могут принять участие в партнерской программе системы. Все, что от вас будет нужно, — это привлечь в систему новых клиентов.  Перейдя на сайт компании, поделиться информацией в социальных сетях о том, что за регистрацию в системе каждый новый клиент получит 25 долларов на свой счет при условии, что на балансе карты будет содержаться не менее 100 долларов. Как только реферал перейдет по вашей пригласительной ссылке и получит платеж в размере 100 долларов, вы получите свой бонус в размере все тех же 25 баксов. Моя партнёрская ссылка.
Перейдя на сайт компании, поделиться информацией в социальных сетях о том, что за регистрацию в системе каждый новый клиент получит 25 долларов на свой счет при условии, что на балансе карты будет содержаться не менее 100 долларов. Как только реферал перейдет по вашей пригласительной ссылке и получит платеж в размере 100 долларов, вы получите свой бонус в размере все тех же 25 баксов. Моя партнёрская ссылка.
к содержанию ↑
Впечатление от работы с системой
Изучив массу отзывов о Payoneer, которые гуляют в сети, я решил поделиться с вами и своим впечатлением от работы с данной системой. В целом, меня порадовала простота регистрации в сервисе и легкость оформления пластика. Могу сказать, что карту мне доставили раньше оговоренного срока, что, несомненно, меня очень порадовало. Что касается снятия денег с карты, то здесь взаимодействие с системой мне не понравилось. Все дело в том, что при попытке снять наличные в банкомате, автоматы выдают состояние баланса в валюте счета. Таким образом, невозможно узнать, сколько точно денег доступно для вывода, а потому, если неверно рассчитал сумму для снятия, можно довольно много спустить на оплате «отказа от снятия средств» и «проверке счета» (напомню, что каждая такая операция стоит доллар, а один вывод средств обходится в 3,15 долларов). Однако, мне кажется, что если приспособиться к столь специфичному моменту, то все будет хорошо.
Регистрация Payoneer
к содержанию ↑
Резюме
Надеюсь, что этот обзор позволит многим фрилансерам, работающим с иностранными компаниями, решить проблему грабительских комиссий. Тестируйте карту, и в комментариях под этой статьей делитесь своими впечатлениями. Мне так же будет интересно узнать, какими аналогами payoneer вы пользуетесь, и, в чем их преимущество перед данной платежной системой. Не забывайте подписываться на обновления блога, ведь впереди вас ждет еще масса всего интересного. До скорых встреч, дорогие друзья!
Если вы нашли ошибку в тексте, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Спасибо за то, что помогаете моему блогу становиться лучше!
guide-investor.com
Калькулятор пайонер — вся информация по блокчейну, криптовалютам и майнингу
В наше время слова «Майнинг», «Блокчейн», «Биткоины» раздаются буквально отовсюду: от пассажиров трамвая до серьёзных бизнесменов и депутатов Госдумы. Разобраться во всех тонкостях и подводных камнях этих и смежных понятий сложно, однако в базе данных на нашем сайте Вы быстро найдёте исчерпывающую информацию, касающуюся всех аспектов.
Калькулятор пайонерВкратце же все необходимые знания будут изложены в этой статье.
Итак, начать стоит с блокчейна. Суть его в том, что компьютеры объединяются в единую сеть через совокупность блоков, содержащую автоматически зашифрованную информацию, попавшую туда. Вместе эти блоки образуют базу данных. Допустим, Вы хотите продать дом. Оформив документы, необходимо идти к нотариусу, затем в присутствии его, заверив передачу своей подписью, Вам отдадут деньги. Это долго, да и к тому же нужно платить пошлину.
Благодаря технологии блокчейна достаточно:
- Договориться.
- Узнать счёт получателя.
- Перевести деньги на счёт получателя.
…и не только деньги. Можно оформить электронную подпись и отправлять документы, любую другую информацию, в том числе и конфиденциальную. Опять же, не нужны нотариусы и другие чиновники: достаточно идентифицироваться Вам и получателю (будь то частное лицо или госучреждение) в своём компьютере.
Транзакция проходит по защищённому каналу связи, никто не видит (в том числе банки и государство), кто, что и кому перевёл.
Возможность взломать исключена из-за огромного количества блоков, описанных выше. Для хакера нужно подобрать шифр для каждого блока, что физически нереально.
Другие возможности использования блокчейна:
- Страхование;
- Логистика;
- Оплата штрафов
- Регистрация браков и многое другое.
С блокчейном тесно связано понятие криптовалюта. Криптовалюта — это новое поколение децентрализованной цифровой валюты, созданной и работающей только в сети интернет. Никто не контролирует ее, эмиссия валюты происходит посредством работы миллионов компьютеров по всему миру, используя программу для вычисления математических алгоритмов.
Вкратце это выглядит так:
1. Вы намереваетесь перевести кому-то деньги.
2. Генерируется математический код, проходящий через уже известные Вам блоки.
3. Множество компьютеров (часто представляющих собой совокупность их, с мощными процессорами и как следствие большей пропускной способностью) обрабатывают цифровую информацию, передавая их на следующие блоки, получая за это вознаграждение (некоторые транзакции можно совершать бесплатно)
4. Математический код доходит до электронного кошелька получателя, на его балансе появляются деньги.
Опять же, как это в случае с блокчейном, переводы криптовалют никем не контролируются.
Хотя база данных открыта, со всеми адресами переводящих и получающих деньги, но владельца того или иного адреса, с которого осуществляется перевод, никто не знает, если только хозяин сам не захочет рассказать.
Калькулятор пайонерРаботающих по подобному принципу валют много. Самой знаменитой является, конечно, биткоин. Также популярны эфириум, ритл, лайткоины, нумитсы, неймкоины и многие другие. Разница у них в разном типе шифрования, обработки и некоторых других параметрах.
Зарабатывают на технологии передачи денег майнеры.
Это люди, создавшие упомянутую выше совокупность компьютерных видеокарт, которая генерирует новые блоки, передающие цифровую информацию — биткоины (или ритлы, или любую другую криптовалюту). За это они получают вознаграждение в виде той же самой криптовалюты.
Существует конкуренция между майнерами, т.к. технология с каждой транзакции запрограммировано усложняется. Сначала можно было майнить с одного компьютера (2008 год), сейчас же такую валюту как биткоин физическим лицам уже просто невыгодно: нужно очень много видеокарт (их все вместе называют фермами), с огромными вычислительными мощностями. Для этого снимаются отдельные помещения, затраты электроэнергии для работы сравнимы с затратами промышленных предприятий.
Зато можно заработать на других, менее популярных, но развивающихся криптовалютах. Также различают соло майнинг и пул майнинг. Соло — это создание своей собственной фермы, прибыль забирается себе. Пул же объединяет других людей с такими же целями. Заработать можно гораздо больше, но придётся уже делиться со всеми.
Перспективами использования технологии блокчейна вообще и криптовалют в частности заинтересовались как и физические лица, так и целые государства.
В Японии криптовалюта узаконена. В России в следующем году собираются принять нормативно-правовые акты о легализации блокчейна, переводов криптовалюты и майнинга. Планируется перевод некоторых операций в рамки блокчейна. Имеет смысл изучить это подробнее, и, при желании, начать зарабатывать. Очевидно, что сейчас информационные технологии будут развиваться и входить в нашу жизнь всё больше и больше.
safe-crypto.me

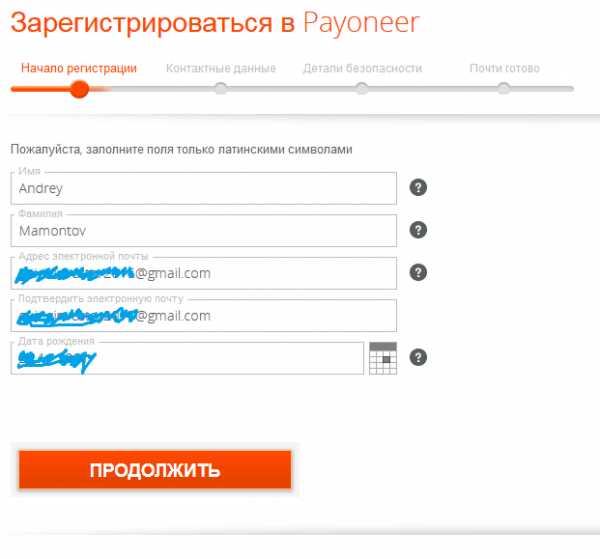
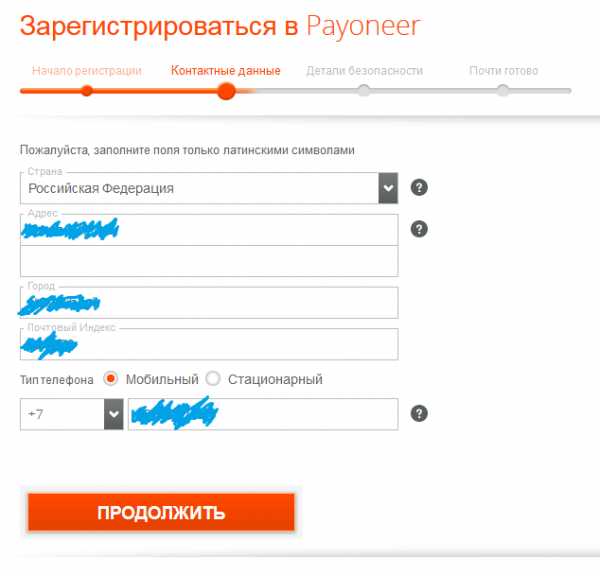 Обязательно указываете индекс, страну, город, улицу, номер дома и квартиры, имя получателя пластика.
Обязательно указываете индекс, страну, город, улицу, номер дома и квартиры, имя получателя пластика. 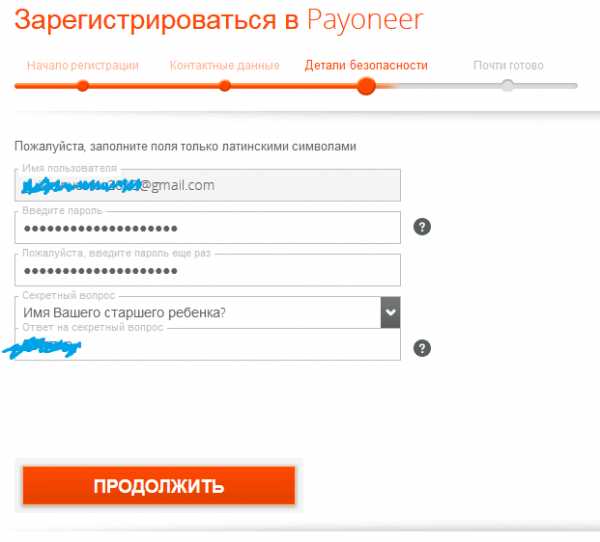 Учитывая то, что сайт англоязычный, вам нужно будет ввести адрес латиницей. Жителям России нужно ждать карту примерно 1-2 недели.
Учитывая то, что сайт англоязычный, вам нужно будет ввести адрес латиницей. Жителям России нужно ждать карту примерно 1-2 недели.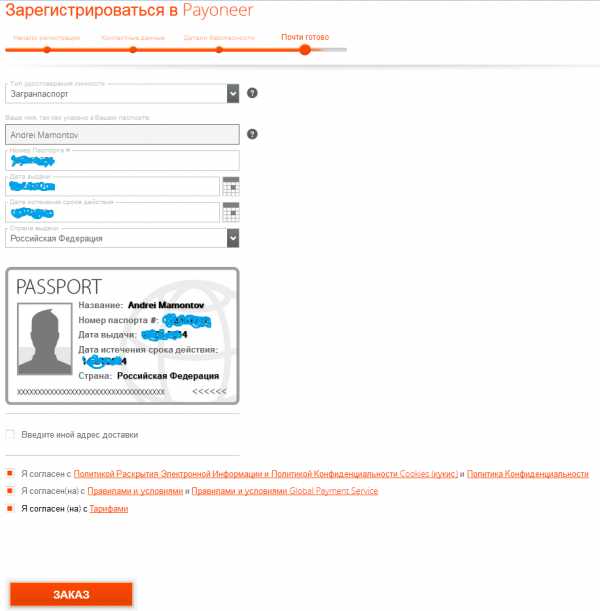 Просто введите в соответствующие поля регистрационной формы номер своего загранпаспорта и все, на этом регистрацию можно считать успешно оконченной. Теперь нам остается только ждать, когда нам доставят карту, и мы сможем начать выводить свой заработок.
Просто введите в соответствующие поля регистрационной формы номер своего загранпаспорта и все, на этом регистрацию можно считать успешно оконченной. Теперь нам остается только ждать, когда нам доставят карту, и мы сможем начать выводить свой заработок.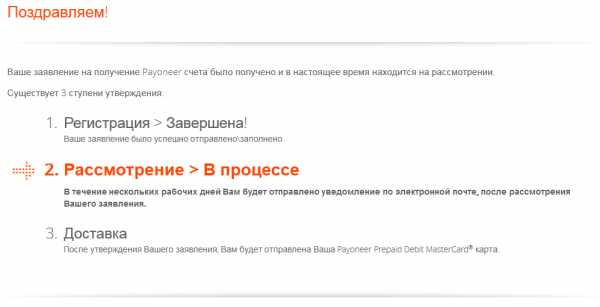
 Для этого потребуется специальный активационный код, который вы найдете в конверте со своей картой. Теперь, когда Payoneer MasterCadr активна и готова к использованию, вам достаточно просто перейти в личный кабинет сервиса и приступить к выводу денег.
Для этого потребуется специальный активационный код, который вы найдете в конверте со своей картой. Теперь, когда Payoneer MasterCadr активна и готова к использованию, вам достаточно просто перейти в личный кабинет сервиса и приступить к выводу денег.
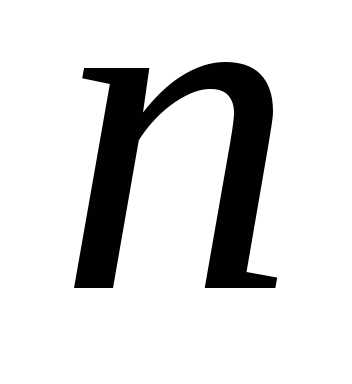 переменных в виде суммы функции, каждая
из которых зависит только от одной
переменной:
переменных в виде суммы функции, каждая
из которых зависит только от одной
переменной: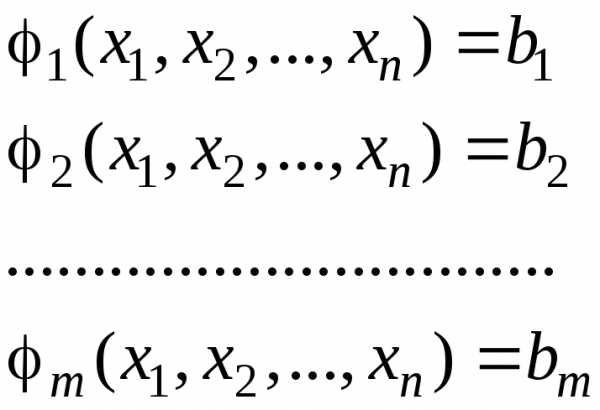
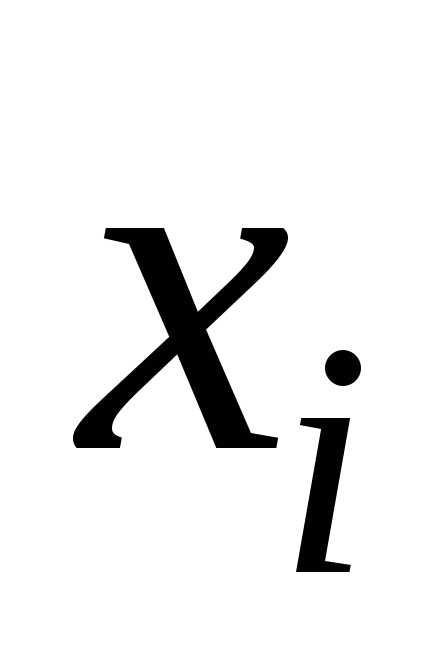 на
на шаге надо учитывать его влияние на
будущее, т.е. учитывать влияние принимаемого
решения на эффективность последующих
шагов. Имеется единственный шаг в решении
задачи в котором можно планировать без
учета влияния решения на последующие
шаги – это последний шаг. Его можно
планировать так, чтобы он изолированно
принес наибольшую выгоду. Поэтому
процесс поиска оптимального решения
начинается от конца к началу.
шаге надо учитывать его влияние на
будущее, т.е. учитывать влияние принимаемого
решения на эффективность последующих
шагов. Имеется единственный шаг в решении
задачи в котором можно планировать без
учета влияния решения на последующие
шаги – это последний шаг. Его можно
планировать так, чтобы он изолированно
принес наибольшую выгоду. Поэтому
процесс поиска оптимального решения
начинается от конца к началу.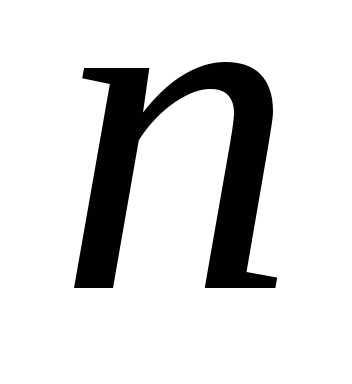 -го
шага, т.е. варианты окончания
-го
шага, т.е. варианты окончания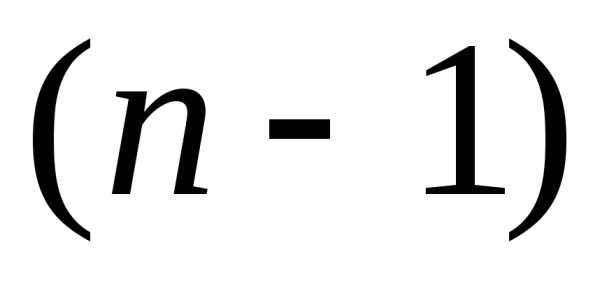 -го
шага. Для каждого варианта находят
такие решения, при которых выигрыш на
последнем шаге будет максимальным. Этот
выигрыш определяется по функциональному
уравнению Беллмана для последнего шага:
-го
шага. Для каждого варианта находят
такие решения, при которых выигрыш на
последнем шаге будет максимальным. Этот
выигрыш определяется по функциональному
уравнению Беллмана для последнего шага: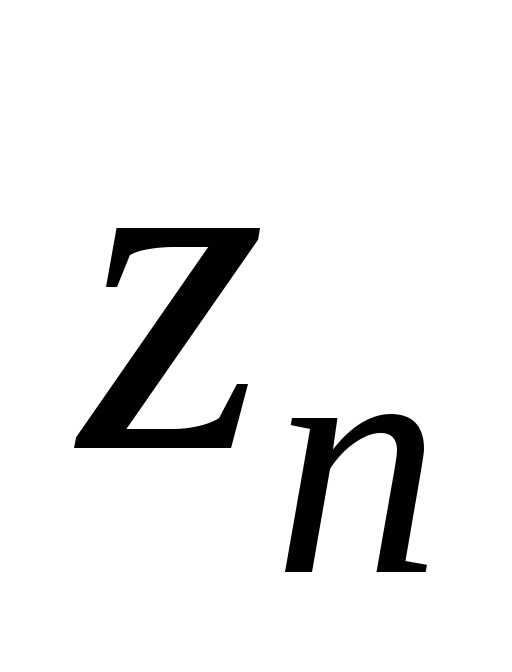 – варианты условий начала
– варианты условий начала -го
шага.
-го
шага.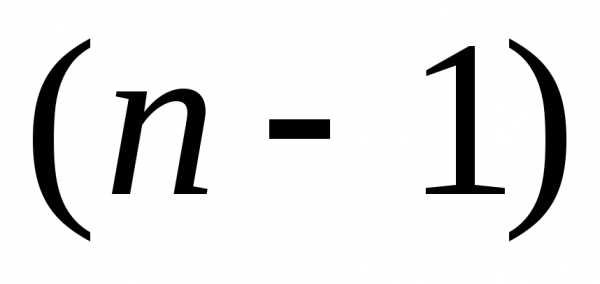 -м
шаге применительно к вариантам условий
начала этого шага, но с учетом решений,
найденных на
-м
шаге применительно к вариантам условий
начала этого шага, но с учетом решений,
найденных на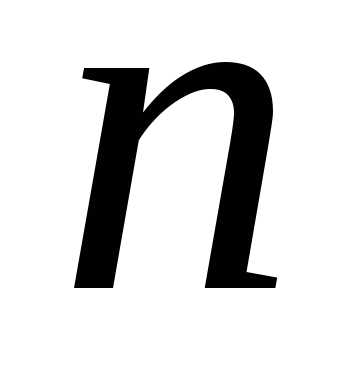 -м
шаге и т. д.
-м
шаге и т. д. – варианты условий начала
– варианты условий начала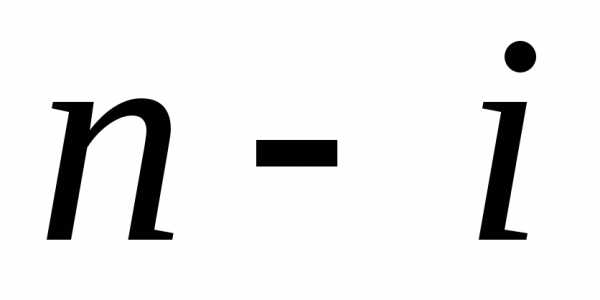 -го
шага;
-го
шага;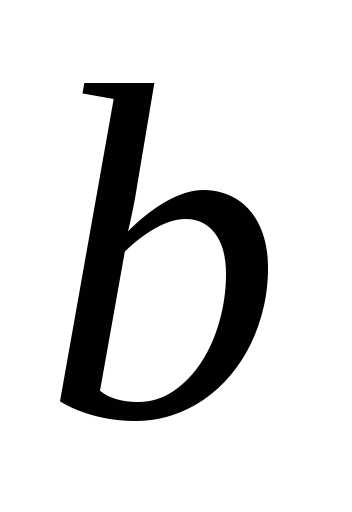 ,
которое можно использовать различными
способами. Пусть
,
которое можно использовать различными
способами. Пусть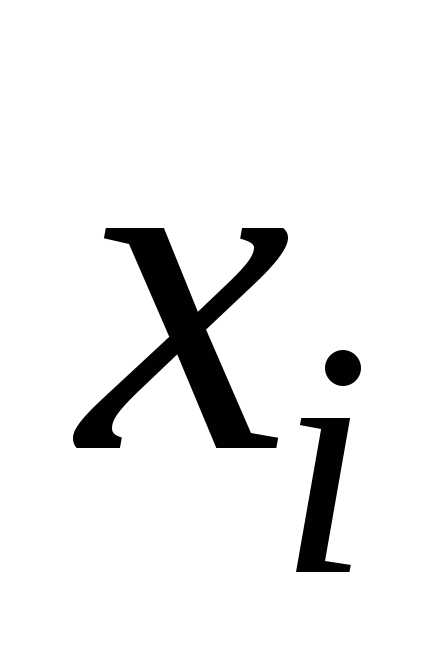 –количестворесурса,используемое
–количестворесурса,используемое 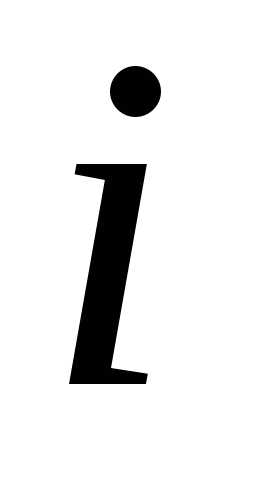 -м
способом,
-м
способом, – доход от использования ресурса
– доход от использования ресурса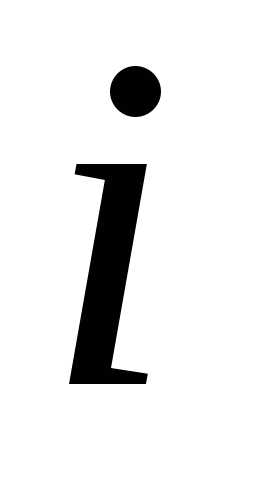 -м
способом ().
-м
способом ().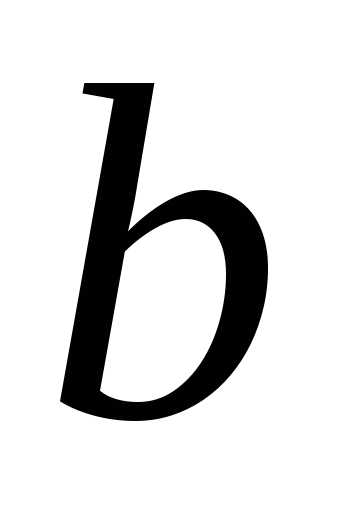 между различными способами, чтобы
суммарный доход был максимальным.
между различными способами, чтобы
суммарный доход был максимальным. . (5.15)
. (5.15)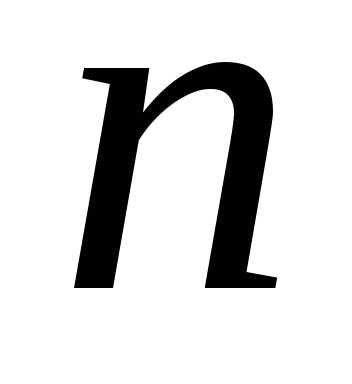 неизвестных, в методе динамического
программирования решается
неизвестных, в методе динамического
программирования решается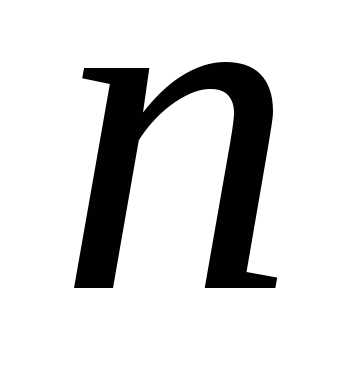 задач, в каждой из которых максимум
находится лишь по одной переменной.
Таким образом, процесс поиска решения
исходной задачи как бы разворачивается
во времени по шагам.
задач, в каждой из которых максимум
находится лишь по одной переменной.
Таким образом, процесс поиска решения
исходной задачи как бы разворачивается
во времени по шагам.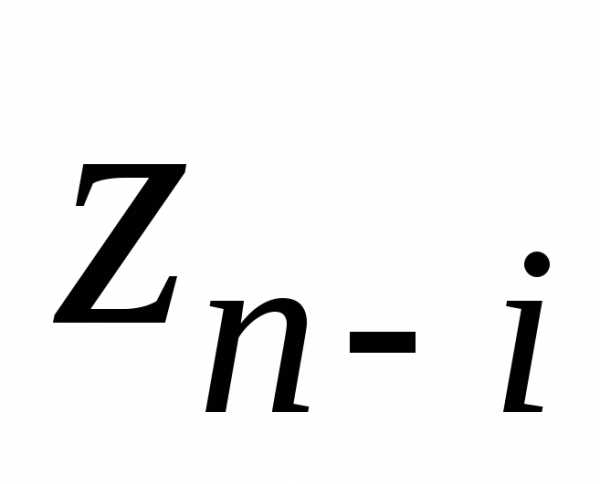 – количество ресурса, оставшееся для
распределения к началу
– количество ресурса, оставшееся для
распределения к началу -го
шага.
-го
шага. .
. .
Таким образом, переменная
.
Таким образом, переменная выражает всевозможные варианты условий
начала последнего шага. Уравнение
Беллмана для последнего шага имеет вид:
выражает всевозможные варианты условий
начала последнего шага. Уравнение
Беллмана для последнего шага имеет вид: 250.
250. x3 = z3.
x3 = z3.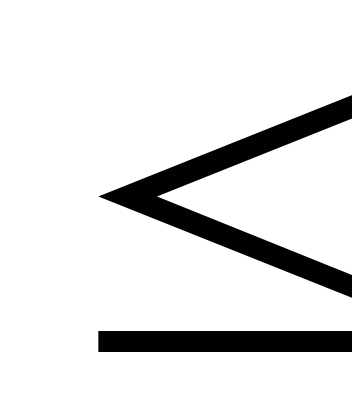 100
100 ,
,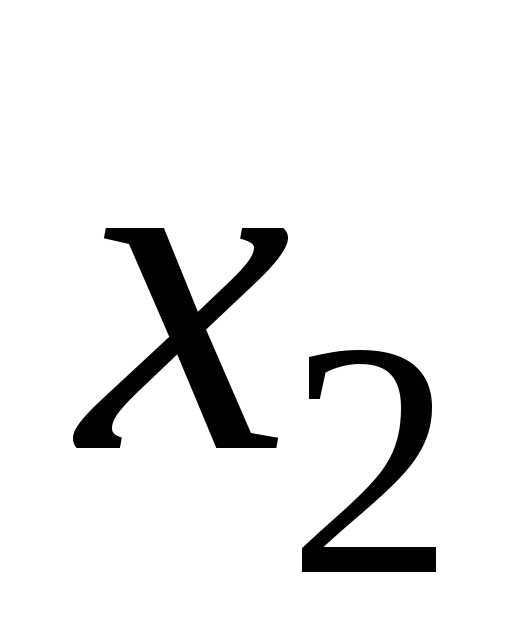 и
и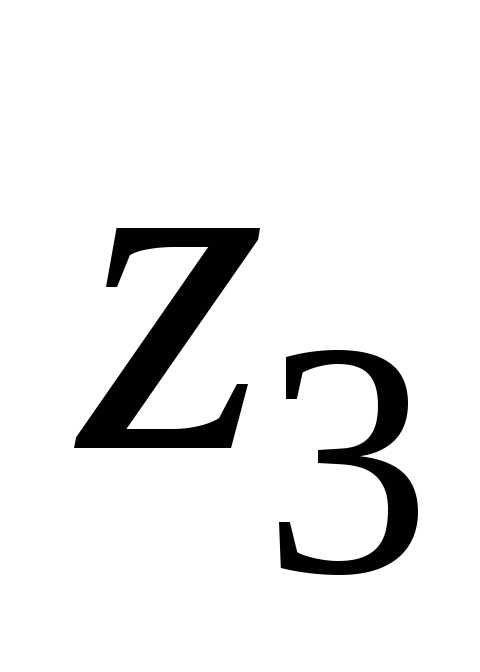 ,
которые в сумме составят величину
,
которые в сумме составят величину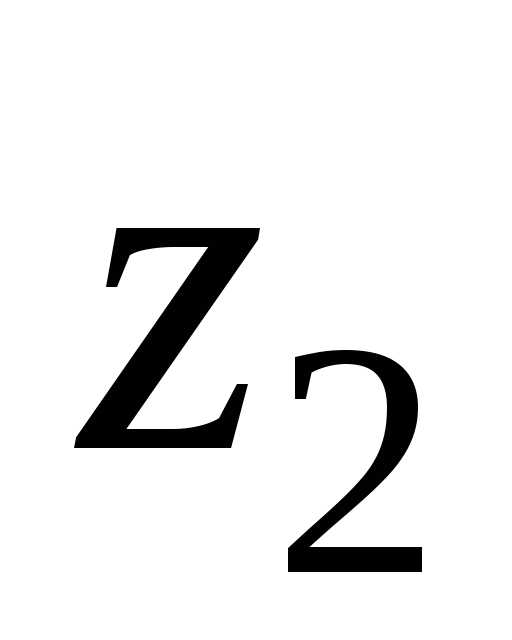 согласно выражению (5.17). При этом
учитываем, что
согласно выражению (5.17). При этом
учитываем, что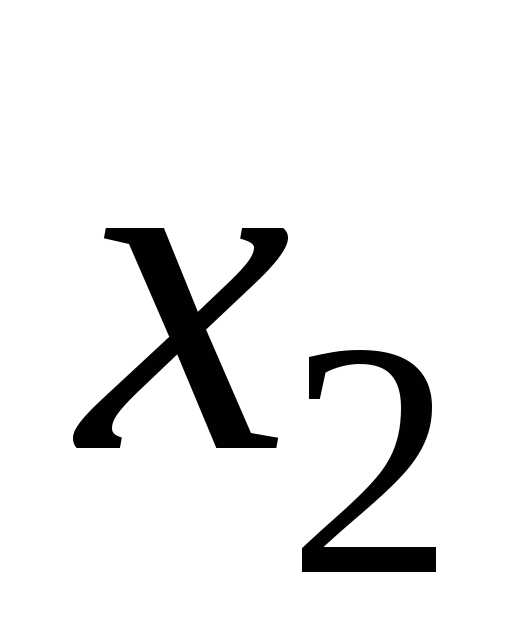 не
должен превышать 100.
не
должен превышать 100.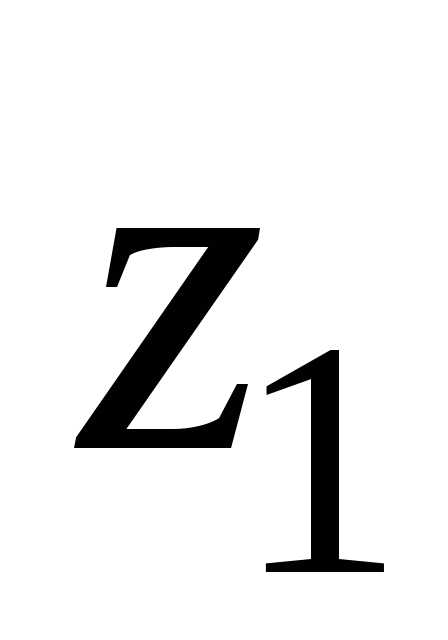 имеет смысл денежных средств для
вложений во все три отделения предприятия
и, следовательно, имеет единственное
значение, равное общей сумме вложений
250 ден. ед. Значения функцииF2(z2 ) будем
брать из последнего столбца таблицы
5.3.
имеет смысл денежных средств для
вложений во все три отделения предприятия
и, следовательно, имеет единственное
значение, равное общей сумме вложений
250 ден. ед. Значения функцииF2(z2 ) будем
брать из последнего столбца таблицы
5.3.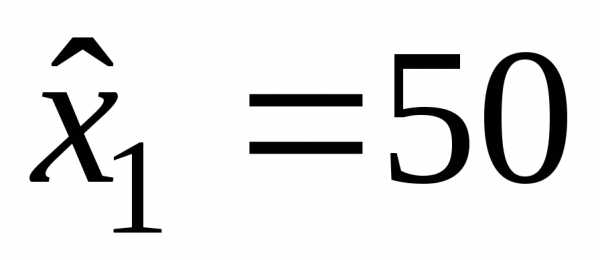 ден.
ед.;
ден.
ед.;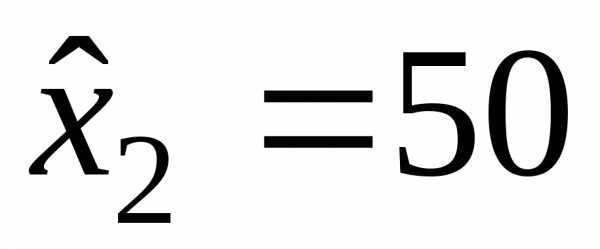 ден.
ед.;
ден.
ед.;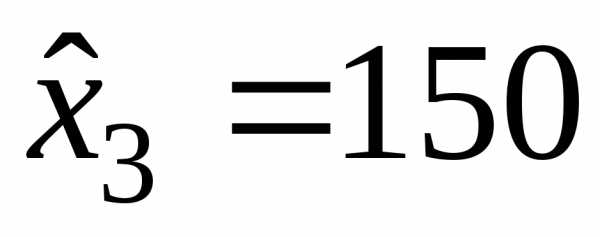 ден. ед..
ден. ед.. ,
в течение которого используется
оборудование, год
,
в течение которого используется
оборудование, год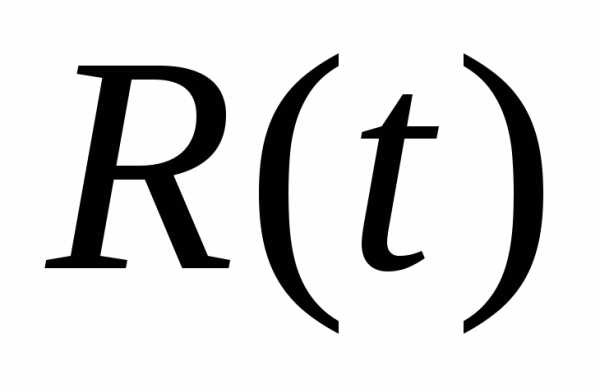 в стоимостном выражении, ден. ед.
в стоимостном выражении, ден. ед.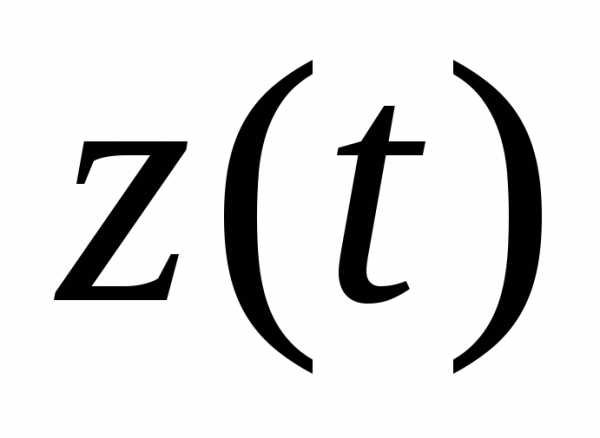 ,
ден. ед.
,
ден. ед. – время службы оборудования;
– время службы оборудования;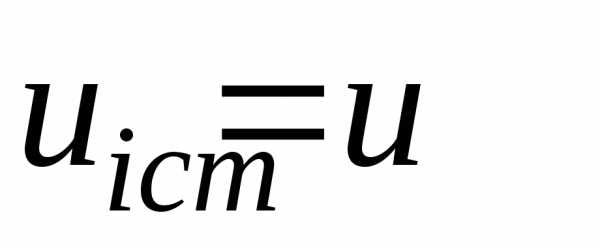 – принятие решения в начале
– принятие решения в начале 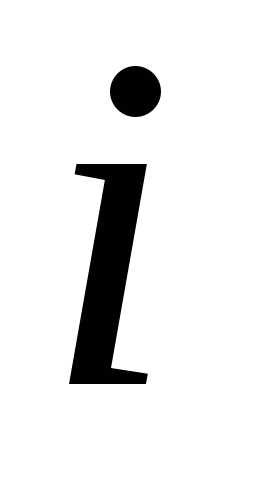 -го
года об использовании имеющегося
оборудования;
-го
года об использовании имеющегося
оборудования;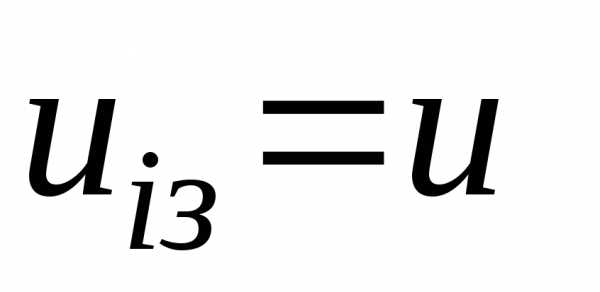 – принятие решения в начале
– принятие решения в начале 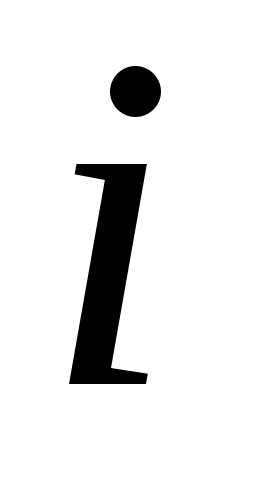 -го
года о замене оборудования;
-го
года о замене оборудования; – стоимость нового оборудования.
– стоимость нового оборудования.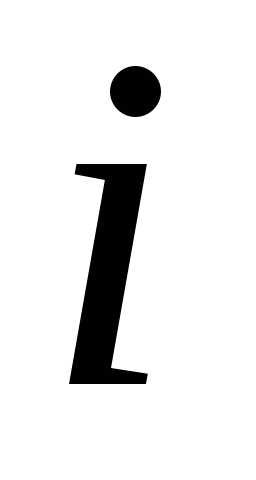 -й
год.
-й
год.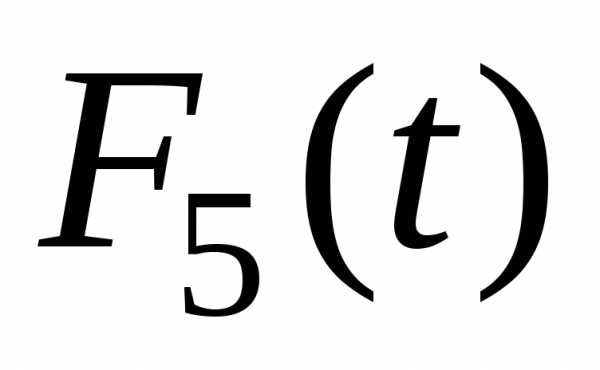 –функция
максимальной прибыли за последний год
в зависимости от возраста оборудования
в начале года
–функция
максимальной прибыли за последний год
в зависимости от возраста оборудования
в начале года  .
.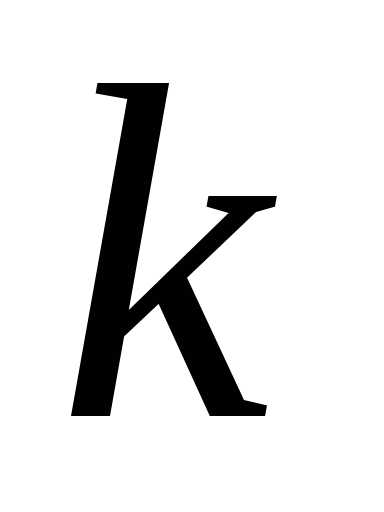 -го
шага
-го
шага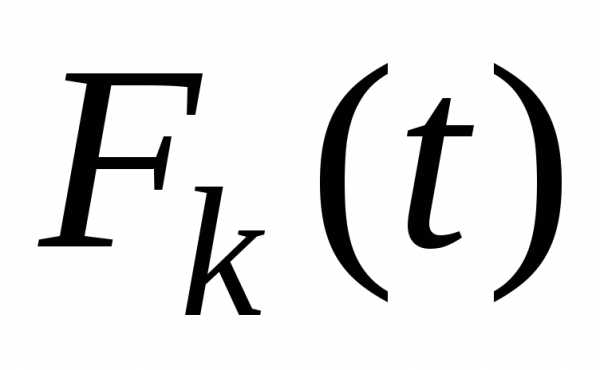 –максимальная
прибыль, начиная с
–максимальная
прибыль, начиная с 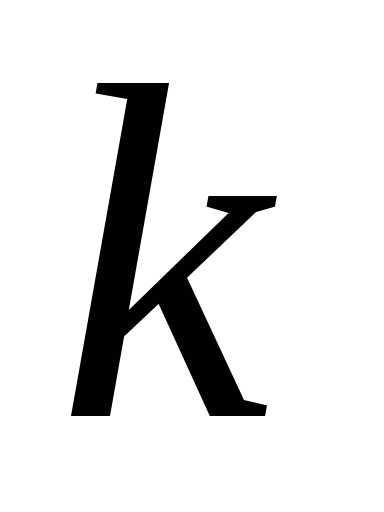 -го
года и до конца периода в зависимости
от возраста оборудования в начале
-го
года и до конца периода в зависимости
от возраста оборудования в начале -го
года.
-го
года. принимает значения: 1, 2, 3, 4. В результате
получаем функцию максимальной прибыли
за последний год в зависимости от
возраста оборудования:
принимает значения: 1, 2, 3, 4. В результате
получаем функцию максимальной прибыли
за последний год в зависимости от
возраста оборудования: принимает значения: 1, 2, 3. Получаем
функцию максимальной прибыли за последние
два года в зависимости от возраста
оборудования:
принимает значения: 1, 2, 3. Получаем
функцию максимальной прибыли за последние
два года в зависимости от возраста
оборудования: принимает значения: 1, 2. Получаем функцию
максимальной прибыли за последние три
года в зависимости от возраста
оборудования:
принимает значения: 1, 2. Получаем функцию
максимальной прибыли за последние три
года в зависимости от возраста
оборудования: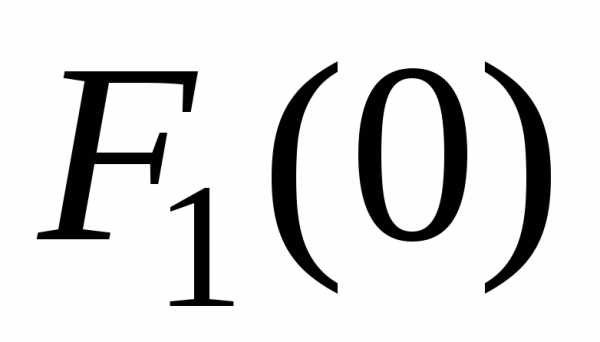 представляет собой максимальную прибыль
предприятия за пятилетний период.
представляет собой максимальную прибыль
предприятия за пятилетний период. .
. .
.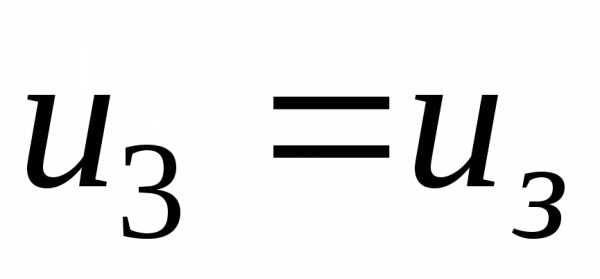 .
.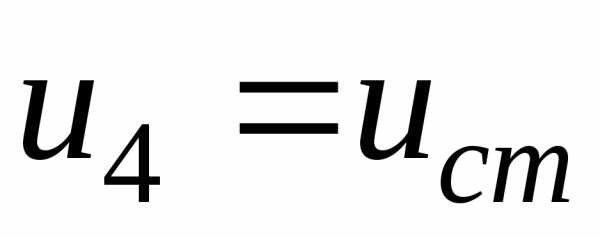 .
.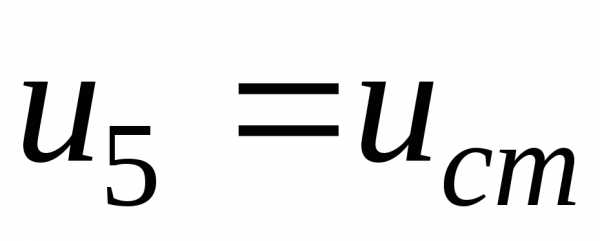 .
.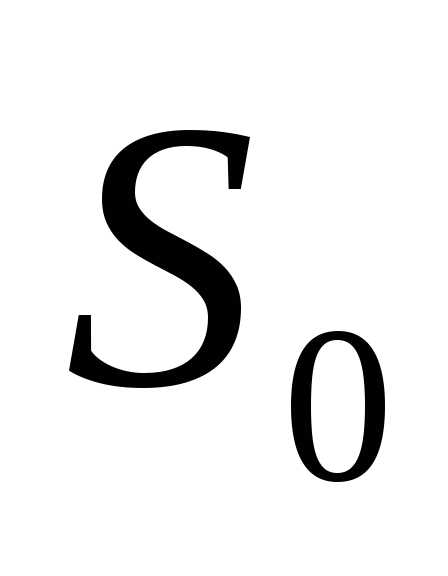 в состояние
в состояние .
.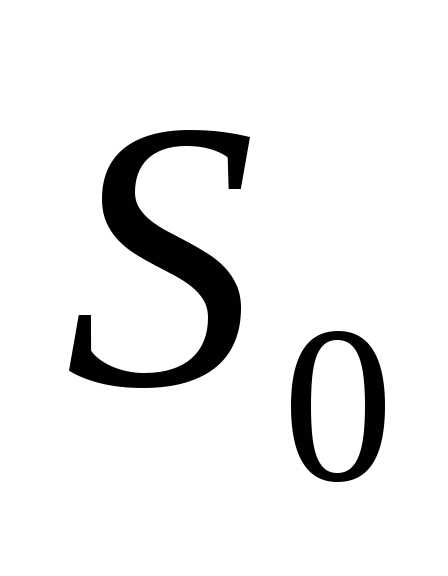 в
в (
(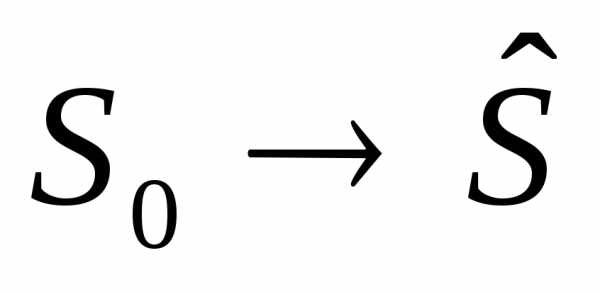 ),
представляет собой совокупностьnпошаговых управлений.
),
представляет собой совокупностьnпошаговых управлений.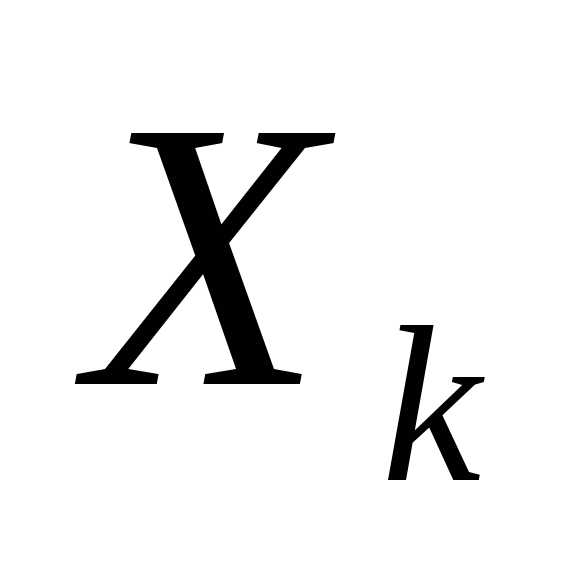 — управление на k-ом шаге и
— управление на k-ом шаге и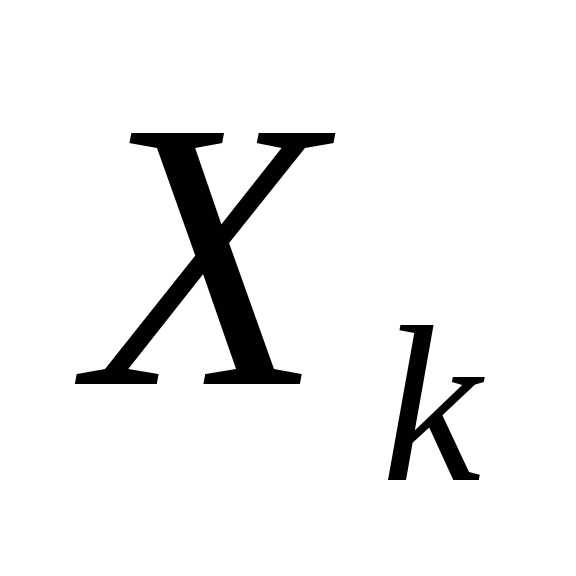 удовлетворяет некоторым ограничениям
и в этом смысле называется допустимым.
удовлетворяет некоторым ограничениям
и в этом смысле называется допустимым.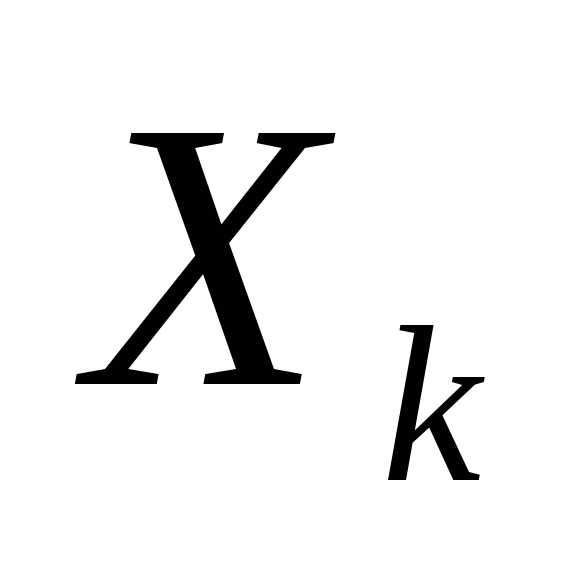 может быть числом, точкой, функцией,
качественным признаком.
может быть числом, точкой, функцией,
качественным признаком.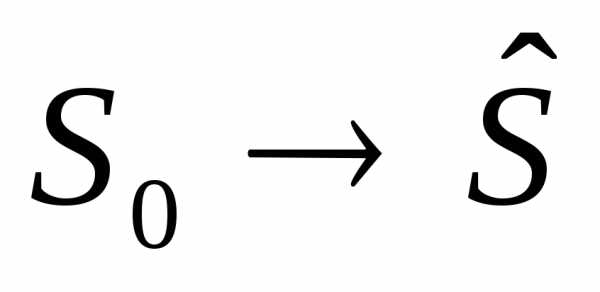 .
.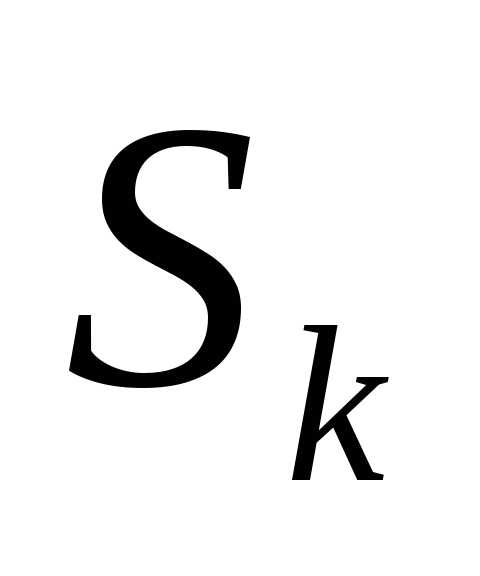 состояние
системы после к-ого шага управления.
состояние
системы после к-ого шага управления.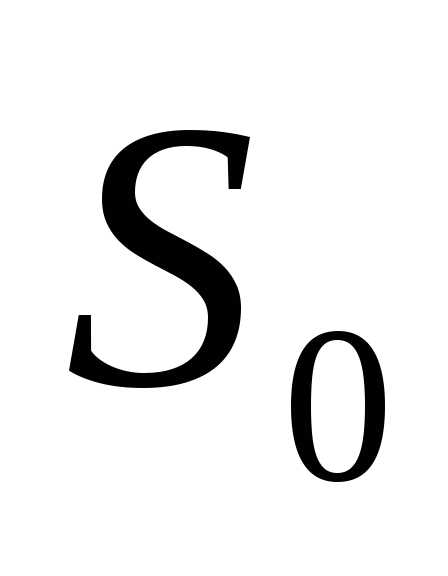 и управления Х.
и управления Х.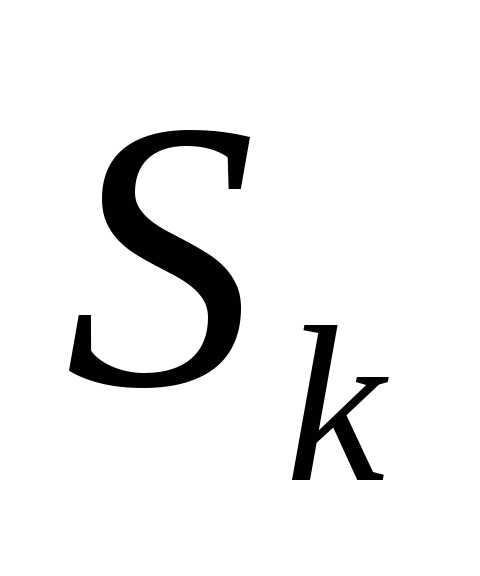 зависит только от предыдущего состояния
зависит только от предыдущего состояния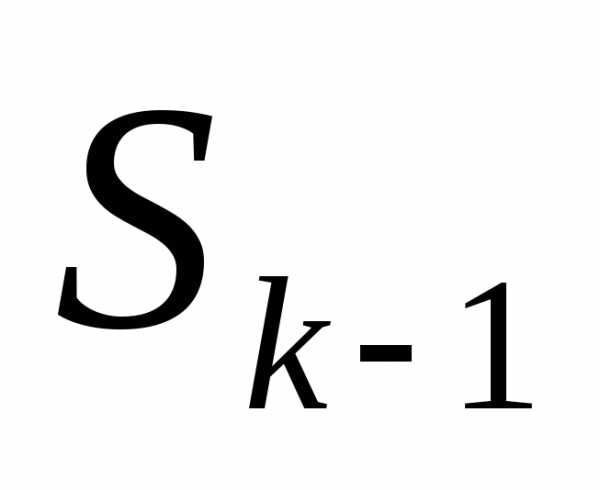 и управления на предыдущем шаге и не
зависит от предшествующих состояний
и управлений. Это требование называется
«отсутствие последствий».- уравнение состояний.
и управления на предыдущем шаге и не
зависит от предшествующих состояний
и управлений. Это требование называется
«отсутствие последствий».- уравнение состояний.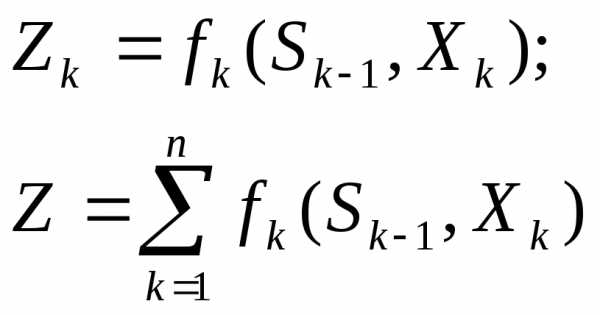
 ,
при котором целевая функция принимает
наибольшее (наименьшее) значение.
,
при котором целевая функция принимает
наибольшее (наименьшее) значение.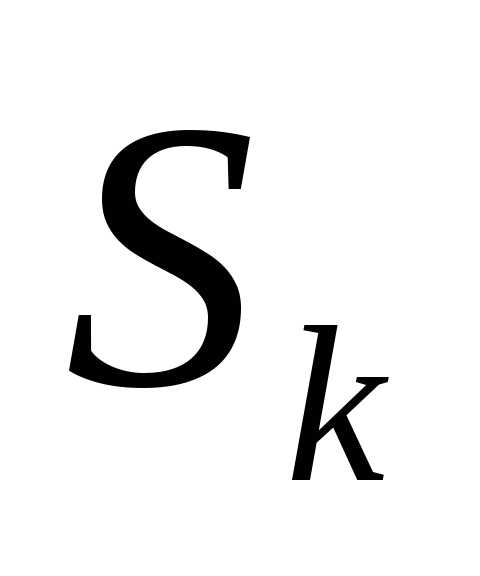 послеk-ого шага зависит
только от предшествующего состояния
послеk-ого шага зависит
только от предшествующего состояния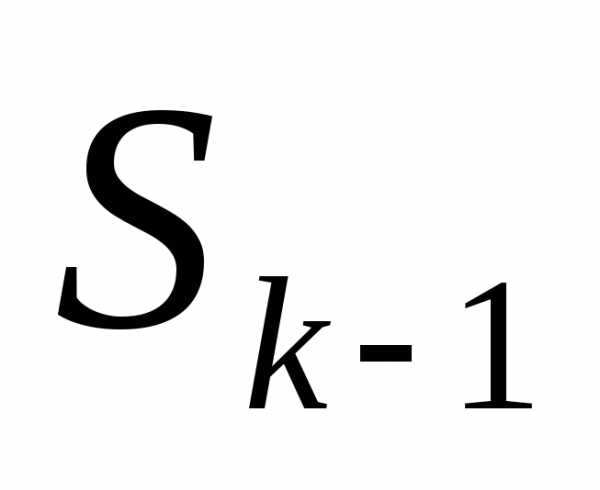 и управления
и управления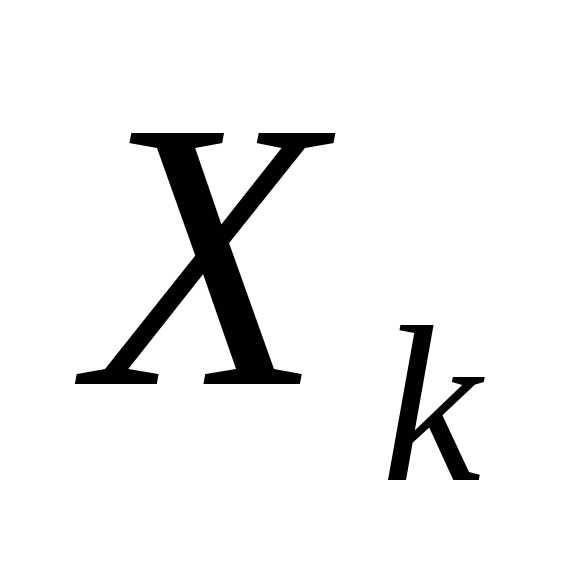 (нет последствий).
(нет последствий).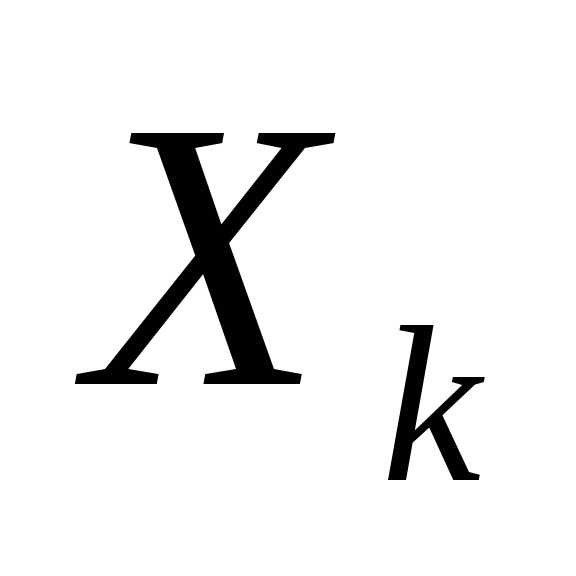 зависит от конечного числа управляющих
переменных, а состояние
зависит от конечного числа управляющих
переменных, а состояние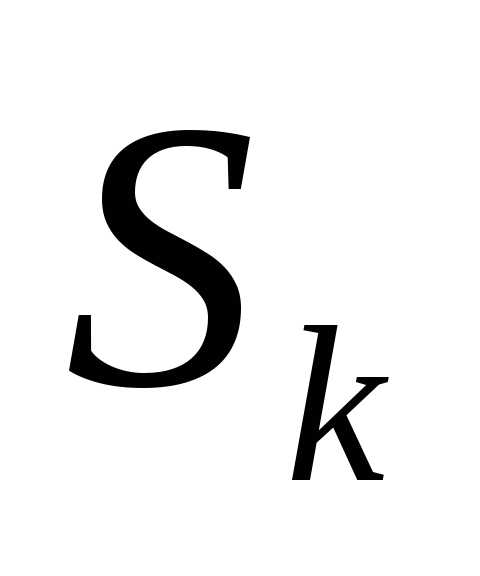 от конечного числа параметров.
от конечного числа параметров.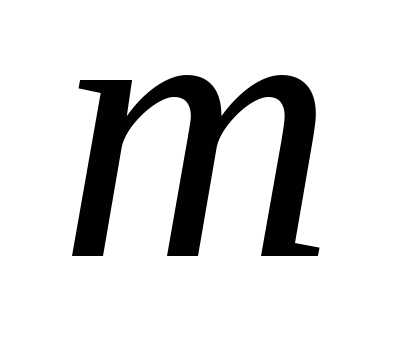 шагов
или этапов, например планирование
деятельности предприятия на несколько
лет, поэтапное планирование инвестиций,
управление производственными мощностями
в течение длительного срока. Показатель
эффективности задачи в целом обозначим
через W, а
показатели эффективности на отдельных
шагах – через
шагов
или этапов, например планирование
деятельности предприятия на несколько
лет, поэтапное планирование инвестиций,
управление производственными мощностями
в течение длительного срока. Показатель
эффективности задачи в целом обозначим
через W, а
показатели эффективности на отдельных
шагах – через  ,
, 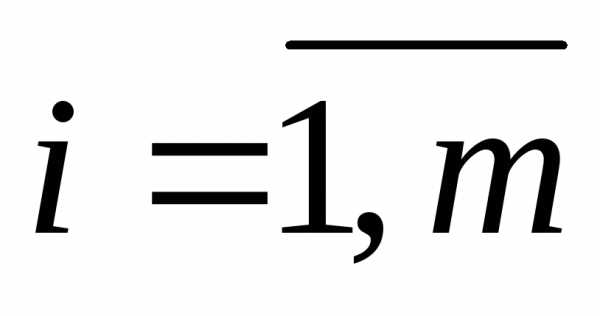 .
Если W обладает свойством аддитивности, т.е.
.
Если W обладает свойством аддитивности, т.е.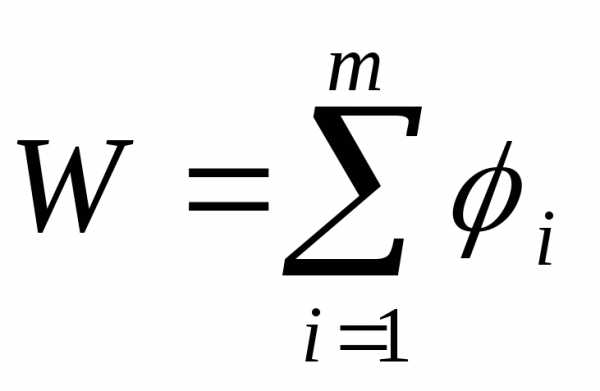 , (5.1.1)
, (5.1.1)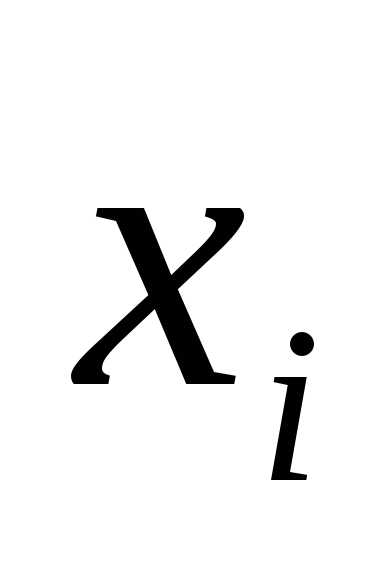 ,
от которой зависят выигрыш на
,
от которой зависят выигрыш на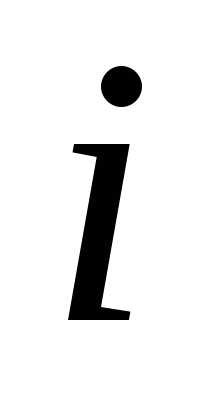 -м шаге
и, следовательно, выигрыш в целом,
называется шаговым управлением,
-м шаге
и, следовательно, выигрыш в целом,
называется шаговым управлением, 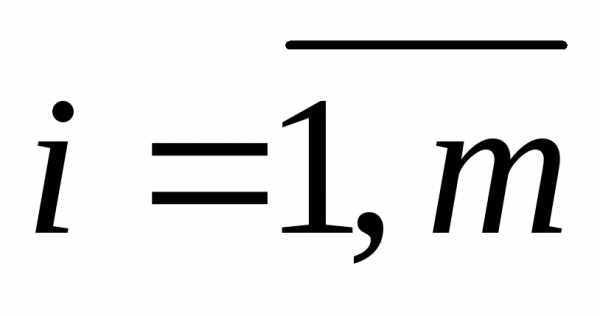 .
.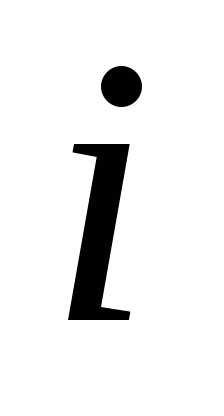 -м
году, необходимо знать, сколько средств
осталось в наличии к этому году и какая
прибыль получена в предыдущем(
-м
году, необходимо знать, сколько средств
осталось в наличии к этому году и какая
прибыль получена в предыдущем(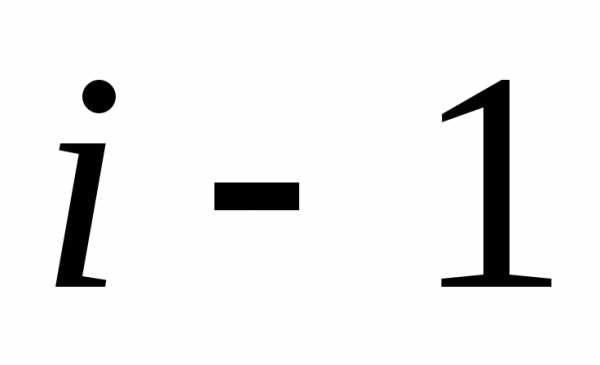 )-м году.
Таким образом, при выборе шагового
управления необходимо учитывать: 1)
возможные исходы предыдущего шага и 2)
влияние управления на все оставшиеся
до конца процесса шаги.
)-м году.
Таким образом, при выборе шагового
управления необходимо учитывать: 1)
возможные исходы предыдущего шага и 2)
влияние управления на все оставшиеся
до конца процесса шаги.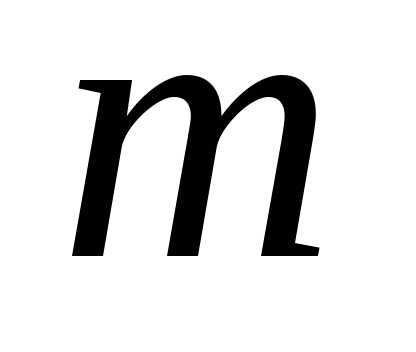 -й шаг,
на котором не надо учитывать возможные
воздействия выбранного управления
-й шаг,
на котором не надо учитывать возможные
воздействия выбранного управления 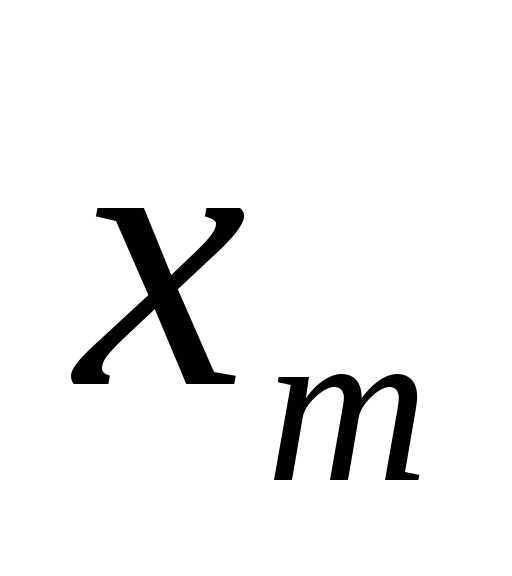 на
все последующие шага, так как эти шаги
просто отсутствуют. Делая предположения
об условиях окончания (
на
все последующие шага, так как эти шаги
просто отсутствуют. Делая предположения
об условиях окончания (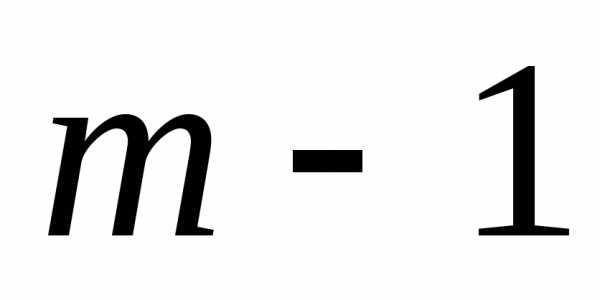 )-гo шага, для каждого из них проводят условную
оптимизацию
)-гo шага, для каждого из них проводят условную
оптимизацию 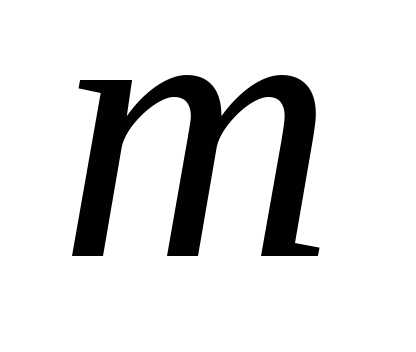 -го шага
и определяют условное оптимальное
управление
-го шага
и определяют условное оптимальное
управление 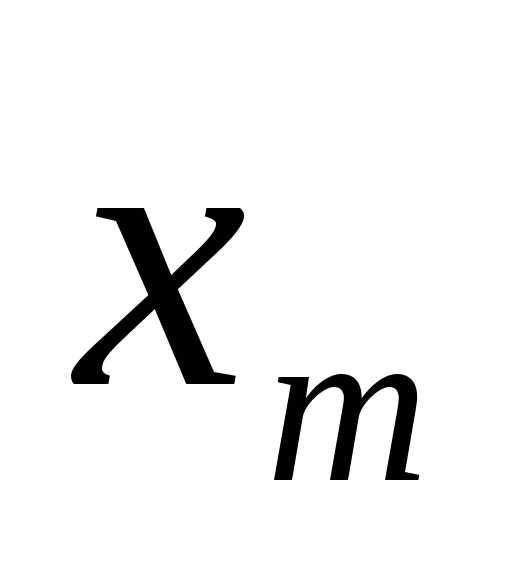 . Аналогично
поступают для (
. Аналогично
поступают для (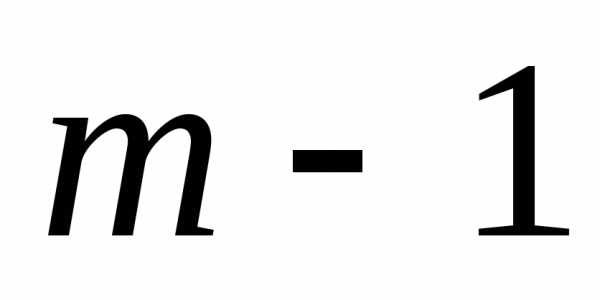 )-го шага, делая предположения об исходах
окончания (
)-го шага, делая предположения об исходах
окончания (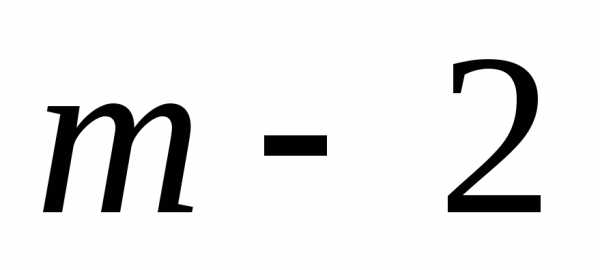 )-го шага и определяя условное оптимальное
управление на (
)-го шага и определяя условное оптимальное
управление на ( )-м шаге, приносящее оптимальный выигрыш
на двух последних шагах – (
)-м шаге, приносящее оптимальный выигрыш
на двух последних шагах – ( )-м и
)-м и  -м. Так
же действуют на всех остальных шагах
до первого. На первом шаге, как правило,
не надо делать условных предположений,
так как состояние системы перед первым
шагом обычно известно.
-м. Так
же действуют на всех остальных шагах
до первого. На первом шаге, как правило,
не надо делать условных предположений,
так как состояние системы перед первым
шагом обычно известно.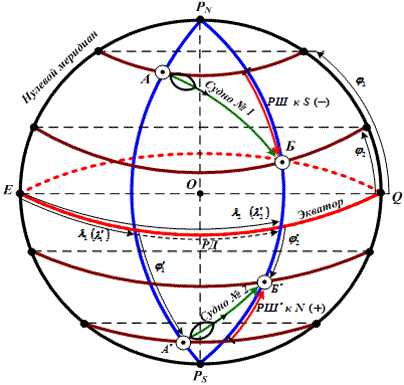




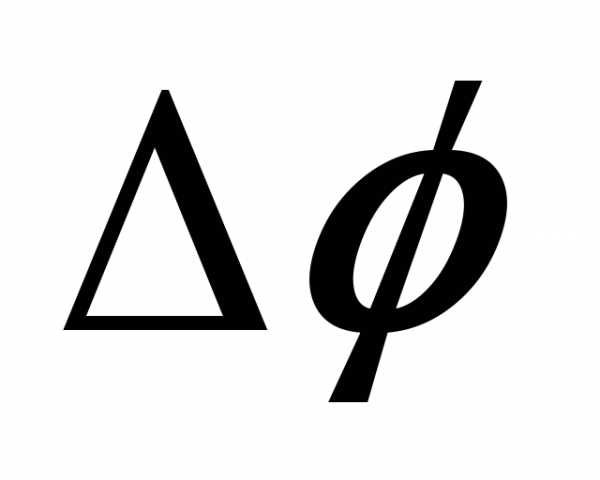















 (1.5)
(1.5)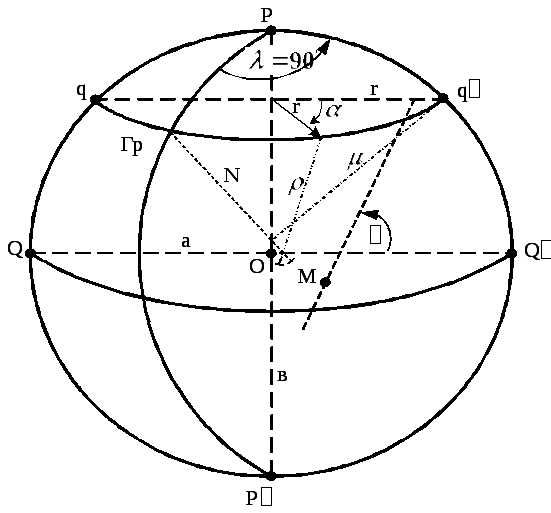
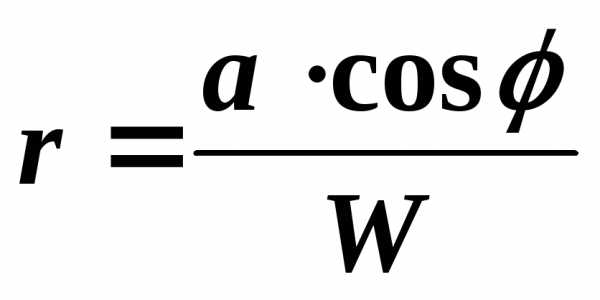 или. (1.6)
или. (1.6) (1.7)
(1.7)
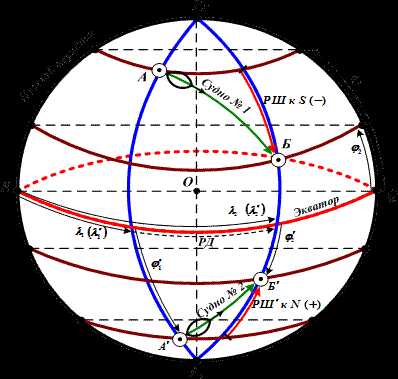
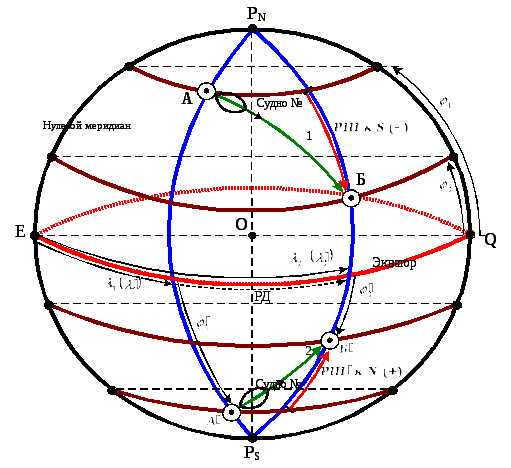
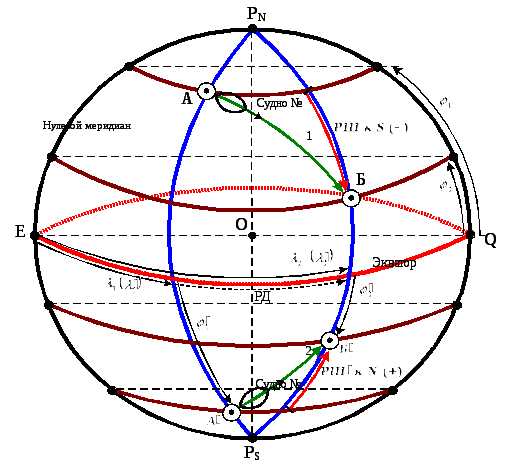
 Истинный курс– двугранный угол между северной частью плоскости истинного меридиана и носовой частью диаметральной плоскости лодки.
Истинный курс– двугранный угол между северной частью плоскости истинного меридиана и носовой частью диаметральной плоскости лодки.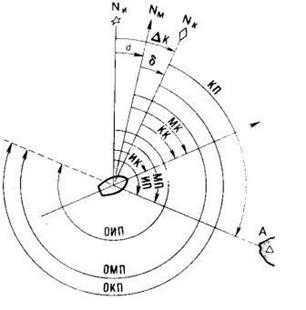






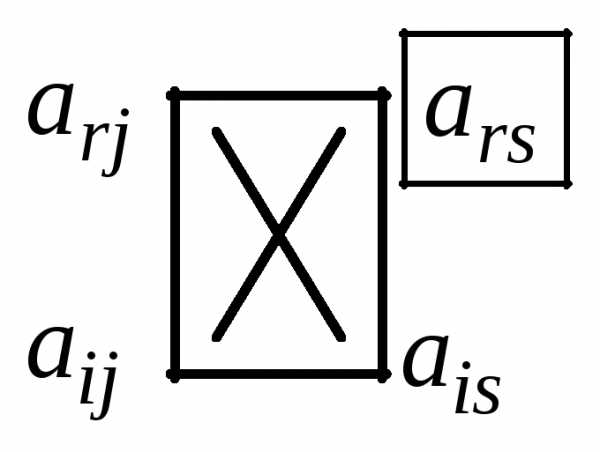
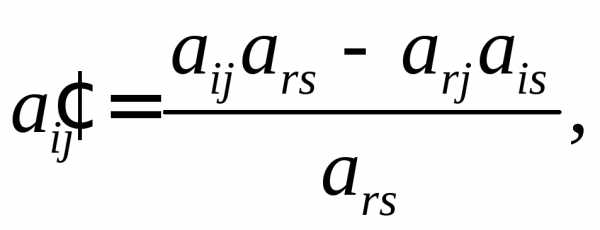
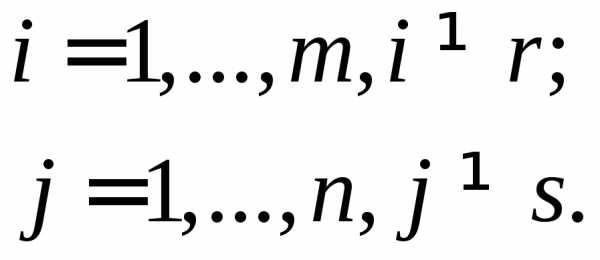 (7)
(7)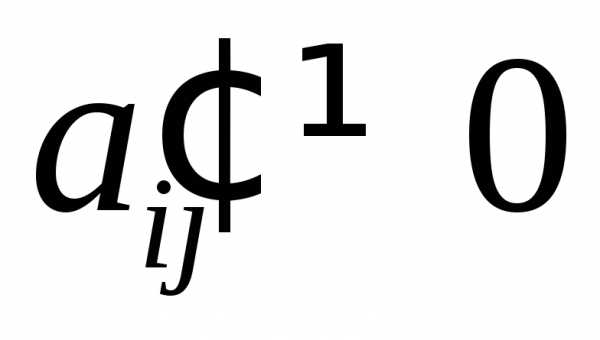 матрицыА
и расположенный в строке и столбце,
которые ещё не были разрешающими. Схему
преобразований 1—4 повторяем до тех
пор, пока все строки (или столбцы) матрицы А не будут использованы как разрешающие.
матрицыА
и расположенный в строке и столбце,
которые ещё не были разрешающими. Схему
преобразований 1—4 повторяем до тех
пор, пока все строки (или столбцы) матрицы А не будут использованы как разрешающие.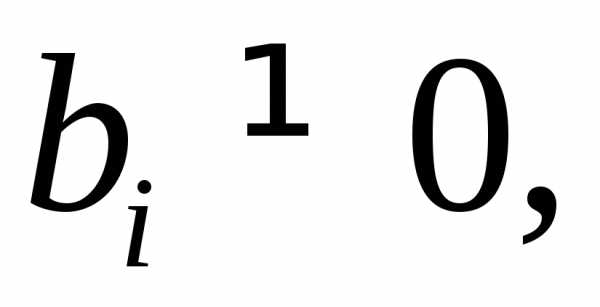
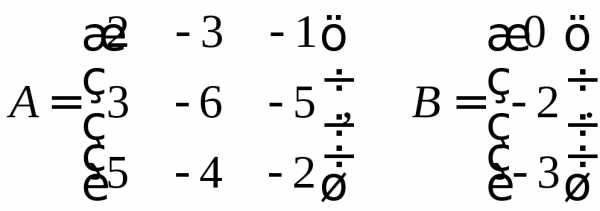
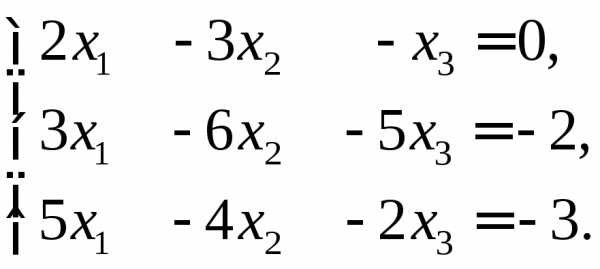
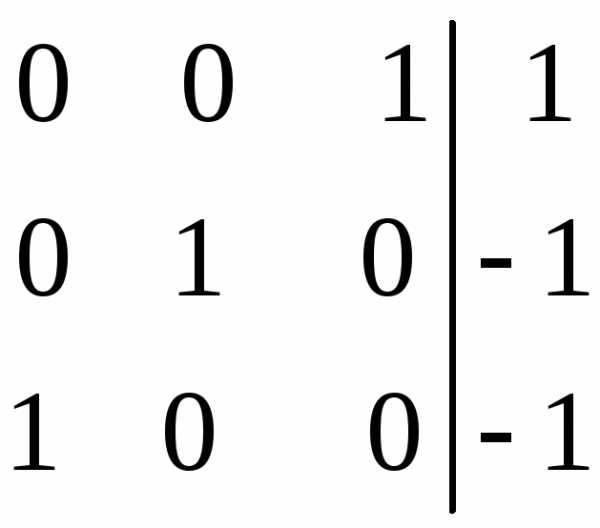
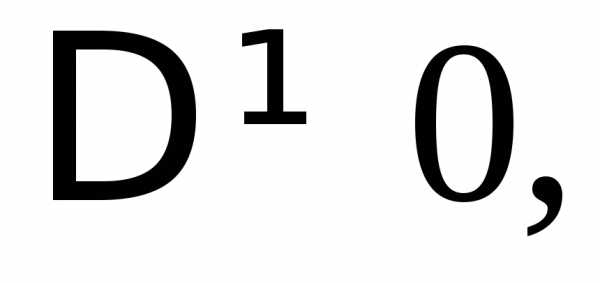 система имеет единственное решение,
которое находим по формулам Крамера
(5):
система имеет единственное решение,
которое находим по формулам Крамера
(5):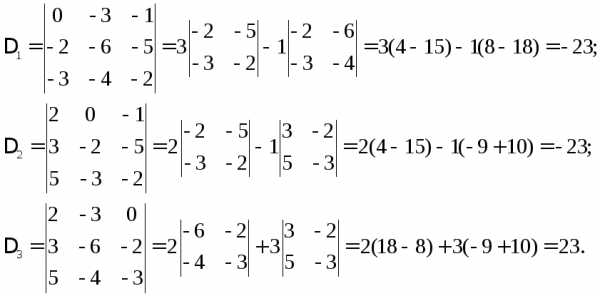
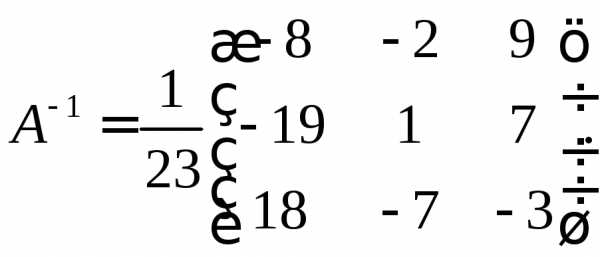
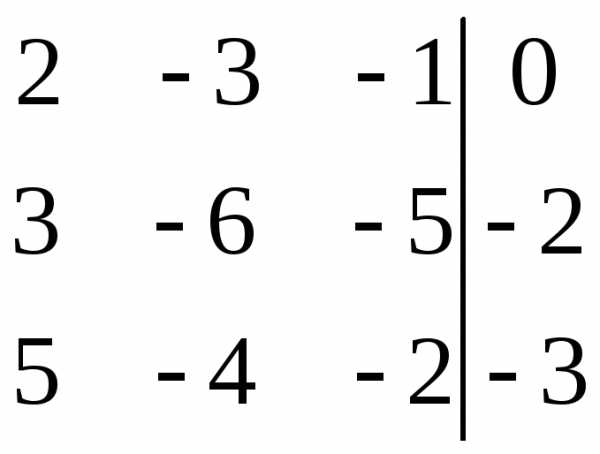
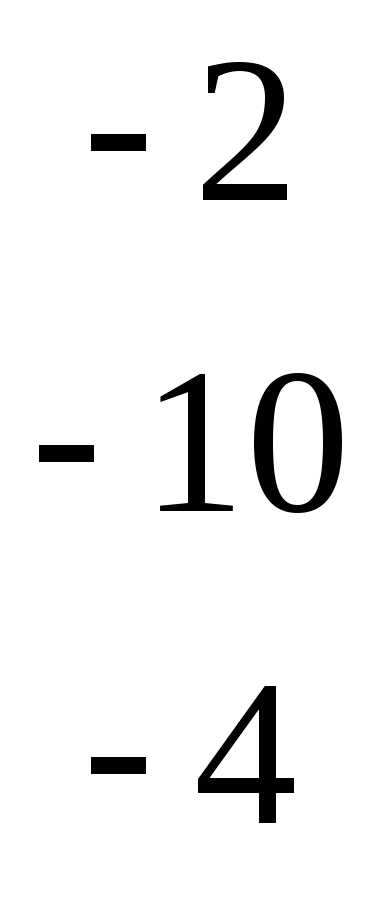
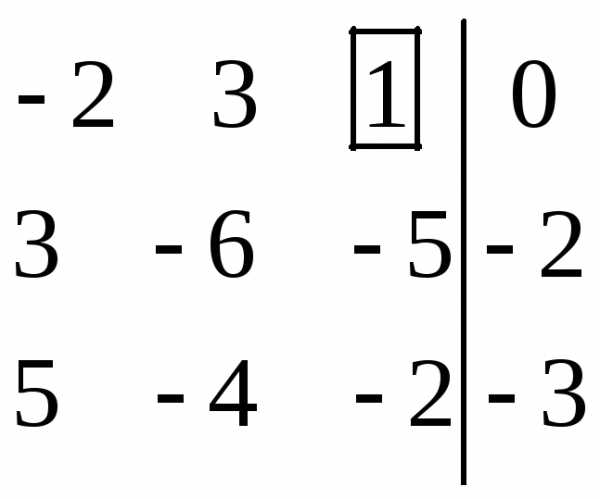
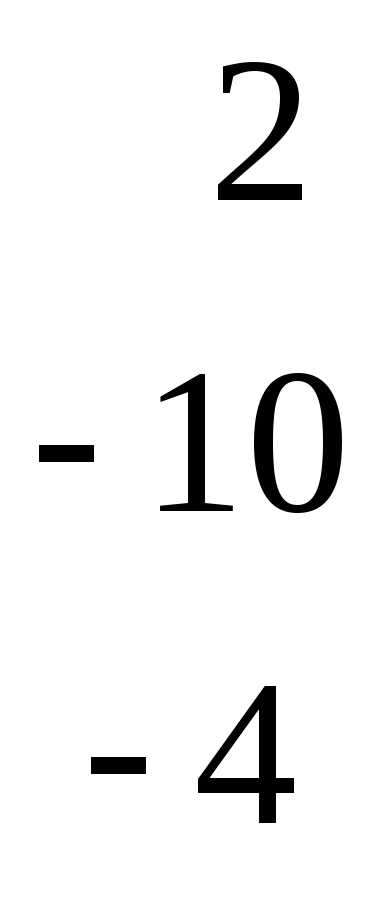
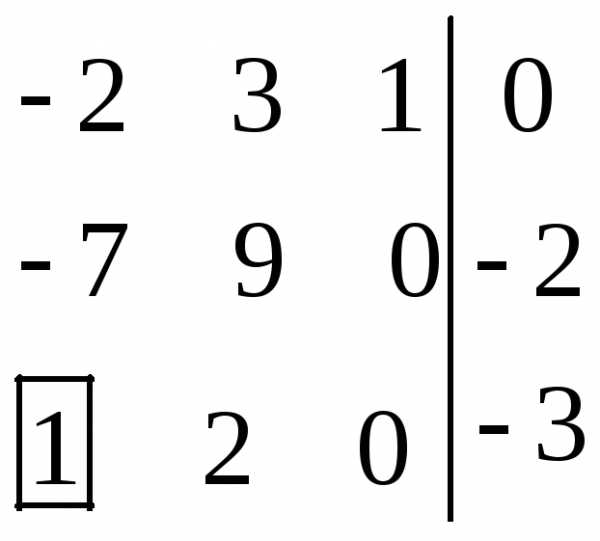
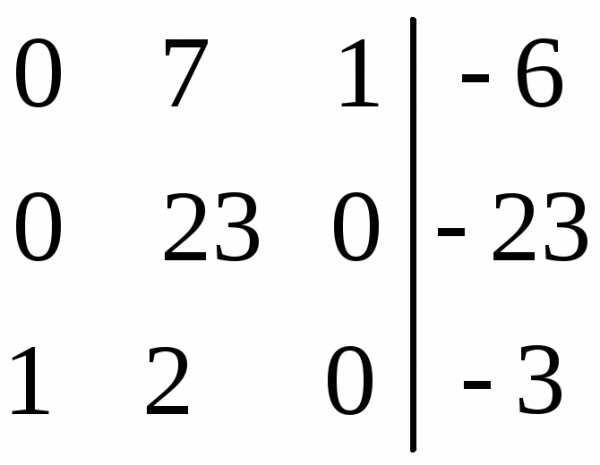
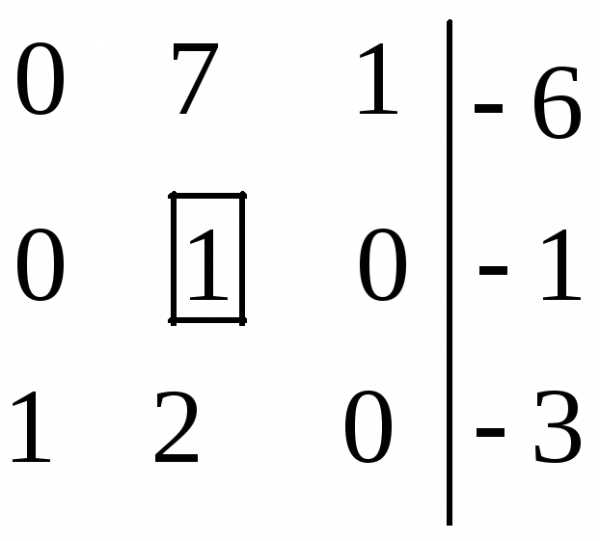

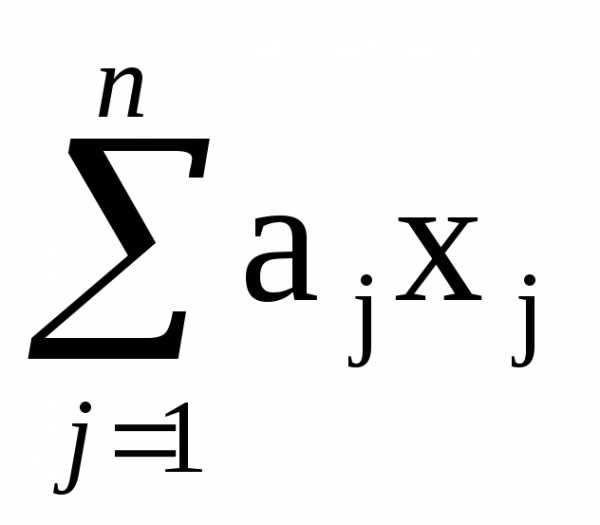 =b.
=b. 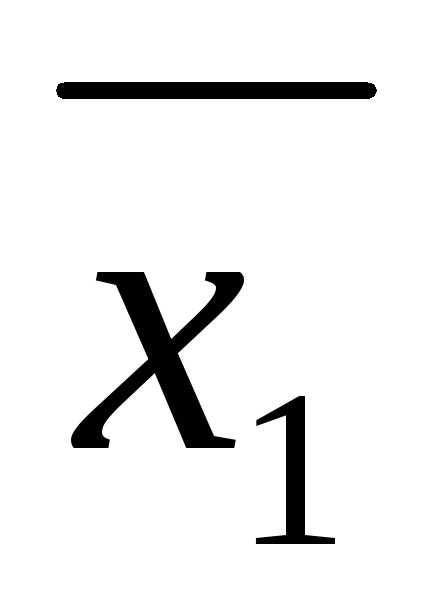 ,
,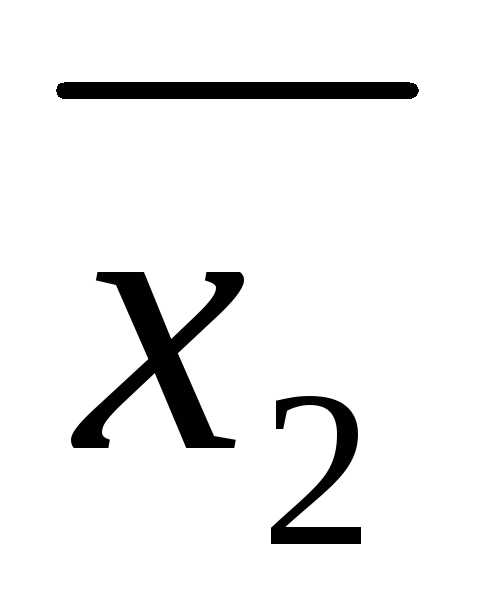 ,…,
,…,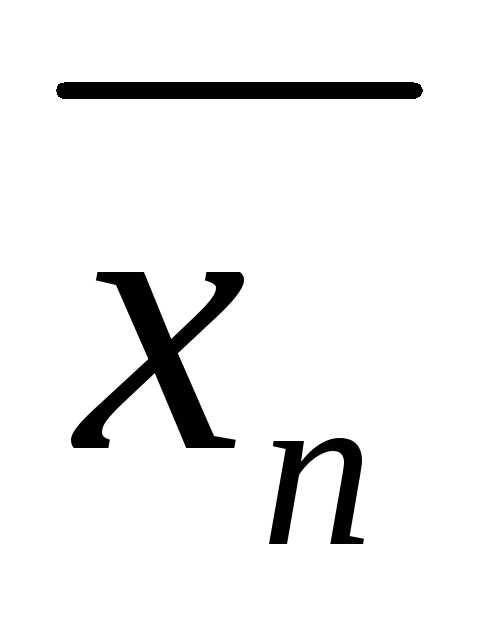 )
значений переменных, который при
подстановке в уравнение (т.е. при замене xjна
)
значений переменных, который при
подстановке в уравнение (т.е. при замене xjна 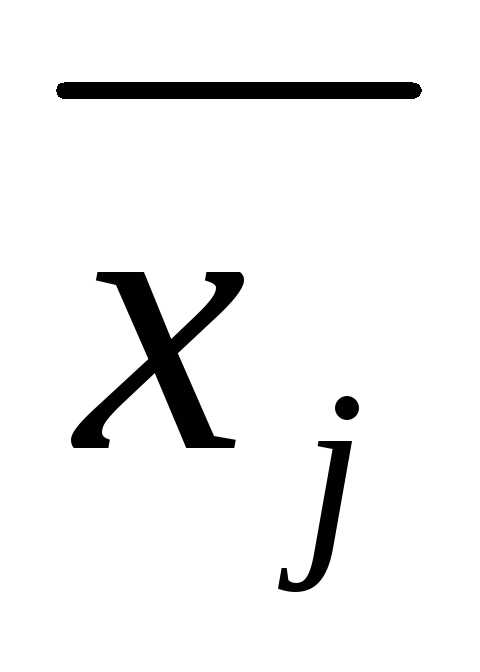 при всехj от 1до n обращает его в тождество. Подчеркнем,
что решение уравнения с n
переменными всегда есть набор из n
чисел и каждый такой набор из n
чисел представляет собой одно решение. Очевидно, что если хотя бы один
коэффициент при переменных не равен 0,
то уравнение (*) имеет решение. В противном
случае решение существует только при
b
= 0, и это все произвольные наборы из n
чисел.
при всехj от 1до n обращает его в тождество. Подчеркнем,
что решение уравнения с n
переменными всегда есть набор из n
чисел и каждый такой набор из n
чисел представляет собой одно решение. Очевидно, что если хотя бы один
коэффициент при переменных не равен 0,
то уравнение (*) имеет решение. В противном
случае решение существует только при
b
= 0, и это все произвольные наборы из n
чисел.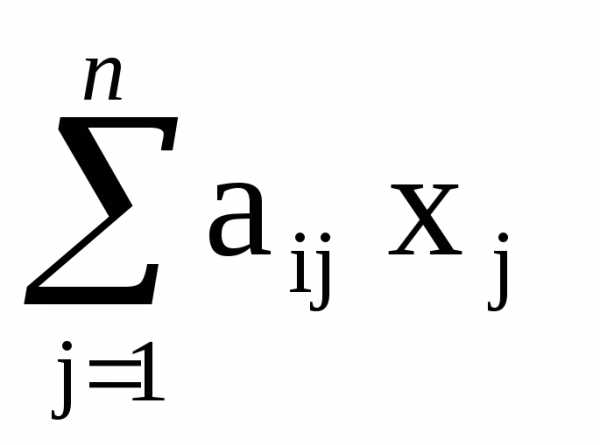 =bi, i = 1,…,m.
=bi, i = 1,…,m.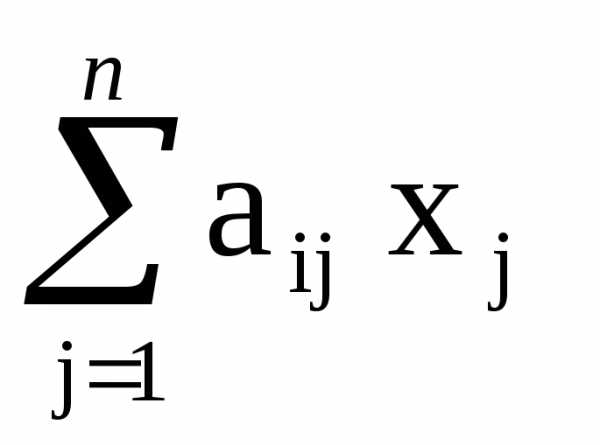 =
0,i = 1,…,m, (10)
=
0,i = 1,…,m, (10)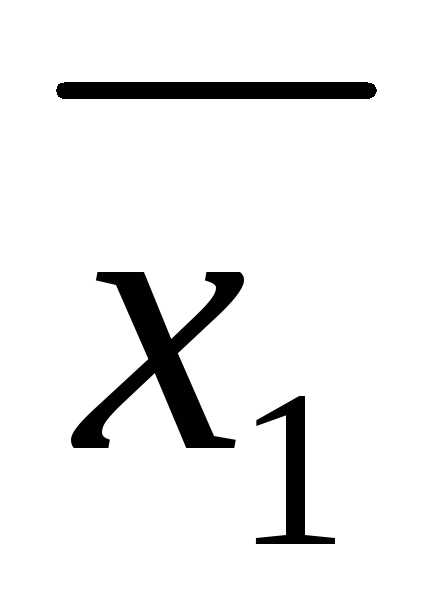 ,
,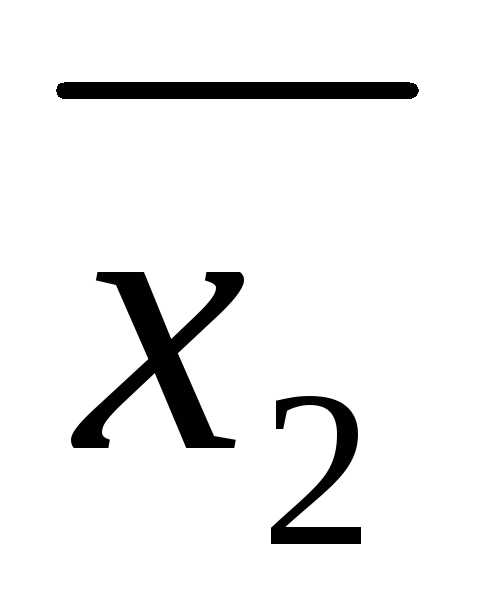 ,…,
,…,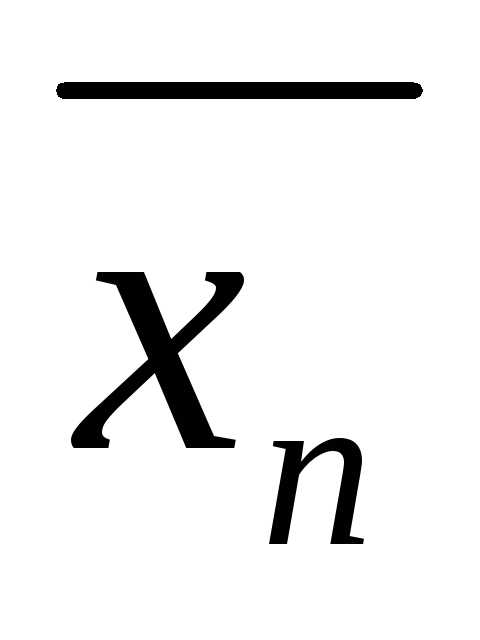 )
значений переменных, который при
подстановке в уравнения системы (1)
(т.е. при замене xjна
)
значений переменных, который при
подстановке в уравнения системы (1)
(т.е. при замене xjна 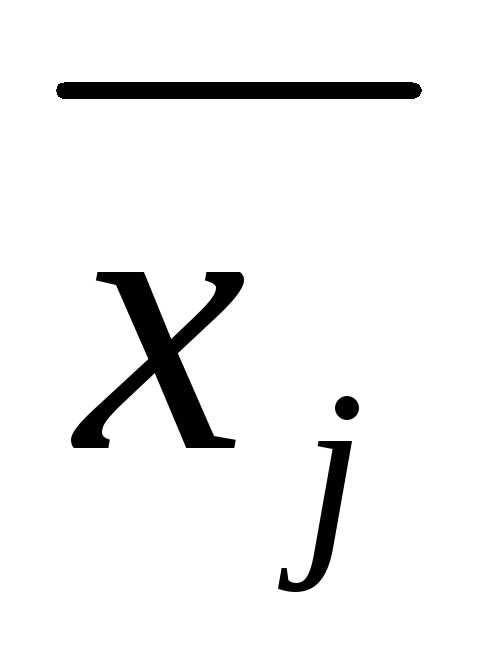 , j
= 1,…,n) все эти уравнения обращает в тождества,
т.е.
, j
= 1,…,n) все эти уравнения обращает в тождества,
т.е. 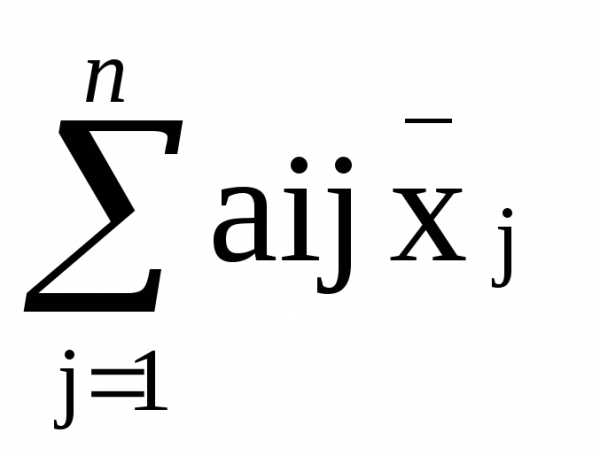 =bi при всех i
= 1,…,m.
=bi при всех i
= 1,…,m. .
. k
k 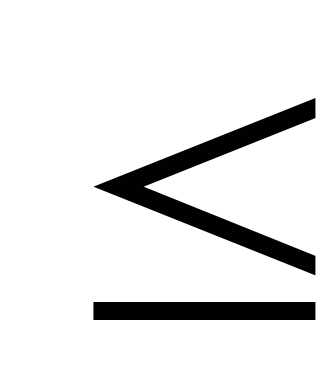 m,
такое, что akj = 0
m,
такое, что akj = 0  j,
то
j,
то 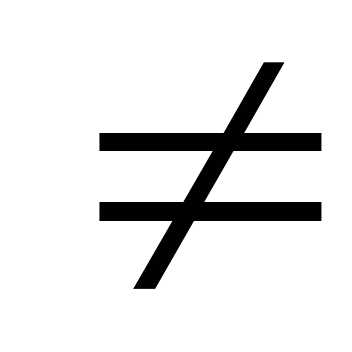 0,
то система (1) несовместна;
0,
то система (1) несовместна; и
прибавим его к первому уравнению. В
результате этого преобразования получим
систему (1’), в которой все уравнения,
начиная со второго, не изменились, а
первое имеет следующий вид
и
прибавим его к первому уравнению. В
результате этого преобразования получим
систему (1’), в которой все уравнения,
начиная со второго, не изменились, а
первое имеет следующий вид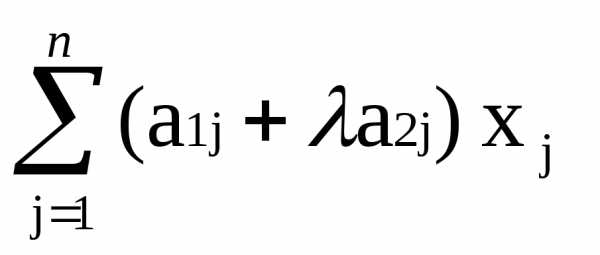 = b1 +
= b1 +  b2.
b2.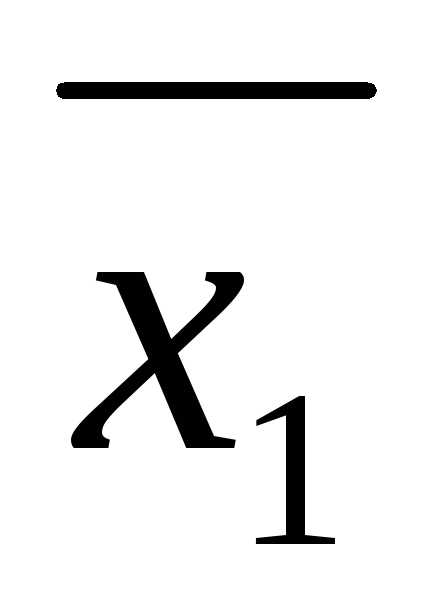 ,
,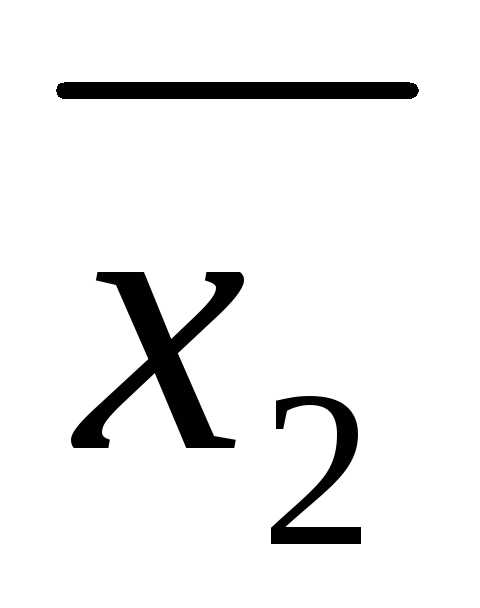 ,…,
,…,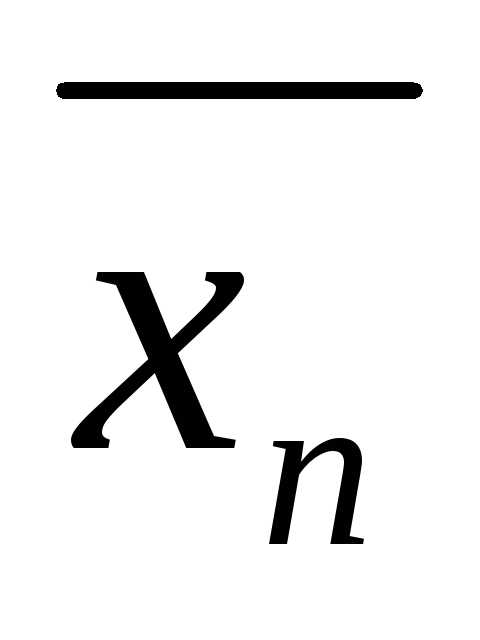 )
значений переменных обращает в тождества
все уравнения системы (1), то он обращает
в тождества и все уравнения системы
(1’). Наоборот, решение (x’1 ,x’2 ,…,x’j , … ,x’n)
системы (1’) является также решением
системы (1), так как система (1) получается
из системы (1’) с помощью аналогичного
преобразования, когда к первому уравнению
системы (1’) прибавляется второе уравнение
системы (1’), умноженное на число (-
)
значений переменных обращает в тождества
все уравнения системы (1), то он обращает
в тождества и все уравнения системы
(1’). Наоборот, решение (x’1 ,x’2 ,…,x’j , … ,x’n)
системы (1’) является также решением
системы (1), так как система (1) получается
из системы (1’) с помощью аналогичного
преобразования, когда к первому уравнению
системы (1’) прибавляется второе уравнение
системы (1’), умноженное на число (- ).
). (в нейm
строк и (n+1)
столбцов), т.е
(в нейm
строк и (n+1)
столбцов), т.е  = (A,
b).
В i
– ой строке матрицы
= (A,
b).
В i
– ой строке матрицы  содержатся всеизвестные параметры, характеризующие i
— ое уравнение системы (1), i
= 1,…, m.
В j
– м столбце матрицы A
содержатся все коэффициенты при
неизвестном xj,
встречающиеся в системе (1).
содержатся всеизвестные параметры, характеризующие i
— ое уравнение системы (1), i
= 1,…, m.
В j
– м столбце матрицы A
содержатся все коэффициенты при
неизвестном xj,
встречающиеся в системе (1). n.
Переставив строки и перенумеровав
переменные (т.е. переставив столбцы),
можно таблицу I(r) представить в виде
n.
Переставив строки и перенумеровав
переменные (т.е. переставив столбцы),
можно таблицу I(r) представить в виде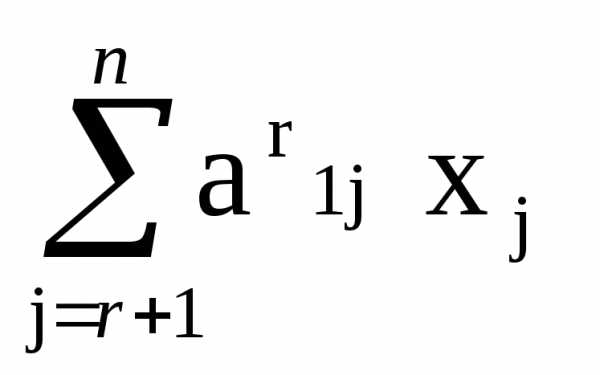 =b(r)1 ,
=b(r)1 ,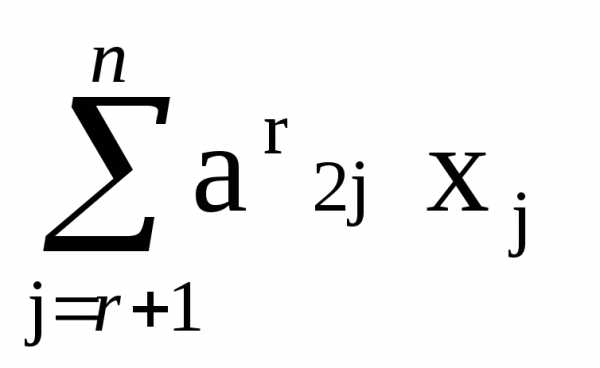 =b(r)2 ,
=b(r)2 ,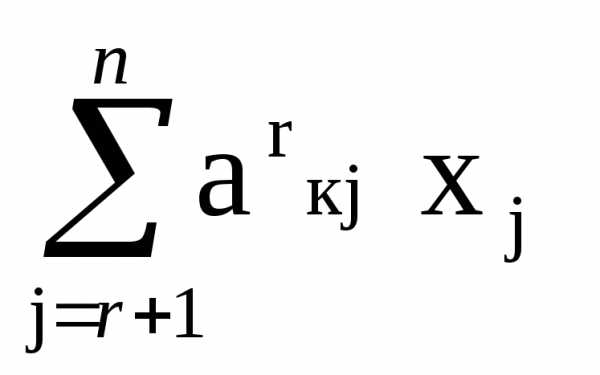 =b(r)r ,
=b(r)r , a(r)ijxj,
i = 1,…,r = m; xj – любое
при
j = (r+1),…,n. (5)
a(r)ijxj,
i = 1,…,r = m; xj – любое
при
j = (r+1),…,n. (5) a(r)ijxj при i
= 1,…, r
= m;
xj – любое при j
=(r+1),…,n.}.
a(r)ijxj при i
= 1,…, r
= m;
xj – любое при j
=(r+1),…,n.}.
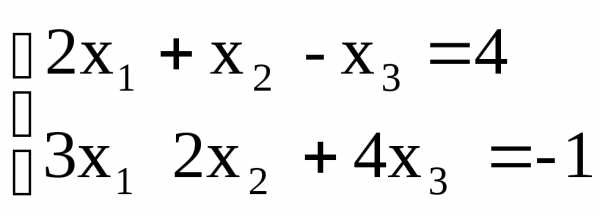
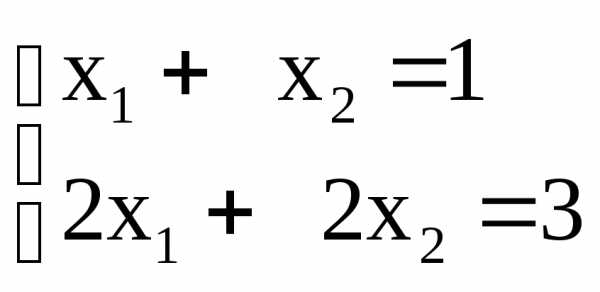
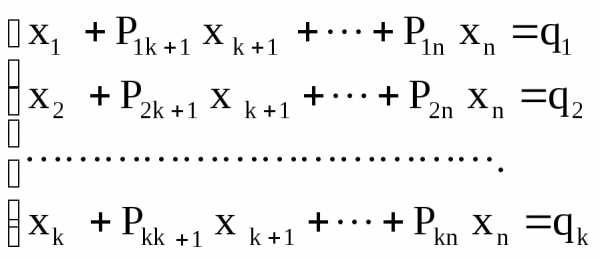 (1.2)
(1.2)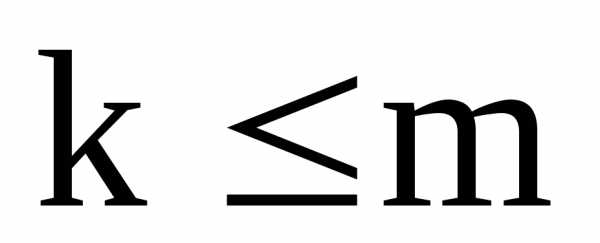 ,
причем строгое неравенство имеет место
тогда, когда на некоторых шагах жордановой
процедуры удалялись уравнения вида
(1.5).
,
причем строгое неравенство имеет место
тогда, когда на некоторых шагах жордановой
процедуры удалялись уравнения вида
(1.5).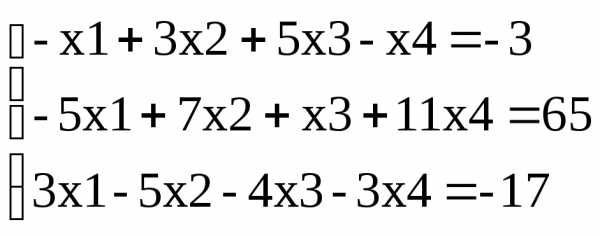

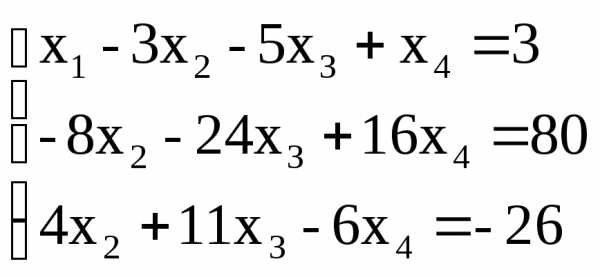
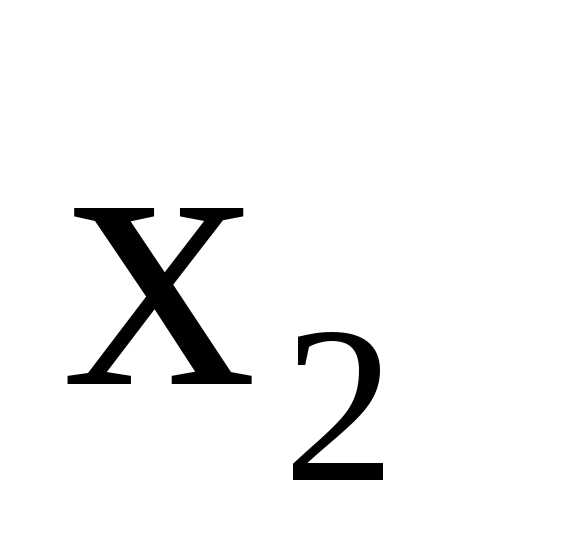 .
Поделив второе уравнение на (-8) и исключив
.
Поделив второе уравнение на (-8) и исключив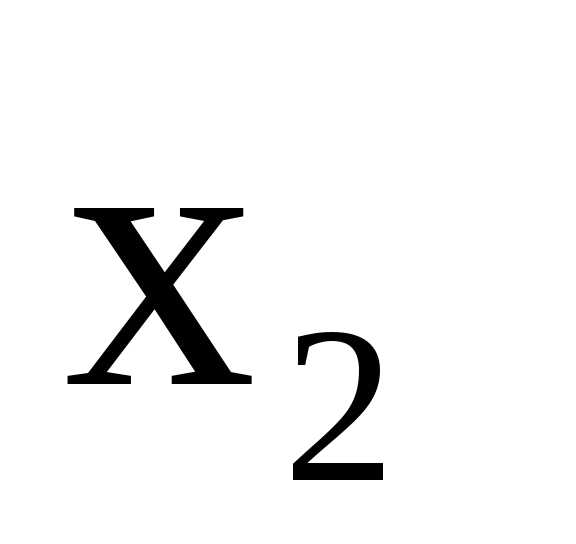 из
первого и третьего уравнений, получим
систему:
из
первого и третьего уравнений, получим
систему: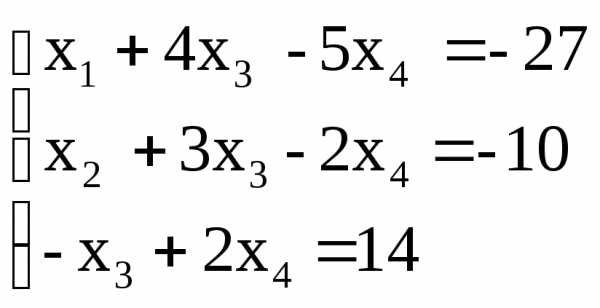
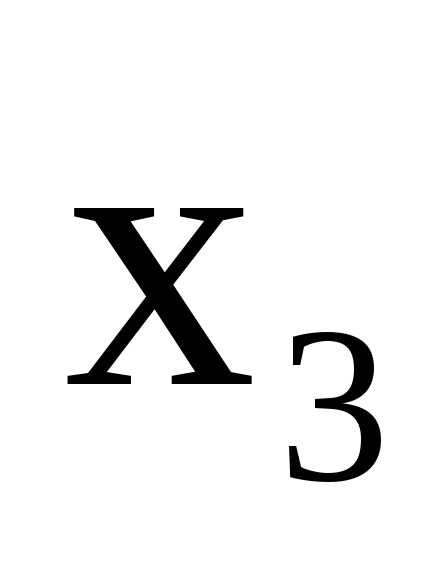 .
Поделим это уравнение на (-1) и исключим
.
Поделим это уравнение на (-1) и исключим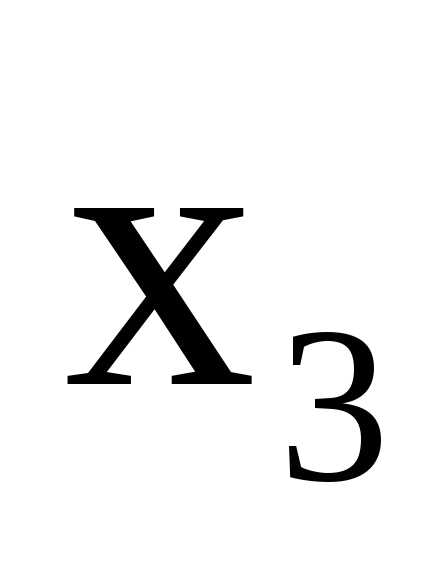 из остальных уравнений. Получим жорданову
форму:
из остальных уравнений. Получим жорданову
форму: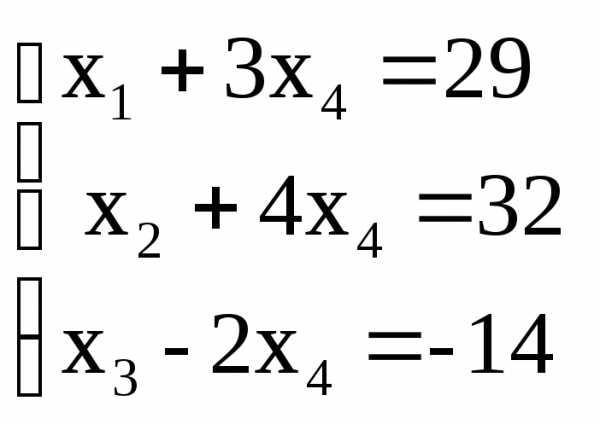
 —
свободной.
—
свободной.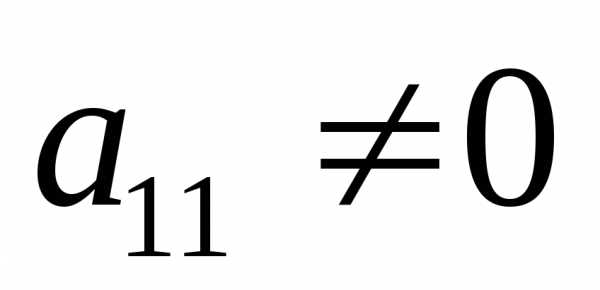 (перестановкой уравнений системы можно
добиться того, что
(перестановкой уравнений системы можно
добиться того, что будет наибольшим по модулю коэффициентом
при
будет наибольшим по модулю коэффициентом
при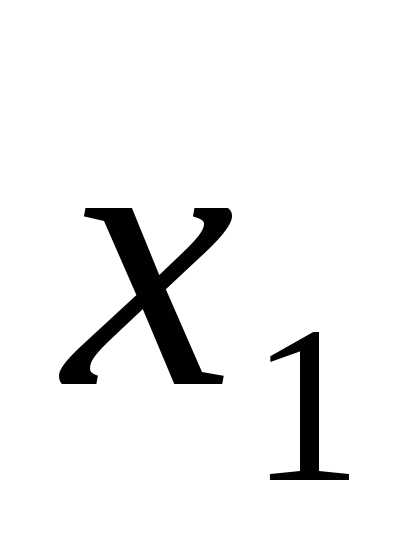 ).
Разделим первое уравнение системы на
).
Разделим первое уравнение системы на ,
во всех остальных уравнениях исключим
,
во всех остальных уравнениях исключим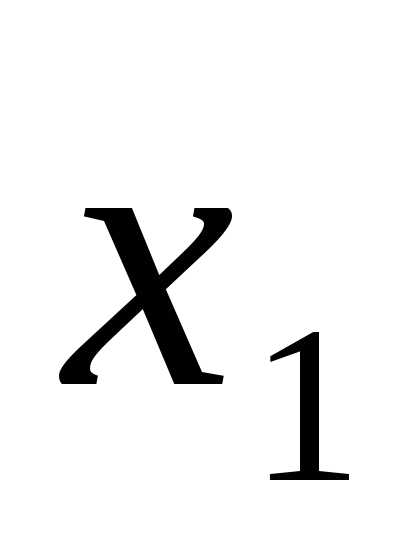 ,
то есть сведем расширенную матрицы
системы к виду
,
то есть сведем расширенную матрицы
системы к виду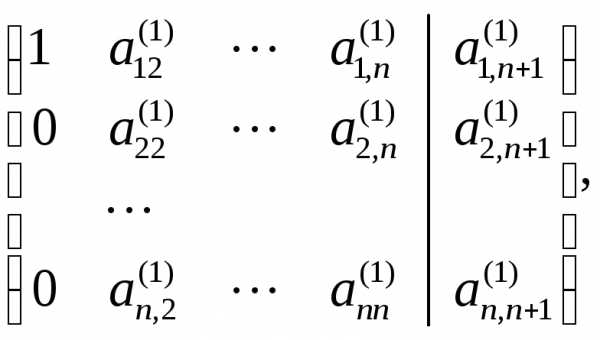
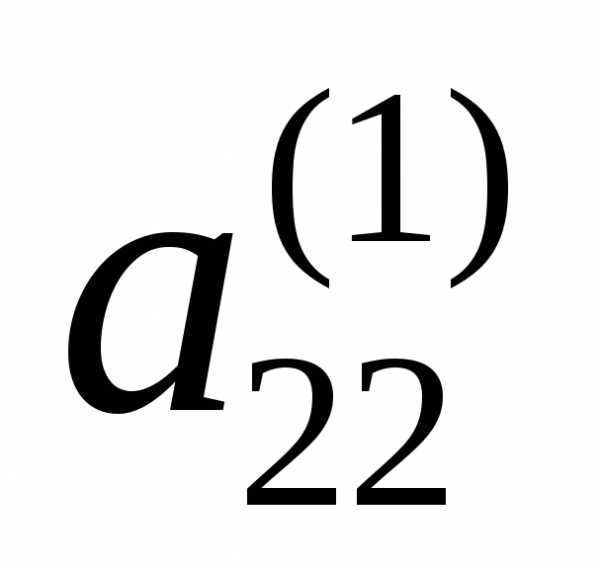 (можно
сделать перестановку строк 2,…,n таким
образом чтобы он был наибольшим по
модулю). Разделим второе уравнение на
(можно
сделать перестановку строк 2,…,n таким
образом чтобы он был наибольшим по
модулю). Разделим второе уравнение на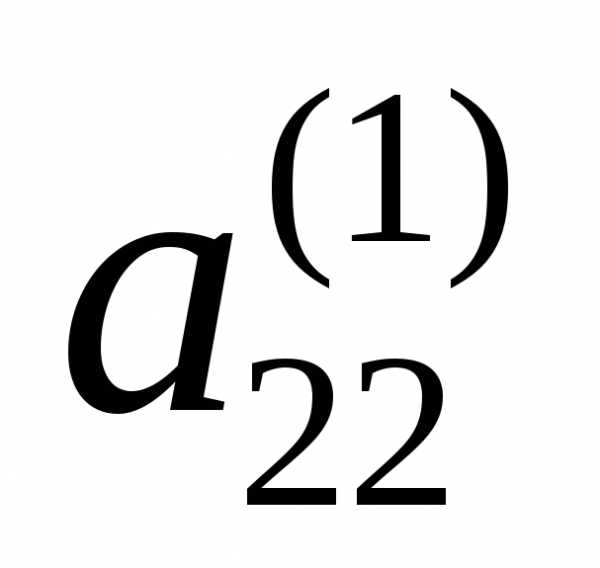 ,
исключим
,
исключим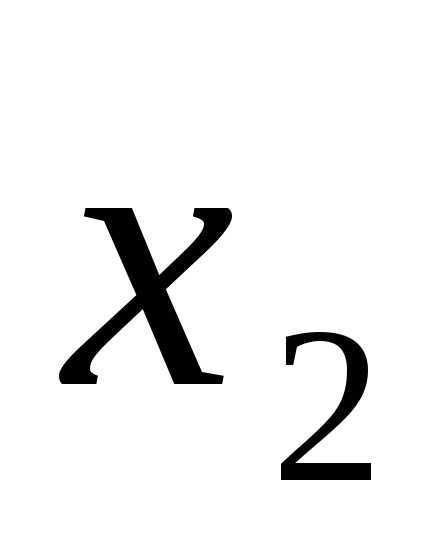 из всех уравнений кроме второго.
из всех уравнений кроме второго.

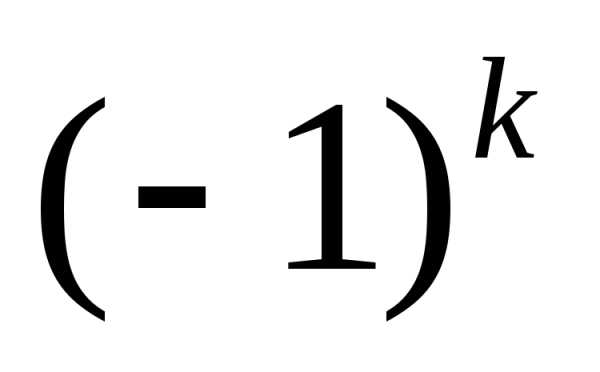 ,
гдек – количество перестановок строк и
столбцов.
,
гдек – количество перестановок строк и
столбцов.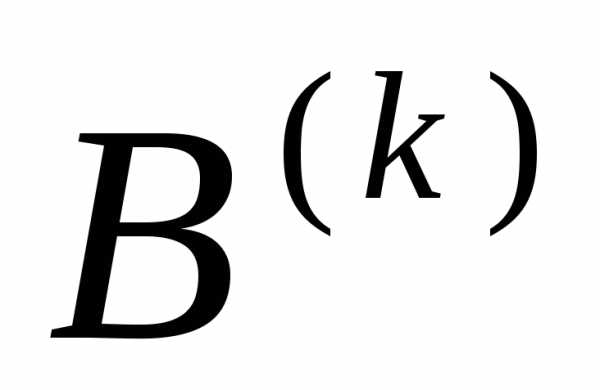 выбирать столбцы единичной матрицы
порядкаn:
выбирать столбцы единичной матрицы
порядкаn: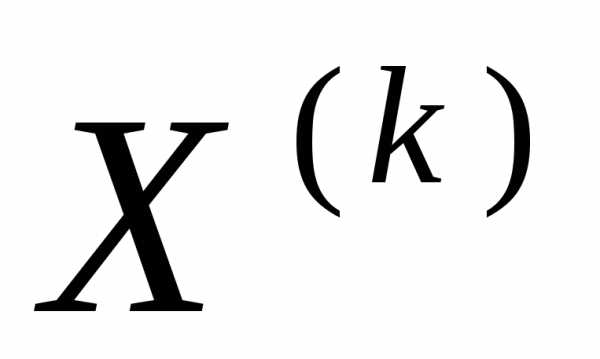 системыбудетк-м
столбцом обратной матрицы
системыбудетк-м
столбцом обратной матрицы 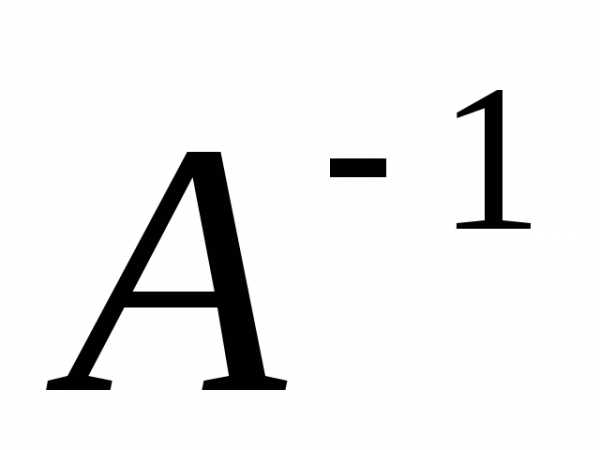 .
.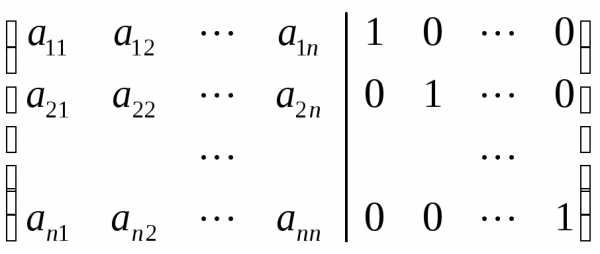 ~после n шагов
~после n шагов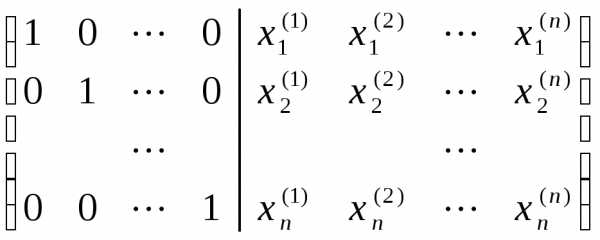 .
.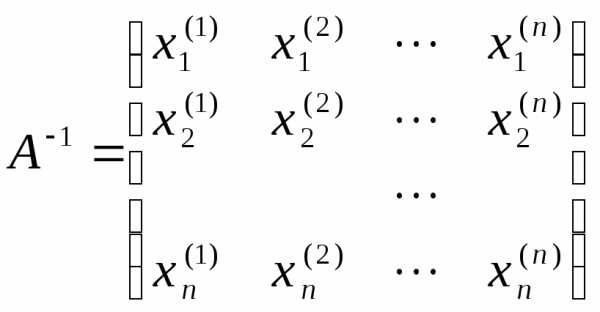 .
.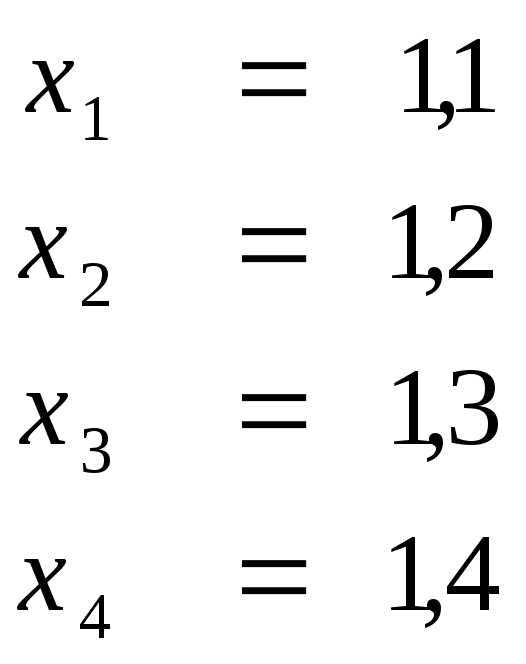 .
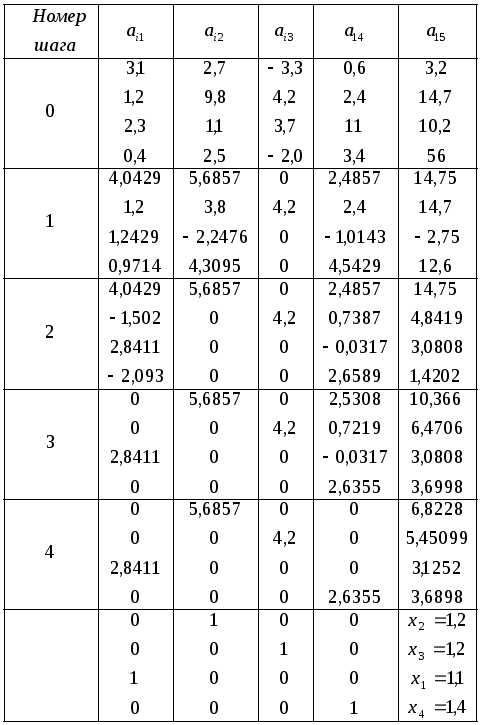
.
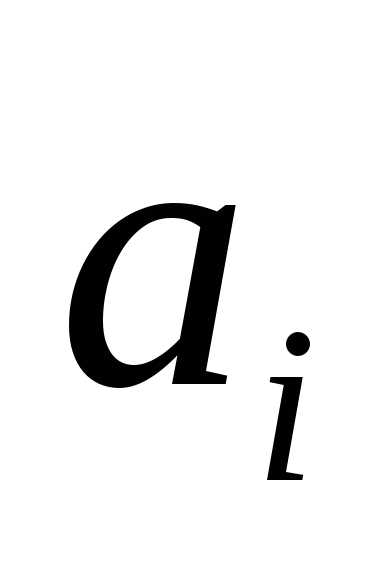 в системе (25). Так как
в системе (25). Так как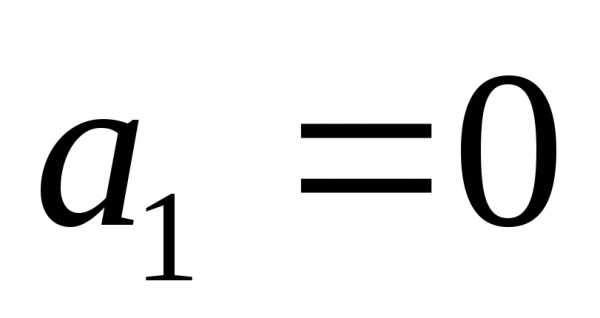 ,
то первое уравнение системы имеет вид
,
то первое уравнение системы имеет вид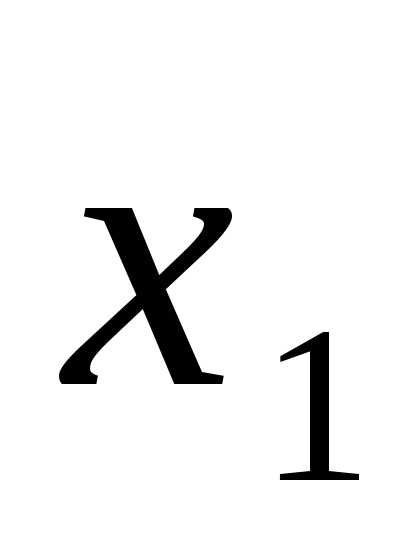 через
через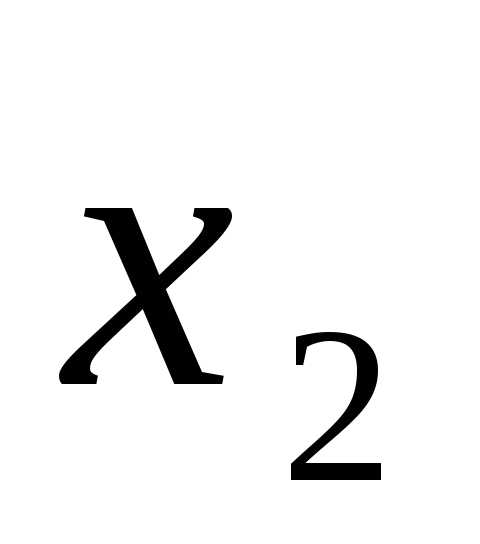 :
: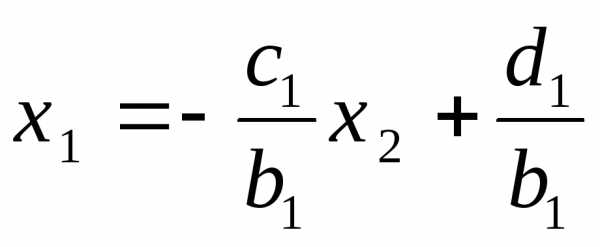 и подставим во второе уравнение системы,
получим уравнение связывающее
и подставим во второе уравнение системы,
получим уравнение связывающее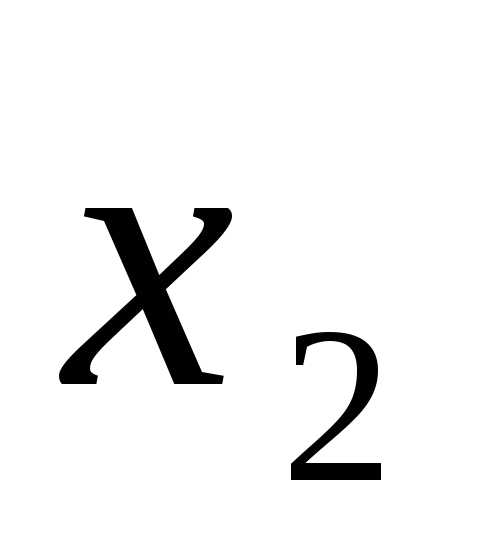 и
и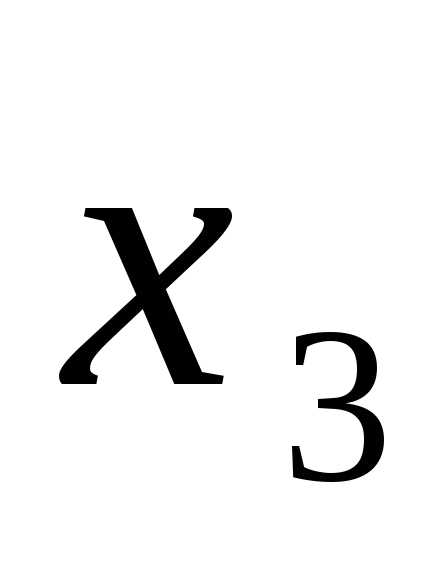 и так далее. Пусть уже получено соотношение
и так далее. Пусть уже получено соотношение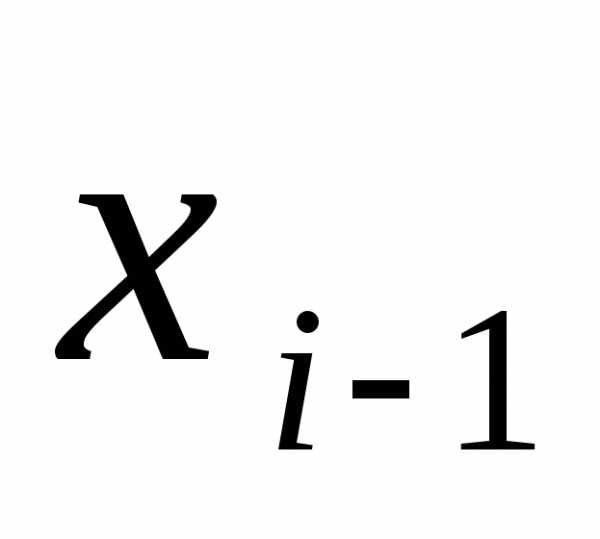 вi-е
уравнение системы (25)
вi-е
уравнение системы (25) в прямом ходе:
в прямом ходе: