Тест: Упрощение буквенных выражений — Математика 5 класс
Упрощение буквенных выражений , нахождение значений буквенных выражений
Математика 5 класс | Автор: Ливанова И.Г. | ID: 3764 | Дата: 31.1.2015
«;} else {document.getElementById(«torf1″).innerHTML=»»;}; if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;}; if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;}; if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;}; if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;}; if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;}; if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;}; if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;}; if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;}; } }Получение сертификата
о прохождении теста
testedu.ru
УПРОЩЕНИЕ ВЫРАЖЕНИЙ 5 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Предмет
Математика
Класс
5
Учитель
Красникова Наталья Николаевна
Тема урока:
Упрощение выражений
Цель урока:
продолжить работу по формированию умений решать уравнения с использованием распределительного свойства умножения относительно сложения и вычитания; продолжить работу над текстовыми задачами, решаемыми с помощью уравнения
Тип урока:
урок комбинированный.
Деятелъностная цель: формирование у учащихся умений упрощать выражения.
Содержательная цель: расширение понятийной базы за счет включения в нее новых элементов.
Образовательные (формирование познавательных УУД):
Отработать навыки чтения и записи числовых и буквенных выражений;
Формировать умение решать задачи способом составления уравнения;
Проверить уровень усвоения изученной темы;
Развивающие (формирование регулятивных УУД)
Развитие навыков самостоятельной деятельности обучавшихся;
Формирование математически грамотной речи. Уметь правильно понимать термины. Развитие математической зоркости.
Воспитательные (формирование коммуникативных и личностных УУД)
Воспитывать интерес к изучаемому предмету;
Воспитывать коллективные взаимоотношения, взаимопонимания;
Развивать самостоятельность, самоконтроль, наблюдательность.
Методы: проблемно-поисковый, словесный, наглядный, практический.
Оборудование: ПК, мультимедийный проектор, листы урока, мел, доска.
Планируемый результат
Личностные:
Формирование познавательного интереса обучающихся к изучению нового материала, к способам обобщения и систематизации знаний.
Воспитание культуры личности.
Развивать навыки сотрудничества.
Познавательные:
Закреплять навыки и умения применять правила упрощений выражений при решении задач и применение свойств умножения,
Систематизировать знания, уметь обобщать и углублять знания , выбирать и формулировать познавательную цель, выражать смысл ситуации с помощью различных примеров.
Предметные:
Уметь в процессе реальной ситуации применять понятие упрощение выражений.
Уметь планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её реализации.
Способствовать приобретению учащимися навыков общения при совместной работе;
Делать выводы на основе обобщения знаний.
Регулятивные:
Самостоятельно формулируют познавательную цель и строят свои действия в соответствии с ней;
Планируют собственную деятельность, определяют средства для её осуществления.
Коммуникативные:
Регулировать собственную деятельность посредством речевых действий;
Уметь слушать и вступать в диалог, воспитывать чувство взаимопомощи;
Уважительное отношение к чужому мнению, культуре учебного труда, требовательное отношение к себе и к своей работе.
Технологии
Технология проблемного обучения, игровые технологии, ИКТ
Форма работы
индивидуальная, фронтальная работа, самостоятельная работа.
Технология проведения
Деятельность учителя
Задания для учащихся, выполнение которых приведет к достижению запланированных результатов
Деятельность учеников
Планируемые результаты
предметные
универсальные учебные действия(УУД)
1
2
3
4
5
6
1. Организационный этап
Создать благоприятный психологический настрой на работу
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
Сегодня вы работаете с листом рефлексии и самооценки. Оцените свою готовность к уроку. – А вот хорошо ли вы считаете в уме, и на сколько вы внимательны, это мы сейчас и проверим! Внимание на экран! Обсуждение и проверка ответов.
Включаются в деловой ритм урока.
Уметь выполнять основные математические действия.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
Регулятивные: организация своей учебной деятельности
Личностные: мотивация учения
Постановка целей и задач урока. Мотивация учебной деятельности учащихся
Цели:
— актуализировать требования
к ученику с позиций учебной
деятельности;
— создать условия для формирования у учеников внутренней потребности во включении в учебную деятельность
Систематизировать изученный материал.
Стимулировать активность ученика на восприятие нового учебного материала.
Подвести к формулированию цели урока и самостоятельному поиску нужной информации.
Но сначала решим несколько упражнений и попробуем назвать тему урока.
1.УСТНО пример А
2.Вычислите устно Б и запишите ответ
15a ∙ 4 =
3b ∙ 12 =
18 ∙ 5b =
11a ∙ 7 =
16 ∙ d ∙ 3 =
x ∙ 5 ∙ 4 ∙ 6 =
3. Упростите В , если возможно:
17m + 5m =
6a – a =
9c + 4c – 6c =
5 + 12n – 2n =
24b + 7a – 5a =
y – 8
Г Верно или не верно
Слушают
Учителя.
Вычисляют устно. Делают записи в листе
Самопроверка.
Самооценивание.
Знать правила упрощения буквенных выражений.
Уметь применять свойства умножения в решении упражнений.
Коммуникативные: уметь совместно договариваться о правилах поведения и общения, следовать им; оформлять свои мысли в устной форме.
Познавательные: уметь использовать модели для решения задач
Найдите пару для выражения, стоящего в левом столбце.
1)5х+13х-4 2)(5+у)*4 3)4а*3
4)15а-а 5)12у-7у-2
6)4х*6*2 7)9*х*5
А)8а Б)4х
В)45х
Г)48х
Д)18х-4
Е)20+4у
Ж)12а
З)5у-2
И)3у
Вычисляют. Сопоставляют величины. Делают записи в листе
Выполняется контроль знаний
Коммуникативные :
Слушать, понимать речь других
Познавательные УУД:
-уметь проводить сравнение по заданным критериям.
.
II. Актуализация и фиксирование индивидуального за-
Затруднения в пробном действии; выявление места и причины затруднения.
Цели:
— организовать фиксирование
учащимися индивидуального
затруднения;
— выявить место (шаг, операцию) затруднения;
— зафиксировать во внешней
речи причину затруднения
Организует
фиксирование
индивидуального затруднения, выявление места и причины
затруднения в речи,
обобщение актуализированных знаний
Какие свойства умножения применяют при решении этих выражений?
Запишите свойства при помощи букв.
Давайте вспомним и запишем
в буквенной форме распределительное свойство умножения относительно сложения и распределительное свойство умножения относительно вычитания:
{а +b ) с = ас + bс
b) с = ac- bc
Назовите тему урока?
Для чего надо уметь упрощать
выражения? Где это пригодится?
Найдите значение выражения:
14у + 380 +у – 380, если у = 20
1 способ (14+1)у+(38-38)=15у
15*20 =300
2 способ 14*20+38+20-38=300
Какой способ более удобный?
Выполните следующие задание удобным способом.
Д)Упростите выражения 1вариант) 3х + 2 + х + 5 =? Х=3
2вариант) 4х – х + 3 + 2 =?х=4
Е) Найдите ошибки при выполнении упрощения буквенного выражения (если они есть)
12в + 4 +13а + в +15 + 12а
1вариант)
12в + 4 +13а + в +15 + 12а = 12в + 25а + 19
2 вариант)
12в + 4 +13а + в +15 + 12а = 38ав + 19
Выполняют
задание
с проговариванием
решения.
Знать распределительное свойство умножения
относительно
сложения и вычитания, сочетательное свойство
свойство умножения.
Уметь упрощать
Выражения.
Познавательные: уметь ориентироваться в своей системе знаний
( уметь отличать новое от уже известного с помощью учителя, преобразовывать информацию из одной формы
в другую).
Коммуникативные: уметь слушать
и понимать речь других, оформлять
мысли в устной и письменной форме.
Регулятивные: уметь проговаривать последовательность действий на уроке, высказывать свое предположение
Организует тематику теста
Молодцы! Ошибки находить вы умеете, но не допускаете ли вы сами ошибок?! Это мы сейчас и проверим. Вам предстоит выполнить тест. Если вы его правильно решите, то узнаете фамилию великого математика. Решая тест, вы должны будете выписать буквы, соответствующие ответам. Приступайте к выполнению задания. ВИЕТ. Эти буквы составили фамилию известного французского математика Франсуа Виета. Он первым начал активно использовать буквы вместо чисел не только в уравнениях, но и в математических выражениях. Имя этого ученого мы еще не раз вспомним в старших класса на уроках алгебры.
Тест. Взаимопроверка, Определяют ответы к заданиям:
1 – В
2 – И
3 – Е
4 — Т
Записывают решение. Самооценка деятельности
Физкультминутка
Организует показ слайдов
— Организация физкультминутки.
Осуществляют пошаговый контроль своих действий, ориентируясь на показ движений
Решите уравнение
13х + 7х = 160
Что нужно сделать перед началом решения?
Упростите левую часть.
Где неизвестное число?
Как найти неизвестный множитель?
Записывают уравнение в листок и находят корень уравнения. Осуществляют пошаговый контроль своих решений.
Выполняют данное задание. Осуществляют самопроверку.
Создание проблемной ситуации.
Задачи: создать проблемную ситуацию; актуализировать опорные знания и умения.
Формулировка задачи через презентацию побуждение к рассуждению и высказыванию своего мнения
Задача №580 стр.88
Прочитайте задачу.
О чем говорится в задаче?
Что сказано про количество стульев?
Что говорится про количество столов? Сколько всего? Обозначай за x то, что требуется найти. Если в вопросе несколько неизвестных, за x обозначай то, которое меньше
Пусть для школы купили x столов. Тогда стульев купили 9x. Всего столов и стульев купили x+9x.
В условии сказано, что всего купили 220 столов и стульев.
Значит, можем составить уравнение:
x+9x=220
10х=220
Х=220:10
Х=22
Что мы нашли?
22 стола купили для школы.
Как найти количество стульев?
Обратите внимание. Что 9*х – количество стульев.
22*9=198 (стульев) купили для школы.
Ответ
Какую тему мы сегодня изучили?
Какие свойства мы применяли при упрощении выражений?
Зачем нужно уметь упрощать выражения?
Сможете вы сами находить и применять эти свойства при решении примеров и уравнений?
Предлагаю самостоятельно решить следующие упражнения.
Учащиеся извлекают необходимую информацию из условия задачи.
Моделируют задачу
Составлять уравнение по условию задачи Уметь решать уравнение.
Учебно-познавательная (переработка, использование информации для решения учебной задачи), коммуникативная (устная, письменная)
Самостоятельное применение полученных знаний.
Задача: закрепление знаний и умений
Подготовила материал
Самостоятельная работа — Каждой группе предлагается задания
1 вариант 2 вариант
Упростите выражение
56х — 34х 64a + 22a
97у + 43у 98b – 75b
7z – 2z + 4 8c + 5c — 5
составьте и решите уравнение
Сумма 2х и 5х равна 156 сумма 18а и 13а равна 31
разность 20у и 3у равна 51 разность 25с и 5с равна 3000
Найдите значение выражения
44х + 25у + 12х — 12у 24а + 36в + 11а — 11в
при х = 1, у = 0 при а = 0, в = 1
По рисунку составьте и решите уравнение
А————В——————-С—————————D
2х 3х 5х
АD= 40 см
Найти АВ Найти ВС
Учащиеся распределяют задания. Выполняют их на листах.
Рефлексия учебной деятельности на уроке.
Цел и:
— организовать рефлексию
и самооценку учениками собственной учебной деятельности
Организует
рефлексию,
самооценку
учебной деятельности
— Подведем итог работы на уроке.
— Какую цель мы ставили? Достигли цели? Назовите тему урока.
— Расскажите, чему вы научились.
— Оцените свою деятельность
на уроке.
Домашнее задание: п. 14, с. 85-88, № 574(а, б,), №618 и № 576(а, б)
Отвечают на вопросы.
Рассказывают, что
узнали. Осуществляют само-
оценку
Формулируют собственную позицию и мнение
Самооценка деятельности на уроке
Осознают мотивацию учебной деятельности и накопление опыта в решении задач
Регулятивные: уметь проговаривать последовательность действий на уроке, оценивать правильность
выполнения действия на уровне адекватной ретроспективной оценки.
Личностные: уметь осуществлять
самооценку на основе критерия успешности учебной деятельности
infourok.ru
Упрощение выражений 5 класс
Цели урока:
совершенствовать умение учащихся выполнять упрощение выражений, продолжить работу по формированию навыка решений задач и уравнений;
развитие познавательной активности, мышления; привитие интереса к предмету.
Ход урока:
Организационный момент.
Здравствуйте, ребята! Садитесь! Откройте свои тетради и запишите число и тему нашего урока. А тема нашего урока — «Упрощение выражений».
Сегодня у нас будет необычный урок. Мы с вами совершим путешествие на остров математики.
Мы поплывем на красивом фрегате под названием «Знание». Я думаю, что вы доверите мне командовать кораблем! Моей задачей будет помочь команде (т.е. вам) не сбиваться с курса и благополучно преодолевать на пути все трудности и подводные течения, и с помощью ваших крепких знаний добраться до конечной цели нашего путешествия — до острова Математики. Ваша задача — слаженно работать, с готовностью следовать за мной по нашей карте (слайд 3). Все препятствия представлены в виде чего?.. Ваши знания, приобретенные на уроках наглядной геометрии, также пригодятся вам сегодня. Успех путешествия будет зависеть от ваших знаний, от выполнения домашнего задания.
Устная работа.
Итак, в путь! Первый остров на нашем пути – это остров Невыученных уроков. Ребята, у кого возникли проблемы при выполнении домашнего задания?
Чтобы обойти этот остров нужно выполнить следующие задания:
Соедините стрелками левую часть, представляющую из себя буквенные выражения, с правой частью, где записаны их названия.
Возьмите первую карточку.
a•b = b•a
распределительное свойство умножения относительно сложения
(a+b)c = ac + bc
переместительное свойство умножения
( a+ b) — c = a + (b — c)
сочетательное свойство сложения
(a — b)c = ac – bc
свойство вычитания числа из суммы
( a + b) — c = (a — c) + b
распределительное свойство умножения относительно вычитания
. Давайте выполним проверку. Если задание выполнено правильно, то ставим + , если неправильно, то — .
Возьмите карточку №2. Соедините стрелками левую и правую часть.
5x + 3x – 4 8a
4a∙3 12a
2a – a + 7a 45x
12x – 7x + 2 8x -4
4x∙6∙2 2 + 5x
9∙x∙5 48x
Давайте выполним проверку. Если задание выполнено правильно, то ставим + , если неправильно, то — .
Математический диктант.
Продвигаемся дальше. И вот снова преграда. На нашем пути подводный риф. Чтобы обойти этот риф нам нужно выполнить математический диктант.
Запишите в тетради — Математический диктант
А сейчас, прочитайте задание и выполните его в тетради! Итак, внимание!
№1. Записать выражение и упростить его:
Сумма 5x и 12x
№ 2. Записать выражение и упростить его:
Произведение 6c и 4
№3. Записать выражение и упростить его:
Произведение 8 и суммы 3xи 5.
№ 4. Записать уравнение и решить его:
Сумма 3y и 5y равна 8.
№ 5. Записать выражение
Разность 12а и 6а
Положили ручки. Закончили работу. Взяли простые карандаши. Давайте выполним проверку. Если задание выполнено правильно, то ставим + , если неправильно, то — .
Посчитайте количество правильных ответов.
Поднимите руки у кого выполнено правильно «5», «4», «3».
Физкультминутка.
Давайте мы немножко отдохнем и проведем физкультминутку.
Дружно встали, потянулись,
Руки на пояс, повернулись.
Вправо, влево, раз, другой,
Повертели головой.
На носочках постояли,
Спинку стрункой подержали.
А теперь, тихонько сели.
Мы еще не все успели!
Решение уравнений.
Чтобы продолжить наше путешествие, нам нужно пополнить запас продовольствия. Займемся рыбалкой. У каждого из вас на столе есть задание в виде рыбки. Возьмите его и решите уравнение в тетради. (Работаем по вариантам.)
К доске пойдет ……………..
Вариант 1
2(х+1)+2х=110
……………….
Вариант 2
3(х+6)+2=110
А теперь отложили свои ручки, повернулись и проверили решение.
Решение задач.
На пути нашего фрегата встретились пираты, чтобы их победить, необходимо решить задачи.
Решите с помощью уравнения задачу. Работа с упражнениями учебника. Открываем учебник на стр. 88. Решаем задачи № 580, 588. Первые пять человек получат дополнительную оценку за урок.
Самостоятельная работа.
Продолжим путь. И вот перед нами остров Знатоков.
У вас на столах лежат листочки с тестами. Возьмите их, подпишите.
Приступайте к выполнению задания. Время истекло. Закончили работу.
Давайте проверим тест.
Задания
Упростите выражение 12с + 28 – 8с +2
А. 14с + 20 Б. 34с В. 4с + 30 Г. 32с + 2
Вычислите 65∙74 — 55∙74
А. 74 Б. 140 В. 740. Г. 10
Найдите значение выражения 4х +5х +х при х=54
А. 54 Б. 5400 В. 540 Г. 486
Решите уравнение 3х + 4х – 3 =18
А. 14; Б. 3; В. 8 Г. 7
Решите задачу: Машина с прицепом перевозит груз весом 312 кг. Груз в машине в 7 раз легче груза в прицепе. Какова масса груза в прицепе?
А. 156. Б. 39. В. 273 Г. Нет правильного ответа.
Время истекло. Закончили работу.
Давайте проверим тест. Если задание выполнено правильно, то ставим + , если неправильно, то — .
Посчитайте количество правильных ответов.
Поднимите руки у кого выполнено правильно «5», «4», «3».
Итог урока.
Мы у цели. Наш фрегат приближается к острову Математика. По итогам урока ребята, вы получите оценку, которая сложится из результатов вашего математического диктанта и теста. Сейчас, давайте проверим вашу зрительную память и знание геометрических фигур, которые мы встретили на пути к острову Математика?
Молодцы, давайте проверим.
Домашнее задание
Ребята, только благодаря вашим знаниям мы благополучно добрались до конечной цели нашего путешествия. Сейчас мы бросим якорь и получим домашнее задание. Открыли дневники и записали задания № 618, 619, 614(а,б). А староста внесет эти задания в электронный дневник.
Ребята, остров Математики таит в себе немало чудес. Вот одно из этих чудес — это послание мудрого древнегреческого ученого Аристотеля :
«Ум заключается не только в знаниях, но и в умении применять знания на деле». Помните об этом ребята и тогда никакие подводные рифы математики вам не будут страшны.
Встали ровненько. Урок закончен. Не забудьте сдать тетради с тестами.
Тест
Упростите выражение 12с + 28 – 8с +2
А. 14с + 20 Б. 34с В. 4с + 30 Г. 32с + 2
Вычислите 65∙74 — 55∙74
А. 74 Б. 140 В. 740. Г. 10
Найдите значение выражения 4х +5х +х при х=54
А. 54 Б. 5400 В. 540 Г. 486
Решите уравнение 3х + 4х – 3 =18
А. 14; Б. 3; В. 8 Г. 7
Решите задачу: Машина с прицепом перевозит груз весом 312 кг. Груз в машине в 7 раз легче груза в прицепе. Какова масса груза в прицепе?
А. 156. Б. 39. В. 273 Г. Нет правильного ответа.
Тест
Упростите выражение 12с + 28 – 8с +2
А. 14с + 20 Б. 34с В. 4с + 30 Г. 32с + 2
Вычислите 65∙74 — 55∙74
А. 74 Б. 140 В. 740. Г. 10
Найдите значение выражения 4х +5х +х при х=54
А. 54 Б. 5400 В. 540 Г. 486
Решите уравнение 3х + 4х – 3 =18
А. 14; Б. 3; В. 8 Г. 7
Решите задачу: Машина с прицепом перевозит груз весом 312 кг. Груз в машине в 7 раз легче груза в прицепе. Какова масса груза в прицепе?
А. 156. Б. 39. В. 273 Г. Нет правильного ответа.
Математический диктант
№1. Записать выражение и упростить его:
Сумма 5x и 12x
№ 2. Записать выражение и упростить его:
Произведение 6c и 4
№3. Записать выражение и упростить его:
Произведение 8 и суммы 3xи 5.
№ 4. Записать уравнение и решить его:
Сумма 3y и 5y равна 8.
№ 5. Записать выражение
Разность 12а и 6а
Математический диктант
№1. Записать выражение и упростить его:
Сумма 5x и 12x
№ 2. Записать выражение и упростить его:
Произведение 6c и 4
№3. Записать выражение и упростить его:
Произведение 8 и суммы 3xи 5.
№ 4. Записать уравнение и решить его:
Сумма 3y и 5y равна 8.
№ 5. Записать выражение
Разность 12а и 6а
Проверим домашнее задание
Соедините стрелками левую часть, представляющую из себя буквенные выражения, с правой частью, где записаны их названия.
a•b = b•a
распределительное свойство умножения относительно сложения
(a+b)c = ac + bc
переместительное свойство умножения
( a+ b) — c = a + (b — c)
сочетательное свойство сложения
(a — b)c = ac – bc
свойство вычитания числа из суммы
( a + b) — c = (a — c) + b
распределительное свойство умножения относительно вычитания
Соедините стрелками левую и правую часть.
5x + 3x – 4 8a
4a∙3 12a
2a – a + 7a 45x
12x – 7x + 2 8x -4
4x∙6∙2 2 + 5x
9∙x∙5 48x
Проверим домашнее задание
Соедините стрелками левую часть, представляющую из себя буквенные выражения, с правой частью, где записаны их названия.
a•b = b•a
распределительное свойство умножения относительно сложения
(a+b)c = ac + bc
переместительное свойство умножения
( a+ b) — c = a + (b — c)
сочетательное свойство сложения
(a — b)c = ac – bc
свойство вычитания числа из суммы
( a + b) — c = (a — c) + b
распределительное свойство умножения относительно вычитания
Соедините стрелками левую и правую часть.
5x + 3x – 4 8a
4a∙3 12a
2a – a + 7a 45x
12x – 7x + 2 8x -4
4x∙6∙2 2 + 5x
9∙x∙5 48x
infourok.ru
Упрощение выражений. 5-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (553,1 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Название представляемой работы: обобщающий урок по теме «Упрощение выражений».
Класс: 5.
Форма учебной работы: классно-урочная.
Цель урока: Организация деятельности учащихся на повторение, обобщение и систематизацию знаний по теме «Упрощение выражений»
Задачи урока:
- Обучающие: повторение, обобщение и систематизация знаний по теме «Упрощение выражений».
- Развивающие: способствование формированию умений применять полученные знания в новой ситуации, развитие математического мышления и речи, развитие навыков использования свойств действий при упрощении выражений.
- Воспитывающие: воспитание интереса к математике, активности, мобильности. Формирование навыков адекватной самооценки деятельности.
Приобретаемые навыки детей: Учащиеся приобретают навыки работы с цифровыми ресурсами, навыки самостоятельной работы, самоконтроля, навыки применения полученных знаний для решения задач.
Особенности роли учителя: Учитель выступает в роли посредника между учащимся и электронными средствами обучения. Так как учителю важно видеть работу каждого, то можно организовать самопроверку всех заданий, если выводить на экран правильно выполненное задание.
Формы организации работы детей: Следить за ходом урока помогает электронная версия урока, сделанная в виде презентации. При этом учащиеся могут сразу увидеть свои ошибки и исправить их. С этой цель правильные решения выводятся на экран для дальнейшего обсуждения.
Технические особенности:
- технические условия: урок проводится в классе, оборудованном мультимедиа проектором.
- используемое оборудование: мультимедийный проектор, экран, компьютер в классе, раздаточный материал.
Описание разработки: Урок с применением ресурсов Единой образовательной коллекции ЦОР. Математика.
Место урока в структуре образовательного процесса: урок по учебному плану в 5 классе по теме «Сложение и вычитание натуральных чисел».
Учебник: «Математика 5. Н.Я.Виленкин, В.И. Жохов и другие.
Форма: комбинированный урок (беседа + практикум) с использованием ИКТ. Обобщение и закрепление материала, решение задач различного уровня сложности, проверка усвоения знаний по теме.
Ход урока
| Деятельность учителя | Деятельность учащихся | Время, мин. |
| Организационный момент Вступительное слово учителя. Слайд 1. Сегодня мы с вами продолжим разговор об упрощении выражений, вспомним, какие свойства нам в этом помогают, решим задачи на применение данных свойств. |
Настраиваются на работу. | 1 |
| Актуализация знаний Задает вопросы по теме, помогая учащимся настроиться на продуктивную деятельность. Слайды 2-4. |
Вспоминают свойства, используют пример для применения сочетательного свойства умножения для упрощения буквенных выражений. Учащиеся могут самостоятельно упрощать выражения в тетради и могут по очереди выходить и писать ответ на доске. Тогда будет поддерживаться дух соревнования, кто быстрее это сделает. Проверяют правильность выполнения задания, готовность двигаться дальше. | 5 |
| Рассмотреть распределительное свойство умножения относительно сложения и вычитания, применить его на конкретных примерах. Слайд 5-6. |
Учащиеся вспоминают распределительное свойство умножения относительно сложения и вычитания и как его использовать при решении удобным способом. Учащиеся могут самостоятельно в тетрадях выполнять задание или выходить по одному и выполнять задание с дальнейшей проверкой. | 3 |
| Записать выражение следующих величин. Слайд 7. |
Учащиеся записывают величины с комментариями. | 1 |
| Используя распределительный закон, преобразовать выражение 2х + 3х. Слайд 8-9. |
Учащиеся комментируют преобразование выражения 2х + 3х с помощью распределительного закона, выполняют упрощение выражений(если это возможно) с дальнейшей проверкой. | 5 |
| Записать математическим языком. Слайд 10. |
Учащиеся с комментариями выполняют записи математическим языком. Проверяют правильность выполнения задания, готовность двигаться дальше. | 3 |
| Упростить выражение и найти его значение. Слайд 11. Проверка правильности выполнения задания с помощью слайда 12. |
Один учащийся у доски выполняет задание, все остальные у себя в тетрадях, далее проверяют правильность выполнения задания и выставление оценки. | 5 |
| Решить уравнение. Слайд 13. |
Учащиеся решают уравнения у себя в тетради и один ученик с комментариями у доски, с дальнейший проверкой правильности решения и выставлением оценки. | 5 |
| Решить задачу с помощью уравнения. Слайд 14-15. |
Учащиеся предлагают свои варианты составления условия задачи и уравнения по данному условию, далее всем классом проверяют правильность составления условия и уравнения по условию задачи. | 10 |
| Учитель подводит итоги урока, рефлексию и объявляет оценки за урок. Слайд 16. |
Учащиеся формулируют итоги урока: повторили, обобщили систематизировали знания по теме «Упрощение выражений» | 2 |
19.12.2012
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Тест: Упрощение выражений — Математика 5 класс
Задания теста позволят проверить предметные результаты по указанной теме, а также отдельные УУД.
Математика 5 класс | ID: 565 | Дата: 1.12.2013
«;} else {document.getElementById(«torf1″).innerHTML=»»;}; if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;}; if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;}; if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;}; if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;}; if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;}; if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;}; if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;}; if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;}; if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;}; } }Получение сертификата
о прохождении теста
testedu.ru
План-конспект урока по алгебре (5 класс) по теме: упрощение выражений 5 класс
Государственное бюджетное образовательное учреждение
средняя общеобразовательная школа №591 Невского района Санкт – Петербурга
Урок математики в 5 классе
по теме «Упрощение выражений»
Учитель математики Елькина Е.С.
Ноябрь 2013 года
Тип урока: Урок обобщения и систематизации знаний
Цели урока:
- Обучающие — повторить, обобщить и систематизировать знания по данной теме, совершенствовать умения и навыки учащихся упрощать выражения,
- Развивающие — способствовать развитию математического слуха, речи, счетных навыков и мышления; развивать познавательный интерес через использование межпредметных связей, культуру математической речи, логическое мышление;
- Воспитательные — побуждать учащихся к само и взаимоконтролю, воспитывать познавательную активность, самостоятельность, упорство в достижении цели.
Задачи урока:
- Закрепить навыки умения упрощать выражения;
- Формировать развитие мышления, счетных навыков;
- Возбудить интерес учебными действиями к урокам математики
Основные средства обучения:
- компьютер, интерактивная доска, карточки в форме рыбок (приложение 1), тесты (приложение 2), домашнее задание (приложение 3), презентация
Ход урока
I. Организационный момент.
Приветствие. Сегодня мы с вами будем закреплять навыки упрощать выражения; продолжим развивать мышление и совершенствовать счетные навыки;
II. Актуализация знаний.
1) Повторение теоретического материала. А какие свойства будут на нашем уроке. Давайте повторим эти свойства — работа со слайдом:
- a+b = b+a — переместительное свойство сложения
- a * b = b * a — переместительное свойство умножения
- (a+b)+c = a+(b+c) — сочетательное свойство сложения
- (a * b) * c = a * (b * c) — сочетательное свойство умножения
- (a+b) * c=ac+bc распределительное свойство умножения относительно сложения
- (a-b)c=ac-bc распределительное свойство умножения относительно вычитания
Законы вспомнили, ну а теперь давайте проверем себя в устном счете. Готовы.
2) Устный счет.
— №591 стр. 89 Какие трудные примеры? Можно ли их вычислить устно?
Решение каждого примера комментируется (каким свойством вы воспользовались?)
— Выполнив следующее задание: (в 1 столбце — задания, во 2 — ответы, найти правильные ответы)
Вопрос. Какое слово получилось? — Упрощение — что означает это слово?
III. Постановка цели и задач урока. Мотивация учебной деятельности.
«Упрощение выражений» — такова тема нашего урока .Записали дату и тему урока в тетрадь. Как вы думаете, зачем нам нужно упрощать выражения? А какова цель нашего урока? (учащиеся отвечают — повторить способы упрощения выражений, закрепить навыки решения уравнений и задач и т.д.)
IV. Подготовка к обобщенной деятельности. Математический диктант
А теперь с помощью математического диктанта проверим, как вы усвоили данные свойства. Я буду читать задание (на экране тоже высвечивается), вы будете записывать математическими знаками и упрощать.
Слайд 6 Записать выражение и упростить:
1 Сумма 5х и 12х (5х+2х=17х)
2. Произведение 6с и 4 (6с*4=24с)
3 Произведение 8 и суммы 3х и 5 (8(3х+5)= 24х + 40)
Записать уравнение и решить
4 Сумма 3у и 5у равна 8 (3у+5у=8; у=1)
5. 6к вдвое меньше, чем 24 (6k* 2 = 24; к=2)
Взаимопроверка. Поменялись тетрадями (у доски поменялись местами), взяли черные ручки и проверяем. (все задания верно – 3 балл, 4 задания верно — 2балла, 3 задания верно 1 балл). Кто получил высший балл? Молодцы.
V. Применение умений и навыков.
Решение уравнений. Где еще применяют упрощение выражений.( Правильно, при решении уравнений).
У каждого из вас на столе есть задание «Решить уравнение» в виде рыбок. (красная – 3 балла, желтая – 2 балла, зеленая – 1 балл). На решение уравнений — 5 минут. Каждый оценивает свои возможности и выбирает, какая рыбка ему по силам. Лучше получить 1 балл, чем 0 баллов. Если кто-то решает раньше времени, то может решить еще оставшиеся.
3 человека, выбравшие разные рыбки, выходят к доске и решают на доске (за доской).
Самопроверка. Затем все проверяем решения (на слайде 8)
- Красная 42х-28х-170=600 (х=55)
- Желтая 4m+5m+m=2350 (m=235)
- Зеленая 65y-31y=102 (y=3)
VI. Физкультпауза.
А теперь небольшая пауза.
Вы видите примеры с ответами на слайдах, если вы согласны, то поднимаете руки вверх, если нет — опускаете вниз.
- 55+20=75,
- 4 * 25=80,
- 100:25 = 4,
- 60 — 22 = 58
. Если вы согласны, то голову наклоняем вниз, если нет — назад
- 15+15 = 30,
- 12 * 6 = 62,
- 99+ 11=110,
- 28 : 7 = 9
VII. Воспроизведение знаний на новом уровне.
Отдохнули, а теперь продолжим. Догадайтесь, каким числом является корень уравнения.
- у + у + у = 15 * 3 (у = 15)
- 4(х+2)=4 * 5+4 * 2 (х = 5)
Чем вы воспользовались?
VIII. умений и знаний в жизненной(проблемной) ситуации
Приближаемся к самому сложному к решению задач .
Для приготовления смеси для рассады берут 1 часть торфа, 2 части перегноя и 5 частей земли. Сколько килограммов торфа, перегноя и земли надо взять для приготовления 72 кг смеси для рассады?
Запишем краткое условие задачи. Обозначаем массу 1 части за х кг.
Что нужно иметь, чтобы приготовить данную смесь? Торф, перегной и землю. Сколько частей торфа? 1 часть — ? кг, сколько перегноя — 2 части — ? кг, земли — 5 частей — ? кг. Всего 72кг.
Как же решить такую задачу? Обозначаем массу 1 части за х кг.
Торфа — х кг, перегноя — 2х кг, земли — 5х кг. Всего (х+2х+5х)кг, что по условию задачи составляет 72 кг. Составим и решим уравнение: Х+2х+5х=72
К доске пойдет::.. решит уравнение и ответит на вопрос задачи (решает за доской). Первые 3 человека, решившие правильно задачу получают дополнительный балл.
Х+2х+5х=72,
9х=72,
х=8 кг — 1 часть — торф
Что нужно еще найти в задаче? Количество земли — 8 * 5 = 40 кг , количество перегноя — 2 * 8=16 кг.
Для тех обучающихся, которые раньше справились с задачей, предлагается решить одну из практических задач, какие решают в повседневной жизни кондитер, фармацевт, строитель (слайды 15 – 18).
IX. Контроль усвоения. Самостоятельная работа в виде теста.
Слайд 19 Выберите верный ответ и обведите его
Вариант 1
1.Укажите верное равенство:
1) (x+4) * 3=x+12;
2) 6(m-10)=6m+60;
3) (2-a) * 8=16-a;
4) 4(k+12)=4k+48
2. Упростить выражение 13 * z * 6
1) 18z
2) 78z,
3) 78,
4) 68
3. Упростить выражение 15х + 12+ 6х:
1) 33х,
2) 15х+ 18,
3) 21х+12,
4) 33
Итог: 423
Вариант 2
1.Укажите верное равенство:
1) (m+7) * 2=m+14;
2) 11(x-10)=11x-110;
3) (15+y) * 3=45+y;
4) 5(12-c)=60+5c
2. Упростить выражение 11 * у * 7
1) 17у
2) 77
3) 77у
4) 117у
3. Упростить выражение 14х- 5+8х:
1) 17х,
2) 22х+5,
3) 27х,
4) 22х-5
Итог: 234
Самопроверка. За каждый правильный ответ 1 балл
X. Итог урока
Подведём итоги нашего урока
1. Знания каких свойств арифметических действий помогли вам справиться с заданиями?
2. Подсчитайте свои баллы за урок:………… 10 – 11 баллов — «5»
9 — 8 баллов — «4»
7 – 6 баллов — « 3»
3.Но сегодня не простой урок, поэтому хочется поставить вам только отличные и хорошие отметки
XI. Домашнее задание. У вас на столе имеются карточки с заданиями (задания карточек по уровням сложности ). Решив верно задания, разукрасим лесовика.
XII. Рефлексия. Остров математики таит в себе немало чудес. «Ум заключается не только в знаниях, но и в умении применять знания на деле» — Аристотель
У вас на столе есть геометрические фигуры. Если вам урок очень понравился, то поднимите круг, если понравился — квадрат, если вам было неуютно — треугольник.
Приложение 1
Приложение 2 Тест.
Фамилия______________________
Имя _________________________
Класс________________________
Выберите верный ответ и обведите его
Вариант 1
1.Укажите верное равенство:
1) ( x+4)•3=x+12; 2) 6(m-10)=6m+60; 3) (2-a)•8=16 — a; 4) 4(k+12)=4k+48
2. Упростить выражение 13•z•6
1) 18z 2) 78z, 3) 78, 4) 68
3. Упростить выражение 15х + 12+ 6х:
1) 33х, 2) 15х+ 18, 3) 21х+12, 4) 33
Итог :
_____________________________________________________________________
Фамилия______________________
Имя _________________________
Класс________________________
Вариант 2
1.Укажите верное равенство:
1) ( m+7)•2=m+14; 2) 11(x-10)=11x-110; 3) (15+y)•3=45+y; 4) 5(12-c)=60+5c
2. Упростить выражение 11•у•7
1) 17у 2) 77 3) 77у 4) 117у
3. Упростить выражение 14х- 5+8х:
1) 17х, 2) 22х+5, 3) 27х, 4) 22х-5
Итог:
Приложение 4
Домашнее задание
Карточка 1
№ | Задания | Ответы |
Упростите выражения | ||
1. | 25а – 17а | 8 – коричневый; 8а – желтый |
2. | 18 b+ 24b | 42 – синий; 42b – красный |
3. | а + 32а | 33а – синий; 33 – зеленый |
4. | 40х – х | 39 – красный; 39х – желтый |
5. | Представьте произведение 25х в виде суммы двух слагаемых, одно из которых равно 12х | 12х + 13 + х – коричневый; (12 +13)х – синий; 12х + 13х – зеленый |
6. | Решите уравнение 9с – с = 104 | 13 – зеленый; 14 – желтый |
7. | Найдите значение выражения 64х + 36х, если х = 183 | 1830 – желтый; 18300 – коричневый; 283 – красный |
Карточка 2
№ | Задания | Ответы |
1. | Представьте в виде произведения 23а – 3а – 12а | 18а – красный; 8а – желтый; 8 – коричневый |
2. | 15b + 15 b + 12 b | 32 – синий; 42b – красный; 42 – желтый |
3. | 3а + а + 29а | 33а – синий; 33 – зеленый |
4. | 100х – 60х – х | 39 – оранжевый; 49х – синий; 39х – желтый |
5. | Представьте произведение 24х в виде суммы двух одинаковых слагаемых | 12х + 12х – зеленый (12 + 12)х – красный; 12х + 12 + х – коричневый; |
6. | Решите уравнение 3х + 5х +2х = 800 | 8 – желтый 80 – зеленый; |
7. | Найдите значение выражения 36х – 20х – 6х, если х =4 | 4 – желтый; 40 – коричневый; 400 – красный |
Карточка 3
№ | Задания | Ответы |
1. | Представьте в виде произведения 3а + 6а – 13 | 9а + 13 – желтый; 22а – коричневый |
2. | 117а – 17 а + 3а | 97а – синий; 103а – красный |
3. | 25+ 6 b + 7 b – b | 37 b – зеленый; 25 + 12b – синий |
4. | 12х + х + 12 + х | 14х + 12 – желтый; 26х – коричневый; |
5. | Представьте произведение 36х в виде суммы трех одинаковых слагаемых | 12х + 12х + 12х – зеленый; 12 + 12 +12 + х – коричневый; (12 +12 + 12)х – красный |
6. | Решите уравнение 3х + 4х – 3 =18 | 4 – желтый; 3 – зеленый |
7. | Найдите значение выражения 35х + 5х – 7, если х =2 | 66 – желтый; 73 – коричневый; |
nsportal.ru
Разработка урока «Упрощение выражений» (5 класс)
МКОУ «Карабаглинская СОШ»
Открытый урок по математике
в 5 классе
на тему:
«Упрощение выражений»
Учитель: Маркарова Н.П.
Тема «Упрощение выражений».
Цель:
Изучить распределительное свойство умножения относительно сложения и вычитания;
развитие познавательной активности, мышления; привитие интереса к предмету;
воспитание самостоятельности.
ХОД УРОКА:
Оргмомент
Учитель Здравствуйте, ребята! Сегодня у нас немного не обычный урок. Мы разделимся на три группы, и в течении всего урока будем работать в группах. Девизом нашего урока будут слова М.В. Ломоносова (Слайд 1)
«Математику уже затем надо учить,
Что она ум в порядок приводит»
М.В. Ломоносов.
Начнем приводить наш ум в порядок с устного счета. (слайд2)
100-55=…*2=…/ 18=…* 15=75
90-71=..* 3=..+ 23=../ 16=5
Вычислите применяя закона арифметических действий.
25 *53*4= (сочетательное свойство умножения)
372+2444+1628= (сочетательное свойство сложения)
Проблемная ситуация для определение темы урока.
Я захотел устроить балл
Ия гостей к себе позвал.
Решил для них испечь пирог
Рецепт никак найти не мог.
Рецепт у друга попросил ,
Но разобраться нету сил.
Я помощи у вас прошу.
Рецепт уж сложный для меня,
Попроще записать нельзя?
(слайд 3)
(слайд4)
Яйца – 4шт. сгущенки – 2 бан.
Муки – 2 ст. масла – 2 пач.
Сахара – 2 ст. сметаны – 1 ст.
— Вы разобрались, молодцы!
(слайд 5)
— Наш пирог будет называться «Путь к успеху»
(слайд 6)
Запишите в тетради число 27.11.2015
Классная работа.
Тема: «Упрощение выражений»
Давайте вместе с вами поставим цель нашего урока, для этого ответим на вопросы.
ЧТО? – (что значит упростить выражение?)
КАК? – (как упрощать выражения?)
ЗАЧЕМ? – (зачем нужно упрощать выражения?)
Получение новых знаний.
В нашем классе есть девочки и мальчики. Девочек у нас 10, а мальчиков 5.
— сколько вас всего (15),
-Как вы узнали? (прибавили)
-Значит выражение (10+5) показывает нам, сколько всего учащихся в нашем классе.
-Давайте представим, что у меня сегодня день рождение и я хочу раздать вам конфеты.
— Будет ли справедливо, если я раздам конфеты только мальчикам? (нет)
— А если я раздам конфеты только девочкам? (нет)
— А как мне поступить? ( нужно раздать всем поровну)
-То есть, я должна дать каждому по 3 конфеты. А что означает выражение по 3 ? ( умножить на 3)
— Запишите выражение (10+5) * 3 = 10*3+5*3=30+15=45
-Это свойство называется распределительным свойством умножения относительно сложения. Запишите это свойство в тетради (слайд 7)
(а+b)*c=ac+bc
-Давайте сравним правую и левую части выражения, как вы думаете возможно ли из правой части получить левую?(да)
-Что для этого нужно сделать? (нужно с вынести за скобки)
-Правильно, с – это общий множитель. Давайте сделаем вывод, как же можно упрощать выражения с помощью распределительного свойства умножения?
1) Можно раскрыть скобки. Для этого каждое число в скобках нужно умножить на множитель и полученные произведения сложить.
2)Можно вынести общий множитель за скобки.
-А разве это свойство действует только для сложения?(для вычитания тоже)
-Попробуйте самостоятельно записать буквенную запись распределительного свойства умножения относительно вычитания. (один ученик записывает на доске)
(a—b)*c=ac—bc (слайд 7)
Первичное закрепление знаний.
—Что значит упростить выражение? (сделать его проще, легче) (слайд 8)
24 * 8= (20+4)*8=20*8+4*8=160+32=192
78*5=(80-2)*5=80*5+2*5=400 -10=390
(Данный слайд, остается как образец на доске. Учащиеся по группа получают задания на карточках)
1 ГРУППА 2 ГРУППА 3 ГРУПА
202*3= 84*6 = 14*3=
198*4 = 79*8= 27*7=
Ответы сверяются по слайду №9
72*17+28*17=(72+28)*17=100*17=1700
(Данный слайд, остается как образец на доске. Учащиеся по группа получают задания на карточках)
1 ГРУППА 2 ГРУППА 3 ГРУПА
977*49+49*23= 603*7+603*93= 69*27+31*27=
438*90-238*90= 263*24-163*24= 202*87-102*87
Ответы сверяются по слайду №11
17а+23а=(17+23)*а=40а или 17а+23а=40а
-Число, стоящее перед буквой называют числовым коэффициентом.
-Слагаемые с одинаковой буквенной частью называют подобными.
-Назовите числовые коэффициенты: 5а; 12с; 24; 6к; 9х; 78у; х
Вывод: Чтобы сложить подобные слагаемые, надо сложить их числовые коэффициенты а буквенную часть переписать.
Слайд №12 как образец остается на доске. Учащиеся по группа получают задания на карточках.
1 ГРУППА 2 ГРУППА 3 ГРУПА
6у -2у +30= 27р +17р -23р= 23а +27а=
84х +15 -20х = 43у – 27у +15у = 48х +х=
Ответы сверяются по слайду №14
Домашнее задание: Стр.91 №608 №609 №611
Рефлексия

infourok.ru












 6 – 2 –5 ПРАВИЛО. Разность двух чисел положительна, если уменьшаемое больше вычитаемого . «
6 – 2 –5 ПРАВИЛО. Разность двух чисел положительна, если уменьшаемое больше вычитаемого . «









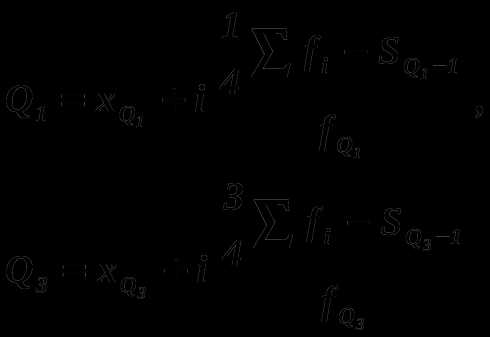
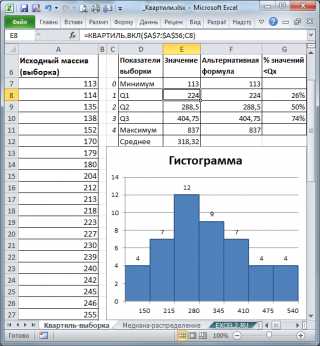


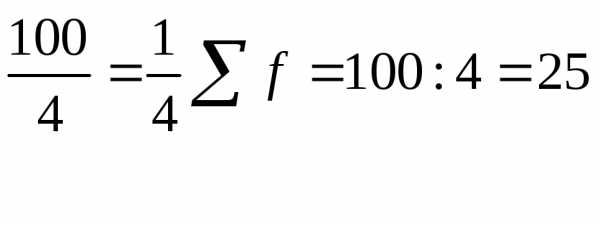 т.е.
интервал 150-200
т.е.
интервал 150-200
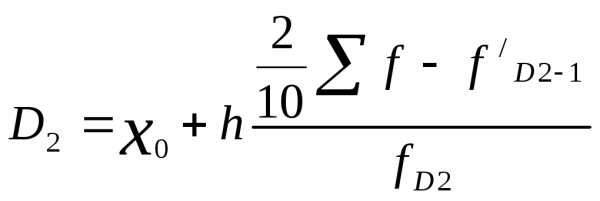

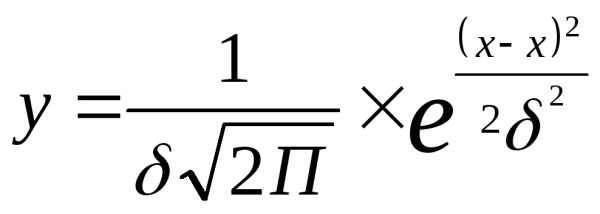


 и средне квадратическое отклонение
и средне квадратическое отклонение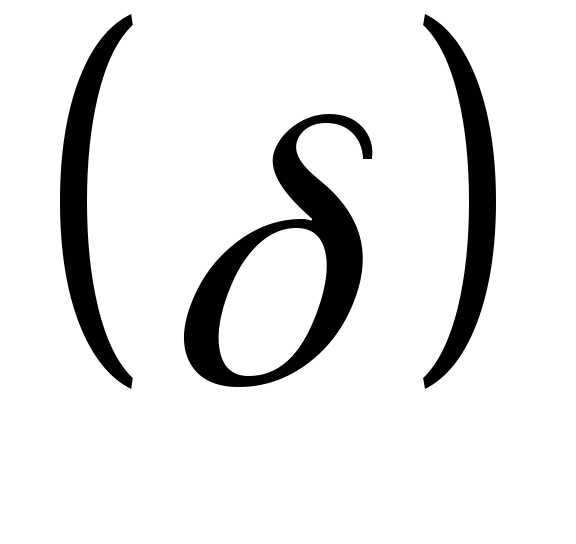 — определяют очертание симметричной
кривой нормального распределения.
— определяют очертание симметричной
кривой нормального распределения.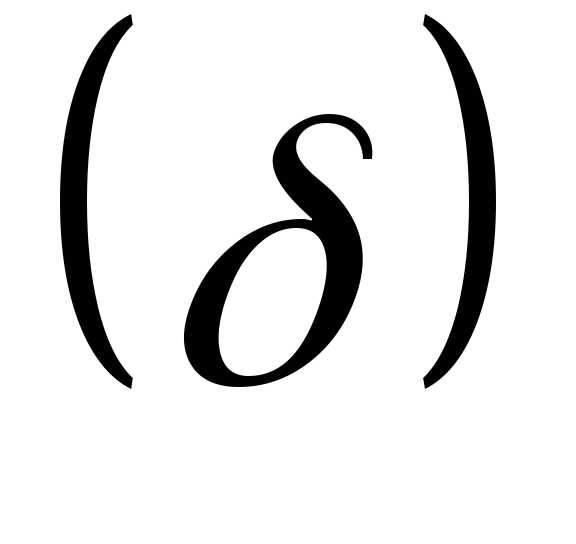 с каждой стороны от средней арифметической,
составляет 0,683 всей площади.
с каждой стороны от средней арифметической,
составляет 0,683 всей площади.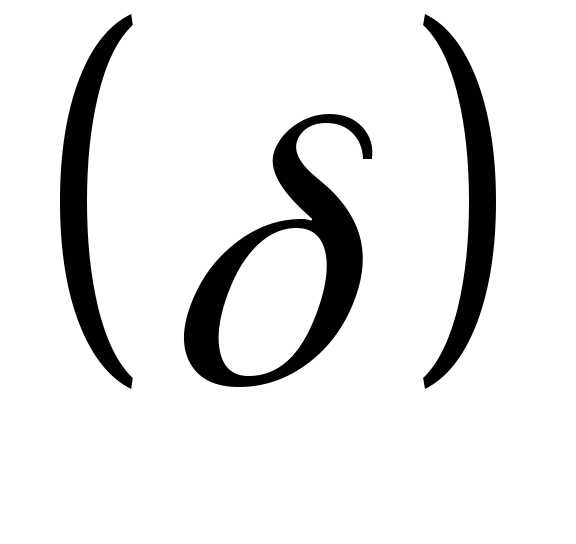 ,
т.е. находятся в пределах (
,
т.е. находятся в пределах ( ).
).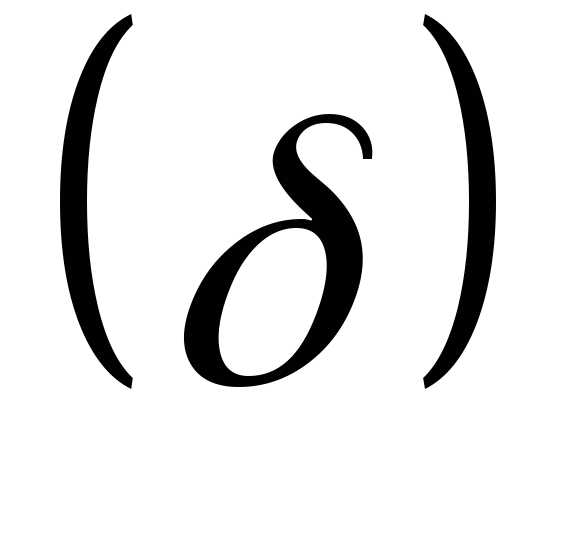 в одну другую сторону от средней
арифметической, составляет 0,954, т.е. всех
единиц совокупности находятся в пределах
в одну другую сторону от средней
арифметической, составляет 0,954, т.е. всех
единиц совокупности находятся в пределах .
Это так называемое правило 3-сигментов,
характерное для нормального распределения.
.
Это так называемое правило 3-сигментов,
характерное для нормального распределения. —
табулированная величина, отыскиваемая
по отклонениям t, а Nh/
—
табулированная величина, отыскиваемая
по отклонениям t, а Nh/ — константа, на к умножаются значения
— константа, на к умножаются значения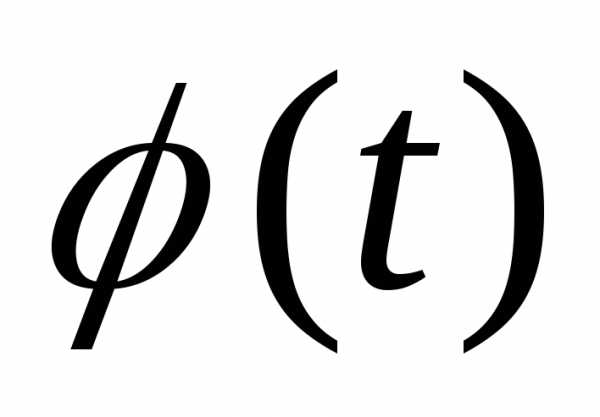 и которая определяет теоретические
частоты исходя из общей численности
единиц совокупности и числа выделяемых
групп. Последовательность расчета
следующая:
и которая определяет теоретические
частоты исходя из общей численности
единиц совокупности и числа выделяемых
групп. Последовательность расчета
следующая:


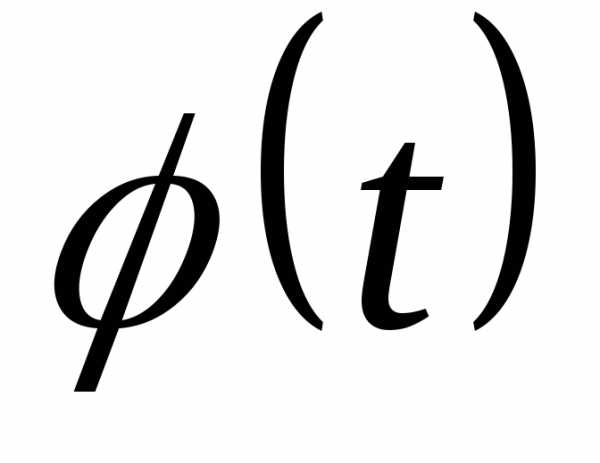
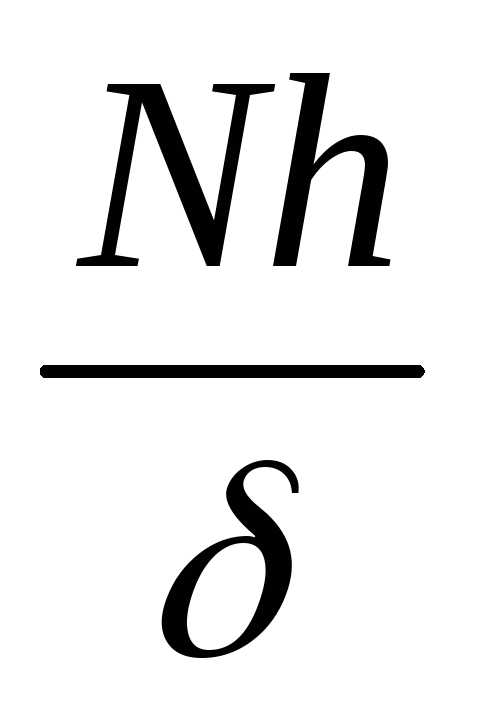
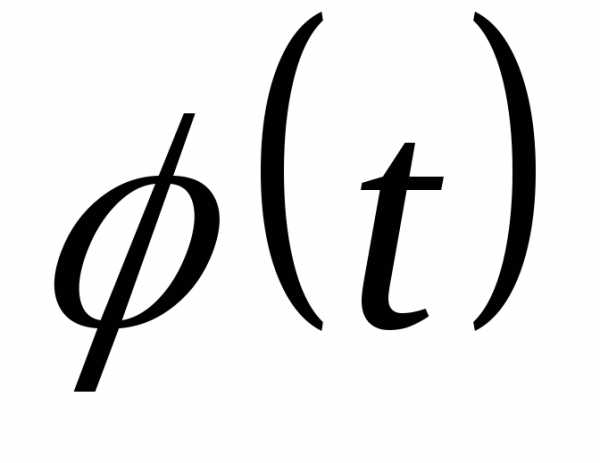 умножаем на константу
умножаем на константу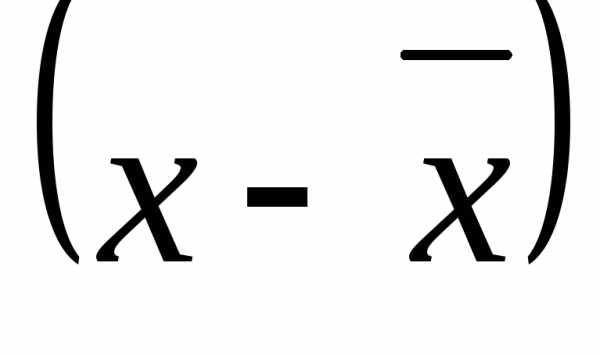
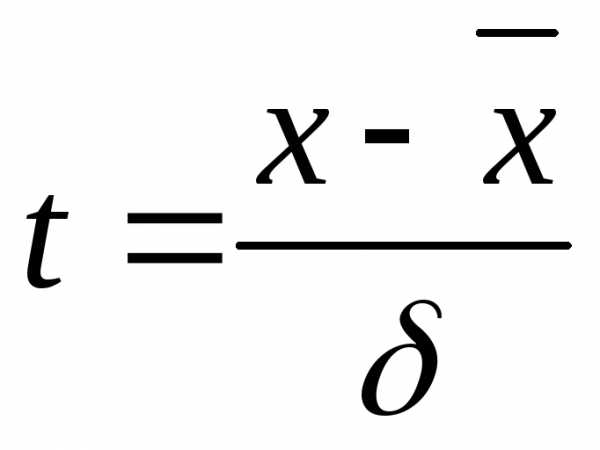

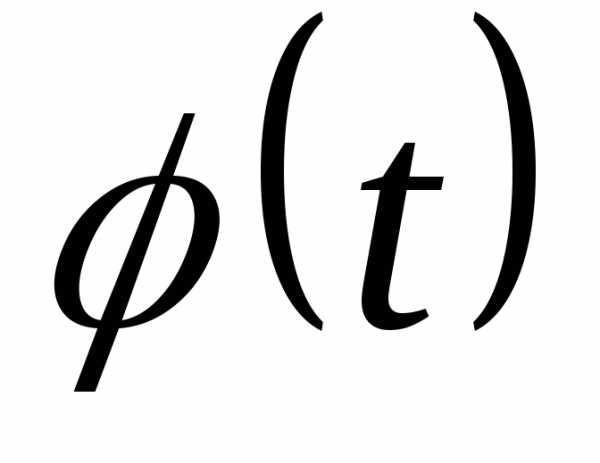 =m/
=m/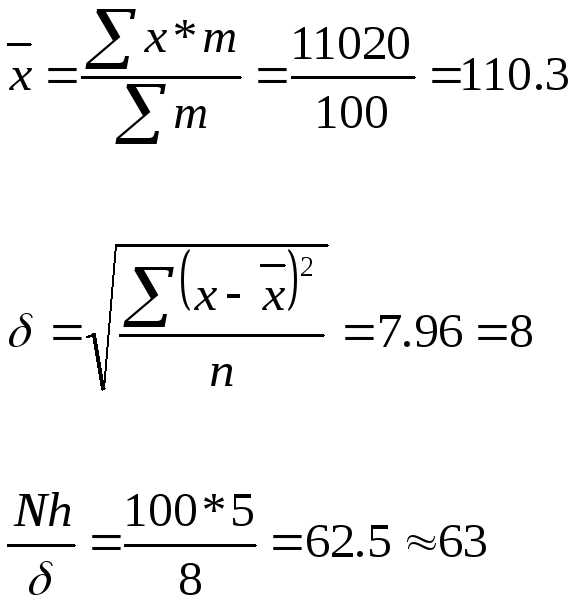







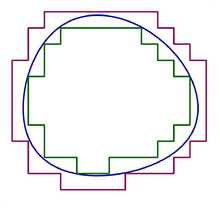 Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере Жордана
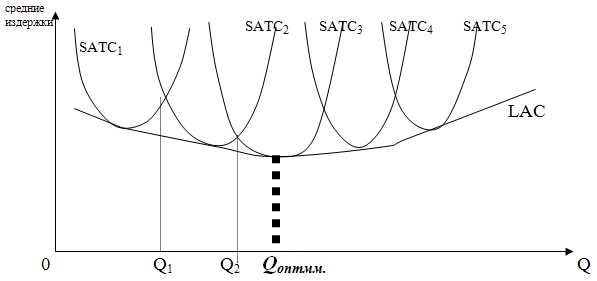
Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере Жордана Увеличение
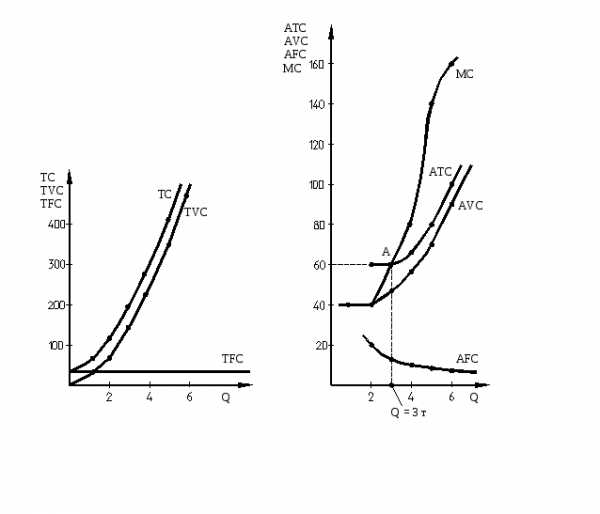
масштаба производства до определенного
размера сопровождается снижением
средних издержек производства, так как действует положительный эффект масштаба.
Затем при
наращивании объема выпуска сверх
определенной массы (4 ед.) средние
издержки производства начинают расти,
так как вступает в
действие закон убывающей
отдачи,
следовательно, меняется уровень доходности предприятия.
Увеличение
масштаба производства до определенного
размера сопровождается снижением
средних издержек производства, так как действует положительный эффект масштаба.
Затем при
наращивании объема выпуска сверх
определенной массы (4 ед.) средние
издержки производства начинают расти,
так как вступает в
действие закон убывающей
отдачи,
следовательно, меняется уровень доходности предприятия.

 Гликоген представляет собой многоразветвленный полисахарид глюкозы, который служит в качестве формы хранения энергии у людей, животных, грибов и бактерий. Полисахаридная структура представляет собой основную форму хранения глюкозы в организме. У людей, гликоген производится и хранится, в основном, в клетках печени и мышцах, гидратированных тремя или четырьмя частями воды. 1) Гликоген функционирует как вторичное долговременное хранилище энергии, причем первичные запасы энергии являются жирами, содержащимися в жировой ткани. Мышечный гликоген превращается в глюкозу мышечными клетками, а гликоген печени превращается в глюкозу для использования по всему телу, включая центральную нервную систему. Гликоген является аналогом крахмала, глюкозного полимера, который функционирует как хранилище энергии в растениях. Он имеет структуру, похожую на амилопектин (компонент крахмала), но более интенсивно разветвленную и компактную, чем крахмал. Оба являются белыми порошками в сухом состоянии. Гликоген встречается в виде гранул в цитозоле / цитоплазме во многих типах клеток и играет важную роль в цикле глюкозы. Гликоген образует запас энергии, который можно быстро мобилизовать для удовлетворения внезапной потребности в глюкозе, но менее компактен, чем энергетические запасы триглицеридов (липидов). В печени, гликоген может составлять от 5 до 6% от массы тела (100-120 г у взрослого человека). Только гликоген, хранящийся в печени, может быть доступен другим органам. В мышцах, гликоген находится в низкой концентрации (1-2% от массы мышц). Количество гликогена, хранящегося в организме, особенно в мышцах, печени и красных кровяных клетках 2), в основном, зависит от тренировок, базового метаболизма и привычек в еде. Небольшое количество гликогена находится в почках и даже меньшее количество – в некоторых глиальных клетках мозга и лейкоцитов. Матка также хранит гликоген во время беременности, чтобы питать эмбрион.
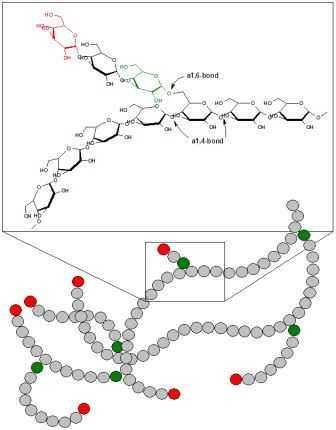
Гликоген представляет собой многоразветвленный полисахарид глюкозы, который служит в качестве формы хранения энергии у людей, животных, грибов и бактерий. Полисахаридная структура представляет собой основную форму хранения глюкозы в организме. У людей, гликоген производится и хранится, в основном, в клетках печени и мышцах, гидратированных тремя или четырьмя частями воды. 1) Гликоген функционирует как вторичное долговременное хранилище энергии, причем первичные запасы энергии являются жирами, содержащимися в жировой ткани. Мышечный гликоген превращается в глюкозу мышечными клетками, а гликоген печени превращается в глюкозу для использования по всему телу, включая центральную нервную систему. Гликоген является аналогом крахмала, глюкозного полимера, который функционирует как хранилище энергии в растениях. Он имеет структуру, похожую на амилопектин (компонент крахмала), но более интенсивно разветвленную и компактную, чем крахмал. Оба являются белыми порошками в сухом состоянии. Гликоген встречается в виде гранул в цитозоле / цитоплазме во многих типах клеток и играет важную роль в цикле глюкозы. Гликоген образует запас энергии, который можно быстро мобилизовать для удовлетворения внезапной потребности в глюкозе, но менее компактен, чем энергетические запасы триглицеридов (липидов). В печени, гликоген может составлять от 5 до 6% от массы тела (100-120 г у взрослого человека). Только гликоген, хранящийся в печени, может быть доступен другим органам. В мышцах, гликоген находится в низкой концентрации (1-2% от массы мышц). Количество гликогена, хранящегося в организме, особенно в мышцах, печени и красных кровяных клетках 2), в основном, зависит от тренировок, базового метаболизма и привычек в еде. Небольшое количество гликогена находится в почках и даже меньшее количество – в некоторых глиальных клетках мозга и лейкоцитов. Матка также хранит гликоген во время беременности, чтобы питать эмбрион.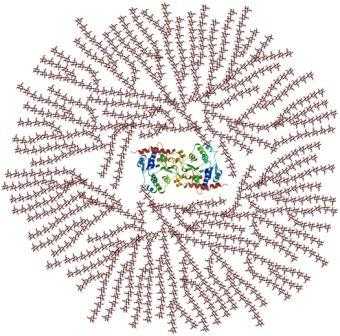 Гликоген представляет собой разветвленный биополимер, состоящий из линейных цепей глюкозных остатков с дальнейшими цепями, разветвляющимися каждые 8-12 глюкоз или около того. Глюкозы связаны линейно с помощью α (1 → 4) гликозидных связей от одной глюкозы к следующей. Ветви связаны с цепями, от которых они отделяются гликозидными связями α (1 → 6) между первой глюкозой новой ветви и глюкозой в цепочке стволовых клеток 3). Из-за того, как синтезируется гликоген, каждая гликогенная гранула имеет в своем составе гликогениновый белок. Гликоген в мышцах, печени и жировых клетках хранится в гидратированной форме, состоящей из трех или четырех частей воды на часть гликогена, связанной с 0,45 миллимолями калия на грамм гликогена.
Гликоген представляет собой разветвленный биополимер, состоящий из линейных цепей глюкозных остатков с дальнейшими цепями, разветвляющимися каждые 8-12 глюкоз или около того. Глюкозы связаны линейно с помощью α (1 → 4) гликозидных связей от одной глюкозы к следующей. Ветви связаны с цепями, от которых они отделяются гликозидными связями α (1 → 6) между первой глюкозой новой ветви и глюкозой в цепочке стволовых клеток 3). Из-за того, как синтезируется гликоген, каждая гликогенная гранула имеет в своем составе гликогениновый белок. Гликоген в мышцах, печени и жировых клетках хранится в гидратированной форме, состоящей из трех или четырех частей воды на часть гликогена, связанной с 0,45 миллимолями калия на грамм гликогена.