Формула естественного прироста населения
Понятие естественного прироста населения
Важнейшим инструментом долгосрочного прогнозирования социально-экономического общественного развития является планирование и анализ прироста населения. Этот показатель чаще всего применяется для расчета величины его трудовых ресурсов, в том числе объема потребностей в них.
При анализе государственной демографической ситуации применяют два основных показателя:
- Механический (миграционный) прирост,
- Естественный прирост.
Формула естественного прироста населения показывает разницу между количеством умерших и родившихся людей за рассматриваемый промежуток времени.
Для максимальной точности данных в расчетах применяют данные статистики, которые дают возможность отследить малейшие изменения. Специальные органы статистики постоянно контролируют показатели рождаемости и смертности, которые имеют документальную основу.
Формула прироста населения
Прирост населения определяется суммированием двух показателей:
- Показатель естественного прироста, представляющий собой разницу между рождаемостью и смертностью за определенный период;
- Показатель миграционного прироста, отражающий разницу между числом прибывших людей на определенную территорию и числом выбывших за рассматриваемый период.
Прирост населения представляет собой разницу текущего уровня демографической ситуации и уровня более раннего периода.
Расчетной единицей может быть промежуток времени долгосрочного (от 5 до 100 лет) и краткосрочного (от нескольких дней до 3 — 5 лет) характера.
Формула естественного прироста населения
Естественный прирост представляет собой разницу между родившимися и умершими гражданами. При этом если рождаемость выше смертности, то можно говорить о расширенном воспроизводстве населения. Если же смертность выше рождаемости, то наблюдается демографический спад и суженное воспроизводство населения.
Существует абсолютная и относительная формула естественного прироста населения.
Формула естественного прироста населения в абсолютных показателяхможет быть определена путем вычитания из объема воспроизводства конца и начала периода.
Данная формула выглядит следующим образом:
ЕП = Р – С
Здесь ЕП – естественный прирост,
Р – количество родившихся людей,
С – количество умерших людей.

Относительную оценку естественного прироста проводят вычислением коэффициентов. В этом случае абсолютная величина является общим числом жителей. Формула естественного прироста населения в относительном выражении вычисляется как разница между родившимися и умершими гражданами за определенный период (то есть абсолютной величиной естественного прироста). Далее эта разница делится на общую численность населения.
Потн. = Пабс. / ЧН
Здесь Потн. – относительный показатель естественного прироста населения,
Пабс. – абсолютный показатель прироста населения, вычисляемый как разность между родившимися и умершими людьми),
ЧН – численность населения.
Примеры решения задач
ru.solverbook.com
Демографические коэффициенты | Primer.by
Демографические коэффициент измеряются в промилле или процентили, обозначаются .
Коэффициент рождаемости
N-число родившихся за год
— среднегодовая численность населения
Коэффициент смертности
M-число умерших за год
— среднегодовая численность населения
Коэффициент естественного прироста
Коэффициент брачности
Бр- число браков за год
— среднегодовая численность населения
Коэффициент разводимости
Разв- число разводов за год
— среднегодовая численность населения
Коэффициент прибытия
Коэффициент выбытия
Коэффициент миграционного (механического) прироста
Коэффициент общего прироста
В знаменателе при расчете общих демографических коэффициентов берется среднегодовая численность всего постоянного населения.
Для нахождения среднегодовой численности населения можно пользоваться несколькими формулами:
Известны численность на начало и на конец года, то пользуются формулой средней арифметической:
Если известна численность населения за несколько равноотстоящих дат, например на 1 число каждого месяца, то пользуются формулой средней хронологической
Если известна численность населения на несколько не равностоящих дат, то пользуются формулой средней взвешенной
, где — полусумма численности населения для соседних дат.
Специальные коэффициенты.
Специальный коэффициент рождаемости
— среднегодовая численность женщин фертильного возраста (15-49 лет)
Коэффициент младенческой смертности
— число умерших детей в возрасте 0 лет.
— число родившихся за этот же период
Более точный результат мы можем получить воспользовавшись формулой Ратса
— число родившихся в прошлом году
— число родившихся в текущем году
Еще более точный результат дает формула:
— число умерших в возрасте до 1 года в текущем году
— число умерших детей до 1 года в прошлом году.
! Как выбрать формулу для вашей задачи? Обратите внимание, что в более точных формулах используются больше данных, следовательно, вы должны использовать ту формулу, для которой достаточно данных.
Коэффициент эффективности воспроизводства населения
Коэффициент жизненности населения (индекс Покровского)
Коэффициент неустойчивости браков
— число разводов за период
— число браков за период
primer.by
9. Расчет общего прироста и перспективной численности населения
Показатели естественного движения населения и миграции используются для оценки общего изменения численности населения и прогнозирования перспективной численности населения.
Оценка общей численности населения производится ежегодно методом демографического баланса на основе итогов последней переписи населения и данных текущего учета естественного и миграционного движения. К численности населения территории по данным последней переписи прибавляют число родившихся и прибывших на данную территорию, вычитают числа умерших и выбывших с данной территории. В расчетах учитывается также изменение численности населения территорий в результате изменения административных границ. Затем от полученного числа отнимают численность населения на начало расчетного периода и получают прирост за данный период. Т.е. можно сказать, что общий прирост населения рассчитывается как сумма естественного прироста и механического прироста (сальдо миграции):
∆общ.пр. = ∆ест.пр. + ∆мех.пр. = N – M + П – В = Sк.г. – Sн.г., (40)
где Sк.г. и Sн.г. численность населения на конец и на начало года (или другого периода, за который рассчитывается прирост) соответственно.
Кроме того, можно рассчитать коэффициент общего прироста населения (Кобщ.пр.) как сумму коэффициентов естественного прироста и механического прироста:
Кобщ.пр. = Кест.пр.+ Кмех.пр. (41)
Или, если раскрыть формулу (41), то:
.(42)
Коэффициент общего прироста можно рассчитать и следующим образом:
(43)
Для планирования социальной и экономической политики важно знать численность населения на планируемый период. Расчет перспективной численности населения является одной из задач статистики населения.
Перспективная численность может быть определена с помощью различных методов в зависимости от того, необходимо ли определить общую перспективную численность или для отдельных возрастных групп, какие цели при этом преследуются. Во всех случаях перспективная численность населения определяется исходя из предположения, что выявленные для определенного периода закономерности изменения численности населения сохранятся в будущем. Но поскольку сами показатели рождаемости, смертности и механического прироста не остаются неизменными и изменяется возрастная структура населения, то перспективные расчеты на длительный период могут содержать ошибки.
Перспективная численность всего населения (общая) может быть рассчитана на основе данных о естественном и механическом приросте населения за анализируемый период и предположении о неизменности выявленной закономерности изменения на прогнозируемый период. Так, если известна численность населения на начало анализируемого периода (Sн.г.) и рассчитан коэффициент общего прироста населения за период, предшествующий анализируемому, то перспективная численность населения через t лет (Sн.г.+t) определяется по следующей формуле:
(44)
Возможен и другой метод расчета перспективной численности, основанный на экстраполяции рядов динамики, выравненных по определенным аналитическим формулам.
Если необходимы детальные данные о перспективной численности населения по отдельным возрастным и половым группам (например, для определения в будущем различных возрастных контингентов, баланса труда и т.д.), то для расчета необходимы сведения о численности и возрастной структуре населения на начало планируемого периода; данные о коэффициентах дожития, рассчитанных на основе таблиц смертности; данные о возрастных коэффициентах рождаемости для женщин в возрасте 15-49 лет. Численность населения по возрастам (кроме нулевого) каждого пола, например через год, рассчитывается с помощью передвижки возрастов. Для этого численность населения каждого возраста и пола умножается на соответствующий коэффициент дожития Рх, в результате определяется возможная (перспективная) численность населения в возрасте х+1 через год и т.д.
Для расчета возможного числа новорожденных через год (возраст 0 лет) возрастные коэффициенты рождаемости умножаются на численность женщин соответствующего возраста (от 15 до 49 лет) в планируемом году. Полученное число детей распределяется по полу на основе сложившихся соотношений: мальчиков 51%, девочек 49%. С учетом коэффициента детской смертности определяется число детей, которые доживут до одного года, дальше расчет ведется с помощью метода передвижки возрастов.
1Когорта – совокупность людей, у которых то или иное демографическое событие (рождение, вступление в брак, рождение первого ребенка и т.п.) произошло в один и тот же год или несколько больший период времени; например, люди, родившиеся в один и тот же год или несколько больший период времени (поколение), вступившие в брак или родившие первого ребенка.
studfiles.net
Решение:
1) Найдем численность наличного населения на конец года (Nк.г.):
Nк.г. = Nн.г. + Р – У + П – В,
где Nн.г. – численность населения на начало года;
Р – число родившихся за год;
У – число умерших за год;
П – число прибывших на данную территорию за год;
В – число выбывших с данной территории за год.
Nк.г. = 400 + 12 – 4 + 6 – 5 = 409 (тыс. чел.)
2) Найдем среднегодовую численность наличного населения ():
404,5 (тыс. чел.)
3) Вычислим показатели естественного движения населения:
а) коэффициент рождаемости (Крожд.):
29,67.
Таким образом, на каждую 1000 человек наличного населения за год рождается 29-30 детей.
б) коэффициент плодовитости (Кплод.):
,
где — среднегодовая численность женщин фертильного (т.е. способного к деторождению) возраста (15-49 лет). По условию задачисоставляет 24% от среднегодовой численности наличного населения, т.е.
97,08.
Таким образом:
123,61.
Таким образом на каждую 1000 женщин фертильного возраста за год рождается 123-124 ребенка.
в) коэффициент смертности (Ксм.):
9,9.
Следовательно, на каждую тысячу человек наличного населения за год умирает 9-10 человек.
г) коэффициент младенческой смертности (Кмл. см.), (смертности детей до 1 года):
45,46.
Таким образом, из каждой 1000 детей до 1 года умирает 45-46 младенцев.
д) коэффициент естественного прироста (Кест. пр.):
Кест. пр. = Крожд. – Ксм. = 29,67 – 9,9 = 19,77или
Кест. пр.19,77.
На каждую 1000 человек наличного населения число родившихся превышает число умерших на 19-20 человек.
е) коэффициент жизненности (Кж.):
Кж3 (раза), т.е. число родившихся превышает число умерших в 3 раза.
4) Вычислим показатели механического движения населения:
а) коэффициент миграции (механического прироста) (Кмигр.):
Кмигр.2,47.
На каждые 1000 человек наличного населения число прибывших на 2-3 человека больше, чем убывших.
Этот коэффициент можно разложить на две составляющие:
Кмигр. приб.14,83.
На каждые 1000 человек наличного населения число прибывших составляет 14-15 человек.
Кмигр. уб.12,36.
Из каждых 1000 человек наличного населения убывает 12-13 человек.
Тогда:
Кмигр. = Кмигр. приб. – Кмигр. уб. = 14,83– 12,36= 2,47.
б) интенсивность механического движения ():
= П + В = 6 + 5 = 11 (тыс. чел.)
в) сальдо механического движения (С0):
С0 = П – В = 6 – 5 = 1 (тыс. чел.)
5) Найдем коэффициент общего прироста наличного населения (Кобщ. Пр.):
Кобщ. пр. = Кест. пр. + Кмигр. = 19,77+ 2,47= 22,24.
На каждую 1000 человек наличного населения общий прирост за год составляет 22-23 человека.
ЗАДАЧА №4.
В области на 01.09.02г. численность детей в возрасте 10-12 лет составили: 10-летних – 62000; 11-летних – 64000; 12-летних – 65000. Вычислить возможный контингент учащихся 9-11 классов на 1 сентября 2006г., если известно, что коэффициент смертности 10-летних – 0,6; 11-летних – 0,5; 12-летних – 0,4; 13-летних – 0,7; 14-летних – 0,8; 15-летних – 1.
Решение:
1)Умножив численность детей на соответствующий коэффициент смертности и исключив полученное число из исходной численности, найдем сколько детей доживет до следующего года. Так например для 10-летних:
620000,0006 = 37 человек – не доживет до 11 лет.
Следовательно,
62000 – 37 = 61963 чел. доживет до 11 лет.
Аналогично для других возрастов.
Для 11-летних:
640000,0005 = 32 чел; 64000 – 32 = 63968 чел. – доживет до 12 лет
Для 12-летних:
650000,0004 = 26 чел; 65000 – 26 = 65974 чел. – доживет до 13 лет
Таким образом, на 01.09.03г. в области будет:
11-летних – 61963 чел.;
12-летних – 63968 чел.;
13-летних – 65974 чел.
2) Аналогично, с учетом новых данных, найдем число школьников на 01.09.04г.
619630,0005 = 31 чел; 61963 – 31 = 61932 чел. – доживет до 12 лет
639680,0004 = 26 чел; 63968 – 26 = 63942 чел. – доживет до 13 лет
659740,0007 = 46 чел; 65974 – 46 = 65928 чел. – доживет до 14 лет
3) Число учеников на 01.09.05г. будет следующее:
619320,0004 = 25 чел; 61932 – 25 = 61907 чел. – 13-летних
639420,0007 = 45 чел; 63942 – 45 = 63897 чел. – 14-летних
659280,0008 = 53 чел; 65928 – 53 = 65875 чел. – 15-летних
4) С учетом новых данных, найдем число учеников на 01.09.06г.
619070,0007 = 43 чел; 61907 – 43 = 61864 чел. – число 14-летних
638970,0008 = 51 чел; 63897 – 51 = 63846 чел. – число 15-летних
658750,001 = 66 чел; 65875 – 66 = 65809 чел. – число 16-летних
Таким образом на 01.09.06г. возможный контингент учащихся
9-х классов – 61864 чел.;
10-х классов – 63846 чел.;
11-х классов – 65809 чел.
ЗАДАЧА №5.
Имеются следующие данные об основных фондах предприятия за отчетный год.
Показатель | Сумма, млн. грн. |
1. Полная первоначальная стоимость основных фондов на начало года (ОФн.г.) | 1720 |
2. Сумма износа на начало года | 458 |
3. За год введены в эксплуатацию новые основные фонды (ОФввед) | 424 |
4. В течении года выбыли, из-за ветхости и износа, основные фонды по стоимости за вычетом износа (ОФизн) | 40 |
5. Полная первоначальная стоимость этих фондов (ОФвыб) | 344 |
6. Среднегодовая норма амортизации, % () | 10,5 |
7. Объем товарной продукции | 2464 |
Определить:
полную первоначальную стоимость основных фондов на конец года;
остаточную стоимость на конец года;
показатели движения основных фондов;
показатели состояния основных фондов на конец года;
показатели использования основных фондов.
studfiles.net
4.3. Показатели механического движения населения
Миграция – передвижение людей через границы территорий с переменой места жительства навсегда или на определенное время.
Перемещение населения внутри страны называется внутренней миграцией, а перемещение населения из одной страны в другую — внешней.
Валовая миграция (брутто-миграция) или миграционный оборот | Показывает общее число мигрирующих жителей (П + В). |
Сальдо миграции или механический прирост | Разница между числом прибывших и выбывших: (П – В) |
Коэффициент прибытия | |
Коэффициент выбытия | |
Коэффициент механического прироста (интенсивности миграции) населения | или Кмех пр = Кприб –— Квыб |
Коэффициент интенсивности миграционного оборота | Характеризует частоту случаев перемены местожительства в совокупности населения за определенный период |
Коэффициент эффективности миграции | |
Коэффициент общего прироста населения | Кобщ = Кест.пр + Кмех.пр |
Типовая задача 2
Механическое движение населения региона характеризуется следующими данными.
Среднегодовая численность населения – 146900 чел.
Прибыло в данный регион – 495 чел.
Выбыло из региона – 216 чел.
Определите:
миграционный прирост;
объем миграции;
коэффициент прибытия;
коэффициент выбытия;
общий коэффициент интенсивности миграции;
коэффициент интенсивности миграционного оборота;
коэффициент эффективности миграции.
Сделайте выводы.
Решение: 1. Миграционный прирост = 495 – 216=279 чел.
2. Объем миграции = 495+216=711 чел.
3. Коэффициент прибытия: %о.
4. Коэффициент выбытия: %о.
5. Общий коэффициент интенсивности миграции:
Кмех пр = Кприб – Квыб = 3,36 – 1,47 = 1,89 %о.
6. Коэффициент миграционного оборота:
%о.
7. Коэффициент эффективности миграции:
%о.
В данном регионе наблюдается прирост населения за счет положительного сальдо миграции.
Типовая задача 3
Численность населения страны на начало года составляла 105599,6 тыс. чел. За год родилось 1311,604 тыс. чел., умерло 2254,856 тыс. чел. Прибыло на постоянное место жительства в страну 2334,034 тыс. чел., убыло 2252,253 тыс. чел. Численность женщин в возрасте от 15 до 49 лет составляла 39097,069 тыс. чел.
На основе приведенных выше данных рассчитайте:
1) численность населения на конец года;
2) среднегодовую численность населения;
3) общие коэффициенты естественного и механического движения населения;
4) коэффициент жизненности Покровского;
5) специальный коэффициент фертильности (плодовитости) женщин;
6) перспективную численность населения через 2 года.
Сделайте выводы.
Решение: 1. Численность населения на конец года:
Sк.г = Sн.г + N – М + П – В = 105599,6 + 1311,604 – 2254,856 + 2334,034 – 2252,253 = 104738,129 (тыс. чел.)
2. Среднегодовая численность населения:
(тыс.чел.)
3. Общие коэффициенты:
— коэффициент рождаемости: %о;
— коэффициент смертности: %о;
— коэффициент естественного прироста (убыли) населения:
%о;
— коэффициент прибытия: %о;
— коэффициент выбытия: %о;
— коэффициент механического прироста:
Кмех пр = Кприб – Квыб = 22,20 – 21,42 = 0,78 %о;
— коэффициент эффективности миграции:
%о;
— коэффициент общего прироста:
Кобщ = Кест.пр + Кмех.пр = -8,97 + 0,78 = -8,19 %о.
4. Коэффициент жизненности Покровского: .
5. Специальный коэффициент фертильности женщин:
%о.
Перспективная численность населения через 2 года:
(тыс. чел.).
Из приведенных и полученных данных следует, что в стране наблюдается естественная убыль населения; численность умерших превышает численность родившихся, причем миграционные процессы не восполняют убыль. Наблюдаются процессы депопуляции населения, при этом большую роль в сложившейся ситуации играет низкий показатель фертильности женщин. Таким образом, через 2 года перспективная численность населения будет меньше фактической.
studfiles.net
Расчет естественного прироста населения. — Alexmed.info
ЗАДАЧА.
Используя данные таблицы, рассчитайте естественный прирост (убыль) населения, напишите вывод о динамике естественного движения населения в городе за 2010-2015 гг.
Динамика показателей естественного движения населения города за 2010-2015 гг.
(на 1000 населения)
| Показатель | Анализируемые годы | |||||
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
| Рождаемость | 9,9 | 9,8 | 10,0 | 10,1 | 10,1 | 10,2 |
| Смертность | 17,1 | 17,0 | 16,9 | 16,8 | 17,0 | 17,1 |
| Естественный прирост (убыль) | -7,2 | -7,2 | -6,9 | -6,7 | -6,9 | -6,9 |
ОТВЕТ:
Естественный прирост населения : рождаемость — смертность. Считаем так каждый год и записываем в таблицу в строке естественного прироста.
Динамика показателей ест. прироста с 2010 г по 2011 г — составляет 0%, так как ест.прирост равный.
Динамика показателей ест.прироста с 2011 по 2012 гг, рассчитываем как показатель наглядности:
7,2 – 100%
6,9 – х %
х = = 95,8%
100% — 95,8% = 4,2%
Динамика показателей ест.прироста с 2012 по 2013 гг, рассчитываем как показатель наглядности:
6,9 – 100%
6,7 – х %
х = = 97,1%
100% — 97,1% = 2,9%
Динамика показателей ест.прироста с 2013 по 2014 гг, рассчитываем как показатель наглядности:
6,7 – 100%
6,9 – х %
х = = 103%
100% — 103% = -3%
Динамика показателей ест.прироста с 2014 по 2015 гг,-0%.
Динамика показателей ест.прироста с 2010 по 2015 гг, рассчитываем как показатель наглядности:
7,2 – 100%
6,9 – х %
х = = 95,8%
100% — 95,8% = 4,2%
Динамика показателей естественного прироста 2010-2011 гг не имеет тенденции к снижению или повышению так как показатель наглядности 0%.
2011-2012 гг имеет тенденцию к снижению на 2,9%. 2013-2014 гг имеет тенденцию к повышению на 3%.
2014 — 2015 гг — 0%.
Динамика показателей ест. движения населения с 2010-2015 гг имеет тенденцию к снижению на 4,1%.
alexmed.info
3. Показатели роста и прироста численности населения
Показатели роста населения наглядно выражают изменения численности населения во времени. Различают показатели роста населения (темпов роста населения) и показатели прироста населения.
Показатели прироста населения могут быть представлены в абсолютных и относительных величинах.
Среди абсолютных различают показатели общего прироста, естественного прироста и миграционного прироста населения.
Относительные показатели прироста можно выразить в виде показателей темпов прироста и коэффициентов.
Темпы прироста — отношение абсолютных величин прироста к численности населения на начало того периода, для которого он исчисляется; а коэффициент общего прироста населения — это отношение абсолютных величин общего прироста населения за определенный промежуток времени к среднему населению:
где Sn — среднее население заданный период, Sn-1 — численность населения на начало периода, Sn-1 , n — численность населения на конец периода. Выражается в процентах (умножается на 100) или промилле (умножается на 1000). Может быть равен нулю, положительным или отрицательным.
Коэффициент естественного прироста населения — это отношение естественного прироста населения к среднему населению за определенный промежуток времени, а также разность коэффициентов рождаемости и смертности:
где N
— М — естественный
прирост населения,  —
среднее население,T—промежуток
времени.
—
среднее население,T—промежуток
времени.
Он может быть и положительным, и отрицательным, со знаком «+» или «—» в зависимости от того, что выше, рождаемость или смертность; может равняться и нулю. Выражается в промилле — %о. Колеблется от 0 до 30-35%о. Коэффициент естественного прироста во всем населении равен разности коэффициентов рождаемости и смертности:
k = n — m.
Если обозначить через S0 и St численность населения в начале и в конце периода, то без учета миграции прирост населения составит:
И, следовательно,
т.е. коэффициент естественного прироста равен годовому приросту, отнесенному к среднему населению.
Коэффициент естественного прироста (или убыли) населения в России в 2000 г. был равен — 6,6 %о (в 1990 г. + 2,2%о).
Коэффициент миграционного прироста измеряется путем сопоставления абсолютных показателей миграции (прибытий, выбытий, чистой и валовой миграции) за определенный срок со средним населением территории. Выражается формулой:
где S— население территории, Мj — прибывшие, Mi — численность выбывших, т.е. отношение чистой миграции к численности населения территории; с — константа, равная 1000 (промилле) или 100 (процент).
Коэффициент миграционного прироста — показатель интенсивности миграции, мера интенсивности миграции. Наиболее распространены коэффициенты миграции по прибытию и по выбытию, рассчитываемые как отношение числа переселившихся на данную территорию и числа выселившихся за определенный период времени (обычно за год) к среднегодовой численности постоянного населения данной территории.
4. Структурные коэффициенты
Демографические коэффициенты класса «Б», или структурные коэффициенты, делятся на показатели нагрузки (соотношения) и показатели доли населения.
Коэффициент демографической нагрузки — обобщенная характеристика возрастной структуры населения, выраженная соотношением отдельных групп (частей) населения между собой и с другими частями, что позволяет судить о «нагруженности» одних групп людей другими. Коэффициент демографической нагрузки показывает, сколько нетрудоспособных приходится на 1000 человек трудоспособного населения, т.е. показывает нагрузку на общество непроизводительного населения.
Наиболее часто употребляются показатели демографической нагрузки, характеризующие соотношения крупных возрастных групп — нетрудоспособного населения 0—14 лет, пожилых и людей старше 60 лет и трудоспособных — 15—59 лет. Кроме того, употребляется отношение числа пожилых людей, или числа детей к числу трудоспособных людей, а также отношение числа пожилых людей к числу детей (последнее служит для оценки степени старения населения).
В 1990 г. в России коэффициент демографической нагрузки был равен 759, в 1999 г. — 711. По прогнозам, к 2005 г. он снизится до 588, после чего к 2015 г. снова возрастет до 696.
Другой вид коэффициентов характеризует доли людей, обладающих определенными признаками в группе населения (например, коэффициент занятости показывает число занятых лиц среди населения данного возраста и пола).
Основная трудность при анализе динамики демографических процессов на основе общих коэффициентов — зависимость их величины не только от характера демографических явлений, но и от специфики возрастной структуры населения, доли в нем различных возрастных групп. Чтобы уменьшить такое влияние, необходимо перейти к исчислению повозрастных (частных) демографических коэффициентов.
Повозрастные коэффициенты чаще исчисляются по пятилетним возрастным группам: 0 — 4 года, 5 — 9 лет,, 10 — 14 лет и т.д. Повозрастные коэффициенты смертности всегда должны рассчитываться раздельно, например, по полу, поскольку для мужчин они всегда существенно больше аналогичных показателей для женщин. Поэтому величина общего коэффициента смертности зависит от соотношения численности мужчин и женщин в населении страны или региона.
Для женщин рассчитывают следующие повозрастные коэффициенты рождаемости:
— коэффициент рождаемости женщин от 15 до 49 лет (так называемый специальный коэффициент рождаемости), как число рождений в среднем на 1000 женщин в этом возрасте;
— повозрастные коэффициенты рождаемости по одногодичным или пятилетним возрастным группам женщин в интервале от 15 до 49 лет.
Повозрастной коэффициент рождаемости женщин в возрасте от 15 до 45 лет в зависимости от возрастной структуры населения и доли женщин детородного возраста в общей численности населения, обычно в 3—5 раз больше величины общего коэффициента рождаемости; максимальная его величина может быть примерно 250—270%о.
studfiles.net


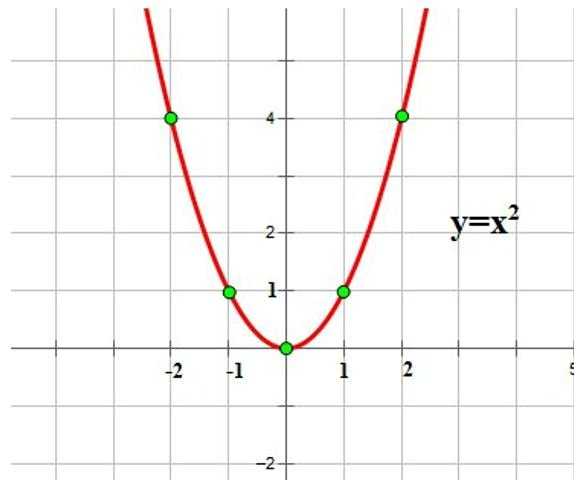
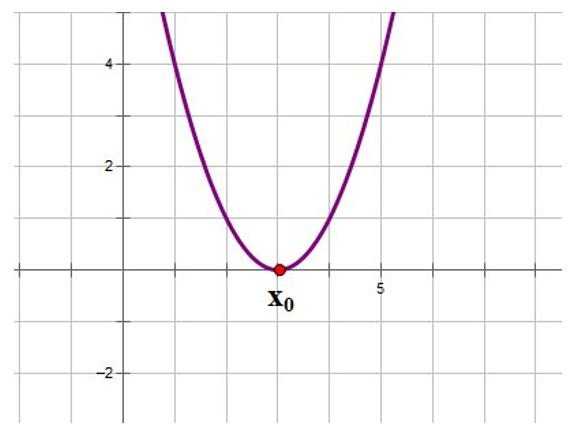
 Характеристика функции у = х2
Характеристика функции у = х2
 Алгоритм построения квадратичной функции
Алгоритм построения квадратичной функции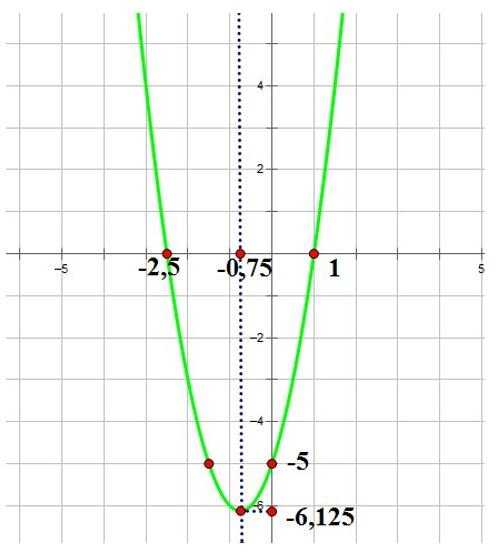


 0 — возрастающей . При х=0 функция принимает своё наименьшее значение . «
0 — возрастающей . При х=0 функция принимает своё наименьшее значение . «
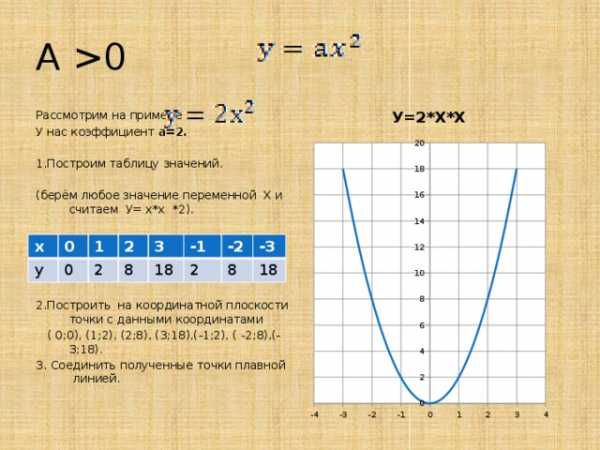 0 Рассмотрим на примере У нас коэффициент а=2. 1.Построим таблицу значений. (берём любое значение переменной Х и считаем У= х*х *2). 2.Построить на координатной плоскости точки с данными координатами ( 0;0), (1;2), (2;8), (3;18),(-1;2), ( -2;8),(-3;18). 3. Соединить полученные точки плавной линией. х 0 у 1 0 2 2 3 8 18 -1 -2 2 -3 8 18 «
0 Рассмотрим на примере У нас коэффициент а=2. 1.Построим таблицу значений. (берём любое значение переменной Х и считаем У= х*х *2). 2.Построить на координатной плоскости точки с данными координатами ( 0;0), (1;2), (2;8), (3;18),(-1;2), ( -2;8),(-3;18). 3. Соединить полученные точки плавной линией. х 0 у 1 0 2 2 3 8 18 -1 -2 2 -3 8 18 «

 0 Графиком функции является парабола. Графиком функции является парабола. Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат ниже оси абсцисс (Ох) – ветви параболы направлены вниз . График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = -18. При х функция является возрастающей , при х 0 — . При х=0 функция принимает своё наибольшее значение ( У max). Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат выше оси абсцисс (Ох) – ветви параболы направлены вверх. График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = 18. При х функция является убывающей , при х 0 — возрастающей . При х=0 функция принимает своё наименьшее значение ( У min). Растяжение вдоль оси Оу при Сжатие к оси Ох при Растяжение вдоль оси Оу при Сжатие к оси Ох при «
0 Графиком функции является парабола. Графиком функции является парабола. Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат ниже оси абсцисс (Ох) – ветви параболы направлены вниз . График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = -18. При х функция является возрастающей , при х 0 — . При х=0 функция принимает своё наибольшее значение ( У max). Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат выше оси абсцисс (Ох) – ветви параболы направлены вверх. График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = 18. При х функция является убывающей , при х 0 — возрастающей . При х=0 функция принимает своё наименьшее значение ( У min). Растяжение вдоль оси Оу при Сжатие к оси Ох при Растяжение вдоль оси Оу при Сжатие к оси Ох при «
 0, то найти корни квадратного трёхчлена по формуле 4. Найти точку пересечения параболы с осью Оу : при х=0, у = С , т.е. ( 0;С). Найти дополнительные точки параболы ( если D Все точки и им симметричные, не забываем отмечать на координатной плоскости. Соединим все отмеченные точки плавной линией — получим график квадратичной функции – параболу. «
0, то найти корни квадратного трёхчлена по формуле 4. Найти точку пересечения параболы с осью Оу : при х=0, у = С , т.е. ( 0;С). Найти дополнительные точки параболы ( если D Все точки и им симметричные, не забываем отмечать на координатной плоскости. Соединим все отмеченные точки плавной линией — получим график квадратичной функции – параболу. «
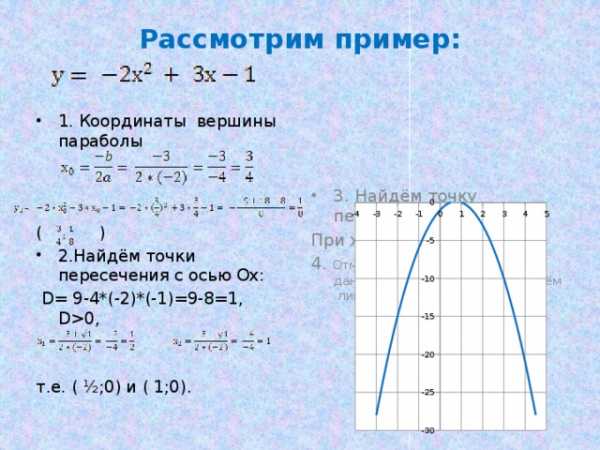 0, т.е. ( ½;0) и ( 1;0). «
0, т.е. ( ½;0) и ( 1;0). «
 0 , то ветви параболы направлены вверх , функция принимает наименьшее значение в абсциссе вершины параболы. Если а ветви параболы направлены вниз , функция принимает наибольшее значение в абсциссе вершины параболы. Ось симметрии параболы – прямая, параллельная оси ординат ( Оу) и проходящая через вершину параболы . Область определения функции – вся числовая ось ( Ох), т.е. х – любое число. Если D = 0 , то парабола имеет с осью Ох всего одну общую точку касания – абсцисса вершины. Если D 0 , то парабола пересекает ось Ох в двух точках ( корни квадратного трёхчлена). Если D , то парабола с осью Ох не пересекается , т.е. находится выше или ниже оси, в зависимости от направления ветвей. «
0 , то ветви параболы направлены вверх , функция принимает наименьшее значение в абсциссе вершины параболы. Если а ветви параболы направлены вниз , функция принимает наибольшее значение в абсциссе вершины параболы. Ось симметрии параболы – прямая, параллельная оси ординат ( Оу) и проходящая через вершину параболы . Область определения функции – вся числовая ось ( Ох), т.е. х – любое число. Если D = 0 , то парабола имеет с осью Ох всего одну общую точку касания – абсцисса вершины. Если D 0 , то парабола пересекает ось Ох в двух точках ( корни квадратного трёхчлена). Если D , то парабола с осью Ох не пересекается , т.е. находится выше или ниже оси, в зависимости от направления ветвей. «

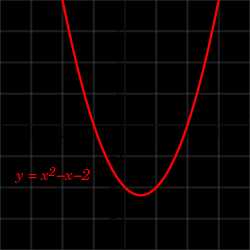 График функции f(x)=x2−x−2{\displaystyle f(x)=x^{2}-x-2}
Эта статья — о числовой функции одной переменной. О функции второй степени с несколькими переменными см. Квадратичная форма; о геометрическом месте точек см. Парабола.
График функции f(x)=x2−x−2{\displaystyle f(x)=x^{2}-x-2}
Эта статья — о числовой функции одной переменной. О функции второй степени с несколькими переменными см. Квадратичная форма; о геометрическом месте точек см. Парабола. на отрезке
на отрезке  линейного однородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами является линейная
комбинация
линейного однородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами является линейная
комбинация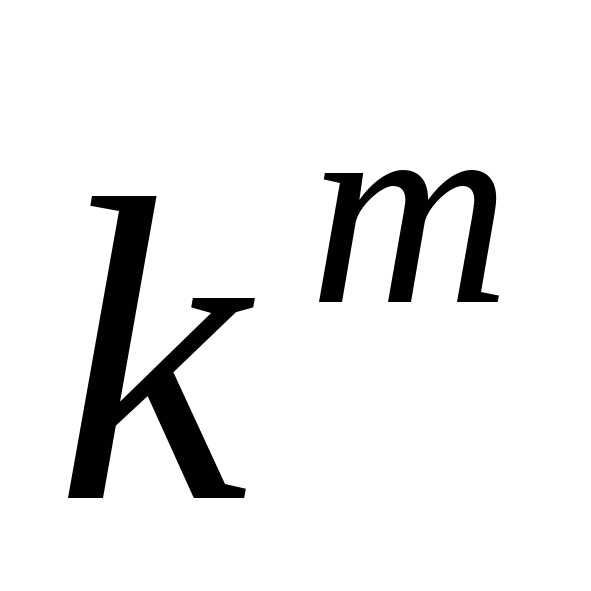 ,
причем сама функция
,
причем сама функция заменяется единицей. Характеристическое
уравнение – это алгебраическое уравнение
степениn.
заменяется единицей. Характеристическое
уравнение – это алгебраическое уравнение
степениn.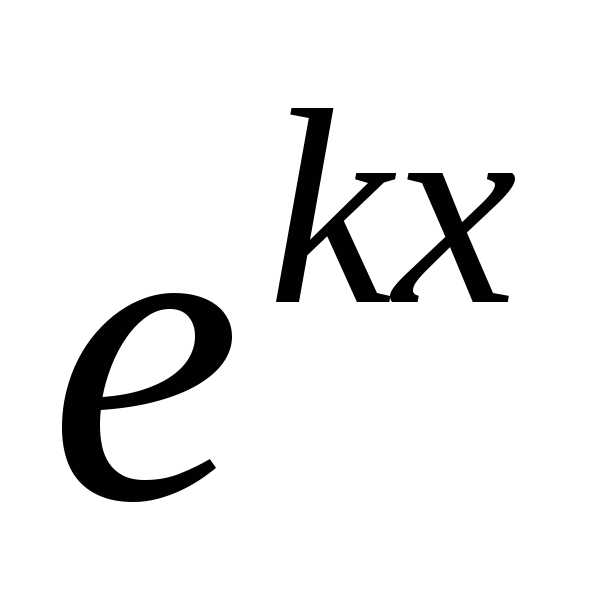 ;
; соответствуют
соответствуют частных решений вида
частных решений вида соответствуют 2
соответствуют 2 частных решений вида
частных решений вида –
заданная функция.
–
заданная функция. на отрезке
на отрезке 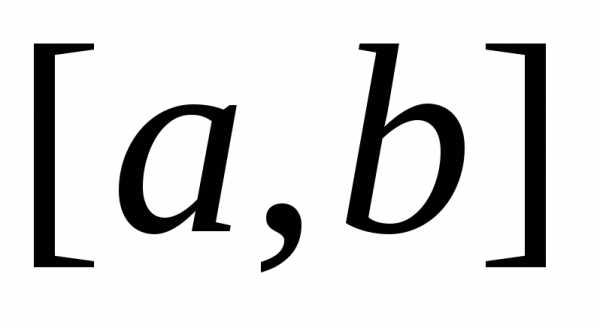 линейного неоднородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами и непрерывной правой
частью
линейного неоднородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами и непрерывной правой
частью 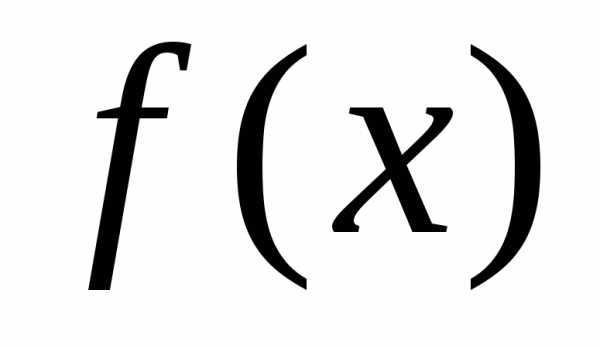 является сумма общего решения
является сумма общего решения неоднородного уравнения:
неоднородного уравнения: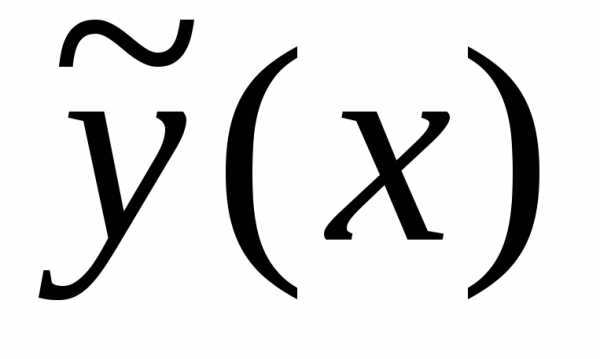 неоднородного уравнения.
неоднородного уравнения. –
многочлен, либо показательная функция,
либо тригонометрические функции
–
многочлен, либо показательная функция,
либо тригонометрические функции 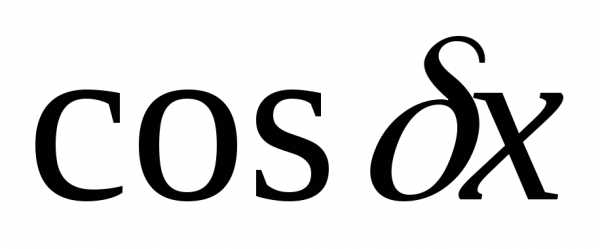 или
или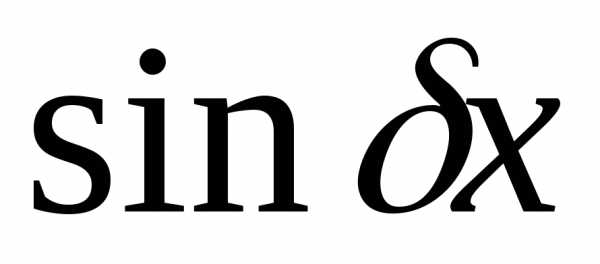 ,
либо линейная комбинация перечисленных
функций, то частное решение
,
либо линейная комбинация перечисленных
функций, то частное решение неоднородного уравнения может быть
найдено методом неопределенных
коэффициентов.
неоднородного уравнения может быть
найдено методом неопределенных
коэффициентов. неоднородного уравнения может быть
найдено методом вариации произвольных
постоянных.
неоднородного уравнения может быть
найдено методом вариации произвольных
постоянных. неоднородного уравнения.
неоднородного уравнения. – действительные постоянные,
– действительные постоянные, и
и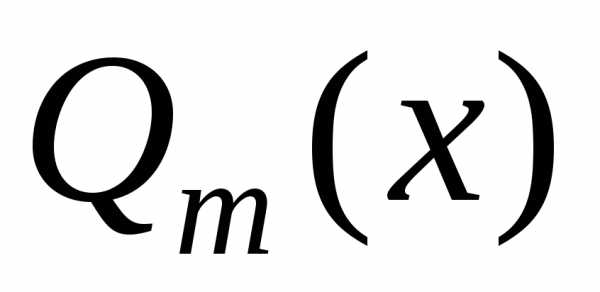 –
многочлены от x соответственно l-й
и m-й
степени.
–
многочлены от x соответственно l-й
и m-й
степени. равно показателю кратности корняв характеристическом уравнении
равно показателю кратности корняв характеристическом уравнении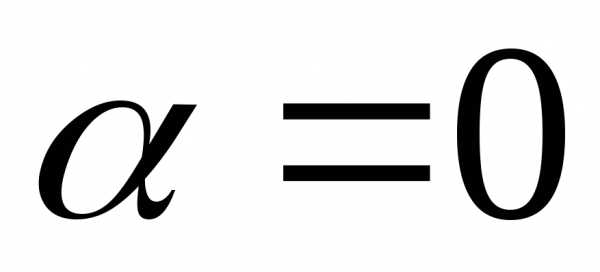 .
.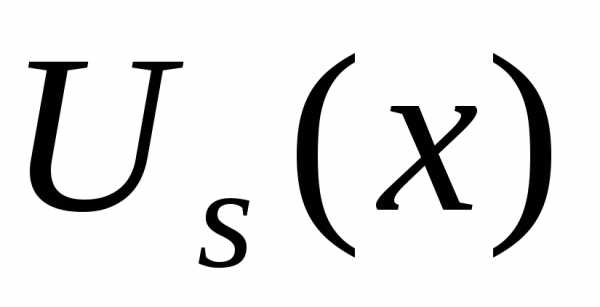 и
и –полные (т.е. содержащие все степени x от 0 до s)
многочлены от x степени s с неопределенными коэффициентами,
причем s равно наибольшему из чисел l и m:
–полные (т.е. содержащие все степени x от 0 до s)
многочлены от x степени s с неопределенными коэффициентами,
причем s равно наибольшему из чисел l и m: входит хотя бы одна из функций
входит хотя бы одна из функций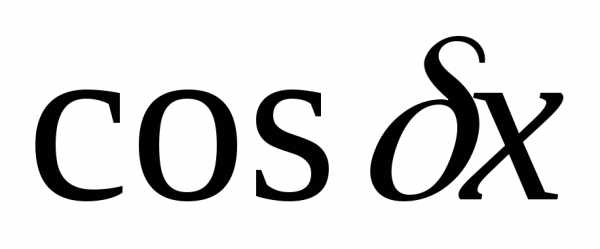 или
или ,
то в решение
,
то в решение надо всегда вводитьобе эти функции.
надо всегда вводитьобе эти функции. вместоy,
вместоy,  вместо
вместо ,
, вместо
вместо и т.д.
и т.д.
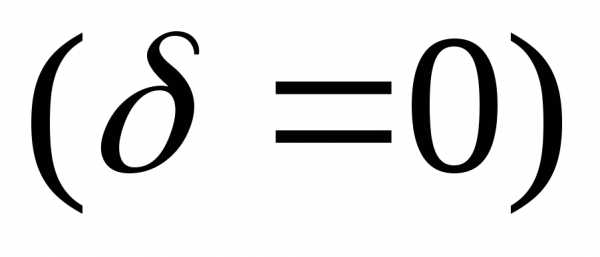 ,
а также согласно принципу наложения
решений для правых частей.
,
а также согласно принципу наложения
решений для правых частей. находим производные
находим производные и
и :
: и найдем их значения:
и найдем их значения: :
: ,
, :
: ,
,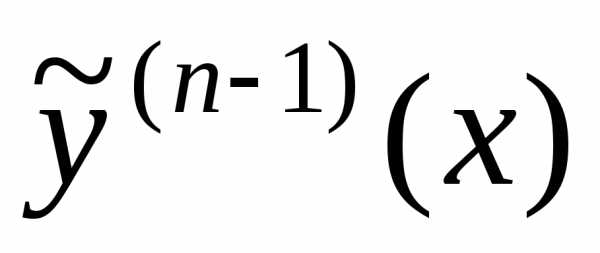 :
: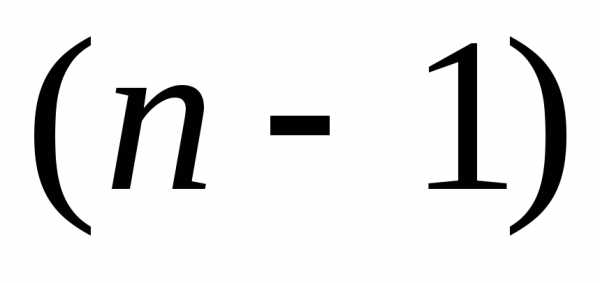 -е
изn искомых уравнений.
-е
изn искомых уравнений.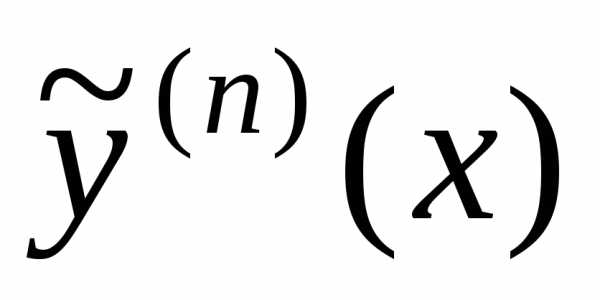 :
: вместоy,
вместоy,  вместо
вместо  ,
,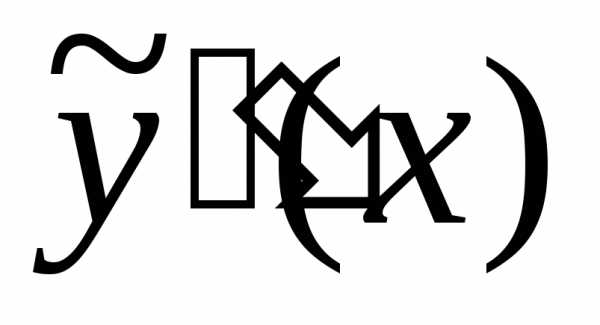 вместо
вместо ,…,
,…, вместо
вместо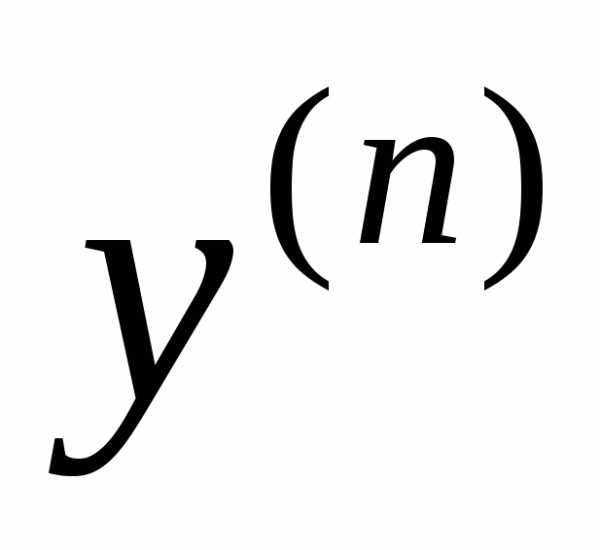 ,
получим последнееn-е
из n искомых
уравнений для определения n неизвестных
функций
:
,
получим последнееn-е
из n искомых
уравнений для определения n неизвестных
функций
:
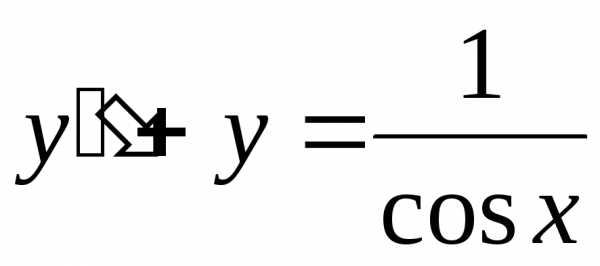 .
. и
и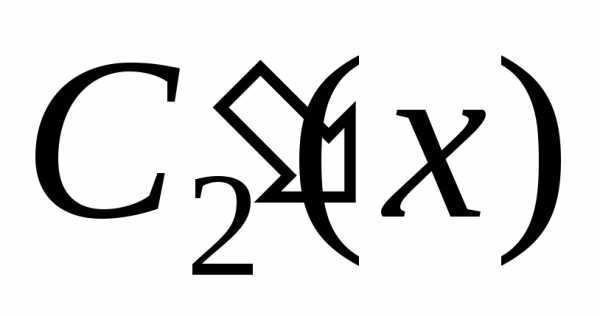 :
: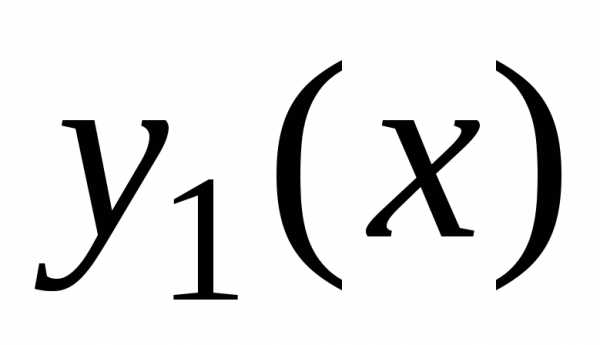 и
и –
линейно независимые решения линейного
однородного дифференциального уравнения
(2.3), то их линейная комбинация,
где
–
линейно независимые решения линейного
однородного дифференциального уравнения
(2.3), то их линейная комбинация,
где и
и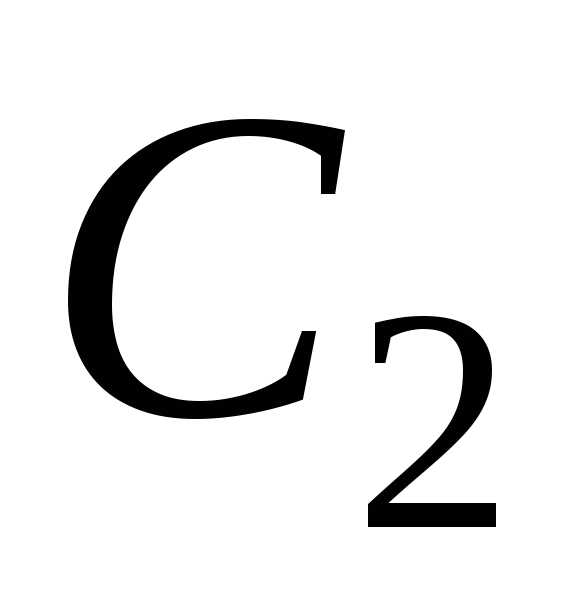 – произвольные
постоянные, является общим решением
этого уравнения.
– произвольные
постоянные, является общим решением
этого уравнения. и
и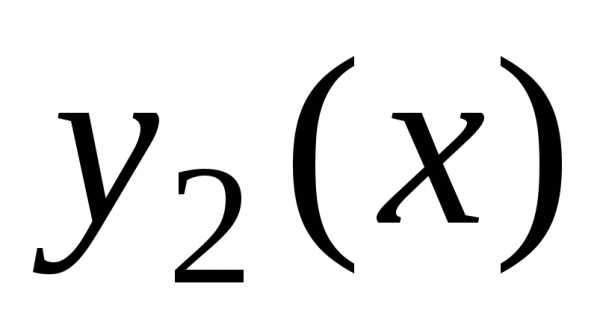 образуют фундаментальную систему решений ЛОДУ (2.3).
образуют фундаментальную систему решений ЛОДУ (2.3). и
и так, чтобы
удовлетворить этим условиям. Запишем
начальные условия в виде:
так, чтобы
удовлетворить этим условиям. Запишем
начальные условия в виде: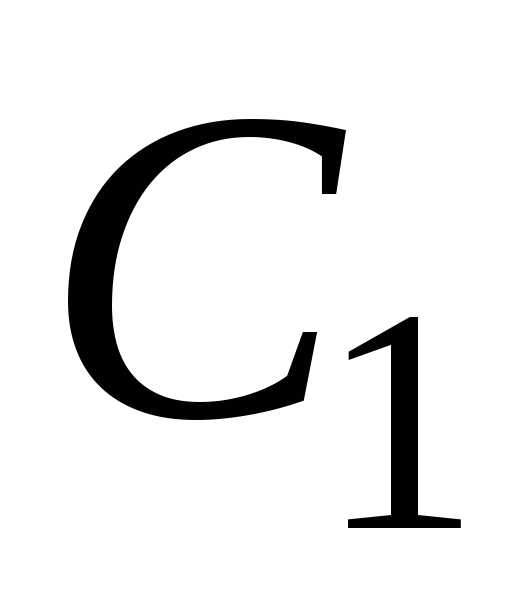 и
и из этой
системы линейных алгебраических
уравнений определяются однозначно, так
как определитель этой системы
из этой
системы линейных алгебраических
уравнений определяются однозначно, так
как определитель этой системы  есть значение определителя Вронского
для линейно независимых решений ЛОДУ
при
есть значение определителя Вронского
для линейно независимых решений ЛОДУ
при :
: и
и – произвольные
постоянные, является общим решением
ЛОДУ
– произвольные
постоянные, является общим решением
ЛОДУ и удовлетворяют данному уравнению. Эти
функции являются линейно независимыми,
так как
и удовлетворяют данному уравнению. Эти
функции являются линейно независимыми,
так как .
Поэтому согласно теореме о структуре
общего решения ЛОДУ 2-го порядка функция
является общим решением данного
уравнения.
.
Поэтому согласно теореме о структуре
общего решения ЛОДУ 2-го порядка функция
является общим решением данного
уравнения. .
Подставляя эту функцию в уравнение
(5.1), после сокращения на
.
Подставляя эту функцию в уравнение
(5.1), после сокращения на ,
получим алгебраическое уравнение,
которое называетсяхарактеристическим:
,
получим алгебраическое уравнение,
которое называетсяхарактеристическим: ,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта
,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта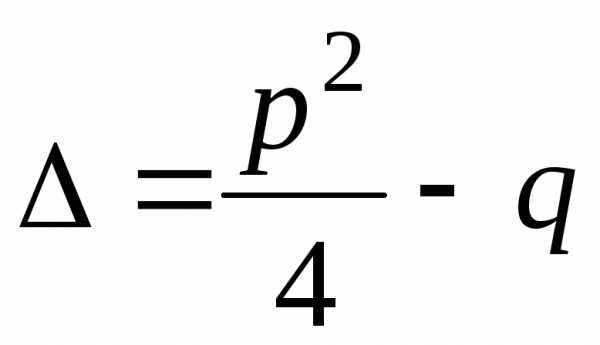 возможны три случая.
возможны три случая. .
Тогда корни характеристического
уравнения различны:
.
Тогда корни характеристического
уравнения различны: 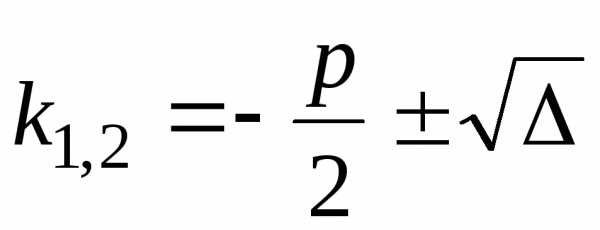 .
Решения
.
Решения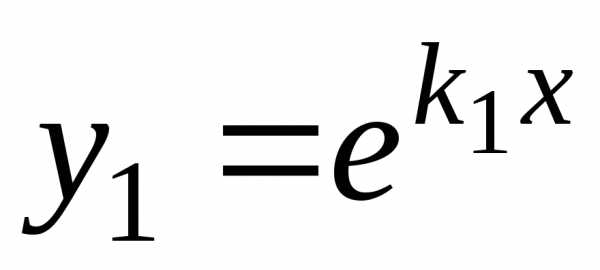 и
и будут линейно независимыми, так как
и общее решение уравнения (5.1) можно
записать в виде
.
будут линейно независимыми, так как
и общее решение уравнения (5.1) можно
записать в виде
.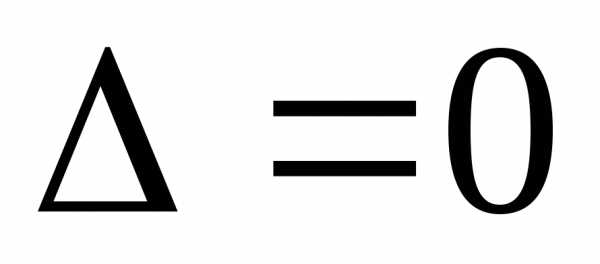 .
В этом случае
.
В этом случае 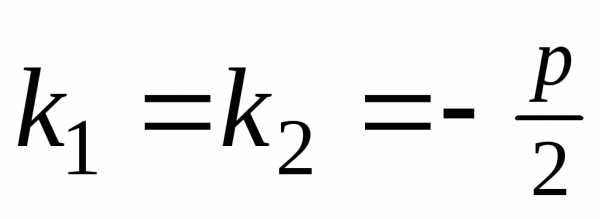 и
и .
В качестве второго линейно независимого
решения можно взять функцию
.
В качестве второго линейно независимого
решения можно взять функцию .
Проверим, что эта функция удовлетворяет
уравнению (5.1).
.
Проверим, что эта функция удовлетворяет
уравнению (5.1).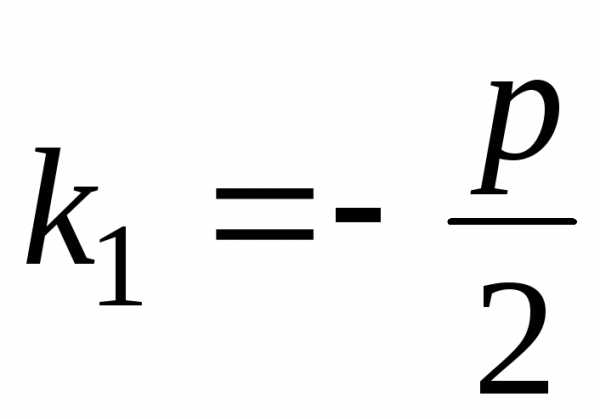 и.
и.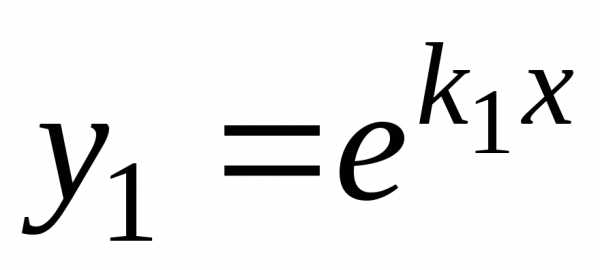 и
и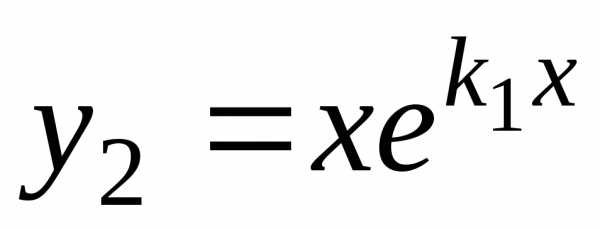 линейно независимы, так как
линейно независимы, так как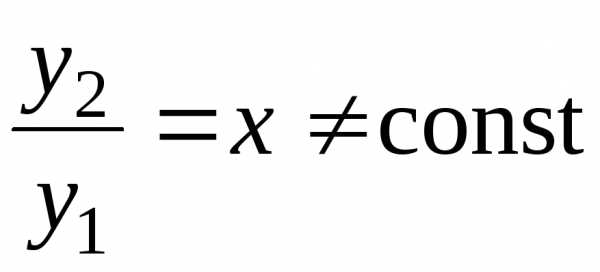 .
Следовательно, общее решение уравнения
(5.1) имеет вид:
.
Следовательно, общее решение уравнения
(5.1) имеет вид: .
В данном случае корни характеристического
уравнения комплексно-сопряжены:
,
где
.
В данном случае корни характеристического
уравнения комплексно-сопряжены:
,
где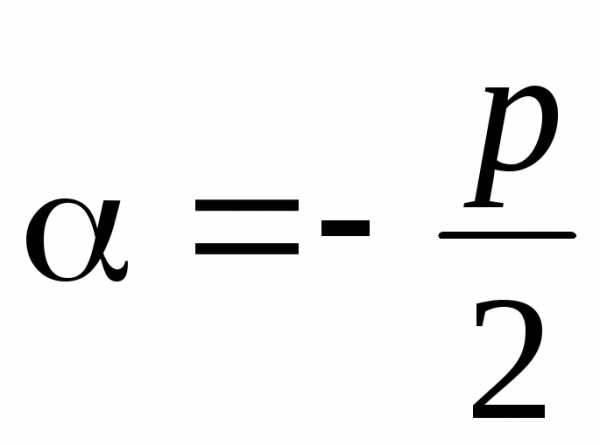 ,
,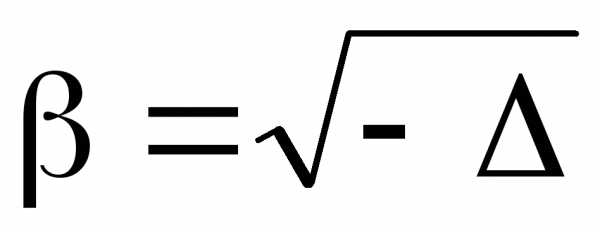 .
Легко проверить, что линейно независимыми
решениями уравнения (5.1) будут функциии
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция
.
Легко проверить, что линейно независимыми
решениями уравнения (5.1) будут функциии
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция  .
. ,
то общее решениебудет иметь вид:
,
то общее решениебудет иметь вид:

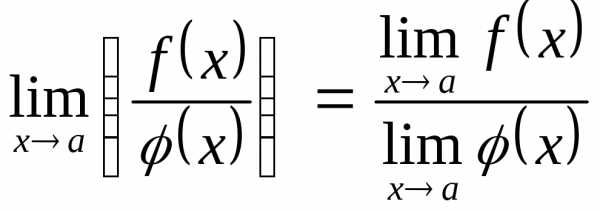 ,
предел частного равен отношению
пределов, если
,
предел частного равен отношению
пределов, если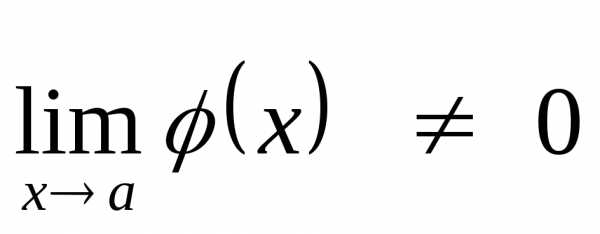 .
.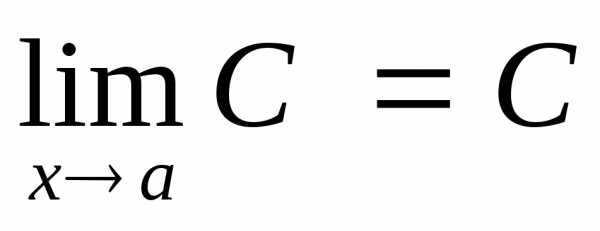 ,
предел постоянной величины равен самой
постоянной.
,
предел постоянной величины равен самой
постоянной. .
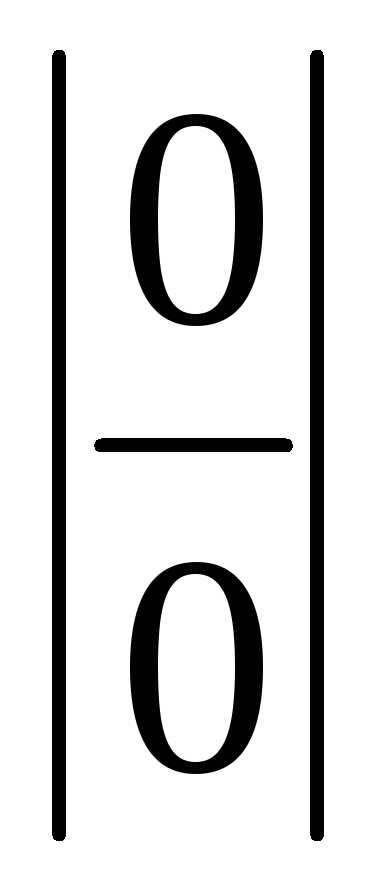
.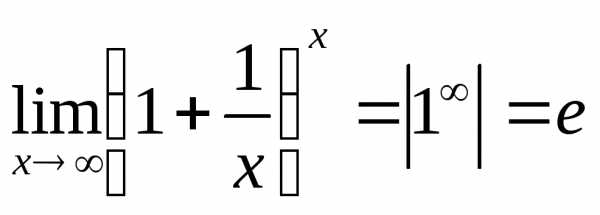 ,
, ,
т.е. является бесконечно малой величиной.
,
т.е. является бесконечно малой величиной.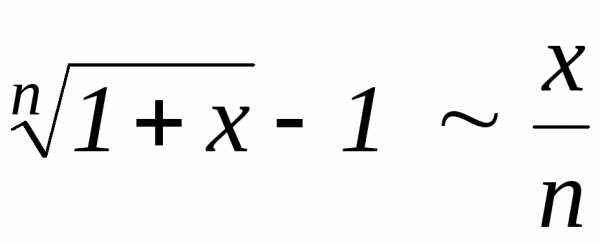
 ,
, 
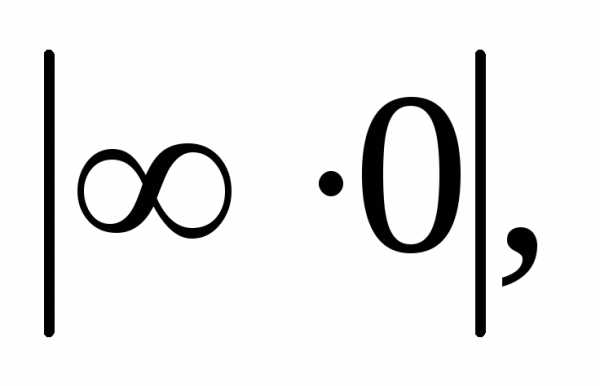
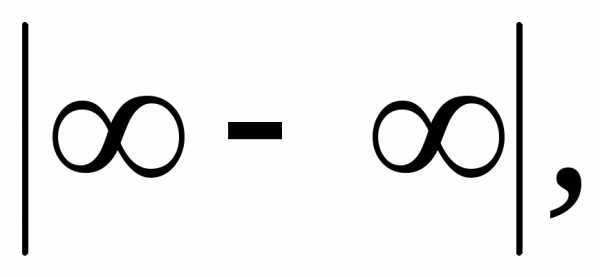
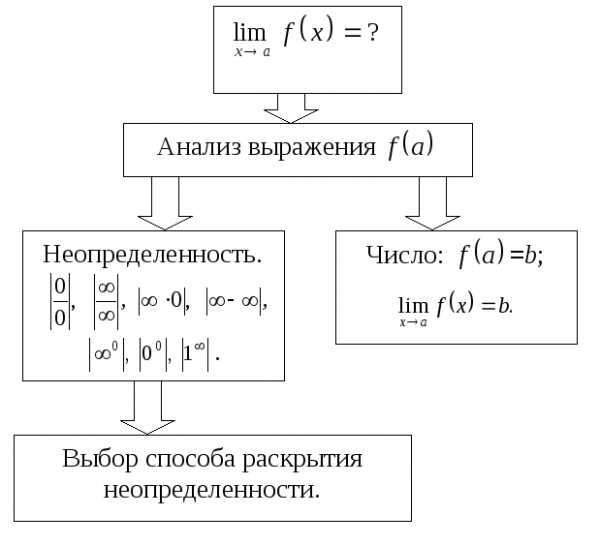
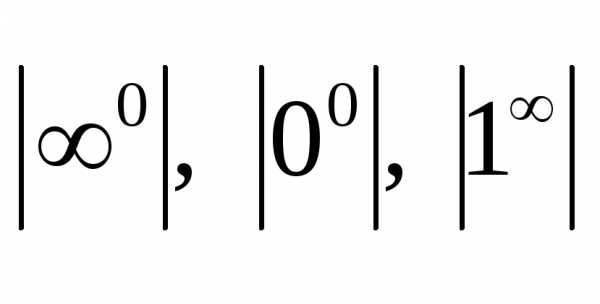 .
.
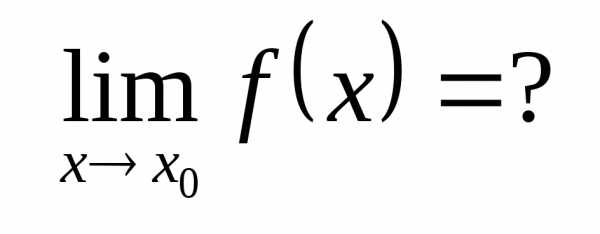 .
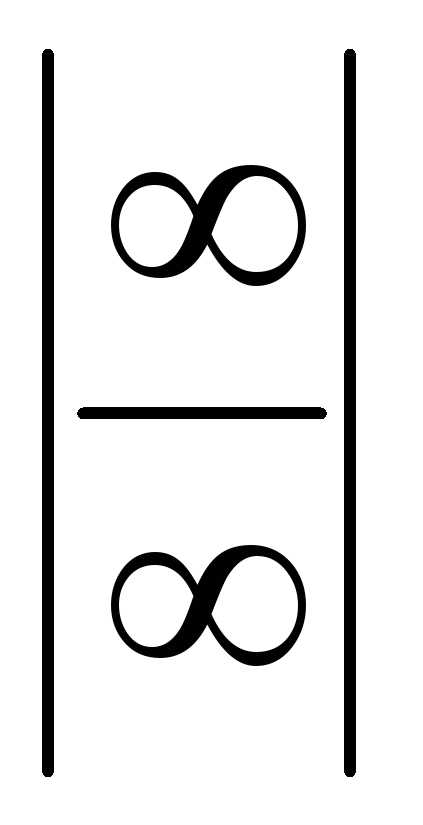
.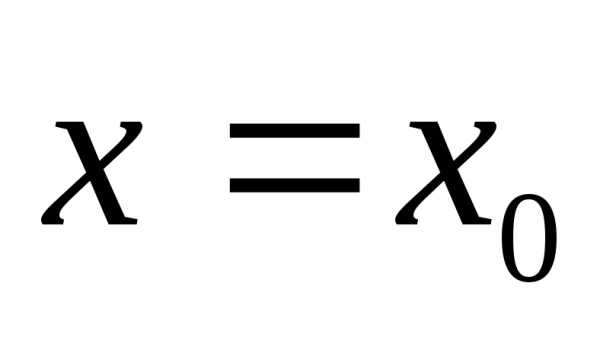 (в том числе и
(в том числе и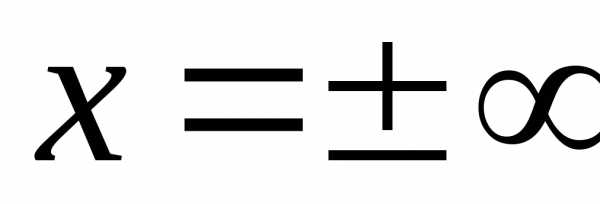 )
в
)
в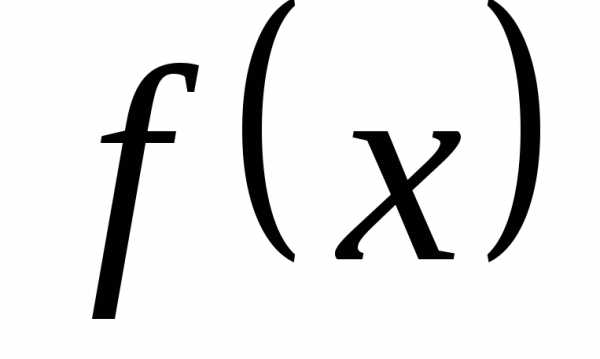 .
.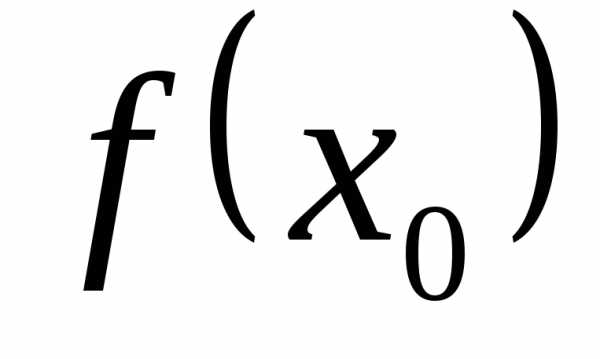 .
.
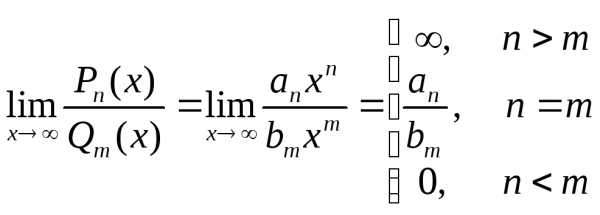
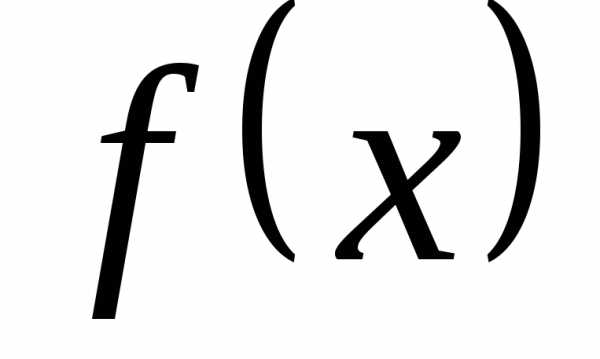 :
: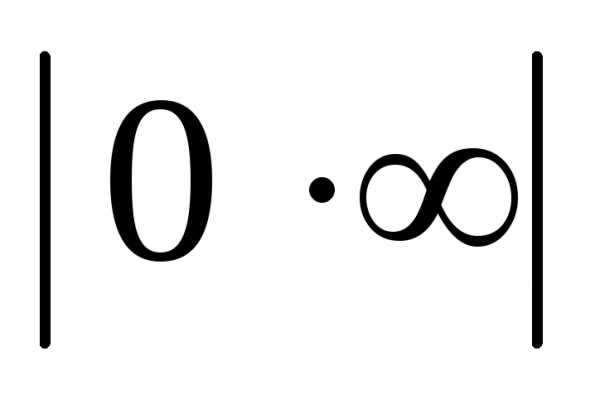
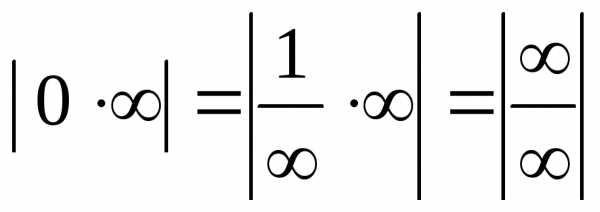 или
или 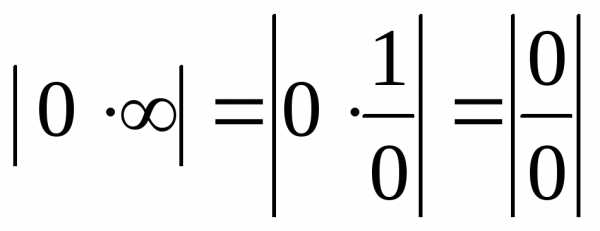 .
.
 ,
то привести к общему знаменателю и
получить
,
то привести к общему знаменателю и
получить .
.
 — бесконечно малая величина.
— бесконечно малая величина.
 Сложение и вычитание четных и нечетных чисел
Сложение и вычитание четных и нечетных чисел






 …
… …
…
 …
… …
…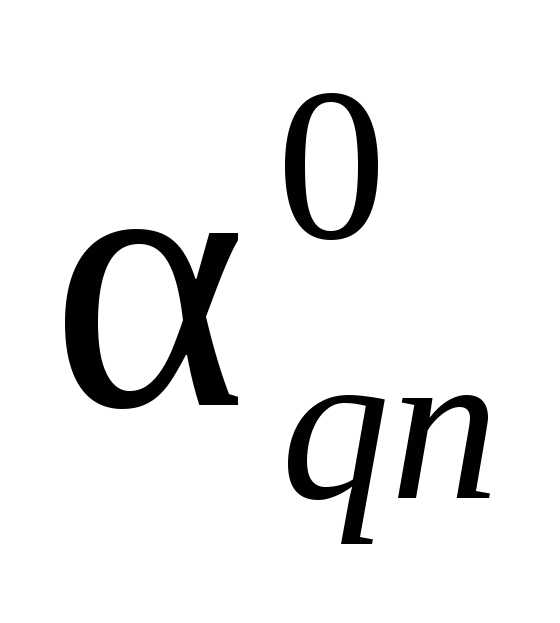
 …
… …
…

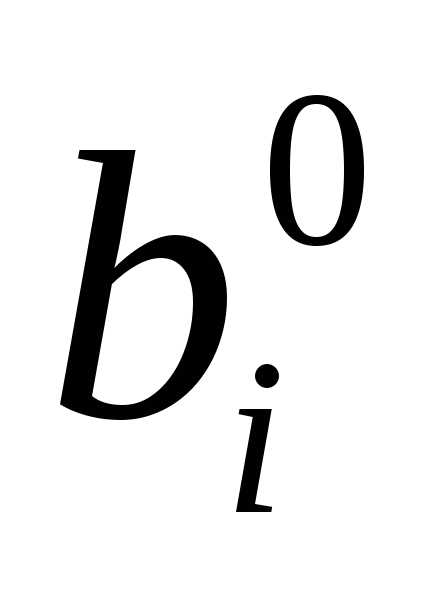
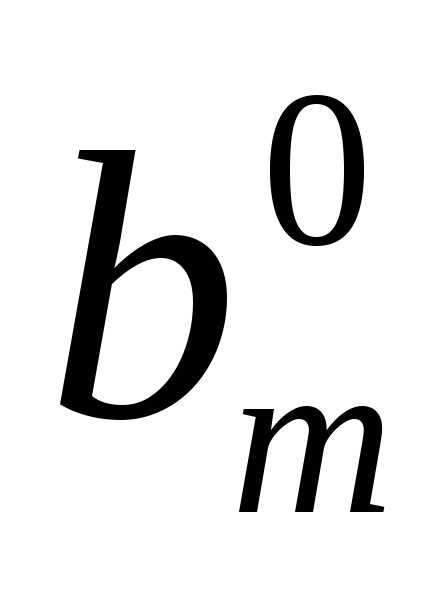
 …
… …
…
 …
…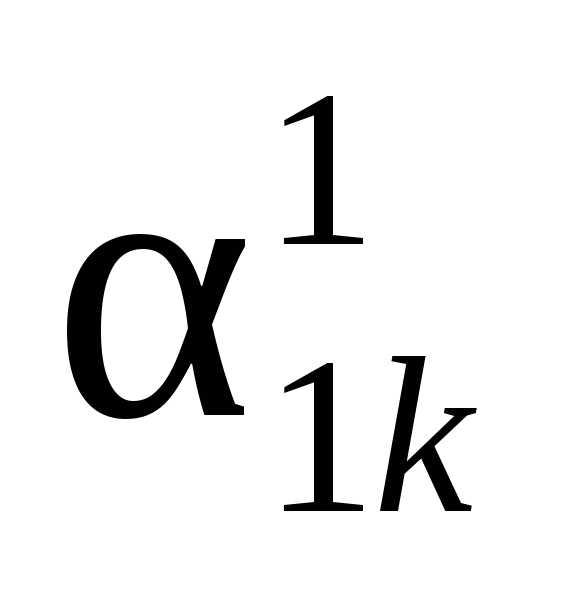 …
…
 …
…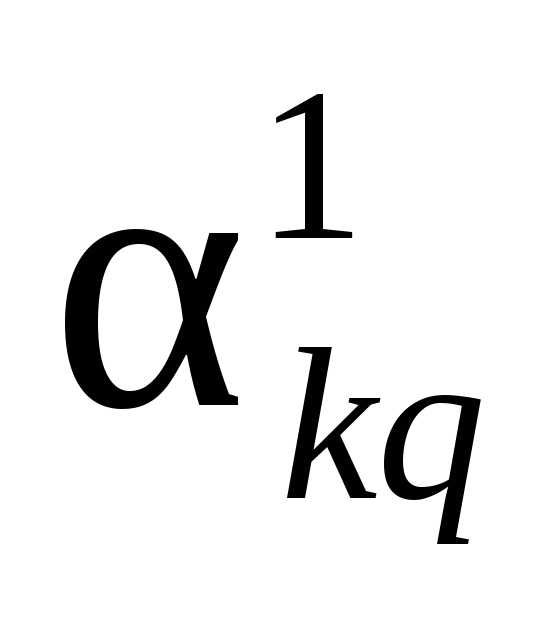 …
…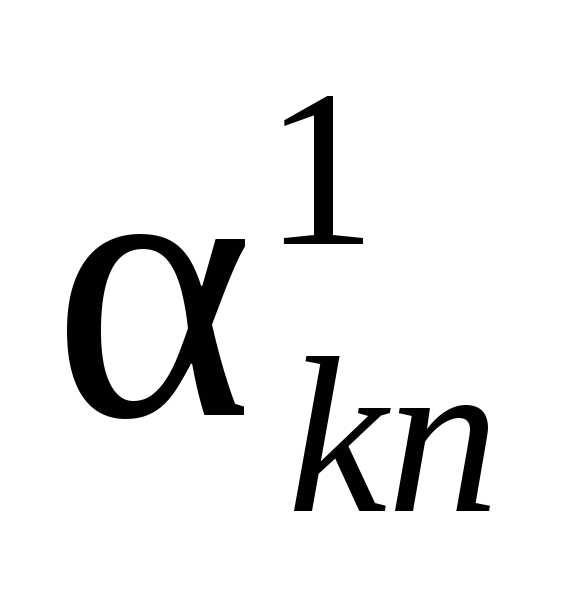
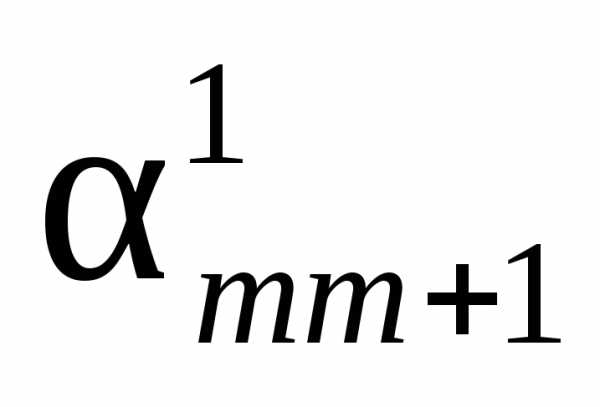 …
…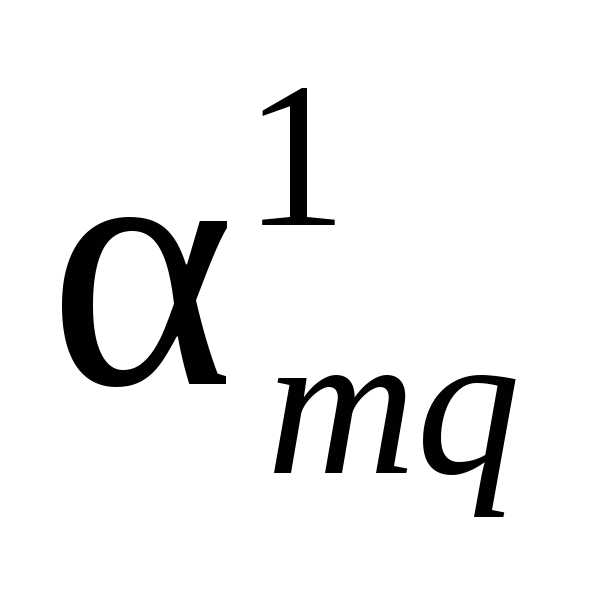 …
…

 …
…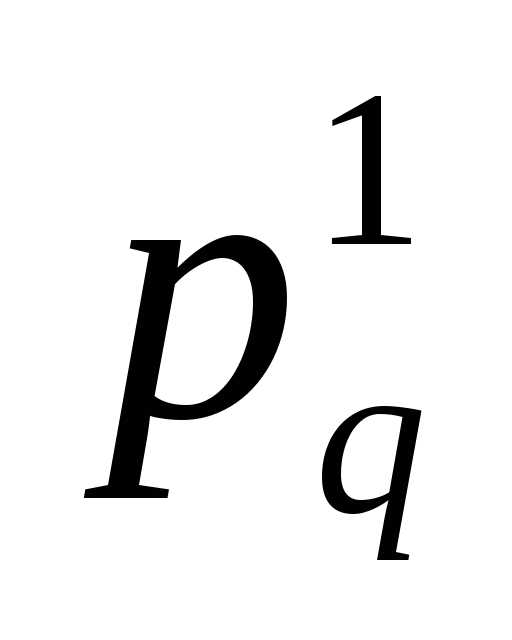 …
…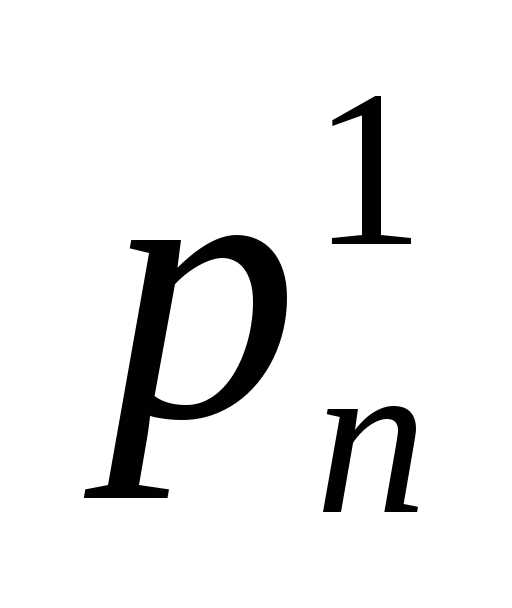

 .
В левом столбце таблицы записываем
основные переменные (базис), в последующих
– коэффициенты
.
В левом столбце таблицы записываем
основные переменные (базис), в последующих
– коэффициенты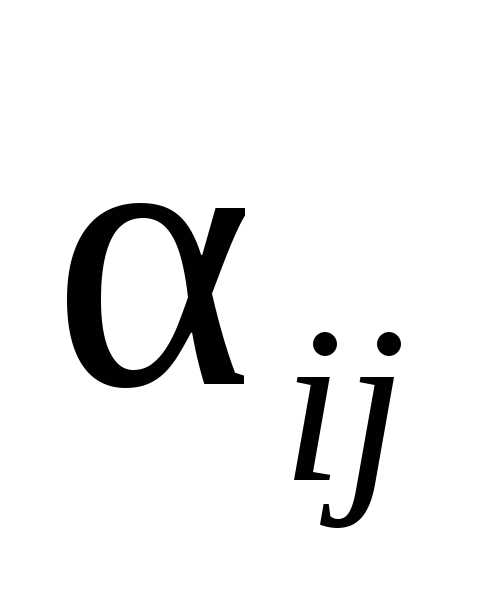 при свободных переменных. В предпоследнем
столбце – свободные члены расширенной
системы.
Последний столбец подготовлен для
оценочных отношений, необходимых для
определения базисной переменной
при свободных переменных. В предпоследнем
столбце – свободные члены расширенной
системы.
Последний столбец подготовлен для
оценочных отношений, необходимых для
определения базисной переменной на основании соотношения (6.29).
на основании соотношения (6.29).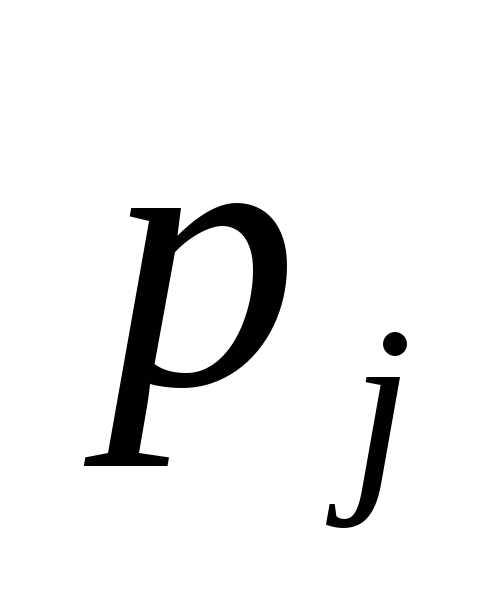 согласно теоремам 6.7,…, 6.9.
согласно теоремам 6.7,…, 6.9. .
Если критерий оптимальности не выполнен
(не выполнены условия теоремы 6.7 или
6.8), то наибольший по модулю отрицательный
коэффициент
.
Если критерий оптимальности не выполнен
(не выполнены условия теоремы 6.7 или
6.8), то наибольший по модулю отрицательный
коэффициент в последней строке определяет разрешающий
(опорный) столбец
в последней строке определяет разрешающий
(опорный) столбец .
. ,
если все
,
если все и
и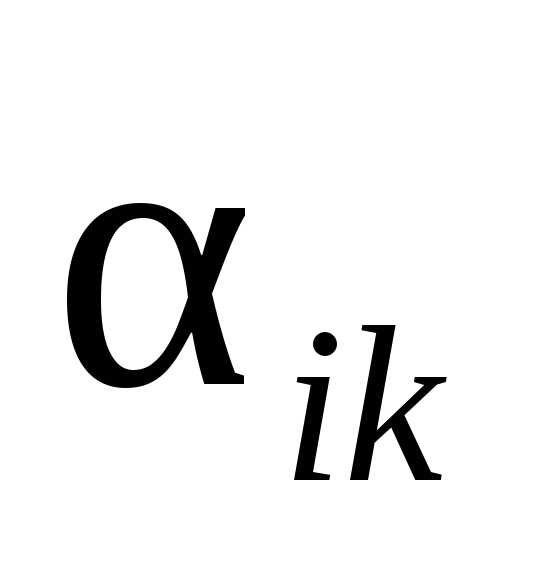 имеют разные знаки;
имеют разные знаки; ,
если все
,
если все и
и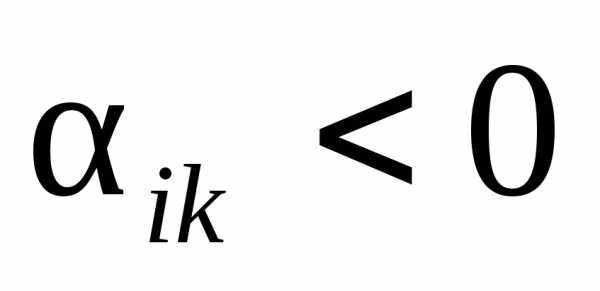 ;
; ,
если
,
если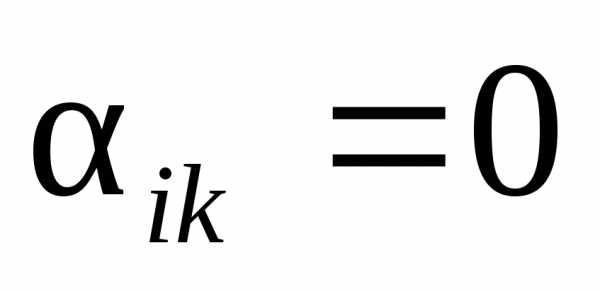 ;
;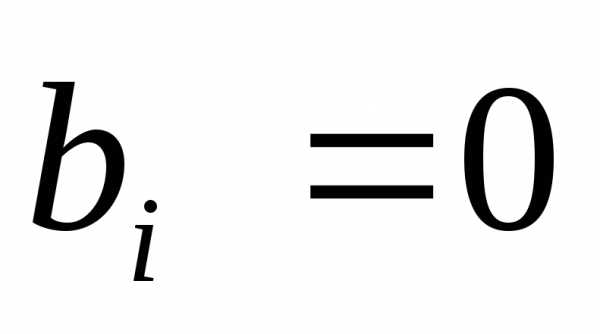 и
и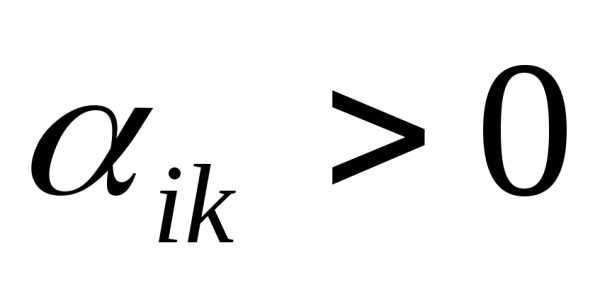 ;
;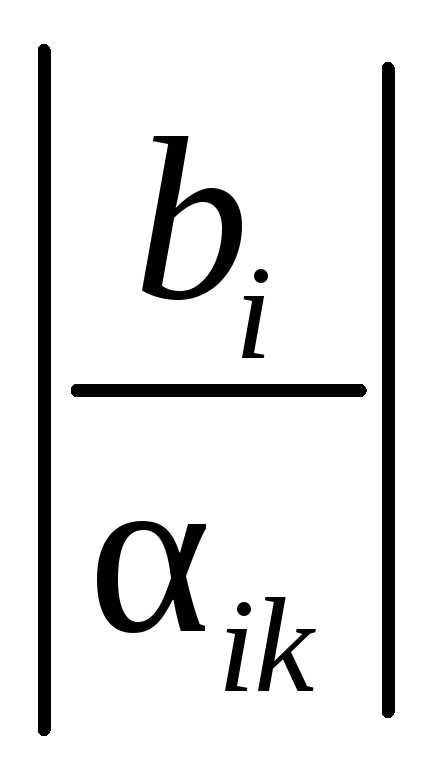 ,
если
,
если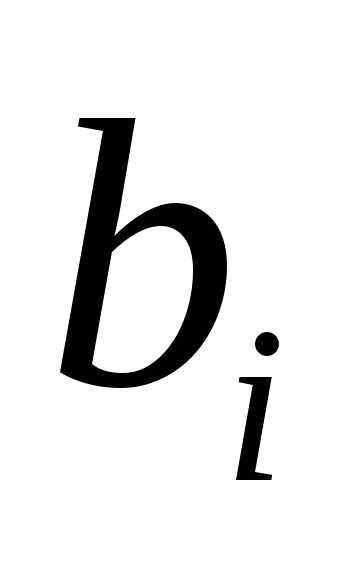 и
и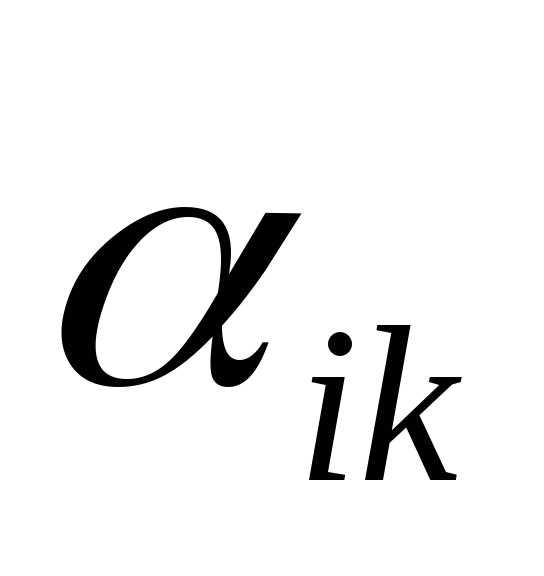 имеют одинаковые знаки.
имеют одинаковые знаки. .
Если конечного минимума нет, то задача
не имеет конечного оптимума (
.
Если конечного минимума нет, то задача
не имеет конечного оптимума (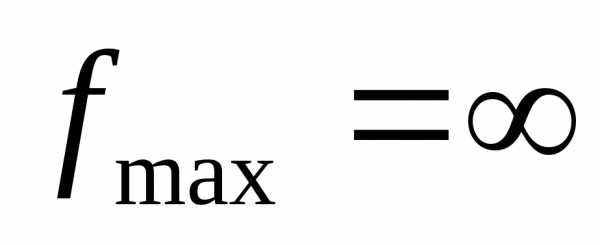 ).
Если минимум конечен, то выбираем строкуq, на которой он достигается (любую,
если их несколько), и называем ее
разрешающей (опорной) строкой. На
пересечении разрешающих строки и столбца
находится разрешающий (опорный) элемент
).
Если минимум конечен, то выбираем строкуq, на которой он достигается (любую,
если их несколько), и называем ее
разрешающей (опорной) строкой. На
пересечении разрешающих строки и столбца
находится разрешающий (опорный) элемент .
.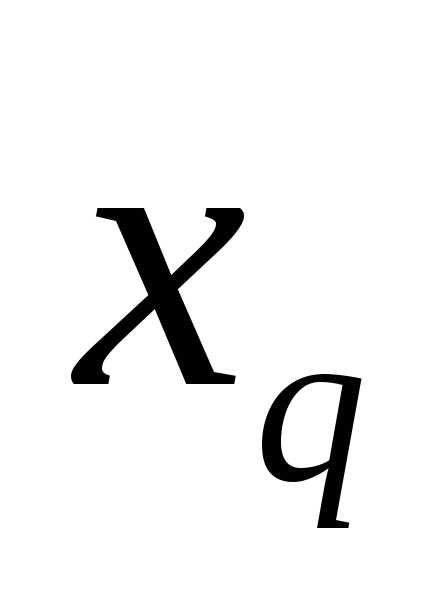 – переменную
– переменную ,
т.е. поменяем местами переменные
,
т.е. поменяем местами переменные и
и ;
; поставить 1;
поставить 1;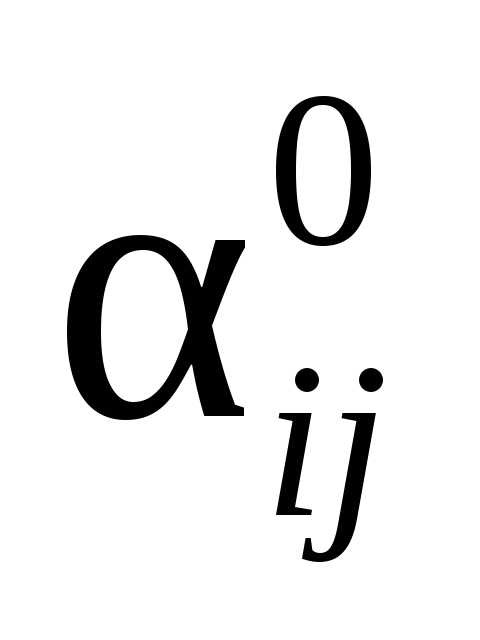 ,
,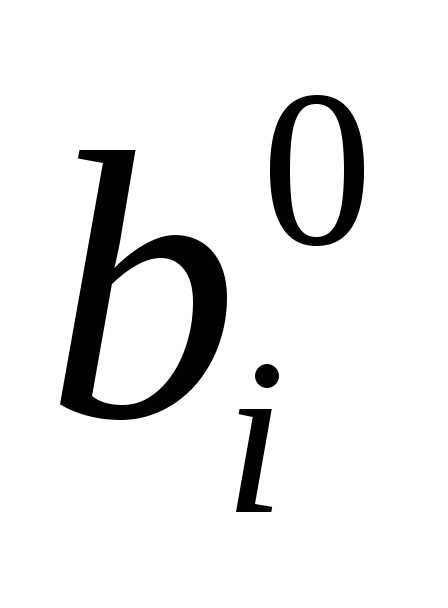 ,
, в новой таблице записать числа
в новой таблице записать числа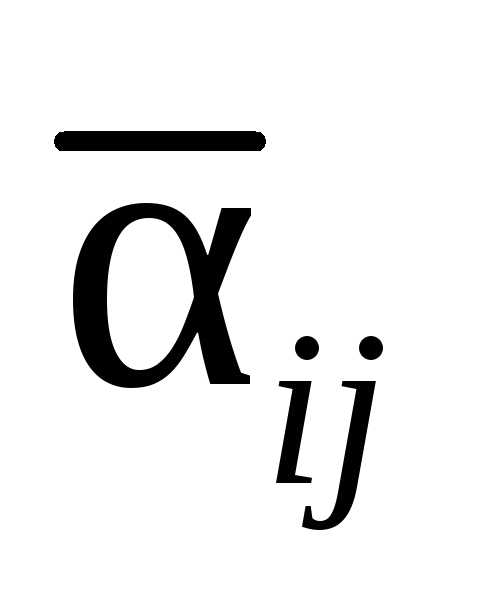 ,
, ,
, ,
которые находятся следующим образом:
,
которые находятся следующим образом: ,
, ,
,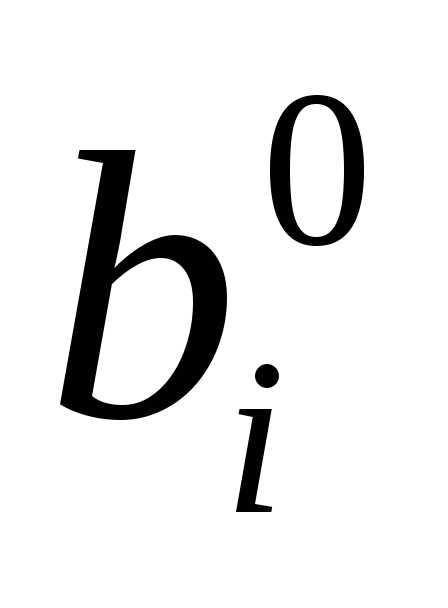 ,
,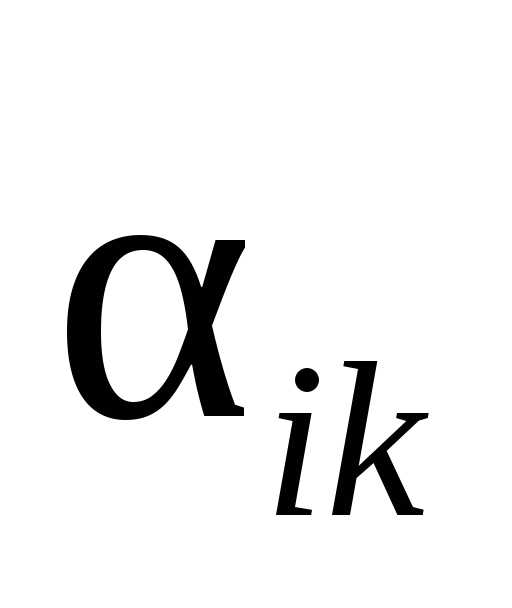 ,
или
,
или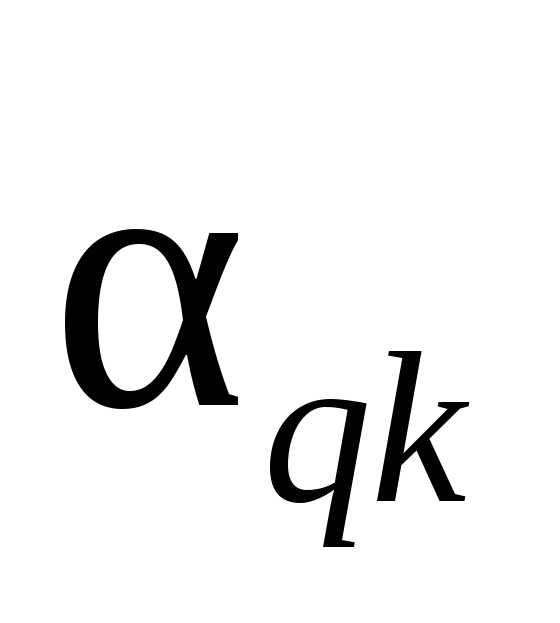 ,
,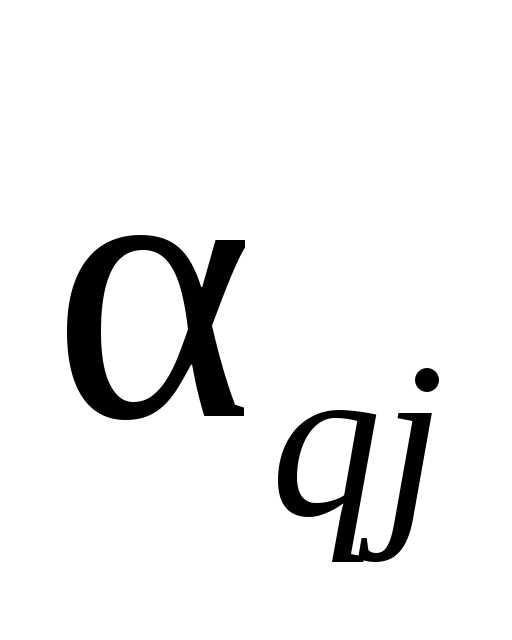 ,
,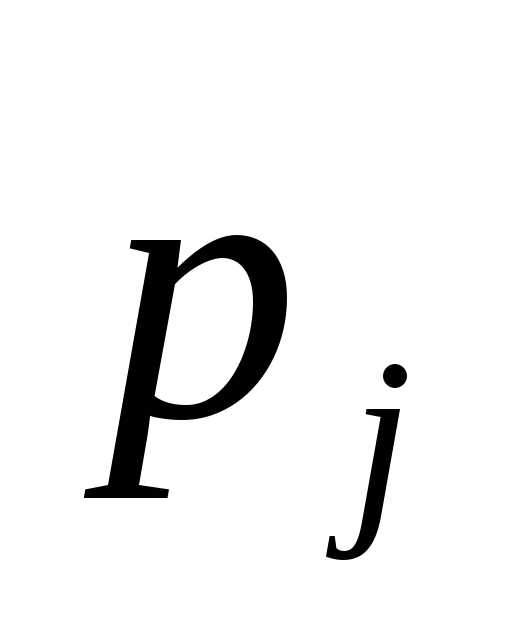 ,
,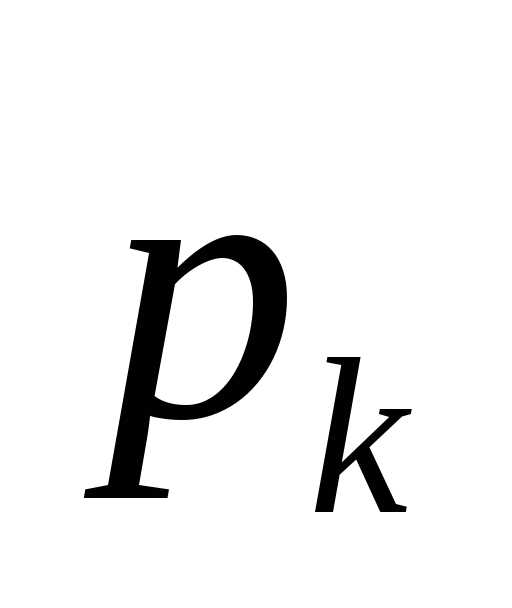 )
перемножаются (произведение, не содержащее
опорного элемента
)
перемножаются (произведение, не содержащее
опорного элемента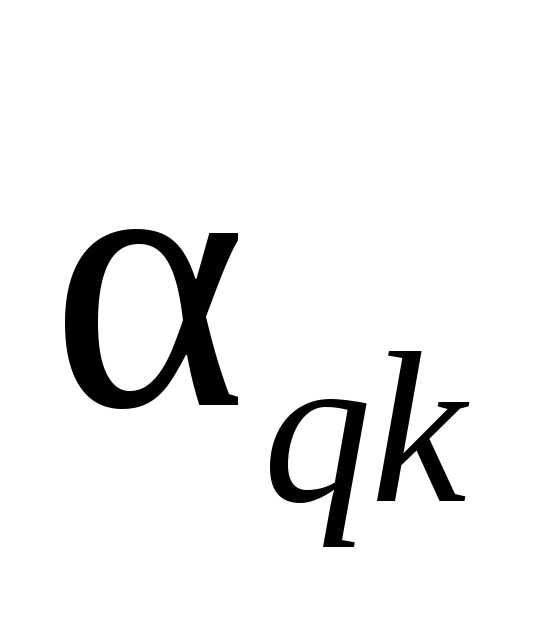 ,
берется со знаком минус) и полученные
произведения складываются;
,
берется со знаком минус) и полученные
произведения складываются;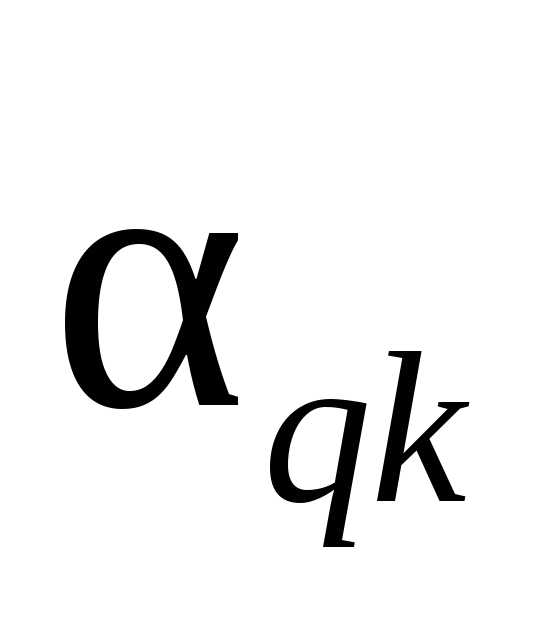 .
.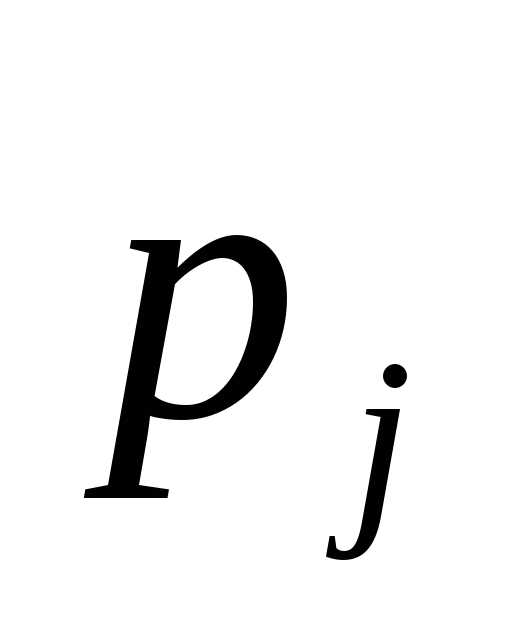 определить, найдено ли оптимальное
значение целевой функции. В случае
отрицательного ответа продолжить
решение (возврат к пункту 6).
определить, найдено ли оптимальное
значение целевой функции. В случае
отрицательного ответа продолжить
решение (возврат к пункту 6).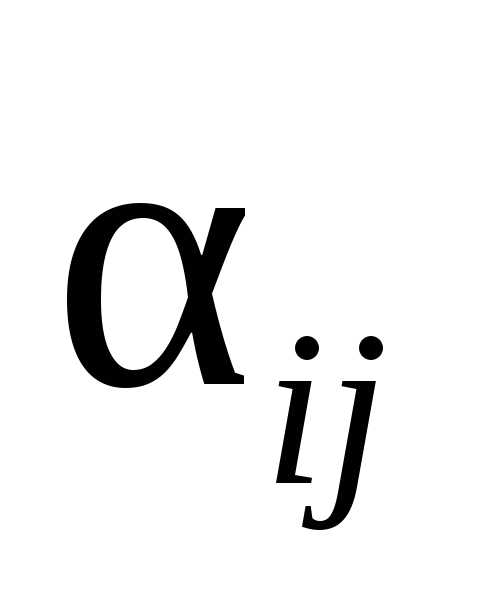 ,
б −
,
б −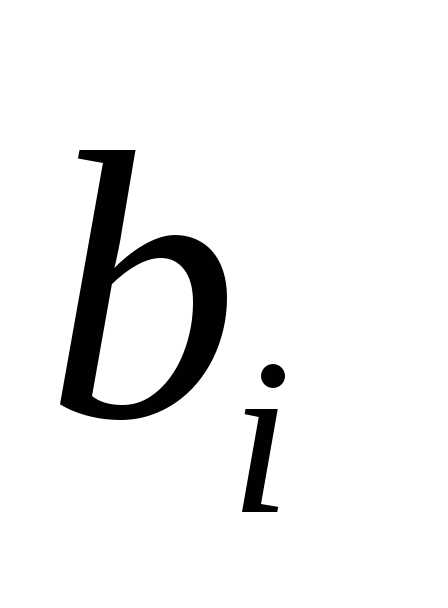 ,
в −
,
в − .
.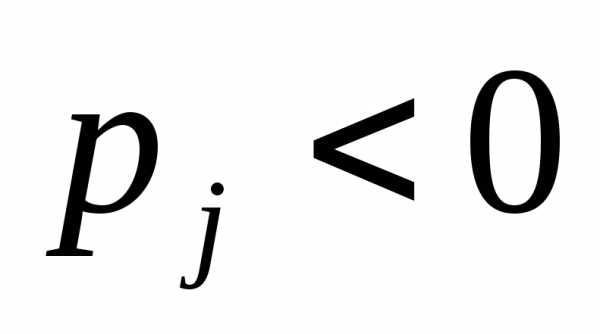 ,
и столбец, соответствующий каждому из
них можно считать опорным. Выберем,
например, первый столбец (этот столбец
отмечен стрелкой). Согласно теореме 6.9
существует допустимое базисное решение.
Опорную строку найдем по правилу (6.29).
В соответствии с пунктом 5 находим
оценочные отношения:,
т.е. это вторая строка. Опорный элемент
,
и столбец, соответствующий каждому из
них можно считать опорным. Выберем,
например, первый столбец (этот столбец
отмечен стрелкой). Согласно теореме 6.9
существует допустимое базисное решение.
Опорную строку найдем по правилу (6.29).
В соответствии с пунктом 5 находим
оценочные отношения:,
т.е. это вторая строка. Опорный элемент обведен рамкой.
обведен рамкой. ).
С учетом (6.29) находим опорную строку:
).
С учетом (6.29) находим опорную строку: обведен рамкой.
обведен рамкой. в последней строке таблицы неотрицательны,
то, согласно теореме 6.9, базисное решение
является точкой минимума в рассматриваемой
задаче, т.е.х* = (3;2;0;0;1),f*
= –15. Графическое решение задачи
представлено на рис. 6.8, откуда видно,
чтох* = (3;2),f* =f(х*) = –15
в последней строке таблицы неотрицательны,
то, согласно теореме 6.9, базисное решение
является точкой минимума в рассматриваемой
задаче, т.е.х* = (3;2;0;0;1),f*
= –15. Графическое решение задачи
представлено на рис. 6.8, откуда видно,
чтох* = (3;2),f* =f(х*) = –15


 (1)
(1)
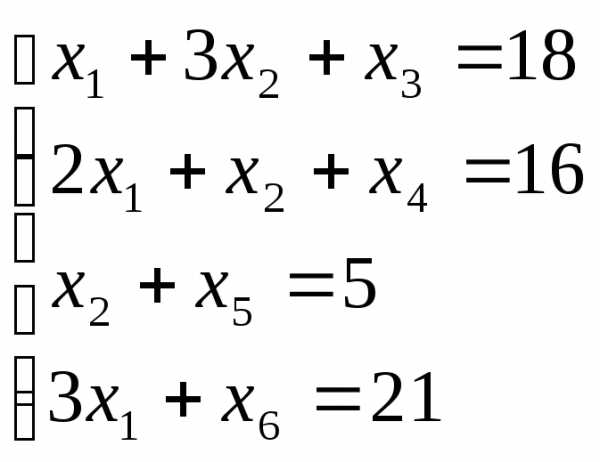
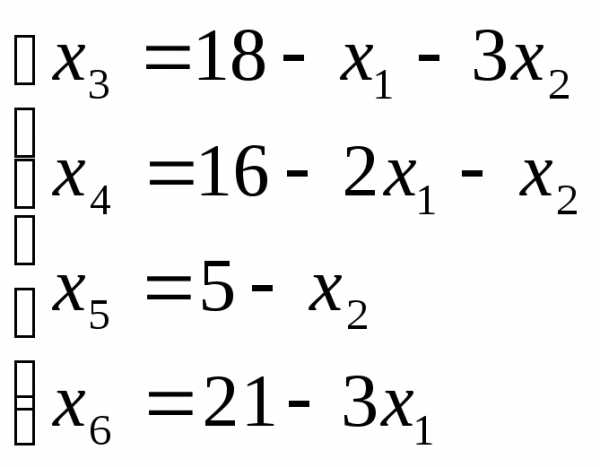 (*)
(*)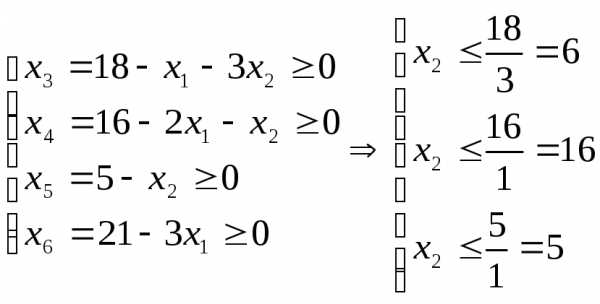


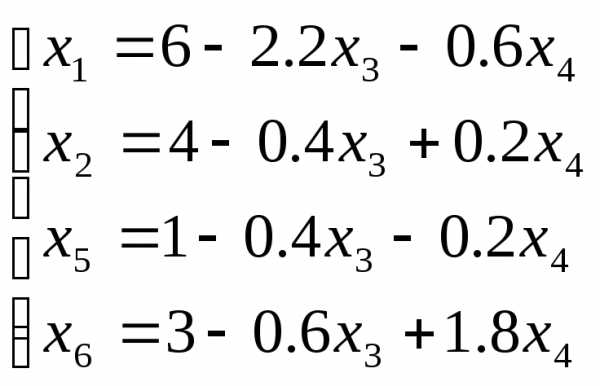
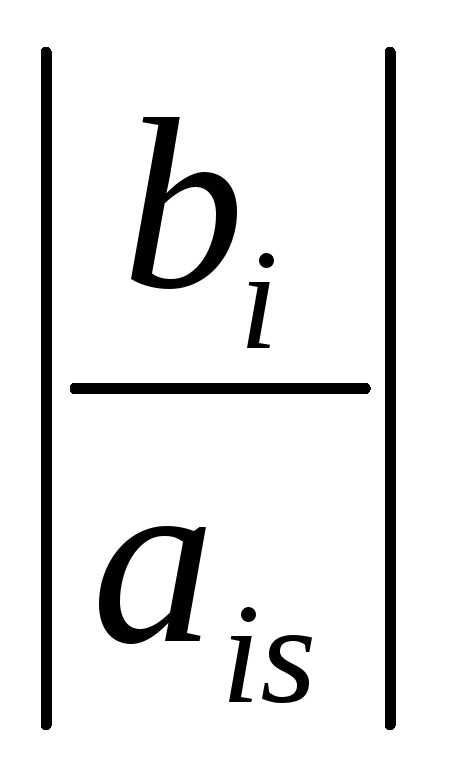 ,
если bi и ais имеют одинаковые знаки.
,
если bi и ais имеют одинаковые знаки. .
Если конечного минимума нет, то задача
не имеет конечного оптимума (zmax=).
Если минимум конечен, то выбираем строку
q,
на которой он достигается (если их
несколько, то любую), и называем ее
разрешающей строкой. На пересечении
разрешающей строки и разрешающего
столбца находится разрешающий элемент
aqs.
.
Если конечного минимума нет, то задача
не имеет конечного оптимума (zmax=).
Если минимум конечен, то выбираем строку
q,
на которой он достигается (если их
несколько, то любую), и называем ее
разрешающей строкой. На пересечении
разрешающей строки и разрешающего
столбца находится разрешающий элемент
aqs. (2)
(2)