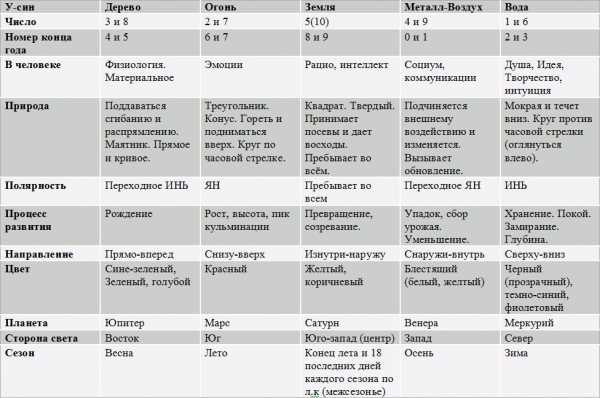
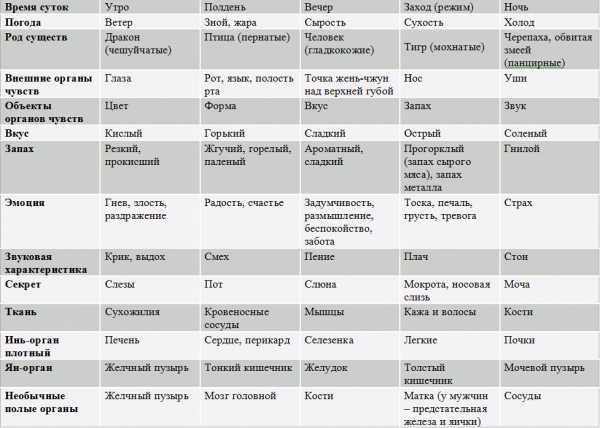
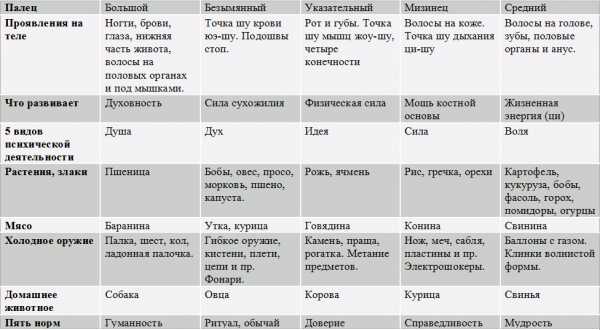
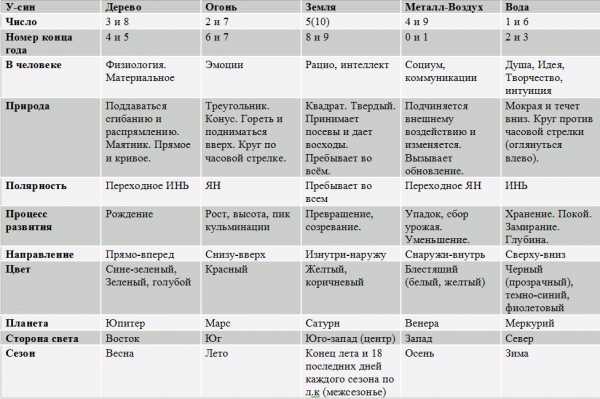
определение, неравенства и их системы
Статья раскрывает тему неравенств, разбираются определения систем и их решения. Будут рассмотрены часто встречающиеся примеры решения систем уравнений в школе на алгебре.
Yandex.RTB R-A-339285-1Определение системы неравенств
Системы неравенств определяют по определениям систем уравнений, значит, что особое внимание уделяется записям и смыслу самого уравнения.
Определение 1Системой неравенств называют запись уравнений, объединенных фигурной скобкой с множеством решений одновременно для всех неравенств, входящих в систему.
Ниже приведены примеры неравенств. Даны два неравенства 2·x−3>0 и 5−x≥4·x−11. Необходимо записать одно уравнение под другим, после чего объединим при помощи фигурной скобки:
2·x-3>0,5-x≥4·x-11
Таким же образом определение систем неравенств представлены в школьных учебниках как для использования одной переменной, так и двух.
Основные виды системы неравенств
Имеет место составление бесконечного множества систем неравенств. Их классифицируют по группам, отличающихся по определенным признакам. Неравенства подразделяют по критериям:
- количество неравенств системы;
- количество переменных записи;
- вид неравенств.
Количество входящих неравенств может насчитывать от двух и более. В предыдущем пункте рассматривался пример решения системы с двумя неравенствами.
2·x-3>0,5-x≥4·x-11
Рассмотрим решение системы с четырьмя неравенствами.
x≥-2,y≤5,x+y+z≥3,z≤1-x2-4·y2
Решение неравенства отдельно не говорит о решение системы в целом. Для решения системы необходимо задействовать все имеющиеся неравенства.
Такие системы неравенств могут иметь одну, две, три и более переменных. В последней изображенной системе это отчетливо видно, там имеем три переменные: x, y, z. Уравнения могут содержать по одной переменной, как в примере, либо по несколько. Исходя из примеров, неравенство x+0·y+0·z≥−2 и 0·x+y+0·z≤5 не считают равнозначными. Школьным программам уделяют внимание решению неравенств с одной переменной.
При записи системы могут быть задействованы уравнения разных видов и с разным количеством переменных. Чаще всего встречаются целые неравенства разных степеней. При подготовке к экзаменам могут встретиться системы с иррациональными, логарифмическими, показательными уравнениями вида:
544-4-x32-2-x≥17,logx216x+2016≤1
Такая система включает в себя показательное и логарифми
zaochnik.com
Задача 15: тонкости решения систем неравенств
В этом видеоуроке я подробно разобрал довольно серьезную задачу 15 из ЕГЭ по математике, которая содержит и логарифмическое, и дробно-рациональное неравенство. Особое внимание уделено теореме Безу (для поиска корней многочлена), а также методике деления многочленов уголком (для разложения на множители).
В этом уроке мы разберем систему из двух неравенств из ЕГЭ по математике:
⎧⎩⎨⎪⎪log7−2x(x+6)≤0x−x−3x+6−x2+27x+90×2+8x+12≤−1\left\{ \begin{align}& {{\log }_{7-2x}}\left( x+6 \right)\le 0 \\& x-\frac{x-3}{x+6}-\frac{{{x}^{2}}+27x+90}{{{x}^{2}}+8x+12}\le -1 \\\end{align} \right.
Решение системы неравенств
Как видите, система состоит из логарифмического неравенства, а также классического дробно-рационального неравенства, однако в процессе решения мы обнаружим, что данное неравенство не так уж и просто, как может показаться на первый взгляд. Начнем с логарифмического. Для этого выпишем его отдельно:
log7−2x(x+6)≤ 0
{{\log }_{7-2x}}\left( x+6 \right)\le \text{ }0
Как и любое логарифмическое неравенство, данная конструкция приводится к каноническому виду, т. е. слева мы оставляем все без изменения, а вот справа запишем следующим образом:
log7−2x(x+6)≤log7−2×1
{{\log }_{7-2x}}\left( x+6 \right)\le {{\log }_{7-2x}}1
Как использовать метод рационализации
Теперь воспользуемся методом рационализации. Напомню, что если у нас есть неравенство вида
logk(x)f(x)⋃logk(x)g(x),
{{\log }_{k\left( x \right)}}f\left( x \right)\bigcup {{\log }_{k\left( x \right)}}g\left( x \right),
то мы можем перейти вот к такой конструкции:
(f(x)−g(x))(k(x)−1)⋃0
\left( f\left( x \right)-g\left( x \right) \right)\left( k\left( x \right)-1 \right)\bigcup 0
Разумеется, в этом неравенстве не учтена область определения логарифма:
f(x)>0
f\left( x \right)>0
g(x)>0
g\left( x \right)>0
1≠k(x)>0
1\ne k\left( x \right)>0
Данные неравенства мы должны просчитать отдельно, а затем пересечь со вторым решением. Но, как правило, учет ОДЗ в решении логарифмических неравенств не представляет, поэтому давайте вернемся к решению элемента нашей системы.
Итак, в роли f(x)f\left( x \right) выступает линейная функция x+6x+6, а в роли g(x)g\left( x \right) выступает просто 1. Поэтому переписываем наше логарифмическое неравенство системы следующим образом:
(x+6−1)(7−2x−1)
\left( x+6-1 \right)\left( 7-2x-1 \right)
Последняя 1 — это та самая x−1x-1, которая стоит во второй скобке. Все это меньше или равно 0. Знак неравенства при выполнении данного преобразования сохраняется. Приведем подобные в каждой скобке:
(x+5)(6−2x)≤0
\left( x+5 \right)\left( 6-2x \right)\le 0
Применение метода интервалов
Очевидно, перед нами простейшее неравенство, которое легко решается методом интервалов. Приравняем каждую скобку к 0:
(+5)=0→=−5
\left( +5 \right)=0\to =-5
6−2=0→2=6
6-2=0\to 2=6
x=3
x=3
Отметим все эти точки (таких точек получилось две) на координатной прямой. При этом заметим, что они являются закрашенными:
Отметим знаки. Для этого возьмем любое число, больше 3. Первым будет стоять «минус». Затем знаки везде чередуются, потому что корней четной кратности нет. Нас интересует знак меньше или равно, т. е. знак «минус». Закрашиваем нужные области. Напомню, что при решении неравенств методом интервалов мы подставляем 1 млрд. в последнее выражение, которое получили перед переходом к уравнениям.
Итак, мы нашли множества. Но, как понимаете, это еще не решение неравенства. Теперь от нас требуется найти область определения логарифма. Для этого выпишем следующие функции:
Erroneous nesting of equation structures
\left[ \begin{align}& x+6>0 \\& 7-2x>0 \\& 7-2x\ne 1 \\\end{align} \right.=>\left[ \begin{align}& x>-6 \\& 7>2x \\& 6\ne 2x \\\end{align} \right.=>\left[ \begin{align}& \\& x<\text{ }3,5 \\& x\ne \text{ }3 \\\end{align} \right.
Итак, мы получили три одновременных требования, т. е. все эти неравенства должны выполняться одновременно. Давайте начертим прямую, параллельную нашему кандидату на ответ:
Мы получили итоговый ответ для первого элемента системы:
(−6;−5]⋃(3;3,5)
\left( -6;-5 \right]\bigcup \left( 3;3,5 \right). На этом моменте у многих учеников возникает вопрос. Взгляните, 3 — с одной стороны она выколота, но с другой стороны, эта же точка закрашена. Так как же отметить ее в результате? Для того, чтобы корректно и раз и навсегда разобраться с этим вопросом, запомните одно простое правило.
Что значит пересечение множеств? Это такое множество, которое одновременно входит и в первое множество и во второе. Другими словами, заполняя картинку, нарисованную ниже, мы ищем такие точки, которые одновременно принадлежат и первой, и второй прямой. Следовательно, если какая-либо точка не принадлежит хотя бы одной из этих прямых, то независимо от того, как она выглядит на второй прямой, она нас не устраивает. И, в частности, с 3, происходит именно такая история: с одной стороны в кандидатах на ответ точка 3 нас устраивает, потому что она закрашена, но с другой стороны 3 выколота в силу области определения логарифма, а, значит, и в итоговом множестве эта точка должна быть выколота. Все, ответ на первое логарифмическое неравенство системы полностью обоснован. Для надежности я еще раз продублирую его:
(−6;−5]⋃(3;3,5)
\left( -6;-5 \right]\bigcup \left( 3;3,5 \right)
Решение дробно-рационального неравенства
Идем далее и решаем дробно-рациональное неравенство из нашей системы. Очевидно, что его мы тоже будем решать методом интервалов. Выпишем его:
x−x−3x+6−x2+27x+90×2+8x+12≤−1x-\frac{x-3}{x+6}-\frac{{{x}^{2}}+27x+90}{{{x}^{2}}+8x+12}\le -1
Теперь перенесем -1 влево:
x+1−x−3x+6−x2+27x+90(x+6)(x+2)≤0x+1-\frac{x-3}{x+6}-\frac{{{x}^{2}}+27x+90}{\left( x+6 \right)\left( x+2 \right)}\le 0
x+11−x−3x+6−x2+27x+90(x+6)(x+2)≤0\frac{x+1}{1}-\frac{x-3}{x+6}-\frac{{{x}^{2}}+27x+90}{\left( x+6 \right)\left( x+2 \right)}\le 0
Приводим всю конструкцию к общему знаменателю:
(x+1)(x+6)(x+2)−(x−3)(x+2)−(x2+27x+90)(x+6)(x+2)≤0\frac{\left( x+1 \right)\left( x+6 \right)\left( x+2 \right)-\left( x-3 \right)\left( x+2 \right)-\left( {{x}^{2}}+27x+90 \right)}{\left( x+6 \right)\left( x+2 \right)}\le 0
Раскроем скобки:
(x+2)((x+1)(x+6)−(x−3))−x2−27x−90(x+6)(x+2)≤0\frac{\left( x+2 \right)\left( \left( x+1 \right)\left( x+6 \right)-\left( x-3 \right) \right)-{{x}^{2}}-27x-90}{\left( x+6 \right)\left( x+2 \right)}\le 0
x3+6×2+9x+2×2+12x+18−x2−27x−90(x+6)(x+2)≤0\frac{{{x}^{3}}+6{{x}^{2}}+9x+2{{x}^{2}}+12x+18-{{x}^{2}}-27x-90}{\left( x+6 \right)\left( x+2 \right)}\le 0
x3+7×2−6x−72(x+6)(x+2)≤0\frac{{{x}^{3}}+7{{x}^{2}}-6x-72}{\left( x+6 \right)\left( x+2 \right)}\le 0
Что можно сказать про полученное неравенство? Во-первых, оно дробно-рациональное, при этом знаменатель уже разложен на множители. Следовательно, наиболее оптимальным вариантом будет решать это неравенство методом интервалов. Однако для того, чтобы решать его методом интервалов, необходимо и числитель разложить на множители. В этом и состоит основная сложность, потому что числитель представляет собой многочлен третьей степени. Кто помнит формулу корней третьей степени? Лично я не помню. Но это нам не потребуется.
Все, что нам потребуется, это теорема Безу, точнее, не сама теорема, а одно из важнейших ее следствии, которое гласит следующее: если многочлен с целыми коэффициентами имеет корень x1{{x}_{1}}, причем он является целым числом, то свободный коэффициент (в нашем случае 72) обязательно будет делиться на x1{{x}_{1}}. Другими словами, если мы хотим найти корни этого кубического уравнения, то все, что нужно, это просто «покопаться» в множителях, на которые раскладывается число 72.
Давайте разложим число 72 на простые множители:
72=8⋅9=2⋅2⋅2⋅3⋅3
72=8\cdot 9=2\cdot 2\cdot 2\cdot 3\cdot 3
Итак, нам нужно перебрать все комбинации двоек т троек, чтобы получить хотя бы один корень нашего кубического выражения. На первый взгляд может показаться, что это комбинаторная задача, однако на самом деле все не так страшно. Давайте начнем с минимального числа:
x=2
x=2
Проверим, является ли 2 ответом. Для этого вспомним, что такое корень. Это такое число, которое будучи подставленным в многочлен, обращает его в 0. Давайте подставим:
(2)=8+28−12−72<0
\left( 2 \right)=8+28-12-72<0
Получаем, что x−2x-2 не подходит. Идем дальше. Давайте возьмем 4:
=4
=4
(4)=64+112−24−72>0
\left( 4 \right)=64+112-24-72>0
x=4x=4 также не является корнем нашей конструкции.
Идем дальше. Какой следующий xx мы будем разбирать? Для ответа на этот вопрос давайте заметим интересный факт: при x−2x-2 наш многочлен был отрицательным, а при x=4x=4 он оказался уже положительным. Это значит, что где-то между точками 2 и 4 наш многочлен пересекает ось xx. Другими словами, где-то на этом отрезке наш он обращается в 0. Это значит, что данная точка будет искомым числом. Давайте подумаем, какое целое число лежит между 4 и 2. Очевидно, что только 3, и 3 присутствует в разложении, следовательно, она действительно может являться корнем нашего выражения. Рассмотрим этот вариант:
x=3
x=3
(3)=27+63−18−72=90−90=0
\left( 3 \right)=27+63-18-72=90-90=0
Прекрасно, наша гипотеза подтвердилась. Действительно, x=3x=3 является корнем нашей конструкции. Но как это поможет нам разложить данный многочлен на множители? Очень просто. Все из той же самой теоремы Безу следует, что если x1{{x}_{1}} является корнем многочлена p(x)p\left( x \right), то значит, что мы можем записать следующее:
x1:p(x)=Q(x)(x−x1)
{{x}_{1}}:p\left( x \right)=Q\left( x \right)\left( x-{{x}_{1}} \right)
Другими словами, зная x1{{x}_{1}} мы можем утверждать, что в разложении нашего выражения на множители обязательно будет присутствовать множитель x1{{x}_{1}}. В нашем случае мы можем записать, что наш многочлен обязательно имеет в своем разложении множитель (x−3)\left( x-3 \right), потому что 3 является его корнем.
Идем дальше. Мы нашли один из корней данного многочлена, но как найти остальные? И здесь нам приходит на помощь деление уголком. Давайте запишем наш исходный многочлен и разделим его:
x3+7×2−6x−72x−3=x2+10x+24\frac{{{x}^{3}}+7{{x}^{2}}-6x-72}{x-3}={{x}^{2}}+10x+24
Другими словами, наше неравенство из системы мы можем переписать следующим образом:
(x+3)(x2+10x+24)(x+6)(x+2)≤0\frac{\left( x+3 \right)\left( {{x}^{2}}+10x+24 \right)}{\left( x+6 \right)\left( x+2 \right)}\le 0
Заметим, что во второй скобке числителя стоит квадратный трехчлен, который тоже очень просто раскладывается на множители, получим:
(x+3)(x+6)(x+4)(x+6)(x+2)≤0\frac{\left( x+3 \right)\left( x+6 \right)\left( x+4 \right)}{\left( x+6 \right)\left( x+2 \right)}\le 0
Вот и все, осталось просто выписать корни:
x=3
x=3
≠−6(2k)
\ne -6\left( 2k \right)
=−4
=-4
≠−2
\ne -2
Давайте отметим все эти точки, которые могут быть решением системы, на координатной прямой xx:
Для того, чтобы определить знаки, берем любое число, больше 3, подставляем в каждую из этих скобок и получаем пять положительных чисел, т. е. справа от 3 стоит знак «плюс». Затем везде знаки меняются, а вот в -6 ничего не меняется, потому что -6 — корень второй кратности. Нас интересуют те области, где знак функции отрицательный, поэтому заштриховываем «минусы».
Итого, мы можем записать решение нашего исходного неравенства — оно будет следующим:
(−∞;−6)⋃(−6;−4]⋃(−2;3]
\left( -\infty ;-6 \right)\bigcup \left( -6;-4 \right]\bigcup \left( -2;3 \right]
Заключительные шаги
Мы решили второе неравенство нашей системы, а теперь осталось решить, собственно, систему, т. е. пересечь полученные нами множества. Для этого я предлагаю построить еще одну прямую, параллельную двум нашим старым прямым, отвечающим за логарифмическое неравенство из системы:

Мы можем записать итоговый ответ второго элемента системы неравенств: (−6;−5]\left( -6;-5 \right]. Теперь можно вернуться к нашей системе и записать итоговое множество:
x∈(−6; −5]
x\in \left( -6;\text{ }-5 \right]
Ключевые моменты
Ключевых моментов в данной задаче сразу несколько:
- Нужно уметь решать логарифмические неравенства с помощью перехода к канонической форме.
- Нужно уметь работать с дробно-рациональными неравенствами. Это вообще материал 8-9 класса, поэтому если вы работаете с логарифмами, то уж с дробно-рациональными неравенствами разберетесь.
- Теорема Безу. Важнейшим следствием из этой теоремы является тот факт, что корни многочлена с целыми коэффициентами являются делителями его свободного члена.
В остальном это несложная, хотя довольно объемная задача на решение системы уравнений. Определенные трудности при решении системы могут возникнуть также в пересечении всех множеств, особенно связанных с точкой 3. Тут все очень просто: достаточно запомнить, что пересечение означает требование одновременного выполнения всех неравенств, т. е. искомая точка должна быть закрашена на всех трех осях. Если хотя бы на одной оси она не закрашена или выколота, то такая точка не может быть частью ответа.
Смотрите также:
- Сравнение корней и учёт области определения в логарифмических неравенства из ЕГЭ.
- Что делать, если в показателе стоит логарифм
- Пробный ЕГЭ-2011 по математике, вариант №8
- Пробный ЕГЭ 2012. Вариант 8 (без производных)
- Пробный ЕГЭ по математике 2015: 3 вариант
- Тест по задачам B14: легкий уровень, 2 вариант
www.berdov.com
StudyPort.Ru — Система неравенств. Решения системы
Системой неравенств называется совокупность неравенств, для которых нужно найти значения неизвестных, удовлетворяющие одновременно всем неравенствам системы.
Значения неизвестных, удовлетворяющие одновременно всем уравнением системы называются решениями системы.
Примеры систем неравенств:
Системы неравенств могут состоять из двух и более неравенств и содержать одну и более переменных. Система неравенств может не иметь решений, иметь несколько решений, иметь бесконечное множество решений.
В школьной программе изучаются системы, содержащие одну переменную.
Для решения различных видов систем разработано много различных методов решения, но в рамках школьного курса рассматривается один самый простой метод. Он заключается в том, что мы решаем каждое неравенство в отдельности, а затем все полученные решения пересекаем на координатной оси.
Примеры решения систем неравенств.
1. Решить систему неравенств
Решим первое неравенство:
x2-4 < 0;
(x-2)(x+2) < 0.
Решим это неравенство методом интервалов.
Решением этого неравенства будет промежуток (-2;2).
Второе неравенство уже решено — пересекаем решения первого и второго неравенства.
Итак, решением системы неравенств будет промежуток (-2;1).
Ответ: (-2;1).
2. Решить систему неравенств
Решим первое неравенство:
Решим второе неравенство:
x-12 < 1;
x < 13.
Пересекаем решения первого и второго неравенства.
Итак, решение системы неравенств — промежуток [8;13).
Ответ: [8;13).
studyport.ru
Система неравенств — решение. Система линейных неравенств
Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.

Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.

Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t1 ≤ t2, то t2 ≥ t1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t1 ≤ t2, то t1 + число ≤ t2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t1≥ t2, t3≥ t4, то t1 + t3≥ t2 + t4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t1 ≤ t2 и число ≤ 0, то число · t1 ≥ число · t2).
- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t1 ≤ t2, t3 ≤ t4, t1, t2, t3, t4 ≥ 0 то t1 · t3 ≤ t2 · t4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t1 ≤ t2 и число ≤ 0, то число · t1 ≥ число · t2).
- Все неравенства обладают свойством транзитивности (например, если t1 ≤ t2 и t2 ≤ t3, то t1 ≤ t3).

Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
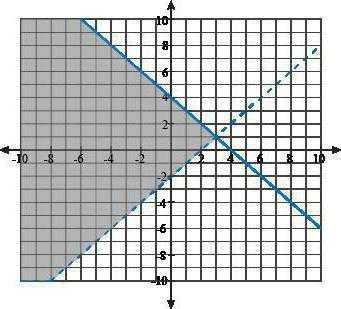
Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х4 — х2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х2«, далее модель переписывают в новом виде. В нашем случае получится t2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.
- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать?
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.

Решебник?
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.
Выводы
Алгебра — это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
fb.ru
Решение системы неравенств с одним неизвестным
Решить систему неравенств — это значит найти значения неизвестного, которые удовлетворяют КАЖДОМУ неравенству системы.
Алгоритм решения системы неравенств с одним неизвестным прост:
1. Сначала решаем каждое неравенство системы по отдельности, и на своей оси. Последнее очень важно: часто при решении системы нелинейных неравенств делают такую ошибку: приравнивают к нулю левые части неравенств, находят корни и все корни наносят на одну ось. ЭТО НЕВЕРНО!
2. Решения всех неравенств совмещаем на одной числовой оси, и находим область, над которой расположено столько «стрелок», сколько неравенств в системе.
Рассмотрим пример. Решим систему неравенств:
Решим каждое неравенство системы, используя метод интервалов:
(1) x2-x-20<0
Найдем корни квадратного трехчлена, стоящего в левой части неравенства: x1=5, x2=-4
Нанесем их на числовую ось:
Расставим знаки. Для этого возьмем число, больше большего корня и подставим вместо х в левую часть неравенства.
Возьмем, например, число 10:
102-10-20>0, следовательно в самом правом промежутке ставим «+». Так как все корни нечетной кратности, знаки меняются при переходе через корни:
Нас интересуют те значения неизвестного, при которых левая часть неравенства меньше 0: Аналогично для второго неравенства:
(2) x2-2x-8<0 :
Выделим область, в которой левая часть неравенства меньше 0:
Аналогично для третьего неравенства:
(3) 2x2+x-45<0
Теперь совместим на одной числовой оси решение трех неравенств:
Мы видим, что три «стрелки», изображающие решения всех трех неравенств проходят над отрезком (-2,4) — это и есть решение нашей системы неравенств.
Ответ: (-2,4)
ege-ok.ru
Решение систем неравенств с одной переменной
Давайте решим задачу: нужно заполнить водой пустой бассейн вместимостью 3000 л. Сколько литров воды в час нужно наливать в бассейн, чтобы через 2 часа он был наполнен более половины и чтобы через 3 часа бассейн не переполнился?
Решение:
Когда необходимо найти такие значения х, при которых одновременно верны два неравенства с одной переменной, их записывают совместно и говорят, что они образуют систему неравенств.
Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства.
Система, которую мы записали для решения задачи – это пример системы линейных неравенств с одной переменной.
Определение:
Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
В виде системы может быть записано и любое двойное неравенство.
Например
Решить систему неравенств – значит найти все её решения или доказать, что решений нет.
Рассмотрим несколько примеров решения систем линейных неравенств с одной переменной.
Пример 1: решим систему неравенств.
Пример 2: решим систему неравенств.
Решение:
Пример 3: решим систему неравенств.
Решение:
Пример 4: решим двойное неравенство.
Решение:
Запишем алгоритм решения систем линейных неравенств с одной переменной.
Для того чтобы решить систему неравенств, надо:
1. Решить каждое из неравенств системы.
2. Изобразить множество решений каждого неравенства на координатной прямой.
3. Найти пересечение промежутков (если оно есть) и записать в виде обозначения промежутка или в виде неравенства, задающего этот промежуток, или сделать вывод об отсутствии решения системы.
Итоги:
videouroki.net
Как изобразить множество решений системы неравенств
В данной статье я отвечаю на очередной вопрос от моих подписчиков. Вопросы приходят разные. Не все из них корректно сформулированы. А некоторые из них сформулированы так, что не сразу получается понять, о чём хочет спросить автор. Поэтому среди огромного множества присылаемых вопросов приходится отбирать действительно интересные, такие «жемчужины», отвечать на которые не просто увлекательно, но ещё и полезно, как мне кажется, для других моих читателей. И сегодня я отвечаю на один из таких вопросов. Как изобразить множество решений системы неравенств?
Это действительно хороший вопрос. Потому что метод графического решения задач в математике — это очень мощный метод. Человек так устроен, что ему удобнее воспринимать информацию с помощью различных наглядных материалов. Поэтому если вы овладеете этим методом, то поверьте, он для вас окажется незаменимым как при решении заданий из ЕГЭ, особенно из второй части, других экзаменов, так и при решении задач оптимизации и так далее, и так далее.
Так вот. Как же нам ответить на этот вопрос. Давайте начнём с простого. Пусть в системе неравенств содержится только одна переменная .
| Пример 1. Изобразите множество решений системы неравенств:
|
Упростим эту систему. Для этого прибавим к обеим частям первого неравенства 7 и поделим обе части на 2, не меняя при этом знак неравенства, так как 2 — положительное число. К обеим частям второго неравенства прибавим 4. В результате получим следующую систему неравенств:
Обычно такую задачу называют одномерной. Почему? Да потому что для того, чтобы изобразить множество её решений, достаточно прямой. Числовой прямой, если быть точным. Отметим точки 6 и 8 на этой числовой прямой. Понятно, что точка 8 будет находиться правее, чем точка 6, потому что на числовой прямой большие числа находятся правее меньших. Кроме того, точка 8 будет закрашенной, так как согласно записи первого неравенства она входит в его решение. Наоборот, точка 6 будет незакрашенной, так как она не входит в решение второго неравенства:
Отметим теперь стрелочной сверху значения , которые меньше или равны 8, как того требует первое неравенство системы, а стрелочкой снизу — значения , которые больше 6, как того требует второе неравенство системы:
Осталось ответить на вопрос, где на числовой прямой находятся решения системы неравенств. Запомните раз и навсегда. Знак системы — фигурная скобка — в математике заменяет союз «И». То есть, переводя язык формул на человеческий язык, можно сказать, что от нас требуется указать значения , которые больше 6 И меньше или равны 8. То есть искомый промежуток лежит на пересечении отмеченных промежутков:
Вот мы и изобразили множество решений системы неравенств на числовой прямой в случае, если в системе неравенств содержится только одна переменная. В этот заштрихованный промежуток входят все значения , при которых все неравенства, записанные в системе, выполняются.
Рассмотрим теперь более сложный случай. Пусть в нашей системе содержатся неравенства с двумя переменными и . В этом случае обойтись только прямой для изображения решений такой системы не получится. Мы выходим за рамки одномерного мира и добавляем к нему ещё одно измерение. Здесь нам понадобится уже целая плоскость. Рассмотрим ситуацию на конкретном примере.
| Пример 2. Изобразите на координатной плоскости множество решений системы неравенств:
|
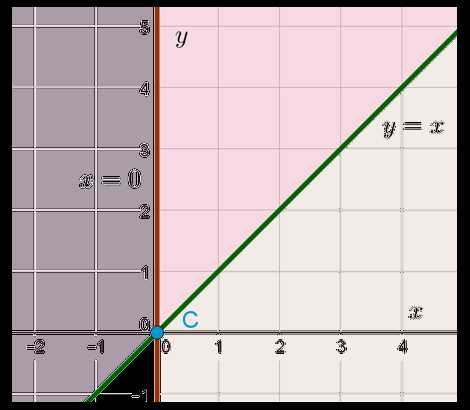
Итак, как же можно изобразить множество решений данной системы неравенств с двумя переменными в прямоугольной системе координат на плоскости? Начнём с самого простого. Зададимся вопросом, какую область этой плоскости задаёт неравенство . Уравнение задаёт прямую, проходящую перпендикулярно оси OX через точку (0;0). То есть фактически это прямая совпадает с осью OY. Ну а раз нас интересуют значения , которые больше или равны 0, то подойдёт вся полуплоскость, лежащая справа от прямой :
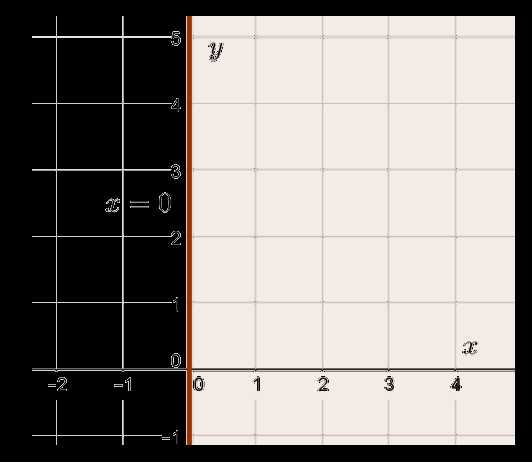
Причём все точки, которые лежат на оси OY, нам тоже подходят, потому что неравенство — нестрогое.
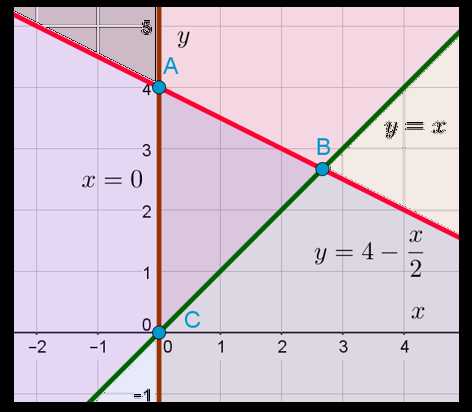
Чтобы понять, какую область на координатной плоскости задаёт третье неравенство, нужно построить график функции . Это прямая, проходящая через начало координат и, например, точку (1;1). То есть фактически это прямая, содержащая биссектрису угла, образующего первую координатную четверть.
А теперь посмотрим на третье неравенство в системе и подумаем. Какую область нам нужно найти? Смотрим: . Знак «больше или равно». То есть ситуация аналогична той, что была в предыдущем примере. Только здесь «больше» означает не «правее», а «выше». Потому что OY — это у нас вертикальная ось. То есть область, задаваемая на плоскости третьим неравенством, — это множество точек, находящихся выше прямой или на ней:
С первым неравенством системы чуть менее удобно. Но после того, как мы смогли определить область, задаваемую третьим неравенством, я думаю, что уже понятно, как нужно действовать.
Нужно представить это неравенство в таком виде, чтобы слева находилась только переменная , а справа — только переменная . Для этого вычтем из обеих частей неравенства и поделим обе части на 2, не меняя при этом знак неравенства, потому что 2 — это положительное число. В результате получаем следующее неравенство:
Осталось только изобразить на координатной плоскости прямую , которая пересекает ось OY в точке A(0;4) и прямую в точке . Последнее я узнал, приравняв правые части уравнений прямых и получив уравнение . Из этого уравнения находится координата точки пересечения, а координата , я думаю вы догадались, равна координате . Для тех, кто всё-таки не догадался, это потому что у нас уравнение одной из пересекающихся прямых: .
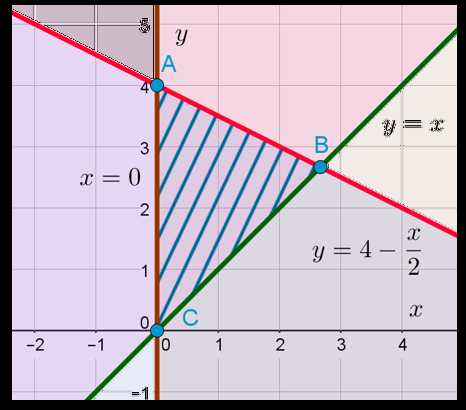
Как только мы нарисовали эту прямую, сразу можно отметить искомую область. Знак неравенства у нас здесь «меньше или равно». Значит, искомая область находится ниже или непосредственно на изображённой прямой:
Ну и последний вопрос. Где же всё-таки находится искомая область, удовлетворяющая всем трём неравенствами системы? Очевидно, что она находится на пересечении всех трёх отмеченных областей. Опять пересечение! Запомните: знак системы в математике означает пересечение. Вот она, эта область:
Ну и последний пример. Ещё более общий. Предположим теперь что у нас не одна переменная в системе и ни две, а аж целых три!
| Пример 3. Изобразите множество решений следующей системы неравенств:
|
Поскольку переменных целых три, то для изображения множества решений такой системы неравенств нам потребуется третье измерение в добавок к двум, с которыми мы работали в предыдущем примере. То есть мы вылезаем из плоскости в пространство и изображаем уже пространственную систему координат с тремя измерениями: X, Y и Z. Что соответствует длине, ширине и высоте.
Начнём с того, что изобразим в этой системе координат поверхность, задаваемую уравнением . По форме оно очень напоминает уравнение окружности на плоскости, только добавляется ещё одно слагаемое с переменной . Несложно догадаться, что это уравнение сферы с центром в точке (1;3;2), квадрат радиуса которой равен 4. То есть сам радиус равен 2.
Тогда вопрос. А что тогда задаёт само неравенство? Для тех, кого этот вопрос ставит в тупик, предлагаю рассудить следующим образом. Переводя язык формул на человеческий, можно сказать, что требуется указать все сферы с центром в точке (1;3;2), радиусы которых меньше или равны 2. Но тогда все эти сферы будут находиться внутри изображённой сферы! То есть фактически данным неравенством задаётся вся внутренняя область изображённой сферы. Если хотите, задаётся шар, ограниченный изображённой сферой:
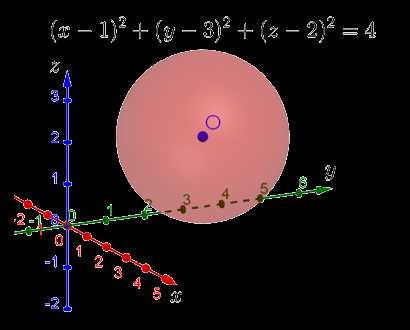
Поверхность, которую задаёт уравнение x+y+z=4 — это плоскость, которая пересекает оси координат в точках (0;0;4), (0;4;0) и (4;0;0). Ну и понятно, что чем больше будет число справа от знака равенства, тем дальше от центра координат будут находиться точки пересечения этой плоскости с осями координат. То есть второе неравенство задаёт полупространство, находящееся «выше» данной плоскости. Используя условный термин «выше», я имею ввиду дальше в сторону увеличения значений координат по осям.
Данная плоскость пересекает изображённую сферу. При этом сечение пересечения — это окружность. Можно даже посчитать, на каком расстоянии от центра системы координат находится центр этой окружности. Кстати, кто догадается, как это сделать, пишите свои решения и ответы в комментариях. Таким образом исходная система неравенств задаёт область пространства, которая находится дальше от этой плоскости в сторону увеличения координат, но заключённая в изображённую сферу:
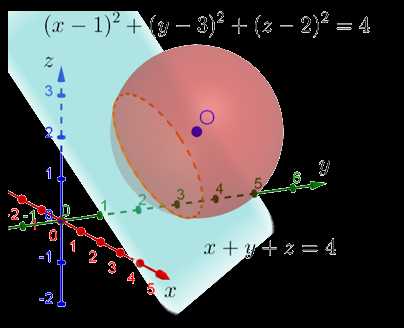
Вот таким образом изображают множество решений системы неравенств. В случае, если переменных в системе больше, чем 3 (например, 4), наглядно изобразить множество решений уже не получится. Потому что для этого потребовалась бы 4-х мерная система координат. Но нормальный человек не способен представить себе, как могли бы располагаться 4 взаимно перпендикулярные оси координат. Хотя у меня есть знакомый, который утверждает, что может сделать это, причём с лёгкостью. Не знаю, правду ли он говорит, может быть и правду. Но всё-таки нормальное человеческое воображение этого сделать не позволяет.
Надеюсь, сегодняшний урок оказался для вас полезным. Чтобы проверить, насколько хорошо вы его усвоили, выполните записанное ниже домашнее задание.
Изобразите множество решений системы неравенств:
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
yourtutor.info
























 1. Сторона квадрата 5 см. Чему равен его периметр? Получаем, что площадь прямоугольника AKOM равна 14 квадратным сантиметрам. Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр. Длина прямоугольника 4см, а ширина – 3см. Чему равна площадь треугольника? 1. Измерьте ширину и длину данного прямоугольника. Что такое периметр? Над доской плакаты с формулами нахождения площади и периметра.
1. Сторона квадрата 5 см. Чему равен его периметр? Получаем, что площадь прямоугольника AKOM равна 14 квадратным сантиметрам. Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр. Длина прямоугольника 4см, а ширина – 3см. Чему равна площадь треугольника? 1. Измерьте ширину и длину данного прямоугольника. Что такое периметр? Над доской плакаты с формулами нахождения площади и периметра.


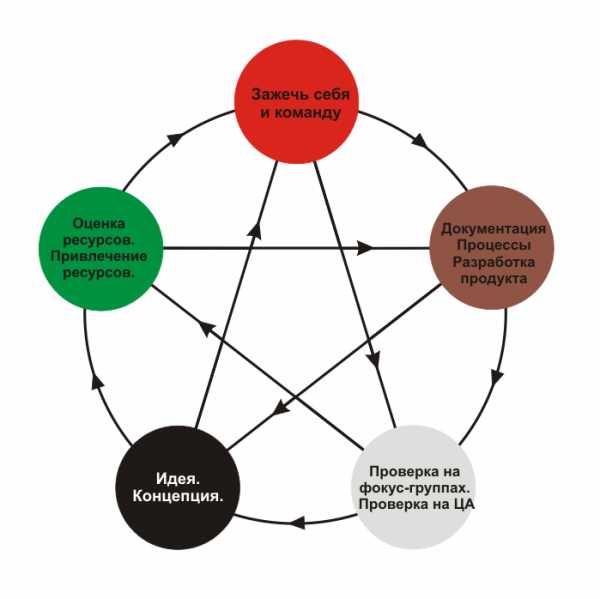
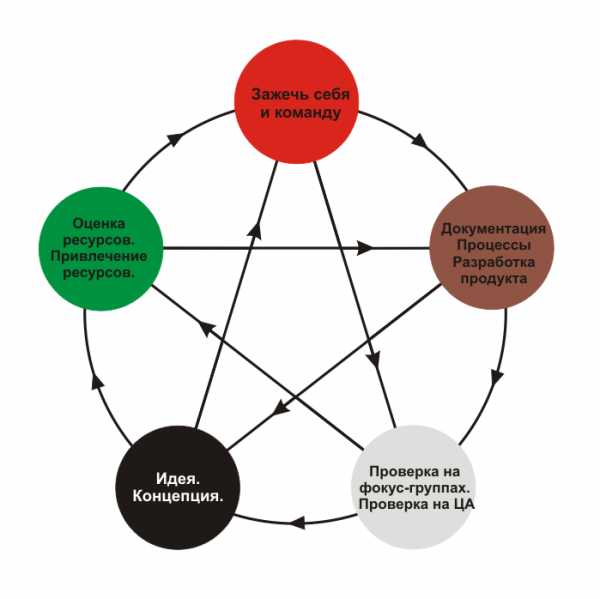
 «Мало знать, надо и применять», гласит народная мудрость. Почему же бывает трудно начать что-то делать, даже если понимаешь, что это нужно?
«Мало знать, надо и применять», гласит народная мудрость. Почему же бывает трудно начать что-то делать, даже если понимаешь, что это нужно?
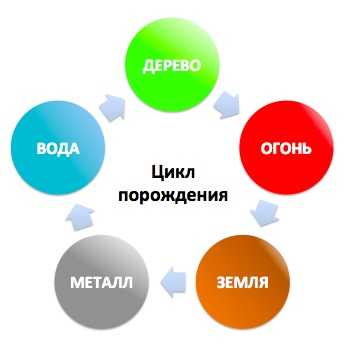
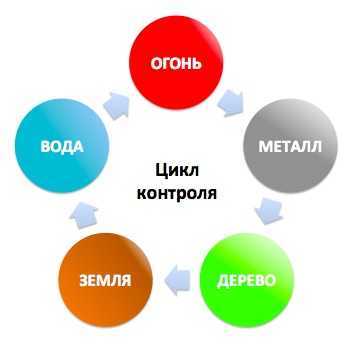
 Питание по системе 5 элементов — древний метод, который помогает людям не только отлично выглядеть и хорошо себя чувствовать , но и получать максимальное количество жизненной энергии и пользы из пищи, способствует оздоровлению и полноценному функционированию всего организма.
Питание по системе 5 элементов — древний метод, который помогает людям не только отлично выглядеть и хорошо себя чувствовать , но и получать максимальное количество жизненной энергии и пользы из пищи, способствует оздоровлению и полноценному функционированию всего организма.



 Кривая производственных возможностей
Кривая производственных возможностей An example PPF with illustrative points marked
An example PPF with illustrative points marked очка
1 — показывает, сколько всего при заданных
условиях мы можем произвести товара 1
(вообще не производя товар 2). Точка 5 —
показывает, сколько мы можем производить
товара 2 (не производя товар1). Точки 2,
3, 4 — показывают возможные комбинации
производства при полном использовании
ресурсов. Точка 6 — показывает равные
доли производства товаров, но при том
она находится ниже кривой производственных
возможностей, то есть при неполном
использовании ресурсов, а значит, наше
производство неоптимально.
очка
1 — показывает, сколько всего при заданных
условиях мы можем произвести товара 1
(вообще не производя товар 2). Точка 5 —
показывает, сколько мы можем производить
товара 2 (не производя товар1). Точки 2,
3, 4 — показывают возможные комбинации
производства при полном использовании
ресурсов. Точка 6 — показывает равные
доли производства товаров, но при том
она находится ниже кривой производственных
возможностей, то есть при неполном
использовании ресурсов, а значит, наше
производство неоптимально. онкая
дуга на графике — изначальная кривая
производственных возможностей.
онкая
дуга на графике — изначальная кривая
производственных возможностей.






